工程光学-浙大2005年答案
05年答案

一、填空题(每小题4分,总共24分)1.56.30 ; 33.70 2.上凸 3.4πn 2e /λ1n 1 4.否 ;是 5.相同; 不同 6. 自然光;线偏振光;部分偏振光二、简答题(每小题6分,总共36分)1.2. 光程变化(1)(1.51)0.010.005(mm)S n d ∆=-=-⨯=相位变化392π2π0.0051020π50010S ϕλ--∆=∆=⨯⨯=⨯ 3.4.5. 这种器件的结构示意图如图所示,让偏振片P 1与P 2的透振方向成450,调整磁感应强度B ,使从法拉第盒出来的光振动面相对P 1转过450。
于是,刚好能通过P 2;但对于从后面光学系统(例如激光放大器等)各界面反射回来的光,经P 2和法拉第盒后,其光矢量与P 1垂直,因此被隔离而不能返回到光源。
6.正午太阳直射,穿过大气层厚度最小。
阳光中被散射掉的短波成分不太多,因此垂直透过大气层后的太阳光基本上呈白色或略带黄橙色。
早晚的阳光斜射,穿过大气层的厚度比正午时厚得多,被大气散射掉的短波成分也多得多,仅剩下长波成分透过大气到达观察者,所以旭日和夕阳呈红色。
三、(10分)解:没插玻璃片之前二光束的光程差为插玻璃片之后二光束的光程差为因此,玻璃片的厚度为-6-40600101.22=1.22=1.464105D λθ⨯=⨯⨯0-40 1.2==8200(m)1.46410d L θ=⨯o o 589355(nm)1.658n λλ===e e 589396(nm)1.486n λλ===01;2I I =221cos ;I I α=23222000221sin cos sin sin 2288cos I I I I I I I ααααα⎫=⎪⇒==⎬=⎪⎭22322πcos sin 2I I I αα⎛⎫=-= ⎪⎝⎭045α∴=P 2 P 1 磁致旋光材料 215r r ∆λ=-=()()212110r r d nd r r d n ∆=--+=---=0.55106(μm)d d λλ=⇒==四、(10分)解:由已知最多接收到7条谱线,但d / a =2有缺级m =2、4的谱线消失。
物理学:工程光学考试答案(题库版)

物理学:工程光学考试答案(题库版)1、名词解释复消色差物镜正确答案:三条谱线之间的轴向色差经过校正的物镜。
2、问答题棱镜和光栅产生的光谱特征有何不同?正确答案:它们光谱主要区别是:(1)光栅光谱是一个均匀排列光谱,(江南博哥)棱镜光谱是一个非均匀排列的光谱。
(2)光栅光谱中个谱线排列是由紫到红(光)棱镜光谱中各谱线排列三由红到紫(光)(3)光栅光谱有级,级与级之间有重叠现象棱镜光谱没有这种现象。
光栅适用的波长范围较棱镜宽。
3、名词解释虚像点正确答案:发撒的出射同心光束的会聚点。
4、单选原子吸收线的劳伦茨变宽是基于()。
A.原子的热运动B.原子与其它种类气体粒子的碰撞C.原子与同类气体粒子的碰撞D.外部电场对原子的影响正确答案:B5、名词解释视场正确答案:物空间中,在某一距离光学系统所能接受的最大物体尺寸,此量值以角度为单位。
6、问答题同一物体经针孔或平面镜所成的像有何不同?正确答案:由反射定律可知,平面镜的物和像是关于镜面对称的。
坐标由右旋坐标系变为像的左旋坐标系,因此像和物左右互易上下并不颠倒。
即物体经平面镜生成等大、正立的虚像。
物体经针孔成像时,物点和像点之间相对与针孔对称。
右旋坐标系惊针孔所成的像仍为右旋坐标系,因此像和物上下左右都是互易的,而且像的大小与针孔到接受屏的距离有关,即物体经针孔生成倒立的实像。
7、填空题发射光谱定性分析,常以()光源激发。
正确答案:直流电弧8、填空题在进行光谱定性全分析时,狭缝宽度宜(),目的是保证有一定的(),而进行定量分析时,狭缝宽度宜(),目的是保证有一定的()。
正确答案:窄;分辨率;宽;照度9、名词解释临界角角正确答案:光密介质到光疏介质出现全反射现象,产生全反射现象时的最小入射角称为临界角。
10、名词解释波像差正确答案:当实际波面与理想波面在出瞳处相切时,两波面间的光程差就是波像差.11、问答题PLC与FBT光分路器相比有哪些优点?正确答案:与传统的采用光纤熔融拉锥工艺制作的器件相比,PLC光分路器具有工作波长宽,通道损耗均匀性体积小,工作温度范围宽,可靠性高等特点,目前是PON接入网中连接OLT和O NU并实现光信号功率分配的首选.12、填空题等离子体光源(ICP)具体有(),()等优点。
工程光学第一章练习参考答案

l 2 ' 15 mm
第一章 16
(2)凸面镀反射膜 r1
l , r 30 , n 1 , n ' 1 n' l' l' n l n' n ' n n ' n r r 1 11 30 15 mm
第一章 16
(3)凹面镀反射膜 (a)在左球面折射
l 2 ' 10 mm
第一章 16
(4)凹面镀反射膜 (a)在左球面折射 (b)在右球面第二次反射
r1
r2
l 2 ' 10 mm
(c)再左球面第三次折射
l 50 mm , r 30 , n 1 . 5 , n ' 1 n' l' 1 l' n l 1 .5 50 n ' n r 1 1 .5 30
n1
I2’
n 1 sin I 1 n 1 sin I 2 ' I1 I 2'
第一章 8
I1’ I1 n 0 sin I 1 n 1 sin I 1 ' n 1 sin I 2 n 2 sin 90 n 2 I 1 ' 90 I 2 I2
n0 n2 n1
3 10 1 . 526
8
1 . 966 10 m / s
8 8
3 10 2 . 417
1 . 241 10 m / s
第一章 4
D=?
h=200mm
全反射问题. (1)
n sin I 1 sin 90 sin I 1 I 41 . 81 n
I
1
工程光学习题参考答案第七章典型光学系统

⼯程光学习题参考答案第七章典型光学系统第七章典型光学系统1.⼀个⼈近视程度是D 2-(屈光度),调节范围是D 8,求:(1)远点距离;(2)其近点距离;(3)配戴100度近视镜,求该镜的焦距;(4)戴上该近视镜后,求看清的远点距离;(5)戴上该近视镜后,求看清的近点距离。
解:① 21-==rl R )/1(m ∴ m l r 5.0-=②P R A -= D A 8= D R 2-= ∴D A R P 1082-=--=-=m P l p 1.01011-=-== ③fD '=1∴m f 1-=' ④D D R R 1-=-='m l R1-=' ⑤P R A '-'= D A 8= D R 1-='D A R P 9-=-'='m l P11.091-=-=' 2.⼀放⼤镜焦距mm f 25=',通光孔径mm D 18=,眼睛距放⼤镜为mm 50,像距离眼睛在明视距离mm 250,渐晕系数为%50=k ,试求(1)视觉放⼤率;(2)线视场;(3)物体的位置。
eye已知:放⼤镜 mm f 25=' mm D 18=放 mm P 50=' mm l P 250='-'%50=K求:①Γ② 2y ③l 解:①fDP '-'-=Γ1 25501252501250-+=''-+'=f P f 92110=-+=②由%50=K 可得: 18.050*2182=='='P D tg 放ωωωtg tg '=Γ∴02.0918.0==ωtg Dytg =ω∴mm Dtg y 502.0*250===ω∴mm y 102= ⽅法⼆:18.0='ωtg mm tg y 45*250='='ω mm l 200-=' mm fe 250='mm l 2.22-= yy l l X '==='=92.22200β mm y 102=③ l P D '-'= mm D P l 20025050-=-=-'='f l l '=-'11125112001=--l mm l 22.22-=3.⼀显微镜物镜的垂轴放⼤率为x3-=β,数值孔径1.0=NA ,共扼距mm L 180=,物镜框是孔径光阑,⽬镜焦距mm f e 25='。
工程光学第二章练习参考答案

f 2' ' f1 f 2'
D2 20 x 0.714286 tg 2 ' 2 0.09920635 f1 108
5.66557
2 11.331
渐晕50%视场
ω
F1’ F2
D2 20 tg 2' 2 0.07936508 f1 108
8
(2)
100
f o' f e' 100 ' fo f' 8 e
f o' 88.89mm ' f e 11.11mm
第七章 (3)
6
-l=-100
l’
1 1 1 l ' 100 11.11 l ' 12.5mm
第七章 (4)
l1 90, l1 ' 270
第二章
4
l1 90,
l1 ' 270
1 1 1 l1 ' l1 f ' f ' 67.5 1 1 1 270 90 f '
第二章
4
1 1 1 l1 ' l1 f ' 1 1 1 l2 ' l2 f'
1 1 1 3l1 l1 f ' 1 1 1 4l 2 l 2 f'
f '1 f '2 f '1 f '2 f ' d f '1 f 2 f '2 240mm
450 f '2 1200 300 450 f '2
第二章 10
f '1 f '2 f '1 f '2 f ' 100 d f '1 f 2 100 50 100 d 100 50 d 100mm
1995-2016年浙江大学841工程光学基础考研真题及答案解析-汇编

1995-2016年浙江大学841工程光学基础考研真题及答案解析-汇编2017版浙江大学《841工程光学基础》全套考研资料我们是布丁考研网浙大考研团队,是在读学长。
我们亲身经历过浙大考研,录取后把自己当年考研时用过的资料重新整理,从本校的研招办拿到了最新的真题,同时新添加很多高参考价值的内部复习资料,保证资料的真实性,希望能帮助大家成功考入浙大。
此外,我们还提供学长一对一个性化辅导服务,适合二战、在职、基础或本科不好的同学,可在短时间内快速把握重点和考点。
有任何考浙大相关的疑问,也可以咨询我们,学长会提供免费的解答。
更多信息,请关注布丁考研网。
以下为本科目的资料清单(有实物图及预览,货真价实):2017年浙江大学《工程光学基础》全套资料包括:一、浙江大学《工程光学基础》历年考研真题及答案解析2016年浙江大学《工程光学基础》考研真题2015年浙江大学《工程光学基础》考研真题2014年浙江大学《工程光学基础》考研真题(含答案解析)2013年浙江大学《工程光学基础》考研真题(含答案解析)2012年浙江大学《工程光学基础》考研真题(含答案解析)2011年浙江大学《工程光学基础》考研真题(含答案解析)2010年浙江大学《工程光学基础》考研真题(含答案解析)2009年浙江大学《工程光学基础》考研真题(含答案解析)2008年浙江大学《工程光学基础》考研真题(含答案解析)2007年浙江大学《工程光学基础》考研真题(含答案解析)2006年浙江大学《工程光学基础》考研真题(含答案解析)2005年浙江大学《工程光学基础》考研真题(含答案解析)2004年浙江大学《工程光学基础》考研真题(含答案解析)2003年浙江大学《工程光学基础》考研真题(含答案解析)2002年浙江大学《工程光学基础》考研真题(含答案解析)2001年浙江大学《工程光学基础》考研真题(含答案解析)2000年浙江大学《工程光学基础》考研真题(含答案解析)1999年浙江大学《工程光学基础》考研真题(含答案解析)1998年浙江大学《工程光学基础》考研真题(含答案解析)1997年浙江大学《工程光学基础》考研真题(含答案解析)1996年浙江大学《工程光学基础》考研真题(含答案解析)1995年浙江大学《工程光学基础》考研真题(含答案解析)二、浙江大学《工程光学基础》期中期末试题汇编三、浙江大学《工程光学基础》考研复习笔记1、浙江大学物理光学笔记2、浙江大学最新光学笔记四、浙江大学《工程光学基础》考研复习题1、习题与答案五、浙江大学《工程光学基础》赠送资料(电子版,发邮箱)1、浙江大学《光学工程基础》复试题目以下为截图及预览:2016年考研真题:2012年考研真题:2012年真题答案解析:期中期末试题:考研复习笔记:。
工程光学习题解答(第1章)

第一章1.举例说明符合光传播基本定律的生活现象及各定律的应用。
答:(1)光的直线传播定律影子的形成;日蚀;月蚀;均可证明此定律.应用:许多精密的测量,如大地测量(地形地貌测量),光学测量,天文测量.(2)光的独立传播定律定律:不同光源发出的光在空间某点相遇时,彼此互不影响,各光束独立传播。
说明:各光束在一点交会,光的强度是各光束强度的简单叠加,离开交会点后,各光束仍按各自原来的方向传播。
2.已知真空中的光速c≈3×108m/s,求光在水(n=1。
333)、冕牌玻璃(n=1。
51)、火石玻璃(n=1。
65)、加拿大树胶(n=1。
526)、金刚石(n=2.417)等介质中的光速。
解:v=c/n(1)光在水中的速度:v=3×108/1。
333=2.25×108 m/s(2)光在冕牌玻璃中的速度:v=3×108/1。
51=1。
99×108 m/s(3)光在火石玻璃中的速度:v=3×108/1。
65=1。
82×108 m/s(4)光在加拿大树胶中的速度:v=3×108/1。
526=1。
97×108 m/s(5)光在金刚石中的速度:v=3×108/2.417=1。
24×108m/s*背景资料:最初用于制造镜头的玻璃,就是普通窗户玻璃或酒瓶上的疙瘩,形状类似“冠”,皇冠玻璃或冕牌玻璃的名称由此而来。
那时候的玻璃极不均匀,多泡沫。
除了冕牌玻璃外还有另一种含铅量较多的燧石玻璃(也称火石玻璃).3.一物体经针孔相机在屏上成像的大小为60mm,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:⇒l=300mm4.一厚度为200mm的平行平板玻璃(设n=1。
5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少?解:本题是关于全反射条件的问题。
工程光学习题参考答案第一章几何光学基本定律

⼯程光学习题参考答案第⼀章⼏何光学基本定律第⼀章⼏何光学基本定律1. 已知真空中的光速c =3810?m/s ,求光在⽔(n=1.333)、冕牌玻璃(n=1.51)、⽕⽯玻璃(n=1.65)、加拿⼤树胶(n=1.526)、⾦刚⽯(n=2.417)等介质中的光速。
解:则当光在⽔中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在⽕⽯玻璃中,n =1.65时,v=1.82 m/s ,当光在加拿⼤树胶中,n=1.526时,v=1.97 m/s ,当光在⾦刚⽯中,n=2.417时,v=1.24 m/s 。
2. ⼀物体经针孔相机在屏上成⼀60mm ⼤⼩的像,若将屏拉远50mm ,则像的⼤⼩变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则⽅向不变,令屏到针孔的初始距离为x ,则可以根据三⾓形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. ⼀厚度为200mm 的平⾏平板玻璃(设n =1.5),下⾯放⼀直径为1mm 的⾦属⽚。
若在玻璃板上盖⼀圆形的纸⽚,要求在玻璃板上⽅任何⽅向上都看不到该⾦属⽚,问纸⽚的最⼩直径应为多少?2211sin sin I n I n =66666.01sin 22==n I745356.066666.01cos 22=-=I88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射⽅式传播时在⼊射端⾯的最⼤⼊射⾓)。
解:位于光纤⼊射端⾯,满⾜由空⽓⼊射到光纤芯中,应⽤折射定律则有: n 0sinI 1=n 2sinI 2 (1)⽽当光束由光纤芯⼊射到包层的时候满⾜全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联⽴得到n 0 .5. ⼀束平⾏细光束⼊射到⼀半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学习题解答第十章光的干涉

第十一章 光的干涉1. 双缝间距为1mm,离观察屏1m,用钠光灯做光源,它发出两种波长的单色光nm 0.5891=λ和nm 6.5892=λ,问两种单色光的第十级亮条纹之间的间距是多少?解:由题知两种波长光的条纹间距分别为961131589105891010D e m d λ---⨯⨯===⨯ 962231589.610589.61010D e m d λ---⨯⨯===⨯ ∴第十级亮纹间距()()65211010589.6589100.610e e m -∆=-=⨯-⨯=⨯2. 在杨氏实验中,两小孔距离为1mm,观察屏离小孔的距离为50cm,当用一片折射率为1.58的透明薄片贴住其中一个小孔时(见图11-17),发现屏上的条纹系统移动了0.5场面,试决定试件厚度。
解:设厚度为h ,则前后光程差为()1n h ∆=- ()1x dn h D∆⋅∴-=230.510100.580.5h --⨯⨯=21.7210h mm -=⨯3. 一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长nm 28.656=λ,空气折射率000276.10=n 。
试求注入气室内气体的折射率。
图11-47 习题2 图解:设气体折射率为n ,则光程差改变()0n n h ∆=- ()02525x d dn n h e D Dλ∆⋅∴-==⋅= 9025656.2810 1.000276 1.0008230.03m n n h λ-⨯⨯=+=+= 4. ** 垂直入射的平面波通过折射率为n 的玻璃板,投射光经投射会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面(见图11-18)的直线发生光波波长量级的突变d ,问d 为多少时,焦点光强是玻璃板无突变时光强的一半。
解:无突变时焦点光强为04I ,有突变时为02I ,设',.d D 200'4cos 2xd I I I Dπλ== ()'104xd m m D λ⎛⎫∴∆==+≥ ⎪⎝⎭又()1n d ∆=- 114d m n λ⎛⎫∴=+ ⎪-⎝⎭5. 若光波的波长为λ,波长宽度为λ∆,相应的频率和频率宽度记为ν和ν∆,证明λλνν∆=∆,对于nm 8.632=λ的氦氖激光,波长宽度nm 8102-⨯=∆λ,求频率宽度和相干长度。
浙江大学2005高代答案

" # $ %
qso
p n n p ) o
n n r rq )
: : ¬ 5 / )« tu 8 + 7 £S ¤¥¦ §7 ¨EF © 7 + ª0« + 0 © 0 ® 55 5 ¯ °
lF f I lF f I
" # $ %
f`mF@
! !
lF ] p F@ C A C C^ q2 cWstu4stvw2 x4y f n( )o +, r z{H| I p l F l I l I 4{ r 4 cWst2 f} r ~r pFI p }F pF
12345 6 789
o 0 ¢* ¢ ¡பைடு நூலகம் +
+ 0
5 ¬ / )7 ª ® ¯ 5 °
! !
12345 6 789
&) # ( # $ 8< ! %./ 0123 45 687 9:%;123 45 7 "! * %' $ '+ , &) &) ? ( ( ( ) 7 > 9:%=1 @$ $ $"&A "! " > * + * + * + ' ' ,> > , , CDE3 F <8 71GH25%IJKLJMNOPG5QRST F <8 7RUVW F ) Q1X%Y 7 QZ[\]59:%^_`La9: b%cd ! %. F$( <#7 * ,>+ F ) i$ # %./ & j kl # ( /F %gh & & > ' 3 4eLaf:%IJ F$! * + ,>Lam F F& ) ) > # # $! ( Ld @$F &i $!#( & > ' '#%n= b%k%F %& L * + * + > > >
(完整版)工程光学习题参考答案第十四章光的偏振和晶体光学.doc

工程光学习题解答第十四章 光的偏振和晶体光学1. 一束自然光以 30 度角入射到玻璃 -空气界面, 玻璃的折射率 n 1.54 ,试计算 ( 1)反射光的偏振度;( 2)玻璃 -空气界面的布儒斯特角; ( 3)以布儒斯特角入射时透射光的偏振度。
解:光由玻璃到空气,n 1 1.54,n 2 1,130o , 2 sin 1n 1sin 1 50.354n 2① r ssin 12tan120.06305sin0.3528, r p12tan12I maxI min22Pr sr p93.80 0I maxI min22r sr p② B1n 2tan 1133 otann 11.54③ 1B时, 290B57 0 , r p 0, r ssin 12 0.4067sin 12T s 1 r s 2 0.8364, T p 1P 1 0.8364 9 0 010.8364注:若n 2 cos 2 , T st s 2 ,T pt p2n 1 cos 1ImaxT p I 0, IminT s I 0故Pt p 2t s 2或 T scos 2(12)t p 2 t s 2T p2. 自然光以布儒斯特角入射到由10 片玻璃片叠成的玻片堆上,试计算透射光的偏振度。
10 片玻璃透射率 T s 1 r s20 0.028解:每片玻璃两次反射,故20.836420而 T p 1,令I min ,则p1 IIm ax1Im axm axII m in m in1 0.02689 0.94761 0.026893. 选用折射率为 2.38 的硫化锌和折射率为 1.38 的氟化镁作镀膜材料,制作用于氟氖激光(632.8nm )的偏振分光镜。
试问(1)分光镜的折射率应为多少?(2)膜层的厚度应为多少?解:( 1)n3sin 45 n2 sin 2n1 n3tg 2 (起偏要求)n2n3 452n2 sin 1 n3n3 2 2n2tg 22 n22 1 tg 2n1 n1 1 n1 n2 n22 n2n2 1 n1 2 2 n2 2 n1 2 1.6883n2(2)满足干涉加强 2 2n2 h2 cos 22 ,2 sin 1 n3 30.1065n2 sin 45则 h2 2 76.84 nmcos2n2 2而1 90 2 59.8934 , h12 228.54 nm 2n1 cos 14. 线偏振光垂直入射到一块光轴平行于界面的方解石晶体上,若光矢量的方向与警惕主截面成( 1)30 度( 2)45 度( 3)60 度的夹角,求o光和e光从晶体透射出来后的强度比?解:垂直入射 1 2 3, S 波与 p 波分阶r s 2 r p 2n1 cos 1 n2 cos 2 n1 n2r sn2 cos n1 n2n1 cos 1 2n2 cos 1 n1 cos 2 n2 n1r pn1 cos n2 n1n2 cos 1 2o 光此时对应 s 波r0 1 n0 ,T0 1 r02 4n0 22 21 n0 1 n02e 光此时对应 p 波r en e 1 , T e1 224n en e1 r e21 n e2T 0 sin 224I 0E s T 0 tg 2n 0 1 n e I eE p 2T e cos 2 T en e1 n 0取 n 0 1.6584 , n e 1.4864则Itg 20.9526I e( 1)30 ,I 01 0.9526 0.3175I e3( 2)45 ,I 00.9526I e( 3)60 ,I 03 0.95262.8578I e5. 方解石晶片的厚度 d 0.013mm ,晶片的光轴与表面成60 度角, 当波长632.8nm的氦氖激光垂直入射晶片时(见图14-64),求( 1)晶片内 o 、 e 光线的夹角;( 2) o 光和 e 光的振动方向; ( 3) o 、 e 光通过晶片后的相位差。
工程光学习题解答

36.2( mm), l F
第二章 理想光学系统
17、有三个薄透镜,其焦距分别为 f1 100mm, f 2 50mm, f 3 50mm, 其间隔 d1 10mm, d 2 10mm 求组合系统的 基点。 h h1 100mm, tan U 2 tan U1 2 解:物方参数 f
lH f
l F l H f 1560mm, l F l H f 1360mm
第二章 理想光学系统
10、解:
f f1f 2
100mm,
f1f 2 f
50mm
d f1 f 2 100mm lH f lH f d f2 d f1 100mm, l F l H f 0
A
OB 50 OB OB 30mm
A
A
n 6、解:0 sin I1 n1 sin I 2 I 2 90 I m
0
n1 sin I m n2 sin 90 sin I m n2 n1 n2 n1
2 2
0
cos I m 1
n0 sin I1 n1 1
H
lH
F2
F1
F
d
l F (lk )
L
f
第二章 理想光学系统
9、已知一透镜 r1 200mm, r2 300mm, d 50mm, n 1.5 , 求其焦距、光焦度、基点位置。 nr1r2 解: f 1440mm 1.44m
( n 1)[ n( r2 r1 ) ( n 1)] 1 f 0.69 D n 1 n d1 120mm, l H f n 1 n d 2 80mm
工程光学基础教程 习题答案(完整)

第一章 几何光学基本定律1. 已知真空中的光速c =3810⨯m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s, 当光在冕牌玻璃中,n=1.51时,v=1.99 m/s, 当光在火石玻璃中,n =1.65时,v=1.82 m/s , 当光在加拿大树胶中,n=1.526时,v=1.97 m/s ,当光在金刚石中,n=2.417时,v=1.24 m/s 。
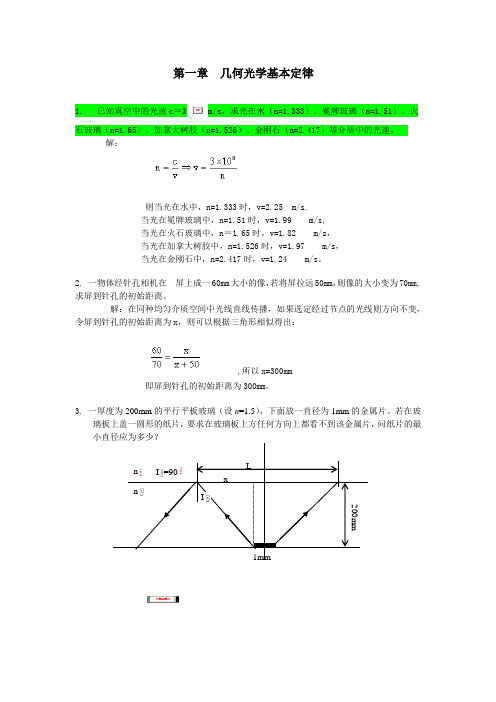
2. 一物体经针孔相机在 屏上成一60mm 大小的像,若将屏拉远50mm ,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x ,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm 。
3. 一厚度为200mm 的平行平板玻璃(设n =1.5),下面放一直径为1mm 的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?2211sin sin I n I n = 66666.01sin 22==n I745356.066666.01cos 22=-=I1mm I 1=90︒n 1 n 2200mmL I 2 x88.178745356.066666.0*200*2002===tgI xmm x L 77.35812=+=4.光纤芯的折射率为1n ,包层的折射率为2n ,光纤所在介质的折射率为0n ,求光纤的数值孔径(即10sin I n ,其中1I 为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有: n 0sinI 1=n 2sinI 2 (1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n 0 .5. 一束平行细光束入射到一半径r=30mm 、折射率n=1.5的玻璃球上,求其会聚点的位置。
工程光学基础 习题参考答案

2、 l = −1000, l'= 4500 / 7, β = −0.4286
1.5 l'
−
1 (−1000)
=
1 300
⇒
1.5 l'
=
1 300
−
1 1000
⇒
l'=
4500 7
=
642.857
3、 l = −100, l' = −225, β = 1.5
似。
20、一球面镜半径 r=-100,求β=0、-0.1×,-0.2×,-1×,1×,5×,10×,∞, 时的物距和像距。 解:
根据公式 β = y' = − l' , 1 + 1 = 2 y l l' l r
所以:
1.β = 0, l' = 0, l = −50 2.β = −0.1, l' = −550, l = −55 3.β = −0.2, l' = −60, l = −300 4.β = −1, l'= −100, l = −100 5.β = 1, l' = 0, l = 0 6.β = 5, l' = −200, l = −40 7.β = 10, l' = −450, l = 45 8.β = ∞, l' = +∞, l = −50
18、一直径为 400mm、折射率为 1.5 的玻璃球中有两个小气泡,一个位于球心, 另一个位于 1/2 半径处。沿两气泡连线方向在球两边观察,问看到气泡在何处? 如果在水中观察,看到气泡又在何处? 解:
(1)求两点成像位置: 如图所示:人观察到的是气泡经过 球面折射后成的像,根据公式 n' − n = n'−n (1-20)位于球心气泡成 l' l r 像位置:
浙大物理光学2005年真题

浙江大学2005年攻读硕士学位研究生入学考试试题考试科目:物理光学编号:注意:答案必须写在答题纸上,写在试卷或草稿上均无效。
一.选择题(2×10=20分)1.欲观察到定域条纹,则首选()A.单色扩展光源B.白光扩展光源C.单色电光源D.白光电光源2.牛顿环装置中,若用平行光垂直照明,则当凸透镜与平板间距拉大时,条纹将()A.外扩 B.向中心收缩 C.无影响3.平行平板干涉中,当平板表面反射率很高时(不考虑吸收),若相邻光束光程差为波长整数倍时,则()A.反射光强等于入射光强B.投射光强等于入射光强C.反射光强随表面反射率增大而增大4.设线数为N1=600的光栅,其零级主极大光强为I1,在其他条件相同情况下,N2=1800的光栅其零级主极大光强为I2,则I2/I1为()A.1/9B.1/3C.3D.95.一束自然光通过¼波片时,一般为()A.线偏振光B.圆偏振光C.椭圆偏振光D.自然光6.以直径d的圆孔作衍射受限系统出瞳,在相干照明时,其截止频率为ρ1,而用非相干光照明时,其截止频率为ρ2,则ρ2/ρ1,为()A.1/4B.1/2C.2D.4E.17.单轴双折射晶体中,一般情况下()A. H,D,S相互垂直B. H,E,k相互垂直C. H,E,S相互垂直D. E,k,S相互垂直8,将一块光栅置于一相干成像系统中,若再其端面上只允许-1和+2级频谱通过,则其光栅的空间频率是()A.与原来相同B.是原来的两倍C.是原来的三倍9.为了观察原子光谱的超精细结构,应首选下列哪个分光系统()A.棱镜B.典型的F-B干涉仪C.典型光栅10.根据菲涅尔衍射波带片理论,当衍射屏只允许中心第一个波带通过时,轴上考察点亮度为I1,而当衍射屏通光孔为无穷大时,轴上考察点亮度为I2,则I2/ I1为( )A.4B.2C.1/2D.1/4二.简答题(4×5=20分)1.写出会聚球面波和发散球面波的波动公式。
工程光学习题参考答案第一章几何光学基本定律
第一章几何光学基本定律1. 已知真空中的光速c =3m/s ,求光在水(n=1.333)、冕牌玻璃(n=1.51)、火石玻璃(n=1.65)、加拿大树胶(n=1.526)、金刚石(n=2.417)等介质中的光速。
解:则当光在水中,n=1.333时,v=2.25 m/s,当光在冕牌玻璃中,n=1.51时,v=1.99 m/s,当光在火石玻璃中,n=1.65时,v=1.82 m/s,当光在加拿大树胶中,n=1.526时,v=1.97 m/s,当光在金刚石中,n=2.417时,v=1.24 m/s。
2. 一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:,所以x=300mm即屏到针孔的初始距离为300mm。
3. 一厚度为200mm的平行平板玻璃(设n=1.5),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形的纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片的最小直径应为多少?1mmI=90nn200mmLIx4.光纤芯的折射率为,包层的折射率为,光纤所在介质的折射率为,求光纤的数值孔径(即,其中为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0.5. 一束平行细光束入射到一半径r=30mm、折射率n=1.5的玻璃球上,求其会聚点的位置。
如果在凸面镀反射膜,其会聚点应在何处?如果在凹面镀反射膜,则反射光束在玻璃中的会聚点又在何处?反射光束经前表面折射后,会聚点又在何处?说明各会聚点的虚实。
解:该题可以应用单个折射面的高斯公式来解决,设凸面为第一面,凹面为第二面。
工程光学基础教程_习题参考答案

工程光学基础教程_习题参考答案工程光学基础教程_习题参考答案第一章光学基本知识与技术1.1 什么是光学?光学在人类生活中有哪些应用?答:光学是研究光的行为和性质的物理学科。
它涉及到光的产生、传播、变换、干涉、衍射、偏振以及光在介质中的行为等问题。
光学在人类生活中有着广泛的应用,如眼镜、镜头、显示器、照明、医疗器械、天文望远镜等。
1.2 光的波动性是如何描述的?答:光的波动性是指光是一种电磁波,具有振幅、频率、波长等特征。
它可以在空间中传播,并且可以表现出干涉、衍射等波动性质。
光的波动性可以通过波长、频率、振幅等参数进行描述。
1.3 什么是光的干涉?举例说明其应用。
答:光的干涉是指两列或两列以上的光波在空间中叠加时,由于光波的叠加产生明暗相间的干涉条纹的现象。
光的干涉在很多领域都有应用,例如光学干涉仪、双缝干涉实验、全息照相、光学通信等。
1.4 什么是光的衍射?举例说明其应用。
答:光的衍射是指光在遇到障碍物或孔径时,会绕过障碍物或孔径边缘,产生明暗相间的衍射图案的现象。
光的衍射在很多领域也有应用,例如光学透镜、衍射光学器件、全息照相、光学存储等。
1.5 什么是光的偏振?举例说明其应用。
答:光的偏振是指光波的电矢量在振动时,只在某个方向上振动,而在其他方向上振动为零的现象。
光的偏振在很多领域也有应用,例如偏振眼镜、偏振片、偏振光学器件等。
第二章光学透镜与成像2.1 什么是透镜?列举几种常见的透镜及其特点。
答:透镜是一种光学器件,它由一块透明材料制成,可以聚焦或发散光线。
常见的透镜包括凸透镜、凹透镜、平凸透镜、平凹透镜等。
2.2 凸透镜的成像原理是什么?如何计算凸透镜的焦距?答:凸透镜的成像原理是光线经过凸透镜后,平行于主轴的光线会聚于一点,这个点称为焦点。
焦距是指从透镜中心到焦点的距离。
凸透镜的焦距可以通过公式 f=1/v+1/u 进行计算,其中f为焦距,u为物距,v为像距。
2.3 凹透镜的成像原理是什么?如何计算凹透镜的焦距?答:凹透镜的成像原理是光线经过凹透镜后,平行于主轴的光线会朝透镜中心方向会聚于一点,这个点称为虚焦点。
工程光学习题解答

工程光学习题解答 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】第一章习题1、已知真空中的光速c=3m/s,求光在水(n=)、冕牌玻璃(n=)、火石玻璃(n=)、加拿大树胶(n=)、金刚石(n=)等介质中的光速。
?解:则当光在水中,n=时,v=m/s,当光在冕牌玻璃中,n=时,v=m/s,当光在火石玻璃中,n=时,v=m/s,当光在加拿大树胶中,n=时,v=m/s,当光在金刚石中,n=时,v=m/s。
2、一物体经针孔相机在屏上成一60mm大小的像,若将屏拉远50mm,则像的大小变为70mm,求屏到针孔的初始距离。
?解:在同种均匀介质空间中光线直线传播,如果选定经过节点的光线则方向不变,令屏到针孔的初始距离为x,则可以根据三角形相似得出:所以x=300mm?即屏到针孔的初始距离为300mm。
3、一厚度为200mm的平行平板玻璃(设n=),下面放一直径为1mm的金属片。
若在玻璃板上盖一圆形纸片,要求在玻璃板上方任何方向上都看不到该金属片,问纸片最小直径应为多少解:令纸片最小半径为x,则根据全反射原理,光束由玻璃射向空气中时满足入射角度大于或等于全反射临界角时均会发生全反射,而这里正是由于这个原因导致在玻璃板上方看不到金属片。
而全反射临界角求取方法为:(1)其中n2=1,n1=,同时根据几何关系,利用平板厚度和纸片以及金属片的半径得到全反射临界角的计算方法为:(2)联立(1)式和(2)式可以求出纸片最小直径x=179.385mm,所以纸片最小直径为358.77mm。
4、光纤芯的折射率为n1、包层的折射率为n2,光纤所在介质的折射率为n0,求光纤的数值孔径(即n0sinI1,其中I1为光在光纤内能以全反射方式传播时在入射端面的最大入射角)。
解:位于光纤入射端面,满足由空气入射到光纤芯中,应用折射定律则有:n0sinI1=n2sinI2(1)而当光束由光纤芯入射到包层的时候满足全反射,使得光束可以在光纤内传播,则有:(2)由(1)式和(2)式联立得到n0 sinI1.5、一束平行细光束入射到一半径r=30mm、折射率n=的玻璃球上,求其会聚点的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
05年答案
一.1.C 2.B 3.B 4.D 5.D 6.C 7.C 8.C 9.B 10.A 二.1.会聚球面波:E=(A/r)exp(-ikr)
发散球面波:E=(A/r)exp(ikr)
2.ε(x)=asin(2えx/d)+t0
3.扩展光源上的两点SS’发出的同倾角的光线经过平板后到达观察屏上时有相同的光程差,故可见度不受影响。
p
4.让偏振光通过¼波片,旋转偏振器,能找到消光位置者为椭圆偏振光
5.望远镜分辨率用θ=1.22λ/D
三.
1.同02年试题
2.条纹移动112个,表示光程差为112λ,而这时两束光程差为(n-1)l,其中l=500mm;
所以(n-1)×500=112×589.3×10-6
3.同01年试题
4.d=1/2000mm,设闪耀角为γ
对一级闪耀波长,2dsinγ=λ则,γ=17.46º
由光栅方程d(sini-sin θ)=m λ i=γ
d(sin γ-sin θ)=m λ 取sin θ=1,得m=-1.17
取sin θ=-1, 得m=2.17
因此,最多可看见500nm 的-1,0,+1,+2级光谱
6.建立如图坐标,
则,投射系数为:
t(x)=rect(x/a)+rect[(x-3/2a-d)/2a]
频谱为E(u)=F[t(x)] a d 2a
=asinc[(ax)/(λz 1)]+
2aexp[-i2えu(3/2a+d)]sinc[(2ax)/ (λz 1)]
I=<E.E*>=a 2sinc 2[(2ax)/ (λz 1)]+4 a 2sinc 2[(ax)/ (λz 1)]+ 4 a 2sinc [(ax)/ (λz 1)] sinc [(2ax)/ (λz 1)]cos[えx(3a+2d)/( λz 1)]
7.同02年试题
8.从起偏器透出偏振光的琼斯矢量为【 】 待测波片的琼斯矩阵为:
m=2
1 法线
0-1
0 1
cos δ/2
1/4波片的矩阵为:
通过1/4波片以后的矩阵为
cos δ/2
=
即出射光为与x 轴成δ/2的线偏振光,利用检偏器确定夹角即可得到待测波片的相位延迟角
9.(1)振幅为2的平面波经过的振幅分布为:
ε(x )=1+cos(2えu 0x) 傅立叶频谱为E(u)=δ(u)+1/2[δ(u+u 0)+ δ(u-u 0)]条纹是平行y 轴的平行直条纹
三个频谱分量对应三个夫琅和费衍射0级和±级极大值,位置为x o ’=0, x ±1’=±u 0λf
一级极大为零级极大强度的1/4
1 -itg δ/2
-itg δ/2 1 1 0 0 i
2 -itg δ/2 -itg δ/2 1 2 0 0 i 1 0
cos δ/2 sin δ/2
(2)I=【1+cos(2えu0x)】2
(3)挡住0级,I= cos2(2えu0x) u=2u0
(4)挡住-1级,I=(1+e-i2えu0x)2=5/4+ cos(2えu0x)
u=u0。
