北师大版高中数学一轮复习第十二章12.1算法与程序框图word版下载
2021高考数学一轮复习统考第12章算法初步、复数、推理与证明第1讲算法初步学案北师大版

第十二章算法初步、复数、推理与证明第1讲算法初步基础知识整合1.算法的框图及结构(1)算法(2)程序框图的图形.通常,程序框图由程序框和流程线组成,一个或几个程序框的组合表示算法中的一(3)三种基本逻辑结构离不开的11基本结构程序框图步骤n错误!(1)输入语句、输出语句、赋值语句的格式与功能语句一般格式功能输入语句14INPUT“提示内容”;变量输入信息输出语句15PRINT“提示内容”;表达式输出信息赋值语句16变量=表达式17将表达式所代表的值赋给变量①IF-THEN格式②IF-THEN-ELSE格式(3)循环语句的格式及框图①UNTI L语句DO循环体LOOP UNTIL条件②WHILE语句WHILE 条件循环体WEND1.注意区分处理框与输入框,处理框主要是赋值、计算,而输入框只是表示一个算法输入的信息.2.循环结构中必有条件结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.3.注意区分当型循环与直到型循环.直到型循环是“先循环,后判断,条件满足时终止循环”,而当型循环则是“先判断,后循环,条件满足时执行循环”.两者的判断框内的条件表述在解决同一问题时是不同的,它们恰好相反.1.(2019·北京高考)执行如图所示的程序框图,输出的s值为( )A.1 B.2C.3 D.4答案 B解析k=1,s=1;第一次循环:s=2,判断k<3,k=2;第二次循环:s=2,判断k<3,k=3;第三次循环:s=2,判断k=3,故输出2.故选B.2.下列程序段执行后,变量a,b的值分别为( )a=15b=20a=a+bb=a-ba=a-bPRINT a,bA.20,15 B.35,35C.5,5 D.-5,-5答案 A解析a=15,b=20,把a+b赋给a,因此得出a=35,再把a-b赋给b,即b=35-20=15.再把a-b赋给a,此时a=35-15=20,因此最后输出的a,b的值分别为20,15.故选A.3.(2019·武昌调研)执行如图所示的程序框图,如果输入的a 依次为2,2,5时,输出的S 为17,那么在判断框中可以填入( )A .k >nB .k <nC .k ≥nD .k ≤n 答案 A解析 第一次输入a =2,此时S =0×2+2=2,k =0+1=1,不满足k =1>n =2;第二次输入a =2,此时S =2×2+2=6,k =1+1=2,不满足k =2>n =2;第三次输入a =5,此时S =6×2+5=17,k =2+1=3,满足k =3>n =2,循环终止,输出的S =17.故选A.4.(2019·湖南郴州模拟)执行如图所示的程序框图,输出S 的值为12时,k 是( )A .5B .3C .4D .2答案 A解析 模拟执行程序,可得每次循环的结果依次为k =2,k =3,k =4,k =5,大于4,可得S =sin 5π6=12,输出S 的值为12.故选A.5.(2020·锦州摸底)若如图所示的程序框图输出的S 是30,则在判断框中M 表示的“条件”应该是( )A .n ≥3B .n ≥4C .n ≥5D .n ≥6 答案 B解析 第一次循环,n =1,S =2;第二次循环,n =2,S =6;第三次循环,n =3,S =14;第四次循环,n =4,S =30,故选B.6.执行如图所示的程序框图,若输入x 的值为1,则输出n 的值为________.答案 3解析第一次:x=1,x2-4x+3=0≤0.第二次:x=2,n=1,x2-4x+3=-1≤0.第三次:x=3,n=2,x2-4x+3=0≤0.第四次:x=4,n=3,x2-4x+3=3>0,输出n,程序结束.核心考向突破考向一算法的基本结构例 1 (2019·全国卷Ⅲ)执行如图所示的程序框图,如果输入的为0.01,则输出s 的值等于( )A .2-124B .2-125C .2-126D .2-127答案 C 解析=0.01,x =1,s =0,s =0+1=1,x =12,x <不成立; s =1+12,x =14,x <不成立; s =1+12+14,x =18,x <不成立; s =1+12+14+18,x =116,x <不成立; s =1+12+14+18+116,x =132,x <不成立; s =1+12+14+18+116+132,x =164,x <不成立; s =1+12+14+18+116+132+164,x =1128,x <成立,此时输出s=2-126.故选C.利用循环结构表示算法应注意的问题(1)注意是利用当型循环结构,还是直到型循环结构.(2)注意准确选择表示累计的变量.(3)注意在哪一步开始循环,满足什么条件不再执行循环体.[即时训练] 1.(2019·天津高考)阅读右边的程序框图,运行相应的程序,输出S的值为( )A.5B.8C.24D.29答案 B解析i=1,S=0,i不是偶数;第一次循环:S=1,i=2<4;第二次循环:i是偶数,j=1,S=5,i=3<4;第三次循环:i不是偶数,S=8,i=4,满足i≥4,输出S,结果为8.故选B.2.(2020·濮阳模拟)执行如图所示的程序框图(其中b=c mod 10表示b等于c除以10的余数),则输出的b为( )A.2 B.4C.6 D.8答案 D解析a=2,b=8,n=1;c=16,a=8,b=6,n=2;c=48,a=6,b=8,n=3;c =48,a=8,b=8,n=4;c=64,a=8,b=4,n=5;c=32,a=4,b=2,n=6;c=8,a=2,b=8,n=7,…,易知该程序框图中a,b的值以6为周期重复出现.又因为2019=6×336+3,所以当n=2019时,b=8.故选D.精准设计考向,多角度探究突破考向二算法的交汇性问题角度1算法与函数的交汇例2 (2019·潍坊模拟)执行右边的程序框图,如果输出的y值为1,则输入的x值为( )A .0B .eC .0或eD .0或1 答案 C解析 程序对应的函数为y =⎩⎪⎨⎪⎧e x,x ≤0,2-ln x ,x >0.若x ≤0,由y =1,得e x=1,得x =0,满足条件;若x >0,由y =2-ln x =1,得ln x =1,即x =e ,满足条件.综上,输入的x 值为0或e ,故选C.角度2 算法与数列的交汇例3 (2020·西宁模拟)执行如图所示的程序框图,若输入n =10,则输出的S 的值是( )A.910B.1011C.1112D.922答案 B解析 模拟程序的运行,可得程序的功能是利用循环结构计算并输出变量S =11×2+12×3+…+110×11的值, 可得S =11×2+12×3+…+110×11=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫110-111=1-111=1011.故选B.角度3 算法与统计的交汇例4 (2019·九江联考)图1是随机抽取的15户居民月均用水量(单位:吨)的茎叶图,月均用水量依次记为A 1,A 2,…,A 15,图2是统计茎叶图中月均用水量在一定范围内的频数的一个程序框图,则输出的n 的值为________.答案7解析由程序框图,知算法的功能是计算15户居民中月均用水量大于2.1的户数,由茎叶图得,在这15户居民中,月均用水量大于2.1的户数为7,故输出的n的值为7.解决算法的交汇性问题的方法循环结构的程序框图与数列、不等式、统计等知识综合是高考命题的一个热点,解决此类问题时应把握三点:一是初始值,即计数变量与累加变量的初始值;二是两个语句,即循环结构中关于计数变量与累加变量的赋值语句;三是一个条件,即循环结束的条件,注意条件与流程线的对应关系.[即时训练] 3.(2020·宁夏银川模拟)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )A .[-6,-2]B .[-5,-1]C .[-4,5]D .[-3,6]答案 D解析 当0≤t ≤2时,S =t -3∈[-3,-1].当-2≤t <0时,2t 2+1∈(1,9],则S ∈(-2,6].综上,当-2≤t ≤2时,S ∈[-3,6],故选D.4.(2019·湖南长沙模拟)如图,给出的是计算1+14+17+…+1100的值的一个程序框图,则图中判断框内的(1)处和执行框中的(2)处应填的语句是( )A .i >100,n =n +1B .i <34,n =n +3C .i >34,n =n +3D .i ≥34,n =n +3答案 C解析 算法的功能是计算1+14+17+…+1100的值,易知1,4,7,…,100成等差数列,公差为3,所以执行框中的(2)处应为n =n +3,令1+(i -1)×3=100,解得i =34,所以终止程序运行的i 值为35,所以判断框内的(1)处应为i >34,故选C.5.在2018~2019赛季NBA 季后赛中,当一个球队进行完7场比赛被淘汰后,某个篮球爱好者对该队的7场比赛得分情况进行统计,如下表:为了对这个队的情况进行分析,此人设计计算σ的算法流程图如图所示(其中x 是这7场比赛的平均得分),求输出的σ的值.解 由题意,知x -=17×(100+104+98+105+97+96+100)=100,由算法流程图可知s =(100-100)2+(104-100)2+(98-100)2+(105-100)2+(97-100)2+(96-100)2+(100-100)2=70.故σ=s7=10. 考向三 基本算法语句例5 (1)(2019·福州质检)下列程序语句的算法功能是( )INPUT a,b,cIF a<b THENa=bEND IFIF a<c THENa=cEND IFPRINT aENDA.输出a,b,c三个数中的最大数B.输出a,b,c三个数中的最小数C.将a,b,c从小到大排列D.将a,b,c从大到小排列答案 A解析由程序语句可知,当比较a,b的大小后,选择较大的数赋给a;当比较a,c的大小后,选择较大的数赋给a,最后输出a,所以此程序的作用是输出a,b,c三个数中的最大数.故选A.(2)运行下面的程序,执行后输出的s的值是( )A.11 B.15C.17 D.19答案 B解析当i=3时,s=7,当i=5时,s=11,当i=7时,s=15,此时不满足“i<6”,所以输出s=15,故选B.基本算法语句应用中需注意的问题(1)赋值号“=”的左、右两边不能对调,A =B 和B =A 的含义及运行结果是不同的. (2)不能利用赋值语句进行代数式的演算(如化简、因式分解等),在赋值语句中的赋值号右边的表达式中每一个“变量”都必须事先赋给确定的值.(3)赋值号与数学中的等号意义不同,比如在数学中式子N =N +1一般是错误的,但在赋值语句中它的作用是将原有的N 的值加上1再赋给变量N ,这样原来的值被“冲”掉.[即时训练] 6.阅读下面的程序:如果上述程序输入的值是51,则运行结果是( ) A .51 B .15 C .105 D .501答案 B解析 因为51÷10=5……1,所以a =5,b =1,x =10×1+5=15.故选B .7.(2019·龙岩质检)如图所示的程序,若最终输出的结果为6364,则在程序中“____?____”处应填入的语句为( )S=0n=2i=1DOS=S+1/nn=2*ni=i+1LOOP UNTIL ?PRINT SENDA.i>=8 B.i>=7C.i<7 D.i<8答案 B解析S=0,n=2,i=1,执行S=12,n=4,i=2;S=12+14=34,n=8,i=3;S=34+18=78,n=16,i=4;S=78+116=1516,n=32,i=5;S=1516+132=3132,n=64,i=6;S=3132+164=6364,n=128,i=7.此时满足题目条件输出的S=6364,∴“?”处应填上i>=7.故选B.(2019·沈阳模拟)程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )A.120 B.84C.56 D.28答案 B解析初始值i=0,n=0,S=0,第一次循环,i=1,n=1,S=1;第二次循环,i=2,n=3,S=4;第三次循环,i=3,n=6,S=10;第四次循环,i=4,n=10,S=20;第五次循环,i=5,n=15,S=35;第六次循环,i=6,n=21,S=56;第七次循环,i=7,n=28,S=84,此时退出循环,输出S=84,故选B.答题启示求解循环结构的程序框图题的“三注意”(1)注意是当型循环结构,还是直到型循环结构;(2)注意选择准确的表示累计的变量;(3)注意在哪一步开始循环,及执行循环体的条件.对点训练“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图所示的程序框图的算法思路就是来源于“欧几里得算法”.执行该程序框图(图中“a MOD b”表示a 除以b的余数),若输入的a,b分别为675,125,则输出的a=()C.50 D.75答案 B解析初始值:a=675,b=125,第一次循环:c=50,a=125,b=50;第二次循环:c=25,a=50,b=25;第三次循环:c=0,a=25,b=0,此时不满足循环条件,退出循环.输出a的值为25,故选B.21。
【走向高考】高考数学总复习 12-1算法与算法框图 课件 北师大版

3.在推理证明的复习中,要准确把握概念,把握好 各种证法的特点和步骤,注意灵活运用. (1)对于合情推理,主要是掌握相关概念,会进行类 比推理,能判断推理的类型. (2) 直接证明与间接证明主要渗透到其他知识板块 中,要注意在复习相应的板块时,培养选择合理证明方法 的能力. 4.熟练准确地进行复数运算是复数学习的重点.
3. 如果执行如图所示的程序框图,那么输出的 k= ( )
A.4 C.6
B.5 D.7
[答案] B
[解析 ] 第一次运行 k= 2,S= 0+ 20= 1; 第二次运行 k= 3, S= 1+ 21= 3; 第三次运行 k= 4, S= 3+ 23= 11; 第四次运行 k= 5, S= 11+ 211>100. 结束循环,输出的 k= 5,故选 B.
1.高考本单元考查的题型主要是选择题和填空题, 分值约在 10~ 15 分之间,属中低档题. 2.重点考查程序框图的“读”或“补”,注重对循 环结构的考查,或与其他知识点相结合的综合考查.
3.预计今后的高考,本单元仍将以程序框图为主, 重点关注程序框图“读”或“补”. 在考查程序框图时经常会与数列、 函数等知识的实际 问题相结合,进一步强化框图问题的实际背景.
(2)流程图形式为
6.循环结构 (1)定义:循环结构是指 从某处开始,按照一定条件,
反复执行处理某步骤的情况. 反复执行的处理步骤称为 循环体.
(2)画循环结构流程图之前,要确定三件事: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的终止条件.
(3)流程图形式为
4.(2011· 福建文,5)阅读下图所示的程序框图,运行 相应的程序,输出的结果是( )
A.3 C.38
2019届一轮复习北师大版理 12.2算法与程序框图 课件(60张)

=2,S=9,S<50⇒x=4,S=73>50,跳出循环,输出 S=73.
栏目 导引
பைடு நூலகம்
第十二章 复数、算法、推理与证明
(2017·高考北京卷)执行如图所示的程序框图,输出的 s 值为 ()
A.2 C.53
B.32 D.85
栏目 导引
第十二章 复数、算法、推理与证明
解析:选 C.运行该程序,k=0,s=1,k<3; k=0+1=1,s=1+1 1=2,k<3; k=1+1=2,s=2+2 1=32,k<3; k=1+2=3,s=32+3 1=53,k=3.输出的 s 值为53.故选 C.
第十二章 复数、算法、推理与证明
(2017·高考全国卷Ⅰ)如图程序框图是为了求出满足 3n
-2n>1 000 的最小偶数 n,那么在 和 两个空白框中,
可以分别填入( )
栏目 导引
第十二章 复数、算法、推理与证明
A.A>1 000 和 n=n+1 B.A>1 000 和 n=n+2 C.A≤1 000 和 n=n+1 D.A≤1 000 和 n=n+2 【解析】 程序框图中 A=3n-2n,故判断框中应填入 A≤1 000,由于初始值 n=0,要求满足 A=3n-2n>1 000 的最小偶数, 故执行框中应填入 n=n+2,选 D. 【答案】 D
语句体 _E__N_D__I_F_ __I_F__条__件__T__H_E__N__
语句体 1 __E_L_S_E___
语句体 2 END IF
栏目 导引
名称
当型
循环
循环 结构
结构 直到 型循
环结
构
第十二章 复数、算法、推理与证明
第12章 算法与程序框图

第一步 投票 第二步 统计票数,如果有一座城市的得票数 超过总票数的一半,那么该城市就获得举办权; 否则将得票数最少的城市淘汰,并转而执行第一步
第三步 输出举办城市
算法步骤 第一步:投票 第二步 统计票数 第三步 输出举办城市
开始 投票
有一座城市的得票数 超过总票数的一半
是
输出该城市为举办城市
P42例5
新课引入
算法是由一系列明确和有限的步骤组成,我们可以用自然语言表示一 个算法,但往往过程复杂,缺乏简洁性,因此必须引入一种使算法表达 的更直观,更准确的方法,这就是今天我们要学习的程序框图。
程序框图基本概念:
程序框图又称流程图,是一种用规定的框、带箭头的线(也称为流程 线或指向线)及文字说明来准确、直观地表示算法的图形。
(2)确切性 算法中的每一个步骤都是确切的,能有效的执行且能得到确定的结果,不能模 棱两可,不存在歧义 (3)可行性(或有效性) 算法的每一个步骤都是可执行的操作,即每一步都可以在有限的时间内完成。 (4)有0个、1个、或多个输入,用于刻画运算对象的初始情况。 (5)有1个或多个输出,用以反映对输入数据加工后的结果,没有输出的算法 是毫无意义的。
结束
将得票数最少 的城市淘汰 否
二、算法的三种基本逻辑结构:
开始 输入n
i=2
①顺序结构 求n除以i的余数r i的值增加1,仍用i表示
③循环结构
i>n-1或r=0?
否
是
是
r=0?
否否
N不是质数
N是质数
②条件结构
结束
算法千差万别,但都是由这 三种基本逻辑结构构成的.
输入n
i=2
求n除以i的余数r
i的值增加1,仍用i表示
12章算法与程序框图

(24,18) (18,6)
(6,12) (6,6)
6就是24和18的最大公约数
循环变量初始化 循环终止条件 循环体
实例四
题意: 某城市对居民的生活用水 实行阶梯式收费,标准为: 每月每户生活用水20m3以 内(含20m3 )为第一级, 按居民生活用水的供水价 格收费;每月每户生活用 水超过20m3且低于或等于 30m3为第二级,超出部分 按供水价格的1.5倍收费; 每月每户生活用水超过 30m3,超过部分按供水价 格的2倍收费,如果该市 居民生活用水的供水价格 为1.24元m3/,另加收城市 附加费用0.06/m3,污水处 理费1.3/m3,水资源费 0.2/m3,请设计一个算法, 输入某户居民某个月的用 水量,输出这个月该户居 民所需缴纳的水费。
当赋予它新的数值,原来的值就被取代。
• 注意: • 1、赋值号左边只能出现变量名,如: x=2,a=b+c,不能出现 2=b, c+1=2 • 2、赋值语句中,只能给一个变量赋值,不能同时给两个变量赋值,如:a=b=5是错误的 。 • 3、赋值号不同于“等号”,赋值号左右可以现现同一个变量,如n=n+1,而等式n=n+1是错误的。 • 4、一个变量可多次赋值,但运算时只跟最后一次赋值相关
题目
起止框 第一步 输入两个数a,b;(输入输出框) 第二步 计算c=a+b;(处理框) 第三步 计算m=c÷2;(处理框) 第四步 输出m;(输入输出框) 起止框
算法
程序框图
实例
起止框
例2: 如图所示程序框图 的功能是( ) A. 求a-b的值 B.求b-a的值 C.求|a-b|的值 D.求 -|a-b|的值
例题
一杯白开水一杯茶水,设计一个算法,将两个怀子中的水对调 ②
2015高考数学(理)一轮复习考点突破课件:12.1算法与程序框图

解决算法语句有三个步骤:首先通读全部语句,
• 把它翻译成数学问题;其次领悟该语句的功能;最后根据语句的功 能运行程序,解决问题.
针对训练 3.(1)(2014· 东北三校模拟)运行如图所示程序的结果为 ( n=10 S=100 DO S=S-n n=n-1 LOOP UNTIL S<=70 PRINT n END )
2
3 解之得,x= (负值舍去); 4 3 综上,输入 x 的值为 . 4 3 【答案】 (1)D (2) 4
• 【归纳提升】 1.解决程序框图问题要注意几个常用变量: • (1)计数变量:用来记录某个事件发生的次数,如i=i+1. • (2)累加变量:用来计算数据之和,如S=S+i. • (3)累乘变量:用来计算数据之积,如p=p×i. • 2 .处理循环结构的框图问题,关键是理解并认请终止循环结构的 条件及循环次数.
1 =2- . k+1
9 当 S= 时,k=4பைடு நூலகம்接着继续计算“k=k+1”,所以 4≤a<5,故 5 选 A. 答案:A
• •
题型三
基本算法语句 (1)(2013· 陕西 ) 根据下列算法语句,当输入 x 为 60 时,输 出y的值为 • ( ) • 输入x;
• A.25 • C.31
B.30 D.61
• (2)(2013·江西)阅读如下程序框图,如果输出i=5,那么在空白矩形 框中应填入的语句为 •( )
• A.S=8*i-2 • C. S=2* i
B.S=2*i-1 D.S=2* i +4
• 【解析】 (1)i=1,S=1;i=2,S=1+2;i=3,S=1+2×(1+2) = 1+ 2+22; i= 4, S=1+ 2×(1+ 2+ 22)= 1+2+ 22+23; „,故 i =10时,S=1+2+22+„+29,故选A. • (2)i=2,S=5;i=3,S<10,排除D;i=4,S=9;i=5,S≥10,排 除A和B,故选C. • 【答案】 (1)A (2)C
北师大版高中数学一轮复习第十二章12.5数学归纳法word版下载

课时作业68 数学归纳法一、选择题1.用数学归纳法证明1+2+…+(2n +1)=(n +1)(2n +1)时,在验证n =1成立时,左边所得的代数式是( ).A .1B .1+3C .1+2+3D .1+2+3+42.用数学归纳法证明不等式1n +1+1n +2+…+12n <1314(n ≥2,n ∈N +)的过程中,由n =k 递推到n =k +1时不等式左边( ).A .增加了一项12(k +1)B .增加了两项12k +1,12k +2C .增加了12k +1和12k +2两项但减少了一项1k +1D .以上各种情况均不对 3.用数学归纳法证明不等式1+12+14+…+12n -1>12764成立时,起始值n 至少应取为( ).A .7B .8C .9D .104.用数学归纳法证明:“(n +1)·(n +2)·…·(n +n )=2n ·1·3·…·(2n -1)”,从“k 到k +1”左端需增乘的代数式为( ).A .2k +1B .2(2k +1) C.2k +1k +1 D.2k +3k +15.在数列{a n }中,a 1=13,且S n =n (2n -1)a n ,通过求a 2,a 3,a 4,猜想a n 的表达式为( ). A.1(n -1)(n +1) B.12n (2n +1) C.1(2n -1)(2n +1) D.1(2n +1)(2n +2)6.设函数f (n )=(2n +9)·3n +1+9,当n ∈N +时,f (n )能被m (m ∈N +)整除,猜想m 的最大值为( ).A .9B .18C .27D .367.对于不等式n 2+n <n +1(n ∈N +),某同学用数学归纳法的证明过程如下:(1)当n =1时,12+1<1+1,不等式成立.(2)假设当n =k (k ∈N +)时,不等式成立,即k 2+k <k +1,则当n =k +1时,(k +1)2+(k +1)=k 2+3k +2<(k 2+3k +2)+(k +2)=(k +2)2=(k +1)+1,∴当n =k +1时,不等式成立,则上述证法( ).A .过程全部正确B .n =1验得不正确C .归纳假设不正确D .从n =k 到n =k +1的推理不正确二、填空题8.用数学归纳法证明“1+a +a 2+…+a n +1=1-a n +21-a(a ≠1,且n ∈N +)”,在验证n =1时,左边计算所得的结果是__________.9.在△ABC 中,不等式1A +1B +1C ≥9π成立;在四边形ABCD 中,不等式1A +1B +1C +1D ≥162π成立;在五边形ABCDE 中,不等式1A +1B +1C +1D +1E ≥253π成立…… 猜想在n 边形A 1A 2…A n 中,有不等式________成立.10.用数学归纳法证明⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15⎝⎛⎭⎫1+17…⎝⎛⎭⎫1+12k -1>2k +12(k >1),则当n =k +1时,左端应乘上__________________________,这个乘上去的代数式共有因式的个数是__________.三、解答题11.设数列{a n}的前n项和为S n,且方程x2-a n x-a n=0有一根为S n-1,n=1,2,3,….(1)求a1,a2;(2)猜想数列{S n}的通项公式,并给出严格的证明.12.(2013届陕西渭南合阳中学月考)已知函数f(n)(n∈N+),满足条件:①f(2)=2,②f(xy)=f(x)·f(y),③f(n)∈N+,④当x>y时,有f(x)>f(y).(1)求f(1),f(3)的值;(2)由f(1),f(2),f(3)的值,猜想f(n)的解析式;(3)证明你猜想的f(n)的解析式的正确性.参考答案一、选择题1.C 解析:左边表示从1开始,连续2n +1个正整数的和,故n =1时,表示1+2+3的和.2.C 解析:当n =k +1时,不等式为1(k +1)+1+1(k +1)+2+…+12(k +1)<1314,∴比当n =k 时增加了12k +1,12k +2项.但最左端少了一项1k +1. 3.B 解析:∵1+12+14+…+127-1=1-⎝⎛⎭⎫1271-12=2-126=27-126=12764, 而1+12+14+ (128)1>12764,故起始值n 至少取8. 4.B 解析:当n =k 时,等式为(k +1)(k +2)·…·(k +k )=2k ×1×3×…×(2k -1), 当n =k +1时,等式为(k +2)(k +3)·…·(k +k )(k +1+k )(k +1+k +1)=2k +1×1×3×…×(2k +1),∴左端增乘(2k +1)(2k +2)k +1=2(2k +1). 5.C 解析:由a 1=13,S n =n (2n -1)a n 求得a 2=115=13×5,a 3=135=15×7,a 4=163=17×9.猜想a n =1(2n -1)(2n +1). 6.D 解析:f (n +1)-f (n )=(2n +11)·3n +2-(2n +9)·3n +1=4(n +6)·3n +1,当n =1时,f (2)-f (1)=4×7×9为最小值,据此可猜想D 正确.7.D 解析:在n =k +1时,没有应用n =k 时的假设,不是数学归纳法.二、填空题8.1+a +a 2 解析:首先观察等式两边的构成情况,它的左边是按a 的升幂顺序排列的,共有n +2项.因此当n =1时,共有3项,应该是1+a +a 2.9.1A 1+1A 2+…+1A n ≥n 2(n -2)π10.⎝⎛⎭⎫1+12k +1⎝⎛⎭⎫1+12k +3·…·⎝⎛⎭⎫1+12k +1-1 2k -1 解析:当n =k 时,⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15·…·⎝ ⎛⎭⎪⎫1+12k -1>2k +12. 当n =k +1时,⎝⎛⎭⎫1+13⎝⎛⎭⎫1+15⎝⎛⎭⎫1+17…⎝ ⎛⎭⎪⎫1+12k -1⎝ ⎛⎭⎪⎫1+12k +1…⎝ ⎛⎭⎪⎫1+12k +1-1>2k +32. ∴左边应乘上⎝ ⎛⎭⎪⎫1+12k +1⎝ ⎛⎭⎪⎫1+12k +3…⎝ ⎛⎭⎪⎫1+12k +1-1,设第一项a 1=2k +1,a n =2k +1-1,d =2,∴n =a n -a 12=2k +1-1-2k -12=2k -1. 三、解答题11.解:(1)当n =1时,x 2-a 1x -a 1=0有一根为S 1-1=a 1-1,于是(a 1-1)2-a 1(a 1-1)-a 1=0,解得a 1=12. 当n =2时,x 2-a 2x -a 2=0有一根为S 2-1=a 2-12, 于是⎝⎛⎭⎫a 2-122-a 2⎝⎛⎭⎫a 2-12-a 2=0,解得a 2=16. (2)由题设知(S n -1)2-a n (S n -1)-a n =0,即S 2n -2S n +1-a n S n =0.当n ≥2时,a n =S n -S n -1,代入上式得S n -1S n -2S n +1=0.(*)由(1)得S 1=a 1=12, S 2=a 1+a 2=12+16=23. 由(*)式可得S 3=34. 由此猜想S n =n n +1,n =1,2,3,…. 下面用数学归纳法证明这个结论.①n =1时已知结论成立.②假设n =k (k ∈N +)时结论成立,即S k =k k +1, 当n =k +1时,由(*)得S k +1=12-S k, 即S k +1=k +1k +2, 故n =k +1时结论也成立.综上,由①,②可知S n =n n +1对所有正整数n 都成立. 12.解:(1)∵f (2)=f (2×1)=f (2)·f (1),又f (2)=2,∴f (1)=1.又∵f (4)=f (2×2)=f (2)·f (2)=4,2=f (2)<f (3)<f (4)=4,且f (3)∈N +.∴f (3)=3.(2)由f (1)=1,f (2)=2,f (3)=3,猜想f (n )=n (n ∈N +).(3)用数学归纳法证明:当n =1时,f (1)=1,函数解析式成立.假设n =k 时,f (k )=k ,函数解析式成立.①若k +1=2m (m ∈N +),f (k +1)=f (2m )=f (2)·f (m )=2m =k +1.②若k +1=2m +1(m ∈N +),f (2m +2)=f [2(m +1)]=f (2)·f (m +1)=2(m +1)=2m +2,2m=f(2m)<f(2m+1)<f(2m+2)=2m+2. ∴f(2m+1)=2m+1=k+1.即当n=k+1时,函数解析式成立.综上可知,f(n)=n(n∈N+)成立.。
【走向高考】高考数学一轮总复习 12-1算法与算法框图课后强化作业 北师大版
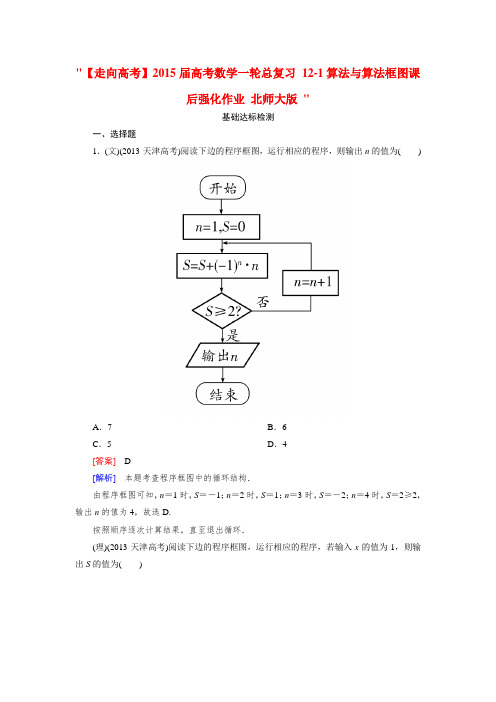
"【走向高考】2015届高考数学一轮总复习12-1算法与算法框图课后强化作业北师大版"基础达标检测一、选择题1.(文)(2013·天津高考)阅读下边的程序框图,运行相应的程序,则输出n的值为()A.7B.6C.5D.4[答案] D[解析]本题考查程序框图中的循环结构.由程序框图可知,n=1时,S=-1;n=2时,S=1;n=3时,S=-2;n=4时,S=2≥2,输出n的值为4,故选D.按照顺序逐次计算结果,直至退出循环.(理)(2013·天津高考)阅读下边的程序框图,运行相应的程序,若输入x的值为1,则输出S的值为()A.64B.73C.512D.585[答案] B[解析]本题考查了程序框图及计算.x=1,S=S+x3=0+13=1;x=2,S=S+x3=1+23=9;x=4,S=S+x3=9+43=9+64=73>50,故输出S.2.(2013·北京高考)执行如图所示的程序框图,输出的S值为()A .1 B.23 C.1321 D.610987[答案] C[解析] 程序运行过程为:i =0,S =1,S =12+12×1+1=23,i =0+1=1,i ≥2不成立;继续下一次循环,S =(23)2+12×23+1=1321,i =1+1=2,由于此时i ≥2成立,故停止循环,输出S 的值1321后结束.3.执行下面的程序框图,如果输入的n 是4,则输出的p 是( )A.8 B.5 C.3 D.2 [答案] C[解析]本小题考查的内容为程序框图中的循环结构.k=1时,p=1,k=2时,p=2,k=3时,p=3.4.执行如图所示的程序框图,输出的S值为()A.2 B.4C.8 D.16[答案] C[解析]当k=0时,满足k<3,因此S=1×20=1;当k=1时,满足k<3,因此S=1×21=2;当k=2时,满足k<3,因此S=2×22=8;当k=3时,不满足k<3,因此输出S=8.5.(文)(2013·江西高考)阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是()A.S<8 B.S<9C.S<10 D.S<11[答案] B[解析]本题考查了程序框图的循环结构.依据循环要求有i=1,S=0;i=2,S=2×2+1=5;i=3,S=2×3+2=8;i=4,S=2×4+1=9,此时结束循环,故应为S<9.(理)(2013·江西高考)阅读如下程序框图,如果输出i=5,那么在空白矩形框内应填入的语句为()[答案] C[解析]i=2时,i不是奇数,S=2×2+1=5<10,继续循环,i=2+1=3,3是奇数,执行“选项”后,需继续循环,故排除D.当i=4时,i不是奇数,S=2×4+1=9<10,继续循环,i=4+1=5,5是奇数,执行“选项”后,应跳出循环,输出i的值5后结束,但2×5-2=8<10,2×5-1=9<10,都需继续循环,故排除A、B选项,但2×5=10<10不成立,故选C.二、填空题6.如图给出一个算法框图,其作用是输入x的值,输出相应的y值.若要使输入的x 值与输出的y值相等.则这样的x值有________个.[答案] 3[解析] 当x ≤2时,x 2=x ,有x =0或x =1; 当2<x ≤5时,2x -3=x ,有x =3; 当x >5时,x =1x ,x 无解.故可知这样的x 有3个.7.(2013·山东高考)执行下面的程序框图,若输入的ε的值为0.25,则输出的n 的值为________.[答案] 3[解析] 本题考查了程序框图和算法等知识. ε=0.25,F 0=1,F 1=2,n =1,此时F 1=F 0+F 1=1+2=3;F 0=F 1-F 0=3-1=2,n =2,∵1F 1=13≤0.25不成立,进入下一循环,F1=F0+F1=2+3=5,F0=F1-F0=5-2=3,n=3,1F1=15≤0.25成立,输出n=3.三、解答题8.国家法定工作日内,每周工作时间满工作量为40h,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为x h,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y元的算法的流程图.(注:满工作量外的工作时间为加班)[解析]算法如下:S1输入工作时间x h;S2若x≤40,则y=8x×(1-10%);否则,y=40×8(1-10%)+(x-40)×10(1-10%).S3输出y值.流程图如下:能力强化训练一、选择题1.(文)(2013·新课标Ⅱ)执行下面的程序框图,如果输入的N=4,那么输出的S=()A .1+12+13+14B .1+12+13×2+14×3×2C .1+12+13+14+15D .1+12+13×2+14×3×2+15×4×3×2[答案] B[解析] 本题考查程序框图的循环结构.由程序框图依次可得,输入N =4, K =1,S =0,T =1→T =1,S =1,K =2;2>4否 T =12,S =1+12,K =3;3>4否T =16,S =1+12+13×2,K =4;4>4否T =14×3×2,S =1+12+13×2+14×3×2,K =5;5>4是,输出S =1+12+13×2+14×3×2,故选B.(理)(2013·新课标Ⅱ)执行下面的程序框图,如果输入的N =10,那么输出的S =( )A .1+12+13+…+110B .1+12!+13!+…+110!C .1+12+13+…+111D .1+12!+13!+…+111![答案] B[解析] 当输入N =10时,由于初值k =1,S =0,T =1,故程序运行过程依次为:T =11=1,S =0+1=1,k =1+1=2,此时不满足k >10→T =12=12!,S =1+12!,k =2+1=3,不满足k >10→T =12!3=13!,S =1+12!+13!,k =3+1=4仍不满足k >10,…,直到k =10时,T =19!10=110!,S =1+12!+13!+ (110),k =11,此时满足k >10,结束循环,输出S =1+12!+13!+ (110)后结束. 2.如果执行如图的框图,输入N =5,则输出的数等于()A.54B.45C.65D.56[答案] D[解析] 本题考查了程序框图的有关知识,并且渗透了裂项求和的方法,在解题时要注意首先弄清楚程序框图的功能,然后看限制条件,题目定位是中档题.根据程序框图可知,该程序框图的功能是计算S =11×2+12×3+13×4+…+1k ×(k +1),现在输入的N =5,所以满足条件k <N 的结果为S =11×2+12×3+13×4+14×5+15×6=(1-12)+(12-13)+…+(15-16)=56,故选D. 3.执行如图所示的流程图,若输出的b 的值为16,则图中判断框内①处应填( )A.3B.4C.5D.2[答案] A[解析]按照流程图依次执行:初始a=1,b=1;第一次循环后,b=21=2,a=1+1=2;第二次循环后,b=22=4,a=2+1=3;第三次循环后,b=24=16,a=3+1=4,而此时应输出b的值,故判断框中的条件应为a≤3,故选A.4.(2013·重庆高考)执行如图所示的程序框图,如果输出s=3,那么判断框内应填入的条件是()A .k ≤6B .k ≤7C .k ≤8D .k ≤9 [答案] B[解析] 本题考查程序框图,主要是循环结构的运行问题.依题意,程序框图是计算s =log 23log 34…log k (k +1)的值,当输出s =3时,即log 2(k +1)=3,所以k =7.由k =k +1知,选B.二、填空题5.如图是计算函数y =⎩⎪⎨⎪⎧ ln (-x ) x ≤-20 -2<x ≤32x x >3的值的程序框图,在①、②、③处应分别填入的是____________________.[答案]y=ln(-x),y=2x,y=0[解析]由程序框图所表达的意义知①②③处应分别填入的是y=ln(-x),y=2x,y=0.6.下图是一个算法流程图,则输出的k的值是________.[答案] 5[解析]第一步,当k=1时,k2-5k+4=1-5+4=0;第二步,当k=2时,k2-5k+4=4-10+4=-2<0;第三步,当k=3时,k2-5k+4=9-15+4=-2<0;第四步,当k=4时,k2-5k+4=16-20+4=0;第五步,当k=5时,k2-5k+4=25-25+4>0,结束循环,输出k=5.三、解答题7.用循环语句来书写1+22+32+…+n2>100的最小自然数n的算法,画出算法流程图.[解析]算法如下:第一步:S=0;第二步:n=1;第三步:S=S+n2;第四步:如果S≤100,使n=n+1,并返回第三步,否则输出n-1.相应的流程图如图所示.。
高考数学一轮复习 第十二章 复数、算法、推理与证明 第2讲 算法与程序框图练习 理 北师大版-北师大

第2讲 算法与程序框图[基础题组练]1.(2020·某某某某模拟)执行如图所示的程序框图,输出K 的值为( )A .99B .98C .100D .101解析:选A.执行程序框图,得K =1,S =0;S =0+lg1+11=lg 2,K =2;S =lg 2+lg 2+12=lg 3,K =3;S =lg 3+lg 3+13=lg 4,K =4;S =lg 4+lg 4+14=lg 5,K =5;…;S =lg 98+lg98+198=lg 99,K =99;S =lg 99+lg 99+199=lg 100=2,退出循环.所以输出K =99,故选A.2.(2020·某某江门调研)执行如图所示的程序框图,若判断框内为“i ≤3”,则输出S =( )A .2B .6C .10D .34解析:选D.因为“i ≤3”,所以执行程序框图,第一次执行循环体后,j =2,S =2,i=2≤3;第二次执行循环体后,j =4,S =10,i =3≤3;第三次执行循环体后,j =8,S =34,i =4>3,退出循环.所以输出S =34.故选D.3.(2020·某某某某质检)执行如图所示的程序框图,若输出的S =2524,则判断框内填入的条件不可以是( )A .k ≤7B .k <7C .k ≤8D .k <8解析:选C.模拟执行程序框图,可得S =0,k =0;k =2,S =12;k =4,S =12+14;k =6,S =12+14+16;k =8,S =12+14+16+18=2524.由题意,此时应不满足条件,退出循环,输出S的值为2524.结合选项可得判断框内填入的条件不可以是“k ≤8”.故选C.4.(2020·某某调研)执行如图所示的程序框图,当输出的值为1时,输入的x 值是( )A .±1B .1或 3C .-3或1D .-1或 3解析:选C.因为输出的值为1,所以根据程序框图可知⎩⎪⎨⎪⎧x >0,2-x 2=1或⎩⎪⎨⎪⎧x ≤0,x 2-2=1,得x =1或x =-3,故选C.5.(2020·某某某某模拟)执行如图所示的程序框图,输出的n 的值是( )A .5B .7C .9D .11解析:选C.法一:执行程序框图,n =1,S =0;S =0+11×3=13,n =3;S =13+13×5=25,n =5;S =25+15×7=37,n =7;S =37+17×9=49,n =9,此时满足S ≥49,退出循环.输出n =9,故选C.法二:由程序框图知,该程序框图的作用是由11×3+13×5+…+1n ×(n +2)=12⎝ ⎛⎭⎪⎫1-13+13-15+…+1n -1n +2=12⎝ ⎛⎭⎪⎫1-1n +2≥49,解得n ≥7,所以输出的n 的值为7+2=9,故选C.6.执行如图所示的程序框图,如果输入的x ,y ,z 的值分别为1,2,3,则输出的S 等于( )A.32 B .163C.158D .154解析:选C.k =6,S =21+2=4,y =1,x =4;k =5,S =24+1=32,y =4,x =32;k =4,S =232+4=163,y =32,x =163;k =3,S =2163+32=158,y =163,x =158;k =2,终止循环,输出的S =158.选C.7.(2020·某某某某四校联考)已知函数f (x )=cos πx3,执行如图所示的程序框图,则输出的S 的值为( )A .670B .1 3412C .671D .672解析:选C.执行程序框图,y =f (1)=cos π3=12,S =0+12=12,n =1+1=2;y =f (2)=cos 2π3=-12,S =12,n =2+1=3;y =f (3)=cos π=-1,S =12,n =3+1=4;y =f (4)=cos 4π3=-12,S =12,n =4+1=5;y =f (5)=cos 5π3=12,S =12+12=1,n =6;y =f (6)=cos 2π=1,S =1+1=2,n =7,…,直到n =2 016时,退出循环.因为函数y =cosn π3是以6为周期的周期函数,2 015=6×335+5,f (2 016)=cos 336π=cos (2π×138)=1,所以输出的S =336×2-1=671.故选C.8.(2020·某某巴蜀中学一模)执行如图所示的程序框图,若输入的a 为24,c 为5,输出的数为3,则输入的b 有可能为( )A .11B .12C .13D .14解析:选B.结合程序框图,若输出的数为3,则经过循环之后的b =a +3=27,由27÷5=5……2,并结合循环结构的特点可得,输入的b 除以5的余数为2,结合选项可得,b 有可能为12,故选B.9.(2020·某某彬州第一次质监)如图1是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14.如图2是统计茎叶图中成绩在一定X围内考试次数的一个程序框图,执行程序框图,输出的结果是( )A.7 B.8C.9 D.10解析:选B.该程序框图的作用是求14次考试成绩超过90分的次数.根据茎叶图可得超过90分的次数为8,故选B.10.(2020·某某三湘名校联盟第一次联考)中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种,如下表:表示一个多位数时,像阿拉伯记数一样,把各个数位的数码从左到右排列,但各位数码的筹式需要纵横相间,个位,百位,万位用纵式表示,十位,千位,十万位用横式表示,以此类推,例如2 268用算筹表示为执行如图所示的程序框图,若输入的x=1,y=2,则输出的S用算筹表示为( )解析:选C.x =1,y =3,i =2;x =2,y =8,i =3;x =14,y =126,i =4.退出循环,输出S =1 764,用算筹表示为,故选C.11.中国古代名著《孙子算经》中的“物不知数”问题:“今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?”即“有数被三除余二,被五除余三,被七除余二,问该数为多少?”为解决此问题,现有同学设计如图所示的程序框图,则框图中的“”处应填入( )A.a -221∈Z B .a -215∈Z C.a -27∈ZD .a -23∈Z解析:选A.根据题意可知,此程序框图的功能是找一个满足下列条件的数a :a =3k +2,a =5n +3,a =7m +2,k ,n ,m ∈Z ,根据程序框图可知,数a 已经满足a =5n +3,n ∈Z ,所以还要满足a =3k +2,k ∈Z 和a =7m +2,m ∈Z 并且还要用一个条件给出,即a -2既能被3整除又能被7整除,所以a -2能被21整除,故在“”处应填入a -221∈Z ,选A.12.程序框图如图,若输入的S =1,k =1,则输出的S 为________.解析:第一次循环,k =2,S =4;第二次循环,k =3,S =11;第三次循环,k =4,S =26;第四次循环,k =5,S =57.此时,终止循环,输出的S =57.答案:5713.如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =________.解析:开始:a =14,b =18,第一次循环:a =14,b =4;第二次循环:a =10,b =4; 第三次循环:a =6,b =4;第四次循环:a =2,b =4; 第五次循环:a =2,b =2.此时,a =b ,退出循环,输出a =2. 答案:214.公元前6世纪的毕达哥拉斯是最早研究完全数的人.完全数是一种特殊的自然数,若一个数所有的真因子(即除了自身以外的约数)的和,恰好等于它本身,则称该数为完全数.如6的真因子有1,2,3,且1+2+3=6,故6是完全数.现为判断一个非零自然数是否是完全数,编拟如下的程序框图,则空白框内应填________.解析:程序框图的循环结构部分的功能是累计非零自然数x 的真因子之和,如果t =xi是整数,那么就将i 这个数累加到变量S 中,所以空白框内应填S =S +i .答案:S =S +i15.若[x ]表示不超过x 的最大整数,则图中的程序框图运行之后输出的结果为________.解析:根据题意,得⎣⎢⎡⎦⎥⎤19940=[4.975]=4,所以该程序框图运行后输出的结果是40个0,40个1,40个2,40个3,40个4的和,所以输出的结果为S =40+40×2+40×3+40×4=400.答案:400[综合题组练]1.执行如图的程序框图,若输入的n 为2 018,则输出的是( )A .前 1 008 个正偶数的和B .前 1 009 个正偶数的和C .前 2 016 个正整数的和D .前 2 018 个正整数的和解析:选B.模拟程序的运行过程知,该程序运行后计算并输出S =2+4+6+…+2 018 的值.故选B.2.“欧几里得算法”是有记载的最古老的算法,可追溯至公元前300年前,如图所示的程序框图的算法思路就是来源于“欧几里得算法”.执行该程序框图(图中“a MOD b ”表示a 除以b 的余数),若输入的a ,b 分别为675,125,则输出的a =( )A .0B .25C .50D .75解析:选B.初始值:a =675,b =125, 第一次循环:c =50,a =125,b =50; 第二次循环:c =25,a =50,b =25; 第三次循环:c =0,a =25,b =0,此时不满足循环条件,退出循环.输出a 的值为25,故选B.3.我国古代数学著作《周髀算经》有如下问题:“今有器中米,不知其数.前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S =1.5(单位:升),则输入k 的值为( )A .4.5B .6C .7.5D .9解析:选B.由程序框图知S =k -k 2-k 2×3-k3×4=1.5,解得k =6,故选B.4.执行如图所示的程序框图,如果输入的a 依次为2,2,5时,输出的s 为17,那么在判断框中可以填入( )A.k<n B.k>nC.k≥n D.k≤n解析:选B.执行程序框图,输入的a=2,s=0×2+2=2,k=1;输入的a=2,s=2×2+2=6,k=2;输入的a=5,s=2×6+5=17,k=3,此时结束循环,又n=2,所以判断框中可以填“k>n”,故选B.5.执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )A.0,0 B.1,1C.0,1 D.1,0解析:选D.当输入x=7时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x成立,故a=1,输出a的值为1.当输入x=9时,b=2,因为b2>x不成立且x不能被b整除,故b=3,这时b2>x不成立且x能被b整除,故a=0,输出a的值为0.6.南宋数学家秦九韶在《数书九章》中提出的秦九韶算法至今仍是多项式求值比较先进的算法.已知f(x)=2 018x2 017+2 017x2 016+…+2x+1,如图所示的程序框图是求f(x0)的值,在“”中应填的语句是( )A.n=i B.n=i+1C.n=2 018-i D.n=2 017-i解析:选C.由秦九韶算法得f(x)=2 018x2 017+2 017x2 016+…+2x+1=(…((2 018x +2 017)x+2 016)x+…+2)x+1,所以程序框图的执行框内应填写的语句是n=2 018-i,故选C.。
高中数学 2.1 流程图课件 北师大版选修12

p是
.
解析:由框图可知,最终输出的 p=1×2×3×4×5×6=720. 答案:720
探究一
探究二
探究三
首页
XX新新知知导导学学 INIINNZHZZHHI DII DDAOAAOOXUXXUUE EE
ZZ重重难难探探究究 HHOONNGGNNAANNTTAANNJIJUIU
DDA当NAA当GNN堂TGGA堂TTNAA检GNN检GGJ测IAJJ测IINAACNNECCEE
1.通过具体实例,进一步认识 程序框图,了解工序流程图; 2.能绘制简单实际问题的流程图, 体会流程图在解决实际问题中的 作用.
思维脉络
12
首页
XX新新知知导导学学 INIINNZHZZHHI DII DDAOAAOOXUXXUUE EE
ZZ重重难难探探究究 HHOONNGGNNAANNTTAANNJIJUIU
DDA当NAA当GNNபைடு நூலகம்TGGA堂TTNAA检GNN检GGJ测IAJJ测IINAACNNECCEE
1.程序流程图 (1)定义:用规定的图形、流程线及文字说明来准确、直观地表示算法
的图形称为程序流程图. (2)画法:通常程序流程图由程序框和流程线组成.一个或几个程序框的
组合表示算法中的一个步骤;流程线按照算法进行的顺序将程序框连接起 来.
程序框图要基于它的算法,在对一个算法进行了透彻分析的基础上设计程 序框图,设计程序框图时要分步进行,把一个大的程序框图分解成若干个小 的部分,按照顺序结构、条件结构、循环结构来局部安排,最后再把各部分 之间进行组装,从而完成完整的程序框图.
探究一
探究二
探究三
首页
XX新新知知导导学学 INIINNZHZZHHI DII DDAOAAOOXUXXUUE EE
2021届北师大版高考理科数一轮复习课件:第十二章 第2讲 算法与程序框图

角度四 完善程序框图
(1)(2019·高考 A.A=2+1 A
全国卷
Ⅰ)
如图是
求2+12+1 12
的程序
框图,
图中
空白框
中应填入
()
B.A=2+A1
C.A=1+12A
D.A=1+21A
(2)如图所示的程序框图是为了求出满足 2+32+43+…+n+n 1<2 019 的最大正整数 n 的值,
问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的 x=0,则输入的 x
值为 A.1156
()
B.34
7 C.8
D.3312
【解析】 (1)第 1 次循环,n=1,S=12;第 2 次循环,n=2,S=12+212;第 3 次循环, n=3,S=12+212+213;第 4 次循环,n=4,S=12+212+213+214=1156.因为输出的结果为1156, 所以判断框的条件为 n<4,所以输入的 a 为 4.故选 D. (2)输入 x,i=1;x←2x-1,i=2;x←2(2x-1)-1=4x-3,i=3;x←2(4x-3)-1=8x -7,i=4;x←2(8x-7)-1=16x-15,i=5,退出循环.依题意可知 16x-15=0,解 得 x=1156.故选 A. 【答案】 (1)D (2)A
(√ ) (√ ) (× ) (√ ) (× )
二、易错纠偏 常见误区 (1)注意循环结构中控制循环的条件; (2)注意区分程序框图是条件结构还是循环结构.
1.若[x]表示不超过 x 的最大整数,执行如图所示的程序框图,则输出 S 的值为________.
解析:由程序框图可以看出,当 n=8 时,S>6 时,程序结束,故输出 S=[ 0]+[ 2]+ [ 4]+[ 6]+[ 8]=7.
高考总复习理数(北师大版)第12章第1节算法与程序框图

第一节算法与程序框图考点高考试题考查内容核心素养程序框图2017·全国卷Ⅰ·T8·5分填充程序框图数学运算2017·全国卷Ⅱ·T8·5分循环结构框图逻辑推理2017·全国卷Ⅲ·T7·5分循环结构框图逻辑推理2016·全国卷Ⅰ·T9·5分框图的功能逻辑推理2016·全国卷Ⅱ·T8·5分循环结构框图逻辑推理2016·全国卷Ⅲ·T7·5分循环结构框图逻辑推理命题分析本节是高考的必考内容,常以选择题、填空题形式出现,考查题型有输出结果,完善程序框图以及判断程序运行功能.1.算法在解决某类问题时,所要执行的一系列可操作或可计算的步骤.现代算法的作用之一是使计算机能代替人完成某些工作.2.算法框图中的符号意义图形符号名称符号表示的意义起止框表示一个算法的起始和结束□输入、输出框表示一个算法输入和输出的信息处理框赋值、执行计算、结果传送判断框判断某一条件是否成立流程线流程进行的方向为了使算法结构更加清晰,可借助图来帮助描述算法.图的特点是直观、清楚,便于检查和交流.通常这样的图叫作框图.4.算法的基本结构名称内容顺序结构选择结构循环结构定义按照步骤依次执行的一个算法,称为具有“顺序结构”的算法,或者称为算法的顺序结构在算法的执行过程中,需要对条件进行判断,判断的结果决定后面的步骤,像这样的结构通常称作选择结构在一些算法中,经常会出现从某处开始,按照一定的条件,反复执行某一处理步骤的情况,像这种需要反复执行循环体的结构称为循环结构算法框图提醒:1.辨明两个易误点(1)易混淆处理框与输入、输出框,处理框主要是赋值、计算,而输入、输出框只是表示一个算法输入或输出的信息.(2)易忽视循环结构中必有选择结构,其作用是控制循环进程,避免进入“死循环”,是循环结构必不可少的一部分.2.识别三种结构的关系顺序结构是每个算法结构都含有的,而对于循环结构有重复性,选择结构具有选择性没有重复性,并且循环结构中必定包含一个选择结构,用于确定何时终止循环体,循环结构和选择结构都含有顺序结构.1.判断下列结论的正误(正确的打“√”,错误的打“×”)(1)算法只能解决一个问题,不能重复使用.()(2)程序框图中的图形符号可以由个人来确定.()(3)输入框只能紧接开始框,输出框只能紧接结束框.()(4)选择结构的出口有两个,但在执行时,只有一个出口是有效的.()答案:(1)×(2)×(3)×(4)√2.(教材习题改编)给出如图算法框图,其功能是()A .求a -b 的值B .求b -a 的值C .求|a -b |的值D .以上都不对解析:选C 由算法框图知其功能是求|a -b |的值.3.阅读如图所示的程序框图,运行相应的程序,输出s 的值等于( )A .-3B .-10C .0D .-2解析:选A 第一次循环:k =0+1=1,满足k <4,s =2×1-1=1; 第二次循环:k =1+1=2,满足k <4,s =2×1-2=0; 第三次循环:k =2+1=3,满足k <4,s =2×0-3=-3; 第四次循环:k =3+1=4,不满足k <4,故输出的s =-3. 4.(2018·济宁模拟)执行如图所示的程序框图,则输出的S 为( )A .-2B .12C .43D .3解析:选D 程序运行如下: S =3,k =1;S =43,k =2;S =12,k =3;S =-2,k =4; S =3,k =5;……发现此程序中的S 值4个一循环,2 017÷4=504……1,则输出的S =3,故选D .顺序结构与选择结构 [明技法]应用顺序结构和选择结构的注意点(1)顺序结构是最简单的算法结构,语句与语句之间、框与框之间是按从上到下的顺序进行的.(2)解决此类问题,只需分清运算步骤,赋值量及其范围进行逐步运算即可.(3)选择结构中条件的判断关键是明确选择结构的功能,然后根据“是”的分支成立的条件进行判断.(4)对选择结构,无论判断框中的条件是否成立,都只能执行两个分支中的一个,不能同时执行两个分支.[提能力]【典例】 (1)运行如图所示程序框图,若输入a ,b 的值分别为log 23和log 32,则输出M 的值是( )A .0B .1C .2D .-1解析:选C∵log23>log32,即a>b,故M=a×b+1=log23×log32+1=2.(2)(2017·山东卷)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0解析:选D当x=7时,∵b=2,∴b2=4<7=x.又7不能被2整除,∴b=2+1=3.此时b2=9>7=x,∴退出循环,a=1,∴输出a=1.当x=9时,∵b=2,∴b2=4<9=x.又9不能被2整除,∴b=2+1=3.此时b2=9=x,又9能被3整除,∴退出循环,a=0.∴输出a=0.故选D.[刷好题]1.阅读如图所示的程序框图,运行相应的程序,若输入x的值为1,则输出y的值为() A.2B.7C .8D .128解析:选C 由程序框图知,y =⎩⎪⎨⎪⎧2x ,x ≥2,9-x ,x <2.∵输入x 的值为1,比2小,∴执行的程序要实现的功能为9-1=8,故输出y 的值为8.2.执行下面的程序框图,如果输入的t ∈[-1,3],则输出的s 属于( )A .[-3,4]B .[-5,2]C .[-4,3]D .[-2,5]解析:选A 由框图知s 是关于t 的分段函数s =⎩⎪⎨⎪⎧3t ,-1≤t <1,4t -t 2,1≤t ≤3,当t ∈[-1,1)时,s ∈[-3,3);当t ∈[1,3]时,s =4t -t 2=4-(t -2)2∈[3,4],故s ∈[-3,4],故选A .循环结构 [析考情]循环结构是高考命题的一个热点问题,多以选择题、填空题的形式呈现,试题难度不大,多为容易题或中档题.[提能力]命题点1:求程序运行后的结果【典例1】(2016·全国卷Ⅱ)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x =2,n =2,依次输入的a 为2,2,5,则输出的S =( )A.7B.12C.17D.34解析:选C由框图可知,输入x=2,n=2,a=2,S=2,k=1,不满足条件;a=2,S=4+2=6,k=2,不满足条件;a=5,S=12+5=17,k=3,满足条件,输出S=17,故选C.命题点2:确定控制循环的变量【典例2】(2017·全国卷Ⅰ)如图所示的程序框图是为了求出满足3n-2n>1 000的最小偶数n,那么在和两个空白框中,可以分别填入()A.A>1 000和n=n+1B.A>1 000和n=n+2C.A≤1 000和n=n+1D.A≤1 000和n=n+2解析:选D因为题目要求的是“满足3n-2n>1 000的最小偶数n”,所以n的叠加值为2,所以内填入“n=n+2”.由程序框图知,当内的条件不满足时,输出n,所以内填入“A≤1 000”.故选D.命题点3:辨析程序框图的功能【典例3】如图所示的程序框图,该算法的功能是()A.计算(1+20)+(2+21)+(3+22)+…+(n+1+2n)的值B.计算(1+21)+(2+22)+(3+23)+…+(n+2n)的值C.计算(1+2+3+…+n)+(20+21+22+…+2n-1)的值D.计算[1+2+3+…+(n-1)]+(20+21+22+…+2n)的值解析:选C初始值k=1,S=0,第1次进入循环体时,S=1+20,k=2;当第2次进入循环体时,S=1+20+2+21,k=3,…;给定正整数n,当k=n时,最后一次进入循环体,则有S=1+20+2+21+…+n+2n-1,k=n+1,终止循环体,输出S=(1+2+3+…+n)+(20+21+22+…+2n-1),故选C.[悟技法]与循环结构有关问题的常见类型及解题策略(1)已知程序框图,求输出的结果,可按程序框图的流程依次执行,最后得出结果.(2)完善程序框图问题,结合初始条件和输出结果,分析控制循环的变量应满足的条件或累加、累乘的变量的表达式.(3)对于辨析程序框图功能问题,可将程序执行几次,即可根据结果作出判断.[刷好题]1.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.35B.20C.18D.9解析:选C按照图中的程序计算,当i=2时,得v=4;当i=1时,得v=2×4+1=9;当i=0时,得v=2×9+0=18;当i=-1时,直接输出v=18,即输出的v值为18.2.(2017·全国卷Ⅱ)执行如图所示的程序框图,如果输入的a=-1,则输出的S=()A.2B.3C.4D.5解析:选B当K=1时,S=0+(-1)×1=-1,a=1,执行K=K+1后,K=2;当K=2时,S=-1+1×2=1,a=-1,执行K=K+1后,K=3;当K=3时,S=1+(-1)×3=-2,a=1,执行K=K+1后,K=4;当K=4时,S=-2+1×4=2,a=-1,执行K=K+1后,K=5;当K=5时,S=2+(-1)×5=-3,a=1,执行K=K+1后,K=6;当K=6时,S=-3+1×6=3,执行K=K+1后,K=7>6,输出S=3,结束循环.故选B.。
高三数学一轮总复习 12-1算法与算法框图同步练习 北师大版

基础巩固一、选择题1.(2012·北京理,4)执行如图所示的程序框图,输出的S值为( )A.2 B.4C.8 D.16[答案]C[解析] 本题考查了算法循环结构的直到型的流程图及整数指数幂的运算.k=0,S=1;k=1,S=1;k=2,S=2;k=3,S=8.循环结束,输出S为8,故选C. 2.执行下面的程序框图,如果输入的n是4,则输出的p是( )A.8 B.5C.3 D.2[答案]C[解析] 本小题考查的内容为程序框图中的循环结构.k=1时,p=1,k=2时,p=2,k=3时,p=3.3.以下是给出的对程序框图的几种说法:①任何一个程序框图都必须有起止框;②输入框只能放在开始框后,输出框只能放在结束框前;③判断框是唯一具有超过一个退出点的符号;④对于一个程序来说,判断框内的条件表达方法是唯一的.其中正确说法的个数是( )A.1 B.2C.3 D.4[答案]C[解析] ①②③正确,④错误.4.(2012·山东理,6)执行下面的程序框图,如果输入a=4,那么输出的n的值为( )A.2 B.3C.4 D.5[答案]B[解析] 本题考查了算法循环结构的直到型的流程图问题.n=0,P=0+40=1,Q=2+1=3;n=1,P=1+41=5,Q=6+1=7;n=2,P=5+42=21,Q=14+1=15,n=3,P>Q.5.如果执行如图所示的程序框图,那么输出的k=( )A.4 B.5C.6 D.7[答案]B[解析] 第一次运行k=2,S=0+20=1;第二次运行k=3,S=1+21=3;第三次运行k=4,S=3+23=11;第四次运行k=5,S=11+211>100.结束循环,输出的k=5,故选B.二、填空题6.(文)(2012·湖南文,14)如果执行如图所示的程序框图,输入x=4.5,则输出的数i=________.[答案] 4[解析] 本题考查程序框图,循环结构等算法知识.i=1,x=4.5-1=3.5;i=2,x=3.5-1=2.5;i=3,x=2.5-1=1.5;i=4,x=1.5-1=0.5,∵0.5<1,∴输出i=4.(理)(2012·湖南理,14)如果执行如图所示的程序框图,输入x=-1,n=3,则输出的数S=________.[答案]-4[解析] 本题主要考查程序框图的功能.根据框图,第一次运行后:S=-3,i=1;第二次运行后:S=5,i=0;第三次运行后:S=-4,i=-1,不满足i≥0,故输出S=-4.7.(2012·晋江月考)如图给出一个算法框图,其作用是输入x的值,输出相应的y值.若要使输入的x值与输出的y值相等.则这样的x值有________个.[答案] 3[解析] 当x≤2时,x 2=x ,有x =0或x =1;当2<x≤5时,2x -3=x ,有x =3;当x>5时,x =1x,x 无解.故可知这样的x 有3个.三、解答题8.国家法定工作日内,每周工作时间满工作量为40h ,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为x h ,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y 元的算法的程序框图.(注:满工作量外的工作时间为加班)[解析] 算法如下: S1 输入工作时间x h ;S2 若x ≤40,则y =8x ×(1-10%);否则,y =40×8(1-10%)+(x -40)×10(1-10%). S3 输出y 值. 程序框图:能 力 提 升一、选择题1.(文)(2012·辽宁文,10)执行如图所示的程序框图,则输出的S 的值是( )A .4 B.32C.23D .-1 [答案] D[解析] 本题考查循环结构.i =1,S =4;i =2时,S =22-4=-1; i =3时,S =22--1=23;i =4时,S =22-23=32;i =5时,S =22-32=4;i =6时,S =22-4=-1, 此时跳出循环,输出S 的值-1.(理)(2012·辽宁理,9)执行如图所示的程序框图,则输出的S 值是( )。
高三数学一轮基础巩固 第12章 第1节 算法与算法框图、基本算法语句(含解析)北师大版

【走向高考】2016届高三数学一轮基础巩固第12章第1节算法与算法框图、基本算法语句北师大版一、选择题1.(文)(2014·北京高考)执行如图所示的程序框图,输出的S值为( )A.1 B.3C.7 D.15[答案] C[解析] 本题考查了程序框图的有关概念.S1:k=0,S=0,S2:S=20=1,k=1,S3:S=1+21=3,k=2,S4:S=3+22=7,k=3,S5:输出S=7.(理)(2014·北京高考)当m=7,n=3时,执行如图所示的程序框图,输出的S值为( )A.7 B.42C.210 D.840[答案] C[解析] 本题考查了程序框图.当m输入的m=7,n=3时,判断框内的判断条件为k<5,故能进入循环的k依次为7,6,5.顺次执行S=S·k,则有S=7·6·5=210,故选C.2.下列算法框图的功能是( )A.求a-b的值B.求b-a的值C.求|a-b|的值D.以上都不对[答案] C[解析] 由判断框中的条件和输出的两种结果易知,框图是求|a-b|的值.3.执行下面的程序框图,如果输入的n是4,则输出的p是( )A.8 B.5C.3 D.2[答案] C[解析] 本小题考查的内容为程序框图中的循环结构.k=1时,p=1,k=2时,p=2,k=3时,p=3.4.(文)阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是( )A.S<8 B.S<9C.S<10 D.S<11[答案] B[解析] 本题考查了程序框图的循环结构.依据循环要求有i=1,S=0;i=2,S=2×2+1=5;i=3,S=2×3+2=8;i=4,S=2×4+1=9,此时结束循环,故应为S<9.(理)阅读如下程序框图,如果输出i=5,那么在空白矩形框内应填入的语句为( )A.S=2*i-2 B.S=2*i-1C.S=2*i D.S=2*i+4[答案] C[解析] i=2时,i不是奇数,S=2×2+1=5<10,继续循环,i=2+1=3,3是奇数,执行“选项”后,需继续循环,故排除D.当i=4时,i不是奇数,S=2×4+1=9<10,继续循环,i=4+1=5,5是奇数,执行“选项”后,应跳出循环,输出i的值5后结束,但2×5-2=8<10,2×5-1=9<10,都需继续循环,故排除A、B选项,但2×5=10<10不成立,故选C.5.(文)(2014·重庆高考)执行如图所示的程序框图,则输出s的值( )A.10 B.17C.19 D.36[答案] C[解析] 本题考查算法的循环结构和层层分析法.k=2,s=2;k=3,s=5;k=5,s=10;k=9,s=19,k=17时,结束循环,此时s=19.(理)(2014·重庆高考)执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45[答案] C[解析] 本题考查了算法与程序框图,第一次循环k =9,s =1×910=910,第二次循环k=8,s =910×89=45 ,第三次循环,k =7,s =710循环后k =6,即可输出,所以满足条件的s >710.所以选C .计算程序框图有关的问题要注意判断框中的条件,同时要注意循环节中各个量的位置.二、填空题6.如图给出一个算法框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等.则这样的x 值有________个.[答案] 3[解析] 当x ≤2时,x 2=x ,有x =0或x =1; 当2<x ≤5时,2x -3=x ,有x =3; 当x >5时,x =1x,x 无解.故可知这样的x 有3个.7.(2014·山东高考)执行下面的程序框图,若输入的x 值为1,则输出的n 的值为________.[答案] 3[解析] 本题考查算法的循环结构框图.x2-4x+3≤0时,1≤x≤3.∴当1≤x≤3时,执行循环分支.当x≥4时,结束循环.初值x=1,n=0时,x=2,此时n=1,x=3,此时n=2,x=4,此时n=3.当x=4时,结束循环,输出n=3.关键看出x=4时结束循环,此时n=3,注意循环条件的使用.8.国家法定工作日内,每周工作时间满工作量为40h,每小时工资8元;如因需要加班,则每小时工资为10元.某人在一周内工作时间为x h,但他须交纳个人住房公积金、失业险(这两项费用为每周总收入的10%).试分析算法步骤并画出其净得工资y元的算法的流程图.(注:满工作量外的工作时间为加班)[解析] 算法如下:S1 输入工作时间x h;S2 若x≤40,则y=8x×(1-10%);否则,y=40×8(1-10%)+(x-40)×10(1-10%).S3 输出y值.流程图如下:一、选择题1.(文)执行下面的程序框图,如果输入的N =4,那么输出的S =( ) A .1+12+13+14B .1+12+13×2+14×3×2C .1+12+13+14+15D .1+12+13×2+14×3×2+15×4×3×2[答案] B[解析] 本题考查程序框图的循环结构.由程序框图依次可得,输入N =4,k =1,S =0,T =1→T =1,S =1,k =2;2>4否 T =12,S =1+12,k =3;3>4否 T =16,S =1+12+13×2,K =4;4>4否 T =14×3×2,S =1+12+13×2+14×3×2,k =5;5>4成立,输出S =1+12+13×2+14×3×2,故选B .(理)执行下面的程序框图,如果输入的N =10,那么输出的S =( )A .1+12+13+…+110B .1+12!+13!+ (110)C .1+12+13+…+111D .1+12!+13!+ (111)[答案] B[解析] 当输入N =10时,由于初值k =1,S =0,T =1,故程序运行过程依次为:T =11=1,S =0+1=1,k =1+1=2,此时不满足k >10→T =12=12!,S =1+12!,k =2+1=3,不满足k >10→T =12!3=13!,S =1+12!+13!,k =3+1=4仍不满足k >10,…,直到k =10时,T=19!10=110!,S =1+12!+13!+...+110!,k =11,此时满足k >10,结束循环,输出S =1+12!+13!+ (110)后结束. 2.如果执行如图的框图,输入N =5,则输出的数等于( )A .54 B .45 C .65 D .56[答案] D[解析] 本题考查了程序框图的有关知识,并且渗透了裂项求和的方法,在解题时要注意首先弄清楚程序框图的功能,然后看限制条件,题目定位是中档题.根据程序框图可知,该程序框图的功能是计算S =11×2+12×3+13×4+…+1k ×k +1,现在输入的N =5,所以满足条件k <N 的结果为S =11×2+12×3+13×4+14×5+15×6=(1-12)+(12-13)+…+(15-16)=56,故选D . 二、填空题3.写出下面算法语句的执行结果________.i =0; S =1;Do i =i +1 S =S *i Loop While S ≤20 输出i . [答案] 4[解析] 第一次循环i =1,S =1×1,第二次S =1×2,第三次S =1×2×3,第四次S =1×2×3×4>20不合题意,而此时i =3+1=4,故输出的i 值为4.4.(2014·浙江高考)若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是________.[答案] 6[解析] 本题考查循环结构运行, 第一次运行结果S =1,i =2 第二次运行结果S =4,i =3, 第三次运行结果S =11,i =4. 第四次运行结果S =26,i =5. 第五次运行结果S =57,i =6. 此时S =57>50,输出i =6.5.(2015·温州第一次测试)按下图所示的程序框图运算,若输入x =20,则输出的k =________.[答案] 3[解析] 由题意得x=20,k=0;k=1,x=39;k=2,x=77;k=3,x=153,循环终止,输出的k=3.三、解答题6.用循环语句来书写1+22+32+…+n2>100的最小自然数n的算法,画出算法流程图.[解析] 算法如下:第一步:S=0;第二步:n=1;第三步:S=S+n2;第四步:如果S≤100,使n=n+1,并返回第三步,否则输出n-1.相应的流程图如图所示.。
高考数学总复习 算法与程序框图学案 理 北师大版

第十二章算法初步、复数学案70算法与程序框图导学目标:1.了解算法的含义,了解算法的思想.2.理解程序框图的三种基本逻辑结构:顺序结构、条件结构、循环结构.自主梳理1.算法通常是指按照一定规则解决某一类问题的________和________的步骤.这些程序或步骤必须是明确和有效的,而且能够在有限步之内完成.2.程序框图又称________,是一种用________、________及____________来准确、直观地表示算法的图形.通常程序框图由________和________组成,一个或几个程序框的组合表示算法中的一个步骤;________带方向箭头,按照算法进行的顺序将________连结起来.3.顺序结构是由________________________组成的,这是任何一个算法都离不开的基本结构.其结构形式为4.条件结构是指算法的流程根据给定的条件是否成立而选择执行不同的流向的结构形式.其结构形式为5.循环结构是指__________________________________________________________.反复执行的步骤称为________.循环结构又分为________________和________________.其结构形式为6.算法的五个特征:概括性、逻辑性、有穷性、不惟一性、普遍性.自我检测1.(2010·陕西)如图所示是求样本x 1,x 2,…,x 10平均数x 的程序框图,图中空白框中应填入的内容为( )A .S =S +x nB .S =S +x nnC .S =S +nD .S =S +1n第1题图 第2题图2.(2010·全国)如果执行如图所示的框图,输入N =5,则输出的数等于( ) A .54 B .45 C .65 D .56 3.(2011·北京)执行如图所示的程序框图,输出的s 值为( )A .-3B .-12C .13D .2第3题图第4题图4.(2011·山东)执行如图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是________.探究点一算法的顺序结构例1已知点P(x0,y0)和直线l:Ax+By+C=0,求点P(x0,y0)到直线l的距离d,写出其算法并画出程序框图.变式迁移1阅读如图的程序框图,若输入的a、b、c分别是21、32、75,则输出的a、b、c分别是()A.75、21、32B.21、32、75C.32、21、75 D.75、32、21探究点二算法的条件结构例2 (2011·杭州模拟)函数y =⎩⎪⎨⎪⎧-2 (x>0)0 (x =0)2 (x<0),写出求该函数的函数值的算法,并画出程序框图.变式迁移2 给出一个如图所示的程序框图,若要使输入的x 值与输出的y 值相等,则这样的x 值的个数是( )A .1B .2C .3D .4 探究点三 算法的循环结构例3写出求1×2×3×4×…×100的一个算法并画出程序框图.变式迁移3(2011·天津和平区模拟)在如图所示的程序框图中,当程序被执行后,输出s的结果是______.1.程序框图主要包括三部分:(1)表示相应操作的框;(2)带箭头的流程线;(3)框内外必要的文字说明,读懂程序框图要从这三个方面研究.流程线反映了流程执行的先后顺序,主要看箭头方向,框内外文字说明表明了操作内容.2.两种循环结构的区别:(1)执行情况不同:当型循环是先判断条件,当条件成立时才执行循环体,若循环条件一开始就不成立,则循环体一次也不执行.而直到型循环是先执行一次循环体,再判断循环条件,循环体至少要执行一次.(2)循环条件不同:当型循环是当条件成立时循环,条件不成立时停止循环,而直到型循环是当条件不成立时循环,直到条件成立时结束循环.(满分:75分)一、选择题(每小题5分,共25分)1.中山市的士收费办法如下:不超过2公里收7元(即起步价7元),超过2公里的里程每公里收2.6元,另每车次超过2公里收燃油附加费1元(不考虑其他因素).相应收费系统的程序框图如图所示,则①处应填()A.y=7+2.6x B.y=8+2.6xC.y=7+2.6(x-2) D.y=8+2.6(x-2)第1题图第2题图2.(2010·福建)阅读如图所示的程序框图,运行相应的程序,输出的i值等于() A.2 B.3 C.4 D.53.(2010·浙江)某程序框图如图所示,若输出的S=57,则判断框内为() A.k>4? B.k>5? C.k>6? D.k>7?第3题图第4题图4.(2010·辽宁)如果执行如图所示的程序框图,输入n=6,m=4,那么输出的p等于() A.720 B.360 C.240 D.1205.阅读下面的程序框图,则输出的S等于()A.14 B.20 C.30 D.55二、填空题(每小题4分,共12分)6.(2011·浙江)若某程序框图如图所示,则该程序运行后输出的k的值是__________.第6题图第7题图7.执行如图所示的程序框图,输出的T=________.8.(2010·江苏改编)如图是一个程序框图,则输出的S的值是________.三、解答题(共38分)9.(12分)(2011·包头模拟)对一个作直线运动在对上述统计数据的分析中,一部分计算见如图所示的程序框图(其中a是这8个数据的平均数),求输出的S的值.10.(12分)(2011·汕头模拟)已知数列{a n}的各项均为正数,观察程序框图,若k=5,k=10时,分别有S=511和S=1021.(1)试求数列{a n}的通项;(2)令b n=2a n,求b1+b2+…+b m的值.11.(14分)已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(x n,y n),…,(1)若程序运行中输出一个数组是(9,t),求t的值;(2)求程序结束时,共输出(x,y)的组数;(3)求程序结束时,输出的最后一个数组.学案70 算法与程序框图自主梳理1.明确 有限 2.流程图 程序框 流程线 文字说明 程序框 流程线 流程线 程序框 3.若干个依次执行的步骤 5.从某处开始,按照一定的条件反复执行某些步骤的情况 循环体 当型(WHILE 型) 直到型(UNTIL 型)自我检测 1.A [由循环结构的程序框图可知需添加的运算为S =x 1+x 2+…+x 10的累加求和.]2.D [第一次运行N =5,k =1,S =0,S =0+11×2,1<5成立,进入第二次运行;k=2,S =11×2+12×3,2<5成立,进入第三次运行;k =3,S =11×2+12×3+13×4,3<5成立,进入第四次运行;k =4,S =11×2+12×3+13×4+14×5,4<5成立,进入第五次运行;k=5,S =11×2+12×3+13×4+14×5+15×6=1-16=56,5<5不成立,此时退出循环,输出S.]3.D [由框图可知i =0,s =2→i =1,s =13→i =2,s =-12→i =3,s =-3→i =4,s =2,循环终止,输出s ,故最终输出的s 值为2.]4.68解析 当输入l =2,m =3,n =5时,不满足l 2+m 2+n 2=0,因此执行:y =70l +21m +15n =70×2+21×3+15×5=278.由于278>105,故执行y =y -105,执行后y =278-105=173,再执行一次y =y -105后y 的值为173-105=68,此时68>105不成立,故输出68.课堂活动区例1解题导引顺序结构是最简单的算法结构,语句与语句之间、框与框之间是按从上到下的顺序进行的.程序框图中一定包含顺序结构.解算法如下:第一步,输入x0,y0及直线方程的系数A,B,C.第二步,计算Z1=Ax0+By0+C.第三步,计算Z2=A2+B2.第四步,计算d=|Z1|.Z2第五步,输出d.程序框图:变式迁移1A[由程序框图中的各个赋值语句可得x=21,a=75,c=32,b=21,故a、b、c分别是75、21、32.]例2解题导引求分段函数函数值的程序框图的画法,如果是分两段的函数,则需引入一个判断框;如果是分三段的函数,则需引入两个判断框.解算法如下:第一步,输入x;第二步,如果x>0,则y=-2;如果x=0,则y=0;如果x<0,则y=2;第三步,输出函数值y.相应的程序框图如图所示.变式迁移2 C [本问题即求函数y =⎩⎪⎨⎪⎧ x 2,x ≤2,2x -3,2<x ≤5,1x ,x>5的值.若x ≤2,由x 2=x 得,x =1或0;若2<x ≤5,由x =2x -3得,x =3;若x>5,由x =1x 得,x =±1,不符合.故符合要求的x 值有3个.] 例3 解题导引 数学中的累加、累乘、累差等重复性操作可以用循环结构来实现.循环结构分当型和直到型两种,二者的区别是:前者是,当满足条件时执行循环体,而后者是“直到”条件满足时结束循环.解 第一步,设S 的值为1.第二步,设i 的值为2.第三步,如果i ≤100执行第四步,否则转去执行第七步.第四步,计算S 乘i 并将结果赋给S.第五步,计数i 加1并将结果赋给i.第六步,转去执行第三步.第七步,输出S 的值并结束算法.根据自然语言描述,程序框图如下:变式迁移3 286解析 数列{a n }:4,7,10,…为等差数列,令a n =4+(n -1)×3=40,得n =13,∴s =4+7+…+40=(4+40)×132=286. 课后练习区1.D [根据题意可知x>2时,收费应为起步价7元+超过2公里的里程收费2.6(x -2)元+燃油附加费1元=8+2.6(x -2).]2.C [由框图可知i =1,s =1×21=2;i =2,s =2+2×22=10;i =3,s =2+2×22+3×23>11,i =i +1=3+1=4.]3.A [当k =1时,k =k +1=2,S =2×1+2=4;当k =2时,k =k +1=3,S =2×4+3=11;当k =3时,k =k +1=4,S =2×11+4=26;当k =4时,k =k +1=5,S =2×26+5=57.此时S =57,循环结束,k =5,所以判断框中应为“k>4?”.]4.B [由框图可知:当n =6,m =4时,第一次循环:p =(6-4+1)×1=3,k =2.第二次循环:p =(6-4+2)×3=12,k =3.第三次循环:p =(6-4+3)×12=60,k =4.第四次循环:p =(6-4+4)×60=360,此时k =m ,终止循环.输出p =360.]5.C [第一次循环:S =12;第二次循环:S =12+22;第三次循环;S =12+22+32;第四次循环:S =12+22+32+42=30.]6.5解析 初始值:k =2,执行“k =k +1”得k =3,a =43=64,b =34=81,a>b 不成立; k =4,a =44=256,b =44=256,a>b 不成立;k =5,a =45=1 024,b =54=625,a>b 成立,此时输出k =5.7.30解析 按照程序框图依次执行为S =5,n =2,T =2;S =10,n =4,T =2+4=6;S =15,n =6,T =6+6=12;S =20,n =8,T =12+8=20;S =25,n =10,T =20+10=30>S ,输出T =30.8.63解析 当n =1时,S =1+21=3;当n =2时,S =3+22=7;当n =3时,S =7+23=15;当n =4时,S =15+24=31;当n =5时,S =31+25=63>33.故S =63.9.解 该程序框图即求这组数据的方差,∵a =44,(2分)∴S =18∑8i =1 (a i -a )2=18[(40-44)2+(41-44)2+…+(48-44)2]=7.(12分) 10.解 由题中框图可知S =1a 1a 2+1a 2a 3+…+1a k a k +1, ∵数列{a n }是等差数列,设公差为d ,则有1a k a k +1=1d (1a k -1a k +1), ∴S =1d (1a 1-1a 2+1a 2-1a 3+…+1a k -1a k +1)=1d (1a 1-1a k +1).(4分) (1)由题意可知,k =5时,S =511;k =10时,S =1021. ∴⎩⎨⎧1d (1a 1-1a 6)=511,1d (1a 1-1a 11)=1021, 解得⎩⎪⎨⎪⎧ a 1=1,d =2或⎩⎪⎨⎪⎧a 1=-1,d =-2(舍去). 故a n =a 1+(n -1)d =2n -1.(8分)(2)由(1)可得b n =2a n =22n -1,∴b 1+b 2+…+b m=21+23+…+22m -1=2(1-4m )1-4=23(4m -1). (12分)11.解 (1)循环体运行结果如下: 输出(1,0)n =3x =3y =-2n<2 011 输出(3,-2)n =5x =9y =-4n<2 011 输出(9,-4)n =7x =27y =-6n<2 011 ∴输出数组(9,t)中的t 值是-4.(4分)(2)计数变量n 的取值为:3,5,7,…,构成等差数列,由3+(m -1)×2=2 011.解得m =1 005,由于当m =1 005时,n =2 011,循环体还要执行一遍,会输出第1 006个数组,然后n =2 013>2 011,跳出循环体.故共输出1 006个数组.(8分)(3)程序输出的数组(x n ,y n )按输出的先后顺序,横坐标x n 组成一个等比数列{x n },首项x 1=1,公比q =3.纵坐标组成一个等差数列{y n },首项y 1=0,公差d =-2.∴x 1 006=31 005,y 1 006=-2×1 005=-2 010.故程序结束时,输出的最后一个数组是(31 005,-2 010).(14分)。
高考数学文科一轮复习北京卷B课件:第十二章 算法初步与框图

11.(2015课标Ⅰ,9,5分)执行下面的程序框图,如果输入的t=0.01,则输出的n= ( ) A.5 B.6 C.7 D.8
答案 C S=1-1 =1 ,m=1 ,n=1;
22 4
S= 1 - 1 = 1 ,m=1 ,n=2;
24 4 8
S= 1 - 1 = 1 ,m= 1 ,n=3;
4 8 8 16
A.0 B.1 C.2 D.3 答案 C 本题主要考查程序框图. 执行程序框图可知:输入N的值为19,19不能被3整除,则N=18; 18大于3且能被3整除,则N=6;6大于3且能被3整除,则N=2;2<3,则输出N的值为2,故选C.e2
4.(2017课标全国Ⅱ,10,5分)执行下面的程序框图,如果输入的a=-1,则输出的S= ( ) A.2 B.3 C.4 D.5
高考文数 (北京市专用)
第十二章 算法初步与框图
五年高考
A组 自主命题·北京卷题组
考点 算法与程序框图
1.(2018北京,3,5分)执行如图所示的程序框图,输出的s值为 ( )
A. 1 B. 5 C. 7 D. 7
2
6
6
12
答案 B 本题主要考查程序框图.
执行程序框图,k=1,s=1,
第一次循环,s=1+(-1)1× 1 =1- 1 = 1 ,k=2;
由程序框图可知k=1,s=2;k=2,s= 3 ;k=3,s= 5 .
2
3
此时k<3不成立,故输出s= 5 .故选C.
3
解题关键 找出循环终止的条件是解题的关键.
3.(2016北京,3,5分,0.95)执行如图所示的程序框图,输出的s值为 ( )
A.8 B.9 C.27 D.36
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业64 算法与程序框图
一、选择题
1.如下框图,当x1=6,x2=9,p=8.5时,x3等于().
A.7 B.8 C.10 D.11
2.(2012江西南昌模拟)若如下程序框图所给的运行结果为S=20,那么判断框中应填入的关于k的条件是().
A.k=9 B.k≤8 C.k<8 D.k>8
3.(2012北京高考)执行如图所示的程序框图,输出的S值为().
A.2 B.4 C.8 D.16
4.阅读如图的程序框图,若输出的S的值等于16,那么在程序框图中的判断框内应填写的条件是().
A.i>5 B.i>6 C.i>7 D.i>8
5.如图是求x1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为().A.S=S·(n+1) B.S=S·x n+1 C.S=S·n D.S=S·x n
6.(2012山东高考)执行下面的程序框图,如果输入a=4,那么输出的n的值为().A.2 B.3 C.4 D.5
7.若下面的程序框图输出的S是126,则①应为().
A.n≤5 B.n≤6 C.n≤7 D.n≤8
二、填空题
8.某程序框图如图所示,则该程序运行后输出的k的值是________.
9. (2012上海十三校联考)根据右面的程序框图,要使得输出的结果在区间[-1,0]上,则输入的x的取值范围是__________.
10.(2012陕西高考改编)下图是计算某年级500名学生期末考试(满分为100分)及格率q的程序框图,则图中空白框内应填入__________.
三、解答题
11. 已知某算法的程序框图如图所示,若将输出的(x,y)值依次记为(x1,y1),(x2,y2),…,(x n,y n),…若程序运行中输出的一个数组是(x,-8),求x的值.
12. 程序框图如图,运行此程序,试求输出的b的值.
参考答案
一、选择题
1.B 解析:∵x 1=6,x 2=9, ∴x 1+x 22=6+92=7.5≠8.5, ∴输出的p =x 2+x 32=9+x 32
=8.5, ∴x 3=8.
2.D 解析:据程序框图可得当k =9时,S =11;k =8时,S =11+9=20.
∴应填入“k >8”.
3.C 解析:初始:k =0,S =1,第一次循环:由0<3,得S =1×20=1,k =1; 第二次循环:由1<3得,
S =1×21=2,k =2;
第三次循环:由2<3得,
S =2×22=8,k =3.
经判断此时要跳出循环.因此输出的S 值为8.
4.A
5.D 解析:这里要求的S 是x 1,x 2,…,x 10的乘积,S 从1开始每循环一次就乘以一个xn ,直到符合S =x 1x 2·…·x n 为止,然后跳出循环,输出S .
6.B 解析:由程序框图知,当n =0时,P =1,Q =3;当n =1时,P =5,Q =7;当n =2时,P =21,Q =15,此时n 增加1变为3,满足P >Q ,循环结束,输出n =3.
7.B 解析:程序是计算21+22+…+2n =126,解得n =6,所以判断框内应填“n ≤6”.
二、填空题
8.5 解析:第1次循环:k =3,a =43,b =34;第2次循环:k =4,a =44,b =44; 第3次循环:k =5,a =45,b =54.
此时,满足条件a >b ,循环终止,因此,输出的k 的值是5.
9.⎣⎡⎦⎤2,52 解析:由程序框图可得输出值y =⎩
⎪⎨⎪⎧ x 2, x <0,4-2x ,x ≥0, 若y ∈[-1,0],则
⎩⎪⎨⎪⎧ -1≤x 2≤0,x <0,或⎩⎪⎨⎪⎧
-1≤4-2x ≤0,x ≥0, 解得2≤x ≤52
. 10.q =M M +N 解析:由框图可知M 表示及格人数,N 表示不及格人数,所以q =M M +N
. 三、解答题
11.解:开始n =1,x 1=1,y 1=0→n =3,x 2=3,y 2=-2→n =5,x 3=9,y 3=-4→n =7,x 4=27,y 4=-6→n =9,x 5=81,y 5=-8,则x =81.
12.解:运行程序各次结果分别为i =10,a =1012,b =a =1012;i =9,a =947
,b =a =947;…;i =5,b =a =613;i =4,a =6<613
,b =a =6;i =3,a =7>6,此时程序结束,故输出b 的值为6.。
