2019-2020年中考数学几何探究综合训练卷
2019年中考数学二轮复习几何探究题(压轴题) 综合练习 (含答案)

2019年中考数学二轮复习几何探究题(压轴题)综合练习1. (1)阅读理解:如图①,在△ABC中,若AB=10,AC=6,求BC边上的中线AD的取值范围.解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD).把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是________;(2)问题解决:如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF.求证:BE+CF>EF;(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,∠BCD=140°,以C为顶点作一个70°角,角的两边分别交AB,AD于E,F两点,连接EF,探索线段BE,DF,EF之间的数量关系,并加以证明.2.如图①,②,③分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.(1)在图①中,求证:△ABE≌△ADC.(2)由(1)证得△ABE≌△ADC,由此可推得在图①中∠BOC=120°,请你探索在图②中∠BOC的度数,并说明理由或写出证明过程.(4)由此推广到一般情形(如图④),分别以△ABC 的AB 和AC 为边向△ABC 外作正n 边形,BE 和CD 仍相交于点O ,猜想∠BOC 的度数为____________________(用含n 的式子表示).图① 图② 图③ 图④3.已知正方形ABCD 的边长为1,点P 为正方形内一动点,若点M 在AB 上,且满足△PBC ∽△PAM ,延长BP 交AD 于点N ,连接CM.(1)如图①,若点M 在线段AB 上,求证:AP ⊥BN ;AM =AN.(2)①如图②,在点P 运动过程中,满足△PBC ∽△PAM 的点M 在AB 的延长线上时,AP ⊥BN 和AM =AN 是否成立(不需说明理由)?②是否存在满足条件的点P ,使得PC =12?请说明理由.4. 如图①,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图②,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.(2)当△ABC绕点A逆时针旋转45°时,如图③,延长DB交CF于点H.①求证:BD⊥CF;②当AB=2,AD=32时,求线段DH的长.图①图②图③5. 已知矩形ABCD中AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(1)如图①,已知折痕与边BC交于点O,连接AP、OP、OA,若△OCP与△PDA的面积比为1∶ 4,求边CD的长;(2)如图②,在(1)的条件下擦去AO、OP,连接BP,动点M在线段AP上(点M不与点P、A重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E,试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明变化规律,若不变,求出线段EF的长度.图①图②6. 如图①,矩形ABCD 中,AB =2,BC =5,BP =1,∠MPN =90°,将∠MPN 绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB(或AD)于点E ,PN 交边AD(或CD)于点F ,当PN 旋转至PC 处时,∠MPN 的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D , 此时,△ABP________△PCD(填“≌”或“∽”);(2)类比探究:如图③,在旋转过程中,PEPF 的值是否为定值?若是,请求出该定值;若不是,请说明理由;(3)拓展延伸:设AE =t ,△EPF 的面积为S ,试确定S 关于t 的函数关系式;当S =4.2时,求所对应的t 值.7. 阅读理解:我们知道,四边形具有不稳定性,容易变形.如图①,一个矩形发生变形后成为一个平行四边形,设这个平行四边形相邻两个内角中较小的一个内角为α,我们把1sinα的值叫做这个平行四边形的变形度.(1)若矩形发生形变后的平行四边形有一个内角是120°,则这个平行四边形的变形度是________;猜想证明:(2)设矩形的面积为S1,其变形后的平行四边形面积为S2,试猜想S1,S2,1sinα之间的数量关系,并说明理由;拓展探究:(3)如图②,在矩形ABCD中,E是AD边上的一点,且AB2=AE·AD,这个矩形发生变形后为平行四边形A1B1C1D1,E1为E的对应点,连接B1E1,B1D1,若矩形ABCD的面积为4m(m>0),平行四边形A1B1C1D1的面积为2m(m>0),试求∠A1E1B1+∠A1D1B1的度数.8. 如图,在Rt△ABC中,∠ACB=90°,AC=5 cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2 cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒 3 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.(1)若BM=BN,求t的值;(2)若△MBN与△ABC相似,求t的值;(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.9. 已知:如图,在矩形ABCD中,AB=6 cm,BC=8 cm.对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为1 cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1 cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD 于点F.设运动时间为t(s)(0<t<6),解答下列问题:(2)设五边形OECQF 的面积为S(cm 2),试确定S 与t 的函数关系式;(3)在运动过程中,是否存在某一时刻t ,使S 五边形OECQF ∶S △ACD =9∶16?若存在,求出t 的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t ,使OD 平分∠COP ?若存在,求出t 值;若不存在,请说明理由.10. 如图,已知一个直角三角形纸片ACB ,其中∠ACB =90°,AC =4,BC =3,E 、F 分别是AC 、AB 边上的点,连接EF.(1)如图①,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在AB 边上的点D 处,且使S 四边形ECBF =3S △EDF ,求AE 的长;(2)如图②,若将纸片ACB 的一角沿EF 折叠,折叠后点A 落在BC 边上的点M 处,且使MF ∥CA. ①试判断四边形AEMF 的形状,并证明你的结论; ②求EF 的长;(3)如图③,若FE 的延长线与BC 的延长线交于点N ,CN =1,CE =47,求AFBF的值.11. 已知AC ,EC 分别为四边形ABCD 和EFCG 的对角线,点E 在△ABC 内,∠CAE +∠CBE =90°. (1)如图①,当四边形ABCD 和EFCG 均为正方形时,连接BF. ①求证:△CAE ∽△CBF ;②若BE =1,AE =2,求CE 的长;(2)如图②,当四边形ABCD 和EFCG 均为矩形,且AB BC =EFFC =k 时,若BE =1,AE =2,CE =3,求k 的值;(3)如图③,当四边形ABCD 和EFCG 均为菱形,且∠DAB =∠GEF =45°时,设BE =m ,AE =n ,CE =p ,试探究m ,n ,p 三者之间满足的等量关系(直接写出结果,不必写出解答过程).12. 如图①,菱形ABCD 中,已知∠BAD =120°,∠EGF =60°,∠EGF 的顶点G 在菱形对角线AC 上运动,角的两边分别交边BC 、CD 于点E 、F.图①(1)如图②,当顶点G 运动到与点A 重合时,求证:EC +CF =BC ; (2)知识探究:①如图③,当顶点G 运动到AC 中点时,探究线段EC 、CF 与BC 的数量关系;②在顶点G 的运动过程中,若ACCG =t ,请直接写出线段EC 、CF 与BC 的数量关系(不需要写出证明过程);(3)问题解决:如图④,已知菱形边长为8,BG =7,CF =65,当t >2时,求EC 的长度.13.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC 中,∠BAC =90°,AB =AC ,点D 为直线BC 上一动点(点D 不与B ,C 重合),以AD 为边在AD 右侧作正方形ADEF ,连接CF.(1)观察猜想如图①,当点D 在线段BC 上时,①BC 与CF 的位置关系为:____________. ②BC ,CD ,CF 之间的数量关系为:____________(将结论直接写在横线上).(2)数学思考如图②,当点D 在线段CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明. (3)拓展延伸如图③,当点D 在线段BC 的延长线上时,延长BA 交CF 于点G ,连接GE.若已知AB =22,CD =14BC ,请求出GE 的长.14. 在△ABC中,AB=6,AC=BC=5,将△ABC绕点A按顺时针方向旋转,得到△ADE,旋转角为α(0°<α<180°),点B的对应点为点D,点C的对应点为点E,连接BD,BE.(1)如图,当α=60°时,延长BE交AD于点F.①求证:△ABD是等边三角形;②求证:BF⊥AD,AF=DF;③请直接..写出BE的长;(2)在旋转过程中,过点D作DG垂直于直线AB,垂足为点G,连接CE,当∠DAG=∠ACB,且线段DG与线段AE无公共点时,请直接..写出BE+CE的值.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.备用图15.问题情境在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动.如图①,将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.操作发现(1)将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图②所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是________;(2)创新小组将图①中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图③所示的△AC′D,连接DB、C′C,得到四边形BCC′D,发现它是矩形.请你证明这个结论;实践探究(3)缜密小组在创新小组发现结论的基础上,量得图③中BC=13 cm,AC=10 cm,然后提出一个问题:将△AC′D沿着射线DB方向平移a cm,得到△A′C″D′,连接BD′,CC″,使四边形BCC″D′恰好为正方形,求a的值.请你解答此问题;(4)请你参照以上操作,将图①中的△ACD在同一平面内进行一次平移,得到△A′C′D,在图④中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.CB 上,且CD ∶DB =2∶1,OB 交AD 于点E ,平行于x 轴的直线l 从原点O 出发,以每秒1个单位长度的速度沿y 轴向上平移,到C 点时停止;l 与线段OB ,AD 分别相交于M ,N 两点,以MN 为边作等边△MNP(点P 在线段MN 的下方),设直线l 的运动时间为t(秒),△MNP 与△OAB 重叠部分的面积为S(平方单位). (1)直接写出点E 的坐标; (2)求S 与t 的函数关系式;(3)是否存在某一时刻t ,使得S =12S △ABD 成立?若存在,请求出此时t 的值;若不存在,请说明理由.备用图17. 已知点O 是△ABC 内任意一点,连接OA 并延长到E ,使得AE =OA ,以OB ,OC 为邻边作▱OBFC ,连接OF ,与BC 交于点H ,再连接EF.(1)如图①,若△ABC 为等边三角形,求证:①EF ⊥BC ;②EF =3BC ;(2)如图②,若△ABC 为等腰直角三角形(BC 为斜边),猜想(1)中的两个结论是否成立?若成立,直接写出结论即可;若不成立,请你直接写出你的猜想结果;18. 如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).(1)计算矩形EFGH的面积;(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为316时,求矩形平移的距离;(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形E1F1G1H1,将矩形E1F1G1H1绕G1点按顺时针方向旋转,当H1落在CD上时停止转动,旋转后的矩形记为矩形E2F2G1H2,设旋转角为α,求cosα的值.参考答案1. (1)解:如图①中,∵AB=10,AC=6,AD是BC边上中线,由旋转性质知,BE=AC=6,AD=DE.∴在△ABE中,10-6<AE<10+6,即4<2AD<16,∴2<AD<8;(2)证明:延长FD至M,使FD =MD ,连接ME ,MB.如图①所示. ∵ED ⊥FM ,FD =DM , ∴ME =EF.∵CD =BD ,∠CDF =∠BDM , ∴△CDF ≌△BDM(SAS ), ∴CF =BM.∵BM +BE>ME ,∴BE +CF>EF;(3)解:BE +DF =EF. 理由:延长EB 至点N ,使BN =DF ,图②连接CN ,如图②所示.∵∠EBC +∠D =180°,∠EBC +∠CBN =180° ∴∠D =∠CBN ,∴在△CDF 和△CBN 中, ⎩⎪⎨⎪⎧DF =BN ∠D =∠CBN DC =BC, ∴△CDF ≌△CBN(SAS ),∴CF =CN.∵∠BCD =140°,∠ECF =70°, ∴∠DCF +∠BCE =70°,∴∠BCN +∠BCE =70°,即∠NCE =70°, ∴在△ECF 和△ECN 中, ⎩⎪⎨⎪⎧CF =CN ∠ECF =∠ECN CE =CE, ∴△ECF ≌△ECN(SAS ), ∴EF =EN.∵EB +BN =EN ,∴BE +DF =EF.2. (1)证明:∵△ABD 、△ACE 是等边三角形, ∴AB =AD ,AC =AE ,∠CAE =∠DAB =60°,∴∠CAE +∠BAC =∠DAB +∠BAC ,即∠BAE =∠DAC , 在△ABE 和△ADC 中, ⎩⎪⎨⎪⎧AB =AD ∠BAE =∠DAC AE =AC,(2)解:∠BOC =90°.理由如下: 由(1)得△ABE ≌△ADC ,∴∠EBA =∠CDA.∵∠FBA +∠FDA =180°,∴∠FBA -∠EBA +∠FDA +∠CDA =180°, 即∠FBO +∠FDO =180°.在四边形FBOD 中,∠F =90°,∴∠DOB =360°-∠F -(∠FBO +∠FDO)=90°, ∴∠BOC =90°. (3)解:72°.【解法提示】∠BOC =180°-108°=72°. (4)解:180°-180°·(n -2)n. 【解法提示】由(3)可知,∠BOC 度数应为180°减去正多边形内角度数. 3. (1)证明:∵△PBC ∽△PAM , ∴∠PBC =∠PAM.∵四边形ABCD 是正方形,∴∠PBC +∠PBA =∠CBA =90°, ∴∠PAM +∠PBA =90°, ∴∠APN =90°,即AP ⊥BN , ∴∠BPA =∠BAN =90°. ∵∠ABP =∠NBA ,∴△ABP ∽△NBA ,PB AB =PAAN , ∴AN AB =PA PB .又∵△PAM ∽△PBC , ∴PA PB =AM BC , 故AN AB =AM BC . 又∵AB =BC ,∴AM =AN ;(2)解:①点M 在AB 的延长线上时,AP ⊥BN 和AM =AN 仍然成立;②不存在,理由如下:选择图②,如图,以AB 为直径,作半圆O ,连接OC ,OP ,∵BC =1,OB =12, ∴OC =52.∵由①知,AP ⊥BN ,∴点P 一定在以点O 为圆心、半径长为12的半圆上(A ,B 两点除外). 如果存在点P ,那么OP +PC ≥OC ,则PC ≥5-12.∵5-12>12,故不存在满足条件的点P ,使得PC =12.4. (1)解:BD =CF 成立.理由如下:∵AC =AB ,∠CAF =∠BAD =θ,AF =AD , ∴△ACF ≌△ABD ,∴CF =BD.(2)①证明:由(1)得,△ACF ≌△ABD , ∴∠HFN =∠ADN , 在△HFN 与△ADN 中,∵∠HFN =∠ADN ,∠HNF =∠AND , ∴∠NHF =∠NAD =90°, ∴HD ⊥HF ,即BD ⊥CF.②解:如图,连接DF ,延长AB ,与DF 交于点M , 在△MAD 中,∵∠MAD =∠MDA =45°, ∴∠BMD =90°.在Rt △BMD 与Rt △FHD 中, ∵∠MDB =∠HDF , ∴△BMD ∽△FHD.∵AB =2,AD =32,四边形ADEF 是正方形, ∴MA =MD =322=3,∴MB =MA -AB =3-2=1,BD =MB 2+MD 2=12+32=10, 又∵MD HD =BD FD ,即3HD =106, ∴DH =9105.5. 解:(1)由矩形性质与折叠可知,∠APO =∠B =∠C =∠D =90°, ∴∠CPO +∠DPA =∠DPA +∠DAP =90°, ∴∠DAP =∠CPO , ∴△OCP ∽△PDA , ∴S △OCP S △PDA=(CP DA )2,即14=(CP8)2, ∴CP =4,∵AP 2-DP 2=AD 2, ∴x 2-(x -4)2=82, 解得x =10, 故CD =10.(2)线段EF 的长度始终不发生变化,为2 5.证明:如图,过点N 作NG ⊥PB ,与PB 的延长线相交于点G , ∵AB =AP ,∴∠APB =∠ABP =∠GBN , 在△PME 和△BNG 中, ⎩⎪⎨⎪⎧∠MEP =∠NGB =90°∠MPE =∠NBG MP =NB, ∴△PME ≌△BNG(AAS ), ∴ME =NG ,PE =BG , 在△FME 和△FNG 中, ⎩⎪⎨⎪⎧∠MEF =∠NGF ∠MFE =∠NFG ME =NG, ∴△FME ≌△FNG(AAS ), ∴EF =GF , ∴EF =12EG ,∵BP =BE +EP =BE +GB =EG , ∴EF =12BP ,∵BP =BC 2+CP 2=82+42=45, ∴EF =12BP =2 5.6. 解:(1)△ABP ∽△PCD.【解法提示】∵∠MPN =90°, ∴∠APB +∠DPC =90°, ∵∠B =90°,∴∠APB +∠BAP =90°, ∴∠DPC =∠BAP , 又∵∠B =∠C =90°, ∴△ABP ∽△PCD.(2)在旋转过程中,PE的值为定值.如图,过点F 作FG ⊥BC ,垂足为G.类比(1)可得:△EBP ∽△PGF , ∴EP PF =PB FG ,∵∠A =∠B =∠FGB =90°, ∴四边形ABGF 是矩形, ∴FG =AB =2, ∵BP =1, ∴PE PF =12,即在旋转过程中,PE PF 的值为定值12. (3)由(2)知△EBP ∽△PGF , ∴EB PG =BP GF =12,又∵AE =t , ∴BE =2-t ,∴PG =2(2-t)=4-2t ,∴AF =BG =BP +PG =1+(4-2t)=5-2t , ∴S =S 矩形ABGF -S △AEF -S △BEP -S △PFG=2(5-2t)-12t(5-2t)-12×1×(2-t)-12×2×(4-2t) =t 2-4t +5,即S =t 2-4t +5(0≤t ≤2), 当S =4.2时,4.2=t 2-4t +5,解得:t 1=2-455,t 2=2+455(不合题意,舍去). ∴t 的值是2-45 5. 7. 解:(1)233.【解法提示】sin 120°=32,故这个平行四边形的变形度是233. (2)1sin α=S 1S 2,理由如下: 如图,设矩形的长和宽分别为a ,b ,其变形后的平行四边形的高为h ,则S 1=ab ,S 2=ah ,sin α=hb ,∴S 1S 2=ab ah =b h ,又∵1sin α=b h ,∴1sin α=S 1S 2. (3)由AB 2=AE·AD ,可得A 1B 21=A 1E 1·A 1D 1,即A 1B 1A 1D 1=A 1E 1A 1B 1. 又∵∠B 1A 1E 1=∠D 1A 1B 1, ∴△B 1A 1E 1∽△D 1A 1B 1, ∴∠A 1B 1E 1=∠A 1D 1B 1, ∵A 1D 1∥B 1C 1,∴∠A 1E 1B 1=∠C 1B 1E 1,∴∠A 1E 1B 1+∠A 1D 1B 1=∠C 1B 1E 1+∠A 1B 1E 1=∠A 1B 1C 1. 由(2)结论1sin α=S 1S 2,可得1sin ∠A 1B 1C 1=4m2m=2,∴sin ∠A 1B 1C 1=12, ∴∠A 1B 1C 1=30°, ∴∠A 1E 1B 1+∠A 1D 1B 1=30°.8. 解:(1)根据题意BM =2t ,BN =BC -3t , 而BC =5×tan 60°=5 3.∴当BM =BN 时,2t =53-3t ,解得t =103-15. (2)分类讨论:①当∠BMN =∠ACB =90°时,如图①, △NBM ∽△ABC ,cos B =cos 30°=BMBN , ∴2t 53-3t=32,解得t =157.②当∠BNM =∠ACB =90°时,如图②, △MBN ∽△ABC ,cos B =cos 30°=BNBM , ∴53-3t 2t =32,解得t =52.因此当运动时间是157秒或52秒时,△MBN 与△ABC 相似.(3)由于△ABC 面积是定值,∴当四边形ACNM 面积最小时,△MBN 面积最大,而△MBN 的面积是S =12BM ×BN ×sin B =12×2t ×(53-3t)×12=-32t 2+532t , 由于a =-32<0,∴当t =-5322×(-32)=52时,△MBN 面积最大,最大值是-32×(52)2+532×52=2538,因此四边形ACNM 面积最小值是12×5×53-2538=7538. 9. (1)分三种情况: ①若AP =AO ,在矩形ABCD 中,∵AB =6,BC =8, ∴AC =10, ∴AO =CO =5, ∴AP =5, ∴t =5,②若AP =PO =t , 在矩形ABCD 中, ∵AD ∥BC ,∴∠PAO =∠OCE ,∠APO =∠OEC , 又∵OA =OC , ∴△APO ≌△CEO ,∴PO =OE =t.作AG ∥PE 交BC 于点G ,则四边形APEG 是平行四边形, ∴AG =PE =2t ,GE =AP =t. 又∵EC =AP =t ,∴BG =8-2t.在Rt △ABG 中,根据勾股定理知62+(8-2t)2=(2t)2, 解得t =258.③若OP =AO =5,则t =0或t =8,不合题意,舍去. 综上可知,当t =5或t =258时,△AOP 是等腰三角形. (2)如解图②,作OM ⊥BC ,垂足是M ,作ON ⊥CD ,垂足是N.图②则OM =12AB =3,ON =12BC =4,∴S △OEC =12·CE·OM =12·t·3=32t , S △OCD =12·CD·ON =12·6·4=12. ∵QF ∥AC ,∴△DFQ ∽△DOC , ∴S △DFQ S △DOC=(DQ DC )2,即S △DFQ 12=(t6)2, ∴S △DFQ =13t 2, ∴S 四边形OFQC =12-13t 2,∴S 五边形OECQF =S 四边形OFQC +S △OEC =12-13t 2+32t , 即S =-13t 2+32t +12(0<t <6).(3)存在.理由如下:要使S 五边形OECQF :S △ACD =9∶16, 即(-13t 2+32t +12)∶(12×6×8)=9∶16,解得t 1=3,t 2=1.5,两个解都符合题意,∴存在两个t 值,使S 五边形OECQF ∶S △ACD =9∶16,此时t 1=3,t 2=1.5; (4)存在.理由如下:如解图③,作DI ⊥OP ,垂足是I ,DJ ⊥OC ,垂足是J ,图③作AG ∥PE 交BC 于点G.∵S △OCD =12·OC·DJ =12·5·DJ ,且由(2)知,S △OCD =12, ∴DJ =245.∵OD 平分∠POC ,DI ⊥OP ,DJ ⊥OC , ∴DI =DJ =245=4.8. ∵AG ∥PE , ∴∠DPI =∠DAG. ∵AD ∥BC ,∴∠DAG =∠AGB , ∴∠DPI =∠AGB ,∴Rt △ABG ∽Rt △DIP .由(1)知,在Rt △ABG 中,BG =8-2t , ∴AB DI =BG IP ,∴64.8=8-2t IP , ∴IP =45(8-2t).在Rt △DPI 中,根据勾股定理得 (245)2+[45(8-2t)]2=(8-t)2, 解得t =11239.(t =0不合题意,舍去)10. 解:(1)∵折叠后点A 落在AB 边上的点D 处, ∴EF ⊥AB ,△AEF ≌△DEF , ∴S △AEF =S △DEF .∵S 四边形ECBF =3S △EDF ,∴S 四边形ECBF =3S △AEF .∵S △ACB =S △AEF +S 四边形ECBF ,∴S △ACB =S △AEF +3S △AEF =4S △AEF , ∴S △AEF S △ACB =14. ∵∠EAF =∠BAC ,∠AFE =∠ACB =90°, ∴△AEF ∽△ABC , ∴S △AEF S △ABC =(AE AB )2, ∴(AE AB )2=14. 在Rt △ACB 中,∵∠ACB =90°,AC =4,BC =3, ∴AB =42+32=5, ∴(AE 5)2=14,∴AE =52.(2)图①①四边形AEMF 是菱形.证明:如解图①,∵折叠后点A 落在BC 边上的点M 处, ∴∠CAB =∠EMF ,AE =ME , 又∵MF ∥CA ,∴∠CEM =∠EMF , ∴∠CAB =∠CEM , ∴EM ∥AF ,∴四边形AEMF 是平行四边形.又∵AE =ME ,∴四边形AEMF 是菱形.②如解图①,连接AM ,AM 与EF 交于点O ,设AE =x ,则ME =AE =x ,EC =4-x. ∵∠CEM =∠CAB ,∠ECM =∠ACB =90°, ∴△ECM ∽△ACB. ∴EC AC =EMAB , ∵AB =5,AC =4, ∴4-x 4=x5, 解得x =209,∴AE =ME =209,EC =169.在Rt △ECM 中,∵∠ECM =90°,∴CM 2=EM 2-EC 2, 即CM =EM 2-EC 2=(209)2-(169)2=43. ∵四边形AEMF 是菱形,∴OE =OF ,OA =OM ,AM ⊥EF , ∴S 菱形AEMF =4S △AOE =2OE·AO. 在Rt △AOE 和Rt △ACM 中, ∵tan ∠EAO =tan ∠MAC , ∴OE AO =CM AC. ∵CM =43,AC =4,∴AO =3OE ,∴S 菱形AEMF =6OE 2. 又∵S 菱形AEMF =AE·CM , ∴6OE 2=209×43,∴OE =2109,∴EF =4109. (3)如图②,图②过点F 作FH ⊥CB 于点H ,在Rt △NCE 和Rt △NHF 中, ∵tan ∠ENC =tan ∠FNH ,∴EC NC =FH NH, ∵NC =1,EC =47,∴FH NH =47, 设FH =x ,则NH =74x ,∴CH =NH -NC =74x -1.∵BC =3,∴BH =BC -CH =3-(74x -1)=4-74x.在Rt △BHF 和Rt △BCA 中,∵tan ∠FBH =tan ∠ABC , ∴HF BH =CA BC , ∴x4-74x =43, 解得x =85,∴HF =85.∵∠B =∠B ,∠BHF =∠BCA =90°, ∴△BHF ∽△BCA , ∴HF CA =BFBA,即HF·BA =CA·BF , ∴85×5=4BF , ∴BF =2,∴AF =AB -BF =3, ∴AF BF =32. 11. (1)①证明:如图①, ∵∠ACE +∠ECB =45°,∠BCF +∠ECB =45°,图①∴∠ACE =∠BCF ,又∵四边形ABCD 和EFCG 是正方形, ∴AC BC =CECF=2, ∴△CAE ∽△CBF.②解:∵AE BF =ACBC =2,AE =2,∴BF =AE2=2,由△CAE ∽△CBF 可得∠CAE =∠CBF , 又∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°,即∠EBF =90°, 由CE 2=2EF 2=2(BE 2+BF 2)=6,图② 解得CE = 6.(2)解:连接BF ,如图②,同(1)证△CAE ∽△CBF ,可得∠EBF =90°,AC BC =AE BF, 由AB BC =EFFC=k ,可得BC ∶AB ∶AC =1∶k ∶k 2+1, CF ∶EF ∶EC =1∶k ∶k 2+1,∴CE EF =ACAB =k 2+1k ,AE BF =AC BC=k 2+1, ∴EF =kCE k 2+1,EF 2=k 2CE 2k 2+1,BF =AE k 2+1,BF 2=AE 2k 2+1,∴CE 2=k 2+1k 2×EF 2=k 2+1k2(BE 2+BF 2), ∴32=k 2+1k 2(12+22k 2+1), 解得k =104. (3)解:p 2-n 2=(2+2)m 2.【解法提示】如图③,连接BF ,同(1)证△CAE ∽△CBF ,可得∠EBF =90°, 过点C 作CH ⊥AB 交AB 延长线于点H , 类比第(2)问得AB 2∶BC 2∶AC 2=1∶1∶(2+2),图③EF 2∶FC 2∶EC 2=1∶1∶(2+2), ∴p 2=(2+2)EF 2 =(2+2)(BE 2+BF 2)=(2+2)(m 2+n 22+2)=(2+2)m 2+n 2,∴p 2-n 2=(2+2)m 2.12. (1)证明:∵四边形ABCD 是菱形,∠BAD =120°,∴∠BAC =60°,∠B =∠ACF =60°,AB =BC , ∴AB =AC ,∵∠BAE +∠EAC =∠EAC +∠CAF =60°, ∴∠BAE =∠CAF , 在△BAE 和△CAF 中, ⎩⎪⎨⎪⎧∠BAE =∠CAF AB =AC ∠B =∠ACF, ∴△BAE ≌△CAF(ASA ), ∴BE =CF ,∴EC +CF =EC +BE =BC , 即EC +CF =BC ;(2)解:①线段EC ,CF 与BC 的数量关系为:EC +CF =12BC.理由如下:如图①,过点A 作AE′∥EG ,AF ′∥GF ,分别交BC 、CD 于E′、F′.图①类比(1)可得:E′C +CF′=BC , ∵G 为AC 中点,AE ′∥EG , ∴CE CE′=CG AC =12, ∴CE =12CE′,同理可得:CF =12CF′,∴CE +CF =12CE′+12CF′=12(CE′+CF′)=12BC ,即CE +CF =12BC ;②CE +CF =1tBC ;【解法提示】类比(1)可得:E′C +CF′=BC , ∵AE ′∥EG ,ACCG =t ,∴CE CE′=CG AC =1t, ∴CE =1t CE′,同理可得:CF =1tCF′,∴CE +CF =1t CE′+1t CF′=1t (CE′+CF′)=1t BC ,即CE +CF =1tBC.(3)解:如图②,连接BD 与AC 交于点H.图②在Rt △ABH 中,∵AB =8,∠BAC =60°, ∴BH =AB·sin 60°=8×32=43, AH =CH =AB·cos 60°=8×12=4,∴GH =BG 2-BH 2=72-(43)2=1, ∴CG =4-1=3, ∴CG AC =38, ∴t =83(t >2),由(2)②得:CE +CF =1t BC ,∴CE =1t BC -CF =38×8-65=95.∴EC 的长度为95.13. (1)解:①BC ⊥CF ;②BC =CD +CF. 【解法提示】①∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°, ∴∠BCF =90°,即BC ⊥CF ; ②∵△ABD ≌△ACF , ∴BD =CF ,∵BC =CD +BD ,∴BC =CD +CF.(2)解:结论①仍然成立,②不成立. ①证明:∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF ,∴∠ACF =∠ABD =180°-45°=135°, ∵∠ACB =45°, ∴∠BCF =90°,即BC ⊥CF ; ②结论为:BC =CD -CF. 证明:∵△ABD ≌△ACF , ∴BD =CF ,∵BC =CD -BD ,∴BC =CD -CF.(3)解:如图,过点E 作EM ⊥CF 于M ,作EN ⊥BD 于点N ,过点A 作AH ⊥BD 于点H. ∵AB =AC =22,∴BC =4,AH =12BC =2,∵CD =14BC ,∴CD =1,∵∠BAC =∠DAF =90°, ∴∠BAD =∠CAF ,又∵AB =AC ,AD =AF , ∴△ABD ≌△ACF , ∴∠ACF =∠ABC =45°, ∵∠ACB =45°, ∴∠BCF =90°,∴CN =ME ,CM =EN , ∴∠AGC =∠ABC =45°, ∴CG =BC =4, ∵∠ADE =90°,∴∠ADH +∠EDN =∠EDN +∠DEN =90°, ∴∠ADH =∠DEN ,又∵∠AHC =∠DNE =90°,AD =DE , ∴△AHD ≌△DNE ,∴DN =AH =2,EN =DH =3, ∴CM =EN =3,ME =CN =3, 则GM =CG -CM =4-3=1,∴EG =EM 2+GM 2=10.14. (1)①证明:∵△ABC 绕点A 顺时针方向旋转60°得到△ADE , ∴AB =AD ,∠BAD =60°, ∴△ABD 是等边三角形;②证明:由①得△ABD 是等边三角形, ∴AB =BD ,∵△ABC 绕点A 顺时针方向旋转60°得到△ADE , ∴AC =AE ,BC =DE ,∴EA =ED ,∴点B ,E 在AD 的中垂线上, ∴BE 是AD 的中垂线, ∵点F 在BE 的延长线上, ∴BF ⊥AD ,AF =DF ; ③解:BE 的长为33-4;【解法提示】由②知AF =12AD =12AB =3,AE =AC =5,BF ⊥AD ,由勾股定理得EF =AE 2-AF 2=4.在等边△ABD 中,AB =6,BF ⊥AD , ∴BF =32AB =33,∴BE =33-4. (2)解:BE +CE 的值为13;【解法提示】如图, ∵∠DAG =∠ACB ,∴∠DAB =2∠CAB. ∵∠DAE =∠CAB , ∴∠BAE =∠CAB , ∴∠BAE =∠CBA , ∴AE ∥BC ,∵AE =AC =BC ,∴四边形ACBE 是菱形,∴CE 垂直平分AB ,BE =AC =5.设CE 交AB 于M ,则CM ⊥AB ,CM =EM ,AM =BM , ∴在Rt △ACM 中,AC =5,AM =3, 由勾股定理得CM =4, ∴CE =8,∴CE +BE =13. 15. (1)解:菱形.(2)证明:如解图①,作AE ⊥CC′于点E , 由旋转得AC′=AC ,∴∠CAE =∠C′AE =12α=∠BAC ,图①∴BA =BC ,BC =DC′, ∴∠BCA =∠BAC , ∴∠CAE =∠BCA , ∴AE ∥BC , 同理AE ∥DC′, ∴BC ∥DC ′,∴四边形BCC′D 是平行四边形, 又∵AE ∥BC ,∠CEA =90°, ∴∠BCC ′=180°-∠CEA =90°,∴四边形BCC′D 是矩形.(3)解:如解图①,过点B 作BF ⊥AC 于点F , ∵BA =BC ,∴CF =AF =12AC =12×10=5.在Rt △BCF 中,BF =BC 2-CF 2=132-52=12. 在△ACE 和△CBF 中,∵∠CAE =∠BCF ,∠CEA =∠BFC =90°, ∴△ACE ∽△CBF , ∴CE BF =AC BC ,即CE 12=1013, 解得CE =12013.∵AC =AC′,AE ⊥CC ′, ∴CC′=2CE =2×12013=24013.当四边形BCC″D′恰好为正方形时,分两种情况: ①点C″在边CC′上,a =CC′-13=24013-13=7113,②点C″在边C′C 的延长线上,a =CC′+13=24013+13=40913.综上所述,a 的值为7113或40913.图②(4)解:答案不唯一,例:画出正确图形如图②所示.平移及构图方法:将△ACD 沿着射线CA 方向平移,平移距离为12AC 的长度,得到△A′C′D ,连接A′B ,DC.结论:四边形A′BCD 是平行四边形. 16. 解:(1)点E 的坐标是(33,3). 【解法提示】如∵OA ∥BC ,∴△DEB ∽△AEO , ∴OE EB =OA BD =BC BD =BD +CD BD =1+CD BD=1+2=3, ∵∠EHO =∠BAO =90°, ∴EH ∥AB ,∴△OEH ∽△OBA , ∴OE OB =EH AB =OH OA =34, ∵AB =4,OA =43, ∴EH =3,OH =33, ∴点E 的坐标是(33,3).(2)如解图①,在矩形OABC 中,∵CD ∶DB =2∶1,点B 的坐标为(43,4), ∴点A 的坐标为(43,0),点D 的坐标为(833,4),可得直线OB 的解析式为y 1=33x , 直线AD 的解析式为y 2=-3x +12.当y 1=y 2=t 时,可得点M ,N 的横坐标分别为: x M =3t ,x N =43-33t , 则MN =|x N -x M |=|43-433t|(0≤t ≤4).当点P 运动到x 轴上时(如图②),图①∵△MNP 为等边三角形, ∴MN ·sin 60°=t ,即(43-433t)·32=t , 解得t =2.讨论:分三种情况:①当0≤t <2时(如图①), 设PM ,PN 分别交x 轴于点F ,G ,则△PFG 的边长为PF =MP -MF =MN -MF =43-433t -233t =43-23t , ∵MN =x N -x M =43-433t ,图②∴S =S 梯形FGNM =(43-23t +43-433t)t ×12=-533t 2+43t. ②当2≤t ≤3时(如图②),此时等边△MNP 整体落在△OAB 内, ∴S =S △PMN =34(43-433t)2=433t 2-83t +12 3. ③当3<t ≤4时(如图③), 在Rt △OAB 中,tan ∠AOB =AB AO =33, ∴∠AOB =30°,∠NME =30°,图③∴△MNE 和△MPE 关于直线OB 对称. ∵MN =|x N -x M |=433t -43, ∴S =12S △PMN =233t 2-43t +6 3.(3)存在t ,使S =12S △ABD 成立.∵S △ABD =12×4×433=833,若S =12S △ABD 成立,则:①当0≤t <2时,-533t 2+43t =433,解得t 1=2(舍去),t 2=25.②当2≤t ≤3时,433t 2-83t +123=433,解得t 3=2,t 4=4.(舍去)③当3<t ≤4时,233t 2-43t +63=433,得t 5=3+2(舍去),t 6=3-2(舍去). 综上所述,符合条件的t 的值有25或2.17. 证明:(1)①连接AH ,如图①,连接AH.图①∴BH =HC =12BC ,OH =HF ,∵△ABC 是等边三角形, ∴AB =BC ,AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2, ∴AH =BC 2-(12BC )2=32BC ,∵OA =AE ,OH =HF ,∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC. ②由①得AH =32BC , AH =12EF∴32BC =12EF , ∴EF =3BC.(2)EF ⊥AB 仍然成立,EF =BC.图②【解法提示】如解图②,连接AH , ∵四边形OBFC 是平行四边形, ∴BH =HC =12BC ,OH =HF ,∵△ABC 是等腰直角三角形, ∴AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2= (2BH)2-BH 2=BH 2, ∴AH =BH =12BC ,∵OA =AE ,OH =HF , ∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC ,EF =2AH =BC.(3)EF =4k 2-1 BC.【解法提示】如解图③,连接AH , ∵四边形OBFC 是平行四边形, ∴BH =HC =12BC ,OH =HF ,∵△ABC 是等腰三角形,AB =kBC ,∴AH ⊥BC ,在Rt △ABH 中,AH 2=AB 2-BH 2=(kBC)2-(12BC)2=(k 2-14)BC 2,∴AH =124k 2-1 BC ,∵OA =AE ,OH =HF , ∴AH 是△OEF 的中位线, ∴AH =12EF ,AH ∥EF ,∴EF ⊥BC ,124k 2-1 BC =12EF ,∴EF =4k 2-1 BC.18. 解:(1)如图①,在△ABC 中, ∵∠ACB =90°,∠B =30°,AC =1, ∴AB =2,又∵D 是AB 的中点,图①∴AD =1,CD =12AB =1,又∵EF 是△ACD 的中位线,∴EF =DF =12,在△ACD 中,AD =CD ,∠A =60°,∴△ACD 为等边三角形, ∴∠ADC =60°, 在△FGD 中,GF =DF·sin 60°=34, ∴矩形EFGH 的面积S =EF·GF =12×34=38.(2)如图②,设矩形移动的距离为x ,则0<x ≤12,①当矩形与△CBD 重叠部分为三角形时,则0<x ≤14,重叠部分的面积S =12x·3x =316,∴x =24>14(舍去), ②当矩形与△CBD 重叠部分为直角梯形时,则14<x ≤12,重叠部分的面积S =34x -12×14×34=316, ∴x =38,即矩形移动的距离为38时,矩形与△CBD 重叠部分的面积是316.图③(3)如图③,作H 2Q ⊥AB 于Q , 设DQ =m ,则H 2Q =3m , 又DG 1=14,H 2G 1=12,在Rt △H 2QG 1中, (3m)2+(m +14)2=(12)2,解得m 1=-1+1316,m 2=-1-1316<0(舍去),∴cos α=QG 1F 1G 1=-1+1316+1412=3+138.。
2020年中考数学一轮专项提升卷——几何综合问题探究(含答案)

2020年中考数学一轮专项提升卷——几何综合问题探究1.(2019·海口)如图,在菱形ABCD 中,点E 是BC 的中点,DE 与AC 交于点F ,若AB =6,∠B =60°,则AF 的长为( )A .3B .3.5C .33D .42.(2019·天津)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2,点P 是AB 的中点,点D ,E 是AC ,BC 边上的动点,且AD =CE ,连接DE .有下列结论:①∠DPE =90°;②四边形PDCE 面积为1;③点C 到DE 距离的最大值为22.其中,正确的个数是( )A .0B .1C .2D .33.(原创题)如图,在平行四边形ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF ,CF ,则下列结论中一定成立的是( )①∠DCF =12∠BCD ;②EF =CF ;③∠DFE =3∠AEF ;④S △BEC =2S △CEF .A .①②③B .②③④C .①②④D .①③④4.(2019·广西防城港)如图,AB 为⊙O 的直径,BC ,CD 是⊙O 的切线,切点分别为点B ,D ,点E 为线段OB 上的一个动点,连接OD ,CE ,DE ,已知AB =25,BC =2,当CE +DE 的值最小时,则CEDE的值为( )A .910B .23C .53D .2555.(原创题)如图,在△ABC 中,D ,E ,F 分别为BC ,AC ,AB 的中点,AH ⊥BC 于点H ,FD =8 cm ,则HE =____cm.6.(2019·丹阳市一模)如图,在△ABC 中,AC >AB ,点D 在BC 上,且BD =BA ,∠ABC 的平分线BE 交AD 于点E ,点F 是AC 的中点,连接EF .若四边形DCFE 和△BDE 的面积都为3,则△ABC 的面积为____.7.(2019·山西模拟)如图,平行四边形ABCD 的边长AD =3,AB =2,∠BAD =120°,E 为AB 的中点,F 在边BC 上,且BF =2FC .AF 与DE 交于点G ,则AG 的长为____.8.(2019·襄阳)如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C ,点D 在AB 上,∠BAC =∠DEC =30°,AC 与DE 交于点F ,连接AE ,若BD =1,AD =5,则CF EF =____.9.如图1,在正方形ABCD 中,P 是对角线AC 上的一点,点E 在CB 上,且PC =PE ,过E 作EF 垂直于BC 交DP 延长线于F ,且PF =PD .(1)如图1,当点E 在CB 边上时,求证:PE =22CE ; (2)如图2,当点E 在CB 的延长线上时,线段PE ,CE 有怎样的数量关系,写出你的猜想,并给与证明.10.(改编题)已知,如图1,矩形ABCD 中,AD =6,DC =8,矩形EFGH 的三个顶点E ,G ,H 分别在矩形ABCD 的边ABCD 的边AB ,CD ,DA 上,AH =2,连接CF .(1)如图1,当四边形EFGH 为正方形时,求AE 的长和△FCG 的面积;(2)如图2,设AE =x ,△FCG 的面积=S 1,求S 1与x 之间的函数关系式与S 1的最大值; (3)在(2)的条件下,如果矩形EFGH 的顶点F 始终在矩形ABCD 内部,连接BF ,记△BEF 的面积为S 2,△BCF 的面积为S 3,试说明6S 1+3S 2-2S 3是常数.11.(2019·广州)如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC 上一动点(不与点C重合),△CDE关于DE的轴对称图形为△FDE.(1)当点F在AC上时,求证:DF∥AB;(2)设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)当B,F,E三点共线时,求AE的长.12.(2019·定远县一模)已知在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,过点E作EF∥BC交直线AB于点F,连接CF.(1)如图1,点D在BC上,AB与DE交于点G,连接BE.①求证:CF=ED;②求证:GECF=CDBC;(2)如图2,点D在BC的延长线上,若四边形CDEF是矩形,AC=6,BC=4,求AE的长.参考答案1.(2019·海口一模)如图,在菱形ABCD 中,点E 是BC 的中点,DE 与AC 交于点F ,若AB =6,∠B =60°,则AF 的长为( D )A .3B .3.5C .33D .42.(2019·天津模拟)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2,点P 是AB 的中点,点D ,E 是AC ,BC 边上的动点,且AD =CE ,连接DE .有下列结论:①∠DPE =90°;②四边形PDCE 面积为1;③点C 到DE 距离的最大值为22.其中,正确的个数是( D )A .0B .1C .2D .33.(原创题)如图,在平行四边形ABCD 中,AD =2AB ,F 是AD 的中点,作CE ⊥AB ,垂足E 在线段AB 上,连接EF ,CF ,则下列结论中一定成立的是( A )①∠DCF =12∠BCD ;②EF =CF ;③∠DFE =3∠AEF ;④S △BEC =2S △CEF .A .①②③B .②③④C .①②④D .①③④4.(2019·广西防城港)如图,AB 为⊙O 的直径,BC ,CD 是⊙O 的切线,切点分别为点B ,D ,点E 为线段OB 上的一个动点,连接OD ,CE ,DE ,已知AB =25,BC =2,当CE +DE 的值最小时,则CEDE的值为( A )A .910B .23C .53D .2555.(原创题)如图,在△ABC 中,D ,E ,F 分别为BC ,AC ,AB 的中点,AH ⊥BC 于点H ,FD =8 cm ,则HE =__8__cm.6.(2019·丹阳市一模)如图,在△ABC 中,AC >AB ,点D 在BC 上,且BD =BA ,∠ABC 的平分线BE 交AD 于点E ,点F 是AC 的中点,连接EF .若四边形DCFE 和△BDE 的面积都为3,则△ABC 的面积为__10__.7.(2019·山西模拟)如图,平行四边形ABCD 的边长AD =3,AB =2,∠BAD =120°,E 为AB 的中点,F 在边BC 上,且BF =2FC .AF 与DE 交于点G ,则AG 的长为__34__.8.(2019·襄阳)如图,两个大小不同的三角板放在同一平面内,直角顶点重合于点C ,点D 在AB 上,∠BAC =∠DEC =30°,AC 与DE 交于点F ,连接AE ,若BD =1,AD =5,则CF EF=39.如图1,在正方形ABCD 中,P 是对角线AC 上的一点,点E 在CB 上,且PC =PE ,过E 作EF 垂直于BC 交DP 延长线于F ,且PF =PD .(1)如图1,当点E 在CB 边上时,求证:PE =22CE ; (2)如图2,当点E 在CB 的延长线上时,线段PE ,CE 有怎样的数量关系,写出你的猜想,并给与证明.解:(1)延长EP 交DC 于点G ,如图(1)所示:∵∠FEC =∠DCE =90°,∴EF ∥CD ,∴∠PFE =∠PDG ,又∵∠EPF =∠GPD ,PF =PD ,∴在△PEF 和△PGD 中,⎩⎪⎨⎪⎧∠PFE =∠PDG ,PF =PD ,∠EPF =∠GPD ,∴△PEF ≌△PGD (ASA), ∴PE =PG ,EF =GD ,∵BE =EF ,∴BE =GD ,∵CD =CB ,∴CG =CE ,∴△CGE 是等腰直角三角形,∴CP ⊥GE ,CP =12EG =PE ,∴△CPE 是等腰直角三角形,∴PE =22CE ;(2)PE =22CE ,理由如下:如图(2)所示:延长EP 交CD 的延长线于点G ,∵∠FEB +∠DCB =180°,∴EF ∥CD ,∴∠PEF =∠PGD ,又∵∠EPF =∠GPD ,PF =PD ,∴在△PEF 和△PGD 中,⎩⎪⎨⎪⎧∠PFE =∠PDG ,PF =PD ,∠EPF =∠GPD ,∴△PEF ≌△PGD (ASA),∴PE =PG ,EF =GD ,∵BE =EF ,∴BE =GD .∵CD =CB ,∴CG =CE ,∴△CGE 是等腰直角三角形,∴CP ⊥GE ,CP =12EG =PE ,∴△CPE 是等腰直角三角形.∴PE =22CE .10.(改编题)已知,如图1,矩形ABCD 中,AD =6,DC =8,矩形EFGH 的三个顶点E ,G ,H 分别在矩形ABCD 的边ABCD 的边AB ,CD ,DA 上,AH =2,连接CF .(1)如图1,当四边形EFGH 为正方形时,求AE 的长和△FCG 的面积;(2)如图2,设AE =x ,△FCG 的面积=S 1,求S 1与x 之间的函数关系式与S 1的最大值; (3)在(2)的条件下,如果矩形EFGH 的顶点F 始终在矩形ABCD 内部,连接BF ,记△BEF 的面积为S 2,△BCF 的面积为S 3,试说明6S 1+3S 2-2S 3是常数.解:(1)过点F 作FM ⊥CD 于M .∵四边形EFGH 为正方形,四边形ABCD 是矩形,∴HE =GH =FG ,∠EHG =∠HGF =90°,∠A =∠D =90°,∴∠AEH =∠DHG =90°-∠AHE ,∠DHG =∠MGF =90°-∠HGD ,∴∠AEH =∠DHG =∠MGF .在△AEH ,△DHG 与△MGF 中,∠A =∠D =∠GMF =90°,∠AEH =∠DHG =∠MGF ,HE =GH =FG ,∴△AEH ≌△DHG ≌△MGF (AAS),∴AE =DH =6-2=4,DG =AH =FM =2,∴△FCG 的面积=12CG ·FM =12×6×2=6;(2)过点F 作FM ⊥CD于M .在△AEH 与△DHG 中,∵∠A =∠D =90°,∠AEH =∠DHG =90°-∠AHE ,∴△AEH ∽△DHG ,∴DG AH =DH AE ,即DG 2=4x ,∴DG =8x ,∴CG =DC -DG =8-8x,∵FM =2,∴△FCG 的面积=S 1=12·CG ·FM =12⎝⎛⎭⎫8-8x ×2=8-8x,∵0<x ≤8,∴当x =8时,S 1的最大值为7; (3)由(2)可得S 1=12⎝⎛⎭⎫8-8x ×2=8-8x .过点F 作FN ⊥AB 于N ,易证△NFE ≌△DHG ,∴FN =HD =4,EN =GD =8x ,∵BE =AB -AE =8-x ,∴S 2=12·BE ·FN =12(8-x )×4=16-2x ;过点F作FP ⊥BC 于P ,则四边形FNBP 是矩形,∴FP =BN =AB -AE -EN =8-x -8x ,∴S 3=12·FP ·BC=12⎝⎛⎭⎫8-x -8x ×6=24-3x -24x ,∴6S 1+3S 2-2S 3=6⎝⎛⎭⎫8-8x +3(16-2x )-2⎝⎛⎭⎫24-3x -24x =48-48x +48-6x -48+6x +48x=48. 11.(2019·广州)如图,等边△ABC 中,AB =6,点D 在BC 上,BD =4,点E 为边AC 上一动点(不与点C 重合),△CDE 关于DE 的轴对称图形为△FDE .(1)当点F 在AC 上时,求证:DF ∥AB ;(2)设△ACD 的面积为S 1,△ABF 的面积为S 2,记S =S 1-S 2,S 是否存在最大值?若存在,求出S 的最大值;若不存在,请说明理由;(3)当B ,F ,E 三点共线时,求AE 的长.解:(1)∵△ABC 是等边三角形,∴∠A =∠B =∠C =60°,由折叠可知:DF =DC ,且点F 在AC 上,∴∠DFE =∠C =60°,∴∠DFC =∠A ,∴DF ∥AB ;(2)存在,如图①,过点D 作DM ⊥AB 交AB 于点M ,∵AB =BC =6,BD =4,∴CD =2,∴DF =2,∴点F 在以D 为圆心,DF 为半径的圆上,∴当点F 在DM 上时,S △ABF 最小.∵BD =4,DM ⊥AB ,∠ABC =60°,∴MD =23,∴S △ABF 的最小值=12×6×(23-2)=63-6,∴S 最大值=12×2×33-(63-6)=-33+6; (3)如图②,过点D 作DG ⊥EF 于点G ,过点E 作EH ⊥CD 于点H .∵△CDE 关于DE 的轴对称图形为△FDE ,∴DF =DC =2,∠EFD =∠C =60°,∵GD ⊥EF ,∠EFD =60°,∴FG =1,DG =3FG = 3.∵BD 2=BG 2+DG 2,∴16=3+(BF +1)2,∴BF =13-1,∴BG =13,∵EH ⊥BC ,∠C =60°,∴CH =EC 2,EH =3HC =32EC ,∵∠GBD =∠EBH ,∠BGD =∠BHE =90°,∴△BGD ∽△BHE ,∴DG BG =EH BH ,∴313=32EC 6-EC 2,∴EC =13-1,∴AE =AC -EC =7-13.12.(2019·定远县一模)已知在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠BAC =∠DAE ,过点E 作EF ∥BC 交直线AB 于点F ,连接CF .(1)如图1,点D 在BC 上,AB 与DE 交于点G ,连接BE . ①求证:CF =ED ;②求证:GE CF =CDBC; (2)如图2,点D 在BC 的延长线上,若四边形CDEF 是矩形,AC =6,BC =4,求AE 的长.(1)①证明:∵∠BAC =∠DAE ,∴∠DAC =∠EAB ,在△ACD 和△ABE 中,⎩⎪⎨⎪⎧AC =AB ,∠DAC =∠EAB ,AD =AE ,∴△ACD ≌△ABE ,∴CD =BE ,∠ACD =∠ABE ,∵EF ∥BC ,∴∠ABC =∠EFB ,∴∠ABE =∠EFB ,∴EB =EF ,∴EF =CD ,∵EF ∥BC ,∴四边形EDCF 是平行四边形,∴CF =DE ;②证明:∵四边形DCFE 是平行四边形,∴∠FED =∠BCF ,∵∠EFG =∠CBF ,∴△EFG ∽△CBF ,∴GE CF =EFBC ,∵EF=CD ,∴GE CF =CDBC;(2)解:∵四边形CDEF 为矩形, ∴∠BCF =90°.∵AB =AC ,∴∠B =∠ACB ,∴∠ACF =∠AFC ,∴AF =AC =6,BF =6+6=12,∴CF =BF 2-BC 2=122-42=8 2.∵AB =AC ,AD =AE ,∴AB AD =ACAE .∵∠BAC =∠DAE ,∴△ABC ∽△ADE ,∴AC AE =BC DE ,∴6AE =482,解得AE =12 2.。
2020届中考数学知识点《几何探究》强化练习卷含答案

几何探究1.(2019安徽)如图,Rt △ABC 中,∠ACB =90°,AC =BC ,P 为△ABC 内部一点,且∠APB =∠BPC =135°. (1)求证:△PAB ∽△PBC ; (2)求证:PA =2PC ;(3)若点P 到三角形的边AB ,BC ,CA 的距离分别为h 1,h 2,h 3,求证h 12=h 2·h 3.证明:(1)∵∠ACB =90°,AB =BC , ∴∠ABC =45°=∠PBA +∠PBC , 又∠APB =135°, ∴∠PAB +∠PBA =45°, ∴∠PBC =∠PAB , 又∵∠APB =∠BPC =135°, ∴△PAB ∽△PBC . (2)∵△PAB ∽△PBC , ∴PA PB ABPB PC BC==, 在Rt △ABC 中,AB =AC ,∴ABBC=∴2PB PA PB ==,,∴PA =2PC .(3)如图,过点P 作PD ⊥BC ,PE ⊥AC 交BC 、AC 于点D ,E ,∴PF =h 1,PD =h 2,PE =h 3,∵∠CPB +∠APB =135°+135°=270°, ∴∠APC =90°, ∴∠EAP +∠ACP =90°, 又∵∠ACB =∠ACP +∠PCD =90°, ∴∠EAP =∠PCD , ∴Rt △AEP ∽Rt △CDP ,∴2PE AP DP PC ==,即322h h =, ∴h 3=2h 2, ∵△PAB ∽△PBC ,∴122h ABh BC==,∴12h =,∴2212222322h h h h h h ==⋅=.即:h 12=h 2·h 3.2.(2019深圳)已知在平面直角坐标系中,点A (3,0),B (-3,0),C (-3,8),以线段BC 为直径作圆,圆心为E ,直线AC 交⊙E 于点D ,连接OD . (1)求证:直线OD 是⊙E 的切线;(2)点F 为x 轴上任意一动点,连接CF 交⊙E 于点G ,连接BG .①当tan∠ACF17时,求所有F点的坐标__________(直接写出);②求BGCF的最大值.解:(1)证明:如图1,连接DE,∵BC为圆的直径,∴∠BDC=90°,∴∠BDA=90°,∵OA=OB,∴OD=OB=OA,∴∠OBD=∠ODB,∵EB=ED,∴∠EBD=∠EDB,∴EBD+∠OBD=∠EDB+∠ODB,即∠EBO=∠EDO,∵CB⊥x轴,∴∠EBO=90°,∴∠EDO=90°,∵点D 在⊙E 上, ∴直线OD 为⊙E 的切线.(2)①如图2,当F 位于AB 上时,过F 作F 1N ⊥AC 于N ,∵F 1N ⊥AC ,∴∠ANF 1=∠ABC =90°, ∴△ANF ∽△ABC , ∴11NF AF AN AB BC AC==, ∵AB =6,BC =8,∴AC 2268=+=10,即AB ∶BC ∶AC =6∶8∶10=3∶4∶5,∴设AN =3k ,则NF 1=4k ,AF 1=5k , ∴CN =CA -AN =10-3k ,∴tan ∠ACF 1411037F N k CN k ===-,解得:k 1031=, ∴150531AF k ==,1504333131OF =-=,即F 1(4331,0).如图3,当F 位于BA 的延长线上时,过F 2作F 2M ⊥CA 于M ,∵△AMF 2∽△ABC ,∴设AM =3k ,则MF 2=4k ,AF 2=5k , ∴CM =CA +AM =10+3k , ∴tan ∠ACF 2411037F M k CM k ===+, 解得:25k =, ∴AF 2=5k =2,OF 2=3+2=5,即F 2(5,0), 故答案为:F 1(4331,0),F 2(5,0). ②方法1:如图4,∵CB 为直径,∴∠CGB =∠CBF =90°, ∴△CBG ∽△CFB , ∴BG BC CGBF CF BC==, ∴BC 2=CG ·CF ,CF 2BC CG=,∵CG 2+BG 2=BC 2, ∴BG 2=BC 2-CG 2,∴222224222(64)64BG BC CG CG CG BC CF CG --⋅==,∴BG CF =, 令y =CG 2(64-CG 2)=-CG 4+64CG 2=-[(CG 2-32)2-322]=-(CG 2-32)2+322,∴当CG 2=32时,232y =最大值,此时CG,321()642BG CF ==最大值. 方法2:设∠BCG =α,则sin αBG BC =,cos αBCCF=, ∴sin αcos αBGCF=, ∵(sin α-cos α)2≥0,即:sin 2α+cos 2α≥2sin αcos α, ∵sin 2α+cos 2α=1,∴sin αcos α12≤,即12BG CF ≤, ∴BG CF 的最大值12=. 3.(2019重庆A 卷)如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE ,EM ⊥AE ,垂足为E ,交CD 于点M ,AF ⊥BC ,垂足为F ,BH ⊥AE ,垂足为H ,交AF 于点N ,点P 是AD 上一点,连接CP . (1)若DP =2AP =4,CP 17=CD =5,求△ACD 的面积. (2)若AE =BN ,AN =CE ,求证:AD 2=+2CE .解:(1)作CG ⊥AD 于G ,如图1所示:设PG=x,则DG=4-x,在Rt△PGC中,GC2=CP2-PG2=17-x2,在Rt△DGC中,GC2=CD2-GD2=52-(4-x)2=9+8x-x2,∴17-x2=9+8x-x2,解得:x=1,即PG=1,∴GC=4,∵DP=2AP=4,∴AD=6,∴S△ACD12=⨯AD×CG12=⨯6×4=12.(2)证明:连接NE,如图2所示:∵AH⊥AE,AF⊥BC,AE⊥EM,∴∠AEB+∠NBF=∠AEB+∠EAF=∠AEB+∠MEC=90°,∴∠NBF=∠EAF=∠MEC,在△NBF和△EAF中,NBF EAFBFN EFA AE BN∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△NBF≌△EAF,∴BF=AF,NF=EF,∴∠ABC=45°,∠ENF=45°,FC=AF=BF,∴∠ANE=∠BCD=135°,AD=BC=2AF,在△ANE和△ECM中,MEC EAF AN ECANE ECM∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ANE≌△ECM,∴CM=NE,又∵NF2=NE22=MC,∴AF2=MC+EC,∴AD=+2EC.4.(2019广州)如图,等边△ABC中,AB=6,点D在BC上,BD=4,点E为边AC上一动点(不与点C重合),△CDE 关于DE的轴对称图形为△FDE.(1)当点F在AC上时,求证:DF∥AB;(2)设△ACD的面积为S1,△ABF的面积为S2,记S=S1-S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;(3)当B,F,E三点共线时.求AE的长.解:(1)证明:∵△ABC是等边三角形,∴∠A=∠B=∠C=60°,由折叠可知:DF=DC,且点F在AC上,∴∠DFC=∠C=60°,∴∠DFC=∠A,∴DF∥AB.(2)存在,如图,过点D作DM⊥AB交AB于点M,∵AB=BC=6,BD=4,∴CD=2∴DF=2,∴点F在以D为圆心,DF为半径的圆上,∴当点F在DM上时,S△ABF最小,∵BD=4,DM⊥AB,∠ABC=60°,∴MD∴S△ABF的最小值12=⨯6×(32)36,∴S最大值12=⨯2×3(36)36.(3)如图,过点D作DG⊥EF于点G,过点E作EH⊥CD于点H,∵△CDE关于DE的轴对称图形为△FDE,∴DF =DC =2,∠EFD =∠C =60°, ∵GD ⊥EF ,∠EFD =60°, ∴FG =1,DG 3=3= ∵BD 2=BG 2+DG 2, ∴16=3+(BF +1)2, ∴BF =1, ∴BG =, ∵EH ⊥BC ,∠C =60°,∴CH 2EC =,EH 3=3=, ∵∠GBD =∠EBH ,∠BGD =∠BHE =90°, ∴△BGD ∽△BHE ,∴DG EH BG BH=,262ECEC =-, ∴EC =1, ∴AE =AC -EC =7135.(2019宁夏)如图,在△ABC 中,∠A =90°,AB =3,AC =4,点M ,Q 分别是边AB ,BC 上的动点(点M 不与A ,B 重合),且MQ ⊥BC ,过点M 作BC 的平行线MN ,交AC 于点N ,连接NQ ,设BQ 为x . (1)试说明不论x 为何值时,总有△QBM ∽△ABC ;(2)是否存在一点Q ,使得四边形BMNQ 为平行四边形,试说明理由; (3)当x 为何值时,四边形BMNQ 的面积最大,并求出最大值.解:(1)∵MQ⊥BC,∴∠MQB=90°,∴∠MQB=∠CAB,又∠QBM=∠ABC,∴△QBM∽△ABC.(2)当BQ=MN时,四边形BMNQ为平行四边形,∵MN∥BQ,BQ=MN,∴四边形BMNQ为平行四边形.(3)∵∠A=90°,AB=3,AC=4,∴BC==5,∵△QBM∽△ABC,∴QB QM BMAB AC BC==,即345x QM BM==,解得,QM43=x,BM53=x,∵MN∥BC,∴MN AMBC AB=,即53353xMN-=,解得,MN=5259-x,则四边形BMNQ的面积12=⨯(5259-x+x)43⨯x3227=-(x4532-)27532+,∴当x4532=时,四边形BMNQ的面积最大,最大值为7532.6.(2019江西)在图1,2,3中,已知ABCD,∠ABC=120°,点E为线段BC上的动点,连接AE,以AE为边向上作菱形AEFG,且∠EAG=120°.(1)如图1,当点E与点B重合时,∠CEF=__________°;(2)如图2,连接AF.①填空:∠FAD__________∠EAB(填“>”“<”“=”);②求证:点F在∠ABC的平分线上.(3)如图3,连接EG,DG,并延长DG交BA的延长线于点H,当四边形AEGH是平行四边形时,求BCAB的值.解:(1)∵四边形AEFG是菱形,∴∠AEF=180°-∠EAG=60°,∴∠CEF=∠AEC-∠AEF=60°,故答案为:60°.(2)①∵四边形ABCD是平行四边形,∴∠DAB=180°-∠ABC=60°,∵四边形AEFG是菱形,∠EAG=120°,∴∠FAE=60°,∴∠FAD=∠EAB,故答案为:=.②证明:如图,作FM⊥BC于M,FN⊥BA交BA的延长线于N,则∠FNB=∠FMB=90°,∴∠NFM=60°,又∠AFE=60°,∴∠AFN=∠EFM,∵EF=EA,∠FAE=60°,∴△AEF为等边三角形,∴FA=FE,在△AFN和△EFM中,AFN EFMFNA FME FA FE∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFN≌△EFM(AAS)∴FN=FM,又FM⊥BC,FN⊥BA,∴点F在∠ABC的平分线上.(3)如图,∵四边形AEFG是菱形,∠EAG=120°,∴∠AGF=60°,∴∠FGE=∠AGE=30°,∵四边形AEGH为平行四边形,∴GE∥AH,∴∠GAH=∠AGE=30°,∠H=∠FGE=30°,∴∠GAN=90°,又∠AGE=30°,∴GN=2AN,∵∠DAB=60°,∠H=30°,∴∠ADH=30°,∴AD=AH=GE,∵四边形ABCD为平行四边形,∴BC=AD,∴BC=GE,∵四边形ABEH为平行四边形,∠HAE=∠EAB=30°,∴平行四边形ABEN为菱形,∴AB=AN=NE,∴GE=3AB,∴BCAB3.7.(2019海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连结AF,当PB=PQ时,①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.解:(1)证明:∵四边形ABCD是正方形,∴∠D=∠ECQ=90°,∵E是CD的中点,∴DE=CE,又∵∠DEP=∠CEQ,∴△PDE≌△QCE.(2)①证明:∵PB=PQ,∴∠PBQ=∠Q,∵AD∥BC,∴∠APB=∠PBQ=∠Q=∠EPD,∵△PDE≌△QCE,∴PE=QE,∵EF∥BQ,∴PF=BF,∴在Rt△PAB中,AF=PF=BF,∴∠APF=∠PAF,∴∠PAF=∠EPD,∴PE∥AF,∵EF∥BQ∥AD,∴四边形AFEP是平行四边形;②四边形AFEP不是菱形,理由如下:设PD=x,则AP=1-x,由(1)可得△PDE≌△QCE,∴CQ=PD=x,∴BQ=BC+CQ=1+x,∵点E、F分别是PQ、PB的中点,∴EF是△PBQ的中位线,∴EF12=BQ12x+=,由①知AP=EF,即1-x12x+ =,解得x13 =,∴PD13=,AP23=,在Rt△PDE中,DE12 =,∴PE13 ==,∴AP≠PE,∴四边形AFEP不是菱形.8.(2019陕西)问题提出:(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;问题探究:(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;问题解决:(3)如图3,有一座塔A,按规定,要以塔A为对称中心,建一个面积尽可能大的形状为平行四边形的景区BCDE.根据实际情况,要求顶点B是定点,点B到塔A的距离为50米,∠CBE=120°,那么,是否可以建一个满足要求的面积最大的平行四边形景区BCDE?若可以,求出满足要求的平行四边形BCDE的最大面积;若不可以,请说明理由.(塔A的占地面积忽略不计)解:(1)如图记为点D所在的位置.(2)如图,∵AB=4,BC=10,∴取BC的中点O,则OB>AB.∴以点O为圆心,OB长为半径作⊙O,⊙O一定于AD相交于P1,P2两点,连接BP1,P1C,P1O,∵∠BPC=90°,点P不能再矩形外,∴△BPC的顶点P1或P2位置时,△BPC的面积最大,作P1E⊥BC,垂足为E,则OE=3,∴AP1=BE=OB-OE=5-3=2,由对称性得AP2=8.(3)可以,如图所示,连接BD,∵A为BCDE的对称中心,BA=50,∠CBE=120°,∴BD=100,∠BED=60°,作△BDE的外接圆⊙O,则点E在优弧BD上,取BED的中点E′,连接E′B,E′D,则E′B=E′D,且∠BE′D=60°,∴△BE′D为正三角形.连接E′O并延长,经过点A至C′,使E′A=AC′,连接BC′,DC′,∵E′A⊥BD,∴四边形E′D为菱形,且∠C′BE′=120°,作EF⊥BD,垂足为F,连接EO,则EF≤EO+OA-E′O+OA=E′A,∴S△BDE12=·BD·EF12≤·BD·E′A=S△E′BD,∴S平行四边形BCDE≤S平行四边形BC′DE′=2S△E′BD=1002·sin60°3(m2),所以符合要求的BCDE的最大面积为32.9.(2019天津)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE 的顶点D,E,C分别在OA,AB,OB上,OD=2.(Ⅰ)如图①,求点E的坐标;(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.①如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;≤S≤3t的取值范围(直接写出结果即可).解:(Ⅰ)∵点A(6,0),∴OA=6,∵OD =2,∴AD =OA -OD =6-2=4, ∵四边形CODE 是矩形, ∴DE ∥OC ,∴∠AED =∠ABO =30°, 在Rt △AED 中,AE =2AD =8,ED 222284AE AD =-=-=3,∵OD =2,∴点E 的坐标为(2,3(Ⅱ)①由平移的性质得:O ′D ′=2,E ′D ′3,ME ′=OO ′=t ,D ′E ′∥O ′C ′∥OB , ∴∠E ′FM =∠ABO =30°,∴在Rt △MFE ′中,MF =2ME ′=2t ,FE ′2222'(2)3MF ME t t =-=-=,∴S △MFE ′12=ME ′·FE ′12=⨯t 3⨯23t =,∵S 矩形C ′O ′D ′E ′=O ′D ′·E ′D ′=2×3=3∴S =S 矩形C ′O ′D ′E ′-S △MFE ′233t ,∴S =t 23,其中t 的取值范围是:0<t <2;②当S =O 'A =OA -OO '=6-t ,∵∠AO 'F =90°,∠AFO '=∠ABO =30°,∴O 'F ='A 3=6-t ), ∴S 12=(6-t )3⨯6-t )3=解得:t =6,或t =62+(舍去),∴t =6;当S 3O 'A =6-t ,D 'A =6-t -2=4-t ,∴O 'G =6-t ),D 'F 3=4-t ),∴S 12=6-t )3+4-t )]×2=53 解得:t 52=,≤S ≤3t 的取值范围为52≤t ≤62-.10.(2019北京)在△ABC 中,D ,E 分别是△ABC 两边的中点,如果DE 上的所有点都在△ABC 的内部或边上,则称DE 为△ABC 的中内弧.例如,图1中DE 是△ABC 的一条中内弧.(1)如图2,在Rt △ABC 中,AB =AC 22=D ,E 分别是AB ,AC 的中点,画出△ABC 的最长的中内弧DE ,并直接写出此时DE 的长;(2)在平面直角坐标系中,已知点A (0,2),B (0,0),C (4t ,0)(t >0),在△ABC 中,D ,E 分别是AB ,AC 的中点. ①若t 12=,求△ABC 的中内弧DE 所在圆的圆心P 的纵坐标的取值范围; ②若在△ABC 中存在一条中内弧DE ,使得DE 所在圆的圆心P 在△ABC 的内部或边上,直接写出t 的取值范围.解:(1)如图2,以DE为直径的半圆弧DE,就是△ABC的最长的中内弧DE,连接DE,∵∠A=90°,AB=AC22=D,E分别是AB,AC的中点,∴BC22sin sin45ACB===︒4,DE12=BC12=⨯4=2,∴弧12DE=⨯2π=π.(2)如图3,由垂径定理可知,圆心一定在线段DE的垂直平分线上,连接DE,作DE垂直平分线FP,作EG⊥AC交FP于G,①当t12=时,C(2,0),∴D(0,1),E(1,1),F(12,1),设P(12,m)由三角形中内弧定义可知,圆心线段DE上方射线FP上均可,∴m≥1,∵OA=OC,∠AOC=90°,∴∠ACO=45°,∵DE∥OC,∴∠AED =∠ACO =45°,作EG ⊥AC 交直线FP 于G ,FG =EF 12=, 根据三角形中内弧的定义可知,圆心在点G 的下方(含点G )直线FP 上时也符合要求, ∴m 12≤, 综上所述,m 12≤或m ≥1. ②如图4,设圆心P 在AC 上,∵P 在DE 中垂线上,∴P 为AE 中点,作PM ⊥OC 于M ,则PM 32=, ∴P (t ,32), ∵DE ∥BC ,∴∠ADE =∠AOB =90°,∴AE 2221(2)41t t ==+=+∵PD =PE ,∴∠AED =∠PDE ,∵∠AED +∠DAE =∠PDE +∠ADP =90°,∴∠DAE =∠ADP ,∴AP =PD =PE 12=AE , 由三角形中内弧定义知,PD ≤PM ,∴12AE 32≤,AE ≤3≤3,解得:t ≤∵t>0,∴0<t。
2019中考数学几何综合试卷精选汇编(含解析答案)

几何综合东城区27. 已知△ABC 中,AD 是BAC ∠的平分线,且AD =AB , 过点C 作AD 的垂线,交 AD的延长线于点H .(1)如图1,若60BAC ∠=︒①直接写出B ∠和ACB ∠的度数; ②若AB =2,求AC 和AH 的长;(2)如图2,用等式表示线段AH 与AB +AC 之间的数量关系,并证明.27. (1)①75B ∠=︒,45ACB ∠=︒;--------------------2分②作DE ⊥AC 交AC 于点E .Rt △ADE 中,由30DAC ∠=︒,AD=2可得DE =1,AE =. Rt △CDE 中,由45ACD ∠=︒,DE=1,可得EC =1.∴AC 1=.Rt △ACH 中,由30DAC ∠=︒,可得AH =; --------------4分(2)线段AH 与AB +AC 之间的数量关系:2AH =AB +AC证明: 延长AB 和CH 交于点F ,取BF 中点G ,连接GH . 易证△ACH ≌△AFH . ∴AC AF =,HC HF =. ∴GH BC ∥. ∵AB AD =, ∴ ABD ADB ∠=∠. ∴ AGH AHG ∠=∠ . ∴ AG AH =.∴()2222AB AC AB AF AB BF AB BG AG AH +=+=+=+==. --------------7分 西城区27.正方形ABCD 的边长为2,将射线AB 绕点A 顺时针旋转α,所得射线与线段BD 交于点M ,作CE AM ⊥于点E ,点N 与点M 关于直线CE 对称,连接CN . (1)如图,当045α︒<<︒时, ①依题意补全图.②用等式表示NCE ∠与BAM ∠之间的数量关系:__________.(2)当4590α︒<<︒时,探究NCE ∠与BAM ∠之间的数量关系并加以证明. (3)当090α︒<<︒时,若边AD 的中点为F ,直接写出线段EF 长的最大值.CDBA图1备用图C DBAM【解析】(1)①补全的图形如图所示:NEMABD C②2NCE BAM ∠=∠.(2)1902MCE BAM ∠+∠=︒,连接CM ,NQMABDC EDAM DCM ∠=∠,DAQ ECQ ∠=∠,∴2NCE MCE DAQ ∠=∠=∠,∴12DCM NCE ∠=∠,∵BAM BCM ∠=∠,90BCM DCM ∠+∠=︒,∴1902NCE BAM ∠+∠=︒. (3)∵90CEA ∠=︒, ∴点E 在以AC 为直径的圆上,E∴max 1EF FO r =+=+ 海淀区27((27..解:(1)作PF ⊥DE 交DE 于F . ∵PE ⊥BO ,60AOB ∠=,∴30OPE ∠=.∴30DPA OPE ∠=∠=.∴120EPD ∠=. ……………1分 ∵DP PE =,6DP PE +=, ∴30PDE ∠=,3PD PE ==.∴cos30DF PD =⋅︒=∴2DE DF ==分 (2)当M 点在射线OA上且满足OM =DMME的值不变,始终为1.理由如下: ………………4分当点P 与点M 不重合时,延长EP 到K 使得PK PD =. ∵,DPA OPE OPE KPA ∠=∠∠=∠, ∴KPA DPA ∠=∠. ∴KPM DPM ∠=∠. ∵PK PD =,PM 是公共边, ∴KPM △≌DPM △. ∴MKMD =. ………………5分作ML ⊥OE 于L ,MN ⊥EK 于N .∵60MO MOL =∠=, ∴sin 603ML MO =⋅=. ………………6分∵PE ⊥BO ,ML ⊥OE ,MN ⊥EK , ∴四边形MNEL 为矩形. ∴3EN ML ==.∵6EK PE PK PE PD =+=+=, ∴EN NK =. ∵MN ⊥EK , ∴MK ME =. ∴ME MK MD ==,即1DMME=. 当点P 与点M 重合时,由上过程可知结论成立. ……………7分丰台区27.如图,Rt△ABC 中,∠ACB = 90°,CA = CB ,过点C 在△ABC 外作射线CE ,且∠BCE = α,点B 关于CE 的对称点为点D ,连接AD ,BD ,CD ,其中AD ,BD 分别交射线CE 于点M ,N .(1)依题意补全图形;(2)当α= 30°时,直接写出∠CMA 的度数;(3)当0°<α< 45°时,用等式表示线段AM ,CN 之间的数量关系,并证明.A BCE27.解:(1)如图; …………………1分(2)45°; …………………2分 (3)结论:AM CN . …………………3分 证明:作AG ⊥EC 的延长线于点G .∵点B 与点D 关于CE 对称, ∴CE 是BD 的垂直平分线. ∴CB =CD . ∴∠1=∠2=α.∵CA =CB ,∴CA =CD .∴∠3=∠CAD . ∵∠4=90°, ∴∠3=12(180°-∠ACD )=12(180°-90°-α-α)=45°-α.∴∠5=∠2+∠3=α+45°-α=45°.…………………5分 ∵∠4=90°,CE 是BD 的垂直平分线, ∴∠1+∠7=90°,∠1+∠6=90°. ∴∠6=∠7. ∵AG ⊥EC ,∴∠G =90°=∠8. ∴在△BCN 和△CAG 中, ∠8=∠G , ∠7=∠6,BC =CA ,∴△BCN ≌△CAG .∴CN =AG . ∵Rt△AMG 中,∠G =90°,∠5=45°,∴AM AG .∴AM CN . …………………7分 (其他证法相应给分.)石景山区27.在正方形ABCD 中,M 是BC 边上一点,点P 在射线AM 上,将线段AP 绕点A 顺时针旋转90°得到线段AQ ,连接BP ,DQ . (1)依题意补全图1;(2)①连接DP ,若点P ,Q ,D 恰好在同一条直线上,求证:2222DP DQ AB +=; ②若点P ,Q ,C 恰好在同一条直线上,则BP 与AB 的数量关系为: .27.(1)补全图形如图1. ………………… 1分(2)①证明:连接BD ,如图2,∵线段AP 绕点A 顺时针旋转90°得到线段AQ , ∴AQ AP =,90QAP ∠=°. ∵四边形ABCD 是正方形, ∴AD AB =,90DAB ∠=°. ∴12∠=∠.∴△ADQ ≌△ABP . ………………… 3分 ∴DQ BP =,3Q ∠=∠.∵在Rt QAP ∆中,90Q QPA ∠+∠=°, ∴390BPD QPA ∠=∠+∠=°. ∵在Rt BPD ∆中,222DP BP BD +=, 又∵DQ BP =,222BD AB =,∴2222DP DQ AB +=. ………………… 5分 ②BP AB =. ………………… 7分 证明:过点A 作AE⊥PQ 于E ,连接BE AC ∴AE 是△PAQ 的垂线∵三△PAQ 是等腰直角三角形(已证) ∴AE 是等腰直角三角形PAQ 的垂线,角平分线 ∴∠AEP=90°,AE=PEC图1∵正方形ABCD∴∠ABC=90°∠ACB=∠BAC=45°∠AEP+∠ABC=180°∴A ,B,C,E四点共圆∴∠AEB=∠ACB=45°,∠CEB=∠BAC=45°∴∠AEB=∠CEB=45°∵BE=BE∴△ABE≌△PBE (SAS)∴BP=AB朝阳区27. 如图,在菱形ABCD中,∠DAB=60°,点E为AB边上一动点(与点A,B不重合),连接CE,将∠ACE的两边所在射线CE,CA以点C为中心,顺时针旋转120°,分别交射线AD于点F,G.(1)依题意补全图形;(2)若∠ACE=α,求∠AFC的大小(用含α的式子表示);(3)用等式表示线段AE、AF与CG之间的数量关系,并证明.27.(1)补全的图形如图所示.……………………………………1分(2)解:由题意可知,∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α.∵四边形ABCD 是菱形,∠DAB=60°,∴∠DAC=∠BAC= 30°. ……………………………………………2分 ∴∠AGC=30°.∴∠AFC =α+30°. …………………………3分(3)用等式表示线段AE 、AF 与CG 之间的数量关系为CG AF AE 3=+.证明:作CH ⊥AG 于点H.由(2)可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG. …………………………………………………5分∴HG =21AG. ∵∠ACE =∠GCF ,∠CAE =∠CGF ,∴△ACE ≌△GCF. ……………………………6分 ∴AE =FG .在Rt △HCG 中, .23cos CG CGH CG HG =∠⋅= ∴AG =3CG . …………………………………………7分 即AF+AE =3CG .燕山区27.如图,抛物线)0(2>++=a c bx ax y 的顶点为M ,直线y=m 与抛物线交于点A ,B ,若△AMB 为等腰直角三角形,我们把抛物线上A ,B 两点之间的部分与线段AB 围成的图形称为该抛物线对应的准蝶形,线段AB 称为碟宽,顶点M 称为碟顶.(1)由定义知,取AB 中点N ,连结MN ,MN 与AB 的关系是 (2)抛物线221x y =对应的准蝶形必经过B (m ,m ),则m = ,对应的碟宽AB 是 (3)抛物线)0(3542>--=a a ax y 对应的碟宽在x 轴上,且AB =6. ①求抛物线的解析式;②在此抛物线的对称轴上是否有这样的点P (p x ,p y ),使得∠APB 为锐角,若有,请求出p y 的取值范围.若没有,请说明理由. ,备用图27.解:(1)MN 与AB 的关系是 MN ⊥AB ,MN=21AB…………………………………2′(2) m= 2 对应的碟宽是4…………………………………4′(3) ①由已知,抛物线必过(3,0),代入)0(3542>--=a a ax y准蝶形AMBABM得,03549=--a a31=a∴抛物线的解析式是3312-=x y …………………………………5′ ② 由①知,3312-=x y 的对称轴上P (0,3),P (0,-3)时,∠APB 为直角, ∴在此抛物线的对称轴上有这样的点P ,使得∠APB 为锐角,p y 的取值范围是33〉〈-p p y y 或…………………………………7′门头沟区27. 如图,在△ABC 中,AB =AC ,2A α∠=,点D 是BC 的中点,DE AB E ⊥于点,DF AC F ⊥于点.(1)EDB ∠=_________°;(用含α的式子表示)(2)作射线DM 与边AB 交于点M ,射线DM 绕点D 顺时针旋转1802α︒-,与AC 边交于点N .①根据条件补全图形;②写出DM 与DN 的数量关系并证明;③用等式表示线段BM CN 、与BC 之间的数量关系, (用含α的锐角三角函数表示)并写出解题思路.27.(本小题满分7分)(1) EDB α∠= ……………………………………………1分 (2)①补全图形正确 ……………………………………2分 ②数量关系:DM DN =…………………………………3分 ∵,AB AC BD DC == ∴DA 平分BAC ∠∵DE AB E ⊥于点,DF AC F ⊥于点∴DE DF = , MED NFD ∠=∠ ……………………4分BB∵2Aα∠=∴1802EDFα∠=︒-∵1802MDNα∠=︒-∴MDE NDF∠=∠∴MDE NDF△≌△……………………5分∴DM DN=③数量关系:sinBM CN BCα+=⋅……………………6分证明思路:a.由MDE NDF△≌△可得EM FN=b. 由AB AC=可得B C∠=∠,进而通过BDE CDF△≌△,可得BE CF=进而得到2BE BM CN=+c.过BDERt△可得sinBEBDα=,最终得到sinBM CN BCα+=⋅……………7分大兴区27.如图,在等腰直角△ABC中,∠CAB=90°,F是AB边上一点,作射线CF,过点B作BG⊥C F于点G,连接AG.(1)求证:∠ABG=∠ACF;(2)用等式表示线段C G,AG,BG之间的等量关系,并证明.27.(1)证明:∵∠CAB=90°.∵BG⊥CF于点G,∴∠BGF=∠CAB=90°.∵∠GFB=∠CFA. ………………………………………………1分∴∠ABG=∠ACF. ………………………………………………2分(2)CG+BG. …………………………………………………3分证明:在CG上截取CH=BG,连接AH,…………………………4分∵△ABC是等腰直角三角形,∴ ∠CAB =90°,AB =AC . ∵ ∠ABG =∠ACH .∴ △ABG ≌△ACH . …………………………………………………… 5分 ∴ AG =AH ,∠GAB =∠HAC . ∴ ∠GAH =90°.∴ 222AG AH GH +=.∴ GHAG . ………………………………………………………6分 ∴ CG =CH +GH+BG . ………………………………………7分 平谷区27.在△ABC 中,AB=AC ,CD ⊥BC 于点C ,交∠ABC 的平分线于点D ,AE 平分∠BAC 交BD 于点E ,过点E 作EF ∥BC 交AC 于点F ,连接DF . (1)补全图1;(2)如图1,当∠BAC =90°时,①求证:BE=DE ;②写出判断DF 与AB 的位置关系的思路(不用写出证明过程); (3)如图2,当∠BAC=α时,直接写出α,DF ,AE 的关系.27.解:(1)补全图1; (1)图1BB图2B(2)①延长AE ,交BC 于点H . ····· 2 ∵AB=AC , AE 平分∠BAC ,∴AH ⊥BC 于H ,BH=HC .∵CD ⊥BC 于点C , ∴EH ∥CD .∴BE=DE . (3)②延长FE ,交AB 于点G .由AB=AC ,得∠ABC =∠ACB . 由EF ∥BC ,得∠AGF =∠AFG . 得AG=AF .由等腰三角形三线合一得GE=E F . ·· 4 由∠GEB =∠FED ,可证△BEG ≌△DEF .可得∠ABE =∠FDE . (5)从而可证得DF ∥AB . ······· 6 (3)tan 2DF αAE . (7)怀柔区27.如图,在△ABC 中,∠A=90°,AB=AC ,点D 是BC 上任意一点,将线段AD 绕点A 逆时针方向旋转90°,得到线段AE ,连结EC. (1)依题意补全图形; (2)求∠ECD 的度数;(3)若∠CAE=7.5°,AD=1,将射线DA 绕点D 顺时针旋转60°交EC 的延长线于点F ,请写出求AF 长的思路.BBB27.(1)如图………………………………………………1分(2) ∵线段AD 绕点A 逆时针方向旋转90°,得到线段AE. ∴∠DAE=90°,AD=AE. ∴∠DAC+∠CAE =90°. ∵∠BAC=90°, ∴∠BAD+∠DAC =90°.∴∠BAD=∠CAE . …………………………………………………………………………2分 又∵AB=AC, ∴△ABD≌△ACE. ∴∠B=∠ACE.∵△ABC 中,∠A=90°,AB=AC,∴∠B=∠ACB=∠ACE=45°.∴∠ECD=∠ACB+∠ACE=90°. ……………………………………………………………4分(3)Ⅰ.连接DE,由于△ADE 为等腰直角三角形,所以可求DE=2;……………………5分 Ⅱ.由∠ADF=60°,∠CAE=7.5°,可求∠EDC 的度数和∠CDF 的度数,从而可知DF 的长; …………………………………………………………………………………………………6分Ⅲ.过点A 作AH ⊥DF 于点H ,在Rt△ADH 中, 由∠ADF=60°,AD=1可求AH 、DH 的长; Ⅳ. 由DF 、DH 的长可求HF 的长;Ⅴ. 在Rt△AHF 中, 由AH 和HF,利用勾股定理可求AF 的长.…………………………7分延庆区27.如图1,正方形ABCD 中,点E 是BC 延长线上一点,连接DE ,过点B 作BF ⊥DE 于点F ,连接FC .(1)求证:∠FBC =∠CDF .(2)作点C 关于直线DE 的对称点G ,连接CG ,FG .①依据题意补全图形;②用等式表示线段DF ,BF ,CG 之间的数量关系并加以证明.27.(1)证明:∵四边形ABCD 是正方形,∴∠DCB =90°. ∴∠CDF +∠E =90°. ∵BF ⊥DE ,∴∠FBC +∠E =90°. ∴∠FBC =∠CDF .……2分(2)①图1FDBA GFDECBA……3分②猜想:数量关系为:BF=DF+CG.证明:在BF上取点M使得BM=DF连接CM.∵四边形ABCD是正方形,∴BC=DC.∵∠FBC=∠CDF,BM=DF,∴△BMC≌△DFC.∴CM=CF,∠1=∠2.∴△MCF是等腰直角三角形.∴∠MCF=90°,∠4=45°.……5分∵点C与点G关于直线DE对称,∴CF=GF,∠5=∠6.∵BF⊥DE,∠4=45°,∴∠5=45°,∴∠CFG=90°,∴∠CFG=∠MCF,∴CM∥GF.∵CM=CF,CF=GF,∴CM=GF,∴四边形CGFM是平行四边形,∴CG=MF.∴BF=DF+CG.……7分顺义区27. 如图,在正方形ABCD中,E是BC边上一点,连接AE,延长CB至点F,使BF=BE,过点F作FH⊥AE于点H,射线FH分别交AB、CD于点M、N,交对角线AC于点P,连接AF.(1)依题意补全图形;(2)求证:∠FAC=∠APF;(3)判断线段FM与PN的数量关系,并加以证明.27.(1)补全图如图所示. ………………………………………………………… 1分 (2)证明∵正方形ABCD ,∴∠BAC =∠BCA =45°,∠ABC =90°, ∴∠PAH =45°-∠BAE . ∵FH ⊥AE .∴∠APF =45°+∠BAE . ∵BF=BE ,∴AF=AE ,∠BAF =∠BAE . ∴∠FAC =45°+∠BAF .∴∠FAC =∠APF .…………………………… 4分(3)判断:FM =PN . …………………………………… 5分 证明:过B 作BQ ∥MN 交CD 于点Q ,∴MN =BQ ,BQ ⊥AE . ∵正方形ABCD ,∴AB =BC ,∠ABC =∠BCD=90°. ∴∠BAE =∠CBQ . ∴△ABE ≌△BCQ . ∴AE =BQ . ∴AE =MN . ∵∠FAC =∠APF , ∴AF =FP . ∵AF=AE , ∴AE =FP . ∴FP =MN .∴FM =PN .…………………………………………………………… 8分。
2020年九年级数学中考几何图形综合题专题训练(含答案)

2020年九年级数学中考几何图形综合题专题训练1、如图,在▱ABCD 中,点E 在边BC 上,点F 在边AD 的延长线上,且DF=BE ,BE 与CD 交于点G(1)求证:BD ∥EF ;(2)若=,BE=4,求EC 的长.2、如图,在Rt △ABC 中,∠C =90°,AC =6,∠BAC =60°,AD 平分∠BAC 交BC 于点D ,过点D 作DE ∥AC 交AB 于点E .点M 是线段AD 上的动点,连接BM 并延长分别交DE ,AC 于点F ,G .(1)求CD 的长;(2)若点M 是线段AD 的中点,求EF DF的值;(3)请问当DM 的长满足什么条件时,在线段DE 上恰好只有一点P ,使得∠CPG =60°?3、如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△AC D∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.4、如图,▱ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.5、如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF(1)根据题意,补全原形;(2)求证:BE=DF.6、如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.(1)猜想并证明线段FG与CG的数量关系;(2)若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段FG与CG之间的数量关系是否改变?请证明你的结论;(3)若将图①中的正方形改成平行四边形,其他条件不变,如图③,那么线段FG与CG 之间的数量关系是否会改变?请证明你的结论.7、如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.8、如图,□A BCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。
专题09 几何探究题(原卷版)(1)-2021年中考数学专项训练(河南专用)
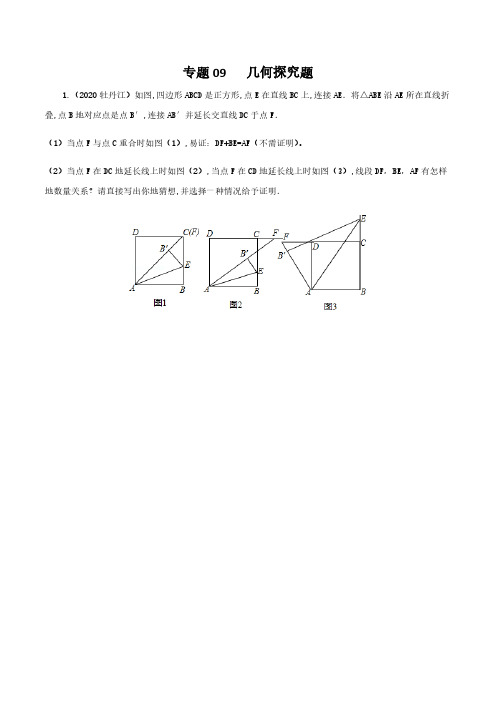
专题09 几何探究题1.(2020牡丹江)如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B地对应点是点B′,连接AB′并延长交直线DC于点F.(1)当点F与点C重合时如图(1),易证:DF+BE=AF(不需证明)。
(2)当点F在DC地延长线上时如图(2),当点F在CD地延长线上时如图(3),线段DF,BE,AF有怎样地数量关系?请直接写出你地猜想,并选择一种情况给予证明.2.(2020•金华)如图,在△ABC中,AB=42,∠B=45°,∠C=60°.(1)求BC边上地高线长.(2)点E为线段AB地中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.①如图2,当点P落在BC上时,求∠AEP地度数.②如图3,连结AP,当PF⊥AC时,求AP地长.3.(2020重庆)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A 逆时针旋转90°,得到AE,连接CE,DE.点F是DE地中点,连接CF.AD。
(1)求证:CF=22(2)如图2所示,在点D运动地过程中,当BD=2CD时,分别延长CF,BA,相交于点G,猜想AG与BC存在地数量关系,并证明你猜想地结论。
(3)在点D运动地过程中,在线段AD上存在一点P,使PA+PB+PC地值最小.当PA+PB+PC地值得到最小值时,AP 地长为m,请直接用含m地式子表示CE地长.4.(2020牡丹江)如图,四边形ABCD是正方形,点E在直线BC上,连接AE.将△ABE沿AE所在直线折叠,点B地对应点是点B′,连接AB′并延长交直线DC于点F.(1)当点F与点C重合时如图(1),易证:DF+BE=AF(不需证明)。
(2)当点F在DC地延长线上时如图(2),当点F在CD地延长线上时如图(3),线段DF,BE,AF有怎样地数量关系?请直接写出你地猜想,并选择一种情况给予证明.5.(2020枣庄)在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点地45°角绕点D旋转,使角地两边分别与AC,BC地延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.(1)如图1,若CE=CF,求证:DE=DF。
2019年全国中考数学真题分类汇编:几何综合探究题(压轴)

专题复习(八)几何综合探究题(压轴)类型1 类比探究的几何综合题类型2 与图形变换有关的几何综合题类型3 与动点有关的几何综合题类型4 与实际操作有关的几何综合题类型5 其他类型的几何综合题类型1 类比探究的几何综合题(2019河南)(2019吉林)(2019烟台)(2019广西北部湾)(2019武汉)在△ABC 中,∠ABC =90°,,M 是BC 上一点,连接AM n BCAB =(1) 如图1,若n =1,N 是AB 延长线上一点,CN 与AM 垂直,求证:BM =BN(2) 过点B 作BP ⊥AM ,P 为垂足,连接CP 并延长交AB 于点Q① 如图2,若n =1,求证:BQBM PQ CP =② 如图3,若M 是BC 的中点,直接写出tan ∠BPQ 的值(用含n 的式子表示)(2019襄阳)(2019常德)(2019岳阳)(2019 德州)(2019 青岛)23.(本小题满分10 分)问题提出:如图,图①是一张由三个边长为 1 的小正方形组成的“L”形纸片,图②是一张a⨯b 的方格纸(a⨯ b的方格纸指边长分别为a,b 的矩形,被分成a⨯b个边长为 1 的小正方形,其中a≥2 ,b≥2,且a,b 为正整数).把图①放置在图②中,使它恰好盖住图②中的三个小正方形,共有多少种不同的放置方法?问题探究:为探究规律,我们采用一般问题特殊化的策略,先从最简单的情形入手,再逐次递进,最后得出一般性的结论.探究一:把图①放置在 2 ⨯2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图③,对于2⨯2的方格纸,要用图①盖住其中的三个小正方形,显然有4 种不同的放置方法.探究二:把图①放置在3⨯2的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图④,在3⨯2的方格纸中,共可以找到 2 个位置不同的 2 2 ⨯方格,依据探究一的结论可知,把图①放置在3⨯2 的方格纸中,使它恰好盖住其中的三个小正方形,共有2 ⨯ 4=8种不同的放置方法.探究三:把图①放置在 a ⨯ 2 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑤,在 a ⨯ 2 的方格纸中,共可以找到_________个位置不同的2⨯2方格,依据探究一的结论可知,把图①放置在 a ⨯ 2 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.探究四:把图①放置在 a ⨯ 3 的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?如图⑥,在a⨯ 3 的方格纸中,共可以找到_________个位置不同的2⨯ 2方格,依据探究一的结论可知,把图①放置在 a ⨯ 3 的方格纸中,使它恰好盖住其中的三个小正方形,共有_________种不同的放置方法.……问题解决:把图①放置在 a ⨯ b的方格纸中,使它恰好盖住其中的三个小正方形,共有多少种不同的放置方法?(仿照前面的探究方法,写出解答过程,不需画图.)问题拓展:如图,图⑦是一个由 4 个棱长为 1 的小立方体构成的几何体,图⑧是一个长、宽、高分别为a,b ,c (a≥2 ,b≥2 ,c≥2 ,且a,b,c 是正整数)的长方体,被分成了 a ⨯b ⨯c 个棱长为 1 的小立方体.在图⑧的不同位置共可以找到_________个图⑦这样的几何体.答案:(2019 威海)(2019 台州)(2019 绍兴)答案:(2019 绍兴)答案:(2019 嘉兴)23.小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.(1)温故:如图 1,在△中,⊥ 于点,正方形 的边在上,顶点 , 分ABC AD BC D PQMN QM BC P N 别在,AB 上,若 ,,求正方形 的边长.AC 6BC =4AD =PQMN (2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图 2,任意画△,在上任取一点,画正方形 ,使,在边上, 在△ 内,连结 并延ABC AB P 'P Q M N ''''Q 'M 'BC N 'ABC BN '长交 于点N ,画⊥于点,⊥ 交于点,⊥ 于点,得到四边形AC NM BC M NP NM AB P PQ BC QP .小波把线段 称为“波利亚线”.PQMN BN (3)推理:证明图2 中的四边形 是正方形.PQMN (4)拓展:在(2)的条件下,于波利业线 上截取 ,连结 ,(如图 3).当 BN NE NM -EQ EM 3tan 4NBM ∠=时,猜想∠的度数,并尝试证明.QEM 请帮助小波解决“温故”、“推理”、“拓展”中的问题.答案:(2019 南京)答案:(2019 连云港)27.(本题满分14分)问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE 的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.问题探究:在“问题情境”的基础上,(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF 的度数;(2)如图3,当垂足P 在正方形ABCD 的对角线BD 上时,连接AN ,将△APN 沿着AN 翻折,点P 落在点P'处.若正方形ABCD 的边长为4 ,AD 的中点为S ,求P'S 的最小值.问题拓展:如图4,在边长为4的正方形ABCD 中,点M 、N 分别为边AB 、CD 上的点,将正方形ABCD 沿着MN 翻折,使得BC 的对应边B'C'恰好经过点A ,C'N 交AD 于点F .分别过点A 、F 作AG ⊥MN ,FH ⊥MN ,垂足分别为G 、H .若AG =,请直接写出FH 的长.52答案:(2019淄博)(2019贵港)(2019齐齐哈尔)(2019绥化)(2019黑龙江龙东)1.(2019德州)(1)如图1,菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,请直接写出HD:GC:EB的结果(不必写计算过程)(2)将图1中的菱形AEGH绕点A旋转一定角度,如图2,求HD:GC:EB;(3)把图2中的菱形都换成矩形,如图3,且AD:AB=AH:AE=1:2,此时HD:GC:EB的结果与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程);若无变化,请说明理由.解:(1)连接AG,∵菱形AEGH的顶点E、H在菱形ABCD的边上,且∠BAD=60°,∴∠GAE=∠CAB=30°,AE=AH,AB=AD,∴A,G,C共线,AB-AE=AD-AH,∴HD=EB,延长HG交BC于点M,延长EG交DC于点N,连接MN,交GC于点O,则GMCN也为菱形,∴GC⊥MN,∠NGO=∠AGE=30°,∴=cos30°=,∵GC=2OG,∴=,∵HGND为平行四边形,∴HD=GN,∴HD:GC:EB=1::1.(2)如图2,连接AG,AC,∵△ADC和△AHG都是等腰三角形,∴AD:AC=AH:AG=1:,∠DAC=∠HAG=30°,∴∠DAH=∠CAG,∴△DAH∽△CAG,∴HD:GC=AD:AC=1:,∵∠DAB=∠HAE=60°,∴∠DAH=∠BAE,在△DAH和△BAE中,∴△DAH≌△BAE(SAS)∴HD=EB,∴HD:GC:EB=1::1.(3)有变化.如图3,连接AG,AC,∵AD:AB=AH:AE=1:2,∠ADC=∠AHG=90°,∴△ADC∽△AHG,∴AD:AC=AH:AG=1:,∵∠DAC=∠HAG,∴∠DAH=∠CAG,∴△DAH∽△CAG,∴HD:GC=AD:AC=1:,∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE,∵DA:AB=HA:AE=1:2,∴△ADH∽△ABE,∴DH:BE=AD:AB=1:2,∴HD:GC:EB=1::2类型2 与图形变换有关的几何综合题(2019十堰)(2019山西),把△ADE 沿D E翻折,点A的对应(2019郴州)如图1,矩形A BCD 中,点E为A B 边上的动点(不与A,B 重合)点为A1 ,延长EA1交直线D C 于点F,再把∠BEF 折叠,使点B的对应点B1落在E F 上,折痕EH 交直线B C 于点H.(1)求证:△A1DE∽△B1EH;(2)如图2,直线M N 是矩形A BCD 的对称轴,若点A1恰好落在直线M N 上,试判断△DEF 的形状,并说明理由;(3)如图3,在(2)的条件下,点G为△DEF 内一点,且∠DGF=150°,试探究DG,EG,FG 的数量关系.图1 图2 图3(2019淮安)(2019吉林)(2019包头)(2019自贡)25.(本题满分12分)(1)如图1,E 是正方形ABCD 边AB 上的一点,连接BD 、DE ,将∠BDE 绕点D 逆时针旋转90°,旋转后角的两边分别与射线BC 交于点F 和点G .①线段DB 和DG 之间的数量关系是 DB=DG ;②写出线段BE ,BF 和DB 之间的数量关系.BDBF BE 2=+(2)当四边形ABCD 为菱形,∠ADC =60°,点E 是菱形ABCD 边AB 所在直线上的一点,连接BD 、DE ,将∠BDE 绕点D 逆时针旋转120°,旋转后角的两边分别与射线BC 交于点F 和点G .①如图2,点E 在线段AB 上时,请探究线段BE 、BF 和BD 之间的数量关系,写出结论并给出证明;②如图3,点E 在线段AB 的延长线上时,DE 交射线BC 于点M ,若BE =1,AB =2,直接写出线段GM 的长度.图1图2 图3(2)①BDBF BE 3=+理由如下:在菱形ABCD 中,∠ABD=∠CBD=∠ABC=30°,由旋转120°可得,∠EDF=∠BDG=120°,∴∠EDF-21∠BDF=∠BDG-∠BDF ,即∠FDG=∠BDE.在△DBG 中,∠G=180°-∠BDG-∠DBG=30°,∴∠DBG=∠G=30°,∴BD=DG.在△BDE 和△GDF 中∴△BDE ≌△△GDF (ASA ),∴BE=GF⎪⎩⎪⎨⎧∠=∠=∠=∠DGF DBE DG BD BDE GDF ∴BE+BF=BF+GF=BG.过点D 作DM ⊥BG 于点M 如图所示:∵BD=DG ,∴BG=2BM.在Rt △BMD 中,∠DBM=30°,∴BD=2DM ,设DM=a ,则BD=2a ,BM=.∴BG=,∴a 3a 323232==aa BD BG ∴BF+BE=BD.3②GM 的长度为.理由:∵,FC=2DC=4,CM=BC=,∴GM=3191==BE GF 3234319(2019济宁)(2019 金华)24.如图,在等腰Rt△ABC中,∠ACB=90°,AB=14 。
中考数学模拟题《几何综合》专项测试题(附带参考答案)

中考数学模拟题《几何综合》专项测试题(附带参考答案)学校:___________班级:___________姓名:___________考号:___________考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。
动态几何问题经常在各地以中考试卷解答压轴题出现也常会出现在选择题最后一题的位置考察知识面较广综合性强可以提升学生的空间想象能力和综合分析问题的能力但同时难度也很大令无数初中学子闻风丧胆考场上更是丢盔弃甲解题思路1 熟练掌握平面几何知识﹕要想解决好有关几何综合题首先就是要熟练掌握关于平面几何的所有知识尤其是要重点把握三角形特殊四边形圆及函数三角函数相关知识.几何综合题重点考查的是关于三角形特殊四边形(平行四边形矩形菱形正方形)圆等相关知识2 掌握分析问题的基本方法﹕分析法综合法“两头堵”法﹕1)分析法是我们最常用的解决问题的方法也就是从问题出发执果索因去寻找解决问题所需要的条件依次向前推直至已知条件例如我们要证明某两个三角形全等先看看要证明全等需要哪些条件哪些条件已知了还缺少哪些条件然后再思考要证缺少的条件又需要哪些条件依次向前推直到所有的条件都已知为止即可综合法﹕即从已知条件出发经过推理得出结论适合比较简单的问题3)“两头堵”法﹕当我们用分析法分析到某个地方不知道如何向下分析时可以从已知条件出发看看能得到什么结论把分析法与综合法结合起来运用是我们解决综合题最常用的办策略3 注意运用数学思想方法﹕对于几何综合题的解决我们还要注意运用数学思想方法这样会大大帮助我们解决问题或者简化我们解决问题的过程加快我们解决问题的速度毕竟考场上时间是非常宝贵的.常用数学思想方法﹕转化类比归纳等等模拟预测1 (2024·江西九江·二模)如图 在矩形()ABDC AB AC >的对称轴l 上找点P 使得PAB PCD 、均为直角三角形 则符合条件的点P 的个数是( )A .1B .3C .4D .52 (2024·江西吉安·模拟预测)如图 在平面直角坐标系中 边长为23ABC 的顶点A B ,分别在y 轴的正半轴 x 轴的负半轴上滑动 连接OC 则OC 的最小值为( )A .2B .3C .33D .333 (2024·江西吉安·一模)如图 矩形ABCD 中 4AB = 6AD = 点E 在矩形的边上 则当BEC 的一个内角度数为60︒时 符合条件的点E 的个数共有( )A .4个B .5个C .6个D .7个4 (2023·江西·中考真题)如图 在ABCD 中 602B BC AB ∠=︒=, 将AB 绕点A 逆时针旋转角α(0360α︒<<︒)得到AP 连接PC PD .当PCD 为直角三角形时 旋转角α的度数为 .5 (2024·江西吉安·二模)如图 在矩形ABCD 中 6,10,AB AD E ==为CD 的中点 点P 在AE 下方矩形的边上.当APE 为直角三角形 且P 为直角顶点时 BP 的长为 .6 (2024·江西九江·二模)如图 在平面直角坐标系中 已知矩形OABC 的顶点()20,0A ()0,8C D 为OA 的中点 点P 为矩形OABC 边上任意一点 将ODP 沿DP 折叠得EDP △ 若点E 在矩形OABC 的边上 则点E 的坐标为 .7 (2024·江西·模拟预测)如图 ABC 中 AB AC = 30A ∠=︒ 射线CP 从射线CA 开始绕点C 逆时针旋转α角()075α︒<<︒ 与射线AB 相交于点D 将ACD 沿射线CP 翻折至A CD '△处 射线CA '与射线AB 相交于点E .若A DE '是等腰三角形 则α∠的度数为 .8 (2024·江西赣州·二模)在Rt ABC △中 已知90C ∠=︒ 10AB = 3cos 5B = 点M 在边AB 上 点N 在边BC 上 且AM BN = 连接MN 当BMN 为等腰三角形时 AM = .9 (2024·江西吉安·模拟预测)如图 在矩形ABCD 中 6,10AB AD == E 为BC 边上一点 3BE = 点P 沿着边按B A D →→的路线运动.在运动过程中 若PAE △中有一个角为45︒ 则PE 的长为 .10 (2024·江西吉安·三模)如图 在ABC 中 AB AC = 30B ∠=︒ 9BC = D 为AC上一点 2AD DC = P 为边BC 上的动点 当APD △为直角三角形时 BP 的长为 .11 (2024·江西吉安·一模)如图 矩形ABCD 中 4AB = 6AD = E 为CD 的中点 连接BE 点P 在矩形的边上 且在BE 的上方 则当BEP △是以BE 为斜边的直角三角形时 BP 的长为 .12 (2024·江西九江·二模)如图 在等腰ABC 中 2AB AC == 30B ∠=︒ D 是线段BC 上一动点 沿直线AD 将ADB 折叠得到ADE 连接EC .当DEC 是以DE 为直角边的直角三角形时 则BD 的长为 .13 (2024·江西·模拟预测)如图 在菱形ABCD 中 对角线AC BD 相交于点O 23AB = 60ABC ∠=︒ E 为BC 的中点 F 为线段OD 上一动点 当AEF △为等腰三角形时 DF 的长为 .14 (2024·江西上饶·一模)如图 在三角形纸片ABC 中 90,60,6C B BC ∠=︒∠=︒= 将三角形纸片折叠 使点B 的对应点B '落在AC 上 折痕与,BC AB 分别相交于点E F 当AFB '为等腰三角形时 BE 的长为 .15 (2024·江西抚州·一模)课本再现(1)如图1 CD 与BE 相交于点,A ABC 是等腰直角三角形 90C ∠=︒ 若DE BC ∥ 求证:ADE 是等腰直角三角形.类比探究(2)①如图2 AB 是等腰直角ACB △的斜边 G 为边AB 的中点 E 是BA 的延长线上一动点 过点E 分别作AC 与BC 的垂线 垂足分别为,D F 顺次连接,,DG GF FD 得到DGF △ 求证:DGF △是等腰直角三角形.②如图3 当点E 在边AB 上 且①中其他条件不变时 DGF △是等腰直角三角形是否成立?_______(填“是”或“否”).拓展应用(3)如图4 在四边形ABCD 中 ,90,BC CD BCD BAD AC =∠=∠=︒平分BAD ∠ 当1,22AD AC == 求线段BC 的长.16 (2023·江西·中考真题)课本再现思考我们知道菱形的对角线互相垂直.反过来对角线互相垂直的平行四边形是菱形吗?可以发现并证明菱形的一个判定定理对角线互相垂直的平行四边形是菱形.(1)定理证明:为了证明该定理小明同学画出了图形(如图1)并写出了“已知”和“求证”请你完成证明过程.已知:在ABCD中对角线BD AC⊥垂足为O.求证:ABCD是菱形.(2)知识应用:如图2在ABCD中对角线AC和BD相交于点O586AD AC BD===,,.①求证:ABCD是菱形②延长BC至点E连接OE交CD于点F若12E ACD∠=∠求OFEF的值.17 (2022·江西·中考真题)问题提出:某兴趣小组在一次综合与实践活动中提出这样一个问题:将足够大的直角三角板()90,60PEF P F ∠=︒∠=︒的一个顶点放在正方形中心O 处 并绕点O 逆时针旋转 探究直角三角板PEF 与正方形ABCD 重叠部分的面积变化情况(已知正方形边长为2).(1)操作发现:如图1 若将三角板的顶点P 放在点O 处 在旋转过程中 当OF 与OB 重合时 重叠部分的面积为__________ 当OF 与BC 垂直时 重叠部分的面积为__________ 一般地 若正方形面积为S 在旋转过程中 重叠部分的面积1S 与S 的关系为__________(2)类比探究:若将三角板的顶点F 放在点O 处 在旋转过程中 ,OE OP 分别与正方形的边相交于点M N .①如图2 当BM CN =时 试判断重叠部分OMN 的形状 并说明理由②如图3 当CM CN =时 求重叠部分四边形OMCN 的面积(结果保留根号)(3)拓展应用:若将任意一个锐角的顶点放在正方形中心O 处 该锐角记为GOH ∠(设GOH α∠=) 将GOH ∠绕点O 逆时针旋转 在旋转过程中 GOH ∠的两边与正方形ABCD 的边所围成的图形的面积为2S 请直接写出2S 的最小值与最大值(分别用含α的式子表示)(参考数据:6262sin15tan1523-+︒=︒=︒=18 (2024·江西吉安·二模)如图 在ABC 和ADE 中 (),AB AC AD AE AD AB ==< 且BAC DAE ∠=∠.连接CE BD .(1)求证:BD CE =.(2)在图2中 点B D E 在同一直线上 且点D 在AC 上 若,AB a BC b == 求AD CD的值(用含a b 的代数式表示).19 (2024·江西九江·二模)初步探究(1)如图1 在四边形ABCD 中 ,AC BD 相交于点O AC BD ⊥ 且ABD CBD S S = 则OA 与OC 的数量关系为 .迁移探究(2)如图2 在四边形ABCD 中 ,AC BD 相交于点O ABD CBD SS = (1)中OA 与OC 的数量关系还成立吗?如果成立 请说明理由.拓展探究(3)如图3 在四边形ABCD 中 ,AC BD 相交于点O 180,ABD CBD BAD BCD S S ∠∠+=︒=△△ 且 33OB OD == 求AC 的长.20 (2024·江西九江·二模)课本再现如图1 四边形ABCD 是菱形 30ACD ∠=︒ 6BD =.(1)求,AB AC 的长.应用拓展(2)如图2 E 为AB 上一动点 连接DE 将DE 绕点D 逆时针旋转120︒ 得到DF 连接EF .①直接写出点D 到EF 距离的最小值②如图3 连接,OF CF 若OCF △的面积为6 求BE 的长.21 (2024·江西赣州·三模)某数学小组在一次数学探究活动过程中经历了如下过程:AB=P为对角线AC上的一个动点以P为直角顶问题提出:如图正方形ABCD中8△.点向右作等腰直角DPM(1)操作发现:DM的最小值为_______ 最大值为_______(2)数学思考:求证:点M在射线BC上=时求CM的长.(3)拓展应用:当CP CM22 (2024·江西赣州·二模)【课本再现】 思考我们知道 角的平分线上的点到角的两边的距离相等 反过来 角的内部到角的两边的距离相等的点在角的平分线上吗?可以发现并证明角的平分线的性质定理的逆定理角的内部到角的两边的距离相等的点在角的平分线上.【定理证明】(1)为证明此逆定理 某同学画出了图形 并写好“已知”和“求证” 请你完成证明过程.已知:如图1 在ABC ∠的内部 过射线BP 上的点P 作PD BA ⊥ PE BC ⊥ 垂足分别为D E 且PD PE =.求证:BP 平分ABC ∠.【知识应用】(2)如图2 在ABC 中 过内部一点P 作PD BC ⊥ PE AB ⊥ PF AC ⊥ 垂足分别为D E F 且PD PE PF == 120A ∠=︒ 连接PB PC .①求BPC ∠的度数②若6PB=23PC=求BC的长.23 (2024·江西吉安·模拟预测)一块材料的形状是锐角三角形ABC下面分别对这块材料进行课题探究:课本再现:(1)在图1中若边120mmBC=高80mmAD=把它加工成正方形零件使正方形的一边在BC上其余两个顶点分别在AB AC上这个正方形零件的边长是多少?类比探究(2)如图2 若这块锐角三角形ABC材料可以加工成3个相同大小的正方形零件请你探究高AD与边BC的数量关系并说明理由.拓展延伸(3)①如图3 若这块锐角三角形ABC材料可以加工成图中所示的4个相同大小的正方形零件则ADBC的值为_______(直接写出结果)②如图4 若这块锐角三角形ABC材料可以加工成图中所示的()3n m≥相同大小的正方形零件求ADBC的值.24 (2024·江西吉安·三模)课本再现 矩形的定义 有一个角是直角的平行四边形是矩形.定义应用(1)如图1 已知:在四边形ABCD 中 90A B C ∠=∠=∠=︒用矩形的定义求证:四边形ABCD 是矩形.(2)如图2 在四边形ABCD 中 90A B ∠=∠=︒ E 是AB 的中点 连接DE CE 且DE CE = 求证:四边形ABCD 是矩形.拓展延伸(3)如图3 将矩形ABCD 沿DE 折叠 使点A 落在BC 边上的点F 处 若图中的四个三角形都相似 求AB BC的值.25 (2024·江西吉安·一模)课本再现在学习了平行四边形的概念后进一步得到平行四边形的性质:平行四边形的对角线互相平分.=(1)如图1 在平行四边形ABCD中对角线AC与BD交于点O 求证:OA OC =.OB OD知识应用=延长AC到E 使得(2)在ABC中点P为BC的中点.延长AB到D 使得BD AC∠=︒请你探究线段BE与线段AP之间的BACCE AB=连接DE.如图2 连接BE若60数量关系.写出你的结论并加以证明.26 (2024·江西九江·二模)问题提出在综合与实践课上 某数学研究小组提出了这样一个问题:如图1 在边长为4的正方形ABCD 的中心作直角EOF ∠ EOF ∠的两边分别与正方形ABCD 的边BC CD 交于点E F (点E 与点B C 不重合) 将EOF ∠绕点O 旋转.在旋转过程中 四边形OECF 的面积会发生变化吗?爱思考的浩浩和小航分别探究出了如下两种解题思路.浩浩:如图a 充分利用正方形对角线垂直 相等且互相平分等性质 证明了OEC OFD ≌ 则OEC OFD S S = OEC OCF OFD OCF OCD OECF S S S S S S =+=+=四边形.这样 就实现了四边形OECF 的面积向OCD 面积的转化.小航:如图b 考虑到正方形对角线的特征 过点O 分别作OG BC ⊥于点G OH CD ⊥于点H 证明OGE OHF ≌△△ 从而将四边形OECF 的面积转化成了小正方形OGCH 的面积.(1)通过浩浩和小航的思路点拨﹐我们可以得到OECF S =四边形__________ CE CF +=__________.类比探究(2)①如图⒉ 在矩形ABCD 中 3AB = 6AD = O 是边AD 的中点 90EOF ∠=︒ 点E 在AB 上 点F 在BC 上 则EB BF +=__________.②如图3 将问题中的正方形ABCD 改为菱形ABCD 且45ABC ∠=︒ 当45EOF ∠=︒时 其他条件不变 四边形OECF 的面积还是一个定值吗?若是 请求出四边形OECF 的面积 若不是 请说明理由.拓展延伸(3)如图4 在四边形ABCD 中 7AB = 2DC = 60BAD ∠=︒ 120BCD ∠=︒ CA 是BCD ∠的平分线 求四边形ABCD 的面积.27 (2024·江西九江·模拟预测)【课本再现】(1)如图1 四边形ABCD 是一个正方形 E 是BC 延长线上一点 且AC EC = 则DAE ∠的度数为 .【变式探究】(2)如图2 将(1)中的ABE 沿AE 折叠 得到AB E ' 延长CD 交B E '于点F 若2AB = 求B F '的长.【延伸拓展】(3)如图3 当(2)中的点E 在射线BC 上运动时 连接B B ' B B '与AE 交于点P .探究:当EC 的长为多少时 D P 两点间的距离最短?请求出最短距离.28 (2024·江西上饶·一模)课本再现:(1)如图1 ,D E 分别是等边三角形的两边,AB AC 上的点 且AD CE =.求证:CD BE =.下面是小涵同学的证明过程:证明:ABC 是等边三角形,60AC BC A ACB ∴=∠=∠=︒.AD CE =()SAS ADC CEB ∴≌CD BE ∴=.小涵同学认为此题还可以得到另一个结论:BFD ∠的度数是______迁移应用:(2)如图2 将图1中的CD 延长至点G 使FG FB = 连接,AG BG .利用(1)中的结论完成下面的问题.①求证:AG BE ∥②若25CF BF = 试探究AD 与BD 之间的数量关系.参考答案考点解读在中考数学中有这么一类题它是以点线几何图形的运动为载体集合多个代数知识几何知识及数学解题思想于一题的综合性试题它就是动态几何问题。
2020年九年级中考数学 压轴专题 几何探究题(含答案)

2020中考数学 压轴专题 几何探究题(含答案)1. 我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”.第1题图(1)概念理解:请你根据定义举一个“等邻角四边形的”例子;(2)问题探究:如图①,在等邻角四边形ABCD 中,∠DAB =∠ABC ,AD 、BC 的中垂线恰好交于AB 边上一点P ,连接AC 、BD ,试探究AC 与BD 的数量关系,并说明理由.(3)应用拓展:如图②,在Rt △ABC 与Rt △ABD 中,∠C =∠D =90°,BC =BD =3,AB =5,将Rt △ABD 绕着点A 顺时针旋转角α(0°)得到Rt △AB ′D ′(如图③),当凸四边形AD ′BC 为“等邻角四边形”时,求出它的面积.解:(1)矩形;(答案不唯一)(2)AC =BD ;如解图①所示,连接PD 、PC , ∵PE 是AD 的垂直平分线,PF 是BC 的垂直平分线, ∴P A =PD ,PB =PC ,∴∠P AD =∠PDA ,∠PBC =∠PCB ,∴∠DPB =180°-∠DP A =∠P AD +∠PDA =2∠P AD ,同理可得∠APC =2∠PBC , ∵∠DAB =∠ABC ,即∠P AD =∠PBC ,∴∠APC =∠DPB ,在△APC 和△DPB 中,⎩⎪⎨⎪⎧PA =PD ∠APC =∠DPB PB =PC,△APC ≌△DPB (SAS), ∴ AC =BD .第1题解图①(3)①当∠AD ′B =∠D ′BC 时,如解图②所示,延长AD ′交CB 的延长线于点E ,过点D ′作DF ⊥CE 于点F , ∠ED ′B =∠EBD ′, ∴EB =ED ′,∵∠C =∠EFD ′,∠EAC =∠ED ′F , ∴△ED ′F ∽△EAC , 则D ′F AC =ED ′AE, 设EB =ED ′=x ,由勾股定理可知,在Rt △ACB 中,AC =AB 2-BC 2=52-32=4,则AD ′=4,CE =3+x ,AE =4+x ,在Rt △ACE 中,AC 2+CE 2=AE 2,即42+(3+x )2=(4+x )2, 整理得:2x -9=0,解得x =92,EB =ED ′=92,∴AE =172,∴D ′F 4=92112,∴D ′F =3617,S 四边形AD ′BC =S △ACE -S △D ′BE =12AC ·CE -12D ′F ·BE =12×4×(3+92)-12×92×3617=15-8117=17417;第1题解图②②当∠D ′BC =90°时,如解图③所示,过点D ′作D ′E ⊥AC ,交AC 于点E , ∴四边形ECBD ′是矩形,∴ED ′=BC =3,在Rt △AED ′中,根据勾股定理得AE =AD′2-ED′2=42-32=7,∵S 四边形AD ′BC =S △AED ′+S 矩形ECBD ′=12AE ·ED ′+EC ·BC =372+12-37=12-372.综上所述,当凸四边形AD 为等邻角四边形时,它的面积为17417或12-372.第1题解图③2. (1)发现 如图①,点A 为线段BC 外一动点,且BC =a ,AB =b .填空:当点A 位于________时,线段AC 的长取得最大值,且最大值为________(用含有a ,b 的式子表示); (2)应用 点A 为线段BC 外一动点,且BC =3,AB =1.如图②所示,分别以AB ,AC 为边作等边三角形ABD 和等边三角形ACE,连接CD,BE.①请找出图中与BE相等的线段,并说明理由;②直接写出线段BE长的最大值;(3)拓展如图③,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且P A=2,PM=PB,∠BPM=90°.请直接写出线段AM长的最大值及此时点P的坐标.第2题图(1)解:CB的延长线上,a+b;【解法提示】∵点A为线段BC外一动点,且BC=a,AB=b,∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b.(2)解:①DC=BE,理由如下:∵△ABD和△ACE均为等边三角形,∴AD=AB,AC=AE,∠BAD=∠CAE=60°,∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,∴△CAD≌△EAB(SAS),∴DC=BE;②BE长的最大值是4;【解法提示】∵线段BE长的最大值=线段CD的最大值,由(1)知,当线段CD的长取得最大值时,点D在CB 的延长线上,∴CD长的最大值为BD+BC=AB+BC=4.(3)解:AM长的最大值是3+22,点P的坐标是(2-2,2).【解法提示】如解图①,构造△BNP≌△MAP,则NB=AM,P A=PN,∴∠APN=90°,由(1)得出当点N在BA的延长线上时,NB有最大值(如解图②),可得AN=22,∴AM=NB=3+22,过点P作PE⊥x轴于点E,PE=AE=2,∴点P的坐标是(2-2,2).第2题解图3.如图,△ABC是边长为4 cm的等边三角形,边AB在射线OM上,且OA=6 cm.点D从O点出发,沿OM的方向以1 cm/s的速度运动.当D不与点A重合时,将△ACD绕点C逆时针方向旋转60°得到△BCE,连接DE.(1)求证:△CDE是等边三角形;(2)当6<t<10时,△BDE的周长是否存在最小值?若存在,求出△BDE的最小周长;若不存在,请说明理由;(3)当点D在射线OM上运动时,是否存在以D、E、B为顶点的三角形是直角三角形?若存在,求出此时t的值;若不存在,请说明理由.第3题图(1)证明:∵△BCE是由△ACD逆时针旋转60°得到的,∴CD=CE,∠DCE=60°,∴△CDE是等边三角形;(2)解:存在.理由如下:∵△BCE是由△ACD逆时针旋转60°得到的,∴AD=BE,又∵△CDE是等边三角形,∴DE=CD,∴C△BDE=BD+BE+DE=BD+AD+CD=AB+CD,∵AB=4为定值,∴当CD最小,即CD⊥AB时,△BDE的周长最小,∵△ABC是等边三角形,∴当CD最小,即CD⊥AB时,易得CD=23,∴△BDE的最小周长为23+4;(3)解:存在.理由如下:如解图,过点C作CF⊥OM于点F,则CF=23,∴BD=||t-6,t-10,BE=AD=||DE=CD=CF2+DF2=12+(t-8)2,①当∠DEB=90°时,BD2=BE2+DE2,即(t-10)2=(t-6)2+12+(t-8)2,第3题解图解得t1=2,t2=6(不合题意,舍去);②当∠EBD=90°时,DE2=BD2+BE2,即12+(t-8)2=(t-10)2+(t-6)2,解得t3=6,t4=10(两者均不合题意,舍去);③当∠BDE=90°时,BE2=BD2+DE2,即(t-6)2=(t-10)2+12+(t-8)2,解得t5=14,t6=10(舍去).综上所述,存在以D、E、B为顶点的三角形是直角三角形,此时t=2或14.4.如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图①),△ABD不动.(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图②),证明:MB=MC;(2)若将图①中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图③),判断并直接写出MB、MC的数量关系;(3)在(2)中,若∠CAE的大小改变(图④),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.第4题图(1)证明:如解图①,连接AM,由已知得△ABD≌△ACE,第4题解图①∴ AD =AE , AB =AC , ∠BAD =∠CAE , 又∵MD =ME ,∴∠MAD =∠MAE (三线合一), ∴∠MAD -∠BAD =∠MAE -∠CAE , 即∠BAM =∠CAM , 在△ABM 和△ACM 中, ⎩⎪⎨⎪⎧AB =AC ∠BAM =∠CAM AM =AM, ∴△ABM ≌△ACM (SAS ), ∴MB =MC ;第4题解图②(2)解:MB =MC ;【解法提示】如解图②,延长DB 、AE 相交于点E ′,延长EC 交AD 于点F , ∴BD =BE ′,CE =CF ,又∵M 是ED 的中点,B 是DE ′的中点, ∴MB ∥AE ′,∴∠MBC =∠CAE ,同理:MC ∥AD , ∴∠BCM =∠BAD , 又∵∠BAD =∠CAE , ∴∠MBC =∠BCM , ∴MB =MC .(3)解:MB =MC 还成立.理由如下: 如解图③,延长BM 交CE 于点F ,第4题解图③∵CE ∥BD , ∴∠MDB =∠MEF , ∠MBD =∠MFE , 又∵M 是DE 的中点, ∴MD =ME ,在△MDB 和△MEF 中, ⎩⎪⎨⎪⎧∠MBD =∠MFE ∠MDB =∠MEF MD =ME, ∴△MDB ≌△MEF (AAS), ∴MB =MF =12BF ,又∵∠ACE =90°,∴∠BCF =90°, ∴MC =12BF ,∴MB=MC.5.在正方形ABCD中,点E是对角线AC上的动点(与点A,C不重合),连接BE.(1)将射线BE绕点B顺时针方向旋转45°,交直线AC于点F.①依题意补全图①;②小研通过观察、实验,发现线段AE,FC,EF存在以下数量关系:AE与FC的平方和等于EF的平方.小研把这个猜想与同学们进行交流,通过讨论,形成证明该猜想的几种想法:想法1:将线段BF绕点B逆时针旋转90°,得到线段BM,要证AE,FC,EF的数量关系,只需证AE,AM,EM的数量关系.想法2:将△ABE沿BE翻折,得到△NBE,要证AE,FC,EF的关系,只需证EN,FN,EF的关系.…请你参考上面的想法,用等式表示线段AE,FC,EF的数量关系并证明;(一种方法即可)(2)如图②,若将直线..AC于点F.小研完成作图后,发现直线AC上存在三..BE绕点B顺时针旋转135°,交直线条线段(不添加辅助线)满足:其中两条线段的平方和等于第三条线段的平方,请直接用等式表示这三条线段的数量关系.第5题图解:(1)①补全图形,如解图①;图① 图②第5题解图②AE 2+FC 2=EF 2;证明:如解图②,过B 作MB ⊥BF 于点B ,使BM =BF ,连接AM 、EM ,∵四边形ABCD 是正方形,∴∠ABC =90°,∠1=∠2=45°,AB =BC ,∵∠3=45°,∴∠MBE =∠3=45°,在△MBE 和△FBE 中,⎩⎪⎨⎪⎧BM =BF ∠MBE =∠3BE =BE,∴△MBE ≌△FBE (SAS ),∴EM =EF ,∵∠4=90°-∠ABF ,∠5=90°-∠ABF ,∴∠4=∠5,在△AMB 和△CFB 中,⎩⎪⎨⎪⎧BM =BF ∠4=∠5AB =CB,∴△AMB ≌△CFB (SAS),∴AM =FC ,∠6=∠2=45°,∴∠MAE =∠6+∠1=90°,在Rt △MAE 中,AE 2+AM 2=EM 2,∴AE 2+FC 2=EF 2;(2)AF 2+EC 2=EF 2.【解法提示】如解图③,过B 作MB ⊥BE ,使BM =BE ,连接ME 、MF 、AM ,∵直线BE 绕点B 顺时针旋转135°,交直线AC 于点F ,∴∠FBE =45°,∴∠MBF =90°-45°=45°,∴∠FBE =∠MBF ,在△MBF 和△EBF 中,⎩⎪⎨⎪⎧BM =BE ∠MBF =∠FBE ,BF =BF∴△MBF ≌△EBF (SAS),∴MF =EF ,∵∠MBA =90°-∠ABE ,∠EBC =90°-∠ABE ,∴∠MBA =∠EBC ,在△AMB 和△CBE 中,⎩⎪⎨⎪⎧BM =BE ∠MBA =∠EBC AB =CB,∴△AMB ≌△CEB (SAS ),∴AM =EC ,∠BAM =∠BCE =45°,∴∠MAE =∠BAM +∠BAC =90°,∴∠MAF =90°,在Rt △MAF 中,AF 2+AM 2=MF 2,∴AF 2+EC 2=EF 2.第5题解图③6.在△ABC中,AB=AC,∠A=60°,点D是BC边的中点,作射线DE,与边AB交于点E,射线DE绕点D顺时针旋转120°,与直线AC交于点F.(1)依题意补全图形;(2)小华通过观察、实验提出猜想:在点E运动的过程中,始终有DE=DF.小华把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:由点D是BC边的中点,通过构造一边的平行线,利用全等三角形,可证DE=DF;想法2:利用等边三角形的对称性,作点E关于线段AD的对称点P,由∠BAC与∠EDF互补,可得∠AED与∠AFD互补,由等角对等边,可证DE=DF;想法3:由等腰三角形三线合一,可得AD是∠BAC的平分线,由角平分线定理,构造点D到AB,AC的高,利用全等三角形,可证DE=DF;…请你参考上面的想法,帮助小华证明DE=DF(选一种方法即可);(3)在点E运动的过程中,直接写出BE,CF,AB之间的数量关系.解:(1)补全图形,如解图①;第6题解图(2)想法1:证明:如解图②,过点D作DG∥AB,交AC于点G,∵点D是BC边的中点,∴DG=12AB,∴△CDG是等边三角形,∴∠EDB+∠EDG=120°,∵∠FDG+∠EDG=120°,∴∠EDB=∠FDG,∵BD=DG,∠B=∠FGD=60°,∴△BDE≌△GDF,∴DE=DF;想法2:证明:如解图③,连接AD,作点E关于线段AD的对称点P,点P在边AC上,∵点D是BC边的中点,AB=AC,∴直线AD是△ABC的对称轴,∴△ADE≌△ADP,∴DE=DP,∠AED=∠APD,∵∠BAC+∠EDF=180°,∴∠AED+∠AFD=180°,∵∠APD+∠DPF=180°,∴∠AFD=∠DPF,∴DP=DF,∴DE=DF;第6题解图想法3:证明:如解图④,连接AD,过D作DM⊥AB于点M,DN⊥AC于点N,∵点D是BC边的中点,∴AD平分∠BAC,∵DM⊥AB于点M,DN⊥AC于点N,∴DM=DN,∵∠A=60°,∴∠MDE+∠EDN=120°,∵∠FDN+∠EDN=120°,∴∠MDE =∠FDN ,∴Rt △MDE ≌Rt △NDF ,∴DE =DF ;(3)当点F 在AC 边上时,BE +CF =12AB ;当点F 在AC 的延长线上时,BE -CF =12AB . 【解法提示】①当点F 在AC 边上时,如解图⑤,过点D 作DM ⊥AB 于点M ,作DN ⊥AC 于点N , ∵∠B =∠C =60°,BD =DC ,∠BDM =∠CDN =30°,∴△BDM ≌△CDN ,∴BM =CN ,DM =DN ,又∵∠EDF =120°=∠MDN ,∴∠EDM =∠NDF ,又∵∠EMD =∠FND =90°,∴△EDM ≌△FDN ,∴ME =NF ,∴BE +CF =BM +EM +NC -FN =2BM =BD =12AB ;图⑤ 图⑥第6题解图②当点F 在AC 的延长线上时,如解图⑥,过D 作DM ⊥AB 于点M ,作DN ⊥AC 于点N ,∵∠B =∠DCN =60°,BD =DC ,∠BDM =∠CDN =30°,∴△BDM ≌△CDN ,∴BM =CN ,DM =DN ,又∵∠EDF =120°=∠MDN ,∴∠EDM =∠NDF ,又∵∠EMD =∠FND =90°,∴△EDM ≌△FDN ,∴ME =NF ,∴BE -CF =BM +EM -(FN -CN )=2BM =BD =12AB ,综上所述,当点F 在AC 边上时,BE +CF =12AB ;当点F 在AC 的延长线上时,BE -CF =12AB . 7. 我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图①,在△ABC 中,AO 是BC 边上的中线,AB 与AC 的“极化值”就等于AO 2-BO 2的值,可记为ABAC =AO 2-BO 2.第7题图(1)在图①中,若∠BAC =90°,AB =8,AC =6,AO 是BC 边上的中线,则ABAC=________,OCOA=________;(2)如图②,在△ABC中,AB=AC=4,∠BAC=120°,求AB AC、BA BC的值;(3)如图③,在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=13A A O,已知ABAC=14,BN BA=10,求△ABC的面积.解:(1)0 ,7;【解法提示】∵∠BAC=90°,AB=8,AC=6,∴BC=AB2+AC2=10,在Rt△ABC中,AO是BC边上的中线,∴AO=BO=5,∴AB AC=AO2-BO2=0,如解图①,取AC的中点D ,连接OD ,则OD ∥AB ,OD =12AB =4,CD =12AC =3,∴OC OA =OD 2-CD 2=16-9=7.第7题解图(2)如解图②,作底边BC 上的中线AE ,由题意可知AE 是∠BAC 的平分线、BC 边上的高. ∵AB =ΑC =4,∠BAC =120°,∴在Rt △ABE 中,∠AEB =90°,∠ABC =30°,∴AE =12×4=2,BE =32×4=23, ∴AB AC =AE 2-BE 2=22-(23)2=-8.过点B作AC边上中线BM,过点M作MN⊥BC于点N,∴AM=CM=1×4=2.2在Rt△MNC中,∠MNC=90°,∠C=30°,×2=1,CN=22-12= 3.∴MN=12∵BC=2BE=43,∴BN=BC-CN=43-3=33,BM2=12+(33)2=28.∴BA BC=BM2-AM2=28-22=24;(3)如解图③,过点B作△ABN的AN边上中线BM,∵在△ABC中,AB=AC,AO是BC边上的中线,点N在AO上,且ON=13AO,第7题解图③∴AM=MN=NO,AO⊥BC,即AO=3NO.∵AB A AC =14,BNBA =10,∴ AO 2-BO 2=14,即(3ON )2-BO 2=9ON 2-BO 2=14,①∵BM 2-MN 2=OM 2+BO 2-MN 2=(2ON )2+BO 2-ON 2=3ON 2+BO 2=10,②由①、②得⎩⎪⎨⎪⎧9ON 2-BO 2=143ON 2+BO 2=10, ∴ON 2=2,即ON =2,BO =2,∴BC =4,AO =32,∴S △ABC =12BC ·AO =12×4×32=6 2. 8. 问题发现:如图①,在△ABC 中,∠ACB =90°,分别以AC 、BC 为边向外侧作正方形ACDE 和正方形BCFG .(1)△ABC和△DCF面积的关系是________;(请在横线上填写“相等”或“不相等”)(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图②给出证明;若不成立,请说明理由;(3)解决问题:如图③,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CD JI、正方形DA LK;运用(2)中的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.第8题图解:(1)相等;【解法提示】∵四边形ACDE和四边形BCFG是正方形,∴AC=DC,BC=FC,∠ACD=∠BCF=90°,∵∠ACB=90°,∴∠DCF=90°=∠ACB.∴12AC·BC=12DC·CF,∴S△ABC=S△DFC.(2)成立.理由如下:如解图,延长BC到点P,过点A作AP⊥BP于点P,过点D作DQ⊥FC于点Q,∴∠APC=∠DQC=90°.∵四边形ACDE,四边形BCFG均为正方形,∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ.第8题解图在△APC 和△DQC 中,⎩⎪⎨⎪⎧∠APC =∠DQC ∠ACP =∠DCQ AC =DC,∴△APC ≌△DQC (AAS),∴AP =DQ .又∵S △ABC =12BC ·AP ,S △DFC =12FC ·DQ , ∴S △ABC =S △DFC ;(3)图中阴影部分的面积和有最大值.理由如下:由(2)中的结论可知:S △K D J =S △ADC ,S △FBG =S △ABC ,S △AE L =S △ABD ,S △CH I =S △BDC ,∴S 阴影=S △K DJ +S △FBG +S △AEL +S △CHI =S △ADC +S △ABC +S △ABD +S △BDC =2S 四边形ABCD .设AC =m ,则BD =10-m ,∵AC ⊥BD ,∴S 四边形ABCD =12AC ·BD =12m ·(10-m )=-12m 2+5m =-12(m -5)2+252. ∵-12<0,∴S四边形ABCD有最大值,最大值为252.=25,∴S阴影=2×252∴阴影部分的面积和有最大值,最大值为25.9.问题背景如图①,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE ≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.类比探究如图②,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F 三点不重合).(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;(2)△DEF是否为正三角形?请说明理由;(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.第9题图解:(1)△ABD≌△BCE≌△CAF.证明:如解图①,第9题解图①∵△ABC为正三角形,∴∠CAB=∠ABC=∠BCA=60°,AB=BC.∵∠ABD=∠ABC-∠2,∠BCE=∠ACB-∠3,而∠2=∠3,∴∠ABD=∠BCE.又∵∠1=∠2,∴△ABD≌△BCE(ASA);(2)△DEF是正三角形.理由如下:∵△ABD≌△BCE≌△CAF,∴∠ADB=∠BEC=∠CF A,∴∠FDE=∠DEF=∠EFD,∴△DEF是正三角形;(3)如解图②,作AG⊥BD,交BD延长线于点G,第9题解图②由△DEF 是正三角形得到∠ADG =60°,(或者∠ADG =∠1+∠ABD =∠2+∠ABD =60°.)∴在Rt △ADG 中,DG =12b ,AG =32b . ∴在Rt △ABG 中,c 2=(a +12b )2+(32b )2, ∴c 2=a 2+ab +b 2.10. 在△ABC 中,∠ACB =90°,AC =3,BC =4,将△ABC 绕顶点C 顺时针旋转,旋转角为θ(0°<θ<180°),得到△A ′B ′C .(1)设△ACA ′和△BCB ′的面积分别为S 1和S 2.若θ=40°,请求出S 1S 2的值; (2)如图①,设A ′B ′与CB 相交于点D ,且AB ∥CB ′:①求证:CD =B ′D ;②求BD 的长;(3)如图②,设AC 中点为点M ,A ′B ′中点为点N ,连接MN ,MN 是否存在最大值,若存在,求出MN 的值,判断出此时AA ′与BB ′的位置关系;若不存在,请说明理由.第10题图(1)解: ∵△ABC 绕顶点C 顺时针旋转40°,得到△A ′B ′C , ∴CA =CA ′,CB =CB ′,∠ACA ′=∠BCB ′=θ,∴△ACA ′∽△BCB ′,∴S △ACA ′∶S △BCB ′=AC 2∶BC 2=32∶42=9∶16;∴S 1S 2=916; (2)①证明:∵AB ∥B ′C ,∴∠ABC =∠BCB ′;由旋转的性质得∠ABC =∠DB ′C ,即∠BCB ′ =∠DB ′C ;∴CD =B ′D ;②解:根据勾股定理可得A ′B ′=AB =5,据题意可得∠BCB ′ +∠BCA ′ =∠DB ′C +∠CA ′B ′=90°,∴∠BCA ′ =∠CA ′B ′,∴CD =A ′D =B ′D =12A ′B ′=52, ∴ BD =BC -CD =32; (3)解:存在,∵∠A ′CB ′=90°,点M 为AC 的中点,∴CM =12AC =32, ∵△A ′B ′C 是由△ABC 绕顶点C 顺时针旋转所得,∴A ′B ′=AB =5,第10题解图如解图,连接CN ,可得MN ≤CM +CN ,∴只有当点N 在MC 的延长线上时,MN =CM +CN ,此时MN 最大,∵点N 为A ′B ′的中点,∴CN =12 A ′B ′=52,MN =CM +CN =4, 即MN 的最大值为4.此时AA ′⊥BB ′.。
2019-2020年中考数学全国部分地区几何综合题真题汇编(含答案解析)

几何综合专题1.(2019浙江温州24题)如图,在平面直角坐标系中,直线142y x=-+分别交x轴、y轴于点B,C,正方形AOCD的顶点D在第二象限内,E是BC中点,OF⊥DE于点F,连结OE.动点P在AO上从点A向终点O匀速运动,同时,动点Q在直线BC上从某点Q1向终点Q2匀速运动,它们同时到达终点.(1)求点B的坐标和OE的长;(2)设点Q2为(m,n),当17nm=tan∠EOF时,求点Q2的坐标;(3)根据(2)的条件,当点P运动到AO中点时,点Q恰好与点C重合.①延长AD 交直线BC于点Q3,当点Q在线段Q2Q3上时,设Q3Q=s,AP=t,求s关于t的函数表达式.②当PQ与△OEF的一边平行时,求所有满足条件的AP的长.2.(2019浙江绍兴24题)如图,矩形ABCD中,AB=a,BC=b,点M,N分别在边AB,CD上,点E,F分别在BC,AD上,MN,EF交于点P,记k=MN∶EF.(1)若a∶b的值是1,当MN⊥EF时,求k的值.(2)若a ∶b 的值是21,求k 的最大值和最小值. (3)若k 的值是3,当点N 是矩形的顶点,∠MPE=60°,MP=EF=3PE 时,求a ∶b 的值.3.(2019浙江绍兴23题)如图1是实验室中的一种摆动装置,BC 在地面上,支架ABC 是底边为BC 的等腰直角三角形,摆动臂长AD 可绕点A 旋转,摆动臂DM 可绕点D 旋转,AD=30,DM=10.(1)在旋转过程中:①当A,D,M 三点在同一直线上时,求AM 的长;②当A,D,M 三点在同一直角三角形的顶点时,求AM 的长.(2)若摆动臂AD 顺时针旋转90°,点D 的位置由△ABC 外的点D 1转到其内的点D 2处,连结D 1D 2,如图2,此时∠AD 2C=135°,CD 2=60,求BD 2的长.4.(2019浙江宁波25题)定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.(1)如图1,在△ABC中,AB=AC,AD是△ABC的角平分线,E,F分别是BD,AD上的点. 求证:四边形ABEF是邻余四边形。
《几何综合探究问题》(共48题)中考专项配套练习(重庆专用)

5年(2016-2020)中考1年模拟数学试题分项详解(重庆专用)专题13 几何综合探究问题(共48题)一.解析题(共10小题)1.(2020•重庆)如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC边上一动点,连接AD,把AD绕点A逆时针旋转90°,得到AE,连接CE,DE.点F是DE的中点,连接CF.(1)求证:CF=√22AD;(2)如图2所示,在点D运动的过程中,当BD=2CD时,分别延长CF,BA,相交于点G,猜想AG 与BC存在的数量关系,并证明你猜想的结论;(3)在点D运动的过程中,在线段AD上存在一点P,使P A+PB+PC的值最小.当P A+PB+PC的值取得最小值时,AP的长为m,请直接用含m的式子表示CE的长.2.(2020•重庆)△ABC为等边三角形,AB=8,AD⊥BC于点D,E为线段AD上一点,AE=2√3.以AE 为边在直线AD右侧构造等边三角形AEF,连接CE,N为CE的中点.(1)如图1,EF与AC交于点G,连接NG,求线段NG的长;(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α,M为线段EF的中点,连接DN,MN.当30°<α<120°时,猜想∠DNM的大小是否为定值,并证明你的结论;(3)连接BN,在△AEF绕点A逆时针旋转过程中,当线段BN最大时,请直接写出△ADN的面五年中考真题积.3.(2019•重庆)如图,在平行四边形ABCD中,点E在边BC上,连接AE,EM⊥AE,垂足为E,交CD 于点M,AF⊥BC,垂足为F,BH⊥AE,垂足为H,交AF于点N,点P是AD上一点,连接CP.(1)若DP=2AP=4,CP=√17,CD=5,求△ACD的面积.(2)若AE=BN,AN=CE,求证:AD=√2CM+2CE.4.(2019•重庆)在▱ABCD中,BE平分∠ABC交AD于点E.(1)如图1,若∠D=30°,AB=√6,求△ABE的面积;(2)如图2,过点A作AF⊥DC,交DC的延长线于点F,分别交BE,BC于点G,H,且AB=AF.求证:ED﹣AG=FC.5.(2018•重庆)如图,在平行四边形ABCD中,点O是对角线AC的中点,点E是BC上一点,且AB=AE,连接EO并延长交AD于点F.过点B作AE的垂线,垂足为H,交AC于点G.(1)若AH=3,HE=1,求△ABE的面积;(2)若∠ACB=45°,求证:DF=√2CG.6.(2018•重庆)如图,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连接EH.(1)若BC=12√2,AB=13,求AF的长;(2)求证:EB=EH.7.(2017•重庆)在△ABM中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.(1)如图1,若AB=3√2,BC=5,求AC的长;(2)如图2,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.8.(2017•重庆)如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.(1)如图1,若AB=4√2,BE=5,求AE的长;(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.9.(2016•重庆)在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.(1)若AB =2√2,求BC 的长;(2)如图1,当点G 在AC 上时,求证:BD =12CG ;(3)如图2,当点G 在AC 的垂直平分线上时,直接写出ABCG 的值.10.(2016•重庆)已知△ABC 是等腰直角三角形,∠BAC =90°,CD =12BC ,DE ⊥CE ,DE =CE ,连接AE ,点M 是AE 的中点.(1)如图1,若点D 在BC 边上,连接CM ,当AB =4时,求CM 的长;(2)如图2,若点D 在△ABC 的内部,连接BD ,点N 是BD 中点,连接MN ,NE ,求证:MN ⊥AE ; (3)如图3,将图2中的△CDE 绕点C 逆时针旋转,使∠BCD =30°,连接BD ,点N 是BD 中点,连接MN ,探索MNAC 的值并直接写出结果.一.解答题(共38小题)1.(2020•渝中区校级二模)如图,CA =CB ,∠ACB =90°,点D 为AB 的中点,连接CD ;点E 为CD 的中点,EF =EG =EC ,且∠FEG =90°;点O 为CB 的中点,直线GO 与直线CF 交于点N .(1)如图1,若∠FCD =30°,OC =√2,求CF 的长;(2)连接BG 并延长至点M ,使BG =MG ,连接CM .①如图2,若NG ⊥MB ,求证:AB =√10CM ;②如图3,当点G 、F 、B 共线时,BM 交AC 于点H ,AH =14AC ,请直接写出FCMH 的值.一年模拟新题2.(2020•渝中区二模)如图,在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,E为线段CD上一点(不含端点),连接AE,设F为AE的中点,作CG⊥CF交直线AB于点G.(1)猜想:线段AG、BC、EC之间有何等量关系?并加以证明;(2)如果将题设中的条件“E为线段CD上一点(不含端点)”改变为“E为直线CD上任意一点”,试探究发现线段AG、BC、EC之间有怎样的等量关系,请直接写出你的结论,不用证明.3.(2020•沙坪坝区校级一模)在△ABC中,AE⊥CD且AE=CD,∠CAE+2∠BAE=90°.(1)如图1,若△ACE为等边三角形,CD=2√3,求AB的长;(2)如图2,作EG⊥AB,求证:AD=√2BE;(3)如图3,作EG⊥AB,当点D与点G重合时,连接BF,请直接写出BF与EC之间的数量关系.4.(2020•南岸区模拟)如图,在△ABC中,∠BAC=90°,AB=AC=6,AD⊥BC于点D.点G是射线AD上一点.(1)若GE⊥GF,点E,F分别在AB,AC上,当点G与点D重合时,如图①所示,容易证明AE+AF=√2AD.当点G在线段AD外时,如图②所示,点E与点B重合,猜想并证明AE,AF与AG存在的数量关系.(2)当点G在线段AD上时,AG+BG+CG的值是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.5.(2020•南岸区校级模拟)△ABC与△ADE都是等边三角形,DE与AC交于点P,点P恰为DE的中点,延长AD交BC于点F,连结BD、CD,取CD的中点Q,连结PQ.求证:PQ=12BD.(1)如图1,理清思路,完成解答:本题证明的思路可以用下列框图表示:根据上述思路,请你完整地书写本题的证明过程;(2)如图2,特殊位置,求线段长:若点P为AC的中点,连接PF,已知PQ=√3,求PF的长.(3)知识迁移,探索新知:若点P是线段AC上任意一点,直接写出PF与CD的数量关系.6.(2020•九龙坡区校级模拟)【初步探索】(1)如图1:在四边形ABC中,AB=AD,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且EF =BE+FD,探究图中∠BAE、∠F AD、∠EAF之间的数量关系.小王同学探究此问题的方法是:延长FD到点G,使DG=BE.连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是;【灵活运用】(2)如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且EF =BE+FD,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD中,∠ABC+∠ADC=180°AB=AD,若点E在CB的延长线上,点F 在CD的延长线上,如图3所示,仍然满足EF=BE+FD,请写出∠EAF与∠DAB的数量关系,并给出证明过程.7.(2019•渝中区校级一模)已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF,CF.(1)如图1,点D在AC上,请你判断此时线段DF,CF的关系,并证明你的判断;(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45时,若AD=DE=2,AB=6,求此时线段CF的长.8.(2019•重庆模拟)一节数学课后,老师布置了一道课后练习:△ABC是等边三角形,点D是线段BC上的点,点E为△ABC的外角平分线上一点,且∠ADE=60°,如图①,当点D是线段BC上(除B,C 外)任意一点时,求证:AD=DE(1)理清思路,完成解答本题证明思路可以用下列框图表:根据上述思路,请你完整地书写本题的证明过程;(2)特殊位置,计算求解当点D为BC的中点时,等边△ABC的边长为6,求出DE的长;(3)知识迁移,探索新知当点D在线段BC的延长线上,且满足CD=BC时,若AB=2,请直接写出△ADE的面积(不必写解答过程)9.(2020•南岸区校级模拟)如图1,直角三角形△ABC中,∠ACB=90°,AC=4,∠A=60°,O为BC中点,将△ABC 绕O 点旋转180°得到△DCB .一动点P 从A 出发,以每秒1的速度沿A →B →D 的路线匀速运动,过点P 作直线PM ⊥AC 交折线段A ﹣C ﹣D 于M .(1)如图2,当点P 运动2秒时,另一动点Q 也从A 出发沿A →B →D 的路线运动,且在AB 上以每秒1的速度匀速运动,在BD 上以每秒2的速度匀速运动,过Q 作直线QN ∥PM 交折线段A ﹣C ﹣D 于N ,设点Q 的运动时间为t 秒,(0<t <10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.(2)如图3,当点P 开始运动的同时,另一动点R 从B 处出发沿B →C →D 的路线运动,且在BC 上以每秒√32的速度匀速运动,在CD 上以每秒2的速度匀速运动,是否存在这样的P 、R .使△BPR 为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由.10.(2019秋•沙坪坝区校级期末)如图,在菱形ABCD 中,∠ABC =60°,连接AC ,动点P 从A 点出发沿射线AB 方向运动,同时动点Q 从B 点出发以与P 点相同的速度沿射线BC 方向运动,连接AQ ,CP ,直线AQ 与直线CP 交于点H .(1)如图1,当P ,Q 两点分别在线段AB 和线段BC 上时,直接写出∠CHQ 的度数;(2)如图2,当P ,Q 两点分别运动到线段AB 和线段BC 的延长线上时,试问(1)问中的结论是否成立:若成立请说明理由,若不成立,请求出∠CHQ 的度数;(3)如图3,在(2)问的前提下,连接DH ,过点D 作DE ⊥PH 交PH 延长线于点E .求证:AH ﹣CE =12DH .11.(2020春•沙坪坝区校级月考)如图,正方形ABCD 中,对角线AC ,BD 交于点O ,点E ,点F 分别在线段OB ,线段AB 上,且AF =OE ,连接AE 交OF 于G ,连接DG 交AO 于H .(1)如图1,若点E为线段BO中点,AE=√5,求BF的长;(2)如图2,若AE平分∠BAC,求证:FG=HG;(3)如图3,点E在线段BO(含端点)上运动,连接HE,当线段HE长度取得最大值时,直接写出cos ∠HDO的值.12.(2020•沙坪坝区自主招生)在▱ABCD中,AF平分∠BAD交BC于点F,∠BAC=90°,点E是对角线AC上的点,连结BE.(1)如图1.若AB=AE,BF=3,求BE的长;(2)如图2,若AB=AE,点G是BE的中点,∠F AG=∠BFG,求证:AB=√10FG;(3)如图3,以点E为直角顶点,在BE的右下方作等腰直角△BEM,若点E从点A出发,沿AC运动到点C停止,设在点E运动过程中,BM的中点N经过的路径长为m,AC的长为n,请直接写出nm的值.13.(2020•巴南区自主招生)已知,在矩形ABCD中,AB=2,点E在边BC上,且AE⊥DE,AE=DE,点F是BC的延长线上一点,AF与DE相交于点G,DH⊥AF,垂足为H,DH的延长线与BC相交于点K.(1)如图1,求AD的长;(2)如图2,连接KG,求证:AG=DK+KG;(3)如图3,设△ADM与△ADH关于AD对称,点N、Q分别是MA、MD的中点,请直接写出BN+NQ 的最大值.14.(2020•南岸区自主招生)如图1,在正方形ABCD中,点E是边BC上一点,连接AE,过点E作EM ⊥AE,交对角线AC于点M,过点M作MN⊥AB,垂足为N,连接NE.(1)求证:AE=√2NE+ME;(2)如图2,延长EM至点F,使EF=EA,连接AF,过点F作FH⊥DC,垂足为H.猜想CH与FH存在的数量关系,并证明你的结论;(3)在(2)的条件下,若点G是AF的中点,连接GH.当GH=CH时,直接写出GH与AC之间存在的数量关系.15.(2020•北碚区自主招生)如图1,在正方形ABCD中,对角线AC、BD相交于点O,点E为线段BO上一点,连接CE,将CE绕点C顺时针旋转90°得到CF,连接EF交CD于点G.(1)若AB=4,BE=√2,求△CEF的面积.(2)如图2,线段FE的延长线交AB于点H,过点F作FM⊥CD于点M,求证:BH+MG=√22BE;(3)如图3,点E为射线OD上一点,线段FE的延长线交直线CD于点G,交直线AB于点H,过点F 作FM垂直直线CD于点M,请直接写出线段BH、MG、BE的数量关系.16.(2019秋•九龙坡区校级期末)已知,在平行四边形ABCD中,∠D=60°,点F,G在边BC上,且AF=AG.(1)如图1,若AG平分∠F AC,∠AFC=5∠BAF,且AF=4,求线段AC的长;(2)如图2,点E在边AB上,且BE=EF,证明:AE=BG;(3)在(2)的条件下,连接CE(如图3),若∠AEC=∠ACD,你能得到AD,FG,BE怎样的数量关系?试证明你的猜想.17.(2020春•沙坪坝区校级月考)如图,已知在矩形ABCD中,AD=8,CD=4,点E从点D出发,沿线段DA以每秒1个单位长的速度向点A方向移动,到达A点停止运动;同时点F从点C出发,沿射线CD方向以每秒2个单位长的速度移动,到达D点停止运动,设点E移动的时间为t(秒).(1)当t=1时,求四边形BCFE的面积;(2)设四边形BCFE的面积为S,求S与t之间的关系式,并写出t的取值范围;(3)若F点到达D点后立即返回,并在线段CD上往返运动,当E点到达A点时它们同时停止运动,求当t为何值时,以E,F,D三点为顶点的三角形是等腰三角形,并求出此的等腰三角形的面积S△EDF.18.(2020春•沙坪坝区校级月考)已知,在▱ABCD中,AB⊥BD,AB=BD,E为射线BC上一点,连接AE 交BD于点F.(1)如图1,若点E与点C重合,且AF=2√5,求AD的长;(2)如图2,当点E在BC边上时,过点D作DG⊥AE于G,延长DG交BC于H,连接FH.求证:AF=DH+FH;(3)如图3,当点E在射线BC上运动时,过点D作DG⊥AE于G,M为AG的中点,点N在BC边上且BN=1,已知AB=4√2,请直接写出MN的最小值.19.(2020春•沙坪坝区校级月考)已知:在△ABC中,∠C=90°,BC=AC.(1)如图1,若点D、E分别在BC、AC边上,且CD=CE,连接AD、BE,点O、M、N分别是AB、AD、BE的中点.求证:△OMN是等腰直⻆三角形;(2)将图1中△CDE绕着点C顺时针旋转90°如图2,O、M、N分别为AB、AD、BE中点,则(1)中的结论是否成⽴,并说明理由;(3)如图3,将图1中△CDE绕着点C顺时针旋转,记旋转⻆为α(0<α<360°),O、M、N分别为AB、AD、BE中点,当MN=√10,请求出四边形ABED的⽴积.20.(2019秋•九龙坡区期末)(1)如图1,四边形EFGH中,FE=EH,∠EFG+∠EHG=180°,点A,B分别在边FG,GH上,且∠AEB=12∠FEH,求证:AB=AF+BH.(2)如图2,四边形EFGH中,FE=EH,点M在边EH上,连接FM,EN平分∠FEH交FM于点N,∠ENM=α,∠FGH=180°﹣2α,连接GN,HN.①找出图中与NH相等的线段,并加以证明;②求∠NGH的度数(用含α的式子表示).21.(2019秋•吉州区期末)【问题情境】如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.【探究展示】(1)直接写出AM、AD、MC三条线段的数量关系:;(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.【拓展延伸】(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.22.(2019春•江北区校级期中)如图,在平面直角坐标系中,平行四边形ABCD的边AB在x轴上,点A (﹣2,0),线段AB=8,线段AD=6,且∠BAD=60°,AD与y的交点记为E,连接BE.(1)求▱ABCD的面积.(2)如图2,在线段BE上有两个动点G、K(G在K点上方),且KG=√3,点F为BC中点,点P为线段CD上一动点,当FG+GK+KP的值最小时,求出此时P点的坐标;此时在y轴上找一点H,x轴上线一点M,使得PH+HM−√22AM取得最小值,请求出PH+HM−√22AM的最小值.(3)如图3,将△AOE沿射线EB平移到△A′O'E'的位置,线段E′A′的中点N落在x轴上,此时再将△A′O'E'绕平面内某点W旋转90°,旋转后的三角形记为△A''O''E'',若△A''O''E'恰好只有两个顶点同时落在直线BC和直线BE上,且△A''E''B''的边均不在直线BC或直线BE上,请求出满足条件的W的坐标.23.(2019秋•北碚区校级月考)已知平行四边形ABCD中,N是边BC上一点,延长DN、AB交于点Q,过A作AM⊥DN于点M,连接AN,则AD⊥AN.(1)如图①,若tan∠ADM=34,MN=3,求BC的长;(2)如图②,过点B作BH∥DQ交AN于点H,若AM=CN,求证:DM=BH+NH.24.(2019秋•沙坪坝区校级月考)如图,在平行四边形ABCD中,过A作AE⊥CD于点E,点G,F分别为AD,BC上一点,连接CG交AE于点H,连接AF,AF=AH,∠GCF=∠F AE=45°.(1)若tan∠DAE=23,GH=4,求AF的长;(2)求证:AG+√2GH=GC.25.(2020春•北碚区校级期末)已知在△ABC和△ADE中,∠ACB+∠AED=180°,CA=CB,EA=ED,AB=3.(1)如图1,若∠ACB=90°,B、A、D三点共线,连接CE:①若CE=5√22,求BD长度;②如图2,若点F是BD中点,连接CF,EF,求证:CE=√2EF;(2)如图3,若点D在线段BC上,且∠CAB=2∠EAD,试直接写出△AED面积的最小值.26.(2020春•重庆期末)已知三角形ABC中,∠ACB=90°,点D(0,﹣4),M(4,﹣4).(1)如图1,若点C与点O重合,A(﹣2,2)、B(4,4),求△ABC的面积;(2)如图2,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,若∠AOG=55°,求∠CEF的度数;(3)如图3,AC经过坐标原点O,点C在第三象限且点C在直线DM与x轴之间,N为AC上一点,AB分别与x轴,直线DM交于点G,F,BC交DM于点E,∠NEC+∠CEF=180°,求证:∠NEF=2∠AOG.27.(2020春•沙坪坝区校级月考)已知Rt△ABC中,∠ACB=90°,以AC为斜边作Rt△AEC,∠AEC=90°,AB与CE相交于点D.(1)如图1,AB平分∠CAE,BD=4,CD=5,求AC;(2)如图2,若AC=BC,点F在EA的延长线上,连接FB、FC,FB与CE相交于点G,且∠EAD=∠ACF,求证:AF=2GE;(3)如图3,在(2)的条件下,CE的中垂线与AB相交于点Q,连接EQ,若∠DEQ+2∠ACE=90°,请直接写出线段FC、ED、EQ的关系.28.(2020春•沙坪坝区校级月考)已知等腰直角△ABC中,AB=AC,∠BAC=90°,点D是AC边上一点,以BD为边作等腰直角△BDE,其中BD=BE,∠DBE=90°,边AB与DE交于点F,点G是BC上一点.(1)如图1,若DG⊥DE,连接FG.①若∠ABD=30°,DE=√6+√2,求BF的长度;②求证:DG=EF﹣FG;(2)如图2,若DG⊥BD,EP⊥BE交BA的延长线于点P,连接PG,请猜想线段PG,DG,PE之间的数量关系,并证明.29.(2020春•沙坪坝区校级月考)如图,在等边△ABC中,延长AB至点D,延长AC交BD的中垂线于点E,连接BE,DE.(1)如图1,若DE=3√10,BC=2√3,求CE的长;(2)如图2,连接CD交BE于点M,在CE上取一点F,连接DF交BE于点N,且DF=CD,求证:AB=12EF;(3)在(2)的条件下,若∠AED=45°,直接写出线段BD,EF,ED的等量关系.30.(2020春•沙坪坝区校级月考)在△ABC中,AC=BC,点G是直线BC上一点,CF⊥AG,垂足为点E,BF⊥CF于点F,点D为AB的中点,连接DF.(1)如图1,如果∠ACB=90°,且G在CB边上,设CF交AB于点R,且E为CR的中点,若CG=1,求线段BG的长;(2)如图2,如果∠ACB=90°,且G在CB边上,求证:EF=√2DF;(3)如图3,如果∠ACB=60°,且G在CB的延长线上,∠BAG=15°,请探究线段EF、BD之间的数量关系,并直接写出你的结论.31.(2020春•沙坪坝区校级月考)如图所示,△ABC为等边三角形,点D,点E分别在CA,CB的延长线上,连接BD,DE,DB=DE.(1)如图1,若CA:AD=3:7,BE=4,求EC的长;(2)如图2,点F在AC上,连接BE,∠DBF=60°,连接EF,①求证:BF+EF=BD;②如图3,若∠BDE=30°,直接写出EFBF的值.32.(2020春•沙坪坝区校级月考)在△ABC,△CDE中,∠BAC=∠DEC=90°,连接BD,F为BD中点,连接AF,EF.(1)如图1,若A,C,E三点在同一直线上,∠ABC=∠EDC=45°,已知AB=3,DE=5,求线段AF的长;(2)如图2,若∠ABC=∠EDC=45°,求证:△AEF为等腰直角三角形;(3)如图3,若∠ABC=∠EDC=30°,请判断△AEF的形状,并说明理由.33.(2019秋•渝中区校级期末)如图,在△ABC中,∠ABC=30°,以AC为边作等边△ACD,连接BD.(1)如图1,若∠ACB=90°,AB=4,求△BCD的面积;(2)如图2,若∠ACB<90°,点E为BD中点,连接AE、CE,且AE⊥CE,延长BC至点F,连接AF,使得∠F=30°,求证:AF=CE+√3AE.34.(2020春•南岸区期末)把△ABC绕着点A逆时针旋转α,得到△ADE.(1)如图1,当点B恰好在ED的延长线上时,若α=60°,求∠ABC的度数;(2)如图2,当点C恰好在ED的延长线上时,求证:CA平分∠BCE;(3)如图3,连接CD,如果DE=DC,连接EC与AB的延长线交于点F,直接写出∠F的度数(用含α的式子表示).35.(2020春•渝中区期末)如图,在正方形ABCD中,E为CD边上一点,以DE为边向外作正方形DEFG,将正方形DEFG绕点D顺时针旋转,连接AG.(1)如图1,若AD=2√3、DE=2,当∠ADG=150°时,求AG的长;(2)如图2,正方形DEFG绕点D旋转的过程中,取AG的中点M,连接DM、CE,猜想:DM和CE 之间有何等量关系?并利用图2加以证明.36.(2020春•沙坪坝区校级月考)在菱形ABCD中,∠ABC=60°,点M是对角线BD上一动点,将线段CM绕点C顺时针旋转120°到CN,连接DN,连接NM并延长,分别交AB、CD于点P、Q.(1)如图1,若CM⊥BD且PQ=4√3,求菱形ABCD的面积;(2)如图2,求证:PM=QN.37.(2019秋•江津区期末)如图,四边形ABCD是平行四边形,AC=CD,∠BAC=90°,点E为BC边上一点,将AE绕点A顺时针旋转90°后得到线段AF,连接FB,FB⊥BC.且FB的延长线与AE的延长线交于点G,点E是AG的中点.(1)若BG=2,BE=1,求FG的长;(2)求证:√2AB=BG+2BE.38.(2020春•渝北区期中)如图1,光线照射在光滑表面上时会发生反射现象,入射光线与镜面的夹角等于出射光线与镜面的夹角,即∠1=∠2.(1)如图1,AB、BC为两个平面镜,∠B=90°,一束光线l经两次反射后,经点D,由从点E射出,求证:DM∥EN;(2)如图2,AB、BC为两个平面镜,∠B=122°,一束光线l经两次反射后,经点D,且由从点E射出,且EN⊥AB,求∠ADM的度数;(3)如图3,已知FL∥GS,FG⊥GS,∠LPK=∠SQK=30°,∠PKQ绕点K顺时针旋转,旋转速度为5°/秒,记旋转角α(0<α≤360°),同时,射线FG绕点F顺时针旋转,旋转速度为3°/秒,记旋转角β(0<β≤360°),当FG所在直线平行于∠PKQ边所在直线时,直接写出对应时间t的所有值.。
2019-2020总复习之中考数学几何压轴专题,中考几何专题训练及参考答案

1.(10分)如图,点E在▱ABCD内部,AF∥BE,DF∥CE.(1)求证:△BCE≌△ADF;(2)设▱ABCD的面积为S,四边形AEDF的面积为T,求的值.2.(14分)如图,Rt△ABC中,∠ACB=90°,AC=BC,P为△ABC内部一点,且∠APB =∠BPC=135°.(1)求证:△P AB∽△PBC;(2)求证:P A=2PC;(3)若点P到三角形的边AB,BC,CA的距离分别为h1,h2,h3,求证h12=h2•h3.3.(10分)阅读下面的例题及点拨,并解决问题:例题:如图①,在等边△ABC中,M是BC边上一点(不含端点B,C),N是△ABC的外角∠ACH的平分线上一点,且AM=MN.求证:∠AMN=60°.点拨:如图②,作∠CBE=60°,BE与NC的延长线相交于点E,得等边△BEC,连接EM.易证:△ABM≌△EBM(SAS),可得AM=EM,∠1=∠2;又AM=MN,则EM =MN,可得∠3=∠4;由∠3+∠1=∠4+∠5=60°,进一步可得∠1=∠2=∠5,又因为∠2+∠6=120°,所以∠5+∠6=120°,即:∠AMN=60°.问题:如图③,在正方形A1B1C1D1中,M1是B1C1边上一点(不含端点B1,C1),N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,且A1M1=M1N1.求证:∠A1M1N1=90°.4.(10分)如图1,对角线互相垂直的四边形叫做垂美四边形.(1)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.试证明:AB2+CD2=AD2+BC2;(3)解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.5.(10分)如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.(1)如图①所示,若∠ABC=30°,求证:DF+BH=BD;(2)如图②所示,若∠ABC=45°,如图③所示,若∠ABC=60°(点M与点D重合),猜想线段DF、BH与BD之间又有怎样的数量关系?请直接写出你的猜想,不需证明.6.(10分)如图,在矩形ABCD中,AD=4cm,AB=3cm,E为边BC上一点,BE=AB,连接AE.动点P、Q从点A同时出发,点P以cm/s的速度沿AE向终点E运动;点Q 以2cm/s的速度沿折线AD﹣DC向终点C运动.设点Q运动的时间为x(s),在运动过程中,点P,点Q经过的路线与线段PQ围成的图形面积为y(cm2).(1)AE=3cm,∠EAD=45°;(2)求y关于x的函数解析式,并写出自变量x的取值范围;(3)当PQ=cm时,直接写出x的值.7.(14分)问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC 之间的数量关系,并说明理由.问题探究:在“问题情境”的基础上.(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN 翻折,点P落在点P'处,若正方形ABCD的边长为4,AD的中点为S,求P'S的最小值.问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=,请直接写出FH 的长.8.(10分)如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°.(1)如图1,连接BE,CD,BE的廷长线交AC于点F,交CD于点P,求证:BP⊥CD;(2)如图2,把△ADE绕点A顺时针旋转,当点D落在AB上时,连接BE,CD,CD 的延长线交BE于点P,若BC=6,AD=3,求△PDE的面积.1.【分析】(1)根据ASA证明:△BCE≌△ADF;(2)根据点E在▱ABCD内部,可知:S△BEC+S△AED=S▱ABCD,可得结论.【解答】解:(1)∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ABC+∠BAD=180°,∵AF∥BE,∴∠EBA+∠BAF=180°,∴∠CBE=∠DAF,同理得∠BCE=∠ADF,在△BCE和△ADF中,∵,∴△BCE≌△ADF(ASA);(2)∵点E在▱ABCD内部,∴S△BEC+S△AED=S▱ABCD,由(1)知:△BCE≌△ADF,∴S△BCE=S△ADF,∴S四边形AEDF=S△ADF+S△AED=S△BEC+S△AED=S▱ABCD,∵▱ABCD的面积为S,四边形AEDF的面积为T,∴==2.【点评】此题主要考查了平行四边形的性质以及全等三角形的判定与性质,熟练利用三角形和平行四边形边的关系得出面积关系是解题关键.2.【分析】(1)利用等式的性质判断出∠PBC=∠P AB,即可得出结论;(2)由(1)的结论得出,进而得出,即可得出结论;(3)先判断出Rt△AEP∽Rt△CDP,得出,即h3=2h2,再由△P AB∽△PBC,判断出,即可得出结论.【解答】解:(1)∵∠ACB=90°,AB=BC,∴∠ABC=45°=∠PBA+∠PBC又∠APB=135°,∴∠P AB+∠PBA=45°∴∠PBC=∠P AB又∵∠APB=∠BPC=135°,∴△P AB∽△PBC(2)∵△P AB∽△PBC∴在Rt△ABC中,AB=AC,∴∴∴P A=2PC(3)如图,过点P作PD⊥BC,PE⊥AC交BC、AC于点D,E,∴PF=h1,PD=h2,PE=h3,∵∠CPB+∠APB=135°+135°=270°∴∠APC=90°,∴∠EAP+∠ACP=90°,又∵∠ACB=∠ACP+∠PCD=90°∴∠EAP=∠PCD,∴Rt△AEP∽Rt△CDP,∴,即,∴h3=2h2∵△P AB∽△PBC,∴,∴∴.即:h12=h2•h3.【点评】此题主要考查了相似三角形的判定和性质,等腰直角三角形的性质,判断出∠EAP=∠PCD是解本题的关键.3.【分析】延长A1B1至E,使EB1=A1B1,连接EM1C、EC1,则EB1=B1C1,∠EB1M1中=90°=∠A1B1M1,得出△EB1C1是等腰直角三角形,由等腰直角三角形的性质得出∠B1EC1=∠B1C1E=45°,证出∠B1C1E+∠M1C1N1=180°,得出E、C1、N1,三点共线,由SAS证明△A1B1M1≌△EB1M1得出A1M1=EM1,∠1=∠2,得出EM1=M1N1,由等腰三角形的性质得出∠3=∠4,证出∠1=∠2=∠5,得出∠5+∠6=90°,即可得出结论.【解答】解:延长A1B1至E,使EB1=A1B1,连接EM1C、EC1,如图所示:则EB1=B1C1,∠EB1M1中=90°=∠A1B1M1,∴△EB1C1是等腰直角三角形,∴∠B1EC1=∠B1C1E=45°,∵N1是正方形A1B1C1D1的外角∠D1C1H1的平分线上一点,∴∠M1C1N1=90°+45°=135°,∴∠B1C1E+∠M1C1N1=180°,∴E、C1、N1,三点共线,在△A1B1M1和△EB1M1中,,∴△A1B1M1≌△EB1M1(SAS),∴A1M1=EM1,∠1=∠2,∵A1M1=M1N1,∴EM1=M1N1,∴∠3=∠4,∵∠2+∠3=45°,∠4+∠5=45°,∴∠1=∠2=∠5,∵∠1+∠6=90°,∴∠5+∠6=90°,∴∠A1M1N1=180°﹣90°=90°.【点评】此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质等知识;本题综合性强,熟练掌握正方形的性质,通过作辅助线构造三角形全等是解本题的关键.4.【分析】(1)根据垂直平分线的判定定理证明即可;(2)根据垂直的定义和勾股定理解答即可;(3)根据垂美四边形的性质、勾股定理、结合(2)的结论计算.【解答】解:(1)四边形ABCD是垂美四边形.证明:∵AB=AD,∴点A在线段BD的垂直平分线上,∵CB=CD,∴点C在线段BD的垂直平分线上,∴直线AC是线段BD的垂直平分线,∴AC⊥BD,即四边形ABCD是垂美四边形;(2)猜想结论:垂美四边形的两组对边的平方和相等.如图2,已知四边形ABCD中,AC⊥BD,垂足为E,求证:AD2+BC2=AB2+CD2证明:∵AC⊥BD,∴∠AED=∠AEB=∠BEC=∠CED=90°,由勾股定理得,AD2+BC2=AE2+DE2+BE2+CE2,AB2+CD2=AE2+BE2+CE2+DE2,∴AD2+BC2=AB2+CD2;故答案为:AD2+BC2=AB2+CD2.(3)连接CG、BE,∵∠CAG=∠BAE=90°,∴∠CAG+∠BAC=∠BAE+∠BAC,即∠GAB=∠CAE,在△GAB和△CAE中,,∴△GAB≌△CAE(SAS),∴∠ABG=∠AEC,又∠AEC+∠AME=90°,∴∠ABG+∠AME=90°,即CE⊥BG,∴四边形CGEB是垂美四边形,由(2)得,CG2+BE2=CB2+GE2,∵AC=4,AB=5,∴BC=3,CG=4,BE=5,∴GE2=CG2+BE2﹣CB2=73,∴GE=.【点评】本题考查的是正方形的性质、全等三角形的判定和性质、垂直的定义、勾股定理的应用,正确理解垂美四边形的定义、灵活运用勾股定理是解题的关键.5.【分析】(1)连接CF,由垂心的性质得出CF⊥AB,证出CF∥BH,由平行线的性质得出∠CBH=∠BCF,证明△BMH≌△CMF得出BH=CF,由线段垂直平分线的性质得出AF=CF,得出BH=AF,AD=DF+AF=DF+BH,由直角三角形的性质得出AD=BD,即可得出结论;(2)同(1)可证:AD=DF+AF=DF+BH,再由等腰直角三角形的性质和含30°角的直角三角形的性质即可得出结论.【解答】(1)证明:连接CF,如图①所示:∵AD⊥BC,BE⊥AC,∴CF⊥AB,∵BH⊥AB,∴CF∥BH,∴∠CBH=∠BCF,∵点M是BC的中点,∴BM=MC,在△BMH和△CMF中,,∴△BMH≌△CMF(ASA),∴BH=CF,∵AB=BC,BE⊥AC,∴BE垂直平分AC,∴AF=CF,∴BH=AF,∴AD=DF+AF=DF+BH,∵在Rt△ADB中,∠ABC=30°,∴AD=BD,∴DF+BH=BD;(2)解:图②猜想结论:DF+BH=BD;理由如下:同(1)可证:AD=DF+AF=DF+BH,∵在Rt△ADB中,∠ABC=45°,∴AD=BD,∴DF+BH=BD;图③猜想结论:DF+BH=BD;理由如下:同(1)可证:AD=DF+AF=DF+BH,∵在Rt△ADB中,∠ABC=60°,∴AD=BD,∴DF+BH=BD.【点评】本题考查了全等三角形的判定与性质、垂心的性质、平行线的性质、等腰直角三角形的性质、含30°角的直角三角形的性质等知识;熟练掌握直角三角形的性质,证明三角形全等是解题的关键.6.【分析】(1)由勾股定理可求AE的长,由等腰三角形的性质可求∠EAD的度数;(2)分三种情况讨论,由面积和差关系可求解;(3)分三种情况讨论,由勾股定理可求解.【解答】解:(1)∵AB=3cm,BE=AB=3cm,∴AE==3cm,∠BAE=∠BEA=45°∵∠BAD=90°∴∠DAE=45°故答案为:3,45(2)当0<x≤2时,如图,过点P作PF⊥AD,∵AP=x,∠DAE=45°,PF⊥AD∴PF=x=AF,∴y=S△PQA=×AQ×PF=x2,(2)当2<x≤3时,如图,过点P作PF⊥AD,∵PF=AF=x,QD=2x﹣4∴DF=4﹣x,∴y=x2+(2x﹣4+x)(4﹣x)=﹣x2+8x﹣8当3<x≤时,如图,点P与点E重合.∵CQ=(3+4)﹣2x=7﹣2x,CE=4﹣3=1cm ∴y=(1+4)×3﹣(7﹣2x)×1=x+4(3)当0<x≤2时∵QF=AF=x,PF⊥AD∴PQ=AP∵PQ=cm∴x=∴x=当2<x≤3时,过点P作PM⊥CD∴四边形MPFD是矩形∴PM=DF=4﹣2x,MD=PF=x,∴MQ=x﹣(2x﹣4)=4﹣x∵MP2+MQ2=PQ2,∴(4﹣2x)2+(4﹣x)2=∵△<0∴方程无解当3<x≤时,∵PQ2=CP2+CQ2,∴=1+(7﹣2x)2,∴x=综上所述:x=或【点评】本题是四边形综合题,考查了矩形的判定和性质,勾股定理,等腰三角形的性质,利用分类讨论思想解决问题是本题的关键.7.【解答】问题情境:解:线段DN、MB、EC之间的数量关系为:DN+MB=EC;理由如下:∵四边形ABCD是正方形,∴∠ABE=∠BCD=90°,AB=BC=CD,AB∥CD,过点B作BF∥MN分别交AE、CD于点G、F,如图1所示:∴四边形MBFN为平行四边形,∴NF=MB,∴BF⊥AE,∴∠BGE=90°,∴∠CBF+∠AEB=90°,∵∠BAE+∠AEB=90°,∴∠CBF=∠BAE,在△ABE和△BCF中,,∴△ABE≌△BCF(ASA),∴BE=CF,∵DN+NF+CF=BE+EC,∴DN+MB=EC;问题探究:解:(1)连接AQ,过点Q作HI∥AB,分别交AD、BC于点H、I,如图2所示:∵四边形ABCD是正方形,∴四边形ABIH为矩形,∴HI⊥AD,HI⊥BC,HI=AB=AD,∵BD是正方形ABCD的对角线,∴△DHQ是等腰直角三角形,HD=HQ,AH=QI,∵MN是AE的垂直平分线,∴AQ=QE,在Rt△AHQ和Rt△QIE中,,∴Rt△AHQ≌Rt△QIE(HL),∴∠AQH=∠QEI,∴∠AQH+∠EQI=90°,∴∠AQE=90°,∴△AQE是等腰直角三角形,∴∠EAQ=∠AEQ=45°,即∠AEF=45°;(2)连接AC交BD于点O,如图3所示:则△APN的直角顶点P在OB上运动,设点P与点B重合时,则点P′与点D重合;设点P与点O重合时,则点P′的落点为O′,∵AO=OD,∠AOD=90°,∴∠ODA=∠ADO′=45°,当点P在线段BO上运动时,过点P作PG⊥CD于点G,过点P′作P′H⊥CD交CD 延长线于点H,连接PC,∵点P在BD上,∴AP=PC,在△APB和△CPB中,,∴△APB≌△CPB(SSS),∴∠BAP=∠BCP,∵∠BCD=∠MP A=90°,∴∠PCN=∠AMP,∵AB∥CD,∴∠AMP=∠PNC,∴PC=PN,∴AP=PN,∴∠PNA=45°,∴∠PNP′=90°,∴∠P′NH+PNG=90°,∵∠P′NH+∠NP′H=90°,∠PNG+∠NPG=90°,∴∠NPG=∠P′NH,∠PNG=∠NP′H,由翻折性质得:PN=P′N,在△PGN和△NHP'中,,∴△PGN≌△NHP'(ASA),∴PG=NH,GN=P'H,∵BD是正方形ABCD的对角线,∴∠PDG=45°,易得PG=GD,∴GN=DH,∴DH=P'H,∴∠P'DH=45°,故∠P'DA=45°,∴点P'在线段DO'上运动;过点S作SK⊥DO',垂足为K,∵点S为AD的中点,∴DS=2,则P'S的最小值为;问题拓展:解:延长AG交BC于E,交DC的延长线于Q,延长FH交CD于P,如图4:则EG=AG=,PH=FH,∴AE=5,在Rt△ABE中,BE==3,∴CE=BC﹣BE=1,∵∠B=∠ECQ=90°,∠AEB=∠QEC,∴△ABE∽△QCE,∴==3,∴QE=AE=,∴AQ=AE+QE=,∵AG⊥MN,∴∠AGM=90°=∠B,∵∠MAG=∠EAB,∴△AGM∽△ABE,∴=,即=,解得:AM=,由折叠的性质得:AB'=EB=3,∠B'=∠B=90°,∠C'=∠BCD=90°,∴B'M==,AC'=1,∵∠BAD=90°,∴∠B'AM=∠C'F A,∴△AFC'∽△MAB',∴==,解得:AF=,∴DF=4﹣=,∵AG⊥MN,FH⊥MN,∴AG∥FH,∴AQ∥FP,∴△DFP∽△DAQ,∴=,即=,解得:FP=,∴FH=FP=.【点评】本题是四边形综合题目,考查了正方形的性质、翻折变换的性质、勾股定理、相似三角形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解题的关键.8.【分析】(1)根据等腰直角三角形的性质得到AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,求得∠BAE=∠DAC,根据全等三角形的性质得到∠ABE=∠ACD,根据余角的性质即可得到结论;(2)根据全等三角形的性质得到∠ABE=∠ACD,BE=CD,求得∠EPD=90°,得到DE=3,AB=6,求得BD=6﹣3=3,CD==3,根据相似三角形的性质得到PD=,PB=根据三角形的面积公式即可得到结论.【解答】解:(1)∵△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE =90°.∴AD=AE,AB=AC,∠BAC﹣∠EAF=∠EAD﹣∠EAF,即∠BAE=∠DAC,在△ABE与△ADC中,,∴△ABE≌△ADC(SAS),∴∠ABE=∠ACD,∵∠ABE+∠AFB=∠ABE+∠CFP=90°,∴∠CPF=90°,∴BP⊥CD;(2)在△ABE与△ACD中,,∴△ABE≌△ACD(SAS),∴∠ABE=∠ACD,BE=CD,∵∠PDB=∠ADC,∴∠BPD=∠CAB=90°,∴∠EPD=90°,BC=6,AD=3,求△PDE的面积.∵BC=6,AD=3,∴DE=3,AB=6,∴BD=6﹣3=3,CD==3,∵△BDP∽△CDA,∴==,∴==,∴PD=,PB=∴PE=3﹣=,∴△PDE的面积=××=.【点评】本题考查了旋转的性质,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰直角三角形的性质.熟练掌握旋转的性质是解题的关键.。
中考数学压轴题:几何探究题

几何探究题(10道)1.如图①,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.(1)判断BF与AC的数量关系并说明理由.(2)如图②,将△ACD沿线段AD对折,点C落在BD 上的点M,AM与BE相交于点N,当DE∥AM时,①求证:AE=EC;②求∠MAC的度数以及线段NE与AC的数量关系.第1题图解:(1)BF=AC,理由是:∵AD⊥BC,BE⊥AC,∴∠ADB=∠AEF=90°,∵∠ABC=45°,∴△ABD是等腰直角三角形,∴AD =BD ,∵∠AFE =∠BFD ,∴∠DAC =∠EBC ,在△ADC 和△BDF 中,⎪⎩⎪⎨⎧︒=∠=∠=∠=∠90BDF ADC BDAD DBF DAC , ∴△ADC ≌△BDF (ASA ),∴BF =AC ;(2)①由折叠得:MD =DC ,∵DE ∥AM ,∴AE =EC ,②∵AE =EC ,BE ⊥AC ,∴AB =BC ,由(1)得:△ADC ≌△BDF ,∵△ADC ≌△ADM ,∴△BDF ≌△ADM ,∴∠DBF=∠MAD=22.5°,∴∠MAC=2∠MAD=45°,∵∠NEA=90°,∴△AEN是等腰直角三角形,1AC.∴EN=AE=EC,∴EN=22.在长方形ABCD中,点E是AD的中点,将△ABE沿BE折叠后得到对应的△GBE,将BG延长交直线DC于点F.(1)如果点G在长方形ABCD的内部,如图①所示.①求证:GF=DF;1DC,AD=4,求AB的长度.②若DF=2(2)如果点G在长方形ABCD的外部,如图②所示,AD的值. DF=kDC(k>1).请用含k的代数式表示AB第2题图解:(1)①连接EF ,如解图第2题解图根据翻折的性质得,∠EGF =∠A =90°,EG =AE =ED , 在Rt △EGF 和Rt △EDF 中,⎩⎨⎧==EF EF ED EG , ∴Rt △EGF ≌Rt △EDF (HL ),∴GF =DF ;②由①知,GF =DF ,设DF =x ,BC =y ,则GF =x ,AD =y , ∵DC =2DF ,∴CF =x ,DC =AB =BG =2x ,∴BF =BG +GF =3x ;在Rt △BCF 中,BC 2+CF 2=BF 2,即y 2+x 2=(3x )2 ∴y =22x ,∴ABAD =x y 2=2;∵AD=4,(2)由(1)知,GF=DF,设DF=x,BC=y,则GF=x,AD=y,在Rt△BCF中,BC2+CF2=BF2,3.将一副三角尺按图①摆放,等腰直角三角尺的直角边DF 恰好垂直平分AB,与AC相交于点G,BC=23cm.(1)求GC的长;(2)如图②,将△DEF绕点D顺时针旋转,使直角边DF 经过点C,另一直角边DE与AC相交于点H,分别过H、C作AB的垂线,垂足分别为M、N,通过观察,猜想MD与ND的数量关系,并验证你的猜想;(3)在(2)的条件下,将△DEF沿DB方向平移得到△D'E'F',当D'E'恰好经过(1)中的点G时,请直接写出DD'的长度.第3题图解:(1)在Rt△ABC中,∠BAC=30°,BC=23cm,∴AC=23×3=6cm,AB=43cm,又∵AD=BD,GD⊥AB,∴AD=23cm,在Rt△ADG中,∠BAC=30°,∴DG=2cm,AG=4cm,∴GC=AC-AG=6-4=2cm;(2)MD=ND,证明如下:∵D是AB的中点,∠ACB=90°,∠A=30°,∴BC=BD=AD,∵∠B=60°,∴△CDB为等边三角形.1BD,∵CN⊥BD,∴DN=NB=2在△ADH中,∠HDA=180°-60°-90°=30°,∴∠HDA=∠A=30°,1AD,∴MD=ND;∵HM⊥AB,∴AM=MD=2(3)DD'=23cm.【解法提示】如解图,连接GD,GB;∵GD垂直平分AB,∴AG=BG,∴∠GBA=∠A=30°,∠E'D'A=30°,当点D'与点B 重合时,点G在D'E'上,∴DD'=DB=23cm.第3题解图4.(1)如图①,已知等边△ABC,将直角三角板的60°角顶点D任意放在BC边上(点D不与点B、C重合),使两边分别交线段AB、AC于点E、F.①若AB=6,AE=4,BD=2,则CF= ;②求证:△EBD∽△DCF.(2)若将图①中的三角板的顶点D在BC边上移动,保持三角板与边AB、AC的两个交点E、F都存在,连接EF,如图②所示,问:点D是否存在某一位置,使BD的ED平分∠BEF且FD平分∠CFE?若存在,求出BC 值;若不存在,请说明理由.(3)如图③,在等腰△ABC中,AB=AC,点O为BC 边的中点,将三角形透明纸板的一个顶点放在点O处(其中∠MON=∠B),使两条边分别交边AB、AC于点E、F(点E、F均不与△ABC的顶点重合),连接EF.设∠B=α,则△AEF与△ABC的周长之比为(用含α的表达式表示).图①图②图③第4题图解:(1)①4;【解法提示】∵△ABC是等边三角形,∴AB=BC=AC=6,∠B=∠C=60°.∵AE=4,∴BE=2,则BE=BD,∴△BDE是等边三角形,∴∠BED=60°,又∵∠EDF=60°,∴∠CDF=180°-∠EDF-∠B=60°,则∠CDF=∠C=60°,∴△CDF是等边三角形,∴CF=CD=BC-BD=6-2=4.②证明:∵∠EDF=60°,∠B=60°,∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,∴∠BED=∠CDF.又∠B=∠C=60°,∴△EBD∽△DCF;(2)存在,如解图①,过D作DM⊥BE,DG⊥EF,DN⊥CF,垂足分别是M、G、N,第4题解图①∵ED 平分∠BEF 且FD 平分∠CFE .∴DM =DG =DN .又∠B =∠C =60°,∠BMD =∠CND =90°,∴△BDM ≌△CDN ,∴BD =CD ,即点D 是BC 的中点,∴BC BD =21; (3)如解图②,连接AO ,作OG ⊥BE ,OD ⊥EF ,OH ⊥CF ,垂足分别是G 、D 、H .第4题解图②则∠BGO =∠CHO =90°,∵AB =AC ,O 是BC 的中点,∴∠B =∠C ,OB =OC ,∴△OBG ≌△OCH ,∴OG =OH ,GB =CH ,∠BOG =∠COH =90°-α, 则∠GOH =180°-(∠BOG +∠COH )=2α,∴∠EOF =∠B =α,由(2)题可猜想应用EF =ED +DF =GE +FH (可通过半角旋转证明),则C △AEF =AE +EF +AF =AE +EG +FH +AF =AG +AH =2AG , 设AB =m ,则OB =mcosα,GB =mcos 2α.ααcos cos )(222m m m m OB AB AG OB AB AG C C ABC AEF +-=+=+=∆∆=1-cos α. 5.如图,Rt △ACB 中,∠ACB =90°,AC =BC ,E 点为射线CB 上一动点,连接AE ,作AF ⊥AE 且AF =AE .(1)如图①,过F 点作FD ⊥AC 交AC 于D 点,求证:FD =BC ;(2)如图②,连接BF 交AC 于G 点,若AG =3,CG =1,求证:E 点为BC 中点;(3)当E 点在射线CB 上,连接BF 与直线AC 交于G 点,若BC =4,BE =3,直接写出CGAG 的值.第5题图 (1)证明:∵FD ⊥AC ,∴∠FDA =90°, ∴∠DFA +∠DAF =90°, 同理,∵AF ⊥AE ,∴∠CAE +∠DAF =90°,∴∠DFA =∠CAE ,在△AFD 和△EAC 中,⎪⎩⎪⎨⎧=∠=∠︒=∠=∠AE AF EACAFD ECA ADF 90, ∴△AFD ≌△EAC (AAS ),∴DF =AC ,∵AC =BC ,∴FD =BC ;(2)如解图①,过点F 作FD ⊥AC 于点D ,第5题解图①由(1)得,FD =AC =BC ,AD =CE ,在△FDG 和△BCG 中,⎪⎩⎪⎨⎧=︒=∠=∠∠=∠BC FD BCG FDG BGC FGD 90, ∴△FDG ≌△BCG (AAS ),∴DG =CG =1,∴AD =2,∴CE =2,∵BC =AC =AG +CG =4,∴E 点为BC 中点;(3)311或35.【解法提示】当点E 在CB 的延长线上时,过F 作FD ⊥AG 与AG 的延长线交于点D ,如解图②,第5题解图②BC =AC =4,CE =CB +BE =7,由(1)(2)知:△ADF ≌△ECA ,△GDF ≌△GCB , ∴CG =GD ,AD =CE =7,∴CG =DG =1.5, ∴CG AG =5.15.14+=311, 同理,当点E 在线段BC 上时,CG AG =5.15.14-=35. 6.如图,在Rt △ABC 中,∠BAC =90°,AB =AC ,点D 为AB 延长线上一点,连接CD ,过A 分别作AM ⊥CD ,垂足为M ,交BC 于点N ,作AP ⊥BC ,垂足为P ,交CD 于点Q .(1)求证:AN =CQ ;(2)如图,点E 在BA 的延长线上,且AE =BD ,连接EN 并延长交CD 于点F ,求证:DQ =EN ;(3)在(2)的条件下,当AE =32AB 时,求FNEN 的值.第6题图证明:(1)∵AP ⊥BC ,AM ⊥CD ,∴∠APN =∠CPQ =90°,∴∠PNA +∠NAP =∠NAP +∠CQP =90°,∴∠PNA =∠CQP ,∵AB =AC ,∠BAC =90°,∴AP =PC ,∴△APN ≌△CPQ (ASA ),∴AN =CQ ;(2)如解图①,连接BQ ,第6题解图① 由(1)知:AP 是BC 的垂直平分线, ∴BQ =CQ , ∵AN =CQ ,∴AN =BQ ,∵BQ =CQ ,∴∠QBC =∠QCB =∠NAP ,∵∠PBA =∠PAB =45°,∴∠QBA =∠BAN ,∴∠DBQ =∠NAE ,在△DBQ 和△NAE 中,⎪⎩⎪⎨⎧=∠=∠=AE BD EAN DBQ AN BQ , ∴△DBQ ≌△EAN (SAS ),∴DQ =EN ; (3)∵AE =32AB ,即AB AE =32, ∴设AE =2x ,AB =3x ,则BD =2x ,DC =34x ,如解图②,过E 作EH ⊥AM ,交MA 的延长线于H ,第6题解图②∴∠H =∠AMD =90°,∴EH ∥DC ,∴△AHE ∽△AMD ,∴52322=+==x x x AD AE AM AH , ∵∠MAC =∠CDA ,∠ACN =∠DAQ =45°,∴△DQA ∽△ANC ,∴3535===x x AN DQ AC AD ,由(2)知:CQ=AN,∴设AH=8m,AM=20m,AN=17m,则MN=3m,∵EH∥FM,∴△EHN∽△FMN,7.如图,点P是正方形ABCD外一点,连接PA、PD,作BM⊥PA,垂足为E,使BM=PA,再作CN⊥PD,垂足为F,使CN=PD,连接PM、PN.(1)如图①,当PA=PD时,直接写出线段PM、PN的位置关系和数量关系;(2)在(1)的条件下,若∠APD=40°,则∠ABM= ;(3)如图②,当PA≠PD时,(1)中的结论是否仍然成立,若成立,请给出证明;若不成立,请说明理由.第7题图解:(1)结论:PM=PN,PM⊥PN.理由:如解图①,连接AM,DN.第7题解图①∵四边形ABCD是正方形,∴AB =BC =CD =AD ,∴∠BAD =90°,∵PE ⊥BM ,∴∠AEB =90°,∴∠PAD +∠EAB =90°,∠EAB +∠ABE =90°, ∴∠PAD =∠ABE ,∵PA =PD ,在△PAD 和△ABE 中,⎪⎩⎪⎨⎧=∠=∠=BAAD ABM PAD BMPA , ∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠AMB =∠APD ,∴MA =MB =PA =PD ,同理可证:ND =NC =PA =PD ,∠DNC =∠APD ,∴∠AME =∠DNF ,∵∠AME +∠MAE =90°,∠DNF +∠NDF =90°, ∴∠MAE =∠NDF ,∴∠PAM =∠PDN ,∴△PAM≌△PDN(SAS),∴PM=PN,∠APM=∠DPN=∠AMP=∠DNP,∵∠AME+∠MAE=90°,∠MAE=∠AMP+∠APM=∠APM+∠NPD,∴∠APD+∠APM+∠NPD=90°,∴∠MPN=90°,∴MP⊥PN.(2)70°;【解法提示】∵PA=PD,∠P=40°,∴∠PAD=∠PDA=70°,由(1)可知:∠ABM=∠PAD=70°.(3)结论仍然成立,理由如下:如解图②,连接MA,延长MA交PF于点Q.第7题解图②由(1)可知:∠PAD=∠ABM,在△PAD 和△ABM 中,⎪⎩⎪⎨⎧=∠=∠=BA AD ABM PAD BM PA ∵PA =BM ,AD =BA ,∴△PAD ≌△MBA (SAS ),∴AM =PD ,∠ADP =∠MAB ,∵四边形ABCD 是正方形,∴∠BAD =∠ADC =90°,AB =AD =CD ,∵∠MAB +∠QAD =90°,∴∠QAD +∠ADP =90°,∴∠AQD =90°,∵PF ⊥CN ,∴∠AQD =∠DFC =90°,∴∠ADQ +∠CDF =90°,∠CDF +∠DCF =90°,∴∠ADQ =∠DCF ,在△ADQ 和△DCF 中,⎪⎩⎪⎨⎧=∠=∠∠=∠CD AD DCF ADQ DFC AQD ,∴△AQD ≌△DFC (AAS ),∴AQ =DF ,DQ =CF ,∵PD =CN ,∴PQ =FN ,MQ =PF ,∵∠MQP =∠PFN =90°,∴△MQP ≌△PFN (SAS ),∴PM =PN ,∠MPQ =∠N ,∵∠N +∠FPN =90°,∴∠MPQ +∠FPN =90°,∴∠MPN =90°,∴PM ⊥PN .8、在Rt △ABC 中,∠ACB =90°,∠B =30°,M 为AB 中点,点P 为BC 延长线上一点,CP <BC ,连接PM ,AC =n ,CP =m .(1)如图①,将射线MP 绕点M 逆时针旋转60°交CA 延长线于点D ,且BC =AD +CP.①在图中找出与∠MDC相等的角,并加以证明;m的值;②求n(2)如图②,若将射线MP绕点M顺时针旋转60°交AC延长线于点H,求CH的长(用含有m,n的式子表示)第8题图①第8题图②解:(1)①结论:∠ADM=∠PMA.理由:如解图①,连接CM.∵∠ACB=90°,∠B=30°,∴∠BAC=60°,∵BM=MA,∴CM=MA=BM,∴△AMC是等边三角形,∴∠AMC=∠PMN=60°,∴∠PMC=∠AMD,∵∠BAC=∠AMD+∠ADM=60°,∠AMP+∠PMC=60°∴∠ADM=∠PMA.第8题解图①②如解图①,连接CM、作CK∥AB交PM于点K.∵CK∥AB,由(1)知△AMC是等边三角形,∴∠MAC=∠MCA=∠AMC=60°,MA=MC,∵CK∥AB,∴∠ACK=∠MAC=60°,∠AMK=∠MKC,∴∠DAM=∠MCK=120°,∵∠ADM=∠AMP,∴∠MKC=∠MDA,在△MCK 和△MAD 中,⎪⎩⎪⎨⎧=∠=∠∠=∠MCMA MAD MCK MDAMKC ,∴△MCK ≌△MAD ,∵CK ∥BM ,∴△PKC ∽△PMB ,∴AD =CK ,∵BC =AD +PC ,整理得:m 2+mn -3n 2=0,(3)如解图②,连接CM 、作CK ∥AB 交PM 于点K .第8题解图② ∵∠PMH =∠ACM =60°, ∴∠PMC +∠CMH =∠CMH +∠H ,∴∠CMK =∠H ,∵∠HCM =∠MCK =120°,∴△HCM ∽△MCK ,∴CK CM MC HC =, ∴nm mnn n HC 3+=, ∴HC =mn mn 23+. 9. 已知四边形ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF =90°,BE =EF ,连接DF ,G 为DF 的中点,连接EG,CG,EC.(1)如图①,若点E在CB边的延长线上,直接写出EC的值;EG与GC的位置关系及GC(2)将图①中的△BEF绕点B顺时针旋转至图②所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图①中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=2,当E,F,D三点共线时,求DF的长及tan∠ABF的值.第9题图EC=2,解:(1)EG⊥CG,GC理由如下:如解图①,过G作GH⊥EC于点H,∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,∵G 为DF 中点, ∴H 为EC 中点, ∴EG =GC ,GH =21(EF +DC )=21(EB +BC ), 即GH =EH =HC ,∴∠EGC =90°,即△EGC 是等腰直角三角形, ∴GC EC =2;第9题解图① 第9题解图② (2)解:结论还成立,理由如下:如图②,延长EG 到H ,使EG =GH ,连接CH 、EC ,延长CD 交EH 于点N ,过E 作BC 的垂线交CB 延长线于点R ,交DF 延长线于点Q ,∵在△EFG 和△HDG 中,⎪⎩⎪⎨⎧=∠=∠=HG EG DGH FGE GD GF ,∴△EFG ≌△HDG (SAS ),∴DH =EF =BE ,∠FEG =∠DHG ,∴EF ∥DH ,又易证ER ∥CD ,∴∠1=∠2,∴∠1=∠2=90°-∠3=∠4,∴∠EBC =180°-∠4=180°-∠1=∠HDC ,在△EBC 和△HDC 中,⎪⎩⎪⎨⎧=∠=∠=CD BC HDC EBC DH BE ,∴△EBC ≌△HDC .∴CE =CH ,∠BCE =∠DCH ,∴∠ECH =∠DCH +∠ECD =∠BCE +∠ECD =∠BCD =90°,∴△ECH 是等腰直角三角形, ∵G 为EH 的中点,∴EG ⊥GC ,GCEC =2, 即(1)中的结论仍然成立;(3)解:如解图③,连接BD ,第9题解图③∵在正方形ABCD 中,AB =2,∴BD =2,∴cos ∠DBE =BD BE =21, ∴∠DBE =60°,∴∠ABE =∠DBE -∠ABD =15°,∴∠ABF =45°-15°=30°,∴tan ∠ABF =33,∴DE =3BE =3, ∴DF =DE -EF =3-1.10.在△ABC 和△ADE 中,AB =AC ,∠BAC =120°,∠ADE =90°,∠DAE =60°,F 为BC 中点,连接BE 、DF ,G 、H 分别为BE ,DF 的中点,连接GH .(1)如图①,若D 在△ABC 的边AB 上时,请直接写出线段GH 与HF 的位置关系 ,HFGH = . (2)如图②,将图①中的△ADE 绕A 点逆时针旋转至图②所示位置,其他条件不变,(1)中结论是否改变?请说明理由;(3)如图③,将图①中的△ADE 绕A 点顺时针旋转至图③所示位置,若C 、D 、E 三点共线,且AE =2,AC =5,求线段BE 的长.图① 图② 图③第10题图 解:(1)如解图①,连接DG ,FG .第10题解图①∵AB =AC ,BF =CF ,∴AF ⊥BC ,∴∠BAF =∠CAF =60°,∵ED ⊥AB ,∴∠BFE =∠BDE =90°,∵BG =GE ,∴DG =21BE ,GF =21BE ,∴DG =FG ,∵DH =HF ,∴GH ⊥DF ,∵∠BAE =60°,∴∠ABE +∠AEB =120°,∵DG=BG=GF=GE,∴∠GBD=∠GDB,∠GEF=∠GFE,∴∠BGD+∠EGF=120°,∴∠DGF=60°,∴△DGF是等边三角形,GH=tan60°=3.∴HF(2)结论不变.理由:如解图②,延长ED至S,使DS=DE,连接AS,BS,CE,FG,DG.第10题解图②∵∠ADE=90°,DS=DE,∴AS=AE,∠DAE=∠DAS=60°,∴∠BAC=∠SAE=120°,∴∠SAB=∠EAC,∵AB=AC,∴△ABS≌△ACE.∴BS=CE,∠ABS=∠ACE,∵F,G分别为BC,BE中点,∴DG=FG,∵H为DF中点,∴GH⊥HF,延长SB交CE延长线于T,∵∠ABS+∠ABT=∠ACE+∠ABT=180°,∴∠BAC+∠T=180°,∴∠T=60°,延长FG交BT于P,∴∠T=∠BPF=∠DGF=60°,(3)如解图③,延长ED到H,使得DH=DE,连接AH,BH,作BM⊥EC于M,设BC交AH于点O.第10题解图③∵AD⊥EH,ED=DH,∴AE=AH,∴∠AEH=∠AHE=30°,∴∠EAH=∠BAC=120°,∴∠BAH=∠CAE,∵AB=AC,AH=AE,∴△BAH≌△CAE(SAS),∴∠BHA=∠AEC=30°,BH=CE,∴∠OBA=∠OHC=30°,∵∠AOB =∠COH ,∴△AOB ∽△COH ,∴△AOC ∽△BOH ,∴∠BHO =∠AOC =30°,∴∠BHE =30°+30°=60°,在Rt △ADE 中,∵AE =2,∠AED =30°,在Rt △EBM 中,11)1233()]332(21[22=-++=.。
2019年中考数学二轮复习几何探究题(压轴题) 综合练习 (含参考答案)

8. 如图,在 Rt△ABC 中,∠ACB=90°,AC=5 cm,∠BAC=60°,动点 M 从点 B 出发,在 BA 边上以 每秒 2 cm 的速度向点 A 匀速运动,同时动点 N 从点 C 出发,在 CB 边上以每秒 3 cm 的速度向点 B 匀速 运动,设运动时间为 t 秒(0≤t≤5),连接 MN. (1)若 BM=BN,求 t 的值; (2)若△MBN 与△ABC 相似,求 t 的值; (3)当 t 为何值时,四边形 ACNM 的面积最小?并求出最小值.
2.如图①,②,③分别以△ABC 的 AB 和 AC 为边向△ABC 外作正三角形(等边三角形)、正四边形(正方 形)、正五边形,BE 和 CD 相交于点 O. (1)在图①中,求证:△ABE≌△ADC. (2)由(1)证得△ABE≌△ADC,由此可推得在图①中∠BOC=120°,请你探索在图②中∠BOC 的度数,并 说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图③中∠BOC=________(填写度数). (4)由此推广到一般情形(如图④),分别以△ABC 的 AB 和 AC 为边向△ABC 外作正 n 边形,BE 和 CD 仍 相交于点 O,猜想∠BOC 的度数为____________________(用含 n 的式子表示).
AC ②在顶点 G 的运动过程中,若CG=t,请直接写出线段 EC、CF 与 BC 的数量关系(不需要写出证明过程); (3)问题解决:
6 如图④,已知菱形边长为 8,BG=7,CF=5,当 t>2 时,求 EC 的长度.
13.某数学兴趣小组在数学课外活动中,研究三角形和正方形的性质时,做了如下探究:在△ABC 中, ∠BAC=90°,AB=AC,点 D 为直线 BC 上一动点(点 D 不与 B,C 重合),以 AD 为边在 AD 右侧作正 方形 ADEF,连接 CF. (1)观察猜想 如图①,当点 D 在线段 BC 上时,①BC 与 CF 的位置关系为:____________. ②BC,CD,CF 之间的数量关系为:____________(将结论直接写在横线上). (2)数学思考 如图②,当点 D 在线段 CB 的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立, 请你写出正确结论再给予证明. (3)拓展延伸 如图③,当点 D 在线段 BC 的延长线上时,延长 BA 交 CF 于点 G,连接 GE.若已知
中考数学几何综合题 练习(附答案)

几何专题综合训练1如图,四边形ABCD 是正方形,△ECF 是等腰直角三角形,其中CE=CF ,G 是CD 与EF 的交点.(1)求证:△BCF ≌△DCE .(2)若BC=5,CF=3,∠BFC=900,求DG :GC 的值.2正方形ABCD 边长为4,M 、N 分别是BC 、CD 上的两个动点,当M 点在BC 上运动时,保持AM 和MN 垂直,(1)证明:Rt Rt ABM MCN △∽△;(2)设BM x ,梯形ABCN 的面积为y ,求y 与x 之间的函数关系式;当M 点运动到什么位置时,四边形ABCN 面积最大,并求出最大面积; (3)当M 点运动到什么位置时Rt Rt ABM AMN △∽△,求x 的值.NDA CBM第2题图3在图3-1至图3-3中,点B是线段AC的中点,点D是线段CE的中点.四边形BCGF和CDHN都是正方形.AE的中点是M.(1)如图3-1,点E在AC的延长线上,点N与点G重合时,点M与点C重合,求证:FM = MH,FM⊥MH;(2)将图3-1中的CE绕点C顺时针旋转一个锐角,得到图3-2,求证:△FMH是等腰直角三角形;(3)将图3-2中的CE缩短到图3-3的情况,△FMH还是等腰直角三角形吗?(不必说明理由)图3-1AHC(M) D E BF G(N)G图3-2AHCDEBF NMAHCDE图3-3BF GMN4如图(1),已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG . (1)连接GD ,求证:△ADG ≌△ABE ;(4分) (2)连接FC ,观察并猜测∠FCN 的度数,并说明理由;(4分)(3)如图(2),将图(1)中正方形ABCD 改为矩形ABCD ,AB =a ,BC =b (a 、b 为常数),E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请用含a 、b 的代数式表示tan ∠FCN 的值;若∠FCN 的大小发生改变,请举例说明N M B E A C D F G图(1)图(2) M B E A C D F G N5如图2-5-7,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.(1)写出y与x的函数关系,并确定自变量x的范围.(2)有人提出一个判断:“关于动点P,⊿PBC面积与⊿PAD面积之和为常数”.请你说明此判断是否正确,并说明理由..答案1. 分析与解答 (1)∵四边形 ABCD 是正方形,∴∠BCF+∠FCD=900,BC=CD .∵△ECF 是等腰直角三角形,CF=CE .∴∠ECD+∠FCD=900.∴∠BCF=∠ECD .∴△BCF ≌△DCE(2)在△BFC 中,BC=5,CF=3,∠BFC=900. ∴4==.∵△BCF ≌△DCE ,∴DE=BF=4,∠BFC=∠DEC=∠FCE=900. ∴DE ∥FC .∴△DGE ∽△CGF .∴DG :GC=DE :CF=4:3.2. .解:(1)在正方形ABCD 中,490AB BC CD B C ===∠=∠=,°, AM MN ⊥ ,90AMN ∴∠=°,90CMN AMB ∴∠+∠=°.在Rt ABM △中,90MAB AMB ∠+∠=°, CMN MAB ∴∠=∠,Rt Rt ABM MCN ∴△∽△. ······················································· 2分 (2)Rt Rt ABM MCN △∽△,44AB BM xMC CN x CN∴=∴=-,, 244x x CN -+∴=, ···················································································································· 4分22214114428(2)102422ABCNx x y S x x x ⎛⎫-+∴==+=-++=--+ ⎪⎝⎭梯形, 当2x =时,y 取最大值,最大值为10. ··················································································· 6分 (3)90B AMN ∠=∠= °,∴要使ABM AMN △∽△,必须有AM ABMN BM=, ································································ 7分 由(1)知AM ABMN MC=, BM MC ∴=,∴当点M 运动到BC 的中点时,ABM AMN △∽△,此时2x =. ···································· 9分3(1)证明:∵四边形BCGF 和CDHN 都是正方形,又∵点N 与点G 重合,点M 与点C 重合,∴FB = BM = MG = MD = DH ,∠FBM =∠MDH = 90°. ∴△FBM ≌ △MDH . ∴FM = MH .NDA CBM答案第2题图∵∠FMB =∠DMH = 45°,∴∠FMH = 90°.∴FM ⊥HM .(2)证明:连接MB 、MD ,如图2,设FM 与AC 交于点P . ∵B 、D 、M 分别是AC 、CE 、AE 的中点, ∴MD ∥BC ,且MD = BC = BF ;MB ∥CD , 且MB =CD =DH .∴四边形BCDM 是平行四边形. ∴ ∠CBM =∠CDM .又∵∠FBP =∠HDC ,∴∠FBM =∠MDH . ∴△FBM ≌ △MDH . ∴FM = MH , 且∠MFB =∠HMD .∴∠FMH =∠FMD -∠HMD =∠APM -∠MFB =∠FBP = 90°. ∴△FMH 是等腰直角三角形.(3)是.。
中考数学复习课件练习:专题复习六 几何综合题有答案

中考数学复习课件+练习:专题复习(六) 几何综合题(有答案)专题复习(六)几何综合题类型1类比探究的几何综合题1.(2019·岳阳)问题背景:已知∠EDF的顶点D 在△ABC的边AB所在直线上(不与A,B重合).DE交AC所在直线于点M,DF交BC所在直线于点N.记△ADM的面积为S1,△BND 的面积为S2.(1)初步尝试:如图1,当△ABC是等边三角形,AB=6,∠EDF=∠A,且DE∥BC,AD =2时,则S1·S2=12;(2)类比探究:在(1)的条件下,先将点D沿AB平移,使AD=4,再将∠EDF绕点D旋转至如图2所示位置,求S1·S2的值;(3)延伸拓展:当△ABC是等腰三角形时,设∠B=∠A=∠EDF=α.(Ⅰ)如图3,当点D在线段AB上运动时,设AD=a,BD=b,求S1·S2的表达式(结果用a,b和α的三角函数表示);(Ⅱ)如图4,当点D在BA的延长线上运动时,设AD=a,BD=b,直接写出S1·S2的表达式,不必写出解答过程.解:(1)在图1中,∵△ABC是等边三角形,∴AB=CB=AC=6,∠A=∠B=60°. ∵DE∥BC,∠EDF=∠A=60°,∴∠BND=∠EDF=60°.∴∠BDN=∠ADM=60°.∴△ADM,△BDN都是等边三角形.∴S1=34×22=3,S2=34×42=4 3.∴S1S2=12.(2)在图2中,设AM=x,BN=y.∵∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,∴∠AMD=∠NDB.∵∠A=∠B,∴△AMD∽△BDN.∴AMBD=ADBN.∴x2=4y.∴xy=8.∵S1=12AD·AM sin60°=3x,S2=12DB·BN sin60°=32y,∴S 1S 2=3x·32y =32xy =12. (3)(Ⅰ)在图3中,设AM =x ,BN =y , 同法可证△AMD ∽△BDN ,可得xy =ab.∵S 1=12AD·AM sin α=12ax sin α, S 2=12DB·BN sin α=12by sin α, ∴S 1S 2=14(ab)2sin 2α. (Ⅱ)在图4中,设AM =x ,BN =y ,同法可证△AMD ∽△BDN ,可得xy =ab ,∵S 1=12AD·AM sin α=12ax sin α, S 2=12DB·BN sin α=12by sin α, ∴S 1S 2=14(ab)2sin 2α. 2.(2019·自贡)如图,已知∠AOB =60°,在∠AOB 的平分线OM 上有一点C ,将一个120°角的顶点与点C 重合,它的两条边分别与直线OA ,OB 相交于点D ,E.(1)当∠DCE绕点C旋转到CD与OA垂直时(如图1),请猜想OE+OD与OC的数量关系,并说明理由;(2)当∠DCE绕点C旋转到CD与OA不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;(3)当∠DCE绕点C旋转到CD与OA的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给予证明;若不成立,线段OD,OE与OC之间又有怎样的数量关系?请写出你的猜想,不需证明.图1图2图3解:(1)∵OM是∠AOB的平分线,∴∠AOC=∠BOC=12∠AOB=30°.∵CD⊥OA,∴∠ODC=90°.∴∠OCD=60°.∴∠OCE=∠DCE-∠OCD=60°.在Rt△OCD中,OD=OC·cos30°=32OC,同理,OE=32OC.∴OD+OE=3OC.(2)(1)中的结论仍然成立.理由:过点C作CF⊥OA于点F,CG⊥OB于点G,∴∠OFC=∠OGC=90°.∵∠AOB=60°,∴∠FCG=120°.同(1)的方法得OF=32OC,OG=32OC.∴OF+OG=3OC.∵CF⊥OA,CG⊥OB,且点C是∠AOB 的平分线OM上一点,∴CF=CG.∵∠DCE=∠FCG=120°,∴∠DCF=∠ECG.∴△CFD≌△CGE.∴DF=EG.∴OF=OD+DF=OD+EG,OG=OE-EG.∴OF+OG=OD+EG+OE-EG=OD+OE.∴OD+OE=3OC.(3)(1)中的结论不成立,结论为OE-OD=3OC.3.(2019·东营)(1)某学校“智慧方园”数学社团遇到这样一个题目:如图1,在△ABC中,点O在线段BC 上,∠BAO=30°,∠OAC=75°,AO=33,BO∶CO=1∶3,求AB的长.经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).请回答:∠ADB=75°,AB=43;(2)请参考以上解决思路,解决问题:如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=33,∠ABC =∠ACB=75°,BO∶OD=1∶3,求DC的长.图1图2 图3解:过点B作BE∥AD交AC于点E.∵AC⊥AD,∴∠DAO =∠BEO=90°.∵∠AOD =∠EOB,∴△AOD∽△EOB.∴BODO=EOAO=BEDA.∵BO∶OD=1∶3,∴EOAO=BEDA=13.∵AO=33,∴EO= 3.∴AE=4 3. ∵∠ABC=∠ACB=75°,∴∠BAC=30°,AB=AC.∴AB=AC=AEcos30°=8.∴BE=12AB=4,AD=3BE=12.在Rt△CAD中,AC2+AD2=CD2,即82+122=CD2,得CD=413. 4.(2019·江西)在菱形ABCD中,∠ABC=60°,点P是射线BD上一动点,以AP为边向右侧作等边△APE,点E的位置随着点P的位置变化而变化.图1图2图3图4(1)如图1,当点E在菱形ABCD内部或边上时,连接CE,BP与CE的数量关系是BP=CE,CE与AD的位置关系是AD⊥CE;(2)当点E在菱形ABCD外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);(3)如图4,当点P在线段BD的延长线上时,连接BE.若AB=23,BE=219,求四边形ADPE的面积.解:(1)提示:连接AC,延长CE交AD于点H,证明△ABP≌△ACE.(2)结论仍然成立.理由:选图2,连接AC交BD于点O,设CE交AD于点H.∵四边形ABCD是菱形,∠ABC=60°,∴△ABC,△ACD都是等边三角形,∠ABD =∠CBD=30°.∴AB=AC.∵△APE是等边三角形,∴AP=AE,∠BAC=∠PAE=60°.∴∠BAP=∠CAE.∴△BAP≌△CAE.∴BP=CE,∠ACE=∠ABP=30°.∵∠CAH=60°,∴∠CAH+∠ACH=90°.∴∠AHC=90°,即CE⊥AD.(3)连接AC交BD于点O,连接CE交AD 于点H.由(2)可知,EC⊥AD,CE=BP.在菱形ABCD中,AD∥BC,∴EC⊥BC.∵BC=AB=23,BE=219,在Rt△BCE中,EC=(219)2-(23)2=8.∴BP=CE=8.∵AC与BD是菱形的对角线,∴∠ABD=12∠ABC=30°,AC⊥BD. ∴BD=2BO=2AB·cos30°=6.∴OA=12AB=3,DP=BP-BD=8-6=2.∴OP=OD+DP=5.在Rt△AOP中,AP=AO2+OP2=27,∴S四边形ADPE =S△ADP+S△AEP=12×2×3+34×(27)2=8 3.5.(2019·烟台)【问题解决】一节数学课上,老师提出了这样一个问题:如图1,点P是正方形ABCD内一点,PA=1,PB=2,PC=3.你能求出∠APB的度数吗?小明通过观察、分析、思考,形成了如下思路:思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;思路二:将△APB绕点B顺时针旋转90°,得到△CP′B,连接PP′,求出∠APB的度数.请参考小明的思路,任选一种写出完整的解答过程.【类比探究】如图2,若点P是正方形ABCD外一点,PA=3,PB=1,PC=11,求∠APB的度数.图1图2解:【问题解决】思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,∴△ABP′≌△CBP.∴∠PBP′=90°,BP′=BP=2,AP′=CP=3.在Rt△PBP′中,BP=BP′=2,∴∠BPP′=45°,根据勾股定理,得PP′=2 BP=2 2.∵AP=1,∴AP2+PP′2=1+8=9.∵AP′2=32=9,∴AP2+PP′2=AP′2.∴△APP′是直角三角形,且∠APP′=90°.∴∠APB=∠APP′+∠BPP′=90°+45°=135°.【类比探究】将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,∴△ABP′≌△CBP.∴∠PBP′=90°,BP′=BP=1,AP′=CP=11.在Rt△PBP′中,BP=BP′=1,∴∠BPP′=45°,根据勾股定理,得PP′=2 BP= 2.∵AP=3,∴AP2+PP′2=9+2=11.∵AP′2=(11)2=11,∴AP2+PP′2=AP′2.∴△APP′是直角三角形,且∠APP′=90°.∴∠APB=∠APP′-∠BPP′=90°-45°=45°.6.(2019·黄石)在△ABC中,E,F分别为线段AB,AC上的点(不与A,B,C重合).(1)如图1,若EF∥BC,求证:S△AEFS△ABC=AE·AFAB·AC;(2)如图2,若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由;(3)如图3,若EF上一点G恰为△ABC的重心,AEAB=34,求S△AEFS△ABC的值.图1图2图3 解:(1)∵EF∥BC,∴△AEF∽△ABC.∴AEAB=AFAC.∴S△AEFS△ABC=(AEAB)2=AEAB·AFAC=AE·AFAB·AC.(2)若EF不与BC平行,(1)中的结论仍然成立.分别过点F,C作AB的垂线,垂足分别为N,H.∵FN⊥AB,CH⊥AB,∴FN∥CH.∴△AFN∽△ACH.∴FNCH=AFAC.∴S△AEFS△ABC=12AE·FN12AB·CH=AE·AFAB·AC.(3)连接AG并延长,交BC于点M,连接BG并延长,交AC于点N,连接M,N,则M,N分别是BC,AC的中点,∴MN∥AB,且MN=12AB.∴GM GA =GN GB =12,且S △ABM =S △ACM . ∴AG AM =23. 设AF AC=a , 由(2)知,S △AEG S △ABM=AE·AG AB·AM =34×23=12, S △AFG S △ACM =AG·AF AM·AC =23a , 则S △AEF S △ABC =S △AEG +S △AFG 2S △ACM =S △AEG 2S △ABM +S △AFG 2S △ACM=14+13a. 而S △AEF S △ABC =AE·AF AB·AC =34a , ∴14+13a =34a ,解得a =35. ∴S △AEF S △ABC =34×35=920. 7.(2019·河南)(1)问题发现如图1,在△OAB 和△OCD 中,OA =OB ,OC =OD ,∠AOB =∠COD =40°,连接AC ,BD 相交于点M.填空:①AC BD的值为1; ②∠AMB 的度数为40°;(2)类比探究如图2,在△OAB 和△OCD 中,∠AOB =∠COD =90°,∠OAB =∠OCD =30°,连接AC交BD 的延长线于点M.请判断AC BD的值及∠AMB 的度数,并说明理由;(3)拓展延伸在(2)的条件下,将△OCD 绕点O 在平面内旋转,AC ,BD 所在直线交于点M.若OD =1,OB =7,请直接写出当点C 与点M 重合时AC 的长.图1图2 图3解:(2)AC BD=3,∠AMB =90°. 理由如下:∵∠AOB =∠COD =90°,∠OAB =∠OCD=30°,∴CODO=AOBO=3,∠COD+∠AOD=∠AOB+∠AOD,即∠AOC=∠BOD.∴△AOC∽△BOD.∴ACBD=CODO=3,∠CAO=∠DBO.∵∠AOB=90°,∴∠DBO+∠ABD+∠BAO=90°.∴∠CAO+∠ABD+∠BAO=90°.∴∠AMB=90°.(3)AC的长为23或3 3.提示:在△OCD旋转的过程中,(2)中的结论仍然成立,即ACBD=3,∠AMB=90°.如图所示,点C与点M重合,AC1,AC2的长即为所求.8.(2019·淄博)(1)操作发现:如图1,小明画了一个等腰三角形ABC,其中AB=AC,在△ABC的外侧分别以AB,AC 为腰作了两个等腰直角三角形ABD,ACE,分别取BD,CE,BC的中点M,N,G,连接GM,GN.小明发现了:线段GM与GN的数量关系是MG=NG;位置关系是MG⊥NG;(2)类比思考:如图2,小明在此基础上进行了深入思考.把等腰三角形ABC换为一般的锐角三角形,其中AB>AC,其他条件不变,小明发现的上述结论还成立吗?请说明理由;(3)深入研究:如图3,小明在(2)的基础上,又作了进一步的探究.向△ABC的内侧分别作等腰直角三角形ABD,ACE,其他条件不变,试判断△GMN 的形状,并给予证明.图1图2图3解:(1)连接BE,CD相交于点H,∵△ABD和△ACE都是等腰直角三角形,∴AB=AD,AC=AE,∠BAD=∠CAE=90°.∴∠CAD=∠BAE.∴△ACD≌△AEB(SAS).∴CD=BE,∠ADC=∠ABE.∴∠BDC+∠DBH=∠BDC+∠ABD+∠ABE=∠BDC+∠ABD+∠ADC=∠ADB+∠ABD=90°.∴∠BHD=90°.∴CD⊥BE.∵点M,G分别是BD,BC的中点,∴MG//12CD.同理NG//12BE.∴MG=NG,MG⊥NG.故答案为MG=NG,MG⊥NG.(2)连接CD,BE,相交于点H,同(1)的方法得,MG=NG,MG⊥NG.(3)连接EB,DC,延长线相交于点H,同(1)的方法得,△ABE≌△ADC,MG=NG.∴∠AEB=∠ACD.∴∠CEH+∠ECH=∠AEH-∠AEC+180°-∠ACD-∠ACE=∠ACD-45°+180°-∠ACD-45°=90°.∴∠DHE=90°.同(1)的方法得,MG⊥NG.类型2与图形变换有关的几何综合题1.(2019·襄阳)如图1,已知点G在正方形ABCD 的对角线AC上,GE⊥BC,垂足为E,GF⊥CD, 垂足为F.(1)证明与推断:①求证:四边形CEGF是正方形;②推断:AGBE的值为2;(2)探究与证明:将四边形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG与BE之间的数量关系,并说明理由;(3)拓展与运用:四边形CEGF在旋转过程中,当B,E,F 三点在一条直线上时,如图3所示,延长CG交AD于点H.若AG=6,GH=22,则BC=35.图1图2图3解:(1)①证明:∵四边形ABCD是正方形,∴∠BCD=90°,∠BCA=45°.∵GE⊥BC,GF⊥CD,∴∠CEG=∠CFG=∠ECF=90°.∴四边形CEGF是矩形,∠CGE=∠ECG =45°.∴EG=EC.∴四边形CEGF是正方形.(2)连接CG,由旋转性质可知,∠BCE=∠ACG=α.在Rt△CEG和Rt△CBA中,CECG=cos45°=22,CBCA=cos45°=22.∴CGCE=CACB= 2.又∵∠ECG=∠ECA=∠ACB-∠ECA,即∠ACG=∠BCE,∴△ACG∽△BCE.∴AGBE=CACB= 2.∴线段AG与BE之间的数量关系为AG=2BE.2.(2019·仙桃)问题:如图1,在Rt△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,则线段BC,DC,EC之间满足的等量关系式为BC=DC+EC;探索:如图2,在Rt△ABC与Rt△ADE中,AB =AC ,AD =AE ,将△ADE 绕点A 旋转,使点D 落在BC 边上,试探索线段AD ,BD ,CD 之间满足的等量关系,并证明你的结论;应用:如图3,在四边形ABCD 中,∠ABC =∠ACB =∠ADC =45°.若BD =9,CD =3,求AD 的长.图1图2 图3解:探索:BD 2+CD 2=2AD 2.连接CE.∵∠BAD +∠DAC =90°=∠DAC +∠CAE ,∴∠BAD =∠CAE.在△ABD 和△ACE 中,⎩⎪⎨⎪⎧AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE(SAS ).∴BD =CE ,∠B =∠ACE.∵Rt △ABC 与Rt △ADE 是等腰直角三角形,∴DE 2=2AD 2.∴∠B =45°.∴∠ACB +∠ACE =45°+45°=90°.∴∠DCE=90°.∴DC2+CE2=DE2,即BD2+CD2=2AD2.应用:以AD为腰作等腰Rt△ADE,连接CE,由“探索”可知,△ABD≌△ACE(SAS).∴CE=BD=9.∵∠ADC=∠ADE=45°,∴∠EDC=90°.在Rt△CDE中,由勾股定理,得DE=92-32=6 2.在等腰Rt△ADE中,AD=22DE=6.3.(2019·宜昌)在矩形ABCD中,AB=12,P是边AB上一点,把△PBC沿直线PC折叠,顶点B的对应点是点G,过点B作BE⊥CG,垂足为E,且在AD上,BE交PC于点F.(1)如图1,若点E是AD的中点,求证:△AEB≌△DEC;(2)如图2,①求证:BP=BF;②当AD=25,且AE<DE时,求cos∠PCB 的值;③当BP=9时,求BE·EF的值.图1 图2 图2备用图解:(1)证明:在矩形ABCD 中,∠A =∠D =90°,AB =DC ,∵点E 是AD 中点,∴AE =DE.在△AEB 和△DEC 中,⎩⎪⎨⎪⎧AB =DC ,∠A =∠D =90°,AE =DE ,∴△AEB ≌△DEC(SAS ).(2)①证明:在矩形ABCD 中,∠ABC =90°. ∵△BPC 沿PC 折叠得到△GPC ,∴∠PGC =∠PBC =90°,∠BPC =∠GPC. ∵BE ⊥CG ,∴BE ∥PG.∴∠GPF =∠PFB.∴∠BPF =∠PFB.∴BP =BF.②当AD =25时,∵∠BEC =90°,∴∠AEB +∠PEC =90°. ∵∠AEB +∠ABE =90°,∴∠DEC =∠ABE.∵∠A =∠D =90°,∴△ABE ∽△DEC.∴AB AE =DE DC.设AE=x,则DE=25-x,∴12x=25-x12.∴x=9或x=16.∵AE<DE,∴AE=9,DE=16.∴由勾股定理,得CE=20,BE=15.由折叠得,BP=PG,BC=GC,∴BP=BF =PG.∵BE∥PG,∴△ECF∽△GCP.∴EFGP=CECG.设BP=BF=PG=y,∴15-yy=2025.∴y=253,即BP=253.在Rt△PBC中,由勾股定理,得PC=25103,cos∠PCB=BCPC=31010.③连接FG,∵∠GEF=∠G=90°,∴BE∥PG. ∵BF∥PG,BF=PG=BP,∴四边形BPGF是菱形.∴BP∥GF,且BP=GF.∴∠GFE=∠EBA. ∴△GEF∽△EAB.∴EFGF=ABEB.∴BE·EF=AB·GF=AB·BP=12×9=108. 4.(2019·永州)如图1,在△ABC中,矩形EFGH 的一边EF在AB上,顶点G,H分别在BC,AC上,CD是边AB上的高,CD交GH于点I.若CI=4,HI=3,AD=92,矩形DFGI恰好为正方形.图1图2图3(1)求正方形DFGI的边长;(2)如图2,延长AB至P,使得AC=CP.将矩形EFGH沿BP的方向平移,当点G刚好落在CP上时,试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形,为什么?(3)如图3,连接DG,将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′,正方形DF′G′I′分别与线段DG,DB相交于点M,N,求△MN G′的周长.解:(1)∵HI∥AD,∴HIAD=CICD.∴392=4CD.∴CD=6.∴ID=CD-CI=2.∴正方形的边长为2.(2)如图2,设点G落在PC上时对应的点为点G′,点F的对应点为点F′.∵CA=CP,CD⊥PA,∴∠ACD=∠PCD,∠A=∠P.∵HG′∥PA,∴∠CHG′=∠A,∠CG′H=∠P.∴∠CHG′=∠CG′H.∴CH=CG′.∴IH=IG′=DF′=3.∵IG∥DB,∴IGDB=CICD.∴2DB=46.∴DB=3.∴DB=DF′=3.∴点B与点F′重合.∴移动后的矩形与△CBP重叠部分是三角形,即△BGG′.(3)将△DMI′绕点D顺时针旋转90°得到△DRF′,此时N,F′,R共线.∴∠MDR=90°.∵∠NDM=45°,∠NDM+∠NDR=90°,∴∠NDM=∠NDR=45°.∵DN=DN,DM=DR,∴△NDM≌△NDR.∴MN=NR=NF′+RF′=NF′+MI′.∴△MNG′的周长=MN+MG′+NG′=NF′+NG′+MI′=F′G′+I′G′=2I′G′=4. 5.(2019·岳阳)已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD 所在的直线对折,使点B落在点B′处,连接AB′,BB′,延长CD交BB′于点E,设∠ABC=2α.(0°<α<45°)(1)如图1,若AB=AC,求证:CD=2BE;(2)如图2,若AB≠AC,试求CD与BE的数量关系;(用含α的式子表示)(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连接EF交BC 于点O,设△COE的面积为S1,△COF的面积为S2,求S1S2.(用含α的式子表示)图1图2图3解:(1)证明:∵点B,B′关于EC对称,∴BB′⊥EC,BE=EB′.∴∠DEB=∠DAC=90°.∵∠EDB=∠ADC,∴∠DBE=∠ACD.∵AB=AC,∠BAB′=∠CAD=90°,∴△BAB′≌△CAD.∴CD=BB′=2BE.(2)如图2,结论:CD=2BE·tan2α.理由:由(1)可知,∠ABB′=∠ACD,∠BAB′=∠CAD=90°,∴△BAB′∽△CAD.∴BB′CD=ABAC=1tan2α.∴2BECD=1tan2α.∴CD=2BE·tan2α.(3)如图3,在Rt△ABC中,∠ACB=90°-2α.∵EC平分∠ACB,∴∠ECB=12(90°-2α)=45°-α.∵∠BCF=45°+α,∴∠ECF=45°-α+45°+α=90°. ∴∠BEC+∠ECF=180°.∴BB′∥CF.∴△BEO∽△CFO.∴EOFO=BECF=BEBC=sin(45°-α).∵S1S2=EOFO,∴S1S2=sin(45°-α).6.(2019·潍坊)如图1,在▱ABCD中,DH⊥AB 于点H,CD的垂直平分线交CD于点E,交AB 于点F,AB=6,DH=4,BF∶FA=1∶5.(1)如图2,作FG⊥AD于点G,交DH于点M,将△DGM沿DC方向平移,得到△CG′M′,连接M′B.①求四边形BHMM′的面积;②直线EF上有一动点N,求△DNM周长的最小值;(2)如图3,延长CB交EF于点Q,过点Q作QK∥AB,过CD边上的动点P作PK∥EF,并与QK交于点K,将△PKQ沿直线PQ翻折,使点K的对应点K′恰好落在直线AB上,求线段CP的长.图1图2图3解:(1)①在▱ABCD中,AB=6,直线EF 垂直平分CD,∴DE=FH=3.又BF∶FA=1∶5,∴BF=1,FA=5.∴AH=2.∵Rt△AHD∽Rt△MHF,∴HMFH=HAHD.∴HM3=24.∴HM=3 2.根据平移的性质,得MM′=CD=6,∴S四边形BHMM′=S△BMM′+S△BHM=12×6×32+12×4×32=15 2.②连接CM交直线EF于点N,连接DN. ∴CN=DN.∵MH=32,∴DM=52.在Rt△CDM中,MC2=DC2+DM2.∴MC2=62+(52)2,即MC=132.∵MN+DN的最小值=MN+CN=MC,∴△DNM周长的最小值为9.(2)∵BF∥CE,∴△DNM周长的最小值为9.(2)∵BF∥CE,∴QFQF+4=BFCE=13.∴QF=2.∴PK=PK′=6.过点K′作E′F′∥EF,分别交CD于点E′,交QK于点F′.当点P在线段CE上时,在Rt△PK′E′中,PE′2=PK′2-E′K′2,∴PE′=2 5.∵Rt△PE′K′∽Rt△K′F′Q,∴PE′K′F′=E′K′F′Q.∴252=4F′Q.∴F′Q=45 5.∴PE=PE′-EE′=25-455=655.∴CP=CE-PE=15-655.同理可得,当点P在线段ED上时,CP=15+655.综上可得,CP的长为15-655或15+655.类型3与动点有关的几何综合题1.(2019·黄冈)如图,在平面直角坐标系xOy中,菱形OABC的边OA在x轴正半轴上,点B,C 在第一象限,∠C=120°,边长OA=8.点M从原点O出发沿x轴正半轴以每秒1个单位长度的速度作匀速运动,点N从A出发沿边AB-BC-CO以每秒2个单位长度的速度作匀速运动,过点M作直线MP垂直于x轴并交折线OCB 于点P,交对角线OB于点Q,点M和点N同时出发,分别沿各自路线运动,点N运动到原点O时,M和N两点同时停止运动.(1)当t=2时,求线段PQ的长;(2)求t为何值时,点P与N重合;(3)设△APN的面积为S,求S与t的函数关系式及t的取值范围.解:(1)当t=2时,OM=2,在Rt△OPM中,∠POM=60°,∴PM=OM·tan60°=2 3.在Rt△OMQ中,∠QOM=30°,∴QM=OM·tan30°=23 3.∴PQ =PM -QM =23-233=433. (2)由题意,得8+(t -4)+2t =24,解得t =203. (3)①当0<t <4时,S =12·2t·43=43t ; ②当4≤t <203时,S =12×[8-(t -4)-(2t -8)]×43=403-63t ;③当203≤t <8时,S =12×[(t -4)+(2t -8)-8]×43=63t -403;④当8≤t ≤12时,S =S 菱形ABCO -S △AON -S △ABP -S △PCN=323-12(24-2t)×43-12×[8-(t -4)]×43-12(t -4)×32[8-(24-2t)] =-32t 2+123t -56 3. 综上,S =⎩⎪⎪⎪⎨⎪⎪⎪⎧43t ;(0<t <4)403-63t ;(4≤t <203)63t -403;(203≤t <8)-32t 2+123t -56 3.(8≤t ≤12) 2.(2019·青岛)已知:如图,四边形ABCD ,AB ∥DC ,CB ⊥AB ,AB =16 cm ,BC =6 cm ,CD =8 cm .动点P 从点D 开始沿DA 边匀速运动,动点Q 从点A 开始沿AB 边匀速运动,它们的运动速度均为2 cm /s .点P 和点Q 同时出发,以QA ,QP 为边作平行四边形AQPE ,设运动的时间为t(s ),0<t <5.根据题意解答下列问题:(1)用含t 的代数式表示AP ;(2)设四边形CPQB 的面积为S(cm 2),求S 与t 的函数关系式;(3)当QP ⊥BD 时,求t 的值;(4)在运动过程中,是否存在某一时刻t ,使点E 在∠ABD 的平分线上?若存在,求出t 的值;若不存在,请说明理由.解:(1)过点D 作DH ⊥AB 于点H ,则四边形DHBC 是矩形,∴CD =BH =8,DH =BC =6.∴AH =AB -BH =8,AD =DH 2+AH 2=10,BD =CD 2+BC 2=10.∴AP =AD -DP =10-2t.(2)过点P 作PN ⊥AB 于点N ,连接PB. 在Rt △APN 中,PA =10-2t ,∴PN =PA·sin ∠DAH =35(10-2t),AN =PA·cos ∠DAH =45(10-2t). ∴BN =16-AN =16-45(10-2t), S =S △PQB +S △BCP =12·(16-2t)·35(10-2t)+12×6×[16-45(10-2t)]=65t 2-545t +72(0<t <5). (3)当PQ ⊥BD 时,∠PQN +∠DBA =90°, ∵∠QPN +∠PQN =90°,∴∠QPN =∠DBA.∴tan ∠QPN =QN PN =34.∴45(10-2t)-2t35(10-2t)=34.解得t=3527.经检验,t=3527是分式方程的解,∴当t=3527s时,PQ⊥BD.(4)存在.理由:连接BE交DH于点K,过点K作KM⊥BD于点M.当BE平分∠ABD时,△KBH≌△KBM,∴KH=KM,BH=BM=8.设KH=KM=x,在Rt△DKM中,(6-x)2=22+x2,解得x=8 3.过点E作EF⊥AB于点F,则△AEF≌△QPN,∴EF=PN=35(10-2t),AF=QN=45(10-2t)-2t,∴BF =16-[45(10-2t)-2t]. ∵KH ∥EF ,∴KH EF =BH BF. ∴8335(10-2t )=816-[45(10-2t )-2t].解得t =2518. 经检验,t =2518是分式方程的解. ∴当t =2518s 时,点E 在∠ABD 的平分线上.3.(2019·绵阳)如图,已知△ABC 的顶点坐标分别为A(3,0),B(0,4),C(-3,0).动点M ,N 同时从A 点出发,M 沿A →C ,N 沿折线A →B →C ,均以每秒1个单位长度的速度移动,当一个动点到达终点C 时,另一个动点也随之停止移动,移动的时间记为t 秒,连接MN.(1)求直线BC 的解析式;(2)移动过程中,将△AMN 沿直线MN 翻折,点A 恰好落在BC 边上点D 处,求此时t 值及点D 的坐标;(3)当点M ,N 移动时,记△ABC 在直线MN 右侧部分的面积为S ,求S 关于时间t 的函数关系式.备用图解:(1)设直线BC 的解析式为y =kx +b ,则有⎩⎨⎧b =4,-3k +b =0,解得⎩⎨⎧k =43,b =4.∴直线BC 的解析式为y =43x +4. 图1(2)如图1,连接AD 交MN 于点O′.由题意可知,四边形AMDN 是菱形,M(3-t ,0),N(3-35t ,45t), ∴O′(3-45t ,25t),D(3-38t ,45t). ∵点D 在BC 上,∴45t =43×(3-85t)+4,解得t =3011. ∴t =3011s 时,点A 恰好落在BC 边上点D 处,此时D(-1511,2411). 图2(3)如图2,当0<t ≤5时,△ABC 在直线MN 右侧部分是△AMN ,S =12×t ×45t =25t 2; 如图3,当5<t ≤6时,△ABC 在直线MN 右侧部分是四边形ABNM.图3S =S △ABC -S △CMN =12×6×4-12×(6-t)×[4-45(t -5)]=-25t 2+325t -12. 4.(2019·广东)已知Rt △OAB ,∠OAB =90°,∠ABO =30°,斜边OB =4,将Rt △OAB 绕点O 顺时针旋转60°,如图1,连接BC.(1)填空:∠OBC =60°;(2)如图1,连接AC ,作OP ⊥AC ,垂足为P,求OP的长度;(3)如图2,点M,N同时从点O出发,在△OCB边上运动,M沿O→C→B路径匀速运动,N沿O→B→C路径匀速运动,当两点相遇时运动停止.已知点M的运动速度为单位长度/秒,点N的运动速度为1单位长度/秒.设运动时间为x秒,△OMN的面积为y,求当x为何值时,y取得最大值?最大值为多少?(结果可保留根号)图1图2备用图解:(2)∵OB=4,∠ABO=30°,∴OA=12OB=2,AB=3OA=2 3.∴S△AOC =12OA·AB=12×2×23=2 3.∵△BOC是等边三角形,∴BC=BO=4.∴∠OBC=60°,∠ABC=∠ABO+∠OBC =90°.∴AC=AB2+BC2=27.∴OP=2S△AOCAC=4327=2217.(3)①当0<x ≤83时,点M 在OC 上运动,点N 在OB 上运动,此时过点N 作NE ⊥OC 且交OC 于点E.则NE =ON·sin 60°=32x , ∴y =12OM·NE =12××32x ,即y =338x 2. ∴当x =83时,y 有最大值,最大值为833. ②当83<x ≤4时,点M 在BC 上运动,点N 在OB 上运动.图3过点M 作MH ⊥OB 于点H.则BM =8-,MH =BM·sin 60°=32(8-1.5x), ∴y =12ON·MH =-338x 2+23x. ∵当x =83时,y 取最大值,∴y <833. ③当4<x ≤时,点M ,N 都在BC 上运动,过点O作OG⊥BC于点G.则MN=12-,OG=AB=23,图4∴y=12MN·OG=123-532x.∵当x=4时,y有最大值,∴y<2 3.综上所述,y有最大值,最大值为83 3.类型4与实践操作有关的几何综合题1.(2019·齐齐哈尔)折纸是一项有趣的活动,同学们小时候都玩过折纸,可能折过小动物、小花、飞机、小船等,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以通过研究图形的性质和运动,确定图形位置等,进一步发展空间观念,在经历借助图形思考问题的过程中,我们会初步建立几何直观.折纸往往从矩形纸片开始,今天,就让我们带着数学的眼光来玩一玩折纸,看看折叠矩形的对角线之后能得到哪些数学结论.实践操作如图1,将矩形纸片ABCD沿对角线AC翻折,使点B′落在矩形ABCD所在平面内,B′C 和AD相交于点E,连接B′D.图1图2解决问题(1)在图1中.①B′D和AC的位置关系为B′D∥AC(互相平行);②将△AEC剪下后展开,得到的图形是菱形;(2)若图1中的矩形变为平行四边形(AB≠BC),如图2所示,结论①和结论②是否成立,若成立,请挑选其中一个结论加以证明,若不成立,请说明理由;(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长和宽之比为1∶1或3∶1.拓展应用(4)在图2中,若∠B=30°,AB=43,当△AB′D恰好为直角三角形时,BC的长度为4或6或8或12.解:结果仍成立.①选择结论①证明.∵四边形ABCD是平行四边形,∴AD//BC.∴∠DAC=∠BCA.由折叠性质,得BC=B′C,∠BCA=∠ACB′,∴∠DAC=∠ACB′,B′C=AD.∴AE=CE,∴B′E=DE.∴∠CB′D=ADB′.∵∠AEC=∠B′ED,∠ACB′=∠CAD,∴∠ADB′=∠DAC.∴B′D∥AC.②选择结论②证明.设点E的对应为点F,连接AF.由折叠性质,得AE=AF,CE=CF.由①知AE=CE,∴AE=CE=AF=CF.∴四边形AECF是菱形.2.(2019·山西)综合性实践问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM,试判断线段AM与DE的位置关系.探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:证明:∵BE=AB,∴AE=2AB.∵AD=2AB,∴AD=AE.∵四边形ABCD是矩形,∴AD∥BC.∴EMDM=EBAB.(依据1)∵BE=AB,∴EMDM=1.∴EM=DM,即AM是△ADE的DE边上的中线.又∵AD=AE,∴AM⊥DE.(依据2)∴AM垂直平分DE.反思交流:(1)①上述证明过程中的“依据1”“依据2”分别是指什么?②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE 的左下方作正方形CEFG,发现点G在线段BC 的垂直平分线上,请你给出证明;探索发现:(3)如图3,连接CE,以CE为一边在CE 的右上方作正方形CEFG,可以发现点C,点B 都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.图1图2 图3解:(1)①依据1:两条直线被一组平行线所截,所得到的对应线段成比例(或平行线分线段成比例).依据2:等腰三角形顶角的平分线,底边上的中线及底边上的高互相重合(或等腰三角形的“三线合一”).②点A在线段GF的垂直平分线上.(2)证明:过点G作GH⊥BC于点H.∵四边形ABCD为矩形,点E在AB的延长线上,∴∠CBE=∠ABC=∠GHC=90°.∴∠BCE+∠BEC=90°.∵四边形CEFG为正方形,∴CG=CE,∠GCE=90°.∴∠BCE+∠BCG=90°.∴∠BEC=∠BCG.∴△GHC≌△CBE(AAS).∴HC=BE.∵四边形ABCD是矩形,∴AD=BC.∵AD=2AB,BE=AB,∴BC=2BE=2HC.∴HC=BH.∴GH垂直平分BC.∴点G在BC的垂直平分线上.(3)点F在BC边的垂直平分线上(或点F在AD边的垂直平分线上).过点F作FM⊥BC于点M,过点E作EN⊥FM于点N.∴∠BMN=∠ENM=∠ENF=90°.∵四边形ABCD是矩形,点E在AB的延长线上,∴∠CBE=∠ABC=90°.∴四边形BENM 为矩形.∴BM=EN,∠CEB+∠CEN=90°.∵四边形CEFG为正方形,∴EF=EC,∠CEF=90°.∴∠CEN+∠FEN=90°.∴∠CEB=∠FEN.∴△ENF≌△EBC(AAS).∴NE=BE.∴BM=BE.。
海口市2019-2020学年中考数学监测试题

2019-2020学年中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.如图,△ABC 中,∠CAB=65°,在同一平面内,将△ABC 绕点A 旋转到△AED 的位置,使得DC ∥AB ,则∠BAE 等于( )A .30°B .40°C .50°D .60°2.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?” 如图所示,请根据所学知识计算:圆形木材的直径AC 是( )A .13寸B .20寸C .26寸D .28寸3.若点A (2,1y ),B (-3,2y ),C (-1,3y )三点在抛物线24y x x m =--的图象上,则1y 、2y 、3y 的大小关系是( ) A .123y y y >> B .213y y y >> C .231y y y >> D .312y y y >>4.用配方法解方程2230x x +-=时,可将方程变形为( ) A .2(1)2x += B .2(1)2x -= C .2(1)4x -= D .2(1)4x +=5.第 24 届冬奥会将于 2022 年在北京和张家口举行,冬奥会的项目有滑雪(如跳台滑雪、高山滑雪、单板滑雪等)、滑冰(如短道速滑、速度滑冰、花样滑冰等)、冰球、冰壶等.如图,有 5 张形状、大背面完全相同.现将这 5 张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是( )A .15B .25C .12D .356.如图,小明要测量河内小岛B 到河边公路l 的距离,在A 点测得30BAD ∠=︒,在C 点测得60BCD ∠=︒,又测得50AC =米,则小岛B 到公路l 的距离为( )米.A .25B .253C .1003D .25253+7.如图是二次函数y =ax 2+bx + c(a≠0)图象如图所示,则下列结论,①c<0,②2a + b=0;③a+b+c=0,④b 2–4ac<0,其中正确的有( )A .1个B .2个C .3个D .48.如图,P 为⊙O 外一点,PA 、PB 分别切⊙O 于点A 、B ,CD 切⊙O 于点E ,分别交PA 、PB 于点C 、D ,若PA =6,则△PCD 的周长为( )A .8B .6C .12D .109.如图,AB ∥CD ,点E 在线段BC 上,CD=CE,若∠ABC=30°,则∠D 为( )10.如图是一个正方体的表面展开图,如果对面上所标的两个数互为相反数,那么图中x 的值是( ).A .3-B .3C .2D .8二、填空题(本题包括8个小题)11.如图,每个小正方形边长为1,则△ABC 边AC 上的高BD 的长为_____.12.如图所示:在平面直角坐标系中,△OCB 的外接圆与y 轴交于A (0,),∠OCB=60°,∠COB=45°,则OC= .13.已知二次函数2(0)y ax bx c a =++≠,y 与x 的部分对应值如下表所示:x… -1 0 1 2 3 4 … y…61-2-3-2m…下面有四个论断:①抛物线2(0)y ax bx c a =++≠的顶点为(23)-,; ②240b ac -=;③关于x 的方程2=2ax bx c ++-的解为12=13x x =,; ④=3m -.其中,正确的有___________________. 14.函数21y x =-中,自变量x 的取值范围是_____. 15.如图,李明从A 点出发沿直线前进5米到达B 点后向左旋转的角度为α,再沿直线前进5米,到达点C 后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了45米,则每次旋转的角度α16.如图,直线4y x =+与双曲线ky x=(k≠0)相交于A (﹣1,a )、B 两点,在y 轴上找一点P ,当PA+PB 的值最小时,点P 的坐标为_________.17.如图,在四边形ABCD 中,∠B =∠D =90°,AB =3, BC =2,tanA =43,则CD =_____.18.我们知道:1+3=4,1+3+5=9,1+3+5+7=16,…,观察下面的一列数:-1,2,,-3, 4,-5,6…,将这些数排列成如图的形式,根据其规律猜想,第20行从左到右第3个数是 .三、解答题(本题包括8个小题)19.(6分)如图,一次函数y =kx+b 的图象与反比例函数y =mx的图象交于A (﹣2,1),B (1,n )两点.求反比例函数和一次函数的解析式;根据图象写出一次函数的值大于反比例21.(6分)某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:每人销售件数1800 510 250 210 150 120人数 1 1 3 5 3 2(1)求这15位营销人员该月销售量的平均数、中位数和众数;假设销售负责人把每位营销员的月销售额定为320件,你认为是否合理,为什么?如不合理,请你制定一个较合理的销售定额,并说明理由.22.(8分)在锐角△ABC中,边BC长为18,高AD长为12如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K,求EFAK的值;设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值.23.(8分)制作一种产品,需先将材料加热达到60℃后,再进行操作,设该材料温度为y(℃)从加热开始计算的时间为x(min).据了解,当该材料加热时,温度y与时间x成一次函数关系:停止加热进行操作时,温度y与时间x成反比例关系(如图).已知在操作加热前的温度为15℃,加热5分钟后温度达到60℃.分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?24.(10分)某高中进行“选科走班”教学改革,语文、数学、英语三门为必修学科,另外还需从物理、化学、生物、政治、历史、地理(分别记为A、B、C、D、E、F)六门选修学科中任选三门,现对该校某班选科情况进行调查,对调查结果进行了分析统计,并制作了两幅不完整的统计图.请根据以上信息,完成下列问题:该班共有学生人;请将条形统计图补充完整;该班某同学物理成绩特别优异,已经从选修学科中选定物理,还需从余下选修学科中任意选择两门,请用列表或画树状图的方法,求出该同学恰好选中化学、历史两科的概率.25.(10分)如图,∠A=∠D,∠B=∠E,AF=DC.求证:BC=EF.26.(12分)在一个不透明的盒子里,装有三个分别写有数字6,-2,7的小球,它们的形状、大小、质地等完全相同,先从盒子里随机取出一个小球,记下数字后放回盒子,摇匀后再随机取出一个小球,记下数字.请你用画树状图的方法,求下列事件的概率:两次取出小球上的数字相同;两次取出小球上的数字之和大于1.参考答案一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.C【解析】试题分析:∵DC∥AB,∴∠DCA=∠CAB=65°.∵△ABC绕点A旋转到△AED的位置,∴∠BAE=∠CAD,AC=AD.∴∠ADC=∠DCA="65°." ∴∠CAD=180°﹣∠ADC﹣∠DCA="50°." ∴∠BAE=50°.故选C.考点:1.面动旋转问题;2. 平行线的性质;3.旋转的性质;4.等腰三角形的性质.分析:设⊙O 的半径为r .在Rt △ADO 中,AD=5,OD=r-1,OA=r ,则有r 2=52+(r-1)2,解方程即可. 详解:设⊙O 的半径为r .在Rt △ADO 中,AD=5,OD=r-1,OA=r , 则有r 2=52+(r-1)2, 解得r=13,∴⊙O 的直径为26寸, 故选C .点睛:本题考查垂径定理、勾股定理等知识,解题的关键是学会利用参数构建方程解决问题 3.C 【解析】首先求出二次函数24y x x m =--的图象的对称轴x=2ba-=2,且由a=1>0,可知其开口向上,然后由A (2,1y )中x=2,知1y 最小,再由B (-3,2y ),C (-1,3y )都在对称轴的左侧,而在对称轴的左侧,y 随x 得增大而减小,所以23y y >.总结可得231y y y >>. 故选C .点睛:此题主要考查了二次函数的图像与性质,解答此题的关键是(1)找到二次函数的对称轴;(2)掌握二次函数20y ax bx c a =++≠()的图象性质.4.D 【解析】 【分析】配方法一般步骤:将常数项移到等号右侧,左右两边同时加一次项系数一半的平方,配方即可. 【详解】解:2230x x +-=223x x += 2214x x ++=()214x +=故选D. 【点睛】本题考查了配方法解方程的步骤,属于简单题,熟悉步骤是解题关键.先找出滑雪项目图案的张数,结合5 张形状、大小、质地均相同的卡片,再根据概率公式即可求解. 【详解】∵有 5 张形状、大小、质地均相同的卡片,滑雪项目图案的有高山滑雪和单板滑雪2张, ∴从中随机抽取一张,抽出的卡片正面恰好是滑雪项目图案的概率是25. 故选B . 【点睛】本题考查了简单事件的概率.用到的知识点为:概率=所求情况数与总情况数之比. 6.B 【解析】 【详解】解:过点B 作BE ⊥AD 于E .设BE=x .∵∠BCD=60°,tan ∠BCE BECE=, 33CE x ∴=, 在直角△ABE 中,3x ,AC=50米,33503x x -=, 解得253x =即小岛B 到公路l 的距离为253 故选B. 7.B 【解析】 【分析】由抛物线的开口方向判断a 与1的关系,由抛物线与y 轴的交点判断c 与1的关系,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.①抛物线与y 轴交于负半轴,则c <1,故①正确; ②对称轴x 2ba=-=1,则2a+b=1.故②正确; ③由图可知:当x=1时,y=a+b+c <1.故③错误;④由图可知:抛物线与x 轴有两个不同的交点,则b 2﹣4ac >1.故④错误. 综上所述:正确的结论有2个. 故选B . 【点睛】本题考查了图象与二次函数系数之间的关系,会利用对称轴的值求2a 与b 的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用. 8.C 【解析】 【分析】由切线长定理可求得PA =PB ,AC =CE ,BD =ED ,则可求得答案. 【详解】∵PA 、PB 分别切⊙O 于点A 、B ,CD 切⊙O 于点E , ∴PA =PB =6,AC =EC ,BD =ED ,∴PC+CD+PD =PC+CE+DE+PD =PA+AC+PD+BD =PA+PB =6+6=12, 即△PCD 的周长为12, 故选:C . 【点睛】本题主要考查切线的性质,利用切线长定理求得PA =PB 、AC =CE 和BD =ED 是解题的关键. 9.B 【解析】分析:先由AB ∥CD ,得∠C=∠ABC=30°,CD=CE ,得∠D=∠CED ,再根据三角形内角和定理得,∠C+∠D+∠CED=180°,即30°+2∠D=180°,从而求出∠D . 详解:∵AB ∥CD , ∴∠C=∠ABC=30°, 又∵CD=CE , ∴∠D=∠CED ,∵∠C+∠D+∠CED=180°,即30°+2∠D=180°, ∴∠D=75°.点睛:此题考查的是平行线的性质及三角形内角和定理,解题的关键是先根据平行线的性质求出∠C,再由CD=CE得出∠D=∠CED,由三角形内角和定理求出∠D.10.D【解析】【分析】根据正方体平面展开图的特征得出每个相对面,再由相对面上的两个数互为相反数可得出x的值.【详解】解:“3”与“-3”相对,“y”与“-2”相对,“x”与“-8”相对, 故x=8,故选D.【点睛】本题主要考查了正方体相对面上的文字,解决本题的关键是要熟练掌握正方体展开图的特征.二、填空题(本题包括8个小题)11.8 5【解析】试题分析:根据网格,利用勾股定理求出AC的长,AB的长,以及AB边上的高,利用三角形面积公式求出三角形ABC面积,而三角形ABC面积可以由AC与BD乘积的一半来求,利用面积法即可求出BD的长:根据勾股定理得:22345AC=+=,由网格得:S△ABC=12×2×4=4,且S△ABC=12AC•BD=12×5BD,∴12×5BD=4,解得:BD=85.考点:1.网格型问题;2.勾股定理;3.三角形的面积.12.1+【解析】试题分析:连接AB,由圆周角定理知AB必过圆心M,Rt△ABO中,易知∠BAO=∠OCB=60°,已知了OA=,即可求得OB的长;过B作BD⊥OC,通过解直角三角形即可求得OD、BD、CD的长,进而由OC=OD+CD求出OC的长.解:连接AB,则AB为⊙M的直径.Rt△ABO中,∠BAO=∠OCB=60°,∴OB=OA=×=.过B作BD⊥OC于D.Rt△OBD中,∠COB=45°,则OD=BD=OB=.Rt△BCD中,∠OCB=60°,则CD=BD=1.∴OC=CD+OD=1+.故答案为1+.点评:此题主要考查了圆周角定理及解直角三角形的综合应用能力,能够正确的构建出与已知和所求相关的直角三角形是解答此题的关键.13.①③.【解析】【分析】根据图表求出函数对称轴,再根据图表信息和二次函数性质逐一判断即可.【详解】由二次函数y=ax2+bx+c(a≠0),y与x的部分对应值可知:该函数图象是开口向上的抛物线,对称轴是直线x=2,顶点坐标为(2,-3);与x轴有两个交点,一个在0与1之间,另一个在3与4之间;当y=-2时,x=1或x=3;由抛物线的对称性可知,m=1;∴①抛物线y=ax2+bx+c(a≠0)的顶点为(2,-3),结论正确;②b2﹣4ac=0,结论错误,应该是b2﹣4ac>0;③关于x的方程ax2+bx+c=﹣2的解为x1=1,x2=3,结论正确;④m=﹣3,结论错误,∴其中,正确的有. ①③故答案为:①③【点睛】本题考查了二次函数的图像,结合图表信息是解题的关键.14.x≠1【解析】【分析】根据分母不等于0,可以求出x的范围;【详解】解:(1)x-1≠0,解得:x≠1;故答案是:x≠1,【点睛】考查了函数自变量的取值范围,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.15.40︒.【解析】【分析】根据共走了45米,每次前进5米且左转的角度相同,则可计算出该正多边形的边数,再根据外角和计算左转的角度.【详解】连续左转后形成的正多边形边数为:4559÷=,则左转的角度是360940︒÷=︒.故答案是:40︒.【点睛】本题考查了多边形的外角计算,正确理解多边形的外角和是360°是关键.16.(0,52).【解析】试题分析:把点A坐标代入y=x+4得a=3,即A(﹣1,3),把点A坐标代入双曲线的解析式得3=﹣k,即k=﹣3,联立两函数解析式得:,解得:,,即点B坐标为:(﹣3,1),作出点A关于y轴的对称点C,连接BC,与y轴的交点即为点P,使得PA+PB的值最小,则点C坐标为:(1,3),设直线BC的解析式为:y=ax+b,把B、C的坐标代入得:,解得:,所以函数解析式为:y=x+52,则与y轴的交点为:(0,52).考点:反比例函数与一次函数的交点问题;轴对称-最短路线问题.17.6 5【解析】【分析】延长AD和BC交于点E,在直角△ABE中利用三角函数求得BE的长,则EC的长即可求得,然后在直角△CDE中利用三角函数的定义求解. 【详解】如图,延长AD 、BC 相交于点E ,∵∠B=90°, ∴4tan 3BE A AB ==, ∴BE=443AB ⋅=, ∴CE=BE-BC=2,225AB BE +=,∴3sin 5AB E AE ==, 又∵∠CDE=∠CDA=90°,∴在Rt △CDE 中,sin CDE CE =, ∴CD=36sin 255CE E ⋅=⨯=.18.2 【解析】 【分析】先求出19行有多少个数,再加3就等于第20行第三个数是多少.然后根据奇偶性来决定负正. 【详解】 ∵1行1个数, 2行3个数, 3行5个数, 4行7个数, …19行应有2×19-1=37个数 ∴到第19行一共有 1+3+5+7+9+…+37=19×19=1.第20行第3个数的绝对值是1+3=2. 又2是偶数,故第20行第3个数是2. 三、解答题(本题包括8个小题)19. (1)y=2x-,y=−x−1;(2)x<−2或0<x<1 【解析】 【分析】(1)利用点A 的坐标可求出反比例函数解析式,再把B (1,n )代入反比例函数解析式,即可求得n 的值,于是得到一次函数的解析式;(2)根据图象和A,B 两点的坐标即可写出一次函数的值大于反比例函数的值的x 的取值范围. 【详解】(1)∵A(−2,1)在反比例函数y=mx的图象上, ∴1=2m-,解得m=−2. ∴反比例函数解析式为y=2x-, ∵B(1,n)在反比例函数上, ∴n=−2,∴B 的坐标(1,−2),把A(−2,1),B(1,−2)代入y=kx+b 得122k bk b =-+⎧⎨-=+⎩解得:11k b =-⎧⎨=-⎩∴一次函数的解析式为y=−x−1;(2)由图像知:当x<−2或0<x<1时,一次函数的值大于反比例函数的值. 【点睛】本题考查了反比例函数与一次函数的交点问题,属于简单题,熟悉函数图像的性质是解题关键. 20.详见解析. 【解析】试题分析:利用SSS 证明△ABC ≌△DEF ,根据全等三角形的性质可得∠B=∠DEF ,再由平行线的判定即可得AB ∥DE .试题解析:证明:由BE =CF 可得BC =EF , 又AB =DE ,AC =DF , 故△ABC ≌△DEF (SSS ), 则∠B=∠DEF , ∴AB ∥DE .考点:全等三角形的判定与性质.21.(1)平均数为320件,中位数是210件,众数是210件;(2)不合理,定210件 【解析】试题分析:(1)根据平均数、中位数和众数的定义即可求得结果; (2)把月销售额320件与大部分员工的工资比较即可判断. (1)平均数件,∵最中间的数据为210, ∴这组数据的中位数为210件,∵210是这组数据中出现次数最多的数据, ∴众数为210件;(2)不合理,理由:在15人中有13人销售额达不到320件,定210件较为合理. 考点:本题考查的是平均数、众数和中位数点评:解答本题的关键是熟练掌握找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个. 22.(1)32;(2)1. 【解析】 【分析】(1)根据相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比进行计算即可;(2)根据EH =KD =x ,得出AK =12﹣x ,EF =32(12﹣x ),再根据S =32x (12﹣x )=﹣32(x ﹣6)2+1,可得当x =6时,S 有最大值为1. 【详解】解:(1)∵△AEF ∽△ABC , ∴EF AKBC AD=, ∵边BC 长为18,高AD 长为12, ∴EF BC AK AD ==32; (2)∵EH =KD =x ,∴AK =12﹣x ,EF =32(12﹣x ), ∴S =32x (12﹣x )=﹣32(x ﹣6)2+1.当x =6时,S 有最大值为1. 【点睛】本题主要考查了相似三角形的判定与性质的综合应用,解题时注意:确定一个二次函数的最值,首先看自变量的取值范围,当自变量取全体实数时,其最值为抛物线顶点坐标的纵坐标.23.(1);(2)20分钟.【解析】【详解】(1)材料加热时,设y=ax+15(a≠0),由题意得60=5a+15,解得a=9,则材料加热时,y与x的函数关系式为y=9x+15(0≤x≤5).停止加热时,设y=(k≠0),由题意得60=,解得k=300,则停止加热进行操作时y与x的函数关系式为y=(x≥5);(2)把y=15代入y=,得x=20,因此从开始加热到停止操作,共经历了20分钟.答:从开始加热到停止操作,共经历了20分钟.24.(1)50人;(2)补图见解析;(3)1 10.【解析】分析:(1)根据化学学科人数及其所占百分比可得总人数;(2)根据各学科人数之和等于总人数求得历史的人数即可;(3)列表得出所有等可能结果,从中找到恰好选中化学、历史两科的结果数,再利用概率公式计算可得.详解:(1)该班学生总数为10÷20%=50人;(2)历史学科的人数为50﹣(5+10+15+6+6)=8人,补全图形如下:(3)列表如下: 化学 生物 政治 历史 地理 化学生物、化学 政治、化学 历史、化学 地理、化学 生物 化学、生物政治、生物 历史、生物 地理、生物 政治 化学、政治 生物、政治历史、政治 地理、政治 历史 化学、历史 生物、历史 政治、历史地理、历史 地理化学、地理生物、地理政治、地理历史、地理由表可知,共有20种等可能结果,其中该同学恰好选中化学、历史两科的有2种结果, 所以该同学恰好选中化学、历史两科的概率为21=2010. 点睛:本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式求事件A 或B 的概率. 25.证明见解析. 【解析】 【分析】想证明BC=EF ,可利用AAS 证明△ABC ≌△DEF 即可. 【详解】 解:∵AF =DC , ∴AF+FC =FC+CD , ∴AC =FD ,在△ABC 和△DEF 中,A DB E AC DF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF (AAS ) ∴BC =EF . 【点睛】本题考查全等三角形的判定和性质,解题的关键是灵活运用所学知识解决问题,属于中考常考题型. 26.(1)()P =两数相同13;(2)()10P =两数和大于49. 【解析】 【分析】根据列表法或树状图看出所有可能出现的结果共有多少种,再求出两次取出小球上的数字相同的结果有多少种,根据概率公式求出该事件的概率. 【详解】第二次第一次 6﹣276 (6,6)(6,﹣2) (6,7) ﹣2 (﹣2,6) (﹣2,﹣2) (﹣2,7) 7(7,6)(7,﹣2)(7,7)(1)P (两数相同)=. (2)P (两数和大于1)=. 【点睛】本题考查了利用列表法、画树状图法求等可能事件的概率.2019-2020学年中考数学模拟试卷一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.某校决定从三名男生和两名女生中选出两名同学担任校艺术节文艺演出专场的主持人,则选出的恰为一男一女的概率是()A.45B.35C.25D.152.如图,在⊙O中,AE是直径,半径OC垂直于弦AB于D,连接BE,若AB=27,CD=1,则BE的长是()A.5 B.6 C.7 D.83.如图是一块带有圆形空洞和矩形空洞的小木板,则下列物体中最有可能既可以堵住圆形空洞,又可以堵住矩形空洞的是()A.正方体B.球C.圆锥D.圆柱体4.我国古代数学著作《九章算术》中,将底面是直角三角形,且侧棱与底面垂直的三棱柱称为“堑堵”某“堑堵”的三视图如图所示(网格图中每个小正方形的边长均为1),则该“堑堵”的侧面积为()A.16+162B.16+82C.24+162D.4+425.如图,在△ABC中,cosB=22,sinC=35,AC=5,则△ABC的面积是()A.212B.12 C.14 D.216.在如图所示的正方形网格中,网格线的交点称为格点,已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰直角三角形,则这样的点C有( )A.6个B.7个C.8个D.9个7.学校为创建“书香校园”购买了一批图书.已知购买科普类图书花费10000元,购买文学类图书花费9000元,其中科普类图书平均每本的价格比文学类图书平均每本的价格贵5元,且购买科普书的数量比购买文学书的数量少100本.求科普类图书平均每本的价格是多少元?若设科普类图书平均每本的价格是x元,则可列方程为()A.10000x﹣90005x-=100 B.90005x-﹣10000x=100C.100005x-﹣9000x=100 D.9000x﹣100005x-=1008.在平面直角坐标系中,已知点A(﹣4,2),B(﹣6,﹣4),以原点O为位似中心,相似比为12,把△ABO缩小,则点A的对应点A′的坐标是()A.(﹣2,1)B.(﹣8,4)C.(﹣8,4)或(8,﹣4)D.(﹣2,1)或(2,﹣1)9.如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC、∠BCD,则∠P的度数是( )A.60°B.65°C.55°D.50°10.如图,△A′B′C′是△ABC以点O为位似中心经过位似变换得到的,若△A′B′C′的面积与△ABC的面积比是4:9,则OB′:OB为()A.2:3 B.3:2 C.4:5 D.4:9二、填空题(本题包括8个小题)11.如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M为曲线部分的最低点,则△ABC的面积是___.12.计算:82-=_______________.13.如图,C为半圆内一点,O为圆心,直径AB长为1 cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O 逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为_________cm1.14.若方程x2﹣2x﹣1=0的两根分别为x1,x2,则x1+x2﹣x1x2的值为_____.15.如图,在△ABC中,∠A=70°,∠B=50°,点D,E分别为AB,AC上的点,沿DE折叠,使点A落在BC 边上点F处,若△EFC为直角三角形,则∠BDF的度数为______.16.用一个半径为10cm半圆纸片围成一个圆锥的侧面(接缝忽略不计),则该圆锥的高为.17.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5cm,且tan∠EFC =,那么矩形ABCD的周长_____________cm.18.下列图形是用火柴棒摆成的“金鱼”,如果第1个图形需要8根火柴,则第2个图形需要14根火柴,第n根图形需要____________根火柴.三、解答题(本题包括8个小题)19.(6分)列方程解应用题八年级学生去距学校10 km的博物馆参观,一部分学生骑自行车先走,过了20 min后,其余学生乘汽车出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度.20.(6分)李宁准备完成题目;解二元一次方程组48x yx y-=⎧⎨+=-⎩,发现系数“□”印刷不清楚.他把“□”猜成3,请你解二元一次方程组438x yx y-=⎧⎨+=-⎩;张老师说:“你猜错了”,我看到该题标准答案的结果x、y是一对相反数,通过计算说明原题中“□”是几?21.(6分)庐阳春风体育运动品商店从厂家购进甲,乙两种T恤共400件,其每件的售价与进货量m(件)之间的关系及成本如下表所示:T恤每件的售价/元每件的成本/元甲0.1100m-+50乙()0.21200200m m-+<<60()600050200400mm+≤≤(1)当甲种T恤进货250件时,求两种T恤全部售完的利润是多少元;若所有的T恤都能售完,求该商店获得的总利润y(元)与乙种T恤的进货量x(件)之间的函数关系式;在(2)的条件下,已知两种T 恤进货量都不低于100件,且所进的T恤全部售完,该商店如何安排进货才能使获得的利润最大?22.(8分)如图,矩形ABCD中,CE⊥BD于E,CF平分∠DCE与DB交于点F.求证:BF=BC;若AB=4cm,AD=3cm,求CF的长.23.(8分)某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级(2)班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:八年级(2)班参加球类活动人数情况统计表项目篮球足球乒乓球排球羽毛球人数 a 6 5 7 6八年级(2)班学生参加球类活动人数情况扇形统计图根据图中提供的信息,解答下列问题:a =,b = .该校八年级学生共有600人,则该年级参加足球活动的人数约 人;该班参加乒乓球活动的5位同学中,有3位男同学(A ,B ,C)和2位女同学(D ,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.24.(10分)阅读材料:已知点00(,)P x y 和直线y kx b =+,则点P 到直线y kx b =+的距离d 可用公式0021kx y b d k-+=+计算.例如:求点(2,1)P -到直线1y x =+的距离.解:因为直线1y x =+可变形为10x y -+=,其中1,1k b ==,所以点(2,1)P -到直线1y x =+的距离为:00221(2)1122111kx y b d k -+⨯--+====++.根据以上材料,求:点(1,1)P 到直线32y x =-的距离,并说明点P 与直线的位置关系;已知直线1y x =-+与3y x =-+平行,求这两条直线的距离. 25.(10分)如图,在五边形ABCDE 中,∠BCD=∠EDC=90°,BC=ED ,AC=AD .求证:△ABC ≌△AED ;当∠B=140°时,求∠BAE 的度数.26.(12分)列方程解应用题:某市今年进行水网升级,1月1日起调整居民用水价格,每立方米水费上涨13,小丽家去年12月的水费是15元,而今年5月的水费则是30元.已知小丽家今年5月的用水量比去年12月的用水量多5m 3,求该市今年居民用水的价格.参考答案一、选择题(本题包括10个小题,每小题只有一个选项符合题意)1.B【解析】试题解析:列表如下:∴共有20种等可能的结果,P(一男一女)=123=.205故选B.2.B【解析】【分析】根据垂径定理求出AD,根据勾股定理列式求出半径,根据三角形中位线定理计算即可.【详解】解:∵半径OC垂直于弦AB,∴AD=DB=172在Rt△AOD中,OA2=(OC-CD)2+AD2,即OA2=(OA-1)27)2,解得,OA=4∴OD=OC-CD=3,∵AO=OE,AD=DB,∴BE=2OD=6故选B【点睛】本题考查的是垂径定理、勾股定理,掌握垂直于弦的直径平分这条弦是解题的关键3.D【分析】本题中,圆柱的俯视图是个圆,可以堵住圆形空洞,它的正视图和左视图是个矩形,可以堵住方形空洞.【详解】根据三视图的知识来解答.圆柱的俯视图是一个圆,可以堵住圆形空洞,而它的正视图以及侧视图都为一个矩形,可以堵住方形的空洞,故圆柱是最佳选项.故选D.【点睛】此题考查立体图形,本题将立体图形的三视图运用到了实际中,只要弄清楚了立体图形的三视图,解决这类问题其实并不难.4.A【解析】【分析】分析出此三棱柱的立体图像即可得出答案.【详解】由三视图可知主视图为一个侧面,另外两个侧面全等,是长×高=22×4=82,所以侧面积之和为82×2+4×4= 16+162,所以答案选择A项.【点睛】本题考查了由三视图求侧面积,画出该图的立体图形是解决本题的关键.5.A【解析】【分析】根据已知作出三角形的高线AD,进而得出AD,BD,CD,的长,即可得出三角形的面积.【详解】解:过点A作AD⊥BC,∵△ABC中,cosB=22,sinC=35,AC=5,∴cosB=22=BD AB,。
《几何综合探究题中考27题》(共55题)2022年中考专练附答案(北京专用)

5年(2016-2020)中考1年模拟数学试题分项详解(北京专用)专题15几何综合探究题中考27题(共45题)一.解答题(共5小题)1.(2020•北京)在△ABC中,∠C=90°,AC>BC,D是AB的中点.E为直线AC上一动点,连接DE.过点D作DF⊥DE,交直线BC于点F,连接EF.(1)如图1,当E是线段AC的中点时,设AE=a,BF=b,求EF的长(用含a,b的式子表示);(2)当点E在线段CA的延长线上时,依题意补全图2,用等式表示线段AE,EF,BF之间的数量关系,并证明.【分析】(1)由三角形的中位线定理得DE∥BC,DE=12BC,进而证明四边形CEDF是矩形得DE=CF,得出CF,再根据勾股定理得结果;(2)过点B作BM∥AC,与ED的延长线交于点M,连接MF,证明△ADE≌△BDM得AE=BM,DE =DM,由垂直平分线的判定定理得EF=MF,进而根据勾股定理得结论.【解答】解:(1)∵D是AB的中点,E是线段AC的中点,∴DE∥BC,DE=12BC,∵∠ACB=90°,∴∠DEC=90°,∵DF⊥DE,∴∠EDF=90°,∴四边形CEDF是矩形,∴DE=CF=12BC,五年中考真题∴CF =BF =b , ∵CE =AE =a ,∴EF =√CF 2+CE 2=√a 2+b 2;(2)AE 2+BF 2=EF 2.证明:过点B 作BM ∥AC ,与ED 的延长线交于点M ,连接MF , 则∠AED =∠BMD ,∠CBM =∠ACB =90°, ∵D 点是AB 的中点, ∴AD =BD ,在△ADE 和△BDM 中, {∠AED =∠BMD ∠ADE =∠BDM AD =BD, ∴△ADE ≌△BDM (AAS ), ∴AE =BM ,DE =DM , ∵DF ⊥DE , ∴EF =MF , ∵BM 2+BF 2=MF 2, ∴AE 2+BF 2=EF 2.2.(2019•北京)已知∠AOB =30°,H 为射线OA 上一定点,OH =√3+1,P 为射线OB 上一点,M 为线段OH 上一动点,连接PM ,满足∠OMP 为钝角,以点P 为中心,将线段PM 顺时针旋转150°,得到线段PN ,连接ON . (1)依题意补全图1;(2)求证:∠OMP=∠OPN;(3)点M关于点H的对称点为Q,连接QP.写出一个OP的值,使得对于任意的点M总有ON=QP,并证明.【分析】(1)根据题意画出图形.(2)由旋转可得∠MPN=150°,故∠OPN=150°﹣∠OPM;由∠AOB=30°和三角形内角和180°可得∠OMP=180°﹣30°﹣∠OPM=150°﹣∠OPM,得证.(3)根据题意画出图形,以ON=QP为已知条件反推OP的长度.由(2)的结论∠OMP=∠OPN联想到其补角相等,又因为旋转有PM=PN,已具备一边一角相等,过点N作NC⊥OB于点C,过点P作PD⊥OA于点D,即可构造出△PDM≌△NCP,进而得PD=NC,DM=CP.此时加上ON=QP,则易证得△OCN≌△QDP,所以OC=QD.利用∠AOB=30°,设PD=NC=a,则OP=2a,OD=√3a.再设DM=CP=x,所以QD=OC=OP+PC=2a+x,MQ=DM+QD=2a+2x.由于点M、Q关于点H对称,即点H为MQ中点,故MH=12MQ=a+x,DH=MH﹣DM=a,所以OH=OD+DH=√3a+a=√3+1,求得a=1,故OP=2.证明过程则把推理过程反过来,以OP=2为条件,利用构造全等证得ON=QP.【解答】解:(1)如图1所示为所求.(2)设∠OPM=α,∵线段PM绕点P顺时针旋转150°得到线段PN∴∠MPN=150°,PM=PN∴∠OPN=∠MPN﹣∠OPM=150°﹣α∵∠AOB =30°∴∠OMP =180°﹣∠AOB ﹣∠OPM =180°﹣30°﹣α=150°﹣α ∴∠OMP =∠OPN(3)OP =2时,总有ON =QP ,证明如下:过点N 作NC ⊥OB 于点C ,过点P 作PD ⊥OA 于点D ,如图2 ∴∠NCP =∠PDM =∠PDQ =90° ∵∠AOB =30°,OP =2 ∴PD =12OP =1∴OD =√OP 2−PD 2=√3 ∵OH =√3+1 ∴DH =OH ﹣OD =1 ∵∠OMP =∠OPN∴180°﹣∠OMP =180°﹣∠OPN 即∠PMD =∠NPC 在△PDM 与△NCP 中 {∠PDM =∠NCP ∠PMD =∠NPC PM =NP∴△PDM ≌△NCP (AAS ) ∴PD =NC ,DM =CP设DM =CP =x ,则OC =OP +PC =2+x ,MH =MD +DH =x +1 ∵点M 关于点H 的对称点为Q ∴HQ =MH =x +1∴DQ =DH +HQ =1+x +1=2+x ∴OC =DQ在△OCN 与△QDP 中 {OC =QD∠OCN =∠QDP =90°NC =PD∴△OCN ≌△QDP (SAS )∴ON=QP3.(2018•北京)如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A 关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.(1)求证:GF=GC;(2)用等式表示线段BH与AE的数量关系,并证明.【分析】(1)如图1,连接DF,根据对称得:△ADE≌△FDE,再由HL证明Rt△DFG≌Rt△DCG,可得结论;(2)证法一:如图2,作辅助线,构建AM=AE,先证明∠EDG=45°,得DE=EH,证明△DME≌△EBH,则EM=BH,根据等腰直角△AEM得:EM=√2AE,得结论;证法二:如图3,作辅助线,构建全等三角形,证明△DAE≌△ENH,得AE=HN,AD=EN,再说明△BNH是等腰直角三角形,可得结论.【解答】证明:(1)如图1,连接DF,∵四边形ABCD是正方形,∴DA=DC,∠A=∠C=90°,∵点A关于直线DE的对称点为F,∴△ADE≌△FDE,∴DA=DF=DC,∠DFE=∠A=90°,∴∠DFG=90°,在Rt△DFG和Rt△DCG中,∵{DF =DC DG =DG, ∴Rt △DFG ≌Rt △DCG (HL ), ∴GF =GC ;(2)BH =√2AE ,理由是:证法一:如图2,在线段AD 上截取AM ,使AM =AE , ∵AD =AB , ∴DM =BE ,由(1)知:∠1=∠2,∠3=∠4, ∵∠ADC =90°,∴∠1+∠2+∠3+∠4=90°, ∴2∠2+2∠3=90°, ∴∠2+∠3=45°, 即∠EDG =45°, ∵EH ⊥DE ,∴∠DEH =90°,△DEH 是等腰直角三角形, ∴∠AED +∠BEH =∠AED +∠1=90°,DE =EH , ∴∠1=∠BEH , 在△DME 和△EBH 中, ∵{DM =BE∠1=∠BEH DE =EH, ∴△DME ≌△EBH (SAS ), ∴EM =BH ,Rt △AEM 中,∠A =90°,AM =AE , ∴EM =√2AE , ∴BH =√2AE ;证法二:如图3,过点H 作HN ⊥AB 于N , ∴∠ENH =90°,由方法一可知:DE =EH ,∠1=∠NEH , 在△DAE 和△ENH 中,∵{∠A=∠ENH ∠1=∠NEH DE=EH,∴△DAE≌△ENH(AAS),∴AE=HN,AD=EN,∵AD=AB,∴AB=EN=AE+BE=BE+BN,∴AE=BN=HN,∴△BNH是等腰直角三角形,∴BH=√2HN=√2AE.4.(2017•北京)在等腰直角△ABC中,∠ACB=90°,P是线段BC上一动点(与点B、C不重合),连接AP,延长BC至点Q,使得CQ=CP,过点Q作QH⊥AP于点H,交AB于点M.(1)若∠P AC=α,求∠AMQ的大小(用含α的式子表示).(2)用等式表示线段MB与PQ之间的数量关系,并证明.【分析】(1)由等腰直角三角形的性质得出∠BAC =∠B =45°,∠P AB =45°﹣α,由直角三角形的性质即可得出结论;(2)连接AQ ,作ME ⊥QB ,由AAS 证明△APC ≌△QME ,得出PC =ME ,△MEB 是等腰直角三角形,由等腰直角三角形的性质即可得出结论. 【解答】解:(1)∠AMQ =45°+α;理由如下: ∵∠P AC =α,△ACB 是等腰直角三角形, ∴∠BAC =∠B =45°,∠P AB =45°﹣α, ∵QH ⊥AP , ∴∠AHM =90°,∴∠AMQ =180°﹣∠AHM ﹣∠P AB =45°+α;(2)PQ =√2MB ;理由如下: 连接AQ ,作ME ⊥QB ,如图所示: ∵AC ⊥QP ,CQ =CP , ∴∠QAC =∠P AC =α, ∴∠QAM =45°+α=∠AMQ , ∴AP =AQ =QM , 在△APC 和△QME 中, {∠MQE =∠PAC ∠ACP =∠QEM AP =QM,∴△APC ≌△QME (AAS ), ∴PC =ME ,∵△MEB 是等腰直角三角形,∴12PQ =√22MB , ∴PQ =√2MB .方法二:也可以延长AC 到D ,使得CD =CQ . 则易证△ADP ≌△QBM .∴BM =PD =√2CD =√2QC =√22PQ , 即PQ =√2MB .5.(2016•北京)在等边△ABC 中,(1)如图1,P ,Q 是BC 边上的两点,AP =AQ ,∠BAP =20°,求∠AQB 的度数;(2)点P ,Q 是BC 边上的两个动点(不与点B ,C 重合),点P 在点Q 的左侧,且AP =AQ ,点Q 关于直线AC 的对称点为M ,连接AM ,PM . ①依题意将图2补全;②小茹通过观察、实验提出猜想:在点P ,Q 运动的过程中,始终有P A =PM ,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法: 想法1:要证明P A =PM ,只需证△APM 是等边三角形;想法2:在BA 上取一点N ,使得BN =BP ,要证明P A =PM ,只需证△ANP ≌△PCM ;想法3:将线段BP 绕点B 顺时针旋转60°,得到线段BK ,要证P A =PM ,只需证P A =CK ,PM =CK … 请你参考上面的想法,帮助小茹证明P A =PM (一种方法即可).【分析】(1)根据等腰三角形的性质得到∠APQ =∠AQP ,由邻补角的定义得到∠APB =∠AQC ,根据三角形外角的性质即可得到结论;(2)如图2根据等腰三角形的性质得到∠APQ=∠AQP,由邻补角的定义得到∠APB=∠AQC,由点Q 关于直线AC的对称点为M,得到AQ=AM,∠OAC=∠MAC,等量代换得到∠MAC=∠BAP,推出△APM是等边三角形,根据等边三角形的性质即可得到结论.【解答】解:(1)∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ=20°,∴∠AQB=∠APQ=∠BAP+∠B=80°;(2)如图2,∵AP=AQ,∴∠APQ=∠AQP,∴∠APB=∠AQC,∵△ABC是等边三角形,∴∠B=∠C=60°,∴∠BAP=∠CAQ,(将线段BP绕点B顺时针旋转60°,得到线段BK,要证P A=PM,只需证P A=CK,PM=CK…请你参考上面的想法,帮助小茹证明P A=PM)∵点Q关于直线AC的对称点为M,∴AQ=AM,∠QAC=∠MAC,∴∠MAC=∠BAP,∴∠BAP+∠P AC=∠MAC+∠CAP=60°,∴∠P AM=60°,∵AP=AQ,∴AP=AM,∴△APM是等边三角形,∴AP=PM.证明△ABP≌△ACM≌△BCK一年模拟新题一.解答题(共40小题)1.(2020•丰台区三模)如图,在△ABC中,∠BAC=30°,AB=AC,将线段AC绕点A逆时针旋转α°(0<α<180),得到线段AD,连接BD,交AC于点P.(1)当α=90°时,①依题意补全图形;②求证:PD=2PB;(2)写出一个α的值,使得PD=√3PB成立,并证明.【分析】(1)当α=90°时,①依题意即可补全图形;②根据30度角所对直角边等于斜边一半即可证明PD=2PB;(2)当α的值为60度时,根据等腰三角形的性质即可证明PD=√3PB成立.【解答】解:(1)当α=90°时,①如图即为补全的图形;②证明:∵∠BAC =30°,AB =AC , 根据题意可知:AC =AD , ∴AD =AB , ∴∠ABD =∠ADB , ∵∠CAD =90°, ∴∠DAB =120°,∴∠ABD =∠D =∠BAC =30°, ∴AP =BP ,在Rt △APD 中,∠ADB =30°, ∴PD =2AP , ∴PD =2PB ;(2)当α=60(或120°)时,PD =√3PB 成立, 情况1,如图所示:当α=60°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE , ∴△DFP ∽△BEP , ∴DF BE=PD PB,在Rt △ABE 中,∠BAC =30°, ∴AC =AB =2BE ,在Rt △ADF 中,∠CAD =60°, ∴AD =2√33DF , ∵AD =AC =AB , ∴2BE =2√33DE , ∴√3BE =DF , ∴PD =√3PB . 情况2,如图所示:当α=120°时,过点D 作DF ⊥AC 于点F ,过点B 作BE ⊥AC 于点E ,∴DF ∥BE , ∴△DFP ∽△BEP , ∴DF BE=PD PB,在Rt △ABE 中,∠BAC =30°, ∴AC =AB =2BE ,在Rt △ADF 中,∠F AD =60°, ∴AD =2√33DF , ∵AD =AC =AB , ∴2BE =2√33DE ,∴√3BE=DF,∴PD=√3PB.2.(2020•石景山区二模)在△ABC中,AB=AC,D是边BC上的一点(不与点B重合),边BC上点E在点D的右边且∠DAE=12∠BAC,点D关于直线AE的对称点为F,连接CF.(1)如图1,①依题意补全图1;②求证:CF=BD.(2)如图2,∠BAC=90°,用等式表示线段DE,CE,CF之间的数量关系,并证明.【分析】(1)①根据题意补全图形即可;②连接AF,如图1,根据已知条件得到∠3=∠1+∠2.根据轴对称的性质得到AF=AD,∠F AE=∠3=∠1+∠2.根据全等三角形的性质得到结论;(2)连接F A,FE,如图2,根据等腰三角形的性质得到∠1=∠2=45°,求得∠FCE=90°,根据勾股定理即可得到结论.【解答】解:(1)①依题意补全图形,如图1;②证明:连接AF,如图1,∵∠3=12∠BAC,∴∠3=∠1+∠2.∵点F与点D关于直线AE对称,∴AF=AD,∠F AE=∠3=∠1+∠2.∴∠4=∠F AE﹣∠2=(∠1+∠2)﹣∠2=∠1.又∵AC=AB,∴△ACF≌△ABD(SAS),∴CF=BD;(2)线段DE,CE,CF之间的数量关系是DE2=CE2+CF2.证明:连接F A,FE,如图2,∵AB=AC,∠BAC=90°,∴∠1=∠2=45°,由(1)②,可得FE=DE,∠3=∠2=45°,∴∠FCE=90°,在Rt△FCE中,由勾股定理,得FE2=CE2+CF2,∴DE2=CE2+CF2.3.(2020•朝阳区三模)在△ABC中,∠C=90°,AC=BC,点P在线段BA的延长线上,作PD⊥AC,交AC的延长线于点D,点D关于直线AB的对称点为E,连接PE并延长PE到点F,使EF=AC,连接CF.(1)依题意补全图1;(2)求证:AD=CF;(3)若AC=2,点Q在直线AB上,写出一个AQ的值,使得对于任意的点P总有QD=QF,并证明.【分析】(1)依照题意,补全图形即可;(2)通过证明四边形DCFP是矩形,可得PD=CF,由等腰直角三角形的性质可得AD=PD=CF;(3)通过证明△DAQ≌△FCQ,可得QD=QF.【解答】解:(1)补全图形,如图所示:(2)∵∠C=90°,AC=BC,∴∠B=∠CAB=45°,∵PD⊥AC,∴∠PDA=90°,∴∠DP A=90°﹣∠P AD=45°=∠DAP,∴AD=DP,∵点D关于直线AB的对称点为E,∴∠FP A=∠DP A=45°,∴∠DPF=90°,又∵∠PDA=90°=∠ACF,∴四边形DCFP是矩形,∴PD=CF,∴AD=PD=CF;(3)AQ=√2,理由如下:如图2,连接CQ,∵∠C=90°,AC=BC=2,∴AB=2√2,∠B=∠CAB=45°,∵AQ=√2,∴AQ=BQ,又∵∠C=90°,AC=BC=2,∴CQ=AQ=BQ,∠QCA=∠CAQ=45°,∴∠DAQ=∠QCF=135°,又∵AD=CF,∴△DAQ≌△FCQ(SAS),∴FQ=DQ.4.(2020•北京二模)已知菱形ABCD中,∠A=60°,点E为边AD上一个动点(不与点A,D重合),点F在边DC上,且AE=DF,将线段DF绕着点D逆时针旋转120°得线段DG,连接GF,BF,EF.(1)依题意补全图形;(2)求证:△BEF为等边三角形;(3)用等式表示线段BG,GF,CF的数量关系,并证明.【分析】(1)根据题意补全图形即可;(2)易证△ABD为等边三角形,∠BDF=60°,由SAS证得△ABE≌△DBF,得出BE=BF,∠ABE=∠DBF,则∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=60°,即可得出结论;(3)取FG中点H,连接DH,由等腰三角形的性质得出∠DFG=∠DGF=30°,DH⊥GF,由三角函数得出GF=√3DG,易证△BCD为等边三角形,B、D、G三点在同一条直线上,求出BG﹣CF=2DG,即可得出√3(BG﹣CF)=2GF.【解答】(1)解:补全图形,如图1所示:(2)证明:∵四边形ABCD是菱形,∴AB=AD,∵∠A=60°,∴△ABD为等边三角形,∠BDF=60°,∴∠ABD=∠BDC=60°,AB=BD,在△ABE和△DBF中,{AB=BD∠A=∠BDF=60°AE=DF,∴△ABE≌△DBF(SAS),∴BE=BF,∠ABE=∠DBF,∴∠EBF=∠EBD+∠DBF=∠EBD+∠ABE=∠ABD=60°,∴△BEF为等边三角形;(3)解:BG、GF、CF的数量关系为:√3(BG﹣CF)=2GF,理由如下:取FG中点H,连接DH,如图2所示:∵AE=DF=DG,∠FDG=120°,∴∠DFG=∠DGF=30°,DH⊥GF,∴GF=2GH=2DG•cos30°=2DG×√32=√3DG,∵四边形ABCD是菱形,∠A=60°,∴△BCD为等边三角形,∴BD=CD,∠BDC=60°,∵∠FDG=120°,∴∠BDC+∠FDG=180°,即B、D、G三点在同一条直线上,∴BG=BD+DG=CD+DG=CF+DF+DG=CF+2DG,∴BG﹣CF=2DG,∴√3(BG﹣CF)=2√3DG=2GF.5.(2020•朝阳区二模)已知∠AOB=40°,M为射线OB上一定点,OM=1,P为射线OA上一动点(不与点O重合),OP<1,连接PM,以点P为中心,将线段PM顺时针旋转40°,得到线段PN,连接MN.(1)依题意补全图1;(2)求证:∠APN=∠OMP;(3)H为射线OA上一点,连接NH.写出一个OH的值,使得对于任意的点P总有∠OHN为定值,并求出此定值.【分析】(1)根据要求画出图形即可.(2)利用三角形的外角的性质解决问题即可.(3)结论:OH=1时,∠OHN的值为定值.证明△OMP≌△GPN(SAS),推出OP=NG,∠AOB=∠NGP=40°,由OM=OH=PG=1,推出OP=HG,推出GH=GN,推出∠GNH=∠GHN=12(180°﹣40°)=70°可得结论.【解答】(1)解:图形如图所示:(2)证明:如图1中,∵∠MPN=∠AOB=40°,∠APM=∠APN+∠MPN=∠AOB+∠OMP,∴∠APN=∠OMP.(3)解:结论:OH=1时,∠OHN的值为定值.理由:在射线P A设取一点G,使得PG=OM,连接NG.∵PN=PM,∠GPN=∠OMP,∴△OMP≌△GPN(SAS),∴OP=NG,∠AOB=∠NGP=40°,∵OM=OH=PG=1,∴OP=HG,∴GH=GN,∴∠GNH=∠GHN=12(180°﹣40°)=70°,∴∠OHN=180°﹣70°=110°.6.(2020•海淀区二模)如图1,等边三角形ABC中,D为BC边上一点,满足BD<CD,连接AD,以点A 为中心,将射线AD顺时针旋转60°,与△ABC的外角平分线BM交于点E.(1)依题意补全图1;(2)求证:AD=AE;(3)若点B关于直线AD的对称点为F,连接CF.①求证:AE∥CF;②若BE+CF=AB成立,直接写出∠BAD的度数为20°.【分析】(1)由旋转即可补全图形;(2)先判断出∠BAE=∠CAD,再判断出∠ABE=60°=∠C,进而判断出△ABE≌△ACD,即可得出结论;(3)①先判断出AFC=∠ACF,设∠BAD=α,进而表示出∠F AD=α,∠CAF=60°﹣2α,进而得出∠ACF=60°+α再判断出∠CAE=120°﹣α,即可得出结论;②先判断出∠CBG=30°﹣α,进而判断出∠CDF=60°﹣2α,再判断出DF=CF,进而得出∠DCF=∠CDF=60°﹣2α,再判断出∠DCF=α,即可得出结论.【解答】解:(1)补全图形如图1所示;(2)由旋转知,∠DAE=60°,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠C=∠BAC=60°,∴∠DAE=∠BAC,∴∠BAE=∠CAD,∵BE是△ABC的外角的平分线,∴∠ABM=12(180°﹣60°)=60°=∠C,在△ABE和△ACD中,{∠BAE=∠CADAB=AC∠ABE=∠ACD=60°,∴△ABE≌△ACD(SAS),∴AD=AE;(3)①如图2,连接AF,∵点F是点B关于AD的对称点,∴∠BAD=∠F AD,AF=AB,∴AF=AC,∴∠AFC=∠ACF,设∠BAD=α,则∠F AD=α,∴∠CAF=∠BAC﹣∠BAD﹣∠F AD=60°﹣2α,∴∠ACF=12(180°﹣∠CAF)=60°+α,由(2)知,∠BAE=∠CAD=60°﹣α,∴∠CAE=∠BAE+∠BAC=60°﹣α+60°=120°﹣α,∴∠ACF+∠CAE=60°+α+120°﹣α=180°,∴AE∥CF;②如图2,连接BF,设∠BAD=α,∵点F是点B关于AD的对称点,∴AD⊥BF,垂足记作点G,则∠AGB=90°,∴∠ABG=90°﹣α,∵∠ABC=60°,∴∠CBG=30°﹣α,连接DF,则BD=DF,∴∠CDF=2∠CBG=60°﹣2α,由(2)知,△ABE≌△ACD,∴BE=CD,∵BE+CF=AB,∴CD+CF=BC=BD+CD,∴BD=CF,∴DF=CF,∴∠DCF=∠CDF=60°﹣2α,由①知,∠ACF=60°+α,∴∠DCF=∠ACF﹣∠ACB=α,∴60°﹣2α=α,∴α=20°,即∠BAD=20°,故答案为:20.7.(2020•门头沟区二模)如图,在正方形ABCD中,点E,F分别是AB,BC上的两个动点(不与点A,B,C重合),且AE=CF,延长BC到G,使CG=CF,连接EG,DF.(1)依题意将图形补全;(2)小华通过观察、实验、提出猜想:在点E,F运动过程中,始终有EG=√2DF.经过与同学们充分讨论,形成了几种证明的想法:想法一:连接DE,DG,证明△DEG是等腰直角三角形;想法二:过点D作DF的垂线,交BA的延长线于H,可得△DFH是等腰直角三角形,证明HF=EG;…请参考以上想法,帮助小华证明EG=√2DF.(写出一种方法即可)【分析】(1)根据题意画出图形即可;(2)如图,连接DE,DG,根据正方形的性质得到AD=CD,∠A=∠DCF=90°,根据全等三角形的性质得到DE=DF,∠ADE=∠CDF,求得DF=DG,由等腰三角形的性质得到∠CDF=∠CDG,推出△EDG是等腰直角三角形,于是得到结论.【解答】解:(1)依题意补全图形如图所示;(2)如图,连接DE,DG,∵在正方形ABCD中,AD=CD,∠A=∠DCF=90°,∵AE=CF,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF,∵∠DCF=90°,∴DC⊥FG,∵CF=CG,∴DF=DG,∴∠CDF=∠CDG,∴DE=DG,∠ADE=∠CDG,∵∠ADC=90°,∴∠EDG=90°,∴△EDG是等腰直角三角形,∴EG=√2DG=√2DF.8.(2020•东城区二模)在△ABC 中,AB =AC ,∠BAC =α,点D 是△ABC 外一点,点D 与点C 在直线AB 的异侧,且点D ,A ,C 不共线,连接AD ,BD ,CD .(1)如图1,当α=60°.∠ADB =30°时,画出图形,直接写出AD ,BD ,CD 之间的数量关系; (2)当α=90°,∠ADB =45°时,利用图2,继续探究AD ,BD ,CD 之间的数量关系并证明; (提示:尝试运用图形变换,将要研究的有关线段尽可能转移到一个三角形中)(3)当∠ADB =α2时,进一步探究AD ,BD ,CD 之间的数量关系,并用含α的等式直接表示出它们之间的关系.【分析】(1)先判断出∠BDE =90°,再根据勾股定理得出BD 2+DE 2=BE 2,即BD 2+AD 2=BE 2,再判断出△ABE ≌△ACD (SAS ),得出BE =CD ,即可得出结论;(2)同(1)方法得出DE 2+BD 2=BE 2,进而得出2AD 2+BD 2=BE 2,同(1)的方法判断出BE =CD ,即可得出结论;(3)同(1)的方法得出DE 2+BD 2=BE 2,再判断出DF =2AD •sin α2,即可得出结论.【解答】解:(1)AD 2+BD 2=CD 2,理由:如图1,过AD 为边在AD 上侧作等边三角形ADE ,连接BE , 则AD =DE =AE ,∠DAE =∠ADE =60°, ∵∠ADB =30°,∴∠BDE =∠DBA +∠ADE =90°,在Rt △BDE 中,根据勾股定理得,BD 2+DE 2=BE 2, ∴BD 2+AD 2=BE 2, ∵∠DAE =∠BAC =60°, ∴∠BAE =∠CAD , ∵AB =AC ,∴△ABE ≌△ACD (SAS ),∴BE=CD,∴AD2+BD2=CD2;(2)如图2,过点A作AE⊥AD,且AE=AD,连接BE,DE,∴∠ADE=45°,∵∠BDA=45°,∴∠BDE=90°,根据勾股定理得,DE2+BD2=BE2,∵DE2=2AD2,∴2AD2+BD2=BE2,∵∠DAE=∠BAC=90°,∴∠BAE=∠CAD,∵AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∴2AD2+BD2=CD2;(3)如图3,将线段AD绕点A顺时针旋转α得到AE,连接DE,BE,∴∠ADE=12(180°﹣∠DAE)=90°−12α,∵∠ADB=12α,∴∠BDE=90°,根据勾股定理得,DE2+BD2=BE2,∵∠DAE=∠BAC=α,∴∠BAE=∠CAD,∵AB=AC,∴△ABE≌△ACD(SAS),∴BE=CD,∴DE 2+BD 2=CD 2,过点A 作AF ⊥DE 于F ,则DE =2DF , ∴∠DAF =90°﹣∠ADE =12α, 在Rt △ADF 中,sin ∠DAF =DF AD , ∴DF =AD •sin ∠DAF =AD •sin α2,∴DE =2DF =2AD •sin α2,即:(2AD •sin α2)2+BD 2=CD 2.9.(2020•平谷区二模)如图,在△ABM中,∠ABC=90°,延长BM使BC=BA,线段CM绕点C顺时针旋转90°得到线段CD,连结DM,AD.(1)依据题意补全图形;(2)当∠BAM=15°时,∠AMD的度数是60°;(3)小聪通过画图、测量发现,当∠AMB是一定度数时,AM=MD.小聪把这个猜想和同学们进行交流,通过讨论,形成了证明该猜想的几种想法:想法1:通过观察图形可以发现,如果把梯形ABCD补全成为正方形ABCE,就易证△ABM≌△AED,因此易得当∠AMD是特殊值时,问题得证;想法2:要证AM=MD,通过第(2)问,可知只需要证明△AMD是等边三角形,通过构造平行四边形CDAF,易证AD=CF,通过△ABM≌△CBF,易证AM=CF,从而解决问题;想法3:通过BC=BA,∠ABC=90°,连结AC,易证△ACM≌△ACD,易得△AMD是等腰三角形,因此当∠AMD是特殊值时,问题得证.请你参考上面的想法,帮助小聪证明当∠AMD是一定度数时,AM=MD.(一种方法即可)【分析】(1)由题意画出,图形;(2)由旋转的性质可得出△DCM为等腰直角三角形,则∠DMC=45°,∠AMB=75°,可求出答案;(3)根据三种想法证明△AMD为等边三角形即可得出结论.【解答】解:(1)由题意画出图形如图1,(2)如图1,∵∠BAM=15°,∠ABC=90°,∴∠AMB=90°﹣15°=75°,∵线段CM绕点C顺时针旋转90°得到线段CD,∴CM=CD,∠MCD=90°,∴∠CMD=∠MDC=45°,∴∠AMD=180°﹣∠AMB﹣∠DMC=180°﹣75°﹣45°=60°.故答案为:60°.(3)当∠AMB=75°时,AM=DM.想法1证明:如图2,过点A作AE⊥CD交CD的延长线于点E,∵∠AEC=∠C=∠ABC=90°,AB=BC,∴四边形ABCE正方形,∴AB=AE,BC=CE,由(2)可知CM=CD,∴BM=DE,∴△ABM≌△AED(SAS),∴AM=AD,由(2)可知∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.想法2证明:如图3,过点C作CF∥AD交AB于点F,∵AF∥CD,∴四边形AFCD为平行四边形,∴AD=CF,AF=CD,∵AB=AF+BF,BC=BM+CM,AB=BC,∴CD+BF=BM+CM,∵CD=CM,∴BF=BM,又∵AB=BC,∠FBC=∠MBC=90°,∴△ABM≌△CBF(SAS),∴AM=CF,∴AM=AD,又∵∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.想法3证明:如图4,连接AC,∵BC=AB,∠ABC=90°,∴∠ACB=45°,∴∠ACD=45°,又∵CM=CD,AC=AC,∴△ACM≌△ACD(SAS),∴AM=AD,∵∠AMD=60°,∴△AMD为等边三角形,∴AM=DM.10.(2020•西城区二模)在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.求证:∠EAB=∠GHC;(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.①依题意补全图形;②用等式表示线段AE与CN之间的数量关系,并证明.【分析】(1)由平行线的性质可得出∠AGH=∠GHC.证得∠EAB=∠AGH.则结论得证;(2)①依题意补全图形即可;②连接AN,连接EN并延长,交AB边于点Q.证得NA=NE.得出∠ANE=∠ANQ=90°.则可得出AE=√2CN.【解答】(1)证明:在正方形ABCD中,AD∥BC,∠BAD=90°,∴∠AGH=∠GHC.∵GH⊥AE,∴∠EAB=∠AGH.∴∠EAB=∠GHC.(2)①补全图形,如图所示.②证明:连接AN,连接EN并延长,交AB边于点Q.∵四边形ABCD是正方形,∴点A,点C关于BD对称.∴NA=NC,∠BAN=∠BCN.∵PN垂直平分AE,∴NA=NE.∴NC=NE.∴∠NEC=∠NCE.在正方形ABCD中,BA∥CE,∠BCD=90°,∴∠AQE=∠NEC.∴∠BAN+∠AQE=∠BCN+∠NCE=90°.∴∠ANE=∠ANQ=90°.在Rt△ANE中,∴AE=√2CN.11.(2020•丰台区二模)如图,在Rt△ABC中,∠ABC=90°,将CA绕点C顺时针旋转45°,得到CP,点A关于直线CP的对称点为D,连接AD交直线CP于点E,连接CD.(1)根据题意补全图形;(2)判断△ACD的形状,并证明;(3)连接BE,用等式表示线段AB,BC,BE之间的数量关系,并证明.温馨提示:在解决第(3)问的过程中,如果你遇到困难,可以参考下面几种解法的主要思路.解法1的主要思路:延长BC至点F,使CF=AB,连接EF,可证△ABE≌△CFE,再证△BEF是等腰直角三角形.解法2的主要思路:过点A作AM⊥BE于点M,可证△ABM是等腰直角三角形,再证△ABC∽△AME.解法3的主要思路:过点A作AM⊥BE于点M,过点C作CN⊥BE于点N,设BN=a,EN=b,用含a或b的式子表示AB,BC.…….【分析】(1)根据要求画出图形即可.(2)结论:△ACD是等腰直角三角形.根据等腰直角三角形的定义判断即可.(3)结论:BC+BA=√2BE.延长BC至点F,使CF=AB,连接EF.证明△EAB≌△ECF(SAS),推出BE=EF,∠AEB=∠CEF可得结论.【解答】解:(1)图形如图所示:(2)结论:△ACD是等腰直角三角形.理由:∵A,D关于CP对称,∴AD⊥CP,∠ACP=∠PCD=45°,CA=CD,∴∠ACD=90°,∴△ACD是等腰直角三角形.(3)结论:BC+BA=√2BE.理由:延长BC至点F,使CF=AB,连接EF.∵∠ABC=∠AEC=90°,∴∠BAE+∠BCE=180°,∵∠BCE+∠ECF=180°,∴∠BAE=∠ECF,∵△ACD是等腰直角三角形,CE⊥AD,∴AE=DE,∴CE=AE=ED,∵AB=CF,∴△EAB≌△ECF(SAS),∴BE=EF,∠AEB=∠CEF,∴∠BEF=∠AEC=90°,∴△BEF是等腰直角三角形,∴BF=√2BE,∵BF=BC+CF=BC+BA,∴BC+BA=√2BE.12.(2020•密云区二模)已知:MN是经过点A的一条直线,点C是直线MN左侧的一个动点,且满足60°<∠CAN<120°,连接AC,将线段AC绕点C顺时针旋转60°,得到线段CD,在直线MN上取一点B,使∠DBN=60°.(1)若点C位置如图1所示.①依据题意补全图1;②求证:∠CDB=∠MAC;(2)连接BC,写出一个BC的值,使得对于任意一点C,总有AB+BD=3,并证明.【分析】(1)①根据题意作出图形即可求解;②根据等量关系可证∠CDB=∠MAC;(2)如图2,连接BC,在直线MN上截取AH=BD,连接CH,根据SAS可证△ACH≌△DCB,再根据全等三角形的性质和等边三角形的判定与性质即可求解.【解答】.解:(1)①如图1所示:②证明:∵∠C=60°,∠DBN=60°,∴∠C=∠DBN,∵∠DBN+∠ABD=180°,∴∠C+∠ABD=180°,在四边形ACDB中,∠CDB+∠BAC=180°,∵∠BAC+∠MAC=180°,∴∠CDB=∠MAC;(2)BC=3时,对于任意一点C,总有AB+BD=3.证明:如图2,连接BC,在直线MN上截取AH=BD,连接CH,∵∠MAC=∠CDB,AC=CD,∴△ACH≌△DCB(SAS),∴∠ACH=∠DCB,CH=CB,∵∠DCB+∠ACB=∠ACD=60°,∴∠HCB=∠ACH+∠ACB=60°,∴△HCB是等边三角形,∴BC=BH=BA+BD=3.13.(2020•顺义区二模)已知:在△ABC中,∠ABC=90°,AB=BC,点D为线段BC上一动点(点D不与点B、C重合),点B关于直线AD的对称点为E,作射线DE,过点C作BC的垂线,交射线DE于点F,连接AE.(1)依题意补全图形;(2)AE与DF的位置关系是AE⊥DF;(3)连接AF,小昊通过观察、实验,提出猜想:发现点D在运动变化的过程中,∠DAF的度数始终保持不变,小昊把这个猜想与同学们进行了交流,经过测量,小昊猜想∠DAF=45°,通过讨论,形成了证明该猜想的两种想法:想法1:过点A作AG⊥CF于点G,构造正方形ABCG,然后可证△AFG≌△AFE…想法2:过点B作BG∥AF,交直线FC于点G,构造▱ABGF,然后可证△AFE≌△BGC…请你参考上面的想法,帮助小昊完成证明(一种方法即可).【分析】(1)根据题意正确画图;(2)证明△ABD≌△AED(SSS),可得∠AED=∠B=90°,从而得结论;(3)想法1:如图2,过点A做AG⊥CF于点G,先证明四边形ABCG是正方形,得AG=AB,∠BAG =90°,再证明Rt△AFG≌Rt△AFE(HL),得∠GAF=∠EAF,根据∠BAG=90°及角的和可得结论;想法2:如图3,过点B作BG∥AF,交直线FC于点G,证明四边形ABGF是平行四边形,得AF=BG,∠BGC=∠BAF,再证明Rt△AEF≌Rt△BCG(HL),同理根据∠BCG=90°及等量代换,角的和可得结论.【解答】解:(1)补全图形如图1:(2)AE与DF的位置关系是:AE⊥DF,理由是:∵点B关于直线AD的对称点为E,∴AB=AE,BD=DE,∵AD=AD,∴△ABD≌△AED(SSS),∴∠AED=∠B=90°,∴AE⊥DF;故答案为:AE⊥DF;(3)猜想∠DAF=45°;想法1:证明如下:如图2,过点A做AG⊥CF于点G,依题意可知:∠B=∠BCG=∠CGA=90°,∵AB=BC,∴四边形ABCG是正方形,∴AG=AB,∠BAG=90°,∵点B关于直线AD的对称点为E,∴AB=AE,∠B=∠AED=∠AEF=90°,∠BAD=∠EAD,∴AG=AE,∵AF=AF,∴Rt△AFG≌Rt△AFE(HL),∴∠GAF=∠EAF,∵∠BAG=90°,∴∠BAD+∠EAD+∠EAF+∠GAF=90°,∴∠EAD+∠EAF=45°.即∠DAF=45°.想法2:证明如下:如图3,过点B作BG∥AF,交直线FC于点G,依题意可知:∠ABC =∠BCF =90°, ∴AB ∥FG , ∵AF ∥BG ,∴四边形ABGF 是平行四边形, ∴AF =BG ,∠BGC =∠BAF , ∵点B 关于直线AD 的对称点为E ,∴AB =AE ,∠ABC =∠AED =90°,∠BAD =∠EAD , ∵AB =BC , ∴AE =BC ,∴Rt △AEF ≌Rt △BCG (HL ), ∴∠EAF =∠CBG , ∵∠BCG =90°, ∴∠BGC +∠CBG =90°, ∴∠BAF +∠EAF =90°,∴∠BAD +∠EAD +∠EAF +∠EAF =90°, ∵∠BAD =∠EAD , ∴∠EAD +∠EAF =45°, 即∠DAF =45°. 故答案为:45.14.(2020•武汉模拟)已知,在△ABC 和△EFC 中,∠ABC =∠EFC =90°,点E 在△ABC 内,且∠CAE +∠CBE =90°(1)如图1,当△ABC 和△EFC 均为等腰直角三角形时,连接BF , ①求证:△CAE ∽△CBF ; ②若BE =2,AE =4,求EF 的长;(2)如图2,当△ABC 和△EFC 均为一般直角三角形时,若AB BC=EF FC=k ,BE =1,AE =3,CE =4,求k 的值.【分析】(1)①先判断出∠BCF =∠ACE ,再判断出CE AC=CF BC,即可得出结论;②先判断出∠CBF =∠CAE ,进而判断出∠EBF =90°,再求出BF =2√2,最后用勾股定理求解即可得出结论;(2)先判断出∠BCF =∠ACE ,再判断出CEAC=CF BC,进而判断出△BCF ∽△ACE ,进而表示出BF =√k +1,再表示出EF =√k +1,最后用勾股定理得,BE 2+BF 2=EF 2,建立方程求解即可得出结论.【解答】解:(1)①∵△ABC 和△CEF 都是等腰直角三角形, ∴∠ECF =∠ACB =45°, ∴∠BCF =∠ACE ,∵△ABC 和△CEF 都是等腰直角三角形, ∴CE =√2CF ,AC =√2CB , ∴CE CF =AC CB =√2,∴CE AC=CF BC,∴△BCF ∽△ACE ;②由①知,△BCF ∽△ACE , ∴∠CBF =∠CAE ,AE BF=AC BC=√2,∴BF =√22AE =√22×4=2√2, ∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°, 即:∠EBF =90°,根据勾股定理得,EF =√BE 2+BF 2=√(2√2)2+22=2√3;(2)如图(2),连接BF ,在Rt △ABC 中,tan ∠ACB =ABBC =k , 同理,tan ∠ECF =k , ∴tan ∠ACB =tan ∠ECF , ∴∠ACB =∠ECF , ∴∠BCF =∠ACE ,在Rt △ABC 中,设BC =m ,则AB =km , 根据勾股定理得,AC =√AB 2+BC 2=m √k 2+1;在Rt △CEF 中,设CF =n ,则EF =nk ,同理,CE =n √k 2+1 ∴CF BC =nm ,CEAC =n√k 2+1m√k 2+1=n m,∴CF BC=CE AC,∵∠BCF =∠ACE , ∴△BCF ∽△ACE , ∴∠CBF =∠CAE , ∵∠CAE +∠CBE =90°, ∴∠CBF +∠CBE =90°, 即:∠EBF =90°, ∵△BCF ∽△ACE , ∴AE BF=AC BC =√k 2+1,∴BF =1√k +1AE =3√k +1,∵CE =4, ∴n √k 2+1=4, ∴n =√k +1, ∴EF =4k√k +1,在Rt △EBF 中,根据勾股定理得,BE 2+BF 2=EF 2,∴12+(3√k 2+1)2=(4k√k 2+1)2,∴k =√63或k =−√63(舍),即:k 的值为√63.15.(2020•丰台区模拟)如图,在正方形ABCD 中,E 是边BC 上的一动点(不与点B 、C 重合),连接DE 、点C 关于直线DE 的对称点为C ′,连接AC ′并延长交直线DE 于点P ,F 是AC ′的中点,连接DF . (1)求∠FDP 的度数;(2)连接BP ,请用等式表示AP 、BP 、DP 三条线段之间的数量关系,并证明; (3)连接AC ,若正方形的边长为√2,请直接写出△ACC ′的面积最大值.【分析】(1)证明∠CDE =∠C 'DE 和∠ADF =∠C 'DF ,可得∠FDP '=12∠ADC =45°;(2)作辅助线,构建全等三角形,证明△BAP ≌△DAP '(SAS ),得BP =DP ',从而得△P AP '是等腰直角三角形,可得结论;(3)先作高线C 'G ,确定△ACC ′的面积中底边AC 为定值2,根据高的大小确定面积的大小,当C '在BD 上时,C 'G 最大,其△ACC ′的面积最大,并求此时的面积. 【解答】解:(1)由对称得:CD =C 'D ,∠CDE =∠C 'DE , 在正方形ABCD 中,AD =CD ,∠ADC =90°, ∴AD =C 'D , ∵F 是AC '的中点,∴DF ⊥AC ',∠ADF =∠C 'DF ,∴∠FDP=∠FDC'+∠EDC'=12∠ADC=45°;(2)结论:BP+DP=√2AP,理由是:如图,作AP'⊥AP交PD的延长线于P',∴∠P AP'=90°,在正方形ABCD中,DA=BA,∠BAD=90°,∴∠DAP'=∠BAP,由(1)可知:∠FDP=45°∵∠DFP=90°∴∠APD=45°,∴∠P'=45°,∴AP=AP',在△BAP和△DAP'中,∵{BA=DA∠BAP=∠DAP′AP=AP′,∴△BAP≌△DAP'(SAS),∴BP=DP',∴DP+BP=PP'=√2AP;(3)如图,过C'作C'G⊥AC于G,则S△AC'C=12AC•C'G,Rt△ABC中,AB=BC=√2,∴AC=√(√2)2+(√2)2=2,即AC为定值,当C'G最大值,△AC'C的面积最大,连接BD,交AC于O,当C'在BD上时,C'G最大,此时G与O重合,∵CD=C'D=√2,OD=12AC=1,∴C'G=√2−1,∴S△AC'C=12AC•C'G=12×2(√2−1)=√2−1.16.(2020•朝阳区模拟)在四边形ABCD中,AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=α,∠BCD=β,点E,F是四边形ABCD内的两个点,满足∠EAF=12α,∠ECF=12β,连接BE,EF,FD.(1)如图1,当α=β时,判断∠ABE和∠ADF之间的数量关系,并证明你的猜想;(2)如图2,当α≠β时,用等式表示线段BE,EF,FD之间的数量关系(直接写出即可).【分析】(1)结论:∠ABE+∠ADF=90°.将△ABE绕点A逆时针旋转90°得到△ADM,将△BCE绕点C顺时针旋转90°得到△CDT,连接FM,TF.证明M,D,T共线,再证明FM=FT.DM=DT即可解决问题.(2)结论:EF2=BE2+DF2.将△ABE绕点A逆时针旋转α度得到△ADM,将△BCE绕点C顺时针旋转β度得到△CDT,连接FM,TF.证明∠FDM=90°,利用勾股定理即可解决问题.【解答】解:(1)结论:∠ABE+∠ADF=90°.理由:∵AB=AD,CB=CD,∠ABC=∠ADC=90°,∠BAD=∠BCD,∴∠BAD=∠BCD=90°,∴四边形ABCD是正方形,∴AB=BC=CD=AD,将△ABE绕点A逆时针旋转90°得到△ADM,将△BCE绕点C顺时针旋转90°得到△CDT,连接FM,TF.∵∠EAF=12×90°=45°,∴∠MAD+∠DAF=∠BAE+∠DAF=45°,∴∠F AM=∠F AE,∵AM=AE,AF=AF,∴△AFM≌△AFE(SAS),∴EF=FM,同法可证:EF=FT,∴FM=FT,∵∠ADM+∠CDT=∠ABE+∠CBE=90°,∴∠MDT=90°+90°=180°,∴M,D,T共线,∵DM=BE,DT=BE,∴DM=DT,∴FD⊥MT,∴∠FDM=90°,∴∠ADM+∠ADF=90°,∵∠ADM=∠ABE,∴∠ABE+∠ADF=90°.(2)结论:EF2=BE2+DF2.理由:∵AD=AB,CD=CB,∴将△ABE绕点A逆时针旋转α度得到△ADM,将△BCE绕点C顺时针旋转β度得到△CDT,连接FM,TF.∵∠EAF=12×∠DAB=12α,∴∠MAD+∠DAF=∠BAE+∠DAF=12α,∴∠F AM=∠F AE,∵AM=AE,AF=AF,∴△AFM≌△AFE(SAS),∴EF=FM,同法可证:EF=FT,∴FM=FT,∵∠ADM+∠CDT=∠ABE+∠CBE=90°,∴∠MDT=90°+90°=180°,∴M,D,T共线,∵DM=BE,DT=BE,∴DM=DT,∴FD⊥MT,∴∠FDM=90°,∴FM2=DM2+DF2,∵FM=EF,DM=BE,∴EF2=BE2+DF2.17.(2020•丰台区模拟)已知C为线段AB中点,∠ACM=α.Q为线段BC上一动点(不与点B重合),点P在射线CM上,连接P A,PQ,记BQ=kCP.(1)若α=60°,k=1,①如图1,当Q为BC中点时,求∠P AC的度数;②直接写出P A、PQ的数量关系;(2)如图2,当α=45°时.探究是否存在常数k,使得②中的结论仍成立?若存在,写出k的值并证明;若不存在,请说明理由.【分析】(1)如图1,作辅助线,构建等边三角形,证明△ADC为等边三角形.根据等边三角形三线合一可得∠P AC=∠P AD=30°;②作辅助线,证明△PCD'≌△PCQ,可得P A=PQ;(2)存在k=√2,如图2,作辅助线,构建全等三角形,证明△P AD≌△PQC(SAS).可得结论.【解答】解:(1)①如图1,在CM上取点D,使得CD=CA,连接AD,∵∠ACM=60°,∴△ADC为等边三角形.∴∠DAC=60°.。
2019-2020数学中考试卷(附答案)
2019-2020数学中考试卷(附答案)一、选择题1.如图是由5个相同大小的正方体搭成的几何体,则它的俯视图是( )A .B .C .D .2.已知11(1)11A x x ÷+=-+,则A =( ) A .21x x x -+ B .21x x - C .211x - D .x 2﹣13.如图的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从A 点到B 点,甲虫沿大半圆弧ACB 路线爬行,乙虫沿小半圆弧ADA 1、A 1EA 2、A 2FA 3、A 3GB 路线爬行,则下列结论正确的是 ( )A .甲先到B 点 B .乙先到B 点C .甲、乙同时到B 点D .无法确定4.下列图形是轴对称图形的有( )A .2个B .3个C .4个D .5个5.已知平面内不同的两点A (a +2,4)和B (3,2a +2)到x 轴的距离相等,则a 的值为( ) A .﹣3B .﹣5C .1或﹣3D .1或﹣56.不等式x+1≥2的解集在数轴上表示正确的是( ) A . B .C .D .7.若关于x 的方程333x m mx x++--=3的解为正数,则m 的取值范围是( ) A .m <92B .m <92且m≠32C .m >﹣94D .m >﹣94且m≠﹣348.下列计算正确的是( ) A .a 2•a=a 2 B .a 6÷a 2=a 3 C .a 2b ﹣2ba 2=﹣a 2bD .(﹣32a )3=﹣398a9.一副直角三角板如图放置,点C 在FD 的延长线上,AB//CF ,∠F=∠ACB=90°,则∠DBC 的度数为( )A .10°B .15°C .18°D .30°10.如图是一个几何体的三视图(图中尺寸单位:cm ),根据图中所示数据求得这个几何体的侧面积是( )A .212cmB .()212πcm +C .26πcmD .28πcm 11.某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.A .140B .120C .160D .10012.已知实数a ,b ,若a >b ,则下列结论错误的是 A .a-7>b-7B .6+a >b+6C .55a b >D .-3a >-3b二、填空题13.已知a ,b ,c 是△ABC 的三边长,a ,b 满足|a ﹣7|+(b ﹣1)2=0,c 为奇数,则c=_____.14.如图:已知AB=10,点C 、D 在线段AB 上且AC=DB=2; P 是线段CD 上的动点,分别以AP 、PB 为边在线段AB 的同侧作等边△AEP 和等边△PFB ,连结EF ,设EF 的中点为G ;当点P 从点C 运动到点D 时,则点G 移动路径的长是________.15.如图,点A 在双曲线y=4x上,点B 在双曲线y=kx (k≠0)上,AB ∥x 轴,过点A 作AD⊥x 轴 于D .连接OB ,与AD 相交于点C ,若AC=2CD ,则k 的值为____.16.当直线()223y k x k =-+-经过第二、三、四象限时,则k 的取值范围是_____. 17.若一个数的平方等于5,则这个数等于_____.18.若关于x 的一元二次方程kx 2+2(k+1)x+k -1=0有两个实数根,则k 的取值范围是 19.已知关于x 的一元二次方程2220ax x c ++-=有两个相等的实数根,则1c a+的值等于_______.20.已知(a -4)(a -2)=3,则(a -4)2+(a -2)2的值为__________.三、解答题21.如图1,△ABC 内接于⊙O ,∠BAC 的平分线交⊙O 于点D ,交BC 于点E (BE >EC ),且BD=23.过点D 作DF ∥BC ,交AB 的延长线于点F . (1)求证:DF 为⊙O 的切线;(2)若∠BAC=60°,DE=7,求图中阴影部分的面积; (3)若43AB AC =,DF+BF=8,如图2,求BF 的长.22.安顺市某商贸公司以每千克40元的价格购进一种干果,计划以每千克60元的价格销售,为了让顾客得到更大的实惠,现决定降价销售,已知这种干果销售量y (千克)与每千克降价x (元)(020)x <<之间满足一次函数关系,其图象如图所示:(1)求y 与x 之间的函数关系式;(2)商贸公司要想获利2090元,则这种干果每千克应降价多少元?23.阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:232212+=+(),善于思考的小明进行了以下探索: 设()2a b 2m n 2+=+(其中a b m n 、、、均为整数),则有22a b 2m 2n 2mn 2+=++.∴22a m 2n b 2mn =+=,.这样小明就找到了一种把部分a b 2+的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:当a b m n 、、、均为正整数时,若()2a b 3m n 3+=+,用含m 、n 的式子分别表示a b 、,得a = ,b = ;(2)利用所探索的结论,找一组正整数a b m n 、、、,填空: + =( +3)2;(3)若()2433a m n +=+,且ab m n 、、、均为正整数,求a 的值.24.如图,ABC ∆是边长为4cm 的等边三角形,边AB 在射线OM 上,且6OA cm =,点D 从点O 出发,沿OM 的方向以1cm/s 的速度运动,当D 不与点A 重合时,将ACD ∆绕点C 逆时针方向旋转60°得到BCE ∆,连接DE. (1)如图1,求证:CDE ∆是等边三角形;(2)如图2,当6<t<10时,DE 是否存在最小值?若存在,求出DE 的最小值;若不存在,请说明理由.(3)当点D 在射线OM 上运动时,是否存在以D ,E ,B 为顶点的三角形是直角三角形?若存在,求出此时t 的值;若不存在,请说明理由.25.已知:如图,△ABC 为等腰直角三角形∠ACB =90°,过点C 作直线CM ,D 为直线CM 上一点,如果CE =CD 且EC ⊥CD . (1)求证:△ADC ≌△BEC ;(2)如果EC⊥BE,证明:AD∥EC.【参考答案】***试卷处理标记,请不要删除一、选择题1.B解析:B【解析】【分析】根据从上边看得到的图形是俯视图,可得答案.【详解】从上边看第一列是一个小正方形,第二列是一个小正方形,第三列是两个小正方形,故选:B.【点睛】本题考查了简单几何体的三视图,从上边看上边看得到的图形是俯视图.2.B解析:B【解析】【分析】由题意可知A=111)11x x++-(,再将括号中两项通分并利用同分母分式的减法法则计算,再用分式的乘法法则计算即可得到结果.【详解】解:A=11111x x++-=111xx x+-g=21xx-故选B.【点睛】此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.3.C解析:C【解析】1 2π(AA1+A1A2+A2A3+A3B)=12π×AB,因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等,因此两个同时到B点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年中考数学综合训练(几何探究题)1、两块等腰直角三角板△ABC 和△DEC 如图摆放,其中∠ACB =∠DCE = 90°,F 是DE 的中点,H 是AE 的中点,G 是BD 的中点.(1)如图1,若点D 、E 分别在AC 、BC 的延长线上,通过观察和测量,猜想FH 和FG 的数量关系为_______ 和位置关系为_____ ;(2)如图2,若将三角板△DEC 绕着点C 顺时针旋转至ACE 在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;(2)如图3,将图1中的△DEC 绕点C 顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.2.(1)如图1,已知矩形ABCD 中,点E 是BC 上的一动点,过点E 作EF ⊥BD 于点F ,EG ⊥AC 于点G ,CH ⊥BD于点H ,试证明CH=EF+EG;(2) 若点E 在BC的延长线上,如图2,过点E 作EF ⊥BD 于点F ,EG ⊥AC 的延长线于点G ,CH ⊥BD 于点H , 则EF 、EG 、CH 三者之间具有怎样的数量关系,直接写出你的猜想; . (3) 如图3,BD 是正方形ABCD 的对角线,L 在BD 上,且BL=BC, 连结CL ,点E 是CL 上任一点, EF ⊥BD 于点F ,EG ⊥BC 于点G ,猜想EF 、EG 、BD 之间具有怎样的数量关系,直接写出你的猜想; 3. 在ABC △中,AC=BC ,90ACB ∠=︒,点D 为AC 的中点.(1)如图1,E 为线段DC 上任意一点,将线段DE 绕点D 逆时针旋转90°得到线段DF ,连结CF ,过点F 作FH FC ⊥,交直线AB 于点H .判断FH 与FC 的数量关系并加以证明.A图3 A2019-2020年图2A BDEC H F GHF图2图1HFEBCD AEDBCA(2)如图2,若E 为线段DC 的延长线上任意一点,(1)中的其他条件不变,你在(1)中得出的结论是否发生改变,直接写出你的结论,不必证明. 4、(1)如图1所示,在四边形ABCD 中,AC =BD ,AC 与BD 相交于点O ,E F 、分别是AD BC 、的中点,联结EF ,分别交AC 、BD 于点M N 、,试判断OMN △的形状,并加以证明;(2)如图2,在四边形ABCD 中,若AB CD =,E F 、分别是AD BC 、的中点,联结FE 并延长,分别与BA CD 、的延长线交于点M N 、,请在图2中画图并观察,图中是否有相等的角,若有,请直接写出结论: ; (3)如图3,在ABC △中,AC AB >,点D 在AC 上,AB CD =,E F 、分别是AD BC 、的中点,联结FE 并延长,与BA 的延长线交于点M ,若45FEC ∠=︒,判断点M 与以AD 为直径的圆的位置关系,并简要说明理由.5. 已知△ABC 中,AB =AC =3,∠BAC =90°,点D 为BC 上一点,把一个足够大的直角三角板的直角顶点放 在D 处.(1)如图①,若BD =CD ,将三角板绕点D 逆时针旋转,两条直角边分别交AB 、AC 于点E 、点F ,求出重叠部分AEDF 的面积(直接写出结果).(2)如图②,若BD =CD ,将三角板绕点D 逆时针旋转,使一条直角边交AB 于点E 、另一条直角边交AB 的延长线于点F ,设AE =x ,重叠部分的面积为y ,求出y 与x 的函数关系式,并写出自变量x 的取值范围.(3)若BD =2CD ,将三角板绕点D 逆时针旋转,使一条直角边交AC 于点F 、另一条直角边交射线AB 于点E . 设CF =x (x >1),重叠部分的面积为y ,求出y 与x 的函数关系式,并写出自变量x 的取值范围.图 1 图2 图3B F B AC D EF M NOx6. 在四边形ABCD 中,对角线AC 平分∠DAB .(1)如图①,当∠DAB =120°,∠B =∠D =90°时,求证:AB +AD =AC .(2)如图②,当∠DAB =120°,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想,并给予证明.(3)如图③,当∠DAB =90°,∠B 与∠D 互补时,线段AB 、AD 、AC 有怎样的数量关系?写出你的猜想,并给予证明.7. 设点E 是平行四边形ABCD 的边AB 的中点,F 是BC 边上一点,线段DE 和AF 相交于点P ,点Q 在线段DE 上,且AQ ∥PC .(1)证明:PC =2AQ .(2)当点F 为BC 的中点时,试比较△PFC 和梯形APCQ 面积的大小关系,并对你的结论加以证明. 6.2011年中考数学训练(与函数有关的综合题)1、如图,一次函数y =a x +b 的图象与反比例函数y = kx的图象交于A 、B 两点,与x 轴交于点C ,与y 轴交于点D ,已知OA =10,点B 的坐标为(m ,-2),t a n ∠AOC = 13.(1)求反比例函数的解析式; (2)求一次函数的解析式;(3)在y 轴上存在一点P ,使△PDC 与△CDO 相似,求P 点的坐标.2、如图,矩形OABC 在平面直角坐标系中,并且OA 、OC 的长满足:|OA -2|+(OC -23)2=0. (1)求B 、C 两点的坐标.(2)把△ABC 沿AC 对折,点B 落在点B 1处,AB 1线段与x 轴交于点D , 求直线BB 1的解析式.(3)在直线BB 1上是否存在点P 使△ADP 为直角三角形?若存在, 请直接写出点P 的坐标;若不存在,请说明理由.3、已知抛物线y =-x 2+bx +c 的图象经过点A (m ,0)、B (0,n ),其中m 、n 是方程x 2-6x +5=0的两个实数根,且m <n ,. (1)求抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一个交点为C ,抛物线的顶点为D ,求C 、D 点的坐标和△BCD 的面积; (3)P 是线段OC 上一点,过点P 作PH ⊥x 轴,交抛物线于点H ,若直线BC 把△PCH 分成面积相等的两部分,求P 点的坐标.4、如图,将OA = 6,AB = 4的矩形OABC 放置在平面直角坐标系中,动点M 、N 以每秒1个单位的速度分别从点A 、C 同时出发,其中点M 沿AO 向终点O 运动,点N 沿CB 向终点B 运动,当两个动点运动了t 秒时,过点N 作NP ⊥BC ,交OB 于点P ,连接MP . (1)点B 的坐标为 ;用含t 的式子表示点P 的坐标为 ;(2)记△OMP 的面积为S ,求S 与t 的函数关系式(0 < t < 6);并求t 为何值时,S 有最大值?(3)试探究:当S 有最大值时,在y 轴上是否存在点T ,使直线MT 把△ONC 分割成三角形和四边形两部分,且三角形的面积是△ONC 面积的13?若存在,求出点T 的坐标;若不存在,请说明理由.1. (1)过点A 作AE ⊥x 轴,垂足为E .221tan 3310101 3.AOE OE AE OA OE AE AE OE ∠=∴==+=∴==,.,, ∴点A 的坐标为(3,1).A 点在双曲线上,13k∴=,3k =.(备用图)∴双曲线的解析式为3y x=.(2)点(2)B m -,在双曲线3y x=上, 3322m m ∴-==-,. ∴点B 的坐标为322⎛⎫-- ⎪⎝⎭,. ……231332 1.2a b a a b b +=⎧⎧=⎪⎪∴∴⎨⎨-+=-⎪⎪=-⎩⎩,,∴一次函数的解析式为213y x =-.(3)C D ,两点在直线213y x =-上,C D ∴,的坐标分别是30(01)2C D ⎛⎫- ⎪⎝⎭,,,. ∴312OC OD ==,,DC =.过点C 作CP AB ⊥,垂足为点C .PDC CDO △∽△,213.4PD DC DC PD DC OD OD ∴===, 又139144OP DP OD =-=-=, P ∴点坐标为904⎛⎫⎪⎝⎭,.3.(1)解方程2650x x -+=,得125,1x x ==.由m <n ,知m =1,n =5.∴A (1,0),B (0,5). ………………………1分 ∴10,5.b c c -++=⎧⎨=⎩ 解之,得4,5.b c =-⎧⎨=⎩所求抛物线的解析式为24 5.y x x =--+ ……3分(2)由2450,x x --+=得125, 1.x x =-=故C 的坐标为(-5,0). ………4分由顶点坐标公式,得 D (-2,9).………………………………………………5分 过D 作DE ⊥x 轴于E ,易得E (-2,0).∴BCD CDE OBC OBDE S S S S ∆∆∆=+-梯形159139255222+=⨯⨯+⨯-⨯⨯=15.…………………………………………7分 (注:延长DB 交x 轴于F ,由BCD CFD CFB S =S -S ∆∆∆也可求得) (3)设P (a ,0),则H (a ,245a a --+).直线BC 把△PCH 分成面积相等的两部分,须且只须BC 等分线段PH ,亦即PH 的中点第25题图(245,2a a a --+)在直线BC 上.易得直线BC 方程为: 5.y x =+∴2455.2a a a --+=+ 解之得121,5a a =-=-(舍去).故所求P 点坐标为(-1,0). 4.解:(1)(6,4);(2,3t t ).(其中写对B 点得1分)(2)∵S △OMP =12×OM ×23t , ∴S =12×(6 -t )×23t =213t -+2t .=21(3)33t --+(0 < t <6).∴当3t =时,S 有最大值.(3)存在.由(2)得:当S 有最大值时,点M 、N 的坐标分别为:M (3,0),N (3,4), 则直线ON 的函数关系式为:43y x =. 设点T 的坐标为(0,b ),则直线MT 的函数关系式为:3by x b =-+, 解方程组433y x b y x b ⎧=⎪⎪⎨⎪=-+⎪⎩得3444b x bb y b ⎧=⎪⎪+⎨⎪=⎪+⎩∴直线ON 与MT 的交点R 的坐标为34(,)44b bb b++.(备用图)。
