二次函数与圆结合的压轴题
中考复习2023年中考数学压轴大题专题二次函数与圆压轴问题

中考复习2023年中考数学压轴大题专题二次函数与圆压轴问题【例1】(2022年江苏省常州市北郊初级中学中考二模数学试题)已知二次函数图象的顶点坐标为A(2,0),且与y轴交于点(0,1),B点坐标为(2,2),点C为抛物线上一动点,以C为圆心,CB为半径的圆交x轴于M,N两点(M在N的左侧).(1)求此二次函数的表达式;(2)当点C在抛物线上运动时,弦MN的长度是否发生变化?若变化,说明理由;若不发生变化,求出弦MN 的长;(3)当△ABM与△ABN相似时,求出M点的坐标.【例2】.(必刷卷05-2022年中考数学考前信息必刷卷(湖南岳阳专用))已知:二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中点A为(﹣1,0),与y轴负半轴交于点C(0,﹣2),其对称轴是直线x=32.(1)求二次函数y=ax2+bx+c的解析式;(2)圆O′经过点△ABC的外接圆,点E是AC延长线上一点,△BCE的平分线CD交圆O′于点D,连接AD、BD,求△ACD的面积;(3)在(2)的条件下,二次函数y=ax2+bx+c的图象上是否存在点P,使得△PDB=△CAD?如果存在,请求经典例题出所有符合条件的P点坐标;如果不存在,请说明理由.【例3】.(2022年江苏省徐州市九年级下学期第二次模拟数学试题)如图,已知二次函数y=ax2+bx+c 的图像与x轴交于A(−1,0),B(2,0)两点,与y轴交于点(0,2).(1)求此二次函数的表达式;(2)点Q在以BC为直径的圆上(点Q与点O,点B,点C均不重合),试探究QO,QB、QC的数量关系,并说明理由.(3)E点为该图像在第一象限内的一动点,过点E作直线BC的平行线,交x轴于点F.若点E从点C出发,沿着抛物线运动到点B,则点F经过的路程为______.x2+bx+c的图象经【例4】(2022年云南省德宏州初中学业水平考试模拟监测数学试题)二次函数y=34过点A(-1,0)和点C(0,-3)与x轴的另一交点为点B.(1)求b,c的值;(2)定义:在平面直角坐标系xOy中,经过该二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.问:√10为半径作△Q,使△Q是二次函数y=在该二次函数图象的对称轴上是否存在一点Q,以点Q为圆心,5634x2+bx+c的坐标圆?若存在,求出点Q的坐标;若不存在,请说明理由;(3)如图所示,点M是线段BC上一点,过点M作MP//y轴,交二次函数的图象于点P,以M为圆心,MP为半径作△M,当△M与坐标轴相切时,求出CMMB的值.专题31二次函数与圆压轴问题1.(湖北省武汉市华中科技大学附属中学2022-2023学年九年级上学期1月考数学试题)如图,已知抛物线经过点A(−1,0),B(3,0),C(0,3)三点,点D是直线BC绕点B逆时针旋转90°后与y轴的交点,点M是线段AB 上的一个动点,设点M的坐标为(m,0),过点M作x轴的垂线交抛物线于点E,交直线BD于点F.(1)求该抛物线所表示的二次函数的解析式;(2)在点M运动过程中,若存在以EF为直径的圆恰好与y轴相切,求m的值;(3)连接AC,将△AOC绕平面内某点G旋转180°后,得到△A1O1C1,点A、O、C的对应点分别是点A1、O1、C1,是否存在点G使得△AOC旋转后得到的△A1O1C1的两个顶点恰好落在抛物线上,若存在,直接写出G 点的坐标;若不存在,请说明理由.2.(专题16二次函数中的相似三角形-【微专题】2022-2023学年九年级数学下册常考点微专题提分精练(人教版))如图,一次函数y=−2x的图象与二次函数y=−x2+3x图象的对称轴交于点B.培优训练(1)写出点B的坐标;(2)将直线y=−2x沿y轴向上平移,分别交x轴于点C、交y轴于点D,点A是该抛物线与该动直线的一个公共点,试求当△AOB的面积取最大值时,点C的坐标;(3)已知点P是二次函数y=−x2+3x图象在y轴右侧部分上的一个动点,若△PCD的外接圆直径为PC,试问:以P、C、D为顶点的三角形与△COD能否相似?若能,请求出点P的坐标;若不能,请说明理由.3.(福建省泉州市鲤城区第七中学2022-2023学年九年级下学期数学期末质量检测)如图(1)所示,y关于x的(x+m)(x−3m)(m>0)图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D二次函数y=−√33m点.以AB为直径作圆,圆心为C.定点E的坐标为(−3,0),连接ED.(1)写出A、B、D三点的坐标;(2)当m为何值时M点在直线ED上?判定此时直线与圆的位置关系;(3)当m变化时,用m表示△AED的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.4.(第5章二次函数(基础、典型、易错、压轴)分类专项训练-2022-2023学年九年级数学考试满分全攻略(苏科版))如图,已知二次函数y=ax2+bx+c的图象与x轴交于A(−1,0),B(2,0)两点,与y轴交于点(0,2).(1)求此二次函数的表达式;(2)点Q在以BC为直径的圆上(点Q与点O,点B,点C均不重合),试探究QO,QB,QC的数量关系,并说明理由.(3)E点为该图象在第一象限内的一动点,过点E作直线BC的平行线,交x轴于点F.若点E从点C出发,沿着抛物线运动到点B,则点F经过的路程为.5.(湖南省长沙麓山外国语实验中学2022-2023学年九年级上学期第三次月考数学试卷)已知二次函数y= ax2+bx+c的图象与x轴交于A,B两点,其中点A为(−1,0),与y轴负半轴交于点C(0,−2),其对称.轴是直线x=32(1)求二次函数y=ax2+bx+c的解析式;(2)圆O′为△ABC的外接圆,点E是AC延长线上一点,∠BCE的平分线CD交圆O′于点D,连接AD、BD,求△ACD的面积;(3)在(2)的条件下,y轴上是否存在点P,使得以P,C,B为顶点的三角形与△BCD相似?如果存在,请求出所有符合条件的P点坐标;如果不存在,请说明理由.6.(湖南省长沙市湖南师大附中博才实验中学2022-2023学年九年级上学期第三次随堂测数学试卷)如图,x2+bx+c与x轴的一个交点A的坐标为(−3,0),以点A为圆心作圆A,与该二次函数的二次函数y=−56图象相交于点B,C,点B,C的横坐标分别为−2,−5,连接AB,AC,并且满足AB⊥AC.过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N.(1)求该二次函数的关系式;(2)经过点B作直线BD,在A点右侧与x轴交于点D,与二次函数的图象交于点E,使得∠ADB=∠ABM,连接AE,求证:AE=AD;(3)若直线y=kx+1与圆A相切,请求出k的值.7.(专题30圆与二次函数结合-【微专题】2022-2023学年九年级数学上册常考点微专题提分精练(人教版))如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,且OA=OC(1)求二次函数的解析式;(2)若以点O为圆心的圆与直线AC相切于点D,求点D的坐标;(3)在(2)的条件下,抛物线上是否存在点P使得以P、A、D、O为顶点的四边形是直角梯形?若存在,直接写出点P坐标;若不存在,请说明理由.8.(北京市朝阳区汇文中学朝阳垂杨柳分校2020-2021学年九年级上学期期中数学试卷)定义:在平面直角坐标系中,图形G 上点P(x,y)的纵坐标y 与其横坐标x 的差y﹣x 称为P 点的“坐标差”,而图形G 上所有点的“坐标差”中的最大值称为图形G 的“特征值”.(1)△点A(1,3)的“坐标差”为;△抛物线y=−x2+3x+3的“特征值”为;(2)某二次函数y=−x2+bx+c(c≠0)的“特征值”为﹣1,点B(m,0)与点C 分别是此二次函数的图象与x 轴和y 轴的交点,且点 B 与点C 的“坐标差”相等.△直接写出m=;(用含c的式子表示)△求此二次函数的表达式.(3)如图,在平面直角坐标系xOy 中,以M(2,3)为圆心,2 为半径的圆与直线y=x 相交于点D、E,请直接写出△M 的“特征值”为.9.(湖南省长沙市中雅培粹学校2022-2023学年九年级上学期第一次月考数学试题)如图,已知抛物线经过点A(−1,0),B(3,0),C(0,3)三点,点D是直线BC绕点B逆时针旋转90°后与y轴的交点,点M是线段AB上的一个动点,设点M的坐标为(m,0),过点M作x轴的垂线交抛物线于点E,交直线BD于点F.(1)求该抛物线所表示的二次函数的解析式;(2)在点M运动过程中,若存在以EF为直径的圆恰好与y轴相切,求m的值;(3)连接AC,将ΔAOC绕平面内某点G旋转180°后,得到ΔA1O1C1,点A、O、C的对应点分别是点A1、O1、C1,是否存在点G使得ΔAOC旋转后得到的ΔA1O1C1的两个顶点恰好落在抛物线上,若存在,求出G点的坐标;若不存在,请说明理由.10.(湖南省长沙市一中双语实验学校2021-2022学年九年级上学期期末数学试题)如图,已知二次函数y= ax2+bx+3的图象与x轴交于点A(1,0)、B(−3,0),与y轴的正半轴交于点C.(1)求二次函数y=ax2+bx+3的表达式;(2)点D是线段OB上一动点,过点D作y轴的平行线,与BC交于点E,与抛物线交于点F,连接CF,探究是否存在点D使得△CEF为直角三角形?若存在,求点D的坐标;若不存在,说明理由;(3)若点P在二次函数图象上,是否存在以P为圆心,√2为半径的圆与直线BC相切,若存在,求点P的坐标;若不存在,说明理由.11.(广东省深圳市龙华区龙华区高峰学校2021-2022学年九年级下学期第三次月考数学试题)如图,已知二次函数y=ax2+bx+c(a<0,c>0)与x轴交于点A、B,与y轴交于点C,且以AB为直径的圆经过点C.(1)若点A(﹣4,0),点B(16,0),求C点坐标和函数关系式.(2)若点D是圆与抛物线的交点(D与A、B、C不重合),在(1)的条件下,坐标轴上是否存在一点P,使得以P、B、C为顶点的三角形与△CBD相似?若存在,请求点P坐标;若不存在,请说明理由.12.(2022年山东省济宁市任城区济宁学院附属中学九年级第二次模拟考试试题)如图,已知二次函数y= ax2+bx+3的图象与x轴交于点A(1,0)、B(−3,0),与y轴的正半轴交于点C(1)求二次函数y=ax2+bx+3的表达式(2)点D是线段OB上一动点,过点D作y轴的平行线,与BC交于点E,与抛物线交于点F,连接CF,BF,探究是否存在点D使得四边形ACFB的面积最大?若存在,求点D的坐标;若不存在,说明理由(3)若点P在二次函数图象上,是否存在以P为圆心,√2为半径的圆与直线BC相切,若存在,直接写点P 的坐标;若不存在,说明理由13.(2022年山东省济宁市金乡县中考二模数学试题)已知二次函数的图象交x轴于点A(3,0),B(-1,0),交y轴于点C(0,-3),P这抛物线上一动点,设点P的横坐标为m.(1)求抛物线的解析式:(2)当△P AC是以AC为直角边的直角三角形时,求点P的坐标:(3)抛物线上是否存在点P,使得以点P为圆心,2为半径的圆既与x轴相切,又与抛物线的对称轴相交?若存在,求出点P的坐标,并求出抛物线的对称轴所截的弦MN的长度;若不存在,请说明理由.(写出过程)14.(江苏省盐城市大丰区新丰初级中学2021-2022学年九年级下学期新课程结束考试数学试题(一模))如图1,在平面直角坐标系中,O为坐标原点,点A、B为抛物线y=x2上的两个动点,且OA△OB.(1)若点B的坐标是(2,m),则点A的坐标是;(2)过点B作BC△x轴,垂足为C,若△AOB与△OBC相似,求cos△OBA.(3)在(1)问的条件下,若点E为二次函数第一象限内抛物线上一动点,EH垂直于X轴于点H,交线段AB 于点F,以EF为直径的圆M与AB交于点R,求当△EFR周长取最大值时E点的坐标;(4)在(3)问的条件下,以BH为直径作圆N,点P为圆N上一动点,连接AP,Q为AP上一点且AQ=12AP,连接HQ,求OQ的最小值;15.(2022年广西河池市凤山县中考模拟(二)数学试题)如图,二次函数y=ax2+4的图象与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,且tan△OAC=1.(1)求二次函数的解析式;(2)若以点O为圆心的圆与直线AC相切于点D,求点D的坐标;(3)在(2)的条件下,抛物线上是否存在点P使得以P、A、D、O为顶点的四边形是直角梯形?若存在,直接写出点P坐标;若不存在,请说明理由.16.(湖北省鄂州市吴都中学2021-2022学年九年级下学期第一次月考数学试题)如图1,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,tan△ACO=13.(1)求这个二次函数的表达式;(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由;(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.17.(2022年新疆维吾尔自治区乌鲁木齐市天山区一模数学试题)如图,已知二次函数y=−14x2+32x+4的图像与x轴交于点A,B,与y轴交于点C,顶点为D,连接BC;(1)求顶点D的坐标;(2)求直线BC的解析式;(3)点E是第一象限内抛物线上的动点,连接BE,CE,求△BCE面积的最大值;(4)以AB为直径,M为圆心作圆M,试判断直线CD与圆M的位置关系,并说明理由18.(专题09二次函数与圆综合问题-挑战2022年中考数学压轴题之学霸秘笈大揭秘)定义:平面直角坐标系xOy中,过二次函数图像与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P(2,2),以P为圆心,√5为半径作圆.请判断△P是不是二次函数y=x2﹣4x+3的坐标圆,并说明理由;(2)已知二次函数y=x2﹣4x+4图像的顶点为A,坐标圆的圆心为P,如图1,求△POA周长的最小值;(3)已知二次函数y=ax2﹣4x+4(0<a<1)图像交x轴于点A,B,交y轴于点C,与坐标圆的第四个交点为D,连接PC,PD,如图2.若△CPD=120°,求a的值.19.(湖南省长沙市青竹湖湘一外国语学校2020-2021学年九年级下学期第二次模拟考试数学试题)已知二次函数的图象经过点A(2,0),B(−4,0),C(0,4),点F为二次函数第二象限内抛物线上一动点,FH⊥x 轴于点H,交直线BC于点D,以FD为直径的圆△M与BC交于点E.(1)求这个二次函数的关系式;(2)当三角形EFD周长最大时.求此时点F点坐标及三角形EFD的周长;(3)在(2)的条件下,点N为△M上一动点,连接BN,点Q为BN的中点,连接HQ,求HQ的取值范围.20.(江苏省宿迁市沭阳县怀文中学2021-2022学年九年级上学期期末数学试题)如图,已知二次函数y= ax2+bx+c的图象与x轴交于A和B(3,0)两点,与y轴交于C(0,−2),对称轴为直线x=5,连接BC,在直4线BC上有一动点P,过点P作y轴的平行线交二次函数的图像于点N,交x轴于点M,(1)求抛物线与直线BC的函数解析式;(2)设点M的坐标为(m,0),求当以PN为直径的圆与y轴相切时m的值:(3)若点P在线段BC上运动,则是否存在这样的点P,使得△CPN与△BPM相似,若存在请直接写出点P 的坐标,若不存在,请写出理由.。
二次函数与圆的综合题(中考数学必考压轴题)
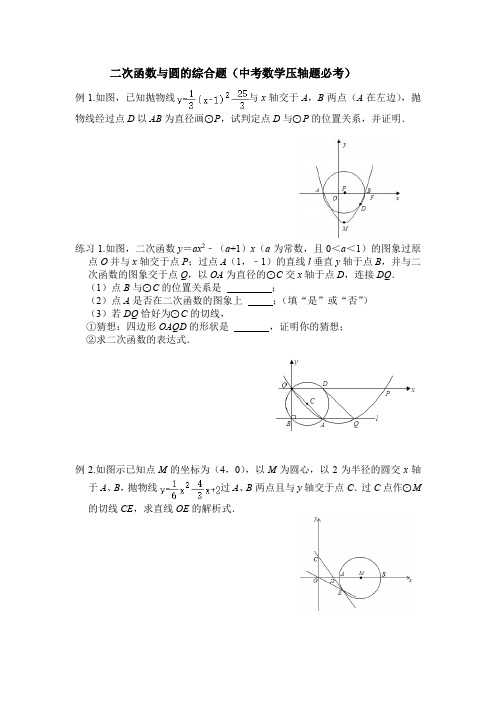
二次函数与圆的综合题(中考数学压轴题必考)例1.如图,已知抛物线与x轴交于A,B两点(A在左边),抛物线经过点D以AB为直径画⊙P,试判定点D与⊙P的位置关系,并证明.练习1.如图,二次函数y=ax2﹣(a+1)x(a为常数,且0<a<1)的图象过原点O并与x轴交于点P;过点A(1,﹣1)的直线l垂直y轴于点B,并与二次函数的图象交于点Q,以OA为直径的⊙C交x轴于点D,连接DQ.(1)点B与⊙C的位置关系是;(2)点A是否在二次函数的图象上;(填“是”或“否”)(3)若DQ恰好为⊙C的切线,①猜想:四边形OAQD的形状是,证明你的猜想;②求二次函数的表达式.例2.如图示已知点M的坐标为(4,0),以M为圆心,以2为半径的圆交x轴于A、B,抛物线过A、B两点且与y轴交于点C.过C点作⊙M 的切线CE,求直线OE的解析式.练习2.平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴,设平行于x轴的直线交抛物线y=﹣x2﹣x+2于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径;若不存在,请说明理由.练习3.如图,抛物线y=﹣x2﹣x+2与x轴交于A(﹣4,0),B(2,0),与y 轴交于点C(0,2).以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.练习4.如图,抛物线y=﹣x2+x+2.经过A、B、C三点,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C,M为抛物线的顶点,试说明直线MC与⊙P的位置关系,并证明你的结论.练习5.如图,抛物线与x轴交于A、B两点,与y轴交于C点.以AB为直径作⊙M.(1)求出M的坐标并证明点C在⊙M上;(2)若P为抛物线上一动点,求出当CP与⊙M相切时P的坐标;练习6.在平面直角坐标系中,已知A(﹣4,0),B(1,0),且以AB为直径的圆交y轴的正半轴于点C,过点C作圆的切线交x轴于点D.(1)求点C的坐标和过A,B,C三点的抛物线的析式;(2)求点D的坐标:(3)设平行于x轴的直线交抛物线于E,F两点,问:是否存在以线段EF为直径的圆,恰好与x轴相切?若存在,求出该圆的半径,若不存在,请说明理由.练习7.如图,在平面直角坐标系中,已知OA=n,OC=m,⊙M与y轴相切于点C,与x轴交于A,B两点,∠ACD=90°,抛物线y=ax2+bx+c经过A,B,C三点.(1)求证:∠OCA=∠OBC;(2)若A(x1,0),B(x2,0),且x1,x2满足x1+x2=5,x1•x2=4,求点C 的坐标和抛物线的解析式;(3)若△ACD≌△ABD,在四边形ABDC内有一点P,且点P到四边形四个顶点的距离之和P A+PB+PC+PD最小,求此时距离之和的最小值及P点的坐标(用含n的式子表示).练习8.已知二次函数y=mx2+(m﹣3)x﹣3(m>0)(1)求证:它的图象与x轴必有两个交点;(2)这条抛物线与x轴交于两点A、B(A在B左),与y轴交于点C,顶点为D,sin∠ABD=,⊙M过A、B、C三点,求⊙M的面积;(3)在(2)的条件下,抛物线上是否存在点P,使P A是⊙M的切线?若存在,求出P点的坐标,若不存在,说明理由.例3.如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(,)两点,点P在该抛物线上运动,以点P为圆心的⊙P总经过定点A(0,2).(1)求a,b,c的值;(2)求证:在点P运动的过程中,⊙P始终与x轴相交;(3)设⊙P与x轴相交于M(x1,0),N(x2,0)(x1<x2)两点,当△AMN 为等腰三角形时,求圆心P的纵坐标.练习9.已知:如图,抛物线y=ax2+bx+1的图象关于y轴对称,且抛物线过点(2,2),点P为抛物线上的动点,以点P为圆心的⊙P与x轴相切,当点P运动对,⊙P始终经过y轴上的一个定点E.(1)求抛物线的解析式;(2)当⊙P的半径为时,⊙P与y轴交于M、N两点,求MN的长;(3)求定点E到直线y=kx﹣8k的距离的最大值.练习10.已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx (a>0)经过A、O两点,且顶点B的纵坐标为﹣2(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连接AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.练习11.已知A是x轴正半轴上一个动点,以线段OA为直径作⊙B,圆心为点B,直径OA=m,线段EF是⊙B的一条弦,EF∥x轴,点C为劣弧EF的中点,过点E作DE垂直于EF,交抛物线C1:y=ax2+bx(a>0)于点G,抛物线经过点O和点A.(1)求证:DG=m;(2)拖动点A,如果抛物线C1与⊙B除点O和点A外有且只有一个交点,求b的值;(3)拖动点A,抛物线C1交⊙B于点O、E、F、A,①求证:DE=m﹣;②直接写出FC2的值(用a,m的代数式表示)练习13.如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A.B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.(1)求∠ACB的大小;(2)写出A,B两点的坐标;(3)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3),求出抛物线的解析式;(4)在该抛物线上是否存在一点D点,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.例4.如图1,抛物线y=ax2+3ax(a为常数,a<0)与x轴交于O,A两点,点B 为抛物线的顶点,点D是线段OA上的一个动点,连接BD并延长与过O,A,B三点的⊙P相交于点C,过点C作⊙P的切线交x轴于点E.(1)①求点A的坐标;②求证:CE=DE;(2)如图2,连接AB,AC,BE,BO,当,∠CAE=∠OBE时,①求证:AB2=AC•BE;②求的值.练习14.如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E 四点,B为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.练习15.如图,二次函数与x轴的一个交点A的坐标为(﹣3,0),以点A为圆心作圆A,与该二次函数的图象相交于点B,C,点B,C的横坐标分别为﹣2,﹣5,连接AB,AC,并且满足AB⊥AC.过点B作BM⊥x轴于点M,过点C作CN⊥x轴于点N.(1)求该二次函数的关系式;(2)经过点B作直线BD,在A点右侧与x轴交于点D,与二次函数的图象交于点E,使得∠ADB=∠ABM,连接AE,求证:AE=AD;(3)若直线y=kx+1与圆A相切,请求出k的值.例5.已知抛物线y=ax2+bx+5(a≠0)经过A(5,0),B(6,1)两点,且与y 轴交于点C.(1)求抛物线y=ax2+bx+5(a≠0)的函数关系式;(2)如图1,连接AC,E为线段AC上一点且横坐标为1,⊙P是△OAE外接圆,求圆心P点的坐标;(3)如图2,连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F;①点E在运动过程中四边形OEAF的面积是否为定值?如果是,请求出这个定值;如果不是,请说明理由;②求出当△AEF的面积取得最大值时,点E的坐标.练习16.如图1,已知抛物线y=﹣x2+bx+c经过点A(1,0),B(﹣5,0)两点,且与y轴交于点C.(1)求b,c的值.(2)在第二象限的抛物线上,是否存在一点P,使得△PBC的面积最大?求出点P的坐标及△PBC的面积最大值.若不存在,请说明理由.(3)如图2,点E为线段BC上一个动点(不与B,C重合),经过B、E、O 三点的圆与过点B且垂直于BC的直线交于点F,当△OEF面积取得最小值时,求点E坐标.练习17.如图1,抛物线y=+bx+c与x轴交于点A(﹣1,0),B(3,0),与y轴交于点C,顶点为D.(1)求抛物线的解析式;(2)如图2,以AB为直径在x轴上方画半圆交y轴于点E,圆心为G,P为半圆上一动点,连接DP,点Q为PD的中点.①判断点C、D与⊙G的位置关系,并说明原因;②当点P沿半圆从点B运动到点A时,求线段AQ的最小值.练习18.如图1,二次函数y=ax2﹣3ax+b(a、b为参数,其中a<0)的图象与x 轴交于A、B两点,与y轴交于点C,顶点为D.(1)若b=﹣10a,求tan∠CBA的值(结果用含a的式子表示);(2)若△ABC是等腰三角形,直线AD与y轴交于点P,且AP:DP=2:3.求抛物线的解析式;(3)如图2,已知b=﹣4a,E、F分别是CA和CB上的动点,且EF=AB,若以EF为直径的圆经过点C,并交x轴于M、N两点,求MN的最大值.课后练习1.抛物线y=ax2+bx﹣4交x轴于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是介于B、C之间的抛物线上的动点(包括B、C两点),点E是△ABP 的外接圆圆心.(1)求抛物线的解析式;(2)如图1,当P为抛物线的顶点时,求圆心E的坐标;(3)如图2,作PH⊥x轴于点H,延长PH交⊙E于点Q,当P从C点出发,沿该抛物线运动到B点,求点Q在这个运动过程中的路径长.2.如图,在正方形OABC中,AB=4,点E是线段OA(不含端点)边上一动点,作△ABE的外接圆交AC于点D.抛物线y=ax2﹣x+c过点O,E.(1)求证:∠BDE=90°;(2)如图1,若抛物线恰好经过点B,求此时点D的坐标;(3)如图2,AC与BE交于点F.①请问点E在运动的过程中,CF•AD是定值吗?如果是,请求出这个值,如果不是,请说明理由;②若,求点E坐标及a的值.。
如何解决圆与函数相结合的压轴题

如何解决圆与函数相结合的压轴题
。 湖 北 阳新 白沙 中学 罗 峻
1 圈与一 次函 数 、 . 二次 函数联 姻
所 以
霸瓣 (l 北 阳如 1 2l 襄 )图。 0湖
在 平 面 直 角 坐 标 系x y 。B 轴 O 中 A 在
( M
:
C
.g 2O O . 因 为 g OC: A. B
\
, / / / 1 \ \
图1
( 。 得 , ,设 P是反 比例 函数 ’ (> )图象 上 的 肌・解曰 F 。 直 ) () , 萼. , 0 :
线 D 的 解 析 式 为 Y=x+ C k m,则 任 意一点 , 以助 圆心 ,O 为半径 的 P长
在 平面 直 角坐标 系 中 , 为 坐标 原点 , 0
y
2 圆 与 一次 函数 、反 比例 函数 .
携 手
为0 C A .所 以AF — AF D f D Oc A.
所 以_ = O' _ F
C
AF AD 所 以8 ( 5 : . n ) 5
:
.
湖 ( 1 蒜 l 21江苏宿迁 ) %. 0 臻2 如图2
,
直 接 写 出 点 P 坐 标 ( 写 求 解 过 的 不
』+ ,解 42 a6 得
I 卜8 + - . 6 b 4 0 -
抛 腰 三 角 形 结 合 后 产 生 角平 分 线.第
() 2 问蕴 涵有 : 双垂 直图形产生三 角
形 相似 、 角平 分 线上 的 点到 角两边 的
物线 的解析 式 为 一 1 _ + . 一 2 4
4 2
距 离相等 . 另外 .本题 自始 至终都 运
二次函数与圆结合的压轴题

二次函数与圆【例题1】 (芜湖市) 已知圆P 的圆心在反比例函数k y x =(1)k >图象上,并与x轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1).(1) 求经过A 、B 、C 三点的二次函数图象的解析式;(2) 若二次函数图象的顶点为D ,问当k 为何值时,四边形ADBP 为菱形. 【例题2】(湖南省韶关市) 25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线32y x =-+与坐标轴交于D 、E 。
设M 是AB 的中点,P 是线段DE 上的动点.(1)求M 、D 两点的坐标;(2)当P 在什么位置时,PA=PB ?求出此时P 点的坐标;(3)过P 作PH ⊥BC ,垂足为H ,当以PM 为直径的⊙F 与BC 相切于点N 时,求梯形PMBH 的面积.【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A 的半径为4,圆心A 的坐标为(2,0),⊙A 与x 轴交于E 、F 两点,与y 轴交于C 、D 两点,过点C 作⊙A 的切线BC ,交x 轴于点B .(1)求直线CB 的解析式;(2)若抛物线y =ax 2+b x +c 的顶点在直线BC 上,与x轴的交点恰为点E 、F ,求该抛物线的解析式;(3)试判断点C 是否在抛物线上?(4) 在抛物线上是否存在三个点,由它构成的三角形与△AOC 相似?直接写出两组这样的点.【例题4】(绵阳市)25.如图,已知抛物线y = ax 2 + bx -3与x 轴交于A 、B两点,与y 轴交于C 点,经过A 、B 、C 三点的圆的圆心M (1,m )恰好在此抛物线的对称轴上,⊙M 的半径为5.设⊙M 与y 轴交于D ,抛物线的顶点为E .(1)求m 的值及抛物线的解析式;(2)设∠DBC = ,∠CBE = ,求sin (-)的值; (3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与△BCE 相似?若存在,请指出点P 的位置,并直接写出点P 的坐标;若不存在,请说明理由. 【例题5】(南充市)25.如图,点M (4,0),以点M 为圆心、2为半径的圆与x 轴交于点A 、B .已知抛物线216y x bx c =++过点A 与B ,与y 轴交于点C .(1)求点C 的坐标,并画出抛物线的大致图象.(2)点Q (8,m )在抛物线216y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ +PB 的最小值.(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.【例题6】(山西省临汾市)26. 如图所示,在平面直角坐标系中,M 经过原点O ,且与x 轴、y 轴分别相交于(60)(08)A B --,,,两点.(1)请求出直线AB 的函数表达式;(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,A MB xyO DE且经过点B ,求此抛物线的函数表达式;(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得115PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由. 【例题7】在△ABC 中,∠A =90°,AB =4,AC =3,M 是AB 上的动点(不与A ,B 重合),过M 点作MN ∥BC 交AC 于点N .以MN 为直径作⊙,并在⊙O 内作内接矩形AMPN .令AM =x . (1)用含x 的代数式表示△MNP 的面积S ; (2)当x 为何值时,⊙O 与直线BC 相切? (3)在动点M 的运动过程中,记△MNP 与梯形BCNM 重合的面积为y ,试求y 关于x 的函数表达式,并求x 为何值时,y 的值最大,最大值是多少? 【例题8】如图,点P 在y 轴上,半径为3的⊙P 分别交x 轴于A 、B 两点,AB=4,交y 轴负半轴于点C ,连接AP 并延长交⊙P 于点D ,过D 作⊙P 的切线分别交x 轴、y 轴于点F 、G ; (1)求直线FG 的解析式;(2)连接CD 交AB 于点E ,求PCD ∠tan 的值;(3)设M 是劣弧BC 上的一个动点,连接DM 交x 轴于点N ,问:是否存在这样的一个常数k ,始终满足AN ·AB+DN ·DM=K ,如果存在,请求出K 的值,如果不存在,请说明理由; AB C D Ex yMO A B C M N D 图 2 O A B C M N P 图 1 O A B C M N P图 3 O。
第13关 以二次函数与圆的问题为背景的解答题(解析版)

第十三关:以二次函数与圆的问题为背景的解答题【总体点评】二次函数在全国中考数学中常常作为压轴题,同时在省级,国家级数学竞赛中也有二次函数大题,很多学生在有限的时间内都不能很好完成。
由于在高中和大学中很多数学知识都与函数知识或函数的思想有关,学生在初中阶段函数知识和函数思维方法学得好否,直接关系到未来数学的学习。
“圆”在初中阶段学习占有重要位置,“垂径定理”、“点与圆的位置关系”的判定与性质、“直线与圆的位置关系”的判定与性质、“正多边形的判定与性质”通常是命题频率高的知识点.由于这部分知识的综合性较强,多作为单独的解答题出现.如果把圆放到直角坐标系中,同二次函数结合,则多作为区分度较高的压轴题中出现.此类题目由于解题方法灵活,考查的知识点全面,体现了方程、建模、转化、数形结合、分类讨论等多种数学思想,得到命题者的青睐【解题思路】二次函数与圆都是初中数学的重点内容,历来是中考数学命题的热点,其本身涉及的知识点就较多,综合性和解题技巧较强,给解题带来一定的困难,而将函数与圆相结合,并作为中考的压轴题,就更显得复杂了.只要我们掌握解决这类问题的思路和方法,采取分而治之,各个击破的思想,问题是会迎刃而解的.解决二次函数与圆的问题,用到的数学思想方法有化归思想、分类思想、数学结合思想,以及代入法、消元法、配方法、代定系数法等。
解题时要注意各知识点之间的联系和数学思想方法、解题技巧的灵活应用,要抓住题意,化整为零,层层深入,各个击破,从而达到解决问题的目的。
【典型例题】经过点A(1,0)和点B(5,0),与y轴【例1】(2019·黑龙江中考真题)如图,抛物线y=ax2+bx−53交于点C.(1)求抛物线的解析式;(2)以点A为圆心,作与直线BC相切的⊙A,请判断⊙A与y轴有怎样的位置关系,并说明理由;(3)在直线BC上方的抛物线上任取一点P,连接PB、PC,请问:△PBC的面积是否存在最大值?若存在,求出这个值和此时点P的坐标;若不存在,请说明理由.【答案】(1)y =−13x 2+2x −53;(2)相交;(3)S △PBC 有最大值12524,此时P 点坐标为(52,54). 【解析】试题分析:(1)把A 、B 两点分别代入抛物线解析可求得a 和b ,可求得抛物线解析式;(2)过A 作AD ⊥BC 于点D ,则AD 为⊙A 的半径,由条件可证明△ABD ∽△CBO ,利用相似三角形的性质可求得AD 的长,可求得半径,进而得出答案;(3)由待定系数法可求得直线BC 解析式,过P 作PQ ∥y 轴,交直线BC 于点Q ,交x 轴于点E ,可设出P 、Q 的坐标,可表示出△PQC 和△PQB 的面积,可表示出△PBC 的面积,再利用二次函数的性质可求得其最大值,容易求得P 点坐标.试题解析:(1)∵抛物线y =ax 2+bx −53经过点A (1,0)和点B (5,0),∴把A 、B 两点坐标代入可得{a +b −53=025a +5b −53=0 ,解得:{a =−13b =2 ,∴抛物线解析式为y =−13x 2+2x −53; (2)相交,理由:过A 作AD ⊥BC 于点D ,如图1,∵⊙A 与BC 相切,∴AD 为⊙A 的半径,由(1)可知C (0,﹣53),且A (1,0),B (5,0),∴OB=5,AB=OB ﹣OA=4,OC=53,在Rt △OBC 中,由勾股定理可得BC=√OC 2+OB 2=√(53)2+52=5√103,∵∠ADB=∠BOC=90°,∠ABD=∠CBO ,∴△ABD ∽△CBO ,∴AD OC=AB BC,即AD53=5√103,解得AD=2√105,即⊙A 的半径为2√105,∵2√105>1,∴⊙A 与y 轴相交;(3)∵C (0,﹣53),∴可设直线BC 解析式为y=kx ﹣53,把B 点坐标代入可求得k=13,∴直线BC 的解析式为y =13x −53,过P 作PQ ∥y 轴,交直线BC 于点Q ,交x 轴于点E ,如图2,设P (x ,−13x 2+2x −53),则Q (x ,13x −53),∴PQ=(−13x 2+2x −53)﹣(13x −53)=−13x 2+53x =−13(x −52)2+2512,∴S △PBC =S △PCQ +S △PBQ =12PQ•OE+12PQ•BE=12PQ (OE+BE )=12PQ•OB=52PQ=−56(x −52)2+12524,∴当x=52时,S △PBC有最大值12524,此时P 点坐标为(52,54),∴当P 点坐标为(52,54)时,△PBC 的面积有最大值.考点:二次函数综合题;探究型;二次函数的最值;最值问题;存在型;压轴题.【例2】(2019·广西中考真题)如图,直线3y x =-交x 轴于点A ,交y 轴于点C ,点B 的坐标为(1,0),抛物线2(0)y ax bx c a =++≠经过,,A B C 三点,抛物线的顶点为点D ,对称轴与x 轴的交点为点E ,点E关于原点的对称点为F ,连接CE ,以点F 为圆心,12CE 的长为半径作圆,点P 为直线3y x =-上的一个动点.(1)求抛物线的解析式; (2)求BDP ∆周长的最小值;(3)若动点P 与点C 不重合,点Q 为⊙F 上的任意一点,当PQ 的最大值等于32CE 时,过,P Q 两点的直线与抛物线交于,M N 两点(点M 在点N 的左侧),求四边形ABMN 的面积.【答案】(1)243y x x =-+-;(2(3【解析】 【分析】(1)直线y=x -3,令x=0,则y=-3,令y=0,则x=3,故点A 、C 的坐标为(3,0)、(0,-3),即可求解; (2)过点B 作直线y=x -3的对称点B′,连接BD 交直线y=x -3于点P ,直线B′B 交函数对称轴与点G ,则此时△BDP 周长=BD+PB+PD=BD+B′B 为最小值,即可求解;(3)如图2所示,连接PF 并延长交圆与点Q ,此时PQ 为最大值,即可求解. 【详解】解:(1)直线3y x =-,令0x =,则3y =-,令0y =,则3x =, 故点,A C 的坐标为(3,0)、(0,3)-,则抛物线的表达式为:()2(3)(1)43y a x x a x x =--=-+, 则33a =-,解得:1a =-,故抛物线的表达式为:243y x x =-+-…①;(2)过点B 作直线3y x =-的对称点'B ,连接BD 交直线3y x =-于点P , 直线'B B 交函数对称轴与点G ,连接'AB ,则此时BDP ∆周长'BD PB PD BD B B =++=+为最小值,(2,1)D ,则点(2,1)G -,即:BG EG =,即点G 是'BB 的中点,过点'(3,2)B -,BDP ∆周长最小值'BD B B =+=;(3)如图2所示,连接PF 并延长交圆与点Q ,此时PQ 为最大值,点,,,,A B C E F 的坐标为(3,0),(1,0),(0,3),(2,0),(2,0)--,则CE =12FQ CE =,则3122PF CE CE =-= 设点(,3)P m m -,点(2,0)F -,22213(2)(3)PF m m ==-+-,解得:1m =,故点(1,2)P -,将点,P F 坐标代入一次函数表达式并解得: 直线PF 的表达式为:2433y x =--…②,联立①②并解得:73x ±=故点,M N 的坐标分别为:,⎝⎭⎝⎭过点,M N 分别作x 轴的垂线交于点,S R ,则ARN SBM ABMN NRSM S S S S ∆∆=--=四边形梯形. 【名师点睛】本题考查的是二次函数综合运用,涉及到一次函数、点的对称性、图形的面积计算等,其中(3),确定PQ 最值时,通常考虑直线过圆心的情况,进而求解.【例3】(2018·青海中考真题)如图,在平面直角坐标系中,四边形ABCD 是以AB 为直径的⊙M 的内接四边形,点A ,B 在x 轴上,⊙MBC 是边长为2的等边三角形,过点M 作直线l 与x 轴垂直,交⊙M 于点E ,垂足为点M ,且点D 平分.(1)求过A ,B ,E 三点的抛物线的解析式; (2)求证:四边形AMCD 是菱形;(3)请问在抛物线上是否存在一点P,使得△ABP的面积等于定值5?若存在,请求出所有的点P的坐标;若不存在,请说明理由.【答案】(1)y=(x+1)2﹣2;(2)证明过程见解析;(3)(2,),(﹣4,).【解析】试题分析:(1)根据题意首先求出抛物线顶点E的坐标,再利用顶点式求出函数解析式;(2)利用等边三角形的性质结合圆的有关性质得出∠AMD=∠CMD=∠AMC=60°,进而得出DC=CM=MA=AD,即可得出答案;(3)首先表示出△ABP的面积进而求出n的值,再代入函数关系式求出P点坐标.试题解析:(1)由题意可知,△MBC为等边三角形,点A,B,C,E均在⊙M上,则MA=MB=MC=ME=2,又∵CO⊥MB,∴MO=BO=1,∴A(﹣3,0),B(1,0),E(﹣1,﹣2),抛物线顶点E的坐标为(﹣1,﹣2),设函数解析式为y=a(x+1)2﹣2(a≠0)把点B(1,0)代入y=a(x+1)2﹣2,解得:a=,故二次函数解析式为:y=(x+1)2﹣2;(2)连接DM,∵△MBC为等边三角形,∴∠CMB=60°,∴∠AMC=120°,∵点D平分弧AC,∴∠AMD=∠CMD=∠AMC=60°,∵MD=MC=MA,∴△MCD,△MDA是等边三角形,∴DC=CM=MA=AD,∴四边形AMCD为菱形(四条边都相等的四边形是菱形);(3)存在.理由如下:设点P的坐标为(m,n)∵S△ABP=AB|n|,AB=4 ∴×4×|n|=5,即2|n|=5,解得:n=±,当时,(m+1)2﹣2=,解此方程得:m1=2,m2=﹣4即点P的坐标为(2,),(﹣4,),当n=﹣时,(m+1)2﹣2=﹣,此方程无解,故所求点P坐标为(2,),(﹣4,).考点:二次函数综合题.【方法归纳】函数知识要理解好数形结合的思想,知识点的掌握中要理解文字解释和图像之间的关系,至于与圆、三角形、方程的综合题,往往最后一问难度大,要建立模型、框架,完善步骤,循序渐进. 【针对练习】1.我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有;②在凸四边形ABCD中,AB=AD且CB≠CD,则该四边形“十字形”.(填“是”或“不是”)(2)如图1,A,B,C,D是半径为1的⊙O上按逆时针方向排列的四个动点,AC与BD交于点E,∠ADB﹣∠CDB=∠ABD﹣∠CBD,当6≤AC2+BD2≤7时,求OE的取值范围;(3)如图2,在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a,b,c为常数,a>0,c<0)与x轴交于A,C两点(点A在点C的左侧),B是抛物线与y轴的交点,点D的坐标为(0,﹣ac),记“十字形”ABCD 的面积为S,记△AOB,△COD,△AOD,△BOC的面积分别为S1,S2,S3,S4.求同时满足下列三个条件的抛物线的解析式;①√S=√S1+√S2;②√S=√S3+√S4;③“十字形”ABCD的周长为12√10.【答案】(1)①菱形,正方形;②不是;(2)12≤OE≤√22(OE>0);(3)y=x2﹣9.【解析】分析:(1)利用“十字形”的定义判断即可;(2)先判断出∠ADB+∠CAD=∠ABD+∠CAB ,进而判断出∠AED=∠AEB=90°,即:AC ⊥BD ,再判断出四边形OMEN 是矩形,进而得出OE 2=2-14(AC 2+BD 2),即可得出结论;(3)由题意得,A (−b−√△2a,0),B (0,c ),C (−b+√△2a,0),D (0,-ac ),求出S=12AC•BD=-12(ac+c )×√△a ,S 1=12OA•OB=-c(√△+b)4a ,S 2=12OC•OD=-c(√△−b)4,S 3=12OA×OD=-c(√△+b)4,S 4=12OB×OC=-c(√△−b)4a,进而建立方程√−c(√△+b)√4a +√−c(√△−b)2=√−c(√△+b)2+√−c(√△−b)√4a,求出a=1,再求出b=0,进而判断出四边形ABCD 是菱形,求出AD=3√10,进而求出c=-9,即可得出结论. 详解:(1)①∵菱形,正方形的对角线互相垂直, ∴菱形,正方形是:“十字形”,∵平行四边形,矩形的对角线不一定垂直, ∴平行四边形,矩形不是“十字形”, 故答案为:菱形,正方形; ②如图,当CB=CD 时,在△ABC 和△ADC 中, {AB =ADCB =CD AC =AC, ∴△ABC ≌△ADC (SSS ), ∴∠BAC=∠DAC , ∵AB=AD , ∴AC ⊥BD ,∴当CB≠CD 时,四边形ABCD 不是“十字形”, 故答案为:不是;(2)∵∠ADB+∠CBD=∠ABD+∠CDB ,∠CBD=∠CDB=∠CAB ,∴∠ADB+∠CAD=∠ABD+∠CAB , ∴180°﹣∠AED=180°﹣∠AEB , ∴∠AED=∠AEB=90°, ∴AC ⊥BD ,过点O 作OM ⊥AC 于M ,ON ⊥BD 于N ,连接OA ,OD ,∴OA=OD=1,OM 2=OA 2﹣AM 2,ON 2=OD 2﹣DN 2,AM=12AC ,DN=12BD ,四边形OMEN 是矩形, ∴ON=ME ,OE 2=OM 2+ME 2, ∴OE 2=OM 2+ON 2=2﹣14(AC 2+BD 2), ∵6≤AC 2+BD 2≤7, ∴2﹣74≤OE 2≤2﹣32, ∴14≤OE 2≤12, ∴12≤OE≤√22; (3)由题意得,A (−b−√△2a,0),B (0,c ),C (−b+√△2a,0),D (0,﹣ac ),∵a >0,c <0, ∴OA=√△+b 2a ,OB=﹣c ,OC=√△−b 2a ,OD=﹣ac ,AC=√△a,BD=﹣ac ﹣c , ∴S=12AC•BD=﹣12(ac+c )×√△a ,S 1=12OA•OB=﹣c(√△+b)4a ,S 2=12OC•OD=﹣c(√△−b)4, S 3=12OA×OD=﹣c(√△+b)4,S 4=12OB×OC=﹣c(√△−b)4a, ∵√S =√S 1+√S 2,√S =√S 3+√S 4, ∴√−c(√△+b)√4a√−c(√△−b)2=√−c(√△+b)2√−c(√△−b)√4a,∴√4a =2,∴a=1,∴S=﹣c √Δ,S 1=﹣c(√△+b)4a ,S 4=﹣c(√△−b)4a, ∵√S =√1+√S 2, ∴S=S 1+S 2+2√S 1S 2, ∴﹣c √Δ=﹣c √Δ2+2√c 2·(−4c)16,∴−c √Δ2=−c √c∴√b 2−4c =√−4c ∴b=0,∴A (√−c ,0),B (0,c ),C (√−c ,0),d (0,﹣c ), ∴四边形ABCD 是菱形, ∴4AD=12√10, ∴AD=3√10, 即:AD 2=90, ∵AD 2=c 2﹣c , ∴c 2﹣c=90,∴c=﹣9或c=10(舍), 即:y=x 2﹣9.【名师点睛】此题是二次函数综合题,主要考查了新定义,平行四边形,矩形,菱形,正方形的性质,全等三角形的判定和性质,三角形的面积公式,求出a=1是解本题的关键.2.(2019·湖南中考真题)如图,抛物线26y ax ax =+(a 为常数,a >0)与x 轴交于O ,A 两点,点B 为抛物线的顶点,点D 的坐标为(t ,0)(﹣3<t <0),连接BD 并延长与过O ,A ,B 三点的⊙P 相交于点C . (1)求点A 的坐标;(2)过点C 作⊙P 的切线CE 交x 轴于点E .①如图1,求证:CE =DE ;②如图2,连接AC ,BE ,BO ,当3a =∠CAE =∠OBE 时,求11OD OE -的值【答案】(1)A(-6,0);(2)①见解析;②1116 OD OE-=【解析】【分析】(1)令y=0,可得ax(x+6)=0,则A点坐标可求出;(2)①连接PC,连接PB延长交x轴于点M,由切线的性质可证得∠ECD=∠COE,则CE=DE;②设OE=m,由CE2=OE•AE,可得m=262tt+,由∠CAE=∠OBE可得BD DOBE OE=,则m=66tt--,综合整理代入11t m--可求出11OD OE-的值.【详解】(1)令ax2+bax=0ax(x+6)=0∴A(-6,0)(2)连接PC,连接PB延长交x轴于MP过O、A、B三点,B为顶点PM OA ∴⊥,90PBC BOM ∠+∠=又∵PC =PBPCB PBC ∴∠=∠,∵CE 为切线90PCB ECD ∴∠+∠=°,又BDP CDE ∠=∠ECD COE ∴∠=∠,∴CE =DE ,(3)设OE =m ,即E (m,0) 由切割定理:CE 2=OE ·AE()()22662t m t m m m t-=⋅+⇒=+①,CAE CBD ∠=∠,已知CAE OBE ∠=∠,CBO EBO ∠=∠ 由角平分线定理:BD DOBE OE=66t t m mt -=⇒=--②由①②得22618360626t tt t t t =⇒++=+--∴t 2=-18t -36211113616t OD OE t m t +-=--=-=, 【点睛】本题是二次函数与圆的综合问题,涉及二次函数图象与x 轴的交点坐标、切线的性质、等腰三角形的判定、切割线定理等知识.把圆的知识镶嵌其中,会灵活运用圆的性质进行计算是解题的关键.3.(2019·浙江中考真题)已知在平面直角坐标系xOy 中,直线1l 分别交x 轴和y 轴于点()()3,0,0,3A B -. (1)如图1,已知P 经过点O ,且与直线1l 相切于点B ,求P 的直径长;(2)如图2,已知直线2: 33l y x =-分别交x 轴和y 轴于点C 和点D ,点Q 是直线2l 上的一个动点,以Q 为圆心,.①当点Q 与点C 重合时,求证: 直线1l 与Q 相切;②设Q 与直线1l 相交于,M N 两点, 连结,QM QN . 问:是否存在这样的点Q ,使得QMN ∆是等腰直角三角形,若存在,求出点Q 的坐标;若不存在,请说明理由.【答案】(1)P 的直径长为(2) ①见解析;②存在这样的点1(3Q -和2(3Q +,使得QMN ∆是等腰直角三角形.【解析】 【分析】(1)连接BC ,证明△ABC 为等腰直角三角形,则⊙P 的直径长=BC=AB ,即可求解;(2)过点C 作CE AB ⊥于点E ,证明CE=ACsin45°=4×2=圆的半径,即可求解; (3)假设存在这样的点Q ,使得QMN ∆是等腰直角三角形,分点Q 在线段CF 上时和点Q 在线段CF 的延长线上两种情况,分别求解即可. 【详解】(1)如图3,连接BC ,∵∠BOC=90°, ∴点P 在BC 上,∵⊙P 与直线l 1相切于点B , ∴∠ABC=90°,而OA=OB , ∴△ABC 为等腰直角三角形,则⊙P 的直径长 (2)如图4过点C 作CE AB ⊥于点E ,图4将0y =代入33y x =-,得1x =, ∴点C 的坐标为()1,0. ∴4AC =, ∵45CAE ∠=︒,∴2CE AC == ∵点Q 与点C 重合,又Q 的半径为∴直线1l 与Q 相切.②假设存在这样的点Q ,使得QMN ∆是等腰直角三角形, ∵直线1l 经过点()()3,0,0,3A B -, ∴l 的函数解析式为3yx .记直线2l 与1l 的交点为F , 情况一:如图5,当点Q 在线段CF 上时, 由题意,得45MNQ ∠=︒. 如图,延长NQ 交x 轴于点G ,图5∵45BAO ∠=︒,∴180454590NGA ∠=︒-︒-︒=︒, 即NG x ⊥轴,∴点Q 与N 有相同的横坐标, 设(),33Q m m -,则(),3N m m +, ∴()333QN m m =+--.∵Q 的半径为∴3(33)m m +--=解得3m =∴336m -=-∴Q 的坐标为(3-. 情况二:当点Q 在线段CF 的延长线上时,同理可得3m =,Q 的坐标为(3+.∴存在这样的点1(3Q -和2(3Q +,使得QMN ∆是等腰直角三角形. 【点睛】本题为圆的综合运用题,涉及到一次函数、圆的切线性质等知识点,其中(2),关键要确定圆的位置,分类求解,避免遗漏.4.(2018·山东中考真题)如图①,在平面直角坐标系中,圆心为P (x ,y )的动圆经过点A (1,2)且与x 轴相切于点B .(1)当x=2时,求⊙P 的半径;(2)求y 关于x 的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.(4)当⊙P 的半径为1时,若⊙P 与以上(2)中所得函数图象相交于点C 、D ,其中交点D (m ,n )在点C 的右侧,请利用图②,求cos ∠APD 的大小.【答案】(1)54;(2)图象为开口向上的抛物线,见解析;(3)点A ;x 轴;(42 【解析】分析:(1)由题意得到AP=PB ,求出y 的值,即为圆P 的半径;(2)利用两点间的距离公式,根据AP=PB ,确定出y 关于x 的函数解析式,画出函数图象即可; (3)类比圆的定义描述此函数定义即可;(4)画出相应图形,求出m 的值,进而确定出所求角的余弦值即可. 详解:(1)由x=2,得到P (2,y ), 连接AP ,PB ,∵圆P与x轴相切,∴PB⊥x轴,即PB=y,由AP=PB=y,解得:y=54,则圆P的半径为54;(2)同(1),由AP=PB,得到(x﹣1)2+(y﹣2)2=y2,整理得:y=14(x﹣1)2+1,即图象为开口向上的抛物线,画出函数图象,如图②所示;(3)给(2)中所得函数图象进行定义:此函数图象可以看成是到点A的距离等于到x轴的距离的所有点的集合;故答案为点A;x轴;(4)连接CD,连接AP并延长,交x轴于点F,交CD于E,设PE=a,则有EF=a+1,,∴D坐标为(,a+1),代入抛物线解析式得:a+1=14(1﹣a2)+1,解得:a=﹣a=﹣2,即PE=﹣在Rt △PED 中,2,PD=1, 则cos ∠APD=PEPD2. 点睛:此题属于圆的综合题,涉及的知识有:两点间的距离公式,二次函数的图象与性质,圆的性质,勾股定理,弄清题意是解本题的关键.5.(2018·江苏中考真题)如图,在平面直角坐标系中,二次函数y=(x -a )(x -3)(0<a<3)的图象与x 轴交于点A 、B (点A 在点B 的左侧),与y 轴交于点D ,过其顶点C 作直线CP ⊥x 轴,垂足为点P ,连接AD 、BC .(1)求点A 、B 、D 的坐标;(2)若△AOD 与△BPC 相似,求a 的值;(3)点D 、O 、C 、B 能否在同一个圆上,若能,求出a 的值,若不能,请说明理由. 【答案】(1)(1)A (a ,0),B (3,0),D (0,3a ).(2)a 的值为73.(3)当D 、O 、C 、B 四点共圆. 【解析】【分析】(1)根据二次函数的图象与x 轴相交,则y=0,得出A (a ,0),B (3,0),与y 轴相交,则x=0,得出D (0,3a ).(2)根据(1)中A 、B 、D 的坐标,得出抛物线对称轴x=32a +,AO=a ,OD=3a ,代入求得顶点C (32a +,-232a -⎛⎫ ⎪⎝⎭),从而得PB=3- 32a +=32a -,PC=232a -⎛⎫ ⎪⎝⎭;再分情况讨论:①当△AOD ∽△BPC 时,根据相似三角形性质得233322a aa a =--⎛⎫ ⎪⎝⎭, 解得:a=3(舍去);②△AOD ∽△CPB ,根据相似三角形性质得233322aaa a =--⎛⎫⎪⎝⎭,解得:a 1=3(舍),a 2=73; (3)能;连接BD ,取BD 中点M ,根据已知得D 、B 、O 在以BD 为直径,M (32,32a )为圆心的圆上,若点C 也在此圆上,则MC=MB ,根据两点间的距离公式得一个关于a 的方程,解之即可得出答案. 【详解】(1)∵y=(x -a )(x -3)(0<a<3)与x 轴交于点A 、B (点A 在点B 的左侧), ∴A (a ,0),B (3,0), 当x=0时,y=3a , ∴D (0,3a );(2)∵A (a ,0),B (3,0),D (0,3a ).∴对称轴x=32a +,AO=a ,OD=3a , 当x= 32a +时,y=-232a -⎛⎫ ⎪⎝⎭, ∴C (32a +,-232a -⎛⎫ ⎪⎝⎭), ∴PB=3-32a +=32a -,PC=232a -⎛⎫ ⎪⎝⎭,①当△AOD ∽△BPC 时, ∴AO OD BP PC=, 即 233322a aa a =--⎛⎫ ⎪⎝⎭,解得:a=3(舍去);②△AOD ∽△CPB , ∴AO OD CP PB=, 即233322aaa a =--⎛⎫⎪⎝⎭, 解得:a 1=3(舍),a 2=73.综上所述:a的值为73;(3)能;连接BD,取BD中点M,∵D、B、O三点共圆,且BD为直径,圆心为M(32,32a),若点C也在此圆上,∴MC=MB,∴22222 3333333222222a a a a⎡⎤+-⎛⎫⎛⎫⎛⎫⎛⎫-++=-+⎢⎥⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦,化简得:a4-14a2+45=0,∴(a2-5)(a2-9)=0,∴a2=5或a2=9,∴a1a2=a3=3(舍),a4=-3(舍),∵0<a<3,∴∴当D、O、C、B四点共圆.【点睛】本题考查了二次函数、相似三角形的性质、四点共圆等,综合性较强,有一定的难度,正确进行分析,熟练应用相关知识是解题的关键.6.(2017·江苏中考真题)如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A 的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.(1)求点P的坐标;(2)求过点A和点E,且顶点在直线CD上的抛物线的函数表达式.【答案】(1) P(1,0).(2) y=x2﹣x﹣.【解析】试题分析:(1)如图,作EF⊥y轴于F,DC的延长线交EF于H.设H(m,n),则P(m,0),PA=m+3,PB=3﹣m.首先证明△ACP∽△ECH,推出,推出CH=2n,EH=2m=6,再证明△DPB ∽△DHE,推出,可得,求出m即可解决问题;(2)由题意设抛物线的解析式为y=a(x+3)(x﹣5),求出E点坐标代入即可解决问题.试题解析:(1)如图,作EF⊥y轴于F,DC的延长线交EF于H.设H(m,n),则P(m,0),PA=m+3,PB=3﹣m.∵EH∥AP,∴△ACP∽△ECH,∴,∴CH=2n,EH=2m=6,∵CD⊥AB,∴PC=PD=n,∵PB∥HE,∴△DPB∽△DHE,∴,∴,∴m=1,∴P(1,0).(2)由(1)可知,PA=4,HE=8,EF=9,连接OP,在Rt△OCP中,PC=,∴CH=2PC=4,PH=6,∴E(9,6),∵抛物线的对称轴为CD,∴(﹣3,0)和(5,0)在抛物线上,设抛物线的解析式为y=a(x+3)(x﹣5),把E(9,6)代入得到a=,∴抛物线的解析式为y=(x+3)(x﹣5),即y=x2﹣x﹣.考点:圆的综合题.7.(2019·山东中考真题)如图,在平面直角坐标系中,抛物线y=ax2+bx+c与⊙M相交于A、B、C、D四点.其中AB两点的坐标分别为(-1,0),(0,-2),点D在x轴上且AD为⊙M的直径.点E是⊙M 与y轴的另一个交点,过劣弧DE上的点F作FH⊥AD于点H,且FH=1.5.(1)求点D的坐标及该抛物线的表达式;(2)若点P是x轴上的一个动点,试求出⊿PEF的周长最小时点P的坐标;(3)在抛物线的对称轴上是否存在点Q,使⊿QCM是等腰三角形?如果存在,请直接写出点Q的坐标;如果不存在,请说明理由.【答案】(1)(4,0),y=12(x+1)(x−4);(2)P(2,0);(3)Q(,),Q(,-),Q(,-4),∴Q(,-).【解析】试题分析:(1)根据题意,设点M的坐标为(m,0),根据两点间的距离公式(半径相等)可以求得m=32,则点D的坐标为(4,0),这样就可以根据交点式来求解抛物线的解析式:y=12(x+1)(x−4)=12x2−32x−2;(2)要在x轴上的找到一点P,使得⊿PEF的周长最小,我们先来看E,F两点,这是两个定点,也就是说EF的长度是不变的,那实际上这个题目就是求PE+PF的最小值,这就变成了轴对称问题中最为经典的“放羊问题”,要解决这一问题首先我们看图中有没有E或F的对称点,根据题意,显然是有E点的对称点B的,那么连接BF与x轴的交点就是我们要求的点P(2,0);(3)首先点M本身就在抛物线对称轴上,其坐标为(32 ,0);点C是点B关于抛物线对称轴的对称点,所以点C的坐标为(3,-2);求Q点的坐标,根据题意可设Q点为(32 ,n).⊿QCM是等腰三角形,则可能有三种情况,分别是QC=MC;QM=MC;QC=QM.根据这三种情况就能求得Q点的坐标可能是(32 ,±52)或(3 2 ,−2516)或(32 ,−4).试题解析:(1)∵A(-1,0),B(0,-2)∴OE=OB=2,OA=1,∵AD是⊙M的直径,∴OE·OB=OA·OD,即:2²=1·OD,OD=4,∴D(4,0),把A(-1,0),B(0,-2),D(4,0)代入得:{a−b+c=0c=−216a+4b+c=0,即,,{a=12b=−32c=−2该抛物线的表达式为:.连接AF,DF,∵FH⊥AD于点H,AD为直径∴△AFH∽△FDH,∴HF²=DH·AH,∵E点与B点关于点O对称,根据轴对称的性质,连接BF交x轴于点P,∵A(-1,0),D(4,0),∴AD=5,设DH=x,则AH=5-x,即1.5²=x(5-x),5x-x²=,4x²-20x+9=0,(2x-1)(2x-9)=0,由AH>DH,∴DH=,∴OH=OD-DH=,∴F(3.5,1.5),设直线BF的解析式为,则3.5k+b=1.5;b=-2,则k=1,b=-2,∴y=x-2,令y=0,则x=-2,∴P(2,0)(3)Q(,),Q(,-),Q(,-4),∴Q(,-).考点:二次函数与圆8.(2019·山东中考真题)如图,在平面直角坐标系xOy中,半径为1的圆的圆心O在坐标原点,且与两坐标轴分别交于A、B、C、D四点.抛物线y=ax2+bx+c与y轴交于点D,与直线y=x交于点M、N,且MA、NC分别与圆O相切于点A和点C.(1)求抛物线的解析式;(2)抛物线的对称轴交x轴于点E,连结DE,并延长DE交圆O于F,求EF的长.(3)过点B作圆O的切线交DC的延长线于点P,判断点P是否在抛物线上,说明理由.(3)点P在抛物线上,理由见解析【答案】(1)(2)3√510【解析】解:(1)∵圆心O在坐标原点,圆O的半径为1,∴点A、B、C、D的坐标分别为A(−1,0)、B(0,−1)、C(1,0)、D(0,1)∵抛物线与直线y=x交于点M、N,且MA、NC分别与圆O相切于点A和点C,∴M(−1,−1)、N(1,1).∵点D、M、N在抛物线上,将D(0,1)、M(−1,−1)、N(1,1)的坐标代入y=ax2+bx+c,得:解之,得:{a=−1 b=1 c=1∴抛物线的解析式为:C(1,0)、D(0,1).(2)∵y=−x2+x+1=−(x−12)2+54∴抛物线的对称轴为x=12,∴OE=12,DE=√14+1=√52.连结BF,∠BFD=90°,∴△BFD∽△EOD,∴DEDB =ODFD,又DE=√52,OD=1,DB=2,∴FD=4√55,∴EF=FD−DE=4√55−√52=3√510.(3)点P在抛物线上.设过D、C点的直线为:y=kx+b,将点C(1,0)、D(0,1)的坐标代入y=kx+b,得:k=−1,b=1,∴直线DC为:y=kx+b.过点P作圆O的切线BP与P轴平行,P点的纵坐标为y=−1,将y=−1代入y=kx+b,得:x=2.∴P点的坐标为y=−1,当x=2时,y=−x2+x+1=−22+2+1=−1,所以,P点在抛物线C(1,0)、D(0,1)上.(1)根据⊙O半径为1,得出D点坐标,再利用CO=1,AO=1,点M、N在直线y=x上,即可求出答案;(2)先利用配方法求出顶点坐标,再根据相似三角形的对应边成比例即可求得结果;(3)先求出直线CD的解析式,即可得到点P的坐标,从而可以判断点P是否在抛物线上.9.(2018·山东中考真题)如图,已知抛物线y=ax2+bx+c(a≠0)经过点A(3,0),B(﹣1,0),C(0,﹣3).(1)求该抛物线的解析式;(2)若以点A为圆心的圆与直线BC相切于点M,求切点M的坐标;(3)若点Q在x轴上,点P在抛物线上,是否存在以点B,C,Q,P为顶点的四边形是平行四边形?若存在,求点P的坐标;若不存在,请说明理由.【答案】(1)y=x2﹣2x﹣3;(2)M(﹣35,﹣65);(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,P的坐标为(,3)或(1,3)或(2,﹣3).【解析】【分析】(1)把A,B,C的坐标代入抛物线解析式求出a,b,c的值即可;(2)由题意得到直线BC与直线AM垂直,求出直线BC解析式,确定出直线AM中k的值,利用待定系数法求出直线AM解析式,联立求出M坐标即可;(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,分两种情况,利用平移规律确定出P的坐标即可.【详解】(1)把A(3,0),B(﹣1,0),C(0,﹣3)代入抛物线解析式得:9303a b ca b cc++=⎧⎪-+=⎨⎪=-⎩,解得:123 abc=⎧⎪=-⎨⎪=-⎩,则该抛物线解析式为y=x2﹣2x﹣3;(2)设直线BC解析式为y=kx﹣3,把B(﹣1,0)代入得:﹣k﹣3=0,即k=﹣3,∴直线BC解析式为y=﹣3x﹣3,∴直线AM解析式为y=13x+m,把A(3,0)代入得:1+m=0,即m=﹣1,∴直线AM解析式为y=13x﹣1,联立得:33113y xy x=--⎧⎪⎨=-⎪⎩,解得:3565xy⎧=-⎪⎪⎨⎪=-⎪⎩,则M(﹣35,﹣65);(3)存在以点B,C,Q,P为顶点的四边形是平行四边形,分两种情况考虑:设Q(x,0),P(m,m2﹣2m﹣3),当四边形BCQP为平行四边形时,由B(﹣1,0),C(0,﹣3),根据平移规律得:﹣1+x=0+m,0+0=﹣3+m2﹣2m﹣3,解得:当时,m2﹣2m﹣﹣2﹣﹣3=3,即P(,3);当m=1时,m 2﹣2m ﹣3=8﹣﹣3=3,即P (1,3); 当四边形BCPQ 为平行四边形时,由B (﹣1,0),C (0,﹣3), 根据平移规律得:﹣1+m=0+x ,0+m 2﹣2m ﹣3=﹣3+0, 解得:m=0或2,当m=0时,P (0,﹣3)(舍去);当m=2时,P (2,﹣3),综上,存在以点B ,C ,Q ,P 为顶点的四边形是平行四边形,P 的坐标为(,3)或(13)或(2,﹣3). 【点睛】此题属于二次函数综合题,涉及的知识有:待定系数法求函数解析式,平行四边形的性质以及平移规律,熟练掌握各自的性质是解本题的关键.10.(2018·湖南中考真题)我们不妨约定:对角线互相垂直的凸四边形叫做“十字形”.(1)①在“平行四边形,矩形,菱形,正方形”中,一定是“十字形”的有 ;②在凸四边形ABCD 中,AB=AD 且CB≠CD ,则该四边形 “十字形”.(填“是”或“不是”) (2)如图1,A ,B ,C ,D 是半径为1的⊙O 上按逆时针方向排列的四个动点,AC 与BD 交于点E ,∠ADB ﹣∠CDB=∠ABD ﹣∠CBD ,当6≤AC 2+BD 2≤7时,求OE 的取值范围;(3)如图2,在平面直角坐标系xOy 中,抛物线y=ax 2+bx+c (a ,b ,c 为常数,a >0,c <0)与x 轴交于A ,C 两点(点A 在点C 的左侧),B 是抛物线与y 轴的交点,点D 的坐标为(0,﹣ac ),记“十字形”ABCD 的面积为S ,记△AOB ,△COD ,△AOD ,△BOC 的面积分别为S 1,S 2,S 3,S 4.求同时满足下列三个条件的抛物线的解析式; ①S =1S 2S +;②S=3S 4S +;③“十字形”ABCD 的周长为1210.【答案】(1)①菱形,正方形;②不是;(2)12OE ≤≤(OE >0);(3)y=x 2﹣9.【解析】 【详解】分析:(1)利用“十字形”的定义判断即可;(2)先判断出∠ADB+∠CAD=∠ABD+∠CAB ,进而判断出∠AED=∠AEB=90°,即:AC ⊥BD ,再判断出四边形OMEN 是矩形,进而得出OE 2=2-14(AC 2+BD 2),即可得出结论; (3)由题意得,A(2b a--,0),B (0,c ),C(2b a-,0),D (0,-ac ),求出S=12AC•BD=-12(ac+c )×a,S 1=12OA•OB=-)4c b a +,S 2=12OC•OD=-)4c b -,S 3=12OA×OD=-)4c b +,S 4=12OB×OC=-)b -,进而建立方程)()()()+=+4b c bc b c b a+---+--,求出a=1,再求出b=0,进而判断出四边形ABCD 是菱形,求出,进而求出c=-9,即可得出结论. 详解:(1)①∵菱形,正方形的对角线互相垂直, ∴菱形,正方形是:“十字形”,∵平行四边形,矩形的对角线不一定垂直, ∴平行四边形,矩形不是“十字形”, 故答案为菱形,正方形; ②如图,当CB=CD时,在△ABC 和△ADC 中,AB AD CB CD AC AC =⎧⎪=⎨⎪=⎩, ∴△ABC ≌△ADC (SSS ),∴∠BAC=∠DAC , ∵AB=AD , ∴AC ⊥BD ,∴当CB≠CD 时,四边形ABCD 不是“十字形”, 故答案为不是;(2)∵∠ADB+∠CBD=∠ABD+∠CDB ,∠CBD=∠CAD,∠CDB=∠CAB , ∴∠ADB+∠CAD=∠ABD+∠CAB , ∴180°﹣∠AED=180°﹣∠AEB , ∴∠AED=∠AEB=90°, ∴AC ⊥BD ,过点O 作OM ⊥AC 于M ,ON ⊥BD 于N ,连接OA ,OD ,∴OA=OD=1,OM 2=OA 2﹣AM 2,ON 2=OD 2﹣DN 2,AM=12AC ,DN=12BD ,四边形OMEN 是矩形, ∴ON=ME ,OE 2=OM 2+ME 2, ∴OE 2=OM 2+ON 2=2﹣14(AC 2+BD 2), ∵6≤AC 2+BD 2≤7,∴2﹣74≤OE 2≤2﹣32,∴14≤OE 2≤12,∴12≤OE≤2;(3)由题意得,A (2b a--,0),B (0,c ),C (2b a-+,0),D (0,﹣ac ),∵a >0,c <0,∴b+,OB=﹣c ,b-,OD=﹣ac ,,BD=﹣ac ﹣c ,∴S=12AC•BD=﹣12(ac+c )×a,S 1=12OA•OB=﹣)4c b a +,S 2=12OC•OD=﹣)4c b -, S 3=12OA×OD=)b +,S 4=12OB×OC=)b -,==)()()()+=+4b c b c b c b a +---+--,, ∴a=1,∴S=﹣S 1=﹣)4c b a +,S 4=﹣)4c b a-,=∴S=S 1+S 2∴﹣+∴=-∴b=0,∴A 0),B (0,c ),C 0),d (0,﹣c ), ∴四边形ABCD 是菱形,∴∴, 即:AD 2=90,∵AD2=c2﹣c,∴c2﹣c=90,∴c=﹣9或c=10(舍),即:y=x2﹣9.点睛:此题是二次函数综合题,主要考查了新定义,平行四边形,矩形,菱形,正方形的性质,全等三角形的判定和性质,三角形的面积公式,求出a=1是解本题的关键.11.(2017·广西中考真题)已知抛物线y1=ax2+bx-4(a≠0)与x轴交于点A(-1,0)和点B(4,0).(1)求抛物线y1的函数解析式;(2)如图①,将抛物线y1沿x轴翻折得到抛物线y2,抛物线y2与y轴交于点C,点D是线段BC上的一个动点,过点D作DE∥y轴交抛物线y1于点E,求线段DE的长度的最大值;(2)在(2)的条件下,当线段DE处于长度最大值位置时,作线段BC的垂直平分线交DE于点F,垂足为H,点P是抛物线y2上一动点,⊙P与直线BC相切,且S⊙P:S△DFH=2π,求满足条件的所有点P的坐标.【答案】(1) 抛物线y1的函数解析式为:y1=x2-3x-4;(2)9;(3)(,),(2),(,4),(2,).【解析】试题分析:(1)将点A(-1,0)和点B(4,0)代入y1=ax2+bx-3即可得到结论;(2)由对称性可知,得到抛物线y2的函数解析式为y2=-x2+3x+4,求得直线BC的解析式为:y=-x+4,设D (m,-m+4),E(m,m2-3m-4),其中0≤m≤4,得到DE=-m+4-(m2-3m-4)=-(m-1)2+9,即可得到结论;(3)由题意得到△BOC是等腰直角三角形,求得线段BC的垂直平分线为y=x,由(2)知,直线DE的解析式为x=1,得到H(2,2),根据S⊙P:S△DFH=2π,得到,由于⊙P与直线BC相切,推出点P在与直线BC的直线上,于是列方程即可得到结论.试题解析:(1)将点A(-1,0)和点B(4,0)代入y1=ax2+bx-3得:a=1,b=-3,∴抛物线y1的函数解析式为:y1=x2-3x-4;(2)由对称性可知,抛物线y2的函数解析式为:y2=-x2+3x+4,∴C(0,4),设直线BC的解析式为:y=kx+q,把B(4,0),C(0,4)代入得,k=-1,q=4,∴直线BC的解析式为:y=-x+4,设D(m,-m+4),E(m,m2-3m-4),其中0≤m≤4,∴DE=-m+4-(m2-3m-4)=-(m-1)2+9,∵0≤m≤4,∴当m=1时,DE max=9;此时,D(1,3),E(1,-6);(3)由题意可知,△BOC是等腰直角三角形,∴线段BC的垂直平分线为:y=x,由(2)知,直线DE的解析式为:x=1,∴F(1,1),∵H是BC的中点,∴H(2,2),∴,,∴S△DFH=1,设⊙P的半径为r,∵S⊙P:S△DFH=2π,∴,∵⊙P与直线BC相切,∴点P在与直线BC的直线上,∴点P在直线y=-x+2或y=-x+6的直线上,∵点P在抛物线y2=-x2+3x+4上,∴-x+2=-x2+3x+4,解得:x1,x2=2-x+2=-x2+3x+4,解得:x3=2+,x4=2,∴符合条件的点P坐标有4个,分别是(,),(2),(,4),(2,4+).【点睛】本题考查了二次函数的综合题,涉及到待定系数法,一次函数、圆的切线等知识点,结合图形正确地选择适当的方法和知识进行解答是关键.12.(2018·山东中考真题)抛物线y=ax2+bx+4(a≠0)过点A(1,﹣1),B(5,﹣1),与y轴交于点C.(1)求抛物线的函数表达式;(2)如图1,连接CB,以CB为边作▱CBPQ,若点P在直线BC上方的抛物线上,Q为坐标平面内的一点,且▱CBPQ的面积为30,求点P的坐标;(3)如图2,⊙O1过点A、B、C三点,AE为直径,点M为上的一动点(不与点A,E重合),∠MBN 为直角,边BN与ME的延长线交于N,求线段BN长度的最大值.。
二次函数与圆的综合压轴题

二次函数与圆的综合压轴题
一、题目描述
本题是一道综合性的数学题,涉及到二次函数和圆的相关知识。
具体要求如下:
给定一个二次函数 $y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$,其中 $a,b,c,r$ 均为已知常数,且 $a\neq0$。
请编写一个函数,判断该二次函数与圆是否有交点,并输出交点的坐标。
二、解题思路
1. 二次函数与圆的关系
首先,我们需要了解二次函数和圆之间的关系。
对于一个二次函数$y=ax^2+bx+c$ 和一个圆 $x^2+y^2=r^2$,它们之间可能存在以下三种情况:
(1)没有交点:当二次函数和圆分离时,它们没有交点。
(2)相切:当二次函数和圆相切时,它们只有一个交点。
(3)相交:当二次函数和圆相交时,它们有两个交点。
接下来,我们需要确定如何求出这些交点的坐标。
2. 求解交点坐标
对于一条直线和一个圆之间的交点坐标可以通过联立直线方程和圆方程求解。
但是对于一个二次函数而言,并不存在明确的直线方程。
因此,在本题中,我们可以通过以下步骤求解交点坐标:
(1)将二次函数和圆的方程联立,得到一个关于 $x$ 的二次方程。
(2)解出该二次方程的根,即为交点的横坐标。
(3)将横坐标代入二次函数或圆的方程中,求出相应的纵坐标。
最后,我们需要根据交点个数输出不同的结果。
如果没有交点,则输出“无交点”;如果有一个交点,则输出该交点坐标;如果有两个交点,则输出两个交点坐标。
三、代码实现
下面是本题的完整代码实现:。
初中数学二次函数与圆相结合的压轴题专题,中考数学二次函数与圆相结合的经典题型讲解及答案解析
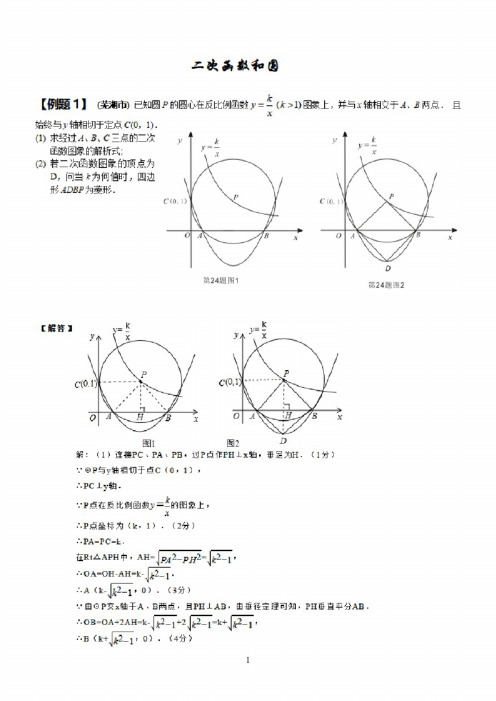
【仲烦1】(我市)已知圆P的圆心在反比例函数y=-(A:>1)上,并与工轴相交于X、3两点.且x始终与]轴相切于定点C(0,1).⑴求经过三点的二次匣1数图象的解析式;(2)若二次函教图象的顶点为D,问当上为何值时'四边形也站尹为菱形.【耕音】解:(1)连接PC、PAx PB,谊P点ffPHXx轴.垂足为H・(1分)与y轴相切于点C(0, 1),.-.PC±y^.•.•P点在反比例函数》二占的囹象上,X•.•P点坐标为(k,1).(2分)•.•PAU.在RtAAPH中,AH=厨2_尸於后一1,•'•A(k-90 ).(3分)•.•由。
P交x轴于A、B两点,且PHJLAB,由垂径击理可知,PH垂直平分AB.AOB=OA+2AH=k•••B3小2_1,0).《4分〉故过A、B两点的抛物线的对称轴为PH所在的直钱斛析式为x=k.可设该抛物线解析式为y=a<x-k)2+h.(5分)又二.抛物线过C(。
,1),B(k-^2_r0),[ak^-^h=1•3|—?昭得a=l,h=1-k^.(7分)•.•抛物线解析式为y=心)2+1上2.(B分)(2)由<1)知抛物线顶点D坐标为(k,l-k2>•・•DH-k2-l.若四边形ADBP为装形.则必有PH=DH.(10分)VPH=1,.•-k2-l=l.又">1,(11分)•・•当k取以时,PD与AB互相垂直平分,则四边形ADBP为菱形•(12分)3【百麒2]翎南省韶关市)25.如图6,在平面直角坐标系中旭边形OABC是矩形,。
虹4应=2,直线),=-":与坐标轴交于D、E。
设M是加的中点,P是线段DE上的动点.(1)求M、D两点的坐标;<2)当P在什么位置时,PA=PB?求出此时P点的坐标j<3)过P作PH1BC,垂足为H,当以PM为直径的OF与BC相切于点N时,求梯形PHBH的面积.图6【分析】(1)因为四边形OABC是逅形,0A=4,AB=2»直线>=r-?与坐标轴交于D、E,M是AB的中点2.所以令y=0,即司术出D的坐标,而AM-1.印以M(4,1);(2)因为PA=PB.断以P是AB的香直平分线和直线ED的交点,而AE的中垂线是y=l,断以P的纵坐标为1,令直线ED的解析式中的y=l,求出的x的值即为相应的P的横坐标;(3〉可设P(x,y>,连将PN、MN、NF,因为点P在y・x-:上,所以P《x,粮据蹦意可2得PNlMNi FN±BCi F是圈心,又因N是钱段HB的中点,HN-NB-—»PH-2-(-x*-)t2 2 2BM=1,利用直径对的圆周角是直甬可得到ZHPX-ZHNP=ZHNP-ZBNM=90°•所以ZHPN=ZB取ph ir£x+| NM,又因ZPHN-ZB-900-所以可得到R tAPNH<^RtANMB•所以—•A2=—^,这BM BN—4-x1—样牧可得到关于X的方程,解之即可求出X的值,而饬求面招的四边形是一个直角梯形,南以Spg=也皿滋或"医号)("6+应)=.21_色叵.2 2 24满答】俄;《1)M", 1),D《9,0);(2分)2(2)V PA=PB>•七点P在线段AB的中毒线上,•.•点P的纵坐标是I,3又•:点P在尸-X-—上,2・.•点P的坐标为(【,1)?(4分)(3)设P(x,y),连接PN、MN、NF,3点P lSy=・x+-上,匕3・'・P(x ,-w+—),2依题意知:PN«LMN>FN^BC,F是圆心,・'・N是线段HB的中点,HN=NB=±M,PH=2.2口,BM=1,<6分)22HPN-ZHNP=NHNP-ZBNM=90°,NHPN=ZBNN1,又ZPHN=ZB=90°5RtAPNH^RtANMBs:HN_PH•'两南,4-x x*.."F=二,-等」22,(8分)x?-12x+14=0»朋得;x-6-j22(^-*>^舍去),k=6-皿=些罕=空也艾竺=一*孕屈,(9分)2【例题31(||-4省白银等7市新课程)28.在直角坐标系中>0A的丰径为4,圆心A曜标为(2, 0),S与X轴交于E、尸两点,与),轴交于(7、D两点,过点(7作0X的切线时,交x轴于点3.(1)求直线C5的解析式:(2)若抛物线.件履7)日€的顶点在直线3C上,与x轴的交点恰为点E、已求该抛物线的解析式J(3)试判断点C是否在抛物线上?(4)在抛物线上是否存在三个点,由它构成的三角形与A4OC相似?直接与出两组这样的点•4[分析】(1>SHAC.根撮区]的李径求出AC. W1B点人的坐麻求出0A,燃后利用勾腹定理列式求出0C・从而得到点C的坐标,再求出ZCAO=60=.然后粮掘直有三甬形两锐角互余米出NB=30。
中考压轴题中的二次函数(三)带答案和详细解析30道解答题.docx

中考压轴题中的二次函数⑶一.解答题(共3()小题)1.(2015*雅安校级一模)己知:如图,抛物线y= - x'+bx+c与x轴,y轴分别相交于点A (-1, 0),B (0, 3)两点,其顶点为D.(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E.求四边形ABDE的面积;(3)AAOB与ABDE是否和似?如果相似,请予以证明;如果不相似,请说明理由.2.(2()15・余姚市模拟)如果抛物线©的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C]上,那么,我们称抛物线C|与C2关联.(1)已知抛物线①y=x2+2x - 1,判断下列抛物线②y=- X2+2X+1; ®y=x2+2x+l与已知抛物线①是否关联,并说明理由.(2)抛物线C】:y=| (x+1) —2,动点P的坐标为(t, 2),将抛物线绕点P (t, 2)旋转180。
得到抛物线C2,若抛物线Ci与C2关联,求抛物线C2的解析式.(3)A为抛物线Ci: y=g(x+l)2-2的顶点,B为与抛物线0关联的抛物线顶点,是否8存在以AB为斜边的等腰直角AABC,使其直角顶点C在y轴上?若存在,求出C点的坐标;若不存在,请说明理由.3.(2015*临淄区校级模拟)设抛物线y=ax2+bx・2与x轴交于两个不同的点A (・1, 0)、B (m, 0),与y轴交于点C.且ZACB=90度.(1)求m的值;(2)求抛物线的解析式,并验证点D (1, -3)是否在抛物线上:(3)已知过点A的直线y=x+l交抛物线于另一点E.问:在x轴上是否存在点P,使以点P、B、D为顶点的三角形与AAEB相似?若存在,请求出所有符合耍求的点P的坐标;若4.(2015*营口模拟)如图,二次函数尸-丄,+bx+c的图象经过点A (4, 0), B (・4,-4),且与y轴交于点C.(1)试求此二次函数的解析式;(2)试证明:ZBAO=ZCAO(H屮O是原点);(3)若P是线段AB±的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图彖及x轴于Q、H两点,试问:是否存在这样的点P,便PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.5.(2()15・杭州模拟)己知经过原点的抛物线y=・2X2+4X(如图所示)与x的另一交点为A 现将它向右平移m (m>0)位,所得抛物线与x轴交于C、D点,与原抛物线交于点P (1)求点P的坐标(可用含m式子表示);(2)设APCD的面积为s,求s关于m关系式;(3)过点P作x轴的平行线交原抛物线于点E,交平移后的抛物线于点F.请问是否存在m,使以点E、0、A、F为顶点的四边形为平行四边形?若存在,求出m的值;若不存在,6.(2()15・温州模拟)如图,已知抛物线y=ax2+bx+c经过A (0, 4), B (4, 0), C (・1, 0)三点.过点A作垂直于y轴的直线1.在抛物线上有一动点P,过点P作直线PQ平行于y轴交直线1于点Q ・连接AP.(1)求抛物线y=ax2+bx+c的解析式;(2)是否存在点P,使得以A、P、Q三点构成的三角形与AAOC相似?如果存在,请求出点P的坐标;若不存在,请说明理由;(3)当点P位于抛物线y=ax2+bx+c的对称轴的右狈9.若将AAPQ沿AP对折,点Q的对7.(2015*來凤县二模)如图1,在平面直角坐标系xOy屮,直线1: y=-|x+K与x轴、y轴分别交于点A和点B (0,・1),抛物线尸吉,+bx+c经过点B,且与直线1的另一个交点乙(2) 点D 在抛物线上,且点D 的横坐标为t (0<t<4).。
压轴题周周练之10:二次函数与圆2

压轴题周周练之10:二次函数与圆2
1、如图,在平面直角坐标系中,已知A (–1,0)、B (3,0),以AB 为直径的⊙M 与y 轴的正半轴交于点C ,抛物线c bx ax y ++=2(a ≠0)经过C 、M 、B 三点.
(1)求点C 的坐标及该抛物线的函数表达式;
(2)若点P 是x 轴下方⊙M 上的一个动点,过点C 作CQ ⊥PC ,交PB 的延长线于点Q . ①当PC 平分∠ACB 时,求△PCQ 的面积;②求△PCQ 的最大面积,并判断此时点Q 是否
2
,抛物线c bx ax y ++=2(a ≠0)经过A 、B 、C 三点.点P 是位到直线
BC 上方抛物线上的一个动点,以点P 为圆心,作⊙P 与直线BC 相切.(1)求抛物线的函数表达式;
(2)若点P 的坐标是(n ,2),试判断⊙P 与抛物线的对称轴的位置关系,并说明理由;
0),∠ACB=90º,tan ∠CAB=21,抛物线c bx ax y ++=2(a ≠0)经过A 、B 、C 三点,E 是抛物线的顶点.⊙M 是△ABC 的外接圆.(1)求抛物线的函数表达式;
(2)判断直线CE 与⊙M 的位置关系,并说明理由;
(3)设⊙M 是与抛物线的另一个交点为D ,P 是位于BD 间抛物线上的一个动点,设点P
的横坐标为x ,△PBC 的面积为S ,求S 与x 之间的函数关系式,并求S 的最大值及此时点P 的坐标.。
2025中考数学二次函数压轴题专题练习21 阿氏圆模型(学生版+解析版)

专题21阿氏圆模型一、知识导航所谓“阿氏圆",是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定值(不力l)的点的栠合叫做圆.如下图,已知A、B两点,点P满足PA:PB=k (k* I),则满足条件的所有的点P构成的图形为圆.pA下给出证明法一:首先了解两个定理(I)角平分线定理:如图,在6-ABC中,AD是乙BAC的角平分线则AB DBAC DCAB DcS BD S ABxDE AB AB DB 证明:一竺丛=---坐上==--,即一一=--s AC/) CD S ACD ACxDF AC. AC DC(2)外角平分线定理;如图,在6.ABC中,外角CAE的角平分线AD交BC的延长线于点D,则AB DB AC DC ^EA,,``B C\\\\IID证明:在B A 延长线上取点E 使得AE=AC ,连接BO,则6.ACD 兰6.AED (SAS), CD=ED 且AD DB ABAB DB 平分乙BDE ,则一一=一一,即一一=一一.DE AE AC DC接下来开始证明步骤:仁',,夕夕2A、、、、、、、、、、、、、MB'N如图,PA:PB=k,作LAPB 的角平分线交AB 于M 点,根据角平分线定理,MA PA —=—=k '故M 点为定MB PB点,即乙APB 的角平分线交AB 于定点;作乙APB 外角平分线交直线AB于N 点,根据外角平分线定理,NA PA—=—=k,故N 点为定点,即乙APB NB PB外角十分线交直线AB 于定点;又乙MPN=90°,定边对定角,故P 点轨迹是以MN 为直径的圆AN法二:达系不妨将点A 、B 两点置于x轴上且关于原点对称,设A (-m, 0),则B (m, 0),设P (x, y), PA=kPB, 即:J (x+m)2+y 2 =k J(x -m)2+ y 2 (x+m)2+y 2 =k 2(x -m )2+k 2y 2 (炉-1)(x2+ y 2)-(2m +2k 2m)x+(k 2-1)矿=02 2m +2k'n /, X-+y-k 2-lx+ni 2 =0解析式满足圆的一般方程,故P点所构成的图形是固,且圆心与AB 共线.除了证明之外,我们还需了解“阿氏圆”的一些性质:(1)PA MA NA —=—=—=k.PB MB NB应用:祁据点A 、B的位置及k的值可确定M 、N及圆心0.OB OP(2) 6.0BPV>/:::,.QPA,即一一=一一,变形为OP 2=OA-OB.OP OA 应用:粮据圆心及半径和A 、B其中一点,可求A 、B另外一点位置.(3)OP OB PA —=—=—=k .OA OP PB应用:已知半径及A 、B中的其中一点,即可知道PA:PB的值.pAN匡I1如图,在L.ABC中,AB=4,AC=2,点D为AB边上一点,当AD=时,L.ACDv>L.ABCC8二二AAC AD觯:若6.ACDV)6.A B C 则有—-=——即AC 2=AB·ADAB AC·: A B =4,AC =2AC2:. AD =—= 1AD故答案为I.2如图,点P 是半径为2的O O 上一动,点,点A 、B为o o 外的定点,连接PA 、P B,点B 与固心0的I距离为4要使PA+�PB 的值最小,如何确定点P,并说明理由.2ABI 思路分析)构造相似三角形,将所求两条线段的和转化为一条线段,此线段与圆的交点即为所求A(详解J连接OB,OP ,在OB 上截取o c 亏1,连接AC 交('0于点P',连接PC.OP OC l ·—=—=-,乙POC =乙BOPOB OP 2 :.�POC BOPPC ll :.—= -,即-PB =PC PB 2· 21:. PA+.:..PB= PA+PC�AC2当点A 、P 、C三点共线时,PA+PC的值最小,最小值为AC的长,即当点P与P'重合时,PA+�PB的2 根据阿氏圆可得OP 2=0B -OC即O P 2 22OC =—=—=1OB 4值最小.23如图,平面直角坐标系中,A(4,0),B(0,3),点E在以原点0为圆心,2力半径的圆上运动,求AE+�BE3 的最小值.y j.... _3一3-,(思路分析)在坐标轴上找一点,构造相似三角形,利用对应边成比例将两条线段的和转化为求一条线段的长,即为最小值.(详解】如图,在y轴上取一点M(O,-:-)4 3 . OE OM 2 4,连接OE,EM, AM,则OE =2,0B =3, OM=-:-3==-OB OE 3又?乙EOM=乙BOE :. EOM =、BOE EM OM 2 2 :.—=—=-,即EM =::::_BEBE OE3. 3 2:. AE+::::_B E=AE+EM切AM3当A 、E 、M三点共线时,AE+BM的值最小,最小值为AM的长在Rt ,.AOM 中,A M =拓夼言夼=幸2:.当E 为线段A.11与o o 的交点时,AE +78E 有最小值为一—-.4而3 3y ·--3-3-'3 2.9 4.如图,已知抛物线y =--x +-x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,44点E的坐标为(2,0),将线段OE绕点0逆时针旋转得到OE',旋转角力a(0°<a<90°),连接BE'、2CE',求BE'+�CE'的敢小值.3(思路分析】由旋转可知E'点的运动轨迹为以原点0为圆心,2为半径的圆在笫一象限内的一段固弧,在y轴上找一点,构造相似三角形,再结合各点坐标求解即可3 9(详解】解.?抛物线的解析式为y=--x 2+-x+34 4 :. B (4,0),C(0,3) ·..点E的坐标为(2,0):.,占、E'的运动轨迹为以原点0为圆心,2为半径的圆在第一象限内的一段圆弧4 如图在y轴上取一点M (O,-::),连接OE',E'M,B M,则OE'=2, OC = 3, OM =-:: 43......3 . E'M OM 2..-=-=-OCOE' 3 又?L.E'OM=乙COE':. E'OM(/) COE'. EM 2 2:.-—=-即E 'M=::..CE 'C E '33 2:. BE'+::..CE'=BE'+E'M�BM当B 、E',M三点共线时,BE'+E'M的值最小,最小值为BM的长·:BM=豆二尸三3)32 4而:.当E'为BM与圆弧的交点时,BE'+7CE'有最小值为3 3I三、中考真题演练I.(2022广东惠州一模)如图1,抛物线y=,矿+bx~4与X轴交于A、B两点,与Y轴交千点C,其中点A的坐标为(-1,0),抛物线的对称轴是迎线x=-.3 2yy图1图2(1)求抛物线的解析式:(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由;(3)如图2,过点B 作BF 上BC 交抛物线的对称轴千点F,以点C 为圆心,2为半径作(,C'点Q 为C上的五一个动点,求--B Q+FQ的最小值.42如图),抛物线)1=成+(a+3)..I,+3(a'1'0)与x轴交于点A(4,0),与y轴交于点B,;{:丘轴上有一动点E(m,O )(0<m<4),过点E作x轴的垂线交直线AB千点N,交抛物线于点P,过点P作PM上AB千点M.y yxX图l(I)求a的值和且线AB的函数表达式:图2C. 6(2)设t:.PMN的周长为C,,t:.A EN的周长为C“若-=-求m的值C 5(3)如图2,在(2)的条件下,将线段OE绕点0逆时针旋转得到OE',旋转角为a (0°<a<90勺,连按E'A 、EB,求E'A+二E'B的最小值.33.(20l9山东中考真题)如图I,在平面直角坐标系中,直线y=-5x+5与x轴,y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴的另一交点为B图1图2(l)求抛物线解析式及B点坐标;(2)若点M为x轴下方抛物线上一动点,连接MA、MB、BC,当点M运动到某一位置时,四边形AMBC 面积最大,求此时点M的坐标及四边形AMBC的面积;(3)如图2,若P点是半径为2的0B上一动点,连接PC、PA,当点P运动到某一位置时,PC+�PA的2值最小,请求出这个最小值,并说明理由.4.(2018广西柳州中考真题)如图,抛物线y= a.x2 +bx+c圭卢轴交千A(.J3,0), 8两点(点8在点A的左侧),与Y轴交于点C,且08=30A=./3oc'LO A C的平分线AD交Y轴于点D,过点A且垂直于AD的均线[交Y轴于点E,点P是X轴下方抛物线上的一个动点,过点P作PF..l.x轴,垂足为F,交直线AD千点H.(l)求抛物线的解析式:(2)设点P的横坐标为111,当FH=HP时,求1/1.的值:I(3)当归线P F为抛物线的对称轴时,以点H为圆心,-H C为半径作1)H,点Q为o H上的一个动点,求2l�AQ+EQ的最小值4x专题21阿氏圆模型一、知识导航所谓“阿氏圆",是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定值(不力l)的点的栠合叫做圆.如下图,已知A、B两点,点P满足PA:PB=k (k* I),则满足条件的所有的点P构成的图形为圆.pA下给出证明法一:首先了解两个定理(I)角平分线定理:如图,在6-ABC中,AD是乙BAC的角平分线则AB DBAC DCAB DcS BD S ABxDE AB AB DB 证明:一竺丛=---坐上==--,即一一=--s AC/) CD S ACD ACxDF AC. AC DC(2)外角平分线定理;如图,在6.ABC中,外角CAE的角平分线AD交BC的延长线于点D,则AB DB AC DC ^EA,,``B C\\\\IID证明:在B A 延长线上取点E 使得AE=AC ,连接BO,则6.ACD 兰6.AED (SAS), CD=ED 且AD DB ABAB DB 平分乙BDE ,则一一=一一,即一一=一一.DE AE AC DC接下来开始证明步骤:仁',,夕夕2A、、、、、、、、、、、、、MB'N如图,PA:PB=k,作LAPB 的角平分线交AB 于M 点,根据角平分线定理,MA PA —=—=k '故M 点为定MB PB点,即乙APB 的角平分线交AB 于定点;作乙APB 外角平分线交直线AB于N 点,根据外角平分线定理,NA PA—=—=k,故N 点为定点,即乙APB NB PB外角十分线交直线AB 于定点;又乙MPN=90°,定边对定角,故P 点轨迹是以MN 为直径的圆AN法二:达系不妨将点A 、B 两点置于x轴上且关于原点对称,设A (-m, 0),则B (m, 0),设P (x, y), PA=kPB, 即:J (x+m)2+y 2 =k J(x -m)2+ y 2 (x+m)2+y 2 =k 2(x -m )2+k 2y 2 (炉-1)(x2+ y 2)-(2m +2k 2m)x+(k 2-1)矿=02 2m +2k'n /, X-+y-k 2-lx+ni 2 =0解析式满足圆的一般方程,故P点所构成的图形是固,且圆心与AB 共线.除了证明之外,我们还需了解“阿氏圆”的一些性质:(1) PA MA NA —=—=—=k .PB MB NB应用:祁据点A 、B的位置及k的值可确定M 、N及圆心0.OB OP(2) 6.0BPV>/:::,.QPA,即一一=一一,变形为OP 2=OA-OB.OP OA 应用:粮据圆心及半径和A 、B其中一点,可求A 、B另外一点位置.(3)OP OB PA —=—=—=k .OA OP PB应用:已知半径及A 、B中的其中一点,即可知道PA:PB的值.pAN匡I1如图,在L.ABC中,AB=4,AC=2,点D为AB边上一点,当AD=时,L.ACDv>L.ABCC8二二AAC AD觯:若6.ACDV)6.A B C 则有—-=——即AC 2=AB·ADAB AC·: AB =4,AC =2AC2:. AD =—= 1AD故答案为I.2如图,点P 是半径为2的O O 上一动点,点A 、B为o o 外的定点,连接PA 、P B,点B 与固心0的I距离为4要使PA+�PB的值最小,如何确定点P,并说明理由.2ABI 思路分析)构造相似三角形,将所求两条线段的和转化为一条线段,此线段与圆的交点即为所求.A(详解J连接OB,OP ,在OB 上截取o c 亏1,连接AC 交('0于点P',连接PC.OP OC l ·—=—=-,乙POC =乙BOPOB OP 2 :.�POC BOPPC ll :.—= -,即-PB =PC PB 2· 21:. PA+.:..PB= PA+PC�AC2当点A 、P 、C三点共线时,PA+PC的值最小,最小值为AC的长,即当点P与P'重合时,PA+�PB的2 根据阿氏圆可得O P 2=0B -O C 即O P 2 22OC =—=—=1OB 4值最小.23如图,平面直角坐标系中,A(4,0),B(0,3),点E在以原点0为圆心,2力半径的圆上运动,求AE+�BE3 的最小值.y j一3-,(思路分析)在坐标轴上找一点,构造相似三角形,利用对应边成比例将两条线段的和转化为求一条线段的长,即为最小值.(详解】如图,在y轴上取一点M(O,-:-)4 3 . OE OM 2 4,连接OE,EM, AM,则OE =2,0B=3, O M=-:-3==-OB OE 3又?乙EOM=乙BOE :. EOM =、BOE EM OM 2 2 :.—=—=-,即EM =::::_BEBE OE3. 3 2:. AE+::::_B E=AE+EM切AM3当A 、E 、M三点共线时,AE+BM的值最小,最小值为AM的长在Rt ,.AOM 中,AM =拓千言夼=孛2:.当E 为线段A.11与o o 的交点时,AE +78E 有最小值为一—-.4而3 3y ·--3-3-'3 2. 94.如图,已知抛物线y =--x +-x+3与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,4 4点E的坐标为(2,0),将线段OE绕点0逆时针旋转得到OE',旋转角力a(0°<a<90°),连接BE'、2CE',求BE'+�CE'的敢小值.3(思路分析】由旋转可知E'点的运动轨迹为以原点0为圆心,2为半径的圆在笫一象限内的一段圆弧,在y轴上找一点,构造相似三角形,再结合各点坐标求解即可3 9(详解】解.?抛物线的解析式为y=--x 2+-x+34 4 :. B (4,0),C(0,3) ·.点E的坐标为(2,0):.,占、E'的运动轨迹为以原点0为圆心,2为半径的圆在第一象限内的一段圆弧4 如图在y轴上取一点M (O,-::),连接OE',E'M,BM,则OE'=2,OC=3, OM=-::43......3 . E'M OM 2..-=-=-OCOE' 3 又?L.E'OM =乙COE':. E'OM(/) COE'. EM 2 2:.-—=-即E 'M=::..CE 'C E '33 2:. B E'+::..CE'=BE'+E'M�BM当B 、E',M三点共线时,BE'+E'M的值最小,最小值为BM的长·:BM =芦言尸=玉3 J3 2 4而:当E'为BM与圆弧的交点时,BE'+7CE'有最小值为3 3I三、中考真题演练I.(2022广东惠州一模)如图1,抛物线y=,矿+bx~4与X轴交于A、B两点,与Y轴交千点C,其中点A的坐标为(-1,0),抛物线的对称轴是迎线x=-.3 2yy图1图2(1)求抛物线的解析式:(2)若点P是直线BC下方的抛物线上一个动点,是否存在点P使四边形ABPC的面积为16,若存在,求出点P的坐标若不存在,请说明理由;(3)如图2,过点B作BF上BC交抛物线的对称轴千点F,以点C为圆心,2为半径作(,C'点Q为C上的五一个动点,求--B Q+F Q的最小值.4【答案】(I)y=入.2-3x-4(2)P{l,6)或(3,4)(3)扫3【分析】(I)根据点A的坐标为(-1,0),抛物线的对称轴是直线x=-.待定系数法求二次函数解析式即可,2(2)先求得直线BC解析式,设P(m,m2-3m-4),则Q(m m-4),过点P作PQ轴交直线BC千点Q,根据S四边彤A BPC= s AOC +S如,等干16建立方程,解一元二次方程即可求得Ill的值,然后求得P的坐标,五(3)在CB上取CE=--,过点E作EG J_OC,构造CQE V>.C BQ,则当F,Q E三点共线时,取得最小值,最小值为FE,勾股定理解直角三形即可.【详解】(I)解:?抛物线y=矿+bx-4与X轴交于A、B两点,与Y轴交于点C,点A的坐标为-l,O),抛物线的对称轴是宜线x=-,3:. C(O,--4),, 4 , 。
二次函数压轴题(与圆综合问题)

二次函数压轴题(与圆综合问题)【典例分析】例1 如图,已知抛物线y=ax2+bx+c(a>0,c<0)交x轴于点A,B,交y轴于点C,设过点A,B,C 三点的圆与y轴的另一个交点为D.(1)如图1,已知点A,B,C的坐标分别为(-2,0),(8,0),(0,-4);①求此抛物线的函数解析式;②若点M为抛物线上的一动点,且位于第四象限,求△BDM面积的最大值;(2)如图2,若a=1,c=-4,求证:无论b取何值,点D的坐标均不改变.思路点拨(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,可得C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,根据根与系数的关系可得OA•OB=4.由A、D、B、C四点共圆可得∠ADC=∠ABC,∠DAB=∠DCB,从而可得△ADO∽∽△CBO,根据相似三角形的性质可得OC•OD=OA•OB=4,从而可得OD=1,即可得到D(0,1),因而无论b 取何值,点D的坐标均不改变.满分解答(1)①∵抛物线y=ax2+bx+c过点A(-2,0),B(8,0),C(0,-4),∴42064804a b ca b cc-+=⎧⎪++=⎨⎪=-⎩,解得14324abc⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩.学#科网∴抛物线的解析式为y=14x2-32x-4;②过点M作ME∥y轴,交BD于点E,连接BC,如图1.∴D(0,4).设直线BD的解析式为y=mx+n.∵B(8,0),D(0,4),∴804m nn+=⎧⎨=⎩,学&科网解得124mn⎧=-⎪⎨⎪=⎩,(2)连接AD、BC,如图2.若a=1,c=-4,则抛物线的解析式为y=x2+bx-4,则C(0,-4),OC=4.设点A(x1,0),B(x2,0),则OA=-x1,OB=x2,且x1、x2是方程x2+bx-4=0的两根,∴OA•OB=-x1•x2=-(-4)=4.考点:圆的综合题例2已知抛物线经过A(3,0), B(4,1)两点,且与y轴交于点C.(1)求抛物线的函数关系式及点C的坐标;(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB 于点F,当△OEF的面积取得最小值时,求点E的坐标.思路点拨(1)用待定系数法求解;(2) 假设存在,分两种情况讨论(3)根据面积公式,列出二次函数,求函数的最值.满分解答(1)将A(3,0),B(4,1)代人得∴∴∴C(0,3) 学科@网②当∠ABP=90O时,过B作BP∥AC,BP交抛物线于点P. ∵A(3,0),C(0,3)∴直线AC的函数关系式为将直线AC向上平移2个单位与直线BP重合.则直线BP的函数关系式为由,得又B(4,1),∴P2(-1,6).综上所述,存在两点P1(0,3), P2(-1,6).(3)∵∠OAE=∠OAF=45O,而∠OEF=∠OAF=45O, ∠OFE=∠OAE=45O,∴∠OEF=∠OFE=45O,∴OE=OF,∠EOF=90O∵点E在线段AC上,∴设E∴=∴===∴当时,取最小值,此时,∴例3如图,在平面直角坐标系中,圆D与y轴相切于点C(0,4),与x轴相交于A、B两点,且AB=6.(1)求D点的坐标和圆D的半径;(2)求sin∠ACB的值和经过C、A、B三点的抛物线对应的函数表达式;(3)设抛物线的顶点为F,证明直线AF与圆D相切.思路点拨(1)连接CD,过点D作DE⊥AB,垂足为E,连接AD.依据垂径定理可知AE=3,然后依据切线的性质可知CD⊥y轴,然后可证明四边形OCDE为矩形,则DE=4,然后依据勾股定理可求得AD的长,故此可求得⊙D的半径和点D的坐标;学科.网(2)先求得A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入可求得a 的值.根据三角形面积公式得:S△ABC=BC×AC sin∠ACB=AB×CO,代入计算即可;(3)求得抛物线的顶点F的坐标,然后求得DF和AF的长,依据勾股定理的逆定理可证明△DAF为直角三角形,则∠DAF=90°,故此AF是⊙D的切线.满分解答(2)如图1所示:∵D(5,4),∴E(5,0),∴A(2,0)、B(8,0).设抛物线的解析式为y=a(x﹣2)(x﹣8),将点C的坐标代入得:16a=4,解得:a,∴抛物线的解析式为y x 2x +4.∵S △ABC =BC ×AC sin ∠ACB =AB ×CO ,∴sin ∠ACB ==.例4如图,已知二次函数()22y x m 4m =--(m >0)的图象与x 轴交于A 、B 两点.(1)写出A 、B 两点的坐标(坐标用m 表示);(2)若二次函数图象的顶点P 在以AB 为直径的圆上,求二次函数的解析式; (3)设以AB 为直径的⊙M 与y 轴交于C 、D 两点,求CD 的长. 思路点拨(1)解关于x 的一元二次方程()22x m 4m 0--=,求出x 的值,即可得到A 、B 两点的坐标。
二次函数背景下的与圆有关的问题(解析版)
备战2020年中考数学压轴题之二次函数专题10 二次函数背景下的与圆有关的问题【方法综述】圆和二次函数都是初中数学重点知识,是压轴题中的常见题目。
而二次函数与圆的结合则常常是高难度的压轴题。
以二次函数为背景的问题中,圆的知识常常以圆的基本知识、与圆有关的位置关系、构造圆和隐形圆为考察内容。
解答要点是结合相关知识,对于已知条件进行数形结合。
【典例示范】类型一 圆的基本性质应用例1:如图,抛物线y =ax 2﹣2ax +m 的图象经过点P (4,5),与x 轴交于A 、B 两点(点A 在点B 的左边),与y 轴交于点C ,且S △P AB =10.(1)求抛物线的解析式;(2)在抛物线上是否存在点Q 使得△P AQ 和△PBQ 的面积相等?若存在,求出Q 点的坐标,若不存在,请说明理由;(3)过A 、P 、C 三点的圆与抛物线交于另一点D ,求出D 点坐标及四边形P ACD 的周长.【答案】(1)y =x 2﹣2x ﹣3;(2)点Q 的坐标为:(﹣2,5)或(﹣13,﹣209);(3). 【思路引导】(1)因为抛物线y =ax 2﹣2ax +m ,函数的对称轴为:x =1,S △P AB =10=12×AB ×y P =12AB ×5,解得AB=4,即可求解;(2)分A 、B 在点Q (Q′)的同侧;点A 、B 在点Q 的两侧两种情况,分别求解即可;(3)过点P 作PO′⊥x 轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A 、P 、C 三点的圆,即可求解.【详解】解:(1)y=ax2﹣2ax+m,函数的对称轴为:x=1,S△P AB=10=12×AB×y P=12AB×5,解得:AB=4,故点A、B的坐标分别为:(﹣1,0)、(3,0),抛物线的表达式为:y=a(x+1)(x﹣3),将点P的坐标代入上式并解得:a=1,故抛物线的表达式为:y=x2﹣2x﹣3…①;(2)①当A、B在点Q(Q′)的同侧时,如图1,△P AQ′和△PBQ′的面积相等,则点P、Q′关于对称轴对称,故点Q′(﹣2,5);②当A、B在点Q的两侧时,如图1,设PQ交x轴于点E,分别过点A、B作PQ的垂线交于点M、N,△P AQ和△PBQ的面积相等,则AM=BN,而∠BEN=∠AEM,∠AME=∠BNE=90°,∴△AME≌△BNE(AAS),∴AE=BE,即点E是AB的中点,则点E(1,0),将点P、E的坐标代入一次函数表达式并解得:直线PQ的表达式为:y=53x﹣53…②,联立①②并解得:x=﹣13或4(舍去4),故点Q(﹣13,﹣209),综上,点Q的坐标为:(﹣2,5)或(﹣13,﹣209);(3)过点P作PO′⊥x轴于点O′,则点O′(4,0),则AO′=PO′=5,而CO′=5,故圆O′是过A、P、C三点的圆,设点D(m,m2﹣2m﹣3),点O′(4,0),则DO′=5,即(m﹣4)2+(m2﹣2m﹣3)2=25,化简得:m(m+1)(m﹣1)(m﹣4)=0,解得:m=0或﹣1或1或4(舍去0,﹣1,4),故:m=1,故点D(1,﹣4);四边形P ACD的周长=P A+AC+CD+PD=【方法总结】本题考查了二次函数与三角形面积、三点共圆、四边形的周长、长度公式,综合性较强,灵活运用二次函数的知识是解题的关键.针对训练1.如图,一次函数y=2x与反比例函数y=kx(k>0)的图象交于A、B两点,点P在以C(-2,0)为圆心,1为半径的圆上,Q是AP的中点(1)若k的值;(2)若OQ长的最大值为32,求k的值;(3)若过点C的二次函数y=ax2+bx+c同时满足以下两个条件:①a+b+c=0;②当a≤x≤a+1时,函数y的最大值为4a,求二次项系数a的值.【答案】(1)2;(2)3225;(3)a的值为-3或2或-4或1.【解析】(1)设A(m,n),∵∴m2+n2=5,∵一次函数y=2x的图象经过A点,∴n=2m,∴m2+(2m)2=5,解得m=±1,∵A在第一象限,∴m=1,∴A(1,2),∵点A在反比例函数y=kx(k>0)的图象上,∴k=1×2=2;(2)如图,连接BP,由对称性得:OA=OB,∵Q是AP的中点,∴OQ=12 BP,∵OQ长的最大值为32,∴BP长的最大值为32×2=3,如图2,当BP过圆心C时,BP最长,过B作BD⊥x轴于D,∵CP=1,∴BC=2,∵B在直线y=2x上,设B(t,2t),则CD=t-(-2)=t+2,BD=-2t,在Rt△BCD中,由勾股定理得:BC2=CD2+BD2,∴22=(t+2)2+(-2t)2,t=0(舍)或-45,∴B(-45,-85),∵点B在反比例函数y=kx(k>0)的图象上,∴k=-45×(-85)=3225;(3)∵抛物线经过点C(-2,0),∴4a-2b+c=0,又∵a+b+c=0,∴b=a,c=-2a,∴y=ax2+ax-2a=a(x+12)2-94a,∵-12<a≤x≤a+1或a≤x≤a+1<-12,当x=a时,取得最大值4a,则a•a2+a•a-2a=4a,解得a=-3或2,当x=a+1时,取得最大值4a,则a(a+1)2+a(a+1)-2a=4a,解得a=-4或1,综上所述所求a的值为-3或2或-4或1.2.对于平面直角坐标系xOy中的点P,Q和图形G,给出如下定义:点P,Q都在图形G上,且将点P的横坐标与纵坐标互换后得到点Q,则称点P,Q是图形G的一对“关联点”.例如,点P(1,2)和点Q(2,1)是直线y=﹣x+3的一对关联点.(1)请写出反比例函数y=6的图象上的一对关联点的坐标:;x(2)抛物线y=x2+bx+c的对称轴为直线x=1,与y轴交于点C(0,﹣1).点A,B是抛物线y=x2+bx+c 的一对关联点,直线AB与x轴交于点D(1,0).求A,B两点坐标.(3)⊙T的半径为3,点M,N是⊙T的一对关联点,且点M的坐标为(1,m)(m>1),请直接写出m的取值范围.【答案】(1)(2,3),(3,2).(2)A,B两点坐标为(﹣1,2)和(2,﹣1).(3)1<m≤1+3√2.【解析】解:(1)∵2×3=3×2=6,∴点(2,3),(3,2)是反比例函数y=6的图象上的一对关联点.x故答案为:(2,3),(3,2).(2)∵抛物线y=x2+bx+c的对称轴为直线x=1,=1,∴﹣b2解得:b=﹣2.∵抛物线y=x2+bx+c与y轴交于点C(0,﹣1),∴c=﹣1,∴抛物线的解析式为y=x2﹣2x﹣1.由关联点定义,可知:点A,B关于直线y=x对称.又∵直线AB与x轴交于点D(1,0),∴直线AB 的解析式为y =﹣x +1.联立直线AB 及抛物线解析式成方程组,得:{y =﹣x +1y =x 2﹣2x ﹣1, 解得:{x 1=−1y 1=2 ,{x 2=−1y 2=2, ∴A ,B 两点坐标为(﹣1,2)和(2,﹣1).(3)由关联点定义,可知:点M ,N 关于直线y =x 对称,∴⊙T 的圆心在直线y =x 上.∵⊙T 的半径为3,∴M 1M 2=√22×2×3=3√2,∴m 的取值范围为1<m≤1+3√2. .3.已知:直线y=-x -4分别交x 、y 轴于A 、C 两点,点B 为线段AC 的中点,抛物线y=ax 2+bx 经过A 、B 两点,(1)求该抛物线的函数关系式;(2)以点B 关于x 轴的对称点D 为圆心,以OD 为半径作⊙D ,连结AD 、CD ,问在抛物线上是否存在点P ,使S △ACP =2S △ACD ?若存在,请求出所有满足条件的点P 的坐标;若不存在,请说明理由;(3)在(2)的条件下,若E 为⊙D 上一动点(不与A 、O 重合),连结AE 、OE ,问在x 轴上是否存在点Q ,使∠ACQ :∠AEO=2:3?若存在,请求出所有满足条件的点Q 的坐标;若不存在,请说明理由.【答案】(1)y=12x2+2x;(2)P坐标为(-3)或(-3+,7);(3)Q坐标为8,0)、(--8,0)、(4,0).【解析】解:(1)∵直线y=-x-4中,y=0时,x=-4;x=0时,y=-4,∴A(-4,0),C(0,-4),∵点B为AC中点,∴B(-2,-2),∵抛物线y=ax2+bx经过A、B两点,∴1640 422a ba b-=⎧⎨-=-⎩,解得:122ab⎧=⎪⎨⎪=⎩,∴抛物线的函数关系式为y=12x2+2x.(2)在抛物线上存在点P使S△ACP=2S△ACD.如图1,连接AD并延长交y轴于点F,∵y=12x2+2x=12(x-2)2-2,∴点B为抛物线的顶点,∵点D为点B关于x轴的对称点,∴D(-2,2)在抛物线的对称轴上,∴DA=DO,∠DAO=∠DOA=45°,∵OA=OC=4,∠AOC=90°,∴∠OAC=45°,∴∠DAC=∠DAO+∠OAC=90°,∴S △ACD =12AC•AD , ∵∠AOF=90°,∴AF 为⊙D 直径,即点F 在⊙D 上,∴AF=2AD ,OF=OA=4即F(0,4),∵S △ACP =2S △ACD =2•12AC•AD=12AC•2AD=12AC•AF , ∴点P 在过点F 且平行于直线y=-x -4的直线上,∴直线PF 解析式为y=-x+4, ∵24122y x y x x =-+⎧⎪⎨=+⎪⎩,解得:1137x y ⎧=--⎪⎨=+⎪⎩;2237x y ⎧=-+⎪⎨=-⎪⎩∴点P 坐标为(-3)或(-7;(3)在x 轴上存在点Q 使∠ACQ :∠AEO=2:3. ∵∠OAD=∠ODA=45°,∴∠ADO=90°,∵点E 在⊙D 上且不与A 、O 重合,∠ACQ :∠AEO=2:3. ①如图2,当点E 在优弧AO 上时,∠AEO=12∠ADO=45°, ∴∠ACQ=23∠AEO=30°,过点Q作QG垂直直线AC于点G,设QG=t,∴Rt△CQG中,CQ=2QG=2t,.∴∠GAQ=∠OAC=45°,∴Rt△AGQ中,AG=QG=t,t.i)若点Q在线段AO上时,如图2:则,解得:-,∴(4=,∴x Q=-8;ii)若点Q在线段OA延长上时,如图3:则AC=CG-t-t=4,解得:t=,∴(4=,∴x Q=-4--8,②当点E在劣弧AO上时,∠AEO=12(360°-∠ADO)=135°,∴∠ACQ=23∠AEO=90°.∵∠CAO=45°,△ACO是等腰直角三角形,∴Q点与A点对称,A (-4,0)∴x Q=4.综上所述:满足条件的点Q有三个,坐标分别为8,0)、(--8,0)、(4,0)4.已知抛物线y=x2+mx﹣2m﹣4(m>0).(1)证明:该抛物线与x轴总有两个不同的交点;(2)设该抛物线与x轴的两个交点分别为A,B(点A在点B的右侧),与y轴交于点C,A,B,C三点都在⊙P上.①试判断:不论m取任何正数,⊙P是否经过y轴上某个定点?若是,求出该定点的坐标;若不是,说明理由;②若点C关于直线x=−m的对称点为点E,点D(0,1),连接BE,BD,DE,△BDE的周长记为l,⊙P2的值.的半径记为r,求lr【答案】(1)证明见解析;(2)①定点F的坐标为(0,1);②10+6√5.5【解析】(1)令y=0,则x2+mx﹣2m﹣4=0,∴△=m2﹣4[﹣2m﹣4]=m2+8m+16,∵m>0,∴△>0,∴该抛物线与x轴总有两个不同的交点;(2)令y=0,则x2+mx﹣2m﹣4=0,∴(x﹣2)[x+(m+2)]=0,∴x=2或x=﹣(m+2),∴A(2,0),B(﹣(m+2),0),∴OA=2,OB=m+2,令x=0,则y=﹣2(m+2),∴C(0,﹣2(m+2)),∴OC=2(m+2),①通过定点(0,1)理由:如图,∵点A,B,C在⊙P上,∴∠OCB=∠OAF,在Rt△BOC中,tan∠OCB=OBOC =m+22(m+2)=12,在Rt△AOF中,tan∠OAF=OFOA =OF2=12,∴OF=1,∴点F的坐标为(0,1);②如图1,由①知,点F(0,1).∵D(0,1),∴点D在⊙P上,∵点E是点C关于抛物线的对称轴的对称点,∴∠DCE=90°,∴DE是⊙P的直径,∴∠DBE=90°,∵∠BED =∠OCB ,∴tan ∠BED =12, 设BD =n ,在Rt △BDE 中,tan ∠BED =BD BE =n BE =12, ∴BE =2n ,根据勾股定理得:DE =√BD 2+BE 2=√5n ,∴l =BD+BE+DE =(3+√5)n ,r =12DE =√52n , ∴l r =√5)√52n =10+6√55. 5..如图①,已知抛物线2139424y x x =-+的顶点为点P ,与y 轴交于点B .点A 坐标为(3,2).点M 为抛物线上一动点,以点M 为圆心,MA 为半径的圆交x 轴于C ,D 两点(点C 在点D 的左侧).(1)如图②,当点M 与点B 重合时,求CD 的长;(2)当点M 在抛物线上运动时,CD 的长度是否发生变化?若变化,求出CD 关于点M 横坐标x 的函数关系式;若不发生变化,求出CD 的长;(3)当△ACP 与△ADP 相似时,求出点C 的坐标.【答案】(1) CD=4;(2)不发生变化,CD=4;(3)点C 坐标为:(1,0),()1-,()1+ 【解析】(1)如图:连结BC ,BD ,由题意得:904B ⎛⎫ ⎪⎝⎭,,(3,2),∴AB =∴2OC ==,∴CD=2OC=4;(2)如图:作MH ⊥x 轴,连结MA ,MC ,设()M x y ,,则半径AM =∴CH ====2=, ∵MH ⊥CD ,∴CD=2CH=4,(3)①当△APC ∽△APD ,即全等时,∴PC=PD ,P 与M 重合,∵P (3,0),CD=4,∴C (1,0)②如图,点M 在点P 的左侧,△APC ∽△DPA ,2PA PD PC =⨯,设PC=x ,x (x -4)=4,解得2x =±,∴()1C -, ③如图,点M 在点P 的右侧△APC ∽△DPA ,2PA PD PC =⨯,设PC=x ,x (x+4)=4,解得2x =-±,∴()C ,综上所述,点C 坐标为:C (1,0);()1C -;()C ; 6.已知抛物线 C 1:y =ax 2 过点(2,2)(1)直接写出抛物线的解析式;(2)如图,△ABC 的三个顶点都在抛物线C 1 上,且边 AC 所在的直线解析式为y =x +b ,若 AC 边上的中线 BD 平行于 y 轴,求AC 2BD 的值;(3)如图,点 P 的坐标为(0,2),点 Q 为抛物线上C 1 上一动点,以 PQ 为直径作⊙M ,直线 y =t 与⊙M 相交于 H 、K 两点是否存在实数 t ,使得 HK 的长度为定值?若存在,求出 HK 的长度;若不存在,请说明理由.【答案】(1)y=12x 2 ;(2)16;(3)见解析.【解析】(1)把点(2,2)坐标代入y =ax2,解得:a =12,∴抛物线的解析式为y =x2;(2)把y =x+b 和y =12x2得:x2﹣2x ﹣2b =0,设A 、C 两点的坐标为(x1,y1)、(x2,y2),则:x1+x2=2,x1•x2=﹣2b ,点D 坐标为(x 1+x 22,y 1+y 22),即D (1,﹣b ),B 坐标为(1,12), AC2=[√2(x2﹣x1)]2=16b+8,BD =12+b , ∴AC 2BD =16;(3)设点Q 坐标为(a ,12a2),点P 的坐标为(0,2),由 P 、Q 坐标得点M 的坐标为(a 2,14a2+1), 设圆的半径为 r ,由P (0,2)、M 两点坐标可得r2=a 24+(14a2﹣1)2=116a4﹣14a2+1,设点M 到直线y =t 的距离为d ,则d2=(a2+1﹣t )=116a4+12a2+1+t2﹣2t ﹣12a2t ,则 HK =2√r 2−d 2=2√(12t −34)a 2+2t −t 2,当12t −34=0 时,HK 为常数,t =32, HK =√3.7.(浙江省湖州市南浔区2017-2018学年九年级上学期期末)已知在平面直角坐标系xOy 中,O 是坐标原点,如图1,直角三角板△MON 中,OM=ON=√3,OQ=1,直线l 过点N 和点N ,抛物线y=ax 2+2√33x+c 过点Q 和点N .(1)求出该抛物线的解析式;(2)已知点P 是抛物线y=ax 2+2√33x+c 上的一个动点.①初步尝试若点P 在y 轴右侧的该抛物线上,如图2,过点P 作PA ⊥y 轴于点A ,问:是否存在点P ,使得以N 、P 、A 为顶点的三角形与△ONQ 相似.若存在,求出点P 的坐标,若不存在,请说明理由;②深入探究若点P 在第一象限的该抛物线上,如图3,连结PQ ,与直线MN 交于点G ,以QG 为直径的圆交QN 于点H ,交x 轴于点R ,连结HR ,求线段HR 的最小值.【答案】(1)y=﹣√33x2+2√33x+√3(2)①(1,4√33)、(3,0)、(5,﹣4√3)②3√2+64【解析】 (1)由题意可知,Q (﹣1,0),N (0,√3),∴c=√3,即y=ax2+2√33x+√3, 将Q (﹣1,0)代入解析式得0=a ﹣2√33+√3,解得a=﹣√33, ∴抛物线解析式是y=﹣√33x2+2√33x+√3; (2)①分三种情况,如图2,情况一:点P 在第一象限时,△APN ∽△ONQ ,设AN=m ,则AP=√3m ,则P 的坐标(√3m ,m+√3),而点P 在抛物线上,代入可得m+√3=﹣√33(√3m )2++2√33(√3m )+√3, 解得m=√33,∴P1(1,4√33); 情况二:点P 恰好在x 轴上,P2(3,0),情况三:P 在第四象限内,同情况一方法可解得P3(5,﹣4√3),②连结CH 和CR ,如图3,∵∠NQ0=60°,∴∠HCR=120°,∵CH=CR ,∴HR=√3CH ,∴HR 最小时,只需要半径最小,即直径最小即可,∴过Q作NM的垂线,垂直时,QG最小,∴用面积法求出,QG=√6+√22,HR最小值=3√2+64.8.如图,在平面直角坐标系中,O为原点,A点坐标为(−8, 0),B点坐标为(2, 0),以AB为直径的圆P与y轴的负半轴交于点C.(1)求图象经过A,B,C三点的抛物线的解析式;(2)设M点为所求抛物线的顶点,试判断直线MC与⊙P的关系,并说明理由.【答案】(1)14x2+32x−4;(2)直线MC与⊙P相切,理由见解析【解析】解:(1)连接AC、BC;∵AB是⊙P的直径,∴∠ACB=90°,即∠ACO+∠BCO=90°,∵∠BCO+∠CBO=90°,∴∠CBO=∠ACO,∵∠AOC=∠BOC=90°,∴△AOC∽△COB,∴AOOC =OC OB,∴OC2=OA·OB=16,∴OC=4,故C(0,﹣4),设抛物线的解析式为:y=a(x+8)(x ﹣2),代入C 点坐标得:a(0+8)(0﹣2)=﹣4,a=14,故抛物线的解析式为:y=14(x+8)(x ﹣2)=14x 2+32x ﹣4;(2)由(1)知:y=14x 2+32x ﹣4=14(x +3)2﹣254;则M(﹣3,﹣254), 又∵C(0, ﹣4),P(﹣3, 0),∴MP=254,PC=5,MC=154,∴MP 2=MC 2+PC 2,即△MPC 是直角三角形,且∠PCM=90°,故直线MC 与⊙P 相切.9.已知抛物线y=ax 2+bx 过点A (1,4)、B (﹣3,0),过点A 作直线AC ∥x 轴,交抛物线于另一点C ,在x 轴上有一点D (4,0),连接CD .(1)求抛物线的表达式;(2)若在抛物线上存在点Q ,使得CD 平分∠ACQ ,请求出点Q 的坐标;(3)在直线CD 的下方的抛物线上取一点N ,过点N 作NG ∥y 轴交CD 于点G ,以NG 为直径画圆在直线CD 上截得弦GH ,问弦GH 的最大值是多少?(4)一动点P 从C 点出发,以每秒1个单位长度的速度沿C ﹣A ﹣D 运动,在线段CD 上还有一动点M ,问是否存在某一时刻使PM+AM=4?若存在,请直接写出t 的值;若不存在,请说明理由.【答案】(1)直线CE 的表达式为y=﹣43x ﹣43;(2)点Q 的坐标为(﹣13,﹣89);(3)弦GH 的最大值81√580;(4)存在,t 的值为3或7【解析】解:(1)∵抛物线y=a x 2+bx 过点A (1,4)、B (﹣3,0),∴{a +b =49a −3b =0,解得:a=1,b=3, ∴抛物线的表达式为y=x 2+3x .(2)当y=4时,有x 2+3x=4,解得:x 1=﹣4,x 2=1,∴点C 的坐标为(﹣4,4),∴AC=1﹣(﹣4)=5.∵A (1,4),D (4,0),∴AD=5.取点E (﹣1,0),连接CE 交抛物线于点Q ,如图1所示.∵AC=5,DE=4﹣(﹣1)=5,AC ∥DE ,∴四边形ACED 为平行四边形,∵AC=AD ,∴四边形ACED 为菱形,∴CD 平分∠ACQ .设直线CE 的表达式为y=mx+n (m≠0),将C (﹣4,4)、E (﹣1,0)代入y=mx+n ,得:{−4m +n =4−m +n =0 ,解得:{m =−43n =−43, ∴直线CE 的表达式为y=﹣43x ﹣43.联立直线CE 与抛物线表达式成方程组,得:{y =−43x −43y =x 2+3x, 解得:{x 1=−4y 1=4 ,{x 2=−13y 2=−89 , ∴点Q 的坐标为(﹣13,﹣89).(3)设直线CD 的表达式为y=kx+c (k≠0),将C (﹣4,4)、D (4,0)代入y=kx+c ,得:{−4k +c =44k +c =0 ,解得:{k =−12c =2 , ∴直线CD 的表达式为y=﹣12x+2.设点N 的坐标为(x ,x2+3x ),则点G 的坐标为(x ,﹣12x+2),∴NG=﹣12x+2﹣(x2+3x )=﹣x2﹣72x+2=﹣(x+74)2+8116,∵﹣1<0,∴当x=﹣74时,NG 取最大值,最大值为8116. 以NG 为直径画⊙O′,取GH 的中点F ,连接O′F ,则O′F ⊥BC ,如图2所示.∵直线CD 的表达式为y=﹣12x+2,NG ∥y 轴,O′F ⊥BC , ∴tan ∠GO′F=GF O′F =12, ∴GF O′G =√12+22=√55, ∴GH=2GF=2√55 O′G=√55NG ,∴弦GH 的最大值为√55×8116=81√580.(4)取点E(﹣1,0),连接CE、AE,过点E作EP1⊥AC于点P1,交CD于点M1,过点E作EP2⊥AD 于点P2,交CD于点M2,如图3所示.∵四边形ACED为菱形,∴点A、E关于CD对称,∴AM=EM.∵AC∥x轴,点A的坐标为(1,4),∴EP1=4.由菱形的对称性可知EP2=4.∵点E的坐标为(﹣1,0),∴点P1的坐标为(﹣1,4),∴CP1=DP2=﹣1﹣(﹣4)=3,又∵AC=AD=5,∴t的值为3或7.10.如图,在平面直角坐标系中,点A(10, 0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB 并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.(1)∠OBA=________°.(2)求抛物线的函数表达式.(3)若P为抛物线上位于第一象限内的一个动点,以P、O、A、E为顶点的四边形面积记作S,则S取何值时,相应的点P有且只有3个?【答案】(1)90;(2)y=−18x2+54x;(3) 以P、O、A、E为顶点的四边形面积S等于16时,相应的点P有且只有3个.【解析】解:(1)90;(2)连接OC,如图1所示,∵由(1)知OB⊥AC,又AB=BC,∴OB是AC的垂直平分线,∴OC=OA=10,在Rt△OCD中,OC=10,CD=8,∴OD=6,∴C(6, 8),B(8, 4)∴OB所在直线的函数关系为y=12x,又∵E点的横坐标为6,∴E点纵坐标为3,即E(6, 3),抛物线过O(0, 0),E(6, 3),A(10, 0),∴设此抛物线的函数关系式为y=ax(x−10),把E点坐标代入得:3=6a(6−10),解得a=−18.∴此抛物线的函数关系式为y=−18x(x−10),即y=−18x2+54x;(3)设点P(p, −18p2+54p),①若点P在CD的左侧,延长OP交CD于Q,如右图2,OP 所在直线函数关系式为:y =(−18p +54)x∴当x =6时,y =−34p +152,即Q 点纵坐标为−34p +152, ∴QE =−34p +152−3=−34p +92,S 四边形POAE =S △OAE +S △OPE =S △OAE +S △OQE −S △PQE =12⋅OA ⋅DE +12QE ⋅OD −12⋅QE ⋅P x •=12×10×3+12×(−34p +92)×6−12•(−34p +92)⋅(6−p ), =−38p 2+94p +15, ②若点P 在CD 的右侧,延长AP 交CD 于Q ,如右图3,P(p, −18p 2+54p),A(10, 0) ∴设AP 所在直线方程为:y =kx +b ,把P 和A 坐标代入得,{10k +b =0pk +b =−18p 2+54p, 解得{k =−18p b =54p. ∴AP 所在直线方程为:y =−18px +54p ,∴当x =6时,y =−18p ⋅6+54p =12P ,即Q 点纵坐标为12P ,∴QE =12P −3,∴S 四边形POAE=S △OAE +S △APE =S △OAE +S △AQE −S △PQE =12⋅OA ⋅DE +12⋅QE ⋅DA −12⋅QE •(P x −6)=12×10×3+12⋅QE •(DA −P x +6)=15+12•(12p −3)⋅(10−p) =−14p 2+4p =−14(p −8)2+16,∴当P 在CD 右侧时,四边形POAE 的面积最大值为16,此时点P 的位置就一个,令−38p 2+94p +15=16,解得,p =3±√573, ∴当P 在CD 左侧时,四边形POAE 的面积等于16的对应P 的位置有两个,综上所知,以P 、O 、A 、E 为顶点的四边形面积S 等于16时,相应的点P 有且只有3个.类型二 与圆有关的位置关系例2.如图1,二次函数y =ax 2﹣2ax ﹣3a (a <0)的图象与x 轴交于A 、B 两点(点A 在点B 的右侧),与y 轴的正半轴交于点C ,顶点为D .(1)求顶点D 的坐标(用含a 的代数式表示);(2)若以AD 为直径的圆经过点C .①求抛物线的函数关系式;②如图2,点E 是y 轴负半轴上一点,连接BE ,将△OBE 绕平面内某一点旋转180°,得到△PMN (点P 、M 、N 分别和点O 、B 、E 对应),并且点M 、N 都在抛物线上,作MF ⊥x 轴于点F ,若线段MF :BF =1:2,求点M 、N 的坐标;③点Q 在抛物线的对称轴上,以Q 为圆心的圆过A 、B 两点,并且和直线CD 相切,如图3,求点Q 的坐标.【答案】(1)(1,﹣4a );(2)①y=﹣x 2+2x+3;②M (52,74)、N (32,154);③点Q 的坐标为(1,﹣)或(1,﹣4﹣).【思路引导】 (1)将二次函数的解析式进行配方即可得到顶点D 的坐标.(2)①以AD为直径的圆经过点C,即点C在以AD为直径的圆的圆周上,依据圆周角定理不难得出△ACD 是个直角三角形,且∠ACD=90°,A点坐标可得,而C、D的坐标可由a表达出来,在得出AC、CD、AD 的长度表达式后,依据勾股定理列等式即可求出a的值.②将△OBE绕平面内某一点旋转180°得到△PMN,说明了PM正好和x轴平行,且PM=OB=1,所以求M、N的坐标关键是求出点M的坐标;首先根据①的函数解析式设出M点的坐标,然后根据题干条件:BF=2MF作为等量关系进行解答即可.③设⊙Q与直线CD的切点为G,连接QG,由C、D两点的坐标不难判断出∠CDQ=45°,那么△QGD为等腰直角三角形,即QD ²=2QG ²=2QB ²,设出点Q的坐标,然后用Q点纵坐标表达出QD、QB的长,根据上面的等式列方程即可求出点Q的坐标.【解析】(1)∵y=ax2﹣2ax﹣3a=a(x﹣1)2﹣4a,∴D(1,﹣4a).(2)①∵以AD为直径的圆经过点C,∴△ACD为直角三角形,且∠ACD=90°;由y=ax2﹣2ax﹣3a=a(x﹣3)(x+1)知,A(3,0)、B(﹣1,0)、C(0,﹣3a),则:AC2=9a2+9、CD2=a2+1、AD2=16a2+4由勾股定理得:AC2+CD2=AD2,即:9a2+9+a2+1=16a2+4,化简,得:a2=1,由a<0,得:a=﹣1,②∵a=﹣1,∴抛物线的解析式:y=﹣x2+2x+3,D(1,4).∵将△OBE绕平面内某一点旋转180°得到△PMN,∴PM∥x轴,且PM=OB=1;设M(x,﹣x2+2x+3),则OF=x,MF=﹣x2+2x+3,BF=OF+OB=x+1;∵BF=2MF,∴x+1=2(﹣x2+2x+3),化简,得:2x2﹣3x﹣5=0解得:x1=﹣1(舍去)、x2=5 2 .∴M(52,74)、N(32,154).③设⊙Q与直线CD的切点为G,连接QG,过C作CH⊥QD于H,如下图:∵C (0,3)、D (1,4),∴CH =DH =1,即△CHD 是等腰直角三角形,∴△QGD 也是等腰直角三角形,即:QD 2=2QG 2;设Q (1,b ),则QD =4﹣b ,QG 2=QB 2=b 2+4;得:(4﹣b )2=2(b 2+4),化简,得:b 2+8b ﹣8=0,解得:b =﹣;即点Q 的坐标为(1,4-+)或(1,4--.【方法总结】此题主要考查了二次函数解析式的确定、旋转图形的性质、圆周角定理以及直线和圆的位置关系等重要知识点;后两个小题较难,最后一题中,通过构建等腰直角三角形找出QD 和⊙Q 半径间的数量关系是解题题目的关键.针对训练1.抛物线y =﹣23x 2+73x ﹣1与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,其顶点为D .将抛物线位于直线l :y =t (t <2524)上方的部分沿直线l 向下翻折,抛物线剩余部分与翻折后所得图形组成一个“M ”形的新图象.(1)点A ,B ,D 的坐标分别为 , , ;(2)如图①,抛物线翻折后,点D 落在点E 处.当点E 在△ABC 内(含边界)时,求t 的取值范围;(3)如图②,当t =0时,若Q 是“M ”形新图象上一动点,是否存在以CQ 为直径的圆与x 轴相切于点P ?若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)A (12,0);B (3,0);D (74,2524);(2)1548≤t≤2548;(3)存在以CQ 为直径的圆与x 轴相切于点P ,点P的坐标为(75-0)、(311,0)、(1,0)或(75+,0). 【解析】解:(1)当y=0时,﹣23x 2+73x ﹣1=0, 解得x 1=12,x 2=3, ∴点A 的坐标为(12,0),点B 的坐标为(3,0), ∵y=﹣23x 2+73x ﹣1=﹣23(x -74)2+2524, ∴点D 的坐标为(74,2524); (2)∵点E 、点D 关于直线y=t 对称,∴点E 的坐标为(74,2t ﹣2524). 当x=0时,y=﹣23x 2+73x ﹣1=﹣1, ∴点C 的坐标为(0,﹣1).设线段BC 所在直线的解析式为y=kx+b ,将B (3,0)、C (0,﹣1)代入y=kx+b ,301k b b +=⎧⎨=-⎩,解得:131k b ⎧=⎪⎨⎪=-⎩, ∴线段BC 所在直线的解析式为y=13x ﹣1. ∵点E 在△ABC 内(含边界),∴2520242517212434tt⎧-≤⎪⎪⎨⎪-≥⨯-⎪⎩,解得:1548≤t≤2548.(3)当x<12或x>3时,y=﹣23x2+73x﹣1;当12≤x≤3时,y=﹣23x2+73x﹣1.假设存在,设点P的坐标为(12m,0),则点Q的横坐标为m.①当m<12或m>3时,点Q的坐标为(m,﹣23x2+73x﹣1)(如图1),∵以CQ为直径的圆与x轴相切于点P,∴CP⊥PQ,∴CQ2=CP2+PQ2,即m2+(﹣23m2+73m)2=14m2+1+14m2+(﹣23m2+73m﹣1)2,整理,得:m1,m2,∴点P 0,0); ②当12≤m≤3时,点Q 的坐标为(m,23x 2-73x +1)(如图2), ∵以CQ 为直径的圆与x 轴相切于点P , ∴CP ⊥PQ ,∴CQ 2=CP 2+PQ 2,即m 2+(23m 2﹣73m+2)2=14m 2+1+14m 2+(23m 2﹣73m+1)2, 整理,得:11m 2﹣28m+12=0,解得:m 3=611,m 4=2, ∴点P 的坐标为(311,0)或(1,0).综上所述:存在以CQ 为直径的圆与x 轴相切于点P ,点P 0)、(311,0)、(1,0)或(75+,0). 2.如图1,抛物线y =ax 2+bx+c 的顶点(0,5),且过点(﹣3,114),先求抛物线的解析式,再解决下列问题:(应用)问题1,如图2,线段AB =d (定值),将其弯折成互相垂直的两段AC 、CB 后,设A 、B 两点的距离为x ,由A 、B 、C 三点组成图形面积为S ,且S 与x 的函数关系如图所示(抛物线y =ax 2+bx+c 上MN 之间的部分,M 在x 轴上):(1)填空:线段AB 的长度d = ;弯折后A 、B 两点的距离x 的取值范围是 ;若S =3,则是否存在点C ,将AB 分成两段(填“能”或“不能”) ;若面积S =1.5时,点C 将线段AB 分成两段的长分别是 ;(2)填空:在如图1中,以原点O 为圆心,A 、B 两点的距离x 为半径的⊙O ;画出点C 分AB 所得两段AC 与CB 的函数图象(线段);设圆心O 到该函数图象的距离为h ,则h = ,该函数图象与⊙O 的位置关系是 .(提升)问题2,一个直角三角形斜边长为c (定值),设其面积为S ,周长为x ,证明S 是x 的二次函数,求该函数关系式,并求x 的取值范围和相应S 的取值范围.【答案】抛物线的解析式为:y =﹣14x 2+5;(1)<x <;(2,相离或相切或相交;(3)相应S 的取值范围为S >14c 2.【解析】解:∵抛物线y =ax 2+bx+c 的顶点(0,5), ∴y =ax 2+5, 将点(﹣3,114)代入, 得114=a×(﹣3)2+5, ∴a =14﹣ , ∴抛物线的解析式为:y =2154x +﹣ ;(1)∵S 与x 的函数关系如图所示(抛物线y =ax 2+bx+c 上MN 之间的部分,M 在x 轴上),在y =2154x +﹣,当y =0时,x 1=x 2=﹣∴M (0),即当x =S =0,∴d 的值为∴弯折后A 、B 两点的距离x 的取值范围是0<x <当S =3 时,设AC =a ,则BC =a ,∴12a (a )=3,整理,得a 2﹣=0, ∵△=b 2﹣4ac =﹣4<0, ∴方程无实数根;当S =1.5时,设AC =a ,则BC =a ,∴12a (a )=1.5,整理,得a 2﹣=0,解得1a 2a∴当a +a当a a +∴若面积S =1.5时,点C 将线段AB +故答案为:0<x <+(2)设AC =y ,CB =x ,则y =﹣1所示的线段PM ,则P (0,,M (0), ∴△OPM 为等腰直角三角形,∴PM OP =, 过点O 作OH ⊥PM 于点H ,则OH =12PM ,∴当0<x 时,AC 与CB 的函数图象(线段PM )与⊙O 相离;当x 时,AC 与CB 的函数图象(线段PM )与⊙O 相切;<x <AC 与CB 的函数图象(线段PM )与⊙O 相交;,相离或相切或相交; (3)设直角三角形的两直角边长分别为a ,b , 则222-a b c a b x c ++=,= , ∵(a+b )2=a 2+b 2+2ab , ∴(x ﹣c )2=c 2+2ab ,∴2111242ab x cx =-, 即S =()22211114244x cx x c c -=-+,∴x 的取值范围为:x >c , 则相应S 的取值范围为S >214c .3.如图,已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点,与y 轴交于C 点,直线BD 交抛物线于点D ,并且()D 2,3,()B 4,0-. (1)求抛物线的解析式;(2)已知点M 为抛物线上一动点,且在第三象限,顺次连接点B 、M 、C ,求BMC 面积的最大值; (3)在(2)中BMC 面积最大的条件下,过点M 作直线平行于y 轴,在这条直线上是否存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆?若存在,求出圆心Q 的坐标;若不存在,请说明理由.【答案】(1)213y x x 222=+-;(2)4;(3)存在,Q 的坐标为()2,4-或()2,1-- 【解析】解:()1将()D 2,3、()B 4,0-的坐标代入抛物线表达式得:422316420a b a b +-=⎧⎨--=⎩,解得:1232a b ⎧=⎪⎪⎨⎪=⎪⎩, 则抛物线的解析式为:213y x x 222=+-; ()2过点M 作y 轴的平行线,交直线BC 于点K ,将点B 、C 的坐标代入一次函数表达式:y k'x b'=+得:04'''2k b b =-+⎧⎨=-⎩,解得:1'2'2k b ⎧=-⎪⎨⎪=-⎩,则直线BC 的表达式为:1y x 22=--, 设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭, 22BMC1113SMK OB 2x 2x x 2x 4x 2222⎛⎫=⋅⋅=----+=-- ⎪⎝⎭, a 10=-<,BMC S∴有最大值,当bx 22a=-=-时, BMCS最大值为4,点M 的坐标为()2,3--;()3如图所示,存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆,切点为N ,过点M 作直线平行于y 轴,交直线AC 于点H ,点M 坐标为()2,3--,设:点Q 坐标为()2,m -, 点A 、C 的坐标为()1,0、()0,2-,OA 1tan OCA OC 2∠==, QH //y 轴,QHN OCA ∠∠∴=,1tan QHN2∠∴=,则sin QHN ∠=,将点A 、C 的坐标代入一次函数表达式:y mx n =+得:02m n n +=⎧⎨=-⎩,则直线AC 的表达式为:y 2x 2=-, 则点()H 2,6--,在Rt QNH 中,QH m 6=+,QN OQ ===QN sin QHNQHm 6∠===+, 解得:m 4=或1-,即点Q 的坐标为()2,4-或()2,1--.4.如图1,对于平面内的点P 和两条曲线L 1、L 2给出如下定义:若从点P 任意引出一条射线分别与L 1、L 2交于Q 1、Q 2,总有PQ 1PQ 2是定值,我们称曲线L 1与L 2“曲似”,定值PQ1PQ 2为“曲似比”,点P 为“曲心”.例如:如图2,以点O ′为圆心,半径分别为r 1、r 2(都是常数)的两个同心圆C 1、C 2,从点O ′任意引出一条射线分别与两圆交于点M 、N ,因为总有O ′MO ′N =r 1r 是定值,所以同心圆C 1与C 2曲似,曲似比为r1r 2,“曲心”为O ′.(1)在平面直角坐标系xOy中,直线y=kx与抛物线y=x2、y=12x2分别交于点A、B,如图3所示,试判断两抛物线是否曲似,并说明理由;(2)在(1)的条件下,以O为圆心,OA为半径作圆,过点B作x轴的垂线,垂足为C,是否存在k值,使⊙O 与直线BC相切?若存在,求出k的值;若不存在,说明理由;(3)在(1)、(2)的条件下,若将“y=12x2”改为“y=1mx2”,其他条件不变,当存在⊙O与直线BC相切时,直接写出m的取值范围及k与m之间的关系式.【答案】(1)两抛物线曲似,理由详见解析;(2)存在k值,使⊙O与直线BC相切,k=±√3;(3)m>1,k2=m2−1.【解析】(1)是,过点A、B作x轴的垂线,垂足分别为D、C,依题意可得A(k,k2)、B(2k,2k2),因此D(k,0)、C(2k,0),∵AD ⊥x 轴、BC ⊥x 轴, ∴AD//BC , ∴OA OB=OD OC=k 2k=12,∴两抛物线曲似,曲似比为12;(2)假设存在k 值,使⊙O 与直线BC 相切, 则OA =OC =2k ,又∵OD =k 、AD =k 2,并且OD 2+AD 2=OA 2, ∴k 2+(k 2)2=(2k)2, 解得:k =√3(负值舍去), 由对称性可取k =−√3, 综上,k =±√3;(3)根据题意得A(k,k 2)、B(mk,mk 2), 因此D(k,0)、C(mk,0), ∵⊙O 与直线BC 相切, ∴OA =OC =mk , 由OA >OD 可得mk >k , 则m >1,由OD =k 、AD =k 2,并且OD 2+AD 2=OA 2, ∴k 2+(k 2)2=(mk)2, 整理,得:k 2=m 2−1.5.已知二次函数图象的顶点在原点O ,对称轴为y 轴.一次函数1y kx =+的图象与二次函数的图象交于A B ,两点(A 在B 的左侧),且A 点坐标为()44-,.平行于x 轴的直线l 过()01-,点.(1)求一次函数与二次函数的解析式;(2)判断以线段AB 为直径的圆与直线l 的位置关系,并给出证明;(3)把二次函数的图象向右平移 2 个单位,再向下平移 t 个单位(t >0),二次函数的图象与x 轴交于 M ,N 两点,一次函数图象交y 轴于 F 点.当 t 为何值时,过 F ,M ,N 三点的圆的面积最小?最小面积是多少?【答案】(1)一次函数的解析式为314y x =-+;二次函数解析式为214y x =. (2)相切,证明见解析(3)当3t =时,过F M N ,,三点的圆面积最小,最小面积为4π. 【解析】()1把()4,4A -代入1y kx =+得34k =-∴一次函数的解析式为314y x =-+ ∴二次函数图象的顶点在原点,对称轴为y 轴,∴二次函数的解析式为2y ax =,将()4,4A -代入解析式得14a =-∴二次函数的解析式为214y x =-()2由231414y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得44x y =-⎧⎨=⎩或114x y =⎧⎪⎨=⎪⎩,11,4B ⎛⎫∴ ⎪⎝⎭,取,A B 的中点317,28P ⎛⎫- ⎪⎝⎭, 过P 作直线l 的垂线,垂足为N ,则3,12N ⎛⎫-- ⎪⎝⎭1725188PN ∴=+=,而直径254AB ∴==12PN AB ∴=,即圓心到直线l 的距离等于半径, 以AB 为直径的圆与直线l 相切.()3平移后二次函数的解析式为()2124y x t =--,令0,y =得()212120,224x t x x --==-=过,,F M N 三点的國的圆心C 一定在平移后抛物线的对称轴.上,要使圓面积最小,圆半径应等于点F 到直线2x =2的距离,点C 坐标为()2,1. 此时,半径为2,面积为4π设圆心为,C MN 的中点为E ,连接,CE CM ,则1CE =,在三角形CEM 中,ME =MN ∴=2134MN x x t =-=∴= ∴当3t 4=时,过,,F M N 三点的圓面积最小,最小面积为4π. 6.如图,在平面角坐标系中,抛物线C 1:y=ax 2+bx ﹣1经过点A (﹣2,1)和点B (﹣1,﹣1),抛物线C 2:y=2x 2+x+1,动直线x=t 与抛物线C 1交于点N ,与抛物线C 2交于点M . (1)求抛物线C 1的表达式;(2)直接用含t 的代数式表示线段MN 的长;(3)当△AMN 是以MN 为直角边的等腰直角三角形时,求t 的值;(4)在(3)的条件下,设抛物线C 1与y 轴交于点P ,点M 在y 轴右侧的抛物线C 2上,连接AM 交y 轴于点k ,连接KN ,在平面内有一点Q ,连接KQ 和QN ,当KQ=1且∠KNQ=∠BNP 时,请直接写出点Q 的坐标.【答案】(1)抛物线C1:解析式为y=x 2+x ﹣1;(2)MN=t 2+2;(3)t 的值为1或0;(4)满足条件的Q 点坐标为:(0,2)、(﹣1,3)、(35,195)、(45,125)【解析】(1)∵抛物线C1:y=ax 2+bx ﹣1经过点A (﹣2,1)和点B (﹣1,﹣1),∴{1=4a −2b −1−1=a −b −1,解得:{a =1b =1 , ∴抛物线C1:解析式为y=x 2+x ﹣1;(2)∵动直线x=t 与抛物线C1交于点N ,与抛物线C2交于点M ,∴点N 的纵坐标为t 2+t ﹣1,点M 的纵坐标为2t 2+t+1,∴MN=(2t 2+t+1)﹣(t 2+t ﹣1)=t 2+2;(3)共分两种情况①当∠ANM=90°,AN=MN 时,由已知N (t ,t 2+t ﹣1),A (﹣2,1),∴AN=t ﹣(﹣2)=t+2,∵MN=t 2+2,∴t 2+2=t+2,∴t1=0(舍去),t2=1,∴t=1;②当∠AMN=90°,AN=MN 时,由已知M (t ,2t 2+t+1),A (﹣2,1),∴AM=t ﹣(﹣2)=t+2,∵MN=t 2+2,∴t 2+2=t+2,∴t 1=0,t 2=1(舍去),∴t=0,故t 的值为1或0;(4)由(3)可知t=1时M 位于y 轴右侧,根据题意画出示意图如图:易得K (0,3),B 、O 、N 三点共线,∵A (﹣2,1),N (1,1),P (0,﹣1),∴点K 、P 关于直线AN 对称,设⊙K 与y 轴下方交点为Q2,则其坐标为(0,2),∴Q2与点O 关于直线AN 对称,∴Q2是满足条件∠KNQ=∠BNP ,则NQ2延长线与⊙K 交点Q1,Q1、Q2关于KN 的对称点Q3、Q4也满足∠KNQ=∠BNP ,由图形易得Q1(﹣1,3),设点Q3坐标为(a ,b ),由对称性可知Q3N=NQ1=BN=2√2,由∵⊙K 半径为1,∴{(a −1)2+(b −1)2=(2√2)2a 2+(b −3)2=12,解得:{a 1=35b 1=195 ,{a 2=−1b 2=3 , 同理,设点Q4坐标为(a ,b ),由对称性可知Q4N=NQ2=NO=√2,∴{(a −1)2+(b −1)2=(√2)2a 2+(b −3)2=12 ,解得:{a 3=45b 3=125 ,{a 4=0b 4=2 , ∴满足条件的Q 点坐标为:(0,2)、(﹣1,3)、(35,195)、(45,125).7.如图,直线2y x =+与抛物线222y x mx m m =-++交于A 、B 两点(A 在B 的左侧),与y 轴交于点C ,抛物线的顶点为D ,抛物线的对称轴与直线AB 交于点M .(1)当四边形CODM 是菱形时,求点D 的坐标;(2)若点P 为直线OD 上一动点,求APB ∆的面积;(3)作点B 关于直线MD 的对称点B ',以点M 为圆心,MD 为半径作M ,点Q 是M上一动点,求2QB '+的最小值. 【答案】(1);(2)3;(3【解析】(1) (,)D m m,OD =, 菱形CODM2OD OC ∴===m ∴= (2)①2y x =+与抛物线222y x mx m m =-++交于,A B 两点,∴联立,222y x mx m m =-++,2y x =+解得1111x m y m =-⎧⎨=+⎩,2224x m y m =+⎧⎨=+⎩ ∵点A 在点B 的左侧(1,1)A m m ∴-+,(2,4)B m m ++AB ∴==∴直线OD 的解析式为y x =,直线AB 的解析式为2y x =+//AB OD ∴,两直线,AB OD 之间距离22h =⨯=11322APBS AB h ∴=⋅=⨯=(3) (1,1)A m m -+,(2,4)B m m ++1AM ∴==2BM ==由M 点坐标(,2)m m +,D 点坐标(,)m m 可知以MD 为半径的圆的半径为(2)2m m +-=取MB 的中点N ,连接,,QB QN QB ',则12MN BM ==⨯=MN QMMN QM QM BM ==QMN BMQ ∠=∠, ~MNQ MQB ∴,2QN MN OB OM ∴==,QN ∴=由三角形三边关系,当,,Q N B '三点共线时QB '+最小, ∵直线AB 的解析式为2y x =+,∴直线AB 与对称轴夹角为45°,∵点,B B '关于对称轴对称, 90BMB '︒∴∠=,由勾股定理得,2QB '+最小值===.8.如图,已知以E(3,0)为圆心,5为半径的☉E 与x 轴交于A ,B 两点,与y 轴交于C 点,抛物线y=ax 2+bx+c(a≠0)经过A ,B ,C 三点,顶点为F.(1)求A ,B ,C 三点的坐标;(2)求抛物线的解析式及顶点F 的坐标;(3)已知M 为抛物线上的一动点(不与C 点重合),试探究:①若以A ,B ,M 为顶点的三角形面积与△ABC 的面积相等,求所有符合条件的点M 的坐标;②若探究①中的M 点位于第四象限,连接M 点与抛物线顶点F ,试判断直线MF 与☉E 的位置关系,并说明理由.【答案】(1)A(-2,0),B(8,0),C(0,-4);(2)抛物线的解析式为y=14x 2-32x -4,F (3,−254);(3)①所点M 的坐标为(6,-4),(√41+3,4),(-√41+3,4);②若M 点位于第四象限,则M 点即为M1点,此时直线MF 和☉E 相切,理由见解析.【解析】(1)由题图可得点A 的横坐标为3-5=-2,点B 的横坐标为3+5=8,连接CE ,则CE=5,又OE=3,。
2023年中考数学压轴题专题10 二次函数与圆存在性问题【含答案】

专题10二次函数与圆存在性问题二次函数是初中数学代数部分最重要的概念之一,是中考数学的重难点;而圆是初中几何中综合性最强的知识内容,它与二次函数都在中考中占据及其重要的地位,两者经常作为压轴题综合考查,能够很好的考查学生的数学综合素养以及分析问题、解决问题的能力.圆心与抛物线的关系、圆上的点和抛物线的关系,其本质就是把位置关系向数量化关系转化.二次函数与圆的综合要数形结合,在读题之前要想到圆中的相关概念、性质及定理,比如圆的定义、垂径定理、圆周角、圆心角、内心、外心、切线、四点共圆的、隐藏圆等;对于二次函数,要熟练掌握解析式的求法和表达形式、顶点、最值、与方程之间的关系,线段长与点的坐标之间的数量转化等.【例1】(2022•闵行区二模)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴相交于点A(﹣1,0),B(3,0),与y轴交于点C.将抛物线的对称轴沿x轴的正方向平移,平移后交x轴于点D,交线段BC于点E,交抛物线于点F,过点F作直线BC的垂线,垂足为点G.(1)求抛物线的表达式;(2)以点G为圆心,BG为半径画⊙G;以点E为圆心,EF为半径画⊙E.当⊙G与⊙E内切时.①试证明EF与EB的数量关系;②求点F的坐标.【例2】(2022•福建模拟)如图,已知抛物线y=ax2+bx+c与x轴相交于A,B两点,点C(2,﹣4)在抛物线上,且△ABC是等腰直角三角形.(1)求抛物线的解析式;(2)过点D(2,0)的直线与抛物线交于点M,N,试问:以线段MN为直径的圆是否过定点?证明你的结论.【例3】(2022•武汉模拟)已知抛物线y=﹣2x2+bx+c(c>0).(1)如图1,抛物线与直线l相交于点M(﹣1,0),N(2,6).①求抛物线的解析式;②过点N作MN的垂线,交抛物线于点P,求PN的长;(2)如图2,已知抛物线y=﹣2x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A,B,C,D(0,n)四点在同一圆上,求n的值.【例4】(2022•上海模拟)在平面直角坐标系xOy中,抛物线y=ax2﹣3ax+2(a<0)交y轴于点A,抛物线的对称轴交x轴于点P,联结PA.(1)求线段PA的长;(2)如果抛物线的顶点到直线PA的距离为3,求a的值;(3)以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B,第一象限内的点Q在⊙P上,且劣弧=2.如果抛物线经过点Q,求a的值.1.(2021•广元)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:x…﹣10123…y…03430…(1)求出这条抛物线的解析式及顶点M的坐标;(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值;(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF 相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.2.(2021•张家界)如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B (8,0).(1)求二次函数的表达式;(2)求顶点A的坐标及直线AB的表达式;(3)判断△ABO的形状,试说明理由;(4)若点P为⊙O上的动点,且⊙O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E的运动时间t的最小值.3.(2021•宜宾)如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.(1)求抛物线的表达式;(2)判断△BCE的形状,并说明理由;(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.4.(2020•雨花区校级一模)如图1,已知抛物线y=ax2﹣12ax+32a(a>0)与x轴交于A,B两点(A在B 的左侧),与y轴交于点C.(1)连接BC,若∠ABC=30°,求a的值.(2)如图2,已知M为△ABC的外心,试判断弦AB的弦心距d是否有最小值,若有,求出此时a的值,若没有,请说明理由;(3)如图3,已知动点P(t,t)在第一象限,t为常数.问:是否存在一点P,使得∠APB达到最大,若存在,求出此时∠APB的正弦值,若不存在,也请说明理由.5.(2020•汇川区三模)如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B (3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.6.(2021•开福区模拟)如图,在平面直角坐标系中,抛物线y=x2﹣bx+c交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).(1)求此抛物线的解析式;(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;(3)在(2)的条件下,设抛物线对称轴l交x轴于点H,△ABD的外接圆圆心为M(如图1),①求点M的坐标及⊙M的半径;②过点B作⊙M的切线交于点P(如图2),设Q为⊙M上一动点,则在点运动过程中的值是否变化?若不变,求出其值;若变化,请说明理由.7.(2020•天桥区二模)如图,抛物线y=ax2+bx+c(a≠0),与x轴交于A(4,0)、O两点,点D(2,﹣2)为抛物线的顶点.(1)求该抛物线的解析式;(2)点E为AO的中点,以点E为圆心、以1为半径作⊙E,交x轴于B、C两点,点M为⊙E上一点.①射线BM交抛物线于点P,设点P的横坐标为m,当tan∠MBC=2时,求m的值;②如图2,连接OM,取OM的中点N,连接DN,则线段DN的长度是否存在最大值或最小值?若存在,请求出DN的最值;若不存在,请说明理由.8.(2020•百色)如图,抛物线的顶点为A(0,2),且经过点B(2,0).以坐标原点O为圆心的圆的半径r=,OC⊥AB于点C.(1)求抛物线的函数解析式.(2)求证:直线AB与⊙O相切.(3)已知P为抛物线上一动点,线段PO交⊙O于点M.当以M,O,A,C为顶点的四边形是平行四边形时,求PM的长.9.(2020•西藏)在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A(﹣2,0),B(4,0)两点,交y轴于点C,点P是第四象限内抛物线上的一个动点.(1)求二次函数的解析式;=,求点P的坐标;(2)如图甲,连接AC,PA,PC,若S△P AC(3)如图乙,过A,B,P三点作⊙M,过点P作PE⊥x轴,垂足为D,交⊙M于点E.点P在运动过程中线段DE的长是否变化,若有变化,求出DE的取值范围;若不变,求DE的长.10.(2020•宜宾)如图,已知二次函数的图象顶点在原点,且点(2,1)在二次函数的图象上,过点F(0,1)作x轴的平行线交二次函数的图象于M、N两点.(1)求二次函数的表达式;(2)P为平面内一点,当△PMN是等边三角形时,求点P的坐标;(3)在二次函数的图象上是否存在一点E,使得以点E为圆心的圆过点F和点N,且与直线y=﹣1相切.若存在,求出点E的坐标,并求⊙E的半径;若不存在,说明理由.11.(2021•嘉兴二模)定义:平面直角坐标系xOy中,过二次函数图象与坐标轴交点的圆,称为该二次函数的坐标圆.(1)已知点P(2,2),以P为圆心,为半径作圆.请判断⊙P是不是二次函数y=x2﹣4x+3的坐标圆,并说明理由;(2)已知二次函数y=x2﹣4x+4图象的顶点为A,坐标圆的圆心为P,如图1,求△POA周长的最小值;(3)已知二次函数y=ax2﹣4x+4(0<a<1)图象交x轴于点A,B,交y轴于点C,与坐标圆的第四个交点为D,连结PC,PD,如图2.若∠CPD=120°,求a的值.12.(2021•常州二模)如图1:抛物线y=﹣x2+bx+c过点A(﹣1,0),点B(3,0),与y轴交于点C.动点E(m,0)(0<m<3),过点E作直线l⊥x轴,交抛物线于点M.(1)求抛物线的解析式及C点坐标;(2)连接BM并延长交y轴于点N,连接AN,OM,若AN∥OM,求m的值.(3)如图2.当m=1时,P是直线l上的点,以P为圆心,PE为半径的圆交直线l于另一点F(点F在x 轴上方),若线段AC上最多存在一个点Q使得∠FQE=90°,求点P纵坐标的取值范围.13.(2021•乐山模拟)如图,抛物线y=ax2+bx+2与直线AB相交于A(﹣1,0),B(3,2),与x轴交于另一点C.(1)求抛物线的解析式;(2)在y上是否存在一点E,使四边形ABCE为矩形,若存在,请求出点E的坐标;若不存在,请说明理由;(3)以C为圆心,1为半径作⊙O,D为⊙O上一动点,求DA+DB的最小值14.(2021•河北区二模)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+3的对称轴是直线x=2,与x 轴相交于A,B两点(点A在点B的左侧),与y轴交于点C.(Ⅰ)求抛物线的解析式及顶点坐标;(Ⅱ)M为第一象限内抛物线上的一个点,过点M作MN⊥x轴于点N,交BC于点D,连接CM,当线段CM=CD时,求点M的坐标;(Ⅲ)以原点O为圆心,AO长为半径作⊙O,点P为⊙O上的一点,连接BP,CP,求2PC+3PB的最小值.15.(2021•长沙模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)的顶点为M,经过C(1,1),且与x轴正半轴交于A,B两点.(1)如图1,连接OC,将线段OC绕点O顺时针旋转,使得C落在y轴的负半轴上,求点C的路径长;(2)如图2,延长线段OC至N,使得ON=,若∠OBN=∠ONA,且,求抛物线的解析式;(3)如图3,抛物线y=ax2+bx+c的对称轴为直线,与y轴交于(0,5),经过点C的直线l:y=kx+m (k>0)与抛物线交于点C、D,若在x轴上存在P1、P2,使∠CP1D=∠CP2D=90°,求k的取值范围.16.(2021秋•上城区校级期中)如图,已知抛物线y=﹣x2+bx+c与x轴交于A、B两点(点A在点B左边),与y轴交于点C,⊙M是△ABC的外接圆.若抛物线的顶点D的坐标为(1,4).(1)求抛物线的解析式,及A、B、C三点的坐标;(2)求⊙M的半径和圆心M的坐标;(3)如图2,在x轴上有点P(7,0),试在直线BC上找点Q,使B、Q、P三点构成的三角形与△ABC相似.若存在,请直接写出点坐标;若不存在,请说明理由.17.(2021秋•西湖区校级期中)我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,﹣3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.(1)求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长;(2)已知点E是“蛋圆”上的一点(不与点A,点B重合),点E关于x轴的对称点是点F,若点F也在“蛋圆”上,求点E坐标;(3)点P是“蛋圆”外一点,满足∠BPC=60°,当BP最大时,直接写出点P的坐标.18.(2021•雨花区二模)如图1,已知圆O的圆心为原点,半径为2,与坐标轴交于A,C,D,E四点,B 为OD中点.(1)求过A,B,C三点的抛物线解析式;(2)如图2,连接BC,AC.点P在第一象限且为圆O上一动点,连接BP,交AC于点M,交OC于点N,当MC2=MN•MB时,求M点的坐标;(3)如图3,若抛物线与圆O的另外两个交点分别为H,F,请判断四边形CFEH的形状,并说明理由.19.(2020•东海县二模)如图,△AOB的三个顶点A、O、B分别落在抛物线C1:y=x2+x上,点A的坐标为(﹣4,m),点B的坐标为(n,﹣2).(点A在点B的左侧)(1)则m=,n=.(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线C2:y=ax2+bx+4经过A'、B'两点,延长OB'交抛物线C2于点C,连接A'C.设△OA'C的外接圆为⊙M.①求圆心M的坐标;②试直接写出△OA'C的外接圆⊙M与抛物线C2的交点坐标(A'、C除外).20.(2022•绿园区二模)在平面直角坐标系中,已知某二次函数的图象同时经过点A(0,3)、B(2m,3)、C(m,m+3).其中,m≠0.(1)当m=1时.①该二次函数的图象的对称轴是直线.②求该二次函数的表达式.(2)当|m|≤x≤|m|时,若该二次函数的最大值为4,求m的值.(3)若同时经过点A、B、C的圆恰好与x轴相切时,直接写出该二次函数的图象的顶点坐标.21.(2022•炎陵县一模)抛物线:y=﹣x2+bx+c与y轴的交点C(0,3),与x轴的交点分别为E、G两点,对称轴方程为x=1.(1)求抛物线的解析式;(2)如图1,过点C作y轴的垂线交抛物线于另一点D,F为抛物线的对称轴与x轴的交点,P为线段OC 上一动点.若PD⊥PF,求点P的坐标.(3)如图1,如果一个圆经过点O、点G、点C三点,并交于抛物线对称轴右侧x轴的上方于点H,求∠OHG的度数;(4)如图2,将抛物线向下平移2个单位长度得到新抛物线L,点B是顶点.直线y=kx﹣k+4(k<0)与抛物线L交于点M、N.与对称轴交于点G,若△BMN的面积等于2,求k的值.22.(2022•杨浦区二模)如图,已知在平面直角坐标系xOy中,抛物线y=﹣+bx+c与x轴相交于点A (4,0),与y轴相交于点B(0,3),在x轴上有一动点E(m,0)(0<m<4),过点E作x轴的垂线交线段AB于点N,交抛物线于点P,过P作PM⊥AB,垂足为点M.(1)求这条抛物线的表达式;(2)设△PMN的周长为C1,△AEN的周长为C2,如果,求点P的坐标;(3)如果以N为圆心,NA为半径的圆与以OB为直径的圆内切,求m的值.【例1】(2022•闵行区二模)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴相交于点A(﹣1,0),B(3,0),与y轴交于点C.将抛物线的对称轴沿x轴的正方向平移,平移后交x轴于点D,交线段BC于点E,交抛物线于点F,过点F作直线BC的垂线,垂足为点G.(1)求抛物线的表达式;(2)以点G为圆心,BG为半径画⊙G;以点E为圆心,EF为半径画⊙E.当⊙G与⊙E内切时.①试证明EF与EB的数量关系;②求点F的坐标.【分析】(1)根据点A、B的坐标,设抛物线y=a(x+1)(x﹣3),再将点C代入即可求出a的值,从而得出答案;(2)①分两种情形,当r⊙G>r⊙E时,则GB﹣EF=GE,则EF=EB,当r⊙G<r⊙E时,则EF﹣GB=GE,设EF=5t,FG=3t,GE=4t,则5t﹣GB=4t,则GB=t<GE=4t,从而得出矛盾;②由.设BD=t,则DE=,利用勾股定理得BE=,则F坐标为(3﹣t,3t),代入抛物线解析式,从而解决问题.【解答】解:(1)∵点A坐标为(﹣1,0),点B坐标为(3,0).设抛物线y=a(x+1)(x﹣3)(a≠0),∵抛物线经过点C(0,4),∴4=﹣3a.解得.∴抛物线的表达式是;(2)①由于⊙G与⊙E内切,当r⊙G<r⊙E时,则EF﹣GB=GE,设EF=5t,FG=3t,GE=4t,则5t﹣GB=4t,∴GB=t<GE=4t,∴点E在线段CB的延长线上.又∵已知点E在线段BC上,∴矛盾,因此不存在.当r⊙G>r⊙E时,则GB﹣EF=GE,又∵GE=GB﹣EB,∴EF=EB;②∵OC⊥OB,FD⊥OB,∴∠COB=∠EDB=90°.∴.∴设BD=t,则DE=;在Rt△BED中,由勾股定理得,.∴,∴F坐标为(3﹣t,3t),∵F点在抛物线上,∴,∴解得,t=0(点F与点B重合,舍去).∴F坐标为(,).【例2】(2022•福建模拟)如图,已知抛物线y=ax2+bx+c与x轴相交于A,B两点,点C(2,﹣4)在抛物线上,且△ABC是等腰直角三角形.(1)求抛物线的解析式;(2)过点D(2,0)的直线与抛物线交于点M,N,试问:以线段MN为直径的圆是否过定点?证明你的结论.【分析】(1)等腰直角三角形斜边中线等于斜边一半,点的坐标,不难求出A、B两点坐标,把点A、B、C 代入二次函数解析式,解三元一次方程组就可得到函数解析式.(2))通过设过点D(2,0)的直线MN解析式为y=k(x﹣2)=kx﹣2k,得到关于x、关于y的方程,利用跟与系数的关系,再得到圆的解析式,待定系数法确定定点的x、y的值,确定定点的坐标.【解答】解:连接AC、BC,过点C作CP垂直于x轴于点P.在Rt△CAB中,AC=BC,CP⊥AB,点C(2,﹣4),∴CP=AP=PB=4,OP=2,∴OA=AP﹣OP=4﹣2=2,OB=OP+PB=4+2=6,∴点A(﹣2,0),点B(6,0),把点A(﹣2,0),点B(6,0),点C(2,﹣4)代入函数解析式得,解得,∴抛物线的解析式为:y=x2﹣x﹣3.故答案为:y=x2﹣x﹣3.(2)设过点D(2,0)的直线MN解析式为y=k(x﹣2)=kx﹣2k,联立直线与抛物线解析式得关于x的等式:kx﹣2k=x2﹣x﹣3,化简得=0,x N+x M=﹣=4(k+1),x N x M==8k﹣12..........①,联立直线与抛物线解析式得关于y的等式:y=(+2)2﹣(+2)﹣3,化简得y2+(﹣﹣1)y﹣4=0,y M+y N=4k2,y M y N=﹣16k2................②,线段MN的中点就是圆的圆心,∴x O=(x N+x M)=2(K+1),代入直线方程得y O=2k2,∴圆心坐标为(2k+2,2k2),直径MN==,把①、②代入上式化简整理得直径MN=,设圆上某一点(x,y)到圆心的距离等于半径,∴=,化简整理得16k2+12﹣8k=x2﹣4kx﹣4x+y2﹣4k2y=﹣4yk2﹣4kx+x2﹣4x+y2,圆过定点,所以与k值无关,看作是关于k的二次等式,k2、k的系数,常量对应相等,得﹣8=﹣4x,x=2,16=﹣4y,y=﹣4,由以上分析,所以以MN为直径的圆过定点(2,﹣4).故答案为:以线段MN为直径的圆过定点(2,﹣4).【例3】(2022•武汉模拟)已知抛物线y=﹣2x2+bx+c(c>0).(1)如图1,抛物线与直线l相交于点M(﹣1,0),N(2,6).①求抛物线的解析式;②过点N作MN的垂线,交抛物线于点P,求PN的长;(2)如图2,已知抛物线y=﹣2x2+bx+c与x轴交于A、B两点,与y轴交于点C,点A,B,C,D(0,n)四点在同一圆上,求n的值.【分析】(1)①把点M(﹣1,0),N(2,6)代入到y=﹣2x2+bx+c中,可得b和c的值.②设P(a,﹣2a2+4a+6),再利用M(﹣1,0),N(2,6),得到MN、PM、PN的表达式,最后利用勾股定理求得a的值.(2)令C(0,c),当y=0时,代入抛物线得x A x B=﹣,根据两角对应相等,可得△AOC∽△DOB,然后再找到对应线段成比例,即得到n的值.【解答】解:(1)①把M(﹣1,0)N(2,6)代入y=﹣2x2+bx+c,得,解得,∴抛物线的解析式为y=﹣2x2+4x+6;②由①,抛物线解析式为:y=﹣2x2+4x+6,设P(a,﹣2a2+4a+6)∵M(﹣1,0),N(2,6),∴MN==3,∴PM=,PN=,又∵PN⊥MN,则PM2=MN2+PN2,(﹣1﹣a)2+(2a2﹣4a﹣b)2=(3)2+(2﹣a)2+(2a2﹣4a)2.整理得:4a2﹣9a+2=0,∴(a﹣2)(4a﹣1)=0.∴a1=2,a2=.当a=2时,P与N重合,∴a=,PN=.(2)证明:设OA=﹣x A,OB=x B,OD=﹣n当y=0时,﹣2x2+bx+c=0,∴x A x B=﹣,∴OA•OB=﹣x A x B=.∵∠CAO=∠BDO,∠ACO=∠DBO∴△AOC∽△DOB∴=∴OA•OB=OC•OD∴=c•(﹣n).∵c≠0∴n=﹣.【例4】(2022•上海模拟)在平面直角坐标系xOy中,抛物线y=ax2﹣3ax+2(a<0)交y轴于点A,抛物线的对称轴交x轴于点P,联结PA.(1)求线段PA的长;(2)如果抛物线的顶点到直线PA的距离为3,求a的值;(3)以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B,第一象限内的点Q在⊙P上,且劣弧=2.如果抛物线经过点Q,求a的值.【分析】(1)分别求出P(,0),A(0,2),由两点间距离公式可求;=×PM×OP=×AP×3,可得a=﹣;(2)抛物线的顶点为M(,2﹣a),由S△APM(3)连接PQ,BP,AM,设Q(t,at2﹣3at+2),求出M(﹣1,0),由垂径定理可得AM=AQ,=①,PQ=AP,得②,联立①②可得a=.【解答】解:(1)y=ax2﹣3ax+2=a(x﹣)2+2﹣a,∴抛物线的对称轴为x=,∴P(,0),令x=0,则y=2,∴A(0,2),∴PA=;(2)由(1)可知抛物线的顶点为M(,2﹣a),∵a<0,∴2﹣a>0,∴S △APM =×PM ×OP =×AP ×3,∴(2﹣a )×=×3,解得a =﹣;(3)连接PQ ,BP ,AM ,∵MP ⊥AB ,∴=,∵=2,∴=,∴AM =AQ ,设Q (t ,at 2﹣3at +2),∵AP =,P (,0),∴M (﹣1,0),∴=①,∵PQ =AP ,∴②,联立①②可得t =或t =﹣1(舍),将t =代入①,可得a =.1.(2021•广元)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与x轴分别相交于A、B两点,与y轴相交于点C,下表给出了这条抛物线上部分点(x,y)的坐标值:x…﹣10123…y…03430…(1)求出这条抛物线的解析式及顶点M的坐标;(2)PQ是抛物线对称轴上长为1的一条动线段(点P在点Q上方),求AQ+QP+PC的最小值;(3)如图2,点D是第四象限内抛物线上一动点,过点D作DF⊥x轴,垂足为F,△ABD的外接圆与DF 相交于点E.试问:线段EF的长是否为定值?如果是,请求出这个定值;如果不是,请说明理由.【分析】(1)运用待定系数法即可求出抛物线解析式,再运用配方法求出顶点坐标;(2)如图1,将点C沿y轴向下平移1个单位得C′(0,2),连接BC′交抛物线对称轴x=1于点Q′,过点C作CP′∥BC′,交对称轴于点P′,连接AQ′,此时,C′、Q′、B三点共线,BQ′+C′Q′的值最小,运用勾股定理即可求出答案;(3)如图2,连接BE,设D(t,﹣t2+2t+3),且t>3,可得DF=t2﹣2t﹣3,BF=t﹣3,AF=t+1,运用圆内接四边形的性质可得∠DAF=∠BEF,进而证明△AFD∽△EFB,利用=,即可求得答案.【解答】解:(1)根据表格可得出A(﹣1,0),B(3,0),C(0,3),设抛物线解析式为y=a(x+1)(x﹣3),将C(0,3)代入,得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,∴该抛物线解析式为y=﹣x2+2x+3,顶点坐标为M(1,4);(2)如图1,将点C沿y轴向下平移1个单位得C′(0,2),连接BC′交抛物线对称轴x=1于点Q′,过点C作CP′∥BC′,交对称轴于点P′,连接AQ′,∵A、B关于直线x=1对称,∴AQ′=BQ′,∵CP′∥BC′,P′Q′∥CC′,∴四边形CC′Q′P′是平行四边形,∴CP′=C′Q′,Q′P′=CC′=1,在Rt△BOC′中,BC′===,∴AQ′+Q′P′+P′C=BQ′+C′Q′+Q′P′=BC′+Q′P′=+1,此时,C′、Q′、B三点共线,BQ′+C′Q′的值最小,∴AQ+QP+PC的最小值为+1;(3)线段EF的长为定值1.如图2,连接BE,设D(t,﹣t2+2t+3),且t>3,∵EF⊥x轴,∴DF=﹣(﹣t2+2t+3)=t2﹣2t﹣3,∵F(t,0),∴BF=OF﹣OB=t﹣3,AF=t﹣(﹣1)=t+1,∵四边形ABED是圆内接四边形,∴∠DAF+∠BED=180°,∵∠BEF+∠BED=180°,∴∠DAF=∠BEF,∵∠AFD=∠EFB=90°,∴△AFD∽△EFB,∴=,∴=,∴EF===1,∴线段EF的长为定值1.2.(2021•张家界)如图,已知二次函数y=ax2+bx+c的图象经过点C(2,﹣3),且与x轴交于原点及点B (8,0).(1)求二次函数的表达式;(2)求顶点A的坐标及直线AB的表达式;(3)判断△ABO的形状,试说明理由;(4)若点P为⊙O上的动点,且⊙O的半径为2,一动点E从点A出发,以每秒2个单位长度的速度沿线段AP匀速运动到点P,再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动,求点E 的运动时间t的最小值.【分析】(1)运用待定系数法即可求出答案;(2)运用配方法将抛物线解析式化为顶点式,得出顶点坐标,运用待定系数法求出直线AB的函数表达式;(3)方法1:如图1,过点A作AF⊥OB于点F,则F(4,0),得出△AFO、△AFB均为等腰直角三角形,即可得出答案,方法2:由△ABO的三个顶点分别是O(0,0),A(4,﹣4),B(8,0),运用勾股定理及逆定理即可得出答案;(4)以O为圆心,2为半径作圆,则点P在圆周上,根据t=AP+PB=PD+PB,可知当B、P、D三点共线时,PD+PB取得最小值,过点D作DG⊥OB于点G,由t=DB=即可求出答案.【解答】解:(1)∵二次函数y=ax2+bx+c(a≠0)的图象经过C(2,﹣3),且与x轴交于原点及点B(8,0),∴c=0,二次函数表达式可设为:y=ax2+bx(a≠0),将C(2,﹣3),B(8,0)代入y=ax2+bx得:,解得:,∴二次函数的表达式为;(2)∵=(x﹣4)2﹣4,∴抛物线的顶点A(4,﹣4),设直线AB的函数表达式为y=kx+m,将A(4,﹣4),B(8,0)代入,得:,解得:,∴直线AB的函数表达式为y=x﹣8;(3)△ABO是等腰直角三角形.方法1:如图1,过点A作AF⊥OB于点F,则F(4,0),∴∠AFO=∠AFB=90°,OF=BF=AF=4,∴△AFO、△AFB均为等腰直角三角形,∴OA=AB=4,∠OAF=∠BAF=45°,∴∠OAB=90°,∴△ABO是等腰直角三角形.方法2:∵△ABO的三个顶点分别是O(0,0),A(4,﹣4),B(8,0),∴OB=8,OA===,AB===,且满足OB2=OA2+AB2,∴△ABO是等腰直角三角形;(4)如图2,以O为圆心,2为半径作圆,则点P在圆周上,依题意知:动点E的运动时间为t=AP+PB,在OA上取点D,使OD=,连接PD,则在△APO和△PDO中,满足:==2,∠AOP=∠POD,∴△APO∽△PDO,∴==2,从而得:PD=AP,∴t=AP+PB=PD+PB,∴当B、P、D三点共线时,PD+PB取得最小值,过点D作DG⊥OB于点G,由于,且△ABO为等腰直角三角形,则有DG=1,∠DOG=45°∴动点E的运动时间t的最小值为:t=DB===5.3.(2021•宜宾)如图1,在平面直角坐标系中,抛物线与x轴分别交于A、B两点,与y轴交于点C(0,6),抛物线的顶点坐标为E(2,8),连结BC、BE、CE.(1)求抛物线的表达式;(2)判断△BCE的形状,并说明理由;(3)如图2,以C为圆心,为半径作⊙C,在⊙C上是否存在点P,使得BP+EP的值最小,若存在,请求出最小值;若不存在,请说明理由.【分析】(1)运用待定系数法即可求得答案;(2)△BCE是直角三角形.运用勾股定理逆定理即可证明;(3)如图,在CE上截取CF=(即CF等于半径的一半),连结BF交⊙C于点P,连结EP,则BF的长即为所求.【解答】解:(1)∵抛物线的顶点坐标为E(2,8),∴设该抛物线的表达式为y=a(x﹣2)2+8,∵与y轴交于点C(0,6),∴把点C(0,6)代入得:a=﹣,∴该抛物线的表达式为y=x2+2x+6;(2)△BCE是直角三角形.理由如下:∵抛物线与x轴分别交于A、B两点,∴令y=0,则﹣(x﹣2)2+8=0,解得:x1=﹣2,x2=6,∴A(﹣2,0),B(6,0),∴BC2=62+62=72,CE2=(8﹣6)2+22=8,BE2=(6﹣2)2+82=80,∴BE2=BC2+CE2,∴∠BCE=90°,∴△BCE是直角三角形;(3)⊙C上存在点P,使得BP+EP的值最小且这个最小值为.理由如下:如图,在CE上截取CF=(即CF等于半径的一半),连结BF交⊙C于点P,连结EP,则BF的长即为所求.理由如下:连结CP,∵CP为半径,∴==,又∵∠FCP=∠PCE,∴△FCP∽△PCE,∴==,即FP=EP,∴BF=BP+EP,由“两点之间,线段最短”可得:BF的长即BP+EP为最小值.∵CF=CE,E(2,8),∴由比例性质,易得F(,),∴BF==.4.(2020•雨花区校级一模)如图1,已知抛物线y=ax2﹣12ax+32a(a>0)与x轴交于A,B两点(A在B 的左侧),与y轴交于点C.(1)连接BC,若∠ABC=30°,求a的值.(2)如图2,已知M为△ABC的外心,试判断弦AB的弦心距d是否有最小值,若有,求出此时a的值,若没有,请说明理由;(3)如图3,已知动点P(t,t)在第一象限,t为常数.问:是否存在一点P,使得∠APB达到最大,若存在,求出此时∠APB的正弦值,若不存在,也请说明理由.【分析】(1)令y=0,求得抛物线与x轴的交点A、B的坐标,令x=0,用a表示C点的坐标,再由三角函数列出a的方程,便可求得a的值;(2)过M点作MH⊥AB于点H,连接MA、MC,用d表示出M的坐标,根据MA=MC,列出a、d的关系式,再通过关系式求得结果;(3)取AB的中点T,过T作MT⊥AB,以M为圆心,MA为半径作⊙M,MT与直线y=x交于点S,P′为直线y=x上异于P的任意一点,连接AP′,交⊙M于点K,连接BK,MP,AP,BP,MB,MA,当P 为直线y=x与⊙M的切点时,∠APB达到最大,利用圆圆周角性质和解直角三角形的知识求得结果便可.【解答】解:(1)连接BC,令y=0,得y=ax2﹣12ax+32a=0,解得,x=4或8,∴A(4,0),B(8,0),令x=0,得y=ax2﹣12ax+32a=32a,∴C(0,32a),又∠ABC=30°,∴tan∠ABC=,解得,a=;(2)过M点作MH⊥AB于点H,连接MA、MC,如图2,∴AH=BH==2,∴OH=6,设M(6,d),∵MA=MC,∴4+d2=36+(d﹣32a)2,得2ad=32a2+1,∴d=16a+=,∴当4时,有,即当a=时,有;(3)∵P(t,t),∴点P在直线y=x上,如图3,取AB的中点T,过T作MT⊥AB,以M为圆心,MA为半径作⊙M,MT与直线y=x交于点S,P′为直线y=x上异于P的任意一点,连接AP′,交⊙M于点K,连接BK,MP,AP,BP,MB,MA,当⊙M与直线y=x相切时,有∠APB=∠AKB>∠AP′B,∴∠APB最大,此时相切点为P,设M(6,d),而T(6,0),∴S(6,6),∴∠PSM=90°﹣∠SOT=45°,又MP=MB=,∴MS==,∵MS+MT=ST=6,∴,解得,d=2(负根舍去),经检验,d=2是原方程的解,也符合题意,∴M(6,2),∴MB=2,∵∠AMB=2∠APB,MT⊥AB,MA=MB,∴∠AMT=∠BMT=∠AMB=∠APB,∴sin∠APB=sin∠BMT=.5.(2020•汇川区三模)如图,在平面直角坐标系上,一条抛物线y=ax2+bx+c(a≠0)经过A(1,0)、B (3,0)、C(0,3)三点,连接BC并延长.(1)求抛物线的解析式;(2)点M是直线BC在第一象限部分上的一个动点,过M作MN∥y轴交抛物线于点N.1°求线段MN的最大值;2°当MN取最大值时,在线段MN右侧的抛物线上有一个动点P,连接PM、PN,当△PMN的外接圆圆心Q在△PMN的边上时,求点P的坐标.【分析】(1)将三个已知点坐标代入抛物线的解析式中列出方程组求得a、b、c,便可得抛物线的解析式;(2)1°用待定系数法求出直线BC的解析式,再设M的横坐标为t,用t表示MN的距离,再根据二次函数的性质求得MN的最大值;2°分三种情况:当∠PMN=90°时;当∠PNM=90°时;当∠MPN=90°时.分别求出符合条件的P点坐标便可.【解答】解:(1)把A、B、C三点的坐标代入抛物线y=ax2+bx+c(a≠0)中,得,解得,,∴抛物线的解析式为:y=x2﹣4x+3;(2)1°设直线BC的解析式为y=mx+n(m≠0),则,解得,,∴直线BC的解析式为:y=﹣x+3,设M(t,﹣t+3)(0<t<3),则N(t,t2﹣4t+3),∴MN=﹣t2+3t=﹣,∴当t=时,MN的值最大,其最大值为;2°∵△PMN的外接圆圆心Q在△PMN的边上,∴△PMN为直角三角形,由1°知,当MN取最大值时,M(),N(),①当∠PMN=90°时,PM∥x轴,则P点与M点的纵坐标相等,∴P点的纵坐标为,当y=时,y=x2﹣4x+3=,解得,x=,或x=(舍去),∴P();②当∠PNM=90°时,PN∥x轴,则P点与N点的纵坐标相等,∴P点的纵坐标为﹣,当y=﹣时,y=x2﹣4x+3=﹣,解得,x=,或x=(舍去),∴P(,);③当∠MPN=90°时,则MN为△PMN的外接圆的直径,∴△PMN的外接圆的圆心Q为MN的中点,∴Q(),半径为,过Q作QK∥x轴,与在MN右边的抛物线图象交于点K,如图②,令y=,得y=x2﹣4x+3=,解得,x=<(舍),或x=,∴K(,),∴QK=>,即K点在以MN为直径的⊙Q外,设抛物线y=x2﹣4x+3的顶点为点L,则l(2,﹣1),连接LK,如图②,则L到QK的距离为,LK=,设Q点到LK的距离为h,则,∴=,∴直线LK下方的抛物线与⊙Q没有公共点,∵抛物线中NL部分(除N点外)在过N点与x轴平行的直线下方,∴抛物线中NL部分(除N点外)与⊙Q没有公共点,∵抛物线K点右边部分,在过K点与y轴平行的直线的右边,∴抛物线K点右边部分与⊙Q没有公共点,综上,⊙Q与MN右边的抛物线没有交点,∴在线段MN右侧的抛物线上不存在点P,使△PMN的外接圆圆心Q在MN边上;综上,点P的坐标为()或().6.(2021•开福区模拟)如图,在平面直角坐标系中,抛物线y=x2﹣bx+c交x轴于点A,B,点B的坐标为(4,0),与y轴于交于点C(0,﹣2).(1)求此抛物线的解析式;(2)在抛物线上取点D,若点D的横坐标为5,求点D的坐标及∠ADB的度数;(3)在(2)的条件下,设抛物线对称轴l交x轴于点H,△ABD的外接圆圆心为M(如图1),①求点M的坐标及⊙M的半径;②过点B作⊙M的切线交于点P(如图2),设Q为⊙M上一动点,则在点运动过程中的值是否变化?若不变,求出其值;若变化,请说明理由.【分析】(1)c=﹣2,将点B的坐标代入抛物线表达式得:0=﹣4b﹣2,解得:b=﹣,即可求解;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图6
x
y F
E H N M
P
D C B A
O
二次函数和圆
【例题1】 (芜湖市)
已知圆P的圆心在反比例函数k
y x
=
(1)k >图象上,并与x轴相交于A 、B 两点. 且始终与y 轴相切于定点C (0,1). (1) 求经过A 、B 、C 三点的二次
函数图象的解析式;
(2) 若二次函数图象的顶点为D,
问当k 为何值时,四边形ADBP 为菱形.
【例题2】(湖南省韶关市)
25.如图6,在平面直角坐标系中,四边形OABC 是矩形,OA=4,AB=2,直线
3
2
y x =-+与坐标轴交于D 、E 。
设M 是AB 的中点,P 是线段DE 上的动点.
(1)求M、D 两点的坐标;
(2)当P在什么位置时,PA=PB?求出此时P 点的坐标;
(3)过P 作PH ⊥B C,垂足为H ,当以PM 为直径的⊙F与BC 相切于点N 时,求梯形P MBH 的面积.
【例题3】(甘肃省白银等7市新课程)28. 在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.
(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x
轴的交点恰为点E、F,求该抛物线的解析式;
(3)试判断点C是否在抛物线上?
(4)在抛物线上是否存在三个点,由它构成的三角形与
△AOC相似?直接写出两组这样的点.
【例题4】(绵阳市)25.如图,已知抛物线y = ax2 + bx-3与x轴交于A、B两点,与y轴交于C点,经过A、B、C三点的圆的圆心M(1,m)恰好在此抛物线的对称轴上,⊙M的半径为5.设⊙M与y轴交于D,抛物线的顶点为E.
(1)求m的值及抛物线的解析式;
(2)设∠DBC = α,∠CBE=β,求sin(α-β)的值;
(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCE相似?若存在,请指出点P的位置,并直接写出点P的坐标;若不存在,请说明理由.
【例题5】(南充市)25.如图,点M(4,0),以点M为圆心、2为半径的圆与x轴交于点A、B.
已知抛物线2
16
y x bx c =
++过点A和B,与y 轴交于点C . (1)求点C 的坐标,并画出抛物线的大致图象.2(ﻫ)点Q (8,m )在抛物线2
16
y x bx c =++上,点P 为此抛物线对称轴上一个动点,求PQ+PB 的最小值.
(3)CE 是过点C 的⊙M 的切线,点E 是切点,求OE 所在直线的解析式.
【例题6】(山西省临汾市)26. 如图所示,在平面直角坐标系中,
M 经过原点O ,且与x 轴、y 轴分别
相交于(60)(08)A B --,,,两点.
(1)请求出直线AB 的函数表达式;
(2)若有一抛物线的对称轴平行于y 轴且经过点M ,顶点C 在M 上,开口向下,且经过点B ,求此抛物线的函数表达式;
(3)设(2)中的抛物线交x 轴于D E ,两点,在抛物线上是否存在点P ,使得1
15
PDE ABC S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.
【例题
7】在△AB C中,∠A =90°,AB =4,AC =3,M 是AB
∥BC 交
A C于点N .以MN 为直径作⊙O ,并在⊙O 内作内接矩形AMPN .(1)用含x 的代数式表示△MNP 的面积S; (2)当x 为何值时,⊙O 与直线BC相切?
x
(3)在动点M 的运动过程中,记△MNP 与梯形BCN M重合的面积为y ,试求y 关于x 的函数表达式,并求x为
何值时,y 的值最大,最大值是多少?
【例题8】如图,点P在y 轴上,半径为3的⊙P 分别交x轴于A、B两点,AB=4,交y 轴负半轴于点C,连
接AP 并延长交⊙P 于点D,过D 作⊙P的切线分别交x 轴、y轴于点F 、G ; (1)求直线FG 的解析式;
(2)连接CD交AB 于点E,求PCD tan 的值; (3)设M是劣弧BC 上的一个动点,连接DM 交x 轴于点N,问:是否存在这样的一个常数k,始终满足AN ·AB+DN ·DM =K,如果存在,请求出K 的值,如果不存在,请说明理由;
A B M N D O
A B C M N P 图 1
O A
B M N 图 3
O。
