数学物理方法题库(兰州大学)
数学物理方法复习资料及参考答案(一)

数学物理方法复习资料及参考答案(一)数学物理方法复习资料及参考答案(一)一、填空题: 1. 复数ii -+11用三角式可表示为(主辐角[)π2,0)。
2. 已知幂级数∑∞=0k kk z a 和∑∞=0k kk z b 的收敛半径分别是1R 和2R ,则幂级数()∑∞=±0k k k k z b a 的收敛半径为:。
3. 勒让德多项式()l P x 的模l N = ()0,1,2,l = 。
4. 在00=z 的邻域上,z e z f 1)(=展开的洛朗级数为:。
5. 函数2)2)(1()(--=z z z z f 的留数)1(resf =。
6. 求解无限长弦的自由振动,设弦的初始位移为)(x ?,初始速度为)(/x a ?-,=),(t x u 。
7. 在00=z 的邻域上,z z f sin )(=的泰勒级数为:。
8. 幂级数()∑∞=-11k k i z k的收敛圆:。
9. 数理方程中的定解条件包括三大类初始条件、和衔接条件。
10. 在本征值问题()()()'''12012--+=-1<<±1??x y xy y x y λ有限中,方程()'''1202--+=x y xy y λ称为__ _ _ __微分方程,该本征值问题的本征值λn =___ _ ,相应本征函数是y x n ()=__________,其中n=___ _ ____,该本征函数称为______ __ _,写出它的表达式(至少一种):___________ _____。
二、简答题:1、孤立奇点分为几类?如何判别?2、简述施图姆-刘维尔本征值问题的共同性质。
三、基础题:1、计算实变函数定积分()()222294x dxI xx ∞=++?2、已知解析函数()f z 的实部233),(xy x y x u -=,0)0(=f ,求虚部和这个解析函数。
数学物理方法习题解答(完整版)

数学物理方法习题解答一、复变函数部分习题解答第一章习题解答1、证明Re z 在z 平面上处处不可导。
证明:令Re z u iv =+。
Re z x =,,0u x v ∴==。
1ux∂=∂,0v y ∂=∂,u v x y ∂∂≠∂∂。
于是u 与v 在z 平面上处处不满足C -R 条件, 所以Re z 在z 平面上处处不可导。
2、试证()2f z z=仅在原点有导数。
证明:令()f z u iv =+。
()22222,0f z z x y u x y v ==+ ∴ =+=。
2,2u u x y x y ∂∂= =∂∂。
v vx y∂∂ ==0 ∂∂。
所以除原点以外,,u v 不满足C -R 条件。
而,,u u v vx y x y∂∂∂∂ , ∂∂∂∂在原点连续,且满足C -R 条件,所以()f z 在原点可微。
()000000x x y y u v v u f i i x x y y ====⎛⎫∂∂∂∂⎛⎫'=+=-= ⎪ ⎪∂∂∂∂⎝⎭⎝⎭。
或:()()()2*000lim lim lim 0z z x y z f z x i y z∆→∆→∆=∆=∆'==∆=∆-∆=∆。
22***0*00limlim lim()0z z z z z z zzz z z z z z zz z=∆→∆→∆→+∆+∆+∆∆==+−−→∆∆∆。
【当0,i z z re θ≠∆=,*2i z e z θ-∆=∆与趋向有关,则上式中**1z zz z∆∆==∆∆】 3、设333322()z 0()z=00x y i x y f z x y ⎧+++≠⎪=+⎨⎪⎩,证明()z f 在原点满足C -R 条件,但不可微。
证明:令()()(),,f z u x y iv x y =+,则()33222222,=00x y x y u x y x y x y ⎧-+≠⎪=+⎨+⎪⎩, 332222220(,)=00x y x y v x y x y x y ⎧++≠⎪=+⎨+⎪⎩。
数学物理方法习题及解答1

数学物理方法习题及解答1试题1一、单项选择题1.复通区域柯西定理()(A )0)(=?dz z f l(B )0)(1=∑?=n i l idz z f (C )0)()(1=+∑??=ni l lidz z f dz z f (l 是逆时针方向,i l 也是逆时针方向)(D)0)()(1=+∑??=ni l lidz z f dz z f (l 是逆时针方向,i l 是顺时针方向)2.周期偶函数:,cos)(10为其中k k k a lxk a a x f ∑∞=+=π:()(A )?=lk d l k f l a 0cos )(1ξπξξ (B )?-=ll k d l k f l a ξπξξcos )(1(C ) ?=lk k d l k f l a 0cos )(1ξπξξδ (D )?lkk d lk f l a 0cos)(2ξπξξδ 3.柯西公式为:()(A )ξξξπd z f i n z f l ?-=)(2!)( (B) ξξξπd z f i z f l ?-=)(21)( (C) ξξξπd z f i z f l n ?-=)()(21)( (D) ξξξπd z f i n z f l n ?-=)()(2!)( 4.在00=z 的邻域上把()=z f 2zz )(sin 展开为()(A )+-+-!6!4!21642z z z(B) +-+-!7!5!31642z z z (C) +-+-6421642z z z(D) +-+-!7!5!31864z z z5.求()z z f sin 1=在z 0=πn 的留数为()(A )!1n (B )n (C )n )1(- (D )16.以下那一个是第一类边界条件()(A ))(),(t f t x u ax == (B ))(,()t f t x u ax n == (C ))()(t f H u ax n u =+= (D )lx ttlx xu Mg t x u ==-=),(7.下列公式正确的为:(A ))()()(0x f dx x x f t =-?+∞∞-δ (B )0)()(0=-?+∞∞-dx x x f t δ (C )∞=-?+∞∞-dx x x f t )()(0δ (D ))()()(0t t f dx x x f =-?+∞∞-δ8.勒让德方程为(A )0)1(2)1(222=++--y l l dx dy x dx yd x(B )0]1)1([2)1(22222=--++--y x m l l dx dy x dx y d x(C )0)(22222=-++y dx dy x dx ym x d x(D )0)(22222=+-+y dxdy x dx y m x d x9.m 阶贝塞尔方程为:(A )0)(22222=--+R m x dx dR x dx R d x (B )0)(22222=-++R m x dx dR x dx R d x (C )0)(22222=+-+R m x dxdR x dx R d x (D )0)(2222=-++R m x dxdR x dx R d x 上 10Z 0是方程W ‘’+P (Z )W ‘+Q (Z )W=0的正则奇点,用级数解法求解时,这个方程的“判定方程“为(A )0)1(21=++---q sp s s (B )0)1(21=++--q sp s s (C )0)1(11=++---q sp s s (D )0)1(22=++---q sp s s二、填空题1、已知解析函数22),()(y x y x u z f -=的实部,则这个解析函数为。
数学物理方法习题答案.pdf
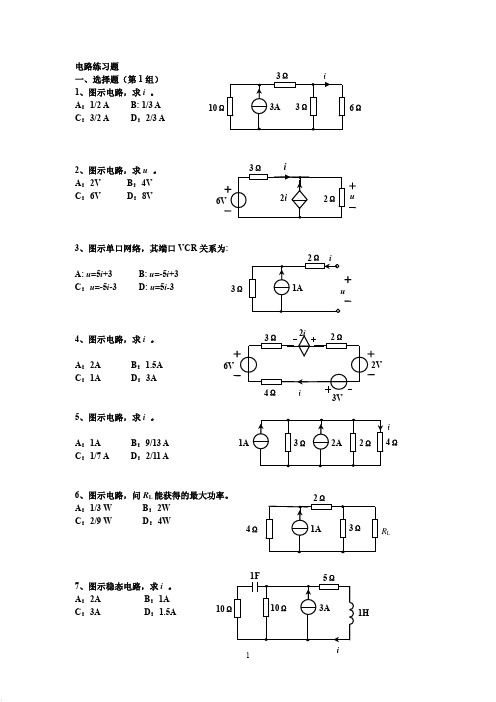
电路练习题一、选择题(第1组)1、图示电路,求i 。
A :1/2 A B: 1/3 A C :3/2 A D :2/3 A2、图示电路,求u 。
A :2VB :4VC :6VD :8V3、图示单口网络,其端口VCR 关系为:A: u =5i +3 B: u =-5i +3 C :u =-5i -3 D: u =5i-34、图示电路,求i 。
A :2AB :1.5AC :1AD :3A5、图示电路,求i 。
A :1AB :9/13 AC :1/7 AD :2/11 A6、图示电路,问R L 能获得的最大功率。
A :1/3 W B :2W C :2/9 W D :4W7、图示稳态电路,求i 。
A :2A B :1AC :3AD :1.5Ai 4ΩR L4Ω6Ω 10Ω1H108、图示稳态电路,问电容中的储能。
A :4J B :2JC :8JD :1J9、图示电路,t < 0时处于稳态, t = 0时,开关切到a , 当t = 5s 时,u c (t )是多少?A :6.3VB :5VC :2.4VD :3.16V10、图示电路,t < 0时处于稳态,t = 0时, 开关断开,求t = 1s 时u c (t )是多少? A :1.47V B :2.94V C: 5V D :4V11、图示电路原处于稳态,在t = 0时, 开关断开,求t = 0.1s 时的电流i (t )。
A :1A B :0 C :0.358A D :0.184 A12、图示正弦稳态电路,求i (t ) 。
A :)452cos(2°+t A B :)452cos(2°−t A C :)452cos(2°−t A D :)452cos(2°+t A13、图示正弦稳态电路中,有效值: I 是10A ,I R 是8A 。
问I c 是多少? A :2A B :18A C :6A D :4Ai(t)1H0.5Ω2ΩA2cos 22t u c1A c (t)2A14、图示正弦稳态电路, 求电阻上的平均功率。
物理数学方法试题及答案

物理数学方法试题及答案一、选择题(每题2分,共10分)1. 以下哪项不是傅里叶变换的性质?A. 线性B. 可逆性C. 尺度变换D. 能量守恒答案:D2. 拉普拉斯变换的收敛区域是:A. 左半平面B. 右半平面C. 全平面D. 虚轴答案:B3. 以下哪项是线性微分方程的特征?A. 可解性B. 唯一性C. 线性叠加原理D. 非线性答案:C4. 在复数域中,以下哪个表达式表示复数的模?A. |z|B. z^2C. z*zD. z/|z|答案:A5. 以下哪个函数是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = sin(x)D. f(x) = cos(x)答案:B二、填空题(每题3分,共15分)1. 傅里叶级数展开中,周期函数的系数可以通过______计算得到。
答案:傅里叶系数2. 拉普拉斯变换中,s = σ + jω代表的是______。
答案:复频域3. 线性微分方程的解可以表示为______的线性组合。
答案:特解4. 复数z = a + bi的共轭复数是______。
答案:a - bi5. 波动方程的一般解可以表示为______和______的函数。
答案:空间变量;时间变量三、简答题(每题5分,共20分)1. 简述傅里叶变换和拉普拉斯变换的区别。
答案:傅里叶变换主要用于处理周期信号,将时间域信号转换到频域;而拉普拉斯变换适用于非周期信号,将时间域信号转换到复频域。
2. 什么是波动方程?请给出其一般形式。
答案:波动方程是描述波动现象的偏微分方程,一般形式为∂²u/∂t² = c²∂²u/∂x²,其中u是波函数,c是波速。
3. 请解释什么是特征值和特征向量,并给出一个例子。
答案:特征值是线性变换中,使得变换后的向量与原向量方向相同(或相反)的标量。
特征向量则是对应的非零向量。
例如,对于矩阵A,如果存在非零向量v和标量λ,使得Av = λv,则λ是A的特征值,v是对应的特征向量。
数学物理方法试题汇总

12届真题1. 求下列各小题(2*5=10分):(1)用几何图形表示0arg(1)4z π<-<; (2)给出序列(1/)sin 6n n z i n π=+的聚点; (3)在复数域中求解方程cos 4z =的解;(4)给出二阶偏微分方程的基本类型;(5)给出解析函数所满足的柯西-黎曼方程。
2.按给定路径计算下列积分(5*2=10分):(1)320Re izdz +⎰,积分路径为线段[0,3]和[3,3+2i]组成的折线;(2)11,==⎰积分路径由z=1出发的。
3.利用留数定理计算下列积分(5*2=10分):(1)241x dx x +∞-∞+⎰; (2)3||1zz e dz z =⎰。
4.求常微分方程20w z w ''-=在0z =邻域内的两个级数解(15分)。
5.求下列线性非奇次偏微分方程的通解:2222u u xy y x y∂∂-=-∂∂(15分)。
6.利用分离变量法求解:(20分)2222000(),|0, |0,0, 0.x x l t t u u x l x t x u u u u t ====⎧∂∂-=-⎪∂∂⎪⎪==⎨⎪∂⎪==∂⎪⎩7.用拉普拉斯变换方法求解半无解问题(20分)220, 0,0,(0,)1, lim (,) 0, (,0)|0, 0.x u u x t t x u t u x t t u x x κ→∞⎧∂∂-=>>⎪∂∂⎪⎪=>⎨⎪=>⎪⎪⎩有界,2005级一、填空(请写在答题纸上,每题6分,共计48分)1. 三维泊松方程是______________________________2. 边界为Γ的区域Ω上函数u 的第二类边界条件为___________________。
3. 极坐标下的二维拉普拉斯方程为__________________________。
4. 定解问题2002||0tt xx t t t u u x u x u ===-∞<<+∞⎧⎪⎨==⎪⎩, ,的解__________________________。
物理数学物理法练习题含答案及解析

物理数学物理法练习题含答案及解析物理和数学是自然界的两个重要学科,它们之间有着紧密的联系。
物理数学是一门研究物理学中的数学方法和应用的学科,对于学习物理学和数学学科的学生来说,理解物理数学的基本概念和方法非常重要。
本文将为大家提供一些物理数学物理法的练习题,并附带答案及解析,希望能帮助大家加深对物理数学物理法的理解。
物理数学物理法练习题一:1. 对于一维的匀强磁场,其磁感应强度与位置关系为B(x)=B0(1-αx),求出在此磁场中的磁场力。
答案:由洛伦兹力公式F=q(v×B),其中q为电荷量,v为速度,B为磁感应强度。
在一维情况下,速度的方向与磁场垂直,即v⊥B。
则磁场力可表示为F=qvB=qvB0(1-αx)。
解析:根据洛伦兹力公式,磁场力的大小与电荷量、速度以及磁感应强度的乘积有关。
在一维匀强磁场中,磁感应强度与位置存在线性关系,根据此关系可以得到磁场力的表达式。
物理数学物理法练习题二:2. 在直角坐标系中,由一个点电荷产生的静电场强度为E=3xi+4yj,其中i和j为单位矢量,求出点电荷的电荷量。
答案:静电场的强度和电荷量的关系由高斯定律给出,即E=ρ/ε0,其中E为静电场强度,ρ为电荷密度,ε0为真空中的介电常数。
在此题中,静电场强度为E=3xi+4yj,代入高斯定律可得ρ/ε0=3xi+4yj。
解析:根据高斯定律,静电场的强度与电荷量的关系是一个线性关系。
通过求解此关系方程组,我们可以确定电荷量的值。
物理数学物理法练习题三:3. 一根长为L的均质细杆,质量为m,绕过其一端的固定轴按垂直于杆的方向以角速度ω旋转,求杆上离轴一端的质点的动能。
答案:质点的动能可表示为K=1/2Iω^2,其中K为动能,I为转动惯量,ω为角速度。
对于质点来说,其距离轴的距离为r=L,转动惯量为I=1/3mL^2。
代入公式,动能可表示为K=1/2(1/3mL^2)ω^2=1/6mL^2ω^2。
解析:根据转动惯量的定义和动能的定义,我们可以通过计算转动惯量和角速度的乘积来确定质点的动能。
数学物理方法习题答案

第11章综合习题11.1,设弦的初始位移为,初始速度为,求解无限长弦的自由振动.[答案 :解即为答朗贝尔公式 ()x ϕ()x ψ11(,)[()()]()d 22x at x at u x t x at x at a ϕϕψξξ+-=++-+⎰pause(0.0000001);end;11.2 半无限长弦的初始位移和速度都是零,端点作微小振动0|sin x u A t ω==,求解弦的振动.【答案 0,();sin (),()x x x u t u A t t a a aω=<=->】 11.3 求解细圆锥形均质杆的纵振动.【提示 作变换 u x =v/】【答案 12()()f x at f x at u x-++=】 11.4 半无限长杆的端点受到纵向力()sin F t A t ω=作用,求解杆的纵振动.【答案 00()()1,()d 221 ()d cos ()2x at at x x at at x x t u a a aA x aA t a YS a YS ϕϕψξξψξξωωω+-++->=+++--⎰⎰】 11.5已知初始电压分布为cos A kx ,cos kx ,求解无线长理想传输线上电压和电流的传播情况,【答案cos (),cos ()A k x at i k x at -=-v =】11.6 在GL CR =条件下求无限长传输线上的电报方程的通解.【答案 11{[()()]()d 22R x at t L x at e x at x at aϕϕψξξ+--++-+⎰】 11.7已知端点通过电阻R 而相接,初始电压分布为cos A kx ,初始电流分布为cos kx .求解半无限长理想传输线上电报方程的解;在什么条件下端点没有反射(遮住情况叫作匹配)?【答案 匹配的条件是0R =本章计算机仿真11.8 试用计算机仿真的方法,将11.2的弦振动规律以图形的分式表示出来.【解】计算机仿真程序w=pi;a=2;A=1.2;x=0:0.01:10;for t=1:0.5:25u=A*sin(pi*(t-x/a));plot(x,u);title('弦振动')xlabel('x')ylabel('u')11.9试用计算机仿真的方法,将11.5中的电压分布和电流分布用图形表示出来.【解】计算机仿真程序w=pi;a=2;A=1.2;k=2*pi;C=0.006;L=0.003;x=0:0.001:10;for t=1:0.5:25subplot(2,1,1);v=A*cos(k*(t-x/a));plot(x,v);title('电压动态分布')xlabel('x')ylabel('v')pause(0.0000001);subplot(2,1,2);i=sqrt(C/L)*A*cos(k*(t-x/a));plot(x,i);title('电流动态分布')xlabel('x')ylabel('i')pause(0.0000001);end;。
数学物理方法复习资料及参考答案(二)

数学物理方法复习资料及参考答案(二)一、选择题:1. 函数()f x 以0z 为中心的Taylor 展开的系数公式为:( )A ξξξπd z f i k C c k ⎰-=)()(20 B !)(0)(k z f C k k =C ξξξπd z f i C c k k ⎰+-=10)()(21 D ξξξπd z f i k C c k k ⎰+-=10)()(2 2。
⎰=-l dz a z )(( ) (其中l 表示以为a 中心ρ为半径的周围)。
A i ⋅πB iC i ⋅-πD 0 3. 非齐次边界条件)(),(0t u t u l x x νμ====,转化为齐次边界条件的方法:( )A )()(tB x t A + B x t A )(C )(t BD x t B x t A )()(2+ 4。
)(t f 是定义在半无界区间),0(∞上的函数,⎩⎨⎧<<<=)(0)0()(t T T t ht f在边界条件0)0(='f 下,把)(t f 展为实数形式傅立叶积分:( ) Aw h 12π B w wT h cos 2π C w wT h sin 2π D wwTh cos 12-π 5. 齐次边界条件0,00====l x x xu u 的本征值和本征函数:( ) A ),3,2,1,0(cos )(,222 ===n l xn C x X l n nn n ππλB ),3,2,1(sin )(,222 ===n l xn C x X l n nn n ππλC ),3,2,1,0()21(cos )(,)21(222 =+=+=n l xn C x X ln n n n ππλD ),3,2,1,0()21(sin )(,)21(222 =+=+=n l xn C x X l n nn n ππλ6. 若集合是( ),则该集合是区域。
A 开集B 连通开集C 连通闭集D 连通集 7. 设a 是)(z f 的可去奇点,则有:( )Alim ()Z af Z →存在且有限 Blim ()Z af Z →不存在C )(z f 在a 点的主要部分只有有限项D )(z f 在a 点的主要部分有无限多项8。
兰州大学高等数学物理类学年第二学期A卷

考试试卷(A卷)
课程名称:高等数学(物理类)任课教师:
学院:专业:年级:
姓名:校园卡号:
题号
一
二
三
四
五
六
七
八
总分
分数
阅卷教师
一填空题(每小题5分,共40分):
1.求方程 的通解。
2.求方程 的通解。
3.求球面 与柱面 交线在 点的切线方程。
4.求直线 与直线 之间的夹角。
四(10分)求球面 在抛物面 之外部分的面积。
五(10分)求由抛物面 和锥面 所围几何体的体积。
六(10分)计算曲面积分 ,其中 为柱面 、抛物面 与坐标面在第一卦限所围几何体的外侧。
七(8分)求表面积为 而体积最大的长方体的体积。
5.计算极限 。
6.求函数 的偏导数。
7.求函数 在 点沿方向角分别是 的方向导数。
8.计算曲线积分 ,其中 是圆周 。
二(12分)已知函数 满足微分方程
(1)求参数 ,利用变换 将原方程变形,使新方程中不出现一阶偏导项;
()再令 ,使新方程变换形式。
三(10分)设 连续可微,而 是由方程 所确定的 的函数,求 。
数学物理方法试卷与答案

《数学物理方法》试卷一、选择题(每题4分,共20分) 1.柯西问题指的是( )A .微分方程和边界条件. B. 微分方程和初始条件. C .微分方程和初始边界条件. D. 以上都不正确. 2.定解问题的适定性指定解问题的解具有( )A .存在性和唯一性. B. 唯一性和稳定性. C. 存在性和稳定性. D. 存在性、唯一性和稳定性.3.牛曼内问题 ⎪⎩⎪⎨⎧=∂∂=∇Γf n u u ,02 有解的必要条件是( )A .0=f .B .0=Γu .C .0=⎰ΓdS f . D .0=⎰ΓdS u .4.用分离变量法求解偏微分方程中,特征值问题⎩⎨⎧==<<=+0)()0(0 ,0)()(''l X X lx x X x X λ的解是( )A .) cos , (2x l n l n ππ⎪⎭⎫ ⎝⎛. B .) sin , (2x l n l n ππ⎪⎭⎫ ⎝⎛. C .) 2)12(cos ,2)12( (2x l n l n ππ-⎪⎭⎫ ⎝⎛-. D .) 2)12(sin,2)12( (2x l n l n ππ-⎪⎭⎫⎝⎛-. 5.指出下列微分方程哪个是双曲型的( ) A .0254=++++y x yy xy xx u u u u u . B .044=+-yy xy xx u u u .C .02222=++++y x yy xy xx u y xyu u y xyu u x .D .023=+-yy xy xx u u u .二、填空题(每题4分,共20分)1.求定解问题⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤==>-==><<=∂∂-∂∂====πππx 0 ,cos 2 ,00 t ,sin 2 ,sin 20 ,0 ,00002222x u u t u t u t x x ut u t t t x x 的解是_____________________________________.2.对于如下的二阶线性偏微分方程0),(),(2),(=++++-fu eu du u y x c u y x b u y x a y x yy xy xx其特征方程为________________________________________________________. 3.二阶常微分方程0)()4341()(1)(2'''=-++x y xx y x x y 的任一特解=y __________ _______________________________________________.4.二维拉普拉斯方程的基本解为________________________________________,三维拉普拉斯方程的基本解为__________________________________________. 5.已知x x x J x x x J cos 2)( ,sin 2)(2121ππ==-,利用Bessel 函数递推公式求=)(23x J _______________________________________.三、(15分)用分离变量法求解如下定解问题22222000, 0, 00, 0, t 0, 0, 0x .x x lt t t u ua x l t t x uu x x u x ul ====⎧∂∂-=<<>⎪∂∂⎪∂∂⎪==>⎨∂∂⎪⎪==≤≤⎪⎩四、(10分)用行波法求解下列问题⎪⎪⎩⎪⎪⎨⎧+∞<<∞-=∂∂=+∞<<∞->=∂∂-∂∂∂+∂∂==.,0 ,3 , ,0 ,03202022222x y u x u x y y uy x u xu y y五、(10分)用Laplace 变换法求解定解问题:⎪⎪⎪⎩⎪⎪⎪⎨⎧<<=>==><<∂∂=∂∂===.20 ,sin ,0 ,0,0 ,20 ,02022x x u t u u t x x ut u t x x π六、(15分)用格林函数法求解下定解问题222200, y 0,() , .y u ux y u f x x =⎧∂∂+=<⎪∂∂⎨⎪=-∞<<+∞⎩七、(10分)将函数()f x x =在区间[0,1]上展成Bessel 函数系(1)11{()}m m J x μ∞=的级数,其中(1)m μ为Bessel 函数1()J x 的正零点,1,2,m = .2008—2009学年第二学期 《数学物理方法》试卷B 答案一、选择题(每题4分,共20分) 1.柯西问题指的是( B )A .微分方程和边界条件. B. 微分方程和初始条件. C .微分方程和初始边界条件. D. 以上都不正确. 2.定解问题的适定性指定解问题的解具有( D )A .存在性和唯一性. B. 唯一性和稳定性. C. 存在性和稳定性. D. 存在性、唯一性和稳定性.3.牛曼内问题 ⎪⎩⎪⎨⎧=∂∂=∇Γf n u u ,02 有解的必要条件是( C )A .0=f .B .0=Γu .C .0=⎰ΓdS f . D .0=⎰ΓdS u .4.用分离变量法求解偏微分方程中,特征值问题⎩⎨⎧==<<=+0)()0(0 ,0)()(''l X X lx x X x X λ的解是( B )A .) cos , (2x l n l n ππ⎪⎭⎫ ⎝⎛. B .) sin , (2x l n l n ππ⎪⎭⎫⎝⎛. C .) 2)12(cos ,2)12( (2x l n l n ππ-⎪⎭⎫ ⎝⎛-. D .) 2)12(sin,2)12( (2x l n l n ππ-⎪⎭⎫⎝⎛-. 5.指出下列微分方程哪个是双曲型的( D ) A .0254=++++y x yy xy xx u u u u u . B .044=+-yy xy xx u u u .C .02222=++++y x yy xy xx u y xyu u y xyu u x .D .023=+-yy xy xx u u u .二、填空题(每题4分,共20分)1.求定解问题⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤==>-==><<=∂∂-∂∂====πππx 0 ,cos 2 ,00 t ,sin 2 ,sin 20 ,0 ,00002222x u u t u t u t x x ut u t t t x x 的解是(x t cos sin 2).2.对于如下的二阶线性偏微分方程0),(),(2),(=++++-fu eu du u y x c u y x b u y x a y x yy xy xx其特征方程为( 0))(,(),(2))(,(22=++dx y x c dxdy y x b dy y x a ). 3.二阶常微分方程0)()4341()(1)(2'''=-++x y xx y x x y 的任一特解=y ( )21(23x J 或0).4.二维拉普拉斯方程的基本解为( r1ln),三维拉普拉斯方程的基本解为( r1).5.已知x x x J x x x J cos 2)( ,sin 2)(2121ππ==-,利用Bessel 函数递推公式求=)(23x J ()s i n )(1(2)cos sin 1(223xxdx d x x x x x x ππ-=- ).三、(15分)用分离变量法求解如下定解问题22222000, 0, 00, 0, t 0, 0, 0x .x x l t t t u ua x l t t x uu x x u x ul ====⎧∂∂-=<<>⎪∂∂⎪∂∂⎪==>⎨∂∂⎪⎪==≤≤⎪⎩解:第一步:分离变量 (4分) 设)()(),(t T x X t x u =,代入方程可得)()()()()()()()(2''''''2''x T a x T x X x X t T x X a t T x X =⇒=此式中,左端是关于x 的函数,右端是关于t 的函数。
兰州大学——数学物理方法期末试卷A

数学物理方法常用的公式(注:仅供参考):拉普拉斯算子作用于标量场在圆柱坐标系和球坐标系下的表示:22222211u u uuzρρρρρϕ⎛⎫∂∂∂∂∇=++⎪∂∂∂∂⎝⎭;22222222111sinsin sinu u uu rr r r r rθθθθθϕ∂∂∂∂∂⎛⎫⎛⎫∇=++⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭勒让德多项式的微分表示:()()21P12!lll l ldx xl dx=-勒让德-傅里叶级数展开:定义在x的区间[]1,1-的至少分段光滑函数()f x可以展开为广义傅里叶级数:()()Pl llf x a x+∞==∑其中,系数()()1121P2l lla f x x dx-+=⎰勒让德多项式的生成函数:()()()()11P cos,0P cos,llllllllrr RRRr Rrθθ+∞+=+∞+=⎧≤<⎪⎪=⎨⎪>⎪⎩∑∑在球坐标下下的梯度表示()()()(),,,,,,11,,sinru r u r u ru r e e er r rθϕθϕθϕθϕθϕθθϕ∂∂∂∇=++∂∂∂r r r一、(本题10分,每小题5分)(1)证明:()k r k∇•=r rr,其中x y zr xe ye ze=++r r r r,kr为常矢量。
(2)计算矢量场2sinx y zA xye z ye yz e=++r r r r的旋度。
二、(本题10分,每小题5分)将下列复数写成代数形式,其中i 为虚数单位,(1 (2)cos 23i π⎛⎫+ ⎪⎝⎭三、(本题10分)已知解析函数()f z 的实部323u x xy =-,且满足()00f =,求该解析函数()f z 。
四、(本题10分) 将函数()2132f z z z =-+以01z =为中心的邻域内做洛朗级数展开。
五、(本题10分) 计算实变函数积分2212cos dxI x πεε=-+⎰, ()01ε<<六、(本题10分)设有一根均匀的柔软的细弦,当它做微小的横振动时,除受内部张力作用外,还受到阻尼力的作用,设阻尼力与速度成正比,比例系数为k ,即单位长度的弦所受阻力(),du x t f kv k dt=-=-。
数学物理方法习题及答案

数学物理⽅法习题及答案数学物理⽅法习题第⼀章:应⽤⽮量代数⽅法证明下列恒等式 1、3r ?= 2、0r ??=3、()()()()()A B B A B A A B A B =?-?-?+?4、21()0r ?=5、()0A = 第⼆章:1、下列各式在复平⾯上的意义是什么? (1)0;2Z a Z b z z -=--=(2)0arg4z i z i π-<<+; 1Re()2z =2、把下列复数分别⽤代数式、三⾓式和指数式表⽰出来。
1;1i i e ++3、计算数值(a 和b 为实常数,x 为实变数)sin5ii ? sin sin()iaz ib za ib e -+4、函数1W z =将z 平⾯的下列曲线变为W 平⾯上的什么曲线?(1)224x y += (2)y x =5、已知解析函数()f z 的实部(,)u x y 或虚部(,)x y υ,求解析函数。
(1)22sin ;,(0)0;,(1)0x u e y u x y xy f u f ?==-+===;(2)(00)f υ==6、已知等势线族的⽅程为22x y +=常数,求复势。
第三章:1、计算环路积分:2211132124sin4(1).(2).11sin (3).(4).()231(5).(1)(3)zz z i z z z z z e dz dzz z ze dz dzz z z dzz z ππ+=+====-+--+-2、证明:21()!2!n n z n l z z e d n i n ξξπξξ=其中l 是含有0ξ=的闭合曲线。
3、估计积分值222iidz z +≤?第四章: 1、泰勒展开(1) ln z 在0z i = (2)11ze-在00z = (3)函数211z z -+在1z = 2、(1)1()(1)f z z z =-在区域01z <<展成洛朗级数。
(2)1()(3)(4)f z z z =--按要求展开为泰勒级数或洛朗级数:①以0z =为中⼼展开;②在0z =的邻域展开;③在奇点的去⼼邻域中展开;④以奇点为中⼼展开。
数学物理方法考题汇总

第一章 一维波动方程的付氏解一.简述偏微分方程,阶,线性非线性,齐次非齐次的概念答:(1)含有未知函数关于自变量的偏导数的等式称为偏微分方程,简称PDE(Partial Differential Equation)(2)偏微分方程的阶:出现在偏微分方程中未知函数偏导数的最大阶数。
(3)方程中各项关于未知函数及其各阶偏导数都是一次的,称为线性;否则称为非线性方程。
(4)不含有未知函数及其偏导数的项称为自由项,自由项为零的方程称为齐次方程,否则称为非齐次方程。
二.P24(8) 指出下列微分方程的阶、线性、齐次性:①(Tricomi 方程): 0xx yy yu u += (2阶线性齐次)②(Klein-Gordon 方程): 220tt u y u c u -∆+=(2阶线性齐次)③(激波方程): 0t x u uu += (1阶非线性齐次) ④(KdV 方程 ): 60t x xxx u uu u -+= (3阶非线性齐次)⑤(多空介质方程): mt u k u =∆ (2阶非线性齐次)三.简述二阶线性偏微分方程的分类方法,P24(9) 对方程111222122+++++=xxxy yy x y a u a u a u b u b u cu f21211220 ()=0 ()<(Laplace,Poisson)a a a >⎧⎪∆≡-⎨⎪⎩双曲型弦振动抛物型热传导0 椭圆型(1)43260+-++=xx xy yy x y u u u u u :双曲线型(2)22(1)(1)0+++++=xx yy x y x u y u xu yu :椭圆型四.何谓发展方程?何谓位势方程?何谓叠加原理?(1) 发展方程: 所描述的物理过程随时间而演变,如:波动方程、热传导方程等;(2) 位势方程:所描述的自然现象是稳恒的,即与时间无关,如:静电场、引力场等。
(3) 几种不同原因综合产生的效果等于这些原因单独产生效果的累加.叠加原理适用于线性方程所描述的物理现象.五.试推导一维波动方程。
数学物理方法样卷

x(t)
=
1 H(t) (2et
−
2 cos 2t
−
) sin 2t
5
三、求解初值问题:
utt = uxx uu|tt|=t=00==x12
(−∞ < x < +∞)
(本小题 15 分)
解: 由达朗贝尔公式:
1 u = [φ(x + at) + φ(x − at)] +
1
∫
x+at
ψ(ξ) dξ
2
l
Xn(x)
=
sin
nπ l
x
Tn(t)
=
Cn
cos
nπa l
t
+
Dn
sin
nπa l
t
利用解的叠加原理, 可得满足方程和边界条件的级数形式解
u(x,
t)
=
∑ ∞
( Cn
cos
nπa t
l
+
Dn
sin
nπa l
) t
sin
nπ l
x
n=0
由初始条件 ut|t=0 , 得 Dn = 0 ,
由
u|t=0
x(t)
=
1 H(t) (et
) − cos t − sin t
2
三、求解初值问题:
utt − a2uxx = 0 uu(t(xx,,00))==ceo−s1x
(−∞ < x < +∞)
(本小题 15 分)
······2 分 ······3 分 ······5 分 ······2 分 ······3 分
X′′(x) + λX(x) = 0
高考物理兰州物理方法知识点基础测试题含答案

高考物理兰州物理方法知识点基础测试题含答案一、选择题1.许多科学家在物理学发展过程中做出了重要贡献,下列叙述中符合物理学史实的是()A.牛顿发现了万有引力定律,通过实验测出了万有引力常量B.哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律C.库仑在前人研究的基础上通过扭秤实验研究得出了库仑定律D.法拉第通过实验得出了欧姆定律2.如图所示,重为G的光滑球在倾角为θ的斜面和竖直墙壁之间处于静止状态.若将此斜面换成材料和质量相同,但倾角θ稍小一些的斜面,以下判断正确的是 ()A.球对斜面的压力增大B.球对斜面的压力减小C.斜面可能向左滑动D.地面受到的压力变小3.在物理学的重大发现中科学家们创造出了许多物理学研究方法,如理想实验法、控制变量法、极限思维法、类比法和科学假说法、建立理想模型法、微元法等等.以下关于所用物理学研究方法的叙述不正确的是()A.牛顿用微元法提出了万有引力定律,并计算出了太阳和地球之间的引力B.根据速度定义式xvt∆=∆,当△t非常非常小时,xt∆∆就可以表示物体在t时刻的瞬时速度,该定义应用了极限思维法C.将插有细长玻璃管的玻璃瓶内装满水.用力捏玻璃瓶,通过细管内液面高度的变化,来反映玻璃瓶发生形变,该实验采用了放大的思想D.在推导匀变速运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,然后把各小段的位移相加,这里采用了微元法4.如图所示,粗糙程度均匀的绝缘空心斜面ABC放置在水平面上,∠CAB=30°,斜面内部O点(与斜面无任何连接)固定有一正点电荷,一带负电的小物体(可视为质点)可以分别静止在M、N、MN的中点P上,OM=ON,OM∥AB,则下列判断正确的是()A.小物体分别在三处静止时所受力的个数一定都是4个B.小物体静止在P点时受到的支持力最大,静止在M、N点时受到的支持力相等C.小物体静止在P点时受到的摩擦力最大D.当小物体静止在N点时,地面给斜面的摩擦力为零5.如图所示,放在粗糙水平桌面上的物体m2,通过跨过定滑轮的绳与物体m1相连,若由静止释放m1,m2的加速度大小为α,现取走m1,用力F向下拉绳,使m2的加速度仍为α,不计滑轮摩擦及绳的质量,则 ( )A.F>m1g B.F<m1gC.F=m1g D.以上三种情况都有可能6.如图所示,两个质量都是m的小球A和B用轻杆连接,斜靠在墙上处于平衡状态。
数学物理方法试题一

备注:请出A、B两套试题并用微机打印,于考试前两周将试题及标准答案送院办公室。第一页,共页
兰州大学物理科学与技术学院物理系1、2专业(班)二年级数学物理方法课程
2003—2004学年第二学期(A)卷期末考试题(150分钟)
考试时间姓名学号
题号
得分
分数
主考教师:徐进章阅卷教师:
一、填空题(30分,没有标明分数值的每空3.5分)
格林函数是,其对称性可表示为:=;科希-黎曼条件(又称C-R条件)为:,是复变函数可导的(1分);用指数形式表示 的值; 在复数平面上具有的物理意义是:;勒让德多项式的母函数为:;已知像函数为 ,其原函数为; 的像函数为;数学物理方程的三类边界条件可用一个数学式表示出来其中第二类边界条件是(1分)的情况。
二、(20分)均匀圆球,半径为 ,初始温度均匀为 ,把它放入温度为 的烘箱,使球面温度保持为 ,求解球内各处温度 的变化情况。
三、(20分)矩形膜,边长为 和 , 边及其对边固定,另两边处于自由个半径为 的空心球,若表面充电到电势为 ,求解球内、外的电势分布。
