自下而上语法分析习题
习题与答案-5-语法分析-自上而下
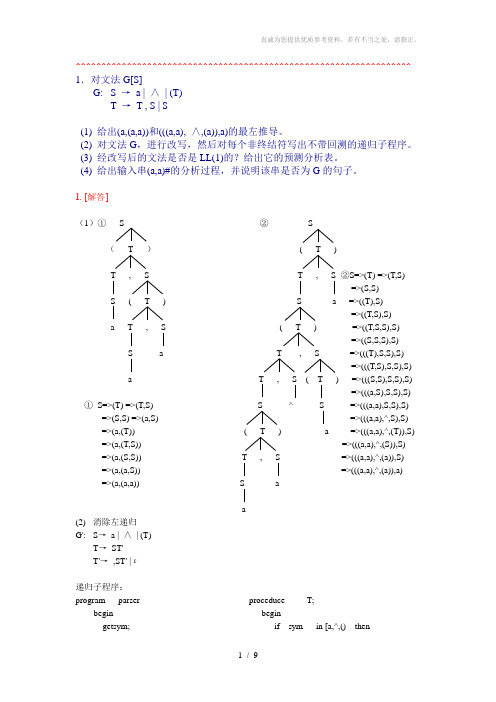
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 1.对文法G[S]G: S →a | ∧| (T)T →T , S | S(1) 给出(a,(a,a))和(((a,a), ∧,(a)),a)的最左推导。
(2) 对文法G,进行改写,然后对每个非终结符写出不带回溯的递归子程序。
(3) 经改写后的文法是否是LL(1)的?给出它的预测分析表。
(4) 给出输入串(a,a)#的分析过程,并说明该串是否为G的句子。
1. [解答](1)①S ②S(T )( T )T , S T , S ②S=>(T) =>(T,S)=>(S,S) S ( T ) S a =>((T),S)=>((T,S),S)a T , S ( T ) =>((T,S,S),S)=>((S,S,S),S) S a T , S =>(((T),S,S),S)=>(((T,S),S,S),S)a T , S ( T ) =>(((S,S),S,S),S)=>(((a,S),S,S),S) ①S=>(T) =>(T,S) S ^ S =>(((a,a),S,S),S)=>(S,S) =>(a,S) =>(((a,a),^,S),S) =>(a,(T)) ( T ) a =>(((a,a),^,(T)),S) =>(a,(T,S)) =>(((a,a),^,(S)),S)=>(a,(S,S)) T , S =>(((a,a),^,(a)),S)=>(a,(a,S)) =>(((a,a),^,(a)),a)=>(a,(a,a)) S aa(2) 消除左递归G': S→a | ∧| (T)T→ST'T'→,ST' |ε递归子程序:program parser proceduce T;begin begingetsym; if sym in [a,^,() thenS beginend; S;proceduce S; T;begin end;if sym=’a’ or sym=’^’ then elsegetsym error;elseif sym=’(‘ end;begin getsym; proceduce T’;T; beginIf sym=’)’ then if sym=’,’ thenGetsym; beginElse getsym;Error; S;End; T;Else end;Error; elseEnd; if sym=’)’ thenelseerror;end;预测分析表不含多重定义入口, 所以该文法是LL(1)文法!(4) 分析栈余留串所用产生式或动作1 #S (a,a)# S—>(T)2 #)T( (a,a)# (匹配3 #)T a,a)# T—>ST’4 #)T’S a,a)# S—>a5 #)T’a a,a)# a匹配6 #)T’ ,a)# T’ —>,ST’7 #)T’S, ,a)# ,匹配8 #)T’S a)# S—>a9 #)T’a a)# a匹配10 #)T’ )# T’—>ε11 #) )# )匹配12 # # 接受因为(a,a)#分析成功所以(a,a)为文法的句子步骤分析栈余留串所用产生式或动作1 #S (a,a# S→(T)2 #)T( (a,a# ( 匹配3 #)T a,a# T→ST’4 #)T’S a,a# S→a5 #)T’a a,a# a 匹配6 #)T’,a# T’→,ST’7 #)T’S, ,a# , 匹配8 #)T’S a# S→a9 #)T’a a# a 匹配10 #)T’# 出错^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 2. G: E →TE'E' →+E |εT →FT'T' →T |εF →PF'F' →*F' |εP →(E) | a | b |∧预测分析表^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 3.已知文法G: S →MH | aH →LSo |εK →dML |εL →eHfM →K | bLM判断G是否是LL(1)文法,如果时,构造LL(1)分析表。
第三章 语法分析

第三章语法分析典型例题 :单项选择题3.1.1. 文法 G: S-xSxly 所识别的语言是 _____ (陕西省 1997 年自考题)a. xyxb. (xyx)*c. xnyxn(n ≥ 0)d. x*yx*3.1.2. 文法 G 描述的语言 L(G) 是指 _____ 。
a. L(G)= {α |S=α,α ∈ VT* }b. L(G)={ α |SA=α , α ∈ VT* }c .L(G)={ α |S=α,α∈ (VT ∪ VN)* } d. L(G)= {α |S=α , α∈ (VT ∪ VN)* }3.1.3. 有限状态自动机能识别_。
a. 上下文无关文法b. 上下文有关文法c. 正规文法d. 短语文法3.1.4. 设 G 为算符优先文法, G 的任意终结符对 a, b 有以下关系成立 ____ 。
a. 若 f(a)g(b) ,则 a bb. 若 f(a)<g(b) ,则 a<bc.a~b 都不一定成立d. a~b 一定成立3.1.5 .茹果文法 G 是无二义的,则它的任何句子α _ _。
(西电 1999 年研究生试题)a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导,但它们对应的语法树相同3.1. 6. 由文法的开始符经。
步或多步推导产生的文法符号序列是 ____ 。
(陕西省 2000 年自考题)a .短语 b. 句柄 c. 句型 d. 句子3.1.7 .文法 G : E-E+TITT-T*P|PP-(E)|I则句型 P+T+i 的句柄和最左素短语分别为 __ _。
a. P+T 和 ib. P 和 P+Tc. i 和 P+T+id. P 和 P3.1.8 .设文法为: S--SA|AA→a|b则对句子 aba ,下面 ____ 是规范推导.a. S=SA=SAA=AAA=aAA=abA=abab. S=SA=SAA=AAA=AAa= Aba =abac. S=SA=SAA=SAa=Sba= Aba =abad. S=SA=Sa=Sba= Aba =aba3.1.9. 文法G: S → b| ∧ |(T)T-T,SIS则 FIRSTVT(T)=____ 。
实验5---语法分析器(自下而上):LR(1)分析法

实验5---语法分析器(自下而上):LR(1)分析法一、实验目的构造LR(1)分析程序,利用它进行语法分析,判断给出的符号串是否为该文法识别的句子,了解LR(K)分析方法是严格的从左向右扫描,和自底向上的语法分析方法。
二、实验内容程序输入/输出示例(以下仅供参考):对下列文法,用LR(1)分析法对任意输入的符号串进行分析:(1)E->E+T(2)E->E—T(3)T->T*F(4)T->T/F(5)F-> (E)(6)F->i输出的格式如下:(1)LR(1)分析程序,编制人:姓名,学号,班级(2)输入一个以#结束的符号串(包括+—*/()i#):在此位置输入符号串(3)输出过程如下:3.对学有余力的同学,测试用的表达式事先放在文本文件中,一行存放一个表达式,同时以分号分割。
同时将预期的输出结果写在另一个文本文件中,以便和输出进行对照。
三、实验方法1.实验采用C++程序语言进行设计,文法写入程序中,用户可以自定义输入语句;2.实验开发工具为DEV C++。
四、实验步骤1.定义LR(1)分析法实验设计思想及算法①若ACTION[sm , ai] = s则将s移进状态栈,并把输入符号加入符号栈,则三元式变成为:(s0s1…sm s , #X1X2…Xm ai , ai+1…an#);②若ACTION[sm , ai] = rj则将第j个产生式A->β进行归约。
此时三元式变为(s0s1…sm-r s , #X1X2…Xm-rA , aiai+1…an#);③若ACTION[sm , ai]为“接收”,则三元式不再变化,变化过程终止,宣布分析成功;④若ACTION[sm , ai]为“报错”,则三元式的变化过程终止,报告错误。
2.定义语法构造的代码,与主代码分离,写为头文件LR.h。
3.编写主程序利用上文描述算法实现本实验要求。
五、实验结果1. 实验文法为程序既定的文法,写在头文件LR.h中,运行程序,用户可以自由输入测试语句。
编译原理-南京大学-自下而上语法分析共102页

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
拉
60、生活的道路一旦选定,事物有规律,这是不 容忽视 的。— —爱献 生
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
编译原理第三版 第五章 自下而上语法分析

a
b a
A a
b A A a a
c A a
d c A a
e B B c c A A a a
S
(2) 分析树: 用树表示“移进 - 归约 ”过程
A A B S
b
A
b
b
d
a
A
直接短语
T i F
句柄
T
T * F F ( E ) i
E + T T F
规范归约
设α是文法G的一个句子, 若序列αn, αn-1, …, α0,满足: (1)αn = α; (2) α0 = S; (3)对任 意i , 0< i ≤n , αi-1 是从αi 将句柄替换成 相应产生左部符号而得到的;则称该序列是一个 规范归约。
1、归约与分析树
(1)移进-归约法: 使用符号栈, 把输入符号逐一移 进栈, 栈顶出现某个产生式右部时归约为左部。
例 :给定文法 G: (1) S→aAcBe (2) A→b (3) A→Ab (4) B→d 输入串 abbcde是否为句子? 归约过程如下: 步骤: 1. 2. 进 进 动作: a b
例:文法G: G[E]: E→E+E|E*E |(E) |i (1) E→E+T│T (2) T→T*F│F (3) F→P↑F│P (4) P→(E)│i 算符优先关系为: 由(4): P→(E) ∴( =) 由(1) (2): E→E+T, T => T*F ∴+<* 由(2) (3): T→T*F, F => P↑F ∴ *<↑ 由(1): E→E+T, E => E+T ∴ +>+ 由(3): F→P↑F, F=> P↑F ∴ ↑ <↑ 由(4): P→(E), E => E+T ∴ ( < +, +>) ... ∴ G为算符优先文法(优先关系表如表5.1所示,P90) #看作终结符号
习题与答案-5-语法分析-自下而上-优先分析

第六章P1163.有文法G[S]:S—>V V—>T|ViT T—>F|T+F F—>)V*|( (1)给出( + ( i ( 的规范推导。
(2)指出句型F+Fi(的短语,句柄,素短语。
(3)G[S]是否OPG?若是,给出(1)中句子的分析过程。
3. G[S]: S—>VV—>T|ViTT—>F|T+FF—>)V*|((1)S S=>V=>ViT=>ViF=>Vi(=>Ti(=>T+Fi(=>T+(i(V =>F+(i(=>(+(I(V i TT FT + F (F (((2) S 短语 F , F+F , ( , F+Fi(句柄 FV 素短语F+F , (V i TT FT + F (F(3) V N FIRSTVT LASTVTF ) ( * (T ) ( + * ( +V ) ( + i * ( + iS ) ( + i * ( + i由V—>ViT得任意(LASTVT(V))>i , i<任意(FIRSTVT(T)) 由#S#得# = ##<任意(FIRSTVT(S)) , 任意(LASTVT(S))># 由T—>T+F得任意(LASTVT(T))>+ +<任意(FIRSTVT(F)) 由F—>)V*得)=* ) < 任意(FIRSTVT(V))任意(LASTVT(V))>* 由此构造运算符优先关系表如下:i + ) * ( #i > < < > < >+ > > < > < >) < < < = <* > > > >( > > > ># < < < < =由关系表中任何两符号只有一种关系知文法为OPG文法步栈当前符号余留串关系动作0 # (+(i(# #<( 移进1 #( + (i(# (>+ 归约2 #N + (i(# #<+ 移进3 #N+ ( i(# +<( 移进4 #N+( i (# (>i 归约5 #N+N i (# +>i 归约6 #N i (# #<i 移进7 #Ni ( # i<( 移进8 #Ni( # (># 移进9 #NiN # i># 归约10 #N # #=# 成功4.已知文法G[S]为:S—>S;G|G G—>G(T)|H H—>a|(S) T—>T+S|S (1)构造G[S]的算符优先关系表,并判断G[S]是否为算符优先文法。
实验三 自下而上语法分析及语义分析

实验三自下而上语法分析及语义分析一、实验目的:通过本实验掌握LR分析器的构造过程,并根据语法制导翻译,掌握属性文法的自下而上计算的过程。
二、实验学时:4学时。
三、实验内容根据给出的简单表达式的语法构成规则(见五),编制LR分析程序,要求能对用给定的语法规则书写的源程序进行语法分析和语义分析。
对于正确的表达式,给出表达式的值。
对于错误的表达式,给出出错位置。
四、实验方法采用LR分析法。
首先给出S-属性文法的定义(为简便起见,每个文法符号只设置一个综合属性,即该文法符号所代表的表达式的值。
属性文法的定义可参照书137页表6.1),并将其改造成用LR分析实现时的语义分析动作(可参照书145页表6.5)。
接下来给出LR分析表。
然后程序的具体实现:●LR分析表可用二维数组(或其他)实现。
●添加一个val栈作为语义分析实现的工具。
●编写总控程序,实现语法分析和语义分析的过程。
注:对于整数的识别可以借助实验1。
五、文法定义简单的表达式文法如下:E->E+T|E-T|TT->T*F|T/F|FF->(E)|i上式中,i 为整数。
六、处理程序例例1: 正确源程序例:23+(45+4)* 40分析结果应为:正确的表达式。
其值为:1983例2: 错误源程序例:5+(56+)-24分析结果应为:错误的表达式:出错位置为)附录:源程序#include <stdio.h>#include"string.h"#include <iostream>using namespace std;#define R 30#define C 20typedef struct elem{char e[4];}Elem; //ACTION表与GoTo表中的元素类型Elem LR[R][C]; //存放ACTION表与GoTo表中的内容typedef struct out{int order; //序号int state[10]; //状态栈char sign[30]; //符号栈char grasen[20]; //产生式char input[30]; //输入串char explen[50]; //解释说明}OutNode; //输出结果中每一行的类型OutNode out[20]; //存放输出结果char Sentence[20]; //存放文法的一个句子char GramSent[10][20]; //存放文法的一组产生式int row,colno; //row为状态个数数,colno为ACTION表与GoTo表列总数int stateTop=0,signTop=0; //状态栈与符号栈的栈顶位置(值与栈中元素的个数相等)void input_GramSent(){int i,num;printf("请输入文法中产生式的个数\n");scanf("%d",&num);for(i=0;i<num;i++){printf("请输入文法的第%d个产生式\n",i);scanf("%s",GramSent+i-1);}printf("请输入文法的一个句子\n");scanf("%s",Sentence);printf("**********************************************************\n");printf("* 文法的产生式如下: *\n");printf("**********************************************************\n");for(i=0;i<num;i++)printf("%s\n",GramSent+i);printf("**********************************************************\n");printf("* 文法的句子如下: *\n");printf("**********************************************************\n");printf("%s\n",Sentence);}void input_LR(int row,int colno) //row为行总数,colno为列总数{int i,j;char mid[4];printf("**********************************************************\n");printf("* 提示:每输入一个元素后就回车 *\n");printf("**********************************************************\n");printf("请输入LR分析表的终结符(包括#)与非终结符\n");for(j=0;j<colno;j++)scanf("%s",LR[0][j].e);for(i=0;i<row;i++){printf("请输入%d号状态所对应的各列的元素,空白的地方用s代替\n",i);for(j=0;j<colno;j++){scanf("%s",mid);if(strcmp(mid,"s")==0||strcmp(mid,"S")==0)strcpy(LR[i+1][j].e," ");elsestrcpy(LR[i+1][j].e,mid);}}}void output_LR(int row,int colno){int i,j;printf("**********************************************************\n"); printf("* LR分析表如下: *\n");printf("**********************************************************\n"); printf("\n");printf(" ");for(j=0;j<colno;j++)printf("%s ",LR[0][j].e);printf("\n");for(i=1;i<=row;i++){printf("%d ",i-1);for(j=0;j<colno;j++)printf("%s ",LR[i][j].e);printf("\n");}printf("\n");}int SignNum(char ch)//给定一个终结符或非终结符,返回其在ACTION表与GoTo表中的列位置int i;char c[2]="0";c[0]=ch;for(i=0;i<colno;i++)if(strcmp(c,LR[0][i].e)==0)return i;return -1;}int CharChangeNum(char* ch)//给定一数字字符串,返回其所对应的数字{int result=0;while(*ch!='\0'){result=result*10+(*ch-'0');ch++;}return result;}int OutResult(int s,int c,int i)//输出结果的第i+1行处理函数,(s 为状态,c为列){char mid[4],gra[20];int s_num,r_num;int n,len,j;strcpy(mid,LR[s+1][c].e);if(strcmp(mid," ")==0){ printf("不能规约\n"); return -2; }if(strcmp(mid,"acc")==0||strcmp(mid,"ACC")==0){ printf("规约成功\n"); return -1; }out[i+1].order=i+2;if(mid[0]=='s'||mid[0]=='S'){s_num=CharChangeNum(mid+1);//s_num为S后的数字for(j=0;j<stateTop;j++)out[i+1].state[j]=out[i].state[j];out[i+1].state[stateTop]=s_num;out[i+1].state[++stateTop]=-1; //完成第i+1行的状态栈赋值strcpy(out[i+1].sign,out[i].sign);out[i+1].sign[signTop]=out[i].input[0];out[i+1].sign[++signTop]='\0'; //完成第i+1行的符号栈的赋值strcpy(out[i+1].grasen," "); //完成第i+1行的产生式的赋值strcpy(out[i+1].input,out[i].input+1); //完成第i+1行的输入符号串的赋值}else if(mid[0]=='r'||mid[0]=='R'){r_num=CharChangeNum(mid+1);//r_num为r后的数字strcpy(gra,*(GramSent+r_num-1));len=strlen(gra);for(j=0;j<len;j++)if(gra[j]=='-' && gra[j+1]=='>')break;n=strlen(gra+j+2);stateTop-=n; signTop-=n;for(j=0;j<stateTop;j++)out[i+1].state[j]=out[i].state[j];j=SignNum(gra[0]);out[i+1].state[stateTop]=CharChangeNum(LR[out[i+1].state[stateTop-1]+1][ j].e);out[i+1].state[++stateTop]=-1; //完成第i+1行的状态栈赋值strcpy(out[i+1].sign,out[i].sign);out[i+1].sign[signTop]=gra[0];out[i+1].sign[++signTop]='\0'; //完成第i+1行的符号栈的赋值strcpy(out[i+1].grasen,gra); //完成第i+1行的产生式的赋值strcpy(out[i+1].input,out[i].input); //完成第i+1行的输入符号串的赋值}return 1;}void OutputResult(int r){int i,j;printf("**********************************************************\n"); printf("* 句子:%s 用LR分析表规约过程如下:*\n",Sentence);printf("**********************************************************\n"); for(i=0;i<=r;i++){j=0;printf("%2d ",out[i].order);while(out[i].state[j]!=-1)printf("%d",out[i].state[j++]);printf(" %s %s %s\n",out[i].sign,out[i].grasen,out[i].input);}}int OutControl()//输出结果的总控函数{int s_num,i=0;out[0].order=1; //序号赋值out[0].state[0]=0; stateTop=1; out[0].state[stateTop]=-1; //状态栈赋值,置栈顶位strcpy(out[0].sign,"#"); signTop=1; //符号栈赋值,置栈顶位strcpy(out[0].grasen," "); //产生式为空strcpy(out[0].input,Sentence); //以下两行为输入串赋值strcat(out[0].input,"#");strcpy(out[0].explen,"0和#进栈"); //解释说明//初使化输出结果的第一行while(1){s_num=SignNum(out[i].input[0]);//if(s_num!=-1)if(OutResult(out[i].state[stateTop-1],s_num,i)!=1)break;i++;}return i;}main(){int r;printf("**********************************************************\n"); printf("* 函数的输入: 文法的产生式,文法句型的一个句子,LR分析表 *\n");printf("* 函数的输出: LR分析器的工作过程与说明 *\n");printf("**********************************************************\n"); printf("请输入LR分析表中终结符与非终结符的总个数\n");scanf("%d",&colno);printf("请输入LR分析表中状态的总个数\n");scanf("%d",&row);input_LR(row,colno);output_LR(row,colno);input_GramSent();r=OutControl(); //r为输出结果的行数OutputResult(r);}七、实验小结这个程序是从网上下载下来的,根据这个实验要求做了些更改,但是总是出现溢出错误,只能运行到LR分析表的部分(如截图),没有找到解决问题的办法。
习题与答案-5-语法分析-自上而下

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 1.对文法G[S]G: S →a | ∧| (T)T →T , S | S(1) 给出(a,(a,a))和(((a,a), ∧,(a)),a)的最左推导。
(2) 对文法G,进行改写,然后对每个非终结符写出不带回溯的递归子程序。
(3) 经改写后的文法是否是LL(1)的?给出它的预测分析表。
(4) 给出输入串(a,a)#的分析过程,并说明该串是否为G的句子。
1. [解答](1)①S ②S(T )( T )T , S T , S ②S=>(T) =>(T,S)=>(S,S) S ( T ) S a =>((T),S)=>((T,S),S)a T , S ( T ) =>((T,S,S),S)=>((S,S,S),S) S a T , S =>(((T),S,S),S)=>(((T,S),S,S),S)a T , S ( T ) =>(((S,S),S,S),S)=>(((a,S),S,S),S)①S=>(T) =>(T,S) S ^ S =>(((a,a),S,S),S)=>(S,S) =>(a,S) =>(((a,a),^,S),S) =>(a,(T)) ( T ) a =>(((a,a),^,(T)),S) =>(a,(T,S)) =>(((a,a),^,(S)),S)=>(a,(S,S)) T , S =>(((a,a),^,(a)),S)=>(a,(a,S)) =>(((a,a),^,(a)),a)=>(a,(a,a)) S aa(2) 消除左递归G': S→a | ∧| (T)T→ST'T'→,ST' |ε递归子程序:program parser proceduce T;begin begingetsym; if sym in [a,^,() thenS beginend; S;proceduce S; T;begin end;if sym=’a’ or sym=’^’ then elsegetsym error;elseif sym=’(‘ end;begin getsym; proceduce T’;T; beginIf sym=’)’ then if sym=’,’ thenGetsym; beginElse getsym;Error; S;End; T;Else end;Error; elseEnd; if sym=’)’ thenelseerror;end;LL(1)文法!(4) 分析栈余留串所用产生式或动作1 #S (a,a)# S—>(T)2 #)T( (a,a)# (匹配3 #)T a,a)# T—>ST’4 #)T’S a,a)# S—>a5 #)T’a a,a)# a匹配6 #)T’ ,a)# T’ —>,ST’7 #)T’S, ,a)# ,匹配8 #)T’S a)# S—>a9 #)T’a a)# a匹配10 #)T’ )# T’—>ε11 #) )# )匹配12 # # 接受因为(a,a)#分析成功所以(a,a)为文法的句子步骤分析栈余留串所用产生式或动作1 #S (a,a# S→(T)2 #)T( (a,a# ( 匹配3 #)T a,a# T→ST’4 #)T’S a,a# S→a5 #)T’a a,a# a 匹配6 #)T’,a# T’→,ST’7 #)T’S, ,a# , 匹配8 #)T’S a# S→a9 #)T’a a# a 匹配10 #)T’# 出错^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 2. G: E →TE'E' →+E |εT →FT'T' →T |εF →PF'F' →*F' |εP →(E) | a | b |∧预测分析表^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ 3.已知文法G: S →MH | aH →LSo |εK →dML |εL →eHfM →K | bLM判断G是否是LL(1)文法,如果时,构造LL(1)分析表。
编译原理作业集-第五章-修订

第五章语法分析—自下而上分析本章要点1. 自下而上语法分析法的基本概念:2. 算符优先分析法;3. LR分析法分析过程;4. 语法分析器自动产生工具Y ACC;5. LR分析过程中的出错处理。
本章目标掌握和理解自下而上分析的基本问题、算符优先分析、LR分析法及语法分析器的自动产生工具YACC等内容。
本章重点1.自下而上语法分析的基本概念:归约、句柄、最左素短语;2.算符优先分析方法:FirstVT, LastVT集的计算,算符优先表的构造,工作原理;3.LR分析器:(1)LR(0)项目集族,LR(1)项目集簇;(2)LR(0)、SLR、LR(1)和LALR(1)分析表的构造;(3)LR分析的基本原理,分析过程;4.LR方法如何用于二义文法;本章难点1. 句柄的概念;2. 算符优先分析法;3. LR分析器基本;作业题一、单项选择题:1. LR语法分析栈中存放的状态是识别________的DFA状态。
a. 前缀;b. 可归前缀;c. 项目;d. 句柄;2. 算符优先分析法每次都是对________进行归约:(a)句柄(b)最左素短语(c)素短语(d)简单短语3. 有文法G=({S},{a},{S→SaS,S→ε},S),该文法是________。
a. LL(1)文法;b.二义性文法;c.算符优先文法;d.SLR(1)文法;4. 在编译程序中,语法分析分为自顶向下分析和自底向上分析两类,和LL(1)分析法属于自顶向下分析;a. 深度分析法b. 宽度优先分析法c. 算符优先分析法d. 递归下降子程序分析法5. 自底向上语法分析采用分析法,常用的是自底向上语法分析有算符优先分析法和LR分析法。
a. 递归b. 回溯c. 枚举d. 移进-归约6. 一个LR(k)文法,无论k取多大,。
a. 都是无二义性的;b. 都是二义性的;c. 一部分是二义性的;d. 无法判定二义性;7. 在编译程序中,语法分析分为自顶向下分析和自底向上分析两类,和LR分析法属于自底向上分析。
第5章 自下而上的语法分析(Tsu版电子教案)

第5章自下而上的语法分析从叶结点出发,步步向上归约。
若能归约到根结点,说明输入串是文法的一个句子,否则输入串存在语法错误。
5.1 自下而上的语法分析概述㈠概述实质上是一种移进归约法,设置一个栈,将输入串符号逐个移进栈内,一旦发现栈顶形成某个产生式的候选式时,立即将栈顶这一部分符号替换(归约)成该产生式的左部符号。
例给定文法G:S→aAcBeA→b | AbB→d和输入串abbcde,其移进归约过程如下所示:移移归移归移移归移归①②③④⑤⑥⑦⑧⑨⑩因最终归约到根结点,输入串abbcde是文法的一个句子。
㈡问题从第④步到第⑤步有二种选择,可将b归约成A,栈顶成aAA;也可将Ab归成A,栈顶成aA,显然后者是正确的,故需精确定义可归约串。
㈢句柄和规范归约①短语②直接短语(简单短语)③句柄继续问题的讨论。
句型aAbcde中存在三个短语,它们是Ab、d和aAbcde,其中Ab和d 是直接短语,句柄是Ab。
不能因为存在规则A→b,就断定b是这个句型的一个短语,b不是句柄,甚至连短语都不是。
④规范归约(最左归约)⑤规范句型⑥规范推导⑦图解法5.2 LR分析法的基本原理㈠前缀㈡活前缀㈢LR分析法的基本思想㈣LR(0)项目(简称项目)在产生式右部的某个位置添加一个园点“.”。
特例,A→ε的项目为A→.。
例文法0.S'→E1.E→aA2.A→cA3.A→d4.E→d这个文法的项目有○1S'→.E ○2S'→E.○3E→.aA ○4E→a.A ○5E→aA.○6A→.cA ○7A→c.A ○8A→cA.○9A→.d ○10A→d.○11E→.d ○12E→d.㈤构造识别活前缀的NFA①将每个项目视为识别活前缀NFA的一个状态。
②规定状态S'→.S为NFA的唯一初态,状态S'→S.为NFA的唯一接受态(S为原文法开始符号,S'为拓广文法开始符号)。
③因在每个状态都可识别出一个活前缀(初态可识别出活前缀ε),故NFA的每个状态都是终态,终态又称为活前缀识别态。
自下而上语法分析习题共28页

16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
END
自下而上语法分析习题
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一
自底向上语法分析测验题

自底向上语法分析测验题
班级学号姓名成绩
一、填空题(共5分)
1.语法分析最常用的两类方法是_ _ ___和__ _ __分析法。
2.语法分析器的输入是__ ___其输出是_ __。
3.一个LR分析器包括三部分:一个总控程序、
和。
4.简单优先分析归约和LR分析法归约的是,算符优先分析
法归约的是。
5.LR分析表包括action表和表,一般会把两张表合并成一张表。
ACTION表包含的动作有移进、接受和报错四种。
二、计算题(每题40分,共80分)
1.构造算符文法G[H]:H→H;M|M M→d|aHb的算符优先关系并对符号串#adb;d#进行分析。
(8分)2已知文法为: S->a|^|(T) T->T,S|S 构造它的LR(1)分析表,并对符号串(a, (a))#进行分析。
(9分)。
编译原理分知识点习题自下而上语法分析 (1)

1.★已知文法G[S]:S→SaA|AA→AbB|BB→cSd|e请证实AacAbcBaAdbed是文法的一个句型,并写出该句型的所有短语、素短语以及句柄。
符号栈S 关系输入串最左素短语S1 S2 S3 S4 S5 S6 S7 R1 R2 R3 R4 R5 R6#< ( a d b ) ##<( < a d b ) ##<(< a > d b ) # d#<( V < d b ) ##<( V<d < b ) ##<( V<d<b > ) # b#<( V<d V > ) # VdV#<( V = ) ##<( =V ) > # (V)# V # 接受因为存在从文法开始符号S到符号串AacAbcBaAdbed的推导过程(如图6.1中的语法树所示),所以符号串AacAbcBaAdbed是文法的句型。
从图6.1中句型A1a1c1 A2b1c2Ba2 A3d1b2ed2的语法树可知,该句型的短语有:A1、B、Ba2 A3、c2Ba2 A3d1、A2b1c2Ba2 A3d1、e、A2b1c2Ba2 A3d1b2e、c1 A2b1c2Ba2 A3d1b2ed2、A1a1c1 A2b1c2Ba2 A3d1b2ed2该句型的素短语有:Ba2 A3、e该句型的句柄为:B2.★已知文法G[S]:S→*AA→0A1|*(1)求文法G的各非终结符号的FIRSTVT集和LASTVT集;(2)构造文法G的优先关系矩阵,并判断该文法是否是算符优先文法;(3)分析句子*0*1,并写出分析过程。
解:本题考查算符优先分析法中的有关知识:非终结符号的FIRSTVT集和LASTVT集的求法、算符优先关系的构造、算符优先文法的定义、算符优先分析过程等。
(1)求文法G的各非终结符号的FIRSTVT集和LASTVT集。
第10章 自下而上的语法分析

49
2. 分析表
由action[s,a]和goto[s,x]两个子表组成。
(1) action表是一个状态(行)和终结符(列)的二 维矩阵,action[s, a]定义了在状态 s 下,当前输入 符号为 a 时应采取的动作。 (2) goto表是一个状态(行)和非终结符(列)的二 维矩阵, goto[s, A]定义了在状态 s 下, 面对非终 结符 A 时应采取的动作。
4
5 6 7 8
02
01 016 0165 0163
#T
#E #E+ #E+i #E+F
+i*i#
+i*i# i*i# *i# *i#
r6
r4
55
(续表) 状态栈 9 符号栈 输入串 *i# 动作
0169
#E+T #E+T*
#E+T*i #E+T*F #E+T #E
s7
s5 r6 r3
10 0 1 6 9 7
19
例:G(E)
E→E+T│T T→T*F│F F→(E) │i 符号串 i+i*i 的规范归约过程。
20
i+i*i F+i*i T+i*i E+i*i
E E + T F i
E → E+T | T T → T*F | F F → (E) | i
T
E+F*i
E+T*i
T F
i
*
F i
E+T*F
E+T
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E
E + T
T T * F F i2 F i3
i1 句型i1*i2+i3的语法树如图: 从语法树可以看出: ET | E+T i1, i2, i3, i1*i2, i1*i2+i3是句型i1*i2+i3的短语 TF | T*F 直接短语有:i1, i2 , i3 Fi | (E) 句柄是: i1
例:考虑如下文法: 求句型 i1 * i2 + i3 的短语、 直接短语和句柄。
ET | E+T
TF | T*F Fi | (E)
从语法分析树来识别: • 一棵子树是由树的某个结点连同 它的所有子孙组成的。 • 子树的所有端末结点自左至右排 列成一个相对子树根的短语。 • 直接短语:只有父子两代结点形 成的短语。 • 句柄:最左子树的直接短语。
如何进行归约?
通过不同的自底向上的分析算法来解释,不同 的算法对可归约串的定义是不同的,但分析过程 都有一个共同的特点:边移进边归约。
规范归约:使用句柄来定义可归约串。
算符优先:使用最左素短语来定义可归约串
规范归约的概念
* • 有文法G,开始符号为S, 如果有S=>xβ y,则xβ y 是文法G的句型,x,y是任意的符号串 * + • 如果有S=>xAy, 且有A=>β ,则β 是句型xβ y相对 于非终结符A的短语 * • 如果有S=>xAy, 且有A->β ,则β 是句型xβ y相对 于A->β 的直接短语 • 位于一个句型最左边的直接短语称为句柄. 注意: 每次归约的部分必须是句柄 (最右推导)。 关键的问题是如何识别句柄
3 检查所构造出来的函数f和g是否与原来的关系矛盾。 若没有矛盾,则f和g就是要求的优先函数,若有矛 盾,则不存在优先函数。
1 对于每个终结符a,令其对应两个符号 fa和ga,画一以所有符号和为结点的方向 图。如果a b,则从fa画一条弧至gb, 如果a b,则画一条弧从gb至fa 。
• 现在必须证明:若a b,则f(a)=g(b);若a b,则f(a)< g(b);若a b,则f(a)> g(b)。
• 有许多优先关系表不存在优先函数,如:
a b a b
不存在对应的优先函数f和g 假定存在f和g,则有 f(a)=g(a),f(a)>g(b), f(b)=g(a),f(b)=g(b) 导致如下矛盾: f(a) > g(b) = f(b) = g(a) = f(a) 如果优先函数存在,则不唯一(无穷多)
• 优点:便于比较,节省空间; • 缺点:原来不存在优先关系的两个终结符,由 于自然数相对应,变成可以比较的。要进行 一些特殊的判断。
• 文法G(E) (1) E→E+T | T (2) T→T*F | F (3) F→P F | P (4) P→(E) | i 的优先函数如下表
+ * ↑ ( ) i # F 2 4 4 0 6 6 0 G 1 3 5 5 0 5 0
(a,(a,a))的最右推导: S (T) (T,S) (T,(T)) (T,(T,S)) (T,(T,a)) (T,(S,a)) (T,(a,a)) (S,(a,a)) (a,(a,a)) (((a,a),^,(a)),a)的最右推导: S (T) (T,S) (S,S) (S,a) ((T),a) ((T,S,S),S) ((S,S,S),S) (((T,S),S,S),S) (((S,S),S,S),S) (((a,S),S,S),S) (((a,a),S,S),S) (((a,a),^,S),S) (((a,a),^,a),S) (((a,a),^,a),a)
• 如果优先函数存在,则可以通过以下三个步骤从优先 表构造优先函数:
1 对于每个终结符a,令其对应两个符号fa和ga,画 一以所有符号和为结点的方向图。如果a b,则 从fa画一条弧至gb,如果a b,则画一条弧从gb至 fa 。
2 对每个结点都赋予一个数,此数等于从该结点出发 所能到达的结点(包括出发点自身)。赋给fa的数作 为f(a),赋给ga的数作为g(a)。
• 上述例子中句子abbcde的规范归约过程是: abbcde, aAbcde, aAcde, aAcBe,S
练习
• 使用下述文法对句型i1*i2+i3进行规范规约:
i1*i2+i3 , F*i2+i3 , T*i2+i3, T*F+i3 , T + i3 , E+i3 , E + F, E+T, E
练习
1、令文法G1为: + E→E+T | T T E T→T*F | F T * F→(E) | i 证明E+T*F是它的一个句型,指出这个句型的所有 短语、直接短语和句柄。
T*F是句型E+T*F相对于T的短语
E
F
E+T*F句型E+T*F相对于E的短语
T*F是句型E+T*F相对于T的直接短语
T*F是句柄
规范归约的定义:
• 假定α是文法G的一个句子,如果序列: αn, αn-1, ……,α0 (=S)满足如下条件,则序列αn, αn-1, ……, α0是一个规范 归约: (1) αn =α 是给定的句子 (2) α0 =S 是文法的开始符号 (3) 对任何i, 0<in,αi-1是从αi经把句柄替换为相应文 法产生式的左部符号而得到的。 • 规范归约是最右推导的逆过程,规范归约又称为最左 归约。
a S
S
S→a
T→S
(((S,a),^,(a)),a)
(((T,a),^,(a)),a) (((T,S),^,(a)),a) (((T),^,(a)),a) ((S,^,(a)),a) ((T,^,(a)),a) ((T,S,(a)),a)
((T,(T)),a) ((T, S),a)
((T),a) T (S,a)S
动作 预备 进 进 归 进 进 进 归 进 进 归 归 进 归 归 进 归
优先函数
• 把每个终结符与两个自然数f()与g()相对 应,使得
若 1 2,则f(1) < g(2) 若 1 2,则f(1) = g(2) 若 1 2,则f(1) > g(2) f称为入栈优先函数,g称为比较优先函数。
第五章
自下而上语法分析方法 习题课
本章要求
1.掌握自下而上分析的基本思想,基本概念 2.掌握算符优先文法、算符优先关系的判定 3.掌握最左素短语、句柄的定义与判定 4.掌握求FirstVT集,LastVT集,学会构造算符优先 关系表,能用算符优先分析法进行表达式分析
问题的提出:
① 在构造语法树的过程中,何时归约? 当可归约串出现在栈顶时就进行归约。 ② 如何知道在栈顶符号串中已经形成可归约串?
. ( T, <. S <. , <. . FIRSTVT(S) = <. T→ ﹤ . .a , , .∧,.>, , (. . > > ) ﹤ ﹤ ﹤
两个终结符之间的优先关系不多 T → T,S LASTVT(T) ﹥ ., 于一种。 .,, ) ﹥ .,, , ﹥ a﹥ , . ,, ∧ ﹥ . . 综上,该文法是算术优先文法。 , 对待特殊地 <. <. #,把它看作句型的开始和结束符 <. .> > .根据#S#同理可得 . . . . . #,∧ ﹥ .# , ) ﹥ # <. # . < <# = .# , .∧ , # ﹤ a﹥ #. a,#﹤ (, ﹤
练 习
2 对下述文法,求句型 E+T * F + i的短语、直接短语、句柄
ET | E+T
TF | T*F Fi | (E) 短语有:i, T * F, E+T * F, E + T * F + i T * F E E + T E + T F
i
直接短语有: i, T * F
句柄是:T * F
输入串(a,(a,a))的算符优先过程。
栈 # #( #(a #(t #(t, #(t,( #(t,(a #(t,(t #(t,(t, #(t,(t,a #(t,(t,s #(t,(t #(t,(t) #(t,s # (t # (t ) # s success
输入字符串 (a,(a,a))# a, (a,a))# , (a,a))# , (a,a))# (a,a))# a,a))# ,a))# ,a))# a))# ))# ))# ))# )# )# )# # #
^ ) (( )) # Sa →(T . , 1、文法是算术文法,且不含ε . . . S →(T) LASTVT(T)﹥ > > > .) 产生式。 . FIRSTVT(T) Sa→(T) ( ﹤ . . . ) , ∧﹥ .),) ﹥ .) , , ﹥ . a﹥ ) > >. .,(﹤ . 2、由优先关系矩阵可知,任何 ^ ﹤ ( . a, ( ﹤ ∧ ( , ( .> , ﹤
• 最右推导又称规范推导,由规范推导所得到的句型称 规范句型,规范推导的逆过程是规范归约。
句型
归约规则
abbcde aAbcde aAcde aAcBe S
(2) Ab (3) A Ab (4) B d (1) S aAcBe
(1)S aAcBe (2)A b (3)A Ab (4)B d
符号栈
句柄 归约规则
a S S→a T→S
输入串:
S T , ) S a )
T S
) a T S S ^ ) ( , T S a ) , T S ( ) , T S ( ( T T S T , ) S a
(
T , S ^ (
