基本初等函数讲义超级全
基本初等函数讲义(超级全)
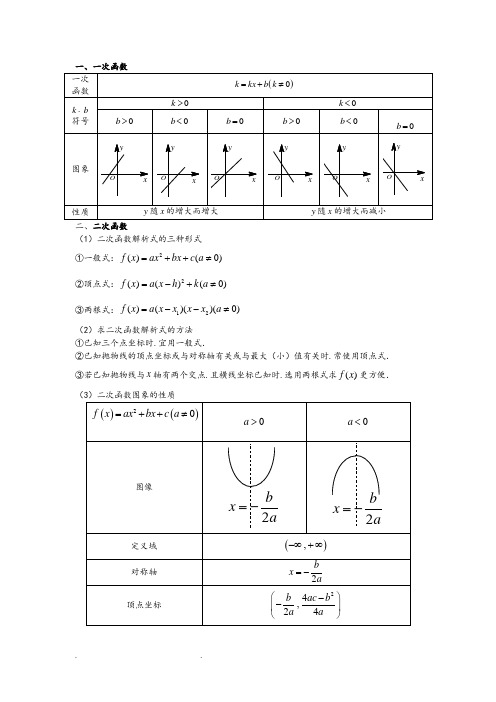
一、一次函数二、二次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法 ①已知三个点坐标时.宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时.常使用顶点式. ③若已知抛物线与x 轴有两个交点.且横线坐标已知时.选用两根式求()f x 更方便. (①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线.对称轴方程为,2x a=-顶点坐标是24(,)24b ac b a a-- ②当0a >时.抛物线开口向上.函数在(,]2b a -∞-上递减.在[,)2ba-+∞上递增.当2b x a =-时.2min 4()4ac b f x a -=;当0a <时.抛物线开口向下.函数在(,]2ba -∞-上递增.在[,)2b a -+∞上递减.当2bx a=-时.2max 4()4ac b f x a -=. 三、幂函数(1)幂函数的定义一般地.函数y x α=叫做幂函数.其中x 为自变量.α是常数. 过定点:所有的幂函数在(0,)+∞都有定义.并且图象都通过点(1,1).(1)根式的概念:如果,,,1nx a a R x R n =∈∈>.且n N +∈.那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(1)对数的定义①若(0,1)xa N a a =>≠且.则x 叫做以a 为底N 的对数.记作log a x N =.其中a 叫做底数.N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)xa x N a N a a N =⇔=>≠>.(2)几个重要的对数恒等式log 10a =.log 1a a =.log b a a b =.(3)常用对数与自然对数常用对数:lg N .即10log N ;自然对数:ln N .即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>.那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A .值域为C .从式子()y f x =中解出x .得式子()x y ϕ=.如果对于y 在C 中的任何一个值.通过式子()x y ϕ=.x 在A 中都有唯一确定的值和它对应.那么式子()x y ϕ=表示x 是y 的函数.函数()x y ϕ=叫做函数()y f x =的反函数.记作1()x fy -=.习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域.即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=.并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上.则'(,)P b a 在反函数1()y f x -=的图象上.④一般地.函数()y f x =要有反函数则它必须为单调函数. 例题一、求二次函数的解析式例1.抛物线244y x x =--的顶点坐标是()A .(2.0)B .(2.-2)C .(2.-8)D .(-2.-8)例2.已知抛物线的顶点为( 1.2).且通过(1.10).则这条抛物线的表达式为()A .()2312y x =-- B .()2312y x =-+ C. ()2312y x =+- D.()2312y x =-+---例3.抛物线y=的顶点在第三象限.试确定m 的取值范围是( ) A .m <-1或m >2 B .m <0或m >-1 C .-1<m <0 D .m <-1例4.已知二次函数()f x 同时满足条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的两根立方和等于17求()f x 的解析式二、二次函数在特定区间上的最值问题例5. 当22x -≤≤时.求函数223y x x =--的最大值和最小值.例6.当0x ≥时.求函数(2)y x x =--的取值范围.例7.当1t x t ≤≤+时.求函数21522y x x =--的最小值(其中t 为常数).222x mx m -++三、幂函数例8.下列函数在(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -=例9.下列幂函数中定义域为{}0x x >的是() A.23y x = B.32y x = C.23y x-= D.32y x-=例10.讨论函数y =52x 的定义域、值域、奇偶性、单调性.并画出图象的示意图.例10.已知函数y =42215x x --.(1)求函数的定义域、值域;(2)判断函数的奇偶性; (3)求函数的单调区间.四、指数函数的运算例11.计算122(2)-⎡⎤-⎣⎦的结果是( ) A、12C、—12例12.等于( ) A 、 B 、C 、 D 、例13.若53,83==ba .则b a233-=___________五、指数函数的性质例14.{|2},{|xM y y P y y ====.则M ∩P () A.{|1}y y > B. {|1}y y ≥ C. {|0}y y > D. {|0}y y ≥ 例15.求下列函数的定义域与值域: (1)442x y -=(2)||2()3x y =例16.函数()2301x y a a a -=+>≠且的图像必经过点 ( )A .(0.1)B .(1.1)C .(2.3)D .(2.4)例17求函数y=2121x x -+的定义域和值域.并讨论函数的单调性、奇偶性.4416a 8a 4a 2a五、对数函数的运算例18.已知32a=.那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -例19.2log (2)log log a a a M N M N -=+.则NM的值为( ) A 、41B 、4C 、1D 、4或1 例20.已知732log [log (log )]0x =.那么12x -等于( )A 、13B C D 例21.2log 13a <.则a 的取值范围是( ) A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭五、对数函数的性质例22.下列函数中.在()0,2上为增函数的是( )A 、12log (1)y x =+B 、2log y =C 、21log y x =D 、2log (45)y x x =-+ 例23.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称例23.求证函数)()lg f x x =是(奇、偶)函数。
《基本初等函数》PPT课件

实
际
问
题
随机数与随机模拟
精选课件ppt
4
组织结构图
某校学生会的组织结构图: 学生会
生
学
活
习
部部
某公司的组织结构图: 总工程师
宣体
文
传育
艺
部部 部
总经理
专家办公室
财
咨
监
信
务
询
理
息
计
部
部
部
划
部 精选课件ppt
开
后
编
发
勤
辑
部
部
部
5
通过结构图理解数列:
函数
化
特 殊
一次函数 指数函数
函数列
类比 类比
推 广
数列
特 殊 化
等差数列 等比数列
精选课件ppt
类比
实数
6
用样本估计总体
变量间的 相互关系
简 单 随 机 抽 样
系 分 用样本 统 层 的频率 抽 抽 分布估 样 样 计总体
用样本 的数字 特征估 计总体 的数字
特征
精选课件ppt
线 性 回 归 分 析
3
《数学3》第3章“概率”的知识结构 图:
随机事件
频率
概率,概率的 意义和性质
应 用
概
率
解
决
古典概型
几何概型
§4.2 结构图
邹城二中 饶兴国
精选课件ppt
1
知识结构图
整数指数幂 有理指数幂 无理指数幂
《数学1》第2章“基本初等函数(Ⅰ)” 的知识结构图:
定义
指数
对数
运算性质
定义 图象与性质
高中数学-必修1-第2章-基本初等函数-讲义

§2.1.1 指数与指数幂的运算(1)1. 了解指数函数模型背景及实用性、必要性;2. 了解根式的概念及表示方法;3. 理解根式的运算性质.4850复习1:正方形面积公式为;正方体的体积公式为 .复习2:(初中根式的概念)如果一个数的平方等于a,那么这个数叫做a的,记作;如果一个数的立方等于a,那么这个数叫做a 的,记作 .二、新课导学※学习探究探究任务一:指数函数模型应用背景探究下面实例及问题,了解指数指数概念提出的背景,体会引入指数函数的必要性.实例1. 某市人口平均年增长率为℅,1990年人口数为a万,则x年后人口数为多少万实例2. 给一张报纸,先实验最多可折多少次你能超过8次吗计算:若报纸长50cm,宽34cm,厚,进行对折x 次后,求对折后的面积与厚度问题1:国务院发展研究中心在2000年分析,我国未来20年GDP(国内生产总值)年平均增长率达℅,则x年后GDP为2000年的多少倍问题2:生物死亡后,体内碳14每过5730年衰减一半(半衰期),则死亡t年后体内碳14的含量P与死亡时碳14关系为57301()2tP=. 探究该式意义小结:实践中存在着许多指数函数的应用模型,如人口问题、银行存款、生物变化、自然科学.探究任务二:根式的概念及运算考察:2(2)4±=,那么2±就叫4的;3327=,那么3就叫27的;4(3)81±=,那么3±就叫做81的 .依此类推,若n x a=,,那么x叫做a 的 .新知:一般地,若n x a=,那么x叫做a的n次方根( n th root ),其中1n>,n*∈N.例如:328=2=.反思:当n为奇数时, n次方根情况如何33-, 记:x=当n为偶数时,正数的n次方根情况例如:81的4次方根就是,记:.强调:负数没有偶次方根;0的任何次方根都是00=.试试:4b a=,则a的4次方根为;3b a=,则a的3次方根为 .新知:(radical),这里n 叫做根指数(radical exponent),a叫做被开方数(radicand).试试:计算2.反思:从特殊到一般,n结论:n a=. 当na=;当n是(0)||(0)a aaa a≥⎧=⎨-<⎩.※典型例题例1求下类各式的值:(1);(2);(3;(4)a b<).变式:计算或化简下列各式.(1(2.推广:(a≥0).※动手试试练1.-练2.化简三、总结提升※学习小结1. n次方根,根式的概念;2. 根式运算性质.※知识拓展1. 整数指数幂满足不等性质:若0a>,则0na>.2. 正整数指数幂满足不等性质:①若1a>,则1na>;01na<<. 其中n∈N*.※自我评价你完成本节导学案的情况为().A. 很好B. 较好C. 一般D. 较差※当堂检测(时量:5分钟满分:10分)计分:).A. 3B. -3C. ±3D. 812. 625的4次方根是().A. 5B. -5C. ±5D. 253.化简2是().A. b-B. bC. b± D.1b4. = .5.计算:3=;1. 计算:(1(2)2. 计算34a a-⨯和3(8)a+-,它们之间有什么关系你能得到什么结论3. 对比()n n nab a b=与()nnna ab b=,你能把后者归入前者吗§2.1.1 指数与指数幂的运算(2)1. 理解分数指数幂的概念;2. 掌握根式与分数指数幂的互化;3. 掌握有理数指数幂的运算.5053复习1:一般地,若n x a=,则x叫做a的,其中1n>,n*∈N. 简记为: .像的式子就叫做,具有如下运算性质:n=;=;= .复习2:整数指数幂的运算性质.(1)m na a=;(2)()m na=;(3)()nab= .二、新课导学※学习探究探究任务:分数指数幂引例:a>01025a a=,则类似可得=;23a== .新知:规定分数指数幂如下*(0,,,1)mna a m n N n=>∈>;*1(0,,,1)mnmna a m n N na-==>∈>.试试:(1)将下列根式写成分数指数幂形式:= ;0,)m N*∈.(2)求值:238;255;436-;52a-.反思:① 0的正分数指数幂为;0的负分数指数幂为 .②分数指数幂有什么运算性质小结:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.指数幂的运算性质:(0,0,,a b r s Q>>∈)ra·r r sa a+=;()r s rsa a=;()r r sab a a=.※典型例题例1 求值:2327;4316-;33()5-;2325()49-.变式:化为根式.例2 用分数指数幂的形式表示下列各式(0)b>:(1)2b b;(2)533b b;(3例3 计算(式中字母均正):(1)211511336622(3)(8)(6)a b a b a b-÷-;(2)311684()m n.小结:例2,运算性质的运用;例3,单项式运算. 例4 计算:(1334a a (0)a >;(2)312103652(2)()m n m n --÷- (,)m n N *∈;(3)÷小结:在进行指数幂的运算时,一般地,化指数为正指数,化根式为分数指数幂,对含有指数式或根式的乘除运算,还要善于利用幂的运算法则.反思:①结论:无理指数幂.(结合教材P 53利用逼近的思想理解无理指数幂意义)② 无理数指数幂(0,)a a αα>是无理数是一个确定的实数.实数指数幂的运算性质如何※ 动手试试 练1. 把851323x --⎫⎪⎪化成分数指数幂.练2. 计算:(1443327; (2三、总结提升 ※ 学习小结①分数指数幂的意义;②分数指数幂与根式的互化;③有理指数幂的运算性质.※ 知识拓展放射性元素衰变的数学模型为:0t m m e λ-=,其中t 表示经过的时间,0m 表示初始质量,衰减后的质量为m ,λ为正的常数.※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 若0a >,且,m n 为整数,则下列各式中正确的是( ).A. m mnna a a ÷= B. m n mn a a a ⋅=C. ()nm m n a a += D. 01n n a a -÷=2.化简3225的结果是( ).A. 5B. 15C. 25D. 125 3. 计算(122--⎡⎤⎢⎥⎣⎦的结果是(). AB .D . 4. 化简2327-= .5. 若102,104mn==,则3210m n -= .1. 化简下列各式: (1)3236()49; (2.2.1⎛- ⎝.§2.1.1 指数与指数幂的运算(练习)1. 掌握n次方根的求解;2. 会用分数指数幂表示根式;3. 掌握根式与分数指数幂的运算.4853复习1:什么叫做根式运算性质像的式子就叫做,具有性质:n=;=;= .复习2:分数指数幂如何定义运算性质①mna=;mna-= .其中*0,,,1a m n N n>∈>②r sa a=;()r sa=;()sab= .复习3:填空.①n为时,(0)||...........(0)xxx≥⎧==⎨<⎩.②求下列各式的值:= ;= ;= ;= ;= ;= ;= .二、新课导学※典型例题例1 已知1122a a-+=3,求下列各式的值:(1)1a a-+;(2)22a a-+;(3)33221122a aa a----.补充:立方和差公式3322()()a b a b a ab b±=±+.小结:①平方法;②乘法公式;③根式的基本性质=(a≥0)等.注意,a≥0十分重要,无此条件则公式不成立.≠.变式:已知11223a a--=,求:(1)1122a a-+;(2)3322a a--.例2从盛满1升纯酒精的容器中倒出13升,然后用水填满,再倒出13升,又用水填满,这样进行5次,则容器中剩下的纯酒精的升数为多少变式:n次后小结:①方法:摘要→审题;探究→结论;② 解应用问题四步曲:审题→建模→解答→作答. ※ 动手试试练1. 化简:11112244()()x y x y -÷-.练2. 已知x +x -1=3,求下列各式的值.(1)1122x x -+; (2)3322x x -+.练 3. 已知12(),0x f x x x π=⋅>,试求.三、总结提升 ※ 学习小结1. 根式与分数指数幂的运算;2. 乘法公式的运用.※ 知识拓展1. 立方和差公式:3322()()a b a b a ab b +=+-+; 3322()()a b a b a ab b -=-++.2. 完全立方公式:33223()33a b a a b ab b +=+++;33223()33a b a a b ab b -=-+-.※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:).354a a (a >0)的值是( ).A. 1B. aC. 15a D. 1710a 3. 下列各式中成立的是( ).A .1777()n n m m =B=C 34()x y + D .=4. 化简3225()4-= .5. 化简2115113366221()(3)()3a b a b a b -÷= .1. 已知32x a b --=+, .2.2n a +=时, 实数a 和整数n 所应满足的条件.§2.1.2 指数函数及其性质(1)学习目标1. 了解指数函数模型的实际背景,认识数学与现实生活及其他学科的联系;2. 理解指数函数的概念和意义;3. 能画出具体指数函数的图象,掌握指数函数的性质(单调性、特殊点).学习过程一、课前准备5457复习1:零指数、负指数、分数指数幂怎样定义的 (1)0a = ; (2)n a -= ;(3)m na = ;m na -= .其中*0,,,1a m n N n >∈>复习2:有理指数幂的运算性质. (1)m n a a = ;(2)()m n a = ; (3)()n ab = .二、新课导学 ※ 学习探究探究任务一:指数函数模型思想及指数函数概念 实例:A .细胞分裂时,第一次由1个分裂成2个,第2次由2个分裂成4个,第3次由4个分裂成8个,如此下去,如果第x 次分裂得到y 个细胞,那么细胞个数y 与次数x 的函数关系式是什么B .一种放射性物质不断变化成其他物质,每经过一年的残留量是原来的84%,那么以时间x 年为自变量,残留量y 的函数关系式是什么讨论:上面的两个函数有什么共同特征底数是什么指数是什么新知:一般地,函数(0,1)x y a a a =>≠且叫做指数函数(exponential function ),其中x 是自变量,函数的定义域为R .反思:为什么规定a >0且a ≠1呢否则会出现什么情况呢试试:举出几个生活中有关指数模型的例子探究任务二:指数函数的图象和性质引言:你能类比前面讨论函数性质时的思路,提出研究指数函数性质的内容和方法吗回顾: 研究方法:画出函数图象,结合图象研究函数性质. 研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.作图:在同一坐标系中画出下列函数图象:1()2x y =, 2x y =讨论:(1)函数2x y =与1()2x y =的图象有什么关系如何由2x y =的图象画出1()2x y =的图象(2)根据两个函数的图象的特征,归纳出这两个指数函数的性质. 变底数为3或13后呢a >1 0<a <1 图 象性 质 (1)定义域:R (2)值域:(0,+∞) (3)过点(0,1),即x =0时,y =1(4)在 R 上是增函数 (4)在R 上是减函数※ 典型例题例1函数()xf x a =(0,1a a >≠且)的图象过点(2,)π,求(0)f ,(1)f -,(1)f 的值.小结:①确定指数函数重要要素是 ; ② 待定系数法.例2比较下列各组中两个值的大小:(1)0.60.52,2; (2)2 1.50.9,0.9-- ; (3)0.5 2.12.1,0.5 ; (4)231π-与.小结:利用单调性比大小;或间接利用中间数.※ 动手试试练1. 已知下列不等式,试比较m 、n 的大小:(1)22()()33m n >; (2) 1.1 1.1m n <.练2. 比较大小:(1)0.70.90.80.8,0.8, 1.2a b c ===;(2)01, 2.50.4,-0.22-, 1.62.5.三、总结提升 ※ 学习小结①指数函数模型应用思想;②指数函数概念;③指数函数的图象与性质;③单调法.※ 知识拓展因为(01)x y a a a =>≠,且的定义域是R , 所以()(01)f x y a a a =>≠,且的定义域与()f x 的定义域相同. 而()(01)x y a a a ϕ=>≠,且的定义域,由()y t ϕ=的定义域确定.学习评价※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 函数2(33)x y a a a =-+是指数函数,则a 的值为( ).A. 1B. 2C. 1或2D. 任意值 2. 函数f (x )=21x a -+ (a >0,a ≠1)的图象恒过定点( ).A. (0,1)B. (0,2)C. (2,1)D. (2,2)3. 指数函数①()x f x m =,②()x g x n =满足不等式 01m n <<<,则它们的图象是( ).4. 比较大小:23( 2.5)- 45( 2.5)-.5. 函数1()19x y =-的定义域为 .课后作业1. 求函数y =1151x x--的定义域.2. 探究:在[m ,n ]上,()(01)x f x a a a =>≠且值域§2.1.2 指数函数及其性质(2)1. 熟练掌握指数函数概念、图象、性质;2. 掌握指数型函数的定义域、值域,会判断其单调性;3. 培养数学应用意识.5760复习1:指数函数的形式是,复习2:在同一坐标系中,作出函数图象的草图:2xy=,1()2xy=,5xy=,1()5xy=,10x y=,1()10x y=.思考:指数函数的图象具有怎样的分布规律二、新课导学※典型例题例1我国人口问题非常突出,在耕地面积只占世界7%的国土上,却养育着22%的世界人口.因此,中国的人口问题是公认的社会问题.2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%.为了有效地控制人口过快增长,实行计划生育成为我国一项基本国策.(1)按照上述材料中的1%的增长率,从2000年起,x年后我国的人口将达到2000年的多少倍(2)从2000年起到2020年我国人口将达到多少小结:学会读题摘要;掌握从特殊到一般的归纳法.试试:2007年某镇工业总产值为100亿,计划今后每年平均增长率为8%, 经过x年后的总产值为原来的多少倍多少年后产值能达到120亿小结:指数函数增长模型.设原有量N,每次的增长率为p,则经过x次增长后的总量y= . 我们把形如xy ka= (,0,1)k R a a∈>≠且的函数称为指数型函数.例2 求下列函数的定义域、值域:(1)21xy=+; (2)y=(3)110.4xy-=.变式:单调性如何小结:单调法、基本函数法、图象法、观察法.试试:求函数y=论其单调性.※ 动手试试练 1. 求指数函数212x y +=的定义域和值域,并讨论其单调性.练2. 已知下列不等式,比较,m n 的大小. (1)33m n <; (2)0.60.6m n >; (3)(1)m n a a a >> ;(4) (01)m n a a a <<<.练3. 一片树林中现有木材30000 m 3,如果每年增长5%,经过x 年树林中有木材y m 3,写出x ,y 间的函数关系式,并利用图象求约经过多少年,木材可以增加到40000m 3.三、总结提升 ※ 学习小结1. 指数函数应用模型(,01)x y ka k R a a =∈>≠且;2. 定义域与值域;2. 单调性应用(比大小).※ 知识拓展形如()(01)f x y a a a =>≠,且的函数值域的研究,先求得()f x 的值域,再根据t a 的单调性,列出简单的指数不等式,得出所求值域,注意不能忽视()0f x y a =>. 而形如()(01)x y a a a ϕ=>≠,且的函数值域的研究,易知0x a >,再结合函数()t ϕ进行研究. 在求值域的过程中,配合一些常用求值域的方法,例如观察法、单调性法、图象法等.学习评价※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 如果函数y =a x (a >0,a ≠1)的图象与函数y =b x(b >0,b ≠1)的图象关于y 轴对称,则有( ). A. a >b B. a <bC. ab =1D. a 与b 无确定关系2. 函数f (x )=3-x-1的定义域、值域分别是( ). A. R , R B. R , (0,)+∞ C. R ,(1,)-+∞ D.以上都不对3. 设a 、b 均为大于零且不等于1的常数,则下列说法错误的是( ).A. y =a x 的图象与y =a -x的图象关于y 轴对称B. 函数f (x )=a 1-x(a >1)在R 上递减 C. 若a 2>a 21-,则a >1 D. 若2x >1,则1x >4. 比较下列各组数的大小:122()5- 320.4-(); 0.763()0.753-(). 5. 在同一坐标系下,函数y =a x , y =b x , y =c x , y =d x 的图象如右图,则a 、b 、c 、d 、1之间从小到大的顺序是 .课后作业1. 已知函数f (x )=a -221x +(a ∈R ),求证:对任何a R ∈, f (x )为增函数.2. 求函数2121x x y -=+的定义域和值域,并讨论函数的单调性、奇偶性.§2.2.1 对数与对数运算(1)1. 理解对数的概念;2. 能够说明对数与指数的关系;3. 掌握对数式与指数式的相互转化.6264复习1:庄子:一尺之棰,日取其半,万世不竭.(1)取4次,还有多长(2)取多少次,还有尺复习2:假设2002年我国国民生产总值为a亿元,如果每年平均增长8%,那么经过多少年国民生产是2002年的2倍(只列式)二、新课导学※学习探究探究任务:对数的概念问题:截止到1999年底,我国人口约13亿. 如果今后能将人口年平均增长率控制在1%,那么多少年后人口数可达到18亿,20亿,30亿讨论:(1)问题具有怎样的共性(2)已知底数和幂的值,求指数怎样求呢例如:由1.01x m=,求x.新知:一般地,如果x a N=(0,1)a a>≠,那么数x叫做以a为底N的对数(logarithm).记作logax N=,其中a叫做对数的底数,N 叫做真数试试:将复习2及问题中的指数式化为对数式.新知:我们通常将以10为底的对数叫做常用对数(common logarithm),并把常用对数10log N简记为lg N在科学技术中常使用以无理数e=……为底的对数,以e为底的对数叫自然对数,并把自然对数logeN简记作ln N试试:分别说说lg5 、、ln10、ln3的意义.反思:(1)指数与对数间的关系0,1a a>≠时,x a N=⇔ .(2)负数与零是否有对数为什么(3)log1a=,logaa= .※典型例题例1下列指数式化为对数式,对数式化为指数式.(1)35125=;(2)712128-=;(3)327a=;(4)2100.01-=;(5)12log325=-;(6)=3-;(7)ln100=.变式:12log32?= =小结:注意对数符号的书写,与真数才能构成整体. 例2求下列各式中x 的值:(1)642log 3x =; (2)log 86x =-;(3)lg 4x =; (4)3ln e x =.小结:应用指对互化求x .※ 动手试试练1. 求下列各式的值.(1)5log 25 ; (2)21log 16; (3)lg 10000.练2. 探究log ?n a a = log ?a N a =三、总结提升 ※ 学习小结①对数概念;②lg N 与ln N ;③指对互化;④如何求对数值※ 知识拓展对数是中学初等数学中的重要内容,那么当初是谁首创“对数”这种高级运算的呢在数学史上,一般认为对数的发明者是十六世纪末到十七世纪初的苏格兰数学家——纳皮尔(Napier ,1550-1617年)男爵. 在纳皮尔所处的年代,哥白尼的“太阳中心说”刚刚开始流行,这导致天文学成为当时的热门学科. 可是由于当时常量数学的局限性,天文学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵时间. 纳皮尔也是当时的一位天文爱好者,为了简化计算,他多年潜心研究大数字的计算技术,终于※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※当堂检测(时量:5分钟满分:10分)计分:1. 若2log3x =,则x =( ). A. 4 B. 6 C. 8 D. 92. log = ( ).A. 1B. -1C. 2D. -2 3. 对数式2log (5)a a b --=中,实数a 的取值范围是().A.(,5)-∞ B .(2,5)C .(2,)+∞D . (2,3)(3,5) 4. 计算:1(3+= .5. 若log 1)1x =-,则x =________,若y =,则y =___________.1. 将下列指数式化成对数式,对数式化成指数式.(1)53243=; (2)51232-=; (3)430a =(4)1() 1.032m =; (5)12log 164=-;(6)2log 1287=; (7)3log 27a =.2. 计算:(1)9log27; (2)3log 243; (3); (3)(2log (2; (4)625.§§2.2.1 对数与对数运算(2)学习目标1. 掌握对数的运算性质,并能理解推导这些法则的依据和过程;2. 能较熟练地运用对数运算法则解决问题..学习过程 一、课前准备 6466 复习1:(1)对数定义:如果x a N =(0,1)a a >≠,那么数 x 叫做 ,记作 . (2)指数式与对数式的互化: xa N =⇔ .复习2:幂的运算性质.(1)m n a a = ;(2)()m n a = ;(3)()n ab = . 复习3:根据对数的定义及对数与指数的关系解答: (1)设log 2a m =,log 3a n =,求m na +; (2)设log a M m =,log a N n =,试利用m 、n 表示log (a M ·)N .二、新课导学 ※ 学习探究探究任务:对数运算性质及推导 问题:由p q p q a a a +=,如何探讨log a MN 和log a M 、log a N 之间的关系问题:设log a M p =, log a N q =,由对数的定义可得:M =p a ,N =q a ∴MN =p a q a =p q a +,∴log a MN =p +q ,即得log a MN =log a M + log a N 根据上面的证明,能否得出以下式子如果 a > 0,a 1,M > 0, N > 0 ,则 (1)log ()log log a a a MN M N =+;(2)log log log a a a MM N N=-;(3) log log ()n a a M n M n R =∈.反思:自然语言如何叙述三条性质 性质的证明思路(运用转化思想,先通过假设,将对数式化成指数式,并利用幂运算性质进行恒等变形;然后再根据对数定义将指数式化成对数式)※ 典型例题例1用log a x , log a y , log a z 表示下列各式:(1)2log a xyz ; (2) 35log a x y z.例2计算: (1)5log 25; (2)0.4log 1;(3)852log (42)⨯; (4)9100探究:根据对数的定义推导换底公式log log log c a c bb a=(0a >,且1a ≠;0c >,且1c ≠;0b >).试试:2000年人口数13亿,年平均增长率1℅,多少年后可以达到18亿 ※ 动手试试练1. 设lg2a =,lg3b =,试用a 、b 表示5log 12.变式:已知lg2=,lg3=,求lg6、lg12.值.练2. 运用换底公式推导下列结论.(1)log log m n a a nb b m=;(2)1log log a b b a =.练 3. 计算:(1)7lg142lg lg7lg183-+-;(2)lg 243lg9.三、总结提升 ※ 学习小结①对数运算性质及推导;②运用对数运算性质;③换底公式.※ 知识拓展① 对数的换底公式log log log b a b NN a =;② 对数的倒数公式1log log a b b a=. ③ 对数恒等式:log log n n a a N N =,log log m n a a nN N=,log log log 1a b c b c a =. ※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 下列等式成立的是( ) A .222log (35)log 3log 5÷=-B .222log (10)2log (10)-=-C .222log (35)log 3log 5+=D .3322log (5)log 5-=-2. 如果lgx =lga +3lgb -5lgc ,那么( ).A .x =a +3b -cB .35abx c=C .35ab x c= D .x =a +b 3-c 33. 若()2lg 2lg lg y x x y -=+,那么( ). A .y x = B .2y x = C .3y x = D .4y x =4. 计算:(1)99log 3log 27+= ;(2)2121log log 22+= .5.计算:15lg 23= .1. 计算:(1;(2)2lg 2lg 2lg5lg5+⋅+.2. 设a 、b 、c 为正数,且346a b c ==,求证: 1112c a b -=.§2.2.1 对数与对数运算(3)学习目标1. 能较熟练地运用对数运算性质解决实践问题;2. 加强数学应用意识的训练,提高解决应用问题的能力.学习过程一、课前准备6669 复习1:对数的运算性质及换底公式.如果 a > 0,a 1,M > 0, N > 0 ,则 (1)log ()a MN = ;(2)log a MN= ;(3) log n a M = .换底公式log a b = .复习2:已知 2log 3 = a , 3log 7 = b ,用 a ,b 表示42log 56.复习3:1995年我国人口总数是12亿,如果人口的年自然增长率控制在℅,问哪一年我国人口总数将超过14亿 (用式子表示)二、新课导学 ※ 典型例题例1 20世纪30年代,查尔斯.里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大. 这就是我们常说的里氏震级M ,其计算公式为:0lg lg M A A =-,其中A 是被测地震的最大振幅,0A 是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是, 计算这次地震的震级(精确到);(2)5级地震给人的振感已比较明显,计算级地震最大振幅是5级地震最大振幅的多少倍(精确到1)小结:读题摘要→寻找数量关系→利用对数计算.例2当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.根据些规律,人们获得了生物体碳14含量P 与生物死亡年数t 之间的关系.回答下列问题: (1)求生物死亡t 年后它机体内的碳14的含量P ,并用函数的观点来解释P 和t 之间的关系,指出是我们所学过的何种函数(2)已知一生物体内碳14的残留量为P ,试求该生物死亡的年数t ,并用函数的观点来解释P 和t 之间的关系,指出是我们所学过的何种函数(3)长沙马王墓女尸出土时碳14的余含量约占原始量的%,试推算古墓的年代反思:① P 和t 之间的对应关系是一一对应;② P 关于t 的指数函数57301()2x P =,则t 关于P的函数为 . ※ 动手试试练1. 计算:(1)0.21log 35-; (2)4912log 3log 2log ⋅-练2. 我国的GDP 年平均增长率保持为%,约多少年后我国的GDP 在2007年的基础上翻两番三、总结提升 ※ 学习小结1. 应用建模思想(审题→设未知数→建立x 与y 之间的关系→求解→验证);2. 用数学结果解释现象.※ 知识拓展在给定区间内,若函数()f x 的图象向上凸出,则函数()f x 在该区间上为凸函数,结合图象易得到1212()()()22x x f x f x f ++≥; 在给定区间内,若函数()f x 的图象向下凹进,则函数()f x 在该区间上为凹函数,结合图象易得到1212()()()x x f x f x f ++≤.※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:25()a -(a ≠0)化简得结果是( ).A .-aB .a 2C .|a |D .a2. 若 log 7[log 3(log 2x )]=0,则12x =( ). A. 3 B.3.已知35a b m ==,且112a b+=,则m 之值为( ).A .15B .2254. 若3a=2,则log 38-2log 36用a 表示为 .5. 已知lg20.3010=,lg1.07180.0301=,则lg2.5=;1102=.1. 化简:(1)222lg5lg8lg5lg20(lg2)3+++;(2)()()24525log 5+log 0.2log 2+log 0.5.2. 若()()lg lg 2lg 2lg lg x y x y x y -++=++,求x y的值.§2.2.2 对数函数及其性质(1)1. 通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;2. 能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;3. 通过比较、对照的方法,引导学生结合图象类比指数函数,探索研究对数函数的性质,培养数形结合的思想方法,学会研究函数性质的方法.7072复习1:画出2x y =、1 ()2x y =的图象,并以这两个函数为例,说说指数函数的性质.复习2:生物机体内碳14的“半衰期”为5730年,湖南长沙马王堆汉墓女尸出土时,碳14的残余量约占原始含量的%,试推算马王堆古墓的年代.(列式)二、新课导学 ※ 学习探究 探究任务一:对数函数的概念讨论:t 与P 的关系 (对每一个碳14的含量P 的取值,通过对应关系log t P =,生物死亡年数t 都有唯一的值与之对应,从而t 是P 的函数)新知:一般地,当a >0且a ≠1时,函数log a y x=叫做对数函数(logarithmic function),自变量是x ; 函数的定义域是(0,+∞).反思:对数函数定义与指数函数类似,都是形式定义,注意辨别,如:22log y x =,5log (5)y x = 都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制 (0a >,且1)a ≠.探究任务二:对数函数的图象和性质 问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗研究方法:画出函数图象,结合图象研究函数性质.研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.试试:同一坐标系中画出下列对数函数的图象. 2log y x =;0.5log y x =.反思: ((2)图象具有怎样的分布规律※ 典型例题例1求下列函数的定义域:(1)2log a y x =;(2)log (3)a y x =-;变式:求函数y =.例2比较大小: (1)ln3.4,ln8.5; (2)0.30.3log 2.8,log 2.7;(3)log 5.1,log 5.9a a .小结:利用单调性比大小;注意格式规范.※ 动手试试练1. 求下列函数的定义域.(1)0.2log (6)y x =--; (2)32log 1y x =-.练2. 比较下列各题中两个数值的大小.(1)22log 3log 3.5和; (2)0.30.2log 4log 0.7和; (3)0.70.7log 1.6log 1.8和; (4)23log 3log 2和.三、总结提升 ※ 学习小结1. 对数函数的概念、图象和性质;2. 求定义域;3. 利用单调性比大小.※ 知识拓展对数函数凹凸性:函数()log ,(0,1)a f x x a a =>≠,12,x x 是任意两个正实数.当1a >时,1212()()()22f x f x x xf ++≤;当01a <<时,1212()()()22f x f x x xf ++≥.学习评价※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 当a >1时,在同一坐标系中,函数x y a -=与log a y x =的图象是( ).2. 函数22log (1)y x x =+≥的值域为( ). A. (2,)+∞ B. (,2)-∞ C. [)2,+∞ D. [)3,+∞3. 不等式的41log 2x >解集是( ). A. (2,)+∞ B. (0,2)B. 1(,)2+∞ D. 1(0,)24. 比大小:(1)log 67 log 7 6 ; (2)log log 2 . 5. 函数(-1)log (3-)x y x =的定义域是 .课后作业1. 已知下列不等式,比较正数m 、n 的大小: (1)3log m <3log n ; (2)0.3log m >0.3log n ; (3)log a m >log a n (a >1)2. 求下列函数的定义域: (1)2log (35)y x =-(2)0.5log 43y x =-§2.2.2 对数函数及其性质(2)1. 解对数函数在生产实际中的简单应用;2. 进一步理解对数函数的图象和性质;3. 学习反函数的概念,理解对数函数和指数函数互为反函数,能够在同一坐标上看出互为反函数的两个函数的图象性质.7273复习1:对数函数log (0,1)a y x a a =>≠且图象和性复习2:比较两个对数的大小.(1)10log 7与10log 12 ; (2)0.5log 0.7与0.5log 0.8.复习3:求函数的定义域.(1)311log 2y x=- ; (2)log (28)a y x =+.二、新课导学 ※ 学习探究探究任务:反函数问题:如何由2x y =求出x反思:函数2log x y =由2x y =解出,是把指数函数2x y =中的自变量与因变量对调位置而得出的. 习惯上我们通常用x 表示自变量,y 表示函数,即写为2log y x =.新知:当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数(inverse function )例如:指数函数2x y =与对数函数2log y x =互为反函数.试试:在同一平面直角坐标系中,画出指数函数2x y =及其反函数2log y x =图象,发现什么性质反思:(1)如果000(,)P x y 在函数2x y =的图象上,那么P 0关于直线y x =的对称点在函数2log y x =的图象上吗为什么(2)由上述过程可以得到结论:互为反函数的两个函数的图象关于 对称.※ 典型例题例1求下列函数的反函数:(1) 3x y =; (2)log (1)a y x =-.小结:求反函数的步骤(解x →习惯表示→定义域)变式:点(2,3)在函数log (1)a y x =-的反函数图象上,求实数a 的值.例2溶液酸碱度的测量问题:溶液酸碱度pH 的计算公式lg[]pH H +=-,其中[]H +表示溶液中氢离子的浓度,单位是摩尔/升.(1)分析溶液酸碱度与溶液中氢离子浓度之间的变化关系(2)纯净水7[]10H +-=摩尔/升,计算其酸碱度.小结:抽象出对数函数模型,然后应用对数函数模型解决问题,这就是数学应用建模思想.※ 动手试试练 1. 己知函数()x f x a k =-的图象过点(1,3)其反函数的图象过点(2,0),求()f x 的表达式.练2. 求下列函数的反函数. (1) y =(2)x (x ∈R );(2)y =log a 2x(a >0,a ≠1,x >0)三、总结提升 ※ 学习小结① 函数模型应用思想;② 反函数概念.※ 知识拓展函数的概念重在对于某个范围(定义域)内的任意一个自变量x 的值,y 都有唯一的值和它对应. 对于一个单调函数,反之对应任意y 值,x 也都有惟一的值和它对应,从而单调函数才具有反函数. 反函数的定义域是原函数的值域,反函数的值域是原函数的定义域,即互为反函数的两个函数,定义学习评价※ 自我评价 你完成本节导学案的情况为( ). A. 很好 B. 较好 C. 一般 D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分: 1. 函数0.5log y x =的反函数是( ). A. 0.5log y x =- B. 2log y x =C. 2x y =D. 1()2x y =2. 函数2xy =的反函数的单调性是( ). A. 在R 上单调递增 B. 在R 上单调递减C. 在(0,)+∞上单调递增D. 在(0,)+∞上单调递减3. 函数2(0)y x x =<的反函数是( ). A. (0)y x x =±> B. (0)y x x => C. (0)y x x =-> D. y x =±4. 函数x y a =的反函数的图象过点(9,2),则a 的值为 .5. 右图是函数1log a y x =,2log a y x=3log a y x=, 4log a y x =的图象,则底数之间的关系为 .课后作业1. 现有某种细胞100个,其中有占总数12的细胞每小时分裂一次,即由1个细胞分裂成2个细胞,按这种规律发展下去,经过多少小时,细胞总数可以超过1010个(参考数据:lg30.477,lg20.301==).2. 探究:求(0)ax by ac cx d+=≠+的反函数,并求出两个函数的定义域与值域,通过对定义域与值域的比较,你能得出一些什么结论§ 对数函数(练习)学习目标。
高中数学-必修1-第2章-基本初等函数-讲义

§ 2.1.1 指数与指数幕的运算(1)1学习目标1. 了解指数函数模型背景及实用性、必要性;2. 了解根式的概念及表示方法;3. 理解根式的运算性质.问题2 :生物死亡后,体内碳 14每过5730年衰减 一半(半衰期),则死亡t 年后体内碳14的含量Pt与死亡时碳14关系为P (I )3730 .探究该式意义2J ..学习过程 一、课前准备(预习教材P 48~ P 50,找出疑惑之处) 复习1:正方形面积公式为 _____________ ;正方体的 体积公式为 一 复习2:(初中根式的概念) 如果一个数的平方等于 a,那么这个数叫做a 的 __________ ,记作 ______________________________ ;如果一个数的立方等于 a ,那么这个数叫做 a 的 __________ ,记作 .二、新课导学 探学习探究 探究任务一:指数函数模型应用背景探究下面实例及问题,了解指数指数概念提出的 背景,体会引入指数函数的必要性 . 实例1.某市人口平均年增长率为%, 1990年人口 数为a 万,则x 年后人口数为多少万小结:实践中存在着许多指数函数的应用模型,如 人口问题、银行存款、生物变化、自然科学 . 探究任务二:根式的概念及运算 考察:(2)24,那么 2就叫4的 _________ ;33 27,那么3就叫27的 _________ ; (3)4 81,那么 3就叫做81的 . 依此类推,若x n a ,,那么x 叫做a 的 .新知:一般地,若x n a ,那么x 叫做a 的n 次方根 (n th root ) ,其中 n 1, n 简记:n a .例如:238,则382.反思:当n 为奇数时,n 次方根情况如何 例如:3 27 3 , 3_273,记:x n a .当n 为偶数时,正数的 n 次方根情况 例如:81的4次方根就是 ___________________ ,记:n a .强调:负数没有偶次方根; 0的任何次方根都是0,即 V0 0 .试试:b 4 a ,则a 的4次方根为 ____________ ;b 3 a ,则a 的3次方根为 _______ —计算:若报纸长 50cm 宽34cm,厚,进行对折 x 次后,求对折后的面积与厚度新知:像&a 的式子就叫做根式 (radical ),这里n叫做根指数(radical exponent ), a 叫做被开方数 (radicand ).试试:计算(2 3)2、、n ( 2)n .问题1:国务院发展研究中心在 2000年分析,我国未来20年GDP 国内生产总值)年平均增长率达%, 则x 年后GD 励2000年的多少倍反思:从特殊到一般,(n a )n 、n /的意义及结果实例2.给一张报纸,先实验最多可折多少次你能 超过8次吗②若0 a 1,则0 a n 1.其中n N*. 结论:(n a)n a.当n是奇数时,n a ;当n是偶数时,n a n |a| a (a 0)a (a 0)%典型例题例1求下类各式的值:(1) 3( a)3; (2) 4( 7)4;(3)6?TT ;(4) 2(a b)2( a b )A.很好B. 较好C.一般D.较差%当堂检测(时量:5分钟满分:10分)计分1. 4( 3)4的值是()A. 3B. —3C.3D.812. 625的4次方根是( ).A. 5B. —5C.± 5D.253.化简(2 b)2是()A. bB. bC. bD.1b4.化简6(a b)6 =5.计算:(3飞)3 =;2孑'7课后作业1.计算:(1)5孑;(2) 37^学习评价探自我评价你完成本节导学案的情况为().变式:计算或化简下列各式•(1)「32 ;(2)3a6 .推广:np a mp n a m( a 0).%动手试试练 1.化简 5 2,6 .7 4”3. 6 4 2. 2.计算a3 a 4和a3( 8),它们之间有什么关系你能得到什么结论练 2.化简2 3 31.5 612 .3.对比(ab)n 前者吗nn ¥,你能把后者归入b二、总结提升%学习小结1. n次方根,根式的概念;2. 根式运算性质.%知识拓展1. 整数指数幕满足不等性质:若a 0,则a n 0.2. 正整数指数幕满足不等性质:①若a 1,则a n 1 ;§ 2.1.1 指数与指数幕的运算(2)上乞二…学习目标 1. 理解分数指数幕的概念; 2. 掌握根式与分数指数幕的互化; 3. 掌握有理数指数幕的运算. 学习过程 一、课前准备 (预习教材P 50~ P 53,找出疑惑之处) 复习1: 一般地,若x na ,则x 叫做a 的 ___________ 其中n 1,n . 简记为: . 像na 的式子就叫做 ________________ ,具有如下 运算性质: (n a)n = _____________ ;戸= ________________ ; np a mp=—一 反思:① 0的正分数指数幕为 __________; 0的负分数指数 幕为 .② 分数指数幕有什么运算性质小结:规定了分数指数幕的意义后,指数的概念就从整 数指数推广到了有理数指数,那么整数指数幕的运 算性质也同样可以推广到有理数指数幕. 指数幕的运算性质: rrr sa • a a (a r )a 0,b 0, r,s Q ) _ rs;r r s(ab) a a探典型例题2例1求值:27乜16 4■3・2 25 3()3. 49复习2:整数指数幕的运算性质. (1) a m |a n _________ ; (2) (a m )n _________ : (3) (ab)n 二、新课导学 探学习探究 探究任务:分数指数幕 ____ _____________ 10引例:a >0 时,5a 10 Q (a 2 )5 a 2 a 5 , 则类似可得3 a 2________________ ; ___ —22好敢a 3)3 a 3,类似可得罷 .变式:化为根式新知: m a 7 m a n规定分数指数幕如下 n a m (a 0,m, n N ,n 1); 1 1 * n r (a 0,m,n N ,n 1). a 例2用分数指数幕的形式表示下列各式 (1) b 2| .b ;(2) b 3; (3) (b 0):3b 4b.m a 7 试试: (1) 2齐 a m将下列根式写成分数指数幕形式: ;盲 —(a0,m--------- ?).例3计算(式中字母均正):211 11 5(1) (3a^b°)( 8a 2b') ( 6a 彗); 1 3(2) (m 帝)16.2 2(2)求值:83 ;55 ;小结:例2,运算性质的运用;例 3,单项式运算. 例4计算: 3a(a 司3、a 43(2m 2n 5)10 (416 332) 7学习评价(i)(2) (3) 0); 1 23 6 m n ) (m,n N );4 64.%自我评价你完成本节导学案的情况为 A.很好B. 较好 C. %当堂检测(时量:5分钟 1.若a 0 ,且m,n 为整数, 是( ).( ) 一般D. 较差 满分:10分)计分: 则下列各式中正确的ma 下m nam nA. a a mnC. a32.化简25°的结果是 A. 5 B. 15 C. 25 B. D.ma an1 amna0 naD. 1253.计算 .2 1 2的结果是( 小结: 正指数,化根式为分数指数幕,对含有指数式或根 式的乘除运算,还要善于利用幕的运算法则 . 在进行指数幕的运算时,一般地,化指数为 A .2 B2 C.24.化简27 ^ =反思: ①的结果 3m5.若 10m 2, 10n 4,则 10结论:无理指数幕.(结合教材P 53利用逼近的思想 理解无理指数幕意义) …迭垃.….课后作业 1.化简下列各式: (1) ②无理数指数幕a (a 0,是无理数)是一个确定 的实数.实数指数幕的运算性质如何 (唧; 49(2)2. 3%动手试试 练1•把 8 5化成分数指数幕.3 练2.计算:(1)詞岡历;(2) 6;(曇孑)4 * 2. 计算:—牯_8临_1阻^算: 3a 2 23 ab 43a 4 1 ' a二、总结提升 %学习小结 ①分数指数幕的意义;②分数指数幕与根式的互 化;③有理指数幕的运算性质 . %知识拓展 放射性元素衰变的数学模型为: 中t 表示经过的时间,m o 表示初始质量,衰减后的 质量为m为正的常数.m m °e 1,其 § 2.1.1 指数与指数幕的运算(练习)'7学习目标J H «r ・ ・m H ruiini ・・m n m ・・m i «m n M ・・r1. 掌握n 次方根的求解;2. 会用分数指数幕表示根式;3. 掌握根式与分数指数幕的运算1- 学习过程—i ■ — — -— — —ll — - - —— —一、课前准备(复习教材P 48~ P 53,找出疑惑之处) 复习1:什么叫做根式运算性质像n a 的式子就叫做 ________________ ,具有性质:(n.a )n = ___________ ; - a =_叩尹=——小结:① 平方法;② 乘法公式;③ 根式的基本性质nP T n a m (a >0)等. 注意,a > 0十分重要,无此条件则公式不成立 例如,6( 8)23_8.1 1变式:已知a 2 a 23,求:1133(1)a 2 a 2 ; (2) a 2 a 2.复习2:分数指数幕如何定义运算性质mm① a"________ ; a n .其中 a 0,m, n N *,n 1② a r |a s ___________ ; (a r )s __________ (ab)s ______ . ___ 复习3:填空.二、新课导学小结:① 方法:摘要T 审题;探究 T 结论;1 立方和差公式: a 3 b 3 (a b)(a2 ab b 2); a 3b 3 (a b)(a 2ab b 2).(1) a a 1 ;(2) a 2 a 2 ;3(3) / 3a 2(3/ 1 1・_a 2a 2补充:立方和差公式 a b (ab)(a 2 ab b 2).变式:n 次后例1已知 时,|x|(X 0) (X 0)② 求下列各式的值:3歹=_6万=vx^=_416=_15_32 =6a 2b 4 =_681 =例2从盛满1升纯酒精的容器中倒出 1升,然后用3 水填满,再倒出1升,又用水填满,这样进行5次,3则容器中剩下的纯酒精的升数为多少求下列各式的值:解应用问题四步曲:审题T建模T解答T作答动手试试(a b)3 a3 3a* 1 2b 3ab2 b3.1. 化简:1 1 1 1(x2 y2) (x4 y4).y学习评价练2.(1) 已知x+x-1 =3,求下列各式的值.1x21X2;(2)3x2练 3. f(x) x ,X1 x20( )一般D. 较差满分:10分)计分:探自我评价你完成本节导学案的情况为A.很好B. 较好探当堂检测(时量:1. 92的值为(C.5分钟).C. 3A. ,3B. 3 332. _ a ( a>0)的值是a 5 a4A. 1B. aC.3.下列各式中成立的是(1A. (—)7 n7m7C. 4 x3y34.化简(25)42 1(x32 _3yrD. 7291a* D.).17a10T9 3315.化简(a3b2)( 3a2b3) (^a6b6)=讥上,课后作业b 2, 求飯—2a 3x―a"6的值.1.已知x a 3§ 2.1.2 指数函数及其性质(1)学习目标1. 了解指数函数模型的实际背景,认识数学与现 实生活及其他学科的联系;2. 理解指数函数的概念和意义;3. 能画出具体指数函数的图象,掌握指数函数的 性质(单调性、特殊点)探究任务二:指数函数的图象和性质引言:你能类比前面讨论函数性质时的思路,提出 研究指数函数性质的内容和方法吗 回顾:研究方法:画出函数图象,结合图象研究函数性质. 研究内容:定义域、值域、特殊点、单调性、最大 (小)值、奇偶性.作图:在同一坐标系中画出下列函数图象:-、课前准备(预习教材P 54~ P 57,找出疑惑之处)复习1:零指数、负指数、分数指数幕怎样定义的 (1) a 0 : (2) a n:mm(3) a n: "Fa.其中 a 0,m, n N ,n1复习2:有理指数幕的运算性质. (1) _______________ a|a ;( 2)(a )___________________ ; (3) (ab)n二、新课导学 探学习探究 探究任务一:指数函数模型思想及指数函数概念 实例:A. 细胞分裂时,第一次由1个分裂成2个,第2 次由2个分裂成4个,第3次由4个分裂成8个, 如此下去,如果第x 次分裂得到y 个细胞,那么细 胞个数y 与次数x 的函数关系式是什么B. —种放射性物质不断变化成其他物质,每经 过一年的残留量是原来的 84%,那么以时间x 年为 自变量,残留量y 的函数关系式是什么 讨论:上面的两个函数有什么共同特征底数是什么 指数是什么新知:一般地,函数 y a x (a 0,且a 1)叫做指数 函数(exponential function ),其中 x 是自 变量,函数的定义域为R.反思:为什么规定a > 0且a 工1呢否则会出现什么 情况呢 讨论:1(1) 函数y 2x 与y q )x 的图象有什么关系如何 由y 2x的图象画出y G )x 的图象(2) 根据两个函数的图象的特征,归纳出这两个 指数函数的性质.变底数为3或1后呢3探典型例题 例1函数f(x)a x ( a 0,且a 1)的图象过点(2,),求 f (0) , f( 1), f(1)的值.试试:举出几个生活中有关指数模型的例子学习过程1 x (2),比较大小: a 0.80",b 0.80:c 02.50.2 1.61 , 0.4 ,2 , 2.5 .2. 探究:在[m n ]上,f(x) a x (a 0且a 1)值域二、总结提升 %学习小结 ①指数函数模型应用思想;②指数函数概念;③指 数函数的图象与性质;③单调法 . %知识拓展因为y a x (a 0,且a 1)的定义域是R,所以 y a"〉(a 0,且a 1)的定义域与f (x)的定义域 相同.而y (a x ) (a 0,且a 1)的定义域,由 y (t)的定义域确定.小结:①确定指数函数重要要素是 ②待定系数法•学习评价例2比较下列各组中两个值的大小:0.60.5(1) 2 ,2 ;(3) 2.10^,0.5Z121 5(2) 0.9 ,0.9 ;(4)2 3与1.( ). 较差5分钟满分:10分)计分: 3)a x 是指数函数,则a 的值为%自我评价你完成本节导学案的情况为A.很好B. 较好C. 一般D.%当堂检测(时量: 1. 函数 y (a 2 3a ( ). A. 1 B. 2 2. 函数 f (x )= ( ). C. 12或2 D. 任意值1 ( a >0, a z 1)的图象恒过定点 小结:禾U 用单调性比大小;或间接利用中间数 探动手试试练1. 已知下列不等式,试比较 m n 的大小:(1)n; (2)m1.1 n1.1 .A. (0,1)B.C. (2,1)D. 3. 指数函数①f(x)(0,2) (2,2)心® 1f XX1[5.函数y1.求函数y =-的定义域. 1练2. (1) (2) 1.2,的定义域为xxm ,②g(x) n 满足不等式).(2.5)5 .24.比较大小:(2.5)30 m n 1,则它们的图象是(§ 2.1.2 指数函数及其性质(2) 说』学习目标J H «r ・・ m n rniini r1. 熟练掌握指数函数概念、图象、性质;2. 掌握指数型函数的定义域、值域,会判断其单调性;3. 培养数学应用意识.小结:学会读题摘要;掌握从特殊到一般的归纳法试试:2007年某镇工业总产值为100亿,计划今后每年平均增长率为8%,经过x年后的总产值为原来的多少倍多少年后产值能达到120亿学习过程一、课前准备(预习教材只7~ P60,找出疑惑之处)复习1:指数函数的形式是_______________________ 其图象与性质如下小结:指数函数增长模型.设原有量N,每次的增长率为p,则经过x次增长后的总量y= ____ 我们把形如y ka x(k R,a 0,且a 1)的函数称为指数型函数.例2求下列函数的定义域、值域:1 (1)y 2x 1;( 2)y( 3)y 0.4厂1.x 1 xy 2, y (-)x 1 xy 10 , y ().10思考:指数函数的图象具有怎样的分布规律小结:单调法、基本函数法、图象法、观察例1我国人口问题非常突出,在耕地面积只占世界7%勺国土上,却养育着22%勺世界人口.因此,中国的人口问题是公认的社会问题. 2000年第五次人口普查,中国人口已达到13亿,年增长率约为1%为了有效地控制人口过快增长,实行计划生育成为我国一项基本国策.(1)按照上述材料中的1%勺增长率,从2000年起,x年后我国的人口将达到2000年的多少倍(2)从2000年起到2020年我国人口将达到多少试试:求函数y (2 x *的定义域和值域,并讨论其单调性.y G)x5变式:单调性如何2%动手试试练1.求指数函数y 2x 1的定义域和值域,并讨论其单调性•练2.已知下列不等式,比较m,n的大小.(1) 3m3n;(2) m0.60.6n;(3) m a a n (a 1);(4) m a a n (0 a 1)练3. —片树林中现有木材30000吊,如果每年增长5%经过x年树林中有木材y m,写出x,y间的函数关系式,并利用图象求约经过多少年,木材可以增加到40000吊.& 学习评价探自我评价你完成本节导学案的情况为( ).A.很好B. 较好C. 一般D. 较差探当堂检测(时量:5分钟满分:10分)计分:1. 如果函数y=a x (a>0, 1)的图象与函数y=b x(b>0,b z 1)的图象关于y轴对称,则有( ).A. a>bB. a<bC. ab=1D. a与b无确定关系2. 函数f(x)=3 —x- 1的定义域、值域分别是().A. R, RB. R, (0,)C. R, ( 1, )D.以上都不对3. 设a、b均为大于零且不等于1的常数,则下列说法错误的是( ).A. y=a x的图象与y=a-x的图象关于y轴对称B. 函数f(x)=a1-x (a>1)在R上递减C. 若a 2 >a 2 1,贝U a>1D. 若2x>1,则x 14. 比较下列各组数的大小:1 3_________ (0.4));______ 血0.75.35. 在同一坐标系下,函数y=a x, y=b x, y=c x, y=d x的图象如右图,贝U a、b、c、d、1之间从小到大的顺序是 .…课后作业21.已知函数f(x)=a— ------------ (a€ R»,求证:对任2x 1 何a R , f (x)为增函数.二、总结提升%学习小结1. 指数函数应用模型y ka x (k R,a 0且a 1);2. 定义域与值域;2.单调性应用(比大小).%知识拓展形如y a f(x) (a 0,且a 1)的函数值域的研究,先求得f (x)的值域,再根据a t的单调性,列出简单的指数不等式,得出所求值域,注意不能忽视y a f(x) 0.而形如y (a x) (a 0,且a 1) 的函数值域的研究,易知a x 0,再结合函数(t)进行研究.在求值域的过程中,配合一些常用求值域的方法,例如观察法、单调性法、图象法等x2.求函数y 2厂」的定义域和值域,并讨论函数2x 1的单调性、奇偶性.§ 221 对数与对数运算(1)学习目标1. 理解对数的概念;2. 能够说明对数与指数的关系;3. 掌握对数式与指数式的相互转化 .新知:一般地,如果a x N (a 0,a 1),那么数x 叫做以a为底 N 的对数(logarithm ).记作x log a N ,其中a 叫做对数的底数,N 叫做真数.试试:将复习2及问题中的指数式化为对数式弋$学习过程-■ .>= ” ■- -■ - -■ .■- » ■一、课前准备(预习教材P 62~ P 64,找出疑惑之处)复习1:庄子:一尺之棰,日取其半,万世不竭 (1 )取4次,还有多长 (2 )取多少次,还有尺 新知:我们通常将以10为底的对数叫做常用对数(common logarithm ),并把常用对数log 10 N 简记 为lg N 在科学技术中常使用以无理数 e= ....... 为底的对数,以e 为底的对数叫自然对数,并把自然 对数log e N 简记作In N试试:分别说说lg5、、ln10、In3的意义.复习2:假设2002年我国国民生产总值为 a 亿元, 如果每年平均增长 8%那么经过多少年国民生产 是2002年的2倍(只列式)二、新课导学 探学习探究 探究任务:对数的概念 问题:截止到1999年底,我国人口约13亿.如果 今后能将人口年平均增长率控制在 1%,那么多少年 后人口数可达到18亿,20亿,30亿反思:(1) 指数与对数间的关系a 0, a 1 时,a x N _____________ . (2) 负数与零是否有对数为什么(3) 也1 _________ , log a a ______ . ___ 探典型例题例1下列指数式化为对数式,对数式化为指数式371a(1) 5 125 ; (2) 2; (3) 327 ;128(4) 100.01 ; (5) log ! 325 ;2(6) = 3 ; (7) In 100=.讨论:(1)问题具有怎样的共性(2) 已知底数和幕的值,求指数 *怎样求呢例如: 由 1.01x m ,求 x .变式: log 1 322独立发明了对数例2求下列各式中x 的值:2(1)log 64 X - ; ( 2) Iog x 8 6 ;3(3)lg x 4 ; ( 4) In e 3 x. 探自我评价 你完成本节导学案的情况为 (A.很好B .较好 C. 一般 D. 较差探当堂检测 (时量: 5分钟 满分: 10分)计分 1.若 log 2 x 3,则x ( ).A. 4B. 6C. 8D. 92. log( m ,-n)(.n 1■ n)= (). A. 1 B.-1 C .2 D.-23.对数式log a 2(5 a ) b 中,实数a 的取值范围是( )A .( ,5)B • (2,5) C. (2,)D• (2,3儿(3,5)4.计算:log: 2 1(3 2.2) .5.若 IogxG/2 1)1,贝y x= _________ ,若log ^8 y ,贝V y = .7®课后作业1. 将下列指数式化成对数式,对数式化成指数式 . 551 a(1) 3 243 ; (2) 2 一 ; (3) 4 3032(4) (-)m 1.03 ;(5) log/64 ;22二、总结提升 探学习小结 ①对数概念;②lg N 与 求对数值探知识拓展对数是中学初等数学中的重要内容,那么当初是 谁首创“对数”这种高级运算的呢在数学史上,一 般认为对数的发明者是十六世纪末到十七世纪初 的苏格兰数学家——纳皮尔( Napier , 1550-1617 年)男爵.在纳皮尔所处的年代,哥白尼的“太阳 中心说”刚刚开始流行,这导致天文学成为当时的 热门学科.可是由于当时常量数学的局限性,天文 学家们不得不花费很大的精力去计算那些繁杂的“天文数字”,因此浪费了若干年甚至毕生的宝贵 时间.纳皮尔也是当时的一位天文爱好者,为了简 化计算,他多年潜心研究大数字的计算技术,终于 2.计算:(1) log 927 ; (2) log 3 243 ; (3) log^81 ;(3)叫、3)(23) ;(4) log 354625.6 log 2 1287 ; (7) log 3 27 a .练2.探究log a a nlog a Na小结:注意对数符号的书写, 与真数才能构成整体 小结:应用指对互化求 x .探动手试试 练1.求下列各式的值.1(1) Iog 5 25 ; (2) log 2 ; (3) |g 10000.16ln N;③指对互化;④如何§§ 221 对数与对数运算(2)'v 学习目标1. 掌握对数的运算性质,并能理解推导这些法则 的依据和过程;2. 能较熟练地运用对数运算法则解决问题 ..1学习过程—1 ■ 1-1~.—— -r-rt™!-.-—.~v —~?rj —1— -.~w™—.-1;—一、课前准备(预习教材P 64~ P 66,找出疑惑之处) 复习1:(1 )对数定义:如果a x N (a 0,a 1),那么数 x 叫做 ___________________ ,记作 ^(2)指数式与对数式的互化:a x N^自然语言如何叙述三条性质 性质的证明思路(运 用转化思想,先通过假设,将对数式化成指数式, 并利用幕运算性质进行恒等变形;然后再根据对数 定义将指数式化成对数式.) 探典型例题例1用log a x , log a y , log a z 表示下列各式: (1 ) log a ;( 2 logaf *复习2:幕的运算性质. (1)a^a n __________ ;(2)(a m )n ______ (3) (ab )n复习3:根据对数的定义及对数与指数的关系解答: (1 )设 log a 2 m , log a 3 n ,求 a m n; (2)设 log a M m , log a N n ,试利用 m 、n 表 示 log a (M • N ). 例2计算: (1) log 5 25 ; (3) log 2 (48 25);(2) log o.4 1 ; (4) lg 9100 .二、新课导学 探学习探究 探究任务:对数运算性质及推导 问题:由a p a q a p q,如何探讨log a MN 和log a M 、 log a N 之间的关系 问题:设 log a M p , log a N q , 由对数的定义可得:M=a p , N =a q* 二 MN a p a q =a p q , log a M 時p +q ,即得 log a MIN log a M + log a N 根据上面的证明,能否得出以下式子 如果 a > 0 , a 1 , M > 0 , N > 0 ,则 (1 ) log a (MN) log a M log a N ; (2) log a M log a M log a N ; N(3) log a M n nlog a M (n R). 探究:根据对数的定义推导换底公式 log a b 3必log c a(a 0 ,且 a 1 ; c 0 ,且 c 1 ; b 0 ).试试:2000年人口数13亿,年平均增长率 1 %, 多少年后可以达到18亿%动手试试反思:1 (2) Iog2 Iog 1 22 2 31 5 -—ig — 52 3① 对数运算性质及推导;②运用对数运算性质;③ 换底公式.探知识拓展① 对数的换底公式log a N② 对数的倒数公式Iog a b2. 设a 、b 、c 为正数,且3a 4b 6c ,求证:c a 2b③ 对数恒等式:log a nN n log a N ,练 1•设 Ig2 a , lg3 b ,试用 a 、b 表示 log 512. log a mN " - Iog a N , Iog a^Iog bd Iog ca 1 . m1学习评价探自我评价你完成本节导学案的情况为 A.很好B. 较好C. 一般D.( ) 较差 计分:变式:已知 Ig2 =, Ig3 =,求 Ig6、Ig12. Ig 3 的 值. A . log 2(3 5) Iog 2 3 Iog 2 5 B . 2iog 2( 10) 2log 2( 10)C. log 2(3 5)log 2^ log 2 5D. 3iog 2( 5) Iog 2 532.女口果 Igx =Iga +3Igb — 5Igc ,那么( 探 当堂检测(时量:5分钟 满分:10分) 1.下列等式成立的是( ) 练2.运用换底公式推导下列结论 (1)Iog a mb n — Iog ab ; m1⑺Iogab 研C. x ab 5 cD. x =a +b 3— 3. 若2lg y 2x Ig x Ig y ,A . yxB . y2xC. y 3x D . y 4x4. 计算: (1) log 9 3log 9 27A . x =a +3b —c3那么(B 3abB x —— 5c3c 5.计算:Ig 练 3.计算:(1)Ig14 Ig 243 Ig9 '2Ig7 Ig7 Ig18;(2)课后作业---- ——1 _1_-_ _• - •-1. 计算:__(1) Ig 习 Ig8 3lg 10lg1.2 (2) lg 22 Ig2 Ig5 Ig5 .log b N log b a 1 log b a .§ 221 对数与对数运算(3)探典型例题例1 20世纪30年代,查尔斯.里克特制订了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级M其计算公式为:Mlg A IgA c,其中A是被测地震的最大振幅,A e是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差).(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是,计算这次地震的震级(精确到);反思:①P和t之间的对应关系是----- 对应;的函数为.%动手试试(2)5级地震给人的振感已比较明显,计算级地震最大振幅是5级地震最大振幅的多少倍(精确到1)左心学习目标1. 能较熟练地运用对数运算性质解决实践问题;2. 加强数学应用意识的训练,提高解决应用问题的能力.二学习过程一、课前准备(预习教材P66~ P69,找出疑惑之处)复习1:对数的运算性质及换底公式.如果a > 0,a 1,M> 0,N > 0 ,则(1)log a(MN)(2). M 叽一N(3)log a M n换底公式log a b _________ . ______ 复习2:已知log23 = a,log a7 = b,用a,b 表示log 42 56.小结:读题摘要T寻找数量关系T利用对数计算.例2当生物死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”•根据些规律,人们获得了生物体碳14含量P与生物死亡年数t之间的关系.回答下列问题:(1)求生物死亡t年后它机体内的碳14的含量P, 并用函数的观点来解释P和t之间的关系,指出是我们所学过的何种函数(2)已知一生物体内碳14的残留量为P,试求该生物死亡的年数t,并用函数的观点来解释P和t 之间的关系,指出是我们所学过的何种函数(3)长沙马王墓女尸出土时碳14的余含量约占原始量的%试推算古墓的年代复习3:1995年我国人口总数是12亿,如果人口的年自然增长率控制在%,问哪一年我国人口总数将超过14亿(用式子表示)、新课导学②P关于t的指数函数P则t关于P练1.计算:(1) 51叽3;(2) log 4 3 log 9 2 log ! 4 32 .2自我评价你完成本节导学案的情况为( ).A.很好B. 较好C.一般D较差当堂检测(时量:5分钟满分:10分)计分:1._log5( a)25(a* 0) 化简得结果是( ).A. —aB. 2 aC. | aID. a2.若log 7 [ log 3 (log 2X)]:=0,则1x2 =( ).A. 3B. 2.3C.22D. 3.23.已知3ab5 m ,且丄a1-2 , b则m之值为( ).A. 15B..15 C . ±、15D.2254.若3a= 2 ,则log 38 - -2log 36i用a表示为5.已知lg20.3010,lg1.0718 0.0301,则练2.我国的GDP年平均增长率保持为%约多少年后我国的GDF在2007年的基础上翻两番lg2.5 ______ ;210_________'7课后作业1.化简:2 2 2(1)lg5 lg8 lg5lg20 (lg2);3(2)Iog25+log 4 0.2 log5 2+log 25O.5 .二、总结提升探学习小结1. 应用建模思想(审题T设未知数T建立之间的关系T求解T验证);2. 用数学结果解释现象.x 2•若lg x y lg x 2y lg 2 lg x lg y ,求一y 的值.x与y探知识拓展在给定区间内,若函数f(x)的图象向上凸出,则函数f(x)在该区间上为凸函数,结合图象易得到x1 x2) f(x1) f(x2);f( )2 2在给定区间内,若函数 f (x)的图象向下凹进,则函数f(x)在该区间上为凹函数,结合图象易得到f( X1 X22f(X1) f(X2)2§ 2.2.2 对数函数及其性质(1)学习目标1. 通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;2. 能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;3. 通过比较、对照的方法,弓I导学生结合图象类比指数函数,探索研究对数函数的性质,培养数形结合的思想方法,学会研究函数性质的方法•.学习过程一、课前准备(预习教材P70~ P72,找出疑惑之处)1复习1:画出y 2x、y (—)x的图象,并以这两2 个函数为例,说说指数函数的性质•注意辨别,如:y 2log2x, y log5(5x) 都不是对数函数,而只能称其为对数型函数;对数函数对底数的限制(a 0,且a 1).探究任务二:对数函数的图象和性质问题:你能类比前面讨论指数函数性质的思路,提出研究对数函数性质的内容和方法吗研究方法:画出函数图象,结合图象研究函数性质. 研究内容:定义域、值域、特殊点、单调性、最大(小)值、奇偶性.试试:同一坐标系中画出下列对数函数的图象.y log2x ;y log 0.5 x.复习2:生物机体内碳14的“半衰期”为5730年, 湖南长沙马王堆汉墓女尸出土时,碳14的残余量约占原始含量的%试推算马王堆古墓的年代•(列式)二、新课导学探学习探究探究任务一:对数函数的概念探典型例题例1求下列函数的定义域:2(1) y log a x ; (2) y log a(3 x);讨论:与的关系(对每一个碳14的含量P的取值,通过对应关系t log ! P ,生物死亡年数t都有唯一的值与之对57302应,从而t是P的函数)新知:一般地,当a>0且a* 1时,函数y log a x叫做对数函数(logarithmic function) ,自变量是x ;函数的定义域是(0, +8).反思:对数函数定义与指数函数类似,都是形式定义,变式:求函数y - log2(3 x)的定义域.例2比较大小:(1) ln3.4, ln8.5 ;(2) log0.32.8, log0.32.7 ;二、总结提升% 1. 学习小结对数函数的概念、图象和性质; 2.求下列函数的定义域:2. 求定义域;(1) y ,log 2(3x 5) ; (2) y ,log °.54x 33. 利用单调性比大小.% 知识拓展对数函数凹凸性:函数 f (x ) log a X, (a 0,a 1), X 1, X 2是任意两个正实数.当 a 1 时,f (X1)f (X2)f (7);2 2 当 o a 1 时,f (X1)f(X2)f (7).2 2^学习评价%自我评价你完成本节导学案的情况为().(3) log a 5.1, log a 5.9. A.很好B. 较好C. 一般D. 较差探 当堂检测(时量:5分钟 满分:10分)计分: 1.当a >1时,在同一坐标系中,函数y a x 与log 2 x (x > 1)的值域为( ).2 log a x 的图象是().2.函数y 小结:利用单调性比大小;注意格式规范 %动手试试 练1.求下列函数的定义域. (1)y log o.2( X 6) ; (2) y 3 log 2X —1 . 练2.比较下列各题中两个数值的大小 . (1) log 23和log 2 3.5 ;(2) log 0.34和 log °.20.7 ; (3) log 0.71.6和 log o.7 1.8 ; (4) log ? 3和 Iog 3 2 . A. (2, )B. ( ,2)C. 2,D. 3,3.不等式的log 4 x1 解集是 ().2A. (2, )B. (0,2)r 11 B. (一, ) D.2(0-) 24.比大小:(1) log 6 log 76; (2) loglog5.函数 y log (x-!)(3 -x )的定义域是:7,课后作业1.已知下列不等式, 比较正数m n 的大小:(1) log s m K log 3 n; (2) log o .3 m > log 0.3n ; (3) log a m o log a n(a > 1)2・§ 2.2.2 对数函数及其性质(2)1学习目标1. 解对数函数在生产实际中的简单应用;2. 进一步理解对数函数的图象和性质;3. 学习反函数的概念,理解对数函数和指数函数互为反函数,能够在同一坐标上看出互为反函数的两个函数的图象性质•学习过程一、课前准备(预习教材P72- P73,找出疑惑之处)复习1 :对数函数y log a x(a 0,且a 1)图象和性质•复习2:比较两个对数的大小.(1)log io7 与log io12 ; (2) log o.5 0.7 与log o.5 0.8.数的自变量新的函数的因变量.我们称这两个函数为反函数(in verse function )例如:指数函数y 2x与对数函数y log2x互为反函数.试试:在同一平面直角坐标系中,画出指数函数y 2x及其反函数y log2x图象,发现什么性质反思:(1)如果巳(冷』0)在函数y 2x的图象上,那么F0关于直线y x的对称点在函数y log2x的图象上吗为什么(2 )由上述过程可以得到结论:互为反函数的两个函数的图象关于_______________ 对称.探典型例题例1求下列函数的反函数:(1)y 3x;(2)y log a(x 1).复习3:求函数的定义域(1) y(2) y log a(2x 8)1 log3 2x二、新课导学探学习探究探究任务:反函数问题:如何由y 2x求出x小结:求反函数的步骤(解x T习惯表示T定义域)变式:点(2,3)在函数y log a(x 1)的反函数图象上,求实数a的值.反思:函数x log2 y由y 2x解出,是把指数函数y 2x中的自变量与因变量对调位置而得出的.习惯上我们通常用x表示自变量,y表示函数,即写为y log2 x.新知:当一个函数是一一映射时,可以把这个函数的因变量作为一个新函数的自变量,而把这个函例2溶液酸碱度的测量问题:溶液酸碱度pH的计算公式pH lg[ H ],其中[H ]表示溶液中氢离。
基本初等函数讲义(超级全)

一、一次函数之阳早格格创做二、二次函数(1)二次函数剖析式的三种形式 ①普遍式:2()(0)f x ax bx c a =++≠ ②顶面式:2()()(0)f x a x h k a =-+≠ ③二根式:12()()()(0)f x a x x x x a =--≠ (2)供二次函数剖析式的要领 ①已知三个面坐标时,宜用普遍式.②已知扔物线的顶面坐标或者与对付称轴有关或者与最大(小)值有关时,常使用顶面式.③若已知扔物线与x 轴有二个接面,且横线坐标已知时,采用二根式供()f x 更便当.(3)二次函数图象的本量①.二次函数2()(0)f x ax bx c a =++≠的图象是一条扔物线,对付称轴圆程为,2bx a =-顶面坐标是24(,)24b ac b a a-- ②当0a >时,扔物线启心进与,函数正在(,]2ba-∞-上递减,正在[,)2b a-+∞上递加,当2bx a =-时,2min 4()4ac b f x a-=;当0a <时,扔物线启心背下,函数正在(,]2b a -∞-上递加,正在[,)2ba-+∞上递减,当2bx a=-时,2max 4()4ac b f x a-=.三、幂函数(1)幂函数的定义普遍天,函数y x α=喊干幂函数,其中x 为自变量,α是常数.(2)幂函数的图象过定面:所有的幂函数正在(0,)+∞皆有定义,而且图象皆通过面(1,1). 四、指数函数(1)根式的观念:如果,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 喊干a 的n 次圆根.(2)分数指数幂的观念①正数的正分数指数幂的意思是:0,,,mnaa m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的背分数指数幂的意思是:1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的背分数指数幂不意思.(3)运算本量①(0,,)r s r s a a a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r=>>∈ab a b a b r R (4)指数函数五、对付数函数(1)对付数的定义①若(0,1)x a N a a =>≠且,则x 喊干以a 为底N 的对付数,记做log a x N =,其中a 喊干底数,N喊干真数.②背数战整不对付数. ③对付数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>.(2)几个要害的对付数恒等式log 10a =,log 1a a =,log b a a b =.(3)时常使用对付数与自然对付数时常使用对付数:lg N ,即10log N ;自然对付数:ln N ,即log e N (其中 2.71828e =…).(4)对付数的运算本量 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN +=②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈④log aNa N =⑤log log (0,)bn a anM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b N N b b a=>≠且(5)对付数函数(6)反函数的观念设函数()y f x =的定义域为A ,值域为C,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对付于y 正在C 中的所有一个值,通过式子()x y ϕ=,x 正在A 中皆有唯一决定的值战它对付应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=喊干函数()y f x =的反函数,记做1()x f y -=,习惯上改写成1()y f x -=.(7)反函数的供法①决定反函数的定义域,即本函数的值域;②从本函数式()y f x =中反解出1()x f y -=;③将1()x f y -=改写成1()y f x -=,并证明反函数的定义域. (8)反函数的本量 ①本函数()y f x =与反函数1()y f x -=的图象关于曲线y x =对付称. ②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 正在本函数()y f x =的图象上,则'(,)P b a 正在反函数1()y f x -=的图象上.④普遍天,函数()y f x =要有反函数则它必须为单调函数.例题一、供二次函数的剖析式244y x x =--的顶面坐标是()A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)例2.已知扔物线的顶面为(-1,-2),且通过(1,10),则那条扔物线的表白式为()A .()2312y x =-- B .()2312y x =-+C.()2312y x =+- D.()2312y x =-+-例3.扔物线y=222xmx m -++的顶面正在第三象限,试决定m的与值范畴是()A .m <-1或者m >2B .m <0或者m >-1C .-1<m <0D .m <-1()f x 共时谦脚条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的二根坐圆战等于17供()f x 的剖析式 二、二次函数正在特定区间上的最值问题例5. 当22x -≤≤时,供函数223y x x =--的最大值战最小值. 例6.当0x ≥时,供函数(2)y x x =--的与值范畴.例7.当1t x t ≤≤+时,供函数21522y x x =--的最小值(其中t 为常数).三、幂函数(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -={}0x x >的是()A.23y x = B.32y x = C.23y x -= D.32y x-=例10.计划函数y =52x 的定义域、值域、奇奇性、单调性,并绘出图象的示企图. 例10.已知函数y =42215x x --.(1)供函数的定义域、值域; (2)推断函数的奇奇性; (3)供函数的单调区间. 四、指数函数的运算122(2)-⎡⎤-⎣⎦的截止是()A、12C 、— D 、—12例12.44等于()A 、16a B 、8a C 、4a D 、2a53,83==ba,则b a233-=___________五、指数函数的本量例14.{|2},{|xM y y P y y ====,则M∩P ()A.{|1}y y >B. {|1}y y ≥C. {|0}y y >D. {|0}y y ≥ 例15.供下列函数的定义域与值域:(1)442x y -=(2)||2()3x y =()2301x y a a a -=+>≠且的图像必通过面 ()A .(0,1)B .(1,1)C .(2,3)D .(2,4) 例17供函数y=2121x x -+的定义域战值域,并计划函数的单调性、奇奇性.五、对付数函数的运算32a =,那么33log 82log 6-用a 表示是()A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a - 例19.2log (2)log log a a a M N M N -=+,则NM 的值为()A 、41B 、4 C 、1 D 、4或者1732log [log (log )]0x =,那么12x-等于()A 、13B C D 例21.2log 13a <,则a 的与值范畴是()A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪⎪⎝⎭⎝⎭五、对付数函数的本量例22.下列函数中,正在()0,2上为删函数的是()A 、12log (1)y x =+B 、2log y =C 、21log y x=D 、2log (45)y x x =-+2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于()A 、x 轴对付称B 、y 轴对付称C 、本面对付称D 、曲线y x =对付称)()lgf x x=是(奇、奇)函数.课下做业1.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象大概是图所示的( )2.对付扔物线y=22(2)x --3与y=-22(2)x -+4的道法不精确的是()A .扔物线的形状相共B .扔物线的顶面相共C .扔物线对付称轴相共D .扔物线的启心目标差异3. 二次函数y=221xx --+图像的顶面正在()A .第一象限B .第二象限C .第三象限D .第四象限4. 如图所示,谦脚a >0,b <0的函数y=2ax bx +的图像是()5.如果扔物线y=26x x c ++的顶面正在x 轴上,那么c 的值为()A .0B .6C .3D .96.一次函数y =ax +b 与二次函数y =ax2+bx +c 正在共一坐标系中的图象大概是( )7.正在下列图象中,二次函数y=ax2+bx +c 与函数y=(ab )x 的图象大概是 ()8.若函数f(x)=(a -1)x2+(a2-1)x +1是奇函数,则正在区间[0,+∞)上f(x)是( )A .减函数B .删函数C .常函数D .大概是减函数,也大概是常函数9.已知函数y =x2-2x +3正在关区间[0,m]上有最大值3,最小值2,则m 的与值范畴是( )A .[1,+∞)B .[0,2]C .[1,2]D .(-∞,2]10、使x2>x3创造的x 的与值范畴是( )A 、x <1且x≠0B 、0<x <1C 、x >1D 、x <111、若四个幂函数y =ax ,y=bx ,y =c x ,y =d x 正在共一坐标系中的图象如左图,则a 、b 、c 、d 的大小关系是( ) A 、d >c >b >a B 、a >b >c >d C 、d >c >a >b D 、a >b >d >c12.若幂函数()1m f x x -=正在(0,+∞)上是减函数,则 ( )A .m >1B .m <1C .m =lD .不克不迭决定 13.若面(),A a b 正在幂函数()n y x n Q =∈的图象上,那么下列论断中不克不迭创造的是A .00a b >⎧⎨>⎩B .00a b >⎧⎨<⎩C.00a b <⎧⎨<⎩ D .00a b <⎧⎨>⎩14.若函数f(x)=log 12(x2-6x +5)正在(a ,+∞)上是减函数,则a 的与值范畴是( )A .(-∞,1]B .(3,+∞)C .(-∞,3)D .[5,+∞)15、设集中2{|3,},{|1,}x S y y x R T y y x x R ==∈==-∈,则S T 是() A 、∅ B 、T C 、S D 、有限集16、函数22log (1)y x x =+≥的值域为()A 、()2,+∞B 、(),2-∞C 、[)2,+∞D 、[)3,+∞17、设1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭,则()A 、312y y y >>B 、213y y y >>C 、132y y y >>D 、123y y y >>18、正在(2)log (5)a b a -=-中,真数a 的与值范畴是()A 、52a a ><或B 、2335a a <<<<或C 、25a <<D 、34a <<19、估计lg52lg2)lg5()lg2(22•++等于() A 、0 B 、1 C 、2 D 、320、已知3log 2a =,那么33log 82log 6-用a 表示是() A 、52a - B 、2a - C 、23(1)a a -+ D 、231a a --21、已知幂函数f(x)过面(2,),则f(4)的值为()A 、12B 、 1C 、2D 、81.扔物线y =8x2-(m -1)x +m -7的顶面正在x 轴上,则m =________.23-=xy 的定义域为___________.()()12m f x m x +=-,如果()f x 是正比率函数,则m=____ ,如果()f x 是反比率函数,则m=______,如果f(x)是幂函数,则m=____.14(1)x --蓄意思,则x ∈___________.35x y <=___________.25525x x y ⋅=,则y 的最小值为___________.7、若2log 2,log 3,m n a a m n a +===. 8、函数(-1)log (3-)x y x =的定义域是. 9、2lg 25lg 2lg50(lg 2)++=.1622<-+x x的解集是__________________________.282133x x --⎛⎫< ⎪⎝⎭的解集是__________________________.103,104x y ==,则10x y -=__________________________.13、已知函数3xlog x (x 0)1f (x),f[f ()]2(x 0)9>⎧=⎨≤⎩,则,的值为 14、函数2)23x (lg )x (f +-=恒过定面2、已知幂函数f (x )=23221++-p p x(p ∈Z )正在(0,+∞)上是删函数,且正在其定义域内是奇函数,供p 的值,并写出相映的函数f (x )、222(3)lg 6x f x x -=-,(1)供()f x 的定义域;(2)推断()f x 的奇奇性.a R ∈,22()()21xx a a f x x R ⋅+-=∈+,试决定a 的值,使()f x 为奇函数.5. 已知函数x 121f (x)log[()1]2=-,(1)供f(x)的定义域;(2)计划函数f(x)的删减性.。
(完整版)基本初等函数知识点及函数的基本性质

定义
函数y logax(a 0且a
1)叫做对数函数
a1
0a1
x1
x1
yx 1
y
y logax
yy logax
图象
(1,0)
O
(1,0)
x
Ox
定义域
(0,,0),即当x
1时,y 0.
奇偶性
非奇非偶
② 对数函数对底数的限制:(a 0,且a1). 三、对数函数的图像和性质:
指数函数及其性质
、指数与指数幂的运算
一)根式的概念
1、如果xna,a R,x R,n1,且n N,那么x叫做a的n次方根.当n是奇数时,a
函数名称
指数函数
定义
函数y ax(a 0且a1)叫做指数函数
图象
a1
0a1
y 1yy ax
(0,1)
Ox
y axy
y 1(0,1)
Ox
定义域
R
值域
(0,+∞)
过定点
在第一象限内,a越小图象越高, 越靠近y轴;
图象影响
在第二象限内,a越大图象越低, 越靠近x轴.
在第二象限内,a越小图象越低, 越靠近x轴.
注意:利用函数的单调性,结合图象还可以看出:
1)
在[a,
b]上,
f (x)
ax(a 0且a
1)值域是[f (a),f(b)]或[f(b),f(a)]
2)
若x
0,则
对数函数及其性质
、对数与对数的运算
一)对数
1.对数的概念: 一般地, 如果ax
N (a
0,a
1),那么数x叫做以.a为.底.N的对数, 记作:
x
必修一_基本初等函数_知识点讲解

基本初等函数第一讲 幂函数1、幂函数的定义一般地,形如y x α=(x ∈R )的函数称为幂函数,其中x 是自变量,α是常数.如11234,,y x y x y x -===等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.注意:y x α=中,前面的系数为1,且没有常数项2、幂函数的图像(1)y x = (2)12y x = (3)2y x = (4)1y x -= (5)3y x =3、幂函数的性质(1)所有的幂函数在(0,+∞)都有定义,并且图象都过点(1,1)(原因:11x=);(2)0>α时,幂函数的图象通过原点,并且在区间),0[+∞上是增函数.特别地,当1>α时,幂函数的图象下凸;当10<<α时,幂函数的图象上凸;(3)0<α时,幂函数的图象在区间),0(+∞上是减函数.在第一象限内,当x 从右边趋向原点时,图象在y 轴右方无限地逼近y 轴正半轴,当x 趋于∞+时,图象在x 轴上方无限地逼近x 轴正半轴.分数指数幂概念 有理指数幂运算性质(0,,)r s r s a a a a r s Q +=>∈;()(0,,)r s rs a a a r s Q =>∈(0,,*,1)a m n N n >∈>且 ()(0,0,)r r r ab a b a b r Q =>>∈第二讲 指数函数1、指数(1)n 次方根的定义若x n =a ,则称x 为a 的n 次方根,“n”是方根的记号.在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是一个负数,0的奇次方根是0;正数的偶次方根是两个绝对值相等符号相反的数,0的偶次方根是0,负数没有偶次方根.(2)方根的性质①当n 为奇数时,n n a =a . ②当n 为偶数时,n n a =|a |=⎩⎨⎧<-≥).0(),0(a aa a(3)分数指数幂的意义①a nm =n m a (a >0,m 、n 都是正整数,n >1). ②an m -=nm a1=nma1(a >0,m 、n 都是正整数,n >1).2、指数函数的定义一般地,函数xy a =(a >0且a ≠1)叫做指数函数,其中x 是自变量,函数的定义域为R . 说明:因为a >0,x 是任意一个实数时,xa 是一个确定的实数,所以函数的定义域为实数集R .n mnm a a=nmn m nm aa a1==-000,0xx a a x a ⎧>⎪=⎨≤⎪⎩x当时,等于若当时,无意义若a <0,如1(2),,8xy x x =-=1先时,对于=等等,6在实数范围内的函数值不存在. 若a =1, 11,xy == 是一个常量, 5,,3,31x x x a y x y y +===+1xx为常数,象y=2-3,y=2等等, 不符合(01)x y a a a =>≠且的形式,所以不是指数函数.3、 指数函数的图像及其性质(1)底数互为倒数的两个指数函数的图象关于y 轴对称.(2)在[,]x a b f x a 上,()=(a >0且a ≠1)值域是[(),()][(),()];f a f b f b f a 或 (3)若0,x f x f x x ≠≠∈则()1;()取遍所有正数当且仅当R;(4)对于指数函数()xf x a =(a >0且a ≠1),总有(1);f a =(5)当a >1时,若1x <2x ,则1()f x <2()f x ;第三讲 对数函数1、 对数(1)对数的概念一般地,若(0,1)xa N a a =>≠且,那么数x 叫做以a 为底N 的对数,记作log a x N =a 叫做对数的底数,N 叫做真数.如:24416,2log 16==则,读作2是以4为底,16的对数. 1242=,则41log 22=,读作12是以4为底2的对数. (2)指数式与对数式的关系:a b =N ⇔log a N =b (a >0,a ≠1,N >0).两个式子表示的a 、b 、N 三个数之间的关系是一样的,并且可以互化.(3)对数运算性质:①log a (MN )=log a M +log a N . ②log a NM =log a M -log a N . ③log a M n=n log a M .(M >0,N >0,a >0,a ≠1) ④对数换底公式:log b N =bNa a log log (a >0,a ≠1,b >0,b ≠1,N >0). (4)两类对数① 以10为底的对数称为常用对数,10log N 常记为lg N .② 以无理数e=2.71828…为底的对数称为自然对数,log e N 常记为ln N .以后解题时,在没有指出对数的底的情况下,都是指常用对数,如100的对数等于2,即lg1002=.2、对数函数的概念一般地,我们把函数log a y x =(a >0且a ≠1)叫做对数函数,其中x 是自变量,函数的定义域是(0,+∞). 3、对数函数的图象及其性质a <11))底数互为倒数的两个对数函数的图象关于x 轴对称.。
基本初等函数知识点

基本初等函数知识点一、引言在数学中,初等函数是由基本初等函数经过有限次的四则运算(加、减、乘、除)以及复合运算得到的函数。
基本初等函数包括常数函数、幂函数、指数函数、对数函数、三角函数以及反三角函数。
本文将详细介绍这些基本初等函数的定义、性质和图像。
二、常数函数定义:常数函数 \( f(x) = c \),其中 \( c \) 是一个实数常数。
性质:常数函数的图像是一条平行于 \( x \) 轴的直线,其所有点的函数值都等于常数 \( c \)。
图像:见附录图1。
三、幂函数定义:幂函数 \( f(x) = x^n \),其中 \( n \) 是实数。
性质:幂函数的性质取决于指数 \( n \) 的值。
当 \( n \) 为正整数时,函数图像是 \( n \) 次幂的曲线;当 \( n \) 为负整数时,函数图像是倒数的幂函数曲线。
图像:见附录图2。
四、指数函数定义:指数函数 \( f(x) = a^x \),其中 \( a > 0 \) 且 \( a\neq 1 \)。
性质:指数函数的底数 \( a \) 决定了函数图像的形状。
当 \( a > 1 \) 时,函数是增长的;当 \( 0 < a < 1 \) 时,函数是衰减的。
图像:见附录图3。
五、对数函数定义:对数函数 \( f(x) = \log_a(x) \),其中 \( a > 0 \) 且\( a \neq 1 \)。
性质:对数函数是指数函数的逆函数。
当 \( a > 1 \) 时,函数是单调增加的;当 \( 0 < a < 1 \) 时,函数是单调减少的。
图像:见附录图4。
六、三角函数1. 正弦函数 \( \sin(x) \)2. 余弦函数 \( \cos(x) \)3. 正切函数 \( \tan(x) \)定义:这些函数与单位圆上的点的坐标有关。
性质:三角函数具有周期性,它们的周期为 \( 2\pi \)。
基本初等函数的导数公式及倒数的运算法则课件

本课件将介绍基本初等函数的导数公式,以及导数的概念和定义。我们将探 讨常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数的导数 公式,并讲解倒数的运算法则。让我们一起深入了解导数和倒数的重要性。
基本初等函数的定义
常数函数
恒定输出的函数,例如f(x) = 3。
指数函数
以常数e为底的指数函数,例如f(x) = e^x。
幂函数
以x为底的指数函数,例如f(x) = x^2。
对数函数
以常数为底的对数函数,例如f(x) = log(base 2)(x)。
导数的概念及定义
导数
描述函数在某一点的瞬时变化率。
定义
导数可以通过极限来定义,即函数的微小变化 与自变量的微小变化之比。
2
导数
cos(x),-sin(x),sec^ 2(x)
3
例子
sin (x)的导数为c os(x)
导数公式:反三角函数的导数
反三角函数
• arcsin(x) • arccos(x) • arctan(x)
导数
• 1/sqrt(1-x^2) • -1/sqrt(1-x^2) • 1/(1+x^2)
导数公式:复合函数的求导法则
导数公式:常数函数的导数源自常数函数 f(x) =c导数 f'(x) =0
导数公式:幂函数的导数
1
幂函数
f(x) = x^n
导数
2
f'(x) =nx^(n-1)
3
例子
f(x) =x^3,导数为f'(x) =3x^2
导数公式:指数函数的导数
1 指数函数
f(x) =e^x
必修一基本初等函数复习PPT课件

18
底数互为倒数的两个 对数函数
y = loga x, y = log1 x
的函数图像关于x轴对a称。
19
当a>1时,a值越大, y=logax的图像越靠近x轴;
当0<a<1时,a值越大, y=logax的图像越远离x轴。
20
4.若loga2<logb2<0,则( B )
(A)0<a<b<1
(B)0<b<a<1
y
叫做幂函数,
其中x是自变
量,α是常数.
O
x
23
幂函数的性质
函数
性质 y=x
y=x2
1
y=x3 y = x 2
y=x-1
定义域 R
R
R [0,+∞) {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶性 奇
偶
奇
单调性
增
[0,+∞)增 (-∞,0]减
增
非奇非偶 奇
(0,+∞)减
常用对数:通常将log10N的对数叫做常用对数,为了简便, N的常用对数记作lgN。
自然对数:通常将使用以无理数e=2.71828…为底的对数
叫
做自然对数,为了简便,
N的自然对数logeN简记作lnN.
12
2024/10/27
13
9.对数恒等式
( ) aloga N = N a 0且a 1,N 0 叫做对数恒等式
10.对数的性质 (1)负数和零没有对数; (2)1的对数是零,即loga1=0; (3)底数的对数等于1,即logaa=1 11.对数的运算法则 如果a>0,a≠1,M>0,N>0,那么
(完整版)基本初等函数知识点及函数的基本性质

指数函数及其性质一、指数与指数幂的运算 (一)根式的概念1、如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a的n次方根用符号n 是偶数时,正数a 的正的n的n次方根用符号0的n 次方根是0;负数a 没有n 次方根.2n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.3、根式的性质:na =;当n 为奇数时,a =;当n 为偶数时,(0)|| (0)a a a a a ≥⎧==⎨-<⎩. (二)分数指数幂的概念1、正数的正分数指数幂的意义是:0,,,m na a m n N +>∈且1)n >.0的正分数指数幂等于0. 2、正数的负分数指数幂的意义是: 1()0,,,mm nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没有意义.注意口诀:底数取倒数,指数取相反数. 3、a 0=1 (a ≠0) a -p = 1/a p (a ≠0;p ∈N *) 4、指数幂的运算性质(0,,)r s r s a a a a r s R +⋅=>∈ ()(0,,)r s rs a a a r s R =>∈ ()(0,0,)r r r ab a b a b r R =>>∈5、0的正分数指数幂等于0,0的负分数指数幂无意义。
二、指数函数的概念一般地,函数)1a ,0a (a y x≠>=且叫做指数函数,其中x 是自变量,函数的定义域为R .注意:○1 指数函数的定义是一个形式定义; ○2 注意指数函数的底数的取值范围不能是负数、零和1.(1)在[a ,b]上,)1a 0a (a )x (f x≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [ (2)若0x ≠,则1)x (f ≠;)x (f 取遍所有正数当且仅当R x ∈ (3)对于指数函数)1a 0a (a )x (f x≠>=且,总有a )1(f =(4)当1a >时,若21x x <,则)x (f )x (f 21< 四、底数的平移对于任何一个有意义的指数函数:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
基本初等函数讲义(超级全)

一、一次函数之相礼和热创作二、二次函数(1)二次函数解析式的三种方式 ①一样平常式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠ (2)求二次函数解析式的方法①已知三个点坐标时,宜用一样平常式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常运用顶点式.③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便.(3)二次函数图象的性子①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2bx a =-顶点坐标是24(,)24b ac b a a-- ②当0a >时,抛物线开口向上,函数在(,]2ba -∞-上递减,在[,)2b a-+∞上递增,当2bx a=-时,2min 4()4ac b f x a-=;当0a <时,抛物线开口向下,函数在(,]2b a -∞-上递增,在[,)2b a-+∞上递减,当2b x a =-时,2max 4()4ac b f x a-=.三、幂函数(1)幂函数的定义一样平常地,函数y x α=叫做幂函数,其中x 为自变量,α是常数.(2)幂函数的图象过定点:全部的幂函数在(0,)+∞都有定义,而且图象都经过点(1,1). 四、指数函数(1)根式的概念:假如,,,1n x a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.(2)分数指数幂的概念①负数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②负数的负分数指数幂的意义是:1()0,,,m m nn aa m n N a -+==>∈且1)n >.0的负分数指数幂没故意义.(3)运算性子①(0,,)r s r s a a a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r r=>>∈ab a b a b r R(4)指数函数五、对数函数(1)对数的定义①若(0,1)x且,则x叫做以a为底N的对数,记作=>≠a N a alog a x N =,其中a 叫做底数,N叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个紧张的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)经常运用对数与自然对数经常运用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4)对数的运算性子 假如0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN +=②减法:log log log a a a MM N N-=③数乘:log log ()n a a n M M n R =∈④log aNa N =⑤log log (0,)bn a anM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.假如对于y 在C 中的任何一个值,经过式子()x y ϕ=,x 在A 中都有独一确定的值和它对应,那么式子()x y ϕ=暗示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x f y -=,风俗上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x f y -=改写成1()y f x -=,并注明反函数的定义域. (8)反函数的性子 ①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称. ②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一样平常地,函数()y f x =要有反函数则它必须为单调函数.例题一、求二次函数的解析式244y x x =--的顶点坐标是()A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)例2.已知抛物线的顶点为(-1,-2),且经过(1,10),则这条抛物线的表达式为()A .()2312y x =-- B .()2312y x =-+C. ()2312y x =+- D.()2312y x =-+-例3.抛物线y=222x mx m -++的顶点在第三象限,试确定m 的取值范围是()A .m <-1或m >2B .m <0或m >-1C .-1<m <0D .m <-1()f x 同时满足条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的两根立方和等于17求()f x 的解析式 二、二次函数在特定区间上的最值成绩例5. 当22x -≤≤时,求函数223y x x =--的最大值和最小值. 例6.当0x ≥时,求函数(2)y x x =--的取值范围.例7.当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数).三、幂函数(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -={}0x x >的是()A.23y x = B.32y x = C.23y x -= D.32y x-=例10.讨论函数y =52x 的定义域、值域、奇偶性、单调性,并画出图象的表示图.例10.已知函数y =42215x x --.(1)求函数的定义域、值域; (2)判别函数的奇偶性; (3)求函数的单调区间. 四、指数函数的运算122(2)-⎡⎤-⎣⎦的结果是()A、12C 、D 、—12例12.44等于() A 、16a B 、8a C 、4a D 、2a53,83==ba,则b a233-=___________五、指数函数的性子 例14.{|2},{|xM y y P y y ====,则M∩P ()A.{|1}y y >B. {|1}y y ≥C. {|0}y y >D. {|0}y y ≥ 例15.求下列函数的定义域与值域: (1)442x y -=(2)||2()3x y =()2301x y a a a -=+>≠且的图像必经过点 ()A .(0,1)B .(1,1)C .(2,3)D .(2,4) 例17求函数y=2121x x -+的定义域和值域,并讨论函数的单调性、奇偶性.五、对数函数的运算32a =,那么33log 82log 6-用a 暗示是()A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -例19.2log (2)log log a a a M N M N -=+,则NM 的值为()A 、41B 、4 C 、1 D 、4或1732log [log (log )]0x =,那么12x-等于()A 、13B D 例21.2log 13a <,则a 的取值范围是()A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞ ⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭D 、220,,33⎛⎫⎛⎫+∞ ⎪⎪⎝⎭⎝⎭五、对数函数的性子例22.下列函数中,在()0,2上为增函数的是() A 、12log (1)y x =+B 、2log y =C 、21log y x=D 、2log (45)y x x =-+2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于() A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称 )()lg f x x =是(奇、偶)函数.课下作业1.已知二次函数y=ax2+bx+c,假如a>b>c,且a+b+c=0,则它的图象可能是图所示的( )2.对抛物线y=22(2)x --3与y=-22(2)x -+4的说法不正确的是()A .抛物线的外形相反B .抛物线的顶点相反C .抛物线对称轴相反D .抛物线的开口方向相反3. 二次函数y=221x x --+图像的顶点在()A .第一象限B .第二象限C .第三象限D .第四象限4. 如图所示,满足a >0,b <0的函数y=2ax bx +的图像是()5.假如抛物线y=26x x c ++的顶点在x 轴上,那么c 的值为()A .0B .6C .3D .96.一次函数y =ax +b 与二次函数y =ax2+bx +c 在同一坐标系中的图象大致是( )7.在下列图象中,二次函数y=ax2+bx +c 与函数y=(ab)x 的图象可能是 ()8.若函数f(x)=(a -1)x2+(a2-1)x +1是偶函数,则在区间[0,+∞)上f(x)是( )A .减函数B .增函数C .常函数D .可能是减函数,也可能是常函数9.已知函数y =x2-2x +3在闭区间[0,m]上有最大值3,最小值2,则m 的取值范围是( )A .[1,+∞)B .[0,2]C .[1,2]D .(-∞,2]10、使x2>x3成立的x 的取值范围是( )A 、x <1且x≠0B 、0<x <1C 、x >1D 、x <111、若四个幂函数y =a x ,y =b x ,y =c x ,y =d x 在同一坐标系中的图象如右图,则a 、b 、c 、d 的大小关系是( )A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c12.若幂函数()1m f x x -=在(0,+∞)上是减函数,则 ( )A .m >1B .m <1C .m =lD .不克不及确定13.若点(),A a b 在幂函数()n y x n Q =∈的图象上,那么下列结论中不克不及成立的是A .00a b >⎧⎨>⎩B .00a b >⎧⎨<⎩C.00a b <⎧⎨<⎩ D .00a b <⎧⎨>⎩14.若函数f(x)=log 12(x2-6x +5)在(a ,+∞)上是减函数,则a 的取值范围是( )A .(-∞,1]B .(3,+∞)C .(-∞,3)D .[5,+∞)15、设集合2{|3,},{|1,}x S y y x R T y y x x R ==∈==-∈,则S T 是()A 、∅B 、TC 、SD 、无限集16、函数22log (1)y x x =+≥的值域为()A 、()2,+∞ B 、(),2-∞ C 、[)2,+∞ D 、[)3,+∞ 17、设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭,则()A 、312y y y >>B 、213y y y >>C 、132y y y >>D 、123y y y >>18、在(2)log (5)a b a -=-中,实数a 的取值范围是()A 、52a a ><或B 、2335a a <<<<或C 、25a <<D 、34a <<19、计算lg52lg2)lg5()lg2(22•++等于() A 、0 B 、1 C 、2 D 、320、已知3log 2a =,那么33log 82log 6-用a 暗示是()A 、52a -B 、2a -C 、23(1)a a -+ D 、231a a --21、已知幂函数f(x)过点(2),则f(4)的值为()A 、12B 、 1C 、2D 、8二、填空题1.抛物线y =8x2-(m -1)x +m -7的顶点在x 轴上,则m =________.23-=x y 的定义域为___________.()()12m f x m x +=-,假如()f x 是反比例函数,则m=____ ,假如()f x 是反比例函数,则m=______,假如f(x)是幂函数,则m=____. 14(1)x --故意义,则x ∈___________.35x y <=___________.25525x x y ⋅=,则y 的最小值为___________. 7、若2log 2,log 3,m n a a m n a +===.8、函数(-1)log (3-)x y x =的定义域是.9、2lg 25lg 2lg50(lg 2)++=.1622<-+x x 的解集是__________________________.282133x x --⎛⎫< ⎪⎝⎭的解集是__________________________.103,104x y ==,则10x y -=__________________________.13、已知函数3x log x (x 0)1f (x),f[f ()]2(x 0)9>⎧=⎨≤⎩,则,的值为 14、函数2)23x (lg )x (f +-=恒过定点三、简答题2、已知幂函数f (x )=23221++-p p x (p ∈Z )在(0,+∞)上是增函数,且在其定义域内是偶函数,求p 的值,并写出相应的函数f (x )、222(3)lg 6x f x x -=-,(1)求()f x 的定义域;(2)判别()f x 的奇偶性. a R ∈,22()()21x x a a f x x R ⋅+-=∈+,试确定a 的值,使()f x 为奇函数. 5. 已知函数x 121f (x)log[()1]2=-,(1)求f(x)的定义域;(2)讨论函数f(x)的增减性.。
基本初等函数讲义超级全
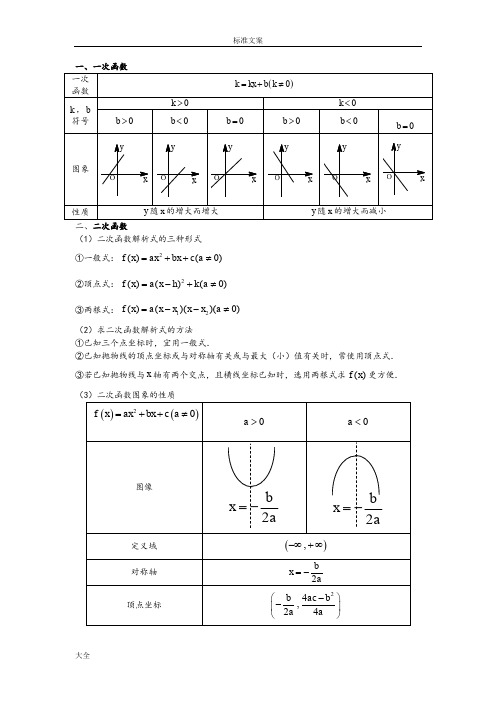
一、一次函数二、二次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2x a=-顶点坐标是24(,)24b ac b a a-- ②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2ba-+∞上递增,当2b x a =-时,2min 4()4ac b fx a -=;当0a <时,抛物线开口向下,函数在(,]2ba -∞-上递增,在[,)2ba-+∞上递减,当2b x a =-时,2max 4()4ac b f x a -=. 三、幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. 过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).(1)根式的概念:如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a NaN =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x fy -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数. 例题一、求二次函数的解析式例1.抛物线244y x x =--的顶点坐标是()A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8) 例2.已知抛物线的顶点为(1,2),且通过(1,10),则这条抛物线的表达式为()A .()2312y x =-- B .()2312y x =-+ C. ()2312y x =+- D.()2312y x =-+---例3.抛物线y=的顶点在第三象限,试确定m 的取值范围是( ) A .m <-1或m >2 B .m <0或m >-1 C .-1<m <0 D .m <-1例4.已知二次函数()f x 同时满足条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的两根立方和等于17求()f x 的解析式二、二次函数在特定区间上的最值问题例5. 当22x -≤≤时,求函数223y x x =--的最大值和最小值.例6.当0x ≥时,求函数(2)y x x =--的取值范围.例7.当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数).222x mx m -++三、幂函数例8.下列函数在(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -=例9.下列幂函数中定义域为{}0x x >的是() A.23y x = B.32y x = C.23y x-= D.32y x-=例10.讨论函数y =52x 的定义域、值域、奇偶性、单调性,并画出图象的示意图.例10.已知函数y =42215x x --.(1)求函数的定义域、值域;(2)判断函数的奇偶性; (3)求函数的单调区间.四、指数函数的运算例11.计算122(2)-⎡⎤-⎣⎦的结果是( ) A、12C、—12例12.等于( ) A 、 B 、C 、 D 、例13.若53,83==ba ,则b a233-=___________五、指数函数的性质例14.{|2},{|xM y y P y y ====,则M ∩P ()A.{|1}y y >B. {|1}y y ≥C. {|0}y y >D. {|0}y y ≥ 例15.求下列函数的定义域与值域: (1)442x y -=(2)||2()3x y =例16.函数()2301x y a a a -=+>≠且的图像必经过点 ( )A .(0,1)B .(1,1)C .(2,3)D .(2,4)例17求函数y=2121x x -+的定义域和值域,并讨论函数的单调性、奇偶性.4416a 8a 4a 2a五、对数函数的运算例18.已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -例19.2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 例20.已知732log [log (log )]0x =,那么12x -等于( )A 、13B C D 例21.2log 13a <,则a 的取值范围是( ) A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭五、对数函数的性质例22.下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+B 、2log y =C 、21log y x =D 、2log (45)y x x =-+ 例23.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称例23.求证函数)()lg f x x =是(奇、偶)函数。
专题1第3讲基本初等函数精品课件大纲人教版课件.ppt

第3讲│ 主干知识整合
2.指数函数 y=ax(a>0,a≠1)的图象和性质 (1)图象:均过定点(0,1),图象均在第一和第二两个象限; 若底数 a>1,则图象是上升的,若底数 0<a<1,则图象是下 降的.但虽然底数都大于 1(或者都大于 0 小于 1),底数取不 同的值,其图象“高低”仍不相同,此时,我们可以根据指 数函数 y=ax 的图象一定过点(1,a)加以区分,显然,在 y 轴 右侧,底数越大,则图象的位置越靠上. (2)性质:定义域均为 R;值域均为(0,+∞);当 a>1 时 为增函数,当 0<a<1 时为减函数.
第3讲│ 要点热点探究
【点评】 本题考查函数、最值等基础知识,同 时考查运用数学知识解决实际问题的能力.解实际应 用题就是在阅读材料、理解题意的基础上,把实际问 题抽象转化成数学问题,然后再用相应的数学知识去 解决.本题涉及分段函数的最值,处理时一定要逐段 进行讨论,对两段的结果进行比较后最后选择正确结 论.
第3讲 基本初等函数
第3讲 基本初等函数
第3讲 │ 主干知识整合
主干知识整合
1.二次函数 f(x)=ax2+bx+c(a≠0)的图象和性质 (1)二次函数的图象 ①二次函数 f(x)=ax2+bx+c(a≠0)的图象是抛物线,对 称轴方程是 x=-2ba,顶点坐标是-2ba,4ac4-a b2. ②当 Δ=b2-4ac>0 时,设 f(x)=ax2+bx+c(a≠0)的图 象 与 x 轴 的 两 交 点为 M(x1,0), N(x2,0), 则 有 |x1 - x2| = b2-4ac |a| .
(1)当 0≤x≤200 时,求函数 v(x)的表达式; (2)当车流密度 x 为多大时,车流量(单位时间内通过桥上 某观测点的车辆数,单位:辆/小时)f(x)=x·v(x)可以达到最大, 并求出最大值.(精确到 1 辆/小时)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、一次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠②顶点式:2()()(0)f x a x h k a =-+≠③两根式:12()()()(0)f x a x x x x a =--≠ (2)求二次函数解析式的方法 ①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (3)二次函数图象的性质①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2x a=-顶点坐标是24(,)24b ac b a a-- ②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2ba-+∞上递增,当2b x a =-时,2min 4()4ac b f x a -=;当0a <时,抛物线开口向下,函数在(,]2ba -∞-上递增,在[,)2b a -+∞上递减,当2bx a=-时,2max 4()4ac b f x a -=. 三、幂函数 (1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. (2)幂函数的图象过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1). 四、指数函数(1)根式的概念:如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 1()0,,,mm n n a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈ (4)指数函数(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…).(4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a NaN =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x fy -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x fy -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y fx -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数. 例题一、求二次函数的解析式例1.抛物线244y x x =--的顶点坐标是()A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8)例2.已知抛物线的顶点为(-1,-2),且通过(1,10),则这条抛物线的表达式为()A .()2312y x =-- B .()2312y x =-+C. ()2312y x =+-D.()2312y x =-+-例3.抛物线y=222x mx m -++的顶点在第三象限,试确定m 的取值围是( ) A .m <-1或m >2 B .m <0或m >-1 C .-1<m <0 D .m <-1例4.已知二次函数()f x 同时满足条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的两根立方和等于17求()f x 的解析式二、二次函数在特定区间上的最值问题例5. 当22x -≤≤时,求函数223y x x =--的最大值和最小值.例6.当0x ≥时,求函数(2)y x x =--的取值围.例7.当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数).三、幂函数例8.下列函数在(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -=例9.下列幂函数中定义域为{}0x x >的是()A.23y x = B.32y x = C.23y x-= D.32y x-=例10.讨论函数y =52x 的定义域、值域、奇偶性、单调性,并画出图象的示意图.例10.已知函数y=42215xx--.(1)求函数的定义域、值域;(2)判断函数的奇偶性;(3)求函数的单调区间.四、指数函数的运算例11.计算122(2)-⎡⎤-⎣⎦的结果是( ) A、12C、—12例12.44等于( ) A 、16a B 、8a C 、4a D 、2a例13.若53,83==ba ,则b a233-=___________五、指数函数的性质例14.{|2},{|xM y y P y y ====,则M∩P() A.{|1}y y > B. {|1}y y ≥ C. {|0}y y > D. {|0}y y ≥ 例15.求下列函数的定义域与值域:(1)442x y -=(2)||2()3x y =例16.函数()2301x y a a a -=+>≠且的图像必经过点 ( )A .(0,1)B .(1,1)C .(2,3)D .(2,4)例17求函数y=2121x x -+的定义域和值域,并讨论函数的单调性、奇偶性.五、对数函数的运算例18.已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -例19.2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 例20.已知732log [log (log )]0x =,那么12x-等于( )A 、13B C D 例21.2log 13a<,则a 的取值围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭五、对数函数的性质例22.下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+B 、2log y =C 、21log y x =D 、2log (45)y x x =-+ 例23.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称例23.求证函数)()lg f x x =是(奇、偶)函数。
课下作业1.已知二次函数y=ax2+bx+c,如果a>b>c,且a+b+c=0,则它的图象可能是图所示的( )2.对抛物线y=22(2)x--3与y=-22(2)x-+4的说法不正确的是()A.抛物线的形状相同 B.抛物线的顶点相同C.抛物线对称轴相同 D.抛物线的开口方向相反3. 二次函数y=221x x--+图像的顶点在()A.第一象限 B.第二象限 C.第三象限 D.第四象限4. 如图所示,满足a>0,b<0的函数y=2ax bx+的图像是()5.如果抛物线y=26x x c++的顶点在x轴上,那么c的值为()A.0 B.6 C.3 D.96.一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图象大致是( )7.在下列图象中,二次函数y=ax2+bx +c 与函数y=(a b)x 的图象可能是()8.若函数f (x )=(a -1)x 2+(a 2-1)x +1是偶函数,则在区间[0,+∞)上f (x )是( )A .减函数B .增函数C .常函数D .可能是减函数,也可能是常函数9.已知函数y =x2-2x +3在闭区间[0,m]上有最大值3,最小值2,则m 的取值围是( )A .[1,+∞) B.[0,2]C .[1,2] D .(-∞,2] 10、使x2>x3成立的x 的取值围是( )A 、x <1且x≠0B 、0<x <1C 、x >1D 、x <111、若四个幂函数y =ax ,y =bx ,y =cx ,y =dx 在同一坐标系中的图象如右图,则a 、b 、c 、d 的大小关系是( )A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c12.若幂函数()1m f x x -=在(0,+∞)上是减函数,则 ( )A .m >1B .m <1C .m =lD .不能确定13.若点(),A a b 在幂函数()n y x n Q =∈的图象上,那么下列结论中不能成立的是A .00a b >⎧⎨>⎩B .00a b >⎧⎨<⎩C.00a b <⎧⎨<⎩ D .00a b <⎧⎨>⎩14.若函数f (x )=log 12(x 2-6x +5)在(a ,+∞)上是减函数,则a 的取值围是( )A .(-∞,1]B .(3,+∞)C .(-∞,3)D .[5,+∞)15、设集合2{|3,},{|1,}x S y y x R T y y x x R ==∈==-∈,则S T 是()A 、∅B 、TC 、SD 、有限集16、函数22log (1)y x x =+≥的值域为()A 、()2,+∞ B 、(),2-∞ C 、[)2,+∞ D 、[)3,+∞17、设1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭,则()A 、312y y y >> B 、213y y y >> C 、132y y y >> D 、123y y y >>18、在(2)log (5)a b a -=-中,实数a 的取值围是()A 、52a a ><或B 、2335a a <<<<或C 、25a <<D 、34a <<19、计算lg52lg2)lg5()lg2(22•++等于() A 、0 B 、1 C 、2 D 、320、已知3log 2a =,那么33log 82log 6-用a 表示是()A 、52a -B 、2a -C 、23(1)a a -+ D 、231a a --21、已知幂函数f(x)过点(2),则f(4)的值为()A 、12B 、 1C 、2D 、8 二、填空题1.抛物线y =8x 2-(m -1)x +m -7的顶点在x 轴上,则m =________.2.函数23-=xy 的定义域为___________.3.设()()12m f x m x +=-,如果()f x 是正比例函数,则m=____ ,如果()f x 是反比例函数,则m=______,如果f(x)是幂函数,则m=____. 4.若14(1)x --有意义,则x ∈___________.5.当35x y <=___________.6.若25525x x y⋅=,则y 的最小值为___________.7、若2log 2,log 3,m na a m n a+===。
