基坑涌水量
基坑涌水量计算书

基坑涌水量计算书
工程信息:
工程名称:未命名工程;方案编制人:张工;编制日期:2019-11-28。
施工单位:建科研
施工;建设地点:和平西桥;地上层数:13;地下层数:3层;建筑高度:40米;建筑面积:10000m2;建设单位:建科研建设公司;设计单位:建科研设计院;监理单位:建科研监理公司;勘查单位:建科研勘察院;总工期:360天;结构类型:框架;
一、基坑类型:
基坑属于均质含水层澘水完整井基坑,且基坑远离边界。
二、基坑简图:
三、计算公式:
其中Q──基坑涌水量;
k──渗透系数,k=5.00;
H──澘水含水层厚度,H=6.70m;
S──基坑水位降深,S=4.00m;
R──降水影响半径,R=46.30m;
r0──基坑等效半径,r0=10.73m。
四、计算结果:
基坑涌水量 Q=353.97m3/d。
基坑涌水量

基坑涌水量
基坑涌水量的计算
1、基坑承压水涌水量按下式估算:
Q =2πk M S 0
r 0=0. 29(a +b ) ) r 0
, R =10S H
式中:Q ——基坑涌水量(m 3/d);
k ——渗透系数,按0.30m/d取值;
S 0——水位降深(m ),按3.90m 考虑;
R ——影响半径(m ),经计算得21.36m ;
r 0——基坑等效半径(m ),经计算得32.04m ;
M 、H ──承压含水层厚度(m),按2.00m ;
a 、
b —分别为基坑的长、短边,按a=60.40m、b=50.00m考虑。
拟开挖基坑计算承压水涌水量Q 1为28.8m 3/d。
2、基坑潜水涌水量按下式估算:
(2H -S ) S Q =1. 366k R lg (1+) r 0
r 0=0. 29(a +b ) , R =2S kH
式中:Q ——基坑涌水量(m 3/d);
k ——渗透系数,按0.002m/d取值;
S ——水位降深(m ),按2.40m 考虑;
R ——影响半径(m ),经计算得0.33m ;
r 0——基坑等效半径(m ),经计算得32.04m ;
H ——含水层厚度(m ),按1.40m ;
a 、
b —分别为基坑的长、短边,按a=60.40m、b=50.00m考虑。
计算基坑潜水涌水量Q 2为3.50m 3/d。
拟开挖基坑计算总涌水量Q 为32.3m 3/d。
潜水基坑涌水量计算书

基坑涌水量计算书
凯特大厦工程;属于框架结构;地上25层;地下0层;建筑高度:0.00m;标准层层高:0.00m ;总建筑面积:0.00平方米;总工期:0天;施工单位:。
本工程由英皇(北京)房地产开发有限公司投资建设,设计,地质勘察,监理,组织施工;由孙士鼎担任项目经理,刘东风担任技术负责人。
一.基坑类型:
基坑属于均质含水层澘水完整井基坑,且基坑靠近隔水边界。
二.基坑简图:
三.计算公式:
其中 Q──基坑涌水量;
k──渗透系数,k=105.03;
S──基坑水位降深,S=5.50m; R──降水影响半径,R=100.83m; r0──基坑等效半径,r0=53.36m。
H──澘水含水层厚度,H=0.80m;
四.计算结果:
基坑涌水量 Q=-4227.62m3/d。
渗透系数+基坑总涌水量计算公式汇总

3. 经验估算法渗透系数k值还可以用一些经验公式来估算,例如1991年哈森提出用有效粒径d10计算较均匀砂土的渗透系数的公式哈森(Hazen)(2-9)1955年,太沙基提出了考虑土体孔隙比e的经验公式太沙基(Kael·Terzaghi 1883~1963),近代土力学及基础工程学的创始人,1883年10月2日生于布拉格(当时属奥地利)。
早期从事钢筋混凝土的研究工作,1912年获奥地利格拉茨高等工业学院博士学位。
1921~1923年,发表了饱和粘土的一维固结理论,提出了有效应力原理。
1925年出版了最早的《土力学》专著。
1929~1938年任维也纳技术大学教授,1938年后任美国哈佛大学教授。
他一生论著有200多篇,代表性的论著有《理论土力学》和《土力学的工程实践》。
1936年太沙基发起成立国际土力学及基础工程协会,并任协会主席至1957年。
(2-10)以上二式中的d10均以mm计,k值的单位是cm/s。
这些经验公式虽然有其实用的一面,但都有其适用条件和局限性,可靠性较差,一般只在作粗略估算时采用。
在无实测资料时,还可以参照有关规范或已建成工程的资料来选定k值,有关常见土的渗透系数参考值如表2-1 。
表2-1 土的渗透系数参考值土的类别渗透系数kcm/s土的类别渗透系数kcm/s粘土<10-7中砂10-2粉质粘土10-5~ 10-6粗砂10-2粉土10-4~ 10-5砾砂10-1粉砂10-3~ 10-4砾石>10-1细砂10-3一、基坑总涌水量计算 按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算: 1、基坑远离水源时:如图1(a )图1符号 意义单位 k 土的渗透系数 m/d H 潜水含水层厚度 m S 基坑水位降深 m R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径, 当基坑为矩形时如下计算:γ0=0.29(a+b) 当基坑为不规则形状时:)1lg()2(366.10r R SS H K Q +-=kH S R 2=kS R 10=πA r =2、基坑近河岸:符号意义单位b 基坑中心到河岸的距离mQ 基坑总涌水量m3/d(二)、均质含水层潜水非完整井基坑涌水量计算:1、基坑远离地面水源:如图2(a)符号意义单位hm(H+h)/2 ml过滤器长度mR 降水影响半径γ基坑等效半径S 基坑水位降深Q 基坑总涌水量m3/d2lg)2(366.1rbSSHkQ-=)2.01lg()1lg(366.122rhllhrRhHkQmmm+-++-=)2(hHhm+=2、基坑近河岸:(含水层厚度不大时) b>M/2 如图2(b )式中:b为基坑中心至河岸的距离,M 为过滤器向下至不透水土层的深度符号 意义单位 M 见表格上说明 m Q基坑总涌水量m 3/d1、基坑远离水源时: 如图3-a符号 意义单位 M 承压水厚度 m S 基坑水位降深 m k 土的渗透系数 m/d R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d]14.0lg 25.066.0lg 2lg [366.12220lM b M l r l l rb s l ks Q -+++=)1lg(73.20r RMSk Q +=2、基坑近河岸:b<0.5γ0 如图3-bb 为基坑中心至河岸的距离 符号意义单位 b 见表上说明 m Q基坑总涌水量m 3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4符号 意义单位 l过滤器长度 m M 承压水厚度 S 基坑水位降深 R 降水影响半径 γ0 基坑等效半径 Q基坑总涌水量m3/d)2lg(73.20r b MS k Q =)2.01lg()1lg(73.20rM l l Mr R MS kQ +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算 如图5图5符号 意义单位 R 降水影响半径 m M 承压水厚度 H hγ0 基坑等效半径 Q基坑总涌水量m3/d)1lg()2(366.102r R h M M H k Q +--=。
渗透系数+基坑总涌水量计算公式汇总

3. 经验估算法渗透系数k值还可以用一些经验公式来估算,例如1991年哈森提出用有效粒径d10计算较均匀砂土的渗透系数的公式哈森(Hazen)(2-9)1955年,太沙基提出了考虑土体孔隙比e的经验公式太沙基(Kael·Terzaghi 1883~1963),近代土力学及基础工程学的创始人,1883年10月2日生于布拉格(当时属奥地利)。
早期从事钢筋混凝土的研究工作,1912年获奥地利格拉茨高等工业学院博士学位。
1921~1923年,发表了饱和粘土的一维固结理论,提出了有效应力原理。
1925年出版了最早的《土力学》专著。
1929~1938年任维也纳技术大学教授,1938年后任美国哈佛大学教授。
他一生论著有200多篇,代表性的论著有《理论土力学》和《土力学的工程实践》。
1936年太沙基发起成立国际土力学及基础工程协会,并任协会主席至1957年。
(2-10)以上二式中的d10均以mm计,k值的单位是cm/s 。
这些经验公式虽然有其实用的一面,但都有其适用条件和局限性,可靠性较差,一般只在作粗略估算时采用。
在无实测资料时,还可以参照有关规或已建成工程的资料来选定k值,有关常见土的渗透系数参考值如表2-1 。
表2-1 土的渗透系数参考值土的类别渗透系数kcm/s土的类别渗透系数kcm/s粘土<10-7中砂10-2粉质粘土10-5~ 10-6粗砂10-2粉土10-4~ 10-5砾砂10-1粉砂10-3~ 10-4砾石>10-1细砂10-3一、基坑总涌水量计算 按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算: 1、基坑远离水源时:如图1(a )图1符号 意义单位 k 土的渗透系数 m/d H 潜水含水层厚度 m S 基坑水位降深 m R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d注:(1)、降水影响半径宜根据试验确定,当基坑安全等级为二、三级时, 当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径, 当基坑为矩形时如下计算:γ0=0.29(a+b) 当基坑为不规则形状时:)1lg()2(366.10r RSS H K Q +-=kH S R 2=kS R 10=πAr =2、基坑近河岸:如图1(b )符号 意义单位 b 基坑中心到河岸的距离m Q基坑总涌水量m 3/d(二)、均质含水层潜水非完整井基坑涌水量计算: 1、基坑远离地面水源: 如图2(a )图2符号 意义单位 h m (H+h)/2 m l 过滤器长度 m R 降水影响半径 γ0 基坑等效半径S 基坑水位降深 Q基坑总涌水量m 3/d02lg)2(366.1r b S S H kQ -=)2.01lg()1lg(366.10022r h l l h r R h H k Q m m m+-++-=)2(h H h m+=2、基坑近河岸:(含水层厚度不大时) b>M/2 如图2(b )式中:b 为基坑中心至河岸的距离,M 为过滤器向下至不透水土层的深度符号 意义单位 M 见表格上说明 m Q基坑总涌水量m 3/d(三)、均质含水层承压水完整井基坑涌水量计算: 1、基坑远离水源时: 如图3-a图3符号 意义单位 M 承压水厚度 m S 基坑水位降深 m k 土的渗透系数 m/d R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d]14.0lg 25.066.0lg 2lg [366.1222lM b M l r l l rb s l ks Q -+++=)1lg(73.20r RMSk Q +=2、基坑近河岸:b<0.5γ0 如图3-b b 为基坑中心至河岸的距离符号 意义单位 b 见表上说明 m Q基坑总涌水量m 3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4图4符号 意义单位 l过滤器长度 m M 承压水厚度 S 基坑水位降深 R 降水影响半径 γ0 基坑等效半径 Q基坑总涌水量m3/d)2lg(73.20r b MS kQ =)2.01lg()1lg(73.20rMl l M r R MS kQ +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算 如图5图5符号 意义单位 R 降水影响半径 m M 承压水厚度 H hγ0 基坑等效半径 Q基坑总涌水量m3/d)1lg()2(366.102r R h M M H kQ +--=。
渗透系数+基坑总涌水量计算公式汇总

渗透系数+基坑总涌水量计算公式汇总————————————————————————————————作者: ————————————————————————————————日期:3. 经验估算法渗透系数k值还可以用一些经验公式来估算,例如1991年哈森提出用有效粒径d10计算较均匀砂土的渗透系数的公式哈森(Hazen)(2-9)1955年,太沙基提出了考虑土体孔隙比e的经验公式太沙基(Kael·Terzaghi1883~1963),近代土力学及基础工程学的创始人,1883年10月2日生于布拉格(当时属奥地利)。
早期从事钢筋混凝土的研究工作,1912年获奥地利格拉茨高等工业学院博士学位。
1921~1923年,发表了饱和粘土的一维固结理论,提出了有效应力原理。
1925年出版了最早的《土力学》专著。
1929~1938年任维也纳技术大学教授,1938年后任美国哈佛大学教授。
他一生论著有200多篇,代表性的论著有《理论土力学》和《土力学的工程实践》。
1936年太沙基发起成立国际土力学及基础工程协会,并任协会主席至1957年。
(2-10)以上二式中的d10均以mm计,k值的单位是cm/s。
这些经验公式虽然有其实用的一面,但都有其适用条件和局限性,可靠性较差,一般只在作粗略估算时采用。
在无实测资料时,还可以参照有关规范或已建成工程的资料来选定k值,有关常见土的渗透系数参考值如表2-1 。
表2-1 土的渗透系数参考值土的类别渗透系数kcm/s土的ﻫ类别渗透系数kcm/s粘土<10-7中砂10-2粉质粘土10-5 ~ 10-6粗砂10-2粉土10-4~10-5砾砂10-1粉砂10-3~ 10-4砾石>10-1细砂10-3一、基坑总涌水量计算 按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算: 1、基坑远离水源时:如图1(a )图1符号 意义单位 k 土的渗透系数 m/d H 潜水含水层厚度 m S 基坑水位降深 m R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d注:(1)、降水影响半径宜根据试验确定,当基坑安全等级为二、三级时, 当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径, 当基坑为矩形时如下计算:γ0=0.29(a +b) 当基坑为不规则形状时:)1lg()2(366.10r R SS H K Q +-=kH S R 2=kS R 10=πAr =ﻬ2、基坑近河岸:如图1(b )符号 意义单位 b 基坑中心到河岸的距离m Q基坑总涌水量m3/d(二)、均质含水层潜水非完整井基坑涌水量计算: 1、基坑远离地面水源: 如图2(a )图2符号 意义单位 h m (H+h)/2 m l 过滤器长度 m R降水影响半径02lg)2(366.1r b S S H kQ -=)2.01lg()1lg(366.10022r h l lh r R h H k Q m m m+-++-=)2(h H h m +=γ0 基坑等效半径 S 基坑水位降深 Q基坑总涌水量m 3/d2、基坑近河岸:(含水层厚度不大时) b>M/2 如图2(b )式中:b 为基坑中心至河岸的距离,M为过滤器向下至不透水土层的深度符号 意义单位 M 见表格上说明 m Q基坑总涌水量m 3/d(三)、均质含水层承压水完整井基坑涌水量计算: 1、基坑远离水源时: 如图3-a图3符号 意义单位 M 承压水厚度 m S基坑水位降深m]14.0lg 25.066.0lg 2lg [366.122200l M b M l r l l r b s l ks Q -+++=)1lg(73.20r RMSk Q +=k 土的渗透系数 m/d R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d2、基坑近河岸:b<0.5γ0 如图3-b b 为基坑中心至河岸的距离符号 意义单位 b 见表上说明 m Q基坑总涌水量m3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4图4符号 意义单位 l过滤器长度 m M 承压水厚度 S 基坑水位降深 R 降水影响半径 γ0 基坑等效半径 Q基坑总涌水量m3/d)2lg(73.20r b MS kQ =)2.01lg()1lg(73.20rMl l M r R MS kQ +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算 如图5图5符号 意义单位 R 降水影响半径 m M 承压水厚度 H hγ0 基坑等效半径 Q基坑总涌水量m3/d)1lg()2(366.102r R h M M H k Q +--=。
涌水量计算公式

Q=#DIV/0! 1.366K*(2H-S)*S/log(1+R/r)对潜水含水层按下式计算R=02*S*SQRT(K*H)对承压含水层按下式计算R=010*S*SQRT(K)r=00.29*(a+b)r=0SQRT(A/3.1415926)Q=#DIV/0! 1.366k*(2H-S)*S/log(2b/r)Q=#DIV/0! 1.366k*(2H-S)*S/log(2(b 1+b 2)*COS(3.1416*(b1-b2)/2/(b1+b2))/3.1416r)Q=#NUM! 1.366k*(2H-S)*S/(2log(r+R)-log(r*(2b+r)))Q=#DIV/0! 1.366k*(H²-h m ²)/(log(1+R/r)+(h m -l)*log(1+0.2*h m /r)/l)2、均质含水层潜水非完整井基坑涌水量计算(1)当基坑远离地面水源一、基坑涌水量计算(2)基坑靠近河岸时(3)基坑位于两地表水体之间或位于补给区与排泄区之间时(4)当基坑靠近隔水边界时当基坑非圆形时,矩形基坑等效半径按下式计算当基坑非圆形时,不规则形状基坑等效半径按下式计算(1)基坑远离地面水源时1、均质含水层潜水完整井基坑涌水量计算Q=#DIV/0!1.366ks*((l+s)/log(2b/r)+l/(log(0.66l/r)+0.25l/M*log(b²/(M²-0.14l²)))Q=#DIV/0! 1.366ks*((l+s)/log(2b/r)+l/(log(0.66l/r)-0.22arsh(0.44l/b))Q=#DIV/0!1.366ks*((l+s)/log(2b/r)+l/(log(0.66l/r)-0.11*l/b))Q=#DIV/0! 2.73k*MS/LOG(1+R/r)Q=#DIV/0! 2.73k*MS/LOG(2b/r)Q=#DIV/0! 2.73k*(2H-S)*S/log(2(b 1+b 2)*COS(3.1416*(b 1+b 2)/2/(b 1+b 2))/3.142r)Q=#DIV/0! 2.73k*MS/(LOG(1+R/r)+(M-l)/l*log(1+0.2*M/r))Q=#DIV/0! 1.366k*((2H-M)*M-h²)/log(1+R/r)q=0120πrlk^(1/3)降水3、均质含水层承压水完整井基坑涌水量计算(1)基坑远离地面水源(2)基坑靠近河岸(3)基坑位于两地表水体之间或位于补给区与排泄区之间时(2)当基坑靠近河岸,含水层厚度不大时(3)当基坑靠近河岸,含水层厚度很大时4、均质含水层承压水非完整井基坑涌水量计算5、均质含水层承压水非完整井基坑涌水量计算n=#DIV/0! 1.1*Q/qK H S R ra bAk H S r bk H S r b1b2k H S r R bk H h m r R l hk b h r s l Mk b h r s larsh (0.44l/b)#DIV/0!k M S R rk M S b rk H S r b1b2 k M S R r l k M H h R rQ q r l k公式中参数Q------基坑涌水量K------土壤的渗透系数H------潜水含水层厚度S------基坑水位降深R------降水影响半径k------土的渗透系数r------基坑等效半径a、b------基坑的长、短边A---------基坑面积(b<R/2)M---------由含水层底板到滤头有效工作部分中点的长度(b>M/2)(b<l)(b>l)M--------承压含水层厚度b<0.5rq-------单井出水量r-------过滤器半径(m)k-------含水层的渗透系数(m/d)。
基坑涌水量计算
20.3 1.0 10.0
21656.04 37748.17 2481.78 38832.37 10766.56 #NUM! 12336.18 12337.08 24.67 0.25 #########
降水井的数量(n) )
圆形基坑半径(r0)
→
52
←输入n值
1.0
4.01
单井井 潜水完整井 管进水 长度 (y0)计 承压完整井 算
######## 基坑中心点水位降 深(S)计算
潜水完整井稳定流
承压水完整井稳定流
##################
100.0 1.0 1.0
←输入b ←输入b1 ←输入b2
要求降深面标高到含水层底面标高的距离(h) 由含水层底板到过滤器有效工作部分中点的长度(M) 过滤器进水部分长度(L)
4、近河基坑降水,含水层厚度很大时,计算涌水量(Q)【当b<L时】
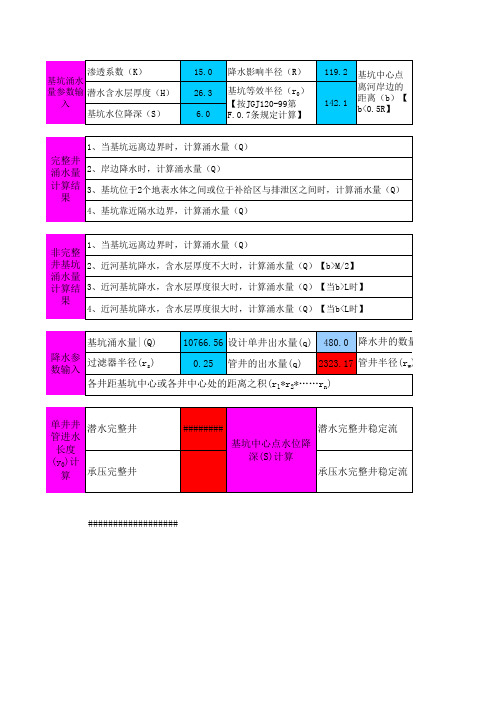
1、当基坑远离边界时,计算涌水量(Q)
基坑涌水量|(Q)
10766.56 设计单井出水量(q) 480.0
降水井的数量
ห้องสมุดไป่ตู้
降水参 过滤器半径(rs) 0.25 管井的出水量(q) 2323.17 管井半径(rw) 数输入 各井距基坑中心或各井中心处的距离之积(r1*r2*……rn)
渗透系数(K) 基坑涌水 量参数输 潜水含水层厚度(H) 入 基坑水位降深(S)
15.0 26.3 6.0
降水影响半径(R) 基坑等效半径(r0) 【按JGJ120-99第 F.0.7条规定计算】
119.2 142.1
基坑中心点 离河岸边的 距离(b)【 b<0.5R】
1、当基坑远离边界时,计算涌水量(Q)
基坑涌水量计算

基坑涌水量计算G.0.1 均质含水层潜水完整井基坑涌水量可按下列规定计算(图G .0.1):1 当基坑远离边界时,涌水量可按式(G.0.1-1)计算:⎪⎪⎭⎫ ⎝⎛+-=011)2(366.1r R g S S H k Q (G.0.1-1) 式中 Q ——基坑涌水量;k ——渗透系数;图G .0.1 均质含水层潜水完整井基坑涌水量计算简图 (a)基坑远离边界;(b)岸边降水;(c)基坑位于两地表水体间;(d)基坑靠近隔水边界H ——潜水含水层厚度;S ——基坑水位降深;R ——降水影响半径;0r ——基坑等效半径,按第G.0.7条规定计算。
2 岸边降水时涌水量可按式(G 。
0。
1-2)计算:21)2(366.1r b g S S H k Q -= b <0.5R (G.0.1-2) 3 当基坑位于两个地表水体之间或位于补给区与排泄区之间时,涌水量可按式(G.0.1-3)计算:⎥⎦⎤⎢⎣⎡+-+-=)(2)(cos )(21)2(366.12121021b b b b r b b g S S H kQ ππ (G.0.1-3) 4 当基坑靠近隔水边界,涌水量可按式(G.0.1-4)计算: )2(1)(21)2(366.1000r b gr r R g S S H k Q +-+-= b ′<0.5R (G.0.1-4) G.0.2 均质含水层潜水非完整井基坑涌水量可按下列规定计算(图G.0.2):1 基坑远离边界时,涌水量可按下式计算:⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+-=00222.01lg 1lg 366.1r h l l h r R H k Q m m mh (G.0.2-1)式中, 2 近河基坑降水,含水层厚度不大时,涌水量可按式(G.0.2-2)计算:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-∙+++=2220014.0lg 25.066.0lg 2lg 366.1l M b M l r l l r b S l kS Q(G .0.2-2)式中 M ——由含水层底板到过滤器有效工作部分中点的长度。
渗透系数+基坑总涌水量计算公式汇总

3. 经验估算法渗透系数k值还可以用一些经验公式来估算,例如1991年哈森提出用有效粒径d10计算较均匀砂土的渗透系数的公式哈森(Hazen)(2-9)1955年,太沙基提出了考虑土体孔隙比e的经验公式太沙基(Kael·Terzaghi 1883~1963),近代土力学及基础工程学的创始人,1883年10月2日生于布拉格(当时属奥地利)。
早期从事钢筋混凝土的研究工作,1912年获奥地利格拉茨高等工业学院博士学位。
1921~1923年,发表了饱和粘土的一维固结理论,提出了有效应力原理。
1925年出版了最早的《土力学》专著。
1929~1938年任维也纳技术大学教授,1938年后任美国哈佛大学教授。
他一生论著有200多篇,代表性的论著有《理论土力学》和《土力学的工程实践》。
1936年太沙基发起成立国际土力学及基础工程协会,并任协会主席至1957年。
(2-10)以上二式中的d10均以mm计,k值的单位是cm/s 。
这些经验公式虽然有其实用的一面,但都有其适用条件和局限性,可靠性较差,一般只在作粗略估算时采用。
在无实测资料时,还可以参照有关规或已建成工程的资料来选定k值,有关常见土的渗透系数参考值如表2-1 。
表2-1 土的渗透系数参考值土的类别渗透系数kcm/s土的类别渗透系数kcm/s粘土<10-7中砂10-2粉质粘土10-5~ 10-6粗砂10-2粉土10-4~ 10-5砾砂10-1粉砂10-3~ 10-4砾石>10-1细砂10-3一、基坑总涌水量计算 按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算: 1、基坑远离水源时:如图1(a )图1符号 意义单位 k 土的渗透系数 m/d H 潜水含水层厚度 m S 基坑水位降深 m R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d注:(1)、降水影响半径宜根据试验确定,当基坑安全等级为二、三级时, 当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径, 当基坑为矩形时如下计算:γ0=0.29(a+b) 当基坑为不规则形状时:)1lg()2(366.10r RSS H K Q +-=kH S R 2=kS R 10=πAr =2、基坑近河岸:如图1(b )符号 意义单位 b 基坑中心到河岸的距离m Q基坑总涌水量m 3/d(二)、均质含水层潜水非完整井基坑涌水量计算: 1、基坑远离地面水源: 如图2(a )图2符号 意义单位 h m (H+h)/2 m l 过滤器长度 m R 降水影响半径 γ0 基坑等效半径S 基坑水位降深 Q基坑总涌水量m 3/d02lg)2(366.1r b S S H kQ -=)2.01lg()1lg(366.10022r h l l h r R h H k Q m m m+-++-=)2(h H h m+=2、基坑近河岸:(含水层厚度不大时) b>M/2 如图2(b )式中:b 为基坑中心至河岸的距离,M 为过滤器向下至不透水土层的深度符号 意义单位 M 见表格上说明 m Q基坑总涌水量m 3/d(三)、均质含水层承压水完整井基坑涌水量计算: 1、基坑远离水源时: 如图3-a图3符号 意义单位 M 承压水厚度 m S 基坑水位降深 m k 土的渗透系数 m/d R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d]14.0lg 25.066.0lg 2lg [366.1222lM b M l r l l rb s l ks Q -+++=)1lg(73.20r RMSk Q +=2、基坑近河岸:b<0.5γ0 如图3-b b 为基坑中心至河岸的距离符号 意义单位 b 见表上说明 m Q基坑总涌水量m 3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4图4符号 意义单位 l过滤器长度 m M 承压水厚度 S 基坑水位降深 R 降水影响半径 γ0 基坑等效半径 Q基坑总涌水量m3/d)2lg(73.20r b MS kQ =)2.01lg()1lg(73.20rMl l M r R MS kQ +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算 如图5图5符号 意义单位 R 降水影响半径 m M 承压水厚度 H hγ0 基坑等效半径 Q基坑总涌水量m3/d)1lg()2(366.102r R h M M H kQ +--=。
渗透系数+基坑总涌水量计算公式汇总

过滤器长度
m
M
承压水厚度
S
基坑水位降深
R
降水影响半径
γ0
基坑等效半径
Q
基坑总涌水量
m3/d
(五)、均质含水层承压-潜水非完整井基坑涌水量计算
如图5
图5
符号
意义
单位
R
降水影响半径
m
M
承压水厚度
H
h
γ0
基坑等效半径
Q
基坑总涌水量
m3/d
1、基坑远离水源时:
如图1(a)
图1
符号
意义
单位
k
土的渗透系数
m/d
H
潜水含水层厚度
m
S
基坑水位降深
m
R
降水影响半径
m
γ0
基坑等效半径
m
Q
基坑总涌水量
m3/d
注:(1)、降水影响半径宜根据试验确定,当基坑安全等级为二、三级时,
当为潜水含水层时:
当为承压水时:
(2)、基坑等效半径当基坑为圆形时就是基坑半径,
γ0
基坑等效半径
S
基坑水位降深
Q
基坑总涌水量
m3/d
2、基坑近河岸:(含水层厚度不大时)
b>M/2如图2(b)
式中:b为基坑中心至河岸的距离,M为过滤器向下至不透水土层的深度
符号
意义
单位
M
见表格上说明
m
Q
基坑总涌水量
m3/d
(三)、均质含水层承压水完整井基坑涌水量计算:
1、基坑远离水源时:
如图3-a
图3
符号
意义
单位
M
承压水厚度
基坑涌水量计算公式
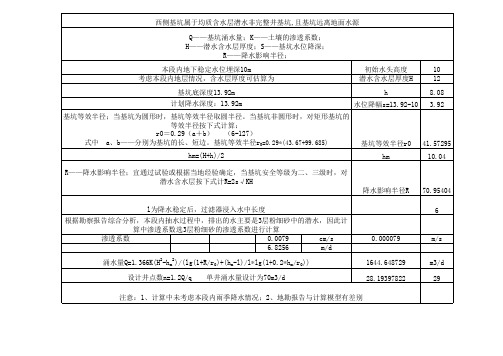
0.000079 1644.648729 28.19397822
m/s m3/d 29
注意:1、计算中未考虑本段内雨季降水情况;2、地勘报告与计算模型有差别
西侧基坑属于均质含水层澘水非完整井基坑,且基坑远离地面水源 Q——基坑涌水量;K——土壤的渗透系数; H——潜水含水层厚度;S——基坑水位降深; R——降水影响半径; 本段内地下稳定水位埋深10m 考虑本段内地层情况,含水层厚度可估算为 基坑底深度13.92m 计划降水深度:13.92m 基坑等效半径;当基坑为圆形时,基坑等效半径取圆半径。当基坑非圆形时,对矩形基坑的 等效半径按下式计算: r0=0.29(a+b) (6-127) 式中 a、b——分别为基坑的长、短边。基坑等效半径r0=0.29*(43.67+99.685) hm=(H+h)/2 R——降水影响半径;宜通过试验或根据当地经验确定,当基坑安全等级为二、三级时,对 潜水含水层按下式计R=2s√KH 降水影响半径R l为降水稳定后,过滤器浸入水中长度 根据勘察报告综合分析,本段内抽水过程中,排出的水主要是3层粉细砂中的潜水,因此计 算中渗透系数选3层粉细砂的渗透系数进行计算 渗透系数 0.0079 cm/s 6.8256 m/d 涌水量Q=1.366K(H2-hm2)/(lg(1+R/r0)+(hm-l)/l*lg(1+0.2*hm/r0)) 设计井点数n=1.2Q/q 单井涌水量设计为70m3/d 70.95404 6 初始水头高度 潜水含水层厚度H h 水位降幅s=13.92-10 10 12 8.08 3.92
渗透系数+基坑总涌水量计算公式汇总

3. 经验估算法渗透系数k值还可以用一些经验公式来估算,例如1991年哈森提出用有效粒径d10计算较均匀砂土的渗透系数的公式哈森(Hazen)(2-9)1955年,太沙基提出了考虑土体孔隙比e的经验公式太沙基(Kael·Terzaghi 1883~1963),近代土力学及基础工程学的创始人,1883年10月2日生于布拉格(当时属奥地利)。
早期从事钢筋混凝土的研究工作,1912年获奥地利格拉茨高等工业学院博士学位。
1921~1923年,发表了饱和粘土的一维固结理论,提出了有效应力原理。
1925年出版了最早的《土力学》专著。
1929~1938年任维也纳技术大学教授,1938年后任美国哈佛大学教授。
他一生论著有200多篇,代表性的论著有《理论土力学》和《土力学的工程实践》。
1936年太沙基发起成立国际土力学及基础工程协会,并任协会主席至1957年。
(2-10)以上二式中的d10均以mm计,k值的单位是cm/s。
这些经验公式虽然有其实用的一面,但都有其适用条件和局限性,可靠性较差,一般只在作粗略估算时采用。
在无实测资料时,还可以参照有关规范或已建成工程的资料来选定k值,有关常见土的渗透系数参考值如表2-1 。
表2-1 土的渗透系数参考值土的类别渗透系数kcm/s土的类别渗透系数kcm/s粘土<10-7中砂10-2粉质粘土10-5~ 10-6粗砂10-2粉土10-4~ 10-5砾砂10-1粉砂10-3~ 10-4砾石>10-1细砂10-3一、基坑总涌水量计算 按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算: 1、基坑远离水源时:如图1(a )图1符号 意义单位 k 土的渗透系数 m/d H 潜水含水层厚度 m S 基坑水位降深 m R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径, 当基坑为矩形时如下计算:γ0=0.29(a+b) 当基坑为不规则形状时:)1lg()2(366.10r R SS H K Q +-=kH S R 2=kS R 10=πA r =2、基坑近河岸:符号意义单位b 基坑中心到河岸的距离mQ 基坑总涌水量m3/d(二)、均质含水层潜水非完整井基坑涌水量计算:1、基坑远离地面水源:如图2(a)符号意义单位hm(H+h)/2 ml过滤器长度mR 降水影响半径γ基坑等效半径S 基坑水位降深Q 基坑总涌水量m3/d2lg)2(366.1rbSSHkQ-=)2.01lg()1lg(366.122rhllhrRhHkQmmm+-++-=)2(hHhm+=2、基坑近河岸:(含水层厚度不大时) b>M/2 如图2(b )式中:b为基坑中心至河岸的距离,M 为过滤器向下至不透水土层的深度符号 意义单位 M 见表格上说明 m Q基坑总涌水量m 3/d1、基坑远离水源时: 如图3-a符号 意义单位 M 承压水厚度 m S 基坑水位降深 m k 土的渗透系数 m/d R 降水影响半径 m γ0 基坑等效半径 m Q基坑总涌水量m 3/d]14.0lg 25.066.0lg 2lg [366.12220lM b M l r l l rb s l ks Q -+++=)1lg(73.20r RMSk Q +=2、基坑近河岸:b<0.5γ0 如图3-bb 为基坑中心至河岸的距离 符号意义单位 b 见表上说明 m Q基坑总涌水量m 3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4符号 意义单位 l过滤器长度 m M 承压水厚度 S 基坑水位降深 R 降水影响半径 γ0 基坑等效半径 Q基坑总涌水量m3/d)2lg(73.20r b MS k Q =)2.01lg()1lg(73.20rM l l Mr R MS kQ +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算 如图5图5符号 意义单位 R 降水影响半径 m M 承压水厚度 H hγ0 基坑等效半径 Q基坑总涌水量m3/d)1lg()2(366.102r R h M M H k Q +--=。
降水井计算

基坑降水计算书一、基坑涌水量计算1、原始条件:计算模型:此井点系统为潜水非完整井,采用基坑外降水。
2、井点管距边坑距离为1.5m ,滤管长度取1.0m ,直径40mm ,配有配套抽水设备;渗透系数(根据勘察报告提供室内渗透系数结合当地经验取值)0.2(m/d )。
3、基坑涌水量计算书3.1基坑开挖深度6.00m ,基坑面积约为9738m 2。
(1)基坑中心处要求降低水位深度S ,取降水后地下水位位于坑底以下1.0m ,则有S=6.00+1.0=7.00m(2)含水层厚度H ’=16m(3)影响半径0R基坑等效半径080.69r m ==(4)基坑涌水量()()3002'1.366298.81lg H S Sm Q k d R r -==⎛⎫⎪⎝⎭二、降水井数量计算1、根据《工程地质手册》公式验算每根井点的允许最大进水量2、井点管的数量经验算,34眼水井管出水量基本能满足基坑总涌水量的要求!三、降水井深度计算降水井深度可以按照以下公式确定:式中:H 1=6.00m (基坑深度)H 2=1.0m (降低水位距离基底要求)H 3=2.0m (水力坡度)H 4=2.0m (水位变化幅度) H 5=1.0m (过滤器长度) H 6=1.0m (沉淀管长度) 根据计算,综合考虑现场条件,又由于降水持续时间长,井内必产生沉砂,因此降水井深度取13米,疏干井深度取14米。
20米。
四、补充方案 1、考虑场地南侧有明水影响,降水井加密布设。
沿基坑周边布置32口降水井,井深13米,另在坑内布置20口14米深疏干井。
2、基坑集水井、电梯坑等处由于开挖较深,可布设轻型井点辅助降水。
3、降水过程中,若该设计方案中降水井不能满足基坑总涌水量,可增设降水井。
基坑总涌水量计算公式汇总

一、基坑总涌水量计算按井管(筒)是否穿透整个含水层分为完整井和非完整井。
按井深分为浅井、中深井和深井。
当水井开凿在承压含水层中,而承压水头又高于地面时称承压井或自流井。
(一)、均质含水层潜水完整井基坑涌水量计算:1、基坑远离水源时:如图1(a )图1符号 意义 单位 k 土的渗透系数 m/d H潜水含水层厚度 m S基坑水位降深 m R降水影响半径 m γ0基坑等效半径 m Q 基坑总涌水量 m 3/d注:(1)、降水影响半径宜根据试验确定,当基坑安全等级为二、三级时,当为潜水含水层时: 当为承压水时: (2)、基坑等效半径当基坑为圆形时就是基坑半径,当基坑为矩形时如下计算:γ0=0.29(a+b)当基坑为不规则形状时:)1lg()2(366.10r R S S H K Q +-=kHS R 2=kS R 10=πA r =02、基坑近河岸:符号意义单位b 基坑中心到河岸的距离mQ 基坑总涌水量m3/d(二)、均质含水层潜水非完整井基坑涌水量计算:1、基坑远离地面水源:如图2(a)符号意义单位hm(H+h)/2 ml过滤器长度mR 降水影响半径γ基坑等效半径S 基坑水位降深Q 基坑总涌水量m3/d2lg)2(366.1rbSSHkQ-=)2.01lg()1lg(366.122rhllhrRhHkQmmm+-++-=)2(hHhm+=2、基坑近河岸:(含水层厚度不大时)b>M/2 如图2(b ) 式中:b为基坑中心至河岸的距离,M 为过滤器向下至不透水土层的深度 符号 意义 单位 M见表格上说明 m Q 基坑总涌水量 m 3/d1、基坑远离水源时:如图3-a符号意义 单位 M承压水厚度 m S基坑水位降深 m k土的渗透系数 m/d R降水影响半径 m γ0基坑等效半径 m Q基坑总涌水量 m 3/d]14.0lg 25.066.0lg 2lg [366.122200lM b M l r l l r b s l ks Q -+++=)1lg(73.20r R MS k Q +=2、基坑近河岸:b<0.5γ0 如图3-b b 为基坑中心至河岸的距离 符号意义 单位 b见表上说明 m Q 基坑总涌水量 m 3/d(四)、均质含水层承压水非完整井基坑涌水量计算 如图4符号意义 单位 l过滤器长度 m M承压水厚度 S基坑水位降深 R降水影响半径 γ0基坑等效半径 Q基坑总涌水量 m3/d)2lg(73.20r b MS k Q =)2.01lg()1lg(73.200r M l l M r R MS k Q +-++=(五)、均质含水层承压-潜水非完整井基坑涌水量计算如图5图5符号意义单位R 降水影响半径m M 承压水厚度Hhγ基坑等效半径Q 基坑总涌水量m3/d)1lg()2(366.12rRhMMHkQ+--=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基坑涌水量的计算
1、基坑承压水涌水量按下式估算:
)(29.0)r 1ln S 2Q 00
b a r R M k +=+
=(π, 式中:Q ——基坑涌水量(m 3/d );
k ——渗透系数,按0.30m/d 取值;
S 0——水位降深(m ),按3.90m 考虑;
R ——影响半径(m ),经计算得21.36m ;
r 0——基坑等效半径(m ),经计算得32.04m ;
M 、H ──承压含水层厚度(m),按2.00m ;
a 、
b —分别为基坑的长、短边,按a=60.40m 、b=50.00m 考虑。
拟开挖基坑计算承压水涌水量Q 1为28.8m 3/d 。
2、基坑潜水涌水量按下式估算:
)(29.0)r 1lg S )2366.1Q 00
b a r R S H k +=+-=((, 式中:Q ——基坑涌水量(m 3/d );
k ——渗透系数,按0.002m/d 取值;
S ——水位降深(m ),按2.40m 考虑;
R ——影响半径(m ),经计算得0.33m ;
r 0——基坑等效半径(m ),经计算得32.04m ;
H ——含水层厚度(m ),按1.40m ;
a 、
b —分别为基坑的长、短边,按a=60.40m 、b=50.00m 考虑。
计算基坑潜水涌水量Q 2为3.50m 3/d 。
拟开挖基坑计算总涌水量Q 为32.3m 3/d 。
H
S R 10=kH
S R 2=。
