南京大学物理学院《633数理方法二》历年考研真题汇编

合集下载

南京大学物理面试题历年集锦

轨道泡
2 地面的静观测者 3好回
是惯性系, 泡泡泡
是在考 g欢lde次严ule泡泡泡4 第一问阴险泡泡泡删除举报广告
2010-11-13 16:24:37 与;e我{i\pi}+1;成 (与;\ma吧hi吧{称……42};成) 第一题看眼就知道了嘛，墙那边类似无穷势垒，另一边类似簧振子，回个肯都学过啊。个形式嘛。
2010-11-13 21:51:58 严a否cal ( 是沉默的高二时被面试的一道题在一个水箱解释回删除举报广告 , 气从箱
奋剂)
到水面和石头从水面到箱
哪个时间短
2010-11-13 21:54:35 断雁嵬蝶 (番茄爱好者) 1泡简述标准模型及子的夸克组
2泡解无限深方势阱
3泡做过的实验回删除举报广告
用任何仪器将一杯水加热到 300K?
你本科的学校多少修车点? 推算学校内
多少自行车
第一道的答案是用手捂泡泡泡泡泡回删除举报广告
2010-11-13 21:36:58 瓂鴮騦 300K 回是都作室温的泡泡泡泡直接放间自然就了
删除举报广告
2010-11-13 21:45:24 ABC ( 小时努力，自会进 ) 一本书看的，忘了谁免试谁了，问题是水的什东西能灭火？回删除举报广告
观测
能观察到加速电子的辐射？ b泡在电子自由落体参照系中
辐射？ c泡你对 a泡b 的回答是矛盾？
3泡匀
磁场中
一个中子
电荷称0！，由于中子的磁矩，
系统
个能级。假设中子一开始处于高能态，请估计高能态自发辐射的半衰期。
4泡
射线中的白子是怎来的？为什一个电中性的 pi我0 子能衰

南京大学物理化学考研真题(含结构化学)

诺循环的 T-s图。
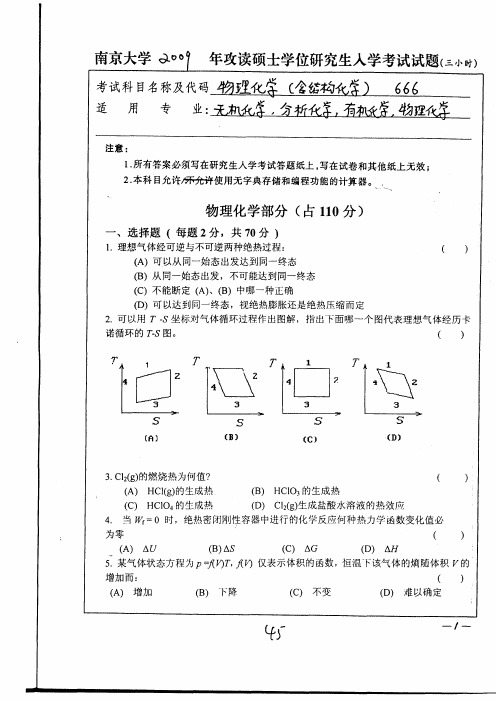
体经历卡
( )
quz
3
S (D9
3,Clzl⒆ 的燃烧热为何值 ? m) HCl(g)的 G) HClO4的 4.当 9/f=0时为零生成热生成热 ⒀ ) HClO3的 rD) c12(⒄ 生成热生成盐酸水溶液的热效应
(
)
,绝热密闭刚性容器中进行的化学反应何种热力学函数变化值必
30.如图在毛细管内装入润湿性液体,当在毛细管内左端加热时,则管内液体将 :( )
, (
↑ 加热
′
右移动 c)不左移动 (B)向移动 (D)因失去平衡而左右来冂移动 m)向 I,其 2m的 31.半径为 I×10ˉ 球形肥皂泡的表面张力为 0.⒆ 5N・ mˉ 附加压力为 : ( ) (c) 2.5N.m-2 (e) 5 N'm-2 (A) 0.025 (D) l0 N.m-2 N.m'' 一毛细管端插入水中 ,毛细管中水面上升 5cm,若将毛细管向下移动 ,留了 3cm 32.将在水面 ,试问水在毛细管上端的行为是 : m)水 (C)毛从毛细管上端溢出细管上端水面呈凹形弯月面 (B)毛 (D)毛 ( 细管上端水面呈凸形弯月面细管上端水面早水平面 )
南京大学 aoo丨
刂年攻读硕士学位研究生入学考试试题 (三咐) 羔 , 6“
考试科目名称及代码毡饧哩倪苄 c兮獭
适用
专
注意 : 1.所有答案必须写在研究生人学考试答题纸上 ,写在试卷和其他纸上无效 ; 2.本科目允许秘使用无字典存储和编程功能的计算器。

南京大学物理学院《633数理方法二》历年考研真题专业课考试试题

目录
2009年南京大学633数理方法二考研真题 2008年南京大学633数理方法二考研真题 2007年南京大学633数学物理方法二考研真题 2006年南京大学333数学物理方法二考研真题 2005年南京大学333数学物理方法二考研真题 2004年南京大学333数学物理方法二考研真题 2000年南京大学333数学物理方法二考研真题
2000年南京大学3法二考研真题
2008年南京大学633数理方法二考研真题
2007年南京大学633数学物理方法二考研真题
2006年南京大学333数学物理方法二考研真题
2005年南京大学333数学物理方法二考研真题
2004年南京大学333数学物理方法二考研真题

南京大学2010年数学分析考研试题及解答

′′
=
′′′
;
利用（1）的结果，得存在),(ba∈ξ，使得
)()(
12
1
)]()()[(
2
1
)()(3ξF
abbFaFabaFbF
′′′
??
′
+
′
?+=,
即)()(
12
1
)]()()[(
2
1
)(3ξf
abbfafabdxxfb
a′
′
??+?=∫．
fxf
Fxf
x
x++→→?
′
==，
从而知(
)Fx在[]0,π上连续，
利用黎曼引理，得()()01
lim0limsin0
22n
nnSfFxnxdxππ→∞→∞????
?=+=
????
????∫，
故有()
()01
limcoscos2cos0
22nfxxxnxdxfπ
π→∞??
++++=
??
??∫?.
七．证明设Ff
aa?
?=?
+++
11
2nnaa?≤?，
()2,3,n=?，
于是{
}na是压缩数列，从而{}na收敛，
设limn
naa→∞=，2
a≥，
则有1
aa=+，210aa??=,15
2
a
+
=.
方法二显然222
a=<，12aa<，
由归纳法，知112na+≤<，1nnaa+≤，
()1,2,3,n=?，

北京大学南京大学量子力学考研试题题库

峪F黢嘁ing
参 C)haptcΓ 1 0ri胥 :ins OfQuantum Physics
α1apter2 M【rtthcmatic1b()ls OfQ11ar、 tt1mλ4ec丨】anics Chaptcr3 POstulatcs OfQuantulvl人丌cchani(;s
C∷haptcr4 ()haptcr5
j的
本
^=o^不
征值和本和f函
数
。
学 (b)在宏农象巾,求箅符
ε的铡i阵表示 ,以及月的本征竹和l本征函数。
)供ε 奋兀二砷 · ⑹ 求从 ⒔农象到捻表象^的和幺i∷ 变换知阵。
(;罗
:(∶
彳a艹￡甫:口
″ι
w
厶 \ 丿
叫
+ d
n
` 丨
‘
\ ︑
R”
●夕
一b' 丶
0
d
丿
一一
6,Ⅵ so″ 】而 ε 阝勿切 /lT伤 nⅠ `卩 c犭 tRf/饣
ቤተ መጻሕፍቲ ባይዱ
J冫幻 /s氵
)l飞 1nlC Ⅱ I。
PA· M· IⅡ rac
C,·
ρ .J· ∫·Sakur缸
sy11a笾冫us
考 7`3eP而
刀c洌es
q厂 Q溺 nFⅣ 饲
∧亻0c向佣
泅
冫4th刚 itiOn
f‘
吹 ,
Ⅳ o初 mQ“ 溺/PrⅡ Jlf姒佗c九四崩 cs,Rc∽ scd Edi⒈ iOn 衤1.
王鸳?矿廴卩嚅
。dFˇ 石 .
饣马∷助赳 η
乙耕 ”:
·
爹亻鲁

历年南京大学考研真题试卷与答案汇总-南京大学考研真题答案-南大考研真题试卷-南大考研真题哪里找？

历年南京大学考研真题试卷与答案汇总-南大考研真题哪里找？金陵南大考研网（南京大学考研在线咨询入口）汇集了南京大学各专业历年考研真题试卷（原版），同时与南京大学专业课成绩前三名的各专业硕士研究生合作编写了配套的真题答案解析，答案部分包括了（解题思路、答案详解）两方面内容。

首先对每一道真题的解答思路进行引导，分析真题的结构、考察方向、考察目的，向考生传授解答过程中宏观的思维方式；其次对真题的答案进行详细解答，方便考生检查自身的掌握情况及不足之处，并借此巩固记忆加深理解，培养应试技巧与解题能力。

具体请点击进入【历年南京大学考研真题答案下载】[金陵南大考研网] 南京大学448汉语写作与百科知识考研真题答案（2010-2017年）[金陵南大考研网] 南京大学建筑设计原理考研真题试卷（2001-2009年）[金陵南大考研网] 南京大学843中外建筑历史与理论考研真题试卷（2001-2009年，不含03）[金陵南大考研网] 南京大学355建筑学基础考研真题（2000、2014-2015年）[金陵南大考研网] 南京大学841分子生物学B考研真题试卷[金陵南大考研网] 南京大学652细胞生物学一考研真题试卷（2000-2011年，不含03、04、10）[金陵南大考研网] 南京大学308护理综合考研真题试卷（2015-2016年）[金陵南大考研网] 南京大学软件基础历年考研真题试卷（2002-2008年）[金陵南大考研网] 南京大学程序设计和数据结构考研真题试卷（1996-2001年）[金陵南大考研网] 南京大学编译原理和操作系统考研真题试卷（1995-2001年）[金陵南大考研网] 南京大学数据结构考研真题试卷（1997-2003年，不含99）[金陵南大考研网] 南京大学操作系统考研真题试卷（1996-2003年，不含01）[金陵南大考研网] 南京大学830工程地质学考研真题试卷（2004-2009年）[金陵南大考研网] 南京大学827构造地质学考研真题试卷（2000-2009年）[金陵南大考研网] 南京大学829地球科学概论考研真题试卷（2002-2009年）[金陵南大考研网] 南京大学826古生物地史学考研真题试卷（2000、2003-2008年）[金陵南大考研网] 南京大学825地球化学考研真题试卷（2003、2005-2009年）[金陵南大考研网] 南京大学824矿床学考研真题试卷（2000、2003-2009、2011年）[金陵南大考研网] 南京大学823矿物学（含结晶学）考研真题试卷（2000、2005-2008年）[金陵南大考研网] 南京大学822地球物理学考研真题试卷（2005-2009年）[金陵南大考研网] 南京大学821岩石学考研真题试卷（2000，2002，2005-2009年）[金陵南大考研网] 南京大学820专业综合考研真题试卷（2003-2009年）[金陵南大考研网] 南京大学856全球变化科学导论考研真题试卷（2007-2008年）[金陵南大考研网] 南京大学857遥感概论考研真题试卷（2007-2009年）[金陵南大考研网] 南京大学847经济地理学考研真题试卷（2005-2009年）[金陵南大考研网] 南京大学816海洋科学导论考研真题试卷（2003-2009年）【历年南京大学考研真题答案下载】[金陵南大考研网] 南京大学811环境科学导论考研真题试卷（2005-2010年）[金陵南大考研网] 南京大学信号与系统考研真题（1995-2002年，不含99、00）[金陵南大考研网] 南京大学艺术/艺术教育理论综合考研真题试卷（08-09）[金陵南大考研网] 南京大学948国际政治学考研真题试卷（2003-2011年，不含10）[金陵南大考研网] 南京大学612法理学考研真题试卷（1996-2015年）[金陵南大考研网] 南京大学中外美术史考研真题试卷（2004-2007年）[金陵南大考研网] 南京大学648艺术综合考研真题与答案（2004-2011年）[金陵南大考研网] 南京大学962管理学与计算机基础考研真题（2005-2013年）[金陵南大考研网] 南京大学961自动控制原理一考研真题（2006-2013年，不含15）[金陵南大考研网] 南京大学922管理与运筹学基础考研真题（2002-2015年，不含13-14）[金陵南大考研网] 南京大学989档案管理理论与方法考研真题试卷（2004-2009）[金陵南大考研网] 南京大学441出版专业基础考研真题与答案[金陵南大考研网] 南京大学335出版综合素质与能力考研真题答案（2011-2012年）[金陵南大考研网] 南京大学619国际关系考研真题试卷（2002-2009年）[金陵南大考研网] 南京大学946研究方法与新闻业务考研真题与部分答案（2005-2011，2015年）[金陵南大考研网] 南京大学959研究方法与传播业务考研真题与部分答案（05-09，11，15-16）[金陵南大考研网] 南京大学620传播史论考研真题与答案（2005-2016年）[金陵南大考研网] 南京大学622新闻传播史论考研真题试卷（2005-2014、2016年）[金陵南大考研网] 南京大学440新闻与传播专业基础考研真题与部分答案（2011-2016）[金陵南大考研网] 南京大学334新闻与传播专业综合能力考研真题试卷（2011-2015）[金陵南大考研网] 南京大学647世界史基础考研真题（2003-2017年）[金陵南大考研网] 南京大学645中国近现代史基础考研真题（2004-2017年）[金陵南大考研网] 南京大学643中国古代史基础考研真题（1995-2016年）[金陵南大考研网] 南京大学348文博综合考研真题试卷与答案（2012、2014年）[金陵南大考研网] 南京大学964英美文学考研真题试卷（2001-2014年）[金陵南大考研网] 南京大学653基础英语考研真题试卷（2002-2015年）[金陵南大考研网] 南京大学211翻译硕士英语考研真题与答案详解（2010-2016年）[金陵南大考研网] 南京大学935语言及论文写作考研真题试卷（2001-2017年）[金陵南大考研网] 南京大学615文学考研真题试卷（1998-2018年）[金陵南大考研网] 南京大学437社会工作实务考研真题试卷（2010-2016年）[金陵南大考研网] 南京大学331社会工作原理考研真题试卷（2010-2016年）[金陵南大考研网] 南京大学954社会保障与社会工作考研真题与答案（2004-2008年）[金陵南大考研网] 南京大学933行政管理学考研真题试卷（1996-2017年）[金陵南大考研网] 南京大学661公共管理基础理论考研真题试卷（2007-2009、2014）[金陵南大考研网] 南京大学976环境与资源保护法学专业综合考研真题试卷（2007-2009年）[金陵南大考研网] 南京大学955诉讼法学专业综合考研真题试卷（2004-2008年）[金陵南大考研网] 南京大学929经济法专业综合二考研真题试卷（1995-2014年）[金陵南大考研网] 南京大学613政治学原理考研真题试卷（1995-2017年）【历年南京大学考研真题答案下载】[金陵南大考研网] 南京大学921管理学原理考研真题试卷（1998-2015年）[金陵南大考研网] 南京大学920会计学考研真题试卷（2003-2018年）[金陵南大考研网] 南京大学919经济学原理考研真题试卷（1994-2017年）[金陵南大考研网] 南京大学434国际商务专业基础考研真题与答案（2011-2017年）[金陵南大考研网] 南京大学938马克思主义发展史考研真题试卷（2007-2008年）[金陵南大考研网] 南京大学918科学思想史（含STS）考研真题试卷（2000-2008年）[金陵南大考研网] 南京大学917宗教艺术考研真题试卷（2000-2008年）[金陵南大考研网] 南京大学914形式逻辑基础考研真题试卷（2000-2009年，不含07）[金陵南大考研网] 南京大学850高分子化学考研真题试卷（2000-2011年）[金陵南大考研网] 南京大学840免疫学考研真题试卷（2000-2009年，不含03）[金陵南大考研网] 南京大学352口腔综合考研真题试卷（2002-2009、2015年）[金陵南大考研网] 南京大学631光学考研真题试卷（2000-2008年）[金陵南大考研网] 南京大学848材料化学基础考研真题试卷（2005-2009年）[金陵南大考研网] 南京大学839材料物理基础考研真题试卷（2000-2009年）[金陵南大考研网] 南京大学833生理学A考研真题试卷（2001-2016年，不含10、11）[金陵南大考研网] 南京大学835生态学考研真题试卷（2000-2009、14-15年）[金陵南大考研网] 南京大学858细胞生物学二考研真题试卷（1999-2010年）[金陵南大考研网] 南京大学669药学基础综合考研真题试卷（2008-2011年）[金陵南大考研网] 南京大学651遗传学考研真题试卷（2005-2011年）[金陵南大考研网] 南京大学642生物化学二考研真题试卷（2000-2011、2016年，不含10）[金陵南大考研网] 南京大学831植物生理学考研真题试卷（2000-2014年）[金陵南大考研网] 南京大学844环境工程学考研真题试卷（2004-2015年）[金陵南大考研网] 南京大学810环境生物学考研真题（2000-2014年）[金陵南大考研网] 南京大学808环境化学考研真题试卷（2000-2013年）[金陵南大考研网] 南京大学634大学化学考研真题试卷（2007-2011年）[金陵南大考研网] 南京大学666仪器分析考研真题试卷（2006-2014年）[金陵南大考研网] 南京大学852有机化学考研真题试卷（1993-2014年）[金陵南大考研网] 南京大学853物理化学考研真题试卷（1997-2011）[金陵南大考研网] 南京大学851信号与系统、模拟电路考研真题（2007-2012年，不含11）[金陵南大考研网] 南京大学804普通物理二考研真题试卷（1999-2009年）[金陵南大考研网] 南京大学803声学基础考研真题试卷（00、02、05-08年）[金陵南大考研网] 南京大学633数理方法二考研真题试卷（2000，2004-2009年）[金陵南大考研网] 南京大学332生物物理考研真题试卷（2001-2009年）[金陵南大考研网] 南京大学629原子核物理考研真题试卷（2000-2010年，不含02）[金陵南大考研网] 南京大学627数学分析考研真题试卷（2006-2013年，不含12）[金陵南大考研网] 南京大学801高等代数考研真题试卷（2005-2014年）[金陵南大考研网] 南京大学432统计学考研真题试卷（2011、2015年）[金陵南大考研网] 南京大学809环境规划与管理考研真题试卷（2004-2011，2016年）[金陵南大考研网] 南京大学930国际法专业综合考研真题（03、04、08、13、15）[金陵南大考研网] 南京大学664体育学综合考研真题试卷（2007-2009年）【历年南京大学考研真题答案下载】[金陵南大考研网] 南京大学813自然地理学考研真题试卷（1997-2011、2014-2016年）[金陵南大考研网] 南京大学663考古学基础考研真题与部分答案（2011-2012年）[金陵南大考研网] 南京大学971日语专业知识综合考研真题试卷（2007-2009年）[金陵南大考研网] 南京大学991西班牙、拉丁美洲文学考研真题（2006-2009年）[金陵南大考研网] 南京大学969德语专业知识综合考研真题试卷（2007-2009年）[金陵南大考研网] 南京大学963英语语言学考研真题与答案（2000-2003，2006-2014年）[金陵南大考研网] 南京大学658基础西班牙语考研真题试卷（2006-2009年）[金陵南大考研网] 南京大学657基础日语考研真题答案（2001-2009年）[金陵南大考研网] 南京大学656基础德语考研真题试卷（2001-2009年）[金陵南大考研网] 南京大学655基础法语考研真题试卷（2010-2010年）[金陵南大考研网] 南京大学654基础俄语考研真题（2003-2009年，不含04、06）[金陵南大考研网] 南京大学264德语考研真题与答案（2001-2009年）[金陵南大考研网] 南京大学262俄语考研真题试卷（2003-2009年）[金陵南大考研网] 南京大学261英语考研真题与答案（2001-2010年）[金陵南大考研网] 南京大学357英语翻译基础考研真题答案（2010-2017年）[金陵南大考研网] 南京大学958东方哲学与宗教概论考研真题试卷（2005-2009年）[金陵南大考研网] 南京大学916宗教学概论（含宗教与文化）考研真题试卷（1995-2009年）[金陵南大考研网] 南京大学915伦理学原理考研真题试卷（2000-2009年，不含04）[金陵南大考研网] 南京大学913现代西方哲学考研真题试卷（2000-2012年，不含04、11）[金陵南大考研网] 南京大学912中国哲学原著（含古代汉语）考研真题试卷（2002-2014年，不含07、10、12、13）[金陵南大考研网] 南京大学911马克思主义哲学史（含原著）考研真题试卷（2004-2009年，不含05）[金陵南大考研网] 南京大学928经济法专业综合一考研真题试卷（2003-2010年）[金陵南大考研网] 南京大学636哲学综合B考研真题试卷（2002-2014年，不含09-10）[金陵南大考研网] 南京大学635哲学综合A考研真题试卷（2002-2014年）[金陵南大考研网] 南京大学265法语考研真题与答案详解（2001-2010年）[金陵南大考研网] 南京大学637哲学综合C考研真题试卷（2002-2014年）[金陵南大考研网] 南京大学926刑法专业综合考研真题试卷（2003-2009、2012年）[金陵南大考研网] 南京大学834分子生物学A考研真题试卷（1996-2013年，不含12）[金陵南大考研网] 南京大学832普通动物学考研真题试卷（2004-2009年）[金陵南大考研网] 南京大学641普通生物学考研真题试卷（2001-2016年）[金陵南大考研网] 南京大学640生物化学一考研真题试卷（1999-2014年，不含11）[金陵南大考研网] 南京大学639普通地质学考研真题试卷（2000-2012年）[金陵南大考研网] 南京大学819土地管理学考研真题（2000-2010年，不含01）[金陵南大考研网] 2019南大815地理信息系统概论考研复习全析（含历年真题，共三册）[金陵南大考研网] 南京大学814人文地理学考研真题（2000-2014年，不含10、12、13年）[金陵南大考研网] 2019南大813自然地理学考研复习全析（含历年真题，共三册）[金陵南大考研网] 南京大学812理论力学考研真题（2000-2009年，不含03））[金陵南大考研网] 2019南大810环境生物学考研复习全析（含历年真题）【历年南京大学考研真题答案下载】[金陵南大考研网] 2019南大808环境化学考研复习全析（含历年真题）[金陵南大考研网] 2019南京大学852有机化学考研复习全析（含历年真题，共三册）[金陵南大考研网] 2019南大853物理化学考研复习全析（含历年真题，共三册）[金陵南大考研网] 南京大学807化工原理考研真题试卷（1998-2014年）[金陵南大考研网] 2019南大考研化工原理重难点与典型题（含考研真题）详解[金陵南大考研网] 2019南大850高分子化学考研复习全析（含历年真题）[金陵南大考研网] 2019南京大学634大学化学考研复习全析（含真题）[金陵南大考研网] 2019南大866信号与通信综合考研复习全析（含真题，共三册）[金陵南大考研网] 2019南大854信号与系统、数字信号处理考研复习全析（共两册）[金陵南大考研网] 2019南大864大学物理一考研复习全析（共四册）[金陵南大考研网] 2019南大867电子技术基础B考研复习全析（共两册）[金陵南大考研网] 2019南京大学802普通物理一考研复习全析（含历年真题）[金陵南大考研网] 2019南京大学648艺术综合考研复习全析（含真题，共两册）[金陵南大考研网] 2019南大961自动控制原理一考研复习全析（含历年真题）[金陵南大考研网] 2019南大922管理与运筹学基础考研复习全析（含历年真题，共三册）[金陵南大考研网] 2019南大962管理学与管理信息系统考研复习全析（含历年真题）（共四册）[金陵南大考研网] 2019南京大学333教育综合考研复习全析（含历年真题）（共六册）[金陵南大考研网] 2019南京大学新闻学考研复习全析（含真题答案，共五册）[金陵南大考研网] 2019南京大学传播学考研复习全析（含真题答案，共五册）[金陵南大考研网] 2019南大348文博综合考研复习全析（含真题与答案）（共四册）[金陵南大考研网] 2019南大653基础英语考研复习全析（含真题与答案）（共五册）[金陵南大考研网] 2019南京大学964英美文学考研复习全析（含真题与答案）[金陵南大考研网] 2019南大357英语翻译基础考研复习全析（含历年真题答案）[金陵南大考研网] 2019南大448汉语写作与百科知识考研复习全析（含真题答案）[金陵南大考研网] 2019南京大学211翻译硕士英语考研复习全析（含真题答案，共五册）[金陵南大考研网] 2019南大考研《影视学专业知识》考试重难点与名校真题详解[金陵南大考研网] 2019南大考研《戏剧戏曲专业知识》考试重难点与名校真题详解[金陵南大考研网] 2019南大考研《艺术理论》考试重难点与名校真题解析[金陵南大考研网] 2019南大934社会学方法考研复习全析（含历年真题）[金陵南大考研网] 南京大学614社会学理论考研真题试卷（2000-2014年）[金陵南大考研网] 2019南大929经济法专业综合二考研复习全析（含历年真题）（共2册）[金陵南大考研网] 2019南大928经济法专业综合一考研复习全析（含历年真题）（共三册）[金陵南大考研网] 2019南大927民商法专业综合考研复习全析（含历年真题）[金陵南大考研网] 2019南大926刑法专业综合考研复习全析（含历年真题）[金陵南大考研网] 2019南大925宪法学与行政法学专业综合考研复习全析（含真题与答案）[金陵南大考研网] 南京大学927民商法专业综合考研真题试卷（2004-2011年）[金陵南大考研网] 《刑事诉讼法学》考试重难点与名校真题详解（陈光中，第五版）[金陵南大考研网] 《宪法》考试重难点与名校真题答案详解（张千帆，法律出版社第二版）[金陵南大考研网] 南京大学925宪法学与行政法学专业综合考研真题与答案（03-09）【历年南京大学考研真题答案下载】[金陵南大考研网] 南京大学924法律史综合考研真题（2003-2009年）[金陵南大考研网] 南京大学923法理专业综合考研真题试卷（2003-2009年）[金陵南大考研网] 南京大学660马克思主义基本原理考研真题试卷（2001-2009年）[金陵南大考研网] 2019南大434国际商务专业基础考研复习全析（含真题与答案）[金陵南大考研网] 2019南京大学431金融学综合考研复习全析（含真题与答案，共五册）[金陵南大考研网] 2019南大911马克思主义哲学史考研复习全析（含历年真题）[金陵南大考研网] 2018南京大学635哲学综合A考研复习全析（含历年真题）[金陵南大考研网] 2019南大445汉语国际教育基础考研复习全析（含真题答案，共三册）[金陵南大考研网] 2019南大354汉语基础考研复习全析（含真题答案，共三册）[金陵南大考研网] 2019南大497法硕联考综合(法学)考研复习全析（含真题答案，共四册）[金陵南大考研网] 2019南大397法硕联考基础(法学)考研复习全析（含真题答案，共三册）[金陵南大考研网] 2019南大498法硕联考综合(非法学)考研复习全析（含真题答案，共四册）[金陵南大考研网] 2019南大398法硕联考基础(非法学)考研复习全析（含真题答案，共三册）[金陵南大考研网] 南京大学263日语考研真题与答案（2001-2010年）[金陵南大考研网] 南京大学431金融学综合考研真题与答案（2002-2017年）[金陵南大考研网] 2019南京大学新闻与传播硕士考研复习全析【含真题答案，共七册】[金陵南大考研网] 2019年南京大学社会保障考研全套资料[金陵南大考研网] 南京大学934社会学方法考研真题试卷（2000-2014，2017年）[金陵南大考研网] 南京大学802普通物理一考研真题试卷（1998-2015年）[金陵南大考研网] 南京大学628量子力学考研真题试卷（1998-2014年）[金陵南大考研网] 2018南京大学考研646国际关系史基础考试解读与真题答案[金陵南大考研网] 2019南京大学考研647世界史基础考试解读与真题答案详解[金陵南大考研网] 南京大学988图书馆学考研真题试卷（2000、2003-2007年）[金陵南大考研网] 南京大学化学专业考研真题试卷（1994-2006年，不含00、03年））[金陵南大考研网] 2019南京大学考研643中国古代史基础考试解读与真题答案详解（共两册）[金陵南大考研网] 2019南京大学考研645中国近现代基础考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研645中国近现代史基础复习全析（含真题答案，共五册）[金陵南大考研网] 2019南京大学考研935语言及论文写作考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研615文学考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研933行政管理学考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研613政治学原理考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研612法理学考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研964英美文学考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研935语言及论文写作复习全析(含真题与答案，共五册) [金陵南大考研网] 2019南京大学考研615文学复习全析(含真题与答案，共六册)[金陵南大考研网] 2019南京大学考研933行政管理学复习全析(含真题与答案，共五册) [金陵南大考研网] 2019南京大学考研613政治学原理复习全析(含真题答案，共三册)[金陵南大考研网] 2019南京大学考研612法理学复习全析(含真题答案，共三册)【历年南京大学考研真题答案下载】[金陵南大考研网] 2019南京大学考研653基础英语考试解读与真题答案详解[金陵南大考研网] 2019南大考研622新闻传播史论应试模拟四套卷与答案详解[金陵南大考研网] 2019南京大学考研622新闻传播史论考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研622新闻传播史论复习全析(含真题与答案) [金陵南大考研网] 2019南京大学考研920会计学考试解读与真题答案详解[金陵南大考研网] 2019南京大学考研920会计学复习全析（含真题与答案）[金陵南大考研网] 2019南京大学考研919经济学原理考试解读与真题答案详解[金陵南大考研网] 2019南大考研919经济学原理复习全析（含真题答案，共五册）[金陵南大考研网] 2019南大考研921管理学原理复习全析（含真题答案，共四册）[金陵南大考研网] 2019南京大学考研921管理学原理考试解读与真题答案详解金陵南大考研网（南京大学考研在线咨询入口）【历年南京大学考研真题答案下载】。

[理学]南京大学2017-2018年数学分析考研试题及解答.pdf

2000年南京大学硕士研究生入学考试数学分析试题一、求下列极限. 1）设nn n x x x ++=+3)1(31,(01>x 为已知),求n n x ∞→lim ； 2)22)(lim 2200y x y x y x +→→；3)201cos lim x xtdt t ++∞→∫； 4)222222021lim cos()xy r x y r e x y dxdy r π+→+≤−∫∫.二、在[]1,1−上有二阶连续导数,0)0(=f ,令xx f x g )()(=,())0()0(,0f g x ′=≠,证明： 1))(x g 在0=x 处连续,且可导,并计算)0(g ′； 2))0(g ′在0=x 处也连续. 二、设t e e t f t ntn 3sin )1()(−−−=,()0≥t ,试证明1）函数序列(){}t f n 在任一有穷区间[]A ,0上和无穷区间[0,)+∞上均一致收敛于0；2）∫+∞−−∞→=−030sin 1lim tdt e e tn t n . 三、设对任一A>0,)(x f 在[]A ,0上正常可积,且0)(0≠∫+∞dt t f 收敛.令(),0,)()()(0≥−=∫∫+∞x dt t f dt t f x x xϕ试证明)(x ϕ在()+∞,0内至少有一个零点.四、计算积分())0(,sin cos ln )(2222>+=∫a dx x x a a I π.五、试求指数λ,使得dy r y x dx r y x λλ22−为某个函数()y x u ,的全微分,并求()y x u ,,其中22y x r +=.六、计算下列曲线积分和曲面积分)1()()()∫+++−++=cdz z y x dy y x dx z y x I ,223其中c 为1222=+y x 与z y x −=+222的交线,从原点看去是逆时针方向.)2()()()2222222:,R c z b y a x S dxdy z dzdx y dydz x I S=−+−+−++=∫∫.七、设()ln nn u x x x =,[]0,1x ∈,(1)试讨论1()n n u x ∞=∑在](0,1上的收敛性和一致收敛性；(2)计算11ln n n x xdx ∞=∑∫.九、设222exp ,0,0(,)0,0,0x t t x f x t t t x−+>> ==> ,0()(,)I x f x t dt ∞=∫ , (0)x > 1）讨论0(,)f x t dt +∞∫在()0,+∞上的一致收敛性,并证明200lim ()2tx I x e dt ++∞−→==∫ 2）计算()I x .2000年南京大学数学分析考研试题的解答一、1、解设xc x c x f ++=)1()(,),0[+∞=∈I x ,其中常数1>c . 因为111)1()()1()(022<−=−≤+−=′<c cc c x c c c x f ,所以f是I 上的压缩函数.对3(1)()3x f x x +=+,13(1)()3n n n nx x f x x ++==+, 1111|||()()||()()|||n n n n n n n n x x f x f x f x x k x x ξ+−−−′−=−=−≤−, 于是111113(1)3(1)32||||||33(3)(3)n n n n n n n n n n x x x x x x x x x x −+−−−++⋅−=−=−++++12||3n n x x −≤−,{}n x 是压缩迭代序列,所以n n x ∞→lim 存在,设lim n n x A →∞=,易知0A ≥；在n n n x x x ++=+3)1(31两边令∞→n 取极限,得到3(1)3A A A+=+,所以A =；故lim n n x →∞=.2、解先求其对数的极限：()2222()(00)limln x,y ,x y x y →+, 由于()()()()222222222211ln ln 022x y x y x y x y x y +≤+⋅++→,((,)0x y →)；所以()2222()(00)limln 0x,y ,x y x y→+=,进而()()222222ln 220()(00)()(00)limlim e=1x yx y x y x,y ,x,y ,xye +→→+== . 3、解由于21cos tdt t+∞∫收敛,于是201cos lim 0x xtdt t++∞→=∫. 4、解 222222021lim cos()xy r x y r ex y dxdy rπ+→+≤−∫∫2222202lim cos()xy r x y r e x y dxdy +→+≤=−∫∫22(0,0)2[cos()]|2xy e x y =−= .二、证明 (1)由于()f x 在[]1,1−上有二阶连续导数, 所以()f x ,(),()f x f x ′′′在[]1,1−上连续；当0x ≠时, ()()f x g x x=,显然()g x 在0x ≠处是连的；在0x =处,'00()()(0)lim ()limlim (0)0x x x f x f x f g x f x x →→→−===−. 有)0()(lim 0g x g x =→；所以()g x 在0x =处连续. 故()g x 在[]1,1−上连续.在0x =处, 00()(0)()(0)(0)lim lim x x f x f g x g x g x x→→′−−′==2000()(0)()(0)()1lim lim lim (0)222x x x f x xf f x f f x f x x →→→′′′′′−−′′====.(2)当0x ≠时, ()()f x g x x =, 2()()()f x x f x g x x ′−′=g . 由于()f x 和()f x ′连续, 故当0x ≠时, ()g x ′存在且连续. 而且, 200()()()()()lim ()limlim 2x x x f x x f x f x x f x f x g x x x →→→′′′′′⋅−⋅+−′==0()1lim (0)(0)22x f x x f g x →′′⋅′′′===. ()g x ′在0x =处连续, 进而()g x ′在[]1,1−上连续.三、引用定理设{()}n f x 在[,)a +∞上有定义,满足：(1)对每一b a >,{()}n f x 在[,]a b 上一致收敛于0；(2)lim ()0n x f x →+∞=,且关于n 是一致的,则{()}n f x 在[,)a +∞上一致收敛于0.1）证明 (1)因为3|()||(1)sin |(1)t t t nnn f t e e t e −−−=−≤−, 显然{}t ne −在任一有穷区间[]A ,0上一致收敛于1, 于是(){}t f n 在任一有穷区间[]A ,0上一致收敛于0；又3|()||(1)sin |t t t nn f t e e t e −−−=−≤,因而lim ()0n t f t →+∞=,且关于n 是一致的,所以(){}t f n 在无穷区间[0,)+∞上一致收敛于0； 2）因为3|()||(1)sin |t ttnn f t e e t e −−−=−≤,且0t e dt +∞−∫收敛,(){}t f n 在任一有穷区间[]A ,0上一致收敛于0利用积分控制收敛定理,得3000lim 1sin lim ()lim ()0tt n n n n n n e e tdt f t dt f t dt +∞+∞+∞−−→∞→∞→∞−=== ∫∫∫. 四、证明显然0(0)()f t dt a ϕ+∞=−=−∫,0lim ()()x x f t dt a ϕ+∞→+∞==∫；存在0A >,当x A ≥时,有()2ax a ϕ<<； )(x ϕ在[0,]A 上连续,(0)()0A ϕϕ<,由闭区间上连续的零点定理, 得)(x ϕ在()+∞,0内至少有一个零点. 五、解dx x b x a )cos sin ln(222202+∫π,0,>b a .记dx x b x a b a I )cos sin ln(),(222202+=∫π,),(b a I 是连续可微函数. 当b a =时,dx x a x a a a I )cos sin ln(),(222202+=∫πa ln π=；当b a ≠时,dxx b x a xa b a I a ∫+=∂∂2022222cos sin sin 2),(πdx bx b a b b x b a b a a ∫+−−+−−=2022222222222sin )(sin )(2π]cos sin 2[2202222222dx x b x a b b a a ∫+−−=ππ]tan tan 2[220222222x d bx a b b a a ∫+−−=ππ ]|)tan arctan(2[22022ππx b a a b b a a −−=b a a b b a a +=−−=1]22[222πππ, 于是C b a b a I ++=)ln(),(π,再由a a a I ln ),(π=,得2ln π−=C ,故2ln),(ba b a I +=π. 六、解设22(,),(,)x x P x y r Q x y r y y λλ==−,12(,)yr y r r P x y x yy λλλ−−∂=∂, 2122(,)xxr x r r Q x y xy λλλ−+∂=−∂,令(,)(,)P x y Q x y y x∂∂=∂∂,得1λ=−；由1u x r x y −∂=∂, 得1()u r y y ϕ=+,代入212u x r y y −∂=−∂,得()y C ϕ=,故1(,)u x y r C y =+ . 七、()()()∫+++−++=cdz z y x dy y x dx z y x I ,223其中c 为1222=+y x 与z y x −=+222的交线,从原点看去是逆时针方向. （1）解 22{(,,):1,21}x y z z x y Σ==−+≤,22{(,):21}D x y x y =+≤(cos ,cos ,cos )n αβγ=r(0,0,1)=, 利用斯托克斯公式,得()()()3cI x z dx x dy x y z dz =++++∫Ñ3cos cos cos dS x y z x zx x y zαβγΣ∂∂∂=∂∂∂+++∫∫3001dS x y z x zx x y zΣ∂∂∂=∂∂∂+++∫∫22(1)(1)Dz dS dxdy Σ=−=+∫∫∫∫2Dy dxdy π=+2122001sin 2d r ππθθ=∫20311cos 2242d πθπθ−=+∫38ππ= . (2)解区域2222)()()(:R c z b y a x ≤−+−+−Ω,利用高斯公式,得222Sx dydz y dzdx z dxdy ++∫∫dxdydz z y x )(2++=∫∫∫Ωdxdydz c b a c z b y a x )]()()()[(2+++−+−+−=∫∫∫Ωdxdydz c b a )(2++=∫∫∫Ω334)(2R c b a π++=3)(38R c b a π++=.八、解 (1)显然1()n n u x ∞=∑在](0,1上收敛,且10,1()()ln ,011n n x u x S x x xx x∞==== << − ∑, ()n u x 在](0,1上连续,而()S x 在](0,1上不连续,所以1()n n u x ∞=∑在](0,1上不一致收敛；(2)11()()ln 1NNN n n x S x u x x x x =−==−∑,显然,对任意01a b <<<,{()}N S x 在[,]a b 上一致收敛,{()}N S x 在(0,1]上连续, |ln ||()|1N x x S x x ≤−,(01)x <<,10|ln |1x x dx x−∫收敛；于是级数可以逐项积分故112001111ln ln (1)n nn n n x x dx x xdx n ∞∞∞=== == +∑∑∑∫∫ . 九、(1)解显然(,)f x t 在(0,)(0,)+∞×+∞上连续,且有20(,)t f x t e−<≤,而2t e dt +∞−∫收敛,从而有0(,)f x t dt +∞∫在()0,+∞上一致收敛；对任意0a B <<<+∞,当0x +→时,(,)f x t 在[,]a B 上一致收敛于2t e −,于是2lim ()lim (,)lim (,)2tx x x I x f x t dt f x t dt e dt ++++∞+∞+∞−→→→====∫∫∫； (2)利用等式20(())b f ax dx x +∞−∫201()f x dx a +∞=∫,)0,(>b a .2()0b ax xedx −−+∞∫20112x e dx a a +∞−==∫ ,)0,(>b a . 可知222()()(,)x t t I x f x t dt edt −++∞+∞==∫∫22()22202xt xxu xteedt ee du e −−+∞+∞−−−−===∫∫.南京大学2001年数学分析考研试题一、求下列极限1）设),2(,43,011≥+==−n a a a n n 求n n a ∞→lim ；2）yx y x e y x 12201lim +−→+∞→++；3）设[],,)(,B b a A C x f B A <<<∈试求∫−+→bah dx hx f h x f )()(lim 04）设)(x f 在)1,0(内可导,且),1,0(,1|)(|∈∀<′x x f 令)2)(1(≥=n n f x n ,试证明n n x ∞→lim 存在有限二、设,1)0(,)(),(2=∈+∞−∞g C x g 令≠−=′=时当时当0,cos )(0),0()(x x xx g x g x f 1）讨论处的连续性；在0)(=x x f 2)求.0)(),(处的连续性在并讨论=′′x x f x f 三、设[][],1,0,1)(0,0)0(,)(1,01∈∀≤′<=∈x x f f C x f 试证明对一切[]1,0∈t ,成立[]∫∫≥ tt dx x f dx x f 032)()(四、求下列积分1）计算反常积分∫+∞−=0sin dx x xe I x ；2)计算曲面积分222I x dydz y dzdx z dxdy Σ=++∫∫,其中Σ为锥面()h z y x ah z ≤≤+=0,22222那部分的外侧.五、求212arctan )(x x x f −=在0=x 处的幂级数展开式,并计算∑∞=+−=012)1(n nn S 之值六、设nnn x x x ++=+11α,1>α,10x ≥. 1) 证明级数11()n n n x x ∞+=−∑绝对收敛；2)求级数()∑∞=+−11n n n x x 之和.七、设4220(,)exp t I dt αβαβ+∞−= + ∫,其中βα,满足不等式43222−≤+−βαα. 1）讨论含参变量积分),(βαI 在区域432:22−≤+−βααD 上的一致收敛性；2）求),(βαI 在区域D 上的最小值.南京大学2001年数学分析考研试题的解答一、 1、解易知111||||4n n n n a a a a +−−=−,{}n a 是压缩迭代序列,所以lim n n a →∞存在,设lim n n a A →∞=,则有34A A +=,1A =,所以lim 1n n a →∞=. 2、解令u =,则有0lim x y u +→+∞→=+∞；由424421202uu u x eeu ey e − ≤+≤==,得2201lim 0x y x ey +→+∞→ +=.3、解 ()f x 在[,]A B 上连续,对任何A a x B <<<,因为 dt t f h t f h x a ∫−+))()((1dt h t f h x a ∫+=)(1dt t f h xa ∫−)(1 dt t f h h x h a ∫++=)(1dt t f h x a ∫−)(1dt t f h h x x ∫+=)(1dt t f h ha a∫+−)(1, 由此,即得)()())()((1lim 0a f x f dt t f h t f h xah −=−+∫→,()A a x B <<< .4、解由题设条件,得 111111|||()(||()()|11(1)n n n x x f f f n n n n n n ξ+′−=−=−≤+++, 121||||||||n p n n n n n n p n p x x x x x x x x +++++−−≤−+−+−L11(1)(1)()111111((1121111n n n p n p n n n n n p n p n n p n<++++−+=−+−++−++++−+=−<+L L 由此即可知{}n x 是一个基本列,所以n n x ∞→lim 存在且有限.二、由于()g x 在(,)−∞+∞上有二阶连续导数,所以()g x ,(),()g x g x ′′′在(,)−∞+∞上连续；0()cos ()sin lim ()limlim (0)(0)1x x x g x x g x xf xg f x →→→′−+′==== 有0lim ()(0)x f x f →=；所以()f x 在0x =处连续. 显然()f x 在0x ≠处连续.故()f x 在(,)−∞+∞上连续.在0x =处, 00()cos (0)()(0)(0)lim lim x x g x xg f x f x f x x→→−′−−′== 200()cos (0)()sin (0)lim lim 2x x g x x xg g x x g x x→→′′′−−+−== 0()cos 1lim ((0)1)22x g x x g →′′+′′==+； (2)当0x ≠时, ()cos ()g x x f x x −=, 2(()sin )(()cos )()g x x x g x x f x x ′+−−′=g . 由于()g x 和()g x ′连续, 故当0x ≠时, ()f x ′存在且连续. 而且, 200(()sin )(()cos )lim ()limx x g x x x g x x f x x →→′+⋅−−′=0(()cos )(()sin )(()sin )lim 2x g x x x g x x g x x x →′′′′+⋅++−+= 0()cos 1lim ((0)1)(0)22x g x x g f →′′+′′′==+= ()f x ′在0x =处连续, 进而()f x ′在(,)−∞+∞上连续.三、假设()f x 在[]0,1上可导,且()0()1,0,1,(0)0f x x f ′<<∀∈=,证明()2300()()>∫∫xxf t dtf t dt ,()0,1∀∈x .证明令()230()()()=−∫∫xxF x f t dtf t dt ,()320()2()()()()2()()′=−=−∫∫xxF x f x f t dt f x f x f t dt f x ,因()0()1,0,1,(0)0f x x f ′<<∀∈=,所以()0>f x ,令20()2()()=−∫xg x f t dt f x ,则[]()2()1()0′′=−>g x f x f x ,即得()(0)0>=g x g , 所以()0′>F x , 则()230()()()(0)0=−>=∫∫xxF x f t dtf t dt F ,()0,1∀∈x ,于是()230()()xxf t dtf t dt >∫∫,()0,1∀∈x .四、(1)计算dx xaxbx e px∫+∞−−0sin sin ,),0(a b p >>. 解因为dyxy xaxbx ba∫=−cos sin sin ,所以dx xax bx epx∫+∞−−0sin sin dx dy xy e b a px)cos (0∫∫+∞−=,由于pxpxexy e−−≤|cos |及dx e px ∫+∞−0收敛,根据魏尔斯特拉斯判别法,得dx xy e px ∫+∞−0cos 在],[b a y ∈上一致收敛,又xy e px cos −在],[),0[b a ×+∞上连续, 所以积分可交换次序,即dx dy xy e bapx )cos (0∫∫+∞−xydx e dy px bacos 0∫∫+∞−=∫+=bady yp p 22p ap b arctan arctan −= 故dx x ax bx e px∫+∞−−0sin sin pap b arctan arctan −= ,任何实数a b p ,,0>. 特别地0sin arctan14xx e dx x π+∞−==∫ .(2)解 (由于Σ不是封闭曲面,需要补充一部分曲面,构成一个封闭曲面.)区域Ω：1222()hx y z h a +≤≤,边界1Σ+Σ=Ω∂,方向朝区域外.2221:,x y a z h Σ+≤=,方向朝上.显然dxdy z dzdx y dydz x 2221++∫∫Σ∫∫Σ=12dxdy z 22222222x y a h dxdy h a a h ππ+≤===∫∫,利用高斯公式,得dxdy z dzdx y dydz x222++∫∫Ω∂dxdydz z y x )(2++=∫∫∫Ω222()2()h ax y z hdzx y z dxdy +≤=++∫∫∫202()ha z z dz h π=⋅∫2212a h π=,再由dxdy z dzdx y dydz x 222++∫∫Ω∂dxdy z dzdx y dydz x 222++=∫∫Σdxdy z dzdx y dydz x 2221+++∫∫Σ,得出dxdy z dzdx y dydz x 222++∫∫Σ2212a h π=− . 五、解 212arctan )(x x x f −=,因为2202()2(1)1n nn f x x x ∞=′==−+∑,(0)0f = 所以210(1)()221n n n f x x n ∞+=−=+∑,(11)x −≤≤,显然21(1)21n n n n ∞+=−+∑在[0,1]上一致收敛,∑∞=+−=012)1(n n n S 21110(1)11lim lim ()212224n n x x n x f x n ππ−−∞+→→=−====+∑ . 六、证明令x x x f ++=1)(α,则有2)1(1)(x x f +−−=′α,αα=)(f , )(x f 在),0(+∞上是严格递减的；当α>x 时,α<)(x f ；当α<x 时,α>)(x f ；若α>1x ,则有 α>−12n x ,α<n x 2,),2,1(L =n ；将11n n n x x x α++=+代入1211n n n x x x α++++=+,得22(1)(1)2n n nx x x ααα+++=++, 由n n n n n x x x x x −++++=−+2)1()1(22αααnn x x 2)1()(22++−=αα,得}{12−n x 单调递减,}{2n x 单调递增,设a x n n =−∞→12lim ,b x n n =∞→2lim ,在121221−−++=n n n x x x α,nn n x x x 22121++=+α中,令∞→n 取极限,得 a a b ++=1α,bb a ++=1α,从而有α==b a ,故α=∞→n n x lim .()11111Nn n N n xx x x x ++=−=−→∑,()N →∞,()111n n n x x x ∞+=−=∑；111|||()()||()()|n n n n n n n x x f x f x f x x ξ+−−′−=−=−,其中n ξ位于n x 与1n x −之间,lim n n ξ→∞=,1lim |()|||11n n f f k αξα→∞−′′==≤=<+, 于是存在正整数N ,当n N ≥时,成立11||||n n n n x x K x x +−−≤−,其中常数01K <<, 由此而来,可知级数11||n n n x x ∞+=−∑收敛,故级数11()n n n x x ∞+=−∑绝对收敛；若1x =则有n x =,此时结论显然可得；若10x ≤<,则有2x >然后就与上面的情况类似了. 七、解 (1)43222−≤+−βαα等价于2221(1)()2αβ−+≤,于是有 221944αβ≤+≤,设422(,,)exp t f t αβαβ−=+, 则有44422exp (,,)exp exp 1944t t t f t αβαβ−−−≤=≤ + ,显然40exp 94t dt +∞−∫是收敛的, 于是(,,)f t dt αβ+∞∫在区域432:22−≤+−βααD 上是一致收敛的；(2)),(βαI ()4400exp exp 414t dt t dt +∞+∞−≥=−∫∫11401()4u e u du +∞−−==, ),(βαI 在区域D 上的最小值1(4 .南京大学2002年数学分析考研试题一求下列极限. (1)(1)cos2lim(sin sin )ln(1)2x x x x xx x →∞+−−+；(2)设()ln()f x x a x =+−,(,)x a ∈−∞,(i)()f x 在(,)a −∞上的最大值；(ii)设1ln x a =,21ln()x a x =−,1()n n x f x +=,(2,3,)n =L ,求lim n n x →∞.二设1()sin ln f x x x=−,试证明()f x 在[2,)+∞内有无穷多个零点. 三设()f x 在0x =的某个邻域内连续,且(0)0f =,0()lim 21cos x f x x→=−,(1)求(0)f ′；(2)求20()lim x f x x→；(3)证明()f x 在点0x =处取得最小值.四设()f x 在0x =的某个邻域内具有二阶连续导数,且0()lim 0x f x x →=,试证明：(1)(0)(0)0f f ′==； (2)级数11()n f n ∞=∑绝对收敛.五计算下列积分 (1)求x ；(2)SI zxdydz xydzdx yzdxdy =++∫∫,其中S 是圆柱面221x y +=,三个坐标平面及旋转抛物面222z x y =−−所围立体的第一象限部分的外侧曲面.六设()[,]f x C a b ∈,()f x 在(,)a b 内可导,()f x 不恒等于常数,且()()f a f b =, 试证明：在(,)a b 内至少存在一点ξ,使()0f ξ′>.七在变力F yzi zxj xyk =++r r r r的作用下,质点由原点沿直线运动到椭球面2222221x y z a b c ++=, 第一象限的点(,,)M ξηζ,问(,,)ξηζ取何值时,F r所做的功W 最大,并求W 的最大值. 八 (1)证明：(1n x xe n −−≤,(,0)n N x n ∗∈≤≤；(2)求20lim (1n n n xx dx n→∞−∫.南京大学2002年数学分析考研试题解答一 (1)解 0(1)cos 2lim (sin sin )2x x xx x x x →+−−+201(1)cos12lim sin sin 2ln(1)x x x x x x x x x x→+−=−+ ln(1)01(ln(1))sin 1222lim2x x x x x e x x x +→+++⋅+=1ln(1)0sin 12lim[(ln(1))12x x x x xe x x x +→=++++ 124=+94=.(2)解 (i)11()1a xf x a x a x−−′=−=−−,当1x a <−时,()0f x ′>,()f x 在(,1]a −∞−上单增, 当1a x a −<<时,()0f x ′<,()f x 在[1,)a a −上单减,所以()f x 在1x a =−处达到最大值,(1)1f a a −=−； (ii)当1a >时,10ln ln(11)1x a a a <==+−<−, 11a x a <−<,210ln()ln 1x a x a a <=−<<−, 32()(1)1x f x f a a =<−=−, 1n x a <−,1n a x <−,1ln()n n n n x x a x x +=+−>,{}n x 单调递增有上界,设lim n n x A →∞=,则有ln()A A a A =+−,1a A −=,1A a =−,所以 lim 1n n x a →∞=−；当1a =时,0n x =,lim 0n n x →∞=；当01a <<时,1ln 0x a =<,1ln ln(11)1x a a a ==+−<−, 11a x <−, 二证明因为1(2102ln(22f n n ππππ+=−>+,1(2)102ln(2)2f n n ππππ−=−−<−,(1,2,)n =L ,显然()f x 在[2,)+∞上连续,由连续函数的介值定理知,存在(2,2)22n n n ππξππ∈−+使得 ()0n f ξ= (1,2,)n =L ,即得()f x 在[2,)+∞上有无穷多个零点.三解 (1)2200()()2lim lim 1cos 1cos x x f x f x x x x x→→==−−,因为20lim21cos x x x →=−,所以20()lim 1x f x x →=, 200()()limlim()0x x f x f x x x x →→=⋅=,00()(0)()lim lim 00x x f x f f x x x→→−==−, 于是(0)0f ′=； (3)由20()lim1x f x x →=知,存在0δ>,当0x δ<<时,2()12f x x >,()(0)f x f >,即知()f x 中在0x =处取得极小值.sup ()x M f x δ≤′′=四、证明 (1)由0()lim ()lim0x x f x f x x x→→=⋅=,知(0)0f =, 由00()(0)()limlim 00x x f x f f x x x→→−==−知(0)0f ′=. (2)22111111((0)(0)()()22n n f f f f f n n n n ξξ′′′′′=++=,211(2M f n n ≤,已知2112n M n∞=∑收敛,其中sup ()x M f x δ≤′′=,于是11(n f n ∞=∑收敛,结论得证.五 (1)解322[(1)]3xx x e dx ′=−∫32222(1)333x x x e dx =−−+33222222(1)(1)3333x x x x e e =−−⋅−+,所以111)1)22xx xe e C=−−−+11(1)(23x x xxe e e C=−−−.(2)解曲面221x y+=,222z x y=−−事物交线为221x y+=,1z=,22221{(,,):1,02,0,0}x y z x y z x y x yΩ=+≤≤≤−−≥≥,22222{(,,):12,02,0,0}x y z x y z x y x yΩ=≤+≤≤≤−−≥≥,其中S是区域1Ω的边界时,利用高斯公式,SI zxdydz xydzdx yzdxdy=++∫∫1()z x y dxdydzΩ=++∫∫∫2122000(cos sin)rd dr z r r rdzπθθθ−=++∫∫∫212222000(cos sin)rdr dz zr r r dπθθθ−=++∫∫∫212200(2)2rdr zr r dzπ−=+∫∫122221[(2)2(2)]22r r r r drπ=−+−∫11352400[44]2[2]4r r r dr r r drπ=−++−∫∫121(212(4635π=−++−7142415π=+.当S是2Ω的边界时,利用高斯公式SI zxdydz xydzdx yzdxdy=++∫∫2()z x y dxdydzΩ=++∫∫∫222000(cos sin)rdz z r r rdπθθθ−=++∫∫222211(2)2(2)]22r r r r drπ=−+−224111[2(22]243r r r drπ=−−+−35212(2435r rπ=+−14241515π=+−.六证明证法一用反证法,假若结论不成立,则对任意(,)x a b∈,都有()0f x′≤,()f x在[,]a b上单调递减,由于f不恒等于常数,所以()f x′不恒等于零,存在一点(,)x a b∈,使得0()0f x′<,()()lim()0x xf x f xf xx x→−′=<−,存在01x x b<<,使得1010()()f x f xx x−<−,10()()f x f x<,因为()()f x f a≤,1()()f b f x≤,所以10()()()()f b f x f x f a≤<≤,这与()()f a f b=矛盾,从而假设不成立,原结论得证.证法 2 由于f在[,]a b上连续,f在[,]a b上取到最大值M和最小值m,且m M<,由于()()f a f b =,所以f 的最大值M 或最小值m 必在(,)a b 内达到. 若f 在0(,)x a b ∈处达到最大值0()()()f a f b f x =<,存在0(,)a x ξ∈使得00()()()()f x f a f x a ξ′−=−,从而有()0f ξ′>；若f 在1(,)x a b ∈处达到最小值1()()()f x f a f b <=,存在11(,)x b ξ∈使得111()()()()f b f x f b x ξ′−=−,从而有()0f ξ′>；结论得证.七解设u xyz =,则有gradu F =r ,所以F r是有势场,()()OMW Fdr u M u O ξηζ==−=∫r r,由于0,0,0x y z ≥≥≥时,222232222)x y z xyz a b c =++≥=,323xyz abc ≤=,等号成立当且仅当x y z a b c ===,所以(,,)ξηζ=时,W 达到最大值,且W 的最大值.八证明 (1)由于当0y ≥时,有1ye y −>−,对任意n N ∗∈,0x n ≤≤,取x y n =,1xn xe n−≥−,所以有(1)x n xe n−≥−；(2)取2(1),0()0,n n x x x n f x n n x −≤≤ = <,有20()x n f x e x −≤≤,20x e x dx +∞−∫收敛,对任意0A >,{()}n f x 在[0,]A 上一致收敛于2x e x −,故由函数列积分的黎曼控制收敛定理,20lim (1nn n x x dx n→∞−∫0lim ()n n f x dx +∞→∞=∫0lim ()n n f x dx +∞→∞=∫20x e x dx +∞−=∫20()xx e dx +∞−′=−∫02()x x e dx +∞−′=∫02x e dx +∞−=∫02()x e dx +∞−′=∫2= .南京大学2003年数学分析考研试题一求下列极限(1)设0a >,求x ；(2)设1x =1n x +=,(1,2,)n =L ,求lim n n x →∞.(3)21lim(1)x x x e x−→∞+⋅. 二过(1,0)P 点作抛物线y =切线,求(1)切线方程；(2)由抛物线、切线及x 轴所围成的平面图形面积； (3)该平面图形分别绕x 轴和y 轴旋转一周的体积. 三对任一00y >,求00()(1)y x y x x ϕ=−在(0,1)中的最大值, 并证明该最大值对任一00y >,均小于1e −.四设()f x 在[0,)+∞上有连续导数,且()0f x k ′≥>,(0)0f <,(k 为常数),试证：()f x 在(0,)+∞内仅有一个零点. 五计算下列积分(1)设120ln(1)()1ax I a dx x +=+∫,(0)a >,求()I a ′和(1)I ； (2)32222()Sxdydz ydzdx zdxdy I x y z ++=++∫∫,其中S 为上半球面2222x y z a ++=,(0)z >的外侧.六设(1),01(),10.n n nxx x x e x ϕ −≤≤= −≤≤ ,()f x 在[1,1]−上黎曼可积, (1)求lim ()n n x ϕ→∞,并讨论{()}n x ϕ在[1,1]−上的一致收敛性；(2)求11lim ()()n n f x x dx ϕ−→∞∫,(要说明理由)七设0()nn n f x a x ∞==∑的收敛半径为R =+∞,令0()nk n k k f x a x ==∑,试证明：(())n f f x 在[,]a b 上一致收敛于(())f f x ,其中[,]a b 为任一有穷闭区间.南京大学2003年数学分析考研试题解答一 (1)解设max{1,}M a =,则有M ≤≤, 由此知,1,01max{1,},1n a M a a a << === ≥ ；(2)解由归纳法,易知2n x <,12x x <,1n n x x +−==,由此知,{}n x 单调递增有界,设lim n n x a →∞=,02a <≤,则有a =2a =,故lim 2n n x →∞=.(3)21lim(1)x x x e x −→∞+⋅ 21(1)lim x x x x e →∞+=1(1)lim xx x x e→∞+ =1[ln(1)1]lim x x xx e +−→∞=, 12[ln(1)1]2311111ln(11lim limlim 12x x xx x x x x x x x ex x +−→∞→∞→∞+−−++==−1lim 21x x x →∞=−+12=−, 故21lim(1)x x x e x −→∞+⋅12=−. 3 解(1)y ′=,设切点为00(,)x y,0x x k y =′==,设切点00(,)x y 的切线方程为0)y x x −=−.将1x =,0y =代入,0)x =−, 002(2)1x x −−=−,03x =,01y =,所求切线方程为11(3)2y x −=−,即1(1)2y x =−. (2)解32212001121(1)212233S x dx udu t tdt =−−=−=−=∫∫∫∫.(3) 3321222120011211[(1)]24326x V x dx dx u du tdt πππππππ=−−=−=−=∫∫∫∫,131122224202[2](21)(44)(441)x V y dy y dy y y dy y y dy ππππ=+−+=++−++∫∫∫∫14016(34)(32)55y y dy πππ=+−=+−=∫.三解 00100()[(1)]y y x y y x x x ϕ−′=−−0100[(1)]y y x y x x −=−−01000[(1)]y y x y y x −=−+, 当0001y x y <<+时,()0x ϕ′>,当0011y x y <<+时,()0x ϕ′<,于是()x ϕ在001yx y =+处达到最大值,000100001000011(((11111(1)y y y y y y y y y y y y ϕ++===+++++.容易证明1()(1)y g y y =+在(0,)+∞上单调递减,11(1)y e y ++>,1111(1)y e y +<+,故有001011(11(1)y y y ey ϕ+=<++.四证明对任意(0,)x ∈+∞,1()()(0)(0)()(0)(0)f x f x f f f x f kx f ξ′=−+=+≥+, 当x 充分大时,有()0f x >,又(0)0f <,由连续函数的介值定理,存在(0,)ξ∈+∞,()0f ξ=, 由()0f x k ′≥>,()f x 在[0,)+∞上严格单调递增,所以()f x 在(0,)+∞内仅有一个零点. 五 (1)解 120()(1)(1)xI a dx ax x ′=++∫1122001[]111x a a dx dx a x ax +=−+++∫∫211[ln 2ln(1)]124a a a π=+−++, 显然(0)0I =,1(1)()I I a da ′=∫111222000ln(1)11ln 212141a a da da da a a a π+=−+++++∫∫∫11(1)ln 2ln 22442I ππ=−+⋅+⋅, 因为(1)ln 28I π=,120ln(1)ln 218x dx x π+=+∫.(2)解 2222{(,,):}x y z x y z a Ω=++≤,222{(,,):,0}D x y z x y a z =+≤=,32222()Sxdydz ydzdx zdxdy I x y z ++=++∫∫31Sxdydz ydzdx zdxdy a =++∫∫31[]S D D a =+−∫∫∫∫∫∫31[30]dxdydz a Ω=+∫∫∫331233a a π=⋅⋅2π=. 六、解 1,0lim ()0,[1,1],0n n x x x x ϕ→∞= = ∈−≠,由于极限函数在[1,1]−上不连续,所以{()}n x ϕ在[1,1]−上不一致收敛；但对任何10,01,a b −<<<<{()}n x ϕ在[1,][,1]a b −U 上一致收敛于0；且|()1n x ϕ≤,根据控制收敛定理,对于()f x 在[1,1]−上黎曼可积,有 11lim ()()0n n f x x dx ϕ−→∞=∫.七、证明由条件知()f x 在(,)−∞+∞上连续,{()}n f x 在任意有限区间上是一致收敛的, 对任意有限区间[,]a b ,{()}n f x 在[,]a b 上一致收敛于()f x ,{()}n f x 在[,]a b 上一致有界,()n f x M ≤,再由()f x 在[,]M M −上一致连续,于是有{(())}n f f x 在[,]a b 上一致收敛于(())f f x .南京大学2004年数学分析考研试题一．求下列极限 1.设n a =+L 求lim n n a →∞；2.ln 2sin x x x e x →++；3. ()()2200lim ln x y x y x y →→++；4. 设(){}222,:r D x y x y r =+≤,0r >,求()2221lim cos rx y r D e x y dxdy r π+−→+∫∫.二．确定最小正数,使下面的不等式成立：()()2222ln x y A x y +≤+,()0,0x y ∀>>.三．设()()1122f x x x = +−,求()()n f x ,并证明级数()()0!0n n n f ∞=∑收敛.四．求333Sx dydz y dzdx z dxdy ++∫∫其中S 是2221x y z ++=的上半球的下侧.五．设()2cos cos cos n n f x x x x =+++L ,（1）当0,2x π ∈ 时,求()lim n n f x →∞,并讨论(){}n f x 在0,2π的一致收敛性；（2）证明:对任一自然数n ,方程()1n f x =在0,3π内有且仅有一个根；（3）若0,3n x π∈是()n f x 的根,求lim n n x →∞.六．设()22xxt f x xe e dt −=∫,(1) 证明 ()f x 在[)0,+∞上有界；(2) 证明221xt x x e dt e ≤−∫,()(),x ∀∈−∞+∞.南京大学2004年数学分析考研试题解答一．1. 解n a ≤≤,1n n ==,1n n →∞==,所以lim 1n n a →∞=；2. 解0ln 2sin xx x e x →++()0112cos lim 1sin x x x e x x ex→+++=+22410+==+. 3. 解因为()()()22220ln x y x y x y ≤++≤+22ln 4ln 0r r r r ==→,()0r →,所以()()2200lim ln 0x y x y x y →→++=.4. 解设(),f x y 在点()0,0的某个邻域内连续,则有 ()()21lim ,0,0rr D f x y dxdy f r π+→=∫∫,()2221lim cos rx y r D e x y dxdy r π+−→+∫∫()220cos 001e −=+=.二．解设()ln r f r r =,()1r ≥,则()10f =,()lim 0r f r →∞=,()21ln rf r r−′=, 当r e =时,有()0f e ′=,当1r e <<时,有()0f r ′>,从而()f r 在[]1,r 上严格单调递增, 当e r <<+∞时,()0f r ′<,从而()f r 在[),e +∞上严格单调递减, 所以()f r 在r e =处达到最大值,对1r ≤<+∞,有()()1f r f e e ≤=, 1ln r r e ≤,()1r ≥, 对01r <<,显然有1ln r r e≤, 故使不等式()()2222ln x y A x y +≤+,()0,0x y ∀>>,成立的最小的正数A 为1e .三．解 ()()1122f x x x = +− 2111522x x=+ + −,()()()()111!2!5212n n n n n n f x x x ++− =++ −, ()()()()111!2!0522nn n n n n f+−+−=+ ,()()()11!5120122n n n n n n u f ++==−+,115151022122n n n u ++<<−:, 而105122n n ∞+=∑是收敛的,所以()()0!0n n n f ∞=∑收敛. 四．解设(){}222,,:1,0V x y z x y z z =++≤≥,(){}22,,:1,0D x y z x y z =+≤= 利用高斯公式,得333S x dydz y dzdx z dxdy ++∫∫333333S D x dydz y dzdx z dxdy x dydz y dzdx z dxdy =−+++++∫∫∫∫上侧 333Dx dydz y dzdx z dxdy +++∫∫()22230Vx y z dxdydz =−+++∫∫∫212220003sin d d r r dr ππθϕϕ=−∫∫∫163255ππ=−⋅⋅=−.五．解 (1)()()2cos 1cos cos cos cos 1cos n nn x x f x x x x x−=+++=−L ,当0,2x π ∈ 时,0cos 1x <<,lim cos 0n n x →∞=,于是有()cos lim 1cos n n x f x x →∞=−,0,2x π∈.()n f x 在0,2π 上连续,显然()0n f n =,(){}0n f 发散,从而知(){}n f x 在0,2π上不一致收敛,对任意02πδ<<,(){}n f x 在,2πδ上一致收敛. 五、设2()cos cos cos n n f x x x x =+++L ,求证:(2) 对任意自然数(2)n n ≥,方程()1n f x =在区间(0,)3π内必有唯一根n x , (3) 并求数列{}n x 的极限n n x ∞→lim .证明 (2) 显(0)1n f n =>,2111(13222n n f π=+++<L ,由连续函数的介值定理,存在(0,)3n x π∈,使得()1n n f x =;显然()0n f x ′<,(0,3x π∈,即()n f x 在(0,)3π上严格单调递减,所以()1n f x =的根是唯一的.(3) 显然1()()n n f x f x +>, 111()()()n n n n n n f x f x f x +++=>, 于1n n x x +<,即得{}n x 单调递增, 203n x x π<≤<,从而lim n n x a →∞=存在,且203x a π<≤≤,lim cos cos n n x a →∞=, 21cos cos 12n x x <≤<,lim(cos )0n n n x →∞=;在cos (1(cos ))()cos (cos )11cos n nn n n n n n nx x f x x x x −=++==−L ,令 n →∞,取极限,得cos 11cos 1cos 2a a a =⇒=−,得3a π=,故lim 3n n x π→∞= .六．证明(1)显然 ()f x 是偶函数,()f x 在[)0,+∞上连续,()220lim limxt xx x x e dtf x e→+∞→+∞=∫222lim2xt x x x e dt xe xe→+∞+=∫22221lim 242x x x x e x e e →+∞=++11022=+=, 于是可知,()f x 在[)0,+∞上有界,且()f x 在[)0,+∞上一致连续；（2）对0x >,设()()221xx t g x e x e dt =−−∫,()00g =,()g x 是偶函数,()222222xxx t x x t g x xe e dt xe xe e dt ′=−−=−∫∫,()00g ′=,()222222220x x x x g x x e e e x e ′′=+−=>,从而有()0g x ′>,()0g x >, 故有221xt x x e dt e ≤−∫,()(),x ∀∈−∞+∞.南京大学2005年数学分析考研试题解答1、求n →∞+. 解解法1 利用几何平均与算术平均不等式,及2!nn n ≥,2224(!)()n n n n n n n n≥=≥=L,limn n→∞+=+∞L .解法2 利用Stolz 定理,原式limn n→∞++=L lim (1)n n n →∞=+−lim n ==+∞.2 、求ln !limln n n n n→∞.解利用Stolz 定理,原式ln(1)lim (1)ln(1)ln n n n n n n →∞+=++−1ln(1)lim 1ln(1)n n n nn →∞++=+⋅1ln(1)lim 1ln(1)ln n n n nn →∞++=++11lim 1ln(1)ln ln(1)ln(1)n n n n n n →∞+=++++1=. 3 求1lim (1)n x n x x dx →∞+∫. 解 11010(1)21n x n x x dx x dx n <+≤=+∫∫,10lim (1)0n x n x x dx →∞+=∫. 4 设21,1()2,1x x g x x x x −≤− = ++>− ,求11(1)lim (n n i x i x g x n n →∞=−−+∑. 解原式10()x g x y dy −=+∫,5、当112p <≤时,证明：344sin ||sin n p n x dx x x ππππ++≥+∫. 证明344sin ||sin n p n x dx x x ππππ+++∫344sin()||()sin()p n u du n u n u πππππ+=+++∫344sin |()(1)sin |p n u du n u u πππ=++−∫, 当344u ππ≤≤时, |()(1)sin |()1(1)1p n p p p n u u n n ππππ++−≤++=++,sin sin4u π≥=, 于是sin |()(1)sin |p n u n u u π≥++− 故有344sin ||sin n p n x dx x x ππππ++≥+∫.南京大学2005年数学分析考研试题一、求下列极限1 设常数1a >,试求极限11lim (1)k nnn k an a k−→∞=+−∑.。

南京大学研究生入学考试复试试题离散数学

严禁用于商业用途?前言??本文收集了1997、1998年和2001年到2007年和2009年南京大学研究生入学考试科目《离散数学》的试卷以及相应试卷答案。

2008年试题未找到 1997年到2007年试题给出本人所做的答案因为离散数学难度大很多答案问过原来教我们离散数学的老师老师也只能给出部分答案所以不能保证全部答案的正确性 2009年试题答案未与同学核对同样不能确保答案正确性故不在此给出。

部分答案有更优解需要同学们自己开发。

??南京大学从2005年开始把《离散数学》作为复试科目满分为80分与《编译原理》同为笔试项目总分150分。

主要考试部分为数理逻辑、集合论、代数结构和图论。

推荐复习时候以南大课件为主课件在网上可以查到有宋方敏和陈道旭两种版本。

通过真题发现很多题目都是课件上证明题的原题而且考试重点与课件也吻合。

??离散数学特点就是难度大上手容易深入难。

代数系统和图论两章难度非常大所以复习好离散数学要有一定的耐心和钻研精神。

?相信天下无难事只怕有心人。

祝愿所有有志考南大CS的同学金榜提名。

????????????????????冷城???????????????????2009年7月??????????1?/?30??严禁用于商业用途?1996年?一试证 ?a.自然数集为无限集中势最小者。

?b.不存在最大的势。

??二任给无向图G 其联结矩阵为A=[aij] 即若存在边(vi,vj)则aij=1否则aij=0 试定义矩阵运算并给出关于A的矩阵的表达式 B=E(A) 使得矩阵B=[bij]满足对于G中的任意两结点vi,vj若其间存在通路则bij=1否则bij=0。

??三任给无向图G ?对G中的边赋予方向得图G’ 试证存在G满足对任意两点v1,v2 G’不论从哪点为始终端均有有向通路到达另一点的充分条件是原图G连通且不存在割边。

??四试分别用永真推理过程和假设推理过程证明 ????(?α→?(?β?→?γ?)?)?→?(?(?α?∧?β?)?→?γ?)??五试给出下式的析合范式和合析范式 ????(?p?→?q?)?→?(?p?→?r?)??六试用谓词演算公式来描述一个代数系统(A,*)为一个群。

新版南京大学数学考研经验考研真题考研参考书

得到拟录取消息的前些天一直忐忑不安，想象着自己失败时的沮丧或者自己成功时的兴奋。

终于尘埃落定，内心激动，又面色平静地拿起手机给每一个关心我的家人和朋友发了这个好消息。

也想在这里写下自己考研路上的点点滴滴，给自己留一个纪念，也希望大家能从中得到一些收获。

立大志者得中志，立中志者得小志，立小志者不得志。

所以我建议刚开始大家就朝着自己喜欢的，最好的学校考虑，不要去担心自己能不能考上的问题，以最好的学校的标准来要求自己去学习。

大家可以去自己想报考的学校官网上下过去的录取分数线，报录比之类的信息给自己一个参考和努力目标。

包括找一些学长学姐问下经验也是很有用的。

备考那个时候无论是老师还是同学们都给了我很多的帮助，让我在备考的路上少走了很多的弯路，尤其是那些珍贵的笔记本，现在回想起来依然很是感动，还好现在成功上岸，也算是没有辜负大家对我的期望。

所以想着成功之后可以写一篇经验贴，希望可以帮助大家。

话不多说，下面跟大家介绍一下我的经验吧。

文末有笔记和真题下载，大家可自取。

南京大学数学的初试科目为：(101)思想政治理论(201)英语一(627)数学分析和(801)高等代数参考书目为：南京大学《数学分析》1996-2017年考研历年真题。

近20年真题，来自官方，真实可靠2、南京大学《数学分析》2000-2010年考研历年真题答案。

最全最新的真题答案，本店独家更新。

3、南京大学《高等代数》1996-2017年考研历年真题。

来自官方，同学们可索要截图！4、南京大学《高等代数》历年考研真题部分答案。

该专业近几年学校官方不出售历年试题。

先说英语吧。

词汇量曾经是我的一块心病，跟我英语水平差不多的同学，词汇量往往比我高出一大截。

从初中学英语开始就不爱背单词。

在考研阶段，词汇量的重要性胜过四六级，尤其是一些熟词僻义，往往一个单词决定你一道阅读能否做对。

所以，一旦你准备学习考研英语，词汇一定是陪伴你从头至尾的一项工作。

考研到底背多少个单词足够？按照大纲的要求，大概是5500多个。