新人教版八年级数学下册教案:方差
人教版数学八年级下册《方差》说课稿2

人教版数学八年级下册《方差》说课稿2一. 教材分析《方差》是人教版数学八年级下册第22章的一节内容。
本节课的主要内容是让学生理解方差的概念,掌握计算方差的方法,并能够运用方差解决实际问题。
教材通过引入数据的波动性,引导学生探究数据的波动大小,从而引出方差的概念。
通过大量的例子,让学生理解方差在实际生活中的应用,培养学生的应用意识。
二. 学情分析八年级的学生已经学习了数据的收集、整理和描述,对平均数、中位数、众数等统计量有一定的了解。
但是,对于方差这一概念,学生可能比较难以理解。
因此,在教学过程中,我将会注重对学生概念的理解和方法的掌握。
三. 说教学目标1.知识与技能目标:理解方差的概念,掌握计算方差的方法,能够运用方差解决实际问题。
2.过程与方法目标:通过合作交流,培养学生探究问题和解决问题的能力。
3.情感态度与价值观目标:培养学生对数据的敏感性,培养学生的应用意识。
四. 说教学重难点1.教学重点:方差的概念和计算方法。
2.教学难点:方差在实际生活中的应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法,引导学生主动探究方差的概念和计算方法。
2.教学手段:利用多媒体课件,展示数据的波动性,帮助学生直观理解方差的概念。
六. 说教学过程1.导入:通过展示一组数据的波动性,引导学生关注数据的波动大小,引出方差的概念。
2.新课导入:介绍方差的定义,引导学生理解方差的意义。
3.方法讲解:讲解方差的计算方法,让学生通过小组合作,共同探究方差的计算步骤。
4.例题讲解:通过一系列的例题,让学生理解方差的应用,培养学生的应用意识。
5.练习巩固:让学生进行练习,巩固对方差的的理解和计算方法的掌握。
6.总结:对本节课的内容进行总结,让学生明确方差的概念和计算方法。
七. 说板书设计板书设计如下:1.定义:一组数据的方差是各个数据与平均数差的平方的平均数。
2.计算方法:a.计算平均数b.计算每个数据与平均数的差c.计算差的平方d.计算平方的平均数八. 说教学评价教学评价主要通过学生的课堂表现、练习情况和课堂讨论来进行。
方差教案初中数学

方差教案初中数学教学目标:1. 理解方差的定义和性质,掌握计算公式。
2. 能够运用方差分析数据,判断数据的稳定性和集中程度。
3. 培养学生的逻辑思维能力和数据分析能力。
教学重点:1. 方差的定义和性质。
2. 方差的计算公式。
教学难点:1. 方差的计算公式的推导。
2. 运用方差分析数据的能力。
教学准备:1. 教学课件或黑板。
2. 练习题。
教学过程:一、导入(5分钟)1. 引导学生回顾数据的波动情况,引入方差的概念。
2. 提问:数据的波动情况如何衡量?引出方差的概念。
二、新课讲解(15分钟)1. 讲解方差的定义:方差是衡量一组数据波动大小的量。
2. 推导方差的计算公式:方差 = (每个数据值 - 平均数)^2 的平均数。
3. 讲解方差的性质:非负数,单位与原数据单位一致。
4. 通过实例讲解如何计算一组数据的方差。
三、练习与讨论(15分钟)1. 让学生独立完成练习题,巩固方差的计算方法。
2. 组织学生进行小组讨论,分享解题过程和心得。
四、方差的实际应用(15分钟)1. 讲解方差在实际生活中的应用,如质量控制、统计分析等。
2. 通过实例分析,让学生学会如何运用方差判断数据的稳定性和集中程度。
五、课堂小结(5分钟)1. 回顾本节课所学内容,让学生总结方差的定义、性质和计算方法。
2. 强调方差在实际生活中的重要性。
六、作业布置(5分钟)1. 布置练习题,让学生巩固方差的概念和计算方法。
2. 鼓励学生查阅相关资料,了解方差在实际应用中的例子。
教学反思:本节课通过讲解方差的定义、性质和计算方法,让学生掌握方差的基本概念和应用。
在教学过程中,注意引导学生主动参与课堂讨论,提高学生的逻辑思维能力和数据分析能力。
同时,结合实际情况,让学生了解方差在生活中的应用,增强学生的学习兴趣。
在作业布置方面,注重培养学生的自主学习能力,鼓励学生查阅资料,拓宽知识面。
八年级数学下册《方差》教案、教学设计

1.方差的概念:教师详细讲解方差的定义,解释方差表示数据离散程度的平方,是衡量数据波动性的重要指标。
2.方差的计算方法:教师通过具体例子,演示方差的计算过程,包括求平均数、计算离差、平方离差、求和、除以数据个数等步骤。
3.方差的性质与意义:讲解方差的性质,如方差是非负的、方差越大表示数据波动性越大等,并解释方差在实际问题中的应用。
4.教学策略:
(1)针对学生的个体差异,实施分层教学,使每个学生都能在原有基础上得到提高。
(2)注重启发式教学,引导学生主动思考、发现问题、解决问题,培养他们的批判性思维。
(3)关注学生的情感态度,及时给予鼓励和指导,帮助他们克服学习中的困难,增强自信心。
(4)利用课后时间,提供丰富的学习资源,鼓励学生进行拓展学习,提高他们的数学素养。
在教学过程中,教师应关注学生的学习情况,及时调整教学策略,使学生在掌握方差相关知识的同时,提高数学素养和综合能力。
二、学情分析
八年级学生已经具备了一定的数学基础,掌握了数据收集、整理、描述和分析的基本方法。在此基础上,学生对方差的概念和计算方法的学习将更为顺利。然而,由于方差的抽象性和计算过程的复杂性,学生在理解和应用方面可能会遇到困难。因此,在教学过程中,教师应关注以下几点:
三、教学重难点和教学设想
(一)教学重难点
1.重点:方差的概念、计算方法及其在实际问题中的应用。
2.难点:方差计算过程中数据的处理,以及对方差意义的深入理解。
(二)教学设想
1.教学方法:
(1)采用情境导入法,通过展示实际生活中的案例,让学生感受数据波动性的存在,从而引出方差的概念。
(2)运用问题驱动法,引导学生探究方差的计算方法,并在实践中加以运用。
新人教版初中八年级数学下册《方差》教案

方差一. 教学目的:1. 了解方差的定义和计算公式。
2. 理解方差概念的产生和形成的过程。
3. 会用方差计算公式来比较两组数据的波动大小。
二. 重点、难点和难点的突破方法:1. 重点:方差产生的必要性和应用方差公式解决实际问题。
2. 难点:理解方差公式三. 例习题的意图分析:1. 教材P125的讨论问题的意图:(1).创设问题情境,引起学生的学习兴趣和好奇心。
(2).为引入方差概念和方差计算公式作铺垫。
(3).介绍了一种比较直观的衡量数据波动大小的方法——画折线法。
(4).客观上反映了在解决某些实际问题时,求平均数或求极差等方法的局限性,使学生体会到学习方差的意义和目的。
2. 教材P154例1的设计意图:(1).例1放在方差计算公式和利用方差衡量数据波动大小的规律之后,不言而喻其主要目的是及时复习,巩固对方差公式的掌握。
(2).例1的解题步骤也为学生做了一个示范,学生以后可以模仿例1的格式解决其他类似的实际问题。
四.课堂引入:除采用教材中的引例外,可以选择一些更时代气息、更有现实意义的引例。
例如,通过学生观看2004年奥运会刘翔勇夺110米栏冠军的录像,进而引导教练员根据平时比赛成绩选择参赛队员这样的实际问题上,这样引入自然而又真实,学生也更感兴趣一些。
五. 例题的分析:教材P154例1在分析过程中应抓住以下几点:1.题目中“整齐”的含义是什么?说明在这个问题中要研究一组数据的什么?学生通过思考可以回答出整齐即波动小,所以要研究两组数据波动大小,这一环节是明确题意。
2.在求方差之前先要求哪个统计量,为什么?学生也可以得出先求平均数,因为公式中需要平均值,这个问题可以使学生明确利用方差计算步骤。
3.方差怎样去体现波动大小?这一问题的提出主要复习巩固方差,反映数据波动大小的规律。
六. 随堂练习:1. 从甲、乙两种农作物中各抽取1株苗,分别测得它的苗高如下:(单位:cm)甲:9、10、11、12、7、13、10、8、12、8;乙:8、13、12、11、10、12、7、7、9、11;问:(1)哪种农作物的苗长的比较高?(2)哪种农作物的苗长得比较整齐?2. 段巍和金志强两人参加体育项目训练,近期的5次测试成绩如下表所示,谁的成绩比较稳定?为什么?参考答案:1.(1)甲、乙两种农作物的苗平均高度相同;(2)甲整齐2.段巍的成绩比金志强的成绩要稳定。
人教版数学八年级下册20.2第1课时《 方差》教学设计

人教版数学八年级下册20.2第1课时《方差》教学设计一. 教材分析《方差》是人教版数学八年级下册20.2第1课时的重要内容。
方差是描述一组数据波动大小,稳定程度的量。
通过学习方差,使学生更好地理解数据的波动情况,为以后学习概率和统计打下基础。
二. 学情分析学生在学习本课时,已经掌握了平均数、标准差等基础知识,能理解数据的波动情况。
但对方差的概念和计算方法可能存在理解上的困难,需要通过实例来引导学生理解方差的概念,并运用计算公式进行计算。
三. 教学目标1.知识与技能:理解方差的概念,掌握方差的计算方法,能计算一组数据的方差。
2.过程与方法:通过实例分析,引导学生理解方差的意义,培养学生的数据分析能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队协作精神,使学生感受到数学在生活中的应用。
四. 教学重难点1.重点:方差的概念,方差的计算方法。
2.难点:方差公式的推导,方差在实际问题中的应用。
五. 教学方法1.情境教学法:通过生活实例,引导学生理解方差的概念。
2.小组合作学习:分组讨论,共同完成方差的计算。
3.激励性评价:鼓励学生积极参与,提高学习积极性。
六. 教学准备1.准备相关的生活实例,用于引导学生理解方差的概念。
2.准备方差的计算练习题,用于巩固所学知识。
3.准备多媒体教学设备,用于展示实例和讲解。
七. 教学过程1.导入(5分钟)通过一个生活实例,如学生的身高数据,引导学生思考:如何描述这些数据的波动情况?引入方差的概念。
2.呈现(10分钟)讲解方差的定义,用公式表示。
并通过动画演示方差的计算过程,让学生直观地理解方差的含义。
3.操练(10分钟)学生分组讨论,共同完成一些方差的计算练习题。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)学生独立完成一些方差的计算题,检验自己对方差的理解。
教师选取部分题目进行讲解,巩固所学知识。
5.拓展(10分钟)引导学生思考:方差在实际生活中有哪些应用?让学生举例说明,进一步体会方差的意义。
人教版数学八年级下册20.2第1课时《方差》说课稿

人教版数学八年级下册20.2第1课时《方差》说课稿一. 教材分析《方差》是人教版数学八年级下册20.2第1课时的一节内容。
本节课的主要内容是让学生了解方差的概念,掌握求一组数据方差的方法,并能够运用方差解决实际问题。
教材通过引入实际例子,让学生感受方差在生活中的应用,培养学生的应用意识。
同时,本节课也为后续学习概率和统计奠定了基础。
二. 学情分析学生在学习本节课之前,已经掌握了平均数、标准差等基本概念,具备了一定的数据分析能力。
但是,对于方差的概念和求法,学生可能较为陌生。
因此,在教学过程中,需要引导学生通过观察、分析、归纳等方法,自主探索方差的含义和求法。
三. 说教学目标1.知识与技能目标:让学生理解方差的概念,掌握求一组数据方差的方法,能够运用方差解决实际问题。
2.过程与方法目标:通过观察、分析、归纳等方法,培养学生自主探索和合作交流的能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,感受数学在生活中的应用,培养学生的应用意识。
四. 说教学重难点1.教学重点:方差的概念和求法,以及方差在实际问题中的应用。
2.教学难点:方差的求法,以及如何运用方差解决实际问题。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法、小组讨论法等,引导学生自主探索和合作交流。
2.教学手段:利用多媒体课件、实物模型等辅助教学,提高学生的学习兴趣和参与度。
六. 说教学过程1.导入新课:通过一个实际问题,引发学生对方差的兴趣,导入新课。
2.自主探索:让学生分组讨论,尝试用自己的方法求解方差,培养学生的自主学习能力。
3.讲解示范:教师讲解方差的定义和求法,并通过示例演示,让学生理解和掌握。
4.练习巩固:布置一些练习题,让学生独立完成,巩固所学知识。
5.应用拓展:让学生运用方差解决实际问题,培养学生的应用意识。
6.总结反思:让学生总结本节课的收获,反思自己的学习过程。
七. 说板书设计板书设计要简洁明了,突出重点。
人教版初中数学方差教案

人教版初中数学方差教案一、教学目标1. 理解方差的概念,掌握方差的计算公式。
2. 能够运用方差分析数据的变化程度,提高数据的准确性和可靠性。
3. 培养学生的逻辑思维能力、数据分析能力及解决问题的能力。
二、教学内容1. 方差的概念:一般地设一组数据x1 , x2 , x3 ,…,xn 的平均数为,则方差为S2=1/n[(x1-)^2 + (x2-)^2 + … + (xn-)^2 ] 。
2. 方差的性质与应用。
三、教学重点与难点1. 重点:方差的概念及其计算公式。
2. 难点:方差的性质与应用。
四、教学过程1. 导入:通过一组数据的波动情况,引发学生对数据变化程度的关注,从而引入方差的概念。
2. 新课讲解:(1) 讲解方差的概念,引导学生理解方差的意义。
(2) 推导方差的计算公式,让学生掌握方差的计算方法。
(3) 讲解方差的性质,如:非负性、对称性、变量扩大或缩小相同的倍数方差不变等。
(4) 结合实际例子,讲解方差的运用,如:判断数据的稳定性、比较不同数据的波动程度等。
3. 练习与讨论:(1) 让学生分组进行练习,巩固方差的概念和计算方法。
(2) 引导学生讨论方差的性质与应用,提高学生的数据分析能力。
4. 总结与反思:让学生回顾本节课所学内容,总结方差的概念、计算方法及应用,反思自己在学习过程中的收获与不足。
五、课后作业1. 请学生完成课后练习题,巩固方差的概念和计算方法。
2. 选取一组实际数据,运用方差进行分析,体会方差在实际问题中的应用。
六、教学反思本节课通过导入、新课讲解、练习与讨论、总结与反思等环节,使学生掌握了方差的概念、计算方法及应用。
在教学过程中,注意调动学生的积极性,引导学生主动参与课堂讨论,提高学生的数据分析能力。
同时,结合课后作业,让学生巩固所学知识,培养学生的实际应用能力。
然而,在教学过程中也存在一些不足,如:对于方差性质的讲解可能不够深入,导致学生理解不够透彻。
在今后的教学中,应加强方差性质的讲解,并通过更多实际例子让学生体会方差在数据分析中的重要作用。
人教版八年级数学下册《方差》教案设计
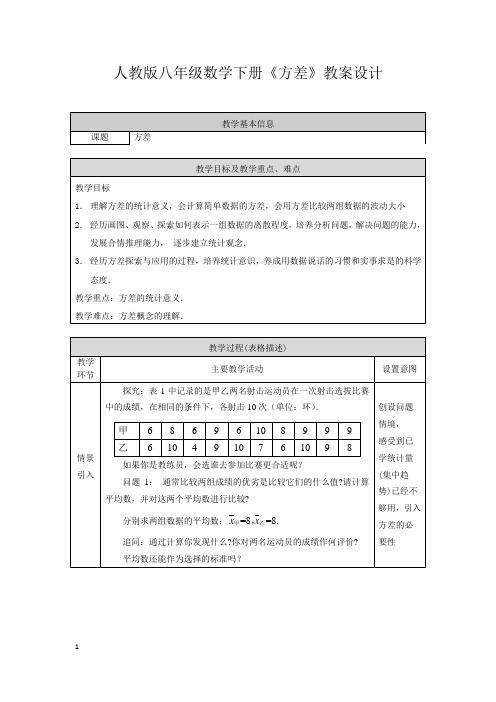
人教版八年级数学下册《方差》教案设计问题2:如何判断两名运动员谁发挥的更稳定呢? 观察统计图,得到如下结论①借助统计图(图1和图2)直观观察数据的波动情况,发现甲的成绩稳定.②观察波动情况,必须先确定波动的标准(什么情况下视为无波动). ③波动程度与每个数据偏离其平均数的“距离”有关.每一个数据的变化都影响着波动的状况,“距离”越远的数对波动的影响越大.问题3:什么样的量能反映一组数据的波动程度呢? 每一个数据的波动状况:用每一个数据与平均数的差来表示. 那么一组数据的整体的波动情况:各数据波动状况的平均值来表示.讨论1:一组数据的波动能否用:计算每一个数据与平均数的差的平均数表示?计算后,发现,此方法的式子的值得零,计算每一个数据与平均数的差的平均数表示数据波动的方法不可行.讨论2:能否利用数学的方法修改一下,来避免正负偏差的相互抵销的这个缺点呢,从而可以衡量数据的波动情况呢?探索分析归纳出两种能描述数据波动的方法: ①先求差的绝对值,再算这些 差的绝对值 的平均数; 也就是,12n x x x x x xn-+-+-②先求差的平方,再算这些差的平方的平均数22212()()()n x x x x x x n-+-+-+教师说明是在统计中常用第二种方法表示数据的波动情况.概括方差的定义n 个数据12,n x x x ,,各数据与它们的平均数x 的差的平方分别为22212()()()n x x x x x x ---,,,, 这些值的平均数叫这组数据的方差,记作2s .2222121()()()n s x x x x x x n ⎡⎤=-+-+-⎣⎦+思考.方差的大小与数据的波动程度有什么关系? 1.当数据分布比较分散时,方差值会怎样?2.当数据分布比较集中时,方差值会怎样?3.方差大小与数据的波动大小有怎样的关系?师生行为:从式子的结构和形的角度得出方差越大,数据的波动越大;方差越小,数据的波动越小.分析方差的概念,便于学生理解和掌握问题4.利用方差公式分析甲乙两名运动员的成绩的波动程度.22222(68)(88)(68)+(98)210s -+-+-+-==甲22222(68)(108)(58)+(88) 3.210s -+-+-+-==乙22s s <∴甲乙甲的数据波动较小,所以甲的成绩比较稳定.可以选甲运动员参加比赛. 总结计算方差的步骤: 1.计算数据的平均数 2. 代入方差公式求值学习计算方差,分析数据的波动(167++-(168++-22s s <∴甲乙甲芭蕾舞团女演员的身高更整齐.思考:用方差解决实际问题的一般步骤: (1)求每组数据的平均数; (2)求方差; (3)比较方差的大小,确定稳定性.10(x +-+________________,________________..用条形图表示下列各组数据,计算并比较它们的平均数和方差,体会方差是怎样刻画数据的波动程度. 6 6;(2) 5 5 6 6 6 7 7;(3) 3 3 4 6 8 9 9; (4) 3 3 3 6 9 9 9. 3. 甲、乙两地9月份上旬的日平均气温如图所示,则甲、乙两地这10天日平均气温的方差的大小关系为22___s s 甲乙(填 > 或 < )4. 已知甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差.根据表中的数据,要从中选择一名成绩好且成绩稳定的运动员参加比赛,应该选择( )A .甲B .乙C .丙D .丁甲 乙 丙 丁 平均数(cm) 185 180 185 180 方差3.63.67.48.1课堂 小结1. 方差怎样计算? 2. 如何理解方差的意义的?3. 用方差来比较两组数据波动大小的条件是?回顾方差的计算公式及方差如何刻画数据波动情况的。
人教初中数学八年级下册20-2-1方差教学设计

人教初中数学八年级下册20-2-1方差教学设计一. 教材分析人教初中数学八年级下册20-2-1方差教学设计,主要介绍了方差的定义、性质和应用。
本节课的内容是学生对方差的理解和掌握,为后续的统计学知识打下基础。
教材通过具体的例子引导学生理解方差的含义,并通过计算练习让学生掌握计算方差的方法。
二. 学情分析学生在学习本节课之前,已经学习了数据的收集、整理和描述的知识,对平均数、中位数等概念有一定的理解。
但对方差的概念和计算方法可能较为陌生。
因此,在教学过程中,需要通过具体的例子和实践活动,帮助学生理解和掌握方差的概念和计算方法。
三. 教学目标1.理解方差的定义和性质;2.掌握计算方差的方法;3.能够应用方差的概念解决实际问题。
四. 教学重难点1.方差的定义和性质;2.计算方差的方法。
五. 教学方法1.实例导入:通过具体的例子引入方差的概念;2.讲解演示:通过讲解和演示,帮助学生理解方差的性质和计算方法;3.练习操练:通过计算练习,让学生掌握计算方差的方法;4.巩固拓展:通过解决实际问题,让学生应用方差的知识;5.小结总结:对所学内容进行总结和归纳;6.家庭作业:布置相关的练习题目,巩固所学知识。
六. 教学准备1.教学课件:制作课件,包括具体的例子、讲解演示、练习题目等;2.教学素材:准备相关的实际问题,供学生巩固拓展使用;3.计算器:为学生准备计算器,用于计算方差。
七. 教学过程1.导入(5分钟)通过一个具体的例子,介绍方差的概念。
例如,比较两组数据的波动大小,引导学生思考如何衡量数据的波动性。
2.呈现(10分钟)讲解方差的定义和性质,演示如何计算方差。
通过详细的解释和示例,让学生理解方差的概念和计算方法。
3.操练(10分钟)让学生进行计算练习,巩固方差的计算方法。
可以布置一些简单的题目,让学生独立完成,然后进行讲解和解析。
4.巩固(10分钟)通过解决实际问题,让学生应用方差的知识。
可以给学生一些实际的数据,让他们计算方差,并解释结果的含义。
20.2.1方差教案2020-2021学年人教版数学八年级下册

一、教学内容
本节课选自人教版数学八年级下册第20章第2节“数据的波动”,具体内容为20.2.1方差。教学内容主要包括:理解和掌握方差的定义及意义,学会计算简单数据的方差;了解方差在描述数据波动程度中的作用,能通过方差对数据的稳定性和集中程度进行判断;掌握使用方差分析实际问题,培养数据分析能力。具体内容包括:
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了方差的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对方差的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
在课堂实践活动环节,分组讨论和实验操作进行得比较顺利,学生们积极参与,展示了他们的思考成果。但我也注意到,有些小组在讨论过程中,成员之间的交流不够充分,可能导致部分学生对方差的实际应用理解不够深入。今后,我需要在这方面多给予引导和关注,鼓励学生们多进行互动交流。
此外,在学生小组讨论环节,我发现有些学生对于方差在实际生活中的应用还是有些迷茫。这可能是因为我们举例不够丰富,或者与学生们的生活实际联系不够紧密。在今后的教学中,我会尝试引入更多与学生生活息息相关的事例,提高他们对方差应用的认识。
突破方法:通过图形、实例等直观方式展示方差的概念,帮助学生建立直观感受。
(2)方差的计算过程:方差的计算步骤相对繁琐,学生容易在计算过程中出现错误。
突破方法:引导学生逐步完成计算过程,强调每个步骤的关键点,并设计相关练习题巩固。
(3)方差在实际问题中的应用:学生可能难以将方差知识应用于实际问题,无法准确判断数据的波动性。
初中人教版方差教案

初中人教版方差教案教学目标:1. 让学生理解方差的定义,掌握方差的计算方法。
2. 培养学生运用方差分析数据的能力,提高学生解决实际问题的能力。
3. 培养学生合作学习、积极探究的精神。
教学重点:1. 方差的概念及计算方法。
2. 运用方差分析数据的能力。
教学难点:1. 方差的计算。
2. 对方差的理解和应用。
教学准备:1. 课件、黑板、粉笔。
2. 学生分组,每组准备数据。
教学过程:一、导入(5分钟)1. 复习相关知识:平均数、标准差。
2. 提问:为什么我们需要方差?方差有什么作用?二、新课导入(15分钟)1. 介绍方差的定义:方差是衡量一组数据波动大小的量。
2. 讲解方差的计算方法:a. 计算平均数。
b. 计算每个数据与平均数的差的平方。
c. 将所有差的平方相加,除以数据个数。
三、实例分析(15分钟)1. 学生分组,每组选择一组数据进行分析。
2. 各组汇报分析结果,教师点评。
四、巩固练习(10分钟)1. 学生独立完成练习题。
2. 教师讲解答案,解析难点。
五、拓展与应用(10分钟)1. 学生分组,运用方差分析实际问题。
2. 各组汇报成果,教师点评。
六、总结(5分钟)1. 回顾本节课所学内容,强调方差的概念和作用。
2. 提醒学生注意方差的计算方法。
七、作业布置(5分钟)1. 课后练习题。
2. 收集生活中的数据,运用方差进行分析。
教学反思:本节课通过实例分析、练习和拓展应用,让学生掌握了方差的概念和计算方法。
在教学过程中,注意引导学生主动参与、积极思考,培养了学生的合作精神和探究能力。
同时,结合生活实际,让学生体会数学的应用价值,提高了学生的学习兴趣。
在今后的教学中,要继续关注学生的学习情况,针对不同学生给予适当的指导,提高学生的数学素养。
同时,注重培养学生的数据处理和分析能力,使学生在解决实际问题时能更好地运用所学的数学知识。
20.2. 2 方差(第一课时)教学设计 2022-2023学年人教版八年级下册数学

20.2.2 方差(第一课时)教学设计一、教学目标1.了解方差的概念和计算方法;2.掌握一维数据和二维数据的方差计算;3.学会运用方差对数据的离散程度进行分析。
二、教学重点1.方差的概念和计算方法;2.一维数据和二维数据的方差计算。
三、教学难点1.运用方差对数据的离散程度进行分析;2.在实际问题中应用方差进行数据处理。
四、教学准备1.教材:人教版八年级下册数学教材;2.教具:黑板、白板、彩色粉笔、教学PPT。
五、教学过程1. 导入与热身教师简要介绍方差的概念,并与学生进行互动对话,引起学生的兴趣和思考。
2. 方差的概念说明•方差:用来衡量数据分布的离散程度。
方差越大,数据的离散程度越大;方差越小,数据的离散程度越小。
•方差的计算公式:对于一维数据,方差的计算公式为:方差 = 平均数与每个数据之差的平方和除以数据个数。
对于二维数据,方差的计算公式为:方差 =平均数与每个数据之差的平方和除以数据个数。
3. 一维数据的方差计算教师通过例题的演示,详细介绍一维数据的方差计算方法,并逐步引导学生进行训练。
4. 二维数据的方差计算教师通过例题的演示,详细介绍二维数据的方差计算方法,并逐步引导学生进行训练。
5. 运用方差进行数据离散程度分析教师通过实际生活中的例子,引导学生运用方差对数据的离散程度进行分析,培养学生的分析思维能力和应用能力。
6. 应用方差进行数据处理教师通过实际问题的讲解,指导学生运用方差对数据进行处理,并帮助学生理解方差在实际问题中的应用价值。
六、课堂小结教师对本节课的重点内容进行小结,并与学生一起复习方差的概念和计算方法。
七、作业布置老师布置相关作业,要求学生运用方差的知识进行数据处理和分析,并指定完成时间。
八、教学反思本节课通过理论讲解和例题演示相结合的方式,引导学生逐步掌握方差的概念、计算方法和应用技巧。
通过与学生的互动对话,增加了学生的参与度和兴趣。
教师在课堂上对学生进行了详细讲解,并进行了及时的总结和梳理,确保学生对方差的学习效果。
人教版数学八年级下册《方差》教学设计2

人教版数学八年级下册《方差》教学设计2一. 教材分析人教版数学八年级下册《方差》是初中数学的重要内容,主要让学生理解方差的概念,掌握求解方差的方法,并能够运用方差解决实际问题。
本节课的教学内容主要包括方差的定义、计算公式及应用。
通过本节课的学习,学生能够理解数据的波动性,并能够利用方差对数据的稳定性进行判断。
二. 学情分析学生在学习本节课之前,已经掌握了数据的收集、整理和分析的基本方法,具备一定的数学运算能力。
但是,对于方差这一概念,学生可能较为陌生,需要通过具体实例来理解其含义。
同时,学生对于数据的波动性及其判断方法也较为模糊,需要通过实例讲解和练习来加深理解。
三. 教学目标1.知识与技能目标:理解方差的概念,掌握求解方差的方法,能够运用方差解决实际问题。
2.过程与方法目标:通过实例分析,培养学生对于数据波动性的认识,提高学生运用数学方法解决实际问题的能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,激发学生探究数学问题的热情。
四. 教学重难点1.教学重点:方差的定义及其计算方法。
2.教学难点:对于数据的波动性的理解和判断。
五. 教学方法采用问题驱动的教学方法,通过实例引入方差的概念,引导学生探究方差的计算方法,并通过实际问题解决来巩固方差的应用。
同时,采用分组讨论和小组合作的方式,培养学生的团队协作能力和解决问题的能力。
六. 教学准备1.教学课件:制作精美的教学课件,包括方差的定义、计算公式及应用实例。
2.教学素材:准备一些实际问题,用于引导学生运用方差解决实际问题。
3.教学设备:投影仪、电脑、黑板等。
七. 教学过程1.导入(5分钟)通过一个实际问题引入方差的概念,如“某班级在一次数学考试中,成绩如下:85, 90, 88, 86, 92, 87, 84, 89, 85, 83。
请计算该班级数学成绩的方差。
”让学生思考如何解决这个问题,从而引出方差的概念。
2.呈现(10分钟)讲解方差的定义和计算公式,并通过课件展示一些实例,让学生理解方差的意义和应用。
人教版初中数学八年级下册《方差》教学设计

人教版初中数学八年级下册《方差》教学设计一. 教材分析人教版初中数学八年级下册《方差》是学生在学习了统计的初步知识、平均数、标准差等概念的基础上,进一步引入方差的概念,通过实例让学生感受方差在实际生活中的应用,培养学生的应用意识。
方差是反映一组数据的波动大小的一个量,方差越大,波动性越大,反之也成立。
本节课通过具体案例让学生感受方差的概念,并学会计算方差,了解方差的意义。
二. 学情分析学生在学习本节课之前,已经掌握了统计的基本知识,平均数、标准差的概念,对数据的处理和分析有一定的了解。
但方差作为一个新的概念,对学生来说比较抽象,需要通过具体的实例让学生感受和理解。
同时,学生对方差的计算方法和意义还需要通过实践来掌握。
三. 教学目标1.了解方差的概念,会计算一组数据的方差。
2.理解方差的意义,能通过方差分析实际问题。
3.培养学生的应用意识,提高学生的数据分析能力。
四. 教学重难点1.重点:方差的概念和计算方法。
2.难点:方差的意义和应用。
五. 教学方法1.采用案例教学法,通过具体的实例让学生感受和理解方差的概念。
2.采用问题驱动法,引导学生思考方差的意义和应用。
3.采用小组合作法,让学生在小组内讨论和探究方差的计算方法。
六. 教学准备1.教学PPT2.实例数据3.小组讨论表格七. 教学过程1.导入(5分钟)通过一个实际问题引出方差的概念:某厂生产的零件,平均长度为10cm,标准差为0.5cm,问这些零件的长度波动性如何?2.呈现(15分钟)呈现一组数据,让学生计算这组数据的方差,并解释方差的意义。
3.操练(15分钟)学生分组,每组选择一组数据,计算方差,并解释方差的意义。
4.巩固(10分钟)学生独立完成教材上的练习题,教师巡回指导。
5.拓展(10分钟)让学生思考方差在实际生活中的应用,如产品质量检测、体育比赛等。
6.小结(5分钟)教师引导学生总结方差的概念、计算方法和意义。
7.家庭作业(5分钟)布置课后练习题,让学生巩固所学知识。
人教版数学八年级下册20.2《方差》(第1课时)说课稿

人教版数学八年级下册20.2《方差》(第1课时)说课稿一. 教材分析人教版数学八年级下册20.2《方差》是学生在学习了数据的收集、整理、描述和分析的基础上,进一步研究数据的波动情况。
方差是衡量一组数据波动大小,稳定程度的量,它反映了数据分布的离散程度。
本节课的内容是在学生掌握了有理数的乘方,算术平均数,数据收集与整理的基础上进行学习的,为后续学习概率,统计等相关知识打下基础。
二. 学情分析学生在七年级时已经接触过方差的概念,但只是停留在感性认识上,没有深入的理解和掌握。
对于方差的计算方法和过程,他们可能还不够熟悉。
因此,在教学过程中,我需要从学生的实际出发,通过实例和练习,引导学生理解和掌握方差的定义,计算方法和应用。
三. 说教学目标1.知识与技能:理解方差的概念,掌握方差的计算方法,能运用方差解决实际问题。
2.过程与方法:通过实例和练习,培养学生的数据分析和处理能力,提高他们的数学思维能力。
3.情感态度价值观:激发学生学习数学的兴趣,培养他们严谨治学的态度,使他们体验到数学在生活中的重要作用。
四. 说教学重难点1.重点:方差的概念,方差的计算方法。
2.难点:方差在实际问题中的应用,对数据的分析和处理。
五.说教学方法与手段本节课我采用讲授法,引导法,实践法,讨论法等多种教学方法。
通过实例和练习,让学生在实践中学习和掌握方差的概念和计算方法。
同时,我还会学生进行小组讨论,分享他们的学习心得和经验,从而提高他们的学习兴趣和效果。
六.说教学过程1.导入:通过一个实际问题,引入方差的概念,激发学生的学习兴趣。
2.讲解:讲解方差的定义,计算方法和步骤,让学生理解和掌握方差的概念。
3.实践:让学生进行练习,巩固所学知识,提高他们的实际操作能力。
4.应用:通过实例,讲解方差在实际问题中的应用,让学生体验到数学的实用性。
5.总结:对本节课的内容进行总结,强调方差的概念和计算方法。
七.说板书设计板书设计要简洁明了,能清晰地展示方差的概念,计算方法和应用。
人教版初中数学八年级下册《方差》说课稿

人教版初中数学八年级下册《方差》说课稿一. 教材分析人教版初中数学八年级下册《方差》是学生在学习了数据的收集、整理和描述的基础上,进一步研究数据的波动情况。
方差的概念和计算方法是本节课的主要内容。
通过学习方差,学生能够更好地理解数据的稳定性和平衡性,为后续的统计学习打下基础。
二. 学情分析学生在学习本节课之前,已经掌握了数据的收集、整理和描述的基本方法,能够理解平均数的含义。
但是,对方差的概念和计算方法可能比较难以理解。
因此,在教学过程中,需要注重引导学生通过实际例子来感受方差的意义,并通过逐步讲解和练习来帮助学生掌握方差的计算方法。
三. 说教学目标1.知识与技能目标:学生能够理解方差的概念,掌握方差的计算方法,并能够运用方差来分析数据的稳定性和平衡性。
2.过程与方法目标:学生通过观察实际例子,培养从实际问题中提出数学问题的能力,并通过合作交流,提高解决问题的能力。
3.情感态度与价值观目标:学生能够积极参与数学学习,培养对数学的兴趣和信心,感受数学与实际生活的联系。
四. 说教学重难点1.重点:方差的概念和计算方法。
2.难点:方差的计算方法的灵活运用。
五. 说教学方法与手段本节课采用情境教学法、引导发现法、讲练结合法等教学方法。
利用多媒体课件、实际例子、练习题等教学手段,帮助学生直观地理解方差的概念和计算方法。
六. 说教学过程1.导入:通过一个实际例子,引导学生思考数据的稳定性问题,引出方差的概念。
2.新课导入:介绍方差的概念和计算方法,通过讲解和示范,让学生理解方差的含义和计算过程。
3.实例分析:通过实际例子,让学生运用方差来分析数据的稳定性和平衡性,巩固对方差的计算方法的掌握。
4.练习与讲解:布置一些练习题,让学生独立完成,然后进行讲解和解析,帮助学生巩固方差的计算方法。
5.课堂小结:对本节课的内容进行总结,强调方差的概念和计算方法的重要性。
七. 说板书设计板书设计主要包括方差的概念、方差的计算方法和方差的运用。
新人教版八年级数学下册教案:方差

20.2 数据的波动程度第1课时方差1.掌握方差的定义和计算公式;(重点)2.会用方差公式进行计算,会比较数据的波动大小.(重点)一、情境导入在生活和生产实际中,我们除了用平均数、中位数和众数来描述一组数据的集中程度外,有时需要了解一组数据的离散程度.乒乓球的标准直径为40mm,质检部门对甲、乙两厂生产的乒乓球的直径进行检测.甲、乙两厂生产的乒乓球中各抽样调查了10只,检测的结果如下(单位:mm):甲厂:40.0,40.1,39.9,40.0,39.8,40.2,40.0,40.1,40.0,39.9;乙厂:40.1,39.8,39.9,40.3,39.8,40.2,40.1,40.2,39.7,39.9.你认为哪个厂生产的乒乓球的直径与标准的误差更小呢?二、合作探究探究点一:方差的计算【类型一】根据数据直接计算方差为了从甲、乙两名同学中选拔一个射击比赛,对他们的射击水平进行了测验,两个在相同条件下各射击10次,命中的环数如下(单位:环):甲:7,8,6,8,6,5,9,10,7,4乙:9,5,7,8,6,8,7,6,7,7(1)求x甲,x乙,s2甲,s2乙;(2)你认为该选择哪名同学参加射击比赛?为什么?解析:方差就是各变量值与其均值差的平方的平均数,根据方差公式计算即可,所以计算方差前要先算出平均数,然后再利用方差公式计算.解:(1)x甲=(7+8+6+8+6+5+9+10+7+4)÷10=7,s2甲=[(7-7)2+(8-7)2+(6-7)2+(8-7)2+(6-7)2+(5-7)2+(9-7)2+(10-7)2+(7-7)2+(4-7)2]÷10=3,x乙=(9+5+7+8+6+8+7+6+7+7)÷10=7,s2乙=[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(6-7)2+(8-7)2+(7-7)2+(6-7)2+(7-7)2+(7-7)2]÷10=1.2;(2)∵s2甲>s2乙,∴乙的成绩稳定,选择乙同学参加射击比赛.方法总结:用“先平均,再求差,然后平方,最后再平均”得到的结果就是方差.【类型二】已知原数据的方差,求新数据的方差已知数据x1,x2,x3,…,x20的平均数是2,方差是14,则数据4x1-2,4x2-2,4x3-2,…,4x20-2的平均数和方差是( )A.2,14B.4,4 C.6,14D.6,4解析:∵x=120(x1+x2+x3+…+x20)=2,x新=120(4x1-2+4x2-2+4x3-2+…+4x20-2)=6;s2=110[(x1-2)2+(x2-2)2+(x 3-2)2+…+(x 20-2)2]=14,s 24x -2=120[(4x 1-2-6)2+(4x 2-2-6)2+(4x 3-2-6)2+…+(4x 20-2-6)2]=14×16=4.故选D.方法总结:掌握数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变,平均数也加或减这个数;当乘以一个数时,方差变成这个数的平方倍,平均数也乘以这个数是本题的关键.【类型三】 根据统计图表判断方差的大小如图是2014年1~12月份某市居民消费价格指数、工业产品出厂价格指数以及原材料等购进价格指数的折线统计图.由统计图可知,三种价格指数方差最小的是( )A .居民消费价格指数B .工业产品出厂价格指数C .原材料等购进价格指数D .不能确定 解析:从折线统计图中可以明显看出居民消费价格指数的波动最小,故方差最小的是居民消费价格指数.故选A.方法总结:折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.探究点二:由方差判断数据的波动程度为了考察甲、乙两种小麦的长势,分别从中抽取10株麦苗,测得苗高如下(单位:cm):甲:12,13,14,13,10,16,13,13,15,11乙:6,9,7,12,11,16,14,16,20,19(1)将数据整理,并通过计算后把下表填全:(2)选择合适的数据代表,说明哪一种小麦长势较好.解析:(1)中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);出现次数最多的这个数即为这组数据的众数;(2)方差越小,数据越稳定,小麦长势较好.所以: (2)因为甲种小麦苗高的方差远小于乙种小麦苗高的方差,故甲种小麦苗高整齐,而两种小麦苗高的中位数和平均数相同,故甲种小麦长势较好.方法总结:平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.三、板书设计 1.方差的概念 2.方差的计算公式通过这节课的教学,让我深刻的体会到只要我们充分相信学生,给学生以最大的自主探索空间,让学生经历数学知识的探究过程,这样既能让学生自主获取数学知识与技能,而且还能让学生达到对知识的深层次理解,更主要的是能让学生在探究过程中学习科学研究的方法,从而增强学生的自主意识,培养学生的探索精神和创新思维.。
最新人教版初中八年级下册数学【教学设计】 方差

方差教学目标:1、知识与技能:了解方差的定义和计算公式。
理解方差概念的产生和形成的过程。
会用方差计算公式来比较两组数据的波动大小。
2、过程与方法:经历探索极差、方差的应用过程,体会数据波动中的极差、方差的求法时以及区别,积累统计经验。
3、情感态度与价值观:培养学生的统计意识,形成尊重事实、用数据说话的态度,认识数据处理的实际意义。
教学重点:方差产生的必要性和应用方差公式解决实际问题。
掌握其求法 教学难点:理解方差公式,应用方差对数据波动情况的比较、判断。
教学过程 一、课题引入2008年北京奥运会上,中国健儿取得了51金,21银,28铜的好成绩,位列金牌榜首位,其中,中国射击队功不可没,取得了四枚金牌如果你是教练:甲,乙两名射击手现要挑选一名射击手参加比赛.若你是教练,你认为挑选哪一位比较适宜?甲,乙两名射击手的测试成绩统计如下:第一次 第二次 第三次 第四次 第五次 甲命中环数 7 8 8 8 9 乙命中环数1061068⑴ 请分别计算两名射手的平均成绩⑵ 请根据这两名射击手的成绩在下图中画出折线统图;⑶ 现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?二、活动探究:乙x =8(环)=8(环)甲x1 2 23 4 54 6 810射击次序1.方差定义:设有n 个数据n x x x ,,, 21,各数据与它们的平均数的差的平方分别是2221)()(x x x x --,,…,,, 2)(x x n -我们用它们的平均数,即用])()()[(1222212x x x x x x nx n -++-+-=来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作2s 。
方差意义:用来衡量一批数据的波动大小在样本容量相同的情况下,方差越大,说明数据的波动越大, 越不稳定归纳总结:(1)方差应用更广泛衡量一组数据的波动大小(2)方差主要应用在平均数相等或接近时(3)方差大波动大,方差小波动小,一般选波动小的2. 因此在上一题的引入中:计算方差的步骤可概括为“先平均,后求差,平方后,再平均”.在刚才的例子中,乙选手的方差为3.2,甲选手的方差为0.4,即S 2甲< S 2乙,因此,甲选手的稳定性比较好,发挥比较稳定,在平均数相同的情况下,建议教练选甲选手参赛三、巩固提高1. 样本5、6、7、8、9、的方差是多少?2. 已知样本数据101,98,102,100,99,则这个样本的方差是( ) A 、0 B 、1 C 、 D 、23. 7,7,7,7,7的方差是多少?方差是( )4. 5、6、7、8、9、的平均数是( ) 方差是( )98,99,100,101,102的平均数是( )方差是( ) 50,60,70,80,90的平均数是( )方差是( ) 5. 3,10,15,18的平均数是( ) 方差是( )53,60,65,68的平均数是( )方差是( )150,500,750,900 的平均数是( )方差是( ) 四、小结()()()()()[]4.0898********1222222=-+-+-+-+-=甲S ()()()()()[]2.388868108681051222222=-+-+-+-+-=甲S(1)知识小结:通过这节课的学习:])()()[(1222212x x x x x x nx n -++-+-=其中,x1,x2 …xn 等代表一组数据, 代表数据的平均值,n 代表数据的个数 (2)方法小结:求一组数据方差的方法;先求平均数,再利用方差公式求方差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
20.2 数据的波动程度
第1课时方差
1.掌握方差的定义和计算公式;(重点)
2.会用方差公式进行计算,会比较数
据的波动大小.(重点)
一、情境导入
在生活和生产实际中,我们除了用平均
数、中位数和众数来描述一组数据的集中程
度外,有时需要了解一组数据的离散程度.
乒乓球的标准直径为40mm,质检部门对
甲、乙两厂生产的乒乓球的直径进行检测.
甲、乙两厂生产的乒乓球中各抽样调查
了10只,检测的结果如下(单位:mm):
甲厂:40.0,40.1,39.9,40.0,39.8,
40.2,40.0,40.1,40.0,39.9;
乙厂:40.1,39.8,39.9,40.3,39.8,
40.2,40.1,40.2,39.7,39.9.
你认为哪个厂生产的乒乓球的直径与
标准的误差更小呢?
二、合作探究
探究点一:方差的计算
【类型一】
根据数据直接计算方差
为了从甲、乙两名同学中选拔一个射击比赛,对他们的射击水平进行了测验,两个在相同条件下各射击10次,命中的环数如下(单位:环):
甲:7,8,6,8,6,5,9,10,7,4
乙:9,5,7,8,6,8,7,6,7,7
(1)求x甲,x乙,s2甲,s2乙;
(2)你认为该选择哪名同学参加射击比赛?为什么?
解析:方差就是各变量值与其均值差的平方的平均数,根据方差公式计算即可,所以计算方差前要先算出平均数,然后再利用方差公式计算.
解:(1)x甲=(7+8+6+8+6+5+9+10+7+4)÷10=7,s2甲=[(7-7)2+(8-7)2+(6-7)2+(8-7)2+(6-7)2+(5-7)2+(9-7)2+(10-7)2+(7-7)2+(4-7)2]÷10=3,x乙=(9+5+7+8+6+8+7+6+7+7)÷10=7,s2乙=[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(6-7)2+(8-7)2+(7-7)2+(6-7)2+(7-7)2+(7-7)2]÷10=1.2;
(2)∵s2甲>s2乙,∴乙的成绩稳定,选择乙同学参加射击比赛.
方法总结:用“先平均,再求差,然后平方,最后再平均”得到的结果就是方差.【类型二】已知原数据的方差,求新
数据的方差
已知数据x1,x2,x3,…,x20的平均数是2,方差是
1
4
,则数据4x1-2,4x2-2,4x3-2,…,4x20-2的平均数和方差是( )
A.2,
1
4
B.4,4 C.6,
1
4
D.6,4
解析:∵x=
1
20
(x1+x2+x3+…+x20)=2,x新=
1
20
(4x1-2+4x2-2+4x3-2+…+4x20-2)=6;s2=
1
10
[(x1-2)2+(x2-2)2+
(x 3-2)2+…+(x 20-2)2]=14,s 2
4x -2=
120[(4x 1-2-6)2
+(4x 2-2-6)2
+(4x 3-2-6)2+…+(4x 20-2-6)2
]=14×16=4.故选
D.
方法总结:掌握数据都加上一个数(或减去一个数)时,方差不变,即数据的波动情况不变,平均数也加或减这个数;当乘以一个数时,方差变成这个数的平方倍,平均数也乘以这个数是本题的关键.
【类型三】 根据统计图表判断方差的
大小
如图是2014年1~12月份某市居
民消费价格指数、工业产品出厂价格指数以及原材料等购进价格指数的折线统计图.由
统计图可知,三种价格指数方差最小的是( )
A .居民消费价格指数
B .工业产品出厂价格指数
C .原材料等购进价格指数
D .不能确定 解析:从折线统计图中可以明显看出居民消费价格指数的波动最小,故方差最小的是居民消费价格指数.故选A.
方法总结:折线图不但可以表示出数量的多少,而且能够清楚地表示出数量的增减变化情况.
探究点二:由方差判断数据的波动程度
为了考察甲、乙两种小麦的长势,
分别从中抽取10株麦苗,测得苗高如下(单位:cm):
甲:12,13,14,13,10,16,13,13,15,11
乙:6,9,7,12,11,16,14,16,20,19
(1)将数据整理,并通过计算后把下表
填全:
(2)选择合适的数据代表,说明哪一种小麦长势较好.
解析:(1)中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);出现次数最多的这个数即为这组数据的众数;(2)方差越小,数据越稳定,小麦长势较好.
所以: (2)因为甲种小麦苗高的方差远小于乙种小麦苗高的方差,故甲种小麦苗高整齐,而两种小麦苗高的中位数和平均数相同,故甲种小麦长势较好.
方法总结:平均数表示一组数据的平均程度;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数);方差是用来衡量一组数据波动大小的量.
三、板书设计 1.方差的概念 2.方差的计算公式
通过这节课的教学,让我深刻的体会到只要我们充分相信学生,给学生以最大的自主探索空间,让学生经历数学知识的探究过程,这样既能让学生自主获取数学知识与技能,而且还能让学生达到对知识的深层次理解,更主要的是能让学生在探究过程中学习科学研究的方法,从而增强学生的自主意识,培养学生的探索精神和创新思维.。
