AMC考题和答案解析

合集下载

amc试题及答案

amc试题及答案1. 问题：已知函数 $ f(x) = 3x^2 - 2x + 5 $，求 $ f(2) $ 的值。

答案：将 $ x = 2 $ 代入函数 $ f(x) $ 中，得到 $ f(2) = 3(2)^2 - 2(2) + 5 = 12 - 4 + 5 = 13 $。

2. 问题：解方程 $ 2x - 5 = 9 $。

答案：首先将方程两边同时加5，得到 $ 2x = 14 $，然后除以2，得到 $ x = 7 $。

3. 问题：如果一个圆的直径是10厘米，那么它的半径是多少？答案：圆的半径是直径的一半，所以半径 $ r = \frac{10}{2} = 5 $ 厘米。

4. 问题：计算 $ \sqrt{49} $。

答案：$ \sqrt{49} = 7 $。

5. 问题：一个班级有30名学生，其中20名是男生。

这个班级的男生比例是多少？答案：男生比例是 $ \frac{20}{30} = \frac{2}{3} $。

6. 问题：如果一个三角形的两个内角分别是 $ 45^\circ $ 和$ 60^\circ $，那么第三个角是多少度？答案：三角形的内角和为 $ 180^\circ $，所以第三个角是$ 180^\circ - 45^\circ - 60^\circ = 75^\circ $。

7. 问题：计算 $ 2^3 $。

答案：$ 2^3 = 2 \times 2 \times 2 = 8 $。

8. 问题：一个数的平方根是4，这个数是多少？答案：这个数是 $ 4^2 = 16 $。

9. 问题：如果一个数的两倍加上3等于15，求这个数。

答案：设这个数为 $ x $，那么 $ 2x + 3 = 15 $。

解这个方程，得到 $ 2x = 12 $，所以 $ x = 6 $。

10. 问题：一个长方形的长是10厘米，宽是5厘米，求它的周长。

美国数学竞赛AMC8 -- 2005年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2005年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:If x is the number, then 2x=60 and x=30. Dividing the number by 2 yields 15.中文解析：按照Connie的计算，这个数乘以2是60，可知这个数是30. 应该做的计算是30除以2，因而正确答案应该是15. 答案是B。

Problem 2Answer: CSolution:Karl paid 5*2.5=$12.5. 20% of this cost that he saved is 12.5*0.2=$2.5.中文解析：Karl按原价买了5个文件夹，支付的费用是：2.5*5=12.5. 折扣价是：1.25*0.8=10。

如果Karl 等一天，可以省2.5元。

答案是C.Problem 3Answer: DSolution:Rotating square ABCD counterclockwise 45° so that the line of symmetry BD is a vertical line makes it easier to see that 4 squares need to be colored to match its corresponding square.中文解析：如上图所示，以BD为对称轴，标蓝色的方块需要涂黑。

共4块，答案是D。

Problem 4Answer: CSolution:The perimeter of the triangle is 6.1+8.2+9.7=24cm. A square's perimeter is four times its side length, since all its side lengths are equal. If the square's perimeter is 24, the side length is24/4=6, and the area is 6*6=36.中文解析：三角形的周长是：6.1+8.2+9.7=24. 正方形的周长和三角形相等，也是24，则其边长是24/4=6. 其面积是：6*6=36. 答案是C。

amc10真题与答案解析

amc10真题与答案解析AMC10真题与答案解析美国数学竞赛（AMC）是一项极具挑战性的数学竞赛，旨在推动学生的数学学习和解决问题的能力。

其中AMC10是为中学生设计的竞赛，是很多学生展现才华并锻炼数学素养的重要机会。

本文将对一道AMC10真题进行解析，帮助读者理解和掌握解题技巧。

以下是一道来自AMC10的真题："In the xy-plane, the graph of$\log_{16}x+\log_{16}y=\tfrac{3}{2}$ is drawn. The line$y=x$ intersects the graph at points $A$ and $B$. What is the length of segment $AB$?"这道题目涉及了对数的性质和直线与曲线的交点问题。

首先，我们先来理解题目所给出的等式。

$\log_{16}x$表示以16为底的对数，可以简化为$\log_2x^4$。

同样地，$\log_{16}y$可以简化为$\log_2y^4$。

所以等式可以写为$\log_2x^4 + \log_2y^4 =\frac{3}{2}$。

我们可以将等式进一步简化为$\log_2 (x^4y^4) =\frac{3}{2}$。

根据对数的性质，我们可以将等式转化为指数形式，得到$x^4y^4 = 2^{\frac{3}{2}}$。

然后我们来解决直线$y=x$与曲线$y=x^4$的交点问题。

我们可以将$x$代入曲线方程中，得到$y=x^4$。

因此，我们可以将交点问题转化为求解以下方程组：$x^4 =x$和$x^4y^4 = 2^{\frac{3}{2}}$。

首先，我们来解原方程$x^4 = x$。

很明显，$x=0$和$x=1$是方程的两个根。

我们可以进一步分析，当$x>1$时，$x^4$的增长速度比$x$快，所以方程没有其他解。

然后，我们来解方程$x^4y^4 = 2^{\frac{3}{2}}$。

美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析：总共花的钱是：12+12*2=36元。

剩余50-36=14元。

答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析：这10个字母的对应关系是： B -0；E-1; S-2; ......K -9. 按照这个对应关系：C-8，L-6，U-7，E-1. 即8671. 答案是A。

Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析：13日是周五，则13-7=6，即6日也是周五，则倒推2月1日是周日。

答案是A。

Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析：大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。

据此，三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。

AMC考题和答案解析

2017 AMC 8 考题及答案Problem 1Which of the following values is largest?Problem 2Alicia, Brenda, and Colby were the candidates in a recent election for student president. The pie chart below shows how the votes were distributed among the three candidates. If Brenda received 36 votes, then how many votes were cast all together?Problem 3What is the value of the expression ?Problem 4When 0.000315 is multiplied by 7,928,564 the product is closest to which of the following?Problem 5What is the value of the expression ? Problem 6If the degree measures of the angles of a triangle are in the ratio , what is the degree measure of the largest angle of the triangle?Problem 7Let be a 6-digit positive integer, such as 247247, whose first three digits are the same as its last three digits taken in the same order. Which of the following numbers must also be a factor of ?Problem 8Malcolm wants to visit Isabella after school today and knows the street where she lives but doesn't know her house number. She tells him, "My house number has two digits, and exactly three of the following four statements about it are true."(1) It is prime.(2) It is even.(3) It is divisible by 7.(4) One of its digits is 9.This information allows Malcolm to determine Isabella's house number. What is its units digit?Problem 9All of Marcy's marbles are blue, red, green, or yellow. One third of her marbles are blue, one fourth of them are red, and six of them are green. What is the smallest number of yellow marbles that Marcy could have?Problem 10A box contains five cards, numbered 1, 2, 3, 4, and 5. Three cards are selected randomly without replacement from the box. What is the probability that 4 is the largest value selected?Problem 11A square-shaped floor is covered with congruent square tiles. If the total number of tiles that lie on the two diagonals is 37, how many tiles cover the floor?Problem 12The smallest positive integer greater than 1 that leaves a remainder of 1 when divided by 4, 5, and 6 lies between which of the following pairs of numbers?Problem 13Peter, Emma, and Kyler played chess with each other. Peter won 4 games and lost 2 games. Emma won 3 games and lost 3 games. If Kyler lost 3 games, how many games did he win?Problem 14Chloe and Zoe are both students in Ms. Demeanor's math class. Last night they each solved half of the problems in their homework assignment alone and then solved the other half together. Chloe had correct answers to only of the problems she solved alone, but overall of her answers were correct. Zoe had correct answers to of the problems she solved alone. What was Zoe's overall percentage of correct answers?Problem 15In the arrangement of letters and numerals below, by how many different paths can one spell AMC8? Beginning at the A in the middle, a path allows only moves from one letter to an adjacent (above, below, left, or right, but not diagonal) letter. One example of such a path is traced in the picture.Problem 16In the figure below, choose point on so that and have equal perimeters. What is the area of ?Problem 17Starting with some gold coins and some empty treasure chests, I tried to put 9 gold coins in each treasure chest, but that left 2 treasure chests empty. So instead I put 6 gold coins in each treasure chest, but then I had 3 gold coins left over. How many gold coins did I have?Problem 18In the non-convex quadrilateral shown below, is a right angle, , , , and .What is the area of quadrilateral ?Problem 19For any positive integer , the notation denotes the product of the integers through . What is the largest integer for which is a factor of the sum?Problem 20An integer between and , inclusive, is chosen at random. What is the probability that it is an odd integer whose digits are all distinct?Problem 21Suppose , , and are nonzero real numbers, and . What are the possible value(s) for ?Problem 22In the right triangle , , , and angle is a right angle. A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?Problem 23Each day for four days, Linda traveled for one hour at a speed that resulted in her traveling one mile in an integer number of minutes. Each day after the first, her speed decreased so that the number of minutes to travel one mile increased by 5 minutes over the preceding day. Each of the four days, her distance traveled was also an integer number of miles. What was the total number of miles for the four trips?Problem 24Mrs. Sanders has three grandchildren, who call her regularly. One calls her every three days, one calls her every four days, and one calls her every five days. All three called her on December 31, 2016. On how many days during the next year did she not receive a phone call from any of her grandchildren?Problem 25In the figure shown, and are line segments each of length 2, and. Arcs and are each one-sixth of a circle with radius 2. What is the area of the region shown?2017 AMC 8 Answer Key1. A2. E3. C5. B6. D7. A8. D9. D10.C11.C12.D13.B14.C15.D16.D17.C18.B19.D20.B21.A22.D23.C24.D。

AMC美国数学竞赛AMC.B 试题及答案解析

2003A M C10 B 1、Which of the following is the same asSolution2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill costSolution3、The sum of 5 consecutive even integers is less than the sum of the rst consecutive odd counting numbers. What is the smallest of the even integersSolution4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias 1.50 each, cannas 2 each, dahlias 2.50 each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her gardenSolution5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawnSolution.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the followingSolution7、The symbolism denotes the largest integer not exceeding . For example. , and . ComputeSolution.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first termSolution9、Find the value of that satisfies the equationSolution10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increasedSolution11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two linesSolution12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s original portionSolution.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of isSolution14、Given that , where both and are positive integers, find the smallest possible value for .Solution15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played isSolution16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the yearSolution.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radiusSolution18、What is the largest integer that is a divisor offor all positive even integersSolution19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicirclesSolution20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .Solution21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacementsSolution22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occurSolution23、A regular octagon has an area of one square unit. What is the area of the rectangleSolution24、The rst four terms in an arithmetic sequence are , , , and, in that order. What is the fth termSolution25、How many distinct four-digit numbers are divisible by and have as their last two digitsSolution。

AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8（美国数学竞赛）历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析：AMC8-2020年：真题 --- 答案---解析（英文解析+中文解析）AMC8 - 2019年：真题----答案----解析（英文解析+中文解析）AMC8 - 2018年：真题----答案----解析（英文解析+中文解析）AMC8 - 2017年：真题----答案----解析（英文解析+中文解析）AMC8 - 2016年：真题----答案----解析（英文解析+中文解析）AMC8 - 2015年：真题----答案----解析（英文解析+中文解析）AMC8 - 2014年：真题----答案----解析（英文解析+中文解析）AMC8 - 2013年：真题----答案----解析（英文解析+中文解析）AMC8 - 2012年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 2010年：真题----答案----解析（英文解析+中文解析）AMC8 - 2009年：真题----答案----解析（英文解析+中文解析）AMC8 - 2008年：真题----答案----解析（英文解析+中文解析）AMC8 - 2007年：真题----答案----解析（英文解析+中文解析）AMC8 - 2006年：真题----答案----解析（英文解析+中文解析）AMC8 - 2005年：真题----答案----解析（英文解析+中文解析）AMC8 - 2004年：真题----答案----解析（英文解析+中文解析）AMC8 - 2003年：真题----答案----解析（英文解析+中文解析）AMC8 - 2002年：真题----答案----解析（英文解析+中文解析）AMC8 - 2001年：真题----答案----解析（英文解析+中文解析）AMC8 - 2000年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 1998年：真题----答案----解析（英文解析+中文解析）AMC8 - 1997年：真题----答案----解析（英文解析+中文解析）AMC8 - 1996年：真题----答案----解析（英文解析+中文解析）AMC8 - 1995年：真题----答案----解析（英文解析+中文解析）AMC8 - 1994年：真题----答案----解析（英文解析+中文解析）AMC8 - 1993年：真题----答案----解析（英文解析+中文解析）AMC8 - 1992年：真题----答案----解析（英文解析+中文解析）AMC8 - 1991年：真题----答案----解析（英文解析+中文解析）AMC8 - 1990年：真题----答案----解析（英文解析+中文解析）AMC8 - 1989年：真题----答案----解析（英文解析+中文解析）AMC8 - 1988年：真题----答案----解析（英文解析+中文解析）析）AMC8 - 1986年：真题----答案----解析（英文解析+中文解析）AMC8 - 1985年：真题----答案----解析（英文解析+中文解析）◆AMC介绍◆AMC（American Mathematics Competitions) 由美国数学协会（MAA）组织的数学竞赛，分为 AMC8 、 AMC10、 AMC12 。

amc数学竞赛试题

amc数学竞赛试题 AMC数学竞赛试题是一种具有挑战性的数学竞赛，旨在激励学生对数学的兴趣和才华，并培养他们解决实际问题的能力。

AMC数学竞赛涵盖广泛的数学领域，是学生们展示数学知识和解题能力的重要场所。

AMC数学竞赛试题一般包括代数、几何、数据分析和概率等多个知识领域。

这些试题通常设计得非常巧妙，要求学生具备深入理解和分析问题的能力。

接下来，我们将通过一些典型的AMC数学竞赛试题，来了解一下其中的难点和解题思路。

首先，我们先来看一道代数题： 1. 给定实数x，如果满足方程|2x+1| + 3x = 5x，则x的值是？解析：首先我们将绝对值分成两种情况：当2x+1≥0时，|2x+1|=2x+1；当2x+1<0时，|2x+1|=-(2x+1)。

然后，我们依次将这两种情况带入原方程，进行化简，最后得到x=1/7。

接下来，我们来看一道几何题： 2. 如图，一个等边三角形内切在一个圆内，然后又在等边三角形内切一个圆，重复这样的操作无穷次。

求最后等边三角形的边长与最初等边三角形的边长的比值。

解析：设最初等边三角形的边长为a，我们可以发现不断嵌套下来，趋近于一个极限值。

假设极限值为L，那么根据相似三角形的性质，我们可以得到L=2L+a，解方程得到L=a/3。

因此，最后等边三角形的边长与最初等边三角形的边长的比值为1/3。

再来看一道数据分析题： 3. 有一组数据集{(1, 2), (2, 4), (3, 6), (4, 8), (5, 10)}，其中横坐标表示时间，纵坐标表示速度。

根据这组数据集，我们能否得到一个准确的速度-时间图像？如果能，请画出图像；如果不能，请说明原因。

解析：我们可以计算出每个点的斜率，也就是速度，发现每个点的速度都是2。

因此，这组数据集得到的速度-时间图像是一个速度恒定的水平直线。

以上只是AMC数学竞赛试题的一小部分示例，它们展示了竞赛中可能遇到的不同类型的问题。

参加AMC数学竞赛不仅可以提高学生的数学水平，还可以锻炼他们的思维能力和解决问题的能力。

美国中学数学竞赛(AMC12-12级)(附答案)

2004 AMC12 试题1. 爱丽每小时的工资为美金20元，其中的1.45%要缴地方税，试问爱丽每小时的工资中要付地方税美金多少分？(美金1元二美金100分)(A) 0.0029 (B) 0.029 (C) 0.29 (D) 2.9 (E) 292. 于AMC2的测验中，每答对一题可得6分，答错可得0分，未作答可得2.5分.假设凯琳在25题中有8题未作答，她至少要答对几题，总分才会不低于100 分？(A) 11(B) 13(C) 14(D) 16(E) 173.滿足x 2y100的正整数序对(x, y)有多少組？(A) 33(B) 49(C) 50(D) 99(E) 1004.白婆婆有6个女儿、没有儿子，有些女儿也恰有6个女儿，其他的女儿没有孩子. 白婆婆有女儿及外孙女共30位，没有外曾孙女. 试问白婆婆的女儿及外孙女中有多少位没有女儿？(A) 22 (B) 23 (C) 24 (D) 25 (E) 265.直线y mx(A) mb 1 (B) 1 mb 0 (C) mb 0 (D) 0 mb 1 (E) mb 16.设u 2 20042005, V 20042005, W 2003 20042004, X 2 20042004Y 20042004, Z 20042003.試问以下何者值最大？(A) U V (B) V W (C) W X (D) X Y (E) Y Z7. 一种代币的游戏，其规那么如下：每回持有最多代币者须分给其他每一位参与游戏者一枚代币，并放一枚代币於回收桶中；当有一位游戏参与者没有代币时，那么游戏结束.假设A、B C三人玩此游戏，在游戏开始时分别持有15、14及13枚代币.试问游戏从开始到结束，共进行了多少回？(A) 36 (B) 37 (C) 38 (D) 39 (E) 409. 有一个将花生酱装在圆桶状瓶子内出售的公司 .市场研究建议瓶子较粗时可增加销售量.假设瓶子的直径增加25%,而体积仍维持不变，那么瓶子的高度应减少百分之多少？(A) 10(B) 25(C) 36(D) 50(E) 6010. 有49个连续整数，它的和为75,則它们排在最中间的数为何？(A) 7(B) 72(C) 73(D) 74(E) 7511. 某国的硬币中有1分、5分、10分及25分四种，在保拉的皮包內硬币的平均值为20分.假设再增加一枚25分的硬币，平均值則增为 21分.試问她的皮包內有多少枚10分的硬币？(A) 0(B) 1(C) 2(D) 3(E) 412. 设A (0, 9) , B (0,12).点A 、B 在直线y x 上, 且AA 与BB 交于点 C (2,8).試问AB的长度是多少？(A) 2(B) 2 2(C) 3(D) 22(E) 3“13. 以S 表示坐标平面上所有的点(a,b)所形成的集合，其中a,b 等于1, 0,或1.試问有多少条相异的直线至少通过集合 S 中的两个点？(A) 8(B) 20(C) 24(D) 27(E) 3614. 三个实数的数列形成一个等差数列，首项是9.假设将第二项加2、第三项加20可使得这三个数变为等比数列，那么这个等比数列中第三项最小可能是多少？(A) 1(B) 4(C) 36(D) 49(E) 8115.小美与小雯在一个圆形的跑道上向相反的方向跑，开始两人分别从8.如下图EAB 及 ABC 为直角，厢 4 , BC 6 , AE 8, AC 与BE 交于D 点.試问差为多少？(A) 2(B) 4(C) 5 (D) 8 (E) 9ADE 与BDC 面积之圆形跑道直径的两端起跑.小美跑了 100公尺时她们第一次相遇；在第一次相遇后小雯跑了 150公尺时她们第二次相遇.假设她们跑的速度都分别维持固定不变，试问此圆形跑道的长度是多少公尺？(A) 250(B) 300(C) 350(D) 400(E) 50016.使函数 log 2004{log 2003{log 2002{log 2001 X}}}有定义的集合为之值是多少？(A) 0(B) 20012002(C) 20022003(D) 20032004{xx c}.試问 c(E) 20012°°丹317.函数f 满足以下性质： (i) f(1) 1,且(ii)对任意的正整数n ,f(2n) n f(n).试问f(2100)之值为何？(A) 1(B) 299(C) 2100(D) 24950 18.如下图，ABCD 是边长2的正方形.在正方形的内部作一个以AB 为直径的半圆，且自C 点引此半圆的切线交AD 边于E 点•试问CE 的长度是多少？(E) 5 ■.5(E) 29999(B) 5 (C) 6 (D)?19.如下图，A B C 三圆彼此外切且均内切于圆等，圆A 的半径1且通过圆D 的圆心.试问圆B 的半径是多少?D.B 、C 两圆相(A)3(B)于(C) 土 (D) |20.从0与1之间的数，随机独立取出两实数a 与b,并将a, b 之和记作c.分别以A, B, C 表示最接近a, b, c 的整数.试问的机率为何？(A) 1(B) !(C) 1(D) 2(E) 443 23421.假设n 02nCOS5,那么Cos2之值是多少？(A) 15 (B) I (C) ±55(D) ?(E)上5522.三个半径为1的球彼此外切且放置在一水平面上，一个半径为2 的大球放在它们的上面 .试问大球的最高点至平面的距离是多少？C 2004 0,且 P (x)=0 有 2004个复数根 z a k b k i , 20042004b k 为实数，a ib i 0,且a kb k .k 1k 1试问以下哪一项可能不是 0 ?2004(A) C 0(B)C2003(C) b z b s L b s 004 (D)a kk 124. 设A 、B 为平面上的两点，其中AB 1.令S 为平面上所有半径是1且能盖住线段AB 之圆的并集，則S 的面积是多少？(A) 2.3(B) -(C) 33(D)卫 3(E) 4 2 33 2325. 对每一个整数n 4,令a n 表示n 进位的循环小数0.133n .把乘积a 4a 5L a 99写成—的形式，其中m P 为正整数，且p 尽可能小.试问mp!之值是多少？(A) 98(B) 101(C) 132(D) 798(E) 962Q屈o J123 52(A) 3(B) 3 -(C) 3 -(D)2349(E) 3 2、223.多项式P(x) GX C 0 ,的系数都是实数, 1 k 2004,其中 a k ,2004(E)C kk 12004C 2004X 2003C 2003XL答案:1 ( E )2 ( C )3 ( B )4 ( E )5 ( B )6 ( A )7 ( B )8 ( B )9 ( C )10 ( C ) 11 ( A )12 ( B )13 ( B )14 ( A )15 ( C ) 16 ( B )17 ( D )18 ( D )19 ( D )20( E ) 21 ( D )22 ( B )23 ( E )24 ( C )25 ( E )。

美国数学竞赛AMC8 -- 2006年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2006年真题解析(英文解析+中文解析) \Problem 1Answer: DSolution:The three prices round to $2, $5, and $10, which has a sum of 17.中文解析：三件商品价格先近似取整，然后求和：2+5+10=17. 答案是D。

Problem 2Answer: CSolution:As the AMC 8 only rewards 1 point for each correct answer, everything is irrelevant except the number Billy answered correctly，13.中文解析：正确的题目每题1分，错误或没做的题目都是0分，做对13题的得分应该是13. 答案是C。

Problem 3Answer: ASolution:When Elisa started, she finished a lap in 25/10=2.5 minutes. Now, she finishes a lap is 24/12=2 minutes. The difference is 2.5-2=0.5中文解析：开始25分钟游10圈，平均2.5分钟游1圈。

后来24分钟游12圈，平均2分钟游1圈。

速度从2.5分钟提高到2分钟，提高了0.5分钟，即1/2 分钟。

答案是A。

Problem 4Answer: BSolution:If the spinner goes clockwise 2+1/4 revolutions and then counterclockwise 3+3/4 revolutions, it ultimately goes counterclockwise 1+1/2 which brings the spinner pointing east.中文解析：最初方向指向西，转整数圈不改变指针方向。

AMC10的真题答案及中文翻译

AMC10的真题答案及中文翻译
1、一张展览票原价为20美元。

Susan使用优惠券购买4张票，享受75折优惠。

Pam使用优惠券购买5张票，享受7折优惠。

Pam比Susan多花了多少美元？
2、一个养鱼缸的底部为矩形，长100cm，宽40cm，高50cm。

水位高度为40cm。

将一个底部为矩形，长40cm，宽20cm，高10cm的砖块放入缸中。

水位上升了多少厘米？
3、两个连续的奇数中，较大的数是较小的数的3倍。

它们的和是多少？
4、一个学校商店售卖7支铅笔和8个笔记本需要4.15美元，售卖5支铅笔和3个笔记本需要1.77美元。

那么16支铅笔和10个笔记本需要多少钱？
5、Euclid高中在2002年有60名学生参加AMC10，在2003年有66名，2004年有70名，2005年有76名，2006年有78名，2007年有85名。

在相邻的哪两年中人数增长的百分率最大？
6、去年，John Q. Public先生继承了一笔遗产。

他需要支付20%的联邦税和剩下的部分中10%的州税。

他需要支付美元的总税费。

这笔遗产有多少美元？
答案：(C) 美元
有多少个正整数对(m, n)，满足m > n且它们的平方差是96？。

amc8历年真题答案解析

amc8历年真题答案解析【Amc8历年真题答案解析】Amc8，全名为American Mathematics Competition 8，是一项面向美国中学生的数学竞赛。

每年11月份举行的Amc8竞赛，旨在通过一系列挑战性的数学问题，培养学生的数学思维能力、创造力和解决问题的能力。

以下是Amc8历年真题的答案解析。

一、2000年真题：1. 答案：C解析：问题要求选择一个在100和999之间的正整数，满足各个数字的平方和等于该数本身。

首先明确数字的范围是100到999，因此只需要考虑三位数。

假设一个三位数为$abc$，那么它满足条件$a^2+b^2+c^2=abc$。

考虑到$a,b,c$的范围在1到9之间，可以通过穷举法逐个尝试。

当$a=2$时，$b=5$和$c=1$，满足条件$2^2+5^2+1^2=251$，因此答案为C。

2. 答案：D解析：问题给出了一个小测试，Tom回答7道题目，其中4道题回答正确。

考虑到每道问题只有两个选择（正确或错误），因此回答7道题目的所有可能性为$2^7=128$。

在这些可能性中，只有一种情况Tom回答了4道题目正确，因此答案为D。

3. 答案：A解析：问题给出了一个图形，包含了一系列长方形。

我们需要计算图形中所有（不重叠）长方形的个数。

首先考虑长方形最小边长为1的情况，可以在图形中找到4个这样的长方形。

然后考虑最小边长为2的情况，可以找到3个长方形。

以此类推，最小边长为3、4、5的情况下，分别可以找到2个、1个、0个长方形。

因此，总共可以找到的长方形个数为$4+3+2+1=10$，答案为A。

4. 答案：C解析：问题给出了一个5乘5的正方形网格，要求从左上角走到右下角，只能向右或向下移动，且不能重复经过同一格。

我们需要计算从左上角到右下角有几条路径。

可以发现，从左上角到右下角，一共需要移动4次向右，4次向下。

因此可以将问题转化为在8个移动中选择4个向右，即$C_8^4=\frac{8!}{4!4!}=70$，答案为C。

AMC12真题和答案解析

AMC12真题和答案解析AMC12，即美国数学竞赛12级，是美国数学协会(American Mathematical Society)举办的一项年度竞赛，旨在选拔优秀的数学学生并促进数学学科的发展。

对于许多对数学有着浓厚兴趣的学子来说，AMC12是一次考验自己数学能力和解题能力的机会。

在AMC12中，每年都会发布一套面向高中生的真题。

这些真题是经过一系列筛选和验证的，确保其具有一定的难度和挑战性。

以下将对一些AMC12真题进行解析，帮助解题过程中可能出现的疑惑。

首先，我们来看一个经典的AMC12真题：问题：在坐标平面上，点A和点B的坐标分别为(2,3)和(4,5)。

如果通过点C(0,k)且垂直于线段AB的直线将线段AB分成两段长度相等的线段，求k的值。

解析：首先，我们可以计算出线段AB的长度为$\sqrt{(4-2)^2+(5-3)^2} = \sqrt{8} = 2\sqrt{2}$。

然后，我们知道通过两点之间的直线的斜率等于这条直线与任一直线垂直的直线的斜率的相反数。

因此，线段AB的直线的斜率为$\frac{5-3}{4-2}=\frac{1}{2}$。

而垂直于直线斜率为$\frac{-2}{1}$的直线的斜率为2。

由此可得直线的斜率为-2。

因为直线过点C(0,k)，可以利用斜截式方程$y=mx+b$来求解。

代入坐标C的值得到$k=2$。

因此，答案为k=2。

接下来，我们再来看一个稍微更复杂一点的问题：问题：给定方程$x^2+3x+2 < 0$，求解x的取值范围。

解析：这是一个关于二次函数的不等式。

我们可以将方程转化为$x^2+3x+2=0$，并求解出方程的根。

通过求解得知$x=-1$和$x=-2$。

因为不等式中的不等号是小于号，因此我们需要找出二次函数的凹凸性。

由于二次函数的系数a大于0，因此它开口朝上，表明当x小于-2或者大于-1时，不等式成立。

因此，x的取值范围为$(-\infty,-2)\cup(-1,\infty)$。

AMC美国数学竞赛AMC.B 试题及答案解析

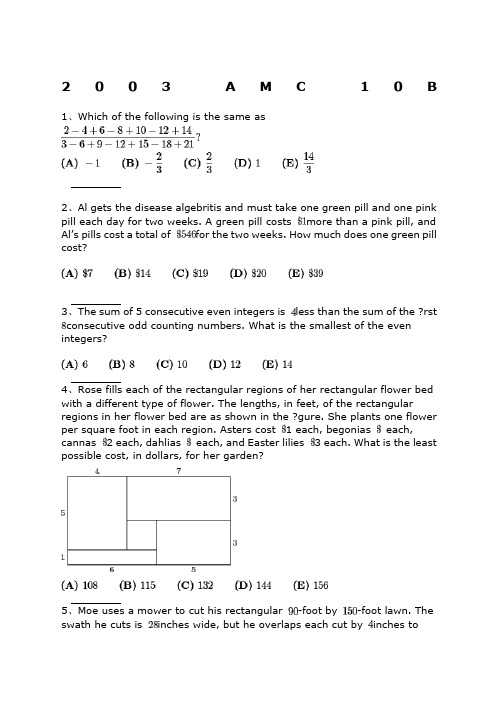
2003A M C10 B 1、Which of the following is the same as2、Al gets the disease algebritis and must take one green pill and one pink pill each day for two weeks. A green pill costs more than a pink pill, and Al’s pills cost a total of for the two weeks. How much does one green pill cost?3、The sum of 5 consecutive even integers is less than the sum of the ?rst consecutive odd counting numbers. What is the smallest of the even integers?4、Rose fills each of the rectangular regions of her rectangular flower bed with a different type of flower. The lengths, in feet, of the rectangular regions in her flower bed are as shown in the ?gure. She plants one flower per square foot in each region. Asters cost 1 each, begonias each, cannas 2 each, dahlias each, and Easter lilies 3 each. What is the least possible cost, in dollars, for her garden?5、Moe uses a mower to cut his rectangular -foot by -foot lawn. The swath he cuts is inches wide, but he overlaps each cut by inches tomake sure that no grass is missed. He walks at the rate of feet per hour while pushing the mower. Which of the following is closest to the number of hours it will take Moe to mow his lawn?.6、Many television screens are rectangles that are measured by the length of their diagonals. The ratio of the horizontal length to the height in a standard television screen is . The horizontal length of a “-inch” television screen is closest, in inches, to which of the following?7、The symbolism denotes the largest integer not exceeding . For example. , and . Compute.8、The second and fourth terms of a geometric sequence are and . Which of the following is a possible first term?9、Find the value of that satisfies the equation10、Nebraska, the home of the AMC, changed its license plate scheme. Each old license plate consisted of a letter followed by four digits. Each new license plate consists of three letters followed by three digits. By how many times is the number of possible license plates increased?11、A line with slope intersects a line with slope at the point . What is the distance between the -intercepts of these two lines?12、Al, Betty, and Clare split among them to be invested in different ways. Each begins with a different amount. At the end of one year they have a total of . Betty and Clare have both doubled their money, whereas Al has managed to lose . What was Al’s origin al portion?.13、Let denote the sum of the digits of the positive integer . For example, and . For how many two-digit values of is ?14、Given that , where both and are positive integers, find the smallest possible value for .15、There are players in a singles tennis tournament. The tournament is single elimination, meaning that a player who loses a match is eliminated. In the first round, the strongest players are given a bye, and the remaining players are paired off to play. After each round, the remaining players play in the next round. The match continues until only one player remains unbeaten. The total number of matches played is16、A restaurant offers three desserts, and exactly twice as many appetizers as main courses. A dinner consists of an appetizer, a main course, and a dessert. What is the least number of main courses that the restaurant should offer so that a customer could have a different dinner each night in the year ?.17、An ice cream cone consists of a sphere of vanilla ice cream and a right circular cone that has the same diameter as the sphere. If the ice cream melts, it will exactly ?ll the cone. Assume that the melted ice cream occupies of the volume of the frozen ice cream. What is the ratio of the cone’s height to its radius?18、What is the largest integer that is a divisor offor all positive even integers ?19、Three semicircles of radius are constructed on diameter of a semicircle of radius . The centers of the small semicircles divide into four line segments of equal length, as shown. What is the area of the shaded region that lies within the large semicircle but outside the smaller semicircles?20、In rectangle , and . Points and are on so that and . Lines and intersect at . Find the area of .21、A bag contains two red beads and two green beads. You reach into the bag and pull out a bead, replacing it with a red bead regardless of the color you pulled out. What is the probability that all beads in the bag are red after three such replacements?22、A clock chimes once at minutes past each hour and chimes on the hour according to the hour. For example, at 1 PM there is one chime and at noon and midnight there are twelve chimes. Starting at 11:15 AM on February , , on what date will the chime occur?23、A regular octagon has an area of one square unit. What is the area of the rectangle ?24、The ?rst four terms in an arithmetic sequence are , , , and, in that order. What is the ?fth term?25、How many distinct four-digit numbers are divisible by and have as their last two digits?。

amc 试卷解析 2023

amc 试卷解析2023一、选择题（每题5分，共25分）已知a 和 b 是两个整数，满足a^2 = b^2 + 28，则 a 和 b 的和的最小可能值为：A. 4B. 6C. 8D. 10E. 12三角形ABC中，AB = 5，AC = 12，BC = 13，则三角形ABC的面积是：A. 15B. 30C. 45D. 60E. 78函数f(x) = 2x^3 - 3x^2 + 5 在x = 1 处的切线斜率为：A. 2B. 4C. 7D. 11E. 13在一个四位数中，千位和百位上的数字之和等于十位和个位上的数字之和。

这样的四位数有多少个？A. 900B. 1800C. 2700D. 3600E. 4500已知数列{a_n} 满足a_1 = 1，a_{n+1} = a_n + 1/a_n，则a_5 的值为：A. 1 + √2B. 2 + √3C. 2 + √5D. 3 + √6E. 3 + √8二、填空题（每题5分，共25分）在平面直角坐标系中，点P(x, y) 到直线Ax + By + C = 0 的距离公式为 d = |Ax + By + C| / √(A^2 + B^2)。

利用此公式，点(2, 3) 到直线3x - 4y + 5 = 0 的距离是_______。

在等差数列{a_n} 中，已知a_1 + a_3 + a_5 = 21，则a_2 + a_4 = _______。

若x 和y 满足方程x^2 + y^2 - 4x + 6y + 12 = 0，则x^2 + y^2 的最小值为_______。

函数y = x^3 - 3x^2 + 2 在区间[-1, 4] 上的最大值为_______。

已知圆C: x^2 + y^2 = 4 和点P(4, 0)，则过点P 且与圆 C 相切的直线的方程为_______。

三、解答题（每题15分，共60分）求证：对于任意正实数 a 和b，都有√(a^2 + b^2) ≥ a + b - √(2ab)。

amc历年试题

AMC试题1. 问题：如果一个正方形的边长是(x + 3)，面积是(x^2 + 10x + 21)，那么(x) 的值是多少？答案：(x = 4)2. 问题：一个三角形有两边长分别为5 和7，这两边的夹角为(60^circ)。

求这个三角形的面积。

答案：面积(= frac{1}{2} times 5 times 7 times sin 60^circ = frac{35sqrt{3}}{4})3. 问题：一个数列的前两项是1 和2，从第三项开始，每一项都是前两项的和。

这个数列的第10 项是多少？答案：第10 项是89（这是一个斐波那契数列）4. 问题：在一个圆内接四边形中，相对的两角之和是多少度？答案：(180^circ)5. 问题：已知(x^2 - 5x + 6 = 0)，求(x^3 - 14x + 24) 的值。

答案：(x^3 - 14x + 24 = (x - 2)(x^2 - 5x + 6) + 12 = 12)（因为(x^2 - 5x + 6 = 0)）6. 问题：一个长方体的三个边长分别为3, 4, 5，求这个长方体的对角线长度。

答案：对角线长度(= sqrt{3^2 + 4^2 + 5^2} = 5sqrt{2})（注意：这不是直角三角形，但对角线仍用三维空间中的距离公式计算）7. 问题：有一个8x8 的国际象棋棋盘，去掉两个相对的角上的方格，问能否用1x2 的多米诺骨牌完全覆盖剩下的方格？答案：不能。

因为去掉两个角后，剩下62 个方格，而每个多米诺骨牌覆盖 2 个方格，所以不可能完全覆盖。

8. 问题：一个正方形的面积是100，如果这个正方形的边长增加了一定的长度，面积变成了121，那么这个长度是多少？答案：原来的边长是10，新的边长是11，所以增加的长度是1。

9. 问题：一个圆的半径是(r)，如果这个圆的半径增加到(2r)，那么这个圆的面积会增加多少倍？答案：原来的面积是(pi r^2)，新的面积是(4pi r^2)，所以面积增加了 4 倍。

amc999990数学竞赛试题

amc999990数学竞赛试题题目一：数列求和问题（200字）某数列的通项公式为An = 2n - 1，求该数列的前n项和Sn。

解析：数列的通项公式An = 2n - 1 表示每一项都比前一项大2，首项为1，公差为2的等差数列。

我们可以利用数列求和公式来求解Sn。

数列求和公式为Sn = (a1 + an) * n / 2，其中a1为首项，an为末项，n为项数。

题目二：函数图像分析问题（200字）已知函数f(x) = x^2 + 2x + 1，求函数的图像在坐标平面内的顶点、对称轴和轴对称点。

解析：函数的顶点即为函数对应的抛物线的顶点，对应的x坐标可通过公式x = -b / (2a) 求解，其中a为二次项系数，b为一次项系数。

对称轴为通过顶点的直线，轴对称点为通过对称轴与抛物线相交的点。

题目三：概率问题（200字）一桶里有5只红球和3只蓝球，从桶中随机抽取2只球。

求抽出的两只球一红一蓝的概率是多少？解析：根据题意，总共有8只球，抽取两只球的所有可能情况为C(8,2) = 28种。

其中，抽出的两只球一红一蓝的情况为C(5,1) * C(3,1) = 15种。

所以，抽出的两只球一红一蓝的概率为15/28。

题目四：几何问题（200字）已知一个三角形ABC，AB = 3 cm，AC = 4 cm，BC = 5 cm，求三角形ABC的面积。

解析：根据已知条件，可以通过海伦公式来计算三角形的面积，海伦公式为S = √(p * (p - a) *(p - b) * (p - c))，其中p为半周长，a、b、c分别为三角形的三边长。

可以计算得到p = (3 + 4 + 5)/2 = 6。

带入公式计算，得到S = √(6*(6-3)*(6-4)*(6-5)) = √(6*3*2*1) = √36 = 6 cm²。

以上给出了四道题目的详细解答，希望能对您的数学学习有所帮助。

如有其他疑问，欢迎提问。

美国数学竞赛AMC8 -- 2019年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 -- 2019年真题解析（英文解析+中文解析）Problem 1Answer: DSolution:We maximize the number of sandwiches Mike and Ike can buy by finding the lowest multiple of 4.5 that is less than 30 This number is 6.Therefore, they can buy 6 sandwiches for 4.5*6=27. They spend the remaining money on soft drinks, so they buy30-27=3 soft drinks. Combining the items, Mike and Ike buy 6+3=9 items.中文解析：4.5*6=27. 因此买6个Sandwiches，剩下的3元钱买3个Drinks.Problem 2Answer: ESolution:Using the diagram we find that the larger side of the small rectangle is 2 times the length of the smaller side. Therefore the longer side is 5*2=10. So the area of the identical rectangles is5*10=50. We have 3 identical rectangles that form the large rectangle. Therefore the area of the large rectangle is 50*3=150.中文解析：长方形的短边的长度是5，则AD=5+5=10. CD=AD=10. 即长方形的长边是10. ABCD的面积是: AB *BC =(10+5)*10=150.答案是E。