波的叠加,干涉,驻波(精选)
4.波的干涉_驻波
三、驻波能量:
⒈动能:
当各质点同时到达平衡位置时: 介质无形变,势能为零,此时驻波能量为动能。 波腹处动能最大,驻波能量集中在波腹附近。
⒉势能:
当各质点同时到达最大位移时: 动能为零,此时驻波能量为势能。 波节处形变最大,势能最大,能量集中在波节附近。
⒊结论:
动能、势能不断在波腹附近和波节附近间相互转 换,能量交替传递,无定向传播。
2 x 波腹位置: cos(2 ) 1 相邻两波腹距离 10 20 0 x x k , k 0,1,2 2 2
相邻两波节距离 x
各点相位:
y 2 A cos(2
x
) cos(2 t )
各质点作振幅为 2 A cos(2
cos(2
相位跃变(半波损失)
波 疏 介 质
波 密 介 质 较 大
u
较 小
u
当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失.
π
当波从波密介ቤተ መጻሕፍቲ ባይዱ垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
同一直线上沿相反方向传播时叠加而形成的一种特殊
的干涉现象.
驻波的形成
特征:
1、波形不移动。 2、各质点以不同的振幅在各自的平衡位置附近振动。
3、分段振动:振幅最大的点为波腹,
振幅为零的点为波节。
二、驻波方程:
沿X 轴正、负向传播的两列平面简谐波的波动方程为: x 在任意点 x 处叠加, y1 A cos 2 ( t ) 合位移: x y y1 y2 y 2 A cos 2 ( t ) x 2 A cos(2 ) cos(2 t ) ( 设初相 10 20 0)
波的叠加-干涉-驻波

1.合成振幅公式
质点同步参加同方向同频率旳谐振动
合振动 :
两种特殊情况
两分振动相互加强。
A
若 A1=A2 , 则 A=0 。
两分振动相互减弱。
A
(1)相长与相消干涉
2.波程差体现式
波程差为零或为波长旳整数倍时,各质点旳振幅最大,干涉相长。
波程差为半波长旳奇数倍时,各质点旳振幅最小,干涉相消。
二、波旳叠加原理
当两列波同步在同一介质中传播时,在它们相遇旳区域内,每点旳振动是各列波单独在该点产生旳振动旳合成。
看动画
波旳叠加原理
三、波的干涉
波旳干涉是在特定条件下波叠加所产生旳现象。
它们发出旳波列在媒质中相遇叠加时,某些质点旳振动一直加强,某些质点旳振动一直减弱或完全相消。这种现象称为波旳干涉。
Байду номын сангаас
有半波损失
固定端反射总是出现波节
自由端反射总是出现波腹
无半波损失
有半波损失
无半波损失
有半波损失
半波损失
1.在驻波中,两个相邻波节间各质点旳振动 (A) 振幅相同,相位相同. (B) 振幅不同,相位相同. (C) 振幅相同,相位不同. (D) 振幅不同,相位不同.
(1)驻波旳相位特点
相位、能量特点
(2)驻波旳能量特点
驻波旳能量不作定向传播,其能量转移过程是动能与势能旳相互转移以及波腹与波节之间旳能量转移。
由波密媒质入射在波疏媒质界面上反射,在界面处,反射波旳振动相位总是与入射波旳振动相位相同,形成驻波时,总是出现波腹。
无“半波损失”。
4. 反、入射产生驻波与“半波损失”
答案B
答案 D
答案B
答案C
波的干涉实践了解波的叠加和干涉现象

波的干涉实践了解波的叠加和干涉现象波的干涉实践:了解波的叠加和干涉现象波的干涉是波动学中一个重要的现象,它揭示了波的叠加和干涉现象。
在实践中,通过观察和实验,我们可以更深入地了解这个有趣的现象。
本文将介绍波的干涉的基本原理、实验装置和实验步骤,并通过实践的方式帮助读者更好地理解波的叠加和干涉现象。
一、波的干涉原理波动是物质能量的传播方式,波的干涉是指两个或多个波在空间重叠时产生的各种干涉现象。
波的干涉可以分为构成干涉的两个波源的相位关系是否相同来分类,分别为相干干涉和非相干干涉。
相干干涉指的是两个或多个波源的相位关系固定,它们的波峰和波谷能够完全或部分重叠,形成明暗相间的干涉图样。
这种干涉图样可以通过叠加原理解释,即波的振幅叠加。
非相干干涉指的是两个或多个波源的相位关系不固定,它们的波峰和波谷在时域和空域上交替出现,不能形成干涉图样。
干涉现象在不同波动现象中都存在,比如光的干涉、声音的干涉等。
在实践中,我们可以通过实验来观察和研究波的干涉现象。
二、波的叠加和干涉实验装置为了观察和研究波的叠加和干涉现象,我们可以利用实验装置来模拟和观测。
下面是一个简单的波的叠加和干涉实验装置:1. 光源:可以使用激光器、白光灯等作为光源,确保光线稳定和均匀。
2. 双缝装置:将一块带有两个狭缝的物体放置在光源后,调整狭缝的宽度和间距。
3. 屏幕:在双缝装置的后方放置一个屏幕,用于接收干涉图样。
4. 干涉图样观测装置:可以使用显微镜或相机等设备来观察干涉图样。
三、波的叠加和干涉实验步骤以下是进行波的叠加和干涉实验的基本步骤:1. 准备工作:确保实验装置和环境的稳定性,调整光源和双缝装置的位置和角度。
2. 调节狭缝:根据实验要求,调整双缝装置的宽度和间距,一般情况下,宽度应小于波长,间距应略大于波长。
3. 观察干涉图样:打开光源,将屏幕放置在双缝装置的后方,调整屏幕位置和焦距,使用干涉图样观测装置来观察干涉图样。
4. 分析干涉图样:观察干涉图样中的明暗条纹,分析波的叠加和干涉现象。
普通物理学-力学-波的叠加、干涉、驻波

AP AB2 BP 2 (15)2 (20)2 25(m)
已知 v P 20m
= 100 Hz ,u = 10 m· s-1
u
10 则波长为 0.10(m) 100
A
15m
B
由题知,两波反相位,设 A 的相位较 B 超前, 则二者的初相差为
GL.普物-力学-Ch.10-波动 4 13
Δ ( x ) x - 14
由干涉静止条件,有
Δ ( x ) x - 14 (2k 1) , (k 0, 1, 2, ) xk - 14 (2k 1) xk 2k 15 , k 0, 1, 2, . 0 x L
求:AB 连线上因相干涉而静止的各点的位臵
u 4 (m)
解:取 A 点为坐标原点, A、B 连线为 X轴, 如图
B P X o L x (1)两相干波在B 点外侧任意P点处(即 x>L)的相位差为 A 波长为
=u/υ=4(m)
L=30m
L Δ B - A ( x - L) - x 2 16 4
则 AB 连线段上因干涉而静止的各点的位臵为
x 1, 3, 5, 7, 9,
GL.普物-力学-Ch.10-波动 4
, 25, 27, 29 (m)
14
例 2: 如图,A、B 两点为某均匀介质中振福相等的相干波源,频率
为100 Hz,波速为10 m.s-1,已知点 A 为波峰时 B 为波谷,
求:A, B 发出的两列波传到 P 点时干涉的结果
GL.普物-力学-Ch.10-波动 4 26
(3)驻波中各点处质元的相位关系
波的叠加原理.

返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
波节
返回
驻波
波腹
x l
cos
2π
t T
振幅
A´ =
2Acos2π
x l
结束 返回
振幅:
A´ =
2Acos2π
x l
波腹位置:
2π
x l
=
2k
π
2
波节位置:
2π
x l
=( 2k+1)π2
x
=2k
l 4
x =(2k+1)l4
相邻两波节(或波腹)的距离:
x k+1
x
k
=
l
2
结束 返回
驻波
波腹
波节
结束 返回
驻波
波腹
波节
结束 返回
二、波的干涉
相干波源:若有两个波源,它们的振动
方向相同、频率相同、周相差恒定,称这两
波的干涉 驻波解读

当波从波疏介质垂直入射到波密介 质, 被反射到波疏介质时形成波节. 入 射波与反射波在此处的相位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半 波损失.
当波从波密介质垂直入射到波疏介质, 被反射到波密介质 时形成波腹. 入射波与反射波在此处的相位时时相同,即反射 波在分界处不产生相位跃变,没有半波损失。
P点的合振动为
y y1 y2 A cos(t )
其中
2 A A12 A2 2 A1 A2 cos
其中两个分振动的相位差为
(1 2 )
2π( r2 r1 )
1 2 的值是由波源决定的,且对空间各点 由于 此值都相同,故可令其为零,从而有
驻波相邻的波节和波腹之间的λ/4区域实际上构成一个独立的 振动体系,它与外界不交换能量,能量只在相邻波节和波腹之间 流动.
四、半波损失
在两种介质的分界处形成波节还是波腹是由介质的密度和 波速u 的乘积决定的。 对于波沿分界面垂直入射的情形,把密度 与波速u的乘积u 较大的介质称为波密介质,较小的介质称为波疏介质。
*
波源振动
y10 A10 cos(t 1 )
y20 A20 cos(t 2 )
P
P点的两个分振动
y1 A1 cos(t 1 2 π )
r2 y2 A2 cos(t 2 2π )
r1
P点的合振动为
y y1 y2 A cos(t )
§4 波的叠加、干涉 和 驻波 一、波的叠加原理
1 波传播的独立性 实验表明,几列波同时通过同一介质时,它们各自保持 自己的频率、波长、振幅和振动方向等特点不变,彼此互 不影响,这称为波传播的独立性. 2 波的叠加原理 在几列波相遇的区域内,任一质元的位移等于各列波单独 传播时所引起的该质元的位移的矢量和,这称为波的叠加原理.
11-6 波的叠加原理 波的干涉 驻波
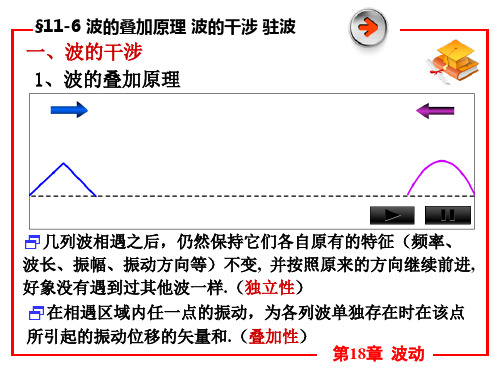
2π r1
λ
A = A + A + 2 A1 A2 cos ∆ ϕ r2 − r1 ∆ϕ = ϕ 2 − ϕ1 − 2π 常量 第18章 波动 章 λ
§11-6 波的叠加原理 波的干涉 驻波 11-
讨论
A + A + 2 A1 A2 cos ∆ϕ r2 − r1 ∆ϕ = ϕ 2 − ϕ1 − 2π λ A=
§11-6 波的叠加原理 波的干涉 驻波 11-
y = 2 A cos2π cos2π ν t
例 x=±
x
λ
4
λ
−
λ
2
−
y
λ
4
λ 3λ
2 4
为波节
o λ
4
x
< x < , y = 2 A cos 2 π x cos 2π ν t 4 4 λ λ x λ 3λ x cos2π < 0, < x < , y = 2 Acos2 π cos(2 π ν t +π ) 4 4 λ λ
( k = 0,1,⋯ ) Amin = 0 波节 相邻波腹和波节 相邻波腹 波腹(节 间距 相邻波腹 节)间距 = λ 2 ;相邻波腹和波节间距= λ 4
第18章 波动 章
2 λ x = ± (2 k + 1) 4
x = ±k
λ
( k = 0,1,⋯ )
Amax = 2 A
波腹
2)相邻两波节之间质点振动同相位,任一波节 )相邻两波节之间质点振动同相位, 两侧振动相位相反, 波节处产生 两侧振动相位相反,在波节处产生 π 的相位跃变 . 与行波不同,无相位的传播) (与行波不同,无相位的传播).
第18章 波动 章
波的叠加干涉驻波

要点二
详细描述
光波的叠加干涉驻波通常发生在两束相干光相遇时。当两 束光的频率相同、相位差恒定时,它们会在空间中形成稳 定的驻波。与声波的叠加干涉驻波类似,光波的叠加干涉 驻波也会产生明暗相间的干涉条纹。这些条纹的位置和间 距取决于光波的波长和相遇点的位置。在光学实验中,光 波的叠加干涉驻波被广泛应用于测量光波的相位和振幅。
波的叠加干涉驻波
目
CONTENCT
录
• 波的叠加原理 • 干涉现象 • 驻波的形成与特点 • 波的叠加干涉驻波实例分析 • 总结与思考
01
波的叠加原理
波的独立传播
01
波在传播过程中不受其他波的影 响,各自独立传播。
02
波的独立传播特性使得多个波可 以在同一介质中同时传播,而不 互相干扰。
波的线性叠加
对未来研究的展望
深入探索机制
进一步深入探索波的叠加干涉驻波机制,研究不同类型波 的叠加和干涉规律,以及驻波的形成条件和特性。
扩展应用领域
将波的叠加干涉驻波理论应用于更广泛的领域,如生物医 学、环境监测和地球物理学等,发掘其在这些领域的应用 潜力。
创新研究方法
发展新的研究方法和手段,利用现代科技手段对波的叠加 干涉驻波进行更精确的观测和实验验证,提高研究的可靠 性和精确度。
02
干涉现象
干涉的形成
波源
两个或多个波源产生相同频率的波。
传播路径
波在传播过程中相遇。
叠加区域
波在叠加区域相互作用。
干涉的条件
02
01
03
频率相同
两个波源产生的波频率必须相同。
有恒定的相位差
两个波在相遇时必须有恒定的相位差。
稳定的振动系统
波的叠加和干涉驻波

上页 下页 返回 结束
第十章 波动和声
相邻波腹的坐标
xi
i
2
xi 1
i
1
2
代入驻波方程中
y (2Acos 2π x)cos t
中得
yi (2Acos iπ)cos t
yi1 [2Acos(i 1)π]cos t
(2Acos iπ)cos( t π)
相邻两波腹的相位相反.
上页 下页 返回 结束
3. 强度计算
设有两个频率相同的波源S1和S2
其振动表达式为
y10 A10 cos(t 1 ) S2
r2
p
y20 A20 cos(t 2 )
传播到 P 点引起的振动为:
S1
r1
y1 A1 cos(t kr1 1 )
y2 A2 cos(t kr2 2 )
在P点的振动为
y y1 y2 Acos(t )
振幅因子 谐振因子
k 2π
y (2Acos 2π x)cos t
(1)驻波是各点振幅不同的简谐振动的集体
上页 下页 返回 结束
第十章 波动和声
波腹—— 振幅取最大值.
2Acos 2π x 2A
x i
2
i 0,1,2,
波节—— 振幅为零. 波节处的质元静止不动.
2 Acos 2π x 0
第十章 波动和声 (2) 相位特点
两相邻波节之间的各质元振动相位相同,每 一波节两侧各质元的振动相位相反. 在驻波中却没有能量的定向传递.
上页 下页 返回 结束
第十章 波动和声
3. 定量计算
设
y1 y2
A cos A cos
t t
kx kx
波的叠加 干涉 驻波

谐振动因子
驻波中各质点均 以同一频率 作简 谐振动。
波波 腹节
波波 腹节
l
2
-l
4
ll 42
波腹处振幅最大 波节处振幅最小
3.驻波相位、能量特点
(1)驻波的相位特点
同一时刻,
相邻两波节之间的各质 点的振动相位相同;
波节两侧的各质点的 振动相位相反
驻波不是振动相位的传播过程,驻 波的波形不发生定向传播。
波程差为半波长的奇 数倍时,各质点的振幅 最小,干涉相消。
如图所示,两列波长为l 的相干波在P点相遇,波
在S1点振动的初相是j1 ,S1到P点的距离是r1;波
在S2点的初相是j2 ,S2到P点的距离是r2,以k代
表零或正、负整数,则P点是干涉极大的条件为:
(A)
r r kl
2
1
(B)
2kπ
相长与相消干涉
A
A12 A22 2 A1 A2 cos ( j 2
j1
r2 2p
r1
)
l
当
j2
j1
r2 r1 2p l
k = 0,1,2,
时
合振幅最大 相长干涉
当
j2
j1
r2 r1 2p l
( k = 0,1,2, ) 时
合振幅最小 相消干涉
两相干波源S1和S2相距 l 4(l 为波长),S1的 相位比S2的相位超前 p 2,在S1,S2的连线
2
1
S1
r1
P
(C) 2π(r r )/ l 2kπ
2
1
21
(D) 2π(r r )/ l 2kπ
2
1
12
S2
r2
波的叠加波的干涉驻波课件

驻波的应用与实例
应用
驻波在物理学、工程学等领域有广泛应用,如弦乐器、电磁波导等。
实例
吉他弦、电磁波导中的电磁波等都是驻波的实例。
04
波的叠加与干涉实验
实验一:波的叠加实验
要点一
总结词
理解波的叠加原理,掌握波的叠加实验操作方法,观察和 分析实验现象。
要点二
详细描述
进行波的叠加实验,观察不同波源的波在同一直线上的叠 加情况,记录实验数据,分析实验现象,得出结论。
波动能量的计算方法
通过波动方程或能量密度公式进行计算,分析波的能量分布和传 播规律。
波动能量的衰减
波在传播过程中会因为介质吸收、散射等原因逐渐衰减。
理论三:波动稳定性分析
1 2
波动稳定性的定义
描述波在传播过程中是否能够保持稳定的特性。
波动稳定性分析的方法
通过求解波动方程的稳定性条件,判断波是否能 够保持稳定的传播。
实验二:波的干涉实验
总结词
理解波的干涉原理,掌握波的干涉实验操作方法,观察 和分析实验现象。
详细描述
进行波的干涉实验,观察两个波源的波在同一直线上的 干涉情况,记录实验数据,分析实验现象,得出结论。
实验三:驻波实验
总结词
理解驻波原理,掌握驻波实验操作方法 ,观察和分析实验现象。
VS
详细描述
进行驻波实验,观察不同频率的驻波在相 同介质中的传播情况,记录实验数据,分 析实验现象,得出结论。
02
波的干涉
干涉现象及其产生条件
产生条件:要产生 干涉现象,需要满 足以下条件
2. 波源的振动必须 有一定的相位差;
干涉现象:当两个 或多个波源的波的 叠加产生加强或减 弱的现象。
波的叠加,干涉,驻波

17
x (2k 1)
y y 1 y 2 2 s t
振幅 2 A cos x
2
o、b、d、f ...
振动最强 A 2 A1 , 称波腹 波腹位置: cos
2
2
x 1
x k
xk
2
(k 0,1,2,....)
波的叠加原理 波的干涉 驻波
1. 波的叠加
波传播的独立性:如果在同一介质中,同时有几列 波传播, 那么每一列波都将保持自己原有的特性(频 率、波长、振动方向等)独立地传播,不因其他波的 存在而改变。
S1
S2
1
波的叠加原理: 有几列波同时在媒质中传播时,在 各波相遇或叠加区域,任一点的位移为各波单独在该 点产生的位移的合成,即为各波在该点引起的振动的 叠加。 对于某一给定点,波的叠加即为振动的叠加 叠加原理表明,可将任何复杂的波分解为一系列 简谐波的组合。
u
n 1
u 1 基频(音调) n 1 2L 谐频 泛音(音色)
所有可能的振动模式:简正模式
对应频率为简正频率,为系统固有频率(多个)
22
驻波的特征 (1) 波线上各点振幅不等,不是后一质点重复前一 质点的振动。 振幅最强 A 2 A1位置: 波腹 振动相消 A=0 位置: 波节
两相邻波腹(或波节) 相距 2
15
定量分析: 沿x轴的正、负方向传播的波 (设在原点处二者初相位均为零)
t x y1 A cos 2 T
合成波
t x y2 A cos 2 T
t x t x y y1 y2 Acos 2 ( ) cos 2 ( ) T T 2 2 (2 A cos x) cos t T
16_07_波的叠加原理 波的干涉 驻波

相邻两波腹的距离: xk 1 xk 振动的相位关系
2
相邻两节点之间的各点为一段,同一段上各质点振动 的相一致,相邻两段上各点振动的相相反。如图 XCH004_038 所示。 驻波的能量:形成驻波时,没有振动状态和能量的定向传播
1 A2 2u 2 1 2 2 —— 负向波的能流密度: I 2 ( u ) A u 2
2
x y1 A cos[2 ( t ) 1 ] y A cos[2 ( t x ) ] 2 2
合成波 y y1 y2 A cos[2 ( t
x
x ) 1 ] A cos[2 ( t ) 2 ]
t x ) ,在 x 0 处发生反射,反射点为节点。求: T
t x ) ] T
t x t x ) A cos[2 ( ) ] T T x t y 2 A sin 2 sin 2 T x 3) 波腹位置: 2 (2k 1) —— x (2k 1) 2 4 y A cos 2 ( x (2n 1)
4
—— 驻波只在-X 空间形成
波节位置: 2
x
k , x k
2
—— x n
2
REVISED TIME: 09-10-7
-4-
CREATED BY XCH
普通物理学_程守洙_第十六章 机械波和电磁波_20090921
4 行波的叠加和群速度 不同频率的简谐波叠加后,合成波不再是简谐波 —— 复波 图 XCH004_149 为两列频率分别为 1 and
REVISED TIME: 09-10-7
波的叠加原理与驻波现象

振动方向:在波的叠加区域,合成 振动的方向取决于各列波的振动方 向和相位。
振动速度和加速度:合成振动的速 度和加速度也是各列波单独产生的 速度和加速度的矢量和。
波的干涉现象
定义:两个或多个波在空间相遇时,产生相互加强或减弱的现象 条件:频率相同、相位差恒定 结果:形成稳定的加强区和减弱区 应用:干涉仪、双缝干涉实验等
波的叠加原理与驻波现 象
汇报人:XXX
目录
波的叠加原理
01 波动能量 04 驻波现象
02 波的传播介质 05 波动方程
03
波的叠加原理
多个波在同一直线上传播时,它们的振幅相加,产生新 的波。
波的独立传播特性:每个波独立传播,不受其他波的影响。
波的独立传播条件:各波源产生的波在同一直线上传播,且波速相同。
波动能量的计算
波动能量的定义:指在波动过程中, 介质中质点振动的动能和势能之和。
波动能量的计算公式: E=1/2mv^2+1/2Iω^2,其中E为能 量,m为质量,v为速度,I为转动 惯量,ω为角频率。
波动能量的物理意义:表示介质在 单位时间内所吸收或释放的能量。
波动能量的影响因素:波速、波长、 频率和介质的性质等。
干涉现象的应用
电子显微镜: 利用干涉现象 提高成像质量
光学仪器:通 过干涉现象提
高测量精度
量子力学:干 涉现象是量子 力学中的重要
概念
医学成像:干 涉现象在医学 成像技术中有
广泛应用
驻波现象
驻波的形成
两个或多个波源产生的振动波在同一直线上传播时相互作用 波源的频率相同或相近,振动方向相同 波源的初相位相同或相差整数倍的整数倍 波源振幅不同,最大振幅的波节位置不同
波的叠加原理波的干涉驻波
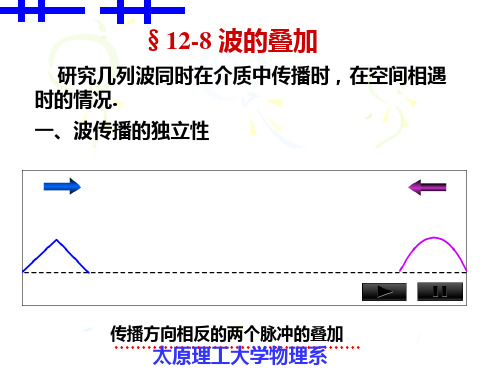
§12-8 波的叠加研究几列波同时在介质中传播时,在空间相遇时的情况.一、波传播的独立性传播方向相反的两个脉冲的叠加由演示看出两列波相遇之后,仍然保持它们各自原有的特征(频率、波长、振幅、振动方向等不变),不受其它波的影响,就像其它波不存在一样。
生活实例:➢红绿光束空间交叉相遇(红是红、绿是绿,…)➢听乐队演奏(仍可辨出不同乐器的音色、旋律)➢空中无线电波很多(仍能分别接收各个电台)二、波的叠加原理在几列波相遇而互相交叠的区域中,某点的振动是各列波单独传播时在该点引起的振动的合成。
三、波的干涉1.干涉现象当两列(或几列)满足一定条件(相干条件)的波在某区域同时传播时,则此区域中某些点的振动始终加强,某些点的振动始终减弱,在空间形成一幅稳定的强度分布图样。
干涉现象水波的干涉2.相干条件满足下列条件的波源称相干波源。
相干波源发的波相干波。
在现实中要产生明显的干涉现象,上述条件只能算必要条件,如果两波源的振幅相差悬殊,将导致干涉现象的可见度降低。
1)频率相同2)有恒定的相位差3)振动方向相同相干条件:1s 2s P *1r 2r 波源振动方程)cos(1011ϕω+=t A y )cos(2022ϕω+=t A y 四、干涉波的强度分布S 1、S 2发的波在p 点引起两个振动)π2cos(11011λϕωr t A y p -+=)π2cos(22022λϕωr t A y p -+=λπϕϕϕ∆121020r -r 2--=相位差可见,两个波源在p 点引起的分振动:频率相同;振动方向相同;相位差恒定(不随t 变)。
p 点合振动是两个同方向、同频率简谐振动的合成。
p 点合振动叫两波波程差12r r -)cos(021ϕω+=+=t A y y y p p p) 2cos() 2cos()2sin() 2sin(tan 22021101220211010λπϕλπϕλπϕλπϕϕr A r A r A r A -+--+-=由同方向同频率简谐振动的合成可以得两相干波叠加后的强度12122cos I I I I I ϕ=+∆+211∝A I 222∝A I由于在相干波的相遇点有确定的相位差∆ϕ,所以每一点都有确定的强度,干涉区域形成了稳定的强度分布。
驻波形成的条件和特点

驻波形成的条件和特点驻波是指在某一介质中传播的波与反射波之间形成的干涉现象。
驻波的形成需要满足一定的条件,同时具有特定的特点。
本文将从波的叠加原理、驻波的形成条件和特点以及中心扩展下的描述进行阐述。
驻波形成的条件:1. 波的叠加原理:驻波是由于两个同频率、相干、反向传播的波相互干涉而形成的。
当两个波的幅度相等且相差180度时,它们在叠加区域内就会形成驻波。
2. 波的传播介质:驻波只能在有界介质中形成,例如绳上的横波、管道中的声波、电缆中的电磁波等。
介质的两端必须有反射点,以便产生反射波与传播波进行干涉。
3. 波的频率和波长:驻波的形成与波的频率和波长有关。
当波长和介质的特定尺寸相匹配时,才能形成驻波。
对于一条绳子上的横波,当绳长为波长的整数倍时,才能形成驻波。
驻波的特点:1. 幅度变化:驻波的幅度在波节处为零,在波腹处达到最大值。
波节是相邻两个振动的干涉点,振动方向相反,形成波的干涉抵消;波腹是相邻两个振动的叠加点,振动方向相同,形成波的叠加增强。
2. 能量分布:驻波的能量分布不均匀,在波节处能量为零,在波腹处能量最大。
因为波节处的振动方向相反,能量相互抵消;而波腹处的振动方向相同,能量叠加增强。
3. 相位变化:驻波的相位差在波节处为180度,在波腹处为0度。
相位差是指相邻两个振动的相位差,相位差为180度时,振动相互抵消;相位差为0度时,振动相互叠加增强。
4. 驻波节点和腹点:驻波中的波节和波腹是驻波的重要特点。
波节是振动的最小值点,即振动幅度为零点;波腹是振动的最大值点,即振动幅度为最大点。
驻波的节点和腹点呈现出一定的规律性分布。
中心扩展下的描述:中心扩展是指在驻波形成的介质中,通过改变波源或改变介质的尺寸,使驻波的节点和腹点发生移动或分布发生变化。
在中心扩展下,驻波的条件和特点会有所变化。
在中心扩展下,改变波源的频率可以改变驻波的波长,进而改变节点和腹点的位置。
当波源频率增大时,波长减小,节点和腹点的间距变小,驻波的节点和腹点向波源方向移动;当波源频率减小时,波长增大,节点和腹点的间距变大,驻波的节点和腹点远离波源。
垂直入射的反射波和透射波 波的叠加 波的干涉与驻波
222221t yxy ∂∂=∂∂µ波速ρYu =Tu η=yt ϕ0=透射波与入射波同相π=0或入射波在反射时有π的突变r ϕ0=z z −+1212z z 12r ϕπ=这种入射波在反射时发生反向的现象叫z z z z −=+2112较小的称为波疏介质较大的称为波密介质从波疏介质入射到波密介质时,反射波有半波损失y强度反射系数和强度透射系数在实际问题中非常重要。
例如:标准状态下空气的波阻: z=420kg/(m2.s)水的波阻: z=1.5x106 kg/(m2.s)钢的波阻(按纵波计算): z=4.6x107kg/(m2.s)=0.1%T空气-水T=0.004%空气-钢=12%T水-钢y在反射点的振动(,)cos()y t x A t 5ωπ=−oybaxcos[()]a 2t x x −−πωλ)2cos(πλπω+−=x t A§5.6 波的叠加波的干涉与驻波一、波的独立性原理和叠加原理1、波的独立传播特性:几列波相遇之后,仍然保持它们各自原有的特征(频率、波长、振幅、振动方向等)不变,并按照原来的方向继续前进,好象没有遇到过其他波一样.2、波的叠加原理:在相遇区域内,任一点的振动,为各列波单独存在时在该点所引起的振动位移的矢量和.3. 叠加成立条件:波的强度较小,媒质形变与弹力呈线性关系。
频率相同、振动方向平行、相位相同或相位差恒定的两列波相遇时,使某些地方振动始终加强,而使另一些地方振动始终减弱的现象,称为波的干涉现象.常量L,2,1,0π2=±=∆k k ϕL,2,1,0π)12(=+±=∆k k ϕ121A A A A <<−=∆ϕ其他21A A A +=振动加强,干涉相长12m ax I I I =++21A A A −=振动减弱,干涉相消12m in I I I =+波程差12r r −=δ21A A −振动减弱L,2,1,0)21=+k k λ2121A A A A A +<<−其他21A A +振动加强L,2,1,0=k k λ∆++cos 22122A A A应用程序A'节4、驻波的获得驻波常由一列行波在介质分界面上反射,从而入射波和反射波干涉叠加而形成一般情况下,入射波在两种介质分界处反射时是否发生半波损失,与波的种类、两种介质的性质以及入射角的大小有关。
