小学四年级奥数(数字与页码问题)
四年级奥数专题 页码问题

第三讲页码问题知识导航页码问题常见的主要有三种题型:一、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;二、已知一本N页的书中,求某个数字出现多少次;三、已知一本N页的书中,求含有某个数字的页码有多少页。
为了清楚起见,我们将n位数的个数、组成所有n位数需要的数字个数。
组成所有不大于n位的数需要的数字个数之间的关系列表如下:不大于该数位所需数字个数个数所需数字个数一位数9 9 9二位数90 180 189三位数900 2700 2889四位数9000 36000 38889五位数90000 450000 488889精典例题例1:一本书共204页,需多少个数字编页码?思路点拨1--9页每页上的页码是一位数,共需数字:1×9=9(个);10--99页每页上的页码是两位数,共需数字:2×90=180(个);100--204页每页上的页码是三位数,共需数字(204-100+1)×3=315(个)。
一本《快乐数学》共250页,则需要多少个数字编页码?例2:印刷厂编印一本辞典的页码,共用了2211个数字。
问:这本书共有多少页?思路点拨因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数字(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页);因为不到三位数的页数有99页,所以这本书共有……模仿练习用了2925个数字编排出一本小说的页码,这本书共有多少页?例3:一本书共有400页,编上页码:1,2,3,4,…,399,400,数字2在这本书的页码中一共出现了多少次?思路点拨分类处理,个位上每十个数字出现一次2,即共有400÷10=40次;十位上每十个数字出现一次2,即共有400÷10=40次;百位上出现了100次。
一本书有500页,数字0在页码中共出现了多少次?例4:有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131。
(完整word版)小学奥数-页码(word文档良心出品)

小学奥数-页码问题页码问题就是根据书的页码而编制出来的一类应用题.编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
页码问题实际上是数论的问题。
一、页码问题的几种题型:(1)已知页码数,要求考生求出书中一共含有多少个数码。
(2)已知页码数,要求考生求此书中某个数码出现的次数。
(3)已知书中包含的数码数,要求考生求出该书的页码数。
(4)已知书中某个数码出现的次数,要求考生求出该书的页码数。
二、页码问题解题基本原理要想要想顺利解答页码问题,首先要弄明白“页码”与“组成它的数码个数”之间的关系。
1.一位数组成的页码共有9个(从1~9),组成所有的一位数需要:(9-1+1)×1=9×1=9(个)数码。
2.两位数共有90个(从10~99),组成所有的两位数需要:2×(99-10+1)=180(个)数码。
3.三位数共有900个(从100~999),组成所有的三位数需要:3×(999-100+1)=2700(个)数码。
4.四位数共有9000个(从1000~9999),组成所有四位数需要:4×(9999-1000+1)=36000(个)数码。
5.9页的书共有:9个数码组成。
6.99页的书共有:9+180=189个数码组成。
7.999页的书共有:2700+180+9=2889个数码组成。
8.9999页的书共有:36000+2700+180+9=38889个数码组成。
三.例题:例1 一本书共204页,需多少个数码编页码?分析与解:1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码:(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码:9+180+315=504(个).例2 一本小说的页码,在排版时必须用2211个数码.问:这本书共有多少页?分析:因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).解:99+(2211-189)÷3=773(页).答:这本书共有773页.例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?分析与解:因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62=62×(62+1)÷2=31×63=1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4 有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131.老师说小明计算错了,你知道为什么吗?分析与解:48页书的所有页码数之和为1+2+…+48=48×(48+1)÷2=1176.按照小明的计算,中间缺的这一张上的两个页码之和为1176-1131=45.这两个页码应该是22页和23页.但是按照印刷的规定,书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两个页码,都是奇数在前,偶数在后,也就是说奇数小偶数大.小明计算出来的是缺22页和23页,这是不可能的.例5 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?分析与解:本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例6 排一本400页的书的页码,共需要多少个数码“0”?分析与解:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”例6、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?解答:这是一个关于循环小数的周期问题。
奥数:页码问题(数论问题)

奥数:页码问题(数论问题)页码问题编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
我们先看一下“数”与“组成它的数码个数”之间的关系.1、一位数的页码有9页,共1×9=9个数字;组成所有的一位数需要9个数码;2、两位数的页码有90页,共90×2=180个数字;需要180个数码3、三位数有900个,全部编上共用900×3=2700个数字,需要3×900=2700(个)数码。
题目会出1、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;2、已知一本N页的书中,求某个数字出现多少次;3、已知一本N页的书中,求含有某个数字的页码有多少页一本书排版时用了N个数字,求这本书有多少页,数字数<2889时,用公式:页码数=数字数/3+36;数字数>2889时,用添加0计算。
例1 一本书共204页,需多少个数码编页码?2.编一本书的书页,用了270个数字(重复的也算,如页码115 用了2个1 和1个5共3个数字),问这本书一共有多少页?N/3+36。
270/3 +36=126。
2.一本小说的页码,在排版时必须用2211 个数码。
问这本书共有多少页?A.773 B.774 C .775 D.7763 .王先生在编一本书,其页数需要用6869 个字,问这本书具体是多少页?A.1999B.9999C.1994D.1995方法一:假设这个页数是A页,则:A+(A-9)+(A-99)+(A-999)=6869 ,求出A=1994方法二:6869>2889,所以,把所有的数字看作是4位数字,不足4位的添O补足4位,l , 2 , 3 , …9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , …99 记为0010 , 0011 , 0012 ,..0099 增加了180 个0100 , 101 ,…999 记为0100 , 0101 ,…0999 增加了900 个O (6869+27+180+900)/4 =1994关于含“1”出现过多少次的问题,总结出的公式就是:总页数的1/10 乘以(数字位-1 ),再加上10 的(数字位数-l)次方。
四年级奥数专题页码问题

四年级奥数专题页码问题知识导航页码问题常见的主要有三种题型:一、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;二、已知一本N页的书中,求某个数字出现多少次;三、已知一本N页的书中,求含有某个数字的页码有多少页。
为了清楚起见,我们将n位数的个数、组成所有n位数需要的数字个数。
组成所有不大于n位的数需要的数字个数之间的关系列表如下:不大于该数位所需数字个数个数所需数字个数一位数9 9 9二位数90 180 189三位数900 2700 2889四位数9000 36000 38889五位数90000 450000 488889精典例题例1:一本书共204页,需多少个数字编页码?思路点拨1--9页每页上的页码是一位数,共需数字:1×9=9(个);10--99页每页上的页码是两位数,共需数字:2×90=180(个);100--204页每页上的页码是三位数,共需数字(204-100+1)×3=315(个)。
模仿练习一本《快乐数学》共250页,则需要多少个数字编页码?例2:印刷厂编印一本辞典的页码,共用了2211个数字。
问:这本书共有多少页?思路点拨因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数字(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页);因为不到三位数的页数有99页,所以这本书共有……模仿练习用了2925个数字编排出一本小说的页码,这本书共有多少页?例3:一本书共有400页,编上页码:1,2,3,4,…,399,400,数字2在这本书的页码中一共出现了多少次?思路点拨分类处理,个位上每十个数字出现一次2,即共有400÷10=40次;十位上每十个数字出现一次2,即共有400÷10=40次;百位上出现了100次。
小四奥数-页码问题(一)

第三讲页码问题一年级姓名学号【知识要点】0、1、2、3、4、5、6、7、8、9是大家最常见、最常用、最熟悉的数,也是当今世界各国通用的数字。
他们是构成十进制数的“零件”。
由一个数字编写的页码是第1页到第9页,共需要用到9个数字。
由两个数字编写的页码是第10页到第99页,共需用到180个数字,由两个数字编写的页码是第100页到第999页,共需用到2700个数字,……依次可类推出其它情况。
【例题】★例1.你知道书上页码排列的规律吗?每张纸上的页码总是正面为,反面为;任意翻开书中的两页,这两页的号码数字是,左边一页为,右边一页为。
一位数有()个,即,两位数有()个,即,三位数有()个,即,四位数有()个,即。
★例2.小明和小智是同学,他们经常在一起探讨数学问题。
一次,小明对小智说:我有一本课外读物,它的页数是一个三位数,个位数字比百位数字大4,十位数字比个位数字也大4,这本课外读物有几页?小智稍加思索就说出了正确答案。
你知道这个答案是多少吗?★例3.一本《成语故事》共有131页,编印这本书的页码共用了多少个数字?★例4.印刷厂编印一本故事书的页码,共用了360个数字,请算一算,这本故事书有多少页?★★例5.一本含有相片的纪实文集的书,共有250页。
其中每两页文字之间有3页是相片插图,也就是3页相片插图前后各有1页文字。
(1)若第1页是文字,这本书含有相片插图的共有多少页?(2)若第1页是相片插图,这本书共有相片插图多少页?【池中戏水】★1.小智也给小明出了一个类似的问题,一本书的页码是一个三位数,百位数字比个位数字大6,十位数字是个位数字与百位数字的平均数,这本书有多少页?★2.一本《快乐数学》共560页,则需要多少个数字编页码?★3.一本书共104页,排页码时要用到多少个数字?★4.用了204个数字编排出一本小书的页码,这本书共有多少页?★5.给一本书编页码,在印刷时必须用到207个铅字(一个铅字代表一个数字),这本书共有多少页?★6.小浩打开数学书做作业,发现这时左右两个页码的和是165,你知道小浩打开的页码是多少吗?为什么?【江中畅游】★7.给一部书编上页码需要689个数字,那么这部书共有多少页?★8.一本书的页码从1~62页,即共有62页,在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次,结果得到的和为2004。
奥数中的数码和页码题目

奥数中的数码和页码题目
数码和页码题目:
题目1:小明参加了一个奥数比赛,他打开试卷,发现每一页都有一个三位数的数码。
如果小明一共翻了100页试卷,每一页的数码都是顺序递增的,试问最后一页的数码是多少?
题目2:在一本奥数题集中,从第一页开始,每一页的页码都是一个四位数。
如果小红翻了20页,她发现每一页的页码的千位数字都是顺序递减的,百位数字都是顺序递增的,个位数字都是0,十位数字都是5,试问小红翻到的最后一页的页码是多少?
题目3:斐波那契数列是一个典型的数列,它的第一项和第二项均是1,之后的每一项是前两项的和。
小明翻开一本奥数题集,数码以斐波那契数列的方式排列在每一页的右下角,第一页的右下角是第三项,第二页是第四项,以此类推。
如果小明翻到第20页,试问右下角的数码是多少?
题目4:某本数学家的传记共有300页。
对于前100页,每一页的数码都是从1开始,顺序递增的。
对于接下来的100页,每一页的数码都是从101开始,顺序递增的。
对于最后100页,每一页的数码都是从201开始,顺序递增的。
试问第50页的数码是多少?
题目5:小华翻开一本奥数参考书,第一页的数码是1,第二页是2,以此类推。
当他翻开第N页时,所有页码的数码之和是675。
试问N是多少?
参考答案:
题目1:最后一页的数码是100。
题目2:小红翻到的最后一页的页码是6590。
题目3:右下角的数码是6765。
题目4:第50页的数码是150。
题目5:N是18。
四年级奥数数页码

比比看谁最细心
给你一本书,从书中你能获得 哪些信息?以我们用的拓展思 维书为例
这本书在出版时就统计好它的字数有231千。这本书 一共有143页,那你知道这143页有多少个数码?
页码不就是数么?还 怎么数呢?这里的数 码和数字有什么区别 么?
算算页码的数字
授课班级:四年十三班
算算页码的数字从哪里入手?
9+180+132=321(个) 答:这143页是由321个数码组成的。
第一关:知识延伸
智力闯关
学校给全校学生换发学生证,每个学生证都有编 号,3001名学生编号从1号起至3001号。问:学生 证编号共有多少个数字?
第三关:能力提升 一本百科全书的页数一共需要. 6869 个数码。 . .. 问:这本书有多少页?
[ 6869-(9+180+2700)] ÷ 4 +9+90+900=1994(页)
答:这本书有1994页。
第四关:看谁算得快 1、一本书一共用了2187个数字组成,这本书有多少页?
9+90+900+[2893-(9+180+2700)÷4] =1000
答:她从1一直写到1000. 2、.排一本小说的页码,需要用2202个数码,这本 书共有多少页? [2202-(9+180)]÷3+9+90=670(页)
四年级奥数详解答案 第23讲 页码问题

四年级奥数详解答案第23讲第二十三讲页码问题一、知识概要页码是指书本每一页(面)上所标注的数目。
(这里的“页”不是指书中的一张纸,而是指一张纸的一面)。
页码问题主要是研究编一本书的页码,一共需要多少个数码,以及知道编一本书的页码所需的数码数量,求这本书页数。
典型的页码问题有如下三类(最基本的):(1)算页码中所用数字个数的和,或是根据已知的页码中所用数字个数的和来求页码。
(2)计算页码中某个数字出现的项数。
(3)计算页码中所有数字的和。
解决页码问题的基本方法是:分段(或分类或分组)计算。
页码个数与组成页码的数码个数之间的关系,如下表所示。
二、典型题目精讲1、一本故事书共180页,需多少个数码编页码?解:数码是指0,1,2,3,4,5,6,7,8,9这十个数字,页码就是由每页上由数码组成的数目。
所以,1~9页有9个数码;10—99页有180个数码;100~180页有81×3=243 (个)数码。
一共有9+180+243=432(个)2、有一本辞典,所编页码共用了3401个数码,这本辞典一共有________页。
解:①1~9页用9个数码;10—99页用了180个数码;100~999用了2700个数码;则1~999页共用数码9+180+2700=2889(个)。
②1000~?页共用数码(3401-2889)=512 (个);则512÷4=128(页)。
故这本辞典共有999+128=1127(页)3、一本漫画共121页,在这本书的页码中数字一共出现了_______次。
解:(分类计算)①在个位上,1出现13次(即1,11,21……101,111,121);②在十位上,1出现20次(即10,11,12……19;110,111,112……119);③在百位上,1出现22次(即100,101,102,……121)。
综合①②③可知,1在书的页码中共出现(13 +20+22)=55(次)。
4、一本书共200页,求页码中全部数字的和。
四年级奥数专题--页码问题

第三讲页码问题知识导航页码问题常见的主要有三种题型:一、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;二、已知一本N页的书中,求某个数字出现多少次;三、已知一本N页的书中,求含有某个数字的页码有多少页。
为了清楚起见,我们将n位数的个数、组成所有n位数需要的数字个数。
组成所有不大于n位的数需要的数字个数之间的关系列表如下:精典例题例1:一本书共204页,需多少个数字编页码?思路点拨1--9页每页上的页码是一位数,共需数字:1×9=9(个);10--99页每页上的页码是两位数,共需数字:2×90=180(个);100--204页每页上的页码是三位数,共需数字(204-100+1)×3=315(个)。
一本《快乐数学》共250页,则需要多少个数字编页码?例2:印刷厂编印一本辞典的页码,共用了2211个数字。
问:这本书共有多少页?思路点拨因为189<2211<2889,所以这本书有几百页。
由前面的分析知道,这本书在排三位数的页码时用了数字(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页);因为不到三位数的页数有99页,所以这本书共有……模仿练习用了2925个数字编排出一本小说的页码,这本书共有多少页?例3:一本书共有400页,编上页码:1,2,3,4,…,399,400,数字2在这本书的页码中一共出现了多少次?思路点拨分类处理,个位上每十个数字出现一次2,即共有400÷10=40次;十位上每十个数字出现一次2,即共有400÷10=40次;百位上出现了100次。
一本书有500页,数字0在页码中共出现了多少次?例4:有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131。
孙老师说小明计算错了,你知道为什么吗?思路点拨48页书的所有页码数之和为:1+2+ …+48=1176;按照小明的计算,中间缺的这一张上的页码之和为1176-1131=45……模仿练习一本书的页码从1至62,即共有62页。
(完整word版)小学奥数页码问题
奥数:页码问题(数论问题)页码问题与图书的页码有亲密联系.事实上,页码问题就是依据书的页码而编制出来的一类应用题.编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数目,求这本书的页数.这是页码问题中的两个基本内容。
页码问题是此刻的奥数比赛以及公事员考试中常有的、常常考试的知识点。
页码问题其实是数论的问题。
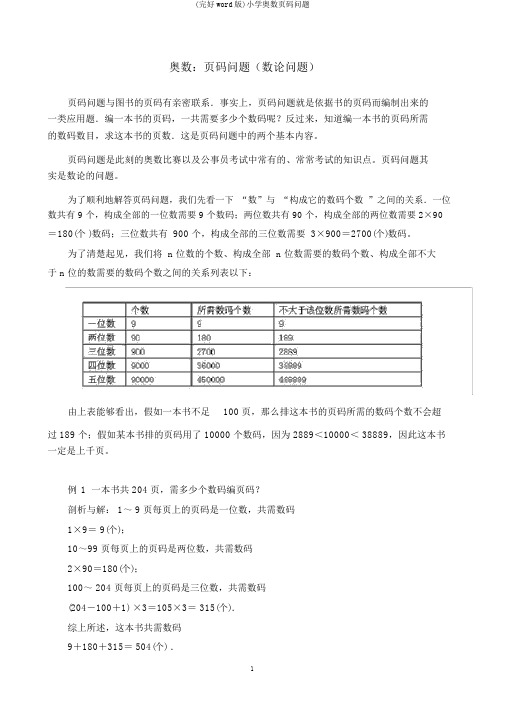
为了顺利地解答页码问题,我们先看一下“数”与“构成它的数码个数”之间的关系.一位数共有 9 个,构成全部的一位数需要 9 个数码;两位数共有 90 个,构成全部的两位数需要 2×90=180(个 )数码;三位数共有 900 个,构成全部的三位数需要 3×900=2700(个)数码。
为了清楚起见,我们将 n 位数的个数、构成全部 n 位数需要的数码个数、构成全部不大于 n 位的数需要的数码个数之间的关系列表以下:由上表能够看出,假如一本书不足100 页,那么排这本书的页码所需的数码个数不会超过 189 个;假如某本书排的页码用了 10000 个数码,因为 2889<10000< 38889,因此这本书一定是上千页。
例1 一本书共 204 页,需多少个数码编页码?剖析与解: 1~ 9 页每页上的页码是一位数,共需数码1×9= 9(个);10~99 页每页上的页码是两位数,共需数码2×90=180(个);100~ 204 页每页上的页码是三位数,共需数码(204-100+1) ×3=105×3= 315(个).综上所述,这本书共需数码9+180+315= 504(个) .例2 一本小的,在排版必用 2211 个数.:本共有多少?剖析:因 189< 2211< 2889,因此本有几百.由前面的剖析知道,本在排三位数的用了数(2211-189)个,因此三位数的数有(2211-189) ÷3= 674( ).因不到三位的数有99 ,因此本共有: 99+674=773( ).解: 99+(2211-189) ÷3=773( ).答:本共有773 .例 3 一本的从 1 至 62,即共有 62 .在把本的各的累加起来,有一个被地多加了一次.果,获得的和数 2000.:个被多加了一次的是几?剖析与解:因本的从 1 至 62,因此本的全之和1+2+⋯+ 61+62= 62×(62+ 1) ÷2= 31×63= 1953.因为多加了一个以后,所获得的和数2000,因此 2000 减去 1953 就是多加了一次的那个,是2000-1953=47.例 4有一本48的,中缺了一,小明将残的相加,获得1131.老小明算了,你知道什么?剖析与解: 48 的全部数之和1+2+⋯+ 48=48×(48+ 1) ÷2=1176.依据小明的算,中缺的一上的两个之和1176-1131= 45.两个是 22 和 23 .可是依据印刷的定,的正文从第 1 起,即数印在正面,偶数印在反面,因此任何一上的两个,都是奇数在前,偶数在后,也就是奇数小偶数大.小明算出来的是缺22 和 23 ,是不行能的.第2000 位上的数字是多少?剖析与解:本似于“用2000 个数能排多少的?”因(2000-189) ÷3=603⋯⋯2,因此2000 个数排到第 99+603+1=703( )的第 2 个数“ 0.”因此本的第 2000 位数是 0.例6 排一本 400 的的,共需要多少个数“0?”剖析与解:将1~400 分四:1~100,101~ 200,201~300, 301~400.在 1~100 中共出 11 次 0,其他各每都比 1~ 100 多出 9 次 0,即每出 20 次0.因此共需要数“ 0”典型例:例 1、13/1995 化成小数后是一个无穷小数,在个无穷小数的小数点后边,从第一位到1995 位,在 1995 个数中,数字 6 共出了多少次?解答:是一个对于循小数的周期。
小学奥数题页码问题练习题

【导语】海阔凭你跃,天⾼任你飞。
愿你信⼼满满,尽展聪明才智;妙笔⽣花,谱下锦绣第⼏篇。
学习的敌⼈是⾃⼰的知⾜,要使⾃⼰学⼀点东西,必需从不⾃满开始。
以下是为⼤家整理的《⼩学奥数题页码问题练习题》供您查阅。
1.⼀页书共380页,印刷⼚的排版⼯⼈编排这本书,仅排页码⼀共要⽤多少个铅字?
2.从“1”⼀直写到“701”:123456789101112……699700701。
共有多少个阿拉伯数字
3.⼀本故事书,仅排页码就⽤去1392个铅字(数字)。
这本书有多少页?
4.在2、4、6、……、396和398这些偶数的数列中,数字“2“⼀个有多少个?
5.排版⼯⼈给⼀本书编排页码,共⽤去942个数字(铅字),这本书有多少页?
6.⾃然数的平⽅按从⼩到⼤排成⼀⾏:14916253649……,那么第112个位置上的数字是多少?
7.设⼩数A = 01234567891011……998999,试问,⼩数点右边第1998位上的数字是⼏?
8.⼀本书共399页,编上页码:1、2、3、4……398、399,问数字“2“在页码中共有多少个?
9.设⼩数B = 024681012……19982000,那么⼩数点右边第2000位上的数字是⼏?
10.有⼀本书中间被撕掉⼀张,余下各页的页码数之和正好是1145。
那么,被撕掉那⼀张的页码数是什么?。
小学奥数精讲:页码问题及其答案

小学奥数精讲:页码问题及其答案一、知识总结:一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180(个)数码;三位数共有900个,组成所有的三位数需要3×900=2700(个)数码。
二、典型例题:例1 一本书共204页,需多少个数码编页码?在排版时必须用2211个数码.问:这本书共有一本小说的页码,在排版时必须用例2 一本小说的页码,多少页?例3 一本书的页码从1至62,即共有62页.在把这本书的各页的页码累加起来时,有一个页码被错误地多加了一次.结果,得到的和数为2000.问:这个被多加了一次的页码是几?例4 将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第2000位上的数字是多少?1 例5 排一本400页的书的页码,共需要多少个数码“0”?”?例6、13/1995 化成小数后是一个无限小数,问在这个无限小数的小数点后面,从第一位到1995位,在这1995个数中,数字6共出现了多少次?共出现了多少次?例7、将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112…问:左起第1000位上的数字是多少?位上的数字是多少?例8、有一本科幻故事书,每四页中,有一页为文字,其余三页为图画。
如果第一页为图画,那么第二、三页也是图画,第四页为文字,第五、六、七页又为图画,七页又为图画,依此类推。
依此类推。
如果第一页为文字,如果第一页为文字,那么第二、那么第二、三、四页为图画,第五页为文字,第六、七、八页又为图画,依此类推。
试问:第五页为文字,第六、七、八页又为图画,依此类推。
试问:(1)假如这本书有96页,且第一页是图画,那么这本书多少页有图画?那么这本书多少页有图画? (2)假如这本书有99页,那么多少页有图画?页,那么多少页有图画?小学奥数精讲:页码问题答案例1、[分析与解] 1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~204页每页上的页码是三位数,共需数码(204-100+1)×3=105×3=315(个).综上所述,这本书共需数码9+180+315=504(个).例2、[分析与解] 因为189<2211<2889,所以这本书有几百页.由前面的分析知道,这个,所以三位数的页数有 本书在排三位数的页码时用了数码(2211-189)个,所以三位数的页数有(2211-189)÷3=674(页).因为不到三位的页数有99页,所以这本书共有:99+674=773(页).例3、[分析与解] ,所以这本书的全书页码之和为 因为这本书的页码从1至62,所以这本书的全书页码之和为1+2+…+61+62 =62×(62+1)÷2 =31×63 =1953.由于多加了一个页码之后,所得到的和数为2000,所以2000减去1953就是多加了一次的那个页码,是2000-1953=47.例4、[分析与解] 本题类似于“用2000个数码能排多少页的页码?”因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”.所以本题的第2000位数是0.例5、[分析与解] 分为四组:将1~400分为四组:1~100,101~200,201~300,301~400.在1~100中共出现11次0,其余各组每组都比1~100多出现9次0,即每组出现20次0.所以共需要数码“0”例6、[分析与解] 这是一个关于循环小数的周期问题。
四年级奥数页码问题

四年级奥数页码问题(总6页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第四讲页码问题知识导航顾名思义,页码问题与图书的页码有密切联系。
事实上,页码问题就是根据书的页码而编制出来的一类应用题。
编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数。
这是页码问题中的两个基本内容。
为了顺利地解答页码问题,我们先看一下“数”与“组成它的数码个数”之间的关系。
一位数共有9个,组成所有的一位数需要9个数码;两位数共有90个,组成所有的两位数需要2×90=180(个)数码;三位数共有900个,组成所有的三位数需要3×900=2700(个),四位数共有9000个,组成所有的四位数共需要4×9000=36000(个)……由上看出,如果一本书不足100页,那么排这本书的页码所需的数码个数不会超过189个;如果某本书排的页码用了10000个数码,因为2889<10000<38889,所以这本书肯定是上千页。
(1)0、1、2、3、4、5、6、7、8、9组成的数字,也是当今世界各国通用的数字,它们是构成十进制的零件,同一个数字由于它在所记的数中的位置不同,所表示的数值不同,这就是“位置值”。
(2)掌握一位数1~9有9个数字,两位数10~99有90*2=180(个)数字,三位数100~999有900*3=2700(个)数字….以此类推。
解答此类问题基本的方法分段、或分类、或分组计算。
精典例题例1:一本书共有200页,在这本书的页码中,共有多少个数字?思路点拨分类思考模仿练习一本书共有1021页,那么共需要多少个数码编页码?例2:一本小说的页码,在排版时必须用2211个数码。
问:这本书共有多少页?思路点拨根据数码找页码的范围。
模仿练习中国一部百科全书上面的页码共用了6909个数字,那么这部书共有多少页?例3:一本书的页码从1至62、即共有62页。
小学四年级奥数(数字与页码问题)

小学四年级奥数第14讲数字与页码知识方法…………………………………………………在日常的编门牌号码中、在编书所用页码中,都会用到数与数字之间的关系。
这样的一些问题,如果用一般的思考方法,往往觉得无法入手,但是只要我们认真思考,善于捕捉数量之同的“蛛丝马迹”,通过合乎情理的运算与推导,就会找出一定的规律,很快地解答这些问题。
重点点拨…………………………………………………【例1】有一个两位数,十位上的数字是个位上数字的3倍。
如果把这两个数字对调位置,组成一个新的两位数,这时两个数的和是132,求原两位数。
分析与解符合十位上的数字是个位上数字的3倍这个条件的两位数有:31,62,93这两个数字对调位置后,得到的是13,26,39,只有39+93=132,所以原来的两位数是93。
【例2】张家的门牌号码是一个三位数,而且三个数宇都不相同,但知道三个数字的和是6,你说说他家的门牌号码是多少?(把所有可能的情况都写出来)分析与解根据三个数字都不相同,但三个数字的和是6,我们找出符合条件的情况:0,1,5组合:150,105,510,501。
0,2,4组合:240,204,420,402。
1,2,3组合:123,132,213,231,312,321。
一共有14种可能。
【例3】一本书共222页,需多少个数码编页码?分析与解1~9页每页上的页码是一位数,共需数码1×9=9(个);10~99页每页上的页码是两位数,共需数码2×90=180(个);100~222页每页上的页码是三位数,共需数码(222-2100+1)×3=369(个)。
9+180+369=558(个)。
答:需要558个数码编页码。
【例4】《民间故事》的正文第一页到最后一页共用了360个数码编页码,这本书的正文有多少页?分析一位数页码只有一位数字,共有1~9这9个数字;两位数页码从10~9,共90个数,180个数字;三位数页码从100~990共900个数,2700个数字。
奥数:页码问题(数论问题)

页码问题编一本书的页码,一共需要多少个数码呢?反过来,知道编一本书的页码所需的数码数量,求这本书的页数.这是页码问题中的两个基本内容。
我们先看一下“数”与“组成它的数码个数”之间的关系.1、一位数的页码有9页,共1×9=9个数字;组成所有的一位数需要9个数码;2、两位数的页码有90页,共90×2=180个数字;需要180个数码3、三位数有900个,全部编上共用900×3=2700个数字,需要3×900=2700(个)数码。
题目会出1、一本书有N页,求排版时用了多少个数字;或者反过来,一本书排版时用了N个数字,求这本书有多少页;2、已知一本N页的书中,求某个数字出现多少次;3、已知一本N页的书中,求含有某个数字的页码有多少页一本书排版时用了N个数字,求这本书有多少页,数字数<2889时,用公式:页码数=数字数/3+36;数字数>2889时,用添加0计算。
例1 一本书共204页,需多少个数码编页码?2.编一本书的书页,用了270个数字(重复的也算,如页码115 用了2个1 和1个5共3个数字),问这本书一共有多少页?N/3+36。
270/3 +36=126。
2.一本小说的页码,在排版时必须用2211 个数码。
问这本书共有多少页?A.773 B.774 C .775 D.7763 .王先生在编一本书,其页数需要用6869 个字,问这本书具体是多少页?A.1999B.9999C.1994D.1995方法一:假设这个页数是A页,则:A+(A-9)+(A-99)+(A-999)=6869 ,求出A=1994方法二:6869>2889,所以,把所有的数字看作是4位数字,不足4位的添O补足4位,l , 2 , 3 , …9 记为0001 , 0002 , 0003 , ..0009 这样增加了3 * 9 = 27 个010 , 11 , 12 , …99 记为0010 , 0011 , 0012 ,..0099 增加了180 个0100 , 101 ,…999 记为0100 , 0101 ,…0999 增加了900 个O(6869+27+180+900)/4 =1994关于含“1”出现过多少次的问题,总结出的公式就是:总页数的1/10 乘以(数字位-1 ),再加上10 的(数字位数-l)次方。
四年级奥数专题页码问题.docx

第三讲页码问题知识导航页码问题常见的主要有三种题型:一、一本书有 N 页,求排版时用了多少个数字;或者反过来,一本书排版时用了 N 个数字,求这本书有多少页;二、已知一本 N 页的书中,求某个数字出现多少次;三、已知一本 N 页的书中,求含有某个数字的页码有多少页。
为了清楚起见,我们将 n 位数的个数、组成所有 n 位数需要的数字个数。
组成所有不大于 n 位的数需要的数字个数之间的关系列表如下 :不大于该数位所需数字个数个数所需数字个数一位数999二位数90180189三位数90027002889四位数90003600038889五位数90000450000488889精典例题例1:一本书共204页,需多少个数字编页码?思路点拨1--9页每页上的页码是一位数,共需数字:1×9=9(个); 10--99页每页上的页码是两位数,共需数字: 2 × 90=180 (个); 100--204页每页上的页码是三位数,共需数字(204-100+1 )× 3=315(个)。
模仿练习一本《快数学》共250 ,需要多少个数字?例2:印刷厂印一本辞典的,共用了2211个数字。
:本共有多少?思路点拨因 189<2211<2889,所以本有几百。
由前面的分析知道,本在排三位数的用了数字( 2211-189 )个,所以三位数的数有( 2211-189 )÷ 3=674();因不到三位数的数有 99 ,所以本共有⋯⋯模仿练习用了 2925 个数字排出一本小的,本共有多少?例3:一本共有400,上:1,2,3,4,⋯,399,400,数字2在本的中一共出了多少次?思路点拨分理,个位上每十个数字出一次2,即共有 400÷ 10=40 次;十位上每十个数字出一次2,即共有400÷ 10=40 次;百位上出了100 次。
模仿练习一本书有 500 页,数字 0 在页码中共出现了多少次?例4:有一本48页的书,中间缺了一张,小明将残书的页码相加,得到1131。
四年级奥数详解答案第23讲页码问题

四年级奥数详解答案第23讲页码问题一、知识概要一位数二位数三位数四位数个数9909009000所用数码(个)自首页起所需数码总数91802700360009189289938889二、典型题目精讲的数目。
所以,1~9页有9个数码;10—99页有180个数码;100~180页有81某3=243(个)数码。
一共有9+180+243=432(个)解:①1~9页用9个数码;10—99页用了180个数码;100~999用了2700个数码;则1~999页共用数码9+180+2700=2889(个)。
②1000~?页共用数码(3401-2889)=512(个);则512÷4=128(页)。
故这本辞典共有999+128=1127(页)解:(分类计算)①在个位上,1出现13次(即1,11,21101,111,121);②在十位解:(分组计算)将0~199分为100组,即0和199,1和198,2和197,98和101,99和100.这样,每组的4个数字之和都是19,100组数字之和是19某100=1900,再加上“200”这三数之和为2,故200页中全部数字之和为1900+2=1902。
解:(分段、分组计算),把1~1236分为2段后再分组计算。
第一段(0~999)分为500第二段(1000~1239)分为120组,即(1000,1239),(1001,1238),(1119,1120);∵每组数字之和是16,∴120组数字之和为16某120=1920。
三、练习巩固与拓展6、将自然数按从小到大的顺序无间隔地排成一个大数:12345678910111213在这个大数的左起500位上的数字是_________。
第二十三讲答案1、解:1某9+2某(99-9)+3某(340-99)=1某9+2某90+3某242=9+180+723=912(个)答:共用了912个数字。
2、解:1某9+2某90=189(个)99+(972-189)÷3=99+783÷3=360(页)答:这本书有360页。
四年级奥数专题之九页码中数字问题

四年级奥数专题之 (11) 页码中的数字问题(1)一本书共132页,在这本书的页码中,共用了多少个数字?
(2)一本科幻小说共320页,问(1)这本科幻小说的页码共要用多少个数字?(2)数字0在页码中共出现了多少次?
(3)排一本学生词典的页码,共用了3829个数字,问这本词典共有几页?
(4)一本儿童时代图书共48页,需要几个数码编页码?
(5)排一本词典的页码共用了2925个数字,请你算一下,这本词典有多少页?
(6)小华翻开数学课本,看了看这两页的页码数,发现它们的乘积是2970,你知道这两个页码数各是多少吗? 7)有一个缺乏道德的人去图书馆看书,他看见书上有些图案很好看,就偷偷地撕下页码为
21 42 84 151 159 160 180的几页,结果被
图书管理员当场发现,责问此人一共撕下几页?
(8)上下两册书的页码共有777个数码,并且上册比下册多7页,上册有多少页?
(9)有一本书的中间被撕掉了一张,余下各页的页码数之和正好是1145,那么,被撕掉的那一张的页码数是几?
(10)有一本196页的书,中间缺了一页,如果将残书的所有页码相加,能不能得到偶数?
(11)一本书100页,计算页码1至100这些自然数中的所有数字的和是多少?。
四年年级奥数题页码问题

2013年四年级奥数题:页码问题例题剖析1.一本书共132页,在这本书的页码中,共用了多少个数字?2.一本书有408页,要把它编出页码1,2,3,4,…,407,408,数字2一共要出现几次?3.排一本辞典的页码共用了2925个数字,请你算一下,这本辞典有多少页?4.有一本书的中间被撕掉了一张,余下各页的页码数之和正好是1145,那么被撕掉的那一张的页码数是几?6.一本书100页,计算页码1﹣100这些自然数中的所有数字的和是多少?练习8.一本科幻小说共320页,问:(1)印这本科幻小说的页码共要多少个数字?(2)数字0在页码中共出现了多少次?9.排一本学生词典的页码,共用了3829个数字,问这本词典共有几页?10.一本故事书的页码,用了49个0,问这本书共有几页?11.一本《新编小学生字典》共563页,需要多少个数码编页码?12.一本书的页码,在排版时用了2691个数码,则这本书一共有多少页?14.一本书的页码从1至82,共有82页,在把这本书的各页的页码累加起来时,有一个页码被错误的多加了一次,结果得到的和为3440.则这个被多加了一次的页码是多少?16.排一本500页的书的页码,共需要多少个0?17.有一本68页的书,中间缺了一张,小杰将残书的页码相加,得到2305,老师说小杰一定算错了,你知道为什么吗?家庭作业:18.一本《儿童时代》共98页,需要多少个数码编页码?19.一本书的页码为1至82页,即共82页.把这本书的各页的页码累加起来时,有一页码漏加了.结果得到的和数为3396.问这个被漏加的页码是几?2013年四年级奥数题:页码问题参考答案与试题解析例题剖析1.一本书共132页,在这本书的页码中,共用了多少个数字?考点:页码问题.专题:传统应用题专题.分析:从1到132页按数的位数分,可以分为:一位数、两位数、三位数.它们分别是1个、2个、3个数字,由此分析解答即可.解答:解:一位数:1页到9页,有9个数字;两位数:10页到99页,有90个数,共180个数字;三位数:100页到132页,有33个数,共99个数字.所以编辑这本书的页码有9+180+99=288个数字.点评:注意分段解决页码问题.2.一本书有408页,要把它编出页码1,2,3,4,…,407,408,数字2一共要出现几次?考点:页码问题.分析:这道题,如果一个一个数出来,是很容易遗漏的,竞赛时间也是不允许的.但如果把1到408分成1到99,100到199,200到299,300到399,400到499,400到408共有5部分,逐个考虑,问题就容易解决了.解答:解:从1到99再分为1到9、10到19、20到29、…90到99共10个部分来分析.显然,20到29这个部分2出现11次,其余都仅各出现1次2,即从1到99共出现20次2;同样的道理,从100到199、300到399都各出现20次2,而从200到299,2出现的次数比从1到99多了百位上的100个2,即出现了120次2;从400到408这部分仅出现1次2.所以,408页的书编页中数字2一共要出现20+40+120+1=181次.点评:因为一个页码为几位数就含有几个数字,所以完成本题据页码的位数进行分析解答比较简单.3.排一本辞典的页码共用了2925个数字,请你算一下,这本辞典有多少页?考点:页码问题.专题:传统应用题专题.分析:成本题可按页码的位数进行分析,1﹣9页9个,10到99页,有90×2=180(个),100﹣999页,有900×3=2700(个),以上共9+180+2700=2889个数字;2925﹣2889=36(个),从1000页起,每页用4个数字,用36个数字的页数为:36÷4=9页,所以,这本词典共有页数:999+9=1008页.解答:解:1﹣9页9个,10到99页,有90×2=180(个),100﹣999页,有900×3=2700(个),以上共9+180+2700=2889个数字;2925﹣2889=36(个),从1000页起,每页用4个数字,用2000个数字的页数为:36÷4=9页;所以,这本词典共有页数:999+9=1008页;答:这本辞典共有1008页.点评:因为一个页码为几位数就含有几个数字,所以完成本题据页码的位数进行分析解答比较简单.4.有一本书的中间被撕掉了一张,余下各页的页码数之和正好是1145,那么被撕掉的那一张的页码数是几?考点:页码问题.专题:传统应用题专题.分析:一本书中间的某一张被撕掉了,这两页的页码数字和应为奇数.余下的各页码数之和是1133,所以这本书的页码总和为偶数.设这本书n页,则n(n+1)÷2>1145,据此分析即可.解答:解:设这本书的页码是从1到n的自然数,正确的和应该是:1+2+…+n=n(n+1),由题意可知,n(n+1)>1145,由估算,当n=48时,n(n+1)=×48×49=1176,1176﹣1145=31,根据书页的页码编排,被撕一张的页码应是奇、偶,其和是奇数,31=15+16.所以,这本书有48页,被撕的一张是第15页和第16页.即这本书共48页,撕掉的是第15页和第16页.点评:解答此题的关键在于弄清被撕掉的两页数字和为奇数.考点:页码问题.专题:传统应用题专题.分析:只要求出组成1~1998共需要多少个数字,即能求出这是一个几位数.根据自然数的排列规律及数位知识进行分析即可.解答:解:1~9共需要9个数字,10~99共需要2×90=180个数字,100~999共需要3×900=1700个数字,1000~1998共需要4×999=3996个数字,所以,这是一个9+180+2700+3996=6885位数.点评:根据自然数的排列规律及数位知识计算出组成这些数的数字的个数是完成本题的关键.6.一本书100页,计算页码1﹣100这些自然数中的所有数字的和是多少?考点:页码问题.专题:探索数的规律.分析:考虑0到99,也就是00到99这100个“两位数”,共用数字100×2=200个,其中,数字0到9出现的次数相等,都是200÷10=20次;因此00到99的所有位数字的和=(0+1+2+ (9)×20=900;再加上100上的数字1即可解决问题.解答:解:00到99这100个“两位数”,共用数字100×2=200个,数字0到9出现的次数相等,都是200÷10=20次;所以00到99的所有位数字的和是(0+1+2+…+9)×20=900;900+1=901;答:1﹣100这些自然数中的所有数字的和是901.点评:注意把一位数看做两位数,使问题简单化统一化.考点:页码问题.专题:传统应用题专题.分析:一位数字1、2、3、4、5、6、7、8、9共占9个位,两位数字10、11、12…99,共有99﹣9个数,所占的位数是(99﹣9)×2,三位数字100、101、102、…999共有999﹣99个数,所占的位数(999﹣99)×3,根据已知得出第666个数字是第638个3位数的第3位,进而得出即可.解答:解:因为共有9个1位数,90个2位数,900个3位数;①666﹣9﹣180=477,所以477÷3=159,因为159是继99后的第159个数,所以此数是258,第三位是8;②1999﹣9﹣180=1810,所以1810÷3=603…1,因为此603是继99后的第603个数所以此数是702,它后面的数字是703,第一位数字是7;答:第666个数字是8,第1999个数字是7.点评:此题主要考查了数字变化规律,根据已知得出变化规律是解题关键.练习8.一本科幻小说共320页,问:(1)印这本科幻小说的页码共要多少个数字?(2)数字0在页码中共出现了多少次?考点:页码问题.专题:传统应用题专题.分析:本题根据自然数的排列组合规律及数位知识进行分析完成即可.解答:解:(1)个位数页码1~9共需要9个数字,两位数页码10~99共需要2×90=180个数字,三位数页码100~320共需要221×3=663个数字.则这本书页码共用了9+180+663=852(个)数字.答:印这本科幻小说的页码共要8个数字.(2)10~99,共出现了9次;100~109,共出现了11次;110~199,共出现了9次;200~209 共出现了11次210~299 共出现了9次300~309 共出现了11次310~320 共出现了2次.共计:9×3+11×3+2=62次答:数字0在页码中共出现了62次.点评:根据自然数的排列组合规律及数位知识分数段进行分析是完成此类题目的关键.9.排一本学生词典的页码,共用了3829个数字,问这本词典共有几页?考点:页码问题.专题:传统应用题专题.分析:完成本题可按页码的位数进行分析,1﹣9页9个,10到99页,有90×2=180(个),100﹣999页,有900×3=2700(个),以上共9+180+2700=2889个数字;3829﹣2889=940(个),从1000页起,每页用4个数字,用940个数字的页数为:940÷4=235所以,这本词典共有页数:999+235=1234页.解答:解:1﹣9页9个,10到99页,有90×2=180(个),100﹣999页,有900×3=2700(个),以上共9+180+2700=2889个数字;3829﹣2889=940(个),从1000页起,每页用4个数字,用2000个数字的页数为:940÷4=235页;所以,这本词典共有页数:999+235=1234页;答:这本辞典共有1234页.点评:因为一个页码为几位数就含有几个数字,所以完成本题据页码的位数进行分析解答比较简单.10.一本故事书的页码,用了49个0,问这本书共有几页?考点:页码问题.专题:传统应用题专题.分析:本题根据自然数的组合排列规律及数位知识分析完成即可.解答:解:1~99共需要9个0,100~199共需要20个0,200~299共需20个0.此时共用了9+20+20=49个零,所以这本书页数可为290~299之间.点评:此类题目根据数段进行分析计算比较简单.11.一本《新编小学生字典》共563页,需要多少个数码编页码?考点:页码问题.分析:本题根据自然数的排列规律及数位知识进行分析即可.解答:解:1~9页共需要 9个数字,10~99共需要2×90=180个数字,100~563共需要3×464=1392个数字,所以,1~563页共需要:9+180+1392=1581(个)数码.点评:根据自然数的排列规律及数位知识计算出组成这些数的数字的个数是完成本题的关键.12.一本书的页码,在排版时用了2691个数码,则这本书一共有多少页?考点:页码问题.专题:传统应用题专题.分析:本题根据自然数的排列规律及数位知识进行分析完成即可.解答:解:个位数页码1~9共需要9个数字;两位数页码10~99共需2×90=180个数字;三位数页码100~999共需3×900=2700个数字;因为2700>2691,2691﹣9﹣180=2502(个),也就是说,三位数字的数有2502个数字;2502÷3=834,说明三位数字的数有834个;834+90+9=933(页);答:这本书共有933页.点评:此题属于页码问题,在解题时应注意分段来解答.考点:页码问题.专题:传统应用题专题.分析:一位数字1、2、3、4、5、6、7、8、9共占9个位,两位数字10、11、12…99,共有99﹣9个数,所占的位数是(99﹣9)×2,三位数字100、101、102、…999共有999﹣99个数,所占的位数(999﹣99)×3,把三种情况的位数加起来,即可得解.解答:解:9+(99﹣9)×2+(999﹣99)×3=9+180+2700=2889,答:这是一个2889位数.点评:解决此题的关键是数清多少个一位数、二位数和三位数,一位数占1个位,二位数占2个位,三位数占3个位,加起来得解.14.一本书的页码从1至82,共有82页,在把这本书的各页的页码累加起来时,有一个页码被错误的多加了一次,结果得到的和为3440.则这个被多加了一次的页码是多少?考点:页码问题.专题:传统应用题专题.分析:一本书的页码从1至82,共有82页,则所有页码之和是1+2+3+…+82,根据高斯求和公式求出所有页码之和后,用3440减去所有页码之和即得这个被多加了一次的页码是多少.解答:解:1+2+3+…+82=(1+82)×82÷2,=83×82÷2,=3403.3440﹣3403=37.答:被多加了一次的页码是37.点评:高斯求和公式:等差数列和=(首项+末项)×项数÷2.考点:页码问题.专题:传统应用题专题.分析:根据自然数的排列规律及数位知识,只要算出2000个数字能组成多少个页码即能知道从左起第2000位上的数字是几.解答:解:组成一位数页码1~9需要9个数字,两位数页码10~99需要2×90=180个数字,此时还剩2000﹣9﹣180=1811个数字,能组成三位数页码1811÷3=603个…2个.即此时能组三位数页码603个,还剩2个数字.则第2000个数字为100+603=703中的第二个数字为0.即左起第2000位上的数字是0.点评:明确自然数的排列规律及数位知识是完成本题的关键.16.排一本500页的书的页码,共需要多少个0?考点:页码问题.专题:传统应用题专题.分析:据自然数的组成结构及排列规律可知,在1~500页中,页码1﹣10间,只有1个0(也即页码10)出现;页码11﹣100间,20、30、40…90逢10的倍数会出现一个0,100页上有2个0,共有10个0;页码101﹣110间,每个页码都有一个0,共有10个0,页码为111﹣200的情况与11﹣100间一样,也是10个0,即101~200之间共20个零;由此可知,201~400之间0的个数与101~200之间的个数是一样的,据此将每个数段的零相加即得数字0在页码中共出现了多少次.解答:解:解:页码1﹣10间,只有1个0(也即页码10)出现;页码11﹣100间,20~90共有8个0,100页上有2个0,共有10个0;页码101﹣110间,共有10个0,页码为111﹣200的情况与11﹣100间一样,也是10个0,即101~200之间共20个零;所以1~500页中,则数码0在页码中出现的次数是1+10+20×4=91个.故答案为:91.点评:根据自然数的排列规律及结构按数段进行分析是完成此类问题的关键.17.有一本68页的书,中间缺了一张,小杰将残书的页码相加,得到2305,老师说小杰一定算错了,你知道为什么吗?考点:页码问题.专题:传统应用题专题.分析:有一本68页的书,则所有页码的和相加的和是1+2+3+…+68=2346,小杰将残书的页码相加,得到2305,2346﹣2305=41,由于中间缺了一张,根据页码的排列规律可知,缺的两页的页码应是相连的,且缺的这张的前一页的页码应是奇数,后一页应是偶数,而41=20+21,前偶后奇,不符合据页码的排列规律.所以错了.解答:解:1+2+3+…+68=(1+68)×68÷2,=69×68÷2,=2346.2346﹣2305=41.41=20+21.前偶后奇,不符合据页码的排列规律,所以错了.点评:明确页码的排列规律是完成此类题目的关键.家庭作业:18.一本《儿童时代》共98页,需要多少个数码编页码?考点:页码问题.专题:传统应用题专题.分析:本题根据自然数的组成规律及数位知识按一位数、两位数、两种情况进行分析计算即可.解答:解:一位数:1~9,共需9个数码;两位数:10~98共需要(98﹣9)×2=178个数码;9+178=187(个)答:需要187个数码编页码.点评:完成本题要注意一位数、两位数、两种情况进行分析计算.19.一本书的页码为1至82页,即共82页.把这本书的各页的页码累加起来时,有一页码漏加了.结果得到的和数为3396.问这个被漏加的页码是几?考点:页码问题.专题:数性的判断专题.分析:由于共82页,则所有页码之和是1+2+3+…+82,由此据高斯求出公式求出所有页码之和,减去3396,即是被漏加的页码是几.解答:解:1+2+3+…+82=(1+82)×82÷2,=83×82÷2,=3403.3403﹣3396=7.答:被漏加的页码是7.点评:高斯求出公式:等差数列和=(首项+末项)×项数÷2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学四年级奥数
第14讲数字与页码
知识方法…………………………………………………
在日常的编门牌号码中、在编书所用页码中,都会用到数与数字之间的关系。
这样的一些问题,如果用一般的思考方法,往往觉得无法入手,但是只要我们认真思考,善于捕捉数量之同的“蛛丝马迹”,通过合乎情理的运算与推导,就会找出一定的规律,很快地解答这些问题。
重点点拨…………………………………………………
【例1】有一个两位数,十位上的数字是个位上数字的3倍。
如果把这两个数字对调位置,组成一个新的两位数,这时两个数的和是132,求原两位数。
分析与解符合十位上的数字是个位上数字的3倍这个条件的两位数有:31,62,93这两个数字对调位置后,得到的是13,26,39,只有39+93=132,所以原来的两位数是93。
【例2】张家的门牌号码是一个三位数,而且三个数宇都不相同,但知道三个数字的和是6,你说说他家的门牌号码是多少?(把所有可能的情况都写出来)
分析与解根据三个数字都不相同,但三个数字的和是6,我们找出符合条件的情况:
0,1,5组合:150,105,510,501。
0,2,4组合:240,204,420,402。
1,2,3组合:123,132,213,231,312,321。
一共有14种可能。
【例3】一本书共222页,需多少个数码编页码?
分析与解1~9页每页上的页码是一位数,共需数码1×9=9(个);
10~99页每页上的页码是两位数,共需数码2×90=180(个);
100~222页每页上的页码是三位数,共需数码(222-2100+1)×3=369(个)。
9+180+369=558(个)。
答:需要558个数码编页码。
【例4】《民间故事》的正文第一页到最后一页共用了360个数码编页码,这本书的正文有多少页?
分析一位数页码只有一位数字,共有1~9这9个数字;两位数页码从10~9,共90个数,180个数字;三位数页码从100~990共900个数,2700个数字。
这本书从第一页到最后一页共用了360个数字,所以这本书的页数是三位数。
360-180-9=171,这剩下的171个数字组成的是三位数页码,所以有171÷3=57(页),一共有99+57=156(页)。
解答360-180-9=171(个171÷3=57(页)99+57=156(页)
答:这本书有156页
【例5】有一本从正文开始一共50页的书,中间缺了一张,小华将这本书的页码相加,得到的和是1254。
老师说小华计算错了,你知道为什么吗?
分析与解50页书的所有页码数之和为
1+2+…+5050×(50+1)÷:21275
按照小明的计算,中间缺的这一张上的两个页码之和为1275-1254=21。
这两个页码应该是10页和11页。
一本书的正文从第1页起,即单数页印在正面,偶数页印在反面,所以任何一张上的两
个页码,都是奇数在前,偶数在后。
小华计算出来的是缺10页和11页,这是不可能的。
【例6】将自然数按从小到大的顺序无间隔地排成一个大数:123456789101112……问:左起第2000位上的数字是多少?
分析与解本题类似于“用2000个数码能排多少页的页码?”
1~9页每页上的页码是一位数,共需数码
10~99页每页上的页码是两位数,共需数码2×90=180(个);
因为(2000-189)÷3=603……2,所以2000个数码排到第99+603+1=703(页)的第2个数码“0”。
所以本题的第2000位数是0。
培优高手…………………………………………………
1.一个两位数,个位上的数字是十位上数字的2倍。
如果把十位上的数字与个位上的数字对调,那么所得的两位数比原来的两位数大36,求原来的两位数。
2.一个两位数,十位上的数字比个位上的数字的3倍还多1,将个位数字与十位数字对调,得到一个新的两位数,这两个两位数的差是45,求这个两位数。
3.某个密码锁由3个非零的数字组成,而且三个数字都不相同,现在知道3个数字的和9,你能找出所有可能的情况吗?
4.某个密码锁由4个数字组成(O除外),而且4个数字都不相同,但知道4个数字的和是14,你能找出所有可能的情况吗?
5.排一本辞典的页码共用了2925个数字,请你算一下,这本辞典有多少页?
6.一本科幻小说共320页,编印这本科幻小说的页码共要用多少个数字?
7.一本书的页码从1至62,即共有62页。
在把这本书的各页页码累积加起来时,有一个页码被错误地多加了一次。
结果,得到的和数为2000。
问:这个被多加了一次的页码是几?
8.将自然数按从小到大的顺序无间隔地排成一个大数:1234568910112……问:左起第1000位上的数字是多少?
9.从1993到5989的所有自然数中,十位数字与个位数字相同的共有多少个?。
