中考数学专题研究(不等式动点问题概率反比例函数函数应用题)

合集下载

中考数学真题分类汇编及解析(十七) 函数与方程、不等式

2x−y+m=0
（2022•荆州中考）如图是同一直角坐标系中函数y1＝2x和y2=2
x的图象．观察图象可得不等式2x＞
2
x的解集为
（）
A．﹣1＜x＜1B．x＜﹣1或x＞1C．x＜﹣1或0＜x＜1D．﹣1＜x＜0或x＞1
【解析】选D．由图象，函数y1＝2x和y2=2
x的交点横坐标为﹣1，1，
所以当﹣1＜x＜0或x＞1时，y1＞y2，即2x＞2 x .
（2022•鄂州中考）数形结合是解决数学问题常用的思想方法．如图，一次函数y＝kx+b（k、b为常数，且k＜
0）的图象与直线y=1
3x都经过点A（3，1），当kx+b＜
1
3x时，根据图象可知，x的取值范围是（）
A．x＞3B．x＜3C．x＜1D．x＞1【解析】选A．由图象可得，
当x＞3时，直线y=1
3x在一次函数y＝kx+b的上方，
所以当kx+b＜1
3x时，x的取值范围是x＞3．
二元一次方程组{y =2x +b y =−3x +6
的解是（）
A ．{x =2y =0
B ．{x =1y =3
C ．{x =−1y =9
D ．{x =3y =1
【解析】选B ．由图象可得直线l 1和直线l 2交点坐标是（4，5），所以方程组组{y =2x +b y =−3x +6
的解为{x =1y =3．（2022•扬州中考）如图，函数y ＝kx +b （k ＜0）的图象经过点P ，则关于x 的不等式kx +b ＞3的解集为 x ＜
﹣1 ．
【解析】由图象可得，
当x ＝﹣1时，y ＝3，该函数y 随x 的增大而减小，
所以不等式kx +b ＞3的解集为x ＜﹣1，
答案：x ＜﹣1。

反比例函数大题(二大题型)—2024年中考数学压轴题专项训练(全国通用)解析版

反比例函数大题（二大题型）通用的解题思路：题型一．反比例函数与一次函数的交点问题反比例函数与一次函数的交点问题（1）求反比例函数与一次函数的交点坐标，把两个函数关系式联立成方程组求解，若方程组有解则两者有交点，方程组无解，则两者无交点．（2）判断正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中的交点个数可总结为：①当k 1与k 2同号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有2个交点；②当k 1与k 2异号时，正比例函数y ＝k 1x 和反比例函数y ＝在同一直角坐标系中有0个交点．题型二．反比例函数综合题（1）应用类综合题能够从实际的问题中抽象出反比例函数这一数学模型，是解决实际问题的关键一步，培养了学生的建模能待定系数法和其他学科中的知识．（2）数形结合类综合题利用图象解决问题，从图上获取有用的信息，是解题的关键所在．已知点在图象上，那么点一定满足这个函数解析式，反过来如果这点满足函数的解析式，那么这个点也一定在函数图象上．还能利用图象直接比较函数值或是自变量的大小．将数形结合在一起，是分析解决问题的一种好方法．题型一．反比例函数与一次函数的交点问题（共25小题）1．（2024•新北区校级模拟）如图，双曲线1k y x =与直线232y x =交于A ，B 两点．点(2,)A a 和点(,3)B b −在双曲线上，点C 为x 轴正半轴上的一点．（1）求双曲线1k y x =的表达式和a ，b 的值；（2）请直接写出使得12y y >的x 的取值范围；（3）若ABC ∆的面积为12，求此时C 点的坐标．【分析】（1）把点(2,)A a 和点(,3)B b −代入232y x =，求出a 与b 的值，再将A 点坐标代入1k y x=，即可求出反比例函数解析式；（2）根据A 与B 横坐标，利用图象求出反比例函数值大于一次函数值时x 的范围即可；（3）根据12ABC AOC BOC S S S ∆∆∆=+=，求出OC 的长，进而得到此时C 点的坐标．【解答】解：（1）直线232y x =过点(2,)A a 和点(,3)B b −， 3232a ∴=⨯=，332b =−， 2b ∴=−．双曲线1k y x=过点(2,3)A ， 236k ∴=⨯=，∴双曲线1k y x =的表达式为16y x=；（2）观察图象，可得当2x <−或02x <<时，反比例函数值大于一次函数值，即使得12y y >的x 的取值范围是2x <−或02x <<；（3）(2,3)A ，(2,3)B −−，12ABC AOC BOC S S S ∆∆∆=+=， ∴11331222OC OC ⨯+⨯=， 4OC ∴=，∴此时C 点的坐标为(4,0)．【点评】此题考查了待定系数法求反比例函数解析式，一次函数与反比例函数的交点问题，函数图象上点的坐标特征，三角形的面积，利用了数形结合的思想，正确求出反比例函数解析式是解本题的关键．2．（2023•苏州）如图，一次函数2y x =的图象与反比例函数(0)k y x x=>的图象交于点(4,)A n ．将点A 沿x 轴正方向平移m 个单位长度得到点B ，D 为x 轴正半轴上的点，点B 的横坐标大于点D 的横坐标，连接BD ，BD 的中点C 在反比例函数(0)k y x x=>的图象上．（1）求n ，k 的值；（2）当m 为何值时，AB OD ⋅的值最大？最大值是多少？【分析】（1）首先将点(4,)A n 代入2y x =可求出n ，再将点A 的坐标代入/y k x =即可求出k ；（2）过点C 作直线EF x ⊥轴于F AB 于E ，先证ECB ∆和FCD ∆全等，得BE DF =，4CE CF ==，进而可求出点(8,4)C ，根据平移的性质得点(4,8)B m +，则4BE DF m ==−，12OD m =−，据此可得出(12)AB DD m m ⋅=−，最后求出这个二次函数的最大值即可．【解答】解：（1）将点(4,)A n 代入2y x =，得：8n =，∴点A 的坐标为(4,8)，将点(4,8)A 代入k y x=，得：32k =．（2）点B 的横坐标大于点D 的横坐标，∴点B 在点D 的右侧．过点C 作直线EF x ⊥轴于F ，交AB 于E ，由平移的性质得：//AB x 轴，AB m =，B CDF ∴∠=∠，点C 为BD 的中点，BC DC ∴=，在ECB ∆和FCD ∆中，B CDF BC DC BCE DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ECB FCD ASA ∴∆≅∆，BE DF ∴=，CE CF =．//AB x 轴，点A 的坐标为(4,8)，8EF ∴=，4CE CF ∴==，∴点C 的纵坐标为4，由（1）知：反比例函数的解析式为：32y x=， ∴当4y =时，8x =，∴点C 的坐标为(8,4)， ∴点E 的坐标为(8,8)，点F 的坐标为(8,0)，点(4,8)A ，AB m =，//AB x 轴，∴点B 的坐标为(4,8)m +，484BE m m ∴=+−=−，4DF BE m ∴==−，8(4)12OD m m ∴=−−=−2(12)(6)36AB OD m m m ⋅=−=−−+∴当6m =时，AB OD ⋅取得最大值，最大值为36．【点评】此题主要考查了反比例函数的图象、二次函数的图象和性质，点的坐标平移等，解答此题的关键是熟练掌握待定系数法求函数的解析式，理解点的坐标的平移，难点是在解答（2）时，构造二次函数求最值．3．（2024•常州模拟）如图，反比例函数1k y x =的图象与一次函数2y k x b =+的图象交于点(1,2)A −，1(4,)2B −．（1）求函数1k y x=和2y k x b =+的表达式；（2）若在x 轴上有一动点C ，当2ABC AOB S S ∆∆=时，求点C 的坐标．【分析】（1）将点(1,2)A −，1(4,)2B −分别代入反比例函数1k y x =和一次函数2y k x b =+的解析式，求解即可；（2）设AB 与y 轴交于点D 作//CE y 轴交AB 于点E ，利用三角形的面积公式，列出方程，求解即可．【解答】解：（1）将点(1,2)A −，1(4,)2B −分别代入反比例函数1k y x =和一次函数2y k x b =+的解析式， 1122k ∴=−⨯=−，222142k b k b −+=⎧⎪⎨+=−⎪⎩， 12k ∴=，21232k b ⎧=−⎪⎪⎨⎪=⎪⎩． ∴反比例函数的解析式为：2y x =，一次函数的解析式为：1322y x =−+．（2）如图，设AB 与y 轴交于点D ，过点C 作//CE y 轴交AB 于点E ，设(,0)C m ，13(,)22E m m ∴−+．13||22CE m ∴=−+．令0x =，则32y =， 3(0,)2D ∴， 32OD ∴=， 11315()[4(1)]2224AOB B A S OD x x ∆∴=⋅−=⨯⨯−−=． 1522ABC AOB S S ∆∆∴==． ∴115()22B A CE x x ⋅−=，即11315||52222m ⋅−+⋅=．解得3m =−或9m =，∴点C 的坐标为(3,0)−或(9,0)．【点评】本题考查了反比例函数与一次函数的交点问题，求三角形的面积，求函数的解析式，正确掌握反比例函数的性质是解题的关键．4．（2024•常州模拟）如图，一次函数1(0)y kx b k =+≠与函数为2(0)m y x x =>的图象交于1(4,1),(,)2A B a 两点．（1）求这两个函数的解析式；（2）根据图象，直接写出满足120y y −>时x 的取值范围；（3）点P 在线段AB 上，过点P 作x 轴的垂线，垂足为M ，交函数2y 的图象于点Q ，若POQ ∆的面积为3，求点P 的坐标．【分析】（1）将A 点坐标代入即可得出反比例函数2(0)m y x x=>，求得函数的解析式，进而求得B 的坐标，再将A 、B 两点坐标分别代入1y kx b =+，可用待定系数法确定一次函数的解析式；（2）由题意即求12y y >的x 的取值范围，由函数的图象即可得出反比例函数的值小于一次函数值的x 的取值范围；（3）由题意，设(,29)P p p −+且142p ……，则4(,)Q p p ，求得429PQ p p=−+−，根据三角形面积公式得到14(29)32POQ S p p p∆=−+−⋅=，解得即可．【解答】解：（1）反比例函数2(0)m y x x=>的图象经过点(4,1)A ， 14m ∴=． 4m ∴=．∴反比例函数解析式为24(0)y x x=>．把1(2B ，)a 代入24(0)y x x=>，得8a =． ∴点B 坐标为1(2，8)，一次函数解析式1y kx b =+图象经过(4,1)A ，1(2B ，8)， ∴41182k b k b +=⎧⎪⎨+=⎪⎩．解得29k b =−⎧⎨=⎩．故一次函数解析式为：129y x =−+．（2）由120y y −>，12y y ∴>，即反比例函数值小于一次函数值．由图象可得，142x <<．（3）由题意，设(,29)P p p −+且142p ……， 4(,)Q p p∴． 429PQ p p∴=−+−． 14(29)32POQ S p p p∆∴=−+−⋅=．解得152p =，22p =． 5(2P ∴，4)或(2,5)．【点评】本题主要考查一次函数与反比例函数交点问题，熟练掌握待定系数法求函数解析式是解题的关键．5．（2024•沭阳县模拟）如图，反比例函数k y x=的图象与一次函数y mx n =+的图象相交于(,1)A a −，(1,3)B −两点．（1）求反比例函数和一次函数的解析式；（2）设直线AB 交y 轴于点C ，点(,0)N t 是x 轴正半轴上的一个动点，过点N 作NM x ⊥轴交反比例函数k y x =的图象于点M ，连接CN ，OM ．若3COMN S >四边形，求t 的取值范围．【分析】（1）将点B ，点A 坐标代入反比例函数的解析式，可求a 和k 的值，利用待定系数法可求一次函数解析式；（2）先求出点C 坐标，由面积关系可求解．【解答】解：（1）反比例函数k y x=的图象与一次函数y mx n =+的图象相交于(,1)A a −，(1,3)B −两点， 13(1)k a ∴=−⨯=⨯−，3k ∴=−，3a =，∴点(3,1)A −，反比例函数的解析式为3y x−=，由题意可得：313m n m n =−+⎧⎨−=+⎩，解得：12m n =−⎧⎨=⎩， ∴一次函数解析式为2y x =−+；（2）直线AB 交y 轴于点C ，∴点(0,2)C ，31222OMN OCN COMN S S S t ∆∆∴=+=+⨯⨯四边形， 3COMN S >四边形， ∴312322t +⨯⨯>， 32t ∴>．【点评】本题考查了反比例函数与一次函数的交点问题，考查了利用待定系数法求解析式，反比例函数的性质等知识，求出两个解析式是解题的关键．6．（2024•宿迁二模）已知函数1y x=的图象与函数(0)y kx k =≠的图象交于点(,)P m n （1）若2m n =，求k 的值和点P 的坐标．（2）当||||m n …时，结合函数图象，直接写出实数k 的取值范围．【分析】（1）由(0)y kx k =≠得n k m =，然后由2m n =可得到k 的值，设(2,)P n n ，将点P 的坐标代入反比例函数解析式可求得n 的值；（2）由(0)y kx k =≠得n k m =，然后结合条件||||m n …可得k 的取值范围．【解答】解：（1）(0)y kx k =≠， 122y n n k x m n ∴====．2m n =，(2,)P n n ∴，21n n ∴=，解得：2n =±．m ∴=P ∴或(．（2）y kx =， y n k x m ∴==，||||m n …，1k ∴…．【点评】本题主要考查的是反比例函数和一次函数的交点问题，掌握待定系数法求函数解析式的方法是解题的关键．7．（2024•泉山区校级模拟）如图，在平面直角坐标系xOy 中，一次函数152y x =+和2y x =−的图象相交于点A ，反比例函数k y x =的图象经过点A ．（1）求反比例函数的表达式；（2）设一次函数152y x =+的图象与反比例函数k y x=的图象的另一个交点为B ，连接OB ，求ABO ∆的面积．【分析】（1）联立方程求得A 的坐标，然后根据待定系数法即可求得；（2）联立方程求得交点B 的坐标，进而求得直线与x 轴的交点，然后利用三角形面积公式求得即可．【解答】解：（1）由1522y x y x ⎧=+⎪⎨⎪=−⎩得24x y =−⎧⎨=⎩，(2,4)A ∴−，反比例函数ky x =的图象经过点A ，248k ∴=−⨯=−，∴反比例函数的表达式是8y x =−；（2）解8152y x y x ⎧=−⎪⎪⎨⎪=+⎪⎩得24x y =−⎧⎨=⎩或81x y =−⎧⎨=⎩，(8,1)B ∴−，由直线AB 的解析式为152y x =+得到直线与x 轴的交点为(10,0)−，111041011522AOB S ∆∴=⨯⨯−⨯⨯=．【点评】本题考查了一次函数和反比例函数的交点问题，通过方程组求得交点坐标是解题的关键．8．（2023•常州）在平面直角坐标系中，一次函数y kx b =+的图象与反比例函数m y x=的图象相交于点(2,4)A 、(4,)B n ．C 是y 轴上的一点，连接CA 、CB ．（1）求一次函数、反比例函数的表达式；（2）若ABC ∆的面积是6，求点C 的坐标．【分析】（1）利用待定系数法求得即可；（2）先求得(0,6)D ，再根据ABC BCDACD S S S ∆∆∆=−得1(42)62CD ⨯⋅−=，进而得出6CD =，据此可得点C 的坐标．【解答】解：（1）点(2,4)A 在反比例函数m y x =的图象上， 248m ∴=⨯=，∴反比例函数解析式为8y x =；又点(4,)B n 在8y x =上，2n ∴=， ∴点B 的坐标为(4,2)，把(2,4)A 和(4,2)B 两点的坐标代入一次函数y kx b =+得2442k b k b +=⎧⎨+=⎩，解得16k b =−⎧⎨=⎩，∴一次函数的解析为6y x =−+．（2）对于一次函数6y x =−+，令0x =，则6y =，即(0,6)D ，根据题意得：1(42)62ABC BCD ACD S S S CD ∆∆∆=−=⨯⋅−=，解得：6CD =，0OC ∴=或12，(0,0)C ∴或(0,12)．【点评】本题主要考查了一次函数与反比例函数交点问题，解题时注意：一次函数与反比例函数交点坐标同时满足一次函数与反比例函数解析式．9．（2024•姜堰区一模）如图，一次函数12y x a =−+的图象与反比例函数2(0)k y k x=>的图象在第一象限相交于点(,)A m n ，(2,3)B m n −．（1）求a 、k 的值；（2）当120y y >>时，直接写出x 的取值范围．【分析】（1）根据反比例函数图象上点的坐标特征，得到3m =，代入A 、B 点的坐标再代入一次函数解析式组成方程组求出n 和a ，最后求出k 值即可；（2）根据函数图象直接写出当120y y >>时自变量取值范围即可．【解答】解：（1）点(,)A m n ，(2,3)B m n −都在反比例函数图象上，3(2)mn n m ∴=⨯−，整理得：2(3)0n m −=，0m ≠，0n ≠，30m ∴−=，解得3m =．(3,)A n ，(1,3)B n 在直线12y x a =−+的图象上，∴623a n a n −+=⎧⎨−+=⎩，解得28n a =⎧⎨=⎩，(3,2)A ∴，(3,2)A 在反比例函数图象上，6k ∴=．8a ∴=，6k =．（2）由（1）可知：(3,2)A ，(1,6)B ，根据函数图象可知，120y y >>时，x 的取值范围为：13x <<．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式是关键．10．（2024•昆山市模拟）如图，一次函数11(0)y k x b k =+≠的图象与反比例函数22(0)k y k x=≠的图象相交于A ，B 两点，其中点A 的坐标为(2,1)−，点B 的坐标为(1,)n ．（1）求这两个函数的表达式；（2）根据图象，直接写出满足21k k x b x+>的取值范围；（3）求ABO ∆的面积．【分析】（1）待定系数法求出两个函数解析式即可；（2）根据图像直接写出不等式的解集即可；（3）根据AOB AOC BOC S S S ∆∆∆=+代入数据计算即可．【解答】解：（1）(2,1)A −，(1,)B n 在反比例函数图象上，221k n ∴=−⨯=，22k n ∴==−，∴反比例函数解析式为：2y x =−， (2,1)A −，(1,2)B −在一次函数图象上，∴11212k b k b +−=⎧⎨+=−⎩，解得111k b =−⎧⎨=−⎩，∴一次函数解析式为：1y x =−−．（2）根据两个函数图象及交点坐标，不等式21k k x b x +>的解集为：2x <−或01x <<．（3）设直线AB 与y 轴的交点为C ，则(0,1)C −即1OC =，1131211222AOB AOC BOC S S S ∆∆∆∴=+=⨯⨯+⨯⨯=．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式．11．（2024•兴化市一模）已知函数1(k y k x =是常数，0)k ≠，函数2392y x =−+．（1）若函数1y 和函数2y 的图象交于点(2,6)A ，点(4,2)B n −．①求k ，n 的值．②当12y y >时，直接写出x 的取值范围．（2）若点(8,)C m 在函数1y 的图象上，点C 先向下平移1个单位，再向左平移3个单位，得点D ，点D 恰好落在函数1y 的图象上，求m 的值．【分析】（1）①根据反比例函数图象上点的坐标特征进行解答即可；②根据图形分布和解答横坐标直接写出不等式解集即可；（2）先根据平移条件得到(5,1)D m −，再根据反比例函数图象上点的坐标特征求出m 值即可．【解答】解：（1）①函数1y 和函数2y 的图象交于点(2,6)A ，点(4,2)B n −，264(2)k n ∴=⨯=⨯−，解得：12k =，5n =． ②由①可知，反比例函数解析式为12y x =，图象分布在第一、三象限，(2,6)A ，(4,3)B 12y y ∴>时，x 的取值范围为：02x <<或4x >．（2）点(8,)C m 在函数1y 的图象上，点C 先向下平移1个单位，再向左平移3个单位，得点D ， (5,1)D m ∴−， D 恰好落在函数1ky x =图象上， 5(1)8m m ∴−=，解得53m =−．【点评】本题考查了反比例函数与一次函数的交点问题，交点坐标满足两个函数解析式是关键．12．（2024•南通模拟）如图，直线AB 交双曲线k y x=于A 、B 两点，交x 轴于点C ，且B 恰为线段AC 的中点，连接OA ．若6OAC S ∆=．求k 的值．【分析】设出点B 的坐标，进而可以表示出点A 和点C 的坐标，再根据OAC ∆的面积即可解决问题．【解答】解：设点B 坐标为(,)k a a ，点B 为线段AC 的中点， ∴22A B ky y a ==，则点A 的坐标为2(,)2a k a ， ∴2A C x x a +=， ∴32C x a =，则点C 坐标为3(,0)2a ．又AOC ∆的面积为6， ∴132622k a a ⋅⋅=，解得4k =，故k 的值为4．【点评】本题考查反比例函数与一次函数的交点问题，熟知反比例函数及一次函数的图象和性质是解题的关键．13．（2024•亭湖区模拟）如图，等腰三角形OAB 中，AO AB =，点B 坐标为(4,0)顶点A 在反比例函数k y x=的图象上，且OAB ∆的面积为12．（1）k = ．（2）过B 点直线对应的解析式为y x b =+与双曲线k y x =在第一，三象限交点分别为点M ，N ． ①求点M ，N 的坐标．②直接写出不等式0k x b x −−…的解集．【分析】（1）过点A 作AC OB ⊥于点C ，利用三角形面积求得AC 即可求得点A 的坐标是(2,6)，将点A 的坐标代入反比例函数表达式，即可求解；（2）①求得一次函数的解析式，与反比例函数解析式联立，解方程组即可求解；②根据图象即可求得．【解答】解：（1）过点A 作AC OB ⊥于点C ，等腰三角形OAB 中，AO AB =，点B 坐标为(4,0)，4OB ∴=，OAB ∆的面积为12， ∴1122OB AC ⋅=，6AC ∴=，(2,6)A ∴，顶点A 在反比例函数k y x =的图象上，解得：2612k =⨯=，故答案为：12；（2）①把B 点的坐标代入y x b =+得：40b +=，4b ∴=−，∴过B 点直线解析式为4y x =−，联立412y x y x =−⎧⎪⎨=⎪⎩，解得62x y =⎧⎨=⎩或26x y =−⎧⎨=−⎩，(6,2)M ∴，(2,6)N −−； ②观察图象，不等式0k x b x −−…的解集是06x <…或2x −…．【点评】本题是反比例函数与一次函数的交点问题，考查了等腰三角形的性质，三角形的面积，待定系数法求反比例函数的解析式，一次函数与反比例函数的交点的求法，函数与不等式的关系，求得A 点的坐标以及数形结合是解题的关键.14．（2024•常熟市模拟）如图，一次函数112y x =−的图象与y 轴相交于B 点，与反比例函数(0,0)k y k x x =≠>图象相交于点(,2)A m ．（1）求反比例函数的表达式；（2）点C 在点A 的左侧，过点C 作y 轴平行线，交反比例函数的图象于点D ，连接BD ．设点C 的横坐标为a ，求当a 为何值时，BCD ∆的面积最大，这个最大值是多少？【分析】（1）根据待定系数法求出反比例函数解析式即可；（2）根据三角形面积公式列出关于a 的代数式，利用二次函数的最值求法求出最大面积即可．【解答】解：（1）点(,2)A m 在一次函数112y x =−的图象上， ∴1122m −=，解得6m =， (6,2)A ∴，点(6,2)A 在反比例函数图象上，6212k ∴=⨯=，∴反比例函数解析式为：12y x =；（2）在一次函数112y x =−中，令0x =，则1y =−，(0,1)B ∴−，点C 的横坐标为a ，点C 的纵坐标为112a −，12(,)D a a ∴，12112CD a a ∴=−+， 1121(1)22BCD S a a a ∆=⨯−+⨯211642a a =−++2125(1)44a =−−+， 104−<，BCD S ∆∴有最大值，当1a =时，最大值254BCD S ∆=．【点评】本题考查了反比例函数与一次函数的交点问题，熟练掌握交点坐标满足两个函数关系式是关键．15．（2024•东海县一模）一次函数5y x =−+与反比例函数k y x=的图象在第一象限交于A ，B 两点，其中(1,)A a ．（1）求反比例函数表达式；（2）结合图象，直接写出5x−+…时，x 的取值范围；（3）若把一次函数5y x =−+的图象向下平移b 个单位，使之与反比例函数k y x =的图象只有一个交点，请直接写出b 的值．【分析】（1）待定系数法求出k 值即可；（2）根据图像和两个函数的交点坐标，直线写出不等式的解集即可；（3）把一次函数5y x =−+的图象向下平移b 个单位得到新的解析式为：5y x b =−+−，联立方程组得到2(5)40x b x −−+=，利用判别式等于0，解出b 值即可．【解答】解：（1）(1,)A a 在一次函数图象上，154a ∴=−+=，即(1,4)A ，(1,4)A 在反比例函数图象上，144k ∴=⨯=，∴反比例函数解析式为：4y x =；（2）联立方程组45y x y x ⎧=⎪⎨⎪=−+⎩，解得14x y =⎧⎨=⎩或41x y =⎧⎨=⎩，(1,4)A ∴，(4,1)B ，根据两个函数图象可知：不等式5kx x −+…的解集为：01x <…或4x …；（3）把一次函数5y x =−+的图象向下平移b 个单位得到新的解析式为：5y x b =−+−，联立方程组54y x b y x =−+−⎧⎪⎨=⎪⎩，消掉得：45x b x −+−=，整理得：2(5)40x b x −−+=，△2(5)160b =−−=， 54b ∴−=±，9b ∴=或1．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式．16．（2024•钟楼区校级模拟）如图，已知反比例函数k y x=的图象与一次函数y ax b =+的图象相交于点(2,3)A 和点(,2)B n −．（1）求反比例函数与一次函数的解析式；（2）直接写出不等式k ax b x >+的解集；（3）若点P 是x 轴上一点，且满足PAB ∆的面积是10，请求出点P 的坐标．【分析】（1）将点A 坐标代入反比例函数解析式求出k ，从而求出点B 坐标，再通过待定系数法求一次函数解析式；（2）通过观察图象交点求解；（3）设点P 坐标为(,0)m ，通过三角形PAB 的面积为10及三角形面积公式求解．【解答】解：（1）将(2,3)代入k y x =得32k=，解得6k =，∴反比例函数解析式为6y x =．26n ∴−=，解得3n =−，所以点B 坐标为(3,2)−−，把(3,2)−−，(2,3)代入y ax b =+得：2332a b a b −=−+⎧⎨=+⎩，解得11a b =⎧⎨=⎩，∴一次函数解析式为1y x =+；（2）由图象可得当3x <−或02x <<时式kax b x >+；（3）设点P 坐标为(,0)m ，一次函数与x 轴交点为E ，把0y =代入1y x =+得01x =+，解得1x =−，∴点E 坐标为(1,0)−．11532222PAB PAE PBE S S S PE PE PE ∆∆∆∴=+=⨯+⨯=， ∴5102PE =，即5|1|102m +=，解得3m =或5m =−．∴点P 坐标为(3,0)或(5,0)−．【点评】本题考查一次函数与反比例函数的结合，解题关键是掌握待定系数法求函数解析式，掌握函数与不等式的关系．17．（2024•姑苏区校级模拟）如图，以x 轴上长为1的线段AB 为宽作矩形ABCD ，矩形长AD 、BC 交直线3y x =−+于点F 、E ，反比例函数(0)k y x x=>的图象正好经过点F 、E ．（1）线段EF 长为；（2）求k 值．【分析】（1）表示出E 、F 的坐标，然后利用勾股定理即可求得EF 的长度；（2）根据反比例函数图象上点的坐标特征得到(3)(1)(2)k m m m m =−+=+−+，解得即可．【解答】解：（1）点F 、E 在直线3y x =−+图象上，∴设(,3)F m m −+，则(1E m +，(1)3)m −++，即(1,2)m m +−+EF ∴．故答案为：（2）反比例函数(0)k y x x=>的图象正好经过点F 、E ， (3)(1)(2)k m m m m ∴=−+=+−+，解得1m =，(3)122k m m ∴=−+=⨯=．【点评】本题是反比例函数与一次函数的交点问题，考查了一次函数图象上点的坐标特征，待定系数法求反比例函数的解析式，求线段的长度，正确表示出点的坐标是解题的关键．18．（2024•昆山市一模）如图，在平面直角坐标系xOy 中，一次函数11(y k x b k =+，b 为常数，且10)k ≠与反比例函数22(k y k x=为常数，且20)k ≠的图象交于点(,6)A m ，(4,3)B −．（1）求反比例函数和一次函数的表达式；（2）当210k k x b x>+>时，直接写出自变量x 的取值范围；（3）已知一次函数1y k x b =+的图象与x 轴交于点C ，点P 在x 轴上，若PAC ∆的面积为9；求点P 的坐标．【分析】（1（2）根据函数图象，写出反比例函数图象在一次函数上方时且在x 轴上方时，自变量的取值范围，即可求解；（3）先求得点C 的坐标，进而根据三角形的面积公式，即可求解．【解答】解：（1）将(4,3)B −代入2k y x=，解得：212k =−，∴反比例函数表达式为12y x =−，将(,6)A m 代入12y x=−，解得：2m =−， (2,6)A ∴−，将(2,6)A −，(4,3)B −代入1y k x b =+，得112643k b k b −+=⎧⎨+=−⎩，解得：1323k b ⎧=−⎪⎨⎪=⎩， ∴一次函数的表达式为：332y x =−+；（2）(2,6)A −，(4,3)B −，根据函数图象可得：当210k k x b x >+>时，20x −<<；（3）332y x =−+，令0y =，解得：2x =，(2,0)C ∴，设(,0)P p ，则|2|PC p =−，PAC ∆的面积为9， ∴1|2|692p ⨯−⨯=，解得：5p =或1−，(5,0)P ∴或(1,0)P −．【点评】本题是反比例函数与一次函数的交点问题，考查了待定系数法求反比例函数的解析式，一次函数19．（2024•盐城模拟）如图，已知一次函数11y k x b =+的图象与反比例函数22k y x=，分别交于点A 和点B ，且A 、B 两点的坐标分别是(1,2)A −−和(2B ．)m ，连接OA 、OB ．（1）求一次函数11y k x b =+与反比例函数22k y x =的函数表达式；（2）求AOB ∆的面积．【分析】（1）用待定系数法求出反比例函数解析式，用AB 两点坐标求出直线解析式即可；（2）求出直线AB 与x 轴的交点M 的坐标，利用AOB BMO AMO S S S ∆∆∆=+代入数据计算即可．【解答】解：（1）点(1,2)A −−在反比例函数图象上，2k ∴=，反比例函数解析式为：2y x=； (2B ．)m 在反比例函数图象上，1m ∴=，即(2,1)B ，点AB 在一次函数11y k x b =+的图象上，∴11221k b k b −+=−⎧⎨+=⎩，解得：111k b =⎧⎨=−⎩，一次函数解析式为：1y x =−，（2）设直线AB 交x 轴于点M ，当0y =，1x =，(1,0)M ，1OM =．所以1131112222AOB BMO AMO S S S ∆∆∆=+=⨯⨯+⨯⨯=．小的分界点．20．（2024•天宁区校级模拟）如图，在平面直角坐标系xOy 中，一次函数2y x b =+的图象与x 轴交于点(1,0)A −，与y 轴交于点B ，与反比例函数(0)k y x x=>的图象交于点C ，且AB BC =．点D 是x 轴正半轴上一点，连接CD ，45ODC ∠=︒．（1）求b 和k 的值；（2）求ACD ∆的面积．【分析】（1）将点A 坐标代入一次函数解析式，求出b 的值，再利用平行线分线段成比例的性质得出1OH OA ==，24CH OB ==，求出C 点坐标，即可求出k 的值；（2）根据45ODC ∠=︒得到DCH ∆是等腰直角三角形，求出AD ，再求ACD ∆的面积即可．【解答】解：（1）将点(1,0)A −代入一次函数2y x b =+，得20b −+=，解得2b =，(0,2)B ∴，2OB ∴=，在22y x =+中，令0y =，则1x =−，(1,0)A ∴−，1OA ∴=，过点C 作CH x ⊥轴于点H ，则//OB ， ∴OA OB AB AH CH AC==， AB BC =， ∴1212AH CH ==， 2AH ∴=，4CH =，1OH OA ∴==，(1,4)C ∴，反比例函数(0)k y x x=>的图象过点C ， 144k ∴=⨯=；（2）45ODC ∠=︒，CH x ⊥轴于点H ，45DCH ∴∠=︒，DCH ∴∆是等腰直角三角形，4DH CH ∴==，1146AD ∴=++=，ACD ∴∆的面积为：11641222AD CH ⋅=⨯⨯=．【点评】本题是反比例函数与一次函数的交点问题，考查了待定系数法求函数的解析式，平行线分线段成比例定理，等腰直角三角形的性质，求出点C 坐标是解决本题的关键．21．（2024•姑苏区校级一模）如图，一次函数1y kx b =+的图象与反比例函数2(0)m y x x=>的图象交于点(4,1)A 和点(2,)B n ．（1）求一次函数和反比例函数解析式；（2）过点B 作BC y ⊥轴于点C ，连接OA ，求四边形OABC 的面积；（3）根据图象直接写出使kx b+<x 的取值范围．【分析】（1）采用待定系数法求函数解析式．先将点A 的坐标代入反比例函数解析式，求出m 值，再将点B 代入反比例函数解析式求出nn 值，然后将A 、B 点坐标代入一次函数解析数即可．（2）四边形OABC 的面积可由一次函数与坐标轴围成的三角形减去两个小三角形的面积得到，求出一次函数与坐标轴的交点即可求出面积．（3）结合图象确定x 的取值范围即可．【解答】解：（1）将点(4,1)A 代入2(0)m y x x =>中，得14m =，解得4m =，故24y x =；将点(2,)B n 代入24y x =，可得422n ==，将(4,1)A ，(2,2)B 代入1y kx b =+，得1422k b k b =+⎧⎨=+⎩，解得123k b ⎧=−⎪⎨⎪=⎩，故1132y x =−+；（2）如图所示，对于一次函数1132y x =−+，令0x =，则13y =，即(0,3)E令10y =，则6x =，即(6,0)D ，6OD ∴=，3OE =，(2,2)B ，BC y ⊥轴，2BC ∴=，321CE =−=，设AOD ∆的高为h ，由(4,1)A 可知1h =，DOE BOE AODOABC S S S S ∆∆∆=−−四边形 111222OD OE BC CE OD h =⨯⨯−⨯⨯−⨯⨯111632161222=⨯⨯−⨯⨯−⨯⨯5=；（3）结合图象可知，当mkx b x +<时， x 的取值范围为02x <<或4x >．【点评】本题主要考查反比例函数和一次函数的图象性质、待定系数法等综合知识，解决本题的关键是求得正确的点的坐标，将四边形OABC 放在大三角形中求解面积．22．（2024•新北区一模）如图，反比例函数(0)k y x x=>与一次函数2y x m =+的图象交于点(1,4)A ，BC y ⊥轴于点D ，分别交反比例函数与一次函数的图象于点B 、C ．（1）求反比例函数和一次函数的表达式；（2）连接AB ，若1OD =，求ABC ∆的面积．【分析】（1）将点A 坐标分别代入两个解析式得到k 、m 值即可；（2）将1y =分别代入两个解析式求出点B 、C 坐标，根据三角形面积公式计算即可．【解答】解：（1）点(1,4)A 在反比例函数图象上，144k ∴=⨯=，∴反比例函数解析式为：4y x=， 2y x m =+的图象过点(1,4)A ，421m ∴=⨯+．解得2m =，∴一次函数解析式为：22y x =+．（2）将1y =代入4y x=得4x =， (4,1)B ∴，将1y =代入22y x =+得12x =−，1(2C ∴−，1)， 194()22BC ∴=−−=， 1927(41)224ABC S ∆∴=⨯⨯−=．【点评】本题考查了一次函数与反比例函数的交点问题，交点坐标满足两个函数解析式．23．（2024•武进区校级模拟）如图，直线3y x =−+与y 轴交于点A ，与x 轴交于点D ，与反比例函数(0)k y k x=≠的图象交于点C ，过点C 作CB x ⊥轴于点B ，3AD AC =．（1）求点A 的坐标及反比例函数的解析式；（2）若点E 是直线3y x =−+与反比例函数(0)k y k x=≠图象的另一个交点，求COE ∆的面积．【分析】（1）求出点A 、点D 的坐标，然后表示出AO 、DO 的长度，再根据//CB y 轴得出DA DO AC OB =，由3AD AC =得出3OD BO =，求出点的横坐标，代入直线解析式求出纵坐标，用待定系数法求出反比例函数解析式；（2）联立两个函数解析式求出点E 坐标，再根据三角形的面积公式求面积即可．【解答】解：（1）直线3y x =−+与y 轴交于点A ，与x 轴交于点D ，(0,3)A ∴，(3,0)D ，即3OA =，3OD =，CB x ⊥轴，//CB y ∴轴， ∴DA DO AC OB=， 3AD AC =，3OD OB ∴=，1OB ∴=，∴点C 的横坐标为1−，点C 在直线3y x =−+上， ∴点(1,4)C −，144k ∴=−⨯=−，∴反比例函数的解析式为4y x=−；（2）联立方程组34y x y x =−+⎧⎪⎨=−⎪⎩，解得14x y =−⎧⎨=⎩或41x y =⎧⎨=−⎩， ∴直线与反比例函数图象的另一个交点E 的坐标为(4,1)−，111115||||313422222COE AOC AOD C D S S S OA x OA x ∆∆∆∴=+=⋅+⋅=⨯⨯+⨯⨯=．【点评】本题考查了一次函数与坐标轴的交点，一次函数与反比例函数的交点，待定系数法求函数解析式，求出反比例函数解析式是解答本题的关键．24．（2024•东海县一模）如图1，在平面直角坐标系中，一次函数y x b =+的图象经过点(2,0)A −，与反比例函数ky x=的图象交于(,4)B a ，C 两点．（1）求一次函数和反比例函数的表达式；（2）点M 是反比例函数图象在第一象限上的点，且4MAB S ∆=，请求出点M 的坐标；（3）反比例函数具有对称性，适当平移就可发现许多神奇的现象．将该双曲线在第一象限的一支沿射线BC 方向平移，使其经过点C ，再将双曲线在第三象限的一支沿射线CB 方向平移，使其经过点B ，平移后的两条曲线相交于P ，Q 两点，如图2，此时平移后的两条曲线围成了一只美丽的“眸”， PQ 为这只“眸”的“眸径”，请求出“眸径” PQ 的长．【分析】（1）用待定系数法分别求一次函数和反比例函数的表达式；（2）由4MAB S ∆=，得点M 满足在与2y x =+M 在y x =或4y x =+上，列方程组求出交点，即可求出点M ；（3）将反比例函数平移后组成方程组求出交点，再求出PQ 长即可．【解答】解：（1）把(2,0)A −代入y x b =+，得02b =−+， 2b ∴=，2y x ∴=+，把(,4)B a 代入2y x =+，得42a =+， 2a ∴=， 248k ∴=⨯=， 8y x∴=， ∴一次函数和反比例函数的表达式分别为：2y x =+，8y x=；（2）令2y x =+中0y =，得2x =−， ∴点(2,0)A −，AB ∴=142MAB S h ∆==⨯，h ∴=M 满足在与2y x =+∴点M 在y x =或4y x =+上，由8y x y x =⎧⎪⎨=⎪⎩，得11x y ⎧=⎪⎨=⎪⎩22x y ⎧=−⎪⎨=−⎪⎩点M 在第一象限， ∴点M坐标为，由48y x y x =+⎧⎪⎨=⎪⎩，得1122x y ⎧=−+⎪⎨=+⎪⎩2222x y ⎧=−−⎪⎨=−⎪⎩ 点M 在第一象限，∴点M坐标为(2−+2+，综上点M坐标为或(2−+2+；（3）平移之后的曲线为：866y x =−+和866y x =+−，由866866y x y x ⎧=+⎪⎪−⎨⎪=−⎪+⎩，得11x y ⎧=⎪⎨=−⎪⎩22x y ⎧=−⎪⎨=⎪⎩，∴点(P −点Q，−，PQ ∴=【点评】本题考查了一次函数及反比例函数的性质的应用，待定系数法的应用及交点的求法是解题关键． 25．（2024•泗阳县校级二模）如图，已知(4,)A n −，(2,4)B −是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点．（1）求反比例函数和一次函数的解析式；（2）求直线AB 与x 轴的交点C 的坐标及AOB ∆的面积；（3）直接写出一次函数的值小于反比例函数值的x 的取值范围．【分析】（1）先把B 点坐标代入代入my x =，求出m 得到反比例函数解析式，再利用反比例函数解析式确定A 点坐标，然后利用待定系数法求一次函数解析式；。

2023年九年级数学中考复习《不等式和不等式组》分类专题集训(附答案)

2023年九年级数学中考复习《不等式和不等式组》分类专题集训(一)不等式过关训练➢典例精讲1．如果关于x的不等式（a+2020）x﹣a＞2020的解集为x＜1，那么a的取值范围是（）A．a＞﹣2020B．a＜﹣2020C．a＞2020D．a＜20202．已知关于x的不等式（a+3b）x＞a﹣b的解集为x＜﹣，则关于x的一元一次不等式bx﹣a＞0的解集为．3．若关于x的不等式ax＜﹣bx+b（a，b≠0）的解集为x＞，则关于x的不等式ax＞2bx+b的解集是．4．已知关于x的不等式3x﹣2a＜4﹣5x有且仅有三个正整数解，则满足条件的整数a的个数是（）A．3个B．4个C．5个D．6个5．若关于x的不等式7x+9＞2x+a的负整数解为﹣2，﹣1，则a的取值范围是．➢课后训练1．已知关于x的不等式（2﹣a）x＞3的解集为，则a的取值范围是（）A．a＞0B．a＜0C．a＞2D．a＜22．若关于x的不等式（2m﹣n）x﹣m＞5n的解集为x＜，则关于x的不等式（m﹣n）x＞m+n的解集为（）A．x＜B．x＞C．x＞5D．x＜53．已知关于x的不等式3（a﹣b）x+a﹣5b＞0的解集为x＜1，则关于x的不等式ax≥4b的解集为．4．若关于x的不等式3x﹣m≤0的正整数解是1，2，3，则m的取值范围是（）A．m≥9B．9＜m＜12C．m＜12D．9≤m＜125．若关于x的不等式2x﹣m≥0的负整数解为﹣1，﹣2．﹣3．则m的取值范围是．(二)不等式组过关训练➢典例精讲一、两同问题1．若关于x的不等式组的解集为x≥2，则m的取值范围是（）A．m≥﹣2B．m≤2C．m＜2D．m＝22．若关于x的不等式组的解集是x＜2，则a的取值范围是（）A．a≥2B．a＜﹣2C．a＞2D．a≤2二、有解、无解问题3．若不等式组有解，则a的取值范围是（）A．a≤B．a≤4C．1≤a≤4D．a≥4．若不等式组无解，则m的取值范围为（）A．m≤8B．m＜8C．m≥8D．m＞8三、整数解问题5．关于x的不等式组的解中恰有4个整数解，则a的取值范围是（）A．18≤a≤19B．18≤a＜19C．18＜a≤19D．18＜a＜196．关于x的不等式组有且只有4个整数解，则常数m的取值范围是．7．若关于x的不等式组的解集中至少有6个整数解，则正数a的最小值是（）A．1B．2C．D．8．（2019•沙坪坝区校级二模）若数m使关于x的一元一次不等式组至多有4个整数解，则非负整数m的值之和是（）A．6B．10C．15D．219．（2022•渝中区校级模拟）如果关于x的不等式组有且仅有2个奇数解，则符合条件的所有整数m的和是（）A．15B．21C．28D．3610.已知关于x的不等式组的所有整数解的和为7，则a的取值范围是．➢课后训练一、两同问题1．不等式组的解集是x＞3，则m的取值范围是（）A．m＞3B．m≥3C．m＜3D．m≤32．若关于x的不等式组的解集是x≤a，则a的取值范围是（）二、有解、无解问题3．若不等式组有解，则实数a的取值范围是（）A．a＜﹣36B．a≤﹣36C．a≥﹣36D．a＞﹣364．若关于x的不等式组无解，则a的取值范围是．三、整数解问题5．若关于x的不等式组恰好只有2个整数解，则所有满足条件的整数a的值之和是（）A．3B．4C．6D．16．关于x的不等式组恰有三个整数解，那么m的取值范围为（）A．﹣1＜m≤0B．﹣1≤m＜0C．0≤m＜1D．0＜m≤17．关于x的不等式组的解集中至少有7个整数解，则整数a的最小值是（）A．4B．3C．2D．18．（2022秋•沙坪坝区校级月考）若数m使关于x的一元一次不等式组至多5个整数解，则则整数m的最大值是（）A．7B．8C．9D．109．（2022秋•渝中区校级月考）若数a使关于y的不等式组恰好有两个奇数解，则符合条件的所有整数a的和是（）A．7B．8C．9D．1010．若关于x的不等式组的所有整数解的和是﹣7，则m的取值范围是．（三）方程与不等式组综合过关训练➢典例精讲1．（2020春•渝中区校级期末）关于x的方程3﹣2x＝3（k﹣2）的解为非负整数，且关于x的不等式组无解，则符合条件的整数k的值的和为（）A．5B．2C．4D．62．若数a使关于x的方程＝﹣﹣1有非负数解，且关于y的不等式组恰好有两个偶数解，则符合条件的所有整数a的和是（）A．﹣22B．﹣18C．11D．123．（2021秋•渝中区校级期末）整数a使得关于x，y的二元一次方程组的解为正整数（x，y均为正整数），且使得关于x的不等式组无解，则所有满足条件的a的和为（）A．9B．16C．17D．304．如果关于x的不等式组的解集为x＞4，且整数m使得关于x，y的二元一次方程组的解为整数（x，y均为整数），则符合条件的所有整数m的和是（）A．﹣2B．2C．6D．10➢课后训练1．（2022秋•九龙坡区校级月考）若整数a使关于x的方程x+2a＝1的解为负数，且使关于的不等式组无解，则所有满足条件的整数a的值之和是（）A．5B．7C．9D．102．（2022秋•沙坪坝区校级期末）若关于x的一元一次不等式组的解集为x≥，且关于y 的方程3y﹣2＝的解为非负整数，则符合条件的所有整数m的积为（）A．2B．7C．11D．103．（2021春•沙坪坝区期末）关于x、y的方程组的解是正整数，且关于t的不等式组有解，则符合条件的整数m的值的和为．参考答案与试题解析➢典例精讲1．如果关于x的不等式（a+2020）x﹣a＞2020的解集为x＜1，那么a的取值范围是（）A．a＞﹣2020B．a＜﹣2020C．a＞2020D．a＜2020【解答】解：∵不等式（a+2020）x﹣a＞2020的解集为x＜1，∴a+2020＜0，解得，a＜﹣2020，故选：B．2．已知关于x的不等式（a+3b）x＞a﹣b的解集为x＜﹣，则关于x的一元一次不等式bx﹣a＞0的解集为x＜﹣．【解答】解：∵不等式（a+3b）x＞a﹣b的解集是x＜﹣，∴a+3b＜0，即a＜﹣3b，∵，即8a＝﹣12b，，∵a+3b＜0，2a+3b＝0，则a＞0，b＜0，∴bx﹣a＞0的解集为x＜﹣．故答案为：x＜﹣．3．若关于x的不等式ax＜﹣bx+b（a，b≠0）的解集为x＞，则关于x的不等式ax＞2bx+b的解集是x ＞﹣1．【解答】解：ax＜﹣bx+b，（a+b）x＜b，∵关于x的不等式ax＜﹣bx+b（a，b≠0）的解集为x＞，∴＝，且a+b＜0，∴a＝b＜0，∴ax＞2bx+b变为﹣bx＞b，∴x＞﹣1，故答案为x＞﹣1．4．已知关于x的不等式3x﹣2a＜4﹣5x有且仅有三个正整数解，则满足条件的整数a的个数是（）A．3个B．4个C．5个D．6个【解答】解：解不等式3x﹣2a＜4﹣5x得：x＜，∵关于x的不等式3x﹣2a＜4﹣5x有且仅有三个正整数解，是1，2，3，∴3＜≤4，解得：10＜a≤14，∴整数a可以是11，12，13，14，共4个，故选：B．5．若关于x的不等式7x+9＞2x+a的负整数解为﹣2，﹣1，则a的取值范围是﹣6≤a＜﹣1．【解答】解：解不等式得：x＞，∵负整数解是﹣1，﹣2，∴﹣3≤＜﹣2．∴﹣6≤a＜﹣1．故答案为：﹣6≤a＜﹣1．➢课后训练1．已知关于x的不等式（2﹣a）x＞3的解集为，则a的取值范围是（）A．a＞0B．a＜0C．a＞2D．a＜2【解答】解：根据题意得：2﹣a＜0，解得：a＞2．故选：C．2．若关于x的不等式（2m﹣n）x﹣m＞5n的解集为x＜，则关于x的不等式（m﹣n）x＞m+n的解集为（）A．x＜B．x＞C．x＞5D．x＜5【解答】解：不等式（2m﹣n）x﹣m＞5n，变形得：（2m﹣n）x＞5n+m，根据已知解集为x＜，得到＝，且2m﹣n＜0，即2m＜n，整理得：4m+20n＝26m﹣13n，即33n＝22m，整理得：3n＝2m，即m＝1.5n，n＜0，代入所求不等式得：0.5nx＞2.5n，解得：x＜5．故选：D．3．已知关于x的不等式3（a﹣b）x+a﹣5b＞0的解集为x＜1，则关于x的不等式ax≥4b的解集为x≤2．【解答】解：不等式移项得：3（a﹣b）x＞5b﹣a，由不等式的解集为x＜1，得到a﹣b＜0，且＝1，整理得：a＜b，且4a＝8b，即a＝2b，∴a＜0，则不等式ax≥4b变形得：x≤＝2，故答案为：x≤2．4．若关于x的不等式3x﹣m≤0的正整数解是1，2，3，则m的取值范围是（）A．m≥9B．9＜m＜12C．m＜12D．9≤m＜12【解答】解：移项，得：3x≤m，系数化为1，得：x≤，∵不等式的正整数解为1，2，3，∴3≤＜4，解得：9≤m＜12，故选：D．5．若关于x的不等式2x﹣m≥0的负整数解为﹣1，﹣2．﹣3．则m的取值范围是﹣8＜m≤﹣6．【解答】解：∵2x﹣m≥0，∴2x≥m，∴x≥，∵不等式组的负整数解为﹣1，﹣2．﹣3，∴﹣4＜≤﹣3，则﹣8＜m≤﹣6，故答案为：﹣8＜m≤﹣6．➢典例精讲一、两同问题1．若关于x的不等式组的解集为x≥2，则m的取值范围是（）A．m≥﹣2B．m≤2C．m＜2D．m＝2【解答】解：，解x﹣m＞0，得：x＞m，解5﹣2x≤1，得：x≥2，∵不等式组的解集是x≥2，∴m＜2，故选：C．2．若关于x的不等式组的解集是x＜2，则a的取值范围是（）A．a≥2B．a＜﹣2C．a＞2D．a≤2【解答】解：解不等式组，由①可得：x＜2，由②可得：x＜a，因为关于x的不等式组的解集是x＜2，所以，a≥2，故选：A．二、有解、无解问题3．若不等式组有解，则a的取值范围是（）A．a≤B．a≤4C．1≤a≤4D．a≥【解答】解：，解不等式①得：x≥1，解不等式②得：x≤4a，又∵不等式组有解，∴4a≥1，解得：a≥，故选：D．4．若不等式组无解，则m的取值范围为（）A．m≤8B．m＜8C．m≥8D．m＞8【解答】解：解不等式＜﹣1得：x＞8，又∵不等式组无解，∴m≤8，故选：A．三、整数解问题5．关于x的不等式组的解中恰有4个整数解，则a的取值范围是（）A．18≤a≤19B．18≤a＜19C．18＜a≤19D．18＜a＜19【解答】解：不等式组整理得：，解得：a﹣2＜x＜21，由不等式组恰有4个整数解，得到整数解为17，18，19，20，∴16≤a﹣2＜17，解得：18≤a＜19，故选：B．6．关于x的不等式组有且只有4个整数解，则常数m的取值范围是．【解答】解：，解不等式①得：x≥﹣1，解不等式②得：x＜m+5，∴原不等式组的解集为﹣1≤x＜m+5，由不等式组的整数解只有4个，得到整数解为﹣1，0，1，2，∴2＜m+5≤3，∴﹣2＜m≤﹣故答案为﹣2＜m≤﹣．7．若关于x的不等式组的解集中至少有6个整数解，则正数a的最小值是（）A．1B．2C．D．【解答】解：解不等式x﹣a≤0，得：x≤a，解不等式2x+3a≥0，得：x≥﹣a，则不等式组的解集为﹣a≤x≤a，∵不等式至少有6个整数解，则a+a≥5，解得a≥2．a的最小值是2．故选：B．8．（2019•沙坪坝区校级二模）若数m使关于x的一元一次不等式组至多有4个整数解，则非负整数m的值之和是（）A．6B．10C．15D．21【解答】解：解不等式组，得﹣1＜x≤，∵至多有4个整数解，＜4，解得m＜7；∴故满足条件的所有非负整数m的值之和为0+1+2+3+4+5+6＝21，故选：D．9．（2019•渝中区校级模拟）如果关于x的不等式组有且仅有2个奇数解，则符合条件的所有整数m的和是（）A．15B．21C．28D．36【解答】解：解不等式组，得：﹣＜x＜，∵不等式组有且仅有2个奇数解，∴-1＜≤1，解得：0＜m≤8，所以所有满足条件的整数m的值为1，2，3，4，5，6，7，8，和为36．故选：D．10.已知关于x的不等式组的所有整数解的和为7，则a的取值范围是7≤a＜9或﹣3≤a＜﹣1．【解答】解：，∵解不等式①得：x，解不等式②得：x≤4，∴不等式组的解集为＜x≤4，∵关于x的不等式组的所有整数解的和为7，∴当时，这两个整数解一定是3和4，∴，∴7≤a＜9，当时，整数解是﹣2，﹣1，0，1，3和4，∴﹣3，∴﹣3≤a＜﹣1，∴a的取值范围是7≤a＜9或﹣3≤a＜﹣1．故答案为：7≤a＜9或﹣3≤a＜﹣1．➢课后训练一、两同问题1．不等式组的解集是x＞3，则m的取值范围是（）A．m＞3B．m≥3C．m＜3D．m≤3【解答】解：解不等式3（x+1）＞12，得：x＞3，∵不等式组的解集为x＞3，∴m≤3，故选：D．2．若关于x的不等式组的解集是x≤a，则a的取值范围是（）A．a≤2B．a＞﹣2C．a＜﹣2D．a≤﹣2【解答】解：解不等式﹣2x﹣1＞3，得：x＜﹣2，解不等式a﹣x≥0，得：x≤a，∵不等式组的解集为x≤a，∴a＜﹣2，故选：C．二、有解、无解问题3．若不等式组有解，则实数a的取值范围是（）A．a＜﹣36B．a≤﹣36C．a≥﹣36D．a＞﹣36【解答】解：不等式组整理得：，由不等式组有解，得到a﹣1＞﹣37，解得：a＞﹣36．故选：D．4．（2020春•陇西县期末）若关于x的不等式组无解，则a的取值范围是a≥﹣2．【解答】解：，解①得：x＞a+3，解②得：x＜1．根据题意得：a+3≥1，解得：a≥﹣2．故答案是：a≥﹣2．三、整数解问题5．若关于x的不等式组恰好只有2个整数解，则所有满足条件的整数a的值之和是（）A．3B．4C．6D．1【解答】解：解不等式组得：＜x＜2，由关于x的不等式组恰好只有2个整数解，得﹣1≤＜0，即0≤a＜4，满足条件的整数a的值为0、1、2、3，整数a的值之和是0+1+2+3＝6，故选：C．6．关于x的不等式组恰有三个整数解，那么m的取值范围为（）A．﹣1＜m≤0B．﹣1≤m＜0C．0≤m＜1D．0＜m≤1【解答】解：，解不等式①可得x＞m，解不等式②可得x≤3，由题意可知原不等式组有解，∴原不等式组的解集为m＜x≤3，∵该不等式组恰好有三个整数解，∴整数解为1，2，3，∴0≤m＜1．故选：C．7．关于x的不等式组的解集中至少有7个整数解，则整数a的最小值是（）A．4B．3C．2D．1【解答】解：，解①得x≤2a，解②得x＞﹣a．则不等式组的解集是﹣a＜x≤2a．∵不等式至少有7个整数解，则2a+a＞7，解得a＞2．整数a的最小值是3．故选：B．8．（2019秋•沙坪坝区校级月考）若数m使关于x的一元一次不等式组至多5个整数解，则则整数m的最大值是（）A．7B．8C．9D．10【解答】解：不等式组的解为，∵至多5个整数解，∴＜5，∴m＜，故选：B．9．（2020秋•渝中区校级月考）若数a使关于y的不等式组恰好有两个奇数解，则符合条件的所有整数a的和是（）【解答】解：不等式组整理得：，解得：＜y＜4，由不等式组有解且恰好有两个奇数解，得到奇数解为3，1，∴﹣1≤＜1，∴﹣3≤a＜5，则满足题意a的值有﹣3，﹣2，﹣1，0，1，2，3，4，5四个，则符合条件的所有整数a的和是9．故选：C．10．若关于x的不等式组的所有整数解的和是﹣7，则m的取值范围是﹣3＜m≤﹣2或2＜m≤3．【解答】解：解不等式+3＞﹣1，得：x＞﹣4.5，∵不等式组的整数解的和为﹣7，∴不等式组的整数解为﹣4、﹣3或﹣4、﹣3、﹣2、﹣1、0、1、2，则﹣3＜m≤﹣2或2＜m≤3，故答案为：﹣3＜m≤﹣2或2＜m≤3．➢典例精讲方程与不等式综合含参问题1．（2020春•渝中区校级期末）关于x的方程3﹣2x＝3（k﹣2）的解为非负整数，且关于x的不等式组无解，则符合条件的整数k的值的和为（）A．5B．2C．4D．6【解答】解：解方程3﹣2x＝3（k﹣2）得x＝，∵方程的解为非负整数，∴≥0，即k≤3，即非负整数k＝1，3，不等式组整理得：，由不等式组无解，得到k＞﹣1，∴﹣1＜k≤3，即整数k＝0，1，2，3，当k＝0时，x＝4.5，不是整数；当x＝2时，k＝1.5，不是整数，两个k的值不符合题意，舍去；综上，k＝1，3，则符合条件的整数k的值的和为4．故选：C．2．若数a使关于x的方程＝﹣﹣1有非负数解，且关于y的不等式组恰好有两个偶数解，则符合条件的所有整数a的和是（）【解答】解：去分母得：3ax+3＝﹣14x﹣6，解得：x＝﹣，∵关于x的方程＝﹣﹣1有非负数解，∴3a+14＜0，∴a＜﹣，不等式组整理得：，解得：＜y＜4，由不等式组有解且恰好有两个偶数解，得到偶数解为2，0，∴﹣2≤＜﹣1，∴﹣7≤a＜﹣3，则满足题意a的值有﹣7，﹣6，﹣5，则符合条件的所有整数a的和是﹣18．故选：B．3．（2019秋•渝中区校级期末）整数a使得关于x，y的二元一次方程组的解为正整数（x，y均为正整数），且使得关于x的不等式组无解，则所有满足条件的a的和为（）A．9B．16C．17D．30【解答】解：解方程组得：，∵方程组的解为正整数，∴a﹣3＝1或a﹣3＝2或a﹣3＝5或a﹣3＝10，解得a＝4或a＝5或a＝8或a＝13；解不等式（2x+8）≥7，得：x≥10，解不等式x﹣a＜2，得：x＜a+2，∵不等式组无解，∴a+2≤10，即a≤8，综上，符合条件的a的值为4、5、8，则所有满足条件的a的和为17，故选：C．4．如果关于x的不等式组的解集为x＞4，且整数m使得关于x，y的二元一次方程组的解为整数（x，y均为整数），则符合条件的所有整数m的和是（）A．﹣2B．2C．6D．10【解答】解：解不等式＞0，得：x＞m，解不等式﹣x＜﹣4，得：x＞4，∵不等式组的解集为x＞4，∴m≤4，解方程组得，∵x，y均为整数，∴m＝4或m＝10或m＝2或m＝﹣4，又m≤4，∴m＝﹣4或m＝4或m＝2，则符合条件的所有整数m的和是2，故选：B．➢课后训练1．（2019秋•九龙坡区校级月考）若整数a使关于x的方程x+2a＝1的解为负数，且使关于的不等式组无解，则所有满足条件的整数a的值之和是（）A．5B．7C．9D．10【解答】解：解方程x+2a＝1得：x＝1﹣2a，∵方程的解为负数，∴1﹣2a＜0，解得：a＞0.5，∵解不等式①得：x＜a，解不等式②得：x≥4，又∵不等式组无解，∴a≤4，∴a的取值范围是0.5＜a≤4，∴整数和为1+2+3+4＝10，故选：D．2．（2020秋•沙坪坝区校级期末）若关于x的一元一次不等式组的解集为x≥，且关于y 的方程3y﹣2＝的解为非负整数，则符合条件的所有整数m的积为（）A．2B．7C．11D．10【解答】解：解不等式≤2x，得：x≥，解不等式2x+7≤4（x+1），得：x≥，∵不等式组的解集为x≥，∴≤，解得m≤5，解方程3y﹣2＝，得：y＝，∵方程的解为非负整数，∴符合m≤5的m的值为2和5，则符合条件的所有整数m的积为10，故选：D．3．（2019春•沙坪坝区期末）关于x、y的方程组的解是正整数，且关于t的不等式组有解，则符合条件的整数m的值的和为5．【解答】解：，①﹣②得：3y＝7﹣m，解得：y＝，把y＝代入①得：x＝，由方程组的解为正整数，得到7﹣m与8+m都为3的倍数，∴m＝1，4，不等式组整理得：，即﹣1≤t≤m，由不等式组有解，得到m＝1，4，综上，符合条件的整数m的值的和为1+4＝5．故答案为：5．。

中考数学复习查补重难点反比例函数与一次函数的综合运用(原卷版)

查补重难点03反比例函数与一次函数的综合运用考点一：反比例函数与一次函数综合反比例函数与一次函数进行综合考查的题型是江苏历年中考数学对于函数考查的重点内容，那么关于反比例函数与一次函数的综合专题当中，我们主要涉及到函数共存问题，交点和不等式（比大小）问题、最值问题以及与几何综合压轴类的题型。

无论是哪一类型的题型，在综合的考察过程当中都是对于反比例函数与一次函数的图像和性质有充分的了解，借助数形结合思想、方程思想、化归思想等。

通过函数的图像来得到我们所需要的求解问题。

在这过程当中，如果对于这两类函数没有全面的了解，那么在解题过程当中就要花费大家很多的时间而导致其解题效率的降低，那么在解决这三大类型的提醒过程当中，该如何利用这些函数的性质来进行解题，该专题可供大家在备考阶段能够进行专项的突破。

题型1.反比例函数和一次函数图像共存问题函数图象共存问题是一次函数和反比例函数当中含有共同的参数，根据分类讨论的形式，由函数的图像特点来判定符合两个函数参数的图形。

解决这类型的题不仅是反比例函数和一次函数进行综合考查，连同二次函数在内的题型进行考查也是比较常见的，所以解决这类型的问题时，我们先要根据一次函数或反比例函数中参数的共性，通过分别进行讨论的形式逐一进行排除，最终确定满足要求的函数图像。

．B ．．．变式1.（2023年湖北省襄阳市中考数学真题）在同一平面直角坐标系中，一次函数y kx =k x的图象可能是（）．B ．C ．D ．变式2.（2022·广西·中考真题）已知反比例函数(0)b y b x=≠的图象如图所示，则一次函数()0y cx a c =-≠和二次函数2(0)y ax bx c a =++≠在同一平面直角坐标系中的图象可能是（）A ．B ．C ．D ．题型2.反比例函数和一次函数的交点问题一次函数图像与反比例函数相关问题，牵扯到的知识点比较多，如求它们的函数解析式，或是通过两者的图像相交，需要考生结合两个函数解析式转化成一元二次方程，从而求得交点坐标等。

(完整版)中考数学动点问题专题讲解

中, 有长度保持不变的线段，这条线段是
2 21
GH= NH= OP=2.
B
3 32
(2) 在 Rt △ POH 中 ,
OH
2
2
OP PH
2
36 x ,
∴
MH
1 OH
1 36
x2 .
2
2
O
在 Rt △ MPH中 ,
MP
PH 2 MH 2
x 2 9 1 x2 1 36 3x 2 .
4
2
P
Ny x
G
MHA 图1
∴ y =GP=2 MP=1 36 3x2 (0< x <6). 33
(3) △ PGH是等腰三角形有三种可能情况 :
① GP=PH时, 1 36 3x 2 3
x , 解得 x
6 . 经检验 , x
② GP=GH时, 1 36 3x 2 2 , 解得 x 0 . 经检验 , x 3
③ PH=GH时, x 2 .
段 , 并求出相应的长度 .
(2) 设 PH x ,GP y , 求 y 关于 x 的函数解析式，并写出函数的定义域
( 即自变量 x 的取值范围 ).
(3) 如果△ PGH是等腰三角形 , 试求出线段 PH的长 .
解:(1) 当点 P 在弧 AB 上运动时 ,OP 保持不变 , 于是线段 GO、GP、 GH
又∠ DAB+∠ADB=∠ ABC=75° ,
∴∠ CAE=∠ADB,
∴△ ADB∽△ EAC, ∴ AB BD , CE AC
D
E
B
C
图2
∴1
x , ∴y
1
.
y1
x

中考数学：反比例函数、不等式、概率综合题

中考数学：反比例函数、不等式、概率综合题
本来以为这道中考第24题会比较难点，没想到居然是个普通难度题，不过确实算是综合了几个方面的内容，还是值得一看的。

（1）求m的取值范围，根据已知m（n-1）≥0可得
mn-m≥0，又点A（m，n）在反比例函数上，所以m不等0，所以6-m≥0，
∴m≤6；
这题放在24题是不是很脑残？
（2）m、n都是正整数，那么根据m的取值范围并结合n=6÷m，可知 m=1，n=6,
m=2，n=3，
m=3，n=2，
m=6，n=1，
一共这四种情况，然后需要验证每个点都在一次函数的什么位置，
m=1，n=6时，在上方；
m=2，n=3时，在下方；
m=3，n=2时，在下方；
m=6，n=1时，在上方；
所以刚好对半关系，有两个点符合，那么概率不就是50%嘛。

题是入门题，相信学过这几个章节内容的同学们，都可以正确解答。

中考数学综合题专题复习【反比例函数】专题解析附答案

一、反比例函数真题与模拟题分类汇编（难题易错题）1．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．2．心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y 随时间x（分钟）的变化规律如下图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：（1）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2）一道数学竞赛题，需要讲19分钟，为了效果较好，要求学生的注意力指标数最低达到36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？【答案】（1）解：设线段AB所在的直线的解析式为y1=k1x+20，把B（10，40）代入得，k1=2，∴y1=2x+20．设C、D所在双曲线的解析式为y2= ，把C（25，40）代入得，k2=1000，∴当x1=5时，y1=2×5+20=30，当，∴y1＜y2∴第30分钟注意力更集中．（2）解：令y1=36，∴36=2x+20，∴x1=8令y2=36，∴，∴∵27.8﹣8=19.8＞19，∴经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目．【解析】【分析】（1）根据一次函数和反比例函数的应用，用待定系数法求出线段AB所在的直线的解析式，和C、D所在双曲线的解析式；把x1=5时和进行比较得到y1＜y2，得出第30分钟注意力更集中；（2）当y1=36时，得到x1=8，当y2=36，得到，由27.8﹣8=19.8＞19，所以经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目.3．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，∴点N的纵坐标为： a2+a+2，即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，∴P（﹣，0）设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣，0）代入y=kx+b，解得k= ，b= ，∴直线PF：y= x+ ，解方程 x2+x+2= x+ ，得x=﹣3或x=2（不合题意，舍去），当x=﹣3时，y= ，∴M（﹣3，）．【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m的值。

人教版九年级数学中考动点问题专项练习及参考答案

人教版九年级数学中考动点问题专项练习例题1. 抛物线223y x x =-++与x 轴相交于A 、B 两点（点A 在B 的左侧），与y轴相交于点C ，顶点为D .⑴ 直接写出A 、B 、C 三点的坐标和抛物线的对称轴；⑵ 连接BC ，与抛物线的对称轴交于点E ，点P 为线段BC 上的一个动点，过点P 作PF DE ∥交抛物线于点F ，设点P 的横坐标为；① 用含m 的代数式表示线段PF 的长，并求出当m 为何值时，四边形PEDF 为平行四边形？② 设BCF ∆的面积为S ，求S 与m 的函数关系式．【答案】⑴()10A -，，()30B ，，()03C ，．抛物线的对称轴是：1x =．⑵①设直线BC 的函数关系式为：y kx b =+．把()()3003B C ，，，分别代入得：303.k b b +=⎧⎨=⎩，解得：13k b =-=，．所以直线BC 的函数关系式为：3y x =-+．当1x =时，132y =-+=，∴()12E ，．当x m =时，3y m =-+， ∴()3P m m -+，．在223y x x =-++中，当1x =时，4y =． ∴()14D ，当x m =时，223y m m =-++∴()223F m m m -++，．∴线段422DE =-=，线段()222333PF m m m m m =-++--+=-+． ∵PF DE ∥∴当PF ED =时，四边形PEDF 为平行四边形．由232m m -+=解得：1221m m ==，．（不合题意，舍去）．因此，当2m =时，四边形PEDF 为平行四边形．②设直线PF 与x 轴交于点M ，由()30B ，，()00O ，，可得：3OB OM MB =+=． ∵BPF CPE S S S ∆∆=+．即()11112222S PF BM PF OM PF BM OM PF OB =⋅+⋅=⋅+=⋅．∴()()221393303222S m m m m m =⨯-+=-+≤≤．例题2. 如图，已知抛物线(1)2)0y a x a =-+≠经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．【答案】（1）∵抛物线2(1))0y a x a =-+≠经过点()20A -，，∴09a =+a =∴二次函数的解析式为：2y =+（2）∵D 为抛物线的顶点∴(1D 过D 作DN OB ⊥于N ，则DN =，3AN =，∴6AD ==∴60DAO ∠=︒∵OM AD ∥①当AD OP =时，四边形DAOP 是平行四边形 ∴6OP =∴()6t s =②当DP OM ⊥时，四边形DAOP 是直角梯形过O 作OH AD ⊥于H ，2AO =，则1AH =（如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =） ∴5OP DH ==，()5t s =③当PD OA =时，四边形DAOP 是等腰梯形 ∴2624OP AD AH =-=-=∴()4t s =综上所述：当6t =、5、4时，对应四边形分别是平行四边形、直角梯形、等腰梯形．（3）由（2）及已知，60OC OB COB OCB =∠=，，°△是等边三角形则62OB OC AD OP t BQ t =====，，，∴()6203OQ t t =-<< 过P 作PE OQ ⊥于E，则PE =∴113322263(62)BCPQ t S t -=⨯⨯⨯-⨯=233633228t ⎛⎫-+⎪⎝⎭ 当32t =时，BCPQ S 的面积最小值为6338 ∴此时33324OQ OP OE ==，=，∴39334443PE QE ===- ∴222233933442PE QE PQ ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭=例题3. 已知⊙O 的半径为3，⊙P 与⊙O 相切于点A ，经过点A 的直线与⊙O 、⊙P 分别交于点B 、C ，cos ∠BAO ＝13．设⊙P 的半径为x ，线段OC 的长为y ．（1）求AB 的长；（2）如图1，当⊙P 与⊙O 外切时，求y 与x 之间的函数关系式，并写出函数的定义域；（3）当∠OCA ＝∠OPC 时，求⊙P 的半径．图1 【答案】（1）如图2，作OE ⊥AB ，垂足为E ，由垂径定理，得AB ＝2AE ．在Rt △AOE 中，cos ∠BAO ＝13AE AO =，AO ＝3，所以AE ＝1．所以AB ＝2．（2）如图2，作CH ⊥AP ，垂足为H ．由△OAB ∽△P AC ，得AO AP AB AC =．所以32x AC =．所以23AC x =．在Rt △ACH 中，由cos ∠CAH ＝13，得1322AH AC CH==．所以1239AH AC x ==，224239CH AC x ==．在Rt △OCH 中，由OC 2＝OH 2＋CH 2，得222422()(3)99y x x =++．整理，得23649813y x x =++．定义域为x ＞0．图2 图3（3）①如图3，当⊙P 与⊙O 外切时，如果∠OCA ＝∠OPC ，那么△OCA ∽△OPC ．因此OA OCOC OP =．所以2OC OA OP =⋅．解方程236493(3)813x x x ++=+，得154x =．此时⊙P 的半径为154．②如图4，图5，当⊙P 与⊙O 内切时，同样的△OAB ∽△P AC ，23AC x =．如图5，图6，如果∠OCA ＝∠OPC ，那么△ACO ∽△APC ．所以AO ACAC AP =．因此2AC AO AP =⋅．解方程22()33x x =，得274x =．此时⊙P 的半径为274．图4 图5 图6例题4. 如图1，在平面直角坐标系中，O为坐标原点，点A的坐标为(0,4)，点B 的坐标为(4,0)，点C的坐标为(－4,0)，点P在射线AB上运动，连结CP与y轴交于点D，连结BD．过P、D、B三点作⊙Q，与y轴的另一个交点为E，延长DQ交⊙Q于F，连结EF、BF．（1）求直线AB的函数解析式；（2）当点P在线段AB（不包括A、B两点）上时．①求证：∠BDE＝∠ADP；②设DE＝x，DF＝y，请求出y关于x的函数解析式；（3）请你探究：点P在运动过程中，是否存在以B、D、F为顶点的直角三角形，满足两条直角边之比为2∶1？如果存在，求出此时点P的坐标；如果不存在，请说明理由．图1【答案】（1）直线AB的函数解析式为y＝－x＋4．（2）①如图2，∠BDE＝∠CDE＝∠ADP；②如图3，∠ADP＝∠DEP＋∠DPE，如图4，∠BDE＝∠DBP＋∠A，因为∠DEP＝∠DBP，所以∠DPE＝∠A＝45°．所以∠DFE＝∠DPE＝45°．因此△DEF是等腰直角三角形．于是得到2y x=．图2 图3 图4（3）①如图5，当BD∶BF＝2∶1时，P(2,2)．思路如下：由△DMB∽△BNF，知122BN DM==．设OD＝2m，FN＝m，由DE＝EF，可得2m＋2＝4－m．解得23m=．因此4(0,)3D．再由直线CD与直线AB求得交点P(2,2)．②如图6，当BD∶BF＝1∶2时，P(8,－4)．思路同上．图5 图6例题5. 在Rt △ABC 中，∠C ＝90°，AC ＝6，53sin =B ，⊙B 的半径长为1，⊙B 交边CB 于点P ，点O 是边AB 上的动点．（1）如图1，将⊙B 绕点P 旋转180°得到⊙M ，请判断⊙M 与直线AB 的位置关系；（2）如图2，在（1）的条件下，当△OMP 是等腰三角形时，求OA 的长；（3）如图3，点N 是边BC 上的动点，如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切，设NB ＝y ，OA ＝x ，求y 关于x 的函数关系式及定义域．图1 图2 图3【答案】（1）在Rt △ABC 中，AC ＝6，53sin =B ，所以AB ＝10，BC ＝8．过点M 作MD ⊥AB ，垂足为D ．在Rt △BMD 中，BM ＝2，3sin 5MD B BM==，所以65MD =．因此MD ＞MP ，⊙M 与直线AB 相离．图4（2）①如图4，MO ≥MD ＞MP ，因此不存在MO ＝MP 的情况．②如图5，当PM ＝PO 时，又因为PB ＝PO ，因此△BOM 是直角三角形．在Rt △BOM 中，BM ＝2，4cos 5BO B BM==，所以85BO =．此时425OA =．③如图6，当OM ＝OP 时，设底边MP 对应的高为OE ．在Rt △BOE 中，BE ＝32，4cos 5BE B BO==，所以158BO =．此时658OA =．图5 图6（3）如图7，过点N 作NF ⊥AB ，垂足为F ．联结ON ．当两圆外切时，半径和等于圆心距，所以ON ＝x ＋y ．在Rt △BNF 中，BN ＝y ，3sin 5B =，4cos 5B =，所以35NF y =，45BF y =．在Rt △ONF 中，4105OF AB AO BF x y =--=--，由勾股定理得ON 2＝OF 2＋NF 2．于是得到22243()(10)()55x y x y y +=--+．整理，得2505040x y x -=+．定义域为0＜x ＜5．图7 图8例题6. 如图1，甲、乙两人分别从A 、B 两点同时出发，点O 为坐标原点．甲沿AO 方向、乙沿BO 方向均以每小时4千米的速度行走，t 小时后，甲到达M 点，乙到达N 点．（1）请说明甲、乙两人到达点O 前，MN 与AB 不可能平行；（2）当t 为何值时，△OMN ∽△OBA ？（3）甲、乙两人之间的距离为MN 的长．设s ＝MN 2，求s 与t 之间的函数关系式，并求甲、乙两人之间距离的最小值．图1【答案】（1）当M 、N 都在O 右侧时，24122OM t t OA-==-，642163ON t t OB-==-，所以OM ON OAOB≠．因此MN 与AB 不平行．（2）①如图2，当M 、N 都在O 右侧时，∠OMN ＞∠B ，不可能△OMN ∽△OBA ．②如图3，当M 在O 左侧、N 在O 右侧时，∠MON ＞∠BOA ，不可能△OMN ∽△OBA ．③如图4，当M 、N 都在O 左侧时，如果△OMN ∽△OBA ，那么ON OA OMOB=．所以462426t t -=-．解得t ＝2．图2 图3 图4（3）①如图2，24OM t =-，12OH t =-，2)MH t =-．(64)(12)52NH ON OH t t t =-=---=-．②如图3，42OM t =-，21OH t =-，1)MH t =-．(64)(21)52NH ON OH t t t =+=-+-=-．③如图4，42OM t =-，21OH t =-，1)MH t =-．(21)(46)52NH OH ON t t t =-=---=-．综合①、②、③，s 222MN MH NH ==+22221)(52)16322816(1)12t t t t t ⎤=-+-=-+=-+⎦．所以当t ＝1时，甲、乙两人的最小距离为12千米．例题7. 已知点 (1，3)在函数ky x=(0x >)的图像上，矩形ABCD 的边BC 在x 轴上，E 是对角线BD 的中点，函数ky x=(0x >)的图像经过A 、E 两点，若45ABD ∠=︒，求E 点的坐标.【解析】点(1，3)在函数k y x=的图像上，3k =.又E 也在函数k y x =的图像上，故设E 点的坐标为(m ，3m). 过E 点作EF x ⊥轴于F ，则3EF m=. 又E 是对角线BD 的中点，62AB CD EF m===. 故A 点的纵坐标为6m ，代入3y x =中，得A 点坐标为 (2m ，6m). 因此22m mBF OF OB m =-=-=.由45ABD ∠=︒，得45EBF ∠=︒，BF EF =. 即有32m m=.解得m =而0m >，故m =则E 点坐标为【答案】例题8. 如图，11POA ∆、212PA A ∆都是等腰直角三角形，点1P 、2P 在函数4y x=(0x >)的图像上，斜边1OA 、12A A 、都在x 轴上，求点2A 的坐标.【解析】分别过点1P 、2P 做x 轴的垂线，根据题意易得1PC OC =，21P D A D =，14PC OC ⋅=，24P D OD ⋅=，得2OA =，所以2A(0).【答案】2A(0).例题9. 如图所示，()()111222P x y P x y ，，，，……，()n n n P x y ，在函数()90y x x=>的图象上，11OP A ∆，212P A A ∆，323P A A ∆，…，1n n n P A A -∆，…都是等腰直角三角形，斜边1121n n OA A A A A -，，…，都在x 轴上，则12n y y y +++=…______________．【解析】由已知易得()133P ，，则13y =，点2P 横坐标为26y +，那么可得()2269y y +=，解得23y =，同理点3P横坐标为3y，那么可得()339y y =，解得3y =依此类推，n P的纵坐标为n y =∴1233n y y y +++=+++……【答案】例题10. 如图，P 是函数12y x=(0x >)图象上一点，直线1y x =-+交x 轴于点A ，交y 轴于点B ，PM Ox ⊥轴于M ，交AB 于E ，PN Oy ⊥轴于N ，交AB 于F.求AF BE ⋅的值.【解析】设点P (x ，y )，过点E 、F 分别作x 轴的垂线，21AF BE xy ⋅==. 【答案】1例题11. 已知：在矩形AOBC 中，4OB =，3OA =．分别以OB OA ，所在直线为x 轴和y 轴，建立如图所示的平面直角坐标系．F 是边BC 上的一个动点（不与BC ，重合），过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E ．（1）求证：AOE △与BOF △的面积相等；（2）记OEF ECF S S S =-△△，求当k 为何值时，S 有最大值，最大值为多少？（3）请探索：是否存在这样的点F ，使得将CEF △沿EF 对折后，C 点恰好落在OB 上？若存在，求出点F 的坐标；若不存在，请说明理由．【答案】（1）证明：设11()E x y ，，22()F x y ，，AOE △与FOB △的面积分别为1S ，2S ，由题意得11k y x =，22k y x =． ∴1111122S x y k ==，2221122S x y k ==．∴12S S =，即AOE △与FOB △的面积相等．（2）由题意知：E F ，两点坐标分别为33k E ⎛⎫ ⎪⎝⎭，，44k F ⎛⎫ ⎪⎝⎭，， ∴11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S =---=---=--△△△△△△矩形∴2112S k k =-+．当161212k =-=⎛⎫⨯- ⎪⎝⎭时，S 有最大值．131412S -==⎛⎫⨯- ⎪⎝⎭最大值．（3）解：设存在这样的点F ，将沿EF 对折后，C 点恰好落在OB 边上的M 点，过点E 作EN OB ⊥，垂足为N ．由题意得：3EN AO ==，143EM EC k ==-，134MF CF k ==-，∵90EMN FMB FMB MFB ∠+∠=∠+∠= ∴EMN MFB ∠=∠．又∵90ENM MBF ∠=∠=， ∴ENM MBF △∽△． ∴EN EM MB MF= ∴11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭==⎛⎫-- ⎪⎝⎭ ∴94MB =．222MB BF MF +=，解得218k =．∴21432k BF ==∴存在符合条件的点F ，它的坐标为21432⎛⎫⎪⎝⎭，．例题12. 如图，点()1A m m +，，()31B m m +-，都在反比例函数ky x=的图象上．（1）求m k ，的值；（2）如果M 为x 轴上一点，N 为y 轴上一点，以点A B M N ，，，为顶点的四边形是平行四边形，试求直线MN 的函数表达式．【解析】（1）由题意可知，()()()131m m m m +=+-．解，得3m =．∴()()3462A B ，，，；∴4312k =⨯=．（2）存在两种情况，如图：①当M 点在x 轴的正半轴上，N 点在y 轴的正半轴上时，设1M 点坐标为()10x ，，1N 点坐标为()10y ，． ∵ 四边形11AN M B 为平行四边形，∴线段11N M 可看作由线段AB 向左平移3个单位，再向下平移2个单位得到的（也可看作向下平移2个单位，再向左平移3个单位得到的）．由（1）知A 坐标为（3，4），B 坐标为（6，2），∴1N 点坐标为042（，-），即102N （，）； 1M 点坐标为（6－3，0），即1M （3，0）．设直线11M N 的函数表达式为12y k x =+，把30x y ==，代入，解得123k =-． ∴ 直线11M N 的函数表达式为223y x =-+．②当M 点在x 轴的负半轴上，N 点在y 轴的负半轴上时，设2M 点坐标为20x （，），2N 点坐标为20y （，）．∵11221122AB N M AB M N AB N M AB M N ∥，∥，＝，＝，∴1221122N M M N N M M N ∥，＝． ∴线段22M N 与线段11N M 关于原点O 成中心对称． ∴2M 点坐标为（-3，0），2N 点坐标为（0，-2）．设直线22M N 的函数表达式为22y k x =-，把30x y =-=，代入，解得223k =-，∴ 直线M 2N 2的函数表达式为223y x =--．所以，直线MN 的函数表达式为223y x =-+或223y x =--．【答案】（1）3m =，12k =；（2）223y x =-+或223y x =--。

初中数学反比例函数及动点问题专题讲解及练习

(K>0)考点二、反比例函数的性质1.2.形状反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;3.位置当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;4.增减性反比例函数的图象,当k>0时,在每一象限内,y随x的增大而减小; 当k<0时,在每一象限内,y随x的增大而增大.5.图象的发展趋势反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.6.对称性反比例函数的图象是关于原点成中心对称的图形.7.任意一组变量的乘积是一个定值,即xy=k.温馨提示：反比例函数的涉及内容1.ⅰ当路程s 一定时，时间t 与速度v的函数关系t=s/v2.ⅱ当矩形面积S一定时，长a与宽b的函数关系a=s/b3.ⅲ当三角形面积S 一定时，三角形的底边y 与高x的函数关系y=2s/x动点问题（重点）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题。

“动点型问题”题型繁多、题意创新，考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等，是近几年中考题的热点和难点。

解决动点问题的关键是“动中求静”。

从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

在动点的运动过程中观察图形的变化情况，理解图形在不同位置的情况，做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

考点一：建立动点问题的函数解析式（或函数图像）函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容。

动点问题反映的是一种函数思想，由于某一个点或某图形的有条件地运动变化，引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系。

初中数学反比例函数动点问题

反比例函数 --－动点、面积专项
k旳图象在第一象限旳分支上有一点A（3，4),P为x轴正半轴上旳1．反比例函数ｙ＝
x
一种动点,（1)求反比例函数解析式. （2)当P在什么位置时,△OPA为直角三角形，求出此时Ｐ点旳坐标.
2、如图，M点是正比例函数y＝kx和反比例函数旳图象旳一种交点.
（1）求这两个函数旳解析式；
（2)在反比例函数旳图象上取一点P,过点P做PA垂直于x轴,垂足为Ａ,点Q 是直线MO上一点，QB垂直于y轴,垂足为B，直线MO上与否存在这样旳点Q,使得△OBQ旳面积是△ＯPＡ旳面积旳２倍？如果存在，祈求出点Q旳坐标,如果不存在，请阐明理由．
3、如图１,已知正比例函数和反比例函数旳图象都通过点M（﹣2，﹣1）,且P(﹣1，﹣2）为双曲线上旳一点,Ｑ为坐标平面上一动点，ＰA垂直于x轴，QB垂直于y轴,垂足分别是A、B．
(１)写出正比例函数和反比例函数旳关系式;
(２)当点Q在直线MO上运动时,直线MO上与否存在这样旳点Q，使得△OＢQ与△ＯAP面积相等如果存在，祈求出点旳坐标,如果不存在,请阐明理由；
(3)如图2,当点Q在第一象限中旳双曲线上运动时,作以OP、OQ为邻边旳平行四边形OPCＱ，求平行四边形OPＣＱ周长旳最小值.。

反比例函数及其应用(共35道)—2023年中考数学真题(全国通用)(解析版)

反比例函数及其应用（35道）一、单选题A ．1B ．2C ．3D ．4【答案】B【分析】延长BA 交y 轴于点D ，根据反比例函数k 值的几何意义得到1212ADO S =⨯=△，3OCBD S =矩形，根据四边形ABCO 的面积等于ADOOCBD S S−矩形，即可得解．【详解】解：延长BA 交y 轴于点D ，∵AB x ∥轴， ∴DA y ⊥轴，∵点A 在函数2(0)y x x =>的图象上，∴1212ADO S =⨯=△，∵BC x ⊥轴于点C ，DB y ⊥轴，点B 在函数3(0)y x x =>的图象上，∴3OCBD S =矩形，∴四边形ABCO 的面积等于312ADOOCBD S S−=−=矩形；故选B ．【点睛】本题考查反比例函数与几何图形的综合应用．熟练掌握反比例函数中k 的几何意义，是解题的关键．A ．321y y y <<B ．132y y y <<C ．312y y y <<D ．231y y y <<【答案】C【分析】先根据函数解析式中的比例系数k 确定函数图象所在的象限，再根据各象限内点的坐标特点及函数的增减性解答．【详解】解：在反比例函数(0)ky k x =<中，0k <，∴此函数图象在二、四象限，420−<−<，∴点()14,A y −，2(2,)B y −在第二象限，10y ∴>，20y >，函数图象在第二象限内为增函数，420−<−<， 120y y ∴<<．30>，3(3,)C y ∴点在第四象限，30y \<，1y ∴，2y ，3y 的大小关系为312y y y <<．故选：C ．【点睛】此题考查的是反比例函数图象上点的坐标特点及平面直角坐标系中各象限内点的坐标特点，比较简单．A ．当3x >时，12y y <B ．当1x <−时，12y y <C ．当03x <<时，12y y >D ．当10x −<<时，12y y <【答案】B【分析】结合一次函数与反比例函数的图象，逐项判断即可得．【详解】解：A 、当3x >时，12y y >，则此项错误，不符合题意； B 、当1x <−时，12y y <，则此项正确，符合题意； C 、当03x <<时，12y y <，则此项错误，不符合题意； D 、当10x −<<时，12y y >，则此项错误，不符合题意；故选：B ．【点睛】本题考查了一次函数与反比例函数的图象，熟练掌握函数图象法是解题关键．A ．123y y y <<B ．312 y y y <<C ．213y y y <<D ．321y y y <<【答案】C【分析】根据反比例函数的图象与性质解答即可．【详解】解：∵30k =>，∴图象在一、三象限，且在每个象限内y 随x 的增大而减小， ∵2101−<−<<， ∴2130y y y <<<．故选：C ．【点睛】本题考查了反比例函数的图象与性质，反比例函数ky x =(k 是常数，0k ≠)的图象是双曲线，当0k >，反比例函数图象的两个分支在第一、三象限，在每一象限内，y 随x 的增大而减小；当 0k <，反比例函数图象的两个分支在第二、四象限，在每一象限内，y 随x 的增大而增大．【答案】A【分析】连接四边形ABCD 的对角线AC BD 、，过D 作DE x ⊥轴，过C 作CF x ⊥轴，直线1y x =−与x 轴交于点M ，如图所示，根据函数图像交点的对称性判断四边形ABCD 是平行四边形，由平行四边形性质及平面直角坐标系中三角形面积求法，确定()11142四边形△ABC COD D S S OM DE CF ===⋅+，再求出直线1y x =−与x 轴交于点()1,0M ，通过联立1y x k y x =−⎧⎪⎨=⎪⎩求出C D 、纵坐标，代入方程求解即可得到答案．【详解】解：连接四边形ABCD 的对角线AC BD 、，过D 作DE x ⊥轴，过C 作CF x ⊥轴，直线1y x =−与x 轴交于点M ，如图所示：根据直线1y x =+、1y x =−与双曲线()0ky k x =>交点的对称性可得四边形ABCD 是平行四边形，()11142四边形△ABC O D C D S S OM DE CF ∴===⋅+，直线1y x =−与x 轴交于点M ， ∴当0y =时，1x =，即()1,0M ，1y x =−与双曲线()0ky k x =>分别相交于点C D 、，∴联立1y x k y x =−⎧⎪⎨=⎪⎩，即1k y y =−，则20y y k +−=，由0k >，解得y =，∴1112⎤⨯⨯−=⎥⎢⎥⎝⎭⎣⎦2=，解得34k =，故选：A ．【点睛】本题考查一次函数与反比例函数综合，涉及平行四边形的判定与性质，熟练掌握平面直角坐标系中三角形面积求法是解决问题的关键．A ．2:3:6B ．6:3:2C ．1:2:3D ．3:2:1【答案】A【分析】首先根据长方体的性质，得出相对面的面积相等，再根据物体的压力不变，结合反比例函数的性质进行分析，即可得出答案．【详解】解：∵长方体物体的一顶点所在A 、B 、C 三个面的面积比是3:2:1， ∴长方体物体的A 、B 、C 三面所对的与水平地面接触的面积比也为3:2:1， ∵FP S =，0F >，且F 一定，∴P 随S 的增大而减小， ∴111::::2:3:6321A B C P P P ==．故选：A ．【点睛】本题考查了反比例函数的性质，解本题的关键在熟练掌握反比例函数的性质．A ．B ．C ．D ．【答案】D【分析】先根据一次函数图象确定a 、b 的符号，进而求出ab 的符号，由此可以确定反比例函数图象所在的象限，看是否一致即可．【详解】解：A 、∵一次函数图象经过第一、二、三象限， ∴00a b >>，， ∴0ab >，∴反比例函数aby x =的图象见过第一、三象限，这与图形不符合，故A 不符合题意；B 、∵一次函数图象经过第一、二、四象限， ∴00a b <>，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形不符合，故B 不符合题意；C 、∵一次函数图象经过第一、三、四象限， ∴00a b ><，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形不符合，故C 不符合题意；D 、∵一次函数图象经过第一、二、四象限， ∴00a b <>，， ∴0ab <， ∴反比例函数aby x =的图象见过第二、四象限，这与图形符合，故D 符合题意；故选D ．【点睛】本题主要考查了一次函数与反比例函数图象和性质，熟练掌握相关性质与函数图象的关系是解决本题的关键．A ．B ．C ．D ．【答案】B 【分析】根据题意11FL F L =代入数据求得245F L =，即可求解．【详解】解：∵11FL F L =，125cm L =，19.8NF =，∴259.8245FL =⨯=， ∴245F L =，函数为反比例函数，当35cm L =时，245735F ==，即245F L =函数图象经过点()35,7．故选：B ．【点睛】本题考查了反比例函数的应用以及函数图象，根据题意求出函数关系式是解题的关键．A ．3B ．4C ．5D ．6【答案】B【分析】由正方形的性质得2BC AB ==，可设2,2k C ⎛⎫ ⎪⎝⎭，1,22k E ⎛⎫+ ⎪⎝⎭，根据21222k k ⎛⎫⨯=⨯+ ⎪⎝⎭可求出k 的值．【详解】解：∵四边形ABCD 是正方形， ∵2,AB BC CD AD ==== ∵点E 为AD 的中点， ∴11,2AE AD ==设点C 的坐标为2,2k ⎛⎫ ⎪⎝⎭，则,222k kBO AO AB BO ==+=+, ∴1,22k E ⎛⎫+ ⎪⎝⎭， ∵点C ，E 在反比例函数ky x =的图象上，∴21222k k ⎛⎫⨯=⨯+ ⎪⎝⎭，解得，4k =，故选：B ．【点睛】本题考查了反比例函数图象上点的坐标特征：反比例函数ky x =（k 为常数，0k ≠）的图象是双曲线，图象上的点()x y ，的横纵坐标的积是定值k ，即xy k =．为半径作圆，当A 与x 轴相切、B 与y 轴相切时，连结【答案】C【分析】过点,A B 分别作,y x 轴的垂线，垂足分别为,E D ，,AE BD 交于点C ，得出B 的横坐标为1，A 的纵坐标为1，设(),1A k ，()1,B k ，则1,1AC k BC k =−=−，根据AB =【详解】解：如图所示，过点A B ，分别作y x ，轴的垂线，垂足分别为E D ，，AE BD ，交于点C ，依题意，B 的横坐标为1，A 的纵坐标为1，设(),1A k ，()1,B k∴()1,1C ，则1,1AC k BC k =−=−，又∵90ACB ∠=︒，AB =∴()()(22211k k −+−=∴13k −=（负值已舍去）解得：4k =，故选：C ．【点睛】本题考查了切线的性质，反比例函数的性质，勾股定理，掌握以上知识是解题的关键．统考中考真题）如图，在平面直角坐标系中，OAB 三个顶点的坐标分别为与OAB 关于直线 A ．23 【答案】A【分析】过点B 作BD x ⊥轴，根据题意得出1,BD OD ==和性质得出2OB AB ==，30BOA BAO ∠∠==︒，利用各角之间的关系180OBA OBD '∠+∠=︒，确定A '，B ，D 三点共线，结合图形确定)2C，然后代入反比例函数解析式即可．【详解】解：如图所示，过点B 作BD x ⊥轴，∵(0,0),O A B ，∴1,BD OD ==∴AD OD =tan BD BOA OD ∠==，∴2OB AB ==，30BOA BAO ∠∠==︒，∴60OBD ABD ∠∠==︒，120OBA ∠=︒， ∵OA B '与OAB 关于直线OB 对称， ∴120OBA '∠=︒， ∴180OBA OBD '∠+∠=︒， ∴A '，B ，D 三点共线， ∴2A B AB '==， ∵A C BC '=， ∴1BC =， ∴2CD =，∴)2C，将其代入(0,0)ky k x x =>>得：k =故选：A ．【点睛】题目主要考查等腰三角形的判定和性质，特殊角的三角函数及反比例函数的确定，理解题意，综合运用这些知识点是解题关键．A ．2B ．2−C ．1D ．1−【答案】A【分析】证明四边形ANOM 是矩形，根据反比例函数的k 值的几何意义，即可解答．【详解】解：AM x ⊥轴于点M ，AN y ⊥轴于直N ，90MON ∠=︒，∴四边形AMON 是矩形，四边形AMON 的面积为2， 2k ∴=，反比例函数在第一、三象限，2k ∴=，故选：A ．【点睛】本题考查了矩形的判定，反比例函数的k 值的几何意义，熟知在一个反比例函数图像上任取一点，过点分别作x 轴，y 轴的垂线段，与坐标轴围成的矩形面积为k是解题的关键．二、填空题【答案】63y x =−【分析】函数图象的平移规则为：上加下减，左加右减，根据平移规则可得答案．【详解】解：将反比例函数6y x =的图象向下平移3个单位可得平移后的解析式为：63y x =−，故答案为：63y x =−．【点睛】本题考查的是函数图象的平移，解题的关键是理解并熟记函数图象的平移规则为：上加下减，左加右减．14．（2023·陕西·统考中考真题）如图，在矩形OABC 和正方形CDEF 中，点A 在y 轴正半轴上，点C ，F 均在x 轴正半轴上，点D 在边BC 上，2BC CD =，3AB =．若点B ，E 在同一个反比例函数的图象上，则这个反比例函数的表达式是．【答案】18y x =【分析】设正方形CDEF 的边长为m ，根据2BC CD =，3AB =，得到()3,2B m ，根据矩形对边相等得到3OC =，推出()3,E m m +，根据点B ，E 在同一个反比例函数的图象上，得到()323m m m⨯=+，得到3m =，推出18y x =．【详解】解：∵四边形OABC 是矩形， ∴3OC AB ==，设正方形CDEF 的边长为m ， ∴CD CF EF m ===， ∵2BC CD =， ∴2BC m =， ∴()3,2B m ，()3,E m m +，设反比例函数的表达式为ky x =，∴()323m m m⨯=+，解得3m =或0m =（不合题意，舍去）， ∴()3,6B ，∴3618=⨯=k ，∴这个反比例函数的表达式是18y x =，故答案为：18y x =．【点睛】本题主要考查了反比例函数，解决问题的关键是熟练掌握矩形性质，正方形性质，反比例函数性质，k 的几何意义．统考中考真题）如图，在平面直角坐标系中，AOC 的边两点．若AOC 的面积是【答案】4【分析】过B ，C 两点分别作y 轴的垂线，垂足分别为D ，E ，设B 点坐标为k m m ⎛⎫ ⎪⎝⎭，，则BD m =，由点B 为AC 的中点，推出C 点坐标为22k m m ⎛⎫ ⎪⎝⎭，，求得直线BC 的解析式，得到A 点坐标，根据AOC 的面积是6，列式计算即可求解．【详解】解：过B ，C 两点分别作y 轴的垂线，垂足分别为D ，E ，∴BD CE ∥， ∴ABD ACE ∽，∴BD ABCE AC =，设B 点坐标为k m m ⎛⎫ ⎪⎝⎭，，则BD m =， ∵点B 为AC 的中点， ∴12BD AB CE AC ==， ∴22CE BD m ==，∴C 点坐标为22k m m ⎛⎫ ⎪⎝⎭，，设直线BC 的解析式为y ax b =+， ∴22k ma b mk ma b m ⎧+=⎪⎪⎨⎪+=⎪⎩，解得2232k a m k b m ⎧=−⎪⎪⎨⎪=⎪⎩， ∴直线BC 的解析式为2322k k y x m m =−+，当0x =时，32ky m =，∴A 点坐标为302k m ⎛⎫ ⎪⎝⎭，，根据题意得132622k m m ⋅⋅=，解得4k =，故答案为：4．【点睛】本题考查了反比例函数的性质、相似三角形的判定及性质、求一次函数解析式、坐标与图形，解题关键是熟练掌握反比例函数的性质及相似三角形的性质．【答案】33【分析】过点B 作BC y ⊥轴于点C ，由旋转的性质得，AO AB =，120OAB ∠=︒，在Rt ABC 中求出BC 、AC 的长，即可得出点B 的坐标，代入反比例函数解析式即可求出k 的值．【详解】解∶过点B 作BC y ⊥轴于点C ，由旋转的性质得，AO AB =，120OAB ∠=︒， ∵点A 的坐标为(0，2)， ∴2AO AB ==， ∵120OAB ∠=︒，∴180********BAC OAB ∠∠=︒−=︒−︒=︒， ∴9030ABC BAC ∠∠=︒−=︒， ∴AC =12AB =1221⨯=，由勾股定理得BC ==∴213OC AO AC =+=+=，∴点B 的坐标为(3)， ∵点B 恰好落在反比例函数ky x =的图象上，∴3k =故答案为∶3【点睛】本题考查了反比例函数图象上点的坐标特征，坐标与图形的变化之旋转，解答本题的关键是求出点B 的坐标．【答案】>【分析】把2x =−和=1x −分别代入反比例函数2y x =中计算y 的值，即可做出判断．【详解】解：∵点()12,A y −和点()21,B y −都在反比例函数2y x =的图象上，∴令2x =−，则1212y ==−−；令=1x −，则2221y ==−−，12−>−，12y y ∴>，故答案为：>．【点睛】本题考查了反比例函数图像上点的坐标特征，计算y 的值是解题的关键．若OAB 的面积为【答案】196/136【分析】由k 的几何意义可得19212k =，从而可求出k 的值．【详解】解：AOB 的面积为||192212k k ==，所以k =196．故答案为：196．【点睛】本题主要考查了k 的几何意义．用k 表示三角形AOB 的面积是本题的解题关键．【答案】3【分析】先把点A 坐标代入求出反比例函数解析式，再把点B 代入即可求出m 的值．【详解】解：∵函数()0ky k x =≠的图象经过点()3,2A −和(),2B m −∴把点()3,2A −代入得326k =−⨯=−，∴反比例函数解析式为6y x −=，把点(),2B m −代入得：62m −−=，解得：3m =，故答案为：3．【点睛】本题考查了待定系数法求反比例函数解析式，反比例函数图象上点的坐标特征，熟知反比例函数图象上的点的坐标一定满足函数解析式是解题的关键．【答案】1.5（满足12k <<都可以）【分析】先判断出一次函数7y x b =−+的图象必定经过第二、四象限，再根据120x x ⋅>判断出反比例函数图象和一次函数图象的两个交点在同一象限，从而可以得到反比例函数的图象经过第二、四象限，即630k −<，最终选取一个满足条件的值即可．【详解】解：70−<，∴一次函数7y x b =−+的图象必定经过第二、四象限，120x x ⋅>，∴反比例函数图象和一次函数图象的两个交点在同一象限， ∴反比例函数63ky x −=（1k >且2k ≠）的函数图象经过第一、三象限，∴630k −>，∴2k <， ∵1k >， ∴12k <<，∴满足条件的k 值可以为1.5，故答案为：1.5（满足12k <<都可以）．【点睛】本题考查一次函数和反比例函数的图形性质，解题的关键是根据120x x ⋅>判断出反比例函数图象和一次函数图象的两个交点在同一象限．的正ABC 的顶点，现将ABC 绕原点【答案】6【分析】画出变换后的图像即可（画AOB 即可），当点A 在y 轴上，点B 、C 在x 轴上时，根据ABC 为等边三角形且AO BC ⊥，可得OB OA=A 、B 分别作x 轴垂线构造相似，则BFO OEA ∽，根据相似三角形的性质得出3AOE S =△，进而根据反比例函数k 的几何意义，即可求解．【详解】当点A 在y 轴上，点B 、C 在x 轴上时，连接AO ，ABC 为等边三角形且AO BC ⊥，则30BAO ∠=︒，∴tan tan30BAO ∠=︒=OB OA=，如图所示，过点,A B 分别作x 轴的垂线，交x 轴分别于点,E F ，AO BO ⊥，90BFO AEO AOB ∠=∠=∠=︒，∴90BOF AOE EAO ∠=︒−∠=∠， ∴BFO OEA ∽，∴213BFO AOES OB S OA ⎛⎫== ⎪⎝⎭， ∴212BFOS−==，∴3AOE S =△， ∴6k =．【点睛】本题考查了反比例函数的性质，k 的几何意义，相似三角形的性质与判定，正确作出辅助线构造相似三角形是解题关键．【答案】2/2−+【分析】过点A 作CD y ⊥轴于点D ，过点B 作BC CD ⊥于点C ，证明DAO CBA ≌，进而根据全等三角形的性质得出,DA CB AC OD ==，根据点(),2A m ，进而得出()2,2B m m +−，根据点,A B 在反比例函数(0)ky x x =>的图象上．列出方程，求得m 的值，进而即可求解．【详解】解：如图所示，过点A 作CD y ⊥轴于点D ，过点B 作BC CD ⊥于点C ，∴90C CDO ∠=∠=︒， ∵,90OA AB OAB =∠=︒， ∴90DAO CAB CBA ∠=︒−∠=∠ ∴DAO CBA ≌ ∴,DA CB AC OD == ∵点A 的坐标为()m,2．∴2AC OD ==，AD BC m == ∴()2,2B m m +−∵,A B 在反比例函数(0)ky x x =>的图象上，∴()()222m m m =+−解得：1m =或1m =（舍去）∴22k m ==故答案为：2．【点睛】本题考查了反比例函数的图象和性质，全等三角形的判定和性质，求得点B 的坐标是解题的关键．【答案】4【分析】根据题意可设点P 的坐标为()22m m ，，则()2D m m ，，把()2D m m ，代入一次函数解析式中求出m 的值进而求出点P 的坐标，再求出k 的值即可．【详解】解：∵PA x ⊥轴于点,A PB y ⊥轴于点,B PA PB =， ∴点P 的横纵坐标相同， ∴可设点P 的坐标为()22m m ，，∵D 为PB 的中点， ∴()2D m m ，，∵()2D m m ，在直线1y x =+上，∴12m m +=， ∴1m =， ∴()22P ，，∵点P 在反比例函数()0ky k x =>的图象上，∴224k =⨯=，故答案为：4．【点睛】本题主要考查了一次函数与反比例函数综合，正确求出点P 的坐标是解题的关键．【答案】6【分析】延长CD 交x 轴于点F ，设,k D a a ⎛⎫ ⎪⎝⎭，利用相似三角形的判定与性质可求得矩形的长与宽，再由矩形的面积即可求和k 的值．【详解】解：延长CD 交x 轴于点F ，如图，由点D 在反比例函数()0k y x x =>的图象上，则设,k D a a ⎛⎫ ⎪⎝⎭，∵矩形ABCD 的边AB 平行于x 轴，AB CD ∥，AD CD ⊥， ∴CD y ⊥轴，AD OF ∥，则kDF a OF a ==，，∵AD OF ∥， ∴CDA CFO △∽△， ∴CD AD ACCF OF OC ==， ∵2AC AO =，∴23AC OC =， ∴2223CD CF DF a ===，2233k AD OF a ==， ∵8AD CD ⋅=，即2283k a a ⨯=，∴6k =，故答案为：6．【点睛】本题考查了相似三角形的判定与性质，反比例函数图象上点的坐标特征，其中相似三角形的判定与性质是关键．则ABP 的面积是【答案】152【分析】把()2,3A −代入到22k y x =可求得2k 的值，再把(),2Bm −代入双曲线函数的表达式中，可求得m 的值，进而利用三角形的面积公式进行求解即可．【详解】∵直线11y k x b =+与双曲线22k y x =（其中120k k ⋅≠）相交于()2,3A−，(),2B m −两点，∴2232k m =−⨯=−∴263k m =−=，，∴双曲线的表达式为：26y x =−，()3,2B −，∵过点B 作BP x ∥轴，交y 轴于点P ， ∴3BP =， ∴1153(32)22ABPS=⨯⨯+=，故答案为152．【点睛】本题是一次函数与反比例函数的交点问题，考查了待定系数法求反比例函数，反比例函数图象上点的坐标特征，三角形的面积，数形结合是解答此题的关键．三、解答题26．（2023·四川绵阳·统考中考真题）如图，设反比例函数的解析式为（k ＞0）．（1）若该反比例函数与正比例函数y=2x 的图象有一个交点的纵坐标为2，求k 的值；（2）若该反比例函数与过点M （﹣2，0）的直线l ：y=kx+b 的图象交于A ，B 两点，如图所示，当△ABO 的面积为时，求直线l 的解析式．【答案】（1）；（2）．【详解】试题分析：（1）由题意可得A（1，2），利用待定系数法即可解决问题；（2）把M（﹣2，0）代入y=kx+b，可得b=2k，可得y=kx+2k，由消去y得到，解得x=﹣3或1，推出B（﹣3，﹣k），A（1，3k），根据△ABO的面积为，可得•23k+•2k=，解方程即可解决问题；试题解析：（1）由题意A（1，2），把A（1，2）代入，得到3k=2，∴．（2）把M（﹣2，0）代入y=kx+b，可得b=2k，∴y=kx+2k，由消去y得到，解得x=﹣3或1，∴B（﹣3，﹣k），A（1，3k），∵△ABO的面积为，∴×2×3k+•2k=，解得k=，∴直线l 的解析式为．考点：反比例函数与一次函数的交点问题．(1)2m =，4a =，求函数3y 的表达式及(2)当a 、m 在满足0a m >>的条件下任意变化时，(3)试判断直线PH 与BC 边的交点是否在函数【答案】(1)函数3y 的表达式为325y x =−+，PGH △的面积为12(2)不变，理由见解析 (3)在，理由见解析【分析】（1）由2m =，4a =，可得(20)A ，，()20B −，，12y x=，22y x −=，则4AB =，当2x =，1212y ==，则()21E ，；当14y =，24x =，解得12x =，则142G ⎛⎫ ⎪⎝⎭，；当24y =，24x −=，解得12x =−，则142H ⎛⎫− ⎪⎝⎭，；待定系数法求一次函数3y 的解析式为325y x =−+，当0x =，35y =，则()05P ，，根据()11154222PGH S ⎡⎤⎛⎫=⨯−−⨯− ⎪⎢⎥⎝⎭⎣⎦△，计算求解即可；（2）求解过程同（1）；（3）设直线PH 的解析式为22y k x b =+，将()01P a +，，m a H a a −⎛⎫⎪⎝⎭，，代入22y k x b =+得，2221b am a k b a a =+⎧⎪−⎨+=⎪⎩，解得221b aa k a m =+⎧⎪⎨=⎪−⎩，即1a x a a m y +−=+，当x m a =−，()11y a m a a a m ⨯+=−+=−，则直线PH 与BC 边的交点坐标为()1m a −，，当x m a =−，21m ay m a −=−=，进而可得结论．【详解】（1）解：∵2m =，4a =，∴(20)A ，，()20B −，，12y x=，22y x −=，∴4AB =，当2x =，1212y ==，则()21E ，；当14y =，24x =，解得12x =，则142G ⎛⎫ ⎪⎝⎭，；当24y =，24x −=，解得12x =−，则142H ⎛⎫− ⎪⎝⎭，；设一次函数3y 的解析式为3y kx b =+，将()21E ，，142G ⎛⎫⎪⎝⎭，，代入3y kx b =+得，21142k b k b +=⎧⎪⎨+=⎪⎩，解得25k b =−⎧⎨=⎩，∴325y x =−+，当0x =，35y =，则()05P ，，∴()1111542222PGH S ⎡⎤⎛⎫=⨯−−⨯−=⎪⎢⎥⎝⎭⎣⎦△； ∴函数3y 的表达式为325y x =−+，PGH △的面积为12；（2）解：PGH △的面积不变，理由如下：∵(0)A m ，，(0)B m a −，，1m y x =，2m ay x −=，∴AB a =，当x m =，11m y m ==，则()1E m ，；当1y a =，m a x =，解得m x a =，则m G a a ⎛⎫⎪⎝⎭，；当2y a =，m a a x −=，解得m a x a −=，则m a H a a−⎛⎫ ⎪⎝⎭，；设一次函数3y 的解析式为113k x b y =+，将()1E m ，，m G a a ⎛⎫ ⎪⎝⎭，，代入113k x b y =+得，11111mk b m k b a a +=⎧⎪⎨+=⎪⎩，解得111a k m b a ⎧=−⎪⎨⎪=+⎩，∴31ax a m y =−++，当0x =，31y a =+，则()01P a +，，∴()11122PGH m m a S a a a a ⎡−⎤⎛⎫=⨯−⨯+−= ⎪⎢⎥⎝⎭⎣⎦△； ∴PGH △的面积不变；（3）解：直线PH 与BC 边的交点在函数2y 的图像上，理由如下：设直线PH 的解析式为22y k x b =+，将()01P a +，，m a H a a −⎛⎫⎪⎝⎭，，代入22y k x b =+得，2221b a m a k b a a =+⎧⎪−⎨+=⎪⎩，解得221b aa k a m =+⎧⎪⎨=⎪−⎩， ∴1ax a a m y +−=+，当x m a =−，()11y am a a a m ⨯+=−+=−，∴直线PH 与BC 边的交点坐标为()1m a −，，当x m a =−，21m ay m a −=−=，∴直线PH 与BC 边的交点在函数2y 的图像上．【点睛】本题考查了正方形的性质，一次函数解析式，反比例函数解析式，交点坐标．解题的关键在于对知识的熟练掌握与灵活运用．(1)求一次函数和反比例函数的表达式； (2)求OAB 的面积；(3)过动点()0T t ，作x 轴的垂线l ，l 与一次函数y x m =−+和反比例函数ky x=的图象分别交于当M 在N 的上方时，请直接写出t 的取值范围．【答案】(1)一次函数的解析式为3y x =−+，反比例函数的解析式为2y x =(2)32(3)0t <或12t << 【分析】（1）把()1，2A 分别代入一次函数和反比例函数求出m k 、的值即可得到答案；（2）联立32y x y x =−+⎧⎪⎨=⎪⎩求出点B 的坐标，令直线AB 与x 交于点C ，由直线AB 求出点C 的坐标，最后由1122AOBAOCBOCA B SSSOC y OC y =−=⋅⋅−⋅⋅，进行计算即可得到答案；（3）直接由函数图象即可得到答案．【详解】（1）解：把()1，2A 代入一次函数y x m =−+，得12m −+=，解得：3m =，∴一次函数的解析式为：3y x =−+，把()1，2A 代入反比例函数ky x =，得21k =，解得：2k =，∴反比例函数的解析式为：2y x =；（2）解：联立32y x y x =−+⎧⎪⎨=⎪⎩，解得：12x y =⎧⎨=⎩或21x y =⎧⎨=⎩，()21B ∴，，令直线AB 与x 交于点C ，如图，，当0y =时，30x −+=，解得：3x =， ()30C ∴，，11113323122222AOBAOCBOCA B SS SOC y OC y ∴=−=⋅⋅−⋅⋅=⨯⨯−⨯⨯=（3）解：由图象可得：，当M 在N 的上方时，t 的取值范围为：0t <或12x <<．【点睛】本题考查了求反比例函数的解析式、求一次函数的解析式、反比例函数与一次函数的交点问题，熟练掌握反比例函数和一次函数的图象与性质，是解题的关键．(1)当气球内的气压超过150KPa 少时气球不会爆炸（球体的体积公式(2)请你利用p 与V 的关系试解释为什么超载的车辆容易爆胎．【答案】(1)气球的半径至少为0.2m 时，气球不会爆炸； (2)由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎【分析】（1）设函数关系式为k p =，用待定系数法可得 4.8p V =，即可得当150p =时， 4.80.032150V ==，从而求出0.2r =；（2）由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎．【详解】（1）设函数关系式为kp V =，根据图象可得：1200.04 4.8k pV ==⨯=， ∴4.8p V =，∴当150p =时，4.80.032150V ==，∴3430.0323r ⨯=，解得：0.2r =，4.80k =>，p ∴随V 的增大而减小，∴要使气球不会爆炸，0.032V ≥，此时0.2r ≥， ∴气球的半径至少为0.2m 时，气球不会爆炸；（2）由于车辆超载，轮胎体积变小，胎内气压增大导致爆胎．【点睛】本题考查反比例函数的应用，涉及立方根等知识，解题的关键是读懂题意，掌握待定系数法求出反比例函数的解析式．轴的对称点，OAC 的面积是【答案】(1)y x =(2)(2P −++或(2P −−−【分析】（1）设,k A m m ⎛⎫ ⎪⎝⎭，可得,k C m m ⎛⎫− ⎪⎝⎭，结合OAC 的面积是8．可得()182k m m m +=，从而可得答案；（2）先求解()2,4A ，()2,4C −，可得直线为28y x =+，联立828y x y x ⎧=⎪⎨⎪=+⎩，再解方程组即可．【详解】（1）解：∵点A 在反比例函数(0)ky k x =≠的图象上，∴设,k A m m ⎛⎫⎪⎝⎭，∵点C 是点A 关于y 轴的对称点，∴,k C m m ⎛⎫− ⎪⎝⎭， ∵OAC 的面积是8．∴()182k m m m +=，解得：8k =；∴反比例函数解析式为：8y x =；（2）∵点A 的横坐标为2时， ∴842A y ==，即()2,4A ，则()2,4C −，∵直线2y x b =+过点C ， ∴44b −+=， ∴8b =，∴直线为28y x =+， ∴828y x y x ⎧=⎪⎨⎪=+⎩，解得：24x y ⎧=−+⎪⎨=+⎪⎩或24x y ⎧=−−⎪⎨=−⎪⎩，经检验，符合题意；∴(2P −++或(2P −−−．【点睛】本题考查的是一次函数与反比例函数的综合应用，轴对称的性质，一元二次方程的解法，熟练的利用图形面积建立方程求解是解本题的关键．(1)求反比例函数的表达式；(2)点D 在反比例函数图象上，且横坐标大于3OBDS=【答案】(1)4y x =(2)132y x =−+【分析】（1）根据四边形OABC 是边长为2的正方形求出点B 的坐标，代入ky x =求出k ；（2）设4,D a a ⎛⎫ ⎪⎝⎭，过点D 作DH x ⊥轴，根据OBD OBH BHD ODH S S S S =+−V V V V 面积列方程，求出点D 坐标，再由待定系数法求出直线BD 的函数表达式．【详解】（1）解：四边形OABC 是边长为2的正方形， ∴4OABC S xy ==正方形， ∴4k =；即反比例函数的表达式为4y x =．（2）解：设4,D a a ⎛⎫ ⎪⎝⎭，过点D 作DH x ⊥轴，点()2,2B ，4,D a a ⎛⎫ ⎪⎝⎭，(),0H a ，∴12OBH S OH AB a=⋅=V 1144(2)(2)222BHD a S DH AH a a a −=⋅=⋅⋅−=V ，122ODH S OH DH =⋅=V3OBD OBH BHD ODH S S S S =+−=V V V V∴4(2)232a a a −+−=，解得：14a =，21a =−，经检验4a =，是符合题意的根，即点()4,1D ，设直线BD 的函数解析式为y kx b =+，得∶ 2241k b k b +=⎧⎨+=⎩，解得：123k b ⎧=−⎪⎨⎪=⎩，即：直线BD 的函数解析式为132y x =−+．【点睛】本题考查了反比例函数的几何意义和待定系数法求一次函数解析式，反比例函数ky x =图象上任意一点做x 轴、y 轴的垂线，组成的长方形的面积等于k，灵活运用几何意义是解题关键．2(1)求反比例函数的解析式；(2)点C 在这个反比例函数图象上，连接【答案】(1)8y x =(2)()4,2C【分析】（1）利用正切值，求出4OB =，进而得到()2,4A ，即可求出反比例函数的解析式；（2）过点A 作AE x ⊥轴于点E ，易证四边形ABOE 是矩形，得到2OE =，4AE =，再证明AED △是等腰直角三角形，得到4DE =，进而得到()6,0D ，然后利用待定系数法求出直线AD 的解析式为6y x =−+，联立反比例函数和一次函数，即可求出点C 的坐标．【详解】（1）解：AB y ⊥轴，90ABO ∴∠=︒，1tan 2AOB =∠，12AB OB ∴=，2AB =，4OB ∴=，()2,4A ∴，点A 在反比例函数()0ky x x =>的图象上，248k ∴=⨯=，∴反比例函数的解析式为8y x =；（2）解：如图，过点A 作AE x ⊥轴于点E ，90ABO BOE AEO ∠=∠=∠=︒，∴四边形ABOE 是矩形，2OE AB ∴==，4OB AE ==，45ADO ∠=︒，AED ∴是等腰直角三角形， 4DE AE ∴==，246OD OE DE ∴=+=+=，()6,0D ∴，设直线AD 的解析式为y kx b =+，2460k b k b +=⎧∴⎨+=⎩，解得：16k b =−⎧⎨=⎩， ∴直线AD 的解析式为6y x =−+，点A 、C 是反比例函数8y x =和一次函数6y x =−+的交点，联立86y x y x ⎧=⎪⎨⎪=−+⎩，解得：24x y =⎧⎨=⎩或42x y =⎧⎨=⎩，()2,4A ， ()4,2C ∴．【点睛】本题是反比例函数综合题，考查了锐角三角函数值，矩形的判定和性质，待定系数法求函数解析式，反比例函数和一次函数交点问题等知识，求出直线AD 的解析式是解题关键．(1)求反比例函数的表达式和点E 的坐标；(2)若一次函数y x m =+与反比例函数的部分时（点M 可与点,D E 重合）【答案】(1)反比例函数解析式为y x =，()22E ，(2)30m −≤≤【分析】（1）根据矩形的性质得到BC OAAB OA ∥，⊥，再由()4,1D 是AB 的中点得到()42B ，，从而得到点E的纵坐标为2，利用待定系数法求出反比例函数解析式，进而求出点E 的坐标即可；（2）求出直线y x m =+恰好经过D 和恰好经过E 时m 的值，即可得到答案．【详解】（1）解：∵四边形OABC 是矩形，∴BC OAAB OA ∥，⊥， ∵()4,1D 是AB 的中点， ∴()42B ，，∴点E 的纵坐标为2，∵反比例函数()0ky x x =>的图象分别与,AB BC 交于点()4,1D 和点E ，∴14k =，∴4k =，∴反比例函数解析式为4y x =，在4y x =中，当42y x ==时，2x =， ∴()22E ，；（2）解：当直线 y x m =+经过点()22E ，时，则22m +=，解得0m =；当直线 y x m =+经过点()41D ，时，则41m +=，解得3m =−；∵一次函数y x m =+与反比例函数()0ky x x =>的图象相交于点M ，当点M 在反比例函数图象上,D E 之间的部分时（点M 可与点,D E 重合）， ∴30m −≤≤．【点睛】本题主要考查了求一次函数解析式，一次函数与反比例函数综合，矩形的性质等等，灵活运用所学知识是解题的关键．【答案】(1)反比例函数的表达式为y x =−；一次函数的表达式为22y x =−+(2)142BC =【分析】（1）利用待定系数法即可求解；（2）先求得直线BC 的表达式为1y =，再分别求得B C 、的坐标，据此即可求解．【详解】（1）解：∵反比例函数()0ky x x =<的图象经过点()1,4A −，∴144k =−⨯=−， ∴反比例函数的表达式为4y x =−；∵一次函数2y x m =−+的图象经过点()1,4A −，∴()421m=−⨯−+，∴2m =，∴一次函数的表达式为22y x =−+；（2）解：∵1OD =， ∴()01D ，，∴直线BC 的表达式为1y =， ∵1y =时，14x =−，解得4x =−，则()41B −，，∵1y =时，122x =−+，解得12x =，则112C ⎛⎫ ⎪⎝⎭，，∴()114422BC =−−=．【点睛】本题考查一次函数、反比例函数图象上点的坐标特征，待定系数法是求函数解析式的基本方法．(1)求反比例函数和一次函数的表达式；(2)求AOB 的面积； (3)请根据图象直接写出不等式【答案】(1)12y x =−，32y x =−+(2)9(3)<2x −或04x <<【分析】（1）把点B 代入反比例函数()0ky k x =≠，即可得到反比例函数的解析式；把点A 代入反比例函数，即可求得点A 的坐标；把点A 、B 的坐标代入一次函数一次函数()0y ax b a =+<即可求得a 、b 的值，从而得到一次函数的解析式；（2）AOB 的面积是AOC 和BOC 的面积之和，利用面积公式求解即可；（3）利用图象，找到反比例函数图象在一次函数图象下方所对应的x 的范围，直接得出结论．【详解】（1）∵点()4,3B −在反比例函数ky x =的图象上，∴34k −=，解得：12k =− ∴反比例函数的表达式为12y x =−．∵(),3A m m −在反比例函数12y x =−的图象上，∴123m m =−−，解得12m =，22m =−（舍去）．∴点A 的坐标为()2,6−．∵点A ，B 在一次函数y ax b =+的图象上，把点()2,6A −，()4,3B −分别代入，得2643a b a b −+=⎧⎨+=−⎩，解得323a b ⎧=−⎪⎨⎪=⎩，∴一次函数的表达式为332y x =−+；（2）∵点C 为直线AB 与y 轴的交点，∴把0x =代入函数332y x =−+，得3y = ∴点C 的坐标为()0,3 ∴3OC =，∴AOB AOC BOC SS S =+ 1122A B OC x OC x =⋅⋅+⋅⋅11323422=⨯⨯+⨯⨯9=．（3）由图象可得，不等式k ax b x <+的解集是<2x −或04x <<．【点睛】此题是反比例函数与一次函数的交点问题，考查了待定系数法求函数的解析式，三角形面积，函数与不等式的关系，求出两个函数解析式是解本题的关键．。

中考数学复习专题--与反比例函数有关的综合问题

中考数学复习专题——与反比例函数有关的综合问题类型一、反比例函数与一次函数结合1.（2017徐州）如图，在平面直角坐标系xOy 中，函数()0y kx b k =+≠与()0my m x=≠的图象相交于点()()2,3,6,1A B --，则不等式mkx b x+>的解集为-------------------------------------（） A ．6x <- B ．60x -<<或2x > C. 2x > D ．6x <-或02x <<2.（2019广东）如图，一次函数b x k y +=1的图象与反比例函数xk y 2=的图象交于A ，B 两点，其中点A 的坐标为（-1，4），点B 的坐标为（4，n ）。

（1）根据图象，直接写出满足xk b x k 21＞+的x 的取值范围；（2）求这两个函数表达式；（3）点P 在线段AB 上，且21：：△△=BOP AOP S S ，求点P 的坐标。

3.（2018北京）在平面直角坐标系中，函数)0(＞x x k y =的图象G 经过点A （4，1），直线l ：b x y +=41与图象G 交于点B ，与y 轴交于点C 。

（1）k= ；（2）横纵坐标均为整数的点叫做整点，记图象G 在点A ，B 之间的部分与线段OA ，OC ，BC 围成的区域（不含边界）为W 。

①当b=-1时，直接写出区域W 的整点个数为个； ②若区域W 内恰有4个整点，结合图象，求b 的取值范围。

类型二、反比例函数与几何图形结合4.（2018徐州）如图，在平面直角坐标系中，函数y kx =与2y x=-的图象交于A 、B 两点，过A 作y 轴的垂线，交函数4y x=的图象于点C ．连接BC ，则△ABC 的面积为----------------------------（） A ．2 B ．4 C ．6 D ．85.（2018连云港）如图，菱形ABCD 的两个顶点B ，D 在反比例函数xky =的图象上，对角线AC 与BD 的交点恰好是坐标原点，已知A （1，1），∠ABC=60°，则k 的值为------------------------------------（） A.-5 B.-4 C.-3 D.-26.（2019无锡模拟）如图，四边形ABCD 的顶点都在坐标轴上，若AB ∥CD ，△ABD 与△ACD 的面积分别为3和6，若双曲线xky =恰好经过BC 的中点E ，则k 的值为---------------------------------------（） A.-2 B.2 C.-1 D.1 7.（2019连云港）如图，函数b x y +-=的图象与函数)0(＜x xky =的图象交于点A （-1，6），并与x 轴交于点C ，点D 是线段AC 上一点，△ODC 与△OAC 的面积比为2：3. （1）k= ，b= ；（2）求点D 的坐标；（3）若将△ODC 绕点O 逆时针旋转，得到△OD ’C ’，其中点D ’落在x 轴负半轴上，判断点C ’是否落在函数)0(＜x xky =的图象上，并说明理由。

2020-2021备战中考数学综合题专题复习【反比例函数】专题解析

2020-2021备战中考数学综合题专题复习【反比例函数】专题解析一、反比例函数1．已知一次函数y=kx+b与反比例函数y= 交于A（﹣1，2），B（2，n），与y轴交于C 点．（1）求反比例函数和一次函数解析式；（2）如图1，若将y=kx+b向下平移，使平移后的直线与y轴交于F点，与双曲线交于D，E两点，若S△ABD=3，求D，E的坐标．（3）如图2，P为直线y=2上的一个动点，过点P作PQ∥y轴交直线AB于Q，交双曲线于R，若QR=2QP，求P点坐标．【答案】（1）解：点A（﹣1，2）在反比例函数y= 的图象上，∴m=（﹣1）×2=﹣2，∴反比例函数的表达式为y=﹣，∵点B（2，n）也在反比例函数的y=﹣图象上，∴n=﹣1，即B（2，﹣1）把点A（﹣1，2），点B（2，﹣1）代入一次函数y=kx+b中，得，解得：k=﹣1，b=1，∴一次函数的表达式为y=﹣x+1，答：反比例函数的表达式是y=﹣，一次函数的表达式是y=﹣x+1；（2）解：如图1，连接AF，BF，∵DE∥AB，∴S△ABF=S△ABD=3（同底等高的两三角形面积相等），∵直线AB的解析式为y=﹣x+1，∴C（0，1），设点F（0，m），∴AF=1﹣m，∴S△ABF=S△ACF+S△BCF= CF×|x A|+ CF×|x B|= （1﹣m）×（1+2）=3，∴m=﹣1，∴F（0，﹣1），∵直线DE的解析式为y=﹣x+1，且DE∥AB，∴直线DE的解析式为y=﹣x﹣1①．∵反比例函数的表达式为y=﹣②，联立①②解得，或∴D（﹣2，1），E（1，﹣2）；（3）解：如图2由（1）知，直线AB的解析式为y=﹣x﹣1，双曲线的解析式为y=﹣，设点P（p，2），∴Q（p，﹣p﹣1），R（p，﹣），PQ=|2+p+1|，QR=|﹣p﹣1+ |，∵QR=2QP，∴|﹣p﹣1+ |=2|2+p+1|，解得，p= 或p= ，∴P（，2）或（，2）或（，2）或（，2）．【解析】【分析】（1）把A的坐标代入反比例函数的解析式可求得m的值，从而可得到反比例函数的解析式；把点A和点B的坐标代入一次函数的解析式可求得一次函数的解析式；（2）依据同底等高的两个三角形的面积相等可得到S△ABF=S△ABD=3，再利用三角形的面积公式可求得点F的坐标，即可得出直线DE的解析式，即可求出交点坐标；（3）设点P（p，2），则Q（p，﹣p﹣1），R（p，﹣），然后可表示出PQ与QR的长度，最后依据QR=2QP，可得到关于p的方程，从而可求得p的值，从而可得到点P的坐标.2．已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是________；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若 = ，则b的值是________．【答案】（1）﹣2（2）3【解析】【解答】解：（1）设点P的坐标为（m，n），则点Q的坐标为（m﹣1，n+2），依题意得：，解得：k=﹣2．故答案为：﹣2．（2）∵BO⊥x轴，CE⊥x轴，∴BO∥CE，∴△AOB∽△AEC．又∵ = ，∴ = = ．令一次函数y=﹣2x+b中x=0，则y=b，∴BO=b；令一次函数y=﹣2x+b中y=0，则0=﹣2x+b，解得：x= ，即AO= ．∵△AOB∽△AEC，且 = ，∴．∴AE= AO= b，CE= BO= b，OE=AE﹣AO= b．∵OE•CE=|﹣4|=4，即 b2=4，解得：b=3 ，或b=﹣3 （舍去）．故答案为：3 ．【分析】（1）设出点P的坐标，根据平移的特性写出Q点的坐标，由点P,Q均在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，即可得出关于k,m,n,b的四元次一方程组，两式作差即可求出k的值；（2）由BO⊥x轴，CE⊥x轴，找出△AOB∽△AEC．再由给定图形的面积比即可求出==，根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长，利用OE=AE﹣AO求出OE的长，再借助反比例函数K的几何意义得出关于b的一元二次方程，解方程即可得出结论。

初中数学中考数学反比例函数综合大题专题——题型分类汇编(

初中数学中考数学反比率函数综合大题专题——题型分类汇编2思虑：如图 10，在直角坐标系中，直线 y kx 1 k 0 与双曲线 y x （x ＞ 0）订交于 P （1，m ）.（1）求 k 的值；（2）若点 Q 与点 P 对于 y=x 成轴对称，则点 Q 的坐标为 Q （）；考点一、反比率函数有关的面积问题1例 1、如图，已知 A(－4， 2 )，B(－1，2)是一次函数 y ＝kx ＋ b(k ≠0)与反比率函数myx (m ≠0，x ＜0)图象的两个交点， AC ⊥ x 轴于点 C ，BD ⊥y 轴于点 D.(1)依据图象直接回答：在第二象限内，当 x 取何值时，一次函数的值大于反比率函数的值？(2)求一次函数的分析式及 m 的值；(3)P 是线段 AB 上一点，连结 PC ， PD ，若△ PCA 和△ PDB 的面积相等，求点 P 的坐标．m1. 如图，一次函数 y ＝kx ＋1(k ≠0)与反比率函数 yx (m ≠0)的图象有公共点 A(1， 2)，直线 l ⊥ x 轴于点 N(3， 0)，与一次函数和反比率函数的图象分别订交于点 B ，C ，连结 AC. (1)求 k 和 m 的值； (2)求点 B 的坐标；(3)求△ ABC 的面积．k2. 如图，已知双曲线 yx 经过点 D(6，1)，点 C是双曲线第三象限上的动点，过点 C 作 CA ⊥x 轴，过点 D 作 DB ⊥y 轴，垂足分别为 A ， B ，连结 AB ，BC.(1)求 k 的值；(2)若△ BCD 的面积为 12，求直线 CD 的分析式；(3)判断 AB 与 CD 的地点关系，并说明原因．3. 如图，在平面直角坐标系中，已知直线AB：y＝kx－3 与反比率函数y8(x＞0)的图象订交于x点 A(8， 1)．(1)求 k 的值；(2)M 是反比率函数图象上一点，横坐标为t (0＜t＜ 8)，过点 M 作 x 轴的垂线交直线 AB 于点 N，则 t为何值时，△ BMN 面积最大，且最大值为多少？4.如图，反比率函数y 2的图象与一次函数y＝kx＋b的图象交于点A、B，点A、B的横坐标分别x为 1、－ 2，一次函数图象与 y 轴交于点 C，与 x 轴交于点 D.(1)求一次函数的分析式；(2)对于反比率函数y 2，当y＜－1时，写出x的取值范围；x(3)在第三象限的反比率函数图象上能否存在一点 P，使得 S△ODP＝ 2S△OCA？若存在，恳求出点 P 的坐标；若不存在，请说明原因．考点二、反比率函数有关的不等式的解集问题例 1、已知，如图，一次函数 y ＝ kx ＋b(k 、b 为常数， k ≠0)的图象与 x 轴、y 轴分别交于 A 、B 两点，且与反比率函数 yn(n 为常数且 n ≠0)的图象在第二象限交于点 C.CD ⊥x 轴，垂足为 D.x若 OB ＝ 2OA ＝3OD ＝6.(1)求一次函数与反比率函数的分析式；(2)求两函数图象的另一个交点坐标； (3)直接写出不等式： kx ＋bn的解集xm1．如图，一次函数 y ＝kx ＋b 的图象与坐标轴分别交于 A ．B 两点，与反比率函数 yx 的图象在第二象限的交点为 C ， CD ⊥ x 轴，垂足为 D ．若 OB ＝2，OD ＝ 4，△ AOB 的面积为 1．(1)求一次函数与反比率函数的分析式；(2)直接写出当 x<0 时， kx ＋b － mx >0 的解集．k 22. 如图，已知一次函数y ＝k x ＋b 的图象与 x 轴、 y 轴分别交于 A ，B 两点，与反比率函数 y 211x(1) 求一次函数 y1＝k1x ＋b 与反比率函数y2k2的分析式；x(2)求△ COD 的面积；(3)直接写出 y1＞y2时自变量 x 的取值范围．3. 如图，已知 A( －4，2)， B(n，－ 4)是一次函数 y＝kx＋ b 和反比率函数y m的图象上的两个交点．x(1)求一次函数和反比率函数的分析式；(2)求△ AOB 的面积；(3)察看图象，直接写出不等式 kx ＋b m＞0 的解集．x考点三、特别三角形、四边形的存在性问题例 1、如图，直线y＝2x－6与反比率函数y k(x＞0)的图象交于点 A(4， 2)，与 x 轴交于点 B.初中数学中考数学反比率函数综合大题专题——题型分类汇编((2)在 x 轴上能否存在点 C，使得 AC＝AB？若存在，求出点 C 的坐标；若不存在，请说明原因．1m2.如图，直线 y1＝4 x＋1 与 x 轴交于点 A，与 y 轴交于点 C，与反比率函数 y2＝x (x>0)的图象交于点 P，过点 P 作 PB⊥x 轴于点 B，且 AC＝BC.(1)求点 P 的坐标和反比率函数y2的分析式；(2)请直接写出 y1>y2时， x 的取值范围；(3)反比率函数 y2图象上能否存在点 D，使四边形 BCPD 为菱形？假如存在，求出点 D 的坐标；假如不存在，说明原因．如图，直线 y＝ 3 x 3与 x， y 轴分别交于点 A，B，与反比率函数 y＝k＞0)图象交于点，D，3x k C过点 A 作 x 轴的垂线交该反比率函数图象于点 E.(1)求点 A 的坐标；(2)若 AE＝AC.①求 k 的值；②试判断点 E 与点 D 能否对于原点O 成中心对称？并说明原因．考点五、线段的最值问题k例 1、如图，反比率函数y＝x (k≠0，x＞ 0)的图象与直线 y＝ 3x 订交于点 C，过直线上点A(1， 3)作 AB⊥x 轴于点 B，交反比率函数图象于点 D，且 AB＝3BD.(1)求 k 的值；(2)求点 C 的坐标；(3)在 y 轴上确立一点 M，使点 M 到 C， D 两点距离之和 d＝MC＋MD 最小，求点 M 的坐标．1.已知正比率函数y＝2x 的图象与反比率函数 y＝k(k≠0)在第一象限内的图象交于点 A，过点 A 作xx 轴的垂线，垂足为点P，已知△ OAP 的面积为 1. (1)求反比率函数的分析式；(2)有一点 B 的横坐标为 2，且在反比率函数图象上，则在 x 轴上能否存在一点 M，使得 MA＋ MB 最小？若存在，恳求出点 M 的坐标；若不存在，请说明原因．2.如图，点 A(－2，n)，B(1，－ 2)是一次函数 y＝ kx＋ b 的图象和反比率函数y m的图象的两个交点x(1)求反比率函数和一次函数的分析式；(2)依据图象写出使一次函数的值小于反比率函数的值的x 的取值范围；(3)若 C 是 x 轴上一动点，设t＝ CB－ CA，求 t 的最大值，并求出此时点 C 的坐标．考点六、反比率函数有关的相像三角形m例 1、如图，直线y＝x＋b与x轴交于点C(4，0)，与y轴交于点B，并与双曲线y＝x(x＜0)交于点A(－1，n)．(1)求直线与双曲线的分析式；(2)连结 OA，求∠ OAB 的正弦值；(3)若点 D 在 x 轴的正半轴上，能否存在以点D、 C、B 组成的三角形△ OAB 相像？若存在求出 D 点的坐标，若不存在，请说明原因．1. 如图，点 B 为双曲线 y k(x＞0)上一点，直线AB平行于y轴，交直线y＝x于点A，交x轴于点D，xk双曲线 y x 与直线y＝x交于点C，若OB2－AB2＝4(1)求 k 的值；(2)点 B 的横坐标为 4 时，求△ ABC 的面积；(3)双曲线上能否存在点P，使△ APC∽△ AOD？若存在，求出点P 的坐标；若不存在，请说明原因．课后专项练习选择以上 3 个题型，分别改编一个题目。

中考考点(3-22)：反比例函数与不等式

中考考点（3-22）：反比例函数与不等式一、选择题1 k x . 如图，正比例函数 y = k x 的图象和反比例函数 y = 的图象都经过点 A (2, −1)，若 y > y ，2 1 1 2 1 2 则 x 的取值范围是 ( )A. −1 < x < 0B. x > 2 D. x < −2 或 0 < x < 2C. −2 < x < 0 或 x > 2二、填空题2 . 若反比例函数的表达式为 y =3 ，则当 x < −1 时，y 的取值范围是． x3 . 如图，抛物线 y = x + 1 与双曲线 y = k 的交点 A 的横坐标是 1，则关于 x 的不等式 2 x k + x 2 + 1 < 0 的解集是． xk x 4 . 反比例函数 y = 的图象与一次函数 y = k x + b 的图象交于 A (−2, −1) 和 B 两点，点 B 的纵坐标为 −3．1 12 2 若 y < y ，则 x 的取值范围是． 1 25 . 如图，已知函数 y = − 3 与 y = ax + bx (a > 0, b > 0) 的图象交于点 P ，点 P 的 2 x3 纵坐标为 1，则关于 x 的不等式 bx + > −ax2 的解集为． x 三、解答题6 . 已知反比例函数 y = m − 5 （m 为常数，m = 5），若这个函数图象的一支位于第二象限． x (1) 求 m 的取值范围．(2) 若 P (−1, a) 在函数 y = 2x + 4 的图象上，又在反比例函数 y = m m − 5 − 5 的图象上，求 m 的值；并求出当 x − 3 < x < −1 时，反比例函数 y = 函数值 y 的取值范围． x7 . 如图，已知一次函数与反比例函数的图象交于点 A (−4, −2) 和 B (a, 4)．(1) 求反比例函数的解析式和点 B 的坐标；(2) 根据图象回答，当 x 在什么范围内时，一次函数的值大于反比例函数的值?第 1 页，共 1 页中考考点（3-22）：反比例函数与不等式—答案一、选择题二、填空题1D2 . −3 < y < 0 3 . −1 < x < 04 . x < −2 或 − 2 < x < 0 解析：∵ 点 A (−2, −1) 在反比例函数 3 的图象上， k 1 y 1 = x k ∴ ∴ ∴ −1 = 1 ， − 2 k 1 = 2， 2 y 1 = ，其图象位于第一、三象限． x2 ∵ ∴ ∴ ∴ 点 B 在反比例函数 y 1 = 的图象上，且点 B 的纵坐标为 −3，x 2 −3 = ，， x 2 x = − Ä ä 3 2 3 点 B 的坐标为 − , −3 ．由反比例函数和一次函数的图象可知，当 y 1 < y 2 时，在第一象限中不满足，在第三象限中满足条件的 x 的2 取值范围是 x < −2 或 − < x < 0．3 5 三、解答题. x < −3 或 x > 0 6 .(1) 依题意得 m − 5 < 0．解得 m < 5．(2) 把 P (−1, a) 代入 y = 2x + 4，可得 a = 2，∴ P (−1, 2)．m − 5 再把 P (−1, 2) 代入 y = 可得 m = 3，y = ， x − 2 ．； x 2 3当 x = −3 时，y = 当 x = −1 时，y = 2． 2 ∴ 当 −3 < x < −1 时， < y < 2．37 . (1) 设反比例函数的解析式为 y = k (k x ∵ ∴ ∴ ∴ 反比例函数图象经过点 A (−4, −2)， k −2 = ， − k = 8， 4 8 反比例函数的解析式为 y = ， x 的图象上， 8 ∵ B (a, 4) 在 y = x 8 ∴ 4 = ， a ∴ ∴ a = 2，点 B 的坐标为 (2, 4)；(2) 根据图象得，当 x > 2 或 −4 < x < 0 时，一次函数的值大于反比例函数的值．答案。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

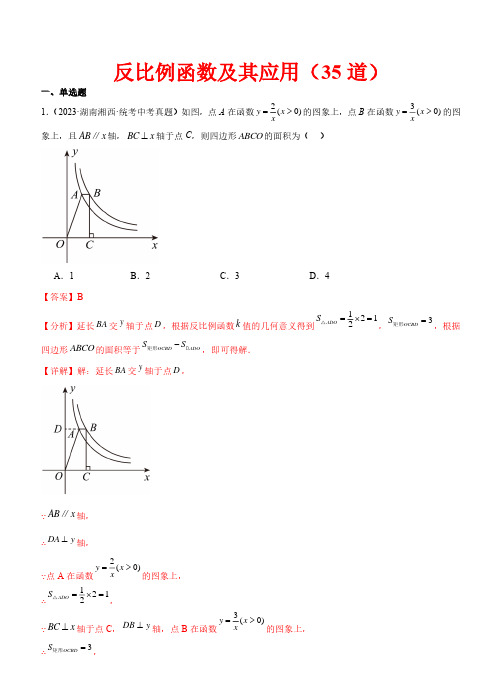
第11题BC A x y1 O y 1＝xy 2＝4x 中考数学4专题研究（不等式、动点问题、概率、反比例函数、函数应用题）1. 不等式组及函数应用题专项训练2. 动点问题专项训练3. 概率专项训练4. 反比例函数问题(2010-7-14)反比例函数问题(2010-7-14)(2010山东聊城）11．函数y 1＝x (x ≥0)，y 2＝4x (x ＞0)的图象如图所示，下列结论：① 两函数图象的交点坐标为A （2，2）； ② 当x ＞2时，y 2＞y 1；③ 直线x ＝1分别与两函数图象交于B 、C 两点，则线段BC 的长为3；④ 当x 逐渐增大时，y 1的值随着x 的增大而增大，y 2的值随着x 的增大而减小．则其中正确的是（）A ．只有①②B ．只有①③C ．只有②④D ．只有①③④（2010湖北咸宁）16．如图，一次函数y ax b =+的图象与x 轴，y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ．有下列四个结论：①△CEF 与△DEF 的面积相等； ②△AOB ∽△FOE ； ③△DCE ≌△CDF ； ④AC BD =．其中正确的结论是．（把你认为正确结论的序号都填上）（2010江苏徐州）25．(本题8分)如图，已知A(n ，-2)，B(1，4)是一次函数y=kx+b 的图象和反比例函数y=xm的图象的两个交点，直线AB 与y 轴交于点C ． (1)求反比例函数和一次函数的关系式； (2)求△AOC 的面积； (3)求不等式kx+b-xm<0的解集(直接写出答案)．（2010江苏南通）21．（本小题满分9分）如图，直线y x m =+与双曲线ky x=相交于A （2，1）、B 两点．（1）求m 及k 的值；A BOxy （第21题）2 1 23 －3 －1 －2 13 －3－1－2 y xDCA B O FE（2）不解关于x 、y 的方程组,,y x m ky x =+⎧⎪⎨=⎪⎩直接写出点B 的坐标；（3）直线24y x m =-+经过点B 吗？请说明理由．2-=x y （2010江苏宿迁）23．（本题满分10分）如图，已知一次函数与反比例函数xy 3=的图象交于A 、B 两点．（1）求A 、B 两点的坐标；（2）观察图象，可知一次函数值小于反比例函数值的x 的取值范围是___________．（把答案直接写在答题卡相应位置上）（2010四川成都）18．如图，已知反比例函数ky x=与一次函数y x b=+的图象在第一象限相交于点(1,4)A k -+．（1）试确定这两个函数的表达式；（2）求出这两个函数图象的另一个交点B 的坐标，并根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围．（2010四川广安）23．如右图，若反比例函数8y x=-与一次函数2y mx =-的图象都经过点(,2)A a ． (1) 求A 点的坐标及一次函数的解析式；(2) 设一次函数与反比例函数图象的另一交点为B ，求B 点坐标，并利用函数图象写出使一次函数的值小于反比例函数的值的x 的取值范围．（2010甘肃兰州）14. 已知点（-1，1y ），（2，2y ），（3，3y ）在反比例函数x k y 12--=的图像上. 下列结论中正确的是 A ．321y y y >> B ．231y y y >> C ．213y y y >> D ． 132y y y >>（2010山东济宁）20．（7分）如图，正比例函数12y x =的图象与反比例函数k y x =(0)k ≠在第一象限的图象交于A 点，过A 点作x 轴的垂线，垂足为M ，已知OAM ∆的面积为1. （1）求反比例函数的解析式；（2）如果B 为反比例函数在第一象限图象上的点（点B 与点A 不重合），且B 点的横坐标为1，在x 轴上求一点P ，使PA PB +最小.（2010山东威海）22．（10分）BA O xy（第23题）OMxyA(第20题)如图，一次函数b kx y +=的图象与反比例函数x my =的图象交于点A ﹙-2，-5﹚，C ﹙5，n ﹚，交y 轴于点B ，交x 轴于点D ．(1) 求反比例函数x m y =和一次函数b kx y +=的表达式； (2) 连接OA ，OC ．求△AOC 的面积．（2010珠海）14.已知：正比例函数y=k 1x 的图象与反比例函数xk y 2=(x>0)的图象交于点M （a,1），MN ⊥x 轴于点N （如图），若△OMN 的面积等于2，求这两个函数的解析式.23．（2010广东广州，23，12分）已知反比例函数y ＝8m x-(m 为常数)的图象经过点A （－1，6）．（1）求m 的值；（2）如图9，过点A 作直线AC 与函数y ＝8m x-的图象交于点B ，与x 轴交于点C ，且AB ＝2BC ，求点C 的坐标．22.(2010湖南常德)已知图7中的曲线函数5m y x-=(m 为常数)图象的一支. (1)求常数m 的取值范围；(2)若该函数的图象与正比例函数2y x =图象在第一象限的交点为A （2，n ）,求点A 的坐标及反比例函数的解析式.（2010湖南郴州）21. （1）求双曲线的解析式；（2）试比较b 与2的大小.（2010江苏苏州）26．(本题满分8(x ＞0)的图象经过点B ． (1)求k 的值；B AOCy xO AB CxyD(2)将正方形OABC 分别沿直线AB 、BC 翻折，得到正方形MABC′、MA′BC ．设线段MC′、NA′分别与函数ky x=(x ＞0)的图象交于点E 、F ，求线段EF 所在直线的解析式．（2010安徽）17. 点P(1，a )在反比例函数xky =的图象上，它关于y 轴的对称点在一次函数42+=x y 的图象上，求此反比例函数的解析式。

概率专项训练1．（2009呼和浩特）有一个正方体，6个面上分别标有1~6这6个整数，投掷这个正方体一次，则出现向上一面的数字是偶数的概率为（）A ．13B ．16C ．12D ．142．（2009青海）将三个均匀的六面分别标有1、2、3、4、5、6的正方体同时掷出，出现的数字分别为a b c 、、，则a b c 、、正好是直角三角形三边长的概率是（）A ．1216B ．172C ．112D ．1363、（20XX 年黄石市）为了防控输入性甲型H1N1流感，某市医院成立隔离治疗发热流涕病人防控小组，决定从内科5位骨干医师中（含有甲）抽调3人组成，则甲一定抽调到防控小组的概率是（）A ．35B ．25C ．45D ．154．（20XX 年枣庄市）布袋中装有1个红球，2个白球，3个黑球，它们除颜色外完全相同，从袋中任意摸出一个球，摸出的球是白球．．的概率是． 5．（20XX 年赤峰市）如右图，是由四个直角边分别是3和4的全等的直角三角形拼成的“赵爽弦图”，小亮随机的往大正方形区域内投针一次，则针扎在阴影部分的概率是6．（2009青海）在一个不透明的布袋中，红色、黑色、白色的玻璃球共有60个，除颜色外，形状、大小、质地等完全相同．小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在15%和45%，则口袋中白色球的个数很可能是个． 7．（20XX 年龙岩）在3 □ 2 □（－2）的两个空格□中，任意填上“+”或“－”，则运算结果为3的概率是． 8．（20XX 年广东省）在一个不透明的布袋中装有2个白球和n 个黄球，它们除颜色不同外，其余均相同．若从中随机摸出一个球，摸到黄球的概率是45，则n __________．9．（20XX年邵阳市）晓芳抛一枚硬币10次，有7次正面朝上，当她抛第11次时，正面向上的概率为______。

10．（20XX年黄石市）汶川大地震时，航空兵空投救灾物质到指定的区域（圆A）如图所示，若要使空投物质落在中心区域（圆B）的概率为12，则B⊙与A⊙的半径之比为．11．(20XX年云南省)在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球，它们除颜色外完全相同，其中红球有2个，黄球有1个，蓝球有1个. 现有一张电影票，小明和小亮决定通过摸球游戏定输赢（赢的一方得电影票）．游戏规则是：两人各摸1次球，先由小明从纸箱里随机摸出1个球，记录颜色后放回，将小球摇匀，再由小亮随机摸出1个球．若两人摸到的球颜色相同，则小明赢，否则小亮赢．这个游戏规则对双方公平吗？请你利用树状图或列表法说明理由．12．（20XX年崇左）一只口袋中放着若干只红球和白球，这两种球除了颜色以外没有任何其他区别，袋中的球已经搅匀，蒙上眼睛从口袋中取出一只球，取出红球的概率是14．（1）取出白球的概率是多少？（2）如果袋中的白球有18只，那么袋中的红球有多少只？13．（2009贺州）一个不透明的布袋里装有4个大小、质地均相同的乒乓球，每个球上面分别标有1，2，3，4．小林先从布袋中随机抽取一个乒乓球（不放回去），再从剩下的3个球中随机抽取第二个乒乓球．（1）请你列出所有可能的结果；（2）求两次取得乒乓球的数字之积为奇数的概率．14．（20XX 年铁岭市）小明和小亮是一对双胞胎，他们的爸爸买了两套不同品牌的运动服送给他们，小明和小亮都想先挑选．于是小明设计了如下游戏来决定谁先挑选．游戏规则是：在一个不透明的袋子里装有除数字以外其它均相同的4个小球，上面分别标有数字1、2、3、4．一人先从袋中随机摸出一个小球，另一人再从袋中剩下的3个小球中随机摸出一个小球．若摸出的两个小球上的数字和为奇数，则小明先挑选；否则小亮先挑选．（1）用树状图或列表法求出小明先挑选的概率；（2）你认为这个游戏公平吗？请说明理由．动点问题专项训练1．（20XX 年重庆）如图，在矩形ABCD 中，AB=2，1BC =，动点P 从点B 出发，沿路线B C D →→作匀速运动，那么ABP △的面积S 与点P 运动的路程x 之间的函数图象大致是（）2．（2009重庆綦江）如图1，在直角梯形ABCD 中，动点P 从点B 出发，沿BC ，CD 运动至点D 停止．设点P 运动的路程为x ，△ABP 的面积为y ，如果y 关于x 的函数图象如图2所示，则△BCD 的面积是（） A ．3 B ．4 C ．5 D ．63．（2009威海）如图，△ABC 和的△DEF 是等腰直角三角形，∠C=∠F=90°，AB=2.DE=4．点B 与点D 重合，点A,B(D),E 在同一条直线上，将△ABC 沿D E →方向平移，至点A 与点E 重合时停止．设点B,D 之间的距离为x ，△ABC 与△DEF 重叠部分的面积为y ，则准确反映y 与x 之间对应关系的图象是（）A ．B ．C ．D ．D C PBA图1C PD 图24．（20XX 年济南）如图，点G 、D 、C 在直线a 上，点E 、F 、A 、B 在直线b 上，若a b Rt GEF ∥，△从如图所示的位置出发，沿直线b 向右匀速运动，直到EG 与BC 重合．运动过程中GEF △与矩形ABCD 重合部分．．．．的面积（S ）随时间（t ）变化的图象大致是（）5．（20XX 年牡丹江）如图，平面直角坐标系中，在边长为1的正方形ABCD 的边上有一动点P 沿A B C D A →→→→运动一周，则P 的纵坐标y 与点P 走过的路程s 之间的函数关系用图象表示大致是（）6．（20XX 年福建莆田）如图1，在矩形ABCD 中，动点P 从点B 出发，沿BC 、CD 、DA 运动至点A 停止，设点P 运动的路程为x ，△ABP 的面积为y ，如果y 关于x 的函数图象如图2所示，则矩形ABCD 的面积是( )A ．10 8．16 C. 20 D ．367．（20XX 年洛江区）如图，三个大小相同的正方形拼成六边形ABCDEF ，一动点P 从点A 出发沿着A →B →C →D →E 方向匀速运动，最后到达点E .运动过程中PEF ∆的面积（s ）随时间（t ）变化的图象大致是（）GDC E F AB a（第4题st O A s t O B C s t O Dst O 1 2 3 4 1 2 y s O 1 2 3 4 1 2 y s O s 1 2 3 4 1 2 y s O 12341 2 y O A BC D A B C DP.·8．（20XX年甘肃兰州）如图8，点A、B、C、D为圆O的四等分点，动点P从圆心O出发，沿O-C-D-O的路线作匀速运动.设运动时间为t秒,∠APB的度数为y度，则下列图象中表示y与t之间函数关系最恰当的是9．（20XX年湖北施恩）13．一张正方形的纸片，剪去两个一样的小矩形得到一个“E”图案，如图4所示，设小矩形的长和宽分别为x、y，剪去部分的面积为20，若2≤x≤10，则y与x的函数图象是:10．（20XX年山西太原）如图，AB是半圆O的直径，点P从点O出发，沿OA AB BO--的路径运动一周．设OP为s，运动时间为t，则下列图形能大致地刻画s与t之间关系的是（）11.（20XX年重庆市江津区）锐角△ABC中，BC＝6,,12=∆ABCS两动点M、N分别在边AB、AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y（y ＞0）,当x＝，公共部分面积y最大，y最大值＝ ,等式组及函数应用题专项训练PAOBstOsO OstOstA．B．C．D．1.（2009，深圳）迎接大运，美化深圳，园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配A、B两种园艺造型共50个摆放在迎宾大道两侧，已知搭配一个A种造型需甲种花卉80盆，乙种花卉40盆，搭配一个B种造型需甲种花卉50盆，乙种花卉90盆．（1）某校九年级（1）班课外活动小组承接了这个园艺造型搭配方案的设计，问符合题意的搭配方案有几种？请你帮助设计出来．（2）若搭配一个A种造型的成本是800元，搭配一个B种造型的成本是960元，试说明（1）中哪种方案成本最低？最低成本是多少元？2.（2009，清远）某饮料厂为了开发新产品，用A种果汁原料和B种果汁原料试制新型甲、乙两种饮料共50千克，设甲种饮料需配制x千克，两种饮料的成本总额为y元．（1）已知甲种饮料成本每千克4元，乙种饮料成本每千克3元，请你写出y与x之间的函数关系式．（2）若用19千克A种果汁原料和17.2千克B种果汁原料试制甲、乙两种新型饮料，下表是试验的相关数据；请你列出关于x且满足题意的不等式组，求出它的解集，并由此分析如何配制这两种饮料，3.（2009，牡丹江）某冰箱厂为响应国家“家电下乡”号召，计划生产A、B两种型号的冰箱100台．经预算，两种冰箱全部售出后，可获得利润不低于4.75万元，不高于4.8万元，两种型号的冰箱生产成本和售价如下表：（1（2）该冰箱厂按哪种方案生产，才能使投入成本最少？“家电下乡”后农民买家电（冰箱、彩电、洗衣机）可享受13%的政府补贴，那么在这种方案下政府需补贴给农民多少元？（3）若按（2）中的方案生产，冰箱厂计划将获得的全部利润购买三种物品：体育器材、实验设备、办公用品支援某希望小学．其中体育器材至多买4套，体育器材每套6000元，实验设备每套3000元，办公用品每套1800元，把钱全部用尽且三种物品都购买的情况下，请你直接写出实验设备的买法共有多少种．4.（2009，铁岭）为迎接国庆六十周年，某校团委组织了“歌唱祖国”有奖征文活动，并设立了一、二、三等奖．学校计划派人根据设奖情况买50件奖品，其中二等奖件数比一等奖件数的2倍还少10件，三等奖所花钱数不超过二等奖所花钱数的1.5倍．各种奖品的单价如下表所示．如果计划一等奖买x件，买50件奖品的总钱数是w元．（1）求w与x的函数关系式及自变量x的取值范围；（2）请你计算一下，如果购买这三种奖品所花的总钱数最少？最少是多少元？5.（2009，齐齐哈尔）某电脑公司经销甲种型号电脑，受经济危机影响，电脑价格不断下降．今年三月份的电脑售价比去年同期每台降价1000元，如果卖出相同数量的电脑，去年销售额为10万元，今年销售额只有8万元．（1）今年三月份甲种电脑每台售价多少元？（2）为了增加收入，电脑公司决定再经销乙种型号电脑，已知甲种电脑每台进价为3500元，乙种电脑每台进价为3000元，公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台，有几种进货方案？（3）如果乙种电脑每台售价为3800元，为打开乙种电脑的销路，公司决定每售出一台乙种电脑，返还顾客现金a元，要使（2）中所有方案获利相同，a值应是多少？此时，哪种方案对公司更有利？(2009，朝阳)某学校计划租用6辆客车送一批师生参加一年一度的哈尔滨冰雕节，感受冰雕艺术的魅力．现有甲、乙两种客车，它们的载客量和租金如下表．设租用甲种客车x辆，租车总费用为y元．（1）求出y（元）与x（辆）之间的函数关系式，指出自变量的取值范围；（2）若该校共有240名师生前往参加，领队老师从学校预支租车费用1650元，试问预支的租车费用是否可以结余？若有结余，最多可结余多少元？6.（2009，抚顺）某食品加工厂，准备研制加工两种口味的核桃巧克力，即原味核桃巧克力和益智核桃巧克力．现有主要原料可可粉410克，核桃粉520克．计划利用这两种主要原料，研制加工上述两种口味的巧克力共50块．加工一块原味核桃巧克力需可可粉13克，需核桃粉4克；加工一块益智核桃巧克力需可可粉5克，需核桃粉14克．加工一块原味核桃巧克力的成本是1.2元，加工一块益智核桃巧克力的成本是2元．设这次研制加工的原味核桃巧克力x块．（1）求该工厂加工这两种口味的巧克力有哪几种方案？（2）设加工两种巧克力的总成本为y元，求y与x的函数关系式，并说明哪种加工方案使总成本最低？总成本最低是多少元？参考答案：1．解：设搭配A种造型x个，则B种造型为(50)x-个，依题意，得：8050(50)34904090(50)2950x xx x+-⎧⎨+-⎩≤≤解得：3331xx⎧⎨⎩≤≥，∴3133x≤≤∵x是整数，x可取31、32、33，∴可设计三种搭配方案：①A 种园艺造型31个，B 种园艺造型19个；②A 种园艺造型32个，B 种园艺造型18个；③A 种园艺造型33个，B 种园艺造型17个．（2）方法一：由于B 种造型的造价成本高于A 种造型成本．所以B 种造型越少，成本越低，故应选择方案③，成本最低，最低成本为：33×800+17×960=42720（元）方法二：方案①需成本：31×800+19×960=43040（元）；方案②需成本：32×800+18×960=42880（元）；方案③需成本：33×800+17×960=42720（元）；∴应选择方案③，成本最低，最低成本为42720元．2. 解：（1）依题意得：43(50)150y x x x =+-=+（2）依题意得：0.50.2(50)19(1)0.30.4(50)17.2(2)x x x x +-⎧⎨+-⎩≤…………≤………解不等式（1）得：30x ≤解不等式（2）得：28x ≥∴不等式组的解集为2830x ≤≤150y x =+，y 是随x 的增大而增大，且2830x ≤≤∴当甲种饮料取28千克，乙种饮料取22千克时，成本总额y 最小，28150178y =+=最小（元）8分 3. 解：（1）设生产A 型冰箱x 台，则B 型冰箱为()100x -台，由题意得：47500(28002200)(30002600)(100)48000x x -+-⨯-≤≤解得：37.540x ≤≤x 是正整数x ∴取38，39或40．22002600(100)400260000y x x x =+-=-+4000-<y ∴随x 的增大而减小∴当40x =时，y 有最小值．即生产A 型冰箱40台，B 型冰箱50台，该厂投入成本最少此时，政府需补贴给农民(280040300060)13%37960()⨯+⨯⨯=元（3）实验设备的买法共有10种．4. 解：（1）1210(210)5[50(210)]x x x x ω=+-+---17200x =+．由02100[50(210)]05[50(210)] 1.510(210)x x x x x x x >⎧⎪->⎪⎨--->⎪⎪---⨯-⎩≤得1020x <≤∴自变量的取值范围是1020x <≤，且x 为整数．（2）∵170k =>，∴ω随x 的增大而增大，当10x =时，有ω最小值．最小值为1710200370ω=⨯+=．答：一等奖买10件，二等奖买10件，三等奖买30件时，所花的钱数最少，最少钱数是370元．5. （1）解：设今年三月份甲种电脑每台售价x 元100000800001000x x=+解得：4000x = 经检验：4000x =是原方程的根，所以甲种电脑今年每台售价4000元．（2）设购进甲种电脑x 台，4800035003000(15)50000x x +-≤≤,解得610x ≤≤因为x 的正整数解为6，7，8，9，10，所以共有5种进货方案（3）设总获利为W 元，(40003500)(38003000)(15)(300)1200015W x a x a x a=-+---=-+- 当300a =时，（2）中所有方案获利相同．此时，购买甲种电脑6台，乙种电脑9台时对公司更有利．6. 解：（1）根据题意，得135(50)410414(50)520x x x x +-⎧⎨+-⎩≤≤ 解得1820x ≤≤ x 为整数181920x ∴=，，当18x =时，50501832x -=-=当19x =时，50501931x -=-=当20x =时，50502030x -=-=∴一共有三种方案：加工原味核桃巧克力18块，加工益智巧克力32块；加工原味核桃巧克力19块，加工益智巧克力31块，加工原味核桃巧克力20块，加工益智巧克力30块．6分（2） 1.22(50)y x x =+-=0.8100x -+0.80-<y ∴随x 的增大而减小∴当20x =时，y 有最小值，y 的最小值为84．∴当加工原味核桃巧克力20块、加工益智巧克力30块时，总成本最低．总成本最低是84元．。