北京市西城区2018-2019学年八年级上期末考试试题及答案

合集下载

北京市西城区2018-2019学年度第一学期期末试卷参考答案及评分标准

北京市西城区2018-2019学年度第一学期期末试卷八年级语文参考答案及评分标准2019．1一．基础·运用（共10分）1．（1）C（2）A （3）B2．答案示例一：请问王老师，您希望学生如何去读书呢？答案示例二：王老师您好，请问您是如何指导学生读书的？）评分标准：语言得体1分，内容1分。

3．“基因编辑婴儿”诞生引发巨大争议。

评分标准：共10分，每小题2分。

二．古诗文阅读（共22分）（一）古诗文默写（共6分）4．烈士暮年5．贫贱不能移6．谁家新燕啄春泥7．惊起一滩鸥鹭8．此中有真意欲辨已忘言评分标准：共6分，每空1分。

（二）古诗阅读（共5分）9．D评分标准：共2分。

10．雄浑、奇美、壮丽晴川历历汉阳树芳草萋萋鹦鹉洲评分标准：共3分，每空1分。

（三）文言文阅读（共10分）11．（1）衡．于虑衡，同“横”，梗塞、不顺。

（2）而后喻．喻，了解，明白。

评分标准：共2分。

每个1分。

12．D评分标准：共2分。

13．示例：了解到这一切之后，就会明白常处忧愁祸患之中可以使人生存，常处安逸快乐之中可以使人死亡。

评分标准：共2分。

14．出身都很贫贱（平凡）或都经过了艰苦磨练；都增长了才干或都成就了不平凡的事业（都成了圣君贤臣、都被明主发现并委以重任）评分标准：共2分，每点1分，答出2点意思对即可。

15．饿其体肤（空乏其身）困于心，衡于虑，而后作评分标准：共2分，每空1分。

附：乙文译文：淮阴侯韩信是江苏淮阴人，还是普通百姓时，经常在别人那里混吃混喝，……有许多人都很讨厌他。

（一天）韩信在城下钓鱼，有几位老太太在河边漂洗丝绵。

有位（在水边漂洗丝绵的）老太太看到他饿了，就拿饭来给他吃，连续漂洗了几十天，天天如此。

韩信非常高兴，对那位老太太说：“我一定会重重地报答您老人家。

”附：丙文译文：西伯姬昌被拘禁而扩写《周易》；孔子受困窘而作《春秋》；屈原被放逐，才写了《离骚》；左丘明失去视力，才有《国语》；孙膑被剜去膝盖骨，《兵法》才撰写出来；吕不韦被贬谪蜀地，后世才流传着《吕氏春秋》；韩非被囚禁在秦国，写出《说难》、《孤愤》；《诗经》三百篇，大都是一些圣贤们抒发愤慨而写作的。

2018-2019学年八年级道德与法治上学期期末检测试题1

2018-2019学年八年级道德与法治上学期期末检测试题一、单项选择（每小题3分，共45分）1. 2017年10月18日上午9时，中国共产党第十九次全国代表大会在京举行。

我市某中学全校师生组织在一起，观看开幕会，聆听习近平同志代表十八大中央委员会向大会作的报告。

这主要表明（）A．我们的社会生活绚丽多彩 B．个人是社会的有机组成部分C．人们对社会生活的感受是一成不变的 D．我们应积极融入社会，关心社会发展2. 感动中国·2017年度人物浙江省已故乡村医生“兰小草”王珏连续15年向社会捐助善款，这种行为（）①这是一种亲社会行为②能体会到分享的快乐③能更好地体现着人生价值④有利于良好社会风气的形成。

A．①②③④ B．②③④C．①②③D．①③④3. 在我省各地开展的“创建文明城市”活动中，不乏中学生的身影，他们清洁社区卫生，劝导文明通行，发放“创文”手册……中学生参与此项活动是（）①提高科学文化素质的主要途径②践行社会主义核心价值观的要求③关心社会的表现，属于亲社会行为④热心公益，服务社会的表现。

A．①②③B．①②④C．①③④D．②③④4. 今天，互联网已经深刻影响我们的生活，在网络上交朋友、发祝福、抢红包、学习医、购物……我们越来越离不开网络。

但同时，网络诈骗、网络售假、网银被盗等也随之出现。

对此，我们应该（）①充分享受网络交往带来的乐趣，把网络作为我们生活的全部②正确认识网络的两面性，用其所长、避其所短③提高自己的安全防范意识，学会自我保护④拒绝使用网络，避免受到伤害。

A. ①②B. ①③C. ②③D. ③④5. 下面漫画给我们的启示有（）①要对自己的网络言论负责，不制造和传播谣言②要学会辨析网络信息，自觉抵制网络谣言③要践行社会主义核心价值观，在网络上传播正能量④网上谣言太多，我们不要相信任何网络信息A. ①②③B. ①③④C. ①②④D. ②③④6. “日月星，花鸟虫，因时序，相平衡；循轨道，行车船，有规矩，成方圆。

北京市西城区三帆中学2018-2019学年八年级(上)期中数学复习试卷(解析版)

北京市西城区三帆中学2018-2019学年八年级（上）期中数学复习试卷一．选择题（每小题3分，满分30分）1．下列图形中不是轴对称图形的是（）A．B．C．D．2．某市有3000名初一学生参加期末考试，为了了解这些学生的数学成绩，从中抽取200名学生的数学成绩进行统计分析．在这个问题中，下列说法：①这3000名初一学生的数学成绩的全体是总体；②每个初一学生是个体；③200名初一学生是总体的一个样本；④样本容量是200．其中说法正确的是（）A．4个B．3个C．2个D．1个3．下列各式变形中，是因式分解的是（）A．a2﹣2ab+b2﹣1＝（a﹣b）2﹣1B．2x2+2x＝2x2（1+）C．（x+2）（x﹣2）＝x2﹣4D．x4﹣1＝（x2+1）（x+1）（x﹣1）4．如图，已知AD是△ABC的BC边上的高，下列能使△ABD≌△ACD的条件是（）A．AB＝AC B．∠BAC＝90°C．BD＝AC D．∠B＝45°5．如图，在Rt△A BC中，∠C＝90°，以顶点A为圆心，适当长为半径画圆弧，分别交AB、AC于点D、E，再分别以点D、E为圆心，大于DE长为半径画圆弧，两弧交于点F，作射线AF交边BC于点G．若CG＝3，AB＝10，则△ABG的面积是（）A．3 B．10 C．15 D．306．如图，△ABC≌△ADE，∠B＝80°，∠C＝30°，∠DAC＝35°，则∠EAC的度数为（）A．40°B．35°C．30°D．25°7．若分式的值为零，则x等于（）A．﹣1 B．1 C．﹣1或1 D．1或28．已知等腰三角形有一个角为100°，那么它的底角为（）A．100°B．40°C．50°D．80°9．如图，△ABC中边AB的垂直平分线分别交BC，AB于点D，E，AE＝3cm，△ADC的周长为9cm，则△ABC的周长是（）A．10cm B．12cm C．15cm D．17cm10．将一张长方形的纸片对折，然后用笔尖在上面扎出字母“B”，再把它展开铺平后，你可以看到的图形是（）A．B．C．D．二．填空题（满分30分，每小题3分）11．如图，AB＝AC，点D，E分别在AB，AC上，CD，BE交于点F，只添加一个条件使△ABE≌△ACD，添加的条件是：．12．化简：a+1+a（a+1）+a（a+1）2+…+a（a+1）99＝．13．如图，AB∥CD，O为∠BAC、∠ACD的平分线的交点，OE⊥AC于E，且OE＝1，则AB与CD之间的距离等于．14．已知x＝﹣2时，分式无意义；x＝4时，分式的值为0，则a+b＝．15．因式分解：（a﹣b）2﹣（b﹣a）＝．16．如图，BD＝CF，FD⊥BC于点D，DE⊥AB于点E，BE＝CD，若∠AFD＝140°，则∠EDF＝．17．化简：＝．18．已知Rt△ABC中，∠C＝90°，AC＝6，BC＝8，将它的一个锐角翻折，使该锐角顶点落在其对边的中点D处，折痕交另一直角边于E，交斜边于F，则△CDE的周长为．19．如图，Rt△ABC中，∠ACB＝90°，∠A＝15°，AB的垂直平分线与AC交于点D，与AB交于点E，连接BD．若AD＝14，则BC的长为．20．如图，在△ABC中，高AD和BE交于点H，且BH＝AC，则∠ABC＝．三．解答题（共1小题，满分8分，每小题8分）21．（8分）分解因式：（1）a2b﹣b3；（2）﹣（x2+2）2+6（x2+2）﹣9四．解答题（共3小题，满分15分，每小题5分）22．（5分）先化简，再求值：（x+2y）（x﹣2y）+（20xy3﹣8x2y2）÷4xy，其中x＝2018，y＝2019．23．（5分）如图，AC∥BD．（1）利用尺规作AB的垂直平分线（保留作图痕迹，不写作法）；（2）若AB的垂直平分线分别交AC、BD于点M、N，连接BM，求证△BMN是等腰三角形．24．（5分）随着互联网的发展，同学们的学习习惯也有了改变，一些同学在做题遇到困难时，喜欢上网查找答案．针对这个问题，某校调查了部分学生对这种做法的意见（分为：赞成、无所谓、反对），并将调查结果绘制成图1和图2两个不完整的统计图．请根据图中提供的信息，解答下列问题：（1）此次抽样调查中，共调查了多少名学生？（2）将图1补充完整；（3）求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数；（4）根据抽样调查结果，请你估计该校1500名学生中有多少名学生持“无所谓”意见．五．解答题（共3小题，满分17分）25．（6分）知识链接：将两个含30°角的全等三角尺放在一起，让两个30°角合在一起成60°，经过拼凑、观察、思考，探究出结论“直角三角形中，30°角所对的直角边等于斜边的一半”．如图，等边三角形ABC的边长为4cm，点D从点C出发沿CA向A运动，点E从B出发沿AB的延长线BF向右运动，已知点D、E都以每秒0.5cm的速度同时开始运动，运动过程中DE与BC相交于点P，设运动时间为x秒．（1）请直接写出AD长．（用x的代数式表示）（2）当△ADE为直角三角形时，运动时间为几秒？（3）求证：在运动过程中，点P始终为线段DE的中点．26．（5分）如图，△ABC中，D是BC的中点，过D点的直线GF交AC于F，交AC的平行线BG于G点，DE⊥DF，交AB于点E，连结EG、EF．（1）求证：BG＝CF；（2）请你判断BE+CF与EF的大小关系，并说明理由．27．（6分）如图，△ABC中，AB＝AC，∠BAC＝50°，P是BC边上一点，将△ABP绕点A逆时针旋转50°，点P旋转后的对应点为P′．（1）画出旋转后的三角形；（2）连接PP′，若∠BAP＝20°，求∠PP′C的度数；六．解答题（共2小题，满分10分）28．（4分）在△ABC中，∠ACB＝90°，AC＝BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图（1）的位置时，求证：①△A DC≌△CEB．②DE＝AD+BE；（2）当直线MN绕点C旋转到图（2）的位置时，求证：DE＝AD﹣BE；（3）当直线MN绕点C旋转到图（3）的位置时，请直接写出DE，AD，BE之间的等量关系．29．（6分）在直角三角形ABC中，若AB＝16cm，AC＝12cm，BC＝20cm．点P从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C →A→B的方向移动，如果点P、Q同时出发，用t（秒）表示移动时间，那么：（1）如图1，请用含t的代数式表示，①当点Q在AC上时，CQ＝；②当点Q在AB上时，AQ＝；③当点P在AB上时，BP＝；④当点P在BC上时，BP＝．（2）如图2，若点P在线段AB上运动，点Q在线段CA上运动，当QA＝AP时，试求出t的值．（3）如图3，当P点到达C点时，P、Q两点都停止运动，当AQ＝BP时，试求出t的值．参考答案一．选择题1．解：A、不是轴对称图形，故本选项符合题意；B、是轴对称图形，故本选项不符合题意；C、是轴对称图形，故本选项不符合题意；D、是轴对称图形，故本选项不符合题意．故选：A．2．解：①这3000名初一学生的数学成绩的全体是总体正确；②每个初一学生的期末数学成绩是个体，故命题错误；③200名初一学生的期末数学成绩是总体的一个样本，故命题错误；④样本容量是200，正确．故选：C．3．解：A a2﹣2ab+b2﹣1＝（a﹣b）2﹣1中不是把多项式转化成几个整式积的形式，故A 错误；B2x2+2x＝2x2（1+）中不是整式，故B错误；C（x+2）（x﹣2）＝x2﹣4是整式乘法，故C错误；Dx4﹣1＝（x2+1）（x2﹣1）＝（x2+1）（x+1）（x﹣1），故D正确．故选：D．4．解：添加AB＝AC，符合判定定理HL；添加BD＝DC，符合判定定理SAS；添加∠B＝∠C，符合判定定理AAS；添加∠BAD＝∠CAD，符合判定定理ASA；选其中任何一个均可．故选：A．5．解：作GH⊥AB于H，由基本尺规作图可知，AG是△ABC的角平分线，∵∠C＝90°，GH⊥AB，∴GH＝CG＝3，∴△ABG的面积＝×AB×GH＝15，故选：C．6．解：∵∠B＝80°，∠C＝30°，∴∠BAC＝180°﹣80°﹣30°＝70°，∵△ABC≌△ADE，∴∠DAE＝∠BAC＝70°，∴∠EAC＝∠DAE﹣∠DAC，＝70°﹣35°，＝35°．故选：B．7．解：依题意得|x|﹣1＝0，且x2﹣3x+2≠0，解得x＝1或﹣1，x≠1和2，∴x＝﹣1．故选：A．8．解：当100°为顶角时，其他两角都为40°、40°，当100°为底角时，等腰三角形的两底角相等，由三角形的内角和定理可知，底角应小于90°，故底角不能为100°，所以等腰三角形的底角为40°、40°．故选：B．9．解：∵△ABC中，边AB的中垂线分别交BC、AB于点D、E，AE＝3cm，∴BD＝AD，AB＝2AE＝6cm，∵△ADC的周长为9cm，∴AC+AD+CD＝AC+BD+CD＝AC+BC＝9cm，∴△ABC的周长为：AB+AC+BC＝15cm．故选：C．10．解：由题意可得，展开后的图形呈轴对称，故选：C．二．填空题（共10小题，满分30分，每小题3分）11．解：∠B＝∠C，理由是：∵在△ABE和△ACD中∴△ABE≌△ACD（ASA），故答案为：∠B＝∠C．12．解：原式＝（a+1）[1+a+a（a+1）+a（a+1）2+…+a（a+1）98] ＝（a+1）2[1+a+a（a+1）+a（a+1）2+…+a（a+1）97]＝（a+1）3[1+a+a（a+1）+a（a+1）2+…+a（a+1）96]＝…＝（a+1）100．故答案为：（a+1）100．13．解：过O作OF⊥AB，OG⊥CD，∵AO为∠BAC的平分线，且OE⊥AC，OF⊥AB，∴OE＝OF＝1，∵CO为∠BAC的平分线，且OE⊥AC，OG⊥CD，∴OG＝O E＝1，∴FG＝OF+OG＝2，∵AB∥CD，∴AB与CD之间的距离等于2，故答案为：214．解：由题意，得﹣2+a＝0，4﹣b＝0，解得a＝2，b＝4．a+b＝2+4＝6，故答案为：6．15．解：原式＝（a﹣b）2+（a﹣b）＝（a﹣b）（a﹣b+1），故答案为：（a﹣b）（a﹣b+1）16．解：∵∠AFD＝140°，∴∠DFC＝40°，∵DE⊥AB，DF⊥BC，∴∠DEB＝∠FDC＝90°，在Rt△BDE和Rt△CFD中，∵，∴Rt△BDE≌Rt△CFD（HL）∴∠BDE＝∠CFD＝40°，∴∠EDF＝180°﹣∠FDC﹣∠BDE＝50°，故答案为：50°．17．解：＝＝；故答案为：．18．解：当角B翻折时，B点与D点重合，DE与EC的和就是BC，也就是说等于8，CD 为AC的一半，故△CDE的周长为8+3＝11；当A翻折时，A点与D点重合．同理DE与EC的和为AC＝6，CD为BC的一半，所以CDE 的周长为6+4＝10．故△CDE的周长为10．19．解：∵DE为线段AB的垂直平分线，∴BD＝AD＝14，∴∠BCD＝2∠A＝30°，∵∠ACB＝90°，∴BC＝BD＝7，故答案为：7．20．解：∵△ABC为锐角三角形，∴高AD和BE在三角形内．∵高AD和BE交于点H，∴∠ADC＝∠BEC＝90°．∵∠EBD+∠BHD＝90°，∠AHE+∠HAE＝90°，∠BHD＝∠AHE，∴∠EAD＝∠EBD，又∵BH＝AC，∠ADC＝∠BDH＝90°，∴△BDH≌△ADC（AAS），∴BD＝AD，∵∠ADB＝90°，∴∠ABC＝45°．故答案为45°三．解答题（共1小题，满分8分，每小题8分）21．解：（1）原式＝b（a2﹣b2）＝b（a+b）（a﹣b）；（2）原式＝﹣[（x2+2）2﹣6（x2+2）+9]＝﹣（x2﹣1）2＝﹣（x+1）2（x﹣1）2．四．解答题（共3小题，满分15分，每小题5分）22．解：原式＝x2﹣4y2+5y2﹣2xy＝x2﹣2xy+y2，＝（x﹣y）2，当x＝2018，y＝2019时，原式＝（2018﹣2019）2＝（﹣1）2＝1．23．（1）解：如图，直线MN即为所求；（2）证明：∵MN垂直平分线段AB，∴MA＝MB，∴∠AMN＝∠BMN，∵AC∥BD，∴∠AMN＝∠BNM，∴∠BMN＝∠BNM，∴BM＝BN，∴△BMN是等腰三角形．24．解：（1）130÷65%＝200，答：此次抽样调查中，共调查了200名学生；（2）反对的人数为：200﹣130﹣50＝20，补全的条形统计图如右图所示；（3）扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数是：×360°＝36°；（4）1500×＝375，答：该校1500名学生中有375名学生持“无所谓”意见．五．解答题（共3小题，满分17分）25．解：（1）由题意得，CD＝0.5x，则AD＝4﹣0.5x；（2）∵△ABC是等边三角形，∴AB＝BC＝AC＝4cm，∠A＝∠ABC＝∠C＝60°．设x秒时，△ADE为直角三角形，∴∠ADE＝90°，BE＝0.5x，AD＝4﹣0.5x，AE＝4+0.5x，∴∠AED＝30°，∴AE＝2AD，∴4+0.5x＝2（4﹣0.5x），∴x＝；答：运动秒后，△ADE为直角三角形；（3）如图2，作DG∥AB交BC于点G，∴∠GDP＝∠BEP，∠DGP＝∠EBP，∠CDG＝∠A＝60°，∠CGD＝∠ABC＝60°，∴∠C＝∠CDG＝∠CGD，∴△CDG是等边三角形，∴DG＝DC，∵DC＝BE，∴DG＝BE．在△DGP和△EBP中，，∴△DGP≌△EBP（ASA），∴DP＝PE，∴在运动过程中，点P始终为线段DE的中点．26．解：（1）∵BG∥AC，∴∠DBG＝∠DCF．∵D为BC的中点，∴BD＝CD又∵∠BDG＝∠CDF，在△BGD与△CFD中，∵∴△BGD≌△CFD（ASA）．∴BG＝CF．（2）BE+CF＞EF．∵△BGD≌△CFD，∴GD＝FD，BG＝CF．又∵DE⊥FG，∴EG＝EF（垂直平分线到线段端点的距离相等）．∴在△EBG中，BE+BG＞EG，即BE+CF＞EF．27．解：（1）旋转后的三角形ACP'如图所示：（2）由旋转可得，∠PAP'＝∠BAC＝50°，AP＝AP'，△ABP≌△ACP'，∴∠APP'＝∠AP'P＝65°，∠AP'C＝∠APB，∵∠BAC＝50°，AB＝AC，∴∠B＝65°，又∵∠BAP＝20°，∴∠APB＝95°＝∠AP'C，∴∠PP'C＝∠AP'C﹣∠AP'P＝95°﹣65°＝30°．六．解答题（共2小题，满分10分）28．解：（1）①∵AD⊥MN，BE⊥MN，∴∠ADC＝∠ACB＝90°＝∠CEB，∴∠CAD+∠ACD＝90°，∠BCE+∠ACD＝90°，∴∠CAD＝∠BCE，∵在△ADC和△CEB中，，∴△ADC≌△CEB（AAS）；②∵△ADC≌△CEB，∴CE＝AD，CD＝BE，∴DE＝CE+CD＝AD+BE；（2）证明：∵AD⊥MN，BE⊥MN，∴∠ADC＝∠CEB＝∠ACB＝90°，∴∠CAD＝∠BCE，∵在△ADC和△CEB中，，∴△ADC≌△CEB（AAS）；∴CE＝AD，CD＝BE，∴DE＝CE﹣CD＝AD﹣BE；（3）当MN旋转到题图（3）的位置时，AD，DE，BE所满足的等量关系是：DE＝BE﹣AD．理由如下：∵AD⊥MN，BE⊥MN，∴∠ADC＝∠CEB＝∠ACB＝90°，∴∠CAD＝∠BCE，∵在△ADC和△CEB中，，∴△ADC≌△CEB（AAS），∴CE＝AD，CD＝BE，∴DE＝CD﹣CE＝BE﹣AD．29．解：（1）①当点Q在AC上时，CQ＝t；②当点Q在AB上时，AQ＝t﹣12；③当点P在AB上时，BP＝16﹣2t；④当点P在BC上时，BP＝2t﹣16；故答案为：t；t﹣12；16﹣2t；2t﹣16；（2）由题意得，12﹣t＝2t，解得，t＝4；（3）∵AQ＝BP∴当点P在线段AB上运动，点Q在线段CA上运动时，12﹣t＝16﹣2t，解得，t＝4，当点P在线段BC上运动，点Q在线段CA上运动时，12﹣t＝2t﹣16，解得，t＝，当点P在线段BC上运动，点Q在线段AB上运动时，t﹣12＝2t﹣16，解得，t＝4（不合题意）则当t＝4或t＝时，AQ＝BP．。

2018-2019学年上期北京市各区期末考试八年级数学分类汇编几何综合题

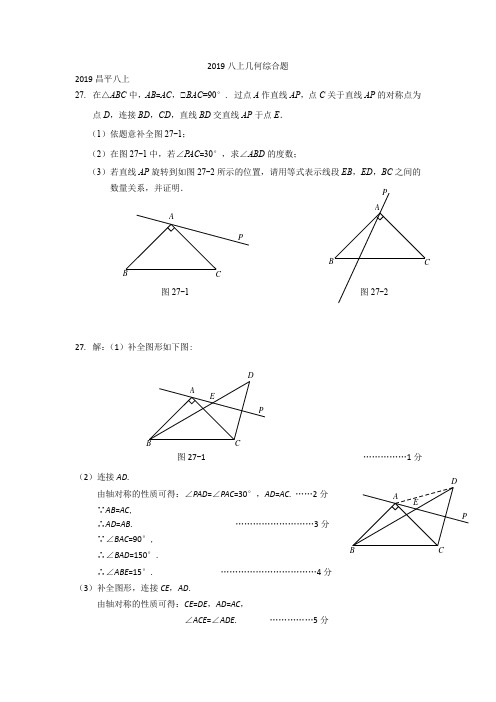
2019八上几何综合题2019昌平八上27. 在△ABC 中，AB =AC ，∠BAC =90°. 过点A 作直线AP ，点C 关于直线AP 的对称点为点D ，连接BD ，CD ，直线BD 交直线AP 于点E ．（1）依题意补全图27-1；（2）在图27-1中，若∠P AC =30°，求∠ABD 的度数；（3）若直线AP 旋转到如图27-2所示的位置，请用等式表示线段EB ，ED ，BC 之间的27. 解：（1）补全图形如下图:（2）连接AD .由轴对称的性质可得：∠PAD =∠PAC =30°，AD =AC . ……2分 ∵AB =AC ,∴AD =AB . ………………………3分 ∵∠BAC =90°,∴∠BAD =150°.∴∠ABE =15°. ……………………………4分（3）补全图形，连接CE ，AD .由轴对称的性质可得：CE =DE ，AD =AC ，∠ACE =∠ADE . ……………5分ABCPED图27-1 ……………1分ABCPED∵AB =AC ， ∴AD =AB . ∴∠ADB =∠ABD . ∴∠ACE =∠ABD . ∵∠ABD +∠ABE =180°， ∴∠ACE +∠ABE =180°. 在四边形ABEC 中，∵∠BAC +∠ABE +∠BEC +∠ACE =360°，又∵∠BAC =90°，∴∠BEC=90°. ……………………………………………………………6分 ∴BE 2+CE 2=BC 2. ∴EB 2+ED 2=BC 2. …………………………………………………………7分2019朝阳八上27．已知C 是线段AB 垂直平分线m 上一动点，连接AC ，以AC 为边作等边三角形ACD ，点D 在直线AB 的上方，连接DB 与直线m 交于点E ，连接BC ，AE ．（1）如图1，点C 在线段AB 上．①根据题意补全图1； ②求证：∠EAC =∠EDC ；（2）如图2，点C 在直线AB 的上方， 0°＜∠CAB ＜30°，用等式表示线段BE ，CE ，DE 之间的数量关系，并证明．27．解：（1）①补全图形如图所示．DPA BCE图1图2②证明：∵直线m是AB的垂直平分线，∴EA=EB，CA=CB．∴∠EAC=∠B．∵△ACD是等边三角形，∴CA=CD．∴CD=CB．∴∠EDC=∠B．∴∠EAC=∠EDC．（2）BE=CE+DE．证明：如图，在EB上截取EF，使EF=CE，连接CF．∵直线m是AB的垂直平分线，∴EA=EB，CA=CB．∴∠EAB=∠EBA，∠CAB=∠CBA．∴∠EAC=∠EBC．∵△ACD是等边三角形，∴CA=CD，∠ACD=60°．∴CD=CB．∴∠EDC=∠EBC．∴∠EDC=∠EAC．∵∠1=∠2，∴∠DEA=∠ACD=60°．∴∠AEB=120°．∵EA=EB，m⊥AB，∴∠AEC=∠BEC=60°．∴△CEF是等边三角形．∴∠CEF=∠CFE=60°．∴△CDF≌△CBE．∴DF=BE．∴BE=CE+DE．2019大兴八上28. 已知:如图, 过等腰直角三角形AB C的直角顶点A作直线AP，点B关于直线AP的对称点为E，连接BE，C E，其中CE交直线AP于点F.（1）依题意补全图形；（2）若∠PAB=16°，求∠ACF的度数；（3）如图，若45°<∠PAB<90°，用等式表示线段AB，FE，FC之间的数量关系，并证明.28.（1）补全图形，如图所示.………………………………1分（2）解：连接AE，∵点E与点B关于直线AP对称，∴对称轴AP是EB的垂直平分线.∴AE=AB，∠EAP=∠BAP=16°…………………………………2分∵等腰直角三角形AB C,∴AB=AC，∠BAC=90°∴AE=AC.∴∠AEC=∠ACF. …………………………………………………3分∴2∠ACF+32°+90°=180°.∴∠ACF=29°……………………………………………………4分（3）AB，FE，FC满足的数量关系：FE2+FC2=2AB2…………………5分证明：连接AE，BF，设BF交AC于点G，∵点E与点B关于直线AP对称，∴对称轴AP是EB的垂直平分线.∴AE=AB，FE=FB.∵AF=AF，∴△AEF≌△ABF∴∠FEA=∠FBA.∵AB=AC，∴AE=AC.∴∠ACE=∠AEC.∴∠ACE=∠ABF. …………………………………………6分又∵∠CGF=∠AGB，∴∠CFB=∠BAC=90°. ………………………………………7分∴FB2+FC2=BC2.∵BC2=2AB2，∴FE2+FC2=2AB2 ………………………………………………8分2019东城八上27．（本小题6分）QPF EDCBA（1）老师在课上给出了这样一道题目：如图（1），等边△ABC 边长为2，过AB 边上一点P 作PE ⊥AC 于E ，Q 为BC 延长线上一点，且AP=CQ ，连接PQ 交AC 于D ，求DE 的长.小明同学经过认真思考后认为，可以通过过点P 作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE 的长. （2）【类比探究】老师引导同学继续研究：1.等边△ABC 边长为2，当P 为BA 的延长线上一点时,作PE ⊥CA 的延长线于点E ，Q 为边BC 上一点，且AP=CQ ，连接PQ 交AC 于D .请你在图（2）中补全图形并求DE 的长.2. 已知等边△ABC ，当P 为AB 的延长线上一点时,作PE ⊥射线AC 于点E ， Q 为（○1BC 边上；○2BC 的延长线上；○3CB 的延长线上）一点，且AP =CQ ，连接PQ 交直线AC 于点D ，能使得DE 的长度保持不变.(将答案的编号填在横线上)图（1）图（2）（备用图）27. 解：（1）DE=1. ………………………1分(2) 1. 正确补全图形. ……………2分过点P 作PF ∥BC 交CA 的延长线与点F . ∴ ∠PF A =∠C .∵ △ABC 是等边三角形， ∴ 可证 △APF 为等边三角形. ∴ AP =PF .C B A C B A又∵ PE ⊥CA 的延长线于点E ， ∴ AE =FE =12AF . ……………3分 ∵ AP=CQ ， ∴ PF =QC .∵ ∠FDP =∠CDQ ，∴ △FDP ≌△CDQ .∴ FD =CD =12CF . ……………4分 ∵ DE =DF -EF =1111222CF AF AC -==. ……………5分2. ○2. ……………6分2019东城八上28. （本小题6分）在平面直角坐标系xOy 中，△ABO 为等边三角形，O 为坐标原点，点A 关于y 轴的对称点为D ，连接AD ，BD ，OD ，其中AD ，BD 分别交y 轴于点E ，P . （1）如图1，若点B 在x 轴的负半轴上时，直接写出BDO ∠的度数；（2）如图2，将△ABO 绕点O 旋转，且点A 始终在第二象限，此时AO 与y 轴正半轴夹角为α，60︒<α<90︒，依题意补全图形，并求出BDO ∠的度数；（用含α的式子表示）（3）在第（2）问的条件下，用等式表示线段BP ，PE ，PO 之间的数量关系.（直接写出结果）图1 图228．解：（1）120°； ……………1分（2）正确画出图形. ……………2分 ∵ ,60AOE DOE AOB α∠=∠=∠=︒,∴ 3602603002BOD αα∠=︒--︒=︒-. …………3分 ∵ BO =BD , ∴ ∠OBD =∠ODB . ∴ 180602BODBDO α︒-∠∠==-︒. ……………4分（3）2PE BP PO =+. ……………6分说明：本试卷中的试题都只给出了一种解法，对于其他解法请参照评分标准相应给分.2019房山八上30. 如图9，BN 是等腰ABC Rt ∆的外角CBM ∠内部的一条射线，090=∠ABC ，CB AB =，点C 关于BN 的对称点为D ，连接AD ，BD ，CD ，其中CD ，AD 分别交射线BN 于点E ，P ．（1）依题意补全图形；（2）若CBN α∠=，求BDA ∠的大小（用含α的式子表示）；（3）用等式表示线段PB ，PA 与PE 之间的数量关系，并证明．30、解：（1） ---------------------------2分FPDEBAO（2）∵∠ABC=90°∴∠MBC=∠ABC=90°∵点C 关于BN 的对称点为D∴BC =BD ，∠CBN=∠DBN=α ---------------------------3分 ∵AB =BC∴AB =BD ---------------------------4分 ∴∠BAD=∠ADB=()α29018021-︒-︒=45°－α ---------------------------5分 (3) 猜想：()PE PB PA +=2 ---------------------------4分证明：过点B 作BQ ⊥BE 交AD 于Q ---------------------------6分 ∵∠BPA=∠DBN+∠ADB ，∠ADB=45°－α，∠DBN=α ∴∠BPA=∠DPE=45°∵点C 关于BN 的对称点为D ∴BE ⊥CD∴PD =2PE ，PQ =2PB ， ---------------------------7分 ∵BQ ⊥BE ，∠BPA=45° ∴∠BPA=∠BQP=45° ∴∠AQB=∠DPB=135° 又∵AB =BD ，∠BAD=∠ADB ∴△AQB ≌△BPD （AAS ） ∴AQ =PD ∵PA =AQ +PQ∴()PE PB PA +=2 ---------------------------8分2019怀柔八上27．如图1，在△ABC 中，AB =AC ， D 为直线BC 上一动点（不与B ，C 重合），在AD 的右侧作△ADE ，使得AE =AD ，∠DAE =∠BAC ，连接CE ．（1）当D 在线段BC 上时，求证:△BAD ≌△CAE ；（2）当点D 运动到何处时，AC ⊥DE ，并说明理由；（3）当CE ∥AB 时，若△ABD 中最小角为20°，直接写出∠ADB 的度数．27．解：（1）∵∠DAE =∠BAC ， ∴∠BAD =∠CAE ． ∵AB=AC ，AD=AE ，∴△BAD ≌△CAE （SAS ）．……………………………………………………2分（2）当D 运动到BC 中点时，AC ⊥DE ． …………………………………………3分∵D 是BC 中点，AB=AC ，∴∠1=∠2． ∵△BAD ≌△CAE ，∴∠1=∠3．∴∠2=∠3． ∵AD=AE ，∴AC ⊥DE ．B EDCBA 图1ABC备用图∴当D 运动到BC 中点时，AC ⊥DE ．……………………………5分（3）∠ADB =20°或40°或100° ．…………………………7分 28．解：（1）如图：…………………………………………………1分（2）在△ACE 和△BCD 中，∴△ACE ≌△BCD （SAS ）． ∴∠1=∠2．∵∠AEC =∠BEF ， ∴∠BFE =∠ACE ．∵∠ACE =90°，∴∠AFB=90°．∴AF ⊥BD ．………………………………………3分（3）数量关系是：CQ =CF ．………………………………………4分过C 作CG ⊥CF 交AF 于G ． ∴∠GCF =90°．∵∠ACB =90°，∴∠3=∠4． ∵∠1=∠2，AC=BC ， ∴△ACG ≌△BCF （ASA ）．∴CG =CF ．∴△CGF 是等腰直角三角形． ∴∠CFG =45°．∴∠CFD =45°．∵点C 与 Q 关于BD 对称，∴CF =FQ ． ∠CFD =∠QFD =45°．∴△CFQ 是等腰直角三角形． ∴CQ =CF ．………………………………………………………7分2019门头沟八上28．已知：△ABC 是等边三角形，D 是直线BC 上一动点，连接AD ，在线段AD 的右侧作射线DP 且使∠ADP =30°，作点A 关于射线DP 的对称点E ，连接DE 、CE ．（1）当点D 在线段BC 上运动时，① 依题意将图1补全；② 请用等式表示线段AB 、CE 、CD 之间的数量关系，并证明；（2）当点D 在直线BC 上运动时，请直接写出AB 、CE 、CD 之间的数量关系，不需证明．21FEBD4321GFEBD∴ △ADE 是等边三角形．…………………………………………………………………3分∴ AD =AE ，∠DAE =∠ADE =60°．又∵△ABC 是等边三角形， ∴ AB =AC=BC ，∠BAC =60°．∴ ∠BAC －∠DAC =∠DAE －∠DAC ，即：∠BAD =∠CAE ．在△BAD 和△CAE 中AB AC BAD CAE AD AE =⎧⎪=⎨⎪=⎩∠∠ ∴△BAD≌△CAE …………………………………………………………………………4分∴ BD =CE∴ AB =BC =BD+CD= CE+CD ．（2）AB = CE+CD ，AB = CE －CD ，AB = CD －CE ．…………………………………………………7分说明：若考生的解法与给出的解法不同，正确者可参照评分参考相应给分．2019密云八上27. 已知：在△ABC 中，∠ABC =45°，CD AB ⊥于点D ，点E 为CD 上一点，且DE=AD ，连接BE 并延长交AC 于点F ，连接DF . （1）求证：BE=AC（2）用等式表示线段FB 、FD 、FC 之间的数量关系，并加以证明.27 . (1) ∵ ∴∵∴ ∴ …………………………1分∴∴ …………………………3分 (2) …………………………4分证明：∵ ∴ ∴ ∴ F EDCBABD CD =BDE CDA BD CD BDC ADC DE AD ∆∆=⎧⎪∠=∠⎨⎪=⎩在和中BDE CDA ∆≅∆BE AC =2FB FD FC =+°90CD AB BDC ADC ⊥∠=∠=°45ABC BDC ∠=∆是等腰直角三角形°DH DF BF H HDF=BDC=90HDF-HDE=BDC-HDE BDH=CDF⊥∠∠∠∠∠∠∠∠作交于FEDC B A∵， ∴∴∴ ∴ ∴∵∴ ………………………………7分2019平谷八上26．阅读下面材料：学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，小聪继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．小聪将命题用符号语言表示为：在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠B =∠E ．小聪想：要想解决问题，应该对∠B 进行分类研究． ∠B 可分为“直角、钝角、锐角”三种情况进行探究．（1）当∠B 是直角时，如图1，在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠B =∠E =90°，则Rt △ABC ≌Rt △DEF （依据：________）（2）当∠B 是锐角时，如图2，BC =EF ，∠B =∠E<90°，在射线EM 上有点D ，使DF =AC ，画出符合条件的点D ，则△ABC 和△DEF 的关系是________；A ．全等B ．不全等C ．不一定全等（3）第三种情况：当∠B 是钝角时，如图3，在△ABC 和△DEF 中，AC =DF ，BC =EF ，BDE CDA ∆≅∆ABEDCF ∠=∠BDH CDF ABE DCF BD DCBDH CDF ∆∆∠=∠⎧⎪=⎨⎪∠=∠⎩在和中BDH CDF ∆≅∆,DH DF BH FC ==HDF ∆是等腰直角三角形HF =图1图2FB FH BH FB FC=+=+∠B =∠E >90°，求证：△ABC ≌△DEF ．26．解：（1）△ABC ≌△DEF （依据：HL ）…………………………………………1分…………………………………………………3分（2）选择C ……………………………………………………4分（3）证明：如图，过点C 作CG ⊥AB 交AB 的延长线于点G ，过点F 作DH ⊥DE 交DE 的延长线于点H ， ∵∠CBA =∠FED ，∴180°﹣∠CBA =180°﹣∠FED ，即∠CBG =∠FEH ， ……………………………………………………………… 5分在△CBG 和△FEH 中，90CBG FEHG H BC EF ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩， ∴△CBG ≌△FEH （AAS ）， ∴CG =FH ，在Rt △ACG 和Rt △DFH 中，AC DFCG FH =⎧⎨=⎩，Rt △ACG ≌Rt △DFH （HL ），∴∠A =∠D ， ………………………………………………………………………6分在△ABC 和△DEF 中，CBA FE A D A D C DF ∠=∠⎧⎪⎨⎪=∠∠⎩=，∴△ABC ≌△DEF （AAS ）．…………………………………………………………7分图32019石景山八上28．ABC △是等边三角形，2AC =，点C 关于AB 对称的点为C '，点P 是直线C B '上的一个动点，连接AP ，作60APD ∠=°交射线．．BC 于点D ．（1）若点P 在线段C B '上（不与点C '，点B 重合）．①如图1，若点P 是线段C B '的中点，则AP 的长为； ②如图2，点P 是线段C B '上任意一点，求证：PD PA =；（2）若点P 在线段C B '的延长线上． ①依题意补全图3；②直接写出线段BD ，AB ，BP 之间的数量关系为：．28．（1． ………………………… 2分 ②证法一：作60BPE ∠=°交AB 于点E ，如图1．…… 3分 ∵ABC △是等边三角形，∴60ABC ∠=°（等边三角形的三个角都是60°）． ∵点C '与点C 关于AB 对称， ∴60C BA CBA BPE '∠=∠=∠°=， ∴460∠=°．∴PBE △ ∴PB PE =（等边三角形的三边都相等）， 5120PBD ∠=∠°=．∵1260∠+∠=°，3260∠+∠=°，∴13∠=∠（等量减等量，差相等）． ………………………… 4分在PBD △和PEA △中，13,,5,PB PE PBD ∠=∠=∠=∠⎧⎪⎨⎪⎩∴PBD △≌PEA △（ASA ）．∴PD PA =（全等三角形的对应边相等）． ……………………… 5分证法二：延长AB 到点E ，使BE BD =，连接PE ，如图2． ……………… 3分 ∵ABC △是等边三角形（已知），∴60ABC ∠=°（等边三角形的三个角都是60°）． ∵点C '与点C 关于AB 对称（已知）， ∴60C BA CBA '∠=∠=°． ∴1120PBD ∠=∠°=．在PBE △和PBD △中，,1,,PB PB PBD BE BD =∠=∠=⎧⎪⎨⎪⎩∴PBE △≌PBD △（SAS ）．∴PE PD =（全等三角形的对应边相等）， ……………………… 4分 3E ∠=∠（全等三角形的对应角相等）． ∵60APF FBD ∠=∠=°， AFP BFD ∠=∠（对顶角相等）， ∴23∠=∠（三角形内角和定理）． ∴2E ∠=∠（等量代换）． ∴PE PA =（等角对等边）．又∵PE PD =（已证），∴PD PA =（等量代换）． ……………………… 5分证法三：延长CB 到点E ，使BE BA =，连接PE ，如图3．可证PEB △≌PAB △（SAS ）．再证PED △是等腰三角形．证法四：连接C A '，在C A '上截取C E C P ''=，连接PE ，如图4．可证PBD △≌AEP △（ASA ）．证法五：过点P 作PM CB ⊥交CB 的延长线于点M ，PN AB ⊥于点N ，如图5．可证PMD △≌PNA △（AAS ）．（2）①补全图形，如图6所示；……… 6分②BD AB BP =+． ……… 7分2019通州八上28. 在等边ABC ∆中，（1）如图1，P ，Q 是BC 边上两点，AP=AQ ，20BAP ∠=︒，求AQB ∠的度数；（2）点,P Q 是BC 边上的两个动点（不与,B C 重合），点P 在点Q 的左侧，且AP AQ =，点Q 关于直线AC 的对称点为M ，连接,.AM PM ①依题意将图2补全； ②求证：.PA PM = 图1 图228. （1）解：∵ △ABC 为等边三角形∴∠B =60°∴∠APC =∠BAP +∠B=80° ∵AP=AQ∴∠AQB=∠APC =80°……………………………..(2分)（2）① 补全图形如图所示. …………………………………..(4分)②证法不唯一CB CB 图4 图5B证明：过点A作AH⊥BC于点H，如图.由△ABC为等边三角形，AP=AQ，可得∠PAB=∠QAC. …………………………………..(5分)∵点Q，M关于直线AC对称，∴∠QAC=∠MAC，AQ=AM∴∠PAB=∠MAC，AQ=AM∴∠PAM=∠BAC=60°…………………………………..(6分)∴△APM为等边三角形∴PA=PM. …………………………………..(7分)2019西城八上26．在△ABC中，AB＝AC，在△ABC的外部作等边三角形△ACD，E为AC的中点，连接DE 并延长交BC于点F，连接BD．（1）如图1，若∠BAC=100°，求∠BDF的度数；（2）如图2，∠ACB的平分线交AB于点M，交EF于点N，连接BN．①补全图2；②若BN=DN，求证：MB=MN．图1 图2（1）解：在等边三角形△ACD中，∠CAD =∠ADC =60°，AD＝AC．∵E为AC的中点，∴∠ADE=12∠ADC＝30°．···················································································2分BDACEF BDACEFMB∵AB＝AC，∴AD＝AB．∵∠BAD=∠BAC+∠CAD＝160°．∴∠ADB=∠ABD＝10°．∴∠BDF=∠ADF -∠ADB＝20°．·····································································4分（2）①补全图形；②证明：连接AN．∵CM平分∠ACB，∴设∠ACM=∠BCM=α．∵AB＝AC，∴∠ABC=∠ACB=2α．在等边三角形△ACD中，∵E为AC的中点，∴DN⊥AC．∴NA=NC．∴∠NAC=∠NCA=α．∴∠DAN=60°+ α．在△ABN和△ADN中，∵,,, AB AD BN DN AN AN=⎧⎪=⎨⎪=⎩∴△ABN≌△ADN．∴∠ABN=∠ADN＝30°，∠BAN=∠DAN＝60°+ α．∴∠BAC＝60°+ 2α．在△ABC中，∠BAC+∠ACB +∠ABC＝180°，∴60°+ 2α+ 2α+2α=180°．∴α=20°．NBD ACEFM∴∠NBC=∠ABC-∠ABN= 10°．∴∠MNB=∠NBC+ ∠NCB=30°．∴∠MNB=∠MBN．∴MB=MN． ···················································································································8分2019延庆八上27.如图，∠MON =45°，点A 是OM 上一点，点B ，C 是ON 上两点，且AB =AC ，作出点B 关于OM 对称的点D ，连接AD ，CD ．（1）按要求补全图形；（2）判断∠DAC = °；（3）判断AD 与DC 的数量关系，并证明．27．解：（1）如图 ………… ……2分（2）∠DAC =90° ………… ……3分（3）AD DC 2=………… ……4分证明：∵点B 与点D 关于AO 对称 ∵BD 被AO 垂直平分 ∵AD =AB 又∵AB =AC∵AD =AC ………… … 5分∵∵ABC =∵ACB =∵O +∵OAB ∵∵BAC =OAB ∠-︒290∵∵DAC =90° ………… … 6分 ∴△ADC 是等腰直角三角形 ∴AD DC 2= …………………7分2019延庆八上28．如图，在△ABC 中，∠ABC =15°，AB =2，BC =2，以AB 为直角边向外作等腰直角△BAD ，且∠BAD=90°；以BC 为斜边向外作等腰直角△BEC ，连接DE ．（1）按要求补全图形；（2）求DE 长；（3）直接写出△ABC 的面积．28．解：（1）如图所示………… ……2分（2）连接DC解：∵△ABD 是等腰直角三角形, AB =2，∠BAD =90°.∴ AB =AD =2 ，∠ABD =45°. 由勾股定理得DB =2.EDCBAFEDCBA∴ ∠DBC =∠ABC +∠ABD =60°. ∵BC =2. ∴ BC =BD .∴△BCD 是等边三角形. ∴BD =CD =2.∴D 点在线段BC 的垂直平分线上. 又∵△BEC 是等腰直角三角形. ∴BE =CE ，∠CEB =45°∴E 点在线段BC 的垂直平分线上. ∴DE 垂直平分BC . ∴BF =21BC =1， ∠BFE =90° ∵∠FBE =∠BEF =45° ∴BF =EF =1Rt △BFD 中，BF =1，BD =2由勾股定理得DF =3∴ DE =DF +EF =13+ ………… ……6分（3）213-………… ……7分2019燕山八上27．已知BC ＝5，AB ＝1，AB ⊥BC ，射线CM ⊥BC ，动点P 在线段BC 上(不与点B ，C 重合)，过点P 作DP ⊥AP 交射线CM 于点D ，连接AD ．(1) 如图1，若BP ＝4，判断△ADP 的形状，并加以证明．(2) 如图2，若BP ＝1，作点C 关于直线DP 的对称点C ′，连接AC ′． ① 依题意补全图2；AB CDM P图2图1PMDCBA②请直接写出线段AC′的长度．27．(1) △ADP是等腰直角三角形．………………………………1分证明：∵BC＝5，BP＝4，∴PC＝1，∵AB＝1，∴PC＝AB．………………………………2分∵AB⊥BC，CM⊥BC，DP⊥AP，∴∠B＝∠C＝90°，∠APB＋∠DPC＝90°，∠PDC＋∠DPC＝90°，∴∠APB＝∠PDC，………………………………3分在△ABP和△PCD中，B CAPB PDC AB PC∠=∠⎧⎪∠=∠⎨⎪=⎩，，，∴△ABP≌△PCD，………………………………4分∴AP＝PD，∵∠APD＝90°，∴△ADP………………………………5分(2) ①依题意补全图2；………………………………6分②AC．………………………………7分2019顺义八上30．数学课上，老师给出了如下问题：已知：如图1，在Rt△ABC中，∠C=90°，AC=BC，延长CB到点D，∠DBE=45°，点F 是边BC上一点，连结AF，作FE⊥AF，交BE于点E．（1）求证：∠CAF=∠DFE；（2）求证：AF=EF．经过独立思考后，老师让同学们小组交流．小辉同学说出了对于第二问的想法：“我想通过构造含有边AF 和EF 的全等三角形，因此我过点E 作EG ⊥CD 于G （如图2所示），如果能证明Rt △ACF 和Rt △FGE 全等，问题就解决了．但是这两个三角形证不出来相等的边，好像这样做辅助线行不通．”小亮同学说：“既然这样做辅助线证不出来，再考虑有没有其他添加辅助线的方法．”请你顺着小亮同学的思路在图3中继续尝试，并完成（1）、（2）问的证明． 30．证明：（1）∵∠C=90°，∵ ∠CAF + ∠1 = 90︒ ． ....................... 1 分 ∵FE ∵AF ，∵ ∠DFE + ∠1 = 90︒ ． ....................... 2 分 ∵ ∠CAF = ∠DFE ． .......................... 3 分（2）在 A C 上截取 A G=BF ，连结 F G ，如图 4． ............................................ 4 分∵AC= BC ，∵ AC - AG = BC -BF ．即 CG= CF ．∵∵C=90°，∵ ∠CGF = ∠CFG = 45︒ ． ∵ ∠AGF = 180︒ - ∠CGF = 135︒ ． ∵∵DBE=45°，∵ ∠FBE = 180︒ - ∠DBE = 135︒ ．∵ ∠AGF = ∠FBE ． ................................................................................. 5 分由： ∠CAF = ∠DFE ． ∵A G F ∵∵FB E （A． ................................................................................................................ 6 分∵AF=EF ． ...................................................................................................7 分G 图3图2图1ACB DEF ACB DEF F EDB CA2019丰台八上28．如图，Rt△ABC中，∠ACB = 90°，AC = BC，点D为AB边上的一个动点(不与点A，B及AB中点重合)，连接CD，点A关于直线CD的对称点为点E，直线BE，CD交于点F.（1）如图1，当∠ACD = 15°时，根据题意将图形补充完整，并直接写出∠BFC的度数；（2）如图2，当45°<∠ACD<90°时，用等式表示线段AC，EF，BF之间的数量关系，并加以证明.图1 图2ACDA BC。

2018-2019学年人教版八年级政治上学期期末测试卷及答案

2018-2019学年人教版八年级政治上学期期末测试卷及答案2018-201年八年级政治上学期期末试题一、单项选择题1.自尊就是自我尊重，指既不向别人卑躬屈膝，也不允许别人歧视、侮辱。

它是一种健康良好的心理状态。

下列名言体现自尊心态的是（）A.以诚感人者，人亦诚而应B.富贵不能淫，贫贱不能移，威武不能屈C.自信者不疑人，人亦信之；自疑者不信人，人亦疑之D.古之立大事者，不惟有超世之才，亦必有坚忍不拔之志2.“人不可以无耻。

无耻之耻，无耻矣。

”XXX的这句话告诉我们（）A.唯有知耻，才有自尊B.世界上并没有羞耻C.人都是知耻的D.自尊是人人都需要的3.2017年9月，八年级学生XXX随打工的父母来到城里，转学到了新学校。

看到周围的同学多才多艺，阳光自信，他觉得自己一无是处，抬不起头来。

你认为他的表现是（）A.①③B.③④C.①②D.①④4.面对纷繁复杂的世界，多少人呼唤“给我一双慧眼吧”，这要求我们（）A.把长辈的一切言行当作我们生活的向导B.学会用良知的标尺加以判断C.追随“社会流行”的文化现象D.学会处世哲学，不可真诚待人5.学会做人，学会辨别是非善恶，比研究专门知识显得更为重要，一个“德盲”远比一个“文盲”对社会更具负面效应。

这段话体现了（）A.注重学会做人，因为有道德的人一定会为社会作出巨大的贡献B.学会做人，明辨是非善恶是很重要的，研究成绩好坏无所谓C.注重学会做人，因为一个文盲不会给社会带来负面效应D.学会做人，明辨是非善恶，才能把握好人生的方向6.为了让自己的游戏人物变得“高大上”，14岁男孩打赏5名游戏主播，让他们为自己代玩手机游戏，花了母亲3070元。

无独有偶，13岁女孩XXX以研究为由，用妈妈的手机偷偷给自己喜欢的网络主播打赏，两个月就花了2万多元。

对于打赏网络主播的现象，你最想对你的同学们说的是（）A.网络直播太可怕，应拒绝从众B.打赏主播新趋势，要主动跟风C.对待流行应理智，需合理有度D.主播挣钱真容易，可弃学尝试7.我们常常想对别人说：“我长大了，请像对大人那样尊重我。

2018-2019学年度第一学期八年级历史试题(含答案)

2018－2019学年度第一学期期末考试八年级历史试题（考试时间：60 分钟分值：100 分）注意事项：1．本试题分第Ⅰ卷和第Ⅱ卷两部分。

第Ⅰ卷为选择题，50分；第Ⅱ卷为非选择题，50分；共100分。

2．答卷前务必将自己的姓名.座号和准考证号按要求填写在答题卡上的相应位置。

3．第Ⅰ卷每题选出答案后，都必须用2B铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，必须先用橡皮擦干净，再改涂其它答案。

4．第Ⅱ卷必需用0.5毫米黑色签字笔书写到答题卡题号所指示的答题区域,不得超出预留范围。

第Ⅰ卷（选择题共50分）一、选择题：本大题共25小题，每小题2分，共50分。

在每小题所列出的四个选项中，只有一项是符合题意的。

1.“自今以后，大皇帝恩准英国人民带同所属家眷，寄居大清沿海之广州、福州、厦门、宁波、上海等五处港口，贸易通商无碍……”上述内容出自下列哪一条约？A．《南京条约》 B．《尼布楚条约》 C．《马关条约》 D．《辛丑条约》2.“到1860年，这个中华文明古国被西方彻底打败并羞辱了……俄国人则既强调贸易收益也强调取得领土。

”“到1860年”，俄国人“取得领土”的条约有①中俄《北京条约》②中俄《改订条约》③中俄《瑷珲条约》④中俄《辛丑条约》A．①② B．①③ C．②④ D．③④3.陈旭麓在《近代中国社会的新陈代谢》中评价近代某一文件时说:“它的价值是为近代思想史提供了一种农民的大同模式。

”这一文件是指A.《资政新篇》B.《天朝田亩制度》C.《北京条约》D.《虎门条约》4.《马关条约》的签订和3000万两白银的“赎辽费”，大大刺激了西方列强，它们在中国掀起了抢夺利权、强租海湾、划分“势力范围”的瓜分中国的狂潮。

当时德国在中国的“势力范围”是A.福建B.长江流域C.长城以北及新疆D.山东5.“中国的首都几次被西方的武装力量所占领，这是近代中国最痛苦的一个时期。

”“中国的首都”曾在下列哪两次战争中被“占领”①鸦片战争②第二次鸦片战争③甲午中日战争④八国联军侵华战争A．①② B．③④ C．②④ D．①③6.蒋廷黻在《中国近代史》中写道：“鸿章窃以为天下事穷则变，变则通……中国欲自强则莫如学习外国利器。

西城区2019-2020学年初二期末英语试题及答案

西城区2019-2020学年初二第一学期期末英语 2020.1听力理解（共20分）一、听下面四段对话或独白。

每段对话或独白后有两道小题, 从每题所给的A,B,C三个选项中选出最佳选项。

每段对话或独白你将听两遍。

（共12分, 每小题1.5分）听下面一段对话, 完成第1至第2小题1. What does the man buy?A. A scarf.B. A hat.C. A T-shirt.2. How much is it?A. 60 dollars.B. 19 dollars.C. 30 dollars.听下面一段对话, 完成第3至第4小题3. What are the speakers going to do finally?A. Go to the cinema.B. Go shopping.C. Go ice skating.4. Where are they going to meet?A. At the shopping center.B. Near the cinema.C. At the school gate.听下面一段对话, 完成第5至第6小题5. What is Sally good at?A. Football.B. Japanese.C. Computers.6. What does Sally want to do?A. Get a job.B. Play sports.C. Study Art.听下面一段独白, 完成第7至第8小题7. Who invented Pompodoro Technique?A. Peter.B. Peter's Dad.C. An Italian man.8. What is the speech mainly about?A. The history of Pompodoro Technique.B. The introduction of Pompodoro Technique.C. The importance of Pompodoro Technique.二、听独白, 记录关健信息。

2018-2019学年最新人教版八年级语文第一学期期末考试试题(含答案)

2018-2019学年度上学期八年级期末语文测试卷考试时间120分钟，试卷满分100分第一部分、积累与运用（30分）I•请把下面的名言工整地抄写在方格里。

（2分）天行健，君子以自强不息。

□□□□□□□□□□□□2下列词语中加点字注音有错误的一项是（）（3分）A、矜持（j m)濒临灭绝（b m）序幕（X⑪笼罩(l eng)B、淘汰（t①拾级而上（sh 0障碍zh M g) 搅拌(jic C、贿赂（I0水泄不通（xi ©掩映(y ing)秧苗(y mg)D、承诺（hu ©矢志不移（sh 1）灼伤（zhu。

遗传(y i)3下列词语中有错别字的一组是（）（3 分）A、无所事事光彩熠熠歇斯底里针锋相对B、耿耿于怀风度翩翩得天独厚一席之地C 、劫后余生手当其冲刀耕火种危言耸听D错综复杂仗义执言大相径庭不言而4.依次填入横线上的词语，正确的一项是（）（3分）1、他觉出其中有什么 ____ ，逼我立即拿来，我只好进屋把书拿出来。

2、为了追求光和热，有人宁愿 _____ 自己的生命。

生命是可爱的。

但寒冷的、寂寞的生，却不如轰轰烈烈的死。

3、最终，这位收买专利权的商人按照合同―了自己的诺言A .奥秘放弃实现B . 秘诀舍弃实现C .秘诀放弃履行D奥秘舍奔履行5、下列句子没有语病的一个是()(3分)A. 我们每个人都应该端正学习科学知识的目的。

B. 我们只有相信自己的能力，才能在各种考验前充满信心。

C •通过全班同学的共同努力，使我们班总成绩在年级组的排位有了大幅度提升。

D.球馆设施齐全，可为乒乓球爱好者提供球拍、球衣、球鞋和衣柜等乒乓器材。

6下面句子没有使用修辞方法的一项是()(3分)A •回望兰亭，难忘残园雨锁，难忘清波泛舟，难忘竹林漫步……B. 每到冬季，流动的飞瀑凝固成一根根冰柱，仿佛一把巨大的竖琴，奏出美妙的乐章。

C. 林子里候多地方还积着厚厚的雪，高山杜鹃花却早已耐不住性子，径自开了起来。

2019.1西城区八年级上学期期末地理(试题及答案)

西城区八年级上学期期末地理2019.01一、你能选对吗？（50分）下列各小题均有四个选项，其中只有一项符合题意要求；每小题2分；请你将答案填写在下面的答题框中（使用机读卡的学校请填写在机读卡上）。

题号 1 2 3 4 5 6 7 8 9 10答案题号11 12 13 14 15 16 17 18 19 20答案题号21 22 23 24 25答案读图1，完成1-4题。

图11.地球表面A.海洋与陆地面积之比约为3:7B.海洋被各大洲分割成均匀的四部分C.大陆与其附近的岛屿合称为洲D.各大洲之间的分界线均为自然界线2.既濒临太平洋又濒临大西洋的大洲有A. 欧洲、北美洲、南美洲B. 北美洲、南美洲、南极洲C. 非洲、北美洲、南美洲D. 北美洲、南美洲、大洋洲3.沟通太平洋和北冰洋的是A. 白令海峡B.巴拿马运河C.马六甲海峡D.苏伊士运河4.四大洋中纬度最高的是A.太平洋B.大西洋C.印度洋D.北冰洋5.读图2“南美洲和非洲的古老地层及动、植物化石相似性图”，作为“大陆漂移学说”的证据，图中显示的信息有①大陆发现古海洋生物的化石②相邻的大陆轮廓形状基本吻合③两块大陆发现相似动、植物化石图2④两块大陆古老地层顺序大致相同A.①②③B. ①②④C.①③④D.②③④读图3，完成6、7题。

6.北半球A.1月份大陆气温最低出现在纬度最高处B.1月份比7月份南北温差更大C.7月份大陆气温最高出现在纬度最低处D.同纬度海洋气温低于陆地气温7.关于影响图中四地气温的主要因素，说法正确的是A.①地1月气温较低，主要受纬度因素影响B.②地1月气温较高，主要受海陆位置因素影响C.③地7月气温较高，主要受地形因素影响D.④地7月气温较低，主要受人类活动因素影响20世纪90年代以来，全球变暖、臭氧层空洞和酸雨日益成为人们普遍关注的全球性环境问题。

据此，完成8、9题。

8.下列漫画反映的是全球性环境问题的有A.①②B.①④C.②③D.③④9. 为缓解②问题的加剧，我们应参与的行动是A.乘坐公共交通工具B.购物时选用环保袋C.控制能源消费数量D.积极推广节水措施读图4“世界65岁及以上人口比例变化趋势图”，完成10、11题。

北京市西城区2018-2019学年八年级上期末数学试卷含答案解析

2018-2019学年北京市西城区八年级（上）期末数学试卷一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．1．图书馆的标志是浓缩了图书馆文化的符号，下列图书馆标志中，不是轴对称的是（）A．B．C．D．2．500米口径球面射电望远镜，简称FAST，是世界上最大的单口径球面射电望远镜，被誉为“中国天眼”．2018年4月18日，FAST望远镜首次发现的毫秒脉冲星得到国际认证，新发现的脉冲星自转周期为0.00519秒，是至今发现的射电流量最弱的高能毫秒脉冲星之一．将0.00519用科学记数法表示应为（）A．0.519×10﹣2B．5.19×10﹣3C．51.9×10﹣4D．519×10﹣63．在△ABC中，AB＝3，AC＝5，第三边BC的取值范围是（）A．10＜BC＜13B．4＜BC＜12C．3＜BC＜8D．2＜BC＜84．如图，∠1+∠2+∠3+∠4+∠5等于（）A．360°B．540°C．720°D．900°5．对于一次函数y＝（k﹣3）x+2，y随x的增大而增大，k的取值范围是（）A．k＜0B．k＞0C．k＜3D．k＞36．下列各式中，正确的是（）A．＝B．＝C．＝D．＝﹣7．如图，已知△ABC，下面甲、乙、丙、丁四个三角形中，与△ABC全等的是（）A．甲B．乙C．丙D．丁8．小东一家自驾车去某地旅行，手机导航系统推荐了两条线路，线路一全程75km，线路二全程90km，汽车在线路二上行驶的平均时速是线路一上车速的1.8倍，线路二的用时预计比线路一用时少半小时，如果设汽车在线路一上行驶的平均速度为xkm/h，则下面所列方程正确的是（）A．＝+B．＝﹣C．＝+D．＝﹣9．如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE 的和最小时，∠CPE的度数是（）A．30°B．45°C．60°D．90°10．如图，线段AB＝6cm，动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动，到达点A后，停止运动；动点Q以1cm/s的速度从B﹣A在线段AB上运动，到达点A后，停止运动．若动点P，Q同时出发，设点Q的运动时间是t（单位：s）时，两个动点之间的距离为s（单位：cm），则能表示s与t的函数关系的是（）A．B．C ．D ．二、填空题（本题共18分，第11～16题，每小题2分，第17题3分，第18题3分）11．若分式的值为零，则x 的值为．12．在平面直角坐标系中，点P （1，﹣2）关于x 轴对称的点的坐标是． 13．计算：20+2﹣2＝．14．如图，在△ABC 中，AB 的垂直平分线MN 交AC 于点D ，连接BD ．若AC ＝7，BC ＝5，则△BDC 的周长是．15．如图，边长为acm 的正方形，将它的边长增加bcm ，根据图形写一个等式．16．如图，在△ABC 中，CD 是它的角平分线，DE ⊥AC 于点 E ．若BC ＝6cm ，DE ＝2cm ，则△BCD 的面积为 cm 2．17．如图，在平面直角坐标系xOy 中，点A 的坐标为（4，﹣3），且OA ＝5，在x 轴上确定一点P ，使△AOP 为等腰三角形．（1）写出一个符合题意的点P 的坐标；（2）请在图中画出所有符合条件的△AOP．18．（1）如图，∠MAB＝30°，AB＝2cm．点C在射线AM上，利用图1，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题．你画图时，选取的BC的长约为cm（精确到0.1cm）．（2）∠MAB为锐角，AB＝a，点C在射线AM上，点B到射线AM的距离为d，BC＝x，若△ABC的形状、大小是唯一确定的，则x的取值范围是．三、解答题（本题共30分，每小题6分）19．（1）分解因式x（x﹣a）+y（a﹣x）（2）分解因式x3y﹣10x2y+25xy20．计算：+21．解方程：+＝122．如图，点A，B，C，D在一条直线上，且AB＝CD，若∠1＝∠2，EC＝FB．求证：∠E＝∠F．23．在平面直角坐标系xOy中，直线l1：y＝3x与直线l2：y＝kx+b交于点A（a，3），点B（2，4）在直线l2上．（1）求a的值；（2）求直线l2的解析式；（3）直接写出关于x的不等式3x＜kx+b的解集．四、解答题（本题共12分，第24题7分，第25题5分）24．在平面直角坐标系xOy中，正方形ABCD的两个顶点的坐标分别为A（﹣2，0），D（﹣2，4），顶点B 在x轴的正半轴上．（1）写出点B，C的坐标；（2）直线y＝5x+5与x轴交于点E，与y轴交于点F．求△EFC的面积．25．阅读下列材料下面是小明同学“作一个角等于60°的直角三角形”的尺规作图过程．已知：线段AB（如图1）求作：△ABC，使∠CAB＝90°，∠ABC＝60°作法：如图2，（1）分别以点A，点B为圆心，AB长为半径画弧，两弧交于点D，连接BD（2）连接BD并延长，使得CD＝BD；（3）连接AC△ABC就是所求的直角三角形证明：连接AD．由作图可知，AD＝BD＝AB，CD＝BD∴△ABD是等边三角形（等边三角形定义）∴∠1＝∠B＝60°（等边三角形每个内角都等于60°）∴CD＝AD∴∠2＝∠C（等边对等角）在△ABC中，∠1+∠2+∠B+∠C＝180°（三角形的内角和等于180°）∴∠2＝∠C＝30°∴∠1+∠2＝90°（三角形的内角和等于180°），即∠CAB＝90°∴△ABC就是所求作的直角三角形请你参考小明同学解决问题的方式，利用图3再设计一种“作一个角等于60°的直角三角形”的尺规作图过程（保留作图痕迹），并写出作法，证明，及推理依据．五、解答题（本题8分）26．在△ABC中，AB＝AC，在△ABC的外部作等边三角形△ACD，E为AC的中点，连接DE并延长交BC 于点F，连接BD．（1）如图1，若∠BAC＝100°，求∠BDF的度数；（2）如图2，∠ACB的平分线交AB于点M，交EF于点N，连接BN．①补全图2；②若BN＝DN，求证：MB＝MN．2018-2019学年北京市西城区八年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．1．图书馆的标志是浓缩了图书馆文化的符号，下列图书馆标志中，不是轴对称的是（）A．B．C．D．【分析】根据轴对称图形的概念解答．【解答】解：A、不是轴对称图形；B、是轴对称图形；C、是轴对称图形；D、是轴对称图形；故选：A．【点评】本题考查的是轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．500米口径球面射电望远镜，简称FAST，是世界上最大的单口径球面射电望远镜，被誉为“中国天眼”．2018年4月18日，FAST望远镜首次发现的毫秒脉冲星得到国际认证，新发现的脉冲星自转周期为0.00519秒，是至今发现的射电流量最弱的高能毫秒脉冲星之一．将0.00519用科学记数法表示应为（）A．0.519×10﹣2B．5.19×10﹣3C．51.9×10﹣4D．519×10﹣6【分析】绝对值小于1的负数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.00519＝5.19×10﹣3．故选：B．【点评】此题主要考查了用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．3．在△ABC中，AB＝3，AC＝5，第三边BC的取值范围是（）A．10＜BC＜13B．4＜BC＜12C．3＜BC＜8D．2＜BC＜8【分析】已知两边，则第三边的长度应是大于两边的差而小于两边的和，这样就可求出第三边长的范围．【解答】解：第三边BC的取值范围是5﹣3＜BC＜5+3，即2＜BC＜8．故选：D．【点评】考查了三角形三边关系，已知三角形的两边，则第三边的范围是：大于已知的两边的差，而小于两边的和．4．如图，∠1+∠2+∠3+∠4+∠5等于（）A．360°B．540°C．720°D．900°【分析】多边形内角和定理：（n﹣2）•180°（n≥3）且n为整数），依此即可求解．【解答】解：（n﹣2）•180°＝（5﹣2）×180°＝3×180°＝540°．故∠1+∠2+∠3+∠4+∠5等于540°．故选：B．【点评】考查了多边形内角和定理，关键是熟练掌握多边形内角和定理：（n﹣2）•180 （n≥3）且n为整数）．5．对于一次函数y＝（k﹣3）x+2，y随x的增大而增大，k的取值范围是（）A．k＜0B．k＞0C．k＜3D．k＞3【分析】一次函数y＝kx+b，当k＞0时，y随x的增大而增大．据此列式解答即可．【解答】解：根据一次函数的性质，对于y＝（k﹣3）x+2，当k﹣3＞0时，即k＞3时，y随x的增大而增大．故选：D．【点评】本题考查了一次函数的性质．一次函数y＝kx+b，当k＞0时，y随x的增大而增大；当k＜0时，y 随x的增大而减小．6．下列各式中，正确的是（）A．＝B．＝C．＝D．＝﹣【分析】根据分式的基本性质解答即可．【解答】解：A、＝，故错误；B、＝+，故错误；C、＝，故正确；D、＝﹣，故错误；故选：C．【点评】本题考查了分式的基本性质，熟记分式的基本性质是解题的关键．7．如图，已知△ABC，下面甲、乙、丙、丁四个三角形中，与△ABC全等的是（）A．甲B．乙C．丙D．丁【分析】根据全等三角形的判定定理作出正确的选择即可．【解答】解：A．△ABC和甲所示三角形根据SA无法判定它们全等，故本选项错误；B．△ABC和乙所示三角形根据SAS可判定它们全等，故本选项正确；C．△ABC和丙所示三角形根据SA无法判定它们全等，故本选项错误；D．△ABC和丁所示三角形根据AA无法判定它们全等，故本选项错误；故选：B．【点评】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．8．小东一家自驾车去某地旅行，手机导航系统推荐了两条线路，线路一全程75km，线路二全程90km，汽车在线路二上行驶的平均时速是线路一上车速的1.8倍，线路二的用时预计比线路一用时少半小时，如果设汽车在线路一上行驶的平均速度为xkm/h，则下面所列方程正确的是（）A．＝+B．＝﹣C．＝+D．＝﹣【分析】设汽车在线路一上行驶的平均速度为xkm/h，则在线路二上行驶的平均速度为1.8xkm/h，根据线路二的用时预计比线路一用时少半小时，列方程即可．【解答】解：设汽车在线路一上行驶的平均速度为xkm/h，则在线路二上行驶的平均速度为1.8xkm/h，由题意得：＝+，故选：A．【点评】本题考查了由实际问题抽象出分式方程，解答本题的关键是，读懂题意，设出未知数，找出合适的等量关系，列出方程．9．如图，△ABC是等边三角形，AD是BC边上的高，E是AC的中点，P是AD上的一个动点，当PC与PE 的和最小时，∠CPE的度数是（）A．30°B．45°C．60°D．90°【分析】连接BE，则BE的长度即为PE与PC和的最小值．再利用等边三角形的性质可得∠PBC＝∠PCB＝30°，即可解决问题；【解答】解：如连接BE，与AD交于点P，此时PE+PC最小，∵△ABC是等边三角形，AD⊥BC，∴PC＝PB，∴PE+PC＝PB+PE＝BE，即BE就是PE+PC的最小值，∵△ABC是等边三角形，∴∠BCE＝60°，∵BA＝BC，AE＝EC，∴BE⊥AC，∴∠BEC＝90°，∴∠EBC＝30°，∵PB＝PC，∴∠PCB＝∠PBC＝30°，∴∠CPE＝∠PBC+∠PCB＝60°，故选：C．【点评】本题考查的是最短线路问题及等边三角形的性质，熟知两点之间线段最短的知识是解答此题的关键．10．如图，线段AB＝6cm，动点P以2cm/s的速度从A﹣B﹣A在线段AB上运动，到达点A后，停止运动；动点Q以1cm/s的速度从B﹣A在线段AB上运动，到达点A后，停止运动．若动点P，Q同时出发，设点Q的运动时间是t（单位：s）时，两个动点之间的距离为s（单位：cm），则能表示s与t的函数关系的是（）A．B．C．D．【分析】根据题意可以得到点P运动的慢，点Q运动的快，可以算出动点P和Q相遇时用的时间和点Q到达终点时的时间，从而可以解答本题．【解答】解：设点Q的运动时间是t（单位：s）时，两个动点之间的距离为s（单位：cm），6＝2t+t解得，t＝2此时，点P离点B的距离为：6﹣2×2＝2cm，点Q离点A的距离为：6﹣2＝4cm，相遇后，点P到达B点用的时间为：2÷2＝1s，此时两个动点之间的距离为3cm，由上可得，刚开始P和Q两点间的距离在越来越小直到相遇时，它们之间的距离变为0，此时用的时间为2s；相遇后，在第3s时点P到达B点，从相遇到点P到达B点它们的距离在变大，1s后P点从B点返回，点P 继续运动，两个动点之间的距离逐渐变小，同时达到A点．故选：D．【点评】本题考查动点问题的函数图象，解题的关键是明确各个时间段内它们对应的函数图象．二、填空题（本题共18分，第11～16题，每小题2分，第17题3分，第18题3分）11．若分式的值为零，则x的值为1．【分析】分式的值为0的条件是分子为0，分母不能为0，据此可以解答本题．【解答】解：，则x﹣1＝0，x+1≠0，解得x＝1．故若分式的值为零，则x的值为1．【点评】本题考查分式的值为0的条件，注意分式为0，分母不能为0这一条件．12．在平面直角坐标系中，点P（1，﹣2）关于x轴对称的点的坐标是（1，2）．【分析】根据关于x轴对称的点的横坐标相等，纵坐标互为相反数，可得答案．【解答】解：点P（1，﹣2）关于x轴对称的点的坐标是（1，2），故答案为：（1，2）．【点评】本题考查了关于x轴对称的点的坐标，利用关于x轴对称的点的横坐标相等，纵坐标互为相反数是解题关键．13．计算：20+2﹣2＝．【分析】根据零指数幂和负指数幂的知识点进行解答．【解答】解：原式＝1+＝．故答案为．【点评】本题主要考查了幂的负指数运算，先把底数化成其倒数，然后将负整指数幂当成正的进行计算，任何非0数的0次幂等于1，比较简单．14．如图，在△ABC中，AB的垂直平分线MN交AC于点D，连接BD．若AC＝7，BC＝5，则△BDC的周长是12．【分析】根据线段的垂直平分线的性质得到DA＝DB，根据三角形的周长公式计算即可．【解答】解：∵NM是AB的垂直平分线，∴DA＝DB，∴△BDC的周长＝BD+CD+BC＝AD+CD+BC＝AC+BC＝12，故答案为：12．【点评】本题考查的是线段的垂直平分线的性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．15．如图，边长为acm的正方形，将它的边长增加bcm，根据图形写一个等式a2+2ab+b2＝（a+b）2．【分析】依据大正方形的面积的不同表示方法，即可得到等式．【解答】解：由题可得，大正方形的面积＝a2+2ab+b2；大正方形的面积＝（a+b）2；∴a2+2ab+b2＝（a+b）2，故答案为：a2+2ab+b2＝（a+b）2．【点评】本题主要考查了完全平方公式的几何背景，即运用几何直观理解、解决完全平方公式的推导过程，通过几何图形之间的数量关系对完全平方公式做出几何解释．16．如图，在△ABC中，CD是它的角平分线，DE⊥AC于点E．若BC＝6cm，DE＝2cm，则△BCD的面积为6cm2．【分析】作DF⊥BC于F，根据角平分线的性质求出DF，根据三角形的面积公式计算即可．【解答】解：作DF⊥BC于F，∵CD是它的角平分线，DE⊥AC，DF⊥BC，∴DF＝DE＝2，∴△BCD的面积＝×BC×DF＝6（cm2），故答案为：6．【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．17．如图，在平面直角坐标系xOy中，点A的坐标为（4，﹣3），且OA＝5，在x轴上确定一点P，使△AOP 为等腰三角形．（1）写出一个符合题意的点P的坐标答案不唯一，如：（﹣5，0）；（2）请在图中画出所有符合条件的△AOP．【分析】（1）根据等腰三角形的性质即可求解；（2）可分三种情况：①AO＝AP；②AO＝PO；③AP＝PO；解答出即可．【解答】解：（1）一个符合题意的点P的坐标答案不唯一，如：（﹣5，0）；（2）如图所示：故答案为：答案不唯一，如：（﹣5，0）．【点评】本题主要考查了作图﹣复杂作图、等腰三角形的判定和坐标与图形的性质，注意讨论要全面，不要遗漏．18．（1）如图，∠MAB＝30°，AB＝2cm．点C在射线AM上，利用图1，画图说明命题“有两边和其中一边的对角分别相等的两个三角形全等”是假命题．你画图时，选取的BC的长约为答案不唯一如：BC＝1.2cm cm（精确到0.1cm）．（2）∠MAB为锐角，AB＝a，点C在射线AM上，点B到射线AM的距离为d，BC＝x，若△ABC的形状、大小是唯一确定的，则x的取值范围是x＝d或x≥a．．【分析】（1）答案不唯一，可以取BC＝1.2cm（1cm＜BC＜2cm）；（2）当x＝d或x≥a时，三角形是唯一确定的；【解答】解：（1）取BC＝1.2cm，如图在△ABC和△ABC′中满足SSA，两个三角形不全等．故答案为：答案不唯一如：BC＝1.2cm．（2）若△ABC的形状、大小是唯一确定的，则x的取值范围是x＝d或x≥a，故答案为x＝d或x≥a．【点评】本题考查全等三角形的判定和性质，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．三、解答题（本题共30分，每小题6分）19．（1）分解因式x（x﹣a）+y（a﹣x）（2）分解因式x3y﹣10x2y+25xy【分析】（1）直接提取公因式（x﹣a）分解因式即可．（2）先提取公因式xy，然后利用完全平方公式进一步进行因式分解．【解答】（1）解：x（x﹣a）+y（a﹣x）＝x（x﹣a）﹣y（x﹣a）＝（x﹣a）（x﹣y）；（2）解：x3y﹣10x2y+25xy＝xy（x2﹣10x+25）＝xy（x﹣5）2．【点评】考查了因式分解﹣提公因式法．当各项系数都是整数时，公因式的系数应取各项系数的最大公约数；字母取各项的相同的字母，而且各字母的指数取次数最低的；取相同的多项式，多项式的次数取最低的．20．计算：+【分析】原式先计算除法运算，再计算加减运算即可求出值．【解答】解：原式＝+•＝+＝+＝．【点评】此题考查了分式的混合运算，熟练掌握运算法则是解本题的关键．21．解方程：+＝1【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：方程两边乘（x﹣3）（x+3），得x（x+3）+6 （x﹣3）＝x2﹣9，解得：x＝1，检验：当x＝1 时，（x﹣3）（x+3）≠0，所以，原分式方程的解为x＝1．【点评】此题考查了解分式方程，利用了转化的思想，解分式方程注意要检验．22．如图，点A，B，C，D在一条直线上，且AB＝CD，若∠1＝∠2，EC＝FB．求证：∠E＝∠F．【分析】求出∠DBF＝∠ACE，AC＝DB，根据SAS推出△ACE≌△DBF，根据全等三角形的性质得出即可．【解答】证明：∵∠1+∠DBF＝180°，∠2+∠ACE＝180°．又∵∠1＝∠2，∴∠DBF＝∠ACE，∵AB＝CD，∴AB+BC＝CD+BC，即AC＝DB，在△ACE和△DBF中，∴△ACE≌△DBF（SAS），∴∠E＝∠F．【点评】本题考查了全等三角形的性质和判定，能求出△ACE≌△DBF是解此题的关键．23．在平面直角坐标系xOy中，直线l1：y＝3x与直线l2：y＝kx+b交于点A（a，3），点B（2，4）在直线l2上．（1）求a的值；（2）求直线l2的解析式；（3）直接写出关于x的不等式3x＜kx+b的解集．【分析】（1）把A（a，3）代入y＝3x可求出a的值；（2）利用待定系数法求直线l2的解析式；（3）写出直线l2：y＝kx+b在直线l1：y＝3x上方所对应的自变量的范围即可．【解答】解：（1）直线l1：y＝3x与直线l2：y＝kx+b交于点A（a，3），所以3a＝3．解得a＝1．（2）由（1）得点A（1，3），直线l2：y＝kx+b过点A（1，3），点B（2，4 ），所以，解得所以直线l2的解析式为y＝x+2.4 分（3）不等式3x＜kx+b的解集为x＜1．【点评】本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y＝kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y＝kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．四、解答题（本题共12分，第24题7分，第25题5分）24．在平面直角坐标系xOy中，正方形ABCD的两个顶点的坐标分别为A（﹣2，0），D（﹣2，4），顶点B 在x轴的正半轴上．（1）写出点B，C的坐标；（2）直线y＝5x+5与x轴交于点E，与y轴交于点F．求△EFC的面积．【分析】（1）根据正方形的性质以及A、D、B的位置即可求得；（2）求得E、F点的坐标，进而求得OB＝2，BC＝4，OF＝5，OE＝1，EB＝3，根据三角形的面积公式和梯形的面积公式求得即可．【解答】解：（1）如图，∵正方形ABCD的两个顶点的坐标分别为A（﹣2，0），D（﹣2，4），顶点B在x轴的正半轴上，∴B（2，0），C（2，4）；（2）∵直线y＝5x+5与x轴交于点E，与y轴交于点F，∴E（﹣1，0），F（0，5），∵B（2，0），C（2，4），∴OB＝2，BC＝4，OF＝5，OE＝1，EB＝3，∴S梯形OBCF＝（OF+BC）•OB＝×（5+4）×2＝9，S△OEF＝OE•OF＝×2×5＝5，S△EBC＝EB•BC＝×3×4＝6，∴S△EFC ＝S梯形OBCF+S△OEF﹣S△EBC＝9+5﹣6＝8．【点评】本题考查一次函数图象上点的坐标特征以及正方形的性质，坐标与图形的性质，求得点的坐标解题的关键．25．阅读下列材料下面是小明同学“作一个角等于60°的直角三角形”的尺规作图过程．已知：线段AB（如图1）求作：△ABC，使∠CAB＝90°，∠ABC＝60°作法：如图2，（1）分别以点A，点B为圆心，AB长为半径画弧，两弧交于点D，连接BD（2）连接BD并延长，使得CD＝BD；（3）连接AC△ABC就是所求的直角三角形证明：连接AD．由作图可知，AD＝BD＝AB，CD＝BD∴△ABD是等边三角形（等边三角形定义）∴∠1＝∠B＝60°（等边三角形每个内角都等于60°）∴CD＝AD∴∠2＝∠C（等边对等角）在△ABC中，∠1+∠2+∠B+∠C＝180°（三角形的内角和等于180°）∴∠2＝∠C＝30°∴∠1+∠2＝90°（三角形的内角和等于180°），即∠CAB＝90°∴△ABC就是所求作的直角三角形请你参考小明同学解决问题的方式，利用图3再设计一种“作一个角等于60°的直角三角形”的尺规作图过程（保留作图痕迹），并写出作法，证明，及推理依据．【分析】根据题意设计“作一个角等于60°的直角三角形”的尺规作图过程，连接DC．得到△DBC是等边三角形，根据等边三角形的性质得到∠B＝60°，根据等腰三角形的性质证明．【解答】解：作法：（1）延长BA至D，使AD＝AB；（2）分别以点 B，点 D 为圆心，BD 长为半径画弧，两弧交于点 C；（3）连接 AC，BC．则△ABC 就是所求的直角三角形，证明：连接 DC．由作图可知，BC＝BD＝DC， ∴△DBC 是等边三角形， ∴∠B＝60°， ∵CD＝CB，AD＝AB， ∴AC⊥BD， ∴△ABC 就是所求作的直角三角形．【点评】本题考查的是等边三角形的性质，基本尺规作图，掌握等边三角形的判定定理和性质定理，等腰三角形的三线合一是解题的关键．五、解答题（本题 8 分） 26．在△ABC 中，AB＝AC，在△ABC 的外部作等边三角形△ACD，E 为 AC 的中点，连接 DE 并延长交 BC 于点 F，连接 BD．（1）如图 1，若∠BAC＝100°，求∠BDF 的度数；（2）如图 2，∠ACB 的平分线交 AB 于点 M，交 EF 于点 N，连接 BN． ①补全图 2； ②若 BN＝DN，求证：MB＝MN．【分析】（1）分别求出∠ADF，∠ADB，根据∠BDF＝∠ADF﹣∠ADB 计算即可；（2）①根据要求画出图形即可；②设∠ACM＝∠BCM＝α，由 AB＝AC，推出∠ABC＝∠ACB＝2α，可得∠NAC＝∠NCA＝α， ∠DAN＝60°+α，由△ABN≌△ADN（SSS），推出∠ABN＝∠ADN＝30°，∠BAN＝∠DAN＝60°+α，∠BAC＝60°+2α，在△ABC 中，根据∠BAC+∠ACB+∠ABC＝180°，构建方程求出 α，再证明∠MNB＝∠MBN 即可解决问题；【解答】（1）解：如图 1 中，在等边三角形△ACD 中， ∠CAD＝∠ADC＝60°，AD＝AC． ∵E 为 AC 的中点， ∴∠ADE＝ ∠ADC＝30°， ∵AB＝AC， ∴AD＝AB， ∵∠BAD＝∠BAC+∠CAD＝160°， ∴∠ADB＝∠ABD＝10°， ∴∠BDF＝∠ADF﹣∠ADB＝20°．（2）①补全图形，如图所示．②证明：连接 AN． ∵CM 平分∠ACB， ∴设∠ACM＝∠BCM＝α， ∵AB＝AC，∴∠ABC＝∠ACB＝2α．在等边三角形△ACD 中， ∵E 为 AC 的中点， ∴DN⊥AC， ∴NA＝NC， ∴∠NAC＝∠NCA＝α， ∴∠DAN＝60°+α，在△ABN 和△ADN 中，∴△ABN≌△ADN（SSS）， ∴∠ABN＝∠ADN＝30°，∠BAN＝∠DAN＝60°+α， ∴∠BAC＝60°+2α，在△ABC 中，∠BAC+∠ACB+∠ABC＝180°， ∴60°+2α+2α+2 α＝180°， ∴α＝20°， ∴∠NBC＝∠ABC﹣∠ABN＝10°， ∴∠MNB＝∠NBC+∠NCB＝30°， ∴∠MNB＝∠MBN， ∴MB＝MN．【点评】本题考查全等三角形的判定和性质，等边三角形的性质，等腰三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．。

2018-2019学年八年级(上)期末数学试卷(有答案和解析)

2018-2019学年八年级（上）期末数学试卷一、选择题（每题3分，共30分）1．如图所示的图案是我国几家银行标志，其中不是轴对称图形的是（）A．B．C．D．2．下列运算中，正确的是（）A．a2•a4＝a8B．a10÷a5＝a2C．（a5）2＝a10D．（2a）4＝8a43．下列变形属于因式分解的是（）A．4x+x＝5x B．（x+2）2＝x2+4x+4C．x2+x+1＝x（x+1）+1D．x2﹣3x＝x（x﹣3）4．石墨烯目前是世界上最薄却也是最坚硬的纳米材料，同时还是导电性最好的材料，其理论厚度仅0.000 000 000 34米，将这个数用科学记数法表示为（）A．0.34×10﹣9B．3.4×10﹣9C．3.4×10﹣10D．3.4×10﹣115．已知图中的两个三角形全等，图中的字母表示三角形的边长，则∠1等于（）A．72°B．60°C．50°D．58°6．如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（）A．13B．16C．8D．107．下列各式成立的是（）A．B．（﹣a﹣b）2＝（a+b）2C．（a﹣b）2＝a2﹣b2D．（a+b）2﹣（a﹣b）2＝2ab8．如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（）A．∠A＝∠D B．BC＝EF C．∠ACB＝∠F D．AC＝DF9．下列三角形：①有两个角等于60°的三角形；②有一个角等于60°的等腰三角形；③三个外角（每个顶点处各取一个外角）都相等的三角形；④一腰上的中线也是这条腰上的高的等腰三角形．其中是等边三角形的有（）A．①②③④B．①②④C．①③D．②③④10．已知x＝3y+5，且x2﹣7xy+9y2＝24，则x2y﹣3xy2的值为（）A．0B．1C．5D．12二、填空题（本大题共6小题，每小题3分，共18分）11．因式分解：2a2﹣8＝．12．若代数式有意义，则实数x的取值范围是．13．一个n边形的内角和是540°，那么n＝．14．如图，Rt△ABC中，∠C＝90°，AD为△ABC的角平分线，与BC相交于点D，若CD＝4，AB ＝15，则△ABD的面积是．15．如图，在△ABC中，AB＝AC，点D在AC上，过点D作DF⊥BC于点F，且BD＝BC＝AD，则∠CDF的度数为．16．如图，△ABC角平分线AE、CF交于点P，BD是△ABC的高，点H在AC上，AF＝AH，下列结论：①∠APC＝90°+ABC；②PH平分∠APC；③若BC＞AB，连接BP，则∠DBP＝∠BAC﹣∠BCA；④若PH∥BD，则△ABC为等腰三角形，其中正确的结论有（填序号）．三、解答题17．（10分）计算（1）（2﹣）0﹣（）﹣2（2）（﹣3a2）3÷6a+a2•a318．（10分）计算（1）（x+1）2﹣（x+1）（x﹣1）（2）﹣x﹣219．（10分）如图，D、C、F、B四点在一条直线上，AB＝DE，AC⊥BD，EF⊥BD，垂足分别为点C、点F，CD＝BF．求证：（1）△ABC≌△EDF；（2）AB∥DE．20．（10分）如图，已知A（﹣2，4），B（4，2），C（2，﹣1）（1）作△ABC关于x轴的对称图形△A1B1C1，写出点C关于x轴的对称点C1的坐标；（2）P为x轴上一点，请在图中找出使△PAB的周长最小时的点P并直接写出此时点P的坐标（保留作图痕迹）．21．（12分）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需要时间与原计划生产450台机器所需时间相同．（1）现在平均每天生产多少台机器；（2）生产3000台机器，现在比原计划提前几天完成．22．（10分）已知代数式．（1）先化简，再求当x＝3时，原代数式的值；（2）原代数式的值能等于﹣1吗？为什么？23．（12分）如图，已知△ABC中AB＝AC，在AC上有一点D，连接BD，并延长至点E，使AE ＝AB．（1）画图：作∠EAC的平分线AF，AF交DE于点F（用尺规作图，保留作图痕迹，不写作法）；（2）在（1）的条件下，连接CF，求证：∠ABE＝∠ACF；（3）若AC＝8，∠E＝15°，求三角形ABE的面积．24．（14分）因式分解是把多项式变形为几个整式乘积的形式的过程．（1）设有多项式x2+2x﹣m分解后有一个因式是x+4，求m的值．（2）若有甲、乙两个等容积的长方体容器，甲容器长为x﹣1，宽为x﹣2．体积为x4﹣x3+ax2+bx ﹣6，（x为整数），乙容器的底面是正方形．①求出a，b的值；②分别求出甲、乙两容器的高．（用含x的代数式表示）25．（14分）在Rt△ABC中，∠B＝90°，AB＝8，CB＝5，动点M从C点开始沿CB运动，动点N从B点开始沿BA运动，同时出发，两点均以1个单位/秒的速度匀速运动（当M运动到B点即同时停止），运动时间为t秒．（1）AN＝；CM＝．（用含t的代数式表示）（2）连接CN，AM交于点P．①当t为何值时，△CPM和△APN的面积相等？请说明理由．②当t＝3时，试求∠APN的度数．2018-2019学年八年级（上）期末数学试卷参考答案与试题解析一、选择题（每题3分，共30分）1．【分析】根据轴对称图形的概念对各选项分析判断即可得解．【解答】解：A、是轴对称图形，故本选项不符合题意；B、不是轴对称图形，故本选项符合题意；C、是轴对称图形，故本选项不符合题意；D、是轴对称图形，故本选项不符合题意．故选：B．【点评】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．2．【分析】根据同底数幂的乘除法则，及幂的乘方法则，结合各选项进行判断即可．【解答】解：A、a2•a4＝a6，计算错误，故本选项错误；B、a10÷a5＝a5，计算错误，故本选项错误；C、（a5）2＝a10，计算正确，故本选项正确；D、（2a）4＝16a4，计算错误，故本选项错误；故选：C．【点评】本题考查了同底数幂的乘除运算及幂的乘方的运算，属于基础题，掌握运算法则是关键．3．【分析】把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式，结合选项进行判断即可．【解答】解：A、是整式的计算，不是因式分解，故本选项错误；B、右边不是整式积的形式，不是因式分解，故本选项错误；C、右边不是整式积的形式，不是因式分解，故本选项错误；D、符合因式分解的定义，故本选项正确．故选：D．【点评】本题考查了因式分解的意义，属于基础题，掌握因式分解的定义是关键．4．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．【解答】解：0.000 000 000 34＝3.4×10﹣10；故选：C．【点评】本题考查用科学记数法表示较小的数，一般形式为a×10﹣n，其中1≤|a|＜10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．5．【分析】根据全等三角形的性质即可求出答案．【解答】解：由于两个三角形全等，∴∠1＝180﹣50°﹣72°＝58°，故选：D．【点评】本题考查了全等三角形的性质，属于基础题型．解答本题的关键是熟练运用全等三角形的性质6．【分析】由于△ABC是等腰三角形，底边BC＝5，周长为21，由此求出AC＝AB＝8，又DE是AB的垂直平分线，根据线段的垂直平分线的性质得到AE＝BE，由此得到△BEC的周长＝BE+CE+CB＝AE+CE+BC＝AC+CB，然后利用已知条件即可求出结果．【解答】解：∵△ABC是等腰三角形，底边BC＝5，周长为21，∴AC＝AB＝8，又∵DE是AB的垂直平分线，∴AE＝BE，∴△BEC的周长＝BE+CE+CB＝AE+CE+BC＝AC+CB＝13，∴△BEC的周长为13．故选：A．【点评】此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．7．【分析】根据完全平方公式和分式的化简判断即可．【解答】解：A、，错误；B、（﹣a﹣b）2＝（a+b）2，正确；C、（a﹣b）2＝a2﹣2ab+b2，错误；D、（a+b）2﹣（a﹣b）2＝4ab，错误；故选：B．【点评】此题考查完全平方公式，关键是根据完全平方公式和分式的化简判断．8．【分析】根据全等三角形的判定，利用ASA、SAS、AAS即可得答案．【解答】解：∵∠B＝∠DEF，AB＝DE，∴添加∠A＝∠D，利用ASA可得△ABC≌△DEF；∴添加BC＝EF，利用SAS可得△ABC≌△DEF；∴添加∠ACB＝∠F，利用AAS可得△ABC≌△DEF；故选：D．【点评】本题考查了全等三角形的判定，掌握全等三角形的判定方法：SSS、ASA、SAS、AAS和HL是解题的关键．9．【分析】根据等边三角形的判定判断，三条边都相等的三角形是等边三角形；三个角都相等的三角形是等边三角形；有一个角是60°的等腰三角形是等边三角形．【解答】解：①两个角为60度，则第三个角也是60度，则其是等边三角形；②有一个角等于60°的等腰三角形是等边三角形；③三个外角相等，则三个内角相等，则其是等边三角形；④根据等边三角形的性质，可得该等腰三角形的腰与底边相等，则三角形三边相等．所以都正确．故选：A．【点评】此题主要考查等边三角形的判定，三条边都相等的三角形是等边三角形；三个角都相等的三角形是等边三角形；有一个角是60°的等腰三角形是等边三角形．10．【分析】依据x﹣3y＝5两边平方，可得x2﹣6xy+9y2＝25，再根据x2﹣7xy+9y2＝24，即可得到xy的值，进而得出x2y﹣3xy2的值．【解答】解：∵x＝3y+5，∴x﹣3y＝5，两边平方，可得x2﹣6xy+9y2＝25，又∵x2﹣7xy+9y2＝24，两式相减，可得xy＝1，∴x2y﹣3xy2＝xy（x﹣3y）＝1×5＝5，故选：C．【点评】本题主要考查了完全平方公式的运用，应用完全平方公式时，要注意：公式中的a，b 可是单项式，也可以是多项式；对形如两数和（或差）的平方的计算，都可以用这个公式．二、填空题（本大题共6小题，每小题3分，共18分）11．【分析】首先提取公因式2，进而利用平方差公式分解因式即可．【解答】解：2a2﹣8＝2（a2﹣4）＝2（a+2）（a﹣2）．故答案为：2（a+2）（a﹣2）．【点评】此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．12．【分析】根据分式有意义的条件可得x﹣3≠0，再解即可．【解答】解：由题意得：x﹣3≠0，解得：x≠3，故答案为：x≠3．【点评】此题主要考查了分式有意义的条件，关键是掌握分式有意义的条件是分母不等于零．13．【分析】根据n边形的内角和为（n﹣2）•180°得到（n﹣2）•180°＝540°，然后解方程即可．【解答】解：设这个多边形的边数为n，由题意，得（n﹣2）•180°＝540°，解得n＝5．故答案为：5．【点评】本题考查了多边的内角和定理：n边形的内角和为（n﹣2）•180°．14．【分析】作DE⊥AB于E，根据角平分线的性质求出DE，根据三角形的面积公式计算即可．【解答】解：作DE⊥AB于E，∵AD是△ABC的角平分线，∠C＝90°，DE⊥AB，∴DE＝CD＝4，∴△ABD的面积＝，故答案为：30【点评】本题考查的是角平分线的性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．15．【分析】设∠A＝α，可得∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，再根据△ABC中，∠A+∠ABC+∠C＝180°，即可得到∠C的度数，再根据DF⊥BC，即可得出∠CDF的度数．【解答】解：∵AB＝AC，BD＝BC＝AD，∴∠ACB＝∠ABC，∠A＝∠ABD，∠C＝∠BDC，设∠A＝α，则∠ABD＝α，∠C＝∠BDC＝2α，∠ABC＝2α，∵△ABC中，∠A+∠ABC+∠C＝180°，∴α+2α+2α＝180°，∴α＝36°，∴∠C＝72°，又∵DF⊥BC，∴Rt△CDF中，∠CDF＝90°﹣72°＝18°，故答案为：18°．【点评】本题主要考查了等腰三角形的性质以及三角形内角和定理的运用，解题时注意：等腰三角形的两个底角相等．16．【分析】①利用三角形的内角和定理以及角平分线的定义即可判断．②利用反证法进行判断．③根据∠DBP＝∠DBC﹣∠PBC＝90°﹣∠ACB﹣（180°﹣∠BAC﹣∠ACB）＝（∠BAC﹣∠ACB），由此即可判断．④利用全等三角形的性质证明CA＝CB即可判断．【解答】解：∵△ABC角平分线AE、CF交于点P，∴∠CAP＝∠BAC，∠ACP＝∠ACB，∴∠APC＝180°﹣（∠CAP+∠ACP）＝180°﹣（∠BAC+∠ACB）＝180°﹣（180°﹣∠ABC）＝90°+∠ABC，故①正确，∵PA＝PA，∠PAF＝∠PAH，AF＝AH，∴△PAF≌△PAH（SAS），∴∠APF＝∠APH，若PH是∠APC的平分线，则∠APF＝60°，显然不可能，故②错误，∵∠DBP＝∠DBC﹣∠PBC＝90°﹣∠ACB﹣（180°﹣∠BAC﹣∠ACB）＝（∠BAC﹣∠ACB），故③错误，∵BD⊥AC，PH∥BD，∴PH⊥AC，∴∠PHA＝∠PFA＝90°，∵∠ACF＝∠BCF，CF＝CF，∠CFA＝∠CFB＝90°，∴△CFA≌△CFB（ASA），∴CA＝CB，故④正确，故答案为①④．【点评】本题考查全等三角形的判定和性质，角平分线的定义等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．三、解答题17．【分析】（1）直接利用零指数幂的性质以及负指数幂的性质分别化简得出答案；（2）直接利用积的乘方运算法则以及整式的乘除运算法则计算得出答案．【解答】解：（1）原式＝1﹣4＝﹣3；（2）原式＝﹣27a6÷6a+a2•a3＝﹣a5+a5＝﹣3a5．【点评】此题主要考查了整式的乘除运算，正确掌握相关运算法则是解题关键．18．【分析】（1）先利用完全平方公式和平方差公式计算，再去括号、合并同类项即可得；（2）根据分式的混合运算顺序和运算法则计算可得．【解答】解：（1）原式＝x2+2x+1﹣（x2﹣1）＝x2+2x+1﹣x2+1＝2x+2；（2）原式＝﹣＝﹣＝．【点评】本题主要考查分式的加减法，解题的关键是熟练掌握分式的加减混合运算顺序和运算法则及完全平方公式、平方差公式．19．【分析】（1）由垂直的定义，结合题目已知条件可利用HL证得结论；（2）由（1）中结论可得到∠D＝∠B，则可证得结论．【解答】证明：（1）∵AC⊥BD，EF⊥BD，∴△ABC和△EDF为直角三角形，∵CD＝BF，∴CF+BF＝CF+CD，即BC＝DF，在Rt△ABC和Rt△EDF中，∴Rt△ABC≌Rt△EDF（HL）；（2）由（1）可知△ABC≌△EDF，∴∠B＝∠D，∴AB∥DE．【点评】本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法（即SSS、SAS、ASA、AAS和HL）和性质（即对应边相等、对应角相等）是解题的关键．20．【分析】（1）分别作出点A、B、C关于x轴的对称点，再顺次连接可得；（2）连接AB1，交x轴于点P，根据图形可得点P的坐标．【解答】解：（1）如图1所示，△A1B1C1即为所求；C1的坐标为（2，1）．（2）如图所示，连接AB1，交x轴于点P，点P的坐标为（2，0）．【点评】本题主要考查作图﹣轴对称变换，解题的关键是熟练掌握轴对称变换的定义和性质．21．【分析】（1）设原计划平均每天生产x台机器，则现在平均每天生产（x+50）台机器，根据工作时间＝工作总量÷工作效率结合现在生产600台机器所需要时间与原计划生产450台机器所需时间相同，即可得出关于x的分式方程，解之经检验后即可得出结论；（2）由提前完成的天数＝工作总量÷原计划工作效率﹣工作总量÷现在工作效率，即可得出结论．【解答】解：（1）设原计划平均每天生产x台机器，则现在平均每天生产（x+50）台机器，依题意，得：＝，解得：x＝150，经检验，x＝150是原方程的解，且符合题意，∴x+50＝200．答：现在平均每天生产200台机器．（2）﹣＝20﹣15＝5（天）．答：现在比原计划提前5天完成．【点评】本题考查了分式方程的应用，找准等量关系，正确列出分式方程是解题的关键．22．【分析】（1）先根据分式的混合运算顺序和运算法则化简原式，再将x的值代入计算可得；（2）根据题意得出＝﹣1，解之求得x的值，再根据分式有意义的条件即可作出判断．【解答】解：（1）原式＝[﹣]•＝（﹣）•＝•＝，当x＝3时，原式＝＝2；（2）若原代数式的值等于﹣1，则＝﹣1，解得x＝0，而x＝0时，原分式无意义，所以原代数式的值不能等于﹣1．【点评】本题主要考查分式的化简求值，解题的关键是熟练掌握分式的混合运算顺序和运算法则及分式有意义的条件．23．【分析】（1）以点A为圆心，以任意长为半径画弧，分别与AC、AE相交，然后以这两点为圆心，以大于它们长度为半径画弧，两弧相交于一点，过点A与这一点作出射线与BE的交点即为所求的点F；（2）求出AE＝AC，根据角平分线的定义可得∠EAF＝∠CAF，再利用“边角边”证明△AEF和△ACF全等，根据全等三角形对应角相等可得∠ABE＝∠ACF；（3）作高线EG，根据三角形的外角性质得∠EAG＝30°，根据直角三角形的性质可得高线EG ＝4，根据三角形面积公式可得结论．【解答】（1）解：如图所示；（2）证明：∵AB＝AC，AE＝AB，∴AE＝AC，∵AF是∠EAC的平分线，∴∠EAF＝∠CAF，在△AEF和△ACF中，，∴△AEF≌△ACF（SAS），∴∠E＝∠ACF，∵AB＝AE，∴∠ABE＝∠E，∴∠ABE＝∠ACF．（3）解：如图，过E作EG⊥AB，交BA的延长线于G，∵AB＝AC＝AE＝8，∴∠ABE＝∠AEB＝15°，∴∠GAE＝∠ABE+∠AEB＝30°，∴EG＝AE＝4，∴三角形ABE的面积＝＝＝16．【点评】本题考查了全等三角形的判断与性质，等腰三角形的性质，角平分线的作法，确定出全等三角形的条件是解题的关键．24．【分析】（1）根据分解因式的定义，假设未知数，进行求解；（2）同上一问，假设未知数，进行求解；然后对体积的表达式进行因式分解，得到乙容器的高；【解答】解：（1）设原式分解后的另一个因式为x+n，则有：x2+2x﹣m＝（x +4）（x +n ）＝x 2+（4+n ）x +4n∴4+n ＝2可得n ＝﹣24n ＝﹣m 可得m ＝8综上所述：m ＝8（2）①设甲容器的高为x 2+mx ﹣3，则有：（x ﹣1）（x ﹣2）（x 2+mx ﹣3）＝x 4﹣x 3+ax 2+bx ﹣6 ∴x •（﹣2）•x 2+（﹣1）•x •x 2+x •x •mx ＝﹣2x 3﹣x 3+mx 3＝（m ﹣3）x 3＝﹣x 3从而得m ﹣3＝﹣1m ＝2原甲容器的体积＝（x ﹣1）（x ﹣2）（x 2+2x ﹣3）＝x 4﹣x 3﹣9x 2+13x ﹣6从而得a ＝﹣9，b ＝13②由乙容器的底面为正方形可得：x 4﹣x 3﹣9x 2+13x ﹣6＝（x ﹣1）（x ﹣2）（x 2+2x ﹣3）＝（x ﹣1）（x ﹣2）（x +3）（x ﹣1）＝（x ﹣1）2（x 2+x ﹣6）故答案为：甲容器的高为x 2+2x ﹣3，乙容器的高为x 2+x ﹣6【点评】该题通过设置未知数，运用多项式乘多项式的方法求解未知数的值．25．【分析】（1）根据路程＝速度×时间，可用含t 的代数式表示BN ，CM 的长，即可用含t 的代数式表示AN 的长；（2）①由题意可得S △ABM ＝S △BNC ，根据三角形面积公式可求t 的值；②过点P 作PF ⊥BC ，PG ⊥AB ，过点A 作AE ⊥CN ，交CN 的延长线于点E ，连接BP ，可证四边形PGBF 是矩形，可得PF ＝BG ，根据三角形的面积公式，可得方程组，求出PG ，PF 的长，根据勾股定理可求PN 的长，通过证△ANE ∽△CNB ，可求AE ，NE 的长，即可求∠APN 的度数．【解答】解：（1）∵M ，N 两点均以1个单位/秒的速度匀速运动，∴CM ＝BN ＝t ，∴AN ＝8﹣t ，故答案为：8﹣t ，t ；（2）①若△CPM 和△APN 的面积相等∴S △CPM +S 四边形BMPN ＝S △APN +S 四边形BMPN ，∴S △ABM ＝S △BNC ，∴＝∴8×（5﹣t ）＝5t∴t ＝∴当t ＝时，△CPM 和△APN 的面积相等；②如图，过点P 作PF ⊥BC ，PG ⊥AB ，过点A 作AE ⊥CN ，交CN 的延长线于点E ，连接BP ，∵PG ⊥AB ，PF ⊥BC ，∠B ＝90°，∴四边形PGBF 是矩形，∴PF ＝BG ，∵t ＝3，∴CM ＝3＝BN ，∴BM ＝2，AN ＝5，∵S △ABM ＝S △ABP +S △BPM ，∴∴16＝8PG +2PF ①∵S △BCN ＝S △BCP +S △BPN ，∴×5×3＝∴15＝3PG +5PF ②由①②组成方程组解得：PG ＝，PF ＝，∴BG ＝∴NG ＝BN ﹣BG ＝3﹣＝在Rt△PGN中，PN＝＝，在Rt△BCN中，CN＝＝∵∠B＝∠E＝90°，∠ANE＝∠BNC∴△ANE∽△CNB∴∴∴AE＝，NE＝∵PE＝EN+PN∴PE＝+＝∴AE＝PE，且AE⊥PE∴∠APN＝45°【点评】本题是三角形综合题，考查了三角形的面积公式，勾股定理，矩形的判定，相似三角形的判定和性质等知识，本题的关键是求出PN的长．。

精品解析：北京市西城区2018-2019学年八年级上学期期末考试历史试题(解析版)

北京市西城区2018—2019学年度第一学期期末试卷八年级历史2019.1试卷满分：100分考试时间：60分钟一、选择题（下列各题的四个选项中，只有一项符合题意。

每小题2分，共50分）1.下图是人民英雄纪念碑的第一幅浮雕“虎门销烟”，与这一事件直接相关的人物是A. 道光帝B. 林则徐C. 陈化成D. 关天培【答案】B【解析】【详解】结合所学知识可知，1838年底，道光帝派力主禁烟的林则徐为钦差大臣，前往广东查禁鸦片。

在林则徐的主持下，1839年6月3日至25日，收缴的鸦片在虎门海滩被当众销毁。

选项B符合题意；道光帝是清朝皇帝；关天培等战死虎门，陈化成在吴淞力竭牺牲；选项ACD不符合题意，故选B。

2.中英《南京条约》规定：“今大皇帝准将香港岛给予大英国君主暨嗣后世袭主位者常远据守主掌……”这一规定使中国丧失了A. 领土主权B. 贸易主权C. 司法主权D. 关税主权【答案】A【解析】【详解】根据题干信息“今大皇帝准将香港岛给予大英国君主暨嗣后世袭主位者常远据守主掌”，结合所学知识可知，中国的领土完整遭到破坏，使中国丧失了主权。

选项A符合题意；选项BCD与题干内容不符，故选A。

3.历史学习要学会区分历史史实和历史结论。

下列各项中，属于历史结论的是A. 英国以“亚罗号事件”为借口发动了第二次鸦片战争B. 1858年，英法联军北上，攻陷大沽炮台，逼近天津C. 第二次鸦片战争使中国的半殖民地化程度进一步加深D. 《北京条约》承认《天津条约》有效外，又增开天津为商埠【答案】C【解析】【详解】结合所学知识可知，史实即历史事实，结论即对历史事件和历史人物的评论。

第二次鸦片战争使中国的半殖民地化程度进一步加深，是说明第二次鸦片战争的影响，属于历史结论。

选项ABD属于历史事实，不符合题意，故选C。

4.第二次鸦片战争前后，强迫清政府签订一系列不平等条约，共割占中国东北和西北150多万平方千米领土的国家是A. 英国B. 法国C. 美国D. 俄国【答案】D【解析】【详解】结合所学知识可知，第二次鸦片战争前后，沙俄俄国强迫清政府签订了一系列不平等条约，共割占中国东北和西北150多万平方千米领土。

北京市西城区2018-2019学年八年级第一学期期末英语试题

一、单选题【区级联考】北京市西城区2018-2019学年八年级第一学期期末英语试题北京初二期末2019-03-21393次1. My aunt bought a hat for ________ on my birthday. I like it very much and wear it every day.A．him B．me C．them D．her2. —What do you know about France, Betty?— France is famous ________ its fine food and wine.A．for B．to C．with D．of3. Mr. Brown is pleased with his new phone, because it runs much ________ than the old one.A．fast B．faster C．fastest D．the fastest4. The Changjiang River is ________ river in China.A．long B．longer C．longest D．the longest5. —Dad, ________ I watch my favorite TV programme at home tonight?—I’m afraid you can’t. We are going to the teahouse.A．can B．should C．must D．need6. The teacher asks us ________ English loudly in class, so that everyone can hear.A．to speak B．speaks C．speaking D．speak7. —What happened to Alice?—She ________ the horse and broke her leg.A．picked up B．fell off C．took away D．lifted up8. I usually go to bed early, but I ________ up late to watch a football game last night.A．stay B．stays C．staying D．stayed9. —Where is Tony? Mr. Li is looking for him.—He ________ basketball on the playground.A．play B．played C．is playing D．plays10. —What did she say just now?—Sorry, I don’t know. I ________ an email at that time.A．write B．will write C．wrote D．was writing二、完型填空11. The Faces of Christmas“ Oh, Sally! Christmas is going to be so terrible this year,” my best friend Laura said to me on the school bus. “ Mom and Dad have to be out of town on Christmas, and I have to stay with my Aunt Jane. She always treats (对待) me like a five-year-old! I wish I had a______family like you, so I could go somewh ere else.”I do have a big family: Mom, Dad, Mary, Jim and I, as well as lots of aunts and uncles. Every Christmas, the whole family get together at our house to have dinner.Later that day, I told Mom about Laura’s______.“ Why don’t you ask Laura to spend Christmas at our house? ” Mom offered.“ Oh, Mom, that would be great! I’m sure Laura would love to come.” I was so excited.“ There will be an extra (额外的) place at the table anyway, because Mary has a chance to go to France with her teachers.” Mom went on while washing dis hes.“No! Mom, she can’t go, or she’ll______Christmas with the family. We’ve always spent it together…” When I wanted to say more, the telephone rang. It was my brother Jim calling. He asked if Mom and Dad wouldn’t______too much if he didn’t come home for Christmas, because he wanted to go skating w ith friends. Of course, Mom and Dad said Jim could go, but I had wanted them to say no.On the afternoon of Christmas Eve, Laura came over, which cheered me up a lot.“Where are Mary and Jim?” she asked me.“They’ve made other______, so they aren’t coming home,” I said. “Christmas just isn’t going to be the same this year______them.”“Of course,” Mom went over and said. “No two Christmases are ever the same. People______—children grow older, new members are added (添加) to the family, and sometimes people die. Do you understand that, Sally?”“ Yes, Mom,” I said. “ I think I do.”Next evening, all my relatives (亲戚) arrived. As I looked around the dinner table, I really began to______what Mom had tried to tell me. I saw the new fa ces of babies, my aunt’s boyfriend, and my best friend, Laura, and I saw the old familiar faces that would always be there. No, I thought. No two Christmase s are ever the same.【小题1】A．big B．happy C．rich D．usual【小题2】A．accident B．advice C．difference D．problem【小题3】A．follow B．miss C．forget D．spend【小题4】A．ask B．speak C．mind D．think【小题5】A．conversations B．plans C．suggestions D．mistakes【小题6】A．against B．around C．between D．without【小题7】A．change B．appear C．improve D．move【小题8】A．imagine B．remember C．understand D．show三、阅读单选12. The Best Classes for KidsKids’ Cooking Price: $ 40Start date: Saturday, Oct 27, 10:00am-12:00pm Location: Sunset Park, BrooklynCome and learn some basics of cooking. Leave with mouthwatering food, such as bread and Sushi.Makerspace Price: $ 75Start date: Monday, Oct 22, 4:00pm-5:30pm Location: Tribeca, ManhattanJoin in daily activities using STEM technology like 3D printers, VR and more!Painting Party Price: $ 50Start date: Thursday, Oct 25, 3:30pm-4:30pm Location: Hoboken, New JerseyLearn about art and culture. Use your imagination to paint.Kids’ Silks Price: $ 45Start date: Tuesday, Oct 23, 3:30pm-4:15pm Location: Gowanus, BrooklynDo exercises in the air and learn basic skills to fly using sil ks.【小题1】Which class can you join if you want to learn something about art and culture?A ．Kids’ Cooking.B ．Makerspace.C ．Painting Party.D ．Kids’ Silks.【小题2】When does Kids’ Cooking start?A ．On Monday, Oct 22.B ．On Tuesday, Oct 23.C ．On Thursday, Oct 25.D ．On Saturday, Oct 27.【小题3】How much do you need to pay for Kids’ Silks if you want to join it?A ．$ 40.B ．$ 45.C ．$ 50.D ．$ 75.13. Scott’s Winter HolidayWinter break was coming soon, and all Scott wanted to do was to go snowboarding. Unluckily, Scott’s parents had booked a weeklong tropical cruise (热带邮轮). But Scott hated warm weather and asked if he could just stay at his best friend’s house to snowboard every day at the local mountain. So he kept talki ng with his parents about it, but they would not change their minds. Family time is important, and it is a tradition that they spend winter break together.When Scott got on the ship with his parents, he walked around to check everything out. He couldn’t believe how great everything was. The dining room loo ked like a palace; the game room had all of his favorite games. Then Scott saw the surfing pool (冲浪池). It wasn’t a big pool, but it had big waves, and the people who were riding the waves made it look like a lot of fun.Scott asked his parents if he could put his swim shorts on so that he could try surfing. They said, “ Of course.” And much to Scott’s surprise, they wanted totry surfing too.When Scott and his parents had their swim suits on, they headed back to the surfing pool. Scott’s dad went first and only lasted about five seconds. Then it was his mom’s turn. She actually made it five seconds longer than his dad did. When it was Scott’s turn, he was excited and nervous. Then the waves starte d. It felt similar to snowboarding but different at the same time. On his first ride, Scott rode for almost 30 seconds. He enjoyed himself a lot.By the time the weeklong cruise was over, Scott had new friends he planned to keep in touch with, a new hobby, and great memories. He told his parents tha t it was his best holiday ever.【小题1】What was Scott’s plan for winter break at first?A．Going surfing.B．Going swimming.C．Going snowboarding.D．Going mountain climbing.【小题2】What do we know from the passage?A．Scott surfed better than his parents.B．Scott taught his parents how to snowboard.C．Scott and his parents went to visit a palace by ship.D．Scott played his favorite games with his best friend.【小题3】Soctt thought his winter break was ________.A．traditional B．boring C．tiring D．enjoyable14. Recently, there have been many reports in newspapers and on TV about big animals coming into towns and cities. There have been bears in Vancouver p arks, leopards on the streets of Mumbai and wild pigs in gardens in Berlin. What happens when big animals come into our cities?Wild animals usually come into cities to look for food. In Cape Town, South Africa, baboons sometimes eat fruit from gardens and go into people’s kitchens and take food from fridges! Baboons are strong animals that scare children. Many people do not like them, but the city can be dangerous for baboons too. So metimes, baboons are hurt in car accidents and human food can kill them. The city council (议会) in Cape Town has a team of Baboon Monitors. Their job i s to find baboons in the city and take them back to the countryside. This makes the city safer for people and it is healthier for the baboons. The problem is th at many baboons will come back to the city to look for food again.In Berlin, Germany, groups of wild pigs sometimes come into the city to look for food. Pigs have come into the city for hundreds of years, but since the wint ers are warmer, there are more pigs now than in the past. Pigs eat flowers and plants in gardens and parks in the city. They also walk in the street and cause t raffic accidents. Some people like the pigs and give them food. But the city council is worried about traffic accidents. They have told people not to give thepigs food and have put up fences (围栏) to stop the pigs from entering the city.In Moscow, Russia, there are about 35, 000 wild dogs. They live in parks, markets and train stations. Some of the dogs were pets that people did not want s o they left them on the streets. Others were born on the streets and have always lived there. Some dogs live alone and others live in packs (成群). A lot of pe ople like them, and they give the dogs food and water. The winter in Moscow is very cold and people usually offer places for dogs to live in.For many animals, cities are dangerous places and they need our help to return to the countryside.【小题1】What can we learn from the second paragraph?A．Many children like playing with baboons.B．Cape Town is a safe place for baboons to stay.C．The city council tried to protect baboons in Cape Town.D．Baboons were born on the streets and have always lived there.【小题2】What do we know about wild pigs in Berlin?A．They make streets dirty.B．They eat fruit from fridges.C．They cause traffic accidents.D．They break fences around gardens.【小题3】What is the best title for the passage?A．Animal Protection B．Animals in the CityC．People and Nature D．Food for Animals15. 阅读短文，根据短文内容，从短文后各题所给的A、B、C、D四个选项中，选择最佳选项。

2018-2019学年第一学期八年级期末考试数学试题(有答案和解析)

2018-2019学年八年级（上）期末数学试卷一、选择题（本题共10小题，每小题4分，共40分）1．点A（﹣3，4）所在象限为（）A．第一象限B．第二象限C．第三象限D．第四象限2．一次函数y＝﹣3x﹣2的图象和性质，述正确的是（）A．y随x的增大而增大B．在y轴上的截距为2C．与x轴交于点（﹣2，0）D．函数图象不经过第一象限3．一个三角形三个内角的度数之比为3：4：5，这个三角形一定是（）A．锐角三角形B．直角三角形C．钝角三角形D．等腰三角形4．下列命是真命题的是（）A．π是单项式B．三角形的一个外角大于任何一个内角C．两点之间，直线最短D．同位角相等5．等腰三角形的底边长为4，则其腰长x的取值范国是（）A．x＞4B．x＞2C．0＜x＜2D．2＜x＜46．已知点A（m，﹣3）和点B（n，3）都在直线y＝﹣2x+b上，则m与n的大小关系为（）A．m＞n B．m＜nC．m＝n D．大小关系无法确定7．把函数y＝3x﹣3的图象沿x轴正方向水平向右平移2个单位后的解析式是（）A．y＝3x﹣9B．y＝3x﹣6C．y＝3x﹣5D．y＝3x﹣18．一个安装有进出水管的30升容器，水管单位时间内进出的水量是一定的，设从某时刻开始的4分钟内只进水不出水，在随后的8分钟内既进水又出水，得到水量y（升）与时间x（分）之间的函数关系如图所示．根据图象信思给出下列说法，其中错误的是（）A．每分钟进水5升B．每分钟放水1.25升C．若12分钟后只放水，不进水，还要8分钟可以把水放完D．若从一开始进出水管同时打开需要24分钟可以将容器灌满9．如图，在△ABC中，点D、E、F分别在边BC、AB、AC上，且BD＝BE，CD＝CF，∠A＝70°，那么∠FDE等于（）A．40°B．45°C．55°D．35°10．如图所示，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD，有下列四个结论：①∠PBC ＝15°，②AD∥BC，③PC⊥AB，④四边形ABCD是轴对称图形，其中正确的个数为（）A．1个B．2个C．3个D．4个二、填空（本大共4小，每小题5分，满分20分）11．函数y＝中，自变量x的取值范围是．12．若点（a，3）在函数y＝2x﹣3的图象上，a的值是．13．已知等腰三角形一腰的垂直平分线与另一腰所在直线的夹角为50°，则此等腰三角形的顶角为．14．如图，CA⊥AB，垂足为点A，AB＝24，AC＝12，射线BM⊥AB，垂足为点B，一动点E从A 点出发以3厘米/秒沿射线AN运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持ED＝CB，当点E经过秒时，△DEB与△BCA全等．三、解答题（本题共2小题，每小题8分，共16分）15．已知一次函数的图象经过A（﹣1，4），B（1，﹣2）两点．（1）求该一次函数的解析式；（2）直接写出函数图象与两坐标轴的交点坐标．16．△ABC在平面直角坐标系中的位置如图所示．（1）在图中画出△ABC与关于y轴对称的图形△A1B1C1，并写出顶点A1、B1、C1的坐标；（2）若将线段A1C1平移后得到线段A2C2，且A2（a，2），C2（﹣2，b），求a+b的值．四、解答题（本大題共2小题，每小题8分，计16分）17．如图，一次函数图象经过点A（0，2），且与正比例函数y＝﹣x的图象交于点B，B点的横坐标是﹣1．（1）求该一次函数的解析式：（2）求一次函数图象、正比例函数图象与x轴围成的三角形的面积．18．如图，P，Q是△ABC的边BC上的两点，且BP＝PQ＝QC＝AP＝AQ，求∠ABC的度数．五、解答题（20分）19．小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：（1）小明家到学校的路程是米．（2）小明在书店停留了分钟．（3）本次上学途中，小明一共行驶了米．一共用了分钟．（4）在整个上学的途中（哪个时间段）小明骑车速度最快，最快的速度是米/分．20．如图，在△ABC中，点D在AB上，点E在BC上，BD＝BE．（1）请你再添加一个条件，使得△BEA≌△BDC，并给出证明．你添加的条件是．（2）根据你添加的条件，再写出图中的一对全等三角形．（只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程）六、解答题（本大题12分）21．P为等边△ABC的边AB上一点，Q为BC延长线上一点，且PA＝CQ，连PQ交AC边于D．（1）证明：PD＝DQ．（2）如图2，过P作PE⊥AC于E，若AB＝6，求DE的长．七、解答题（本大题12分）22．某校运动会需购买A，B两种奖品，若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元．（1）求A、B两种奖品的单价各是多少元？（2）学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式．求出自变量m的取值范围，并确定最少费用W的值．八、解答題（本大题14分23．在平面直角坐标系中，O是坐标原点，A（2，2），B（4，﹣3），P是x轴上的一点（1）若PA+PB的值最小，求P点的坐标；（2）若∠APO＝∠BPO，①求此时P点的坐标；②在y轴上是否存在点Q，使得△QAB的面积等于△PAB的面积，若存在，求出Q点坐标；若不存在，说明理由．参考答案与试题解析一、选择题（本题共10小题，每小题4分，共40分）1．【分析】应先判断出所求的点的横纵坐标的符号，进而判断点A所在的象限．【解答】解：因为点A（﹣3，4）的横坐标是负数，纵坐标是正数，符合点在第二象限的条件，所以点A在第二象限．故选B．【点评】解决本题的关键是记住平面直角坐标系中各个象限内点的符号，第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．2．【分析】根据一次函数的图象和性质，依次分析各个选项，选出正确的选项即可．【解答】解：A．一次函数y＝﹣3x﹣2的图象y随着x的增大而减小，即A项错误，B．把x＝0代入y＝﹣3x﹣2得：y＝﹣2，即在y轴的截距为﹣2，即B项错误，C．把y＝0代入y＝﹣3x﹣2的：﹣3x﹣2＝0，解得：x＝﹣，即与x轴交于点（﹣，0），即C项错误，D．函数图象经过第二三四象限，不经过第一象限，即D项正确，故选：D．【点评】本题考查了一次函数图象上点的坐标特征，一次函数的图象，一次函数的性质，正确掌握一次函数图象的增减性和一次函数的性质是解题的关键．3．【分析】由题意知：把这个三角形的内角和180°平均分了12份，最大角占总和的，根据分数乘法的意义求出三角形最大内角即可．【解答】解：因为3+4+5＝12，5÷12＝，180°×＝75°，所以这个三角形里最大的角是锐角，所以另两个角也是锐角，三个角都是锐角的三角形是锐角三角形，所以这个三角形是锐角三角形．故选：A．【点评】此题考查了三角形内角和定理，解题时注意：三个角都是锐角，这个三角形是锐角三角形；有一个角是钝角的三角形是钝角三角形；有一个角是直角的三角形是直角三角形．4．【分析】根据单项式、三角形外角性质、线段公理、平行线性质解答即可．【解答】解：A、π是单项式，是真命题；B、三角形的一个外角大于任何一个与之不相邻的内角，是假命题；C、两点之间，线段最短，是假命题；D、两直线平行，同位角相等，是假命题；故选：A．【点评】本题考查了命题与定理：命题写成“如果…，那么…”的形式，这时，“如果”后面接的部分是题设，“那么”后面解的部分是结论．命题的“真”“假”是就命题的内容而言．任何一个命题非真即假．要说明一个命题的正确性，一般需要推理、论证，而判断一个命题是假命题，只需举出一个反例即可．5．【分析】根据等腰三角形两腰相等和三角形中任意两边之和大于第三边列不等式，求解即可．【解答】解：∵等腰三角形的底边长为4，腰长为x，∴2x＞4，∴x＞2．故选：B．【点评】本题考查等腰三角形的性质，等腰三角形中两腰相等，以及三角形的三边关系．6．【分析】根据一次函数y＝﹣2x+b图象的增减性，结合点A和点B纵坐标的大小关系，即可得到答案．【解答】解：∵一次函数y＝﹣2x+b图象上的点y随着x的增大而减小，又∵点A（m，﹣3）和点B（n，3）都在直线y＝﹣2x+b上，且﹣3＜3，∴m＞n，故选：A．【点评】本题考查了一次函数图象上点的坐标特征，正确掌握一次函数图象的增减性是解题的关键．7．【分析】根据平移性质可由已知的解析式写出新的解析式即可．【解答】解：根据题意，直线向右平移2个单位，即对应点的纵坐标不变，横坐标减2，所以得到的解析式是y＝3（x﹣2）﹣3＝3x﹣9．故选：A．【点评】此题主要考查了一次函数图象与几何变换，能够根据平移迅速由已知的解析式写出新的解析式：y＝kx左右平移|a|个单位长度的时候，即直线解析式是y＝k（x±|a|）；当直线y＝kx上下平移|b|个单位长度的时候，则直线解析式是y＝kx±|b|．8．【分析】根据前4分钟计算每分钟进水量，结合4到12分钟计算每分钟出水量，可逐一判断．【解答】解：每分钟进水：20÷4＝5升，A正确；每分钟出水：（5×12﹣30）÷8＝3.75 升；故B错误；12分钟后只放水，不进水，放完水时间：30÷3.75＝8分钟，故C正确；30÷（5﹣3.75）＝24分钟，故D正确，故选：B．【点评】本题考查函数图象的相关知识．从图象中获取并处理信息是解答关键．9．【分析】首先根据三角形内角和定理，求出∠B+∠C的度数；然后根据等腰三角形的性质，表示出∠BDE+∠CDF的度数，由此可求得∠EDF的度数．【解答】解：△ABC中，∠B+∠C＝180°﹣∠A＝110°；△BED中，BE＝BD，∴∠BDE＝（180°﹣∠B）；同理，得：∠CDF＝（180°﹣∠C）；∴∠BDE+∠CDF＝180°﹣（∠B+∠C）＝180°﹣∠FDE；∴∠FDE＝（∠B+∠C）＝55°．故选：C．【点评】此题主要考查的是等腰三角形的性质以及三角形内角和定理．有效地进行等角的转移时解答本题的关键．10．【分析】（1）先求出∠BPC的度数是360°﹣60°×2﹣90°＝150°，再根据对称性得到△BPC 为等腰三角形，∠PBC即可求出；（2）根据题意：有△APD是等腰直角三角形；△PBC是等腰三角形；结合轴对称图形的定义与判定，可得四边形ABCD是轴对称图形，进而可得②③④正确．【解答】解：根据题意，∠BPC＝360°﹣60°×2﹣90°＝150°∵BP＝PC，∴∠PBC＝（180°﹣150°）÷2＝15°，①正确；根据题意可得四边形ABCD是轴对称图形，∴②AD∥BC，③PC⊥AB正确；④也正确．所以四个命题都正确．故选：D．【点评】本题考查轴对称图形的定义与判定，如果一个图形沿着一条直线对折，两侧的图形能完全重合，这个图形就是轴对称图形．折痕所在的这条直线叫做对称轴．二、填空（本大共4小，每小题5分，满分20分）11．【分析】由二次根式中被开方数为非负数且分母不等于零求解可得．【解答】解：根据题意，得：，解得：x≤2且x≠﹣2，故答案为：x≤2且x≠﹣2．【点评】本题主要考查函数自变量的取值范围，函数自变量的范围一般从三个方面考虑：（1）当函数表达式是整式时，自变量可取全体实数；（2）当函数表达式是分式时，考虑分式的分母不能为0；（3）当函数表达式是二次根式时，被开方数非负．12．【分析】把点（a，3）代入y＝2x﹣3得到关于a的一元一次方程，解之即可．【解答】解：把点（a，3）代入y＝2x﹣3得：2a﹣3＝3，解得：a＝3，故答案为：3．【点评】本题考查了一次函数图象上点的坐标特征，正确掌握代入法是解题的关键．13．【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形，不可能是等腰直角三角形，所以应分开来讨论．【解答】解：当为锐角时，如图∵∠ADE＝50°，∠AED＝90°，∴∠A＝40°当为钝角时，如图∠ADE＝50°，∠DAE＝40°，∴顶角∠BAC＝180°﹣40°＝140°，故答案为40°或140°．【点评】本题考查了等腰三角形的性质及三角形内角和定理，分类讨论是正确解答本题的关键．14．【分析】设点E经过t秒时，△DEB≌△BCA；由斜边ED＝CB，分类讨论BE＝AC或BE＝AB 或AE＝0时的情况，求出t的值即可．【解答】解：设点E经过t秒时，△DEB≌△BCA；此时AE＝3t分情况讨论：（1）当点E在点B的左侧时，BE＝24﹣3t＝12，∴t＝4；（2）当点E在点B的右侧时，①BE＝AC时，3t＝24+12，∴t＝12；②BE＝AB时，3t＝24+24，∴t＝16．（3）当点E与A重合时，AE＝0，t＝0；综上所述，故答案为：0，4，12，16．【点评】本题考查了全等三角形的判定方法；分类讨论各种情况下的三角形全等是解决问题的关键．三、解答题（本题共2小题，每小题8分，共16分）15．【分析】（1）利用待定系数法容易求得一次函数的解析式；（2）分别令x＝0和y＝0，可求得与两坐标轴的交点坐标．【解答】解：（1）∵图象经过点（﹣1，4），（1，﹣2）两点，∴把两点坐标代入函数解析式可得，解得，∴一次函数解析式为y＝﹣3x+1；（2）在y＝﹣3x+1中，令y＝0，可得﹣3x+1＝0，解得x＝；令x＝0，可得y＝1，∴一次函数与x轴的交点坐标为（，0），与y轴的交点坐标为（0，1）．【点评】本题主要考查待定系数及函数与坐标轴的交点，掌握待定系数法求函数解析式的步骤是解题的关键．16．【分析】（1）根据轴对称的性质确定出点A1、B1、C1的坐标，然后画出图形即可；（2）由点A1、C1的坐标，根据平移与坐标变化的规律可规定出a、b的值，从而可求得a+b的值．【解答】解：（1）如图所示：A1（2，3）、B1（3，2）、C1（1，1）．（2）∵A1（2，3）、C1（1，1），A2（a，2），C2（﹣2，b）．∴将线段A1C1向下平移了1个单位，向左平移了3个单位．∴a＝﹣1，b＝0．∴a+b＝﹣1+0＝﹣1．【点评】本题主要考查的轴对称变化、坐标变化与平移，根据根据平移与坐标变化的规律确定出a、b的值是解题的关键．四、解答题（本大題共2小题，每小题8分，计16分）17．【分析】（1）根据点B在函数y＝﹣x上，点B的横坐标为﹣1，可以求得点B的坐标，再根据一次函数过点A和点B即可求得一次函数的解析式；（2）将y＝0代入（1）求得的一次函数的解析式，求得该函数与x轴的交点，即可求得一次函数图象、正比例函数图象与x轴围成的三角形的面积．【解答】解：（1）∵点B在函数y＝﹣x上，点B的横坐标为﹣1，∴当x＝﹣1时，y＝﹣（﹣1）＝1，∴点B的坐标为（﹣1，1），∵点A（0，2），点B（﹣1，1）在一次函数y＝kx+b的图象上，∴，得，即一次函数的解析式为y＝x+2；（2）将y＝0代入y＝x+2，得x＝﹣2，则一次函数图象、正比例函数图象与x轴围成的三角形的面积为：＝1．【点评】本题考查两条直线相交或平行问题、待定系数法求一次函数解析式，解答本题的关键是明确题意，利用数形结合的思想解答．18．【分析】根据等边三角形的性质，得∠PAQ＝∠APQ＝∠AQP＝60°，再根据等腰三角形的性质和三角形的外角的性质求得∠ABC＝∠BAP＝∠CAQ＝30°，从而求解．【解答】解：∵BP＝PQ＝QC＝AP＝AQ，∴∠PAQ＝∠APQ＝∠AQP＝60°，∠B＝∠BAP，∠C＝∠CAQ．又∵∠BAP+∠ABP＝∠APQ，∠C+∠CAQ＝∠AQP，∴∠ABC＝∠BAP＝∠CAQ＝30°．【点评】此题主要考查了运用等边三角形的性质、等腰三角形的性质以及三角形的外角的性质．五、解答题（20分）19．【分析】（1）因为y轴表示路程，起点是家，终点是学校，故小明家到学校的路程是1500米；（2）与x轴平行的线段表示路程没有变化，观察图象分析其对应时间即可．（3）共行驶的路程＝小明家到学校的距离+折回书店的路程×2．（4）观察图象分析每一时段所行路程，然后计算出各时段的速度进行比较即可．【解答】解：（1）∵y轴表示路程，起点是家，终点是学校，∴小明家到学校的路程是1500米．（2）由图象可知：小明在书店停留了4分钟．（3）1500+600×2＝2700（米）即：本次上学途中，小明一共行驶了2700米．一共用了14分钟．（4）折回之前的速度＝1200÷6＝200（米/分）折回书店时的速度＝（1200﹣600）÷2＝300（米/分），从书店到学校的速度＝（1500﹣600）÷2＝450（米/分）经过比较可知：小明在从书店到学校的时候速度最快即：在整个上学的途中从12分钟到14分钟小明骑车速度最快，最快的速度是450 米/分【点评】本题考查了函数的图象及其应用，解题的关键是理解函数图象中x轴、y轴表示的量及图象上点的坐标的意义．20．【分析】本题是开放题，应先确定选择哪对三角形，再对应三角形全等条件求解．【解答】解：添加条件例举：BA＝BC；∠AEB＝∠CDB；∠BAC＝∠BCA；证明例举（以添加条件∠AEB＝∠CDB为例）：∵∠AEB＝∠CDB，BE＝BD，∠B＝∠B，∴△BEA≌△BDC．另一对全等三角形是：△ADF≌△CEF或△AEC≌△CDA．故填∠AEB＝∠CDB；△ADF≌△CEF或△AEC≌△CDA．【点评】三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．六、解答题（本大题12分）21．【分析】（1）过点P作PF∥BC交AC于点F；证出△APF也是等边三角形，得出∠APF＝∠BCA＝60°，AP＝PF＝AF＝CQ，由AAS证明△PDF≌△QDC，得出对应边相等即可；（2）过P作PF∥BC交AC于F．同（1）由AAS证明△PFD≌△QCD，得出对应边相等FD＝CD，证出AE+CD＝DE＝AC，即可得出结果．【解答】（1）证明：如图1所示，点P作PF∥BC交AC于点F；∵△ABC是等边三角形，∴△APF也是等边三角形，∴∠APF＝∠BCA＝60°，AP＝PF＝AF＝CQ，∴∠FDP＝∠DCQ，∠FDP＝∠CDQ，在△PDF和△QDC中，，∴△PDF≌△QDC（AAS），∴PD＝DQ；（2）解：如图2所示，过P作PF∥BC交AC于F．∵PF∥BC，△ABC是等边三角形，∴∠PFD＝∠QCD，△APF是等边三角形，∴AP＝PF＝AF，∵PE⊥AC，∴AE＝EF，∵AP＝PF，AP＝CQ，∴PF＝CQ．在△PFD和△QCD中，，∴△PFD≌△QCD（AAS），∴FD＝CD，∵AE＝EF，∴EF+FD＝AE+CD，∴AE+CD＝DE＝AC，∵AC＝6，∴DE＝3．【点评】本题考查了等腰三角形的判定与性质、全等三角形的判定与性质、平行线的性质；熟练掌握等边三角形的性质，证明三角形全等是解决问题的关键．七、解答题（本大题12分）22．【分析】（1）设A奖品的单价是x元，B奖品的单价是y元，根据条件建立方程组求出其解即可；（2）根据总费用＝两种奖品的费用之和表示出W与m的关系式，并有条件建立不等式组求出x 的取值范围，由一次函数的性质就可以求出结论．【解答】解（1）设A奖品的单价是x元，B奖品的单价是y元，由题意，得，解得：．答：A奖品的单价是10元，B奖品的单价是15元；（2）由题意，得W＝10m+15（100﹣m）＝﹣5m+1500∴，解得：70≤m≤75．∵m是整数，∴m＝70，71，72，73，74，75．∵W＝﹣5m+1500，∴k＝﹣5＜0，∴W随m的增大而减小，＝1125．∴m＝75时，W最小∴应买A种奖品75件，B种奖品25件，才能使总费用最少为1125元．【点评】本题考查了一次函数的性质的运用，二元一次方程组的运用，一元一次不等式组的运用，解答时求一次函数的解析式是关键．八、解答題（本大题14分23．【分析】（1）根据题意画坐标系描点，根据两点之间线段最短，求直线AB解析式，与x轴交点即为所求点P．（2）①作点A关于x轴的对称点A'，根据轴对称性质有∠APO＝∠A'PO，所以此时P、A'、B在同一直线上．求直线A'B解析式，与x轴交点即为所求点P．②法一，根据坐标系里三角形面积等于水平长（右左两顶点的横坐标差）与铅垂高（上下两顶点的纵坐标差）乘积的一半，求得△PAB的面积为12，进而求得△QAP的铅垂高等于6，再得出直线BQ上的点E坐标为（2，8）或（2，﹣4），求出直线BQ，即能求出点Q坐标．法二，根据△QAB与△PAB同以AB为底时，高应相等，所以点Q在平行于直线AB、且与直线AB距离等于P到直线AB距离的直线上．这样的直线有两条，一条即过点P且与AB平行的直线，另一条在AB上方，根据平移距离相等即可求出．所求直线与y轴交点即点Q．【解答】解：（1）∵两点之间线段最短∴当A、P、B在同一直线时，PA+PB＝AB最短（如图1）设直线AB的解析式为：y＝kx+b∵A（2，2），B（4，﹣3）∴解得：∴直线AB：y＝﹣x+7当﹣x+7＝0时，得：x＝∴P点坐标为（，0）（2）①作点A（2，2）关于x轴的对称点A'（2，﹣2）根据轴对称性质有∠APO＝∠A'PO∵∠APO＝∠BPO∴∠A'PO＝∠BPO∴P 、A '、B 在同一直线上（如图2）设直线A 'B 的解析式为：y ＝k 'x +b '解得：∴直线A 'B ：y ＝﹣x ﹣1当﹣x ﹣1＝0时，得：x ＝﹣2∴点P 坐标为（﹣2，0）②存在满足条件的点Q法一：设直线AA '交x 轴于点C ，过B 作BD ⊥直线AA '于点D （如图3）∴PC ＝4，BD ＝2∴S △PAB ＝S △PAA '+S △BAA '＝设BQ 与直线AA '（即直线x ＝2）的交点为E （如图4）∵S △QAB ＝S △PAB则S △QAB ＝＝2AE ＝12∴AE ＝6∴E 的坐标为（2，8）或（2，﹣4）设直线BQ 解析式为：y ＝ax +q或解得：或∴直线BQ ：y ＝或y ＝∴Q 点坐标为（0，19）或（0，﹣5）法二：∵S △QAB ＝S △PAB∴△QAB 与△PAB 以AB 为底时，高相等即点Q 到直线AB 的距离＝点P 到直线AB 的距离i ）若点Q 在直线AB 下方，则PQ ∥AB设直线PQ ：y ＝x +c ，把点P （﹣2，0）代入解得c ＝﹣5，y ＝﹣x ﹣5即Q （0，﹣5）ii ）若点Q 在直线AB 上方，∵直线y ＝﹣x ﹣5向上平移12个单位得直线AB ：y ＝﹣x +7∴把直线AB：y＝﹣x+7再向上平移12个单位得直线AB：y＝﹣x+19∴Q（0，19）综上所述，y轴上存在点Q使得△QAB的面积等于△PAB的面积，Q的坐标为（0，﹣5）或（0，19）【点评】本题考查了两点之间线段最短，轴对称性质，求直线解析式，求三角形面积，平行线之间距离处处相等．解题关键是根据题意画图描点，直角坐标系里三角形面积的求法（）是较典型题，两三角形面积相等且等底时，高相等即第三个顶点在平行于底的直线上．。

2018-2019学年人教版八年级上期末考试英语试题含答案

2018-2019 学年度第一学期期末教学质量检测八年级英语试题（时间：120分钟，满分120分）友情提示：亲爱的同学，你好！今天是你展示才能的时候，只要你仔细审题、认真答题，你就会有出色的表现！请注意以下事项：1.考生务必将姓名、考场、考号填涂在答题卡规定的位置上。

2.第1-50题是选择题，每小题选出答案后，用2B铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号。

答案不能答在试卷上。

3.所有题目均在答题卡上作答，考试结束后，将答题卡上交。

第I卷（共55分）第一部分听力（25分）I.根据你所听到的对话，选择正确的选项。

每小题将听到一段对话，每段对话听两遍。

你将有10秒钟的时间完成有关小题和也读下一小题。

（共10小题，每小题1分，共10分）2. W3. W4. HA. B. C.5. W hoisthetallestofthethree?A.Nick.B.Jim.C.Sam.6. D oesthemanhaveenoughmoneytobuythebookintheend?A.Wedon’tknow.B.Yes,hedoes.C.No,hedoesn ’t.7. W hatdoesFangMingusuallydoonweekends?A.Hedoesshopping.B.Heplaysthepiano.C.Wedon ’tknow.8. W hoisTimmycalling?A.Peter.B.Tom.C.Betty.9. W hattimedoesthetrainleave?A.6:05.B.6:15.C.6:25.10. WhatcantheydoinBeachParktomorrow?A.Theycangobirdwatching.B.Theycangofishingandswim.C.Theycangobirdwatchingandswim.II. 听对话和问题，选择正确答案。

部编版2018-2019学年上学期期末考试八年级语文试卷(含答案)

部编版2018-2019学年上学期期末考试八年级语文试卷（含答案）一、积累与运用（33分）1．下列各组词中字形和加点字的读音完全正确．．的一项（）（2分）A．纤．维（q iān）喧嚣藏污纳垢．（gòu）旁逸斜出B．诏．令（zhào) 婆娑春寒料峭． (xiào) 重峦叠障C．丘壑．（hè）题跋杳．无消息（yǎo）筋疲力尽D．轩．榭（xuān）狼籍舳．舻相接（zhóu）潜滋暗长2．下列句子中，加点的词语使用恰当．．的一项是（）（2分）A．当海啸到来时，很多人都在默默无闻．．．．中，完全没有察觉到灾难的来临。

B．拙政园内，花树俯仰生姿．．．．，蜂蝶轻飞曼舞。

游客徜徉其中，流连忘返。

C．现在，诈骗的手段是层出不穷，而且诈骗手法别具匠心．．．．，令人防不胜防。

D．时间真如行云流水．．．．，还记得刚入初中时的豪言壮语，转眼间，初二学年已过去一半。

3．下列句子中，没有．．语病的一句是（）（2分）A．笔记本电脑显示了快捷、稳定、方便而日渐成为人们日常工作中的重要工具。

B．林老师的课不仅让在后排观摩的老师们受益匪浅，而且牢牢地吸引了全班学生。

C．司法大数据显示，近年来，10%的交通事故案件发生的原因为开车看手机造成的。

D．看到山林中的老枫树伸开它依然翠绿的手掌时，我不禁想起大慈大悲的千手观音。

4．下列句子组成语段，顺序排列最恰当．．的一项是（ )（2分）①考察表明，塔里木地区有非常长的聚水期。

②早在30万年前，塔里木盆地和柴达木盆地还是连在一起的大海，后来这里的地壳逐渐抬升。

③这一时期一直持续了数万年，使得塔里木地区积聚了大量地下水。

④但还是个湿润地带，降水比较丰富，草原、沼泽密布。

⑤为什么塔里木盆地地下会形成巨大的地下水库呢？A．①③②④⑤ B．⑤①②④③ C．⑤②①④③ D．①⑤②④③5．下列对语文知识和传统文化常识解析正确的一项是（）（2分）A．“商鞅立木、尾生抱柱、一诺千金、烽火戏诸侯”都是中国古人诚信守信的故事。

2018—2019学年度人教版八年级上学期期末教学质量监测语文试题(含参考答案)

2018—2019学年度上学期期末教学质量监测八年级语文试题请将所有答案填写在答题纸上一、积累运用（30分）1.下列词语中加点字每组读音都不相同的一项是（）（2分）A.狼藉．/慰藉．倦．怠/镌．刻遏．制／简明扼．要步履蹒跚．/春意阑珊．B.纤．维/拉纤．滞．留/窒．息记载．／千载．难逢鹤．立鸡群/以邻为壑．C.嶙．峋/遴．选倔．强/诀．别阻挡．／锐不可当．坦荡如砥．/同仇敌．忾D.濒．临/频．繁轩昂．/盎．然悄．然／春寒料峭．不屑．一顾/惟妙惟肖．2.下列各组词语中汉字书写完全正确的一项是( )(2分)A.仲裁娴熟不折不挠坦荡如砥B.浩翰踌躇巧妙绝伦为富不仁C.慰勉蒙寐连绵不断自出新裁D.雕镂推祟惮精竭虑诚惶成恐3.下列句子中加点词语使用有误的一项是( )(2分)A.燕子矶是一座山，山上丹崔翠壁，磴道盘曲，燕头跨江而出，宛然．．一只燕子，因而得名。

B.这部小说情节跌宕起伏，抑扬顿挫．．．．，具有很强的感染力。

C.今年“十·一”国庆节期间，前往苍马山观光的游客络绎不绝．．．．。

D.据调查：在各种不文明行为中，市民对不遵守交通法规乱闯红灯的行为深恶痛疾．．．．。

4.下列表述不正确的一项是（）（2分）A．新闻特写兼有新闻和文学的特点，要相对完整地记叙新闻事件，生动形象地展现新闻现场。

B．汪曾祺，江苏省高邮人，著有小说《受戒》《大淖记事》，被誉为“抒情的人道主义者，中国最后一个纯粹的文人，中国最后一个士大夫。

”C．《蝉》的作者法布尔，法国昆虫学家、作家，作品《昆虫故事》，又称《昆虫记》，世人称为“昆虫界的荷马”。

D.茅盾，现代作家，原名沈德鸿，字雁冰。

主要作品有长篇小说《蚀》《虹》《子夜》《腐蚀》；中篇小说《路》《三人行》；短篇小说《春蚕》《秋收》《残冬》《林家铺子》等。

5. 名著阅读（8分）【甲】几乎每次进餐后，它都要整理一下仪容。

譬如用前腿上的跗节把触须和上颚里里外外清扫干净。

【乙】嗉囊装满后，它用喙尖抓抓脚底，用沾着唾液的爪擦擦脸和眼睛，然后闭着双眼或者躺在沙上消化食物。

2018-2019学年第一学期期末质量调研八年级语文试卷及答案

2018-2019学年第一学期期末质量调研八年级语文试题第一部分积累运用（20分）1.根据拼音写汉字或给加点的汉字注拼音。

（2分）（1）街上行人摩肩接踵．，络yì不绝。

【】【】（2）雨季则有青头菌．、牛肝菌，味极鲜yú。

【】【】2.名著阅读。

（3分）有这样一只不知危险无所畏惧的灰颜色的蝗虫占着那只螳螂迎面跑了过来……蝗螂把它的翅膀极庹张开，它的翅竖了超来，并且直立得好像帆船一样。

翅膀整在它的后背上，蝗梆将身体的上端弯齿超来，样子很像一根弯曲着手柄的拐杖，并且不时地上下起落着。

(1)这段文字出自法国昆虫学家法布尔的《_ _ 》。

（1分）(2)本选段细致入微地刻画了螳螂时的动作，生动地表现了螳螂的特点。

（2分）3．阅读下面这则消息，为其拟写一个标题（15个字以内）。

（2分）据新华社报道，国家新闻出版广电总局日前下发《关于进一步加强电视上星综合频道节目管理的通知》，要求严格控制未成年人参与真人秀节目，不得借真人秀节目炒作包装明星，尤其不得在娱乐访谈、娱乐报道等节目中宣传炒作明星子女，防止包装造“星”、一夜成名。

通知中强调，总局将从节目数量、节目内容、播出时间等方面对真人秀节目进行引导调控，原则上不允许再制作播出明星子女参与的真人秀节目。

45．阅读下面几则材料，按要求回答后面的问题。

（4分)材料一：四川省乐山市峨边彝族自治县新林镇的一座山顶，每年都有游客自驾来休闲度假，即使在冬季，也有一些“背包客”。

这里森林茂密，空气干净，良好的生态吸引了大家，他们一来就会住上好几天。

在森林资源极为丰富的四川省，越来越多的市民开始选择进森林休假、疗养。

走进大山，不仅可以静心，而且可以“洗肺”，这是普通农家乐无法比拟的。

随着城市生活压力加大、休闲疗养意识增强，城镇居民去深山老林“洗肺”会成为热门项目。

材料二：森林康养产业的潜力远不只是简单的森林旅游。

四川省民政厅福利慈善处马江说，随着老龄化社会加速到来，很多退休人员要到生态环境好的地方休闲，同时疗养和保健也是他们重要的消费需求，他们是森林康养非常重要的消费人群。