三角形培优训练题集锦
三角形认识培优

1、下列条件:①∠A+∠B=∠C,②∠A:∠B:∠C=2:3:4,③∠A=90°-∠B,④∠A=∠B= 12∠C;其中能判断△ABC是直角三角形的有()个A、1B、2C、3D、42、如图,在△ABC中,CD⊥BC于点C,点D在AB的延长线上,则CD是△ABC的()A、BC边上的高B、AB边上的高C、AC边上的高D、以上都不对3、已知不等腰三角形的两边长分别是2cm和9cm,如果第三边长是整数,那么第三边长为()cmA、8B、10C、8或10D、8或9或104、下列说法中正确的是()①三角形三条中线都在三角形内部,②三角形三条角平分线都在三角形内部,③三角形三条高都在三角形内部;A、①②③B、①②C、②③D、①③5、如图所示,在△ABC中,已知点D,E,F分别为BC,AD,CE的中点,且S△BEF=4cm2,则△AEC的面积是()cm2A、 B、 C、4 D、56、以下列长度的线段为边,能构成三角形的是()A、3,6,9B、3,5,9,C、2,6,4D、4,6,97、在△ABC中,∠A:∠B:∠C=12:7:5,则△ABC是()A、钝角三角形B、锐角三角形C、直角三角形D、等腰三角形8、如图,将纸片△ABC沿着DE折叠压平,则()A、∠A =∠1+∠2;B、∠A =12(∠1+∠2);C、∠A =13(∠1+∠2);D、∠A =14(∠1+∠2)9、如图,△ABC中,∠A,∠B,∠C的外角分别记为α,β和γ,若α:β:γ=3:4:5,则∠A:∠B:∠C=()A、3:2:1;B、1:2:3;C、3:4:5;D、5:4:310、如图,BP是△ABC中∠ABC的平分线,CP是∠ACB领补角的平分线,若∠ABP=20°,∠ACP=50°,则∠A+∠P=()A、 70°B、80°C、90°D、100°11、如图,若直线l1∥l2,∠A=125°,∠B=85°,则∠1+∠2=()A、30°B、35°C、36°D、40°12、如图,△ABC中,∠ABC=50°,∠ACB=60°,点E在BC延长线上,∠ABC的平分线BD与∠ACE的平分线相较于点D,连接AD,则下列结论不正确的是()A、∠ACE=70°B、∠ACE= 90°C、∠ACE=35°D、∠ACE=55°13、如图,已知△ABC中,∠A =∠ACB,CP平分∠ACB,BD、CD分别为△ABC的外角平分线,给出以下结论:①CP⊥CD;②∠D=90°- 12∠A;③PD∥AC,其中正确结论的个数是()个A、0B、1C、2D、314、如图,∠ABC=31°,又∠BAC的平分线AE与∠FCB的平分线CE 相交于E点,则∠AEC的度数为()A、°B、°C、°D、20°15、如图,△ABC中,∠BAC=90°,AD⊥BC,∠ABC的平分线BE交AD于点F,AG平分∠DAC,给出下列结论:①∠BAD=∠C;②∠AEF=∠AFE;③∠EBC=∠C;④AG⊥EF,其中正确结论的序号是()A、②③④;B、①③④;C、①②④;D、①②③16、三角形三边长分别为8,19,a,则最长边a的取值范围是______________17、如图,∠A=65°,∠B=75°,将纸片一角折叠,使得点C落在△ABC内,若∠2=33°,则∠1=_____________18、用9根相同的火柴棒拼成一个三角形,火柴棒不允许剩余、折叠、折断,则能摆出_____________个不同的三角形19、如图,在6×6正方形网格中,每个小正方形的边长为1,格点上已有两个点A、B,再找一个格点C,使得△ABC的面积为2,这样的C点有_____________个20、在长方形网格中,每个小长方形长为2,宽为1,A、B两点是格点,再找一个格点C,使得△ABC的面积为2,满足条件的C点有_____________个21、如图,a∥b,∠1+∠2=75°,则∠3+∠4=_____________22、如图1是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE=____________23、如图,D、E分别是△ABC的边AB、BC上的点,AD=2BD,BE=CE,设△ADC面积为S1,△ACE面积为S2,若S△ABC=6,则S1 -S2=____________24、小亮家离校1km,小明家离校3km,如果小亮家和小明家距离xkm,则x的取值范围是_____________25、如图,BM是△ABC中AC边上的中线,AB=5cm,BC=3cm,那么△ABM和△BCM的周长之差是_____________26、已知AD为△ABC的中线,E为AD的中点,若△ABC的面积为20,BD=4,求点E到BC的距离27、如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,若∠BDC=140°,∠BGC=110°,求∠A的度数28、如图,已知∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于F点,(1)当∠OCD=50°时(如图1),试求∠F(2)当点C、D在射线OA,OB上任意移动时(不与点O重合)(如图2),∠F的度数是否发生变化,若变化,说明理由;若不变,求出∠F的度数。
人教版数学八年级上册第11章《三角形》培优测试题(含答案)

第11章《三角形》培优测试题一.选择题(共10小题)1.下面分别是三根小木棒的长度,能摆成三角形的是()A.5cm,8cm,2cm B.5cm,8cm,13cmC.5cm,8cm,5cm D.2cm,7cm,5cm2.如图,在△ABC中,∠ACB=100°,∠A=20°,D是AB上一点,将△ABC沿CD 折叠,使B点落在AC边上的B′处,则∠ADB′等于()A.40°B.20°C.55°D.30°3.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30,∠2=20°,则∠B=()A.20°B.30°C.40°D.50°4.三角形的三个内角的度数之比为2:3:7,则这个三角形最大内角一定是()A.75°B.90°C.105°D.120°5.在△ABC中,若AB=9,BC=6,则第三边CA的长度可以是()A.3B.9C.15D.166.如图,AD,CE为△ABC的角平分线且交于O点,∠DAC=30°,∠ECA=35°,则∠ABO等于()A.25°B.30°C.35°D.40°7.若正多边形的一个外角是60°,则该正多边形的内角和为()A.360°B.540°C.720°D.900°8.如图,图中直角三角形共有()A.1个B.2个C.3个D.4个9.有公共顶点A,B的正五边形和正六边形按如图所示位置摆放,连接AC交正六边形于点D,则∠ADE的度数为()A.144°B.84°C.74°D.54°10.如图,AE平分△ABC外角∠CAD,且AE∥BC,给出下列结论:①∠DAE=∠CAE;②∠DAE=∠B;③∠CAE=∠C;④∠B=∠C;⑤∠C+∠BAE=180°,其中正确的个数有()A.5个B.4个C.3个D.2个二.填空题(共8小题)11.三角形三边长分别为3,2a﹣1,4.则a的取值范围是.12.如图,在△ABC中,D、E分别是AB、AC上的点,点F在B C的延长线上,DE∥BC,∠A=44°,∠1=57°,则∠2= .13.在△ABC中,BO平分∠ABC,CO平分∠ACB,当∠A=50°时,∠BOC= .14.一个n边形的每个内角都为144°,则边数n为.15.在△ABC中,∠C=∠A=∠B,则∠A= 度.16.如图,AE是△ABC的角平分线,AD⊥BC于点D,若∠BAC=128°,∠C=36°,∠DAE 度.17.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=20°,则∠B= .18.如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点,若∠A=60°,则∠BMN的度数是.三.解答题(共7小题)19.(1)已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.(2)一个正多边形的内角和为1800°,求这个多边形的边数.20.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于E,∠BAC=60°,∠ABE=25°.求∠DAC的度数.21.如图①所示,为五角星图案,图②、图③叫做蜕变的五角星.试回答以下问(1)在图①中,试证明∠A+∠B+∠C+∠D+∠E=180°;(2)对于图②或图③,还能得到同样的结论吗?若能,请在图②或图③中任选其一证明你的发现;若不能,试说明理由.22.如图,已知△ABC中,高为AD,角平分线为AE,若∠B=28°,∠ACD=52°,求∠EAD的度数.23.如图,在△ABC中,AD平分∠BAC交BC于点D,AE⊥BC,垂足为E,且CF∥AD.(1)如图1,若△ABC是锐角三角形,∠B=30°,∠ACB=70°,则∠CFE= 度;(2)若图1中的∠B=x,∠ACB=y,则∠CFE= ;(用含x、y的代数式表示)(3)如图2,若△ABC是钝角三角形,其他条件不变,则(2)中的结论还成立吗?请说明理由.24.如图,BG∥EF,△ABC的顶点C在EF上,AD=BD,∠A=23°,∠BCE=44°,求∠ACB的度数.25.【探究】如图①,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.(1)若∠ABC=50°,∠ACB=80°,则∠A= 度,∠P= 度(2)∠A与∠P的数量关系为,并说明理由.【应用】如图②,在△ABC中,∠ABC的平分线与∠ACB的平分线相交于点P.∠ABC的外角平分线与∠ACB的外角平分线相交于点Q.直接写出∠A与∠Q的数量关系为.参考答案一.选择题1. C.2. A.3. D.4. C.5. B.6. A.7. C.8. C.9. B.10. A.二.填空题11. 1<a<4.12.101°.13.115°.14. 10.15.60.16. 10.17.30°.18.50°.三.解答题19.解:(1)设此三角形三个内角的比为x,2x,3x,则x+2x+3x=180,6x=180,x=30,则三个内角分别为30°、60°、90°,相应的三个外角分别为150°、120°、90°.(2)设这个多边形的边数是n,则(n﹣2)•180°=1800°,解得n=12.故这个多边形的边数为12.20.解:∵BE平分∠ABC,∴∠ABC=2∠ABE=2×25°=50°,∵AD是BC边上的高,∴∠BAD=90°﹣∠ABC=90°﹣50°=40°,∴∠DAC=∠BAC﹣∠BAD=60°﹣40°=20°.21.解:(1)证明:如图①,设BD、AD与CE的交点为M、N;△MBE和△NAC中,由三角形的外角性质知:∠DMN=∠B+∠E,∠DNM=∠A+∠C;△DMN中,∠DMN+∠DNM+∠D=180°,故∠A+∠B+∠C+∠D+∠E=180°.(2)结论仍然成立,以图③为例;延长CE交AD于F,设CE与BD的交点为M;同(1)可知:∠DMF=∠B+∠E,∠DFM=∠A+∠C;在△DMF中,∠D+∠DMF+∠DFM=180°,∴∠A+∠B+∠C+∠D+∠E=180°.22.解:∵AD为高,∠B=28°,∴∠BAD=62°,∵∠ACD=52°,∴∠BAC=∠ACD﹣∠B=24°,∵AE是角平分线,∴∠BAE=BAC=12°,∴∠EAD=∠BAD﹣∠BAE=50°.23.解:(1)∵∠B=30°,∠ACB=70°,∴∠BAC=180°﹣∠B﹣∠ACB=80°,∵AD平分∠BAC,∴∠BAD=40°,∵AE⊥BC,∴∠AEB=90°∴∠BAE=60°∴∠DAE=∠BAE﹣∠BAD=60°﹣40°=20°,∵CF∥AD,∴∠CFE=∠DAE=20°;故答案为:20;(2)∵∠BAE=90°﹣∠B,∠BAD=∠BAC=(180°﹣∠B﹣∠BCA),∴∠CFE=∠DAE=∠BAE﹣∠BAD=90°﹣∠B﹣(180°﹣∠B﹣∠BCA)=(∠BCA ﹣∠B)=y﹣x.故答案为: y﹣x;(3)(2)中的结论成立.∵∠B=x,∠ACB=y,∴∠BAC=180°﹣x﹣y,∵AD平分∠BAC,∴∠DAC=∠BAC=90°﹣x﹣y,∵CF∥AD,∴∠ACF=∠DAC=90°﹣x﹣y,∴∠BCF=y+90°﹣x﹣y=90°﹣x+y,∴∠ECF=180°﹣∠BCF=90°+x﹣y,∵AE⊥BC,∴∠FEC=90°,∴∠CFE=90°﹣∠ECF=y﹣x.24.解:∵AD=BD,∠A=23°,∴∠ABD=∠A=23°,∵BG∥EF,∠BC E=44°,∴∠DBC=∠BCE=44°,∴∠ABC=44°+23°=67°,∴∠ACB=180°﹣67°﹣23°=90°.25.解:(1)∵∠ABC=50°,∠ACB=80°,∴∠A=50°,∵∠ABC的平分线与∠ACB的平分线相交于点P,∴∠CBP=∠ABC,∠BCP=∠ACB,∴∠BCP+∠CBP=(∠ABC+∠ACB)=×130°=65°,∴∠P=180°﹣65°=115°,故答案为:50,115;(2).证明:∵BP、CP分别平分∠ABC、∠ACB,∴,,∵∠A+∠ABC+∠ACB=180°∠P+∠PBC+∠PCB=180°,∴,∴,∴;(3).理由:∵∠ABC的外角平分线与∠ACB的外角平分线相交于点Q,∴∠CBQ=(180°﹣∠ABC)=90°﹣∠ABC,∠BCQ=(180°﹣∠ACB)=90°﹣∠ACB,∴△BCQ中,∠Q=180°﹣(∠CBQ+∠BCQ)=180°﹣(90°﹣∠ABC+90°﹣∠ACB)=(∠ABC+∠ACB),又∵∠ABC+∠ACB=180°﹣∠A,∴∠Q=(180°﹣∠A)=90°﹣∠A.。
初一下学期三角形培优专题训练

初一下学期三角形培优专题训练专题一:8字形图型1. 如图所示•求 / A+Z B+Z C+Z D+Z E的大小。
3 .如图:Z A+Z B+Z C+Z D+Z E+Z F 等于()A、180° B 、360 ° C 、270 ° D 、540°A+Z B+Z C+Z D+Z E+Z F 的大小.4.已知,如图, A B C D E F的度数为B C D E F G n度DE是Z CDB的平分线,ZA1 + Z2 +Z3 +Z 4+Z 5+Z 6+Z 7=6. 如图,7. 如图Z&如图AE是Z CAB的平分线,90 ,则n=C=40°,Z E=35° .求Z B的度数.ECEB2•如图是一个六角星,其中AOE60 , A5.如图所示.求Z专题二:燕尾形图型1. (2010?帛州)如图,/ BDC=98,A. 61°B. 60°2. 如图所示,已知/ 1=20°,/ 2=25°A. 60°B. 70 °3. 如图,已知DABC边BC延长线上一点,DF丄AB于F交AC于E, / A=35° ,? / D=42°求/ ACD的度数.4. 如图,直线DE交厶ABC的边AB、AC于D E,/ACB= 74°,/ AED= 48°,则/ BDF的度数是—5.知:如图,点E在AC上,点F在AB上, BE CF交于点O且/ C—/B= 20°,/ EO F/ A= 70°,求/ C的度数.6.下图,BE是/ ABD的角平分线,CF是/ ACD的角平分线,BE与CF交于点G,点/BDC=140 , / BGC=110,则/ A的度数为()A. 70°B. 75C.80°D.85°:C=38,/ /B=23°,/ A的度数是()C.37°D. 39°,/ A=35,则/ BDC的度数为()C.80°D. 85°专题三:双垂直型1 如图所示,在△ ABC 中,/ ACB=90,/ ABC=25 , CDLAB 于 D,则/ AC ________________ 度2.图,在△ ABC 中,/ ACB=90 , CDLAB,垂足为 D.下列说法不正确的是( )A.与/ 1互余的角只有/ 2 B .Z A 与/ B 互余C.Z 仁/ B D.若/ A=2/ 1,则/ B=30°3 .如图,AC 丄BD, DE I AB,下列叙述正确的是()4 如图,△ ABC 中,Z BAC=90 , AD 丄BC 于 D, E 是 AD 上一点, 求证:Z BED>Z C5. 如图,在 VABC C 中, ACB 90 , CD 1 2A.Z A=Z BB.Z B=Z DC.Z A=ZDD.AB , AF 是角平分线,交 CD 于点E ,求证专题四:三角形三条角平分线型1如图①,BD CD 是/ ABC 和/ACB 的角平分线且相交于点 D,请猜想/ A 与/ BDC 之间的 数量关系,并说明理由。
三角形培优题型

专题一:8字形图型如图,90A B C D E F G n ∠+∠+∠+∠+∠+∠+∠=⋅︒,求 n 的大小专题二:飞镖形图型 如图,BE 是∠ABD 的角平分线,CF 是∠ACD 的角平分线,BE 与CF 交于点G ,∠BDC =140°,∠BGC =110°,则∠A 的度数为________专题三:双垂直型 如图,在ABC ∆中,90ACB CD AB AF ∠=︒⊥,,是角平分线,交CD 于点E ,求证12∠=∠专题四:三角形角平分线型如图,点M 是△ABC 两个内角平分线的交点,点N 是△ABC 两个外角平分线的交点,如果∠CMB :∠CNB =3:2,那么∠CAB = 度专题五:同一边上角平分线与高线结合型 1.2.如图,在△ABC 中,AD 是角平分线,AE 是高,已知∠BAC =2∠B ,∠B =2∠DAE ,求∠ACB 的度数。
专题六:图形的折叠问题如图所示,将沿着DE 翻折,若,则.专题七:三角形高与面积的计算在△ABC 中,点D 为边BC 的中点,点E 为线段AD 上一点,且满足AE =2ED ,则△ABC 与△BDE 的面积之比为 。
专题八:三角形三边关系与周长1.若一个等腰三角形的三边长均为整数,且周长为10,则底边长为2.等腰三角形一边长为cm 5,另一边为cm 10,则它的周长是 cm 。
3.已知:△ABC 中,AB =AC ,BD 是AC 边上的中线,如果D 点把三角形ABC 的周长分为12cm 和15cm 两部分,则此三角形腰长为__________.4.若a ,b ,c 分别是三角形的三边,化简│a -b -c │+│b -c -a │-│c -a +b │5.已知等腰三角形的底边长为8cm ,一腰的中线把三角形的周长分为两部分,其中一部分比另一部分长2cm ,则这个三角形的腰长为____________。
专题九:综合题型1.一个n 边形切去一个角后所得多边形的内角和为1800°,则这个多边形的边数是______________.2.如图,△ABC 中,AE 、BF 是角平分线,它们相交于点O .(∠ABC >∠C ), (1)试说明∠BOA=90°+∠C ;(2)当AD 是高,判断∠DAE 与∠C 、∠ABC 的关系,并说明理由.ABC △1280∠+∠=°B ∠= A EDCBG F12。
全等三角形专题培优(带答案)

全等三角形专题培优考试总分: 110 分考试时间: 120 分钟卷I(选择题)一、选择题(共 10 小题,每小题 2 分,共 20 分)1.如图为个边长相等的正方形的组合图形,则A. B.C. D.2.下列定理中逆定理不存在的是()A.角平分线上的点到这个角的两边距离相等B.在一个三角形中,如果两边相等,那么它们所对的角也相等C.同位角相等,两直线平行D.全等三角形的对应角相等3.已知:如图,,,,则不正确的结论是()A.与互为余角B.C.D.4.如图,是的中位线,延长至使,连接,则的值为()A. B. C. D.5.如图,在平面直角坐标系中,在轴、轴的正半轴上分别截取、,使;再分别以点、为圆心,以大于长为半径作弧,两弧交于点.若点的坐标为,则与的关系为()A. B.C. D.6.如图,是等边三角形,,于点,于点,,则下列结论:①点在的角平分线上;②;③;④.正确的有()A.个B.个C.个D.个7.如图,直线、、″表示三条相互交叉的公路,现计划建一个加油站,要求它到三条公路的距离相等,则可供选择的地址有()A.一处B.二处C.三处D.四处8.如图,是的角平分线,则等于()A. B.C. D.9.已知是的中线,且比的周长大,则与的差为()A. B.C. D.10.若一个三角形的两条边与高重合,那么它的三个内角中()A.都是锐角B.有一个是直角C.有一个是钝角D.不能确定卷II(非选择题)二、填空题(共 10 小题,每小题 2 分,共 20 分)11.问题情境:在中,,,点为边上一点(不与点,重合),交直线于点,连接,将线段绕点顺时针方向旋转得第1页,共7页第2页,共7页………外………○……………………○……………………○※※请※※不※※答※※题※………内………○……………………○……………………○到线段(旋转角为),连接.特例分析:如图.若,则图中与全等的一个三角形是________,的度数为________.类比探究:请从下列,两题中任选一题作答,我选择________题. :如图,当时,求的度数; :如图,当时,①猜想的度数与的关系,用含的式子表示猜想的结果,并证明猜想;②在图中将“点为边上的一点”改为“点在线段的延长线上”,其余条件不变,请直接写出的度数(用含的式子表示,不必证明)12.如图,正方形纸片的边长为,点、分别在边、上,将、分别沿、折叠,点、恰好都落在点处,已知,则的长为________.13.在中,为的平分线,于,于,面积是,,,则的长为________.14.在中,,的垂直平分线与所在的直线相交所得到锐角为,则等于________.15.如图,平分,于,于,,则图中有________对全等三角形.16.如图,在中,,点从点出发沿射线方向,在射线上运动.在点运动的过程中,连结,并以为边在射线上方,作等边,连结. 当________时,;请添加一个条件:________,使得为等边三角形; ①如图,当为等边三角形时,求证:;②如图,当点运动到线段之外时,其它条件不变,①中结论还成立吗?请说明理由.17.如图,从圆外一点引圆的两条切线,,切点分别为,.如果,,那么弦的长是________.18.如图,在中,,,是的平分线,平分交于,则________.19.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图,在中,,平分,, 求的长.小聪思考:因为平分,所以可在边上取点,使,连接.这样很容易得到,经过推理能使问题得到解决(如图). 请回答:是________三角形.的长为________.参考小聪思考问题的方法,解决问题: 如图,已知中,,,平分,,.求的长.20.如图,在和中,,,若要用“斜边直角边..”直接证明,则还需补充条件:________.三、解答题(共 7 小题 ,每小题 10 分 ,共 70 分 )21.如图,已知为等边三角形,为延长线上的一点,平分,,求证:为等边三角形.22.尺规作图(不要求写作法,保留作图痕迹)如图,作①的平分线;②边上的中线;22.一块三角形形状的玻璃破裂成如图所示的三块,请你用尺规作图作一个三角形,使所得的三角形和原来的三角形全等.(不要求写作法,保留作图痕迹.不能在原图上作三角形)22.如图:在正方形网格中有一个,按要求进行下列画图(只能借助于网格):①画出中边上的高(需写出结论).②画出先将向右平移格,再向上平移格后的.23.平行四边形中,,点为边上一点,连结,点在边所在直线上,过点作交于点.如图,若为边中点,交延长线于点,,,,求;如图,若点在边上,为中点,且平分,求证:;如图,若点在延长线上,为中点,且,问中结论还成立吗?若不成立,那么线段、、满足怎样的数量关系,请直接写出结论.24.如图,直线与轴、轴分别交于、两点,直线与直线关于轴对称,已知直线的解析式为,求直线的解析式;过点在的外部作一条直线,过点作于,过点作于,请画出图形并求证:;沿轴向下平移,边交轴于点,过点的直线与边的延长线相交于点,与轴相交于点,且,在平移的过程中,①为定值;②为定值.在这两个结论中,有且只有一个是正确的,请找出正确的结论,并求出其值.25.如图:,,过点,于,于,.求证:.第3页,共7页第4页,共7页26.如图,点,在上,,,,与交于点.求证:;试判断的形状,并说明理由.27.如图,已知点是平分线上一点,,,垂足为、吗?为什么?是的垂直平分线吗?为什么? 答案 1.B 2.D 3.D 4.A 5.B 6.D 7.D 8.A 9.B 10.B11.[ “”, “” ][ “” ] 12.[ “” ] 13.[ “” ] 14.[ “或” ]15.[ “” ] 16.[ “;” ][ "添加一个条件,可得为等边三角形; 故答案为:;①∵与是等边三角形, ∴,,, ∴, 即, 在与中, , ∴, ∴;②成立,理由如下; ∵与是等边三角形, ∴,,, ∴, 即, 在与中, , ∴, ∴." ] 17.[ “” ] 18.[ “” ]19.[ "解:是等腰三角形, 在与中,, ∴, ∴,, ∵, ∴, ∴,∴是等腰三角形;" ][ "的长为, ∵中,,, ∴, ∵平分, ∴,在边上取点,使,连接, 则,∴, ∴, ∴,在边上取点,使,连接, 则, ∴,, ∵, ∴, ∴, ∵,∴." ]\"go题库\"20.[ “” ]21.证明:∵为等边三角形,∴,,即,∵平分,∴,在和中,,∴,∴,,又,∴,∴为等边三角形.22.解:如图所示:;如图所示:即为所求;;①如图所示:即为所求;②如图所示:即为所求;..23.解:如图,在平行四边形中,,∴,∵在中,为的中点,,∴,又∵,∴,故可设,,则中,,解得,∴,又∵,,∴为的中点,∴;如图,延长交的延长线于点,则,∵,∴,又∵平分,∴,∴是等腰直角三角形,∴,又∵,∴,∴,,又∵为的中点,∴,∴,∴,∵,∴;第5页,共7页第6页,共7页…○…………装订…………○…※※请※※不※※内※※答※※题※※…○…………装订…………○…若点在延长线上,为中点,且,则中的结论不成立,正确结论为:. 证明:如图,延长交的延长线于点,则,∵, ∴, ∴, 又∵, ∴, ∴,,又∵为的中点, ∴, ∴, ∴, ∵, ∴.24.解:∵直线与轴、轴分别交于、两点, ∴,,∵直线与直线关于轴对称, ∴∴直线的解析式为:;如图..∵直线与直线关于轴对称, ∴,∵与为象限平分线的平行线, ∴与为等腰直角三角形, ∴, ∵, ∴ ∴ ∴,,∴;①对,过点作轴于,直线与直线关于轴对称∵,, 又∵, ∴, 则, ∴ ∴ ∴ ∴ ∴.25.证明:连接, ∵, ∴, ∵, ∴, ∴, ∵,, ∴, 在和中,∴.26.证明:∵,∴,即.又∵,,∴,∴.解:为等腰三角形理由如下:∵,∴,∴,∴为等腰三角形.27.解:.理由:∵是的平分线,且,,∴,∴;是的垂直平分线.理由:∵,在和中,,∴,∴,由,,可知点、都是线段的垂直平分线上的点,从而是线段的垂直平分线.第7页,共7页。
人教版 八年级数学 第12章 全等三角形 培优训练 (含答案)

人教版八年级数学第12章全等三角形培优训练一、选择题1. 下列各组的两个图形属于全等图形的是()2. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE相交于点M,则∠DCE等于()A.∠B B.∠A C.∠EMF D.∠AFB3. 如图所示,P是∠BAC内一点,且点P到AB,AC的距离PE,PF相等,则△PEA≌△PF A的依据是()A.HL B.ASA C.SSS D.SAS4. 根据下列条件,能画出唯一的△ABC的是()A.AB=3,BC=4,AC=8 B.AB=4,BC=3,∠A=30°C.AB=5,AC=6,∠A=50°D.∠A=30°,∠B=70°,∠C=80°5. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上6. 如图,有一张三角形纸片ABC,已知∠B=∠C=x°,按下列方案用剪刀沿着箭头方向剪开,可能得不到全等三角形纸片的是()7. 现已知线段a,b(a<b),∠MON=90°,求作Rt△ABO,使得∠O=90°,OA=a,AB=b.小惠和小雷的作法分别如下:小惠:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点A为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.小雷:①以点O为圆心、线段a的长为半径画弧,交射线ON于点A;②以点O为圆心、线段b的长为半径画弧,交射线OM于点B,连接AB,△ABO即为所求.则下列说法中正确的是()A.小惠的作法正确,小雷的作法错误B.小雷的作法正确,小惠的作法错误C.两人的作法都正确D.两人的作法都错误8. 如图,点G在AB的延长线上,∠GBC,∠BAC的平分线相交于点F,BE⊥CF 于点H.若∠AFB=40°,则∠BCF的度数为()A.40°B.50°C.55°D.60°二、填空题9. 如图,在Rt△ABC中,∠C=90°,∠B=20°,以点A为圆心,小于AC的长为半径画弧与AB,AC分别交于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧相交于点P,连接AP并延长交BC于点D,则∠ADB=°.10. 如图,在△ABC中,AD⊥BC于点D,要使△ABD≌△ACD,若根据“HL”判定,还需要添加条件:____________.11. 如图,若AB=AC,BD=CD,∠A=80°,∠BDC=120°,则∠B=________°.12. 在△ABC中,AB=4,AC=3,AD是△ABC的角平分线,则△ABD与△ACD 的面积之比是________.13. (2019•南通)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=__________度.14. 如图所示,已知AD∥BC,则∠1=∠2,理由是________________;又知AD =CB,AC为公共边,则△ADC≌△CBA,理由是______,则∠DCA=∠BAC,理由是__________________,则AB∥DC,理由是________________________________.15. 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB,垂足为E.若△DBE的周长为20,则AB=________.16. 如图,△ABC的两条外角平分线BP,CP相交于点P,PE⊥AC交AC的延长线于点E.若△ABC的周长为11,PE=2,S△BPC =2,则S△ABC=.三、解答题17. 育新中学校园内有一块直角三角形(Rt△ABC)空地,如图所示,园艺师傅以角平分线AD为界,在其两侧分别种上了不同的花草,在△ABD区域内种植了一串红,在△ACD区域内种植了鸡冠花,并量得两直角边AB=20 m,AC=10 m,分别求一串红与鸡冠花两种花草的种植面积.18. 如图,已知△ACF≌△DBE,且点A,B,C,D在同一条直线上.若AD=16,BC=10,求AB的长.19. 我们把两组邻边分别相等的四边形叫做“筝形”.如图,四边形ABCD是筝形,其中AB=AD,CB=CD,P是对角线AC上除A,C外的任意一点.求证:∠ABP =∠ADP.20. 如图,已知AP∥BC,∠P AB的平分线与∠CBA的平分线相交于点E,过点E 的直线分别交AP,BC于点D,C.求证:AD+BC=AB.21. (1)如图①,在△ABC中,∠BAC=90°,AB=CA,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE.(2)如图②,将(1)中的条件改为:在△ABC中,AB=CA,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角,则结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由.人教版八年级数学第12章全等三角形培优训练-答案一、选择题1. 【答案】A2. 【答案】A[解析] ∵△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,∴∠DCE=∠B.故选A.3. 【答案】A4. 【答案】C[解析] 对于选项A来说,AB+BC<AC,不能画出△ABC;对于选项B来说,可画出△ABC为锐角三角形或者钝角三角形;对于选项C来说,已知两边及其夹角,△ABC是唯一的;对于选项D来说,△ABC的形状可确定,但大小不确定.5. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.6. 【答案】C[解析] 选项A中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项B中由全等三角形的判定定理“SAS”证得图中两个小三角形全等.选项C中,如图①,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.这两个角所对的边是BE和CF,而已知条件给的是BD=CF=3,故不能判定两个小三角形全等.选项D中,如图②,∵∠DEC=∠B+∠BDE,∴x°+∠FEC=x°+∠BDE.∴∠FEC=∠BDE.又∵BD=CE=2,∠B=∠C,∴△BDE≌△CEF.故能判定两个小三角形全等.7. 【答案】A[解析] AB=b,AB是斜边,小惠作的斜边长是b符合条件,而小雷作的是一条直角边长是b.故小惠的作法正确,小雷的作法错误.8. 【答案】B[解析] 如图,过点F分别作FZ⊥AE于点Z,FY⊥CB于点Y,FW⊥AB于点W.∵AF平分∠BAC,FZ⊥AE,FW⊥AB,∴FZ=FW.同理FW=FY.∴FZ=FY.又∵FZ⊥AE,FY⊥CB,∴∠FCZ=∠FCY.由∠AFB=40°,易得∠ACB=80°.∴∠ZCY=100°.∴∠BCF=50°.二、填空题9. 【答案】125[解析] 由题意可得AD平分∠CAB.∵∠C=90°,∠B=20°,∴∠CAB=70°.∴∠CAD=∠BAD=35°.∴∠ADB=180°-20°-35°=125°.10. 【答案】AB =AC11. 【答案】20[解析] 如图,过点D 作射线AF.在△BAD 和△CAD 中,⎩⎨⎧AB =AC ,AD =AD ,BD =CD ,∴△BAD ≌△CAD(SSS). ∴∠BAD =∠CAD ,∠B =∠C.∵∠BDF =∠B +∠BAD ,∠CDF =∠C +∠CAD , ∴∠BDF +∠CDF =∠B +∠BAD +∠C +∠CAD , 即∠BDC =∠B +∠C +∠BAC. ∵∠BAC =80°,∠BDC =120°, ∴∠B =∠C =20°.12. 【答案】4∶3【解析】如解图,过D 作DE ⊥AB ,DF ⊥AC ,垂足分别为E 、F ,∵AD 是∠BAC 的平分线,∴DE =DF(角平分线上的点到角两边的距离相等),设DE=DF=h,则S△ABDS△ACD =12AB·h12AC·h=43.13. 【答案】70【解析】∵∠ABC=90°,AB=AC,∴∠CBF=180°–∠ABC=90°,∠ACB=45°,在Rt△ABE和Rt△CBF中,AB CBAE CF=⎧⎨=⎩,∴Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=25°,∴∠ACF=∠ACB+∠BCF=45°+25°=70°,故答案为:70.14. 【答案】两直线平行,内错角相等SAS全等三角形的对应角相等内错角相等,两直线平行15. 【答案】20[解析] 由角平分线的性质可得CD=DE.易证Rt△ACD≌Rt△AED,则AC=AE,DE+DB=CD+DB=BC=AC=AE,故DE+DB+EB =AE+EB=AB.16. 【答案】7[解析] 过点P作PF⊥BC于点F,PG⊥AB于点G ,连接AP.∵△ABC的两条外角平分线BP,CP相交于点P,∴PF=PG=PE=2.∵S△BPC=2,∴BC·2=2,解得BC=2.∵△ABC的周长为11,∴AC+AB=11-2=9.∴S △ABC =S △ACP +S △ABP -S △BPC =AC ·PE+AB ·PG-S △BPC =×9×2-2=7.三、解答题17. 【答案】解:如图,过点D 作DE ⊥AB 于点E ,DF ⊥AC 于点F. ∵AD 是∠BAC 的平分线,∴DE =DF. ∵AB =20 m ,AC =10 m ,∴S △ABC =12×20×10=12×20·DE +12×10·DF ,解得DE =203(m).∴△ACD 的面积=12×10×203=1003(m 2),△ABD 的面积=12×20×203=2003(m 2).故一串红的种植面积为2003 m 2,鸡冠花的种植面积为1003 m 2.18. 【答案】解:∵△ACF ≌△DBE ,∴AC=DB.∴AC-BC=DB-BC ,即AB=CD.∵AD=16,BC=10,∴AB=CD=(AD-BC )=3.19. 【答案】证明:在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,AC =AC ,CB =CD , ∴△ABC ≌△ADC.∴∠BAP =∠DAP.在△BAP 和△DAP 中,⎩⎨⎧AB =AD ,∠BAP =∠DAP ,AP =AP , ∴△BAP ≌△DAP.∴∠ABP =∠ADP.20. 【答案】证明:如图,在AB 上截取AF =AD ,连接EF.∵AE 平分∠PAB ,∴∠DAE =∠FAE.在△DAE 和△FAE 中,⎩⎨⎧AD =AF ,∠DAE =∠FAE ,AE =AE ,∴△DAE ≌△FAE(SAS).∴∠AFE =∠ADE.∵AD ∥BC ,∴∠ADE +∠C =180°.又∵∠AFE +∠EFB =180°,∴∠EFB =∠C.∵BE 平分∠ABC ,∴∠EBF =∠EBC.在△BEF 和△BEC 中,⎩⎨⎧∠EFB =∠C ,∠EBF =∠EBC ,BE =BE ,∴△BEF ≌△BEC(AAS).∴BF =BC.∴AD +BC =AF +BF =AB.21. 【答案】解:(1)证明:∵BD ⊥直线m ,CE ⊥直线m , ∴∠BDA =∠AEC =90°.∴∠BAD +∠ABD =90°.∵∠BAC =90°,∴∠BAD +∠CAE =90°. ∴∠CAE =∠ABD.在△ADB 和△CEA 中,⎩⎨⎧∠ABD =∠CAE ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.(2)成立.证明:∵∠BDA =∠BAC =α,∴∠DBA +∠BAD =∠BAD +∠EAC =180°-α. ∴∠DBA =∠EAC.在△ADB 和△CEA 中,⎩⎨⎧∠DBA =∠EAC ,∠BDA =∠AEC ,AB =CA ,∴△ADB ≌△CEA(AAS).∴BD =AE ,AD =CE.∴DE =AE +AD =BD +CE.。
全等三角形培优专题训练

探索三角形全等1、一长方形纸片沿对角线剪开,得到两三角形纸片,再将这两纸片摆成如以下图形式,使点B 、F 、C 、D 在同一条直线上.⑴求证:AB ⊥ED ;⑵假设PB =BC ,请找出图中与此条件有关的一对全等三角形,并给予证明2、如图,在△ABC 中,AC =BC ,∠ACB =90°,AD 平分∠BAC ,BE ⊥AD 交AC 的延长线于F ,E 为垂足,那么结论:①AD =BF ;②CF =CD ;③AC +CD =AB ;④BE =CF ;⑤BF =2BE.其中正确的选项是〔 〕3、如图,点C在线段AB上,DA ⊥AB,EB⊥AB,FC⊥AB,且DA=BC,EB=AC,FC=AB,∠AFB=51°,求∠DFC的度数.中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线M、N上,且OE=OF.⑴图中共有几对全等三角形,请把它们都写下来;⑵求证:∠MAE=∠NCF全等三角形的应用全等三角形常用来转移线段和角,用它来证明:①线段和角的等量关系②线段和角的和差倍分关系③直线与直线的平行或垂直等位置关系1、如图,BD、CE分别是△ABC的边AC和AB上的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.试判断AP与AQ的关系,并证明.2、如图,AD是△ABC的高,E为AC上一点,BE交AD于点F,且BF=AC,FD=CD,求证:BE⊥ACB3、如图,在△ABC中,AB=AC,AD=AE,∠BAC=∠DAC=90°.⑴当点D在AC上时,如图①,线段BD,CE有怎样的数量和位置关系"证明你猜测的结论.⑵将图①中的△ADE绕点A顺时针旋转α角(0°<α<90°) ,如图②,线段BD、CE有怎样的数量关系和位置关系?问明理由.4、在△ABC中,AB=AC,点D是直线BC上一点〔不与B、C重合〕,以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.⑴如图①,当点D在线段BC上时,假设∠BAC=90°,那么∠BCE=_______度.⑵设∠BAC=α,∠BCE=βa、如图②,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.②B①①b、当点D在直线BC上移动时,α,β之间有怎样的数量关系?请直接写出你的结论.辅助线作法之连接法在几何证明中,常通过添加辅助线来构造全等三角形.常见的添加辅助线方法有:连接法、截长补短法、倍长中线法、翻折法、旋转法以及利用特殊条件构造全等三角形等等.1、如图,△ABC的两条高BD,CE相交于点P,且PD=PE.证明∶AC=ABA2、AB =DE ,BC =EF ,∠B =∠E ,AF =CD 求证:AC ∥DF3、如图,AB 交CD 于点O ,AD 、CB 的延长线相交于点E ,且OA =OC ,EA =EC.∠A =∠C 吗?点O 在∠AEC 的平分线上吗?辅助线作法之倍长中线法在题目条件中含有中线的问题,我们常用的辅助线就是将中线延长一倍,其目的是为了得一对BE全等三角形,将分散的条件集中到一个三角形中去.1、△ABC中,AB=5,AC=3,求中线AD的取值围.2、如图,在△ABC中,AD是∠BAC的平分线,又是BC上的中线求证:AB=ACBB3、在△ABC 中,D 是边BC 上的一点,且CD =AB ,∠BAD =∠BDA ,AE 是△ABD 的中线.求证∶AC =2AE4、△ABC 中,D 为BC 的中点,DE ⊥DF 交AB ,AC 于点E ,F.求证:BE +CF >EF辅助线作法之截长补短法截长法:在第三条线段上截下一段使其等于两条线段中的一条,再证明剩余局部与另一条相等. 补短法:把两条线段中的一条补到另一条线段上去,证明所得新线段与第三条线段相等.B1、AC ∥BD ,EA ,EB 分别平分∠CAB 和∠DBA ,点E在CD 上.求证:AB =AC +BD2、在四边形ABCD 中,AC 平分∠BAD ,CE ⊥AB 于点E ,且AE =½〔AB +AD 〕.求证∶∠B +∠D =180°ABD3、如图,△ABC中,∠A=90°,AB=AC,D为AC的中点,AE⊥BD于E,延长AE交BC 于F.求证:∠ADB=∠CDF4、如图,∠C=90°,AC=BC,AD是∠BAC的角平分线.求证∶AC+CD=AB12、如图,AB=CD=AE=BC+DE=2,∠ABC=∠AED=90°,求五边形ABCDE的面积.B辅助线作法之利用特殊条件构造全等三角形2、如图,在△ABC 中,AC =½AB ,AD 平分∠BAC ,且AD =BD求证:CD ⊥AC全等三角形在动态几何中的运用1、如图,△ABC 的边BC 在直线l 上,AC ⊥BC ,且AC =BC.△EFP 的边FP 也在直线l 上,边EF 与边AC 重合,且EF =FP.⑴在图①中,请你通过观察、测量、猜测并写出AB 与AP 所满足的数量关系和位置关系; ⑵将△EFP 沿直线l 向左平移到图②的位置时,EP 交AC 于点Q,连接AP,BQ.猜测并写出BQ 与AP 所满足的数量关系和位置关系,并证明你的猜测;⑶将△EFP 沿直线l 向左平移到图③的位置时,EP 的延长线交AC 的延长线于点Q,连接AP,BQ.你认为⑵中所猜测的BQ 与AP 的数量关系和位置关系还成立吗"假设成立,给出证明;假设不成立,请说明理由.B探究角平分线1、如图,△ABC 的外角∠ACD 的平分线CP 与角∠ABC 的平分线BP 相交于点P ,假设∠BPC =40°,那么∠CAP =_____________.2、如图,∠B =∠C =90°,M 是BC 的中点,DM 平分∠ADC.求证:AM 平分∠DAB3、如图,在△ABC 中,∠BAC =90°,AB =AC,BE 平分∠ABC,CE ⊥BE.求证:CE =12BD4、如图,在△ABC 中,AD 平分∠BAC ,BD =CD 求证:∠B =∠CBB5、如图,在Rt △ABC 中,∠C =90°,AC =BC ,AD 是∠BAC 的平分线,交BC 于D ,DE ⊥AB 于E ,假设AB =10cm ,那么△DBE 的周长是多少?6、AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE =DG ,△ADG 和△AED 的面积分别为50和39,那么△EDF 的面积为多少?7、如图,△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F.求证:BE =CFB8、在△ABC 中,AD 是∠BAC 的平分线,E 、F 分别为AB 、AC 上的点,且∠EDF +∠BAF =180°⑴求证:DE =DF⑵如果把最后一个条件改为AE >AF ,且∠AED +∠AFD =180°,那么结论还成立吗?9、如图,AB =AC ,BE ⊥AC 于E ,CF ⊥AB 于F ,BE 与CF 交于点D求证:点D 在∠BAC 的平分线上.10、如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,以下结论正确的选项是( )A.AB-AD>CB-CDB.AB-AD=CB-CDC.AB-AD<CB-CDD.AB-CD与CB-CD的大小关系不确定11、如图,△ABC中,∠B=60°,∠BAC,∠BCA的平分线AD,CE相交于点O.求证:DC+AE=AC12、如图,△ABC,P为角平分线AD、BE、CF的交点,过点P作PG⊥BC于G点。
培优专题2:巧用三角形的外角解决问题

大小为 75° . 来自9. [推理能力]如图, D , E , F 分别是△ ABC 三边延长线上的点,∠ D +∠ E +∠ F =107°,求∠1+∠2+∠3的度数.
◉答案 解:易知∠ D +∠3=∠ CAB ,∠ E +∠1=∠ ABC ,∠ F +∠2=∠ ACB ,∴∠ D +∠ E +∠ F +∠1+∠2+∠3=∠ CAB +∠ ABC +∠ ACB =180°.∵∠ D +∠ E +∠ F
第6题图
7. [一题多解]如图,直线 AB ∥ EF ,点 C 是直线 AB 上一点,点 D 是直线 AB 外一
点,若∠ BCD =95°,∠ CDE =25°,则∠ DEF 的度数是
120° .
第7题图
8. [一题多解]如图,△ EFG 的三个顶点 E , F 和 G 分别在平行线 AB , CD 上, FH 平分∠ EFG ,交线段 EG 于点 H ,若∠ AEF =36°,∠ BEG =57°,则∠ EHF 的
第一章 三角形
培优专题2:巧用三角形的外角解决问题
1. (贺州校级一模)如图,∠ A ,∠1,∠2的大小关系是( BB )
A. ∠ A >∠1>∠2
B. ∠2>∠1>∠ A
C. ∠ A >∠2>∠1
D. ∠2>∠ A >∠1
第1题图
2. 如图,在△ ABC 中,点 D 在边 AB 上, BE ∥ AC ,连接 ED . 若∠ A =56°, ∠ E =48°,则∠ ADE =( D )D
A. 94°
B. 98°
第2题图 C. 102°
D. 104°
3. 图①是一路灯的实物图,图②是该路灯的平面示意图,则图②中∠ CBN 的度数
《三角形》培优专题

第三周培优专题《三角形》1出题人:陈乐宇 审题人:刘凯迪班级: 姓名: 学号:一、热身题1、三角形的三个内角中,锐角的个数不少于( )A. 1 个B. 2 个C. 3个D. 不确定2. △ABC 中,∠A :∠B :∠C=1:2:3,CD ⊥AB 于点D ,若BC=a ,则AD 等于( )A a B a C a D a (1232323)3. 下列命题的逆命题是真命题的是( )A. 对顶角相等B. 若a=b ,则|a|=|b|C. 末位是零的整数能被5整除D. 直角三角形的两个锐角互余4. 如图,△ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,则∠A 的度数为( )A. 30°B. 36°C. 45°D. 70°二、渐入佳境1. 等腰三角形的腰长为2cm ,面积等于1平方cm ,则它的顶角的度数为________。
2. 已知,如图,O 是△ABC 的∠ABC 、∠ACB 的角平分线的交点,OD ∥AB 交BC 于D ,OE ∥AC 交BC 于E ,若BC=10cm ,则△ODE 的周长________。
3. 如图,在Rt △ABC 中,∠B=90°,∠A=40°,AC 的垂直平分线MN 与AB 相交于D 点,则∠BCD 的度数是________。
第2题 第3题 第4题4. 如图,∠AOP=∠BOP=15°,PC ∥OA ,PD ⊥OA ,若PC=4,则PD 的长为________。
三、思维大考验1、如图,AD⊥CD,AB=10,BC=20,∠A=∠C=30°,求AD、CD的长。
2.如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高。
求证:AD垂直平分EF。
3、如图1,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN、MC交于点E,BM、CN相交于点F.图1 图2(1)求证:AN=BM;(2)求证:△CEF为等边三角形;(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在图2中补出符合要求的图形,并判断第(1)、(2)两小题的结论是否仍然成立。
全等三角形经典培优题型(含标准答案)
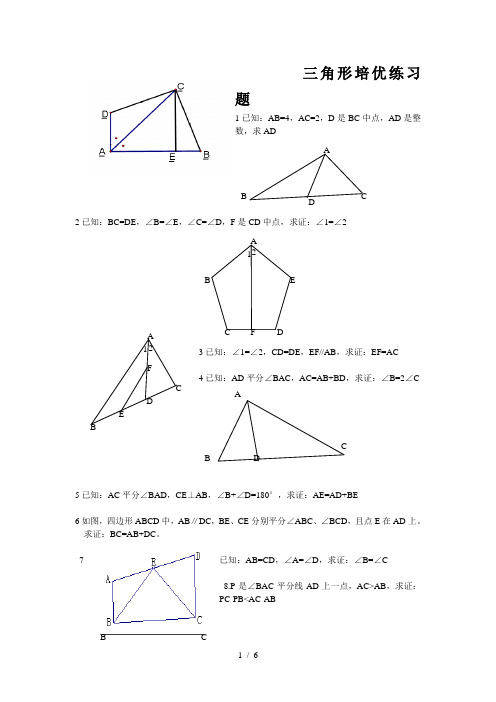
三角形培优练习题1已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD2已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠23已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC4已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠C5已知:AC 平分∠BAD ,CE ⊥AB ,∠B+∠D=180°,求证:AE=AD+BE6如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
求证:BC=AB+DC 。
已知:AB=CD ,∠A=∠D ,求证:∠B=∠C78.P 是∠BAC 平分线AD 上一点,AC>AB ,求证:PC-PB<AC-ABCDBA BC DEF 2 1ADBCA B CD ABACDF2 1 E9已知,E 是AB 中点,AF=BD ,BD=5,AC=7,求DC10.如图,已知AD ∥BC ,∠P AB 的平分线与∠CBA 的平分线相交于E ,CE 的连线交AP 于D .求证:AD +BC =AB .11如图,△ABC 中,AD 是∠CAB 的平分线,且AB =AC +CD ,求证:∠C =2∠B12如图:AE 、BC 交于点M ,F点在AM 上,BE∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
13已知:如图,AB =AC ,BD ⊥AC ,CE ⊥AB ,垂足分别为D 、E ,BD 、CE 相交于点F 。
求证:BE =CD .14在△ABC 中,︒=∠90ACB ,BC AC =,直线MN 经过点C ,且MN AD ⊥于D ,MN BE ⊥于E .(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①ADC ∆≌CEB ∆;②BE AD DE +=;(2)当直线MN 绕点C 旋转到图2的位置时,(1)中的结论还成立吗?若成立,请给出证明;若不成立,说明理由.15如图所示,已知AE ⊥AB ,AF ⊥AC ,AE=AB ,AF=AC 。
相似三角形培优难题集锦(含答案)
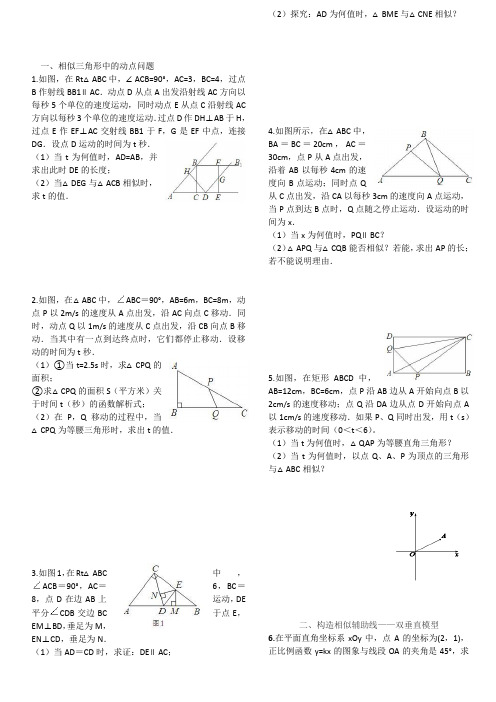
一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A 以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t<6)。
三角形培优训练100题集锦(一)2024

三角形培优训练100题集锦(一)【引言概述】三角形是数学中的一个重要几何概念,对于学生的数学培优训练具有重要意义。
本文整理了一份包含一百道三角形相关题目的训练集锦,旨在帮助学生系统地掌握三角形的性质、定理和计算方法,提高解题能力。
以下将从五个大点来阐述这份题集的内容。
【大点1:三角形基础知识】1. 三角形的定义及分类2. 三角形内角和的性质3. 三角形边长关系:三角不等式定理4. 三角形的周长和面积计算公式5. 三角形的特殊点:重心、垂心、外心、内心、费马点等【大点2:三角形的相似与全等】1. 相似三角形的性质2. 判定三角形相似的方法3. 三角形的全等的条件4. 利用相似三角形或全等三角形解题的方法5. 实际问题中的应用:测量、定位、相似比例等【大点3:三角形的角与线段关系】1. 角的平分线与垂直平分线的特点2. 三角形的角平分线定理3. 三垂线定理与垂心定理4. 外角与内角的关系5. 角与弧的关系及其应用:圆周角、弦切角、弧度制等【大点4:三角形的特殊性质与定理】1. 等腰三角形的性质与判定2. 直角三角形的性质与判定3. 正三角形的性质及计算4. 等边三角形的性质及计算5. 锐角三角形和钝角三角形的性质及判定【大点5:三角形的应用问题】1. 三角形的角度测量与边长测量2. 三角形在建筑工程中的应用:测量高度、角度与距离3. 三角形在地理学中的应用:测量地底深度、地图测量等4. 三角形在航空航天领域的应用:导航、角度计算等5. 三角形在日常生活中的应用:地理问题、旅行导航、地震角度计算等【总结】通过对本文中所整理的三角形培优训练100题集锦的学习,同学们将能够掌握三角形的基础知识,灵活运用三角形的相似与全等等性质和定理,熟练解决三角形的角与线段关系问题,理解各种特殊三角形的性质,并能够应用三角形的知识解决实际问题。
这将为学生的数学学习和思维能力的提高提供坚实的基础。
全等三角形经典培优题型(含答案)

全等三角形经典培优题型(含答案)1.已知三角形ABC中,AB=4,AC=2,D是BC的中点,AD是整数,求AD的长度。
解:由题意可得AD=AB-DB,又BD=DC=AC/2=1,故AB=AD+DB=AD+1,代入AB=4得AD=3.2.已知四边形BCDE中,BC=DE,∠B=∠E,∠C=∠D,F是CD的中点,证明∠1=∠2.解:由于BC=DE,且∠B=∠E,所以△BCE≌△EDC,从而∠1=∠BCE=∠EDC=∠2.3.已知四边形ABCD中,∠1=∠2,CD=DE,EF//AB,证明EF=AC。
解:由于EF//AB,所以△EFC∼△ABC,从而EF/AC=FC/BC,而CD=DE,所以FC=CD,代入得EF/AC=CD/BC,又由于∠1=∠2,所以△BCD∼△ECD,从而CD/BC=ED/AC,代入得EF/AC=ED/AC,即EF=AC。
4.已知三角形ABC中,AD平分∠BAC,AC=AB+BD,证明∠B=2∠C。
解:由于AD平分∠BAC,所以∠BAD=∠CAD,从而∠B=∠BAD+∠ABD=∠CAD+∠ACD,又由于AC=AB+BD,所以BD=AC-AB,代入得∠B=∠CAD+∠ACD=∠CAD+∠ABC,又由于∠CAD=∠CAB,所以∠B=∠CAB+∠ABC=2∠C。
5.已知三角形ABC中,AC平分∠BAD,CE⊥AB,∠B+∠D=180°,证明AE=AD+BE。
解:由于AC平分∠BAD,所以∠CAD=∠CAB,从而△ABE∼△DCE,所以AE/AD=BE/CD,又由于∠B+∠D=180°,所以CD=AB,代入得AE/AD=BE/AB,即AE=AD·(BE/AB),又由于CE⊥AB,所以△CEB为直角三角形,从而BE/AB=CE/AC,代入得AE=AD·(CE/AC),又由于AC平分∠BAD,所以△ACD∼△ABC,从而CE/AC=CD/AB,代入得AE=AD·(CD/AB),又由于CD=AB-BD,所以AE=AD·((AB-BD)/AB),即AE=AD+BE·(AB/AD-1),又由于AB>AD,所以AB/AD-1<AB/AD,从而AE<AD+BE·(AB/AD),即AE<AD+BE。
初一下学期三角形培优专题

B.15度
C.20度
D.不能确定
5.如图,三角形ABC中,AD平分∠BAC,EG⊥AD,且分别交AB、AD、AC及BC的延长线于点E、H、F、G,下列四个式子中正确的是( )
A.∠1=1∕2(∠2-∠3)
B.∠1=2(∠2-∠3)
C.∠G=1∕2(∠3-∠2)
D.∠G=1∕2∠1
专题八:平行线型
A.∠A=∠B
B.∠B=∠D
C.∠A=∠D
D.∠A+∠D=90°
4如图,△ABC中,∠BAC=90°,AD⊥BC于D,E是AD上一点,求证:∠BED>∠C
5.如图,在 中, 是角平分线,交 于点 ,求证
专题四:三角形三条角平分线型
1.如图①,BD、CD是∠ABC和∠ACB的角平分线且相交于点D,请猜想∠A与∠BDC之间的数量关系,并说明理由。
(1)试找出∠1、∠2、∠3之间的关系并说出理由;
(2)如果点P在A、B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A、B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A、B不重合)
5.如下图,AB∥CD,直线a交AB、CD分别于点E、F,点M在EF上,p是直线CD上的一个动点,(点P不与F重合)
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
专题十三:三角形三边关系与周长
1.若一个等腰三角形的三边长均为整数,且周长为10,则底边长为
2.周长为16的三角形的三边长都是整数,这样的三角形有个
3.三角形三条边长是三个连续的自然数,周长小于19,则满足条件的三角形有个
4.三角形三条边长均为整数,其中两边长之差为7,三角形的周长是奇数,则第三边长可能为
相似三角形培优专题训练

相似三角形培优专题训练1.给定平行四边形ABCD,点G在边DC的延长线上,AG交BC于点E,BG交CD于点F。
证明△AGD∽△EGC∽△EAB。
2.给定△ABC,AB=AC,∠A=36°,BD是角平分线。
证明△ABC∽△BCD。
3.给定△ABC,D为内点,ED、AD分别与BC、AB相交,以BC为边在△ABC外作∠XXX∠ABD,∠XXX∠BAD。
证明△DBE∽△ABC。
4.给定矩形ABCD,BC=3AB,E、F是BC边上的三等分点,连结AE、AF、AC。
证明图中不存在非全等的相似三角形。
5.给定△ABC,AC上截取AD,CB延长线上截取BE,使AD=BE。
证明DF•AC=BC•FE。
6.给定△ABC,∠BAC=90°,M是BC的中点,DM⊥BC于点E,交BA的延长线于点D。
证明(1)MA=MD•ME;(2)2MD²=AD²+4AE²。
7.给定△ABC,AD为中线,CF为任一直线,CF交AD于点E,交AB于点F。
证明AE:ED=2AF:FB。
8.给定正方形ABCD,E、F分别是XXX和AD上的点,且。
证明∠XXX∠XXX。
9.给定平行四边形ABCD,AR、BR、CP、DP各为四角的平分线。
证明SQ∥AB,RP∥BC。
10.给定四边形XXX和四边形BDFE,其中AB∥ED,BC∥FE。
证明AF∥CD。
11.给定直角三角形ABC,BCDE是正方形,AE交BC于点F,FG∥AC交AB于点G。
证明FC=FG。
12.给定锐角三角形ABC,C的平分线交AB于点E,交斜边上的高AD于点O,过O引BC的平行线交AB于点F。
证明OE=OF。
第1章《三角形的初步知识》培优提升卷含答案

第1章《三角形的初步认识》培优提升卷班级______ 姓名_______一、选择题(每题3分,共30分)1.现有四根木棒,长度分别为4cm ,6cm ,8cm ,10cm ,从中任取三根木棒,能组成三角形的个数为( )A .1个B .2个C .3个D .4个2.如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则∠+∠12 的度数为( )A.120°B. 180°C. 240°D. 300°第2题 第4题 第5题 3.根据下列已知条件,能惟一画出△ABC 的是( )A .AB =3,BC =4,CA =8 B .AB =4,BC =3,∠A =30° C .∠A =60°,∠B =45°,AB =4D .∠C =90°,AB =64.如图,A ,B ,C ,D ,E ,F 是平面上的6个点,则∠A +∠B +∠C +∠D +∠E +∠F 的度数是( ) A. 180° B.360° C.540° D.720°5.如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD 的度数是( ) A . 15°B . 25°C . 30°D . 10°6.下列命题:(1)无限小数是无理数 (2)绝对值等于它本身的数是非负数 (3) 垂直于同一直线的两条直线互相平行 (4) 有两边和其中一边的对角对应相等的两个三角形全等, (5)面积相等的两个三角形全等,是真命题的有( ) A.1个 B.2个 C.3个 D.4个2160°7.如图,在△ABC 和△DEB 中,已知AB=DE ,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )A.BC=EC ,∠B=∠EB. BC=ECC. BC=DC ,∠A=∠DD.∠B=∠E,∠A=∠D8.如图,在△ABC 中,AD 是角平分线,AE 是高,已知∠BAC =2∠B ,∠B =2∠DAE ,那么∠ACB 为( )A. 80°B. 72°C. 48°D. 36°第7题 第8题 第10题9.若三角形的周长为18,且三边都是整数,则满足条件的三角形的个数有( )A 、4个B 、5个C 、6个D 、7个10.如图所示,点B 、C 、E 在同一条直线上,△ABC 与△CDE 都是等边三角形,则下列结论不一定成立的是( )A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA 二、填空题(每题4分,共24分)11.已知三角形的三边长分别是3、x 、9,则化简135-+-x x =12.如图,长方形ABCD 中(AD>AB),M 为CD 上一点,若沿着AM 折叠,点N 恰落在BC 上,则∠ANB+∠MNC=___________13.如图,在△ABC 中,∠B =47°,三角形的外角∠DAC 和∠ACF 的平分线交于点E ,则∠AEC =______°BFDE ACDCBAE第12题 第13题 第16题14.在△ABC中,AB=8,AC=6,则BC边上的中线AD 的取值范围是15.已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥C.其中为真命题的是__________.(填写所有真命题的序号)16.在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=900,E是BC的中点,DE平分∠ADC,∠CED=35°,,则∠EAB是多少度?大家一起热烈地讨论交流,小英第一个得出正确答案,是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ED F CB A三角形培优训练专题【三角形辅助线做法】图中有角平分线,可向两边作垂线。
也可将图对折看,对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
【常见辅助线的作法有以下几种】1、遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”。
2、遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”。
3、遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理。
4、过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”。
5、截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明。
这种作法,适合于证明线段的和、差、倍、分等类的题目。
6、已知某线段的垂直平分线,那么可以在垂直平分线上的某点向该线段的两个端点作连线,出一对全等三角形。
7、特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答。
1、已知,如图△ABC中,AB=5,AC=3,求中线AD的取值范围.2、如图,△ABC中,E、F分别在AB、AC上,DE⊥DF,D是中点,试比较BE+CF与EF的大小.3、如图,△ABC中,BD=DC=AC,E是DC的中点,求证:AD平分∠BAE.ED CBA4、以ABC∆的两边AB、AC为腰分别向外作等腰Rt ABD∆和等腰Rt ACE∆,90,BAD CAE∠=∠=︒连接DE,M、N分别是BC、DE的中点.探究:AM与DE的位置关系及数量关系.(1)如图①当ABC∆为直角三角形时,探究:AM与DE的位置关系和数量关系;(2)将图①中的等腰Rt ABD∆绕点A沿逆时针方向旋转︒θ(0<θ<90)后,如图②所示,(1)问中得到的两个结论是否发生改变?并说明理由.5、如图,ABC∆中,AB=2AC,AD平分BAC∠,且AD=BD,求证:CD⊥AC.CDBACBACBA6、如图,AD ∥BC ,EA,EB 分别平分∠DAB,∠CBA ,CD 过点E ,求证;AB =AD+BC 。
7、如图,已知在△ABC 内,060BAC ∠=,040C ∠=,P ,Q 分别在BC ,CA 上,并且AP ,BQ分别是BAC ∠,ABC ∠的角平分线。
求证:BQ+AQ=AB+BP8、如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠,求证: 0180=∠+∠C A9、如图在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,求证;AB-AC >PB-PC10、11、 AD为△ABC的角平分线,直线MN⊥AD于A.E为MN上一点,△ABC周长记为AP,△EBC周长记为BP.求证BP>AP.12、已知:△ABC和△ADE是两个不全等的等腰直角三角形,其中BA=BC,DA=DE,联结EC,取EC的中点M,联结BM和DM.(1)如图1,如果点D、E分别在边AC、AB上,那么BM、DM的数量关系与位置关系是;(2)将图1中的△ADE绕点A旋转到图2的位置时,判断(1)中的结论是否仍然成立,并说明理由.CBAEMMEABCDCB13、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD,CE 相交于点O ,求证:OE=OD14、如图,△ABC 中,AD 平分∠BAC ,DG ⊥BC 且平分BC ,DE ⊥AB 于E ,DF ⊥AC 于F. (1)说明BE=CF 的理由;(2)如果AB=a ,AC=b ,求AE 、BE 的长.15、如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;(2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
ED G F C BAOP AM NE B CDF AE FB D 图①图②图③FED CB A BC16、 正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.17、D 为等腰Rt ABC ∆斜边AB 的中点,DM ⊥DN,DM,DN 分别交BC,CA 于点E,F 。
(1) 当MDN ∠绕点D 转动时,求证DE=DF 。
(2) 若AB=2,求四边形DECF 的面积。
18、 如图,ABC ∆是边长为3的等边三角形,BDC ∆是等腰三角形,且0120BDC ∠=,以D 为顶点做一个060角,使其两边分别交AB 于点M ,交AC 于点N ,连接MN ,求AMN ∆的周长。
_ A19、已知四边形ABCD 中,AB AD ⊥,BC CD ⊥,AB BC =,120ABC =o∠,60MBN =o∠,MBN ∠绕B 点旋转,它的两边分别交AD DC ,(或它们的延长线)于E F ,. 当MBN ∠绕B 点旋转到AE CF =时(如图1),易证AE CF EF +=.当MBN ∠绕B 点旋转到AE CF ≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段AE CF ,,EF 又有怎样的数量关系?请写出你的猜想,不需证明.20、已知2,PB=4,以AB 为一边作正方形ABCD,使P 、D 两点落在直线AB 的两侧. (1)如图,当∠APB=45°时,求AB 及PD 的长;(2)当∠APB 变化,且其它条件不变时,求PD 的最大值,及相应∠APB 的大小.(图1) AB CD E F MN(图2)A B CDE FMN(图3)AB C D E F MN21、在等边ABC ∆的两边AB 、AC 所在直线上分别有两点M 、N ,D 为ABC V 外一点,且︒=∠60MDN ,︒=∠120BDC ,BD=DC. 探究:当M 、N 分别在直线AB 、AC 上移动时,BM 、NC 、MN 之间的数量关系及AMN ∆的周长Q 与等边ABC ∆的周长L 的关系.图1 图2 图3(I )如图1,当点M 、N 边AB 、AC 上,且DM=DN 时,BM 、NC 、MN 之间的数量关系是 ; 此时=LQ; (II )如图2,点M 、N 边AB 、AC 上,且当DM ≠DN 时,猜想(I )问的两个结论还成立吗?写出你的猜想并加以证明;(III ) 如图3,当M 、N 分别在边AB 、CA 的延长线上时,若AN=x ,则Q= (用x 、L 表示).22、如图2-7-1,△ABC 和△DCE 均是等边三角形,B 、C 、E 三点共线,AE 交CD 于G ,BD 交AC 于F 。
求证:① AE=BD;② CF=CG.23、如图2-7-2,在正方形ABCD中,M是AB的中点,MN⊥MD,BN平分∠CBE。
求证:MD=MN。
24、如图2-7-3,△ABC中,∠ABC=2∠C,∠BAC的平分线交BC于D。
求证:AB+BD=AC25、如图2-7-4,△ABC中,AC>AB,AD平分∠BAC,P为AD上任一点,连结PB、PC。
求证:PC-PB<AC-AB。
26、如图2-7-5,从等腰Rt△ABC的直角顶点C向中线BD作垂线,交BD于F,交AB于E,连结DE。
求证:∠CDF=∠ADE。
27、在△ABC 中,∠ACB =90°,AC =BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E.(1)当直线MN 绕点C 旋转到图1的位置时,求证: ①△ADC ≌△CEB ;②DE =AD +BE ; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE =AD -BE ;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE 、AD 、BE 具有怎样的等量关系?请写出这个等量关系,并加以证明。
28、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与B 、C 重合),斜边和∠ACM 的平分线CF 交于点F (1)如图(1)当点E 在BC 边中点位置时1) 猜想AE 与EF 满足的数量关系是 。
2) 连结点E 与AB边得中点N,猜想BE和CF满足的数量关系是3) 请证明你的上述猜想(2)如图(2)当点E在BC边得任意位置时:此时AE和EF有怎样的数量关系,并说明你的理由?E图(1)NFMCBAE图(2)FA29、已知AC 平分∠MAN ,∠MAN=120º,(1)在图(1)中,若∠ABC=∠ADC=90º,求证:AB+AD=AC 。
(2)在图(2)中,若∠MAN=120º,∠ABC+∠ADC=180º,则(1)中的结论还成立吗?若成立请你给出证明,若不成立请说明理由?30、如图1,在ABC △中,点P 为BC 边中点,直线a 绕顶点A 旋转,若点B P 、在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接.PM PN 、 (1)延长MP 交CN 于点E (如图2),①求证:BPM CPE △≌△;②求证:PM PN =; (2)若直线a 绕点A 旋转到图3的位置时,点B P 、在直线a 的同侧,其它条件不变.此时PM PN =还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变,请直接判断PM PN =还成立吗?不必说明理由.图(1)CD B N MA 图(2)C DB N M A 题图1 题图2 题图331、如图1,已知正方形ABCD 的边CD 在正方形DEFG 的边DE 上,连接AE GC ,. (1)试猜想AE 与GC 有怎样的位置关系,并证明你的结论.(2)将正方形DEFG 绕点D 按顺时针方向旋转,使点E 落在BC 边上,如图2,连接AE 和GC .你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.32、已知等边△ABC 和点P ,设点P 到△ABC 三边AB 、AC 、BC 的距离分别为h 1、h 2、h 3,△ABC 的高为h 。
