弹塑性理论习题讲解
弹塑性力学部分习题及答案

1 εij = (ui, j +uj,i ) 2
σji, j
(i, j =12,3) ,
E 1 ν = 2(uj,ij +ui, jj ) +1−2νuk,kjδij (1+ν)
5Байду номын сангаас
20112011-2-17
题1-3
E 1 ν (uj,ij +ui,jj ) + σji, j = uk,ki 2 (1+ν) 1−2ν
3
2c
l
y
解: 1、将 Φ 代入
∇ 4Φ =0 满足, 为应力函数。 满足, Φ 为应力函数。
2、求应力(无体力) 求应力(无体力)
20112011-2-17 20
题1-13 3 3F xy q 2 Φ= xy− 2 + y 4c 3 2 c
2
o
x
2c
l
y
2
∂φ 3F xy ∂φ σx = 2 = − 3 +q, σy = 2 =0, ∂y 2c ∂x y2 ∂φ 3F τxy =− = − 1− 2 ∂x∂y 4c c
z l y
F = −ρg bz
x
x
20112011-2-17
8
题1-5 等截面直杆(无体力作用),杆轴 等截面直杆(无体力作用),杆轴 ), 方向为 z 轴,已知直杆的位移解为
u =−kyz v =kxz
w=k ( x, y) ψ
为待定常数, 其中 k 为待定常数,ψ(x‚y)为待定函数, 为待定函数 试写出应力分量的表达式和位移法方程。 试写出应力分量的表达式和位移法方程。
2
弹塑性力学最后例题

u y
2
]dxdy
经推导得:
U = E 4 1 - n2
(
)
p2 b
å
n
k= 1
k 2B k2
3
(3)由 =0 变分方程确定系数 Bk :
Bk 0 k 1 Bk
n
即 或:
U =
0 Bk
k 1,2 n
E 4 1 - n2
(
)
p2 b
å
n
k= 1
k 2B k2
抖 U = 抖 Bk = -
V = Bk
ò f v dA
y k
ò
b
0
b = rg cos k p - 1) ( kp
k py r g sin dy b
(k = 1, 2 L n )
4
得:
E 2 1- n
(
2
)
p 2k 2 ? Bk b
2b rg pk
(k = 1, 3, 5 L )
这是k个独立方程,可求出k个待定系数 Bk。 解得:
Bk = 4 1 - n 2 b2 k pE
3 3
(
)
rg
(k = 1, 3, 5 L )
(4) 位移解答
u 0
b 处的竖向位移为: 令: y 2
b
4 (1 2 )b2 y 1 3 y 1 5 y v( y ) g (sin 3 sin 3 sin ) 3 E b 3 b 5 b
6
题3 张量证明
求证 证明
J 2 Sij ij
J 2 J 2 Skl ij Skl ij S kl 1 S S mn mn 2 ij 1 pp kl kl 3
(完整版)弹塑性力学习题题库加答案
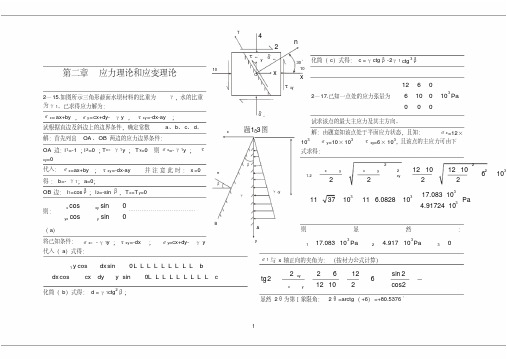
第二章应力理论和应变理论2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为:σx =ax+by ,σy =cx+dy-γy ,τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件:OA 边:l 1=-1 ;l 2=0 ;T x=γ1y ;T y =0 则σx =-γ1y ;τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0得:b=-γ1;a=0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0 则:cos sin 0cossinx xy yxy………………………………(a )将己知条件:σx=-γ1y ;τxy =-dx ;σy =cx+dy-γy代入(a )式得:1cossin 0cossin0y dx bdx cxdyy cL L L L L L L L L L L L L L L L L L化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1ctg 3β2—17.己知一点处的应力张量为312606100100Pa试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103σy =10×103 τxy =6×103,且该点的主应力可由下式求得:222231.2333312101210610222217.0831011371011 6.0828104.9172410xyxyxyPa则显然:3312317.08310 4.917100Pa Paσ1 与x 轴正向的夹角为:(按材力公式计算)22612sin 22612102cos2xy xytg 显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376°δy题图1-3τxyx 30°10n24xO10yTτ30°δ30°xO γyβBA n βγ1y则:θ=+40.2688B 40°16'或(-139°44')2—19.己知应力分量为:σx =σy =σz =τxy =0,τzy =a ,τzx =b ,试计算出主应力σ1、σ2、σ3并求出σ2的主方向。
弹塑性理论习题讲解

2-7已知某点的应力状态为 过该点斜截面法线 的方向余弦为 ,试求斜截面上切应力 的表达式。
2-8物体中某点的应力状态为 求该点主应力的大小和主轴方向。
2-9已知物体中某点的应力状态为 ,斜截面法线的方向余弦为 ,试求斜截面上切应力的大小。
2-10半径为 的球,以常速度 在粘性流体中沿 轴方向运动。球面上点A( )受到的表面力为 , , ,式中 为流体的静水压力。试求球所受的总力量。
图8-9
8-2悬臂梁(0≤x≤1,-c≤y≤c),左端固定,沿下边界受均匀分布剪力,而上边界和右端不受载荷时,可用应力函数 得出解答。这个解答在哪些方面是不完善的?将应力表达式与由拉伸和弯曲的初等公式得到的表达式作一比较,见图8-10。
图8-10
8-3悬臂梁受均布荷重 的作用,梁长 ,高2c,求应力分布。见图8-11。
2-11已知物体中某点的应力状态为 ,斜截面法线的方向余弦为 ,试证明斜截面上的正应力 及剪应力 分别为 、 。
习题3
3-1若位移 是坐标的一次函数,则在整个物体中各点的应变都是一样的,这种变形叫均匀变形。设有以O为中心的曲面,在均匀变形后成为球面,
问原来的曲面 是怎样的一种曲面?
3-2证明 , , , (其中 和 是微小的常数),不是一个可能的应变状态。
提示:边界条件中出现 项时,应设 。
图8-11图8-12
8-4有简支梁长 ,高 ,受均布荷重 的作用,求应力分布,见图8-12。
8-5简支梁长 ,高 ,试证由于自重 所产生的应力分布为
,
,
,
式中 。
提示: , , 是方程组的一组特解,然后把有体积力的问题变为无体积力的问题求解。
弹塑性力学习题解答

塑性:弹性:2-16设有任意形状的等厚度薄板,体力可以不计,在全部边界上(包括孔口边界上)受有均匀压力q 试证q y x -==σσ 及0=xy τ能满足平衡微分方程、相容方程和应力边界条件,也能满足位移单值条件,因而就是正确的解答。
证明: 〔1〕将应力分量q y x -==σσ,0=xy τ和0==y x f f 分别代入平衡微分方程、相容方程⎪⎪⎩⎪⎪⎨⎧=+∂∂+∂∂=+∂∂+∂∂00y x xy yy x y yx x x f f τστσ 〔a 〕 0)1())((2222=∂∂+∂∂+-=+∂∂+∂∂)(y f x f yx y x y x μσσ 〔b 〕 显然〔a 〕、〔b 〕是满足的〔2〕对于微小的三角板dy dx A ,,都为正值,斜边上的方向余弦),cos(x n l =,),cos(y n m =,将q y x -==σσ,0=xy τ代入平面问题的应力边界条件的表达式⎪⎩⎪⎨⎧=+=+)()()()(s f l m s f m l y s xy y x s yx x τστσ 〔c 〕 那么有),cos(),cos(x n q x n x -=σ),cos(),cos(y n q y n y -=σ所以q x -=σ,q y -=σ。
对于单连体,上述条件就是确定应力的全部条件。
〔3〕对于多连体,应校核位移单值条件是否满足。
该题为平面应力的情况,首先,将应力分量q y x -==σσ及0=xy τ代入物理方程,得形变分量q E x )1(-=με,q Ey )1(-=με,0=xy γ 〔d 〕 然后,将〔d 〕的变形分量代入几何方程,得q Ex u )1(-=∂∂μ,q E y v )1(-=∂∂μ,0=∂∂+∂∂y u x v 〔e 〕 前而式的积分得到 )()1(1y f qx E u +-=μ,)()1(2x f qy Ev +-=μ 〔f 〕 其中的1f 和2f 分别是y 和x 的待定函数,可以通过几何方程的第三式求出,将式〔f 〕代入〔e 〕的第三式得 dxx df dy y df )()(21=- 等式左边只是y 的函数,而等式右边只是x 的函数。
弹塑性力学部分习题及答案

e kk
2019/8/31
4
题1-3
e kk
ij (1 E )( ij 1 2 e ij) (i,j 1 ,2 ,3 )
j,i j (1 E )( j,i j 1 2 k,jk ij ) (i,j 1 ,2 ,3 )
i1 2ui,j
j
Guj,jiGi,ju j
代入 j,ij F b i0 (i,j 1 ,2 ,3 )
得
G 2 u i G u j,j iF b i0在 V 上
2019/8/31
7
题1-4 等截面柱体在自重作用下,应力解为
x=y=xy=yz=zx=0 , z=gz,试求位移。
,且设 ur 表达式为
ur C1rC r2(18 E 2)2r3
b
ra
x
试由边界条件确定 C1 和 C2 。
y
解: 边界条件为: (r)r=a=0, (r)r=b=0
应力r(平面
应力问题):
r 1E2(ddrururr)
2019/8/31
32
题1-16 由边界条件确定 C1 和 C2 :
v g l x y E
y
l
式中 E、 为弹性模量和泊松系数。
试(1)求应力分量和体积力分量;
hh
(2)确定各边界上的面力。
x
解: 1、求应变
x u x E g l x , y y v E g (l x )
2019/8/31
15
x
x=ax、y=ax、xy= -ax
3、求应变
x=ax、y=a(2x+y-l-h)、 xy= -ax
弹塑性力学试卷及弹性力学教材习题及解答

二、填空题:(每空2分,共8分)1、在表征确定一点应力状态时,只需该点应力状态的-------个独立的应力分量,它们分别是-------。
(参照oxyz直角坐标系)。
2、在弹塑性力学应力理论中,联系应力分量与体力分量间关系的表达式叫---------方程,它的缩写式为-------。
三、选择题(每小题有四个答案,请选择一个正确的结果。
每小题4分,共16分。
)1、试根据由脆性材料制成的封闭圆柱形薄壁容器,受均匀内压作用,当压力过大时,容器出现破裂。
裂纹展布的方向是:_________。
A、沿圆柱纵向(轴向)B、沿圆柱横向(环向)C、与纵向呈45°角D、与纵向呈30°角2、金属薄板受单轴向拉伸,板中有一穿透形小圆孔。
该板危险点的最大拉应力是无孔板最大拉应力__________倍。
A、2B、3C、4D、53、若物体中某一点之位移u、v、w均为零(u、v、w分别为物体内一点,沿x、y、z直角坐标系三轴线方向上的位移分量。
)则在该点处的应变_________。
A、一定不为零B、一定为零C、可能为零D、不能确定4、以下________表示一个二阶张量。
A、B、C、D、四、试根据下标记号法和求和约定展开下列各式:(共8分)1、;(i ,j = 1,2,3 );2、;五、计算题(共计64分。
)1、试说明下列应变状态是否可能存在:;()上式中c为已知常数,且。
2、已知一受力物体中某点的应力状态为:式中a为已知常数,且a>0,试将该应力张量分解为球应力张量与偏应力张量之和。
为平均应力。
并说明这样分解的物理意义。
3、一很长的(沿z轴方向)直角六面体,上表面受均布压q作用,放置在绝对刚性和光滑的基础上,如图所示。
若选取=ay2做应力函数。
试求该物体的应力解、应变解和位移解。
(提示:①基础绝对刚性,则在x=0处,u=0 ;②由于受力和变形的对称性,在y=0处,v=0 。
)题五、3图4、已知一半径为R=50mm,厚度为t=3mm的薄壁圆管,承受轴向拉伸和扭转的联合作用。
弹塑性力学习题及问题详解

本教材习题和参考答案与局部习题解答第二章2.1计算:(1)pi iq qj jk δδδδ,(2)pqi ijk jk e e A ,(3)ijp klp ki lj e e B B 。
答案 (1)pi iq qj jkpk δδδδδ=;答案 (2)pqi ijk jk pq qp e e A A A =-;解:(3)()ijp klp ki ljik jl il jk ki lj ii jj ji ij e e B B B B B B B B δδδδ=-=-。
2.2证明:假如ijji a a =,如此0ijk jk e a =。
〔需证明〕a 、b 和c 是三个矢量,试证明:2[,,]⋅⋅⋅⋅⋅⋅=⋅⋅⋅a a a b a cb a b b bc a b c c a c b c c证:因为123111123222123333i i i i i i i i i i i i i ii ii i a a a b a c b a b b b c c a c b c c a a a a b c b b b a b c c c c a b c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦, 所以123111123222123333123111123222123333det det()i ii i i i i ii i i i i ii ii i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c a a a a b c b b b a b c c c c a b c ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即得 1231112123222123333[,,]i i i i i i i i i i i i i i i i i i a a a b a c a a a a b c b a b b b c b b b a b c c a c b c c c c c a b c ⋅⋅⋅⋅⋅⋅=⋅⋅⋅==a a a b a c b a b b b c a b c c a c b c c 。
弹塑性力学习题答案

第二章 习题解答2-1解:已知 0,0,===-==y x xy y xf f q τσσ1)⎪⎪⎩⎪⎪⎨⎧+∂∂+∂∂+∂∂+∂∂xy y yxx x y yx τστσ23()()⎩⎨⎧++s xy y s yx x l m m l σστστσ 有:lq t x -=代入(*4理、几何方程得:E x u x ==∂∂ε11E y v y ==∂∂ε0==∂∂+∂∂xy yux v γ ()()⇒=+∴0dyy df dx x dg 类似于教材题2-3,可求出 ()()wx v x g wy u y f +=-=00,001;1v wx qy Ev u wy qx Eu ++--=+---=∴υυ从v u ,表达式可见,位移分量是坐标的单值函数,满足位移单值条件。
综合1)~4),。
q xy y x 为问题的正确解答0,=-==τσσ2-2x =σxy τ注意:y x ,代入均满足。
2)验证相容方程:0)(2=+∇y x σσ 亦满足。
3)验证应力边界条件: i) 主要边界:()0,2=±=h y yx yτσ满足ii) 次要边界:()()()()()⎪⎪⎪⎩⎪⎪⎪⎨⎧===⎰⎰⎰-=-=-=222222320)1(0h h lx xy h h l x x h h l x x Pdy ydy dy τσσ (1)、(2)满足,(3)式左=⎰-===⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛-223332212*41*618218hh P h I P h h I P dy y h I P 右 结论:所列xy y x τσσ,,满足平衡方程、相容方程;在主要边界上严格满足应力边界条件,次要边界近似满足应力边界条件,又为单连体,故在圣维南原理的前提下为问题的正确解。
2-3、证明:1)由,,yVf xV fy x∂∂-=∂∂-=则平衡微分方程为: ()()⎪⎪⎩⎪⎪⎨⎧=∂τ∂+∂-σ∂=∂τ∂+∂-σ∂⇒⎪⎪⎩⎪⎪⎨⎧=∂∂-∂τ∂+∂σ∂=∂∂-∂τ∂+∂σ∂0x y V 0yx V 0y V x y 0x V y x yx y xyx yx y xy x (*) 类似于题2-10的推证过程,(*)式的通解为:y x x V yV 2xy 22y 22x ∂∂ϕ∂-=τ∂ϕ∂=-σ∂ϕ∂=-σ;;即: yx V xV y2xy 22y 22x ∂∂ϕ∂-=τ+∂ϕ∂=σ+∂ϕ∂=σ;;2) 对于平面应力问题,相容方程为:()()⎪⎪⎭⎫⎝⎛∂∂+∂∂+-=+∇y f x f y x y xυσσ12即:2222 2-4、x, y n l σσ2==2l 应力主向成∴l σn3-3、解: 1由x=0得: 2由 得: Fx Ex Cx Bx Ax y ++++=∴注:公式中已略去ϕ中与应力分量无关的一次项和常数项。
弹塑性力学部分习题及答案

厚壁筒应力问题
要点一
总结词
厚壁筒应力问题主要考察了弹塑性力学中厚壁筒结构的应 力分析和变形计算。
要点二
详细描述
厚壁筒应力问题涉及到厚壁筒结构在受到内压、外压或其 他复杂载荷作用时的应力分布和变形情况。在解题过程中 ,需要运用弹塑性力学的相关理论,如应力分析、应变分 析等,来求解结构的应力分布和变形情况。同时,还需要 考虑厚壁筒结构的特殊性,如不同材料的组合、多层结构 等,对结构应力和变形的影响。
02
弹塑性力学基础知识
应力和应变
基本概念
详细描述:应力和应变是弹塑性力学中的基本概念。应力表示物体内部相邻部分之间的相互作用力,而应变则表示物体在应 力作用下的变形程度。
屈服条件与应力-应变关系
屈服准则与流动法则
详细描述:屈服条件决定了材料在应力作用下的屈服点,是判断材料是否进入塑性状态的重要依据。 应力-应变关系则描述了材料在受力过程中应力与应变的变化规律。
弹塑性力学特点
弹塑性力学具有广泛的应用背景,涉及到众多工程领域,如结构工程、机械工 程、航空航天等。它既适用于脆性材料,也适用于塑性材料,并考虑了材料的 非线性特性。
弹塑性力学的基本假设
连续性假设
小变形假设
假设固体内部是连续的,没有空隙或 裂纹。
假设物体在外力作用下发生的变形是 微小的,不会影响物体内部应力分布。
弹塑性力学部分习题及答 案
• 弹塑性力学概述 • 弹塑性力学基础知识 • 弹塑性力学典型习题解析 • 弹塑性力学部分习题的定义与特点
弹塑性力学的定义
弹塑性力学是一门研究固体在受到外力作用时,其内部应力、应变和位移之间 关系的学科。它主要关注材料在受力过程中发生的弹性变形和塑性变形。
弹塑性力学-陈明祥版的-课后习题答案++

◆ 所有与坐标系选取无关的量,统称为物理恒量。
◆ 在一定单位制下,只需指明其大小即足以被说明
的物理量,统称为标量。例如温度、质量、功等。
◆ 在一定单位制下,除指明其大小还应指出其方向
的物理量,称为矢量。例如速度、加速度等。
x j xk
(I-25)
4.张量的分解
张量一般是非对称的。若张量 ai的j 分量满足
aij a ji
(I-27)
则 aij称为对称张量。 如果 的分ai量j 满足
aij a ji
(I-28)
则称为反对称张量。显然反对称张量中标号重复的
分量(也即主对角元素)为零,即 a11 a22 。a33 0
弹塑性力学与材料力学同属固体力学的 分支学科,它们在分析问题解决问题的基本 思路上都是一致的,但在研究问题的基本方 法上各不相同。其基本思路如下:
(1) 受力分析及静力平衡条件 (力的分析)
物体受力作用处于平衡状态,应当满足的条件 是什么?(静力平衡条件)
(2) 变形的几何相容条件 (几何分析)
材料是均匀连续的,在受力变形后仍应是连续 的。固体内既不产生“裂隙”,也不产生“重叠 ”, 此时材料变形应满足的条件是什么?(几何相 容条件)
建立起普 遍适用的理 论与解法。
1、涉及数学理论较复杂,并以其理论与解
法的严密性和普遍适用性为特点;
2、弹塑性的工程解答一般认为是精确的;
3、可对初等力学理论解答的精确度和可靠
进行度量。
四、 弹塑性力学的基本任务
可归纳为以下几点: 1.建立求解固体的应力、应变和位移分布规律的 基本方程和理论; 2.给出初等理论无法求解的问题的理论和方法, 以及对初等理论可靠性与精确度的度量; 3.确定和充分发挥一般工程结构物的承载能力, 提高经济效益; 4.为进一步研究工程结构物的强度、振动、稳定 性、断裂等力学问题,奠定必要的理论基础。
弹塑性力学作业(含答案)

2—15.如图所示三角形截面水坝材料的比重为γ,水的比重为γ1。
己求得应力解为: σx =ax+by ,σy =cx+dy-γy , τxy =-dx-ay ;试根据直边及斜边上的边界条件,确定常数a 、b 、c 、d 。
解:首先列出OA 、OB 两边的应力边界条件: OA 边:l 1=-1 ;l 2=0 ;T x = γ1y ; T y =0 则σx =-γ1y ; τxy =0代入:σx =ax+by ;τxy =-dx-ay 并注意此时:x =0得:b=-γ1;a =0;OB 边:l 1=cos β;l 2=-sin β,T x =T y =0 则:cos sin 0cos sin 0x xy yxy σβτβτβσβ+=⎧⎨+=⎩………………………………(a )将己知条件:σx= -γ1y ;τxy =-dx ; σy =cx+dy-γy 代入(a )式得:化简(b )式得:d =γ1ctg 2β;化简(c )式得:c =γctg β-2γ1 ctg 3β2—17.己知一点处的应力张量为31260610010000Pa ⎡⎤⎢⎥⨯⎢⎥⎢⎥⎣⎦试求该点的最大主应力及其主方向。
解:由题意知该点处于平面应力状态,且知:σx =12×103 σy =10×103 τxy =6×103,且该点的主应力可由下式求得: 则显然:3312317.08310 4.917100PaPa σσσ=⨯=⨯=σ1 与x 轴正向的夹角为:(按材力公式计算)显然2θ为第Ⅰ象限角:2θ=arctg (+6)=+80.5376° 则:θ=+40.268840°16' 或(-139°44') 5-2:给出axy ϕ=;(1):捡查ϕ是否可作为应力函数。
(2):如以ϕ为应力函数,求出应力分量的表达式。
(3):指出在图示矩形板边界上对应着什么样的边界力。
(坐标如图所示) 解:将axy ϕ=代入40ϕ∇=式得:220ϕ∇∇= 满足。
(完整版)弹塑性力学习题题库加答案.docx
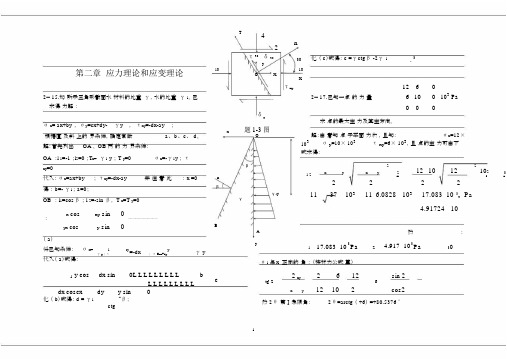
第二章 应力理论和应变理论2— 15.如 所示三角形截面水 材料的比重 γ,水的比重 γ 1。
己求得 力解 :σ x = ax+by , σy =cx+dy- γy , τxy =-dx-ay ;根据直 及斜 上的 界条件,确定常数 a 、b 、c 、 d 。
解:首先列出OA 、 OB 两 的 力 界条件:OA :l 1=-1 ;l 2=0 ;T x= γ1 y ; T y =0σx =-γ1y ; τxy =0代入: σx =ax+by ; τxy =-dx-ay 并 注 意 此 : x =0得 : b=- γ1; a=0;OB : l 1=cos β ; l 2=-sin β, T x =T y =0:x cosxy sin0 yx cosy sin⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( a )将己知条件: σ x=1xy=-dxyγ y-γ y ; τ; σ =cx+dy-代入( a )式得:1 y cos dx sin0L L L L L L L L L bdx coscxdyy sin L L L L L L L L L化 ( b )式得: d = γ12β;ctgT4n2τ 30° δ 30°30°化 ( c )式得: c =γctg β -2γ 13y10x10Ox12 6τxy103 Pa2— 17.己知一点 的 力 量6 10 00 0δ y求 点的最大主 力及其主方向。
x题1-3 图解:由 意知 点 于平面 力状 ,且知:σx =12×O103σ y =10× 103 τ xy =6× 103,且 点的主 力可由下式求得:β212 101221.2xyxy21023n 22xy22610βγ 1y113710311 6.0828 10317.083 10 3 Paγ34.91724 10BA然:y117.083 10 3Pa2 4.917 10 3Pa30σ 1 与 x 正向的 角 : (按材力公式 算)c2 xy2 6 12 sin 2tg 2121026xycos2然 2θ 第Ⅰ象限角: 2θ=arctg ( +6) =+80.5376 °则:θ=+40.2688 B 40° 16'或(-139° 44')2— 19.己知应力分量为:σx=σy=σz=τxy=0,τzy=a,τzx=b,试计算出主应力σ1、σ2、σ3 并求出σ2 的主方向。
弹塑性力学部分习题及答案

解
根据梁的弯曲变形公式,y = Fx/L(L - x),其中y为挠度,F 为力,L为梁的长度。代入题目给定的数据,得y = (frac{300 times (4 - x)}{8})。当x = 2时,y = (frac{300 times (4 - 2)}{8}) = 75mm。
习题三答案及解析
解析
和变形情况。
04
弹塑性力学弹塑性力学的基本假设。
答案
弹塑性力学的基本假设包括连续性假设、均匀性假设、各向同性假设和非线性假设。连 续性假设认为物质是连续的,没有空隙;均匀性假设认为物质的性质在各个位置都是相 同的;各向同性假设认为物质的性质在不同方向上都是相同的;非线性假设认为弹塑性
习题二答案及解析
01 02 03 04
解析
选择题主要考察基本概念的理解,如能量守恒定律、牛顿第二定律等 。
填空题涉及简单的力学计算,如力的合成与分解、牛顿第二定律的应 用等。
计算题要求应用能量守恒定律和牛顿第二定律进行计算,需要掌握基 本的力学原理和公式。
习题三答案及解析
01
答案
02
选择题
03
1. A
2. 解
根据牛顿第二定律,F = ma,其中F为力,m为质量,a 为加速度。代入题目给定的数据,得a = (frac{400}{5}) = 80m/s(}^{2})。再根据运动学公式s = ut + (frac{1}{2})at(}^{2}),得s = 10 × 2 + (frac{1}{2} times 80 times (2)^2) = 108m。
04
计算题要求应用胡克定律和动量守恒定律进行计算,需要掌握基本的 力学原理和公式。
习题二答案及解析
弹塑性力学习题解答

塑性:弹性:2-16设有任意形状的等厚度薄板,体力可以不计,在全部边界上(包括孔口边界上)受有均匀压力q 试证q y x -==σσ 及0=xy τ能满足平衡微分方程、相容方程和应力边界条件,也能满足位移单值条件,因而就是正确的解答。
证明: (1)将应力分量q y x -==σσ,0=xy τ和0==y x f f 分别代入平衡微分方程、相容方程⎪⎪⎩⎪⎪⎨⎧=+∂∂+∂∂=+∂∂+∂∂00y x xy yy x y yxxx f f τστσ (a ) 0)1())((2222=∂∂+∂∂+-=+∂∂+∂∂)(y f x f yx y x y x μσσ (b )显然(a )、(b )是满足的(2)对于微小的三角板dy dx A ,,都为正值,斜边上的方向余弦),cos(x n l =,),cos(y n m =,将q y x -==σσ,0=xy τ代入平面问题的应力边界条件的表达式⎪⎩⎪⎨⎧=+=+)()()()(s f l m s f m l y s xy y x s yx x τστσ (c ) 则有),cos(),cos(x n q x n x -=σ ),cos(),cos(y n q y n y -=σ 所以q x -=σ,q y -=σ。
对于单连体,上述条件就是确定应力的全部条件。
(3)对于多连体,应校核位移单值条件是否满足。
该题为平面应力的情况,首先,将应力分量q y x -==σσ及0=xy τ代入物理方程,得形变分量q E x )1(-=με,q Ey )1(-=με,0=xy γ (d ) 然后,将(d )的变形分量代入几何方程,得q Ex u )1(-=∂∂μ,q E y v )1(-=∂∂μ,0=∂∂+∂∂y u x v (e )前而式的积分得到 )()1(1y f qxE u +-=μ,)()1(2x f qy Ev +-=μ (f ) 其中的1f 和2f 分别是y 和x 的待定函数,可以通过几何方程的第三式求出,将式(f )代入(e )的第三式得 dxx df dy y df )()(21=-等式左边只是y 的函数,而等式右边只是x 的函数。
弹塑性力学习题解

第二章 习题解
5.
为什么在推导相容方程时,使用了平衡方 程。在应力求解时的三个方程中,用两个 平衡方程和一个相容方程,这是否矛盾?
答:不矛盾。这是因为在推导相容方程时,为了简化方 程,对平衡方程求导,消去相容方程中的剪应力分量。 通过能满足相容方程的正应力分量,再求解出的剪应力 分量,不一定能满足平衡方程。因为对偏微分方程积分, 相差一任意函数。
2
第三章 习题解
2.
试证明,如果体力虽然不是常量,但却是有势的力,即
X
其中V是势函数,则应力分量亦可用应力函数φ表示成 为 2 2 2
x
V x
Y
V , y
试导出相应的相容方程。 证明:
y
2
V, y
x
2
V , xy
xy
因体力不等于零的情况下的平衡方程的解,可分解为齐次方程 解和特解。而: 2 2 2
b2 1 2 r r2 qa b 1 2 a
b2 1 2 r 2 qa b 1 2 a
因为方程中不包含材料常数,在平面应变情况下,它们 不变。平面应变情况下的轴向应力分量为:
第四章 习题解
b 1 2 a 由于问题的轴对称性, 剪应力分量为零。
z r
第二章 习题解
1.
说明弹性力学两个平面问题的异同。
答:相同点:两者均是数学上的二维问题,两者的独立应 力分量都是xy坐标面内的应力分量,所受边界力均平行于 xy坐标面。所得到的弹性力学方程除弹性常数不同外,形 式上相同。 不同点:平面应力问题的结构为一很薄的平板,边界 z xz yz 0。 力对称分布于平分板厚的中面,应力分量 平面应变问题的结构是一很长的直线柱体,边界力垂直于 柱体轴线并沿轴线长度不变化,由于柱体很长可以认为轴 向位移为零,从而轴向应变为零,弹性力学变量有下列关 系: w 0, z 0, z 0, xz yz 0
弹塑性力学第十一章标准详解
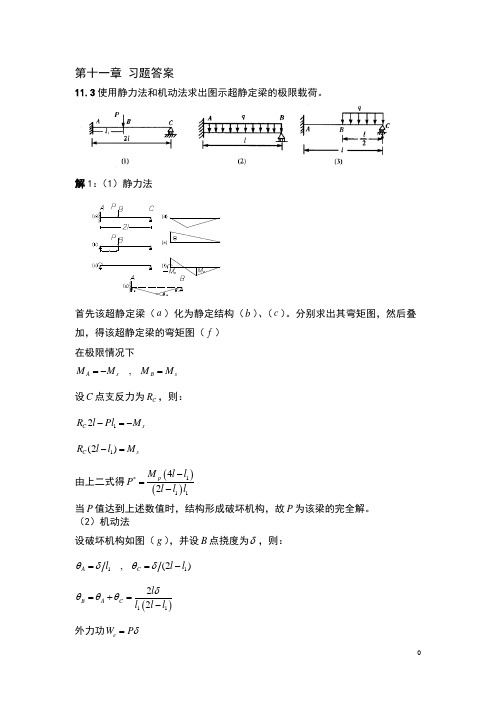
第十一章 习题答案11.3使用静力法和机动法求出图示超静定梁的极限载荷。
解1:(1)静力法首先该超静定梁(a )化为静定结构(b )、(c )。
分别求出其弯矩图,然后叠加,得该超静定梁的弯矩图(f ) 在极限情况下,A sB s M M M M =-=设C 点支反力为C R ,则:12C s R l Pl M -=- 1(2)C s R l l M -=由上二式得()()11142p M l l P l l l *-=-当P 值达到上述数值时,结构形成破坏机构,故P 为该梁的完全解。
(2)机动法设破坏机构如图(g ),并设B 点挠度为δ,则:11,(2)A C l l l θδθδ==-()1122B A C l l l l δθθθ=+=-外力功e W P δ=内力功()11142i A A B B s l l W M M M l l l θθδ-=+=-由e i W W =,可得极限载荷上限为()11142s l l P M l l l *-=-由于在P *作用下,()s s M M x M -≤≤,故上式所示载荷为完全解的极限载荷。
解2:(1)静力法先将该超静定梁化为静定梁(b )、(c ),分别作弯矩图,叠加得该超静定梁的弯矩图(f )设A 点为坐标原点,此时弯矩方程为:()()()212B M x R l x q l x =---在极限状态时,有()0,0s x M M ==- ()11,s x x M x M == 令()0dM x dx=得1()B q l x R -= (1) 而212B s R l ql M -=- (2)()()21112B s R l x q l x M ---= (3)联立解(1)、(2)、(3)得2122s s M qM ql l ⎛⎫=- ⎪⎝⎭解得21122s M q l⎡=⎣取较大的值,可得0211.66sM q l ≈ 在以上0q 值作用下,梁已形成破坏机构,故其解为完全解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-7已知某点的应力状态为 过该点斜截面法线 的方向余弦为 ,试求斜截面上切应力 的表达式。
2-8物体中某点的应力状态为 求该点主应力的大小和主轴方向。
2-9已知物体中某点的应力状态为 ,斜截面法线的方向余弦为 ,试求斜截面上切应力的大小。
2-10半径为 的球,以常速度 在粘性流体中沿 轴方向运动。球面上点A( )受到的表面力为 , , ,式中 为流体的静水压力。试求球所受的总力量。
5-9如已知材料的屈服极限按如下规律变化 ,试求此等厚度自由旋转圆盘在极限状态下的转速 以及径向和环向的应力表达式。
5-10已知理想均质弹塑性材料制成的圆盘,此材料服从特雷斯卡屈服条件,如 为极限状态时的转速,而 为盘中某一点进入塑性时的转速,试分别求出带中心圆孔圆盘和不带中心圆孔圆盘的 / 值各为多少?
2-11已知物体中某点的应力状态为 ,斜截面法线的方向余弦为 ,试证明斜截面上的正应力 及剪应力 分别为 、 。
习题3
3-1若位移 是坐标的一次函数,则在整个物体中各点的应变都是一样的,这种变形叫均匀变形。设有以O为中心的曲面,在均匀变形后成为球面,
问原来的曲面 是怎样的一种曲面?
3-2证明 , , , (其中 和 是微小的常数),不是一个可能的应变状态。
习题2
2-1受拉的平板,一边上有一凸出的尖齿,如图2.1。试证明齿尖上完全没有应力。
图2.1
2-2物体中某点的应力状态为 ,求三个不变量和三个主应力的大小。
2-3有两个坐标系,试证明 。
2-4M点的主应力为 。一斜截面的法线v与三个主轴成等角,求 、 及 。
2-5已知某点的应力状态为 ,求该点主应力的大小和主轴方向。
习题5
5-1已知理想弹塑性材料的受弯杆件,设计截面为:(a)正方形,(b)圆形,(c)内外径比为 的圆环,(d)正方形沿对角线受弯,(e)工字型;其尺寸如图5-17所示。试求塑性极限弯矩与弹性极限弯矩之比 各为多少?
图5-17
5-2设有理想弹塑性材料的矩形截面杆件的高度为 ,宽度为 受外力作用,当弹性核 时,试求此时弯矩值为多少?
图5-19图5-20
5-7在题5-6中,当 时,试给出卸载后,在弹性区和塑性区应力的表达式。
5-8已知内半径为a,外半径为b的自由旋转环盘(如图5-21所示),材料的屈服极限为,试用特雷斯卡屈服条件求出此旋转环盘在极限状态时的表达式,并求出的最大值。给出a趋近于零或趋近于b(薄环情况)的的最大值。
图5-21
3-3将一个实体非均匀加热到温度T,而T是 、 、 的函数。如果假设每一单元体的热膨胀都不受约束,那么各应变分量为 , ,其中 是热膨胀系数,是常数。试证明,这种情况只有当T是 、 、 的线性函数时才会发生。
3-4参照下图,
设 , ,而 ,试证:
3-5已知欧拉应变 的6个分量,证明小变形的线应变和剪应变为
4-2设体积力为常量,试证明:
。
式中 , 。
4-3设体积力为常量,试证明:
。
4-4试推导,用应力法把有体积力问题化成无体积力问题的基本方程和边界条件。
4-5用应力法解释弹性力学问题,基本方程为什么也是9个而不6个?
4-6推导密切尔——贝尔特拉米方程的过程中,曾用过平衡方程,为什么解题时,用应力法,基本方程中还有平衡方程?
(a)单向受力状态, ,
(b)纯剪受力状态, 。
3-17已知薄壁圆筒承受拉应力 及扭矩的作用,若使用米泽斯屈服条件,试求薄壁圆筒屈服时扭转应力应为多大?并给出此时塑性应变增量的比值。
3-18若有两向应力状态 ,试求各应变分量的值。
习题4
4-1设已知对各向同性材料的应力应变关系为 ,试证其应力主轴与应变主轴是一致的。
5-11已知半径为b的等厚度的实心旋转圆盘,由不可压缩材料制成,材料服从特雷斯卡屈服条件,如盘中所有点都同时进入塑性状态,则屈服条件的表达式应取何形式?此时极限转速 应为多大?
5-12设有理想弹塑性材料制成的厚壁圆筒,内半径为a,外半径为b,承受内压 的作用,试求此后圆筒开始进入塑性状态时和完全进入塑性状态时的压力比值为多少?
5-3已知矩形截面的简支梁,其高为 ,宽为 ,在梁上 范围内承受均
布载荷的作用如图5-18所示。试求此梁中间截面开始进入塑型时的外载荷 以及极限载荷 的值,分别求出 和 两种情况时的弹塑性分界线的表达式。
5-4若已知理想弹塑性材料的剪切屈服极限为 ,如用此材料支撑半径为R的受扭圆轴,试求当 和 时,扭矩M值的大小。 为弹塑性分解半径。
3-14已知两端封闭的薄壁圆筒,半径为r,厚度为t,承受内压及轴向拉应力的作用,试求此时圆管的屈服条件,并画出屈服条件的图。
3-15已知半径为r,厚度为t的薄壁圆筒,承受轴向拉伸和扭转的联合作用,设在加载过程中,保持 ,试求此圆管在按米泽斯屈服条件屈服时,轴向拉伸力P和扭矩M的表达式。
3-16在如下两种情况下,试给出塑性应变增量的比值。
,
3-6已知: , , ,求: .
3-7试证: .
3-8设某点的拉格朗日应变为
试求:(a)主应变;
(b)最大主应变对应的主轴方向;
(c)最大剪应变分量 .
3-9刚性位移与刚体位移有什么区别?
3-10试用应力分量写出轴对称极坐标平面应变状态条件下的协调方程。
3-11如图3-11所示,试用正方体(a×a×a)证明不可压缩物体的泊松比 。
图5-18
5-5试求外半径为b,内半径为a的圆管(如图5-19所示)。在扭矩的作用下,塑性极限扭矩和弹性极限扭矩之比为多大?如为薄壁管,则扭矩之比又为多大?
5-6已知理想弹塑性材料制成的空心圆轴(如图5-20所示),内半径为a,外半径为b,若内外半径之比为 ,即,试求使截面最外层屈服时的 和使截面达到完全屈服时的扭矩 的值各为2将橡皮方块放在与它同样体积的铁盒内,在上面用铁盖封闭,使铁盖上面承受均匀压力 的作用,如图3-12所示。假设铁盒与铁盖可以看作为刚体,在橡皮与铁之间没有摩擦力,试求铁盒内侧面所受到的压力以及橡皮块的体积应变。若将橡皮块换成刚体或不可压缩体时,其体积应变将有什么变化?
图3-11图3-12
3-13设 为主应力偏量,试证明用主应力偏量表示米泽斯屈服条件,其形式为
