三校生高考数学模拟试卷3
2025届江西省南昌三校高三第三次模拟考试数学试卷含解析

2025届江西省南昌三校高三第三次模拟考试数学试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.抛掷一枚质地均匀的硬币,每次正反面出现的概率相同,连续抛掷5次,至少连续出现3次正面朝上的概率是( ) A .14B .13C .532D .3162.函数的图象可能是下面的图象( )A .B .C .D .3.阅读名著,品味人生,是中华民族的优良传统.学生李华计划在高一年级每周星期一至星期五的每天阅读半个小时中国四大名著:《红楼梦》、《三国演义》、《水浒传》及《西游记》,其中每天阅读一种,每种至少阅读一次,则每周不同的阅读计划共有( ) A .120种B .240种C .480种D .600种4.如图所示的程序框图,当其运行结果为31时,则图中判断框①处应填入的是( )A .3?i ≤B .4?i ≤C .5?i ≤D .6?i ≤5.已知集合{}10A x x =+≤,{|}B x x a =≥,若A B R =,则实数a 的值可以为( )A .2B .1C .0D .2-6.若复数z 满足()1i z i +=(i 是虚数单位),则z 的虚部为( ) A .12B .12-C .12i D .12i -7.函数2|sin |2()61x f x x=+ )A .B .C .D .8.如图是计算11111++++246810值的一个程序框图,其中判断框内应填入的条件是( )A .5k ≥B .5k <C .5k >D .6k ≤9.已知函数()5sin 12f x x π⎛⎫=+ ⎪⎝⎭,要得到函数()cos g x x =的图象,只需将()y f x =的图象( )A .向左平移12π个单位长度 B .向右平移12π个单位长度C .向左平移512π个单位长度 D .向右平移512π个单位长度 10.已知实数x ,y 满足2212x y +≤,则2222267x y x y x +-++-+的最小值等于( )A .625B .627C 63-D .962-11.总体由编号为01,02,...,39,40的40个个体组成.利用下面的随机数表选取5个个体,选取方法是从随机数表(如表)第1行的第4列和第5列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )A .23B .21C .35D .3212.()6321x x x ⎫-⎪⎭的展开式中的常数项为( ) A .-60B .240C .-80D .180二、填空题:本题共4小题,每小题5分,共20分。
上海数学三校生高考模拟卷-3
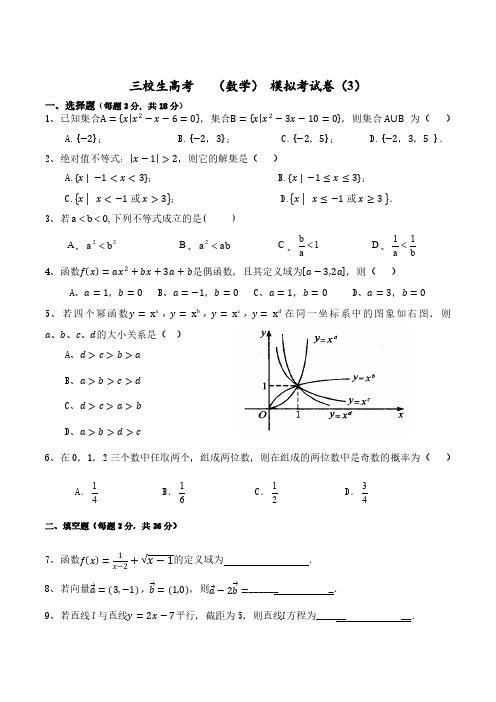
三校生高考 (数学) 模拟考试卷(3)一、选择题(每题3分, 共18分)1、已知集合A =*x |x 2−x −6=0+,集合B =*x |x 2−3x −10=0+,则集合 A⋃B 为( )A.{−2};B.{−2,3};C.{−2,5};D.{−2,3,5 }.2、绝对值不等式:|x −1|>2,则它的解集是( )A.*x | −1<x <3+;B.*x | −1≤x ≤3+;C.{x | x <−1或 x >3};D.{x | x ≤−1或 x ≥3 }.3、若,0<<b a 下列不等式成立的是( )A 、22b a <B 、ab a <2C 、1<a bD 、b a 11<4、函数f (x )=ax 2+bx +3a +b 是偶函数,且其定义域为,a −3,2a -,则( )A 、a =1,b =0B 、a =−1,b =0C 、a =1,b =0D 、a =3,b =05、若四个幂函数y =a x ,y =b x ,y =c x ,y =d x 在同一坐标系中的图象如右图,则a 、b 、c 、d 的大小关系是( )A 、d >c >b >aB 、a >b >c >dC 、d >c >a >bD 、a >b >d >c6、在0,1,2三个数中任取两个,组成两位数,则在组成的两位数中是奇数的概率为() A .14 B .16 C .12 D .34二、填空题(每题3分,共36分)7、函数f (x )=1x−2+√x −1的定义域为 .8、若向量a ⃗=(3,−1),b ⃗⃗=(1,0),则a ⃗−2b ⃗⃗=______ _.9、若直线 与直线y =2x −7平行,截距为5,则直线 方程为______ __.10、不等式(x+2)(x−7)<0的解集为.11、等差数列*a+中,若a=2,a2+a=13,则数列公差d= ___ __.12、有6名男生,4名女生,现选3名参加比赛,要求至少一男一女,则有种不同选法.13、在∆ABC中,已知sinA:sinB:sinC=3:5:7,且最大边长为14,则∆ABC的面积是 .14、已知角 α 终边上一点 P(−3,4),则 sinα+cosα=。
三校生高考模拟数学试卷

一、选择题(本大题共20小题,每小题5分,共100分)1. 下列函数中,在实数域内单调递增的是()A. y = -x^2 + 2xB. y = 2^xC. y = log2xD. y = √x2. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为()A. 10B. 15C. 20D. 253. 若复数z满足|z - 1| = |z + 1|,则复数z的实部是()A. 0B. 1C. -1D. 无法确定4. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减5. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极小值为()A. -1B. 0C. 1D. 26. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 107. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 4868. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x9. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定10. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减11. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 212. 下列方程组中,有唯一解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1013. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48614. 下列函数中,在区间(0,+∞)上为增函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x15. 若复数z满足|z - 1| = |z + 1|,则复数z的虚部是()A. 0B. 1C. -1D. 无法确定16. 下列命题中,正确的是()A. 函数y = x^3在R上单调递增B. 等差数列{an}的通项公式为an = a1 + (n - 1)dC. 若a > b > 0,则a^2 > b^2D. 函数y = log2x在(0,+∞)上单调递减17. 已知函数f(x) = x^3 - 3x^2 + 2,则f(x)的极大值为()A. -1B. 0C. 1D. 218. 下列方程组中,无解的是()A. x + y = 1B. 2x + 3y = 6C. 3x - 4y = 2D. 4x - 5y = 1019. 已知等比数列{an}的首项a1 = 2,公比q = 3,则第10项a10的值为()A. 18B. 54C. 162D. 48620. 下列函数中,在区间(0,+∞)上为减函数的是()A. y = x^2B. y = 2^xC. y = log2xD. y = √x二、填空题(本大题共10小题,每小题5分,共50分)21. 已知等差数列{an}的前n项和为Sn,若S10 = 100,S20 = 300,则第15项a15的值为______。
三校生高考数学模拟试卷

三校生高考数学模拟试卷一、选择题(本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设集合A = {xx^2 - 3x + 2 = 0},B={1, 2},则A与B的关系是()A. A⊂neqq BB. A = BC. A⊃neqq BD. A∩ B=varnothing2. 函数y=√(x - 1)的定义域是()A. (-∞,1]B. [1,+∞)C. (-∞, 0]D. [0,+∞)3. 若sinα=(3)/(5),且α是第二象限角,则cosα的值为()A. (4)/(5)B. -(4)/(5)C. (3)/(4)D. -(3)/(4)4. 过点(1,2)且斜率为3的直线方程为()A. y - 2 = 3(x - 1)B. y+2=3(x + 1)C. y - 2=-3(x - 1)D. y+2=-3(x + 1)5. 二次函数y = x^2+2x - 3的对称轴为()A. x = - 1B. x = 1C. x = 2D. x=-26. 已知向量→a=(1,2),→b=(3,-1),则→a·→b等于()A. 1B. -1C. 5D. -57. 在等差数列{a_n}中,若a_1=1,d = 2,则a_5的值为()A. 9B. 10C. 11D. 128. 若x>0,则函数y = x+(1)/(x)的最小值是()A. 1B. 2C. 3D. 49. 从5名男生和3名女生中选3人参加某项活动,要求既有男生又有女生,则不同的选法有()种。
A. 45B. 30C. 15D. 1010. 若f(x)是定义在R上的奇函数,当x>0时,f(x)=x^2+1,则f(-1)的值为()A. -2B. 2C. -1D. 1二、填空题(本大题共5小题,每小题4分,共20分)11. 计算log_28=_。
12. 椭圆frac{x^2}{16}+frac{y^2}{9}=1的长半轴长a = _。
最新三校生数学高考模拟试卷

三校生数学高考模拟试卷一、是非选择题。
(对的选A ,错的选B。
每小题3分,共30分)1.如果A={0.1.2.3},B={1},则B ∈A …………………………………………( ) 2.已知直线上两点A (-3,3),B (3,-1),则直线AB 的倾斜角为65π( ) 3.lg 2+lg5=lg7………………………………………………………………………( ) 4.函数f(x)=245x x -+的定义域是【-1,5】…………………………( )5.sin750·sin3750=41-……………………………………………………………( )6.在等比数列{a n }中,a 1=31,a 4=89,则数列的公比为23…………………( )7.若向量32=+,则∥……………………………………( )8.双曲线13422=-y x 的渐近线方程为x y 23±=,焦距为2………………( ) 9.直线l ⊥平面α,直线m ∥平面β,若l ∥m ,则α⊥β………………( )10.二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………( )二、选择题(每小题5分,共40分) 11.函数f(x)=lg(x-3)的定义域是 ( )A.RB.(-3,3)C.(-∞,-3)∪(3,+∞)D.【0,+∞) D.112.以点M (-2,3)为圆心且与x 轴相切的圆的方程( )A.(x +2)2+(y -3)2=4 B . (x -2)2+(y +3)2=4C.(x +2)2+(y -3)2=9 D . (x -2)2+(y +3)2=913.10件产品中,3件次品,甲、乙两人依次各取一件产品,按取后放回,求恰有一件次品的概率为( ) A.10021 B. 241 C. 4521 D. 502114.若函数f(x)在定义域R 上是奇函数,且当x ﹥0时,f(x)=2410x x -,则f(-2)=( ).A. -104B.104C. 1D.10-1215.a=2是直线(a 2-2)x +y=0和直线2x +y +1=0互相平行的( ).A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16.设数列{a n }的前n 项和为2n s n=,则a 8=()A.64B.49C.16D.1517.在直角坐标系中,设A (-2,3),B (-3,-3),现沿x 轴把直角坐标系折成直二面角,则AB 的长为( )A.6B.5C.19D.118.a =(1,2),b =(x ,5),且b a⊥2,则x= ( )A .10B .-10 C.25 D.25-三、填空题(每题5分,共30分)19.已知x ∈(ππ,-),已知sinx=21, 则x= _ 已知tanx=-1,则x= _20.已知正方形ABCD 的边长为2,AP ⊥平面ABCD ,且AP=4,则点P 到BD 的距离 21.过圆3622=+y x 上一点(4,52)的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排,其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级: 姓名: 座号:四、解答题(第25、26、题,每小题10分,第27.28题,每小题15分,共50分)255=8=,<b a ,> =32π,求()()b a b a -∙+2。
三校生第三次模考数学试卷

(三校生)第三次模考数 学 试 卷试卷分值:150分 考试时间:120分钟一.是非选择题(本大题共10小题,每小题3分,共30分。
对的选A ,错的选B ) 1. 设全集{1,2,3,4,5}U =,集合{1,4}A =,则U C A 的所有子集个数是8. ()AB2. 函数y =[1,)-+∞ ()AB 3. 已知数列{}n a 满足1lg 2n n a a +=+且11a =,则其通项公式为1(1)lg 2n a n =+- 4. 函数2sin y x π=的最小正周期为π ()AB5. ()AB 6. 正方体1111ABCD A BC D -中,异面直线1BC 与1CD 所成角为45 ()AB7. 与原点距离为2,斜率为1的直线方程是10x y -+= ()AB 8. 一枚硬币连续抛掷三次,至少有两次正面向上的概率是12()AB 9. 设随机变量ξ的概率分布为()(1,2,3,4)5a P k k k ξ===,则125a = ()AB 10.在8(1)(1)x x -+的展开式中,5x 的系数是14- ()AB 二.单项选择题(本大题共8小题,每小题5分,共40分)11.已知向量(3,2)a =-与(6,)b λ=共线,则λ的值为 ( ).1144A B C D --12.sin()cos cos()sin x y y x y y -+-= ( ) .s i n s i n .c o s s i n .s i n .A x y B x y C x D x13.直线10x y ++=的倾斜角是 ( )32....4443A B C D ππππ-14.0.3222,0.3,log 0.3的大小关系是 ( )20.320220.320.3222.0.3log 0.32.log 0.30.32.2log 0.30.3.log 0.320.3A B C C <<<<<<<<15.两条直线没有公共点是两条直线为异面直线的 ( ).A 充分条件 .B 必要条件 .C 充要条件 .D 既不充分也不必要条件 16.设{}n a 为等差数列,已知25836a a a ++=,则5a = ( ) .12.24.36.A B C D 17.甲,乙两人各进行一次射击,如果甲击中的概率为0.6,乙击中的概率为0.7,那么 甲,乙两人至少有一人击中的概率是 ( ) .0.86.0.42.0.88.0.90A B C D18.若回归直线方程为 1.23y x a =+,其中样本中心点为(4,5),则a =( ).4.5.0.08.0.09A B C D三.填空题(本大题共6小题,每小题5分,共30分)19.已知向量(1,2),(,4)a b m ==-且//a b ,则()______.a a b += 20.在三角形ABC 中,1cos ,23A a ==,则sin _____.Bb= 21.圆22410x x y +++=的圆心到直线310x y +-=的距离为_____. 22.在等比数列{}n a 中,已知355a a =,那么1357____.a a a a =23.平面//α平面β,,,a b αβ⊂⊂则直线,a b 的位置关系是__________.24.椭圆22214x y a +=与双曲线2212x y a -=有相同的焦点,则a 的值为____.四.解答题(本大题共6小题,25—28每小题8分,29—30每小题9分,共50分) 25.已知一等差数列的第3项为2,前10项的和为95,问11是否为这个数列中的项?若是,求出是第几项。
最新三校生数学高考模拟试卷教学内容

三校生数学高考模拟试卷一、是非选择题。
(对的选A ,错的选B。
每小题3分,共30分)1.如果A={0.1.2.3},B={1},则B ∈A …………………………………………( ) 2.已知直线上两点A (-3,3),B (3,-1),则直线AB 的倾斜角为65π( ) 3.lg 2+lg5=lg7………………………………………………………………………( ) 4.函数f(x)=245x x -+的定义域是【-1,5】…………………………( )5.sin750·sin3750=41-……………………………………………………………( )6.在等比数列{a n }中,a 1=31,a 4=89,则数列的公比为23…………………( )7.若向量32=+,则∥……………………………………( )8.双曲线13422=-y x 的渐近线方程为x y 23±=,焦距为2………………( ) 9.直线l ⊥平面α,直线m ∥平面β,若l ∥m ,则α⊥β………………( )10.二项式1033⎪⎭⎫⎝⎛-x x 展开式中二项式系数最大的项是第五项…………………( )二、选择题(每小题5分,共40分) 11.函数f(x)=lg(x-3)的定义域是 ( )A.RB.(-3,3)C.(-∞,-3)∪(3,+∞)D.【0,+∞) D.112.以点M (-2,3)为圆心且与x 轴相切的圆的方程( )A.(x +2)2+(y -3)2=4 B . (x -2)2+(y +3)2=4C.(x +2)2+(y -3)2=9 D . (x -2)2+(y +3)2=913.10件产品中,3件次品,甲、乙两人依次各取一件产品,按取后放回,求恰有一件次品的概率为( ) A.10021 B. 241 C. 4521 D. 502114.若函数f(x)在定义域R 上是奇函数,且当x ﹥0时,f(x)=2410x x -,则f(-2)=( ).A. -104B.104C. 1D.10-1215.a=2是直线(a 2-2)x +y=0和直线2x +y +1=0互相平行的( ).A.充分条件 B.必要条件 C.充要条件 D.即不充分也不必要条件 16.设数列{a n }的前n 项和为2n s n=,则a 8=()A.64B.49C.16D.1517.在直角坐标系中,设A (-2,3),B (-3,-3),现沿x 轴把直角坐标系折成直二面角,则AB 的长为( )A.6B.5C.19D.118.a =(1,2),b =(x ,5),且b a⊥2,则x= ( )A .10B .-10 C.25 D.25-三、填空题(每题5分,共30分)19.已知x ∈(ππ,-),已知sinx=21, 则x= _ 已知tanx=-1,则x= _20.已知正方形ABCD 的边长为2,AP ⊥平面ABCD ,且AP=4,则点P 到BD 的距离 21.过圆3622=+y x 上一点(4,52)的切线方程为 _ _22.椭圆1422=+y x 的离心率为23.4名男生和2名女生站成一排,其中2名女生站在两端的站法有 种24.函数1422+-=x x y 的值域为 班级: 姓名: 座号:四、解答题(第25、26、题,每小题10分,第27.28题,每小题15分,共50分) 255=8=,<b a ,> =32π,求()()b a b a -•+2。
数学试卷三校生高考

一、选择题(每题4分,共40分)1. 已知函数f(x) = x^2 - 2x + 1,那么f(2)的值为()A. 1B. 3C. 0D. -12. 下列函数中,是奇函数的是()A. f(x) = x^2B. f(x) = |x|C. f(x) = x^3D. f(x) = x^43. 已知等差数列{an}的公差为d,若a1 + a2 + a3 = 9,a1 + a2 + a3 + a4 = 18,则d的值为()A. 2B. 3C. 4D. 54. 在△ABC中,角A、B、C的对边分别为a、b、c,若a^2 + b^2 = c^2,则△ABC是()A. 直角三角形B. 锐角三角形C. 钝角三角形D. 等腰三角形5. 下列方程中,有唯一解的是()A. x^2 + x + 1 = 0B. x^2 - 2x + 1 = 0C. x^2 + 2x + 1 = 0D. x^2 - 4x + 3 = 06. 已知等比数列{an}的公比为q,若a1 + a2 + a3 = 12,a1 a2 a3 = 27,则q的值为()A. 3B. 2C. 1D. -17. 下列函数中,在定义域内单调递增的是()A. f(x) = x^2B. f(x) = 2^xC. f(x) = log2xD. f(x) = x^38. 已知函数f(x) = x^2 - 3x + 2,那么f(-1)的值为()A. 0B. 1C. 2D. -19. 在△ABC中,角A、B、C的对边分别为a、b、c,若a = 3,b = 4,c = 5,则△ABC的面积为()A. 6B. 8C. 10D. 1210. 下列方程中,有无数解的是()A. x^2 + y^2 = 1B. x^2 + y^2 = 4C. x^2 + y^2 = 9D. x^2 + y^2 = 16二、填空题(每题4分,共40分)1. 已知等差数列{an}的首项为a1,公差为d,那么第n项an = _______。
三校生高考数学模拟试卷3

三校生高考数学模拟试卷3三校生高考数学模拟试卷3对于许多即将参加三校生高考的同学们来说,数学是一门至关重要的科目。
而在高考前,进行模拟考试是非常必要的。
最近,我们学校组织了一次高考数学模拟试卷3的考试,旨在帮助同学们熟悉考试形式和提升应试能力。
在本文中,我将分享一些有关这次模拟试卷的看法和体会。
首先,让我们来了解一下什么是三校生高考。
三校生高考是指中等职业学校、中等技术学校和职业高中的毕业生参加的高考。
与普通高考相比,三校生高考在考试科目、考试形式和内容上都有所不同。
其中,数学科目在三校生高考中占有较大比重,对于很多同学来说也是相对较难的一门课程。
在这次模拟试卷3的考试中,我们遇到了各种类型的题目,包括计算题、应用题和证明题等。
总体来说,这次模拟试卷的难度适中,但也有一些比较有挑战性的题目。
从题型上来看,填空题和选择题的比例较大,这也符合三校生高考数学的实际考试情况。
在备考过程中,我发现自己在一些基础知识方面还需要加强。
例如,在这次模拟试卷中,有一道关于三角函数的题目,如果对相关概念掌握不够扎实,就很难顺利解答。
此外,我还需要提高自己的解题速度和准确率,特别是在做一些计算题和应用题时,需要更加细心和耐心。
为了提高自己的数学成绩,我采取了一些具体的措施。
首先,我会对每个知识点进行系统的学习和复习,确保自己对基础知识有更加深入的理解。
其次,我会通过做题来巩固自己的知识,特别是做一些历年高考数学真题和模拟试卷,这样可以更好地了解自己的薄弱环节,并针对性地进行提高。
最后,我会积极参加各种数学竞赛和辅导班,这样可以与其他同学进行交流和学习,同时也可以拓展自己的解题思路和方法。
总之,这次高考数学模拟试卷3的考试对我来说是一次非常有价值的经历。
通过这次考试,我更加清晰地了解了自身的数学水平,同时也发现了自己在备考过程中需要加强的地方。
我相信,在未来的备考过程中,我会更加努力地学习和提高自己的数学能力,争取在高考中取得优异的成绩。
【高教版】江西省2020年三校生高考数学全真模拟题(三)

江西省2020年三校生高考数学全真模拟题(三)命题人:赖斌 审核人:李发彬 命题时间:2019.3 份数:95第Ⅰ卷(选择题 共70分)一、是非选择题:本大题共10小题,每小题3分,共30分.对每小题的命题做出判断,对的选A ,错的选B.1、R ∈2…………………………………………………………………………………(A B )2、若a>b,则-5a>-5b ………………………………………………………………………(A B )3、函数42)(x x x f +=是一个偶函数……………………………………………………(A B )4、81632=…………………………………………………………………………………(A B ) 5、若)3,1(-=a )2,2(,-=a 则)1,1(=+b a ……………………………………………(A B )6、过直线外一点,可以作无数个平面与这条直线平行…………………………………(A B )7、如果,54sin =a 则53cos -=α………………………………………………………(A B )8、由数字1,2,3,4,5可以组成60个数字不重复的三位数………………………………(A B ) 9、5>x 是3>x 的必要不充分条件……………………………………………………(A B )10、椭圆14322=+y x 的焦点坐标为(-1,0),(1,0)……………………………………(A B ) 二、单项选择题:本大题共8小题,每小题5分,共40分。
11、函数x y lg =的定义域是( ) .A .()+∞∞-,B .[0,+∞]C .(0,+∞)D .(1,+∞) 12.式子log 39的值为( ) .A .1B .2C .3D .9 13.已知锐角α的终边经过点(1,1),那么角α为( ) . A .30° B .90° C .60° D .45°14、已知一个圆的半径是2,圆心点是A (1,0),则该圆的方程是( ) . A .4)1(22=+-y x B .4)1(22=++y x C. 2)10(22=+-y x D .2)1(22=++y x 15、已知a=4, b=9,则a 与b 的等比中项是( ) . A .6 B . -6 C .±6 D .±61 16、同时抛掷两枚均匀的硬币,出现 两个反面的概率是( ) .A .21 B .31 C .41 D .51 17、设椭圆14522=+y x 的两个焦点分别是F 1、F 2,AB 是经过F 1的弦,则△ABF 2的周长是( ) .A .25B .45C .252+D .254+ 18、如图,直线PA 垂直于直角三角形ABC 所在的平面,且∠ABC=90°,在△PAB ,△PBC,,△PAC 中,直角三角形的个数是( ) .A .0B .1C .2D . 3第Ⅱ卷(非选择题 共80分)三、填空题:本大题共6小题,每小题5分,共30分.19、cos 300°=______________________ .20、设a =x 2+2x ,b =x 2+x +2,若x >2,则a 、b 的大小关系是_________________ . 21、已知正方体的表面积是54cm 2,则它的体积是________________ .22、已知双曲线162x -192=y 则它的离心率是____________ . 23、四本不同的图书,分给四个同学,每人一本,则不同的分法有________种(用数字作答). 24、当a >0且a ≠1时,函数f(x)=a x -2-3的图象必过定点______________ .四、解答题:本大题共6小题,25~28小题每小题8分,29~30小题每小题9分,共50分.解答应写出过程或步骤.25、已知)5,3(-=a,),15(m b -=(1)当实数m 为何值时,b a ⊥;(2)当实数m 为何值时b a// .班级:_____________________姓名:_____________________座位号:_________________***************************密*********************封*********************线****************************26、已知数列{}n a 满足a 1=1, a 2=3,a n+2+a 2=2a n +1(n ∈N *) (1)求a 3,a 4的值; (2)求数列{}n a 的前N 项和S .27、现用长8m 的铝合金制作一个矩形窗户的边框,问怎样设计,才能既使铝合金恰好用完,又使窗户的面积最大?28、已知函数f(x)=lg xx+-11.(1)f(-31)+f(-32)的值;(2)求证:函数f (x )为奇数函数;(3)解不等式f (x )<129、如图,已知矩形ABCD ,MA ⊥平面ABCD ,若AB=MA=1,AD=3。
江西省贵溪市实验中学2021届高三三校生第三次模考考试数学试卷 (解析版)

2021年江西省鹰潭市贵溪实验中学三校生高考数学三模试卷一、是非选择题(共10小题).对的选A,错的选B。
1.与的等比中项是2.(判断对错)2.a>b是ac2>bc2充要条件.(判断对错)3.小明有4个电子邮箱,他要发3个电子邮件,发送方法的种数为43.(判断对错)4.圆x2+y2+4x+2y﹣5=0的圆心坐标为(2,﹣1).(判断对错)5.若直线a与平面α垂直,则a与平面α内的所有直线都垂直.(判断对错)6.将函数y=sin2x的图象向右平移个单位可得到函数的图象.(判断对错)7.已知集合A={x|x≤0},且A∩B=A,则集合B可能是{x|x≤﹣1}.(判断对错)8.已知f(x)是定义在R上的奇函数,当x>0时,f(x)=log3x,则f(﹣3)=1.(判断对错)9.已知一个正方体的所有顶点在一个球面上,若该球的表面积12π,则正方体的体积为8.(判断对错)10.已知函数f(x)=ax2+bx+c,关于x的不等式f(x)<0的解集为(﹣1,3),则f(4)>f(0)>f(1).(判断对错)二、单项选择题(共8小题).11.已知集合A={0,2},B={﹣2,﹣1,0,1,2},则A∪B=()A.{0,2}B.{1,2}C.{0}D.{﹣2,﹣1,0,1,2}12.已知点(﹣4,3)是角α终边上的一点,则sin(π﹣α)=()A.B.C.D.13.在等比数列{a n}中,a3、a15是方程x2﹣7x+12=0的两个根,则的值为()A.B.2C.﹣2D.414.已知(1+x)n的展开式中,第三项与第十项的二项式系数相等,则二项式系数和为()A.212B.211C.210D.2915.设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是()A.若m∥α,n∥α,则m∥n B.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β16.已知椭圆C:+=1的一个焦点为(2,0),则C的离心率为()A.B.C.D.17.定义运算:a*b=,则函数f(x)=1*2x的图象大致为()A.B.C.D.18.长方体ABCD﹣A1B1C1D1,AB=4,AD=2,,则异面直线A1B1与AC1所成角的余弦值为()A.B.C.D.三.填空题(共6小题).19.函数y=的定义域为.20.已知向量=(﹣1,2),=(m,1),若向量+与垂直,则m=.21.过点(1,3)且平行于直线x+2y+3=0的直线方程为.22.已知函数f(x)=log2(x2+a),若f(3)=1,则a=.23.过抛物线y2=6x的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=5,那么|AB|等于.24.在锐角三角形△ABC中,S△ABC=2,AB=5,AC=1,则BC=.四、解答题:本大题共6小题,25-28小题每小题8分,29-30小题每小题8分,共50分;解答应写出过程或步骤。
广东省东莞市三校2022年高考考前模拟数学试题含解析

2021-2022高考数学模拟试卷注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.答题时请按要求用笔。
3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折暴、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“乐”不排在第一节,“射”和“御”两门课程不相邻,则“六艺”课程讲座不同的排课顺序共有( )种. A .408B .120C .156D .2402.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2πC .76π D .π3.已知双曲线C :22221(0,0)x y a b a b-=>>的左、右两个焦点分别为1F ,2F ,若存在点P 满足1212::4:6:5PF PF F F =,则该双曲线的离心率为( )A .2B .52C .53D .54.若函数32()39f x x ax x =++-在3x =-时取得极值,则a =( ) A .2B .3C .4D .55.已知x ,y 满足不等式组2202100x y x y x +-≤⎧⎪--≤⎨⎪≥⎩,则点(),P x y 所在区域的面积是( )A .1B .2C .54D .456.已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边经过点()1,2P ,则cos2θ=( ) A .35B .45-C .35D .457.大衍数列,米源于我国古代文献《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释我国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.已知该数列前10项是0,2,4,8,A .22n n -B .212n -C .212n (-)D .22n8.若实数,x y 满足不等式组121210x y x y x y +≥-⎧⎪-≤-⎨⎪--≤⎩,则234x y -+的最大值为( )A .1-B .2-C .3D .29.设{|210}S x x =+>,{|350}T x x =-<,则S T ( )A .∅B .1{|}2x x <-C .5{|}3x x >D .15{|}23x x -<< 10.已知函数()()3cos 0f x x x ωωω=+>,对任意的1x ,2x ,当()()1212f x f x =-时,12min2x x π-=,则下列判断正确的是( )A .16f π⎛⎫= ⎪⎝⎭B .函数()f x 在,62ππ⎛⎫⎪⎝⎭上递增C .函数()f x 的一条对称轴是76x π=D .函数()f x 的一个对称中心是,03π⎛⎫⎪⎝⎭11.已知函数()1f x +是偶函数,当()1,x ∈+∞时,函数()f x 单调递减,设12a f ⎛⎫=- ⎪⎝⎭,()3b f =,()0c f =,则a b c 、、的大小关系为() A .b a c <<B .c b d <<C .b c a <<D .a b c <<12.若复数z 满足(1)12i z i +=+,则||z =( )AB .32CD .12二、填空题:本题共4小题,每小题5分,共20分。
【高教版】2020年三校生高考模拟考试数学试卷(三)

24、以椭圆焦点 F1、 F2 为直径的两个端点的圆,恰好过椭圆的两顶点,则这个椭圆的离心率
是____________________ .
四、解答题:本大题共 6 小题,25~28 小题每小题 8 分,29~30 小题每小题 9 分,共 50 分. 解答应写出过程或步骤. 25、已知集合 A {x x2 ax 15 0} ,B {x x2 5x b 0} ,如果 A B {3},求 a,b 及 A B .
)
A .{x x 1}
B . {x x 0}
C . {x x 1} D . {x x 1}
16、在等差数列{an}中,a3 a8 16 ,则 S10 …………………… . 68
C . 48
D . 36
17、若直线 x 3y 1 0 与 ax y 1 0 互相垂直,则 a …………………………(
3
6、若直线的倾斜角为
,且过点 (1,2) ,则直线的方程为 x
y 1 0 ………(A
B)
4
7、正方体 ABCD A1B1C1D1 中,异面直线 BC 与 DD1 所成的角为 90o …………(A B)
8、等比数列{an}中, a1 2 , a5 16 ,则 q 2 …………………………………(A B)
21、已知 5 件产品中有 3 件正品,2 件次品,若从中任取一件产品,则取出的产品是正品的概
率等于______________;
22、已知
a
3,
b
2
,则
a
与
b
的夹角为 45o
,则
a
b
_____________;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年三校生高考模拟考试(三)
数 学 试 题
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。
用2B 铅笔将试卷类型填涂在答题卡相应位置上。
将条形码横贴在答题卡右上角“条形码粘贴处”。
2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的,答案无效。
4.考生必须保持答题卡的整洁。
考试结束后,将答题卡交回。
一、选择题:(本大题共20小题,每小题2分,满分40分.在每小题给出的四个选项中,
只有一项符合题目要求).
1.已知集合{}2,A a =,{}4B =,且{}1,2,4A B =则a =( )
A .4
B .3
C .2
D .1
2.函数0.2log (1)x -的定义域为( )
A (1,2)
B ](
1,2 C []1,2 D )1,2⎡⎣
3.已知,a b 是实数,则“0a =”是“()30a b -=”的( )
A .充分非必要条件
B .必要非充分条件
C .充分必要条件
D .非充分非必要条件
4.不等式2560x x --≤的解集是( )
A . {}23x x -≤≤
B .{}61x x -≤≤
C . {}16x x -≤≤
D .{}16x x x ≥≤或
5.下列函数中,在区间(0,+∞)上为增函数的是( )
A .y =x +1
B .y =(x -1)2
C .y =2-x
D .y =log 0.5(x +1)
6.函数cos 2y x ⎛⎫=- ⎪⎝⎭π在区间,43ππ⎡⎤⎢⎥⎣⎦
上的最大值是( ) A .1 B .32 C .22 D .1
2
7.已知向量a =(3,1),b =(-2,1),则2a b -=( )。
A 、64
B 、65
C 、65
D 、64
8.数列{}n a 中,452,2a a ==,则数列{}n a 的前8项和等于 ( )
A .16
B .15
C .14
D .13
9.2
(sin 2cos 2)1y x x =--是 ( ) A .最小正周期为π2的偶函数
B .最小正周期为π2的奇函数
C .最小正周期为π的偶函数
D .最小正周期为π的奇函数
10.函数()f x 是奇函数,()y f x =的图象经过点()2,5-,则下列等式恒成立的是
A . ()25f -=
B .()25f -=-
C . ()52f -=
D .()52f -=-
11.抛物线y x 82
-=的准线方程是 ( )
A .4=y
B .4-=y
C .2=y
D .2-=y
12.已知向量(3,5)a =,(2,)b x =,且a b ⊥,则x =( )
A 、65
B 、65-
C 、 56
D 、56-
13.直线l 的倾斜角是4
π,在x 轴上的截距为2,则直线l 的方程是( ) A .20x y +-= B .20x y ++= C .20x y -+= D .20x y --=
14.双曲线19
252
2=-y x 上的一点到左焦点的距离是6,则它到右焦点的距离( ). A 、16 B 、4或-16 C 、4 D 、-4或16
15.等差数列}{n a 中,,105=a 且3321=++a a a ,则有( )
A .3,21=-=d a
B .3,21==d a
C .2,31=-=d a
D .2,31-==d a
16.过点A (2,3),且垂直于直线2x +y -5=0的直线方程是( ).
A 、 x -2y +4=0
B 、y -2 x +4=0
C 、2x -y -1=0
D 、 2x +y -7=0
17. 函数()4sin cos ()f x x x x R =∈的最大值是( ).
A. 1
B. 2
C. 4
D. 8
18.已知角α终边上的一点4cos ),4,3(k P =
-α,则k 的值是( ) A .516- B .5
12 C .4- D .3- 19.函数sin 2y x =的图象按向量(,1)6a=π-
平移后的图象对应的函数为( ). A 、sin(2)13y x π=-
- B 、sin(2)16y x π=++ C 、sin(2)16y x π=-- D 、sin(2)13
y x π=++ 20. 已知数列{}n a 的前n 项和1
n n S n =+,则5a = ( ). A. 142 B. 130 C. 45 D. 56
二、填空题:本大题共5小题,每小题4分,满分20分.
21.已知等比数列{}n a ,满足0n a >()*n N ∈且579a a =,则6a =
.
22. 已知向量a 和b 的夹角为34
π,且|||3==a b ,则⋅=a b .
23.圆2240x x y -+=的圆心到直线40x +-=的距离是 。
24.()f x 是定义在(0,+∞)上的增函数,则不等式()(23)f x f x >-的解集 是 。
25.若sin 6παα⎛⎫-= ⎪⎝⎭
,则tan =α .
三、解答题:本大题共5小题,满分40分.解答题应写出文字说明、证明过程或演算步骤.
26. 在ABC ∆中,,,a b c 分别是A B C ,,∠∠∠的对边,已知3,4b c ==,1cos A=3.
(1)求a 的值; (2)求sinC 的值.
27.设函数()f x m n =⋅,其中向量(2sin ,3cos )m x x =-, (sin 2cos ,2cos )n x x x =+-
求:(1) f(x)的最小正周期 (2) 函数的最小值和以及相应的x,其中
(0,)2x π∈
28.已知椭圆x2a2+y2b2
=1(a >b >0)的右焦点为F(c,0).且c =2。
(1)若椭圆的两准间的距离为焦距的4倍,求椭圆的方程;
(2)过该椭圆的右焦点的直线的斜率为-1,求直线与椭圆所截得的线段的长度。
29. B 船位于A 船正东26公里处,现A 、B 两船同时出发,A 船以每小时12公里的速度
朝正北方向行驶,B 船以每小时5公里的速度朝正西方向行驶,那么何时两船相距最近,最近距离是多少
30.已知数列{}n a 满足111,22,(*)n n a a a n N +==+∈。
(1)求4a
(2)证明数列
{}2n a +是等比数列.并求数列{}n a 的通项公式。
