蒙特卡洛算法详讲(最新整理)
蒙特卡洛光线追踪法

蒙特卡洛光线追踪法一、介绍蒙特卡洛光线追踪法蒙特卡洛光线追踪法(Monte Carlo Ray Tracing)是一种基于概率统计的光线追踪算法,它通过随机采样来模拟光线在场景中传播的过程,从而实现对场景的真实感渲染。
与传统的光线追踪算法相比,蒙特卡洛光线追踪法具有更高的灵活性和更强的适应性,可以处理复杂场景、多次散射等问题。
二、蒙特卡洛光线追踪法原理1. 光线追踪在光线追踪中,我们从观察点出发向屏幕上每个像素发射一条射线,并计算该射线与场景中物体的交点。
如果存在交点,则从该交点出发向场景中发射新的反射或折射光线,并继续递归地进行计算。
2. 蒙特卡洛方法在传统的光线追踪中,我们需要对每个像素发射大量的射线才能得到较为真实的渲染效果。
而在蒙特卡洛光线追踪中,我们采用随机采样的方法来模拟光线的传播过程,从而减少了计算量。
具体来说,我们在每个像素上随机发射一定数量的光线,并计算这些光线与场景中物体的交点。
然后,根据一定的概率分布函数来确定光线反射或折射的方向,并继续递归地进行计算。
最终,将所有采样得到的颜色值进行平均,即可得到该像素的最终颜色值。
3. 全局照明在蒙特卡洛光线追踪中,我们还需要考虑全局照明问题。
具体来说,在每个交点处,我们需要计算该点与场景中其他物体之间的能量传输情况,并将其贡献到最终颜色值中。
为了实现全局照明效果,我们可以使用两种方法:直接光照和间接光照。
直接光照是指从交点处向场景中所有可见灯源发射一条阴影射线,并计算该射线与灯源之间的能量传输情况。
而间接光照则是指从交点处向场景中随机发射一条新的光线,并计算该光线与场景中其他物体之间的能量传输情况。
三、蒙特卡洛光线追踪法优缺点1. 优点(1)真实感渲染:蒙特卡洛光线追踪法可以模拟光线在场景中的真实传播过程,从而得到更加真实的渲染效果。
(2)适应性强:蒙特卡洛光线追踪法可以处理复杂场景、多次散射等问题,具有更高的灵活性和适应性。
(3)易于扩展:由于采用随机采样的方法,因此可以很容易地扩展到并行计算和分布式计算等领域。
蒙特卡洛算法
蒙特卡洛算法1. 蒙特卡洛⽅法的基本思想蒙特卡罗⽅法⼜叫统计模拟⽅法,它使⽤随机数(或伪随机数)来解决计算的问题,是⼀类重要的数值计算⽅法。
该⽅法的名字来源于世界著名的赌城蒙特卡罗,⽽蒙特卡罗⽅法正是以概率为基础的⽅法。
⼀个简单的例⼦可以解释蒙特卡罗⽅法,假设我们需要计算⼀个不规则图形的⾯积,那么图形的不规则程度和分析性计算(⽐如积分)的复杂程度是成正⽐的。
⽽采⽤蒙特卡罗⽅法是怎么计算的呢?⾸先你把图形放到⼀个已知⾯积的⽅框内,然后假想你有⼀些⾖⼦,把⾖⼦均匀地朝这个⽅框内撒,散好后数这个图形之中有多少颗⾖⼦,再根据图形内外⾖⼦的⽐例来计算⾯积。
当你的⾖⼦越⼩,撒的越多的时候,结果就越精确。
2.例⼦蒙特卡洛算法显然可⽤于近似计算圆周率:让计算机每次随机⽣成两个0到1之间的数,看这两个实数是否在单位圆内。
⽣成⼀系列随机点,统计单位圆内的点数与圆外的点数,内接圆⾯积和正⽅形⾯积之⽐为PI:4,PI为圆周率。
,当随机点取得越多时,其结果越接近于圆周率。
下⾯给出c++版本的实现:#include<iostream>#include<cstdio>#include<cstdlib>#include<cmath>using namespace std;double in,out,ans;double x,y,dis;double getrand(){double ran=0;int t=rand()%10000;ran=(double)t/10000;return ran;}int main(){int time=0;scanf("%d",&time);for(int i=1;i<=time;i++){x=getrand()*2;y=getrand()*2;dis=sqrt((1-x)*(1-x)+(1-y)*(1-y));if(dis>1) out++;else in++;}ans=4*in/(in+out);printf("%lf",ans);return0;}如图,当time的值取1*10^9时,PI的值表⽰为3.040527,这个值和真实值仍有较⼤区别,主要原因在cstdlib库中的rand_max,即随机数值的最⼤范围仅为32767。
蒙特卡洛近似法

蒙特卡洛近似法蒙特卡洛近似法是一种利用随机抽样的方法来估计复杂计算问题的解的算法。
该算法以蒙特卡洛赌场为名,因为它的基本原理就是通过大量的随机采样来逼近真实情况,就像在赌场玩游戏一样。
下面将从算法的原理、应用场景和优缺点三个方面来详细介绍蒙特卡洛近似法。
一、算法原理蒙特卡洛近似法是一种随机化算法。
它的基本思想是,对于一个计算问题,我们无法直接求出它的解,但是可以采用随机抽样的方法来逼近它的解。
具体来说,算法流程如下:1. 对于需要求解的问题,我们可以将其转化为某个随机变量的期望。
例如,我们需要求解一个随机变量的期望值 E(X),可以表示为 E(X) =∫xf(x)dx,其中 f(x) 是 X 的概率密度函数。
这样,我们的问题就转化为求解这个期望值。
2. 为了估计这个期望值,我们可以通过随机抽样的方法来模拟 X 的分布。
具体来说,我们可以生成 n 个服从 f(x) 分布的随机变量X1,X2,…,Xn,然后根据它们的平均值来估计 E(X),即E(X) ≈(X1+X2+…+Xn)/n。
3. 当样本数 n 越来越大时,我们得到的估计值会越来越接近真实值。
这是因为根据大数定律,样本均值会以概率1收敛到期望值。
二、应用场景蒙特卡洛近似法在科学计算和工程问题中有着广泛的应用。
其典型应用包括:1. 财务分析:用于预测金融市场的波动性和风险。
2. 物理仿真:用于计算复杂的物理系统的行为,例如量子力学、原子结构和热力学。
3. 生物医学:用于评估疾病治疗和预防方法的效果,以及进行药物筛选和基因研究。
4. 工程设计:用于设计、建模和测试高风险系统,例如火箭、核反应堆和汽车碰撞测试。
三、优缺点蒙特卡洛近似法具有以下优点:1. 精度高:当样本数趋近于无穷大时,该算法能够提供接近真实值的估计。
2. 算法简单:该算法只需要进行随机抽样和简单的平均计算,算法流程简单易懂。
3. 可处理高维问题:该算法能够处理高维的计算问题,没有维度的限制。
主元素问题蒙特卡洛算法

主元素问题蒙特卡洛算法主元素问题主元素问题是指在一个序列中,出现次数超过一半的元素被称为主元素。
该问题可以通过多种算法进行解决,如暴力枚举、哈希表、排序和分治等。
其中,蒙特卡洛算法是一种随机化算法,可以用于求解主元素问题。
蒙特卡洛算法蒙特卡洛算法是一种基于随机采样的方法,常用于求解复杂问题。
该算法通过随机采样来估计某个数学量的值,并且可以控制误差范围。
在主元素问题中,我们可以使用蒙特卡洛算法来估计序列中出现次数超过一半的元素是否存在。
具体实现1. 随机选择一个数作为候选主元素。
2. 遍历整个序列,统计候选主元素出现的次数。
3. 如果候选主元素出现次数超过了序列长度的一半,则认为该候选主元素是真正的主元素。
4. 如果候选主元素出现次数没有超过序列长度的一半,则重新选择一个数作为候选主元素并重复步骤2和3。
分析蒙特卡洛算法虽然不能保证总能找到主元素,但是可以保证找到的主元素是正确的概率非常高。
具体来说,假设候选主元素在序列中出现的次数为k,则根据概率学知识可知,随机选择一个数后,该数成为候选主元素并且在序列中出现了k次的概率为C(n,k)/2^n,其中n为序列长度。
当k>n/2时,该概率大于1/2,因此可以认为候选主元素是真正的主元素。
而当k<=n/2时,需要多次随机选择才能找到真正的主元素。
代码实现下面给出蒙特卡洛算法的Python代码实现:```pythonimport randomdef majority_element(nums):candidate = Nonecount = 0for num in nums:if count == 0:candidate = numif num == candidate:count += 1else:count -= 1return candidatedef monte_carlo_majority_element(nums):while True:candidate = random.choice(nums)if nums.count(candidate) > len(nums) // 2:return candidatenums = [1, 2, 3, 4, 5, 5, 5]print(majority_element(nums)) # 输出:5print(monte_carlo_majority_element(nums)) # 输出:5```上述代码中,majority_element函数使用了Boyer-Moore投票算法求解主元素问题,monte_carlo_majority_element函数使用了蒙特卡洛算法求解主元素问题。
蒙特卡洛树算法 ucb1算法公式两项的含义

蒙特卡洛树算法ucb1算法公式两项的含义摘要:一、蒙特卡洛树算法(MCTS)简介二、UCB1算法原理及公式含义1.探索与利用的平衡2.公式推导与解释三、MCTS在实际应用中的优势与局限四、总结与展望正文:一、蒙特卡洛树算法(MCTS)简介蒙特卡洛树算法(Monte Carlo Tree Search,简称MCTS)是一种随机模拟算法,广泛应用于博弈、机器学习等领域。
它通过多次随机模拟进行搜索,逐步构建一颗搜索树,并根据搜索树的结果来选择最优策略。
MCTS算法在每一步都会重复进行多次随机模拟,对每个状态进行探索,并选择具有较高UCB1值的策略。
二、UCB1算法原理及公式含义1.探索与利用的平衡UCB1(Upper Confidence Bound 1)算法在MCTS中起到平衡探索与利用的作用。
探索是指尝试新的状态或策略,以发现更好的结果;利用则是对已有的状态或策略进行重复试验,以提高结果的准确性。
UCB1算法在每一步通过计算每个状态的期望回报,平衡探索与利用的关系。
2.公式推导与解释UCB1算法的核心公式如下:π_i = argmax_a (Q_i(a) + c * √(N_i(a) * log(N)))其中,π_i表示在第i次迭代时选择的动作;Q_i(a)表示状态i下选择动作a的期望回报;N_i(a)表示状态i下选择动作a的试验次数;N表示总的试验次数;c为调节探索与利用的参数。
公式中的第一部分Q_i(a)表示利用已有数据得到的期望回报,第二部分√(N_i(a) * log(N))表示探索部分,随着试验次数的增加,探索部分逐渐减小,以实现探索与利用的平衡。
三、MCTS在实际应用中的优势与局限1.优势:- 适用于大规模问题,因为MCTS可以在每次迭代中快速剪枝,减少计算量。
- 能应对动态环境,因为MCTS可以根据新数据不断更新策略。
- 具有较好的泛化能力,因为MCTS通过随机模拟进行搜索,能较好地处理不确定性问题。
蒙特卡洛算法的计算原理

蒙特卡洛算法的计算原理今天来聊聊蒙特卡洛算法的计算原理。
我最初接触到蒙特卡洛算法的时候,就像是进入了一个充满概率魔法的世界。
你想想看啊,生活中有这么个场景,假如你想知道一个不规则形状池塘的面积。
你可能会觉得很头疼,因为它不是规规矩矩的正方形或者圆形,很难直接计算。
这时候蒙特卡洛算法的思想就有点像咱们来个随机大作战。
咱们可以先找个已知面积的大长方形框住这个池塘,比如这个长方形就是100平方米。
然后呢,就开始让一群小伙伴随便往这个长方形区域里扔石头(这就相当于随机生成点)。
大家扔了很多很多石头之后,我们就数一数落在池塘里的石头数量和总共扔出的石头数量。
假设总共扔了1000块石头,落在池塘里的有600块,那按照比例,这个池塘的面积就大概是60平方米啦。
这种看似简单粗糙的随机模拟的方法,背后就是蒙特卡洛算法的基本思想。
说到这里,你可能会问:“这在数学和计算机里有什么理论依据呢?”其实它是基于概率论中的大数定律。
大数定律简单来说,就是当随机试验的次数足够多的时候,某些事件发生的频率就会非常接近它的概率。
蒙特卡洛算法就是不断地进行随机试验,让结果越来越接近那个准确的解。
打个比方吧,蒙特卡洛算法就像在一个装满彩球的大箱子里猜特定颜色球的数量。
每次随机拿出一个球,记录颜色后再放回去。
刚开始的时候,预测结果可能偏差很大,但拿的次数越多,就越接近真实的颜色比例,进而能算出那种颜色球的大致数量。
蒙特卡洛算法在很多实际应用中都超级有用。
比如说金融领域里风险评估。
股票的价格波动受到众多复杂因素的影响,就像一个超级复杂的不规则图形。
这时候用蒙特卡洛算法,把影响股票价格的各类因素当成那些随机扔的点,通过大量的模拟(多组随机数据运行股票价格模型),就能得到股票价格在一定情况下波动范围的大概情形,从而评估风险。
在物理学里模拟粒子运动也是如此。
在一个有着复杂磁场、电场的空间里,粒子的运动轨迹很难通过确定的方程式算出来。
蒙特卡洛算法就可以随机模拟粒子在这个空间里的运动,不停地试验不同的起始状态、不同的运动方向等,通过大量的模拟就能得到粒子可能的分布、运动范围等信息。
蒙特卡罗方法讲解

蒙特卡罗方法讲解
蒙特卡洛方法(Monte Carlo Method)又称几何表面积法,是用来解决统计及数值分析问题的一种算法。
蒙特卡洛方法利用了随机数,其特点是算法简单,可以解决复杂的统计问题,并得到较好的结果。
蒙特卡洛方法可以被认为是统计学中一种具体的模拟技术,可以通过模拟仿真的方式来估算一个问题的可能解。
它首先利用穷举或随机的方法获得随机变量的统计数据,然后针对该统计数据利用数理统计学的方法获得解决问题的推断性结果,例如积分、概率等。
蒙特卡洛方法在计算机科学中的应用非常广泛,可以用来模拟统计物理、金融工程、统计数据反演、运行时参数优化以及系统可靠性计算等问题,因此广泛被用于许多不同的领域。
蒙特卡洛方法的基本思想是:将一个难以解决的复杂问题,通过把它分解成多个简单的子问题,再用数学方法求解这些子问题,最后综合这些简单问题的结果得到整个问题的解。
蒙特卡洛方法的这种思路,也称作“积分”,即将一个复杂的问题,分解成若干小问题,求解它们的结果,再综合起来,得到整体的结果。
蒙特卡洛方法以蒙特卡罗游戏为基础,用统计学的方法对游戏进行建模。
蒙特卡洛计算方法

蒙特卡洛计算方法我折腾了好久蒙特卡洛计算方法,总算找到点门道。
说实话,蒙特卡洛计算方法这事儿,我一开始也是瞎摸索。
刚开始接触的时候,我就感觉这好像是一种特别玄乎的东西,就像在一个大雾弥漫的森林里,完全不知道路在哪儿。
我听人家说这个蒙特卡洛计算方法是一种随机模拟之类的东西。
我就想,随机?那岂不是就像抓阄?比如我要算一个不规则图形的面积,我最开始的想法可傻了,我想我就随便在一个已知面积的大矩形里扔好多小石子,然后看看落在那个不规则图形里的小石子占总小石子的比例,再用这个比例去乘那个大矩形的面积,感觉这样就能算出不规则图形的面积了。
后来我发现,这想法是有点对,但在实际操作里可难了。
比如说,怎么确保小石子扔得足够随机呢?我手动扔石子的时候,太难保证那种完全的随机性了。
而且数石子也是个大问题,要是形状特别复杂,想要数清楚落在不规则图形里的石子数,简直是噩梦。
后来我才知道,这蒙特卡洛方法在计算机里的运用可高明多了。
它是用大量的随机数来模拟某个过程。
就好像你想知道一个城市里平均每家的收入情况。
那你就不能真的一家一家去问对吧,那就好像我一颗一颗数石子那么蠢。
这时候蒙特卡洛方法呢,就像是从这个城市里随机抽取好多好多家庭,这个抽取得有技术,要确保是随机抽取,就像抽签得保证每个签被抽到的概率相等一样。
然后用这些抽取到的家庭的收入情况来估算整个城市的平均家庭收入。
我还犯过一个错,我在做一个关于概率分布的蒙特卡洛模拟的时候,生成的随机数范围搞错了。
我以为是从0到1,结果应该是1到100,这就导致我后面算出的结果完全是错的。
我当时还纳闷怎么数值这么奇怪呢,找了半天,才恍然大悟原来是随机数的范围出了问题。
这蒙特卡洛计算方法呀,重要的一点就是生成的随机数要足够随机,数量也要足够多。
就像是我们想通过抽样知道一锅汤的咸淡,如果只尝一口汤,可能不准,但多尝几口,而且每次尝的那一口都要是随机从锅里舀的,那这样得到的结果就靠谱多了。
还有一点就是,要清楚自己模拟的目的是什么。
马尔可夫链蒙特卡洛算法的详细步骤解析

马尔可夫链蒙特卡洛算法的详细步骤解析马尔可夫链蒙特卡洛算法(Markov Chain Monte Carlo,MCMC)是一种基于统计的随机模拟算法,用于从复杂的概率分布中抽取样本。
在实际应用中,MCMC算法被广泛用于概率推断、参数估计、贝叶斯统计等问题的求解。
本文将详细解析MCMC算法的步骤及其原理,以便读者能够更好地理解和应用该算法。
1. 马尔可夫链MCMC算法的核心是马尔可夫链。
马尔可夫链是一个随机过程,具有“无记忆”的性质,即未来的状态只依赖于当前的状态,与过去的状态无关。
假设我们要从一个概率分布π(x)中抽取样本,可以构造一个转移核函数Q(x'|x),表示在当前状态为x时,下一个状态为x'的概率。
若满足细致平稳条件,即π(x)Q(x'|x) =π(x')Q(x|x'),则该马尔可夫链的平稳分布即为π(x)。
MCMC算法利用马尔可夫链的平稳分布来抽取样本。
2. Metropolis-Hastings算法Metropolis-Hastings算法是MCMC算法的一种经典实现。
其步骤如下:(1)初始化:选择一个初始状态x(0)。
(2)抽样:根据转移核函数Q(x'|x)抽取候选状态x'。
(3)接受-拒绝:计算接受概率α = min{1, π(x')Q(x|x') /π(x)Q(x'|x)}。
以α为概率接受候选状态x',否则保持当前状态x。
(4)迭代:重复步骤(2)和(3),直到达到设定的抽样次数。
Metropolis-Hastings算法通过接受-拒绝的方式生成符合目标分布π(x)的样本,但其效率较低。
因此,后续提出了各种改进算法,如Gibbs抽样、Hamiltonian Monte Carlo等。
3. Gibbs抽样Gibbs抽样是一种特殊的MCMC算法,适用于多维变量的联合分布抽样。
其步骤如下:(1)初始化:选择一个初始状态x(0)。
一文详解蒙特卡洛(MonteCarlo)法及其应用

⼀⽂详解蒙特卡洛(MonteCarlo)法及其应⽤概述蒙特卡罗⽅法是⼀种计算⽅法。
原理是通过⼤量随机样本,去了解⼀个系统,进⽽得到所要计算的值。
它⾮常强⼤和灵活,⼜相当简单易懂,很容易实现。
对于许多问题来说,它往往是最简单的计算⽅法,有时甚⾄是唯⼀可⾏的⽅法。
它诞⽣于上个世纪40年代美国的"曼哈顿计划",名字来源于赌城蒙特卡罗,象征概率。
π的计算第⼀个例⼦是,如何⽤蒙特卡罗⽅法计算圆周率π。
正⽅形内部有⼀个相切的圆,它们的⾯积之⽐是π/4。
现在,在这个正⽅形内部,随机产⽣10000个点(即10000个坐标对 (x, y)),计算它们与中⼼点的距离,从⽽判断是否落在圆的内部。
如果这些点均匀分布,那么圆内的点应该占到所有点的π/4,因此将这个⽐值乘以4,就是π的值。
通过R语⾔脚本随机模拟30000个点,π的估算值与真实值相差0.07%。
⽆意识统计学家法则(Law of the unconscious statistician)这是本⽂后续会⽤到的⼀个定理。
作为⼀个预备知识,我们⾸先来介绍⼀下它。
先来看⼀下维基百科上给出的解释。
In probability theory and statistics, the law of the unconscious statistician (sometimes abbreviated LOTUS) is a theorem used to calculate the 期望值 of a function of a 随机变量 when one knows the probability distribution of but one does not explicitly know the distribution of . The form of the law can depend on the form in which one states the probability distribution of the 随机变量 .If it is a discrete distribution and one knows its PMF function (but not ), then the 期望值 of iswhere the sum is over all possible values of .If it is a continuous distribution and one knows its PDF function (but not ), then the 期望值 of isLOTUS到底表达了⼀件什么事呢?它的意思是:已知随机变量的概率分布,但不知道的分布,此时⽤LOTUS公式能计算出函数的数学期望。
蒙特卡洛(Monte Carlo)算法
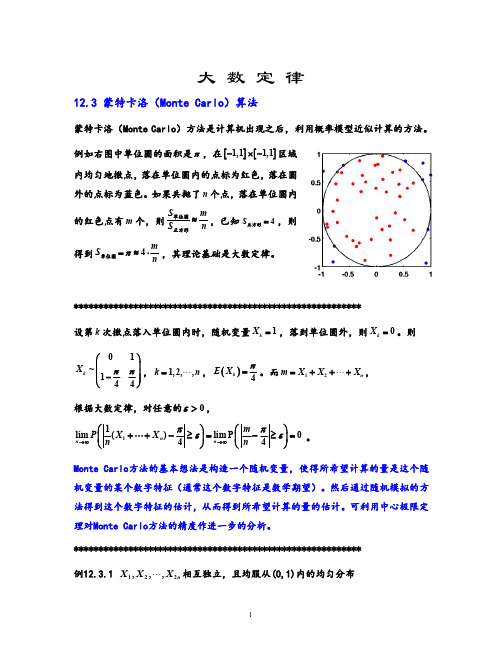
大数定律12.3蒙特卡洛(Monte Carlo)算法蒙特卡洛(Monte Carlo)方法是计算机出现之后,利用概率模型近似计算的方法。
例如右图中单位圆的面积是π,在[][]1,11,1-⨯-区域内均匀地撒点,落在单位圆内的点标为红色,落在圆外的点标为蓝色。
如果共抛了n 个点,落在单位圆内的红色点有m 个,则S mS n ≈单位圆正方形,已知4S =正方形,则得到4m S nπ=≈⋅单位圆,其理论基础是大数定律。
**********************************************************设第k 次撒点落入单位圆内时,随机变量1k X =,落到单位圆外,则0k X =。
则01~144k X ππ⎛⎫ ⎪ ⎪- ⎪⎝⎭,1,2,,k n = ,()4k E X π=。
而12n m X X X =+++ ,根据大数定律,对任意的0>ε,11lim ()lim P 044n n n m P X X n n ππεε→∞→∞⎛⎫⎛⎫++-≥=-≥= ⎪ ⎪⎝⎭⎝⎭。
Monte Carlo方法的基本想法是构造一个随机变量,使得所希望计算的量是这个随机变量的某个数字特征(通常这个数字特征是数学期望)。
然后通过随机模拟的方法得到这个数字特征的估计,从而得到所希望计算的量的估计。
可利用中心极限定理对Monte Carlo方法的精度作进一步的分析。
**********************************************************例12.3.1n X X X 221,,, 相互独立,且均服从(0,1)内的均匀分布⎩⎨⎧<+=-其他,01,422212k k k X X Y ,n k ,,2,1 =,(1)对任意给定的正整数n ,证明nY Y Y Y n +++= 21的期望为π;(2)用中心极限定理估计100n =时,()1.0<-πY P ;(3)用切比雪夫不等式估计,n 取多大时,可保证()9.01.0≥<-πY P 。
马尔可夫链蒙特卡洛算法的详细步骤解析(Ⅲ)

马尔可夫链蒙特卡洛算法的详细步骤解析1. 蒙特卡洛模拟的基本原理蒙特卡洛模拟是指通过随机抽样的方法来估计一些数学问题的解。
它的基本原理是利用大量的随机样本来近似估计和计算数学问题的解。
在实际应用中,蒙特卡洛模拟通常用于求解无法通过解析方法得到精确解的问题。
2. 马尔可夫链的基本概念马尔可夫链是指一个具有马尔可夫性质的随机过程。
这种性质是指给定当前的状态,未来的状态只与当前状态有关,而与过去的状态无关。
马尔可夫链具有平稳分布和转移矩阵等基本属性。
3. 马尔可夫链蒙特卡洛算法的基本思想马尔可夫链蒙特卡洛算法是一种基于马尔可夫链的蒙特卡洛模拟方法。
其基本思想是通过构建一个满足平稳分布的马尔可夫链,利用该链的平稳分布来估计和计算数学问题的解。
该算法的核心在于构建马尔可夫链和利用该链进行随机抽样。
4. 马尔可夫链蒙特卡洛算法的详细步骤(1)初始化:选择一个合适的初始状态,并根据转移概率矩阵进行状态转移,直到达到平稳分布。
(2)平稳分布的估计:通过对平稳分布进行随机抽样,估计得到平稳分布的近似值。
(3)数学问题的解估计:利用平稳分布的近似值来估计和计算数学问题的解。
5. 马尔可夫链蒙特卡洛算法的应用马尔可夫链蒙特卡洛算法在估计和计算复杂的数学问题上具有广泛的应用。
例如在金融领域中,可以用该算法来估计股票价格的随机波动;在统计学中,可以用该算法来估计参数的置信区间等。
6. 马尔可夫链蒙特卡洛算法的优缺点(1)优点:该算法可以用于估计和计算各种复杂的数学问题,且不需要事先对问题进行特定的假设和简化。
(2)缺点:该算法需要大量的计算和存储资源,并且在某些情况下可能收敛速度较慢。
7. 马尔可夫链蒙特卡洛算法的改进针对算法的收敛速度较慢的问题,可以通过改进马尔可夫链的构建方式和转移概率矩阵来提高算法的效率。
例如可以采用多链并行的方式来构建马尔可夫链,以加快算法的收敛速度。
8. 结语马尔可夫链蒙特卡洛算法是一种基于马尔可夫链的蒙特卡洛模拟方法,通过构建满足平稳分布的马尔可夫链来估计和计算数学问题的解。
哈密顿蒙特卡洛算法

哈密顿蒙特卡洛算法(Hamiltonian Monte Carlo, HMC)是一种用于统计推断的强大马尔可夫链蒙特卡洛(MCMC)方法。
它在许多复杂的统计模型,特别是贝叶斯统计中,表现出了卓越的性能。
HMC结合了物理学中的哈密顿动力学与蒙特卡洛采样技术,有效地解决了传统MCMC方法在处理高维分布时面临的困难。
首先,我们来了解一下蒙特卡洛方法。
蒙特卡洛方法是一类通过随机数(或更一般地,伪随机数)进行数值计算的方法。
在统计物理、粒子输运、真空技术、激光技术、生物医学等多个领域都有广泛应用。
蒙特卡洛方法的基本思想是通过大量随机抽样来估计某个难以直接计算的量。
例如,我们可以用蒙特卡洛方法估算圆周率π的值,或者求解复杂的定积分问题。
然而,传统的蒙特卡洛方法在处理高维分布时效率较低。
为了克服这一问题,哈密顿蒙特卡洛算法应运而生。
HMC算法利用了物理学中的哈密顿动力学原理。
在哈密顿系统中,系统的状态由位置变量和动量变量共同描述,而系统的演化则遵循哈密顿方程。
HMC算法将这些物理概念引入到统计采样中,通过模拟哈密顿动力系统的演化过程来生成样本。
具体来说,HMC算法从一个给定的初始状态开始,然后在每一步中,根据哈密顿方程更新位置和动量。
这个过程相当于在目标分布上进行一次“模拟”的物理运动。
经过一段时间后,系统达到一个新的状态,这个状态被接受作为样本的一部分。
通过重复这个过程,HMC算法可以生成一系列样本,这些样本渐进地服从目标分布。
HMC算法的关键在于如何选择合适的哈密顿函数以及如何模拟哈密顿动力系统的演化。
一般来说,我们需要根据目标分布的特点来构造哈密顿函数,以确保生成的样本能够准确地反映目标分布的特性。
同时,我们还需要选择合适的数值积分方法来模拟哈密顿方程的演化过程,以保证算法的精度和效率。
相比于传统的蒙特卡洛方法,HMC算法具有更高的采样效率和更好的样本质量。
它能够有效地探索高维空间中的复杂分布,并生成与目标分布更为接近的样本。
第六讲 蒙特卡洛方法

伪随机数
• 实际应用的随机数通常都是通过某些数学公式计 算而产生的伪随机数。
n k T ( n , n 1 , , n k 1 ), n 1,2,
• 这样的伪随机数从数学意义上讲已经一点不是随 机的了。 • 只要伪随机数能够通过随机数的一系列的统计检 验(证明其均匀性和独立性),我们就可以把它 当作真随机数而放心地使用。这样我们就可以很 经济地、重复地产生出随机数。
• 产生均匀伪随机数的方法有平均取中法、乘同余 法。
平均取中法
• 该方法首先给出一个2r位的数,取它的中间 的 r 位数码作为第一个伪随机数;然后将第 一个伪随机数平方构成一个新的2r 位数, 再取中间的r 位数作为第二个伪随机数…。 如此循环便得到一个伪随机数序列。类似 上述方法,利用十进制公式表示2r 位数的 递推公式。
和 同样服从[0,1]的均匀分布,
x 1
MC方法概述
• 为了得到具有一定精确度的近似解,所需随机试 验的次数是很多的,通过人工方法作大量的试验 相当困难,甚至是不可能的。因此,蒙特卡罗方 法的基本思想虽然早已被人们提出,却很少被使 用。本世纪四十年代以来,由于电子计算机的出 现,使得人们可以通过电子计算机来模拟随机试 验过程,把巨大数目的随机试验交由计算机完成, 使得蒙特卡罗方法得以广泛地应用,在现代化的 科学技术中发挥应有的作用。
• 如已知某变量x满足正态分布(高斯分布), 要求抽样变量序列x1,x2,x3,…xN,使之满足给 定的分布。
直接抽样法
• 当随机变量的分布函数已知或可以通过分 布密度函数积分得到,且比较简单。这时 可采用直接随机抽样法 • 如试按以下分布密度函数,对随机变量进 行抽样。
e x x 0 0 f ( x) else 0
蒙洛卡特算法

蒙洛卡特算法蒙洛卡特算法是一种基于随机抽样技术的数值计算方法,广泛应用于风险评估、金融衍生品定价、物理模拟等众多领域。
本文将对蒙洛卡特算法的原理、应用以及优势进行介绍。
一、蒙洛卡特算法原理蒙特卡洛算法是一种随机化算法,基于随机抽样的方法获取样本来求解问题。
直接蒙特卡洛算法是一种非常原始的方法,将问题转化为一个期望值,使用随机抽样的方法进行估计。
而蒙洛卡特算法则是通过改进直接蒙特卡洛算法,使得随机抽样的效率更高。
具体来说,蒙洛卡特算法首先通过随机抽样的方法生成多个独立的随机数序列,这些序列称为样本。
然后,将这些样本输入到函数中进行计算,最后对计算结果进行统计分析得到估计值。
蒙洛卡特算法有以下几个特点:1. 独立性。
样本之间应该是相互独立的,这意味着每个样本都是完全独立于其他样本的,并且可以多次使用。
2. 随机性。
随机抽样的过程应该是完全随机的,这意味着每个样本的值应该是随机的,并且应该具有相同的概率分布。
3. 代表性。
样本应该是代表性的,这意味着样本的数量应该足够大,以及样本应该来自于整个概率分布的区域。
4. 收敛性。
当样本数量足够大时,蒙洛卡特算法会收敛于真值。
二、蒙洛卡特算法应用1. 风险评估。
用蒙洛卡特算法进行风险评估,可以帮助投资者更加准确地评估投资的风险。
2. 金融衍生产品定价。
蒙洛卡特算法可以帮助金融衍生产品的定价,例如期权、期货等。
3. 物理模拟。
使用蒙洛卡特算法可以模拟物理系统,例如量子场论、蒙特卡洛模拟等。
4. 优化模型。
蒙洛卡特算法可以用于优化模型,例如寻找一个函数的最小值或最大值。
三、蒙洛卡特算法优势1. 可分布计算。
蒙洛卡特算法允许在分布式计算环境下运行,这使得它能够利用并行计算的优势来提高计算效率。
2. 适应高维数据。
相比于其他的数值计算方法,蒙洛卡特算法在处理高维数据时表现更加优秀。
3. 不要求导数。
相比较于一些需要求导数的数值计算方法,例如最优化算法和差分方程算法,蒙洛卡特算法不需要对函数进行求导。
(完整版)蒙特卡洛算法详讲

(完整版)蒙特卡洛算法详讲Monte Carlo 法§8.1 概述Monte Carlo 法不同于前⾯⼏章所介绍的确定性数值⽅法,它是⽤来解决数学和物理问题的⾮确定性的(概率统计的或随机的)数值⽅法。
Monte Carlo ⽅法(MCM ),也称为统计试验⽅法,是理论物理学两⼤主要学科的合并:即随机过程的概率统计理论(⽤于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。
它是⽤⼀系列随机数来近似解决问题的⼀种⽅法,是通过寻找⼀个概率统计的相似体并⽤实验取样过程来获得该相似体的近似解的处理数学问题的⼀种⼿段。
运⽤该近似⽅法所获得的问题的解in spirit 更接近于物理实验结果,⽽不是经典数值计算结果。
普遍认为我们当前所应⽤的MC 技术,其发展约可追溯⾄1944年,尽管在早些时候仍有许多未解决的实例。
MCM 的发展归功于核武器早期⼯作期间Los Alamos (美国国家实验室中⼦散射研究中⼼)的⼀批科学家。
Los Alamos ⼩组的基础⼯作刺激了⼀次巨⼤的学科⽂化的迸发,并⿎励了MCM 在各种问题中的应⽤[2]-[4]。
“Monte Carlo ”的名称取⾃于Monaco (摩纳哥)内以赌博娱乐⽽闻名的⼀座城市。
Monte Carlo ⽅法的应⽤有两种途径:仿真和取样。
仿真是指提供实际随机现象的数学上的模仿的⽅法。
⼀个典型的例⼦就是对中⼦进⼊反应堆屏障的运动进⾏仿真,⽤随机游动来模仿中⼦的锯齿形路径。
取样是指通过研究少量的随机的⼦集来演绎⼤量元素的特性的⽅法。
例如,)(x f 在b x a <<上的平均值可以通过间歇性随机选取的有限个数的点的平均值来进⾏估计。
这就是数值积分的Monte Carlo ⽅法。
MCM 已被成功地⽤于求解微分⽅程和积分⽅程,求解本征值,矩阵转置,以及尤其⽤于计算多重积分。
任何本质上属随机组员的过程或系统的仿真都需要⼀种产⽣或获得随机数的⽅法。
蒙特卡洛树蚁群算法

蒙特卡洛树蚁群算法摘要:1.蒙特卡洛树蚁群算法的概述2.蒙特卡洛树蚁群算法的原理3.蒙特卡洛树蚁群算法的应用领域4.蒙特卡洛树蚁群算法的优缺点5.蒙特卡洛树蚁群算法的发展前景正文:蒙特卡洛树蚁群算法是一种基于自然界生物群体行为的优化算法,它结合了蒙特卡洛方法和蚁群算法的优点,广泛应用于组合优化、信号处理、机器学习等领域。
本文将从以下几个方面介绍蒙特卡洛树蚁群算法。
一、蒙特卡洛树蚁群算法的概述蒙特卡洛树蚁群算法(Monte Carlo Tree Ant Colony Optimization, MCTACO)是一种模拟自然界蚂蚁觅食行为的优化算法。
它通过模拟蚂蚁在树状结构中的搜索行为,寻找最优解。
该算法继承了蚁群算法的群体搜索策略和蒙特卡洛方法的随机模拟策略,使其在解决复杂问题时具有较高的效率。
二、蒙特卡洛树蚁群算法的原理1.蚂蚁搜索策略:在算法中,蚂蚁通过释放信息素来标记路径,并根据路径上的信息素浓度来选择下一步的行动。
这种策略使得蚂蚁在搜索过程中能够共享信息,减少重复搜索,提高搜索效率。
2.蒙特卡洛方法:蒙特卡洛方法通过随机抽样来估计问题空间的解。
在MCTACO 中,蚂蚁的搜索过程就是一系列随机抽样过程,通过大量抽样来逼近最优解。
3.树状结构:MCTACO 采用树状结构来表示问题空间,使得算法具有较好的扩展性。
同时,树状结构也使得算法在搜索过程中具有较好的导向性。
三、蒙特卡洛树蚁群算法的应用领域蒙特卡洛树蚁群算法在许多领域都取得了显著的应用成果,主要包括:1.组合优化:如旅行商问题(Traveling Salesman Problem, TSP)、装载问题(Vehicle Routing Problem, VRP)等。
2.信号处理:如信号调制与解调、图像处理等。
3.机器学习:如数据挖掘、模式识别等。
四、蒙特卡洛树蚁群算法的优缺点优点:1.具有良好的搜索能力,适用于解决复杂问题。
2.具有较高的搜索效率,能够在较短时间内找到较优解。
蒙特卡洛算法公式方程

蒙特卡洛算法公式方程蒙特卡洛算法公式方程,听起来是不是有点让人头大?但别怕,其实它没有那么可怕,咱们一起来瞧瞧。
先说说啥是蒙特卡洛算法吧。
简单来说,它就像是在一个大迷宫里,通过不断地扔骰子、碰运气,来找到出口的方法。
想象一下,你在一个超级大的花园里找一朵特别的花,但是花园太大了,你不知道从哪儿开始找。
这时候,你就闭上眼睛随便走,走的过程中不断地记录和分析,说不定就能找到那朵花啦。
蒙特卡洛算法里有一个特别重要的公式方程,那就是通过随机抽样来估计某个值。
比如说,咱们要算一个不规则图形的面积。
这图形弯弯绕绕的,不好直接算。
那咱们就在一个大的矩形框里,随机地撒很多很多的小点。
然后数一下落在这个不规则图形里的点有多少,再根据总的点数和落在图形里的点数比例,就能估算出这个图形的面积啦。
我记得有一次,我给学生们讲这个的时候,有个小家伙特别可爱。
他瞪着大眼睛问我:“老师,这是不是就像闭着眼睛抓糖果,抓到多少算多少呀?”我笑着说:“对呀,差不多就是这个意思,只不过我们要更聪明地抓,还要算出大概能抓多少。
”那咱们再深入一点说这个公式方程。
它其实就是通过大量的随机试验,来逼近真实的结果。
就好像你要知道一个罐子里有多少颗糖,你又不能一颗一颗地数,那你就每次随机抓一把,多抓几次,然后根据抓到的平均数量来估计罐子里糖的总数。
在实际应用中,蒙特卡洛算法可厉害啦。
比如在金融领域,预测股票价格的走势;在物理研究中,模拟粒子的运动;在工程设计里,优化复杂系统的性能等等。
再举个例子吧,假设我们要设计一个新的桥梁,要考虑各种不确定的因素,像风的影响、车辆的重量等等。
这时候蒙特卡洛算法就派上用场啦,通过模拟大量可能的情况,找到最可靠的设计方案。
回到学习蒙特卡洛算法公式方程上,大家千万不要被它的外表吓到。
就像爬山一样,一步一步来,总能爬到山顶看到美丽的风景。
多做一些练习题,多思考一些实际的例子,慢慢地就能掌握其中的奥秘啦。
总之,蒙特卡洛算法公式方程虽然看起来有点复杂,但只要我们用心去理解,多动手实践,就一定能搞明白它,让它成为我们解决问题的好帮手!。
蒙特卡洛树算法

蒙特卡洛树算法
【最新版】
目录
1.蒙特卡洛树算法的定义与原理
2.蒙特卡洛树算法的应用领域
3.蒙特卡洛树算法的优缺点
4.我国在蒙特卡洛树算法方面的研究进展
正文
蒙特卡洛树算法(Monte Carlo Tree Search,简称 MCTS)是一种随机模拟算法,其核心思想是通过多次随机模拟进行搜索和选择,从而在复杂问题中找到最优解。
该算法在很多领域都有广泛的应用,如计算机视觉、机器学习、经济学、物理学等。
蒙特卡洛树算法的工作原理是:首先,根据问题建立一棵搜索树,然后从根节点开始,在每个节点进行随机抽样,根据抽样结果选择最优的子节点进行扩展。
重复这个过程,直到找到叶子节点,即问题的最优解。
由于随机抽样的不确定性,蒙特卡洛树算法需要进行多次模拟,最后根据多次模拟的结果选取最优解。
蒙特卡洛树算法具有很多优点,例如具有较强的鲁棒性,能够应对不确定性和非线性问题。
同时,该算法具有较高的搜索效率,能够快速找到问题的最优解。
然而,蒙特卡洛树算法也存在一定的缺点,如计算复杂度较高,需要进行大量的随机抽样和模拟,因此在处理大规模问题时,算法的运行时间较长。
我国在蒙特卡洛树算法方面也取得了很多研究进展。
近年来,我国学者在蒙特卡洛树算法的改进、加速和应用等方面进行了深入研究,提出了许多创新性的方法和算法。
这些研究成果不仅丰富了蒙特卡洛树算法的理论体系,还为我国在相关领域的技术进步和产业发展做出了重要贡献。
总之,蒙特卡洛树算法是一种具有广泛应用和重要价值的随机模拟算法。
在计算机科学和工程领域,该算法为解决复杂问题提供了一种高效且鲁棒的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Monte Carlo 法§8.1 概述Monte Carlo 法不同于前面几章所介绍的确定性数值方法,它是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法。
Monte Carlo 方法(MCM ),也称为统计试验方法,是理论物理学两大主要学科的合并:即随机过程的概率统计理论(用于处理布朗运动或随机游动实验)和位势理论,主要是研究均匀介质的稳定状态[1]。
它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。
运用该近似方法所获得的问题的解in spirit 更接近于物理实验结果,而不是经典数值计算结果。
普遍认为我们当前所应用的MC 技术,其发展约可追溯至1944年,尽管在早些时候仍有许多未解决的实例。
MCM 的发展归功于核武器早期工作期间Los Alamos (美国国家实验室中子散射研究中心)的一批科学家。
Los Alamos 小组的基础工作刺激了一次巨大的学科文化的迸发,并鼓励了MCM 在各种问题中的应用[2]-[4]。
“Monte Carlo ”的名称取自于Monaco (摩纳哥)内以赌博娱乐而闻名的一座城市。
Monte Carlo 方法的应用有两种途径:仿真和取样。
仿真是指提供实际随机现象的数学上的模仿的方法。
一个典型的例子就是对中子进入反应堆屏障的运动进行仿真,用随机游动来模仿中子的锯齿形路径。
取样是指通过研究少量的随机的子集来演绎大量元素的特性的方法。
例如,在上的平均值可以)(x f b x a <<通过间歇性随机选取的有限个数的点的平均值来进行估计。
这就是数值积分的Monte Carlo 方法。
MCM 已被成功地用于求解微分方程和积分方程,求解本征值,矩阵转置,以及尤其用于计算多重积分。
任何本质上属随机组员的过程或系统的仿真都需要一种产生或获得随机数的方法。
这种仿真的例子在中子随机碰撞,数值统计,队列模型,战略游戏,以及其它竞赛活动中都会出现。
Monte Carlo 计算方法需要有可得的、服从特定概率分布的、随机选取的数值序列。
§8.2 随机数和随机变量的产生[5]-[10]全面的论述了产生随机数的各类方法。
其中较为普遍应用的产生随机数的方法是选取一个函数,使其将整数变换为随机数。
以某种方法选取)(x g 0x ,并按照产生下一个随机数。
最一般的方程具有如下形式:)(1k k x g x =+)(x gm c ax x g mod )()(+=(8.1)其中 初始值或种子()=0x 00>x 乘法器()=a 0≥a 增值()=c 0≥c模数=m对于数位的二进制整数,其模数通常为。
例如,对于31位的计算机即可取t t 2m 。
这里和都是整数,且具有相同的取值范围。
所1312-a x ,0c 0,,x m c m a m >>>需的随机数序便可由下式得 {}n xm c ax x n n mod )(1+=+(8.2)该序列称为线性同余序列。
例如,若且,则该序列为70===c a x 10=m 7,6,9,0,7,6,9,0…… (8.3)可以证明,同余序列总会进入一个循环套;也就是说,最终总会出现一个无休止重复的数字的循环。
(8.3)式中序列周期长度为4。
当然,一个有用的序列必是具有相对较长周期的序列。
许多作者都用术语乘同余法和混合同余法分别指代和时的线性同余法。
选取和的法则可参见[6,10]。
0=c 0≠c c a x ,,0m 这里我们只关心在区间内服从均匀分布的随机数的产生。
用字符来)1,0(U 表示这些数字,则由式(8.2)可得mx U n 1-=(8.4)这样仅在数组中取值。
(对于区间(0,1)内的随机数,U {}m m m m /)1(,......,/2,/1,0-一种快速检测其随机性的方法是看其均值是否为0.5。
其它检测方法可参见[3,6]。
)产生区间内均匀分布的随机数,可用下式),(b a XU a b a X )(-+=(8.5)用计算机编码产生的随机数(利用式(8.2)和(8.4))并不是完全随机的;事实上,给定序列种子,序列的所有数字都是完全可预测的。
一些作者为强调U 这一点,将这种计算机产生的序列称为伪随机数。
但如果适当选取和,序c a ,m 列的随机性便足以通过一系列的统计检测。
它们相对于真随机数具有可快速产U 生、需要时可再生的优点,尤其对于程序调试。
Monte Carlo 程序中通常需要产生服从给定概率分布的随机变量。
)(x F X 该步可用[6],[13]-[15]中的几种方法加以实现,其中包括直接法和舍去法。
直接法(也称反演法或变换法),需要转换与随机变量相关的累积概率函X 数(即:为的概率)。
显然表明,通)()(x X prob x F ≤=)(x F x X ≤1)(0≤≤x F过产生(0,1)内均匀分布随机数,经转换我们可得服从分布的随机样本。
U )(x F X 为了得到这样的具有概率分布的随机数,不妨设,即可得)(x F X )(x F U =)(1U F X -=(8.6)其中具有分布函数。
例如,若是均值为呈指数分布的随机变量,且X )(x F X μ∞<<-=-x e x F x 0,1)(/μ(8.7)在中解出可得)(x F U =X)1ln(U X --=μ(8.8)由于本身就是区间(0,1)内的随机数,故可简写为)1(U -U X ln μ-=(8.9)有时(8.6)式所需的反函数不存在或很难获得。
这种情况可用舍去法来)(1x F -处理。
令为随机变量的概率密度函数。
令时的,dxx dF x f )()(=X b x a >>0)(=x f 且上界为(即:),如图8.1所示。
我们产生区间(0,1)内的两个)(x f M M x f ≤)(随机数,则),(21U U11)(U a b a X -+=M U f 21=(8.10)分别为在(a,b)和(0,M)内均匀分布的随机数。
若)(11X f f ≤(8.11)则为的可选值,否则被舍去,然后再试新的一组。
如此运用舍去法,1X X ),(21U U 所有位于以上的点都被舍去,而位于上或以下的点都由)(x f )(x f 来产生。
11)(U a b a X -+=1X图8.1 舍去法产生概率密度函数为的随机变量)(x f 例8.1 设计一子程序使之产生0,1之间呈均匀分布的随机数。
用该程序产生U 随机变,其概率分布由下式给定Θπθθθ<<-=0),cos 1(21)(T 解:生成的子程序如图8.2所示。
该子程序中,U ,0,21474836471221==-=c m 且。
应用种子数(如1234),主程序中每调用一次子程序,就会生1680775==a 成一个随机数。
种子数可取1到间的任一整数。
U m0001C**********************************************************0002 C PROGRAM FOR GENERATING RANDOM VARIABLESWITH0003 C A GIVEN PROBABILITY DISTRIBUTION 0004C********************************************************** 0005 0006 DOUBLE PRECISION ISEED 0007 0008 ISEED=1234.D0 0009 DO 10 I=1,100 0010 CALL RANSOM(ISEED,R) 0011 THETA=ACOSD(1.0-2.0*R) 0012 WRITE(6,*)I,THETA 0013 10 CONTINUE 0014 STOP 0015 END0001C********************************************************** 0002 C SUBROUTINE FOR GENERATING RANDOM NUMBERS IN0003 C THE INTERVAL (0,1) 0004C********************************************************** 0005 0006 SUBROUTINE RANDOM (ISEED,R) 0007 DOUBLE PRECISION ISDDE,DEL,A 0008 DATA DEL,A/2147483647.D0,16807.D0/ 0009 0010 ISDDE=DMOD(A*ISDDE,DEL) 0011 R=ISDDE/DEL 0012 RETURN 0013 END图8.2 例8.1的随机数生成器 图8.2的子程序只是为了说明本章所介绍的一些概念。
大多数计算机都有生成随机数的子程序。
为了生成随机变量,令Θ)cos 1(21)(Θ-=Θ=T U 则有)21(cos )(11U U T -==Θ--据此,一系列具有给定分布的随机变量便可由图8.2所示主程序中生成。
Θ§8.3 误差计算Monte Carlo 程序给出的解按大量的检测统计都达到了平均值。
因此,该解中包含了平均值附近的浮动量,而且不可能达到100%的置信度。
要计算Monte Carlo 算法的统计偏差,就必须采用与统计变量相关的各种统计方法。
我们只简要介绍期望值和方差的概念,并利用中心极限定理来获得误差估计[13,16]。
设是随机变量。
则的期望值或均值定义为X X x⎰∞∞-=dx x xf x )((8.12)这里是的概率密度分布函数。
如果从中取些独立的随机样本)(x f X )(x f ,那么的估计值就表现为个样本值的均值。
N x x x ,...,,21x N∑==Nn nxNx11ˆ(8.13)是的真正的平均值,而只是的有着准确期望值的无偏估计。
虽然x X xˆx x ˆ的期望值等于,但。
因此,我们还需要的值在附近的分布测度。
x x x≠ˆx ˆx 为了估计以及在附近的的值的分布,我们需要引入的方差,其定义X xˆx X 为与差的平方的期望值,即X x⎰∞∞--=-==dx x f x x x x x Var )(()()(222σ(8.14)由,故有2222)(x x x x x x +-=-⎰⎰⎰∞∞-∞∞-∞∞-+-=dx x f x dx x xf x dx x f x x )()(2)()(222σ(8.15)或者 222)(x x x -=σ(8.16)方差的平方根称为标准差,即 2/122)()(x x x -=σ(8.17)标准差给出了在均值附近的分布测度,并由此给出了误差幅度的阶数。
