用二分法求方程
用二分法求方程近似解的两个注意点

用二分法求方程近似解的两个注意点用二分法求方程近似解需要注意以下两个点:1.用二分法求函数零点的一般步骤:第一步:确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε; 第二步:求区间[a,b]的中点c ;第三步:计算f(c):(1)若f(c)=0,则c 就是函数的零点;(2)若f(a)·f(c)<0,则令b =c (此时零点x 0∈(a ,c));(3)若f(c)·f(b)<0,则令a =c (此时零点x 0∈(c ,b)).根据这个步骤,各次区间的取舍根据的就是函数零点的存在性定理,即舍去区间端点函数值同号的区间,取区间端点函数值异号的区间.2.精确度与计算次数的关系:精确度是方程近似解的一个重要指标,它由计算次数决定.若初始区间是(a,b ),那么经过n 次取中点后,区间的长度是n b a 2||-,只要这个区间的长度小于精确度ε,那么这个区间内的任意一个值都可以作为方程的近似解,因此计算次数和精确度满足关系n b a 2||-<ε,即n >]||[log 2εb a -,其中[ ]表示取整数,如[2.5]=2,][π=3等.【例1】用二分法求方程x x 1ln =在(1,2)上的近似解,取中点c=1.5,则下一个有根区间是 .【分析】由区间端点处函数值的符号,根据函数零点的存在性定理解决.【解析】令f(x)=x x 1ln-, 则f(1)=-1<0,f(2)=,01ln 2ln 212ln =>=-e )25.1(ln 31325.1ln )5.1(2-=-=f <0, 所以f(1.5)·f(2)<0,故下一个有根区间是(1.5,2)故填(1.5,2).【点评】用二分法求方程的近似解时,每一次取中点后,下一个有根区间的判断原则是:若中点函数值为零,则这个中点就是方程的解;若中点函数值不等于零.则下一个有根区间是区间端点函数值异号的区间.【例2】在用二分法求方程的近似解时,若初始区间是(1,5),精确度要求是0.001,则需要计算的次数是 .【解析】根据计算精确度与区间长度和计算次数的关系确定.设需计算n 次,则n 满足n 24<0.001,即2n >4000.由于211=2048,212=4096,故计算12次就可以满足精确度要求.故填12.【点评】在用二分法求方程的近似解时,精确度与计算次数、区间长度之间存在紧密的联系,可以根据其中两个量求得另一个.当然,在实际求解过程中也可能用不到12次,也许11次,甚至10次即可解决问题,但前提是到结束时,区间的两个端点精确到与所要求的精确度的近似值相同.。
二分法求方程的根

二分法求方程的根二分法是求解函数零点的一种简单而又有效的方法。
它适用于xx、xx、xx等情况下,能够快速找出函数的根,对于计算机程序中的解析和数学问题研究都有很大帮助。
接下来,我们就来介绍一下利用二分法求方程的根。
求解方程的根,首先需要通过一些数学手段,将问题转化为一个函数问题。
假设我们需要求解函数$f(x)=0$的根,其中$x$为实数,我们可以将其转化为$f(x)>0$和$f(x)<0$两种情况的判断。
这样的话,就可以寻找一个区间$[a,b]$,在这个区间内,$f(x)>0$的$x$和$f(x)<0$的$x$广泛地分布在$a$和$b$这两个点的两侧,此时我们就可以运用二分法,在这个区间$[a,b]$内寻找函数$f(x)=0$的根。
在使用二分法之前,要定义好区间$[a,b]$,并进行初始化。
通常情况下,我们可以采用等距离的方式将区间分成$n$份,其中$n$为我们估计的一个比较小的值,但要保证区间内$f(x)>0$和$f(x)<0$的值分别在区间的两侧。
然后在处理过程中,每进行一次迭代,区间长度就会缩短一半,这样可以不断逼近根。
接下来就可以按照下述步骤进行计算:1. 首先,选定区间$[a,b]$,将区间分为$n$份($n$为自己估计的一个小数),如果$f(a)>0$且$f(b)<0$,则继续下一步骤,否则退出。
2. 对于区间$[a,b]$,将其一分为二,这里我们选定中间点为$c=\dfrac{a+b}{2}$,并对区间左半部分$[a,c]$和右半部分$[c,b]$进行讨论。
3. 判断$f(c)>0$还是$f(c)<0$,如果是$f(c)>0$,则根位于左半部分$[a,c]$;如果是$f(c)<0$,则根位于右半部分$[c,b]$。
4. 再次对左半部分$[a,c]$和右半部分$[c,b]$进行二分,不断缩短区间长度,逼近根。
5. 重复执行步骤3和4,直到区间长度小于一定的精度,或者达到迭代的最大次数。
用二分法求方程的近似解(带练习)

4.5.2用二分法求方程的近似解1.二分法的概念对于在区间[a,b]上图象连续不断且f(a)f(b)<0的函数y=f(x),通过不断地把它的零点所在区间一分为二,使所得区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.用二分法求函数零点近似值的步骤给定精确度ε,用二分法求函数y=f(x)零点x0的近似值的一般步骤如下:(1)确定零点x0的初始区间[a,b],验证f(a)f(b)<0.(2)求区间(a,b)的中点__c__.(3)计算f(c),并进一步确定零点所在的区间:①若f(c)=0(此时x0=c),则__c__就是函数的零点;②若f(a)f(c)<0(此时x0∈(a,c)),则令b=c;③若f(c)f(b)<0(此时零点x0∈(c,b)),则令a=c.(4)判断是否达到精确度ε:若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤(2)~(4).以上步骤可借助口诀记忆:定区间,找中点,中值计算两边看;同号去,异号算,零点落在异号间;周而复始怎么办?精确度上来判断.1.已知函数f(x)的图象如图,其中零点的个数与可以用二分法求解的零点的个数分别为()A.4,4 B.3,4C.5,4 D.4,3D解析:图象与x轴有4个交点,所以零点的个数为4;左右函数值异号的零点有3个,所以可以用二分法求解的零点个数为3,故选D.2.若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精确度为0.01,则对区间(1,2)至少二等分( )A .5次B .6次C .7次D .8次C 解析:设对区间(1,2)至少二等分n 次,初始区间长为1. 第1次二等分后区间长为12;第2次二等分后区间长为122;第3次二等分后区间长为123;…第n 次二等分后区间长为12n .根据题意,得12n <0.01,∴n >log 2100. ∵6<log 2100<7, ∴n ≥7.故对区间(1,2)至少二等分7次.【例1】下面关于二分法的叙述中,正确的是( ) A .用二分法可求所有函数零点的近似值B .用二分法求方程的近似解时,可以精确到小数点后的任一位C .二分法无规律可循,无法在计算机上完成D .只能用二分法求函数的零点B 解析:用二分法求函数零点的近似值,需要有端点函数值符号相反的区间,故选项A 错误;二分法是一种程序化的运算,可以在计算机上完成,故选项C 错误;求函数的零点的方法还有方程法、函数图象法等,故选项D 错误.故选B.运用二分法求函数的零点应具备的条件(1)函数图象在零点附近连续不断.(2)在该零点左右函数值异号.只有满足上述两个条件,才可用二分法求函数的零点.1.下列关于函数f(x),x∈[a,b]的命题中,正确的是()A.若x0∈[a,b]且满足f(x0)=0,则x0是f(x)的一个零点B.若x0是f(x)在[a,b]上的零点,则可以用二分法求x0的近似值C.函数f(x)的零点是方程f(x)=0的根,但f(x)=0的根不一定是函数f(x)的零点D.用二分法求方程的根时,得到的都是近似解A解析:使用二分法必须满足二分法的使用条件,B不正确;f(x)=0的根也一定是函数f(x)的零点,C不正确;用二分法求方程的根时,得到的也可能是精确解,D不正确,只有A正确.2.已知下列四个函数图象,其中能用二分法求出函数零点的是()A解析:由二分法的定义与原理知A选项正确.【例2】利用二分法求方程x2-x-1=0的近似解(精确度为0.3).解:令f(x)=x2-x-1,由于f(0)=-1<0,f(1)=-1<0,f(2)=1>0,故可取区间(1,2)作为计算的初始区间.用二分法逐次计算,列表如下:零点所在区间中点的值中点函数值(1,2) 1.5 -0.25(1.5,2) 1.75 0.312 5(1.5,1.75) 1.625 0.015 625∵|1.75-1.5|=0.25<0.3,∴方程x2-x-1=0的近似解可取1.5或1.75.二分法的步骤证明函数f(x)=2x+3x-6在区间(1,2)内有唯一一个零点,并求出这个零点.(精确度为0.1)证明:∵函数f(x)=2x+3x-6,∴f(1)=-1<0,f(2)=4>0.∴f(x)在区间(1,2)内有零点.又∵f(x)是增函数,∴函数f(x)=2x+3x-6在区间(1,2)内有唯一的零点.设该零点为x0,则x0∈(1,2),取x1=1.5,f(1.5)≈1.33>0,f(1)·f(1.5)<0,∴x0∈(1,1.5).取x2=1.25,f(1.25)≈0.128>0,f(1)·f(1.25)<0,∴x0∈(1,1.25).取x3=1.125,f(1.125)≈-0.44<0,f(1.125)·f(1.25)<0,∴x0∈(1.125,1.25).取x4=1.187 5,f(1.187 5)≈-0.16<0,f(1.187 5)·f(1.25)<0,∴x0∈(1.187 5,1.25).∵|1.25-1.187 5|=0.062 5<0.1,∴可取x0=1.25,则该函数的零点近似解为1.25.探究题1某方程在区间D=(2,4)内有一无理根,若用二分法求此根的近似值,要使所得的近似值的精确度达到0.1,则应将区间D等分的次数至少是________次.5解析:第一次等分,则根在区间(2,3)内或(3,4)内,此时精确度ε>0.1;不妨设根在(2,3)内,第二次等分,则根在区间(2,2.5)内或(2.5,3)内,此时精确度ε>0.1;不妨设根在(2,2.5)内,第三次等分,则根在区间(2,2.25)内或(2.25,2.5)内,此时精确度ε>0.1;不妨设根在(2,2.25)内,第四次等分,则根在区间(2,2.125)内或(2.125,2.25)内,此时精确度ε>0.1;不妨设根在(2,2.125)内,第五次等分,则根在区间(2,2.062 5)内或(2.062 5,2.125)内,此时精确度ε<0.1.满足题目要求,故至少要等分5次.探究题2在用二分法求函数f(x)的一个正实数零点时,经计算,f(0.64)<0,f(0.72)>0,f(0.68)<0,则函数的一个精确到0.1的正实数零点的近似值为()A.0.68 B.0.72 C.0.7 D.0.6C解析:已知f(0.64)<0,f(0.72)>0,则函数f(x)的零点的初始区间为[0.64,0.72],又0.68=12×(0.64+0.72),且f(0.68)<0,所以零点在区间[0.68,0.72],且该区间的左、右端点精确到0.1所取的近似值都是0.7.因此,0.7就是所求函数的一个正实数零点的近似值.1.根据函数的零点与相应方程的解的关系,求函数的零点与求相应方程的解是等价的.求方程f(x)=0的近似解,即按照用二分法求函数零点近似值的步骤求解.2.区分好“精确度”与“精确到”.3.现实生活中,有很多问题可以用二分法来解决,例如线路断路、地下管道的堵塞、水管的泄漏等.在26枚崭新的金币中,有一枚外表与真金币完全相同的假币(质量轻一点),现在只有一台天平,应用适当的方法最多称几次就可以发现这枚假币?将26枚金币平均分成两份,放在天平上,假币在轻的那13枚金币里面;将这13枚金币拿出1枚,将剩下的12枚平均分成两份,若天平平衡,则假币一定是拿出的那一枚,若不平衡,则假币一定在轻的那6枚金币里面;将这6枚金币平均分成两份,则假币一定在轻的那3枚金币里面;将这3枚金币任意拿出2枚放在天平上,若平衡,则剩下的那一枚是假币,若不平衡,则轻的那一枚是假币.依据上述分析,最多称4次就可以发现这枚假币.用二分法求方程的近似解练习(30分钟60分)1.(5分)定义在R上的函数f(x)的图象是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)f(b)<0,用二分法求x0时,当fa+b2=0时,函数f(x)的零点是() A.(a,b)外的点B.a+b2C.区间a,a+b2或a+b2,b内的任意一个实数D.x=a或bB解析:由fa+b2=0知a+b2是零点,且在(a,b)内.2.(5分)为了求函数f(x)=2x+3x-7的一个零点,某同学利用计算器得到自变量x和函数f(x)的部分对应值,如表所示.x 1.25 1.312 5 1.375 1.437 5 1.51.562 5f(x) -0.871 6 -0.578 8 -0.281 30.021 01 0.328 43 0.641 15则方程2x+3x=7的近似解(精确到0.1)可取为()A.1.32 B.1.39 C.1.4 D.1.3C解析:由题意可知f(x)为增函数.由f(1.375)•f(1.437 5)<0,可知方程2x+3x=7的近似解可取为1.4.故选C.3.(5分)若函数f(x)=x3+x2-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下.f(1)≈-2 f(1.5)≈0.625 f(1.25)≈-0.984f(1.375)≈-0.260 f(1.437 5)≈0.162 f(1.406 25)≈-0.054那么方程x3+x2-2x-2=0的一个近似根(精确度为0.05)可以是()A.1.25 B.1.375 C.1.42 D.1.5C解析:由表格可得,函数f(x)=x3+x2-2x-2的零点在(1.406 25,1.437 5)之间,且1.437 5-1.406 25<0.05.结合选项可知,方程x3+x2-2x-2=0的一个近似根(精确度为0.05)可以是1.42.故选C.4.(5分)用二分法求方程ln x-2+x=0在区间[1,2]上零点的近似值时,先取区间中点c=32,则下一个含根的区间是32,2.5.(5分)某同学在借助计算器求“方程lg x=2-x的近似解(精确到0.1)”时,设f(x)=lg x+x-2,算得f(1)<0,f(2)>0;在后面的过程中,他用二分法又取了4个x的值,计算了其函数值的正负,并得出判断,方程的近似解是x≈1.8.那么他再取的x的4个值依次是________.1.5,1.75,1.875,1.812 5解析:第一次用二分法计算得区间(1.5,2),第二次得区间(1.75,2),第三次得区间(1.75,1.875),第四次得区间(1.75,1.812 5).6.(5分)利用计算器,列出部分自变量和函数值的对应值如表:x -1.6 -1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0y=2x 0.329 9 0.378 9 0.435 3 0.5 0.574 30.659 8 0.757 9 0.870 6 1y=x2 2.56 1.96 1.44 1 0.64 0.36 0.16 0.04 0 若方程2x=x2有一个根位于区间(a,a+0.4)(a在表格中第一行里的数据中取值),则a 的值为________.-1或-0.8解析:令f(x)=2x-x2,由表中的数据可得f(-1)<0,f(-0.6)>0,f(-0.8)<0, f(-0.4)>0,∴方程的根在区间(-1,-0.6)与(-0.8,-0.4)内.∴a=-1或a=-0.8.7.(5分)用二分法求方程x2=2的正实根的近似解(精确度为0.001)时,如果选取初始区间是[1.4,1.5],则达到精确度要求至少需要计算________次.7解析:设至少需要计算n次,则n满足0.12n<0.001,即2n>100,因为n∈N*,且27=128,故要达到精确度要求至少需要计算7次.8.(12分)以下是用二分法求方程x3+3x-5=0的一个近似解(精确度为0.1)的不完整的过程,请补充完整,并写出结论.设函数f(x)=x3+3x-5,其图象在(-∞,+∞)上是连续不断的一条曲线.先求值,f(0)=________,f(1)=________,f(2)=________,f(3)=________.所以f(x)在区间________内存在零点x0,填表:区间中点m f(m)的符号区间长度解:f(0)=-5,f(1)=-1,f(2)=9,f(3)=31,f(x)在区间(1,2)内存在零点x0,填表为区间中点m f(m)的符号区间长度(1,2) 1.5 + 1(1,1.5) 1.25 +0.5(1,1.25) 1.125 -0.25(1,125,1.25) 1.187 5 +0.125(1.125,1.187 5) 0.062 5因为|1.187 5-1.125|=0.062 5<0.1,所以原方程的近似解可取为1.187 5.9.(13分)求方程x2-2x-1=0的一个大于零的近似解(精确度为0.1).解:设f(x)=x2-2x-1,先画出函数图象的草图,如图所示.因为f(2)=-1<0,f(3)=2>0,所以在区间(2,3)上,方程x2-2x-1=0有一解,记为x1,取2和3的中间数2.5,因为f(2.5)=0.25>0,所以x1∈(2,2.5),再取2与2.5的中间数2.25,因为f(2.25)=-0.437 5<0,所以x1∈(2.25,2.5),如此继续下去,得f(2.375)<0,f(2.437 5)>0,则x1∈(2.375,2.4375),因为|2.437 5-2.375|=0.062 5<0.1.所以此方程大于零的近似解为2.437 5.。
《用二分法求方程的近似解》教学设计

《用二分法求方程的近似解》教学设计【教学目标】1. 理解二分法求方程近似解的基本原理和步骤。
2. 能够运用二分法求解简单的方程。
3. 培养学生的问题分析和解决问题的能力。
【教学准备】1. 课件、教学录像等教学辅助工具。
2. 题目:使用二分法求解方程x^3 - 2x - 5 = 0的根。
【教学过程】一、导入(5分钟)1. 教师提问:“在前面的学习中,我们学过了如何使用代入法求解方程,请问还有其他方法可以求解方程吗?”2. 引导学生思考,然后教师简要介绍二分法的基本原理。
二、概念讲解(10分钟)1. 教师通过示意图等方式,讲解二分法求方程近似解的基本思想和步骤。
2. 强调二分法的基本原理是通过不断将待求解区间进行二分,直到找到近似解为止。
3. 提醒学生在运用二分法时需要确定初始的待求解区间。
三、示例演练(20分钟)1. 教师出示题目:“使用二分法求解方程x^3 - 2x - 5 = 0的根。
”2. 以班级为单位进行讨论,确定初步的待求解区间。
3. 教师引导学生运用二分法求解方程的近似解,并进行实时解答。
4. 教师解释二分法求解方程的具体步骤,并引导学生完成。
5. 教师进行总结,强调二分法在求解方程近似解中的重要性。
四、巩固练习(15分钟)1. 教师提供一组方程,要求学生运用二分法求解方程的近似解。
2. 学生独立完成练习,并在一定时间内互相讨论、交流。
3. 教师根据学生的表现和问题进行答疑和指导。
五、拓展应用(15分钟)1. 拓展应用让学生运用二分法解决实际问题,如求解方程在某个区间内的根的个数。
2. 强调根和解在二分法中的关系,并引导学生思考和讨论。
3. 学生独立完成实际问题的求解,并主动分享解题过程和思路。
六、小结(5分钟)1. 教师对本节课的学习内容进行小结,强调二分法的应用领域和实际意义。
2. 教师对学生的表现进行评价和肯定,鼓励学生在日常生活中积极运用所学知识。
【教学反思】本节课通过概念讲解、示例演练、巩固练习和拓展应用等环节,帮助学生初步了解和掌握二分法求解方程近似解的基本原理和步骤。
用二分法求方程的近似解(高中数学)

[解] 因为 f(-1)>0,f(-2)<0,且函数 f(x)=x3-3x2-9x+1 的图象 是连续的曲线,根据函数零点的存在性定理可知,它在区间[-2,-1]内 有零点,用二分法逐步计算,列表如下:
22
端点(中点)
________.
11
合作探究 提素养
12
二分法的概念 【例 1】 已知函数 f(x)的图象如图所示,其中零点的个数与可以用 二分法求解的个数分别为( )
A.4,4
B.3,4
C.5,4
D.4,3
D [图象与 x 轴有 4 个交点,所以零点的个数为 4;左右函数值异号
的零点有 3 个,所以用二分法求解的个数为 3,故选 D.]
内的唯一零点时,精确度为 0.001, 长度|b-a|小于精确度ε时,便可结束
则结束计算的条件是( )
计算.]
A.|a-b|<0.1
B.|a-b|<0.001
C.|a-b|>0.001
D.|a-b|=0.001
3.已知函数 y =f(x)的图象如图所 示,则不能利用二分 法求解的零点是 ________.
由于|1.75-1.687 5|=0.062 5<0.1,所以函数的正数
零点的近似值可取为1.687 5.
26
利用二分法求方程近似解的过程图示
27
1.二分法就是通过不断地将所选区间一分为二,使区间的两个端点 逐步逼近零点,直至找到零点附近足够小的区间,根据所要求的精确度, 用此区间的某个数值近似地表示真正的零点.
2.并非所有函数都可以用二分法求其零点,只有满足: (1)在区间[a,b]上连续不断; (2)f(a)·f(b)<0, 上述两条的函数方可采用二分法求得零点的近似值.
用二分法求方程的近似解知识点

用二分法求方程的近似解知识点二分法是一种常用的求方程近似解的数值计算方法,运用这种方法可以找到函数方程f(x)=0在给定区间[a,b]上的一个根。
本文将对二分法的原理、步骤及其应用进行详细介绍。
一、原理二分法的原理基于数学中的零点定理,也叫做中间值定理。
该定理表明:如果一个连续函数f(x)在区间[a,b]上有f(a)和f(b)异号,即f(a)·f(b)<0,则在该区间内至少存在一个根。
基于这一定理,我们可以通过不断将给定区间一分为二,并判断中点函数值与零的位置关系,从而确定新的区间,直到满足精度要求或者迭代次数达到指定值。
这样可以在给定的精度范围内逐步缩小根的位置。
二、步骤下面是使用二分法求解方程根的一般步骤:1.选择一个区间[a,b],确保f(a)·f(b)<0。
这样可以保证函数在区间[a,b]内至少有一个根。
2.计算区间中点m=(a+b)/23.计算函数在中点处的值f(m)。
4.判断f(m)和0的关系:a.如果f(m)等于0,那么m就是方程的一个根;b.如果f(m)与f(a)异号,那么存在根的区间变为[a,m],重复步骤2-4;c.如果f(m)与f(b)异号,那么存在根的区间变为[m,b],重复步骤2-45.重复步骤2-4,直到达到所需的精度要求或者迭代次数达到指定值。
三、应用二分法在解决方程问题中有广泛的应用,特别是对于无法用解析法求解的非线性方程、高次多项式等复杂函数,二分法可以提供一个近似解。
此外,二分法还可以用于其他数值计算问题。
例如,在一些求极值的问题中,我们可以通过求解函数导数方程的根来找到极值点。
这时,同样可以使用二分法来近似求解。
四、注意事项在使用二分法求解方程时,需要注意以下几点:1.确保函数在给定区间上是连续且有定义的。
2.选择合适的初始区间[a,b]。
如果起始区间过大,则可能导致求解时间过长;如果起始区间过小,则可能无法找到根。
通常情况下,可以通过分析函数图像或者利用已知的条件进行初步估计。
python二分法求解方程

python二分法求解方程在Python中,可以使用二分法来求解方程。
二分法是一种寻找目标值的有效算法,可以用于不断缩小搜索范围,直到找到满足条件的解。
对于一个单调递增或递减函数f(x),我们可以通过以下步骤使用二分法来求解方程f(x) = 0的解:1. 确定搜索区间。
首先需要找到一个包含解的区间,可以通过观察函数的图像或者使用其他方法来确定一个大致的搜索范围。
2. 设置精度。
由于浮点数运算存在舍入误差,因此我们需要设置一个足够小的精度值来判断是否找到了解。
一般情况下,可以使用一个很小的数作为终止条件,例如0.00001。
3. 运用二分法进行搜索。
根据中值定理,如果f(x)在[a, b]上连续,且f(a)与f(b)异号,则存在一个c属于(a, b),使得f(c) = 0。
我们可以选择搜索区间的中点作为c的初始猜测值。
4. 判断中点是否为解。
计算中点的函数值f(c),如果f(c)的绝对值小于我们设置的精度,则认为c是解,算法结束。
否则,根据f(c)与f(a)或f(b)的符号关系,更新搜索区间。
5. 更新搜索区间。
如果f(c)与f(a)符号相同,则解位于[c, b]区间中,否则解位于[a, c]区间中。
更新搜索区间,将a或b的值重新设为c,重复步骤3和4,直到找到解或者搜索区间足够小。
下面是一个使用二分法求解方程的示例代码:```pythondef binary_search(f, a, b, precision):while (b - a) > precision:c = (a + b) / 2if f(c) == 0:return celif f(c) * f(a) < 0:b = celse:a = creturn (a + b) / 2# 定义需要求解的方程,例如求解x^2 - 4 = 0的解def equation(x):return x ** 2 - 4# 设置搜索区间和精度a = 0b = 10precision = 0.00001# 调用二分法函数求解方程result = binary_search(equation, a, b, precision)# 打印结果print("The solution is: ", result)```这个示例代码演示了如何使用二分法求解方程x^2 - 4 = 0的解。
用二分法求方程的近似解(很实用)通用课件

使用数学软件实现二分法
总结词
数学软件如Matlab、Mathematica等提 供了强大的符号计算和数值计算功能, 适合用于实现二分法。
VS
详细描述
这些数学软件通常提供了内置的二分法函 数,可以直接调用。用户只需要输入方程 的形式和初始区间,软件会自动调用二分 法函数来求解近似解。
使用在线工具实现二分法
二分法的原理
总结词
二分法基于函数的连续性和零点的存在性定理,通过不断缩小搜索区间来逼近零点。
详细描述
二分法利用了函数在区间端点上的函数值异号的性质,每次迭代都将搜索区间缩小一半,从而以较快 的速度逼近零点。这个过程一直持续到找到满足精度要求的零点或者搜索区间长度小于某个阈值。
二分法的适用范围
总结词
二分法适用于寻找连续函数在某个区间内的零点。
详细描述
二分法要求函数在零点所在的区间内连续,且在区间的端点上的函数值异号。对于一些不满足这些条件的函数, 如分段函数或有多个零点的函数,二分法可能无法找到正确的零点。因此,在使用二分法之前,需要先对函数进 行适当的分析和验证。
02
二分法的基本步骤
确定初始区间
首先需要确定方程有解的初始区间 ,可以通过代入法或观察法得到。
计算中点
在初始区间内取中点,并计算中点 的函数值。
判断中点性质
根据中点的函数值与区间端点的函 数值进行比较,确定下一步的搜索 区间。
迭代搜索
不断重复上述步骤,每次将搜索区 间缩小一半,直到达到所需的精度 要求。
求函数的零点
01
确定初始区间
同样需要确定函数有零点的初 始区间。
02
计算中点
在初始区间内取中点,并计算 中点的函数值。
用二分法求方程的近似解的方法

用二分法求方程的近似解的方法二分法(又称折半法)是一种常用于求解方程近似解的数值计算方法。
它基于一个非常重要的思想:如果在一个区间内的函数值在两个端点处取值的符号不同,那么在该区间内一定存在一个根,即方程在该区间内至少有一个解。
二分法的基本原理是将求解的区间不断缩小,每次将区间一分为二,并找出中间点的函数值。
根据中间点的函数值与两个端点的函数值的符号关系,确定新的区间。
通过不断缩小区间的范围,最终找到一个满足精度要求的近似解。
下面将详细介绍二分法的步骤及相关注意事项。
步骤1:选择一个区间[a,b],其中a和b是方程的根的近似区间。
确保方程在a和b点的函数值异号,即f(a)*f(b)<0。
如果不满足这个条件,需要重新选择一个区间。
步骤2:求出区间的中点c,计算f(c)的值。
步骤3:根据f(c)的符号与f(a)的符号的关系,更新区间。
如果f(c)与f(a)的符号相同,则新的区间是[c,b]。
如果f(c)与f(a)的符号不同,则新的区间是[a,c]。
步骤4:重复步骤2和步骤3,直到满足精度要求为止。
一般可以设置一个容差范围eps,当区间的长度小于eps时,即认为求解已经足够精确。
注意事项:1.在选择初始区间[a,b]时,需要确保方程在这个区间内有一个解。
通常可以通过画出函数曲线或分析函数的性质来确定初始区间。
2.在每次更新区间时,要保证新的区间仍然满足f(a)*f(b)<0。
如果不满足,需要选择一个新的区间,并重新开始算法。
3. 二分法是一种迭代算法,需要根据精度的要求来设置迭代次数。
通常可以通过判断区间长度是否小于eps来确定迭代的终止条件。
4.二分法并不能保证找到方程在给定区间内的所有解,而只能找到一个解。
如果方程有多个解,需要根据需要修改初始区间,并多次运行二分法来找到所有的解。
总结:二分法是一种简单而有效的求解方程近似解的方法。
通过不断缩小区间的范围,并利用函数值的符号关系来确定新的区间,可以找到一个满足精度要求的近似解。
用二分法求方程的近似解知识点

用二分法求方程的近似解1.二分法:对于区间[a,b]上连续不断、且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).函数零点的性质是二分法求函数变号零点近似值的重要依据.必须是满足区间[a,b]上连续不断、且f(a)f(b)<0这两个条件的函数才能用二分法求得零点的近似值.2.用二分法求函数零点给定精确度ε,用二分法求函数f(x)零点近似值的步骤如下:1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;2.求区间(a,b)的中点;3.计算 f(x1):(1)若f(x1)=0,则x1就是函数的零点;(2)若f(a)· f(x1)<0,则令b= x1(此时零点x0∈(a, x1) );(3)若f(x1)· f(b)<0,则令a= x1(此时零点x0∈( x1,,b)); 4.判断是否达到精确度ε,即若|a-b|< ε,则得到零点近似值a(或b),否则重复步骤2~4.3.用二分法求方程近似解不解方程,如何求方程x2-2x-1=0的一个正的近似解(精确到0.1),,,,怎样理解是否达到精度要求了?设函数的零点为x0,则a<x0<b.作出数轴,在数轴上标出a、b、x0对应的点.所以0<x0-a<b-a, a-b<x0-b<0.由于|a-b|<ε,所以|x0-a|<b-a<ε, x0-b<|a-b|<ε,即a或b作为函数的零点x0的近似值都达到给定的精确度ε.由函数的零点与相应方程根的关系,我们可用二分法来求方程的近似解.由于计算量较大,而且是重复相同的步骤,因此,我们可以通过设计一定的计算程序,借助计算器或计算机完成计算.在计算器或计算机中安装一个方程数值解法的程序,当我们输入相应的方程,并给出精确度(有效数字)后,计算器或计算机就会依据程序进行运算了.例借助计算器或计算机用二分法求方程2x+3x=7的近似解(精确到0.1).解原方程即2x+3x-7 =0,令f(x)=2x+3x-7,借助计算器或计算机作出该函数的图象与对应值表.解原方程即2x+3x-7 =0,令f(x)=2x+3x-7,借助计算器或计算机作出该函数的图象与对应值表.观察图表,可知: f(1)· f(2)<0,说明这个函数在区间(1,2)内由零点.下面是求方程近似解的框图,根据框图,可选择一种计算机语言,写出程序,并在计算机上运行后得出结果.4.二分法不仅仅用于求函数的零点和方程的根,它在现实生活中也有许多重要的应用,常用于:查找线路电线、水管、气管等管道线路故障,实验设计、资料查询等。
数值计算课后规范标准答案2
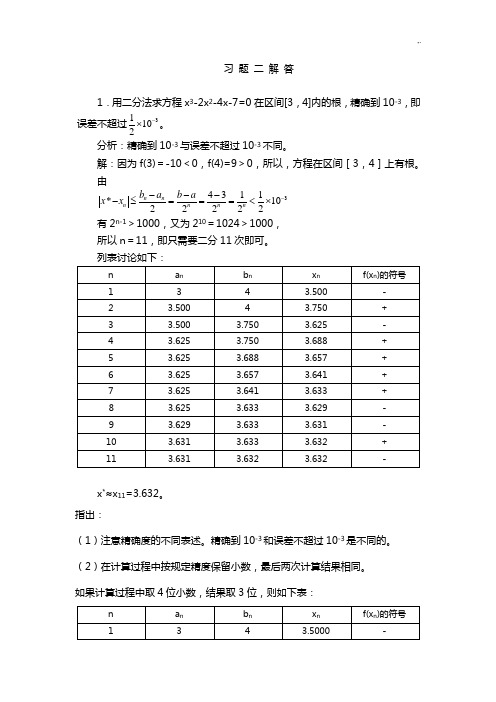
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
用二分法求方程的近似解

用二分法求方程的近似解引言在解决一些数学问题中,经常需要求解一个方程的近似解。
其中一种常用的方法是二分法。
二分法是一种逐步逼近的算法,通过不断将搜索区间缩小来寻找方程的解。
本文将介绍二分法的基本原理,并结合一个具体的例子来演示如何使用二分法求解方程的近似解。
二分法的基本原理二分法基于一个重要的性质,即如果一个函数在某个区间上是单调递增或单调递减的,则在该区间上存在一个唯一解。
基于这个性质,二分法的基本原理可以总结为以下几步:1.确定一个初始搜索区间,该区间需要包含方程解的范围。
2.每次将搜索区间划分为两个子区间。
3.判断解是否在左子区间还是右子区间中。
4.不断重复步骤2和步骤3,直到搜索区间足够小,或者找到了近似解。
实例演示假设我们要求解方程 f(x) = 0 的近似解,其中函数 f(x) 是一个连续的单调递增函数。
下面我们使用二分法来求解方程x^2 - 4 = 0的近似解。
首先,我们需要定义初始搜索区间。
根据方程x^2 - 4 = 0的特点,我们可以发现,方程的解位于区间 [-3, 3] 内,因为 (-2)^2 = 4 和 (2)^2 = 4。
因此,我们将初始搜索区间定义为 [-3, 3]。
接下来,我们每次将搜索区间划分为两个子区间,并判断解位于哪个子区间中。
假设我们定义每个子区间的长度不超过 0.01。
然后,我们可以按照以下步骤进行迭代:1.将搜索区间 [-3, 3] 划分为两个子区间:[-3, 0] 和 [0, 3]。
2.计算子区间的中点,分别为 -1.5 和 1.5。
3.判断解是否位于左子区间 [-3, -1.5] 中。
由于方程是单调递增的,我们可以判断解不在该子区间中。
4.判断解是否位于右子区间 [-1.5, 0] 中。
由于方程是单调递增的,我们可以判断解位于该子区间中。
5.更新搜索区间为 [0, 1.5]。
6.重复步骤1到步骤5,直到搜索区间足够小。
通过不断缩小搜索区间的长度,最终我们可以得到一个足够接近方程解的近似解。
用二分法求方程的近似解(基础知识+基本题型)(含解析)

4.5.2用二分法求方程的近似解(基础知识+基本题型)知识点一 二分法的概念对于在区间[]a b ,上连续不断且f (a )•f (b )﹤0 的函数y=f(x ),通过不断地把函数f (x )的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法. 提示(1)逐步逼近的思想:采用二分法,使区间逐步缩小,使函数的零点所在的范围逐步缩小,也就是逐渐逼近函数的零点,当区间长度小到一定程度时,即a b —﹤ε(ε为精确度),就得到近似解.(2)可行性:从其操作过程看,方法是可行的,是可以解决待求问题的,更可以借助科学工具完成求解. (3)二分法的理论依据:如果函数y= f(x )是连续不断的,且f(a )及f(b )的符号相反(a <b ),那么方程f(x )=0在a 与b 之间至少存在一个跟.知识点二 二分法的步骤给定精确度ε,用二分法求函数f(x )零点近似值的步骤如下: (1)确定区间[]a b ,,验证f (a )•f (b )﹤0,给定精确度ε; (2)求区间(a ,b )的中点c; (3)计算f (c );①若f (c )=0,则c 就是函数的零点;②若f (a )•f (c )﹤0,则令b=c (此时零点0x ∈(a ,c )); ③若f (c )•f (b )﹤0,则令a=c (此时零点0x ∈(c ,b )).(4)判断是否达到精确度ε,即若|a-b ︱﹤ε,则得到零点近似值a (或b );否则重复(2)—(4).考点一 用二分法判断根的存在区间例1方程322360x x x -+-=在区间[]2,4-上的根必定在( )A .[]2,1-上B .5,42⎡⎤⎢⎥⎣⎦上C .71,4⎡⎤⎢⎥⎣⎦上D .75,42⎡⎤⎢⎥⎣⎦上解析:设32()236f x x x x =-+-, 则(2)88660,(4)64321260f f -=----<=-+->,因为2412-+=且(1)12360f =-+-<,所以函数()f x 在[]1,4上必有零点。
用二分法求方程课件

二分法的基本思想
二分法的基本思想是通过不断将搜索区间一分为二,并根据 函数值在左右端点的符号来判断根所在的子区间,从而逐步 逼近根的近似值。
在每次迭代过程中,选取当前搜索区间的中点,并根据函数 值在该点的正负来判断根所在的子区间,然后舍弃非根所在 的子区间,继续在剩余的子区间上重复该过程,直到达到预 设的精度要求。
定的鲁棒性。
缺点
收敛速度慢
二分法的收敛速度取决于初始区间的 大小和方程的性质,对于一些复杂的 方程,可能需要多次迭代才能得到精 确解。
需要判断根的存在性
对初始区间选择敏感
二分法的收敛速度和精度与初始区间 的选择密切相关,如果初始区间选择 不当,可能会影响最终的求解结果。
在使用二分法之前,需要先判断方程 是否在给定的区间内有根,否则可能 无法收敛。
复杂的非线性方程时具有一定的优势。
END
THANKS
感谢观看
KEEP VIEW
计算中点
在初始区间内选择一个中点,通常是区间的中点。 中点的计算是二分法求解方程的关键步骤之一,需要精确计算中点的坐标。
判断中点处的函数值
判断中点处的函数值是二分法求解方程的重要步骤,根据 函数值的不同情况,可以决定下一步的行动。
如果函数值异号,说明解在区间内,继续进行下一步;如 果函数值同号,说明解不在区间内,需要重新选择初始区 间或调整中点位置。
PART 05
二分法的改进和变种
变种方法一:插值二分法
总结词
通过插值多项式来逼近方程的根,从而提高二分法的收敛速度。
详细描述
插值二分法是在二分法的基础上,利用插值多项式来逼近方程的根。通过构造插值多项式,可以更精 确地估计方程的根的位置,从而加快二分法的收敛速度。
用二分法求方程的近似解

用二分法求方程的近似解一、二分法的定义对于区间[]b a ,上的连续不断且0b f a f )<()(∙的函数)(x f y =,通过不断地把它的零点所在区间一分为二,使得区间的两个端点逐步逼近零点,进而得到近似解的方法叫做二分法二、用二分法求函数)(x f y =零点x 0的近似值的一般步骤1、确定零点x 0的初始区间[]b a ,,验证0b f a f )<()(∙.2.求区间),(b a 中点c .3.计算)(c f ,并进一步确定零点所在区间:(1)若0c f =)((此时,c x 0=),则c 就是函数零点;(2)若0c f a f )<()(∙(此时,),(c a x 0∈),则令c b =(3)若0b f c f )<()(∙(此时,),(b c x 0∈),则令c a =.4.判断是否达到精确度ε:若ε<b a -,则得到零点的近似值为a(或b );否则重复步骤2~4三、总结通过不断地把函数的零点所在区间一分为二,使得区间的两个端点逐步逼近零点,得到零点近似值.对于在某一区间上函数图象连续不断,且区间端点的函数值的乘积符号为负的函数,都可以利用这种方法来求零点的近似值四、题型二分法的定义与应用例1若函数y=f(x)的一个正零点附近的函数值用二分法计算,其参考数据如下:f(1)=-2,f(1.25)=-0.984,f(1.375)=-0.260,f(1.40625)=-0.054,f(1.4375)=0.162,f(1.5)=0.625,那么方程f(x)=0的一个近似根(精确度0.1)为()A.1.2B.1.3C.1.4D.1.5解:因为f(1)<0,f(1.5)>0,所以f(1)f(1.5)<0,所以函数在(1,1.5)内有零点,因为1.5-1=0.5>0.1;因为f(1.25)<0,所以f(1.25)f(1.5)<0,所以函数在(1.25,1.5)内有零点,因为1.5-1.25=0.25>0.1;因为f(1.375)<0,所以f(1.375)f(1.5)<0,所以函数在(1.375,1.5)内有零点,因为1.5-1.375=0.125>0.1;因为f(1.4375)>0,所以f(1.4375)f(1.375)<0,所以函数在(1.375,1.4375)内有零点,因为1.4375-1.375=0.0625<0.1;所以方程f(x)=0的一个近似根(精确度0.1)是区间(1.375,1.4375)内的任意一个值(包括端点值).故选:C.例2已知函数x e x x f --=)(的部分函数值如表所示:例3若函数f(x)=x³+x²-2x-2的一个正数零点附近的函数值用二分法计算,其参考数据如下:f(1)=—2f(1.5)=0.625f(1.25)=—0.984f(1.375)=—0.260f(1.4375)=0.162f(1.40625)=—0.054那么方程x³+x²-2x-2=0的一个近似根(精确度为0.05)可以是()A.1.25B.1.375C.1.42D.1.5解:由表格可得,函数f(x)=x³+x²-2x-2的零点在(1.40625,1.4375)之间;结合选项可知,方程x³+x²-2x-2=0的一个近似根(精确度为0.05)可以是1.42;故选:C.例4设函数f(x)=x ²-2,用二分法求f(x)=0的一个近似解时,第1步确定了一个区间为),(231,到第3步时,求得的近似解所在的区间应该是()A 、),(231B 、,(2345C 、),(23811D 、,(1623811解:令(x)=x ²-2,则f(1)=-1<0,则023f >(,016745f <-=)(;所以到第二步求得的近似解所在的区间应该是,(2345;0647811f <-=)(,由023f 811f <((知到第3步时,求得的近似解所在的区间应该是在),(23811故选:C.例5已知图象连续不断的函数y=f(x)在区间(a,b)(b-a=1)上有唯一零点,如果用二分法求这个零点(精确度为0.1)的近似值,那么将区间(a,b)等分的次数至少是().解:设至少需要将区间(a,b)等分n 次,则1.02ab n ≤-,即10121n ≤所以n ≥4,即将区间(a,b)等分的次数至少是4次.故答案为:4.例6用二分法求函数f(x)=x³+5的零点可以取的初始区间是()A.[-2,1]B.[-1,0]C.[0,1]D.[1,2]解:二分法求变号零点时所取初始区间[a,b],应满足使f(a)·f(b)<0.由于本题中函数f(x)=x³+5,由于f(-2)=-3,f(1)=6,显然满足f(-2)f(1)<0,故函数f(x)=x³+5的零点可以取的初始区间是[-2,1],故选:A.。
用二分法求方程的近似解

必备知识·自主学习
1.二分法的概念 (1)二分法:对于在区间[a,b]上图象连续不断且f(a)·f(b)<0的函数y=f(x), 通过不断地把它的零点所在区间_一__分__为__二__,使所得区间的两个端点逐步逼近 零点,进而得到零点_近__似__值__的方法叫做二分法. (2)本质:利用零点存在定理,将零点所在的范围尽量缩小,得到符合一定精确度 要求的零点的近似值. (3)应用:求函数的零点、方程的根的近似解.
0.125 0.097 8
0.156 25 0.379 7
0.187 5 0.664 7
根据上述数据,可得f(x)=5x+7x-2的一个零点近似值(精确度0.05)不可能为
()
A.0.625
B.0.093 75
C.0.125
D.0.096
2.用二分法求方程2x+3x-7=0在区间[1,3]内的根,取区间的中点为x0=2,那么下 一个有根的区间是________. 【解题导引】1.首先确定零点所在的区间,再根据相关的概念判断所取的零点 是否正确. 2.依据f(1),f(2),f(3)的符号作出判断.
2.下列图象与x轴均有交点,其中不能用二分法求函数零点的是 ( )
【解析】选A.只有A中图象与x轴交点两侧的函数值不变号,都是正值,因此不 能用二分法.
3.(教材二次开发:例题改编)若函数f(x)=x3+x2-2x-2的一个零点(正数)附近的 函数值用二分法逐次计算,参考数据如表:
x
1
f(x) -2
2.关于利用方程的根求参数的范围 (1)首先将方程变形为等号两边均为初等函数的等式,设出两个函数,作出两个 函数的图象,根的个数即为图象交点的个数,利用图象确定参数的范围; (2)解题思维过程:方程解的个数⇒函数交点个数⇒方程根的个数,方法是数形 结合法.
二分法求方程近似解的过程

二分法求方程近似解的过程
二分法是一种常用的求方程近似解的有效方法,它的基本思想是
用区间法,轮流缩短解所在的区间。
这种方法的优点是速度快,准确
性高。
二分法求方程近似解的步骤如下:
首先,确定方程,并确定原函数f(x)在一段闭区间内有且仅有一个零点。
其次,取这段区间的中点作为解的猜测值(称为根);再次,计算函数f(x)的值f(x0),用f(x0)的值判断f(x)的根位于哪一段区间,然后以此确定新的区间范围;最后,重复上述步骤,即以新区间
为依据取中点作为猜测值,计算函数值,最终使根收敛于函数零点。
此时,舍入值可以视为对方程的近似解。
二分法求方程近似解既快又准确,因此被广泛应用于解决复杂的
数学问题。
但是,要使用二分法求方程近似解,想要取得最佳解,必
须认真地确定函数的定义域、确定函数的取值范围,同时要考虑舍入
误差的影响等内容。
只有全面综合考虑,才能使二分法求方程近似解
效果最佳。
二分法求方程

二分法求方程一、引言在数学中,解方程是一个重要的问题。
对于一些简单的方程,可以通过代数方法来求解。
但是对于一些复杂的方程,代数方法可能无法得到精确解,需要使用数值方法来求解。
本文将介绍二分法求解方程的方法。
二、二分法原理二分法又称折半法,是一种在有序数组中查找某一特定元素的搜索算法。
其基本思想是:将有序数组从中间分开成两部分,如果要查找的元素比中间元素大,则在右半部分继续查找;如果要查找的元素比中间元素小,则在左半部分继续查找;如果要查找的元素恰好等于中间元素,则直接返回。
三、二分法求解方程步骤1. 确定区间首先需要确定一个包含根的区间[a, b]。
通常情况下,可以通过观察函数图像或者利用初值定理来确定一个大致的区间。
2. 求出区间中点将区间[a, b]从中点m=(a+b)/2处划分成两个子区间[a, m]和[m, b]。
3. 判断根所在子区间计算f(m)的值,并与0进行比较。
如果f(m)=0,则m即为方程的解;如果f(m)>0,则根在子区间[a, m]中;如果f(m)<0,则根在子区间[m, b]中。
4. 缩小区间根据上一步的判断结果,将包含根的子区间作为新的搜索区间,重复步骤2和步骤3,直到找到满足精度要求的解。
四、二分法求解方程示例假设要求解方程x^3-2x-5=0在[2, 3]内的一个近似解。
1. 确定区间观察函数图像可知,方程在[2, 3]内有且仅有一个实根。
2. 求出区间中点m=(a+b)/2=2.53. 判断根所在子区间f(m)=m^3-2m-5=-1.875<0,因此根在子区间[m, b]=[2.5, 3]中。
4. 缩小区间重复步骤2和步骤3:m=(a+b)/2=2.75f(m)=m^3-2m-5=1.015625>0,因此根在子区间[a, m]=[2, 2.75]中。
m=(a+b)/2=2.375f(m)=m^3-2m-5=-0.6484375<0,因此根在子区间[m, b]=[2.375, 2.75]中。
最新数值计算课后答案2
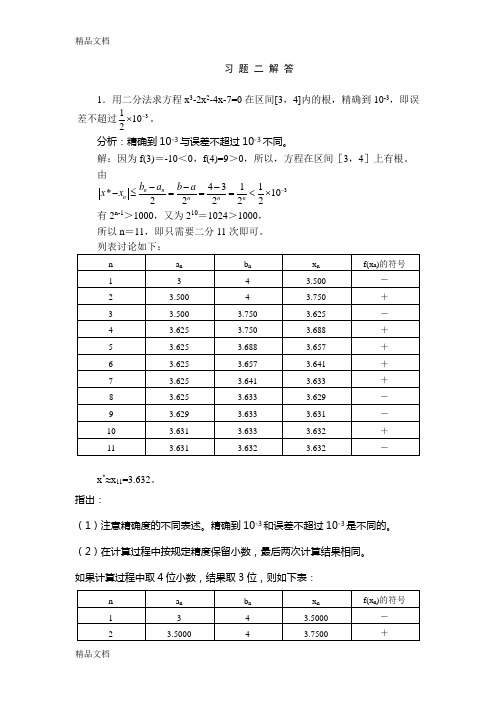
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根;因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
二分法求解3次方程

二分法求解3次方程二分法求解3次方程是一种常见的数学解题方法,它通过将方程式转化为自变量的一元函数,并通过不断逼近根的方法求得方程的根。
本文将会详细地介绍使用二分法求解3次方程的步骤。
1.将3次方程式转化为一元函数式对于3次方程,我们可以将其转化为通常的一元函数y=f(x),其中x为自变量,y为因变量。
例如,对于3次方程x^3 + 2x^2 - 3 = 0,我们可以将其转化为函数y=f(x) = x^3 + 2x^2 - 3。
这里的y就是方程在当前x值下的解。
2.通过二分法确定自变量的解对于3次方程,我们可以对自变量进行二分法处理。
简单来说,二分法就是将自变量的解分成两部分,分别处理每个部分,直到求得可接受的精度为止。
详细来说,二分法如下:(1)确定自变量的上下界。
通过给定的初始值或观察曲线,确定自变量的上下界,将其分别用x1和x2表示,保证方程在(x1,x2)内存在根的解。
(2)将自变量中点的值带入函数中得到y值,判断其与0的大小关系。
如果y值大于0,则根存在于(x1,x2)的左半边,反之则在右半边。
(3)根据上一步的判断,重新确定自变量的上下界。
如果y值大于0,则新的上界是中点x的值,否则,新的下界是中点x的值。
(4)对于新的上下界,重新求出中点x,并带入函数中得到y值,然后重复步骤(2)和步骤(3),直到满足给定的精度为止。
3.计算方程的解通过不断进行二分法处理,我们可以求得3次方程的解。
此时,在获得可接受的精度范围内,我们可以将x的值代入原方程中,计算出相应的y值,即为方程的根。
综上所述,二分法求解3次方程需要将方程式转化成一元函数式,然后通过逐渐逼近自变量的解来计算方程的根。
这种方法简单、易于实践,是解决多项式方程式的一种有效方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5 5.60944 2.53125 2.5625 2.546875 0.028617117 0.03125
5
6 7.79176 2.53125 2.546875 2.5390625 0.009919918 0.015625
y
0
7 9.94591 2.53125 2.5390625 2.5351563 0.000567772 0.0078125
小于0.1呢?为什么?
(4)怎样确定零点的近似值?假如精确度为0.01呢?
(5)什么是二分法?请你总结出用二分法求方程近似解的一般 步骤。
二分法定义:对于在区间[a,b]上连续不断、且f(a)·f(b)<0的函数y=f(x),
通过不断把函数f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,
你能求下列方程的解吗? (1) x2 6x 9 0
(2) ln x 2x 6 0
(3) 2x 3x 7
若求不出,对于方程(2)由上一节学习的知识,我 们知道它的解在区间(2,3)内,有进一步缩小解的范围 的方法吗?
求方程 ln x 2x 6 0 的近似解(误差小于0.1)。
y 20
15
10
5
y
0-5 0246810
-10
-15
区间
(2,3)
中点的值 中点函数近似值
a-b
2.5
-0.084
1
(2.5,3)
2.75
0.512
0.5
(2.5,2.75) (2.5,2.625) (2.5,2.5625)
2.625 2.5625 2.53125
0.215 0.066 -0.009
0.1 -5.6282265 1
2
1.5 0.328427125
1
0.5 -4.0857864 1
1.5
1.25 -0.87158577 0.5
1
-2
1.25
1.5
1.375 -0.281320891 0.25
2
3
1.375
1.5
1.4375 0.021011094 0.125
3
10
1.375 1.4375 1.40625 -0.130776714 0.0625
探究交流问题:
(1)你是如何确定函数 f (x) ln x 2x 6 的零点大致所在
的区间(2,3)的? (2)你又如何进一步缩小零点所在的区间呢? (3)用该方法分到什么时候才能使零点与零点的近似值误差 小于0.1呢?为什么? (4)怎样确定零点的近似值?假如精确度为0.01呢? (5)什么是二分法?请你总结出用二分法求方程近似解的一
0.25 0.125 0.0625
(2.53125,2.5625) (2.53125,2.546875) (2.53125,2.5390625)
2.546875 2.5390625 2.53515625
0.029 0.010 0.001
0.03125 0.015625 0.0078125
(3)用该方法分到什么时候才能使零点与零点的近似值误差
x0
1
2
3
4
5
6
7
f (x) -6
-2
3
10 21 40 75 142
观察得 f (1) f (2) 0 ,因此这个函数在区间(1,2)
内有零点 x0.
取区间y(1,2)的中点x1 1.5,用计算器算得 f 1.5 0.33.
因为 f 1 f 1.5 0 ,所以 x0 1,1.5 .
再 因取为区f 间1.2(51 , f1.15.5)的 中x0,所点以x2
般步骤。
求方程 ln x 2x 6 0 的近似解(误差小于0.1)。
探究交流问题:
(1)你是如何确定函数 f (x) ln x 2x 6 的零点大致所在的区间(2,3)的?
y
0
2
3x
(2)你又如何进一步缩小零点所在的区间呢?
y
0
x
用二分法求方程㏑x+2x-6=0的近似解
x
y
区
间
中点 中点函数值 精确度
0
2
4
6
8
10
8 12.0794 2.53125 2.53515625 2.5332031 -0.004109191 0.00390625 -5
9 14.1972 2.53125 2.53320313 2.5322266 -0.006447895 0.00195313 -10
2.53125 -0.0088 2.53125 2.53222656 2.5317383 -0.007617303 0.00097656 2.539063 0.00992 2.53125 2.53173828 2.5314941 -0.008202021 0.00048828 -15
进而得到零点近似值的方法叫二分法。
给定精确度ε ,用二分法求函数f(x)零点近似值的步骤:
1、确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε
2、求区间(a,b)的中点c
3、计算f(c) (1) 若f(c)=0,则c就是函数的零点 (2) 若f(a)f(c)<0,则令b= c(此时零点x0∈(a,c)) (3) 若f(c)f(c)<0,则令a= c(此时零点x0∈(c,b))
4、判断是否达到精确度ε,即若|a-b|< ε,则得到零点的近似值a(或b);否 则重复2~4
用二分法求方程 2 x 3 x 7的近似解(精确度0.1)
解: 原方程即2 x 3 x 7 0 ,令 f ( x) 2 x 3x 7
作出函数 f ( x) 2 x 3x 7 的对应值表与图象。
1.25, 算得 f 1.25 x0 1.25,1.5 .
0.87
.
同理o可得,x0 1.375,1.5 , x0 1.375,1.4375
由于 1.375 1.4375 0.0625 0.1 ,所以原方程的近
似解为1.4375
用二分法求方程2^x+3x-7=0的近似解
x
y
区
间
中点 中点函数值 精确度
y
0.01 -10.585 2
3
2.5 -0.083709268 1
1
-4
2.5
3
2.75 0.511600912 0.5
20
2 -1.3069 2.5
2.75 2.625 0.215080896 0.25
15
3 1.09861 2.5
2.625 2.5625 0.065983344 0.125
10 4 3.38629 2.5 2.5625 2.53125 -0.008786748 0.0625
4
21 1.40625 1.4375 1.421875 -0.055039952 0.03125
