小波去噪实例
小波分析在信号去噪中的应用(最新整理)

小波分析在信号去噪中的应用摘要:利用小波方法去噪,是小波分析应用于实际的重要方面。
小波去噪的关键是如何选择阈值和如何利用阈值来处理小波系数,通过对几种去噪方法不同阀值的选取比对分析和基于MATLAB 信号去噪的仿真试验,比较各种阀值选取队去噪效果的影响。
关键词:小波去噪;阀值;MATLAB 工具1、 小波去噪模型的建立如果一个信号被噪声污染后为,那么基本的噪声模型就可以表示为()f n ()s n ()()()s n f n e n σ=+式中:为噪声;为噪声强度。
最简单的情况下为高斯白噪声,且=1。
()e n σ()e n σ小波变换就是要抑制以恢复,从而达到去除噪声的目的。
从统计学的()e n ()f n 观点看,这个模型是一个随时间推移的回归模型,也可以看作是在正交基上对函数无参估计。
小波去噪通常通过以下3个步骤予以实现:()f n a)小波分解;b)设定各层细节的阈值,对得到的小波系数进行阈值处理;c)小波逆变换重构信号。
小波去噪的结果取决于以下2点:a)去噪后的信号应该和原信号有同等的光滑性;b)信号经处理后与原信号的均方根误差越小,信噪比越大,效果越好。
如何选择阈值和如何利用阈值来量化小波系数,将直接影响到小波去噪结果。
2、小波系数的阈值处理2.1由原始信号确定阈值小波变换中,对各层系数降噪所需的阈值一般是根据原信号的信噪比来决定的。
在模型里用这个量来表示,可以使用MATLAB 中的wnoisest 函数计算得到σσ值,得到信号的噪声强度后,根据下式来确定各层的阈值。
thr =式中n 为信号的长度。
2.2基于样本估计的阈值选取1)无偏似然估计(rigrsure):是一种基于Stein 无偏似然估计原理的自适应阈值选择。
对于给定的阈值T ,得到它的似然估计,再将似然T 最小化,就得到了所选的阈值,这是一种软件阈值估计。
2)阈值原则(sqtwlolg):固定阈值T 的计算公式为。
3)启发式阈值原则(heursure):是无偏似然估计和固定阈值估计原则的折中。
小波去噪方法及步骤

小波去噪方法及步骤
本文主要介绍小波分解与重构法、非线性小波变换阈值法、平移不变量小波法以及小波变换模极大值法这4种常用的小波去噪方法。
将它们分别用于仿真算例的去噪处理,并对这几种方法的应用场合、去噪性能、计算速度和影响因素等方面进行比较。
选择了Matlab软件中的仿真信号Blocks作为原始信号,信号长度(即采样点数)N=2048,如图1a所示。
由于该信号中含有若干不连续点和奇异点,因此用以下几种方法对图1b中叠加了高斯白噪声的Blocks信号(信噪比为7)进行去噪处理,能够很清楚地比较出这几种方法的去噪性能。
图1 原始信号和含噪信号的时域波形
一、小波去噪方法
1、小波分解与重构法去噪
小波分解与重构的快速算法,即Mallet算法。
据这一算法,若fk为信号f (t)的离散采样数据,fk=c0,k,则信号f(t)的正交小波变换分解公式为:。
推荐-小波分析的光谱数据去噪 精品

基于小波分析的光谱数据去噪1.1 课题背景及意义光谱分析法是以辐射能与物质组成和结构之间的内在联系及表现形式—光谱的测量为基础,利用光谱来分析样品的物质组成,属性或者物态信息的技术。
由于光谱分析技术具有分析速度快,精度高,结果稳定,无破坏等优点,在化工、农业、医学等领域得到越来越广泛的应用[1],[2]。
由于在光谱测量过程会中受到仪器,样品背景,各种干扰等随机因素的影响,得到的光谱数据中不可避免的含有噪声,如果不加以处理,会影响校正模型建立的质量和未知样品预测结果的准确性。
通过对光谱数据的去噪预处理,可以减少噪声的影响,提高模型的稳定性。
通常采用的去噪方法包括平滑,傅立叶分析等。
其中光谱平滑的目的是消除高频随机误差,其基本思路是在平滑点的前后各取若干点来进行“平均”或“拟合”,以求得平滑点的最佳估计值,消除随机噪声,这一方法的基本前提是随机噪声在处理“窗口”内的均值为零。
这种平滑的方法可有效地平滑高频噪声,提高信噪比,但是它对有效信号也进行平滑,容易造成信号失真,降低了光谱分辨率,而且光谱的两端不能进行平滑,因此存在一定的局限性。
傅立叶分析对数据处理应用的主要目的是加快信息的提取过程,通过压缩数据使得信息提取更加有效,同时去除干扰和噪声。
在传统的信号处理中,傅立叶分析是数据预处理的主要手段,但是傅立叶分析只能获得信号的整个频谱,不能得到信号的局部特性,不能充分刻画动态的非平稳信号的特征[3]。
而小波分析可以把各种频率组成的混合信号按照不同的分辨尺度分解成一系列不同频率的块信号。
由此可对特殊频率范围内的噪声进行滤波处理,小波分析灵活滤波的特性是其它方法无法比拟的。
小波分析是从傅立叶分析的基础上发展以来的,通过引入可变的尺度因子和平移因子,在信号分析时具有可调的时频窗口,巧妙地解决了时频局部化矛盾,弥补了傅立叶分析的不足,为信号处理提供了一种多分辨率下的动态分析手段。
由于小波分析对信号的分时分频的精细表达和多分辨率分析的特点,即有用信号和噪声信号在不同尺度上呈现不同的视频特征或者传播行为,根据这些特征的不同,可以将有用信号提取出来。
信号处理之小波去噪方法介绍

本文对各种去噪方法进行了比较,总结了两大类方法的基本思想及实现流程,详细介绍了应用最广的小波阈值去噪。
一、小波去噪主要方法1、基于小波分频的去噪方法——主要用来压制面波等规则干扰;2、小波域去噪方法——主要用于压制随机干扰,目前主要有三种方法: a) 模极大值去噪方法(Mallat 和Zhang ,1992)b) 尺度相关性分析方法(Xu ,1994)c) 小波阈值收缩方法(Dohono 和Johnstone ,1994)其中,小波阈值去噪方法能在最小均方误差意义下得到信号的近似最优估计,计算速度快,适应性广,因此应用最广泛。
二、方法实现的总体流程1、基于小波分频的去噪方法小波时频分析使信号在空间域和频率域同时具有良好的局部分析性质。
小波变换可以将信号分解到各个不同的尺度或各个不同的频段上,并且通过伸缩、平移聚焦到信号的任一细节加以分析。
小波分析的这些特长,结合传统的傅立叶去噪方法,为地球物理信号去噪提供了有效途径。
对于离散序列信号,其小波变换采用 Mallat 快速算法, 信号经尺度j =1,2,…,J 层分解后,得到)(2R L 中各正交闭子空间(1W 、2W 、…、J W 、J V ), 若j j V A ∈代表尺度为j 的低频部分, j j W D ∈代表高频部分,则信号可以表示为J J D D A t f +++= 1)(,据此可重构出信号在尺度j =J 时的低频部分和j =1,2,…,J 的高频部分。
如果地震数据中的干扰波频率与有效波的频率成分是分开的,通过小波分频很容易消除干扰波;如果两种频率成分存在混叠,也可以用小波分频方法提取混叠部分,再用传统方法分离有效和干扰波。
这样可以最大限度的保留有效波能量。
2、小波域去噪方法小波域去噪方法是利用信号和噪声的小波系数在小波域不同特性来进行的。
信号和噪声的小波系数幅值随尺度变化的趋势不同,随着尺度的增加,噪声的小波系数很快衰减,而信号的小波系数基本不变。
小波图像去噪及matlab分析
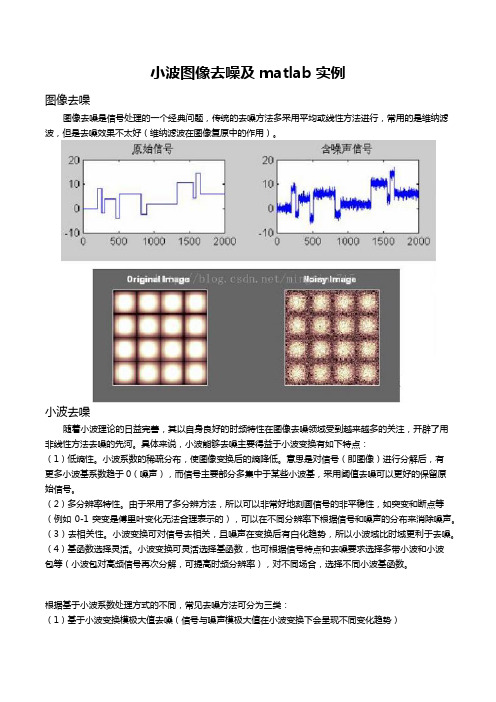
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题,传统的去噪方法多采用平均或线性方法进行,常用的是维纳滤波,但是去噪效果不太好(维纳滤波在图像复原中的作用)。
小波去噪随着小波理论的日益完善,其以自身良好的时频特性在图像去噪领域受到越来越多的关注,开辟了用非线性方法去噪的先河。
具体来说,小波能够去噪主要得益于小波变换有如下特点:(1)低熵性。
小波系数的稀疏分布,使图像变换后的熵降低。
意思是对信号(即图像)进行分解后,有更多小波基系数趋于0(噪声),而信号主要部分多集中于某些小波基,采用阈值去噪可以更好的保留原始信号。
(2)多分辨率特性。
由于采用了多分辨方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等(例如0-1突变是傅里叶变化无法合理表示的),可以在不同分辨率下根据信号和噪声的分布来消除噪声。
(3)去相关性。
小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪。
(4)基函数选择灵活。
小波变换可灵活选择基函数,也可根据信号特点和去噪要求选择多带小波和小波包等(小波包对高频信号再次分解,可提高时频分辨率),对不同场合,选择不同小波基函数。
根据基于小波系数处理方式的不同,常见去噪方法可分为三类:(1)基于小波变换模极大值去噪(信号与噪声模极大值在小波变换下会呈现不同变化趋势)(2)基于相邻尺度小波系数相关性去噪(噪声在小波变换的各尺度间无明显相关性,信号则相反)(3)基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法,应用广泛,因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值,设w是小波系数的大小,wλ是施加阈值后小波系数大小,λ为阈值。
(1)硬阈值当小波系数的绝对值小于给定阈值时,令其为0,而大于阈值时,保持其不变,即:(2)软阈值当小波系数的绝对值小于给定阈值时,令其为0,大于阈值时,令其都减去阈值,即:如下图,分别是原始信号,硬阈值处理结果,软阈值处理结果。
小波理论及小波滤波去噪方法

要点二
详细描述
小波硬阈值去噪法是小波阈值去噪法的一种,通过对小波 系数应用硬阈值函数进行处理,能够有效地去除噪声。硬 阈值函数的特点是在阈值处将小波系数分为两部分,保留 大于阈值的系数,置小于阈值的系数为零,具有简单易行 的优点。然而,硬阈值函数在处理过程中存在不连续性, 可能会引入新的噪声或信号失真。
通过软阈值函数处理小波系数,实现去噪的小波去噪方法。
详细描述
小波软阈值去噪法是在小波阈值去噪法的基础上发展而来的,通过对小波系数应用软阈值函数进行处理,能够更 好地保留信号的细节信息,提高去噪效果。软阈值函数的特点是在阈值处平滑过渡,避免了硬阈值函数的不连续 性。
小波硬阈值去噪法
要点一
总结词
通过硬阈值函数处理小波系数,实现去噪的小波去噪方法 。
03
小波滤波去噪的优缺点
优点
多尺度分析
小波变换能够同时提供信号在 时间和频率域的信息,允许在
多个尺度上分析信号。
去噪效果好
小波变换具有很好的局部化特 性,能够有效地将信号和噪声 在不同尺度上分离,从而实现 去噪。
自适应性
小波变换能够根据信号的特性 自适应地选择合适的小波基和 分解尺度,以更好地适应信号 的特性。
小波理论及小波滤波去噪 方法
• 小波理论概述 • 小波滤波去噪方法 • 小波滤波去噪的优缺点 • 小波滤波去噪的改进方法 • 小波滤波去噪的实例分析
01
小波理论概述
小波的定义与特性
小波是一种特殊的函数,具有局部性和波动性, 能够在时间和频率两个维度上进行分析。
小波具有可伸缩性,能够适应不同的频率分析需 求。
实例一:图像去噪
总结词
图像去噪是小波滤波去噪方法的重要应用之一,通过小波变换对图像进行多尺度分析, 有效去除噪声,提高图像质量。
小波分析的语音信号噪声消除方法

基于小波分析的语音信号噪声消除方法及MATLAB 实现一、 实验内容噪声污染是我们生产、生活中普遍存在的问题。
在某些环境中,噪声的影响给人们的生活和工作带来了极大不便,尤其在语音信号处理中,噪声甚至使人们正常的生活和工作无法进行。
因此,消除噪声干扰具有极为重要的研究意义和广泛的应用前景。
小波分析理论是一种新兴的信号处理理论,它在时间上和频率上都有很好的局部性,这使得小波分析非常适合于时-频分析,借助时- 频局部分析特性,小波分析理论已经成为信号去噪中的一种重要的工具。
利用小波方法去噪,是小波分析应用于实际的重要方面。
小波去噪的关键是如何选择阈值和如何利用阈值来处理小波系数,通过对小波阈值化去噪的原理介绍,运用MATLAB 中的小波工具箱,对一个含噪信号进行阈值去噪,实例验证理论的实际效果,证实了理论的可靠性。
本文简述了几种小波去噪方法,其中的阈值去噪的方法是一种实现简单、效果较好的小波去噪方法。
实验内容包括:(1) 分别利用软阈值法和硬阈值法对含噪信号进行去噪,并进行效果对比。
(2) 分别使用FFT 和小波分析方法对含噪信号进行去噪处理,并进行效果对比。
二、 实验原理1. 小波去噪原理分析1.1. 小波去噪原理叠加性高斯白噪声是最常见的噪声模型,受到叠加性高斯白噪声“污染”的观测信号可以表示为:i i i y f z σ=+ 1,...,,i n = (1.1) 其中y i 为含噪信号,i f 为“纯净”采样信号,z i 为独立同分布的高斯白噪声~(0,1)iid i z N ,σ为噪声水平,信号长度为n. 为了从含噪信号y i 中还原出真实信号i f ,可以利用信号和噪声在小波变换下的不同的特性,通过对小波分解系数进行处理来达到信号和噪声分离的目的。
在实际工程应用中,有用信号通常表现为低频信号或是一些比较平稳的信号,而噪声信号则通常表现为高频信号,所以我们可以先对含噪信号进行小波分解(如进行三层分解):321312211CD CD CD CA CD CD CA CD CA S +++=++=+= (1.2)图1 三层小波分解示意图其中i cA 为分解的近似部分, 为i cD 分解的细节部分,321,,i =,则噪声部分通常包含在1cD ,2cD ,3cD 中,用门限阈值对小波系数进行处理,重构信号即可达到去噪的目的。
基于小波分析的信号去噪

基于小波分析的信号去噪一、实验目的1、掌握小波分析的原理;2、利用小波分析进行信号去噪,并编写Matlab 程序。
二、实验内容1、使用不同小波函数对信号去噪,比较消噪效果;2、采取不同分解层数对信号去噪,比较消噪效果;3、阈值设定方法对信号去噪的影响;三、实验原理小波分析方法是一种窗口大小(即窗口面积)固定但其形状可改变,时间窗和频率窗都可改变的时频局部化分析方法。
即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被誉为数学显微镜。
正是这种特性,使小波变换具有对信号的自适应性。
原则上讲,传统上使用傅里叶分析的地方,都可以用小波分析取代。
小波分析优于傅里叶变换的地方是,它在时域和频域同时具有良好的局部化性质。
小波函数的定义:设()t ψ为平方可积函数,即())(2R L t ∈ψ,若其傅里叶变换()ωψ∧(()ωψ∧是()t ψ的傅里叶变换)满足∞<=⎰∧ωωωψψd C R 2)(称()t ψ为一个基本小波或母小波(Mother Wavelet ),并称上式为小波函数的允许条件。
与标准的傅立叶变换相比,小波分析中用到的小波函数不具有唯一性,对于一个时频分析问题,如何选者最佳的小波基函数是一个重要的问题。
常用的小波函数有Haar 小波、dbN 小波、Morl 小波、Mexh 小波、Meyer 小波等,不同的小波函数对应不同的尺度函数和性能。
从下图中可以看出小波变换与傅立叶变换在时频窗口特性上有很大的不同,更显示了上述小波变换的特点。
图6-1 小波变换的时频分析窗小波变换的多分辨率分析实际上就是对一个频带信号进行低频分解,对每一步分解出来的低频部分在分解,使频率分辨率越来越高,其目的是构造一个理想的正交小波基。
小波包分析实际上就是对与多分辨率分析没有分解的高频信号也进行逐层分解,进一步提高时频分辨率。
小波分析地这些原理与特点与测控领域中的滤波原理非常相似,常常被用于信号噪声的消除。
(完整word版)基于小波变换的图像去噪

基于小波变换的图像去噪姓名:兰昆伟学号:********指导老师:***专业:电子信息工程课题背景及意义人类传递信息的主要媒介是语音和图像。
据统计,在人类接收的信息中,听觉信息占20%,视觉信息占60%…。
其中图像信息以其信息量大,传输速度快,作用距离远等一系列优点成为人类获取信息的重要来源和利用信息的重要手段。
一幅图像所包含的信息量和直观性是声音、文字所无法比拟的。
然而,图像在生成和传输的过程中会受到各种噪声的干扰,图像的质量会受到损害,这对图像后续更高层次的处理是十分不利的。
因此,在图像的预处理阶段,很有必要对图像进行去噪,这样可以提高图像的信噪比,突出图像的期望特征。
图像噪声的主要来源有三个方面:一是敏感元器件内部产生的高斯噪声。
这是由于器件中的电子随机热运动而造成的电子噪声,这类噪声很早就被人们成功的建模并研究。
一般用零均值高斯白噪声来表征。
二是光电转换过程中的泊松噪声。
这类噪声是由光的统计本质和图像传感器中光电转换过程引起的,在弱光情况下,影响更为严重。
常用只有泊松密度分布的随机变量作为这类噪声的模型。
三是感光过程中产生的颗粒噪声。
在显微镜下检查可发现,照片上光滑细致的影调,在微观上呈现的是随机的颗粒性质。
对于多数应用,颗粒噪声用高斯过程(白噪声)作为有效模型。
小波变换具有良好的时频局部化性质,为解决这一问题提供了良好的工具。
随着小波理论的不断发展完善,其良好的时频特性使其在图像去噪领域中得到了广泛的应用。
理论和实验证明,信号与噪声在小波域有着不同的传播特性,信号的小波变换模极大值将随尺度的增大而增大或不变,而噪声的小波变换模极大值将随尺度的增大而减小,充分利用这些特点,在小波变换域中能十分有效地把信号和噪声区别开来。
因此,基于小波变换的去噪方法能够在噪声剔除的同时保护图像信号边缘,具有很好的应用前景和极大的发展潜力。
发展历程及现状为克服傅立叶分析不能同时作时频局部化分析的缺点,1964年,Gabor提出了窗口傅立叶变换,1910年Haar提出最早的Haar小波规范正交基,开辟了通往小波的道路。
基于小波分析的信号去噪方法

浙江海洋学院学报(自然科学版)第30卷文章编号:1008-830X(2011)02-0150-05基于小波分析的信号去噪方法刘志松(浙江海洋学院数理与信息学院,浙江舟山316004)摘要:介绍了小波变换出现的背景及应用意义、信号去噪效果的标准及小波变换去噪的基本原理和方法。
利用MATLAB 软件特别是MATLAB 小波工具箱编写仿真程序,结果表明小波变换在信号去噪中的有效性和优越性。
关键词:Fourier 变换;小波变换;MATLAB;信号去噪中图分类号:N911.7文献标识码:ASignal De-Noising Based on the Wavelet TransformLIU Zhi-song(School of Mathematics ,Physics and Information Science of Zhejiang Ocean University ,Zhoushan 316004,China)Abstract:In this paper ,background and significance of wavelet are introduced.It recalled the standard of the effect of signal de-noising and the basic principles and methods of wavelet transform de-noising.Final -ly ,MATLAB wavelet toolbox was used to show the effect and superiority of wavelet transform in signal de-noising.Key words:fourier transform;wavelet transform;MATLAB;signal de-noising1910年Haar 构造了紧支撑Haar 函数系,但是直到80年代人们才真正开始研究小波,1986年,Mallat和Meyer 提出了多分辨分析理论(Multi-resolution Analysis ,简记MRA ),为小波的构造提供了一般的途径。
小波变换的图像去噪

PSNR
18.8334
19.4146
17.2939
14.8055
五.小波基函数对去噪效果的影响
小波基函数对去噪效果的影响分析
通过实验直观效果图及峰值信噪比可知,对图像 采用haar小波基函数进行分解效果最佳,峰值信 噪比最大,所以在以下的实验中选用haar小波基 函数。
小波基函 数 sym4小波 db10小波 coif2小波 bior4.4小 波 bior2.2小 波 haar小波
完毕
Thank
you
二.本案例设计思路
基于小波多分辨分析的图像去噪是小波理论中的一 项重要的内容,它是解决去噪问题的一种非常有效手段, 本案例采用了对比的方法,对cameraman图像加入高斯 噪声,利用haar小波函数对该图像和信号进行二级分解, 分别用小波变换对该图像进行去噪,并采用空域滤波和 频域低通滤波对其去噪,给出了仿真结果,从视觉直观 图和峰值信噪比这一参数上进行了分析对比,比较其效 果,目的就是体现小波变换对信号和图像去噪比起其他 算法的优势。
PSNR
20.9041
20.5123
21.0996
20.3081
20.7512
24.6331
六. 小波变换图像去噪仿真结果
小波图像去噪仿真结果分析
从消噪结果来看,用小波变换进行图像消噪 所得的图像主观效果更好,从它们的峰值信噪 比来看,用小波变换进行图像消噪所得的图像 的峰值信噪比更大,这些都说明小波变换的图 像去噪效果更好。
去噪方法 峰值信噪比/dB
中值去噪 巴特沃斯低通去噪
小波去噪4
个人总结
在数学上,小波去噪问题的本质是一个函数 逼近问题,即如何在有小波母函数伸缩和平移所 展成的函数空间中,根据提出的衡量准则,寻找 对原语音信号和图像的最佳逼近,以完成原语音 信号和图像和噪声的区分; 从信号的角度看,小波去噪是一个信号滤波 的问题,尽管在很大程度上小波去噪可以看成是 低通滤波,但是由于在去噪后,还能成功地保留 语音信号和图像特征,所以在这一点上优于传统 的低通滤波器。所以可见,小波去噪实际上是特 征提取和低通滤波功能的综合。
一种优化的小波包去噪方法在超声波信号降噪中的应用

一种优化的小波包去噪方法在超声波信号降噪中的应用摘要:有效去除信号中的噪声是地球物理勘探领域中一个较重要的研究内容。
常规的频率域和时间域滤波方法不能去除超声波数据中噪声而保持信号的初至波形不发生畸变,而基于小波包基的信号去噪方法却是一种较好的方法。
该算法以小波包分析为基础,根据最小代价原理研究信号分解的最佳小波包基,对不同频率的系数采用不同的阈值进行量化,利用量化后的系数重构得到去噪后的信号。
实验结果表明,该方法去除噪声的同时并不改变原信号的相位,也不会产生波形的畸变,在超声波探测中取得了较好的应用,是一种较为理想的去噪手段。
关键词:小波包变换超声去噪最佳小波包基1引言目前,无论在工程应用还是理论研究中,去除信号噪声都是一个热门话题。
超声波检测是国内外应用广泛、使用频率很高且发展很快的一种工业无损检测方法。
它对所检测材料中的疏松、分层、缝隙等缺陷十分敏感。
超声回波或透射波信号中含有大量有关缺陷性质的信息,但由于信号在激励、传输过程中不同程度地受到随机噪声的污染,这些干扰信号会给信号的处理带来误差,严重时甚至会造成缺陷的误检和漏检。
所以如何进行降噪处理,从混有噪声的信号中提取反映缺陷本质特征的信号,一直是信号处理中的重要内容。
尽管目前有许多降噪算法,如空域复合法、频率复合法、解卷积、自适应滤波、倒谱分析方法、人工神经网络和裂谱分析法等【1】,但是它们中的绝大多数仅在时域或频域分析信号【2】。
超声波无损检测信号通常是一种被探头中心频率调制的时频有限的非平稳宽带信号,因此用时频分析中的小波包分解进行信号的降噪处理将十分有效。
2小波包变换介绍小波变换(Wavelet transform)是20世纪80年代中期出现的时频域信号分析工具。
小波包变换是小波变换的推广,与小波变换相比,小波包变换能够提供一种更加精细的分析方法,即离散小波变换的尺度是二进制变化的,所以在高频频段其频率分辨率差;而在低频频段其时间分辨率差。
图像小波去噪方法

图像小波去噪去噪方法摘要:小波分析由于在时域、频域同时具有良好的局部化性质和多分辨率分析的特点,成为信号分析的一个强有力的工具。
木文首先介绍了小波分析的基木理论知识,然后介绍邻域平均法、时域频域低通滤波法、中值滤波法以及自适应平滑滤波法四种传统去噪方法,针对传统去噪方法的不足之处,提出了用小波变换和小波包对图像信号进行去噪处理。
通过Matlab仿真,得到了这两种方法的去噪效果的优缺点。
结果表明,小波包去噪方法无论是在视觉效果还是信噪比都比小波变换更好。
关键词:小波变换、小波包、图像去噪Abstract : Wavelet analysis in time domain and frequency domain due to the excellent localized properties and multi-resolution analysis of the characteristics of the signal analysis,become a powerful tool.This paper introduces the basic theories of wavelet analysis,then introduces neighborhood averaging method and time domain frequency domain low-pass filtering method,median filtering method and adaptive smoothing filtering method four traditional de-noising method,and compare to conventional de-noising method deficiency,put forward by wavelet transform and wavelet packet to deal with the noise of image signal.Through the simulation of Matlab,the advantages and disadvantages of the two methods could be demonstrated.Results show that the denoising method of wavelet packets in visual effect or signal-to-noise ratio is better than the wavelet transform.Keywords: Wavelet transform; Wavelet packet; Image de-nosing1 引言图像消噪是一种研究颇多的图像预处理技术,根据实际信号(图像是二维信号)和噪声的不同特点,人们提出了各式各样的去噪方法,其中最为直观的方法是根据噪声能景一般集中于高频,而信号频谱则分布于一个有限区间的这一特点,采用低通滤波的方法来进行去噪,例如滑动平均窗滤波、Wiener:线性滤波、中值滤波等。
小波阈值去噪方法在多普勒雷达测速系统中的应用

小波阈值去噪方法在多普勒雷达测速系统中的应用一、绪论介绍多普勒雷达测速系统的基本原理和应用,引入小波阈值去噪方法的重要性和优势。
二、小波阈值去噪方法的原理及流程介绍小波变换、阈值选取和噪声去除的流程,详细解析小波阈值去噪方法的原理。
三、基于小波阈值去噪的多普勒雷达测速系统信号处理详细介绍如何将小波阈值去噪方法应用到多普勒雷达测速系统信号处理中,包括信号预处理、滤波和参数提取等。
四、应用实例及实验结果分析基于实验数据,实现了基于小波阈值去噪的多普勒雷达测速系统信号处理,并进行了结果分析和比较,验证了该方法的有效性和优势。
五、总结与展望总结了本文的主要内容和创新点,提出了未来的研究方向和应用前景。
第一章:绪论随着无线通信技术的迅速发展,多普勒雷达测速技术在航空、物流、交通、安防等领域越来越广泛地应用。
多普勒雷达测速系统通过分析目标反射回来的电磁波的频率和幅值等特征参数,实现对目标运动状态,如速度、方向、加速度等的精确测量,具有高精度、高可靠性和无需干预被测目标的优点。
在多普勒雷达测速系统中,信号处理对测速性能的影响非常大。
由于测速信号常常受到外界干扰,例如噪声、杂波等,导致系统精度下降、误差增加。
因此,如何提高测速信号质量、降低噪声干扰,是多普勒雷达测速技术研究的重要问题。
小波阈值去噪方法是一种常用的噪声去除方法,其基本原理是分析信号的局部特征,如频谱、时间域上的奇异性,将信号分解为不同尺度的小波函数,利用小波系数的非零值特性,通过选取合适的阈值,抑制小波系数中干扰信号的贡献。
由于小波阈值去噪方法具有区域性和多分辨性的特点,可有效地去除噪声,同时保留信号有用的信息。
在多普勒雷达测速系统中,很多研究学者通过小波阈值去噪方法对信号进行去噪处理,可以实现更准确的目标速度、加速度等测量结果。
这种方法优于传统的滤波方法,其主要优点为:保留噪声低频成分,避免干扰信号的失真;在高频范围内实现有选择性的抑制,保留目标信号的高频信息,提高了测速技术的抗干扰能力和精度。
小波去噪

小波去噪一、小波去噪中信号阈值的估算信号去噪是信号处理领域的经典问题之一。
传统的去噪方法主要包括线性滤波方法和非线性滤波方法,如中值滤波和wiener 滤波等。
传统去噪方法的不是在于使信号变换后的熵增高、无法刻画信号的非平稳特性并且无法得到信号的相关性。
为了克服上述缺点,人们开始使用小波变换解决信号去噪问题。
小波变换具有下列良好特性:(1) 低熵性:小波系数的稀疏分布,使信号变换后的熵降低;(2) 多分辨率特性:可以非常妤地刻画信号的非平稳特性,如边缘、尖峰、断点等;(3) 去相关性:可取出信号的相关性,且噪声在小波变换后有白化趋势,所以比时域更利于去噪;(4) 选基灵活性:由于小波变换可以灵活选择基函数,因此可根据信号特点和去噪要求选择适合小波。
小波在信号去噪领域已得到越来越广泛的应用。
阈值去噪方法是一种实现简单、效果较好的小波去噪方法。
阈值去噪方法的思想就是对小波分解后的各层系数中模大于和小于某阈值的系数分别处理,然后对处理完的小波系数再进行反变换,重构出经过去噪后的信号。
下面从阈值函数和阈值估计两方面对阈值去噪方法进行介绍。
1.阈值函数常用的阈值函数主要是硬阈值函数和软阈值函数。
(1)硬阈值函数。
表达式为)|(|)(T w wI w >=η,如图4.18所示,其中横坐标表示信号的原始小波系数,纵坐标表示阈值化后的小波系数。
(2)软阈值函数。
表达式为)|(|))sgn(()(T w I T w w w >-=η,如图4.19所示,其中横坐标表示信号的原始小波系数,纵坐标表示阈值化后的小波系数。
一般来说,硬阈值方法可以很好地保留信号边缘等局部特征,软阈值处理相对要平滑,但会造成边缘模糊等失真现象。
为了克服上述缺陷,最近提出了一种半软阈值函数,如图4.20所示。
它可以兼顾软阈值和硬阈值方法的优点,其表达式为)|(|)||()|(|)sgn()(2211212T w wI T w T I T T T w T w w >+<<--=η其中210T T <<。
Matlab小波去噪实例

4.6 小波去噪举例[4,6]4.6.1 MATLAB中用wnoise函数测试去噪算法% waveletnoise.msqrt_snr=3;init=231434;[x,xn]=wnoise(3,11,sqrt_snr,init); % WNOISE generate noisy wavelet test data.% X= WNOISE(FUN,N) returns values of the test function given by FUN, on a % 2^N sample of [0,1].% [X,XN] = WNOISE(FUN,N,SQRT_SNR) returns values of the test function% given by FUN and rescaled such that std(x) = SQRT_SNR (standard% deviation). The returned vector XN contains the same test vector X corrupted% by an additive Gaussian white noise N(0,1).% Then XN has a signal-to-noise ratio of (SQRT_SNR^2).% [X,XN] = WNOISE(FUN,N,SQRT_SNR,INIT) returns previous vectors X % and XN, but the generator seed is set to INI value.subplot(3,2,1),plot(x)title('original test function')subplot(3,2,2),plot(xn)title('noised function')% 产生一个长为2**11点,包含高斯白噪声的正弦信号,噪声的的标准%偏差为3。
小波平移不变量法去噪的快速算法(含程序)

编程实现平移不变量去噪的快速算法,结合例子验证该方法的去噪性能[程序说明]:共包含三个M 函数文件,分别是:shift_left函数,实现信号序列向左循环平移一位;shift_right 函数,实现信号序列向右循环平移一位,这两个函数在程序实现和功能上都很简单,在此不再赘述;TI_Denoise 函数,是该算法的主函数,用快速算法实现含噪信号的TI 去噪。
以下是该函数的帮助文档,比较清楚地说明了各参数的意义和该函数的用法:% Fast TI_Denoising of 1-d signal with wavelet thresholding.% Usage% y=TI_Denoise(signal,wavename,L)% Inputs% signal 1-d noisy signal, length(signal)= 2^J. J must be an positive integer.% wavename name of wavelet% L Low-Frequency cutoff for shrinkage. L <= J.% Outputs% y the signal after being denoised另外一个文件main 调用了TI_Denoise 函数,分别用不同种类的小波,对系统自带的几个含噪信号进行了平移不变量去噪,并将去噪前后的信号显示出来。
其中的signal 可以选用系统本身带有的几个含噪信号之一,小波wavename 和分解级数L 也可任意选择(L<=J),以此对各种条件下的TI 去噪性能进行比较。
具体的M 程序文件见附件。
[算法流程]:TI 小波去噪的功能基本上全是在TI_Denoise 函数中实现的,主要流程如下:1. 快速TI 前向小波分解原理与课本上一致,不再赘述;这里调用了shift_left 函数,来对各分辨级上的低频信号进行平移;做小波变换时,直接调用了dwt,并将延拓方式设为周期型’per’,保证了分解后系数的总数目不变;每一级dwt 后的系数均直接存入TI 表中,这里将每一级的低频系数也存入了TI表中,置于第一列,到下一级时再将其更新,直至最后一级的低频系数存入,则不再发生变化。
