四点共圆练习
四点共圆精选习题及答案

四点共圆精选习题及答案作为一种古老而神秘的数学理论,圆形一直是数学家们探究和研究的对象之一。
而在圆形领域中,四点共圆更是一个受到广泛关注和深入研究的问题。
四点共圆是指在平面上给出任意四个点,能否通过一个圆将这四个点完美地围起来。
今天我们精选了几个四点共圆的习题,希望能给大家带来一些启示。
题目一:已知在平面直角坐标系中,四点 A(0,0),B(0,2),C(4,0),D(x,y)。
若四点在同一圆上,则点 D 的坐标为多少?解题思路:根据四点共圆基本知识,可以列出以下方程组:(x-2)²+y²=r²x²+(y-2)²=r²(x-4)²+y²=r²x²+y²=r²将方程组联立,消去 r,最终得到 x²+y²=5²,即点 D 的坐标为(3,4)或(−3,4)。
题目二:在平面直角坐标系中,四个点 A,B,C,D 分别为(7,0),(0,7),(−7,0) 和(0,−7)。
请证明:四点共圆。
解题思路:根据四点共圆定理,四个点共圆当且仅当它们构成的任意三角形的外接圆都存在。
可得三个三角形 ABC、ACD 和ABD 的外接圆都是以原点为圆心的半径为7 的圆,因此四点 A、B、C、D 构成的圆也一定存在。
题目三:在平面直角坐标系中,四点 A,B,C,D 分别为(−3,4),(−4,−3),(4,−3) 和(−1,−2)。
请计算过点 C 的直径的长度。
解题思路:通过计算可以知道,连接点 C 和其他三个点构成的三角形外接圆的圆心坐标分别为(−1,−1)、(−1,0) 和 (0,1),因此过点 C 的直径所在的直线应为直线 y=x-1。
可得直线 y=x-1 与直线x=4、直线x=−3 和直线y=−3 的交点分别为 (4, 3)、(−3,−4) 和(0,−1),因此该直径的长度为√145。
初二秋.第2讲.四点共圆(二)

P A
连接 P B、P Q、 P C、 P R, ∵ △ ABC 是等腰三角形,PQ ∥ AC ,PR ∥ AB , ∴ QB QP , RP RC , BQP A PRC . ∵ P ,P 关于直线 QR 对称,∴ QP QB QP ,
RP RP RC , ∴ Q 是 △BPP 的外心, R 是
∵
I1
是
连 接 AI C ,AI B ,BI C , BI B , DI D ∵ I A ,I B ,I C ,I D 1 都 是 内 心 , ∴ AIC B 90 ADB , 2 1 AID B 90 ACB , ∴ A、B、 I D、I C 四 点 2 共圆,∴ AIC I D ABI D 180 . 同 理 , A、D、 I B 、IC 四 点 共 圆 , 则 AIC I B ADI B 180 .
A F D O I H E C
所 以 ABO OBD CBE , ABC ABE (90 A) 30 ∵ , BOC 2 BAC 120 1 BIC 90 BAC 120 , 2 BHC EHF 180 A 120 则 知 B、 O、 I、 H、 BOC BIC BHC ,于是, C 五 点 共 圆 .此 时 , OBC OCB 30 , CIH CBH , OIC 180 OBC 150 故 OIH 150 . ⑴ (150 ) (30 ) 120 OIH ABC (定值) ⑵ OIH ACB (定值)
四点共圆例题及问题详解

例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.证明菱形ABCD的对角线AC和BD相交于点O,连接OE、OF、OG、OH.∵AC和BD 互相垂直,∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中,E、F、G、H,分别是AB、BC、CD、DA的中点,即E、F、G、H四点共圆.(2)若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆.例2 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.证明∵DE⊥AB,DF⊥AC,∴∠AED+∠AFD=180°,即A、E、D、F四点共圆,∠AEF=∠ADF.又∵AD⊥BC,∠ADF+∠CDF=90°,∠CDF+∠FCD=90°,∠ADF=∠FCD.∴∠AEF=∠FCD,∠BEF+∠FCB=180°,即B、E、F、C四点共圆.(3)若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆.证明在△ABC中,BD、CE是AC、AB边上的高.∴∠BEC=∠BDC=90°,且E、D在BC的同侧,∴E、B、C、D四点共圆.∠AED=∠ACB,∠A=∠A,∴△AED∽△ACB.上述三种方法是证“四点共圆”的基本方法,至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了.【例1】在圆内接四边形ABCD中,∠A-∠C=12°,且∠A∶∠B=2∶3.求∠A、∠B、∠C、∠D的度数.解∵四边形ABCD内接于圆,∴∠A+∠C=180°.∵∠A-∠C=12°,∴∠A=96°,∠C=84°.∵∠A∶∠B=2∶3,∠D=180°-144°=36°.利用圆内接四边形对角互补可以解决圆中有关角的计算问题.【例2】已知:如图1所示,四边形ABCD内接于圆,CE∥BD交AB的延长线于E.求证:AD·BE=BC·DC.证明:连结AC.∵CE∥BD,∴∠1=∠E.∵∠1和∠2都是所对的圆周角,∴∠1=∠2.∠1=∠E.∵四边形ABCD内接于圆,∴∠EBC=∠CDA.∴△ADC∽△CBE.AD∶BC=DC∶BE.AD·BE=BC· DC.本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件,进而得到结论.关于圆内接四边形的性质,还有一个重要定理.现在中学课本一般都不列入,现介绍如下:定理:圆内接四边形两条对角线的乘积等于两组对边乘积的和.已知:如图2所示,四边形ABCD内接于圆.求证:AC·BD=AB·CD+AD·BC.证明:作∠BAE=∠CAD,AE交 BD于 E.∵∠ABD=∠ACD,即 AB·CD=AC·BE.①∵∠BAE+∠CAE=∠CAD+∠CAE,∴∠BAC=∠EAD.又∠ACB=∠ADE,AD·BC=AC·DE.②由①,②得AC·BE+AC·DE=AB·CE+AD·BCAC·BD=AB·CD+AD·BC这个定理叫托勒密(ptolemy)定理,是圆内接四边形的一个重要性质.这个证明的关键是构造△ABE∽△ACD,充分利用相似理论,这在几何中是具有代表性的.在数学竞赛中经常看到它的影子,希望能引起我们注意.命题“菱形都内接于圆”对吗?命题“菱形都内接于圆”是不正确的.所以是假命题.理由是:根据圆的内接四边形的判定方法之一,如果一个四边形的一组对角互补,那么这个四边形内接于圆.这个判定的前提是一组对角互补,而菱形的性质是一组对角相等.而一组相等的角,它们的内角和不一定是180°.如果内角和是180°,而且又相等,那么只可能是每个内角等于90°,既具有菱形的性质,且每个内角等于90°,那末这个四边形一定是正方形.而正方形显然是菱形中的特例,不能说明一般情形.判定四边形内接于圆的方法之二,是圆心到四边形四个顶点的距离相等.圆既是中心对称图形,又是轴对称图形,它的对称中心是圆心.菱形同样既是中心对称图形,又是轴对称图形,它的对称中心是两条对角线的交点.但菱形的对称中心到菱形各个顶点的距离不一定相等.所以,也无法确定菱形一定内接于圆;如果菱形的对称中心到菱形各边顶点的距离相等,再加上菱形的对角线互相垂直平分这些性质,那么这个四边形又必是正方形.综上所述,“菱形都内接于圆”这个命题是错误的.5圆的内接四边形例1 已知:如图7-90,ABCD是对角线互相垂直的圆内接四边形,通过对角线的交点E与AB垂直于点H的直线交CD于点M.求证:CM=MD.证明∠MEC与∠HEB互余,∠ABE与∠HEB互余,所以∠MEC=∠ABE.又∠ABE=∠ECM,所以∠MEC=∠ECM.从而CM=EM.同理MD=EM.所以CM=MD.点评本例的逆命题也成立(即图中若M平分CD,则MH⊥AB).这两个命题在某些问题中有时有用.本例叫做婆罗摩笈多定理.例2 已知:如图7-91,ABCD是⊙O的内接四边形,AC⊥BD,分析一如图7-91(a),由于E是AB的中点,从A引⊙O的需证明GB=CD.但这在第七章ξ1.4圆周角中的例3已经证明了.证明读者自己完成.*分析二如图7-91(b),设AC,BD垂直于点F.取CD的有OE∥MF.从而四边形OEFM应该是平行四边形.证明了四边形OEFM是平行四边形,问题也就解决了.而证明四边形OEFM是平行四边形已经没有什么困难了.*分析三如图7-91(b),通过AC,BD的交点F作AB的垂线交CD于点M.连结线段EF,MO.由于OE⊥AB,FM⊥AB,所以OE∥FM.又由于EF⊥CD(见例1的点评),MO⊥CD,所以EF∥MO.所以四边形OEFM为平行四边形.从而OE=MF,而由例3 求证:圆内接四边形对边乘积的和等于对角线的乘积,即图中AB·CD+BC·AD=AC·BD.分析在AB·CD+BC·AD=AC·BD中,等号左端是两个乘积的和,要证明这种等式成立,常需把左端拆成两个单项式来证明,即先考虑AB·CD和BC·AD各等于什么,然后再考虑AB·CD+BC·AD是否等于AC·BD.而要考虑AB·CD和BC·AD各等于什么,要用到相似三角形.为此,如图7-92,作AE,令∠BAE=∠CAD,并且与对角线BD相交于点E,这就得到△ABE∽△ACD.由此求得AB·CD=AC·BE.在圆中又出现了△ABC∽△AED,由此又求得BC·AD=AC·ED.把以上两个等式左右各相加,问题就解决了.证明读者自己完成.点评本例叫做托勒玫定理.它在计算与证明中都很有用.意一点.求证:PA=PB+PC.分析一本例是线段和差问题,因此可用截取或延长的方法证明.如图7-93(a),在PA上取点M,使PM=PB,剩下的问题是证明MA=PC,这只要证明△ABM≌△CBP就可以了.证明读者自己完成.分析二如图7-93(a),在PA上取点M,使MA=PC,剩下的问题是证明PM=PB,这只要证明△BPM是等边三角形就可以了.证明读者自己完成.分析三如图7-93(b),延长CP到M,使PM=PB,剩下的问题是证明PA=MC,这只要证明△PAB≌△CMB就可以了.证明读者自己完成.读者可仿以上的方法拟出本例的其他证明.*本例最简单的证明是利用托勒玫定理(例3).证明由托勒玫定理得PA·BC=PB·AC+PC·AB,由于BC=AC=AB,所以有PA=PB+PC.例2 如图7—116,⊙O1和⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:CE∥DF.分析:要证明CE∥DF.考虑证明同位角(或内错角)相等或同旁内角互补.由于CE、DF分别在两个圆中,不易找到角的关系,若连结AB,则可构成圆内接四边形,利用圆内接四边形的性质定理可沟通两圆中有关角的关系.证明:连结AB.∵ABEC是圆内接四边形,∵ADFB是圆内接四边形,∴∠BAD+∠F=180°,∴∠E+∠F=180°.∴CE∥CF.说明:(1)本题也可以利用同位角相等或内错角相等,两直线平行证明.如延长EF至G,因为∠DFG=∠BAD,而∠BAD=∠E,所以∠DFG=∠E.(2)应强调本题的辅助线是为了构成圆内接四边形,以利用它的性质,导出角之间的关系.(3)对于程度较好的学生,还可让他们进一步思考,若本题不变,但不给出图形,是否还有其他情况?问题提出后可让学生自己画图思考,通过讨论明确本题还应有如图7—117的情况并给予证明.例3 如图7—118,已知在△ABC中,AB=AC,BD平分∠B,△ABD的外接圆和BC 交于E.求证:AD=EC.分析:要证AD=EC,不能直接建立它们的联系,考虑已知条件可知∠ABD=∠DBE,容易看出.若连结DE,则有AD=DE.因此只要证DE=EC.由于DE和EC为△DEC的两边,所以只要证∠EDC=∠C.由已知条件可知∠C=∠ABC.因此只要证∠EDC=∠ABC.因为△EDC是圆内接四边形ABED的一个外角,所以可证∠EDC=∠ABC.问题可解决.证明:连结DE.∵BD平分∠ABC,∴,AD=DE.∵ABED是圆内接四边形,∵AB=AC,∴∠ABC=∠C,∴∠EDC=∠C.于是有DE=EC.因此AD=EC.四、作业1.如图7—120,在圆内接四边形ABCD中,AC平分BD,并且AC⊥BD,∠BAD=70°18′,求四边形其余各角.2.圆内接四边形ABCD中,∠A、∠B、∠C的度数的比为2∶3∶6,求四边形各内角的度数.3.如图7—121,AD是△ABC外角∠EAC的平分线,AD与三角形的外接圆交于点D.求证:DB=DC.作业答案或提示:1.∠ABC=∠ADC=90°,∠BCD=109°42′.2.∠A=45°,∠B=67.5°,∠C=135°,∠D=112.5°.3.提示:因为∠DBC=∠DAC,∠EAD=∠DCB,∠EAD=∠DAC,所以∠DBC=∠DCB,因此DB=DC.判定四点共圆的方法引导学生归纳判定四点共圆的方法:(1)如果四个点与一定点距离相等,那么这四个点共圆.(2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆.(3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆.(4)如果两个直角三角形有公共的斜边,那么这两个三角形的四个顶点共圆(因为四个顶点与斜边中点距离相等).3.如图7—124,已知ABCD为平行四边形,过点A和B的圆与 AD、BC分别交于E、F.求证:C、D、E、F四点共圆.提示连结EF.由∠B+∠AEF=180°,∠B+∠C=180°,可得∠AEF=∠C.四点共圆的应用山东宁阳教委教研室栗致根四点共圆在平面几何证明中应用广泛,熟悉这种应用对于开阔证题思路,提高解题能力都是十分有益的.一用于证明两角相等例1 如图1,已知P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,OP交AB 于E.求证:∠APC=∠BPD.证明连结OA,OC,OD.由射影定理,得AE2=PE·EO,又AE=BE,则AE·BE =PE·EO……(1);由相交弦定理,得AE·BE=CE·DE……(2);由(1)、(2)得CE·ED=PE·EO,∴ P、C、O、D四点共圆,则∠1=∠2,∠3=∠4,又∠2=∠4.∴∠1=∠3,易证∠APC=∠BPD(∠4=∠EDO).二用于证明两条线段相筹例2 如图2,从⊙O外一点P引切线PA、PB和割线PDC,从A点作弦AE平行于DC,连结BE交DC于F,求证:FC=FD.证明连结AD、AF、EC、AB.∵PA切⊙O于A,则∠1=∠2.∵AE∥CD,则∠2=∠4.∴∠1=∠4,∴P、A、F、B四点共圆.∴∠5=∠6,而∠5=∠2=∠3,∴∠3=∠6.∵AE∥CD,∴EC=AD,且∠ECF=∠ADF,∴△EFC≌△AFD,∴FC=FD.三用于证明两直线平行例3 如图3,在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC.证明连结EC.在△ABE和△ACE中,∵AE=AE,AB=AC,∠BAE=∠CAE,∴△AEB≌AEC,∴∠5=∠1=∠2,∴B、C、H、E四点共圆,∴∠6=∠3.在△GEB 和△GEC中,∵GE=GE,∠BEG=∠CEG,EB=EC,∴△GEB≌△GEC,∴∠4=∠2=∠3,∴∠4=∠6.∴EH∥GC.四用于证明两直线垂直证明在△ABD和△BCE中,∵AB=BC,∠ABD=∠BCE,BD=CE,则△ABD≌△BCE,∴∠ADB=∠BEC,∴P、D、C、E四点共圆.设DC的中点为O连结OE、DE.易证∠OEC=60°,∠DEO=30°∴∠DEC=90°,于是∠DPC=90°,∴ CP⊥AD.五用于判定切线例5 如图5,AB为半圆直径,P为半圆上一点,PC⊥AB于C,以AC为直径的圆交PA于D,以BC为直径的圆交PB于E,求证:DE是这两圆的公切线.证明连结DC、CE,易知∠PDC=∠PEC=90°,∴ P、D、C、E四点共圆,于是∠1=∠3,而∠3+∠2=90°,∠A+∠2=90°,则∠1=∠A,∴DE是圆ACD 的切线.同理,DE是圆BCE的切线.因而DE为两圆的公切线六用于证明比例式例6 AB、CD为⊙O中两条平行的弦,过B点的切线交CD的延长线于G,弦PA、PB分别交CD于E、F.证明如图6.连结BE、PG.∵BG切⊙O于B,则∠1=∠A.∵AB∥CD,则∠A=∠2.于是∠1=∠2,∴P、G、B、E四点共圆.由相交弦定理,得EF·FG=PF·FB.在⊙O中,由相交弦定理,得CF·FD=FP·FB.七用于证明平方式例7 ABCD为圆内接四边形,一组对边AB和DC延长交于P点,另一组对边AD和BC延长交于Q点,从P、Q引这圆的两条切线,切点分别是E、F,(如图 7)求证:PQ2=QF2+PE2.证明作△DCQ的外接圆,交PQ于M,连结MC,∵∠1=∠2=∠3,则P、B、C、M四点共圆.由圆幂定理得PE2=PC·PD=PM·PQ,QF2=QC·QB=QM·QP,两式相加得PE2+QF2=PM·PQ+ QM·QP=PQ(PM+QM)=PQ·PQ=PQ2∴PQ2=PE2+QF2.八用于解计算题例8如图8,△ABC的高AD的延长线交外接圆于H,以AD为直径作圆和AB、AC分别交于E、F点,EF交 AD于 G,若 AG=16cm,AH=25cm,求 AD的长.解连结DE、DF、BH.∵∠1=∠2=∠C=∠H,∴B、E、G、H四点共圆.由圆幂定理,得AE·AB=AG·AN.在△ABD中,∵∠ADB=90°,DE⊥AB,由射影定理,得AD2=AE·AB,∴AD2=AG·AH=16×25=400,∴AD=20cm.九用于证明三点共线例9如图9,D为△ABC外接圆上任意一点,E、F、G为D点到三边垂线的垂足,求证:E、F、G三点在一条直线上.证明连结EF、FG、BD、CD.∵∠BED=∠BFD=90°,则B、E、F、D四点共圆,∴∠1=∠2,同理∠3=∠4.在△DBE和△DCG中,∵∠DEB=∠DGC,∠DBE=∠DCG,故∠1=∠4,易得∠2=∠3,∴ E、F、G三点在一条直线上.十用于证明多点共圆例10如图10,H为△ABC的垂心,H1、H2、H3为H点关于各边的对称点,求证:A、B、C、H1、H2、H3六点共圆.证明连结AH2,∵H与H2关于AF对称,则∠1=∠2.∵A、F、D、C四点共圆,则∠2=∠3,于是∠1=∠3,∴A、H2、B、c四点共圆,即H2在△ABC的外接圆上.同理可证,H1、H3也在△ABC的外接圆上.∴A、B、C、H1、H2、H3六点共圆.托勒密定理的数形转换功能山东临沂市四中姜开传临沂市第一技校刘久松圆内接四边形两组对边乘积的和等于其对角线的乘积,即在四边形 ABCD 中,有AB·CD+AD·BC=AC·BD,这就是著名的托勒密定理.本刊1996年第2期给出了它的几种证法,作为续篇,本文就其数形转换功能举例说明如下:1 “形”转换为“数”对于某些几何问题,特别是圆内接多边形问题,如果能根据题设中隐含的数量关系,利用托勒密定理可将“形”转换为“数”,从而达到用代数运算来代替几何推理的目的.例1已知正七边形A1A2 (7)(第21届全俄数学奥林匹克竞赛题)对于这道竞赛题,原证较繁,但通过深挖隐含条件,利用托勒密定理可改变整个解题局面,使证题步骤简缩到最少.如图1,连 A1A5、A3A5,则A1A5=A1A4、A3A5=A1A3.在四边形A1A3A4A5中,由托勒密定理,得A3A4·A1A5+A4A5·A1A3=A1A4·A3A5,即A1A2·A1A4+A1A2·A1A3=A1A3·A1A4,两边同除以A1A2·A1A3·A1A4即得结论式.例2 如图2,A、B、C、D四点在同一圆周上,且BC=CD=4,AE=6,线段BE和DE的长都是整数,则BD的长等于多少?(1988年全国初中数学联赛题)此题若用其它方法解,往往使人一筹莫展.若运用托勒密定理,可使问题化难为易.由△CDE∽△BAE和△CBE∽△DAE,得由托勒密定理,得BD(AE+CE)=4(AB+AD),亦即 CE(AE+CE)=16.设CE=x,整理上式,得x2+6x-16=0.解得x=2(负值已舍),故BE·DE=CE·AE=12.∵BD<BC+CD=8,例3一个内接于圆的六边形,其五个边的边长都为81,AB是它的第六边,其长为31,求从B出发的三条对角线长的和.(第九届美国数学邀请赛试题)原解答过程冗长.若通过托勒密定理的桥梁作用,把“形”转换为“数”,可使问题化繁为简.如图3,设BD=a, BE=b,BF=c,连AC、CE、AE,则CE=AE=BD=a,AC=BF =c.在四边形BCDE中,由托勒密定理,得81b+812=a2①同理81b+31·81=ac ②31a+81a=bc ③解①、③、③组成的方程组,得a=135,b=144,c=105故 a+b+c=384.2 “数”转换为“形”对于某些代数问题,若结构与托勒密定理相似,通过构造圆内接四边形,可把“数”转换为“形”,然后利用“形”的性质,使问题得到解决.这种解法构思巧妙,方法独特,富于创新,出奇制胜.例4 解方程若按常规方法解这个无理方程,过程繁冗.若由方程的结构特征联想到托勒密定理,则构造直径AC=x(x≥11)的圆及圆内接四边形ABCD,使BC=2,CD=11,如图 4,于是由托勒密定理,得在△BCD中,由余弦定理,得经检验x=14是原方程的根.求证: a2+b2=1.这道名题已有多种证法,而且被视为用三角换无法解代数问题的典范.下面再给出一各几何证法.易知0≤a、b≤1且a、b不全为零.当a、b之一为零时,结论显然成立.当a、b全不为零时,由已知等式联想到托勒密定理,作直径AC=1的圆及圆内接四与已知等式比较,得BD=1,即BD也为圆的直径,故a2+b2=1例6设a>c,b>c,c>0,此题若用常规方法证明也不轻松.下面利用托勒密定理给出它的一个巧证.由托勒密定理,得巧用托勒密定理证题河北晋州市数学论文研究协会张东海王素改在解证某些数学题时,如能巧用托勒密定理,可使解证过程简洁清新,兹举例说明.托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.一、构造“圆”,运用定理【例1】设a,b,x,y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证作直径AB=1的圆,在AB的两侧任作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x, AD=y.(图1)由勾股定理知a,b,x,y满足条件.根据托勒密定理,有AC·BD+BC·AD=AB·CD.∵ CD≤1,∴ax+by≤1.二、利用无形圆,运用定理【例2】等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.已知:梯形 ABCD中,AD=BC,AB∥CD.求证:BD2=BC2+AB·CD.证∵等腰梯形内接于圆,由托勒密定理,有AC·BD=AD·BC+AB·CD.∵AD=BC,AC=BD,∴BD2=BC2+AB·CD.(图略)【例 3】已知:边长为 1的正七边形ABCDEFG中,对角线 AD=a,BG=b(a≠b).求证:(a+b)2(a-b)=ab2.证连结BD,GE,BE,DG,则 BD=EG=GB=b,DG=BE=DA=a, DE=AB=AG=1.(如图2)在四边形ABDG中,由托勒密定理,有AD·BG=AB·DG+BD·AG,即ab=a+b (1)同理在四边形BDEG中,得BE·DG=DE·BG+BD·EG,即a2=b+b2 (2)将(2)变形为b=a2-b2 (3)(1)×(3),得ab2=(a+b)(a2-b2).故ab2=(a+b)2(a-b).三、构造圆内接四边形,运用定理【例4】在△ABC中,∠A的内角平分线AD交外接圆于D.连结BD.求证:AD·BC=BD·(AB+AC).证(如图3) 连结DC.由托勒密定理.有AD·BC=AB·CD+AC·BD.又∵∠1=∠2,∴BD=DC.∴AD·BC=AB·CD+AC·BD=BD(AB+AC).即AD·BC=BD·(AB+AC).圆内接四边形的面积公式黑龙江绥化五中任天民设圆内接四边形ABCD中各边为a,b,c,d.连结 BD.由∠A+∠C=180°,可以推出sinA=sinC,cosA=-cosC.并且S四边形ABCD=S△ABD+S△BCD所以这样我们得出了圆内接四边形面积的计算公式.在上面的公式中,如果设某一边为零,(不仿设d=0)此时四边形变成三角形,该公式恰是计算三角形面积的海伦公式.圆内接四边形面积公式的得出是受三角形面积公式的启发,通过联想探索出来的,而且两者在形式上又是那么的相近.这种现象在数学中不胜枚举,如果同学们都能从特殊规律去探索一般规律,再从一般规律去认识特殊规律.那么对数学能力的培养将大有裨益.四条边定长四边形面积的最大值上海市育群中学李甲鼎四条边为定长的四边形不具稳定性,但在某种特定的位置下,它能内接于圆,成为圆内接四边形.并且此时达到变化过程中面积最大值.下文证明这个事实.已知:四边形ABCD中:AB=a,BC=b,CD=c,DA=d求证:四边形ABCD中有唯一四边形能内接于圆,且此时面积达到最大值.证明:(1)先证四边形四边定长,有唯一的四边形内接于圆,设∠ABC=α,∠ADC=β,AC=x.令α+β=π,即cosα+cosβ=0x的解唯一确定,代入(1)(2)后cosα、cosβ也随之唯一确,在α,β∈(0,π)的条件下α、β也同时唯一确定.∴四边形四边定长,对角互补,四边形是唯一的.即所得到的四边形为圆内接四边形.(2)当四边定长的四边形内接于圆时,此四边形面积最大.∵四边形ABCD的面积由余弦定理得a2+b2-2abcosα=x2=c2+d2-2cdcosβ显然当α+β=π时(即为圆内接四边形时)S2达到最大值,即S最大.一个几何定理的应用江苏省徐州矿务局庞庄职校张怀林定理:如图1,在圆接四边形ABCD中弦AD平分∠BAC,则2ADcosα=AB+AC.证明连接BD、DC、BC,设已知圆半径为R,则由正弦定理有:BD=DC=2Rsinα,BC=2Rsin2α.由托勒密定理有AB·CD+AC·BD=AD·DC.∴(AB+AC)·2Rsinα=AD·2Rsin2α.则 2AD·cosα=AB+AC.下面举例说明它的应用.例1如图2,已知锐角△ABC的∠A平分线交BC于L,交外接圆于N,过L 分别作LK⊥AB,LM⊥AC,垂足分别为K、M.求证:四边形AKNM的面积等于△ABC 的面积.(第28届IMO)证明由已知得∠BAN=∠CAN,由定理有 2ANcosα=AB+AC,=AN·AL·cosα·sinα=AN·AK·sinα=AN·AM·sinα=2S△AKN=2S△AMN.∴S△ABC=S四边形AKNM.(第21届全苏奥数)证明作正七边形外接圆,如图3所示.由定理有2c·cosα=b+c,又在等腰△A1A2A3中有2a·cosα=b.例3在△ABC中,∠C=3∠A,a=27,c=48,则b的值是____.(第36届AHSME试题) 解如图4.作△ABC的外接圆,在取三等分点D、E,连CD、CE.由已知得:∠ACD=∠DCE=∠ECB=∠A,CD=AB=48,由定理有 2CE·cosA=CB+CD ①2CD·cosA=CE+AC ②又2CB·cosA=CE ③由②、③得:b=AC=CE·(CD-CB)/CB=35.托勒密定理及其应用河北省晋州市数学论文研究协会刘同林托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).已知:圆内接四边形ABCD,求证:AC·BD=AB·CD+AD·BC.证明:如图1,过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP.①+②得 AC(BP+DP)=AB·CD+AD·BC.即AC·BD=AB·CD+AD·BC.这就是著名的托勒密定理,在通用教材中习题的面目出现,不被重视.笔者认为,既然是定理就可作为推理论证的依据.有些问题若根据它来论证,显然格外简洁清新.兹分类说明如下,以供探究.一、直接应用托勒密定理例1如图2,P是正△ABC外接圆的劣弧上任一点(不与B、C重合),求证:PA=PB+PC.分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA·BC=PB·AC+PC·AB,∵AB=BC=AC.∴PA=PB+PC.二、完善图形借助托勒密定理例2证明“勾股定理”:在Rt△ABC中,∠B=90°,求证:AC2=AB2+BC2证明:如图3,作以Rt△ABC的斜边AC为一对角线的矩形ABCD,显然ABCD 是圆内接四边形.由托勒密定理,有AC·BD=AB·CD+AD·BC.①又∵ABCD是矩形,∴AB=CD,AD=BC,AC=BD.②把②代人①,得AC2=AB2+BC2.例3如图4,在△ABC中,∠A的平分线交外接∠圆于D,连结BD,求证:AD·BC=BD(AB+AC).证明:连结CD,依托勒密定理,有AD·BC=AB·CD+AC·BD.∵∠1=∠2,∴ BD=CD.故 AD·BC=AB·BD+AC·BD=BD(AB+AC).三、利用“无形圆”借助托勒密定理例4等腰梯形一条对角线的平方等于一腰的平方加上两底之积.如图5,ABCD中,AB∥CD,AD=BC,求证:BD2=BC2+AB·CD.证明:∵等腰梯形内接于圆,依托密定理,则有AC·BD=AD·BC+AB·CD.又∵ AD=BC,AC=BD,∴BD2=BC2+AB·CD.四、构造图形借助托勒密定理例5若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明:如图6,作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x,AD=y.由勾股定理知a、b、x、y是满足题设条件的.据托勒密定理,有AC·BD+BC·AD=AB·CD.∵CD≤AB=1,∴ax+by≤1.五、巧变原式妙构图形,借助托勒密定理例6已知a、b、c是△ABC的三边,且a2=b(b+c),求证:∠A=2∠B.分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c.证明:如图 7,作△ABC的外接圆,以 A为圆心,BC为半径作弧交圆于D,连结BD、DC、DA.∵AD=BC,∴∠ABD=∠BAC.又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.依托勒密定理,有BC·AD=AB·CD+BD·AC.①而已知a2=b(b+c),即a·a=b·c+b2.②∴∠BAC=2∠ABC.六、巧变形妙引线借肋托勒密定理例7在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4,析证:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图8,作△ABC的外接圆,作弦BD=BC,边结AD、CD.在圆内接四边形ADBC中,由托勒密定理,有AC·BD+BC·AD=AB·CD易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC,关于圆内接四边形的若干共点性质浙江绍兴县鲁迅中学范培养设四边形ABCD内接于圆O,其边AB与DC的延长线交于P,AD与BC的延长线交于Q,由P作圆的两切线PM、PN,切点分别为M、N;由Q作圆的两切线QE、QF,切点分别为E、F(如图1).则有以下一些共点性质:性质1 AC、BD、EF三直线共点.证明:如图1,设AC交EF于K1,则K1分EF所成的比为设BD交EF于K2,同理可得K2分EF所成的比为由(5)、(6)可得(1)=(2),故K1、K2分EF所成的比相等.∴K1、K2重合,从而AC、BD、EF三直线共点.类似地 AC、BD、MN三直线共点,因此有以下推论 AC、BD、EF、MN四直线共点.性质2 AB、DC、EF三直线共点于P.(此性质等同于1997年中国数学奥林匹克第二试第四题)这里用上述证明性质1的方法证之.证明:如图2.设DC与EF的延长线交于P1,则P1分EF所成的比为设AB与EF的延长线交于P2,则P2分EF所成的比为由(5)、(6)可得(7)=(8),故P1、P2分EF所成的比相等.∴P1、P2重合,从而AB、DC、EF三直线共点于P.推论 AD、BC、NM三直线共点于Q.性质 3 EM、NF、PQ三直线共点.证明:如图3,设EM的延长线交PQ于G1,妨上证法,G1分PQ所成的比为设NF的延长线交PQ于G2,则G2分PQ所成的比为(这里E、F、P三点共线及N、M、Q三点共线在性质2及推论中已证).由△PME∽△PFM得由(11)、(12)及QE=QF、PN=PM可得(9)=(10),故G1、G2分PQ所成的比相等.∴G1、G2重合,从而EM、NF、PQ三直线共点.性质4如果直线EN和MF相交,那么交点在直线PQ上,即 EN、MF、PQ三直线共点.证明从略,妨性质3的证法可得.性质5 EM、NF、AC三直线共点.证明:如图4,类似于性质1的证明,设EM与AC的延长线交于G3,则G3分AC所成的比为设NF与AC的延长线交于G4,则G4分AC所成的比为由(15)、(18)、(19)可得(13)=(14),故G3、G4分AC所成的比相等.∴G3、G4重合,从而 EM、NF、AC 三直线共点.推论EM、NF、AC、PQ四直线共点.限于篇幅,仅列以上五条共点性质.有兴趣的读者不妨再探索其它共点性质例3在边长为a的正七边形ABCDEFG中,两条不相等的对角线长分别为t,m.证明如图4,连结AD、CE,令AE=t,AC=m,在圆内接四边形ACDE中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma.托勒密定理及其应用河北省晋州市数学论文研究协会康美娈彭立欣托勒密定理圆内接四边形的两条对角线的乘积(两条对角线所包矩形的面积),等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形面积之和).证明如图1,过C作CP使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.∴AC·BP=AD·BC ①又∠ACB=∠DCP,∠5=∠6,∴AC·DP=AB·CD.②①+②得AC(BP+PD)=AD·BC+AB·CD.故AC·BD=AD·BC+AB·CD.托勒密定理在教材中仅以习题的形式出现,若以此定理为根据,可使许多问题解证过程别具一格.例1已知P是正△ABC的外接圆劣弧上任意一点.求证:PA=BP+PC.证明如图2,ABPC是圆内接四边形,根据托勒密定理,有PA·BC=PB·AC+PC·AB.∵AB=BC=AC,∴PA=PB+PC.例2证明等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.证明如图3,设在梯形ABCD中,AD=BC,AB∥CD.∵等腰梯形内接于圆,∴AC·BD=AD·BC+AB·CD.又AD=BC,AC=BD,∴BD2=BC2+AB·CD.例3在边长为a的正七边形ABCDEFG中,两条不相等的对角线长分别为t,m.证明如图4,连结AD、CE,令AE=t,AC=m,在圆内接四边形ACDE中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma.例4已知 a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明作直径AB=1的圆,在AB两侧作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x,DA=y(如图5).依勾股定理知a、b、x、y是满足题设条件的.依托勒密定理有AC·BD+BC·AD=AB·CD.又∵CD≤AB=1,∴ax+by≤1.例5△ABC的三个内角 A、 B、 C的对边分别为a、b、c,且a2=b(b+c).求证:A=2B.分析将a2=b(b+c)变形为a·a=b·b+b·c,可联想到托勒密定理,进而构造一个圆内接等腰梯形,使两腰为b,两对角线为a,一底边为c.证明如图6,作△ABC的外接圆.以A为圆心,以BC为半径画弧交圆于D,连结BD、DA、DC.。
(完整版)四点共圆例题及答案

例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.证明菱形ABCD的对角线AC和BD相交于点O,连接OE、OF、OG、OH.∵AC和BD 互相垂直,∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中,E、F、G、H,分别是AB、BC、CD、DA的中点,即E、F、G、H 四点共圆.(2) 若四边形的两个对角互补( 或一个外角等于它的内对角) ,则四点共圆.例 2 如图,在△ ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.证明∵ DE⊥AB,DF⊥AC,∴∠ AED+∠ AFD=180°,即A、E、D、F 四点共圆,∠AEF=∠ADF.又∵ AD⊥BC,∠ ADF+∠ CDF=90°,∠CDF+∠ FCD=90°,∠ADF=∠FCD.∴∠ AEF=∠FCD,∠BEF+∠ FCB=180°,即B、E、F、C 四点共圆.(3) 若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆.证明在△ ABC中,BD、CE是AC、AB边上的高.∴∠ BEC=∠BDC=9°0 ,且E、D在BC的同侧,∴E、B、C、D四点共圆.∠AED=∠ACB,∠A=∠A,∴△ AED∽△ ACB.上述三种方法是证“四点共圆”的基本方法,至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了.【例1】在圆内接四边形ABCD中,∠ A-∠C=12°,且∠ A∶∠ B=2∶3.求∠ A、∠B、∠C、∠D的度数.解∵四边形ABCD内接于圆,∴∠ A+∠C=180°.∵∠A-∠C=12°,∴∠ A=96°,∠ C=84°.∵∠ A∶∠ B=2∶3,∠D=180°-144°=36°.利用圆内接四边形对角互补可以解决圆中有关角的计算问题.【例2】已知:如图 1 所示,四边形ABCD内接于圆,CE∥BD交AB的延长线于E.求证:AD· BE=BC· DC.证明:连结AC.∵CE∥BD,∴∠ 1=∠E.∵∠1和∠2 都是所对的圆周角,∴∠ 1=∠2.∠1=∠E.∵四边形ABCD内接于圆,∴∠ EBC=∠CDA.∴△ ADC∽△ CBE.AD∶BC=D∶C BE.AD· BE=BC· DC.本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件,进而得到结论.关于圆内接四边形的性质,还有一个重要定理.现在中学课本一般都不列入,现介绍如下:定理:圆内接四边形两条对角线的乘积等于两组对边乘积的和.已知:如图2所示,四边形ABCD内接于圆.求证:AC·BD=AB·CD+AD·BC.证明:作∠ BAE=∠CAD,AE交BD于E.∵∠ ABD=∠ACD,即AB· CD=A·C BE.①∵∠BAE+∠CAE=∠CAD+∠CAE,∴∠ BAC=∠EAD.又∠ ACB=∠ADE,AD· BC=AC·DE.②由①,②得AC·BE+AC·DE=AB· CE+AD· BCAC·BD=AB·CD+AD·BC这个定理叫托勒密(ptolemy) 定理,是圆内接四边形的一个重要性质.这个证明的关键是构造△ ABE∽△ ACD,充分利用相似理论,这在几何中是具有代表性的.在数学竞赛中经常看到它的影子,希望能引起我们注意.命题“菱形都内接于圆”对吗?命题“菱形都内接于圆”是不正确的.所以是假命题.理由是:根据圆的内接四边形的判定方法之一,如果一个四边形的一组对角互补,那么这个四边形内接于圆.这个判定的前提是一组对角互补,而菱形的性质是一组对角相等.而一组相等的角,它们的内角和不一定是180°.如果内角和是180°,而且又相等,那么只可能是每个内角等于90°,既具有菱形的性质,且每个内角等于90°,那末这个四边形一定是正方形.而正方形显然是菱形中的特例,不能说明一般情形.判定四边形内接于圆的方法之二,是圆心到四边形四个顶点的距离相等.圆既是中心对称图形,又是轴对称图形,它的对称中心是圆心.菱形同样既是中心对称图形,又是轴对称图形,它的对称中心是两条对角线的交点.但菱形的对称中心到菱形各个顶点的距离不一定相等.所以,也无法确定菱形一定内接于圆;如果菱形的对称中心到菱形各边顶点的距离相等,再加上菱形的对角线互相垂直平分这些性质,那么这个四边形又必是正方形.综上所述,“菱形都内接于圆”这个命题是错误的.5 圆的内接四边形例 1 已知:如图7-90 ,ABCD是对角线互相垂直的圆内接四边形,通过对角线的交点E与AB垂直于点H的直线交CD于点M.求证:CM=M.D证明∠MEC与∠ HEB互余,∠ ABE与∠HEB互余,所以∠ MEC∠= ABE.又∠ ABE= ∠ECM,所以∠ MEC∠= ECM.从而CM=E.M同理MD=E.M所以CM=M.D点评本例的逆命题也成立(即图中若M平分CD,则MH⊥ AB).这两个命题在某些问题中有时有用.本例叫做婆罗摩笈多定理.例 2 已知:如图7-91 ,ABCD是⊙O的内接四边形,AC⊥BD,分析一如图7-91(a),由于E是AB的中点,从A引⊙ O的需证明GB=C.D 但这在第七章ξ 1.4 圆周角中的例3已经证明了.证明读者自己完成.* 分析二如图7-91(b),设AC,BD垂直于点F.取CD的有OE∥ MF.从而四边形OEFM应该是平行四边形.证明了四边形OEFM是平行四边形,问题也就解决了.而证明四边形OEFM是平行四边形已经没有什么困难了.*分析三如图7-91(b),通过AC,BD的交点F作AB的垂线交CD于点M.连结线段EF,MO.由于OE⊥AB,FM⊥AB,所以OE∥FM.又由于EF⊥CD(见例 1 的点评),MO⊥CD,所以EF∥MO.所以四边形OEFM为平行四边形.从而OE=M,F 而由例 3 求证:圆内接四边形对边乘积的和等于对角线的乘积,即图中AB·CD+B·C AD=AC·BD.分析在AB·CD+B·CAD=AC·BD中,等号左端是两个乘积的和,要证明这种等式成立,常需把左端拆成两个单项式来证明,即先考虑AB·CD和BC·AD各等于什么,然后再考虑AB· CD+B·C AD是否等于AC·BD.而要考虑AB· CD和BC· AD各等于什么,要用到相似三角形.为此,如图7-92 ,作AE,令∠ BAE=∠CAD,并且与对角线BD相交于点E,这就得到△ ABE∽△ACD.由此求得AB·CD=A·C BE.在圆中又出现了△ ABC∽△ AED,由此又求得BC·AD=AC· ED.把以上两个等式左右各相加,问题就解决了.证明读者自己完成.点评本例叫做托勒玫定理.它在计算与证明中都很有用.意一点.求证:PA=PB+P.C分析一本例是线段和差问题,因此可用截取或延长的方法证明.如图7-93(a),在PA上取点M,使PM=P,B 剩下的问题是证明MA=P,C 这只要证明△ ABM≌△CBP就可以了.证明读者自己完成.分析二如图7-93(a),在PA上取点M,使MA=P,C 剩下的问题是证明PM=P,B 这只要证明△ BPM是等边三角形就可以了.证明读者自己完成.分析三如图7-93(b),延长CP到M,使PM=PB,剩下的问题是证明PA=M,C 这只要证明△ PAB≌△ CMB就可以了.证明读者自己完成.读者可仿以上的方法拟出本例的其他证明.* 本例最简单的证明是利用托勒玫定理(例3).证明由托勒玫定理得PA·BC=PB·AC+PC·AB,由于BC=AC=A,B所以有PA=PB+P.C例 2 如图7—116,⊙ O1 和⊙ O2都经过A、B两点,经过点A的直线CD与⊙ O1交于点C,与⊙ O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙ O2交于点F.求证:CE∥DF.分析:要证明CE∥DF.考虑证明同位角(或内错角)相等或同旁内角互补.由于CE、DF 分别在两个圆中,不易找到角的关系,若连结AB,则可构成圆内接四边形,利用圆内接四边形的性质定理可沟通两圆中有关角的关系.证明:连结AB.∵ABEC是圆内接四边形,∴∠ BAD=∠E.∵ADFB是圆内接四边形,∴∠ BAD+∠ F=180°,∴∠ E+∠ F=180°.∴CE∥CF.说明:(1) 本题也可以利用同位角相等或内错角相等,两直线平行证明.如延长EF至G,因为∠ DFG=∠BAD,而∠BAD=∠E,所以∠ DFG=∠E.(2) 应强调本题的辅助线是为了构成圆内接四边形,以利用它的性质,导出角之间的关系.(3) 对于程度较好的学生,还可让他们进一步思考,若本题不变,但不给出图形,是否还有其他情况?问题提出后可让学生自己画图思考,通过讨论明确本题还应有如图7—117的情况并给予证明.例 3 如图7—118,已知在△ ABC中,AB=AC,BD平分∠ B,△ ABD的外接圆和BC 交于E.求证:AD=EC.分析:要证AD=EC,不能直接建立它们的联系,考虑已知条件可知∠ ABD=∠DBE,容易看出.若连结DE,则有AD=D.E 因此只要证DE=EC.由于DE和EC为△ DEC的两边,所以只要证∠ EDC=∠ C.由已知条件可知∠ C=∠ ABC.因此只要证∠ EDC=∠ABC.因为△ EDC是圆内接四边形ABED的一个外角,所以可证∠ EDC=∠ ABC.问题可解决.证明:连结DE.∵ BD平分∠ ABC,∵ABED是圆内接四边形,∴∠ EDC=∠ABC.∵AB=AC,∴∠ ABC=∠C,∴∠ EDC=∠ C.于是有DE=EC.因此AD=EC.四、作业1.如图7—120,在圆内接四边形ABCD中,AC平分BD,并且AC⊥BD,∠ BAD=70°18′,求四边形其余各角.2.圆内接四边形ABCD中,∠ A、∠ B、∠ C的度数的比为2∶3∶6,求四边形各内角的度数.3.如图7—121,AD是△ABC外角∠EAC的平分线,AD与三角形的外接圆交于点D.求证:DB=D.C作业答案或提示:1.∠ABC=∠ADC=9°0 ,∠ BCD=10°9 42′.2.∠A=45°,∠ B=67.5°,∠ C=135°,∠ D=112.5°.3.提示:因为∠ DBC=∠DAC,∠EAD=∠DCB,∠EAD=∠DAC,所以∠ DBC=∠DCB,因此DB=D.C判定四点共圆的方法引导学生归纳判定四点共圆的方法:(1) 如果四个点与一定点距离相等,那么这四个点共圆.(2) 如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆.(3) 如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆.(4) 如果两个直角三角形有公共的斜边,那么这两个三角形的四个顶点共圆( 因为四个顶点与斜边中点距离相等) .3.如图7—124,已知ABCD为平行四边形,过点A和B的圆与AD、BC分别交于E、F.求证:C、D、、提示连结EF.由∠ B+∠ AEF=180 °,∠ B +∠ C=180°,可得∠ AEF= ∠C.四点共圆的应用山东宁阳教委教研室栗致根四点共圆在平面几何证明中应用广泛,熟悉这种应用对于开阔证题思路,提高解题能力都是十分有益的.一用于证明两角相等例 1 如图1,已知P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,OP 交AB 于E.求证:∠ APC=∠ BPD.证明连结OA,OC,OD.由射影定理,得AE2=PE·EO,又AE=BE,则AE·BE =PE·EO⋯⋯(1) ;由相交弦定理,得AE·BE=CE·DE⋯⋯(2) ;由(1) 、(2) 得CE·ED=PE·EO,∴ P、C、O、D四点共圆,则∠ 1=∠2,∠3=∠4,又∠ 2=∠ 4.∴∠ 1=∠3,易证∠ APC=∠ BPD(∠ 4=∠ EDO.)二用于证明两条线段相筹例 2 如图2,从⊙ O外一点P 引切线PA、PB和割线PDC,从 A 点作弦AE 平行于DC,连结BE交DC于F,求证:FC=FD.证明连结AD、AF、EC、AB.∵PA切⊙O于A,则∠ 1=∠ 2.∵ AE∥ CD,则∠ 2=∠ 4.∴∠1=∠4,∴P、A、F、B四点共圆.∴∠ 5=∠ 6,而∠5=∠2=∠3,∴∠3=∠6.∵AE∥CD,∴EC=AD,且∠ECF=∠ADF,∴△EFC≌△AFD,∴FC=FD.用于证明两直线平行例 3 如图3,在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥ GC.证明连结EC.在△ ABE和△ACE中,∵AE=AE,AB=AC,∠BAE=∠CAE,∴ △AEB≌AEC,∴∠5=∠1=∠2,∴B、C、H、E四点共圆,∴∠ 6=∠3.在△ GEB 和△ GEC中,∵ GE=GE,∠BEG=∠CEG,EB=EC,∴△GEB≌△GEC,∴∠ 4=∠2 =∠ 3,∴∠ 4=∠ 6.∴ EH∥ GC.四用于证明两直线垂直证明在△ ABD和△BCE中,∵AB=BC,∠ABD=∠BCE,BD=CE,则△ABD≌△ BCE,∴∠ ADB=∠ BEC,∴P、D、C、E四点共圆.设DC的中点为O连结OE、DE.易证∠ OEC=60°,∠ DEO=30°∴∠ DEC=90°,于是∠ DPC=9°0 ,∴ CP⊥AD.五用于判定切线例 5 如图5,AB为半圆直径,P为半圆上一点,PC⊥AB于C,以AC为直径的圆交PA 于D,以BC为直径的圆交PB于E,求证:DE是这两圆的公切线.证明连结DC、CE,易知∠ PDC=∠ PEC=90°,∴ P、D、C、E四点共圆,于是∠ 1=∠3,而∠3+∠ 2=90°,∠ A+∠ 2=90°,则∠ 1=∠ A,∴DE是圆ACD 的切线.同理,DE是圆BCE的切线.因而DE为两圆的公切线六用于证明比例式例 6 AB、CD为⊙ O中两条平行的弦,过B点的切线交CD的延长线于G,弦PA、PB分别交CD于E、F.证明如图6.连结BE、PG.∵BG切⊙ O于B,则∠ 1=∠ A.∵AB∥CD,则∠A=∠2.于是∠1=∠2,∴P、G、B、E四点共圆.由相交弦定理,得EF·FG=PF·FB.在⊙ O中,由相交弦定理,得CF· FD=FP·FB.七用于证明平方式例7 ABCD为圆内接四边形,一组对边AB和DC延长交于P 点,另一组对边AD和BC延长交于Q点,从P、Q引这圆的两条切线,切点分别是E、F,(如图7)求证:PQ2=QF2+PE2.证明 作△ DCQ 的外接圆,交 PQ 于 M ,连结 MC ,∵∠ 1=∠2=∠ 3,则 P 、B 、 C 、M 四点共圆.由圆幂定理得 PE 2=PC ·PD =PM · PQ ,QF 2=QC ·QB = QM ·QP ,两 式相加得 PE 2+ QF 2=PM ·PQ + QM ·QP=PQ (P +MQM )=PQ ·PQ=P 2Q∴PQ 2=PE 2+QF 2.八 用于解计算题例 8 如图 8,△ ABC 的高 AD 的延长线交外接圆于 H ,以 AD 为直径作圆和 AB 、 AC 分别交于 E 、F 点, EF 交 AD 于 G ,若 AG=16cm ,AH=25cm ,求 AD 的长.解 连结 DE 、DF 、BH .∵∠ 1=∠2=∠ C=∠H ,∴B 、E 、G 、H 四点共圆.由圆 幂定理,得 AE ·AB =AG ·AN .在△ ABD 中,∵∠ ADB=90°,DE ⊥AB ,由射影定理, 得 AD 2= AE ·AB ,∴ AD 2=AG ·AH = 16×25= 400,∴ AD=20cm .九 用于证明三点共线例 9 如图 9, D 为△ABC 外接圆上任意一点,垂足,求证: E 、F 、G 三点在一条直线上. 证明 连结 EF 、FG 、BD 、CD .∵∠ BED=∠BFD=90°,则 B 、E 、F 、D 四点共 圆,∴∠ 1=∠ 2,同理∠ 3=∠4.在△DBE 和△DCG 中,∵∠DEB =∠DGC ,∠DBE =∠DCG ,故∠1=∠4,E 、F 、G 为 D 点到三边垂线的易得∠2=∠ 3,∴ E、F、G三点在一条直线上.十用于证明多点共圆例10 如图10,H为△ABC的垂心,H1、H2、H3为H点关于各边的对称点,求证:A、B、C、H1、H2、H3六点共圆.证明连结AH2,∵H与H2 关于AF对称,则∠ 1=∠2.∵A、F、D、C四点共圆,则∠ 2=∠ 3,于是∠ 1=∠3,∴A、H2、B、c 四点共圆,即H2在△ ABC的外接圆上.同理可证,H1、H3也在△ ABC的外接圆上.∴ A、B、C、H1、H2、H3六点共圆.相关资源加到收藏夹添加相关资源托勒密定理的数形转换功能山东临沂市四中姜开传临沂市第一技校刘久松圆内接四边形两组对边乘积的和等于其对角线的乘积,即在四边形ABCD 中,有AB·CD+AD·BC=AC·BD,这就是著名的托勒密定理.本刊1996 年第 2 期给出了它的几种证法,作为续篇,本文就其数形转换功能举例说明如下:1 “形”转换为“数”对于某些几何问题,特别是圆内接多边形问题,如果能根据题设中隐含的数量关系,利用托勒密定理可将“形”转换为“数”,从而达到用代数运算来代替几何推理的目的.例 1 已知正七边形A1A2⋯A7 ,(第21 届全俄数学奥林匹克竞赛题)对于这道竞赛题,原证较繁,但通过深挖隐含条件,利用托勒密定理可改变整个解题局面,使证题步骤简缩到最少.如图1,连A1A5、A3A5,则A1A5=A1A4、A3A5=A1A3.在四边形A1A3A4A5 中,由托勒密定理,得A3A4·A1A5+A4A5·A1A3=A1A4·A3A5,即A1A2·A1A4+A1A2·A1A3=A1A3·A1A4,两边同除以A1A2·A1A3·A1A4 即得结论式.例2 如图2,A、B、C、D四点在同一圆周上,且BC=CD=4,AE=6,线段BE和DE的长都是整数,则BD的长等于多少?(1988 年全国初中数学联赛题)此题若用其它方法解,往往使人一筹莫展.若运用托勒密定理,可使问题化难为易.由△ CDE∽△ BAE和△ CBE∽△ DAE,得由托勒密定理,得BD(AE+CE)=4(AB+AD),亦即CE(AE+CE)=16.设CE=x,整理上式,得x +6x-16=0.解得x=2(负值已舍),故BE·DE=CE·AE=12.∵BD<BC+CD=8,例 3 一个内接于圆的六边形,其五个边的边长都为81,AB 是它的第六边,其长为31,求从B出发的三条对角线长的和.(第九届美国数学邀请赛试题)原解答过程冗长.若通过托勒密定理的桥梁作用,把“形”转换为“数”,可使问题化繁为简.如图3,设BD=a,BE=b,BF=c,连AC、CE、AE,则CE=AE=BD=a,AC=BF=c.在四边形BCDE中,由托勒密定理,得81b+812=a2①同理81b+31· 81=ac ②31a+81a=bc ③解①、③、③组成的方程组,得a=135,b=144,c=105故 a +b+c=384.2 “数”转换为“形”对于某些代数问题,若结构与托勒密定理相似,通过构造圆内接四边形,可把“数”转换为“形”,然后利用“形”的性质,使问题得到解决.这种解法构思巧妙,方法独特,富于创新,出奇制胜.例 4 解方程若按常规方法解这个无理方程,过程繁冗.若由方程的结构特征联想到托勒密定理,则构造直径AC=x(x≥11) 的圆及圆内接四边形ABCD,使BC=2,CD=11,如图4 ,于是由托勒密定理,得经检验 x=14 是原方程的根.求证: a 2+ b 2=1.易知 0≤a 、b ≤1 且 a 、b 不全为零.当 a 、b 之一为零时,结论显然成立. 当 a 、b 全不为零时,由已知等式联想到托勒密定理,作直径 AC =1 的圆及圆内接四与已知等式比较,得 BD = 1,即 BD 也为圆的直径,故 a 2+b 2=1 例 6 设 a >c ,b >c ,c >0,此题若用常规方法证明也不轻松.下面利用托勒密定理给出它的一个巧证.这道名题已有多种证法, 再给出一各几何证法.而且被视为用三角换无法解代数问题的典范.在△ BCD 中,由余弦定理,得由托勒密定理,得巧用托勒密定理证题河北晋州市数学论文研究协会张东海王素改在解证某些数学题时,如能巧用托勒密定理,可使解证过程简洁清新,兹举例说明.托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.一、构造“圆”,运用定理【例1】设a,b,x,y 是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证作直径AB=1的圆,在AB的两侧任作Rt△ACB和Rt△ ADB,使AC=a,BC=b,BD=x,AD=y.(图1)由勾股定理知a,b,x,y 满足条件.根据托勒密定理,有AC·BD+BC·AD=AB·CD.∵ CD≤1,∴ ax+by≤1.二、利用无形圆,运用定理【例2】等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.已知:梯形ABCD中,AD=BC,AB∥CD.求证:BD2=BC2+AB·CD.证∵等腰梯形内接于圆,由托勒密定理,有AC·BD=AD·BC+AB·CD.∵AD=BC,AC=BD,∴BD2=BC2+AB·CD.(图略)【例 3 】已知:边长为 1 的正七边形ABCDEFG中,对角线AD=a,BG=b (a≠ b).求证:(a+b)2(a -b)=ab2.证连结BD,GE,BE,DG,则BD=EG=GB=b,DG=B=E DA=a,DE=AB=AG=.1( 如图2)在四边形ABDG中,由托勒密定理,有AD·BG=AB·DG+BD·AG,即ab=a+ b (1)同理在四边形BDEG中,得BE·DG=D·E BG+BD·EG,即a2=b+b2 (2)将(2) 变形为b=a2-b2 (3)(1) ×(3) ,得ab2=(a +b)(a 2-b2).故ab2=(a +b) 2(a -b) .三、构造圆内接四边形,运用定理例4】在△ ABC中,∠ A的内角平分线AD交外接圆于D.连结BD.求证:AD·BC=BD·(AB+AC).证(如图3)连结DC.由托勒密定理.有AD·BC=AB·CD+AC·BD.又∵∠ 1=∠2,∴ BD=D.C∴AD·BC=AB·CD+AC· BD=BD(A+B AC).即AD·BC=BD· (AB+AC).圆内接四边形的面积公式黑龙江绥化五中任天民设圆内接四边形ABCD中各边为a,b,c,d.连结BD.由∠ A+∠ C=180°,可以推出sinA=sinC ,cosA=-cosC.并且S 四边形ABCD=S△ABD+S△ BCD所以这样我们得出了圆内接四边形面积的计算公式.在上面的公式中,如果设某一边为零,(不仿设d=0)此时四边形变成三角形,该公式恰是计算三角形面积的海伦公式.圆内接四边形面积公式的得出是受三角形面积公式的启发,通过联想探索出来的,而且两者在形式上又是那么的相近.这种现象在数学中不胜枚举,如果同学们都能从特殊规律去探索一般规律,再从一般规律去认识特殊规律.那么对数学能力的培养将大有裨益.四条边定长四边形面积的最大值上海市育群中学李甲鼎四条边为定长的四边形不具稳定性,但在某种特定的位置下,它能内接于圆,成为圆内接四边形.并且此时达到变化过程中面积最大值.下文证明这个事实.已知:四边形ABCD中:AB=a,BC=b,CD=c,DA=d求证:四边形ABCD中有唯一四边形能内接于圆,且此时面积达到最大值.证明:(1) 先证四边形四边定长,有唯一的四边形内接于圆,设∠ ABC=α,∠ADC=β,AC=x.令α+β =π,即cosα+cosβ=0x 的解唯一确定,代入(1)(2) 后cosα、cosβ也随之唯一确,在α,β∈(0 ,π )的条件下α、β也同时唯一确定.∴四边形四边定长,对角互补,四边形是唯一的.即所得到的四边形为圆内接四边形.(2) 当四边定长的四边形内接于圆时,此四边形面积最大.∵四边形ABCD的面积由余弦定理得a2+b2-2abcosα=x2=c2+d2-2cdcosβ显然当α+β =π时( 即为圆内接四边形时 )S 2达到最大值,即 S 最大.一个几何定理的应用江苏省徐州矿务局庞庄职校 张怀林定理:如图 1,在圆接四边形 ABCD 中弦 AD 平分∠ BAC ,则 2ADcos α=AB + AC .证明 连接 BD 、DC 、BC ,设已知圆半径为 R ,则由正弦定理有:BD =DC = 2Rsin α, BC =2Rsin2 α.由托勒密定理有AB ·CD+AC · BD=AD ·DC . ∴(AB+AC) · 2Rsin α=AD ·2Rsin2 α. 则 2AD ·cos α=AB +AC . 下面举例说明它的应用.例 1 如图 2,已知锐角△ ABC 的∠A 平分线交 BC 于 L ,交外接圆于 N ,过 L 分别作 LK ⊥AB , LM ⊥AC ,垂足分别为 K 、M .求证:四边形 AKNM 的面积 等于△ ABC 的面积.(第 28 届 IMO )证明 由已知得 ∠BAN= ∠CAN ,由定理有2ANcos α=AB+AC,=AN·AL·cosα· sinα =AN ·AK ·sinα=AN·AM·sinα=2S △AKN=2S △AMN.∴S△ABC=S 四边形AKNM.(第21 届全苏奥数)证明作正七边形外接圆,如图 3 所示.由定理有2c · cos α=b+c ,又在等腰△ A1A2A3中有2a·cosα=b.例 3 在△ABC 中,∠C=3∠A ,a =27,c =48,则 b 的值是 ____ .(第 36 届 AHSME 试题 )解 如图 4 .作△ ABC 的外接圆,在 取三等分点由已知得: ∠ACD=∠DCE=∠ECB=∠A ,CD=AB=48 , 由定理有2CE · cosA=CB+CD ① 2CD ·cosA =CE+AC ②又 2CB ·cosA=CE ③由②、③得: b=AC=CE ·(CD-CB)/CB=35 .托勒密定理及其应用 河北省晋州市数学论文研究协会刘同林托勒密定理:圆内接四边形中,两条对角线的乘积 (两对角线所包矩形的面 积 )等于两组对边乘积之和 (一组对边所包矩形的面积与另一组对边所包矩形的 面积之和 ).已知:圆内接四边形 ABCD , 求证: AC ·BD =AB ·CD +AD ·BC .D 、E ,连 CD 、CE .证明:如图1,过C 作CP 交BD 于P,使∠1=∠2,又∠3=∠4,∴△ACD ∽△ BCP .又∠ ACB= ∠DCP ,∠ 5=∠6,∴△ ACB ∽△ DCP .①+②得AC(BP +DP)=AB ·CD+AD·BC.即AC·BD=AB ·CD+AD·BC.这就是著名的托勒密定理,在通用教材中习题的面目出现,不被重视.笔者认为,既然是定理就可作为推理论证的依据.有些问题若根据它来论证,显然格外简洁清新.兹分类说明如下,以供探究.、直接应用托勒密定理例1 如图2,P是正△ABC 外接圆的劣弧上任一点(不与B、C重合),求证:PA=PB +PC .分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA·BC=PB ·AC+PC ·AB,∵AB=BC=AC .∴PA=PB+PC .二、完善图形借助托勒密定理例 2 证明“勾股定理”:在Rt△ABC 中,∠ B=90°,求证:AC2=AB2+BC2证明:如图3,作以Rt△ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.由托勒密定理,有AC·BD=AB ·CD+AD·BC.① 又∵ ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD .② 把②代人①,得AC2=AB 2+BC2.例 3 如图4,在△ ABC 中,∠ A 的平分证:AD·BC=BD(AB +AC).证明:连结CD,依托勒密定理,有AD ∵∠ 1=∠2,∴ BD=CD .故AD·BC=AB ·BD+AC·BD= BD(AB +AC).三、利用“无形圆”借助托勒密定理例 4 等腰梯形一条对角线的平方等于一腰的平方加上两底之积.线交外接∠圆于D,连结BD ,求BC=AB·CD+AC·BD.如图5,ABCD 中,AB∥CD,AD=BC ,求证:BD2=BC2+AB·CD.证明:∵等腰梯形内接于圆,依托密定理,则有AC·BD=AD ·BC+AB·CD.又∵ AD=BC ,AC=BD ,∴BD2=BC 2+AB·CD.四、构造图形借助托勒密定理例 5 若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by ≤1 .证明:如图6,作直径AB=1 的圆,在AB 两边任作Rt△ACB 和Rt△ADB ,使AC=a,BC=b ,BD =x,AD=y.由勾股定理知a、b、x、y 是满足题设条件的.据托勒密定理,有AC·BD +BC·AD=AB ·CD.∵CD≤AB =1,∴ax+by≤1.五、巧变原式妙构图形,借助托勒密定理例 6 已知a、b、c 是△ ABC 的三边,且 a =b(b +c),求证:∠ A=2∠ B.分析:将 a =b(b +c)变形为a·a=b ·b +bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c.证明:如图7,作△ ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D,连结BD、DC、DA .∵AD=BC ,∴∠ ABD= ∠BAC .又∵∠ BDA= ∠ ACB(对同弧),∴∠ 1=∠2.依托勒密定理,有BC·AD=AB ·CD+BD·AC.①而已知a2=b(b +c),即a·a=b·c+b2.②∴∠ BAC=2 ∠ABC.六、巧变形妙引线借肋托勒密定理例7 在△ABC 中,已知∠ A∶∠ B∶∠ C=1 ∶2∶4,析证:将结论变形为AC·BC+AB·BC=AB ·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图8,作△ ABC 的外接圆,作弦BD=BC ,边结AD、CD.在圆内接四边形ADBC 中,由托勒密定理,有AC ·BD+BC ·AD=AB ·CD 易证AB=AD ,CD=AC,∴AC·BC+BC·AB=AB ·AC,关于圆内接四边形的若干共点性质浙江绍兴县鲁迅中学范培养设四边形ABCD 内接于圆O,其边AB 与DC 的延长线交于P,AD 与BC 的延长线交于Q,由P 作圆的两切线PM 、PN,切点分别为M、N;由Q 作圆的两切线QE、QF,切点分别为E、F(如图1).则有以下一些共点性质:性质 1 AC 、BD、EF 三直线共点.证明:如图1,设AC 交EF 于K1,则K1分EF 所成的比为设BD 交EF 于K2,同理可得K2 分EF 所成的比为由(5)、(6)可得(1)=(2),故K1、K2分EF 所成的比相等.∴K1、K2 重合,从而AC、BD、EF 三直线共点.类似地AC、BD、MN 三直线共点,因此有以下推论AC、BD 、EF、MN 四直线共点.性质 2 AB 、DC 、EF 三直线共点于P.(此性质等同于1997 年中国数学奥林匹克第二试第四题)这里用上述证明性质 1 的方法证之.证明:如图2.设DC 与EF 的延长线交于P1,则P1分EF 所成的比为设AB 与EF 的延长线交于P2,则P2分EF 所成的比为由(5)、(6)可得(7)=(8),故P1、P2分EF 所成的比相等.∴P1、P2 重合,从而AB、DC 、EF 三直线共点于P.推论AD、BC 、NM 三直线共点于Q.性质 3 EM 、NF、PQ 三直线共点.证明:如图3,设EM 的延长线交PQ 于G1,妨上证法,G1分PQ 所成的比设NF 的延长线交PQ 于G2,则G2 分PQ 所成的比为(这里E、F、P 三点共线及N、M、Q 三点共线在性质 2 及推论中已证).由△ PME ∽△ PFM 得由(11)、(12)及QE=QF 、PN=PM可得(9)=(10) ,故G1、G2分PQ 所成的比相等.∴G1、G2 重合,从而EM 、NF、PQ 三直线共点.性质 4 如果直线EN 和MF 相交,那么交点在直线PQ 上,即EN 、MF、PQ 三直线共点.证明从略,妨性质 3 的证法可得.性质 5 EM 、NF、AC 三直线共点.证明:如图4,类似于性质 1 的证明,设EM 与AC 的延长线交于G3,则G3分AC 所成的比为设NF 与AC 的延长线交于G4,则G4 分AC 所成的比为由(15)、(18)、(19)可得(13)=(14) ,故G3、G4分AC 所成的比相等.∴G3、G4 重合,从而EM、NF、AC 三直线共点.推论EM、NF 、AC、PQ 四直线共点.限于篇幅,仅列以上五条共点性质.有兴趣的读者不妨再探索其它共点性质例 3 在边长为 a 的正七边形ABCDEFG 中,两条不相等的对角线长分别为t,m .证明如图4,连结AD 、CE,令AE=t,AC =m,在圆内接四边形ACDE 中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma .托勒密定理及其应用河北省晋州市数学论文研究协会康美娈彭立欣托勒密定理圆内接四边形的两条对角线的乘积(两条对角线所包矩形的面积),等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形面积之和).证明如图1,过 C 作CP 使∠1=∠2,又∠3=∠4,∴△ ACD ∽△ BCP .∴AC·BP=AD ·BC ①又∠ ACB= ∠DCP ,∠ 5=∠6,∴AC·DP=AB ·CD.②①+②得AC(BP+PD)=AD ·BC+AB ·CD.故AC·BD=AD ·BC+AB ·CD.托勒密定理在教材中仅以习题的形式出现,若以此定理为根据,可使许多问题解证过程别具一格.例 1 已知P 是正△ ABC 的外接圆劣弧上任意一点.求证:PA=BP+PC.证明如图2,ABPC 是圆内接四边形,根据托勒密定理,有PA·BC=PB·AC+PC ·AB.∵AB=BC=AC, ∴PA=PB+PC.例 2 证明等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.证明如图 3 ,设在梯形ABCD 中,AD=BC ,AB∥CD .∵等腰梯形内接于圆,∴AC·BD=AD ·BC+AB ·CD.又AD=BC,AC=BD,∴BD2=BC 2+AB·CD.例 3 在边长为 a 的正七边形ABCDEFG 中,两条不相等的对角线长分别为t,m.证明如图4,连结AD 、CE,令AE=t,AC =m,在圆内接四边形ACDE中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma .例 4 已知a、b、x、y 是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明作直径AB=1 的圆,在AB 两侧作Rt△ACB 和Rt △ADB ,使AC=a,BC=b ,BD=x,DA=y(如图5).依勾股定理知a、b、x、y 是满足题设条件的.依托勒密定理有AC·BD+BC·AD=AB·CD.又∵ CD≤AB=1 ,∴ ax+by ≤1.例 5 △ABC 的三个内角A、B、 C 的对边分别为a、b、c,且a2=b(b +c).求证:A=2B .分析将a2=b(b +c)变形为a·a=b·b+b·c,可联想到托勒密定理,进而构造一个圆内接等腰梯形,使两腰为b,两对角线为a,一底边为c.证明如图 6 ,作△ ABC 的外接圆.以A为圆心,以BC 为半径画弧交圆于D,连结BD、DA、DC .则BD=AC=b .据托勒密定理有BC·AD=AB ·CD+BD·AC.①又已知a2=b(b+c),即a·a=b ·b+b·c.② 比较①、②,有CD=b=BD .于是∠ BAC=2 ∠ABC ,即A=2B.。
四点共圆例题及答案

四点共圆的应用例1 如图1,已知P 为⊙O 外一点,PA 切⊙O 于A ,PB 切⊙O 于B ,OP 交AB 于E . 求证:∠APC =∠BPD .例2 如图2,从⊙O 外一点P 引切线PA 、PB 和割线PDC ,从A 点作弦AE 平行于DC ,连结BE 交DC 于F ,求证:FC =FD .例3 如图3,在△ABC 中,AB=AC ,AD ⊥BC ,∠B 的两条三等分线交AD 于E 、G ,交AC 于F 、H .求证:EH ∥GC .PP例4 如图4,⊿ABC 为等边三角形,D 、E 分别为BC 、AC 边上的点,且BD=31BC,CE=31AC,AD 与BE 相交于P 点。
求证:CP ⊥AD例5 如图5,AB 为半圆直径,P 为半圆上一点,PC ⊥AB 于C ,以AC 为直径的圆交PA 于D ,以BC 为直径的圆交PB 于E ,求证:DE 是这两圆的公切线.例6 AB 、CD 为⊙O 中两条平行的弦,过B 点的切线交CD 的延长线于G ,弦PA 、PB 分别交CD于E 、F .求证:FGFDCF EF例7 ABCD 为圆内接四边形,一组对边AB 和DC 延长交于P 点,另一组对边AD 和BC 延长交于Q点,从P 、Q 引这圆的两条切线,切点分别是E 、F ,(如图 7)求证:PQ 2=QF 2+PE 2.例8 如图8,△ABC 的高AD 的延长线交外接圆于H ,以AD为直径作圆和AB 、AC 分别交于E 、F 点,EF 交 AD 于 G ,若 AG=16cm ,AH=25cm ,求 AD 的长.例9 如图9,D 为△ABC 外接圆上任意一点,E 、F 、G 为D 点到三边垂线的垂足,求证:E 、F 、G 三点在一条直线上.例10 如图10,H 为△ABC 的垂心,H 1、H 2、 H 3为H 点关于各边的对称点,求证:A 、B 、 C 、H 1、H 2、H 3六点共圆.11、已知PQRS 是圆内接四边形,∠PSR =90°,过点2BQ 作PR 、PS 的垂线,垂足分别为点H 、K.求证:HK 平分QS.12.AB 为⊙O 的直径,点C 在⊙O 上且OC ⊥AB,P 为⊙O 上一点,位于点B 、C 之间,直线CP 与AB 的延长线交于点Q,过Q 作直线与AB 垂直,交直线AP 于点R. 求证:BQ =QR.13.如图10,在△ABC 中,AD ⊥BC,BE ⊥CA,AD 与BE 交于点H,P 为 边AB 的中点,过点C 作CQ ⊥PH,垂足为Q.求证:2PE =PH ·PQ.R。
四点共圆(专项练习)

四点共圆(专项练习)一、单选题1.如图①,若BC 是Rt △ABC 和Rt △DBC 的公共斜边,则A 、B 、C 、D 在以BC 为直径的圆上,则叫它们“四点共圆”.如图①,△ABC 的三条高AD 、BE 、CF 相交于点H ,则图①中“四点共圆”的组数为( )A .2B .3C .4D .62.如图,已知AB=AC=AD ,①CAD=20°,则①CBD 的度数是( )A .10°B .15°C .20°D .25°3.如图,圆上有A 、B 、C 、D 四点,其中80BAD ∠=︒,若弧ABC 、弧ADC 的长度分别为7π、11π,则弧BAD 的长度为( )A .4πB .8πC .10πD .15π4.如图,四边形ABCD 内接于O ,AB CD =,A 为BD 中点,60BDC ∠=︒,则ADB ∠等于( )A .40︒B .50︒C .60︒D .70︒5.如图,在ABC ∆中,90BAC ∠=︒,AB =AC =5,点D 在AC 上,且2AD =,点E 是AB 上的动点,连结DE ,点F ,G 分别是BC ,DE 的中点,连接AG ,FG ,当AG =FG 时,线段DE 长为( )A 13B 52C 41D .46.如图,在四边形ABCD 中,AC 、BD 为对角线,点M 、E 、N 、F 分别为AD 、AB 、BC 、CD 边的中点,下列说法:①当AC BD =时,M 、E 、N 、F 四点共圆.①当AC BD ⊥时,M 、E 、N 、F 四点共圆.①当AC BD =且AC BD ⊥时,M 、E 、N 、F 四点共圆.其中正确的是( )A .①①B .①①C .①①D .①①①7.锐角ABC 的三条高AD 、BE 、CF 交于H ,在A 、B 、C 、D 、E 、F 、H 七个点中.能组成四点共圆的组数是( )A .4组B .5组C .6组D .7组二、填空题 8.如图,正五边形ABCDE 内接于①O ,则①ADE 的度数是 _____.9.如图,四边形ABCD 是①O 的内接四边形,若①O 半径为4,且①C =2①A ,则BD 的长为__.10.如图,将ABC 绕点A 顺时针旋转25°得到AEF ,EF 交BC 于点N ,连接AN ,若57C ∠=︒,则 ANB ∠=__________.11.如图,AB 是Rt ABC 和Rt ABD △的公共斜边,AC=BC ,32BAD ∠=,E 是AB 的中点,联结DE 、CE 、CD ,那么ECD ∠=___________________.三、解答题12.如图所示,AB AC AD ==,60BAC ∠=︒,求BDC ∠.13.如图所示,正方形ABCD中,BD为对角线,点E为BD上一点,过E作EF AE⊥,=.交DC于F,求证:AE FE∠=∠.14.如图,四边形ABED是圆的内接四边形,延长AD、BE相交于点C,已知C EDC=;(1)求证:AB AC(2)若AB是四边形ABED外接圆的直径,求证:BE ED=.15.如图,AB=AC,AE=AF,①BAC=①EAF=90°,BE、CF交于M,连AM.①求证:BE=CF;①求证:BE①CF;①求①AMC的度数.16.如图,①ABC中,BE①AC,CF①AB,垂足分别为E、F,M为BC的中点.(1)求证:ME=MF.(2)若①A=50°,求①FME的度数.17.如图所示,在平行四边形ABCD中,点E为AB,BC的垂直平分线的交点,若∠=︒,求AECD60∠.18.定义:有一个角是其对角一半的圆的内接四边形叫做圆美四边形,其中这个角叫做美角.已知四边形ABCD是圆美四边形.(1)求美角A∠的度数;(2)如图1,若O 的半径为5,求BD 的长;(3)如图2,若CA 平分BCD ∠,求证:BC CD AC +=.19.如图1,在正方形ABCD 中,点F 在边BC 上,过点F 作EF BC ⊥,且()FE FC CE CB =<,连接CE 、AE ,点G 是AE 的中点,连接FG .(1)用等式表示线段BF 与FG 的数量关系:______;(2)将图1中的CEF △绕点C 按逆时针旋转,使CEF △的顶点F 恰好在正方形ABCD 的对角线AC 上,点G 仍是AE 的中点,连接FG 、DF .①在图2中,依据题意补全图形;①用等式表示线段DF 与FG 的数量关系并证明.20.如图所示,在①ABC 中,AB=AC ,任意延长CA 到P ,再延长AB 到Q ,使AP=BQ , 求证:①ABC 的外心O 与点A 、P 、Q 四点共圆.21.如图,已知A,B,C,D四点共圆,且AC=BC.求证:DC平分①BDE.22.如图,已知矩形ABCD.求证:A、B、C、D四点共圆.23.在正方形ABCD中,M是BC边上一点,点P在射线AM上,将线段AP绕点A顺时针旋转90︒得到线段AQ,连接BP,DQ.=;(1)如图1,求证:BP DQ(2)如图2,若点P,B,D三点共线,求证:A,Q,P,D四点共圆;AD ,求BP的长.(3)若点P,Q,C三点共线,且324.如图,在Rt ABC中,①BAC=90°,①ABC=40°,将ABC绕A点顺时针旋转得到ADE,使D点落在BC边上.(1)求①BAD的度数;(2)求证:A、D、B、E四点共圆.25.如图1,ABC中,AC=BC=4,①ACB=90°,过点C任作一条直线CD,将线段BC沿直线CD翻折得线段CE,直线AE交直线CD于点F.直线BE交直线CD于G点.(1)小智同学通过思考推得当点E在AB上方时,①AEB的角度是不变的,请按小智的思路帮助小智完成以下推理过程:①AC=BC=EC,①A、B、E三点在以C为圆心以AC为半径的圆上,①①AEB=①ACB,(填写数量关系)①①AEB=°.(2)如图2,连接BF,求证A、B、F、C四点共圆;(3)线段AE最大值为,若取BC的中点M,则线段MF的最小值为.26.阅读以下材料,并完成相应的任务:西姆松定理是一个平面几何定理,其表述为:过三角形外接圆上异于三角形顶点的任意一点作三边或其延长线的垂线,则三垂足共线(此线常称为西姆松线).数学兴趣小组的同学们尝试证明该定理.如图1,已知ABC内接于①O,点P在①O上(不与点A、B、C重合),过点P分别作AB,BC,AC的垂线,垂足分别为D,E,F求证:点D,E,F在同一条直线上以下是他们的证明过程:如图1,连接PB ,PC ,DE ,EF ,取PC 的中点Q ,连接QE ,QF , 则12PQ CQ PC EQ FQ ====(依据1), ①E ,F ,P ,C 四点共圆.①180FCP FEP ∠+∠=︒(依据2).又①180ACP ABP ∠+∠=︒,①FEP ABP ∠=∠.①90BDP BEP ∠=∠=︒,①B ,D ,P ,E 四点共圆.①DBP DEP ∠=∠(依据3).①180ABP DBP ∠+∠=︒,①180FEP DEP ∠+∠=︒(依据4).①点D ,E ,F 在同一条直线上.任务:(1)填空:①依据1指的的是中点的定义及______;①依据2指的是______;①依据3指的是______;①依据4指的是______.(2)善于思考的小英发现当点P 是BC 的中点时,BD CF =.请你利用图2证明该结论的正确性.27.[发现]如图①ACB=①ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)[思考]如图①,如果①ACB=①ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A,B,C三点的圆上吗?我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在圆O外,要么在圆O内,以下该同学的想法说明了点D不在圆O外.请结合图①证明点D也不在①O内.[结论]综上可得结论:如图①,如果①ACB=①ADB=a(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:点A、B、C、D四点共圆.[应用]利用上述结论解决问题:如图①,已知△ABC中,①C=90°,将△ACB绕点A顺时针旋转一个角度得△ADE,连接BE CD,延长CD交BE于点F,(1)求证:点B、C、A、F四点共圆;(2)求证:BF=EF.图①28.定义:如果同一平面内的四个点在同一个圆上,那么我们把这称为四点共圆.(1)下列几何图形的四个顶点构成四点共圆的有.(填序号)①平行四边形;①菱形;①矩形;①正方形;①等腰梯形.(2)已知①ABC中,①A=40°,如图1,平面上一点D,使得A、B、C、D四点共圆,试求①BDC的度数.(3)若△ABC的外接圆为⊙O,半径为r,平面上有两点E、F,分别与△ABC的三个顶点构成四点共圆(E在AB的左侧,F点在AC的右侧),如图2.①试判断∠E+∠F﹣∠BAC 的值是否为定值?如果是,请求出这个值;如果不是,请说明理由;②若BC弦的长度与⊙O的半径r2:1,并且边AB经过圆心O,如图3,试求五边形AEBCF的最大面积(用含r的式子表示).参考答案1.D【分析】根据两个直角三角形公共斜边时,四个顶点共圆,结合图形求解可得. 解:如图,以AH 为斜边的两个直角三角形,四个顶点共圆(A 、F 、H 、E ), 以BH 为斜边的两个直角三角形,四个顶点共圆(B 、F 、H 、D ), 以CH 为斜边的两个直角三角形,四个顶点共圆(C 、D 、H 、E ), 以AB 为斜边的两个直角三角形,四个顶点共圆(A 、E 、D 、B ), 以BC 为斜边的两个直角三角形,四个顶点共圆(B 、F 、E 、C ), 以AC 为斜边的两个直角三角形,四个顶点共圆(A 、F 、D 、C ), 共6组. 故选D .【点拨】本题考查四点共圆的判断方法.解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆.2.A解:如图,AB=AC=AD ①20CAD ∠=︒11201022CBD CAD ∴∠=∠=⨯︒=︒,故选A . 3.C 【分析】先求出圆的周长,再根据圆内接四边形的性质可得100C ∠=︒,然后根据圆周角定理可得弧BAD所对圆心角的度数,最后根据弧长的定义即可得.解:弧ABC、弧ADC的长度分别为7π、11π∴圆的周长为71118πππ+=80BAD∠=︒100C∴∠=︒(圆内接四边形的对角互补)∴弧BAD所对圆心角的度数为2200C∠=︒则弧BAD的长度为200 1810360ππ⨯=故选:C.【点拨】本题考查了圆周角定理、弧长的定义、圆内接四边形的性质,熟记圆的相关定理与性质是解题关键.4.A【分析】根据AB CD=,A为BD中点求出①CBD=①ADB=①ABD,再根据圆内接四边形的性质得到①ABC+①ADC=180°,即可求出答案.解:①A为BD中点,①AB AD=,①①ADB=①ABD,AB=AD,①AB CD=,①①CBD=①ADB=①ABD,①四边形ABCD内接于O,①①ABC+①ADC=180°,①3①ADB+60°=180°,①ADB∠=40°,故选:A.【点拨】此题考查圆周角定理:在同圆中等弧所对的圆周角相等、相等的弦所对的圆周角相等,圆内接四边形的性质:对角互补.5.A【分析】连接DF,EF,过点F作FN①AC,FM①AB,结合直角三角形斜边中线等于斜边的一半求得点A,D,F,E四点共圆,①DFE=90°,然后根据勾股定理及正方形的判定和性质求得AE 的长度,从而求解.解:连接DF ,EF ,过点F 作FN ①AC ,FM ①AB①在ABC ∆中,90BAC ∠=︒,点G 是DE 的中点, ①AG =DG =EG 又①AG =FG①点A ,D ,F ,E 四点共圆,且DE 是圆的直径 ①①DFE =90°①在Rt ①ABC 中,AB =AC =5,点F 是BC 的中点, ①CF =BF =1522BC =FN =FM =52又①FN ①AC ,FM ①AB ,90BAC ∠=︒ ①四边形NAMF 是正方形 ①AN =AM =FN =52又①90NFD DFM ∠+∠=︒,90DFM MFE ∠+∠=︒ ①NFD MFE ∠=∠ ①①NFD ①①MFE ①ME =DN =AN -AD =12①AE =AM +ME =3①在Rt ①DAE 中,DE 2213AD AE +故选:A .【点拨】本题考查直径所对的圆周角是90°,四点共圆及正方形的判定和性质和用勾股定理解直角三角形,掌握相关性质定理正确推理计算是解题关键.6.C 【分析】连接EM、MF、FN、NE,连接EF、MN,交于点O,利用三角形中位线定理可证到四边形ENFM是平行四边形;然后根据条件判定四边形ENFM的形状,就可知道M、E、N、F四点是否共圆.解:连接EM、MF、FN、NE,连接EF、MN,交于点O,如图所示.①点M、E、N、F分别为AD、AB、BC、CD边的中点,①EM①BD①NF,EN①AC①MF,EM=NF=12BD,EN=MF=12AC.①四边形ENFM是平行四边形.①当AC=BD时,则有EM=EN,所以平行四边形ENFM是菱形.而菱形的四个顶点不一定共圆,故①不一定正确.①当AC①BD时,由EM①BD,EN①AC可得:EM①EN,即①MEN=90°.所以平行四边形ENFM是矩形.则有OE=ON=OF=OM.所以M、E、N、F四点共圆,故①正确.①当AC=BD且AC①BD时,同理可得:四边形ENFM是正方形.则有OE=ON=OF=OM所以M、E、N、F四点共圆,故①正确.故选C.【点拨】本题考查了四点共圆、三角形的中位线定理、平行四边形的判定与性质、矩形的判定与性质、菱形的判定与性质、正方形的判定与性质等知识.熟练掌握平行四边形、矩形、菱形、正方形的判定定理是解题关键.7.C【分析】根据两个直角三角形公共斜边时,四个顶点共圆,完整选择.解:如图,以AH为斜边的两个直角三角形,四个顶点共圆(A、F、H、E),以BH为斜边的两个直角三角形,四个顶点共圆(B、F、H、D),以CH为斜边的两个直角三角形,四个顶点共圆(C、D、H、E),以AB为斜边的两个直角三角形,四个顶点共圆(A、E、D、B),以BC为斜边的两个直角三角形,四个顶点共圆(B、F、E、C),以AC为斜边的两个直角三角形,四个顶点共圆(A、F、D、C),共6组.故选C.【点拨】本题考查四点共圆的判断方法.解题关键是明确有公共斜边的两个直角三角形的四个顶点共圆.8.36°##36度【分析】先利用正多边形的性质求出①AED度数、再利用等腰三角形的性质以及三角形内角和定理求解即可.解:①正五边形ABCDE内接于①O,①AE=ED,①AED=()5-21805⨯︒=108°,①①ADE =①EAD =12(180°-108°)=36°,故答案为:36°.【点拨】本题考查正多边形与圆,等腰三角形的性质,三角形内角和定理等知识,解题的关键是记住正多边形的内角和公式.9.3【分析】连接OB ,OD ,利用内接四边形的性质得出①A=60°,进而得出①BOD=120°,利用含30°的直角三角形的性质解答即可.解:连接OB ,OD ,过O 作OE①BD ,①四边形ABCD 是①O 的内接四边形,①C=2①A , ①①C+①A=3①A=180°, 解得:①A=60°, ①①BOD=120°, 在Rt △BEO 中,OB=4, 3 3 故答案为:3【点拨】此题考查内接四边形的性质,关键是利用内接四边形的性质得出①A=60°. 10.102.5° 【分析】先根据旋转的性质得到25CAF ∠=︒,25CNF ENB ∠=∠=︒,得到点A 、N 、F 、C 共圆,再利用77.5ANC AFC ∠=∠=︒,根据平角的性质即可得到答案;解:如图,AF 与CB 相交于点O ,连接CF ,根据旋转的性质得到:AC=AF ,57F C ∠=∠=︒,25CAF ∠=︒,25CNF ENB ∠=∠=︒, ①点A 、N 、F 、C 共圆, ①1802577.52ACF AFC ︒-︒∠=∠==︒, 又①点A 、N 、F 、C 共圆, ①77.5ANC AFC ∠=∠=︒,①18077.5102.5ANB ∠=︒-︒=︒(平角的性质), 故答案为:102.5°【点拨】本题主要考查了旋转的性质、平角的性质、点共圆的判定,掌握平移的性质是解题的关键;11.13 【分析】先证明A 、C 、B 、D 四点共圆,得到①DCB 与①BAD 的是同弧所对的圆周角的关系,得到①DCB 的度数,再证①ECB=45°,得出结论.解:①AB 是Rt①ABC 和Rt①ABD 的公共斜边,E 是AB 中点,①AE=EB=EC=ED ,①A 、C 、B 、D 在以E 为圆心的圆上, ①①BAD=32°, ①①DCB=①BAD=32°,又①AC=BC ,E 是Rt①ABC 的中点, ①①ECB=45°,①①ECD=①ECB -①DCB=13°. 故答案为:13.【点拨】本题考查直角三角形的性质、等腰三角形性质、圆周角定理和四点共圆问题,综合性较强.12.30°. 【分析】由AB=AC=AD ,可得B ,C ,D 在以A 为圆心,AB 为半径的圆上,然后由圆周角定理,证得①CAD=2①CBD ,①BAC=2①BDC ,继而可得①CAD=2①BAC .解:①AB=AC=AD ,①B ,C ,D 在以A 为圆心,AB 为半径的圆上, ①①CAD=2①CBD ,①BAC=2①BDC , ①①CBD=2①BDC ,①BAC=60°, ①①CAD=2①BAC=120°. ①①BDC=30°.【点拨】此题考查了圆周角定理.注意得到B ,C ,D 在以A 为圆心,AB 为半径的圆上是解此题的关键.13.见分析. 【分析】先根据正方形的性质可得①CDA=90°,再根据EF AE ⊥得到①AEF=90°,从而得证A ,E ,F ,D 共圆,45EAF BDC ∠=∠=︒,继而得出AE=FE.解:在正方形ABCD 中,90ADC ∠=︒,①BDC=45°①EF AE ⊥ ①90AEF ∠=︒ ①①ADC+①AEF=180° ①A ,E ,F ,D 共圆, ①45EAF BDC ∠=∠=︒, ①45EAF EFA ∠=∠=︒ ①AE FE =.【点拨】本题考查了正方形的性质,四点共圆,以及等腰三角形的判定,熟练掌握相关知识是解题的关键14.(1)见分析;(2)见分析. 【分析】(1)根据圆内接四边形对角互补证得①B =①C ,从而利用等角对等边证得AB =AC ; (2)连接AE ,将证明弧相等转化为弧相对的圆周角相等来实现. 解:(1)①四边形ABED 是圆内接四边形,①①B+①ADE=180° 又①①EDC+①ADE=180° ①①EDC=①B 又①①EDC=①C①①B=①C①AB=AC(2)连接AE①AB是圆的直径①①AEB=90°又①AB=AC①AE平分①BAC①①BAE=①EAD①BE DE【点拨】本题考查圆内接四边形及圆的有关性质,解题的关键是知道圆内接四边形及圆的有关性质.15.(1)见分析;(2)见分析;(3)135°解:试题分析:①证①BEA①①CFA.①①ABE=①ACF,①①CMB=①CAB=90°.①作AG①BE于G,AH①CF于H,证①AGB①①AHC,AG=AH,①AMG=45°,可得①AMC=135°试题解析:(1)①①BAC=①EAF=90°①①BAE=①CAF①AE=AF,AB=AC,①三角形BAE 全等于三角形CAF,① BE=CF(2)①①AEB=①AFC设CF与AE相交于点H 则①MHE = ①AHF①三角形EMH与三角形HAF的内角和都为180°① ①EMF = ①EAF即BE①CF(3)①①ABE=①ACF① A ,B ,C ,M 四点共圆① ①AMC+①ABC=180°①AB=AC ,①BAC=90°,①ABC=45°① ①AMC=180°--①ABC=135°也可以作AG①BE 于G ,AH①CF 于H ,证①AGB①①AHC ,AG =AH ,①AMG =45°,可得①AMC =135.16.(1)证明见分析(2)80°.试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半得到ME=12BC ,MF=12BC ,得到答案;(2)根据四点共圆的判定得到B 、C 、E 、F 四点共圆,根据圆周角定理得到答案. (1)证明:①BE①AC ,CF①AB ,M 为BC 的中点,①ME=12BC ,MF=12BC ,①ME=MF ;(2)解:①CF①AB ,①A=50°,①①ACF=40°,①BE①AC ,CF①AB ,①B 、C 、E 、F 四点共圆,①①FME=2①ACF=80°.【点拨】1.直角三角形斜边上的中线;2.等腰三角形的判定与性质.17.120AEC ∠=︒【分析】由点E 为AB ,BC 的垂直平分线的交点知,EA EB EC ==,所以A ,B ,C 在以E 为圆心,EA 为半径的圆上,由圆的性质知2AEC ABC ∠=∠,再由平行四边形的性质,问题得解.解:连结EB ,①点E 为AB ,BC 的垂直平分线的交点①EA EB EC ==,①A ,B ,C 在以E 为圆心,EA 为半径的圆上,作出辅助圆,由圆的性质知2AEC ABC ∠=∠,又平行四边形ABCD 中,60ABC D ∠=∠=︒①2120AEC ABC ∠=∠=︒【点拨】作辅助圆,可以将直线型问题转化为曲线型问题,为我们解决问题时提供更开阔思路,更简捷的方法.18.(1)60°;(2)53(3)见分析【分析】(1)根据美角的定义可得12A C ∠=∠,然后根据圆内接四边形的性质即可求出结论; (2)连接DO 并延长,交O 与点E ,连接BE ,根据同弧所对的圆周角相等可得①E=①A=60°,然后根据直径所对的圆周角是直角可得①DBE=90°,最后利用锐角三角函数即可求出结论;(3)延长CB 至F ,使BF=DC ,连接AF 、BD ,先证出①ABD 为等边三角形,然后利用SAS 证出①ABF①①ADC ,从而得出AF=AC ,①F=①DCA=60°,再证出①ACF 为等边三角形,利用等边三角形的性质和等量代换即可得出结论.解:(1)根据题意可得:12A C ∠=∠,而①A +①C=180° ①①A=60°(2)连接DO 并延长,交O 与点E ,连接BE①①E=①A=60°①DE 为O 的直径,O 的半径为5,①①DBE=90°,DE=10在Rt①DBE 中,353 (3)延长CB 至F ,使BF=DC ,连接AF 、BD由(1)可知:①BAD=60°,①BCD=2①BAD=120° ①CA 平分BCD ∠,①①BCA=①DCA=12BCD ∠=60° ①①ABD=①DCA=60°①①ADB=180°-①ABD -①BAD=60°①①ABD 为等边三角形①AB=AD根据圆内接四边形的性质可得①ABF=①ADC在①ABF 和①ADC 中BF DC ABF ADC AB AD =⎧⎪∠=∠⎨⎪=⎩①①ABF①①ADC①AF=AC ,①F=①DCA=60°①①FAC=180°-①F -①ACF=60°①①ACF 为等边三角形①CF=AC①BC +BF=AC①BC +CD=AC【点拨】此题考查的是新定义类问题、圆内接四边形的性质、圆周角定理及推论、锐角三角函数、等边三角形的判定及性质和全等三角形的判定及性质,掌握新定义、圆内接四边形的性质、圆周角定理及推论、锐角三角函数、等边三角形的判定及性质和全等三角形的判定及性质是解决此题的关键.19.(1)2BF FG=;(2)①画图见分析;①2DF FG,证明见分析【分析】(1)先判断出①AGB①①CGB,得到①GBF=45°,再判断出①EFG①①CFG,得到①GFB =45°,从而得到①BGF为等腰直角三角形,即可.(2)①画图2即可;①如图2,连接BF、BG,证明①ADF①①ABF得DF=BF,根据直角三角形斜边中线的性质得:AG=EG=BG=FG,由圆的定义可知:点A、F、E、B在以点G为圆心,AG长为半径的圆上,①BGF=2①BAC=90°,所以①BGF是等腰直角三角形,可得结论.解:(1)BF2FG,理由是:如图1,连接BG,CG,①四边形ABCD为正方形,①①ABC=90°,①ACB=45°,AB=BC,①EF①BC,FE=FC,①①CFE=90°,①ECF=45°,①①ACE=90°,①点G是AE的中点,①EG=CG=AG,①BG=BG,①①AGB①①CGB(SSS),①①ABG=①CBG=12①ABC=45°,①EG=CG,EF=CF,FG=FG,①①EFG①①CFG(SSS),①①EFG=①CFG=12(360°﹣①BFE)=12(360°﹣90°)=135°,①①BFE=90°,①①BFG=45°,①①BGF为等腰直角三角形,①BF2FG.故答案为:BF2;(2)①如图2所示,①2=;理由如下:DF FG如图2,连接BF、BG,①四边形ABCD是正方形,①AD=AB,①ABC=①BAD=90°,AC平分①BAD,①①BAC=①DAC=45°,①AF=AF,①①ADF①①ABF(SAS),①DF=BF,①EF①AC,①ABC=90°,点G是AE的中点,①AG=EG=BG=FG,①点A、F、E、B在以点G为圆心,AG长为半径的圆上,①BF BF=,①BAC=45°,①①BGF=2①BAC=90°,①①BGF是等腰直角三角形,①BF2FG,①DF2FG.【点拨】本题是四边形综合题,主要考查了正方形的性质,直角三角形斜边中线的性质,全等三角形的判定和性质,圆的性质,判断①BGF为等腰直角三角形是解本题的关键,作出辅助线是解本题的难点.20.见分析解:试题分析:先作①ABC的外接圆①O,并作OE①AB于E,OF①AC于F,连接OP、OQ、OB、OA,证出BE=AF,OE=OF,再证Rt①OPF①Rt①OQE,得到①P=①Q即可得到答案.证明:作①ABC的外接圆①O,并作OE①AB于E,OF①AC于F,连接OP、OQ、OB、OA,①O是①ABC的外心,①OE=OF,OB=OA,由勾股定理得:BE2=OB2﹣OE2,AF2=OA2﹣OF2,①BE=AF,①AP=BQ,①PF=QE,①OE①AB,OF①AC①①OFP=①OEQ=90°,①Rt①OPF①Rt①OQE,①①P=①Q,①O、A、P、Q四点共圆.即:①ABC的外心O与点A、P、Q四点共圆.【点拨】本题主要考查了四点共圆,勾股定理,全等三角形的性质和判定,确定圆的条件等知识点,作辅助线构造全等三角形证①P=①Q是解此题的关键.21.证明见分析.【分析】根据圆周角定理和圆内接四边形的性质得到①2=①1,①3=①ABC,由等腰三角形的性质得到①1=①ABC ,等量代换得到①2=①3,于是得到结论.证明:①A ,B ,C ,D 四点共圆,①①2=①1,①3=①ABC ,①AC=BC ,①①1=①ABC ,①①2=①3,①DC 平分①BDE .【点拨】本题考查了圆周角定理,圆内接四边形的性质,角平分线的判定,熟练掌握圆周角定理是解题的关键.22.见分析【分析】连接AC 、BD ,根据矩形的性质可得OA=OB=OC=OD ,即可得结论.解:连接AC 、BD 交于O 点,①四边形ABCD 为矩形,①AC BD =.①OA OB OC OD ===.①A 、B 、C 、D 到点O 的距离相等,①A 、B 、C 、D 在以O 为圆心,OA 为半径的圆上.即A 、B 、C 、D 四点共圆.【点拨】本题考查了矩形的性质及圆的认识,熟练掌握矩形的性质,理解四点共圆的意义是解题关键.23.(1)见分析;(2)见分析;(3)3BP =【分析】(1)证明AQD APB ≌即可得出答案;(2)根据全等三角形的性质以及圆内接四边形对角和为180︒即可得出结论; (3)证明PAQ △为等腰直角三角形,得出45APC ∠=︒,然后得出2ABC APC ∠=∠,根据圆周角定理可得点P 在圆B 上,结论可得.解:(1)根据旋转的性质可得AP AQ =,90PAQ ∠=︒,①90BAD ∠=︒,①DAQ BAP ∠=∠,①AB AD =,①()AQD APB SAS ≌,①BP DQ =;(2)①AQD APB ≌,①Q APB ∠=∠,①点P ,B ,D 三点共线,①180APD APB ∠+∠=︒,①180Q APD ∠+∠=︒,①A ,Q ,P ,D 四点共圆;(3)①AP AQ =,90PAQ ∠=︒,①PAQ △为等腰直角三角形,①45APC ∠=︒,以点B 为圆心,BA 为半径作B ,①90ABC ∠=︒,45APC ∠=︒,①2ABC APC ∠=∠,①点P 在圆B 上,①3BP BC ==.【点拨】本题考查了全等三角形的判定与性质,四点共圆,圆周角定理等知识,熟练掌握基础知识是解本题的关键.24.(1)10°;(2)见分析【分析】(1)由三角形内角和定理和已知条件求得①C的度数,由旋转的性质得出AC=AD,即可得出①ADC=①C,最后由外角定理求得①BAD的度数;(2)由旋转的性质得到①ABC=①AED,由四点共圆的判定得出结论.解:(1)①在Rt ABC中,①BAC=90°,①ABC=40°,①①C=50°,①将ABC绕A点顺时针旋转得到ADE,使D点落在BC边上,①AC=AD,①①ADC=①C=50°,①①ADC=①ABC+①BAD=50°,①①BAD=50°-40°=10°证明(2)①将ABC绕A点顺时针旋转得到ADE,①①ABC=①AED,①A、D、B、E四点共圆.【点拨】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定,解题的关键是理解旋转后的图形与原图形对应边相等,对应角相等.25.(1)1,45;(2)见分析;(3)8,2222【分析】(1)根据同弧所对的圆周角等于圆心角的一半解答;(2)由题意知,CD垂直平分BE,连接BF,则BF=EF,求得①EBF=①AEB=45°,利用外角的性质得到①AFB=①EBF+①AEB=90°,即可得到结论;(3)当点A、C、E在一条直线上时,线段AE最大,最大值为4+4=8,当MF①BC时线段MF最小,根据BC的中点M,得到CF=BF,设BG=FG=x,则2x,CG2 +1)x,由勾股定理得222+=,求出2842CG BG BCx=-222+=,即可求BM MF BF出222MF=.(1)解:①AC=BC=EC,①A、B、E三点在以C为圆心以AC为半径的圆上,①ACB,①①AEB=12①①AEB=45°.,45;故答案为:12(2)解:由题意知,CD 垂直平分BE ,连接BF ,则BF=EF ,①①EBF =①AEB =45°.①①AFB =①EBF +①AEB =90°.①①ACB =90°,①A 、B 、F 、C 在以AB 为直径的圆上,即A 、B 、F 、C 四点共圆;(3)解:当点A 、C 、E 在一条直线上时,线段AE 最大,最大值为4+4=8,当MF ①BC 时线段MF 最小,①BC 的中点M ,①CF=BF , 设BG=FG=x ,则2,CG 2x ,①222CG BG BC +=,①222(21)4x x ⎡⎤+=⎣⎦, 得2842x =-①222BM MF BF +=,①2222(2)MF x +=,得222MF =,故答案为:8,222 . .【点拨】此题考查了圆周角定理,四点共圆的判定及性质,线段垂直平分线的性质,勾股定理,等腰直角三角形的性质,熟记各知识点并熟练应用解决问题是解题的关键.26.(1)①直角三角形斜边上的中线等于斜边的一半;①圆内接四边形对角互补;①同弧或等弧所对的圆周角相等;①等量代换(2)见分析【分析】(1)根据直角三角形斜边上的中线的性质,圆内接四边形的性质,同弧或等弧所对的圆周角相等进行求解即可;(2)如图,连接P A,PB,PC,只需要证明Rt Rt△≌△即可证明结论.PBD PCF(1)解:①直角三角形斜边上的中线等于斜边的一半;①圆内接四边形对角互补;①同弧或等弧所对的圆周角相等;①等量代换;(2)证明:如图,连接P A,PB,PC.①点P是BC的中点,①BP PC=.①BP PC∠=∠.=,PAD PAC又①PD AD⊥,PF AC⊥,①PD PF=.①Rt Rt△≌△(HL).PBD PCF=.①BD CF【点拨】本题主要考查了圆内接四边形的性质,直角三角形斜边上的中线的性质,全等三角形的性质与判定,弧,弦,圆周角的关系,同弧或等弧所对的圆周角相等等等,正确作出辅助线和熟知相关知识是解题的关键.27.【思考】证明见分析;【应用】(1证明见分析;(2)证明见分析试题分析:【思考】假设点D在①O内,利用圆周角定理及三角形外角的性质,可证得与条件相矛盾的结论,从而证得点D不在①O内;[应用](1)由旋转的性质可得①ACD=①ABE,故B、C、A、F四点共圆,(2)由圆内接四边形的性质得①BCA+①BF A=180°即可证明.【思考】【证】如图,假设点D 在①O 内,延长AD 交①O 于点E ,连接BE ;则①AEB =①ACB①①ADB 是△DBE 的一个外角①①ADB >①AEB①①ADB >①ACB这与条件①ACB =①ADB 矛盾①点D 不在①O 内【证】(1)①AC =AD ,AB =AE ,①①ACD =①ADC ,①ABE =①AEB ,①①CAB =①DAE ,①①CAD =①BAE ,①2①ACD +①CAD =180°,2①ABE +①BAE =180°,①①ACD =①ABE ,①B 、C 、A 、F 四点共圆,(2)①B 、C 、A 、F 四点共圆,①①BF A +①BCA =180°,①①ACB =90°,①①BF A =90°,①AF ①BE ,①AB =AE ,①BF =EF .【点拨】本题综合考查了圆周角定理、反证法、三角形外角的性质、点和圆的位置关系等知识,熟练掌握性质定理是解题的关键.28.(1)①①①;(2)①BDC 的度数为140°或 40°;232 【分析】 (1)由“对角互补的四边形是圆的内接四边形”,即可得出答案;(2)分点D在BC上和点D在AB、AC上两种情况讨论,即可求出①BDC的度数;(3)①由圆内接四边形的性质可得①E+①AFB=180°,由①BAC=①BFC,可得①E+①AFC =①E+①AFB+①BFC=①E+①AFB+①BAC=180°+①BAC,进而可得①E+①AFC﹣①BAC=180°;①由AB经过圆心O,BC弦的长度与①O的半径r21,可得①ABC为等腰直角三角形,S五边形AEBCF=S△ABE+S△ABC+S△ACF,当①ABE及①ACF面积最大时,五边形AEBCF的最大面积,E为AB中点时,①ABE面积最大,F为AC中点时,①ACF面积最大,求出①ABE及①ACF面积最大值,最后把三个三角形的面积相加,即可求出五边形AEBCF的最大面积.(1)解:①矩形、正方形、等腰梯形的对角互补,①矩形、正方形、等腰梯形的四个顶点构成四点共圆,故答案为:①①①;(2)解:如图4,当点D在BC上时,①A、B、D、C四点共圆,①①A+①D=180°,①①BAC=40°,①①BDC=180°﹣40°=140°,如图5和图6,当点D在AB或AC上时,①①BAC=40°,①①BDC=①BAC=40°,综上所述,①BDC的度数为140°或40°;(3)解:①如图7,连接BF,①四边形AEBF是圆内接四边形,①①E+①AFB=180°,又①①BAC=①BFC,①①E+①AFC=①E+①AFB+①BFC=①E+①AFB+①BAC=180°+①BAC,①①E+①AFC﹣①BAC=180°,即①E+①F﹣①BAC=180°;①①AB经过圆心,①AB是①O的直径,①①ACB=90°,①BC:OB2:1,OB=r,①BC2r,①AB=2r,①AC222r,AB BC①BC=AC,①①ABC是等腰直角三角形,①S五边形AEBCF=S△ABE+S△ABC+S△ACF,①当①ABE及①ACF面积最大时,五边形AEBCF的最大面积,此时,E为AB中点时,①ABE面积最大,F为AC中点时,①ACF面积最大,如图8,连接OE,连接OF交AC于H,①OE①AB,OF①AC,①AH=CH,①OH=12BC2r,①S△ABE的最大值为:12•AB•OE=12×2r×r=r2,S△ACF的最大值为:12•AC•FH=122r×(r22r2﹣12×r2,①S五边形AEBCF的最大值为:r2+r222﹣12×r223+2.【点拨】本题考查了四点共圆,掌握四点共圆及圆周角的性质是解决问题的关键.。
中考数学总复习《四点共圆问题》专题(含答案)

如图,在 中, , 中, ,若 三点在同一直线 上. 连接 、 ,点 、 、 分别为 、 、 的中点.求证 .
在梯形ABCD中, , , , 分别在 , 上, .
求证: .
如图 和 中, ,求证点 , , , 四点在同一个圆上.
(1)当点 在 内时,延长 交 于 ,连结 ,则有
如图,在△ABC中,分别以AB,AC为直径在 ABC外作半圆 和半圆 ,其中 和 分别为两个半圆的圆心.F是边BC的中点,点D和点E分别为两个半圆圆弧的中点.过点A作半圆 的切线,交CE的延长线于点Q,过点Q作直线FA的垂线,交BD的延长线于点P,连结PA.
求证:PA是半圆 的切线.
如图,在四边形ABCD中,已知∠BAD=60°,∠ABC=90°,∠BCD=120°,对角线AC,BD交于点E,且DE=2EB,F为AC的中点.
求证:(1)∠FBD=30°;(2)AD=DC.
四点共圆问题答案解析
一、解答题
(1)∵ ,∴ ,
∴ ,∴ 四点共圆.
(2) 连结 ,设 相交于
由(1)可知 是圆的直径,
又∵ 是平行四边形,∴ 是 中点,
∴ 是圆心,∴ ,
∵ ,∴ .
取 的中点 ,连接 ,故
【解析】取斜边中点,利用斜边中线等于斜边长一半,然后利用证明方法一.
∵ 是 的切线,∴ ,
∴ ,
∵ ,
∴ ,
∴ 四点共圆,
∵ ,∴ .
连结ห้องสมุดไป่ตู้,
∵ ,
∴ ,
∴ ,
∵ ,
∴ 四点共圆, 四点共圆,
∴ 五点共圆,
∴ .
四点共圆经典题

四点共圆【知识要点】四点共圆的判定方法:1、若四个点到一定点的距离相等,则这四个点在同一个圆上(即这四点共圆)。
2、若一个四边形的一组对角的和等于180度,则这个四边形的四个顶点共圆。
3、若一个四边形的一个外角等于它的内对角,则这个四边形的四个顶点共圆。
4、若两个点在一条线段的同旁,并且和这条线段的两端连线所夹的角相等,那么这两个点和这条线的两个端点共圆。
5、若AB 、CD 两线段相交于P 点,且PD PC PB PA ⋅=⋅,则A 、B 、C 、D 四点共圆。
6、若AB 、CD 两线段延长后相交于P 点,且PD PC PB PA ⋅=⋅,则A 、B 、C 、D 四点共圆。
7、若四边形两组对边乘积的和等于对角线的乘积,则四边形的四个顶点共圆。
二、直角边相交的“双直角”类说明:我说的“双直角”特指如下两种情况;相对“双直角”(如图1);同侧“双直角”(如图2).其特点是:A 连公共斜边,作斜边上的中线,得5个等腰三角形;B 四点共圆,据同弧上圆周角相等得到很多等角.1.如图5–2–3,∠ABC =∠ADC =90°,M 、N 分别是线段AC 、BD 的中点. 求证:MN ⊥BD .2.如图5–2–7,在锐角△ABC 中,∠BAC =60°,BD 、CE 为高,F 是BC 的中点,连接DE 、EF 、FD .则在:①EF =FD ;②AD ︰AB =AE ︰AC ;③△DEF 是等边三角形;④BE +CD =BC ;⑤当∠ABC =45°是,BE =2DE .这五个结论中一定AB C DOA B C D O 图1 图2 图5–2–3 B C DANM正确的个数是( )A .2B .3C .4D .53.已知ABC ∆中,D 为AB 边上的任意一点,AC DF //交BC 于点F ,α=∠=∠=∠ACB ABC CDE BC AE ,//,(1)如图1,当是等边三角形。
时,求证:ABC 60∆=α(2)如图2,当()()DE CE DE⊥==2;2CD 145时,求证: α(3)如图3,当α为锐角时,请直接写出线段CE 与DE 的数量关系是:=DE CEAB C E F D图5–2–7。
四点共圆例题及答案

四点共圆例题及答案四点共圆是一个基本的几何概念,指的是在同一平面上有四个点,可以在一个圆上找到这四个点构成的圆周。
这个概念在几何学中非常重要,因为它可以用来解决许多几何问题。
在本文中,我们将展示一些常见的四点共圆例题及答案,希望对几何学爱好者有所帮助。
题目1:如图,ABCD为一矩形,O为AC的中点,P、Q分别为AB、CD上一点,连OP、OQ。
证明O、P、Q、D四点共圆。
答案1:首先,连接BD,可以得到三角形BOD。
因为ABCD是一个矩形,所以BD是矩形的对角线,即BD=AC。
由于O是AC的中点,所以OD=1/2AC=1/2BD。
因此,OD是矩形的中线,而且OD平分角BOD。
所以,∠BOD=2∠POQ。
另一方面,因为PO、QD分别是∠BOD的平分线,所以∠POD=1/2∠BOD、∠QOD=1/2∠BOD。
这样,我们可以得到:∠POQ=∠POD+∠QOD=1/2∠BOD+1/2∠BOD=∠BOD所以,O、P、Q、D四点共圆,且这个圆的圆心是OD的中点。
题目2:如图,在平面上有四个点ABCD,能否用尺规作出过这四点的圆?答案2:可以,下面是具体的做法:1.连接AB、BC、CD和DA,得到一个矩形ABCD。
2.以AB为直径作圆,得到圆O1。
3.以BC为直径作圆,得到圆O2。
4.在线段AC上取一点E,使得AE=AB,连BE,作线段BE的中垂线,交O1于点F,交O2于点G。
5.以FG为直径作圆,得到过四点ABCD的圆。
题目3:如图,在平面上有一圆O,点A、B、C在这个圆上,点D在圆内,且以AD、BD、CD为边的三角形相似。
证明:四点A、B、C、D共圆。
答案3:设AB与CD的交点为E,BC与AD的交点为F。
因为三角形ABC在圆O上,所以∠AEB=∠ACB,又因为三角形CBD在圆O上,所以∠CEB=∠CDB,而∠AEB+∠CEB=180,所以∠ACB+∠CDB=180。
同理可得∠AFC+∠BFD=180。
因为三角形ABC和三角形AFB相似,所以∠AEB=∠AFC,同理∠BFD=∠CDB。
(完整版)四点共圆例题及答案

例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H四点共圆.证明菱形ABCD的对角线AC和BD相交于点O,连接OE、OF、OG、OH.∵AC和BD 互相垂直,∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中,E、F、G、H,分别是AB、BC、CD、DA的中点,即E、F、G、H四点共圆.(2)若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆.例2 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.证明∵DE⊥AB,DF⊥AC,∴∠AED+∠AFD=180°,即A、E、D、F四点共圆,∠AEF=∠ADF.又∵AD⊥BC,∠ADF+∠CDF=90°,∠CDF+∠FCD=90°,∠ADF=∠FCD.∴∠AEF=∠FCD,∠BEF+∠FCB=180°,即B、E、F、C四点共圆.(3)若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆.证明在△ABC中,BD、CE是AC、AB边上的高.∴∠BEC=∠BDC=90°,且E、D在BC的同侧,∴E、B、C、D四点共圆.∠AED=∠ACB,∠A=∠A,∴△AED∽△ACB.上述三种方法是证“四点共圆”的基本方法,至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了.【例1】在圆内接四边形ABCD中,∠A-∠C=12°,且∠A∶∠B=2∶3.求∠A、∠B、∠C、∠D的度数.解∵四边形ABCD内接于圆,∴∠A+∠C=180°.∵∠A-∠C=12°,∴∠A=96°,∠C=84°.∵∠A∶∠B=2∶3,∠D=180°-144°=36°.利用圆内接四边形对角互补可以解决圆中有关角的计算问题.【例2】已知:如图1所示,四边形ABCD内接于圆,CE∥BD交AB的延长线于E.求证:AD·BE=BC·DC.证明:连结AC.∵CE∥BD,∴∠1=∠E.∵∠1和∠2都是所对的圆周角,∴∠1=∠2.∠1=∠E.∵四边形ABCD内接于圆,∴∠EBC=∠CDA.∴△ADC∽△CBE.AD∶BC=DC∶BE.AD·BE=BC· DC.本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件,进而得到结论.关于圆内接四边形的性质,还有一个重要定理.现在中学课本一般都不列入,现介绍如下:定理:圆内接四边形两条对角线的乘积等于两组对边乘积的和.已知:如图2所示,四边形ABCD内接于圆.求证:AC·BD=AB·CD+AD·BC.证明:作∠BAE=∠CAD,AE交 BD于 E.∵∠ABD=∠ACD,即 AB·CD=AC·BE.①∵∠BAE+∠CAE=∠CAD+∠CAE,∴∠BAC=∠EAD.又∠ACB=∠ADE,AD·BC=AC·DE.②由①,②得AC·BE+AC·DE=AB·CE+AD·BCAC·BD=AB·CD+AD·BC这个定理叫托勒密(ptolemy)定理,是圆内接四边形的一个重要性质.这个证明的关键是构造△ABE∽△ACD,充分利用相似理论,这在几何中是具有代表性的.在数学竞赛中经常看到它的影子,希望能引起我们注意.命题“菱形都内接于圆”对吗?命题“菱形都内接于圆”是不正确的.所以是假命题.理由是:根据圆的内接四边形的判定方法之一,如果一个四边形的一组对角互补,那么这个四边形内接于圆.这个判定的前提是一组对角互补,而菱形的性质是一组对角相等.而一组相等的角,它们的内角和不一定是180°.如果内角和是180°,而且又相等,那么只可能是每个内角等于90°,既具有菱形的性质,且每个内角等于90°,那末这个四边形一定是正方形.而正方形显然是菱形中的特例,不能说明一般情形.判定四边形内接于圆的方法之二,是圆心到四边形四个顶点的距离相等.圆既是中心对称图形,又是轴对称图形,它的对称中心是圆心.菱形同样既是中心对称图形,又是轴对称图形,它的对称中心是两条对角线的交点.但菱形的对称中心到菱形各个顶点的距离不一定相等.所以,也无法确定菱形一定内接于圆;如果菱形的对称中心到菱形各边顶点的距离相等,再加上菱形的对角线互相垂直平分这些性质,那么这个四边形又必是正方形.综上所述,“菱形都内接于圆”这个命题是错误的.5圆的内接四边形例1 已知:如图7-90,ABCD是对角线互相垂直的圆内接四边形,通过对角线的交点E与AB垂直于点H的直线交CD于点M.求证:CM=MD.证明∠MEC与∠HEB互余,∠ABE与∠HEB互余,所以∠MEC=∠ABE.又∠ABE=∠ECM,所以∠MEC=∠ECM.从而CM=EM.同理MD=EM.所以CM=MD.点评本例的逆命题也成立(即图中若M平分CD,则MH⊥AB).这两个命题在某些问题中有时有用.本例叫做婆罗摩笈多定理.例2 已知:如图7-91,ABCD是⊙O的内接四边形,AC⊥BD,分析一如图7-91(a),由于E是AB的中点,从A引⊙O的需证明GB=CD.但这在第七章ξ1.4圆周角中的例3已经证明了.证明读者自己完成.*分析二如图7-91(b),设AC,BD垂直于点F.取CD的有OE∥MF.从而四边形OEFM应该是平行四边形.证明了四边形OEFM是平行四边形,问题也就解决了.而证明四边形OEFM是平行四边形已经没有什么困难了.*分析三如图7-91(b),通过AC,BD的交点F作AB的垂线交CD于点M.连结线段EF,MO.由于OE⊥AB,FM⊥AB,所以OE∥FM.又由于EF⊥CD(见例1的点评),MO⊥CD,所以EF∥MO.所以四边形OEFM为平行四边形.从而OE=MF,而由例3 求证:圆内接四边形对边乘积的和等于对角线的乘积,即图中AB·CD+BC·AD=AC·BD.分析在AB·CD+BC·AD=AC·BD中,等号左端是两个乘积的和,要证明这种等式成立,常需把左端拆成两个单项式来证明,即先考虑AB·CD和BC·AD各等于什么,然后再考虑AB·CD+BC·AD是否等于AC·BD.而要考虑AB·CD和BC·AD各等于什么,要用到相似三角形.为此,如图7-92,作AE,令∠BAE=∠CAD,并且与对角线BD相交于点E,这就得到△ABE∽△ACD.由此求得AB·CD=AC·BE.在圆中又出现了△ABC∽△AED,由此又求得BC·AD=AC·ED.把以上两个等式左右各相加,问题就解决了.证明读者自己完成.点评本例叫做托勒玫定理.它在计算与证明中都很有用.意一点.求证:PA=PB+PC.分析一本例是线段和差问题,因此可用截取或延长的方法证明.如图7-93(a),在PA上取点M,使PM=PB,剩下的问题是证明MA=PC,这只要证明△ABM≌△CBP就可以了.证明读者自己完成.分析二如图7-93(a),在PA上取点M,使MA=PC,剩下的问题是证明PM=PB,这只要证明△BPM是等边三角形就可以了.证明读者自己完成.分析三如图7-93(b),延长CP到M,使PM=PB,剩下的问题是证明PA=MC,这只要证明△PAB≌△CMB就可以了.证明读者自己完成.读者可仿以上的方法拟出本例的其他证明.*本例最简单的证明是利用托勒玫定理(例3).证明由托勒玫定理得PA·BC=PB·AC+PC·AB,由于BC=AC=AB,所以有PA=PB+PC.例2 如图7—116,⊙O1和⊙O2都经过A、B两点,经过点A的直线CD与⊙O1交于点C,与⊙O2交于点D.经过点B的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:CE∥DF.分析:要证明CE∥DF.考虑证明同位角(或内错角)相等或同旁内角互补.由于CE、DF分别在两个圆中,不易找到角的关系,若连结AB,则可构成圆内接四边形,利用圆内接四边形的性质定理可沟通两圆中有关角的关系.证明:连结AB.∵ABEC是圆内接四边形,∵ADFB是圆内接四边形,∴∠BAD+∠F=180°,∴∠E+∠F=180°.∴CE∥CF.说明:(1)本题也可以利用同位角相等或内错角相等,两直线平行证明.如延长EF至G,因为∠DFG=∠BAD,而∠BAD=∠E,所以∠DFG=∠E.(2)应强调本题的辅助线是为了构成圆内接四边形,以利用它的性质,导出角之间的关系.(3)对于程度较好的学生,还可让他们进一步思考,若本题不变,但不给出图形,是否还有其他情况?问题提出后可让学生自己画图思考,通过讨论明确本题还应有如图7—117的情况并给予证明.例3 如图7—118,已知在△ABC中,AB=AC,BD平分∠B,△ABD的外接圆和BC 交于E.求证:AD=EC.分析:要证AD=EC,不能直接建立它们的联系,考虑已知条件可知∠ABD=∠DBE,容易看出.若连结DE,则有AD=DE.因此只要证DE=EC.由于DE和EC为△DEC的两边,所以只要证∠EDC=∠C.由已知条件可知∠C=∠ABC.因此只要证∠EDC=∠ABC.因为△EDC是圆内接四边形ABED的一个外角,所以可证∠EDC=∠ABC.问题可解决.证明:连结DE.∵BD平分∠ABC,∴,AD=DE.∵ABED是圆内接四边形,∵AB=AC,∴∠ABC=∠C,∴∠EDC=∠C.于是有DE=EC.因此AD=EC.四、作业1.如图7—120,在圆内接四边形ABCD中,AC平分BD,并且AC⊥BD,∠BAD=70°18′,求四边形其余各角.2.圆内接四边形ABCD中,∠A、∠B、∠C的度数的比为2∶3∶6,求四边形各内角的度数.3.如图7—121,AD是△ABC外角∠EAC的平分线,AD与三角形的外接圆交于点D.求证:DB=DC.作业答案或提示:1.∠ABC=∠ADC=90°,∠BCD=109°42′.2.∠A=45°,∠B=67.5°,∠C=135°,∠D=112.5°.3.提示:因为∠DBC=∠DAC,∠EAD=∠DCB,∠EAD=∠DAC,所以∠DBC=∠DCB,因此DB=DC.判定四点共圆的方法引导学生归纳判定四点共圆的方法:(1)如果四个点与一定点距离相等,那么这四个点共圆.(2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆.(3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆.(4)如果两个直角三角形有公共的斜边,那么这两个三角形的四个顶点共圆(因为四个顶点与斜边中点距离相等).3.如图7—124,已知ABCD为平行四边形,过点A和B的圆与 AD、BC分别交于E、F.求证:C、D、E、F四点共圆.提示连结EF.由∠B+∠AEF=180°,∠B+∠C=180°,可得∠AEF=∠C.四点共圆的应用山东宁阳教委教研室栗致根四点共圆在平面几何证明中应用广泛,熟悉这种应用对于开阔证题思路,提高解题能力都是十分有益的.一用于证明两角相等例1 如图1,已知P为⊙O外一点,PA切⊙O于A,PB切⊙O于B,OP交AB 于E.求证:∠APC=∠BPD.证明连结OA,OC,OD.由射影定理,得AE2=PE·EO,又AE=BE,则AE·BE =PE·EO……(1);由相交弦定理,得AE·BE=CE·DE……(2);由(1)、(2)得CE·ED=PE·EO,∴ P、C、O、D四点共圆,则∠1=∠2,∠3=∠4,又∠2=∠4.∴∠1=∠3,易证∠APC=∠BPD(∠4=∠EDO).二用于证明两条线段相筹例2 如图2,从⊙O外一点P引切线PA、PB和割线PDC,从A点作弦AE平行于DC,连结BE交DC于F,求证:FC=FD.证明连结AD、AF、EC、AB.∵PA切⊙O于A,则∠1=∠2.∵AE∥CD,则∠2=∠4.∴∠1=∠4,∴P、A、F、B四点共圆.∴∠5=∠6,而∠5=∠2=∠3,∴∠3=∠6.∵AE∥CD,∴EC=AD,且∠ECF=∠ADF,∴△EFC≌△AFD,∴FC=FD.三用于证明两直线平行例3 如图3,在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC.证明连结EC.在△ABE和△ACE中,∵AE=AE,AB=AC,∠BAE=∠CAE,∴△AEB≌AEC,∴∠5=∠1=∠2,∴B、C、H、E四点共圆,∴∠6=∠3.在△GEB 和△GEC中,∵GE=GE,∠BEG=∠CEG,EB=EC,∴△GEB≌△GEC,∴∠4=∠2=∠3,∴∠4=∠6.∴EH∥GC.四用于证明两直线垂直证明在△ABD和△BCE中,∵AB=BC,∠ABD=∠BCE,BD=CE,则△ABD≌△BCE,∴∠ADB=∠BEC,∴P、D、C、E四点共圆.设DC的中点为O连结OE、DE.易证∠OEC=60°,∠DEO=30°∴∠DEC=90°,于是∠DPC=90°,∴ CP⊥AD.五用于判定切线例5 如图5,AB为半圆直径,P为半圆上一点,PC⊥AB于C,以AC为直径的圆交PA于D,以BC为直径的圆交PB于E,求证:DE是这两圆的公切线.证明连结DC、CE,易知∠PDC=∠PEC=90°,∴ P、D、C、E四点共圆,于是∠1=∠3,而∠3+∠2=90°,∠A+∠2=90°,则∠1=∠A,∴DE是圆ACD 的切线.同理,DE是圆BCE的切线.因而DE为两圆的公切线六用于证明比例式例6 AB、CD为⊙O中两条平行的弦,过B点的切线交CD的延长线于G,弦PA、PB分别交CD于E、F.证明如图6.连结BE、PG.∵BG切⊙O于B,则∠1=∠A.∵AB∥CD,则∠A=∠2.于是∠1=∠2,∴P、G、B、E四点共圆.由相交弦定理,得EF·FG=PF·FB.在⊙O中,由相交弦定理,得CF·FD=FP·FB.七用于证明平方式例7 ABCD为圆内接四边形,一组对边AB和DC延长交于P点,另一组对边AD和BC延长交于Q点,从P、Q引这圆的两条切线,切点分别是E、F,(如图 7)求证:PQ2=QF2+PE2.证明作△DCQ的外接圆,交PQ于M,连结MC,∵∠1=∠2=∠3,则P、B、C、M四点共圆.由圆幂定理得PE2=PC·PD=PM·PQ,QF2=QC·QB=QM·QP,两式相加得PE2+QF2=PM·PQ+ QM·QP=PQ(PM+QM)=PQ·PQ=PQ2∴PQ2=PE2+QF2.八用于解计算题例8如图8,△ABC的高AD的延长线交外接圆于H,以AD为直径作圆和AB、AC分别交于E、F点,EF交 AD于 G,若 AG=16cm,AH=25cm,求 AD的长.解连结DE、DF、BH.∵∠1=∠2=∠C=∠H,∴B、E、G、H四点共圆.由圆幂定理,得AE·AB=AG·AN.在△ABD中,∵∠ADB=90°,DE⊥AB,由射影定理,得AD2=AE·AB,∴AD2=AG·AH=16×25=400,∴AD=20cm.九用于证明三点共线例9如图9,D为△ABC外接圆上任意一点,E、F、G为D点到三边垂线的垂足,求证:E、F、G三点在一条直线上.证明连结EF、FG、BD、CD.∵∠BED=∠BFD=90°,则B、E、F、D四点共圆,∴∠1=∠2,同理∠3=∠4.在△DBE和△DCG中,∵∠DEB=∠DGC,∠DBE=∠DCG,故∠1=∠4,易得∠2=∠3,∴ E、F、G三点在一条直线上.十用于证明多点共圆例10如图10,H为△ABC的垂心,H1、H2、H3为H点关于各边的对称点,求证:A、B、C、H1、H2、H3六点共圆.证明连结AH2,∵H与H2关于AF对称,则∠1=∠2.∵A、F、D、C四点共圆,则∠2=∠3,于是∠1=∠3,∴A、H2、B、c四点共圆,即H2在△ABC的外接圆上.同理可证,H1、H3也在△ABC的外接圆上.∴A、B、C、H1、H2、H3六点共圆.相关资源加到收藏夹添加相关资源托勒密定理的数形转换功能山东临沂市四中姜开传临沂市第一技校刘久松圆内接四边形两组对边乘积的和等于其对角线的乘积,即在四边形 ABCD 中,有AB·CD+AD·BC=AC·BD,这就是著名的托勒密定理.本刊1996年第2期给出了它的几种证法,作为续篇,本文就其数形转换功能举例说明如下:1 “形”转换为“数”对于某些几何问题,特别是圆内接多边形问题,如果能根据题设中隐含的数量关系,利用托勒密定理可将“形”转换为“数”,从而达到用代数运算来代替几何推理的目的.例1已知正七边形A1A2 (7)(第21届全俄数学奥林匹克竞赛题)对于这道竞赛题,原证较繁,但通过深挖隐含条件,利用托勒密定理可改变整个解题局面,使证题步骤简缩到最少.如图1,连 A1A5、A3A5,则A1A5=A1A4、A3A5=A1A3.在四边形A1A3A4A5中,由托勒密定理,得A3A4·A1A5+A4A5·A1A3=A1A4·A3A5,即A1A2·A1A4+A1A2·A1A3=A1A3·A1A4,两边同除以A1A2·A1A3·A1A4即得结论式.例2 如图2,A、B、C、D四点在同一圆周上,且BC=CD=4,AE=6,线段BE和DE的长都是整数,则BD的长等于多少?(1988年全国初中数学联赛题)此题若用其它方法解,往往使人一筹莫展.若运用托勒密定理,可使问题化难为易.由△CDE∽△BAE和△CBE∽△DAE,得由托勒密定理,得BD(AE+CE)=4(AB+AD),亦即 CE(AE+CE)=16.设CE=x,整理上式,得x2+6x-16=0.解得x=2(负值已舍),故BE·DE=CE·AE=12.∵BD<BC+CD=8,例3一个内接于圆的六边形,其五个边的边长都为81,AB是它的第六边,其长为31,求从B出发的三条对角线长的和.(第九届美国数学邀请赛试题)原解答过程冗长.若通过托勒密定理的桥梁作用,把“形”转换为“数”,可使问题化繁为简.如图3,设BD=a, BE=b,BF=c,连AC、CE、AE,则CE=AE=BD=a,AC=BF =c.在四边形BCDE中,由托勒密定理,得81b+812=a2①同理81b+31·81=ac ②31a+81a=bc ③解①、③、③组成的方程组,得a=135,b=144,c=105故 a+b+c=384.2 “数”转换为“形”对于某些代数问题,若结构与托勒密定理相似,通过构造圆内接四边形,可把“数”转换为“形”,然后利用“形”的性质,使问题得到解决.这种解法构思巧妙,方法独特,富于创新,出奇制胜.例4 解方程若按常规方法解这个无理方程,过程繁冗.若由方程的结构特征联想到托勒密定理,则构造直径AC=x(x≥11)的圆及圆内接四边形ABCD,使BC=2,CD=11,如图 4,于是由托勒密定理,得在△BCD中,由余弦定理,得经检验x=14是原方程的根.求证: a2+b2=1.这道名题已有多种证法,而且被视为用三角换无法解代数问题的典范.下面再给出一各几何证法.易知0≤a、b≤1且a、b不全为零.当a、b之一为零时,结论显然成立.当a、b全不为零时,由已知等式联想到托勒密定理,作直径AC=1的圆及圆内接四与已知等式比较,得BD=1,即BD也为圆的直径,故a2+b2=1例6设a>c,b>c,c>0,此题若用常规方法证明也不轻松.下面利用托勒密定理给出它的一个巧证.由托勒密定理,得巧用托勒密定理证题河北晋州市数学论文研究协会张东海王素改在解证某些数学题时,如能巧用托勒密定理,可使解证过程简洁清新,兹举例说明.托勒密定理:圆内接四边形中,两条对角线的乘积等于两组对边乘积之和.一、构造“圆”,运用定理【例1】设a,b,x,y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证作直径AB=1的圆,在AB的两侧任作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x, AD=y.(图1)由勾股定理知a,b,x,y满足条件.根据托勒密定理,有AC·BD+BC·AD=AB·CD.∵ CD≤1,∴ax+by≤1.二、利用无形圆,运用定理【例2】等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.已知:梯形 ABCD中,AD=BC,AB∥CD.求证:BD2=BC2+AB·CD.证∵等腰梯形内接于圆,由托勒密定理,有AC·BD=AD·BC+AB·CD.∵AD=BC,AC=BD,∴BD2=BC2+AB·CD.(图略)【例 3】已知:边长为 1的正七边形ABCDEFG中,对角线 AD=a,BG=b(a≠b).求证:(a+b)2(a-b)=ab2.证连结BD,GE,BE,DG,则 BD=EG=GB=b,DG=BE=DA=a, DE=AB=AG=1.(如图2)在四边形ABDG中,由托勒密定理,有AD·BG=AB·DG+BD·AG,即ab=a+b (1)同理在四边形BDEG中,得BE·DG=DE·BG+BD·EG,即a2=b+b2 (2)将(2)变形为b=a2-b2 (3)(1)×(3),得ab2=(a+b)(a2-b2).故ab2=(a+b)2(a-b).三、构造圆内接四边形,运用定理【例4】在△ABC中,∠A的内角平分线AD交外接圆于D.连结BD.求证:AD·BC=BD·(AB+AC).证(如图3) 连结DC.由托勒密定理.有AD·BC=AB·CD+AC·BD.又∵∠1=∠2,∴BD=DC.∴AD·BC=AB·CD+AC·BD=BD(AB+AC).即AD·BC=BD·(AB+AC).圆内接四边形的面积公式黑龙江绥化五中任天民设圆内接四边形ABCD中各边为a,b,c,d.连结 BD.由∠A+∠C=180°,可以推出sinA=sinC,cosA=-cosC.并且S四边形ABCD=S△ABD+S△BCD所以这样我们得出了圆内接四边形面积的计算公式.在上面的公式中,如果设某一边为零,(不仿设d=0)此时四边形变成三角形,该公式恰是计算三角形面积的海伦公式.圆内接四边形面积公式的得出是受三角形面积公式的启发,通过联想探索出来的,而且两者在形式上又是那么的相近.这种现象在数学中不胜枚举,如果同学们都能从特殊规律去探索一般规律,再从一般规律去认识特殊规律.那么对数学能力的培养将大有裨益.四条边定长四边形面积的最大值上海市育群中学李甲鼎四条边为定长的四边形不具稳定性,但在某种特定的位置下,它能内接于圆,成为圆内接四边形.并且此时达到变化过程中面积最大值.下文证明这个事实.已知:四边形ABCD中:AB=a,BC=b,CD=c,DA=d求证:四边形ABCD中有唯一四边形能内接于圆,且此时面积达到最大值.证明:(1)先证四边形四边定长,有唯一的四边形内接于圆,设∠ABC=α,∠ADC=β,AC=x.令α+β=π,即cosα+cosβ=0x的解唯一确定,代入(1)(2)后cosα、cosβ也随之唯一确,在α,β∈(0,π)的条件下α、β也同时唯一确定.∴四边形四边定长,对角互补,四边形是唯一的.即所得到的四边形为圆内接四边形.(2)当四边定长的四边形内接于圆时,此四边形面积最大.∵四边形ABCD的面积由余弦定理得a2+b2-2abcosα=x2=c2+d2-2cdcosβ显然当α+β=π时(即为圆内接四边形时)S2达到最大值,即S最大.一个几何定理的应用江苏省徐州矿务局庞庄职校张怀林定理:如图1,在圆接四边形ABCD中弦AD平分∠BAC,则2ADcosα=AB +AC.证明连接BD、DC、BC,设已知圆半径为R,则由正弦定理有:BD=DC=2Rsinα,BC=2Rsin2α.由托勒密定理有AB·CD+AC·BD=AD·DC.∴(AB+AC)·2Rsinα=AD·2Rsin2α.则2AD·cosα=AB+AC.下面举例说明它的应用.例1如图2,已知锐角△ABC的∠A平分线交BC于L,交外接圆于N,过L分别作LK⊥AB,LM⊥AC,垂足分别为K、M.求证:四边形AKNM的面积等于△ABC的面积.(第28届IMO)证明由已知得∠BAN=∠CAN,由定理有2ANcosα=AB+AC,=AN·AL·cosα·sinα=AN·AK·sinα=AN·AM·sinα=2S△AKN=2S△AMN.∴S△ABC=S四边形AKNM.(第21届全苏奥数)证明作正七边形外接圆,如图3所示.由定理有2c·cosα=b+c,又在等腰△A1A2A3中有2a·cosα=b.例3在△ABC中,∠C=3∠A,a=27,c=48,则b的值是____.(第36届AHSME试题)解如图4.作△ABC的外接圆,在取三等分点D、E,连CD、CE.由已知得:∠ACD=∠DCE=∠ECB=∠A,CD=AB=48,由定理有2CE·cosA=CB+CD ①2CD·cosA=CE+AC ②又2CB·cosA=CE ③由②、③得:b=AC=CE·(CD-CB)/CB=35.托勒密定理及其应用河北省晋州市数学论文研究协会刘同林托勒密定理:圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和).已知:圆内接四边形ABCD,求证:AC·BD=AB·CD+AD·BC.证明:如图1,过C作CP交BD于P,使∠1=∠2,又∠3=∠4,∴△ACD ∽△BCP.又∠ACB=∠DCP,∠5=∠6,∴△ACB∽△DCP.①+②得AC(BP+DP)=AB·CD+AD·BC.即AC·BD=AB·CD+AD·BC.这就是著名的托勒密定理,在通用教材中习题的面目出现,不被重视.笔者认为,既然是定理就可作为推理论证的依据.有些问题若根据它来论证,显然格外简洁清新.兹分类说明如下,以供探究.一、直接应用托勒密定理例1如图2,P是正△ABC外接圆的劣弧上任一点(不与B、C重合),求证:PA=PB+PC.分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为繁冗.若借助托勒密定理论证,则有PA·BC=PB·AC+PC·AB,∵AB=BC=AC.∴PA=PB+PC.二、完善图形借助托勒密定理例2证明“勾股定理”:在Rt△ABC中,∠B=90°,求证:AC2=AB2+BC2证明:如图3,作以Rt△ABC的斜边AC为一对角线的矩形ABCD,显然ABCD是圆内接四边形.由托勒密定理,有AC·BD=AB·CD+AD·BC.①又∵ABCD是矩形,∴AB=CD,AD=BC,AC=BD.②把②代人①,得AC2=AB2+BC2.例3如图4,在△ABC中,∠A的平分线交外接∠圆于D,连结BD,求证:AD·BC=BD(AB+AC).证明:连结CD,依托勒密定理,有AD·BC=AB·CD+AC·BD.∵∠1=∠2,∴BD=CD.故AD·BC=AB·BD+AC·BD=BD(AB+AC).三、利用“无形圆”借助托勒密定理例4等腰梯形一条对角线的平方等于一腰的平方加上两底之积.如图5,ABCD中,AB∥CD,AD=BC,求证:BD2=BC2+AB·CD.证明:∵等腰梯形内接于圆,依托密定理,则有AC·BD=AD·BC+AB·CD.又∵AD=BC,AC=BD,∴BD2=BC2+AB·CD.四、构造图形借助托勒密定理例5若a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明:如图6,作直径AB=1的圆,在AB两边任作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x,AD=y.由勾股定理知a、b、x、y是满足题设条件的.据托勒密定理,有AC·BD+BC·AD=AB·CD.∵CD≤AB=1,∴ax+by≤1.五、巧变原式妙构图形,借助托勒密定理例6已知a、b、c是△ABC的三边,且a2=b(b+c),求证:∠A=2∠B.分析:将a2=b(b+c)变形为a·a=b·b+bc,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b,两对角线为a,一底边为c.证明:如图7,作△ABC的外接圆,以A为圆心,BC为半径作弧交圆于D,连结BD、DC、DA.∵AD=BC,∴∠ABD=∠BAC.又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.依托勒密定理,有BC·AD=AB·CD+BD·AC.①而已知a2=b(b+c),即a·a=b·c+b2.②∴∠BAC=2∠ABC.六、巧变形妙引线借肋托勒密定理例7在△ABC中,已知∠A∶∠B∶∠C=1∶2∶4,析证:将结论变形为AC·BC+AB·BC=AB·AC,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.如图8,作△ABC的外接圆,作弦BD=BC,边结AD、CD.在圆内接四边形ADBC中,由托勒密定理,有AC·BD+BC·AD=AB·CD易证AB=AD,CD=AC,∴AC·BC+BC·AB=AB·AC,关于圆内接四边形的若干共点性质浙江绍兴县鲁迅中学范培养设四边形ABCD内接于圆O,其边AB与DC的延长线交于P,AD与BC 的延长线交于Q,由P作圆的两切线PM、PN,切点分别为M、N;由Q作圆的两切线QE、QF,切点分别为E、F(如图1).则有以下一些共点性质:性质1 AC、BD、EF三直线共点.证明:如图1,设AC交EF于K1,则K1分EF所成的比为设BD交EF于K2,同理可得K2分EF所成的比为由(5)、(6)可得(1)=(2),故K1、K2分EF所成的比相等.∴K1、K2重合,从而AC、BD、EF三直线共点.类似地AC、BD、MN三直线共点,因此有以下推论AC、BD、EF、MN四直线共点.性质2 AB、DC、EF三直线共点于P.(此性质等同于1997年中国数学奥林匹克第二试第四题)这里用上述证明性质1的方法证之.证明:如图2.设DC与EF的延长线交于P1,则P1分EF所成的比为设AB与EF的延长线交于P2,则P2分EF所成的比为由(5)、(6)可得(7)=(8),故P1、P2分EF所成的比相等.∴P1、P2重合,从而AB、DC、EF三直线共点于P.推论AD、BC、NM三直线共点于Q.性质 3 EM、NF、PQ三直线共点.证明:如图3,设EM的延长线交PQ于G1,妨上证法,G1分PQ所成的比为设NF的延长线交PQ于G2,则G2分PQ所成的比为(这里E、F、P三点共线及N、M、Q三点共线在性质2及推论中已证).由△PME∽△PFM得由(11)、(12)及QE=QF、PN=PM可得(9)=(10),故G1、G2分PQ所成的比相等.∴G1、G2重合,从而EM、NF、PQ三直线共点.性质4如果直线EN和MF相交,那么交点在直线PQ上,即EN、MF、PQ三直线共点.证明从略,妨性质3的证法可得.性质5 EM、NF、AC三直线共点.证明:如图4,类似于性质1的证明,设EM与AC的延长线交于G3,则G3分AC所成的比为设NF与AC的延长线交于G4,则G4分AC所成的比为由(15)、(18)、(19)可得(13)=(14),故G3、G4分AC所成的比相等.∴G3、G4重合,从而EM、NF、AC 三直线共点.推论EM、NF、AC、PQ四直线共点.限于篇幅,仅列以上五条共点性质.有兴趣的读者不妨再探索其它共点性质例3在边长为a的正七边形ABCDEFG中,两条不相等的对角线长分别为t,m.证明如图4,连结AD、CE,令AE=t,AC=m,在圆内接四边形ACDE 中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma.托勒密定理及其应用河北省晋州市数学论文研究协会康美娈彭立欣托勒密定理圆内接四边形的两条对角线的乘积(两条对角线所包矩形的面积),等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形面积之和).证明如图1,过C作CP使∠1=∠2,又∠3=∠4,∴△ACD∽△BCP.∴AC·BP=AD·BC ①又∠ACB=∠DCP,∠5=∠6,∴AC·DP=AB·CD.②①+②得AC(BP+PD)=AD·BC+AB·CD.故AC·BD=AD·BC+AB·CD.托勒密定理在教材中仅以习题的形式出现,若以此定理为根据,可使许多问题解证过程别具一格.例1已知P是正△ABC的外接圆劣弧上任意一点.求证:PA=BP+PC.证明如图2,ABPC是圆内接四边形,根据托勒密定理,有PA·BC=PB·AC+PC·AB.∵AB=BC=AC,∴PA=PB+PC.例2证明等腰梯形一条对角线的平方,等于一腰的平方加上两底之积.证明如图3,设在梯形ABCD中,AD=BC,AB∥CD.∵等腰梯形内接于圆,∴AC·BD=AD·BC+AB·CD.又AD=BC,AC=BD,∴BD2=BC2+AB·CD.例3在边长为a的正七边形ABCDEFG中,两条不相等的对角线长分别为t,m.证明如图4,连结AD、CE,令AE=t,AC=m,在圆内接四边形ACDE 中,据托勒密定理,有AD·CE=AE·CD+AC·DE,即tm=ta+ma.例4已知a、b、x、y是实数,且a2+b2=1,x2+y2=1.求证:ax+by≤1.证明作直径AB=1的圆,在AB两侧作Rt△ACB和Rt△ADB,使AC=a,BC=b,BD=x,DA=y(如图5).依勾股定理知a、b、x、y是满足题设条件的.依托勒密定理有AC·BD+BC·AD=AB·CD.又∵CD≤AB=1,∴ax+by≤1.例5△ABC的三个内角A、B、C的对边分别为a、b、c,且a2=b(b+c).求证:A=2B.分析将a2=b(b+c)变形为a·a=b·b+b·c,可联想到托勒密定理,进而构造一个圆内接等腰梯形,使两腰为b,两对角线为a,一底边为c.证明如图6,作△ABC的外接圆.以A为圆心,以BC为半径画弧交圆于D,连结BD、DA、DC.。
专题06四点共圆(专项训练)(原卷版)
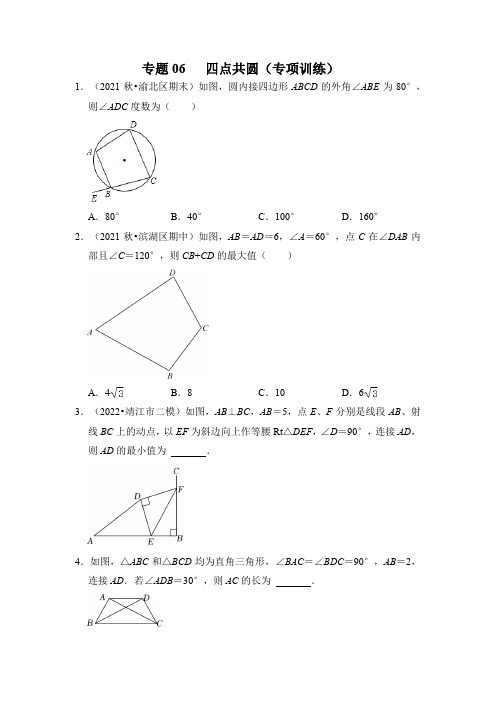
专题06 四点共圆(专项训练)1.(2021秋•渝北区期末)如图,圆内接四边形ABCD的外角∠ABE为80°,则∠ADC度数为()A.80°B.40°C.100°D.160°2.(2021秋•滨湖区期中)如图,AB=AD=6,∠A=60°,点C在∠DAB内部且∠C=120°,则CB+CD的最大值()A.4B.8C.10D.6 3.(2022•靖江市二模)如图,AB⊥BC,AB=5,点E、F分别是线段AB、射线BC上的动点,以EF为斜边向上作等腰Rt△DEF,∠D=90°,连接AD,则AD的最小值为.4.如图,△ABC和△BCD均为直角三角形,∠BAC=∠BDC=90°,AB=2,连接AD.若∠ADB=30°,则AC的长为.5.如图,在四边形ABCD中,BD=6,∠BAD=∠BCD=90°,则四边形ABCD 面积的最大值为.6.如图,在△ABC和△ACD中,∠ABC=∠ADC=45°,AC=6,则AD的最大值为.7.如图,△ABC中,AB=AC,∠BAC=90°,点D是BC的中点,点E,F分别为AB,AC边上的点,且∠EDF=90°,连接EF,则∠DEF的度数为.8.(2022秋•萧山区月考)如图,以C为公共顶点的Rt△ABC和Rt△CED中,∠ACB=∠CDE=90°,∠A=∠DCE=30°,且点D在线段AB上,则∠ABE =30°,若AC=10,CD=9,则BE=.9.(2021秋•宽城区期末)【问题原型】如图①,在⊙O中,弦BC所对的圆心角∠BOC=90°,点A在优弧BC上运动(点A不与点B、C重合),连结AB、AC.(1)在点A运动过程中,∠A的度数是否发生变化?请通过计算说明理由.(2)若BC=2,求弦AC的最大值.【问题拓展】如图②,在△ABC中,BC=4,∠A=60°.若M、N分别是AB、BC的中点,则线段MN的最大值为.10.(2022秋•仪征市期中)【问题提出】苏科版九年级(上册)教材在探究圆内接四边形对角的数量关系时提出了两个问题:1.如图(1),在⊙O的内接四边形ABCD中,BD是⊙O的直径.∠A与∠C、∠ABC与∠ADC有怎样的数量关系?2.如图(2),若圆心O不在⊙O的内接四边形ABCD的对角线上,问题(1)中发现的结论是否仍然成立?(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系,请帮助他完善问题1的证明:∵BD是⊙O的直径,∴,∴∠A+∠C=180°,∵四边形内角和等于360°,∴.(2)请回答问题2,并说明理由;【深入探究】如图(3),⊙O的内接四边形ABCD恰有一个内切圆⊙I,切点分别是点E、F、G、H,连接GH,EF.(3)直接写出四边形ABCD边满足的数量关系;(4)探究EF、GH满足的位置关系;(5)如图(4),若∠C=90°,BC=3,CD=2,请直接写出图中阴影部分的面积.10.(2022•遵义)综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.提出问题:如图1,在线段AC同侧有两点B,D,连接AD,AB,BC,CD,如果∠B=∠D,那么A,B,C,D四点在同一个圆上.探究展示:如图2,作经过点A,C,D的⊙O,在劣弧AC上取一点E(不与A,C重合),连接AE,CE,则∠AEC+∠D=180°(依据1)∵∠B=∠D∴∠AEC+∠B=180°∴点A,B,C,E四点在同一个圆上(对角互补的四边形四个顶点共圆)∴点B,D在点A,C,E所确定的⊙O上(依据2)∴点A,B,C,D四点在同一个圆上反思归纳:(1)上述探究过程中的“依据1”、“依据2”分别是指什么?依据1:;依据2:.(2)如图3,在四边形ABCD中,∠1=∠2,∠3=45°,则∠4的度数为.拓展探究:(3)如图4,已知△ABC是等腰三角形,AB=AC,点D在BC上(不与BC 的中点重合),连接AD.作点C关于AD的对称点E,连接EB并延长交AD 的延长线于F,连接AE,DE.①求证:A,D,B,E四点共圆;②若AB=2,AD•AF的值是否会发生变化,若不变化,求出其值;若变化,请说明理由.11.如图,在△ABC中,以AB为直径作⊙O交AC于点D,交BC于点E,CE =BE,过点E作EF⊥AC于点F,FE的延长线交AB的延长线于点G,连接DE.(1)求证:FG是⊙O的切线;(2)求证:EG2=AG•BG;(3)若BG=1,EG=,求sin∠CDE的值.。
四点共圆练习试题
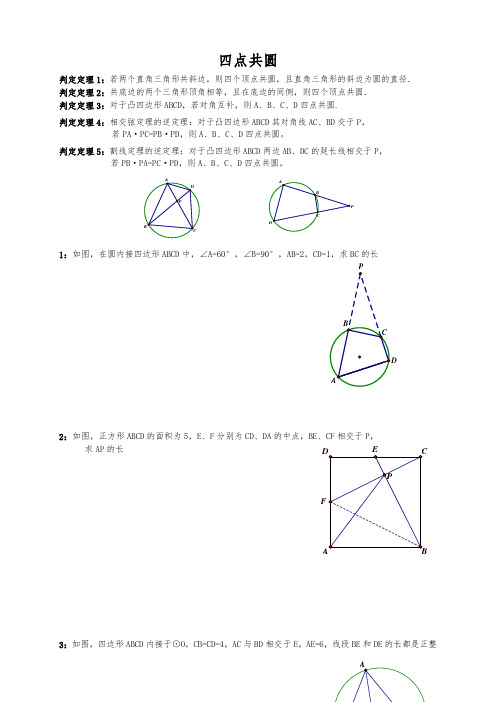
四点共圆判定定理1:若两个直角三角形共斜边,则四个顶点共圆,且直角三角形的斜边为圆的直径. 判定定理2:共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆. 判定定理3:对于凸四边形ABCD ,若对角互补,则A 、B 、C 、D 四点共圆. 判定定理4:相交弦定理的逆定理:对于凸四边形ABCD 其对角线AC 、BD 交于P ,若PA ·PC=PB ·PD ,则A 、B 、C 、D 四点共圆。
判定定理5:割线定理的逆定理:对于凸四边形ABCD 两边AB 、DC 的延长线相交于P ,若PB ·PA=PC ·PD ,则A 、B 、C 、D 四点共圆。
1:如图,在圆内接四边形ABCD 中,∠A=60°,∠B=90°,AB=2,CD=1,求BC 的长2:如图,正方形ABCD 的面积为5,E 、F 分别为CD 、DA 的中点,BE 、CF 相交于P ,求AP 的长3:如图,四边形ABCD 内接于⊙O ,CB=CD=4,AC 与BD 相交于E ,AE=6,线段BE 和DE 的长都是正整F数,求BD 的长4:如图,OQ ⊥AB ,O 为△ABC 外接圆的圆心,F 为直线OQ 与AB 的交点,BC 与OQ 交于P 点,A 、C 、Q 三点共线,求证:OA 2=OP·OQ5:如图,P 是⊙O 外一点,PA 与⊙O 切于点A ,PBC 是⊙O 的割线,AD ⊥PO 于D ,求证:PB :BD=PC :CD6:如图,直线AB 、AC 与⊙O 分别相切于B 、C 两点,P 为圆上一点,P 到AB 、AC 的距离分别为6cm 、4cm ,求P 到BC 的距离A7: 在半⊙O 中,AB 为直径,直线CD 交半圆于C 、D ,交AB 延长线于M (MB<MA ,AC<MD ),设 K 是△AOC 与△DOB 的外接圆除点O 外的另一个交点,求证:∠MKO=90°8:如图,在圆内接四边形ABCD 中,AB=AD ,∠BAD=60°,AC=a ,求:四边形ABCD 的面积(用a 表示)一、选择题1、设ABCD 为圆内接四边形,现给出四个关系式:(1)sinA=sinC ; (2)sinA+sinC=0;(3)cosB+cosD=0; (4)cosB=cosD ;其中总能成立的关系式的个数是( )A 、一个;B 、两个;C 、三个;D 、四个; 2、下面的四边形有外接圆的一定是( )A 、平行四边形;B 、梯形;C 、等腰梯形;D 、两个角互补的四边形; 3、四边形ABCD 内接于圆,∠A :∠B :∠C=7:6:3,则∠D 等于( )A 、36º;B 、72º;C 、144º;D 、54º;4、如图1,在四边形ABCD 中,AB=BC=AC=AD ,AH ⊥CD 于H ,CP ⊥BC 交AH 于P ,若AB =AP=1,则BD 等于( )A、; B 、2; C 、3; D;5、对于命题:①内角相等的圆内接五边形是正五边形;②内角相等的圆内接四边形是正四边形。
四点共圆练习题(精.选)

word.CF EAH B N M C A B 四点共圆练习题1. 如图,ABC ∆三边上的高交于H ,H 不于任一顶点重合,则以A 、B 、C 、D 、E 、F 、H中某四个点可以确定的圆共有多少个?2. 在梯形ABCD 中,AB ‖DC ,DC AB >,K 、M 分别在AD 、BC 上,CBK DAM ∠=∠,求证:CKB DMA ∠=∠3. 正方形ABCD 的中心为O ,面积为21989cm ,P 为正方形内一点,︒=∠45OPB ,14:5:=PB PA ,求PB 。
4.如图8,△ABC 的高AD 的延长线交外接圆于H ,以AD 为直径作圆和AB 、AC 分别交于E 、F 点,EF 交 AD 于 G ,若 AG=16cm ,AH=25cm ,求 AD 的长.5. 如图,在平行四边形ABCD 中,BC AM ⊥于M ,CD AN ⊥于N ,若13=AB ,5=BM ,9=MC ,求MN 的长度6.如图所示,棱形ABCD 的对角线AC,BD 相交于点O,四条边AB,BC,CD,DA 的中点为E,F,G ,H.求证:E,F,G ,H 四点共圆7. 如图2,从⊙O 外一点P 引切线PA 、PB 和割线PDC ,从A 点作弦AE 平行于DC ,连结BE 交DC 于F ,求证:FC =FD .BC MK DA CBOPDA FEDABOC8.在△ABC中,AB=AC,AD⊥BC,∠B的两条三等分线交AD于E、G,交AC于F、H.求证:EH∥GC.9.如图,△ABC为等边三角形,D,E分别为BC,AC边上的点,且BD=13BC,CE=13AC,AD与BE相交于点P,求证:CP⊥AD10.锐角△ABC中,BD,CE分别是AC,AB边上的高线,EM⊥BD于M,DN⊥CE于N.求证:MN//BC.11.在△ABC中,,B C∠∠的平分线相交于T, ,B C∠∠的外角平分线相交于P.求证:()12BPC ABC ACB∠=∠+∠12.如图所示,如果五边形ABCDE中,.ABC ADE AEC ADB∠=∠∠=∠且求证:BAC DAE∠=∠.13.四边形ABCD内接于圆,通过M和N分别表示直线AB和CD,BC与AD的交点,设1B是已知圆同过点B、M、N三点的圆的异于B的交点,求证:直线1B D平分线段MN.最新文件仅供参考已改成word文本。
四点共圆(习题)

圆内接四边形与四点共圆思路一:用圆的定义:到某定点的距离相等的所有点共圆。
→若连在四边形的三边的中垂线相交于一点,那么这个四边形的四个顶点共圆。
(这三边的中垂线的交点就是圆心)。
产生原因:圆的定义:圆可以看作是到定点的距离等于定长的点的集合。
基本模型:AO=BO=CO=DO ⇔ A、B、C、D四点共圆(O为圆心)思路二:从被证共圆的四点中选出三点作一个圆,然后证另一个点也在这个圆上,即可证明这四点共圆.→要证多点共圆,一般也可以根据题目条件先证四点共圆,再证其他点也在这个圆上。
思路三:运用有关性质和定理:①对角互补,四点共圆:对角互补的四边形的四个顶点共圆。
产生原因:圆内接四边形的对角互补。
基本模型:∠=+B)⇔ A、B、C、D四点共圆180∠D=180∠+∠DA(或0②张角相等,四点共圆:线段同侧两点与这条线段两个端点连线的夹角相等,则这两个点和线段的两个端点共四个点共圆。
产生原因:在同圆或等圆中,同弧所对的圆周角相等.方法指导:把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角(即:张角)相等(同弧所对的圆周角相等),从而即可肯定这四点共圆.∠⇔ A、B、C、D四点共圆=CAB∠CDB③同斜边的两个直角三角形的四个顶点共圆,其斜边为圆的直径.产生原因:直径所对的圆周角是直角。
=C⇔ A、B、C、D四点共圆∠D∠=90④外角等于内对角,四点共圆:有一个外角等于其内对角的四边形的四个顶点共圆。
产生原因:圆内接四边形的外角等于内对角。
基本模型:∠⇔ A、B、C、D四点共圆=ECD∠B1。
如图,已知ABC ∆的两条角平分线AD 和CE 相交于H ,060B ∠=,F 在AC 上,且AE AF =.证明:B ,D,H ,E 四点共圆:证明:CE 平分DEF ∠。
2.如图,AC ⊥BC ,CE ⊥AB ,CF ⊥AD.求证:∠AFE=∠B.3.已知在凸五边形ABCDE 中,3BAE BC CD DE α∠===,,且1802BCD CDE α∠=∠=︒-,求证:BAC CAD DAE ∠=∠=∠. E D C B A ED C B A4、如图,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB 的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD与∠BCE都是锐角,且∠ACD=∠BCE,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP。
高中数学四点共圆例题及答案

例1 如图,E、F、G、H分别是菱形ABCD各边的中点.求证:E、F、G、H 四点共圆.证明菱形ABCD的对角线AC和BD相交于点O,连接OE、OF、OG、OH.∵AC和BD 互相垂直,∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中,E、F、G、H,分别是AB、BC、CD、DA的中点,即E、F、G、H四点共圆.(2)若四边形的两个对角互补(或一个外角等于它的内对角),则四点共圆.例2 如图,在△ABC中,AD⊥BC,DE⊥AB,DF⊥AC.求证:B、E、F、C四点共圆.证明∵DE⊥AB,DF⊥AC,∴∠AED+∠AFD=180°,即A、E、D、F四点共圆,∠AEF=∠ADF.又∵AD⊥BC,∠ADF+∠CDF=90°,∠CDF+∠FCD=90°,∠ADF=∠FCD.∴∠AEF=∠FCD,∠BEF+∠FCB=180°,即B、E、F、C四点共圆.(3)若两个三角形有一条公共边,这条边所对的角相等,并且在公共边的同侧,那么这两个三角形有公共的外接圆.证明在△ABC中,BD、CE是AC、AB边上的高.∴∠BEC=∠BDC=90°,且E、D在BC的同侧,∴E、B、C、D四点共圆.∠AED=∠ACB,∠A=∠A,∴△AED∽△ACB.上述三种方法是证“四点共圆”的基本方法,至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了.【例1】在圆内接四边形ABCD中,∠A-∠C=12°,且∠A∶∠B=2∶3.求∠A、∠B、∠C、∠D的度数.解∵四边形ABCD内接于圆,∴∠A+∠C=180°.∵∠A-∠C=12°,∴∠A=96°,∠C=84°.∵∠A∶∠B=2∶3,∠D=180°-144°=36°.利用圆内接四边形对角互补可以解决圆中有关角的计算问题.【例2】已知:如图1所示,四边形ABCD内接于圆,CE∥BD交AB 的延长线于E.求证:AD·BE=BC·DC.证明:连结AC.∵CE∥BD,∴∠1=∠E.∵∠1和∠2都是所对的圆周角,∴∠1=∠2.∠1=∠E.∵四边形ABCD内接于圆,∴∠EBC=∠CDA.∴△ADC∽△CBE.AD∶BC=DC∶BE.AD·BE=BC· DC.本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件,进而得到结论.关于圆内接四边形的性质,还有一个重要定理.现在中学课本一般都不列入,现介绍如下:定理:圆内接四边形两条对角线的乘积等于两组对边乘积的和.已知:如图2所示,四边形ABCD内接于圆.求证:AC·BD=AB·CD +AD·BC.证明:作∠BAE=∠CAD,AE交 BD于 E.∵∠ABD=∠ACD,即 AB·CD=AC·BE.①∵∠BAE+∠CAE=∠CAD+∠CAE,∴∠BAC=∠EAD.又∠ACB=∠ADE,AD·BC=AC·DE.②由①,②得AC·BE+AC·DE=AB·CE+AD·BCAC·BD=AB·CD+AD·BC这个定理叫托勒密(ptolemy)定理,是圆内接四边形的一个重要性质.这个证明的关键是构造△ABE∽△ACD,充分利用相似理论,这在几何中是具有代表性的.在数学竞赛中经常看到它的影子,希望能引起我们注意.命题“菱形都内接于圆”对吗?命题“菱形都内接于圆”是不正确的.所以是假命题.理由是:根据圆的内接四边形的判定方法之一,如果一个四边形的一组对角互补,那么这个四边形内接于圆.这个判定的前提是一组对角互补,而菱形的性质是一组对角相等.而一组相等的角,它们的内角和不一定是180°.如果内角和是180°,而且又相等,那么只可能是每个内角等于90°,既具有菱形的性质,且每个内角等于90°,那末这个四边形一定是正方形.而正方形显然是菱形中的特例,不能说明一般情形.判定四边形内接于圆的方法之二,是圆心到四边形四个顶点的距离相等.圆既是中心对称图形,又是轴对称图形,它的对称中心是圆心.菱形同样既是中心对称图形,又是轴对称图形,它的对称中心是两条对角线的交点.但菱形的对称中心到菱形各个顶点的距离不一定相等.所以,也无法确定菱形一定内接于圆;如果菱形的对称中心到菱形各边顶点的距离相等,再加上菱形的对角线互相垂直平分这些性质,那么这个四边形又必是正方形.综上所述,“菱形都内接于圆”这个命题是错误的.。
四点共圆专项练习(1)学生版
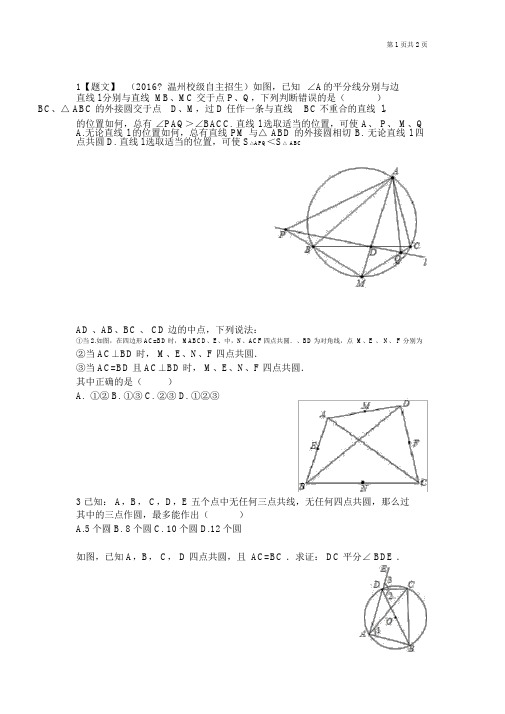
第1页共2页1【题文】(2016?温州校级自主招生)如图,已知∠A的平分线分别与边直线 l 分别与直线 MB、MC 交于点 P、Q,下列判断错误的是()BC、△ ABC 的外接圆交于点D、M,过 D 任作一条与直线BC 不重合的直线 l,的位置如何,总有∠PAQ>∠BACC. 直线 l 选取适当的位置,可使 A、 P、 M、QA.无论直线 l 的位置如何,总有直线 PM 与△ ABD 的外接圆相切B. 无论直线 l 四点共圆 D. 直线 l 选取适当的位置,可使 S△APQ<S△ABCAD 、AB、BC 、 CD 边的中点,下列说法:①当2.如图,在四边形AC=BD时, MABCD、E、中,N、ACF四点共圆.、BD为对角线,点 M、E 、 N、 F 分别为②当 AC⊥BD 时, M、E、N、F 四点共圆.③当 AC=BD 且 AC⊥BD 时, M、E、N、F 四点共圆.其中正确的是()A.①②B. ①③C. ②③D. ①②③3已知: A,B, C,D,E 五个点中无任何三点共线,无任何四点共圆,那么过其中的三点作圆,最多能作出()A.5个圆B. 8个圆C. 10个圆D.12个圆如图,已知 A,B, C, D 四点共圆,且 AC=BC .求证: DC 平分∠ BDE .第2页共2页4 如图,四边形ABCD 中,∠ B= ∠D=90°,点 E 为 AC 的中点,则 A,B ,C,D四点共圆吗?5如图,在△ ABC 中, AD⊥BC,DE⊥AB,DF ⊥AC.求证: B、E、F、C 四点共圆.6 如图,在△ ABC 中, CA=CB ,O 为外心, I 为内心, D 为 BC 上的点,且BI⊥ DO .(1)证明: B、 I、O、 D 四点共圆;(2)证明: ID∥AC .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四点共圆
判定定理1:若两个直角三角形共斜边,则四个顶点共圆,且直角三角形的斜边为圆的直径. 判定定理2:共底边的两个三角形顶角相等,且在底边的同侧,则四个顶点共圆.
判定定理3:对于凸四边形ABCD ,若对角互补,则A 、B 、C 、D 四点共圆.
判定定理4:相交弦定理的逆定理:对于凸四边形ABCD 其对角线AC 、BD 交于P ,
若PA ·PC=PB ·PD ,则A 、B 、C 、D 四点共圆。
判定定理5:割线定理的逆定理:对于凸四边形ABCD 两边AB 、DC 的延长线相交于P ,
若PB ·PA=PC ·PD ,则A 、B 、C 、D 四点共圆。
1:如图,在圆内接四边形ABCD 中,∠A=60°,∠B=90°,AB=2,CD=1,求BC 的长
2:如图,正方形ABCD 的面积为5,E 、F 分别为CD 、DA 的中点,BE 、CF 相交于P ,
求AP 的长
F
3:如图,四边形ABCD 内接于⊙O ,CB=CD=4,AC 与BD 相交于E ,AE=6,线段BE 和DE 的长
都是正整数,求BD 的长
4:如图,OQ ⊥AB ,O 为△ABC 外接圆的圆心,F 为直线OQ 与AB 的交点,BC 与OQ 交于P 点,
A 、C 、Q 三点共线,求证:OA 2=OP·OQ
5:如图,P 是⊙O 外一点,PA 与⊙O 切于点A ,PBC 是⊙O 的割线,AD ⊥PO 于D ,
求证:PB :BD=PC :CD
6:如图,直线AB 、AC 与⊙O 分别相切于B 、C 两点,P 为圆上一点,P 到AB 、AC 的距离分别为
6cm 、4cm ,求P 到BC 的距离
7: 在半⊙O 中,AB 为直径,直线CD 交半圆于C 、D ,交AB 延长线于M (MB<MA ,AC<MD ),
设 K 是△AOC 与△DOB 的外接圆除点O 外的另一个交点,求证:∠MKO=90°
8:如图,在圆内接四边形ABCD 中,AB=AD ,∠BAD=60°,AC=a ,求:四边形ABCD 的面积(用
a 表示)
一、选择题
1、设ABCD 为圆内接四边形,现给出四个关系式:(1)sinA=sinC ; (2)sinA+sinC=0;
(3)cosB+cosD=0; (4)cosB=cosD ;其中总能成立的关系式的个数是( )
A 、一个;
B 、两个;
C 、三个;
D 、四个;
2、下面的四边形有外接圆的一定是( )
A 、平行四边形;
B 、梯形;
C 、等腰梯形;
D 、两个角互补的四边形;
3、四边形ABCD 内接于圆,∠A :∠B :∠C=7:6:3,则∠D 等于( )
A 、36º;
B 、72º;
C 、144º;
D 、54º;
4、如图1,在四边形ABCD 中,AB=BC=AC=AD ,AH ⊥CD 于H ,CP ⊥BC 交AH 于
P
,若AB =AP=1,则BD 等于( )
A
、; B 、2; C 、3; D
; 5、对于命题:①内角相等的圆内接五边形是正五边形; ②内角相等的圆内接四边形是正四边形。
以下四个结论 中正确的是( )
A 、①,②都对;
B 、①对,②错;
C 、①错,②对;
D 、①,②都错;
二、填空题
6、如图2,△ABC 中,∠B=60º,AC=3cm ,则△ABC 的外接圆半径为 。
7、如图3,△ABC 中,∠ACB=65º,BD ⊥AC 于D ,CE ⊥AB 于E ,则∠AED= ,∠CED= 。
8、如图4,△ABC 中,AD 是∠BAC 的平分线,延长AD 交△ABC 的外接圆于E ,已知AB=a ,BD=b ,BE=c ,则AE= ,DE = 。
9
、如图5,正方形ABCD 的中心为O ,面积为19892cm ,P 为正方形内一点,且∠OPB=45º,PA :
PB =5:14,则PB= 。
10、如图6,四边形ABCD 内接于以AD 为直径的圆中,若AB 和BC 的长度各为1,
72CD =,那么AD= 。
三、解答题
11、如图7,在△ABC 中,AD 为高线,DE ⊥AB 于E ,DF ⊥AC 于F 。
求证:B 、C 、F 、E 四点共圆。
图1图5图4图3图2图6
12、如图9, AB 为圆的直径,AD 、BC 为圆的两条弦,且BD 与AC 相交于E 。
求证:AC ·AE+BD ·BE=AB 2。
13、如图,圆O 的直径为5,在圆O 上位于直径AB 的异侧有定点C 和动点P ,已知BC :CA =4:3,点P 在半圆弧AB 上运动(不与A 、B 两点重合),过点C 作CP 的垂线CD 交PB 的延长线于D 点.
(1)求证:AC ·CD=PC ·BC ;
(2)当点P 运动到AB 弧中点时,求CD 的长;
图9
A
(3)当点P运动到什么位置时,△PCD的面积最大?并求出这个最大面积S。
