第四章北航 材料力学 全部课件 习题答案
工程力学--材料力学北京科大东北大学版第4版习题答案
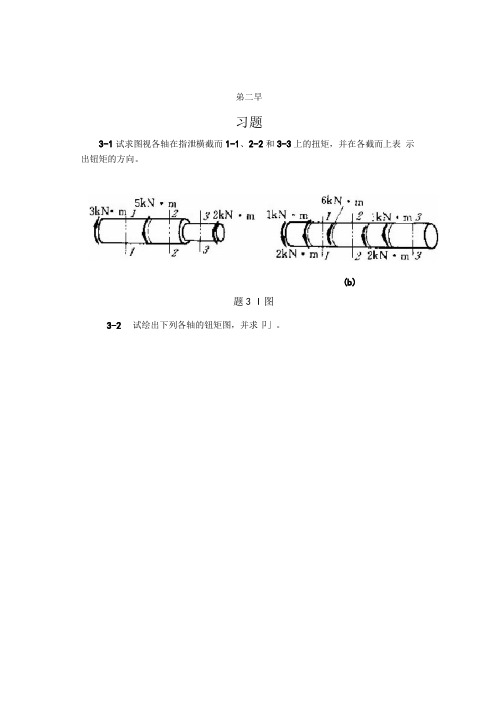
弟二早习题3-1试求图视各轴在指泄横截而1-1、2-2和3-3上的扭矩,并在各截而上表示出钮矩的方向。
(b)题3 I图3-2 试绘出下列各轴的钮矩图,并求卩」。
2mD cfr@=©=33-3 ma=2OON.m 9mb=4OON.m 9mc=6OON 9m. (b)3-4 一传动轴如图所示,已知 ma=130N ・・cm, mb=300N.cm, mc=i, md=70N.cm;^段轴的直径分别为:Dab=5cm, Dbc=7.5cm, Dcd=5cm(1) 画出扭矩图;(2) 求1 •仁2・2、3・3截而的最大切应力。
3-5图示的空心圆轴,外径D=8cm,内径d=6.25cm,承受扭矩m=1000N.m. (1) 求(2) 绘出横截面上的切应力分布图: (3)求单位长度扭转角,已知G=80000Mpa.3-6已知变截而钢轴上的外力偶矩^=1800N.m, Wf=1200N.m,试求最大切应力和最大相对扭矩。
已知G=80dbpa ・3M试绘下列各轴的扭矩(a)题3-6图3-7 一钢轴的转矩n=240/min.传递功率^=44.1kN.m.已知[^=40Mpa,=1W,6=80*MPa,试按强度和冈帔条件汁算轴的直径解:轴的直径由强度条件确左,rf>60-7wn o3-8图示实心轴通过牙嵌离合器把功率传给空心轴。
传递的功率ft=7.5kw,轴的转速n=100r/min,试选择实心轴直径占和空心轴外径“。
已知%心入5,题L8图3-9图示AB轴的转速n=120r/min,从B轮上输入功率丹=40kw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传疋。
已知锥齿轮的节圆直径=600mm:各轴直径为^-=100111111, “=80mm, “=60fnfn, KLzOlWPa,试对各轴进行强度校核。
3-10船用推进器的轴,一段是实心的,直径为280mm,另一段是空心的,其内径为外径的一半。
《材料力学》第四篇课后习题参考答案

反思与改进
不足之处
在解题过程中,我发现自己在 某些知识点上还存在理解不够 深入的问题,需要进一步加强 学习。
改进方向
在未来的学习中,我将更加注 重理论与实践的结合,通过更 多的实际案例来加深对知识点 的理解。
学习计划调整
针对自己的不足之处,我将制 定更为详细的学习计划,加强 针对性的练习和复习,以提高 自己的学习效果。
总结词
考虑非线性效应
详细描述
本题目需要考虑非线性效应对结构性能的影响,如大变形 、塑性变形等,需要运用材料力学的基本理论,对这些非 线性效应进行分析和计算。
总结词
结合实际工程背景
详细描述
本题目需要结合实际工程背景,对结构进行详细的分析和 设计。需要考虑实际工程中的各种因素,如施工条件、环 境因素等,以确保结构的可靠性和安全性。
这种方法需要熟练掌握 材料力学的基本概念和 公式,对问题的理解要 深入,能够准确判断和 选择适用的公式。
解析方法二
01
图解法
02
图解法
03
图解法
04
图解法
解析方法三
数学解析法
数学解析法是通过建立数学模型,将实际问题转 化为数学问题,利用数学工具进行求解。
•·
这种方法需要具备较高的数学水平,能够建立准 确的数学模型,并选择适当的数学方法进行求解 。
05
总结与反思
学习总结
80%
知识掌握情况
通过完成课后习题,我深入理解 了材料力学中的基本概念和原理 ,掌握了解决实际问题的基本方 法。
100%
解题能力提升
通过不断练习和反思,我提高了 自己的解题能力和思维逻辑性, 能够更加熟练地运用所学知识解 决复杂问题。
材料力学第四版课后答案课件

02 材料力学基础知识
CHAPTER
详细描述
材料力学是工程学科中的一门基础学科,主要研究材料在力作用下的行为,包括材料的 变形、断裂、疲劳等。对于工程师来说,了解材料力学的基本原理和知识是必不可少的
,因为这些原理和知识被广泛应用于各种工程领域,如建筑、机械、航空航天等。
材料力学的基本假设与原理
总结词
材料力学基于一些基本假设和原理,如连续性、均匀 性、各向同性等,通过这些假设和原理来描述材料的 力学行为。
材料力学第四版课后答案课件
目录
CONTENTS
• 材料力学概述 • 材料力学基础知识 • 材料力学基本分析方法 • 材料力学中的能量方法 • 材料力学的应用实例 • 材料力学第四版课后答案解析
01 材料力学概述
CHAPTER
材料力学的定义与重要性
总结词
材料力学是研究材料在力作用下变形、破坏和恢复的学科,对于工程设计和安全至关重 要。
材料力学的发展历程
• 总结词:材料力学的发展经历了多个阶段,从最早的实验观察到现代的数值模拟和智能化技术应用。
• 详细描述:材料力学的发展历程可以追溯到古代,当时的人们通过实践经验积累了一些关于材料性质的认识。然而,真正的材料力学研究始于18世纪,当时的一些科学家开始系统地研 究材料的力学行为。随着科学技术的发展,材料力学的研究也不断深入,涉及到更广泛的应用领域。现代的材料力学研究已经与数学、物理、化学等多个学科交叉融合,形成了许多新 的研究方向和应用领域。同时,随着计算机技术和数值模拟方法的快速发展,现代的材料力学研究也更加依赖于计算机模拟和智能化技术。这些技术的发展为材料力学的研究提供了更 广阔的空间和更深入的认识。
详细描述
材料力学的研究基于一些基本假设和原理。连续性假 设认为材料可以被看作连续的介质,而不是由单个原 子或分子组成。均匀性假设则认为在材料的宏观尺度 上,材料的性质是均匀的,不会因位置的不同而有所 变化。是相同的,不会因方向的不同而有所变化。这些 基本假设和原理为材料力学的研究提供了基础。
北航材料力学课后习题答案

σ max = 117MPa (在圆孔边缘处)
2-15 图示桁架,承受载荷 F 作用,已知杆的许用应力为[σ ]。若在节点 B 和 C 的
位置保持不变的条件下,试确定使结构重量最轻的α 值(即确定节点 A 的最佳位置)。
解:1.求各杆轴力
题 2-15 图
设杆 AB 和 BC 的轴力分别为 FN1 和 FN2 ,由节点 B 的平衡条件求得
分别为
FN
=
1 2
σmax A
=
1 2
× (100 ×106 Pa) × (0.100m × 0.040m)
=
2.00 ×105 N
=
200kN
Mz
=
FN
(
h 2
−
h )
3
=பைடு நூலகம்
1 6
FN h
=
1 × (200 ×103 N) × (0.100m) 6
= 3.33×103 N ⋅ m
=
3.33kN ⋅ m
2-5 .........................................................................................................................................................2
= 0.2 ×10−3 m 0.100m
= 2.00 ×10−3
rad
α AB
= 0.1×10−3 m = 1.00 ×10−3 0.100m
rad
得 A 点处直角 BAD 的切应变为
γ A = γ BAD = α AD − α AB = 1.00 ×10−3 rad
材料力学第四章习题选及其解答.docx

4-1. 试求图示各梁中截面1、2、3上的剪力和弯矩,这些截面无限接近于截面C或D 。
设p 、q 、a 均为已知。
解:(c )(1)截开1截面,取右段,加内力(22112322qaa qa a P M qaqa P Q -=⨯-⨯-==+=(3)截开2截面,取右段,加内力(4)求内力2222122qaM a qa a P M qaqa P Q -=+⨯-⨯-==+=(d )(1)求约束反力N R N R D A 300 100==(2)截开1截面,取左段,加内力(d)B(f)B(c)M=qa 2M M M=qa 2B(3)求1截面内力NmR M N R Q A A 202.010011-=⨯-=-=-=(4)截开2截面,取左段,加内力(5)求2截面内力NmR M N R Q A A 404.010022-=⨯-=-=-=(6)截开3截面,取右段,加内力(7)求3截面内力NmP M N P Q 402.020023-=⨯-===(f )(1)求约束反力qa R qa R D C 25 21==(2)截开1截面,取左段,加内力Q 1M 12BMB(3)求1截面内力2112121 qa a qa M qa Q -=⨯-=-=(4)截开2截面,取右段,加内力(5)求2截面内力222223qa M a P M qaR P Q D -=-⨯=-=-= 4-3. 已知图示各梁的载荷P 、q 、M0和尺寸a 。
(1)列出梁的剪力方程和弯矩方程;(2)作剪力图和弯矩图;(3)确定∣Q ∣max 和∣M ∣max 。
q(c)M 0=qa 2 (d)(f)(e) (g)q(h)1BM (a)(b) Bq解:(a )(1)求约束反力Pa M P R A A == 2(2)列剪力方程和弯矩方程⎪⎩⎪⎨⎧∈=-⨯-+⨯=∈-=+⨯=⎩⎨⎧∈=-=∈==),0[ )(2)(],0( 2)(]2,( 02)(),0( 2)(2222211111222111a x Pa a x P M x R x M a x Pa Px M x R x M a a x P R x Q a x P R x Q A A A A A A (3)画Q 图和M 图(4)最大剪力和最大弯矩值(i)q(j)BP=20kN(l)q(k)qM xxPa M P Q ==max max 2(b )(1)求约束反力223 qa M qa R B B ==(2)列剪力方程和弯矩方程⎪⎪⎩⎪⎪⎨⎧∈-⨯-=∈-=⎩⎨⎧∈-=∈-=)2,[ )2()(],0[ 21)()2,[ )(],0[ )(2222121112221111a a x a x qa x M a x qx x M a a x qa x Q a x qx x Q (3)画Q 图和M 图(4)最大剪力和最大弯矩值2maxmax 23 qa M qa Q == (c )(1)求约束反力qBxxqM 0=qa 2M2 2qa M qa R A A ==(2)直接画Q 图和M 图(3)最大剪力和最大弯矩值2max max 2qa M qa Q ==(d )(1)求约束反力P R R B A == 0(2)直接画Q 图和M 图(3)最大剪力和最大弯矩值Pa M P Q ==max maxxxxx。
材料力学-北京交通大学-4章答案
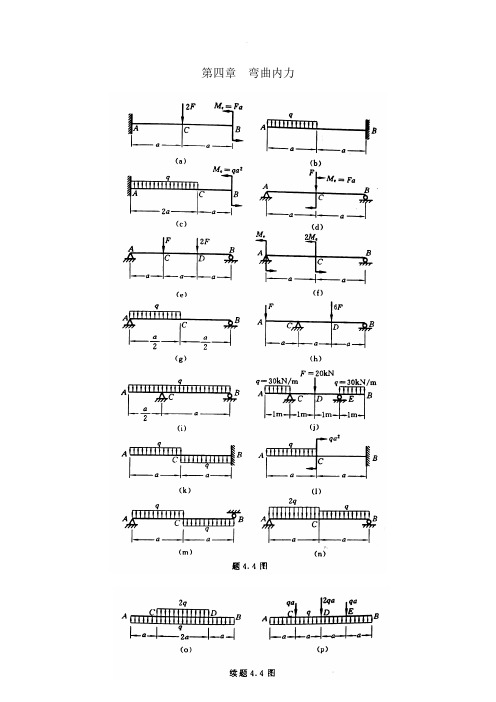
第四章弯曲内力4.4 设已知题4.4图(a)~(p)所示各梁的载荷 F 、q 、e M 和尺寸a ,(1)列出梁的剪力方程和弯矩方程;(2)作剪力图和弯矩图;(3)确定maxSF 及max M 。
解:(a)如题4.4图(a)所示。
剪立如题4.4图(a 1)所示坐标系。
(1)列剪力方程和弯矩方程。
应用题4.1(a)解法二提供的列剪力方程和弯矩方程的方法。
AC 段 ()()20S F x F x a =<<()()()20M x F x a x a =-<≤CB 段 ()()02S F x a x a =≤≤()()2M x Fa a x a =≤<(2)作剪力图、弯矩图,如题4.4图(a 2)所示。
(3)梁的最大剪力和弯矩为max2SF F =, max M Fa =(b) 如题4.4图(b)所示。
解法同4.4(a)。
剪立题4.4图(b 1)所示坐标系。
(1)列剪力方程和弯矩方程。
AC 段 ()()0S F x qx x a =-≤≤()()2102M x qx x a =-≤≤CB 段 ()()2S F x qa a x a =-≤<()()22a M x qa x a x a ⎛⎫=--≤< ⎪⎝⎭(2) 作剪力图、弯矩图,如题4.4图(b 2)所示。
(3) 梁的最大剪力和弯矩为maxSF qa =, 2max32Mqa =(c) 如题4.4图(c)所示。
解法同4.4(a)。
剪立题4.4图(c 1)所示坐标系。
(1)列剪力方程和弯矩方程。
CB 段 ()()023S F x a x a =≤≤()()223M x qa a x a =≤<AC 段 ()()()202S F x q a x x a =-<≤()()()2212022M x q a x qa x a =--+<≤(2) 作剪力图、弯矩图,如题4.4图(c 2)所示。
第四章北航的材料力学全部课件习题答案

第四章 扭 转4-5 一受扭薄壁圆管,外径D = 42mm ,内径d = 40mm ,扭力偶矩M = 500N •m ,切变模量G =75GPa 。
试计算圆管横截面与纵截面上的扭转切应力,并计算管表面纵线的倾斜角。
解:该薄壁圆管的平均半径和壁厚依次为mm 122 mm 5.20)22(210=-==+=d D d D R δ,于是,该圆管横截面上的扭转切应力为189.4MPa Pa 10894.1m001.00.02052πN 500π282220=⨯=⨯⨯==δτR T 依据切应力互等定理,纵截面上的扭转切应力为 MPa 4.189=='ττ 该圆管表面纵线的倾斜角为rad 102.53rad 1075104.189396-⨯=⨯⨯==G τγ 4-7 试证明,在线弹性范围内,且当R 0/δ≥10时,薄壁圆管的扭转切应力公式的最大误差不超过4.53%。
解:薄壁圆管的扭转切应力公式为δR Tτ20π2=设βδR =/0,按上述公式计算的扭转切应力为3220π2π2δβTδR T τ== (a)按照一般空心圆轴考虑,轴的内、外直径分别为 δR D δR d +=-=002 2,极惯性矩为 )4(2π])2()2[(32π)(32π2200404044p δR δR δR δR d D I +=--+=-=由此得)14(π)12()2()4(π)2(23022000p max ++=++=+=ββδβδδδT R R R TδR I T τ (b)比较式(a)与式(b),得)12(214)12()14(ππ222332max++=++⋅=ββββββδδβT Tττ 当100==δβR 时,9548.0)1102(10211042max=+⨯⨯⨯+⨯=ττ可见,当10/0≥δR 时,按薄壁圆管的扭转切应力公式计算τ的最大误差不超过4.53%。
4-8 图a 所示受扭圆截面轴,材料的γτ-曲线如图b 所示,并可用mC /1γτ=表示,式中的C 与m 为由试验测定的已知常数。
(完整版)材料力学课后习题答案
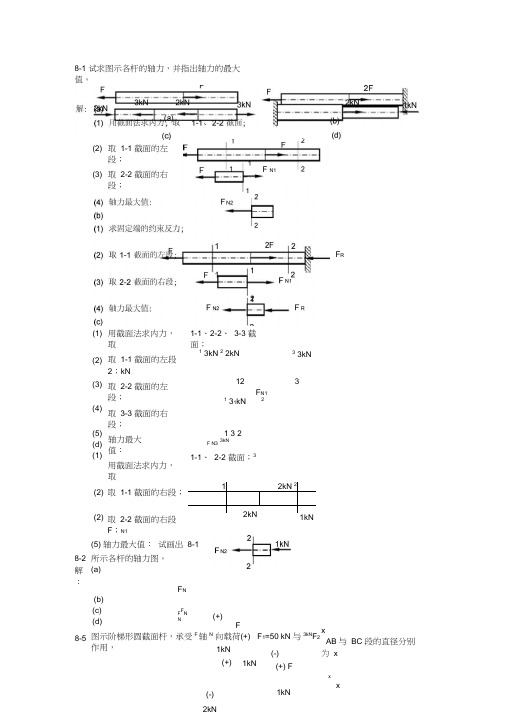
xx8-1 试求图示各杆的轴力,并指出轴力的最大值。
取 1-1 截面的左段;(2) (3) F N1取 2-2 截面的右段;F R用截面法求内力,取1-1、2-2、 3-3 截面;(1) (2) (3) (4)(5)(d)(1)取 1-1 截面的左段2;kN 取 2-2 截面的左段;取 3-3 截面的右段;轴力最大值: 用截面法求内力,取13kN 2 2kN33kN12 3F N11 31kN 21 32 F N33kN1-1、 2-2 截面;38-2 解:8-5 (2) (2) 取 1-1 截面的右段; 取 2-2 截面的右段F ;N112kN 22kN(5) 轴力最大值: 试画出 8-1所示各杆的轴力图。
(a) (b) (c) (d)F NF FN N(+)F图示阶梯形圆截面杆,承受F 轴N 向载荷(+) F 1=50 kN 与3kNF 2作用, 1kN (+) 1kN(-)(+) Fx AB 与 BC 段的直径分别为 x (-)1kN2kNd 1=20 mm 和 d 2=30 mm ,如欲使 AB 与 BC 段横截面上的正应力相同,试求载荷 F 2 之值。
(2) 求 1-1、 2-2 截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷 F=10 kN 作用,杆的横截面面积 A=1000 mm 2,粘接面的方位 角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
l 1l 2解: (1) 用截面法求 AB 、 BC 段的轴力;(2) 分段计F 算个杆向变形;FAC 杆缩短。
2F8-22 图示桁架,杆 1与A 杆 2的横截面面积与材料均相B 同,在节点 A 处承受C 载荷 F 作用。
从解: 8-6 解: (1) 用截面法求出 F 11-1、2-2 截面的轴力;(2) 求 1-1、 2-2 截面的正应A 力 ,利用正应力相B 同 ;题 8-5 图所示圆截面杆,已知载荷 1F 1=200 kN ,F 2=1020 kN ,CAB 段的直径 d 1=40 mm ,如 欲使 AB 与 BC 段横截面上的正应力相同,试求 BC 段的直径。
工程力学材料力学第四完整版本习题答案解析
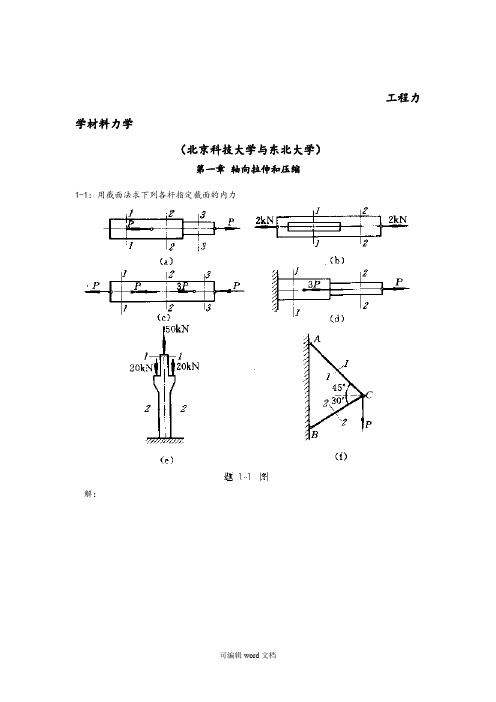
工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
北航材料力学课件-第四章 扭转

shaft
tube
0.1mm 500mm
2 104
由物理方程:
shaft tube 2 104
E E shaft
tube
l
,
由平衡方程(设想沿横截面截开): A tube tube A shaft shaft 0
Atube : Ashaft 6
tube 4.67MPa, shaft 28MPa
第四章 扭转
本章主要研究: 圆截面轴的扭转应力与变形 圆截面轴的扭转强度与刚度 矩形等非圆截面轴扭转 薄壁截面轴扭转
Page 9
第四章 扭转
§4-1 引言
工程中的扭转问题 下图:汽车传动轴
上图:扭转实验机
Page10
扭转实例
第四章 扭转
F F
Page11
第四章 扭转
A
M
B
M M
归纳与比较: 1、由实例归纳受扭圆轴的外力与变形特征; 2、与拉压杆比较。
A:
2M
D3
,
16
M
B :
D3
14
16
max
Page43
第四章 扭转
4、刚度校核
m 2M a
A
BM
3M
dD
a
a
a
a
x
T
M
T 2M x a
B
2M
A
x
max
max
A:
2M
GD4
,
注意
32
单位换算
M
B :
D4G
14
32
max
设计轴,可按 , 分别设计,取较大者
Page40
第四章 扭转
北航材力课件第四章
x
3、强度校核
T W p m ax
d D a a a a
AB,CD段为危险段
2M A: 3 D 16 M B : D 3 (1 4 ) 16
T A B
C 2M D M
max max
x
A
A
d G dx
A
2dA T
定义
A
2 dA I P
极惯性矩
圆轴扭转角变化率
d T dx GI P
Page14
BUAA
MECHANICS OF MATERIALS
d G dx
d T dx GI P
圆轴扭转剪应力一般公式
T IP
分布:与 成正比
M 2M M
T l GI P
M l1 M l 2 GI P GI P
m
mx dx 0 GI P
l
x
Page29
BUAA
MECHANICS OF MATERIALS
圆轴扭转刚度条件
M 2M M
M l1 M l 2 GI P GI P
工程实际中,通常是限制扭转角沿轴线的变化率。 许用扭转角变化率: []
作业:3-14, 3-18, 3-20
Page35
BUAA
MECHANICS OF MATERIALS
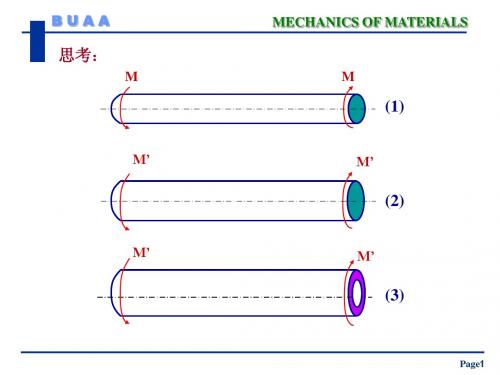
思考:
M M
(1)
M’
M’
(2)
M’ M’
(3)
Page1
BUAA
MECHANICS OF MATERIALS
本 讲 内 容
§3-4 §3-5 §3-6 §3-7 圆轴扭转横截面上的应力 极惯性矩与抗扭截面系数 圆轴扭转破坏与强度条件 圆轴扭转变形与刚度计算
材料力学第四章作业答案

材料力学第四章作业答案-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII4-1 试作下列各轴的扭矩图。
(a)(b)4-4 图示圆截面空心轴,外径D=40mm ,内径d=20mm ,扭矩m kN T ⋅=1,试计算mm 15=ρ的A 点处的扭矩切应力A τ以及横截面上的最大和最小的扭转切应力。
解:P A I T ρς= )1(3244απ-=D I p 又mm 20d = D=40mm 5.0==∴Dd α 41244310235500)5.01(32)1040(14.3m I p --⨯=-⨯⨯⨯= MPa Pa I T P A 7.63107.6310235500101510161233=⨯=⨯⨯⨯⨯==∴--ρτ P W T =max τ 9433431011775)5.01(16)1040(14.3)1(16--⨯=-⨯⨯⨯=-=απD W P a Pa W T P MP 9.84109.841011775101693max=⨯=⨯⨯==∴-τ 当2'd =ρ时 MPa Pa I T P 4.42104.4210235500101010161233'min =⨯=⨯⨯⨯⨯==--ρτ4-6 将直径d=2mm ,长l=4m 的钢丝一端嵌紧,另一端扭转一整圈,已知切变模量G=80GPa ,试求此时钢丝内的最大切应力m ax τ。
解:r G ⋅=τ dx d R r R ϕ⋅=∴ R=mm d 12= 3331057.1414.321012101---⨯=⨯⨯⨯=⨯⨯=⋅=∴l dx d R r R πϕ MPa Pa r G 6.125106.1251057.11080639=⨯=⨯⨯⨯=⋅=∴-τ(方法二:πϕ2=, l=4 ,P GI Tl =ϕ ,324d I P π=,rIp W p = ,l Gd W T P πτ==max )4-7 某钢轴直径d=80mm ,扭矩m kN T ⋅=4.2,材料的许用切应力MPa 45][=τ,单位长度许用扭转角m /)(5.0][ =θ,切变模量G=80GPa ,试校核此轴的强度和刚度。
工程力学材料力学第四版(北京科技大学与东北大学)习题答案重点

工程力学材料力学(北京科技大学与东北大学)第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解:(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注(轴向拉伸为正,压缩为负)1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解:σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。
解:下端螺孔截面:σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面:σ2=2P S =8.72MPa 上端双螺孔截面:σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4:一桅杆起重机如图所示,起重杆AB为一钢管,其外径D=20mm,内径d=18mm;钢绳CB的横截面面积为0.1cm2。
已知起重量P=2000N,试计算起重机杆和钢丝绳的应力。
解:受力分析得:F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5:图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:QNl lEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9:用一板状试样进行拉伸试验,在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
北航材料力学-习题集解-【全答案】(52页)
— 61 —
F Nx
dx
C
M dM
FNx dFNx
(b)
M C 0 , M dM M pdx
h 0 2
∴
ph dM dx 2
2-7
| M | max 。
试作 2-6 题中梁的轴力图和弯矩图, 并确定 | FNx | max 和
FN
l
x
pl
解: | FNx | max pl (固定端)
习题 2-4 图
( ql )
C
A
B
M 5 4
Fy 0 , FRA
M C FRB
1 ql (↓) , 4
1 1 l ql l ql 2 (+) 4 4
(a-1)
(b-1)
M A ql 2
A
M 2
C
D
E
M 2
B
M 2
M
A
C
1 4
B
M
3
— 59 —
| M | max
(d) M B 0
3 2 ql 2 1 ql l 0 2
( gl)
D
l
(c)
(d)
FRA 2l q 3l
FRA
FQ
FQ
( gl)
1.25
5 ql (↑) 4
A
B
1
C
A
(c-1)
D
B
0.75
C
1
3 Fy 0 , FRB ql (↑) 4 q MB 0 , MB l2 2 25 2 ql MD 0, MD 32 5 | FQ | max ql 4 25 2 | M | max ql 32 (e) Fy 0 ,FRC = 0 3 l M C 0 , ql l ql M C 0 2 2
工程力学--材料力学(北京科大、东北大学版)第4版4-6习题答案
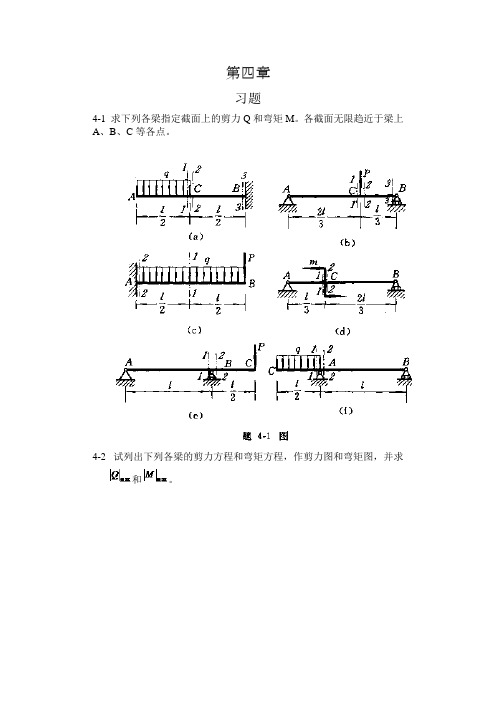
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
4-2 试列出下列各梁的剪力方程和弯矩方程,作剪力图和弯矩图,并求和。
4-3 用叠加法作以下各梁的弯矩图。
并求出。
4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
4-5 不列剪力方程和弯矩方程,作以下各梁的剪力图和弯矩图,并求出和。
4-6 用合适的方法作下列各梁的剪力图和弯矩图。
4-7 试根据载荷、剪力图和弯矩图之间的关系,检查下列各梁的剪力图和弯矩图是否正确,并对错误之处加以改正。
4-8 作下列构件的内力图。
4-9 在梁上行走的小车二轮的轮压均为P ,如图所示。
问小车行至何位置时梁内的弯矩最大?最大弯矩值是多少?设小车的轮距为c,大梁的跨度为。
参考答案4-1 解:题(b)(1)求支反力(见图)由,l-P l=0 =由,(2)剪力按计算剪力的规则(3)弯矩按计算弯矩的规则其它各题的答案:(a)(c)(d)(e)(f)4-2 解:题c(1)剪力和弯矩方程以左端A为原点,任一截面距左端的距离为x(图)\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图(3)与值由及得=200N =950题(f)(1)求支反力(见图)由,600-1004040=0=由,q4020-60=0=校核:+=2667+1333=4000N=q40=10040 所以支反力计算正确(2)剪力和弯矩方程以左端为原点,任一截面距左端的距离为x,则得剪力方程:弯矩方程(2)剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由,即剪力的条件求得Q(x)=3333-100x=0x=33.3cm(4)及由及得=2667N ,=355其他各题的答案:(a)=ql =(b)(d)(e)(g)(h)(i)(j)4-3 解:题c分别作、q单独作用时的弯矩图(图、),然后将此二图叠加得总的弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(
d 1/ m (3m 1)T ) d dx 2πCm( ) ( 3m 1) / m 2
(e)
将式(e)代入式(b),并注意到 T=M ,最后得扭转切应力公式为
M 1/ m 2πm d (3 m 1)/m ( ) 3m 1 2 横截面上的切应力的径向分布图示如图 4-8。
R0
此管不是薄壁圆管。
D 80 6 mm 37mm, δ 6mm R0 10 2 2
80- 6 2 68 0.85 80 80
max2
由此得 M 的许用值为
M2 16M 2 [ 2 ] Wp2 πD 3 (1 4 )
[M 2 ]
第四章 扭 转
4-5
一受扭薄壁圆管,外径 D = 42mm,内径 d = 40mm,扭力偶矩 M = 500N•m,切
变模量 G=75GPa。试计算圆管横截面与纵截面上的扭转切应力,并计算管表面纵线的倾斜角。 解:该薄壁圆管的平均半径和壁厚依次为
1 D d D d R0 ( ) 20.5mm, 1mm 2 2 2 2 2 于是,该圆管横截面上的扭转切应力为 T 500N 1.894108 Pa 189.4MPa 2 2 2 2πR0 2π 0.0205 0.001m
式中的 C 与 m 为由试验测定的已知常数。试建立扭转切应力公式,并画横截面上的切应力分
题 4-8 图 解:所研究的轴是圆截面轴,平面假设仍然成立。据此,从几何方面可以得到
d dx 根据题设,轴横截面上距圆心为 ρ 处的切应力为
(a)
τ ρ C(
由静力学可知,
d 1/ m ) dx
2
T T 0 2 2
M y 0,Fz
8Tl 8Tl 0 3πd 3πd 4Tl 4Tl M z 0,Fy4 l Fy3 l 3πd 3πd 0 l Fx1 (2ez1 )
既然是力偶系,力的平衡方程(共三个)自然满足,这是不言而喻的。 上述讨论中,所有的 T 在数值上均等于 M 。
设 Fy3 作用线到竖向半径 O1E 的距离为 e z2 (见图 b) ,由
Fy3 ez2
得
d /2 3 T π/2 2 cos d d T 0 0 Ip 8
ez 2
T 3πd 3πd 0.295d 8 4T 32
同理,可算出另半个右端面 O1FE 以及左端面 AOB、OCB 上的竖向分布内力的合力为
T (2 1) T δ T ( R0 ) (2 R0 ) 2 2 Ip 2 πR0 (4 R0 ) π 3 (4 2 1)
τ max
(b)
比较式(a)与式(b),得
τ τ max
当
T 2π 2
3
π 3 (4 2 1) 4 2 1 T (2 1) 2 (2 1)
1 d 4Tl Fx1 τ max ( l) 2 2 2 πd
同理,得截面 OCFO1 上分布内力的合力为
Fx2
方向示如图 c。
4Tl πd 2
设 Fx1 与Fx2 作用线到 x 轴线的距离为 ez1 ,容易求出
2 d d ez1 3 2 3 根据图 b,可算出单元体右端面上水平分布内力的合力为
Fy4 Fy1 Fy2
4T 3πd
方向均示如图 c。它们的作用线到所在面竖向半径的距离均为 e z2 。 由图 c 可以看得很清楚,该单元体在四对力的作用下处于平衡状态,这四对力构成四个 力偶,显然,这是一个空间力偶系的平衡问题。
M x 0,Fy
4
(2ez2 ) Fz2 e y Fy1 (2ez2 ) Fz1 e y
M A M B 2M A 2M
即
M A MB M
(b)解:此为静不定轴,可解除右端约束,代之以支反力偶矩 M B ,示如图 4-21b。
依据
d T ( x ) 4M dx GI p Gπ (d A cx)3
得截面 A 和 B 间的扭转角为
cx) 2M (d A cx) 2 | l0 3 0 πGδc A cx)
l
2Ml 1 1 2Ml (d A d B ) ( 2 2 ) 2 πGδ (d B d A ) d B d A πGδd 2 A dB
ey
T 3πd 3πd 0.295d 4 8T 32
同理, Fz1 作用线到水平直径 AC 的距离也同此值。 根据图 b,还可算出半个右端面 DO1 E 上竖向分布内力的合力为
Fy3
π / 2 d / 2 Tρ
0
0
Ip
π 4T sin( θ ) ρdρ dθ 2 3πd
3.72 108 Pa 372MPa
结论: max [ ] ,该弹簧满足强度要求。
4-20
图示圆锥形薄壁轴 AB,两端承受扭力偶矩 M 作用。设壁厚为,横截面 A 与
B 的平均直径分别为 dA 与 dB,轴长为 l,切变模量为 G。试证明截面 A 和 B 间的扭转角为
A/ B
d1
3
16ml π[τ ]
(a)
BC 段上的最大扭矩在截面 B 处,其值为
Tmax2 ml2
由该截面的扭转强度条件得
d2
2.最轻重量设计 轴的总体积为
3
16ml2 π[τ ]
16ml2 2 / 3 π π 2 π 16ml 2 / 3 V d12 (l l2 ) d 2 l2 [( ) (l l 2 ) ( ) l2 ] 4 4 4 π[τ ] π[τ ]
πD 3 (1 4 )[ 2 ] π 0.0803 (1 0.854 ) 40 106 Nm 16 16 1.922103 N m 1.922kN m
可见,扭力偶矩 M 的许用值为
[ M ] [ M 2 ] 1.922kN m
4-13
图示阶梯形轴,由 AB 与 BC 两段等截面圆轴组成,并承受集度为 m 的均匀分
4-11
如图所示,圆轴 AB 与套管 CD 用刚性突缘 E 焊接成一体,并在截面 A 承受扭
力偶矩 M 作用。圆轴的直径 d = 56mm,许用切应力[ 1 ]=80MPa,套管的外径 D = 80mm,壁 厚 = 6mm,许用切应力[ 2 ]= 40MPa。试求扭力偶矩 M 的许用值。
R0
10 时,
max
4 102 1 0.9548 2 10 (2 10 1)
1
可见,当 R0 / δ 10 时,按薄壁圆管的扭转切应力公式计算 τ 的最大误差不超过 4.53%。
4-8
布图。
图 a 所示受扭圆截面轴,材料的 曲线如图 b 所示,并可用 C 1/ m 表示,
7
4-21
为已知常数。
图示两端固定的圆截面轴,承受扭力偶矩作用。试求支反力偶矩。设扭转刚度
题 4-21 图 (a)解:此为静不定轴,但有对称条件可以利用。 设 A 与 B 端的支反力偶矩分别为 M A和M B ,它们的转向与扭力偶矩 M 相反。由于左右 对称,故知
M A MB
由 M x 0 可得
2 Ml (d A d B ) 2 2 πG d A dB
题 4-20 图 证明:自左端 A 向右取坐标 x ,轴在 x 处的平均半径为
d dA 1 1 R0 ( x ) (d A B x ) (d A cx) 2 l 2
式中,
c
截面 x 的极惯性矩为
d B d A l
1 πδ 3 I p 2πR0 2π [ (d A cx)]3 (d A cx)3 2 4
D = 40mm,弹簧丝的直径 d = 7mm,许用切应力[ ]= 480MPa,试校核弹簧的强度。
6
m
故需考虑曲率的影响,此时,
D 40 5.71 10 d 7
max
8FD(4m+2) 8 1.00 103 0.040 (4 5.71 2)N πd 3 (4m 3) π 0.0073 (4 5.71 3)m2
根据极值条件
dV 0 dl2
得
(
由此得
16ml 2/3 16m 2/3 5 2 / 3 ) ( ) l2 0 π[ ] π[ ] 3
3 l2 ( ) 3/2 l 0.465l 5
从而得
(b)
3 l1 l l2 [1 ( ) 3/2 ]l 0.535l 5
Fz2
同理,左端面上的合力为
π d /2 T
0 0
π 8T cos( θ ) ρdρdθ Ip 2 3πd
8T 3πd
Fz1
方向亦示如图 c。
设 Fz2 作用线到水平直径 DF 的距离为 e y (见图 b) ,由
3
Fz2 e y
得
T Ip
0 cos
π
2
d /2 π T ( )d 3d 0 2 4
布的扭力偶矩作用。为使轴的重量最轻,试确定 AB 与 BC 段的长度 l1 与 l2 以及直径 d1 与 d2。 已知轴总长为 l,许用切应力为[ ]。
题 4-13 图
5
解:1.轴的强度条件 在截面 A 处的扭矩最大,其值为
Tmax1 ml
由该截面的扭转强度条件
max1
得
Tmax1 16ml [τ ] Wp1 πd13
依据切应力互等定理,纵截面上的扭转切应力为 τ τ 189.4MPa 该圆管表面纵线的倾斜角为
