正交试验表查询 比较全
常用的正交实验表

常用的正交实验表正交实验表是一种用于设计实验的工具,它可以帮助研究人员在尽可能少的试验次数内获得尽可能多的信息。
正交实验表的设计基于正交性原则,即每个因素的变化都是独立的,不会对其他因素产生影响。
常用的正交实验表有L9、L12、L16、L18等。
L9正交实验表是一种常用的正交实验表,它包含9个试验点,可以用于研究3个因素的影响。
L9实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现3次,保证了每个因素的变化都是独立的。
使用L9实验表进行实验时,研究人员需要确定3个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L12正交实验表是一种包含12个试验点的正交实验表,可以用于研究4个因素的影响。
L12实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现4次,保证了每个因素的变化都是独立的。
使用L12实验表进行实验时,研究人员需要确定4个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L16正交实验表是一种包含16个试验点的正交实验表,可以用于研究4个因素的影响。
L16实验表的设计基于正交性原则,每个因素有4个水平,每个水平都出现4次,保证了每个因素的变化都是独立的。
使用L16实验表进行实验时,研究人员需要确定4个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L18正交实验表是一种包含18个试验点的正交实验表,可以用于研究5个因素的影响。
L18实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现6次,保证了每个因素的变化都是独立的。
使用L18实验表进行实验时,研究人员需要确定5个因素和它们的水平,然后按照实验表中的设计进行实验。
正交试验常用表

正交试验常用表正交试验是一种常用的试验设计方法,用于研究多个因素对实验结果的影响。
在进行正交试验时,需要使用正交试验表来安排实验方案。
正交试验表是根据正交设计原理编制的一种表格,能够全面、均匀地考察各个因素对结果的影响,从而减少试验次数,提高试验效果。
正交试验表通常由因素列和水平列组成。
因素列是指需要研究的各个因素,如温度、压力、时间等,而水平列则是指每个因素的不同水平,如高、中、低。
通过在因素列和水平列中选择相应的因素和水平,可以建立适合实验的正交试验表。
正交试验表的编制有一定的规则和原则。
首先,正交试验表应该保证各个因素和水平之间的均衡性。
也就是说,每个因素的每个水平应该尽可能地出现在不同的试验中,以避免因素之间的相互影响。
其次,正交试验表应该考虑到可重复性。
也就是说,同一个试验应该能够进行多次,以验证结果的可信度。
最后,正交试验表还需要考虑到实验的实际可行性和经济性。
也就是说,试验的次数和条件应该在可接受范围内,以避免过多的资源浪费。
正交试验表的应用范围非常广泛。
在工业生产中,正交试验表可以用于选择最佳的工艺参数,优化生产工艺,提高产品质量和产量。
在科学研究中,正交试验表可以用于探究各个因素对研究结果的影响,从而提出新的理论或解释现象。
在市场调研中,正交试验表可以用于确定消费者对产品的喜好和需求,为产品开发提供依据。
正交试验表的使用需要注意一些问题。
首先,正交试验表只能用于研究定量因素,而不能用于研究定性因素。
其次,正交试验表只能提供各个因素对结果的主要影响,而不能提供因素之间的相互作用效应。
最后,正交试验表只能作为一种初步的试验设计方法,需要结合实际情况进行调整和改进。
总之,正交试验表是一种非常实用的试验设计工具,能够全面、均衡地考察各个因素对结果的影响。
在进行正交试验时,我们需要根据实际情况选择合适的正交试验表,并注意表格的均衡性、可重复性和可行性。
通过合理地利用正交试验表,我们可以减少试验次数,提高试验效果,从而为工业生产、科学研究和市场调研提供可靠的依据。
正交试验常用表

正交试验常用表
正交试验常用表是一种用来设计和分析实验的工具。
它通过系统地变化不同因素的水平,来观察它们对实验结果的影响。
正交试验常用表有助于减少实验的数量和复杂度,同时提高实验结果的可靠性和可解释性。
在正交试验常用表中,每一行代表一个试验条件,每一列代表一个因素的水平。
通过选择正交试验常用表中的特定行和列,可以确定每个试验条件下因素水平的组合。
这样,只需进行少量试验即可覆盖所有可能的因素组合,节省了时间和资源。
正交试验常用表的设计原则是互斥性和均衡性。
互斥性要求每个试验条件下,每个因素只有一个水平发生变化,以确保因素之间的效应能够独立评估。
均衡性要求每个因素的每个水平在试验条件中出现的次数相等,以避免因素间的偏倚。
正交试验常用表的设计需要考虑实验目标和因素的数量。
通常,我们希望能够观察到每个因素的主效应和交互效应,因此需要选择合适的正交试验常用表。
例如,如果有3个因素,我们可以选择一个L9正交试验常用表,其中每个因素有3个水平,每个水平出现3次。
在进行正交试验时,需要按照正交试验常用表中的设计进行实验,并记录实验结果。
然后,通过统计分析方法,如方差分析,来评估因素对实验结果的影响,并确定主效应和交互效应。
正交试验常用表在工程、制造和科学研究等领域广泛应用。
它可以帮助研究人员确定最佳的工艺参数、产品设计和优化方案,以提高产品质量和效率。
正交试验常用表是一种有效的实验设计工具,它可以帮助研究人员减少实验数量和复杂度,提高实验结果的可靠性和可解释性。
通过合理选择和应用正交试验常用表,可以更好地设计和分析实验,以促进科学研究和工程应用的发展。
常用正交试验计算表_显著性判断及表头安排等

0
0
0
0
C
A×C
L4
L5
1
1
2
2
1
1
2
2
1
2
2
1
1
2
2
1
B×C L6 1 2 2 1 1 2 2 1
-
-
-
-
-
L7
L8
L9
L10
L11
1
2
2
1
2
1
1
2
8
8
8
8
0
0
0
0
15.3 14.8
14.9
15
0
0
0
0
14.5
15
14.9
14.8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
234.09 219.04 222.01
L3
4
4
2
3
12
1#
8
3#
2
2
1
1
B
A×B
L2
L3
1
1
1
1
2
2
2
2
1
2
1
2
2
1
2
1
L n(m
结果1 kij^2 结果1^2
Qj=
1 r
m Kij2
i=1
n
T= x i
i=1
CT
T2 n
n
QT=
x
2 i
正交试验设计常用的正交表

16
221211221 1 2 1 2 2 1
精彩文档
实用标准文案
L16(215)二列间的交互作用表
精彩文档
实用标准文案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14
(2) 1 6
4 5 10 11 8 9 14 15 12 13
B
(A×B)1 C×D
(A×B)2
(A×B)3
C
(A×C)1 B×D
B
(A×B)1 C×D
(A×B)2 C×E
(A×B)3
C
(A×C)1 B×D
9
10
11
12
13
3
(A×C)2 (A×C)3 B×C
4
(A×C)2
(A×C)3
B×C (A×D)1
D
(A×D)3 (A×D)2
5
(A×C)2 B×E
(A×C)3
1
1111111111111
2
1111122222222
3
1222211112222
4
1222222221111
5
2112211221122
6
2112222112211
7
2221111222211
8
2221122111122
9
3121212121212
10
3121221212121
11
3212112122121
1
2
3
4
5
6
7
列
列
号
号
(1) 3
正交试验设计常用正交表

(1) L 4(23)列123号试 验号 1 1 1 12 1 2 23 2 1 24221随意两列间的交互作用为此外一列。
(2) L 8(2 7)列1234567 号试1 1 1 1 1 1 验号 11 21 1 12 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 1 72 2 1 1 2 2 1 82212112L 8(2 7) 二列间的交互作用表1234567列列号3 2 64 7 6 号( 1)( 2)1 5 7 4 5 ( 3)7 6 5 4 ( 4)1 2 3( 5)3 2( 6)1 ( 7)L8(2 7) 表头设计因列号子数 2 3 4 5 6 13 A B A × B C A ×C B × C4 A BA × BCA ×CB × CC× D B × D A × D4 ABA × BCA ×CDC×D B× D B × CA B A × B C A ×CD5 A × ED× E C×D C× E B× D B ×EB × C(3) L 8(4 ×24)列号试验1 2 3 4 5号1 1 1 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 18 4 2 1 1 2 L8(4 ×2 4) 表头设计因列号子数 2 3 4 512 A B (A× B)1 (A ×B)2 (A ×B) 33 A B C4 A B C D5 A B C D E7DA ×DEA ×D(4) L 12 (2 11)列1 2 3 4 5 6 7 8 9 10 11 号试验1 1 1 1 1 1 1 1 1 1 1号12 1 1 1 1 1 2 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 110 2 2 2 1 1 1 1 2 2 1 211 2 2 1 2 1 2 1 1 1 2 212 2 2 1 1 2 1 2 1 2 2 1 (5) L 16 (2 15)列1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 号试验号11 1 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 1 1 2 2 2 2 2 2 2 23 1 1 1 2 2 2 2 1 1 1 1 2 2 2 24 1 1 1 2 2 2 2 2 2 2 2 1 1 1 15 1 2 2 1 1 2 2 1 1 2 2 1 1 2 26 1 2 2 1 1 2 2 2 2 1 1 2 2 1 17 1 2 2 2 2 1 1 1 1 2 2 2 2 1 18 1 2 2 2 2 1 1 2 2 1 1 1 1 2 29 2 1 2 1 2 1 2 1 2 1 2 1 2 1 210 2 1 2 1 2 1 2 2 1 2 1 2 1 2 111 2 1 2 2 1 2 1 1 2 1 2 2 1 2 112 2 1 2 2 1 2 1 2 1 2 1 1 2 1 213 2 2 1 1 2 2 1 1 2 2 1 1 2 2 114 2 2 1 1 2 2 1 2 1 1 2 2 1 1 215 2 2 1 2 1 1 2 1 2 2 1 2 1 1 216 2 2 1 2 1 1 2 2 1 1 2 1 2 2 1L16 (2 15 ) 二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14(2) 1 6 4 5 10 11 8 9 14 15 12 13(3) 7 6 5 4 11 10 9 8 15 14 13 12(4) 1 2 3 12 13 14 15 8 9 10 11(5) 3 2 13 12 15 14 9 8 11 10(6) 1 14 15 12 13 10 11 8 9(7) 15 14 13 12 11 10 9 8(8) 1 2 3 4 5 6 7(9) 3 2 5 4 7 6(10) 1 6 7 4 5(11) 7 6 5 4(12) 1 2 3(13) 3 2(14) 1L16 (2 15 ) 表头设计15413121111987654321数号列子因EE F××C BE×AEF×BD D D F××××C C C AEE×CD D D E××××B B B AD D DE F××× × ×A A AB CD D DE×DC C C F××××B B B EC C C F××××A A A DC C CB B B E××××A A A DB B BA A A4 5 6E F G E F G H× × ×× ×× ×C B A C B A DG GF FD F G D F G H× × ×× ×× ×C A A C A A EE ED E G D E G H× × ×× ×× ×B AC B A C FD E F D E F H× × ×× ×× ×A B C A B C GD DHC F G C F G H× × ×× ×× ×B E D B E D AC F G C F G H× × ×× ×× ×A D E A D E BC CB E G B E G H× × ×× ×× ×A D F A D F CB BA A7 8(6) L 16 (4 ×212)列1 2 3 4 5 6 7 8 9 10 11 12 13 号试验号11 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 2 2 23 1 2 2 2 2 1 1 1 1 2 2 2 24 1 2 2 2 2 2 2 2 2 1 1 1 15 2 1 1 2 2 1 1 2 2 1 1 2 26 2 1 1 2 2 2 2 1 1 2 2 1 17 2 2 2 1 1 1 1 2 2 2 2 1 18 2 2 2 1 1 2 2 1 1 1 1 2 29 3 1 2 1 2 1 2 1 2 1 2 1 210 3 1 2 1 2 2 1 2 1 2 1 2 111 3 2 1 2 1 1 2 1 2 2 1 2 112 3 2 1 2 1 2 1 2 1 1 2 1 213 4 1 2 2 1 1 2 2 1 1 2 2 114 4 1 2 2 1 2 1 1 2 2 1 1 215 4 2 1 1 2 1 2 2 1 2 1 1 216 4 2 1 1 2 2 1 1 2 1 2 2 1L16 (4 ×212 )表头设计因列号子数 1 2 3 4 5 6 73 A B (A ×B) 1 (A× B)2 (A ×B)3 C (A ×C)14 A B(A ×B) 1(A× B)2 (A ×B)3 C(A ×C)1C× D B× D5 A B(A ×B) 1 (A× B)2(A ×B)3 C(A ×C)1C× D C× E B× D因列号子数8 9 10 11 12 133 (A × C)2 (A × C)3 B × C4 (A × C)2 (A × C)3B × CD (A ×D) 3 (A×D) 2(A×D)1(A × C)2 B × C D E (A × E)15 (A × C)3 (A×D)1B× E (A ×E)3 (A ×D) 3 (A×D) 2(A × E)229列试验号 12345678910111213141516 (8) L 16 (4 3×26)1 2 3 4 5 6 7 8 9 10 11号1 1 1 1 1 1 1 1 1 111 2 1 1 1 2 2 2 2 2 21 32 2 2 1 1 1 2 2 21 42 2 2 2 2 2 1 1 12 1 1 2 2 1 2 2 1 2 22 2 1 2 2 2 1 1 2 1 12 3 2 1 1 1 2 2 2 1 12 4 2 1 1 2 1 1 1 2 23 1 2 1 2 2 1 2 2 1 23 2 2 1 2 1 2 1 1 2 13 3 1 2 1 2 1 2 1 2 13 4 1 2 1 1 2 1 2 1 24 1 2 2 1 2 2 1 2 2 14 2 2 2 1 1 1 2 1 1 24 3 1 1 2 2 2 1 1 1 24 4 1 1 2 1 1 2 2 2 1123456789列试验号号 1 1 1 1 1 1 1 1 1 12 1 2 2 1 1 2 2 2 23 1 3 3 2 2 1 1 2 24 1 4 4 2 2 2 2 1 15 2 1 2 2 2 1 2 1 26 2 2 1 2 2 2 1 2 17 2 3 4 1 1 1 2 2 18 2 4 3 1 1 2 1 1 29 3 1 3 1 2 2 2 2 110 3 2 4 1 2 1 1 1 211 3 3 1 2 1 2 2 1 212 3 4 2 2 1 1 1 2 113 4 1 4 2 1 2 1 2 214 4 2 3 2 1 1 2 1 115 4 3 2 1 2 2 1 1 116 4 4 1 1 2 1 2 2 2(9) L 16 (4 4×23)列试验号 12345678910111213141516 (10) L16 (45)试验号1 2 3 4 5 6 7号1 1 1 1 1 111 2 2 2 1 2 21 3 3 32 1 21 4 4 42 2 12 1 23 2 2 12 2 1 4 2 1 22 3 4 1 1 2 22 43 2 1 1 13 1 34 1 2 23 24 3 1 1 13 3 1 2 2 2 13 4 2 1 2 1 24 1 4 2 2 1 24 2 3 1 2 2 14 3 2 4 1 1 14 4 1 3 1 2 2 列1 2 3 4 51号1 1 1 112 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2(11) L16 (8×28)列1 2 3 4 5 6 7 8 9号试验号 1 1 1 1 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 210 5 2 1 2 1 2 1 2 111 6 1 2 1 2 2 1 2 112 6 2 1 2 1 1 2 1 213 7 1 2 2 1 1 2 2 114 7 2 1 1 2 2 1 1 215 8 1 2 2 1 2 1 1 216 8 2 1 1 2 1 2 2 1 (12) L20 (219)列1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 号试1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 验1 1号2 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 13 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 24 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 25 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 16 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 17 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 28 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 29 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 210 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 211 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 112 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 213 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 114 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 215 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 116 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 117 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 118 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1(13) L9 (34)试验号(14) L18 (2×37)列试验号号123456789101112131415161718 列1 2 3 4号1 1 1 112 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 8 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 1 1 3 3 3 3 3 3 1 2 1 1 2 2 3 3 1 2 2 2 3 3 1 1 1 2 3 3 1 1 2 2 1 3 1 2 1 3 2 3 1 3 2 3 2 1 3 11 3 3 1 32 1 22 1 13 3 2 2 1 2 1 2 1 1 3 3 2 2 1 3 2 2 1 1 3 2 2 1 2 3 1 3 2 2 2 2 3 1 2 1 3 2 2 3 1 2 3 2 1 2 3 1 3 2 3 1 2 2 3 2 1 3 1 2 3 2 3 3 2 1 2 3 1(15) L 27 (3 13)列号试 1 2 3 4 5 6 7 8 9 10 11 12 13 验号1 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2 L27 (3 13 )表头设计因列号子数 1 2 3 4 5 63 A B (A ×B) 1 (A× B)2 C (A ×C) 14 A B(A ×B) 1(A× B)2 C(A ×C) 1(C×D) 2 (B×D)2因列号子数8 9 10 11 12 133 (B ×C)1 D (A×D)1 (B × C)2 (B×D)1 (C× D) 14(B ×C)1(A×D)1 (B × C)2(A × D)27(A ×C)2(A ×C)2L27 (3 13 ) 二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1)3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)111(16) L25 (56)1 2 3 4 5 6列 1 1 1 1 1 11试号验号2 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 310 2 5 1 2 3 411 3 1 3 5 2 412 3 2 4 1 3 513 3 3 5 2 4 114 3 4 1 3 5 215 3 5 2 4 1 316 4 1 4 2 5 317 4 2 5 3 1 418 4 3 1 4 2 519 4 4 2 5 3 120 4 5 3 1 4 221 5 1 5 4 3 222 5 2 1 5 4 323 5 3 2 1 5 424 5 4 3 2 1 525 5 5 4 3 2 1(17) L32 (231)1 3 0 3 92 8 2 7 2 6 2 5 2 4 23 2 2 2 1 2 0 2 9 1 8 1 7 1 6 1 5 14 1 3 1 2 1 1 1 0 1 9 8 7 65 4 3 2 1 2 2 1 2 1 1 2 2 1 1 2 1 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 1 2 2 1 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 1 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 21 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1号号1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6验列1 1 1 1 1 1 1试。
正交试验设计常用正交表

正交试验设计常用正交表1) 试验编号:1、2、3、4任意两列间的交互作用为另外一列。
2) 试验编号:1、2、3、4、5、6、7、8二列间的交互作用表:1列2号-3号2列3号-2号3列2号-1号4列6号-5号5列4号-7号6列7号-6号7列5号-4号3) 试验编号:1、2、3、4、5表头设计:列号因子数1.A2.B3.A×B4.C5.A×C4) 试验编号:1、2、3、4、5表头设计:列号因子数1.A2.B3.(A×B)14.(A×B)25.(A×B)36.E5) 试验编号:1、2、3、4、5、6、7、8、9 5) L___.215) n TableIn this table。
the numbers in the first row and first column represent the ns of the columns being analyzed。
The numbers in the cells ___.It is important to note that some of the paragraphs in the original text are missing or ___。
it is difficult to rewrite them without more n。
However。
the remaining paragraphs ___ clarity:Paragraph 1: ___.Paragraph 2: The numbers in the first row and first column represent the ns of the columns being analyzed。
The numbers in the cells ___.Paragraph 3: It is important to note that some of the paragraphs in the original text are missing or ___。
三因素两水平正交试验表

三因素两水平正交试验表
咱们先来说说什么是因素呢?就好比你做三明治,面包、火腿和蔬菜就是因素。
那什么是水平呢?比如说面包有白面包和全麦面包这两种,这就是面包这个因素的两个水平啦。
火腿呢,有普通火腿和烟熏火腿,这也是两个水平。
蔬菜有生菜和黄瓜,这同样是两个水平。
比如说,我们班有个小组要做一个小实验。
他们想知道不同的土壤(因素一,水平是沙质土和黏质土)、不同的浇水频率(因素二,水平是每天浇一次水和三天浇一次水)、不同的光照时长(因素三,水平是6小时光照和12小时光照)对小植物生长的影响。
要是他们一个一个去试所有的组合,那要花费好多时间和精力呢。
可是有了这个正交试验表,就简单多啦。
这个表就像一个小清单,告诉他们按照一定的顺序去做实验就好。
就像按照一个特殊的食谱做点心一样。
他们按照这个表做实验,很快就得到了一些结果。
比如说,在沙质土、每天浇一次水、6小时光照的情况下,小植物长得还不错。
在黏质土、三天浇一次水、12小时光照的时候,植物的生长又有不同的情况。
通过这个正交试验表,他们不需要试完所有的8种组合,就能大概知道哪些因素对植物生长的影响比较大啦。
就像你在玩搭积木。
你有不同形状的积木(这就是因素),每种形状还有不同的颜色(这就是水平)。
你想搭出一个最漂亮又最稳固的城堡。
如果没有一个好的方法,你就只能乱搭一通。
但是有了类似正交试验表这样的方法,你就可以有计划地去搭,很快就能找到搭出好城堡的诀窍啦。
四因素四水平正交试验表

四因素四水平正交试验表(Four Factors Four Levels Orthogonal Array)是一种试验设计方法,它能够通过设计合适的试验方案,有效地筛选出影响目标因素的关键因素,并确定其最佳组合条件,以提高产品的质量和效率。
在传统试验设计中,需要考虑多个因素对目标变量的影响,这些因素之间可能存在相互作用,同时每个因素又有多个水平需要考虑。
这种情况下,要确定每个因素的最佳水平组合,需要进行大量的试验,耗费时间和人力成本较高。
而利用进行试验设计,可以通过少量的试验数据就能够得出每个因素的最佳水平组合,从而实现精细化的试验设计。
是基于正交阵理论和组合设计理论建立的试验设计方法。
正交阵是一种特殊的矩阵,具有平衡和等距的特性,能够将多个因素的不同水平进行“配对”,使得每个因素的不同水平都能够在试验中进行充分的观察和比较,从而确定最佳的因素水平组合。
通过进行试验设计,需要先确定试验的目标变量和试验因素。
确定试验因素时需要考虑可能的相互作用,以及可能存在的高低优势。
然后根据正交阵的原理,选择适合的正交试验表,安排试验方案。
在试验过程中,需要进行数据采集和分析,根据分析结果确定每个因素的最佳水平组合。
最终得到的结果可以用于优化产品设计、提高生产效率和优化工艺流程。
是一种高效精准的试验设计方法,能够大大缩短试验周期,降低试验成本,提高试验效果。
它不仅在工业领域得到广泛应用,在医学、环境保护、社会科学等领域也有着重要的应用价值。
总之,是一种经典的试验设计方法,利用它可以快速有效地确定最佳因素的水平组合,从而实现有效优化产业的实现,是科学技术领域的重要工具。
正交试验设计表

正交试验设计表
正交试验设计表是一种有效的实验设计方法,可以在最小的试验次数下,系统地研究多个因素对试验结果的影响。
该表包含由正交数组组成的矩阵,每个数组表示一个试验组合。
通过对每个试验组合进行实验,可以分析不同因素之间的相互作用,确定最优的试验条件。
下面是一个简单的正交试验设计表示例:
| 因素/水平 | A1 | A2 | A3 | B1 | B2 |
| --- | --- | --- | --- | --- | --- |
| C1 | 1 | 1 | 2 | 2 | 2 |
| C2 | 2 | 2 | 1 | 1 | 2 |
| C3 | 1 | 2 | 1 | 2 | 1 |
在上表中,因素A有3个水平,因素B有2个水平,因素C有3个水平。
通过正交试验设计表,可以生成15个试验组合,每个组合包含一个因素A的水平、一个因素B的水平和一个因素C的水平。
例如,第一组试验组合是A1B1C1,第二组试验组合是A1B1C2,以此类推。
在进行实验时,可以根据自己的需要选择其中的一部分或全部试验组合进行研究。
正交试验设计表是一种高效的实验设计方法,在工程、科学和医学等领域广泛应用。
通过合理地利用正交试验设计表,可以快速、准确地确定最佳试验方案,提高实验效率和成果质量。
- 1 -。
常用正交表对照图
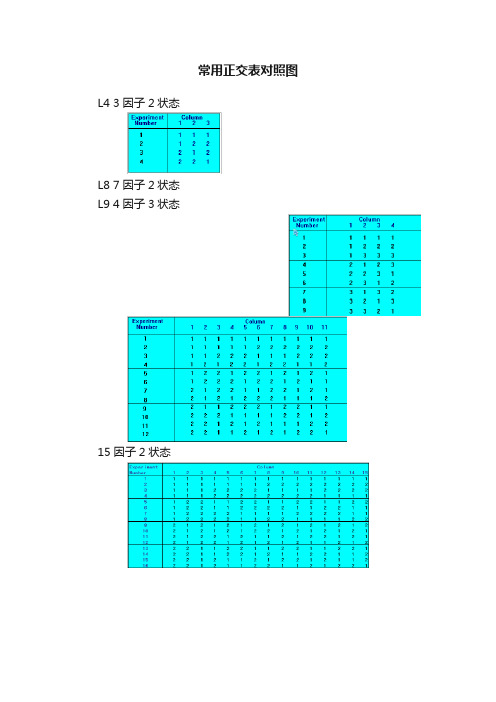
常用正交表对照图L4 3因子2状态L8 7因子2状态L9 4因子3状态15因子2状态1因子2状态和7因子3状态L18 7因子3状态7试验号\列号 1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 2 2 23 1 3 3 3 3 3 34 2 1 1 2 2 3 35 2 2 2 3 3 1 16 2 3 3 1 1 2 27 3 1 2 1 3 2 38 3 2 3 2 1 3 19 3 3 1 3 2 1 210 1 1 3 3 2 2 111 1 2 1 1 3 3 212 1 3 2 2 1 1 313 2 1 2 3 1 3 214 2 2 3 1 2 1 315 2 3 1 2 3 2 116 3 1 3 2 3 1 217 3 2 1 3 1 2 3183****3113因子3状态32因子两状态1因子2状态和11因子5状态1因子2状态和25因子3状态31因子2状态21因子4状态L18 6因子3状态和1因子6状态因子1 因子2 因子3 因子4 因子5 因子6 因子7 实验1 0 0 0 00 0 0 实验2 0 1 2 2 0 1 1 实验3 0 2 1 2 1 0 2 实验4 0 1 1 0 2 2 3 实验5 0 2 0 1 2 1 4 实验6 0 0 2 1 1 2 5 实验7 1 1 1 1 1 1 0 实验8 1 2 0 0 1 2 1 实验9 1 0 2 0 2 1 2 实验10 1 2 2 1 0 0 3 实验11 1 0 1 2 0 2 4 实验12 1 1 0 2 2 0 5 实验13 2 2 2 2 2 2 0 实验14 2 0 1 1 2 0 1 实验15 2 1 0 1 0 2 2 实验16 2 0 0 2 1 1 3 实验17 2 1 2 0 1 0 4 实验18 2 2 1 0 0 1 5L8 4因子2状态和1因子4状态0 因子1 因子2 因子3 因子4 因子5实验1 1 1 1 1 1实验2 1 2 2 2 2实验3 2 1 1 2 2实验4 2 2 2 1 1实验5 3 1 2 1 2实验6 3 2 1 2 1实验7 4 1 2 2 1实验8 4 2 1 1 2L12 4因子2状态和1因子3状态L12(3×24)试验号\列号 1 2 3 4 51 1 1 1 1 12 1 1 1 2 23 1 2 2 1 24 1 2 2 2 15 2 1 2 1 16 2 1 2 2 27 2 2 1 2 28 2 2 1 2 29 3 1 2 1 210 3 1 1 2 111 3 2 1 1 212 3 2 2 2 1L12 2因子2状态和1因子6状态2试验号\列号 1 2 31 2 1 12 5 1 23 5 2 14 2 2 25 4 1 16 1 1 27 1 2 18 4 2 29 3 1 110 6 1 211 6 2 112 3 2 2L49 8因子7状态8试验号\列号 1 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 2 2 2 2 2 2 23 1 3 3 3 3 3 3 34 1 4 4 4 4 4 4 46 1 6 6 6 6 6 6 67 1 7 7 7 7 7 7 78 2 1 2 3 4 5 6 79 2 2 3 4 5 6 7 111 2 4 5 6 7 1 2 312 2 5 6 7 1 2 3 413 2 6 7 1 2 3 4 514 2 7 1 2 3 4 5 615 3 1 3 5 7 2 4 616 3 2 4 6 1 3 5 717 3 3 5 7 2 4 6 118 3 4 6 1 3 5 7 219 3 5 7 2 4 6 1 320 3 6 1 3 5 7 2 421 3 7 2 4 6 1 3 522 4 1 4 7 3 6 2 523 4 2 5 1 4 7 3 624 4 3 6 2 5 1 4 725 4 4 7 3 6 2 5 126 4 5 1 4 7 3 6 227 4 6 2 5 1 4 7 328 4 7 3 6 2 5 1 429 5 1 5 2 6 3 7 430 5 2 6 3 7 4 1 531 5 3 7 4 1 5 2 632 5 4 1 5 2 6 3 733 5 5 2 6 3 7 4 134 5 6 3 7 4 1 5 235 5 7 4 1 5 2 6 336 6 1 6 4 2 7 5 337 6 2 7 5 3 1 6 438 6 3 1 6 4 2 7 539 6 4 2 7 5 3 1 641 6 6 4 2 7 5 3 142 6 7 5 3 1 6 4 243 7 1 7 6 5 4 3 244 7 2 1 7 6 5 4 345 7 3 2 1 7 6 5 446 7 4 3 2 1 7 6 547 7 5 4 3 2 1 7 648 7 6 5 4 3 2 1 7L16 4因子4状态和3因子2状态列号1 2 3 4 5 6 7 试验号1 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 2。
