常用正交试验计算表_显著性判断及表头安排等
常用的正交实验表

常用的正交实验表正交实验表是一种用于设计实验的工具,它可以帮助研究人员在尽可能少的试验次数内获得尽可能多的信息。
正交实验表的设计基于正交性原则,即每个因素的变化都是独立的,不会对其他因素产生影响。
常用的正交实验表有L9、L12、L16、L18等。
L9正交实验表是一种常用的正交实验表,它包含9个试验点,可以用于研究3个因素的影响。
L9实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现3次,保证了每个因素的变化都是独立的。
使用L9实验表进行实验时,研究人员需要确定3个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L12正交实验表是一种包含12个试验点的正交实验表,可以用于研究4个因素的影响。
L12实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现4次,保证了每个因素的变化都是独立的。
使用L12实验表进行实验时,研究人员需要确定4个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L16正交实验表是一种包含16个试验点的正交实验表,可以用于研究4个因素的影响。
L16实验表的设计基于正交性原则,每个因素有4个水平,每个水平都出现4次,保证了每个因素的变化都是独立的。
使用L16实验表进行实验时,研究人员需要确定4个因素和它们的水平,然后按照实验表中的设计进行实验。
通过对实验结果的分析,研究人员可以确定每个因素对结果的影响以及它们之间的交互作用。
L18正交实验表是一种包含18个试验点的正交实验表,可以用于研究5个因素的影响。
L18实验表的设计基于正交性原则,每个因素有3个水平,每个水平都出现6次,保证了每个因素的变化都是独立的。
使用L18实验表进行实验时,研究人员需要确定5个因素和它们的水平,然后按照实验表中的设计进行实验。
正交试验常用表

正交试验常用表正交试验是一种常用的试验设计方法,用于研究多个因素对实验结果的影响。
在进行正交试验时,需要使用正交试验表来安排实验方案。
正交试验表是根据正交设计原理编制的一种表格,能够全面、均匀地考察各个因素对结果的影响,从而减少试验次数,提高试验效果。
正交试验表通常由因素列和水平列组成。
因素列是指需要研究的各个因素,如温度、压力、时间等,而水平列则是指每个因素的不同水平,如高、中、低。
通过在因素列和水平列中选择相应的因素和水平,可以建立适合实验的正交试验表。
正交试验表的编制有一定的规则和原则。
首先,正交试验表应该保证各个因素和水平之间的均衡性。
也就是说,每个因素的每个水平应该尽可能地出现在不同的试验中,以避免因素之间的相互影响。
其次,正交试验表应该考虑到可重复性。
也就是说,同一个试验应该能够进行多次,以验证结果的可信度。
最后,正交试验表还需要考虑到实验的实际可行性和经济性。
也就是说,试验的次数和条件应该在可接受范围内,以避免过多的资源浪费。
正交试验表的应用范围非常广泛。
在工业生产中,正交试验表可以用于选择最佳的工艺参数,优化生产工艺,提高产品质量和产量。
在科学研究中,正交试验表可以用于探究各个因素对研究结果的影响,从而提出新的理论或解释现象。
在市场调研中,正交试验表可以用于确定消费者对产品的喜好和需求,为产品开发提供依据。
正交试验表的使用需要注意一些问题。
首先,正交试验表只能用于研究定量因素,而不能用于研究定性因素。
其次,正交试验表只能提供各个因素对结果的主要影响,而不能提供因素之间的相互作用效应。
最后,正交试验表只能作为一种初步的试验设计方法,需要结合实际情况进行调整和改进。
总之,正交试验表是一种非常实用的试验设计工具,能够全面、均衡地考察各个因素对结果的影响。
在进行正交试验时,我们需要根据实际情况选择合适的正交试验表,并注意表格的均衡性、可重复性和可行性。
通过合理地利用正交试验表,我们可以减少试验次数,提高试验效果,从而为工业生产、科学研究和市场调研提供可靠的依据。
常用的正交表

正交表(Orthogonal Array)是一种设计实验的工具,特别适用于研究多因素对试验结果的影响。
正交表可以帮助科学家在有限的实验次数内获得较为全面的信息。
以下是一些常用的正交表:
1.L型正交表:
•L9:包含9个试验点,用于三因素的初步研究。
•L16:包含16个试验点,用于四因素的初步研究。
2.Taguchi正交表:
•L8:包含8个试验点,用于三因素的优化实验。
•L27:包含27个试验点,用于三因素的详细研究。
3.Plackett-Burman正交表:
•PB12:包含12个试验点,用于初步筛选12个因素中的重要因素。
•PB20:包含20个试验点,用于更多因素的初步筛选。
4.Box-Behnken正交表:
•3因素3水平的Box-Behnken正交表:用于优化实验,适用于三因素的研究。
5.中心合成法正交表:
•CCC-2:用于三因素的优化实验。
•CCC-3:用于四因素的优化实验。
6.格兰杰正交表:
•4水平格兰杰正交表:用于四因素的研究。
•5水平格兰杰正交表:用于五因素的研究。
7.斯坦纳正交表:
•S5:用于五因素的研究。
•S6:用于六因素的研究。
这些是一些常见的正交表,具体选择应根据实验设计的需要以及研究的因素数量来确定。
在设计实验时,科学家可以根据实际情况选择最适合的正交表,以达到经济高效地获取试验信息的目的。
常用正交试验计算表_显著性判断及表头安排等

8 14.5 15.3
0 0 210.25 234.09 0 0 54.15
60.15
0
0 29.8 111.005 114.3
8 12.4 17.4
0 0 153.76 302.76 0 0 38.52
75.78
0
0
8 14.9 14.9
0 0 222.01 222.01 0 0 57.67
56.63
SSj=Qj CT
Vj
SSj dfj
1、在因素 使用方法: 水平表填入
各水平 2、在正交 表中填入选 择的正交表 形式,常用 正交表在《 常用正交表 、交互作用 表、表头设 计》中选取 粘贴 3、填入试 验结果 4、在K值计 算区域输入 希望统计的 结果列名称 5、手工更 改MSE**的 计算与F判 据的两个自 由度选项 6、获得显 著与否的结 论 7、正交表 的使用及数 据处理参考 资料见上 图例说明: 不建议更改 的部分 需要判断, 更改的部分 根据需要更 改的部分
225
0
0
0
0
210.25 225
222.01 219.04
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
60.15 56.2
56.63
58.02
0
0
0
0
54.15 58.1
57.67
56.28
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
正交试验设计常用正交表
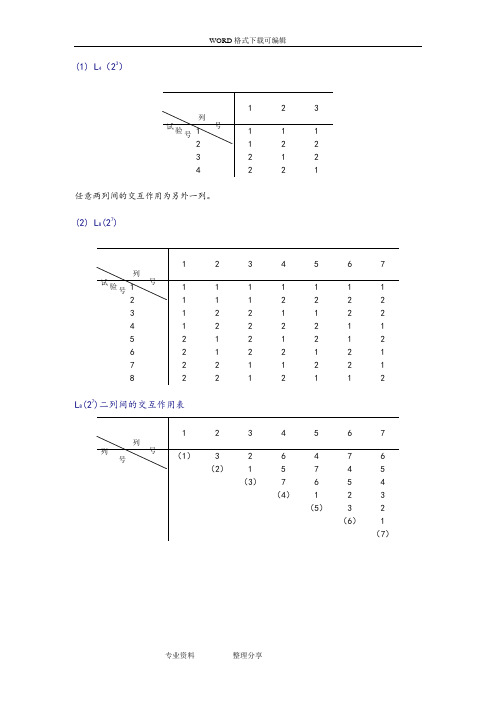
(1) L 4(23)任意两列间的交互作用为另外一列。
(2) L 8(27)L 8(27)二列间的交互作用表1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 22112 3 4 5 6 7 1 1 11 1 1 1 12 1 1 1 2 2 2 23 1 2 2 1 1 2 24 1 2 2 2 2 1 15 2 1 2 1 2 1 26 2 1 2 2 1 2 17 2 2 1 1 2 2 1 8221211212 3 4 5 6 7(1) 3 2 6 4 7 6 (2) 1 5 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1(7)列 号 试验 号列号试验 号列号列号L 8(27)表头设计1 2 3 4 5 6 7 3 A B A ×B C A ×C B ×C 4 A B A ×B C ×D C A ×C B ×D B ×C A ×D D 4 A B C ×D A ×B C B ×D A ×C D B ×C A ×D 5 A D ×EB C ×DA ×BC ×EC B ×DA ×CB ×ED A ×E B ×CE A ×D(3) L 8(4×24)L 8(4×24)表头设计1 2 3 4 52 A B (A ×B)1 (A ×B)2 (A ×B)3 3 A B C4 A B C D 5ABCDE1 2 3 4 5 1 11 1 1 12 1 2 2 2 23 2 1 1 2 24 2 2 2 1 15 3 1 2 1 26 3 2 1 2 17 4 1 2 2 1 842112列号因 子 数列号 试验 号列号因 子 数(4) L 12 (211)(5) L 16 (215)1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 1 21 1 1 1 12 2 2 2 2 23 1 1 2 2 2 1 1 1 2 2 24 1 2 1 2 2 1 2 2 1 1 25 1 2 2 1 2 2 1 2 1 2 16 1 2 2 2 1 2 2 1 2 1 17 2 1 2 2 1 1 2 2 1 2 18 2 1 2 1 2 2 2 1 1 1 29 2 1 1 2 2 2 1 2 2 1 1 10 2 2 2 1 1 1 1 2 2 1 2 11 2 2 1 2 1 2 1 1 1 2 2 122 2 1 1 2 1 2 1 2 2 11 2 3 4 5 6 7 8 9 10 11 12 13 14 151 1 1 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 1 1 2 2 2 2 2 2 2 23 1 1 1 2 2 2 2 1 1 1 1 2 2 2 24 1 1 1 2 2 2 2 2 2 2 2 1 1 1 15 1 2 2 1 1 2 2 1 1 2 2 1 1 2 26 1 2 2 1 1 2 2 2 2 1 1 2 2 1 17 1 2 2 2 2 1 1 1 1 2 2 2 2 1 18 1 2 2 2 2 1 1 2 2 1 1 1 1 2 29 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 10 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 11 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 12 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 13 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 14 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 15 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 162 2 1 2 1 1 2 2 1 1 2 1 2 2 1列号试验 号列号试验 号L16(215)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1 ) 3 2 5 4 769 8 11101312 15 14 (2)1 6 4510 11 891415 12 13(3)7 6 5411 10 981514 13 12(4)1 2312 13 14 15 89 10 11(5)3213 12 151498 11 10(6)114 15 12131011 8 9(7)15 14 13121110 9 8(8)1 234 5 67(9)325 4 76(10)16 7 45(11)7 6 54(12)1 23(13)32(14)1L 16(215)表头设计15EC ×E B ×FC ×E B ×F A ×GC ×E B ×F A ×GD ×H14 A ×EGG13 B ×E F F F 12 C ×D C ×D C ×D A ×FC ×D A ×F A ×GC ×D A ×F A ×GE ×H11 C ×E EEE10 B ×D B ×D B ×D A ×EB ×D A ×EC ×GB ×D A ×EC ×G F ×H9 A ×D A ×D A ×D B ×E C ×FA ×DB ×EC ×F A ×D B ×E C ×FG ×H 8 D D D D D7 D ×E H 6 B ×C B ×C B ×C E ×F B ×C E ×F D ×G B ×C E ×F D ×G A ×H5 A ×C A ×C A ×C D ×F A ×C D ×F E ×G A ×C D ×F E ×G B ×H 4 C C C C C 3A ×B A ×B A ×B D ×E A ×B D ×E F ×G A ×B D ×E F ×GC ×H2 B B BBB1 A A A A A 列号 因子数4 5 6 7 8(6) L16(4×212)L16 (4×212)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2(A×B)3 C (A×C)14 A B (A×B)1C×D(A×B)2(A×B)3 C(A×C)1B×D5 A B (A×B)1C×D(A×B)2C×E(A×B)3 C(A×C)1B×D8 9 10 11 12 13 3 (A×C)2(A×C)3B×C4 (A×C)2(A×C)3B×C(A×D)1D (A×D)3(A×D)25(A×C)2B×E(A×C)3B×C(A×D)1(A×E)2D(A×E)3E(A×D)3(A×E)1(A×D)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 2 2 23 1 2 2 2 2 1 1 1 1 2 2 2 24 1 2 2 2 2 2 2 2 2 1 1 1 15 2 1 1 2 2 1 1 2 2 1 1 2 26 2 1 1 2 2 2 2 1 1 2 2 1 17 2 2 2 1 1 1 1 2 2 2 2 1 18 2 2 2 1 1 2 2 1 1 1 1 2 29 3 1 2 1 2 1 2 1 2 1 2 1 210 3 1 2 1 2 2 1 2 1 2 1 2 111 3 2 1 2 1 1 2 1 2 2 1 2 112 3 2 1 2 1 2 1 2 1 1 2 1 213 4 1 2 2 1 1 2 2 1 1 2 2 114 4 1 2 2 1 2 1 1 2 2 1 1 215 4 2 1 1 2 1 2 2 1 2 1 1 216 4 2 1 1 2 2 1 1 2 1 2 2 1 列号试验号列号因子数列号因子数(8) L16 (43×26)1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 12 1 2 1 1 1 2 2 2 2 2 23 1 3 2 2 2 1 1 1 2 2 24 1 4 2 2 2 2 2 2 1 1 15 2 1 1 2 2 1 2 2 1 2 26 2 2 1 2 2 2 1 1 2 1 17 2 3 2 1 1 1 2 2 2 1 18 2 4 2 1 1 2 1 1 1 2 29 3 1 2 1 2 2 1 2 2 1 210 3 2 2 1 2 1 2 1 1 2 111 3 3 1 2 1 2 1 2 1 2 112 3 4 1 2 1 1 2 1 2 1 213 4 1 2 2 1 2 2 1 2 2 114 4 2 2 2 1 1 1 2 1 1 215 4 3 1 1 2 2 2 1 1 1 216 4 4 1 1 2 1 1 2 2 2 11 2 3 4 5 6 7 8 91 1 1 1 1 1 1 1 1 12 1 2 2 1 1 2 2 2 23 1 3 3 2 2 1 1 2 24 1 4 4 2 2 2 2 1 15 2 1 2 2 2 1 2 1 26 2 2 1 2 2 2 1 2 17 2 3 4 1 1 1 2 2 18 2 4 3 1 1 2 1 1 29 3 1 3 1 2 2 2 2 110 3 2 4 1 2 1 1 1 211 3 3 1 2 1 2 2 1 212 3 4 2 2 1 1 1 2 113 4 1 4 2 1 2 1 2 214 4 2 3 2 1 1 2 1 115 4 3 2 1 2 2 1 1 116 4 4 1 1 2 1 2 2 2列号试验号列号试验号(10) L16 (45)1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 21 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2列号试验号列号试验号(12) L 20 (219)12 3 4 5 6 7 8 9 1 1 11 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 2 10 5 2 1 2 1 2 1 2 1 11 6 1 2 1 2 2 1 2 1 12 6 2 1 2 1 1 2 1 2 13 7 1 2 2 1 1 2 2 1 14 7 2 1 1 2 2 1 1 2 15 8 1 2 2 1 2 1 1 2 168211212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 191 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 12 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 13 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 24 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 25 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 16 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 17 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 28 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 29 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 10 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 11 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 12 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 13 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 1 14 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 15 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 16 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 17 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 18 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 19 2 1 2 2 1 1 2 2 2 21 2 1 2 1 1 1 1 2 列号 试验 号列 号 试 验 号(13) L9 (34)(14) L18 (2×37)1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 1 2 2 2 2 2 23 1 1 3 3 3 3 3 34 1 2 1 1 2 2 3 35 1 2 2 2 3 3 1 16 1 2 3 3 1 1 2 27 1 3 1 2 1 3 2 38 1 3 2 3 2 1 3 19 1 3 3 1 3 2 1 210 2 1 1 3 3 2 2 111 2 1 2 1 1 3 3 212 2 1 3 2 2 1 1 313 2 2 1 2 3 1 3 214 2 2 2 3 1 2 1 315 2 2 3 1 2 3 2 116 2 3 1 3 2 3 1 217 2 3 2 1 3 1 2 318 2 3 3 2 1 2 3 1列号试验号列号试验号(15) L27 (313)L27 (313)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2 C (A×C)1(A×C)24 A B (A×B)1(C×D)2(A×B)2 C(A×C)1(B×D)2(A×C)28 9 10 11 12 13 3 (B×C)1 D (A×D)1(B×C)2(B×D)1(C×D)14(B×C)1(A×D)2(A×D)1(B×C)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2列号试验号列号因子数列号因子数L27 (313)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1 )3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)1111 2 3 4 5 61 1 1 1 1 1 12 1 2 2 2 2 23 1 3 3 3 3 34 1 4 4 4 4 45 1 5 5 5 5 56 2 1 2 3 4 57 2 2 3 4 5 18 2 3 4 5 1 29 2 4 5 1 2 3 10 2 5 1 2 3 4 11 3 1 3 5 2 4 12 3 2 4 1 3 5 13 3 3 5 2 4 1 14 3 4 1 3 5 2 15 3 5 2 4 1 3 16 4 1 4 2 5 3 17 4 2 5 3 1 4 18 4 3 1 4 2 5 19 4 4 2 5 3 1 20 4 5 3 1 4 2 21 5 1 5 4 3 2 22 5 2 1 5 4 3 23 5 3 2 1 5 4 24 5 4 3 2 1 5 255 5 4 3 2 1列 号 试验 号31122121122112122130122121122112122129122121121221211228122121121221211227 122112212112211226 1 22112212112211225 1 2 2 112211221122124 1 2 2 1 12211221122123 1 2 1 2 2 1 212121121222 1 2 1 2 2 1 2 12121121221 1 2 1 2 2 1 2 1 1212212120 1 2 1 2 2 1 2 1 1 2 12212119 1 2 1 2 1 2 1 2 2 1 2 1 212118 1 2 1 2 1 2 1 2 2 1 2 1 2 12117 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 16 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 15 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 14 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 13 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 12 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 11 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 10 1122112222112211 9 11221122112211228 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 7 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 6 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 21 1 1 1 1 1 1 12 2 2 2 2 2 2 2WORD 格式下载可编辑11111111111111111列号试验号12345678910111213141516。
正交试验设计常用的正交表

16
221211221 1 2 1 2 2 1
精彩文档
实用标准文案
L16(215)二列间的交互作用表
精彩文档
实用标准文案
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
(1) 3 2 5 4 7 6 9 8 11 10 13 12 15 14
(2) 1 6
4 5 10 11 8 9 14 15 12 13
B
(A×B)1 C×D
(A×B)2
(A×B)3
C
(A×C)1 B×D
B
(A×B)1 C×D
(A×B)2 C×E
(A×B)3
C
(A×C)1 B×D
9
10
11
12
13
3
(A×C)2 (A×C)3 B×C
4
(A×C)2
(A×C)3
B×C (A×D)1
D
(A×D)3 (A×D)2
5
(A×C)2 B×E
(A×C)3
1
1111111111111
2
1111122222222
3
1222211112222
4
1222222221111
5
2112211221122
6
2112222112211
7
2221111222211
8
2221122111122
9
3121212121212
10
3121221212121
11
3212112122121
1
2
3
4
5
6
7
列
列
号
号
(1) 3
正交试验设计常用正交表分析

选用正交表。
根据提供的因素和水平进行正交表的选择, 选择的方法为试验的水平作为正 交表的水平, 试验的各个因素小于或等于正交表的列数,表格中没有数据的项空掉即可。
可以数据公式分析影响因子,也可以软件表征结果(1) L 4(23)任意两列间的交互作用为另外一列(2) L 8(27)L 8(27)二列间的交互作用表1 2 3 1 1 1 1 2 1 2 2 3 2 1 2 4 2211 2 3 4 5 6 7 1 1 1 1 1 1 1 1 2 1 1 1 2 2 2 2 3 1 2 2 1 1 2 2 4 1 2 2 2 2 1 1 5 2 1 2 1 2 1 2 6 2 1 2 2 1 2 1 7 2 2 1 1 2 2 1 822121121 2 3 4 5 6 7(1) 3 2 6 4 7 6 (2) 1 5 7 4 5 (3) 7 6 5 4 (4) 1 2 3 (5) 3 2 (6) 1 (7)列号 试验 号 列号试验 号列号列号L 8(27)表头设计1 2 3 4 5 6 7 3 A B A ×B C A ×C B ×C 4 A B A ×B C ×D C A ×C B ×D B ×C A ×D D 4 A B C ×D A ×B C B ×D A ×C D B ×C A ×D 5 A D ×EB C ×DA ×BC ×EC B ×DA ×CB ×ED A ×E B ×CE A ×D(3) L 8(4×24)L 8(4×24)表头设计1 2 3 4 52 A B (A ×B)1 (A ×B)2 (A ×B)3 3 A B C4 A B C D 5ABCDE1 2 3 4 5 1 1 1 1 1 1 2 1 2 2 2 2 3 2 1 1 2 2 4 2 2 2 1 1 5 3 1 2 1 2 6 3 2 1 2 1 7 4 1 2 2 1 842112列号因 子 数列号试 验号列号因 子数(4) L 12 (211)(5) L 16 (215)1 2 3 4 5 6 7 8 9 10 11 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 2 2 2 2 3 1 1 2 2 2 1 1 1 2 2 2 4 1 2 1 2 2 1 2 2 1 1 2 5 1 2 2 1 2 2 1 2 1 2 1 6 1 2 2 2 1 2 2 1 2 1 1 7 2 1 2 2 1 1 2 2 1 2 1 8 2 1 2 1 2 2 2 1 1 1 2 9 2 1 1 2 2 2 1 2 2 1 1 10 2 2 2 1 1 1 1 2 2 1 2 11 2 2 1 2 1 2 1 1 1 2 2 12221121212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 6 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 7 1 2 2 2 2 1 1 1 1 2 2 2 2 1 1 8 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 9 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 10 2 1 2 1 2 1 2 2 1 2 1 2 1 2 1 11 2 1 2 2 1 2 1 1 2 1 2 2 1 2 1 12 2 1 2 2 1 2 1 2 1 2 1 1 2 1 2 13 2 2 1 1 2 2 1 1 2 2 1 1 2 2 1 14 2 2 1 1 2 2 1 2 1 1 2 2 1 1 2 15 2 2 1 2 1 1 2 1 2 2 1 2 1 1 2 16221211221121221列号试 验号 列号试 验 号L16(215)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13 14 15(1 ) 3 2 5 4 769 8 11101312 15 14 (2)1 6 4510 11 891415 12 13(3)7 6 5411 10 981514 13 12(4)1 2312 13 14 15 89 10 11(5)3213 12 151498 11 10(6)114 15 12131011 8 9(7)15 14 13121110 9 8(8)1 234 5 67(9)325 4 76(10)16 7 45(11)7 6 54(12)1 23(13)32(14)1L 16(215)表头设计15EC ×E B ×FC ×E B ×F A ×GC ×E B ×F A ×GD ×H14 A ×EGG13 B ×E F F F 12 C ×D C ×D C ×D A ×FC ×D A ×F A ×GC ×D A ×F A ×GE ×H11 C ×E EEE10 B ×D B ×D B ×D A ×EB ×D A ×EC ×GB ×D A ×EC ×G F ×H9 A ×D A ×D A ×D B ×E C ×FA ×DB ×EC ×F A ×D B ×E C ×FG ×H 8 D D D D D7 D ×E H 6 B ×C B ×C B ×C E ×F B ×C E ×F D ×G B ×C E ×F D ×G A ×H5 A ×C A ×C A ×C D ×F A ×C D ×F E ×G A ×C D ×F E ×G B ×H 4 C C C C C 3A ×B A ×B A ×B D ×E A ×B D ×E F ×G A ×B D ×E F ×GC ×H2 B B BBB1 A A A A A 列号 因子数4 5 6 7 8(6) L16 (4×212)L16 (4×212)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2(A×B)3 C (A×C)14 A B (A×B)1C×D(A×B)2(A×B)3 C(A×C)1B×D5 A B (A×B)1C×D(A×B)2C×E(A×B)3 C(A×C)1B×D8 9 10 11 12 13 3 (A×C)2(A×C)3B×C4 (A×C)2(A×C)3B×C(A×D)1D (A×D)3(A×D)25(A×C)2B×E(A×C)3B×C(A×D)1(A×E)2D(A×E)3E(A×D)3(A×E)1(A×D)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 1 2 2 2 2 2 2 2 23 1 2 2 2 2 1 1 1 1 2 2 2 24 1 2 2 2 2 2 2 2 2 1 1 1 15 2 1 1 2 2 1 1 2 2 1 1 2 26 2 1 1 2 2 2 2 1 1 2 2 1 17 2 2 2 1 1 1 1 2 2 2 2 1 18 2 2 2 1 1 2 2 1 1 1 1 2 29 3 1 2 1 2 1 2 1 2 1 2 1 210 3 1 2 1 2 2 1 2 1 2 1 2 111 3 2 1 2 1 1 2 1 2 2 1 2 112 3 2 1 2 1 2 1 2 1 1 2 1 213 4 1 2 2 1 1 2 2 1 1 2 2 114 4 1 2 2 1 2 1 1 2 2 1 1 215 4 2 1 1 2 1 2 2 1 2 1 1 216 4 2 1 1 2 2 1 1 2 1 2 2 1 列号试验号列号因子数列号因子数(8) L16 (43×26)1 2 3 4 5 6 7 8 9 10 111 1 1 1 1 1 1 1 1 1 1 12 1 2 1 1 1 2 2 2 2 2 23 1 3 2 2 2 1 1 1 2 2 24 1 4 2 2 2 2 2 2 1 1 15 2 1 1 2 2 1 2 2 1 2 26 2 2 1 2 2 2 1 1 2 1 17 2 3 2 1 1 1 2 2 2 1 18 2 4 2 1 1 2 1 1 1 2 29 3 1 2 1 2 2 1 2 2 1 210 3 2 2 1 2 1 2 1 1 2 111 3 3 1 2 1 2 1 2 1 2 112 3 4 1 2 1 1 2 1 2 1 213 4 1 2 2 1 2 2 1 2 2 114 4 2 2 2 1 1 1 2 1 1 215 4 3 1 1 2 2 2 1 1 1 216 4 4 1 1 2 1 1 2 2 2 11 2 3 4 5 6 7 8 91 1 1 1 1 1 1 1 1 12 1 2 2 1 1 2 2 2 23 1 3 3 2 2 1 1 2 24 1 4 4 2 2 2 2 1 15 2 1 2 2 2 1 2 1 26 2 2 1 2 2 2 1 2 17 2 3 4 1 1 1 2 2 18 2 4 3 1 1 2 1 1 29 3 1 3 1 2 2 2 2 110 3 2 4 1 2 1 1 1 211 3 3 1 2 1 2 2 1 212 3 4 2 2 1 1 1 2 113 4 1 4 2 1 2 1 2 214 4 2 3 2 1 1 2 1 115 4 3 2 1 2 2 1 1 116 4 4 1 1 2 1 2 2 2列号试验号列号试验号(10) L16 (45)1 2 3 4 5 6 71 1 1 1 1 1 1 12 1 2 2 2 1 2 23 1 3 3 3 2 1 24 1 4 4 4 2 2 15 2 1 2 3 2 2 16 2 2 1 4 2 1 27 2 3 4 1 1 2 28 2 4 3 2 1 1 19 3 1 3 4 1 2 210 3 2 4 3 1 1 111 3 3 1 2 2 2 112 3 4 2 1 2 1 213 4 1 4 2 2 1 214 4 2 3 1 2 2 115 4 3 2 4 1 1 116 4 4 1 3 1 2 21 2 3 4 51 1 1 1 1 12 1 2 2 2 23 1 3 3 3 34 1 4 4 4 45 2 1 2 3 46 2 2 1 4 37 2 3 4 1 28 2 4 3 2 19 3 1 3 4 210 3 2 4 3 111 3 3 1 2 412 3 4 2 1 313 4 1 4 2 314 4 2 3 1 415 4 3 2 4 116 4 4 1 3 2列号试验号列号试验号(12) L 20 (219)1 2 3 4 5 6 7 8 9 1 11 1 1 1 1 1 1 12 1 2 2 2 2 2 2 2 23 2 1 1 1 1 2 2 2 24 2 2 2 2 2 1 1 1 15 3 1 1 2 2 1 1 2 26 3 2 2 1 1 2 2 1 17 4 1 1 2 2 2 2 1 18 4 2 2 1 1 1 1 2 29 5 1 2 1 2 1 2 1 2 10 5 2 1 2 1 2 1 2 1 11 6 1 2 1 2 2 1 2 1 12 6 2 1 2 1 1 2 1 2 13 7 1 2 2 1 1 2 2 1 14 7 2 1 1 2 2 1 1 2 15 8 1 2 2 1 2 1 1 2 168211212211 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 11 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 12 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 13 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 24 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 25 1 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 16 2 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 17 2 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 28 2 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 29 2 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 10 1 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 11 2 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 12 1 2 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 13 2 1 1 1 1 2 2 1 2 2 1 1 1 2 2 2 1 2 1 14 1 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 15 1 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 16 1 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 17 1 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 18 2 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 19 2 1 2 2 1 1 2 2 2 2 1 2 1 2 1 1 1 1 2 列号 试验 号列 号 试验 号(13) L9 (34)(14) L18 (2×37)1 2 3 41 1 1 1 12 1 2 2 23 1 3 3 34 2 1 2 35 2 2 3 16 2 3 1 27 3 1 3 28 3 2 1 39 3 3 2 11 2 3 4 5 6 7 81 1 1 1 1 1 1 1 12 1 1 2 2 2 2 2 23 1 1 3 3 3 3 3 34 1 2 1 1 2 2 3 35 1 2 2 2 3 3 1 16 1 2 3 3 1 1 2 27 1 3 1 2 1 3 2 38 1 3 2 3 2 1 3 19 1 3 3 1 3 2 1 210 2 1 1 3 3 2 2 111 2 1 2 1 1 3 3 212 2 1 3 2 2 1 1 313 2 2 1 2 3 1 3 214 2 2 2 3 1 2 1 315 2 2 3 1 2 3 2 116 2 3 1 3 2 3 1 217 2 3 2 1 3 1 2 318 2 3 3 2 1 2 3 1列号试验号列号试验号(15) L27 (313)L27 (313)表头设计1 2 3 4 5 6 73 A B (A×B)1(A×B)2 C (A×C)1(A×C)24 A B (A×B)1(C×D)2(A×B)2 C(A×C)1(B×D)2(A×C)28 9 10 11 12 13 3 (B×C)1 D (A×D)1(B×C)2(B×D)1(C×D)14(B×C)1(A×D)2(A×D)1(B×C)21 2 3 4 5 6 7 8 9 10 11 12 131 1 1 1 1 1 1 1 1 1 1 1 1 12 1 1 1 1 2 2 2 2 2 2 2 2 23 1 1 1 1 3 3 3 3 3 3 3 3 34 1 2 2 2 1 1 1 2 2 2 3 3 35 1 2 2 2 2 2 2 3 3 3 1 1 16 1 2 2 2 3 3 3 1 1 1 2 2 27 1 3 3 3 1 1 1 3 3 3 2 2 28 1 3 3 3 2 2 2 1 1 1 3 3 39 1 3 3 3 3 3 3 2 2 2 1 1 110 2 1 1 3 1 2 3 1 2 3 1 2 311 2 1 2 3 2 3 1 2 3 1 2 3 112 2 1 3 3 3 1 2 3 1 2 3 1 213 2 2 1 1 1 2 3 2 3 1 3 1 214 2 2 2 1 2 3 1 3 1 2 1 2 315 2 2 3 1 3 1 2 1 2 3 2 3 116 2 3 1 2 1 2 3 3 1 2 2 3 117 2 3 2 2 2 3 1 1 2 3 3 1 218 2 3 3 2 3 1 2 2 3 1 1 2 319 3 1 3 2 1 3 2 1 3 2 1 3 220 3 1 3 2 2 1 3 2 1 3 2 1 321 3 1 3 2 3 2 1 3 2 1 3 2 122 3 2 1 3 1 3 2 2 1 3 3 2 123 3 2 1 3 2 1 3 3 2 1 1 3 224 3 2 1 3 3 2 1 1 3 2 2 1 325 3 3 2 1 1 3 2 3 2 1 2 1 326 3 3 2 1 2 1 3 1 3 2 3 2 127 3 3 2 1 3 2 1 2 1 3 1 3 2列号试验号列号因子数列号因子数L27 (313)二列间的交互作用表1 2 3 4 5 6 7 8 9 10 11 12 13(1 )3 2 2 6 5 5 9 8 8 12 11 114 4 3 7 7 6 10 10 9 13 13 12 (2)1 1 8 9 10 5 6 7 5 6 74 3 11 12 13 11 12 13 8 9 10(3)1 9 10 8 7 5 6 6 7 52 13 11 12 12 13 11 10 8 9(4)10 8 9 6 7 5 7 5 612 13 11 13 11 12 9 10 8(5)1 1234 2 4 37 6 11 13 12 8 10 9(6)1 423 3 2 45 13 12 11 10 9 8(7)3 4 2 4 3 212 11 13 9 8 10(8)1 123 410 9 5 7 6(9)1 42 38 7 6 5(10)3 4 26 5 7(11)1 113 12(12)1111 2 3 4 5 6 1 1 1 1 1 1 1 2 1 2 2 2 2 2 3 1 3 3 3 3 3 4 1 4 4 4 4 4 5 1 5 5 5 5 5 6 2 1 2 3 4 5 7 2 2 3 4 5 1 8 2 3 4 5 1 2 9 2 4 5 1 2 3 10 2 5 1 2 3 4 11 3 1 3 5 2 4 12 3 2 4 1 3 5 13 3 3 5 2 4 1 14 3 4 1 3 5 2 15 3 5 2 4 1 3 16 4 1 4 2 5 3 17 4 2 5 3 1 4 18 4 3 1 4 2 5 19 4 4 2 5 3 1 20 4 5 3 1 4 2 21 5 1 5 4 3 2 22 5 2 1 5 4 3 23 5 3 2 1 5 4 24 5 4 3 2 1 5 25554321列 号 试 验 号31122121122112122130122121122112122129122121121221211228122121121221211227 122112212112211226 1 22112212112211225 1 2 2 112211221122124 1 2 2 1 12211221122123 1 2 1 2 2 1 212121121222 1 2 1 2 2 1 2 12121121221 1 2 1 2 2 1 2 1 1212212120 1 2 1 2 2 1 2 1 1 2 12212119 1 2 1 2 1 2 1 2 2 1 2 1 212118 1 2 1 2 1 2 1 2 2 1 2 1 2 12117 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 16 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 15 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 14 1 1 2 2 2 2 1 1 2 2 1 1 1 1 2 2 13 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 12 1 1 2 2 2 2 1 1 1 1 2 2 1 1 2 2 11 1 1 2 2 1 1 2 2 2 2 1 1 2 2 1 1 101122112222112211 911221122112211228 1 1 2 2 1 1 2 2 1 1 2 2 1 1 2 2 7 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 6 1 1 1 1 2 2 2 2 2 2 2 2 1 1 1 1 5 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 4 1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 211111111111111111列号试验号12345678910111213141516。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
0
0
0
C
A×C
L4
L5
1
1
2
2
1
1
2
2
1
2
2
1
1
2
2
1
B×C L6 1 2 2 1 1 2 2 1
-
-
-
-
-
L7
L8
L9
L10
L11
1
2
2
1
2
1
1
2
8
8
8
8
0
0
0
0
15.3 14.8
14.9
15
0
0
0
0
14.5
15
14.9
14.8
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
234.09 219.04 222.01
L3
4
4
2
3
12
1#
8
3#
2
2
1
1
B
A×B
L2
L3
1
1
1
1
2
2
2
2
1
2
1
2
2
1
2
1
L n(m
结果1 kij^2 结果1^2
Qj=
1 r
m Kij2
i=1
n
T= x i
i=1
CT
T2 n
n
QT=
x
2 i
i=1
25 26 27 28 29 30 31 32 N K1 K2 K3 K4 K1j^2 K2j^2 K3j^2 K4j^2 KX21 KX22 KX23 KX24 T CT QT
225
0
0
0
0
210.25 225
222.01 219.04
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
60.15 56.2
56.63
58.02
0
0
0
0
54.15 58.1
57.67
56.28
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
111.085 111.01
0.0800 0.0050
1
1
0.08 0.005
8 14.5 15.3
0 0 210.25 234.09 0 0 54.15
60.15
0
0 29.8 111.005 114.3
8 12.4 17.4
0 0 153.76 302.76 0 0 38.52
75.78
0
0
8 14.9 14.9
0 0 222.01 222.01 0 0 57.67
56.63
L13
L14
L15
3
3
3
3
L12
L13
L14
L15
4
4
4
4
12
13
14
15
0
0
0
0
0
0
0
0
-
-
-
-
L12
L13
L14
L15 结果1 结果2 结果3 结果1^2 结果2^2
3.1
3.5
9.61 12.25
2.9
3.2
8.41 10.24
4.3
4.2
18.49 17.64
4.2
4
17.64
16
3.3
3.4
试验号 n L1
1
L1
K值统计
2
条件区
L1
3
L1
4
因素
k
1
水平1
14
因素水平 表
水平2 水平3 水平4
16
水平数
2
Df
1
表头设计
表头设计
列号
k
A
试验号 n L1
1
1
2
1
3
1
4
1
5
2
6
2
7
2
8
2
9
10
11
12
13
正交表
14 15
16
17
18
19
20
21
22
23
24
L2
L3
1
1
L2
L3
2
2
L2
L3
3
3
L2
SSj=Qj CT
Vj
SSj dfj
1、在因素 使用方法: 水平表填入
各水平 2、在正交 表中填入选 择的正交表 形式,常用 正交表在《 常用正交表 、交互作用 表、表头设 计》中选取 粘贴 3、填入试 验结果 4、在K值计 算区域输入 希望统计的 结果列名称 5、手工更 改MSE**的 计算与F判 据的两个自 由度选项 6、获得显 著与否的结 论 7、正交表 的使用及数 据处理参考 资料见上 图例说明: 不建议更改 的部分 需要判断, 更改的部分 根据需要更 改的部分
10.89 11.56
3.1
3.2
9.61 10.24
4.6
4.9
21.16 24.01
4.3
4.6
18.49 21.16
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
#DIV/0!
111.005
0.0000 1 0
111.01 #DIV/0!
0.0050 #DIV/0!
1
0
0.005 #DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
32 1 1
异常显著
2 9 9
不显著
0 5.117355029 10.56143105
#DIV/0! 0
#DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
#DIV/0!
#DIV/0! 0
#DIV/0!
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
0
0
不显著
2 不显著
#DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0! #DIV/0!
/view/13531cb00c22590102029dc2.html
L12
L13
L14
L15
1
1
1
1
L12
L13
L14
L15
2
2
2
2
L12
L n(mk)正交表及计算表格
L4
L5
L6
L7
L8
L9
1
1
1
1
1
1
L4
L5
L6
L7
L8
L9
2
2
2
2
2
2
L4
L5
L6
L7
L8
L9
3
3
3
3
3
3
L4
L5
L6
L7
L8
L9
4
4
4
4
4
4
4
5
6
7
8
9
1
1
1
1
1
1
1
1
2
2
2
2
0
0
1
1
1
1
0
0
L10
L11
1
1
L10
L11
2
2
L10
L11
3
3
L10
L11
4
4
10
11
算MSE**
0.0025
1250
0
0.05
F
0.01
F
F判据结论 异常显著 异常显著 不显著
参考资料:
/view/13531cb00c225901020
