算法课件六分支定界
第六章 分支限界法.ppt

13
单源最短路径问题
1. 问题描述
下面以一个例子来说明单源最短路径问题:在下 图所给的有向图G中,每一边都有一个非负边权。要 求图G的从源顶点s到目标顶点t之间的最短路径。
14
单源最短路径问题
1. 问题描述
下图是用优先队列式分支限界法解有向图G的 单源最短路径问题产生的解空间树。其中,每一个结 点旁边的数字表示该结点所对应的当前路长。
// 取下一扩展结点
i++;}
// 进入下一层
}
26
装载问题
3. 算法的改进
结点的左子树表示将此集装箱装上船,右子树 表示不将此集装箱装上船。设bestw是当前最优解; ew是当前扩展结点所相应的重量;r是剩余集装箱 的重量。则当ew+rbestw时,可将其右子树剪去, 因为此时若要船装最多集装箱,就应该把此箱装 上船。
(2)回溯求解TSP也是盲目的(虽有目标函数,也 只有找到一个可行解后才有意义)
7
解空间树的动态搜索
分支限界法首先确定一个合理的限界函数,并根据限 界函数确定目标函数的界[down, up]; 然后按照广度优先策略遍历问题的解空间树,在某一 分支上,依次搜索该结点的所有孩子结点,分别估算 这些孩子结点的目标函数的可能取值(对最小化问题, 估算结点的down,对最大化问题,估算结点的up)。 如果某孩子结点的目标函数值超出目标函数的界,则 将其丢弃(从此结点生成的解不会比目前已得的更 好),否则入待处理表。
A->E->Q->M
21
单源最短路径问题
Dijakstra算法和分支限法在解决该问题的异同:
优先队列式分支限界法的搜索方式是根据活结点的优先级确 定下一个扩展结点。结点的优先级常用一个与该结点有关的 数值p来表示。最大优先队列规定p值较大的结点点的优先级 较高。在算法实现时通常用一个最大堆来实现最大优先队列, 体现最大效益优先的原则。类似地,最小优先队列规定p值 较小的结点的优先级较高。在算法实现时,常用一个最小堆 来实现,体现最小优先的原则。采用优先队列式分支定界算 法解决具体问题时,应根据问题的特点选用最大优先或最小 优先队列,确定各个结点点的p值。
分支定界法

分支定界法分支定界法,也称为分界定义法,是为了确定并将客观事物归类的一种逻辑基础规范。
它是一组文本规范,用于描述和分类客观事物,以及它们之间的关系。
它分析客观事物的共性,从这些共性,弄清楚客观事物以及它们之间的关系,形成分支定义法。
分支定界法最初创造于18世纪的德国,由卡尔文贝因茨(Karl von Bennizs)提出,他的著作 Theorie der classifikation(分类理论)发表于1790年。
他的主要思想是:通过对客观事物的共性的分析,将客观事物归类,并形成一系列的分类方法。
分支定界法一般包括三个层次:主类,亚类,次类。
主要是将客观事物按照一定的共性划分到不同的类别中,然后在每个主类中进行更详细的分析,形成子类,从而将客观事物更细致地分类。
分支定界法有很多优点。
首先,它可以更好地适应新出现的客观事物,以及客观事物可能出现的新情况。
这是因为,分支定界法有着一系列的分类方法,不仅具有某种共性,而且有着不同的子类,这些子类可以更好地形成客观事物之间的关系,并且有利于新类别的形成。
此外,分支定界法还可以帮助人们进行判断。
分界定义法是一种可以把客观事物细致分类的方法,从而可以更好地去判断两个客观事物之间是否有关系,或者相似度如何,从而帮助我们做出判断。
然而,分支定界法也有一定的局限性。
有时,分支定界法所指定的客观事物重叠,或者具有相同的共性,这会降低分类的准确性。
此外,它也会忽略一些客观事物的细微差别,这可能会影响分类的结果。
总之,分支定界法是一种有效的客观事物归类方法。
它可以更好地划分客观事物的共性,也可以更直观地反映客观事物之间的关系,从而有效地把客观事物归类。
此外,它还可以帮助我们做出判断,但它也有一定的局限性,必须在不同的客观事物之间上尽量保持准确性和细微差别。
5.2 分支界定解法PowerPoint 演示文稿

已完成的求解过程和所得到的计算结果可用框 图来表示,见下图。
x2≤3
B
x1=2.25 x2=3.75 y=41.25
x2≥4
UB=41.25 LB=0
B1 x1=3 x2=3 y=39
B2 x1=1.8 x2=4 y=41
UB=41 LB=39
13
3.定界:由图可知。界为max { 39,41 } = 41。于是
4
③如果相应线性规划有最优解, 但不符合原整数规划问题的整数条件, 则这个最优解不是原整数规划的最优解,
记此最优值为原整数规划问题Z*的上界, 然后, 用观察法求出下界, 转入第二步。
5
第二步:
主要特征是分支。 具体作法: 从相应线性规划的最优解中, 任意选择一个不满足原整数规划整数条件
的决策变量xj=bj
x2 4
x1 1
x1, x2 0
5 x 1 9 x 2 45
B21
x1 x2 6
x2 4
B22
x1 2 x1, x2
0
解B21得:最优解(x1,x2)=(1,4),最优值ymax=40. 解B22得: B22无可行解。
14
至此,已完成的求解过程和所得到的计算结果运用 框图来表示,如图所示:
UB=14 LB=14
22
例2:A问题为
MaxZ=40x1+90x2 9x1+7x2≤56 7x1+20x2 ≤70 x1,x2≥0 x1,x2 都为整数
B问题为 MaxZ=40x1+90x2 9x1+7x2≤56 7x1+20x2 ≤70 x1,x2≥0
23
问题B
Z=356
x1=4.81 ,x2=1.82 Z=356
6.2 分支定界解法

①若LP无可行解,则IP也没有可行解;
②若LP有最优解且满足整数要求,则即为IP的最优解; ③若LP有最优解但不满足整数要求,则转下一步;
2. 进行迭代:
①分支与定界:在LP的最优解中任选一个非整数解的变量 xi =b,在LP问题加上约束:
xi [b]和xi [b]+1
组成两个新的LP问题,称为分枝。
5 x1 7 x2 35 5 x1 7 x2 35 4 x 9 x 36 4 x 9 x 36 1 2 1 2 s.t . s.t . x2 2 x2 2 x 5 x 4 1 1 x1 , x2 0. x1 , x2 0. B11的最优解 x1 4, x2 2, z11 14. * 14 z 14.4. 3 2 B12的最优解 x1 5, x2 1 , z12 14 . 7 7
Page 23
x z 32 z1,对B 21进行分枝,增加约束x1 4及x1 5得:
B 211 : max z 4 x1 3 x2
10
A
B211:X=(4,6), z5=34
6
B1
1.2 x1 0.8 x2 10 2 x1 2.5 x2 25 s.t . x1 4,x2 6,x1 4 x1 , x2 0 B212:X=(5,5), 即x1 4 ,可行域是一条线段 z =35
问题B的解中有一个非整数变量 x2=2 6/17。于是在原问题中 增 加 两 个 约 束 条 件 : x2≤2 和 x2≥3 , 将 原 问 题 分 解 为 B1 和 B2(即两支)。 B 1 : max z 2 x1 3 x2 B 2 : max z 2 x1 3 x2
整数规划及分支定界法42页PPT

谢谢!
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
整数规划及分支定界法 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 孔子
整数规划及分支定界法42页PPT

2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
整数规划及分支定界法 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
谢谢!
பைடு நூலகம்
36、自己的鞋子,自己知道紧在哪里。——西班牙
37、我们唯一不会改正的缺点是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
40、学而不思则罔,思而不学则殆。——孔子
分支定界法原理简介

分支定界法原理简介分支定界法是一种广义搜索算法,人工使用非常繁琐,但由于计算机的运算速度快的特点,这种算法十分适合计算机进行。
分支定界法是计算机最擅长的广义搜索穷举算法。
基本思想:1. 松弛模型的最优解要优于其相应的整数规划的解由于松弛模型可行解的区域(多边形)包含了对应的整数规划的可行解的集合(多边形内的整数点),因而松弛模型的解要优于整数规划的解。
这就是说,如果问题是求最大值的,则松弛模型最优解对应的目标函数值必大于或等于整数规划最优解对应的目标函数值;如果问题是求最小值的,则松弛模型的最优解对应的目标函数值必小于或等于整数规划最优解对应的目标函数值。
由此可以推出:2. 松弛模型的最优解如果是整数解,则必然也是整数规划的最优解。
3. 松弛模型的最优解如果不是整数解,则如果问题是求最大值的,松弛模型最优解的目标函数值是整数规划最优解目标函数值的一个上界;如果问题是求最小值的,则松弛模型最优解的目标函数值是整数规划最优解目标函数值的一个下界。
我们用例子来说明用分支定界法求解整数规划的步骤。
例 求下面整数规划的最优解1212121212max 4090s.t. 975672070 ,0x ,Z x x x x x x x x x =++≤+≤≥为整数解 从上述各约束条件可见,是一个可行解,对应的松弛模型目标函数值。
本问题是一个求最大值的问题,因而整数规划最优解的目标函数的下界可以取为0,即取整数规划模型最优值的下界(0,0)0Z =0Z =。
先考虑此整数规划问题的线性松弛模型0:其解为 松弛模型0 0123564.811.82Z x x ===由于松弛模型解的目标函数值是整数规划模型最优值的一个上界,可以取此处的0Z 为整数规划模型最优值的一个上界356Z =。
由于该松弛模型解不是整数解,分原问题为和两个子模型:子模型1和子模型2。
14x ≤15x ≥子模型1子模型2 14≤x 15≥x1123494.002.10Z x x ===2123495.001.57Z x x ===子模型1的形式: 121212112max 4090s.t. 975672070 4x ,0Z x x x x x x x x =++≤+≤≤≥子模型2的形式:121212112max 4090s.t. 975672070 5x ,0Z x x x x x x x x =++≤+≤≥≥所求整数规划模型的最优值不会超过这两个子模型的最优值中大的那个,即349。
分支界定算法

分支定界(branch and bound) 算法是一种在问题的解空间树上搜索问题的解的方法。
但与回溯算法不同,分支定界算法采用广度优先或最小耗费优先的方法搜索解空间树,并且,在分支定界算法中,每一个活结点只有一次机会成为扩展结点。
利用分支定界算法对问题的解空间树进行搜索,它的搜索策略是:1 .产生当前扩展结点的所有孩子结点;2 .在产生的孩子结点中,抛弃那些不可能产生可行解(或最优解)的结点;3 .将其余的孩子结点加入活结点表;4 .从活结点表中选择下一个活结点作为新的扩展结点。
如此循环,直到找到问题的可行解(最优解)或活结点表为空。
从活结点表中选择下一个活结点作为新的扩展结点,根据选择方式的不同,分支定界算法通常可以分为两种形式:1 .FIFO(First In First Out) 分支定界算法:按照先进先出原则选择下一个活结点作为扩展结点,即从活结点表中取出结点的顺序与加入结点的顺序相同。
2 .最小耗费或最大收益分支定界算法:在这种情况下,每个结点都有一个耗费或收益。
如果要查找一个具有最小耗费的解,那么要选择的下一个扩展结点就是活结点表中具有最小耗费的活结点;如果要查找一个具有最大收益的解,那么要选择的下一个扩展结点就是活结点表中具有最大收益的活结点。
又称分支定界搜索法。
过程系统综合的一类方法。
该法是将原始问题分解,产生一组子问题。
分支是将一组解分为几组子解,定界是建立这些子组解的目标函数的边界。
如果某一子组的解在这些边界之外,就将这一子组舍弃(剪枝)。
分支定界法原为运筹学中求解整数规划(或混合整数规划)问题的一种方法。
用该法寻求整数最优解的效率很高。
将该法原理用于过程系统综合可大大减少需要计算的方案数日。
分支定界法的思想是:首先确定目标值的上下界,边搜索边减掉搜索树的某些支,提高搜索效率。
在竞赛中,我们有时会碰到一些题目,它们既不能通过建立数学模型解决,又没有现成算法可以套用,或者非遍历所有状况才可以得出正确结果。
分支定界法步骤

分支定界法步骤嘿,咱今儿个就来唠唠这分支定界法的步骤。
你说这分支定界法啊,就像是在一个迷宫里找出口,得一步步来,还得有策略呢!首先呢,得有个目标函数,就像你要去一个地方,得知道往哪儿走才是对的呀。
然后根据这个目标函数,把问题给划分成一个个小部分,这就好比把迷宫分成了好多条路。
接下来,就开始在这些小部分里探索啦。
咱得给每个部分设定一个界限,就像给每条路设个关卡一样,超过了这个界限,咱就先不考虑啦。
这一步可得仔细咯,不能马虎。
然后呢,咱就选择一个最有希望的部分继续深入。
这就像在迷宫里选了一条感觉最有可能走到出口的路。
沿着这条路走啊走,看看能不能找到更好的结果。
要是在这个过程中发现了一个比之前更好的解,那可就太棒啦!赶紧把它记下来,这说不定就是咱要找的答案呢。
有时候啊,走着走着发现路走不通了,咋办呢?那就得换条路试试呀,不能在一棵树上吊死嘛。
这分支定界法啊,就像是一场冒险,每一步都充满了未知和挑战。
你得有耐心,还得有智慧,才能在这复杂的迷宫里找到正确的方向。
你想想看,要是没有这一步步的分析和探索,那岂不是像无头苍蝇一样乱撞呀?那可不行,咱得有方法,有策略地去解决问题。
在实际应用中,这分支定界法可帮了大忙呢!它能帮我们解决很多复杂的问题,让我们能更高效地找到最优解。
所以说呀,这分支定界法的步骤可真不简单,每一步都得认真对待。
就像建房子一样,一砖一瓦都得放好,才能建成坚固的大厦。
咱在运用分支定界法的时候,也得这样,一步一个脚印,踏踏实实地去做,才能得到满意的结果呀!你说是不是这个理儿呢?。
运筹学_分支定界法课件

m ax Z x1 5 x2
m ax Z x1 5 x2
x1 x2 2
( IP 1)
5
x1 x1
6
x2
30 4
x1
1
x 1 , x 2 0 且 为 整 数
x1 x2 2
( IP
2)
5
x1 x1
6
x2
30 4
x1
2
x 1 , x 2 0 且 为 整 数
现在只要求出(LP1)和(LP2)的最优解即可。
x1
x1 5x2 Z
运筹学_分支定界法
x1=18/11, x2 =40/11
Z(0) =218/11≈(19.8)
x2
即Z 也是(IP)最大值的上限。
m ax Z x1 5 x2
3
x1 x2 2
5
x1 x1
6
x2
30 4
x 1 , x 2 0
⑵ 5x16x2 30 ⑴ x1 x2 2
#
运筹学_分支定界法
例一:用分枝定界法求解整数规划问题(用图解法计算)
m ax Z x1 5 x2
x1 x2 2
5
x1
6
x2
30
x1
4
x 1 , x 2 0 且 全 为 整 数
记为(IP)
解:首先去掉整数约束,变成一般线性规划问题
m ax Z x1 5 x2
x1 x2 2
5
x1 x1
6
x2
30 4
3
x1
1
x 1 , x 2 0 且 为 整 数
1
⑵ 5x16x2 30 ⑴ x1 x2 2
A
⑶ x1 4
1
分支定界法

以下内容基本为转载内容:1. 模型整数规划的模型与线性规划基本相同,只是额外的添加了部分变量为整数的约束。
2. 求解步骤整数规划求解的基本框架是分支定界法(Branch and bound,BnB)。
首先去除整数约束得到“松弛模型”,使用线性规划的方法求解。
若有某个变量不是整数,在松弛模型上分别添加约束:x<=floor(A)和x>=ceil(A)然后再分别求解,这个过程叫做分支。
当节点求解结果中所有变量都是整数时,停止分支。
这样不断迭代,形成了一棵树。
定界,指的是叶子节点产生后,相当于给问题定了一个下界。
之后在求解过程中一旦某个节点的目标函数值小于这个下界,那就直接pass,不用再进行分支了;每次新产生叶子节点,则更新下界。
3. python算法实现import mathfrom scipy.optimize import linprogimport sysdef integerPro(c,A,b,Aeq,beq,t=1.0E-12):res=linprog(c,A_ub=A,b_ub=b,A_eq=Aeq,b_eq=beq)if(type(res.x)is float):#produces error codebestX=[sys.maxsize]*len(c)else:bestX=res.xbestVal=sum([x*y for x,y in zip(c,bestX)])if all(((x-math.floor(x))<t or(math.ceil(x)-x)<t)for x in bestX): return(bestVal,bestX)else:ind=[i for i,x in enumerate(bestX)if(x-math.floor(x))>t and (math.ceil(x)-x)>t][0]newCon1=[0]*len(A[0])newCon2=[0]*len(A[0])newCon1[ind]=-1newCon2[ind]=1newA1=A.copy()newA2=A.copy()newA1.append(newCon1)newA2.append(newCon2)newB1=b.copy()newB2=b.copy()newB1.append(-math.ceil(bestX[ind]))newB2.append(math.floor(bestX[ind]))r1=integerPro(c,newA1,newB1,Aeq,beq)r2=integerPro(c,newA2,newB2,Aeq,beq)if r1[0]<r2[0]:return r1else:return r2例子:输入c=[3,4,1]A=[[-1,-6,-2],[-2,0,0]]b=[-5,-3]Aeq=[[0,0,0]]beq= [0]print(integerPro(c,A,b,Aeq,beq))输出(8.0,array([2.,0., 2.]))其中8是目标函数值,2,0,2是3个整数变量的值。
分支定界法
s.t.xr br
x 0, x为整数
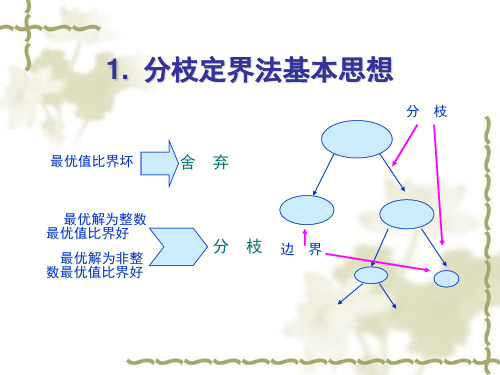
1. 分枝定界法基本思想续
❖ 分枝方法示意图
1. 分枝定界法基本思想续
❖ 定界
1. 当前得到的最好整数解的目标函数值
2. 分枝后计算松弛的线性规划的最优解
➢ 整数解且目标值小于原有最好解的值则替代原有 最好解
➢ 整数解且目标值大于原有最好解的值则 删除该分 支其中无最优解
➢ 非整数解且目标值小于原有最好解的值则继续分 支
➢ 非整数解且目标值大于等于原有最好解的值则删 除该分支其中无最优解
2. 分枝定界法计算步骤
2. 分枝定界法计算步骤-例题
❖
例3.3.1
minZ
( x1
x2 )
s.t.44
x1 x1
2x2 2 x2
1 11
2x2 1
x1x2 整数
例x3.(33,5.) 1z 解 4答 0
T0
z z 3x52xz(2,1()1,332.2)5xx((xPP2))(21.25,12) (2Px) (P1 ) (xP(x)P1) 3 x 无解(2,x32) 2无z 解(P )72 5 1 5 13 T T 1 3 115 T 2 3 12 1 6 2 2 T 2 4
1. 分枝定界法基本思想ห้องสมุดไป่ตู้
分枝
最优值比界坏
舍弃
最优解为整数 最优值比界好
最优解为非整 数最优值比界好
分 枝 边界
1. 分枝定界法基本思想续
0
N
I
B1N
cB B1b B 1b
xr br Z
br xr br 1
1. 分支定界法基本思想续
❖ 分枝的方法 min c x
分支定界

5 x1 7 x2 35 4 x 9 x 36 1 2 s.t . x2 2 x1 , x2 0
5 x1 7 x2 35 问题 B 2 : 4 x 9 x 36 1 2 s.t . x2 3 x1 , x2 0
5 x1 7 x2 35 s.t . 4 x1 9 x2 36 x , x 0, 全部为整数 1 2
解 :step1
确定与整数规划问题(记为问题 A)对应的松
弛线性规划问题 (记为问题 B):
max z 2 x1 3 x2
5 x1 7 x2 35 s.t . 4 x1 9 x2 36 x , x 0 1 2
i 1, 2, , p
则约束条件组可表示为
n aij x j bi Myi , i 1, 2,, p j 1 p yi p q i 1 y 0,1; i 1, 2,, p i
例 3.4.2 固定支出问题 考察 n 种产品的产品计划问题。假定生产某种产品 j 就 发生单位可变成本 c j ,另外,不管产品 j 生产多少,还需 支出固定成本 k j ,但若不生产产品 j 也就无需支出固定成 本。因此,如何制定产品计划,使得总生产成本最小。
step2 先求出问题 B 的解,用单纯形方法得 问题 B 的最优解为:
x1 3
12 17
,
x2 2
6 17
,
* z0
14
8 17
step3
用观察法找问题 A的—个整数解,一般可取
x1 0, x2 0 ,进行试探,求得其目标函数值 z 0 ,以 z * 表示问题
A 的最优目标函数值;这时有 0 z* 14 8 step4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
LOGO
布线问题适合采用队列式分支限界法来解决。 从起始位置 a开始将它作为第一个扩展结点。与该结点相邻并且可达 的方格被加入到活结点队列中,并且将这些方格标记为1,表示它们到a的 距离为1 接着从活结点队列中取出队首作为下一个扩展结点,并将与当前扩展 结点相邻且未标记过的方格标记为 2,并存入活节点队列。这个过程一直 继续到算法搜索到目标方格b或活结点队列为空时为止(表示没有通路)
(2)将剩余的集装箱装上第二艘轮船。
示例4:布线问题
LOGO
问题描述:印刷电路板将布线区域划分成 n*m个方格阵列。精确 的电路布线问题要求确定连接方格 a 的中点到方格 b 的中点的最短布 线方案。在布线时,电路只能沿直线或直角布线。为了避免线路相 交,已布了线的方格做了封锁标记,其他线路不允许穿过被封锁的 方格
A B
20
LOGO
活节点表
B C C E
C
×
20 15 30 15 15
E F G
F G
35
E
×
35
解1:[1,0,0], 收益40 F G 解2:[0,1,1], 收益50 NULL G
9
最大收益-分支定界思想
LOGO
使用一个最大堆:其中的 E-节点按照每个活节点收益值 的降序,或是按照活节点任意子树的叶节点所能获得的收 益估计值的降序从队列中取出。 FIFO分支-限界算法用队存储活结点,优先队列式分支限 界法用堆存储活结点,以保证比较优良的结点先被扩展。 且对于优先队列式分支限界算法,一旦扩展到叶结点就已 经找到最优解,可以停止搜索。
LOGO
广度优先搜索算法,一般需存储产生的所有结 点,占用的存储空间要比深度优先搜索大得多, 因此,程序设计中,必须考虑溢出和节省内存 空间的问题。 但广度优先搜索法一般无回溯操作,即入栈和 出栈的操作,所以运行速度比深度优先搜索快。
4
2. 分支限界法
LOGO
采用广度优先产生状态空间树的结点,并使用剪 枝函数的方法称为分支限界法。 所谓“分支”是采用广度优先的策略,依次生 成扩展结点的所有分支(即:儿子结点)。 所谓“限界”是在结点扩展过程中,计算结点 的上界(或下界),边搜索边减掉搜索树的某 些分支,从而提高搜索效率
17
LOGO
优先队列式分支限界法程序框架
设T为状态空间树的根结点;~C(x)为耗费估计函数; 初始化优先队列Q; 计算~C(T),并将T入队; 循环,直到队列Q空(无解): 结点e出队; 若e是回答结点,则 输出解或求解路径,求解结束; 否则 检查e的所有子结点x: 若x满足约束条件,则 计算~C(x),并将x入队; 记录搜索路径;
LOGO
通常深度优先搜索法不全部保留结点,扩展完 的结点从数据存储结构栈中弹出删去,这样, 一般在数据栈中存储的结点数就是解空间树的 深度,因此它占用空间较少。 所以,当搜索树的结点较多,用其它方法易产 生内存溢出时,深度优先搜索不失为一种有效 的求解方法。
3
1. 概述
方法2:广度优先搜索
使用最小堆存储活节点
【注】活节点表采用堆结构 E-节点 B E D H
24 29
LOGO
活节点表 E D C D J K C H J K I C 路径13241,25
30 35 40 11
6 26 14 19
4
55
21
【定界函数】如果一个 节点的定界值不比当前 最优旅行更小,则将被 删除而不被展开!
18
LOGO
示例3 :装载问题
1. 问题描述
有一批共个集装箱要装上2艘载重量分别为C1和C2的轮船,其中集
LOGO
装箱i的重量为Wi,且
w
i 1
n
i
c1 c2
装载问题要求确定是否有一个合理的装载方案可将这个集装箱装上 这2艘轮船。如果有,找出一种装载方案。 容易证明:如果一个给定装载问题有解,则采用下面的策略可得到 最优装载方案。 (1)首先将第一艘轮船尽可能装满;
LOGO
最开始,队列中的活结点为标1的格 子,随后经过一个轮次,活结点变为标2 的格子,以此类推,一旦b方格成为活节 点便表示找到了最优方案。为什么这条路 径一定就是最短的呢?这是由于我们这个 搜索过程的特点所决定的,假设存在一条 由a至b的更短的路径,b结点一定会更早 地被加入到活结点队列中并得到处理。
11
示例2:旅行商问题
FIFO分支定界
E-节点
B C E F G H I J K
LOGO
活节点表
C D E
×
×
D E F G F G H I J K 路径12341,59 路径12431,66 路径13241,25 路径1342,不展开 路径14231,25 路径1432,不展开
13
示例2解法2:最小耗费法
必做:旅行商问题、0-1背包问题任选一题完成 选做:印刷电路板排列问题 提交代码和报告 报告内容:分析所实现问题的程序执行过程
25
LOGO
LOGO
LOGO
LOGO
LOGO
LOGO
5
分支限界算法思想
对E-节点的扩充方式:引入活节点表
LOGO
【思想】每个活节点有且仅有一次机会变成 E-节点。 当一个节点变为E-节点时,则生成从该节点移动一 步即可到达的所有新节点。在生成的节点中,抛弃 那些不可能导出(最优)可行解的节点,其余点 加入活节点表,然后从表中选择一个节点作为下一 个E-节点。 从活节点表中取出所选择的节点并进行扩充,直到 找到解或活动表为空,扩充过程才结束。
LOGO
问题:FIFO搜索或LIFO搜索也可以通过加入“限界” 策略加速搜索,与优先队列式分支限界法——LC-检索 的区别在哪儿呢? 答案:由于FIFO搜索或LIFO搜索是盲目地扩展结点, 当前最优解距真正的最优解距离较大,作为“界”所起 到的剪枝作用很有限,不能有效提高搜索速度。
作业
LOGO
实现旅行商问题的分支限界FIFO、优先队列求解 实现0-1背包问题的分支限界FIFO、优先队列求 解 *印刷电路板排列问题 要求:
14
0-1背包问题解3:最大收益法
LOGO
假设有4个物品,重量分别是(4,7,5,3), 价值分别是(40,42,25,12),背包容量是 W=10。 单位重量价值分别为:(10,6,5,4)
LOGO
LOGO
队列式分支限界法程序框架
设T为状态空间树的根结点;初始化队列Q; 将T入队; 循环,直到队列Q空(无解): 结点e出队; 若e是回答结点,则 输出解或求解路径; 否则 检查e的所有子结点x: 若x满足约束条件,则 将x入队; 记录搜索路径;
采用广度优先搜索策略的目的是:尽早发现剪枝点。
10
堆
n 个元素的序列 {k1, k2 , , kn }
当且仅当满足下述关系时,称之为堆
LOGO
ki k 2i ki k 2i 1
或
ki k 2i ki k 2i 1
n i 1,2, , 2
6
几种常见的分支限界法 不同的活结点表形成不同的分枝限界法:
LOGO
FIFO分支限界法(队列式分支限界法):活结 点表是先进先出队列
LIFO分支限界法:活结点表是堆栈
最小耗费或最大收益法分支限界法(优先队列 式分支限界法):活结点表是优先权队列,LC 分支限界法将选取具有最高优先级的活结点出 队列,成为新的扩展结点。
LOGO
1 概述 2 分支限界法 3 应用举例
1
1. 概述
搜索法
LOGO
在动态产生问题的解空间,并搜索问题的可行 解或最优解。 在生成的结点中,抛弃那些不满足约束条件 (或者说不可能导出最优可行解)的结点。
搜索方式
深度优先搜索 广度优先搜索
2
1. 概述
方法1:深度优先搜索
7
FIFO分支定界法
LOGO
在解空间树上的FIFO法,类似从根节点出发的 BFS方法; 与BFS的区别在于:在FIFO分支定界中,不可行 的节点不会被搜索!
8
示例1:0/1背包问题解1
n=3, w=[20,15,15], p=[40,25,25], c=30 E-节点 FIFO分支定界
