中考数学压轴题专题费马点
备战2024年中考数学压轴题之二次函数篇(全国通用)专题13 二次函数-费马点求最小值(学生版)

第十三讲二次函数--费马点最值必备知识点费马点:三角形内的点到三个顶点距离之和最小的点【结论】如图,点M 为锐角△ABC 内任意一点,连接AM 、BM 、CM ,当M 与三个顶点连线的夹角为120°时,MA+MB+MC的值最小【证明】以AB 为一边向外作等边三角形△ABE ,将BM 绕点B 逆时针旋转60°得到BN ,连接EN .∵△ABE 为等边三角形,∴AB =BE ,∠ABE =60°.而∠MBN =60°,∴∠ABM =∠EBN .在△AMB 与△ENB 中,∵,∴△AMB ≌△ENB (SAS ).连接MN .由△AMB ≌△ENB 知,AM =EN .∵∠MBN =60°,BM =BN ,∴△BMN 为等边三角形.∴BM =MN .知识导航∴AM+BM+CM=EN+MN+CM.∴当E、N、M、C四点共线时,AM+BM+CM的值最小.此时,∠BMC=180°﹣∠NMB=120°;∠AMB=∠ENB=180°﹣∠BNM=120°;∠AMC=360°﹣∠BMC﹣∠AMB=120°.分别以△ABC的AB、AC为一边向外作等边△ABE和等边△ACF,连接CE、BF,设交点为M,则点M即为△ABC的费马点。
点P 为锐角△ABC 内任意一点,连接AP 、BP 、CP ,求xAP+yBP+zCP 最小值解决办法:第一步,选定固定不变线段;第二步,对剩余线段进行缩小或者放大。
如:保持BP 不变,xAP+yBP+zCP=)(y CP yz BP AP y x ,如图所示,B 、P 、P 2、A 2四点共线时,取得最小值。
例:点P 为锐角△ABC 内任意一点,∠ACB=30°,BC=6,AC=5,连接AP 、BP 、CP ,求3AP+4BP+5CP 的最小值【分析】将△APC 绕C 点顺时针转90°到△A 1P 1C ,过P 2作P 1A 1的平行线,交CA 1于点A 2,且满足A 2P 2:P 1A 1=3:4.在Rt △PCP 2中,设PC=a ,由△CA 2P 2∽△CA 1P 1得CP 2=3a/4,则PP2=5a/4。
中考数学压轴题费马点

《费马点》解题思路费马点是指平面内到三角形三个顶点距离之和最小的点,这个最小的距离叫做费马距离.若三角形的内角均小于120°,那么三角形的费马点与各顶点的连线三等分费马点所在的周角;若三角形内有一个内角大于等于120°,则此钝角的顶点就是到三个顶点距离之和最小的点.一、若三角形有一个内角大于等于120°,则此钝角的顶点即为该三角形的费马点如图在4ABC中,N BAC N120。
,求证:点A为4ABC 的费马点证明:如图,在△ABC内有一点P延长BA至C,使得AC=AC,作N CAP =N CAP,并且使得AP=AP,连结PP贝IJ4APC四△APC, PC=PC 因为N BAC N120。
所以N PAP=/CAC W60所以在等腰4PAP中,AP N PP所以PA+PB+PC N PP+PB+PC〉BC=AB+AC所以点A为4ABC的费马点二、若三角形的内角均小于120°,则以三角形的任意两边向外作等边三角形,两个等边三角形外接圆在三角形内的交点即为该三角形的费马点.如图,在4ABC中三个内角均小于120°,分别以AB、AC为边向外作等边三角形,两个等边三角形的外接圆在4ABC内的交点为O,求证: 点。
为4ABC的费马点证明:在4ABC内部任意取一点O,;连接OA、OB、OC将4AOC绕着点A逆时针旋转60°,得到A AO, 口连接。
,则O' D=OC所以△AO。
,为等边三角形,OO'=AO所以0A+0C+0B=00,+0B+0/ D则当点B、。
、。
/、D四点共线时,OA+OB+OC最小此时ABAC为边向外作等边三角形,两个等边三角形的外接圆在△ABC内的交点即为点O如图,在4ABC中,若N BAC、N ABC、N ACB均小于120°, O为费马点,则有N AOB=N BOC=N COA=120°,所以三角形的费马点也叫三角形的等角中心例1 如图,在平面直角坐标系中,点A的坐标为(一6, 0), 点B的坐标为(6, 0),点C的坐标为(6, 4内),延长AC至点D 使得CD=AC,过点DE作DE//AB,交BC的延长线于点E,设G为y 轴上的一点,点P从直线y=无x+6城3与y轴的交点M出发,先沿y轴到达点G,再沿GA到达点A,若点P在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定点G的位置,使点P按照上述要求到达A所用的时间最短解解・.・t= GM GA 2GA + GM 2 v v 2 v・•・当2GA+GM最小时,时间最短如图,假设在OM上存在一点G,则BG=AG・・.MG+2AG=MG+AG+BG把4MGB绕点B顺时针旋转60°,得到A M,G/ B,连结GG', MM, ・・・A GG' B、A MM,B都为等边三角形则GG'=G,B=GB又・・・M, G,=MG・・.MG+AG+BG=M/ G’+GG’+AG二•点A、M/为定点・・・AM,与OM的交点为G,此时MG+AG+BG最小・••点G的坐标为(0, 2S)例2 A、B、C、D四个城市恰好为一个正方形的四个顶点,要建立一个公路系统使得每两个城市之间都有公路相通,并是整个公路系统的总长度为最小,则应当如何修建?解:如图,将4ABP绕点N逆时针旋转60°,得到A EBM;同样,将△DCQ绕点C顺时针旋转60°,得到△FCN,连结AE、DF,则A ABE、△DCF均为等边三角形,连结PM、QN,则△BPM,^CQN均为等边三角形所以当点E,M,P,Q,N,F共线时,整个公路系统的总长取到最小值,为线段EF的长,如图,此时点P, Q在EF上,1= 2 = 3= 4 = 30 .进阶训练1.如图,在ABC中,ABC=60 , AB=5, BC=3, P是ABC 内一点,求PA+PB+PC的最小值,并确定当PA+PB+PC取得最小值时,APC的度数.答案:PA+PB+PC的最小值为7,此时APC=120【提示】如图,将APB绕点B逆时针旋转60 ,得到A'BP', 连结PP',A'C.过点A'作A'E BC,交CB的延长线于点E.解Rt A' EC求A'C的长,所得即为PA+PB+PC的最小值.2.如图,四边形ABCD是正方形,ABE是等边三角形,M为对角线BD上任意一点,将BM绕点B逆时针旋转60得到BN,连结AM, CM, EN(1)当M在何处时,AM+CM的值最小?(2)当M在何处时,AM+BM+CM的值最小?请说明理由;(3)当AM+BM+CM的最小值为,:3 i时,求正方形的边长.答案:(1)当点M落在BD的中点时,AM+CM的值最小,最小值为AC的长;(2)连结CE,当点M位于BD与CE的交点处时.AM+BM+CM的值最小,最小值为CE的长.(3)正方形的边长为我.【提示】(3)过点E作EF BC,交CB的延长线于点F,解Rt EFC 即可.。
[全]中考数压轴题之费马点模型详解
![[全]中考数压轴题之费马点模型详解](https://img.taocdn.com/s3/m/a15ddf7202d276a201292e64.png)
中考数压轴题之费马点模型详解如图,在四边形ABCD中,ZB=60°,AD=30°,AB=BC.(1)求Z4+ZC的度数;(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;(3)若AB=l i点E在四边形ABCD内部运动,且满足?IE?=BE2*CE2)求点E运动路径的长度.这期这道题并不是中考真题,我也没找到是哪里的模考题,但是不影响这道题的重要性,这种类型的题目,同学们如果做过总结,会发现很简单,如果不做总结,考试时间都给你想你也想不出来,下面我们就来看看这道题吧第一问,求匕A+zC的度数,这个很简单,就是270。
第二问让我们连接BD,探究一下三条边之间的关系A这关系看不出来,我们能够拿尺子量一下,发现不是加和关系,那么考虑勾股定理关系,发现就是它。
这里要注意一下,有的题目会让我们猜测关系,但是关系往往不是那么容易看出来的,所以我们有必要借助一些工具,比如刻度尺,量角器这些来进行辅助猜测。
既然判断出是勾股定理关系,那么我们该怎么证明呢?首先想到是要把它们放到一个三角形当中去,不过这个三角形在哪里呢?这边就需要同学们积累一下了,遇到这种边相等,且存在勾股定理关系的,我们要想到旋转。
A我们将红色的三角形绕点B顺时针旋转60。
到蓝色的三角形的位置,因为BA=BC,所以旋转过来刚好能重合,我去居然这么巧!其实就是因为相等才想到旋转的,这种技巧需要大家记忆,否则你考试很难考自己想出来的。
之后我们就发现,AD=CD',BD=BD',不过好像还是没有把这三条边放到一个三角形当中去,不急,我们还要连接DD,,这样^DD,就是等边三角形,怎么突然它就是等边三角形了?因为我旋转了60°,而且BD=BD',所以它自然是等边三角形。
那么后面就简单了,BD与DD'是相等的,所以三条边都转化到了A CDD'当中,那么问题就转化为证明/DCD'=90°了。
专题40中考最值难点突破费马点问题(原卷版)

专题40 中考最值难点突破费马点问题(原卷版)模块一典例剖析+针对训练费马点问题解题技巧:旋转变换.类型一费马点模型典例1(2020秋•仓山区校级期中)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点,此时P A+PB+PC的和最小,称为△ABC的费马距离.(1)若点P是等边三角形三条高的交点,点P(填是或不是)该三角形的费马点.(2)如图(2),分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD相交于P点.求证:P点为△ABC的费马点.(3)若图(2)中,AB=5,AC=4,BC=a,BD=b,则△ABC的费马距离=.针对训练1.(2021春•滨海县期中)如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B 点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)当M点在何处时,2AM的值最小,并说明理由;(3)当M点在何处时,2AM+BM的值最小,并说明理由.2.(2021春•历下区期末)【操作发现】(1)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.①请按要求画图:将ABC绕点A按顺时针方向旋转90°,点B的对应点为B',点C的对应点为C′;②连接BB′,此时∠ABB′=°;【问题解决】在某次数学兴趣小组活动中,小明同学遇到了如下问题:(2)如图2,在等边△ABC中,点P在内部,且P A=3,PC=4,∠APC=150°,求PB的长.经过同学们的观察、分析、思考、交流,对上述问题形成了如下想法:将△APC绕点A按顺时针方向旋转60°,得到△ABP′,连接PP′,寻找P A、PB、PC三边之间的数量关系.…请参考他们的想法,完成该问题的解答过程;【学以致用】(3)如图3,在等腰直角△ABC中,∠ACB=90°,P为△ABC内一点,且P A=5,PC=2√2,∠BPC =135°,求PB;【思维拓展】(4)注意:从以下①②中,你任意选择一道题解答即可.①等腰直角△ABC中,∠ACB=90°,P为△ABC内部一点,若BC=4,则AP+BP+CP的最小值=;②如图4,若点P是正方形ABCD外一点,P A=3,PB=√3,PC=√15,求∠APB的度数.3.(2019春•金水区校级期中)在△ABC中,∠ACB=90°,点P为△ABC内一点.(1)如图1,连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.如果BP⊥CE,BP=3,AB=6,则CE=.(2)如图2,连接P A,PB,PC,当AC=BC=8时,求P A+PB+PC的最小值.类型二费马点模型变式典例2(2021春•碑林区校级期中)[问题发现]如图①,在△OAB中,OB=3,若将△OAB绕点O逆时针旋转120°得△OA′B′,连接BB'.则BB'=.[问题探究]如图②,已知△ABC是边长为4√3的等边三角形,以BC为边向外作等边△BCD,P为△ABC 内一点,将线段CP绕点C逆时针旋转60°,P的对应点为Q.求P A+PB+PC的最小值.[实际应用]如图③,在长方形ABCD中,其中AB=600,AD=800,点P是长方形内一动点,且S△P AD =2S△PBC,点Q为△ADP内的任意一点,是否存在一点P和一点Q,使得AQ+DQ+PQ有最小值?若存在,请求出这个最小值,并求出此时PQ的长度,若不存在,请说明理由.针对训练1.(2021•雁塔区校级模拟)【问题情境】如图1,在△ABC中,∠A=120°,AB=AC,BC=5√3,则△ABC的外接圆的半径值为.【问题解决】如图2,点P为正方形ABCD内一点,且∠BPC=90°,若AB=4,求AP的最小值.【问题解决】如图3,正方形ABCD是一个边长为3√3cm的隔离区域设计图,CE为大门,点E在边BC上,CE=√3cm,点P是正方形ABCD内设立的一个活动岗哨,到B、E的张角为120°,即∠BPE=120°,点A、D为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点Q,使得Q到A、D、P三个岗哨的距离和最小,试求QA+QD+QP的最小值.(保留根号或结果精确到1cm,参考数据√3≈1.7,10.52=110.25).模块二2023中考押题预测一.选择题1.(2017秋•义乌市月考)已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermatpoint).已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为√2的等腰直角三角形DEF的费马点,则PD+PE+PF=()A.2√3B.1+√3C.6D.3√32.(2022春•山亭区期中)如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.40°B.30°C.50°D.65°二.填空题3.(2019秋•开福区校级月考)法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时P A+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CP A=120°,如图,点P为锐角△ABC的费马点,且P A=3,PC=4,∠ABC=60°,则费马距离为.4.(2019秋•梁溪区期末)如图,已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为1+√3,则这个正方形的边长为.5.(2021•丹东)已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果△ABC是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足∠APB=∠BPC=∠CP A=120°.(例如:等边三角形的费马点是其三条高的交点).若AB=AC=√7,BC=2√3,P为△ABC的费马点,则P A+PB+PC =;若AB=2√3,BC=2,AC=4,P为△ABC的费马点,则P A+PB+PC=.6.(2022秋•洪山区校级期中)如图,以等边△ABC的一边BC为底边作等腰△BCD,已知AB=3,CD=BD=√3,且∠BDC=120°,在△BCD内有一动点P,则PB+PC+PD的最小值为.7.(2022秋•大冶市期末)如图,D是等边三角形ABC外一点,连接AD,BD,CD,已知BD=8,CD=3,则当线段AD的长度最小时,①∠BDC=;②AD的最小值是.三.解答题8.(2009•湖州)自选题:若P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点.(1)若点P为锐角△ABC的费马点,且∠ABC=60°,P A=3,PC=4,则PB的值为;(2)如图,在锐角△ABC外侧作等边△ACB′连接BB′.求证:BB′过△ABC的费马点P,且BB′=P A+PB+PC.9.问题探究:(1)如图1,已知,在四边形ABCD中,AB=BC,AD=DC,则对角线AC、BD的位置关系是.(2)如图2,已知,在△ABC中,AC=BC,∠ACB=90°.△ABC内一动点E到A、B、C三点的距离之和的最小值为2,求AC的长.问题解决:(3)如图3,在平面直角坐标系xOy中,△ABC三个顶点的坐标分别为A(﹣6,0),B(6,0),C(0,4√3),延长AC至点D,使CD=12AC,过点D作DE⊥y轴于点E.设G为y轴上一点,点P从点E出发,先沿y轴到达G点,再沿GA到达A点.若点P在直线GA上运动速度为定值v,在y轴上运动速度为2v,试确定点G的位置,使P点按照上述要求到达A点所用的时间最短,并求此时点G的坐标.10.(2017•利辛县一模)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点.(1)若点P是等边三角形三条中线的交点,点P(填是或不是)该三角形的费马点.(2)如果点P为锐角△ABC的费马点,且∠ABC=60°.求证:△ABP∽△BCP;(3)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD交于P点.如图(2)①求∠CPD的度数;②求证:P点为△ABC的费马点.12.(2022春•兰溪市校级月考)定义:在一个等腰三角形底边的高线上所有点中,到三角形三个顶点距离之和最小的点叫做这个等腰三角形的“近点”,“近点”到三个顶点距离之和叫做这个等腰三角形的“最近值”.【基础巩固】(1)如图1,在等腰Rt△ABC中,∠BAC=90°,AD为BC边上的高,已知AD上一点E满足∠DEC =60°,AC=4√6,求AE+BE+CE=;【尝试应用】(2)如图2,等边三角形ABC边长为4√3,E为高线AD上的点,将三角形AEC绕点A逆时针旋转60°得到三角形AFG,连接EF,请你在此基础上继续探究求出等边三角形ABC的“最近值”;【拓展提高】(3)如图3,在菱形ABCD中,过AB的中点E作AB垂线交CD的延长线于点F,连接AC、DB,已知∠BDA=75°,AB=6,求三角形AFB“最近值”的平方.。
初中数学精品试题:费马点问题

费马点问题
例1 ( 2013 年常州中考) 如图2,在Rt△ABC 中,∠C = 90°,AC = 1,BC = 3,
点O 为Rt△ABC 内一点,连接AO,BO,CO,且∠AOC = ∠COB = ∠BOA = 120°,按下列要求画图( 保留画图痕迹) :
以点B 为旋转中心,将△AOB 绕点 B 顺时针方向旋转60°,得到△A'O'B( 其中点A、O 的对应点分别为点A'、O') ,并回答下列问题:
∠ABC = ; ∠A'BC = ; OA + OB+ OC =
例 2 ( 2016 年朝阳中考) 小颖在学习“两点之间,线段最短”查阅资料时发现: △ABC 内总存在一点P 与三个顶点的连线的夹角相等,此时该点到三个顶
点的距离之和最小
例3 ( 2010 年宁德中考) 如图,四边形ABCD是正方形,△ABE 是等边三角形,M 为对角线BD( 不含 B 点) 上任意一点,将BM 绕点 B 逆时针旋转60°得到BN,连接EN、AM、CM.
( 1) 求证: △AMB ≌△ENB;
( 2) ① 当M 点在何处时,AM + CM 的值最小;
② 当M 点在何处时,AM + BM + CM 的值最小,并说明理由;
( 3) 当AM + BM + CM 的最小值为3+ 1 时,求正方形的边长。
中考复习之线段和差最值之费马点问题-附练习题含参考答案
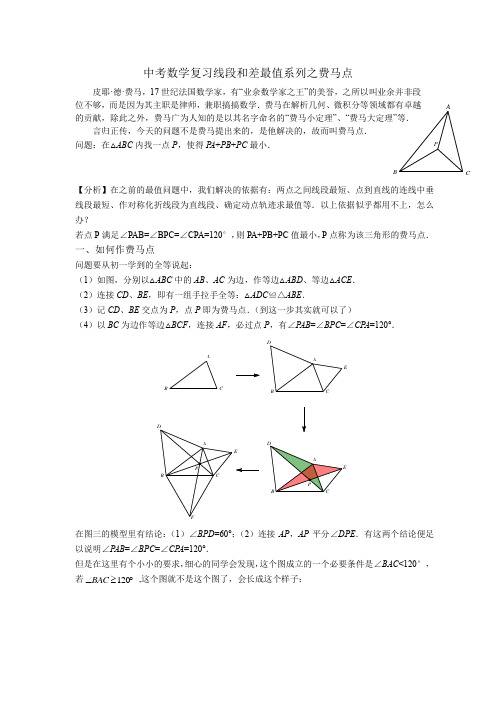
ABCP中考数学复习线段和差最值系列之费马点皮耶·德·费马,17世纪法国数学家,有“业余数学家之王”的美誉,之所以叫业余并非段位不够,而是因为其主职是律师,兼职搞搞数学.费马在解析几何、微积分等领域都有卓越的贡献,除此之外,费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等.言归正传,今天的问题不是费马提出来的,是他解决的,故而叫费马点. 问题:在△ABC 内找一点P ,使得P A +PB +PC 最小.【分析】在之前的最值问题中,我们解决的依据有:两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等.以上依据似乎都用不上,怎么办?若点P 满足∠PAB=∠BPC=∠CPA=120°,则PA+PB+PC 值最小,P 点称为该三角形的费马点.一、如何作费马点问题要从初一学到的全等说起:(1)如图,分别以△ABC 中的AB 、AC 为边,作等边△ABD 、等边△ACE . (2)连接CD 、BE ,即有一组手拉手全等:△ADC ≌△ABE .(3)记CD 、BE 交点为P ,点P 即为费马点.(到这一步其实就可以了)(4)以BC 为边作等边△BCF ,连接AF ,必过点P ,有∠P AB =∠BPC =∠CP A =120°.在图三的模型里有结论:(1)∠BPD =60°;(2)连接AP ,AP 平分∠DPE .有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°.但是在这里有个小小的要求,细心的同学会发现,这个图成立的一个必要条件是∠BAC <120°,若120BAC ∠≥︒ ,这个图就不是这个图了,会长成这个样子:EB ACAB CDE此时CD 与BE 交点P 点还是我们的费马点吗?显然这时候就不是了,显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和.所以,是的,你想得没错,此时三角形的费马点就是A 点!当然这种情况不会考的,就不多说了.二、为什么是这个点为什么P 点满足∠P AB =∠BPC =∠CP A =120°,P A +PB +PC 值就会最小呢?归根结底,还是要重组这里3条线段:P A 、PB 、PC 的位置,而重组的方法是构造旋转!在上图3中,如下有△ADC ≌△ABE ,可得:CD =BE .类似的手拉手,在图4中有3组,可得:AF =BE =CD .巧的,它们仨的长度居然一样长!更巧的是,其长度便是我们要求的P A +PB +PC 的最小值,这一点是可以猜想得到的,毕竟最小值这个结果,应该也是个特别的值! 接下来才是真正的证明:考虑到∠APB =120°,∴∠APE =60°,则可以AP 为边,在PE 边取点Q 使得PQ =AP ,则△APQ 是等边三角形.△APQ 、△ACE 均为等边三角形,且共顶点A ,故△APC ≌△AQE ,PC =QE . 以上两步分别转化P A =PQ ,PC =QE ,故P A +PB +PC =PB +PQ +QE =BE .没有对比就没有差别,我们换个P 点位置,如下右图,同样可以构造等边△APQ ,同样有△APC ≌△AQE ,转化P A =PQ ,PC =QE ,显然,P A +PB +PC =PB +PQ +QE >BE .还剩下第3个问题!如果说费马点以前还算是课外的拓展内容,那现在,已经有人把它搬上了中考舞台!【中考再现】问题背景:如图1,将△ABC 绕点A 逆时针旋转60°得到△ADE ,DE 与BC 交于点P ,可推出结论:P A +PC =PE .问题解决:如图2,在△MNG 中,MN =6,∠M =75°,MG=O 是△MNG 内一点,则点O 到△MNG 三个顶点的距离和的最小值是______.【分析】本题的问题背景实际上是提示了解题思路,构造60°的旋转,当然如果已经了解了费马点问题,直接来解决就好了!如图,以MG 为边作等边△MGH ,连接NH ,则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值.(此处不再证明)过点H 作HQ ⊥NM 交NM 延长线于Q 点,根据∠NMG =75°,∠GMH =60°,可得∠HMQ =45°,∴△MHQ 是等腰直角三角形, ∴MQ =HQ =4,∴NH== 练习题1.如图,在△ABC 中,△ACB=90°,AB=AC=1,P 是△ABC 内一点,求P A +PB +PC 的最小值.2. 如图,已知矩形ABCD ,AB =4,BC =6,点M 为矩形内一点,点E 为BC 边上任意一点,则MA +MD +ME 的最小值为______.NG图2图1ABCD EPHGN M464Q HGN MABCDME3.如图,矩形ABCD中,AB=10,BC=15,现在要找两点E、F,则EA+EB+EF+FC+FD的最小值为__________4.如图,等腰Rt∆ABC中,AB=4,P为∆ABC内部一点,则PA+PB+PC的最小值为_______5.如图,∆ABC中,AB=4,,∠ABC=75°,P为∆ABC内的一个动点,连接PA、PB、PC,则PA+PB+PC的最小值为________6.如图,P为正方形ABCD对角线BD上一动点,若AB=2,则PA+PB+PC的最小值为______7.在Rt∆ABC中,∠ACB=90°,AC=1,,点O为Rt∆ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC=_______8.如图,在四边形ABCD中,∠B=60°,AB=BC=3,AD=4,∠BAD=90°,点P是四边形内部一点,则PA+PB+PD的最小值是______9.如图,点P是矩形ABCD对角线BD上的一个动点,已知AB=2,,则PA+PB+PC 的最小值为_______10.如图,菱形ABCD的对角线AC上有一动点P,BC=6,∠ABC=150°,则PA+PB+PD的最小值为__________11.已知,在∆ABC中,∠ACB=30°点P是ABC内一动点,则PA+PB+PC的最小值为__________12.如图,设点P到等边三角形ABC两顶点A、B的距离分别为2则PC的最大值为______13.如图,设点P到正方形ABCD两顶点A、D的距离为2PC的最大值为________14.如图,设点P到正方形ABCD两顶点A、D的距离为2则PO的最大值为_________.15.如图,在Rt∆ABC中,∠BAC=90⁰,AB=AC,点D是BC边上一动点,连接AD,把AD 绕点A逆时针旋转90⁰,得到AE,连接CE、DE,点F是DE的中点,连接CF问题:在点D运动的过程中,在线段AD上存在一点P,使PA+PB+PC的值最小,当PA+PB+PC 取最小值时,AP的长为m,用含有m的式子表示CE的长.参考答案1.7.8.7 9.3 10. 12.2+13.2+1 15.32m +。
中考数学复习专题:几何最值模型—费马点专题
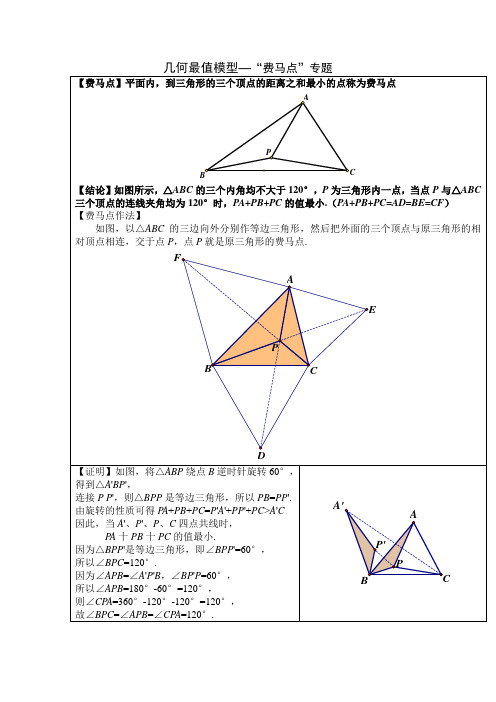
【费马点】平面内,到三角形的三个顶点的距离之和最小的点称为费马点【结论】如图所示,△ABC 的三个内角均不大于120°,P 为三角形内一点,当点P 与△ABC 三个顶点的连线夹角均为120°时,PA +PB +PC 的值最小.(PA +PB +PC=AD=BE=CF ) 【费马点作法】如图,以△ABC 的三边向外分别作等边三角形,然后把外面的三个顶点与原三角形的相对顶点相连,交于点P ,点P 就是原三角形的费马点.【证明】如图,将△ABP 绕点B 逆时针旋转60°,得到△A 'BP ',连接P P ',则△BPP 是等边三角形,所以PB =PP '. 由旋转的性质可得P A +PB +PC =P 'A '+PP '+PC >A 'C 因此,当A '、P '、P 、C 四点共线时,P A 十PB 十PC 的值最小.因为△BPP '是等边三角形,即∠BPP '=60°, 所以∠BPC =120°.因为∠APB =∠A 'P 'B ,∠BP 'P =60°, 所以∠APB =180°-60°=120°,则∠CP A =360°-120°-120°=120°, 故∠BPC =∠APB =∠CP A =120°.CBAPPDFECBAA'P'ABCP费马点结论:1) 对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点; 2) 对于有一个角超过120°的三角形,费马点就是这个内角的顶点. 费马问题解决问题的方法是运用旋转变换.1) 利用旋转把三条共点线段转化成折线段, 2) 利用两点之间线段最短 构造直角三角形,利用勾股定理 模型巧记求到三角形三个顶点距离和的最小值,只需要以三角形的一条边为边作等边三角形,那么原三角形的第三个顶点和等边三角形的第三个顶点的距离就是最小值 例1、P 是边长是2的等边△ABC 内的一点, 求PA+PB+PC 的最小值【分析】把△APC 绕A 逆时针旋转60°,得到△AP'C',连接PP' 易知△APP'是等边三角形∴PC=P'C∴∠CAC'=60°∴P A+PB+PC=PB+PP'+PC’当且仅当BPP'C '共线时取得最小值∵AB =2;∴AD =1;BD =3∴.C'D =3∴BC =23 点评:①用旋转把三条共点线段转化成折线段 ②利用两点之间线段最短③构造直角三角形,利用勾股定理例2、P 是边长是1的正方形ABCD 内的一点, 求PA+PB+PC 的最小值【分析】把△APB 绕B 逆时针旋转,得到△BP'A',连接PP' ∴△BPP '是等边三角形 ∴BP=BP ' ∴∠PBP '=60°∴P A+PB+PC=P'A'+PP'+PC ,当且仅当CPP'A'共线时取得最小值∵AB =AB '=1;A'P'PCBA∴A'M =12;BM =32;∴CM =232;CA '=622例3、P 是△ABC 内的一点,BC=6,AC=5,∠ACB =30°, 求P A+PB+PC 的最小值 【分析】把△APC 绕C 顺时针旋转60°,得到△CP'A',连接PP' ∴△CPP '是等边三角形 ∴CP=PP'∴∠PCP '=60°∴P A+PB+PC=P 'A'+PB+PP '当且仅当BPP ’A ’共线时取得最小值 ∵CA=CA '=5;CB=6,∠ACB =30° ∴∠A 'CB =60° ∴A 'B =61什么是加权费马点问题?标准的费马点问题式中的三条线段的系数全为1。
中考数学几何模型专题12费马点问题(学生版) 知识点+例题

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题12费马点问题-年8月17日﹣1665年1月12日),生于法国南部图卢兹(Toulouse )附近的波蒙•德•罗曼,被誉为业余数学家之王.1643年,费马曾提出了一个著名的几何问题:给定不在一条直线上的三个点A ,B ,C ,求平面上到这三个点的距离之和最小的点的位置.另一位数学家托里拆利成功地解决了这个问题:如图1,△ABC (三个内角均小于120°)的三条边的张角都等于120°,即满足∠APB =∠BPC =∠APC =120°的点P ,就是到点A ,B ,C 的距离之和最小的点,后来人们把这个点P 称为“费马点”. 下面是“费马点”的证明过程:如图2,将△APB 绕着点B 逆时针旋转60°得到△A ′P ′B ,使得A ′P ′落在△ABC 外,则△A ′AB 为等边三角形,∴P ′B =PB =PP ′,于是P A +PB +PC =P ′A ′+PP ′+PC ≥A ′C ,∴当A ',P ',P ,C 四点在同一直线上时P A +PB +PC 有最小值为A 'C 的长度,∵P ′B =PB ,∠P 'BP =60°,∴△P 'BP 为等边三角形,则当A ',P ',P ,C 四点在同一直线上时,∠BPC =180°﹣∠P 'PB =180°﹣60°=120°,∠APB =∠A 'PB =180°﹣∠BP 'P =180°﹣60°=120°,∠APC =360°﹣∠BPC ﹣∠APC =360°﹣120°﹣120°=120°,∴满足∠APB =∠BPC =∠APC =120°的点P ,就是到点A ,B ,C 的距离之和最小的点;ABC 所在平面上一点,且∠APB =∠BPC =∠CP A =120°,则点P 叫做△ABC 的费马点.(1)如点P为锐角△ABC的费马点.且∠ABC=60°,P A=3,PC=4,求PB的长.(2)如图(2),在锐角△ABC外侧作等边△ACB′连接BB′.求证:BB′过△ABC的费马点P,且BB′=P A+PB+PC.(3)已知锐角△ABC,∠ACB=60°,分别以三边为边向形外作等边三角形ABD,BCE,ACF,请找出△ABC的费马点,并探究S△ABC与S△ABD的和,S△BCE与S△ACF的和是否相等.【例2】探究问题:(1)阅读理解:①如图(A),在已知△ABC所在平面上存在一点P,使它到三角形顶点的距离之和最小,则称点P为△ABC的费马点,此时P A+PB+PC的值为△ABC的费马距离;②如图(B),若四边形ABCD的四个顶点在同一圆上,则有AB•CD+BC•DA=AC•BD.此为托勒密定理;(2)知识迁移:①请你利用托勒密定理,解决如下问题:如图(C),已知点P为等边△ABC外接圆的上任意一点.求证:PB+PC=P A;②根据(2)①的结论,我们有如下探寻△ABC(其中∠A、∠B、∠C均小于120°)的费马点和费马距离的方法:第一步:如图(D),在△ABC的外部以BC为边长作等边△BCD及其外接圆;第二步:在上任取一点P′,连接P′A、P′B、P′C、P′D.易知P′A+P′B+P′C=P′A+(P′B+P′C)=P′A+;第三步:请你根据(1)①中定义,在图(D)中找出△ABC的费马点P,并请指出线段的长度即为△ABC的费马距离.(3)知识应用:2010年4月,我国西南地区出现了罕见的持续干旱现象,许多村庄出现了人、畜饮水困难,为解决老百姓的饮水问题,解放军某部来到云南某地打井取水.已知三村庄A、B、C构成了如图(E)所示的△ABC(其中∠A、∠B、∠C均小于120°),现选取一点P打水井,使从水井P到三村庄A、B、C所铺设的输水管总长度最小,求输水管总长度的最小值.【例3】如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的正半轴上,∠ODB=30°,OE为△BOD的中线,过B、E两点的抛物线与x轴相交于A、F两点(A在F的左侧).(1)求抛物线的解析式;(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;(3)点P为△ABO内的一个动点,设m=P A+PB+PO,请直接写出m的最小值,以及m 取得最小值时,线段AP的长.1.已知:到三角形3个顶点距离之和最小的点称为该三角形的费马点.如果△ABC是锐角(或直角)三角形,则其费马点P是三角形内一点,且满足∠APB=∠BPC=∠CP A=120°.(例如:等边三角形的费马点是其三条高的交点).若AB=AC=,BC=2,P为△ABC的费马点,则P A+PB+PC=;若AB=2,BC=2,AC=4,P为△ABC的费马点,则P A+PB+PC=.2.在△ABC中,若其内部的点P满足∠APB=∠BPC=∠CP A=120°,则称P为△ABC的费马点.如图所示,在△ABC中,已知∠BAC=45°,设P为△ABC的费马点,且满足∠PBA=45°,P A=4,则△P AC的面积为.3.如图,在边长为6的正方形ABCD中,点M,N分别为AB、BC上的动点,且始终保持BM=CN.连接MN,以MN为斜边在矩形内作等腰Rt△MNQ,若在正方形内还存在一点P,则点P到点A、点D、点Q的距离之和的最小值为.4.如果点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点.已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点.若点P是腰长为的等腰直角三角形DEF的费马点,则PD+PE+PF=.5.法国数学家费马提出:在△ABC内存在一点P,使它到三角形顶点的距离之和最小.人们称这个点为费马点,此时P A+PB+PC的值为费马距离.经研究发现:在锐角△ABC中,费马点P满足∠APB=∠BPC=∠CP A=120°,如图,点P为锐角△ABC的费马点,且。
(中考数学二轮强化专题)第10讲 费马点问题

第十讲线段和最小之“费马点问题”问题背景“费马点”——就是到三角形三个顶点的距离之和最小的点.“费马点”问题在中考考查时主要隐藏在求PA+PB+PC的最小值问题,通常将某三角形绕点旋转一定的角度,从而将三条线段转化在同一条直线上,利用两点之间线段最短解决问题.模型分析1、对于一个各角不超过120°的三角形,“费马点”是对各边的张角都是120°的点;2、对于有一个角超过120°的三角形,费马点就是这个内角的顶点.费马点P使它到△ABC三个顶点的距离之和PA+PB+PC最小,这就是所谓的“费马”问题.【模型计算】如图,将△APC绕点A逆时针旋转60°到△AP′C′,则可以构造出等边三角形APP′,从而得到AP=PP′,CP=C′P′,所以将PA+PB+PC的值转化为PP′+PB+P′C′的值,则线段BC′的长即为所求的最小值.经典例题剖析例1.如图,在△ABC中,P为平面内一点,连结P A,PB,PC,分别以PC和AC为一边向右作等边三角形△PCM和△ACD.【探究】求证:PM=PC,MD=P A【应用】若BC=a,AC=b,∠ACB=60°,则P A+PB+PC的最小值是______________(用a,b 表示)例2.如图,矩形ABCD中,AB=2√3,BC=6,P为矩形内一点,连接P A,PB,PC,则P A+PB+PC 的最小值是________________。
强化练习1.如图,已知正方ABCD内一动点E到A、B、C三点的距离之和的最小值为1+√3,则这个正方形的边长为______.2.问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:P A+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=4√2.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是________.3.如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM.(1)求证:△AMB≌△ENB;(2)①当M点在何处时,AM+CM的值最小;②当M点在何处时,AM+BM+CM的值最小,并说明理由;(3)当AM+BM+CM的最小值为√3+1时,求正方形的边长.。
中考数学压轴系列--费马点

对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.△三个顶点的距离之和PA+PB+PC最小?这就是下面简单说明如何找点P使它到ABC所谓的费尔马问题.图1解析:如图1,把△APC绕A点逆时针旋转60°得到△AP′C′,连接PP′.则△APP′为等边三角形,AP= PP′,P′C′=PC,所以PA+PB+PC= PP′+ PB+ P′C′.点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC′为定长,所以当B、P、P′、C′四点在同一直线上时,PA+PB+PC最小.这时∠BPA=180°-∠APP′=180°-60°=120°,∠APC=∠A P′C′=180°-∠AP′P=180°-60°=120°,∠BPC=360°-∠BPA-∠APC=360°-120°-120°=120°△的每一个内角都小于120°时,所求的点P对三角形每边的张角都因此,当ABC是120°,可在AB、BC边上分别作120°的弓形弧,两弧在三角形内的交点就是P点;当有一内角大于或等于120°时,所求的P点就是钝角的顶点.费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.1.( 株洲)已知P 是边长为1的正方形ABCD 内的一点,求PA+PB+PC 的最小值.2.( 北京)如图. 在平面直角坐标系xOy 中. 点B 的坐标为(0,2). 点D 在x 轴的正半轴上. 30ODB ∠=︒. OE 为△BOD 的中线. 过B 、E 两点的抛物线23y ax x c =++与x 轴相交于A 、F 两点(A 在F 的左侧).等边△OMN 的顶点M 、N 在线段AE 上,点P 为△ABO 内的一个动点. 设m PA PB PO =++.请直接写出m 的最小值, 以及m 取得最小值时, 线段AP 的长. (备用图)图2图1B3.( 延庆)小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC 是一个可以变化的角)中,AB=2,AC=4,以BC 为边在BC 的下方作等边△PBC,求AP 的最大值。
中考数学试卷费马点

的位置关系是()A. 共线B. 共圆C. 共点D. 无规律2. 已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. DE=EF=FDB. ∠ABC=∠DEFC. AB+BC+CA=DE+EF+FDD. ABC≌DEF3. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定不成立?()A. AB=ACB. ∠ABC=∠DEFC. DE=EF=FDD. ABC≌DEF4. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. ∠ABC=∠DEFB. ∠ABD=∠BCDC. ∠ACF=∠BCED. ∠BAC=∠BCF5. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()A. AB=ACB. ∠ABC=∠DEFC. AB+BC+CA=DE+EF+FDD. ABC≌DEF二、填空题6. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么点D、E、F 的位置关系是()7. 已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()8. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定不成立?()9. 在三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()10. 已知三角形ABC中,点D、E、F分别满足AD=BD,BE=CE,CF=AF,那么下列哪个结论一定成立?()三、解答题点D、E、F在同一直线上。
12. (15分)已知三角形ABC的边长分别为a、b、c,点D、E、F分别满足AD=BD,BE=CE,CF=AF,求证:DE=EF=FD。
专题06 费马点求最小值(解析版)

中考数学压轴题--二次函数第6节 费马点求最小值内容导航方法点拨PQ EABC QPABCE△APC ≌△AQE ,且△APQ 为等边三角形, ∴PC=QE ,AP=PQ ∴AP+BP+CP=BP+PQ+QE当B 、P 、Q 、E 共线时,AP+BP+CP 和最小例题演练题组1:费马点在三角形中运用例1.如图,在△ABC 中,P 为平面内一点,连结P A ,PB ,PC ,分别以PC 和AC 为一边向右作等边三角形△PCM和△ACD.【探究】求证:PM=PC,MD=P A【应用】若BC=a,AC=b,∠ACB=60°,则P A+PB+PC的最小值是(用a,b表示)【解答】【探究】证明:∵以PC和AC为一边向右作等边三角形△PCM和△ACD,∴PM=PC,AC=CD,PC=CM,∠PCM=∠ACD=60°,∴∠PCA=∠MCD,在△ACP和△DCM中,,∴△ACP≌△DCM(SAS),∴MD=P A;【应用】解:连接BD,如图所示:∵△APC≌△DCM,∴∠ACP=∠DCM,AC=CD=b,∴∠ACP+∠PCB=∠DCM+∠PCB,∴∠DCM+∠PCB=∠ACB=60°,∴∠BCD=∠DCM+∠PCB+∠PCM=60°+60°=120°,作DF⊥BC于F,则∠CFD=90°,在Rt△CDF中,∵∠DCF=180°﹣120°=60°,CD=b,∴∠CDF=30°,∴CF=AC=b,DF=CF=b,∴BF=a+b,∴BD===;当B、P、M、D共线时,P A+PB+PC的值最小,即P A+PB+PC的最小值为:;故答案为:.练1.1问题提出(1)如图①,在△ABC中,BC=2,将△ABC绕点B顺时针旋转60°得到△A′B′C′,则CC′=;问题探究(2)如图②,在△ABC中,AB=BC=3,∠ABC=30°,点P为△ABC内一点,连接P A、PB、PC,求P A+PB+PC的最小值,并说明理由;问题解决(3)如图③,在四边形ABCD中,AD∥BC,AB=6,AD=4,∠ABC=∠BCD=60°.在四边形ABCD内部有一点,满足∠APD=120°,连接BP、CP,点Q为△BPC内的任意一点,是否存在一点P和一点Q,使得PQ+BQ+CQ有最小值?若存在,请求出这个最小值;若不存在,请说明理由.【解答】解:(1)如图①,由旋转的性质可知:△BCC′是等边三角形,∴CC′=BC=2,故答案为2.(2)如图②,将△ABP绕点B逆时针旋转60°得到△BFE,连接PF,EC.由旋转的性质可知:△PBF是等边三角形,∴PB=PF,∵P A=EF,∴P A+PB+PC=PC+PF+EF,∵PC+PF+EF≥EC,∴当P,F在直线EC上时,P A+PB+PC的值最小,易证BC=BE=BA=3,∠CBE=90°,∵EB⊥BC,∴EC=BC=3,∴P A+PB+PC的最小值为3.(3)如图③﹣1中,将△PBQ绕点B逆时针旋转60°得到△EBG,则PQ=EG,△BQG是等边三角形,∴BQ=QG,PQ=EG,∴PQ+BQ+CQ=EG+GQ+QC≥EC,∴EC的值最小时,QP+QB+QC的值最小,如图③﹣2中,延长BA交CD的延长线于J,作△ADJ的外接圆⊙O,将线段BO,BP绕点B逆时针旋转60°得到线段BO′,BE,连接EO′,OB,OP.易证△BEO′≌△BPO(SAS),∴EO′=OP,∵∠APD+∠AJD=180°,∴A,P,D,J四点共圆,∴OP=,∴EO′=,∴点E的运动轨迹是以O′为圆心,为半径的圆,∴当点E在线段CO′上时,EC的值最小,最小值=CO′﹣EO′,连接OO′,延长OO′到R,使得O′R=OO′,连接BR,则∠OBR=90°,作RH⊥CB交CB 的延长线于H,O′T⊥CH于T,OM⊥BC于M.在Rt△OBM中,BM=5,OM=,∴OB==,∴BR=OB=14,由△BHR∽△OMB,∴=,∴RH=5,∵HR∥O′T∥OM,OO′=RO′,∴TM=TH,∴O′T==,∴BT==3,∴CO′==,∴CO′﹣EO′=﹣=.∴QP+QB+QC的最小值为.题组2:费马点在四边形中运用例2.如图,P为正方形ABCD内的动点,若AB=2,则P A+PB+PC的最小值为.【解答】解:将△BPC绕点B顺时针旋转60°,得到△BP'C',∴BP=BP',∠PBP'=60°,△BPC≌△BP'C',∴△BPP'是等边三角形,PC=P'C',∠PBC=∠P'BC',BC=BC'=2,∴BP=PP',∴P A+PB+PC=AP+PP'+P'C',∴当线段AP,PP',P'C'在一条直线上时,P A+PB+PC有最小值,最小值是AC'的长,过点C'作C'E⊥AB交AB的延长线于E,∵∠ABP+∠PBP'+∠P'BC'=60°+∠ABP+∠PBC=150°,∴∠EBC'=30°,∴EC'=1,BE=EC'=,∴AE=2+,∴AC'===+,故答案为:+.练2.1如图,四边形ABCD是正方形,△ABE是等边三角形,M为对角线BD上任意一点,将BM 绕点B逆时针旋转60°得到BN,连接BN、AM、CM.(1)求证:△AMB≌△ENB;(2)若正方形的边长为,正方形内是否存在一点P,使得P A+PB+PC的值最小?若存在,求出它的最小值;若不存在,说明理由.【解答】解:(1)如图1,∵四边形ABCD为正方形,△ABE为等边三角形,∴BE=BA,BA=BC,∠ABE=60°;∵∠MBN=60°,∴BE=BA,∠MBN=∠ABE,∴∠MBA=∠NBE;在△AMB与△ENB中,,∴△AMB≌△ENB(SAS),(2)顺时针旋转△BPC60度,可得△PBE为等边三角形.即得P A+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小P A+PB+PC=AF.BM=BF•cos30°=BC•cos30°=,则AM=+=,∵AB=BF,∠ABF=150°∴∠BAF=15°既得AF==+1.例3.如图,在平面直角坐标系xOy中,点B的坐标为(0,2),点D在x轴的正半轴上,∠ODB =30°,OE为△BOD的中线,过B、E两点的抛物线与x轴相交于A、F两点(A在F的左侧).(1)求抛物线的解析式;(2)等边△OMN的顶点M、N在线段AE上,求AE及AM的长;(3)点P为△ABO内的一个动点,设m=P A+PB+PO,请直接写出m的最小值,以及m取得最小值时,线段AP的长.【解答】解:(1)过E作EG⊥OD于G(1分)∵∠BOD=∠EGD=90°,∠D=∠D,∴△BOD∽△EGD,∵点B(0,2),∠ODB=30°,可得OB=2,;∵E为BD中点,∴∴EG=1,∴∴点E的坐标为(2分)∵抛物线经过B(0,2)、两点,∴,可得;∴抛物线的解析式为;(3分)(2)∵抛物线与x轴相交于A、F,A在F的左侧,∴A点的坐标为∴,∴在△AGE中,∠AGE=90°,(4分)过点O作OK⊥AE于K,可得△AOK∽△AEG∴∴∴∴∵△OMN是等边三角形,∴∠NMO=60°∴;∴,或;(6分)(写出一个给1分)(3)如图;以AB为边做等边三角形AO′B,以OA为边做等边三角形AOB′;易证OE=OB=2,∠OBE=60°,则△OBE是等边三角形;连接OO′、BB′、AE,它们的交点即为m最小时,P点的位置(即费马点);∵OA=OB′,∠B′OB=∠AOE=150°,OB=OE,∴△AOE≌△B′OB;∴∠B′BO=∠AEO;∵∠BOP=∠EOP′,而∠BOE=60°,∴∠POP'=60°,∴△POP′为等边三角形,∴OP=PP′,∴P A+PB+PO=AP+OP′+P′E=AE;即m最小=AE=;如图;作正△OBE的外接圆⊙Q,根据费马点的性质知∠BPO=120°,则∠PBO+∠BOP=60°,而∠EBO=∠EOB=60°;∴∠PBE+∠POE=180°,∠BPO+∠BEO=180°;即B、P、O、E四点共圆;易求得Q(,1),则H(,0);∴AH=;由割线定理得:AP•AE=OA•AH,即:AP=OA•AH÷AE=×÷=.故:m可以取到的最小值为当m取得最小值时,线段AP的长为.(如遇不同解法,请老师根据评分标准酌情给分)练3.1如图,抛物线y=ax2+bx+过点A(1,0),B(5,0),与y轴相交于点C.(1)求抛物线的解析式;(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点O到二次函数图象的垂直距离是线段OC的长.已知点E为抛物线对称轴上的一点,且在x轴上方,点F为平面内一点,当以A,B,E,F为顶点的四边形是边长为4的菱形时,请求出点F到二次函数图象的垂直距离.(3)在(2)中,当点F到二次函数图象的垂直距离最小时,在以A,B,E,F为顶点的菱形内部是否存在点Q,使得AQ,BQ,FQ之和最小,若存在,请求出最小值;若不存在,请说明理由.【解答】解:(1)∵抛物线y=ax2+bx+过点A(1,0),B(5,0),∴0=a+b+0=25a+5b+∴a=,b=﹣3∴解析式y=x2﹣3x+(2)当y=0,则0=x2﹣3x+∴A(1,0),B(5,0)∴对称轴直线x=3,顶点坐标(3,﹣2),AB=4∵抛物线与y轴相交于点C.∴C(0,)如图1①如AB为菱形的边,则EF∥AB,EF=AB=4,且E的横坐标为3∴F的横坐标为7或﹣1∵AE=AB=4,AM=2,EM⊥AB∴EM=2∴F(7,2),或(﹣1,2)∴当x=7,y=×49﹣7×3+=6∴点F到二次函数图象的垂直距离6﹣2②如AB为对角线,如图2∵AEBF是菱形,AF=BF=4∴AB⊥EF,EM=MF=2∴点F到二次函数图象的垂直距离﹣2+2(3)当F(3,﹣2)时,点F到二次函数图象的垂直距离最小如图3,以BQ为边作等边三角形BQD,将△BQF绕B逆时针旋转60°到△BDN位置,连接AN,作PN⊥AB于P∵等边三角形BQD∴QD=QB=BD,∵将△BQF绕B逆时针旋转60°到△BDN位置∴NB=BF=4,∠FBN=60°,DN=FQ∵AQ+BQ+FQ=AQ+QD+DN∴当AQ,QD,DN共线时AQ+BQ+FQ的和最短,即最短值为AN的长.∵AF=BF=4=AB,∴∠ABF=60°∴∠NBP=60°且BN=4,∴BP=2,PN=2∴AP=6在Rt△ANP中,AN==4∴AQ+BQ+FQ的和最短值为4.。
初三数学中考模型之费马点问题

费马点的问题定义:数学上称,到三角形 3 个极点距离之和最小的点为费马点。
它是这样确立的:1. 假如三角形有一个内角大于或等于 120°,这个内角的极点就是费马点;2. 假如 3 个内角均小于 120°,那么在三角形内部对 3 边张角均为 120°的点,是三角形的费马点。
3. 费马点与 3 个极点连成的线段是交流 3 点的最短路线,简单理解,这个路线是独一的。
我们称这一结果为最短路线原理。
性质:费马点有以下主要性质:1.费马点到三角形三个极点距离之和最小。
2.费马点连结三极点所成的三夹角皆为 120°。
3.费马点为三角形中能量最低点。
4.三力均衡时三力夹角皆为 120°,因此费马点是三力均衡的点。
例 1::△ ABH 是等边三角形。
求证: GA+GB+GH 最小证明:∵△ABH 是等边三角形。
G 是其重心。
∴∠AGH= ∠AGB= ∠BGH=120 °。
以 HB 为边向右上方作等边三角形△ DBH.以 HG 为边向右上方作等边三角形△ GHP.∵ AH=BH=AB=12.∴∠AGH=120 ° , ∠HGP=60° .∴ A、G、P 三点一线。
再连 PD 两点。
∵△ABH 、△GHP 和△BDH 都是等边三角形 ,∠GHB=30 ° .∴∠PHD=30 ° ,.在△HGB 和△HPD 中∵ HG=HP∠GHB= ∠PHD;HB=HD ;∴△HGB ≌△HPD;〔SAS〕∴∠HPD= ∠HGB=120 °;∵∠HPG=60° .∴ G、P、D 三点一线。
∴ AG=GP=PD, 且同在一条直线上。
∵ GA+GH+GB=GA+GP+PD=AD.∴ G 点是等边三角形内到三个极点的距离之和最小的哪一点,费马点。
也就是重心。
例 2::△ ABC 是等腰三角形, G 是三角形内一点。
∠ AGC= ∠AGB= ∠BGC=120 °。
2024学年初中数学几何(费马点模型)模型专项练习(附答案)

2024学年初中数学几何(费马点模型)模型专项练习1.数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点.现定义:菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点.例如:菱形ABCD,P是对角线BD上一点,E、F是边BC和CD上的两点,若点P满足PE与PF之和最小,则称点P为类费马点.(1)如图1,在菱形ABCD中,AB=4,点P是BD上的类费马点①E为BC的中点,F为CD的中点,则PE+PF= .②E为BC上一动点,F为CD上一动点,且∠ABC=60°,则PE+PF= .(2)如图2,在菱形ABCD中,AB=4,连接AC,点P是△ABC的费马点,(即P A,PB,FC之和最小),①当∠ABC=60°时,BP= .②当∠ABC=30°时,你能找到△ABC的费马点P吗?画图做简要说明,并求此时P A+PB+PC的值.2.阅读材料:平面几何中的费马问题是十七世纪法国数学家、被誉为业余数学家之王的皮埃尔•德•费马提出的一个著名的几何问题.1643年,在一封写给意大利数学家和物理学家托里拆利的私人信件中,费马提出了下面这个极富挑战性和趣味性的几何难题,请求托里拆利帮忙解答: 给定不在一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最短的点P的位置.托里拆利成功地解决了费马的问题.后来人们就把平面上到一个三角形的三个顶点A,B,C距离之和最小的点称为△ABC的费马﹣托里拆利点,也简称为费马点或托里拆利点.问题解决:(1)费马问题有多种不同的解法,最简单快捷的还是几何解法.如图1,我们可以将△BPC 绕点B顺时针旋转60°得到△BDE,连接PD,可得△BPD为等边三角形,故PD=PB,由旋转可得DE=PC,因此P A+PB+PC=P A+PD+DE,由可知,P A+PB+PC的最小值与线段的长度相等;(2)如图2,在直角三角形△ABC内部有一动点P,∠BAC=90°,∠ACB=30°,连接P A,PB,PC,若AB=2,求P A+PB+PC的最小值;(3)如图3,菱形ABCD的边长为4,∠ABC=60°,平面内有一动点E,在点E运动过程中,始终有∠BEC=90°,连接AE、DE,在△ADE内部是否存在一点P,使得P A+PD+PE最小,若存在,请直接写出P A+PD+PE的最小值;若不存在,请说明理由.3.若点P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC的费马点.当三角形的最大角小于120°时,可以证明费马点就是“到三角形的三个顶点的距离之和最小的点”.即P A+PB+PC最小.(1)如图1,向△ABC外作等边三角形△ABD,△AEC.连接BE,DC相交于点P,连接AP.①证明:点P就是△ABC费马点;②证明:P A+PB+PC=BE=DC;(2)如图2,在△MNG中,MN=4,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是.4.如图,在菱形ABCD中,∠ABC=60°,点E、F分别是AB、BC上的动点,连接DE、DF、EF.(1)如图1,连接AF,若AF⊥BC,E为AB的中点,且EF=2,求DF的长;(2)如图2,若BE=BF,G为DE的中点,连接AF、AG、FG,求证:AG⊥FG;(3)如图3,若AB=4,将△BEF沿EF翻折得到△EFP(始终保持点P在菱形ABCD的内部),连接AP、BP及CP,请直接写出当P A+PB+PC值最小时PB的长.参考答案1.数学上称“费马点”是位于三角形内且到三角形三个顶点距离之和最短的点.现定义:菱形对角线上一点到该对角线同侧两条边上的两点距离最小的点称为类费马点.例如:菱形ABCD,P是对角线BD上一点,E、F是边BC和CD上的两点,若点P满足PE与PF之和最小,则称点P为类费马点.(1)如图1,在菱形ABCD中,AB=4,点P是BD上的类费马点①E为BC的中点,F为CD的中点,则PE+PF= .②E为BC上一动点,F为CD上一动点,且∠ABC=60°,则PE+PF= .(2)如图2,在菱形ABCD中,AB=4,连接AC,点P是△ABC的费马点,(即P A,PB,FC之和最小),①当∠ABC=60°时,BP= .②当∠ABC=30°时,你能找到△ABC的费马点P吗?画图做简要说明,并求此时P A+PB+PC的值.【详细解答】解:(1)①取AB的中点E',连接PE',∵四边形ABCD是菱形,∴BC=AB=CD,∠ABP=∠CBP,∵点E,E'分别是AB,BC的中点,∴BE=BE',在△BEP和△BE'P中,,∴△BEP≌△BE'P(SAS),∴PE=PE',1∴PE+PF=PE'+PF,∴当E'、P、F三点共线时,PE+PF最小值为E'F的长,∵AE'=DF,AE'∥DF,∴四边形AE'FD是平行四边形,∴E'F=AB=4,∴PE+PF=4,故答案为:4;②由①知PE+PF=E'F,若E、F为动点,则E'F的最小值为AB与CD之间的距离,∴过点C作CH⊥AB于H,在Rt△BCH中,sin∠CBH =,∴CH=2,∵点P是BD上的类费马点∴PE+PF的最小值为2;故答案为:2;(2)①如图2,将△BPC绕点B顺时针旋转60°得△BP'C',连接PP',∴BP=BP',PC=P'C',∠PBP'=60°,∴△BPP'是等边三角形,∴PP'=PB,∴P A+PB+PC=P A+PP'+P'C',∴当P、P'在线段AC'上时,P A+PB+PC最小值为AC'的长,2∴连接AC',AC'与BD的交点为P点, ∵AB=BC=4,∠ABC=120°,∴∠BAP=∠ABP=30°,AC'=4, ∴AP=BP,同理BP'=CP',∴BP=AC'=;故答案为:;②如图3,将△BPC绕点B顺时针旋转60°得△BP'C',连接PP',∴BP=BP',PC=P'C',∠PBP'=60°,∠CBC'=60°,∴△BPP'是等边三角形,∴PP'=PB,∴P A+PB+PC=P A+PP'+P'C',∴当P、P'在线段AC'上时,P A+PB+PC最小值为AC'的长,且线段AC'在△ABC内部的线段即为费马点P,∵∠ABC'=90°,AB=BC'=4,∴AC'=,∴此时P A+PB+PC的最小值为4.2.阅读材料:平面几何中的费马问题是十七世纪法国数学家、被誉为业余数学家之王的皮埃尔•德•费马提出的一个著名的几何问题.1643年,在一封写给意大利数学家和物理学家托里拆利的私人信件中,费马提出了下面这个极富挑战性和趣味性的几何难题,请求托里拆利帮忙详细解答: 给定不在一条直线上的三个点A,B,C,求平面上到这三个点的距离之和最短的点P的位置.托里拆利成功地解决了费马的问题.后来人们就把平面上到一个三角形的三个顶点A,B,3C距离之和最小的点称为△ABC的费马﹣托里拆利点,也简称为费马点或托里拆利点.问题解决:(1)费马问题有多种不同的解法,最简单快捷的还是几何解法.如图1,我们可以将△BPC 绕点B顺时针旋转60°得到△BDE,连接PD,可得△BPD为等边三角形,故PD=PB,由旋转可得DE=PC,因此P A+PB+PC=P A+PD+DE,由可知,P A+PB+PC的最小值与线段的长度相等;(2)如图2,在直角三角形△ABC内部有一动点P,∠BAC=90°,∠ACB=30°,连接P A,PB,PC,若AB=2,求P A+PB+PC的最小值;(3)如图3,菱形ABCD的边长为4,∠ABC=60°,平面内有一动点E,在点E运动过程中,始终有∠BEC=90°,连接AE、DE,在△ADE内部是否存在一点P,使得P A+PD+PE 最小,若存在,请直接写出P A+PD+PE的最小值;若不存在,请说明理由.【详细解答】解:(1)将△BPC绕点B顺时针旋转60°得到△BDE,连接PD,可得△BPD 为等边三角形,故PD=PB,由旋转可得DE=PC,因此P A+PB+PC=P A+PD+DE,由两点之间线段最短可知,P A+PB+PC的最小值与线段AE的长度相等.故答案为:两点之间线段最短,AE.(2)如图,将△ABP绕点B顺时针旋转60°得到△EBF,连接PF,CE,作EH⊥CA交CA的延长线于H.4在Rt△ABC中,∵∠ABC=30°,AB=2,∴BC=2AC=4,AB=AC=2,由旋转的旋转可知:P A=EF,△PBF,△ABE是等边三角形, ∴PF=PB,∴P A+PB+PC=EF+FP+PC,∵EF+FP+PC≥CE,∴当C,P,F,E共线时,P A+PB+PC的值最小,∵∠BAC=90°,∠CAE=60°,∴∠HAE=180°﹣90°﹣60°=30°,∵EH⊥AH,AE=AB=2,∴EH =AE=1,AH=EH =,∴CE ===2,∴P A+PB+PC的最小值为2.故答案为2.(3)如图3中,将△ADP绕点A逆时针旋转90°得到△TAH,连接PH,DT,CT.5∵四边形ABCD是菱形,∴AB=BC=CD=AD,∵∠ABC=60°,∴△ABC,△ADC都是等边三角形,∵∠BEC=90°,∴点E在以BC为直径的⊙O上运动,连接OT,OE,则OE=BC=2,由旋转的性质可知,△P AH,△ADT都是等边三角形,P A=PH,HT=PD, ∵OE+PE+PH+TH≥OT,∴PE+P A+PD≥OT﹣OE,∵TA=TD=AC=CD=AD=4,∴CT⊥AD,∵AD∥BC,∴CT⊥BC,CT=4,∴OT==2,∴PE+P A+PD≥2﹣2,∴PA+PD+PE的最小值为2﹣2.3.若点P为△ABC所在平面上一点,且∠APB=∠BPC=∠CP A=120°,则点P叫做△ABC 的费马点.当三角形的最大角小于120°时,可以证明费马点就是“到三角形的三个顶点6的距离之和最小的点”.即P A+PB+PC最小.(1)如图1,向△ABC外作等边三角形△ABD,△AEC.连接BE,DC相交于点P,连接AP.①证明:点P就是△ABC费马点;②证明:P A+PB+PC=BE=DC;(2)如图2,在△MNG中,MN=4,∠M=75°,MG=3.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是.【详细解答】(1)证明:①如图1﹣1中,作AM⊥CD于M,AN⊥BE于N设AB交CD于O.∵△ADB,△ACE都是等边三角形,∴AD=AB,AC=AE,∠DAB=∠CAE=60°,∴∠DAC=∠BAE,∴△ADC≌△ABE(SAS),∴CD=BE,S△DAC=S△ABE,∠ADC=∠ABE,∵AM⊥CD,AN⊥BE,∴•CD•AM =•BE•AN,∴AM=AN,∴∠APM=∠APN,∵∠AOD=∠POB,∴∠OPB=∠DAO=60°,∴∠APN=∠APM=60°,∴∠APC=∠BPC=∠APC=120°,7∴点P是就是△ABC费马点.②在线段PD上取一点T,使得P A=PT,连接AT.∵∠APT=60°,PT=P A,∴△APT是等边三角形,∴∠P AT=60°,AT=AP,∵∠DAB=∠TAP=60°,∴∠DAT=∠BAP,∵AD=AB,∴△DAT≌△BAP(SAS),∴PB=DT,∴PD=DT+PT=P A+PB,∴P A+PB+PC=PD+PC=CD=BE.(2)解:如图2:以MG为边作等边三角形△MGD,以OM为边作等边△OME.连接ND,作DF⊥NM,交NM的延长线于F.∵△MGD和△OME是等边三角形∴OE=OM=ME,∠DMG=∠OME=60°,MG=MD,∴∠GMO=∠DME在△GMO和△DME中,,∴△GMO≌△DME(SAS),∴OG=DE∴NO+GO+MO=DE+OE+NO∴当D、E、O、N四点共线时,NO+GO+MO值最小,∵∠NMG=75°,∠GMD=60°,∴∠NMD=135°,∴∠DMF=45°,∵MG=3∴MF=DF=,∴NF=MN+MF=4+=,∴ND===,∴MO+NO+GO最小值为,故答案为,4.如图,在菱形ABCD中,∠ABC=60°,点E、F分别是AB、BC上的动点,连接DE、DF、EF.(1)如图1,连接AF,若AF⊥BC,E为AB的中点,且EF=2,求DF的长;(2)如图2,若BE=BF,G为DE的中点,连接AF、AG、FG,求证:AG⊥FG;(3)如图3,若AB=4,将△BEF沿EF翻折得到△EFP(始终保持点P在菱形ABCD的内部),连接AP、BP及CP,请直接写出当P A+PB+PC值最小时PB的长.【详细解答】解:(1)方法1、如图1,∵AF⊥BC,∴∠AFB=90°,∵E为AB的中点,∴AE=BE,∴EF=BE=AB=2,∵∠ABC=60°,∴BF=EF=BC,∴CF=EF=2,过点D作DG⊥BC交BC的延长线于G,在Rt△CDG中,∠DCG=180°﹣∠BCD=60°,∴∠CDG=30°,CG=CD=2,DG=CG=2,∴FG=CF+CG=4,在Rt△DFG中,DF==2;方法2、∵AF⊥BC,∴∠AFB=90°,∵点E是AB的中点,∴AE=BE,在Rt△ABF中,EF=BE=AB,∴AB=4,∵四边形ABCD是菱形,∴AD=AB=4,∠BAD=180°﹣∠ABC=120°,在Rt△ABF中,∠ABC=60°,∴∠BAF=30°,∴AF=2,∠DAF=∠BAD﹣∠BAF=90°,在Rt△ADF中,根据勾股定理得,DF==2;(2)方法1、如图2,延长AG交CD于H,连接AC,FH, ∵AB∥CD,∴∠AEG=∠HDG,∵G为DE的中点,∴EG=DG,在△AEG和△DHG中,,∴△AEG≌△DHG,∴AG=HG,AE=DH,∵AB=BC=CD,BE=BF,∴FC=DH,BF=CH,在△AFC和△AHD中,,∴△AFC≌△AHD,∴AH=AF,同理:△ABF≌△ACH,∴∠BAF=∠CAH,∴∠F AH=∠F AC+∠CAH=∠F AC+∠BAF=∠BAC=60°, ∴△AFH是等边三角形,∵AG=HG,∴AG⊥FG.方法2、延长AG交CD于H,连接FH,∵四边形ABCD是菱形,∴AB=CD,AB∥CD,∴∠EAG=∠DHG,∠AEG=∠HDG,∵点G是DE中点,∴EG=DG,∴△AEG≌△HDG,∴AG=HG,AE=DH,∴BE=CH,∵BE=BF,∠ABC=60°,∴△BEF是等边三角形,∴∠BEF=60°,EF=BE,∴∠AEF=∠FCH,EF=CH,∴△AEF≌△FCH,∴AF=HF,∵AG=HG,∴FG⊥AG,(3)如图a,在△ABC中,P为其中任意一点.连接AP,BP,得到△ABP.以点B为旋转中心,将△ABP逆时针旋转60°,得到△EBD∵旋转60°,且BD=BP,∴△DBP为一个等边三角形∴PB=PD∴P A+PB+PC=DE+PD+PC∴当E、D、P、C四点共线时,为P A+PB+PC最小.如图3,当B、P、G、D四点共线时,P A+PB+PC值最小,最小值为BD. ∵将△APC绕点C顺时针旋转60°,得到△DGC,∴△APC≌△DGC,∴CP=CG,∠PCG=60°,∴△PCG是等边三角形,∴PG=CG=CP,∠GPC=∠CGP=60°.∵菱形ABCD中,∠ABP=∠CBP=∠ABC=30°,∴∠PCB=∠GPC﹣∠CBP=60°﹣∠30°=30°,∴∠PCB=∠CBP=30°,∴BP=CP,同理,DG=CG,∴BP=PG=GD.连接AC,交BD于点O,则AC⊥BD.在Rt△BOC中,∵∠BOC=90°,∠OBC=30°,BC=4,∴BO=BC•cos∠OBC=4×=2,∴BD=2BO=4,∴BP=BD=.即当P A+PB+PC值最小时PB的长为.。
“费马点”与中考试题

“费马点”与中考试题(一)费马,法国业余数学家,拥有业余数学之王的称号,他是解析几何的发明者之一.费马点——就是到三角形的三个顶点的距离之和最小的点.费尔马的结论:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点,对于有一个角超过120°的三角形,费马点就是这个内角的顶点.下面简单说明如何找点P使它到三个顶点的距离之和PA+PB+PC最小?这就是所谓的费马问题.图1解析:如图1,把△APC绕A点逆时针旋转60°得到△AP′C′,连接PP′.则△APP′为等边三角形,AP= PP′,P′C′=PC,所以PA+PB+PC= PP′+ PB+ P′C′.点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC′为定长,所以当B、P、P′、C′ 四点在同一直线上时,PA+PB+PC最小.这时∠BPA=180°-∠APP′=180°-60°=120°,∠APC=∠A P′C′=180°-∠AP′P=180°-60°=120°,∠BPC=360°-∠BPA-∠APC=360°-120°-120°=120°因此,当的每一个内角都小于120°时,所求的点P对三角形每边的张角都是120°,可在AB、BC边上分别作120°的弓形弧,两弧在三角形内的交点就是P点;当有一内角大于或等于120°时,所求的P点就是钝角的顶点.费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.本文列举近年“费马点”走进中考试卷的实例,供同学们学习参考.例1 (广东中考题)已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为,求此正方形的边长.图2图3分析:连接AC,发现点E到A、B、C三点的距离之和就是到三个顶点的距离之和,这实际是费尔马问题的变形,只是背景不同.解如图2,连接AC,把△AEC绕点C顺时针旋转60°,得到△GFC,连接EF、BG、AG,可知△EFC、△AGC都是等边三角形,则EF=CE.又FG=AE,∴AE+BE+CE = BE+EF+FG(图4).∵点B、点G为定点(G为点A绕C点顺时针旋转60°所得).∴线段BG即为点E到A、B、C三点的距离之和的最小值,此时E、F两点都在BG 上(图3).设正方形的边长为,那么BO=CO=,GC=, GO=.∴BG=BO+GO=+.∵点E到A、B、C三点的距离之和的最小值为.∴+=,解得=2.注本题旋转△AEB、△BEC也都可以,但都必须绕着定点旋转,读者不妨一试.例2 (北京中考题)如图4,在平面直角坐标系中,△ABC三个顶点的坐标分别为,,,延长AC到点D, 使CD=,过点D作DE∥AB交BC的延长线于点E.(1)求D点的坐标;(2)作C点关于直线DE的对称点F,分别连结DF、EF,若过B点的直线将四边形CDFE分成周长相等的两个四边形,确定此直线的解析式;(3)设G为y轴上一点,点P从直线与y轴的交点出发,先沿y轴到达G 点,再沿GA到达A点,若P点在y轴上运动的速度是它在直线GA上运动速度的2倍,试确定G点的位置,使P点按照上述要求到达A点所用的时间最短.分析和解:(1)D点的坐标(3,)(过程略).(2)直线BM的解析式为(过程略).图4(3)如何确定点G的位置是本题的难点也是关健所在.设Q点为y轴上一点,P在y 轴上运动的速度为v,则P沿M→Q→A运动的时间为,使P点到达A点所用的时间最短,就是MQ+AQ最小,或MQ+2AQ最小.解法1 ∵BQ=AQ,∴MQ+2AQ最小就是MQ+AQ+BQ最小,就是在直线MO 上找点G使他到A、B、M三点的距离和最小.至此,再次发现这又是一个费尔马问题的变形,注意到题目中等边三角形的信息,考虑作旋转变换.把△MQB绕点B顺时针旋转60°,得到△M′Q′B,连接QQ′、MM′(图5),可知△QQ′B、△MM′B都是等边三角形,则QQ′=BQ.又M′Q′=MQ,∴MQ+AQ+BQ= M′Q′+ QQ′+AQ.∵点A、M′为定点,所以当Q、Q′两点在线段A M′上时,MQ+AQ+BQ最小.由条件可证明Q′点总在AM′上,所以 A M′与OM的交点就是所要的G点(图6).可证OG=MG.图5 图6 图7解法 2 考虑MQ+AQ最小,过Q作BM的垂线交BM于K,由OB=6,OM=,可得∠BMO=30°,所以QK=MQ.要使MQ+AQ最小,只需使AQ+QK最小,根据“垂线段最短”,可推出当点A、Q、K在一条直线上时,AQ+QK最小,并且此时的QK垂直于BM,此时的点Q即为所求的点G(图7).过A点作AH⊥BM于H,则AH与y轴的交点为所求的G点.由OB=6,OM=,可得∠OBM=60°,∴∠BAH=30°在Rt△OAG中,OG=AO·tan∠BAH=∴G点的坐标为(0,)(G点为线段OC的中点).例 3 (湖州中考题)若点P 为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°, 则点P叫做△ABC的费马点.(1)若P为锐角△ABC的费马点,且∠ABC=60°,PA=3,PC=4, 则PB的值为;(2)如图8,在锐角△ABC的外侧作等边△ACB′,连结BB′.求证:BB′ 过△ABC 的费马点P,且BB′=PA+PB+PC.图8解:(1)利用相似三角形可求PB的值为.(2)设点P为锐角△ABC的费马点,即∠APB=∠BPC=∠CPA=120°如图8,把△ACP绕点C顺时针旋转60°到△B′CE,连结PE,则△EPC为正三角形.∵∠B′EC = ∠APC =120°,∠PEC=60°∴∠B′EC+∠PEC=180°即 P、E、B′三点在同一直线上∵∠BPC=120°,∠CPE=60°,∴∠BPC +∠CPE =180°,即 B、P、E 三点在同一直线上∴B、P、E、B′四点在同一直线上,即BB′ 过△ABC的费马点P.又PE=PC,B′E= PA,∴BB′=E B′+PB+PE=PA+PB+PC.注通过旋转变换,可以改变线段的位置,优化图形的结构.在使用这一方法解题时需注意图形旋转变换的基础,即存在相等的线段,一般地,当题目出现等腰三角形(等边三角形)、正方形条件时,可将图形作旋转60°或90°的几何变换,将不规则图形变为规则图形,或将分散的条件集中在一起,以便挖掘隐含条件,使问题得以解决.费尔马问题是个有趣的数学问题,这些问题常常可通过旋转变换来解决.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题9 费马点
破解策略
费马点是指平面内到三角形三个顶点距离之和最小的点,这个最小的距离叫做费马距离.
若三角形的内角均小于120°,那么三角形的费马点与各顶点的连线三等分费马点所在的周角;若三角形内有一个内角大于等于120°,则此钝角的顶点就是到三个顶点距离之和最小的点.
1.若三角形有一个内角大于等于120°,则此钝角的顶点即为该三角形的费马点
如图在△ABC中,∠BAC≥120°,求证:点A为△ABC的费马点证明:
如图,在△ABC内有一点P延长BA至C,使得AC=AC,作∠CAP=∠CAP,并且使得AP =AP,连结PP
则△APC≌△APC,PC=PC
因为∠BAC≥120°
所以∠PAP=∠CAC≤60
所以在等腰△PAP中,AP≥PP
所以PA+PB+PC≥PP+PB+PC>BC=AB+AC
所以点A为△ABC的费马点
2.若三角形的内角均小于120°,则以三角形的任意两边向外作等边三角形,两个等边三角形外接圆在三角形内的交点即为该三角形的费马点.
如图,在△ABC中三个内角均小于120°,分别以AB、AC为边向外作等边三角形,两个等边三角形的外接圆在△ABC内的交点为O,求证:点O为△ABC的费马点
证明:在△ABC内部任意取一点O,;连接OA、OB、OC
将△AOC绕着点A逆时针旋转60°,得到△AO′D连接OO′则O′D=OC
所以△AOO′为等边三角形,OO′=AO
所以OA+OC+OB=OO′+OB+O′D
则当点B、O、O′、D四点共线时,OA+OB+OC最小
此时ABAC为边向外作等边三角形,两个等边三角形的外接圆在△ABC内的交点即为点O
如图,在△ABC中,若∠BAC、∠ABC、∠ACB均小于120°,O为费马点,则有∠AOB=∠BOC =∠COA=120°,所以三角形的费马点也叫三角形的等角中心
例1 如图,在平面直角坐标系中,点A 的坐标为(-6,0),点B 的坐标为(6,0),点C 的坐标为(6,34),延长AC 至点D 使得CD =AC ,过点DE 作DE //AB ,交BC 的延长线于点E ,设G 为y 轴上的一点,点P 从直线y =3-x +36与y 轴的交点M 出发,先沿y 轴到达点G ,再沿GA 到达点A ,若点P 在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定点G 的位置,使点P 按照上述要求到达A 所用的时间最短
解:∵t =
v
GM
v v GM 22GA GA 2+=
+ ∴当2GA +GM 最小时,时间最短
如图,假设在OM 上存在一点G ,则BG =AG ∴MG +2AG =MG +AG +BG
把△MGB 绕点B 顺时针旋转60°,得到△M ′G ′B ,连结GG ′,MM ′ ∴△GG ′B 、△MM ′B 都为等边三角形 则GG ′=G ′B =GB 又∵M ′G ′=MG
∴MG +AG +BG =M ′G ′+GG ′+AG ∵点A 、M ′为定点
∴AM ′与OM 的交点为G ,此时MG +AG +BG 最小 ∴点G 的坐标为(0,32)
例2 A 、B 、C 、D 四个城市恰好为一个正方形的四个顶点,要建立一个公路系统使得每两个城市之间都有公路相通,并是整个公路系统的总长度为最小,则应当如何修建?
解:如图,将△ABP 绕点N 逆时针旋转60°,得到△EBM ;同样,将△DCQ 绕点C 顺时针旋转60°,得到△FCN ,连结AE 、DF ,则△ABE 、△DCF 均为等边三角形,连结PM 、QN ,则△BPM ,△CQN 均为等边三角形
所以当点E ,M ,P ,Q ,N ,F 共线时,整个公路系统的总长取到最小值,为线段EF 的长,如图,此时点P ,Q 在EF 上,1=2=3=
4=30.
F
N
E
M
B C
A
D
P
Q
进阶训练
1.如图,在ABC 中,ABC =60,AB =5,BC =3,P 是ABC 内一点,求PA +PB +
PC 的最小值,并确定当PA +PB +PC 取得最小值时,APC 的度数.
B
C
A
P
答案:PA +PB +PC 的最小值为7,此时APC =120.
P'
A'
P
A
C
B E
【提示】如图,将
APB 绕点B 逆时针旋转60,得到A 'BP ',连结PP ',A 'C .过点
A '作A 'E BC ,交C
B 的延长线于点E .解Rt A 'E
C 求A 'C 的长,所得即为PA +PB +PC 的
最小值.
2. 如图,四边形ABCD 是正方形,ABE 是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B 逆时针旋转60
得到BN ,连结AM ,CM ,EN .
(1)当M 在何处时,AM +CM 的值最小?
(2)当M 在何处时,AM +BM +CM 的值最小?请说明理由; (3)当AM +BM +CM 31时,求正方形的边长.
N
E
M
答案:(1)当点M 落在BD 的中点时,AM +CM 的值最小,最小值为AC 的长; (2)连结CE ,当点M 位于BD 与CE 的交点处时.AM +BM +CM 的值最小,最小值为CE
的长.
(3)正方形的边长为2.
【提示】(3)过点E 作EF BC,交CB的延长线于点F,解Rt EFC即可.
N
E
M。
