高一数学上学期期中联考试题及答案
2024-2025学年浙江省“钱塘联盟”高一第一学期期中联考数学科试题(含答案)

2024-2025学年浙江省“钱塘联盟”高一第一学期期中联考数学科试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A ={−2,1,2},B ={x|(x +2)(x−1)≤0},则A ∩B =( )A. (−2,1)B. [−2,1]C. {−2,1}D. {−2,1,2}2.设x ∈R ,则“|x−2|<1”是“x 2+x−2>0”的( )A. 充分而不必要条件 B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件3.命题“∀x ≥1,x 2≥2”的否定是( )A. ∀x ≥1,x 2<2 B. ∃x ≥1,x 2<2C. ∀x <1,x 2≥2 D. ∃x <1,x 2<24.下列说法正确的是( )A. 若a >b ,则ac 2>bc 2B. 若a >b >0,m >0,则ma <mb C. 若a >b ,c >d ,则ac >bdD. 若−2<a <3,1<b <2则−3<a−b <15.已知f(x)是定义在[−1,1]上的增函数,且f(x−1)<f(1−3x),则x 的取值范围是( )A. [0,12)B. (0,12)C. (12,1]D. [−1,12)6.在同一坐标系内,函数y =x a 和y =ax−1a 的图象可能是( )A. B. C. D.7.正数x ,y 满足x +2y =2,则x +8yxy 的最小值为( )A. 4B. 7C. 8D. 98.已知函数f(x)=x−1,g(x)=2x ,记F(x)=max{f(x),g(x)}={f(x),f(x)≥g(x)g(x),f(x)<g(x),则下列关于函数的说法不正确的是( )A. 当x ∈(0,2)时,F(x)=2x B. 函数F(x)的最小值为−2C. 函数F(x)在(−1,0)上单调递减D. 若关于x 的方程F(x)=m 恰有两个不相等的实数根,则−2<m <−1或m >1二、多选题:本题共3小题,共18分。
湖北省鄂东南省级示范高中教育教学改革联盟学校2024-2025学年高一上学期期中联考数学试题含答案

2024年秋季鄂东南省级示范高中教育教学改革联盟学校期中联考高一数学试卷(答案在最后)命题学校:考试时间:2024年11月11日上午08:00—10:00试卷满分:150分一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各组对象不能构成集合的是()A.中国古代四大发明B.所有无理数C.2024年高考数学难题D.小于π的正整数【答案】C 【解析】【分析】根据题意利用集合中元素具有确定性的性质,对选项逐一判断可得结论.【详解】对于A ,中国古代四大发明是指造纸术、指南针、火药、印刷术,满足集合定义,即A 能构成集合;对于B ,所有无理数定义明确,即B 能构成集合;对于C ,2024年高考数学难题定义不明确不具有确定性,不符合集合的定义,即C 构不成集合;对于D ,小于π的正整数只有1,2,3,具有确定性,满足集合定义,即D 能构成集合.故选:C2.已知集合103x A x x ⎧⎫+=≤⎨⎬-⎩⎭,{}1B x x =≥,则A B = ()A.{}13x x -<< B.{}13x x <<C.{}13x x ≤≤ D.{}13x x ≤<【答案】D 【解析】【分析】解不等式化简集合A ,再利用交集的定义求解即得.【详解】依题意,1{|0}{|13}3x A x x x x +=≤=-≤<-,而{}1B x x =≥,所以{}13A B x x ⋂=≤<.故选:D3.已知函数()2222()1m m f x m m x --=--是幂函数,且在(0,+∞)上递增,则实数m =()A.2B.1- C.4D.2或1-【答案】B 【解析】【分析】利用幂函数的定义求出m 值,再由单调性验证即得.【详解】因函数()2222()1m m f x m m x --=--是幂函数,则211m m --=,即220m m --=,解得1m =-或2m =,当1m =-时,函数()f x x =在(0,+∞)上递增,则1m =-,当2m =时,函数2()f x x -=在(0,+∞)上递减,不符合要求,实数1m =-.故选:B4.已知()f x 是定义在[]1,1-上的减函数,且()()113f x f x -<-,则x 的取值范围是()A.12,23⎛⎤⎥⎝⎦B.10,2⎛⎫ ⎪⎝⎭C.10,2⎡⎫⎪⎢⎣⎭D.20,3⎡⎤⎢⎥⎣⎦【答案】A 【解析】【分析】根据()f x 的定义域以及单调性可得1x -,13x -满足的条件,由此即可解得x 的范围.【详解】由题意,函数()f x 是定义在[]1,1-上的减函数,因为()()113f x f x -<-,得1311131111x x x x -<-⎧⎪-≤-≤⎨⎪-≤-≤⎩,解得1223x <≤,所以x 的取值范围是12,23⎛⎤⎥⎝⎦.故选:A.5.若0a >,0b >,23a b +=,则12a b+的最小值为()A.1B.3C.6D.9【答案】B 【解析】【分析】利用乘“1”法即可求出最值.【详解】根据题意可得()12112122121453;333a b a b a b a b b a ⎛⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝当且仅当22a bb a=即1,1a b ==时,等号成立,此时最小值为3.故选:B.6.我国著名数学家华罗庚曾说:“数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休”.在数学的学习和研究中,常用函数的图象来研究函数的性质,也常用函数的解析式来研究函数图象的特征.下面的图象对应的函数可能是()A.()11f x x =-B.()11f x x =-C.()311f x x =+ D.()211f x x =+【答案】B 【解析】【分析】首先由函数的定义域排除CD ,再由01x <<时,()0f x <排除A ,即可得答案.【详解】由图象可知,函数的定义域为(,1)(1,1)(1,)-∞-⋃-⋃+∞,因为()311f x x =+的定义域为(,1)(1,)-∞-⋃-+∞,所以排除C ,因为()211f x x =+的定义域为R ,所以排除D ,因为当01x <<时,()101f x x =<-,所以排除A ,故选:B7.已知函数22()24f x x ax a =-+-,若关于x 的不等式(())0f f x <的解集为空集,则实数a 的取值范围是()A.(),8-∞- B.[]8,6-- C.(],6∞-- D.(),6-∞-【答案】C 【解析】【分析】令()t f x =,求出不等式()0<f t 的解,再代入判断列式求解.【详解】函数2()()44f x x a =--≥-,设()t f x =,不等式(())0f f x <为()0<f t ,即2()40t a --<,解得22a t a -<<+,依题意,22()42a x a a -<--<+无解,即不等式22()6a x a a +<-<+无解,因此60a +≤,解得6a ≤-,所以实数a 的取值范围是6a ≤-.故选:C8.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的美誉.函数()[]f x x =称为高斯函数,其中x ∈R ,[]x 表示不超过x 的最大整数,例如:[]21.1-=-,[]2.52=,则方程][[21]4x x x ++=的所有大于零的解之和为()A.12 B.34C.32D.74【答案】D 【解析】【分析】x ∀∈R ,k ∃∈Z ,使211k x k ≤+<+,可得122k kx -≤<,2242k x k -≤<,分类讨论k 为奇数和偶数的情况,求出k 的值,再代入求解即可.【详解】x ∀∈R ,k ∃∈Z ,使211k x k ≤+<+,则[21]x k +=,于是122k kx -≤<,2242k x k -≤<,若k 为奇数,则12k -∈Z ,1[]2k x -=,1[21]42[]k x k x x -++=+=,则312222k k k --≤<,解得13k -<≤,1k =或3k =,当1k =时,102x ≤<,[]0x =,[21]1x +=,104x +=,解得11[0,42x =∈,当3k =时,312x ≤<,[]1x =,[21]3x +=,314x +=,解得31[1,2x =∈;若k 为偶数,则2k ∈Z ,则[]12kx =-,[21]14[]2k x k x x ++=+-=,则322122kk k -≤-<,解得2k -2<≤,0k =或2k =,当0k =时,102x -≤<,[]1x =-,[21]0x +=,104x -+=,解得11[,0)42x =-∈-,当2k =时,112x ≤<,[]0x =,[21]2x +=,024x +=,解得11[,1)22x =∈,所以所有大于零的解之和为1171424++=.故选:D【点睛】结论点睛:“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种,然后根据此新定义去解决问题,有时还需要用类比的方法去理解新的定义,这样有助于对新定义的透彻理解.但是,透过现象看本质,它们考查的还是基础数学知识,所以说“新题”不一定是“难题”,掌握好三基,以不变应万变才是制胜法宝.二、选择题:本题共3小题,每小题6分,共18'分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.有下列四种说法,正确的说法有()A.奇函数图象不一定过坐标原点B.命题“x ∀∈R ,210x x ++>”的否定是“x ∃∈R ,210x x ++<”C.若,,a b c ∈R ,则“22ab cb >”的充要条件是“a c >”D.定义在R 上的函数()y f x =对任意两个不等实数a ,b ,总有()()0f a f b a b->-成立,则()y f x =在R 上是增函数【答案】AD 【解析】【分析】对A 举反例即可;对B ,利用全称命题的否定为特称命题即可判断;对C ,举反例0b =即可;对D ,根据单调性的定义即可判断.【详解】对于A ,奇函数的图象不一定过坐标原点,如()()10f x x x=≠是奇函数,它的图象不过原点,所以A 正确;对于B ,命题“x ∀∈R ,210x x ++>”的否定是“2R,10x x x ∃∈++≤”,B 错误;对于C ,若0b =,则由a c >不能推出²²ab cb >,故“a c >”不是“²²”ab cb >的充要条件,故C 错误;对于D ,根据题意知,a b >时,()()f a f b >,a b <时,()()f a f b <,由单调性的定义知,=在R 上是增函数,D 正确.故选:AD.10.已知关于x 的不等式20ax bx c ++≤的解集为{|2x x ≤-或3}x ≥,则下列说法正确的是()A.0a > B.0ax c +>的解集为{}6x x <C.8430a b c ++>D.20cx bx a ++<的解集为11{|}23x x -<<【答案】BCD 【解析】【分析】根据给定条件,可得6,,0c a b a a =-=-<,再给一元二次不等式的求解逐项判断即得.【详解】由不等式20ax bx c ++≤的解集为{|2x x ≤-或3}x ≥,得0a <且2,3-是方程²0ax bx c ++=的两个根,则3(2),3(2)c ba a⨯-=+-=-,即6,c a b a =-=-,对于A ,0a <,A 错误;对于B ,不等式0ax c +>为60ax a ->,而0a <,解得6x <,B 正确;对于C ,843843(6)140a b c a a a a ++=-+-=->,C 正确;对于D ,不等式²0cx bx a ++<为260ax ax a --+<,即2610x x +-<,解得1123x -<<,D 正确.故选:BCD11.已知函数()f x 的定义域为R ,对任意实数x ,y 满足:()()()1f x y f x f y -=-+,且()10f =.当0x >时,()1f x <.则下列选项正确的是()A.()01f =B.()21f =-C.()1f x -为奇函数 D.()f x 为R 上的增函数【答案】ABC 【解析】【分析】对A 直接赋值0x y ==即可;对B ,赋值2,1x y ==即可;对C ,利用奇偶性定义判断即可;对D ,根据单调性的判断方法判断即可.【详解】对于A ,由题可知()()()0001f f f =-+,故()01f =,故A 正确;对于B ,由题可知()()()()()()21211122111f f f f f f -=-+==-=-,,故B 正确;对于C ,()()()()0012f x f f x f x -=-+=-,故()()()111f x f x f x ⎡⎤--=---⎣⎦,为奇函数,故C 正确;对于D ,当12x x >时,()()()12121f x f x f x x -=--,∵1>2,∴1−2>0,∴1−2−1<0∴是R 上的减函数,故D 错误.故选:ABC.二、填空题:本题共3小题,每小题5分,共15分.12.函数()()01f x x =++的定义域为______.【答案】()(],11,3-∞-- 【解析】【分析】根据每个式子有意义的条件分别求出自变量x 的取值范围,再求交集即可.【详解】因为()()01f x x =+,所以3010x x -≥⎧⎨+≠⎩,解得3x ≤且1x ≠-,所以函数的定义域为(()(],11,3∞--⋃-.故答案为:()(],11,3∞--⋃-.13.已知集合,,1y A x x ⎧⎫=⎨⎬⎩⎭,{}2,,0B x x y =+,若A B =,则2x y +=_________.【答案】2-【解析】【分析】根据题意利用集合中元素的互异性分类讨论即可求得结果.【详解】依题意可知0x ≠,由于A B =可知0y =,此时{},0,1A x =,{}2,,0B x x =所以21x =,解得1x =-或1x =(舍去)即22x y +=-.故答案为:2-14.设函数22,2()26,2x x x f x x x ⎧-≤=⎨-+>⎩关于x 的方程()f x a =有三个不等实根123,,x x x ,且123x x x <<,则123223x x x ++的取值范围是_________.【答案】29[13,2【解析】【分析】画出函数图象,数形结合得到122x x +=,37[3,2x ∈,求出答案.【详解】画出函数()f x 的图象,观察图形知,仅当10a -<≤时,方程()f x a =有三个不等实根,分别对应直线y a =与图象三个交点的横坐标,其中两个交点位于二次函数图象上,不妨设123x x x <<,显然12,x x 关于1x =对称,则122x x +=,另一个交点位于直线26y x =-+上,在26y x =-+中,当10y -<≤时,732x ≤<,即37[3,2x ∈,因此12321224,3[9,)2x x x +=∈,所以12329223[13,2x x x ++∈.故答案为:29[13,2三、解答题:本题共5小题,共77分.解答应写出文字、证明过程或演算步骤.15.设全集U =R ,已知集合{}2430A x x x =-+≤,{}1B x m x m =≤≤+.(1)若A B =∅ ,求实数m 的取值范围;(2)若“x B ∈”是“x A ∈”的充分条件,求实数m 的取值范围.【答案】(1){|0m m <或3}m >(2){|12}m m ≤≤【解析】【分析】(1)先求出集合A ,然后结合集合的交集运算即可求解;(2)由题意得B A ⊆,然后结合集合的包含关系即可求解.【小问1详解】由²430x x -+≤,解得13x ≤≤,所以{|13}A x x =≤≤.因为A B =∅ ,且B ≠∅,所以11m +<或3m >,得0m <或3m >,所以实数m 的取值范围是{|0m m <或3}m >;【小问2详解】因为“x B ∈”是“x A ∈”的充分条件,所以B A ⊆,所以113m m ≥⎧⎨+≤⎩,解得12m ≤≤,所以实数m 的取值范围是{|12}m m ≤≤.16.用篱笆在一块靠墙的空地围一个面积为2的等腰梯形菜园,如图所示,用墙的一部分做下底AD ,用篱笆做两腰及上底,且腰与墙成60︒,当等腰梯形的腰长为多少时,所用篱笆的长度最小?并求出所用篱笆长度的最小值.【答案】等腰三角形腰长为20m ,所用篱笆长度的最小值为60m .【解析】【分析】建立函数模型,利用基本不等式求解.【详解】设()()m 0AB a a =>,上底()()m 0BC b b =>,分别过点B ,C 作下底的垂线,垂足分别为E ,F ,则2BE a=,2a AE DF ==,则下底22a a AD b a b =++=+,该等腰梯形的面积()()2224b a b S a a b a ++=⋅=+=,所以()21200a b a +=,则6002a b a =-,所用篱笆长为6006003226022a a l a b a a a =+=+-=+≥=,当且仅当60032aa =即()20m a =,()20mb =时取等号.所以,当等腰梯形的腰长为20m 时,所用篱笆长度最小,其最小值为60m .17.函数()f x 的定义域为{}0D x x =∈≠R ,且满足对于任意12,x x D ∈,有()()()1212f x x f x f x ⋅=+,当1x >时,()0f x >.(1)证明:()f x 是偶函数;(2)如果()41f =,解不等式()23f x -<.【答案】(1)证明见解析(2)(62,2)(2,66)-⋃【解析】【分析】(1)令12,1x x x ==-,121x x ==-从而得到()()f x f x -=,即可证明;(2)通过赋值代换得(|2|)(64)f x f -<,再证明其单调性,从而得到不等式组,解出即可.【小问1详解】因对定义域内的任意12,x x D ∈,有()()()1212f x x f x f x ⋅=+,令12,1x x x ==-,则有()()(1)f x f x f -=+-,又令121x x ==-,得2(1)(1)f f -=,再令121x x ==,得(1)0f =,从而(1)0f -=,于是有()()f x f x -=,所以()f x 是偶函数.【小问2详解】由于(4)1f =,所以3111(4)(4)(4)(444)(64)f f f f f =++=++=⨯⨯=,于是不等式(2)3f x -<可化为(2)(64)f x f -<,由(1)可知函数()f x 是偶函数,则不等式可化为(|2|)(64)f x f -<,设120x x <<,则()()()()()222121111111x x x f x f x f x f x f x f x f f x x x ⎡⎤⎛⎫⎛⎫⎛⎫-=-⨯=-+=-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎣⎦,由于120x x <<,所以211x x >,所以210x f x ⎛⎫> ⎪⎝⎭,所以()()120f x f x -<,所以()()12f x f x <,所以()f x 在(0,)+∞上是增函数,所以可得26420x x ⎧-<⎪⎨-≠⎪⎩,解得62662x x -<<⎧⎨≠⎩,所以不等式(2)3f x -<的解集为(62,2)(2,66)-⋃.18.已知函数()322x ax b f x x --=+为R 上的奇函数,且()21f -=.(1)求实数,a b 的值;(2)试判断函数()f x 在区间()1,+∞的单调性,并说明理由;(3)求函数()()()21g x f x mf x ⎡⎤=--⎣⎦(其中33x -≤≤)的值域.【答案】(1)7a =,0b =;(2)函数()f x 在区间()1,+∞单调递增,理由见解析;(3)答案见解析【解析】【分析】(1)根据奇偶性定义以及函数值解方程可得结果;(2)利用单调性定义按照步骤即可证明()f x 在区间1,+∞单调递增;(3)由换元法得出函数()g x 的表达式,再由(2)中的结论得出其在33x -≤≤上的单调性,利用二次函数性质分类讨论即可得出结果.【小问1详解】根据题意可得()00f =,即()02b f x =-=,可得0b =;再由()21f -=可得()82142a f x -+==+,解得7a =;当7a =,0b =可得()3272x x f x x -=+,经检验此时()f x 满足()()3272x x f x f x x -+-==-+,为奇函数,所以7a =,0b =【小问2详解】取任意()12,1,x x ∞∈+,且12x x <,则()()()()()()()()323233112221112112222212124242442222x x x x x x x x x x f x f x x x x x -+--+---=-=++++()()()()22221212121222129221422x x x x x x x x x x -+++-=++;由()12,1,x x ∞∈+,12x x <可得120x x -<,2222121212922140x x x x x x +++->;所以()()120f x f x -<,即可得()()12f x f x <,即函数()f x 在区间1,+∞的单调递增;【小问3详解】由()()()()6612,12,3,31111f f f f =--==-=-,由(2)得当[]12,0,1x x ∈时,2222121212210,092214x x x x x x x x <+++<-<,所以()()120f x f x ->,即()()12f x f x >,所以函数()f x 在0,1上单调递减;因此函数()f x 在0,1上单调递减,在1,+∞上单调递增,又函数()f x 为上的奇函数,所以函数()f x 的减区间为[]1,1-,递增区间为()(),11,∞∞--⋃+,当33x -≤≤时,()22f x -≤≤,令()()22f x t t =-≤≤,有()2221124m m g x t mt t ⎛⎫=--=--- ⎪⎝⎭,①当22m ≤-时,即4m ≤-,()()()()223,232g x g m g x g m ≥-=+≤=-,此时函数()g x 的值域为[]23,32m m +-;②当202m -<≤时,即40m -<≤时,可得()()()2minmax 1,23224m m g x g g x g m ⎛⎫==--==- ⎪⎝⎭,此时函数()g x 的值域为21,32;4m m ⎡⎤---⎢⎥⎣⎦③当022m <<时,即04m <<时,()()()2minmax 1,22324m m g x g g x g m ⎛⎫==--=-=+ ⎪⎝⎭,此时函数()g x 的值域为21,23;4m m ⎡⎤--+⎢⎥⎣⎦④当22m ≥时,即4≥m ,()()()()223,232g x g m g x g m ≤-=+≥=-,此时函数()g x 的值域为[]32,23m m -+,综上所述,4m ≤-时,其值域为[]23,32m m +-;当40m -<≤时,值域为21,32;4m m ⎡⎤---⎢⎥⎣⎦当04m <<时,值域为21,234m m ⎡⎤--+⎢⎥⎣⎦;当4≥m 时,值域为[]32,23m m -+【点睛】关键点点睛:本题关键在于利用换元法得出函数()g x 的表达式,再证明得出函数的单调性,利用二次函数性质分类讨论即可得出结果函数()g x 的值域.19.已知n 为正整数,集合(){}{}12,,,0,1,1,2,,n n i M x x x x i n =⋅⋅⋅∈=⋅⋅⋅,对于n M 中任意两个元素()12,,,n a a a α=⋅⋅⋅和()12,,,n b b b β=⋅⋅⋅,定义:()1122,,,n n a b a b a b αβ-=--⋅⋅⋅-;()1122,n nd a b a b a b αβ=-+-+⋅⋅⋅+-(1)当3n =时,设()1,0,1α=,()1,1,0β=,写出αβ-,并计算(),d αβ;(2)若集合S 满足3S M ⊆,且,S αβ∀∈,(),2d αβ=,求集合S 中元素个数的最大值,写出此时的集合S ,并证明你的结论;(3)若,n M αβ∈,且(),d k αβ=,任取n M γ∈,求(),d αγβγ--的值.【答案】(1)()0,1,1αβ-=,(),2d αβ=(2)最大值是4,证明见解析(3)(),d kαγβγ--=【解析】【分析】(1)根据定义直接求解即可;(2)根据定义,结合反证法进行求解即可;(3)根据定义,结合绝对值的性质进行证明即可.【小问1详解】当3n =时,设()1,0,1α=,()1,1,0β=,则()0,1,1αβ-=,所以(),0112d αβ=++=;【小问2详解】最大值是4.理由如下:此时()()()(){}0,0,0,0,1,1,1,0,1,1,1,0S =或()()()(){}0,0,1,0,1,0,1,0,0,1,1,1S =.若还有第5个元素,则必有()()1,0,0,0,1,1和()()0,0,1,1,1,0和()()0,1,0,1,0,1和()()1,1,1,0,0,0之一出现,其对应的(,)3d αβ=,不符合题意.【小问3详解】设()12,,,n a a a α=⋅⋅⋅,()12,,,n b b b β=⋅⋅⋅,()12,,,n c c c γ=⋅⋅⋅,所以{},,0,1i i i a b c ∈,{}0,1i i a b -∈,(1i =,2,3,)n ,从而()1122,,,n n n a b a b a b M αβ-=--⋅⋅⋅-∈,又()11112222,n n n n d a c b c a c b c a c b c αγβγ--=---+---+⋅⋅⋅+---,当0i c =时,i i i i i i a c b c a b ---=-;当1i c =时,()()11i i i i i i i i a c b c a b a b ---=---=-,所以()(),,d d αγβγαβ--=,所以(),d k αγβγ--=.。
天津市2023-2024学年高一上学期期中联考数学试题含答案

2023~2024学年度第一学期期中联考高一数学(答案在最后)本试卷满分150分,考试用时120分钟.一、选择题(共9题,每题5分,满分45分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合{}1A x x =>,{}15B x x =-<<,则A B = ()A.{}15x x -<<B.{}15x x <<C.{}1x x >- D.{}1x x >【答案】B 【解析】【分析】利用交集的定义可求得集合A B ⋂.【详解】因为{}1A x x =>,{}15B x x =-<<,则{}15A B x x ⋂=<<.故选:B.2.设:0p x >,:13q x <<,则p 是q 的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】利用集合的包含关系判断可得出结论.【详解】因为{}0x x >{}13x x <<,因此,p 是q 的必要不充分条件.故选:B.3.不等式25240x x +-<的解集是()A.{8x x <-或}3x >B.{3x x <-或}8x >C.{}38x x -<< D.{}83x x -<<【答案】D 【解析】【分析】利用一元二次不等式的解法求解即可.【详解】因为()()2524380x x x x +-=-⋅+<,所以83x -<<,即不等式25240x x +-<的解集是{}83x x -<<.故选:D.4.已知0.91.213, 1.2,3a b c -⎛⎫=== ⎪⎝⎭,则,,a b c 的大小关系是()A.a c b <<B.c b a<< C.c<a<bD.b<c<a【答案】D 【解析】【分析】运用介值法及指数函数单调性比较大小即可.【详解】因为01.21b ==,0.90.9133c -⎛⎫== ⎪⎝⎭,又因为3x y =在R 上单调递增,1.20.90>>,所以 1.20.903331>>=,即a c b >>.故选:D.5.函数2(21)31f x x x +=-+,则(3)f =()A.1- B.1C.2- D.2【答案】A 【解析】【分析】由解析式代入计算函数值即可.【详解】设213x +=,得1x =,则(3)1311f =-+=-.故选:A.6.设()f x 为R 上的奇函数,且当0x <时,()31f x x =-,则()()04f f +=()A.11B.11- C.13D.13-【答案】C 【解析】【分析】由()f x 为R 上的奇函数可得()00f =,()()44f f =--,代入计算即可求解.【详解】因为()f x 为R 上的奇函数,所以()00f =,()()44f f =--,又当0x <时,()31f x x =-,所以()()()4443113f f =--=--⨯-=,所以()()0401313f f +=+=.故选:C.7.已知幂函数()f x x α=的图象过点15,5⎛⎫ ⎪⎝⎭,则函数()(3)()g x x f x =-在区间1,13⎡⎤⎢⎥⎣⎦上的最小值是()A.-1B.-2C.-4D.-8【答案】D 【解析】【分析】先求出幂函数的解析式,从而得出()g x 的表达式,然后再求()g x 的最小值.【详解】因为幂函数()f x x α=的图像过点15,5⎛⎫ ⎪⎝⎭,所以155α=,得1α=-,所以1()f x x =,则3()(3)()1g x x f x x =-=-显然在区间1,13⎡⎤⎢⎥⎣⎦上单调递增,所以所求最小值为11983g ⎛⎫=-=- ⎪⎝⎭.故选:D8.设(),0,a b ∈+∞,则下面的不等式不正确的是()A.2b a a b+≥ B.1122a b a b+≥++C.222a b ab +≥ D.22b a a ba b+≥+【答案】B 【解析】【分析】根据不等式的性质以及基本不等式,结合特例法逐项判定,即可求解.【详解】对于A ,(),0,a b ∈+∞,由2b a a b +≥=,当且仅当a b =时,等号成立,正确;对于B ,取1a b ==,1121122213a b a b+=+=<+=+=+,不正确;对于C ,由222a b ab +≥,当且仅当a b =时,等号成立,正确;对于D ,由不等式33222()()0a b a b ab a b a b +--=+-≥,可得3322a b a b ab +≥+,当且仅当a b =时,等号成立,两边同除ab ,可得22b a a b a b+≥+成立,正确;故选:B9.已知函数()32e 1xf x x =-+,则不等式()()212f x f x +->-的解集为()A.1,3⎛⎫+∞ ⎪⎝⎭B.()1,+∞ C.1,3⎛⎫-∞ ⎪⎝⎭D.(),1-∞【答案】A 【解析】【分析】由题意可得()()2f x f x -+=-,问题转化为()()21f x f x ->-,再判断函数()f x 的单调性,利用单调性求解即可得解.【详解】()32e 1x f x x =-+ ,()()33222e 1e 1x xf x x x -∴-=--=-+-++,()()2f x f x ∴-+=-,所以不等式()()212f x f x +->-可转化为()()21f x f x ->-,又3y x =在R 上单调递增,e x y =在R 上单调递增,进而2e 1xy =-+在R 上单调递增,所以函数()f x 在R 上单调递增,21x x ∴->-,解得13x >,所以原不等式的解集为1,3⎛⎫+∞ ⎪⎝⎭.故选:A.二、填空题(共6题,每题5分,满分30分,将答案填写在答案卡上)10.命题p :01x ∃≥,2000x x -<,则命题p 的否定为______.【答案】1x ∀≥,20x x -≥,【解析】【分析】根据存在量词命题的否定为全称量词命题易求.【详解】根据存在量词命题的否定为全称量词命题知:命题p :01x ∃≥,2000x x -<的否定为1x ∀≥,20x x -≥.故答案为:1x ∀≥,20x x -≥11.函数()()01x f x x+=的定义域为______.【答案】()(]1,00,2- 【解析】【分析】根据解析式有意义列不等式组求解可得.【详解】由题可知220100x x x x ⎧-++≥⎪+≠⎨⎪≠⎩,解得12x -<≤且0x ≠,所以()f x 的定义域为()(]1,00,2- .故答案为:()(]1,00,2- 12.已知:13p x -<<,:12q x m -<<+,若p 是q 的充分不必要条件,则实数m 的取值范围是_______.【答案】()1,+∞【解析】【分析】由已知条件可得出集合的包含关系,可得出关于实数m 的不等式组,由此可解得实数m 的取值范围.【详解】因为p 是q 的充分不必要条件,则{}13x x -<<{}12x x m -<<+,所以,23m +>,解得1m >.因此,实数m 的取值范围是()1,+∞.故答案为:()1,+∞.13.已知函数()221f x x ax a =-++-在区间[]01,上的最大值是2,则实数=a ______.【答案】1-或2.【解析】【分析】由函数对称轴与区间关系,分类讨论求出最大值且等于2,解关于a 的方程,即可求解.【详解】函数()22221()1f x x ax a x a a a =-++-=--+-+,对称轴方程为为x a =;当0a ≤时,max ()(0)12,1f x f a a ==-==-;当2max 01,()()12a f x f a a a <<==-+=,即21510,2a a a +--==(舍去),或152a =(舍去);当1a ≥时,max ()(1)2f x f a ===,综上1a =-或2a =.故答案为:1-或2.【点睛】本题考查二次函数的图像与最值,考查分类讨论思想,属于中档题.14.已知0a >,0b >,且1ab =,则11822a b a b+++的最小值为______.【答案】4【解析】【分析】根据题意,将原式化为2822a b a b+++,再由基本不等式,即可得到结果.【详解】因为0a >,0b >,且1ab =,所以1188284222222ab ab a b a b a b a b a b a b +++=++=+≥==+++,当且仅当2822a b a b +=+时,即212a b ⎧=-⎪⎨=+⎪⎩或212a b ⎧=⎪⎨=-⎪⎩时,等号成立,所以11822a b a b+++的最小值为4.故答案为:415.已知函数()()()()214112x a x a x f x a x ⎧-+<⎪=⎨≥⎪⎩,满足对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,则实数a 的取值范围为______.【答案】21,112⎡⎫⎪⎢⎣⎭【解析】【分析】根据分段函数的单调性列式求解.【详解】对任意的实数12x x ≠,都有()()12120f x f x x x -<-成立,所以函数()f x 在R 上为减函数,可得21002142a a aa a ⎧⎪-<⎪>⎨⎪⎪-+≥⎩,解得21112a ≤<,所以实数a 的取值范围为21,112⎡⎫⎪⎢⎣⎭.故答案为:21,112⎡⎫⎪⎢⎣⎭三、解答题(共5题,满分75分.必要的文字说明,解答过程和演算步骤不能省略)16.(1)计算()1122013342⎛⎫⎛⎫-⨯- ⎪⎪⎝⎭⎝⎭(2)计算7log 23log lg 25lg 47+++.【答案】(1)52-.(2)112.【解析】【分析】(1)利用实数指数幂的运算性质计算即可;(2)利用对数的运算性质计算即可.【详解】(1)原式11232221315221412222⎡⎤⎛⎫⎛⎫=--⨯+=-+=-⎢⎥ ⎪⎪⎝⎭⎝⎭⎢⎥⎣⎦.(2)原式()32333311log 32lg 52lg 222lg 5lg 222lg102222222=+++=+++=++=++=.17.已知集合{}2135A x a x a =-≤≤+,{}320B x x =≤≤.(1)当2a =时,求A B ⋂,A B ⋃;(2)求能使A B A = 成立的a 的取值范围.【答案】(1){}311A B x x ⋂=≤≤,{}320A B x x ⋃=≤≤.(2)6a <-或25a ≤≤.【解析】【分析】(1)利用交集、并集运算求解即可;(2)由A B A = 得A B ⊆,分类讨论列不等式组求解即可.【小问1详解】当2a =时,{}311A x x =≤≤,又{}320B x x =≤≤,所以{}311A B x x ⋂=≤≤,{}320A B x x ⋃=≤≤.【小问2详解】因为A B A = ,所以A B ⊆,又集合{}2135A x a x a =-≤≤+,{}320B x x =≤≤,当A =∅时,2135a a ->+,即6a <-,这时A B ⊆.当A ≠∅时,有21352133520a a a a -≤+⎧⎪-≥⎨⎪+≤⎩,解得25a ≤≤.综上,实数a 的取值范围为6a <-或25a ≤≤.18.设函数()21f x mx mx =--.(1)若对于一切实数(),0x f x <恒成立,求m 的取值范围;(2)解不等式()()21221f x m x x m <-+--.【答案】18.(]4,0-19.答案见解析.【解析】【分析】(1)分成二次项系数为0和不为0两种情况,当二次项系数不为0时满足开口向下且Δ0<;(2)因式分解后对参数m 分类讨论即可.【小问1详解】①若0m =,此时10-<恒成立;②若0m ≠,要使得210mx mx --<恒成立,则2Δ40m m m <⎧⎨=+<⎩,解得40m -<<,所以(]4,0m ∈-;【小问2详解】()2211221mx mx m x x m --<-+--,即()2220x m x m -++<,即()()20x x m --<,若m>2,则解集为()2,m ;若2m =,此时不等式无解;若2m <,则解集为()m,219.已知函数()321x af x =-+是定义域在R 上的奇函数.(1)求实数a 的值;(2)判断函数()f x 的单调性并证明;(3)若对任意的[]1,2t ∈-,不等式()()2220f t f t k -+-<恒成立,求实数k 的取值范围.【答案】(1)6(2)()f x 在(),-∞+∞上是增函数,证明见解析(3)()6,+∞【解析】【分析】(1)根据函数奇偶性得(0)302af =-=,解得a 的值;最后代入验证;(2)根据指数函数的单调性可直接下结论,然后利用单调性的定义证明;(3)根据函数奇偶性与单调性将不等式化简为222k t t >+-对于[1,2]t ∈-恒成立,再根据恒成立转化为对应函数最值问题,最后根据函数最值得结果.【小问1详解】函数()321xaf x =-+是定义域在R 上的奇函数,由(0)302a f =-=,得6a =,即有()()321632121x x x f x -=-=++,下面检验:()()()()()()32132123122121212x xxx xx xxf x fx ------⋅--====-+++⋅,且定义域为R 关于原点对称,所以()f x 为奇函数,故符合;【小问2详解】()f x 在(),-∞+∞上是增函数.证明如下:设任意12x x <,()()()()()12121212622663321212121x x x x x x f x f x -⎛⎫⎛⎫-=---= ⎪ ⎪++++⎝⎭⎝⎭,由于12x x <,则12022x x <<,即有()()()121262202121x x x x -<++,则有()()12f x f x <,故()f x 在(),-∞+∞上是增函数;【小问3详解】因为对任意的[]1,2t ∈-,不等式()()2220f t f t k -+-<恒成立,所以2(2)(2)f t f t k -<--对于[]1,2t ∈-恒成立,因为()f x 是定义域在R 上的奇函数,所以2(2)(2)f t f k t -<-对于[]1,2t ∈-恒成立,又()f x 在R 上是增函数,所以222t k t -<-,即222k t t >+-对于[1,2]t ∈-恒成立,而函数()222g t t t =+-在[]1,2-上的最大值为()26g =,所以6k >,所以实数k 的取值范围为()6,+∞.20.已知函数()f x 的定义域为R ,并且满足下列条件:①()11f -=;②对任意,R x y ∈,都有()()()f x y f x f y +=+;③当0x >时,()0f x <.(1)证明:()f x 为奇函数.(2)解不等式()()2222f x x f x +-->-.(3)若()255f x m mt ≤--对任意的[]1,1x ∈-,[]1,1t ∈-恒成立,求实数m 的取值范围.【答案】(1)证明见解析(2)()4,1-(3)(][),66,-∞-⋃+∞【解析】【分析】(1)用赋值法先求出()0f ,再令y x =-即可得证;(2)先证明函数在R 上是减函数,再求得()22f =-,最后将不等式()()2222f x x f x +-->-转化为2340x x +-<求解即可;(3)将题意转化为2560m mt -->,[]1,1t ∈-恒成立即可.【小问1详解】由题意函数()f x 的定义域为R ,定义域关于原点对称,令0x y ==,则(00)(0)(0)2(0)f f f f +=+=,故(0)0f =.令y x =-,则()()()0f x x f x f x -=+-=,故()()f x f x -=-.故()f x 为奇函数.【小问2详解】任取12,R x x ∈,且12x x >.由题意120x x ->,()120f x x -<,()()()()1121122f x f x x x f x x f x =-+=-+,故()()()12120f x f x f x x -=-<,即()()12f x f x <,又12x x >,故()f x 在R 上为减函数.因为()11f -=,所以()11f =-,()()211112f f =+=--=-,故()()2222f x x f x +-->-即()()()2222f x x f x f ++->,即2222x x x ++-<,化简可得2340x x +-<,解得()4,1x ∈-.【小问3详解】由(2)知()f x 在[]1,1-上为减函数,故()f x 在[]1,1-上最大值为()11f -=.要使()255f x m mt ≤--对任意的[]1,1x ∈-,[]1,1t ∈-恒成立,则2551m mt --≥,即2560mt m -+-≥对任意[]1,1t ∈-恒成立.又256y mt m =-+-是关于t 的一次函数,故只需()2251605160m m m m ⎧-⨯-+-≥⎨-⨯+-≥⎩,。
江西省部分学校2024-2025学年高一上学期11月期中考试数学试题(含解析)

江西省2024—2025学年上学期第一次模拟选科联考高一数学试卷共4页,19小题,满分150分。
考试用时120分钟。
注意事项:1.考查范围:必修第一册第一章至第三章第二节。
2.答卷前,考生务必将自己的姓名、准考证号等填写在答题卡指定位置上。
3.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
4.考生必须保持答题卡的整洁。
考试结束后,请将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知全集,集合,,则A.{2,3,4,5}B.{1,3,4}C.{3,4}D.{3}2.已知命题,,则为A., B.,C., D.,3.已知为定义在R 上的奇函数,当时,,则A. B.C. D.4.已知是幂函数,若,则a =A.B.2C.4D.65.若A. B. C. D.6.已知定义在R 上的函数满足,且,且,,则A. B.C. D.7.若关于x 的不等式的解集为,且,则实数m 的值为}{1,2,3,4,5U =2}{1,M =}2,{3,4N =()U M N = ð:1p x ∃>320x ->p ⌝1x ∀…320x ->1x ∀…320x -…1x ∀>320x -<1x ∀>320x -…()f x 0x >31()1f x x x =-+(1)f -=12-1232-3292()(4)m f x m x -=-()2f a =121a <-=5(1)a -+5(1)a +6(1)a -+6(1)a +()f x (5)(5)f x f x +=-12,(5,)x x ∀∈+∞12x x ≠121[(()()x x x f --2]()0f x >(5.5)(4.5)f f >(2.7)(3.2)f f <(7.3)(7.9)f f >(2.7)(5.2)f f >220()21x m x m m +-+-<12(,)x x 12112x x +=A.-4B.-1C.1D.48.已知函数若存在实数x ,使,则实数a 的取值围为A. B.C. D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列计算中正确的是A.C. D.10.使成立的一个充分条件可以是A.且 B.且C.且 D.且11.已知函数的定义域为R ,且的图象关于原点对称,的图象关于y 轴对称,则A. B.C.函数是增函数D.三、填空题:本题共3小题,每小题5分,共15分.12.已知函数,则________.13.已知幂函数的图象过点,则________.14.对于任意实数x ,表示不小于x 的最小整数,例如(1.2)=2,,表示不大于x 的最大整数,例如[1.2]=1,.已知定义在R 上的函数,若集合,则集合A 中所有元素的和为________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)已知函数在上单调递减,其中,且.(1)求的解析式;(2)求函数,的值域.16.(15分)已知集合,,且.23,2,(),2,x ax a x f x a x ⎧-++>⎪=…()0f x <(,1)-∞-(,2)(6,)-∞-+∞(,6)(1,)-∞--+∞(,1)(6,)-∞-+∞ 1144-=2=±23(8)4-=23184-=3a b c ->a c >2b c >-2a c >b c >-2a c >b c>-3a c >2b c>()f x (2)4y f x =+-(4)4y f x x =++(2)4f =(6)12f =-()f x (8)(4)824f x f x x -+-=-30,()()1,0,x f x g x x x x ==-<⎪⎩…((1))g f -=()m f x x =3(3,33[(2)]f =()x (0.2)0-=[]x 0.21[]-=-()(2)[3]f x x x =⋅4|(),23A y y f x x ⎧⎫==-<-⎨⎬⎩⎭…()af x b x=+(0,)+∞24a =(1)1f =()f x 2()2()[()]g x f x f x =+[1,4]x ∈(4,29]A m =+{|2233}B x m x m =-+……12B ∈(1)当时,求实数m 的取值范围;(2)设;,若p 是q 的必要不充分条件,求实数m 的取值范围.17.(15分)已知定义在R 上的奇函数与偶函数满足,若.(1)求的解析式;(2)求关于x 的不等式的解集.18.(17分)某糕点连锁店现有五家分店,出售A ,B 两款糕点,A 为特价糕点,为吸引顾客,按进价销售.已知用16000元购进A 糕点与用22000元购进B 糕点的重量相同,且B 糕点每斤的进价比A 糕点每斤的进价多6元.(1)求A ,B 两种糕点每斤的进价;(2)经市场调查发现,B 糕点每斤售价30元时,每月可售出3120斤,售价每提高1元,则每月少售出120斤,售价每降低1元,则每月多售出120斤,糕点店不会低于进价销售.则B 糕点每斤定价为多少元时,糕点店通过卖B 糕点获得的月利润最大?最大是多少?(3)因为使用进价销售的A 糕点物美价廉,所以深受顾客青睐,五个分店每月的总销量为10000斤.今年年初该连锁店用50万购进一批设备,用于生产A 糕点.已知每斤糕点的原材料价格为8元,若生产A 糕点n 个月()所用的原材料之外的各种费用总计为万元,若只考虑A 糕点,记该连锁店前n 个月的月平均利润为z 万元,求z 的最大值.19.(17分)对非空数集A 及实数k ,定义,,已知.(1)当时,若集合A 为单元素集,求A ;(2)当时,若集合,求ab 的所有取值构成的集合;(3)若A 中有3个元素,求实数k 的取值范围.16A ∉:p t A ∈:q t B ∈()f x ()g x ()()2||2f x g x x x +=++()()()h x f x g x =⋅()h x 2(3)(3)0h x tx h x t -+-<*n ∈N 211324n n +2{|,}A k x x a k a A ==-∈ {|,}A k x x k a a A ⊗==-∈A k A k =⊗ 1k =3k ={,}A a b =江西省2024—2025学年上学期第一次模拟选科联考高一数学参考答案及评分细则1.【答案】A【解析】,故选A.2.【答案】D【解析】根据存在量词命题的否定是全称量词命题,得,.故选D.3.【答案】B【解析】因为为定义在R 上的奇函数,所以.故选B.4.【答案】C【解析】因为是幂函数,所以,得,故时,.故选C.5.【答案】C【解析】当时,.故选C.6.【答案】D【解析】由题意得函数在上单调递减,在上单调递增.对选项A ,,A 错误;对选项B ,因为函数在上单调递减,所以,B 错误;对选项C ,因为函数在上单调递增,所以,C 错误;对选项D ,因为,函数在上单调递减,故,D 正确.故选D.7.【答案】B【解析】因为关于x 的不等式的解集为,所以关于x 的方程有两个不相等的实数根,所以,解得,且,,所以,解得.故选B.8.【答案】D【解析】当时,,即,因为,所以,故有解,{3,4,5}{2,3,4}{2,3,4,5}()U M N == ð:1p x ⌝∀>320x -…()f x 311(1)(1)1112f f ⎛⎫-=-=--= ⎪+⎝⎭92()(4)m f x m x-=-41m -=5m =12()f x x ==2=4a =1a <-10a +<3(1)a =--3(1)a =+=336(1)(1)(1)a a a --+=-+()f x (,5)-∞(5,)+∞(5.5)(50.5)f f =+=(50.5)(4.5)f f -=()f x (,5)-∞(2.7)(3.2)f f <()f x (5,)+∞(7.3)(7.9)f f >(5.2)(5f f =+0.2)(50.2)(4.8)f f =-=()f x (,5)-∞(2.7)(4.8)(5.2)f f f >=220()21x m x m m +-+-<12(,)x x 220()21x m x m m +-+-=12,x x 22[2(1)]41()440m m m m ∆=--⨯⋅-=-+>1m <122(1)x x m +=--212x x m m =-1221212112(1)2x x m x x x x m m+--+===-1m =-2x >230x ax a -++<23(1)x a x +<-2x >11x ->231x a x +>-即,因为,当且仅当,即时等号成立,故;当时,有解,即有解,也即,因为单调递增,故时,取最大值-1,故.综上,实数a的取值范围为.故选D.9.【答案】ACD (每选对1个得2分)【解析】对于A ,,A 正确;对于B,B 错误;对于C ,,C 正确;对于D ,,D 正确.故选ACD.10.【答案】AC (每选对1个得3分)【解析】充分性成立,即选项能推出,对于A ,,又,同向不等式相加得,A 成立;对于B ,令,,,满足且,但,B 不成立;对于C ,,又,同向不等式相加得,,C 成立;对于D ,令,,,满足且,但,D 不成立.故选AC.11.【答案】ABD (每选对1个得2分)【解析】A 选项,的定义域为R ,因为的图象关于原点对称,所以为奇函数,所以,故,令,得,A 正确;B 选项,由的图象关于y 轴对称,得为偶函数,所以,即,令,得,得,B 正确;C 选项,因为,C 错误;D 选项,因为,所以,因为,令,得,即,故,,D 正确.故选ABD.12.【答案】-8【解析】,.13.【答案】64【解析】由,所以.14.【答案】67【解析】当时,;当时,,,2min31x ax ⎛⎫+>⎪-⎝⎭223(11)341226111x x x x x x +-++==-+++=--- (4)11x x -=-3x =6a >2x …0a +<a <max (a <y =2x =y =1a <-(,1)(6,)-∞-+∞ 1144-=2=23(8)4-==232311848-===3a b c ->22b c b c <-⇒->a c >3a b c ->3a =7b =1c =-2a c >b c >-433a b c -=-<-=b c b c <-⇒->2a c >3a b c ->5a =8b =1c =-3a c >2b c >33a b c -=-=()f x (2)4y f x =+-(2)4y f x =+-(2)4(2)40f x f x --++-=(2)(2)8f x f x -++=0x =(2)4f =(4)4y f x x =++(4)4y f x x =++(4)4(4)4f x x f x x --=++(4)(4)8f x f x x -=++2x =4(2)(6)16f f ==+(6)12f =-(2)(6)f f >(2)(2)8f x f x -++=()8(4)f x f x =--(4)(4)8f x f x x -=++4x t -=()(8)328f t f t t =-+-()(8)328f x f x x =-+-8(4)(8)328f x f x x --=-+-(8)(4)824f x f x x -+-=-(1)112f -=--=-3((1))(2)(2)8g f g -=-=-=-333m =3m =-3()f x x =333(3(36[(2)](22264f ⨯====2x =-()(4)[6](4)(6)24f x =-⋅-=-⨯-=523x -<<-10423x -<<-(2)3x =-,,;当时,,,,,;当时,,,,,.综上,,集合A 中所有元素的和为67.15.解:(1)由得,(2分)因为函数在上单调递减,所以,故.(5分)由得,所以.(7分)(2),(10分)当时,,,,所以函数,的值域为.(13分)【评分细则】值域写成集合或区间形式均给分.16.解:(1)因为,所以,得,(2分)又因为,所以,即,(5分)故当时,m 的取值范围是.(7分)(2)因为,所以,,若p 是q 的必要不充分条件,则B 是A 的真子集,(10分)故(12分)解得.故实数m 的取值范围是.(15分)【评分细则】结果写成集合或区间或不等式形式均给分.17.解:(1)因为,即,又,得,,(4分)635x -<<-[3]6x =-()(2)[3](3)(6)18f x x x =⋅=-⨯-=5332x -- (10)233x --……(2)3x =-9532x --……[3]5x =-()(2)[3](3)(5)15f x x x =⋅=-⨯-=3423x -<<-8323x -<<-(2)2x =-9342x -<<-[3]5x =-()(2)[3](2)(5)10f x x x =⋅=-⨯-={24,18,15,10}A =24a =2a =±()af x b x=+(0,)+∞0a >2a =(1)21f b =+=1b =-2()1f x x=-222424()2()[()]211g x f x f x x x x ⎛⎫=+=-+-=- ⎪⎝⎭[1,4]x ∈2[1,16]x ∈241,44x ⎡⎤∈⎢⎥⎣⎦2131,34x ⎡⎤-∈-⎢⎥⎣⎦2()2()[()]g x f x f x =+[1,4]x ∈3,34⎡⎤-⎢⎥⎣⎦12B ∈221233m m -+……37m ……16A ∉2916m +<72m <16A ∉73,2⎡⎫⎪⎢⎣⎭37m ……A O ≠B O ≠224,3329,m m m ->⎧⎨++⎩…36m <…(3,6]()()2||2f x g x x x -+-=-+-+()()2||2f x g x x x -+=-++()()2||2f x g x x x +=++()2f x x =()||2g x x =+所以.(5分)(2)因为,所以为奇函数,(7分)又当时,单调递增,故函数在R 上单调递增.(9分)则不等式,可化为,即,即,(11分)①若,即时,;②若,即时,不等式无解;③若,即时,,综上,当时,解集为,当时,解集为,当时,解集为.(15分)【评分细则】1.第一问求出和的解析式分别给2分;2.第一问结果写成分段函数形式不扣分;3.第二间结果不写成集合或区间形式扣1分,未总结,但结果正确均给满分,三种情况每少一种情况扣1分.18.解:(1)设A 糕点每斤的进价为a 元,B 糕点每斤的进价为元,所以,解得,所以A 糕点每斤的进价为16元,B 糕点每斤的进价为22元.(4分)(2)设B 糕点每斤涨价元,蛋糕店通过B 糕点获得的月利润为y 元.由题意,(6分)当时,y 有最大值.(8分)所以B 糕点每斤定价为39元时,月利润最大,最大为34680元.(9分)(3)设前n 个月的总利润为w ,因为A 糕点每斤售价为16元,每月可售出10000斤,故每月可收入16万元,其中原材料为8万元,则,(12分)月平均利润万元,(15分)()()()2(||2)h x f x g x x x =⋅=+()2()(||2)2(||2)()h x x x x x h x -=--+=-+=-()h x 0x …2()24h x x x =+()h x 2(3)(3)0h x tx h x t -+-<2(3)(3)(3)h x tx h x t h t x -<--=-23(3)0x t x t +--<(3)(1)0x t x -+<13t <-3t <-13tx <<-13t=-3t =-13t >-3t >-13t x -<<3t <-|13t x x ⎧⎫<<-⎨⎬⎩⎭3t =-∅3t >-|13t x x ⎧⎫-<<⎨⎬⎩⎭()f x ()g x (6)a +16000220006a a =+16a =(8)x x -…22(3022)(3120120)120216024960120(9)34680y x x x x x =+--=-++=--+9x =22*111311685050()324324w n n n n n n n ⎛⎫=--+-=-+-∈ ⎪⎝⎭N 503131215.2532444w n z n n ==--+-+==…当且仅当,即时等号成立,(16分)所以z 的最大值为5.25.(17分)【评分细则】1.第二问未配方,只要结果正确,就给分;2.第三问未说明等号成立条件扣1分.19.解:(1)时,设,由,得,所以,即,得或1,故或.(4分)(2)时,,由,得,得或即或(5分)当时,是方程的两根,故,(6分)当时,两式相减得,由集合中元素的互异性得,所以,故,即,同理,故是方程的两根,所以,(7分)故ab 的所有取值构成的集合为.(8分)(3)设,由,得,①若故是方程的三个不等的实数根,而此方程最多有两个实数根,不可能有三个实数根,故不成立;(11分)②若,当时,,令,得,(12分)对,,两式相减得,因为,所以,代入,得,同理,5032n n=40n =1k ={}A a =11A A =⊗ 2{1}{1}a a -=-211a a -=-220a a +-=2a =-{2}A =-1}{A =3k ={,}A a b =33A A =⊗ 22{3,3}{3,3}a b a b --=--2233,33a a b b ⎧-=-⎨-=-⎩2233,33,a b b a ⎧-=-⎨-=-⎩2260,60a a b b ⎧+-=⎨+-=⎩226,6,a b b a ⎧=-⎨=-⎩2260,60a ab b ⎧+-=⎨+-=⎩,a b 260x x +-=6ab =-226,6a b b a⎧=-⎨=-⎩22a b a b -=-a b ≠1a b +=266(1)5a b a a =-=--=+250a a --=250b b --=,a b 250x x --=5ab =-{6,5}--{,,}A a b c =A k A k =⊗ 222{,,}{,,}a k b k c k k a k b k c ---=---222,,,a k k a b k k b c k k c ⎧-=-⎪-=-⎨⎪-=-⎩,,a b c 220x x k +-=222,,,a k kb b k k ac k k c ⎧-=-⎪-=-⎨⎪-=-⎩2c k k c -=-220c c k +-=180k ∆=+ (1)8k -…2a k k b -=-2b k k a -=-22a b a b -=-a b ≠1a b +=2a k k b -=-2120a a k -+-=2120b b k -+-=故为方程的两个不相等的实根,令,得,(13分)当时,与均有两个不相等的实根,且这两个方程的根不完全相同,故符合题意;(14分)③若则,根据集合中元素的互异性,两两不相等,不妨设,(ⅰ)当时,,又,所以,这与矛盾,故不成立;(ⅱ)当时,,又,所以,这与矛盾,故不成立;(ⅲ)当时,,又,所以,这与矛盾,故不成立;(ⅳ)当时,,又,所以,这与矛盾,故不成立.(16分)综上,实数k 的取值范围是.(17分)【评分细则】1.第一问只得出一种情况,扣2分;结果不写成集合形式,扣1分;2.第二问求出ab 的一个值,给2分,最后结果不写成集合形式,扣1分;3.第三问结果写成不等式、集合或区间形式,结果正确即给满分.,a b 2120x x k -+-=14(12)0k '∆=-->38k >38k >2120x x k -+-=220x x k +-=222,,,a k k b b k k c c k k a ⎧-=-⎪-=-⎨⎪-=-⎩2222a b b c c a k +=+=+=,,a b c a b c >>0a b c >>>22a b >b c >22c a b b ++>22c a b b ++=0a b c >>>22a b >b c >22c a b b ++>22c a b b ++=0a b c >>>22b c <c a <22b c a c ++<22b c a c ++=0a b c >>>22b c <c a <22b c a c ++<22b c a c ++=3,8⎛⎫+∞ ⎪⎝⎭。
福建省漳州市十校联盟2024-2025学年高一上学期期中质量检测联考数学试题含答案
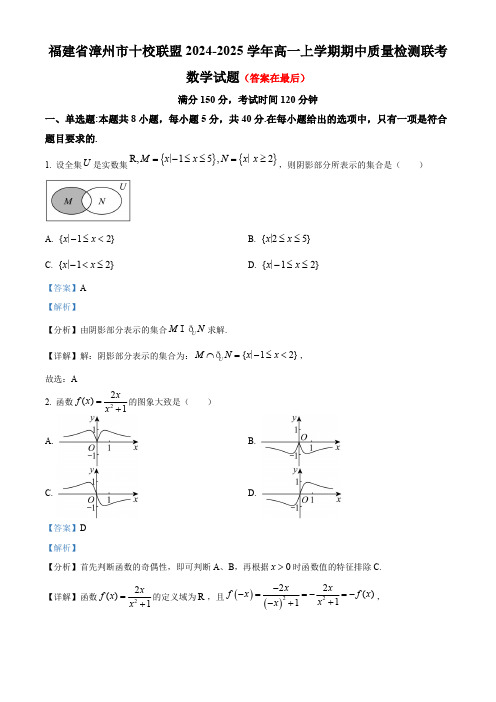
福建省漳州市十校联盟2024-2025学年高一上学期期中质量检测联考数学试题(答案在最后)满分150分,考试时间120分钟一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.设全集U 是实数集{}{}R,15,2M x x N x x =-≤≤=≥∣∣,则阴影部分所表示的集合是()A.{12}x x -≤<∣B.{25}xx ≤≤∣C.{12}xx -<≤∣ D.{12}xx -≤≤∣【答案】A 【解析】【分析】由阴影部分表示的集合U M N I ð求解.【详解】解:阴影部分表示的集合为:{12}U M xx N ≤⋂=-<∣ð,故选:A 2.函数22()1xf x x =+的图象大致是()A. B.C. D.【答案】D 【解析】【分析】首先判断函数的奇偶性,即可判断A 、B ,再根据0x >时函数值的特征排除C.【详解】函数22()1x f x x =+的定义域为R ,且()()2222()11x x f x f x x x --==-=-+-+,所以22()1xf x x =+为奇函数,函数图象关于原点对称,故排除A 、B ;又当0x >时()0f x >,故排除C.故选:D3.下列不等式中,可以作为“30x -<”的一个必要不充分条件是()A.14x <<B.4x <C.1x <D.02x <<【答案】B 【解析】【分析】由必要不充分条件的概念逐项判断即可.【详解】对于A:14x <<为30x -<既不充分也不必要条件;对于B :4x <为30x -<的必要不充分条件;对于C:1x <为30x -<的充分不必要条件;对于D :02x <<为30x -<的充分不必要条件;故选:B4.若336a b +=,则a b +的取值范围是()A.(1,2]-B.[]0,2C .(2,)+∞ D.(,2]-∞【答案】D 【解析】【分析】根据基本不等式的应用可得3≥2a b +≤.【详解】易知30,30a b >>,所以336a b +=≥=,即可得3≥2393a b +≤=,所以2a b +≤,当且仅当1a b ==时,等号成立.故选:D5.幂函数()223()1m m f x m m x +-=--在(0,)+∞上是增函数,则实数m 的值为()A.2或1-B.1-C.2D.2-或1-【答案】C 【解析】【分析】根据幂函数的定义及幂函数的单调性,可得221130m m m m ⎧--=⎨+->⎩,进而求解即可.【详解】由题意得,221130m m m m ⎧--=⎨+->⎩,解得2m =.故选:C.6.若命题“2R,20x ax ax ∃∈-+≤”是假命题,则实数a 的取值范围是()A.{04}aa <<∣ B.{}08aa ≤≤∣C.{08}aa ≤<∣ D.{04}aa ≤<∣【答案】C 【解析】【分析】转化为x ∀∈R ,220ax ax -+>为真命题,分类讨论,结合判别式符号列不等式求解即可.【详解】命题:p x ∃∈R ,220ax ax -+≤为假命题,即x ∀∈R ,220ax ax -+>为真命题.当0a =时:20>恒成立;当0a ≠时:满足2Δ80a a a >⎧⎨=-<⎩,解得08a <<.综上,实数a 的取值范围是[)0,8,故选:C7.已知函数()16,2,2x x a x f x ax -⎧-≤=⎨>⎩在定义域上是单调递减函数,求实数a 的取值范围为()A.2,15⎡⎫⎪⎢⎣⎭ B.1,13⎛⎫ ⎪⎝⎭C.1,13⎡⎫⎪⎢⎣⎭ D.2,15⎛⎫⎪⎝⎭【答案】A 【解析】【分析】分段函数是减函数,各个函数在对应区间上单调递减,且(],2-∞对应函数右端点函数值大于或等于()2,+∞对应函数的左端点函数值,建立不等式后解得a 的取值范围.【详解】由题意可知:()6g x x a =-在(],2-∞上单调递减,又∵()6g x x a =-关于直线6x a =对称,∴()g x 在(],6a -∞上单调递减,∴62a ≥,∴13a ≥;()1x h x a -=在()2,+∞上单调递减,∴01a <<;且()()22g h ≥即26a a -≥,∴27a ≥或25a ≤,∴215a ≤<.故选:A.8.已知函数()f x 为定义在R 上的偶函数,12,(,0)x x ∀∈-∞,且()()12211221,4x f x x f x x x x x -<>-,且(2)4,(0)0f f -=-=,求不等式()4f x <-的解集为()A.[2,2]-B.(2,0)(0,2)-C.(2,0)(2,)-+∞D.(2,2)-【答案】B 【解析】【分析】构造函数()4()+=f x g x x,由已知条件确定它的奇偶性与单调性,然后利用其性质分类讨论解不等式.【详解】12,(,0)x x ∀∈-∞,且()()12211221,4x f x x f x x x x x --,则()()12212140x f x x f x x x -->-,()()122121[4][4]0x f x x f x x x +-+>-,所以212121()4()4f x f x x x x x ++->-,设()4()+=f xg x x,则2121(0)()g x x x g x ->-,21()()g x g x >,因此(,0)x -∞时,()g x 是增函数,又因为()f x 是偶函数,所以()4()4()()f x f x g x g x x x-++-==-=--,所以()g x 是奇函数,因此()g x 在(0,)+∞上也是增函数,(2)4(2)02f g -+-==-,则(2)(2)0=--=g g ,()4f x <-,()40f x +<,0x <时,()40f x x +>,即()0g x >,所以20x -<<,0x >时,()40f x x+<,即()0g x <,所以0<<2,综上,不等式的解集为()()2,00,2-⋃,故选:B .【点睛】方法点睛:本题考查函数的奇偶性与单调性解不等式,解题时主要要构造新函数()4()+=f xg x x,利用它的性质求解.在题中出现1221()()x f x x f x -时,构造新函数需要通过提取(或分子分母同除以或不等式两边同除以)21x x 得出2121()()f x f x x x -,当然本题中不等式右边不为0,因此需先移项变形,再确定构造的函数.二、多选题:本题共3小题,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,选对但不全的得部分分,有选错或不选的得0分.9.中国古代重要的数学著作《孙子算经》下卷有题:“今有物,不知其数.三三数之,剩二;五五数之,剩三;七七数之,剩二.问:物几何?”现有如下表示:已知{}*32,N A xx n n ==+∈∣,{}*53,N B x x n n ==+∈∣,{}*72,N C x x n n ==+∈∣,若()a A B C ∈⋂⋂,则下列选项中符合题意的整数a 为()A.23B.68C.128D.233【答案】ACD 【解析】【分析】依题意可知整数a 除以3余数为2,除以5余数为3,除以7余数为2;对选项逐一验证即可得出结论.【详解】根据题意可知,A B C ⋂⋂代表的是除以3余数为2,除以5余数为3,除以7余数为2的整数;对于A ,可知23372,23543,23732÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅,即A 正确;对于B ,可得683222,685133,68795÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅,不合题意,即B 错误;对于C ,可得1283422,1285253,1287182÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅,即C 正确;对于D ,易知2333742,2335463,2337332÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅÷=⋅⋅⋅⋅⋅⋅.可知D 正确.故选:ACD10.若0,0,2a b a b >>+=,则下列不等式对一切满足条件的a ,b 恒成立的是()A.222a b ab +≤B.222a b +≥C.+≤ D.112a b+≥【答案】ABD 【解析】【分析】A 选项,222b a a a b b +=,利用基本不等式求出最大值;B 选项,由基本不等式得()()22224a b a b +≥+=,求出222a b +≥;C 选项,()224a b ≤+=2≤,C 错误;D 选项,利用基本不等式“1”的妙用求出最小值.【详解】A 选项,()()222222ab a b b a a b a b ab ++≤+===,当且仅当1a b ==时,等号成立,故A 正确;B 选项,()()22222224a bab ab a b +≥++=+=,故222a b +≥,当且仅当1a b ==时,等号成立,B 正确;C 选项,()224=+++=a b a b 2≤,当且仅当1a b ==时,等号成立,C 错误;D 选项,()11111111122222b a a b a b a b a b ⎛⎛⎫⎛⎫+=++=+++≥+= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当b aa b=,即1a b ==时,等号成立,D 正确.故选:ABD11.已知函数()f x 的定义域为R ,且满足2()()e e x x f x f x ---=+,则下列命题正确的是()A.函数()f x 的图像关于(0,0)对称B.函数()f x 的图像关于y 轴对称C.函数()f x 的最小值2D.()()0.10.123f f >-【答案】BC 【解析】【分析】依题意求出函数()f x 的解析式,可得其为偶函数,判断出A 错误,B 正确;再由基本不等式可得C 正确,利用奇偶性和单调性可得D 错误.【详解】由2()()e e x x f x f x ---=+可得2()()e e x x f x f x ---=+;两式联立可得()e e x x f x -=+,易知函数()f x 满足()()e e xxf x f x -=+=-,可知()f x 为偶函数,即可得A 错误,B 正确;易知e 0x >,所以()1e 2e x x f x =+≥=,当且仅当0x =时,等号成立,可得C 正确;当[)0,x ∈+∞时,根据对勾函数以及偶函数性质可得,()f x 为单调递增;易知()()0.10.133f f -=,且0.10.123<,所以()()()0.10.10.1233f f f <=-,即D 错误.故选:BC三、填空题:本题共3小题,每小题5分,共15分.12.计算:314316(0.125)(1181-⎛⎫-+-= ⎪⎝⎭___________.【答案】1927-【解析】【分析】根据分数指数幂运算法则计算可得结果.【详解】易知原式()()()314343132278190.510.512172323--⎛⎫⎛⎫⎛⎫=-+=-+=-+=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;故答案为:1927-13.定义运算,,a a ba b b a b≤⎧⊗=⎨>⎩,已知函数()(132)3x f x x =-⊗,则()f x 的最大值为___________.【答案】9【解析】【分析】根据a b ⊗的含义及函数132y x =-与函数3x y =的单调性可得分段函数()f x 的解析式及单调性,可得最大值.【详解】由题意得,a b ⊗表示a 与b 的最小值,∵132y x =-在R 上单调递减,3x y =在R 上单调递增,且2x =时,1323x x -=,∴当2x ≤时,3132x x ≤-,当2x >时,3132x x >-,∴op =3,≤213−2s >2,∴()f x 在(,2)-∞上单调递增,在(2,)+∞上单调递减,∴max ()(2)9f x f ==.故答案为:9.14.若函数2231()3ax x f x ++⎛⎫= ⎪⎝⎭的值域是10,9⎛⎤ ⎥⎝⎦,则f (x )的单调递增区间是________.【答案】(,1]-∞-【解析】【分析】令g (x )=ax 2+2x +3,由f (x )的值域确定g (x )的值域,从而求出a 值,利用复合函数单调性的性质可得答案.【详解】令g (x )=ax 2+2x +3,由于f (x )的值域是10,9⎛⎤ ⎥⎝⎦,所以g (x )的值域是[2,+∞).因此有0,12424a a a>⎧⎪-⎨=⎪⎩解得a =1,这时g (x )=x 2+2x +3,2231()3x x f x ++⎛⎫= ⎪⎝⎭,由于g (x )的单调递减区间是(-∞,-1],所以f (x )的单调递增区间是(-∞,-1].故答案为:(,1]-∞-【点睛】本题考查复合函数的单调性,考查指数函数性质的应用,属于基础题.四、解答题:本大题共5小题,共77分.解答应写出文字说明,证明过程或演算步骤.15.已知集合|A x y ⎧==⎨⎩,103|2B x x x ⎧⎫=⎨⎬⎩⎭+>-.(1)求()R A B ⋃ð;(2)若{6}C xa x a =-≤≤∣,且A C A = ,求实数a 的取值范围.【答案】(1)()1A ,(0,)2R B ⎛⎤⋃=-∞-⋃+∞ ⎥⎝⎦ð(2)[4,6]【解析】【分析】(1)先化简集合A ,B ,再利用集合的并集和补集运算求解;(2)由A C A = ,得到A C ⊆求解.【小问1详解】解:由040x x >⎧⎨-≥⎩,得04x <≤.所以A (0,4]=,由2103x x +>-,得:2110,332x x x +<∴-<<-.所以1,32B ⎛⎫=-⎪⎝⎭,1,[3,)2R B ⎛⎤=-∞-⋃+∞ ⎥⎝⎦ð.所以,()1A ,(0,)2R B ⎛⎤⋃=-∞-⋃+∞ ⎥⎝⎦ð;【小问2详解】由A C A = ,得A C ⊆,所以604a a -≤⎧⎨≥⎩,解得64a a ≤⎧⎨≥⎩即46a ≤≤.所以实数a 的取值范围[4,6].16.已知2()(2)(,)f x ax a x b a b R =-++∈(1)若不等式()0f x <的解集为(1,3)-,求a ,b 的值;(2)若b =2,且0a >求关于x 的不等式()0f x >的解集.【答案】(1)2,6a b ==-(2)答案见解析【解析】【分析】(1)由不等式的解集得相应一元二次方程的解,结合韦达定理求解;(2)不等式变形为2(1)0x x a ⎛⎫--> ⎪⎝⎭,再根据2a与1的大小分类讨论得出不等式的解集.【小问1详解】因为()0f x <的解集为(1,3)-,所以0a >,且1-和3是方程2(2)0ax a x b -++=的两个实数根.2(1)3,(1)3a ba a+∴-+=-⨯=,解得:2,6a b ==-.【小问2详解】当2b =时,2()(2)2(2)(1)f x ax a x ax x =-++=--()0f x >等价于(2)(1)0ax x -->因为0a >,得2(1)0x x a ⎛⎫--> ⎪⎝⎭当21a =,即2a =时,不等式为2(1)0x ->,得1x ≠,当21a <,即2a >时,解不等式得2x a <或1x >,当21>a,即02a <<时,解不等式得1x <或2x a >,综上,当2a =时,不等式的解集为(,1)(1,)-∞⋃+∞.当2a >时,不等式的解集为2,(1,)a ⎛⎫-∞+∞ ⎪⎝⎭.当02a <<时,不等式的解集为2(,1),a ⎛⎫-∞+∞ ⎪⎝⎭.17.漳州市是中国重要的食用菌生产基地之一,食用菌产业得益于得天独厚的气候环境和土壤条件.某乡镇企业于2025年准备投资种植一批目前市场上较受欢迎的鸡枞菌.根据研究发现:种植鸡枞菌,一年需投入固定成本55万元,第一年最大产量50万斤,每生产x 万斤,需投入其他成本()c x 万元,211010,0366()160021285,3650x x x c x x x x ⎧++≤≤⎪⎪=⎨⎪+-<≤⎪⎩,根据市场调查,鸡枞菌的市场售价每万斤20万元,且全年所有产量都能全部售出.(利润=收入-固定成本-其它成本)(1)写出2025年利润f x ()(万元)与产量x (万斤)的函数解析式;(2)求2025年鸡枞菌产量x 为多少万斤时,该企业所获利润最大,求出利润最大值.【答案】(1)211065,0366()1600230,3650x x x f x x x x ⎧-+-≤≤⎪⎪=⎨⎪--+<≤⎪⎩(2)2025年产量为40万斤时,该企业所获利润最大,利润最大值为150万元【解析】【分析】(1)由利润=收入-固定成本-其它成本,根据题意求解;(2)由(1)的结论,利用二次函数的性质和基本不等式求解.【小问1详解】解:由题意可知:当036x ≤≤时,2211()20101055106566f x x x x x x ⎛⎫=-++-=-+- ⎪⎝⎭,当3650x <≤时,16001600()202128555230,f x x x x x x ⎛⎫=-+--=--+ ⎪⎝⎭211065,0366()1600230,3650x x x f x x x x ⎧-+-≤≤⎪⎪∴=⎨⎪--+<≤⎪⎩.【小问2详解】由211065,0366()1600230,3650x x x f x x x x ⎧-+-≤≤⎪⎪=⎨⎪--+<≤⎪⎩,①当036x ≤≤时,2211()1065(30)8566f x x x x =-+-=--+当30x =时,()f x 取得大值,最大值为85,②当3650x <≤时,1600()230230150f x x x ⎛⎫=-++≤-= ⎪⎝⎭,当且仅当1600x x=即40x =时,()f x 取得最大值50,由①②可得:当40x =时,()f x 取得最大值150,综上所述,2025年产量为40万斤时,该企业所获利润最大,利润最大值为150万元.18.设函数2x x f a ka x -=-()(0a >且1,R)a k ≠∈,若()f x 是定义在R 上的奇函数且8(1)3f =.(1)求k 和a 的值;(2)判断()f x 的单调性(无需证明),并求关于m 的不等式()2(1)50f m f m ++-+<成立时实数m 的取值范围;(3)已知函数22()2(),[0,1]x x g x a a f x x -=+-∈,求()g x 的值域.【答案】(1)1,32k a ==(2)在R 上单调递增,()(),23,-∞-⋃+∞(3)341,9⎡⎤⎢⎥⎣⎦【解析】【分析】(1)利用函数奇偶性以及函数值即可解得k 和a 的值;(2)由复合函数单调性可判断()f x 在R 上单调递增,利用单调性以及奇偶性解不等式可得实数m 的取值范围;(3)利用换元法将函数整理成二次函数形式,判断出其单调性,再由二次函数性质可得结果.【小问1详解】因为()f x 是R 上奇函数,所以()()f x f x -=-,即22x x x x a ka a ka ---=-+,整理得:()(12)0x x k a a --+=所以1120,2k k -==.所以()x x f x a a -=-,检验可知符合题意;又18(1)3f a a =-=,即28103a a --=,解得3a =或13a =-(舍)所以1,32k a ==.【小问2详解】由(1)可知()33x x f x -=-,易知指数函数3x y =为单调递增,函数3x y -=为单调递减,利用复合函数单调性可得()f x 在R 上单调递增,又因为()f x 为R 上的奇函数,所以()()22(1)55f m f m f m +<--+=-所以215m m +<-,即260m m -->,解得2m <-或3m >.所以()f x 在R 上单调递增,m 的取值范围是−∞,−2∪3,+∞【小问3详解】()2222()2()2,[0,1]x x x x x x g x a a f x a a a a x ---=+-=+--∈所以()22()33233x x x x g x --=+--()()2332332,[0,1]x x x x x --=---+∈令33x x t -=-,由(2)易知33x x t -=-在0,1上单调递增,所以8t 0,3⎡⎤∈⎢⎥⎣⎦记22822(1)1,0,3y t t t t ⎡⎤=-+=-+∈⎢⎥⎣⎦当时min 1,1t y ==;当83t =时,max 349y =.所以()g x 的值域是341,9⎡⎤⎢⎥⎣⎦.19.我们知道,函数()y f x =的图象关于坐标原点成中心对称图形的充要条件是函数()y f x =为奇函数,有同学发现可以将其推广为:函数()y f x =的图象关于点(,)P a b 成中心对称图形的充要条件是函数()y f x a b =+-为奇函数.给定函数4()1f x x x c=-++.(1)写出函数()f x 图象的对称中心(只写出结论即可,不需证明);(2)当2c =时,①判断函数()f x 在区间(2,)-+∞上的单调性,并用定义证明;②已知函数g(1)1x +-是奇函数,且当[0,1]x ∈时,2()22g x x mx m =-+,若对任意1[0,2]x ∈,总存在2[0,2]x ∈,使得()()12g x f x =,求实数m 的取值范围.【答案】(1)(,1)c c --(2)①函数()f x 在区间(2,)-+∞上单调递增,证明见解析;②[0,1].【解析】【分析】(1)由函数成中心对称的充要条件可得()4()1f x c c x x---=-为奇函数,可得对称中心;(2)①根据单调性定义按照步骤即可证明函数()f x 在区间(2,)-+∞上单调递增;②依题意并根据二次函数性质得出两函数的值域之间的包含关系,限定出最值之间的不等关系,解不等式即可求得结果.【小问1详解】根据题意可知,函数4()1f x x x c =-++是由函数4y x x =-向左平移c 个单位,向上平移1个单位得到的;所以()4()1f x c c x x---=-为奇函数,可得函数()f x 图象的对称中心是(,1)c c --.【小问2详解】当2c =时,4()12f x x x =-++.①函数()f x 在区间(2,)-+∞上单调递增;证明如下:12,(2,)x x ∀∈-+∞,且12x x <,()()()()()12121212124441112222f x f x x x x x x x x x ⎛⎫-=-+-+-=-+ ⎪ ⎪++++⎝⎭,因为122x x -<<,所以12120,20,20x x x x -<+>+>,所以()()1241022x x +>++,所以()()120f x f x -<,即()()12f x f x <.所以()f x 在(2,)-+∞单调递增,②因为(1)1g x +-是奇函数,所以()g x 关于点(1,1)对称,设()g x 在[0,2]上的值域为,()A f x 在[0,2]上的值域为B .因为对任意1[0,2]x ∈,总存在2[0,2]x ∈,使得()()12g x f x =,所以A B ⊆,由①可知()f x 在[0,2]上单调递增,又(0)1,(2)2f f =-=,所以[1,2]B =-,又222()22()2,[0,2]g x x mx m x m m m x =-+=--+∈,当0m <时,()g x 在[0,1]上单调递增,又g(1)1,()g x =关于点(1,1)对称,所以函数()g x 在(1,2]也单调递增,故()g x 在[0,2]上单调递增,又因为g(0)2,(2)2(0)22m g g m ==-=-,故[2,22]A m m =-,因为A B ⊆,所以21222m m ≥-⎧⎨-≤⎩,得0m ≥,又0m <,所以此时m 不存在.当01m ≤≤时,g()x 在(0,)m 单调递减,在(,1)m 单调递增,又g()x 的对称中心为(1,1),所以g()x 在(1,2)m -单调递增,在(2,2]m -单调递减,所以[min{(2),()},max{(0),(2)}]A g g m g g m =-,要使A B ⊆,只需()()()222022121g g m g m m m ⎧=-=-≥-⎪⎨=-+≥-⎪⎩,且()()()202222222g m g m g m m m ⎧=≤⎪⎨-=-=-+≤⎪⎩,解得01m ≤≤,又01,m ≤≤所以01m ≤≤,当1m >时,()g x 在[0,1]单调递减,所以()g x 在(1,2]单调递减,所以()g x 在[0,2]单调递减,所以[22,2]A m m =-,所以22122m m -≥-⎧⎨≤⎩,所以1m ≤,又1m >,所以此时m 不存在,综上:01m ≤≤,即m 的范围是[0,1].【点睛】关键点点睛:本题关键在于根据二次函数性质得出两函数的值域之间的包含关系,限定出最值之间的不等关系,解不等式即可求得结果.。
2024-2025学年浙江省“ S9 联盟”高一第一学期期中联考数学试题(含答案)

2024-2025学年浙江省“ S9 联盟”高一第一学期期中联考数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合A={x|−1<x<1},B={x|0≤x≤2},则A∩B=( )A. {x|−1<x<2}B. {x|−1<x≤2}C. {x|0≤x<1}D. {x|0≤x≤2}2.已知命题p:∀x∈R,x2+a−1≥0,若p为真命题,则a的取值范围是( )A. (−∞,1)B. (−∞,1]C. (1,+∞)D. [1,+∞)3.下列结论正确的是( )A. 若a>b,m>n,则a−m>b−nB. 若m>0,则12>1+m2+mC. 7−6<6−5D. 若1a >1b,则a<b4.“x>2”是“2x<1”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5.已知函数f(x)=x(1−x),x∈[0,1],且f(x)最大值为( )A. 0B. −14C. 14D. 126.已知函数f(x)=x2−2ax+3在(−∞,2]上是减函数,则实数a的取值范围为( )A. (−∞,−1]B. [−1,+∞)C. (−∞,2]D. [2,+∞)7.函数f(x)的部分图像如图,则f(x)的解析式可能是( )A. f(x)=1|x−1|B. f(x)=1||x|−1|C. f(x)=1|x+1|D. f(x)=1|x|+18.已知函数f(x)的定义域为(2,+∞),值域为R,则( )A. 函数f(x2+2)的定义域为RB. 函数f(x2+2)−2的值域为RC. 函数f(x2+2x+3)的定义域和值域都是RD. 函数f(f(x))的定义域和值域都是R二、多选题:本题共3小题,共18分。
在每小题给出的选项中,有多项符合题目要求。
浙江省“浙南名校联盟”2024-2025学年高一上学期期中联考数学试题含解析

2024-2025学年浙江省“浙南名校联盟”高一上期中联考数学试题❖一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.(答案在最后)1.已知集合{|31}A x x =-<<,2{|4}B x x =<,则A B = ()A.{}1,0- B.{}2,1,0,1--C.{|21}x x -<< D.{|32}x x -<<【答案】D 【解析】【分析】先化简集合B ,再求出两集合的并集即可.【详解】由2{|4}{|22}B x x x x =<=-<<,{|31}A x x =-<<,得{|32}A B x x =-<< .故选:D.2.要建造一个容积为31200m ,深为6m 的长方形无盖蓄水池,池壁的造价为95元2/m ,池底的造价为135元2/m ,问水池总造价最低时,水池的长a 与宽b 分别为()A.a =,b = B.10a =,20b =C.20a =,10b = D.15a =,15b =【答案】A 【解析】【分析】设水池的长为a m ,宽为b m ,总造价为z 元;从而可得12002006ab ==,()95226135z a b ab =+⨯+⨯,结合基本不等式求最值即得.【详解】设水池的长为a m ,宽为b m ;总造价为z 元;则12002006ab ==,故200b a=;95(22)61351140()27000z a b ab a b =+⨯+⨯=++11402700027000≥⨯=+当且仅当a =b =.故选:A.3.若2313a ⎛⎫= ⎪⎝⎭,1313b ⎛⎫= ⎪⎝⎭,1323c ⎛⎫= ⎪⎝⎭,则a 、b 、c 的大小关系是()A.a b c >>B.b c a >>C.c b a >>D.c a b>>【答案】C 【解析】【分析】利用指数函数13xy ⎛⎫= ⎪⎝⎭的单调性可得出a 、b 的大小关系,利用幂函数13y x =在 欧 ∞上的单调性可得出b 、c 的大小关系,由此可得出a 、b 、c 的大小关系.【详解】因为13xy ⎛⎫= ⎪⎝⎭在 上为减函数,故21331133⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,即a b <,又13y x =在 欧 ∞上为增函数,故11332133⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭,即c b >,故c b a >>.故选:C.4.已知函数()2f x 的定义域为[]0,4,则()31xf -的定义域为()A.[]0,8 B.[]0,2C.[]0,80 D.80,31⎡⎤-⎣⎦【答案】B 【解析】【详解】先由题意求出()f x 的定义域,进而可求()31xf -的定义域.【解答】因为函数()2f x 的定义域为[]0,4,由[]0,4x ∈,可得[]20,8x ∈,即()f x 的定义域为[]0,8,对于函数()31xf -,需使0318x ≤-≤,解得[]0,2x ∈,故()31xf -的定义域为[]0,2.故选:B.5.“2R,10x ax ax ∃∈-+≤”是假命题,则实数a 的取值范围为()A.()0,4 B.[)0,4 C.[]0,4 D.(]0,4【答案】B 【解析】【分析】利用特称命题及其否定形式的真假结合二次不等式恒成立问题计算即可.【详解】由特称命题的否定形式及真假可知:“2R,10x ax ax ∃∈-+≤”为假则其否定形式“2R,10x ax ax ∀∈-+>”为真命题,显然当0a =时符合题意,当0a ≠时,由一元二次不等式的恒成立问题得2Δ40a a a >⎧⎨=-<⎩,解之得()0,4a ∈,综上可得[)0,4a ∈.故选:B6.“幂函数()()211m f x m m x-=--在()0,∞+单调递减”是“1m =-”的()A.充分不必要条件B.充要条件C.必要不充分条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据幂函数的定义求出m 的值,再根据充分必要条件的定义判断即可.【详解】若()f x 为幂函数,则211m m --=,解得1m =-或2m =,因当1m =-时,()2f x x -=在()0,∞+上单调递减,符合题意;当2m =时,()f x x =在()0,∞+上单调递增,不合题意.故由“幂函数()()211m f x m m x-=--在()0,∞+单调递减”当且仅当“1m =-”成立,即“幂函数()()211m f x m m x-=--在()0,∞+单调递减”是“1m =-”的充要条件.故选:B .7.已知()34122x xf x x m -=+-⋅,123f ⎛⎫= ⎪⎝⎭,则13f ⎛⎫-= ⎪⎝⎭()A.2-B.4- C.6- D.4【答案】C 【解析】【分析】由已知求得13313121432mm ⎛⎫+-= ⎪⎝⎭⋅,代入计算,即可得13f ⎛⎫- ⎪⎝⎭.【详解】由题意,得13313114122332f m -⎛⎫⎛⎫=+-= ⎪ ⎪⎝⎭⎝⎭⋅,则113333113314112143322m m m -⎛⎫⎛⎫+=+-= ⎪ ⎪⎝⎭⎝⎭⋅⋅,注意到11113333331133114122213322,m m m m m ----⎛⎫⎛⎫-=-=-=-+ ⎪ ⎪⎝⎭⎝⎭⋅⋅则113333113311411212242633322f mm m ---⎛⎫⎛⎫⎛⎫-=-+-=--+-=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⋅⋅.故选:C8.()2269,01,1(),1,2x x x x m x f x x -+⎧-+≤≤⎪=⎨>⎪⎩若()f x 的最大值为()3f ,则m 的取值范围为()A.3,14⎡⎤-⎢⎥⎣⎦B.53,44⎡⎤-⎢⎥⎣⎦C.33,44⎡⎤-⎢⎥⎣⎦D.5,14⎡⎤-⎢⎥⎣⎦【答案】A 【解析】【分析】先求出()()max 31f x f ==,得当01x ≤≤时,21x x m -+≤恒成立,分离参数,利用二次函数的性质即可求解.【详解】当1x >时,()()2236911()22x xx f x --+⎛⎫== ⎪⎝⎭,因为12xy ⎛⎫= ⎪⎝⎭是减函数,()23y x =-在()1,3递减,在()3,+∞递增,则当1x >时,()f x 在()1,3递增,在()3,+∞递减,故当1x >时,()()max 31f x f ==,则当01x ≤≤时,21x x m -+≤恒成立,则当01x ≤≤时,2211x x m x x -+-≤≤-++恒成立,又当01x ≤≤时,2213124x x x ⎛⎫-+-=--- ⎪⎝⎭,则当12x =时,()2max314x x -+-=-;当01x ≤≤时,2215124x x x ⎛⎫-++=--+ ⎪⎝⎭,且当0x =时,211x x -++=;当1x =时,211x x -++=则当0x =时,()2min11x x -++=,故m 的取值范围为3,14⎡⎤-⎢⎥⎣⎦故选:A二、多选题:本题共3小题,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得2分,有选错的得0分.9.下列结论错误的是()A.若()()12f f <,则()f x 在[]1,2上单调递增B.()223f x x x =+-在[)0,+∞上单调递增C.()1f x x=在定义域内单调递减D.若()224,1,3,1x ax x f x a x x ⎧---≤⎪=⎨+->⎪⎩在R 上单调递增,则a 的取值范围为(]3,1--【答案】ACD 【解析】【分析】由单调性的定义可得A 错误;由二次函数的性质可得B 正确;由单调函数的规定可得C 错误;由分段函数的单调性结合二次函数和分式型函数的性质可得D 错误;【详解】对于A 、不符合任意性,故A 错误;对于B 、()()222314f x x x x =+-=+-,在()1,-∞递增,故B 正确;对于C 、()1f x x=在(),0-∞和()0,∞+递减,不能说在定义域内单调递减,故C 错误;对于D 、由题意,得2130312141a a a a ⎧⎪-≥⎪+>⎨⎪+⎪--⨯-≤-⎩,解得21a -≤≤-,故D 错误;故选:ACD.10.已知,0a b >,22a b ab ++=,则下列结论正确的是()A.ab的最大值为6- B.2a b +的最大值为4-C.1112+++a b 的最小值为1 D.411a b++的最小值为4【答案】AD 【解析】【分析】对于A ,B ,直接利用基本不等式即可求解;对于C ,由题设等式可得22ba b-=+,代入消元后根据对勾函数的性质可判断;对于D ,代入消元后根据基本不等式即可判断.【详解】对于A,由22a b ab ab =++≥,可得20ab +-≤,即得220-++≤,因,0a b >,解得02≤,故6ab ≤-2b a =时等号成立,由222a b a b ab =⎧⎨++=⎩,可得12a b ⎧=-⎪⎨=⎪⎩,故当且仅当1a =-,2b =时,ab取得最大值为6-,故A 正确;对于B ,因122222a b ab a b +=-=-⋅⋅2122()22a b +≥-⋅,当且仅当2b a =时等号成立,令20t a b =+>,代入上式,可得21224t t ≥-⋅,即28160t t +-≥,解得4t ≥-,故当且仅当1a =-,2b =时,2a b +取得最小值为4-,故B 错误;对于C ,由22a b ab ++=,可得22ba b-=+,由0a >,可得02<<b ,故11112121224212b b a b b b b++=+=+-++++++.令()22,4m b =+∈,则得11114()1244m m a b m m+=+=+++,函数在()2,4上单调递增,故112111242a b +>+=++,即C 错误;对于D ,4141122112b b a b b b b+=+=++-+++24≥+=,当且仅当1b =,13a =时等号成立,故411a b++的最小值为4,故D 正确.故选:AD .11.存在函数()f x 满足对任意的x ∈R 都有()A.()2222f x x x x -=+ B.()2212f x x x +=+-C.()2e e2x xf xx--=- D.()e23xxf =+【答案】BCD 【解析】【分析】对于A ,令0x =与2x =即可判断;对于B ,配方、换元即可判断;对于C ,换元,根据函数的单调性及函数的定义即可判断;对于D ,换元即可判断.【详解】对于A ,令0x =,可得()00f =;令2x =,可得()08f =,矛盾,故A 错误;对于B ,()22221111x x x x +=+-=+-,所以()21112fx x +-=+-.令211t x =+-,则)11x t +=≥-,所以()()21f t t =≥-,所以()()21f x x =≥-,故B 正确;对于C ,设e e x x t -=-,e =x m ,则1=-t m m,e x m = 是增函数,x 与m 一一对应,又1(0)t m m m=->也是增函数,m 与t 也是一一对应,x ∴与t 为一一对应,同时22y x x =-符合函数定义,故C 正确;对于D ,令()e 0xt t =>,则ln x t =,所以()()ln 230t f t t =+>,所以()()ln 230x f x x =+>,故D 正确;故选:BCD.三、填空题:本题共3小题,每小题5分,共15分.12.log 2lg 2lg2lg5lg52++⋅++的值为__________.【答案】3【解析】【分析】利用对数、指数运算性质即可求解.【详解】原式()2lg2lg2lg5lg5=+⋅++2lg 2lg5213=++=+=故答案为:313.()122f x x x =-+-,则不等式()32f x ≤的解集为__________.【答案】313,26⎡⎤⎢⎥⎣⎦【解析】【分析】分类讨论去绝对值,求解即可.【详解】当1x <时,()()12253f x x x x =-+-=-,由()32f x ≤,可得3532x -≤,解得76x ≥,故x 不存在;当12x ≤≤时,()()1223f x x x x =-+-=-,由()32f x ≤,可得332x -≤,解得32x ≥,故322x ≤≤;当2x >时,()()12235f x x x x =-+-=-,由()32f x ≤,可得3352x -≤,解得136≤x ,故1326x <≤,综上,31326x ≤≤,故答案为:313,26⎡⎤⎢⎥⎣⎦.14.已知a ,b ,0c >,1b c +=,则4b ca abc bc+++的最小值为__________.【答案】5【解析】【分析】由基本不等式得41b c a abc bc ++≥-+,再结合已知利用基本不等式求出4b c bc +的最小值可得解.【详解】()()4411111b c b ca a abc bc bc a +++=++-≥=++①,当且仅当24(1)b ca bc++=时取等号,()441414559b c b c b c bc c b c b c b +⎛⎫=+=++=++≥= ⎪⎝⎭,即49b c bc +≥②,当且仅当4b cc b=时,即13b =,23c =时取等号,将②式代入①式得412315b c a abc bc ++≥-=⨯-=+,当且仅当2a =,13b =,23c =时取等号.故答案为:5.四、解答题:本题共5小题,共60分.解答应写出文字说明,证明过程或演算步骤.15.已知(]71,21,{|1}5A a aB x x =+-=≤--.(1)若3a =,{|25}U x x =-<≤,求()U A B ⋂ð;(2)设命题:p x A ∈,命题:q x B ∈,若命题q 是命题p 的必要不充分条件,求a 的取值范围.【答案】(1)(){|245}U A B x x x ⋂=-<≤=或ð(2)()2,3【解析】【分析】(1)根据不等式求出集合B ,然后依据集合的运算求出结果即可;(2)根据已知命题q 是命题p 的必要不充分条件可得集合关系,进而求出结果【小问1详解】2{|0}{|25}5x B x x x x +=≤=-≤<-;当3a =时,(]4,5{|45}A A B x x =∴=<< (){|245}U A B x x x ∴=-<≤= 或ð.【小问2详解】由题意得AB ,则121,215,12a a a a +<-⎧⎪-<⎨⎪+≥-⎩即233a a a >⎧⎪<⎨⎪≥-⎩,得23a <<.故a 的取值范围是()2,3.16.已知()f x 是定义在R 上的奇函数,当0x >时,()32xf x x =+.(1)求函数()f x 的解析式;(2)求不等式()3f x >的解集;(3)R a ∈,解关于x 的不等式()()2220f ax ax f x +++>.【答案】(1)332,0()0,0,2,0x x x x f x x x x -⎧+>⎪==⎨⎪-<⎩(2)()1,+∞(3)答案见解析【解析】【分析】(1)利用定义域为R 的奇函数()f x ,当0x >时,()32xf x x =+,可求0x <时的解析式;(2)结合函数单调性进行求解即可;(3)()()2220f ax ax f x +++>等价于()()222.f ax ax f x +>--又()f x 在R 上单调递增,所以222ax ax x +>--,即()2220ax a x +++>,然后解不等式即可.【小问1详解】当0x =时,()0f x =.当0x <时,0x ->,()33()22xx f x x x ---=-+=-+,所以()32x f x x -=-.332,0()0,0,2,0x x x x f x x x x -⎧+>⎪∴==⎨⎪-<⎩【小问2详解】由题意得当0x >时,()f x 单调递增且()1f x >,()00f =,在[)0,∞+上单调递增,又()f x 为奇函数, 在R 上单调递增,()()31f x f >= .1x ∴>即()3f x >的解集为 欧 ∞.【小问3详解】()()2220f ax ax f x +++>等价于()()222f ax ax f x +>--.又()f x 在R 上单调递增,222ax ax x ∴+>--,即()2220ax a x +++>.①当0a =时,220x +>,解得1x >-,∴原不等式解集为()1,∞-+;②当0a <时,原不等式可化为()210x x a ⎛⎫++< ⎪⎝⎭,解得21x a-<<-,∴原不等式解集为21,a ⎛⎫-- ⎪⎝⎭.③当0a >时,原不等式可化为()210x x a ⎛⎫++> ⎪⎝⎭,()2i 1a-=-时,即2a =时,原不等式解集为()(),11,∞∞--⋃-+;()2ii 1a ->-时,即2a >时,原不等式解集为()2,1,a ∞∞⎛⎫--⋃-+ ⎪⎝⎭;()2iii 1a -<-时,即2a <时,原不等式解集为()2,1,a ∞∞⎛⎫--⋃-+ ⎪⎝⎭;17.温州市初中毕业生体育学业测试项目中,耐力类(男生1000米/女生800米)为必考项目.现一体重为50kg 的小明准备做四分钟的跑步训练,其分为两个阶段,第一阶段为前一分钟的稳定阶段,第二阶段为后三分钟的疲劳阶段.假设小明稳定阶段做速度为16m /v s =的匀速运动,该阶段每千克体重消耗体力111160Q t v =⨯△(1t 表示该阶段所用时间),疲劳阶段变为22630t v =-的减速运动(2t 表示该阶段所用时间),由于速度降低,体力得到一定恢复,该阶段每千克体重消耗体力222260t v Q t ⨯=+△.假定小明可用于跑步消耗的初始体力为0700kJ Q =,不考虑其他因素,所用时间为t (单位s ),请回答下列问题:(1)写出小明剩余体力Q 关于时间t 的函数()Q t ;(2)小明在四分钟内何时体力达到最低,最低值是多少;(3)小明在三分整时,恰好跑完840米,若此时他准备做匀速冲刺阶段,此阶段每千克体重消耗体力33333)11(400200Q v v t =+)△((3t 表示该阶段所用时间),问在保证体力未消耗完的前提下,小明能否在3分40前跑完一千米?【答案】(1)()7005,060,48050100,6024030t t Q t t t t -≤≤⎧⎪=⎨⎛⎫⋅+-<≤ ⎪⎪⎝⎭⎩(2)第120秒时,体力为最小值300kJ(3)不能【解析】【分析】(1)分类讨论当060t ≤≤时,当60240t <≤时,得到解析式;(2)当060t ≤≤时,()Q t 为一次函数且单调递减,当60240t <≤时,结合基本不等式求解;(3)当180t =时,此时()10003Q t =要使在三分四十前到达,需要34v ≥,求解即可.【小问1详解】当060t ≤≤时,()670050700560Q t t t =-⋅⋅=-.当60240t <≤时,()()60606480304005050100606030t t t Q t t t-⎛⎫-⋅- ⎪⎛⎫⎝⎭=-⋅=⋅- ⎪-+⎝⎭.综上()7005,060,48050100,6024030t t Q t t t t -≤≤⎧⎪=⎨⎛⎫⋅+-<≤ ⎪⎪⎝⎭⎩.【小问2详解】当060t ≤≤时,()Q t 为一次函数且单调递减,∴此过程()min ()60400Q t Q ==,当60240t <≤时,()480501005010030030t Q t t ⎛⎫=⋅+-≥⋅=⎪⎝⎭,当且仅当48030t t =,即120t =时取“=”.由于300400<,第120秒时,体力最小值为300kJ【小问3详解】当180t =时,此时()480180100050100180303Q t ⎛⎫=⋅+-=⎪⎝⎭.冲刺时,体力消耗量为33331150(()4002)00v v t ⋅+32333311160(()20()4084)v v v v =+⋅=+,要使在三分四十前到达,需要34v ≥,23100020()403603v ∴+≥>,所以小明不能在3分40前跑完一千米.18.已知()122x x a f x b++=+是奇函数.(1)求a ,b 的值;(2)若()f x 的定义域为R ,判断()f x 的单调性并证明;(3)在第二问的条件下,()22g x x mx =-,对任意的1R x ∈,存在[]20,4x ∈,使得()()12f x g x =,求m 的取值范围.【答案】(1)2a =-,1b =或2a =,1b =-(2)()f x 在R 上单调递增,证明见解析(3)74⎤⎥⎦【解析】【分析】(1)直接根据奇函数的定义求解即可;(2)利用作差法来证明函数的单调性;(3)先记1R x ∈时,()1f x 的值域为A ,[]20,4x ∈时,()2g x 的值域为B ,然后得出A B ⊆,再求出()2,2A =-,得到max ()2g x ≥,min ()2g x ≤-,对m 进行分类讨论即可求出m 的取值范围.【小问1详解】由题意得()00f =或()0f 不存在,①当()00f =时,()2001a f b +==+,2a =-,()1222x x f x b+-=+,又()()11f f =--,即4212122b b --=-++,1b ∴=,经检验()12221x x f x +-=+为奇函数,2a ∴=-,1b =满足条件;②当()0f 不存在时,1b =-,()1221x x f x a ++-=,又()()11f f =--,即1412211a a ++=---,2a ∴=,经检验()12221x x f x ++=-为奇函数,2a ∴=,1b =-满足条件;【小问2详解】()f x 定义域为R ,()12221x x f x +-∴=+,任取1x ,2R x ∈,12x x <,()()1212121112222222212121212121x x x x x x f x f x ++--⎛⎫⎛⎫-=-=⋅--- ⎪ ⎪++++⎝⎭⎝⎭()()122112112244021212121x x x x x x -⎛⎫=-=⋅< ⎪++++⎝⎭,()()()12,f x f x f x ∴<∴在R 上单调递增;【小问3详解】记1R x ∈时,()1f x 的值域为A ,[]20,4x ∈时,()2g x 的值域为B ,由题意得A B ⊆,令21(1)xt t =+>,则()()()121222422,221x x t f x t t +---===-∈-+,()2,2A ∴=-,又A B ⊆,max ()2g x ∴≥,min () 2.g x ≤-①当2m ≥时,()()max 00g x g ==不符合题意,②当02m ≤<,()max ()41682g x g m ==-≥,()2min ()2g x g m m ==-≤-,即21682202m m m -≥⎧⎪-≤-⎨⎪≤<⎩,74m ≤≤,③当0m <时,()min ()002g x g ==≤-不成立,综上所述:m的取值范围为74⎤⎥⎦.【点睛】关键点点睛:本题第三问的关键是由集合间的包含关系对m 进行分类讨论.19.设k 是正整数,A 是*N 的非空子集(至少有两个元素),如果对于A 中的任意两个元素x ,y ,都有x y k -≠,则称A 具有性质()P k .(1)试判断集合{}1,2,4,5B =,{}1,5,6C =是否具有性质()2P ?并说明理由;(2)若集合{}{}1211,,,1,2,,20A a a a =⊆ ,证明A 不可能具有性质()5P ;(3)若集合{}1,2,,1000A ⊆ 且具有性质()4P 和()7P ,求A 中元素个数的最大值.【答案】(1){}1,2,4,5B =不具有性质()2P ,{}1,5,6C =具有性质()2P ,理由见解析(2)证明见解析(3)455个.【解析】【分析】(1)根据定义判断,B C 是否具有性质()2P 即可;(2)将集合{}1,2,,20 中的元素分为10个集合,进行求解即可;(3)先说明连续11项中集合A 中最多选取5项,然后求出集合A 中共有455个元素,即可.【小问1详解】422-= ,B ∴不具有性质()2P .512-≠ ,612-≠,652-≠,C ∴具有性质()2P ;【小问2详解】将集合{}1,2,,20 中的元素分为如下10个集合,{}1,6,{}2,7,{}3,8,{}4,9,{}5,10,{}11,16,{}12,17,{}13,18,{}14,19,{}15,20.所以从集合{}1,2,,20 中取11个元素,那么这10个集合至少有一个集合要选2个数,存在两个元素其差为5,A ∴不可能具有性质()5P ;【小问3详解】先说明连续11项中集合A 中最多选取5项,以1,2,3…,11为例.将这11个数分为{}1,8,{}2,9,{}3,10,{}4,11,{}5,{}6,{}77个集合,①5,6,7同时选,因为具有性质()4P 和()7P ,所以选5则不选1,9;选6则不选2,10;选7则不选3,11;则只剩4,8.故1,2,3…,11中属于集合A 的元素个数不超过5个.②5,6,7选2个,若只选5,6,则1,2,9,10,7不可选,又{}4,11只能选一个元素,3,8可以选,故1,2,3…,11中属于集合A 的元素个数不超过5个.若选5,7,则只能从2,4,8,10中选,但4,8不能同时选,故1,2,3…,11中属于集合A 的元素个数不超过5个.若选6,7,则2,3,10,11,5不可选,又{}1,8只能选一个元素,4,9可以选,故1,2,3…11中属于集合A 的元素个数不超过5个.③5,6,7中只选1个,又四个集合{}1,8,{}2,9,{}3,10,{}4,11每个集合至多选1个元素,故1,2,3…,11中属于集合A 的元素个数不超过5个.由上述①②③可知,连续11项自然数中属于集合A 的元素至多只有5个,如取1,4,6,7,9.因为1000901110=⨯+,则把每11个连续自然数分组,前90组每组至多选取5项;从991开始,最后10个数至多选取5项,故集合A 的元素最多有915455⨯=个.给出如下选取方法:从1,2,3…,11中选取1,4,6,7,9;然后在这5个数的基础上每次累加11,构造90次.此时集合A 的元素为:1,4,6,7,9;12,15,17,18,20;23,26,28,29,31; ;2014,2017,2019,2020,2022,991,994,996,997,999共455个元素.经检验可得该集合符合要求,故集合A 的元素最多有455个.【点睛】关键点点睛:本题第三问的关键点在于根据集合新定义对集合A的中元素进行分类,可先取其中连续11项进行讨论较为简单.。
2024-2025学年福建省龙岩市一级校联盟高一上学期11月期中联考数学试题(含答案)

2024-2025学年福建省龙岩市一级校联盟高一上学期11月期中联考数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合M={−1,1,2},N={x|x2≤2x},则M∩N= ( )A. {0,1}B. {1,2}C. {−1,0,1,2}D. {−1,0,2}2.命题“∃x<0,x+3>3x”的否定为( )A. ∀x<0,x+3≤3xB. ∀x<0,x+3>3xC. ∃x≥0,x+3>3xD. ∃x≥0,x+3≤3x3.若P:x<2,则P的一个充分不必要条件为( )A. x<3B. x<2C. −8<x<2D. −10<x≤24.函数y=2x2−2x2+2的图象大致为( )A. B.C. D.5.已知函数y=f(x)的定义域为[−1,2],则函数y=f(x+1)x−1的定义域为( )A. [−2,1]B. [−2,1)C. [0,3]D. (1,3]6.已知f(x)={(a−3)x+4,x≤2,2ax,x>2是R上的减函数,则实数a的取值范围是( )A. [2,3)B. (2,3)C. (0,3)D. (0,3]7.已知正数m,n满足3m⋅9n=9,则2m +3n的最小值为( )A. 26B. 4+23C. 8+43D. 8+238.已知y =f(x)是R 上的偶函数,对于任意的x ∈R ,都有f(x +4)=f(x)+f(2)成立,且f(1)=−3,当x 1,x 2∈[0,2]且x 1≠x 2时,都有f(x 1)−f(x 2)x 1−x 2>0成立.现给出下列命题:①f(−11)=−3;②函数y =f(x)图象的一条对称轴为x =2;③函数y =f(x)在[−6,−5]上为严格增函数;④方程f(x)=0在[−9,9]上有4个根.其中正确的命题个数为( )A. 1B. 2C. 3D. 4二、多选题:本题共3小题,共18分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省温州市十校联合体-高一数学上学期期中联考试题新人教A版
一、选择题(本大题共10小题,每小题4分,满分40分。
在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列集合与表示同一集合的是(▲)
A.
B.
C.
D.
2.下列给出的四个图形中,是函数图象的有(▲)
A.①② B. ①③④ C. ②③④ D. ①②③④
3.若的定义域为A,的定义域为B,那么(▲)
A. B. C. D.
4.已知,则(▲)(为自然对数的底数)
A. B. 1 C. D. 0
5.设函数若是奇函数,则的值是(▲)
A. B. C. D.
6.有四个幂函数:①②③④.某同学研究了其中的一个函数,他给出这个函数的三个性质:(1)偶函数;(2)值域是;(3)在上是增函数.如果他给出的三个性质中,有两个正确,一个错误,则他研究
的函数是(▲)
A.① B. ② C. ③ D. ④
7.设,,,则的大小关系是(▲)
A. B. C. D.
8.定义域为的偶函数的部分图象如图所示,则在上,下列函数中
与的单调性不同的是(▲)
A. B.
C. D.
9.函数的值域为,则实数的取值范围是(▲)A. B. C. D.
10.当时,不等式恒成立,则实数的取值范围是(▲) A. B. C. D.
二、填空题(本大题共7小题,每小题4分,满分28分)
11.设,,若,则实数▲ . 12.函数的定义域是▲(用区间表示).
13.已知函数若,则的值为▲ .
14.计算的结果是▲ .
15.已知函数在上是增函数,则实数的取值范围是▲ .
16.已知函数,若,则▲ . 17.已知若,则▲ .
2013学年第一学期十校联合体期中联考
高一数学答题卷
座位号
(完卷时间100分钟,总分120分,不得使用计算器
.......)
一、选择题(本大题共10小题,每小题4分,满分40分。
在每小题给出的四个选项中,只
11.____________ 12. 13.____________________
14.____________ 15.______________ 16.______________ 17.____________________ 三、解答题(本大题共5小题,满分52分。
解答应写出文字说明、证明过程或演算步骤)
18.(本小题满分8分)设全集,集合,.
(1)求;;
(2)已知集合,若,求的值.
19.(本小题满分10分)已知幂函数的图象过点.
(1)求的解析式;
(2)若函数在上的最大值比最小值大1,求实数的值.
20.(本小题满分12分)已知函数.
(1)求的值;
(2)画出函数的图象,并根据图象写出函数的值域和单调区间;
(3)若方程有四个根,求实数的取值范围,并求出这四个根的和.
21.(本小题满分10分)已知是二次函数,若,且
(1)求函数的解析式;
(2)记集合,,若,求实数的取值范围.
22.(本小题满分12分)已知函数是定义在实数集R上的
奇函数.
(1)求的值,判断在R上的单调性并用定义证明;
(2)当时,恒成立,求实数的取值范围.
2013学年第一学期十校联合体高一期中联考
数学答案
三、解答题(本大题共5小题,满分52分。
解答应写出文字说明、证明过程或演算步骤)18.(本小题满分8分)设全集,集合,.
(1)求;;
(2)已知集合,若,求的值.
19.(本小题满分10分)已知幂函数的图象过点.
(1)求的解析式;
(2)若函数在上的最大值比最小值大1,求实数的值.
解:(1)设,由……………………4分(2)当时,由符合题意………3分当时,由也符合题意
所以实数的值是或…………………………3分20.(本小题满分12分)已知函数.
(1)求的值;
(2)画出函数的图象,并根据图象写出函数的值域和单调区间;
(3)若方程有四个根,求实数的取值范围,并求出这四个根的和.
解:(1)…………………………2分(2)值域是,…………………………1分单调增区间和,…………………………2分
减区间和…………………………2分
(2)
分
(说明:增区间写成扣1分,减区间写成也扣1分)(3)因为方程有四个根,
所以根据图象可得实数的取值范围是,…………………2分
由图象判断是偶函数,所以这四个根的和是0. …………………1分
21.(本小题满分10分)已知是二次函数,若,且
(1)求函数的解析式;
(2)记集合,,若,求的取值范围.
解:(1)设,由得………………1分
………………3分
22.(本小题满分12分)已知函数是定义在实数集R上的
奇函数.
(1)求的值,判断在R上的单调性并用定义证明;
(2)当时,恒成立,求实数的取值范围.
(2)
令,
对于恒成立……………1分令
则
所以的取值范围是……………3分
(说明:用其它方法解答也可)。
