向量法证明三点共线的又一方法及应用
求证三点共线的方法

求证三点共线的方法
三点共线指的是在平面直角坐标系中,三个点的坐标可以表示为一条直线上的点,也就是说,这三个点处于同一条直线上。
证明三点共线的方法主要有以下几种。
一、使用向量方法证明:
设三个点分别为A(x1, y1), B(x2, y2), C(x3, y3),则向量AB=(x2-x1, y2-y1),向量AC=(x3-x1, y3-y1)。
若向量AB和向量AC共线,则有向量AB=k向量AC,其中k为常数。
同时,k=(x2-x1)/(x3-x1)=(y2-y1)/(y3-y1)。
如果k的值相同,则可以得知向量AB与向量AC共线,即点A、B、C三点共线。
斜率指的是两个点之间的纵坐标和横坐标之差的比值。
设三个点分别为A(x1, y1), B(x2, y2), C(x3, y3),则有斜率公式
如果k1 = k2,则点A、B、C三点共线。
对于三个点A(x1, y1),B(x2, y2),C(x3, y3),三点共线可以用行列式表示:
|x1 y1 1|
|x2 y2 1| = 0
|x3 y3 1|
以上四种方法是证明三点共线的主要方法。
一般情况下,使用向量方法或者斜率方法比较简单易懂,行列式方法或距离方法稍微有点繁琐。
在实际应用中,需要根据具体问题选择合适的方法进行证明。
(完整版)平面向量中“三点共线定理”妙用

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且1x y +=。
特别地有:当点P 在线段AB 上时,0,0x y >> 当点P 在线段AB 之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为S n ,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O ),则S 200=( ) A .100B .101C .200D .201解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200()1002a a S +==,故选A 。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:4424y x y xx y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB = m AM ,AC =n AN ,则m +n 的值为 .解:因为O 是BC 的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是△OAB 的重心,P 、Q 分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线. 设OA x OP =,OB y OQ =,证明:yx 11+是定值; 图3图4图2证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y ∴+= 113x y ∴+= 11x y∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与BF 相交于G 点,记AB a =,AD b =,则AG =_______A .2177a b + B. 2377a b + C. 3177a b + D. 4277a b +分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B 以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
平面向量中三点共线的证明及其应用

平面向量中三点共线的证明及其应用在平面向量中,三点共线说明这三个点满足下面的条件:重合、向垂直、和向平行。
如果三点共线,这意味着他们在同一条线上,且在同一条平面空间内。
三点共线的证明有两种方式-零空间的方法和二维的方法。
在零空间的方法中,每个点的位置可以用三个极坐标系表示,r,θ,φ是相应的极角度和极坐标(或旋转角度)。
用三维立体的形式表示每个点的位置,我们可以使用下面的表达式来表示:其中,x=r*cosθ*sinφ,y=r*cosθ*cosφ,z=r*sinθ由于这三个点共线,它们将在三维中共同满足右边的方程:a*x+b*y+c*z=0可以看出,这个方程具有三个参数-a,b,c,这意味着它可以用来描述和表示任何三点共线的情况。
另一种方法是二维法,它直接使用三点的平面坐标来证明三点共线。
在这里,两个点的坐标用(x1,y1)和(x2,y2)表示,而另一个点的坐标用(x,y)表示。
为了证明三点共线,需要满足方程m*(x1-x2)+n*(y1-y2)=0在这里,m和n是方程的参数。
如果这个方程能够成立,意味着第三个点(x,y)与其余两个点在同一条线上。
三点共线的数学原理在日常生活中得到广泛的应用。
其中最常见的应用是画图和土木计算,通常需要三角测量。
绘图包括绘制几何形状、图像和其他图案,这些图案通常与空间位置有关,因此必须确保三点共线,以便得出正确的结论。
土木计算中也经常会遇到三点共线的问题,例如评估桥梁的结构安全性时,在桥梁的两端设置两个支撑,这就是一个三点共线的示例。
总之,三点共线是一个重要的数学原理,具有重要的应用。
研究人员、土木工程师,甚至是普通的绘图师都会经常使用这个原理。
高中数学教学论文 向量法证明三点共线的又一方法及应用

向量法证明三点共线的又一方法及应用平面向量既具有数量特征,又具有图形特征,学习向量的应用,可以启发同学们从新的视角去分析、解决问题,有益于培养创新能力. 下面就一道习题的应用探究为例进行说明.原题 已知OB λOA μOC =+u u u r u u u r u u u r ,其中1λμ+=. 求证:A 、B 、C 三点共线思路:通过向量共线(如AB k AC =u u u r u u u r )得三点共线.证明:如图,由1λμ+=得1λμ=-,则 (1)OB λOA μOC μOA μOC =+=-+u u u r u u u r u u u r u u u r u u u r∴()OB OA μOC OA -=-u u u r u u u r u u u r u u u r ∴AB μAC =u u u r u u u r∴A 、B 、C 三点共线.思考:1. 此题揭示了证明三点共线的又一向量方法,点O 具有灵活性;2. 反之也成立(证明略):若A 、B 、C 三点共线,则存在唯一实数对λ、μ,满 足OB λOA μOC =+u u u r u u u r u u u r ,且1λμ+=.揭示了三点贡献的又一个性质;3. 特别地,12λμ==时,1()2OB OA OC =+u u u r u u u r u u u r ,点B 为AC u u u r 的中点,揭示了OAC V中线OB 的一个向量公式,应用广泛.应用举例 例1 如图,平行四边形ABCD 中,点M 是AB 的中点,点N 在BD 上,且13BN BD =. 利用向量法证明:M 、N 、C 三点共线. 思路分析:选择点B ,只须证明BN λBM μBC =+u u u r u u u u r u u u r ,且1λμ+=. 证明:由已知BD BA BC =+u u u r u u u r u u u r ,又点N 在BD 上,且13BN BD =,得 1111()3333BN BD BA BC BA BC ==+=+u u u r u u u r u u u r u u u r u u u r u u u r 又点M 是AB 的中点, 12BM BA ∴=u u u u r u u u r ,即2BA BM =u u u r u u u u rD A B C M N2133BN BM BC ∴=+u u u r u u u u r u u u r 而21133+= ∴M 、N 、C 三点共线.点评:证明过程比证明MN mMC =u u u u r u u u u r 简洁.例2如图,平行四边形OACB 中,13BD BC =,OD 与AB 相交于E ,求证:. 14BE BA =. 思路分析:可以借助向量知识,只须证明:14BE BA =u u u r u u u r ,而BA BO BC =+u u u r u u u r u u u r ,又O 、D 、E 三点共线,存在唯一实数对λ、μ,且1λμ+=,使BE λBO μBD =+u u u r u u u r u u u r ,从而得到BE u u u r 与BA u u u r 的关系. 证明:由已知条件,BA BO BC =+u u u r u u u r u u u r ,又B 、E 、A 三点共线,可设BE k BA =u u u r u u u r ,则BE k BO k BC =+u u u r u u u r u u u r ①又O 、E 、D 三点共线,则存在唯一实数对λ、μ,使BE λBO μBD =+u u u r u u u r u u u r ,且1λμ+=. 又13BD BC =u u u r u u u r 13BE λBO μBC ∴=+u u u r u u u r u u u r ②根据①、②得 131k λk μλμ=⎧⎪⎪=⎨⎪+=⎪⎩,解得141434k λμ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩ 14BE BA ∴=u u u r u u u r 14BE BA ∴= 点评:借助向量知识,充分运用三点共线的向量性质解决问题,巧妙、简洁. D O AC E B。
高考数学复习点拨:向量证明三线共点与三点共线问题

用向量证明三线共点与三点共线问题山东 徐鹏三线共点、三点共线是几何中经常遇到的问题,直接证明往往很困难,用向量法解决则简捷得多.证明A 、B 、C 三点共线,只要证明AB 与AC 共线即可,即证明AC AB λ=.证明三线共点一般须证两线交点在第三条直线上. 例1. 证明:若向量OA 、OB 、OC 的终点A 、B 、C 共线,则存在实数λ、μ,且1=+μλ,使得OB OA OC μλ+=;反之,也成立.证明:如图1,若OA 、OB 、OC 的终点A 、B 、C 共线,则AB //BC ,故存在实数m,使得AB m BC =,又OB OC BC -=,OA OB AB -=,故)(OA OB m OB OC -=-,OB m OA m OC )1(++-=.令,1,m m +=-=μλ则存在,1,,=+μλμλ且使得OB OA OC μλ+=. 若OB OA OC μλ+=,其中,1=+μλ则λμ-=1,OB OA OC )1(λλ-+=.从而有OC -OB =λ(OA -OB ),即BA BC λ=.又因为BA BC 和有公共点B,所以A 、B 、C 三点共线,即向量OA 、OB 、OC 的终点A 、B 、C 共线.例2. 证明:三角形的三条中线交于一点.证明:如图2,D 、E 、F 分别是ABC ∆三边上的中A O BC图1点.设BE BG AD AG G BE AD b CB a CA μ===⋂==,,,.设.则=-+-=++-=+-=+=)21()21()()(b a a b CA BC a b BE a b BG AB AG μμμ b a )1(1(21μμ-+-),又b a b a CD AC AD AG λλλλλ21)21()(+-=+-=+== ⎪⎪⎩⎪⎪⎨⎧==⎪⎪⎩⎪⎪⎨⎧-=-=-3232121121μλμλμλ解得所以 则b a b a a AD a AG CA CG 3131)21(3232+=+-+=+=+= b a CF 2121+=,所以CF CG 32=,所以G 在中线CF 上,所以三角形三条中线交于一点. A BCEDF图2 G。
向量中三点共线常用结论

向量中三点共线常用结论向量是数学中的重要概念,在几何学、物理学、力学等学科中都有广泛的应用。
当三个点的向量共线时,有一些常用的结论可以帮助我们更好地理解和应用向量的概念。
首先,我们来谈谈共线的定义。
当三个点的向量可以通过放缩得到相等的向量时,它们就是共线的。
也就是说,三个点的向量可以表示为k倍于另一个向量的形式,其中k为一个实数。
在三维空间中,我们可以将共线的三个点的向量表示为OA = a,OB = b,OC = c。
其中,O为坐标原点,A、B、C为三个点。
常用的共线判定方法有两种,即向量共线定理和点共线定理。
首先是向量共线定理。
如果三个向量a,b和c共线,那么存在一个实数k,使得c = ka + (1-k)b。
我们可以将这个公式理解为,c可以由a和b经过一定的比例缩放得到。
其次是点共线定理。
如果三个点A、B、C共线,那么它们的向量OA、OB和OC是共线的。
反之亦成立,即如果OA、OB和OC共线,那么点A、B、C也是共线的。
这个定理可以帮助我们在实际问题中通过向量的共线性判断点的共线性。
在实际应用中,我们常常会遇到一些与共线性相关的问题。
例如,在几何学中,我们希望判断三个点是否在一条直线上,可以通过计算它们的向量是否共线来得出结论。
如果计算出的向量共线,则可以判断三个点是共线的;反之,如果向量不共线,则可以判断三个点不共线。
另一个应用是在物理学中,我们常常用向量来描述力的作用。
如果有多个力作用在同一个物体上,我们可以通过判断这些力的向量是否共线来判断它们是否可以合成为一个力。
如果力的向量共线,则可以将它们合成为一个力;反之,如果力的向量不共线,则无法合成为一个力。
在解决问题时,我们可以运用这些常用的共线结论。
首先,我们可以通过计算向量是否共线来确定点的共线性。
其次,我们可以通过判断向量的共线性来确定力的合成。
最后,我们还可以利用共线性来解决其他几何学、物理学和力学等问题。
总之,向量的共线性是数学中的一个重要概念,有着广泛的应用。
三点共线与三线共点的证明方法

三点共线与三线共点的证明方法三个点共线指的是这三个点同时在一条直线上,也可以说是三个点在同一条直线上。
三线共点指的是通过三个不共线的点分别画一条直线,这三条直线交于同一点。
三点共线的证明方法主要有以下几种:1.直线方程法:设三个点分别为A(x1,y1),B(x2,y2),C(x3,y3)。
利用直线方程的一般式Ax+By+C=0来确定三个点是否共线。
具体步骤如下:-计算直线AB的方程:A1x+B1y+C1=0(其中A1=y2-y1,B1=x1-x2,C1=x2y1-x1y2)-将点C的坐标代入直线AB的方程:A1x3+B1y3+C1=0-如果等式成立,则三个点共线;如果不成立,则不共线。
2.坐标法:设三个点分别为A(x1,y1),B(x2,y2),C(x3,y3)。
根据点的坐标特点,通过计算三个点的斜率来判断是否共线。
具体步骤如下:-计算AB和BC两个线段的斜率:k1=(y2-y1)/(x2-x1),k2=(y3-y2)/(x3-x2)-如果k1=k2,则三个点共线;如果k1≠k2,则不共线。
3.向量法:设三个点分别为A(x1,y1),B(x2,y2),C(x3,y3)。
通过判断向量AB和向量AC的平行性来确定三个点是否共线。
具体步骤如下:-计算向量AB和向量AC的分量:AB=(x2-x1,y2-y1),AC=(x3-x1,y3-y1)-如果向量AB和向量AC平行,则三个点共线;如果不平行,则不共线。
三线共点的证明方法有以下几种:1.十字交叉法:通过在纸上画出三个不共线的点A、B、C,然后通过直尺(或者铅笔加线板)在三个点上分别连线,如果三条线段交叉于同一点,则三个点共线。
2.逆向思维法:设三个点为A、B、C。
可以通过逆向思维,即假设不共线,来反证明三条线段共点。
首先连线AB、AC,得到两条直线,然后通过延长AB和AC,使其相交于点D。
如果D与C重合,则三线共点;如果D与C不重合,则不共点。
由于三个点不共线,所以最后的结论是D与C不重合,即三线不共点。
平面向量中的三点共线结论的应用
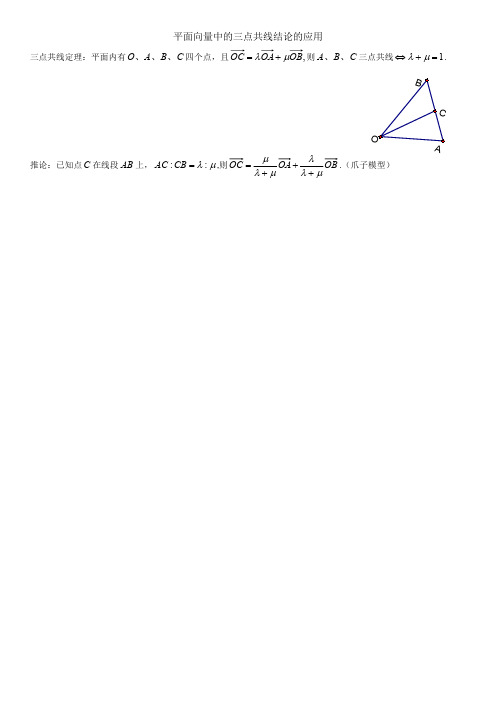
若,3.已知B 为OAC 边AC 上一点,且满足OC y OA x OB +=4,不等式222313x y m m x y +≥-++恒成立时,实数m 的最值范围为___________.巩固练习1.在ABC ∆中,4AB =,O 为三角形的外接圆的圆心,若),(R y x AC y AB x AO ∈+=且21x y +=,则ABC ∆的面积的最大值为_____.2.在P AB ∆中,,60,9,80=∠==APB PB P A 点C 满足PB y P A x PC +=,且,0,0,532≥≥=+y x y x 其中则||PC 的最大值为______,最小值为______.3.已知ABC ∆的外心为O 满足AC y AB x AO +=,若,10,6==AC AB 且,5102=+y x 则=∠BAC cos ______.例5.如图,M 为△ABC 的中线AD 的中点,过点M 的直线分别交线段AB 、AC 于点P 、Q 两点,设AP xAB =,AQ y AC =,记()y f x =,设32()32g x x a x a =++,[0,1]x ∈,若对任意11[,1]3x ∈,总存在2[0,1]x ∈,使得12()()f x g x =成立,则实数a 的取值范围为______.巩固练习2.(2022·辽宁葫芦岛·高三期末)如图,在等腰ABC 中,已知2AB AC ==,120A ∠= ,E ,F 分别是边AB ,AC 上的点,且AE AB λ= ,AF AC μ=,其中λ,R μ∈,且21λμ+=,若线段EF ,BC 的中点分别为M ,N ,则MN的最小值是()A .77B .217C .2114D .213.(2023·全国·高三专题练习)直角三角形ABC 中,P 是斜边BC 上一点,且满足2BP PC =,点M 、N 在过点P 的直线上,若AM m AB = ,AN nAC =,()0,0m n >>,则下列结论错误的是()A .12m n+为常数B .m n +的最小值为169C .2m n +的最小值为3D .m 、n 的值可以为12m =,2n =巧用杠杆原理处理三角形中的向量问题数值,各线段上得如图所示各点的标数则根据杠杆平衡原理可,已知三角形中的赋值标数法,d,cNC AN b a MB AM ==点数值乘数值等于点数值乘线段上,段数值乘积相等。
平面向量中“三点共线定理”妙用

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B、P三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x ,y使得:OP xOA yOB =+且1x y +=。
特别地有:当点P在线段AB 上时,0,0x y >> 当点P 在线段A B之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为Sn,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O),则S 200=( ) A .100ﻩﻩﻩﻩB.101 ﻩC.200 ﻩﻩﻩD.201解:由平面三点共线的向量式定理可知:a1+a 200=1,∴1200200200()1002a a S +==,故选A。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y x x y ∴>> 由基本不等式可知:4424y x y x x y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是B C的中点,过点O 的直线分别交直线AB 、AC于不同的两点M 、N,若AB = m AM ,AC =nAN ,则m +n 的值为 .解:因为O 是B C的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是图3图4图2△OAB 的重心,P 、Q 分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线.设OA x OP =,OB y OQ =,证明:yx 11+是定值; 证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y∴+= 113x y ∴+= 11x y ∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与B F相交于G 点,记AB a =,AD b =,则AG =_______A.2177a b +B. 2377a b +C. 3177a b + D. 4277a b + 分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
平面向量三点共线定理的推论及空间推广

平面向量三点共线定理的推论及空间推广三点共线定理,又称三点确定一直线,它是平面几何学中一个基本定理。
它宣称,假设有三个不同的点,它们一定能构成一条直线。
本文主要介绍三点共线定理的推论及平面的推广,并且进一步评论该定理在空间几何中的推广。
一、三点共线定理:1. 定义:三点共线定理,又称三点确定一直线,是指,任意三个不同点,它们一定能构成一条直线。
2. 推论:(1)若由不同的三点确定的直线上含有两点,那么其余一点必然也在这条直线上。
(2)如果有一条直线上含有两点,则另一点也必然在这条直线上。
3. 例子:我们从A、B、C三点可以确定一条直线,若在这条直线上发现了B1点,B1点必然和A、C也在这条直线上。
二、平面推广:1.定理:三点共线定理也同样拓展到了平面中,即:任意三个不同点,必定能构成一个平面或一个平行于某平面的直线。
2.推论:(1)若由不同的三点所确定的平面上含有两点,那么另一点必定也在这个平面上。
(2)如果一个平面上含有两点,则另一点也必定在这个平面上。
3.例子:三个点A、B、C在一个平面上,若在这个平面上发现了B1点,那么A、C也必定在这个平面上,这样就可以确定这个平面。
三、空间推广:1.定理:三点共线定理可以拓展到空间几何中,即:任意三个不同点,必定能构成一个平面或一个空间中的直线。
2.推论:(1)若由不同的三点所确定的平面上含有两点,那么另一点必定也在这个平面上。
(2)如果一个平面上含有两点,则另一点也必定在这个平面上。
3.例子:如果三个点A、B、C全都在空间中,若空间中发现了B1点,那么A、C也必定在平面上,这样就可以确定这个平面。
总结:三点共线定理是一个基本定理,指任意三个不同点,一定能构成一条直线,并且这个定理在平面和空间几何中都能成立,一个平面或一个空中的直线,它的推论雷同,即:若有两点,另一点也在这个平面或这条直线上。
证明三点共线的向量定理

证明三点共线的向量定理证明三点共线的向量定理1. 引言在几何学中,共线是指多个点在同一条直线上。
证明三点共线的向量定理是一种常用的方法,它利用向量的性质来判断三个点是否在同一条直线上。
本文将深入探讨这个定理,通过提供详细的解释和举例,帮助您全面了解这一概念。
2. 向量的基本概念在开始证明之前,我们先了解一些基本的向量概念。
向量是有大小和方向的量,通常用箭头来表示。
向量可以表示为有序数对 (a, b),其中a 和 b 分别表示向量在水平和垂直方向上的分量。
在这里,我们使用巴斯克定理,这是一个三角学中的基本定理,通过它我们可以找到一个向量的模长和方向。
3. 证明三点共线的向量定理现在我们来证明三个点是否共线的向量定理。
假设有三个点A(x1, y1)、B(x2, y2) 和 C(x3, y3)。
根据向量的定义,我们可以将向量 AB 表示为向量 a = (x2 - x1, y2 - y1),向量 BC 表示为向量 b = (x3 - x2, y3 -y2)。
如果这两个向量是平行的,那么向量 a 和向量 b 的比例关系为 a= k * b,其中 k 是一个常数。
这意味着点 A、B 和 C 共线。
为了证明这一点,我们可以计算向量 a 和向量 b 的比值,如果比值等于常数 k,那么三个点就共线。
具体计算如下:a = (x2 - x1, y2 - y1)b = (x3 - x2, y3 - y2)k = a / b = (x2 - x1) / (x3 - x2) = (y2 - y1) / (y3 - y2)如果比值 k 等于常数,那么三个点 A、B 和 C 就共线。
4. 举例说明为了更好地理解上述证明过程,我们举个例子来计算三个点是否共线。
假设有三个点 A(1, 2)、B(3, 4) 和 C(5, 6)。
我们可以计算向量 a 和向量 b 的比值:a = (3 - 1, 4 - 2) = (2, 2)b = (5 - 3, 6 - 4) = (2, 2)k = a / b = (2 - 1) / (2 - 1) = 1由于比值 k 等于常数 1,所以点 A、B 和 C 是共线的。
平面向量中“三点共线定理”妙用

的最小值是
3、在平行四边形ABCD中,O是对角线AC与BD的交点,E是BC边的中点,连接DE交AC于点F。已知 ,则 ( )
A. B. C. D.
4、(2014届东江中学高三年级理科第三次段考)在平行四边形ABCD中,E、F分别是BC、CD的中点,DE交AF于H,记 、 分别为a、b,则 =()
A. B. C. D.
解: 三点共线,又
,故选C
例4(07年江西高考题理科)如图3,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB、AC于不同的两点M、N,若 =m , =n ,则m+n的值为.
解: 因为O是BC的中点,故连接AO,如图4,由向量加法的平行四边形法则可知:
,
又 三点共线,
例1(06年江西高考题理科第7题)已知等差数列{an}的前n项和为Sn,若 ,且A、B、C三点共线,(设直线不过点O),则S200=( )
A.100B.101C.200D.201
解:由平面三点共线的向量式定理可知:a1+a200=1,∴ ,故选A。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
8、如图所示:A,B,C是圆O上的三个点,CO的延长线与线段AB交于圆内一点D,若
则有:( )
变式:如图所示:A,B,C是圆O上的三个点,CO的延长线与线段AB的延长线交于圆外一点F,若
则有:( )
A. B. C. D.
分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F、G、B以及E,G,C三点在一条直线上,可用平面内三点共线定理求解。
解: 三点共线, 由平面内三点共线定理可得:存在唯一的一对实数x使得
平面向量中“三点共线定理”妙用讲解学习

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点的O ,存在唯一的一对实数x,y 使得:OP xOA yOB =+且1x y +=。
特别地有:当点P 在线段AB 上时,0,0x y >> 当点P 在线段AB 之外时,0xy <笔者在经过多年高三复习教学中发现,运用平面向量中三点共线定理与它的两个推广形式解决高考题,模拟题往往会使会问题的解决过程变得十分简单!本文将通过研究一些高考真题、模拟题和变式题去探究平面向量中三点共线定理与它的两个推广形式的妙用,供同行交流。
例1(06年江西高考题理科第7题)已知等差数列{a n }的前n 项和为S n ,若1200OB a OA a OC =+,且A 、B 、C 三点共线,(设直线不过点O ),则S 200=( ) A .100B .101C .200D .201解:由平面三点共线的向量式定理可知:a 1+a 200=1,∴1200200200()1002a a S +==,故选A 。
点评:本题把平面三点共线问题与等差数列求和问题巧妙地结合在一起,是一道经典的高考题。
例2 已知P 是ABC ∆的边BC 上的任一点,且满足R y x AC y AB x AP ∈+=.,,则yx 41+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线AP xAB yAC =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y xx y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:4424y x y xx y x y+≥⨯=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,13AN NC =,点P 是BC 上的一点,若211AP mAB AC =+,则实数m 的值为( ) A .911 B. 511 C. 311 D. 211解:,,B P N 三点共线,又2284111111AP mAB AC mAB AN mAB AN =+=+⨯=+ 8111m ∴+= 311m ∴=,故选C 例4(07年江西高考题理科)如图3,在△ABC 中,点O 是BC 的中点,过点O 的直线分别交直线AB 、AC 于不同的两点M 、N ,若AB = m AM ,AC =n AN ,则m +n 的值为 .解:因为O 是BC 的中点,故连接AO ,如图4,由向量加法的平行四边形法则可知:1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22m nAO AM AN ∴=+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是△OAB 的重心,P 、Q分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线. 设OA x OP =,OB y OQ =,证明:yx 11+是定值; 图3图4图2证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+ 又,,P G Q 三点共线,11133x y ∴+= 113x y ∴+= 11x y∴+为定值3例6(汕头市东山中学2013届高三第二次模拟考试)如图6所示,在平行四边形ABCD 中,13AE AB =,14AF AD =,CE 与BF 相交于G 点,记AB a =,AD b =,则AG =_______A .2177a b + B. 2377a b + C. 3177a b + D. 4277a b +分析:本题是以平面几何为背景,为载体,求向量的问题,所以我们很容易联想到点F 、G 、B 以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
如何证明三点共线向量法

如何证明三点共线向量法嘿,大家好,今天咱们聊聊三点共线这个有趣的话题。
说到三点共线,很多人脑海里第一反应可能是那些枯燥的几何公式,哦,天哪,听着就想打个瞌睡。
不过,今天我想用一种轻松幽默的方式来带大家走进这个世界,保证让你觉得“哎哟,这个有意思”。
想象一下,你和你的好朋友们正在公园里散步,突然看到前面有三棵树,哇,这不是一幅画吗?你们可能就站在那里,打着哈哈,拍着照,仿佛这些树就是你们的合照背景。
这时候你可能就会想,这三棵树,它们是不是在一条直线上呢?说实话,生活中我们随时随地都能遇到三点共线的情况。
比方说,三个人在一起,聊着天,哈哈大笑,感觉就是一条线,那就是生活的趣味啊!咱们从数学的角度来聊聊怎么证明这三点共线。
向量法是个简单又实用的工具。
想象一下,你手里有一个向量,就像一把钥匙,打开了数学世界的门。
假设你有三个点A、B和C,首先我们得给这些点起个绰号,比如说“老大”、“老二”和“老三”。
然后,咱们就可以分别从老大出发到老二和老三,形成两个向量AB和AC。
这样一来,这俩向量就像是你手里的两把剪刀,可以轻松地切割出一个平面。
如果这两个向量在同一条线上,那它们就可以用一个共同的比例关系来表达。
换句话说,咱们可以说AB和AC是平行的,或者更简单地说,它们是在同一条线上。
如果你感觉有点懵,那没关系,想象一下两条在海滩上走的腿,走得越远,越像一条直线。
就是这个道理!再说说什么是共线,简单来说,就是三点如果满足一定的比例关系,就可以认为它们是共线的。
这里面就有个“小秘密”,如果你能找到一个数k,使得向量AB = k × 向量AC,那这三点就真的可以算作在同一条线上了。
这种感觉就像是找到了通往宝藏的地图,哈哈,想想都激动。
那我们再回到实际生活中,假设你跟朋友们去爬山,你们三个人正好在一条直线上。
要是这个时候你们拍个合照,看看背后那美丽的风景,哎,正好在三点共线的状态下,那绝对是一幅绝佳的风景画!这个时候,如果有小伙伴们偏离了这条线,哎呀,那就显得有些格格不入了,是不是?有些人可能会问,为什么三点共线这么重要呢?这不光是数学上的一个概念,生活中我们也经常用到。
三点共线向量式及应用

经验交流2014-03普通高中课程标准实验教科书《数学》必修4(人教B 版)第97页以例题的形式给出了三点共线向量式:例题已知A 、B 是直线l 上任意两点,O 是l 外一点。
求证:对直线l 上任意一点P ,存在实数t ,使关于基底的分解式为并且满足式的点P 一定在l 上。
为了方便学生记忆和运用,常将上述内容改写为:在平面中A 、B 、C 三点共线的充要条件是OA =xOB+yOC O 为平面内任意一点),其中x+y =1。
一、应用于平面几何求值问题例1如图1,点G 是三角形ABO 的重心,PQ 是过G 的分别交OA 、OB 于P 、Q 的一条线段,且OP =mOA ,OQ=nOB ,(m 、n ∈R )。
求1m +1n的值。
分析:本题是一道典型的平面几何证明题,但用平面几何方法则过程很复杂。
连结OG 交AB 于D ,注意到图中有两组三点共线,分别为A 、D 、B ;P 、G 、Q ,于是可以用三点共线向量式进行求解。
由A 、D 、B 三点共线及D 是中点有AP =tAB=t (OB -OA ),①由点G 是三角形ABO 的重心可知OD =32OG ,由题设有OA =1m OP ,OB =1nOQ 为了使用第二组共线关系,在①式左右两端同时替换得:32OG =12m OP +12n OQ ,即QC =13m OP +13n OQ由P 、G 、Q 三点共线得13m +13n =1即1m +1n=3。
二、应用于立体几何证明问题例2(2013年浙江卷理科20题)如图2,在四面体A -BCD 中,AD ⊥平面BCD ,BC ⊥CD ,AD =2,BD =22√.M 是AD 的中点,P 是BM 的中点,点Q 在线段AC 上,且AQ =3QC .(1)证明:PQ ∥平面BCD ;分析:本题(1)是一道典型的立体几何问题转化为平面几何证明,笔者尝试用三点共线向量式来求解,过程较为简洁,不妨作为一种解法来储备。
平面向量中“三点共线定理”妙用

平面向量中“三点共线定理”妙用对平面内任意的两个向量b a b b a//),0(,≠的充要条件是:存在唯一的实数λ,使b a λ=由该定理可以得到平面内三点共线定理:三点共线定理:在平面中A 、B 、P 三点共线的充要条件是:对于该平面内任意一点。
OB a OA a OC =+,且A ) A 。
y4+ 的最小值是解:点P 落在ABC 的边BC 上 ∴B ,P,C 三点共线A P x AB y =+ 1x y ∴+= 且x>0,y>014141444()1()()145y x y x x y x y x y x y x y x y∴+=+⨯=+⨯+=+++=++ x>0,y>040,0y xx y ∴>> 由基本不等式可知:44y x x y +≥=,取等号时4y xx y =224y x ∴=2y x ∴=±0,0x y >>2y x∴=1x y +=12,33x y ∴==,符合所以yx 41+的最小值为9 点评:本题把平面三点共线问题与二元函数求最值、基本不等式巧妙地结合在一起, 较综合考查了学生基本功.例3(湖北省2011届高三八校第一次联考理科)如图2,在△ABC 中,2284AP mAB AC mAB AN mAB AN =+=+⨯=+8111m += ,若AB = m AM 因为,由向量加法的平行1()2AO AB AC ∴=+m AB AM =,AC nAN =1()2AO mAM nAN ∴=+22AO AM AN =+又,,M O N 三点共线,∴由平面内三点共线定理可得:122m n+= 2m n ∴+=例5(广东省2010届高三六校第三次联)如图5所示:点G 是△OAB 的重心,P 、Q分别是边OA 、OB 上的动点,且P 、G 、Q 三点共线. 设x =,OB y OQ =,证明:yx 11+是定值;证明:因为G 是OAB 的重心,211()()323OG OA OB OA OB ∴=⨯+=+1OP xOAOA OP x=∴= 1OQ yOBOB OQ y=∴=111111()()3333OG OA OB OP OQ OG OP OQ x y x y∴=+=+∴=+111111,1AF AD =,CE 与,则AG =_______7b + B. 377a b + C. 31a b + D. 想到点F 、G 、B 以及E,G,C 三点在一条直线上,可用平面内三点共线定理求解。
三点共线向量公式

三点共线向量公式
三点共线向量公式:x2-x1y3-y1=x3-x1y2-y1。
三点共线指的是三点在同一条直线上。
可以设三点为A、B、C,利用向量证明:λAB=AC(其中λ为非零实数)。
Ax1,y1,Bx2,y2,Cx3,y3
向量AB=x2-x1,y2-y1,向量AC=x3-x1,y3-y1
A、B、C共线得:向量AB//向量AC
x2-x1y3-y1=x3-x1y2-y1
所以A、B、C共线:x2-x1y3-y1=x3-x1y2-y1
方法一:取两点确立一条直线,计算该直线的解析式.代入第三点坐标看是否满足该
解析式(直线与方程)。
方法二:设三点为A、B、C,利用向量证明:λAB=AC(其中λ为非零实数)。
方法三:利用点差法求出AB斜率和AC斜率,相等即三点共线。
方法四:用梅涅劳斯定理。
方法五:利用几何中的公理“如果两个不重合的平面有一个公共点,那么它们有且只
有一条过该点的公共直线”.可知:如果三点同属于两个相交的平面则三点共线。
方法六:运用公(定)理“过直线外一点有且只有一条直线与已知直线平行(垂直)”.其实就是同一法。
感谢您的阅读,祝您生活愉快。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量法证明三点共线的又一方法及应用
蒋李萍 2011年10月24日
平面向量既具有数量特征,又具有图形特征,学习向量的应用,可以启发同学们从新的视角去分析、解决问题,有益于培养创新能力. 下面就一道习题的应用探究为例进行说明.
原题 已知OB λOA μOC =+,其中1λμ+=. 求证:A 、B 、C 三点共线 思路:通过向量共线(如AB k AC =)得三点共线. 证明:如图,由1λμ+=得1λμ=-,则
(1)OB λOA μOC μOA μOC =+=-+ ∴()OB OA μOC OA -=- ∴AB μAC =
∴A 、B 、C 三点共线.
思考:1. 此题揭示了证明三点共线的又一向量方法,点O 具有灵活性;
2. 反之也成立(证明略):若A 、B 、C 三点共线,则存在唯一实数对λ、μ,满
足OB λOA μOC =+,且1λμ+=.揭示了三点共线的又一个性质; 3. 特别地,12λμ==
时,1
()2
OB OA OC =+,点B 为AC 的中点,揭示了OAC
中线OB 的一个向量公式,应用广泛.
应用举例:
例1 如图,平行四边形ABCD 中,点M 是AB 的中点,点N 在BD 上,且1
3
BN BD =. 利用向量法证明:M 、N 、C 三点共线.
思路分析:选择点B ,只须证明BN λBM μBC =+,且1λμ+=. 证明:由已知BD BA BC =+,又点N 在BD 上,且1
3
BN BD =
,得 1111()3333BN BD BA BC BA BC ==+=+
又点M 是AB 的中点,
1
2BM BA ∴=,即2BA BM =
21
33BN BM BC ∴=+
而21133
+= ∴M 、N 、C 三点共线.
D
A
B
C
M
N
点评:证明过程比证明MN mMC =简洁. 例2如图,平行四边形OACB 中,13BD BC =
,OD 与AB 相交于E ,求证:. 1
4
BE BA =. 思路分析:可以借助向量知识,只须证明:14
BE BA =,而
BA BO BC =+,又O 、D 、E 三点共线,存在唯一实数对λ、μ,
且1λμ+=,使BE λBO μBD =+,从而得到BE 与BA 的关系.
证明:由已知条件,BA BO BC =+,又B 、E 、A 三点共线,可设BE k BA =,则
BE k BO k BC =+①
又O 、E 、D 三点共线,则存在唯一实数对λ、μ,使BE λBO μBD =+,且1λμ+=. 又13
BD BC =
1
3
BE λBO μBC
∴=+②
根据①、②得
131k λk μλμ=⎧⎪⎪=⎨⎪+=⎪⎩,解得141434k λμ⎧=⎪⎪⎪=⎨⎪
⎪=⎪⎩
1
4BE BA ∴=
1
4BE BA ∴=
点评:借助向量知识,充分运用三点共线的向量性质解决问题,巧妙、简洁. 练习题:
D O
A
C
E
B
ﻩ。
