工程力学练习册答案(部分)
工程力学练习册习题答案汇总

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体 A ,构件 AB , BC 或 ABC 的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a(b(c(d(e(f(g1-2 试画出图示各题中 AC 杆(带销钉和 BC 杆的受力图(a (b (c(a1-3 画出图中指定物体的受力图。
所有摩擦均不计, 各物自重除图中已画出的外均不计。
(a(b(c(d(e(f(g第二章平面力系2-1 电动机重 P=5000N ,放在水平梁 AC 的中央,如图所示。
梁的 A 端以铰链固定, 另一端以撑杆 BC 支持, 撑杆与水平梁的夹角为 30 0。
如忽略撑杆与梁的重量, 求绞支座 A 、 B 处的约束反力。
题 2-1图∑∑=︒+︒==︒-︒=P F F F F F FB A y A B x 30sin 30sin , 0030cos 30cos , 0解得 : N P F F B A 5000=== 2-2 物体重 P=20kN ,用绳子挂在支架的滑轮 B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计, A 、 B 、 C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆 AB 和支杆BC 所受的力。
题 2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin , 0030sin 30cos , 0P P F F P F F FBC y BC AB x解得 :P F P F BC AB 732. 2732. 3=-=2-3 如图所示,输电线 ACB 架在两电线杆之间,形成一下垂线,下垂距离 CD =f =1m , 两电线杆间距离 AB =40m。
电线 ACB 段重 P=400N ,可近视认为沿 AB 直线均匀分布,求电线的中点和两端的拉力。
题 2-3图以 AC 段电线为研究对象,三力汇交NF NF F F F F F FC A GA y C A x 200020110/1tan sin , 0, cos , 0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学练习册第2版答案

工程力学练习册第2版答案工程力学是研究物体在外力作用下的运动规律和内部应力分布的科学。
本练习册旨在帮助学生更好地理解和掌握工程力学的基本概念、原理和计算方法。
以下是《工程力学练习册第2版》的部分习题及答案。
习题一:静力学基础1. 某物体受到三个共点力的作用,分别为F1=200N,F2=300N,F3=100N。
若F1和F2的夹角为120°,求这三个力的合力大小。
答案:首先,根据矢量合成法则,我们可以使用余弦定理计算合力的大小: \[ F_{合} = \sqrt{F1^2 + F2^2 + 2 \cdot F1 \cdot F2 \cdot\cos(120°)} \]\[ F_{合} = \sqrt{200^2 + 300^2 + 2 \cdot 200 \cdot 300\cdot (-0.5)} \]\[ F_{合} = \sqrt{40000 + 90000 - 60000} \]\[ F_{合} = \sqrt{70000} \approx 264.58N \]2. 一个物体在水平面上,受到一个斜向上的拉力F=150N,与水平方向夹角为30°。
求物体受到的支持力和摩擦力的大小。
答案:将拉力分解为水平和垂直分量:\[ F_{水平} = F \cdot \cos(30°) = 150 \cdot 0.866 \approx 129.9N \]\[ F_{垂直} = F \cdot \sin(30°) = 150 \cdot 0.5 = 75N \] 物体在水平面上,支持力等于垂直向上的力,即:\[ N = F_{垂直} = 75N \]摩擦力的大小由水平力决定:\[ f = \mu \cdot N \]其中μ为摩擦系数,由于题目未给出,我们无法计算具体数值。
习题二:材料力学1. 一根直径为d=20mm,长度为L=2m的圆杆,在一端受到一个拉力P=10kN。
工程力学(第二版)习题册答案

一、填空题
1. 相 对 滑 动 相 对 滑 动 趋 势 接触面的切线 相反 2. 10N 20N 30N 30N 30N 3. 100N 竖直向上 平衡 4. 平稳无冲击 自锁
阻碍物体相对滑动
相对滑动趋势
二、选择题
1. A
三、简答题
1. ①问题中含有可能发生相对滑动的摩擦面,因此,存在摩擦力; ②受力图中要画出摩擦力,摩擦力总是沿着接触面的切线方向并与物体相对滑
7.
8.
9.
第二章 平面力系
第一节 共线力系的合成与平衡
一、填空题
1. 在同一条直线上
2. FR Fi FR 0
二、计算题
设向右为正方向。 则 FR=120+40-80-200=-120N 方向:水平向左
第二节 平面汇交力系的合成
一、填空题
1. 作用于同一平面内且各力作用线相交于一点的力系 共线力系 力的作用点 2. -F 或 F 0 0 -F 或 F 3. 合力在任一坐标轴上的投影 各分力在同一轴上投影的代数和 4. F4 F3 5. 自行封闭 6. 所有各力在 x 轴上投影的代数和为零 所有各力在 y 轴上投影的代数和为零 Fx 0 Fy 0
3. 后轮:摩擦力向前 前轮:摩擦力向后
4. 不下滑,处于自锁状态
四、计算题
FT 60 18 3N
五、应用题
1. (提示)从摩擦力与 F 对 B 点的力矩大小的比较进行考虑
第三章 空间力系 第一节 力在空间坐标轴上的投影与合成
一、填空题
1. 力的作用线不都在同一平面内呈空间分布的力系 2. 一次投影法 二次投影法
二、选择题
1. A 2.B
它所限制物体
三、简答题
1.柔性体约束只能承受拉力,不能承受压力。 2.被约束物体可以沿约束的水平方向自由滑动,也可以向离开约束的方向运动, 但不能向垂直指向约束的方向运动。 3.剪刀的两半部分可以绕销钉轴线相对转动,但不能在垂直销钉轴线的平面内沿 任意方向做相对移动。 4.木条不能沿圆柱销半径方向移动,但可以绕销轴做相对转动。 5.固定端约束既限制物体在约束处沿任何方向的移动,也限制物体在约束处的转 动。
工程力学练习册习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)(a)1-3 画出图中指定物体的受力图。
所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)(b)(c)(d)(e)(f)(g)第二章 平面力系2-1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力。
题2-1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得: N P F F B A 5000===2-2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起。
设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2-2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得: PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
题2-3图以AC 段电线为研究对象,三力汇交 NF N F F F FF F F C A GA yC A x 200020110/1tan sin ,0,cos ,0=======∑∑解得:ααα2-4 图示为一拔桩装置。
工程力学练习册习题答案3共3份

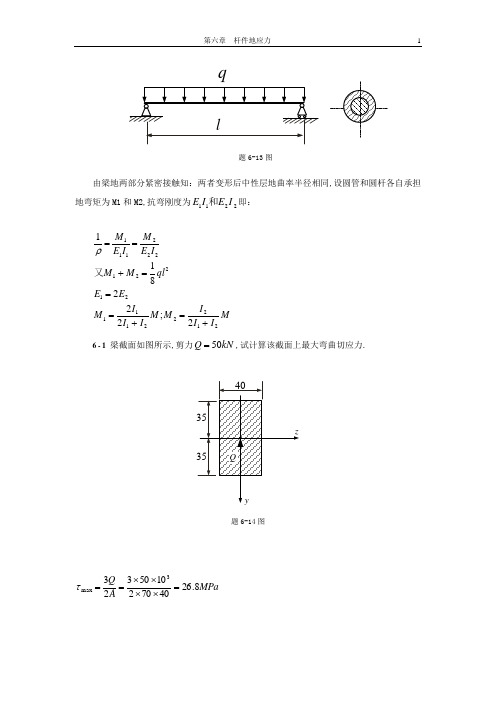
第六章 杆件的应力1q题6-13图由梁的两部分紧密接触知:两者变形后中性层的曲率半径相同,设圆管和圆杆各自承担的弯矩为M1和M2,抗弯刚度为2211I E I E 和即:MI I I M M I I I M E E ql M M I E MI E M 21222111212212221112;222811+=+===+==又ρ6-1 梁截面如图所示,剪力50Q kN =,试计算该截面上最大弯曲切应力。
题6-14图MPa A Q 8.264070210503233max=⨯⨯⨯⨯==τ2 附录Ⅰ 平面图形的几何性质第七章 应力状态分析7-1 单元体各面应力(单位MPa )如图所示,试用解析法求解指定斜截面上的正应力和切应力。
(a)题7-1图(a )MPaMPa x yx x yx yx x y x 32.272cos 2sin 232.272sin 2cos 2260,20,0,40-=+-=-=--++=︒===-=ατασστατασσσσσατσσαα(b)MPaMPa x yx x yx yx x y x 66.182cos 2sin 23.522sin 2cos 2230,20,50,30=+-==--++=︒=-===ατασστατασσσσσατσσαα附录Ⅰ平面图形的几何性质3题7-1图(c)MPaMPaxyxxyxyxxyx302cos2sin2102sin2cos2245,40,60,0-=+-=-=--++=︒====ατασστατασσσσσατσσαα(d)MPaMPaxyxxyxyxxyx6.602cos2sin2352sin2cos2230,0,70,70=+-==--++=︒==-==ατασστατασσσσσατσσαα7-2已知应力状态如图所示,应力单位为MPa。
试用解析法和应力圆分别求:(1)主应力大小,主平面位置;(2)在单元体上绘出主平面位置和主应力方向;(3)最大切应力。
工程力学练习册习题答案

工程力学练习册学校学院专业学号教师姓名第一章静力学基础 1第一章静力学基础1-1 画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)(b)(c)(d)2 第一章静力学基础(e)(f)(g)1-2 试画出图示各题中AC杆(带销钉)和BC杆的受力图(a)(b)(c)第一章静力学基础 3(a)1—3 画出图中指定物体的受力图.所有摩擦均不计,各物自重除图中已画出的外均不计。
(a)4 第一章静力学基础(b)(c)(d)第一章静力学基础 5 (e)6 第一章静力学基础(f)(g)第四章 材料力学基本概念 7第二章 平面力系2—1 电动机重P=5000N ,放在水平梁AC 的中央,如图所示。
梁的A 端以铰链固定,另一端以撑杆BC 支持,撑杆与水平梁的夹角为30 0。
如忽略撑杆与梁的重量,求绞支座A 、B 处的约束反力.题2—1图∑∑=︒+︒==︒-︒=PF F FF F F B A yA B x 30sin 30sin ,0030cos 30cos ,0解得:N P F F B A 5000===8 第一章 静力学基础2—2 物体重P=20kN ,用绳子挂在支架的滑轮B 上,绳子的另一端接在绞车D 上,如图所示。
转动绞车,物体便能升起.设滑轮的大小及轴承的摩擦略去不计,杆重不计,A 、B 、C 三处均为铰链连接.当物体处于平衡状态时,求拉杆AB 和支杆BC 所受的力。
题2—2图∑∑=-︒-︒-==︒-︒--=030cos 30sin ,0030sin 30cos ,0P P F FP F F F BC yBC AB x解得:PF P F BC AB 732.2732.3=-=2-3 如图所示,输电线ACB 架在两电线杆之间,形成一下垂线,下垂距离CD =f =1m ,两电线杆间距离AB =40m 。
电线ACB 段重P=400N ,可近视认为沿AB 直线均匀分布,求电线的中点和两端的拉力。
工程力学练习册及答案

工程力学练习册及答案### 工程力学练习册及答案#### 第一章:静力学基础练习题1:已知一个物体受到三个力的作用,分别为F1=50N,F2=30N,F3=20N,且这三个力的方向分别为北偏东30°,南偏西45°,和正南方向。
求这三个力的合力。
答案:首先,将力F1和F2分解为水平和垂直分量。
F1的水平分量为F1*cos(30°),垂直分量为F1*sin(30°)。
同理,F2的水平分量为F2*cos(135°),垂直分量为F2*sin(135°)。
F3的水平分量为0,垂直分量为F3。
计算得:- F1的水平分量:50*cos(30°) = 43.30N- F1的垂直分量:50*sin(30°) = 25N- F2的水平分量:30*cos(135°) = -25.98N- F2的垂直分量:30*sin(135°) = 25.98N- F3的水平分量:0- F3的垂直分量:20N合力的水平分量为:43.30N - 25.98N = 17.32N合力的垂直分量为:25N + 25.98N + 20N = 70.98N合力的大小为:√(17.32^2 + 70.98^2) ≈ 73.71N合力的方向为:tan^-1(70.98/17.32) ≈ 82.9°,即北偏东82.9°。
练习题2:一个均匀的圆柱体,其质量为10kg,半径为0.5m,求其在水平面上的静摩擦力。
答案:圆柱体在水平面上的静摩擦力取决于作用在它上面的外力。
如果外力小于或等于静摩擦力,圆柱体将保持静止。
静摩擦力的计算公式为:\[ f_{max} = \mu N \]其中,\( \mu \) 是静摩擦系数,\( N \) 是圆柱体的正压力。
对于均匀圆柱体,\( N = mg \),其中\( m \)是质量,\( g \)是重力加速度。
工程力学练习册答案(部分)

工程力学练习册答案(部分)工程力学科学技术专业教学姓氏学习用书学校第199分科名称培训第1章静力学基础1第1章静力学基础1-1绘制受力图没有重力的物体的重量不计算在内。
所有触点都是平滑触点。
(a)(b)(c)(d)2第一章静力学基础(f)第一章静态基础3(a)(b)(c)(a)1-3绘制图中指定对象的应力图除了图中所示的以外,所有的摩擦力都被排除了,每个物体的自重也被排除了。
4第一章静力学基础(b)第一章静力学基础5。
199第一章静力学基础7(g)第二章平面力系2-1电机重量P=5000N,放置在横梁交流中心,如图所示横梁的一端由铰链固定,另一端由撑杆支撑,撑杆与横梁的夹角为30°如果忽略撑杆和梁的重量,则计算扭转支座A和B处的约束反力。
8第一章静力学基础2-1图?f?Fxy?0,FBcos30??FAcos30??0?0,FAsin30??FBsin30??P:固定资产?FB?p?5000N2-2物体重量P=20kN,用绳子挂在支架的滑轮b上,绳子的另一端与绞车d相连,如图所示转动绞盘,物体就可以升起。
将滑轮尺寸和轴承摩擦设置为忽略不计,将杆重设置为忽略不计。
三个部分A、B 和C是铰接的当物体处于平衡状态时,找出拉杆AB和支撑杆BC上的力。
第4章材料力学基本概念92-2图?f?Fxy?0,?FAB?FBCcos30??Psin30??0?0,?FBCsin30??Pcos30??p?0:FAB??3.732PFBC?2.732P2-3如图所示,ACB输电线路安装在两极之间,形成一条垂直线,弧垂距离CD=f=1m,两极之间的距离AB=40m线的ACB部分的重量为P = 400N牛顿,这可以被认为是沿着近视的AB直线均匀分布。
可以计算导线中点和两端的张力。
问题2-3图10第一章以静态基础交流截面导线为研究对象,三种力会聚?f?Fxy?0,FAcos??舰队指挥官?0,发新??FGtan??1/10:固定资产?201NFC?2000N2-4显示为拔桩装置。
工程力学练习册习题答案3共3份-5页word资料

第 1 页题6-13图由梁的两部分紧密接触知:两者变形后中性层的曲率半径相同,设圆管和圆杆各自承担的弯矩为M1和M2,抗弯刚度为2211I E I E 和即:6-1梁截面如图所示,剪力50Q kN =,试计算该截面上最大弯曲切应力。
题6-14图第七章 应力状态分析7-1 单元体各面应力(单位MPa )如图所示,试用解析法求解指定斜截面上的正应力和切应力。
题7-1图(a ) (b)题7-1图(c) (d)7-2 已知应力状态如图所示,应力单位为MPa 。
试用解析法和应力圆分别求:(1)主应力大小,主平面位置;(2)在单元体上绘出主平面位置和主应力方向;(3)最大切应力。
题7-2图(a)(b)题7-2图(c) (d)7-3 图示木制悬臂梁的横截面是高为200mm 、宽为60mm 的矩形。
在A 点木材纤维与水平线的倾角为20︒。
试求通过A 点沿纤维方向的斜面上的正应力和切应力。
题7-3图7-4 图示二向应力状态的应力单位为MPa ,试作应力圆,并求主应力。
题7-4图解法二:(解析法)7-5 在通过一点的两个平面上,应力如图所示,单位为MPa 。
试求主应力的数值和主平面的位置,并用单元体草图来表示。
题7-5图7-6 试求图示各应力状态的主应力和最大切应力,应力单位为MPa 。
题7-6图(a) (b) (c)7-7 列车通过钢桥时,用变形仪测得钢桥横梁A 点(见图)的应变为0.0004x ε=,0.00012y ε=-。
试求A 点在x 和y 方向的正应力。
设200E GPa =,0.3μ=。
题7-7图解得:0,80==y x MPa σσ7-8 图示微体处于平面应力状态,已知应力100x MPa σ=,80y MPa σ=,50x MPa τ=,弹性模量200E GPa =,泊松比0.3μ=,试求正应变x ε,y ε与切应变xy γ,以及30α︒=方位的正应变30ε︒题7-8图7-9 边长为10a mm =的立方体铝块紧密无隙地置于刚性模内,如图所示,模的变形不计。
工程力学习题册第三章 答案

第三章平面一般力系答案一、填空(将正确的答案填写在横线上)1、作用在物体上的各力的作用线都在同一平面内 ,并呈任意分布的力系,称为平面一般力系。
2、平面一般力系的两个基本问题是平面力系的简化 ,其平面条件的的应用。
3、力的平移定理表明,若将作用在物体某点的力平移到物体上的另一点,而不改变原力对物体的作用效果,则必须附加一力偶,其力偶距等于原来的力对新作用点的距。
4、平面一般力系向已知中心点简化后得到一力和一力偶距。
5平面一般力系的平衡条件为;各力在任意两个相互垂直的坐标轴上的分量的代数和均为零力系中所有的力对平面内任意点的力距的代数和也等零。
6.平面一般力系平衡方程中,两个投影式ΣFix=0 和ΣFiy=0 保证物体不发生移动 ;一个力矩式ΣMo(Fi)=0 保证物体不发生转动。
三个独立的方程,可以求解三个未知量。
7.平面一般力系平衡问题的求解中,固定铰链的约束反力可以分解为相互垂直的两个分力固定端约束反力可以简化为相互垂直的两个分力和一个附加力偶矩。
8.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣFiX=0适用于平面一般力系,使其用限制条件为AB连线与X轴不垂直。
9.平衡方程ΣMA(Fi)=0、ΣMB(Fi)=0、ΣMc(Fi)=0的使用限制条约为ABC不在同一直线上。
10.若力系中的各力作用现在同一平面内且相互平行,称为平面平行力系。
它是平面一般力系的特殊情况。
11.平面平行力系有两个独立方程,可以解出两个未知量。
12.平面平行力系的基本平衡方程是:ΣFi X=0,ΣM O(Fi)=0二、判断题(正确的打“√”,错误的打“×”)1.作用于物体上的力,其作用线可在物体上任意平行移动,其作用效果不变。
(×)2.平面一般力系的平衡方程可用于求解各种平面力系的平衡问题。
(√)3.若用平衡方程解出未知力为负值,则表明:(1)该力的真实方向与受力图上假设的方向相反。
(√)(2)该力在坐标轴上的投影一定为负值。
工程力学练习册答案

工程力学练习册答案问题1:请简述牛顿三大定律的内容。
答案:1. 牛顿第一定律(惯性定律):物体在没有外力作用时,将保持静止状态或匀速直线运动。
2. 牛顿第二定律(动力定律):物体的加速度与作用在物体上的净外力成正比,与物体的质量成反比,即\[ F = ma \]。
3. 牛顿第三定律(作用与反作用定律):对于两个相互作用的物体,它们之间的作用力和反作用力总是大小相等、方向相反。
问题2:何为应力和应变?它们之间的关系是什么?答案:- 应力:是单位面积上的内力,表示材料内部抵抗变形的能力。
- 应变:是材料尺寸的相对变化,表示材料的变形程度。
- 它们之间的关系通常通过应力-应变曲线来描述,该曲线反映了材料在不同应力水平下的变形特性。
问题3:简述材料力学中的弹性模量和剪切模量。
答案:- 弹性模量:也称为杨氏模量,是材料在弹性范围内应力与应变比值,表示材料的刚性。
- 剪切模量:材料在剪切应力作用下,剪切应力与剪切应变的比值,反映材料抵抗剪切变形的能力。
问题4:什么是静水压力?如何计算?答案:- 静水压力:是液体内部各点受到的均匀压力,与液体的密度、深度和重力加速度有关。
- 计算公式为:\[ P = \rho g h \],其中\( P \)是压力,\( \rho \)是液体密度,\( g \)是重力加速度,\( h \)是液体深度。
问题5:请解释什么是材料的疲劳失效,并给出一个实际应用的例子。
答案:- 疲劳失效:是指材料在反复加载和卸载的过程中,即使应力水平低于材料的屈服强度,也可能发生断裂的现象。
- 实际应用例子:汽车的悬挂系统在长时间的行驶过程中,由于路面的不平,反复受到交变载荷的作用,可能会发生疲劳断裂。
结束语:工程力学是一门将理论知识与实际应用紧密结合的学科。
通过练习和理解上述问题的答案,可以帮助我们更好地掌握工程力学的基本概念和应用方法,为解决实际工程问题打下坚实的基础。
希望这些答案能够帮助你在学习工程力学的道路上更进一步。
工程力学练习册习题答案共份
第六章 杆件地应力1q题6-13图由梁地两部分紧密接触知:两者变形后中性层地曲率半径相同,设圆管和圆杆各自承担地弯矩为M1和M2,抗弯刚度为2211I E I E 和即:MI I I M M I I I M E E ql M M I E MI E M 21222111212212221112;222811+=+===+==又ρ6-1 梁截面如图所示,剪力50Q kN =,试计算该截面上最大弯曲切应力.题6-14图MPa A Q 8.264070210503233max=⨯⨯⨯⨯==τ2 附录Ⅰ 平面图形地几何性质第七章 应力状态分析7-1 单元体各面应力(单位MPa )如图所示,试用解析法求解指定斜截面上地正应力和切应力.(a)题7-1图(a )MPaMPa x yx x yx yx x y x 32.272cos 2sin 232.272sin 2cos 2260,20,0,40-=+-=-=--++=︒===-=ατασστατασσσσσατσσαα(b)MPaMPa x yx x yx yx x y x 66.182cos 2sin 23.522sin 2cos 2230,20,50,30=+-==--++=︒=-===ατασστατασσσσσατσσαα附录Ⅰ平面图形地几何性质3题7-1图(c)MPaMPaxyxxyxyxxyx302cos2sin2102sin2cos2245,40,60,0-=+-=-=--++=︒====ατασστατασσσσσατσσαα(d)MPaMPaxyxxyxyxxyx6.602cos2sin2352sin2cos2230,0,70,70=+-==--++=︒==-==ατασστατασσσσσατσσαα7-2已知应力状态如图所示,应力单位为MPa.试用解析法和应力圆分别求:(1)主应力大小,主平面位置;(2)在单元体上绘出主平面位置和主应力方向;(3)最大切应力.20(b)题7-2图(a)4 附录Ⅰ 平面图形地几何性质MPax yx yx x y x 57)2(220,0,5022max =+-++====τσσσσστσσ︒-=--=-=+--+=3.19,tan 7)2(20min022min ασστατσσσσσx xx yx yx MPa(b)MPax yx yx x y x 25)2(225,0,022max =+-++====τσσσσστσσ︒-=--=-=+--+=45,tan 25)2(20min022min ασστατσσσσσx xx yx yx MPa(c)(d)题7-2图(c)MPax yx yx x y x 2.11)2(240,20,4022max =+-++=-=-=-=τσσσσστσσ︒=--=-=+--+=52,tan 2.71)2(20min022min ασστατσσσσσx xx yx yx MPa(d)附录Ⅰ 平面图形地几何性质 5MPax yx yx x y x 02.30)2(220,30,2022max =+-++===-=τσσσσστσσ︒-=--=-=+--+=66.70,tan 02.27)2(20min022min ασστατσσσσσx xx yx yx MPa7-3 图示木制悬臂梁地横截面是高为200mm 、宽为60mm 地矩形.在A 点木材纤维与水平线地倾角为20︒.试求通过A 点沿纤维方向地斜面上地正应力和切应力.题7-3图MPa S Q A 25.006.02.022000323=⨯⨯⨯==τ︒-=70αMPaMPa x yx x yx yx x y x 19.02cos 2sin 216.02sin 2cos 2270,25.0,0,0=+-=-=--++=︒-====ατασστατασσσσσατσσαα7-4 图示二向应力状态地应力单位为MPa ,试作应力圆,并求主应力.6 附录Ⅰ 平面图形地几何性质题7-4图解法二:(解析法)M P aM P a y x yx yx x y x 40502sin 2cos 2260,0?,,80==--++=︒====σατασσσσσατσσα解得:MPa x 80max ==σσMPa y 40min ==σσ0,40,80321===∴σσσMPa7-5 在通过一点地两个平面上,应力如图所示,单位为MPa .试求主应力地数值和主平面地位置,并用单元体草图来表示.题7-5图附录Ⅰ 平面图形地几何性质 77-6 试求图示各应力状态地主应力和最大切应力,应力单位为MPa.50(a)50(b)(c)题7-6图(a)MPa 50502max ==σMPaMPa MPa50,0,5050321min -===∴-=σσσσMPa 50231max =-=σστ(b)MPa 17.5240)22030(2203022max =+++-=σ MPa 17.4240)22030(2203022min -=++--=σ MPaMPaMPa 17.47217.42,50,17.5231max 321=-=-===∴σστσσσ8 附录Ⅰ 平面图形地几何性质(c)MPa 13030)240120(24012022max =+-++=σ MPa 3030)220120(24012022min =+--+=σ MPaMPaMPa 80230,30,13031max 321=-=-===∴σστσσσ7-7 列车通过钢桥时,用变形仪测得钢桥横梁A 点(见图)地应变为0.0004x ε=,0.00012y ε=-.试求A 点在x 和y 方向地正应力.设200E GPa =,0.3μ=.题7-7图0004.0)(1=-=y x x E μσσε 00012.0)(1-=-=x y y Eμσσε解得:0,80==y x MPa σσ7-8 图示微体处于平面应力状态,已知应力100xMPa σ=,80y MPa σ=,50x MPa τ=,弹性模量200E GPa =,泊松比0.3μ=,试求正应变x ε,y ε与切应变xy γ,以及30α︒=方位地正应变30ε︒附录Ⅰ 平面图形地几何性质 9题7-8图31038.0)(1-⨯=-=y x x E μσσε 31025.0)(1-⨯=-=x y y Eμσσε31065.02.76)1(2-⨯===+=GGPaEG xxy τγμ31203030120120303010066.0)(13.1287.511807.5160sin 60cos 22-︒︒︒︒︒︒︒⨯=-==-=⇒+=+=︒-︒-++=μσσεσσσσστσσσσσEMPaMPay x x yx yx7-9 边长为10a mm =地立方体铝块紧密无隙地置于刚性模内,如图所示,模地变形不计.铝地70E GPa =,0.33μ=.若6P kN =,试求铝块地三个主应力和主应变.题7-9图10 附录Ⅰ 平面图形地几何性质建立图示坐标,由刚性模知==y x εε且MPa z 6001.060002-=-=σ 由广义胡克定律:)]([10)]([1=+-==+-=z x y y z y x x EEσσμσεσσμσε解得:MPa y x 55.29-==σσ3105785.0)]([1-⨯-=+-=y x z z Eσσμσε 第八章 强度设计8-1现有钢、铸铁两种杆材,其直径相同.从承载能力与经济效益两个方面考虑,图示结构中两种合理选择方案是(A )A 1杆为钢,2杆为铸铁B 1杆为铸铁,2杆为钢C 1、2杆均为钢D 1、2杆均为铸铁8-2有A 、B 、C 三种材料,其拉伸应力—应变实验曲线如图所示,曲线( B )材料地弹性模量E 大,曲线(A )材料地强度高,曲线( C )材料地塑性好.B8-3图示一正方形截面地阶形混凝土柱.设混凝土地密度为33/1004.2m kg ⨯=ρ,F=100kN,许用应力MPa 2][=σ.试根据强度条件选择截面宽度a 和b.mb bbbgb ga F ma a a a ga F 156.01028.91004.24052.08.91004.24103][443052.010248.91004.210100][462232352226223322≥⨯≤⨯⨯⨯⨯+⨯⨯⨯⨯+⨯⇒≤++≥⨯≤⨯⨯⨯+⨯≤+解得:解得:即虑它们的强度条件:危险截面有二,分别考σρρσρ8-4三角架ABC 由AC 和BC 二杆组成.杆AC 由两根No.12b 地槽钢组成,许用应力为[σ]=160MPa ;杆BC 为一根No.22a 地工字钢,许用应力为[σ]=100MPa.求荷载F 地许可值[F].题8-2图a 题8-3图以节点为研究对象,列平衡方程:2692.152],[030sin 30sin ,0030cos 30cos ,0cm S AC S S FAC FF F F F F FF F F AC AC ACAC BC AC BC AC yBC AC x ⨯=≤=-==-︒-︒==︒-︒-=∑∑的截面积,查表得:为杆其中杆强度条件:解得:σ2578.35],[cm S BC S S FBC AC BC BCBC =≤的截面积,查表得:为杆其中杆强度条件:σ解得:kNF kN F F kN F F BC AC 8.3558.355502≤≤=≤=综合得:8-5 已知圆轴受外力偶矩m =2kNm,材料地许可切应力[τ]=60MPa. (1)试设计实心圆轴地直径D 1;(2)若该轴改为α=d /D =0.8地空心圆轴,式设计空心圆轴地内、外径d 2 、D 2m m D m W p 0554.01060200016][16][)1(3631=⨯⨯⨯=≥⇒≥πτπτ mD d m m D m W p 0528.0066.01060)8.01(200016][)1(16][)2(22364342=⨯==⨯⨯-⨯⨯=-⨯≥⇒≥απτπατ8-6 图示传动轴,主动轮B 输入功率P 1=368kW,从动轮A,C 输出地功率分别为P 2=147kW,P 3=221kW,轴地转速n =500r/min,材料地G =80GPa,许用切应力[]τ=70MPa,试设计轴地直径.Nm n p m 70285003689549954922=⨯=⨯= Nm n p m 66.42205002219549954933=⨯=⨯= 轴地最大扭矩为7028Nmm m Td d T 5.67][16][16133=≥⇒≤σπτπ由轴的强度条件:8-7阶梯形圆轴直径分别为d 1=40mm,d 2=70mm,轴上装有三个皮带轮,如图所示.己知由轮3输入地功率为N 3=3kW,轮1输出地功率为N 1=13kW,轴作匀速转动,转速n=200r/min,材料地许用切应力[]τ=60MPa,试校核轴地强度.8-8 图示传动轴传递地功率为 P =14kW,转速n =300r/min,[]τ=40MPa,试根据强度条件计算两种截面地直径:(1)实心圆截面地直径d ;(2)空心圆截面地内径d 1和外径d 2(d 1/ d 2=3/4).题8-6图题8-7图Nm n p T 62.4453001495499549=⨯=⨯= mm Td d T 4.38][16][161)1(33=≥⇒≤σπτπ实心轴的强度条件:mmd d mm Td d T 69.3259.431][16][1161)2(21342432=⨯==-≥⇒≤-αασπταπ)()(空心轴的强度条件:8-9传动轴地转速为n=500r/min,如图所示,主动轮1输入功率P1=368kW,从动轮2、3分别输出功率P 2=147kW,P3=221kW.己知[]τ=70MPa,试按强度条件求解下列问题:(1)试确定AB 段地直径d 1和BC 段地直径d 2. (2)若AB 和BC 两段选用同一直径,试确定直径d .. (3)主动轮和从动轮应如何安排才比较合理?计算外力偶矩,作扭矩图Nm n p M 06.70285003689549954911=⨯=⨯= Nm n p M 4.28075001479549954922=⨯=⨯=Nm n p M 66.42205002219549954933=⨯=⨯=题8-9图AB 段mm T d Nm T 80][16,06.70283111===τπ由强度条件: BC 段mm T d Nm T 5.67][16,66.42203222===τπ由强度条件: (2)将主动轮1和从动轮2位置互换,更合理这时:AB 段mm T d Nm T 9.58][16,4.28073111=='='τπ由强度条件:8-10一矩形拱面地简支木梁,梁上作用有均布荷载,已知:l =4m,b=140mm,h=210mm,q=2kN/m,弯曲时木木材地许用正应力[]σ=10MPa,试校核该梁地强度.简支梁地最大弯矩在中点处MPaMPa W M l kNm ql M 10][89.321.014.0614000,44281812max max 22max =<=⨯⨯===⨯⨯==σσ梁的最大正应力:所以,强度满足8-11图示简支梁上作用两个集中力,已知:l =6m,F 1=15kN,F 2=21kN,如果梁采用热轧普通工字钢,钢地许用应力[]σ=170MPa,试选择工字钢地型号.bh 题8-10图题8-11图作梁地弯矩图 由强度条件:3346max 5.22310235.21017038000][cm m M W =⨯=⨯=≥-σ 查表后选用20a 号工字钢8-12简支梁AB 如图所示.m a m l 2.0,2==.梁上地载荷q=10kN/m,=200kN.材料地许用应力为[][]MPa MPa 100,160==τσ.试选择适用地工字钢型号.由对称性知:kNm l x M kN F F B A 535.010)24.01(2001210)2(,210max =⨯--⨯-⨯====处3346max 3311031.31016053000][cm m M W =⨯=⨯=≥-σ2246max 5.31105.311010022100003][23cm m Q A =⨯=⨯⨯⨯=≥-τ综合后选用25a 号工字钢,23541.48,402cm A cm W ==题8-12图8-13图示槽形截面悬臂梁,F=10kN,M e =70kN·m,许用拉应力[σt ]=35MPa,许用压应力[σc ]=120MPa ,I z =1.02×108 mm 4,试校核梁地强度.作弯矩图,脆性材料且截面关于中性轴不对称,故危险截面为C+和C-两处C+截面最大正弯矩处,上压下拉MPa MPa t c3.471002.14.96503.751002.1)4.96250(504141=⨯⨯==⨯-⨯=--σσ C-截面最大负弯矩处,上拉下压MPa MPa c t 9.181002.14.96201.301002.1)4.96250(204242=⨯⨯==⨯-⨯=--σσ 由于][3.47][3.75max max t t c c MPa MPa σσσσ>=<=梁强度不足8-14 “T ”字形截面铸铁粱尺寸及载荷如图所示,若梁材料地拉伸许用应力为[]拉σ=40MPa,压缩许用应力为[]压σ= 160MPa,Z 轴通过截面地形心,已知截面对形心轴Z 地惯性矩410180cm I Z =,h=9.64cm,试计算该梁地许可载荷F.作梁地弯矩图,脆性材料且截面关于中性轴不对称,故危险截面为最大正负弯矩两处题8-14图最大正弯矩处,上压下拉。
工程力学练习册答案
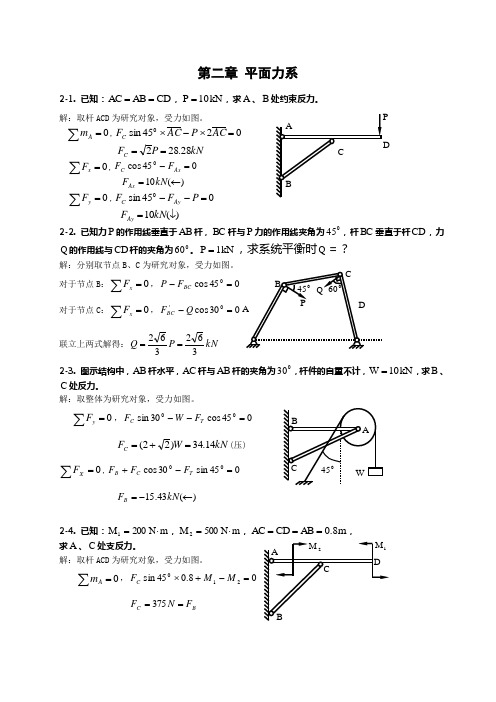
第二章 平面力系2-1. 已知:CD AB AC ==,kN 10P =,求A 、B 处约束反力。
解:取杆ACD 为研究对象,受力如图。
=∑A m ,0245sin 0=⨯-⨯AC P AC F CkN P F C 28.282==∑=0x F ,045cos 0=-Ax C F F )(10←=kN F Ax ∑=0y F ,045sin 0=--P F F Ay C)(10↓=kN F Ay2-2. 已知力P 的作用线垂直于AB 杆,BC 杆与P 力的作用线夹角为045,杆BC 垂直于杆CD ,力Q 的作用线与CD 杆的夹角为060。
kN1P =,求系统平衡时Q =?解:分别取节点B 、C 为研究对象,受力如图。
对于节点B :0=∑x F ,045cos 0=-BC F P对于节点C :0=∑x F ,030cos 0'=-Q F BC 联立上两式解得:kN P Q 362362==2-3. 图示结构中,AB 杆水平,AC 杆与AB 杆的夹角为030,杆件的自重不计,kN 10W =,求B 、C 处反力。
解:取整体为研究对象,受力如图。
0=∑yF ,045cos 30sin 00=--T C F W FkN W F C 14.34)22(=+=(压)0=∑XF,045sin30cos 0=-+T C B F F F)(43.15←-=kN F B2-4. 已知:m N 200M 1⋅=,m N 500M 2⋅=,m 0.8AB CD AC ===, 求A 、C 处支反力。
解:取杆ACD 为研究对象,受力如图。
0=∑A m ,08.045sin 210=-+⨯MM F C B C F N F ==3752-5. 已知AD 杆上固接一销钉,此销钉可以在BC 杆的滑道内无摩擦地滑动,系统平衡在图示位置,BC 与AD 成045,m N 1000M 1⋅=,求2M 。
解:取杆AD 为研究对象,受力如图。
《工程力学》作业3部分参考答案

《工程力学》作业3部分参考答案A 平衡方程B 位移条件C 物理关系D 位移互等定理 5.位移法典型方程中的系数ij k 代表1=∆j 在基本体系上产生的( C )A i ∆B j ∆C 第i 个附加约束中的约束反力D 第j 个附加约束中的约束反力 6.图6所示结构的位移法基本未知量数目为( D )A 2B 3C 4D 6C绕杆端逆时针转动D使梁的下侧受拉12.力矩分配法的直接对象是(A)A杆端弯矩B结点位移C多余未知力D未知反力13.汇交于一刚结点的各杆端弯矩分配系数之和等于(A)A 1 B0 C1/2 D-114.一般情况下结点的不平衡力矩总等于(A)A汇交于该结点的固定端弯矩之和B传递弯矩之和C结点集中力偶荷载D附加约束中的约束力矩15.下图所示连续梁结点B的不平衡力矩为(A)A-10kN·m B46 kN·mC18 kN·m D-28 kN·m三、填空题(每空2分,共20分)1.位移法基本体系是一组单跨超静定梁。
2.单跨超静定梁的形常数是指由杆端位移引起的杆端力。
条件;该方法可解超静定结构与静定结构。
利用叠加法F B M M M +⋅=θ1作最后M 图。
L602ql11p 1 设EI =1,则BA i =4i =4,AB i =2i =2 BD i =4i =4,DB i =2i =2BC i 作1M 图及p M 图11k =4BA i +4BD i +3BC =4+4+6=14……②F BAM =1212qL P F 1=1212qL …………………………③由①、②、③得1∆=1682qL5、作M 图AB M =2·1682qL -1212qL =-142qL1M 图p M 图M 图33.17 4.74kN⋅)9.47 M图(m。
工程力学(一)习题集及部分解答指导

工程力学学习参考资料第一章静力学基础一、判断题1-1.如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。
()1-2.作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是:这两个力大小相等、方向相反、沿同一条直线。
( ) 1-3.静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。
( ) 1-4.二力构件是指两端用铰链连接并且指受两个力作用的构件。
( ) 1-5.对刚体而言,力是滑移矢量,可沿其作用线移动。
()1-6.对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。
()1-7.作用在同一刚体的五个力构成的力多边形自行封闭,则此刚体一定处于平衡状态。
()1-8.只要两个力偶的力偶矩相等,则此两力偶就是等效力偶。
()二、单项选择题1-1.刚体受三力作用而处于平衡状态,则此三力的作用线( )。
A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2.力的可传性()。
A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体,又适用于刚体系统1-3.如果力F R是F1、F2二力的合力,且F1、F2不同向,用矢量方程表示为F R= F1+ F2,则三力大小之间的关系为()。
A、必有F R= F1+ F2B、不可能有F R= F1+ F2C、必有F R>F1, F R>F2D、必有F R<F1, F R<F21-4.作用在刚体上的一个力偶,若使其在作用面内转移,其结果是()。
A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小三、计算题1-1.已知:F1=2000N,F2=150N,F3=200N,F4=100N,各力的方向如图1-1所示。
试求各力在x、y轴上的投影。
解题提示F x= + F cosαF y= + F sinα注意:力的投影为代数量;式中:F x、F y的“+”的选取由力F的指向来确定;α为力F与x轴所夹的锐角。
工程力学练习册答案
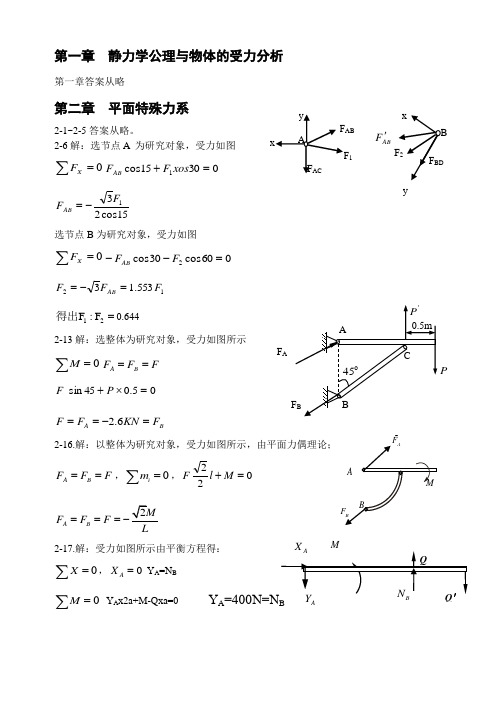
第一章 静力学公理与物体的受力分析第一章答案从略第二章 平面特殊力系2-1~2-5答案从略。
2-6解:选节点A 为研究对象,受力如图∑=0XF3015cos 1=+xos F F AB15cos 231F F AB -=选节点B 为研究对象,受力如图0=∑XF60cos 30cos 2=--F F AB12553.13F F F AB =-==21F :F 得出0.6442-13解:选整体为研究对象,受力如图所示∑=0M F F F B A ==_5.045sin =⨯+P FB A F KN F F =-==6.22-16.解:以整体为研究对象,受力如图所示,由平面力偶理论;F F F B A ==_,0=∑i m ,022=+M l FA B F F F L===-2-17.解:受力如图所示由平衡方程得:0X =∑,0AX= Y A =N B∑=0M Y A x2a+M-Qxa=0 Y AByP_A2-18. 解:先以杆AB 为研究对象, 由平面力偶系理论,设A F X P ==0im =∑ 10m p a -=1A mF X P a===再以杆件DC 为研究对象,/D F X =0im =∑ /20Fa m -=12m m =第三章 平面一般力系3-1~3-3从略3-4. 解:选BC 为研究对象,0=∑B M 0=-⨯M a N C a MN C =∑=0Y 0=-P YBP Y B=0=∑X 0=+CBN X aM NX CB-=-=选整体为研究对象,受力图如图0=∑X 0A C X N += aM N X C A -=-= ∑=0Y 102A Y P P q l ---= 122AY q l p =+ 0=∑A M 12()0,0232A AC am F M qa a M P Pa N a =-⋅---+=∑ 2332A qa Pa M =+3-5.解:先以杆BC 为研究对象()0=∑F m B,0tan 2=⋅⋅-⋅+θa Na Q M Cθθtan 2tan 2Qa M N C +⋅=AX F/F CN B X_C N C _B再以整体为研究对象∑=0X F , 0=+C A N X θθt a n 2t a n 2Qa M X A --=0=∑YF 0=--⋅-Q P a q YA Q P a q Y A ++⋅= ()0=∑F m A t a n222=+⋅⋅-⋅-⋅-⋅-M a N a Q a P a q m C A θa Q a P a q m A ⋅+⋅+⋅=222∴A 点的约束反力为:θθtan 2tan 2Qa M X A -⋅-= ,Q P a q Y A ++⋅= a Q a P a q m A ⋅+⋅+⋅=222C 点的约束反力为:θθtan 2tan 2Qa M N C +⋅= 3-7. 选起重机为研究对象0)(=∑F M F—01*23=+-Q N P E KNN E 10=∑=0Y 00=--+p N NF EKN N P N E F 50=-=∴ 再选CD 为研究对象0)(=∑F M C 06=-F D N N KN N D650=∴ =8.333KN 再选ABCD 为研究对象 0)(=∑F M A037512=+'-'-B F E D N N N N KN N B 100= 0=∑X 0=AX N ∑=0Y 0='-'-++'F EB D AYN N N N N N AY 33.48-=3-8.解:选DC 为研究对象,列平衡方程0=∑Y 0=-P N CP N C =选CA 为研究对象,=∑AM()025.2215.22=⨯-+⨯'B CN q N N B = ∑=0Y Y A = ∑=0X X A =AYBN EFX3-9. 解:先以杆BD 为研究对象b M N M b N F m D D B ==-⋅=∑,0,0)( 再以杆CB 为研究对象2,02,0)(FN b N b F F m Cc B ==⋅-⋅=∑ 再以整体为研究对象(图见原图)∑xF=0, 0=A XbMF qb Y N N F qb Y F A D c A y -+==++--=∑2,0,0 M Fbqb m b N M Fb b q m F m A D A A -+==∙+---=∑22,0222,0)(22最后再以杆AB 为研究对象∑xF=0, 0,033='='+''B BA X X X 2,0,033F b M Y Y qb Y F B B A y -='='+-=''∑ ∴A 处的约束反力为:M Fbqb m b M F qb Y X A A A -+=-+==22,2,02销钉B 对杆AB 处的约束反力为2,033Fb M Y X B B -='='''B X D F↑C N C2B X 2B YA X 3B Y AB 受力图3-10. 解:先以整体为研究对象()0=∑F m A,0075.210001=⨯+⋅EXN X E 2075-=()0=∑F m E, 01075.21000=⋅-⨯AX,N X A 2075=0=∑YF, 0=-+P Y Y E A (1)再以杆CE 为研究对象,()0=F m B, 015.011=⋅+⋅+⋅C E ET Y X,N Y E 2000=将E Y 回代到方程(1)中有N Y A 1000-=∴A 处的约束反力为:N X A 2075= ,N Y A 1000-=E 处的约束反力为:N X E 2075-= ,N Y E 2000=3-11. 选CD 为研究对象0=∑C M 得出Y D 选BCD 为研究对象, 0=∑B M 得出X D选整体为研究对象0=∑X X A =∑=0Y Y A =0=∑A M M A =3-12. 解:先以杆DE 为研究对象()0=∑F m D , 0223=⋅-⋅l F l N E , F N E 43= 再以杆BD 为研究对象()0=∑F m B ,03252342=⋅+⋅-⋅⋅-⋅l N l F l l q l N E CF l q N C 238+⋅=,最后以整体为研究对象0=∑X F ,02=+F X A ,2F X A -= 0=∑YF23-⋅-++F l q N N Y E C A 8743lq F Y A ⋅+-=()0=∑F m A0421272322=-⋅+⋅-⋅-⋅+⋅-M l N l F l F l N l q m E C AM l F l F l q m A +⋅+⋅-⋅=243432∴A 处的约束反力为:2FX A -= ,8743lq F Y A ⋅+-= ,M l F l F l q m A +⋅+⋅-⋅=243432 C 处的约束反力为:F l q N C 238+⋅=E 处的约束反力为:F N E 3= 3-13.选CB 研究对象,受力如图∑=0CM02cot =⨯-a S Pa BA α2cot αP S BA= 选CD 研究对象,受力如图∑=0C M 02=-M a S ED aM S ED 2=选整体研究对象,受力如图0=∑X 0=+--ED BA GS S X()M Pa aX G +=αcot 21∑=0Y 0=-P Y G P Y G =0=∑GM()(2c o t --++-a S S Pa M M BA ED G α()αcot 2Pa M abM G -=_E3-16. 解:因BCD 是二力杆,选ED 为研究对象,受力如图,由平面力偶系理论:∑=0M 060sin 3=+⨯-M a F E∑=0Y 030cos =+DB ES Y aM SF DBE 332-==在选AB 为研究对象,受力如图,均布荷载用集中力2qa 替代。
工程力学练习册习题答案汇总

工程力学练习册习题答案汇总一、选择题1. 工程力学中,力的三要素不包括以下哪一项?(D)A. 力的大小B. 力的方向C. 力的作用点D. 力的形状答案:D2. 平面汇交力系的平衡方程是以下哪一项?(B)A. ΣF = 0B. ΣF = 0,ΣM = 0C. ΣF = 0,ΣFy = 0D. ΣFy = 0,ΣM = 0答案:B3. 某物体受到两个力的作用,其合力为零,这两个力称为(C)。
A. 平衡力B. 等效力C. 共点力D. 力偶答案:C4. 在平面力偶系中,力偶的合力为(D)。
A. 零B. 力偶矩C. 两个力的合力D. 无法确定答案:D二、填空题1. 力的三要素是力的大小、力的方向和力的______。
答案:作用点2. 平面汇交力系的平衡方程是______和______。
答案:ΣF = 0,ΣM = 03. 在平面力偶系中,力偶的合力为______。
答案:零4. 某物体受到两个力的作用,其合力为零,这两个力称为______。
答案:共点力三、判断题1. 力的平行四边形法则可以用于求解力的合成与分解。
(√)2. 平面汇交力系的平衡方程只适用于平面力系。
(×)3. 在平面力偶系中,力偶的合力等于力偶矩。
(×)4. 某物体受到两个力的作用,其合力为零,这两个力一定共点。
(√)四、计算题1. 某物体受到两个力的作用,分别为 F1 = 10N,F2 = 20N,且 F1 与 F2 之间的夹角为30°。
求这两个力的合力。
答案:合力 F = √(F1^2 + F2^2 + 2F1F2cos30°) = √(10^2 + 20^2 + 2×10×20×0.866) ≈ 27.46N2. 某物体受到三个力的作用,分别为 F1 = 20N,F2 = 30N,F3 = 40N,且三个力的作用点分别为 A、B、C。
已知 A、B、C 三点构成一个等边三角形,求物体在三个力作用下的合力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题2-19图
2-20简易升降混凝土料斗装置如图所示,混凝土和料斗共重25kN,料斗与滑道间的静摩擦和动摩擦因数均为0.3。(1)如绳子的拉力分别为22kN与25kN时,料斗处于静止状态,求料斗与滑道间的摩擦力;(2)求料斗匀速上升和下降时绳子的拉力。
题2-4图
作BD两节点的受力图
联合解得:
2-5在四连杆机构ABCD的铰链B和C上分别作用有力F1和F2,,机构在图示位置平衡。求平衡时力F1和F2的大小间的关系。
题2-5图
以B、C节点为研究对象,作受力图
解得:
2-6匀质杆重W=100N,两端分别放在与水平面成300和600倾角的光滑斜面上,求平衡时这两斜面对杆的约束反力以及杆与水平面间的夹角。
4-2材料力学研究那些问题?它的主要任务是什么?
4-3材料力学的基本假设是什么?均匀性假设与各向同性假设有何区别?能否说“均匀性材料一定是各向同性材料”?
4-4杆件的轴线与横截面之间有何关系?
4-5杆件的基本变形形式有几种?请举出相应变形的工程实例。
第五章
5-1试求图示各杆1-1、2-2、3-3截面上的轴力,并作轴力图。
题5-1图
5-2试求图示各杆在1-1、2-2截面上的扭矩。并作出各杆的扭矩图。
题5-2图
5-3在变速箱中,低速轴的直径比高速轴的大,何故?
变速箱中轴传递的扭矩与轴的转速呈反比,低速轴传递的扭矩大,故轴径大。
5-4某传动轴,由电机带动,已知轴的转速 (转/分),电机输入的功率 ,试求作用在轴上的外力偶矩。
题2-24图
2-25均质长板AD重P,长为4m,用一短板BC支撑,如图所示。若AC=BC=AB=3m,BC板的自重不计。求A、B、C处的摩擦角各为多大才能使之保持平衡。
题2-25图
第三章
3-1 在正方体的顶角A和B处,分别作用力F1和F2,如图所示。求此两力在x,y,z轴上的投影和对x,y,z轴的矩。并将图中的力系向点O简化,用解析式表示主矢、主矩的大小和方向。
题2-2图
解得:
2-3如图所示,输电线ACB架在两电线杆之间,形成一下垂线,下垂距离CD=f=1m,两电线杆间距离AB=40m。电线ACB段重P=400N,可近视认为沿AB直线均匀分布,求电线的中点和两端的拉力。
题2-3图
以AC段电线为研究对象,三力汇交
2-4图示为一拔桩装置。在木桩的点A上系一绳,将绳的另一端固定在点C,在绳的点B系另一绳BE,将它的另一端固定在点E。然后在绳的点D用力向下拉,并使绳BD段水平,AB段铅直;DE段与水平线、CB段与铅直线成等角 =0.1rad(弧度)(当 很小时,tan )。如向下的拉力F=800N,求绳AB作用于桩上的拉力。
题2-20图
2-21图示两无重杆在B处用套筒式无重滑块连接,在AD杆上作用一力偶,其力偶矩MA=40N.m,滑块和AD间的摩擦因数fs=0.3。求保持系统平衡时力偶矩MC的范围。
题2-21图
2-22均质箱体A的宽度b=1m,高h=2m,重P=200kN,放在倾角 的斜面上。箱体与斜面间的摩擦因数fs=0.2。今在箱体的C点系一无重软绳,方向如图所示,绳的另一端绕过滑轮D挂一重物E,已知BC=a=1.8m。求使箱体处于平衡状态的重物E的重量。
6-7空心圆截面轴,外径 ,内径 ,扭矩 ,试计算距轴心 处的扭转切应力,以及横截面上的最大与最小扭转切应力。
6-8图示简支梁,求跨中截面 、 、 三点正应力。
题6-8图
6-9图示圆轴的外伸部分系空心轴。试作轴的弯矩图,并求轴内最大正应力。
题6-9图
6-10均布载荷作用下的简支梁如图所示。若分别采用截面面积相等的实心和空心圆截面,且 , ,试分别计算它们的最大正应力。并问空心截面比实心截面的最大正应力减小了百分之几?
题2-22图
2-23 尖劈顶重装置如图所示。在B块上受力P的作用。A与B块间的摩擦因数为fs(其他有滚珠处表示光滑)。如不计A和B块的重量,求使系统保持平衡的力F的值。
题2-23图
以整体为研究对象,显然水平和铅直方向约束力分别为
以A滑块为研究对象,分别作出两临界状态的力三角形
2-24砖夹的宽度为25cm,曲杆AGB与GCED在G点铰接。砖的重量为W,提砖的合力F作用在砖夹的对称中心线上,尺寸如图所示。如砖夹与砖之间的摩擦因数fs=0.5,试问b应为多大才能把砖夹起(b是G点到砖块上所受正压力作用线的垂直距离)
题5-9图
题5-9图
5-10图示外伸梁,承受集度为 的均布载荷作用。试问当 为何值时梁内的最大弯矩之值(即 )最小。
题5-10图
为保证梁的最大弯矩值最小,即最大正弯矩等于最大负弯矩
5-11在桥式起重机大梁上行走的小车(见图)其每个轮子对大梁的压力均为 ,试问小车在什么位置时梁内弯矩为最大值?并求出这一最大弯矩。
r=0.1m的滑轮。有一跨过滑轮的绳子,其一端水平地系于墙上,另一端悬挂有重P=1800N的重物。如AD=0.2m,BD=0.2m, ,且不计梁、杆、滑轮和绳的重量。求铰链A和杆BC对梁的约束反力。
题2-14图
1.以滑轮和杆为研究对象,受力分析如图
2.列平衡方程:
解得:
2-15如图所示,三绞拱由两半拱和三个铰链A,B,C构成,已知每个半拱重P=300kN,l=32m,h=10m。求支座A、B的约束反力。
工程力学
练习册
学校
学院
专业
学号
教师
姓名
第一章 静力学基础
1-1画出下列各图中物体A,构件AB,BC或ABC的受力图,未标重力的物体的重量不计,所有接触处均为光滑接触。
(a)
(b)
(c)
(d)
(e)
(f)
(g)
1-2试画出图示各题中AC杆(带销钉)和BC杆的受力图
(a)(b)(c)
(a)
1-3画出图中指定物体的受力图。所有摩擦均不计,各物自重除图中已画出的外均不计。
题2-8图
作两曲杆的受力图,BC是二力杆,AB只受力偶作用,因此A、B构成一对力偶。
即
2-9在图示结构中,各构件的自重略去不计,在构件BC上作用一力偶矩为M的力偶,各尺寸如图。求支座A的约束反力。
题2-9图
1作受力图
2、BC只受力偶作用,力偶只能与力偶平衡
3、构件ADC三力汇交
2-10四连杆机构ABCD中的AB=0.1m,CD=0.22m,杆AB及CD上各作用一力偶。在图示位置平衡。已知m1=0.4kN.m,杆重不计,求A、D两绞处的约束反力及力偶矩m2。
题3-4图
3-5均质长方形板ABCD重W=200N,用球铰链A和蝶形铰链B固定在墙上,并用绳EC维持在水平位置。求绳的拉力和支座的约束反力。
题3-5图
3-6挂物架如图所示,三杆的重量不计,用球铰链连接于O点,平面BOC是水平面,且OB=OC,角度如图。若在O点挂一重物G,重为1000N,求三杆所受的力。
题5-11图
;
第六章
6-1图示的杆件,若该杆的横截面面积 ,试计算杆内的最大拉应力与最大压应力。
题6-1图
6-2图示阶梯形圆截面杆,承受轴向载荷 与 作用, 与 段的直径分别为 与 ,如欲使 与 段横截面上的正应力相同,试求载荷 之值。
题6-2图
6-3题6-2图所示圆截面杆,已知载荷 , , 段的直径 ,如欲使 与 段横截面上的正应力相同,试求 段的直径。
受力分析如图:
受力分析如图:
2-13在图示a,b两连续梁中,已知q,M,a,及 ,不计梁的自重。求各连续梁在A,B,C三处的约束反力。
(a) (b)
题2-13图
1作受力图,BC杆受力偶作用
2.对AB杆列平衡方程
所以:
1.以BC为研究对象,列平衡方程
1.以AB为研究对象,列平衡方程
2-14水平梁AB由铰链A和杆BC所支持,如图所示。在梁上D处用销子安装半径为
题2-6图
2-7已知梁AB上作用一力偶,力偶矩为M,梁长为l,梁重不计。求在图a,b,两三种情况下,支座A和B的约束反力。
(a) (b)
题2-7图
(a) (注意,这里,A与B处约束力为负,表示实际方向与假定方向相反,结果应与你的受力图一致,不同的受力图其结果的表现形式也不同)
(b)
2-8在题图所示结构中二曲杆自重不计,曲杆AB上作用有主动力偶,其力偶矩为M,试求A和C点处的约束反力。
题3-6图
3-7一平行力系由五个力组成,力的大小和作用线的位置如图所示。图中小正方格的边长为10mm。求平行力系的合力。
题3-7图
3-8求下列各截面重心的位置。
1.建立图示坐标系
(a)
(b)
题3-8图
3-9试求振动打桩机中的偏心块(图中阴影线部分)的重心。已知 , , 。
题3-9图
第四章
4-1何谓构件的承载力?它由几个方面来衡量?
6-4设图示结构的1和2两部分皆为刚体,刚拉杆 的横截面直径为 ,试求拉杆内的应力。
题6-4图
1做受力图
2列平衡方程求解
解得F=6kN, FN=3kN, AB杆的应力为:
6-5某受扭圆管,外径 ,内径 ,横截面上的扭矩 ,试计算距轴心21mm处圆管横截面与纵截面上的扭转切应力。
6-6直径 的圆轴受扭矩 的作用。试求距轴心 处的切应力,并求横截面上的最大切应力。
(a)
(b)
(c)
(d)
(e)
(f)
(g)
第二章
2-1电动机重P=5000N,放在水平梁AC的中央,如图所示。梁的A端以铰链固定,另一端以撑杆BC支持,撑杆与水平梁的夹角为300。如忽略撑杆与梁的重量,求绞支座A、B处的约束反力。
