表A.6 皮尔逊相关的临界值(完整版)
皮尔逊相关系数的含义与计算
皮尔逊相关系数的含义与计算皮尔逊相关系数是统计学中常用的衡量两个变量之间相关性的指标。
它能够量化变量之间的线性相关程度，帮助我们了解它们之间的关系。
皮尔逊相关系数是以其提出者卡尔·皮尔逊的名字命名的，被广泛应用于各个领域，如经济学、社会学、心理学和生物学等。
含义和解释皮尔逊相关系数的取值范围是-1到1之间。
当系数值为1时，表示两个变量之间存在完全正向线性相关关系；当系数值为-1时，则表示两个变量之间存在完全负向线性相关关系；而当系数值为0时，则表示两个变量之间不存在线性相关关系。
所以，皮尔逊相关系数的绝对值越接近于1，表示两个变量之间的线性相关性越强。
不仅可以用皮尔逊相关系数来判断两个变量之间的相关性，还可以通过系数的正负来判定相关关系的方向。
当系数为正时，变量之间有正向相关；当系数为负时，则表明变量之间呈负向相关。
计算方法计算皮尔逊相关系数需要以下步骤：计算每个变量的平均值。
假设我们有两个变量X和Y，分别有n个数据点。
则X的平均值记为X_mean，Y的平均值记为Y_mean。
接下来，计算每个数据点与对应变量的平均值之差。
记为(X-X_mean)和(Y-Y_mean)。
然后，计算每个差值的乘积。
计算的公式为(X-X_mean)*(Y-Y_mean)。
将所有计算得到的乘积相加，得到总和Σ((X-X_mean)*(Y-Y_mean))。
计算每个差值的平方，并对所有平方值进行相加。
得到总和Σ((X-X_mean)2)和Σ((Y-Y_mean)2)。
将总和Σ((X-X_mean)(Y-Y_mean))除以√(Σ((X-X_mean)^2))√(Σ((Y-Y_mean)^2))，即为皮尔逊相关系数。
示例为了更好地理解皮尔逊相关系数的计算过程，我们以体重和身高之间的关系为例进行演示。
计算身高和体重的平均值：身高的平均值X_mean=(165+170+175+180+185)/5=175cm体重的平均值Y_mean=(60+65+70+75+80)/5=70kg接下来，计算每个数据点与平均值之差：(X-X_mean)=(165-175,170-175,175-175,180-175,185-175)=(-10,-5,0,5,10)(Y-Y_mean)=(60-70,65-70,70-70,75-70,80-70)=(-10,-5,0,5,10)然后，计算每个差值的乘积：(X-X_mean)(Y-Y_mean)=(-10-10,-5*-5,0*0,5*5,10*10)=(100,25,0,25,100)将所有计算得到的乘积相加，得到总和Σ((X-X_mean)*(Y-Y_mean))=250计算每个差值的平方，并对所有平方值进行相加：Σ((X-X_mean)^2)=100+25+0+25+100=250Σ((Y-Y_mean)^2)=100+25+0+25+100=250计算皮尔逊相关系数：pearson_correlation=Σ((X-X_mean)(Y-Y_mean))/(√(Σ((X-X_mean)^2))√(Σ((Y-Y_mean)^2)))=250/(√(250)*√(250))=250/(15.81*15.81)≈0.628由于皮尔逊相关系数的取值范围为-1到1，这个结果说明身高和体重之间存在一定程度的正向线性相关关系，但并不是完全强相关。
斯皮尔曼等级相关系数二
Pearson（皮尔逊）相关系数相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度。
如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：(1)、当相关系数为0时，X和Y两变量无关系。
(2)、当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间。
(3)、当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间。
相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度：相关系数0.8-1.0 极强相关0.6-0.8 强相关0.4-0.6 中等程度相关0.2-0.4 弱相关0.0-0.2 极弱相关或无相关Pearson（皮尔逊）相关系数1、简介皮尔逊相关也称为积差相关（或积矩相关）是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。
假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：公式一：公式二：公式三：公式四：以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。
2、适用范围当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：(1)、两个变量之间是线性关系，都是连续数据。
(2)、两个变量的总体是正态分布，或接近正态的单峰分布。
(3)、两个变量的观测值是成对的，每对观测值之间相互独立。
3、Matlab实现皮尔逊相关系数的Matlab实现（依据公式四实现）：[cpp]view plaincopy1.function coeff = myPearson(X , Y)2.% 本函数实现了皮尔逊相关系数的计算操作3.%4.% 输入：5.% X：输入的数值序列6.% Y：输入的数值序列7.%8.% 输出：9.% coeff：两个输入数值序列X，Y的相关系数10.%11.12.13.if length(X) ~= length(Y)14. error('两个数值数列的维数不相等');15.return;16.end17.18.fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X);19.fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 /length(X)));20.coeff = fenzi / fenmu;21.22.end %函数myPearson结束也可以使用Matlab中已有的函数计算皮尔逊相关系数：[cpp]view plaincopy1.coeff = corr(X , Y);。
相关系数检验临界值表文献
相关系数检验临界值表文献
相关系数检验临界值表是在统计学中用于判断两个变量之间相关性显著性的重要工具。
一般来说，我们使用Pearson相关系数或Spearman等级相关系数来衡量两个变量之间的相关性。
在进行相关系数检验时，我们需要比较计算得到的相关系数与临界值来判断相关性是否显著。
对于Pearson相关系数，一般使用t检验或者F检验来判断相关系数的显著性。
临界值表可以在统计学的相关教科书或者专业的统计学文献中找到。
一般来说，临界值表会根据所选的显著性水平（通常是0.05或0.01）和自由度来给出相应的临界值。
临界值表的构建是基于统计学原理和大量的模拟实验得出的，因此是经过严格验证和确认的。
在实际应用中，可以根据所用的统计软件或者统计工具来查找相应的临界值表，比如SPSS、R、Python中的stats模块等都提供了相应的临界值表供用户参考。
此外，也可以通过一些在线的统计学资源或者统计学论坛来获取相关系数检验临界值表的信息。
在使用临界值表时，需要注意所选的显著性水平和自由度，以确保选择正确的临界值进行判断。
总之，相关系数检验临界值表是统计学中非常重要的工具，可以帮助我们判断变量之间的相关性是否显著。
在实际应用中，可以通过各种途径获取相应的临界值表来进行相关系数检验。
临界相关系数
临界相关系数一、介绍临界相关系数是统计学中的一个重要概念，用于衡量两个变量之间的相关程度。
在统计分析中，我们经常需要确定两个变量之间的关联性，以便更好地理解和解释数据。
临界相关系数提供了一种衡量这种关联性的方法，可以帮助我们确定变量之间是否存在显著的相关性。
二、相关系数的定义相关系数是用来度量两个变量之间关联程度的统计量。
在实际应用中，最常用的相关系数是皮尔逊相关系数，也叫做线性相关系数。
皮尔逊相关系数的取值范围是-1到1，其中1表示完全正相关，-1表示完全负相关，0表示没有线性相关关系。
三、临界相关系数的概念临界相关系数是一种对皮尔逊相关系数进行显著性检验的方法。
在统计学中，我们通常希望判断观察到的相关系数是否具有统计显著性，即是否可以推断出变量之间的相关关系不是由于随机因素引起的。
临界相关系数提供了一个临界值，如果观察到的相关系数超过了这个临界值，我们可以认为这个相关系数是显著的。
四、计算临界相关系数计算临界相关系数需要先确定显著性水平，通常用α表示。
常见的显著性水平有0.05和0.01。
然后，根据样本量n和自由度df，查找对应的临界值。
临界相关系数可以在统计表格中找到，也可以使用统计软件进行计算。
五、临界相关系数的应用临界相关系数的应用非常广泛。
在社会科学研究中，临界相关系数可以用来分析调查问卷数据，帮助研究人员了解变量之间的关联性。
在金融领域，临界相关系数可以用来分析股票之间的关联性，帮助投资者进行风险管理和资产配置。
在医学研究中，临界相关系数可以用来分析疾病和遗传因素之间的关系，帮助医生制定治疗方案。
六、临界相关系数的局限性临界相关系数虽然在统计分析中起着重要作用，但也存在一些局限性。
首先，临界相关系数只能用来衡量线性关系，对于非线性关系无法准确判断。
其次，临界相关系数只能用来判断变量之间的关联性，无法确定因果关系。
最后，临界相关系数只能用来判断两个变量之间的关联性，对于多个变量之间的关系无法进行分析。
皮尔逊相关性分析
皮尔逊相关性分析皮尔逊相关性分析（Pearson correlation analysis）是统计学中常用的一种分析方法，用于衡量两个变量之间的相关程度。
它基于皮尔逊相关系数，可以评估变量之间的线性关系强度和方向。
本文将介绍皮尔逊相关性分析的原理、应用和计算方法。
一、原理皮尔逊相关系数是一种衡量两个变量之间相关性的统计量，取值范围从-1到1。
当相关系数为1时，表示两个变量完全正相关；当相关系数为-1时，表示两个变量完全负相关；当相关系数为0时，表示两个变量之间没有线性关系。
皮尔逊相关系数的计算公式如下：r = ∑((X_i - X)(Y_i - Ȳ)) / sqrt(∑((X_i - X)^2)∑((Y_i - Ȳ)^2))其中，r为皮尔逊相关系数，X_i和Y_i分别为两个变量的观测值，X和Ȳ分别为两个变量的均值。
二、应用皮尔逊相关性分析广泛应用于各个领域，可以帮助我们了解变量之间的关联程度，进而指导决策和分析。
以下是一些皮尔逊相关性分析的常见应用场景：1. 经济学在经济学中，我们可以使用皮尔逊相关性分析来研究不同经济指标之间的关系，例如国内生产总值（GDP）与消费支出、投资支出之间的相关性，以及失业率与通货膨胀率之间的相关性。
2. 市场营销在市场营销领域，皮尔逊相关性分析可以帮助我们了解不同广告渠道对销售额的影响程度，以及产品价格与销售量之间的相关性。
通过分析这些相关性，我们可以优化市场推广策略，提高销售业绩。
3. 医学研究医学研究中，我们可以使用皮尔逊相关性分析来研究不同因素对某种疾病发病率的影响。
例如，我们可以研究吸烟与肺癌之间的相关性，或者BMI指数与心血管疾病之间的相关性。
通过这些研究结果，我们可以更好地预防和治疗疾病。
三、计算方法进行皮尔逊相关性分析时，需要获取两个变量的相关数据，并使用统计软件进行计算。
下面以SPSS软件为例，介绍具体的计算步骤：1. 打开SPSS软件，并导入数据文件。
附表（临界值表）
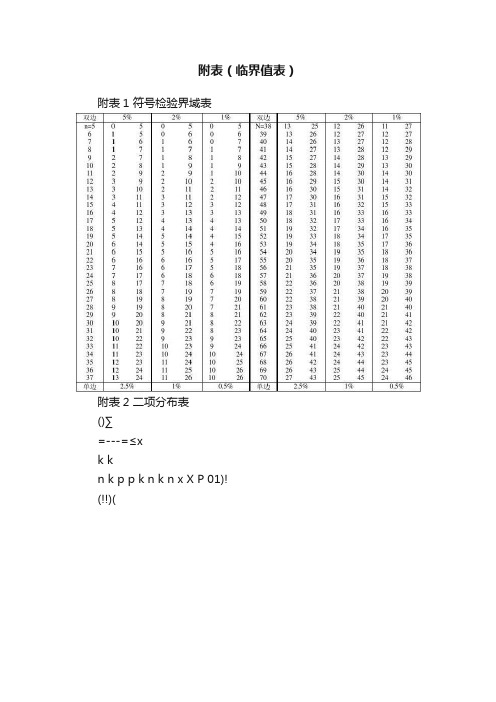
附表（临界值表）附表1 符号检验界域表附表2 二项分布表()∑=---=≤xk kn k p p k n k n x X P 01)!(!!)(附表3 标准正态分布表[])(1)(21)(22Z z dweZ W ZΦ-=-Φ-Φ-∞-?π附表4 威尔科克森带符号的秩和检验临界值（T值）表这里T是最大整数，即P（T≤t/n）≤a累积的单尾概率附表5 秩和检验临界值表括号数值表示样本容量（n1,n2）附表6 曼.怀特尼检验（U的临界值）单尾0.025或双尾0.05单尾0.05或双尾0.1附表7 游程检验的临界值表附表8 关于最长游程检验的临界值表当n1,n2≤25时,W a的值P(W≥W a)≤a Ⅰa=0.01Ⅱa=0.05附表9 游程长度平方和检验的临界值表附表10 X2分布表本表对自由度n的X2分布给出上侧分位数(X2a)表，P(X2n>X2a)=α附表11 Kolmogorov—Smirnov拟合优度检验临界值D n表附表12 Kolmogorov----Smirnov双样本检验中D的分子K D的临界值表(小样本) n1=n2≤30附表12续 Kolmogorov----Smirnov双样本检验中D的临界值表附表13 Spearman检验统计量的临界值近似右尾临界值r s*；P(r s>r s*)≤a；n=4--30注意：r s*的相应左尾临界值为-r s*附表14 Kendall检验统计量的临界值当n>60时,T的近似数可以由下式得到：W p≌X p18)52)(1(+-nnn式中X p的值可以从标准正态分布中得到。
上表中只给出肯达尔统计检验量T的数值W p，即T的数值的上界，而下界数可由以下关系式得出：W p=-W p临界域为：T>W p或T<-W p附表15 Kendall协和系数中S的临界值表附表16 Cruskall---Wallis检验统计量的临界值附表17 上、下游程分布的数目。
pearson(皮尔逊)相关系数
pearson(皮尔逊)相关系数皮尔逊相关系数是一种衡量两个变量之间线性关系的指标。
它是构建在统计学原理的基础上的，可以帮助人们确定两个变量之间的强度和方向。
它也是最常被使用的相关系数之一，适用于两个连续性变量。
1. 理解皮尔逊相关系数的概念：皮尔逊相关系数是一种衡量两个变量之间强度和方向的统计指标。
它的值在-1到1之间，0表示没有线性关系，正值表示正相关，负值表示负相关。
具体来说，当第一个变量增加时，如果第二个变量也增加，则称它们之间存在正相关；当第一个变量增加时，如果第二个变量减少，则称它们之间存在负相关。
2. 计算皮尔逊相关系数：皮尔逊相关系数的计算需要用到协方差和方差，公式如下：r = cov(X,Y) / (SD(X) * SD(Y))其中，r为皮尔逊相关系数，cov(X,Y)是X和Y的协方差，SD(X)和SD(Y)是X和Y的标准差。
3. 判断皮尔逊相关系数的显著性：如果想要知道皮尔逊相关系数是否显著，需要计算t值。
t值的计算公式如下：t = r * sqrt(n-2) / sqrt(1 - r^2)其中，n是样本个数。
当t值大于临界值时，皮尔逊相关系数就是显著的。
4. 了解皮尔逊相关系数的优缺点：皮尔逊相关系数有以下优点：计算简单、易于理解、适用范围广。
但它也有缺点，比如它只能测量线性关系，不能测量非线性关系，而且对异常值比较敏感。
在实际应用中，皮尔逊相关系数被广泛用于研究各种现象。
比如在医学领域中，可以用它研究两种疾病之间是否有关系；在经济学领域中，可以用它研究两个变量之间的关系，比如货币供应和通货膨胀之间的关系。
总之，皮尔逊相关系数是统计学中一个重要的工具，可以帮助人们更好地理解数据之间的关系。
相关系数临界值
相关系数临界值相关系数是统计学中常用的一种度量两个变量之间关系强度的指标。
它可以告诉我们两个变量之间的相关程度，从而帮助我们分析和理解数据之间的关系。
在进行相关性分析时，我们需要考虑相关系数的临界值，以确定关系是否显著。
本文将详细介绍相关系数的临界值，并讨论其在不同领域中的应用。
相关系数的临界值是指在给定显著性水平下，用于判断相关系数是否达到统计显著的阈值。
常用的显著性水平有0.05和0.01，分别代表了95%和99%的置信水平。
在使用相关系数进行分析时，我们希望找到的相关系数超过临界值，以确保所得到的结果不是由于随机误差引起的。
在统计学中，最常用的相关系数是皮尔逊相关系数。
在样本较大且满足正态分布的情况下，我们可以使用标准正态分布表来确定临界值。
对于显著性水平为0.05的双侧检验，临界值为±1.96；对于显著性水平为0.01的双侧检验，临界值为±2.58。
这意味着如果计算得到的相关系数大于1.96或小于-1.96，我们可以拒绝原假设，认为两个变量之间存在显著的相关关系。
然而，在样本较小、不满足正态性假设或相关系数的近似分布不明确的情况下，我们需要使用不同的方法来确定相关系数的临界值。
蒙特卡洛模拟是常用的一种方法，通过生成大量的随机数来模拟相关系数的分布。
根据蒙特卡洛模拟的结果，我们可以确定相应显著性水平下的临界值。
相关系数的临界值在不同领域中有着广泛的应用。
在社会科学研究中，相关性分析常用于探究人口统计学数据之间的关系，例如性别与收入、教育程度与就业率等。
临界值的确定可以帮助研究者确定变量之间的关系是否具有实际意义，从而进行更深入的分析。
在金融领域中，相关系数的临界值可以用于衡量资产之间的相关性。
例如，在投资组合管理中，我们希望找到相关系数较低的资产来构建多元化的投资组合，以降低风险。
临界值的使用可以帮助投资者确定哪些资产之间的关系是显著的，从而作出更明智的投资决策。
此外，在医学研究中，相关系数的临界值可以用于评估疾病的风险因素。
皮 尔逊相关性分析
皮尔逊相关性分析在统计学的广袤领域中，皮尔逊相关性分析是一项非常重要的工具，它帮助我们理解和揭示两个变量之间线性关系的强度和方向。
无论是在社会科学、自然科学，还是在日常生活的各种数据分析中，皮尔逊相关性分析都有着广泛的应用。
那么，什么是皮尔逊相关性分析呢？简单来说，它是一种用来衡量两个连续变量之间线性关联程度的统计方法。
想象一下，我们有两个变量，比如一个人的身高和体重。
我们想知道这两个变量之间是不是存在着某种规律，是身高越高体重就越重，还是两者之间没有明显的关系？这时候，皮尔逊相关性分析就派上用场了。
皮尔逊相关性系数（通常用 r 表示）的取值范围在－1 到 1 之间。
当 r 接近 1 时，表示两个变量之间存在很强的正线性相关关系，也就是说，一个变量的增加往往伴随着另一个变量的增加。
比如，我们研究学生的学习时间和考试成绩，发现学习时间越长，考试成绩往往越高，那么这两个变量之间可能就存在较强的正相关。
相反，当 r 接近－1 时，则表示两个变量之间存在很强的负线性相关关系，即一个变量的增加会伴随着另一个变量的减少。
举个例子，我们考察一个地区的气温和羽绒服的销量，随着气温的升高，羽绒服的销量通常会下降，这两个变量之间就可能存在较强的负相关。
而当 r 接近 0 时，则表明两个变量之间几乎不存在线性关系。
比如一个人的鞋子尺码和他的数学成绩，这两者之间很可能没有什么直接的线性关联。
为了更清楚地理解皮尔逊相关性分析，我们来看看它是如何计算的。
其实，这个计算过程涉及到一些数学公式，但我们可以用比较通俗的方式来解释。
大致来说，它是通过计算两个变量的协方差除以它们各自的标准差的乘积得到的。
协方差反映了两个变量变化的一致性程度，如果两个变量的变化趋势一致，协方差就为正；如果变化趋势相反，协方差就为负；如果两个变量相互独立，协方差就接近于 0 。
标准差则衡量了一个变量的离散程度，也就是数据的分散程度。
在实际应用中，皮尔逊相关性分析有着诸多重要的意义。
波段 皮尔逊相关系数-概述说明以及解释
波段皮尔逊相关系数-概述说明以及解释1.引言1.1 概述波段分析是一种技术分析方法，常用于股市、期货及金融市场的投资交易中。
它通过观察价格图表上的波动和震荡周期，以及相关的技术指标，来预测市场的价格走势和交易机会。
波段分析主要关注价格的短期波动，通常涵盖数天到数周的时间跨度。
皮尔逊相关系数是一种统计学方法，用来衡量两个变量之间的线性关系的强弱。
它的取值范围从-1到1，其中-1表示完全负相关，0表示无相关，1表示完全正相关。
皮尔逊相关系数常被用于研究变量之间的相关性，如股票收益率与经济指标的关系等。
本文将重点探讨波段分析和皮尔逊相关系数在金融市场中的应用。
首先，我们将简要介绍波段的定义和应用。
然后，我们将详细阐述皮尔逊相关系数的原理和计算方法。
最后，我们将总结波段与皮尔逊相关系数之间的关系，并展望未来研究的方向。
通过研究波段和皮尔逊相关系数，我们可以更好地理解和把握金融市场的行情走势，提高投资决策的准确性和效益。
本文的研究将为投资者和分析师提供有益的参考和指导，帮助他们做出更明智的投资决策，并为金融市场的稳定发展做出贡献。
文章结构是指文章整体的框架和组织方式，它包括引言、正文和结论等部分。
本文的结构如下：1. 引言1.1 概述1.2 文章结构1.3 目的2. 正文2.1 波段的定义和应用2.2 皮尔逊相关系数的介绍3. 结论3.1 波段与皮尔逊相关系数的关系总结3.2 对波段和皮尔逊相关系数的未来研究展望在文章结构部分，我们介绍了这篇长文的整体结构和各个部分的内容安排。
引言部分主要是引领读者进入主题，概述研究对象和研究目的，并简要介绍文章的结构。
正文部分是文章的核心内容，分为两个小节，分别介绍了波段的定义和应用，以及皮尔逊相关系数的介绍。
结论部分对前文的内容进行总结，并对波段和皮尔逊相关系数未来的研究方向进行展望。
文章结构的合理安排可以使读者更好地理解文章的内容，同时也有助于作者将自己的思路进行清晰的表达。
皮尔逊相关系数的学习
皮尔逊相关系数的学习在统计学中，皮尔逊积矩相关系数（英语：Pearson product-moment correlation coefficient，又称作 PPMCC或PCCs, 文章中常用r或Pearson’s r表示）用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间。
在自然科学领域中，该系数广泛用于度量两个变量之间的相关程度。
它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的。
这个相关系数也称作“皮尔森相关系数r”。
皮尔逊相关系数的定义两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商。
假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：公式一：1公式二：2公式三：3公式四：4以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。
皮尔逊相关系数的解释皮尔逊相关系数理解有两个角度1、以高中课本为例，将两组数据首先做Z分数处理之后，然后两组数据的乘积和除以样本数。
Z分数一般代表正态分布中数据偏离中心点的距离。
等于变量减掉平均数再除以标准差。
标准差则等于变量减掉平均数的平方和再除以样本数最后再开方。
所以我们可以将公式依次精简为：3以下为python的实现：123 4 5 6 7 8 9 10 11 12 13 14 15 16 17from math import sqrt#返回p1和p2的皮尔逊相关系数def sim_pearson(prefs,p1,p2):#得到双方曾评价过的物品列表si = {}for item in prefs[p1]:if item in prefs[p2]:si[item] = 1#得到列表元素个数n = len(si)#如果两者没有共同之处，则返回1 if not n:return 1#对所有偏好求和2、 按照大学的线性数学（几何学）的解释，可以看做是两组数据的向量夹角的余弦。
cca皮尔森相关系数
cca皮尔森相关系数
摘要：
1.皮尔森相关系数的定义和意义
2.皮尔森相关系数的计算方法和公式
3.皮尔森相关系数的应用和示例
4.皮尔森相关系数的局限性和注意事项
正文：
皮尔森相关系数，又称作皮尔逊相关系数，是由英国数学家卡尔·皮尔逊在19 世纪末20 世纪初提出的一种衡量两个变量之间线性相关程度的统计指标。
皮尔森相关系数的取值范围在-1 到1 之间，当相关系数为1 时，表示两个变量完全正相关；当相关系数为-1 时，表示两个变量完全负相关；当相关系数为0 时，表示两个变量之间不存在线性相关关系。
皮尔森相关系数的计算方法是通过公式：r = ∑((x_i-平均x)*(y_i-平均y))/√∑(x_i-平均x)^2 * ∑(y_i-平均y)^2 来进行的，其中x_i 和y_i 代表每一个样本的数值，平均x 和平均y 代表所有样本数值的平均值。
皮尔森相关系数的应用十分广泛，它可以用于衡量各种变量之间的相关性，如经济学中的物价指数和经济增长率，生物学中的生物体长度和体重，甚至是社会科学中的学生成绩和家庭收入等。
然而，皮尔森相关系数也有其局限性。
首先，它只能用来衡量线性关系的强度，对于非线性关系无法准确衡量。
其次，它的值受到样本数量和样本分布的影响，有时可能会出现误判。
皮尔逊相关性分析
皮尔逊相关性分析皮尔逊相关性分析是一种广泛应用于探索两个连续变量之间关系强度和方向的方法。
术语“相关性”指的是两个或更多事物相互关联的程度。
在统计学中，特别指变量间的线性关系，这就需要皮尔逊相关性分析这一工具，用于衡量和解释此类关系。
首先，我们来了解一下皮尔逊相关系数。
皮尔逊相关系数是一种度量两个变量之间线性关系强度和方向的值，它的取值范围在-1到1之间。
这个系数的大小说明了变量之间的关系强度，正负号则表明关系的方向。
超过0的系数表示正相关，也就是一个变量增加，另一个也会增加。
小于0的系数表示两者为负相关，当一个变量增加时，另一个会减少。
比如，人的身高和体重通常是正相关；而车辆的燃油消耗量和其行驶的速度则是负相关。
基于皮尔逊相关性分析的计算方法，我们可以进行更深入的探讨。
计算两个变量X和Y的皮尔逊相关系数的公式为: r = Σ(Xi - X平均) * (Yi - Y平均) / [(n - 1) * sX *sY] 其中，Xi和Yi是X和Y的各观测值，sX和sY是X和Y的样本标准差。
在这里，我们把变量的每个观察值减去其平均值，意味着我们正在处理的数据是中心化的。
在实际研究中运用皮尔逊相关性分析时，有几点需要注意。
首先，除非两个变量是线性关系，否则皮尔逊系数可能会低估真实的关联。
其次，皮尔逊相关系数很大程度上依赖于样本。
一组样本内所观测到的关联可能不会反映总体的真实情况，所以我们需要通过抽样误差来判断关联的精确度。
再者，我们应时刻警惕假相关。
即使皮尔逊系数很高，我们也不能轻易推断两者之中存在因果关系。
综上所述，皮尔逊相关性分析是衡量变量间线性关系的重要工具，不仅能帮助我们理解变量间的联系，但同时也需注意其局限性和应用时的注意事项。
只有透彻理解并熟练掌握，在实际应用中才能发挥其应有的价值。
皮尔逊相关系数知识讲解
精品文档简单相关系数又称皮尔逊相关系数，它描述了两个定距变量间联系的紧密程度。
样本的简单相关系数一般用r 表示，计算公式为：其中n 为样本量，分别为两个变量的观测值和均值。
r 描述的是两个变量间线性相关强弱的程度。
r的取值在-1与+1之间，若r> 0，表明两个变量是正相关，即一个变量的值越大，另一个变量的值也会越大；若r v 0,表明两个变量是负相关，即一个变量的值越大另一个变量的值反而会越小。
r 的绝对值越大表明相关性越强，要注意的是这里并不存在因果关系。
若r=0，表明两个变量间不是线性相关，但有可能是其他方式的相关（比如曲线方式）利用样本相关系数推断总体中两个变量是否相关, 可以用t 统计量对总体相关系数为0 的原假设进行检验。
若t 检验显著,则拒绝原假设,即两个变量是线性相关的；若t 检验不显著,则不能拒绝原假设,即两个变量不是线性相关的皮尔逊相关系数又称“皮尔逊积矩相关系数” ,对两个定距变量（例如,年龄和身高）的关系强度的测量，简写T。
这一测量也可用作对显著性的一种检验，其方法是检验解消假设：总体中的T值为0。
若样本T实际上不等于0，则解消假设可加否定，从而我们可以满意地看到, 这两个变量不是无关的, 在统计显著性层次上它们是有关的。
例如, 若我们有一个较大的样本，并发现一个高的样本值T（例如，90）,那么我们不妨否定这一解消假设：这个样本是来自一个其真正的T值为0的总体，因为假若真正的总体值是0，我们就不可能单纯碰巧取得一个如此高的样本。
T的变化从-1 （全负关系），通过0 （无关系或无关性），到+1（全正关系）。
从直线关系和曲线关系之间的关系来说，T是对直线关系的一种测量。
对T 有两个主要的解释：（1）T 2 =所解释的方差额。
（2）T测量围绕回归线散布的程度，也就是说,它告诉我们,我们用回归线可预测的准确程度有多大。
1 、建立数据库2 、按analyze ---- correlate ------ bivarizte 顺序单击菜单项,展开一个对话框,在correlationcoefficients中就有Pearson相关系数的选项简单相关系数又称皮尔逊相关系数, 它描述了两个定距变量间联系的紧密程度。
Pearson相关系数简介
2.相关类型：
3.作用：粗略地给出了两个变量的关联类型与程度
通过相关散布图的形状，我们大概可以判 断变量之间相关程度的强弱、方向和性质，但 并不能得知其相关的确切程度。
为精确了解变量间的相关程度，还需作进 一步统计分析，求出描述变量间相关程度与变 化方向的量数，即相关系数。总体相关系数用 p表示，样本相关系数用r表示。
2
XX
X2
X2
n
lYY
2
Y Y
Y2
Y2
n
l XY
X
X Y
Y
XY
X Y
n
例13-1
测得某地15名正常成年人的血铅X和24小 时的尿铅Y，试分析血铅与24小时尿铅之 间是否直线相关。
15名自愿者的血铅和24小时尿铅测量值（μmol/L）
编号 X
Y 编号 X
Y
1 0.11 0.14 9 0.23 0.24
17.189 1 r2
n2
3. v=15-2=13，查界值表,P<0.001，拒绝H0，认为血 线性相关的前提条件是X、Y都服从正态分布（双 变量正态分布）
2. 当散点图有线性趋势时，才可进行线性相关分析 3. 必须在假设检验认为相关的前提下才能以r的大
用水平轴x上的数代表父亲身高垂直轴y上的数代表儿子的身高1078个点所形成的图形是一个散点它的形状象一块橄榄状的云中间的点密集边沿的点稀少其主要部分是一个椭圆
两变量关联性分析
pearson相关系数介绍
世间万物是普遍联系的
医学上，许多现象之间也都有相互联系，例 如：身高与体重、体温与脉搏、年龄与血压、 产前检查与婴儿体重、乙肝病毒与乙肝等。 在这些有关系的现象中，它们之间联系的程 度和性质也各不相同。
皮尔逊相关系数表
皮尔逊相关系数表
皮尔逊相关系数表是用来衡量两个变量之间线性相关程度的统计方法，取值范围在-1到1之间。
用数学公式表示为：
r = (Σ(X-μx)(Y-μy))/√(Σ(X-μx)²Σ(Y-μy)²)
其中，X和Y是两个变量的值，μx和μy分别是X和Y的平
均值。
根据皮尔逊相关系数的取值，可以有以下判断：
- 当r=1时，表示两个变量完全正相关；
- 当r=0时，表示两个变量之间没有线性相关关系；
- 当r=-1时，表示两个变量完全负相关。
此外，皮尔逊相关系数还可以根据r的绝对值大小来判断相关
程度的强弱：
- 当|r|≈1时，表示相关性强；
- 当|r|≈0时，表示相关性弱。
一般情况下，根据常见的经验判断，r的绝对值大于0.7时，
认为相关性较强；当r的绝对值大于0.3时，认为相关性较弱。