高等数学复旦大学出版第三版上册课后答案习...
高等数学上复旦第三版 课后习题答案

283高等数学上(修订版)(复旦出版社)习题六 无穷数级 答案详解1.写出下列级数的一般项: (1)1111357++++ ;(2)22242462468x x x x x ++++⋅⋅⋅⋅⋅⋅ ;(3)35793579a a a a -+-+ ;解:(1)121n U n =-; (2)()2!!2n n xU n =;(3)()211121n n n a U n ++=-+; 2.求下列级数的和: (1)()()()1111n x n x n x n ∞=+-+++∑;(2)()1221n n n n ∞=+-++∑;(3)23111555+++ ; 解:(1)()()()()()()()111111211n u x n x n x n x n x n x n x n =+-+++⎛⎫-=⎪+-++++⎝⎭284从而()()()()()()()()()()()()()()11111211212231111111211n S x x x x x x x x x n x n x n x n x x x n x n ⎛-+-= +++++++⎝⎫++-⎪+-++++⎭⎛⎫-=⎪++++⎝⎭因此()1lim 21n n S x x →∞=+,故级数的和为()121x x +(2)因为()()211n U n n n n =-+-++- 从而()()()()()()()()324332215443211211211221n S n n n n n n n n =-+-----+-++---+-++-=+-++-=+-+++所以lim 12n n S →∞=-,即级数的和为12-. (3)因为21115551115511511145n nn n S =+++⎡⎤⎛⎫-⎢⎥ ⎪⎝⎭⎣⎦=-⎡⎤⎛⎫=-⎢⎥ ⎪⎝⎭⎣⎦ 从而1lim 4n n S →∞=,即级数的和为14. 3.判定下列级数的敛散性: (1) ()11n n n ∞=+-∑;(2)()()11111661111165451n n +++++⋅⋅⋅-+ ; (3) ()23133222213333n n n --+-++- ;285(4)311115555n +++++ ; 解:(1) ()()()3212111n S n n n =+++-+--=+-从而lim n n S →∞=+∞,故级数发散. (2) 1111111115661111165451111551n S n n n ⎛⎫=-+-+-++-⎪-+⎝⎭⎛⎫=- ⎪+⎝⎭从而1lim 5n n S →∞=,故原级数收敛,其和为15. (3)此级数为23q =-的等比级数,且|q |<1,故级数收敛. (4)∵15n n U =,而lim 10n n U →∞=≠,故级数发散. 4.利用柯西审敛原理判别下列级数的敛散性:(1) ()111n n n +∞=-∑;(2)1cos 2nn nx∞=∑; (3)1111313233n n n n ∞=⎛⎫+- ⎪+++⎝⎭∑. 解:(1)当P 为偶数时,()()()()122341111112311111231111112112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n p n n n +++++++++++----=++++++++-+--=++++⎛⎫⎛⎫-=----- ⎪ ⎪+-+-++++⎝⎭⎝⎭<+当P 为奇数时,286()()()()1223411111123111112311111112311n n n pn n n n p U U U n n n n pn n n n pn p n p n n n n +++++++++++----=++++++++-+-+=++++⎛⎫⎛⎫-=---- ⎪ ⎪+-++++⎝⎭⎝⎭<+因而,对于任何自然数P ,都有12111n n n p U U U n n++++++<<+ , ∀ε>0,取11N ε⎡⎤=+⎢⎥⎣⎦,则当n >N 时,对任何自然数P 恒有12n n n pU U U ε++++++< 成立,由柯西审敛原理知,级数()111n n n +∞=-∑收敛. (2)对于任意自然数P ,都有()()()1212121cos cos cos 12222111222111221121112212n n n p n n n p n n n p n p n p nU U U x n p x xn n ++++++++++++++++=+++≤+++⎛⎫- ⎪⎝⎭=-⎛⎫=- ⎪⎝⎭<于是, ∀ε>0(0<ε<1),∃N =21log ε⎡⎤⎢⎥⎣⎦,当n >N 时,对任意的自然数P都有12n n n p U U U ε++++++< 成立,由柯西审敛原理知,该级数收敛. (3)取P =n ,则287()()()()()121111113113123133213223231131132161112n n n pU U U n n n n n n n n n n ++++++⎛⎫=+-+++- ⎪++++++⋅+⋅+⋅+⎝⎭≥++++⋅+≥+> 从而取0112ε=,则对任意的n ∈N ,都存在P =n 所得120n n n p U U U ε++++++> ,由柯西审敛原理知,原级数发散.5.用比较审敛法判别下列级数的敛散性. (1)()()111465735n n ++++⋅⋅++ ;(2)22212131112131nn +++++++++++ (3)1πsin 3n n ∞=∑;(4) 3112n n∞=+∑;(5)()1101nn a a∞=>+∑;(6)()1121nn ∞=-∑.解:(1)∵ ()()21135n U nn n =<++而211n n ∞=∑收敛,由比较审敛法知1n n U ∞=∑收敛. (2)∵221111n n n U n n n n++=≥=++ 而11n n∞=∑发散,由比较审敛法知,原级数发散.(3)∵ππsinsin 33lim lim ππ1π33n nn n n n→∞→∞=⋅=288而1π3n n ∞=∑收敛,故1πsin 3n n ∞=∑也收敛.(4)∵33321112n U nnn=<=+ 而3121n n∞=∑收敛,故3112n n∞=+∑收敛.(5)当a >1时,111n n n U a a =<+,而11n n a ∞=∑收敛,故111nn a∞=+∑也收敛. 当a =1时,11lim lim 022n n n U →∞→∞==≠,级数发散. 当0<a <1时,1lim lim 101n n n n U a →∞→∞==≠+,级数发散. 综上所述,当a >1时,原级数收敛,当0<a ≤1时,原级数发散.(6)由021limln 2xx x →-=知121lim ln 211nx n→∞-=<而11n n∞=∑发散,由比较审敛法知()1121nn ∞=-∑发散.6.用比值判别法判别下列级数的敛散性:(1) 213n n n ∞=∑;(2)1!31nn n ∞=+∑; (3)232333*********nn n +++++⋅⋅⋅⋅ ; (1) 12!n n n n n ∞=⋅∑解:(1) 23n n n U =,()2112311lim lim 133n n n n n n U n U n ++→∞→∞+=⋅=<, 由比值审敛法知,级数收敛.289(2) ()()111!311lim lim 31!31lim 131n n n n n nn n n U n U n n ++→∞→∞+→∞++=⋅++=⋅++=+∞所以原级数发散.(3) ()()11132lim lim 2313lim 21312n nn n n n n nn U n U n n n +++→∞→∞→∞⋅=⋅⋅+=+=> 所以原级数发散.(4) ()()1112!1lim lim 2!1lim 21122lim 1e 11n nn n n n n nnn n n U n n U n n n n n +++→∞→∞→∞→∞⋅+=⋅⋅+⎛⎫= ⎪+⎝⎭==<⎛⎫+ ⎪⎝⎭故原级数收敛.7.用根值判别法判别下列级数的敛散性:(1) 1531nn n n ∞=⎛⎫⎪+⎝⎭∑;(2)()[]11ln 1nn n ∞=+∑;(3) 21131n n n n -∞=⎛⎫⎪-⎝⎭∑;(4) 1nn n b a ∞=⎛⎫⎪⎝⎭∑,其中a n →a (n →∞),a n ,b ,a 均为正数.解:(1)55lim lim 1313n n n n n U n →∞→∞==>+, 故原级数发散.(2) ()1lim lim 01ln 1n n n n U n →∞→∞==<+,290故原级数收敛.(3)121lim lim 1931nn nn n n U n -→∞→∞⎛⎫==< ⎪-⎝⎭, 故原级数收敛.(4) limlim nn n n n nb b b a a a →∞→∞⎛⎫== ⎪⎝⎭, 当b <a 时,ba <1,原级数收敛;当b >a 时,b a>1,原级数发散;当b =a 时,b a=1,无法判定其敛散性.8.判定下列级数是否收敛?若收敛,是绝对收敛还是条件收敛?(1)1111234-+-+ ;(2)()()1111ln 1n n n ∞-=-+∑;(3) 2341111111153535353⋅-⋅+⋅-⋅+ ;(4)()21121!n n n n ∞-=-∑; (5)()()1111n n R n αα∞-=∈-∑;(6) ()11111123nn n n ∞=⎛⎫-++++ ⎪⎝⎭∑ . 解:(1)()111n n U n -=-,级数1n n U ∞=∑是交错级数,且满足111n n >+,1lim 0n n →∞=,由莱布尼茨判别法级数收敛,又11121n n n U n∞∞===∑∑是P <1的P级数,所以1n n U ∞=∑发散,故原级数条件收敛.(2)()()111ln 1n n U n -=-+,()()1111ln 1n n n ∞---+∑为交错级数,且()()11ln ln 12n n >++,()1lim 0ln 1n n →∞=+,由莱布尼茨判别法知原级数收敛,但由于()11ln 11n U n n =≥++291所以,1n n U ∞=∑发散,所以原级数条件收敛.(3)()11153n n n U -=-⋅民,显然1111115353n n n n n n U ∞∞∞=====⋅∑∑∑,而113nn ∞=∑是收敛的等比级数,故1n n U ∞=∑收敛,所以原级数绝对收敛.(4)因为2112lim lim 1n n n n nU U n ++→∞→∞==+∞+. 故可得1n n U U +>,得lim0n n U →∞≠, ∴lim 0n n U →∞≠,原级数发散. (5)当α>1时,由级数11n nα∞=∑收敛得原级数绝对收敛. 当0<α≤1时,交错级数()1111n n n α∞-=-∑满足条件:()111n n αα>+;1lim 0n n α→∞=,由莱布尼茨判别法知级数收敛,但这时()111111n n n nn αα∞∞-===-∑∑发散,所以原级数条件收敛.当α≤0时,lim0n n U →∞≠,所以原级数发散. (6)由于11111123n nn ⎛⎫⋅>++++ ⎪⎝⎭而11n n∞=∑发散,由此较审敛法知级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 发散. 记1111123n U nn ⎛⎫=⋅++++ ⎪⎝⎭ ,则292()()()()()()1222111111123111111112311111111231110n n U U n n n n n n n n n n n n n n +⎛⎫⎛⎫-=-++++- ⎪⎪+⎝⎭⎝⎭+⎛⎫=-++++ ⎪⎝⎭++⎛⎫⎛⎫-=++++ ⎪ ⎪⎝⎭+++⎝⎭>即1n n U U +>又01111lim lim 12311d n n n n U n n x n x→∞→∞⎛⎫=++++ ⎪⎝⎭=⎰ 由0111lim d lim 01t t t t x t x→+∞→+∞==⎰ 知lim 0n n U →∞=,由莱布尼茨判别法,原级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 收敛,而且是条件收敛.9.判别下列函数项级数在所示区间上的一致收敛性.(1) ()1!1nn x n ∞=-∑,x ∈[-3,3]; (2) 21nn x n ∞=∑,x ∈[0,1];(3) 1sin 3n n nx∞=∑,x ∈(-∞,+∞); (4)1!nxn e n -∞=∑,|x |<5; (5)3521cos n nxn x∞=+∑,x ∈(-∞,+∞)解:(1)∵()()3!!11nnx n n ≤--,x ∈[-3,3],而由比值审敛法可知()13!1nn n ∞=-∑收敛,所以原级数在 [-3,3]上一致收敛.(2)∵221nx n n≤,x ∈[0,1],293而211n n∞=∑收敛,所以原级数在[0,1]上一致收敛. (3)∵1sin 33n n nx ≤,x ∈(-∞,+∞),而113nn ∞=∑是收敛的等比级数,所以原级数在(-∞,+∞)上一致收敛. (4)因为5!!nnx ee n n -≤,x ∈(-5,5), 由比值审敛法可知51!nn e n ∞=∑收敛,故原级数在(-5,5)上一致收敛.(5)∵53523cos 1nxn xn≤+,x ∈(-∞,+∞),而5131n n∞=∑是收敛的P -级数,所以原级数在(-∞,+∞)上一致收敛.10.若在区间Ⅰ上,对任何自然数n .都有|U n (x )|≤V n (x ),则当()1n n V x ∞=∑在Ⅰ上一致收敛时,级数()1n n U x ∞=∑在这区间Ⅰ上也一致收敛.证:由()1n n V x ∞=∑在Ⅰ上一致收敛知, ∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,于是,∀ε>0,∃N (ε)>0,使得当n >N 时,∀x ∈Ⅰ有|U n +1(x )+U n +2(x )+…+U n +p (x )|≤V n +1(x )+V n +2(x )+…+V n +p (x ) ≤|V n +1(x )+V n +2(x )+…+V n +p (x )|<ε,因此,级数()1n n U x ∞=∑在区间Ⅰ上处处收敛,由x 的任意性和与x 的无关294性,可知()1n n U x ∞=∑在Ⅰ上一致收敛.11.求下列幂级数的收敛半径及收敛域:(1)x +2x 2+3x 3+…+nx n +…; (2)1!nn x n n ∞=⎛⎫⎪⎝⎭∑;(3)21121n n x n -∞=-∑; (4)()2112nn x n n∞=-⋅∑; 解:(1)因为11limlim 1n n n n a n a n ρ+→∞→∞+===,所以收敛半径11R ρ==收敛区间为(-1,1),而当x =±1时,级数变为()11n n n ∞=-∑,由lim(1)0n x nn →-≠知级数1(1)nn n ∞=-∑发散,所以级数的收敛域为(-1,1).(2)因为()()1111!11lim lim lim lim e 1!11nn n n n n n n n na n n n a n n n n ρ-+-+→∞→∞→∞→∞⎡⎤+⎛⎫⎛⎫==⋅===+ ⎪⎢⎥ ⎪+⎝⎭+⎝⎭⎣⎦ 所以收敛半径1e R ρ==,收敛区间为(-e,e).当x =e 时,级数变为1e nn n n n∞=∑;应用洛必达法则求得()10e e1lim 2xx x x →-+=-,故有111lim 12n n n a n a +→∞⎛⎫-=-<⎪⎝⎭由拉阿伯判别法知,级数发散;易知x =-e 时,级数也发散,故收敛域为(-e,e).(3)级数缺少偶次幂项.根据比值审敛法求收敛半径.211212221lim lim 2121lim21n n n n n nn U x n U n x n x n x ++-→∞→∞→∞-=⋅+-=⋅+= 所以当x 2<1即|x |<1时,级数收敛,x 2>1即|x |>1时,级数发散,故295收敛半径R =1.当x =1时,级数变为1121n n ∞=-∑,当x =-1时,级数变为1121n n ∞=--∑,由1121lim 012n n n→∞-=>知,1121n n ∞=-∑发散,从而1121n n ∞=--∑也发散,故原级数的收敛域为(-1,1). (4)令t =x -1,则级数变为212nn t n n∞=⋅∑,因为()()2122lim lim 1211n n n na n na n n ρ+→∞→∞⋅===⋅++ 所以收敛半径为R =1.收敛区间为 -1<x -1<1 即0<x <2.当t =1时,级数3112n n ∞=∑收敛,当t =-1时,级数()31112n n n ∞=-⋅∑为交错级数,由莱布尼茨判别法知其收敛.所以,原级数收敛域为 0≤x ≤2,即[0,2] 12.利用幂级数的性质,求下列级数的和函数: (1)21n n nx∞+=∑;(2) 22021n n x n +∞=+∑;解:(1)由()321lim n n n x n x nx++→∞+=知,当|x |=<1时,原级数收敛,而当|x |=1时,21n n nx ∞+=∑的通项不趋于0,从而发散,故级数的收敛域为(-1,1).记 ()23111n n n n S nxxnxx ∞∞+-====∑∑易知11n n nx∞-=∑的收敛域为(-1,1),记()111n n S n xx ∞-==∑296则()1011xn n x S x x x∞===-∑⎰ 于是()()12111x S x x x '⎛⎫== ⎪-⎝⎭-,所以()()()3211x S x x x =<-(2)由2422221lim 23n n n x n x n x++→∞+=⋅+知,原级数当|x |<1时收敛,而当|x |=1时,原级数发散,故原级数的收敛域为(-1,1),记()2221002121n n n n x x S x x n n ++∞∞====++∑∑,易知级数21021n n x n +∞=+∑收敛域为(-1,1),记()211021n n x S x n +∞==+∑,则()21211n n S x x x∞='==-∑, 故()1011d ln 21xx S x x x +'=-⎰ 即()()1111ln 021x S S x x +-=-,()100S =,所以()()()11ln 121x xS xS x x x x+==<-13.将下列函数展开成x 的幂级数,并求展开式成立的区间: (1)f (x )=ln(2+x ); (2)f (x )=cos 2x ; (3)f (x )=(1+x )ln(1+x ); (4)()221x f x x=+;(5)()23xf x x=+; (6)()()1e e 2x x f x -=-; (7)f (x )=e x cos x ;(8)()()212f x x =-.解:(1)()()ln ln 2ln 2ln 11222x x f x x ⎛⎫⎛⎫===++++ ⎪ ⎪⎝⎭⎝⎭由于()()0ln 111n nn x x n ∞==+-+∑,(-1<x ≤1)故()()110ln 11221n nn n x x n +∞+=⎛⎫=+- ⎪⎝⎭+∑,(-2≤x ≤2)297因此()()()11ln ln 22121n nn n x x n +∞+==++-+∑,(-2≤x ≤2) (2)()21cos 2cos 2x f x x +==由()()20cos 1!2nnn x x n ∞==-∑,(-∞<x <+∞)得()()()()()220042cos 211!!22n n n nn n n x x x n n ∞∞==⋅==--∑∑ 所以()()22011()cos cos 222114122!2n nn n f x x x x n ∞===+⋅=+-∑,(-∞<x <+∞) (3)f (x )=(1+x )ln(1+x ) 由()()()10ln 111n nn x x n +∞==+-+∑,(-1≤x ≤1)所以()()()()()()()()()()()()()1120111111111111111111111111111n nn n n nn n n n n nn n n n n n n n n n x f x x n x x n n x x x n n n n x xn n x xn n +∞=++∞∞==++∞∞+==+∞+=-∞+==+-+=+--++=++--+++--=+⋅+-=++∑∑∑∑∑∑∑ (-1≤x ≤1)(4)()2222111x f x x xx==⋅++由于()()()2211!!2111!!21n n n n x n x∞=-=+-+∑ (-1≤x ≤1)298故()()()()221!!2111!!2n n n n x f x x n ∞=⎛⎫-+=- ⎪⎝⎭∑()()()()2211!!211!!2n n n n x xn ∞+=-=+-∑ (-1≤x ≤1) (5)()()()()2202111313133133nn n n nn n xf x x x x x x ∞=+∞+==⋅+⎛⎫=⋅- ⎪⎝⎭=-<∑∑(6)由0e !nxn x n ∞==∑,x ∈(-∞,+∞)得()01e !n nxn x n ∞-=⋅-=∑,x ∈(-∞,+∞)所以()()()()()()0002101e e 2112!!1112!,!21x x n n n n n n n n n n f x x x n n x n x x n -∞∞==∞=+∞==-⎛⎫-=- ⎪⎝⎭=⋅⎡⎤--⎣⎦=∈-∞+∞+∑∑∑∑(7)因为e cos x x 为()()1e cos sin x x i e x i x +=+的实部, 而()()[]()10002011!1!ππ2cos sin !44ππ2cos sin !44nxi n nn n nn n n n n ex i n x i n x i n x n n i n ∞+=∞=∞=∞==+=+⎡⎤⎛⎫=+ ⎪⎢⎥⎝⎭⎣⎦⎛⎫=⋅+ ⎪⎝⎭∑∑∑∑299取上式的实部.得2π2cos4cos !n xn n n e x x n ∞==⋅∑(-∞<x <+∞)(8)由于()1211n n nx x ∞-==-∑ |x |<1而()211412f x x =⋅⎛⎫- ⎪⎝⎭,所以()111001422n n n n n n x x f n x --∞∞+==⋅⎛⎫=⋅= ⎪⎝⎭∑∑ (|x |<2) 14.将()2132f x x x =++展开成(x +4)的幂级数.解:21113212x x x x =-++++而()()()0101113411431314413334713nn nn n x x x x x x x ∞=∞+==+-++=-⋅+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<∑∑又()()()0101122411421214412224622nn nn n x x x x x x x ∞=∞+==+-++=-+-+⎛+⎫⎛⎫=-< ⎪⎪⎝⎭⎝⎭+=--<<-∑∑300所以()()()()()2110011013244321146223n nn n n n nn n n f x x x x x x x ∞∞++==∞++==++++=-+⎛⎫=-+-<<- ⎪⎝⎭∑∑∑15.将函数()3f x x =展开成(x -1)的幂级数. 解:因为()()()()()2111111!2!m nmm mm m m x xx x n---+=++++++-<<所以()()[]()()()33221133333331121222222211111!2!!n f x x x n x x x n ==+-⎛⎫⎛⎫⎛⎫⎛⎫----+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭=+++++---(-1<x -1<1) 即()()()()()()()()()()()()()2323133131313251111111222!23!2!3152111022!n nnnn n f x x x x x n n x x n ∞=⋅⋅⋅⋅⋅⋅--+--=+++++----⋅⋅⋅⋅⋅⋅--=+-<<⋅∑ 16.利用函数的幂级数展开式,求下列各数的近似值: (1)ln3(误差不超过0.0001); (2)cos20(误差不超过0.0001)解:(1)35211ln 213521n x x x x x x n -+⎛⎫=+++++ ⎪--⎝⎭,x ∈(-1,1)令131x x +=-,可得()11,12x =∈-,301故()35211111112ln3ln 212325222112n n -+⎡⎤+++++==⎢⎥⋅⋅⋅-⎣⎦-又()()()()()()()()()()2123212121232521242122112222123222212112222123252111222212112211413221n n n n n n n n n n n r n n n n n n n n n n +++++++++-⎡⎤++=⎢⎥⋅⋅++⎣⎦⎡⎤⋅⋅++=+++⎢⎥⋅⋅+++⎣⎦⎛⎫<+++ ⎪⎝⎭+=⋅+-=+ 故5810.000123112r <≈⨯⨯61010.000033132r <≈⨯⨯. 因而取n =6则35111111ln32 1.098623252112⎛⎫=≈++++ ⎪⋅⋅⋅⎝⎭(2)()()2420ππππ909090cos 2cos 11902!4!!2nn n ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭==-+-++-∵24π906102!-⎛⎫ ⎪⎝⎭≈⨯;48π90104!-⎛⎫⎪⎝⎭≈ 故2π90cos2110.00060.99942!⎛⎫⎪⎝⎭≈-≈-≈17.利用被积函数的幂级数展开式,求定积分0.5arctan d xx x⎰(误差不超过0.001)的近似值.302解:由于()3521arctan 13521n n x x x x x n +=-+-++-+ ,(-1≤x ≤1) 故()2420.50.5000.5357357arctan d d 113521925491111111292252492nx x x x x x x n x x x x ⎡⎤=-+-++-⎢⎥+⎣⎦⎛⎫=-+-+ ⎪⎝⎭=-⋅+⋅-⋅+⎰⎰ 而3110.013992⋅≈,5110.0013252⋅≈,7110.0002492⋅≈. 因此0.535arctan 11111d 0.487292252x x x ≈-⋅+⋅≈⎰ 18.判别下列级数的敛散性:(1)111n nnn nn n +∞=⎛⎫+ ⎪⎝⎭∑;(2)21cos 32n n nx n ∞=⎛⎫ ⎪⎝⎭∑; (3)()1ln 213nn n n ∞=+⎛⎫+ ⎪⎝⎭∑.解:(1)∵122111n nnnnn nn n n n n n n +⎛⎫>= ⎪+⎝⎭⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭ 而()22211221lim lim 10111nnn n n n nn n --++→∞→∞⎡⎤⎛⎫-⎛⎫==≠+⎢⎥⎪ ⎪+⎝⎭+⎝⎭⎣⎦故级数2211nn n n ∞=⎛⎫⎪+⎝⎭∑发散,由比较审敛法知原级数发散. (2)∵2cos 3022n nnx n n ⎛⎫⎪⎝⎭<≤ 由比值审敛法知级数12n n n ∞=∑收敛,由比较审敛法知,原级数21cos 32nn nx n ∞=⎛⎫ ⎪⎝⎭∑303收敛. (3)∵()()ln ln 220313nnn n n ++<<⎛⎫+ ⎪⎝⎭ 由()()()()11ln 33lim lim 3ln 21ln 3lim3ln 2113nn n n n nn U n U n n n ++→∞→∞→∞+=⋅++=+=< 知级数()1ln 23nn n ∞=+∑收敛,由比较审敛法知,原级数()1ln 213n n n n ∞=+⎛⎫+ ⎪⎝⎭∑收敛. 19.若2lim n nn U →∞存在,证明:级数1n n U ∞=∑收敛. 证:∵2lim n n n U →∞存在,∴∃M >0,使|n 2U n |≤M , 即n 2|U n |≤M ,|U n |≤2M n而21n Mn ∞=∑收敛,故1n n U ∞=∑绝对收敛. 20.证明,若21n n U ∞=∑收敛,则1nn U n∞=∑绝对收敛. 证:∵222211111222n n n nU U n U U n n n+=⋅≤=+⋅而由21n n U ∞=∑收敛,211n n∞=∑收敛,知 22111122n n U n ∞=⎛⎫+⋅ ⎪⎝⎭∑收敛,故1n n U n∞=∑收敛, 因而1nn U n∞=∑绝对收敛.30421.若级数1n n a ∞=∑与1n n b ∞=∑都绝对收敛,则函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.证:U n (x )=a n cos nx +b n sin nx ,∀x ∈R 有()cos sin cos sin n n n n n n n U a nx b nx a nx b nx a b x =+≤+≤+由于1n n a ∞=∑与1n n b ∞=∑都绝对收敛,故级数()1n n n a b ∞=+∑收敛.由魏尔斯特拉斯判别法知,函数项级数()1cos sin n n n a nx b nx ∞=+∑在R 上一致收敛.22.计算下列级数的收敛半径及收敛域:(1) 1311nn n n x n ∞=⎛⎫+ ⎪+⎝⎭∑;(2)()1πsin12nnn x ∞=+∑; (3) ()2112nn n x n ∞=-⋅∑解:(1)()111lim 1331lim 3123311311lim lim lim 22313e e 3n n nn nn nnn n n a a n n n n n n n n n n ρ+→∞+→∞→∞→∞→∞-=+⎛⎫⎛⎫++=⋅ ⎪ ⎪+⎝⎭+⎝⎭⎛⎫++++⎛⎫+=⋅⋅ ⎪ ⎪++⎝⎭+⎝⎭=⋅⋅=∴133R ρ==, 又当33x =±时,级数变为()113133311333nnnn n n n n n n ∞∞==⎛⎫⎛⎫⎛⎫++=±± ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭∑∑, 因为33333lim 033nn n en -→∞⎛⎫+=≠ ⎪+⎝⎭305所以当33x =±,级数发散,故原级数的收敛半径33R =,收敛域(-33,33). (2) 111ππsin122lim lim lim ππ2sin 22n n n n n n nnna a ρ+++→∞→∞→∞==== 故12R ρ==,又∵πsinπ2limsin 2lim ππ0π22n n n n n n→∞→∞⋅==≠.所以当(x +1)=±2时,级数()1πsin12n n n x ∞=+∑发散, 从而原级数的收敛域为-2<x +1<2,即-3<x <1,即(-3,1)(3) ()212121lim lim 221n n n n n na n a n ρ++→∞→∞⋅===⋅+ ∴2R =,收敛区间-2<x -1<2,即-1<x <3. 当x =-1时,级数变为()2111nn n∞=-∑,其绝对收敛,当x =3时,级数变为211n n ∞=∑,收敛. 因此原级数的收敛域为[-1,3]. 23.将函数()0arctan d xtF t x t=⎰展开成x 的幂级数. 解:由于()21arctan 121n nn t t n +∞==-+∑306所以()()()()()20002212000arctan d d 121d 112121nxx n n n n xnnn n t t F t t x t n t x t n n ∞=+∞∞====-+==--++∑⎰⎰∑∑⎰(|x |≤1)24.判别下列级数在指定区间上的一致收敛性:(1)()113n nn x ∞=-+∑,x ∈[-3,+∞); (2)1n n n x ∞=∑,x ∈(2,+∞); (3)()()222211n nx x n n ∞=⎡⎤+++⎣⎦∑,x ∈(-∞,+∞);解:(1)考虑n ≥2时,当x ≥-3时,有()1111133333nn n n nx x --=<<+-+ 而1113n n ∞-=∑收敛,由魏尔斯特拉斯判别法知,级数()113nnn x ∞=-+∑在[-3,+∞)上一致收敛. (2)当x >2时,有2n nn nx=< 由1112lim 122n n nn n +→∞+=<知级数12n n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数1n n nx ∞=∑在(2,+∞)上一致收敛. (3)∀x ∈R 有()()()22224322111nn n x n n nx n n n ≤<=⎡⎤+⋅+++⎣⎦而311n n ∞=∑收敛,由魏尔斯特拉斯判别法知,级数()()222211n n x x n n ∞=⎡⎤+++⎣⎦∑在(-∞,+∞)上一致收敛. 25.求下列级数的和函数:307(1)()211121n n n x n ∞-=--∑; (2)2121n n x n +∞=+∑; (3)()11!1n n nxn ∞-=-∑; (4)()11n n x n n ∞=+∑.解:(1)可求得原级数的收敛半径R =1,且当|x |=1时,级数()111121n n n ∞-=--∑是收敛的交错级数,故收敛域为[-1,1] 记()()()()22111111112121n n n n n n x x S x xS x x n n -∞∞--=====----∑∑ 则S 1(0)=0,()()122121111n n n S x x x∞--='==-+∑ 所以()()1121d arctan 01xS S x x x x-==+⎰ 即S 1(x )=arctan x ,所以S (x )=x arctan x ,x ∈[-1,1].(2)可求得原级数的收敛半径R =1,且当|x |=1时,原级数发散.记()21021n n x S x n +∞==+∑则()22011n n S x x x ∞='==-∑ ()200111d d ln 121xxx S x x x x x +'==--⎰⎰,即()()11ln 021xS S x x+-=-,S (0)=0 所以()11ln 21xS x x+=-,(|x |<1)(3)由()11!lim lim 0!1n n n n n a n n a n +→∞→∞+==-知收敛域为(-∞,+∞).记()()11!1n n n S x x n ∞-==-∑则()()()1011d e !!11nn xx n n x x S x x x x n n -∞∞=====--∑∑⎰,所以()()()e 1e x x S x x x '==+,(-∞<x <+∞)(4)由()()()112lim111n n n n n →∞++=+知收敛半径R =1,当x =1时,级数变为308()111n n n ∞=+∑,由()2111n n n <+知级数收敛,当x =-1时,级数变为()()111n n n n ∞=-+∑是收敛的交错级数,故收敛域为[-1,1].记()()11nn x S x n n ∞==+∑则S (0)=0,()()111n n x xS x n n +∞==+∑,()[]1111n n x xS x x∞-=''==-∑ (x ≠1) 所以()[]()0d ln 1xxS x x x ''=--⎰ 即()[]()ln 1xS x x '=--()[]()()()00d ln 1d 1ln 1xxxS x x x x x x x '=--=--+⎰⎰ 即()()()1ln 1xS x x x x =--+当x ≠0时,()()111ln 1S x x x⎛⎫=+-- ⎪⎝⎭,又当x =1时,可求得S (1)=1(∵()1lim lim 111n n S x n →∞→∞⎛⎫=-= ⎪+⎝⎭) 综上所述()()[)()0,01,1111ln 1,1,00,1x S x x x x x =⎧⎪==⎪⎨⎛⎫⎪+--∈- ⎪⎪⎝⎭⎩ 26.设f (x )是周期为2π的周期函数,它在(-π,π]上的表达式为()32π0,0π.x f x x x -<≤⎧=⎨<≤⎩ 试问f (x )的傅里叶级数在x =-π处收敛于何值?解:所给函数满足狄利克雷定理的条件,x =-π是它的间断点,在x =-π处,f (x )的傅里叶级数收敛于()()[]()33ππ11π22π222f f -+-+-=+=+30927.写出函数()21π00πx f x x x --≤≤⎧=⎨<≤⎩的傅里叶级数的和函数. 解:f (x )满足狄利克雷定理的条件,根据狄利克雷定理,在连续点处级数收敛于f (x ),在间断点x =0,x =±π处,分别收敛于()()00122f f -++=-,()()2πππ122f f -++-=,()()2πππ122f f -+-+--=,综上所述和函数.()221π00π102π1π2x x x S x x x --<<⎧⎪<<⎪⎪=-=⎨⎪⎪-=±⎪⎩28.写出下列以2π为周期的周期函数的傅里叶级数,其中f (x )在[-π,π)上的表达式为:(1)()π0π,4ππ0;4x f x x ⎧≤<⎪⎪=⎨⎪--≤<⎪⎩(2)()()2πx π=-≤≤f x x ;(3)()ππ,π,22ππ,,22ππ,π;22⎧--≤<-⎪⎪⎪=-≤<⎨⎪⎪≤<⎪⎩x f x x x x (4)()()cosππ2=-≤≤x f x x .310解:(1)函数f (x )满足狄利克雷定理的条件,x =n π,n ∈z 是其间断点,在间断占处f (x )的傅里叶级数收敛于()()ππ0044022f f +-⎛⎫+- ⎪+⎝⎭==,在x ≠n π,有()π0π-ππ011π1πcos d cos d cos d 0ππ4π4n a f x nx x nx x nx x -⎛⎫==-+= ⎪⎝⎭⎰⎰⎰ ()π0π-ππ011π1πsin d sin d sin d ππ4π40,2,4,6,,1,1,3,5,.n b f x nx x nx x nx xn n n-⎛⎫==-+ ⎪⎝⎭=⎧⎪=⎨=⎪⎩⎰⎰⎰于是f (x )的傅里叶级数展开式为()()11sin 2121n f x n x n ∞==--∑(x ≠n π) (2)函数f (x )在(-∞,+∞)上连续,故其傅里叶级数在(-∞,+∞)上收敛于f (x ),注意到f (x )为偶函数,从而f (x )cos nx 为偶函数,f (x )sin nx 为奇函数,于是()π-π1sin d 0πn b f x nx x ==⎰,2π20-π12πd π3a x x ==⎰,()()ππ22-π0124cos d cos d 1ππnn a f x nx x x nx x n ===-⋅⎰⎰ (n =1,2,…) 所以,f (x )的傅里叶级数展开式为:()()221π41cos 3nn f x nx n∞==+-⋅∑ (-∞<x <∞)(3)函数在x =(2n +1)π (n ∈z )处间断,在间断点处,级数收敛于0,当x ≠(2n +1)π时,由f (x )为奇函数,有a n =0,(n =0,1,2,…)311()()()πππ2π002222πsin d sin d sin d ππ212π1sin 1,2,π2n nb f x nx x x nx x nx x n n n n ⎡⎤==+⎢⎥⎣⎦=--+=⎰⎰⎰ 所以()()12112π1sin sin π2n n n f x nx n n ∞+=⎡⎤=-⋅+⎢⎥⎣⎦∑ (x ≠(2n +1)π,n ∈z )(4)因为()cos 2xf x =作为以2π为周期的函数时,处处连续,故其傅里叶级数收敛于f (x ),注意到f (x )为偶函数,有b n =0(n =1,2,…),()()ππ-π0π0π1212cos cos d cos cos d π2π2111cos cos d π2211sin sin 12211π224110,1,2,π41n n x xa nx x nx xn x n x x n x n x n n n n +==⎡⎤⎛⎫⎛⎫=++- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎡⎤⎛⎫⎛⎫+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥=+⎢⎥+-⎢⎥⎣⎦⎛⎫=-= ⎪-⎝⎭⎰⎰⎰所以f (x )的傅里叶级数展开式为:()()12124cos 1ππ41n n nxf x n ∞+==+--∑ x ∈[-π,π]29.将下列函数f (x )展开为傅里叶级数: (1)()()πππ42x f x x =--<<(2)()()sin 02πf x x x =≤≤解:(1) ()ππ0-ππ11ππcos d d ππ422x a f x nx x x -⎛⎫==-= ⎪⎝⎭⎰⎰[]()ππππ-π-πππ1π11cos d cos d x cos d π4242π1sin 001,2,4n x a nx x nx x nx x nx n n--⎛⎫=-=- ⎪⎝⎭=-==⎰⎰⎰312()ππππ-π-π1π11sin d sin d xsin d π4242π11n n x b nx x nx x nx x n-⎛⎫=-=- ⎪⎝⎭=-⋅⎰⎰⎰故()()1πsin 14n n nxf x n∞==+-∑ (-π<x <π)(2)所给函数拓广为周期函数时处处连续, 因此其傅里叶级数在[0,2π]上收敛于f (x ),注意到f (x )为偶函数,有b n =0,()ππ0πππ011cos0d sin d ππ24sin d ππa f x x x x x x x --====⎰⎰⎰ ()()()()()()ππ0ππ02222cos d sin cos d ππ1sin 1sin 1d π211π10,1,3,5,4,2,4,6,π1n na f x nx x x nx x n x n x x n n n n -===+--⎡⎤⎣⎦-⎡⎤=+-⎣⎦-=⎧⎪-=⎨=⎪-⎩⎰⎰⎰所以()()2124cos2ππ41n nxf x n ∞=-=+-∑ (0≤x ≤2π) 30.设f (x )=x +1(0≤x ≤π),试分别将f (x )展开为正弦级数和余弦级数. 解:将f (x )作奇延拓,则有a n =0 (n =0,1,2,…)()()()()ππ0022sin d 1sin d ππ111π2πn nb f x nx x x nx x n==+--+=⋅⎰⎰从而()()()1111π2sin πnn f x nx n∞=--+=∑ (0<x <π)313若将f (x )作偶延拓,则有b n =0 (n =1,2,…)()()ππ00222cos d 1cos d ππ0,2,4,64,1,3,5,πn a f x nx x x nx x n n n ==+=⎧⎪=-⎨=⎪⎩⎰⎰ ()()ππ0π012d 1d π2ππa f x x x x -==+=+⎰⎰ 从而()()()21cos 21π242π21n n xf x n ∞=-+=--∑ (0≤x ≤π) 31.将f (x )=2+|x | (-1≤x ≤1)展开成以2为周期的傅里叶级数,并由此求级数211n n∞=∑的和. 解:f (x )在(-∞,+∞)内连续,其傅里叶级数处处收敛,由f (x )是偶函数,故b n =0,(n =1,2,…)()()11010d 22d 5a f x x x x -==+=⎰⎰()()()1112cos d 22cos d 0,2,4,64,1,3,5,πn a f x nx x x nx xn n n -==+=⎧⎪-=⎨=⎪⎩⎰⎰所以()()()221cos 21π542π21n n xf x n ∞=-=--∑,x ∈[-1,1]取x =0得,()2211π821n n ∞==-∑,故 ()()22222111111111π48212n n n n n n n n ∞∞∞∞=====+=+-∑∑∑∑ 所以211π6n n∞==∑31432.将函数f (x )=x -1(0≤x ≤2)展开成周期为4的余弦级数.解:将f (x )作偶延拓,作周期延拓后函数在(-∞,+∞)上连续,则有b n =0 (n =1,2,3,…)()()220201d 1d 02a f x x x x -==-=⎰⎰ ()()()222022221ππcos d 1cos d 2224[11]π0,2,4,6,8,1,3,5,πn nn x n xa f x x x x n n n n -==-=--=⎧⎪=⎨-=⎪⎩⎰⎰ 故()()()22121π81cos π221n n xf x n ∞=-=-⋅-∑(0≤x ≤2)33.设()()011,0,2cos π1222,1,2n n x x a f x s x a n x x x ∞=⎧≤≤⎪⎪==+⎨⎪-<<⎪⎩∑,-∞<x <+∞,其中()12cos πd n a f x n x x =⎰,求52s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作偶延拓到[-1,1],再以2为周期延拓到(-∞,+∞)将f (x )展开成余弦级数而得到 s (x ),延拓后f (x )在52x =-处间断,所以515511122222221131224s f f f f +-+-⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-=-+-=-+-⎢⎥⎢⎥ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎛⎫=+= ⎪⎝⎭34.设函数f (x )=x 2(0≤x <1),而()1s i n πn n s x b nx ∞==∑,-∞<x <+∞,其中()12sin πd n b f x n x x =⎰ (n =1,2,3,…),求12s ⎛⎫- ⎪⎝⎭. 解:先对f (x )作奇延拓到,[-1,1],再以2为周期延拓到(-∞,+∞),并将315f (x )展开成正弦级数得到s (x ),延拓后f (x )在12x =-处连续,故.211112224s f ⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. 35.将下列各周期函数展开成为傅里叶级数,它们在一个周期内的表达式分别为:(1)f (x )=1-x 2 1122x ⎛⎫-≤< ⎪⎝⎭;(2)()21,30,1,0 3.x x f x x +-≤<⎧=⎨≤<⎩解:(1) f (x )在(-∞,+∞)上连续,故其傅里叶级数在每一点都收敛于f (x ),由于f (x )为偶函数,有b n =0 (n =1,2,3,…)()()112221002112d 41d 6a f x x x x -==-=⎰⎰, ()()()()112221021222cos2n πd 41cos2n πd 11,2,πn n a f x x x x x x n n -+==--==⎰⎰所以()()12211111cos 2π12πn n f x n x n +∞=-=+∑ (-∞<x <+∞)(2) ()()303033011d 21d d 133a f x x x x x --⎡⎤==++=-⎢⎥⎣⎦⎰⎰⎰, ()()()()330330221πcos d 331π1π21cos d cos d 3333611,1,2,3,πn nn xa f x x n x n x x x x n n --==++⎡⎤=--=⎣⎦⎰⎰⎰316()()()()33033011πsin d 331π1π21sin d sin d 333361,1,2,πn n n xb f x x n x n x x x x n n --+==++=-=⎰⎰⎰ 而函数f (x )在x =3(2k +1),k =0,±1,±2,…处间断,故()()()122116π6π11cos 1sin 2π3π3n n n n x n x f x n n ∞+=⎧⎫⎡⎤=-+--+-⎨⎬⎣⎦⎩⎭∑ (x ≠3(2k +1),k =0,±1,±2,…)36.把宽为τ,高为h ,周期为T 的矩形波(如图所示)展开成傅里叶级数的复数形式.解:根据图形写出函数关系式()0,22,220,22T t u t h t T t ττττ⎧-≤<-⎪⎪⎪=-≤<⎨⎪⎪≤≤⎪⎩()()22022111d d d 2T l T l h c u t t u t t h t l T T Tτττ---====⎰⎰⎰ ()()π2π222π2π22222π2211e d e d 212πe d e d 2ππsin e 2ππn T n i t l i t l T T n l n n i t i t T T n i t T c u t t u t tl T h T n h t i t T T n i T h h n n i n T τττττττ----------==-⎛⎫⎛⎫==⋅- ⎪ ⎪⎝⎭⎝⎭⎛⎫⎡⎤=-= ⎪⎣⎦⎝⎭⎰⎰⎰⎰。
高等数学上_复旦大学出版_习题五答案
(16) 对于任意的 y∈[0,h],过点(0,y)且垂直于 y 轴的平面截该立体为一椭圆,且该椭圆的半轴为: A a B b x1=A y , 同理可得该椭圆的另一半轴为: x 2 = B y. h h 故该椭圆面积为 A a B b A ( y )= x 1 x 2 = A y B y h h 从而立体的体积为
2 0 2 2
1 y
1+ y ′ 2 d x =2
0
1+
1 dx y2
=2
2 1 y2 1+ y 2 d =2 1+ y 2 d y y 2 0 0 2
= y 1+ y 2 +ln (y + 1+ y 2 ) =2 5 +ln(2+ 5)
0
(2) y =ln x , 3 ≤x≤ 8 ; 解:l = = (3) y =
∴D =
1 a 0
(x x 2 ax )d x
1 1 1 a = (1 a )· x2 x3 3 0 2 = 1 1 a )3 6( 1 9 1 a )3 = 6( 2 得 a=2. (13) 4. 求下列旋转体的体积: (1) 由 y = x 2 与 y 2 = x 3 围成的平面图形绕 x 轴旋转;
习题五
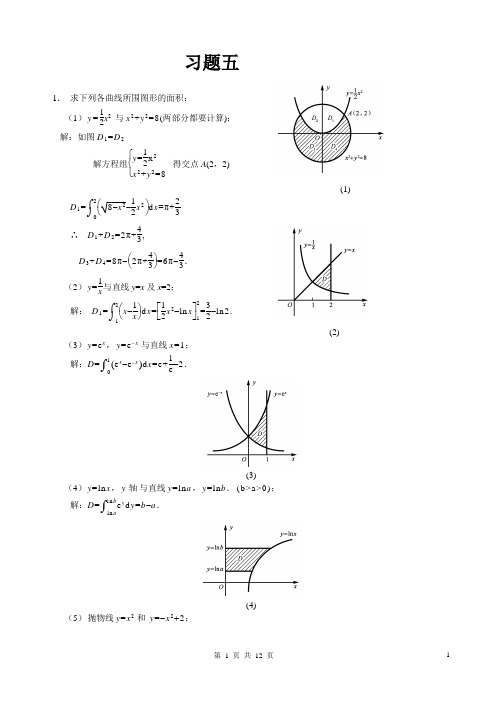
1. 求下列各曲线所围图形的面积: 1 (1) y = x2 与 x 2 + y 2 =8(两部分都要计算); 2 解:如图 D 1 = D 2
Байду номын сангаас
y = 1 x 2 解方程组 2 得交点 A(2,2) x 2 + y 2 =8
(1) 1 2 D 1 = 8 x 2 x 2 d x =π+ 2 3 0 4 ∴ D 1 + D 2 =2 π + , 3 4 4 D 3 + D 4 =8 π 2 π + =6 π . 3 3 1 (2) y = 与直线 y=x 及 x=2; x
复旦高数答案习题3

1. 验证:函数 f ( x) ln sinx 在 [ ,
π 5π ] 上满足罗尔定理的条件,并求出相应的 ,使 6 6
f ( ) 0 .
π 5π π 5π π 5π 在 ( , ) 上可导, 且 f ( ) f ( ) ln 2 , ] 上连续, 6 6 6 6 6 6 π 5π π 5π 即在 [ , ] 上满足罗尔定理的条件, 由罗尔定理, 至少存在一点 ( , ), 使 f ( ) 0 . 6 6 6 6 cos x π π 5π π 事实上,由 f ( x) cot x 0 得 x ( , ), 故取 ,可使 f ( ) 0 . sin x 2 6 6 2
证: f ( x) ln sin x 在区间 [ , 2. 下列函数在指定区间上是否满足罗尔定理的三个条件?有没有满足定理结论中的 ?
x2 , ⑴ f ( x) 0,
⑵ f ( x) x 1 , ⑶ f ( x) 解:⑴
0 x 1, x 1,
[0,1] ;
2 2
⑶ 原式= lim
ex 1 ex 1 1 lim lim . x x x x x 0 e 1 xe x 0 2e xe x 0 2 x 2
⑷ 原式= lim
x a
cos x cos a . 1
⑸ 原式= lim
mx m1 m m n a . x a nx n 1 n
f ( x) f (a) 0, xa
f (a) f (c) f (b) ,故由罗尔定理知,1 (a, c) ,使得 f (1 ) 0 , 2 (c, b) ,
使得 f ( 2 ) 0 ,又 f ( x) 在 [1 , 2 ] 上连续,在 (1 , 2 ) 内可导,由罗尔定理知,
高等数学复旦大学出版第三版上册课后答案习题全

x x x x , 1 分别表示不超过 , 1 的最大整数. 20 20 20 20
14. 已知水渠的横断面为等腰梯形,斜角 =40°,如图所示.当过水断面 ABCD 的面积为定值 S0 时,求湿周 L(L=AB+BC+CD)与水深 h 之间的函数关系式,并指明其定义域.
106 106 106 件,库存数为 件,库存费为 0.05 元. x 2x 2x
3
106 0.05 设总费用为,则 y 10 x . 2x
13. 邮局规定国内的平信,每 20g 付邮资 0.80 元,不足 20 g 按 20 g 计算,信件重量不得超过 2kg, 试确定邮资 y 与重量 x 的关系. 解: 当 x 能被 20 整除,即 [
x
7. 证明: f ( x) 2 x 1 和 g ( x)
3
3
x 1 互为反函数. 2
证:由 y 2 x 1 解得 x
3
3
y 1 , 2
2
故函数 f ( x) 2 x 1 的反函数是 y
3
3
x 1 ( x R ) , 这与 g ( x) 2
3
x 1 是同一个函 2
3
又由 1 cos x 1 得 0 1 cos x 2 , 即 0 y 2 , 故可得反函数的定义域为 [0,2], 所以 , 函数 y 1 cos x, x [0, π] 的反函
3
数为 y arccos 3 x 1
(0 x 2) .
9. 判断下列函数在定义域内的有界性及单调性:
(2) f ( x) e
2 x
e 2 x sin( x) e 2 x e 2 x sin x (e 2 x e 2 x sin x) f ( x)
关于 高等数学课后习题答案 复旦大学出版社 李开复编

高等数学(上)第一章 函数与极限1. 设⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛ 2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ;⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ 3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
4. 设数列{}nx 有界, 又,0lim =∞→nn y证明: .0lim =∞→nnn yx5. 根据函数的定义证明: ⑴ ()813lim 3=-→x x(2) 0sin lim =+∞→x x x6. 根据定义证明: 当0→x 时,函数x x y 21+=是无穷大.问x 应满足什么条件时,才能使?104>y 7. 求极限:⑴13lim223+-→x x x =0⑵ ()hx h x h 22lim-+→=x h h x h h 2)2(lim 0=+→⑶13lim 242+-+∞→x x x x x =0(4) ()2121lim nn n -+++∞→Λ=212)1(lim 2=-∞→n n n n (5)⎪⎭⎫ ⎝⎛---→311311lim x x x =1)1)(1(31lim 221-=++--++→x x x x x x(6) ()223222lim -+→x x x x =∞8. 计算下列极限: ⑴ xxx 1sinlim 20→=0⑵ x x x arctan lim ∞→=0arctan .1lim =∞→x xx 9. 计算下列极限:⑴ x x x ωsin lim 0→=ϖϖϖϖ=→.sin lim 0xx x ⑵ x x x 3tan lim 0→=33cos 1.3sin lim 0=→xx x x ⑶ xx xx sin 2cos 1lim 0-→=2sin .sin 2lim 20=→xx xx(4)xx x 321⎪⎭⎫ ⎝⎛-∞→lim =6620)21(lim ---→=⎥⎦⎤⎢⎣⎡-e x xx(5)()xx x 121+→lim =22.210)21(lim e x xx =+→(6)xx x x ⎪⎭⎫ ⎝⎛--∞→13lim =21)2.(21)121(lim -+--∞→=-+e xxx10. 利用极限存在准则证明:⑴ 11211lim 222=⎪⎭⎫⎝⎛++++++∞→πππn n nn n n Λ故原式=1⑵ 数列ΛΛ,222,22,2+++的极限存在,并求其极限.11. 当0→x 时, 22x x -与32x x -相比, 哪一个是较高阶的无穷小12. 当1→x 时, 无穷小x -1和()2121x -是否同阶是否等价13. 证明: 当0→x 时, 有2~1sec 2x x -.14. 利用等价无穷小的代换定理, 求极限:xx x x 30sin sin tan lim-→.15. 讨论()201212x x f x x x ⎧≤<=⎨-≤≤⎩ 的连续性, 并画出其图形.16. 指出下列函数的间断点属于哪一类.若是可去间断点,则补充或改变函数的定义使其连续.⑴2,123122==+--=x x x x x y⑵ 11311=⎩⎨⎧>-≤-=x x xx x y1x y ==017. 讨论函数()xx x x f nnn 2211lim +-=∞→的连续性, 若有间断点,判别其类型。
高等数学上复旦大学出版习题1答案.pdf

x1
=
sin
x2
,即 A 中不同的元素
x1,
x2
有相同的
像,∴f 不是单射.
综上所述, f 为满射,但不是单射.
(3)∵∀x1, x2 ∈ A , 且 x1 ≠ x2 ,有 ex1 ≠ ex2 ,即 A 中不同的元素有不同的像,∴f 是单射.
又∵ 0 ∈ B,∀x ∈ A, ex ≠ 0 ,即 B 中的元素 0 没有原像,∴f 不是满射.
2. 设 X = {1, 2,3, 4,5, 6}, A = {1, 2,3}, B = {2, 4, 6},C = {1,3,5} ,求 A∪ B ∪ C, A ∩ B ∩C , CXA,CXA∪CXB,
CXA∩CXB.
解: A∪ B ∪ C = {1, 2,3}∪{2, 4, 6}∪{1,3,5} = X
⎨ ⎩
x
≠
0
所以函数的定义域是 (−∞, 0) ∪ (0, 4].
(2)要使函数有意义,必须
所以函数的定义域是[-3,0) ∪(0,1) . (3)要使函数有意义,必须
⎧ x+3≥0
⎧x ≥ −3
⎪⎨lg(1− x) ≠ 0
即
⎪ ⎨
x
≠
0
⎪⎩ 1− x > 0
⎪⎩ x < 1
x2 −1≠ 0 即 x ≠ ±1
(2)不正确. 例如: A={1,2},B={1},C={1,3}有 A∩B=A∩C={1},但 B≠C.
4. 判定下列映射哪些是满射,哪些是单射,哪些是一一映射?
(1) A=(-∞,+∞),B=(-∞,+∞), f : x ∈ A |→ y = x3 ∈ B ;
(2) A=(-∞,+∞),B=[-1,1], f : x ∈ A |→ y = sin x ∈ B ;
高等数学复旦大学出版第三版课后答案

206习题十1. 根据二重积分性质,比较ln()d D x y σ+⎰⎰与2[ln()]d D x y σ+⎰⎰的大小,其中:(1)D 表示以(0,1),(1,0),(1,1)为顶点的三角形; (2)D 表示矩形区域{(,)|35,02}x y x y ≤≤≤≤.解:(1)区域D 如图10-1所示,由于区域D 夹在直线x +y =1与x +y =2之间,显然有图10-112x y ≤+≤从而 0l n ()x y ≤+<故有2l n ()[l n ()]x y x y+≥+ 所以 2l n ()d [l n ()]dD Dx yx y σσ+≥+⎰⎰⎰⎰(2)区域D 如图10-2所示.显然,当(,)x y D ∈时,有3x y +≥.图10-2从而 ln(x +y )>1 故有2l n ()[l n ()]x y x y+<+207所以 2l n ()d [l n ()]dD Dx yx y σσ+<+⎰⎰⎰⎰2. 根据二重积分性质,估计下列积分的值: (1),{(,)|02,02}I D x y x y σ==≤≤≤≤⎰⎰;(2)22sin sin d ,{(,)|0π,0π}D I x y D x y x y σ==≤≤≤≤⎰⎰; (3)2222(49)d ,{(,)|4}D I x y D x y x y σ=++=+≤⎰⎰. 解:(1)因为当(,)x y D ∈时,有02x ≤≤, 02y ≤≤因而 04xy ≤≤.从而22≤故2d D D σσσ≤≤⎰⎰⎰⎰⎰⎰即2d d DDσσσ≤≤⎰⎰⎰⎰而 d D σσ=⎰⎰ (σ为区域D 的面积),由σ=4 得8σ≤≤⎰⎰(2) 因为220sin 1,0sin 1x y ≤≤≤≤,从而220sin sin 1x y ≤≤故 220d sin sin d 1d D D D x y σσσ≤≤⎰⎰⎰⎰⎰⎰ 即220sin sin d d D D x y σσσ≤≤=⎰⎰⎰⎰ 而2πσ=所以2220sin sin d πD x y σ≤≤⎰⎰(3)因为当(,)x y D ∈时,2204x y ≤+≤所以22229494()925x y x y ≤++≤++≤故 229d (49)d 25d D D D x y σσσ≤++≤⎰⎰⎰⎰⎰⎰ 即229(49)d 25Dx y σσσ≤++≤⎰⎰208而2π24πσ=⋅=所以2236π(49)d 100πDx y σ≤++≤⎰⎰3. 根据二重积分的几何意义,确定下列积分的值: (1)222(,{(,)|};D a D x y x y a σ=+≤⎰⎰(2)222,{(,)|}.D x y x y a σ=+≤⎰⎰解:(1)(,D a σ⎰⎰在几何上表示以D 为底,以z 轴为轴,以(0,0,a )为顶点的圆锥的体积,所以31(π3Da a σ=⎰⎰ (2)σ⎰⎰在几何上表示以原点(0,0,0)为圆心,以a为半径的上半球的体积,故32π.3a σ=⎰⎰ 4.设f (x ,y )为连续函数,求2220021lim(,)d ,{(,)|()()}πDr f x y D x y x x y y r r σ→=-+-≤⎰⎰.解:因为f (x ,y )为连续函数,由二重积分的中值定理得,(,),D ξη∃∈使得2(,)d (,)π(,)Df x y f r f σξησξη=⋅=⋅⎰⎰又由于D 是以(x 0,y 0)为圆心,r 为半径的圆盘,所以当0r →时,00(,)(,),x y ξη→ 于是:0022200000(,)(,)11lim(,)d limπ(,)lim (,)ππlim (,)(,)Dr r r x y f x y r f f r r f f x y ξησξηξηξη→→→→=⋅===⎰⎰5. 画出积分区域,把(,)d D f x y σ⎰⎰化为累次积分: (1) {(,)|1,1,0}D x y x y y x y =+≤-≤≥;(2)2{(,)|2,}D x y y x x y =≥-≥209(3)2{(,)|,2,2}D x y y y x x x=≥≤≤解:(1)区域D 如图10-3所示,D 亦可表示为11,01y x y y -≤≤-≤≤.所以1101(,)d d (,)d yD y f x y y f x y x σ--=⎰⎰⎰⎰(2) 区域D 如图10-4所示,直线y =x -2与抛物线x =y 2的交点为(1,-1),(4,2),区域D 可表示为22,12y x y y ≤≤+-≤≤.图10-3 图10-4所以2221(,)d d (,)d y D yf x y y f x y x σ+-=⎰⎰⎰⎰(3)区域D 如图10-5所示,直线y =2x 与曲线2y x=的交点(1,2),与x =2的交点为(2,4),曲线2y x=与x =2的交点为(2,1),区域D 可表示为22,1 2.y x x x≤≤≤≤图10-5210所以2221(,)d d (,)d xD xf x y x f x y y σ=⎰⎰⎰⎰.6. 画出积分区域,改变累次积分的积分次序: (1) 2220d (,)d yyy f x y x⎰⎰; (2)e ln 1d (,)d xx f x y y ⎰⎰;(3) 1320d (,)d yy f x y x-⎰; (4)πsin 0sin2d (,)d xx x f x y y -⎰⎰;(5) 1233001d (,)d d (,)d yyy f x y y y f x y x -+⎰⎰⎰⎰.解:(1)相应二重保健的积分区域为D :202,2.y y x y ≤≤≤≤如图10-6所示.图10-6D 亦可表示为:04,.2xx y ≤≤≤所以2224002d (,)d d (,)d .yx yy f x y x x f x y y =⎰⎰⎰⎰(2) 相应二重积分的积分区域D :1e,0ln .x y x ≤≤≤≤如图10-7所示.图10-7D 亦可表示为:01,e e,y y x ≤≤≤≤211所以e ln 1e10ed (,)d d (,)d y xx f x y y y f x y x =⎰⎰⎰⎰(3) 相应二重积分的积分区域D为:01,32,y x y ≤≤≤≤-如图10-8所示.图10-8D 亦可看成D 1与D 2的和,其中 D 1:201,0,x y x ≤≤≤≤D 2:113,0(3).2x y x ≤≤≤≤-所以2113213(3)2001d (,)d d (,)d d (,)d yx x y f x y x x f x y y x f x y y --=+⎰⎰⎰⎰⎰.(4) 相应二重积分的积分区域D 为:0π,sinsin .2xx y x ≤≤-≤≤如图10-9所示.图10-9D 亦可看成由D 1与D 2两部分之和,其中 D 1:10,2arcsin π;y y x -≤≤-≤≤ D 2:01,arcsin πarcsin .y y x y ≤≤≤≤-所以πsin 0π1πarcsin 0sin 12arcsin 0arcsin 2d (,)d d (,)d d (,)d xyx y yx f x y y y f x y x y f x y x ----=+⎰⎰⎰⎰⎰⎰(5) 相应二重积分的积分区域D 由D 1与D 2两部分组成,其212中 D 1:01,02,y x y ≤≤≤≤D 2:13,03.y x y ≤≤≤≤-如图10-10所示.图10-10D 亦可表示为:02,3;2xx y x ≤≤≤≤- 所以()1233230012d ,d d (,)d d (,)d yyxxy f x y x y f x y x x f x y y --+=⎰⎰⎰⎰⎰⎰7.解:因为(,)Df x y d σ⎰⎰为一常数,不妨设(,)Df x y C =⎰⎰则有(,)x y f xy C =+从而有(,)()x y Df xy f uv C dudv =++⎰⎰而{}2(,)0 1.0D x y x y x =≤≤≤≤21(,)00()u x y f xy uv C dv du ⎡⎤∴=+⎰⎰+⎣⎦2120012u xy uv cv du ⎡⎤=+⎰+⎢⎥⎣⎦ 152012xy u cu du ⎡⎤=+⎰+⎢⎥⎣⎦163011123xy u cu ⎡⎤=++⎢⎥⎣⎦11123xy C =++18C ∴=故(,)18x y f xy ∴=+8. 计算下列二重积分:213(1) 221d d ,:12,;Dx x y D x y x y x≤≤≤≤⎰⎰ (2) e d d ,x yD x y ⎰⎰D由抛物线y 2 = x ,直线x =0与y =1所围;(3) d ,x y ⎰⎰D 是以O (0,0),A (1,-1),B (1,1)为顶点的三角形; (4) cos()d d ,{(,)|0π,π}D x y x y D x y x x y +=≤≤≤≤⎰⎰.解:(1)()22222231221111d d d d d d xx D x x x x x x y x y x x x x y yy ==-=-⎰⎰⎰⎰⎰⎰2421119.424x x ⎡⎤=-=⎢⎥⎣⎦(2) 积分区域D 如图10-12所示.图10-12D 可表示为:201,0.y x y ≤≤≤≤所示22110000ed d de d d e d()xx x y y yyyD xx y y x y y y==⎰⎰⎰⎰⎰⎰ 2111100ed (e 1)d e d d y x y y yy y y y y y y y ==-=-⎰⎰⎰⎰1111120000011de d e e d .22yy yy y y y y y =-=--=⎰⎰⎰ (3) 积分区域D 如图10-13所示.214图10-13D 可表示为:01,.x x y x ≤≤-≤≤所以2110d d arcsin d 2xxxx y x y x y x x --⎡==+⎢⎣⎰⎰⎰⎰⎰ 112300ππ1πd .2236x x x ==⋅=⎰ ππππ0πππ0(4)cos()d d d cos()d [sin()]d [sin(π)sin 2]d (sin sin 2)d 11.cos cos 222x Dxx y x y x x y y x y xx x x x x x x x +=+=+=+-=--⎡⎤==+⎢⎥⎣⎦⎰⎰⎰⎰⎰⎰⎰9. 计算下列二次积分:10112111224(1)d d ;(2)d e d d e d .yy y xxyxy x xy x y x +⎰⎰⎰⎰解:(1)因为sin d x x x⎰求不出来,故应改变积分次序。
高等数学教材答案第三册

高等数学教材答案第三册第一章:函数的极限与连续1.1 极限的概念与性质在高等数学教材的第三册中,第一章主要介绍了函数的极限与连续。
第一节讲解了极限的概念与性质。
极限是高等数学中的重要概念,用于描述函数在某一点上的趋近情况。
一系列性质被推导出来,如极限的唯一性、局部有界性、局部保号性等。
1.2 极限的运算法则第二节介绍了极限的运算法则。
这些法则包括四则运算法则、乘法法则、除法法则、复合函数的极限法则等。
这些法则为计算极限提供了方便的方法和准确的结果。
1.3 单调有界数列的极限第三节探讨了单调有界数列的极限。
通过引入上界和下界的概念,讨论了单调递增和单调递减数列的极限,并给出了相应的定理和推论。
1.4 无穷小量与无穷大量第四节介绍了无穷小量与无穷大量。
无穷小量是在极限过程中趋近于零的函数,无穷大量则是趋近于无穷大的函数。
在讨论极限的同时,通过引入这两个概念,对极限的计算和性质进行了更深入的研究。
1.5 极限存在准则第五节讲解了极限存在的准则。
对于函数来说,极限存在的条件是非常重要的。
通过介绍保号性和零号夹逼准则等几个重要的极限存在条件,加深了读者对极限存在的理解。
第二章:导数与微分2.1 导数的概念与性质第一节主要介绍了导数的概念与性质。
导数是刻画函数局部变化率的重要工具,也是微分学的核心概念之一。
通过定义与推导,引出了导数的几何意义和物理意义,并讨论了导数的一些基本性质。
2.2 导数的计算与应用第二节讲解了导数的计算与应用。
通过引入导数的四则运算法则、链式法则、反函数法则等,使读者能够更加熟练地计算各种函数的导数,并应用导数解决实际问题。
2.3 高阶导数与高阶微分第三节介绍了高阶导数与高阶微分。
高阶导数是导数的推广,定义了二阶导数、三阶导数等概念。
高阶微分则是对函数进行高阶逼近的工具,通过引入泰勒公式,讨论了高阶微分的性质和计算方法。
2.4 隐函数与参数方程的导数第四节研究了隐函数与参数方程的导数。
关于高等数学课后习题答案复旦大学出版社李开复编

高等数学(上)第一章 函数与极限1. 设⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x , 求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛ 2. 设()x f 的定义域为[]1,0,问:⑴()2x f ; ⑵()x f sin ;⑶()()0>+a a x f ; ⑷()()a x f a x f -++ ()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ 3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
4. 设数列{}nx 有界, 又,0lim =∞→nn y证明: .0lim =∞→nnn yx5. 根据函数的定义证明: ⑴ ()813lim 3=-→x x(2) 0sin lim =+∞→x x x6. 根据定义证明: 当0→x 时,函数x x y 21+=是无穷大.问x 应满足什么条件时,才能使?104>y 7. 求极限:⑴13lim223+-→x x x =0⑵ ()hx h x h 22lim-+→=x h h x h h 2)2(lim 0=+→⑶13lim 242+-+∞→x x x x x =0(4) ()2121lim nn n -+++∞→Λ=212)1(lim 2=-∞→n n n n (5)⎪⎭⎫ ⎝⎛---→311311lim x x x =1)1)(1(31lim 221-=++--++→x x x x x x(6) ()223222lim -+→x x x x =∞8. 计算下列极限: ⑴ xxx 1sinlim 20→=0⑵ x x x arctan lim ∞→=0arctan .1lim =∞→x xx 9. 计算下列极限:⑴ x x x ωsin lim 0→=ϖϖϖϖ=→.sin lim 0xx x ⑵ x x x 3tan lim 0→=33cos 1.3sin lim 0=→xx x x ⑶ xx xx sin 2cos 1lim 0-→=2sin .sin 2lim 20=→xx xx(4)xx x 321⎪⎭⎫ ⎝⎛-∞→lim =6620)21(lim ---→=⎥⎦⎤⎢⎣⎡-e x xx(5)()xx x 121+→lim =22.210)21(lim e x xx =+→(6)xx x x ⎪⎭⎫ ⎝⎛--∞→13lim =21)2.(21)121(lim -+--∞→=-+e xxx10. 利用极限存在准则证明:⑴ 11211lim 222=⎪⎭⎫⎝⎛++++++∞→πππn n nn n n Λ故原式=1⑵ 数列ΛΛ,222,22,2+++的极限存在,并求其极限.11. 当0→x 时, 22x x -与32x x -相比, 哪一个是较高阶的无穷小?12. 当1→x 时, 无穷小x -1和()2121x -是否同阶?是否等价?13. 证明: 当0→x 时, 有2~1sec 2x x -.14. 利用等价无穷小的代换定理, 求极限:xx x x 30sin sin tan lim-→.15. 讨论()201212x x f x x x ⎧≤<=⎨-≤≤⎩ 的连续性, 并画出其图形.16. 指出下列函数的间断点属于哪一类.若是可去间断点,则补充或改变函数的定义使其连续.⑴2,123122==+--=x x x x x y⑵ 11311=⎩⎨⎧>-≤-=x x xx x y1x y ==017. 讨论函数()xx x x f nnn 2211lim +-=∞→的连续性, 若有间断点,判别其类型。
高等数学上册课后习题答案

高等数学上册课后习题答案高等数学上册课后习题答案高等数学是一门重要的学科,对于理工科的学生来说尤为重要。
在学习高等数学的过程中,课后习题是巩固知识、提高能力的重要途径。
然而,由于课后习题的难度较大,很多学生常常无法独立完成,因此有一份课后习题答案是非常有必要的。
下面将为大家提供高等数学上册课后习题的答案。
第一章极限与连续1.1 习题答案1. 设函数f(x) = x^2 + 3x - 2,则f(-1) = (-1)^2 + 3(-1) - 2 = 2 - 3 - 2 = -3。
2. 设函数f(x) = 2x^2 + 3x - 5,则f(2) = 2(2)^2 + 3(2) - 5 = 8 + 6 - 5 = 9。
3. 设函数f(x) = x^3 + 2x^2 + x,则f(0) = 0^3 + 2(0)^2 + 0 = 0。
4. 设函数f(x) = 3x^2 - 4x + 1,则f(1) = 3(1)^2 - 4(1) + 1 = 3 - 4 + 1 = 0。
5. 设函数f(x) = x^3 - 2x,则f(-2) = (-2)^3 - 2(-2) = -8 + 4 = -4。
1.2 习题答案1. 设函数f(x) = 2x^2 + 3x - 1,则f(1) = 2(1)^2 + 3(1) - 1 = 2 + 3 - 1 = 4。
2. 设函数f(x) = x^3 - 2x + 1,则f(-1) = (-1)^3 - 2(-1) + 1 = -1 + 2 + 1 = 2。
3. 设函数f(x) = 3x^2 - 4x + 2,则f(0) = 3(0)^2 - 4(0) + 2 = 2。
4. 设函数f(x) = 4x^3 - 3x^2 + 2x,则f(2) = 4(2)^3 - 3(2)^2 + 2(2) = 32 - 12 +4 = 24。
5. 设函数f(x) = x^3 + x^2 + x,则f(-2) = (-2)^3 + (-2)^2 + (-2) = -8 + 4 - 2 = -6。
最新版高等数学课后习题标准答案(复旦大学出版社)(李开复编)

高等数学(上)第一章 函数与极限1. 设⎪⎩⎪⎨⎧≥<=3||,03|||,sin |)(ππϕx x x x ,求).2(446ϕπϕπϕπϕ、、、⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛6sin )6(ππϕ=21= 224sin )4(==ππϕ()0222)4sin()4(==-=-ϕππϕ2. 设()x f 的定义域为[]1,0,问:⑴()2x f ;⑵()x f s i n ; ⑶()()0>+a a x f ; ⑷()()a x f a x f -++()0>a 的定义域是什么?(1)][;,-的定义域为所以知-11)(,111022x f x x ≤≤≤≤ []ππππ)12(,2)(sin ),()12(21sin 0)2(+∈+≤≤≤≤k k x f Z k k x k x 的定义域为所以知由][a a a x f ax a a x -+-≤≤≤+≤1,)(110)3(-的定义域为所以知-由][φ时,定义域为当时,定义域为当从而得-知由211,210111010)4(>-≤<⎩⎨⎧+≤≤-≤≤⎩⎨⎧≤-≤≤+≤a a a a a x a a x a a x a x3. 设()⎪⎩⎪⎨⎧>-=<=111011x x x x f ,()xe x g =,求()[]x gf 和()[]x fg ,并做出这两个函数的图形。
⎪⎪⎩⎪⎪⎨⎧>=<==⎪⎩⎪⎨⎧>-=<=⎪⎩⎪⎨⎧>-=<=-1,1,11,)]([.)20,10,00,1)]([1)(,11)(,01)(,1)]([.)11)(x e x x e e x f g x x x x g f x g x g x g x g f x f 从而得4.设数列{}nx 有界,又,0lim =∞→nn y证明:.0lim =∞→n n n y x{}结论成立。
从而时,有,当自然数即又有对有界,∴=<=-<>∃>∀=≤∀>∃∴∞→ ..0)(,0,0lim ,,0εεεεMM y x y x My N n N y Mx n M x n n n n n n n n n5. 根据函数的定义证明: ⑴()813lim 3=-→x x8)13(lim 813303,033,33813,03=-<--<-<>∀<-<-=-->∀→x x x x x x x 所以成立时,恒有,当=取故即可。
复旦大学第三版数学分析答案

一﹑细心填一填,你一定能行(每空2分,共20分)1.当 = 时,分式的值为零.2.某种感冒病毒的直径为0.0000000031米,用科学记数法表示为.3.请你写出一个图象在第一、三象限的反比例函数.4.随机从甲、乙两块试验田中各抽取100株麦苗测量高度,计算平均数和方差的结果为:,,,,则小麦长势比较整齐的试验田是(填“甲”或“乙”).5.如图,□ABCD中,AE,CF分别是∠BAD,∠BCD的角平分线,请添加一个条件使四边形AECF为菱形.6.计算.7.若点()、、都在反比例函数的图象上,则的大小关系是.8.已知梯形ABCD中,AD∥BC,∠ABC=60°,BD=2 ,AE为梯形的高,且BE=1,•则AD=______.9.如图,中,,,,分别以为直径作三个半圆,那么阴影部分的面积为(平方单位).10.如图,矩形ABCD的对角线BD过O点,BC∥x轴,且A(2,-1),则经过C点的反比例函数的解析式为.二﹑精心选一选,你一定很棒(每题3分,共30分)11.下列运算中,正确的是A. B. C. D.12.下列说法中,不正确的是A.为了解一种灯泡的使用寿命,宜采用普查的方法B.众数在一组数据中若存在,可以不唯一C.方差反映了一组数据与其平均数的偏离程度D.对于简单随机样本,可以用样本的方差去估计总体的方差13.能判定四边形是平行四边形的条件是A.一组对边平行,另一组对边相等 B.一组对边相等,一组邻角相等C.一组对边平行,一组邻角相等 D.一组对边平行,一组对角相等14.反比例函数在第一象限的图象如图所示,则k的值可能是A.1 B.2 C.3 D.415.在平面直角坐标系中,已知点A(0,2),B(,0),C(0,),D(,0),则以这四个点为顶点的四边形是A.矩形B.菱形 C.正方形 D.梯形16.某校八年级(2)班的10名团员在“情系灾区献爱心”捐款活动中,捐款情况如下(单位:元):10 8 12 15 10 12 11 9 10 13.则这组数据的A.平均数是11 B.中位数是10 C.众数是10.5 D.方差是3.917.一个三角形三边的长分别为15cm,20cm和25cm,则这个三角形最长边上的高为A.15cmB.20cmC.25cmD.12cm18.已知,反比例函数的图像经过点M(k+2,1)和N(-2, ),则这个反比例函数是A. B. C. D.19.如图所示,有一张一个角为600的直角三角形纸片,沿其一条中位线剪开后,不能拼成的四边形是A.邻边不等的矩形B.等腰梯形C.有一角是锐角的菱形D.正方形20.甲、乙两班举行跳绳比赛,参赛选手每分钟跳绳的次数经统计计算后填入下表:班级参加人数中位数方差平均次数甲 35 169 6.32 155乙 35 171 4.54 155某同学根据上表分析得出如下结论:①甲、乙两班学生跳绳成绩的平均水平相同,②乙班优秀的人数多于甲班优秀的人数(每分钟跳绳次数≥170为优秀),③甲班的成绩的波动情况比乙班的成绩的波动大。
