中考数学计算题集锦
中考数学计算题100道(58页)

中考数学计算题100道(58页)一、选择题1. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定2. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 03. 下列哪个数不是素数?A. 2B. 3C. 44. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定5. 下列哪个数是质数?A. 4B. 6C. 76. 如果一个数的平方是正数,那么这个数是什么?B. 负数C. 07. 下列哪个数是合数?A. 2B. 3C. 58. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 09. 下列哪个数是素数?A. 4B. 6C. 710. 如果一个数的平方是负数,那么这个数是什么?A. 正数B. 负数C. 011. 下列哪个数不是素数?A. 2B. 3C. 412. 如果一个数是偶数,那么它的平方根也是偶数吗?B. 不是C. 不一定13. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 014. 下列哪个数是质数?A. 4B. 6C. 715. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定16. 下列哪个数是合数?A. 2B. 3C. 517. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 018. 下列哪个数是素数?A. 4B. 6C. 719. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 020. 下列哪个数不是素数?A. 2B. 3C. 421. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定22. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 023. 下列哪个数是质数?A. 4B. 6C. 724. 如果一个数是奇数,那么它的平方是奇数吗?B. 不是C. 不一定25. 下列哪个数是合数?A. 2B. 3C. 526. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 027. 下列哪个数是素数?A. 4B. 6C. 728. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 029. 下列哪个数不是素数?A. 2B. 3C. 430. 如果一个数是偶数,那么它的平方根也是偶数吗?B. 不是C. 不一定31. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 032. 下列哪个数是质数?A. 4B. 6C. 733. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定34. 下列哪个数是合数?A. 2B. 3C. 535. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 036. 下列哪个数是素数?A. 4B. 6C. 737. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 038. 下列哪个数不是素数?A. 2B. 3C. 439. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定40. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 041. 下列哪个数是质数?A. 4B. 6C. 742. 如果一个数是奇数,那么它的平方是奇数吗?B. 不是C. 不一定43. 下列哪个数是合数?A. 2B. 3C. 544. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 045. 下列哪个数是素数?A. 4B. 6C. 746. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 047. 下列哪个数不是素数?A. 2B. 3C. 448. 如果一个数是偶数,那么它的平方根也是偶数吗?B. 不是C. 不一定49. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 050. 下列哪个数是质数?A. 4B. 6C. 751. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定52. 下列哪个数是合数?A. 2B. 3C. 553. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 054. 下列哪个数是素数?A. 4B. 6C. 755. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 056. 下列哪个数不是素数?A. 2B. 3C. 457. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定58. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 059. 下列哪个数是质数?A. 4B. 6C. 760. 如果一个数是奇数,那么它的平方是奇数吗?B. 不是C. 不一定61. 下列哪个数是合数?A. 2B. 3C. 562. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 063. 下列哪个数是素数?A. 4B. 6C. 764. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 065. 下列哪个数不是素数?A. 2B. 3C. 466. 如果一个数是偶数,那么它的平方根也是偶数吗?B. 不是C. 不一定67. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 068. 下列哪个数是质数?A. 4B. 6C. 769. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定70. 下列哪个数是合数?A. 2B. 3C. 571. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 072. 下列哪个数是素数?A. 4B. 6C. 773. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 074. 下列哪个数不是素数?A. 2B. 3C. 475. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定76. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 077. 下列哪个数是质数?A. 4B. 6C. 778. 如果一个数是奇数,那么它的平方是奇数吗?B. 不是C. 不一定79. 下列哪个数是合数?A. 2B. 3C. 580. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 081. 下列哪个数是素数?A. 4B. 6C. 782. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 083. 下列哪个数不是素数?A. 2B. 3C. 484. 如果一个数是偶数,那么它的平方根也是偶数吗?B. 不是C. 不一定85. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 0. 下列哪个数是质数?A. 4B. 6C. 787. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定88. 下列哪个数是合数?A. 2B. 3C. 589. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 090. 下列哪个数是素数?A. 4B. 6C. 791. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 092. 下列哪个数不是素数?A. 2B. 3C. 493. 如果一个数是偶数,那么它的平方根也是偶数吗?A. 是的B. 不是C. 不一定94. 如果一个数的立方是负数,那么这个数是什么?A. 正数B. 负数C. 095. 下列哪个数是质数?A. 4B. 6C. 796. 如果一个数是奇数,那么它的平方是奇数吗?A. 是的B. 不是C. 不一定97. 下列哪个数是合数?A. 2B. 3C. 598. 如果一个数的平方是正数,那么这个数是什么?A. 正数B. 负数C. 099. 下列哪个数是素数?A. 4B. 6C. 7100. 如果一个数的立方是正数,那么这个数是什么?A. 正数B. 负数C. 0中考数学计算题100道(58页)二、填空题1. 一个正方形的边长是5厘米,那么它的面积是多少平方厘米?2. 一个长方形的长是8厘米,宽是4厘米,那么它的面积是多少平方厘米?3. 一个圆的半径是3厘米,那么它的面积是多少平方厘米?4. 一个三角形的底是6厘米,高是4厘米,那么它的面积是多少平方厘米?5. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?6. 一个正方体的边长是4厘米,那么它的体积是多少立方厘米?7. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?8. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?9. 一个球的半径是4厘米,那么它的体积是多少立方厘米?10. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?11. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?12. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?13. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?14. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?15. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?16. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?17. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?18. 一个球的半径是4厘米,那么它的体积是多少立方厘米?19. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?20. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?21. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?22. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?23. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?24. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?25. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?26. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?27. 一个球的半径是4厘米,那么它的体积是多少立方厘米?28. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?29. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?30. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?31. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?32. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?33. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?34. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?35. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?36. 一个球的半径是4厘米,那么它的体积是多少立方厘米?37. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?38. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?39. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?40. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?41. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?42. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?43. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?44. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?45. 一个球的半径是4厘米,那么它的体积是多少立方厘米?46. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?47. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?48. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?49. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?50. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?51. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?52. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?53. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?54. 一个球的半径是4厘米,那么它的体积是多少立方厘米?55. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?56. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?57. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?58. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?59. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?60. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?61. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?62. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?63. 一个球的半径是4厘米,那么它的体积是多少立方厘米?64. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?65. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?66. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?67. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?68. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?69. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?70. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?71. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?72. 一个球的半径是4厘米,那么它的体积是多少立方厘米?73. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?74. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?75. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?76. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?77. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?78. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?79. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?80. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?81. 一个球的半径是4厘米,那么它的体积是多少立方厘米?82. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?83. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?84. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?85. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?87. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?88. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?89. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?90. 一个球的半径是4厘米,那么它的体积是多少立方厘米?91. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?92. 一个等腰三角形的底是6厘米,腰是5厘米,那么它的面积是多少平方厘米?93. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的面积是多少平方厘米?94. 一个菱形的对角线分别是8厘米和6厘米,那么它的面积是多少平方厘米?95. 一个梯形的上底是5厘米,下底是8厘米,高是3厘米,那么它的面积是多少平方厘米?96. 一个正方体的对角线长是10厘米,那么它的体积是多少立方厘米?97. 一个长方体的长是8厘米,宽是4厘米,高是2厘米,那么它的体积是多少立方厘米?98. 一个圆柱的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?99. 一个球的半径是4厘米,那么它的体积是多少立方厘米?100. 一个圆锥的底面半径是3厘米,高是5厘米,那么它的体积是多少立方厘米?。
中考数学计算题训练

中考数学计算题训练中考数学计算题专项训练一、训练一1.计算:1) sin45° - 1/2 + 3/8;2) 2×(-5) + 23 - 3÷4 + 2^2 + (-1)^4 + (5-2) - |-3|;3) -1-16+(-2)^2/(2×1) + 1001+12-33×tan30°;6) -2+(-2)+2sin30°;8) (-1)-16+(-2)^2/[(2×1)+(1×1)]。
2.计算:[-1/2 + 1/3×(-tan45°)] + 3/2.3.计算:1/3 - 2^-1 - (2010-2012+(-1)^-1)/(1001+12-33×tan30°)。
4.计算:18-[cos60°/(2-1-4sin30°)]+[(2-2)/(2-1)]。
5.计算:[cos60°/(-1)]-1^20+|2-8|-2^-1×(tan30°-1)。
二、训练二(分式化简)1.化简:2x/(x^2-4x-2) - 1/(x-2)。
2.化简:(1+1/(x-2))/(x^2-4)。
3.化简:(1-a)/(2a-1) ÷ [(a^2+2a+1)/(3-a^5)]。
4.化简:[(a-1)/(a^2-1)] ÷ [(a-1)/(2a-1)],其中a≠-1.5.化简:[2x/(x+1)(x-1)] + [1/2(x-1)]。
6.化简:[1/(x-2)^2] ÷ [1/(x^2-4x+1)],其中x≠1.7.化简:[1-(a-1)/(2a)] ÷ [(a^2+2a)/(a-1)],其中a≠a。
8.化简:[2/(a+2)-(a-2)/(a-1)] ÷ [2/(a+1)-2/(a-2)],其中a为整数且-3<a<2.9.化简:[(11/2)x+2]/(x-y) + [9/(x^2+2xy+y^2)],其中x=1,y=-2.10.化简:[(1/2)-(1/12)x]/[2/(x-4)-x/(x^2-4)],其中x=2(tan45°-cos30°)-1.三、训练三(求解方程)1.解方程x-4x+1=0.2.解分式方程(3x-2)/(x+1) + (2x+1)/(x-2) =3.3.解方程:x^3-2x^2+5x-6=0.4.解方程:(x-1)/(x+1) + (x+1)/(x-1) = 4.5.解方程:(x-2)/(x+1) + (x+1)/(x-2) = 2.四、解不等式1.解不等式 $x+2>1$,得 $x>-1$,整数解为 $x\in(-1,+\infty)$。
初三中考数学试卷计算题全

一、选择题(每题3分,共15分)1. 若方程x^2 - 5x + 6 = 0的解为x1和x2,则x1 + x2的值为()A. 2B. 3C. 5D. 62. 在直角坐标系中,点A(2,3)关于y轴的对称点坐标为()A.(-2,3)B.(2,-3)C.(-2,-3)D.(2,3)3. 若a、b是方程x^2 - 4x + 3 = 0的两个根,则a^2 + b^2的值为()A. 7B. 8C. 9D. 104. 在等腰三角形ABC中,底边BC的长度为8,腰AC的长度为6,则三角形ABC的面积为()A. 24B. 18C. 14D. 125. 若x + y = 5,x - y = 1,则x^2 - y^2的值为()A. 24B. 16C. 12D. 8二、填空题(每题3分,共15分)6. 若方程2x - 3 = 5的解为x = 4,则方程3x - 6 = y的解为y = _______。
7. 在等边三角形ABC中,若AB = AC = BC = 5,则三角形ABC的周长为 _______。
8. 若函数f(x) = 2x - 1的图象经过点P(3,f(3)),则点P的坐标为 _______。
9. 若平行四边形ABCD的对角线AC和BD相交于点O,且AC = 10,BD = 8,则三角形AOD的面积为 _______。
10. 若x,y是方程x^2 - 2x - 3 = 0的两个根,则x^2 + y^2的值为 _______。
三、解答题(每题10分,共30分)11. (1)若方程x^2 - 2x - 3 = 0的两个根为a和b,求a + b和ab的值。
(2)若方程x^2 - mx + n = 0有两个相等的实数根,求m和n的值。
12. (1)在直角坐标系中,点A(-2,3)关于原点的对称点坐标为B,求点B的坐标。
(2)若直线y = 2x + 1与y轴的交点为C,求点C的坐标。
13. (1)已知等腰三角形ABC的底边BC的长度为8,腰AC的长度为6,求三角形ABC的面积。
(完整版)初中数学中考计算题复习含答案
1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71 220130 3|1|012013567 8 10 111213+|3|+1 151612120130+||222+412 17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一.解答题(共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简,第二项利用负数的绝对值等于它的相反数计算法则计算,第四项利用负指数幂法则计算,第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4 17112013|7|+01211211115218原式第一项利用立方根的定义化简,第二项利用二次根式的化简公式化简,第三项利用零指数幂法则计算,1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021)原式第一项利用负数的绝对值等于它的相反数计算,第二项先计算乘方运算,再计算除法运算,第2131234622212121121313122312+11)原式第一项利用负数的绝对值等于它的相反数计算,第二项利用特殊角的三212172+1+324121)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负指数幂法则21+13+3213212512+112112+126121)原式第一项利用特殊角的三角函数值化简,第二项利用零指数幂法则计算,212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113.解方程(本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析:原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。
初中数学中考计算题复习(最全)-含答案

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x—.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3.30.化简并求值:•,其中x=21.. 2。
初中数学中考计算题复习(最全)-含答案

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x—.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3. 30.化简并求值:•,其中x=21.. 2。
(完整版)初三中考数学计算题训练及答案

1 23 8 3 ﹣ ﹣1.计算:22+|﹣1|﹣ 9.2 计算:( 13)0 -( 2 )-2 + tan45°13.计算:2×(-5)+23-3÷2.4. 计算:22+(-1)4+(5-2)0-|-3|;5.计算: Sin 450 -+ 6.计算: - 2 + (-2)0 + 2 s in 30︒ .( 1)0 + ∣2 3∣ + 2sin 60° 7.计算 ,8.计算:a(a-3)+(2-a)(2+a)∣﹣5∣ + 22﹣( + 1)00 39.计算:10. 计算: -- (-2011) + 4 ÷(-2)11.解方程 x 2﹣4x+1=0.12.解分式方程2 =x + 23x - 23 13.解方程:x=2x-1.14.已知|a﹣1|+ab + 2=0,求方裎x+bx=1 的解.x 315.解方程:x2+4x-2=0 16.解方程:x - 1 - 1 - x = 2.{2x+3<9-x,) 17.(2011.苏州)解不等式:3﹣2(x﹣1)<1.18.解不等式组:2x-5>3x.⎧x - 2 6(x + 3) ⎧⎪x + 2 > 1, 19.解不等式组⎨( -1)- 6 ≥ 4(x +1) 20.解不等式组⎨x +1 < 2.⎩5 x ⎩⎪ 2初中计算题训练2 12 1 2 1 21 2 1 2答案1.解: 原式=4+1﹣3=22.解:原式=1-4+1=-2.3.解:原式=-10+8-6=-84.解:原式=4+1+1-3=3。
1 5.解:原式= -2 + 2 = 2 . 6. 解:原式=2+1+2× =3+1=4.2 27. 解:原式=1+2﹣ 3+2× 2 =1+2﹣ 3+ 3=3.8.解: a (a - 3)+ (2 - a )(2 + a )= a 2 - 3a + 4 - a 2 =4 - 3a9. 解:原式=5+4-1=810. 解:原式= 3 -1- 1=0.2211. 解:(1)移项得,x 2﹣4x=﹣1,配方得,x 2﹣4x+4=﹣1+4,(x ﹣2)2=3,由此可得 x ﹣2=± 3,x =2+3,x =2﹣ 3;(2)a=1,b=﹣4,c=1.b 2﹣4ac=(﹣4)2﹣4×1×1=12>0.4 ± 12x=2 =2± 3, x =2+ 3,x =2﹣ 3.12.解:x=-10 13.解:x=314. 解:∵|a﹣1|+1b + 2=0,∴a﹣1=0,a=1;b+2=0,b=﹣2.1 ∴x ﹣2x=1,得 2x 2+x ﹣1=0,解得 x =﹣1,x =2. 1 1经检验:x =﹣1,x =2是原方程的解.∴原方程的解为:x =﹣1,x =2. 15.解: x =-4 ±16 + 8 = -4 ± 2 6 = - 2 ± 2 216. 解:去分母,得 x +3=2(x -1) . 解之,得 x =5. 经检验,x =5 是原方程的解. 17. 解:3﹣2x+2<1,得:﹣2x <﹣4,∴x>2. 18.解:x <-519.解: x ≥ 1520. 解:不等式①的解集为 x >-1;不等式②的解集为 x +1<4 x <3故原不等式组的解集为-1<x <3.2 36。
汇总)初中数学中考计算题(最全)-含答案

汇总)初中数学中考计算题(最全)-含答案.doc1.解答题(共30小题)1.1 计算题:① 2+3=5;②解方程:x+5=10,解得x=5.1.2 计算:π+(π﹣2013)=2π-2013.1.3 计算:|1﹣|﹣2cos30°+(﹣)×(﹣1)2013|=|1-|-2cos30°+(-1)×(-1)2013||=|1-|-2×√3/2+1||=|1-√3+1|=|2-√3|。
1.4 计算:﹣(-2)+(-3)=1.1.5 计算:√(5+2√6)+√(5-2√6)=√2+√3.1.6 计算:(2+√3)(2-√3)=1.1.7 计算:(1+√2)²=3+2√2.1.8 计算:(1-√3)²=4-2√3.1.9 计算:(√2+1)²=3+2√2.1.10 计算:(√2-1)²=3-2√2.1.11 计算:(3+√5)(3-√5)=4.1.12 计算:(√3+1)(√3-1)=2.1.13 计算:(√2+√3)²=5+2√6.1.14 计算:﹣(π﹣3.14)+|﹣3|+(﹣1)2013+tan45°=0.1.15 计算:√3+√2-√6=√3-√2+√6.1.16 计算或化简:1)计算2﹣1﹣tan60°+(π﹣2013)+|﹣|=-tan60°-2011;2)(a﹣2)²+4(a﹣1)﹣(a+2)(a﹣2)=-3a²+10a-6.1.17 计算:1)(﹣1)2013﹣|﹣7|+(√2)﹣1=-√2-8;2)(2+√3)÷(√3-1)=1+√3.1.18 计算:(1+√2)(1-√2)=﹣1.1.19 解方程:x²+2x+1=0,解得x=-1.1.20 计算:1)tan45°+sin230°﹣cos30°•tan60°+cos245°=√2-1;2)(√2+1)²-(√2-1)²=4√2.1.211)|﹣3|+16÷(﹣2)³+(2013﹣)﹣tan60°=2010;2)解方程:(1-2x)²=3,解得x=√2﹣1.1.222)求不等式组:{x²-2x0},解得0<x<1.1.232)先化简,再求值:(√3+1)÷(√3-1)=2.1.241)计算:tan30°=√3/3;2)解方程:x²-2x+1=0,解得x=1.1.25 计算:1)√2-√3+√6=(√2-1)(√3-1);2)先化简,再求值:(√2+1)²+(√2-1)²=8.1.261)计算:(1-√2)÷(1+√2)=-1+√2;2)解方程:x²-2x+2=0,解得x=1-√3.1.27 计算:1)(√2+√3)²-(√2-√3)²=4√6;2)先化简,再求值:(x²+2x+1)÷(x²-1)=1+x。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考计算题集锦
一、计算题
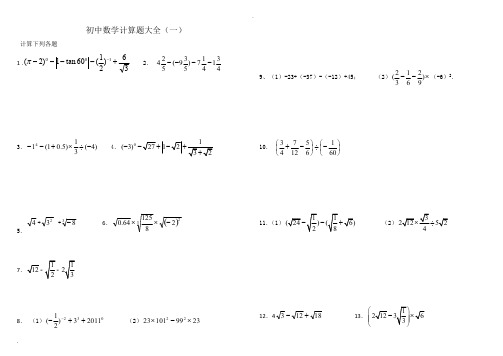
1.计算:102010)51()5(97)1(-+-⨯+---π 2. 1
021()2)(2)3
---
3.计算:22
+|﹣1|﹣错误!未找到引用源。
4. 计算:2×(-5)+23-3÷12 5.计算:22+(-1)4+(5
-2)0-|-3|;
6.计算:a(a-3)+(2-a)(2+a)
7.计算:错误!未找到引用源。
8.. 计算:()()0332011422
---+÷- 9、计算:1021
()2)(2)3--+-
10. )]4
1()52
[()3(-÷-÷- 11.74)431()1651()56(⨯-÷-⨯- 12. )3
1
5141(601+-÷
13.5145203-
+ 14.7531
31234+-
二、中考分式化简与求值
1、
.2
5
624322+-+-÷+-a a a a a 选一个使原代数式有意义的数带入求值.
2、先化简22(1)11
a a
a a a -+÷+-,再从1,-1中选一个你认为合适的数作为a 的值代入求值。
3、先化简,再求值:222
11()x y x y x y x y
+÷-+-,其中1,1x y ==
4、先化简,再求值: a -2a 2
-4 +1
a +2
,其中a =3.
5、先化简,再求值:)1
1(x -÷1
122
2-+-x x x ,其中x =2.
6、先化简,再求值:(x – 1x )÷ x +1
x
,其中x = 2+1.
7、先化简,再求值:11
1222122
2-++++÷--x x x x x x ,其中12+=x .
8、先化简,再求值:a
a a a a -+-÷--2
244)111(,其中1-=a
9、先化简,再求值:2
4)2122(+-÷
+--x x
x x ,其中34 +-=x .
10.先化简22()5525x x x x x x -÷---,然后从不等组23212x x --⎧⎨⎩
≤的解集中,选取一个你认为符合题意....的x 的值代入求值.
三、解分式方程 1、.2
31-=x x x 2、
x x x -=+--23
123 3、2111x x x x
++=
+ 4、 423-x -2-x x
=21。
5、x x ─ 1 ─ 2 x ─ 2x ─ 1 = 0
6、21
133x x x -=---
7、x 2
-3x -1=x
x 3122-. 8 、
71766x x x -+=-- 9、
2141111x x x x x -++=+-- 10.2223122
211
x x x x x x x x ---=+++-
11、2
135
111x x x
=---+ 12.222224x x a x a x a a x -=+--
13.2122
21
x x x x x -+=
+-+
14、解方程:当2
410x x -+=,方程062212
2
=-+++x x x x 的值是多少?
15、已知 ,求
的值。
四、解不等式组;
2、解不等式组:12,1
32,2
x x x ->⎧⎪
⎨-≤+⎪⎩………………①
…………②
3、解不等式组⎩
⎨⎧+>>-120
26x x x ,并把解集在数轴上表示出来.
5、解不等式组12(1)532122
x x x --⎧⎪
⎨-<+⎪⎩≤,并把解集在数轴上表示出来.
6、解不等式组3(2)41213
x x x x --≤⎧⎪
+⎨>-⎪⎩ .
7、求满足不等式组⎩
⎨⎧≤->+②x ①
x 1083152 的整数解
17、已知)1(645)25(3+-<++x x x ,化简:x x 3113--+。
