MATLAB回归预测模型

合集下载

matlab回归建模过程

matlab回归建模过程摘要：一、回归建模概述- 回归分析的定义- 回归建模的目的和意义二、MATLAB 回归建模过程- 一元线性回归- 数学模型定义- 模型参数估计- 检验、预测及控制- 多元线性回归- 数学模型定义- 模型参数估计- 多元线性回归中检验与预测- 逐步回归分析三、MATLAB 回归建模应用案例- 案例一：一元线性回归分析- 案例二：多元线性回归分析- 案例三：逐步回归分析正文：一、回归建模概述回归分析是一种研究变量之间关系的统计方法，通过建立一个数学模型，描述自变量与因变量之间的线性关系。

回归建模在实际应用中有着广泛的应用，如经济学、生物学、社会学等学科的研究中，可以帮助我们更好地理解变量之间的关系，并对未来趋势进行预测和控制。

MATLAB 是一种广泛应用于科学计算和数据分析的编程语言，提供了丰富的回归建模工具箱，可以帮助我们快速、高效地进行回归建模分析。

二、MATLAB 回归建模过程1.一元线性回归一元线性回归是最简单的回归分析方法，适用于只有一个自变量和一个因变量的情况。

在MATLAB 中，我们可以使用回归分析工具箱中的`regress`函数进行一元线性回归建模。

（1）数学模型定义一元线性回归的数学模型可以表示为：y = a + bx其中，y 表示因变量，x 表示自变量，a 和b 分别表示回归系数。

（2）模型参数估计在MATLAB 中，我们可以使用`regress`函数对模型参数进行估计。

函数的原型为：b = regress(y, x)其中，y 表示因变量向量，x 表示自变量向量，b 表示回归系数向量。

（3）检验、预测及控制在得到回归系数向量b 后，我们可以进行回归检验、预测以及控制。

2.多元线性回归多元线性回归适用于有多个自变量和因变量的情况。

在MATLAB 中，我们可以使用回归分析工具箱中的`polyfit`函数进行多元线性回归建模。

（1）数学模型定义多元线性回归的数学模型可以表示为：y = a0 + a1x1 + a2x2 + ...+ anxn其中，y 表示因变量，x1、x2、...、xn 表示自变量，a0、a1、a2、...、an 分别表示回归系数。

matlab随机森林回归预测算法

随机森林是一种常用的机器学习算法，它在回归和分类问题中都有很好的表现。

而在Matlab中，也提供了随机森林回归预测算法，能够帮助用户解决实际问题中的预测和建模需求。

下面我们将就Matlab中的随机森林回归预测算法展开详细的介绍。

一、随机森林的原理随机森林是一种集成学习算法，它由多棵决策树组成。

在构建每棵决策树时，会随机选择样本和特征进行训练，最后将多棵决策树的结果综合起来，形成最终的预测结果。

这样的做法可以有效地减少过拟合的风险，同时具有很高的预测准确性。

随机森林的优点主要包括：具有很好的鲁棒性，对于数据中的噪声和缺失值有很强的适应能力；能够处理高维数据和大规模数据，不需要对数据进行特征选择和降维；具有很好的泛化能力，不易发生过拟合。

二、Matlab中的随机森林回归预测算法Matlab提供了一个强大的集成学习工具箱，其中包括了随机森林回归预测算法。

用户可以很方便地使用这个工具箱进行数据建模和预测。

1. 数据准备在使用Matlab进行随机森林回归预测之前，首先需要准备好数据。

数据应该包括自变量和因变量，可以使用Matlab的数据导入工具将数据导入到工作空间中。

2. 构建随机森林模型在数据准备好之后，可以使用Matlab的fitrensemble函数来构建随机森林模型。

该函数可以指定树的数量、最大深度、最小叶子大小等参数，也可以使用交叉验证来优化模型的参数。

3. 模型预测一旦模型构建完成，就可以使用predict函数对新的数据进行预测了。

通过输入自变量的数值，就可以得到相应的因变量的预测值。

4. 模型评估在得到预测结果之后，通常需要对模型进行评估，以了解模型的预测能力。

可以使用Matlab提供的各种评估指标函数，如均方误差（MSE）、决定系数（R-squared）、平均绝对误差（MAE）等来评估模型的表现。

5. 参数调优如果模型的表现不佳，可以尝试使用交叉验证、网格搜索等方法对模型的参数进行调优，以提高模型的预测准确性。

matlab建立多元线性回归模型并进行显著性检验及预测问题

matlab建立多元线性回归模型并进行显着性检验及预测问题例子;x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';X=[ones(16,1) x]; 增加一个常数项Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]'; [b,bint,r,rint,stats]=regress(Y,X) 得结果：b = bint = stats = 即对应于b的置信区间分别为[，]、[,]; r2=, F=, p= p<, 可知回归模型y=+ 成立. 这个是一元的，如果是多元就增加X的行数！function [beta_hat,Y_hat,stats]=regress(X,Y,alpha)% 多元线性回归(Y=Xβ+ε)MATLAB代码%？% 参数说明% X：自变量矩阵，列为自变量，行为观测值% Y：应变量矩阵，同X% alpha：置信度，[0 1]之间的任意数据% beta_hat：回归系数% Y_beata：回归目标值，使用Y-Y_hat来观测回归效果% stats：结构体，具有如下字段% =[fV,fH]，F检验相关参数，检验线性回归方程是否显着% fV：F分布值，越大越好，线性回归方程越显着% fH：0或1，0不显着；1显着(好)% =[tH,tV,tW]，T检验相关参数和区间估计，检验回归系数β是否与Y有显着线性关系% tV：T分布值，beta_hat(i)绝对值越大,表示Xi对Y显着的线性作用% tH：0或1，0不显着；1显着% tW：区间估计拒绝域，如果beta(i)在对应拒绝区间内，那么否认Xi对Y显着的线性作用% =[T,U,Q,R]，回归中使用的重要参数% T：总离差平方和，且满足T=Q+U% U：回归离差平方和% Q：残差平方和% R∈[0 1]：复相关系数，表征回归离差占总离差的百分比，越大越好% 举例说明% 比如要拟合y=a+b*log(x1)+c*exp(x2)+d*x1*x2，注意一定要将原来方程线化% x1=rand(10,1)*10;% x2=rand(10,1)*10;% Y=5+8*log(x1)+*exp(x2)+*x1.*x2+rand(10,1); % 以上随即生成一组测试数据% X=[ones(10,1) log(x1) exp(x2) x1.*x2]; % 将原来的方表达式化成Y=Xβ，注意最前面的1不要丢了% [beta_hat,Y_hat,stats]=mulregress(X,Y,%% 注意事项% 有可能会出现这样的情况，总的线性回归方程式显着的=1)，% 但是所有的回归系数却对Y的线性作用却不显着=0)，产生这种现象的原意是% 回归变量之间具有较强的线性相关，但这种线性相关不能采用刚才使用的模型描述，% 所以需要重新选择模型%C=inv(X'*X);Y_mean=mean(Y);% 最小二乘回归分析beta_hat=C*X'*Y; % 回归系数βY_hat=X*beta_hat; % 回归预测% 离差和参数计算Q=(Y-Y_hat)'*(Y-Y_hat); % 残差平方和U=(Y_hat-Y_mean)'*(Y_hat-Y_mean); % 回归离差平方和T=(Y-Y_mean)'*(Y-Y_mean); % 总离差平方和，且满足T=Q+UR=sqrt(U/T); % 复相关系数，表征回归离差占总离差的百分比，越大越好[n,p]=size(X); % p变量个数，n样本个数% 回归显着性检验fV=(U/(p-1))/(Q/(n-p)); % 服从F分布，F的值越大越好fH=fV>finv(alpha,p-1,n-p); % H=1，线性回归方程显着(好)；H=0，回归不显着% 回归系数的显着性检验chi2=sqrt(diag(C)*Q/(n-p)); % 服从χ2(n-p)分布tV=beta_hat./chi2; % 服从T分布，绝对值越大线性关系显着tInv=tinv+alpha/2,n-p);tH=abs(tV)>tInv; % H(i)=1，表示Xi对Y显着的线性作用；H(i)=0，Xi对Y的线性作用不明显% 回归系数区间估计tW=[-chi2,chi2]*tInv; % 接受H0，也就是说如果在beta_hat(i)对应区间中，那么Xi与Y线性作用不明显stats=struct('fTest',[fH,fV],'tTest',[tH,tV,tW],'TUQR',[T,U,Q,R]);。

matlab建立多元线性回归模型并进行显著性检验及预测问题

matlab建立多元线性回归模型并进行显著性检验及预测问题例子;x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';X=[ones(16,1) x]; 增加一个常数项 Y=[88 85 88 91 92 93 93 95 96 98 97 9698 99 100 102]'; [b,bint,r,rint,stats]=regress(Y,X) 得结果：b = bint = stats = 即对应于b的置信区间分别为[，]、[,]; r2=, F=, p= p<, 可知回归模型 y=+ 成立. 这个是一元的，如果是多元就增加X的行数！function [beta_hat,Y_hat,stats]=regress(X,Y,alpha)% 多元线性回归(Y=Xβ+ε)MATLAB代码%% 参数说明% X：自变量矩阵，列为自变量，行为观测值% Y：应变量矩阵，同X% alpha：置信度，[0 1]之间的任意数据% beta_hat：回归系数% Y_beata：回归目标值，使用Y-Y_hat来观测回归效果% stats：结构体，具有如下字段% =[fV,fH]，F检验相关参数，检验线性回归方程是否显著% fV：F分布值，越大越好，线性回归方程越显著% fH：0或1，0不显著；1显著(好)% =[tH,tV,tW]，T检验相关参数和区间估计，检验回归系数β是否与Y有显著线性关系% tV：T分布值，beta_hat(i)绝对值越大,表示Xi对Y显著的线性作用% tH：0或1，0不显著；1显著% tW：区间估计拒绝域，如果beta(i)在对应拒绝区间内，那么否认Xi对Y显著的线性作用% =[T,U,Q,R]，回归中使用的重要参数% T：总离差平方和，且满足T=Q+U% U：回归离差平方和% Q：残差平方和% R∈[0 1]：复相关系数，表征回归离差占总离差的百分比，越大越好% 举例说明% 比如要拟合 y=a+b*log(x1)+c*exp(x2)+d*x1*x2，注意一定要将原来方程线化% x1=rand(10,1)*10;% x2=rand(10,1)*10;% Y=5+8*log(x1)+*exp(x2)+*x1.*x2+rand(10,1); % 以上随即生成一组测试数据% X=[ones(10,1) log(x1) exp(x2) x1.*x2]; % 将原来的方表达式化成Y=Xβ，注意最前面的1不要丢了% [beta_hat,Y_hat,stats]=mulregress(X,Y,%% 注意事项% 有可能会出现这样的情况，总的线性回归方程式显著的=1)，% 但是所有的回归系数却对Y的线性作用却不显著=0)，产生这种现象的原意是% 回归变量之间具有较强的线性相关，但这种线性相关不能采用刚才使用的模型描述，% 所以需要重新选择模型%C=inv(X'*X);Y_mean=mean(Y);% 最小二乘回归分析beta_hat=C*X'*Y; % 回归系数βY_hat=X*beta_hat; % 回归预测% 离差和参数计算Q=(Y-Y_hat)'*(Y-Y_hat); % 残差平方和U=(Y_hat-Y_mean)'*(Y_hat-Y_mean); % 回归离差平方和T=(Y-Y_mean)'*(Y-Y_mean); % 总离差平方和，且满足T=Q+UR=sqrt(U/T); % 复相关系数，表征回归离差占总离差的百分比，越大越好[n,p]=size(X); % p变量个数，n样本个数% 回归显著性检验fV=(U/(p-1))/(Q/(n-p)); % 服从F分布，F的值越大越好fH=fV>finv(alpha,p-1,n-p); % H=1，线性回归方程显著(好)；H=0，回归不显著% 回归系数的显著性检验chi2=sqrt(diag(C)*Q/(n-p)); % 服从χ2(n-p)分布tV=beta_hat./chi2; % 服从T分布，绝对值越大线性关系显著tInv=tinv+alpha/2,n-p);tH=abs(tV)>tInv; % H(i)=1，表示Xi对Y显著的线性作用；H(i)=0，Xi 对Y的线性作用不明显% 回归系数区间估计tW=[-chi2,chi2]*tInv; % 接受H0，也就是说如果在beta_hat(i)对应区间中，那么Xi与Y线性作用不明显stats=struct('fTest',[fH,fV],'tTest',[tH,tV,tW],'TUQR',[T,U,Q,R]) ;。

matlab中的偏最小二乘法(pls)回归模型,离群点检测和变量选择

matlab中的偏最小二乘法（pls）回归模型，离群点检测和变
量选择
在MATLAB中，可以使用以下函数实现偏最小二乘法回归模型、离群点检测和变量选择：
1. 偏最小二乘法（PLS）回归模型：
- `plsregress`：该函数用于计算偏最小二乘法（PLS）回归模型。

它可以输出回归系数、预测结果以及其他性能指标。

2. 离群点检测：
- `mahal`：该函数用于计算多元正态分布下的马氏距离，可以作为离群点的度量。

- `outlier`：该函数用于检测一维数据的离群点。

3. 变量选择：
- `plsregress`的输出结果中可以通过使用交叉验证和预测误差来选择最优的变量数量。

- `plsregress`的输出结果中的回归系数中可以通过设置阈值来选择较大的变量。

具体用法可以参考MATLAB的文档和示例代码。

均值回归模型参数估计 matlab代码

均值回归模型是一种常见的统计建模方法，它通过对自变量和因变量之间的平均关系进行建模来进行参数估计。

在实际的数据分析和建模过程中，我们经常需要使用MATLAB来进行均值回归模型的参数估计和分析。

本文将针对均值回归模型参数估计的MATLAB代码进行详细的介绍和解释。

1. 均值回归模型简介均值回归模型是一种简单但常用的统计建模方法，它假设自变量与因变量之间的关系是通过均值来进行描述的。

均值回归模型的基本形式可以表示为：Y = β0 + β1*X + ε其中，Y表示因变量，X表示自变量，β0和β1分别表示回归方程的截距和斜率参数，ε表示误差项。

均值回归模型的目标就是通过对数据进行拟合来估计出最优的β0和β1参数，从而描述自变量和因变量之间的关系。

2. MATLAB代码实现在MATLAB中，我们可以使用regress函数来进行均值回归模型参数的估计。

regress函数的基本语法如下：[b,bint,r,rint,stats] = regress(y,X)其中，y表示因变量的数据向量，X表示自变量的数据矩阵，b表示回归系数的估计值，bint表示回归系数的置信区间，r表示残差向量，rint表示残差的置信区间，stats是一个包含了回归统计信息的向量。

3. 代码示例下面是一个使用MATLAB进行均值回归模型参数估计的简单示例：```MATLAB生成随机数据X = randn(100,1);Y = 2*X + randn(100,1);均值回归模型参数估计[b,bint,r,rint,stats] = regress(Y,X);打印回归系数估计值fprintf('回归系数估计值:\n');disp(b);打印回归统计信息fprintf('回归统计信息:\n');disp(stats);```在这个示例中，我们首先生成了一个随机的自变量X和一个根据线性关系生成的因变量Y。

然后使用regress函数对这些数据进行了均值回归模型参数的估计，并打印出了回归系数的估计值和一些回归统计信息。

遗传算法回归预测matlab程序

遗传算法回归预测matlab程序1. 简介遗传算法是一种基于生物遗传机制的优化算法，它模拟了自然界中的遗传、变异、适应与选择机制。

在数据预测领域，遗传算法被广泛应用于回归分析，它能够通过不断迭代优化模型参数，找到最优的拟合曲线，从而实现对未知数据的准确预测。

而在matlab程序中，遗传算法回归预测模型的实现也成为了一种常见的工具，深受数据分析和预测领域的从业者所青睐。

2. 遗传算法回归预测原理遗传算法回归预测模型基于遗传算法的优化能力，通过不断迭代调整模型参数，使其与真实数据的差距最小化。

其基本原理包括以下几个步骤：2.1. 个体编码：将回归模型的参数进行二进制编码，构成种裙的个体。

2.2. 适应度评估：采用回归模型拟合真实数据，计算个体的适应度，即拟合度。

2.3. 选择操作：根据个体的适应度进行选择，将适应度高的个体保留下来，作为父代参与繁殖。

2.4. 交叉操作：对选择出来的父代进行交叉操作，产生新的个体，并保留一定概率的变异操作。

2.5. 新一代个体重复步骤2.2~2.4，直至达到预设的迭代次数或收敛条件。

3. 遗传算法回归预测matlab程序实现步骤在matlab中实现遗传算法回归预测模型，通常可以按以下步骤进行操作：3.1. 导入数据：首先需要导入需要进行回归预测的数据，并进行数据预处理，包括归一化、标准化等操作。

3.2. 初始化种裙：根据回归模型的参数范围，随机初始化种裙的个体，并进行个体编码。

3.3. 适应度评估：利用回归模型对种裙中的个体进行拟合，计算其适应度。

3.4. 选择、交叉、变异操作：根据个体的适应度进行选择、交叉、变异操作，产生新一代的个体。

3.5. 迭代操作：重复进行选择、交叉、变异操作，直至达到预设的迭代次数或收敛条件。

3.6. 获取最优解：得到迭代过程中适应度最高的个体，即为最优解，用于构建回归模型进行预测。

4. 遗传算法回归预测matlab程序示例代码下面是一个简单的遗传算法回归预测matlab程序示例代码：```matlab导入数据data = load('data.txt');X = data(:, 1);y = data(:, 2);m = length(y);初始化种裙populationSize = 100;numParams = 2;population = zeros(populationSize, numParams);for i = 1:populationSizepopulation(i, :) = rand(1, numParams);end迭代参数优化numIterations = 100;for iter = 1:numIterations适应度评估fitness = zeros(populationSize, 1);for i = 1:populationSizeparams = population(i, :);yPredicted = params(1) * X + params(2);fitness(i) = 1 / (m * 2) * sum((yPredicted - y).^2); end选择、交叉、变异操作[fitness, indices] = sort(fitness);population = population(indices, :);newPopulation = zeros(populationSize, numParams);for i = 1:populationSizeparent1 = population(mod(i, populationSize) + 1, :);parent2 = population(mod(i + 1, populationSize) + 1, :); crossoverPoint = randi([1, numParams - 1]);child = [parent1(1:crossoverPoint),parent2(crossoverPoint+1:end)];mutationPoint = randi([1, numParams]);child(mutationPoint) = rand(1);newPopulation(i, :) = child;endpopulation = newPopulation;end获取最优解bestParams = population(1, :);yPredicted = bestParams(1) * X + bestParams(2);plot(X, y, 'ro', X, yPredicted, 'b-');```5. 总结遗传算法回归预测matlab程序的实现，基于遗传算法的优化能力，可以有效地对回归模型进行参数优化，从而实现对未知数据的准确预测。

第三讲 MATLAB预测(1)回归分析

ˆ 489.2946 s t 2 65.8896 t 9.1329
方法二
化为多元线性回归：
t=1/30:1/30:14/30;
s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48];
3
1
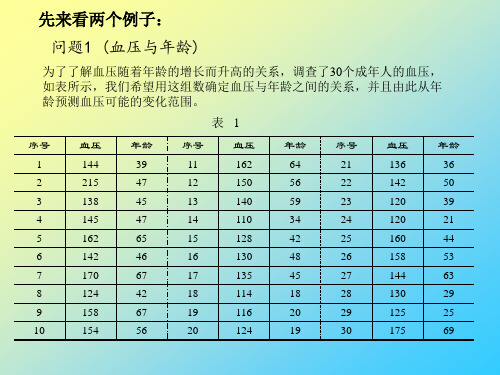
模型：记血压为 y ，年龄为 x1 ，体重指数为 x2 ，吸烟习惯为 x3 ，用Matlab将 y 与 x2 的数据做散点图，看出大致也呈线性关系，建立模型： y 0 1 x1 2 x2 3 x3 由数据估计系数 0，2，3，4 ，也可看做曲面拟合（其实为超平面）
T=[ones(14,1) t‘ (t.^2)'];
[b,bint,r,rint,stats]=regress(s',T); b,stats
得回归模型为：
ˆ 9.1329 65.8896 s t 489.2946 t2
预测及作图
Y=polyconf(p,t,S) plot(t,s,'k+',t,Y,'r')
（二）多元二项式回归
命令：rstool（x，y，’model’, alpha）
nm矩阵
n维列向量
显著性水平
（缺省时为0.05）
由下列 4 个模型中选择 1 个（用字符串输入，缺省时为线性模型）： linear（线性）： y 0 1 x1 m xm purequadratic（纯二次）： interaction（交叉）： y
其中 x=（x1，x2，„，xn），y=（y1，y2 ，„，yn）； m m-1 p=（a1，a2，„，am+1）是多项式 y=a1x +a2x +„+amx+am+1 的系数；S 是一个矩阵，用来估计预测误差.

Matlab技术回归分析方法

Matlab技术回归分析方法简介：回归分析是一种常用的数据分析方法，用于建立变量之间的关系模型。

Matlab是一种功能强大的数值计算软件，提供了丰富的函数和工具包，用于实现回归分析。

本文将介绍几种常见的Matlab技术回归分析方法，并探讨其应用场景和优缺点。

一、线性回归分析：线性回归分析是回归分析的经典方法之一，用于研究变量之间的线性关系。

在Matlab中，可以使用`fitlm`函数来实现线性回归分析。

该函数通过最小二乘法拟合出最优的线性模型，并提供了各种统计指标和图形展示功能。

线性回归分析的应用场景广泛，例如预测销售额、研究市场需求等。

然而，线性回归假设自变量和因变量之间存在线性关系，当数据呈现非线性关系时，线性回归会失效。

为了解决非线性关系的问题，Matlab提供了多种非线性回归分析方法，如多项式回归、指数回归等。

二、多项式回归分析：多项式回归分析是一种常见的非线性回归方法，用于建立多项式模型来描述变量之间的关系。

在Matlab中，可以使用`fitlm`函数中的`polyfit`选项来实现多项式回归分析。

多项式回归在处理非线性关系时具有很好的灵活性。

通过选择不同的多项式次数，可以适应不同程度的非线性关系。

然而，多项式回归容易过拟合，导致模型过于复杂，对新数据的拟合效果不佳。

为了解决过拟合问题，Matlab提供了正则化技术，如岭回归和Lasso回归，可以有效控制模型复杂度。

三、岭回归分析：岭回归是一种正则化技术，通过添加L2正则项来控制模型的复杂度。

在Matlab中，可以使用`fitlm`函数的`Regularization`选项来实现岭回归分析。

岭回归通过限制系数的大小，减少模型的方差，并改善模型的拟合效果。

然而，岭回归不能自动选择最优的正则化参数，需要通过交叉验证等方法进行调优。

四、Lasso回归分析：Lasso回归是另一种常用的正则化技术，通过添加L1正则项来控制模型的复杂度。

在Matlab中，可以使用`fitlm`函数的`Regularization`选项来实现Lasso回归分析。

数学建模回归分析matlab版

案例一：股票价格预测
总结词
基于历史销售数据，建立回归模型预测未来销售量。
详细描述
收集公司或产品的历史销售数据，包括销售额、销售量、客户数量等，利用Matlab进行多元线性回归分析，建立销售量与时间、促销活动、市场环境等因素之间的回归模型，并利用模型预测未来销售量。
案例二：销售预测
基于历史人口数据，建立回归模型预测未来人口增长趋势。
非线性模型的评估和检验
非线性回归模型是指因变量和自变量之间的关系不是线性的，需要通过非线性函数来拟合数据。
非线性回归模型
Matlab提供了非线性最小二乘法算法，可以用于估计非线性回归模型的参数。
非线性最小二乘法
03
CHAPTER
线性回归分析
一元线性回归分析是用来研究一个因变量和一个自变量之间的线性关系的统计方法。
回归分析在许多领域都有广泛的应用，如经济学、生物学、医学、工程学等。
它可以帮助我们理解变量之间的关系，预测未来的趋势，优化决策，以及评估模型的性能和可靠性。
回归分析的重要性
模型评估指标
用于评估模型性能的统计量，如均方误差（MSE）、均方根误差（RMSE）等。
误差项
实际观测值与模型预测值之间的差异，通常用 ε 表示。
总结词
对数回归模型的一般形式为 (y = a + blnx) 或 (y = a + bln(x))，其中 (y) 是因变量，(x) 是自变量，(a) 和 (b) 是待估计的参数。在Matlab中，可以使用 `log` 函数进行对数转换，并使用 `fitlm` 或 `fitnlm` 函数进行线性化处理，然后进行线性回归分析。
详细描述
多项式回归模型是一种非线性回归模型，适用于因变量和自变量之间存在多项式关系的情况。

MATLAB回归分析工具箱使用方法

MATLAB回归分析工具箱使用方法回归分析是一种用于探索变量之间关系的统计方法。

它可以通过分析一个或多个自变量（也称为预测变量或解释变量）与一个因变量（也称为响应变量或预测变量）之间的关系来进行预测和解释。

在MATLAB中，进行回归分析需要使用统计和机器学习工具箱。

下面是使用MATLAB回归分析工具箱的一般步骤：1.准备数据：首先，你需要准备你要进行回归分析的数据。

数据应包括自变量和因变量。

你可以将数据存储在MATLAB的工作空间中。

2. 导入数据：如果你的数据存储在外部文件中，如Excel文件或CSV文件，你可以使用MATLAB的导入工具将数据导入到MATLAB中。

3.拟合模型：在回归分析中，你需要选择适当的模型来拟合你的数据。

MATLAB提供了多种回归模型，如线性回归、多项式回归、广义线性模型等。

你可以根据你的数据类型和需求选择适当的模型。

4. 拟合模型参数：一旦你选择了合适的模型，你需要拟合模型参数。

在MATLAB中，你可以使用"fitlm"函数来拟合线性模型，使用"fitrgp"函数来拟合高斯过程回归模型。

这些函数将返回一个拟合模型的对象。

5.模型评估：拟合模型后，你可以对模型进行评估。

MATLAB提供了一些工具来评估模型的好坏，如决定系数（R²）、均方根误差（RMSE）等。

你可以使用这些指标来判断你的模型是否满足你的需求。

6. 预测：一旦你拟合了你的模型并评估了模型的好坏，你可以使用模型来进行预测。

你可以使用"predict"函数来预测新的自变量对应的因变量。

除了上述步骤外，MATLAB还提供了一些其他的回归分析工具箱的功能，如特征选择、模型比较、交叉验证等。

你可以根据你的需求来选择适当的功能和方法。

总结起来，使用MATLAB回归分析工具箱进行回归分析的一般步骤包括数据准备、数据导入、选择模型、拟合模型参数、模型评估和预测。

利用 Matlab作回归分析

利用 Matlab 作回归分析一元线性回归模型：2,(0,)y x N αβεεσ=++求得经验回归方程：ˆˆˆyx αβ=+ 统计量：总偏差平方和：21()n i i SST y y ==-∑，其自由度为1T f n =-；回归平方和：21ˆ()n i i SSR y y ==-∑，其自由度为1R f =；残差平方和：21ˆ()n i i i SSE y y ==-∑，其自由度为2E f n =-；它们之间有关系：SST=SSR+SSE 。

一元回归分析的相关数学理论可以参见《概率论与数理统计教程》，下面仅以示例说明如何利用Matlab 作回归分析。

【例1】为了了解百货商店销售额x 与流通费率（反映商业活动的一个质量指标，指每元商品流转额所分摊的流通费用）y 之间的关系，收集了九个商店的有关数据，见下表1.试建立流通费率y 与销售额x 的回归方程。

表1 销售额与流通费率数据【分析】：首先绘制散点图以直观地选择拟合曲线，这项工作可结合相关专业领域的知识和经验进行，有时可能需要多种尝试。

选定目标函数后进行线性化变换，针对变换后的线性目标函数进行回归建模与评价，然后还原为非线性回归方程。

【Matlab数据处理】：【Step1】：绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。

510152025图1 销售额与流通费率数据散点图根据图1，初步判断应以幂函数曲线为拟合目标，即选择非线性回归模型，目标函数为：(0)b y ax b =< 其线性化变换公式为：ln ,ln v y u x == 线性函数为：ln v a bu =+【Step2】：线性化变换即线性回归建模（若选择为非线性模型）与模型评价% 线性化变换u=log(x)';v=log(y)';% 构造资本论观测值矩阵mu=[ones(length(u),1) u];alpha=0.05;% 线性回归计算[b,bint,r,rint,states]=regress(v,mu,alpha)输出结果：b =[ 2.1421; -0.4259]表示线性回归模型ln=+中：lna=2.1421，b=-0.4259；v a bu即拟合的线性回归模型为=-；y x2.14210.4259bint =[ 2.0614 2.2228; -0.4583 -0.3934]表示拟合系数lna和b的100(1-alpha)%的置信区间分别为：[2.0614 2.2228]和[-0.4583 -0.3934]；r =[ -0.0235 0.0671 -0.0030 -0.0093 -0.0404 -0.0319 -0.0016 0.0168 0.0257]表示模型拟合残差向量；rint =[ -0.0700 0.02300.0202 0.1140-0.0873 0.0813-0.0939 0.0754-0.1154 0.0347-0.1095 0.0457-0.0837 0.0805-0.0621 0.0958-0.0493 0.1007]表示模型拟合残差的100(1-alpha)%的置信区间；states =[0.9928 963.5572 0.0000 0.0012] 表示包含20.9928SSR R SST==、方差分析的F 统计量/963.5572//(2)R E SSR f SSR F SSE f SSE n ===-、方差分析的显著性概率((1,2))0p P F n F =->≈；模型方差的估计值2ˆ0.00122SSE n σ==-。

在Matlab中进行回归分析和预测模型的技术

在Matlab中进行回归分析和预测模型的技术在当今数据驱动的社会中，回归分析和预测模型成为了数据科学领域中不可或缺的技术。

在这方面，Matlab作为一个功能强大且广泛应用的数学软件包，为进行回归分析和预测模型提供了丰富的工具和函数。

本文将探讨在Matlab中使用回归分析进行数据建模和预测的技术。

首先，回归分析是一种通过建立一个数学方程来描述变量之间关系的统计方法。

它常用于研究自变量（也称为预测变量）与因变量之间的关系。

在Matlab中，回归分析主要通过线性回归模型来实现。

线性回归模型假设因变量与自变量之间存在线性关系。

在Matlab中，可以使用regress函数来拟合线性回归模型。

该函数可以通过最小二乘法估计回归系数，使得预测变量与实际观测值之间的残差平方和最小化。

除了线性回归模型，Matlab还提供了其他类型的回归模型，如多项式回归模型、岭回归模型和弹性网络回归模型等。

多项式回归模型通过增加自变量的多项式项来处理非线性关系。

岭回归模型和弹性网络回归模型则通过引入正则化项来解决多重共线性问题，提高模型的鲁棒性和预测能力。

在进行回归分析时，特征工程是一个重要的环节。

特征工程涉及到对原始数据进行处理和转换，以提取对模型建立和预测有用的特征。

在Matlab中，可以利用数据预处理工具箱来进行特征工程。

数据预处理工具箱提供了一系列函数和工具来处理数据中的缺失值、异常值和重复值，进行特征选择和降维，并进行数据标准化和归一化等操作。

通过合理的特征工程，可以提高模型的性能和准确度。

除了回归分析，预测模型在许多实际应用中也起着重要的作用。

预测模型可以根据历史数据和趋势来预测未来的趋势和行为。

在Matlab中，可以利用时间序列分析和神经网络等方法进行预测建模。

时间序列分析是一种用于预测未来数值的统计方法，广泛应用于经济学、金融学和气象学等领域。

在Matlab中，时间序列分析主要通过自回归（AR）模型和移动平均（MA）模型来实现。

matlab多元回归预测

matlab多元回归预测英文回答：In multivariate regression analysis, we aim to predict a dependent variable based on multiple independent variables. This technique is widely used in various fields, including finance, economics, and social sciences.To perform multivariate regression analysis in MATLAB, we can use the "fitlm" function. This function fits alinear regression model to the data and provides various statistical measures and predictions.Let's say we have a dataset with three independent variables (X1, X2, X3) and one dependent variable (Y). We can start by loading the data into MATLAB and creating a design matrix:matlab.data = load('data.mat');X = [data.X1, data.X2, data.X3];Y = data.Y;Next, we can use the "fitlm" function to fit the linear regression model:matlab.model = fitlm(X, Y);Once the model is fitted, we can obtain various statistics and predictions. For example, we can check the coefficients of the independent variables:matlab.coefficients = model.Coefficients;disp(coefficients);We can also make predictions using the model. Let's say we have a new set of independent variables (X1_new, X2_new, X3_new) for which we want to predict the dependent variable:matlab.X_new = [X1_new, X2_new, X3_new];Y_predicted = predict(model, X_new);disp(Y_predicted);This will give us the predicted values of the dependent variable based on the new independent variables.中文回答：在多元回归分析中，我们旨在基于多个自变量来预测一个因变量。

MATLAB 回归分析regress,nlinfit,stepwise函数

MATLAB 回归分析regress,nlinfit,stepwise函数matlab回归分析regress,nlinfit,stepwise函数回归分析1．多元线性重回在matlab统计工具箱中使用命令regress()实现多元线性回归，调用格式为b=regress(y，x)或[b，bint，r，rint，statsl=regess(y，x，alpha)其中因变量数据向量y和自变量数据矩阵x按以下排列方式输入对一元线性重回，挑k=1即可。

alpha为显著性水平(缺省时预设为0.05)，输入向量b，bint为回归系数估计值和它们的置信区间，r，rint为残差及其置信区间，stats就是用作检验重回模型的统计数据量，存有三个数值，第一个就是r2，其中r就是相关系数，第二个就是f统计数据量值，第三个就是与统计数据量f对应的概率p，当p拒绝h0，回归模型成立。

图画出来残差及其置信区间，用命令rcoplot(r，rint)实例1：已知某湖八年来湖水中cod浓度实测值(y)与影响因素湖区工业产值(x1)、总人口数(x2)、捕鱼量(x3)、降水量(x4)资料，建立污染物y的水质分析模型。

(1)输出数据x1=[1.376,1.375,1.387,1.401,1.412,1.428,1.445,1.477]x2=[0.450,0.475,0.485,0.50 0,0.535,0.545,0.550,0.575]x3=[2.170,2.554,2.676,2.713,2.823,3.088,3.122,3.262]x4=[0.8922,1.1610,0.5346,0.9589,1.0239,1.0499,1.1065,1.1387]y=[5.19,5.30,5.60，5.82，6.00,6.06，6.45，6.95](2)留存数据(以数据文件.mat形式留存，易于以后调用)savedatax1x2x3x4yloaddata(抽出数据)(3)继续执行重回命令x=[ones(8,1)，]；[b，bint，r，rint，stats]=regress得结果：b=(-16.5283，15.7206，2.0327，-0.2106，-0.1991)’stats=(0.9908，80.9530，0.0022)即为=-16.5283+15.7206xl+2.0327x2-0.2106x3+0.1991x4r2=0.9908，f=80.9530，p=0.00222．非线性重回非线性回归可由命令nlinfit来实现，调用格式为[beta,r,j]=nlinfit(x，y，'model’，beta0)其中，输人数据x，y分别为n×m矩阵和n维列向量，对一元非线性回归，x为n维列向量model是事先用m-文件定义的非线性函数，beta0是回归系数的初值，beta是估计出的回归系数，r是残差，j是jacobian矩阵，它们是估计预测误差需要的数据。

matlab二元逻辑回归-概述说明以及解释

matlab二元逻辑回归-概述说明以及解释1.引言引言部分是文章的开篇，通常用来介绍文章的主题和研究背景，为读者提供一个整体的了解。

在本文中，引入的主题是"matlab二元逻辑回归"。

在概述部分，我们可以简要介绍二元逻辑回归的定义和应用，引出本文的研究内容和目的。

json"1.1 概述":{"二元逻辑回归是一种统计学习方法，用于建立一个预测模型来描述一个二元随机变量的概率分布。

在实际应用中，二元逻辑回归常用于解决分类问题，例如判断一个邮件是否为垃圾邮件、一个患者是否患有某种疾病等。

通过对数据进行建模和训练，我们可以利用二元逻辑回归模型来进行分类预测。

Matlab作为一种强大的科学计算软件，提供了丰富的工具和函数用于进行数据分析和建模。

本文将重点介绍在Matlab中如何实现二元逻辑回归，并通过一个实例来演示其应用。

通过学习本文，读者将了解二元逻辑回归的基本概念，掌握在Matlab 中如何进行二元逻辑回归建模和预测，以及了解该方法在实际应用中的优缺点和发展方向。

"}1.2 文章结构本文主要分为引言、正文和结论三个部分。

在引言部分中，将对二元逻辑回归进行概述，介绍文章结构和目的。

正文部分将详细介绍二元逻辑回归的概念和在Matlab中的应用，包括算法原理和实现步骤。

同时，将通过一个实例来帮助读者更好地理解二元逻辑回归的使用方法。

在结论部分，将总结二元逻辑回归在Matlab中的应用，并进行优缺点分析，最后展望未来发展方向，为读者提供一个全面的了解和展望。

1.3 目的:本文的目的是探讨在Matlab中如何实现二元逻辑回归，并通过实际案例展示其应用场景。

我们将深入讨论二元逻辑回归的概念和原理，并通过Matlab代码实现具体的操作步骤。

通过本文的阐述，读者可以更加深入了解二元逻辑回归在数据分析和预测中的作用，以及在Matlab环境下如何灵活运用这一技术。

matlab里ar模型的参数解释

Matlab中的AR模型（自回归模型）是一种常见的时间序列建模方法，用于预测未来的数值。

AR模型的参数解释对于理解模型的预测能力和对时间序列数据的理解至关重要。

在本文中，我将深入探讨Matlab中AR模型的参数解释，并共享我对这个主题的个人观点和理解。

1. AR模型简介AR模型是建立在时间序列数据上的统计模型，在Matlab中可以通过ar模块来进行建模和参数估计。

AR模型假设未来的数值是过去若干个数值的线性组合，其中过去的数值被称为滞后项。

AR模型的一般形式可以表示为：y(t) = c + Σφ(i)y(t-i) + ε(t)其中，y(t)是在时刻t的数值，c是常数项，φ(i)是AR模型的参数，ε(t)是白噪声误差。

在这个模型中，φ(i)表示了过去数值对当前数值的影响程度，参数的大小和符号对模型的预测能力和数据的理解都有着重要的影响。

2. AR模型的参数解释在Matlab中，使用ar模块可以对AR模型的参数进行估计和解释。

对于一个已经建立的AR模型，可以使用以下代码来获取模型的参数：```matlabmdl = ar(data, p); % data是时间序列数据，p是滞后阶数parameters = mdl.a;```在这段代码中，ar函数用于建立AR模型，data是输入的时间序列数据，p是滞后阶数，mdl.a用于获取模型的参数。

得到模型的参数后，可以通过观察参数的值和符号来解释模型对数据的影响。

3. 参数解释的重要性对AR模型的参数进行解释对于理解模型的预测能力和对时间序列数据的影哿至关重要。

参数的大小和符号表明了过去数值对当前数值的影响程度，这对于理解数据的变化规律和趋势预测有着重要的意义。

参数的解释可以帮助我们发现数据背后的规律和规则，为进一步分析和应用提供了重要的参考。

深入理解AR模型的参数解释对于在实际问题中的应用和分析具有重要的意义。

4. 我对AR模型参数解释的个人观点和理解在我的个人看来，AR模型的参数解释是对时间序列数据的理解和分析过程中不可或缺的一部分。

MATLAB回归分析

MATLAB回归分析回归分析是一种通过建立数学模型来研究变量之间的关系的统计方法。

在MATLAB中，我们可以使用回归分析工具箱来进行回归分析。

回归分析的目标是找到一个能够最好地描述自变量和因变量之间关系的数学模型。

在这篇文章中，我们将介绍回归分析的基本原理、MATLAB中的回归分析工具箱的使用以及如何解释回归分析的结果。

回归分析的基本原理回归分析建立在线性回归的基础上。

线性回归假设因变量与自变量之间存在一个线性关系。

回归分析通过找到最佳拟合线来描述这种关系。

最常用的回归方程是一元线性回归方程，它可以表示为：y=β0+β1x+ε，其中y是因变量，x是自变量，β0和β1是回归系数，ε是误差项。

- regress函数：用于计算多元线性回归模型，并返回回归系数、截距和残差。

例如，[B, BINT, R]=regress(y, X)用于计算因变量y和自变量矩阵X之间的回归模型。

- fitlm函数：用于拟合线性回归模型并返回拟合对象。

例如，mdl= fitlm(X, y)用于拟合因变量y和自变量矩阵X之间的线性回归模型，并返回mdl拟合对象。

- plot函数：用于绘制回归分析的结果。

例如，plot(mdl)用于绘制fitlm函数返回的拟合对象mdl的结果。

- coefCI函数：用于计算回归系数的置信区间。

例如，CI =coefCI(mdl)用于计算拟合对象mdl中回归系数的置信区间。

解释回归分析的结果回归分析的结果通常包括拟合曲线、回归系数以及模型的可靠性指标。

拟合曲线描述了自变量和因变量之间的关系。

回归系数可以用来解释自变量对因变量的影响。

模型的可靠性指标包括截距、回归系数的显著性检验以及相关系数等。

拟合曲线可以通过调用plot函数来绘制。

回归系数可以通过调用coef函数来获取。

对回归系数的显著性检验可以利用置信区间来判断，如果置信区间包含0，则说明回归系数不显著。

相关系数可以通过调用corrcoef函数来计算。

二阶回归模型 matlab 五元二次

二阶回归模型是数学和统计学中常用的模型之一，它可以通过建立变量之间的二次关系来描述数据的变化规律。

在Matlab中，我们可以利用多项式函数来构建二阶回归模型，并通过最小二乘法求解模型参数。

本文将详细介绍在Matlab中如何使用五元二次回归模型进行数据分析。

一、二阶回归模型介绍二阶回归模型是指自变量的最高次数为二次方的回归模型。

它的一般形式可以表示为：y = β0 + β1x1 + β2x2 + β3x3 + β4x4 + β5x5 + β6x1^2 +β7x2^2 + β8x3^2 + β9x4^2 + β10x5^2 + β11x1x2 + β12x1x3 + β13x1x4 + β14x1x5 + β15x2x3 + β16x2x4 + β17x2x5 + β18x3x4 + β19x3x5 + β20x4x5其中，y是因变量，x1、x2、x3、x4、x5是自变量，β0至β20是模型的参数。

二、Matlab中的二阶回归模型在Matlab中，我们可以使用polyfit函数来拟合二阶回归模型。

具体步骤如下：1. 将数据准备为矩阵形式，其中每一行代表一个数据点，包括因变量y和自变量x1、x2、x3、x4、x5。

2. 使用polyfit函数拟合数据，语法为：p = polyfit(X,y,2)其中，X是自变量矩阵，y是因变量向量，2表示二次回归模型。

3. 获取模型参数，包括截距和系数：beta0 = p(3);beta1 = p(2);...beta20 = p(1);4. 得到回归方程：y = beta0 + beta1*x1 + beta2*x2 + beta3*x3 + beta4*x4 + beta5*x5 + beta6*x1^2 + beta7*x2^2 + beta8*x3^2 +beta9*x4^2 + beta10*x5^2 + beta11*x1*x2 + beta12*x1*x3 + beta13*x1*x4 + beta14*x1*x5 + beta15*x2*x3 + beta16*x2*x4 + beta17*x2*x5 + beta18*x3*x4 + beta19*x3*x5 + beta20*x4*x5三、五元二次回归模型实例接下来，我们通过一个实例来演示在Matlab中使用五元二次回归模型进行数据分析。