统计学多元回归分析实例

合集下载

多元回归模型及其应用

多元回归模型及其应用多元回归模型是统计学中的一种常见方法，它可以帮助我们分析多个自变量与一个因变量之间的关系。

在实际应用中，多元回归模型在预测和解释变量之间的复杂关系方面非常重要。

本文将介绍多元回归模型的基本概念、构建方法和应用场景。

一、多元回归模型的基本概念多元回归模型是指，用于分析多个自变量和一个因变量之间关系的一种统计模型。

假设我们有一个因变量Y和k个自变量X1、X2…Xk，我们可以建立下面的模型来描述它们之间的关系：Y = β0 + β1X1 + β2X2 + … + βkXk + ε其中，β0是截距项，β1、β2、…、βk是自变量的系数，ε是误差项。

误差项代表了模型中无法被自变量解释的部分，通常假设误差项符合正态分布。

二、多元回归模型的构建方法1. 变量选择在构建多元回归模型时，选择自变量非常重要。

首先要考虑每个自变量与因变量的相关性，只有当自变量与因变量的相关性显著时，才有可能对因变量做出有用的解释。

此外，还要考虑多个自变量之间的相关性，若存在高度相关的自变量，这将会让回归模型变得不稳定。

2. 模型拟合模型拟合是指，通过计算模型参数，将模型调整到最适合样本数据的状态。

在多元回归模型中，可以用最小二乘法来拟合模型，该方法试图让模型预测的值与实际值之间的差异最小化。

3. 模型评估模型评估是指对多元回归模型的性能进行评估，主要包括判断模型的拟合效果、检验自变量系数的显著性以及判断模型是否存在过拟合等。

一些常见的评估指标包括拟合优度(R2)、均方根误差(RMSE)、Akaike信息准则(AIC)和贝叶斯信息准则(BIC)等。

三、多元回归模型的应用场景多元回归模型可以应用于许多领域，例如社会科学、自然科学和商业领域等。

以下是一些应用场景的举例：1. 销售预测在商业领域，多元回归模型可以用于预测销售数量。

我们可以通过收集历史销售数据和相关的自变量来建立回归模型，例如促销活动、价格、产品质量等。

这些自变量能够帮助我们解释销售数量的变化，并预测未来销售趋势。

统计学中的多元回归分析

统计学中的多元回归分析多元回归分析是一种在统计学中广泛使用的分析方法，用于研究一个或多个自变量对一个因变量的影响。

它可以帮助我们理解变量之间的关系，并预测因变量的值。

在本文中，我们将介绍多元回归分析的概念、方法和应用。

一、概念和基本假设多元回归分析是一种统计建模的技术，它通过建立数学关系模型，描述一个或多个自变量如何与一个因变量相关联。

在多元回归分析中，我们假定自变量和因变量之间存在线性关系，并基于这一假设进行分析。

此外，我们还假设误差项之间是独立且服从正态分布的。

二、多元回归模型多元回归模型可以写成如下形式：Y = β0 + β1*X1 + β2*X2 + … + βn*Xn + ε其中，Y代表因变量，X1至Xn代表自变量，β0至βn代表回归系数，ε代表误差项。

回归系数表示了自变量对因变量的影响程度。

我们可以通过估计回归系数来获得关于自变量与因变量之间关系的更多信息。

三、回归系数的估计估计回归系数是多元回归分析中的重要步骤，常用的方法包括最小二乘法和最大似然法。

最小二乘法通过最小化观测值与回归方程预测值之间的差异来估计回归系数。

最大似然法则基于给定观测数据时回归系数最有可能的取值，求解回归系数的估计值。

四、解释回归方程在进行多元回归分析时，除了估计回归系数，还需要解释回归方程及其统计显著性。

常见的指标包括回归方程的R²值、调整R²值、F统计量以及各个自变量的t统计量等。

R²值表示回归模型可以解释因变量变异程度的百分比，越接近1表示模型拟合效果较好。

F统计量则用于检验自变量的联合显著性。

五、多元共线性问题多元回归分析中常常会遇到多元共线性问题，即自变量之间存在高度相关性，对回归系数的估计造成困扰。

为了检测和解决多元共线性问题，可以使用方差膨胀因子和条件数等指标进行诊断，并采取相应的修正措施。

六、实例分析下面通过一个实例来演示多元回归分析的应用。

假设我们想研究一个地区的人均GDP与教育水平、医疗水平和就业率之间的关系。

统计学中的多元回归分析方法

统计学中的多元回归分析方法统计学是一门研究收集、整理和解释数据的学科，而多元回归分析是其中一种重要的方法。

本文将针对统计学中的多元回归分析方法进行详细讨论和解释。

一、引言多元回归分析是一种用于研究多个自变量与一个因变量之间关系的统计方法。

通过建立一个数学模型，它可以被用来预测或解释因变量的变化。

多元回归分析方法可以帮助我们理解不同自变量与因变量之间的影响程度和相关性。

二、多元回归模型多元回归模型可以表示为Y = β0 + β1X1 + β2X2 + ... + βnXn + ε，其中Y是因变量，X1至Xn是自变量，β0至βn是回归系数，ε是误差项。

回归系数表示了自变量对因变量的影响程度，而误差项则表示了模型无法解释的部分。

三、多元回归分析步骤1. 数据准备：收集所需自变量和因变量的数据，并进行预处理，如缺失值填充和异常值处理。

2. 模型选择：根据研究目的和数据特点选择适当的多元回归模型。

3. 参数估计：利用最小二乘法或其他估计方法估计回归系数，找到最优解。

4. 模型检验：通过统计检验和评估指标，检验模型的拟合程度和显著性。

5. 解释结果：解释回归系数的意义和影响，评估模型的可解释性。

6. 预测应用：利用得到的模型对未知数据进行预测，评估模型的预测效果。

四、多元共线性多元共线性是指自变量之间存在高度相关性的情况，会影响回归系数的估计和解释结果的准确性。

通过相关系数矩阵和方差膨胀因子等方法，可以检测和解决多元共线性问题。

五、模型评估指标在多元回归分析中，常用的模型评估指标包括决定系数（R-squared）、调整决定系数（Adjusted R-squared）、标准误差（Standard Error）、F统计量（F-statistic）等。

这些指标可以评估模型的拟合优度和显著性。

六、案例应用以房价预测为例，假设我们想通过多个自变量（如房屋面积、位置、卧室数量等）来预测房屋的价格。

通过收集相关数据并进行多元回归分析，可以建立一个房价预测模型，并根据回归系数解释不同自变量对于房价的影响程度。

多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法，它可以用来研究多个自变量与因变量之间的关系。

在实际应用中，多元线性回归模型可以帮助我们理解不同自变量对因变量的影响程度，从而进行预测和决策。

下面，我们将通过一个实际案例来介绍多元线性回归模型的应用。

案例背景：某电商公司希望了解其产品销售额与广告投入、季节因素和竞争对手销售额之间的关系，以便更好地制定营销策略和预测销售额。

数据收集：为了分析这一问题，我们收集了一段时间内的产品销售额、广告投入、季节因素和竞争对手销售额的数据。

这些数据将作为我们多元线性回归模型的输入变量。

模型建立：我们将建立一个多元线性回归模型，以产品销售额作为因变量，广告投入、季节因素和竞争对手销售额作为自变量。

通过对数据进行拟合和参数估计，我们可以得到一个多元线性回归方程，从而揭示不同自变量对产品销售额的影响。

模型分析：通过对模型的分析，我们可以得出以下结论：1. 广告投入对产品销售额有显著影响，广告投入越大，产品销售额越高。

2. 季节因素也对产品销售额有一定影响，不同季节的销售额存在差异。

3. 竞争对手销售额对产品销售额也有一定影响，竞争对手销售额越大，产品销售额越低。

模型预测：基于建立的多元线性回归模型，我们可以进行产品销售额的预测。

通过输入不同的广告投入、季节因素和竞争对手销售额，我们可以预测出相应的产品销售额，从而为公司的营销决策提供参考。

结论：通过以上分析，我们可以得出多元线性回归模型在分析产品销售额与广告投入、季节因素和竞争对手销售额之间关系时的应用。

这种模型不仅可以帮助我们理解不同因素对产品销售额的影响，还可以进行销售额的预测，为公司的决策提供支持。

总结：多元线性回归模型在实际应用中具有重要意义，它可以帮助我们理解复杂的变量关系，并进行有效的预测和决策。

在使用多元线性回归模型时，我们需要注意数据的选择和模型的建立，以确保模型的准确性和可靠性。

通过以上案例，我们对多元线性回归模型的应用有了更深入的理解，希望这对您有所帮助。

spss多元回归分析案例

spss多元回归分析案例SPSS多元回归分析案例。

在统计学中，多元回归分析是一种用于探究多个自变量与因变量之间关系的方法。

通过多元回归分析，我们可以了解不同自变量对因变量的影响程度，以及它们之间的相互作用情况。

在本篇文档中，我将通过一个实际案例来介绍如何使用SPSS软件进行多元回归分析。

案例背景：假设我们是一家电子产品公司的市场营销团队，在推出新产品之前，我们希望了解不同因素对产品销量的影响。

我们收集了一些数据，包括产品的售价、广告投入、竞争对手的售价、季节等因素，以及产品的销量作为因变量。

数据准备：首先，我们需要将数据录入SPSS软件中。

在SPSS中，我们可以通过导入Excel文件的方式将数据导入到软件中，并进行必要的数据清洗和处理。

确保数据的准确性和完整性对于后续的多元回归分析非常重要。

模型建立：接下来，我们需要建立多元回归模型。

在SPSS中，我们可以通过依次选择“分析”-“回归”-“线性回归”来进行多元回归分析。

在“因变量”栏中输入销量，然后将所有自变量依次输入到“自变量”栏中。

在建立模型之前，我们还需要考虑是否需要进行变量转换或交互项的添加，以更好地拟合数据。

模型诊断：建立模型后，我们需要对模型进行诊断，以确保模型的准确性和有效性。

在SPSS中，我们可以通过查看残差的正态性、异方差性以及自相关性来进行模型诊断。

如果模型存在严重的偏差或违反了多元回归分析的假设，我们需要进行相应的修正或改进。

模型解释：最后，我们需要解释多元回归模型的结果。

在SPSS的输出结果中，我们可以看到各个自变量的系数、显著性水平、调整R方等统计指标。

通过这些指标，我们可以了解不同自变量对销量的影响程度，以及它们之间的相互作用情况。

同时，我们还可以进行各种假设检验，来验证模型的有效性和可靠性。

结论：通过以上多元回归分析，我们可以得出不同自变量对产品销量的影响程度，以及它们之间的相互作用情况。

这些结果对于我们制定产品的定价策略、广告投放策略以及市场营销策略都具有重要的指导意义。

回归分析实例范文

回归分析实例范文回归分析是一种统计方法，用于研究两个或多个变量之间的关系。

它可以帮助我们了解变量之间的相关性，以及一个变量对另一个变量的影响程度。

以下是一个回归分析的实例，以说明如何运用回归分析来探索变量之间的关系。

假设我们有两个变量：广告费用（x）和销售额（y）。

我们对其中一产品进行了市场调研，收集了一些数据，如下所示：广告费用（万元），销售额（万元）-----------，-----------4，1002，508，2006，15010，250我们的目标是确定广告费用与销售额之间的关系，以及预测未来的销售额。

首先，我们可以通过绘制散点图来观察两个变量之间的关系。

从散点图中可以看出，广告费用与销售额之间存在着正相关关系，即广告费用越高，销售额也越高。

接下来，我们可以使用回归分析来量化这种关系。

在回归分析中，我们假设存在一个线性关系，即销售额（y）与广告费用（x）之间的关系可以用一条直线来表示。

我们希望找到一条最佳拟合线，使得该直线尽可能地通过数据点。

通过回归分析，我们可以得到以下回归方程，用于预测销售额：y=β0+β1*x其中，β0表示截距，β1表示斜率。

回归分析还可以计算出拟合优度（R²），来评估模型的拟合程度。

R²的取值范围为0到1，越接近1表示模型的拟合程度越好。

现在，我们来计算回归方程和拟合优度。

首先，我们需要计算β1和β0。

β1可以通过以下公式来计算：β1 = ∑((xi - x平均)*(yi - y平均)) / ∑((xi - x平均)²)β0可以通过以下公式计算：β0=y平均-β1*x平均其中，x平均和y平均分别表示广告费用和销售额的平均值。

计算得到β1≈20计算得到β0≈5因此，回归方程为：y=5+20*x接下来，我们计算拟合优度（R²）。

拟合优度可以通过以下公式计算：R²=SSR/SSTO其中，SSR（回归平方和）表示拟合线解释的总方差SSR = ∑((yi - y预测)²)SSTO（总平方和）表示实际观测值和实际平均值之间的总方差，可以通过以下公式计算：SSTO = ∑((yi - y平均)²)计算得到SSR≈850计算得到SSTO≈1166.67因此，拟合优度（R²）为：R²=850/1166.67≈0.73拟合优度为0.73，说明回归模型可以解释销售额的73%的变异性。

多元统计学回归分析优秀课件

逐步回归，逐个地把显著的变量加入；把不显著的变量去掉。
在DPS中的逐步回归分析
在DPS中，数据格式和线性回归相同：一行一个样本，一列一个变量，因变量放在最右边。
17
逐步回归：调整
值达到最大
R
下一页
18
19
分析结果和线性回归相同。
20
自变量中有定性变量的回归
学生高1成绩受初3成绩影响数据中，如果还考虑家庭收入，但它是“低”，“中”，“高”，即用1，2，3来代表的定性变量。这时需要含定性变量的回归分析，这时的回归模型是：
标准回归系数标准误 t值 p值
0.0692 2.0483 0.0546
0.5925
0.0000 4.2275 0.0005
0.2727
0.0019 2.3637 0.0289
-0.0011
0.0007 0.0095 0.9925
-0.4477
0.0108 3.2080 0.0046
从多个解释变量里面挑选“重要”因子建立回归方程，逐步回归。
H 0: 10 H 1: 10
▪ 统计软件，如DPS给出了这个检验的结果： ▪ t检验统计量为9.089，而p-值为0.000。
因变量Y的波动，被解释变量X可以解释的比例，叫做决定系数（ coefficient of determination），用R2表示。本例的R2=0.632；说明高一成绩的波动，大约有63％可由初3成绩来解释（或者说是由初 3成绩来决定）。
例：学生高一成绩，能否被初三的成绩来解释？
高1和初3成绩关系 100
90
80
70
60
50
40
40

多元统计分析案例分析

多元统计分析案例分析多元统计分析是指采用多个统计方法和技术对数据进行综合分析的一种分析方法。

它可以帮助研究者揭示出多个变量之间的复杂关系，并进一步分析它们的影响和作用。

下面以一份市场调研报告为例，介绍如何运用多元统计分析进行案例分析。

案例背景：饮料公司在上海市开展了一项市场调研，调查了300名消费者对其产品的购买行为和偏好。

调研对象包括消费者的年龄、性别、收入水平、产品购买频率、产品品牌偏好等变量。

1.数据准备：将调研数据录入电脑，确保数据的准确性和完整性。

对于缺失值进行处理，可以采用删除、插补等方法。

2.描述性统计分析：首先对数据进行描述性统计分析，包括计算平均值、标准差、频数等。

了解数据的分布情况和基本统计信息，例如了解不同性别的样本比例，不同年龄段的购买频率等。

3.相关性分析：通过相关系数分析来研究各个变量之间的关系，包括变量间的线性相关性和非线性相关性。

可以计算皮尔逊相关系数或斯皮尔曼相关系数来评估变量之间的关联程度。

4.回归分析：通过回归分析可以研究一个或多个自变量对因变量的影响程度。

可以先进行单变量回归分析，确定哪些自变量对因变量有显著影响。

然后进行多元回归分析，建立一个多元回归模型，研究多个自变量对因变量的综合影响。

5.研究假设检验：通过假设检验来验证研究假设的可靠性。

例如，可以进行t检验或方差分析来判断一些自变量对因变量的影响是否显著。

6.因素分析：可以利用因素分析来研究多个自变量之间的共同特征。

通过提取主成分或因子，将原始变量转化为更少的几个综合变量，以便对数据进行更简洁的分析和解释。

7.聚类分析：通过聚类分析可以将样本划分为不同的类别或群体，以研究不同自变量组合的消费者群体特征和购买行为。

8.判别分析：通过判别分析可以建立分类模型，将样本分为多个已知类别，以研究哪些自变量最能有效地区分不同群体。

9.结果解释和报告撰写：将多元统计分析的结果进行解释和总结，并撰写报告。

报告中应包括对分析方法的描述、数据的描述和分析结果的解释。

统计学多元回归分析实例

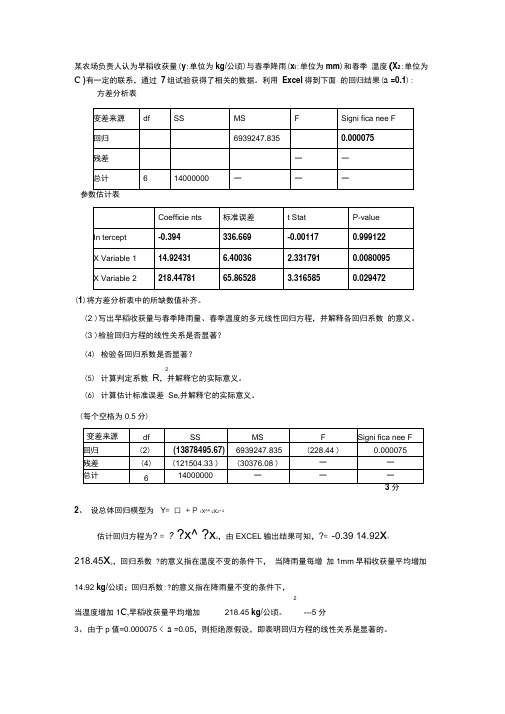
某农场负责人认为早稻收获量(y:单位为kg/公顷)与春季降雨(x i:单位为mm)和春季温度(X2:单位为C )有一定的联系，通过7组试验获得了相关的数据。

利用Excel得到下面的回归结果(a =0.1):方差分析表(1)将方差分析表中的所缺数值补齐。

(2 )写出早稻收获量与春季降雨量、春季温度的多元线性回归方程，并解释各回归系数的意义。

(3 )检验回归方程的线性关系是否显著？(4)检验各回归系数是否显著？2(5)计算判定系数R，并解释它的实际意义。

(6)计算估计标准误差Se,并解释它的实际意义。

(每个空格为0.5分)2、设总体回归模型为Y= 口+ P 1X^^ 2X2+ &?x^ ?x2，由EXCEL输出结果可知，?= -0.39 14.92x1估计回归方程为? = ?218.45x2，回归系数 ?的意义指在温度不变的条件下，当降雨量每增加1mm早稻收获量平均增加14.92 kg/公顷；回归系数:?的意义指在降雨量不变的条件下，2当温度增加1C,早稻收获量平均增加218.45 kg/公顷。

---5 分3、由于p值=0.000075 < a =0.05，则拒绝原假设，即表明回归方程的线性关系是显著的。

4、由于各回归系数的P值均小于a ( 0.05 ),所以各回归系数是显著的。

---2 分5、2二§臾二1387849567二0.99，表示早稻收获量的总变异中有99%的部分可以由降R SST 14000000雨量、温度的联合变动来解释。

---4 分6、S =」SS E =V MST = J30376.08 =174.29(k为自变量个数)，是总体回归模型e n - k -1中随机扰动项&的标准差的无偏估计量，用来衡量回归方程拟合程度的分析指标，S e越大，拟合程度越低；S e越小，拟合程度越高• —4 分。

商务统计学课件-多元线性回归分析实例应用

6.80
13.65
14.25
27
8.27
6.50
13.70
13.65
28
7.67
5.75
13.75
13.75
29
7.93
5.80
13.80
13.85
30
9.26
6.80
13.70
14.25
销售周期
1
销售价格/元
其他公司平均销售价格
/元
多元线性回归分析应用
多元线性回归分析应用
解
Y 表示牙膏销售量，X 1 表示广告费用，X 2表示销售价格， X 3
个自变量之间的线性相关程度很高，回归方程的拟合效果较好。
一元线性回归分析应用
解
广告费用的回归系数检验 t1 3.981 ，对应的 P 0.000491 0.05
销售价格的回归系数检验 t2 3.696 ，对应的 P 0.001028 0.05
其它公司平均销售价格的回归系数检验
…
14
1551.3
125.0
45.8
29.1
15
1601.2
137.8
51.7
24.6
16
2311.7
175.6
67.2
27.5
17
2126.7
155.2
65.0
26.5
18
2256.5
174.3
65.4
26.8
万元
表示其他公司平均销售价格。建立销售额的样本线性回归方程如
下：
Yˆi 15.044 0.501X 1i 2.358 X 2i 1.612 X 3i
一元线性回归分析应用

多元线性回归分析案例

多元线性回归分析案例多元线性回归分析是统计学中常用的一种分析方法，它可以用来研究多个自变量对因变量的影响，并建立相应的数学模型。

在实际应用中，多元线性回归分析可以帮助我们理解变量之间的关系，预测未来的趋势，以及制定相应的决策。

本文将通过一个实际案例来介绍多元线性回归分析的基本原理和应用方法。

案例背景。

假设我们是一家电子产品制造公司的市场营销团队，我们想要了解产品销量与广告投入、产品定价和市场规模之间的关系。

我们收集了过去一年的数据，包括每个月的产品销量（千台）、广告投入（万元）、产品定价（元/台）和市场规模（亿人）。

数据分析。

首先，我们需要对数据进行描述性统计分析，以了解各变量的分布情况和相关性。

我们计算了产品销量、广告投入、产品定价和市场规模的均值、标准差、最大最小值等统计量，并绘制了相关性矩阵图。

通过分析发现，产品销量与广告投入、产品定价和市场规模之间存在一定的相关性，但具体的关系还需要通过多元线性回归分析来验证。

多元线性回归模型。

我们建立了如下的多元线性回归模型：\[Sales = \beta_0 + \beta_1 \times Advertising + \beta_2 \times Price + \beta_3 \times MarketSize + \varepsilon\]其中，Sales表示产品销量，Advertising表示广告投入，Price表示产品定价，MarketSize表示市场规模，\(\beta_0, \beta_1, \beta_2, \beta_3\)分别为回归系数，\(\varepsilon\)为误差项。

模型验证。

我们利用最小二乘法对模型进行参数估计，并进行了显著性检验和回归诊断。

结果表明，广告投入、产品定价和市场规模对产品销量的影响是显著的，模型的拟合效果较好。

同时，我们还对模型进行了预测能力的验证，结果表明模型对未来产品销量的预测具有一定的准确性。

决策建议。

人口统计学中的多元回归分析

人口统计学中的多元回归分析随着社会的发展，人口的多元化和复杂化越来越明显。

人口统计学作为一门对人口数量、结构和分布等方面进行系统地研究和分析的学科，成为了解人口现象和规律的主要学科之一。

而多元回归分析是人口统计学中一种广泛应用的方法，可以帮助我们更加深入地了解人口现象和变化规律。

一、多元回归分析的概念和意义多元回归分析是通过制定数学模型来分析两个或两个以上变量之间的关系，并确定它们之间的相关性质。

在人口统计学中，多元回归分析常常用于研究人口数量、结构、分布等方面的影响因素和相互关系。

多元回归分析的结果可以帮助我们预测未来的人口变化趋势，制定相关政策和措施，以调整和优化人口结构，实现经济和社会的可持续发展。

二、多元回归分析的模型和假设多元回归分析的基本模型为：Y = β0 + β1X1 + β2X2 +…+ βkXk + ε其中，Y表示因变量，即需要分析的人口现象；X1、X2、…、Xk表示自变量，即影响人口现象的各种因素；β0、β1、β2…、βk表示各个自变量的回归系数，即各个自变量对因变量的贡献大小；ε则表示误差项，即未被回归模型解释的不确定因素。

多元回归分析的假设主要包括以下几点：1. 自变量和因变量之间是线性关系2. 各自变量之间不存在多重共线性（即不相互独立）3. 误差项具有零均值和常量方差4. 误差项之间不存在自相关（即不相互依赖）通过建立合适的多元回归模型，并进行数据拟合和检验，可以判断各个变量是否显著影响因变量，以及它们的影响大小和方向。

三、应用举例以人口数量与城市化程度之间的关系为例。

通过选取适当的自变量，如城市人口增长率、大学生人数、劳动力人口比例等，建立多元回归模型，可以分析这些因素对人口数量的影响。

模型拟合好之后，可以得到不同自变量的回归系数，从而可以判断不同因素对人口数量的影响程度。

如劳动力人口比例的系数为正，说明劳动力人口的增加可以促进人口数量的增长；而大学生人数的系数为负，说明大学生越多，人口数量越少，因为他们更愿意在大城市就业，而非返回农村。

多元线性回归实习实际例题分析

多元线性回归分析实习线性回归过程（Linear Regression）可用于分析一个或多个自变量与一个因变量之间的线性数量关系，并可进行回归诊断分析。

●[例题3.1]某地29名13岁男童身高x1（cm），体重x2（kg），肺活量y（L）的实测值数据见表3.1，试建立肺活量与身高、体重的回归关系。

[ 操作过程]①[ 数据格式] 见数据文件< 多元线性回归例题.sav >该数据库有4列29行，即4个变量、29个记录（Observation），每个变量占1列，每个记录占1行，该数据格式为一般多元分析的数据格式。

②[ 过程]单击后可弹出线性回归对话框。

该对话框内有诸多选项，现分别介绍。

③[ 选项]◆因变量。

只能选入1个因变量，本例选入变量“肺活量”。

◆自变量。

可以是1个或多个，本例选入变量“身高、体重”。

◆当选择不同组合的自变量进行回归分析时，可保存每次选择的自变量，用按钮和按钮可分别向前、向后翻找各种自变量的组合。

◆选择回归模型拟合的分析方法，有5种可供选择。

Enter 强迫引入法，即一般回归分析，所选自变量全部进入方程，为系统默认方式。

Stepwise 逐步回归法，加入有显著性意义的变量和剔除无显著性意义的变量，直到所建立的方程式中不再有可加入和可剔除的变量为止。

Remove 强迫剔除法。

根据设定的条件剔除自变量。

Backward向后逐步法。

所选自变量全部进入方程，根据Options对话框中设定的标准在计算过程中逐个剔除变量，直到所建立的方程式中不再含有可剔除的变量为止。

Forward：向前逐步法。

根据Options对话框中设定的标准在计算过程中逐个加入单个变量，直到所建立的方程式中不再有可加入的变量为止。

◆选择符合某变量条件的观察单位进行分析，每次只能选入1位范围，有6种方式供选择，在Value框内输入设定值。

equal to 等于设定值。

not equal to不等于设定值。

less than小于设定值。

统计学中的多元回归与方差分析

统计学中的多元回归与方差分析多元回归是指多个自变量（影响因素）对一个因变量（效果）的影响进行定量分析的方法。

方差分析则是一种用于分析因变量被一些分类变量影响的方法。

虽然两种方法的应用场景不尽相同，但是它们都很重要，是统计学中的基础知识之一。

一、多元回归多元回归分析常用于解释因变量如何受到多个自变量的影响。

例如，一个经济学家可能想要知道一个人购买食品的数量与哪些因素有关。

他可能会考虑许多不同的自变量，如收入、食品价格、家庭规模、家庭成员的年龄、偏好等。

他可能会尝试研究这些变量与购买食品数量之间的关系，并尝试建立一个数学模型来预测购买食品数量。

这就是多元回归分析所涵盖的内容。

在这个例子中，我们将购买的食品数量称为因变量，自变量包括收入、食品价格、家庭规模、家庭成员的年龄和偏好等。

我们假设这些自变量互相独立，不会相互影响。

我们还假设它们与因变量之间的关系是线性的。

在多元回归分析中，我们尝试建立一个包含所有自变量的方程来解释因变量的变化。

二、方差分析方差分析也称为变量分析或ANOVA，是用于分析因变量受到一些分类变量影响的方法。

例如，在一组实验中，我们可能会测试不同的肥料品牌对玉米的产量是否有影响。

我们还可能想比较不同的播种密度，田间间隔以及其他因素的影响。

我们可以使用方差分析来确定这些因素对玉米产量的影响程度。

在执行方差分析时，我们首先要将数据分成不同的组，然后计算每组的平均值。

接下来，我们将计算每组的平均值，以确定这些差异是否达到了统计上的显著性。

如果这些差异是显著的，我们可以确定哪些因素是造成差异的原因。

三、多元方差分析有时，我们需要同时考虑多个因素对因变量的影响。

在这种情况下，我们使用多元方差分析。

这种方法可以确定每个因素对因变量的影响大小，并确定这些差异是否具有统计学意义。

总体而言，多元回归和方差分析都是统计学家经常使用的方法。

多元回归允许我们探究因变量与多个自变量的关系，而方差分析则允许我们了解因变量受到分类变量的影响程度。

多元线性回归模型实验报告

多元线性回归模型实验报告实验报告：多元线性回归模型1.实验目的多元线性回归模型是统计学中一种常用的分析方法，通过建立多个自变量和一个因变量之间的模型，来预测和解释因变量的变化。

本实验的目的是利用多元线性回归模型，分析多个自变量对于因变量的影响，并评估模型的准确性和可靠性。

2.实验原理多元线性回归模型的基本假设是自变量与因变量之间存在线性关系，误差项为服从正态分布的随机变量。

多元线性回归模型的表达形式为：Y=b0+b1X1+b2X2+...+bnXn+ε，其中Y表示因变量，X1、X2、..、Xn表示自变量，b0、b1、b2、..、bn表示回归系数，ε表示误差项。

3.实验步骤（1）数据收集：选择一组与研究对象相关的自变量和一个因变量，并收集相应的数据。

（2）数据预处理：对数据进行清洗和转换，排除异常值、缺失值和重复值等。

（3）模型建立：根据收集到的数据，建立多元线性回归模型，选择适当的自变量和回归系数。

（4）模型评估：通过计算回归方程的拟合优度、残差分析和回归系数的显著性等指标，评估模型的准确性和可靠性。

4.实验结果通过实验，我们建立了一个包含多个自变量的多元线性回归模型，并对该模型进行了评估。

通过计算回归方程的拟合优度，我们得到了一个较高的R方值，说明模型能够很好地拟合观测数据。

同时，通过残差分析，我们检查了模型的合理性，验证了模型中误差项的正态分布假设。

此外，我们还对回归系数进行了显著性检验，确保它们是对因变量有显著影响的。

5.实验结论多元线性回归模型可以通过引入多个自变量，来更全面地解释因变量的变化。

在实验中，我们建立了一个多元线性回归模型，并评估了模型的准确性和可靠性。

通过实验结果，我们得出结论：多元线性回归模型能够很好地解释因变量的变化，并且模型的拟合优度较高，可以用于预测和解释因变量的变异情况。

同时，我们还需注意到，多元线性回归模型的准确性和可靠性受到多个因素的影响，如样本大小、自变量的选择等，需要在实际应用中进行进一步的验证和调整。

多元线性回归方法及其应用实例

多元线性回归方法及其应用实例多元线性回归方法（Multiple Linear Regression）是一种广泛应用于统计学和机器学习领域的回归分析方法，用于研究自变量与因变量之间的关系。

与简单线性回归不同，多元线性回归允许同时考虑多个自变量对因变量的影响。

多元线性回归建立了自变量与因变量之间的线性关系模型，通过最小二乘法估计回归系数，从而预测因变量的值。

其数学表达式为：Y=β0+β1X1+β2X2+...+βnXn+ε，其中Y是因变量，Xi是自变量，βi是回归系数，ε是误差项。

1.房价预测：使用多个自变量（如房屋面积、地理位置、房间数量等）来预测房价。

通过建立多元线性回归模型，可以估计出各个自变量对房价的影响权重，从而帮助房产中介或购房者进行房价预测和定价。

2.营销分析：通过分析多个自变量（如广告投入、促销活动、客户特征等）与销售额之间的关系，可以帮助企业制定更有效的营销策略。

多元线性回归可以用于估计各个自变量对销售额的影响程度，并进行优化。

3.股票分析：通过研究多个自变量（如市盈率、市净率、经济指标等）与股票收益率之间的关系，可以辅助投资者进行股票选择和投资决策。

多元线性回归可以用于构建股票收益率的预测模型，并评估不同自变量对收益率的贡献程度。

4.生理学研究：多元线性回归可应用于生理学领域，研究多个自变量（如年龄、性别、体重等）对生理指标（如心率、血压等）的影响。

通过建立回归模型，可以探索不同因素对生理指标的影响，并确定其重要性。

5.经济增长预测：通过多元线性回归，可以将多个自变量（如人均GDP、人口增长率、外商直接投资等）与经济增长率进行建模。

这有助于政府和决策者了解各个因素对经济发展的影响力，从而制定相关政策。

在实际应用中，多元线性回归方法有时也会面临一些挑战，例如共线性（多个自变量之间存在高度相关性）、异方差性（误差项方差不恒定）、自相关（误差项之间存在相关性）等问题。

为解决这些问题，研究人员提出了一些改进和扩展的方法，如岭回归、Lasso回归等。

多元线性回归模型案例

多元线性回归模型案例多元线性回归是统计学中常用的一种回归分析方法，它可以用来研究多个自变量对因变量的影响程度，是一种多元变量之间关系的分析方法。

在实际应用中，多元线性回归模型可以用来预测和解释各种现象，比如销售额、市场份额、股票价格等。

下面我们通过一个实际案例来介绍多元线性回归模型的应用。

假设我们有一个电商平台的数据，其中包括了用户的年龄、性别、购买次数和消费金额等信息。

我们想通过这些信息来建立一个多元线性回归模型，以预测用户的消费金额。

首先，我们收集了一定数量的数据样本，并进行了数据清洗和预处理工作，确保数据的准确性和完整性。

接下来，我们需要建立多元线性回归模型。

在多元线性回归模型中，我们以消费金额作为因变量，而年龄、性别和购买次数作为自变量。

我们假设消费金额与这些自变量之间存在线性关系，然后通过最小二乘法来估计模型参数。

最终得到的多元线性回归模型可以表示为：Y = β0 + β1X1 + β2X2 + β3X3 + ε。

其中，Y代表消费金额，X1、X2、X3分别代表年龄、性别和购买次数，β0、β1、β2、β3是模型的参数，ε是误差项。

通过建立多元线性回归模型，我们可以得到各个自变量对因变量的影响程度，从而进行预测和分析。

比如，我们可以利用模型来预测不同年龄、性别和购买次数的用户的消费金额，以便进行精准营销和产品定位。

另外，我们还可以通过模型来分析各个自变量之间的相关性，从而深入了解用户的消费行为规律。

在实际应用中，多元线性回归模型还可以进行模型检验和优化。

我们可以利用残差分析、方差膨胀因子等方法来检验模型的拟合效果和自变量的共线性问题，从而提高模型的准确性和稳定性。

总的来说，多元线性回归模型是一种强大的分析工具，可以用来研究多个自变量对因变量的影响，进行预测和解释。

在实际应用中，我们可以根据具体的问题和数据特点来选择合适的自变量，建立多元线性回归模型，并进行模型检验和优化，以实现精准分析和预测。

医学统计学：多元线性回归分析

多元线性回归分析
一、多元线性回归方程的概念二、多元线性回归分析步骤三、标准化偏回归系数四、自变量的筛选五、回归方程的总体评价六、多元线性回归的应用七、应用多元线性回归分析时需注意的事项
一. 多元线性回归方程的概念
表达式：
b0为回归方程的常数项； p为自变量的个数；
b1、b2、bp为偏回归系数（Partial regression
多元线性回归方程也是按最小二乘法原则获得，即：
(Y Yˆ)2 Y (b0 b1X1 b2 X2 bm Xm)2 为最小
C oe f fi c ie n tsa
Unstandardized Coefficients
Model
1
(Constant)
B
Std. Error
5.943
2.829
表明至少有一个自变量与应变量之间存在线性回归关系。
A NO V Ab
Model
1
Regression
Residual
Sum of Squares 133.711
88.841
df
Mean Square
4
33.428
22
4.038
F 8.278
Total
222.552
26
a. Predictors: (Constant), 糖化血红蛋白, 甘油三脂, 胰岛素, 总胆固醇
表 15-2
总胆固醇（ mmol/L）
X1 5.68 3.79 6.02 4.85 4.60 6.05 4.90 7.08 3.85 4.65 4.59 4.29 7.97 6.19 6.13 5.71 6.40 6.06 5.09 6.13 5.78 5.43 6.50 7.98 11.54 5.84 3.84

多元线性回归模型案例

多元线性回归模型案例多元线性回归模型是统计学中常用的一种回归分析方法，它可以用来研究多个自变量对因变量的影响。

在实际应用中，多元线性回归模型可以帮助我们理解和预测各种复杂的现象，比如销售额和广告投入、学生成绩和学习时间等等。

接下来，我们将通过一个实际的案例来详细介绍多元线性回归模型的应用。

案例背景：假设我们是一家电子产品公司的市场营销团队，我们想要了解广告投入、产品定价和促销活动对销售额的影响。

为了实现这个目标，我们收集了一段时间内的销售数据，并且记录了每个月的广告投入、产品定价和促销活动的情况。

现在，我们希望利用这些数据来建立一个多元线性回归模型，从而分析这些因素对销售额的影响。

数据收集：首先，我们需要收集相关的数据。

在这个案例中，我们收集了一段时间内的销售额、广告投入、产品定价和促销活动的数据。

这些数据可以帮助我们建立多元线性回归模型，并且进行相关的分析。

建立模型：接下来，我们将利用收集到的数据来建立多元线性回归模型。

在多元线性回归模型中，我们将销售额作为因变量，而广告投入、产品定价和促销活动作为自变量。

通过建立这个模型，我们可以分析这些因素对销售额的影响，并且进行预测。

模型分析：一旦建立了多元线性回归模型，我们就可以进行相关的分析。

通过分析模型的系数、拟合优度等指标，我们可以了解每个自变量对销售额的影响程度，以及整个模型的拟合情况。

这些分析结果可以帮助我们更好地理解销售额的变化规律，以及各个因素之间的关系。

模型预测：除了分析模型的影响，多元线性回归模型还可以用来进行预测。

通过输入不同的自变量数值，我们可以预测对应的销售额。

这样的预测结果可以帮助我们制定更加合理的市场营销策略，从而提高销售业绩。

模型评估：最后，我们需要对建立的多元线性回归模型进行评估。

通过对模型的残差、预测误差等进行分析，我们可以了解模型的准确性和可靠性。

如果模型的预测效果不理想，我们还可以通过改进模型结构、增加自变量等方式来提高模型的预测能力。