MATLAB仿真程序

合集下载

matlab2010b电机仿真

matlab2010b电机仿真在MATLAB 2010b中进行电机仿真可以使用Simulink和Simscape Power Systems工具箱。

下面是一个简单的示例，演示了如何使用Simulink建立并运行一个电机仿真模型。

1. 打开MATLAB 2010b软件。

2. 在Simulink库浏览器中找到电机建模组件。

可以在“Simulink”标签下的“Electrical”部分找到一些相关组件，如“Induction Motor”和“DC Motor”等。

3. 双击相应的组件，将其拖动到模型编辑器中。

可以使用这些组件来构建一个电机模型。

4. 连接电机建模组件的输入和输出端口。

例如，可以将一个输入信号传递到电机的控制端口，将输出信号连接到电机的运动端口。

5. 配置电机的参数。

双击电机组件，可以打开参数对话框，并设置电机的参数，如转矩、速度、电压等。

6. 添加其他必要的组件和连接，以完成电机模型的搭建。

7. 单击模型编辑器中的“运行”按钮，开始仿真电机模型。

可以通过观察仿真结果和信号波形来分析电机的行为和性能。

注意：MATLAB 2010b版本可能需要安装额外的工具箱才能进行电机仿真。

可以在软件安装目录下的“toolbox”文件夹中查找相关的工具箱，并确保其已经安装和激活。

此外，Simscape Power Systems工具箱也提供了一系列电机模型和仿真组件，可以用于建立更精细和复杂的电机系统模型。

可以按照类似的步骤，使用Simscape Power Systems工具箱中的电机组件进行仿真。

希望以上信息对您有帮助！。

matlab电路仿真教程

matlab电路仿真教程Matlab是一种功能强大的软件，用于进行电路仿真和分析。

通过Matlab，用户可以轻松地进行电路分析、验证和优化。

在本教程中，我将介绍如何使用Matlab进行电路仿真，并提供一些实例来帮助您更好地理解。

首先，我们需要了解Matlab中的电路仿真工具。

Matlab提供了许多函数和工具箱，用于电路建模和仿真。

其中最常用的是Simulink和Circuits工具箱。

Simulink是一个可视化的仿真环境，用于建立和模拟电路系统。

Circuits工具箱则提供了一些基本电路元件和函数，用于电路建模和分析。

要开始使用Matlab进行电路仿真，首先需要安装Matlab和Simulink软件，并确保您具有有效的许可证。

然后，打开Matlab并导航到Simulink库。

在Simulink库中，您将找到许多电路元件，例如电阻器、电容器和电感器，以及电压源和电流源。

将合适的元件拖放到工作区域中，然后连接它们以构建您的电路。

在电路建模完成后，您需要为电路设置适当的参数。

例如，您可以指定电阻、电容和电感的值，以及电压源和电流源的值。

您还可以添加信号源和观察点，以便在仿真期间监视电路的行为。

一旦您完成了电路建模和参数设置，接下来就可以对其进行仿真了。

在Simulink工具箱中，有几种不同类型的仿真可用，例如时域仿真和频域仿真。

通过选择合适的仿真类型，并设置仿真时间和步长，您可以开始执行仿真并观察电路的响应。

在仿真完成后，您可以使用Matlab绘图工具箱中的一些函数来绘制和分析电路响应。

例如，您可以绘制电压随时间的变化曲线，或者计算电源输出和负载电流之间的关系。

通过使用Matlab的分析工具，您还可以进行降阶、优化和参数估计等进一步分析。

让我们通过一个简单的示例来说明如何使用Matlab进行电路仿真。

假设我们有一个简单的RC电路，其中包括一个电阻器和一个电容器。

我们想要了解电容器的电压如何随时间变化。

matlab 光纤sbs仿真程序

matlab 光纤sbs仿真程序光纤SBS（Stimulated Brillouin Scattering，受激布里渊散射）是一种重要的非线性光学效应，在光通信系统中具有广泛的应用。

为了更好地理解和研究光纤SBS的特性和影响因素，我们可以使用MATLAB进行光纤SBS的仿真。

在进行光纤SBS仿真之前，我们首先需要了解光纤SBS的基本原理。

光纤SBS是一种非线性光学过程，当一束高功率的激光光束通过光纤时，会与光纤中的声子模式发生相互作用，从而产生新的光学波长。

这种相互作用过程中，激光光束中的光子会被散射成为新的频率和波矢的声子，从而产生散射光。

光纤SBS的效应会导致光信号的失真和损耗，因此在光通信系统设计中需要进行充分的考虑。

在MATLAB中进行光纤SBS仿真可以通过建立合适的数学模型和参数设置来实现。

首先，我们需要定义光纤的基本参数，如长度、折射率、光纤的非线性系数等。

然后，我们可以通过输入光信号的频率、功率和波形等信息来模拟光纤中的光场传输过程。

在仿真过程中，我们可以考虑光纤的非线性效应和声子模式的影响，从而得到光纤中的散射光信号。

为了更好地理解光纤SBS的影响，我们可以通过改变光纤的参数和输入光信号的特性来进行不同情况下的仿真实验。

例如，我们可以改变光纤的长度、直径和折射率等参数，观察散射光的频率和强度的变化。

此外，我们还可以改变输入光信号的频率、功率和波形等特性，研究它们对光纤SBS效应的影响。

通过光纤SBS的仿真实验，我们可以得到光纤SBS效应的一些重要特性和参数。

例如，我们可以得到光纤SBS的阈值功率和阈值频率，即当输入光功率或频率超过一定的阈值时，光纤SBS效应会变得明显。

此外，我们还可以得到光纤SBS的增益谱和散射光的功率谱密度等信息，从而更好地了解光纤SBS的特性和应用。

在进行光纤SBS仿真时，我们还可以结合其他光纤效应和系统参数进行综合分析。

例如，我们可以考虑光纤的色散效应、非线性效应和衰减等因素，从而研究它们与光纤SBS效应的相互作用。

实验一典型环节的MATLAB仿真

实验一典型环节的MATLAB仿真一、实验目的1．熟悉MATLAB桌面和命令窗口，初步了解SIMULINK功能模块的使用方法。

2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。

3．定性了解各参数变化对典型环节动态特性的影响。

二、SIMULINK的使用MATLAB中SIMULINK是一个用来对动态系统进行建模、仿真和分析的软件包。

利用SIMULINK功能模块可以快速的建立控制系统的模型，进行仿真和调试。

1．运行MATLAB软件，在命令窗口栏“>>”提示符下键入simulink命令，按Enter 键或在工具栏单击按钮，即可进入如图1-1所示的SIMULINK仿真环境下。

2．选择File菜单下New下的Model命令，新建一个simulink仿真环境常规模板。

3．在simulink仿真环境下，创建所需要的系统。

以图1-2所示的系统为例，说明基本设计步骤如下：1）进入线性系统模块库，构建传递函数。

点击simulink下的“Continuous”，再将右边窗口中“Transfer Fen”的图标用左键拖至新建的“untitled”窗口。

图1-1 SIMULINK仿真界面图1-2 系统方框图2）改变模块参数。

在simulink 仿真环境“untitled ”窗口中双击该图标，即可改变传递函数。

其中方括号的数字分别为传递函数的分子、分母各次幂由高到低的系数，数字之间用空格隔开；设置完成后，选择OK ，即完成该模块的设置。

3）建立其它传递函数模块。

按照上述方法，在不同的simulink 的模块库中，建立系统所需的传递函数模块。

例：比例环节用“Math ”右边窗口“Gain ”的图标。

4）选取阶跃信号输入函数。

用鼠标点击simulink 下的“Source ”，将右边窗口中“Step ”图标用左键拖至新建的“untitled ”窗口，形成一个阶跃函数输入模块。

5）选择输出方式。

海杂波matlab仿真程序

海杂波matlab仿真程序海杂波（sea clutter）是雷达信号处理中的一个重要问题，也是海洋环境中的一个常见现象。

海杂波指的是雷达接收到的来自海面的回波信号中的杂波部分，它主要由海浪、海浪与海面之间的散射物、海洋生物等引起。

海杂波会对雷达系统的性能产生影响，因此对海杂波进行研究和仿真具有重要意义。

Matlab是一种常用的科学计算软件，它提供了丰富的工具和函数，可以用来进行海杂波的仿真和分析。

在海杂波仿真中，我们可以通过模拟海洋环境中的各种因素，来生成与实际海杂波相似的信号。

这样可以帮助我们更好地理解海杂波的特性，并为雷达系统的设计和性能评估提供参考。

海杂波的特点是多变性和复杂性。

海洋环境中的海浪和散射物会引起回波信号的频率和相位的变化，这使得海杂波的特性难以准确描述。

因此，在进行海杂波的仿真时，我们需要考虑到这些因素，并结合实际的海洋环境数据进行模拟。

海杂波的仿真可以帮助我们研究海洋环境中的信号处理算法和雷达系统的性能。

通过对海杂波的仿真，我们可以评估不同算法对海杂波的抑制效果，并选择最优的算法来提高雷达系统的性能。

同时，海杂波的仿真还可以用于雷达系统的性能测试和验证，以确保系统能够正常工作。

海杂波的仿真还可以帮助我们研究海洋环境中的其他问题，例如海洋生物的检测和跟踪。

海洋生物在雷达回波中会产生特定的特征，通过对海杂波的仿真，我们可以研究这些特征，并开发相应的算法来检测和跟踪海洋生物。

除了海杂波的仿真，Matlab还可以用于海杂波数据的处理和分析。

通过对海杂波数据的处理和分析，我们可以提取出海杂波的特征和统计信息，从而更好地理解海杂波的性质。

这些信息可以用于雷达系统的设计和性能评估，并为海洋环境的监测和预测提供参考。

海杂波的仿真是雷达信号处理中的一个重要问题。

通过使用Matlab 进行海杂波的仿真和分析，我们可以更好地理解海杂波的特性，并为雷达系统的设计和性能评估提供参考。

海杂波的仿真还可以帮助我们研究海洋环境中的其他问题，例如海洋生物的检测和跟踪。

模糊pid matlab(simulink)仿真详细步骤

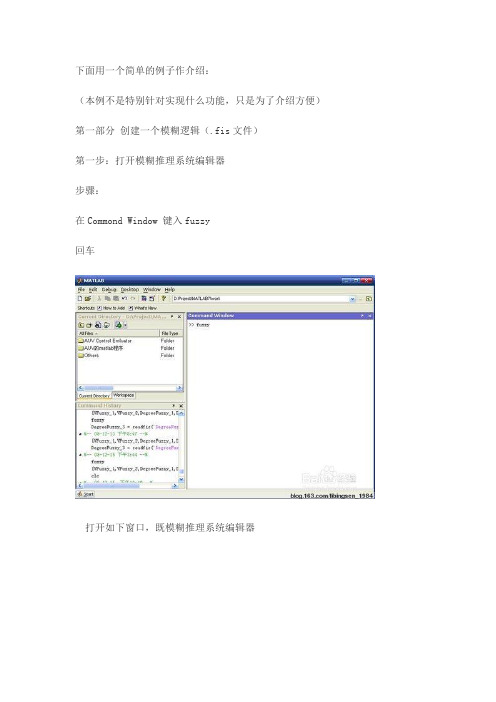
下面用一个简单的例子作介绍：（本例不是特别针对实现什么功能，只是为了介绍方便）第一部分创建一个模糊逻辑（.fis文件）第一步：打开模糊推理系统编辑器步骤：在Commond Window 键入fuzzy回车打开如下窗口，既模糊推理系统编辑器第二步：使用模糊推理系统编辑器本例用到两个输入，两个输出，但默认是一个输人，一个输出步骤：1、添加一个输入添加一个输出得如下图2、选择Input、output(选中为红框)，在Name框里修改各输入的名称并将And method 改为prod，将Or method 改为 probor提示：在命名时’_’在显示时为下标，可从上图看出。

第三步：使用隶属函数编辑器该编辑器提供一个友好的人机图形交互环境，用来设计和修改模糊推理系中各语言变量对应的隶属度函数的相关参数，如隶属度函数的形状、范围、论域大小等，系统提供的隶属度函数有三角、梯形、高斯形、钟形等，也可用户自行定义。

步骤：1、双击任何一个输入量（In_x、In_y）或输出量打开隶属度函数编辑器。

2、在左下处Range和Display Range处添加取值范围，本例中In_x和In_y的取值范围均为[0 10], Out_x和Out_y的取值范围均为[0 1]3、默认每个输入输出参数中都只有3个隶属度函数，本例中每个输入输出参数都需要用到五个，其余几个需要自己添加：选中其中一个输入输出参数点击Edit菜单，选Add MFS…打开下列对话框将MF type设置为trimf(三角形隶属度函数曲线，当然你也需要选择其他类型) 将Number of MFs 设置为2点击OK按钮同样给其他三个加入隶属度函数4、选中任何一个隶属度函数（选中为红色），在Name 中键入名称，在Type中选择形状，在Params中键入范围，然后回车如下图：5、关闭隶属函数编辑器第四步：使用规则编辑器通过隶规则编辑器来设计和修改“IF...THEN”形式的模糊控制规则。

基于matlab的机械结构仿真程序

基于matlab的机械结构仿真程序基于Matlab的机械结构仿真程序是一种用于模拟和分析机械系统动态行为的工具。

通过使用Matlab编程语言和Simulink仿真环境，我们可以构建出具有各种结构和运动特性的机械系统，并对其进行仿真和优化。

以下是一个基于Matlab的机械结构仿真程序的探讨：1. 简介在介绍这个仿真程序之前，我们首先明确一下机械结构仿真的定义和意义。

机械结构仿真是指通过建立数学模型和运用仿真技术，对机械系统进行虚拟化，以便通过模拟和分析机械系统的行为，获得系统的性能指标和设计优化。

2. Matlab的仿真环境Matlab是一种强大的科学计算软件，具有丰富的工具箱和编程语言。

Simulink是Matlab的一个附属工具，用于建立、模拟和分析动态系统。

Simulink提供了一个直观的图形化界面，使得机械结构仿真程序的搭建更加便捷。

3. 机械结构建模在进行机械结构仿真前，我们需要首先建立机械系统的数学模型。

这包括建立机械结构的几何模型、物理模型和动力学模型。

通过使用Matlab的数学工具箱，可以方便地表示机械结构的运动学和动力学方程，从而实现仿真程序的搭建。

4. 动力学仿真一旦机械结构的数学模型建立完毕，我们可以使用Matlab的仿真工具对机械系统的动态行为进行仿真。

仿真可以模拟机械结构在不同工况下的运动和响应，例如负载变化、初始条件变化等。

通过对仿真数据的分析，我们可以获得机械系统的性能指标，如速度、加速度、力矩等。

5. 仿真结果分析仿真结果的分析是机械结构仿真程序中非常重要的一环。

通过使用Matlab的数据处理和可视化工具，我们可以对仿真结果进行综合分析。

通过绘制机械系统的运动轨迹图、动力学响应曲线和频谱图，我们可以更直观地理解系统的行为特性，并进一步对机械结构进行优化。

6. 优化设计基于仿真结果的分析，我们可以对机械结构的设计进行优化。

通过改变机械结构的几何参数、材料选择和工艺参数等，可以改善系统的性能和可靠性。

MATLAB机器人仿真程序

MATLAB机器人仿真程序哎呀，说起 MATLAB 机器人仿真程序，这可真是个有趣又充满挑战的领域！我还记得有一次，我带着一群学生尝试做一个简单的机器人行走仿真。

那时候，大家都兴奋极了，眼睛里闪着好奇的光。

我们先从最基础的开始，了解 MATLAB 这个工具的各种函数和命令。

就像是给机器人准备好各种“零部件”，让它能顺利动起来。

比如说，我们要设定机器人的初始位置和姿态，这就好像是告诉机器人“嘿，你从这里出发，站好啦！”然后，再通过编程来控制它的运动轨迹。

有的同学想让机器人走直线，有的同学想让它拐个弯，还有的同学想让它走个复杂的曲线。

在这个过程中，可遇到了不少问题呢。

有个同学不小心把坐标设置错了，结果机器人“嗖”地一下跑到了不知道哪里去，大家哄堂大笑。

还有个同学在计算速度和加速度的时候出了差错，机器人的动作变得奇奇怪怪的，像是在跳“抽筋舞”。

不过，大家并没有气馁，而是一起努力找错误，修改代码。

终于，当我们看到那个小小的机器人按照我们设想的轨迹稳稳地行走时，那种成就感简直无法形容。

回到 MATLAB 机器人仿真程序本身，它其实就像是一个神奇的魔法盒子。

通过输入不同的指令和参数，我们可以创造出各种各样的机器人运动场景。

比如说，我们可以模拟机器人在不同地形上的行走，像是平坦的地面、崎岖的山路或者是湿滑的冰面。

这时候，我们就要考虑摩擦力、重力等各种因素对机器人运动的影响。

想象一下，机器人在冰面上小心翼翼地走着，生怕滑倒，是不是很有趣？而且，MATLAB 机器人仿真程序还能帮助我们优化机器人的设计。

比如说，如果我们发现机器人在某个动作上消耗了太多的能量，或者动作不够灵活，我们就可以通过调整程序中的参数来改进。

这就像是给机器人做了一次“整形手术”，让它变得更完美。

另外，我们还可以用它来进行多机器人的协同仿真。

想象一下，一群机器人在一起工作，有的负责搬运东西，有的负责巡逻，它们之间需要相互配合，避免碰撞。

这就需要我们精心设计它们的通信和协调机制，让它们像一支训练有素的团队一样高效工作。

matlab通信仿真实例

matlab通信仿真实例在Matlab中进行通信系统的仿真，可以涉及到多种不同的通信技术和协议，包括调制解调、信道编码、多址接入等。

以下以OFDM系统为例，介绍Matlab 中通信仿真的实例。

OFDM（正交频分复用）是一种常用于现代通信系统中的技术，它将高速数据流分割成多个较低速的子流，并将每个子流分配到不同的子载波上。

优点是能够抵抗多径效应和频率选择性衰落，并提供高数据速率。

首先，我们需要创建一个包含OFDM系统参数的结构体。

例如：ofdmParam.M = 16; % 子载波数量ofdmParam.K = 4; % 用于混合多路复用的用户数量ofdmParam.N = ofdmParam.M * ofdmParam.K; % 总子载波数量ofdmParam.CP = 16; % 循环前缀长度接下来，我们可以生成用于OFDM仿真的数据流。

例如，我们可以使用随机整数生成器生成一系列整数，并将其转换为复数形式的调制符号：data = randi([0, ofdmParam.M-1], 1, ofdmParam.N);dataMod = qammod(data, ofdmParam.M);然后，我们可以创建一个包含OFDM信号的函数。

在OFDM系统中，生成的数据符号将分配到不同的子载波上，然后在时域中通过插入循环前缀进行叠加：function[ofdmSignal] = createOFDMSignal(dataMod, ofdmParam) ofdmSignal = [];for k = 0:ofdmParam.K-1% 提取相应的数据符号，并进行IFFTofdmData =ifft(dataMod(k*ofdmParam.M+1:(k+1)*ofdmParam.M));% 添加循环前缀ofdmDataWithCP = [ofdmData(end-ofdmParam.CP+1:end), ofdmData];% 将OFDM符号添加到OFDM信号中ofdmSignal = [ofdmSignal, ofdmDataWithCP];endend将OFDM信号传输到信道中，我们可以使用加性高斯白噪声（AWGN）信道模型来模拟实际通信环境：EbNo = 10; % 信噪比snr =10*log10(ofdmParam.N*ofdmParam.M/(ofdmParam.N*ofdmParam.M+1 )*(10^(EbNo/10)));ofdmSignalNoisy = awgn(ofdmSignal, snr, 'measured');最后，我们可以对接收到的OFDM信号进行解调和信号恢复。

MATLAB仿真

第2章 MATLAB仿真与其它高级语言相比较，MATLAB具有独特的优势： (1) MATLAB是一种跨平台的数学语言。采用MATLAB 编写的程序可以在目前所有的操作系统上运行 ( 只要这些系统上安装了MATLAB平台)。MATLAB程序不依赖于计算机类型和操作系统类型。
(2) MATLAB是一种超高级语言。MATLAB平台本身是用C语言写成的，其中汇集了当前最新的数学算法库，是许多专业数学家和工程学者多年的劳动结晶。 MATLAB 意味着站在巨人的肩膀上观察和处理问题，所以在编程效率，程序的可读性、可靠性和可移植性上远远超过了常规的高级语言。这使得 MATLAB 成为了进行科学研究和数值计算的首选语言。
第2章 MATLAB仿真 MATLAB中可以方便地进行复数运算，例如计算
5
a b
2
，其中，a=15+j3，b=5e j2。
>>a=15+j*3,b=5*exp(j*2),(a.^2+b).^(1/5)［回车］ 6. MATLAB 提供了极为便利的数据可视化手段，可以作出任意函数的图像。作为快速入门，在此以一个
二维作图为例，作出函数 y=e-x/10sinx 在 x∈［ -1,10 ］范
第2章 MATLAB仿真 (5) MATLAB具有强大的绘图功能。利用MATLAB的绘图功能，可以轻易地获得高质量的(印刷级)曲线图。具有多种形式来表达二维、三维图形，并具有强大的动画功能，可以非常直观地表现抽象的数值结果。这也是 MATLAB广为流行的重要原因之一。 (6) MATLAB具有串口操作、声音输入输出等硬件操控能力。随着版本的提高，这种能力还会不断加强，使得人们利用计算机和实际硬件相连接的半实物仿真的梦想得以轻易实现。 (7) MATLAB程序可以直接映射为DSP芯片可接受的代码，大大提高了现代电子通信设备的研发效率。

MATLAB环境下的仿真软件

MATLAB环境下的仿真软件MATLAB是一种功能强大的数学仿真软件，它能够进行各种领域的仿真模拟和数据分析。

在MATLAB环境下，用户可以使用编程语言对各种数学问题进行建模，并且能够方便地进行数据可视化和结果分析。

本文将介绍MATLAB环境下的仿真软件的基本特点和相关应用。

首先，MATLAB环境下的仿真软件具有以下几个基本特点：1. 编程语言：MATLAB使用自身的编程语言，它结合了许多其他编程语言的特点，如C、FORTRAN等。

用户可以使用MATLAB编写脚本文件，便于对仿真模型进行建模、逻辑控制和可视化处理。

2. 广泛的库函数：MATLAB提供了丰富的库函数，用户可以直接调用这些函数进行数学计算、数据处理和图形绘制等。

这些库函数包括线性代数、信号处理、图像处理、数值计算等各个领域。

3. 图形界面：MATLAB提供了友好的图形界面，使用户能够轻松地进行模型建立、仿真运行和结果分析。

用户可以通过拖动、点击操作来创建和编辑仿真模型，同时实时查看仿真结果。

4. 数据可视化：MATLAB具有强大的数据可视化功能，可以将仿真结果以各种形式呈现，如二维曲线图、三维图形、动画等。

这些图形能够直观地展示仿真结果，方便用户进行分析和比较。

5. 跨学科应用：MATLAB广泛应用于各个学科领域，包括工程、物理、化学、生物、经济等。

用户可以根据自己的需求，选择相应的工具箱进行模型建立和仿真。

在MATLAB环境下，仿真软件可以应用于多个领域，下面以几个具体的案例来说明：1. 电路仿真：用户可以使用MATLAB的电路仿真工具箱，对电路进行模拟和分析。

用户可以通过电路图的方式建立模型，然后通过设置参数和初始条件，进行仿真运行。

仿真结果可以呈现电压、电流等变化曲线，方便用户进行电路分析和优化设计。

2. 控制系统仿真：用户可以使用MATLAB的控制系统工具箱，对控制系统进行建模和仿真。

用户可以通过传递函数或状态空间模型来描述控制系统，然后进行仿真运行。

OFDM MATLAB仿真程序

OFDM.m: OFDM Simulator (outer function)clear all;A = [1 1/exp(1) 1/exp(2)]; % power delay profileN = 64; % number of symbols in a single OFDM symbolGI = 16; % guard intervalMt = 1; % number of Tx antennasMr = 1; % number of Rx antennassig2 = 1e-3; % noise varianceM = 8; % max constellation bit numberMgap = 10.^(1:(1.7/10):2.7); % gapBtot = 100*Mt; % total # bits per OFDM symbolTransmitIter = 50; % # iterations of symbol transmissions for each channel instance ChannelIter = 100; % # iterations of independent identically distributed channel instances GapIter = length(Mgap);load ENC2.matload ENC4.matload ENC16.matload ENC64.matload ENC256.matTotEbNo = [];Errors =[];EbNo = [];for lGap = 1:GapIterlGapgap = Mgap(lGap);totalErrors = 0;for lChan = 1:ChannelIter% create channel[H h_f]=create_channel(Mt, Mr, A, N+GI);% decompose each subchannel in the frequency domain[U S V] = svd_decompose_channel(Mt, Mr, h_f, N);% bitloading[bits_alloc,energy_alloc] = BitLoad(S,Btot,Mt*N,gap,sig2,M);%energy_alloc=energy_alloc/(mean(energy_alloc));%energy_alloc=ones(1,128);for lTrans = 1:TransmitIter% bits to transmitx = (randn(1,Btot)>0);% modulatex_mod = modulate(x,bits_alloc,energy_alloc, s2,s4,s16,s64,s256);% precode modulated signalx_pre = precode(Mt, x_mod, V, N);% ifft, with cyclic prefix for each antennaofdm_symbol =[];for i=1:Mtofdm_symbol = [ofdm_symbol; ifft_cp_tx_blk(x_pre(i:Mt:Mt*(N-1)+i),N,GI)];endofdm_symbol2 = reshape(ofdm_symbol,Mt*(N+GI),1);% channely = transpose(channel(sig2, Mt, Mr, ofdm_symbol2, H, N+GI));% fftrec_symbol =[];for i=1:Mtrec_symbol = [rec_symbol; fft_cp_rx_blk(y(i:Mt:Mt*(N+GI-1)+i),N,GI)];endrec_symbol2 = reshape(rec_symbol,1,Mt*N);% shape received signalshaped_vals = shape(rec_symbol2, Mr, U, N);% demodulatey_demod = demodulate(shaped_vals, bits_alloc, energy_alloc, S, s2,s4,s16,s64,s256, c2,c4,c16,c64,c256); % comparisontotalErrors = totalErrors + sum(xor(y_demod,x));endEbNo = [EbNo sum(energy_alloc)/Btot/sig2];endErrors = [Errors totalErrors/Btot/ChannelIter/TransmitIter]TotEbNo = [TotEbNo mean(EbNo)]EbNo = [];endsemilogx(TotEbNo, Errors);xlabel('Eb/No');ylabel('BER');title('SISO link, adaptive rate and power')save SISO_adaptive2.mat Errors EbNocreate_channel.m: Generates a Rayleigh fading frequency-selective channel, parametrized by the antenna configuration, the OFDM configuration, and the power-delay profile.function [H, H_f]=create_channel(Mt, Mr, A, N);% function [H, H_f]=create_channel(Mt, Mr, A, N);%% A - vector containing the power-delay profile (real values)% Mt - number of Tx antennas% Mr - number of Rx antennas% N - number of vector symbols to be sent in a single OFDM symbol Tx% ie: N MIMO transmissions in one OFDM symbol% This is for Rayleigh frequency-selective fading, which assumes complex % Gaussian matrix elements with in-phase and quadrature components independent.% Assume iid matrix channel elements, and further, independent channel taps % define the channel tapsH_int = 1/sqrt(2)*(randn(Mr*length(A),Mt) + j*randn(Mr*length(A),Mt));H_int2=[];for i = 1:length(A)H_int2 = [H_int2;sqrt(A(i))*H_int((i-1)*Mr+1:i*Mr,:)];end%h_f = fft(H_int2',64);%%H = H_int2';H_int2 = [H_int2;zeros((N-length(A))*Mr,Mt)];H_f = zeros(Mr,Mt*(N-16));for i = 1:Mtfor j = 1:Mrh_f = fft(H_int2(j:Mr:(N-16-1)*Mr+j,i));for k = 1:(N-16)H_f(j,i+(k-1)*Mt) = h_f(k);endendendH=[H_int2];for i = 1:N-1H=[H,[zeros(Mr*i,Mt);H_int2(1:(N-i)*Mr,:)]];endsvd_decompose_channel.m: Since full channel knowledge is assumed, transmission is across parallel singular value modes. This function decomposes the channel into these modes.function [U, S, V] = svd_decompose_channel(Mt, Mr, h_f, N);% [U S V] = svd_decompose_channel(Mt, Mr, h_f, N);%% Function decomposes the channel at each subcarrier into its SVD components %% Mt - # Tx antennas% Mr - # Rx antennas% h_f - MIMO impulse response - Mr rows, Mt*L columns, where L is the number of% channel taps% N - # subcarriersU = [];S = [];V = [];for i = 1:N[Utmp Stmp Vtmp] = svd(h_f(:,(i-1)*Mt+1:i*Mt));U=[U Utmp];V=[V Vtmp];S=[S Stmp];endS = sum(S,1);BitLoad.m: Apply the bit-loading algorithm to achieve the desired bit and energy allocation for the current channel instance.function [bits_alloc,energy_alloc] =BitLoad(subchan_gains,total_bits,num_subc,gap,noise,M)% Bit Loading Algorithm% ---------------------%% Inputs :% subchan_gains : SubCarrier Gains% total_bits : Total Number of bits% num_subc : Number of Subcarriers% gap : Gap of the system% noise : Noise Power% M : Max Constellation Size% Outputs:% bits_alloc : Bits allocation for each subchannel% power_alloc : Total Power allocation% ---------------------------------------------------------------% Compute SNR's for each channelSNR = ComputeSNR(subchan_gains,noise,gap);% This function just initializes the system with a particular bit% allocation and energy allocation using Chow's Algorithm. This is% further efficientize using Campello's Algorithm[bits_alloc, energy_alloc] = chow_algo(SNR,num_subc,M);% Form the Energy Increment Table based on the present channel% gains for all the subchannels in order to be used by Campello% Algorithmenergytable = EnergyTableInit(SNR,M);% Efficientize the algorithm using the Campello's algorithm[bits_alloc,energy_alloc] =campello_algo(bits_alloc,energy_alloc,energytable,total_bits,num_subc,M );ComputeSNR.m: Given the subcarrier gains, this simple function generates the SNR values of each channel (each singular value on each tone is a separate channel). function SNR = ComputeSNR(subcar_gains,noise,gap)SNR = abs((subcar_gains.^2)./(noise*gap));chow_algo.m: Apply Chow's algorithm to generate a particular bit and energy allocation.% Chow's Algorithm% ----------------% This is based on the paper by Chow et al titled%% A Practical Discrete Multitone Transceiver Loading Algorithm% for Data Transmission over Spectrally Shaped Channels.IEEE Trans% on Communications. Vol. 43, No 2/3/4, pp. 773-775, Feb/Mar/Apr 1995 function [bits_alloc, energy_alloc] = chow_algo(SNR,num_subc,M)for i = 1:num_subc% Assuming each of the subchannels has a flat fading, we get initial estimate % of the bits for each subchanneltempbits = log2(1 + abs(SNR(i))); % bits per two dimension. roundtempbits = round(tempbits); % round the bitsif (roundtempbits > 8) % Limit them between 2 and 15 roundtempbits = 8;endif (mod(roundtempbits,2)== 1 & roundtempbits ~= 1)roundtempbits = roundtempbits -1;endif roundtempbits > 0 % Calculate the Energy required for the subchannelenergy_alloc(i) = (2^roundtempbits-1)/SNR(i) ;elseenergy_alloc(i) = 0;endbits_alloc(i) = roundtempbits; % Update the BitSubChan end% end of functionEnergyTableInit.m: Given the SNR values, form a table of energy increments for each channel.function energytable = EnergyTableInit(SNR,M);% Inputs:% subcar_gains : Subcarrier Gains% M : max Constellation Size% Gap : Gap of the system% Noise : Noise Power% Outputs:% energytable : Energytable%% Based on the Subcarrier Gains, we calculate the energy% increment required by each subcarrier for transmitting% 1,2 ,4 ,6,8 bits.% Energy = 2^(i-1)/subcar_gains;% ------------------------------------------------------%subcar_gains = (subcar_gains.^2)/(Gap*Noise);energytable = abs((1./SNR)'*(2.^([1:M+1]-1)));% Increase the energy value for constellation size of more than M to% a very high value so that it is not assigned.energytable(:,M+1) = Inf*ones(size(energytable(:,M+1)));for i = 3:2:Menergytable(:,i) = (energytable(:,i) +energytable(:,i+1))/2;energytable(:,i+1) = energytable(:,i);end%energytable = [ones(1,size(energytable,1))' energytable];campello_algo.m: Apply Campello's algorithm to converge to the optimal bit and energy allocation for the given channel conditions.% campello_algo.m% --------------% This function is used by Campello's algorithm to allocate bits and energy for% each subchannel optimally.function [bits_alloc, energy_alloc] =campello_algo(bits_alloc,energy_alloc,energytable,total_bits,num_subc,M)bt = sum(bits_alloc);% We can't transmit more than M*(Number of subchannel) bitsif total_bits > M*num_subctotal_bits = M*num_subc;endwhile (bt ~= total_bits)if (bt > total_bits)max_val = 0;max_ind = ceil(rand(1)*num_subc);for i = 1:num_subcif bits_alloc(i) ~= 0temp = energytable(i,bits_alloc(i)) ;elsetemp = 0;endif (temp > max_val)max_val = temp;max_ind = i;endendif (bits_alloc(max_ind) > 0)bits_alloc(max_ind) = bits_alloc(max_ind) -1;energy_alloc(max_ind) = energy_alloc(max_ind) - max_val;bt = bt-1;endelsemin_val = Inf;min_ind = ceil(rand(1)*num_subc);for i = 1:num_subcif bits_alloc(i) ~=0 & bits_alloc(i) <9temp = energytable(i,bits_alloc(i) + 1);elsetemp = Inf;endif (temp < min_val)min_val = temp;min_ind = i;endendif (bits_alloc(min_ind) < 8)bits_alloc(min_ind) = bits_alloc(min_ind) +1;if (min_val==inf)min_val = energytable(min_ind,bits_alloc(min_ind));endenergy_alloc(min_ind) = energy_alloc(min_ind) +min_val;bt = bt+1;endendendfor i = 1:length(bits_alloc)if (mod(bits_alloc(i),2) == 1 & bits_alloc(i) ~=1)[bits_alloc,energy_alloc] =ResolvetheLastBit(bits_alloc,energy_alloc,i,energytable,num_subc);endendResolvetheLastBit.m: An optimal bit-loading of the last bit requires a unique optimization.function [bits_alloc, energy_alloc] =ResolvetheLastBit(bits_alloc,energy_alloc,index,energytable,num_subc) max_val = 0;for i = 1:num_subcif (i ~= index & bits_alloc(i) == 1)if bits_alloc(i) ~= 0temp = energytable(i,bits_alloc(i)) ;endif (temp > max_val)max_val = temp;max_ind = i;endendendmin_val = Inf;for i = 1:num_subcif (i~= index & bits_alloc(i) == 1)if bits_alloc(i) ~=0temp = energytable(i,bits_alloc(i) + 1);endif (temp < min_val)min_val = temp;min_ind = i;endendendif (min_val < max_val)bits_alloc(min_ind) = bits_alloc(min_ind) + 1;bits_alloc(index) = bits_alloc(index) - 1;energy_alloc(index) = energy_alloc(index) - min_val; elsebits_alloc(max_ind) = bits_alloc(max_ind) - 1;bits_alloc(index) = bits_alloc(index) + 1;energy_alloc(index) = energy_alloc(index) + max_val; end。

如何在Matlab中进行模拟仿真

如何在Matlab中进行模拟仿真在科学和工程领域中，模拟仿真是一种非常重要的工具，可以帮助实现对现实世界复杂问题的理解和分析。

而在这方面，Matlab是一个功能强大且广泛使用的软件平台，它提供了丰富的工具和函数，便于进行模拟仿真。

本文将介绍如何在Matlab中进行模拟仿真，并探讨其中的一些关键技巧和注意事项。

首先，要进行模拟仿真，我们需要有一个模型。

模型是对待研究问题的一种简化和抽象，它可以是数学方程、系统方程或者演化规则等形式。

在Matlab中，可以使用符号计算工具箱对模型进行推导和建立。

通过定义变量、方程和初始条件，可以将实际问题转化为计算机可以处理的形式。

一旦建立了模型，就可以开始进行仿真了。

在Matlab中，可以使用数值计算工具箱中的函数来求解微分方程、差分方程和代数方程等。

例如，ode45函数可以用于求解常微分方程，而ode15s函数则适合求解刚性方程。

此外，还有丰富的工具函数可以用于求解常微分方程组、偏微分方程和随机过程等。

除了求解方程，Matlab还提供了许多其他的工具和函数，用于分析和处理仿真结果。

例如，可以使用绘图函数来可视化仿真结果，帮助我们更好地理解问题。

Matlab中的绘图函数可以实现各种类型的图形，包括线图、散点图、柱状图、等高线图等。

此外，还可以使用统计工具箱中的函数进行数据分析和参数估计。

在进行模拟仿真时，我们还需要注意一些技巧和注意事项。

首先，要注意选择合适的数值方法和精度。

不同的问题可能需要不同的数值方法，而选择适当的数值方法可以提高求解效率和准确性。

此外，要注意数值方法的稳定性和收敛性。

有时候，仿真结果可能会出现数值误差，这时可以考虑使用更高精度的方法或者增加计算步长来改善结果。

其次，要注意仿真中的参数选择和设置。

参数的选择会影响仿真结果的准确性和可靠性。

有时候，我们需要进行参数敏感性分析，即通过改变参数的值来观察仿真结果的变化情况。

这可以帮助我们了解模型的行为和性质，并指导进一步的研究和设计。

(完整版)合成孔径雷达点目标仿真MATLAB程序

合成孔径雷达成像系统点目标仿真源程序：clcclose allC=3e8; %光速Fc=1e9; %载波频率lambda=C/Fc; %波长%成像区域Xmin=0;Xmax=50;Yc=10000;Y0=500;%SAR基本参数V=100; %雷达平台速度H=0; %雷达平台高度R0=sqrt(Yc^2+H^2);D=4; %天线孔径长度Lsar=lambda*R0/D; %合成孔径长度Tsar=Lsar/V; %合成孔径时间Ka=-2*V^2/lambda/R0;%线性调频率Ba=abs(Ka*Tsar);PRF=2*Ba; %脉冲重复频率PRT=1/PRF;ds=PRT; %脉冲重复周期Nslow=ceil((Xmax-Xmin+Lsar)/V/ds);%脉冲数Nslow=2^nextpow2(Nslow); %量化为2的指数sn=linspace((Xmin-Lsar/2)/V,(Xmax+Lsar/2)/V,Nslow); %创建时间向量PRT=(Xmax-Xmin+Lsar)/V/Nslow; %更新PRF=1/PRT; % 更新脉冲重复频率fa=linspace(-0.5*PRF,0.5*PRF,Nslow);Tr=5e-6; %脉冲宽度Br=30e6; %调频信号带宽Kr=Br/Tr; %调频率Fsr=2*Br; %快时间域取样频率dt=1/Fsr; %快时间域取样间隔Rmin=sqrt((Yc-Y0)^2+H^2);Rmax=sqrt((Yc+Y0)^2+H^2+(Lsar/2)^2);Nfast=ceil(2*(Rmax-Rmin)/C/dt+Tr/dt);Nfast=2^nextpow2(Nfast);tm=linspace(2*Rmin/C,2*Rmax/C+Tr,Nfast);dt=(2*Rmax/C+Tr-2*Rmin/C)/Nfast; %更新Fsr=1/dt;fr=linspace(-0.5*Fsr,0.5*Fsr,Nfast);DY=C/2/Br; %距离分辨率DX=D/2; %方位分辨率Ntarget=3; %目标数目Ptarget=[Xmin,Yc,1 %目标位置Xmin,Yc+10*DY,1Xmin+20*DX,Yc+50*DY,1];K=Ntarget; %目标数目N=Nslow; %慢时间采样数M=Nfast; %快时间采样数T=Ptarget; %目标位置%合成孔径回波仿真Srnm=zeros(N,M);for k=1:1:Ksigma=T(k,3);Dslow=sn*V-T(k,1);R=sqrt(Dslow.^2+T(k,2)^2+H^2);tau=2*R/C;Dfast=ones(N,1)*tm-tau'*ones(1,M);phase=pi*Kr*Dfast.^2-(4*pi/lambda)*(R'*ones(1,M));Srnm=Srnm+sigma*exp(j*phase).*(0<Dfast&Dfast<Tr).*((abs(Dslow)<Lsar/2)'*ones(1,M));end%距离压缩tr=tm-2*Rmin/C;Refr=exp(j*pi*Kr*tr.^2).*(0<tr&tr<Tr);%距离压缩参考函数F_Refr=fft((Refr));Sr=zeros(N,M);for k2=1:1:Mtemp1=fft(Srnm(k2,:));FSrnm=temp1.*conj(F_Refr);Sr(k2,:)=ifft(FSrnm);end%方位压缩ta=sn-(Xmin+Xmax)/2/V;Refa=exp(j*pi*Ka*ta.^2).*(abs(ta)<Tsar/2); %方位压缩参考函数F_Refa=fft(Refa);Sa=zeros(N,M);for k3=1:1:Mtemp2=fft(Sr(:,k3));F_Sa=temp2.*conj(F_Refa.');Sa(:,k3)=fftshift(ifft(F_Sa));endrow=tm*C/2;col=sn*V;%绘图%回波雷达数据figure(1)subplot(211)imagesc(abs(Srnm));title('SAR data')subplot(212)imagesc(angle(Srnm))%灰度图figure(2)colormap(gray)imagesc(row,col,255-abs(Sr));title('距离压缩'),xlabel('距离向'),ylabel('方位向');figure(3)colormap(gray)imagesc(row,col,255-abs(Sa));title('方位压缩'),xlabel('距离向'),ylabel('方位向');%轮廓图figure(4)Ga=abs(Sa);a=max(max(Ga));contour(row,col,Ga,[0.707*a,a],'b');grid onx1=sqrt(H^2+min(abs(Ptarget(:,2))).^2)-5*DY;x2=sqrt(H^2+max(abs(Ptarget(:,2))).^2)+5*DY;y1=min(Ptarget(:,1))-5*DX;y2=max(Ptarget(:,1))+5*DX;axis([x1,x2,y1,y2])%三维成像图figure(5)mesh(Ga((400:600),(200:500)));axis tightxlabel('Range'),ylabel('Azimuth');仿真结果图：图4. 1 点目标原始回波数据图4. 2 距离压缩后成像图图4. 3 方位压缩后成像图（点阵目标成像灰度图）图4. 4 点阵目标成像轮廓图。

弹道仿真matlab程序

弹道仿真matlab程序英文回答：As a software engineer, I have experience in developing simulation programs using MATLAB. One of the applications that I have worked on is a ballistic trajectory simulation program. This program calculates the trajectory of a projectile based on its initial conditions and the forces acting on it.To begin with, the program takes input parameters such as the initial velocity, launch angle, and atmospheric conditions. These parameters are used to calculate the initial velocity components in the x and y directions. The program then uses numerical integration techniques, such as Euler's method or the Runge-Kutta method, to calculate the position and velocity of the projectile at each time step.During the simulation, the program takes into account various factors that affect the trajectory of theprojectile. These include the gravitational force, air resistance, and wind speed and direction. The program uses mathematical models to calculate the effect of these forces on the projectile's motion.For example, let's say we want to simulate thetrajectory of a cannonball. We input the initial conditions, such as the initial velocity of the cannonball and the launch angle. The program then calculates the initial velocity components in the x and y directions. As the simulation progresses, the program takes into account the gravitational force pulling the cannonball downwards andthe air resistance slowing it down. It also considers the effect of wind, if any, on the trajectory. The program continues to calculate the position and velocity of the cannonball at each time step until it reaches the ground.The output of the simulation program includes the trajectory of the projectile, which can be visualized using MATLAB's plotting capabilities. This allows us to analyze and study the behavior of the projectile under different conditions.中文回答：作为一名软件工程师，我有使用MATLAB开发仿真程序的经验。

matlab通信原理仿真教程

matlab通信原理仿真教程
Matlab通信原理仿真教程如下：
1. 导入Simulink和Communications Toolbox。

Simulink是MATLAB的一个扩展，用于建模、仿真和分析动态系统。

Communications Toolbox
是用于通信系统仿真的附加工具箱。

2. 创建通信系统模型。

在Simulink中，可以使用各种模块来创建通信系统
模型，例如信号源、调制器、解调器、信道和噪声源等。

3. 配置模块参数。

根据所需的通信系统参数，配置各个模块的参数。

例如，在调制器模块中，可以选择所需的调制类型（如QPSK、QAM等），并设
置相应的参数。

4. 运行仿真。

在Simulink中，可以使用“开始仿真”按钮来运行仿真。

Simulink将自动进行系统建模和仿真，并显示结果。

5. 分析仿真结果。

使用MATLAB中的各种工具和分析函数来处理仿真结果，例如频谱分析、误码率计算等。

以上是Matlab通信原理仿真教程的基本步骤，具体实现过程可能会因不同的通信系统和仿真需求而有所不同。

建议参考Matlab官方文档和相关教程进行学习。

MATLAB_6.5模拟仿真教程

模块功能说明：
求取信号的绝对值
求取信号的绝对值
4.Math（数学运算库）
数学运算库以及其中各模块的功能如图 4 6 所示。
输出强制系统输入为零的代数状态
输出强制系统输入为零的代数状态
按位逻辑运算按位逻辑运算逻辑真值查找逻辑真值查找输出输入复数的幅值与相位输出输入复数的幅值与相位
且可以直接将模块库中的模块拖动或者拷贝
到用户的系统模型中以构建动态系统模型。
4.2.1 Simulink公共模块库
Simulink公共模块库是Simulink中最为基础、最为通用的模块库，它可以被应用到不同的专业领域中。Simulink公共模块库共包含9个模块库，如图4.2所示。下面分别介绍各个模块的功能： 1. Continuous（连续系统模块库）连续系统模块库以及其中各模块的功能如图4.3所示。 2. Discrete（离散系统模块库）离散系统模块库以及其中各模块的功能如图4.4所示。
Matlab simulink仿真软件
Simulnk是Matalb作为重要的组件之一，它向用户提供一个动态建模、仿真和综合分析的集成环境。在此环境中，用户无需书写大量的程序，而只需通过简单直观的鼠标操作，选取适当的模块，就可构造出复杂的仿真模型。
主要优点：
适应面广，可构造的系统包括：线性、非线性；离散、连续及混合系统；单任务、多任务离散事件系统。
模块功能说明：数据类型转换器信号分解器
数据类型转换器信号分解器
从 Goto 模块中获得信号函数调用发生器
从Goto模块中获得信号
号与系统模
块库）
函数调用发生器向Goto模块传递信号

matlab仿真工具基本操作

matlab仿真工具基本操作Matlab是一种功能强大的数学仿真工具，它提供了丰富的功能和工具箱，可以用于各种科学计算、数据分析和模型仿真等领域。

本文将介绍Matlab仿真工具的基本操作，帮助读者快速上手使用该工具。

一、Matlab的安装与启动在开始使用Matlab之前，首先需要将其安装在计算机上。

用户可以从MathWorks官方网站下载Matlab的安装程序，并按照安装向导进行操作。

安装完成后，可以通过桌面上的快捷方式或者在命令行中输入"matlab"来启动Matlab。

二、Matlab的界面与基本操作Matlab的界面由多个窗口组成，包括命令窗口、编辑器窗口、工作空间窗口、命令历史窗口等。

用户可以通过菜单栏、工具栏或者命令行来执行各种操作。

1. 命令窗口：用户可以在命令窗口中直接输入Matlab命令，并按下Enter键执行。

Matlab会立即给出相应的结果，并显示在命令窗口中。

2. 编辑器窗口：用户可以在编辑器窗口中编写Matlab脚本文件，以便进行更复杂的操作。

脚本文件可以保存为.m文件，并通过命令窗口中的"run"命令或者点击编辑器窗口中的运行按钮来执行。

3. 工作空间窗口：工作空间窗口显示了当前Matlab工作空间中的变量列表。

用户可以通过命令行或者脚本文件来创建、修改和删除变量，并在工作空间窗口中查看其值和属性。

4. 命令历史窗口：命令历史窗口记录了用户在命令窗口中输入的所有命令，方便用户查找和重复使用。

三、Matlab的数学计算功能Matlab提供了丰富的数学计算函数，可以进行向量和矩阵运算、符号计算、微积分、线性代数、概率统计等操作。

用户可以通过命令行或者脚本文件来调用这些函数，并进行各种数学计算。

1. 向量和矩阵运算：Matlab中可以方便地定义和操作向量和矩阵。

用户可以使用矩阵运算符（如+、-、*、/）对向量和矩阵进行加减乘除等运算，还可以使用内置函数（如transpose、inv、det）进行转置、求逆和求行列式等操作。

使用MATLAB进行数学建模和仿真的步骤和注意事项

使用MATLAB进行数学建模和仿真的步骤和注意事项随着科技的发展，数学建模和仿真在工程、科学、经济等领域中扮演着至关重要的角色。

MATLAB作为一种强大的数学建模和仿真工具，在各种研究领域都广泛应用。

本文将介绍使用MATLAB进行数学建模和仿真的步骤和注意事项，帮助读者更好地进行数学模型的开发和仿真实验。

一、数学建模的步骤1. 确定问题和目标：首先明确所要解决的问题和需要达到的目标。

这一步是建立数学模型的基础，为后续的步骤提供方向。

2. 收集数据和背景信息：收集与问题相关的数据和背景信息，包括实验数据、文献资料等。

这些信息将作为建模的依据和参考，有助于更好地理解问题和找到解决方案。

3. 建立数学模型：选择合适的数学方法和工具，将问题转化为数学表达式。

根据问题的特点和需求，可以选择不同的数学模型，如代数方程、微分方程、优化模型等。

4. 参数估计和模型验证：根据已有的数据和背景信息，对模型的参数进行估计，并通过实验数据验证模型的准确性和适用性。

如果需要对模型进行修改和改进，可以返回第三步进行调整。

5. 模型求解和分析：使用MATLAB进行模型求解和分析。

根据建立的数学模型，利用数学工具和算法，得到问题的解或结果。

可以使用MATLAB各种内置函数和工具箱，例如符号计算工具箱、优化工具箱等。

6. 结果评估和应用：对模型的结果进行评估和分析，判断模型的有效性和可行性。

根据实际问题的需求，将模型结果应用于实际情况中，提供决策和解决方案。

二、MATLAB数学建模和仿真的注意事项1. 确定合适的数学工具：MATLAB提供了丰富的数学工具和函数，可以满足不同问题的需求。

在建模过程中，需要根据具体的问题特点和要求，选择合适的数学工具和函数。

同时，要善于利用MATLAB的帮助文档和在线资源，充分了解和掌握所使用的函数和工具的功能和使用方法。

2. 数据准备和预处理：良好的数据质量对于建模的准确性和仿真的可靠性至关重要。