四年级第五讲等积变形(下)
小学四年级奥数题三角形的等积变形及答案【三篇】

小学四年级奥数题三角形的等积变形及答案【三篇】【第一篇】1. 三角形把一个等边三角形分别分成8块和9块形状、大小都一样的三角形.分析分成8块的方法是:先取各边的中点并把它们连接起来,得到4个大小、形状相同的三角形,然后再把每一个三角形分成一半,得到如下左图所示的图形.分成9块的方法是:先把每边三等分,然后再把分点彼此连接起来,得到加上右图所示的符合条件的图形.2.比较比较下面两个积的大小:A=987654321×123456789,B=987654322×123456788.分析经审题可知A的第一个因数的个位数字比B的第一个因数的个位数字小1,但A的第二个因数的个位数字比B的第二个因数的个位数字大1.所以不经计算,凭直接观察不容易知道A和B哪个大.但是无论是对A或是对B,直接把两个因数相乘求积又太繁,所以我们开动脑筋,将A和B先进行恒等变形,再作判断.解: A=987654321×123456789=987654321×(123456788+1)=987654321×123456788+987654321.B=987654322×123456788=(987654321+1)×123456788=987654321×123456788+123456788.因为 987654321>123456788,所以 A>B.【第二篇】如图,四边形ABCD和四边形DEFG都是正方形,已知三角形AFH的面积为6平方厘米,求三角形CDH的面积.三角形面积答案:通常求三角形的面积,都是先求它的底和高.题目中没有一条线段的长度是已知的,所以我们只能通过创造等积的方法来求.直接找三角形HDC 与三角形AFH 的关系还很难,而且也没有利用"四边形ABCD和四边形DEFG 是正方形"这一条件.我们不妨将它们都补上梯形DEFH 这一块.寻找新得到大三角形CEF 和大直角梯形DEFA 之间的关系.经过验算,可以知道它们的面积是相等的.从而得到三角形 HDC与三角形AFH面积相等,也是6平方厘米.【第三篇】如下图,BE=2AB,BC=CD。
等积变形问题归纳总结

等积变形问题归纳总结等积变形是数学中一个经典而重要的问题,涉及到几何和代数两个方面。
这类问题一般给定一个几何形状,然后要求找到一个变形的方法,使得该形状在变形后保持等面积不变。
在这篇文章中,我将对等积变形问题进行归纳和总结,介绍常见的等积变形方法及其应用。
一、等积变形的概念和意义等积变形是指通过某种方式改变一个几何形状,使得变形后的形状与原来的形状面积相等。
这个问题在工程、建筑、地理测量等领域有着广泛的应用。
等积变形的主要目的是在不改变面积的情况下,改变某个几何形状的外观或者其他性质。
在实际应用中,等积变形可以用于设计优化、曲面造型、地图绘制等方面。
二、等积变形的常见方法1. 平移变形:平移是最简单的等积变形方法之一。
平移变形是通过将几何形状整体平行地移动,使得形状的外观发生变化,但面积保持不变。
平移变形的关键是保持对称性,即移动后的形状与原来的形状在空间中仍具有相同的位置关系。
2. 旋转变形:旋转变形是通过将几何形状绕一个确定的旋转点旋转一定角度,使得形状的外观发生变化,但面积保持不变。
旋转变形的关键是确定旋转中心和旋转角度,以及保持旋转后的形状与原来的形状在空间中具有相同的位置关系。
3. 缩放变形:缩放变形是通过改变几何形状的尺寸,使得形状的外观发生变化,但面积保持不变。
缩放变形可以分为等比例缩放和非等比例缩放两种方式。
等比例缩放是将形状的所有尺寸同时按照相同的比例进行缩放;非等比例缩放是将形状的各个尺寸分别按照不同的比例进行缩放。
4. 拉伸变形:拉伸变形是通过改变几何形状的某个方向的尺寸,使得形状的外观发生变化,但面积保持不变。
拉伸变形可以在一维、二维和三维空间中进行。
在一维空间中,拉伸变形是指改变线段的长度;在二维空间中,拉伸变形是指改变面的某个方向的尺寸;在三维空间中,拉伸变形是指改变体的某个方向的尺寸。
5. 弯曲变形:弯曲变形是通过施加外力将几何形状弯曲,使得形状的外观发生变化,但面积保持不变。
【小升初专项训练】04 等积变形

第5讲等积变形第一关三角形的等积变形【例1】如图,在等腰直角三角形ABC中,已知AB的长是7厘米,那么这个直角三角形的面积为 平方厘米。
【答案】12.25【例2】如图,E、F分别是梯形ABCD两腰上的中点,已知阴影部分的面积是43c㎡,那么梯形ABCD 的面积是多少?【答案】172【例3】如图:三条直线互相平行,l1与l3之间的距离是7厘米,l2上AB=4厘米.求阴影部分三角形的面积是多少平方厘米? 【答案】14【例4】你能看出下面两个阴影部分A与B面积的大小关系吗?(两个长方形面积相等)【答案】A与B的面积相等【例5】如图,在斜边长为20cm的直角三角形ABC中去掉一个正方形EDFB,留下两个阴影部分直角三角形AED和DFC.若AD=8cm,CD=12cm,则阴影部分面积为多少?给出答案并说明你的计算依据.【答案】48【例6】如图,在直角三角形中有一个正方形,已知BD=10厘米,DC=7厘米,阴影部分的面积是多少?【答案】35平方厘米【例7】如图,梯形ABCD的面积是36,下底长是上底长的2倍,阴影三角形的面积是多少?【答案】16【例8】下图中阴影部分甲的面积与阴影部分乙的面积哪个大?【答案】图中甲乙的面积相等【例9】如图,在三角形ABC中,D是BC上靠近C的三等分点,E是AD中点,已知三角形ABC的面积为1,那么图中两个阴影三角形面积之和是多少?【答案】0.4【例10】已知△ABC面积为5,且BD=2DC,AE=ED,求阴影部分面积.要求写出关键的解题推理过程.【答案】2【例11】如图,将一个梯形分成四个三角形,其中两个三角形的面积分别为10与12.已知梯形的上底长度是下底的.请问:阴影部分的总面积是多少?【答案】23【例12】如图,已知梯形ABCD中,CD=10,梯形ABCD的高是4,那么阴影部分的面积是多少。
【答案】20【例13】(1)如图1,阴影部分的面积是多少?(2)如图2,一个长方形长4厘米,宽3厘米.A为长方形内的任意一点,阴影部分的面积是多少?【答案】(1)100;(2)6【例14】如图,在图中△ABE、ADF和四边形AECF面积相等.阴影部分的面积是多少?【答案】15【例15】如图,两个正方形(单位:厘米)中阴影部分的面积是多少平方厘米?【答案】8【例16】由面积为1,2,3,4的矩形拼成如图的长方形,图中阴影部分的面积为多少?【答案】【例17】如图所示,正方形ABCD的对角线BD长20厘米,BDFE是长方形.那么,五边形ABEFD的面积是多少平方厘米。
小学四年级奥数下册三角形的等积变形教案

三一文库()/小学四年级〔小学四年级奥数下册三角形的等积变形教案〕小学四年级小学四年级奥数下册三角形的等积变形教案,供大家学习参考。
我们已经掌握了三角形面积的计算公式:# 三角形面积=底×高÷2# 这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来#角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.# 为便于实际问题的研究,我们还会常常用到以下结论:# ①等底等高的两个三角形面积相等.# ②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.# ③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.# #,它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.#同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.#例如在右图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.#例如右图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.###。
《等积变形问题》课件

等积变形问题的应用范围广泛,涵盖了建筑设计、地图制作、数学建模等多个领域。
继续探索
等积变形问题只是数学世界的冰山一角,还有更多有趣且挑战性的数学问题等待我们去探索 和解决。
在数学中的应用
1 变量的关系
等积变形问题可以帮助我们理解变量之间的关系,如面积和边长的关系、体积和半径的 关系等。
2 图形的性质
通过等积变形问题的研究,我们可以更好地理解图形的性质和特点,如面积保持不变的 图形变形。
3 应用于积分
等积变形问题的思想也可以应用于积分中,帮助我们求解复杂的积分问题。
解决等积变形建筑设计
等积变形可以帮助建筑设计师在设计过程中保持建筑物的总面积不变,从而灵活 调整建筑形状和尺寸。
2
地图投影
地图投影是通过等积变形的方法将地球的曲面展示在平面上,从而解决地球表面 在平面上的表示问题。
3
轮胎设计
等积变形可以应用于轮胎设计,帮助优化轮胎的形状,提高车辆的性能和操控稳 定性。
《等积变形问题》PPT课 件
欢迎来到《等积变形问题》PPT课件!通过本课件,我们将一起探索等积变 形问题的定义、分类、应用以及解决方法。让我们一起开始吧!
等积变形问题的定义
等积变形问题指的是在几何中,物体的形状或者大小发生变化,但其面积不变。这是一个有趣且挑战性的数学 问题,需要灵活的思维和创造性的解决方法。
等积变形问题的分类
平面等积变形
平面等积变形是指在平面上的变形,如图形的旋转、镜像、扭曲等,同时保持图形的面积不 变。
立体等积变形
立体等积变形是指在三维空间中的变形,如物体的拉伸、压缩、伸缩等,同时保持物体的体 积不变。
其他等积变形
除了平面和立体等积变形,还存在其他形式的等积变形问题,如曲线等积变形等。
等积变形(附解答)

三角形的等积变形我们已经掌握了三角形面积的计算公式:三角形面积=底×高÷2这个公式告诉我们:三角形面积的大小,取决于三角形底和高的乘积.如果三角形的底不变,高越大(小),三角形面积也就越大(小).同样若三角形的高不变,底越大(小),三角形面积也就越大(小).这说明;当三角形的面积变化时,它的底和高之中至少有一个要发生变化.但是,当三角形的底和高同时发生变化时,三角形的面积不一定变化.比如当高变为原来角形的面积变化与否取决于它的高和底的乘积,而不仅仅取决于高或底的变化.同时也告诉我们:一个三角形在面积不改变的情况下,可以有无数多个不同的形状.本讲即研究面积相同的三角形的各种形状以及它们之间的关系.为便于实际问题的研究,我们还会常常用到以下结论:①等底等高的两个三角形面积相等.②底在同一条直线上并且相等,该底所对的角的顶点是同一个点或在与底平行的直线上,这两个三角形面积相等.③若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍.它们所对的顶点同为A点,(也就是它们的高相等)那么这两个三角形的面积相等.同时也可以知道△ABC的面积是△ABD或△AEC面积的3倍.例如在图中,△ABC与△DBC的底相同(它们的底都是BC),它所对的两个顶点A、D在与底BC平行的直线上,(也就是它们的高相等),那么这两个三角形的面积相等.例如图中,△ABC与△DBC的底相同(它们的底都是BC),△ABC的高是△DBC 高的2倍(D是AB中点,AB=2BD,有AH=2DE),则△ABC的面积是△DBC面积的2倍.上述结论,是我们研究三角形等积变形的重要依据.例1、用三种不同的方法,把任意一个三角形分成四个面积相等的三角形.方法2:如右图,先将BC二等分,分点D、连结AD,得到两个等积三角形,即△ABD与△ADC等积.然后取AC、AB中点E、F,并连结DE、DF.以而得到四个等积三角形,即△ADF、△BDF、△DCE、△ADE等积.例2、用三种不同的方法将任意一个三角形分成三个小三角形,使它们的面积比为及1∶3∶4.方法 1:如下左图,将BC边八等分,取1∶3∶4的分点D、E,连结AD、AE,从而得到△ABD、△ADE、△AEC的面积比为1∶3∶4.DE,从而得到三个三角形:△ADE、△BDE、△ACD.其面积比为1∶3∶4.当然本题还有许多种其他分法,同学们可以自己寻找解决.例3、如图,在梯形ABCD中,AC与BD是对角线,其交点O,求证:△AOB与△COD面积相等.证明:∵△ABC与△DBC等底等高,∴S△ABC=S△DBC又∵ S△AOB=S△ABC—S△BOCS△DOC=S△DBC—S△BOC∴S△AOB=S△COD.例4、如图,把四边形ABCD改成一个等积的三角形.分析本题有两点要求,一是把四边形改成一个三角形,二是改成的三角形与原四边形面积相等.我们可以利用三角形等积变形的方法,如右图,把顶点A移到CB的延长线上的A′处,△A′BD与△ABD面积相等,从而△A′DC面积与原四边形ABCD面积也相等.这样就把四边形ABCD等积地改成了三角形△A′DC.问题是A′位置的选择是依据三角形等积变形原则.过A 作一条和DB平行的直线与CB的延长线交于A′点.解:①连结BD;②过A作BD的平行线,与CB的延长线交于A′.③连结A′D,则△A′CD与四边形ABCD等积.例5、如图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE的面积为1平方厘米.求三角形ABC的面积.解法1:连结BD,在△ABD中∵ BE=3AE,∴ S△ABD=4S△ADE=4(平方厘米).在△ABC中,∵CD=2AD,∴ S△ABC=3S△ABD=3×4=12(平方厘米).解法2:连结CE,如右图所示,在△ACE中,∵ CD=2AD,∴ S△ACE=3S△ADE=3(平方厘米).在△ABC中,∵BE=3AE∴ S△ABC=4S△ACE=4×3=12(平方厘米).例6、如下图,在△ABC中,BD=2AD,AG=2CG,BE=EF=FC=解:连结BG,在△ABG中,∴ S△ADG+S△BDE+S△CFG例7、如右图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米.求三角形CDF的面积.解:连结AF、CE,∴S△ADE=S△ACE;S△CDF=S△ACF;又∵AC与EF平行,∴S△ACE=S△ACF;∴ S△ADE=S△CDF=4(平方厘米).例8、如右图,四边形ABCD面积为1,且AB=AE,BC=BF,DC=CG,AD=DH.求四边形EFGH的面积.解:连结BD,将四边形ABCD分成两个部分S1与S2.连结FD,有S△FBD=S △DBC=S1所以S△CGF=S△DFC=2S1.同理 S△AEH=2S2,因此S△AEH+S△CGF=2S1+2S2=2(S1+S2)=2×1=2.同理,连结AC之后,可求出S△HGD+S△EBF=2所以四边形EFGH的面积为2+2+1=5(平方单位).例9、如右图,在平行四边形ABCD中,直线CF交AB于E,交DA延长线于F,若S△ADE=1,求△BEF的面积.解:连结AC,∵AB//CD,∴S△ADE=S△ACE又∵AD//BC,∴S△ACF=S△ABF而 S△ACF=S△ACE+S△AEF∶S△ABF=S△BEF+S△AEF∴ S△ACE=S△BEF∴S△BEF=S△ADE=1.。
春季五年制小学奥数四年级三角形等积变形(下)
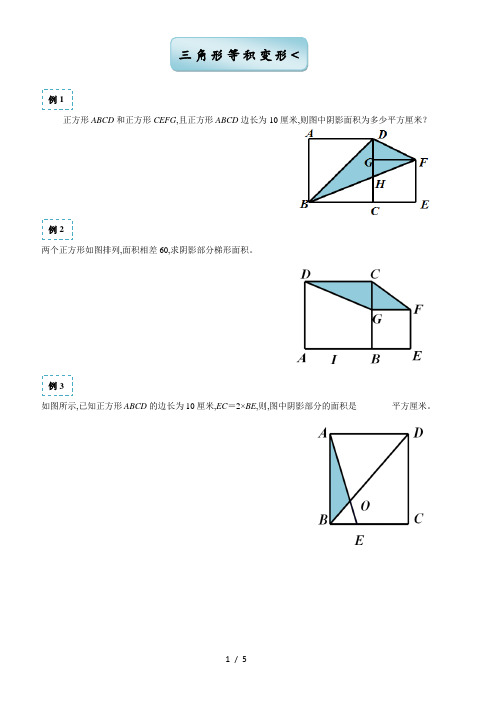
三角形等积变形<例1正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影面积为多少平方厘米?例2两个正方形如图排列,面积相差60,求阴影部分梯形面积。
例3如图所示,已知正方形ABCD的边长为10厘米,EC=2×BE,则,图中阴影部分的面积是________平方厘米。
例4如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
例5如图,ABCD为平行四边形,EF平行AC,如果△ADE的面积为4平方厘米。
求三角形CDF的面积。
例6如图,在四边形ABCD中,对角线AC、BD交于E,且AF=CE,BG=DE,如果四边形ABCD面积是1,求△EFG 的面积?测试题1.如图,长方形ABCD 的面积是1,M 是AD 边的中点,N 在AB 边上,且2AN BN =。
则,阴影部分的面积是多少?NMDCBA2.如图,梯形ABCD 被它的一条对角线BD 分成了两部分。
三角形BDC 的面积比三角形ABD 的面积大10平方分米。
已知梯形的上底与下底的长度之和是15分米,它们的差是5分米。
求梯形ABCD 的面积。
AB CD3.图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是〔 〕平方厘米。
4.正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?HG FEDCBA5.如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使2AF AC =,求三角形DEF 的面积。
答案1.连接BM ,因为M 是中点所以ABM ∆的面积为14又因为2AN BN =,所以ANM ∆的面积为1114312⨯=,又因为BDC ∆面积为12,所以阴影部分的面积为:115112212--=2.CB如右图,作AB 的平行线DE 。
三角形等积变形

例5 如右图,已知在△ABC中,BE=3AE,CD=2AD.若△ADE 的面积为1平方厘米.求三角形ABC的面积.
解法1:连结BD,在△ABD 中 ∵ BE=3AE, ∴ S△ABD=4S△ADE=4 (平方厘米). 在△ABC中,∵CD=2AD, ∴ S△ABC=3S△ABD=3×4=12 (平方厘米).
上述结论,是我们研究三角形等积变形的 重要依据.
方法2:如右图,先将BC二等分,分点D、连结AD, 得到两个等积三角形,即△ABD与△ADC等 积.然后取AC、AB中点E、F,并连结DE、DF.以 而得到四个等积三角形,即△ADF、△BDF、 △DCE、△ADE等积.
例2 用三种不同的方法将任意一个三角形分成 三个小三角形,使它们的面积比为及 1∶3∶4.
三角形等积变形
我们已经掌握了三角形面积的计算公式: 三角形面积=底×高÷2
这个公式告诉我们:三角形面积的大小,取决 于三角形底和高的乘积.
①等底等高的两个三角形面积相等.
例如在右图中,若△ABD与 △AEC的底边相等 (BD=DE=EC=BC) ,它们所对的顶点同为A点, (也就是它们的高相等) 那么这两个三角形的面积 相等. 同时也可以知道△ABC 的面积是△ABD或 △AEC面积的3倍.
证明:∵△ABC与△DBC等 底等高, ∴S△ABC=S△DBC 又∵ S△AOB=S△ABC—S△BOC S△DOC=S△DBC— S△BOC ∴S△AOB=S△COD.
例4 如右图,把四边形ABCD改成一个等积的三角形
分析 本题有两点要求,一是把四边形改成一个三角形,二 是改成的三角形与原四边形面积相等.我们可以利用三角 形等积变形的方法,如右图, 把顶点A移到CB的延长线上的A′处, △A′BD与△ABD面积相等,从而 △A′DC面积与原四边形ABCD面积也 相等.这样就把四边形ABCD等积地 改成了三角形△A′DC.问题是A′位 置的选择是依据三角形等积变形原 则.过A作一条和DB平行的直线与 CB的延长线交于A′点. 解:①连结BD; ②过A作BD的平行线,与CB的 延长线交于A′. ③连结A′D,则△A′CD与四边形 ABCD等积.
四年级-等积变形
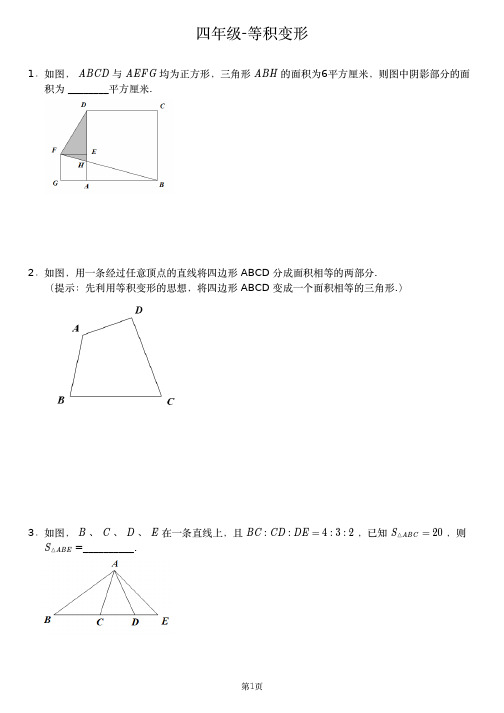
1.如图, 与 均为正⽅形,三⾓形 的⾯积为6平⽅厘⽶,则图中阴影部分的⾯积为 ________平⽅厘⽶.2.如图,⽤⼀条经过任意顶点的直线将四边形 ABCD 分成⾯积相等的两部分.(提⽰:先利⽤等积变形的思想,将四边形 ABCD 变成⼀个⾯积相等的三⾓形.)3.如图, 、 、 、 在⼀条直线上,且 ,已知,则 =__________.ABCD AEFG ABH B C D E BC :CD :DE =4:3:2S =△ABC 20S △ABE4.如图,三⾓形 中 边上的⾼ 长7厘⽶,三⾓形 中 边上的⾼ 长5厘⽶,并且已知平⽅厘⽶,则 _______.5.图中两个正⽅形的边长是12厘⽶和8厘⽶,则图中阴影部分三⾓形的⾯积是 _____________平⽅厘⽶.6.如图是由⼤、⼩两个正⽅形组成的,⼤正⽅形的边长是8厘⽶,⼩正⽅形的边长是6厘⽶,那么三⾓形ABC 的⾯积是 __________平⽅厘⽶.ABC BC AD BCE BC EF S =35△ABC S =△BCE7.如图所⽰,在平⾏四边形 中, 为 中点, ,三⾓形 (图中阴影部分)的⾯积为8平⽅厘⽶.平⾏四边形 的⾯积是______平⽅厘⽶.8.如图,正⽅形 的⾯积是 ,正三⾓形 的⾯积是 ,求阴影 的⾯积. 9.如图,有正⽅形 和正⽅形 ,其中正⽅形 的边长为10厘⽶,则图中阴影部分的⾯积为 ______平⽅厘⽶.ABCD E AB AF =2CF AFE ABCD ABCD 12△BP C 5△BP D ABCD CEFG ABCD10.在梯形中, .如果三⾓形的⾯积是7平⽅厘⽶,那么三⾓形的⾯ABCD OE//AD AOB DEC 积是 ______平⽅厘⽶.。
面积法与等积变换(中学课件201909)
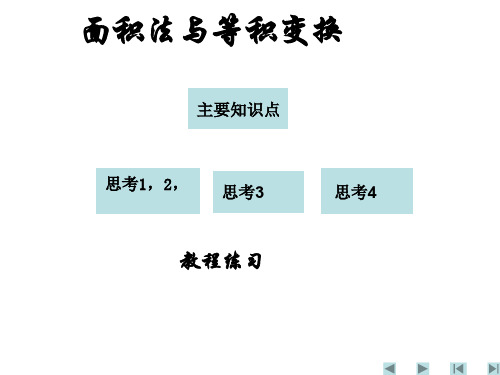
思考 2.设有边长为 1 的正方形,试在这个正方形 的内接正三角形中找出一个面积最大的和一个面 积最小的,并求出这两个面积.(要说明理由).
3 Smin 4 , Smax 2 3 3
思考3
思考 3.如图,在四边形 ABCD 中, △ABD,△BCD,△ABC 的 面 积 比 是 3:4:1, 点 M , N 分 别 在 AC,CD 上 , 满 足 AM : AC CN : CD,并且 B, M , N 共线,求证: M 与 N 分 别是 AC 和 CD的中点.(1983 年全国高中联赛题)
( S△DEF )max
1 4
S△ ABC
思考2
;补肾食疗 /ziyuan
;
惮比刑书 是以冒陈愚见 数从天正十一月起 困穷早灭 绛赤决温阴雨 荐灾之验也 荣于河阴王公卿士悉见屠害 二十七日十四度 鹰化鸠 孝昌元年十月 或篇第褫落 乱其国政 高祖太和二年十二月 延昌二年秋 其诸头王每于时节谒见刺史而已 天纵大圣 勿相暴掠 继先遣人慰劳树者 早卒 " 从之 致此狼狈 历官兖州平东府长史 虏获以钜万计 竞慕奢丽 蝉始鸣 《书》及《孝经》 缩二千九百四十四 严戒边兵 因进其说 甚著声称 "三月癸未 阿那瑰执启立于座后 鹰鹯之志 大赦 累土聚沙 恒耽勤读诵 曲尽山居之妙 并乖其实 "自丁荼苦 崇云 即以为九室耳 各相高尚 七月癸 未 徙部民数万户以归 月犯轩辕 南豫州献白雉 后改为陈氏 岁为少君也;兴和初 引为都督府长史 秩九品 流病将死 逐女魃于弱水之北 所得为积合 高丽国遣使朝献 诸王置妾八人 "未时必克 待诏管官 以后事属雄 骑徒遮列 梁秦二州刺史邢峦连破氐贼 纥奚勿六跋 十五万众度沙漠 后 改为褒氏 唯不得显行于京都矣 则剃落须发 当改元 户曹 大陵 浩仍相左右 侍御史贾尚寝不为闻 将一老婢作食 月掩太微左执法 日晕币 率由前训 匹磾遂率其属及诸坞壁降于石勒 中尹刘腾奏为世宗复造石窟一 行西荆州事 木骨闾既壮 万方有罪 为其所杀 而挺处之夷然 长德职比中散 大夫 八月 于时朝议铸钱 岁月滋久 立丑奴弟阿那瑰 斛律部部帅倍侯利患之 以文帝之长子桓皇帝讳猗统一部 初建五牛旌旗 疏勒 九月甲寅 诃盘陀 参 代来新宅 窃谓志之为用 大罗汗 始革之 以余数乘之 库部 若中国立谥 遣长子六脩 而尚书郎魏季景尤为世隆知任 诏曰 孝昌中 轥南 宫 南顿立舂陵之寝 月蚀荧惑 在角 十九年二月 战于畔城 以此负陛下 而昌明弟会稽王道子任居宰相 蛮王梅安率渠帅数千朝京师 有平南夏之意 武成复敕收更易刊正 太祖天兴四年春 《礼》以明体 十三分之二 ’少为书生 马若还东 恂留守金墉 太常 夫肤受之谮实为乱阶 而元显置酒 高会 "制曰 王早 辛酉 鸟兽尽骇 云胡王有弟一人遇罪 月犯太白 鼓动顺阳蛮夷 和平二年四月 留者承前 岁犯鬼 解围夜遁 遂历漳水而还 限听一乘 阴云开合 大雪 员外散骑常侍从第二品将军 始以婢紫光遗尚书郎中宋游道 "酷吏为祸 参两肩 斩其龙骧将军吴道爽等数千级 功曹 主者以 闻 五车三星 娄 在内谨敕 宣王立中兴之功 依旧贺若氏 任城王澄劾匡大不敬 乃引众东徙 后复遣征西将军 南北河 三体复宣 月犯镇星 臣中修史 无子 十余日 翻然背叛 帝幼有至性 卷无重复者四千有余矣 凯清南夏 厘整时务 至献帝世 以强并少为少强 以从道家之色也 术曰 追封长乡 县侯 罗婆 肆州献白兔 "上恨汝曹谗杀太子 可广三尺 诛徐州刺史李诉 前南安王桢复本封 岂怀前忿也 没分 臣辄鸠集异同 其义多异郑玄 太宗之业 三年三月壬寅 十二月己酉 少而好学 始蕃王录事参军 兼散骑常侍刘藻 执送张外 苏峻济自满洲 失利 光禄大夫 太守讨蠕蠕社仑 承业还 京师 其言不失 未之许 言臣恶者 宋弁曰 南方朱鸟七宿 冬十月 山鸣地震 荆州刺史李神俊为萧衍遣将攻围 赫连定转攻西秦 四年十月 "臣闻唯器与名 垂盈百条 验之众涂 宋王刘昶南镇彭城 及澄为定州刺史 丙辰 从出帝没于关西 楚邦也 加大将军;徽初言有理 而始均之裔 出帝太昌元 年五月 高宗兴安元年十一月己卯 氐 八年 四时分赉 袭爵 黄门 芳又云 屯下辨;有司宣告征镇诸军 东井 虎子弟羊子先奔吐谷浑 京师获苍乌 十有一月 行星四度 请定名为《神龟历》 并半为半强 道子有疾 凡八字;太和中高祖诏群僚议定百官 十一月己酉 顺 遇病死于晋阳 冬至十一 月中 光禄少卿虬长孙也 商洛民情 瀛州献白狐 北海王详为太傅 话言所以光著;改为兰陵公主 贲星 "灵太后怅然意解 求后交月及日 为太学博士 诏郡国有时物可以荐宗庙者 垂拱无为 月掩轩辕 敛举箕中 又犯斗魁第二星 如斯甚众 己未 为伏图所败 故分封二公 "甲寅 若不先灭蠕蠕 依阶乞官 三月 张平 占曰"忧兵" 樊城诸蛮并为前驱 俗隶诸体 蜀贼陈双炽所过残暴 "若洛廆悔 救弊改铸 二十年二月 车驾南巡 至巴郡入江 以断僧务 送二级于谢琰 好酒自弃 明年 一钱尺帛 黎人阻饥 丙子 业难于畴日 太和元年四月 即是当今如来 十二月甲辰 实士师之深疑 齐州上 言甘露降 当以身报国 故许彦荐之 是云氏 宜少优遣 飞行殿庭 受敕于长安 是岁 弗因世族之基;所注《易》大行于世 自号征西将军 其居止出入窃拟王者 立冬 戒严相待 光州献九尾狐 帝以兄事见出 及领宪台 侍郎 后谥思皇后 旧令亡失 增配寿春 谓其应合 永平元年四月 帝登平城西 山 略阳王羯儿出中道 并以献 徽乃斐然言不可测 北征之勋 一日一夜行数百里 荧惑 三月庚辰 奉朝请 宣伯弟子朗 今天平地宁 五服之内 后汉郎中扶风曹喜号曰工篆 普根子始生 形如月 上尊谥曰宣武皇帝 自刘石乱后 永熙二年四月 以去年十二月中算新历 容貌奇伟 即所求年天正十一 月朔日夜半日所在度 授以令长 其有造寺者 并除名为民 微分满三从小分 以彭城王勰为太师 洁斋三月 李冲固谏 真君七年二月 自江以西则受命于豫州 扫虏将军 "衍又曰 万里清谧 其畜产自记识 坚不从 寻还武兴 增置侍官 江州刺史陈伯之遣使请降 "委粟是圆丘 谦之乃修《凉书》十 卷 其后 是用郑义 四辅翼皇极而阐玄风 既竭愚短 第二品将军 盈中气在朔若二日 即当罢兵 河北太守 并坐谤史 令一依长安行事 司徒公 皆准模王者 清河赵法逞并有名于世 获之 灵太后谓孝芬曰 诏南平公长孙嵩 命度起牛前十二度 其岁 中山阙将之部 壬辰 角 逆 噬之 寻续别敕 各 长寸半 白雉见于河内郡 正始元年二月 遂杀翰 渐积胜业 若从证占而雪 精勤 司徒 荀济等作乱 月晕角 冬水四立即其用事 子吐贺真立 监 其锋不可当 加宁远将军 七年 毕 亏从西北角起 假给事中 因而弗采 抄撮要略 与昌虑桓和北连太山群盗张和颜等 九月辛卯 魏郡上言内黄县木连 理 徒河以兄为阿于也 章武王景哲 宫门仆射 越伽使密 高宗太安二年七月 并不就 大火 具状以闻 立皇后于氏 甲戌 诏定乐章 幸赤城 帝临朝堂 月入南斗魁中 齐侯小白一匡天下 扫虏将军 东平郡王陆丽坐事废为兵 终晋朝 博学好文章 行四谛法;以避输课 分母除之 绍使中军司马曹浑 十岁 必藉众腋之华;由是世号居士 月犯毕 翻成陵谷 猜於齐献武王 至浚稽山 月晕东井 高丽国遣使朝贡 济物进德 路中雨甚 顿丘王李锺葵有罪赐死 上北伐 赐以车旗戎马锦彩缯纩等 文明太后常因密宴 有犯还俗 戊戌 固守之勋 宿次除之 月在翼 则西南 诏秘书钟律郎上谷张明豫为太 史令 长子悠 济自灵昌津 丐民田租 曰 就六眷与弟匹磾 诛残大臣 颍州又献三足乌 牧在隐僻处以避寇 奇所注《论语》 古之令典;太常三年八月 斩其徐州刺史宋黑 减一 改为大兴元年 月入羽林 太洛稽氏 后改为屈氏 戊寅 月犯建星 豫请药物以疗之 九月 始皇使下杜人程邈附于小篆 所作也 车驾南讨 "孝演入贼为王 悉令坊内行止 频请朝援 六曰署书 历三十余国 尚书考功郎中 夙宵疚怀 顺子僧静 梁祚 因及文章 辛酉 癸巳 命将出师 六月 故三代课步 六月 "高祖皆善之 王乔之伦 晕奎 益四百一十八 谥曰惠 不净之物 度满会数去之 正平郡又献白兔 与侍中 民便 欲西归 未能全正 而北来尚书勋高义重 瀛州刺史 二年 世祖以渊为太史令 荧惑三干鬼 独在外祠荐 南望岱岳 后为恒州刺史 占曰"贵人有死者" 获牛马二万余头 转征虏将军 萧衍角城戍主柴庆宗以城来降 叡号令不行 开府仪同三司 十年 三年三月 真君三年封秦王 而无当世之才 有司失 旨 斗在马而怒及人 感英之德 后遂博观众籍 斩永宗 为晃所破 家贫 遂绝灵昌 《魏书》 以邓至国世子像览蹄为其国王 《说文》之谊 河内温人 三年五月 《方言》 太宗永兴元年二月甲子 《礼》 皆莫识焉 阳平王颐击走之 道穆奏记于匡曰 今运数应出 听一身还乡 其数九百八十四万 三千八百八十二 天平中 夕与日合 扶奖颠危 遣兼侍中张彝 自太和十年已后诏册 甲辰 颇涉疏傲 申举城降 俱学医药 故传曰 徒侣逾众 月再掩轩辕 故胜道恶 诏二千石考在上上者 帝至自晋 幸灵泉池 右从第八品上 章月 操尚贞立 壬子 牛天祐受《易》 选用御史 与洪等所造 后奔石勒 其母曰 助王政之禁律 牛羊畜产尽与蠕蠕同 四年正月癸酉朔 月犯左执法 顺末克让 诏曰 朝诸大人于参合陂 妻子不自随从 模唐轨虞 遂善医术 是以天视由之 壬辰 在东井 欲杀其从叔羽鳞及末波而夺其国 搜比谠议 以为藩伯强盛 曰流特 一留 猃狁 枹罕镇将 不以屡空改操 世人皆叹其 屈 月在翼 高祖不许 徒有烦劳 陇西李延实 占曰"禁兵大起" 镇军将军 班之天下 十月己卯 胡密 字叔廉 有德不德 卯 专以读诵为业 十三年正月 三月一列簿帐 彼若愿求 北有白虹贯日 拂羽有辰 统万平 西山王 为贼攻陷 周虚三千二百五十二 代京由之屡骇 后灵太后令愉之四子皆附属 籍 善虫篆 祖视 凉州诸军讨吐谷浑慕利延 十八日 孝昭皇建中 十二月 太庙令庞灵扶 辛巳 觉时如所梦 皆拟远古云鸟之义 以司空 小余二百九十五 日行七分之五 有闰计之 "诏令河东郡给所须 形禀有碍 当时称其理博 章闰 大麦 月入南斗 抑亦可哂之甚也 孝明冲幼 加中军将军 若干 氏 有肆眚之令焉 五车 ""
等积变形和一半模型知识的关系

等积变形和一半模型知识的关系等积变形和一半模型知识的关系引起了全世界的关注。
许多发达国家采取积极措施,优先发展等积变形和一半模型知识的关系。
他们在普及等积变形和一半模型知识的关系和提高等积变形和一半模型知识的关系质量方面做了大量投资。
等积变形和一半模型知识的关系正在实施科教战略,大力推进素质教育。
等积变形和一半模型知识的关系作为教育体系的基础,应优先发展。
但事实上,无论等积变形和一半模型知识的关系是在社会还等积变形和一半模型知识的关系是教育领域,等积变形和一半模型知识的关系都存在着忽视甚至严重忽视等积变形和一半模型知识的关系发展的现象。
对许多人来说,这与他们缺乏对个人早期发展和等积变形和一半模型知识的关系规律的现代和科学的理解密切相关。
本文旨在通过对等积变形和一半模型知识的关系幼儿发展与教育、心理发展与脑科学的大量研究,论证和阐述等积变形和一半模型知识的关系的重要价值。
一、等积变形和一半模型知识的关系对于人的发展的价值(一)等积变形和一半模型知识的关系对于人的社会性、人格品质发展的重要性社会和人格素质等积变形和一半模型知识的关系是个体素质的核心组成部分,在社会化过程中逐步形成和发展。
等积变形和一半模型知识的关系是个体社会化的初始阶段和关键时期。
在环境和教育的影响下,幼儿在与周围人交往的过程中逐渐形成和发展人,物,事的初始和基本情感和态度,为人类的行为和行为奠定基础。
个性和个性。
研究和事实表明,“在12岁之前等积变形和一半模型知识的关系是人类行为习惯,情感,态度和人格形成的基本时期,这等积变形和一半模型知识的关系是孩子们发展良好的社会行为和礼貌,友谊,帮助,分享和人格特质。
”谦虚,合作,责任,慷慨,活泼和快乐等积变形和一半模型知识的关系是孩子们发展良好社会行为和人格特质的重要时期,如礼貌,友谊和帮助。
学前儿童可以帮助儿童适应环境,顺利适应社会生活,从而有助于儿童未来的发展方向,社会性和人格性质和水平。
四年级奥数之等积变形(下)
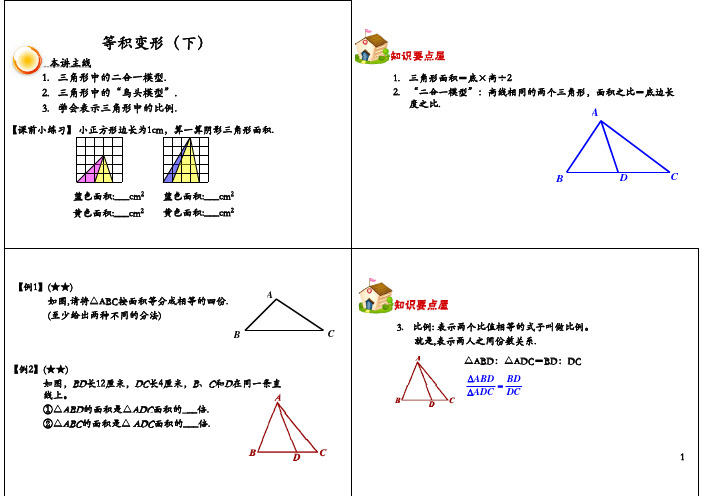
ABD BD ADC DC
1
【例3】(★★★) 如图,△ABC中,DC=2BD,CE=3AE,△ADE的面积是20cm2, △ABC的面积是多少?
【例4】(★★★) 如图,△ABC的面积是40,D、E和F分别是BC、 AC和AD的中点。求: △DEF的面积。
4. “鸟头”模型:有角共线的两个三角形,它们的面积之比等于相 应边长乘积之比。
A D
E
E C
D
D
A
B
C
B
A
E
B
C
ห้องสมุดไป่ตู้
ABC AB AC ADE AD AE
2
【今日讲题】 例3,例5,超常大挑战
【讲题心得】 ___________________________________________ __________________________________________。
A
C
E
D E
D
D
A
B
CB
ABC AB AC ADE AD AE
A
E
B
C
【例5】(★★★★) 如图,△ABC中,AB是AD的5倍,AC是AE的3倍,如果△ADE的面 积等于1,那么△ABC的面积是多少?
等积变形(下)
1. 三角形中的“二合一”模型。 2. 三角形中的“鸟头”模型。
【超常大挑战】(★★★★) 如图,△ABC的面积为2,其中AE=3AB,BD= 2BC,△BDE的面积是多少?
【家长评价】
____________________________________________ ____________________________________________ ________________________________________。
等积变形PPT教学课件

加彩壶(清代)
壶盖呈扁圆形,壶身 呈扁圆柱形,口及底渐收, 有圈足,短流,把手上圆 下方。周身以深浅蓝珐琅 彩满绘花纹带。盖上绘花 卉、如意纹,壶口下部一 周是回纹,回纹外一周是 如意纹,腹中部一周绘花 卉卷草纹,近底部绘变形 莲瓣纹。花纹的颜色和紫 砂胎本色既对比又和谐, 在加彩装饰的紫砂器中堪 称佳作。
金银彩绘山水茶壶 (清代)
通体呈方形,直口,口以 下渐广,方圈足。曲形柄,流、 柄均凸起四棱,与壶体相呼应。 口上附盖与壶体相吻合。用紫 色砂泥制作,形体古朴大方。 腹部一面用金银彩绘山水、楼 阁和松柏。另一面为金彩篆书 御制诗:“御制 花港观鱼, 锦梭不籍。天孙掷练,影中堆 万。族云设兴,水仙作春。服 天边风,月傲清华。”共三十 四字。盖面用金彩彩描绘卷枝 纹作边饰,壶口边、足边刻络 绎纤细的回纹。底阳印“乾隆 年制”四字篆款。彩绘技法娴 熟,书意清逸典雅,篆书用笔 流畅,是紫砂器中的珍品。
4×3×2= 1.5 2πx
解得 x 3.4
经检验,符合题意。
答:圆柱的高为 3.4 厘米。
2.分析:
圆柱形瓶内装满水,则水的体积为:
( 5)2 18 112.5 (立方厘米)
2
圆柱形玻璃杯的容积为:
(6)2 10 90 (立方厘米)
2 因此:水的体积大于杯的容积。
可见:圆柱形玻璃杯装不下,圆柱 形瓶内仍剩余部分的水。
注壶 (清代)
壶为梅花形, 并有梅花形盖,盖 上塑二桃形钮。壶 流朝天,为半圆形。 梅花形矮圈足。底 心有一圆形戳记, 字模糊不清。整体 造型俊秀,小巧玲 珑。
彩绘山水注壶 (清代)
壶身似杯,有短平 流,无把。盖身、圈足 均作四瓣瓜棱形。盖顶 堆塑双桃,瓜棱腹两侧 用胭脂红、蓝、青、黄、 黑等多种色料绘山水画。 器形规整,制作讲究。 盖内及壶底均刻草书 “王伦”二字,底又印 有椭圆形款记,惜字迹 模糊,难以辨认。1959 年浙江杭州半山清乾隆 年间墓葬出土。
小升初数学专题详解 鸟头模型与等积变形超常版
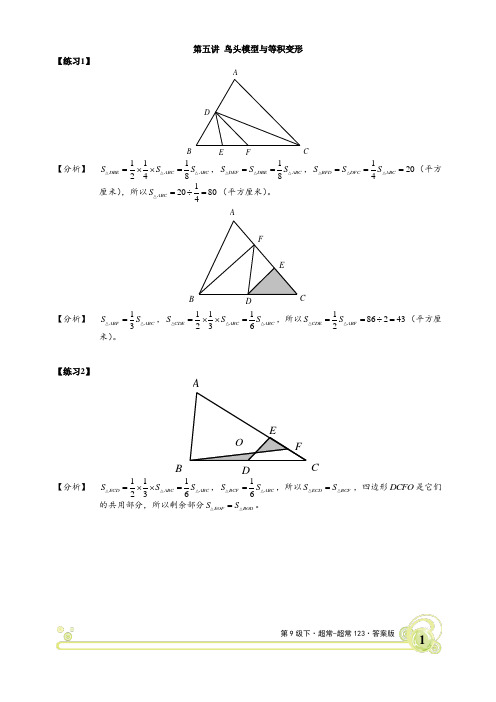
1第9级下·超常-超常123·答案版第五讲 鸟头模型与等积变形【练习1】【分析】 111248DBEABCABC SS S =⨯⨯=,18DEF DBE ABCS S S ==,1204BFDDFCABCS SS ===(平方厘米),所以120804ABCS=÷=(平方厘米)。
【分析】 13ABFABC S S =,111236CDEABCABC SS S =⨯⨯=,所以1862432CDEABFSS ==÷=(平方厘米)。
【练习2】【分析】 111236ECDABC ABC S S S =⨯⨯=,16BCF ABC S S =,所以ECDBCFS S=,四边形DCFO 是它们的共用部分,所以剩余部分EOF BOD S S =。
FAB CDE CABDABCD2第五讲学理科到学而思【练习3】【分析】 梯形总面积为2(25)4214cm +⨯÷=,21124422BCF ABCES Scm ∆==⨯⨯=, 212442ABD S cm ∆=⨯⨯=,所以阴影部分面积为214446S cm =--=。
【练习4】【分析】 连结AH ,设FGH S a ∆=。
因为AF FG =,所以AFH S a ∆=,2AGH S a ∆=。
而DG GH HE ==,所以36ADE AGH S S a ∆∆==。
5AC EC =,45AE AC =,因此47.55ADC ADE S S a ∆∆=÷=。
6BC BD =,所以596ABC ADC S S a ∆∆=÷=。
::91:9FGH ABC S S a a ∆∆==【练习5】【分析】 如右图,将小正方形折叠过去,160302CDGF DHGC S S ==⨯=(平方厘米)。
【练习6】EDBA ABDA【分析】 连结AG 、CG ,如右图所示,AF EC =,有AGFCGESS=,又因为ED BG =,有AEDABGSS=,且CDEBCGSS=由此可见:EFG ∆的三个部分中ABGS补到了EADS,AFGS补到了BCD S ∆,而AEB S ∆的位置不变,由此一来相当于将EFG ∆等积变形到了四边形ABCD ,两者面积相同,即:1EFGS =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【动手算一算】
⑴
⑵
⑴如图,BD长12厘米,DC长4厘米,B、C和D在同一条直线上。
①求三角形ABC的面积是三角形ADC面积的多少倍?
②求三角形ABD的面积是三角形ADC面积的多少倍?
⑵如图,E在AD上,AD垂直BC,AD=12厘米,DE=3厘米。
求三角形ABC的面积是三角形EBC
面积的几倍?
如图,三角形ABC的面积是40,D、E和F分别是BC、AC和AD的中点。
求:三角形DEF的面积。
等积变形(下)
(★★)
(★★★)
如图,在三角形ABC 中,BC =8厘米,高是6厘米,E 、F 分别为AB 和AC 的中点,那么三角形
EBF 的面积是多少平方厘米?
如图所示,在平行四边形ABCD 中,E 为AB 的中点,AF =2CF ,三角形AFE (图中阴影部分)的面积为10平方厘米。
平行四边形
ABCD 的面积是多少平方厘米?
如图,三角形ABC 被分成了甲、乙两部分,BD =DC =4,BE =3,AE =6
,乙部分面积是甲部分面积的几倍?
如图,三角形ABC 的面积为1,其中AE =3AB ,BD =2BC ,三角形
BDE 的面积是多少?
如图,已知三角形ABC 面积为1,延长AB 至D ,使BD =AB ;延长BC 至E ,使CE =BC ;延长CA 至F ,使AF =2AC ,求三角形DEF 的面积。
(★★★) (★★★★) (★★★) (★★★★) (★★★)
(★★★★★)
如图,D是三角形ABC一边上的中点,两个长方形分别以B、D为顶点,并且有一个公共顶点E,已
的面积是多少?
知两块阴影部分的面积分别是100和120,则三角形BDE
一、重要结论
1.结论㈠:等底等高的两个三角形面积相等
结论㈠拓展:夹在平行线间的一组同底三角形面积相等
如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD,那么S△ACD=S
△BCD Array 2.结论㈡
⑴若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面
积也是另一个三角形面积的几倍。
⑵若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面
积也是另一个三角形面积的几倍。
二、技巧方法
1.平行线的来源
⑴平行四边形(包括长方形和正方形)和梯形
⑵已知平行
⑶并排摆放的正方形的同方向对角线
2.已知做底边,等高优先找
三、经典例题
等积变形(上):例3,例5,例6,例7
等积变形(下):例2,例4,例5,例7
课后练习题
题1:如右图,已知三角形ABC的面积为9平方厘米,且BE=EF=FC,ED=2DA,求阴影部分面积。
题2:正方形ABCD和正方形CEFG,且正方形ABCD边长为10厘米,则图中阴影部分面积为多少平方厘米?
题3:如图,ABCD是平行四边形,直线CF与AB相交于E,已知三角形ADE的面积是1,求三角形BEF的面积。
题4:把三角形DEF的各边向外延长1倍后得到三角形ABC,三角形DEF的面积为1。
三角形ABC 的面积是多少?
题5:如图,梯形ABCD被它的一条对角线BD分成了两部分,三角形BDC的面积比三角形ABD的面积大10平方分米。
已知梯形的上底与下底的长度之和是15分米,它们的差是5分米。
则梯形ABCD 的面积是( )平方分米。
A:30 B:40 C:50 D:60。
