有向图的强连通分量
连通图的割点、割边(桥)、块、缩点,有向图的强连通分量

连通图的割点、割边(桥)、块、缩点,有向图的强连通分量一、基本概念无向图割点:删掉它之后(删掉所有跟它相连的边),图必然会分裂成两个或两个以上的子图。
块:没有割点的连通子图割边:删掉一条边后,图必然会分裂成两个或两个以上的子图,又称桥。
缩点:把没有割边的连通子图缩为一个点,此时满足任意两点间都有两条路径相互可达。
求块跟求缩点非常相似,很容易搞混,但本质上完全不同。
割点可以存在多个块中(假如存在k个块中),最终该点与其他点形成k个块,对无割边的连通子图进行缩点后(假设为k个),新图便变为一棵k个点由k-1条割边连接成的树,倘若其中有一条边不是割边,则它必可与其他割边形成一个环,而能继续进行缩点。
有割点的图不一定有割边,如:3是割点,分别与(1,2)和(4,5)形成两个无割点的块有割边的图也不定有割点,如:w(1,2)为割边,有向图强连通分量:有向图中任意两点相互可达的连通子图,其实也相当于无向图中的缩点二、算法无向图借助两个辅助数组dfn[],low[]进行DFS便可找到无向图的割点和割边,用一个栈st[]维护记录块和“缩点”后连通子图中所有的点。
dfn[i]表示DFS过程中到达点i的时间,low[i]表示能通过其他边回到其祖先的最早时间。
low[i]=min(low[i],dfn[son[i]])设 v,u之间有边w(v,u),从v->u:如果low[u]>=dfn[v],说明v的儿子u不能通过其他边到达v的祖先,此时如果拿掉v,则必定把v的祖先和v的儿子u,及它的子孙分开,于是v便是一个割点,v和它的子孙形成一个块。
如果low[u]>dfn[v]时,则说明u不仅不能到达v的祖先,连v也不能通过另外一条边直接到达,从而它们之间的边w(v,u)便是割边,求割边的时候有一个重边的问题要视情况处理,如果v,u之间有两条无向边,需要仍视为割边的话,则在DFS的时候加一个变量记录它的父亲,下一步遇到父结点时不扩展回去,从而第二条无向重边不会被遍历而导致low[u]==dfn[v] ,而在另外一些问题中,比如电线连接两台设备A,B 如果它们之间有两根电线,则应该视为是双连通的,因为任何一条电线出问题都不会破坏A和B之间的连通性,这个时候,我们可以用一个used[]数组标记边的id,DFS时会把一条无向边拆成两条有向边进行遍历,但我们给它们俩同一个id号,在开始遍历v->u前检查它的id是否在上一次u->v 时被标记,这样如果两点之间有多条边时,每次遍历都只标记其中一条,还可以通过其他边回去,形成第二条新的路求割点的时候,维护一个栈st 每遍历到一个顶点v则把它放进去,对它的子孙u如果dfn[u]为0,则表示还没有遍历到则先DFS(u),之后再判断low[u]和dfn[v],如果low[u]>=dfn[v],则把栈中从栈顶到v这一系列元素弹出,这些点与v 形成一个块,如果u的子孙x也是一个割点,这样做会不会错把它们和v,u放在一起形成一个块呢,这种情况是不会发生的,如果发现x是一个割点,则DFS 到x那一步后栈早就把属于x的子孙弹出来了,而只剩下v,u的子孙,它们之间不存在割点,否则在回溯到v之前也早就提前出栈了!画一个图照着代码模拟一下可以方便理解。
Kosaraju算法

求有向图的强连通分量的经典算法——Kosaraju算法一、Kosaraju算法步骤:Step1、对有向图G做dfs(深度优先遍历),记录每个结点结束访问的时间Step2、将图G逆置,即将G中所有弧反向。
Step3、按Step1中记录的结点结束访问时间从大到小对逆置后的图做dfs Step4、得到的遍历森林中每棵树对应一个强连通分量。
相关概念:在dfs(bfs)算法中,一个结点的开始访问时间指的是遍历时首次遇到该结点的时间,而该结点的结束访问时间则指的是将其所有邻接结点均访问完的时间。
二、Kosaraju算法求解过程实例下面结合实例说明Kosaraju算法的基本策略。
图1给出了一个有向图G。
图1 有向图GStep1:假设从DFS在遍历时按照字母顺序进行,根据Kosaraju算法,在步骤1中我们得到的遍历顺序可以表达为[A,[C,[B,[D,D],B],C],A][E,[F,[G,[H,H],G],F],E]在遍历序列中每一个结点出现了两次,其中第一次出现的时间为该结点的开始访问时间,第二次出现的时间为该结点的结束访问时间。
Step2:根据算法第2步,将图G逆置,得到对应的反向图G’如图2所示。
Step3:根据步骤1得到的遍历序列,按照结点结束访问时间递减排序后的结果为EFGHACBD下面,按照该结点序列顺序对逆置图G ’所深度优先遍历,得到的深度优先遍历森林如图3所示。
森林中共有4棵树,其中(a)和(d)只有一个结点,这里认为单结点也是一个强联通分量(在实际应用中可以根据实际需要将这种情况过滤掉)。
三、算法讨论问题1:以上图为例,第一遍搜索得到以A 为根的子序列(设为S1)和以E 为根的子树序列(设为S2),图反向后,再从E 开始搜索,能搜到的元素肯定不会包含S1的元素,为什么?答:因为S1中的点都不能到达E ,而第二遍搜索就是看哪些点能到达E ,所以搜不到S1中的点。
问题2:图反向后对A 进行深搜,尽管E 能到达A ,为什么搜不到E ?因为第一遍深搜时,A 不能达到E ,所以E 肯定位于A 的右边,而第二遍深搜是按照结束时间进行搜索的,在搜索A 之前,已经搜完E ,对E 设置了已经遍历标志,所以不会把E 并入A 的强联通分量。
强连通分量(超详细!!!)

强连通分量(超详细)⼀、定义在有向图G中,如果两个顶点u,v间有⼀条从u到v的有向路径,同时还有⼀条从v到u的有向路径,则称两个顶点强连通。
如果有向图G的每两个顶点都强连通,称G是⼀个强连通图。
有向⾮强连通图的极⼤强连通⼦图,称为强连通分量。
图中,⼦图{1,2,3,4}为⼀个强连通分量,因为顶点1,2,3,4两两可达。
{5},{6}也分别是两个强连通分量。
⼆、tarjan算法时间复杂度是O(N+M)四条边:树枝边:DFS时经过的边,即DFS搜索树上的边。
前向边:与DFS⽅向⼀致,从某个结点指向其某个⼦孙的边。
后向边:与DFS⽅向相反,从某个结点指向其某个祖先的边。
(返祖边)横叉边:从某个结点指向搜索树中的另⼀⼦树中的某结点的边。
Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的⼀棵⼦树。
搜索时,把当前搜索树中未处理的节点加⼊⼀个堆栈,回溯时可以判断栈顶到栈中的节点是否为⼀个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的⼦树能够追溯到的最早的栈中节点的次序号。
由定义可以得出,Low(u)=Min {Low(u), Low(v) } (u,v)为树枝边,u为v的⽗节点 . Low(u)=Min {Low(u), DFN(v) } DFN(v),(u,v)为指向栈中节点的后向边(指向栈中结点的横叉边) }当结点u搜索结束后,若DFN(u)=Low(u)时,则以u为根的搜索⼦树上所有还在栈中的节点是⼀个强连通分量。
算法过程:从节点1开始DFS,把遍历到的节点加⼊栈中。
搜索到节点u=6时,DFN[6]=LOW[6],找到了⼀个强连通分量。
退栈到u=v为⽌,{6}为⼀个强连通分量。
初始化时Low[u]=DFN[u]=++index返回节点5,发现DFN[5]=LOW[5],退栈后{5}为⼀个强连通分量。
返回节点3,继续搜索到节点4,把4加⼊堆栈。
发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。
强连通算法--Tarjan个人理解+详解

强连通算法--Tarjan个⼈理解+详解⾸先我们引⼊定义:1、有向图G中,以顶点v为起点的弧的数⽬称为v的出度,记做deg+(v);以顶点v为终点的弧的数⽬称为v的⼊度,记做deg-(v)。
2、如果在有向图G中,有⼀条<u,v>有向道路,则v称为u可达的,或者说,从u可达v。
3、如果有向图G的任意两个顶点都互相可达,则称图 G是强连通图,如果有向图G存在两顶点u和v使得u不能到v,或者v不能到u,则称图G 是强⾮连通图。
4、如果有向图G不是强连通图,他的⼦图G2是强连通图,点v属于G2,任意包含v的强连通⼦图也是G2的⼦图,则乘G2是有向图G的极⼤强连通⼦图,也称强连通分量。
5、什么是强连通?强连通其实就是指图中有两点u,v。
使得能够找到有向路径从u到v并且也能够找到有向路径从v到u,则称u,v是强连通的。
然后我们理解定义:既然我们现在已经了解了什么是强连通,和什么是强连通分量,可能⼤家对于定义还是理解的不透彻,我们不妨引⼊⼀个图加强⼤家对强连通分量和强连通的理解:标注棕⾊线条框框的三个部分就分别是⼀个强连通分量,也就是说,这个图中的强连通分量有3个。
其中我们分析最左边三个点的这部分:其中1能够到达0,0也能够通过经过2的路径到达1.1和0就是强连通的。
其中1能够通过0到达2,2也能够到达1,那么1和2就是强连通的。
.........同理,我们能够看得出来这⼀部分确实是强连通分量,也就是说,强连通分量⾥边的任意两个点,都是互相可达的。
那么如何求强连通分量的个数呢?另外强连通算法能够实现什么⼀些基本操作呢?我们继续详解、接着我们开始接触算法,讨论如何⽤Tarjan算法求强连通分量个数:Tarjan算法,是⼀个基于Dfs的算法(如果⼤家还不知道什么是Dfs,⾃⾏百度学习),假设我们要先从0号节点开始Dfs,我们发现⼀次Dfs 我萌就能遍历整个图(树),⽽且我们发现,在Dfs的过程中,我们深搜到了其他强连通分量中,那么俺们Dfs之后如何判断他喵的哪个和那些节点属于⼀个强连通分量呢?我们⾸先引⼊两个数组:①dfn【】②low【】第⼀个数组dfn我们⽤来标记当前节点在深搜过程中是第⼏个遍历到的点。
求有向图的强连通分量个数(kosaraju算法)

求有向图的强连通分量个数(kosaraju算法)求有向图的强连通分量个数(kosaraju算法)1. 定义连通分量:在⽆向图中,即为连通⼦图。
上图中,总共有四个连通分量。
顶点A、B、C、D构成了⼀个连通分量,顶点E构成了⼀个连通分量,顶点F,G和H,I分别构成了两个连通分量。
强连通分量:有向图中,尽可能多的若⼲顶点组成的⼦图中,这些顶点都是相互可到达的,则这些顶点成为⼀个强连通分量。
上图中有三个强连通分量,分别是a、b、e以及f、g和c、d、h。
2. 连通分量的求解⽅法对于⼀个⽆向图的连通分量,从连通分量的任意⼀个顶点开始,进⾏⼀次DFS,⼀定能遍历这个连通分量的所有顶点。
所以,整个图的连通分量数应该等价于遍历整个图进⾏了⼏次(最外层的)DFS。
⼀次DFS中遍历的所有顶点属于同⼀个连通分量。
下⾯我们将介绍有向图的强连通分量的求解⽅法。
3. Kosaraju算法的基本原理我们⽤⼀个最简单的例⼦讲解Kosaraju算法显然上图中有两个强连通分量,即强连通分量A和强连通分量B,分别由顶点A0-A1-A2和顶点B3-B4-B5构成。
每个连通分量中有若⼲个可以相互访问的顶点(这⾥都是3个),强连通分量与强连通分量之间不会形成环,否则应该将这些连通分量看成⼀个整体,即看成同⼀个强连通分量。
我们现在试想能否按照⽆向图中求连通分量的思路求解有向图的强连通分量。
我们假设,DFS从强连通分量B的任意⼀个顶点开始,那么恰好遍历整个图需要2次DFS,和连通分量的数量相等,⽽且每次DFS遍历的顶点恰好属于同⼀个连通分量。
但是,我们若从连通分量A中任意⼀个顶点开始DFS,就不能得到正确的结果,因为此时我们只需要⼀次DFS就访问了所有的顶点。
所以,我们不应该按照顶点编号的⾃然顺序(0,1,2,……)或者任意其它顺序进⾏DFS,⽽是应该按照被指向的强连通分量的顶点排在前⾯的顺序进⾏DFS。
上图中由强连通分量A指向了强连通分量B。
强连通分量与模拟链表

强联通分量与模拟链表作者:逸水之寒1.强连通分量强连通分量的定义是:在有向图中,u可以到达v,但是v不一定能到达u,如果u,v 到达,则他们就属于一个强连通分量。
求强连通分量最长用的方法就是Kosaraju算法,比较容易理解而且效率很高,本文对强连通分量的求法均采用Kosaraju算法。
其主要思想:首先对原图G进行深搜形成森林(树),然后选择一棵树进行第二次深搜,注意第一次是要判断节点A能不能通向节点B,而第二次要判断的是节点B能不能通向A,能遍历到的就是一个强连通分量。
(附录给出伪代码)Kosaraju算法如果采用了合适的数据结构,它的时间复杂度是O(n)的。
相关题目有很多,例如USACO 5.3.3,2009NOIP Senior No.3。
下面将以USACO 5.3.3 schlnet 举例说明。
Preblem 1. Network of Schools (USACO 5.3.3 schlnet\IOI96 No.3)A number of schools are connected to a computer network. Agreements have been developed among those schools: each school maintains a list of schools to which it distributes software (the "receiving schools"). Note that ifB is in the distribution list of school A, then A does not necessarily appear in the list of school B.You are to write a program that computes the minimal number of schools that must receive a copy of the new software in order for the software to reach all schools in the network according to the agreement (Subtask A). As a further task, we want to ensure that by sending the copy of new software to an arbitrary school, this software will reach all schools in the network. To achieve this goal we may have to extend the lists of receivers by new members. Compute the minimal number of extensions that have to be made so that whatever school we send the new software to, it will reach all other schools (Subtask B). One extension means introducing one new member into the list of receivers of one school.INPUT FORMATThe first line of the input file contains an integer N: the number of schools in the network (2<=N<=100). The schools are identified by the first N positive integers. Each of the next N lines describes a list of receivers. The line i+1 contains the identifiers of the receivers of school i. Each list ends with a 0. An empty list contains a 0 alone in the line.SAMPLE INPUT (file schlnet.in)52 43 04 5 01 0OUTPUT FORMATYour program should write two lines to the output file. The first line should contain one positive integer: the solution of subtask A. The second line should contain the solution of subtask B.SAMPLE OUTPUT (file schlnet.out)12分析:本题需要将强连通分量进行缩点,具体做法可以先求出所有的强连通分量,然后重新建立图,将一个强连通分量用一个点在新图中表示出来。
数据结构第7章-答案

一、单选题C01、在一个图中,所有顶点的度数之和等于图的边数的倍。
A)1/2 B)1 C)2 D)4B02、在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A)1/2 B)1 C)2 D)4B03、有8个结点的无向图最多有条边。
A)14 B)28 C)56 D)112C04、有8个结点的无向连通图最少有条边。
A)5 B)6 C)7 D)8C05、有8个结点的有向完全图有条边。
A)14 B)28 C)56 D)112B06、用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A07、用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A)栈 B)队列 C)树 D)图A08、一个含n个顶点和e条弧的有向图以邻接矩阵表示法为存储结构,则计算该有向图中某个顶点出度的时间复杂度为。
A)O(n) B)O(e) C)O(n+e) D)O(n2)C09、已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是。
A)0 2 4 3 1 5 6 B)0 1 3 6 5 4 2 C)0 1 3 4 2 5 6 D)0 3 6 1 5 4 2B10、已知图的邻接矩阵同上题,根据算法,则从顶点0出发,按广度优先遍历的结点序列是。
A)0 2 4 3 6 5 1 B)0 1 2 3 4 6 5 C)0 4 2 3 1 5 6 D)0 1 3 4 2 5 6D11、已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是。
A)0 1 3 2 B)0 2 3 1 C)0 3 2 1 D)0 1 2 3A12、已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是。
A)0 3 2 1 B)0 1 2 3 C)0 1 3 2 D)0 3 1 2A13、图的深度优先遍历类似于二叉树的。
A)先序遍历 B)中序遍历 C)后序遍历 D)层次遍历D14、图的广度优先遍历类似于二叉树的。
数据结构第7章复习题

ab edcf第七章图一、选择题1.图中有关路径的定义是()。
A.由顶点和相邻顶点序偶构成的边所形成的序列 B.由不同顶点所形成的序列C.由不同边所形成的序列 D.上述定义都不是2.设无向图的顶点个数为n,则该图最多有()条边。
A.n-1 B.n(n-1)/2 C. n(n+1)/2 D.0 E.n23.一个n个顶点的连通无向图,其边的个数至少为()。
A.n-1 B.n C.n+1 D.nlogn;4.n个结点的完全有向图含有边的数目()。
A.n*n B.n(n+1) C.n/2 D.n*(n-l)5.在一个无向图中,所有顶点的度数之和等于所有边数()倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的()倍。
A.1/2 B.2 C.1 D.46.下面结构中最适于表示稀疏无向图的是(),适于表示稀疏有向图的是()。
A.邻接矩阵 B.逆邻接表 C.邻接多重表 D.十字链表 E.邻接表7.下列哪一种图的邻接矩阵是对称矩阵?()A.有向图 B.无向图 C.AOV网 D.AOE网8. 设如左图所示,在下面的5个序列中,符合深度优先遍历的序列有多少?()a eb d fc a c fde b a e df c b a e fd c b aef d b cA.5个 B.4个 C.3个 D.2个9.下面哪一方法可以判断出一个有向图是否有环(回路):A.深度优先遍历 B. 拓扑排序 C. 求最短路径 D. 求关键路径10. 下面是求连通网的最小生成树的prim算法:集合VT,ET分别放顶点和边,初始为( 1 ),下面步骤重复n-1次: a:( 2 );b:( 3 );最后:( 4 )。
(1).A.VT,ET为空 B.VT为所有顶点,ET为空C.VT为网中任意一点,ET为空 D.VT为空,ET为网中所有边(2).A. 选i属于VT,j不属于VT,且(i,j)上的权最小B.选i属于VT,j不属于VT,且(i,j)上的权最大C.选i不属于VT,j不属于VT,且(i,j)上的权最小D.选i不属于VT,j不属于VT,且(i,j)上的权最大(3).A.顶点i加入VT,(i,j)加入ET B. 顶点j加入VT,(i,j)加入ET C. 顶点j加入VT,(i,j)从ET中删去 D.顶点i,j加入VT,(i,j)加入ET(4).A.ET 中为最小生成树 B.不在ET中的边构成最小生成树 C.ET中有n-1条边时为生成树,否则无解 D.ET中无回路时,为生成树,否则无解11. (1). 求从指定源点到其余各顶点的迪杰斯特拉(Dijkstra)最短路径算法中弧上权不能为负的原因是在实际应用中无意义;(2). 利用Dijkstra求每一对不同顶点之间的最短路径的算法时间是O(n3) ;(图用邻接矩阵表示)(3). Floyd求每对不同顶点对的算法中允许弧上的权为负,但不能有权和为负的回路。
有向图的强连通分量及应用

图G T ) ,能遍历 到的顶点就是一个强连通分量。余 下部分和原来 顶弹出 ,所以,得到 出栈 的顶点序列为 v 2 , v 4 , v 3 , v 1 ;再从最后
的森林一起组成一个新的森林 ,继 续步骤 2 直 到没有顶点为止 。 具体求解步骤如下: 其所有邻接 点的访 问都完成 ( 即出栈)的顺序将顶 点排列起来 。
代码为 :
v o i d r ed f s ( mt x 1
_
w h i l e ( e > 0 &&e l f a g [ e ] —= o 1 {
i n t k _ b [ e ] ;
i f ( ! l f a g [ k ] ) d f § ( k ) ; e - n e x t [ e ] ;
1 K o s a r a j u 算法
形成 的 D F S 树森林 嘲。
Ko s a r a j u算 法基于 以下 思想:强连 通分量 一 定是某种 D F S 弹 出,并进入栈 s t a c k 1 ,如图 ( b ) 所示 。 将v 2 从栈顶弹出后,再 这 个算法可 以说是最容 易理解 ,最通 用的算法 ,其 比较关 邻接点 从而从系统栈 弹出,并进入栈 s t a c k l ,如 图 ( c ) 所示 。将 键 的部分是 同时应 用 了原 图 G和反 图 G T 嘲。步骤 1 :先对 原 图 v 4 从栈顶弹 出后 ,顶点 v 3不存在未访 问的邻接点从而从系统栈
图( e ) 所示。这 就是该有向图的两个强连通分量的顶点集 。
பைடு நூலகம்
{ l f a g [ x 】 = 1 ;
i n t e = p [ x 】 ;
( 啦 一个有商翻
∞ 将 肚糟璜弹出
强连通分量的定义

强连通分量的定义
强连通分量是图论中的一个概念,指的是在有向图中,若任意两个顶点都存在一条有向路径,则这个有向图就是强连通的。
而强连通分量则指的是有向图中的极大强连通子图,即在该子图中任意两个顶点都是强连通的,并且该子图不能再加入其他的顶点或边使其仍然保持强连通。
在实际应用中,强连通分量有着广泛的应用。
比如在电路设计中,可以将电路看作一个有向图,每个元件看作一个顶点,元件之间的电线则看作一条有向边。
那么在这个电路中,如果存在一个强连通分量,则说明这些元件可以构成一个独立的电路模块,可以方便地进行测试和维护。
此外,在社交网络分析、路网规划等领域,强连通分量也有着重要的应用。
在实际应用中,我们可以通过深度优先搜索(DFS)或者Tarjan算法来求解一个有向图的强连通分量。
具体来说,DFS 算法可以通过遍历有向图来寻找所有的强连通分量;而Tarjan 算法则是一种更高效的算法,可以在O(V+E)的时间复杂度内求解一个有向图的所有强连通分量。
总之,强连通分量是图论中一个重要的概念,在实际应用中有着广泛的应用。
通过深入学习和理解这个概念,我们可以更好地应用它来解决实际问题。
图论常见模型与分析

例题分析
先求传递闭包 对于边(u,v),若存在一点k,使得uk且
kv,则边(u,v)是不必要的 易得一个O(n^3)的算法
证明?
23
Stack.push(u)
// 将节点u压入栈中
for each (u, v) in E
// 枚举每一条边
if (v is not visted) // 如果节点v未被访问过(树边)
tarjan(v)
// 继续向下找
Low[u] = min(Low[u], Low[v])
else if (v in S)
有向图G’,使G和G’的传递闭包相同。 图的传递闭包是指,若存在边AB, BC,
则必存在边AC N <= 100, M <= 10000
20
例题分析
Input 33 12 23 13 Output 2
Input 46 12 21 23 32 34 43 Output 4
21
例题分析
求强连通分量,缩点…… 在同一强连通分量内部,最少需要几条边? 不同分量之间的边,有哪一种是不必要的?
强连通分量相关
概念:有向图的强连通分量(SCC)是指,对 于强连通分量里面的任意两个点u,v,都存 在从u到v的路和从v到u的路
算法:复杂度均为O(V+E)
Kosaraju (两次dfs) Tarjan / Gabow (一次dfs)
1
Tarjan
对图进行DFS,每个SCC都是DFS树的一个子树。 在搜索时用堆栈维护当前正在处理的结点,栈顶 的若干元素即组成一个SCC。
18
例题分析
最终解法:
对原图求SCC并缩点,设新点i中最高价格点 为H[i],最低价格点为L[i]。在新的DAG图上 有DP:
图论_连通_连通分量

图论_连通_连通分量 强连通图 : 强连通分量就是本⾝ 有向图 ---> ⾮强连通图 : 多个强连通分量图---> 连通图 : 连通分量就是本⾝ ⽆向图 ---> ⾮连通图 : 多个连通分量路径 : 顾名思义.路径长度 : 路径上边的数量.路径 : 顾名思义.路径长度 : 路径上边的数量.连通 : ⽆向图顶点A可以到顶点B,则称A,B连通.强连通 : 有向图中,两个顶点间⾄少存在⼀条互相可达路径,则两个顶点强连通连通图 : 图中任意两点都连通的图.强连通图 : 有向图的任意两点都强连通.连通分量 : ⽆向图的极⼤连通⼦图称为连通分量.连通图只有⼀个连通分量,即⾃⾝强连通分量: 强连通图有向图的极⼤强连通⼦图.强连通图的强连通分量只有⼀个,即强连通图本⾝.基图 : 将有向图的所有边替换成⽆向边形成的图.弱连通图 : 基图是连通图的有向图.(即,连通的有向图)求图的连通分量的⽬的,是为了确定从图中的⼀个顶点是否能到达图中的另⼀个顶点,也就是说,图中任意两个顶点之间是否有路径可达。
求强连通分量有多种算法.我⽤的Tarjan算法. 复杂度O(V+E)这两个博客写得不错:https:///reddest/p/5932153.htmlhttps:///shadowland/p/5872257.htmlint dfn[16]; // 时间戳int dfn_num = 0; // 时间int low[16]; // 节点u所能访问到的最⼩时间戳int inSt[16]; // 节点u是否在栈中.int st[16];int top = 0;// 我们维护的信息.int col[16]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[16]; // 每个颜⾊值所拥有的块数./*第⼀步: 访问当前节点的所有⼦节点: ⼦节点有三种第⼀种: 未访问过的, 我们对它进⾏访问, 同时设置它的时间戳dfn[u]和low[u]为++ndfn_num,以及进栈.第⼆种: 访问过的,并且在栈中,我们直接更新我们当前节点的low[] --> 注意应该⽤low[u] 和 dfn[v]⽐较.第三种: 访问过的,并且不在栈中的, 我们直接跳过.因为这个时候,所以它已经染⾊了,属于⼀个连通块了.第⼆步: 如果dfn[u] == low[u] 说明已经找到⼀个连通块了.这时候我们要将栈顶元素弹出,直到当前节点. 记得也要修改inSt, 同时维护我们需要的信息.*/void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;} while (st[top--] != u);}}View Code加上2个板⼦题./problem/1332/题⽬很简单: 要你求出最⼤的强连通块,如果有多个则输出字典序最⼩的⼀个.#include <cstdio>#include <cstring>#include <algorithm>using namespace std;const int maxn = 5e4+500;struct Edge {int lst;int to;}edge[maxn<<1];int head[maxn];int qsz = 1;inline void add(int u, int v) {edge[qsz].lst = head[u];edge[qsz].to = v;head[u] = qsz++;}int dfn[maxn]; // 时间戳int dfn_num = 0; // 时间int low[maxn]; // 节点u所能访问到的最⼩时间戳int inSt[maxn]; // 节点u是否在栈中.int st[maxn];int top = 0;// 我们维护的信息.int col[maxn]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[maxn]; // 每个颜⾊值所拥有的块数.int id[maxn];void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;id[col_num] = u;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;id[col_num] = min(id[col_num], st[top]);} while (st[top--] != u);}}int main(){memset(id, 0x3f, sizeof(id));int n, i, u, v, m, t;scanf("%d%d", &n, &m);for (i=1; i<=m; ++i) {scanf("%d%d%d", &u, &v, &t);add(u, v);if (t==2) add(v, u);}for (i=1; i<=n; ++i)if (!dfn[i]) Tarjan(i);int mm = 0, tcol = -1;for (i=1; i<=col_num; ++i)if (mm < size[i]) {mm = size[i];tcol = i;} else if (m == size[i]) {if (id[tcol] > id[i])tcol = i;}// printf("%d \n", tcol);printf("%d\n", mm);for (i=1; i<=n; ++i)if (col[i] == tcol) printf("%d ", i);printf("\n");return0;}View Codehttps:///problem/HYSBZ-1051题⽬: 求出所有⽜都欢迎的⽜的个数. 我们可以把所有连通块求出,然后把⼀个连通块看成⼀个点,即缩点. 然后找到出度为零的点(连通块), 如果有且只有⼀个,那么连通块的点数就是答案,否则答案为零.#include <cstdio>#include <algorithm>using namespace std;struct Edge {int lst;int to;}edge[50500];int head[10100];int qsz = 1;inline void add(int u, int v) {edge[qsz].lst = head[u];edge[qsz].to = v;head[u] = qsz++;}int dfn[10100]; // 时间戳int dfn_num = 0; // 时间int low[10100]; // 节点u所能访问到的最⼩时间戳int inSt[10100]; // 节点u是否在栈中.int st[10100];int top = 0;// 我们维护的信息.int col[10100]; // 给节点染⾊, 同⼀个连通块的节点应该是同⼀个颜⾊的.int col_num = 0; // 颜⾊值.int size[10100]; // 每个颜⾊值所拥有的块数./*第⼀步: 访问当前节点的所有⼦节点: ⼦节点有三种第⼀种: 未访问过的, 我们对它进⾏访问, 同时设置它的时间戳dfn[u]和low[u]为++ndfn_num,以及进栈.第⼆种: 访问过的,并且在栈中,我们直接更新我们当前节点的low[] --> 注意应该⽤low[u] 和 dfn[v]⽐较. 第三种: 访问过的,并且不在栈中的, 我们直接跳过.因为这个时候,所以它已经染⾊了,属于⼀个连通块了. 第⼆步: 如果dfn[u] == low[u] 说明已经找到⼀个连通块了.这时候我们要将栈顶元素弹出,直到当前节点. 记得也要修改inSt, 同时维护我们需要的信息.*/void Tarjan(int u) {int v, i;dfn[u] = low[u] = ++dfn_num; //添加时间戳.st[++top] = u; // 进栈inSt[u] = true; // 标⽰在栈for (i=head[u]; i; i=edge[i].lst) {v = edge[i].to;if (!dfn[v]) {Tarjan(v);low[u] = min(low[u], low[v]);} else if (inSt[v]) {low[u] = min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {col_num++;do {inSt[st[top]] = false;col[st[top]] = col_num;size[col_num]++;} while (st[top--] != u);}}bool ou[10010];int main(){// freopen("E:\\input.txt", "r", stdin);int n, i, j, u, v, m;scanf("%d%d", &n, &m);for (i=1; i<=m; ++i) {scanf("%d%d", &u, &v);add(u, v);}for (i=1; i<=n; ++i)if (!dfn[i])Tarjan(i);// 缩点操作int cnt = 0, res = 0;for (i=1; i<=n; ++i) {if (ou[col[i]]) continue;for (j=head[i]; j; j=edge[j].lst) {v = edge[j].to;if (col[i] != col[v]) {ou[col[i]] = true;break;}}}for (i=1; i<=col_num; ++i) {if (!ou[i]) {res = size[i];cnt++;}if (cnt > 1) {res = 0;break;}}printf("%d\n", res);return0;}View Code。
(精选)北大PKU 慕课 EDX 数据结构与算法 第八章图 quiz答案与解析

第八章图PROBLEM 1(1/1 分)下图中的强连通分量的个数为多少个?How many strongly connected graphs in the under graph?33 - 正确33Explanation有向图强连通的极大子图称为该有向图的强连通分支或者强连通分量。
分别为最左边1个点组成的极大子图,中间4个点组成的极大子图和最右边1个点组成的极大子图。
分别为最左边1个点,中间4个点和最右边1个点。
Maximal strongly connected subgraphs of a directed graph are called strongly connected components of this directed graph.They are the subgraph consist of the left-most vertex, the subgraph consist of 4 vertices in the middle, ,and the subgraph consist of the right-most vertex respectively.PROBLEM 2(1/1 分)下面关于图的说法正确的有 (多选)The right statements of graphs in the following are: (There are more than one correct answers)对于无向图,所有结点的度数加起来一定是偶数。
As for undirected graphs, the sum of degrees of all vertices is definitely even number., 将有向图的一个强连通分量中的边全部反向仍然是强连通分量。
Reversion all the edges of a strongly connected component of a directed graph, then the subgraph is still a strongly connected component., - 正确对于无向图,所有结点的度数加起来一定是偶数。
强连通分量

强连通分量【引言】本文讲述了求强连通分量的T arjan算法的思想以及一般过程,鉴于T arjan算法比较抽象,很多人明白怎么做但不理解为什么,所以本文以作者对T arjan算法的理解为主,供读者参考。
【正文】一、强连通分量的概念及性质。
概念:对于一个有向图G,存在点集P使得P中任意两点可以互相到达,则称P为一个强连通分量。
性质:如果对于一个点v,在v可以到达的点中,可以回到v的点和v一定属于同一个强连通分量;不可以回到v的点和v一定不属于一个强连通分量。
二、T arjan思想1.初步思想:利用搜索算法找到点v可以到达的所有点,再判断这些点中哪些可以回到v,并对符合条件的点进行染色,染成同色的点组成一个强连通分量。
2.深搜性质的利用:首先对点来做一些定义:白色点:表示该点还没有被访问过。
灰色点:表示正在处理该点发出的边,还没处理完。
黑色点:表示该点发出的所有边都处理完了。
深搜序:表示所有点由白变灰的顺序。
附属点:某点v从刚刚变成灰色到刚刚变成黑色这段时间内访问并处理过的所有点(不包括那些在v之前变灰或变黑的点,那些点在这段时间内只访问但没处理)性质1:从开始处理点v到处理完点v,所有的附属点都从白变黑。
性质2:在开始处理点v之前的那个时刻,所有的灰色点都可以到达点v,称这些灰色点为祖先点,并且这些祖先点构成一条链。
性质3:对于性质2所述的那些灰色点,在深搜序中靠前的点一定可以到达靠后的点。
这些性质有助于理解后面的思想。
3.引入进一步思想:首先是想法:对于当前点v,和它在同一个强连通分量里的点一定可以到达它。
这些点可以分为两部分:(1)性质2中那些灰色的点(祖先点) (2)其他可以到达v的点对于(2)那部分点,又可以分为两部分:和v在同一个强连通分量里的:这部分点将会变成v的附属点,所以不必考虑。
不和v在同一个强连通分量里的:这部分点显然不在考虑范畴内,但一会儿要用到。
所以,我们只需要考虑性质2中的祖先点!!!也就是说,v的附属点中,可以直接或间接到达那些祖先点的点,和v一定属于同一个强连通分量(通俗点说,就是v可以到它,它可以到 v的祖先,v的祖先又可以到v)。
Tarjan算法
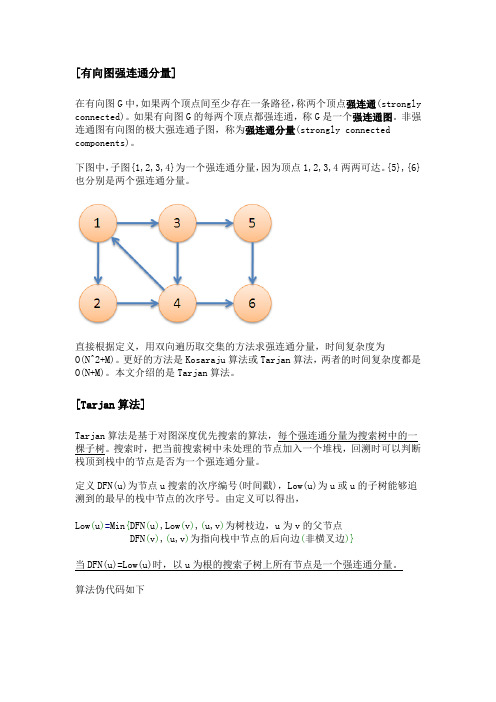
[有向图强连通分量]在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(strongly connected)。
如果有向图G的每两个顶点都强连通,称G是一个强连通图。
非强连通图有向图的极大强连通子图,称为强连通分量(strongly connected components)。
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达。
{5},{6}也分别是两个强连通分量。
直接根据定义,用双向遍历取交集的方法求强连通分量,时间复杂度为O(N^2+M)。
更好的方法是Kosaraju算法或Tarjan算法,两者的时间复杂度都是O(N+M)。
本文介绍的是Tarjan算法。
[Tarjan算法]Tarjan算法是基于对图深度优先搜索的算法,每个强连通分量为搜索树中的一棵子树。
搜索时,把当前搜索树中未处理的节点加入一个堆栈,回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。
定义DFN(u)为节点u搜索的次序编号(时间戳),Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。
由定义可以得出,Low(u)=Min{DFN(u),Low(v),(u,v)为树枝边,u为v的父节点DFN(v),(u,v)为指向栈中节点的后向边(非横叉边)}当DFN(u)=Low(u)时,以u为根的搜索子树上所有节点是一个强连通分量。
算法伪代码如下tarjan(u){DFN[u]=Low[u]=++Index // 为节点u设定次序编号和Low初值Stack.push(u)// 将节点u压入栈中for each (u, v) in E // 枚举每一条边if(v is not visted)// 如果节点v未被访问过tarjan(v)// 继续向下找Low[u]= min(Low[u], Low[v])else if(v in S)// 如果节点u还在栈内Low[u]= min(Low[u], DFN[v])if(DFN[u]== Low[u])// 如果节点u是强连通分量的根repeatv = S.pop// 将v退栈,为该强连通分量中一个顶点print vuntil (u== v)}接下来是对算法流程的演示。
2-sat问题的tarjan算法

2-sat问题是一种布尔可满足性问题,即判断一个由布尔变量和它们的逻辑运算构成的合取范式是否存在可满足的赋值。
在计算机科学和逻辑学中,2-sat问题具有重要的理论和实际意义。
为了解决2-sat问题,人们提出了许多有效的算法,其中tarjan算法是一种经典且高效的解决方法。
1. tarjan算法的概述tarjan算法是由美国的计算机科学家Robert Tarjan在1972年提出的,它主要用于解决有向图中的强连通分量问题。
在2-sat问题中,可以将布尔变量和它们的逻辑运算构成的合取范式转化为一个有向图。
然后利用tarjan算法来求解图中的强连通分量,从而判断2-sat问题是否可满足。
2. tarjan算法的原理tarjan算法的核心是利用深度优先搜索(DFS)来遍历图中的节点,并且通过维护一个栈来记录搜索路径上的节点。
在DFS的过程中,通过比较节点的深度和搜索路径上的节点的深度来判断是否存在环路,从而找到强连通分量。
利用tarjan算法求解2-sat问题的关键在于将逻辑运算转化为有向图,同时构建出正确的搜索路径和深度信息,以便进行强连通分量的判断。
3. tarjan算法的优势与其他算法相比,tarjan算法具有许多优势。
tarjan算法的时间复杂度为O(V+E),其中V为图中的节点数,E为图中的边数。
这意味着即使在大规模的图中,tarjan算法也能够在合理的时间内得到结果。
tarjan算法的实现相对比较简单,只需要进行一次DFS遍历和一些基本的数据结构操作即可完成。
另外,tarjan算法的结果也比较容易理解和解释,对于2-sat问题的求解具有很好的可解释性。
4. tarjan算法的应用由于tarjan算法在解决2-sat问题中具有较高的效率和可靠性,因此它在实际的计算机科学和工程领域得到了广泛的应用。
在编译原理中,可以利用tarjan算法进行程序的静态分析和优化;在人工智能和图像处理中,可以利用tarjan算法对逻辑规则进行推理和推导;在电路设计和布线规划中,也可以利用tarjan算法对逻辑电路进行布线和优化。
连通分量——精选推荐

连通分量图论连通分量0.1 概述图论中,或者説OI中研究的连通分量主要有三种:强连通分量、点双连通分量、边双连通分量。
本⽂并不打算着重讲述tarjan算法的具体实现,默认读者已掌据此前置知识。
1.1 强连通分量强连通分量是指:在有向图中,强连通分量中的任意两点(u,v),存在u→v和v→u的两条不同路径。
极⼤强连通分量:⽆法继续扩张的强连通分量。
在通常语境下,⼀般默认“强连通分量”指的就是"极⼤强连通分量"算法实现:tarjan算法可以做到O(n)效率地求解。
1.2 例题:[USACO15JAN]草鉴定Grass Cownoisseur可以发现,将图缩点染⾊后,⼀个分量内的点之间可以任意到达。
即:答案的最⼩值等于1号草场所处分量的⼤⼩。
在已经缩点后的图上计算由1号草场所在分量向其余分量求最长路dis1,再求由其余分量向1号草场所在分量的最长路dis2(建反边)对于原图上存在的⼀条边u→v,如果这两个点同处⼀个连通分量上,在这条边上逆⾏⼀次是没有任何意义的;但是如果这两个点并不在⼀个连能分量上,那么可以:先⾛到v所在的分量dis1[v分量],再逆⾏回到u分量,然后回到1号草场分量dis2[u分量],最后逛完1号分量siz[1号分量]。
因此:ans=max(ans,dis1[v]+dis2[u]+size[1分量]2.1 点双连通分量点双连通分量指:⽆向图中,分量中的任意两点间存在经过的点完全不相同的两条路径。
2.2 性质割点起到类似“分割”的作⽤,分割两个点双连通分量。
⼀个割点最多出现在两个点双连通分量上,⽽⾮割点则最多出现在⼀个点双连通分量上。
注意到这⼀条性质后,其实点双连通分量的求解就不是⼀个难事了。
⼀个点双连通分量最早会在割点或者图的根上被探测到。
当tarjan找到⼀个割点后,将栈中的所有点和这个割点归纳到⼀个点双连通分量中。
栈中的所有点弹出,但这个割点不弹出。
void tarjan(int u){DFN[u]=LOW[u]=++DFN[0]; sta[++top]=u; in[u]=true;int cnt=0;tor(i,u){int v=edge[i];if(!DFN[v]){cnt++;tarjan(v);LOW[u]=min(LOW[u],LOW[v]);if(LOW[v]>=DFN[u]){tot++;if(u!=root) ge[u]=true;while(sta[top]!=u){in[sta[top]]=false;lis[tot].push_back(sta[top]);top--;}lis[tot].push_back(u);}}else if(in[v]) LOW[u]=min(LOW[u],DFN[v]);}if(u==root&&cnt>=2) ge[u]=true;}2.3 例题:[HNOI2012]矿场搭建对图做⼀次点双连通分量的归纳,分情况讨论。
强连通分量的三种算法

有向图中, u可达v不一定意味着v可达u. 相互可达则属于同一个强连通分量(S trongly Connected Component, SCC)最关键通用部分:强连通分量一定是图的深搜树的一个子树。
一、Kosaraju算法1. 算法思路基本思路:这个算法可以说是最容易理解,最通用的算法,其比较关键的部分是同时应用了原图G和反图GT。
(步骤1)先用对原图G进行深搜形成森林(树),(步骤2)然后任选一棵树对其进行深搜(注意这次深搜节点A能往子节点B走的要求是EAB存在于反图GT),能遍历到的顶点就是一个强连通分量。
余下部分和原来的森林一起组成一个新的森林,继续步骤2直到没有顶点为止。
改进思路:当然,基本思路实现起来是比较麻烦的(因为步骤2每次对一棵树进行深搜时,可能深搜到其他树上去,这是不允许的,强连通分量只能存在单棵树中(由开篇第一句话可知)),我们当然不这么做,我们可以巧妙的选择第二深搜选择的树的顺序,使其不可能深搜到其他树上去。
想象一下,如果步骤2是从森林里选择树,那么哪个树是不连通(对于GT来说)到其他树上的呢?就是最后遍历出来的树,它的根节点在步骤1的遍历中离开时间最晚,而且可知它也是该树中离开时间最晚的那个节点。
这给我们提供了很好的选择,在第一次深搜遍历时,记录时间i离开的顶点j,即numb[i] =j。
那么,我们每次只需找到没有找过的顶点中具有最晚离开时间的顶点直接深搜(对于GT来说)就可以了。
每次深搜都得到一个强连通分量。
隐藏性质:分析到这里,我们已经知道怎么求强连通分量了。
但是,大家有没有注意到我们在第二次深搜选择树的顺序有一个特点呢?如果在看上述思路的时候,你的脑子在思考,相信你已经知道了!!!它就是:如果我们把求出来的每个强连通分量收缩成一个点,并且用求出每个强连通分量的顺序来标记收缩后的节点,那么这个顺序其实就是强连通分量收缩成点后形成的有向无环图的拓扑序列。
为什么呢?首先,应该明确搜索后的图一定是有向无环图呢?废话,如果还有环,那么环上的顶点对应的所有原来图上的顶点构成一个强连通分量,而不是构成环上那么多点对应的独自的强连通分量了。
强连通分量

结论 • 这让我们就将简化版问题给解决了~
• 首先,统计出图中出度为0的点。
• 如果这样的点只有一个,那么从该点 出发反向dfs遍历图。如果可以遍历 所有点,那么说明这个点就是题目要 求的点。
• 时间复杂度o(n+e)
不要高兴的太早
• 上面的结论在有环图是否适用呢?
• 很可惜,结论不成立。 • 因为大牛可以互相仰慕,所以若最受欢迎 的牛与其他牛互相仰慕,这些牛都是最受 欢迎的牛。这样,满足条件的点出度可能 不为0,也不止有一个。
Kosaraju算法(黑书286)
• 算法步骤(正确性证明略)
– 对有向图进行DFS,记录下顶点变黑的时间 A[i]。
– 改变图 的每一条边的方向,生成新图GT。
– 按上次DFS 顶点变黑的时间A[i]由大到小顺 序对GT进行DFS。遍历结果构成森林W 。
– W 中每棵树的结点构成了有向图的一个 强连通分量。
G(6) E(2)
• 得到A[i]从大 到小的顺序: •FGACDEB
D(3)
演示
• 改变图G 的每一条边 的方向,生成新图GT • 按A[i]由大到小顺序
A (5)
C(4) B(1) F(7)
FGACDEB
对GT进行第二次DFS
G(6) E(2)
• 得到森林w
• FG||ACB||DE
D(3)
演示
• 关于缩点法的进一步深入讨论,请参考周 源2005年信息学奥赛冬令营论文。
部分用到强连通分量的题目
• POJ 2186 Popular Cows (基础) • POJ 2553 The Bottom of a Graph (alpc OJ 1274)(基础) • POJ 1236 Network of Schools (基础) • 2010中南赛 light sources(alpc OJ) (基础) • POJ 2762 Going from u to v or from v to u? (中等,弱连通分量 ) • POJ 3160 Father Christmas flymouse(难,DP题) • POJ 1904 King‘s Quest (难,推荐,非缩点,匹配思想与强连通分量的转化)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告
课程名称数据结构
实验项目名称有向图的强连通分量
班级与班级代码14计算机实验班
实验室名称(或课室)实验楼803 专业计算机科学与技术
任课教师
学号:
姓名:
实验日期:2015年12 月03 日
广东财经大学教务处制
姓名实验报告成绩
评语:
指导教师(签名)
年月日说明:指导教师评分后,实验报告交院(系)办公室保存。
一、实验目的与要求
采用邻接表存储的有向图。
二、实验内容
(1)创建N个节点的空图
DiGraph CreateGraph(int NumVertex)//创建一个N个节点的空图
{
DiGraph G;
G = malloc( sizeof( struct Graph ) );
if( G == NULL ) FatalError( "Out of space!!!" );
G->Table = malloc( sizeof( struct TableEntry ) * NumVertex );
if( G->Table == NULL )
FatalError( "Out of space!!!" );
G->NumVertex = NumVertex;
G->NumEdge = 0;
int i;
for (i=0;i<NumVertex;i++)
{
G->Table[i].Header=MakeEmpty(NULL);
G->Table[i].V=i;
}
return G;
}
(2)在图G上执行DFS,通过对DFS生成森林的后序遍历对G的顶点编号。
//后序DFS遍历图G,并将节点按后序遍历的顺序编号
int *PostDFS(DiGraph G)
{
int NumVertex=G->NumVertex;
int visited[NumVertex];
int i;
for (i=0;i<NumVertex;i++)
{
visited[i]=0;//初始化,所有节点都未被访问过
}
int *post = malloc( sizeof( int ) * NumVertex );//用于存放后序DFS遍历时,节点的编号
if( post == NULL ) FatalError( "Out of space!!!" );
int postCounter=0;
//定义一个内嵌的DFS函数
void DFS (Vertex v)//从节点v出发执行DFS
{
visited[v]=1;//标记该节点被访问
Position P = Header( G->Table[v].Header );
if( !IsEmpty( G->Table[v].Header ) )
{
do//对节点v的所有邻接点递归调用DFS
{
P = Advance( P );
Vertex w=Retrieve( P );
if (visited[w]==0)//v的邻接点w未被访问过
{
DFS(w);
}
} while( !IsLast( P, G->Table[v].Header ) );
}
post[v]=postCounter;
postCounter++;
}
Vertex j;
for (j=0;j<NumVertex;j++)//从每个节点出发进行DFS,因为图G有可能不是连通的
{
if (visited[j]==0) DFS(j);
}
return post;
}
(3)求图G的强连通分量
int *StrongConnectedComponent(DiGraph G)//求图G的强连通分量
{
//DFS后序遍历图G,并将节点按后序遍历的顺序编号存入post数组
int *post=PostDFS(G);
//求图G的逆置GR
DiGraph GR=ReverseGraph(G);
//按post编号从大到小顺序在GR上执行DFS,所得连通分量就是原图G的强连通分量
int NumVertex=GR->NumVertex;
int visited[NumVertex];
int i;
for (i=0;i<NumVertex;i++)
{
visited[i]=0;//初始化,所有节点都未被访问过
}
int *sccID = malloc( sizeof( int ) * NumVertex );//用于标记强连通分量的数组
if( sccID == NULL ) FatalError( "Out of space!!!" );
int sccCounter=0;
//定义一个内嵌的DFS函数
void DFS (Vertex v)//从节点v出发执行DFS
{
visited[v]=1;//标记该节点被访问
sccID[v]=sccCounter;
Position P = Header( GR->Table[v].Header );
if( !IsEmpty( GR->Table[v].Header ) )
{
do//对节点v的所有邻接点递归调用DFS
{
P = Advance( P );
Vertex w=Retrieve( P );
if (visited[w]==0)//v的邻接点w未被访问过
{
DFS(w);
}
} while( !IsLast( P, GR->Table[v].Header ) );
}
}
int m;
for (m=NumVertex-1;m>=0;m--)//按post编号从大到小顺序在GR上执行DFS,因为图G有可能不是连通的
{
Vertex n;
for (n=0;n<NumVertex;n++)
{
if (post[n]==m)//节点n的编号为当前最大值
{
if (visited[n]==0)
{
DFS(n);
sccCounter++;
}
}
}
}
return sccID;
}
(4)测试函数
main()
{
DiGraph G=CreateGraph(10);
//插入15条边,参见教科书P248,图9-74
InsertEdge(G,0,1);
InsertEdge(G,0,3);
InsertEdge(G,1,2);
InsertEdge(G,1,5);
InsertEdge(G,2,0);
InsertEdge(G,2,3);
InsertEdge(G,2,4);
InsertEdge(G,3,4);
InsertEdge(G,5,2);
InsertEdge(G,6,5);
InsertEdge(G,6,7);
InsertEdge(G,7,5);
InsertEdge(G,7,9);
InsertEdge(G,8,7);
InsertEdge(G,9,8);
//插入15条边结束
printf("输出图...\n");
OutputGraph(G);
printf("\n输出图的逆置...\n");
DiGraph GR=ReverseGraph(G);
OutputGraph(GR);
printf("\n输出后序DFS编号...\n");
int *pp=PostDFS(G);
int i;
for (i=0;i<G->NumVertex;i++)
printf("%d---",pp[i]);
printf("\n\n输出强连通分量编号...\n");
int *scc=StrongConnectedComponent(G);
for (i=0;i<G->NumVertex;i++)
printf("%d~~~",scc[i]);
printf("\n\n");
}
(5)测试截图
四、实验中的问题及解决办法,疑问和猜想。
五、实验总结
(1)加深对程序语言和算法的理解。
(2)知识量不够,语法不会用。
