苏科版九年级下册数学 7.5解直角三角形同步练习

合集下载

苏科版九年级数学下册 7.5 解直角三角形同步测试题

7.5 解直角三角形同步测试题（满分120分；时间：120分钟）一、选择题（本题共计10 小题，每题3 分，共计30分，）1. 在Rt△ABC中，∠C=90∘，若斜边上的高为ℎ，sin A=35，则AB的长等于（）A.5 4ℎB.53ℎ C.2512ℎ D.1225ℎ2. 已知Rt△ABC中，∠C=90∘，sin A=45，BC=8，则AC等于（）A.6B.323C.10D.123. 如图AD⊥CD，AB=13，BC=12，CD=3，AD=4，则sin B=()A.5 13B.1213C.35D.454. 如图，在△ABC中，∠C=90∘，∠B=50∘，AB=10，则BC的长为（）A.10tan50∘B.10cos50∘C.10sin50∘D.10cos50∘5. 在△ABC中，∠A=150∘，AB=2，AC=4，则tan B的值是（）A.√3+1B.√3−12C.√3−1 D.√3+126. 如图，在△ABC中，斜边BC上的高AD=4，cos B=45，则AC=()A.6B.163C.5D.47. 已知Rt△ABC中，∠C＝90∘，AB＝2√5，tan A=12，则BC的长是（）A.2B.8C.2√5D.4√58. 如图，四边形ABCD中，∠A=135∘，∠B=∠D=90∘，BC=2√3，AD=2，则四边形ABCD的面积是（）A.4√2B.4√3C.4D.69. 如图，在Rt△ABC中，∠ACB=90∘，CD⊥AB于D，AC=2√2，AB=2√3，设∠BCD=α，那么cosα的值是（）A.√22B.√2 C.√33D.√6310. 在如图所示的方格纸中，点A、B、C都在方格线的交点．则∠ACB=()A.120∘B.135∘C.150∘D.165∘二、填空题（本题共计10 小题，每题3 分，共计30分，）11. 如图，Rt△ABC中，∠C=90∘，D是BC上一点，AD=BD，tan∠ADC=4，AB=4√5，3则CD=________．12. 如图，在四边形ABCD中，∠A=30∘，∠C=90∘，∠ADB=105∘，sin∠BDC=√3，AD=24．则DC的长=________．13. 如图，在△ABC中，∠B=60∘，AB=2，BC=1+√3，求∠ACB的度数为________．14. 如图，已知∠ABD=∠C=90∘，AD=12，AC=BD，∠BAD=30∘，则BC=________．，则BD的长为15. Rt△ABC中，∠C＝90∘，CD为斜边AB上的高，若BC＝4，sin A=23________．16. 如图，在△ABC中，∠A=30∘，∠B=45∘，AC=2√3，则CB的长为________．，AB=15，17. 如图，△ABC中，∠ACB=90∘，tan A=43AC=________．，AD=1．则BC的长18. 在△ABC中，AD是BC边上的高，∠C=45∘，sin B=13________．19. 如图所示，∠AOB是放置在正方形网格中的一个角，则sin∠AOB的值是________．20. 如图，在△ABC和△ACD中，∠B=∠D，tan B=1，BC=5，CD=3，∠BCA=90∘−21∠BCD，则AD=________．2三、解答题（本题共计7 小题，共计60分，）21. 如图，已知∠MON=25∘，矩形ABCD的边BC在OM上，对角线AC⊥ON．当AC=5时，求AD的长．（参考数据：sin25∘=0.42；cos25∘=0.91；tan25∘=0.47，结果精确到0.1）22. 如图，在△ABC中，AB=AC，它的一个外角为80∘，底角平分线CD的长为20√3，3求腰上的高CE的长．23. 已知，Rt△ABC中，∠C=90∘，∠A=30∘，BC=3，D为AC边上一点，∠BDC=45∘，求AD的长．24. 已知：在△ABC中，∠ACB=90∘，CD⊥AB于D，BE:AB=3:5，若CE=√2，cos∠ACD=4，求tan∠AEC的值及CD的长．525. 如图所示，在Rt△ABC中，AB=10，sin A=3，求BC的长和tan B的值．526. 如图，AD是△ABC的高，CD＝16．BD＝12，∠C＝35∘．求∠B（可以使用计算器，精确到1∘）．27. 如图，在Rt△ABC中，∠B=90∘，sin A=5，点D在AB边上，且∠BDC=45∘，BC=5．13（1）求AD长；（2）求∠ACD的正弦值．参考答案一、选择题（本题共计10 小题，每题 3 分，共计30分）1.【答案】C【解答】解：如图，CD为斜边AB上的高，在Rt△ABC中，sin A=BCAB =35，设BC=3k，则AB=5k，根据勾股定理，得AC=√AB2−BC2=4k；在Rt△ACD中，sin A=CDAC =ℎAC=35，AC=53ℎ，∵ 4k=53ℎ，∵ k=512ℎ，∵ AB=5×512ℎ=2512ℎ．故选C．2.【答案】A【解答】解：如图，在Rt△ACB中，∵ sin A=BCAB，∵ 8AB =45，∵ AB=10，∵ AC=√AB2−BC2=6．故选A．3.【答案】A【解答】解：由勾股定理知，AC2=CD2+AD2=25，∵ AC=5．∵ AC2+BC2=169=AB2，∵ △CBA是直角三角形．∵ sin B=ACAB =513．故选A．4.【答案】B【解答】解：∵ cos B=BCAB，∵ BC=AB cos B=10cos50∘．故选B．5.【答案】B【解答】解：如图所示：过点C作CD⊥BA于点D，∵ ∠A=150∘，∵ ∠CAD=30∘，∵ AC=4，∠CDA=90∘，∵ CD=2，AD=√42−22=2√3，∵ tan B=CDBD =2√3+2=√3−12．故选：B．6.【答案】C【解答】解：∵ ∠A=90∘，AD为BC上的高，∵ ∠BDA=90∘，∵ ∠B+∠BAD=∠BAD+∠CAD=90∘，∵ ∠B=∠CAD，∵ cos B=45，∵ cos∠CAD=45，∵ ADAC =45，∵ AD=4，∵ AC=5，故选C．7.【答案】A【解答】解：∵ Rt△ABC中，∠C＝90∘，AB＝2√5，tan A=12，∵ 设BC=a，则AC=2a，∵ a2+(2a)2=(2√5)2，解得，a=2或a=−2（舍去），∵ BC=2，故选A．8.【答案】C【解答】解：如图，分别延长CD，BA交于点E．∵ ∠DAB=135∘，∵ ∠EAD=∠C=∠E=45∘，∵ BE=BC=2√3，AD=ED=2，∵ 四边形ABCD的面积=S△EBC−S△ADE=12BC⋅BE−12AD⋅DE，=12×2√3×2√3−12×2×2，=6−2，=4．故选C．9.【答案】D【解答】解：∵ Rt△ABC中，∠ACB=90∘，CD⊥AB于D，∵ ∠B+∠A=90∘，∠B+∠BCD=90∘，∵ ∠A=∠BCD=α，∵ cosα=ACAB =√22√3=√63．故选D．10.【答案】B【解答】解：设网格边长为1则AC=√10，BC=√5，AB=5由余弦定理得cos∠ACB=AC2+BC2−AB22AC⋅BC=−√22∵ ∠ACB=135∘故选B．二、填空题（本题共计10 小题，每题 3 分，共计30分）11.【答案】3【解答】解：在Rt△ACD中，tan∠ADC=ACCD =43，设AC=4x，CD=3x，∵ AD=√AC2+CD2=5x，∵ BD=AD=5x，∵ BC=BD+CD=8x，在Rt△ABC中，AC=4x，BC=8x，∵ AB=√AC2+BC2=4√5x，而AB=4√5，∵ 4√5x=4√5，解得x=1，∵ CD=3x=3．故答案为3．12.【答案】√2【解答】解：作DH⊥AB于H，如图，∵ ∠A=30∘，∵ ∠ADB=60∘，DH=12AD=2，∵ ∠ADB=105∘，∵ ∠BDH=45∘，∵ △BDH为等腰直角三角形，∵ BD=√2DH=2√2，在Rt△BCD中，∵ sin∠BDC=BCBD =√32，∵ BC=2√2×√32=√6，∵ CD=√BD2−BC2=√2．故答案为√2．13.【答案】45∘【解答】解：作AH⊥BC，如图，在Rt△ABH中，∵ cos∠B=BHAB，∵ BH=2cos60∘=1，∵ AH=√AB2−BH2=√3，∵ BC=1+√3，∵ CH=BC−BH=1+√3−1=√3，在Rt△ACH中，∵ tan C=AHCH =√3√3=1，∵ ∠C=45∘．故答案为45∘．14.【答案】6√2【解答】解：已知∠ABD=∠C=90∘，AD=12，AC=BD，∠BAD=30∘，∵ BD=12AD=12×12=6，∵ AC=BD=6，在直角三角形ABD中，根据勾股定理得：AB=√AD2−BD2=√122−62=6√3，在直角三角形ACB中，根据勾股定理得：BC=√AB2−AC2=√(6√3)2−62=6√2．故答案为：6√2．15.【答案】83【解答】∵ 在Rt△ABC中，BC＝4，sin A=23，∵ AB＝6，∵ AC＝2√5，∵ CD是斜边AB上的高线，∵ CD=4√53，∵ BD=√BC2−CD2=83．16.【答案】√6【解答】解：过C作CD⊥AB，交AB于点D，在Rt△ACD中，∠A=30∘，AC=2√3，∵ CD=12AC=√3.在Rt△BCD中，∠B=45∘，CD=√3，∵ CB=√2CD=√6.故答案为：√6.17.【答案】9【解答】解：∵ ∠ACB=90∘，tan A=BCAC =43，∵ 设BC=4x，则AC=3x，∵ AB=√BC2+AC2=15，∵ 15=√(4x)2+(3x)2，解得：x2=9，∵ x1=3或x2=−3（不合题意，舍去），∵ AC=3x=9；故答案为：9．18.【答案】2√2+1【解答】解：∵ 在△ABC中，AD是BC边上的高，∵ AD⊥BC，即∠ADB=∠ADC=90∘，在Rt△ACD中，∠C=45∘，∵ ∠DAC=45∘，∵ DC=AD=1，在Rt△ABD中，sin B=13，AD=1，∵ sin B=ADAB =13，即AB=3，根据勾股定理得：BD=√32−12=2√2，则BC=BD+DC=2√2+1，故答案为：2√2+119.【答案】√22【解答】解：如图，连接AB．∵ OA=AB=√10，OB=2√5，∵ OB2=OA2+AB2，∵ ∠OAB=90∘，∵ △AOB是等腰直角三角形，∵ ∠AOB=45∘，∵ sin∠AOB=√22.故答案为：√22.20.【答案】2√5【解答】解法一：如图1，延长DC至Q，使CQ=BC=5，连接AQ，过A作AH⊥DQ于H，则DQ=DC+CQ=CD+BC=3+5=8，∵ ∠BCA+∠ACQ+∠BCQ=180∘，∵ ∠BCA=90∘−12∠BCD，设∠BCD=x∘，则∠BCA=90−12x∘，∵ ∠ACQ=180∘−x∘−(90∘−12x)=90−12x∘=∠BCA，∵ AC=AC，∵ △BCA≅△QCA，∵ ∠B=∠Q=∠D，∵ AD=AQ，∵ AH⊥DQ，∵ DH=QH=12QD=4，tan∠B=tan∠Q=AHQH =AH4=12，∵ AH=2，∵ AQ=AD=2√5；解法二：如图2，在BC上取一点F，使BF=CD=3，连接AF，∵ CF=BC−BF=5−3=2，过F作FG⊥AB于G，∵ tan B=12=FGBG，设FG=x，BG=2x，则BF=√5x，∵ √5x=3，x=√5，即FG=√5，延长AC至E，连接BD，∵ ∠BCA=90∘−12∠BCD，∵ 2∠BCA+∠BCD=180∘，∵ ∠BCA+∠BCD+∠DCE=180∘，∵ ∠BCA=∠DCE，∵ ∠ABC=∠ADC，∵ A、B、D、C四点共圆，∵ ∠DCE=∠ABD，∠BCA=∠ADB，∵ ∠ABD=∠ADB，∵ AB=AD，在△ABF和△ADC中，∵ {AB=AD∠ABC=∠ADCBF=CD，∵ △ABF≅△ADC(SAS)，∵ AF=AC，过A作AH⊥BC于H，∵ FH=HC=12FC=1，由勾股定理得：AB2=BH2+AH2=42+AH2①，S△ABF=12AB⋅GF=12BF⋅AH，∵ AB√5=3AH，∵ AH=√5，∵ AH2=AB25②，把②代入①得：AB2=16+AB25，解得：AB=±2√5，∵ AB>0，∵ AD=AB=2√5，三、解答题（本题共计7 小题，每题10 分，共计70分）21.【答案】解：延长AC交ON于点E，如图，∵ AC⊥ON，∵ ∠OEC=90∘，在Rt△OEC中，∵ ∠O=25∘，∵ ∠OCE=65∘，∵ ∠ACB=∠OCE=65∘，∵ 四边形ABCD是矩形，∵ ∠ABC=90∘，AD=BC，在Rt△ABC中，∵ cos∠ACB=BC，AC∵ BC=AC⋅cos65∘=5×0.42=2.1，∵ AD=BC=2.1．【解答】解：延长AC交ON于点E，如图，∵ AC⊥ON，∵ ∠OEC=90∘，在Rt△OEC中，∵ ∠O=25∘，∵ ∠OCE=65∘，∵ ∠ACB=∠OCE=65∘，∵ 四边形ABCD是矩形，∵ ∠ABC=90∘，AD=BC，在Rt△ABC中，∵ cos∠ACB=BC，AC∵ BC=AC⋅cos65∘=5×0.42=2.1，∵ AD=BC=2.1．22.【答案】解：∵ AB=AC，∵ ∠ABC=∠ACB，∵ ∠CAE=80∘，∵ ∠ABC=∠ACB=40∘，∵ CD平分∠ACB，∵ ∠BCD=20∘，∠CDE=∠BCD+∠ABC=20∘+40∘=60∘，∵ CE=sin∠EDC⋅CD=sin60∘⋅20√33=√32⋅20√33=10．【解答】解：∵ AB=AC，∵ ∠ABC=∠ACB，∵ ∠CAE=80∘，∵ ∠ABC=∠ACB=40∘，∵ CD平分∠ACB，∵ ∠BCD=20∘，∠CDE=∠BCD+∠ABC=20∘+40∘=60∘，∵ CE=sin∠EDC⋅CD=sin60∘⋅20√33=√32⋅20√33=10．23.【答案】解：∵ 在Rt△ABC中，∠C=90∘，∠A=30∘，BC=3，∵ AB=6，AC=3√3，∵ ∠BDC=45∘，∵ ∠DBC=45∘，∵ CD=BC=3，∵ AD=AC−CD=3√3−3．【解答】解：∵ 在Rt△ABC中，∠C=90∘，∠A=30∘，BC=3，∵ AB=6，AC=3√3，∵ ∠BDC=45∘，∵ ∠DBC=45∘，∵ CD=BC=3，∵ AD=AC−CD=3√3−3．24.【答案】解：在Rt△ACD与Rt△ABC中，∵ ∠ABC+∠CAD=90∘，∠ACD+∠CAD=90∘，∵ ∠ABC=∠ACD，∵ cos∠ABC=cos∠ACD=45，在Rt△ABC中，BCAB =45，令BC=4k，AB=5k，则AC=3k，由BE:AB=3:5，知BE=3k，则CE=k，且CE=√2，则k=√2，AC=3√2．∵ Rt△ACE中，tan∠AEC=ACCE=3，∵ Rt△ACD中，cos∠ACD=CDAC =45，∵ CD=12√25．【解答】解：在Rt△ACD与Rt△ABC中，∵ ∠ABC+∠CAD=90∘，∠ACD+∠CAD=90∘，∵ ∠ABC=∠ACD，∵ cos∠ABC=cos∠ACD=45，在Rt△ABC中，BCAB =45，令BC=4k，AB=5k，则AC=3k，由BE:AB=3:5，知BE=3k，则CE=k，且CE=√2，则k=√2，AC=3√2．∵ Rt△ACE中，tan∠AEC=ACCE=3，∵ Rt△ACD中，cos∠ACD=CDAC =45，∵ CD=12√25．25.【答案】解：在Rt△ABC中，∵ ∠C=90∘，AB=10，sin A=35，∵ BCAB =35，∵ BC=6，AC=√AB2−BC2=√102−62=8，∵ tan B=ACBC =86=43．【解答】解：在Rt△ABC中，∵ ∠C=90∘，AB=10，sin A=35，∵ BCAB =35，∵ BC=6，AC=√AB2−BC2=√102−62=8，∵ tan B=ACBC =86=43．26.【答案】∵ AD⊥BC，∵ ∠ADC＝∠ADB＝90∘，在Rt△ACD中，AD＝CD⋅tan C＝16×0.70≈12.20，在Rt△ABD中，tan B=ADBD =12.2012≈1，∵ ∠B＝45∘．【解答】∵ AD⊥BC，∵ ∠ADC＝∠ADB＝90∘，在Rt△ACD中，AD＝CD⋅tan C＝16×0.70≈12.20，在Rt△ABD中，tan B=ADBD =12.2012≈1，∵ ∠B＝45∘．27.【答案】∵ ∠B=90∘，∠BDC=45∘，∵ BC=BD=5，∵ sin A=513，∵ AB=12，∵ AD=AB−BD=12−5=7；过A作AE⊥CE交CD延长线于点E，∵ △ADE是等腰直角三角形，∵ AE=DE=7√22，则sin∠ACD=7√226．【解答】∵ ∠B=90∘，∠BDC=45∘，∵ BC=BD=5，∵ sin A=5，13∵ AB=12，∵ AD=AB−BD=12−5=7；过A作AE⊥CE交CD延长线于点E，∵ △ADE是等腰直角三角形，，∵ AE=DE=7√22．则sin∠ACD=7√226。

苏科版九下 7.5解直角三角形同步课时训练(word版含答案)

7.5解直角三角形同步课时训练一、单选题1．如图，四边形ABCD 中，∠BAD=∠ADC=90°，，点P 在四边形ABCD 的边上．若P 到BD 的距离为32，则点P 的个数为（）.A ．1B ．2C ．3D ．42．如图，在Rt △ABC 中，∠C ＝90°，AB ＝4，sinA ＝12，则BC 的长为（）A ．2B ．3C D ．3．如图，第一象限内的点A 在反比例函数1y x=的图象上，第二象限内的点B 在反比例函数(0) k y k x =≠的图象上，且OA OB ⊥，sin A =，则k 的值为（）A ．12-B ．4-C ．D ．3-4．如图，在△ABC 中，∠C ＝90°，AC ＝32，AB 的垂直平分线MN 交AC 于点D ，连接BD ，若sin ∠CBD ＝79，则BC 的长是（）A ．16B ．C ．D ．85．如图，在四边形ABCD 中，∠ACB ＝∠CAD ＝90°，AC ＝CB ，sin ∠ACD ＝35，则tan ∠BDC 的值是（）A B ．6C ．1637D ．16256．如图，390,10,17,cos 5EFG EF OG FGO ∠=︒==∠=，则点F 的坐标是（）A ．278,4⎛⎫⎪⎝⎭B ．()8,12C ．336,4⎛⎫ ⎪⎝⎭D ．()6,107．如图，在Rt ABC ∆中，90,2C BC AB ∠=︒==，则B 等于（）A ．15︒B ．20︒C ．30D ．60︒8．小明沿着坡度为1:2的山坡向下走了1000m ，则他下降了（）A ．B ．500mC ．D ．1000m9．如图，在ABC 中，AD 平分BAC ∠，//DE AC 交AB 于点E ，//DF AB 交AC 于点F ，且AD 交EF 于点O ，若8AF EF ==，则sin DAC ∠的值为（）A ．13B ．2C ．12D ．210．如图，Rt ABC △中，90ACB ∠=︒，CD AB ⊥，4tan 3B =，若10BC =，则AD 的长为（）A ．6B ．323C ．7.5D ．10二、填空题11．如图，已知直线2y x =-与抛物线2522y ax x =+-与x 轴交于点,A B （点B在点A 左侧），与y 轴交于点C ．点P 是x 轴上一动点，点N 为直线AC 上一点，则CP PN +的最小值为________．12．如图，在矩形ABCD 的AB 边取一点E ，将ADE 沿DE 折叠，使得点A 落在BC 边上点F 处，延长EF ，与CDF ∠的角平分线交于点G ，DG 交BC 于点H ，已知AB =12FH BC =时，点G 到直线ED 的距离为_________．13．如图，在△ABC中，AB＝AC＝5，BC＝8，点D是边BC上（不与B，C重合）一动点，∠ADE＝∠B＝α，DE交AC于点E，若△DCE为直角三角形，则BD的值为_____．=，则14．如图△ABC是O的内接三角形，60BAC∠=︒，D是BC的中点，AD a四边形ABDC的面积为________．15．如图，在边长为1的菱形ABCD中，∠ABC＝60°，将△ABD沿射线BD方向平移，得到△EFG，连接EC、GC．求EC＋GC的最小值为______．'''位置，此时AC'的中点恰好与D 16．如图，将矩形ABCD绕点A旋转至矩形AB C D点重合，AB'交CD于点E．若DE＝2，则AC的长为_____．三、解答题17．如图，在平行四边形ABCD 中，15AB =，AD DB ⊥，4tan 3A ∠=．点P ，Q 是射线BD 上两个动点，点Q 以每秒3个单位的速度从点B 向终点D 运动，23PQ BQ =，点P 和点B 始终在点Q 两侧，过点P 作PH AB ⊥于点H ，连接HQ ，以PH 、HQ 为邻边作平行四边形PHQG ，设点Q 的运动时间为(s)t ．（1）PH =________（用含t 的代数式表示）；（2）当点G 落在DC 上时，求t 值；（3）点O 为线段BD 中点，当直线OG 平行或垂直于BCD △一边时，求PQG 与BCD △重叠部分的面积；（4）若经过点G 的直线将平行四边形ABCD 的面积两等分，同时该直线将平行四边形PHQG 的面积分成1:3的两部分，直接写出t 的值． 18．如图，△ABC 中，AB=AC ，以AC 为直径的O 交BC 于点D ，点E 为AC 延长线上一点，且DE 是O 的切线．（1）求证：∠CDE=12∠BAC ；（2）连接AD ，若tan ∠CAD=13，CE=4，求O 的半径．19．如图，在ABC 中，AD 是BC 边上的高，E 是AC 边的中点，41312sin 5BC AD B ===，，．（1）求线段CD 的长；（2）求tan 2ADE ∠的值．20．如图，四边形ABCD 中，90B ∠=︒，2AB =，8CD =，AC CD ⊥，1sin 3ACB ∠=．（1）求AC 的长．（2）求tan cos DAC DAC ∠⋅∠的值．参考答案1．B 2．A 3．A 4．B 5．C 6．B 7．C 8．A 9．C 10．B11．12．613．4或254．14．241516．17．（1）3t ；（2）32t =；（3）2720或154或17625；（4）1811或1813【详解】解：（1）∵∠90=15ADB AB =︒，，tan BD A AD ∠==43， ∴9AD =，12BD = 在△ADB 和△PHB 中，∠90ADB PHB ABD PBH =∠=︒∠=∠， ∴△ADBPHB ∆∴AB AD PB PH =，即AD PBPH AB⋅= ∵25533PB BQ PQ BQ BQ BQ t =+=+==∴45315tPH t == 故答案为：3t （2）当点G 落在DC 上时， ∵4tan 3A ∠=， ∴4sin 5A ∠=，3sin 5CDB ∠=, 在Rt ADB 中，90ADB ∠=︒4sin 5DB A AB ∠==， ∴4125DB AB ==∴在Rt AQG 中，90AGQ ∠=︒()31235GQ t =-，同理355PH t =， ∵PH GQ =,∴()33123555t =t - ∴32t =（3）①当//OG DC 时，3t 4=，22141212327232555420S t t t ⎛⎫=⋅⋅⋅==⨯=⎪⎝⎭ ②当//OG BC 或OG DB ⊥时，54t =，2214121251523255544S t t t ⎛⎫=⋅⋅⋅==⨯= ⎪⎝⎭③当OG DC ⊥时，2t =，22121831762326529525S ⎛⎫=⨯-⨯⨯⨯-⨯=⎪⎝⎭ （4）∵经过点G 的直线将平行四边形ABCD 的面积平分，∴这条直线经过平行四边形ABCD的对角线的交点，即BD的中点O．①如图，当直线OG经过PH的中点R时，直线OG将平行四边形PHQG的面积分成1:3的两部分，∵PH//GQ，∴12 PR POGQ OQ==，∴561 632 tt-= -∴1813t=；②如图，当直线OG经过HQ的中点N时，直线OG将平行四边形PHQG的面积分成1:3的两部分，∵PG//HQ，∴12 NQ OQPG PO==，∴631 562tt-=-，∴1811 t=；综上所述，满足条件的t的值为1811或1813．18．（1）见解析；（2）16．【详解】解：（1）如图，连接OD，AD，∵AC是直径，∴∠ADC=90°，∴AD⊥BC，∵AB=AC，∴∠CAD=∠BAD=12∠BAC，∵DE是⊙O 的切线，∴OD⊥DE，∴∠ODE=90︒，∴∠ADC=∠ODE，∴∠CDE=∠ADO，∵OA= OD，∴∠CAD=∠ADO，∴∠CDE =∠CAD，∴∠CDE=∠CAD=12∠BAC；（2）解：∵AB=AC，AD⊥BC，∴BD=CD，∵tan∠CAD= 13，∴AD=3CD，∴设DC=x，则AD=3x，∴=，∵∠CDE=∠CAD，∠DEC=∠AED，∴△CDE ∽△DAE ， ∴CE DC DE DE AD AE ==，即 43x DE DE x AE== ， ∴DE=12，AE=36，∴AC=AE-CE=32，∴⊙O 的半径为16．19．（1）4，（2）34 【详解】解：（1）∵4sin 5B =∴45AD AB =， ∵12AD =，∴15AB =，9BD ==，1394CD =-=；（2）过点D 作DF ⊥AC ，垂足为F ，∵12AD =，4CD =，∴AC ==， ∵1122AD CD AC DF ⋅=⋅，∴DF =∵E 是AC 边的中点，∴12AE DE AC ===EF ==， ∵AE DE =，∴∠EAD =∠EDA ，∴∠DEF =2∠ADE ，3tan 2tan 4DF ADE DEC EF ∠=∠==；20．（1）6AC =；（2）4.5【详解】解：（1）190,2,sin ,3B AB ACB ∠=︒=∠= 1,3AB AC ∴= 即：21,3AC = 6,AC ∴=经检验：6AC =符合题意；（2）,8,6,AC CD CD AC ⊥==10,AD ∴===8463tan ,cos ,63105DC AC DAC DAC AC AD ∴∠===∠=== 434tan cos .355DAC DAC ∴∠⋅∠=⨯=。

2022-2023学年苏科版九年级数学下册《7-5解直角三角形》同步达标测试题(附答案)

2022-2023学年苏科版九年级数学下册《7.5解直角三角形》同步达标测试题（附答案）一．选择题（共8小题，满分32分）1．在平面直角坐标系中，点A （sin30°，﹣cos60°）关于y 轴对称的点的坐标是（）A ．（﹣，﹣）B ．（，）C ．（，）D ．（﹣，﹣）2．已知在Rt △ABC 中，∠C ＝90°，∠A ＝α，AC ＝3，那么AB 的长等于（）A ．3tan αB tan 3C ．D ． 3．如图，点A 、B 、C 均在4x 4的正方形网格的格点上，则tan ∠BAC ＝（）A ．B ．C ．D ． 4．在△ABC 中，BC ＝+1，∠B ＝45°，∠C ＝30°，则△ABC 的面积为（）A ．B ．+1C ．D ．+15．已知△ABC 中，∠C ＝90°，tan A ＝，D 是AC 上一点，∠CBD ＝∠A ，则cos ∠CDB 的值为（）A ．B ．C ．D ．26．如图所示，在Rt △ABC 中，∠C ＝90°，，点D 在BC 边上，CD ＝AC ，AB ＝26，则BD 的长为（）A ．10B ．12C ．14D ．167．如图，在△ABC中，DC平分∠ACB，BD⊥CD于点D，∠ABD＝∠A，若BD＝1，AC ＝7，则tan∠CBD的值为（）A．5B．C．3D．8．如图，在平面直角坐标系中放置三个长为3，宽为1的矩形，则tan∠BAC＝（）A．2B．C．3D．二．填空题（共8小题，满分40分）9．已知△ABC，∠A＝30°，AB＝4，BC＝2，则△ABC的面积为．10．如图，点P在线段BC上，AB⊥BC，DP⊥AP，CD⊥DP，如果BC＝10，AB＝2，tan C ＝，那么DP的长是．11．如图所示的网格是正方形网格，则tan∠P AB+tan∠PBA＝，∠P AB+∠PBA ＝°（点A，B，P是网格线交点）．12．如图，在四边形ABCD中，AB＝2，BC＝CD＝2，∠B＝90°，∠C＝120°，则线段AD的长为．13．在△ABC中，AB＝BC＝5，，设BC的垂直平分线与AB的交点为D，的值为．14．已知△ABC是以AB为一腰的等腰三角形，AB＝5，tan∠BAC＝，则△ABC的底边长为．15．如图，△ABC中，∠ACB＝90°，AC＝BC，点D、点E分别在AB、AC上，连接CD、ED，ED＝CD，tan∠ADE＝，BD＝，则AB＝．16．如图，在边长为1的正方形网格中，点B、C、D在格点上，连接BD并延长，交网格线于点A，则sin∠ADC＝．三．解答题（共6小题，满分48分）17．如图，在△ABC中，∠B＝30°，AB＝6，AD⊥BC于点D且，求BC的长．18．如图，已知在△ABC中，∠A＝45°，∠B＝60°，AB＝8，求△ABC的面积．19．△ABC中，∠B＝45°，∠BAC＝15°，AC＝10cm，求BC边的长度．20．如图，已知Rt△ABC中，∠BAC＝90°，BC＝6，AC＝4，以A为圆心，AB为半径画圆，与边BC交于另一点D．（1）求BD的长；（2）连接AD，求∠DAC的余弦值．21．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，sin∠ABC＝，D是边AB上一点，且CD＝CA，BE⊥CD，垂足为点E．（1）求∠EBD的正弦值；（2）求AD的长．22．如图，在Rt△AOB中，∠AOB＝90°，以O为圆心，OB的长为半径的圆交边AB于点D，点C在边OA上且CD＝AC，延长CD交OB的延长线于点E．（1）求证：CD是圆的切线；（2）已知sin∠OCD＝，AB＝4，求AC长度及阴影部分面积．参考答案一．选择题（共8小题，满分32分）1．解：∵sin30°＝，cos60°＝，∴点（sin30°，﹣cos60°）关于y轴对称的点的坐标是（﹣，﹣），故选：D．2．解：∵cos A＝，∠A＝α，AC＝3，∴AB＝＝．故选：C．3．解：如图，过点B作BD⊥AC，垂足为D．由格点三角形可知：AC＝＝4，AB＝＝2．∵S△ABC＝×4×4﹣×4×2＝8﹣4＝4，S△ABC＝AC•BD＝×4×BD＝2BD．∴2BD＝4，∴BD＝．∴AD＝＝＝3．∴tan∠BAC＝＝＝．故选：A．4．解：过A点作AD⊥BC于点D，∵∠B＝45°，∴∠BAD＝45°＝∠B，∴AD＝BD，设BD＝x，则AD＝x，∵∠C＝30°，∴tan C＝，∴，∵BC＝+1，∴x+x＝+1，∴x＝1，即AD＝1，∴．故选：A．5．解：∵∠CBD＝∠A，∴tan∠CBD＝tan A＝，设CD＝a，∴tan∠CBD＝＝∴BC＝2a，在Rt△CBD中，BD＝＝＝a，∴cos∠CDB＝＝＝．故选：A．6．解：在Rt△ABC中，∠C＝90°，，AB＝26，∴BC＝AB cos B＝26×＝24，∴AC＝＝＝10，∵CD＝AC，∴CD＝10，∴BD＝BC﹣CD＝24﹣10＝14，故选：C．7．解：如图，延长BD交AC于点E．∵DC平分∠ACB，BD⊥CD于点D，∴∠CDE＝∠CDB＝90°，∠DCE＝∠DCB．在△DCE和△DCB中，，∴△DCE≌△DCB（SAS）．∴BD＝ED＝1．∵∠ABD＝∠A，∴AE＝BE＝2．∵AC＝7，∴CE＝AC﹣AE＝5．∴CD＝＝＝2．∴tan∠CBD＝＝＝2．故选：B．8．解：如图，过C作CE⊥AB于E，延长AF交BC于D，依题意BC＝3，AD＝BD＝2，CD＝1，在Rt△ADC中，AC＝＝，在Rt△ADB中，AB＝＝2，∵S△ABC＝AD×BC＝CE×AB，∴CE＝，∴AE＝＝，∴tan∠BAC＝＝3．故选：C．二．填空题（共8小题，满分40分）9．解：分情况讨论：如图1，过点B作BD⊥AC，垂足为D，∵∠A＝30°，∴BD＝＝＝2，∴AD＝＝＝2，在Rt△BCD中，CD＝＝＝2，∴AC＝AD﹣CD＝2﹣2，∴S△ABC＝＝＝2﹣2；如图2，过点B作BD⊥AC，垂足为D，∵∠A＝30°，∴BD＝＝＝2，∴AD＝＝＝2，在Rt△BCD中，CD＝＝＝2，∴AC＝AD+CD＝2+2，∴S△ABC＝＝＝2+2．综上，△ABC的面积为2﹣2或2+2．故答案为：（2﹣2）或（2+2）．10．解：∵DP⊥AP，CD⊥DP，∴AP∥CD，∴∠C＝∠APB，∵AB⊥BC，∴tan∠APB＝，∵tan C＝，∴＝，∴BP＝4，∴PC＝BC﹣BP＝10﹣4＝6，在Rt△CDP中，tan C＝，CD＝＝，∴＝，解得：DP＝或DP＝﹣（不合题意舍去），故答案为：．11．解：如图，过点P作PM⊥AB于M．在Rt△APM中，tan∠P AB＝＝，在Rt△BPM中，tan∠PBA＝＝，∴tan∠P AB+tan∠PBA＝+＝；延长AP到格点C，连接BC，∵PC＝BC＝＝，PB＝＝，∴PC2+BC2＝PB2，∴△PBC是等腰直角三角形，∴∠CPB＝45°，∵∠CPB＝∠P AB+∠PBA，∴∠P AB+∠PBA＝45°．故答案为：，45．12．解：如图，连接AC．在Rt△ABC中，∵∠B＝90°，AB＝2，BC＝2，∴tan∠ACB＝＝＝，∴∠ACB＝30°，∴AC＝2AB＝4．∵∠BCD＝120°，∴∠ACD＝∠BCD﹣∠ACB＝120°﹣30°＝90°．在Rt△ADC中，∵∠ACD＝90°，AC＝4，CD＝2，∴AD＝＝＝2．故答案为2．13．解：如图，设BC的垂直平分线交BC于E，∵DE是BC的垂直平分线，∴BE＝EC，DE⊥BC，∵tan∠ABC＝＝，∴设DE＝4x，BE＝3x，∴BC＝6x＝AB，∵DB＝＝＝5x，∴AD＝AB﹣DB＝x，∴＝，故答案为：．14．解：①如图，当AC为腰时，过点B作BD⊥AC，∵tan∠BAC＝，∴，设BD＝3x，AD＝4x，在Rt△ABD中，AD2+BD2＝AB2，即（4x）2+（3x）2＝52，解得：x＝（舍去负值），∴AD＝4，BD＝3，∴CD＝AC﹣AD＝1，∴BC＝；②当BC为腰时，过点B作BD⊥AC，如图，∵tan∠BAC＝，∴，设BD＝3x，AD＝4x，在Rt△ABD中，AD2+BD2＝AB2，即（4x）2+（3x）2＝52，解得：x＝1（舍去负值），∴AD＝4，∴AC＝2AD＝8．综上所述，△ABC的底边长为或8．故答案为：或8．15．解：如图，过点D作DQ⊥AC于点Q，DP⊥BC于点P，过点作ET⊥AD于点T．∵CA＝CB，∠ACB＝90°，∴∠A＝∠B＝45°，∴AT＝ET，DP＝PB，BD＝，∴PB＝DP＝1，∵tan∠ADE＝＝，∴可以假设ET＝k，DT＝3k，∴AD＝4k，∴AE＝k，AQ＝DQ＝2k，∴EQ＝AQ﹣AE＝k，∵DE＝DC，DQ⊥EC，∴EQ＝CQ＝PD＝1，∴k＝1，∴k＝，∴AD＝4k＝2，∴AB＝AD+DB＝3，16．解：延长CD，交另一格点E，连接BE，如图，由题意可得：△BCE是等腰直角三角形，∠BDE＝∠ADC，∵BE＝，BD＝，∴sin∠ADC＝sin∠BDE＝．故答案为：．三．解答题（共6小题，满分48分）17．解：∵AD⊥BC于点D．∴∠ADB＝∠ADC＝90°∴△ABD，△ADC为直角三角形．∵Rt△ADB中，∠B＝30°，AB＝6∴，∴，∵Rt△ADC中，，∴．∴CD＝2．∴．18．解：如图，过点C作CD⊥BC于点D，则∠ADC＝∠BDC＝90°，∵∠B＝60°，∠CAD＝45°，∴∠BCD＝30°，∠ACD＝45°，∴AD＝CD，设BD＝x，则CD＝x，∵AB＝8，∴AD＝8﹣x，∴CD＝8﹣x，∴x＝8﹣x，解得x＝4﹣4，∴CD＝8﹣4，∴S△ABC＝•AB•CD＝×8×（8﹣4）＝32﹣16．19．解：过点A作AD⊥BC，交BC的延长线于点D．∵∠B＝45°，∠BAC＝15°，∠ADC＝90°，∴∠DCA＝60°，∠BAD＝45°．在Rt△ACD中，∵cos∠DCA＝＝cos60°＝，sin∠DCA＝＝sin60°＝，AC＝10，∴CD＝5，AD＝5．在Rt△ABD中，∵∠BAD＝∠B，∴BD＝AD＝5．∴BC＝BD﹣CD＝5﹣5．20．解：（1）过点A作AH⊥BD于H，如图1所示：∵Rt△ABC，∠BAC＝90°，BC＝6，AC＝4，∴AB＝＝＝2，∵AB•AC＝BC•AH，∴AH＝＝＝，∴BH＝＝＝，∵AH⊥BD，∴BH＝HD＝，∴BD＝；（2）过点D作DM⊥AC于M，如图2所示：由（1）得：AH＝，BD＝，AB＝2，∴AD＝AB＝2，CD＝BC﹣BD＝6﹣＝，∵AH•CD＝DM•AC，∴DM＝＝＝，在Rt△ADM中，由勾股定理得：AM＝＝＝，∴cos∠DAC＝＝＝．21．解：（1）∵AC＝CD，∴∠CAD＝∠ADC＝∠EDB，又∵在Rt△EDB中，∠EDB+∠EBD＝90°，在Rt△ABC中，∠CAD+∠ABC＝90°，∴∠EBD＝∠ABC，∴sin∠EBD＝sin∠ABC＝；（2）过点C作CF⊥AB于点F，如图所示：在Rt△ACB中，cos∠CAB＝＝sin∠ABC＝，∴在Rt△AFC中，cos∠CAF＝＝＝，∴AF＝1，又∵△CAD为等腰三角形，CF⊥AD，∴AD＝2AF＝2．22．（1）证明：如图，连接OD，∵AC＝CD，∴∠A＝∠ADC＝∠BDE，∵∠AOB＝90°，∴∠A+∠ABO＝90°，又∵OB＝OD，∴∠OBD＝∠ODB，∴∠ODB+∠BDE＝90°，即OD⊥EC，∵OD是半径，∴EC是⊙O的切线；（2）解：在Rt△COD中，由于sin∠OCD＝，设OD＝4x，则OC＝5x，∴CD＝＝3x＝AC，在Rt△AOB中，OB＝OD＝4x，OA＝OC+AC＝8x，AB＝4，由勾股定理得，OB2+OA2＝AB2，即：（4x）2+（8x）2＝（4）2，解得x＝1或x＝﹣1（舍去），∴AC＝3x＝3，OC＝5x＝5，OB＝OD＝4x＝4，∵∠ODC＝∠EOC＝90°，∠OCD＝∠ECO，∴△COD∽△CEO，∴＝，即＝，∴EC＝，∴S阴影部分＝S△COE﹣S扇形＝××4﹣＝﹣4π＝，答：AC＝3，阴影部分的面积为．。

苏科版九年级下册数学下册 7.5解直角三角形练习

C BA 锐角三角函数章节------解直角三角形（含答案）知识梳理：1 三边之间的关系： a²+b²=c²2 两锐角之间的关系： ∠A+∠B=903. 边与角之间的关系：sinA=角A 的对边角A 的斜边 cosA=角A 的邻边角A 的斜边 tanA=角A 的对边角A 的邻边总结：由直角三角形中的已知元素求出其他未知元素的过程，叫做解直角三角形。

例题讲解：例1. 如图，已知正方形ABCD 的边长为2，如果将线段BD 绕着点B 旋转后，点D 落在CB 的延长线上的D ′处，那么tan ∠BAD ′等于（）(A)．1 (B)．√ (C)．√22 (D)．2√例2、如果a 是锐角，且cosa=45，那么sina 的值是（）．（A ）925 （B ） 45 （C ）35 （D ）1625例3、等腰三角形底边长为10㎝，周长为36cm ，那么底角的余弦等于（）．（A ）513 （B ）1213 （C ）1013 （D ）512例4、在Rt △ABC 中，∠C ＝90°，下列式子中正确的是（）．（A ）sinA=sinB （B ）sinA=cosB（C ）tanA=tanB （D ）cotA=cotB例5、已知α为锐角，tan （90°－α）=√3，则α的度数为（）（A ）30° （B ）45° （C ）60° （D ）75°例6、如果∠a 是等边三角形的一个内角，那么cos a 的值等于（）．（A ）12 （B ）√22 （C ）√32 （D ）1例7、如图，在△ABC 中，若∠A ＝30°，∠B ＝45°，AC ＝√22，则BC ＝例8、如图，沿倾斜角为30︒的山坡植树，要求相邻两棵树的水平距离AC 为2m ，那么相邻两棵树的斜坡距离AB 为 m 。

(精确到0.1m)例9、求值：sin 245°- cos60°+ tan60°·cos 230°例10、如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为60°，路基高度为5.8米，求路基下底宽（精确到0.1米）.例11、如图，某一水库大坝的横断面是梯形ABCD ，坝顶宽CD ＝5米，斜坡AD ＝16米，坝高 6米，斜坡BC 的坡度i=1：3.求斜坡AD 的坡角∠A （精确到1分）和坝底宽AB ．（精确到0.1米）例12、某中学有一块三角形形状的花圃ABC,现可直接测到∠A=30°,AC=40米,BC=25米, 请你求出这块花圃可能的面积(结果保留根号)D CBA巩固练习：1．如图，在Rt△ABC 中，除∠C＝90°外，其余______个元素之间存在以下关系： (l)三边之间的关系：____________（也就是__________定理）；(2)两个锐角之间的关系：____________；(3)边角之间的关系：sin A ＝________，cos A ＝________，tan A ＝_________．2．如图，在梯形ABCD 中，AD ∥BC ，∠B ＝30°，∠C ＝60°，AD ＝4，AB ＝3√3，则底BC 的长为_______．3．在△ABC 中，∠C ＝90°，a ＝3，c ＝2√3，则∠B ＝________．4．在△ABC 中，∠C ＝90°，∠A ＝45°，c ＝6，则b ＝________．5．在Rt△ABC 中，∠C ＝90°，BC ＝√5，AC ＝√15，则∠A 的度数为 ( )A ．90°B ．60°C ．45°D ．30°6．在Rt△ABC 中，∠C ＝90°，则在下列边角之间的关系中，正确的是 ( )A ．b ＝c sin AB ．a ＝b tan AC ．a ＝b tan BD ．b ＝c cos B7．在△ABC 中，∠C ＝90°，tan A ＝13，则sin B 的值为 ( )A ．√1010B ．23C ．34D ．√10√10 8．如图，在△ABC 中，cosB=√22，sinC ＝35，AC ＝5，则△ABC 的面积是( )A ．212 B ．12 C ．14 D ．219．如图，为了测量河两岸A、B两点的距离，在与AB垂直的方向点C处测得AC＝a，∠ACB＝α，则AB的长为( ) A．a．sin α B．a．tan αC．a．cos αD．33 tan10.在Rt△ABC中，∠C＝90°．根据下列条件解直角三角形：(1)已知c＝20，∠A＝45°；(2)已知a＝36，∠B＝30°；(3)已知a＝19，c＝19√2；(4)a＝6√2，b＝66．11．如图，在菱形ABCD中，AE⊥BC于E点，EC＝1，sinB＝513．求四边形ABCD的周长．12．如图，在△ABC中，∠C＝90°，D是BC的中点，∠ADC＝60°，AC＝√3，求△ABD的周长．13．如图，某居民楼I高20米，窗户朝南，该楼内一楼住户的窗台到地面的距离CM为2米，窗户CD高1.8米．现计划在I楼的正南方向距I楼30米处新建一居民楼Ⅱ．当正午时刻太阳光线与地面成30°角时，要使Ⅱ楼的影子不影响I楼所有住户的采光，新建Ⅱ楼最高只能盖多少米？14．在Rt△ABC中，∠C＝90°，b＋c＝24，∠A－∠B＝30°，解此直角三角形．15．如图，在△ABC中∠C＝90°，∠A＝45°，D为AC上一点，∠BDC＝60°，AD＝2，求BC 的长．16．已知等腰三角形的底边长为20 cm，面积为100√3cm2，求此三角形各内角的度数．317．如图，⊙O的直径AB与弦CD相交于点E，弧BC=弧BD，⊙O的切线BF与弦AD的，求线段AD、CD的长．延长线相交于点F，连接BC，若⊙O的半径为4，cos∠BCD＝3418.如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取√3＝1.732，结果精确到1m）巩固练习答案：1．5 (1) a 2＋b 2 ＝c 2 勾股 (2) ∠A ＋∠B ＝90° (3)a c b c ab 2．103．30° 4．5．D 6．B 7．D 8．A 9．B10．(1)∠B ＝45°，a ＝10√b ＝10(2)∠A ＝60°，b ＝12，c ＝24 (3)∠A ＝45°，∠B ＝45°，b ＝19(4)∠A ＝30°，∠B ＝60°，c ＝11．可以求得边长为13，则四边形ABCD 的周长为52.12．△ABD的周长为3+13．新建居民楼Ⅱ最高只能盖（10√3＋2）米14. ∠A ＝60°，∠B ＝30°，a ＝，b ＝8，c ＝1615．BC＋116．三个内角分别为30°、30°、120°17．AD ＝6， CD ＝18. 设CE ＝x m ，则由题意可知BE ＝x m ，AE ＝(x ＋100)m ．在Rt △AEC 中，tan ∠CAE ＝AE CE ，即tan30°＝100+x x∴33100=+x x ，3x ＝3(x ＋100)解得x ＝50＋503＝136.6∴CD ＝CE ＋ED ＝(136.6＋1.5)＝138.1≈138(m)。

苏科版初中数学九年级下册《7.5 解直角三角形》同步练习卷

苏科新版九年级下学期《7.5 解直角三角形》同步练习卷一．选择题（共16小题）1．如图，在△ABC中，AB＝AC，BC＝12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD＝x，tan∠ACB＝y，则（）A．x﹣y2＝3B．2x﹣y2＝9C．3x﹣y2＝15D．4x﹣y2＝21 2．如图，在△ABC中，AC⊥BC，∠ABC＝30°，点D是CB延长线上的一点，且BD＝BA，则tan∠DAC的值为（）A．2+B．2C．3+D．33．如图，在△ABC中，AD⊥BC，垂足为点D，若AC＝6，∠C＝45°，tan ∠ABC＝3，则BD等于（）A．2B．3C．3D．24．如图，△ABC中AB＝AC＝4，∠C＝72°，D是AB中点，点E在AC上，DE⊥AB，则cos A的值为（）A．B．C．D．5．如图，在Rt△ABC中，∠B＝90°，∠A＝30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（）A．B．C．D．6．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是（）A．B．4C．8D．47．在Rt△ABC中，∠C＝90°，sin A＝，BC＝6，则AB＝（）A．4B．6C．8D．108．在Rt△ABC中，∠C＝90°，sin A＝，AC＝6cm，则BC的长度为（）A．6cm B．7cm C．8cm D．9cm9．如图，以原点O为圆心，半径为1的弧交坐标轴于A，B两点，P是上一点（不与A，B重合），连接OP，设∠POB＝α，则点P的坐标是（）A．（sinα，sinα）B．（cosα，cosα）C．（cosα，sinα）D．（sinα，cosα）10．如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（）A．B．C．D．211．在△ABC中，AB＝12，AC＝13，cos∠B＝，则BC边长为（）A．7B．8C．8或17D．7或1712．如图，在直角△BAD中，延长斜边BD到点C，使DC＝BD，连接AC，若tan B＝，则tan∠CAD的值（）A．B．C．D．13．如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）A．1，2，3B．1，1，C．1，1，D．1，2，14．如图，若△ABC和△DEF的面积分别为S1、S2，则（）A．S1＝S2B．S1＝S2C．S1＝S2D．S1＝S2 15．在Rt△ACB中，∠C＝90°，AB＝10，sin A＝，cos A＝，tan A＝，则BC的长为（）A．6B．7.5C．8D．12.516．在直角三角形ABC中，已知∠C＝90°，∠A＝40°，BC＝3，则AC＝（）A．3sin40°B．3sin50°C．3tan40°D．3tan50°二．填空题（共20小题）17．如图，点D为△ABC的AB边上的中点，点E为AD的中点，△ADC为正三角形，给出下列结论，①CB＝2CE，②tan∠B＝，③∠ECD＝∠DCB，④若AC＝2，点P是AB上一动点，点P到AC、BC边的距离分别为d1，d2，则d12+d22的最小值是3．其中正确的结论是（填写正确结论的番号）．18．四边形ABCD中，BD是对角线，∠ABC＝90°，tan∠ABD＝，AB＝20，BC＝10，AD＝13，则线段CD＝．19．如图，在△ABC中，AC＝6，BC＝10，tan C＝，点D是AC边上的动点（不与点C重合），过D作DE⊥BC，垂足为E，点F是BD的中点，连接EF，设CD＝x，△DEF的面积为S，则S与x之间的函数关系式为．20．已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积等于．21．如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则tan∠AOD＝．22．如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则∠BAC的正弦值是．23．如图，在Rt△ABC中，∠C＝90°，点D是AB的中点，ED⊥AB交AC于点E．设∠A＝α，且tanα＝，则tan2α＝．24．△ABC中，AB＝12，AC＝，∠B＝30°，则△ABC的面积是．25．在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D都在格点处，AB与CD相交于O，则tan∠BOD的值等于．26．如图，Rt△ABC中，∠C＝90°，BC＝15，tan A＝，则AB＝．27．如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C＝1，tan∠BA2C ＝，tan∠BA3C＝，计算tan∠BA4C＝，…按此规律，写出tan∠BA n C＝（用含n的代数式表示）．28．已知△ABC中，tan B＝，BC＝6，过点A作BC边上的高，垂足为点D，且满足BD：CD＝2：1，则△ABC面积的所有可能值为．29．如图，在直角坐标系中，点A，B分别在x轴，y轴上，点A的坐标为（﹣1，0），∠ABO＝30°，线段PQ的端点P从点O出发，沿△OBA的边按O→B →A→O运动一周，同时另一端点Q随之在x轴的非负半轴上运动，如果PQ ＝，那么当点P运动一周时，点Q运动的总路程为．30．如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα＝，则t的值是．31．如图，△ABC中，AD平分∠BAC，AC＝AD＝2，AB＝3，cos∠ABC的值为．32．BD为等腰△ABC的腰AC上的高，BD＝1，tan∠ABD＝，则CD的长为．33．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD的值是．34．已知在△ABC中，AB＝AC＝8，∠BAC＝30°，将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于．35．如图，Rt△ABC中，∠C＝90°，∠B＝30°，BC＝6，则AB的长为．36．如图，在Rt△ABC中，∠C＝90°，∠B＝37°，BC＝32，则AC＝．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）三．解答题（共14小题）37．阅读下列材料：如图1，在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，可以得到：S△ABC＝ab sin C＝ac sin B＝bc sin A证明：过点A作AD⊥BC，垂足为D．在Rt△ABD中，sin B＝∴AD＝c•sin B∴S＝a•AD＝ac sin B△ABC＝ab sin C同理：S△ABCS△ABC＝bc sin A∴S＝ab sin C＝ac sin B＝bc sin A△ABC（1）通过上述材料证明：＝＝（2）运用（1）中的结论解决问题：如图2，在△ABC中，∠B＝15°，∠C＝60°，AB＝20，求AC的长度．（3）如图3，为了开发公路旁的城市荒地，测量人员选择A、B、C三个测量点，在B点测得A在北偏东75°方向上，沿笔直公路向正东方向行驶18km到达C点，测得A在北偏西45°方向上，根据以上信息，求A、B、C三点围成的三角形的面积．（本题参考数值：sin15°≈0.3，sin120°≈0.9，≈1.4，结果取整数）38．如图①，在Rt△ABC中，以下是小亮探究与之间关系的方法：∵sin A＝，sin B＝∴c＝，c＝∴＝根据你掌握的三角函数知识．在图②的锐角△ABC中，探究、、之间的关系，并写出探究过程．39．如图，已知△ABC中，AB＝BC＝5，tan∠ABC＝．（1）求边AC的长；（2）设边BC的垂直平分线与边AB的交点为D，求的值．40．如图，在△ABC中，BC＝12，tan A＝，∠B＝30°；求AC和AB的长．41．把（sinα）2记作sin2α，根据图1和图2完成下列各题．（1）sin2A1+cos2A1＝，sin2A2+cos2A2＝，sin2A3+cos2A3＝；（2）观察上述等式猜想：在Rt△ABC中，∠C＝90°，总有sin2A+cos2A＝；（3）如图2，在Rt△ABC中证明（2）题中的猜想：（4）已知在△ABC中，∠A+∠B＝90°，且sin A＝，求cos A．42．某游乐场部分平面图如图所示，C、E、A在同一直线上，D、E、B在同一直线上，测得A处与E处的距离为80 米，C处与D处的距离为34米，∠C ＝90°，∠ABE＝90°，∠BAE＝30°．（≈1.4，≈1.7）（1）求旋转木马E处到出口B处的距离；（2）求海洋球D处到出口B处的距离（结果保留整数）．43．如图，四边形ABCD是一片水田，某村民小组需计算其面积，测得如下数据：∠A＝90°，∠ABD＝60°，∠CBD＝54°，AB＝200m，BC＝300m．请你计算出这片水田的面积．（参考数据：sin54°≈0.809，cos54°≈0.588，tan54°≈1.376，≈1.732）44．如图，在四边形ABCD中，∠BCD是钝角，AB＝AD，BD平分∠ABC，若CD＝3，BD＝，sin∠DBC＝，求对角线AC的长．45．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝3，点D在边AC上，且AD＝2CD，DE⊥AB，垂足为点E，联结CE，求：（1）线段BE的长；（2）∠ECB的余切值．46．如图，已知四边形ABCD中，∠ABC＝90°，∠ADC＝90°，AB＝6，CD ＝4，BC的延长线与AD的延长线交于点E．（1）若∠A＝60°，求BC的长；（2）若sin A＝，求AD的长．（注意：本题中的计算过程和结果均保留根号）47．如图，△ABC中，AD⊥BC，垂足是D，若BC＝14，AD＝12，tan∠BAD＝，求sin C的值．48．如图方格纸中每个小正方形的边长均为1，点A，B在小正方形的顶点上．（1）在图中画出△ABC（点C在小正方形的顶点上），使∠ABC＝90°，tan∠A ＝2．（2）直接写出△ABC的周长和面积．49．如图，AD是△ABC的中线，tan B＝，cos C＝，AC＝．求：（1）BC的长；（2）sin∠ADC的值．50．如图①所示，将直尺摆放在三角板上，使直尺与三角板的边分别交于点D，E，F，G，已知∠CGD＝42°（1）求∠CEF的度数；（2）将直尺向下平移，使直尺的边缘通过三角板的顶点B，交AC边于点H，如图②所示，点H，B在直尺上的读数分别为4，13.4，求BC的长（结果保留两位小数）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）苏科新版九年级下学期《7.5 解直角三角形》同步练习卷参考答案与试题解析一．选择题（共16小题）1．如图，在△ABC中，AB＝AC，BC＝12，E为AC边的中点，线段BE的垂直平分线交边BC于点D．设BD＝x，tan∠ACB＝y，则（）A．x﹣y2＝3B．2x﹣y2＝9C．3x﹣y2＝15D．4x﹣y2＝21【分析】过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，根据线段垂直平分线求出DE＝BD＝x，根据等腰三角形求出BQ＝CQ＝6，求出CM＝QM ＝3，解直角三角形求出EM＝3y，AQ＝6y，在Rt△DEM中，根据勾股定理求出即可．【解答】解：过A作AQ⊥BC于Q，过E作EM⊥BC于M，连接DE，∵BE的垂直平分线交BC于D，BD＝x，∴BD＝DE＝x，∵AB＝AC，BC＝12，tan∠ACB＝y，∴＝＝y，BQ＝CQ＝6，∴AQ＝6y，∵AQ⊥BC，EM⊥BC，∴AQ∥EM，∵E为AC中点，∴CM＝QM＝CQ＝3，∴EM＝3y，∴DM＝12﹣3﹣x＝9﹣x，在Rt△EDM中，由勾股定理得：x2＝（3y）2+（9﹣x）2，即2x﹣y2＝9，故选：B．【点评】本题考查了线段垂直平分线性质，等腰三角形的性质，勾股定理，解直角三角形等知识点，能正确作出辅助线是解此题的关键．2．如图，在△ABC中，AC⊥BC，∠ABC＝30°，点D是CB延长线上的一点，且BD＝BA，则tan∠DAC的值为（）A．2+B．2C．3+D．3【分析】通过解直角△ABC得到AC与BC、AB间的数量关系，然后利用锐角三角函数的定义求tan∠DAC的值．【解答】解：如图，∵在△ABC中，AC⊥BC，∠ABC＝30°，∴AB＝2AC，BC＝＝AC．∵BD＝BA，∴DC＝BD+BC＝（2+）AC，∴tan∠DAC＝＝＝2+．故选：A．【点评】本题考查了解直角三角形，利用锐角三角函数的概念解直角三角形问题．3．如图，在△ABC中，AD⊥BC，垂足为点D，若AC＝6，∠C＝45°，tan∠ABC＝3，则BD等于（）A．2B．3C．3D．2【分析】根据三角函数定义可得AD＝AC•sin45°，从而可得AD的长，再利用正切定义可得BD的长．【解答】解：∵AC＝6，∠C＝45°，∴AD＝AC•sin45°＝6×＝6，∵tan∠ABC＝3，∴＝3，∴BD＝＝2，故选：A．【点评】此题主要考查了解直角三角形，关键是掌握三角函数定义．4．如图，△ABC中AB＝AC＝4，∠C＝72°，D是AB中点，点E在AC上，DE⊥AB，则cos A的值为（）A．B．C．D．【分析】先根据等腰三角形的性质与判定以及三角形内角和定理得出∠EBC＝36°，∠BEC＝72°，AE＝BE＝BC．再证明△BCE∽△ABC，根据相似三角形的性质列出比例式＝，求出AE，然后在△ADE中利用余弦函数定义求出cos A的值．【解答】解：∵△ABC中，AB＝AC＝4，∠C＝72°，∴∠ABC＝∠C＝72°，∠A＝36°，∵D是AB中点，DE⊥AB，∴AE＝BE，∴∠ABE＝∠A＝36°，∴∠EBC＝∠ABC﹣∠ABE＝36°，∠BEC＝180°﹣∠EBC﹣∠C＝72°，∴∠BEC＝∠C＝72°，∴BE＝BC，∴AE＝BE＝BC．设AE＝x，则BE＝BC＝x，EC＝4﹣x．在△BCE与△ABC中，，∴△BCE∽△ABC，∴＝，即＝，解得x＝﹣2±2（负值舍去），∴AE＝﹣2+2．在△ADE中，∵∠ADE＝90°，∴cos A＝＝＝．故选：C．【点评】本题考查了解直角三角形，等腰三角形的性质与判定，三角形内角和定理，线段垂直平分线的性质，相似三角形的判定与性质，难度适中．证明△BCE∽△ABC是解题的关键．5．如图，在Rt△ABC中，∠B＝90°，∠A＝30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（）A．B．C．D．【分析】设BC＝x，由含30°角的直角三角形的性质得出AC＝2BC＝2x，求出AB＝BC＝x，根据题意得出AD＝BC＝x，AE＝DE＝AB＝x，作EM ⊥AD于M，由等腰三角形的性质得出AM＝AD＝x，在Rt△AEM中，由三角函数的定义即可得出结果．【解答】解：如图所示：设BC＝x，∵在Rt△ABC中，∠B＝90°，∠A＝30°，∴AC＝2BC＝2x，AB＝BC＝x，根据题意得：AD＝BC＝x，AE＝DE＝AB＝x，作EM⊥AD于M，则AM＝AD＝x，在Rt△AEM中，cos∠EAD＝＝＝；故选：B．【点评】本题考查了解直角三角形、含30°角的直角三角形的性质、等腰三角形的性质、三角函数；通过作辅助线求出AM是解决问题的关键．6．如图，在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，则BC的长是（）A．B．4C．8D．4【分析】根据cos B＝及特殊角的三角函数值解题即可．【解答】解：∵在Rt△ABC中，∠C＝90°，∠B＝30°，AB＝8，cos B＝，即cos30°＝，∴BC＝8×＝4；故选：D．【点评】本题考查了三角函数的定义及特殊角的三角函数值，是基础知识，需要熟练掌握．7．在Rt△ABC中，∠C＝90°，sin A＝，BC＝6，则AB＝（）A．4B．6C．8D．10【分析】在直角三角形ABC中，利用锐角三角函数定义表示出sin A，将sin A的值与BC的长代入求出AB的长即可．【解答】解：在Rt△ABC中，∠C＝90°，sin A＝＝，BC＝6，∴AB＝＝＝10，故选：D．【点评】此题考查了解直角三角形，熟练掌握锐角三角函数定义是解本题的关键．8．在Rt△ABC中，∠C＝90°，sin A＝，AC＝6cm，则BC的长度为（）A．6cm B．7cm C．8cm D．9cm【分析】根据三角函数的定义求得BC和AB的比值，设出BC、AB，然后利用勾股定理即可求解．【解答】解：∵sin A＝＝，∴设BC＝4x，AB＝5x，又∵AC2+BC2＝AB2，∴62+（4x）2＝（5x）2，解得：x＝2或x＝﹣2（舍），则BC＝4x＝8cm，故选：C．【点评】本题考查了三角函数与勾股定理，正确理解三角函数的定义是关键．9．如图，以原点O为圆心，半径为1的弧交坐标轴于A，B两点，P是上一点（不与A，B重合），连接OP，设∠POB＝α，则点P的坐标是（）A．（sinα，sinα）B．（cosα，cosα）C．（cosα，sinα）D．（sinα，cosα）【分析】过P作PQ⊥OB，交OB于点Q，在直角三角形OPQ中，利用锐角三角函数定义表示出OQ与PQ，即可确定出P的坐标．【解答】解：过P作PQ⊥OB，交OB于点Q，在Rt△OPQ中，OP＝1，∠POQ＝α，∴sinα＝，cosα＝，即PQ＝sinα，OQ＝cosα，则P的坐标为（cosα，sinα），故选：C．【点评】此题考查了解直角三角形，以及坐标与图形性质，熟练掌握锐角三角函数定义是解本题的关键．10．如图，在平面直角坐标系中，直线OA过点（2，1），则tanα的值是（）A．B．C．D．2【分析】设（2，1）点是B，作BC⊥x轴于点C，根据三角函数的定义即可求解．【解答】解：设（2，1）点是B，作BC⊥x轴于点C．则OC＝2，BC＝1，则tanα＝＝．故选：C．【点评】本题考查了三角函数的定义，理解正切函数的定义是关键．11．在△ABC中，AB＝12，AC＝13，cos∠B＝，则BC边长为（）A．7B．8C．8或17D．7或17【分析】首先根据特殊角的三角函数值求得∠B的度数，然后分锐角三角形和钝角三角形分别求得BD和CD的长后即可求得线段BC的长．【解答】解：∵cos∠B＝，∴∠B＝45°，当△ABC为钝角三角形时，如图1，∵AB＝12，∠B＝45°，∴AD＝BD＝12，∵AC＝13，∴由勾股定理得CD＝5，∴BC＝BD﹣CD＝12﹣5＝7；当△ABC为锐角三角形时，如图2，BC＝BD+CD＝12+5＝17，故选：D．【点评】本题考查了解直角三角形的知识，能从中整理出直角三角形是解答本题的关键，难点为分类讨论，难点中等．12．如图，在直角△BAD中，延长斜边BD到点C，使DC＝BD，连接AC，若tan B＝，则tan∠CAD的值（）A．B．C．D．【分析】延长AD，过点C作CE⊥AD，垂足为E，由tan B＝，即＝，设AD＝5x，则AB＝3x，然后可证明△CDE∽△BDA，然后相似三角形的对应边成比例可得：，进而可得CE＝x，DE＝，从而可求tan ∠CAD＝＝．【解答】解：如图，延长AD，过点C作CE⊥AD，垂足为E，∵tan B＝，即＝，∴设AD＝5x，则AB＝3x，∵∠CDE＝∠BDA，∠CED＝∠BAD，∴△CDE∽△BDA，∴，∴CE＝x，DE＝，∴AE＝，∴tan∠CAD＝＝．故选：D．【点评】本题考查了锐角三角函数的定义，相似三角形的判定和性质以及直角三角形的性质，是基础知识要熟练掌握，解题的关键是：正确添加辅助线，将∠CAD放在直角三角形中．13．如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）A．1，2，3B．1，1，C．1，1，D．1，2，【分析】A、根据三角形三边关系可知，不能构成三角形，依此即可作出判定；B、根据勾股定理的逆定理可知是等腰直角三角形，依此即可作出判定；C、解直角三角形可知是顶角120°，底角30°的等腰三角形，依此即可作出判定；D、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，依此即可作出判定．【解答】解：A、∵1+2＝3，不能构成三角形，故选项错误；B、∵12+12＝（）2，是等腰直角三角形，故选项错误；C、底边上的高是＝，可知是顶角120°，底角30°的等腰三角形，故选项错误；D、解直角三角形可知是三个角分别是90°，60°，30°的直角三角形，其中90°÷30°＝3，符合“智慧三角形”的定义，故选项正确．故选：D．【点评】考查了解直角三角形，涉及三角形三边关系，勾股定理的逆定理，等腰直角三角形的判定，“智慧三角形”的概念．14．如图，若△ABC和△DEF的面积分别为S1、S2，则（）A．S1＝S2B．S1＝S2C．S1＝S2D．S1＝S2【分析】过A点作AG⊥BC于G，过D点作DH⊥EF于H．在Rt△ABG中，根据三角函数可求AG，在Rt△ABG中，根据三角函数可求DH，根据三角形面积公式可得S1，S2，依此即可作出选择．【解答】解：过A点作AG⊥BC于G，过D点作DH⊥EF于H．在Rt△ABG中，AG＝AB•sin40°＝5sin40°，∠DEH＝180°﹣140°＝40°，在Rt△DHE中，DH＝DE•sin40°＝8sin40°，S1＝8×5sin40°÷2＝20sin40°，S2＝5×8sin40°÷2＝20sin40°．则S1＝S2．故选：C．【点评】本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系，关键是作出高线构造直角三角形．15．在Rt△ACB中，∠C＝90°，AB＝10，sin A＝，cos A＝，tan A＝，则BC的长为（）A．6B．7.5C．8D．12.5【分析】根据三角函数的定义来解决，由sin A＝＝，即可得BC．【解答】解：∵∠C＝90°，AB＝10，∴sin A＝，∴BC＝AB×＝10×＝6．故选：A．【点评】本题考查了解直角三角形和勾股定理的应用，注意：在Rt△ACB中，∠C＝90°，则sin A＝，cos A＝，tan A＝．16．在直角三角形ABC中，已知∠C＝90°，∠A＝40°，BC＝3，则AC＝（）A．3sin40°B．3sin50°C．3tan40°D．3tan50°【分析】利用直角三角形两锐角互余求得∠B的度数，然后根据正切函数的定义即可求解．【解答】解：∠B＝90°﹣∠A＝90°﹣40°＝50°，又∵tan B＝，∴AC＝BC•tan B＝3tan50°．故选：D．【点评】本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．二．填空题（共20小题）17．如图，点D为△ABC的AB边上的中点，点E为AD的中点，△ADC为正三角形，给出下列结论，①CB＝2CE，②tan∠B＝，③∠ECD＝∠DCB，④若AC＝2，点P是AB上一动点，点P到AC、BC边的距离分别为d1，d2，则d12+d22的最小值是3．其中正确的结论是①③④（填写正确结论的番号）．【分析】由题意可得△BCE是含有30°的直角三角形，根据含有30°的直角三角形的性质可判断①②③，易证四边形PMCN是矩形，可得d12+d22＝MN2＝CP2，根据垂线段最短，可得CP的值即可求d12+d22的最小值，即可判断④．【解答】解：∵D是AB中点∴AD＝BD∵△ACD是等边三角形，E是AD中点∴AD＝CD，∠ADC＝60°＝∠ACD，CE⊥AB，∠DCE＝30°∴CD＝BD∴∠B＝∠DCB＝30°，且∠DCE＝30°，CE⊥AB∴∠ECD＝∠DCB，BC＝2CE，tan∠B＝故①③正确，②错误∵∠DCB＝30°，∠ACD＝60°∴∠ACB＝90°若AC＝2，点P是AB上一动点，点P到AC、BC边的距离分别为d1，d2，∴四边形PMCN是矩形∴MN＝CP∵d12+d22＝MN2＝CP2∴当CP为最小值，d12+d22的值最小∴根据垂线段最短，则当CP⊥AB时，d12+d22的值最小此时：∠CAB＝60°，AC＝2，CP⊥AB∴CP＝∴d12+d22＝MN2＝CP2＝3即d12+d22的最小值为3故④正确故答案为①③④【点评】本题考查了解直角三角形，等边三角形的性质和判定，利用垂线段最短求d12+d22的最小值是本题的关键．18．四边形ABCD中，BD是对角线，∠ABC＝90°，tan∠ABD＝，AB＝20，BC＝10，AD＝13，则线段CD＝17或．【分析】作AH⊥BD于H，CG⊥BD于G，根据正切的定义分别求出AH、BH，根据勾股定理求出HD，得到BD，根据勾股定理计算即可．【解答】解：当∠ADB为锐角时，作AH⊥BD于H，CG⊥BD于G，∵tan∠ABD＝，∴＝，设AH＝3x，则BH＝4x，由勾股定理得，（3x）2+（4x）2＝202，解得，x＝4，则AH＝12，BH＝16，在Rt△AHD中，HD＝＝5，∴BD＝BH+HD＝21，∵∠ABD+∠CBD＝90°，∠BCG+∠CBD＝90°，∴∠ABD＝∠BCG，∴＝，又BC＝10，∴BG＝6，CG＝8，∴DG＝BD﹣BG＝15，∴CD＝＝17，当∠ADB为钝角时，CD′＝＝，故答案为：17或．【点评】本题考查的是勾股定理、锐角三角函数的定义，掌握解直角三角形的一般步骤、理解锐角三角函数的定义是解题的关键．19．如图，在△ABC中，AC＝6，BC＝10，tan C＝，点D是AC边上的动点（不与点C重合），过D作DE⊥BC，垂足为E，点F是BD的中点，连接EF，设CD＝x，△DEF的面积为S，则S与x之间的函数关系式为S＝x2．【分析】可在直角三角形CED中，根据DE、CE的长，求出△BED的面积即可解决问题．【解答】解：（1）在Rt△CDE中，tan C＝，CD＝x∴DE＝x，CE＝x，∴BE＝10﹣x，＝×（10﹣x）•x＝﹣x2+3x．∴S△BED∵DF＝BF，＝x2，∴S＝S△BED故答案为S＝x2．【点评】本题考查解直角三角形，三角形的面积等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．20．已知△ABC中，AB＝10，AC＝2，∠B＝30°，则△ABC的面积等于15或10．【分析】作AD⊥BC交BC（或BC延长线）于点D，分AB、AC位于AD异侧和同侧两种情况，先在Rt△ABD中求得AD、BD的值，再在Rt△ACD中利用勾股定理求得CD的长，继而就两种情况分别求出BC的长，根据三角形的面积公式求解可得．【解答】解：作AD⊥BC交BC（或BC延长线）于点D，①如图1，当AB、AC位于AD异侧时，在Rt△ABD中，∵∠B＝30°，AB＝10，∴AD＝AB sin B＝5，BD＝AB cos B＝5，在Rt△ACD中，∵AC＝2，∴CD＝＝＝，则BC＝BD+CD＝6，∴S＝•BC•AD＝×6×5＝15；△ABC②如图2，当AB、AC在AD的同侧时，由①知，BD＝5，CD＝，则BC＝BD﹣CD＝4，∴S＝•BC•AD＝×4×5＝10．△ABC综上，△ABC的面积是15或10，故答案为15或10．【点评】本题主要考查解直角三角形，解题的关键是熟练掌握三角函数的运用、分类讨论思想的运算及勾股定理．21．如图，在边长为1的小正方形网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点O，则tan∠AOD＝2．【分析】首先连接BE，由题意易得BF＝CF，△ACO∽△BKO，然后由相似三角形的对应边成比例，易得KO：CO＝1：3，即可得OF：CF＝OF：BF＝1：2，在Rt△OBF中，即可求得tan∠BOF的值，继而求得答案．【解答】解：如图，连接BE，∵四边形BCEK是正方形，∴KF＝CF＝CK，BF＝BE，CK＝BE，BE⊥CK，∴BF＝CF，根据题意得：AC∥BK，∴△ACO∽△BKO，∴KO：CO＝BK：AC＝1：3，∴KO：KF＝1：2，∴KO＝OF＝CF＝BF，在Rt△OBF中，tan∠BOF＝＝2，∵∠AOD＝∠BOF，∴tan∠AOD＝2．故答案为：2【点评】此题考查了相似三角形的判定与性质，三角函数的定义．此题难度适中，解题的关键是准确作出辅助线，注意转化思想与数形结合思想的应用．22．如图，在4×4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则∠BAC的正弦值是．【分析】先根据勾股定理的逆定理判断出△ABC的形状，再由锐角三角函数的定义即可得出结论．【解答】解：∵AB2＝32+42＝25、AC2＝22+42＝20、BC2＝12+22＝5，∴AC2+BC2＝AB2，∴△ABC为直角三角形，且∠ACB＝90°，则sin∠BAC＝＝，故答案为：．【点评】本题考查的是勾股定理的逆定理以及锐角三角函数，熟知在一个三角形中，如果两条边长的平方之和等于第三边长的平方，那么这个三角形是直角三角形是解答此题的关键．23．如图，在Rt△ABC中，∠C＝90°，点D是AB的中点，ED⊥AB交AC于点E．设∠A＝α，且tanα＝，则tan2α＝．【分析】根据题目中的数据和锐角三角函数可以求得tan2α的值，本题得以解决．【解答】解：连接BE，∵点D是AB的中点，ED⊥AB，∠A＝α，∴ED是AB的垂直平分线，∴EB＝EA，∴∠EBA＝∠A＝α，∴∠BEC＝2α，∵tanα＝，设DE＝a，∴AD＝3a，AE＝，∴AB＝6a，∴BC＝，AC＝∴CE＝AC﹣AE＝，∴tan2α＝，故答案为：．【点评】本题考查解直角三角形、线段垂直平分线，解答本题的关键是明确题意，找出所求问题需要的条件，利用解直角三角形的相关知识解答．24．△ABC中，AB＝12，AC＝，∠B＝30°，则△ABC的面积是21或15．【分析】过A作AD⊥BC于D（或延长线于D），根据含30度角的直角三角形的性质得到AD的长，再根据勾股定理得到BD，CD的长，再分两种情况：如图1，当AD在△ABC内部时、如图2，当AD在△ABC外部时，进行讨论即可求解．【解答】解：①如图1，作AD⊥BC，垂足为点D，在Rt△ABD中，∵AB＝12、∠B＝30°，∴AD＝AB＝6，BD＝AB cos B＝12×＝6，在Rt△ACD中，CD＝＝＝，∴BC＝BD+CD＝6+＝7，则S＝×BC×AD＝×7×6＝21；△ABC②如图2，作AD⊥BC，交BC延长线于点D，由①知，AD＝6、BD＝6、CD＝，则BC＝BD﹣CD＝5，＝×BC×AD＝×5×6＝15，∴S△ABC故答案为：21或15．【点评】本题主要考查了解直角三角形，勾股定理，本题关键是得到BC和AD 的长，同时注意分类思想的运用．25．在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D都在格点处，AB与CD相交于O，则tan∠BOD的值等于3．【分析】根据平移的性质和锐角三角函数以及勾股定理，通过转化的数学思想可以求得tan∠BOD的值，本题得以解决．【解答】解：方法一：平移CD到C′D′交AB于O′，如右图所示，则∠BO′D′＝∠BOD，∴tan∠BOD＝tan∠BO′D′，设每个小正方形的边长为a，则O′B＝，O′D′＝，BD′＝3a，作BE⊥O′D′于点E，则BE＝，∴O′E＝＝，∴tan BO′E＝，∴tan∠BOD＝3，故答案为：3．方法二：连接AM、NL，在△CAH中，AC＝AH，则AM⊥CH，同理，在△MNH中，NM＝NH，则NL⊥MH，∴∠AMO＝∠NLO＝90°，∵∠AOM＝∠NOL，∴△AOM∽△NOL，∴，设图中每个小正方形的边长为a，则AM＝2a，NL＝a，∴＝2，∴，∴，∵NL＝LM，∴，∴tan∠BOD＝tan∠NOL＝＝3，故答案为：3．方法三：连接AE、EF，如右图所示，则AE∥CD，∴∠F AE＝∠BOD，设每个小正方形的边长为a，则AE＝，AF＝，EF＝a，∵，∴△F AE是直角三角形，∠FEA＝90°，∴tan∠F AE＝，即tan∠BOD＝3，故答案为：3．【点评】本题考查解直角三角形，解答本题的关键是明确题意，作出合适的辅助线，利用勾股定理和等积法解答．26．如图，Rt△ABC中，∠C＝90°，BC＝15，tan A＝，则AB＝17．【分析】根据∠A的正切求出AC，再利用勾股定理列式计算即可得解．【解答】解：∵Rt△ABC中，∠C＝90°，tan A＝，BC＝15，∴＝，解得AC＝8，根据勾股定理得，AB＝＝＝17．故答案为：17．【点评】本题考查了解直角三角形，勾股定理，主要利用了锐角的正切等于对边比邻边．27．如图，把n个边长为1的正方形拼接成一排，求得tan∠BA1C＝1，tan∠BA2C ＝，tan∠BA3C＝，计算tan∠BA4C＝，…按此规律，写出tan∠BA n C＝（用含n的代数式表示）．【分析】作CH⊥BA4于H，根据正方形的性质、勾股定理以及三角形的面积公式求出CH、A4H，根据正切的概念求出tan∠BA4C，总结规律解答．【解答】解：作CH⊥BA4于H，由勾股定理得，BA4＝＝，A4C＝，△BA4C的面积＝4﹣2﹣＝，∴××CH＝，解得，CH＝，则A4H＝＝，∴tan∠BA4C＝＝，1＝12﹣1+1，3＝22﹣2+1，7＝32﹣3+1，∴tan∠BA n C＝，故答案为：；．【点评】本题考查的是正方形的性质、勾股定理的应用以及正切的概念，掌握正方形的性质、熟记锐角三角函数的概念是解题的关键．28．已知△ABC中，tan B＝，BC＝6，过点A作BC边上的高，垂足为点D，且满足BD：CD＝2：1，则△ABC面积的所有可能值为8或24．【分析】分两种情况，根据已知条件确定高AD的长，然后根据三角形面积公式即可求得．【解答】解：如图1所示：∵BC＝6，BD：CD＝2：1，∴BD＝4，∵AD⊥BC，tan B＝，∴＝，∴AD＝BD＝，∴S＝BC•AD＝×6×＝8；△ABC如图2所示：∵BC＝6，BD：CD＝2：1，∴BD＝12，∵AD⊥BC，tan B＝，∴＝，∴AD＝BD＝8，＝BC•AD＝×6×8＝24；∴S△ABC综上，△ABC面积的所有可能值为8或24，故答案为8或24．【点评】本题考查了解直角三角形，以及三角函数的定义，三角形面积，分类讨论思想的运用是本题的关键．29．如图，在直角坐标系中，点A，B分别在x轴，y轴上，点A的坐标为（﹣1，0），∠ABO＝30°，线段PQ的端点P从点O出发，沿△OBA的边按O→B →A→O运动一周，同时另一端点Q随之在x轴的非负半轴上运动，如果PQ ＝，那么当点P运动一周时，点Q运动的总路程为4．【分析】首先根据题意正确画出从O→B→A运动一周的图形，分四种情况进行计算：①点P从O→B时，路程是线段PQ的长；②当点P从B→C时（QC ⊥AB，C为垂足），点Q从O运动到Q，计算OQ的长就是运动的路程；③点P从C→A时，点Q由Q向左运动，路程为QQ′；④点P从A→O时，点Q运动的路程就是点P运动的路程；最后相加即可．【解答】解：在Rt△AOB中，∵∠ABO＝30°，AO＝1，∴AB＝2，BO＝＝，①当点P从O→B时，如图1、图2所示，点Q运动的路程为，②如图3所示，QC⊥AB，则∠ACQ＝90°，即PQ运动到与AB垂直时，垂足为P，当点P从B→C时，∵∠ABO＝30°∴∠BAO＝60°∴∠OQD＝90°﹣60°＝30°∴cos30°＝∴AQ＝＝2∴OQ＝2﹣1＝1则点Q运动的路程为QO＝1，③当点P从C→A时，如图3所示，点Q运动的路程为QQ′＝2﹣，④当点P从A→O时，点Q运动的路程为AO＝1，∴点Q运动的总路程为：+1+2﹣+1＝4故答案为：4【点评】本题主要是应用三角函数定义来解直角三角形，此题的解题关键是理解题意，正确画出图形；线段的两个端点看成是两个动点，将线段移动问题转化为点移动问题．30．如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα＝，则t的值是．【分析】过点A作AB⊥x轴于B，根据正切等于对边比邻边列式求解即可．【解答】解：过点A作AB⊥x轴于B，∵点A（3，t）在第一象限，∴AB＝t，OB＝3，又∵tanα＝＝＝，∴t＝．故答案为：．【点评】本题考查了锐角三角函数的定义，过点A作x轴的垂线，构造出直角三角形是利用正切列式的关键，需要熟记正切＝对边：邻边．31．如图，△ABC中，AD平分∠BAC，AC＝AD＝2，AB＝3，cos∠ABC的值为．【分析】根据三角形角平分线定理得到＝，设BD＝3x，CD＝2x，过AE⊥CD于E，解直角三角形即可得到结论．【解答】解：∵AD平分∠BAC，∴＝，∴设BD＝3x，CD＝2x，过AE⊥CD于E，∵AD＝AC，∴DE＝CE＝x，∴BE＝4x，∴AB2﹣BE2＝AC2﹣CE2，∴32﹣（4x）2＝22﹣x2，∴x＝，∴BE＝，∴cos∠ABC＝，故答案为：．【点评】本题考查了三角形角平分线定理，解直角三角形，等腰三角形的性质，熟练掌握三角形的角平分线定理是解题的关键．32．BD为等腰△ABC的腰AC上的高，BD＝1，tan∠ABD＝，则CD的长为2或2﹣或．【分析】分两种情况：①如图1，∠A为钝角，AB＝AC，在R t△ABD中，根据锐角三角函数的定义即可得到结果；②如图2，∠A为锐角，AB＝AC，在R t △ABD中根据锐角三角函数的定义即可得到结果；③如图3，∠A为底角，由tan∠ABD＝，得到∠ABD＝60°于是得到∠A＝30°，求得∠C＝120°，在R t△BCD中根据锐角三角函数的定义即可得到结果．【解答】解：分三种情况：①如图1，∠A为钝角，AB＝AC，在R t△ABD中，∵BD＝1，tan∠ABD＝，∴AD＝，AB＝2，∴AC＝2，∴CD＝2+，②如图2，∠A为锐角，AB＝AC，在R t△ABD中，∵BD＝1，tan∠ABD＝，∴AD＝，AB＝2，∴AC＝2，∴CD＝2﹣，③如图3，∠A为底角，∵tan∠ABD＝，∴∠ABD＝60°，∴∠A＝30°，∴∠C＝120°，∴∠BCD＝60°∵BD＝1，∴CD＝；④∠C为锐角且为顶角时，如图4，∵BD⊥AC，∴∠ADB＝90°，∵tan∠ABD＝，∴∠ABD＝60°，∴∠A＝30°，∵∠CBA＝∠A＝30°，∴∠C＝120°＞90°，∴这种情况不存在；综上所述；CD的长为：2或2﹣或，故答案为：2或2﹣或．【点评】本题考查了等腰三角形的性质，解直角三角形，难点在于要分情况讨论．33．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB，垂足为D，则tan∠BCD的值是．【分析】先求得∠A＝∠BCD，然后根据锐角三角函数的概念求解即可．【解答】解：在Rt△ABC与Rt△BCD中，∠A+∠B＝90°，∠BCD+∠B＝90°．∴∠A＝∠BCD．∴tan∠BCD＝tan∠A＝＝＝．故答案为．【点评】本题考查了解直角三角形，三角函数值只与角的大小有关，因而求一个角的函数值，可以转化为求与它相等的其它角的三角函数值．34．已知在△ABC中，AB＝AC＝8，∠BAC＝30°，将△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，延长线段AD，交原△ABC的边BC的延长线于点E，那么线段DE的长等于4﹣4．【分析】作CH⊥AE于H，根据等腰三角形的性质和三角形内角和定理可计算出∠ACB＝（180°﹣∠BAC）＝75°，再根据旋转的性质得AD＝AB＝8，∠CAD＝∠BAC＝30°，则利用三角形外角性质可计算出∠E＝45°，接着在Rt△ACH中利用含30度的直角三角形三边的关系得CH＝AC＝4，AH＝CH＝4，所以DH＝AD﹣AH＝8﹣4，然后在Rt△CEH中利用∠E＝45°得到EH＝CH＝4，于是可得DE＝EH﹣DH＝4﹣4．【解答】解：作CH⊥AE于H，如图，∵AB＝AC＝8，∴∠B＝∠ACB＝（180°﹣∠BAC）＝（180°﹣30°）＝75°，∵△ABC绕点A旋转，使点B落在原△ABC的点C处，此时点C落在点D处，∴AD＝AB＝8，∠CAD＝∠BAC＝30°，∵∠ACB＝∠CAD+∠E，∴∠E＝75°﹣30°＝45°，在Rt△ACH中，∵∠CAH＝30°，。

九年级数学下册第7章 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习2 (新版)苏科版

—————————— 教育资源共享步入知识海洋 ————————[7.5 第2课时解直角三角形的应用]一、选择题1．在Rt △ABC 中，∠C ＝90°，∠B ＝35°，AB ＝7，则BC 的长为( ) A ．7sin35° B.7cos35°C ．7cos35°D ．7tan35°2．如图K －31－1，点A (3，t )在第一象限，OA 与x 轴所夹的锐角为α，tan α＝32，则t 等于( )图K －31－1A ．0.5B ．1.5C ．4.5D ．23．等腰三角形的顶角为120°，腰长为2 cm ，则它的底边长为链接听课例2归纳总结( )A. 3 cmB.4 33cmC ．2 cmD ．2 3 cm 4．如图K －31－2，⊙O 的直径AB ＝2，弦AC ＝1，点D 在⊙O 上，则∠D 的度数为( )图K －31－2A ．30°B ．45°C ．60°D ．75°5．如图K －31－3，在△ABC 中，∠BAC ＝90°，AB ＝AC ，D 为边AC 的中点，DE ⊥BC 于点E ，连接BD ，则tan ∠DBC 的值为( )图K －31－3A.13B.2－1 C ．2－ 3 D.14 二、填空题6．如图K －31－4，在平面直角坐标系xOy 中，O 为坐标原点，点P 的坐标为(5，12)，那么OP 与x 轴正半轴所夹的锐角为________．(精确到0.1°)图K －31－47．如图K －31－5，在菱形ABCD 中，AC ＝6，BD ＝8，则sin ∠ABC ＝________．图K －31－58．如图K －31－6，在△ABC 中，∠A ＝30°，∠B ＝45°，AC ＝2 3，则AB 的长为________．图K －31－69．2018·安徽四模如图K －31－7，在△ABC 中，AB ＝AC ，AH ⊥BC ，垂足为H ，如果AH ＝BC ，那么tan ∠BAH 的值是________．图K －31－710．2017·黑龙江在△ABC 中，AB ＝12，AC ＝39，∠B ＝30°，则△ABC 的面积是________．三、解答题11．2018·淮南模拟如图K －31－8，在△ABC 中，∠A ＝30°，cos B ＝45，AC ＝6 3.求AB 的长.链接听课例2归纳总结图K －31－812．如图K －31－9，在平面直角坐标系内，O 为原点，点A 的坐标为(10，0)，点B 在第一象限内，BO ＝5，sin ∠BOA ＝35.求：(1)点B 的坐标； (2)cos ∠BAO 的值．图K －31－913．2018·广安改编如图K －31－10，已知AB 是⊙O 的直径，P 是BA 延长线上一点，PC 切⊙O 于点C ，连接AC ，CG 是⊙O 的弦，CG ⊥AB ，垂足为D .(1)求证：∠PCA ＝∠ABC ；(2)过点A 作AE ∥PC 交⊙O 于点E ，连接BE .若cos P ＝45，PC ＝10，求BE 的长．图K －31－10阅读理解在锐角三角形ABC 中，∠A ，∠B ，∠ACB 的对边分别是a ，b ，c .如图K －31－11所示，过点C 作CD ⊥AB 于点D ，则cos A ＝AD b，即AD ＝b cos A ，图K －31－11∴BD ＝c －AD ＝c －b cos A .在Rt △ADC 和Rt △BDC 中，有CD 2＝AC 2－AD 2＝BC 2－BD 2， ∴b 2－b 2cos 2A ＝a 2－(c －b cos A )2，整理，得a 2＝b 2＋c 2－2bc cos A ，(1)同理可得b2＝a2＋c2－2ac cos B，(2)c2＝a2＋b2－2ab cos∠ACB. (3)这个结论就是著名的余弦定理，在以上三个等式中有六个元素a，b，c，∠A，∠B，∠ACB，若已知其中的任意三个元素，可求出其余的另外三个元素．如：在锐角三角形ABC中，∠A，∠B，∠C的对边分别是a，b，c，已知∠A＝60°，b ＝3，c＝6，则由(1)式可得a2＝32＋62－2×3×6cos60°＝27，∴a＝3 3，则∠B，∠C可由式子(2)，(3)分别求出，在此略．根据以上阅读理解，请你试着解决如下问题：已知锐角三角形ABC的三边a，b，c(a，b，c分别是∠A，∠B，∠C的对边)分别是7，8，9，求∠A，∠B，∠C的度数．(结果精确到1°)详解详析[课堂达标]1．[解析] C 在Rt △ABC 中，cos B ＝BCAB ，所以BC ＝AB ·cos B ＝7cos 35°.故选C .2．[解析] C 如图，过点A 作AB ⊥x 轴于点B.∵点A(3，t)在第一象限， ∴AB ＝t ，OB ＝3. 又∵tan α＝AB OB ＝t 3＝32，∴t ＝4.5. 故选C .3．[解析] D 如图，过点A 作AD ⊥BC 于点D ，则∠BAD ＝∠CAD ＝60°，BD ＝DC.∵AD ⊥BC ，∴∠B ＝30°.∵AB ＝2 cm ， ∴AD ＝1 cm ，BD ＝ 3 cm ， ∴BC ＝2 3 cm .故选D .4．[解析] C ∵AB 是⊙O 的直径，∴∠ACB ＝90°.∵AC ＝1，AB ＝2，∴sin ∠ABC ＝ACAB ＝12，∴∠ABC ＝30°，∠A ＝60°，∴∠D ＝60°，故选C . 5．[解析] A ∵在△ABC 中，∠BAC ＝90°，AB ＝AC ， ∴∠ABC ＝∠C ＝45°，BC ＝2AC. 又∵D 为边AC 的中点， ∴AD ＝DC ＝12AC.∵DE ⊥BC 于点E ， ∴∠CDE ＝∠C ＝45°， ∴DE ＝EC ＝22DC ＝24AC ， ∴tan ∠DBC ＝DEBE ＝24AC 2AC －24AC ＝13. 故选A .6．[答案] 67.4°[解析] 如图，过点P 作PA ⊥x 轴，垂足为A.由勾股定理，得OP ＝122＋52＝13，∴cos ∠POA ＝513，∴∠POA ≈67.4°.7．[答案] 2425[解析] 过点A 作AE ⊥BC ，垂足为E ，由AC ＝6，BD ＝8，根据勾股定理得AB ＝32＋42＝5，菱形ABCD 的面积＝12AC·BD＝BC·AE，即12×6×8＝5×AE ，得AE ＝245，所以sin ∠ABC＝AE AB ＝2455＝2425. 8．[答案] 3＋ 3[解析] 如图，过点C 作CD ⊥AB 于点D ，则∠ADC ＝∠BDC ＝90°. ∵∠B ＝45°，∴∠BCD ＝∠B ＝45°， ∴CD ＝BD.∵∠A ＝30°，AC ＝2 3， ∴CD ＝3， ∴BD ＝CD ＝ 3.由勾股定理，得AD ＝AC 2－CD 2＝3， ∴AB ＝AD ＋BD ＝3＋ 3.9．[答案] 12[解析] 设AH ＝BC ＝2x.∵AB ＝AC ，AH ⊥BC ，∴BH ＝CH ＝12BC ＝x ，∴tan ∠BAH ＝BH AH ＝x 2x ＝12.10．[答案] 21 3或15 3[解析] (1)当∠ACB 为锐角时，如图①，过点A 作AD ⊥BC ，垂足为D.在Rt △ABD 中，∵AB ＝12，∠B ＝30°， ∴AD ＝12AB ＝6，BD ＝AB·cos B ＝12×32＝6 3.在Rt △ACD 中，CD ＝AC 2－AD 2＝（39）2－62＝3， ∴BC ＝BD ＋CD ＝6 3＋3＝7 3，则S △ABC ＝12BC·AD＝12×7 3×6＝21 3；(2)当∠ACB 为钝角时，如图②，过点A 作AD ⊥BC ，交BC 的延长线于点D.由(1)知，AD ＝6，BD ＝6 3，CD ＝3，则BC ＝BD －CD ＝5 3，∴S △ABC ＝12BC·AD＝12×5 3×6＝15 3.故答案为21 3或15 3.11．解：如图，过点C 作CD ⊥AB 于点D.∵∠A ＝30°，∴CD ＝12AC ＝3 3，AD ＝AC ·cos A ＝9.∵cos B ＝45，∴设BD ＝4x ，则BC ＝5x.由勾股定理，得CD ＝3x.由题意，得3x ＝3 3，解得x ＝3， ∴BD ＝4 3，∴AB ＝AD ＋BD ＝9＋4 3.12．解：(1)如图，过点B 作BH ⊥OA ，垂足为H.在Rt △OHB 中，∵BO ＝5，sin ∠BOA ＝35，∴BH ＝BO·sin ∠BOA ＝5×35＝3，∴OH ＝BO 2－BH 2＝4， ∴点B 的坐标为(4，3)．(2)∵OA ＝10，OH ＝4，∴AH ＝6. 在Rt △AHB 中， ∵BH ＝3，AH ＝6， ∴AB ＝BH 2＋AH 2＝3 5， ∴cos ∠BAO ＝AH AB ＝2 55.13．解：(1)证明：连接OC.∵PC 与⊙O 相切于点C ，∴∠PCO ＝90°，∴∠PCA ＋∠OCA ＝90°. ∵AB 是⊙O 的直径，∴∠ACB ＝90°， ∴∠OCB ＋∠OCA ＝90°， ∴∠PCA ＝∠OCB.∵OC ＝OB ，∴∠OCB ＝∠ABC ， ∴∠PCA ＝∠ABC.(2)∵cos P ＝PC OP ＝45，PC ＝10，∴OP ＝252，∴OC ＝OP 2－CP 2＝152，∴AB ＝15.∵AE ∥PC ，∴∠BAE ＝∠P.∵AB 是⊙O 的直径，∴∠E ＝90°， ∴AE ＝A B·cos ∠BAE ＝15×45＝12，∴BE ＝AB 2－AE 2＝9. [素养提升][解析] 此题只要把三边长代入余弦定理公式即可求出三角的余弦值，从而求出三角．解：由(1)得72＝82＋92－2×8×9cos A ，则cos A ＝23，∠A ≈48°.由(2)得82＝72＋92－2×7×9cos B ，则cos B ＝1121，∠B ≈58°，∴∠C ＝180°－∠A －∠B ≈74°.。

苏科版九年级下册数学 7.5解直角三角形同步练习

7.5解直角三角形同步练习一．选择题1．如图，在△ABC中，CA＝CB＝4，cos C＝，则sin B的值为（）A．B．C．D．2．如图，A、B、C分别是小正方形的三个顶点，且每个小正方形的边长均为1，则sin∠BAC的值为（）A．B．C．1D．3．如图，在等腰直角三角形ABC中，∠C＝90°，AC＝6，D是BC上一点，若tan∠DAB＝，则AD的长为（）A．2B．C．2D．84．如图，延长Rt△ABC的斜边AB到点D，使BD＝AB，连接CD，若tan∠BCD＝，则tan A 的值是（）A．1B．C．9D．5．如图，在△ABC中，∠ACB＝90°，sin A＝，CD平分∠ACB，则∠BDC的度数是（）A．45°B．60°C．70°D．75°6．如图，在平面直角坐标系中，直线OA过点（4，2），则tanα的值是（）A．B．C．D．27．如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，且BE＝2AE，已知AD＝3，tan ∠BCE＝，那么CE等于（）A．2B．3﹣2C．5D．48．将一副三角板如图摆放在一起，组成四边形ABCD，连接AC，则tan∠ACD的值等于（）A．2B．2+C．1+D．29．如图，Rt△ABC中，∠CAB＝90°，在斜边CB上取点M，N（不包含C、B两点），且tan B ＝tan C＝tan∠MAN＝1，设MN＝x，BM＝n，CN＝m，则以下结论能成立的是（）A．m＝n B．x＝m+n C．x＞m+n D．x2＝m2+n2 10．如图，△ABC中，AB＝AC＝5，BC＝8，若∠BPC＝∠BAC，则cos∠BPC＝（）A．B．C．D．二．填空题11．在△ABC中，AB＝AC，若cos A＝，则＝．12．在Rt△ABC中，∠B＝90°，AC＝5，BC＝3，P为线段AB上一点，且CP＝，则sin ∠PCA的值为．13．如图，在△ABC中，AB＝AC，sin B＝，延长BC至点D，使CD：AC＝1：3，则tan∠CAD ＝．14．已知在△ABC中，tan B＝，BC＝6，过点A作BC边上的高，垂足为D，且＝2，则△ABC的面积为．15．如图，在△ABC中，AB＝AC，BD是AC边上的中线，AE⊥BC，垂足为点E，交BD于F，cos∠ABC＝，AB＝13．则tan∠DBC的值为．三．解答题16．如图，在Rt△ABC中，设a，b，c分别为∠A，∠B，∠C的对边，∠C＝90°，b＝8，∠A 的平分线AD＝，求∠B，a，c的值．17．如图，Rt△ABC中，∠A＝90°，AD、AE分别是BC边的中线和高，若cos B＝，BC＝10．（1）求AB的长；（2）求AE的长；（3）求sin∠ADB的值．18．【问题背景】如图1，在边长为1的正方形网格中，连结格点A、B和C、D，AB和CD相交于点P，求tan∠CPB的值．小马同学是这样解决的：连结格点B、E可得BE∥CD，则∠ABE ＝∠CPB，连结AE，那么∠CPB就变换到Rt△ABE中．则tan∠CPB的值为．【探索延伸】如图2，在边长为1的正方形网格中，AB和CD相交于点P，求sin∠APD的值．参考答案一．选择题1．解：过点A作AD⊥BC，垂足为D，如图所示．在Rt△ACD中，CD＝CA•cos C＝1，∴AD＝＝；在Rt△ABD中，BD＝CB﹣CD＝3，AD＝，∴AB＝＝2，∴sin B＝＝．故选：D．2．解：连接BC，∵每个小正方形的边长均为1，∴AB＝，BC＝，AC＝，∵AB2+BC2＝AC2，∴△ABC是直角三角形，∴sin∠BAC＝＝＝，故选：B．3．解：如图，过点D作DE⊥AB于点E，∵等腰直角三角形ABC中，∠C＝90°，AC＝6，∴AB＝6，∠B＝45°，且DE⊥AB∴∠EDB＝∠B＝45°，∴DE＝BE，∵tan∠DAB＝＝，∴AE＝5DE，∵AB＝AE+BE＝5DE+DE＝6DE＝6∴DE＝，AE＝5∴AD＝＝2故选：C．4．解：如图，过B作BE∥AC交CD于E．∵AC⊥BC，∴BE⊥BC，∠CBE＝90°，∴BE∥AC．∵AB＝BD，∴AC＝2BE．又∵tan∠BCD＝，设BE＝x，则BC＝3x，AC＝2x，∴tan A＝＝＝．故选：D．5．解：∵在△ABC中，∠ACB＝90°，sin A＝，CD平分∠ACB，∴∠A＝30°，∠ACD＝45°，∵∠BDC＝∠A+∠ACD，∴∠BDC＝75°，故选：D．6．解：过点（4，2）作直线CD⊥x轴交OA于点C，交x轴于点D，∵在平面直角坐标系中，直线OA过点（4，2），∴OD＝4，CD＝2，∴tanα＝，故选：A．7．解：∵tan∠BCE＝，∴∠BCE＝30°，∴∠B＝60°，又∵在Rt△ABD中，AD＝3，∴BD＝3，AB＝6，∵BE＝2AE，∴BE＝4，AE＝2，在Rt△BEC中，BE＝4，∠BCE＝30°∴CE＝4，故选：D．8．解：如图作AH⊥CB交CB的延长线于H．∵∠ABD＝90°，∠DBC＝45°，∴∠ABH＝45°，∵∠AHB＝90°，∴△ABH是等腰直角三角形，∴AH＝BH，设AH＝BH＝a，则AB＝a，BD＝a，BC＝CD＝a，CH＝a+a，∵∠AHB＝∠DCB＝90°，∴AH∥DC，∴∠ACD＝∠CAH，∴tan∠ACD＝tan∠CAH＝＝+1，故选：C．9．解：∵tan B＝tan C＝tan∠MAN＝1，∴∠B＝∠C＝∠MAN＝45°，∵∠CAB＝90°，∴AC＝AB，将△BAM绕点A顺时针旋转90°至△ACN′，点B与点C重合，点M落在N′处，连接NN′，则有AN′＝AM，CN′＝BM，∠1＝∠3，∵∠MCN＝45°，∴∠1+∠2＝45°，∴∠2+∠3＝45°，∴∠NAN′＝∠MAN．在△MAN与△NAN′中，，∴△MAN≌△NCN′（SAS），∴MN＝NN′．由旋转性质可知，∠ACN′＝∠B＝45°，∴∠NCN′＝∠ACN′+∠ACB＝90°，∴NN'2＝NC2+N'C2，即x2＝n2+m2，故选：D．10．解：过点A作AE⊥BC于点E，如图所示：∵AB＝AC＝5，∴BE＝BC＝×8＝4，∠BAE＝∠BAC，∵∠BPC＝∠BAC，∴∠BPC＝∠BAE．在Rt△BAE中，由勾股定理得AE＝＝＝3，∴cos∠BPC＝cos∠BAE＝＝．故选：C．二．填空题11．解：过B点作BD⊥AC于点D，∵cos A＝，∴，设AD＝4x，则AB＝5x，∴，∵AB＝AC，∴AC＝5x，∴CD＝5x﹣4x＝x，∴BC＝，∴，故答案为：．12．解：如图，作PD⊥AC于点D，在Rt△ABC中，∠B＝90°，AC＝5，BC＝3，∴AB＝＝4，在Rt△CBP中，CP＝，BC＝3，∴BP＝＝，∴AP＝AB﹣BP＝，∵sin∠A＝＝，即＝，∴PD＝，∴sin∠PCA＝＝×＝．故答案为：．13．解：过点D作DE⊥AC，与AC的延长线交于点E，∵AB＝AC，∴∠B＝∠ACB，∵∠DCE＝∠ACB，∴∠DCE＝∠B，∵sin B＝，∴，不妨设DE＝4x，则CD＝5x，∴，∵CD：AC＝1：3，∴AC＝3CD＝15x，∴AE＝AC+CE＝18x，∴tan∠CAD＝，故答案为14．解：当△ABC是锐角三角形时，如图1，∵BC＝6，＝2，∴BD＝4，∵tan B＝，∴＝，∴AD＝，∴S△ABC＝＝＝8；当△ABC是钝角三角形时，如图2，∵BC＝6，＝2，∴BD＝12，∵tan B＝，∴＝，∴AD＝8，∴S△ABC＝＝＝24，综上，△ABC的面积为8或24，故答案为8或24．15．解：过点D作DG⊥BC于点G，∵AB＝AC＝13，cos∠ABC＝，∴BE＝5，由勾股定理可知：AE＝12，∵AE⊥BC，∴BE＝EC＝5，∵D是AC的中点，DG∥AE，∴DG是△AEC的中位线，∴DG＝AE＝6，EG＝CE＝，∴BG＝，在Rt△BDG中，tan∠DBC＝＝＝，故答案为：三．解答题16．解：∵∠C＝90°，b＝8，∠A的平分线AD＝，∴cos∠CAD＝＝，∴∠CAD＝30°，∴∠CAB＝60°，∴∠B＝30°，∴c＝2b＝16，a＝＝＝8，即∠B＝30°，a＝8，c＝16．17．解：（1）在Rt△ABC中，∠A＝90°，cos B＝，BC＝10，∴AB＝BC•cos B＝10×＝6．（2）在Rt△ABC中，∠A＝90°，BC＝10，AB＝6，∴AC＝＝＝8．∵AE是BC边的高，∴AC•AB＝BC•AE，即×8×6＝×10AE，∴AE＝．（3）Rt△ABC中，AD是BC边的中线，BC＝10，∴AD＝BC＝5．在Rt△AED中，∠AED＝90°，AD＝5，AE＝，∴sin∠ADB＝＝＝．18．解：（1）如图1，∵BE∥CD，∴∠ABE＝∠CPB，∴tan∠ABE＝tan∠CPB，∵∠AEB＝90°，∴tan∠CPB＝tan∠ABE＝＝＝3，故答案为3．（2）如图2，连接CE，DE，作DM⊥CE于M．∵BC∥AE，BC＝AE，∴四边形ABCE是平行四边形，∴CE∥AB，∴∠APD＝∠ECD．∵△ECD的面积＝3×4﹣×1×4﹣×2×3﹣×1×3＝，∴CE•DM＝，∵CE＝，∴DM＝，∴sin∠APD＝sin∠ECD＝＝÷＝．。

苏科版九年级数学下册 7.5 解直角三角形同步练习

7.5解直角三角形【方法点拨】解直角三角形（Rt △ABC ,∠C ＝90°）（1）三边之间的关系：a 2+b 2=c 2．（2）两锐角之间的关系：∠A ＋∠B ＝90°．（3）边角之间的关系（4）解直角三角形中常见类型：①已知一边一锐角．②已知两边． 1. 已知：在Rt △ABC 中，∠C =90°，b =3c =4，解Rt △ABC 。

2．已知在ABC △中，90C ∠=，设sinB n =，当B ∠是最小的内角时，n 的取值范围是 A ．20n <<B ．102n << C ．30n << D ．30n << 3．如图，△ABC 中，AB =AC ，点D 在AC 上，DE ⊥BC ，垂足是E ， A ．21 B ．37 C ．773 D ．434．如图，在RtΔABC 中，∠C ＝90O ，AC ＝6，AC 边上的中线BD ＝21，解这个RtΔABC ．ABC D学校班级姓考试-----------------------------------------------------------密---------------------------------封----------------------------------线--------------------------------------CA B5．如图，Rt△ABC中，∠C＝90°，D是BC上一点，∠DAC=30°，BD＝2，AB＝23，求AC的长6. 如图，从热气球C处测得地面A、B两点的俯角（视线与水平线夹角）分别为30°、45°，如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，求AB两点的距离。

7. 如图，在△ABC中，∠A=30°，tanB=31，BC=10,求AB的长。

九年级数学解直角三角形同步练习同步练习

苏科九下《7.5解直角三角形》同步练习一选择题1、如图，已知正方形ABCD 的边长为2，如果将线段BD 绕着点B 旋转后，点D 落在CB 的延长线上的D ′处，那么tan ∠BAD ′等于（） (A)．1(B)．2 (C)．22(D)．22 2、如果α是锐角，且54cos =α，那么αsin 的值是（）．（A ）259 （B ） 54 （C ）53 （D ）2516 3、等腰三角形底边长为10㎝，周长为36cm ，那么底角的余弦等于（）．（A ）513 （B ）1213 （C ）1013 （D ）5124、. 以下不能构成三角形三边长的数组是 ( )（A ）（1，3，2）（B ）（3，4，5）（C ）（3，4，5）（D ）（32，42，52）5、在Rt △ABC 中，∠C ＝90°，下列式子中正确的是（）．（A ）B A sin sin = （B ）B A cos sin = （C ）B A tan tan = （D ）B A cot cot =6、在矩形ABCD 中，DE ⊥AC 于E ，设∠ADE=α，且53c o s =α,AB = 4, 则AD 的长为（）．（A ）3 （B ）316 （C ）320 （D ）5167、某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a 元，则购买这种草皮至少要（）．（A ）450a 元（B ）225a 元（C ）150a 元（D ）300a 元 8、已知α为锐角，tan （90°－α）α的度数为（）（A ）30° （B ）45° （C ）60° （D ）75°9、在△ABC 中，∠C =90°，BC =5，AB =13，则sin A 的值是( ) （A ）135 （B ）1312 （C ）125 （D ）51210、如果∠a 是等边三角形的一个内角，那么cos a 的值等于（）．A BCDE︒15020米30米（A ）21 （B ）22 （C ）23 （D ）1 二填空题1、如图，在△ABC 中，若∠A ＝30°，∠B ＝45°，AC ＝22，则BC ＝ 2、如图，沿倾斜角为30︒的山坡植树，要求相邻两棵树的水平距离AC 为2m ，那么相邻两棵树的斜坡距离AB 为 m 。

苏科版数学九年级下册7.5《解直角三角形》同步练习

2、在△ABC中，∠C= ，tanA+tanB=6,S△ABC=8,求斜边c的长？
3、在△ABC中，∠C= ，b+c=24,∠A－∠B=300,解这个直角三角形.
某施工人员在离地面高度为5米的C处拉引电线杆，若固定点离电线杆3米，如图所示，则至少需要多长的缆线AC才能拉住电线杆？
并球缆线AC与地面的夹角（结果保留两位小数）。
6、如图，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，到达后必须立即卸货，此时接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西600的方向移动，距台风中心200海里的圆形区域（包括边界）均会受到影响。（1）问B处是否会受到台风的影响？请说明理由。（2）为避免受到台风的影响，该船应在多少小时内卸完货物。
在△ABC中，∠C= ，已知边a=10和∠A=400，解这个直角三角形。
4、⊙O的半径为10，求⊙O的内接正八边形的边长（精确到0.1）
课中参与：
1、在△ABC中，∠C= ，已知斜边c和一条直角边b，求直角边a的关系式是_，求∠A的关系式是_，求∠B的关系式是_。
在△ABC中，∠C= ，AB=10 ，AC=10，则∠B=，BC=。
已知在边长a的正方形ABCD中，E是AD的中点，
BH⊥CE垂足为H，求∠CBH的余弦值。
3、如图，在△ABC中，∠C= ，D是BC上一点。∠B= ，
∠ADC= ，BD=15。求AC。
4、如图，在△ABC中，∠B为钝角，AB=1，AC=4，S△ABC=1,求∠A及tanC.
5、如图,一块四边形的土地ABCD,测得其中∠ABC=1200,AB⊥AD,BC⊥CD,AB=60 m,CD=100 m,求这块土地的面积。

苏科版九年级下册数学 7.5解直角三角形同步练习

7.5解直角三角形同步练习一．选择题1．在Rt△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、∠C的对边，，则a：b：c为（）A．1：2：3B．2：：3C．2：3：D．2：：2．如图，设∠AOC＝α，∠BOC＝β，P为射线OC上一点，PD⊥OA于D，PE⊥OB于E，则等于（）A．B．C．D．3．菱形的边长为4，有一个内角40°，则较短的对角线是（）A．4sin40°B．4sin20°C．8sin20°D．8cos20°4．如图，在平面直角坐标系中，AB＝3，连结AB并延长至C，连结OC，若满足OC2＝BC⋅AC，tanα＝2，则点C的坐标为（）A．（﹣2，4）B．（﹣3，6）C．（﹣，）D．（﹣，）5．如图，在Rt△ABC中，∠CAB＝90°，AD⊥BC于点D，BD＝2，tan∠C＝，则线段AC的长为（）A．10B．8C．D．6．如图所示，在△ABC中，∠C＝90°，AC＝16cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC＝，则BD的长是（）A．4cm B．6cm C．8cm D．10cm7．如图，在Rt△ABC中，∠C＝90°，sin A＝，D为AB上一点，且AD：DB＝3：2，过点D作DE⊥AC于E，连结BE，则tan∠CEB的值等于（）A．B．2C．D．8．如图，在等腰Rt△ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝，则AD的长为（）A．2B．C．D．19．如图，在Rt△ABC中，∠ACB＝90°，tan B＝，CD为AB边上的中线，CE平分∠ACB，则的值（）A．B．C．D．10．在直角坐标系中，点A的坐标为（3，0），点B是y轴正半轴上的一点，点C是第一象限内一点，且AC＝2，设tan∠BOC＝m，则m的最小值是（）A．1B．C．D．二．填空题11．如图，BD是△ABC的高，AB＝，BC＝2，tan A＝1，则CD＝．12．如图，等腰Rt△ABP的斜边AB＝2，点M、N在斜边AB上．若△PMN是等腰三角形且底角正切值为2，则MN＝．13．如图，BE是△ABC的角平分线，F是AB上一点，∠ACF＝∠EBC，BE、CF相交于点G．若sin∠AEB＝，BG＝4，EG＝5，则S△ABE＝．14．如图．在边长为1的3×5正方形网格中，点A、B、C、D都在格点上，则tan∠1是．15．如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC，垂足为点D，线段AE与线段CD相交于点F且AE＝AB，连接DE，∠E＝∠C，若AD＝2DE，则cos∠BAD的值为．三．解答题16．已知：如图，在Rt△ABC中，∠ACB＝90°，BC＝12，cos B＝，D、E分别是AB、BC边上的中点，AE与CD相交于点G．（1）求CG的长；（2）求tan∠BAE的值．17．如图，已知在△ABC中，∠ACB＝90°，sin B＝，延长边BA至点D，使AD＝AC，联结CD．（1）求∠D的正切值；（2）取边AC的中点E，联结BE并延长交边CD于点F，求的值．18．如图，已知△ABC中，∠ACB＝90°，D是边AB的中点，P是边AC上一动点，BP与CD相交于点E．（1）如果BC＝6，AC＝8，且P为AC的中点，求线段BE的长；（2）联结PD，如果PD⊥AB，且CE＝2，ED＝3，求cos A的值；（3）联结PD，如果BP2＝2CD2，且CE＝2，ED＝3，求线段PD的长．参考答案一．选择题1．解：设BC＝2x，则AB＝3x，AC＝；∴a：b：c＝BC：AC：AB＝2：：3．故选：B．2．解：由正弦的概念知，＝＝．故选A．3．解：由菱形的性质知，菱形的对角线互相垂直平分，且平分一组对角，设较短的对角线的一半为X，则sin20°＝∴X＝4sin20°∴较短的对角线长是8sin20°．故选：C．4．解：∵∠C＝∠C，∵OC2＝BC•AC，即，∴△OBC∽△OAC，∴∠A＝∠COB，∵α+∠COB＝90°，∠A+∠ABO＝90°，∴∠ABO＝α，∵tanα＝2，∴tan∠ABO＝，∴OA＝2OB，∵AB＝3，由勾股定理可得：OA2+OB2＝AB2，即，解得：OB＝3，∴OA＝6．∴tan∠A＝＝．如图，过点C作CD⊥x轴于点D，∵tanα＝2，∴设C（﹣m，2m），m＞0，∴AD＝6+m，∵tan∠A＝，∴＝，∴＝，解得：m＝2，经检验，m＝2是原方程的解．∴点C坐标为：（﹣2，4）．故选：A．5．解：∵∠CAB＝90°，AD⊥BC于点D，∴∠B+∠C＝90°，∠B+∠BAD＝90°，∴∠BAD＝∠C．在Rt△ABD中，∠ADB＝90°，BD＝2，∵tan∠BAD＝＝，∴AD＝2BD＝4，∴AB＝＝2．在Rt△ABC中，∠CAB＝90°，AB＝2，∵tan∠C＝＝，∴AC＝2AB＝4．故选：D．6．解：∵cos∠BDC＝＝，可设DC＝3x，BD＝5x，又∵MN是线段AB的垂直平分线，∴AD＝DB＝5x，又∵AC＝16cm，∴3x+5x＝16，解得，x＝2cm，∴BD＝5x＝10cm，故选：D．7．解：在Rt△AED中，∵sin A＝＝，∴可以假设AD＝15k，DE＝9k，则AE＝12k，∵AD：DB＝3：2，∴DB＝10k，∵DE∥BC，∴＝＝，∴＝＝，∴BC＝15k，AC＝20k，∴EC＝AC﹣AE＝8k，∴tan∠CEB＝＝，故选：D．8．解：作DE⊥AB于E，如图，∵∠C＝90°，AC＝BC＝6，∴△ACB为等腰直角三角形，AB＝AC＝6，∴∠A＝45°，在Rt△ADE中，设AE＝x，则DE＝x，AD＝x，在Rt△BED中，tan∠DBE＝＝，∴BE＝5x，∴x+5x＝6，解得x＝，∴AD＝×＝2．故选：A．9．解：如图，过点E和点D作EF⊥AC，DG⊥AC于点F和G，∴EF∥DG，∴＝，∵CE平分∠ACB，∴∠ECF＝ACB＝45°，∵∠EFC＝90°，∴∠FEC＝45°，∴EF＝FC，∴AF＝AC﹣FC＝AC﹣EF，∵CD为AB边上的中线，∴DG∥BC，DG＝BC，∴EF∥BC，∴∠AEF＝∠B，∴tan∠AEF＝tan∠B＝，∴＝，即＝，解得EF＝AC，∵＝，∴BC＝AC，∴＝＝＝．∴＝＝．故选：D．10．解：C在以A为圆心，以2为半径作圆周上，只有当OC与圆A相切（即到C点）时，∠BOC最小，AC＝2，OA＝3，由勾股定理得：OC＝，∵∠BOA＝∠ACO＝90°，∴∠BOC+∠AOC＝90°，∠CAO+∠AOC＝90°，∴∠BOC＝∠OAC，tan∠BOC＝tan∠OAC＝＝，随着C的移动，∠BOC越来越大，∵C在第一象限，∴C不到x轴上，即∠BOC＜90°，∴tan∠BOC≥，∴m的最小值是，故选：B．二．填空题11．解：∵tan A＝1，∴∠A＝45°，∵BD⊥AD，∴∠D＝90°，∴AD＝BD，∵AB＝，∴AD＝BD＝，∴CD＝＝＝1，故答案为1．12．解：如图1中，当PM＝PN时，过点P作PH⊥AB于H．∵P A＝PB，∠APB＝90°，PH⊥AB，∴AH＝BH＝1，∴PH＝HA＝HB＝1，∵tan∠PMN＝2＝，∴MH＝NH＝，∴MN＝1．如图2中，当MP＝MN时，设MP＝MN＝x．∵tan∠MNP＝＝2，∴NH＝，在Rt△PHM中，则有x2＝（x﹣）2+12，解得x＝，∴MN＝，当NP＝NM时，同法可得MN＝，综上所述，满足条件的MN的值为1或．13．解：如图，过点B作BT⊥AC于T，连接EF．∵BE平分∠ABC，∴∠ABE＝∠CBE，∵∠ECG＝∠ABE，∴∠ECG＝∠CBE，∵∠CEG＝∠CEB，∴△ECG∽△EBC，∴＝＝，∴EC2＝EG•EB＝5×（5+4）＝45，∵EC＞0，∴EC＝3，在Rt△BET中，∵sin∠AEB＝＝，BE＝9，∴BT＝，∴ET＝＝＝，∴CT＝ET+CE＝，∴BC＝＝＝6，∴CG＝＝10，∵∠ECG＝∠FBG，∴E，F，B，C四点共圆，∴∠EFG＝∠CBG，∵∠FGE＝∠BGC，∴△EGF∽△CGB，∴＝，∴＝，∴EF＝3，∵∠AFE＝∠ACB，∠EAF＝∠BAC，∴△EAF∽△BAC，∴＝＝＝，设AE＝x，则AB＝2x，∵∠FBG＝∠ECG，∠BGF＝∠CGE，∴△BGF∽△CGE，∴＝，∴＝，∴BF＝，∵AE•AC＝AF•AB，∴x（x+3）＝（2x﹣）•2x，解得x＝，∴AE＝ET＝，∴点A与点T重合，∴AB＝2AE＝，∴S△ABE＝×AB×AE＝××＝．故答案为．14．解：如图，取格点E，连接DE、BE，则DE∥AC，∴∠1＝∠BDE，∵BE2＝DE2＝12+22＝5，BD2＝12+32＝10，∴BE2+DE2＝BD2，∴△BDE是直角三角形，∠BDE＝∠DBE＝45°，则tan∠1＝tan∠BDE＝1，故答案为：1．15．解：取AD的中点G，连接BG，如图所示：则AG＝DG，AD＝2AG，∵AD＝2DE，∴DE＝AG，∵∠BAC＝90°，AD⊥BC，∴∠ABC+∠C＝∠ABC+∠BAG＝90°，∴∠C＝∠BAG，∵∠C＝∠E，∴∠BAG＝∠E，在△ABG和△EAD中，，∴△ABG≌△EAD（SAS），∴BG＝AD＝2DE＝2DG，∴BD＝＝＝DG，∴AB＝＝＝DG，∴cos∠BAD＝＝＝；故答案为：．三．解答题16．解：（1）∵在Rt△ABC中，∠ACB＝90°，BC＝12，cos B＝，∴，∵D是斜边AB上的中点，∴，又∵点E是BC边上的中点，∴点G是△ABC的重心，∴；（2）∵点E是BC边上的中点，∴，过点E作EF⊥AB，垂足为F，∵在Rt△BEF中，cos B＝，BF＝BE•cos B＝，∴，∵AF＝AB﹣BF＝18﹣4＝14，∴tan∠BAE＝．17．解：（1）过点C作CG⊥AB，垂足为G，∵∠ACB＝90°，∴∠ACG＝∠B，在△ABC中，sin B＝，设AC＝3x，则AB＝5x，BC＝4x，∴sin∠ACG＝＝＝sin B，∴AG＝x，CG＝x，∴DG＝DA+AG＝3x+x＝x，在Rt△DCG中，tan∠D＝＝；（2）过点C作CH∥DB，交BF的延长线于点H，则有△CHF∽△DBF，又有E是AC的中点，可证△CHE≌△ABE，∴HC＝AB＝5x，由△CHF∽△DBF得：＝＝＝．18．解：（1）∵P为AC的中点，AC＝8，∴CP＝4，∵∠ACB＝90°，BC＝6，∴BP＝2，∵D是边AB的中点，P为AC的中点，∴点E是△ABC的重心，∴BE＝BP＝；（2）如图1，过点B作BF∥CA交CD的延长线于点F，∴，∵BD＝DA，∴FD＝DC，BF＝AC，∵CE＝2，ED＝3，则CD＝5，∴EF＝8，∴＝，∴＝，∴＝，设CP＝k，则P A＝3k，∵PD⊥AB，D是边AB的中点，∴P A＝PB＝3k∴BC＝2k，∴AB＝2k，∵AC＝4k，∴cos A＝；（3）∵∠ACB＝90°，D是边AB的中点，∴CD＝BD＝AB，∵PB2＝2CD2，∴BP2＝2CD•CD＝BD•AB，∵∠PBD＝∠ABP，∴△PBD∽△ABP，∴∠BPD＝∠A，∵∠A＝∠DCA，∴∠DPE＝∠DCP，∵∠PDE＝∠CDP，∴△DPE∽△DCP，∴PD2＝DE•DC，∵DE＝3，DC＝5，∴PD＝．。

苏科版九年级数学下册第7章 7.5 《解直角三角形》同步测试题

=
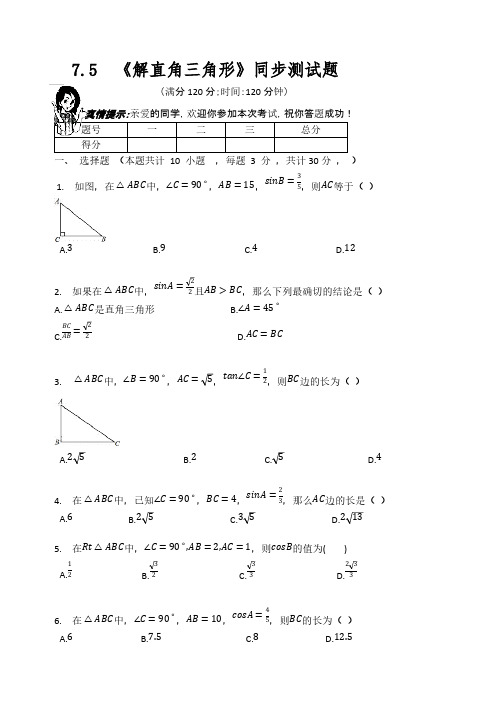
2
3，那么
�� ＝________．
13. 如图，在 △ ��中，∠�� = 30 ∘ ，∠�� = 45 ∘ ，�� = 2 3，则�� △ �� = ________．
（1）写出��与��之间的函数关系式；（2）当��的长等于多少时，点��与点��重合．
20.
如图，在��
△
��中，∠��
=
90
∘
，��是��边上的中线，��∠��
=
3
5，则��∠��的
）
A. △ ��是直角三角形
B.∠�� = 45 ∘
��
C.��
=
2 2
D.�� = ��
3.
△ ��中，∠�� = 90 ∘ ，�� =
22.
已知：如图， △ ��中，∠�� = 90 ∘ ，�� ⊥ ��于��，�� = 10，�� = 6．求：
��∠��的值及��的长．

九年级数学下册第7章锐角三角函数7.5解直角三角形7.5.1解直角三角形同步练习2(新版)苏科版

第1课时解直角三角形的意义]一、选择题1．如图K －30－1，在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，那么以下关系式错误的选项是( )图K －30－1A ．a ＝b tan AB ．b ＝c cos AC ．a ＝c sin AD ．c ＝bsin A2．在以下条件下，不能解直角三角形的是( ) A ．一直角边和一锐角 B ．一斜边和一锐角 C ．两边 D ．两锐角3．在Rt △ACB 中，∠C ＝90°，AB ＝10，sin A ＝35，cos A ＝45，tan A ＝34，那么BC 的长为( )链接听课例3归纳总结 A ．6 B ．7.5 C ．8 D ．4．2021·宜昌如图K －30－2，要测量小河两岸相对的两点P ，A 的距离，可以在小河边取PA 的垂线PB 上一点C ，测得PC ＝100米，∠PCA ＝35°，那么小河宽PA 等于( )图K－30－2A．100sin35°米 B．100sin55°米C．100tan35°米 D．100tan55°米二、填空题5．在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，c＝8，∠B＝30°，那么∠A＝________，a＝________，b＝________．6．如图K－30－3，在地面上的点A处测得树顶B的仰角为α，AC＝7米，那么树高BC 为________米．图K－30－37．如图K－30－4，在Rt△ABC中，∠C＝90°，∠B＝37°，BC＝32，那么AC＝________．(参考数据：sin37°≈，cos37°≈，tan37°≈0.75)图K－30－48．在Rt△ABC中，∠C＝90°，∠A＝60°，BC＝2 3，BD是中线，那么BD的长是________．三、解答题9．如图K－30－5，在△ABC中，∠C＝90°，∠B＝37°.假设BC＝3，求AC，AB的长．(结果保存小数点后一位，参考数据：sin37°≈，cos37°≈，tan37°≈0.75)链接听课例1归纳总结图K－30－510．在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，∠A＝60°，c ＝8 3.解这个直角三角形.链接听课例1归纳总结探究题2021·无锡模拟如图K－30－6，在Rt△ABC中，∠CAB＝90°，在斜边CB上取点M，N(不包含C，B两点)，且tan B＝tan C＝tan∠MAN＝1，设MN＝x，BM＝n，CN＝m，那么以下结论能成立的是( )图K－30－6A．m＝n B．x＝m＋nC．x＞m＋n D．x2＝m2＋n2详解详析[课堂达标] 1．D2．[解析] D 解直角三角形，需一角一边或两边．3．[解析] A 如图，∵∠C ＝90°， ∴sin A ＝BCAB，∴BC ＝AB ·sin A ＝10×35＝6.应选A .4．[解析] C 在Rt △PCA 中，∠APC ＝90°，tan ∠PCA ＝PAPC ，∴PA ＝PC·tan ∠PCA ＝100tan 35°米．5．60° 4 3 4 6．[答案] 7tan α[解析] 在Rt △ABC 中，因为tan α＝BCAC ，所以BC ＝AC·tan α＝7tan α，故答案为7tan α. 7．[答案] 24[解析] 由题意知tan B ＝tan 37°＝AC32≈，解得AC ＝24.8．[答案] 13[解析] 由正切定义，先求出AC 的长，再求出DC 的长，由勾股定理求出BD ＝13. 9．[解析] 根据正切函数和余弦函数的定义即可得到结论．解：∵∠C ＝90°， ∴∠B ＝37°. 又∵BC ＝3，∴AC ＝BC·tan 37°≈， AB ＝BCcos 37°≈3.8.10．解：∠B ＝90°－60°＝30°. ∵sin A ＝ac，∴a ＝c·sin A ＝8 3×sin 60°＝8 3×32＝12， ∴b ＝c 2－a 2＝〔8 3〕2－122＝4 3.[素养提升][解析] D ∵tan B ＝tan C ＝tan ∠MAN ＝1， ∴∠B ＝∠ACB ＝∠MAN ＝45°. ∵∠CAB ＝90°， ∴AC ＝AB.将△BAM 绕点A 顺时针旋转90°至△ACN′，点B 与点C 重合，点M 落在点N′处，连接NN′，那么AN′＝AM ，CN ′＝BM ，∠1＝∠3. ∵∠MAN ＝45°，∠CAB ＝90°， ∴∠1＋∠2＝45°， ∴∠2＋∠3＝45°， ∴∠N ′AN ＝∠MAN. 在△MAN 与△NAN′中， ∵⎩⎪⎨⎪⎧AM ＝AN′，∠MAN ＝∠N′AN，AN ＝AN ，∴△MAN ≌△N ′AN(SAS )， ∴MN ＝NN′.由旋转的性质可知，∠ACN ′＝∠B ＝45°， ∴∠NCN ′＝∠ACN′＋∠ACB ＝90°，∴NN ′2＝NC 2＋N′C 2，即x 2＝m 2＋n 2. 应选D .。

九年级数学下册第7章锐角三角函数 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习1 (新版)苏科版

第7章锐角三角函数7.5 第2课时构造直角三角形解题知识点构造直角三角形解题1．如图7－5－12，在△ABC中，AB＝AC，AH⊥BC，垂足为H，如果AH＝BC，那么sin ∠BAC的值是( )A.54B.45C.35D.537－5－127－5－132．如图7－5－13，圆的内接正五边形ABCDE的边长为a，圆的半径为r，下列等式成立的是( )A．a＝2r·sin36° B．a＝2r·cos36°C ．a ＝r ·sin36°D ．a ＝2r ·sin72°3．如图7－5－14，在△ABC 中，AB ＝3，BC ＝2，∠B ＝60°，则△ABC 的面积等于( ) A.3 32 B.32C. 3 D ．3 37－5－147－5－154．如图7－5－15，在四边形ABCD 中，∠B ＝∠D ＝90°，AB ＝3，BC ＝2，tan A ＝43，则CD ＝________．5．如图7－5－16，正三角形ABC 内接于⊙O ，若AB ＝2 3 cm ，求⊙O 的半径．图7－5－166．2018·自贡如图7－5－17，在△ABC 中，BC ＝12，tan A ＝34，∠B ＝30°，求AC和AB 的长．图7－5－177．如图7－5－18，已知∠B ＝37°，AB ＝20，C 是射线BM 上一点．(1)在下列条件中，可以唯一确定BC 长的是________(填写所有符合条件的序号)； ①AC ＝13；② tan ∠ACB ＝125；③连接AC ，△ABC 的面积为126.(2)在(1)的答案中，选择一个作为条件，画出草图，求BC (参考数据： sin37°≈0.60, cos37°≈0.80, tan37°≈0.75)．图7－5－18第7章锐角三角函数7.5 第2课时构造直角三角形解题1．B [解析] 过点B 作BD ⊥AC 于点D ，设AH ＝BC ＝2x .∵AB ＝AC ，AH ⊥BC ，∴BH ＝CH ＝12BC ＝x .根据勾股定理，得AC ＝AH 2＋CH 2＝（2x ）2＋x 2＝5x .由S △ABC ＝12BC ·AH ＝12AC ·BD ，得12·2x ·2x ＝12·5x ·BD ，解得BD ＝4 55x ，∴sin ∠BAC ＝BD AB ＝4 55x 5x ＝45.2．A [解析] 如图，作OF ⊥BC 于点F . ∵∠COF ＝360°÷5÷2＝36°， ∴CF ＝r ·sin36°， ∴a ＝2r ·sin36°.故选A.3．A [解析] △ABC 的面积为12AB ·BC ·sin B ＝12×3×2×sin60°＝12×3×2×32＝3 32. 故选A.4.65 [解析] 延长AD 和BC 交于点E .∵在Rt △ABE 中，tan A ＝BE AB ＝43，AB ＝3，∴BE ＝4，∴EC ＝BE －BC ＝4－2＝2.∵△ABE 和△CDE 中，∠B ＝∠EDC ＝90°，∠E ＝∠E ，∴∠DCE ＝∠A ，∴在Rt △CDE 中，tan ∠DCE ＝tan A ＝DE CD ＝43，∴设DE ＝4x ，则CD ＝3x .在Rt △CDE 中，EC 2＝DE 2＋CD 2，∴4＝16x 2＋9x 2，∴x ＝25(负值舍去)，则CD ＝65.5．解：如图，过点O 作OD ⊥BC 于点D ，连接BO .∵正三角形ABC 内接于⊙O ，∴点O 既是三角形的内心也是外心，∴∠OBD ＝30°，BD ＝CD ＝12BC ＝12AB ＝ 3 cm ，∴ cos30°＝BDBO ＝3BO，解得BO ＝2(cm)，即⊙O 的半径为2 cm.6．[解析] 通过作高构造直角三角形，在Rt △BCD 和Rt △ACD 中利用特殊角的三角函数值和勾股定理即可求解．解：如图所示，过点C 作CD ⊥AB 于点D ，在Rt △BCD 中，∵∠B ＝30°，BC ＝12，∴sin B ＝CD BC ＝CD 12＝sin30°＝12，∴CD ＝6；cos B ＝BD BC ＝BD 12＝cos30°＝32，∴BD ＝6 3.在Rt △ACD 中，tan A ＝34，CD ＝6，∴tan A ＝CD AD ＝6AD ＝34，∴AD ＝8，∴AC ＝AD 2＋CD 2＝82＋62＝10，AB ＝AD ＋BD ＝8＋6 3. 即AC 的长为10，AB 的长为8＋6 3. 7．解：(1)②③(2)画图略．若选②，作AD ⊥BM 于点D ，则∠ADB ＝∠ADC ＝90°. 在Rt △ABD 中，∠ADB ＝90°，∴AD ＝AB · sin B ≈12，BD ＝AB ·cos B ≈16. 在Rt △ACD 中，∠ADC ＝90°， ∴CD ＝ADtan ∠ACB≈5，∴BC ＝BD ＋CD ≈21.若选③，作CE ⊥AB 于点E ，则∠BEC ＝90°.由S △ABC ＝12AB ·CE ，得CE ＝12.6.在Rt △BEC 中，∠BEC ＝90°， ∴BC ＝CEsin B≈21.。

九年级数学下册第7章锐角三角函数7.5解直角三角形7.5.2构造直角三角形解题同步练习1(新版)苏科

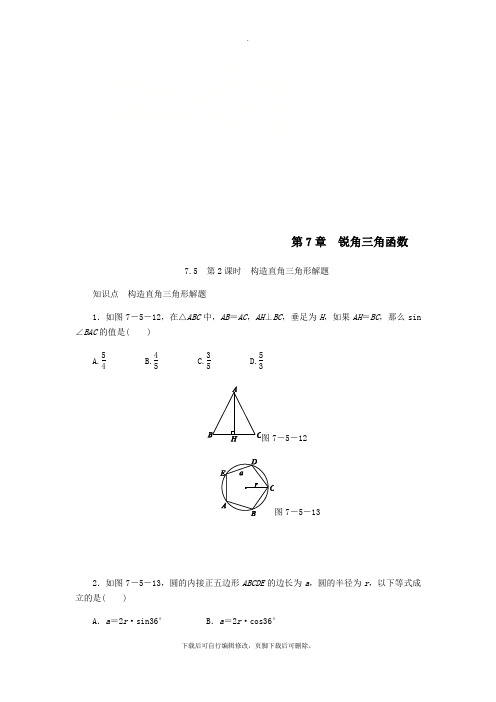
第7章锐角三角函数7.5 第2课时构造直角三角形解题知识点构造直角三角形解题1．如图7－5－12，在△ABC中，AB＝AC，AH⊥BC，垂足为H，如果AH＝BC，那么sin ∠BAC的值是( )A.54B.45C.35D.53图7－5－12图7－5－132．如图7－5－13，圆的内接正五边形ABCDE的边长为a，圆的半径为r，以下等式成立的是( )A．a＝2r·sin36° B．a＝2r·cos36°C ．a ＝r ·sin36°D ．a ＝2r ·sin72°3．如图7－5－14，在△ABC 中，AB ＝3，BC ＝2，∠B ＝60°，那么△ABC 的面积等于( ) A.3 32 B.32C. 3 D ．3 37－5－147－5－154．如图7－5－15，在四边形ABCD 中，∠B ＝∠D ＝90°，AB ＝3，BC ＝2，tan A ＝43，那么CD ＝________．5．如图7－5－16，正三角形ABC 内接于⊙O ，假设AB ＝2 3 cm ，求⊙O 的半径．图7－5－166．2021·自贡如图7－5－17，在△ABC 中，BC ＝12，tan A ＝34，∠B ＝30°，求AC和AB 的长．图7－5－177．如图7－5－18，∠B ＝37°，AB ＝20，C 是射线BM 上一点．(1)在以下条件中，可以唯一确定BC 长的是________(填写所有符合条件的序号)； ①AC ＝13；② tan ∠ACB ＝125；③连接AC ，△ABC 的面积为126.(2)在(1)的答案中，选择一个作为条件，画出草图，求BC (参考数据： sin37°≈0.60, cos37°≈0.80, tan37°≈)．图7－5－18第7章锐角三角函数7.5 第2课时构造直角三角形解题1．B [解析] 过点B 作BD ⊥AC 于点D ，设AH ＝BC ＝2x .∵AB ＝AC ，AH ⊥BC ，∴BH ＝CH ＝12BC ＝x .根据勾股定理，得AC ＝AH 2＋CH 2＝〔2x 〕2＋x 2＝5x .由S △ABC ＝12BC ·AH ＝12AC ·BD ，得12·2x ·2x ＝12·5x ·BD ，解得BD ＝4 55x ，∴sin ∠BAC ＝BD AB ＝4 55x 5x ＝45.2．A [解析] 如图，作OF ⊥BC 于点F . ∵∠COF ＝360°÷5÷2＝36°， ∴CF ＝r ·sin36°， ∴a ＝2r ·sin36°.应选A.3．A [解析] △ABC 的面积为12AB ·BC ·sin B ＝12×3×2×sin60°＝12×3×2×32＝3 32. 应选A.4.65 [解析] 延长AD 和BC 交于点E .∵在Rt △ABE 中，tan A ＝BE AB ＝43，AB ＝3，∴BE ＝4，∴EC ＝BE －BC ＝4－2＝2.∵△ABE 和△CDE 中，∠B ＝∠EDC ＝90°，∠E ＝∠E ，∴∠DCE ＝∠A ，∴在Rt △CDE 中，tan ∠DCE ＝tan A ＝DE CD ＝43，∴设DE ＝4x ，那么CD ＝3x .在Rt △CDE 中，EC 2＝DE 2＋CD 2，∴4＝16x 2＋9x 2，∴x ＝25(负值舍去)，那么CD ＝65.5．解：如图，过点O 作OD ⊥BC 于点D ，连接BO .∵正三角形ABC 内接于⊙O ，∴点O 既是三角形的内心也是外心，∴∠OBD ＝30°，BD ＝CD ＝12BC ＝12AB ＝ 3 cm ，∴ cos30°＝BDBO ＝3BO，解得BO ＝2(cm)，即⊙O 的半径为2 cm.6．[解析] 通过作高构造直角三角形，在Rt △BCD 和Rt △ACD 中利用特殊角的三角函数值和勾股定理即可求解．解：如下图，过点C 作CD ⊥AB 于点D ，在Rt △BCD 中，∵∠B ＝30°，BC ＝12，∴sin B ＝CD BC ＝CD 12＝sin30°＝12，∴CD ＝6；cos B ＝BD BC ＝BD 12＝cos30°＝32，∴BD ＝6 3.在Rt △ACD 中，tan A ＝34，CD ＝6，∴tan A ＝CD AD ＝6AD ＝34，∴AD ＝8，∴AC ＝AD 2＋CD 2＝82＋62＝10，AB ＝AD ＋BD ＝8＋6 3. 即AC 的长为10，AB 的长为8＋6 3. 7．解：(1)②③(2)画图略．假设选②，作AD ⊥BM 于点D ，那么∠ADB ＝∠ADC ＝90°. 在Rt △ABD 中，∠ADB ＝90°，∴AD ＝AB · sin B ≈12，BD ＝AB ·cos B ≈16. 在Rt △ACD 中，∠ADC ＝90°， ∴CD ＝ADtan ∠ACB≈5，∴BC ＝BD ＋CD ≈21.假设选③，作CE ⊥AB 于点E ，那么∠BEC ＝90°.由S △ABC ＝12AB ·CE ，得CE ＝12.6.在Rt △BEC 中，∠BEC ＝90°， ∴BC ＝CEsin B≈21.。

九年级数学下册第7章锐角三角函数 7.5 解直角三角形 7.5.1 解直角三角形同步练习2 (新版)苏科版

[7.5 第1课时解直角三角形的意义]一、选择题1．如图K －30－1，已知在Rt △ABC 中，∠C ＝90°，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，则下列关系式错误的是( )图K －30－1A ．a ＝b tan AB ．b ＝c cos AC ．a ＝c sin AD ．c ＝bsin A2．在下列条件下，不能解直角三角形的是( ) A ．已知一直角边和一锐角 B ．已知一斜边和一锐角 C ．已知两边 D ．已知两锐角3．在Rt △ACB 中，∠C ＝90°，AB ＝10，sin A ＝35，cos A ＝45，tan A ＝34，则BC 的长为( )链接听课例3归纳总结A ．6B ．7.5C ．8D ．12.54．2018·宜昌如图K －30－2，要测量小河两岸相对的两点P ，A 的距离，可以在小河边取PA 的垂线PB 上一点C ，测得PC ＝100米，∠PCA ＝35°，则小河宽PA 等于( )图K－30－2A．100sin35°米 B．100sin55°米C．100tan35°米 D．100tan55°米二、填空题5．在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，c＝8，∠B＝30°，则∠A＝________，a＝________，b＝________．6．如图K－30－3，在地面上的点A处测得树顶B的仰角为α，AC＝7米，则树高BC 为________米．图K－30－37．如图K－30－4，在Rt△ABC中，∠C＝90°，∠B＝37°，BC＝32，则AC＝________．(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)图K－30－48．已知在Rt△ABC中，∠C＝90°，∠A＝60°，BC＝2 3，BD是中线，则BD的长是________．三、解答题9．如图K－30－5，在△ABC中，∠C＝90°，∠B＝37°.若BC＝3，求AC，AB的长．(结果保留小数点后一位，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)链接听课例1归纳总结图K－30－510．在Rt△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，∠A＝60°，c＝8 3.解这个直角三角形.链接听课例1归纳总结探究题2018·无锡模拟如图K－30－6，在Rt△ABC中，∠CAB＝90°，在斜边CB上取点M，N(不包含C，B两点)，且tan B＝tan C＝tan∠MAN＝1，设MN＝x，BM＝n，CN＝m，则以下结论能成立的是( )图K－30－6A．m＝n B．x＝m＋nC．x＞m＋n D．x2＝m2＋n2详解详析[课堂达标] 1．D2．[解析] D 解直角三角形，需已知一角一边或两边．3．[解析] A 如图，∵∠C ＝90°， ∴sin A ＝BCAB，∴BC ＝AB ·sin A ＝10×35＝6.故选A .4．[解析] C 在Rt △PCA 中，∠APC ＝90°，tan ∠PCA ＝PAPC ，∴PA ＝PC·tan ∠PCA ＝100tan 35°米．5．60° 4 3 4 6．[答案] 7tan α[解析] 在Rt △ABC 中，因为tan α＝BCAC ，所以BC ＝AC·tan α＝7tan α，故答案为7tan α. 7．[答案] 24[解析] 由题意知tan B ＝tan 37°＝AC32≈0.75，解得AC ＝24.8．[答案] 13[解析] 由正切定义，先求出AC 的长，再求出DC 的长，由勾股定理求出BD ＝13. 9．[解析] 根据正切函数和余弦函数的定义即可得到结论．解：∵∠C ＝90°， ∴∠B ＝37°. 又∵BC ＝3，∴AC ＝BC·tan 37°≈2.3， AB ＝BCcos 37°≈3.8.10．解：∠B ＝90°－60°＝30°. ∵sin A ＝ac，∴a ＝c·sin A ＝8 3×sin 60°＝8 3×32＝12， ∴b ＝c 2－a 2＝（8 3）2－122＝4 3.[素养提升][解析] D ∵tan B ＝tan C ＝tan ∠MAN ＝1， ∴∠B ＝∠ACB ＝∠MAN ＝45°. ∵∠CAB ＝90°， ∴AC ＝AB.将△BAM 绕点A 顺时针旋转90°至△ACN′，点B 与点C 重合，点M 落在点N′处，连接NN′，则AN′＝AM ，CN ′＝BM ，∠1＝∠3. ∵∠MAN ＝45°，∠CAB ＝90°， ∴∠1＋∠2＝45°， ∴∠2＋∠3＝45°， ∴∠N ′AN ＝∠MAN. 在△MAN 与△NAN′中， ∵⎩⎪⎨⎪⎧AM ＝AN′，∠MAN ＝∠N′AN，AN ＝AN ，∴△MAN ≌△N ′AN(SAS )， ∴MN ＝NN′.由旋转的性质可知，∠ACN ′＝∠B ＝45°， ∴∠NCN ′＝∠ACN′＋∠ACB ＝90°，∴NN ′2＝NC 2＋N′C 2，即x 2＝m 2＋n 2. 故选D .。

苏科版九年级下册数学 7.5解直角三角形 同步练习

苏科版九年级数学下册 7.5 解直角三角形 同步测试题

苏科版 九下 7.5解直角三角形同步课时训练(word版含答案)

2022-2023学年苏科版九年级数学下册《7-5解直角三角形》同步达标测试题(附答案)

苏科版九年级下册数学 下册 7.5解直角三角形练习

苏科版初中数学九年级下册《7.5 解直角三角形》同步练习卷

九年级数学下册 第7章 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习2 (新版)苏科版

苏科版九年级下册数学 7.5解直角三角形 同步练习

苏科版九年级数学下册 7.5 解直角三角形同步练习

九年级数学解直角三角形同步练习同步练习

苏科版数学九年级下册7.5《解直角三角形》同步练习

苏科版九年级下册数学 7.5解直角三角形 同步练习

苏科版九年级数学下册 第7章 7.5 《解直角三角形》同步测试题

九年级数学下册第7章锐角三角函数7.5解直角三角形7.5.1解直角三角形同步练习2(新版)苏科版

九年级数学下册 第7章 锐角三角函数 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习1 (新版)苏科版

九年级数学下册第7章锐角三角函数7.5解直角三角形7.5.2构造直角三角形解题同步练习1(新版)苏科

九年级数学下册 第7章 锐角三角函数 7.5 解直角三角形 7.5.1 解直角三角形同步练习2 (新版)苏科版

苏科版九年级下册数学 7.5解直角三角形同步练习

苏科版九年级数学下册 7.5 解直角三角形同步测试题

苏科版九下 7.5解直角三角形同步课时训练(word版含答案)

苏科版九年级下册数学下册 7.5解直角三角形练习

九年级数学下册第7章 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习2 (新版)苏科版

苏科版九年级下册数学 7.5解直角三角形同步练习

苏科版九年级下册数学 7.5解直角三角形同步练习

苏科版九年级数学下册第7章 7.5 《解直角三角形》同步测试题

九年级数学下册第7章锐角三角函数 7.5 解直角三角形 7.5.2 构造直角三角形解题同步练习1 (新版)苏科版

九年级数学下册第7章锐角三角函数 7.5 解直角三角形 7.5.1 解直角三角形同步练习2 (新版)苏科版