结构动力学的刚度系数柔度系数汇总.
▲ 结构刚、柔度概念强化和灵活应用

(2l )3 l3 48EI 6 EI
3)B点竖向刚度
6EI k0 3 l
1
6EI k k0 3 l
[例3]求图示结构C点的竖向刚度k。
C EI
l EI l EI EA=∞ EI l
Δ=1
k
6i/l
k
12i/l2
(刚度示意图)
解: 由图示可见,相当于四根两端固支梁并联。
i2
4
i1 1
i2 2
结 束
(第二版)作业: 8 —21(反弯点法)
解: 悬臂梁自由端:
1
k11 A k0 k11
EI
l3 A 3EI
3EI kA 3 l
l
3EI l3
刚度并联,两者叠加:
3EI k11 k0 3 l
k0
[例2]求图示结构B点的竖向刚度。
A
E1I1=∞
B
EA=∞
A
E1I1=∞
(等效图)
B k0
EI l /2 l /2
l
解: 1)作等效图 2)简支梁中点柔度
12i2 k2 2 h2
总刚度:
k
P 1 1 1
k1 k2
12i1 k1 2 h1
串联一般公式:
n 1 1 1 1 1 k k1 k2 kn j 1 k j
▲ 楼层刚度与位移法刚度系数的关系
EI∞
k21 k2
1
k22 k2
总侧移刚度:
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度:
h2
h1i1Βιβλιοθήκη i2k k左柱 k右柱
结构力学柔度计算公式

结构力学柔度计算公式结构力学柔度计算公式是对结构体系中的柔度进行计算的公式。
柔度是指结构在外力作用下发生变形的能力,是结构体系的一项重要性能指标。
通过计算柔度可以了解结构的变形情况,评估结构的稳定性和抗风、抗震能力,为结构设计和分析提供依据。
柔度的计算公式与结构的类型、边界条件、受力形式等因素有关。
下面将分别介绍几种常见的结构类型的柔度计算公式。
杆系结构的柔度计算公式杆系结构是指由杆件组成的结构,例如悬臂梁、桁架等。
对于杆系结构,柔度可以通过弹性力学的方法进行计算。
根据弹性力学理论,杆件的柔度与杆件的材料力学性质、截面形状、长度等因素有关。
常见的杆系结构柔度计算公式如下:F = k * δ其中,F表示结构受力,k表示柔度系数,δ表示结构的变形量。
柔度系数k可以通过杆件的材料力学性质和几何参数计算得到。
板系结构的柔度计算公式板系结构是指由薄板组成的结构,例如平板、薄壳等。
对于板系结构,柔度可以通过板的弯曲理论进行计算。
根据板的弯曲理论,板的柔度与板的材料力学性质、尺寸、支撑条件等因素有关。
常见的板系结构柔度计算公式如下:F = k * δ其中,F表示结构受力,k表示柔度系数,δ表示结构的变形量。
柔度系数k可以通过板的材料力学性质和几何参数计算得到。
梁系结构的柔度计算公式梁系结构是指由梁组成的结构,例如悬臂梁、梁柱系统等。
对于梁系结构,柔度可以通过梁的弯曲理论进行计算。
根据梁的弯曲理论,梁的柔度与梁的材料力学性质、截面形状、长度、支撑条件等因素有关。
常见的梁系结构柔度计算公式如下:F = k * δ其中,F表示结构受力,k表示柔度系数,δ表示结构的变形量。
柔度系数k可以通过梁的材料力学性质和几何参数计算得到。
上述三种结构类型的柔度计算公式都遵循相同的基本原理,即柔度与受力和变形量之间的关系。
通过合理选择柔度计算公式,可以准确计算出结构的柔度,进而评估结构的性能和稳定性。
需要注意的是,结构力学柔度计算公式只是结构分析的一部分,结构的实际变形情况还需要考虑材料的非线性特性、接触约束、温度变化等因素的影响。
结构力学专题七(单自由度体系的动力计算)

设: 2
k11 m
1
m11
运动方程: y(t) 2 y(t) 0
1、运动方程的解
y(t) c1sin t c2 cos t
(a)
或 y(t) csin( t )(ຫໍສະໝຸດ )当 y0、y0 为已知时
y(t)
y 0
sin
t
y
0
cos
t
(c)
方程(a)、(b)、(c)称为位移方程。
2、位移方程的几何意义
A1 5cm2
W 0.1kN
3m
(1)求竖向振动时的频率和周期,
(2)设: y0 10cm(向下),y0 0;
求: t
4
90
时质体的绝对位移。
A2 10cm2
4m
补2(选作):求图示体系的自振频率:
m
EI
m
k
l
l
l EI
FP (t)
EI
l/2 l/2
三、举例与讨论
例1: 建立图示体系运动微分方程 FP (t)
m EI
l/2 l/2
方程:
L3 48EI
(my(t)
cy(t))
y(t)
L3 48EI
FP (t)
my(t) cy(t)
48EI L3
y(t)
FP (t)
例2: 建立图示体系运动微分方程
FP (t)
EI0
m
h EI
EI
方程:
my(t) cy(t)
m
EI FP (t)
l/2 l/2
例3: 求图示体系的自振频率。
FP (t)
EI0
m
h EI
EI
结力(下)复习(结构动力学)解析

k11
k12
12m1
1 7.5661
8.欲使图示体系的自振频率增大,在下述办法中可采用:
A.增大质量m; C.减小梁的EI;
m EI
B.将质量m 移至梁的跨中位置 ; D.将铰支座改为固定支座 。
k 1
m m
(D )
9.图 示 体 系 的 自 振 频 率 3EI1 / (mh3) 。 ( )
m
EI=oo
EI1
EI1
h
k 6EI1 , k 6EI1
h3
m mh3
10.图示体系 EI 2105 kN m2, 20s-1, k 3105 N/m, P 5103 N, W 10kN。 求质点处最大动位移和最大动弯矩 。
Psin t
k W
2m
2m
解:
1 (1 21 2 1 2) 1 1
Psin t
A
W
l /2
l /2
3l 16 5l 32 M1
解:自振频率
B
1 ( 1 l l 3l 1 l l 2 l 2)
EI 2 4 32 2 4 2 3 4
l3 ( 1 3 ) EI 48 256
要点:
结构动力学
1. 单自由度体系的自由振动,自振频率 (刚度法和柔度法) 2. 单自由度体系的强迫振动,动力系数,动内力和动位
移幅值(振幅) 3. 多自由度体系的自由振动的频率及主振型的计算 (刚度
法和柔度法) 4. 多自由度体系受同步简谐动荷作用下的动内力和动位
移幅值的计算
掌握所涉及到的所有公式。
2 1 [( k11 k22 ) ( k11 k22 )2 4(k11k22 k12k21) ]
2 m1 m2
结构动力学的刚度系数柔度系数通用课件

扭曲刚度系数计算
扭曲刚度系数定义
01
扭曲刚度系数是衡量结构在扭曲载荷下抵抗变形的能力的系数。
扭曲刚度系数的计算公式
02
扭曲刚度系数可以通过结构材料的弹性模量和截面极惯性矩计
算得出。
扭曲刚度系数的物理意义
03
扭曲刚度系数越大,表示结构在扭曲载荷下的变形越小,结构
的抗扭能力越强。
复合受力下的刚度系数计算
分析方法
通过对处理后的数据进行统计分析、曲线拟合、模式识别等,可以进一步分析结构的动力学特性,包括固有频率、 阻尼比等参数。此外,还可以通过对比不同结构的响应数据,评估不同结构的动力学性能。
实验结果及讨论
实验结果
实验测得了不同结构在不同激振条件下的响 应数据,包括加速度和位移。通过对数据进 行处理和分析,得到了不同结构的刚度系数 和柔度系数以及相关的动力学参数。
刚度系数和柔度系数是结构动力学中两个重要的概念,可以反映结构的刚度和柔度性质。
本文通过理论和实例分析,对结构动力学中的刚度系数和柔度系数进行了详细阐述,并介绍了它们在工 程实际中的应用和意义。
对未来研究的展望
随着科学技术的发展,结构动力学的研究领域将不断扩大,对刚度系数和柔度系数 的认识也将更加深入。
复合受力下的柔度系数的计算
复合受力下的柔度系数可以通过结构在复合力作用下的变形量进行计算。
03
复合受力下的柔度系数的影响因素
复合受力下的柔度系数受到材料性质、截面形状、边界条件等因素的影
响。
04
刚度系数与柔度系数的应用
在结构设计中的应用
刚度系数
在结构设计中,刚度系数是用来衡量结构抵抗变形的能力。通过计算和分析刚度 系数,可以确定结构的稳定性、承载能力和振动特性。
《结构力学》-龙驭球-10-动力学(6)

频率与反对称主振型的自振频率相等时才发
Y1
D1 D0
,
Y2
D2 D0
生共振。
不会趋于无穷大,不发生共振, 共振区只有一个。
Y1 FI1 / m1 2 Y2 FI 2 / m2 2
4.当 1 或 2 时
(11 1/ m1 2 )FI1 12 FI 2 1P 0 Y1 Y2
21FI1 ( 22 1/ m2 2 )FI 2 2P 0
§10-6 两个自由度体系在简谐荷载下的受迫振动
1、刚度法
m1 y..1 k11 y1 k12 y2 m2 y..2 k21 y1 k22 y2
F0P1(t) F0P2 (t)
如FP1(t) FP1 sint FP2 (t) FP2 sint
y1(t) Y1 sint 在平稳阶段,各质点也作简谐振动: y2 (t) Y2 sint
当 m1 = m2 = m,k1 = k2 = k
Y1
FP
(k
D0
2m)
D0 (2k m 2 )(k m 2 ) k 2
Y2
FP k D0
D0
k2k11k2k22132 mk2m1kmk2222k1m2k22mm 24
2 mD214 FPk1 2k22 2m2 m2D(2mk22 FP32 mkk11 2 2m41)
已知:m1 m2 m, 3.415
EI ml 3
解: Y1 11 (Fp FI1 ) 12 FI 2
Y2 21 (Fp FI1 ) 22 FI 2
Y1 FI1 / m1 2 Y2 FI 2 / m2 2
Fp sin t
m1
m2
l / 3 y1 lE/I3y2 l / 3
▲ 结构动力计算期末复习

—— 振动微分方程
2.位移方程法(柔度法)
FP=1
静平衡位置为原点 方程与重力无关 单位力引起的位移
δ
δ=1/k
m
(1)确定柔度系数 δ
I (t ) my
y
(2)规定位移的正向(定坐标)
(3)标出惯性力(沿正向)
(4)写出位移方程(考虑结构的位移协调)
y(t ) I (t ) my(t ) —— 惯性力引起的位移
1 192 EI 134.16s 1 m 5ml 3
1 1
2 2
1.552
3)求yDmax , MDmax
yD max 5l 3 1.552 20 103 5 43 P P 5.75 103 m 192 EI 192 90 105
4.弄懂共振原理,以及阻尼对共振区的重大影响。
三.两个(多个)自由度体系的自由振动 1.会列振动方程,并用矩阵式表示,刚、柔度法均掌握;
m1 0 0 1 k11 y k m2 y2 21 k12 y1 0 y 0 k22 2
62.8 2
2
0.33
2)动力荷载幅值所引起的静位移 P P y st P k m 2 4.9 9.8 1000 0.1 mm 2 123 62.6
Psinθt
m 1m
3)最大动力位移 [ y( t )]Dmax yst 0.033mm 4)振幅
——
(3)方法选择
柔度法
取决于结构的 刚度系数 柔度系数
谁较容易求得。
静定结构,图乘法求δ
顺利求解刚(柔)度系数是自由振动分析的关键!
▲ 结构刚、柔度概念强化和灵活应用

6EI k0 = = 3 δ l
1
6EI k = k0 = 3 l
[例3]求图示结构 点的竖向刚度k。 3]求图示结构C点的竖向刚度 。 求图示结构 点的竖向刚度 C EI l EI l EI EA=∞ EI l
刚度示意图) (刚度示意图)
∆=1
k
6i/l
k
12i/l2
解: 由图示可见,相当于四根两端固支梁并联。 由图示可见,相当于四根两端固支梁并联。
k0
[例2]求图示结构 点的竖向刚度。 2]求图示结构B点的竖向刚度。 求图示结构 点的竖向刚度
A
E1I1=∞
B EA=∞ EI
A
E1I1=∞(等效图) 等效图)Fra bibliotekB k0
l /2
l /2
l
解: 1)作等效图 ) 2)简支梁中点柔度 )
(2l )3 l3 δ= = 48 EI 6 EI
3)B点竖向刚度 ) 点竖向刚度
h1
i1
i2
h2
k = k左柱 + k右柱 =
∞ h
总侧移刚度: 总侧移刚度:
i1
i2
k = k左柱 + k右柱
n
12 i1 12 i2 = 2 + 2 h h
并联一般公式: 并联一般公式:
k = ∑kj
j =1
(2)串联 )
∆ P h2 h1 k2 ∆1 ∆2
1 ∆1 = P iδ1 = Pi k1
结构刚、 ▲ 结构刚、柔度概念强化和灵活应用
1. 刚、柔度概念
δ 1
柔度δ 单位力引起的位移。 柔度 —— 单位力引起的位移。 力偶) 转角) (力偶) (转角)
1 k
6《结构动力学》-第六章
x2
x3
k4
x4
k5
x5
m2
k3
m3
m4
m5
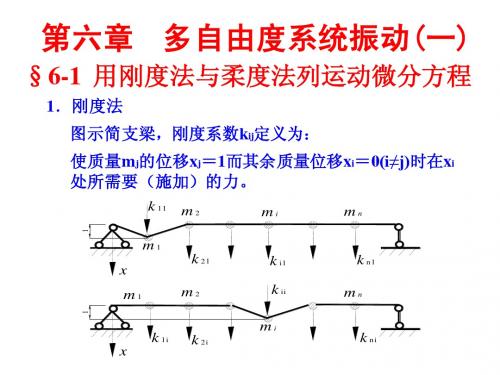
解:首先用力使m1产生单位位移,并用力使其余质量不动, 首先用力使 产生单位位移,并用力使其余质量不动, 则需要给m 的力为k 的弹性力和, 则需要给 1的力为 1与k2的弹性力和,即k11=k1+k2。此时 m2需加力为 2,沿x的负方向,即k21=-k2,其余质量不必 需加力为k 的负方向, 的负方向 施加任何力, 施加任何力,即k31=k41=k51=0。 。 用类似方法可得其余刚度系数,于是有: 用类似方法可得其余刚度系数,于是有:
m2上加单位力,各质量的位移分别为: 上加单位力,各质量的位移分别为:
a12 = 1 k1 a 22 = 1 1 + k1 k 2 a 32 = a 22 = 1 1 + k1 k 2
〈例〉求图示三自由度系统的刚度矩阵和柔度矩阵。 求图示三自由度系统的刚度矩阵和柔度矩阵。
k1
m1
x1 k2
x2
x3 m3
LL
用矩阵符号可写成: 用矩阵符号可写成:
LL
mn &&n = −k n1 x1 − k n 2 x2 − LL − k nn xn + Fn (t ) x
& [M ]{X& }+ [K ]{X } = {F (t )}
〈例〉求图示五自由度系统的刚度矩阵。 求图示五自由度系统的刚度矩阵。
k1
m1
x1 k2
或写成: 或写成:
& {X } + [A][M ]{X& } = {0}
在刚度矩阵[K]非奇异条件下,柔度矩阵 与刚度矩 在刚度矩阵 非奇异条件下,柔度矩阵[A]与刚度矩 非奇异条件下 存在如下的互逆关系: 阵[K]存在如下的互逆关系: 存在如下的互逆关系
结构动力学计算

变化,且作相位相同的同步运动,即它们在同一时刻均达极值;
➢ 由于在运动的任一瞬时质体都处于平衡状态,于是可在幅值
处建立运动方程,此时方程中将不含时间t,把微分方程转化为
代数方程,使计算得以简化。
例7. 求图示体系的自振频率
m1 m
B
EI C
m2
1 3
m
m l22kl2
A
0 .5 l
l
kD 0 .5 l
在质量上沿位移方向施加惯性力; 求外力(包括惯性力)引起的质量的位移; 令该位移等于体系的位移;
例2. 用柔度法建立体系的运动方程
m
l EI EI
l
O
y
my y
ym y
my 1 y 0
2l 3
11 3EI
my(t)32E l3Iy(t)0
P=1
图乘法
?
l
例3:用柔度法列运动方程
m y(t)
12 EI h3
6 EI h2
1
6 EI
k
h2
12 EI
h3
6 EI h2
k m
24EI mh3
T 2
练习3:计算图示结构水平振动和竖直振动时 的自振 频率,自重忽略不计。
m
EI常 数
l
l
l
Horizontal Vibration: -----Flexibility Method
Anti-symmetrical Load +symmetrical Structure
✓ 自振频率计算公式
k m
1
m
tan1
y
0 0
v
0
✓ 计算k或δ:静力学知识 l 3 1 8EI
结构动力学多自由度

pbT
~ fpa
paT ~fpb paT ~fpb T pbT ~f T pa pbT ~fpa
故 ~f 、 k 均为对称矩阵。
单元刚度矩阵
单元刚度系数表示由单位节点位移所引起的节点力。
单元刚度系数由虚位移法求得。
例如,课本P106图11-5所示简支梁中,令a端发生单位转角, 并给该处一竖向虚位移,零外力所做的功,等于内力所做的 功。
表示一个自由度发生相应单位位移而其他节点不动时在结构中所 产生的的力。
弹性特性
柔度的定义:
~ fij —在j坐标施加单位荷载而引起的i坐标的挠度。
则任意荷载组合下: vi ~fi1 p1 ~fi2 p2 ~fiN pN
用矩阵表示:
v1
vi
v N
略去阻尼矩阵和施加的荷载向量的影响: mv kv 0
假定以上多自由度体系的振动是简谐振动:
v(t) vˆ sin(t )
vˆ 表示体系的形状,不随时间变化。
v 2vˆ sin(t ) 2v 2mvˆ sin(t ) kvˆ sin(t ) 0
k 2m vˆ 0
无阻尼自由振动—振动频率分析
k 2m vˆ 0
即: k 2m 0
上式的N个根,表述体系可能存在的N个振型的频率。
1
2
3
WE va pa v1 k13
Lபைடு நூலகம்
WI v1 0 EI ( x) 1''( x) 3''( x)dx
理论力学中的刚度与柔度分析

理论力学中的刚度与柔度分析理论力学是研究物体在外力作用下的力学性质和相互作用的学科。
在力学中,刚度和柔度是描述物体对外力响应的重要参数。
本文将重点介绍刚度和柔度的概念、计算方法以及在工程中的应用。
一、刚度的概念与计算方法刚度是指物体抵抗形变的能力。
当物体受到外力作用时,如果能够保持形状不发生变化,即具有很高的抵抗形变能力,我们称该物体具有高的刚度。
刚度可以用来衡量物体对力的响应程度,是一个标志物体强度和刚性的指标。
在理论力学中,刚度通常用弹性系数表示。
最常见的是弹性模量,也称为杨氏模量,用E表示。
弹性模量描述了物体受力时的应变与应力之间的关系。
弹性模量越大,物体的刚度就越高。
计算刚度的方法有多种,其中最常用的是针对杆件和弹簧的刚度计算公式。
对于杆件,刚度可以通过杨氏模量和截面形状来计算。
例如,对于长度为L、截面面积为A的杆件,其刚度可以通过以下公式计算:刚度 = 弹性模量 ×截面积/长度对于弹簧,刚度可以通过弹性系数和弹簧的形状参数来计算。
例如,对于线性弹簧,其刚度可以表示为:刚度 = 弹性系数 ×弹簧长度/形变刚度的计算方法因物体的形状和材料特性而异,需要根据具体情况进行选择和计算。
二、柔度的概念与计算方法柔度是指物体在受到外力作用时发生形变的程度。
与刚度相反,柔度越高,物体对外力的响应越灵敏,形变程度越大。
在理论力学中,柔度可以用来衡量物体的柔软度和弯曲性。
柔度的计算方法与刚度类似,同样涉及物体的形状、尺寸和材料特性。
对于弹性材料,柔度可以用杨氏模量的倒数来表示。
也就是说,柔度可以表示为:柔度 = 1/弹性模量柔度越高,即弹性模量越小,物体的弯曲性越大,形变程度越严重。
对于弹簧,柔度可以通过弹性系数的倒数来表示。
即:柔度 = 1/弹性系数柔度的计算方法类似于刚度,需要根据具体情况进行选择和计算。
三、刚度与柔度在工程中的应用刚度和柔度在工程中具有广泛的应用。
它们在结构设计、材料选择以及机械性能评估等方面发挥着重要的作用。
结构力学应用-结构动力学

(小阻尼) 令
有阻尼的自振频率
1
2
y(t ) e
t
y0 y0 ( y0 cos t sin t )
*写成
y(t ) b e
2 0
t
sin(t )
(14-12)
y0 y0 2 其中 b y ( )
柔度法(力法)
MY KY 0 MY Y 0
10、按柔度法求解
振型方程: ([ ][ 2 [ 1 M ]){Y } 00} ([ I ] M ] ][ [ I ]){Y } { 2 频率(特征)方程
D [ ][ M ] [ I ] 0
y0 tg y0 y0
位移-时间曲线如图示:
阻尼比——阻尼的基本参数: a.阻尼对频率(周期)的影响
k
2m
1 2
T T 1 2 T
0.2
T T
b、阻尼对振幅的影响
be
t
——振幅随时间逐渐衰减
11m1
1
12 m2
(k )
0 0
(14 63)
{Y }
(k )
Y1 Y2
(k )
11m1 k 12 m2
12 m2
k2
(k=1、2)
结构的刚度和质量分布 ——对称 其主振型 ——对称、反对称 计算自振频率: ——分别就正、反对称情况 ——取半跨结构计算 ——两个单自由度问题计算 显然,振型分别为: [1 1]T、[1 -1]T
1
0.2,
yn ln 2 j yn j 相隔j个周期: 1
结构动力学多自由度

求解系数:由质量矩阵和刚度矩阵的正交性,阻尼矩阵的一般形式为:
不耦合的运动方程—有阻尼
同理:
故:
不耦合的运动方程—有阻尼
另一种方法:
不耦合的运动方程—有阻尼
体系的对角广义质量矩阵:
不耦合的运动方程—有阻尼
在上式中,每一振型对阻尼矩阵起的作用与振型的阻尼比成比例。因此,任何无阻尼的振型对阻尼矩阵不起作用。
对每一项乘一个未知的时间函数li(t),并且将这个乘积在时间间隔t1到t2积分:
由于变分为零:
令:
Lagrange运动方程可改写为:
规格化的主振型矩阵:
无阻尼多自由度结构体系自由振动方程:
第i 阶振型的特解:
这样的特解有n个!
振型的物理意义
将N个振型中的每一振型形式,用F表示N个振型所组成的方阵。
以上矩阵为结构的振型矩阵,为一N*N方阵。
各项前乘 ,可得:
即:
注意:即使质量矩阵和柔度矩阵都是对称的,它们的乘机也是不对称的!
几何约束条件:
Hamilton原理:
动能可以用广义坐标和它们的一次导数表示,位能可以单独用广义坐标表示。非保守力在广义坐标的一组任意变分所引起的虚位移上所做的虚功,可以表示为这些变分的线性函数。
代入Hamilton原理公式:
由分部积分公式:
由:
故:
Lagrange运动方程:
由算例:
此时:
Lagrange运动方程写为:
假定弯矩—位移关系:
上式中,第一项由保守力产生,第二项由非保守力产生。
非保守力所做的虚功:
假定非保守力仅限于横向分布荷载p(x,t),这些力的虚功为:
非保守力所做的总虚功为:
其中:
刚度系数和柔度系数的关系

刚度系数和柔度系数的关系嘿,朋友们!今天咱来聊聊刚度系数和柔度系数这俩家伙呀!你说这刚度系数呢,就像是个硬骨头,特别倔强,不容易变形。
想象一下,那就是一根特别结实的铁棍,你怎么掰它都很难让它弯曲。
它呀,代表着材料抵抗变形的能力,越强就越难让它有啥变化。
而柔度系数呢,简直就是刚度系数的反义词啦!它就像个面团似的,可以随意被揉捏变形。
它反映的是材料容易变形的程度呀。
咱举个例子哈,比如说弹簧。
那弹簧就是柔度系数比较大的典型。
你轻轻一拉,它就能变长好多,很容易就变形啦。
但要是换成一块铁板,那可就不一样咯,你得使多大劲才能让它有点变化呀,这就是刚度系数大的表现。
你说这俩家伙是不是很有意思呀?它们就像一对欢喜冤家。
有时候我们需要刚度系数大的材料,比如建大桥呀,那可不能软了吧唧的,得稳稳当当的。
可有时候呢,又需要柔度系数大的,像一些需要缓冲的地方,就得能屈能伸。
刚度系数和柔度系数的关系呀,就好像白天和黑夜,相互对立又相互依存。
没有绝对的好与坏,只有在合适的地方发挥合适的作用。
咱在生活中不也常常遇到这样类似的情况嘛!有时候我们得像刚度系数一样坚定,不轻易被外界改变;可有时候呢,又得像柔度系数一样灵活,能适应各种变化。
比如说在职场上,该坚持原则的时候就得刚,可遇到一些特殊情况也得学会变通呀。
再想想,人际关系不也是这样嘛!和有些人相处,你就得硬气点,不能随便被欺负;可和另一些人呢,就得柔和点,不然关系不就僵啦。
所以呀,我们得学会把握好这个度,根据不同的情况灵活运用刚度系数和柔度系数的特点。
不能一味地刚,也不能一味地柔,得刚柔并济才行呀!这就好像走路,一条腿太硬走不快,一条腿太柔又走不稳,得两条腿配合好了,才能稳稳当当往前走不是?总之,刚度系数和柔度系数这俩概念虽然是在物理学里的,但咱在生活中也能找到好多类似的道理呀。
我们要学会在不同的场景下,发挥出它们的优势,让我们的生活更加美好,更加顺利呀!你们说是不是这个理儿呢?。
▲ 结构刚柔度系数复习.ppt

§13-1 动力计算的特点和动力自由度 §13-2 单自由度体系的自由振动
▲ 结构的刚、柔度系数复习 §13-3 单自由度体系的强迫振动 §13-4 阻尼对振动的影响 §13-5 两个自由度体系的自由振动 §13-7 两个自由度体系在简谐荷载下的
强迫振动 §13-11 近似法求自振频率
k m
48 EI ml 3
T 2 ml 3
48 EI
结束
(第二版)作业: 10 — 4、5
三、自由振动微分方程的解
y(t) Asin( t )
四、结构的自振周期和频率
静定结构,图乘法求δ
k 1 m m
T 2
五、例题
m EI
l /2
l /2
1
[例1] 计算图示结构的频率和周期。
解:(柔度法)
1 m
l3
48EI
48EI ml 3
T 2 ml3
24EI 5ml 3
1y 2
y
(位移几何关系)
ky
A
m(1 y) 2
my
(惯性力和弹力)
[例10] 建立图示结构的振动方程,并计算自振频率、周期。
k
k
m
EI
EI
Δ=1
l
6i/l
EA=∞
EI
EI
l
l
12i/l2
解:
刚度并联:
k
4 12i
/
l2
48 EI l3
48 EI 振动方程 my ky 0 即 my l 3 y 0
3EI h3
3EI h3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、自由振动微分方程的解
y(t ) Asin( t )
四、结构的自振周期和频率
k 1 m m
T
2
五、例题
m
l /2 1 EI l /2
[例1] 计算图示结构的频率和周期。 (柔度法) 解:
1 m
l 48EI
ml 3 T 2 48EI
3
48 EI ml 3
1
k22 k2
k12 k2
k2
EI∞
k11 k1 k2
1
k1
k1 、k2 —— 楼层刚度(本楼层单位侧移所需的侧向力) k11 、k12 、k21 、k22 —— 位移法的刚度系数 kij
kij
—— 第j 个结点位移发生单位位移(其它结点位移均锁固)时, 在第i 个结点位移处产生的反力。
h EI EI
3EI 3EI 6EI k k左柱 k右柱 3 3 3 h h h
总侧移刚度:
h2
h1
i1
i2
k k左柱 k右柱
3 i1 3 i2 2 2 h1 h2
∞ h
总侧移刚度:
i1
i2
12 i1 12 i2 k k左柱 k右柱 2 2 h h
(刚度并联,两者叠加)
k
k11 k
EI
1
l
3EI l3
k11 m
3 EI
l3
k m
[例7]计算图示刚架的频率和周期。
1
m EI1= I I h
k
解: (刚度法)
由柱刚度并联 得:
12 EI 24 EI k 2 3 3 h h
k 24 EI m mh3
mh3 T 2 2 EI
2
[例8]建立图示结构的振动方程,并计算自振频率。
A l /2
2m
EI=∞
m k
l /4
解: (刚度法) 由∑MA=0 得:
l /2
4 y (位移几何关系) 5 4 k ( y) 5 2m
1
[例2] 计算图示结构的水平和竖向振动频率。
m
H
1
解:
V
E,I E,A
1 H m H
l3 其中 H 3EI
l 其中 v EA
A,E,I
l
1 V mV
[例3] 图示三根单跨梁,EI为常数,在梁中点有集中质量m , 不考虑梁的质量,试比较三者的自振频率。 m m m
1 1 1 1 k k1 k2 k3
3)计算顶端侧移
1 1 1 P P k1 k2 k3 2 2 h3 P h12 h2 24 i1 i2 i3
▲单自由度体系的自由振动要点回顾
一、自由振动 二、振动微分方程的建立
由图示可知:
k11=k1+k2
k12=k21=-k2
k22=k2
3. 应用举例
P
求图示三层刚架的顶端侧移。
解: 1)计算各楼层(侧移)刚度
i3 i2
i3 i2
12i1 k1 2 2 h1
12i2 k2 2 2 h2
12i3 k3 2 2 h3
(柱并联)
i1
i1
2)计算楼顶点(侧移)柔度
(1)刚度法 (2)柔度法
——
ky 0 my
y 2 y 0
——
研究作用于被隔离的质量上的力,建立 平衡方程,需要用到刚度系数。 研究结构上质点的位移,建立位移协调方程, 需要用到柔度系数。
超静定结构,查表(形常数)
取决于结构的
刚度系数 柔度系数
谁较容易求得。
静定结构,图乘法求δ
l/2 l/2
3 l/ 16
l/2
l/2
P=1
l/2
l/2
1 ,先求δ 解: m
l 1 48EI
3
l/
2
3l /32 7l5 2 P=1 768EI
l3 3 192 EI
1
48 EI ml 3
3 192 EI 1 l 2 768 l EI 3l l 5l 7l 2 2 (2 3 )3 EI 6 2ml 16 2 32 768 EI 7 ml 3
5
1 87.35 S 1 m
[例5]求图示结构的自振圆频率。
A
h
m
I→∞ EI C
解:先求δ
B
l
1 lh 2h lh 2 EI 2 3 3EI
1
h h
1 3EI 2 m11 mlh
[例6]求图示结构的自振频率。 解:先求k11
k11 m
3EI k11 k 3 l
▲ 结构的刚、柔度系数 复习
1. 刚、柔度概念
δ 1
补充内容
柔度 —— 单位力引起的位移。 (力偶) (转角)
1 k
刚度 —— 单位位移所需施加的力。 (转角) (力偶)
两者的互逆关系:
K δ
k 1
1
单自由度时:
● 熟记几种简单情况的刚、柔度
δ 1
悬臂梁自由端: l3 3EI
k1
、k2 — 楼层刚度
12i2 k2 2 h2
总刚度:
k
P 1 1 1
k1 k2
12i1 k1 2 h1
串联一般公式:
n 1 1 1 1 1 k k1 k2 kn j 1 k j
▲ 楼层刚度与位移法刚度系数的关系
EI∞
k21 k2
并联一般公式:
k kj
j 1
n
(2)串联
Δ P h2 k2 Δ1 Δ2
1 1 P 1 P k1
楼面刚度 为无穷大 视同刚臂
1 2 P 2 P k2
h1
k1
1 1 1 1 1 2 P P P k1 k2 k1 k2
k
3EI l3
i
1 k
两端固支梁侧移刚度: 12 EI 12i k 3 2 l l
i
1
一固一铰支梁的侧移刚度:(同悬臂梁) 1 3EI 3i k 3 2 l l k 简支梁中点柔度、刚度:
l3 48EI 48E联、串联刚度 (1)并联 总侧移刚度:
据此可得:ω1 ׃ω2 ׃ω3= 1 ׃1.512 ׃2
结构约束越强,则刚度越大, 其自振动频率也越大。
[例4] 图示桁架,E=206GPa , A=0.002m2 , mg=40KN , 计算自振频率。( g取10m/s2 )
1
(柔度法) 解:
3
m 4 4
( Fn )i2 li 243 EA 18EA i 1
