《大学物理A(II)》第9次作业解答
《大学物理》第二版-课后习题标准答案-第九章

《大学物理》第二版-课后习题答案-第九章————————————————————————————————作者:————————————————————————————————日期:习题精解9-1.在气垫导轨上质量为m 的物体由两个轻弹簧分别固定在气垫导轨的两端,如图9-1所示,试证明物体m 的左右运动为简谐振动,并求其振动周期。
设弹簧的劲度系数为k 1和k 2. 解:取物体在平衡位置为坐标原点,则物体在任意位置时受的力为 12()F k k x =-+ 根据牛顿第二定律有2122()d xF k k x ma m dt=-+==化简得21220k k d x x dt m++= 令212k k mω+=则2220d x x dt ω+=所以物体做简谐振动,其周期1222mT k k ππω==+9-2 如图9.2所示在电场强度为E 的匀强电场中,放置一电偶极矩P=ql 的电偶极子,+q 和-q 相距l ,且l 不变。
若有一外界扰动使这对电荷偏过一微小角度,扰动消息后,这对电荷会以垂直与电场并通过l 的中心点o 的直线为轴来回摆动。
试证明这种摆动是近似的简谐振动,并求其振动周期。
设电荷的质量皆为m ,重力忽略不计。
解 取逆时针的力矩方向为正方向,当电偶极子在如图9.2所示位置时,电偶极子所受力矩为sin sin sin 22l lM qE qE qEl θθθ=--=- 电偶极子对中心O 点的转动惯量为2221222l l J m m ml ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭由转动定律知2221sin 2d M qEl J ml dtθθβ=-==•化简得222sin 0d qEdt mlθθ+= 当角度很小时有sin 0θ≈,若令22qEmlω=,则上式变为222sin 0d dtθωθ+= 所以电偶极子的微小摆动是简谐振动。
而且其周期为222mlT qEππω== 9-3 汽车的质量一般支承在固定与轴承的若干根弹簧上,成为一倒置的弹簧振子。
大学物理2A答案

第1页,共2页第2页,共2页院系: 专业班级: 学号: 姓名: 座位号:2011-2012学年第一学期期末考试试卷答案与评分标准《大学物理2》(A )卷一、选择题(每小题2分,共30分)1、B2、C3、D4、A5、C6、A7、B8、D9、D 10、C 二、填空题(每小题2分,共10分) 1、10,π2 2、 (=1,2,3...)2nn λ3、22 (=0,1,2,...)Δdn k k λ==4、-31.210⨯5、1000三、判断题:(每小题1分,共10分)1. T2. T3. F4. F5. F6. F7. T8. T9. F 10. T 四、计算题(本大题共4个小题,共50分)1、解:(1)波动方程:](cos[ϕω+-=u x t A y----------------------------------3分ω = 2π/T = π u = λ/T =1m/s -----------------------------------2分00==x t 0,0>∂∂==ty y v2π-=ϕ ---------------------2分2π)(πcos[0.1--=x t y ---------------------------------1分(2)波的表达式,由]2π)(πcos[0.1--=x t y得]π2πcos[0.1x y -=xπsin = -----------------------------------1分s 0.1=t波形图-------------------------3分(3)m 5.0=x 处质点的运动方程 由2π)(πcos[0.1--=x t y 得]πcos[π-=t y--------------------------3分2、解:(1)一侧的第2条暗纹与另一侧的第2条暗纹间为(2K+1)个条纹间距,由λ∆d x d '=, ----------------------------------2分可得()22Δ2+1λd x k d'=----------------------------------3分()2221∆'x dλd k =+500 nm= ----------------------------------1分(2)中央明纹中心距离最邻近的暗纹中心的距离为半个条纹间距,则1'15 m m2d x λ.d'∆== ----------------------------------4分3、解:(1)分子速率在0到02υ范围内,由归一化条件:0002 202()2a N N f d d ad υυυυυυυυυυ==+⎰⎰⎰ 得03υN a =---------------------3分(2)0003/2/2227/12a N d ad N υυυυυυυυ∆=+=⎰⎰ --------------------------------3分(3)分子速率平方的平均值: 222/()dN N f d υυυυυ∞∞==⎰⎰;0022321122()22k a a m m d d N Nυυυευυυυυυ==+⎰⎰203631υm =--------------4分4、解:(1)循环系统所做的功:2810W P V =∆⋅∆=⨯J --------------------4分 (2)系统吸收的热量:1()()ab da P b a V a d Q Q Q C T T C T T =+=-+-53()()22b b a a a a d d P V P V P V P V =-+-25210=⨯J ----------------------------------8分效率:115.4%W Q η=≈ -----------------------------3分/y 课程代码: 22002172 适用班级: 09数学与应用数学 命题教师: 杨亦云 任课教师: 杨亦云。
大学物理课后习题答案第九章

第9章 电稳感应和电磁场 习题及答案1. 通过某回路的磁场与线圈平面垂直指向纸面内,磁通量按以下关系变化:23(65)10t t Wb -Φ=++⨯。
求2t s =时,回路中感应电动势的大小和方向。
解:310)62(-⨯+-=Φ-=t dtd ε 当s t 2=时,V 01.0-=ε由楞次定律知,感应电动势方向为逆时针方向2. 长度为l 的金属杆ab 以速率υ在导电轨道abcd 上平行移动。
已知导轨处于均匀磁场B ϖ中,B ϖ的方向与回路的法线成60°角,如图所示,B ϖ的大小为B =kt (k 为正常数)。
设0=t 时杆位于cd 处,求:任一时刻t 导线回路中感应电动势的大小和方向。
解:任意时刻通过通过回路面积的磁通量为202160cos t kl t Bl S d B m υυ==⋅=Φρρ导线回路中感应电动势为 t kl tmυε-=Φ-=d d 方向沿abcda 方向。
3. 如图所示,一边长为a ,总电阻为R 的正方形导体框固定于一空间非均匀磁场中,磁场方向垂直于纸面向外,其大小沿x 方向变化,且)1(x k B +=,0>k 。
求: (1)穿过正方形线框的磁通量;(2)当k 随时间t 按t k t k 0)(=(0k 为正值常量)变化时,线框中感生电流的大小和方向。
解:(1)通过正方形线框的磁通量为⎰⎰=⋅=Φa S Badx S d B 0ρρ⎰+=a dx x ak 0)1()211(2a k a +=(2)当t k k 0=时,通过正方形线框的磁通量为)211(02a t k a +=Φ 正方形线框中感应电动势的大小为dt d Φ=ε)211(02a k a += 正方形线框线框中电流大小为)211(02a R k a R I +==ε,方向:顺时针方向4.如图所示,一矩形线圈与载有电流t I I ωcos 0=长直导线共面。
设线圈的长为b ,宽为a ;0=t 时,线圈的AD 边与长直导线重合;线圈以匀速度υρ垂直离开导线。
大学物理(下) No.9作业解析

《大学物理》作业 No.9原子结构 激光 固体一、选择题1. 氢原子中处于3d 量子态的电子,描述其量子态的四个量子数(n , l , m l , m s )可能取的值为[ D ] (A) (3,1,1,-1/2) (B) (1,0,1,-1/2)(C) (2,1,2,1/2) (D) (3,2,0,1/2)解:3d 量子态的量子数取值为n =3,l =2,21,2,1,0±=±±=s l m m 。
2. 在氢原子的K 壳层中,电子可能具备的量子数(n , l , m l , m s )是[ A ] (A) (1,0,0,1/2) (B) (1,0,-1,1/2)(C) (1,1,0,-1/2) (D) (2,1,0,-1/2)解:K 壳层n =1,l =0,l m =0,2/1±=s m 。
3. P 型半导体中杂质原子所形成的局部能级(也称受主能级),在能级结构中应处于[ C ] (A) 满带中。
(B) 导带中。
(C) 禁带中,但接近满带顶。
(D) 禁带中,但接近导带底。
4. 与绝缘体相比较,半导体能带结构的特点是[ D ] (A) 导带也是空带。
(B) 满带与导带重合。
(C) 满带中总是有空穴,导带中总是有电子。
(D) 禁带宽度较窄。
5. 激发本征半导体中传导电子的几种方法有 (1) 热激发,(2) 光激发,(3) 用三价元素掺杂,(4) 用五价元素掺杂。
对于纯锗和纯硅这类本征半导体,在上述方法中能激发其传导电子的只有[ D ] (A) (1)和(2)。
(B) (3)和(4)。
(C) (1)(2)和(3)。
(D) (1)(2)和(4)。
6. 硫化镉(CdS)晶体的禁带宽度为2.42eV ,要使这种晶体产生本征光电导,则入射到晶体上的光的波长不能大于(普朗克常量s J 1063.634⋅⨯=-h ,基本电荷C 1060.119-⨯=e )[ D ] (A) 650nm 。
大学物理课后习题答案第九章

外。当>0时,求:杆两端的感应电动势的大小和方向。
解:
故
∵
故
(即从)
14.一同轴电缆由两个同轴圆筒构
成,内筒半径为1.00mm,外筒半径为
7.00mm,求每米该同轴电缆的自感系
数(两筒的厚度可忽略)。
解:设电流由内筒流出、外筒流回,由安培环路定理得
内、外筒之间,
内、外筒之间每米长度所通过的磁通量:
每米同轴电缆的自感系数:
O x
O x
解:建立图示坐标系,长直导线在右边产生的磁感应强度大小为 时刻通过线圈平面的磁通量为
任一时刻线圈中的感应电动势为
5.如图所示,在两平行载流的无限长直导线的平面内有一矩形线 圈。两导线中的电流方向相反、大小相等,且电流以的变化率增大, 求:
(1)任一时刻线圈内所通过的磁通量; (2)线圈中的感应电动势。 解:(1) 任一时刻通过线圈平面的磁通量为
第9章 电稳感应和电磁场 习题及答案
1. 通过某回路的磁场与线圈平面垂直指向纸面内,磁通量按以下 关系变化:。求时,回路中感应电动势的大小和方向。
解: 当时, 由楞次定律知,感应电动势方向为逆时针方向
2. 长度为的金属杆以速率在导电轨道上平行 移动。已知导轨处于均匀磁场中,的方向与回路的 法线成60°角,如图所示,的大小为=(为正常 数)。设时杆位于处,求:任一时刻导线回路中感 应电动势的大小和方向。
解:(1)通过正方形线框的磁通量为 (2)当时,通过正方形线框的磁通量为 正方形线框中感应电动势的大小为 正方形线框线框中电流大小为
,方向:顺时针方向 4.如图所示,一矩形线圈与载有电流长直导线 共面。设线圈的长为,宽为;时,线圈的边与长直 导线重合;线圈以匀速度垂直离开导线。求任一时 刻线圈中的感应电动势的大小。
大学物理作业9.1

(A) qd / 0 (C)qd / 2 0
答:C
(B) qd / 0
(D) qd / 20
第三页,编辑于星期六:十六点 二十六分。
大学物理
6、电荷分布在有限空间内,则任意两点P1、P2之间 的电势差取决于
(A) 从P1移到P2的试探电荷电量的大小
dU
1
4 0
dq
L d
x
kxdx
40 L d
x
UP
k
4 0
L 0
xdx
L d x
k
4 0
L 0
L
L
d
d
x
1dx
k (L d ) ln L d L
40
d
第十二页,编辑于星期六:十六点 二十六分。
大学物理
2、半径R为的圆弧形细塑料棒,两端空隙为d ( R d), 总电荷量为q的正电荷均匀地分布在棒上。求圆心O处场 强的大小和方向。
外有一同心的半径为R的均匀带电球面B,带电量
为 q2 ,则A、B两球面间的电势差为q1 (1 1。) 4 0 r R
第九页,编辑于星期六:十六点 二十六分。
大学物理
7、 两段形状相同的圆弧如图所示对称放置,圆弧
半径为R,圆心角为,均匀带电,线密度分别为
和 ,则圆心O点的场强大小为 0 。电势
大学物理
(3)半径相同处的电势相等
rR
U1
R r
E1
dl
R r dr
r 2 0
4 0
R2 r2
rR
U2
R r E2 dl
R R2 dr R2 ln r
《大学物理学》第二版下册习题解答

第九章 静电场中的导体9.1 选无穷远处为电势零点,半径为R 的导体球带电后,其电势为U 0,则球外离球心距离为r 处的电场强度的大小为(A) 302rU R . (B) R U 0. (C) 20rRU . (D) r U 0. [ C ] 9.2如图所示,一厚度为d 的“无限大”均匀带电导体板,电荷面密度为σ ,则板的两侧离板面距离均为h 的两点a 、b 之间的电势差为:(A) 0. (B)2εσ. (C) 0εσh . (D) 02εσh. [ A ]9.3 一个未带电的空腔导体球壳,内半径为R .在腔内离球心的距离为d 处( d < R ),固定一点电荷+q ,如图所示. 用导线把球壳接地后,再把地线撤去.选无穷远处为电势零点,则球心O 处的电势为 (A) 0 . (B)dq04επ.(C)R q 04επ-. (D) )11(4Rd q -πε. [ D ]9.4 在一不带电荷的导体球壳的球心处放一点电荷,并测量球壳内外的场强分布.如果将此点电荷从球心移到球壳内其它位置,重新测量球壳内外的场强分布,则将发现: (A) 球壳内、外场强分布均无变化. (B) 球壳内场强分布改变,球壳外不变. (C) 球壳外场强分布改变,球壳内不变.(D) 球壳内、外场强分布均改变. [ B ]9.5在一个孤立的导体球壳内,若在偏离球中心处放一个点电荷,则在球壳内、外表面上将出现感应电荷,其分布将是:(A) 内表面均匀,外表面也均匀. (B) 内表面不均匀,外表面均匀. (C) 内表面均匀,外表面不均匀.(D) 内表面不均匀,外表面也不均匀. [ B ]9.6当一个带电导体达到静电平衡时: (A) 表面上电荷密度较大处电势较高. (B) 表面曲率较大处电势较高. (C) 导体内部的电势比导体表面的电势高.(D) 导体内任一点与其表面上任一点的电势差等于零. [ D ]9.7如图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q .设无限远处为电势零点,试求: (1) 球壳内外表面上的电荷. (2) 球心O 点处,由球壳内表面上电荷产生的电势. (3) 球心O 点处的总电势.解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q .(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+9.8有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷.如图所示,试求: (1) 导体板面上各点的感生电荷面密度分布.(2) 面上感生电荷的总电荷.解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为σ.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()024cos 0220=++=⊥εσεθb r q E P π 2分 ∴ ()2/3222/b r qb +-=πσ 1分(2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()2/322/d d b r qbrdr S Q +-==σ总电荷为 ()q brrdrqb dS Q S-=+-==⎰⎰∞2/322σ 2分O9.9 如图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为q A 和q B 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净带电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为σ. ()()0004///4/d εεσπ++π⋅==⎰⎰a q a q R S U U B A S P A∵0d =⋅⎰⎰AS S σ∴ ()()04///επ+=a q a q U B A P9.10三个电容器如图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C第十章 静电场中的电介质10.1 关于D的高斯定理,下列说法中哪一个是正确的? (A) 高斯面内不包围自由电荷,则面上各点电位移矢量D为零.(B) 高斯面上处处D为零,则面内必不存在自由电荷.(C) 高斯面的D通量仅与面内自由电荷有关.(D) 以上说法都不正确. [ C ]10.2一导体球外充满相对介电常量为εr 的均匀电介质,若测得导体表面附近场强为E ,则导体球面上的自由电荷面密度σ为(A) ε 0 E . (B) ε 0 ε r E .(C) ε r E . (D) (ε 0 ε r - ε 0)E . [ B ]10.3 一平行板电容器中充满相对介电常量为εr 的各向同性均匀电介质.已知介质表面极化电荷面密度为±σ′,则极化电荷在电容器中产生的电场强度的大小为:(A) 0εσ'. (B) r εεσ0'. (C) 02εσ'. (D)rεσ'. [ A ]10.4一平行板电容器始终与端电压一定的电源相联.当电容器两极板间为真空时,电场强度为0E ,电位移为0D,而当两极板间充满相对介电常量为εr 的各向同性均匀电介质时,电场强度为E ,电位移为D,则(A) r E E ε/0 =,0D D =. (B) 0E E =,0D D rε=.(C) r E E ε/0 =,r D D ε/0 =. (D) 0E E =,0D D=. [ B ]10.5如图所示, 一球形导体,带有电荷q ,置于一任意形状的空腔导体中.当用导线将两者连接后,则与未连接前相比系统静电场能量将 (A) 增大. (B) 减小.(C) 不变. (D) 如何变化无法确定. [ B ]q10.6将一空气平行板电容器接到电源上充电到一定电压后,断开电源.再将一块与极板面积相同的各向同性均匀电介质板平行地插入两极板之间,如图所示. 则由于介质板的插入及其所放位置的不同,对电容器储能的影响为:(A) 储能减少,但与介质板相对极板的位置无关. (B) 储能减少,且与介质板相对极板的位置有关. (C) 储能增加,但与介质板相对极板的位置无关.(D) 储能增加,且与介质板相对极板的位置有关. [ A ]介质板10.7静电场中,关系式 P E D+=0ε(A) 只适用于各向同性线性电介质. (B) 只适用于均匀电介质. (C) 适用于线性电介质.(D) 适用于任何电介质. [ D ]10.8一半径为R 的带电介质球体,相对介电常量为εr ,电荷体密度分布ρ = k / r 。
大学物理第9章 题库答案2(修改)

大学物理第9章题库答案2(最新修改)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March第九章 电磁场填空题 (简单)1、在竖直放置的一根无限长载流直导线右侧有一与其共面的任意形状的平面线圈,直导线中的电流由上向下,当线圈以垂直于导线的速度背离导线时,线圈中的感应电动势 ,当线圈平行导线向上运动时,线圈中的感应电动势 。
(填>0,<0,=0)(设顺时针方向的感应电动势为正)(<0, =0)2、磁场的高斯定律表明磁场是 ,因为磁场发生变化而引起电磁感应,是不同于回路变化时产生的 。
相同之处是 。
(无源场,动生电动势,磁通量发生改变)3、只要有运动电荷,其周围就有 产生;而法拉弟电磁感应定律表明,只要 发生变化,就有 产生。
(磁场,磁通量,感应电动势)4、一磁铁自上向下运动,穿过一闭合导体回路,(如图7),当磁铁运动到a 处和b 处时,回路中感应电流的方向分别是 和 。
(逆时针,顺时针)5、电磁感应就是由 生 的现象,其主要定律为 ,其中它的方向是由 定律来决定,即 。
(磁,电,电磁感应定律,楞次,见p320)6、当穿过某回路中的磁通量发生变化时,电路中 (填一定或不一定)产生感应电流;电路中 (填一定或不一定)产生感应电动势。
(不一定, 一定)7、在电磁感应中,感应电动势的大小与闭合回路的磁通量 成正比。
(对时间的变化率)8、在竖直放置的一根无限长载流直导线右侧有一与其共面的任意形状的平面线圈,直导线中的电流由上向下,当线圈平行导线向下运动时,线圈中的感应电动势 , 当线圈以垂直于导线的速度靠近导线时,线圈中的感应电动势 。
(填>0,<0,=0)(设顺时针方向的感应电动势为正)(=0,>0)9、将条形磁铁插入与冲击电流计串连的金属环中,有-5q=2.010c ⨯的电荷通过电流计,若连接电流计的电路总电阻25R =Ω,则穿过环的磁通量的变化=∆Φ Wb 。
大学物理_第九章_课后答案

µ0 I , r 为管外一点到螺线管轴 2πr
题 9-4 图 9-5 如果一个电子在通过空间某一区域时不偏转, 能否肯定这个区域中没有磁场?如果它发 生偏转能否肯定那个区域中存在着磁场? 解:如果一个电子在通过空间某一区域时不偏转,不能肯定这个区域中没有磁场,也可能存 在互相垂直的电场和磁场, 电子受的电场力与磁场力抵消所致. 如果它发生偏转也不能肯定 那个区域存在着磁场,因为仅有电场也可以使电子偏转. 9-6 已知磁感应强度 B = 2.0 Wb· m 的均匀磁场, 方向沿 x 轴正方向, 如题 9-6 图所示. 试求:(1)通过图中 abcd 面的磁通量;(2)通过图中 befc 面的磁通量;(3)通过图中 aefd 面 的磁通量. 解: 如题 9-6 图所示
题 9-7 图 9-7 如题9-7图所示, AB 、 CD 为长直导线, BC 为圆心在 O 点的一段圆弧形导线,其半 径为 R .若通以电流 I ,求 O 点的磁感应强度. 解:如题 9-7 图所示, O 点磁场由 AB 、 BC 、 CD 三部分电流产生.其中
⌢
⌢
AB 产生
� B1 = 0
CD 产生 B2 =
9-13 一根很长的铜导线载有电流10A,设电流均匀分布.在导线内部作一平面 S ,如题9-13 图所示.试计算通过S平面的磁通量(沿导线长度方向取长为1m的一段作计算).铜的磁导率
µ = µ0 .
解:由安培环路定律求距圆导线轴为 r 处的磁感应强度
� B ∫ ⋅ dl = µ 0 ∑ I
l
B 2πr = µ 0
B0 =
�
µ 0 ev = 13 T 4πa 2
电子磁矩 Pm 在图中也是垂直向里,大小为
Pm =
e 2 eva πa = = 9.2 × 10 − 24 A ⋅ m 2 T 2
大学物理课后答案9-10-推荐下载

依照电场叠加原理可以求得各区域电场强度的大小和方向.因而正确答案为(B). 9-2 下列说法正确的是( ) (A)闭合曲面上各点电场强度都为零时,曲面内一定没有电荷 (B)闭合曲面上各点电场强度都为零时,曲面内电荷的代数和必定为零 (C)闭合曲面的电通量为零时,曲面上各点的电场强度必定为零 (D)闭合曲面的电通量不为零时,曲面上任意一点的电场强度都不可能为零 分析与解 依照静电场中的高斯定理,闭合曲面上各点电场强度都为零时,曲面内电荷的 代数和必定为零,但不能肯定曲面内一定没有电荷;闭合曲面的电通量为零时,表示穿入 闭合曲面的电场线数等于穿出闭合曲面的电场线数或没有电场线穿过闭合曲面,不能确定 曲面上各点的电场强度必定为零;同理闭合曲面的电通量不为零,也不能推断曲面上任意
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置各试时类卷,管调需路控要习试在题验最到;大位对限。设度在备内管进来路行确敷调保设整机过使组程其高1在中正资,常料要工试加况卷强下安看与全22过,22度并22工且22作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
《大学物理A(II)》-第9次作业解答

w
R s
B
dr
M dM s B r dr
3 0 0
方向沿轴线向上,受磁力矩 dM= dpm Bsin/2= sw Br3dr
I 2 (Ua Ub )/R Blv/R2 ,
由N流向N’.
M N a B v R1 l R2 b M' N'
(2)外力提供的功率等于两电阻上消耗的 焦耳热功率.
P RI R I
2 1 1
2 2 2
2 2 2
R1 R2 Blv R1 R2 2 2 2 R1 R2 故 Blv P0 , R1 R2
2
轴线上单位长度受力:
0 I h Fx 0 2 cosd 0 2 R
2
0 I h Fy 0 2 sin d 2 R 2 0 I 2 R
2
y
B
dF
x
沿y轴负向。
9、一半径为 R 的薄圆盘,放在磁感应强度为 B 的均匀磁场中, B 的方向与盘面平行,如图所示, 圆盘表面的电荷面密度为 s ,若圆盘以角速度 w 绕其轴线转动,试求作用在圆盘上的磁力矩。
dF
0 I dB dl 2R R
y
轴线上长为h的一段受磁力 B 2 0 I h dF IhdB 2 2 dl dF 2 R 2 0 I h dFx dF cos( ) 2 2 dl cos 2 R
x
0 I h dFy dF sin( ) 2 2 dl sin 2 R
大学物理(下)第九章作业与解答

第九章真空中的静电场一. 选择题1. 关于电场强度的定义,下列说法正确的是(A) 电场中某点场强的方向就是点电荷放在该点所受电场力的方向(B) 场强可由定义,其中为试验电荷,可正可负,为试验电荷所受电场力(C) 以点电荷为中心的球面上各点场强相同(D) 以上说法都不正确[ ]2. 有一边长为a的正方形平面,在其中垂线上距中心O点a/2处,有一电量为q的正点电荷,如图示,则通过该平面的电场强度通量为(A)(B)(C)(D) [ ]3. 点电荷Q被曲面S所包围,从无穷远处引入另一点电荷q至曲面外一点,则引入前后(A) 通过曲面S的电通量不变,曲面上各点场强不变(B) 通过曲面S的电通量变化,曲面上各点场强变化(C) 通过曲面S的电通量不变,曲面上各点场强变化(D) 通过曲面S的电通量变化,曲面上各点场强不变[ ]4. 已知一高斯面所包围的体积内电荷的代数和,则可以肯定(A) 高斯面上各点场强均为零(B) 穿过高斯面上每一面元的电场强度通量均为零(C) 穿过整个高斯面的电场强度通量为零(D) 以上说法都不正确[ ]5. 一具有球对称分布的电场E-r关系曲线如图所示,该电场是下列哪种带电体产生的(A) 半径为R均匀带电球面(B) 半径为R均匀带电球体(C) 半径为R非均匀带电球体(D) 无法判断[ ]6. 真空中有一半径为R的细圆环,均匀分布有正电荷q,若无穷远处电势为零,则环心处的场强和电势的值为(A) (B)(C) (D) [ ]7. 电荷分布在有限空间内,则任意两点A和B之间的电势差取决于(A) 从A移到B的试验电荷电量的大小(B) A和B处电场强度的大小和方向(C) 试验电荷由A移到B的路径(D) 由A移到B电场力对单位电荷所做的功[ ]8. 在点电荷+q的电场中,若取图中P点处为电势零点,则M点的电势为(A) (B)(C) (D) [ ]9. 真空中有一点电荷Q,在与它相距r的a点处有一试验电荷q,现使试验电荷q从a点沿半圆弧轨道运动到b点,如图示,则电场力对q做功为(A) (B)(C) (D) 0 [ ]二. 填空题10. 电量为的试验电荷放在电场中某点时,受到的向下的力,则该点的电场强度大小为______________,方向_______________.( 3N/C ;向上 )11. 如图,在点电荷q和–q电场中,做三个高斯面、、,则____________,____________,____________.(; 0 ; )12. 长为L的均匀带电细棒,电荷线密度为λ,求距细棒为x的一点的场强,当时,E =____________,当时,E =____________.(; )13. 图中曲线表示一具有球对称电场的电势分布U-r曲线,r表示离对称中心的距离,该电场是____________________________的电场.( 半径为R均匀带正电球面)14. 边长a为的正方形顶点处各放置电量为q的四个点电荷,无穷远处电势为零,则正方形中心处的电势为_______________________.( )15. 静电场中,场强沿任意闭合路径的线积分等于零,其数学表示式是________________,这表明静电场中的电场线特征是_________________________.( ;不可能闭合 )16. 场强不变的空间,电势_____________为常数,电势不变的空间,场强_____________为零.(填“一定”或“不一定”) ( 不一定;一定)三. 计算题17. 如图所示,真空中一长为L的均匀带电细杆,总电荷为q,试求在细杆延长线上距杆的一端距离为d的P点的电场强度.解:如解图,取杆左端为原点,x轴向右为正在带电细杆任意位置x处取一小段线元,其电量它在点P产生的电场强度方向沿x轴正向由于所有小段电荷元在P点产生的场强方向相同,所以方向沿x轴正向18. 用绝缘细线弯成半径R的半圆环,其上均匀地分布着电荷Q,试求环心处的电场强度.解:如解图,建立坐标系Oxy在环上任意位置(与x轴成角)取一段圆弧线元,其电量方向如图,在圆环对称处同样取一段圆弧线元,其在环心处场强与对称分布,它们在x轴上分量抵消为零,由此可知,总场强沿y轴负向,则方向沿y轴负向19. 如图所示,在点电荷q的电场中,取半径为R的圆形平面,设q在垂直于平面并通过圆心O的轴线上A处,A点与圆心O点的距离为d. 试计算通过此平面的电场强度通量.解:如题解图,过圆平面的电通量与通过以A为球心,r =AB为半径,以圆平面的周界为周界的球冠的电通量相同,该球冠面积为根据高斯定理,通过半径r=AB的整个球面的电通量为且均匀分布,所以通过球冠的电通量为20. 半径为R的无限长圆柱体上电荷均匀分布,圆柱体单位长度的电荷为λ. 用高斯定理求圆柱体内外距轴线距离为r处的电场强度.解:电场分布具有柱对称性,方向沿径向.作同轴圆柱形高斯面,高为l ,半径为r,如题解图.由高斯定理当r > R 时,当r < R 时,21. 两无限大均匀带电平板,其电荷面密度分别为σ(σ>0)及-σ,板间距为d,如图示.求:(1)Ⅰ、Ⅱ、Ⅲ三个区域的电场强度;(2)两板间的电势差.解:(1)无限大均匀带电平板电场为匀强场,方向垂直平面面密度为σ的平面两侧电场大小为面密度为-σ的平面两侧电场大小为则Ⅰ区Ⅱ区(方向向右)Ⅲ区(2)两板间电势差为22. 如图,电荷q均匀分布在长为2L的细杆上,求在杆中垂线上距杆为d的P点处的电势(设无限远处电势为零).解:如题解图,建立坐标系,在任意位置x处取线元d x,其电量其在P点电势为。
大学物理第9章答案

大学物理第9章答案 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN综合练习题一、填空题1、把一根导线弯成形状固定的平面曲线放在均匀磁场B 中,绕其一端α点以角速率ω逆时针方向旋转,转轴与B 平行,如图9-52所示。
则整个回路电动势为 ,ab 两端的电动势为 。
2、引起动生电动势的非静电力是力,其非静电场强度k E = 。
3、如图9-53所示,在通有电流为I 的长直导线近旁有一导线段ab 长l ,离长直导线距离d ,当它沿平行于长直导线的方向以速度υ平移时,导线中的i ε=____ 。
4、感应电场是由 产生的,它的电场线是 的,它对导体中的自由电荷的作用力大小为 。
5、如图9-54所示,导体AB 长为L ,处在磁感应强度为B 的匀强磁场中,磁感应线垂直纸面向里,AB 搁在支架上成为电路的一部分。
当电路接通时,导体AB 弹跳起来,此时导体AB 中的电流方向为 。
6、 半径为r 的小导线圆环置于半径为R 的大导线圆环的中心,二者在同一平面内。
且r R <<。
若在大导线圆环中通有电流0sin i I t ω=,其中ω,0I 为常量,t 为时间。
则任意时刻,小导线圆环中感应电动势的大小为 。
7、一个折成角形的金属导线aoc (ao oc l ==)位于xoy 平面中,磁感强度为B 的匀强磁场垂直于xoy 平面,如图9-55所示。
当aoc 以速度υ沿x 轴正方向运动时,导线a ,c 两点的电势差ac V = ;当aoc 以速度υ沿y 轴正方向运动时,导线上o ,a 两点的电势差oa V = 。
8、自感为0.25H 的线圈中,当电流在(1/16)s 内由2A 均匀减少到零时,线圈中自感电动势的大小为 。
图9-52图-539、在磁感强度为B 的磁场中,以速率υ垂直切割磁力线运动的—长度为L 的金属杆,相当于 。
它的电动势为 ,产生此电动势的非静电力是 。
二、选择题1、如图9-56所示,当闭合线圈ABCD 以速度υ平行长直导线运动时,判断下哪种说法是正确的: ( )A 、线圈磁通不变,线圈上电动势处处相等,故无电流;B 、AB 、CD 切割磁力线,线圈的动生电动势不为零,线圈中存在感应电流;C 、线圈中AB 、CD 存在动生电动势,但线圈总的动生电动势为零,故无感应电流;D 、以上说法都不对。
大学物理课后习题答案-9答案
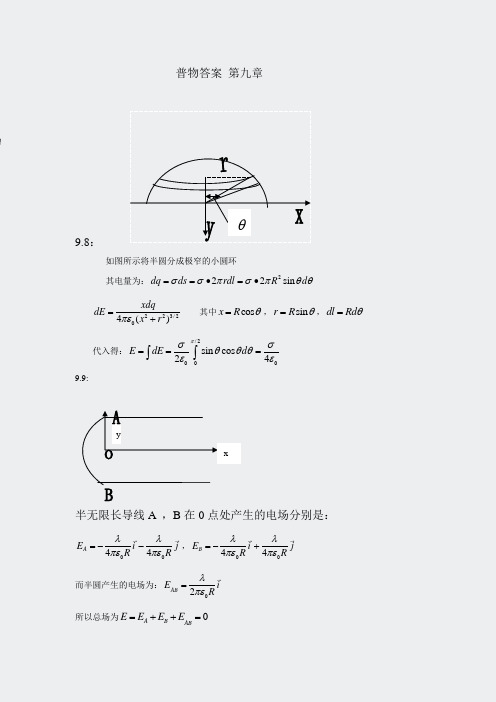
普物答案 第九章9.8:如图所示将半圆分成极窄的小圆环其电量为:222sin dq ds rdl R d σσπσπθθ==•=• 223/204()xdq dE x r πε=+ 其中cos x R θ=,sin r R θ=,dl Rd θ= 代入得:/2000sin cos 24E dE d πσσθθθεε===⎰⎰ 9.9:半无限长导线A ,B 在0点处产生的电场分别是:0044A E i j R R λλπεπε=--,0044B E i j R Rλλπεπε=-+ 而半圆产生的电场为:02AB E i Rλπε= 所以总场为0A B ABE E E E =++= xyθ9.25:(1)0004346c qqqU l l l πεπεπε=-=-••,00U =0000()6c q q A q U U lπε=•-= (2)000()6c q q A q U U lπε∞'=-•-=9.28:利用高斯定理得: 111220122200()()4()4r R q E R r R rq q r R r πεπε⎧⎪<⎪⎪=<<⎨⎪⎪+>⎪⎩0.3230.20.3900a U E dr E dr V ∞=+=⎰⎰,30.5450b U E dr V ∞==⎰9.29:设AB ,DE 段对0点的电势为1U ,2U ,圆弧对0点的电势为3U 21200ln 244RR dx U U x λλπεπε===⎰ 30044BDRd U R λθλπεε==⎰ 所以有1230(2ln 2)4U U U U λππε=++=+9.31:(1):我们在导线上任取微元dx ,电量为:2Q dq dx l= 它产生的电势220124Q dx l dU x y πε=+ 由叠加原理得:220ln 4l ll y l Q U dU l y πε-++==⎰ 2204dU Q E dy y l y πε=-=+ 方向:y 轴正方向 (2):0124Q dl l dU x l πε'='-, 0ln 8q x l U dU dU x l πε+===-⎰ 2204()dU Q E dx x l πε=-=- 方向:x 轴正方向dxxy9.32: 与前面类似的,我们取平行与底面的细圆环,面积为:22sin ds rdl l dl ππθ==00sin 42ds dU dl l σσθπεε•== 积分得: 21R 00)22R U dU dl σσεε===-⎰⎰21(R R9.33:在半径r 处取宽度为dr 的同心圆环,其电量为2rdr σπ•00242rdr dr dU r σπσπεε•== 代入数据得: 309102b a dr U V σε==⨯⎰r ldlr。
大学物理第九章练习 参考答案

第九章 电磁感应 电磁场理论练 习 一一.选择题1. 在一线圈回路中,规定满足如图1所示的旋转方向时,电动势ε,磁通量Φ为正值。
若磁铁沿箭头方向进入线圈,则有( B )(A ) d Φ /dt < 0, ε < 0 ; (B ) d Φ /dt > 0, ε < 0 ; (C ) d Φ /dt > 0, ε > 0 ; (D ) d Φ /dt < 0, ε > 0。
2. 一磁铁朝线圈运动,如图2所示,则线圈内的感应电流的方向(以螺线管内流向为准)以及电表两端电势U A 和U B 的高低为( C )(A ) I 由A 到B ,U A >U B ; (B ) I 由B 到A ,U A <U B ; (C ) I 由B 到A ,U A >U B ; (D ) I 由A 到B ,U A <U B 。
3. 一长直螺线管,单位长度匝数为n ,电流为I ,其中部放一面积为A ,总匝数为N ,电阻为R 的测量线圈,如图3所示,开始时螺线管与测量线圈的轴线平行,若将测量线圈翻转180°,则通过测量线圈某导线截面上的电量∆q 为( A )(A ) 2μ0nINA /R ; (B ) μ0nINA /R ; (C ) μ0NIA /R ; (D ) μ0nIA /R 。
4. 尺寸相同的铁环和铜环所包围的面积中,磁通量的变化率相同,则环中( A ) (A )感应电动势相同,感应电流不同; (B )感应电动势不同,感应电流相同; (C )感应电动势相同,感应电流相同; (D )感应电动势不同,感应电流不同。
二.填空题1.真空中一长度为0l 的长直密绕螺线管,单位长度的匝数为n ,半径为R ,其自感系数L可表示为0220l R n L πμ=。
2. 如图4所示,一光滑的金属导轨置于均匀磁场B 中,导线ab 长为l ,可在导轨上平行移动,速度为v ,则回路中的感应电动势ε=θsin Blv ,a 、b 两点的电势a U < b U (填<、=、>),回路中的电流I=R Blv /sin θ,电阻R 上消耗的功率P=R Blv /)sin (2θ。
大学物理II练习册答案9

大学物理II练习册答案9大学物理练习九一.选择题:1.下面列出的真空中静电场的场强公式,其中哪个是正确的?(A) 点电荷q 的电场:204r qE επ= .(r 为点电荷到场点的距离)(B) “无限长”均匀带电直线(电荷线密度)的电场:r r E302ελπ=(r为带电直线到场点的垂直于直线的矢量)(C) “无限大”均匀带电平面(电荷面密度)的电场:02εσ=E(D) 半径为R 的均匀带电球面 (电荷面密度) 外的电场:r rR E302εσ= (r为球心到场点的矢量) [ D ]2. 取一闭合积分回路L ,使三根载流导线穿过它所围成的面。
现改变三根导线之间的相互间隔,但不越出积分回路,则 [ B ](A) 回路L 内的∑I 不变,L 上各点的B不变。
(B) 回路L 内的∑I 不变,L 上各点的B改变。
(C) 回路L 内的∑I 改变,L 上各点的B不变。
(D) 回路L 内的∑I 改变,L 上各点的B改变。
3.磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上,图(A)~ (E)哪一条曲线表示B- x 的关系? [ B ]4.一铜板厚度为D=1.00mm ,放置在磁感应强度为B=1.35T 的匀强磁场中,磁场方向垂直于导体的侧表面,如图所示,现测得铜板上下两面电势差为V U 51010.1-?=,已知铜板中自由电子数密度3281020.4-?=m n ,电子电量C e 191060.1-?=,则此铜板中的电流为 [ B ](A) 82.2A. (B) 54.8A. (C) 30.8A. (D) 22.2A.二.填空题:1.有一长直金属圆筒,沿长度方向有稳恒电流I 通过,在横截面上电流均匀分布。
筒内空腔各处的磁感应强度大小为 0 ;筒外空间中离轴线r 处2.如图,平行的无限长直载流导线A 和B ,电流强度为I ,垂直纸面向外,两根载流导线之间相距为a ,则(1)AB 中点(p 点)的磁感应强度=p B0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B1 B2 0w 4
b
d 3 2wdr 2
o
a
B3
ab
0
2
2wdr 2r
0w ln 2
b a
B
0w 2
ln
b a
I
I
A
B
[A]
7、如图,水平面内有两条相距 l 的平行长直光滑裸导线
MN、M’ N’,其两端分别与电阻R1、R2 相连;匀强磁场 B 垂直于图面向里;裸导线 ab 垂直搭在平行导线上,并在外 力作用下以速率v平行于导线向右作匀速运动.裸导线 MN、M’ N’ 与 ab 的电阻均不计.
(1) 求电阻 R1、R2 中的电流 I1 与 I2,并说明其流向.
0 2
I
2
2h R2
dl
dF
x
dF x
dF
cos(
)
0 2
I
2
2h R2
dl
cos
dF y
dF
sin(
)
0 2
I
2
2h R2
dl
sin
轴线上单位长度受力:
Fx
0
0 I 2h 2 2R
cosd
0
Fy
0
0 I 2h 2 2R
自由滑动.当 ab 在外力 F 作用下,向左运
动时,下面的描述那一个是正确的 ?
(A) cd 也向左运动.
(B) cd 内有电流流过,由 d 向 c .
(C) cd 向右运动.
(D)磁场对 ab 导线的作用力向右.
a
c
B
(D)ab边转出纸外,bc边转入纸内。
a
d
Bb
c
[A]
6、有两个半径相同的圆环形载流导线A、B,它们可以 自由转动和移动,把它们放在相互垂直的位置上,如 图所示,将发生以下哪一种运动?
(A)A、B均发生转动和平动,最后两线圈电流同方向 并紧靠一起。
(B)A不动,B在磁力作用下发生转动和平动。 (C)A、B都在运动,但运动的趋势不能确定。 (D)A和B都在转动,但不平动,最后两线圈磁矩同方向 平行。
(C) H L3 d l I (D) H L4 d l I
2I •
L1 I
L2
L3
L4
[D]
4、有一无限长通电流的扁平铜片,宽度为
a,厚度不计,电流 I 在铜片上均匀分布,
在铜片外与铜片共面,离铜片右边缘为 b处
的 P 点(如图)的磁感应 B 的大小为:
(A)
0
2 a b
解: B=B1+B2+B3
b
B1、B2 分别为带电的大
o
半圆线圈和小半圆线圈
a
转动产生的磁感应强度,
B3为带电线段b-a转动产生的磁感应强
度.
1
wb , 2
B1
01
2b
0wb 2b 2
0w
4
2
wa 2
b
o
a
B2
0wa 2a 2
0w
为矩形,芯子材料的磁导率为 ,圆环内
外半径分别为 R1 和 R2, 求:(1)芯子中的B值和芯子截面磁通量。 (2)在 r < R1和 r > R2 处的 B 值。
解:(1)由安培环流定理
L H dl H 2r NI
R1
R2 o
b
H NI
2r B H NI
(B) 0 ln a b 2a b
(C) 0 ln a b 2b a
(D)0Leabharlann 2 1 2
a
b
I a
b
P
[B]
5、如图,匀强磁场中有一矩形通电线圈, 它的平面与磁场平行,在磁场作用下,线 圈发生转动,其方向是
(A)ab边转入纸内,cd边转出纸外。 (B)ab边转出纸外,cd边转入纸内。 (C)ab边转入纸内,bc边转出纸外。
P
bd
[A]
3、如图,流出纸面的电流为 2I ,流进纸 面的电流为 I ,则下述各式中那一个是正 确的?
(A) H L1 d l 2I (B) H L2 d l I
有与轴线上的长直导线载有等值反向的电
流 I 。试求轴线上长直导线单位长度所受
磁力。
解:取如图坐标,柱
面电流密度为 I
R
/ R,在半圆柱面上 I
I
取宽度为 dl 平行与
y
轴线的窄条,它在轴
线上产生磁感应强 度。
B
dF
x
dB 0 I dl 2R R
y
轴线上长为h的一段受磁力 B
dF IhdB
1、如图,匀强磁场B中有一个边长为a 的正方形线圈,线圈平面与磁场方向平行且按
如图所示方式放置,则线圈每边受到的磁场力
2 BIa
大小为____2_______,线圈所受的磁力矩大小
为__B__I_a_2___。
45°
r
B
2、如图所示,导轨置于水平面内,磁场方
向垂直向上,导线 ab 和 cd 可以在导轨上
(2) 设外力提供的功率不能超过某值 P0 ,求导线 ab 的最
大速率.
M N
a
vB
R1 l
R2
b M' N'
解:(1)导线 ab 中的动生电动势 e =Blv ,不计
导线电阻时, a、b 两点间电势差
U a Ub e Blv
2R
R1
R2 o
b
磁通量
m
B dS
NIb 2
ln R2 R1
由安培环路定理知:在r R 和r R 处
H 0 B 0
11、有一闭合回路由半径为 a 和 b 的两个 同心共面半圆连接而成,如图其上均匀分布
线密度为 的电荷,当回路以匀角速度 w 绕
过 o 点垂直于回路平面的轴转动时,求圆心 o 点处的磁感强度的大小.
转动形成电流
dI=w dq / 2 =swrdr 磁矩dpm=r2dI =sw r3dr
w
dr
Rs
B
方向沿轴线向上,受磁力矩
dM= dpm R
M 0 dM
Bsin/2= sw
s B R r3dr 0
Br3dr
s BR4
4
方向为
10、如图所示,为一均匀密绕的环形螺线 管,匝数为 N ,通电电流为 I ,其横截面积
故 I1 (U a Ub )/R Blv/R 1, 由M流向M’.
I 2 (U a Ub )/R Blv/R 2 , 由N流向N’.
M N
a
vB
R1 l
R2
b
M' N'
(2)外力提供的功率等于两电阻上消耗的
焦耳热功率.
P
R1
I
2 1
R2
I
2 2
B 2l 2v 2 R1 R2 R1R2
M N a vB
R1 l R2 b
M' N'
故
B 2l 2v 2
R1 R2 R1R2
P0 ,
最大速率
vm
1 Bl
R1R 2P0 . R1 R2
8、一半径为 R 的无限长半圆柱面导体,载
sin
d
0 I 2 2R
沿y轴负向。
y
B
dF
x
9、一半径为 R 的薄圆盘,放在磁感应强度为 B 的均匀磁场中, B 的方向与盘面平行,如图所示,
圆盘表面的电荷面密度为 s ,若圆盘以角速度 w
绕其轴线转动,试求作用在圆盘上的磁力矩。
解:取半径为 r, 宽为dr的圆环电
量dq=s 2rdr
