《作业精编》九年级数学上册北师大版第二章_21花边有多宽
北师大版数学九年级上册2.1.1《花边有多宽》教案

北师大版数学九年级上册2.1.1《花边有多宽》教案一. 教材分析《花边有多宽》是北师大版数学九年级上册第2章《相似多边形》的第1节内容。
本节课主要通过探究梯形的相似性质,让学生掌握相似多边形的判定方法,并能够运用相似性质解决实际问题。
此内容是学生在学习了七年级和八年级的相关知识基础上进行的,对学生空间想象能力和逻辑思维能力的培养具有重要意义。
二. 学情分析九年级的学生已经具备了一定的数学基础,对于多边形的性质和图形的变换有一定的了解。
但是,对于相似多边形的判定和应用可能还比较模糊。
因此,在教学过程中,需要注重引导学生从直观到抽象的认识过程,让学生在探究中理解相似多边形的性质,提高他们的空间想象能力和解决问题的能力。
三. 教学目标1.理解相似多边形的概念,掌握相似多边形的性质。
2.能够运用相似性质解决实际问题。
3.培养学生的空间想象能力和逻辑思维能力。
4.提高学生运用数学知识解决实际问题的能力。
四. 教学重难点1.重点:相似多边形的概念和性质。
2.难点:相似多边形的判定方法和应用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究相似多边形的性质。
2.利用多媒体辅助教学,展示图形的变化,帮助学生直观理解相似性质。
3.运用实例讲解,让学生在实际问题中运用相似性质解决问题。
4.采用小组合作学习,培养学生的团队协作能力和沟通能力。
六. 教学准备1.多媒体教学设备。
2.梯形图形的相关教具。
3.练习题和学习资料。
七. 教学过程1.导入(5分钟)利用多媒体展示一些梯形图形,引导学生观察并提出问题:“这些梯形有什么共同的特点?”让学生思考并回答,从而引出相似多边形的概念。
2.呈现(10分钟)通过展示梯形的相似性质,让学生观察并总结出相似多边形的性质。
引导学生从直观到抽象的认识过程,让学生在探究中理解相似多边形的性质。
3.操练(10分钟)让学生分组合作,利用相似性质对给定的梯形进行变换,并观察变换后的梯形与原梯形的关系。
北师大版数学九年级上册2.1.2《花边有多宽》说课稿

北师大版数学九年级上册2.1.2《花边有多宽》说课稿一. 教材分析《花边有多宽》是北师大版数学九年级上册第2.1.2节的内容。
这一节的主要内容是让学生掌握圆的周长和直径的关系,并能够运用这个关系解决实际问题。
教材通过引入花边的宽度问题,引导学生探究圆的周长和直径的关系,进而得出圆的周长公式。
这个内容在数学学习中非常重要,因为它不仅涉及到圆的基本性质,还涉及到数学的探究方法和解决问题的策略。
二. 学情分析九年级的学生已经掌握了圆的基本知识,对圆的周长和直径有一定的了解。
他们在学习这一节内容时,已经有了一定的数学基础和探究能力。
但是,他们对圆的周长和直径的关系的理解可能还比较浅显,需要通过实际问题来深化他们的理解。
此外,他们可能对数学的探究方法还不够熟悉,需要通过实践活动来培养他们的探究能力。
三. 说教学目标1.知识与技能:让学生掌握圆的周长和直径的关系,能够运用这个关系解决实际问题。
2.过程与方法:通过实践活动,培养学生的探究能力和合作能力。
3.情感态度与价值观:让学生体验数学的乐趣,增强他们对数学的兴趣和自信心。
四. 说教学重难点重点:圆的周长和直径的关系,圆的周长公式的应用。
难点:圆的周长公式的推导过程,对圆的周长和直径的关系的理解。
五. 说教学方法与手段在这一节课中,我将采用问题驱动的教学方法,引导学生通过实践活动探究圆的周长和直径的关系。
我会使用多媒体手段,如PPT和网络资源,来辅助我的教学。
六. 说教学过程1.导入:通过展示一些实际问题,如花边的宽度,引起学生对圆的周长和直径的关系的兴趣。
2.探究:让学生分组进行实践活动,通过测量和计算得出圆的周长和直径的关系。
3.讲解:根据学生的探究结果,讲解圆的周长公式的推导过程。
4.练习:让学生进行一些相关的练习题,巩固他们对圆的周长和直径的关系的理解。
5.总结:让学生总结他们在实践活动中的发现和体验,加强对圆的周长和直径的关系的理解。
七. 说板书设计板书设计将包括以下内容:1.圆的周长和直径的关系公式2.圆的周长公式的推导过程3.实际问题解决策略八. 说教学评价教学评价将包括以下几个方面:1.对圆的周长和直径的关系的理解程度2.运用圆的周长公式解决实际问题的能力3.实践活动中的参与度和合作能力九. 说教学反思在课后,我将对自己的教学进行反思,看是否达到了教学目标,学生是否掌握了圆的周长和直径的关系,以及他们在实践活动中的表现。
北师大版数学九年级上册2.1.2《花边有多宽》教案

北师大版数学九年级上册2.1.2《花边有多宽》教案一. 教材分析《花边有多宽》这一节是北师大版数学九年级上册第2.1.2节的内容,主要是让学生通过实际问题,掌握用代数方法解决几何问题的思路和方法。
本节课的内容与生活实际紧密相连,有利于激发学生的学习兴趣,培养学生的实际问题解决能力。
二. 学情分析九年级的学生已经具备了一定的代数和几何基础,对于解决实际问题也有一定的经验。
但是,他们在解决实际问题时,往往缺乏条理性和逻辑性,不能很好地将实际问题转化为数学问题。
因此,在教学过程中,需要引导学生学会将实际问题转化为数学问题,并运用代数方法解决。
三. 教学目标1.理解并掌握用代数方法解决几何问题的基本思路和方法。
2.能够将实际问题转化为数学问题,并运用代数方法解决。
3.培养学生的逻辑思维能力和实际问题解决能力。
四. 教学重难点1.教学重点:用代数方法解决几何问题的基本思路和方法。
2.教学难点:如何将实际问题转化为数学问题,并运用代数方法解决。
五. 教学方法采用问题驱动法,引导学生通过实际问题,发现并总结用代数方法解决几何问题的思路和方法。
同时,采用小组合作学习的方式,培养学生的团队协作能力和实际问题解决能力。
六. 教学准备1.准备相关的实际问题,用于引导学生思考和讨论。
2.准备课件,用于辅助教学。
七. 教学过程1.导入(5分钟)教师通过展示一些实际问题,如“花边的宽度是多少?”、“一块长方形铁皮的面积是多少?”等,引导学生思考如何用代数方法解决这些问题。
2.呈现(10分钟)教师引导学生通过观察和分析实际问题,发现并总结用代数方法解决几何问题的思路和方法。
教师在这个过程中,对学生进行引导和启发,帮助学生理解和掌握。
3.操练(10分钟)教师给出一些具体的实际问题,让学生独立或小组合作地进行解决。
教师在这个过程中,对学生进行指导,帮助学生解决遇到的问题。
4.巩固(10分钟)教师通过一些练习题,让学生巩固所学的内容。
九年级数学上册 2.1花边有多宽(第2课时)教案 北师大版

2.1花边有多宽(二)教学目标(一)教学知识点1.探索一元二次方程的解或近似解.2.培养学生的估算意识和能力.(二)能力训练要求1.经历方程解的探索过程,增进对方程解的认识,发展估算意识和能力.(三)情感与价值观要求通过师生的共同活动,激发学生探求知识的欲望,从而加强学生估算意识和能力的培养.教学重点探索一元二次方程的解或近似解.教学难点培养学生的估算意识和能力.教学方法分组讨论法教具准备投影片五X第一X:花边有多宽(记作投影片§2.1.2 A)第二X:议一议(记作投影片§2.1.2 B)第三X:上节课的问题(记作投影片§ 2.1.2 C)第四X:做一做(记作投影片§ 2.1.2 D)第五X:小亮的求解过程(记作投影片§2.1.2 E)教学过程I.创设现实情景,引入新课[师]前面我们通过实例建立了一元二次方程,并通过观察归纳出一元二次方程的有关概念,大家来回忆一下.[生甲]把只含有一个未知数并且都可以化为ax2+bx+c=0(a、b、c为常数,a≠0)的整式方程叫做一元二次方程.[生乙]一元二次方程的一般形式是ax2+bx+c=O(a、b、c为常数,a≠0).其中ax2称为二次项,bx称为一次项,c为常数项;a和b分别称为二次项系数和一次项系数.[师]很好,现在我们来看上节课的问题:花边有多宽.(出示投影片§ 2.1.2 A)一块四周镶有宽度相等的花边的地毯,如下图所示,它的长为8 m,宽为5 m,如果地毯中央长方形图案的面积为18 m2,那么花边有多宽?[师生共析]我们设花边的宽度为x,m,那么地毯中央长方形图案的长为(8-2x)m,宽为(5-2x)m.根据题意,就得到方程(8-2x)(5-2x)=18.[师]大家想一下:能求出这个方程中的未知数x吗?……[师]这节课我们继续来探讨“花边有多宽”.Ⅱ.讲授新课[师]要求地毯的花边有多宽,由前面我们知道:地毯花边的宽x(m)满足方程(8-2x)(5-2x)=18.可以把它化为2x2-13x+11=0.由此可知:只要求出2x2-13x+11=0的解,那么地毯花边的宽度即可求出.如何求呢?[生]可以选取一些值代入方程,看能否有使得方程左、右两边的值都相等的数值.如果有,则可求出花边的宽度.[师]噢,那如何选取数值呢?大家来分组讨论讨论.(出示投影片§2.1.2 B)1.x可能小于0吗?说说你的理由.2.x可能大于4吗?可能大于2.5吗?说说你的理由,并与同伴进行交流.3.x的值应选在什么X围之内?4.完成下表:5.你知道地毯花边的宽x(m)是多少吗? 还有其他求解方法吗?与同伴进行交流.[生甲]因为x表示地毯的宽度,所以不可能取小于0的数.[生乙]x既不可能大于4,也不可能大于2.5.因为如果x大于4,那么地毯的长度8-2x就小于0,如果x大于2.5时,那么地毯的宽度同样是小于0.[生丙]x的值应选在0和2.5之间.[生丁]表中的值为:当x=0时,2x2-13x+11=11(依次类推),即[生戊]由上面的讨论可以知道:当x=1时,2x2-13x+11=0,正好与右边的值相等.所以由此可知:x =1是方程2x2-13x+11=0的解,从而得知;地毯花边的宽为1 m.[生己]我没有把原方程化为一般形式,而是把18分解为6× 8.然后凑数:8-2x=6,5-2x=3,两个一元一次方程的解正好为同解,x=1.这样,地毯花边的宽度就可以求出来,即它为1 m.[师]同学们讨论得真棒,接下来大家来看上节课的另一实际问题,(出示投影片§ 2.1.2 C)如图,一个长为10 m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8 m,如果梯子的顶端下滑1 m,那么梯子的底端滑动多少米?[师]上节课我们通过设未知数得到满足条件的方程,即梯子底端滑动的距离x(m)满足方程(x+6)2+72=102.把这个方程化为一般形式为x2+12x-15=0.那么你知道梯子底端滑动的距离是多少吗?即你能求出x吗?同学们来做一做.(出示投影片§2.1.2 D)1.小明认为底端也滑动了1 m,他的说法正确吗?为什么?2.底端滑动的距离可能是2 m吗?可能是3 m吗?为什么?3.你能猜出滑动距离x(m)的大致X围吗?4.x的整数部分是几?十分位是几?[生甲]小明认为底端也滑动了1 m,他的说法不正确.因为当x=1时,x2+12x-15=-2≠0,即x=1不满足方程,所以他的说法不正确.[生乙]底端滑动的距离既不可能是2 m,也不可能是3 m.因为当x=2时,x2+12x-15=13≠0,当x=3时,x2+12x-15=30≠0,即x=2,x=3都不满足方程,所以都不可能.[生丙]因为梯子滑动的距离是正值,所以我选取了一些值,列表如下:x 0 1 2 3 4x2+12x-15 -15 -2 13 30 49由表中可知,当x=1,x=2时,x2+12x-15的值分别为-2,13,而0介于负数和正数之间,所以我猜测;的大致X围是在1和2之间.[生丁]由刚才的讨论可知:x的大致X围是在1和2之间,所以x的整数部分是1.我在1和2之间取了一些值,如下表:由表中可知:x在1.1和1.2之间,所以x的十分位是1.[师]同学们回答得很好,下面来看小亮的求解过程.(出示投影片§2.1.2 E) 小亮把他的求解过程整理如下:所以1<x<1.5.进一步计算:所以1.1<x<1.2.因此J的整数部分是1,十分位是1.你们的结果怎样呢?[生齐声]与他的一样.[师]很好,对于这两个问题的具体解决,我们是先根据实际问题确定了其解的大致X围,然后通过具体计算进行两边“夹逼”,逐步获得了问题的解或近似解.“夹逼”思想是数学中近似计算的重要思想,大家应了解.接下来,我们来解决上节课的第2个问题,以巩固本节课所学的知识.Ⅲ.课堂练习课本P46随堂练习1.五个连续整数,前三个数的平方和等于后两个数的平方和,你能求出这五个整数分别是多少吗?解:设五个连续整数中的第一个数为x,则根据题意,可得方程x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2.把它化为一般形式:x2-8x-20=0.可列表如下:所以x=-2或x=10.因此,这五个连续整数依次为-2,-1,0,1,2或10,11,12,13,14.Ⅳ.课时小结本节课我们通过解决实际问题,探索了一元二次方程的解或近似解,并了解了近似计算的重要思想——“夹逼”思想.Ⅴ.课后作业(一)课本P46习题2.2 1、2(二)1.预习内容:P47~P482.预习提纲(1)复习完全平方公式(2)会用开平方法解形如(x+m)2=n(n≥0)的方程.Ⅵ.活动与探究梯子底端滑动的距离x(m)满足方程x2+12x-15=0,我们已经能猜出滑动距离x(m)的大致X围是1和2之间,并且知道x的整数部分是1,十分位是1,那么你能求出x的百分位吗?[过程]这道题也是一个求方程的近似解的题,要求学生估计近似解,从中体会无限逼近的思想,并进一步促进学生对方程解的理解,发展其估算意识.[结果]根据方程x2+12x-15=0,可列表:所以1.14<x<1.15.因此,x的百分位是4.板书设计§花边有多宽(二)一、地毯花边的宽x(m)满足方程(8-2x)(5-2x)=18,即2x2-13x+11=0.注:x>0,8-2x>0,5-2x>0.二、梯子底端滑动的距离x(m)满足方程(x+6)2+72=102,即x2+12x-15=0.所以1<x<2.x的整数部分是1,所以x的整数部分是1,十分位是1.三、课堂练习四、课时小结五、课后作业。
北师大版数学九年级上册2.1《花边有多宽》教案1

北师大版数学九年级上册2.1《花边有多宽》教案1一. 教材分析《花边有多宽》这一节是人教版九年级上册第二单元《几何图形》中的一节内容。
本节课主要让学生通过观察、操作、思考、交流等活动,掌握花边的宽度,发展学生的空间观念和几何思维能力。
教材通过生活中的实例,引出花边的宽度,然后让学生通过实际操作,探索求解花边宽度的方法,从而培养学生的实践能力和解决问题的能力。
二. 学情分析九年级的学生已经具备了一定的几何基础知识,对几何图形有一定的认识。
同时,学生的空间想象能力和动手操作能力也在逐步发展。
但是,对于一些复杂的花边图案,学生可能还比较难以理解和计算。
因此,在教学过程中,教师需要关注学生的个体差异,引导学生通过实际操作,逐步理解和掌握花边的宽度求解方法。
三. 教学目标1.知识与技能目标:让学生掌握花边的宽度求解方法,能够运用所学知识解决实际问题。
2.过程与方法目标:通过观察、操作、思考、交流等活动,培养学生的空间观念和几何思维能力。
3.情感态度与价值观目标:激发学生对数学的兴趣,培养学生的团队合作意识和问题解决能力。
四. 教学重难点1.重点:花边的宽度求解方法。
2.难点:对于复杂花边图案的理解和计算。
五. 教学方法1.采用问题驱动的教学方法,引导学生通过观察、操作、思考、交流等活动,探索花边的宽度求解方法。
2.运用多媒体辅助教学,展示花边图案,提高学生的空间想象力。
3.分组合作学习,培养学生的团队合作意识。
六. 教学准备1.多媒体教学设备。
2.花边图案实物或图片。
3.剪刀、直尺、彩笔等动手操作工具。
七. 教学过程1.导入(5分钟)教师展示一些花边图案实物或图片,引导学生观察并思考:如何才能知道这些花边的宽度呢?通过这个问题,激发学生的学习兴趣,引出本节课的主题。
2.呈现(10分钟)教师提出具体的问题:给定一个花边图案,如何求解其宽度?然后引导学生分组讨论,共同探索求解方法。
3.操练(10分钟)每组学生选取一个花边图案,使用剪刀、直尺、彩笔等工具,进行实际操作,尝试求解花边的宽度。
北师大版数学九年级上册2.1《花边有多宽》教学设计1

北师大版数学九年级上册2.1《花边有多宽》教学设计1一. 教材分析《花边有多宽》这一节是北师大版数学九年级上册第二章《相似》的第一课时。
本节课主要通过探究花边的宽度,让学生理解相似图形的性质,掌握相似比的计算方法,并能够运用相似比解决实际问题。
教材通过生活中的实例引入相似的概念,激发学生的学习兴趣,培养学生运用数学解决实际问题的能力。
二. 学情分析九年级的学生已经掌握了相似图形的概念,对图形的变换也有了一定的了解。
但学生在计算相似比时,可能还不太熟练,需要通过大量的练习来提高。
此外,学生解决实际问题的能力有待提高,需要教师在教学中进行引导和培养。
三. 教学目标1.知识与技能:理解相似图形的性质,掌握相似比的计算方法,能够运用相似比解决实际问题。
2.过程与方法:通过观察、操作、猜想、验证等方法,培养学生的动手操作能力和推理能力。
3.情感态度价值观:培养学生运用数学解决实际问题的意识,提高学生对数学的兴趣。
四. 教学重难点1.重点:理解相似图形的性质,掌握相似比的计算方法。
2.难点:运用相似比解决实际问题。
五. 教学方法1.情境教学法:通过生活中的实例引入相似的概念,激发学生的学习兴趣。
2.引导发现法:教师引导学生观察、操作、猜想、验证,培养学生独立思考的能力。
3.实践操作法:让学生通过实际操作,加深对相似图形性质的理解。
4.合作学习法:学生分组讨论,培养学生的团队协作能力。
六. 教学准备1.教学课件:制作课件,展示花边的图片和相关的数学知识。
2.练习题:准备一些关于相似比计算和实际问题的练习题,用于课堂练习和巩固。
3.教学道具:准备一些花边的实物,用于展示和操作。
七. 教学过程1.导入(5分钟)教师通过展示一些花边的图片,引导学生观察花边的形状和宽度,激发学生的学习兴趣。
2.呈现(10分钟)教师介绍相似图形的概念,解释相似比的含义,并通过举例让学生理解相似比的应用。
3.操练(15分钟)教师引导学生分组讨论,每组选择一幅花边的图片,计算花边的相似比,并解释原因。
北师大版数学九年级上册2.1《花边有多宽》教学设计2

北师大版数学九年级上册2.1《花边有多宽》教学设计2一. 教材分析《花边有多宽》这一节是北师大版数学九年级上册第二章《相似》的第一课时,是在学生已经学习了相似三角形的性质,相似多边形的性质,成比例线段的基础上进行学习的。
本节课主要是通过实例让学生理解并掌握相似多边形的性质,能够运用相似多边形的性质解决实际问题。
二. 学情分析九年级的学生已经具备了一定的几何知识,对相似多边形的性质有一定的了解。
但是,对于如何运用相似多边形的性质解决实际问题,学生可能还存在一定的困难。
因此,在教学过程中,教师需要通过具体的实例,引导学生理解和运用相似多边形的性质,提高学生的解决问题的能力。
三. 教学目标1.知识与技能:让学生理解并掌握相似多边形的性质,能够运用相似多边形的性质解决实际问题。
2.过程与方法:通过实例,培养学生观察、分析、解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的探究精神。
四. 教学重难点1.重点:让学生理解和掌握相似多边形的性质。
2.难点:如何引导学生运用相似多边形的性质解决实际问题。
五. 教学方法1.情境教学法:通过具体的实例,引导学生理解和运用相似多边形的性质。
2.问题驱动法:通过提问,激发学生的思考,引导学生探究相似多边形的性质。
3.小组合作法:在解决实际问题的过程中,鼓励学生进行小组合作,共同解决问题。
六. 教学准备1.准备相关的实例,用于引导学生理解和运用相似多边形的性质。
2.准备一些实际问题,用于巩固学生对相似多边形的性质的理解。
七. 教学过程1.导入(5分钟)通过展示一些实际问题,让学生观察并思考:这些问题可以通过相似多边形的性质来解决吗?从而引出本节课的主题——相似多边形的性质。
2.呈现(10分钟)教师通过具体的实例,引导学生理解和掌握相似多边形的性质。
例如,可以通过展示两张相似的图形,让学生观察并回答:这两张图形的对应边是否成比例?对应角是否相等?3.操练(10分钟)教师提出一些实际问题,让学生运用相似多边形的性质进行解决。
北师大版-数学-九年级上册-2.1 花边有多宽 作业5

2.1 花边有多宽一、选择题1.方程3x 2=3x 的解是 A.x =0 B.x =1C.x =0或x =1D.x =-1或x =02.已知一元二次方程的两实根为1和-43,则此方程为 A.x 2-04341=+xB.x 2+04341=+x C.4x 2-x -3=0 D.4x 2-x +3=03.如果方程x 2+k 2-16=0与x 2-3k +12=0有相同的实数根,那么k 的值是 A.-7 B.-7或4 C.-4 D.4 4.下列方程中是一元二次方程的共有几个 ①3x 2+1=0 ②3x 2-(5-1)x =3 ③x 2+x3+1=0 ④x x 42-+3=0 A.1 B.2 C.3 D.45.方程(x -3)2=3-x 的根是A.x =2B.x =4C.x =3D.x =2或x =36.方程(m 2-m -2)x 2+mx +3=0是关于x 的一元二次方程,则m 满足 A.m ≠2 B.m ≠-1C.m ≠2且m ≠-1D.m ≠2或m ≠-17.若方程kx 2-4x +3=0是关于x 的方程,且有实根,则k 的非负整数值为 A.0,1 B.0,1,2 C.1 D.1,2,38.把2x 2+4x -1化成a (x +h)2+k 的形式为A.2(x +1)2-3B.2(x +1)2-2C.2(x +2)2-3D.2(x +2)2-99.若方程4x 2+(a 2-3a -10)x +4a =0的两根互为相反数,则a 的值是 A.5或-2 B.5C.-2D.非以上答案10.方程(x -p )2=q (q >0)的根是 A.x =p ±q B.x =-p ±q C.x =±p +qD.x =±(p +q )二、填空题1.方程33212-=+x x 化为一般形式为__________. 2.一元二次方程x 2+2x -m =0,当m =__________时,方程有两个相等的实根;当m __________时,方程有两个不等实根;当m =__________时,方程有一个根为0.3.如果-3是方程3x 2+kx -6=0的一个根,那么k 的值为__________,另一个根为__________.4.两个相邻正整数的平方和比这两个数中较小的数的2倍大51,则这两个数是__________.三、解答题1.求证:对于任意实数m ,关于x 的方程(x -2)(x -1)=m 2有两个不相等的实数根.2.不解方程2x 2-6x +1=0,(1)求此方程的两根的倒数和. (2)求两根差的平方. 四、应用问题一块矩形耕地,大小尺寸如右图,要在这块地上横纵分别挖2条和4条水渠,如果水渠的宽相等,且余下的面积为9600平方米,问水渠要挖多宽?参考答案一、1.C 2.C 3.B 4.B 5.D 6.D 7.A 8.A 9.A 10.A二、1.2x 2-3x -9=02.-1 >-1 03.7324.5,6 三、1.提示:化成标准一元二次方程,用Δ=b 2-4ac >0 2.(1)略解由根与系数关系得x 1+x 2=3,x 1·x 2=21, 6132111212121==⋅+=+x x x x x x (2)(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=32-4×21=9-2=7 四、略。
(北师大版)九年级上册数学第二章《一元二次方程》2.1花边有多宽(导学案)

花边有多宽【学习目标】1.在具体情境中,理解一元二次方程相关概念及其解的概念;2.通过自主探索和小组合作,会列出问题情境中的方程,并学会估算一元二次方程的解; 3.积极参与数学学习活动,对数学有好奇心和求知欲,在数学活动中,获得成功的体验,锻炼克服困难的意志,建立自信心。
【使用说明和学法指导】1.用15分钟左右的时间认真阅读、探究课本基础知识,并借助《教材解读》自主学习,用双色笔勾画出一元二次方程的相关概念。
2.认真完成课前导学案的问题; $3.初步评价自己完成学习目标情况,并把自己的疑问写出来,以求课堂上解决。
【课前导学】 一、探究新知:知识点1 一元二次方程定义解读:1、只含有一个未知数x 的_________方程,并且都可以转化成______________(a 、b 、c 为常数,a ______0)的形式,这样的方程叫做一元二次方程。
2、相关概念:二次项是______,一次项是______,c 叫做_________。
3、反思:(1) 由于一元二次方程的最高次数为______,所以必须满足a ______0;(2) 由于一元二次方程的一般形式是_____________________,所以在化为一般形式时,一定要使得方程的右边是_______。
只有把方程转化为一般形式后,才可确定是否是一元二次方程。
^【自我测评】1. 辨析下列方程是否为一元二次方程,不是的请说明原因:①310x -=;②0132=-x③0132=+xx ;④)2)(1(122--=-x x x ;⑤215)73)(25(x x x =-+;⑥x y x 322=+2.把方程:x x x -=--3)5(2化成一般形式为__________________,其二次项系数为_____,一次项系数为________,常数项为________。
3.若2)1(222+-=++x c bx ax ,则a =______,b =_______,c =_______。
北师大版数学九年级上册2.1《花边有多宽》教案2

北师大版数学九年级上册2.1《花边有多宽》教案2一. 教材分析《花边有多宽》这一节内容是北师大版数学九年级上册第二章的第一课时,主要学习了用坐标表示点、直线和圆的位置关系,以及函数的性质。
通过这一节内容的学习,学生能够理解坐标与图形之间的关系,掌握用坐标表示点的方法,了解直线和圆的方程,以及理解函数的概念。
二. 学情分析九年级的学生已经掌握了初中阶段的基本数学知识,对于图形的认识和坐标的学习已经有了一定的基础。
但是,对于坐标与图形之间的关系,以及直线和圆的方程的理解还需要加强。
此外,学生对于函数的概念可能还比较陌生,需要通过实例来帮助理解。
三. 教学目标1.知识与技能:学生能够理解坐标与图形之间的关系,掌握用坐标表示点的方法,了解直线和圆的方程,以及理解函数的概念。
2.过程与方法:学生通过观察、实践和思考,培养数形结合的思维方式,提高解决问题的能力。
3.情感态度价值观:学生能够积极参与数学学习,体验数学的乐趣,培养对数学的热爱。
四. 教学重难点1.教学重点:学生能够理解坐标与图形之间的关系,掌握用坐标表示点的方法,了解直线和圆的方程。
2.教学难点:学生对于函数的概念的理解,以及如何应用坐标解决实际问题。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过问题驱动引导学生思考,通过案例教学让学生深入了解坐标与图形之间的关系,通过小组合作学习培养学生的团队协作能力和解决问题的能力。
六. 教学准备1.教师准备:准备好相关的教学案例和实例,制作好PPT,准备好黑板和粉笔。
2.学生准备:学生需要预习相关的内容,了解坐标与图形之间的关系,以及直线和圆的方程。
七. 教学过程1.导入(5分钟)通过展示一些生活中的实例,如地图上的位置、商场里的商品摆放等,引导学生思考坐标与图形之间的关系。
提问:你们知道这些实例中坐标的作用吗?通过这个问题,激发学生的兴趣,引出本节课的主题。
2.呈现(15分钟)教师通过PPT展示直线和圆的方程,以及函数的概念。
21花边有多宽2北师大版九年级上

三、梯子底端滑动的距离x(m)满足方程
2 2 2
(x+6) +7 =10 也就是x2+i2x —15=0
(1)你能猜出滑动距离x(m)的大致范围吗?
(2)x的整数部分是几?十分位是几?
倡使用计算器。
四、课堂练习
课本P46随堂练习
1 •五个连续整数,前三个数的平方和等于后两个数的平方和,你能求出这五个整数分别是多少吗?
五、课时小结
本节课我们通过解决实际问题,探索了一元二次方程的解或近似解,并了解了近似计算的重要思想一一“夹逼”思想.
六、课后作业
(一)课本P46习题2. 2 I、2
(二)1.预习内容:P47—P48
板书设计:
一、地毯花边的宽x(m),满足方程(8—
2x)(5 —2x)=18
二、梯子底端滑动的距离x(m)满足方
程(x+6) 2+72=102
三、练习
四、小结
进一步计算
注意:(1)估算的精度不适过高。
(2)计算时提
因此x的整数部分是1,十分位是1。
北师大版九上2.1《花边有多宽》word教案
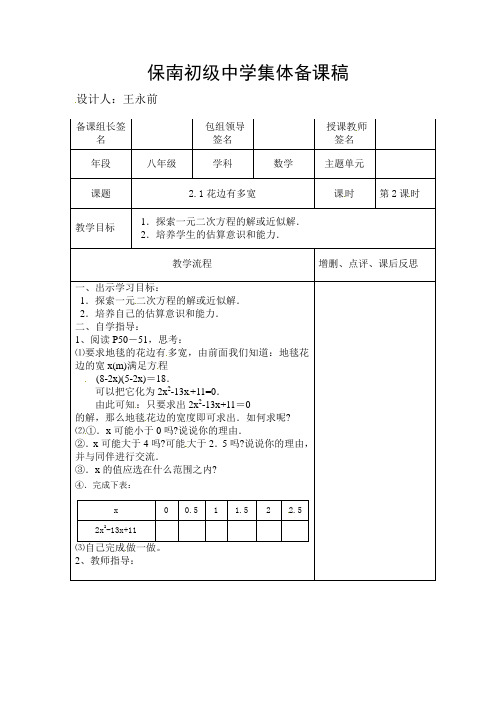
④.完成下表:
x
0
0.5
1
1.5
2
2.5
2x2-13x+11
⑶自己完成 做一做。
2、教师指导:
保南初级中学集体备课稿
设计人:王永前
⑴要求地毯的花边有 多宽,由前面我们知道:地毯花边的宽x(m)满足方 程
(8-2x)(5-2x)=18.
可以把它化为2x2-13x +11=0.
由此可知 :只要求出2x2-13x+11=0
的解,那么地毯 花边的宽度即可求出.如何求呢?
⑵ ①.x可能小于0吗?说说你的理由.
②.x可能大于4吗?可能 大于2.5吗?说说你的理由,并与同伴进行交流.
备课组长签名
包组领导签名
授课教 师签名
年段
八年级
学科
数学ห้องสมุดไป่ตู้
主题单元
课题
2.1花边有多宽
课 时
第2课 时
教学目标
1.探索一元二次方程的解或近似解.
2.培养学生的估算意识和能力.
教学流程
增删、点评、课后反思
1、出示学习目标:
1.探索一元 二次方程的解或近似解.
2.培养自己的估算意识和能力.
2、自学指导:
1、阅读P50-51,思考:
北师九年级数学上第二章2.1花边有多宽同步练习及答案

北师九年级数学上第二章§2.1花边有多宽同步练习及答案一、填空题1.一元二次方程的一般形式是__________.2.将方程-5x 2+1=6x 化为一般形式为__________.3.将方程(x +1)2=2x 化成一般形式为__________.4.方程2x 2=-8化成一般形式后,一次项系数为__________,常数项为__________.5.方程5(x 2-2x +1)=-32x +2的一般形式是__________,其二次项是__________,一次项是__________,常数项是__________.6.若ab ≠0,则a 1x 2+b1x =0的常数项是__________. 7.如果方程ax 2+5=(x +2)(x -1)是关于x 的一元二次方程,则a __________.8.关于x 的方程(m -4)x 2+(m +4)x +2m +3=0,当m __________时,是一元二次方程,当m __________时,是一元一次方程.二、选择题1.下列方程中,不是一元二次方程的是( )A.2x 2+7=0B.2x 2+23x +1=0C.5x 2+x1+4=0 D.3x 2+(1+x )2+1=0 2.方程x 2-2(3x -2)+(x +1)=0的一般形式是( )A.x 2-5x +5=0B.x 2+5x +5=0C.x 2+5x -5=0D.x 2+5=03.一元二次方程7x 2-2x =0的二次项、一次项、常数项依次是( )A.7x 2,2x ,0B.7x 2,-2x ,无常数项C.7x 2,0,2xD.7x 2,-2x ,04.方程x 2-3=(3-2)x 化为一般形式,它的各项系数之和可能是( ) A.2 B.-2 C.32- D.3221-+5.若关于x 的方程(ax +b )(d -cx )=m (ac ≠0)的二次项系数是ac ,则常数项为( )A.mB.-bdC.bd -mD.-(bd -m )6.若关于x 的方程a (x -1)2=2x 2-2是一元二次方程,则a 的值是( )A.2B.-2C.0D.不等于27.若x =1是方程ax 2+bx +c =0的解,则( )A.a +b +c =1B.a -b +c =0C.a +b +c =0D.a -b -c =08.关于x 2=-2的说法,正确的是( )A.由于x 2≥0,故x 2不可能等于-2,因此这不是一个方程B.x 2=-2是一个方程,但它没有一次项,因此不是一元二次方程C.x 2=-2是一个一元二次方程D.x 2=-2是一个一元二次方程,但不能解三、解答题现有长40米,宽30米场地,欲在中央建一游泳池,周围是等宽的便道及休息区,且游泳池与周围部分面积之比为3∶2,请给出这块场地建设的设计方案,并用图形及相关尺寸表示出来。
