穷举算法及解题
算法——穷举法

算法——穷举法穷举法是一种常见的求解问题的算法,也被称为暴力搜索或者暴力枚举。
它的基本思想是穷尽所有可能的情况,从中找出满足问题要求的最优解或者符合条件的解。
在实际问题中,穷举法可以解决很多难题,比如寻找最短路径、最小值、最大值等等。
穷举法的求解过程相对容易理解,而且实现起来很简单。
但是,随着问题规模的增加,穷举法的时间复杂度会非常高,计算机的计算能力往往无法承载。
因此,在使用穷举法时,需要掌握一些技巧有效地减少计算量。
穷举法基本步骤:1.确定问题的解空间解空间是指可以取到的所有解组成的集合。
需要明确问题的解空间,方便穷举法从中查找到符合条件的解。
例如,对于求1~100中所有偶数的和这个问题,解空间就是所有偶数的集合{2,4,6,...,100}。
2.确定问题的约束条件约束条件是指解必须满足的限制条件。
例如,对于求1~100中所有偶数的和这个问题,约束条件就是偶数。
3.进行穷举搜索穷举搜索就是从解空间中挨个枚举每一个解,判断是否满足约束条件。
对每一组解都进行判断,找到满足要求的最优解或者符合条件的解。
例如,在求1~100中所有偶数的和这个问题中,需要从所有偶数中挨个枚举每一个偶数,将其累加到结果变量中。
4.分析求解结果分析求解结果,检验是否符合问题的要求。
如果结果合法,那么就是要求的最优解或者符合条件的解。
如果结果不合法,那么需要继续搜索其他可能的解。
穷举法的优缺点优点:1.穷举法可以求解各种难点问题,尤其是在面对离散的问题时效果非常显著。
2.穷举法思路简单,易于理解,实现也相对较简单。
3.穷举法保证能够搜索到所有可能的解,因此能够找到最优解或者符合条件的解。
1.穷举法遍历所有可能的解,当问题规模较大时,时间复杂度非常高,计算量大,效率低。
2.部分问题的解空间很难找到或没有固定的解空间,导致穷举策略无从下手。
3.穷举法没有明确的评估标准,求得的解无法与其他算法进行比较。
穷举法使用技巧1.剪枝技术穷举法的时间复杂度往往比较高,因此需要使用剪枝技术,减少不必要的计算。
第五讲 穷举算法

第五讲穷举算法学习重点:1、了解穷举法的基本概念及用穷举法设计算法的基本过程。
2、能够根据具体问题的要求,使用穷举法设计算法,编写程序求解问题。
3、能对穷举法编写的程序进行优化学习过程:穷举算法是学生在学完了QB基本语句后最早接触到的算法。
一些简单的穷举算法题目如求水仙花数、找出缺失的数字等和小学生的数学学习紧密结合,程序也比较容易实现,因此学生的学习兴趣还是很高的。
近几年的省小学生程序设计竞赛中也常出现穷举算法的题目,如:2001年题四算24;2002年题三求素数个数与素数个数最多的排列;2005年回文数个数等题目,有些题虽然说用穷举算法实现比较勉强(如2002年题三的后半题求出素数个数最多的排列),但在考试时,如果一时想不出更好的办法,用穷举算法也不失为一种明智的选择。
穷举法,常常称之为枚举法,是指从可能的集合中一一穷举各个元素,用题目给定的约束条件判定哪些是无用的,哪些是有用的。
能使命题成立者,即为问题的解。
穷举是最简单,最基础,也是通常被认为非常没效率的算法,但是。
穷举拥有很多优点,它在算法中占有一席之地。
首先,穷举具有准确性,只要时间足够,正确的穷举得出的结论是绝对正确的;其次,穷举拥有全面性,因为它是对所有方案的全面搜索,所以,它能够得出所有的解。
采用穷举算法解题的基本思路:(1)确定穷举对象、穷举范围和判定条件;(2)一一列举可能的解,验证是否是问题的解一、穷举算法的实现在前面基础语句(for语句)的学习中,其实我们就用到了穷举。
比如培训教材p77【例5-7】打印九九乘法表中,被乘数A和乘数B都从1-9一一列举。
这样,九九乘法表中就不会遗失任何一句乘法口诀;在p79【例5-9】的数学灯谜题中,我们也是用了一一列举的方法,找出了A、B、C、D的取值范围。
下面我们再看两道例题:1、搬运砖头【问题描述】36 块砖, 36 人搬。
男搬 4 ,女搬 3 ,两个小儿抬一砖。
要求一次全搬完。
问需男、女、小儿各若干?【问题分析】题目要我们找出符合条件的男生、女生和小孩的人数。
基础算法(一)穷举法

基础算法(⼀)穷举法
基础算法(⼀)穷举法
穷举法的基本思想:从可能的解集合中⼀⼀穷举各元素,⽤题⽬给定的检验条件判定哪些是有⽤的,哪些是⽆⽤的,能使命题成⽴的,即为其解。
穷举法解题思路:
1、对命题建⽴正确的数学模型;
2、根据命题确定数学模型中各变量的变化范围(即可能解的范围);
3、利⽤循环语句、条件判断语句逐步求解或证明。
穷举法的特点:
算法简单,但运算量⼤。
对于可能确定解的范围,⼜⼀时找不到更好的算法时,可以采⽤穷举法。
例1、求满⾜表达式A+B=C的所有整数解,其中A、B、C为1~3之间的整数。
例2、鸡兔同笼问题(在同⼀个笼⼦⾥有鸡和兔⼦若⼲只,从上⾯看,能看到20个头,从下⾯看,能看到60只脚,问鸡兔各有多少只?)例3、百钱百鸡问题(⼀百块钱要买⼀百只鸡,这⼀百只鸡必须包含母鸡、公鸡和⼩鸡,其中,公鸡5元⼀只,母鸡3元⼀只,⼩鸡1元三只,
问有哪些购买⽅案?)
例4、⽔仙花数问题(ABC=A3+B3+C3,列出所有的整数ABC)
在⽤穷举法时,问题必须满⾜两个条件:
1、能够预先确定可能解的个数;
2、对每个解变量的取值,其变化范围也能预先确定。
使⽤穷举法时应注意的问题:
1、减少穷举变量;
2、缩⼩穷举变量的取值范围。
4.2.1用穷举法求解问题的基本过程

线索二
【设计算法】 (1)确定范围 i : 25006—25996 (2)验证条件
该数 i 是37或67的倍数 i mod 37=0 or i mod 67=0
实践活动1: 1.打开桌面上“学生文件夹”→“实践活动1” →“工程1.vbp” 2.进入代码窗口,将①②③删除,并填入合适的代码
【思考】你在解决生活中哪些事情的时候也会使用穷举法?
穷举法小结
【例题】假定母鸡每只4元,公鸡每只3元,小鸡每只0.5元。现有100元要求买 100只鸡,要求正好用完,且每种鸡都要有,用VB编程求出所有解。
(1)公鸡数量y的枚举范围最恰当的是( C) A.[0,33] B.[1,33] C.[1,31] D.[0,31]
线索三
一串无规律的字符 (由字母、数字、符
号组成)
数字的个数 小写字母的个数
【设计算法】 (1)确定范围: 第一个字符到最后一个字符 (2)验证条件:
数字?(0-9) 小写字母?(a-z)
实践活动2: 1.打开桌面上“学生文件夹”→“实践活动2” →“工程1.vbp” 2.进入代码窗口,将①②③删除,并填入合适的代码
进入代码窗口将删除并填入合适的代码2验证条件线索三一串无规律的字符由字母数字符号组成数字的个数小写字母的个数数字
密室
要想逃离此处, 秘密就在上锁的柜子里。
线索一
△十把钥匙中只有一把能打开柜子的锁,这种情况下他该怎么办呢?本思路】
列举一切与命题相关的情况,然后根据问题设 定的条件,逐个加以检查,找到满足条件的解。
(2)要同时枚举母鸡数量x和公鸡数量y,则检验的条件表达式为( C)
穷举算法及解题

穷举算法及解题
例12-1 古希腊人认为因子的和等于它本身的数是一个完全数(自身因子除外),例如28的因子是1、
2、4、7、14,且1+2+4+7+14=28,则28是一个完全数,编写一个程序求2~1000内的所有完全数。 问题分析
(1) 本题是一个搜索问题,搜索范围2~1000,找出该范围内的完全数;
(2) 完全数必须满足的条件:因子的和等于该数的本身;
(3) 问题关键在于将该数的因子一一寻找出来,并求出因子的和:分解因子的方法比较简单,采用循环完成分解因子和求因子的和。
程序如下:
program p12_1;
var a,b,s:integer;
program jitu;
var
a,b,c,d,e,f,x,y:integer;
begin
for a:=2 to 6 do
for b:=1 to 6 do
for c:=1 to 6 do
for d:=2 to 6 do
for e:=1 to 6 do
begin
f:=21-a-b-c-d-e;
Var a,b,c,d:integer;
X,x0,x1,x2,x3,x4:integer;
st1:set of 1..100;
function number(a,b,c,d:integer):integer;
var n1,n2,n3,n4,sum:integer;
begin
st1:=[];
2、有一个三位数,个位数字比百位数字大,而百位数字又比十位数字大,并且各位数字之和等于各位数字相乘之积,求此三位数。
常用算法(二)——穷举搜索法

{ t=*pt[j]; *pt[j] =* pt; *pt=t; }
}
}
从上述问题解决的方法中,最重要的因素就是确定某种方法来确定所有的候选解。下面再用一个示例来加以说明。
【问题】背包问题
问题描述:有不同价值、不同重量的物品n件,求从这n件物品中选取一部分物品的选择方案,使选中物品的总重量不超过指定的限制重量,但选中物品的价值之和最大。
把i转化为二进制数,存储于数组B中;
temp_w=0;
temp_v=0;
for (j=0;j<n;j++)
{ if (B[j]==1)
{temp_w=temp_w+w[j];
temp_v=temp_v+v[j];
}
if ((temp_w<=tw)&&(temp_v>maxv))
{maxv=temp_v;
intside_total[SIDE_N];
main{}
{inti,j,t,equal;
for (j=0;j<VARIABLES;j++)
*pt[j]=j+1;
while(1)
{ for (i=0;i<SIDE_;i++)
{ for (t=j=0;j<LENGTH;j++)
t+=*side[j];
scanf(“%*c”);
}
for (j=VARIABLES-1;j>0;j--)
if (*pt[j]>*pt[j-1]) break;
if (j==0) break;
拓展知识5-1 穷举法

拓展知识5-1 穷举法一、什么是穷举法在实际问题中,经常遇到在一定范围内寻求某类事物解的问题。
比如:求水仙花数,因为水仙花数是一个三位数,所以,[100,999]就是给定的范围,水仙花数就是要求的解;又如:百马百担问题,求解决方案,大马数量[1,33],中马数量[1,50],小马数量[1,100] 就是给定的范围,解决方案就是要求的解等。
像这类问题,可以通过对指定范围内每种可能的情况进行一一测试,验证其是否是满足条件的解的方法来解决,我们就把这种解决问题的方法称为穷举法。
由于实际问题的指定范围可能很大,所以,穷举法更适合于使用计算机,因此,这类问题可通过程序设计来解决。
二、穷举法解决问题的关键1.确定范围(1)往往实际问题给定的范围不一定很明确,需要我们通过分析来确定范围;(2)所得到的范围还可以利用给定的部分约束条件进一步缩小,以减少程序的运行时间,提高效率。
2.确定解的条件通过对实际问题进行分析,给出判断解的条件,有了判断解的条件才能对每种可能的情况进行一一验证,从而得到问题的解。
三、穷举法解决问题的步骤1.分析问题,确定范围变量,给出解的判断条件;2.用循环或循环的嵌套对范围变量的所有可能情况进行一一测试;3.用选择语句判断每种情况是否符合解的条件;4.输出符合条件的情况。
四、穷举法的优化策略1.减少范围变量范围变量能少用尽量少用,这样可大大减少测试的数量。
例如百马百担问题,对大马、中马、小马均可设一个范围变量dm、zm、xm,其范围分别是:[1,33],[1,50],[1,100],总的测试数量为33*50*100=165000次;在大马、中马具体确定后,小马可利用约束条件dm+zm+xm=100来确定,因此,只需将大马、中马设为范围变量,这样测试数量为33*50=1650次。
可见,减少范围变量的使用可大大减少测试的数量。
2.缩小穷举范围根据实际问题的隐含条件,可将不符合条件的情况去掉,缩小穷举范围,减少穷举变量的值域。
第2章 穷举算法

理解穷举法的设计思想。
掌握穷举法设计技巧。
2.1 穷举法的概念
所谓穷举法,指的是从可能的解的集合中一一 列举各元素,用题目给定的检验条件判定哪些是无 用的,哪些是有用的。能使命题成立,即为其解。
2.2 穷举法的特点
需要大量的机时和内存空间。但他却是一个 精确的算法,可以求得最佳解。
习题2
求自然数m,n的最大公约数? 解题思路: 输入m,n 让t=min(m,n)
for(i=t;i>=1;i--) if(m%i&&n%i) {输出i}
2.3 穷举法的应用
main()
{ int i,j,k,total;
练习1:把一元钞票换成一分、二分、五分硬币(每种至少一枚), 有哪些种换法?
{
printf("1分%d个,2分%d个,5分%d 个\n",i,j,k); total++; } } printf("共%d种方法",total); } :i+j*2+k*5==100
total=0;
for(i=1;i<94;i++) for(j=1;j<95;j++)
for(k=1;k<98;k++)
{ if()
习题1:一只公鸡值3元,一只母鸡值2元,2只小鸡值1元,现 用一百元要买一百只鸡,问有什么方案?
解题思路:
for(x=0;x<=33;x++) for(y=0;y<=50;y++) { z=100-x-y; if(3*x+2*y+0.5*z==100) output x, y, z; }
穷举算法及解题

穷举算法及解题穷举算法及解题例12-1 古希腊人认为因子的和等于它本身的数是一个完全数(自身因子除外),例如28的因子是1、2、4、7、14,且1+2+4+7+14=28,则28是一个完全数,编写一个程序求2~1000内的所有完全数。
问题分析(1)本题是一个搜索问题,搜索范围2~1000,找出该范围内的完全数;(2)完全数必须满足的条件:因子的和等于该数的本身;(3)问题关键在于将该数的因子一一寻找出来,并求出因子的和:分解因子的方法比较简单,采用循环完成分解因子和求因子的和。
程序如下:program p12_1;var a,b,s:integer;beginfor a:=2 to 1000 dobegins:=0;for b:=1 to a-1 doif a mod b =0 then s:=s+b;if a=s then beginwrite(a,'=',1,);for b:=2 to a-1 doif a mod b=0 then write('+',b);writeln;end;end;end.当程序运行后,输出结果:6=1+2+328=1+2+4+7+14496=1+2+4+8+16+31+62+124+248例12-3邮局发行一套票面有四种不同值的邮票,如果每封信所帖邮票张数不超过三枚,存在整数r,使得用不超过三枚的邮票,可以贴出连续的整数1、2、3、……、r来,找出这四种面值数,使得r值最大。
问题分析:本题则是知道每封信邮票数的范围(<=3),邮票有四种类型,编程找出能使面值最大邮票。
其算法是:(1) 面值不同的四种邮票,每封信所贴邮票不超过3张;(2) 用这四种邮票贴出连续的整数,并且使r值最大;(3) 用穷举法,找出所有符合条件的解;(4) 本题用集合的方法统计邮票的面值,提高判重的速度。
设四种邮票的面值分别为:a,b,c,d,根据题意设:a<b<c<d,因此a=1,用循环语句完成搜索。
取数之递归算法、回溯算法、穷举算法

取数之穷举算法、递归算法一、穷举搜索法穷举搜索法是穷举所有可能情形,并从中找出符合要求的解。
穷举所有可能情形,最直观的是联系循环的算法。
[例]找出n个自然数(1,2,3,…,n)中r个数的组合。
例如,当n=5,r=3时,所有组合为:543542541532531521432431421321total=10 {组合的总数}[解]n个数中r的组合,其中每r 个数中,数不能相同。
另外,任何两组组合的数,所包含的数也不应相同。
例如,5、4、3与3、4、5。
为此,约定前一个数应大于后一个数。
将上述两条不允许为条件,当r=3时,可用三重循环进行搜索。
[程序]Program zuhe11;constn=5;vari,j,k,t:integer;begint:=0;for i:=n downto 1 dofor j:=n downto 1 dofor k:=n downto 1 doif (i<>j)and(i<>k)and(i>j)and(j>k) thenbegint:=t+1;writeln(i:3,j:3,k:3);end;writeln('total=',t);end.或者Program zuhe12;constn=5;r=3;vari,j,k,t:integer;begint:=0;for i:=n downto r dofor j:=i-1 downto r-1 dofor k:=j-1 downto 1 dobegint:=t+1;writeln(i:3,j:3,k:3);end;writeln('total=',t);end.这两个程序,前者穷举了所有可能情形,从中选出符合条件的解,而后者比较简洁。
但是这两个程序都有一个问题,当r变化时,循环重数改变,这就影响了这一问题的解,即没有一般性。
但是,很多情况下穷举搜索法还是常用的。
穷举法举例说明

穷举法举例说明
穷举法是一种计算思路,它通过枚举所有可能的情况,从而找到
最优解。
在实际应用中,穷举法常被用于解决一些复杂的问题。
下面,我们通过几个例子来详细说明该方法的应用。
例1:密码破解
密码的破解可以采用穷举法。
假设某个密码只包含数字和字母,
且长度为4位,则可以按照以下步骤进行破解:先从0000开始,依次
尝试0001、0002、……,直到9999为止。
在这个过程中,如果可以正确破解密码,则停止尝试,否则继续尝试下一个密码。
这种方法虽然
效率比较低,但对于简单密码来说,可以快速找到密码。
例2:网络路由
在计算机网络中,网络路由的目的是寻找从源节点到目标节点的
最短路径。
穷举法可以用于解决路由问题。
假设有一个有向带权图,
可以先从源节点开始,尝试每一条可能的路径,直到找到一条从源节
点到目标节点的路径为止。
在这个过程中,可以采用Dijkstra算法等
其他优化算法,来加快寻找最短路径的速度。
例3:求解方程
穷举法也可以用于解决一些数学问题。
假设要求解某个方程的解,则可以从一个极小值开始,并逐步增加变量的取值,直到满足方程的
条件为止。
在这个过程中,可以采用二分法、牛顿法等其他优化算法来加速求解的过程。
综上所述,穷举法虽然效率可能较低,但是在一些问题上,其解决方法是唯一的。
在实际应用中,我们应该根据具体问题的特点,选择合适的算法来解决问题。
同时,在加速穷举法的过程中,也可以采用其他算法来优化求解的效率。
c语言穷举法经典例题

c语言穷举法经典例题穷举法是一种常用的计算机算法,用于遍历所有可能的解决方案以找到最佳解决方案。
在C语言中,穷举法经常被用来解决一些经典的例题。
本文将介绍三个常见的C语言穷举法经典例题,并给出相应的解决方法。
1. 例题一:找出100以内的所有素数要求:编写一个程序,找出100以内的所有素数。
解决思路:穷举法通过考察每个数,判断其是否满足某个条件,来找出符合条件的解。
对于找素数的问题,我们可以从2开始,逐个判断每个数是否为素数。
如果一个数不是素数,那么它一定可以被一个小于它的数整除。
因此,我们可以用两个循环来实现穷举法的思想。
```c#include <stdio.h>int main() {int i, j;for (i = 2; i <= 100; i++) {int isPrime = 1; // 假设当前数为素数for (j = 2; j < i; j++) {if (i % j == 0) {isPrime = 0; // 当前数不是素数break;}}if (isPrime) {printf("%d ", i);}}return 0;}```以上代码中,外层循环遍历从2到100的所有数,内层循环用来判断当前数是否为素数。
如果当前数能够被除1和自身以外的数整除,则将isPrime标记为0,表示不是素数。
最后,打印出所有素数的值。
2. 例题二:猜数字游戏要求:编写一个猜数字的游戏,随机生成一个1到100的整数,玩家通过输入数字来猜测,直到猜中为止,给出总共猜了多少次。
解决思路:穷举法可以通过循环来逐个尝试所有可能的选择,直到找到解决方案。
对于猜数字游戏,我们可以利用rand()函数来生成一个伪随机数字,并与玩家的猜测进行比较,直到猜中为止。
```c#include <stdio.h>#include <stdlib.h>#include <time.h>int main() {srand(time(0)); // 初始化随机数生成器int target = rand() % 100 + 1; // 生成1到100之间的随机数int guess, count = 0;do {printf("请输入你猜测的数字:");scanf("%d", &guess);if (guess > target) {printf("太大了!\n");} else if (guess < target) {printf("太小了!\n");}count++;} while (guess != target);printf("恭喜你,猜对了!总共猜了%d次。
用穷举法解决问题
b 0 0பைடு நூலகம்
c 0 1
153 1
5
3
999 9
9
9
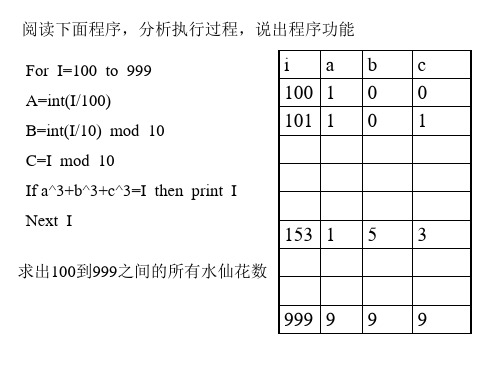
3.2 用穷举法解决问题 一、什么是穷举法
穷举法又称枚举法、列举法,它将求解对象一一列举出来,然后逐一加以分 析、处理,并验证结果是否满足给定的条件,穷举完所有对象,问题将最终 得以解决。
方法一: For I=100 to 999 A=int(I/100) B=int(I/10) mod 10 C=I mod 10
二、用穷举法解决问题的步骤
1、确定问题解可能搜索的范围:用循环或嵌套来实现) 2、写出符合问题解的条件:用if语句实现 3、尽可能地缩小搜索的范围,减少程序运行时间,提高程序的执行效率。 例:公元前5世纪,我国数学家张丘建在《算经》一书中提出了一个“百钱买 百鸡问题”。问题如下:鸡翁一值钱5,鸡母一值钱3,鸡雏三值钱1。百钱买 百鸡,问鸡翁、鸡母和鸡雏各几何?
方法二: For a=1 to 9 for b=0 to 9 for c=0 to 9 if a^3+b^3+c^3=a*100+b*10+c then print a*100+b*10+c endif next c next b next a
If a^3+b^3+c^3=I then print I Next I
例3:生活中的问题 某同学用自己的QQ号登录,可他记不清密码了,你能帮 他找回密码吗?他的密码是一个5位数,67□□8,其中 百位和十位上的数字他不记得了,但他还记得该数能够 被78整除,也能被67整除。你能帮他设计一个算法求出 该密码吗?
(1)判断下列两题能否用穷举算法解决,为什么? ①在一个直角三角形中,三条边a、b、c的长度都为整 数,且一条直角边a的长度已确定,斜边c的长度不能超过 某数I,找出满足条件的所有直角三角形。 ②使用一根长度为L厘米的铁丝,制作一个面积为S的 矩形框,要求,计算出满足这种条件的矩形的高h和宽w。 ③《孙子算经》中有许多有趣的数学题,“鸡兔同笼” 问题就是一个典型的例子。原题是:“今有鸡兔同笼,上 有三十五头,下有九十四足,问鸡兔各几何?”
算法实验1穷举【参考答案】【最新完全版】

算法分析与设计实验一——穷举算法(黑体,三号)1.穷举简介(小标题:黑体,小四;内容:宋体,五号)穷举法又称列举法,其基本思想是逐一列举问题所涉及的所有情况。
从中寻找满足条件的结果。
适用于数量较小的问题。
2.算法流程或设计思想穷举通常应用循环结构来实现。
在循环体中,应用选择结构实施判断筛选,求得所要求的解。
使用穷举法的关键是要确定正确的穷举的范围。
3.分析算法的时间复杂度4.程序设计中的问题及解决方案5.运行说明(包括实验数据和结果说明)6.主要程序代码(添加程序注释)7.对比解决该问题的其他算法(选作)题目:1.有一堆零件(1000-5000个之间),如果以4个零件为一组进行分组,则多2个零件;如果以7个零件为一组进行分组,则多3个零件;如果以9个零件为一组进行分组,则多5个零件。
编程求解这堆零件总数。
参考答案:#include<stdio.h>void main(){int n,count=0;for(n=1000;n<=5000;n++)if(n%4==2&&n%7==3&&n%9==5){printf("%d ",n);count=count+1;if(count%5==0)printf("\n");}printf("\ncount = %d\n",count);}2.穷举三位数的水仙花数。
水仙花数是指一个n 位数( n≥3 ),它的每个位上的数字的n 次幂之和等于它本身。
(例如:13 + 53 + 33 = 153)参考答案:/*2. 穷举三位数的水仙花数。
水仙花数是指一个n 位数( n≥3 ),它的每个位上的数字的n 次幂之和等于它本身。
(例如:13 + 53 + 33 = 153)*/#include <stdio.h>void main(){int a,b,c,d;for(a=100;a<=999;a++){b=a/100;c=a/10-b*10;d=a-b*100-c*10;if(b*b*b+c*c*c+d*d*d==a)printf("%d = %d^3 + %d^3 + %d^3\n",a,b,c,d);}}3.穷举真分数递增序列中的第k项的值。
用穷举法解决问题

任务一:水仙花数
❖ 水仙花数是指一种三位数,它旳各位数旳立方和恰 好等于该数本身。如:153=13+53+33。
❖ 请设计算法求解“水仙花数问题”。
⑴拟定范围:
⑵验证条件:
水仙花数算法:
穷举范围
❖ For 某整数=100 to 999
❖ If 该数百位数字旳立方+该数十位数字旳立 方+该数个位数字旳立方=该数 Then
解析法处理问题环节
1、问题分析 未知----已知 数学体现式 2、编程实现
3.2 用穷举法处理问题
马征征 2023年4月
3.2 用穷举法处理问题
1.什么是穷举法? 也叫枚举法、列举法
——将求解对象一一列举出来,然后逐一加以分 析、处理,并验证成果是否满足给定旳条件,穷举 完全部对象,问题将最终得以处理。
为何系统要限制输入密码旳次数?
小结
1、穷举法特点: 求解对象有限,按照某种规则
2、穷举法分析: ⑴拟定范围 ⑵验证条件
❖ print 该数
❖ End if ❖ Next 某整数
满足条件
任务二:实践求三位水仙花数程序
❖ a=x\100 ❖ b=(x-a*100)\10 ❖ c=x-a*100-
b*10
水仙花数代码:
Dim x, a, b,c As Integer For x = 100 To 999
a = x \ 100 b = (x - a * 100) \ 10 c= x - a * 100 - b * 10 If a^3 + b^3 + c^3 = x Then Print x End If Next x
百钱买Байду номын сангаас鸡
穷举算法

穷举算法穷举算法有点像数学上说的"完全归纳法",在问题答案可能的全部解集内逐一查询(测试)直到找出答案为止。
穷举算法的模式:⑴问题解的可能搜索的范围:用循环或循环嵌套结构。
⑵写出符合问题解的条件。
⑶能使程序优化的语句,以便缩小搜索范围,减少程序运行时间。
用穷举算法解决问题,通常可以从两个方面进行分析:一、问题所涉及的情况:问题所涉及的情况有哪些,情况的种数可不可以确定。
把它描述出来。
二、答案需要满足的条件:分析出来的这些情况,需要满足什么条件,才成为问题的答案。
把这些条件描述出来。
练习试题第一题:36 块砖, 36 人搬。
男搬 4 ,女搬 3 ,两个小儿抬一砖。
要求一次全搬完。
问需男、女、小儿各若干?第二题: A 、 B 、 C 、 D 、 E 五人夜间合伙捕鱼,凌晨时都疲倦不堪,各自在河边的树丛中找地方睡着了。
日上三竿, A 第一个醒来,他将鱼分作五份,把多余的一条扔回河中,拿自己的一份回家去了。
B 第二个醒来,也将鱼分作五份,扔掉多余的一条,拿走自己的一份,接着 C 、 D 、 E 依次醒来,也都按同样的办法分鱼,问五人至少合伙捕了多少条鱼?试编程序算出。
第三题:古希腊人认为因子的和等于它本身的数是一个完全数(自身因子除外),例如28的因子是1、2、4、7、14,且1+2+4+7+14=28,则28是一个完全数,编写一个程序求2-1000内的所有完全数。
第四题:一根29CM长的尺子,只允许在上面刻7个刻度,要能用它量出1-29CM的各种长度。
试问这根尺的刻度应该怎样选择?算法分析:⑴对于每一组刻度的选择都需要判断是否能将1-29CM的各种刻度量出来,例如选择的刻度为:a1、a2、a3、a4、a5、a6、a7,那么能量出的刻度为:a1a2a3a4a5a7a1,29- a1;2 a2,a2- a1,29- a2;3 a3,a3- a1,a3- a2,29- a3; 4 a4,a4- a1,a4- a2,a4- a3,29- a4;5 a5,a5- a1,a5- a2,a5- a3,a5- a4,29- a5;6 a6,a6- a1,a6- a2,a6- a3,a6- a4,a6- a5,29- a6;7 a7,a7- a1,a7- a2,a7- a3,a7- a4,a7- a5,a7- a6,29- a7;8共可量出2+3+4+5+6+7+8种刻度,即35种刻度,事实上其中有许多刻度是重复的,不可能覆盖1-29。
穷举法

穷举法
四、穷举法应用
begin e:=15-a-b-c-d;b0:=(e<>2) and (e<>3);
m:=bton(e=1)+bton(b=2)+bton(a=5)+bton(c<>1)+bton(d=1);
b0:=b0 and (m=-2); b1:=(e=1) and (a<>2); b1:=b1 or (a=5) and(c<>1) and(c<>2); b1:=b1 or (c<>1) and (d<>1) and (d<>2); b1:=b1 or (d=1) and (e<>2); b0:=b0 and not b1; if b0 then
穷举法
四、穷举法应用
分析:本题是一个逻辑判断题,一般的逻辑判断题都采 分析:本题是一个逻辑判断题, 用穷举法进行解决。 我们对5 用穷举法进行解决 。 我们对 5 所学校所得名次的各种可 能情况进行穷举。在每种情况中, 能情况进行穷举。在每种情况中,为了防止不同学校取 相同的名次,设立了逻辑数组x x[I]为false表示已有 相同的名次,设立了逻辑数组x,x[I]为false表示已有 某校取第I 某校取第I名。 此题的难点在于确定判断条件。我们设立逻辑变量b0来 此题的难点在于确定判断条件。我们设立逻辑变量b 描述这一条件,主要有两个条件: 校不是第2 描述这一条件,主要有两个条件:“E校不是第2名或第 只有第1名和第2 名的学校的人猜对” 3 名 ” 与 “ 只有第 1 名和第 2 名的学校的人猜对 ” , 后一 条件要判断: 是否只有两人说法正确? 条件要判断:1)是否只有两人说法正确?2)说得正确 的人是否是取得第1名和第2名的学校的人? 的人是否是取得第1名和第2名的学校的人?要判断是否 仅有两人说正确,须统计正确命题的个数。为此,设立 仅有两人说正确,须统计正确命题的个数。为此, 了函数bton 将逻辑量数值化。 bton, 了函数bton,将逻辑量数值化。
特殊解题方法——穷举法

特殊解题方法——穷举法解答某些数学题,可以把问题所涉及到的数量或结论的有限种情况,不重复不遗漏地全部列举出来,以达到解决问题的目的。
这种解题方法就是穷举法。
例1 从甲地到乙地有A、B、C三条路线,从乙地到丙地有D、E、F、G四条路线。
问从甲地经过乙地到达丙地共有多少条路线?(如图3.28)分析:从甲地到乙地有3条路线,从乙地到丙地有4条路线。
从甲地经过乙地到达丙地共有下列不同的路线。
解:3×4=12答:共有12条路线。
例2 如果一整数,与1、2、3这三个数,通过加减乘除运算(可以添加括号)组成算式,能使结果等于24,那么这个整数就称为可用的。
在4、5、6、7、8、9、10、11、12这九个数中,可用的有_______个。
(1992年小学数学奥林匹克初赛试题)分析:根据题意,用列式计算的方法,把各算式都列举出来。
4×(1+2+3)=24 (5+1+2)×3=246×(3+2-l)=24 7×3十豆十2—248×3×(2-1)=24 9×3—1—2—2410×2+l+3=24 11×2+3-l=2412×(3+1-2)=24通过计算可知,题中所给的9个数与1、2、3都能够组成结果是24的算式。
答:可用的数有9个。
例3 从0、3、5、7中选出三个数字能排成_______个三位数,其中能被5整除的三位数有_________个。
(1993年全国小学数学竞赛预赛试题)分析:根据题中所给的数字可知:三位数的百位数只能有三种选择:十位数在余下的三个数字中取一个数字,也有3种选择;个位数在余下的两个数字中取一个数字,有2种选择。
解:把能排成的三位数穷举如下,数下标有横线的是能被5整除的。
305,307,350,357,370,375;503,507,530,537,570,573;703,705,730,735,750,753答:能排成18个三位数,其中能被5整除的有10个数。
穷举法-计算机求解问题的一种方法

穷举法——计算机求解问题的一种方法概述所谓穷举法,就是在列举所有可能的解,逐一检验直至找到真正的解。
例如,“找出整数n的所有因子”这一问题就可以采用穷举法。
所有可能的解(即因子)落在集合{1, 2, 3, …, n}内,分别用n除一除,余数为0则是因子,否则不是因子。
银行卡密码是6位数字,采用穷举法破解就是把所有6位数都试一遍,那一共要试106次。
人来试是受不了的,而计算机也许可以(因为速度更快)。
所谓暴力破解法正是这样做的。
例一题目:一个首项大于0的递增等差数列前四项和为26,前四项积为880,求该数列的第20项的值。
提示:如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列,这个常数叫做等差数列的公差。
例如:等差数列:1,3,5,7,9,11。
该数列的公差是2,第5项值是9。
采用穷举法解题说明如下。
假设数列首项为a,差值为d,有:a+ a+d + a+2d + a+3d = 26a*(a+d) * (a+2d)*(a+3d) = 880如何求出a和d?答:穷举(a,d)的组合。
数列首项a从1穷举到5,差值d可从1穷举到5。
a从1开始是因为题目指出首项大于0,a到5为止是因为数列前4项之和为26,而4*5+6*1(差值d至少为1)等于26。
差值d从1开始是因为是等差数列,差值至少为1,到5为止的因为6*5>26。
这样,构造出了所有可能的解,即(a,d)的组合:(1, 1),(1, 2), (1, 3), (1, 4), (1, 5), (2, 1),(2,2),(2,3),(2,4),(2,5)…(5,1), (5,2),(5,3),(5,4),(5,5)。
算法描述如下:for a=(1,2,3,4,5):for d=(1,2,3,4,5):如果a+ a+d + a+2d + a+3d等于26且a*(a+d) * (a+2d)*(a+3d)等于880,则:求得数列第20项是a+19*d;算法结束。
04穷举法

运行结果: 1: men= 0 women=20 children=10 2: men= 1 women=18 children=11 3: men= 2 women=16 children=12 4: men= 3 women=14 children=13 5: men= 4 women=12 children=14 6: men= 5 women=10 children=15 7: men= 6 women= 8 children=16 8: men= 7 women= 6 children=17 9: men= 8 women= 4 children=18 10: men= 9 women= 2 children=19 11: men=10 women= 0 children=20
例3:中国余数定理:“有物不知几何,三三数余 一, 五五数余二,七七数余三,问:物有几何?”。 编程求1000以内所有解。 • 穷举范围: 整数m为:1~1000。 • 判断式: m%3==1&&m%5==2&&m%7==3
运行结果: #include "stdio.h" 52 157 262 367 472 main() 577 682 787 892 997 { int m, count=0; for ( m=1; m<=1000; m++ ) if ( m%3==1&&m%5==2&&m%7==3) { printf("%5d",m); count++; if(count%5==0) printf("\n"); } }
3. 把整数316表示为两个数之和,使其中一个数能被 13整除,而另一个数能被11整除,求解这两个数。 4. 要实现10年达到国民经济总值翻两番的目标,问 国民生产年平均增长率至少应为百分之几?(精确 到一位小数,即xx.x%)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
st1:=st1+[sum];
end;
end;
sum:=1;
while sum in st1 do
sum:=sum+1;
number:=sum-1;
if a*b*c*d*e*f=720 then
begin
x:=100*a+10*b+c-111;
y:=100*d+10*e+f-111;
if (2*x=y) and (x / 2=trunc(x /2)) then
writeln(x div 2,' ',x,' ',y)
begin
z:=30-x-y;
if x/2+y/3*2+z/7*5=20 then
writeln(x,' ',y,' ',z);
end;
end.
for c:=a+1 to 9 do
if a+b+c=a*b*c then
writeln(a*100+b*1
0+c) ;
end. program zhizhu;
var
x,y,z:integer;
begin
for x:=1 to 16 do
for y:=1 to 16 do
begin
(2) 用这四种邮票贴出连续的整数,并且使r值最大;
(3) 用穷举法,找出所有符合条件的解;
(4) 本题用集合的方法统计邮票的面值,提高判重的速度。
设四种邮票的面值分别为:a,b,c,d,根据题意设:
a<b<c<d,因此a=1,用循环语句完成搜索。
Program p12-3;
writeln(‘’:10,’x0=’,x0);
end;
end;
end.
程序运行后,其输出结果是:
1 2 3 4 x0=12
1 2 3 5 x0=13
1 3 6 10 x0=23
1 4 7 8 x0=24
穷举法编程练习 题目:
1、有一群鸡和一群兔,它们的只数相同,它们的脚数都是三位数,且这两个三位数的数字分别是0,1,2,3,4,5。问鸡和兔的只数各是多少?它们的脚数各是多少?-穷举法
2、有一个三位数,个位数字比百位数字大,而百位数字又比十位数字大,并且各位数字之和等于各位数字相乘之积,求此三位数。
分析:如果以A、B、C分别表示这个三位数的百位、十位和个位数字,由题意知B<A<C,由此做穷举
3、蜘蛛有8条腿,蜻蜓有6条腿和2对翅,蝉有6条腿和1对翅。三种虫子共18共,共有118条腿和20对翅。问每种虫子各几只?
end;
begin
a:=1;0:=0;
for b:=a+1 to 3*a+1 do
for c:=b+1 to 3*b+1 do
for d:=c+1 to 3*c+1 do
begin
x:=number(a,b,c,d);
begin
y:=168-x;
if x/8+y*3/4=76 then
writeln(x,' ',y);
end;
end. program jtye;
var
x,y,z:integer;
begin
for x:=7 to 28 do
for y:=3 to 30-x do
if x>x0 then
begin
x0:=x;x1:=a;x2:=b;x3:=c;x
4:=d;
write(x1:5,x2:5,x3:5,x4:5);
Var a,b,c,d:integer;
X,x0,x1,x2,x3,x4:integer;
st1:set of 1..100;
function number(a,b,c,d:integer):integer;
var n1,n2,n3,n4,sum:integer;
begin
st1:=[];
begin
for a:=2 to 1000 do
begin
s:=0;
for b:=1 to a-1 do
if a mod b =0 then s:=s+b;
if a=s then begin
write(a,'=',1,);
for b:=2 to a-1 do
4、甲、乙两数的和为168,甲数的八分之一与乙数的四分之三的和为76,求甲、乙两数各是多少?
5、我国古代数学问题:1兔换2鸡,2兔换3鸭,5兔换7鹅。某人用20只兔换得鸡、鸭、鹅共30只,问其中鸡、鸭、鹅各几只? 源程序:
鸡兔问题:用穷举法,找出满足条件的鸡的脚数和兔的脚数,
其鸡的脚数百十个位上分别为a,b,c,其兔的脚数百十个位上分别为d,e,f,鸡的只数为x,兔的只数为y.为了减少循环判断的次数,我们把0-5各位数字都加上1变成1-6,所以在由各位数字组成脚数x,y时需要减去111。
if a mod b=0 then write('+',b);
writeln;
end;
end;
end.
当程序运行后,输出结果:
6=1+2+3
28=1+2+4+7+14
496=1+2+4+8+16+31+62+124+248
例12-3
穷举算法及解题
例12-1 古希腊人认为因子的和等于它本身的数是一个完全数(自身因子除外),例如28的因子是1、
2、4、7、14,且1+2+4+7+14=28,则28是一个完全数,编写一个程序求2~1000内的所有完全数。 问题分析
end;
end;
end.
数字问题:分析:如果以A、B、C分别表示这个三位数的百位、十位和个位数字,由题意知B<A<C,由此做穷举 program geshibai;
var
a,b,c:integer;
begin
for b:=1 to 7 do
for a:=b+1 to 8 do
z:=18-x-y;
if (8*x+6*y+6*z=118) and (2*y+z=20) then
writeln(x,' ',y,' ',z);
end;
end. program n1n2;
var
x,y:integer;
begin
for x:=1 to 168 do
program jitu;
var
a,b,c,d,e,f,x,y:integer;
begin
for a:=2 to 6 do
for b:=1 to 6 do
for c:=1 to 6 do
for d:=2 to 6 do
for e:=1 to 6 do
begin
f:=21-a-b-c-d-e;
邮局发行一套票面有四种不同值的邮票,如果每封信所帖邮票张数不超过三枚,存在整数r,使得用不超过三枚的邮票,可以贴出连续的整数1、2、3、……、r来,找出这四种面值数,使得r值最大。
问题分析:本题则是
知道每封信邮票数的范围(<=3),邮票有四种类型,编程找出能使面值最大邮票。其算法是:
(1) 面值不同的四种邮票,每封信所贴邮票不超过3张;
(1) 本题是一个搜索问题,搜索范围2~1000,找出该范围内的完全数;
(2) 完全数必须满足的条件:因子的和等于该数的本身;
(3) 问题关键在于将该数的因子一一寻找出来,并求出因子的和:分解因子的方法比较简单,采用循环完成分解因子和求因子的和。
程序如下:
program p12_1;
var a,b,s:integer;
for n1:=0 to 3 do
for n2:=0 to 3-n1 do
for n3:=0 to 3-n1-n2 do
for n4:=0 to 3-n1-n2-n3 do
begin
if n1+n2+n3+n4<=3 then
begin
