ANSYS Maxwell 2D求解齿槽转矩的几种方法
ANSYSMaxwell2D求解齿槽转矩地几种方法

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
ANSYS-Maxwell-2D求解齿槽转矩、饱和电感、饱和磁链的几种方法

齿槽转矩、一、问题描述1.齿槽转矩T cog :当永产生的转矩即为T cog ,它是是永磁电机特有的问题之关键问题。
2.饱和电感:绕组存在导致绕组电感变化。
考虑高电机模型精度有重要意3.饱和磁链:绕组交链存在饱和现象。
二、基于Maxwell 2d 的求Maxwell 2D 可以有效对于求Tcog,方法很多为模板,介绍3种方法。
打开该案例后,首先Settings 中设置“Fract 算例,将新算例的类型修例,删除RMxprt 算例,按1.静磁场扫描转子旋转角首先,选中转子轭和4在弹出窗口中将旋转角度弹出的窗口中,定义变量磁链等随电流变化的规律ANSYS Maxwell 求解、饱和电感、饱和磁链永磁电机绕组不通电时,永磁体和定子是永磁体与电枢齿之间相互作用力的之一,是高性能永磁电机设计和制造中在电感,当电机负载不同时,铁心的虑不同负载电流、不同转子角度下的绕意义。
链有磁链,跟电感一样,磁链也受电流求解T cog 的方法仿真得出永磁电机电磁方案的齿槽转多。
本文以R17.2 RMxprt 中的自带案例先将系统中的案例另存到工作目录ions 1”,计算并生成Maxwell 2D 修改为静磁场算例,并分别再复制一按照图1重命名各个算例。
图1 算例重命名角度的方法个永磁体,做旋转操作(选菜单Edit 度设置为一个新变量“my_ang”(如图量“my_ang”的初值为“0 deg”。
律,则类似地在输入电流的地方,将电链的方法子铁芯之间相互作用的切向分量引起的。
T cog 中必须考虑和解决的的磁饱程度会有差异,绕组电感变化,对提流、转子角度的影响,转矩、电感、磁链。
例4极24槽“assm-1”录下,然后在Design 瞬态场算例。
复制该一次静磁场和瞬态场算t->Arrange->Rotate),图2),并确定;在新(如要求转矩、电感、电流定义为新变量。
)图2 旋转转子然后,选中模型中的“Band”区域,选菜单“Maxwell2D->Parameters->Assign-> Torque” 中,定义求解转矩(如要求电感或磁链,则选“…->Matrix…”,另外在此前还要先定义有电流的区域“Excitations->Assign Current”),如图3所示。
ANSYS Mawell 2D求解齿槽转矩的几种方法

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
AoIHKOZ。
mX01jiM。
GCQjxmD。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
PG3z2Zu。
VAY8dQ1。
Wyt3k7x。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
pz4EOlT。
Y0US14Y。
rS3jYMp。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
W0ppFM8。
Q5qvbs7。
dgJ9Gfx。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
ANSYS转矩施加三种方法

转矩一般有三种施加的方法:第一种,将矩转换成一对一对的力偶,直接施加在对应的节点上面.第二种,在构件中心部位建立一个节点,定义为MASS21单元,然后跟其他受力节点耦合,形成刚性区域,就是用CERIG命令.然后直接加转矩到主节点,即中心节点上面第三种,使用MPC184单元.是在构件中心部位建立一个节点,跟其他受力节点分别形成多根刚性梁,,从而形成刚性面.最后也是直接加载荷到中心节点上面,通过刚性梁来传递载荷.上面三种方法计算的结果基本一致,我做过实验的.只不过是后两种情况都是形成刚性区域,但是CERIG命令是要在小变形或者小旋转才能用,只支持静力,线形分析.而第三种方法适用多种情况,不仅支持大应变,还支持非线形情况。
前言做一个总结意义!!!原因:最近网上有较多的朋友在咨询关于实体加载的方法目的:希望这个问题不再成为大家的疑惑的一部分!!!!!!!!!!!!!!!!一、说说施加方法思路1:矩或扭矩说白了就是矩,所谓矩就是力和力臂的乘积。
施加矩可以等效为施加力;思路2:直接施加弯矩或扭矩,此时需要引入一个具有旋转自由度的节点;二、在ANSYS中实现的方法这里说说3个基本方法,当然可以使用这3个方法的组合方法,组合方法就是对3个基本方法的延伸,但原理仍不变。
方法1:引入mass21,利用cerig命令Ex1:/prep7block,0,1,0,1,0,2k,9,0.5,0.5,2.5mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3r,2,1e-6et,1,45et,2,21keyopt,2,3,0lesize,all,0.2vmesh,allksel,s,,,9type,2real,2kmesh,allallselnsel,s,loc,z,2,3NPLOTCERIG,node(0.5,0.5,2.5),ALL,ALL, , , , allsel/SOLUf,node(0.5,0.5,2.5),my,100e3FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve方法2:利用mpc184单元/prep7block,0,1,0,1,0,2mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3et,2,184keyopt,2,1,1lesize,all,0.2vmesh,alln,1000,0.5,0.5,2.5type,2mat,2*do,i,1,36e,1000,36+i*enddoallselallsel/SOLUf,node(0.5,0.5,2.5),my,100e3 FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve方法3:使用rbe3命令/prep7block,0,1,0,1,0,2k,9,0.5,0.5,2.5mp,ex,1,2e10mp,prxy,1,0.2mp,prxy,1,0.3r,2,1e-6et,1,45keyopt,2,3,0lesize,all,0.2vmesh,allksel,s,,,9type,2real,2kmesh,allallsel*dim,sla,array,36*do,i,1,36sla(i)=i+36*enddo*dim,sla2,array,36*do,i,1,36sla2(i)=i+36*enddoallselrbe3,node(0.5,0.5,2.5),all,sla,sla2allsel/SOLUf,node(0.5,0.5,2.5),my,100e3FINISH/SOLnsel,s,loc,z,0d,all,allallselsolve三、使用结论方法1和方法2的结果一致,方法3偏大。
齿槽转矩测试方法(一)

齿槽转矩测试方法(一)齿槽转矩测试简介齿槽转矩测试是一种常用的测试方法,用于评估机械设备的转动精度和承载能力。
本文将介绍齿槽转矩测试的各种方法,包括静态测试、动态测试以及衍生的相关技术。
1. 静态测试方法静态测试方法主要用于测试设备在静止状态下的转矩特性。
以下是一些常用的静态测试方法:•直接法:通过直接施加力矩,测量设备的转动阻力。
这种方法简单直接,适用于轻负荷和低转速的设备。
•浮动法:使用气浮技术对设备进行支撑,测量设备在不同转速下的转矩。
这种方法适用于高转速设备和需要较高精度的测试。
•受力法:通过加载外部力矩,测量设备的变形和应力,从而间接计算出齿槽转矩。
这种方法适用于需要考虑设备变形和应力的情况。
2. 动态测试方法动态测试方法主要用于测试设备在运动状态下的转矩特性。
以下是一些常用的动态测试方法:•自激振动法:通过设备自身的振动特性,间接估计设备的转矩。
这种方法简便易行,适用于一些特殊情况,如无法直接加载力矩的情况。
•力/力矩传感器法:使用力传感器或力矩传感器直接测量设备受到的力或力矩。
这种方法准确可靠,适用于需要高精度测量的情况。
3. 相关技术除了上述的测试方法外,还有一些衍生的相关技术可以用于齿槽转矩测试:•数字化仿真技术:通过建立数学模型,对设备的转矩特性进行模拟和分析。
这种技术可以提供详细的转矩分布、变形分析等信息,但需要准确的设备参数和工况输入。
•红外测温技术:通过红外热像仪对设备进行测温,从而了解设备运行状态和转矩特性。
这种技术无接触,适用于需要远程监测和快速测试的场景。
结论齿槽转矩测试是评估机械设备性能的重要方法之一。
根据实际需求,可选择合适的静态或动态测试方法进行测试。
同时,借助相关的技术手段,也能对设备的转矩特性进行更加准确和全面的评估。
在进行测试之前,确保测试条件和设备参数的准确性,以获得可信的测试结果。
4. 注意事项和应用领域•注意事项:–齿槽转矩测试需要专业设备和经验丰富的技术人员进行操作和解读结果。
利用麦克斯韦张量法分析永磁电动机齿槽转矩

共振的现象。由于影响齿槽转矩 的因素很多 , 如齿槽 的数量 、 齿槽形 状以及磁钢 的极 弧系数 等 , 因此很 难分 析齿槽
转矩。利用麦克斯韦张量法来分析齿槽转矩 , 简单明 了, 而可以定性地认识齿槽转矩 , 从 为电机设计提供理论参考 。 关键词 : 齿槽转矩 ; 麦克斯韦张量 ; 共振
换 的 电磁装置 。在 电机 内建 立进 行 机 电能量所 必需
利 用 它来形 象地 描述 磁 场 的机械 力 。 由于 影 响齿 槽 转 矩 的因 素非 常 多 , 齿槽 的形 如
状 、 隙 的大小 、 极 的 形 状 和分 布 等 因素 有 关 , 气 磁 所 以利 用 解析 函数 的方 法就 显 得非 常复 杂 和 困难 , 因 此 这里 运 用 麦 克 斯 韦 张 量 法 来 定 性 地 解 释齿 槽 转 矩 。 同时利用 麦 克 斯 韦法 与虚 位 移 法 的 等 价性 , 运 用虚 位移 法来 计算 齿槽 转 矩 的整体 数值 。
中 图 分 类 号 : M3 1 T 5 文献标识码 : A 文 章 编 号 :04 7 1 (0 0 1 — 0 7 0 10 — 0 8 2 1 )2 0 2 - 4
Cog i g To q g n r ue Anayss f r a ntM a ne i o or i a l i or Pe m ne g tc M t s Usng M xwelTe o l ns r ZHANG - a SHI Ka Er p n,
触持电棚 20 第 2 0 年 1期 1
…
…
一
利 用 麦 克 斯 韦张 量 法分 析 永磁 电动 机 齿 槽 转 矩
张二 攀 , 卡 石
( 南京师 范大学 , 江苏南京 20 1 ) 1而产生 的 , 它会引起 转矩脉动 , 甚至 可能发生 与 电机
基于ANSOFT的永磁同步伺服电机齿槽转矩分析

①r 0第 32 卷 第 4 期 佳 木 斯 大 学 学 报 ( 自 然 科 学 版 ) Vol . 32 No . 4 2014 年 07 月 Journal of Jiamusi University ( Natural Science Edition) July 2014文章编号: 1008 - 1402( 2014) 04 - 0559 - 04基于 ANSOFT 的永磁同步伺服电机齿槽转矩分析黄金霖1 , 易 靓2 , 曹光华1( 1. 安徽机电职业技术学院电气工程系,安徽 芜湖 241000; 2. 江西理工大学电气工程与自动化学院,江西 赣州 341000)摘 要: 齿槽转矩是永磁电机的固有属性,引起电机的转矩波动,产生振动和噪声. 为减小齿槽 转矩,提高永磁伺服电机的控制精度,在研究永磁电机齿槽转矩产生机理的基础上,根据永磁电 机齿槽转矩的解析式,研究定子齿部开辅助槽和转子磁极偏移对永磁电机齿槽转矩的影响; 利用 有限元软件 ANSOFT ,建立 36 槽 8 极永磁伺服电机的有限元分析模型,计算不同尺寸辅助槽和 磁极偏心距离时的齿槽转矩,分析辅助槽尺寸和磁极偏心距离对齿槽转矩的影响. 研究结果表 明,合理的辅助槽尺寸和磁极偏心距离可有效削弱永磁伺服电机的齿槽转矩. 关键词: 齿槽转矩; 磁极偏心; 辅助槽; 永磁电机中图分类号: TM303 文献标识码: A随着矢量控制算法、电力电子器件和计算机 控制技术的不断发展,永磁伺服电机的应用越来越 广. 在数控机床、小型机器人、机械传动设备以及混 合电动汽车等领域,永磁伺服电机已经代替传统的 异步电机和直流电机,成为许多领域必不可少的传 其中,μ0 是空气磁导率.根据式( 1) 、( 2) 以及气隙磁密随着电机定转 子相对位置角和沿气隙切向不同位置分布的解析 表达式,得到齿槽转矩的表达式为: 动设备[1].T= -12πL Fe ( R2 - R2)∞nG B sinnz α 永磁伺服电机结构与普通异步电机相比,转子 永磁体取代了传统的转子绕组,转子永磁体的存 cog2μ0α∫B dV = 4μ2 1∑ n = 1 nzn 2p( 3)在,使得电机的效率和功率密度高; 与此同时,转子 永磁体与定子槽相互作用,产生齿槽转矩,使得电 机转矩波动增加,产生振动与噪声,影响伺服电机 的控制精度. 齿槽转矩是永磁电机特有的属性,因 此,怎样减小永磁电机的齿槽转矩成为相关专家学 者研究的重点之一[2].1 齿槽转矩产生机理齿槽转矩是永磁电机固有属性,是指电机空载 运行时,永磁体磁极和定子铁心之间的相互作用而 产生的转矩. 它体现了磁极与电枢槽口之间相互作 用力的切向分量的波动[3].根据其定义,可得出齿槽转矩的计算表达式如下:T = - Wcogθ气隙与永磁体磁场中的能量又可以表示为:由式 3 可知,永磁电机的齿槽转矩随着定子槽 数、永磁体的尺寸、极弧系数等值的变化而变化,式 3 为齿槽转矩的削弱提供了理论研究依据[4].2 有限元模型的建立2. 1 电机结构本文设计一台 36 槽 8 极永磁同步伺服电机,以此 为 研 究 对 象,利用有限元分析软 件 Ansoft Mawell 14. 0,研究定子齿开辅助槽、磁极偏移对永 磁同步伺服电机齿槽转矩的影响,提出减小齿槽转 矩的一些方法. 电机的技术指标和具体尺寸分别如 表 1,2 所示. 根据主要尺寸,建立电机的有限元分析模型,1 2W = W air + W PM =2μ ∫B dV( 2)如图 1 所示. 电机由定子铁芯、定子绕组、永磁体、①收稿日期: 2014 - 04 - 30基金项目: 国家自然科学基金青年基金项目( 51267006) ; 江西省自然科学基金项目( 20122BAB206031) . 作者简介: 黄金霖( 1988 - ) ,女,江西赣州人,硕士研究生,助教,研究方向: 永磁电机的设计与分析.定子外径 122. 3mm 转子外径 78mm 定子内径 80mm 转子内径 30mm 定子槽数36 磁极对数 4 减重孔个数8气隙长度 / mm1h 560 佳 木 斯 大 学 学报 ( 自 然 科 学 版 ) 2014 年转子铁心和转轴等部分组成; 永磁同步伺服电机对 控制精度的要求较高,为减小电机的转动惯量,采 用转子开减重孔的结构.表 1 永磁同步伺服电机的技术指标对永磁体的磁动势和磁导分别进行傅里叶分 解,得到:Λ( θ) = ∑Λn cos( kQ θ)( 5) nF 2( θ,θ ,l) = f cos2pv( θ - θ )( 6)额定功率 / kW 4. 5 额定电压 / V 220 额定转速 / rpm 3000 额定转矩 / N . m14. 33表 2 电机的主要尺寸∑ vv式中 θ0 为永磁电机中,定子某齿的中心轴线 与磁极中心线的的初始角度,θ 是磁极与某固定定 子齿相差的角度; Q 为定子槽数,p 为磁极对数,Λn 为 第 n 次磁导谐波幅值,f v 为第 n 次磁动势谐波幅值. 将式( 5) ,( 6) 带入式( 2) 中得到: n12πT cog = - 式中,D4 D α l ∑Λn f n I ∫0 cosn θcos( θ - θ0) d θ ( 7)枢直径,n 为定子槽数 Q 与磁极对数 2p图 1 电机结构图2. 2 空载磁场分布建好模型后,确定合适的求解场,分配正确的 材料属性,施加边界条件,选择合适的激励源方式, 确定所需的时间步长,得出电机的空载磁通分布如 图 2 所示.图 2 永磁同步伺服电机空载磁通分布图 网格剖分时应注意,齿槽转矩的大小受网格剖分的 影响较大,应该精确剖分电机的 band 和气隙部分.3 定子齿开槽减小齿槽转矩由磁路的基础知识,永磁体的磁导为μ0a 电的最小公倍数. 由式( 7) 可知,只有当磁动势的谐波次数与磁导的谐波次数相同时,永磁电机才会产 生齿槽转矩; 且随着谐波次数的增加,与之对应的 磁势谐波与磁导谐波幅值随之减小,则齿槽转矩也 减小,当在每个定子齿上开 m 个槽,相当槽数由 Q 增 加 为 ( m + 1) Q , 则 当 LCM( ( Q + 1) m ,2p) / LCM( Q ,2p) 不等于 1 时,就增加了基本齿槽 转矩次数,则降低了齿槽转矩,其中 LCM( Q ,2p) 为 Q 与 2p 的最小公倍数.文献 5 研究表明,定子齿开辅助槽可有效的减 小永磁伺服电机的齿槽转矩,达到减小电机的振动 和噪声的目的[5]. 开辅助槽时,应注意辅助槽的间 隔相等,大小相等,均匀分布在定子齿上.图 3 不同结构的辅助槽3. 1 辅助槽槽型对齿槽转矩的影响辅助槽的形状和电机的定转子槽一样,也可以 选择不同的槽型结构,确定具体槽型尺寸的前提 下,分别选取不同的槽型结构( 三角形槽、矩形槽、 圆形槽) ,如图 3 所示. 对其进行有限元分析,分析不 同槽型结构对永磁同步伺服电机齿槽转矩的影响.三种 辅助槽型尺寸分别为矩形槽槽宽为 1mm ,槽深为 0. 4mm; 三角形槽的槽宽为 2mm ,槽 深为 0. 8mm; 圆形槽的半径为 0. 5mm . 得到的齿槽 Λ( θ) =m ( 4)+ g( θ)转矩波形图如图 4 所示.第4 期黄金霖,等: 基于ANSOFT 的永磁同步伺服电机齿槽转矩分析561图4 不同槽型结构的齿槽转矩波形由图 4 可知,不同槽型的辅助槽,永磁电机齿槽转矩幅值的大小不同.其中,矩形槽降低齿槽转矩的效果最好,圆形槽次之,三角形槽最差.图5 槽口宽度对齿槽的影响图6 槽深对齿槽转矩的影响3.2 辅助槽尺寸对齿槽转矩的影响定子齿开辅助槽虽可有效减小永磁电机的齿槽转矩,但辅助槽的尺寸对齿槽转矩有较大影响,选择合适的尺寸可以进一步减小永磁电机齿槽转矩[6]; 若槽口和槽深选择不当,反而会增大电机的齿槽转矩.建立定子齿开矩形槽的永磁同步伺服电动机有限元分析模型,研究不同辅助槽型尺寸对电机齿槽转矩的影响,得出齿槽转矩波形图.图 5 与图6给出了辅助槽的槽口宽度和槽深,对电机齿槽转矩的影响.由图5、6可知,永磁电机的齿槽转矩随着辅助槽槽口宽度的增大先增大后减小再增大,当辅助槽槽口的宽度为0.6mm 时,即为定子槽口宽度的一半时,齿槽转矩达到最小值; 齿槽转矩随着辅助槽槽深的增大先减小后增大,当辅助槽深为0.4mm时,齿槽转矩达到最小值.此外,开辅助槽时,辅助槽要均匀的分布在电枢齿上,辅助槽的槽口宽度和槽深要选取合适,太深会导致齿部磁密过大,太浅达不到明显的效果.图7 磁极偏心结构图8 偏心电机的齿槽转矩波形图9 偏心电机的空载反电势波形4 磁极偏心对齿槽转矩的影响开辅助槽虽可有效的降低齿槽转矩,但加工难度较高,而且定子齿开辅助槽会产生高次谐波,有些场合对电机的控制精度要求很高,开辅助槽一般不能满足需要.对于表面式结构的永磁伺服电机,r 562 佳 木 斯 大 学 学 报 ( 自 然 科 学 版 ) 2014 年还可以采用磁极偏心的结构来减小永磁电机的齿槽转矩[7,8].不采用采用偏心磁极的结构时,其气隙径向磁 密为h m( 1) 定子齿部开辅助槽可有效减小永磁电机 的齿槽转矩; ( 2) 辅助槽型的形状影响齿槽转矩的 大小,其中矩形槽的效果最好,三角形槽最差; ( 3 ) 辅助槽的尺寸影响齿槽转矩的变化,随着辅助槽深 度的增加,齿槽转矩的幅值先减小,后增大; 随着辅 B( θ) = B r ( θ)( 8) h m + g( θ)助槽槽口宽度的增大,齿槽转矩先增大,再减小,最采用偏心磁极的结构时,永磁电机的永磁体内 外径不同心( 如图 7 所示) ,外圆的圆心为,半径为 Ro1 ,内圆的圆心为,半径为 Ro2 . O 1 和 O 2 之间的距 离为永磁体的偏心距离,用 h_px 表示.其气隙磁密的径向分布为:后增大; ( 4 ) 在保证永磁伺服电机性能的条件下, 采用磁极偏心的结构可有效的降低永磁电机的齿槽 转矩. 参考文献:h_px h _p x[1] 刘细平,郑爱华,王晨. 偏心与此同步伺服电动机优化设计 B'( θ) = B r ( θ) h_px + g( θ) ' = B r ( θ) h m + g( θ) [J ]. 微特电机,2012,40( 10) : 23 - 25. [2] Kyu Yun Hwang ,Hai Lin ,Se Hyun Rhyu . A Study on the Novel=h_pxB ( θ)h m h mm θh m= B r '( θ)h + g( θ)m ( 9)Coefficient Modeling for a Skewed Permanent Magnet and Over-hang Structure for Optimal Design of Brushless DC Motor [J ].I EEE Transactions on Magnetics ,2012,48( 5) : 1918 - 1923.由公式( 3) 和( 9) 可知,当 Ro1 和 Ro2 等参数不 变时,永磁电机齿槽转矩的大小只与气隙磁密的分 布有关,因此只要改变磁极形状,使得相应的径向 磁密分布减小,就可减小齿槽转矩[9,10].建立偏心永磁伺服电机的有限元分析模型,分 析磁极偏心的距离对齿槽转矩的影响,如图 8 所 示. 图 9 是磁极偏心时,电机空载反电势的波形图.由图 8 可知,磁极偏心距离 h_px = 15mm 时, 电机的齿槽转矩达到最小值; 由图 9 可知,改变磁 极的偏心距离,电机空载反电势的大小基本不变, 波形正弦性保持较好. 因此,合适的磁极偏心距离 可有效削弱永磁电机的齿槽转矩.5 结 论本文在研究齿槽转矩解析式的基础上,采用有 限元分析的方法,提出减小齿槽转矩的一些方法, 研究表明:[3] 王秀和. 永磁电机[M ]. 2 版. 北京: 中国电力出版社,2007. [4] 王秀和,丁婷婷,杨玉波. 自起动永磁同步电动机齿槽转矩的研究[J ]. 中国电机工程学报,2005,25( 18) : 166 - 170. [5] 夏加宽,于冰. 定子齿开槽对永磁电机齿槽转矩的影响[J ].微电机,2010,43( 7) : 13 - 16. [6] 罗宏浩,廖自力. 永磁电机齿槽转矩的谐波分析与最小化设计[J ]. 电机与控制学报,2010,14( 4) : 36 - 40. [7] 杨玉波,王秀和,张鑫等. 磁极偏移削弱永磁电机齿槽转矩方 法[J ]. 中国电机工程学报,2006,21( 10) : 22 - 25.[8] Zhu Z Q . Evaluation of Superposition Technique for Calculating Cogging Torque in Permanent Magnet Brush Less Machines [J ].I EEE ,Trans . on magnetics . 2006,42( 5) : 1597 - 1603.[9] Nakamura K ,Fujimoto H ,Fujitsuna M . Torque Ripple Suppres- sionControl for Pm Motor with Current Control based on PTC .I n: Proc 0f Power Electronics . Conference ( IPEC ) ,Sapporo , 2010: 1077 - 1082.[10] 杨玉波,王秀和,丁婷婷. 基于单一磁极宽度变化的内置式 永磁同步电 动 机 齿 槽 转 矩 削 弱 方 法[J ]. 电 工 技 术 学 报, 2009,24( 7) : 41 - 45.Cogging Torque Analysis of Permanent Magnet SynchronousMotor Based on ANSOFTHUANG Jin - lin 1, YI Liang 2, CHAO Guang - hua1( 1. Department of Electrical Engineering ,Anhui Technological College of Machinery and Electricity ,Wuhu 241000,China; 2. School of Electrical Engineering and Automation ,Jiangxi University of Science and Technology ,Ganzhou 341000,China)Abstract: Cogging torque could cause the motor 's torque ripple occurred ,and lead to mechanical vibration and acoustic noise . In order to weaken the PMSM 's cogging torque and improved control precision ,this paper based on the study of cogging torque 's generating mechanism ,according to the analysis formula of cogging torque , the impact of assist slot and PM eccentric distance affected the cogging torque was researched . The FEA software ANSOFT was used ,the FEA model of 36 slots 8 pole was established ,the cogging torque of different assist slot 's size and PM eccentric distance has been calculated ,and the influence of assist slot 's size and PM eccentric dis- tance to cogging torque were analyzed . The results indicate that a reasonable assist slot size and eccentric dis- tance could help to reduce the PMSM 's cogging torque .Key words: cogging torque; eccentric; assist slot; permanent magnet machines。
几种简单的齿槽转矩测量方法

F N h o i , o gh n , I G Y n i A ucu , N ig eg E G Z abn WU K nse g D N u f ,H N G i n WA G Qn pn g e h ( a a un yn c n ea dT c nlg nier gC . t , a a 6 0 C N) D l nG ag agSi c n eh o yE g e n o ,Ld D l n16 0 , H i e o n i i 1
置, 即稳定平衡点 ; 电磁转矩为零 , 偏离时都有 回复到
该位 置 的作 用 转 矩 , 趋 于 另一 相 邻 的稳 定 平 衡 点 。 或
可 见转 矩 的作 用方 向是交 变 的 , 常 所说 的定 位 转矩 通
是 指交 变 幅值 。 由于 定位 转 矩 主 要源 于定 子齿 槽 , 所 以也被 叫做齿 槽转 矩 , 者 叫做齿槽 定位 转矩 。 或 在 永磁 电动 机 中 , 槽转 矩常 常成 为引起 振动 、 齿 噪 声 和提 高控 制精 度 困难 的基 本 原 因。 因此 , 何 测 量 如 齿 槽转 矩也 是受 到相 当关注 的 问题 。本 文介绍 几种 齿
的位 置 。正 因为这样 , 常把 永 磁 电 动机 不 通 电且 绕 常 组开 路情 况下 转动转 子 的转矩称 为定 位转 矩 。 定位 转矩 的产 生主要 源于定 子齿槽 的存 在 。当永 磁转 子 的磁极 与定 子齿 槽 的相对 位 置 不 同时 , 主磁 路
槽转 矩 的测 量方 法 。
( )4 — 1 1 :4 5 .
图 1 杠杆测量法
杠 杆测 量法是 一种 非常 简单 、 直观 、 易实 现的测 量
方法 , 但是 精度很 难保证 , 以常在 测量要 求精 度不 高 所 或者 条件 受 限 时采 用 。测 量 时 需 注 意 几 点 : 1 杠 杆 ()
ANSYS Maxwell 2D求解齿槽转矩的几种方法

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
ANSYSMaxwell2D求解齿槽转矩的几种方法

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
齿槽转矩_精品文档

齿槽转矩引言在机械工程中,齿槽转矩是一个重要的概念。
它是指在一个旋转系统中,由于齿轮或传动齿轮的齿槽受到力或扭矩作用而引起的转矩。
了解和设计齿槽转矩对于机械系统的正常运行和优化至关重要。
本文将介绍齿槽转矩的基本概念、计算方法以及在实际应用中的重要性。
一、齿槽转矩的定义齿槽转矩是指在齿轮或传动齿轮的齿槽上受到的力或扭矩,它是齿轮传动中扭矩的一种表现形式。
齿槽转矩的大小取决于施加在齿轮上的力或扭矩的大小以及齿轮的几何形状和材料的特性等因素。
二、齿槽转矩的计算方法齿槽转矩的计算涉及到几何学、力学和材料科学等多个学科的知识。
以下是常用的几种计算方法:1. 力的分解法:将作用在齿槽上的力或扭矩分解为垂直于齿槽方向和平行于齿槽方向的分量,然后计算每个分量对应的转矩,最后将两个分量的转矩进行叠加得到总转矩。
2. 动平衡法:利用动力学的平衡原理,通过计算齿轮系统中各个部件的动力平衡方程,推导出齿槽转矩与其他参数之间的关系,从而计算得到齿槽转矩的数值。
3. 有限元法:利用有限元分析软件,将齿槽和齿轮系统建模为一系列有限元,在施加力或扭矩的作用下进行有限元分析,通过计算每个有限元上的应力和应变,最终得到齿槽转矩的数值。
4. 经验公式法:根据实际工程经验,总结出一些与齿槽转矩有关的经验公式,通过输入一些基本参数,例如齿轮的模数、齿数、齿轮宽度等,就可以快速估算出齿槽转矩的数值。
三、齿槽转矩的重要性齿槽转矩在机械系统中扮演着重要的角色。
它直接关系到齿轮传动系统的传动效率和可靠性。
下面列举了齿槽转矩的几个重要性方面:1. 传动效率:齿槽转矩会引起齿轮的损耗和摩擦,降低传动的效率。
通过准确计算和优化设计齿槽转矩,可以最大程度地减少这种能量损耗,提高传动系统的效率。
2. 强度分析:齿槽转矩直接作用于齿轮的齿槽上,如果齿槽的强度不足,会导致齿槽破裂或变形,进而引发整个传动系统的故障。
因此,准确计算和评估齿槽转矩对齿轮齿槽强度的影响,对于保证传动系统的可靠性和寿命具有重要意义。
【杂谈Maxwell】Maxwell2D等效斜槽

【杂谈Maxwell】Maxwell2D等效斜槽1 前言为了抑制振动和噪声,电机采用斜槽是一种常见的结构形式,其的仿真严格来说是一个3D问题,但由于3D仿真时间与资源的限制,采用2D的等效的方式,亦有一定的计算精度,其等效的原理如图1所示,即将轴向分成多个错位段,每段对应一个2D工程,对2D工程的结果进行相加求平均。
原斜槽示意等效斜槽示意图1在ANSYS Maxwell R17版本前,2D等效斜槽是通过对转子初始相位角进行参数化,求解多个工程,然后在后处理中进行处理完成的,在ANSYS Maxwell R17版本起,可以通过一个斜槽的设置,仅求解一个工程即可完成等效,本文对两种方法分别进行讲解。
本文以一台4极24槽永磁电机为例,电机轴向斜1个定子槽,电机的1/4模型如图2所示:图22 R17之前版本整体思路是对转子初始相位角进行参数化,然后在后处理中利用对曲线“统计”中的“平均”得到结果,具体操作如下:(1)在MotionSetup中将转子初始位置设置为一个变量(名称任意),如①所示:图3图4电机的初始角度为7.5°,这里同样将变量的初始值设置为7.5deg ,如图5所示。
图5(2)参数化变量“Ini_deg”图6如图7所示,在①中选择之前设置的初始相位角变量“Ini_deg”,在②选择添加变量的方式为是:个数,③中设置变量的初始值,④中设置变量的结束值,本文斜一个定子槽,对于24槽电机,即360/24=15°,且一般为了与不斜槽的结果做比较,保证结果的相位一直,一般是在初始转子位置角(本例为7.5°)的正负两侧选择起始值,即参数化变量的范围是:开始:(7.5-360/15/2)=0°结束:(7.5+360/15/2)=15°⑤是变量的个数,一般设置为7个或以上就能保证等效的精度,这里设置为7,然后点⑥(这里为了演示,起始之前已经添加好了变量,故Add为灰色,首次添加,Add不是灰的),然后点击⑦图7(3)求解,如图8所示。
齿槽转矩
关于齿槽转矩的计算
由于模型保密,我采用的赵博书上第四章的例子。
齿槽转矩由于是永磁电机绕组不通电时永磁体与铁芯之间作用产生的转矩。
因此,网格剖分对齿槽转矩影响很大,一般采用导入静态场网格的方法求解齿槽转矩。
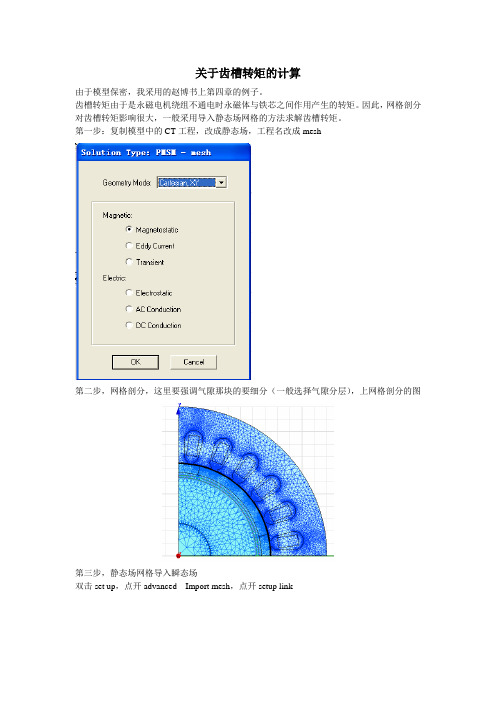
第一步:复制模型中的CT工程,改成静态场,工程名改成mesh
第二步,网格剖分,这里要强调气隙那块的要细分(一般选择气隙分层),上网格剖分的图
第三步,静态场网格导入瞬态场
双击set up,点开advanced Import mesh,点开setup link
点use this project ,source design 选择mesh 工程
第四步,将motion setup的angular velocity改成1deg_per_sec
另外,需要注意的地方是,选择time的时候要合适,还有导入网格的时候模型一定要一致,不然会导致计算错误。
计算结果。
ANSYSMaxwellD求解齿槽转矩的几种方法

ANSYS Maxwell 2D求解齿槽转矩的几种方法齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt算例,按照图1重命名各个算例。
图1? 算例重命名1静磁场扫描转子旋转角度首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2? 旋转转子然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3? 定以转矩求解在“Analysis”中添加1个“Setup”,设置迭代精度误差为%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长 deg,如图4所示。
图4? Optimetrics扫描范围设置设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5? 结果调用界面重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6? 扫描转子旋转角度所得齿槽转矩曲线值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
基于ANSYS的齿槽力矩分析

基于ANSYS的永磁力矩电机齿槽力矩分析与研究曹红飞(国营林泉电机厂,贵阳 550008)摘要:为了降低起动电压和提高低速运行的平稳性,在永磁力矩电机设计时应特别注意减小齿槽力矩。
本文以某永磁直流力矩电机设计改进为例,运用ANSYS软件建立2D模型,对电机电磁场进行分析,对影响电机齿槽力矩的关键参数(如极弧系数、气隙大小等)进行优化设计,得出电机的齿槽力矩和关键参数的关系。
关键词:永磁电机齿槽力矩 ANSYSAnalysis and study of Cogging torque in permanentmagnet torque motor Based on ANSYSCao Hong-fei(Linquan Motor,Guiyang 550008 ,China)Abstract:In the process of designing the permanent magnet torque motor,we must be center our attention on the Cogging torque because of reducing the Start-up V oltage and increasing the stabilization of low-speed .The paper take the permanent magnet torque motor as a example,creating the 2D model based on ANSYS to analysis electromagnetic fields, optimizing the key parameters of influencing the Cogging torque,find out the relationgship between the Cogging torque and the key parameters.。
基于Ansoft Maxwell的内置式Ⅴ型永磁电机齿槽转矩优化

基于Ansoft Maxwell 的内置式V 型永磁电机齿槽转矩优化*吴铭刘成武(福建工程学院,福建福州35011)摘要:作为永磁电机制造不可忽视的性能指标,齿槽转矩是永磁电机向高性能高精度迈进前亟需解决的关键一步。
文章基于能量法和傅里叶展开,解析推导出内置式V 型永磁电机的齿槽转矩理论表达式,从较直观的角度分析了齿槽转矩的产生规律,研究了不等厚磁极、开辅助槽和辅助凸部、槽口尺寸变化引起齿槽转矩波动的影响,并与Ansoft Max⁃well 有限元分析软件结合仿真各优化策略下的内置式电机齿槽转矩。
研究表明,采用不等厚磁极、开辅助凹槽和辅助凸部、适当选取辅助槽尺寸均能减弱齿槽转矩对电机的影响。
关键词:齿槽转矩;有限元;内置式电机;优化策略中图分类号:TM351文献标识码:A文章编号:1672-4801(2020)02-058-05DOI:10.19508/ki.1672-4801.2020.02.017*福建省自然科学基金资助项目(2018J01628)作者简介:吴铭(1996—),男,硕士生,研究方向为永磁电机振动与噪声、电磁场分析。
刘成武(1975—),男,教授,博士,研究方向为机械结构多学科优化设计、汽车NVH 。
随着控制技术的迅速成熟和高性能永磁材料的问世,永磁电机结合驱动控制系统普遍应用在新能源汽车市场。
永磁体磁场与定子齿槽相互作用产生齿槽转矩,系统的控制精度会受其引起的振动和噪声波及。
齿槽转矩是高性能永磁电机研发中不容忽视的重要课题,降低甚至消除齿槽转矩将会对行业影响深远。
在关于齿槽转矩的削弱方法和优化策略方面,近些年取得了大量研究成果。
文献[1]从永磁电机的气隙磁导模型入手解析出能够减小齿槽转矩的合适槽口宽度,但提出的槽口宽度运用到实际价值不高。
文献[2]探究了傅里叶分解系数是否受定子齿槽口宽度影响,研究表明使气隙磁导平方的傅里叶分解系数降低的槽口宽度能减小齿槽转矩;但作者仅从改变相对气隙磁导的角度削弱齿槽转矩,存在一定局限性。
齿槽转矩

关于齿槽转矩的计算
由于模型保密,我采用的赵博书上第四章的例子。
齿槽转矩由于是永磁电机绕组不通电时永磁体与铁芯之间作用产生的转矩。
因此,网格剖分对齿槽转矩影响很大,一般采用导入静态场网格的方法求解齿槽转矩。
第一步:复制模型中的CT工程,改成静态场,工程名改成mesh
第二步,网格剖分,这里要强调气隙那块的要细分(一般选择气隙分层),上网格剖分的图
第三步,静态场网格导入瞬态场
双击set up,点开advanced Import mesh,点开setup link
点use this project ,source design 选择mesh 工程
第四步,将motion setup的angular velocity改成1deg_per_sec
另外,需要注意的地方是,选择time的时候要合适,还有导入网格的时候模型一定要一致,不然会导致计算错误。
计算结果。
斜槽分析maxwell2D斜槽设置

斜槽分析maxwell2D斜槽设置
斜槽系数的分析和绕组系数分析是一样的,可以放在圆周内去计算。
可以参考电机学第四章
齿谐波频率:
v = k*(Z/P)+/- 1
Z为槽数,也是齿数,P是极对数。
一齿加一槽,形成一个齿谐波。
而一对极对应一个基波,所以如果在一对极中有两个槽,那就有两个齿谐波。
+/-1 目前不知道为啥
斜槽系数 = 0.5个齿距??
这句话怎么理解?
上述基波齿谐波齿数理解:转子转一圈,基波转了P(极对数)圈,再考虑有12个槽,所以齿谐波转了12*P(12*5=60圈),从机械角度来看。
360/60 = 6° 也就是一个齿谐波占据了机械角度6°而一个齿槽360/12 = 30°,所以为了消除齿谐波,斜槽不需要斜一个齿,只需要 6/30=0.2个齿即可
maxwell 2D中等效斜槽操作
注:通过上面理论分析可以求出齿槽谐波的机械角度为theta 则start和stop = -theta/2 , theta/2 ;count一般为10以上这样计算更准确。
齿槽转矩计算

齿槽转矩计算齿槽转矩是机械工程中常用的一个概念,它描述了在齿轮传动中产生的转矩大小。
齿槽转矩的计算对于机械设计和分析非常重要,它能够帮助工程师确定齿轮的尺寸和材料,以确保传动系统的可靠性和效率。
在进行齿槽转矩计算之前,我们需要明确几个关键参数。
首先是齿轮的模数(齿距除以π),它描述了齿轮齿槽的大小。
其次是齿轮的齿数,它决定了齿轮的直径和转速。
还有齿轮的材料,它对齿槽转矩的承载能力有重要影响。
齿槽转矩的计算可以通过以下公式进行:T = K * m * Z * F其中,T表示齿槽转矩,K是一个修正系数,m是模数,Z是齿数,F 是齿槽承载力。
修正系数K考虑了齿轮的几何形状和接触条件。
它的值可以通过经验公式或者有限元分析得出。
对于常见的齿轮,修正系数通常在0.8到1.5之间。
模数m是齿槽的大小,它直接决定了齿轮的尺寸。
通常,模数的选择需要考虑到齿轮的强度和齿面接触疲劳寿命。
齿数Z表示齿轮的齿数,它决定了齿轮的直径。
齿数越多,齿轮的直径越大,转矩的承载能力也就越高。
齿槽承载力F是齿轮齿槽的最大承载能力,它是一个与材料和几何形状相关的参数。
齿槽承载力可以通过材料的强度和齿槽的几何形状来计算。
通过以上公式和参数,我们可以计算出齿槽转矩的大小。
这个数值对于机械设计和分析非常重要,它可以帮助工程师选择合适的齿轮尺寸和材料,以确保传动系统的可靠性和效率。
齿槽转矩的计算是机械工程中一个复杂而重要的问题。
它需要考虑多个参数和公式,并进行准确的计算。
通过合理选择齿轮的尺寸和材料,我们可以提高传动系统的可靠性和效率,同时降低成本和维护费用。
在实际应用中,工程师需要根据具体情况进行齿槽转矩的计算,并结合其他因素进行综合考虑。
只有在全面考虑了材料、几何形状和接触条件等因素后,才能得出准确的齿槽转矩数值,从而保证传动系统的安全可靠性。
齿槽转矩的计算是机械工程中一个重要的问题。
它需要考虑多个参数和公式,并进行准确的计算。
通过合理选择齿轮的尺寸和材料,我们可以提高传动系统的可靠性和效率,从而实现机械设备的稳定运行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ANSYS Maxwell 2D求解齿槽转矩的几种方法
齿槽转矩是永磁电机特有的问题之一,是高性能永磁电机设计和制造中必须考虑和解决的关键问题。
其表现是当永磁电机绕组不通电时,永磁体和定子铁芯之间相互作用产生的转矩,它是永磁体与电枢齿之间相互作用力的切向分量引起的。
Maxwell 2D可以有效仿真得出永磁电机电磁方案的齿槽转矩,且方法较多。
本文以R17.2 RMxprt中的自带案例4极24槽“assm-1”为模板,介绍3种方法。
打开该案例后,首先将系统中的案例另存到工作目录下,然后在DesignSettings 中设置“Fractions 1”,计算并生成Maxwell 2D瞬态场算例。
复制该算例,将新算例修改为静磁场算例,并分别再复制一次静磁场和瞬态场算例,删除RMxprt 算例,按照图1重命名各个算例。
图1 算例重命名
1静磁场扫描转子旋转角度
首先选中转子轭和4个永磁体,做旋转操作,在弹出窗口中设置旋转角度为变量“my_ang”,并定义变量初始值为“0 deg”,如图2所示。
图2 旋转转子
然后选中模型“Band”,在“Parameters”中定义求解转矩,如图3所示。
图3 定以转矩求解
在“Analysis”中添加1个“Setup”,设置迭代精度误差为0.1%,最后在“Optimetrics”中设置变量“my_ang”的扫描范围为线性步长[0 deg ,20 deg],步长0.2 deg,如图4所示。
图4 Optimetrics扫描范围设置
设置完成后即可求解,求解完成后按照图5的设置,查看静磁场分析报告。
因为本电机的轴向长度为65mm,而Maxwell 2D XY平面静磁场求解的对象默认长度为1m,因此需要在求解结果中加入“/1000*65”的运算。
图5 结果调用界面
重命名该结果报告为“Cogging_ Torque”,齿槽转矩结果如图6所示。
图6 扫描转子旋转角度所得齿槽转矩曲线
值得注意的是,RMxprt一键有限元生成的表贴式永磁体充磁方向为径向充磁,其充磁方向由极坐标定义,即N极充磁方向为R的正方向,S极充磁方向为R的负方向,参考坐标系为“Global”坐标。
而实际工程中常常会遇到平行充磁的电机,对于平行充磁最常用的处理方式是建立参考坐标系,永磁体的充磁方向参考特定参考坐标系的X轴正方向。
而在上述操作中,参考坐标系无法跟随转子旋转,使用本方法分析平行充磁时的结果将是错误的,因此可以利用第2种方法分析齿槽转矩。
打开“2_Cogging_Torque_MS_Stator”算例,首先选择“Stator”和所有的线圈,做旋转操作,设置旋转角度为变量“my_Stator_ang”,变量初始值为“0 deg”,如图7所示。
图7 旋转定子
按照算例“1_Cogging_Torque_MS_Rotor”的方法设置“Torque1”和“Setup1”,在“Optimetrics”中设置图8所示扫描范围。
图8 Optimetrics扫描范围设置
求解完成后查看齿槽转矩结果,如图9、10所示。
图9 齿槽转矩调用界面
图10 扫描转子旋转角度所得齿槽转矩曲线
本方法中,永磁体不旋转,因此充磁方向不改变,分析结果对于任意方式定义的充磁方向均有效。
3瞬态场求解空载低速旋转转矩多周期仿真
打开瞬态场算例“3_Cogging_Torque_TR_2Period”,首先修改模型转速为“1 deg_per_sec”,初始角修改为“-20 deg”,然后在网格划分中设置合理划分规则,再将“Excitations”删除(右键Delete All),将求解设置修改为图11所示。
图11 求解设置
本算例中求解2个以上周期,在前面一半时间以“1s”为仿真步长,快速达到稳定;后面一半时间以“0.2s”为仿真步长,得到较高精度。
结果如图12所示
图12 2周期瞬态场齿槽转矩仿真结果
单周期仿真
打开瞬态场算例“4_Cogging_Torque_TR_1Period”,设置初始角为“0 deg”,转速为“1deg_per_sec”,求解设置如图13所示
图13 1周期求解设置
本算例求解时长包含1个齿槽转矩周期,结果如图14所示。
图14 1周期瞬态场齿槽转矩仿真结果
将静磁场仿真结果导出,并做简单的数据编辑后,导入到同一个结果窗口下,如图15所示,二者结果吻合度较高。
图15 静磁场仿真结果对比
瞬态场仿真结果对比
将瞬态场仿真结果导出,并做简单的数据编辑后,导入到同一个结果窗口下,如图16所示,2条曲线完全重合。
图16 瞬态场仿真结果对比
将4个仿真结果完全导入到同一个结果窗口,瞬态场和静磁场结果趋势基本相同,有较小误差。
图17 静磁场和瞬态场仿真结果对比
5总结
在上述的静磁场计算中,每一步计算都要重新迭代网格,速度较慢,并且需要Optimetrics License支持。
静磁场求解的对象模型默认长度是1m,在后处理中需要做特殊处理。
平行充磁和径向充磁需要区别对待。
而瞬态场的1个周期和2个周期的计算结果相同;另外测试过,转速1deg/sec和1min/sec的计算结果相同;计算中网格只需要划分一次,且不需要Optimetrics License支持。
结果对比时将结果文件导出为csv文件,修改题头和数值单位,并导入到一个结果显示窗口中,直接对比。
图18 导出文件。
