塑性矩计算公式范文

流变参数塑形指数计算公式

流变参数塑形指数计算公式流变学是研究物质在外力作用下的变形和流动规律的一门学科，它在化工、材料、食品等领域有着广泛的应用。

其中，流变参数塑性指数是描述物质在外力作用下的变形特性的重要参数之一。

本文将介绍流变参数塑性指数的计算公式及其在实际应用中的意义。

流变参数塑性指数是描述物质在外力作用下的变形特性的一个重要参数，它可以用来评价物质的流变性能。

在实际应用中，塑性指数可以帮助工程师和科研人员了解物质在不同应力下的变形特性，从而指导工程设计和材料选择。

流变参数塑性指数的计算公式如下：\[ N = \frac{\tau_{y}}{K} \]其中，N为塑性指数，τy为屈服应力，K为流变模量。

屈服应力是描述物质在外力作用下开始发生塑性变形的应力值，它是塑性变形发生的临界点。

流变模量是描述物质在外力作用下的变形特性的一个重要参数，它可以反映物质的变形硬度。

流变参数塑性指数的计算公式是通过屈服应力和流变模量的比值来描述物质的塑性变形特性的。

在实际应用中，流变参数塑性指数的计算可以通过实验测试得到。

首先，需要对物质进行流变学实验，通过施加不同的应力，测量物质的变形量和应力值，从而得到物质的屈服应力和流变模量。

然后，将这两个参数代入计算公式中，就可以得到物质的塑性指数。

流变参数塑性指数在实际应用中具有重要的意义。

首先，它可以帮助工程师和科研人员了解物质在不同应力下的变形特性，从而指导工程设计和材料选择。

其次，塑性指数还可以用来评价物质的加工性能和稳定性，对于材料加工和生产具有重要的指导意义。

此外，塑性指数还可以用来评价物质的性能变化和老化情况，对于材料的质量控制和品质评价具有重要的意义。

总之，流变参数塑性指数是描述物质在外力作用下的变形特性的重要参数，它可以通过实验测试得到。

在实际应用中，塑性指数可以帮助工程师和科研人员了解物质的变形特性，指导工程设计和材料选择，评价物质的加工性能和稳定性，评价物质的性能变化和老化情况。

塑性计算方法及适用范围(精)

c 由于超静定结构具有多余约束，某一支座进入破坏阶段时，只是少一个多余联系，整个结构并未破坏。
d 按弹性理论计算法计算时，支座弯矩总是远ቤተ መጻሕፍቲ ባይዱ于跨中弯矩，支座配筋拥挤，构造复杂，施工不便。
塑性内力重分布的计算方法
对于均布荷载作用下，等跨连续板、次梁考虑塑性内力重分布的弯矩，可按下列公式计算：（1）控制截面的弯矩： M=am（g+q）l02 式中 am—弯矩系数，板和次梁按表6-4数据采用。
式中 αm—弯矩系数，板和次梁按表 6-4 数据采用。
表 6-4 连续梁及连续单向板弯矩计算系数 m
截面位置
边
支承情况
端支
座
梁板搁置墙上
0
－
板
整浇刚性连
1/16
接
－
梁
1/24
－梁与柱刚性连接
1/16
跨边跨
中 1/11
1/14
1/14
第二跨
第二支座
第二跨中
二跨连续－1/10 三跨以上连续－ 1/16
外
内
侧
侧
0.55 0.55
钢筋混凝土连续梁板考虑塑性内力重分布的设计方法按弹性理论计算法的缺陷： a 钢筋砼是两种材料组成的非匀质弹性体，在构件的截面设计中己充分考虑了其塑性性能，按破坏阶段的构件截面计算方法与按弹性理论计算的结构内力是互不协调的，材料强度未能得到充分发挥。
b 弹性理论计算法是按活荷载的最不利位置时的内力包络图来配筋的，但各跨中和各支座截面的最大内力实际上并不能同时出现。
1/11
中间跨
中间支中间跨
座
中
－1/14 1/16
(2) 控制截面的剪力

弹塑性_塑性力学基本方程和解法

在加载过程中物体各点处的偏应力分量 sij 保持比例不变。在工程允许精度下，也可推
广应用于稍为偏离简单加载的情况。
以上各种理论中涉及的一些假设，例如：塑性应变偏量的增在单一的函数关系等假设，都得到了常用金属材
料大量试验的验证。
z 强化规律对于理想弹塑性材料，材料一旦屈服，其应力状态点在主应力空间中就落在屈服
变形， Hα 也不变，于是
∂f ∂σ ij
除等向强化外，有些强化材料表现为随动强化（图 7.7b），即，在强化过程中，屈
服面的大小和形状保持不变，只随塑性变形的发展而在应力空间中平移。还有些材料
在强化过程中随动强化与等向强化同时发生，称为混合强化。
由于在应力和强化参数空间中，表示应力状态的应力点只可能位于后继屈服面
（或加载面）上或其内，不可能位于曲面之外，若加载面是一个正则曲面，则有
⎯2⎯
研究生学位课弹塑性力学电子讲义
姚振汉
⎧ε = 0 ⎨⎩σ = σ s
当 σ <σs 当 ε >0
(2)
图 7.5 理想弹塑性和刚塑性
当考虑材料强化性质时，可在理想弹塑性模型的基础上加以改进，采用线性强化弹塑性模型来近似：
⎧σ = Eε
⎨⎩σ = σ s +E1 (ε − εs )
当 ε ≤εs 当 ε >εs
(5)
⎯3⎯
第七章塑性力学的基本方程与解法
其中 k 可由单向拉伸或其它材料试验测得的σ s 确定， k = σ s 2 。当不能确定主应力的排序时，在以三个主应力为坐标轴的应力空间中，由特雷斯卡条件所包围的弹性状态的应力空间为
σ1 −σ 2 ≤ 2k, σ 2 −σ 3 ≤ 2k, σ 3 −σ1 ≤ 2k

塑性力学常用公式

塑性力学常用公式1. 偏张量及其不变量 1.1应力偏张量13ij ij kk ijS σσδ=-第二不变量及应力强度（V on Mises 应力）22222222112222333311122331221'21'[()()()6()]6'3'ij ij ijij J S S J J S J σσσσσστττσσ==-+-+-+++∂=∂=1.2应变偏张量13ij ij kk ije εεδ=-第二不变量及应变强度（等效应变）2222222211222233331112233121'213'[()()()()]624'3ij ijI e e I I εεεεεεγγγε==-+-+-+++=2. 屈服条件V on Mises 屈服条件2()03'ij s J σσσσ-==其中Tresca 屈服条件max ()02sij στσ-=其中13max 2σστ-=是最大剪应力123σσσ≥≥是三个主应力。

3. 增量本构关系3.1理想塑性材料加载面：()ij sσσσ≡增量关系：()ευσυσδλ⎡⎤=+-+⎣⎦011ij ij kk ij ijd d d d S E流动因子：000=00=0s s ij ij ps ij ij S d d d S d σσσσσλλσσσ⎧<<⎪=⎨≥=⎪⎩或，000T ep T e D d d D σαλεσαασ=矩阵形式ασσασεεσαασ⎛⎫=-= ⎪⎝⎭0000T e ee ep Te D D d D d D d D3.2线性等向强化材料加载面:()()()0p ij ij s h d ϕσσσσε=-+=⎰增量关系：()ευσυσδλ⎡⎤=+-+⎣⎦011ij ij kk ij ij d d d d S E流动因子：000000()0()=000()=00ij ij ij ij p ij ij ij S d d d S d ϕσϕσσλλϕσσ⎧<≤⎪=⎨>>⎪⎩或，029114()p kl kld S d hλσσ=矩阵形式0002111()4()Tep e d F F d d hεσσασσασσ==+0()ep d D d σσε=3.3线性随动强化材料加载面：()()0p ij ij ij s c ϕσσσεσ=--=增量关系：()011()pij ij kk ij ij ij d d d d S c E ευσυσδλε⎡⎤=+-+-⎣⎦000000()0()=0()0()=0()0pij ij ij ij ij pp ij ij ij ij S c d d d S c d ϕσϕσεσλλϕσεσ⎧<-≤⎪=⎨->⎪⎩或，023()2p p kl kl kl sd S c d c λεσσ=-矩阵形式00(,)((,))p p ep e p d F d F F d εσεσσεσ==+0(,)p ep d D d σσεε=4. 增量形式的弹塑性力学边值问题体内：T ep d Ldud D d L d dF εσεσ==+=边界：du nd dp σ==。

(完整版)弹塑性力学公式

应力应变关系:弹性模量 || 广义虎克定律 1.弹性模量a 弹性模量单向拉伸或压缩时正应力与线应变之比,即E σε=b 切变模量切应力与相应的切应变之比,即G τγ=c 体积弹性模量三向平均应力0()3x y z σσσσ++=与体积应变θ(=εx +εy +εz )之比, 即K σθ=d 泊松比单向正应力引起的横向线应变ε1的绝对值与轴向线应变ε的绝对值之比,即1ενε= 2.广义虎克定律 a.弹性力学基本方程在弹性力学一般问题中，需要确定15个未知量，即6个应力分量，6个应变分量和3个位移分量。

这15个未知量可由15个线性方程确定，即 (1)3个平衡方程(或用脚标形式简)写为:22()0jijii x u f tσρ∂∂++-=∂∂(,,,)i j x y z =(2)6个变形几何方程,或简写为:1()2ji ij j iu u E x x ∂∂=+∂∂(,,,)i j x y z =(3)6个物性方程简写为:0132ij ij E G E νσσδ=-2ij ij ijG σελθδ=+(,,,)i j x y z ={1()0()()i j ij i j δ=≠=2.边界条件x x xx xy xy xz xzF l l l σττ=++y yz xx y xy yz xzF l l l τσσ=++z zz xx xy xy z xzF l l l ττσ=++式中，l nj =cos(n,j)为边界上一点的外法线n 对j 轴的方向余弦 b 位移边界问题在边界S x 上给定的几何边界条件为*x x u u = *y y u u =*z z u u = 式中，u i 为表面上给定的位移分量Cauchy 公式： T x = σ x l + τ xy m +τ zx n T y = τ xy l+σ y m +τ zy n T y =τ xz l+τ y z m +σ z n22)(n x z n n n T l T T nT T T στ=+++=边界条件：()()()x xy xz s x xy y yz s y xz yz z s zl m n T l m n T l m n T στττστττσ++=++=++= 平衡微分方程：000yx x zxx xy y zyy yz xz zz F x y z F x y z F x y zτσττστττσ∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂∂∂∂+++=∂∂∂ 主应力、不变量，偏应力不变量321231230x y zx xy y z zxyz yx y zy xz x z x xy xzyx y yzzx zy z I I I I I I σσσσσσστσστττσττσσστττστττσ-+-==++=++= 1231();3m i i m s σσσσσσ=++=-()()()112322222223016()6x y y z z xxy yz zx J ss s J J σσσσσστττ=++=⎡⎤=-+-+-+++⎢⎥⎣⎦=偏应力张量行列式的秩八面体812381()3σσσστ=++等效应力σ=体积应变x y z θεεε=++12312()Ev vεσσσ-=++几何方程：;;;x xy y yz z xy u u v x y x v v w y z y w u w z z xεγεγεγ∂∂∂==+∂∂∂∂∂∂==+∂∂∂∂∂∂==+∂∂∂ 12ij ij εγ=变形协调方程22222y xyx xy y xετε∂∂∂+=∂∂∂物理方程()()()12(1);12(1);12(1);x x y z xyxy y y x z yz yz z z y x zx zx v v E E v v E Ev v E Eεσσσγτεσσσγτεσσσγτ+⎡⎤=-+=⎣⎦+⎡⎤=-+=⎣⎦+⎡⎤=-+=⎣⎦偏应力与偏应变的关系 3;2m m ij ij K s Ge σε==平面应变问题()()()()()'x '''''''2111111112(1)2(1);0;110;x y x y y y x y x xy xyxy z zy zx zy zx z x y v v v v Ev v v v E v v E E E v E v v v v εσσσσεσσσσγττεγγττσσσ⎡⎤=-=--⎣⎦-⎡⎤=-=--⎣⎦-++=====--=====+ 平面应力问题()()()x 11;2(1)01;0x y y y x xy xyzy zx zy zx z x y z v v E Ev Evεσσεσσγτγγττεσσσ=-=-+======-+= 平面问题方程：平衡方程：00yxx x xy yy F x y F x yτστσ∂∂++=∂∂∂∂++=∂∂几何方程;;x y xy u v u v x y y xεεγ∂∂∂∂===+∂∂∂∂ 边界条件;x yx x xy y y l m T l m T σττσ+=+=位移边界条件;x x y y u u u u ==协调方程平面应变22222y xyxxy y xετε∂∂∂+=∂∂∂平面应力222220;0;0z z zxy x y εεε∂∂∂===∂∂∂平面问题应力解（直角坐标系）22222x x y y xy F xy F y x xy ϕσϕσϕτ∂=-∂∂=-∂∂=-∂协调方程：222222222()()()0x y x y x yϕσσ∂∂∂∂+=++=∂∂∂∂ 平面问题应力解（极坐标系）平衡微分方程：10210r r r r r r F r r r F r r rθθθθθθτσσσθτστθ∂-∂+++=∂∂∂∂+++=∂∂ 几何方程：1;1r r r r r u u u r r r u u u r r rθθθθθεεθγθ∂∂==+∂∂∂∂=+-∂∂ 本构方程：()()r 11;2(1)r r rrv v E E v Eθθθθθεσσεσσγτ=-=-+= 变形协调：22222211()0r r rr θ∂∂∂++=∂∂∂已知应力函数ϕ，求应力2222222211;111()r r r r r r r r r r r θθϕϕϕσσθϕϕϕϕτθθθ∂∂∂=+=∂∂∂∂∂∂∂=-+=-∂∂∂∂∂ 平面应变下：()()[]()()[]r (1)112(1)112r r Eu u u u E u u u u θθθσεεσεε=-++-=-++-屈服条件Tresca 屈服条件()12111s022ij sf k σσσστ-=-===单轴拉伸：k ;纯剪切：k Mises 屈服条件()()()()222222222222016()6K K ij x y y z z x xy yz zx s sf J k J σσσσσσστττσ=-=⎡⎤=-+-+-+++⎢⎥⎣⎦=单轴拉伸：;纯剪切：1、理想弹塑性材料的加卸载准则：()()0,0;0,0;ij ij ijij ij ij ff df d ff df d σσσσσσ∂===∂∂==<∂加载卸载2、硬化材料的加卸载准则：()()()0,0;0,0;0,0;ij ij ij ij ij ij ij ij ij ff d f f d ff d βββσεσσσεσσσεσσ∂=>∂∂==∂∂=<∂，加载，中性加载，卸载。

第九章塑性力学简单实例

• 圆杆的位移,应变和应力采用圆柱坐标,位移分量 a 为: ur 0 zra z u zr r uz 0 o x 其中为单位长度扭角. 应变 z r , 其它为零. 应力除 z (它的大小与 z 有关,是 r 的函数)不等于零外, 其它为零. 注意: 这个问题满足简单加载条件. 另外, 应力满足平衡条件, 也满足圆杆侧面的边界条件. 根据Saint-Venant原理杆两端的边界条件可以只在合力方面得到满足.
5) 残余应力在 T 作用下, 按弹性计算得到 2Tr z R4
3)弹性极限扭角( rs R
e
s
):
RG 3
弹性极限扭矩为
Te
由卸载前的应力减去上式的剪应力得到残余应力.见前页图.
R 3 s
2 3
4-5 非圆截面杆的塑性极限扭矩在圆杆的弹塑性扭转中, 截面上的最大剪应力产生在距圆心最远处的外边界上, 且在扭转过程中截面无翘曲. 对于非圆截面杆件, 前述两个结论不适用. 此时杆件截面将发生翘曲, 及扭转中横截面不再保持平面, 但刚性转动的假定仍然成立, 而因此得到的最大剪应力产生在距形心最近处. 先讨论非圆截面杆的弹性扭转. y zr 1.弹性分析
b y
M
M
x o
h/2
z h/2
y
y
• 基本关系式按照梁的初等弯曲理论: 平截面和小变形, 并且材料不可压缩,即 1/ 2 ,它们的应力和应变表示为
截面上的应力分布情况( 距离):
是梁的中性面到弹塑性分界面的
梁截面上要满足的条件
1. 对于理想弹塑性材料
• 截面上的弯矩是
是弹性区对中性轴的惯性矩,

资料塑性变形力学计算

（a）
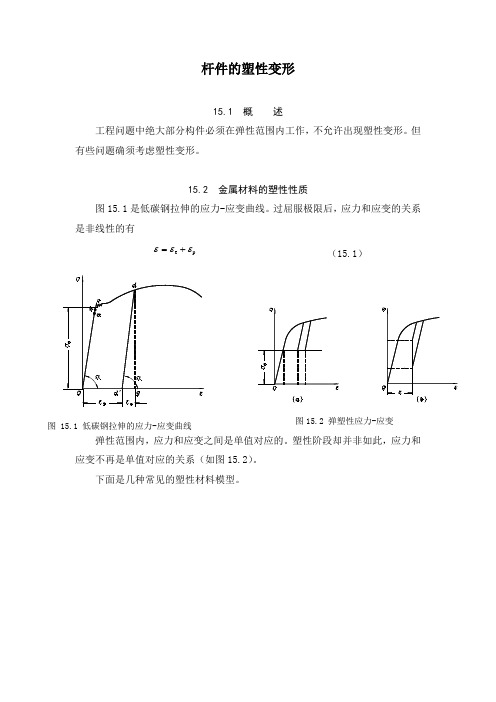
在二向应力状态下，，以上条件变为
，，（b）
塑性条件（b）在平面中是一个六角形，如图15.19所示。在三向应力的情况下，塑性条件（a）在应力空间中是六个平面。这就是特雷斯卡塑性条件的几何表示。如图15.20所示。柱面以内的点代表不发生塑性形变的应力状态，而柱面上的点代表进入塑性形变的应力状态。这样的柱面称为塑性曲面。
解：以和分别表和杆的轴力，表杆的轴力。令，，得
(e)
当载荷逐渐增加时，杆的应力首先达到，这时的载荷即为。由（）式的第二式得
由此解出
载荷继续增加，中间杆的轴力保持为 ,两侧杆件仍然是弹性的。直至两侧的杆件的轴力也达到，相应的载荷即为极限载荷。这时由节点的平衡方程知
加载过程中，载荷与点位移的关系已表示于图15.9 中。
式中m和皆为常量。试导出实心圆轴扭转时应力和变形的计算公式。
解：根据圆轴扭转的平面假设，可以直接引用3.4中的（）式，求得横截ቤተ መጻሕፍቲ ባይዱ上任意点处的剪应变为
(d)
式中是扭转角沿轴线的变化率，为横截面上一点到圆心的距离，即为该点剪应变。（）式表明，沿横截面半径，各点的剪应变是按直线规律变化的（图15.11 ）。由（）、（）两式求出
例15.6在矩形截面梁形成塑性区后，将载荷卸尽，试求梁截面边缘处的应力。设材料是理想弹塑性的。
解：当矩形截面梁的横截面上出现塑性区时，应力分布表示于图15.14 。根据公式（15.7），截面上的弯矩为
这时梁内的最大应力为。
卸载过程相当于把与上列弯矩数值相等、方向相反的另一弯矩加于梁上，且它引起的应力按线弹性公式计算，即最大应力为
按照第四强度理论，材料的塑性条件为公式（15.3），即

弹性截面模量跟塑性截面模量的解释跟算法

弹性截面模量与塑性截面模量的解释与算法
塑性截面模量为截面各组成部分对中和轴的面积距。

与塑性截面模量相应的中和轴为：截面面积的平分线（与弯曲主轴平行，如工字型截面的强轴X-X ），对矩形截面计算公式为2/4pnx W bh =；
弹性截面模量为截面惯性矩与截面上受拉或受压边缘至形心轴距离的比值，弹性截面模量的中和轴为：整个截面关于经此轴线的截面面积矩为零，横截面在此轴线弯曲正应力为零（可用截面各组成面积对某一翼缘边的面积距之和与整个截面面积的比值确定中和轴离该翼缘边的距离进行计算）。

对矩形截面计算公式为2/6enx W bh =；
一般而言，有全截面塑性发展的截面特性=弹性理论截面特性×塑性发展系数，即pnx enx x W W γ=⋅，对于矩形截面， 1.5x γ=。

(完整版)塑性铰长度及转动能力计算

塑性較长度及转动能力计算塑性铰长度及转动能力计算延性是指结构或构件在承载能力没有显著下降的情况下承受变形的能力，度量延性的一个重要指标就是塑性铰长度。

钢筋混凝土塑性设计的关键问题是弯矩调幅系数的取值,而弯矩调幅系数大小与等效塑性铰区长度成正比,因此合理确定钢筋混凝土受弯构件的等效塑性铰区长度是至关重要的课题之一。

国内外许多学者通过试验研究给出了不同的等效塑性铰区长度计算公式（见表1）。

但由于试验构件数量的局限性,所给出的公式总是有一定的适用范围。

如Corley 、Mottock 和Baker 的公式仅适用与临界截面到反弯点的距离Z 与截面有效高度h0之比大于5.4, 且剪力较小的情况。

坂静雄和朱伯龙的公式没有考虑Z 和剪力的影响,若其他条件相同且Z 值不同时,由此公式计算出的等效塑性铰区长度为定值,这显然是不合理的。

Sawyer 假设构件中的最大弯矩是极限弯矩,推导出弯矩大于截面屈服弯矩My 区段内的等效塑性铰区长度值（理论等效塑性铰区长度）,并假定等效塑性铰区的扩展范围为0.25 h0 ,他考虑了弯矩分布对等效塑性铰区长度的影响,但扩展长度为定值的假设是不合理的。

因此,有必要综合考虑影响等效塑性铰区长度的主要因素建立更为准确、适用范围更广泛的等效塑性铰区长度的计算公式,以合理的估算塑性铰区的塑性转动能力。

1、塑性铰区长度钢筋混凝土简支梁在集中荷载 P 的作用范围 l p0 内由于存在着许多弯剪裂缝,致使该范围内的钢筋应力、应变基本相同。

这表明在l p0 区段内均具有最大弯矩截面的曲率。

超越 l p 0区段,曲率就逐渐下降到屈服曲率 y ,因此 l p0两侧曲率为 y 的截面之间的距离 l p 就是塑性铰区长度 ,见图 1。

因而,当截面的塑性转角一定时 ,等效塑性铰区长度与极限曲率u和屈服曲率 y 的差成正比。

大量试验结果表明 ,当采用试验测得的极限曲率 u 和屈服曲率 y 建立起来的等效塑性铰区长度计算公式计算塑性铰区的转角时 ,所得到的结果是偏于保守的在分析构件的塑性转动能力时 ,无论弯矩 - 曲率关系采用二折线或三折线关系,一2、塑性铰区长度的影响因素（1）截面极限曲率 u 和屈服曲率 y 的影响等效塑性铰区长度等于所考察截面极限转角极限曲率 u 与屈服曲率 y 之差,即:u与屈服转角 y 之差除以l p u y uy(1)图 1 在集中荷载 P 作用下钢筋混凝土简支梁的曲率随梁长的变化2 ）临界截面到反弯点距离Z 的影响般认为非弹性（塑性）曲率集中分布于弯矩值大于屈服弯矩M y 且小于极限弯矩M u 的区段内,该区段称为塑性铰区。

05003塑性弯矩

弹塑性和塑性工作阶段(1)塑性极限弯矩、塑性铰与截面形状系数截面边缘部分进入有限状态后，当弯矩继续增加，弹性核心部分减小。

当整个截面都进入塑性状态时，得塑性极限弯矩为：M p= W pn f y式中W pn——净截面塑性抵抗矩这时梁截面已不能负担更大的弯矩，而变形则将继续增加，梁左右部分在弯径方向产生相对转动，这种现象称为形成塑性铰。

图1 梁截面的塑性抵抗矩W pn =S n1+S n2=2S n式中S n1、S n2分别为上、下半净截面对塑性中和轴(面积一部分轴)的面积矩；S n2为上或下半净截面(A n/2)对形心轴的面积矩(图1)。

对矩形截面，W= I/(h/2)=bh2/6，W pn=2S=2(bh/2)h/4=bh2/4，W pn =1.5 W n。

对工形截面或格构式截面，边缘纤维屈服时，全部截面的应力基本上都已接近f y，故W pn≈W n，计算可得W pn =(1.1～1.2) W n，翼缘愈大时取偏低值。

W pn / W n (或W pn/ W)称为截面形状系数。

(2)截面塑性发展系数钢梁设计中只考虑截面内部分发展塑性，否则①梁的挠度将过大；② 钢梁腹板较薄，会有一定剪应力，有时还有局部压应力，故应限制塑性弯曲应力的范围以免综合考虑的折算应力太大；③ 过分发展塑性变形对钢梁的整体稳定和板件的局部稳定不利。

因此设计时不采用塑性W pn ，而代以稍偏小的γW ，γ为截面塑性发展系数，取1<γ< W pn / W n 。

经归并简化后，GBJ17-88规定，设计时采用的γ值见表1。

表1 截面塑性发展系数γx 、γy 值表中γ原则上归为四类：(a)γ=1.2——适用于所考虑边缘纤维处没有加宽翼缘的截面(如矩形截面、工字形截面绕弱轴弯曲等)，这些截面有较大的塑性发展潜力。

(b)γ=1.05——适用于所考虑边缘纤维为加宽翼缘的截面(如矩形截面、工字形截面，这些截面发展塑性变形增大抵抗弯矩的潜力较小。

联轴器扭矩计算公式

联轴器扭矩计算公式联轴器是一种广泛应用于机械传动领域的装置，用于连接两个轴并传递扭矩。

在设计和选择联轴器时，了解其扭矩计算公式是非常重要的。

本文将介绍联轴器扭矩计算公式的相关知识，并探讨其应用。

一、联轴器扭矩计算公式的基本原理联轴器扭矩的计算基于扭矩平衡的原理。

当两个轴通过联轴器连接时，扭矩在轴和联轴器之间传递。

扭矩的传递会导致联轴器产生变形，产生一定的应力。

因此，通过计算联轴器的扭矩，可以评估其是否能够满足设计要求。

联轴器扭矩计算公式的推导基于材料力学和弹性力学的原理。

根据联轴器的几何形状和材料特性，可以得到以下扭矩计算公式：1. 弹性联轴器的扭矩计算公式对于弹性联轴器，其扭矩计算公式可以表示为：T = K × τ × d × l其中，T为联轴器的扭矩，K为联轴器的扭矩系数，τ为剪切应力，d为联轴器的直径，l为联轴器的长度。

2. 弹性塑性联轴器的扭矩计算公式对于弹性塑性联轴器，其扭矩计算公式可以表示为：T = K × τ × d × l × η其中，T为联轴器的扭矩，K为联轴器的扭矩系数，τ为剪切应力，d为联轴器的直径，l为联轴器的长度，η为联轴器的强度折减系数。

三、联轴器扭矩计算公式的应用联轴器扭矩计算公式的应用可以帮助工程师评估联轴器的性能和可靠性，从而选择合适的联轴器。

在应用过程中，需要确定联轴器的参数，如直径、长度和材料特性，并结合实际工况计算扭矩。

1. 确定联轴器的参数在计算扭矩之前，需要准确地确定联轴器的参数。

这包括联轴器的直径、长度和材料特性。

直径和长度是联轴器的几何参数，直接影响联轴器的刚度和传递扭矩的能力。

材料特性包括联轴器的材料强度和弹性模量，对联轴器的可靠性和变形特性有重要影响。

2. 计算扭矩根据联轴器的几何参数和工作条件，可以计算扭矩。

利用联轴器扭矩计算公式，将参数代入公式中进行计算。

根据计算结果，可以评估联轴器是否能够满足设计要求。

金属力学性能之塑性指标

塑性：是指金属材料在载荷作用下产生最大塑性变形而不破坏的能力。

①伸长率：δ
试样受拉力断裂后，总伸长量与原始长度的比值的百分率称为伸长率（延伸率）
相同符号才能进行比较，同一钢材的δ5与δ10值不同，大约为δ5的1.2倍。

为了防止采用屈强比高的钢材，对锅炉钢板的伸长率规定δ5不得小于18%，以此来限定屈强比。

②断面收缩率：Ψ（%）
试样受拉力断裂后，试样截面的缩减量与原截面之比的百分率称为断面收缩率。

断面收缩率不受试件标距长度的影响（无长短之分），对于锅炉压力容器材料的伸长率一般要求10%以上。

伸长率和断面收缩率表明材料在静态或缓慢拉伸应力作用下的韧性，良好的塑性即可使材料冷压成型性好，重要的受压零件可防止超载时发生脆性断裂，但对塑性的要求有一定限度并非越大越好。

青岛丰东热处理有限公司专业提供热处理服务，可为客户提供化学热处理(渗碳、渗氮、碳氮共渗)、真空热处理、等离子热处理(离子渗氮)、常规热处理(含深冷处理)等四大领域的热处理加工服务。

欢迎新老客户来电咨询，电话：4006577217。

“青岛丰东热处理”微信公众号提供热“新鲜”的处理行业动态及资讯，如果您对热处理相关知识感兴趣，欢迎关注我们，青岛丰东期待与您共同进步！。

塑性本构方程

第八章塑形本构关系
引言:
塑性变形规律的复杂性, 到目前为止这个塑性本构关系问题还没有得到满意的解决.经典塑性本构关系的理论分为两大类: (1)全量理论, 又称为形变理论, 它认为在塑性状态下仍有应力和应变全量之间的关系. 包括：
Hencky(亨奇)理论（1924）：不考虑弹性变形和材料硬化。（理想刚塑形模型）
(1)理想塑性材料的加载和卸载准则.
理论塑性材料是无硬化的, 屈服条件与加载历史无关,, 初始屈服面和后继屈服面是重合的. 即如图所示
弹性状态; 加载
加载;
卸载卸载. 法线方向的梯度方向屈服面
(2)硬化材料的加,卸载准则. 对于硬化材料,后继屈服面和初始屈服面不同, 与塑性变形的大小和历史有关.
其中 d 为一个大于零的比例系数.称为与屈服条件相关联的塑性流动法则.也称为塑性应变增量的正交流动法则对研究塑性力学的本构关系有重要意义.
p d • Drucker公设的第二式是加载准则. 它的几何意义是当 ij 不为零时, d ij 的方向必须指向加载面外法线一侧, 即 f d d ij 0 ij
Shield和Ziegler指出, 建立塑性本构关系需要考虑三个基本要素: (1)初始屈服条件;(2)流动法则;(3)加载条件. 其中(1) 在第六章已经解决, 本章要解决第(2) ;(3)点. yy
§8-1 塑性应变增量
进入塑性状态后，应变不仅取决于应力状态 ij ，而且还取决于达到该应力状态的历史，描述历史引入一个内变量。
f d d ij
p ij
因为 d 0 , 所以
f d ij 0 ij
这就是加载准则.
二、Ilyushin共设

弹性截面模量与塑性截面模量的例析

弹性截面模量与塑性截面模量的解释与算法
塑性截面模量为截面各组成部分对中和轴的面积距。

与塑性截面模量相应的中和轴为：截面面积的平分线（与弯曲主轴平行，如工字型截面的强轴X-X ），对矩形截面计算公式为2/4pnx W bh =；
弹性截面模量为截面惯性矩与截面上受拉或受压边缘至形心轴距离的比值，弹性截面模量的中和轴为：整个截面关于经此轴线的截面面积矩为零，横截面在此轴线弯曲正应力为零（可用截面各组成面积对某一翼缘边的面积距之和与整个截面面积的比值确定中和轴离该翼缘边的距离进行计算）。

对矩形截面计算公式为2/6enx W bh =；
一般而言，有全截面塑性发展的截面特性=弹性理论截面特性×塑性发展系数，即pnx enx x W W γ=⋅，对于矩形截面， 1.5x γ=。

箱型梁截面塑性抵抗矩分析

箱型梁截面塑性抵抗矩分析作者：李奕金彭加欣来源：《卷宗》2015年第08期摘要：箱型梁是工程中广泛应用的构件，为了更直接的取得工程需要截面塑性抵抗矩，本文截面塑性抵抗矩为变量，对比腹板高度与翼缘高度的增幅，分析出增大腹板高度，能较大幅度的提高梁的抗弯强度，为设计者进行塑性设计时选择合理截面尺寸提供数据参考。

关键词：箱型梁；截面塑性抵抗矩；影响程度；增幅1.引言箱型梁结构美观、施工便利、结构具有较大的抗弯刚度和抗扭刚度而被广泛应用于公路和市政桥梁中[1]。

然而大多数设计者在进行截面设计时单纯考虑梁弹性破坏的情况，导致材料的浪费，也增加了工程造价。

本文以塑性理论为基，避免繁琐的计算[2]，仅考虑箱型梁截面在仅承受弯矩的作用下产生理想的塑性破坏[3]，根据实际情况仅分析梁承受竖直方向荷载时，通过分析对于x轴的截面塑性抵抗矩wpx的变化对截面几何尺寸参数影响程度，反推出截面几何尺寸参数对其塑性抵抗矩的影响大小。

如图1所示箱型梁的截面示意图，箱型梁的截面塑性抵抗矩公式为：Wpx=Bt（h+t）+0.5dh2式中：h—腹板高度；d—腹板宽度； t—翼缘高度； B—翼缘宽度。

从表达式看出：箱型梁的截面塑性抵抗矩是由其4个几何参数决定的，腹板宽度对截面塑性抵抗矩的影响较小；同时在实际工程中，为了方便设计施工梁截面的翼缘宽度往往为标准化尺寸，因此以腹板宽度和翼缘宽度为定值，只考虑箱型梁截面塑性抵抗矩的变化对腹板高度和翼缘高度的影响。

以箱型梁的截面塑性抵抗矩为自变量，依次以腹板高度和翼缘高度为因变量，保持其它几何尺寸参数不变，通过该几何参数的增量可以反推出该几何参数对箱型梁的截面塑性抵抗矩的影响大小。

2.计算分析2.1 腹板高度h的变化取d=50mm，t=50mm，B=500mm， Wpx为自变量，从2.00×107mm3开始，以1.50×106mm3递增，则Wpx和 S与h的关系如表1：可得：随着塑性抵抗矩Wpx增大，腹板高度h越来越大，但是其增幅越来越小，增幅范围大体在2%～6%。

弹塑性矩阵推导

考虑材料的塑性，其增量形式的本构关系可表达为p d σ=(D -D )d ε (1)式(1)中，D 为弹性矩阵，p D 为塑性矩阵。

弹性矩阵D 的形式为422000333242000333224000333000000000000000K G K G K G K G K G K G K G K G K G G G G ⎡⎤+--⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥=⎢⎥--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦D (2) 体积模量3(12)E K μ=-，剪切模量2(1)E G μ=+。

在应变空间内，塑性矩阵可表达为1()T f fA ∂∂=∂∂p D D D σσ(3) 式中，()()T T p f f f fA B ∂∂∂∂=--∂∂∂∂D D σσσσ(4) f为屈服函数；p σ为塑性应力，p p =σD ε；1/2(()())T p T p T p f f f f B f f f ωθε∂∂⎧⎪∂∂⎪∂∂⎪'=⎨∂∂⎪∂∂∂⎪⎪∂∂∂⎩σσI σσσ(5) [111000]T '=I ；p ω为塑性功；p θ为塑性体应变；p ε为等效塑性应变；κ为反映加载历史的参数。

对于Drucker-Prager 模型，其屈服条件为10f I α== (6)1x y z I σσσ=++，22222221()2x y z xy yz zxJ S S S S S S =+++++，α为材料常数。

f α∂''=+∂I σ (7) 222Txyzxyyzzx S S S S S S '⎡⎤=⎣⎦S(8)()3f K αα∂'''==+∂DD I I σ(9) 2()()(3)9T T T f f A K K G ααα∂∂'''===+∂∂D I I σσ (10) 1()T f fA ∂∂=∂∂p D D D σσ22222222112123113211212311321121231131121121121(3)(3)999(9)(T TT T T TK K K GK G K G K G J m mn ml S m S m S m mn n nl S n S n S n ml nl l S l S l S l S m S n S l ααααααβββββββββββββ''=++''''=++++=p D I I I I S SS211211222311221321231231231122231231132232113113113113212113223113)()()S S S S S S m S n S lS S S S S S m S n S l S S S S S ββββββββββββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⋅⋅⎢⎥⎢⎥⋅⋅⎢⎥⋅⋅⎢⎥⎣⎦令43p K G =+，23q K G =- 弹塑性矩阵可表达为2112123113211212311321121231132112112112112112223112213123123123112223()(p m q mn q mlS m S m S mq mnp n q nl S n S n S n q ml q nl p l S l S l S l S m S n S l G S S S S S S m S n S lS S G βββββββββββββββββββββββ------------------=-=-----⋅-⋅----⋅-ep p D D D 21231132232113113113113212113223113)()S S S S m S n S lS S S S G S ββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⋅⎢⎥----⋅-⋅-⎢⎥⎣⎦令1β=，2β=，1112m S ββ=+，1222n S ββ=+，1332l S ββ=+2211222211129(9)()x x x x K G K G J S m ααββ⎣⎦++==+=p2222212221112122299(9)()()y x x yx y K G S S S K G K G J S S mnαααββββ⎡⎤=+++⎣⎦++=+=++=p D222221321112133299(9)()()z x x zx z K G S S S K G K G J S S S S mlαααββββ⎡⎤=+⎣⎦++=++=++=p D221421112112112(9))()xy x xyx xy G S S K G J S S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D221521112123123(9))()yz x yzx yz G S S S K G J S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D221621112113113(9))()zx x zxx zx G S S S K G J S S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D222222121112122299(9)()()x y y xx y K G S S K G K G J S S mnαααββββ⎡⎤=+⎣⎦++=+=++=p D2222222212229(9)()y y y y K G K G J S S n ααββ⎣⎦++=+=+=p222222321222133299(9)()()z y y Zy z K G S S S K G K G J S S S nlαααββββ⎡⎤=+++⎣⎦++=++=++=p D222421222112112(9))()xy y xyy xy G S S K G J S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D222521222123123(9))()yz y yzy yz G S S K G J S S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D222621222113113(9))()zx y zxy zx G S S K G J S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D222223121112133299(9)()()x z z xx z K G S S S K G K G J S S S S mlαααββββ⎡⎤=+⎣⎦++=++=++=p D222223221222133299(9)()()y z z yy z K G S S S K G K G J S S S nlαααββββ⎡⎤=+++⎣⎦++=++=++=p D2233222213329(9)()z z z z K G K G J S S l ααββ⎣⎦++==+=p223421332112112(9))()xy z xyz xy G S S K G J S S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D223521332123123(9))()yz z yzz yz G S S K G J S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D223621332113113(9))()zx z zxz zx G S S S K G J S S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D224121112112112(9)()xy xy xx xy G S S K G J S S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D224221222112112(9)()xy xy yy xy G S S S K G J S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D224321332112112(9)()xy xy zz xy G S S S K G J S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D22211244)()xyxy S β⎡⎤===⎣⎦p D11222345xy yz xy yz S S S S S ββ⎡⎤===⋅⎣⎦p D11221346xy zx xy zx S S S ββ⎡⎤===⋅⎣⎦p D225121112123123(9))()yz yz xx yz G S S K G J S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D225221222123123(9))()yz yz yy yz G S S S K G J S S S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D225321332123123(9))()yz yz zz yz G S S K G J S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D11222354xy yz xy yz S S S S ββ⎡⎤===⋅⎣⎦p D22212355)()yz yz S β⎡⎤===⎣⎦p D11322356yz zx yz zx S S S S S ββ⎡⎤===⋅⎣⎦p D226121112113113(9))()zx zx xx zx G S S K G J S S S mαββββ⎡⎤=+⎣⎦+==+⋅=p D226221222113113(9))()zx zx yy zx G S S K G J S S S nαββββ⎡⎤=+⎣⎦+==+⋅=p D226321332113113(9))()zx zx zz zx G S S S K G J S S S S lαββββ⎡⎤=+⎣⎦+==+⋅=p D11321264zx xy zx xy S S S ββ⎡⎤===⋅⎣⎦p D11322365zx yz zx yz S S S S S ββ⎡⎤===⋅⎣⎦p D22211366)()zxzx S S β⎡⎤===⎣⎦p D。

弯管力矩计算公式资料

第二节管材弯曲一、材弯曲变形及最小弯曲半径二、管材截面形状畸变及其防止三、弯曲力矩的计算管材弯曲工艺是随着汽车、摩托车、自行车、石油化工等行业的兴起而发展起来的，管材弯曲常用的方法按弯曲方式可分为绕弯、推弯、压弯和滚弯；按弯曲加热与否可分为冷弯和热弯；按弯曲时有无填料(或芯棒)又可分为有芯弯管和无芯弯管。

图6—19、图6—20、图6—21和图6—22分别为绕弯、推弯、压弯及滚弯装置的模具示意图。

图6—19在弯管机上有芯弯管1—压块2—芯棒3—夹持块4—弯曲模胎5—防皱块6—管坯图6—20 型模式冷推弯管装置图6—21 V 形管件压弯模 1—压柱 2—导向套 3—管坯 4—弯曲型模 1—凸模 2—管坯 3—摆动凹模图6—22三辊弯管原理1—轴2、4、6—辊轮3—主动轴5—钢管一、材弯曲变形及最小弯曲半径管材弯曲时，变形区的外侧材料受切向拉伸而伸长，内侧材料受到切向压缩而缩短，由于切向应力θσ及应变θε沿着管材断面的分布是连续的，可设想为与板材弯曲相似，外侧的拉伸区过渡到内侧的压缩区，在其交界处存在着中性层，为简化分析和计算，通常认为中性层与管材断面的中心层重合，它在断面中的位置可用曲率半径ρ表示(图6—23)。

管材的弯曲变形程度，取决于相对弯曲半径D R 和相对厚度D t (R 为管材断面中心层曲率半径，D 为管材外径，t 为管材壁厚)的数值大小，D R 和D t 值越小，表示弯曲变形程度越大(即D R 和D t 过小)，弯曲中性层的外侧管壁会产生过度变薄，甚至导致破裂；最内侧管壁将增厚，甚至失稳起皱。

同时，随着变形程度的增加，断面畸变(扁化)也愈加严重。

因此，为保证管材的成形质量，必须控制变形程度在许可的范围内。

管材弯曲的允许变形程度，称为弯曲成形极限。

管材的弯曲成形极限不仅取决于材料的力学性能及弯曲方法，而且还应考虑管件的使用要求。

对于一般用途的弯曲件，只要求管材弯曲变形区外侧断面上离中性层最远的位置所产生的最大伸长应变m ax ε不致超过材料塑性所允许的极限值作为定义成形极限的条件。

截面弹性抵抗矩

截面弹性抵抗矩
根据材料力学，在弹性工作范围内，W=M/σ。

式中，W——构件截面的弹性扺抗矩，一般简称为抵抗矩，mm^3；M——弯矩，N.mm；σ——构件截面边缘纤维处的弯曲正应力，N/mm^2。

由此可知，截面扺抗矩W的物理意义：W等于弯矩M与截面边缘纤维处弯曲正应力σ的比值。

说明：在塑性工作阶段，要用截面塑性抵抗矩Wp。

截面模量（抵抗矩）：截面对其形心轴的惯性矩与截面上最远点至形心轴距离比值。

截面抵抗矩：一种是塑性截面抵抗矩(塑性设计时采用),一种是弹性截面抵抗矩(弹性设计时采用)。

截面抵抗矩是截面本身所具有的特性，与外力无关，所以要用W=2Ix/h计算，当然这个公式也只是适用于对称截面，对于非对称截面，应以除以h/2，而是除以中和轴到外边缘的距离。

弹塑性矩阵推导(全面版)资料

弹塑性矩阵推导（全面版）资料考虑材料的塑性，其增量形式的本构关系可表达为p d σ=(D-D )d ε (1)式(1)中，D 为弹性矩阵，p D 为塑性矩阵。

弹性矩阵D 的形式为422000333242000333224000333000000000000K G K GK G K G K GK G K GK GK G G G G ⎡⎤+--⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥=⎢⎥--+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦D (2) 体积模量3(12)E K μ=-，剪切模量2(1)EG μ=+。

在应变空间内，塑性矩阵可表达为1()T f fA ∂∂=∂∂p D D D σσ(3) 式中，()()T T p f f f fA B ∂∂∂∂=--∂∂∂∂D D σσσσ(4) f为屈服函数；p σ为塑性应力，p p =σD ε；1/2(()())T p T p T p f f f f B f f f ωθε∂∂⎧⎪∂∂⎪∂∂⎪'=⎨∂∂⎪∂∂∂⎪⎪∂∂∂⎩σσI σσσ(5) [111000]T '=I ；p ω为塑性功；p θ为塑性体应变；p ε为等效塑性应变；κ为反映加载历史的参数。

对于Drucker-Prager 模型，其屈服条件为10f I α== (6)1x y z I σσσ=++，22222221()2x yz xy yz zx J S S S S S S =+++++，α为材料常数。

f α∂''=∂I σ (7) 222Txyzxyyzzx S S S S S S '⎡⎤=⎣⎦S(8)()3f K αα∂'''==+∂DD I I σ(9) 2()()(3)9T T T f f A K K G ααα∂∂'''===+∂∂D I I σσ (10) 1()T f fA ∂∂=∂∂p D D D σσ22222222112123113211212311321121231131121121121(3)(3)999(9)(T TT T T TK K K GK G K G K G J m mn ml S m S m S m mn n nl S n S n S n ml nl l S l S l S l S m S n S l ααααααβββββββββββββ''=+++''''=++++=p D I I I I S SS211211222311221321231231231122231231132232113113113113212113223113)()()S S S S S S m S n S lS S S S S S m S n S l S S S S S ββββββββββββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⋅⋅⎢⎥⎢⎥⋅⋅⎢⎥⋅⋅⎢⎥⎣⎦令43p K G =+，23q K G =- 弹塑性矩阵可表达为2112123113211212311321121231132112112112112112223112213123123123112223()(p m q mn q mlS mS m S m q mnp n q nl S n S n S nq ml q nl p l S l S l S l S m S n S l G S S S S S S m S n S lS S G βββββββββββββββββββββββ------------------=-=-----⋅-⋅----⋅-ep p D D D 21231132232113113113113212113223113)()S S S S m S n S lS S S S G S ββββββββββ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⋅⎢⎥----⋅-⋅-⎢⎥⎣⎦令1β=，2β=1112m S ββ=+，1222n S ββ=+，大型矩阵系统◆ELL系列ELL**V##(视频矩阵)ELL**A##(音频矩阵)ELL**RV##(环通视频矩阵)通道选择输入：8XN+64 最大256路输出：4XN+8 最大32路产品介绍：ELL系列视、音频主机采用大规模音视频切换专用芯片作为音频视频切换矩阵电路的多路多通道切换设备，溶合了先进的矩阵切换技术和计算机技术，可以给用户提供卓越的整体性能。

塑性矩计算公式范文

流变参数塑形指数计算公式

塑性计算方法及适用范围(精)

弹塑性_塑性力学基本方程和解法

塑性力学常用公式

(完整版)弹塑性力学公式

第九章 塑性力学简单实例

资料塑性变形力学计算

弹性截面模量跟塑性截面模量的解释跟算法

(完整版)塑性铰长度及转动能力计算

05003塑性弯矩

联轴器扭矩计算公式

金属力学性能之塑性指标

塑性本构方程

弹性截面模量与塑性截面模量的例析

箱型梁截面塑性抵抗矩分析

弹塑性矩阵推导

弯管力矩计算公式资料

截面弹性抵抗矩

弹塑性矩阵推导(全面版)资料

第九章塑性力学简单实例