绥化市中考数学试卷及答案
(中考精品卷)黑龙江省绥化市中考数学真题(解析版)

二○二二年绥化市初中毕业学业考试数学试题一、单项选择题(本题共12个小题,每小题3分,共36分)1. 化简12-,下列结果中,正确的是( ) A. 12 B. 12- C. 2 D. -2【答案】A【解析】【分析】根据绝对值的运算法则,求出绝对值的值即可. 【详解】解:1122-= 故选:A .【点睛】本题考查根据绝对值的意义求一个数的绝对值,求一个数的绝对值:①当a 是正数时,│a │=a ;②当a 是负数时,│a │=-a ;③当a =0时,│0│=0.掌握求一个数的绝对值的方法是解答本题的关键.2. 下列图形中,既是轴对称图形又是中心对称图形的是()A. B. C. D. 【答案】D【解析】【分析】根据中心对称图形与轴对称图形的概念进行判断即可.【详解】解:A .是轴对称图形,不是中心对称图形,故本选项不符合题意; B .是轴对称图形,不是中心对称图形,故本选项不符合题意;C .不是轴对称图形,是中心对称图形,故本选项不符合题意;D .既是轴对称图形,又是中心对称图形,故本选项符合题意.故选:D .【点睛】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.3. 下列计算中,结果正确的是( )A. 22423x x x +=B. ()325x x = 2=- D.2=±【答案】C【解析】【分析】根据合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,即可一一判定.【详解】解:A.22223x x x +=,故该选项不正确,不符合题意;B.()326x x =,故该选项不正确,不符合题意;2=-,故该选项正确,符合题意;2=,故该选项不正确,不符合题意;故选:C . 【点睛】本题考查了合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,熟练掌握和运用各运算法则是解决本题的关键.4. 下列图形中,正方体展开图错误的是( )A. B. C. D.【答案】D【解析】【分析】利用正方体及其表面展开图的特点解题.【详解】D 选项出现了“田字形”,折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,A 、B 、C 选项是一个正方体的表面展开图.故选:D .【点睛】此题考查了几何体的展开图,只要有“田”“凹”字的展开图都不是正方体的表面展开图.5. 2x -+在实数范围内有意义,则x 的取值范围是( )A. 1x >-B. 1x -…C. 1x -…且0x ≠D. 1x -…且0x ≠【答案】C【解析】 【分析】根据二次根式被开方数不能为负数,负整数指数幂的底数不等于0,计算求值即可;【详解】解:由题意得:x +1≥0且x ≠0,∴x ≥-1且x ≠0,故选: C .【点睛】本题考查了二次根式的定义,负整数指数幂的定义,掌握其定义是解题关键. 6. 下列命题中是假命题的是( )A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半B. 如果两个角互为邻补角,那么这两个角一定相等C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D. 直角三角形斜边上的中线等于斜边的一半【答案】B【解析】【分析】利用三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质分别判断后即可确定正确的选项.【详解】解:A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半,是真命题,故此选项不符合题意;B. 如果两个角互为邻补角,那么这两个角不一定相等,故此选项是假命题,符合题意;C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,是真命题,故此选项不符合题意;D. 直角三角形斜边上的中线等于斜边的一半,是真命题,故此选项不符合题意; 故选:B【点睛】考查了命题与定理的知识,解题的关键是了解三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质.7. 如图,线段OA 在平面直角坐标系内,A 点坐标为()2,5,线段OA 绕原点O 逆时针旋转90°,得到线段OA ',则点A '的坐标为( )A. ()5,2-B. ()5,2C. ()2,5-D. ()5,2-【答案】A【解析】【分析】如图,逆时针旋转90°作出OA ',过A 作AB x ⊥轴,垂足为B ,过A '作A B x ''⊥轴,垂足为B ',证明()A OB BOA AAS '∠ ≌,根据A 点坐标为()2,5,写出5AB =,2OB =,则5OB '=,2A B '=,即可写出点A 的坐标.【详解】解:如图,逆时针旋转90°作出OA ',过A 作AB x ⊥轴,垂足为B ,过A '作A B x ''⊥轴,垂足为B ',∴90A BO ABO ∠'=∠=︒,OA OA '=,∵18090A OB AOB A OA '∠+∠=︒-∠'=︒,90AOB A ∠+∠=︒,∴A OB A ∠'=∠,∴()A OB BOA AAS '∠ ≌,∴OB AB '=,A B OB '=,∵A 点坐标为()2,5,∴5AB =,2OB =,∴5OB '=,2A B '=,∴()5,2A '-,故选:A .【点睛】本题考查旋转的性质,证明A OB BOA '∠ ≌是解答本题的关键.8. 学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是( )A. 该组数据的中位数为98B. 该组数据的方差为0.7C. 该组数据的平均数为98D. 该组数据的众数为96和98 【答案】D【解析】【分析】首先对数据进行重新排序,再根据众数,中位数,平均数,方差的定义进行求值计算即可.【详解】解:数据重新排列为:96,96,97,98, 98,∴数据的中位数为:97,故A 选项错误; 该组数据的平均数为9696979898975++++= ,故C 选项错误; 该组数据的方差为:()()()()()22222196979697979798979897=0.85⎡⎤-+-+-+-+-⎣⎦,故B 选项错误;该组数据的众数为:96和98,故D 选项正确;故选:D .【点睛】本题主要考查数据中名词的理解,掌握众数,中位数,平均数,方差的定义及计算方法是解题的关键.9. 有一个容积为243m 的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径2倍的粗油管向油罐注油,直至注满,注满油的全过程共用30分钟,设细油管的注油速度为每分钟x 3m ,由题意列方程,正确的是( )A. 1212304x x +=B. 1515244x x +=C. 3030242x x +=D. 1212302x x+= 【答案】A【解析】【分析】由粗油管口径是细油管的2倍,可知粗油管注水速度是细油管的4倍.可设细油管的注油速度为每分钟x 3m ,粗油管的注油速度为每分钟4x 3m ,继而可得方程,解方程即可求得答案.【详解】解:∵细油管的注油速度为每分钟x 3m ,∴粗油管的注油速度为每分钟4x 3m , ∴1212304x x+=. 故选:A .【点睛】此题考查了分式方程的应用,准确找出数量关系是解题的关键.10. 已知二次函数2y ax bx c =++的部分函数图象如图所示,则一次函数24y ax b ac =+-与反比例函数42a b c y x++=在同一平面直角坐标系中的图象大致是( )A. B.C. D.【答案】B【解析】【分析】根据2y ax bx c =++的函数图象可知,0a >,240b ac ->,即可确定一次函数图象,根据2x =时,420y a b c =++>,即可判断反比例函数图象,即可求解.【详解】解:∵二次函数2y ax bx c =++的图象开口向上,则0a >,与x 轴存在2个交点,则240b ac ->,∴一次函数24y ax b ac =+-图象经过一、二、三象限,二次函数2y ax bx c =++的图象,当2x =时,420y a b c =++>,∴反比例函数42a b c y x++=图象经过一、三象限 结合选项,一次函数24y ax b ac =+-与反比例函数42a b c y x++=在同一平面直角坐标系中的图象大致是B 选项故选B 【点睛】本题考查了一次函数,二次函数,反比例函数的图象与性质,掌握二次函数的图象与系数的关系是解题的关键.11. 小王同学从家出发,步行到离家a 米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y (单位:米)与出发时间x (单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )A. 2.7分钟B. 2.8分钟C. 3分钟D. 3.2分钟【答案】C【解析】【分析】先根据题意求得A 、D 、E 、F 的坐标,然后再运用待定系数法分别确定AE 、AF 、OD 的解析式,再分别联立OD 与AE 和AF 求得两次相遇的时间,最后作差即可.【详解】解: 如图:根据题意可得A (8,a ),D (12,a ),E (4,0),F (12,0) 设AE 的解析式为y =kx +b ,则048k b a k b =+⎧⎨=+⎩ ,解得4a k b a⎧=⎪⎨⎪=-⎩ ∴直线AE 的解析式为y =4a x -3a 同理:直线AF 的解析式为:y =-4a x +3a ,直线OD 的解析式为:y =12a x 联立124a y x a y x a ⎧=⎪⎪⎨⎪=-⎪⎩,解得62x a y =⎧⎪⎨=⎪⎩ 联立1234a y x a y x a ⎧=⎪⎪⎨⎪=-+⎪⎩,解得934x a y =⎧⎪⎨=⎪⎩ 两人先后两次相遇的时间间隔为9-6=3min .故答案为C .【点睛】本题主要考查了一次函数的应用,根据题意确定相关点的坐标、求出直线的解析式成为解答本题的关键.12. 如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x <….则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x =-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A. 0个B. 1个C. 2个D. 3个【答案】C【解析】 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式; (2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==, ∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽, ∴AB AM AP AB=, ∵2AB =,AP x =,PM y =, ∴22x y x -=, 解得:4y x x =-, 故(1)正确;(2)当4AP =时,541DP AD AP =-=-=, ∴12DC DP AP AB ==, 又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=, ∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ===,∵FPM APB ∠=∠,∴FPM APB ∽, ∴MF PF PM AB AP PB==,∴24MF PF ==∴MF =,PF =∴BF BP PF =-=-=∴3tan 4MF EBP BF ∠=== 故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.二、填空题(本题共10个小题,每小题3分,共30分)13. 一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为14,则这个箱子中黄球的个数为______个. 【答案】15【解析】【分析】设黄球个数为x 个,根据概率计算公式列出方程,解出x 即可.【详解】解:设:黄球的个数为x 个, 5154x =+ 解得:15x =,检验:将15x =代入520x +=,值不为零,∴15x =是方程的解,∴黄球的个数为15个,故答案为:15.【点睛】本题考查概率计算公式,根据题意列出分式方程并检验是解答本题的关键. 的14. 因式分解:()()269m n m n +-++=________.【答案】()23m n +-【解析】【分析】将()m n +看做一个整体,则9等于3得的平方,逆用完全平方公式因式分解即可.【详解】解:()()269m n m n +-++ ()()22233m n m n =+-⨯⨯++()23m n =+-.【点睛】本题考查应用完全平方公式进行因式分解,整体思想,能够熟练逆用完全平方公式是解决本题的关键.15. 不等式组360x x m ->⎧⎨>⎩的解集为2x >,则m 的取值范围为_______. 【答案】m ≤2【解析】【分析】先求出不等式①的解集,再根据已知条件判断m 范围即可. 【详解】解:360x x m ->⎧⎨>⎩①②, 解①得:2x >,又因为不等式组的解集为x >2∵x >m ,∴m ≤2,故答案为:m ≤2.【点睛】本题考查了解一元一次不等式组,能根据不等式的解集和已知得出m 的范围是解此题的关键.16. 已知圆锥的高为8cm ,母线长为10cm ,则其侧面展开图的面积为_______.【答案】60πcm 2【解析】【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2.【详解】解:圆锥的高为8cm ,母线长为10cm ,由勾股定理得,底面半径=6cm ,底面周长=12πcm ,侧面展开图的面积=12×12π×10=60πcm 2.故答案为:60πcm 2.【点睛】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.17. 设1x 与2x 为一元二次方程213202x x ++=的两根,则()212x x -的值为________. 【答案】20【解析】【分析】利用公式法求得一元二次方程的根,再代入求值即可; 【详解】解:∵213202x x ++= △=9-4=5>0,∴13x =-+23x =-,∴()212x x -=((223320-++==,故答案为:20;【点睛】本题考查了一元二次方程的解,掌握公式法解一元二次方程是解题关键. 18. 定义一种运算;sin()sin cos cos sin αβαβαβ+=+,sin()sin cos cos sin αβαβαβ-=-.例如:当45α=︒,30β=︒时,()sin 4530︒+︒=12=,则sin15︒的值为_______.【解析】 【分析】根据sin()sin cos cos sin αβαβαβ-=-代入进行计算即可.【详解】解:sin15sin(4530)︒=︒-︒=sin 45cos30cos 45sin 30︒︒︒︒-12【点睛】此题考查了公式的变化,以及锐角三角函数值的计算,掌握公式的转化是解题的关键.,且有公共顶点A,则19. 如图,正六边形ABCDEF和正五边形AHIJK内接于O的度数为______度.BOH【答案】12【解析】【分析】连接AO,求出正六边形和正五边形的中心角即可作答.【详解】连接AO,如图,∵多边形ABCDEF是正六边形,∴∠AOB=360°÷6=60°,∵多边形AHIJK是正五边形,∴∠AOH=360°÷5=72°,∴∠BOH=∠AOH-∠AOB=72°-60°=12°,故答案为:12.【点睛】本题考查了正多边形的中心角的知识,掌握正多边形中心角的计算方法是解答本题的关键.20. 某班为奖励在数学竞赛中成绩优异的同学,花费48元钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4元,乙种奖品每件3元,则有______种购买方案.【答案】3##三【解析】【分析】设购买甲种奖品x 件,乙种奖品y 件,列出关系式,并求出3124y x =-,由于1≥x ,1y ≥且x ,y 都是正整数,所以y 是4的整数倍,由此计算即可.【详解】解:设:购买甲种奖品x 件,乙种奖品y 件,4348x y +=,解得3124y x =-, ∵1≥x ,1y ≥且x ,y 都是正整数,∴y 是4的整数倍,∴4y =时,341294x ⨯=-=, 8y =时,381264x ⨯=-=, 12y =时,3121234x ⨯=-=, 16y =时,3161204x ⨯=-=,不符合题意, 故有3种购买方案,故答案为:3.【点睛】本题考查列关系式,根据题意判断出y 是4的整数倍是解答本题的关键. 21. 如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PK OA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221+【解析】【分析】解直角三角形分别求得11PK,22P K,33P K,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA⊥,11OPK∴△是直角三角形,在11Rt OPK中,60AOB∠=︒,11OP=,12111tan60PP PK OP∴==⋅︒=11PK OA⊥,22P K OA⊥,1122PK P K∴∥,2211OP K OPK∴△∽△,222111P K OPPK OP∴=,=221P K∴=,同理可得:2331P K =+,3441P K =,……, 11n n n P K -∴=+,2022202320231P K ∴=,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.22. 在长为2,宽为x (12x <<)的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x 的值为________. 【答案】65 或32【解析】【分析】分析题意,根据x 的取值范围不同,对剩下矩形的长宽进行讨论,求出满足题意的x 值即可.【详解】解:第一次操作后剩下的矩形两边长为2x - 和x , (2)22x x x --=- ,又12x <<Q ,220x ∴-> ,2x x ∴-> ,则第一次操作后,剩下矩形的宽为2x -,所以可得第二次操作后,剩下矩形一边为2x - ,另一边为:(2)22x x x --=- ,∵第三次操作后,剩下的纸片恰为正方形,∴第二次操作后剩下矩形的长是宽的2倍,分以下两种情况进行讨论:①当222x x --> ,即43x <时 ,第三次操作后剩下的矩形的宽为22x - ,长是2x - ,则由题意可知:22(22)x x -=- ,解得:65x = ; ②当222x x --< ,即43x >时, 第三次操作后剩下的矩形的宽为2x - ,长是22x - ,由题意得:222(2)x x -=- , 解得:32x = , 65x ∴= 或者32x = .故答案为:65 或32. 【点睛】本题考查了矩形的性质,正方形的性质以及分类讨论的数学思想方法,熟练掌握矩形,正方形性质以及分类讨论的方法是解题的关键.三、解答题(本题共6个小题,共54分)23. 已知:ABC .(1)尺规作图:用直尺和圆规作出ABC 内切圆的圆心O ;(只保留作图痕迹,不写作法和证明)(2)如果ABC 的周长为14cm ,内切圆的半径为1.3cm ,求ABC 的面积.【答案】(1)作图见详解(2)9.1【解析】【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;(2)利用割补法,连接OA ,OB ,OC ,作OD ⊥AB ,OE ⊥BC ,OF ⊥AC ,这样将△ABC 分成三个小三角形,这三个小三角形分别以△ABC 的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.【小问1详解】解:如下图所示,O 为所求作点,【小问2详解】解:如图所示,连接OA ,OB ,OC ,作OD ⊥AB ,OE ⊥BC ,OF ⊥AC ,∵内切圆的半径为1.3cm ,∴OD =OF =OE =1.3,∵三角形ABC 的周长为14,∴AB +BC +AC =14, 则111222ABC AOB COB AOC S S S S AB OD BC OE AC OF =++=⋅⋅+⋅⋅+⋅⋅△△△△ 111.3() 1.3149.122AB BC AC =⨯⨯++=⨯⨯= 故三角形ABC 的面积为9.1.【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.24. 如图所示,为了测量百货大楼CD 顶部广告牌ED 的高度,在距离百货大楼30m 的A 处用仪器测得30DAC ∠=︒;向百货大楼的方向走10m ,到达B 处时,测得48EBC ∠=︒,仪器高度忽略不计,求广告牌ED 的高度.(结果保留小数点后一位)1.732≈,sin 480.743︒≈,cos 480.669︒≈,tan 48 1.111︒≈)【答案】4.9m【解析】【分析】先求出BC 的长度,再分别在Rt △ADC 和Rt △BEC 中用锐角三角函数求出EC 、DC ,即可求解.【详解】根据题意有AC =30m ,AB =10m ,∠C =90°,则BC =AC -AB =30-10=20,在Rt △ADC 中,tan 30tan 30DC AC A =⨯∠=⨯=o ,在Rt △BEC 中,tan 20tan 48EC BC EBC =⨯∠=⨯o ,∴20tan 48DE EC DC =-=⨯-o即20tan 4820 1.11110 1.732 4.9DE =⨯-≈⨯-⨯=o故广告牌DE 的高度为4.9m .【点睛】本题考查了解直角三角形的应用,掌握锐角三角函数的性质是解答本题的关键. 25. 在平面直角坐标系中,已知一次函数11y k x b =+与坐标轴分别交于()5,0A ,50,2B ⎛⎫ ⎪⎝⎭两点,且与反比例函数22k y x =的图象在第一象限内交于P ,K 两点,连接OP ,OAP △的面积为54.(1)求一次函数与反比例函数的解析式;(2)当21y y >时,求x 的取值范围;(3)若C 为线段OA 上的一个动点,当PC KC +最小时,求PKC 的面积.【答案】(1)115,22y x =-+22.y x= (2)01x <<或4x >,(3)65【解析】 【分析】(1)先运用待定系数法求出直线解析式,再根据OAP △的面积为54和直线解析式求出点P 坐标,从而可求出反比例函数解析式;(2)联立方程组并求解可得点K 的坐标,结合函数图象可得出x 的取值范围; (3)作点K 关于x 轴的对称点K ',连接KK ',PK '交x 轴于点C ,连接KC ,则PC +KC 的值最小,求出点C 的坐标,再根据PKC AKM KMC PAC S S S S ∆∆∆∆=--求解即可.【小问1详解】解:∵一次函数11y k x b =+与坐标轴分别交于()5,0A ,50,2B ⎛⎫ ⎪⎝⎭两点, ∴把()5,0A ,50,2B ⎛⎫ ⎪⎝⎭代入11y k x b =+得, 1505,2k b b +=⎧⎪⎨=⎪⎩,解得,11252k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴一次函数解析式为115,22y x =-+ 过点P 作PH x ⊥轴于点H ,∵(5,0),A∴5, OA=又5,4PAOS∆=∴15 524PH⨯⨯=∴1,2 PH=∴151 222x-+=,∴4,x=∴1 (4,2 P∵1(4,2P在双曲线上,∴21 42,2k=⨯=∴22 .yx=【小问2详解】解:联立方程组得,15222y xyx⎧=-+⎪⎪⎨⎪=⎪⎩解得,111 2x y =⎧⎨=⎩,22412xy=⎧⎪⎨=⎪⎩∴(1,2),k根据函数图象可得,反比例函数图象直线上方时,有01x <<或4x >,∴当21y y >时,求x 的取值范围为01x <<或4x >,【小问3详解】解:作点K 关于x 轴的对称点K ',连接KK '交x 轴于点M ,则K '(1,-2),OM =1, 连接PK '交x 轴于点C ,连接KC ,则PC +KC 的值最小,设直线PK '的解析式为,y mx n =+ 把1(4,(1,2)2P K '-代入得,2142m n m n +=-⎧⎪⎨+=⎪⎩解得,56176m n ⎧=⎪⎪⎨⎪=-⎪⎩∴直线PK '的解析式为517,66y x =- 当0y =时,106657x -=,解得,751x =, ∴17(,0)5C ∴175OC = ∴17121,55MC OC OM =-=-= 178555AC OA OC =-=-= 514AM OA OM =-=-=,∴PKC AKM KMC PAC S S S S ∆∆∆∆=--1112181422225252=⨯⨯-⨯⨯-⨯⨯ 122455=-- 65= 【点睛】本题主要考查了反比例函数与一次函数的综合,正确作出辅助线是解答本题的关在键.26. 我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.(1)如图一,在等腰ABC 中,AB AC =,BC 边上有一点D ,过点D 作DE AB ⊥于E ,DF AC ⊥于F ,过点C 作CG AB ⊥于G .利用面积证明:DE DF CG +=.(2)如图二,将矩形ABCD 沿着EF 折叠,使点A 与点C 重合,点B 落在B ′处,点G 为折痕EF 上一点,过点G 作GM FC ⊥于M ,GN BC ⊥于N .若8BC =,3BE =,求GM GN +的长.(3)如图三,在四边形ABCD 中,E 为线段BC 上的一点,EA AB ⊥,ED CD ⊥,连接BD ,且AB AE CD DE=,BC =,3CD =,6BD =,求ED EA +的长. 【答案】(1)证明见解析(2)4(3【解析】【分析】(1)根据题意,利用等面积法ABC ABD ACD S S S ∆∆∆=+,根据等腰ABC 中,AB AC =,即可得到结论;(2)根据题中条件,利用折叠性质得到AFE CFE ∠=∠,结合矩形ABCD 中AD BC ∥得到AFE FEC ∠=∠,从而有CFE FEC ∠=∠,从而确定EFC ∆是等腰三角形,从而利用(1)中的结论得到=GM GN FH +,结合勾股定理及矩形性质即可得到结论;(3)延长BA CD 、交于F ,连接EF ,过点B 作BG FC ⊥于G ,根据AB AE CD DE =,EA AB ⊥,ED CD ⊥,得到ABC ∆是等腰三角形,从而由(1)知ED EA BG +=,在Rt BCG ∆中,BG ==,在Rt BDG ∆中,6BD =,BG ==BG ==求解得1x =,从而得到结论.【小问1详解】证明:连接AD ,如图所示:在等腰ABC 中,AB AC =,BC 边上有一点D ,过点D 作DE AB ⊥于E ,DF AC ⊥于F ,过点C 作CG AB ⊥于G , ∴由ABC ABD ACD S S S ∆∆∆=+得111222AB CG AB ED AC FD ⋅=⋅+⋅, ∴DE DF CG +=;【小问2详解】解:连接CG ,过点F 作FH BC ⊥于H ,如图所示:根据折叠可知AFE CFE ∠=∠,在矩形ABCD 中,AD BC ∥,则AFE FEC ∠=∠,CFE FEC ∴∠=∠,即EFC ∆等腰三角形,是在等腰EFC ∆中,FC EC =,EF 边上有一点G ,过点G 作GM FC ⊥于M ,GN BC ⊥于N ,过点F 作FH BC ⊥于H ,由(1)可得=GM GN FH +,在Rt ABE ∆中,90B ∠=︒,3,835BE AE EC BC BE ===-=-=,则4AB ===,在四边形ABHF 中,90B BAF FHB ∠=∠=∠=︒,则四边形ABHF 为矩形, 4FH AB ∴==,即4GM GN FH AB +===;【小问3详解】解:延长BA CD 、交于F ,连接EF ,过点B 作BG FC ⊥于G ,在四边形ABCD 中,E 为线段BC 上的一点,EA AB ⊥,ED CD ⊥,则90BAE CDE ∠=∠=︒,又 AB AE CD DE=, ∴ABE DCE ∆∆ ,ABE C ∴∠=∠,即ABC ∆是等腰三角形,∴由(1)可得ED EA BG +=,设=GD x ,90EDC BGC ∠=∠=︒ ,BC =,3CD =,在Rt BCG ∆中,BG ==,在Rt BDG ∆中,6BD =,BG ==,∴BG ==1x =,BG ∴==ED EA BG +==【点睛】本题考查几何综合,涉及到等腰三角形的判定与性质、等面积求线段关系、折叠的性质、勾股定理求线段长、相似三角形的判定与性质等知识点,读懂题意,掌握(1)中的证明过程与结论并运用到其他情境中是解决问题的关键.27. 如图所示,在O 的内接AMN 中,90MAN ∠=︒,2AM AN =,作AB MN ⊥于点P ,交O 于另一点B ,C 是¼AM 上的一个动点(不与A ,M 重合),射线MC 交线段BA 的延长线于点D ,分别连接AC 和BC ,BC 交MN 于点E .(1)求证:CMA CBD △∽△.(2)若10MN =, MCNC =,求BC 的长. (3)在点C 运动过程中,当3tan 4MDB ∠=时,求ME NE 的值. 【答案】(1)证明见解析(2)(3)32【解析】【分析】(1)利用圆周角定理得到∠CMA =∠ABC ,再利用两角分别相等即可证明相似; (2)连接OC ,先证明MN 是直径,再求出AP 和NP 的长,接着证明COE BPE △∽△,利用相似三角形的性质求出OE 和PE ,再利用勾股定理求解即可; (3)先过C 点作CG ⊥MN ,垂足为G ,连接CN ,设出34GM x CG x ==,,再利用三角函数和勾股定理分别表示出PB 和PG ,最后利用相似三角形的性质表示出EG ,然后表示出ME 和NE ,算出比值即可.【小问1详解】解:∵AB ⊥MN ,∴∠APM =90°,∴∠D +∠DMP =90°,又∵∠DMP +∠NAC =180°,∠MAN =90°, ∴∠DMP +∠CAM =90°,∴∠CAM =∠D ,∵∠CMA =∠ABC ,∴CMA CBD △∽△.【小问2详解】连接OC ,∵90MAN ∠=︒,∴MN 是直径,∵10MN =,∴OM =ON =OC =5,∵2AM AN =,且222A M A N M N +=,∴AN AM == ∵1122AMN S AM AN MN AP =⋅=⋅△, ∴4AP =,∴4BP AP ==,∴2NP ==,∴523OP =-=,∵ MCNC =, ∴OC ⊥MN ,∴∠COE =90°,∵AB ⊥MN ,∴∠BPE =90°,∴∠BPE =∠COE ,又∵∠BEP =∠CEO ,∴COE BPE △∽△ ∴CO OE CE BP PE BE==, 即54OE CE PE BE == 由3OE PE OP +==,∴5433OE PE ==,,∴CE ===,BE ===∴BC =+=【小问3详解】过C 点作CG ⊥MN ,垂足为G ,连接CN , ∵MN 是直径,∴∠MCN =90°,∴∠CNM +∠DMP =90°,∵∠D +∠DMP =90°,∴∠D =∠CNM , ∵3tan 4MDB ∠=, ∴3tan 4CNM ∠=, 设34GM x CG x ==,,∴5CM x =, ∴203x CN =, ∴163x NG =,∴253x NM = ∴256x OM ON ==, ∵2AM AN =,且222A M A N M N +=,∴AN x =,AM x =, ∵1122AMN S AM AN MN AP =⋅=⋅△, ∴103AP x PB ==, ∴53NP x =, ∴16511333PG x x x =-=, ∵∠CGE =∠BPE =90°,∠CEG =∠BEP , ∴CGE BPE △∽△, ∴CG GE CE BP PE BE==, 即4103x GE CE PE BE x == ∴2GE x =,53PE x =∴5ME x =,103x NE =, ∴:3:2ME NE =, ∴ME NE 值为32. 的【点睛】本题考查了圆的相关知识、相似三角形的判定与性质、三角函数、勾股定理等知识,涉及到了动点问题,解题关键是构造相似三角形,正确表示出各线段并找出它们的关系,本题综合性较强,属于压轴题.28. 如图,抛物线2y ax bx c =++交y 轴于点()0,4A -,并经过点()6,0C ,过点A 作AB y ⊥轴交抛物线于点B ,抛物线的对称轴为直线2x =,D 点的坐标为()4,0,连接AD ,BC ,BD .点E 从A 点出发,以每秒个单位长度的速度沿着射线AD 运动,设点E 的运动时间为m 秒,过点E 作EF AB ⊥于F ,以EF 为对角线作正方形EGFH .(1)求抛物线的解析式;(2)当点G 随着E 点运动到达BC 上时,求此时m 的值和点G 的坐标;(3)在运动的过程中,是否存在以B ,G ,C 和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G 的坐标,如果不存在,请说明理由.【答案】(1)214433y x x =--(2)165m =,2412,55G ⎛⎫- ⎪⎝⎭ (3)368,55⎛⎫- ⎪⎝⎭或(3,-3)1216,55⎛⎫- ⎪⎝⎭或426,55⎛⎫- ⎪⎝⎭ 【解析】【分析】(1)利用待定系数法求解析式即可;(2)求出直线BC 解析式,通过△EGF 为等腰直角三角形表示出G 点坐标,将G 点代入BC 解析式即可求得m 的值,从而求得G 点坐标;(3)将矩形转化为直角三角形,当△BGC 是直角三角形时,当△BCG 为直角三角形时,当△CBG 为直角三角形时,分情况讨论分别列出等式求得m 的值,即可求得G 点坐标.【小问1详解】将点A (0,-4)、C (6,0)代入解析式2y ax bx c =++中,以及直线对称轴2x =,可得4036622c a b c b a ⎧⎪-=⎪=++⎨⎪⎪-=⎩, 解得13434a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩, ∴抛物线的解析式为214433y x x =--; 【小问2详解】∵A (0,-4),D ()4,0,∴△AOD 为等腰直角三角形,∵AB y ⊥轴交抛物线于点B ,∴B (4,-4),设直线BC 解析式为y =kx +b ,将B (4,-4),C (6,0)代入解析式得, 4406k b k b -=+⎧⎨=+⎩,解得212k b =⎧⎨=-⎩, ∴直线BC 解析式为y =2x -12,由题意可得AE =,△ADB 为等腰直角三角形,∴AF EF AE m ===, ∵四边形EGFH 正方形,∴△EGF 为等腰直角三角形, ∴11,422G m m m ⎛⎫+-+ ⎪⎝⎭, 点G 随着E 点运动到达BC 上时,满足直线BC 解析式y =2x -12, ∴11421222m m m ⎛⎫-+=+- ⎪⎝⎭, ∴165m =,此时2412,55G ⎛⎫- ⎪⎝⎭; 【小问3详解】B (4,-4),C (6,0),11,422G m m m ⎛⎫+-+ ⎪⎝⎭, ∴()()222640420BC =-++=,22222313144442222BG m m m m ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,222223131604642222CG m m m m ⎛⎫⎛⎫⎛⎫⎛⎫=-++-=-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 要使以B ,G ,C 和平面内的另一点为顶点的四边形是矩形,需满足:当△BGC 是直角三角形时,222BG CG BC +=, 22223131464202222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫-++-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 解得,1245m =,22m =, 此时G 368,55⎛⎫- ⎪⎝⎭或(3,-3); 当△BCG 为直角三角形时,222BC CG BG +=,22223131206442222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-+-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 为解得,285m =, 此时G 426,55⎛⎫- ⎪⎝⎭; 当△CBG 为直角三角形时,222BC BG CG +=,22223131204642222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-+=-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 解得,85m =, 此时G 1216,55⎛⎫- ⎪⎝⎭; 综上所述:点G 坐标为368,55⎛⎫-⎪⎝⎭或(3,-3)1216,55⎛⎫- ⎪⎝⎭或426,55⎛⎫- ⎪⎝⎭. 【点睛】本题是二次函数的综合题,考查了待定系数法求解析式、等腰直角三角形的性质和判定,动点运动问题,存在矩形问题,利用数形结合,注意分情况讨论是解题的关键。
2023年黑龙江省绥化市中考数学真题(解析)

二〇二三年绥化市初中毕业学业考试数学试题一、单选题1.【答案】C【解析】解:A 选项,是轴对称图形,不是中心对称图形,故A 选项不合题意;B 选项,是轴对称图形,不是中心对称图形,故B 选项不符合题意;C 选项,既是轴对称图形又是中心对称图形,故C 选项合题意;D 选项,不是轴对称图形,是中心对称图形,故D 选项不合题意.故选:C .2.【答案】D【解析】解:052-+516=+=,故选:D .3.【答案】B【解析】根据题意,该几何体的左视图为:,故选B .4.【答案】A【解析】解:90.000000001110-=⨯.故选:A .5.【答案】D【解析】解:A 选项,333()pq p q =--,故该选项不正确,不符合题意;B 选项,43222x x x x x ⋅+⋅=,故该选项不正确,不符合题意;C 5=,故该选项不正确,不符合题意;D 选项,()326a a =,故该选项正确,符合题意;故选:D .6.【答案】C【解析】解:依题意,190345∠+︒=∠+︒,∵125∠=︒,∴370∠=︒,故选:C .7.【答案】D【解析】解:A 选项,若方差22s s >乙甲,则乙组数据的波动较小,故该选项不正确,不符合题意;B 选项,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项不正确,不符合题意;C 选项,三角形三条中线的交点叫做三角形的重心,故该选项不正确,不符合题意;D 选项,角的内部到角的两边的距离相等的点在角的平分线上,故该选项正确,符合题意;故选:D .8.【答案】B【解析】解:A 选项,该组数据的样本容量是1224%50÷=,故该选项不正确,不符合题意;B 选项,8090x ≤<的人数为:5041212715----=,41525+<,4151225++>,该组数据的中位数落在90~100这一组,故该选项正确,符合题意;C 选项,90~100这组数据的组中值是95,故该选项不正确,不符合题意;D 选项,110~120这组数据对应的扇形统计图的圆心角度数为736050.450⨯︒=︒,故该选项不正确,不符合题意;故选:B .9.【答案】C【解析】设()3,B m ,∵点B ,C 的横坐标都是3,2BC =,AC 平行于x 轴,点D 在AC 上,且其横坐标为1,∴()()3,2,1,2C m D m ++,∴32m m =+,解得1m =,∴()3,1B ,∴313k =⨯=,故选C .10.【答案】B【解析】解:设乙车单独运送这批货物需x 天,由题意列方程11111424x ⎛⎫++= ⎪⎝⎭,故选:B .11.【答案】A【解析】解:如图所示,连接BD ,过点B 作BE AD ⊥于点E ,当04t <<时,M 在AB 上,菱形ABCD 中,60A ∠=︒,4AB =,∴AB AD =,则ABD △是等边三角形,∴122AE ED AD ===,BE ==∵2,AM x AN x ==,∴2AM ABAN AE==,又A A ∠=∠∴AMN ABE ∽∴90ANM AEB ∠=∠=︒∴MN ==,∴2122y x x ==当48t ≤<时,M 在BC 上,∴1122y AN BE x =⨯=⨯=,综上所述,04t <<时的函数图象是开口向上的抛物线的一部分,当48t ≤<时,函数图象是直线的一部分,故选:A .12.【答案】D【解析】∵四边形ABCD 是正方形,∴90BAD ADE ∠=∠=︒,AB AD =∵BFAE⊥∴90ABF BAF DAE ∠=︒-∠=∠∴cos cos ABF EAD ∠=∠即BF ADAB AE=,又AB AD =,∴2AB BF AE =⋅,故①正确;设正方形的边长为a ,∵点E 为边CD 的中点,∴2a DE =,∴1tan tans 2ABF EAD ∠=∠=,在Rt ABE △中,AB a ===,∴55AF a =在Rt ADE △中,52AE ==∴55352510EF AE AF a =-=-=,∵AB DE ∥∴GAB GED ∽∴2AG ABGE DE==∴1536GE AE a ==∴25615FG AE AF GE a a a a =--=--=∴53522515aAF FG ==∴:2:3BGF BAF S S =△△,故②正确;∵AB a =,∴22222BD AB AD a =+=,如图所示,过点H 分别作,BF AE 的垂线,垂足分别为,M N,又∵BF AE ⊥,∴四边形FMHN 是矩形,∵FH 是BFG ∠的角平分线,∴HM HN =,∴四边形FMHN 是正方形,∴FN HM HN ==∵25252,515BF AF a FG a ===∴13MH FG BM BF ==设MH b =,则34BF BM FM BM MH b b b =+=+=+=在Rt BMH中,BH ==,∵5BF a =∴2545a b =解得:510b a =∴52102BH a a ==,∴22222B a D BD HD a a =-⋅⨯=,故④正确.故选:D .二、填空题13.【答案】()()x y x z +-【解析】解:2x xy xz yz +--=()()()()x x y z x y x y x z +-+=+-,故答案为:()()x y x z +-.14.【答案】5x ≥-且0x ≠##0x ≠且5x ≥-【解析】∵式子5x x有意义,∴50x +≥且0x ≠,∴5x ≥-且0x ≠,故答案为:5x ≥-且0x ≠.15.【答案】12##0.5【解析】解:列表如下,1234111 1=1213142221=212=232142=333 1=3 2313=344441=42 2=43414=共有16种等可能结果,符合题意的有8种,∴第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是81162=,故答案为:12.16.【答案】23-【解析】解:∵一元二次方程256x x x +=+,即2460x x --=,的两根为1x 与2x ,∴121246x x x x +==-,,∴1211+x x 12124263x x x x +===--,故答案为:23-.17.【答案】12x -##12x-+【解析】解:2222142442x x x x x x x x x+--⎛⎫-÷⎪--+-⎝⎭()()()()()2221242x x x x x x x x x +----=⨯--()()2222442x x x x x x x x ---+=⨯--12x =-;故答案为:12x -.18.【答案】22π3cm 3⎛⎫-⎪⎝⎭【解析】解:如图所示,连接,OA OC ,设,AB CO 交于点D∵将 AB 沿弦AB 翻折,使点C 与圆心O 重合,∴AC AO =,OC AB ⊥又OA OC =∴OA OC AC ==,∴AOC 是等边三角形,∴60AOC ∠=︒,1OD CD ==,∴AD ==,∴阴影部分面积)226012π22πcm 36023AOC AOC S S =-=⨯-⨯= 扇形故答案为:22πcm 3⎛-⎝.19.【答案】(62,2)a b --【解析】解:如图所示,过点,C C '分别作x 轴的垂线,CD C D ''垂足分别为,D D ',∵ABC 与AB C ''△的相似比为12∶,点A 是位似中心,(2,0)A ∴2AD AD '=∵(,)C a b ,∴2,AD a CD b =-=,∴24,2A D a C D b '''=-=,∴()224,0D a '-+∴C '(62,2)a b --故答案为:(62,2)a b --.20.【答案】3+##3【解析】解:∵E 为高BD 上的动点.∴1302CBE ABC ∠=∠=︒∵将CE 绕点C 顺时针旋转60︒得到CF .ABC 是边长为6的等边三角形,∴,60,CE CF ECF BCA BC AC =∠=∠=︒=∴CBE CAF ≌∴30CAF CBE ∠=∠=︒,∴F 点在射线AF 上运动,如图所示,作点C 关于AF 的对称点C ',连接DC ',设CC '交AF 于点O ,则=90AOC ∠︒在Rt AOC 中,30CAO ∠=︒,则132CO AC ==,则当,,D F C '三点共线时,FC FD +取得最小值,即FC FD F C F D CD ''''+=+=∵6CC AC '==,ACO C CD '∠=∠,CO CD =∴ACO C CD ' ≌∴90C DC AOC '∠=∠=︒在C DC ' 中,C D '===∴CDF 周长的最小值为3CD FC CD CD DC '++=+=+故答案为:3+21.【答案】22n n -##22n n -+【解析】解:依题意,()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-,,∴123n a a a a ++++= ()21432122n n n n n n +-==-=-,故答案为:22n n -.22.【答案】44+-【解析】解:如图所示,过点A 作AM BC ⊥于点M ,∵等腰ABC ,120BAC ∠=︒,2AB =.∴30ABC ACB ∠=∠=︒,∴112AM AB ==,BM CM ===∴BC =,如图所示,当ABC 以点B 为旋转中心逆时针旋转45︒,过点B 作BEA B '⊥交A D '于点E ,∵120BAC ∠=︒,∴60DA B '∠=︒,30A EB '∠=︒,在Rt A BE ' 中,24A E A B ''==,BE ==∵等腰ABC ,120BAC ∠=︒,2AB =.∴30ABC ACB ∠=∠=︒,∵ABC 以点B 为旋转中心逆时针旋转45︒,∴45ABA '∠=︒,∴180********DBE ∠=︒-︒-︒-︒=︒,1804530105A BD '∠=︒-︒-︒=︒在A BD ' 中,1801806010515D DA B A BD ∠=︒-∠-∠=︒-︒-︒=''︒,∴D EBD ∠=∠,∴EB ED ==,∴4A D A E DE ''=+=+如图所示,当ABC 以点B 为旋转中心顺时针旋转45︒,过点D 作DF BC '⊥交BC '于点F ,在BFD △中,45BDF CBC ∠'=∠=︒,∴DF BF=在Rt DC F ' 中,30C '∠=︒∴3'3DF FC =∴BC BF =+=∴3DF BF ==-∴26DC DF '==-∴624A D C D A C ''''=-=-=-,综上所述,A D '的长度为4-或4+,故答案为:4-或4+.三、解答题23.【答案】(1)见解析(2)75EDF ∠=︒或105︒【解析】(1)解:如图所示,①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画弧,两弧交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O 交于,E F 两点,作直线,PE PF ,则直线,PE PF 即为所求;(2)如图所示,点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒,∵,PE PF 是O 的切线,∴90PEO PFO ∠=∠=︒,∴360909030150EOF ∠=︒-︒-︒-︒=︒,当点D 在优弧 EF 上时,1752EDF EOF ∠=∠=︒,当点D 在劣弧 EF上时,18075105EDF ∠=︒-︒=︒,∴75EDF ∠=︒或105︒.24.【答案】(1)河两岸之间的距离是20+米(2)5tan 2CPE ∠=【解析】(1)解:如图所示,过点C 作CM EF ⊥于点M ,设CM a =米,∵30CBE ∠=︒∴3tan tan 303CM CBM PB ∠==︒=,∴MB =,在Rt MCD △中,tan tan 451CM CDM MD∠==︒=,∴MD MC a ==∴40BD MB MD a =-=-=解得:20a =答:河两岸之间的距离是20米;(2)解:如图所示,依题意,4012)52PB BD DP =+=+=+,∴((20528MP MB PB =-=+=+,在Rt CMP △中,5tan2CM CPM MP ∠==,∴5tan 2CPE ∠=.25.【答案】(1)每辆A 型车、B 型车坐满后各载客40人、55人(2)共有4种租车方案,租8辆A 型车,2辆B 型车最省钱(3)在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米【解析】(1)解:设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意得5231034340x y x y +=⎧⎨+=⎩解得4055x y =⎧⎨=⎩答:每辆A 型车、B 型车坐满后各载客40人、55人.(2)设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意得()()500600105500405510420m m m m ⎧+-≤⎪⎨+-≥⎪⎩解得:2583m ≤≤m 取正整数,∴5m =,6,7,8∴共有4种租车方案设总租金为w 元,则500600(10)1006000w m m m =+-=-+ 1000-<w ∴随着m 的增大而减小∴8m =时,w 最小∴租8辆A 型车,2辆B 型车最省钱.(3)设s kt =甲,1s k t b =+乙.由题意可知,甲车的函数图象经过(4,300);乙车的函数图象经过(0.5,0),(3.5,300)两点.∴75s t =甲,10050s t =-乙25s s -=乙甲,即100507525t t --=解得3t =或3007525t -=解得113t =所以,在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米.26.【答案】(1)见解析(2)y =(或2(416x y x -=+)(3)1023【解析】(1)证明:∵四边形ABCD 为矩形,∴AD BF ∥,∴D DCF ∠=∠,∵G 为CD 中点,∴DG CG =,在ADG △和△FCG 中D GCF DG CG AGD FGC ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴(ASA)ADG FCG △≌△;(2)∵四边形ABCD 为矩形,∴90ABC ∠=︒,∵CE AF ⊥,∴90CEF ABC ∠=︒=∠,∵F F ∠=∠,∴CEF ABF △∽△,∴CE CF AB AF=,∵4AB =,BF x =,∴在Rt ABF 中,AF ==,∵CE y =,∴4y =∴y =2(416x y x -=+);(3)过点E 作EN BF ⊥于点N ,∵四边形ABCD 为矩形,且3AD =,∴3AD BC ==,∵4AB =,1CF =,∴AB BF =,∴ABF △为等腰直角三角形,∴45CFE BAF ∠=∠=︒,∵CE AF ⊥,∴CEF △为等腰直角三角形,∴45ECF ∠=︒,∵EN CF ^,∴EN 平分CF ,∴12CN NF NE ===,在Rt BNE 中,∵222BE BN EN =+,∴2BE ==,∵45ECF BAF ︒∠=∠=,∴135BAM BCE ∠=∠=︒,∵BM BE ⊥,∴90MBA ABE ∠+∠=︒,∵90ABE EBC ∠+∠=︒,∴MBA EBC ∠=∠,∴BAM BCE △∽△,∴43BM BA BE BC ==,43522=,∴1023BM =.27.【答案】(1)见解析(2)见解析(3)215【解析】(1) ABC ∠和AMC ∠是 AC 所对的圆周角,∴ABC AMC Ð=Ð,AHM CHB Ð=Ð,∴AMH CBH ,∴AH MH CH BH=,∴MH CH AH BH ⋅=⋅.(2)连接OC ,交AB 于点F ,MC 与ND 为一组平行弦,即:MC ND ∥,∴OND OMC Ð=Ð, OM OC =,∴OMC OCM ∠=∠, 90OND AHM∠+∠=︒,∴90OCM AHM OCM CHB Ð+Ð=Ð+Ð=°,∴90HFC ∠=︒,∴OC AB ⊥,∴OC 是AB 的垂直平分线,∴ =AC BC.(3)连接DM 、DG ,过点D 作DE MN ⊥,垂足为E ,设点G 的对称点G ',连接G D ¢、G N ',DG DG '=,G ND GND ¢Ð=Ð,∴ 'DM DG = ,∴DG DM ¢=,∴DG DM =,∴DGM 是等腰三角形,DE MN ⊥,∴GE ME =, DN CM ∥,∴CMN DNM Ð=Ð,MN 为直径,∴90MDN ∠=︒,∴90MDE EDN ∠+∠=︒,DE MN ⊥,∴90DEN ∠=︒,∴90DNM EDN Ð+Ð=°,∴3sin sin sin 5EDM DNM CMN Ð=Ð=Ð=,在Rt MND △中,15MN =,∴3sin 5MD DNM MN Ð==,∴3155MD =,∴9MD =,在Rt MED 中,3sin 5ME EDM MDÐ==,∴395ME =∴275ME =,∴2721215255NG MN MG MN ME =-=-=-´=∴215NG =故答案为:215.28.【答案】(1)211462y x x =++,36y x =+(2)满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -(3)当133m =时,12CD PD +的最大值为24【解析】(1)解:把(6,0)A -,(2,0)B -,(0,6)C 代入21y ax bx c =++得36604206a b c a b c c -+=⎧⎪-+=⎨⎪=⎩解得1246a b c ⎧=⎪⎪=⎨⎪=⎪⎩∴211462y x x =++把(2,0)B -代入6y kx =+得3k =∴36y x =+(2)满足条件的E 、F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -解:①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ⊥,12F F BC ⊥,使12E B E B BC ==,12CF CF BC ==,连接11E F 、22E F .过点1E 作11E H x ⊥轴于1H .∵1111,90BE CB BOC E H B E BC =∠=∠=︒=∠,又111190BE H E BH CBO ∠=︒-∠=∠,∴11(AAS)BE H CBO △≌△,∴112E H BO ==,16H B OC ==∴1(8,2)E -同理可得,2(4,2)E -②以BC 为正方形的对角线时,过BC 的中点G 作33EF BC ⊥,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形,过点3E 作3E N y ⊥轴于点N ,过点B 作3BM E N ⊥于点M∵3333,90CE BE CNE E MB =∠=∠=︒,又33390BE M CE N E CN∠=︒-∠=∠∴33(AAS)CE N E BM △≌△∴3CN E M =,3BM E N=∵BC =∴3E G BG ==∴3E B =在3Rt E NC △中,22233E C CN E N =+∴222(6)CN CN =+-解得2CN =或4当4CN =时,3(2,2)E ,此时点E 在点F 右侧故舍去;当2CN =时,3(4,4)E -.综上所述:1(8,2)E -,2(4,2)E -,3(4,4)E -(3)∵211462y x x =++向右平移8个单位长度得到抛物线()()22184862y x x =-+-+当20y =,即()()21848602x x -+-+=解得:122,6x x ==∴(2,0)M ,(6,0)N ∵2y 过M ,N ,C 三点∴221462y x x =-+在直线NC 下方的抛物线2y 上任取一点P ,作PH x ⊥轴交NC 于点H ,过点H 作HG y ⊥轴于点.G∵(6,0)N ,(0,6)C ∴ON OC=∴CON 是等腰直角三角形∵45CHG ∠=︒,90GHP ∠=︒∴45PHD ∠=︒又PD CN⊥∴HPD 是等腰直角三角形∴22HD DP HP ==∵点P 在抛物线2y 上,且横坐标为m∴CG GH m==∴2CH m=∵6CN y x =-+∴(,6)H m m -+∴2211646322HP m m m m m ⎛⎫=-+--+=-+ ⎪⎝⎭∴222123232242HD DP m m m ⎛⎫==-+=-+ ⎪⎝⎭∴211332322222242CD PD CH HD PD CH PD m m m ⎛⎫+=++=+=+-+ ⎪ ⎪⎝⎭2321316928324m ⎛⎫=--+ ⎪⎝⎭∴当133m =时,12CD PD +的最大值为24.。
2024年黑龙江省绥化市中考数学试卷(附答案解析)

2024年黑龙江省绥化市中考数学试卷(附答案解析)一、单项选择题(本题共12个小题,每小题3分,共36分)1.(3分)实数﹣的相反数是()A.2025B.﹣2025C.﹣D.【解答】解:﹣的相反数是,故选:D.2.(3分)下列所述图形中,是轴对称图形但不是中心对称图形的是()A.平行四边形B.等腰三角形C.圆D.菱形【答案】B.分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.3.(3分)某几何体是由完全相同的小正方体组合而成,如图是这个几何体的三视图,那么构成这个几何体的小正方体的个数是()A.5个B.6个C.7个D.8个【答案】A.4.(3分)若式子有意义,则m的取值范围是()A.m≤B.m≥﹣C.m≥D.m≤﹣【解答】解:由题意得:2m﹣3≥0,解得:m≥,故选:C.5.(3分)下列计算中,结果正确的是()A.(﹣3)﹣2=B.(a+b)2=a2+b2C.=±3D.(﹣x2y)3=x6y3【解答】解:(﹣3)﹣2=,则A符合题意;(a +b )2=a 2+2ab +b 2,则B不符合题意;=3,则C 不符合题意;(﹣x 2y )3=﹣x 6y 3,则D 不符合题意;故选:A .6.(3分)小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是﹣2和﹣5.则原来的方程是()A .x 2+6x +5=0B .x 2﹣7x +10=0C .x 2﹣5x +2=0D .x 2﹣6x ﹣10=0【答案】B .7.(3分)某品牌女运动鞋专卖店,老板统计了一周内不同鞋码运动鞋的销售量如表:鞋码3637383940平均每天销售量/双1012201212如果每双鞋的利润相同,你认为老板最关注的销售数据是下列统计量中的()A .平均数B .中位数C .众数D .方差【解答】解:因为众数是在一组数据中出现次数最多的数,又根据题意,每双鞋的销售利润相同,鞋店为销售额考虑,应关注卖出最多的鞋子的尺码,这样可以确定进货的数量,所以该店主最应关注的销售数据是众数.故选:C .8.(3分)一艘货轮在静水中的航速为40km /h ,它以该航速沿江顺流航行120km 所用时间,与以该航速沿江逆流航行80km 所用时间相等,则江水的流速为()A .5km /hB .6km /hC .7km /hD .8km /h【解答】解:设江水的流速为x km /h ,则沿江顺流航行的速度为(40+x )km /h ,沿江逆流航行的速度为(40﹣x )km /h ,根据题意得:=,解得:x =8,∴江水的流速为8km /h .故选:D .【点评】本题考查了分式方程的应用,找准等量关系,正确列出分式方程是解题的关键.9.(3分)如图,矩形OABC各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比缩小,则顶点B在第一象限对应点的坐标是()A.(9,4)B.(4,9)C.(1,)D.(1,)【分析】根据位似变换的性质解答即可.【解答】解:∵以原点O为位似中心,将矩形OABC按相似比缩小,点B的坐标为(3,2),∴顶点B在第一象限对应点的坐标为(3×,2×),即(1,),故选:D.10.(3分)下列叙述正确的是()A.顺次连接平行四边形各边中点一定能得到一个矩形B.平分弦的直径垂直于弦C.物体在灯泡发出的光照射下形成的影子是中心投影D.相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等【分析】选项A根据中点四边形的定义以及矩形的判定方法解答即可;选项B根据垂径定理判断即可;选项C根据中心投影的定义判断即可;选项D根据圆心角、弧、弦、弦心距的关系定理判断即可.【答案】C.11.(3分)如图,四边形ABCD是菱形,CD=5,BD=8,AE⊥BC于点E,则AE的长是()A.B.6C.D.12【解答】解:∵四边形ABCD是菱形,CD=5,BD=8,∴BC=CD=5,BO=DO=4,OA=OC,AC⊥BD,∴∠BOC=90°,在Rt△OBC中,由勾股定理得:OC===3,∴AC=2OC=6,∵菱形ABCD的面积=AE•BC=BD×AC=OB•AC,∴AE===,故选:A.12.(3分)二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,则下列结论中:①>0;②am2+bm≤a﹣b(m为任意实数);③3a+c<1;④若M(x1,y)、N(x2,y)是抛物线上不同的两个点,则x1+x2≤﹣3.其中正确的结论有()A.1个B.2个C.3个D.4个【解答】解:由题意,∵抛物线开口向下,∴a<0.又抛物线的对称轴是直线x=﹣=﹣1,∴b=2a<0.又抛物线交y轴正半轴,∴当x=0时,y=c>0.∴<0,故①错误.由题意,当x=﹣1时,y取最大值为y=a﹣b+c,∴对于抛物线上任意的点对应的函数值都≤a﹣b+c.∴对于任意实数m,当x=m时,y=am2+bm+c≤a﹣b+c.∴am2+bm≤a﹣b,故②正确.由图象可得,当x=1时,y=a+b+c<0,又b=2a,∴3a+c<0<1,故③正确.由题意∵抛物线为y=ax2+bx+c,∴x1+x2=﹣=﹣=﹣2>﹣3,故④错误.综上,正确的有②③共2个.故选:B.二、填空题(本题共10个小题,每小题3分,共30分)13.(3分)我国疆域辽阔,其中领水面积约为370000km2,把370000这个数用科学记数法表示为.【解答】解:370000=3.7×105,故答案为:3.7×105.14.(3分)分解因式:2mx2﹣8my2=.【分析】先提取公因式再运用公式法进行因式分解即可得出答案.【解答】解:原式=2m(x2﹣4y2)=2m(x+2y)(x﹣2y).故答案为:2m(x+2y)(x﹣2y).15.(3分)如图,AB∥CD,∠C=33°,OC=OE.则∠A=°.【解答】解:∵OC=OE,∠C=33°,∴∠E=∠C=33°,∴∠DOE=∠E+∠C=66°,∵AB∥CD,∴∠A=∠DOE=66°,故答案为:66.16.(3分)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50m,则这栋楼的高度为m(结果保留根号).【解答】解:由题意得:AD⊥BC,在Rt△ACD中,∠CAD=60°,AD=50m,∴CD=AD•tan60°=50(m),在Rt△ABD中,∠BAD=45°,∴BD=AD•tan45°=50(m),∴BC=BD+CD=(50+50)m,∴这栋楼的高度为(50+50)m,故答案为:(50+50).17.(3分)化简:÷(x﹣)=.【解答】解:原式=÷=•=,故答案为:.18.(3分)用一个圆心角为126°,半径为10cm的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为__cm.【解答】解:扇形的弧长==7π(cm),故圆锥的底面半径为7π÷2π=(cm).故答案为:.19.(3分)如图,已知点A(﹣7,0),B(x,10),C(﹣17,y),在平行四边形ABCO中,它的对角线OB与反比例函数y=(k≠0)的图象相交于点D,且OD:OB=1:4,则k=.【分析】作BE⊥x轴,DG⊥x轴,根据点的坐标及相似三角形性质可求出点D坐标继而求出k值.【解答】解:如图,作BE⊥x轴,DG⊥x轴,垂足分别为E、G,∵点A(﹣7,0),B(x,10),C(﹣17,y),∴BE=10,OF=17,OA=7,∴EF=BC=OA=7,∴OE=17+7=24,∵BE∥DG,∴△ODG∽△OBE,∵OD:OB=1:4,∴=,∴,∴D(﹣,6),∵点D在反比例函数图象上,∴k=﹣=﹣15.故答案为:﹣15.20.(3分)如图,已知∠AOB=50°,点P为∠AOB内部一点,点M为射线OA、点N为射线OB上的两个动点,当△PMN的周长最小时,则∠MPN=.【解答】解:作P点关于OB的对称点E,连接EP,EO,EM;∴EM=MP,∠MPO=∠OEM,∠EOM=∠MOP,作P点关于OA的对称点F,连接NF,PF,OF,∴PN=FN,∠OPN=∠OFN,∠PON=∠NOF,∴PM+PN+MN=EM+NF+MN≥EF,当E,M,N,F共线时,△PMN周长最短,又∵∠EOF=∠EOM+∠MOP+∠PON+∠NOF,∠AOB=∠MOP+∠PON,∴∠EOF=2∠AOB,又∵∠AOB=50°,∴∠EOF=100°,∴在△EOF中,∠OEM+∠OFN+∠EOF=180°,∴∠OEM+∠OFN=180°﹣100°=80°,∵∠MPO=∠OEM,∠OPN=∠OFN,∴∠MPO+∠OPN=80°,∵∠MPN=∠MPO+OPN=80°,故答案为:80°.21.(3分)如图,已知A1(1,﹣),A2(3,﹣),A3(4,0),A4(6,0),A5(7,),A6(9,),A7(10,0),A8(11,﹣)…,依此规律,则点A2024的坐标为.【答案】(2891,).22.(3分)在矩形ABCD中,AB=4cm,BC=8cm,点E在直线AD上,且DE=2cm,则点E到矩形对角线所在直线的距离是或或cm.【解答】解:如图1,过点E作EF⊥BD于点F,∵四边形ABCD是矩形,∴∠BAD=∠ABC=∠ADC=90°,AC=BD,AD=BC,AB=CD,∵AB=4cm,BC=8cm,∴由勾股定理得cm,∴BD=cm,∵∠EFD=∠BAD=90°,∠EDF=∠BDA,∴△DEF∽△DBA,∴,∴,∴EF=cm;如图2,过点E作EM⊥AC于点M,∵AD=BC=8cm,DE=2cm,∴AE=6cm,∵∠AME=∠ADC=90°,∠EAM=∠CAD,∴△AEM∽△ACD,∴,∴∴EM=cm;如图3,过点E作EN⊥BD的延长线于点N,∴∠END=∠BAD=90°,∴∠EDN=∠BDA,∴△END∽△BAD,∴,∴,∴EN=cm;如图4,过点E作EH⊥AC的延长线于点H,∴∠AHE=∠ADC=90°,∴∠EAH=∠CAD,∴△AHE∽△ADC,∴,∵AD=BC=8cm,DE=2cm,∴AE=10cm,∴,∴EH=cm;综上,点E到矩形对角线所在直线的距离是cm或cm或cm,故答案为:或或.三、解答题(本题共6个小题,共54分)23.(7分)已知:△ABC.(1)尺规作图:画出△ABC的重心G.(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,连接AG,BG.已知△ABG的面积等于5cm2,则△ABC的面积是cm2.【解答】解:(1)分别作出AB边和BC边的垂直平分线,与AB和BC边分别交于点N和点M,连接AM和CN,如图所示,点G即为所求作的点.(2)∵点G是△ABC的重心,∴AG=2MG,∵△ABG的面积等于5cm2,∴△BMG的面积等于2.5cm2,∴△ABM的面积等于7.5cm2.又∵AM是△ABC的中线,∴△ABC的面积等于15cm2.故答案为:15.24.(7分)为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动、为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图请根据统计图中的信息,解答下列问题:(1)参加本次问卷调查的学生共有人;(2)在扇形统计图中,A组所占的百分比是,并补全条形统计图.(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示,请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.【解答】解:(1)参加本次问卷调查的学生共有12÷20%=60(人).故答案为:60.(2)A组的人数为60﹣20﹣10﹣12=18(人),∴在扇形统计图中,A组所占的百分比是18÷60×100%=30%.故答案为:30%.补全条形统计图如图所示.(3)列表如下:A B C DA(A,B)(A,C)(A,D)B(B,A)(B,C)(B,D)C(C,A)(C,B)(C,D)D(D,A)(D,B)(D,C)共有12种等可能的结果,其中选中的2个社团恰好是B和C的结果有:(B,C),(C,B),共2种,∴选中的2个社团恰好是B和C的概率为=.25.(9分)为了响应国家提倡的“节能环保”号召,某共享电动车公司准备投入资金购买A、B两种电动车.若购买A种电动车25辆、B种电动车80辆,需投入资金30.5万元;若购买A种电动车60辆、B 种电动车120辆,需投入资金48万元.已知这两种电动车的单价不变.(1)求A、B两种电动车的单价分别是多少元?(2)为适应共享电动车出行市场需求,该公司计划购买A、B两种电动车200辆,其中A种电动车的数量不多于B种电动车数量的一半.当购买A种电动车多少辆时,所需的总费用最少,最少费用是多少元?(3)该公司将购买的A、B两种电动车投放到出行市场后,发现消费者支付费用y元与骑行时间x min 之间的对应关系如图.其中A种电动车支付费用对应的函数为y1;B种电动车支付费用是10min之内,起步价6元,对应的函数为y2.请根据函数图象信息解决下列问题.①小刘每天早上需要骑行A种电动车或B种电动车去公司上班.已知两种电动车的平均行驶速度均为300m/min(每次骑行均按平均速度行驶,其它因素忽略不计),小刘家到公司的距离为8km,那么小刘选择B种电动车更省钱(填写A或B).②直接写出两种电动车支付费用相差4元时,x的值5或40.【解答】解:(1)设A、B两种电动车的单价分别为x元、y元,由题意得,,解得:,答:A、B两种电动车的单价分别为1000元、3500元.(2)设购买A种电动车m辆,则购买8种电动车(200﹣m)辆,m(200﹣m),解得:m≤,设所需购买总费用为w元,则w=1000m+3500(200﹣m)=﹣2500m+700000,∵﹣2500<0,∴w随着m的增大而减小,∵m取正整数,∴m=66时,w最少,=700000﹣2500x66=535000(元),∴w最少答:当购买A种电动车66辆时所需的总费用最少,最少费用为535000元.(3)①∵两种电动车的平均行驶速度均为300m/min,小刘家到公司的距离为8km,∴所用时间=26(分钟),根据函数图象可得当x>20时,y2<y1更省钱,∴小刘选择B种电动车更省钱,故答案为:B.②设y1=k1x,将(20,8)代入得,8=20k1,解得:k1=,∴y1=x,当0<x≤10时,y2=6,当x>10时,设y2=k2x+b2,将(10,6)、(20,8)代入得,,解得:,∴y2=x+4,依题意,当0<x<10时,y2﹣y1=4,即6﹣x=4,解得:x=5,当x>10时,|y2﹣y1|=4,即|x+4﹣x|=4,解得:x=0(舍去)或x=40,故答案为:5或40.【点评】本题考查了二元一次方程组的应用,一次函数的应用,找到等量关系是解题的关键.26.(10分)如图1,O是正方形ABCD对角线上一点,以O为圆心,OC长为半径的⊙O与AD相切于点E,与AC相交于点F.(1)求证:AB与⊙O相切;(2)若正方形ABCD的边长为+1,求⊙O的半径;(3)如图2,在(2)的条件下,若点M是半径OC上的一个动点,过点M作MN⊥OC交于点N.当CM:FM=1:4时,求CN的长.【解答】(1)证明:如图,连接OE,过点O作OG⊥AB于点G,∵⊙O与AD相切于点E,∴OE⊥AD,∵四边形ABCD是正方形,AC是正方形的对角线,∴∠BAC=∠DAC=45°,∴OE=OG,∵OE为⊙O的半径,∴OG为⊙O的半径,∵OG⊥AB,∴AB与⊙O相切;(2)解:如图,∵AC为正方形ABCD的对角线,∴∠DAC=45°,∵⊙O与AD相切于点E,∴∠AEO=90°,∴由(1)可知AE=OE,设AE=OE=OC=OF=R,在Rt△AEO中,∵AE2+EO2=AO2,∴AO2=R2+R2,∵R>0,∴,又∵正方形ABCD的边长为+1,在Rt△ADC中,∴,∵OA+OC=AC,∴,∴,∴⊙O的半径为;(3)解:如图,连接FN,ON,设CM=k,∵CM:FM=1:4,∴CF=5k,∴OC=ON=2.5k,∴OM=OC﹣CM=1.5k,在Rt△OMN中,由勾股定理得:MN=2k,在Rt△CMN中,由勾股定理得:,又∵,∴,∴.【点评】本题考查了圆的综合应用,其中掌握圆的相关知识点、正方形的性质、角平分线性质勾股定理的计算等知识点的应用是本题的解题关键.27.(10分)综合与实践问题情境在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片△ABC和△DEF满足∠ACB=∠EDF=90°,AC=BC=DF=DE=2cm.下面是创新小组的探究过程.操作发现(1)如图1,取AB的中点O,将两张纸片放置在同一平面内,使点O与点F重合.当旋转△DEF纸片交AC边于点H、交BC边于点G时,设AH=x(1<x<2),BG=y,请你探究出y与x的函数关系式,并写出解答过程.问题解决(2)如图2,在(1)的条件下连接GH,发现△CGH的周长是一个定值.请你写出这个定值,并说明理由.拓展延伸(3)如图3,当点F在AB边上运动(不包括端点A、B),且始终保持∠AFE=60°.请你直接写出△DEF纸片的斜边EF与△ABC纸片的直角边所夹锐角的正切值2+或2﹣(结果保留根号).【解答】解:(1)如图:∵∠ACB=∠EDF=90°,且AC=BC=DF=DE=2cm,∴∠A=∠B=∠DFE=45°,∴∠AFH+∠BFG=∠BFG+∠FGB=135°,∴∠AFH=∠FGB,∴△AFH∽△BGF,∴,∴AH•BG=AF•BF,在Rt△ACB中,AC=BC=2,∴,∵O是AB的中点,点O与点F重合,∴,∴,∴,∴y与x的函数关系式为;(2)△CGH的周长定值为2,理由如下:∵AC=BC=2,AH=x,BG=y,∴CH=2﹣x,CG=2﹣y,在Rt△HCG中,∴===,将(1)中xy=2代入得:=,∵1<x<2,y=,∴1<y<2,∴x+y>2,∴GH=x+y﹣2,∴△CHG的周长=CH+CG+GH=2﹣x+2﹣y+x+y﹣2=2;(3)①过点F作FN⊥AC于点N,作FH的垂直平分线交FN于点M,连接MH,如图:∵∠AFE=60°,∠A=45°,∴∠AHF=75°,∴FM=MH,∵∠FNH=90°,∴∠NFH=15°,∵FM=MH,∴∠NFH=∠MHF=15°,∴∠NMH=30°,在Rt△MNH中,设NH=k,∴MH=MF=2k,∴MN==k,∴FN=MF+MN=(2+)k,在Rt△FNH中,;②过点F作FN⊥BC于点N,作FG的垂直平分线交BG于点M,连接FM,∵∠AFE=60°,∠B=45°,∴∠FGB=∠AFE﹣∠B=15°,∵GM=MF,∴∠FGB=∠GFM=15°,∴∠FMB=30°,在Rt△FNM中,设FN=k,∴GM=MF=2k,由勾股定理得MN==k,∴GN=GM+MN=(2+)k,在Rt△FNG中,,综上所述,tan或,故答案为:2+或2﹣.【点评】本题考查几何变换综合应用,涉及相似三角形判定与性质,等腰直角三角形性质及应用,锐角三角函数,勾股定理及应用等知识,解题的关键是作辅助线,构造直角三角形解决问题.28.(11分)综合与探究如图,在平面直角坐标系中,已知抛物线y=﹣x2+bx+c与直线相交于A,B两点,其中点A(3,4),B (0,1).(1)求该抛物线的函数解析式;(2)过点B作BC∥x轴交抛物线于点C.连接AC,在抛物线上是否存在点P使tan∠BCP=tan∠ACB.若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.(提示:依题意补全图形,并解答)(3)将该抛物线向左平移2个单位长度得到y1=a1x2+b1x+c1(a1≠0),平移后的抛物线与原抛物线相交于点D,点E为原抛物线对称轴上的一点,F是平面直角坐标系内的一点,当以点B,D,E,F为顶点的四边形是菱形时,请直接写出点F的坐标.【解答】解:(1)∵抛物线y=﹣x2+bx+c过点A(3,4),B(0,1),∴,解得:,∴该抛物线的函数解析式为y=﹣x2+4x+1;(2)存在.理由如下:∵BC∥x轴,且B(0,1),∴点C的纵坐标为1,∴1=﹣x2+4x+1,解得:x1=0(舍去),x2=4,∴C(4,1),过点A作AQ⊥BC于Q,设直线CP交y轴于点M,如图,在Rt△ACQ中,∵A(3,4),∴Q(3,1),∵tan∠BCP=tan∠ACB,∴tan∠BCP=×=×=,∵BC=4,∠CBM=90°,∴=tan∠BCP=,∴BM=BC=×4=2,∴|y M﹣1|=2,∴y M=3或﹣1,∴M1(0,3),M2(0,﹣1),∴直线CM1的解析式为y=﹣x+3,直线CM2的解析式为y=x﹣1,由,解得,(舍去),由,解得,(舍去),∴P1(,),P2(﹣,﹣),综上所述,满足条件的点P的坐标为P1(,),P2(﹣,﹣);(3)∵y=﹣x2+4x+1=﹣(x﹣2)2+5,∴原抛物线的对称轴为直线x=2,顶点坐标为(2,5),∵将该抛物线向左平移2个单位长度得到新抛物线y′,∴y′=﹣x2+5,联立得,解得:,∴D(1,4),又B(0,1),设E(2,t),F(m,n),当BD、EF为对角线时,则,解得:,∴F(﹣1,3);当BE、DF为对角线时,则,解得:或,∴F(1,4)与点D重合,不符合题意,舍去,或F(1,﹣2);当BF、DE为对角线时,则,解得:或,∴F(3,4﹣)或F(3,4+);综上所述,点F的坐标为(﹣1,3)或(1,﹣2)或(3,4﹣)或(3,4+).。
2024年黑龙江省绥化市中考数学试题(解析版)

二〇二四年绥化市初中毕业学业考试数学试题考生注意:1.考试时间120分钟2.本试题共三道大题,28个小题,总分120分3.所有答案都必须写在答题卡上所对应的题号后的指定区域内一、单项选择题(本题共12个小题,每小题3分,共36分)请在答题卡上用2B 铅笔将你的选项所对应的方框涂黑1.实数12025-的相反数是()A.2025B.2025- C.12025-D.12025【答案】D 【解析】【分析】本题考查了相反数的定义,熟练掌握相反数的定义是解题的关键.【详解】解:实数12025-的相反数是12025,故选:D .2.下列所述图形中,是轴对称图形但不是中心对称图形的是()A.圆B.菱形C.平行四边形D.等腰三角形【答案】D 【解析】【分析】根据轴对称图形与中心对称图形的概念进行判断即可.【详解】A 、是轴对称图形,也是中心对称图形,故此选项错误;B 、是轴对称图形,也是中心对称图形,故此选项错误;C 、不是轴对称图形,是中心对称图形,故此选项错误;D 、是轴对称图形,不是中心对称图形,故此选项正确,故选D .【点睛】本题考查了中心对称图形与轴对称图形的概念.辨别轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;.辨别中心对称图形的关键是要寻找对称中心,旋转180度后与原图重合.3.某几何体是由完全相同的小正方体组合而成,下图是这个几何体的三视图,那么构成这个几何体的小正方体的个数是()A.5个B.6个C.7个D.8个【答案】A 【解析】【分析】此题主考查了三视图,由主视图易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由主视图和左视图可得第二层立方体的个数,相加即可.【详解】解:由三视图易得最底层有3个正方体,第二层有2个正方体,那么共有325+=个正方体组成.故选:A .4.23m -有意义,则m 的取值范围是()A.23m ≤B.32m ≥-C.32m ≥D.23m ≤-【答案】C 【解析】【分析】本题考查了二次根式有意义的条件,根据题意可得230m -≥,即可求解.23m -有意义,∴230m -≥,解得:32m ≥,故选:C .5.下列计算中,结果正确的是()A.()2139--=B.()222a b a b +=+C.93=± D.()3263x y x y -=【答案】A 【解析】【分析】本题考查了负整数指数幂,完全平方公式,算术平方根,积的乘方,据此逐项分析计算,即可求解.【详解】解:A.()2139--=,故该选项正确,符合题意;B.()2222a b a ab b +=++,故该选项不正确,不符合题意;C.3=,故该选项不正确,不符合题意;D.()3263x y x y -=-,故该选项不正确,不符合题意;故选:A .6.小影与小冬一起写作业,在解一道一元二次方程时,小影在化简过程中写错了常数项,因而得到方程的两个根是6和1;小冬在化简过程中写错了一次项的系数,因而得到方程的两个根是2-和5-.则原来的方程是()A.2650x x ++=B.27100x x -+=C.2520x x -+=D.26100x x --=【答案】B 【解析】【分析】本题考查了一元二次方程根与系数的关系,根据题意得出原方程中127x x +=,1210x x =,逐项分析判断,即可求解.【详解】解:∵小影在化简过程中写错了常数项,得到方程的两个根是6和1;∴12617x x +=+=,又∵写错了一次项的系数,因而得到方程的两个根是2-和5-.∴1210x x =A.2650x x ++=中,126x x +=-,125x x =,故该选项不符合题意;B.27100x x -+=中,127x x +=,1210x x =,故该选项符合题意;C.2520x x -+=中,125x x +=,122x x =,故该选项不符合题意;D.26100x x --=中,126x x +=,1210x x =-,故该选项不符合题意;故选:B .7.某品牌女运动鞋专卖店,老板统计了一周内不同鞋码运动鞋的销售量如表:鞋码3637383940平均每天销售量/双1012201212如果每双鞋的利润相同,你认为老板最关注的销售数据是下列统计量中的()A.平均数B.中位数C.众数D.方差【分析】此题主要考查统计的有关知识,了解平均数、中位数、众数、方差的意义;平均数、中位数、众数是描述一组数据集中程度的统计量;方差是描述一组数据离散程度的统计量.销量大的尺码就是这组数据的众数.【详解】解:由于众数是数据中出现次数最多的数,故老板最关注的销售数据的统计量是众数.故选:C .8.一艘货轮在静水中的航速为40km /h ,它以该航速沿江顺流航行120km 所用时间,与以该航速沿江逆流航行80km 所用时间相等,则江水的流速为()A.5km /hB.6km /hC.7km /hD.8km /h【答案】D 【解析】【分析】此题主要考查了分式方程的应用,利用顺水速=静水速+水速,逆水速=静水速-水速,设未知数列出方程,解方程即可求出答案.【详解】解:设江水的流速为km/h x ,根据题意可得:120804040x x=+-,解得:8x =,经检验:8x =是原方程的根,答:江水的流速为8km/h .故选:D .9.如图,矩形OABC 各顶点的坐标分别为()0,0O ,()3,0A ,()3,2B ,()0,2C ,以原点O 为位似中心,将这个矩形按相似比13缩小,则顶点B 在第一象限对应点的坐标是()A.()9,4 B.()4,9 C.31,2⎛⎫⎪⎝⎭D.21,3⎛⎫⎪⎝⎭【分析】本题考查了位似图形的性质,根据题意B 的坐标乘以13,即可求解.【详解】解:依题意,()3,2B ,以原点O 为位似中心,将这个矩形按相似比13缩小,则顶点B 在第一象限对应点的坐标是21,3⎛⎫ ⎪⎝⎭故选:D .10.下列叙述正确的是()A.顺次连接平行四边形各边中点一定能得到一个矩形B.平分弦的直径垂直于弦C.物体在灯泡发出的光照射下形成的影子是中心投影D.相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等【答案】C 【解析】【分析】本题考查了矩形的判定,垂径定理,中心投影,弧、弦与圆心角的关系,根据相关定理逐项分析判断,即可求解.【详解】A.顺次连接平行四边形各边中点不一定能得到一个矩形,故该选项不正确,不符合题意;B.平分弦(非直径)的直径垂直于弦,故该选项不正确,不符合题意;C.物体在灯泡发出的光照射下形成的影子是中心投影,故该选项正确,符合题意;D.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦心距也相等,故该选项不正确,不符合题意;故选:C .11.如图,四边形ABCD 是菱形,5CD =,8BD =,AE BC ⊥于点E ,则AE 的长是()A.245B.6C.485D.12【答案】A【分析】本题考查了勾股定理,菱形的性质,根据勾股定理求得OC ,进而得出6AC =,进而根据等面积法,即可求解.【详解】解:∵四边形ABCD 是菱形,5CD =,8BD =,∴142DO BD ==,AC BD ⊥,5BC CD ==,在Rt CDO △中,3CO ==,∴26AC OC ==,∵菱形ABCD 的面积为12AC BD BC AE ⨯=⨯,∴18624255AE ⨯⨯==,故选:A .12.二次函数()20y ax bx c a =++≠的部分图象如图所示,对称轴为直线=1x -,则下列结论中:①0b c>②2am bm a b +≤-(m 为任意实数)③31a c +<④若()1,M x y 、()2,N x y 是抛物线上不同的两个点,则123x x +≤-.其中正确的结论有()A.1个B.2个C.3个D.4个【答案】B 【解析】【分析】本题考查了二次函数的图象的性质,根据抛物线的开口方向,对称轴可得a<0,20b a =<即可判断①,=1x -时,函数值最大,即可判断②,根据1x =时,0y <,即可判断③,根据对称性可得122x x +=-即可判段④,即可求解.【详解】解:∵二次函数图象开口向下∴a<0∵对称轴为直线=1x -,∴12bx a=-=-∴20b a =<∵抛物线与y 轴交于正半轴,则0c >∴0bc<,故①错误,∵抛物线开口向下,对称轴为直线=1x -,∴当=1x -时,y 取得最大值,最大值为a b c -+∴2am bm c a b c ++≤-+(m 为任意实数)即2am bm a b +≤-,故②正确;∵1x =时,0y <即0a b c ++<∵2b a =∴20a a c ++<即30a c +<∴31a c +<,故③正确;∵()1,M x y 、()2,N x y 是抛物线上不同的两个点,∴,M N 关于=1x -对称,∴1212x x +=-即122x x +=-故④不正确正确的有②③故选:B二、填空题(本题共10个小题,每小题3分,共30分)请在答题卡上把你的答案写在所对应的题号后的指定区域内13.中国的领水面积约为370000km 2,将数370000用科学记数法表示为:__________.【答案】3.7×105【解析】【详解】科学记数法是指:a ×10n ,且1≤a <10,n 为原数的整数位数减一,370000=3.7×510.故答案为:3.7×105.14.分解因式:2228mx my -=______.【答案】()()222m x y x y +-【解析】【分析】本题考查了因式分解,先提公因式2m ,然后根据平方差公式因式分解,即可求解.【详解】解:2228mx my -=()2224m x y -=()()222m x y x y +-故答案为:()()222m x y x y +-.15.如图,AB CD ∥,33C ∠=︒,OC OE =.则A ∠=______︒.【答案】66【解析】【分析】本题考查了平行线的性质,等边对等角,三角形外角的性质,根据等边对等角可得33E C ∠=∠=︒,根据三角形的外角的性质可得66DOE ∠=︒,根据平行线的性质,即可求解.【详解】解:∵OC OE =,33C ∠=︒,∴33E C ∠=∠=︒,∴66DOE E C ∠=∠+∠=︒,∵AB CD ∥,∴66A DOE =∠=︒∠,故答案为:66.16.如图,用热气球的探测器测一栋楼的高度,从热气球上的点A 测得该楼顶部点C 的仰角为60︒,测得底部点B 的俯角为45︒,点A 与楼BC 的水平距离50m AD =,则这栋楼的高度为______m (结果保留根号).【答案】(50+##()50+【解析】【分析】本题考查解直角三角形—仰角俯角问题.注意准确构造直角三角形是解答此题的关键.根据题意得456050m BAD CAD AD ∠=︒∠=︒=,,,然后利用三角函数求解即可.【详解】解:依题意,456050m BAD CAD AD ∠=︒∠=︒=,,.在Rt △ABD 中,tan 4550150m BD AD =⋅︒=⨯=,在Rt ACD △中,tan 6050CD AD =⋅︒==,∴(m 50BC BD CD =+=+.故答案为:(50+.17.计算:22x y xy y x x x ⎛⎫--÷-= ⎪⎝⎭_________.【答案】1x y-【解析】【分析】本题考查了分式的混合运算.先算括号内的减法,把除法变成乘法,再根据分式的乘法法则进行计算即可.【详解】解:22x y xy y x x x ⎛⎫--÷- ⎪⎝⎭222x y x xy y x x--+=÷2()x y x x x y -=-1x y=-,故答案为:1x y-.18.用一个圆心角为126︒,半径为10cm 的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为______cm .【答案】72【解析】【分析】本题考查了弧长公式,根据圆锥的底面圆的周长等于侧面的弧长,代入数据计算,即可求解.【详解】解:设这个圆锥的底面圆的半径为cm R ,由题意得,12610π2π180R ⨯⨯=解得:7cm 2R =故答案为:72.19.如图,已知点()7,0A -,(),10B x ,()17,C y -,在平行四边形ABCO 中,它的对角线OB 与反比例函数()0ky k x=≠的图象相交于点D ,且:1:4OD OB =,则k =______.【答案】15-【解析】【分析】本题考查了反比例函数与平行四边形综合,相似三角形的性质与判定,分别过点,B D ,作x 的垂线,垂足分别为,F E ,根据平行四边形的性质得出()2410B -,,证明ODE OBF △∽△得出6OE =,2.5DE =,进而可得()6,2.5D -,即可求解.【详解】如图所示,分别过点,B D ,作x 的垂线,垂足分别为,F E ,∵四边形AOCB 是平行四边形,点()7,0A -,(),10B x ,()17,C y -,∴7OA BC ==,∴24x =-,即()2410B -,,则24OF =,10BF =∵DE x ⊥轴,BF x ⊥轴,∴DE BF∥∴ODE OBF △∽△∴14OE OD DE OF OB BF ===∴6OE =, 2.5DE =∴()6,2.5D -∴6 2.515k =-⨯=-故答案为:15-.20.如图,已知50AOB ∠=︒,点P 为AOB ∠内部一点,点M 为射线OA 、点N 为射线OB 上的两个动点,当PMN 的周长最小时,则MPN ∠=______.【答案】80︒##80度【解析】【分析】本题考查了轴对称-最短路线问题,等腰三角形的性质,三角形内角和定理的应用;作关于OA ,OB 的对称点12P P ,.连接12OP OP ,.则当M ,N 是12PP 与OA ,OB 的交点时,PMN 的周长最短,根据对称的性质可以证得:150OPM OPM ∠=∠=︒,12OP OP OP ==,根据等腰三角形的性质即可求解.【详解】解:作P 关于OA ,OB 的对称点12P P ,.连接12OP OP ,.则当M ,N 是12PP 与OA ,OB 的交点时,PMN 的周长最短,连接12PO P O 、,1PP 关于OA 对称,∴11112POP MOP OP OP PM PM OPM OPM ∠=∠==∠=∠,,,同理,222P OP NOP OP OP ∠=∠=,,12122(210)0POP POP P OP MOP NOP AOB ∴∠=∠+∠=∠+∠=∠=︒,12OP OP OP ==,∴12POP △是等腰三角形.∴2140OP N OPM ∠=∠=︒,∴2180MPN MPO NPO OP N OPM ∠=∠+∠=∠+∠=︒故答案为:80︒.21.如图,已知(11,A ,(23,A ,()34,0A ,()46,0A ,(5A ,(6A ,()710,0A ,(811,A …,依此规律,则点2024A 的坐标为______.【答案】(2891,【解析】【分析】本题考查了点坐标的规律探究.解题的关键在于根据题意推导出一般性规律.根据题意可知7个点坐标的纵坐标为一个循环,7n A 的坐标为()10,0n ,据此可求得2024A 的坐标.【详解】解:∵(11,A ,(23,A ,()34,0A ,()46,0A ,(5A ,(6A ,()710,0A ,(811,A …,,∴可知7个点坐标的纵坐标为一个循环,7n A 的坐标为()10,0n ,(71101,n A n ++∵202472891÷=⋅⋅⋅,∴2023A 的坐标为()2890,0.∴2024A 的坐标为(2891,故答案为:(2891,.22.在矩形ABCD 中,4cm AB =,8cm BC =,点E 在直线AD 上,且2cm DE =,则点E 到矩形对角线所在直线的距离是______cm .【答案】255或655或25【解析】【分析】本题考查了矩形的性质,解直角三角形,设,AC BD 交于点O ,点1E 在线段AD 上,2E 在AD 的延长线上,过点AC 作AC ,BD 的垂线,垂足分别为123,,F F F ,进而分别求得垂线段的长度,即可求解.【详解】解:∵四边形ABCD 是矩形,4AB =,8BC =,∴8AD BC ==,4CD AB ==,∴22224845AC AD CD =+=+=∴45sin 545CD CAD AC ∠===,825cos 545CAD ∠==,41tan 82CAD ∠==如图所示,设,AC BD 交于点O ,点1E 在线段AD 上,2E 在AD 的延长线上,过点AC 作AC ,BD 的垂线,垂足分别为123,,F F F ∵AO DO=∴OAD ODA∠=∠当E 在线段AD 上时,∴1826AE AD DE =-=-=在11Rt AE F 中个,111565sin 655E F AE CAD =⋅∠==∵OAD ODA∠=∠在12Rt E F D 中,12112525sin 255E F DE E DF =∠=⨯=;当E 在射线AD 上时,在2Rt DCE 中,221tan 42DCE ∠==∴CAD DCE∠=∠∴90DCE DCA ∠+∠=︒∴2E C AC⊥∴2E C ===在23Rt DE F中,232232sin 55E F DE E DF DE =⨯∠=⨯=综上所述,点E 到对角线所在直线的距离为:255或5或或655或三、解答题(本题共6个小题,共54分)请在答题卡上把你的答案写在所对应的题号后的指定区域内23.已知:ABC.(1)尺规作图:画出ABC 的重心G .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,连接AG ,BG .已知ABG 的面积等于25cm ,则ABC 的面积是______2cm .【答案】(1)见解析(2)15【解析】【分析】本题考查了三角形重心的性质,画垂线;(1)分别作,BC AC 的中线,交点即为所求;(2)根据三角形重心的性质可得23ABG ABD S S = ,根据三角形中线的性质可得2215cm ABC ABD S S == 【小问1详解】解:作法:如图所示①作BC 的垂直平分线交BC 于点D②作AC 的垂直平分线交AC 于点F③连接AD 、BF 相交于点G④标出点G ,点G 即为所求【小问2详解】解:∵G 是ABC 的重心,∴23AG AD =∴23ABG ABD S S = ∵ABG 的面积等于25cm ,∴27.5cm ABD S = 又∵D 是BC 的中点,∴2215cmABC ABD S S == 故答案为:15.24.为了落实国家“双减”政策,某中学在课后服务时间里,开展了音乐、体操、诵读、书法四项社团活动.为了了解七年级学生对社团活动的喜爱情况,该校从七年级全体学生中随机抽取了部分学生进行“你最喜欢哪一项社团活动”的问卷调查,每人必须选择一项社团活动(且只能选择一项).根据调查结果,绘制成如下两幅统计图.请根据统计图中的信息,解答下列问题:(1)参加本次问卷调查的学生共有______人.(2)在扇形统计图中,A组所占的百分比是______,并补全条形统计图.(3)端午节前夕,学校计划进行课后服务成果展示,准备从这4个社团中随机抽取2个社团汇报展示.请用树状图法或列表法,求选中的2个社团恰好是B和C的概率.【答案】(1)60(2)30%,作图见解析(3)1 6【解析】【分析】本题考查了条形统计图与扇形统计图信息关联,列表法或画树状图法求概率;(1)根据D组的人数除以占比得出总人数;(2)根据总人数求得A组的人数,进而求得占比,以及补全统计图;(3)根据列表法或画树状图法求概率,即可求解.【小问1详解】解:参加本次问卷调查的学生共有1220%60÷=(人);【小问2详解】解:A组人数为6020101218---=人A组所占的百分比为:18100%30% 60⨯=补全统计图如图所示,【小问3详解】画树状图法如下图列表法如下图A B C DA(),B A(),C A(),D AB(),A B(),C B(),D BC(),A C(),B C(),D CD(),A D(),B D(),C D由树状图法或列表法可以看出共有12种结果出现的可能性相等,选中的2个社团恰好是B和C的情况有两种.∴P(选中的2个社团恰好是B和C)21 126 ==.25.为了响应国家提倡的“节能环保”号召,某共享电动车公司准备投入资金购买A、B两种电动车.若购买A种电动车25辆、B种电动车80辆,需投入资金30.5万元;若购买A种电动车60辆、B种电动车120辆,需投入资金48万元.已知这两种电动车的单价不变.(1)求A、B两种电动车的单价分别是多少元?(2)为适应共享电动车出行市场需求,该公司计划购买A、B两种电动车200辆,其中A种电动车的数量不多于B种电动车数量的一半.当购买A种电动车多少辆时,所需的总费用最少,最少费用是多少元?(3)该公司将购买的A、B两种电动车投放到出行市场后,发现消费者支付费用y元与骑行时间minx之间的对应关系如图.其中A种电动车支付费用对应的函数为1y;B种电动车支付费用是10min之内,起步价6元,对应的函数为2y.请根据函数图象信息解决下列问题.①小刘每天早上需要骑行A 种电动车或B 种电动车去公司上班.已知两种电动车的平均行驶速度均为300m /min (每次骑行均按平均速度行驶,其它因素忽略不计),小刘家到公司的距离为8km ,那么小刘选择______种电动车更省钱(填写A 或B ).②直接写出两种电动车支付费用相差4元时,x 的值______.【答案】(1)A 、B 两种电动车的单价分别为1000元、3500元(2)当购买A 种电动车66辆时所需的总费用最少,最少费用为535000元(3)①B②5或40【解析】【分析】本题考查了二元一次方程组的应用,一元一次不等式的应用,一次函数的应用;(1)设A 、B 两种电动车的单价分别为x 元、y 元,根据题意列二元一次方程组,解方程组,即可求解;(2)设购买A 种电动车m 辆,则购买B 种电动车()200m -辆,根据题意得出m 的范围,进而根据一次函数的性质,即可求解;(3)①根据函数图象,即可求解;②分别求得12,y y 的函数解析式,根据214y y -=,解方程,即可求解.【小问1详解】解:设A 、B 两种电动车的单价分别为x 元、y 元由题意得,258030500060120480000x y x y +=⎧⎨+=⎩解得10003500x y =⎧⎨=⎩答:A 、B 两种电动车的单价分别为1000元、3500元【小问2详解】设购买A 种电动车m 辆,则购买8种电动车()200m -辆,由题意得:()12002m m ≤-解得:2003m ≤设所需购买总费用为w 元,则()100035002002500700000w m m m =+-=-+25000-< ,w 随着m 的增大而减小,m 取正整数66m ∴=时,w 最少∴700000250066535000w =-⨯=最少(元)答:当购买A 种电动车66辆时所需的总费用最少,最少费用为535000元【小问3详解】解:①∵两种电动车的平均行驶速度均为300m /min ,小刘家到公司的距离为8km ,∴所用时间为80002263003=分钟,根据函数图象可得当20x >时,21y y <更省钱,∴小刘选择B 种电动车更省钱,故答案为:B .②设11y k x =,将()20,8代入得,1820k =解得:25k =∴125y x =;当010x <≤时,26y =,当10x >时,设222y k x b =+,将()10,6,()20,8代入得,2222610820k b k b =+⎧⎨=+⎩解得:22154k b ⎧=⎪⎨⎪=⎩∴2145y x =+依题意,当010x <<时,214y y -=即2645x -=解得:5x =当10x >时,214y y -=即124455x x +-=解得:0x =(舍去)或40x =故答案为:5或40.26.如图1,O 是正方形ABCD 对角线上一点,以O 为圆心,OC 长为半径的O 与AD 相切于点E ,与AC 相交于点F .(1)求证:AB 与O 相切.(2)若正方形ABCD 1,求O 的半径.(3)如图2,在(2)的条件下,若点M 是半径OC 上的一个动点,过点M 作MN OC ⊥交 CE 于点N .当:1:4CM FM =时,求CN 的长.【答案】(1)证明见解析(2(3)2105【解析】【分析】(1)方法一:连接OE ,过点O 作OG AB ⊥于点G ,四边形ABCD 是正方形,AC 是正方形的对角线,得出OE OG =,进而可得OG 为O 的半径,又OG AB ⊥,即可得证;方法二:连接OE ,过点O 作OG AB ⊥于点G ,根据正方形的性质证明()AAS AOE AOG ≌得出OE OG =,同方法一即可得证;方法三:过点O 作OG AB ⊥于点G ,连接OE .得出四边形AEOG 为正方形,则OE OG =,同方法一即可得证;(2)根据O 与AD 相切于点E ,得出90AEO ∠=︒,由(1)可知AE OE =,设AE OE OC OF R ====,在Rt AEO △中,勾股定理得出AO =,在Rt ADC 中,勾股定理求得AC ,进而根据OA OC AC +=建立方程,解方程,即可求解.(3)方法一:连接ON ,设CM k =,在Rt OMN △中,由勾股定理得:2MN k =,在Rt CMN 中,由勾股定理得:CN =,结合题意522FC k R ====得出225k =,即可得出CN =;方法二:连接FN ,证明CNM CFN ∽△△得出2CN CM CF =⋅,进而可得12255CM CF ==,同理可得CN方法三:连接FN ,证明CNM CFN ∽△△得出2NC MC FC =⋅,设CM k =,则5FC k =,进而可得NC =,进而同方法一,即可求解.【小问1详解】方法一:证明:连接OE ,过点O 作OG AB ⊥于点G ,O 与AD 相切于点E ,∴OE AD ⊥.四边形ABCD 是正方形,AC 是正方形的对角线,∴45BAC DAC ∠=∠=︒,∴OE OG =,OE 为O 的半径,OG ∴为O 的半径,OG AB ⊥,AB ∴与O 相切.方法二:证明:连接OE ,过点O 作OG AB ⊥于点G ,O 与AD 相切于点E ,∴OE AD ⊥,∴90AEO AGO ∠=∠=︒,四边形ABCD 是正方形,∴45BAC DAC ∠=∠=︒,又 AO AO =,∴()AAS AOE AOG ≌,∴OE OG =,OE 为O 的半径,OG ∴为O 的半径,OG AB ⊥,AB ∴与O 相切.方法三:证明:过点O 作OG AB ⊥于点G ,连接OE .AD 与O 相切,OE 为O 半径,∴OE AE ⊥,∴90AEO ∠=︒,OG AB ⊥,∴90AGO ∠=︒,又 四边形ABCD 为正方形,∴90BAD ∠=︒,∴四边形AEOG 为矩形,又AC 为正方形的对角线,∴45EAO GAO AOE ∠=∠=∠=︒,∴OE AE =,∴矩形AEOG 为正方形,∴OE OG =.又OE 为O 的半径,OG ∴为O 的半径,又 OG AB ⊥,AB ∴与O 相切.【小问2详解】解:AC 为正方形ABCD 的对角线,∴45DAC ∠=︒,O 与AD 相切于点E ,∴90AEO ∠=︒,∴由(1)可知AE OE =,设AE OE OC OF R ====,在Rt AEO △中,222AE EO AO +=,∴222AO R R =+,0R >,∴AO =,又 正方形ABCD 1.在Rt ADC 中,∴)1AC ==+, OA OC AC +=,∴)1R +=,∴R =.∴O 的半径为.【小问3详解】方法一:解:连接ON ,设CM k =,:1:4CM FM =,∴5CF k =,∴ 2.5OC ON k ==,∴ 1.5OM OC CM k =-=.在Rt OMN △中,由勾股定理得:2MN k =,在Rt CMN 中,由勾股定理得:CN =,又 522FC k R ====,∴225k =.∴55CN ==.方法二:解:连接FN ,CF 为O 的直径,∴90CNF ∠=︒,∴90FNM CNM ∠+∠=︒,MN AC ⊥,∴90NFM FNM ∠+∠=︒,∴NFM CNM ∠=∠,NCM FCN ∠=∠,∴CNM CFN ∽△△,∴2CN CM CF =⋅,:1:4CM FM =,5CF CM =,∴CN =, 22CF R ===∴12255CM CF ==,方法三:解:连接FN ,CF 为O 的直径,∴90CNF ∠=︒,∴90FNM CNM ∠+∠=︒,MN AC ⊥,∴90NFM FNM ∠+∠=︒,∴NFM CNM ∠=∠,NCM FCN ∠=∠,∴CNM CFN ∽△△,∴NC FC MC NC=,∴2NC MC FC =⋅,:1:4CM FM =,∴:1:5CM FC =,设CM k =,则5FC k =,∴25NC k k =⨯,∴NC =.又 522FC k R ====,∴225k =,【点睛】本题考查了切线的性质与判定,正方形的性质,全等三角形的性质与判定,勾股定理,垂径定理,相似三角形的性质与判定,正确的添加辅助线是解题的关键.27.综合与实践问题情境在一次综合与实践课上,老师让同学们以两个全等的等腰直角三角形纸片为操作对象.纸片ABC 和DEF 满足90ACB EDF ∠=∠=︒,2cm AC BC DF DE ====.下面是创新小组的探究过程.操作发现(1)如图1,取AB 的中点O ,将两张纸片放置在同一平面内,使点O 与点F 重合.当旋转DEF 纸片交AC 边于点H 、交BC 边于点G 时,设()12AH x x =<<,BG y =,请你探究出y 与x 的函数关系式,并写出解答过程.问题解决(2)如图2,在(1)的条件下连接GH ,发现CGH 的周长是一个定值.请你写出这个定值,并说明理由.拓展延伸(3)如图3,当点F 在AB 边上运动(不包括端点A 、B ),且始终保持60AFE ∠=︒.请你直接写出DEF 纸片的斜边EF 与ABC 纸片的直角边所夹锐角的正切值______(结果保留根号).【答案】(1)()212y x x=<<,见解析;(2)2,见解析;(3)2+或2【解析】【分析】(1)根据题意证明AFH BGF ∽△△,得出关系式AH BG AF BF ⋅=⋅,进而求得AB AF BC ===,代入比例式,即可求解;(2)方法一:勾股定理求得GH ,将将(1)中2xy =代入得2GH x y =+-,进而根据三角形的周长公式,即可求解;方法二:证明AOH BGO ∽△△,HAO HOG ∽△△,过O 作OM AH ⊥交AH 于点M ,作OP HG ⊥交HG 于点P ,作ON GB ⊥交GB 于点N .证明OMH OPH △≌△,OPG ONG △≌△,得出HG MH GN =+,得出112CM CN BC ===,进而根据三角形的周长公式可得CHG △的周长2212CM CN CM =+==⨯=.方法三:过O 作OM AH ⊥交AH 于点M ,作ON GB ⊥交GB 于点N ,在NB 上截取一点Q ,使NQ MH =,连接OC .得出OMH ONQ △≌△,OHG OQG △≌△,则HG GQ GN MH ==+,同方法二求得112CM CN BC ===,进而即可求解;(3)分两种情况讨论,EF 于,AC BC 的夹角;①过点F 作FN AC ⊥于点N ,作FH 的垂直平分线交FN于点M ,连接MH ,在Rt MNH △中,设NH k =,由勾股定理得,(2FN MN MF k =+=+,进而根据正确的定义,即可求解;②过点F 作FN BC ⊥于点N ,作FG 的垂直平分线交BG 于点M ,连接FM ,在Rt FNM △中,设FN k =,同①即可求解..【详解】操作发现解:(1)∵90ACB EDF ∠=∠=︒,且2cm AC BC DF DE ====.∴45A B DFE ∠=∠=∠=︒,∴135AFH BFG BFG FGB ∠+∠=∠+∠=︒,∴AFH FGB ∠=∠,∴AFH BGF ∽△△,∴AF AH BG BF=,∴AH BG AF BF ⋅=⋅.在Rt ACB △中,2AC BC ==,∴AB ===∵O 是AB 的中点,点O 与点F 重合,∴AF BF ==,∴xy =,∴()212y x x=<<.问题解决(2)方法一:解:CGH 的周长定值为2.理由如下:∵2AC BC ==,AH x =,BG y =,∴2CH x =-,2CG y =-,在Rt HCG 中,∴GH ===.将(1)中2xy =代入得:∴2GH x y ===+-.∵()22222244x y x y xy x y +=++=++≥,又∵12x <<,∴2x y +>,∴2GH x y =+-.∵CHG △的周长CH CG GH =++,∴CHG △的周长2222x y x y =-+-++-=.方法二:解:CGH 的周长定值为2.理由如下:∵ABC 和DEF 是等腰直角三角形,∴45A B E EOD ∠=∠=∠=∠=︒,∵180AOH BOG EOD ∠+∠+∠=︒,∴135AOH BOG ∠+∠=︒,在AOH △中,45A ∠=︒,∴135AOH AHO ∠+∠=︒,∴AHO BOG ∠=∠,∴AOH BGO ∽△△,∴AO OH AH BG OG OB==,AOH OGB ∠=∠,AHO BOG ∠=∠,∵O 为AB 的中点,∴AO BO =,∴OH AH OG AO=,又∵45A EOD ∠=∠=︒,∴HAO HOG ∽△△,AHO OHG ∠=∠,OGB OGH ∠=∠,∴过O 作OM AH ⊥交AH 于点M ,作OP HG ⊥交HG 于点P ,作ON GB ⊥交GB 于点N .∴OM OP ON ==.又∵OH OH =,OG OG =,∴OMH OPH △≌△,OPG ONG △≌△,∴HM PH =,PG NG =,∴HG MH GN =+.∵CHG △的周长CH CG GH CH CG MH GN CM CN =++=+++=+.又∵AO OB =,OM ON =,45A B ∠=∠=︒,∴AOM BON ≌,∴AM BN =,∵90C ∠=︒,90AMO ∠=︒,∴OM BC ∥,∵O 是AB 的中点,∴点M 是AC 的中点,同理点N 是BC 的中点.∴112CM CN BC ===,∴CHG △的周长2212CM CN CM =+==⨯=.方法三:解:CGH 的周长定值为2.理由如下:过O 作OM AH ⊥交AH 于点M ,作ON GB ⊥交GB 于点N ,在NB 上截取一点Q ,使NQ MH =,连接OC .∵ABC 是等腰直角三角形,O 为AB 的中点,∴OC 平分ACB ∠,∴OM ON =,∴OMH ONQ △≌△,∴OH OQ =,MOH NOQ ∠=∠.∵45HOG Ð=°,90ACB ∠=︒,∴90MON ∠=︒,45MOH GON ∠+∠=︒,∴45GOQ ∠=︒,∴HOG GOQ ∠=∠,∵OG OG =,∴OHG OQG △≌△,∴HG GQ GN MH ==+,∴CHG △的周长CH CG GH CH CG MH GN CM CN =++=+++=+.又∵AO OB =,OM ON =,45A B ∠=∠=︒,∴AOM BON ≌,∴AM BN =.∵90C ∠=︒,90AMO ∠=︒,∴OM BC ∥.∵O 是AB 的中点,∴点M 是AC 的中点,同理点N 是BC 的中点.∴112CM CN BC ===,∴CHG △的周长2212CM CN CM =+==⨯=.拓展延伸(3)2+或2①解:∵60AFE ∠=︒,45A ∠=︒,∴75AHF ∠=︒,过点F 作FN AC ⊥于点N ,作FH 的垂直平分线交FN 于点M ,连接MH ,∴FM MH =,∵90FNH ∠=︒,∴15NFH ∠=︒,∵FM MH =,∴15NFH MHF ∠=∠=︒,∴=30NMH ∠︒,在Rt MNH △中,设NH k =,∴2MH MF k ==,由勾股定理得,MN ==,∴(2FN MN MF k =+=+,∴在Rt FNH △中,(2tan tan 752k FN FHNNH k +∠=︒===+②解:∵60AFE ∠=︒,45A ∠=︒,∴15FGB ∠=︒,过点F 作FN BC ⊥于点N ,作FG 的垂直平分线交BG 于点M ,连接FM .∵GM MF =,∴15FGB GFM ∠=∠=︒,∴30FMB ∠=︒,在Rt FNM △中,设FN k =,∴2GM MF k ==,由勾股定理得,MN ==,∴(2GN GM MN k =+=+,∴在Rt FNG △中,tan tan152FN FGN GN ∠=︒===-.∴tan 2FHN ∠=+或tan 2FGN ∠=.【点睛】本题考查了相似三角形的性质与判定,全等三角形的性质与判定,解直角三角形,旋转的性质,函数解析式,熟练掌握相似三角形的性质与判定,解直角三角形是解题的关键.28.综合与探究如图,在平面直角坐标系中,已知抛物线2y x bx c =-++与直线相交于A ,B 两点,其中点()3,4A ,()0,1B .(1)求该抛物线的函数解析式.(2)过点B 作BC x ∥轴交抛物线于点C ,连接AC ,在抛物线上是否存在点P 使1tan tan 6BCP ACB ∠=∠.若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.(提示:依题意补全图形,并解答)(3)将该抛物线向左平移2个单位长度得到()2111110y a x b x c a =++≠,平移后的抛物线与原抛物线相交于点D ,点E 为原抛物线对称轴上的一点,F 是平面直角坐标系内的一点,当以点B 、D 、E 、F 为顶点的四边形是菱形时,请直接写出点F 的坐标.【答案】(1)241y x x =-++(2)存在,点P 坐标为1111,24P ⎛⎫ ⎪⎝⎭,215,24P ⎛⎫-- ⎪⎝⎭,补图见解析(3)()11,3F -、(23,4F -、(33,4F +、()41,2F -【解析】【分析】(1)待定系数法求解析式即可求解;(2)根据平行线的性质可得2141c y x x ==-++,求得()4,1C ,进而分别求得()3,4A ,()3,1Q ,根据1tan tan 6BCP ACB ∠=∠可得1tan 2BCP ∠=,设直线CP 交y 轴于点M ,则()10,3M ,()20,1M -.进而可得1C M ,2CM 的解析式为1132CM y x =-+,2112CM y x =-,连接1C M 交抛物线于1P ,连接2CM 交抛物线于2P ,进而联立抛物线与直线解析式,解方程,即可求解.(3)①以BD 为对角线,如图作BD 的垂直平分线1ME 交BD 于点M 交直线2x =于1E ,设()12,E y ,根据两点距离公式可得2y =,根据中点坐标公式可得()11,3F -,②以BD 为边,如图以B 为圆心,BD 为半径画圆交直线2x =于点2E ,3E ;连接2BE ,3BE ,根据勾股定理求得2,BD BE ,进而得出(22,1E ,(32,1E +,根据平移的性质得出(23,4F ,(33,4F +,③以BD 为边,如图以点D 为圆心,BD 长为半径画圆交直线2x =于点4E 和5E ,连接4DE ,5DE ,则45DE DE BD ===,过点D 作45DH E E ⊥于点H ,则1DH =,在4Rt DHE △和5Rt DHE △中,由勾股定理得453HE HE ==,则()42,1E 、()52,7E ,根据45tan tan 3DBE E DH ∠=∠=,可得45DBE E DH ∠=∠,过点B 作44BF DE ∥,过4E 作44E F BD ∥,4BF 和44E F 相交于点4F ,4BE 的中点()1,1G .根据中点坐标公式可得()41,2F -;【小问1详解】解:∵把点()3,4A ,()0,1B 代入2y x bx c =-++得9341b c c -++=⎧⎨=⎩,解得41b c =⎧⎨=⎩,∴241y x x =-++.【小问2详解】存在.理由:∵BC x ∥轴且()0,1B ,∴2141c y x x ==-++,∴10x =(舍去),24x =,∴()4,1C .过点A 作AQ BC ⊥于点Q ,在Rt ACQ 中,∵()3,4A ,∴()3,1Q ,∵1tan tan 6BCP ACB ∠=∠,∴111tan 3662AQ BCP CQ ∠=⨯=⨯=.设直线CP 交y 轴于点M ,4BC =,90CBM ∠=︒,∴()10,3M ,()20,1M -.连接1C M 交抛物线于1P ,连接2CM 交抛物线于2P ,∴1C M ,2CM 的解析式为1132CM y x =-+,2112CM y x =-,∴1213241CM y x y x x ⎧=-+⎪⎨⎪=-++⎩,解得()12124x x ⎧=⎪⎨⎪=⎩舍去,或2211241CM y x y x x ⎧=-⎪⎨⎪=-++⎩,解得()34124x x ⎧=-⎪⎨⎪=⎩舍去.∴把112x =,312x =-代入241y x x =-++得1114y =,354y =-,∴1111,24P ⎛⎫ ⎪⎝⎭,215,24P ⎛⎫-- ⎪⎝⎭.综上所述,满足条件的点P 坐标为1111,24P ⎛⎫⎪⎝⎭,215,24P ⎛⎫-- ⎪⎝⎭.【小问3详解】()11,3F -、(23,4F、(33,4F +、()41,2F -.方法一:①以BD 为对角线,如图作BD 的垂直平分线1ME 交BD 于点M 交直线2x =于1E ∵()0,1B ,()1,4D ,∴15,22M ⎛⎫ ⎪⎝⎭.设()12,E y ,∵11DE BE =,∴()()22221421y y +-=+-,∴2y =,∴()12,2E ,∵M 是11E F 的中点,∴()11,3F -.。
2023年黑龙江省绥化市中考数学试卷含答案解析

绝密★启用前2023年黑龙江省绥化市中考数学试卷学校:___________姓名:___________班级:___________考号:___________注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上,写在试卷上无效。
3.考试结束后,本试卷和答题卡一并交回。
一、选择题(本大题共12小题,共36.0分。
在每小题列出的选项中,选出符合题目的一项) 1.下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.2.计算|−5|+20的结果是( ) A. −3B. 7C. −4D. 63.如图是一个正方体,被切去一角,则其左视图是( )A.B.C.D.4.纳米是非常小的长度单位,1nm=0.000000001m,把0.000000001用科学记数法表示为( )A. 1×10−9B. 1×10−8C. 1×108D. 1×1095.下列计算中,结果正确的是( )A. (−pq)3=p3q3B. x⋅x3+x2⋅x2=x8C. √ 25=±5D. (a2)3=a66.将一副三角板按如图所示摆放在一组平行线内,∠1=25°,∠2=30°,则∠3的度数为( )A. 55°B. 65°C. 70°D. 75°7.下列命题中叙述正确的是( )A. 若方差s甲2>s乙2,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上8.绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是( )A. 该组数据的样本容量是50人B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D. 110~120这组数据对应的扇形统计图的圆心角度数为51°9.在平面直角坐标系中,点A在y轴的正半轴上,AC平行于x轴,点B,C的横坐标都是3,BC=2,点D在AC上,且其横坐标为1,若反比例函数y=k(x>0)的图象x经过点B,D,则k的值是( )A. 1B. 2C. 3D. 3210.某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( )A. 14+12x=1 B. 14+12(14+1x)=1C. 14(1+12)+1x=1 D. 14+(14+12)1x=111.如图,在菱形ABCD中,∠A=60°,AB=4,动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A−B−C向终点C运动;点N以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是( )A. B.C. D.12.如图,在正方形ABCD中,点E为边CD的中点,连接AE,过点B作BF⊥AE于点F,连接BD交AE于点G,FH平分∠BFG交BD于点H.则下列结论中,正确的个数为( )①AB2=BF⋅AE②S△BGF:S△BAF=2:3③当AB=a时,BD2−BD⋅HD=a2A. 0个B. 1个C. 2个D. 3个二、填空题(本大题共10小题,共30.0分) 13.因式分解:x 2+xy −xz −yz = ______ . 14.若式子√ x+5x有意义,则x 的取值范围是______ .15.在4张完全相同的卡片上,分别标出1,2,3,4.从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是______ . 16.已知一元二次方程x 2+x =5x +6的两根为x 1与x 2,则1x 1+1x 2的值为______ .17.化简:(x+2x 2−2x −x−1x 2−4x+4)÷x−4x 2−2x= ______ .18.如图,⊙O 的半径为2cm ,AB 为⊙O 的弦,点C 为AB⏜上的一点,将AB ⏜沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为______ .(结果保留π与根号)19.如图,在平面直角坐标系中,△ABC 与△AB′C′的相似比为1:2,点A 是位似中心,已知点A(2,0),点C(a,b),∠C =90°.则点C′的坐标为______ .(结果用含a ,b 的式子表示)20.如图,△ABC 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60°得到CF.连接AF ,EF ,DF ,则△CDF 周长的最小值是______ .21.在求1+2+3+⋯+100的值时,发现:1+100=101,2+99=101…,从而得到1+2+3+⋯+100=101×50=5050.按此方法可解决下面问题.图(1)有1个三角形,记作a 1=1;分别连接这个三角形三边中点得到图(2),有5个三角形,记作a 2=5;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作a3=9;按此方法继续下去,则a1+a2+a3+⋯+a n=______ .(结果用含n的代数式表示)22.已知等腰△ABC,∠A=120°,AB=2.现将△ABC以点B为旋转中心旋转45°,得到△A′BC′,延长C′A′交直线BC于点D.则A′D的长度为______ .三、解答题(本大题共6小题,共54.0分。
绥化市中考数学试卷及答案

二○○八年绥化市初中毕业学业考试数 学 试 卷考生注意:1.考试时间120分钟2.全卷共三道大题,总分120分一、填空题(每空3分,满分33分)1.在抗震救灾过程中,共产党员充分发挥了先锋模范作用,截止5月28日17时,全国党员已缴纳特殊党费26.84亿元,用科学记数法表示为 元(结果保留两个有效数字). 2.函数31xy x -=-中,自变量x 的取值范围是 . 3.如图,BAC ABD ∠=∠,请你添加一个条件: ,使OC OD =(只添一个即可).4.如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm ,弧长是6πcm ,那么围成的圆锥的高度是 cm . 5.如图,某商场正在热销2008年北京奥运会的纪念品,小华买了一盒福娃和一枚奥运徽章,已知一盒福娃的价格比一枚奥运徽章的价格贵120元,则一盒福娃价格是 元.6.有一个正十二面体,12个面上分别写有1~12这12个整数,投掷这个正十二面体一次,向上一面的数字是3的倍数或4的倍数的概率是 .7.在半径为5cm 的圆中,两条平行弦的长度分别为6cm 和8cm ,则这两条弦之间的距离为 .8.一幅图案.在某个顶点处由三个边长相等的正多边形镶嵌而成.其中的两个分别是正方形和正六边形,则第三个正多边形的边数是 .9.如图,矩形ABCD 中,3AB =cm ,6AD =cm ,点E 为AB 边上的任意一点,四边形EFGB 也是矩形,且2EF BE =,则AFC S =△ 2cm .D OC B A 第3题图 O B A 第4题图 5cmADCEF GB第9题图2341 6 5 第6题图一共花了170元 第5题图10.三角形的每条边的长都是方程2680x x -+=的根,则三角形的周长是 .11.如图,菱形111AB C D 的边长为1,160B ∠=;作211AD B C ⊥于点2D ,以2AD 为一边,做第二个菱形222AB C D ,使260B ∠=;作322AD B C ⊥于点3D ,以3AD 为一边做第三个菱形333AB C D ,使360B ∠=;依此类推,这样做的第n个菱形n n n AB C D 的边n AD 的长是 . 二、选择题(每题3分,满分27分)12.下列各运算中,错误的个数是( )①01333-+=- ②523-= ③235(2)8a a = ④844a a a -÷=-A .1B .2C .3D .413.用电器的输出功率P 与通过的电流I 、用电器的电阻R 之间的关系是2P I R =,下面说法正确的是( ) A .P 为定值,I 与R 成反比例 B .P 为定值,2I 与R 成反比例 C .P 为定值,I 与R 成正比例D .P 为定值,2I 与R 成正比例14.为紧急安置100名地震灾民,需要同时搭建可容纳6人和4人的两种帐篷,则搭建方案共有( ) A .8种 B .9种 C .16种 D .17种 15.对于抛物线21(5)33y x =--+,下列说法正确的是( ) A .开口向下,顶点坐标(53), B .开口向上,顶点坐标(53), C .开口向下,顶点坐标(53)-,D .开口向上,顶点坐标(53)-,16.下列图案中是中心对称图形的是( )17.关于x 的分式方程15mx =-,下列说法正确的是( ) A .方程的解是5x m =+ B .5m >-时,方程的解是正数1D B 3第11题图AC 2B 2C 3D 3 B 1D 2C 1 A . B . C .D .第16题图C .5m <-时,方程的解为负数D .无法确定18.5月23日8时40分,哈尔滨铁路局一列满载着2400吨“爱心”大米的专列向四川灾区进发,途中除3次因更换车头等原因必须停车外,一路快速行驶,经过80小时到达成都.描述上述过程的大致图象是( )第18题图 19.已知5个正数12345a a a a a ,,,,的平均数是a ,且12345a a a a a >>>>,则数据123450a a a a a ,,,,,的平均数和中位数是( )A .3a a ,B .342a a a +, C .23562a a a +,D .34562a a a +,20.如图,将ABC △沿DE 折叠,使点A 与BC 边的中点F 重合,下列结论中:①EF AB∥且12EF AB =;②BAF CAF ∠=∠; ③12ADFE S AF DE =四边形;④2BDF FEC BAC ∠+∠=∠,正确的个数是( )A .1B .2C .3D .4三、解答题(满分60分) 21.(本小题满分5分)先化简:224226926a a a a a --÷++++,再任选一个你喜欢的数代入求值. 22.(本小题满分6分)如图,方格纸中每个小正方形的边长都是单位1.(1)平移已知直角三角形,使直角顶点与点O 重合,画出平移后的三角形. (2)将平移后的三角形绕点O 逆时针旋转90,画出旋转后的图形.第20题图t B. C . D .(3)在方格纸中任作一条直线作为对称轴,画出(1)和(2)所画图形的轴对称图形,得到一个美丽的图案.23.(本小题满分6分) 有一底角为60的直角梯形,上底长为10cm ,与底垂直的腰长为10cm ,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm ,第三个顶点落在下底上.请计算所作的三角形的面积. 24.(本小题满分7分)A B C ,,三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表一和图一: 表一(1)请将表一和图一中的空缺部分补充完整.(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图二(没有弃权票,每名学生只能推荐一个),请计算每人的得票数.(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.图二 9590 8580 7570 分数/分 图一竞选人 A B C武警战士乘一冲锋舟从A 地逆流而上,前往C 地营救受困群众,途经B 地时,由所携带的救生艇将B 地受困群众运回A 地,冲锋舟继续前进,到C 地接到群众后立刻返回A 地,途中曾与救生艇相遇.冲锋舟和救生艇距A 地的距离y (千米)和冲锋舟出发后所用时间x (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.(1)请直接写出冲锋舟从A 地到C 地所用的时间. (2)求水流的速度.(3)冲锋舟将C 地群众安全送到A 地后,又立即去接应救生艇.已知救生艇与A 地的距离y (千米)和冲锋舟出发后所用时间x (分)之间的函数关系式为11112y x =-+,假设群众上下船的时间不计,求冲锋舟在距离A 地多远处与救生艇第二次相遇?26.(本小题满分8分)已知:正方形ABCD 中,45MAN ∠=,MAN ∠绕点A 顺时针旋转,它的两边分别交CB DC ,(或它们的延长线)于点M N ,. 当MAN ∠绕点A 旋转到BM DN =时(如图1),易证BM DN MN +=. (1)当MAN ∠绕点A 旋转到BM DN ≠时(如图2),线段BM DN ,和MN 之间有怎样的数量关系?写出猜想,并加以证明.(2)当MAN ∠绕点A 旋转到如图3的位置时,线段BM DN ,和MN 之间又有怎样的数量关系?请直接写出你的猜想.BBMBCNCNM CNM 图1图2图3A A A D D D x (分)某工厂计划为震区生产A B ,两种型号的学生桌椅500套,以解决1250名学生的学习问题,一套A 型桌椅(一桌两椅)需木料30.5m ,一套B 型桌椅(一桌三椅)需木料30.7m ,工厂现有库存木料3302m . (1)有多少种生产方案?(2)现要把生产的全部桌椅运往震区,已知每套A 型桌椅的生产成本为100元,运费2元;每套B 型桌椅的生产成本为120元,运费4元,求总费用y (元)与生产A 型桌椅x (套)之间的关系式,并确定总费用最少的方案和最少的总费用.(总费用=生产成本+运费) (3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由. 28.(本小题满分10分) 如图,在平面直角坐标系中,点(30)C -,,点A B ,分别在x 轴,y轴的正半轴上,且满足10OA -=.(1)求点A ,点B 的坐标.(2)若点P 从C 点出发,以每秒1个单位的速度沿射线CB 运动,连结AP .设ABP △的面积为S ,点P 的运动时间为t 秒,求S 与t 的函数关系式,并写出自变量的取值范围. (3)在(2)的条件下,是否存在点P ,使以点A B P ,,为顶点的三角形与AOB △相似?若存在,请直接写出点P 的坐标;若不存在,请说明理由.x二○○八年黑龙江省绥化市初中毕业学业考试数学试卷参考答案及评分标准一、填空题,每空3分,满分33分(多答案题全对得3分,否则不得分) 1.92.710⨯2.3x ≤且1x ≠3.C D ∠=∠或ABC BAD ∠=∠或AC BD =或OAD OBC ∠=∠ 4.45.1456.127.1cm 或7cm 8.12 9.910.6或10或1211.12n -⎛ ⎝⎭二、选择题,每题3分,满分27分.12.C 13.B 14.A 15.A 16.B 17.C 18.D 19.D 20.B三、解答题,满分60分.21.解:224226926a a a a a --÷++++ 2(2)(2)2(3)2(3)2a a a a a +-+=++- ····································································· (1分)242633a a a a ++=-+++ ·················································································· (2分) 23a =+ ·································································································· (3分) n 取3-和2以外的任何数,计算正确都可给分. ············································ (5分) 22.平移正确,给2分;旋转正确,给2分;轴对称正确,给2分,计6分.23.解:当15BE =cm 时,ABE △的面积是250cm ; 当15CF =cm 时,BCF △的面积是275cm ;当15BE =cm 时,BCE △的面积是2cm .(每种情况,图给1分,计算结果正确1分,共6分) 24.解:(1)90;补充后的图如下(每项1分,计2分)(2)A :30035105⨯=% B :30040120⨯=% C :3002575⨯=%(方法对1分,计算结果全部正确1分,计2分)(3)A :854903105392.5433⨯+⨯+⨯=++(分)B :954803120398433⨯+⨯+⨯=++(分)C :90485375384433⨯+⨯+⨯=++(分)B 当选(方法对1分,计算结果全部正确1分,判断正确1分,计3分) 25.解:(1)24分钟 ················································································· (1分) (2)设水流速度为a 千米/分,冲锋舟速度为b 千米/分,根据题意得24()20(4424)()20b a a b -=⎧⎨-+=⎩ ·············································································· (3分) 解得1121112a b ⎧=⎪⎪⎨⎪=⎪⎩B9590 85 80 7570分数/分竞选人A B C答:水流速度是112千米/分. ······································································ (4分) (3)如图,因为冲锋舟和水流的速度不变,所以设线段a 所在直线的函数解析式为56y x b =+ ····························································································· (5分) 把(440),代入,得1103b =-∴线段a 所在直线的函数解析式为511063y x =- ············································ (6分)由11112511063y x y x ⎧=-+⎪⎪⎨⎪=-⎪⎩求出20523⎛⎫ ⎪⎝⎭,这一点的坐标 ·············································· (7分)∴冲锋舟在距离A 地203千米处与救生艇第二次相遇. ···································· (8分) 26.解:(1)BM DN MN +=成立. ························································· (2分)如图,把AND △绕点A 顺时针90,得到ABE △,则可证得E B M ,,三点共线(图形画正确) ···· (3分) 证明过程中,证得:EAM NAM ∠=∠ ···························· (4分)证得:AEM ANM △≌△ ························ (5分)ME MN ∴= ME BE BM DN BM =+=+DN BM MN ∴+= ·················································································· (6分) (2)DN BM MN -= ············································································· (8分) 27.解:(1)设生产A 型桌椅x 套,则生产B 型桌椅(500)x -套,由题意得0.50.7(500)30223(500)1250x x x x +⨯-⎧⎨+⨯-⎩≤≥ ···································································· (2分) 解得240250x ≤≤ ················································································· (3分) 因为x 是整数,所以有11种生产方案. ························································ (4分) (2)(1002)(1204)(500)2262000y x x x =+++⨯-=-+ ····························· (6分)220-<,y 随x 的增大而减少.x (分)B ME A C N D∴当250x =时,y 有最小值. ··································································· (7分) ∴当生产A 型桌椅250套、B 型桌椅250套时,总费用最少.此时min 222506200056500y =-⨯+=(元) ··············································· (8分) (3)有剩余木料,最多还可以解决8名同学的桌椅问题. ······························ (10分) 28.解:(1)2310OB OA --=230OB ∴-=,10OA -= ······································································· (1分) OB ∴=,1OA =点A ,点B分别在x 轴,y 轴的正半轴上(10)(0A B ∴,, ·················································································· (2分)(2)求得90ABC ∠= ············································································· (3分)(0(t t S t t ⎧<⎪=⎨->⎪⎩ ≤(每个解析式各1分,两个取值范围共1分) ················································ (6分)(3)1(30)P -,;21P ⎛-⎝;31P ⎛⎝;4(3P (每个1分,计4分) ··········································································································· (10分)注:本卷中所有题目,若由其它方法得出正确结论,酌情给分.。
2022年黑龙江省绥化市中考数学真题(附答案)

二○二二年绥化市初中毕业学业考试数学试题一、单项选择题(本题共12个小题,每小题3分,共36分)1. 化简12-,下列结果中,正确的是( ) A. 12 B. 12- C. 2 D. -2【答案】A【解析】【分析】根据绝对值的运算法则,求出绝对值的值即可. 【详解】解:1122-= 故选:A .【点睛】本题考查根据绝对值的意义求一个数的绝对值,求一个数的绝对值:①当a 是正数时,│a │=a ;②当a 是负数时,│a │=-a ;③当a =0时,│0│=0.掌握求一个数的绝对值的方法是解答本题的关键. 2. 下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D. 【答案】D【解析】【分析】根据中心对称图形与轴对称图形的概念进行判断即可.【详解】解:A .是轴对称图形,不是中心对称图形,故本选项不符合题意;B .是轴对称图形,不是中心对称图形,故本选项不符合题意;C .不是轴对称图形,是中心对称图形,故本选项不符合题意;D .既是轴对称图形,又是中心对称图形,故本选项符合题意.故选:D .【点睛】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.3. 下列计算中,结果正确的是( )A. 22423x x x +=B. ()325x x = 2=- 2=±【答案】C【解析】【分析】根据合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,即可一一判定.【详解】解:A.22223x x x +=,故该选项不正确,不符合题意;B.()326x x =,故该选项不正确,不符合题意;2=-,故该选项正确,符合题意;2=,故该选项不正确,不符合题意;故选:C .【点睛】本题考查了合并同类项法则、幂的乘方运算法则、开立方运算、求一个数的算术平方根,熟练掌握和运用各运算法则是解决本题的关键.4. 下列图形中,正方体展开图错误的是( )A. B. C. D.【答案】D【解析】【分析】利用正方体及其表面展开图的特点解题.【详解】D 选项出现了“田字形”,折叠后有一行两个面无法折起来,从而缺少面,不能折成正方体,A 、B 、C 选项是一个正方体的表面展开图.故选:D .【点睛】此题考查了几何体的展开图,只要有“田”“凹”字的展开图都不是正方体的表面展开图.5. 2x -在实数范围内有意义,则x 的取值范围是( )A. 1x >-B. 1x -C. 1x -且0x ≠D. 1x -且0x ≠【答案】C【解析】【分析】根据二次根式被开方数不能为负数,负整数指数幂的底数不等于0,计算求值即可;【详解】解:由题意得:x+1≥0且x≠0,∴x≥-1且x≠0,故选:C.【点睛】本题考查了二次根式的定义,负整数指数幂的定义,掌握其定义是解题关键.6. 下列命题中是假命题的是()A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半B. 如果两个角互为邻补角,那么这两个角一定相等C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D. 直角三角形斜边上的中线等于斜边的一半【答案】B【解析】【分析】利用三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质分别判断后即可确定正确的选项.【详解】解:A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半,是真命题,故此选项不符合题意;B. 如果两个角互为邻补角,那么这两个角不一定相等,故此选项是假命题,符合题意;C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,是真命题,故此选项不符合题意;D. 直角三角形斜边上的中线等于斜边的一半,是真命题,故此选项不符合题意;故选:B【点睛】考查了命题与定理的知识,解题的关键是了解三角形的中位线定理、邻补角性质、切线长定理以及直角三角形斜边上的中线的性质.2,5,线段OA绕原点O逆时针旋转90°,得到线段7. 如图,线段OA在平面直角坐标系内,A点坐标为()OA',则点A'的坐标为()A. ()5,2-B. ()5,2C. ()2,5-D. ()5,2- 【答案】A【解析】【分析】如图,逆时针旋转90°作出OA ',过A 作AB x ⊥轴,垂足为B ,过A '作A B x ''⊥轴,垂足为B ',证明()A OB BOA AAS '∠≌,根据A 点坐标为()2,5,写出5AB =,2OB =,则5OB '=,2A B '=,即可写出点A 的坐标.【详解】解:如图,逆时针旋转90°作出OA ',过A 作AB x ⊥轴,垂足为B ,过A '作A B x ''⊥轴,垂足为B ',∴90A BO ABO ∠'=∠=︒,OA OA '=,∵18090A OB AOB AOA '∠+∠=︒-∠'=︒,90AOB A ∠+∠=︒,∴A OB A ∠'=∠,∴()A OB BOA AAS '∠≌,∴OB AB '=,A B OB '=,∵A 点坐标为()2,5,∴5AB =,2OB =,∴5OB '=,2A B '=,∴()5,2A '-,故选:A .【点睛】本题考查旋转的性质,证明AOB BOA '∠≌是解答本题的关键.8. 学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是( )A. 该组数据的中位数为98B. 该组数据的方差为0.7C. 该组数据的平均数为98D. 该组数据的众数为96和98【答案】D【解析】【分析】首先对数据进行重新排序,再根据众数,中位数,平均数,方差的定义进行求值计算即可.【详解】解:数据重新排列为:96,96,97,98, 98,∴数据的中位数为:97,故A 选项错误; 该组数据的平均数为9696979898975++++= ,故C 选项错误; 该组数据的方差为:()()()()()22222196979697979798979897=0.85⎡⎤-+-+-+-+-⎣⎦,故B 选项错误;该组数据的众数为:96和98,故D 选项正确;故选:D .【点睛】本题主要考查数据中名词的理解,掌握众数,中位数,平均数,方差的定义及计算方法是解题的关键.9. 有一个容积为243m 的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径2倍的粗油管向油罐注油,直至注满,注满油的全过程共用30分钟,设细油管的注油速度为每分钟x 3m ,由题意列方程,正确的是( )A. 1212304x x +=B. 1515244x x +=C. 3030242x x +=D. 1212302x x+= 【答案】A【解析】【分析】由粗油管口径是细油管的2倍,可知粗油管注水速度是细油管的4倍.可设细油管的注油速度为每分钟x 3m ,粗油管的注油速度为每分钟4x 3m ,继而可得方程,解方程即可求得答案.【详解】解:∵细油管的注油速度为每分钟x 3m ,∴粗油管的注油速度为每分钟4x 3m , ∴1212304x x+=. 故选:A .【点睛】此题考查了分式方程的应用,准确找出数量关系是解题的关键.10. 已知二次函数2y ax bx c =++的部分函数图象如图所示,则一次函数24y ax b ac =+-与反比例函数42a b c y x++=在同一平面直角坐标系中的图象大致是( )A. B.C. D.【答案】B【解析】【分析】根据2y ax bx c =++的函数图象可知,0a >,240b ac ->,即可确定一次函数图象,根据2x =时,420y a b c =++>,即可判断反比例函数图象,即可求解.【详解】解:∵二次函数2y ax bx c =++的图象开口向上,则0a >,与x 轴存在2个交点,则240b ac ->,∴一次函数24y ax b ac =+-图象经过一、二、三象限,二次函数2y ax bx c =++的图象,当2x =时,420y a b c =++>, ∴反比例函数42a b c y x++=图象经过一、三象限 结合选项,一次函数24y ax b ac =+-与反比例函数42a b c y x++=在同一平面直角坐标系中的图象大致是B 选项故选B 【点睛】本题考查了一次函数,二次函数,反比例函数的图象与性质,掌握二次函数的图象与系数的关系是解题的关键.11. 小王同学从家出发,步行到离家a 米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y (单位:米)与出发时间x (单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )A. 2.7分钟B. 2.8分钟C. 3分钟D. 3.2分钟【答案】C【解析】【分析】先根据题意求得A 、D 、E 、F 的坐标,然后再运用待定系数法分别确定AE 、AF 、OD 的解析式,再分别联立OD 与AE 和AF 求得两次相遇的时间,最后作差即可.【详解】解: 如图:根据题意可得A (8,a ),D (12,a ),E (4,0),F (12,0) 设AE 的解析式为y =kx +b ,则048k b a k b =+⎧⎨=+⎩ ,解得4a k b a⎧=⎪⎨⎪=-⎩ ∴直线AE 的解析式为y =4a x -3a 同理:直线AF 的解析式为:y =-4a x +3a ,直线OD 的解析式为:y =12a x 联立124a y x a y x a ⎧=⎪⎪⎨⎪=-⎪⎩,解得62x a y =⎧⎪⎨=⎪⎩ 联立1234a y x a y x a ⎧=⎪⎪⎨⎪=-+⎪⎩,解得934x a y =⎧⎪⎨=⎪⎩ 两人先后两次相遇的时间间隔为9-6=3min .故答案为C .【点睛】本题主要考查了一次函数的应用,根据题意确定相关点的坐标、求出直线的解析式成为解答本题的关键.12. 如图,在矩形ABCD 中,P 是边AD 上的一个动点,连接BP ,CP ,过点B 作射线,交线段CP 的延长线于点E ,交边AD 于点M ,且使得ABE CBP =∠∠,如果2AB =,5BC =,AP x =,PM y =,其中25x <.则下列结论中,正确的个数为( )(1)y 与x 的关系式为4y x x=-;(2)当4AP =时,ABP DPC ∽;(3)当4AP =时,3tan 5EBP ∠=.A. 0个B. 1个C. 2个D. 3个【答案】C【解析】 【分析】(1)证明ABM APB ∽,得AB AM AP AB=,将2AB =,AP x =,PM y =代入,即可得y 与x 的关系式; (2)利用两组对应边成比例且夹角相等,判定ABP DPC ∽;(3)过点M 作MF BP ⊥垂足为F ,在Rt APB △中,由勾股定理得BP 的长,证明FPM APB ∽,求出MF ,PF ,BF 的长,在Rt BMF △中,求出tan EBP ∠的值即可.【详解】解:(1)∵在矩形ABCD 中,∴AD BC ∥,90A D ∠=∠=︒,5BC AD ==,2AB DC ==, ∴APB CBP ∠=∠,∵ABE CBP =∠∠,∴ABE APB ∠=∠,∴ABM APB ∽, ∴AB AM AP AB=, ∵2AB =,AP x =,PM y =, ∴22x y x -=, 解得:4y x x =-, 故(1)正确;(2)当4AP =时,541DP AD AP =-=-=, ∴12DC DP AP AB ==, 又∵90A D ∠=∠=︒,∴ABP DPC ∽,故(2)正确;(3)过点M 作MF BP ⊥垂足为F ,∴90A MFP MFB ∠=∠=∠=︒,∵当4AP =时,此时4x =,4413y x x =-=-=, ∴3PM =,在Rt APB 中,由勾股定理得:222BP AP AB =+,∴BP ==,∵FPM APB ∠=∠,∴FPM APB ∽, ∴MF PF PM AB AP PB==,∴24MF PF ==,∴5MF =,5PF =∴55BF BP PF =-==,∴3tan 4MF EBP BF ∠=== 故(3)不正确;故选:C .【点睛】本题主要考查相似三角形的判定和性质,勾股定理的应用,矩形的性质,正确找出相似三角形是解答本题的关键.二、填空题(本题共10个小题,每小题3分,共30分)13. 一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为14,则这个箱子中黄球的个数为______个. 【答案】15【解析】【分析】设黄球个数为x 个,根据概率计算公式列出方程,解出x 即可.【详解】解:设:黄球的个数为x 个,5154x =+ 解得:15x =,检验:将15x =代入520x +=,值不为零,∴15x =是方程的解,∴黄球的个数为15个,故答案为:15.【点睛】本题考查概率计算公式,根据题意列出分式方程并检验是解答本题的关键.14. 因式分解:()()269m n m n +-++=________.【答案】()23m n +-【解析】【分析】将m n 看做一个整体,则9等于3得的平方,逆用完全平方公式因式分解即可.【详解】解:()()269m n m n +-++ ()()22233m n m n =+-⨯⨯++ ()23m n =+-.【点睛】本题考查应用完全平方公式进行因式分解,整体思想,能够熟练逆用完全平方公式是解决本题的关键.15. 不等式组360x x m ->⎧⎨>⎩的解集为2x >,则m 的取值范围为_______. 【答案】m ≤2【解析】【分析】先求出不等式①的解集,再根据已知条件判断m 范围即可.【详解】解:360x x m ->⎧⎨>⎩①②, 解①得:2x >,又因为不等式组的解集为x >2∴x >m ,∴m ≤2,故答案为:m ≤2.【点睛】本题考查了解一元一次不等式组,能根据不等式的解集和已知得出m 的范围是解此题的关键. 16. 已知圆锥的高为8cm ,母线长为10cm ,则其侧面展开图的面积为_______.【答案】60πcm 2【解析】【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2.【详解】解:圆锥的高为8cm ,母线长为10cm ,由勾股定理得,底面半径=6cm ,底面周长=12πcm , 侧面展开图的面积=12×12π×10=60πcm 2.故答案为:60πcm 2.【点睛】本题利用了勾股定理,圆的周长公式和扇形面积公式求解.17. 设1x 与2x 为一元二次方程213202x x ++=的两根,则()212x x -的值为________. 【答案】20【解析】【分析】利用公式法求得一元二次方程的根,再代入求值即可; 【详解】解:∵213202x x ++= △=9-4=5>0,∴13x =-23x =-,∴()212x x -=((223320-==, 故答案为:20;【点睛】本题考查了一元二次方程的解,掌握公式法解一元二次方程是解题关键.18. 定义一种运算;sin()sin cos cos sin αβαβαβ+=+,sin()sin cos cos sin αβαβαβ-=-.例如:当45α=︒,30β=︒时,()sin 4530︒+︒=1222+=,则sin15︒的值为_______.【解析】【分析】根据sin()sin cos cos sin αβαβαβ-=-代入进行计算即可.【详解】解:sin15sin(4530)︒=︒-︒=sin 45cos30cos45sin30︒︒︒︒-12-=44-=.4.故答案为:4【点睛】此题考查了公式的变化,以及锐角三角函数值的计算,掌握公式的转化是解题的关键.∠的度数为19. 如图,正六边形ABCDEF和正五边形AHIJK内接于O,且有公共顶点A,则BOH______度.【答案】12【解析】【分析】连接AO,求出正六边形和正五边形的中心角即可作答.【详解】连接AO,如图,∵多边形ABCDEF是正六边形,∴∠AOB=360°÷6=60°,∵多边形AHIJK是正五边形,∴∠AOH=360°÷5=72°,∴∠BOH=∠AOH-∠AOB=72°-60°=12°,故答案为:12.【点睛】本题考查了正多边形的中心角的知识,掌握正多边形中心角的计算方法是解答本题的关键.20. 某班为奖励在数学竞赛中成绩优异的同学,花费48元钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4元,乙种奖品每件3元,则有______种购买方案.【答案】3##三【解析】【分析】设购买甲种奖品x 件,乙种奖品y 件,列出关系式,并求出3124y x =-,由于1≥x ,1y ≥且x ,y 都是正整数,所以y 是4的整数倍,由此计算即可.【详解】解:设:购买甲种奖品x 件,乙种奖品y 件, 4348x y +=,解得3124y x =-, ∵1≥x ,1y ≥且x ,y 都是正整数,∴y 是4的整数倍,∴4y =时,341294x ⨯=-=, 8y =时,381264x ⨯=-=, 12y =时,3121234x ⨯=-=, 16y =时,3161204x ⨯=-=,不符合题意, 故有3种购买方案,故答案为:3.【点睛】本题考查列关系式,根据题意判断出y 是4的整数倍是解答本题的关键.21. 如图,60AOB ∠=︒,点1P 在射线OA 上,且11OP =,过点1P 作11PKOA ⊥交射线OB 于1K ,在射线OA 上截取12PP ,使1211PPPK =;过点2P 作22P K OA ⊥交射线OB 于2K ,在射线OA 上截取23P P ,使2322P P P K =.按照此规律,线段20232023P K 的长为________.20221+【解析】【分析】解直角三角形分别求得11PK,22P K,33P K,……,探究出规律,利用规律即可解决问题.【详解】解:11PK OA⊥,11OPK∴△是直角三角形,在11Rt OPK中,60AOB∠=︒,11OP=,12111tan60PP PK OP∴==⋅︒=11PK OA⊥,22P K OA⊥,1122PK P K∴∥,2211OP K OPK∴△∽△,222111P K OPPK OP∴=,11=,221P K∴=,同理可得:2331P K =+,3441P K =+,……, 11n n n P K -∴=,2022202320231P K ∴=+,20221.【点睛】本题考查了图形的规律,解直角三角形,平行线的判定,相似三角形的判定与性质,解题的关键是学会探究规律的方法.22. 在长为2,宽为x (12x <<)的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x 的值为________. 【答案】65 或32【解析】【分析】分析题意,根据x 的取值范围不同,对剩下矩形的长宽进行讨论,求出满足题意的x 值即可.【详解】解:第一次操作后剩下的矩形两边长为2x - 和x , (2)22x x x --=- ,又12x <<,220x ∴-> ,2x x ∴-> ,则第一次操作后,剩下矩形的宽为2x -,所以可得第二次操作后,剩下矩形一边为2x - ,另一边为:(2)22x x x --=- ,∵第三次操作后,剩下的纸片恰为正方形,∴第二次操作后剩下矩形的长是宽的2倍,分以下两种情况进行讨论:①当222x x --> ,即43x <时 ,第三次操作后剩下的矩形的宽为22x - ,长是2x - ,则由题意可知:22(22)x x -=- , 解得:65x = ;②当222x x --< ,即43x >时, 第三次操作后剩下的矩形的宽为2x - ,长是22x - ,由题意得:222(2)x x -=- , 解得:32x = , 65x ∴= 或者32x = .故答案为:65 或32. 【点睛】本题考查了矩形的性质,正方形的性质以及分类讨论的数学思想方法,熟练掌握矩形,正方形性质以及分类讨论的方法是解题的关键.三、解答题(本题共6个小题,共54分)23. 已知:ABC .(1)尺规作图:用直尺和圆规作出ABC 内切圆的圆心O ;(只保留作图痕迹,不写作法和证明)(2)如果ABC 的周长为14cm ,内切圆的半径为1.3cm ,求ABC 的面积.【答案】(1)作图见详解(2)9.1【解析】【分析】(1)根据角平分线的性质可知角平分线的交点为三角形内切圆的圆心,故只要作出两个角的角平分线即可;(2)利用割补法,连接OA ,OB ,OC ,作OD ⊥AB ,OE ⊥BC ,OF ⊥AC ,这样将△ABC 分成三个小三角形,这三个小三角形分别以△ABC 的三边为底,高为内切圆的半径,利用提取公因式可将周长代入,进而求出三角形的面积.【小问1详解】解:如下图所示,O 为所求作点,【小问2详解】解:如图所示,连接OA ,OB ,OC ,作OD ⊥AB ,OE ⊥BC ,OF ⊥AC ,∵内切圆的半径为1.3cm ,∴OD =OF =OE =1.3,∵三角形ABC 的周长为14,∴AB +BC +AC =14, 则111222ABC AOB COB AOC S S S S AB OD BC OE AC OF =++=⋅⋅+⋅⋅+⋅⋅△△△△ 111.3() 1.3149.122AB BC AC =⨯⨯++=⨯⨯= 故三角形ABC 的面积为9.1.【点睛】本题考查三角形的内切圆,角平分线的性质,割补法求几何图形的面积,能够将角平分线的性质与三角形的内切圆相结合是解决本题的关键.24. 如图所示,为了测量百货大楼CD 顶部广告牌ED 的高度,在距离百货大楼30m 的A 处用仪器测得30DAC ∠=︒;向百货大楼的方向走10m ,到达B 处时,测得48EBC ∠=︒,仪器高度忽略不计,求广告牌ED 的高度.(结果保留小数点后一位)1.732≈,sin 480.743︒≈,cos480.669︒≈,tan 48 1.111︒≈)【答案】4.9m【解析】【分析】先求出BC 的长度,再分别在Rt △ADC 和Rt △BEC 中用锐角三角函数求出EC 、DC ,即可求解.【详解】根据题意有AC =30m ,AB =10m ,∠C =90°,则BC =AC -AB =30-10=20,在Rt △ADC 中,tan 30tan 30DC AC A =⨯∠=⨯=,在Rt △BEC 中,tan 20tan 48EC BC EBC =⨯∠=⨯, ∴20tan 4810DE EC DC =-=⨯-即20tan 481020 1.11110 1.732 4.9DE =⨯-≈⨯-⨯=故广告牌DE 的高度为4.9m .【点睛】本题考查了解直角三角形的应用,掌握锐角三角函数的性质是解答本题的关键. 25. 在平面直角坐标系中,已知一次函数11y k x b =+与坐标轴分别交于()5,0A ,50,2B ⎛⎫ ⎪⎝⎭两点,且与反比例函数22k y x =的图象在第一象限内交于P ,K 两点,连接OP ,OAP △的面积为54.(1)求一次函数与反比例函数的解析式;(2)当21y y >时,求x 的取值范围;(3)若C 为线段OA 上的一个动点,当PC KC +最小时,求PKC 的面积.【答案】(1)115,22y x =-+22.y x= (2)01x <<或4x >,(3)65【解析】 【分析】(1)先运用待定系数法求出直线解析式,再根据OAP △的面积为54和直线解析式求出点P 坐标,从而可求出反比例函数解析式;(2)联立方程组并求解可得点K 的坐标,结合函数图象可得出x 的取值范围;(3)作点K 关于x 轴的对称点K ',连接KK ',PK '交x 轴于点C ,连接KC ,则PC +KC 的值最小,求出点C 的坐标,再根据PKC AKM KMC PAC S S S S ∆∆∆∆=--求解即可.【小问1详解】解:∵一次函数11y k x b =+与坐标轴分别交于()5,0A ,50,2B ⎛⎫ ⎪⎝⎭两点, ∴把()5,0A ,50,2B ⎛⎫ ⎪⎝⎭代入11y k x b =+得, 1505,2k b b +=⎧⎪⎨=⎪⎩,解得,11252k b ⎧=-⎪⎪⎨⎪=⎪⎩, ∴一次函数解析式为115,22y x =-+ 过点P 作PH x ⊥轴于点H ,∵(5,0),A∴5,OA 又5,4PAO S ∆=∴15524PH ⨯⨯= ∴1,2PH = ∴151222x -+=, ∴4,x = ∴1(4,)2P ∵1(4,)2P 在双曲线上, ∴2142,2k =⨯= ∴22.y x= 【小问2详解】 解:联立方程组得,15222y x y x ⎧=-+⎪⎪⎨⎪=⎪⎩解得,1112x y =⎧⎨=⎩ ,22412x y =⎧⎪⎨=⎪⎩∴(1,2),k根据函数图象可得,反比例函数图象直线上方时,有01x <<或4x >,∴当21y y >时,求x 的取值范围为01x <<或4x >,【小问3详解】解:作点K 关于x 轴的对称点K ',连接KK '交x 轴于点M ,则K '(1,-2),OM =1,连接PK '交x 轴于点C ,连接KC ,则PC +KC 的值最小,设直线PK '的解析式为,y mx n =+把1(4,),(1,2)2P K '-代入得,2142m n m n +=-⎧⎪⎨+=⎪⎩解得,56176m n ⎧=⎪⎪⎨⎪=-⎪⎩∴直线PK '的解析式为517,66y x =- 当0y =时,106657x -=,解得,751x =, ∴17(,0)5C ∴175OC = ∴17121,55MC OC OM =-=-= 178555AC OA OC =-=-= 514AM OA OM =-=-=,∴PKC AKM KMC PAC S S S S ∆∆∆∆=--1112181422225252=⨯⨯-⨯⨯-⨯⨯ 122455=-- 65= 【点睛】本题主要考查了反比例函数与一次函数的综合,正确作出辅助线是解答本题的关键. 26. 我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.(1)如图一,在等腰ABC 中,AB AC =,BC 边上有一点D ,过点D 作DE AB ⊥于E ,DF AC ⊥于F ,过点C 作CG AB ⊥于G .利用面积证明:DE DF CG +=.(2)如图二,将矩形ABCD 沿着EF 折叠,使点A 与点C 重合,点B 落在B ′处,点G 为折痕EF 上一点,过点G 作GM FC ⊥于M ,GN BC ⊥于N .若8BC =,3BE =,求GM GN +的长.(3)如图三,在四边形ABCD 中,E 为线段BC 上的一点,EA AB ⊥,ED CD ⊥,连接BD ,且AB AECD DE=,BC =3CD =,6BD =,求ED EA +的长. 【答案】(1)证明见解析(2)4(3【解析】【分析】(1)根据题意,利用等面积法ABC ABD ACD S S S ∆∆∆=+,根据等腰ABC 中,AB AC =,即可得到结论;(2)根据题中条件,利用折叠性质得到AFE CFE ∠=∠,结合矩形ABCD 中AD BC ∥得到AFE FEC ∠=∠,从而有CFE FEC ∠=∠,从而确定EFC ∆是等腰三角形,从而利用(1)中的结论得到=GM GN FH +,结合勾股定理及矩形性质即可得到结论;(3)延长BA CD 、交于F ,连接EF ,过点B 作BG FC ⊥于G ,根据AB AE CD DE=,EA AB ⊥,ED CD ⊥,得到ABC ∆是等腰三角形,从而由(1)知ED EA BG +=,在Rt BCG ∆中,BG ==Rt BDG ∆中,6BD =,BG =BG ==1x =,从而得到结论.【小问1详解】证明:连接AD ,如图所示:在等腰ABC 中,AB AC =,BC 边上有一点D ,过点D 作DE AB ⊥于E ,DF AC ⊥于F ,过点C 作CG AB ⊥于G ,∴由ABC ABD ACD S S S ∆∆∆=+得111222AB CG AB ED AC FD ⋅=⋅+⋅, ∴DE DF CG +=; 【小问2详解】解:连接CG ,过点F 作FH BC ⊥于H ,如图所示:根据折叠可知AFE CFE ∠=∠,在矩形ABCD 中,AD BC ∥,则AFE FEC ∠=∠,CFE FEC ∴∠=∠,即EFC ∆等腰三角形,在等腰EFC ∆中,FC EC =,EF 边上有一点G ,过点G 作GM FC ⊥于M ,GN BC ⊥于N ,过点F 作FH BC ⊥于H ,由(1)可得=GM GN FH +,在Rt ABE ∆中,90B ∠=︒,3,835BE AE EC BC BE ===-=-=,则4AB ==,在四边形ABHF 中,90B BAF FHB ∠=∠=∠=︒,则四边形ABHF 为矩形,4FH AB ∴==,即4GM GN FH AB +===;【小问3详解】解:延长BA CD 、交于F ,连接EF ,过点B 作BG FC ⊥于G ,在四边形ABCD 中,E 为线段BC 上的一点,EA AB ⊥,ED CD ⊥,则90BAE CDE ∠=∠=︒, 又AB AECD DE=, ∴ABE DCE ∆∆,ABE C ∴∠=∠,即ABC ∆是等腰三角形,∴由(1)可得ED EA BG +=,设=GD x ,90EDC BGC ∠=∠=︒,BC =3CD =,在Rt BCG ∆中,BG ==在Rt BDG ∆中,6BD =,BG =,∴BG ==1x =,BG ∴=ED EA BG +==【点睛】本题考查几何综合,涉及到等腰三角形的判定与性质、等面积求线段关系、折叠的性质、勾股定理求线段长、相似三角形的判定与性质等知识点,读懂题意,掌握(1)中的证明过程与结论并运用到其他情境中是解决问题的关键.27. 如图所示,在O 的内接AMN 中,90MAN ∠=︒,2AM AN =,作AB MN ⊥于点P ,交O 于另一点B ,C 是AM 上的一个动点(不与A ,M 重合),射线MC 交线段BA 的延长线于点D ,分别连接AC 和BC ,BC 交MN 于点E .(1)求证:CMA CBD △∽△.(2)若10MN =,MC NC =,求BC 的长.(3)在点C 运动过程中,当3tan 4MDB ∠=时,求ME NE 的值. 【答案】(1)证明见解析(2)(3)32【解析】【分析】(1)利用圆周角定理得到∠CMA =∴ABC ,再利用两角分别相等即可证明相似;(2)连接OC ,先证明MN 是直径,再求出AP 和NP 的长,接着证明COE BPE △∽△,利用相似三角形的性质求出OE 和PE ,再利用勾股定理求解即可;(3)先过C 点作CG ⊥MN ,垂足为G ,连接CN ,设出34GM x CG x ==,,再利用三角函数和勾股定理分别表示出PB 和PG ,最后利用相似三角形的性质表示出EG ,然后表示出ME 和NE ,算出比值即可.【小问1详解】解:∵AB ⊥MN ,∴∠APM =90°,∴∠D +∠DMP =90°,又∵∠DMP +∠NAC =180°,∠MAN =90°,∴∠DMP +∠CAM =90°,∴∠CAM =∠D ,∴∠CMA =∴ABC ,∴CMA CBD △∽△.【小问2详解】连接OC ,∵90MAN ∠=︒,∴MN 是直径,∵10MN =,∴OM =ON =OC =5,∵2AM AN =,且222AM AN MN +=,∴AN AM == ∵1122AMN S AM AN MN AP =⋅=⋅△, ∴4AP =,∴4BP AP ==,∴2NP ==,∴523OP =-=,∵MC NC =,∴OC ⊥MN ,∴∴COE =90°,∵AB ⊥MN ,∴∴BPE =90°,∴∴BPE =∠COE ,又∵∴BEP =∠CEO ,∴COE BPE △∽△ ∴CO OE CE BP PE BE==, 即54OE CE PE BE == 由3OE PE OP +==,∴5433OE PE ==,,∴CE ===BE ===∴BC ==【小问3详解】过C 点作CG ⊥MN ,垂足为G ,连接CN , ∵MN 是直径,∴∴MCN =90°,∴∴CNM +∠DMP =90°,∵∴D +∠DMP =90°,∴∴D =∠CNM , ∵3tan 4MDB ∠=, ∴3tan 4CNM ∠=, 设34GM x CG x ==,,∴5CM x =, ∴203x CN =,∴163x NG =, ∴253x NM =, ∴256x OM ON ==, ∵2AM AN =,且222AM AN MN +=,∴AN x =,AM x =, ∵1122AMN S AM AN MN AP =⋅=⋅△, ∴103AP x PB ==, ∴53NP x =, ∴16511333PG x x x =-=, ∵∴CGE =∠BPE =90°,∴CEG =∠BEP , ∴CGE BPE △∽△, ∴CG GE CE BP PE BE==, 即4103x GE CE PE BEx == ∴2GE x =,53PE x = ∴5ME x =,103x NE =, ∴:3:2ME NE =, ∴MENE 值为32.【点睛】本题考查了圆的相关知识、相似三角形的判定与性质、三角函数、勾股定理等知识,涉及到了动点问题,解题关键是构造相似三角形,正确表示出各线段并找出它们的关系,本题综合性较强,属于压轴题.28. 如图,抛物线2y ax bx c =++交y 轴于点()0,4A -,并经过点()6,0C ,过点A 作AB y ⊥轴交抛物线于点B ,抛物线的对称轴为直线2x =,D 点的坐标为()4,0,连接AD ,BC ,BD .点E 从A 点出发,个单位长度的速度沿着射线AD 运动,设点E 的运动时间为m 秒,过点E 作EF AB ⊥于F ,以EF 为对角线作正方形EGFH .(1)求抛物线的解析式;(2)当点G 随着E 点运动到达BC 上时,求此时m 的值和点G 的坐标;(3)在运动的过程中,是否存在以B ,G ,C 和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G 的坐标,如果不存在,请说明理由.【答案】(1)214433y x x =-- (2)165m =,2412,55G ⎛⎫- ⎪⎝⎭ (3)368,55⎛⎫- ⎪⎝⎭或(3,-3)1216,55⎛⎫- ⎪⎝⎭或426,55⎛⎫- ⎪⎝⎭ 【解析】【分析】(1)利用待定系数法求解析式即可;(2)求出直线BC 解析式,通过△EGF 为等腰直角三角形表示出G 点坐标,将G 点代入BC 解析式即可求得m 的值,从而求得G 点坐标;(3)将矩形转化为直角三角形,当△BGC 是直角三角形时,当△BCG 为直角三角形时,当△CBG 为直角三角形时,分情况讨论分别列出等式求得m 的值,即可求得G 点坐标.【小问1详解】将点A (0,-4)、C (6,0)代入解析式2y ax bx c =++中,以及直线对称轴2x =,可得4036622c a b c b a ⎧⎪-=⎪=++⎨⎪⎪-=⎩, 解得13434a b c ⎧=⎪⎪⎪=-⎨⎪=-⎪⎪⎩, ∴抛物线的解析式为214433y x x =--; 【小问2详解】∵A (0,-4),D ()4,0,∴△AOD 为等腰直角三角形,∵AB y ⊥轴交抛物线于点B ,∴B (4,-4),设直线BC 解析式为y =kx +b ,将B (4,-4),C (6,0)代入解析式得,4406k b k b -=+⎧⎨=+⎩,解得212k b =⎧⎨=-⎩, ∴直线BC 解析式为y =2x -12,由题意可得AE =,△ADB 为等腰直角三角形,∴2AF EF AE m ===, ∵四边形EGFH 正方形,∴△EGF 为等腰直角三角形, ∴11,422G m m m ⎛⎫+-+ ⎪⎝⎭, 点G 随着E 点运动到达BC 上时,满足直线BC 解析式y =2x -12, ∴11421222m m m ⎛⎫-+=+- ⎪⎝⎭, ∴165m =,此时2412,55G ⎛⎫- ⎪⎝⎭; 【小问3详解】B (4,-4),C (6,0),11,422G m m m ⎛⎫+-+ ⎪⎝⎭, ∴()()222640420BC =-++=,22222313144442222BG m m m m ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,222223131604642222CG m m m m ⎛⎫⎛⎫⎛⎫⎛⎫=-++-=-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 要使以B ,G ,C 和平面内的另一点为顶点的四边形是矩形,需满足:当△BGC 是直角三角形时,222BG CG BC +=,22223131464202222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫-++-+-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 解得,1245m =,22m =,此时G 368,55⎛⎫- ⎪⎝⎭或(3,-3); 当△BCG 为直角三角形时,222BC CG BG +=,22223131206442222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-+-=-+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 解得,285m =, 此时G 426,55⎛⎫- ⎪⎝⎭; 当△CBG 为直角三角形时,222BC BG CG +=,22223131204642222m m m m ⎛⎫⎛⎫⎛⎫⎛⎫+-+=-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 解得,85m =, 此时G 1216,55⎛⎫- ⎪⎝⎭; 综上所述:点G 坐标为368,55⎛⎫-⎪⎝⎭或(3,-3)1216,55⎛⎫- ⎪⎝⎭或426,55⎛⎫- ⎪⎝⎭. 【点睛】本题是二次函数的综合题,考查了待定系数法求解析式、等腰直角三角形的性质和判定,动点运动问题,存在矩形问题,利用数形结合,注意分情况讨论是解题的关键.。
2023年绥化市中考数学试卷及答案
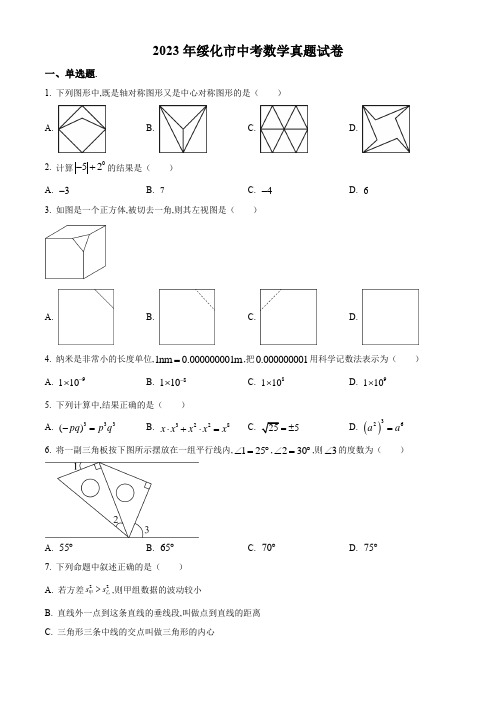
2023年绥化市中考数学真题试卷一、单选题.1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D. 2. 计算052-+的结果是( )A. 3-B. 7C. 4-D. 6 3. 如图是一个正方体,被切去一角,则其左视图是( )A. B. C. D. 4. 纳米是非常小的长度单位,1nm 0.000000001m =,把0.000000001用科学记数法表示为( )A. 9110-⨯B. 8110-⨯C. 8110⨯D. 9110⨯ 5. 下列计算中,结果正确的是( )A. 333()pq p q -=B. 3228x x x x x ⋅+⋅=C. 5=±D. ()326a a = 6. 将一副三角板按下图所示摆放在一组平行线内,125∠=︒,230∠=︒,则3∠的度数为( )A. 55︒B. 65︒C. 70︒D. 75︒7. 下列命题中叙述正确的是( )A. 若方差22s s >乙甲,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上8. 绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是()A. 该组数据的样本容量是50人B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D. 110~120这组数据对应的扇形统计图的圆心角度数为51︒9. 在平面直角坐标系中,点A在y轴的正半轴上,AC平行于x轴,点B,C的横坐标都是3,2BC=,点D在AC上,且其横坐标为1,若反比例函数kyx=(0x>)的图像经过点B,D,则k的值是()A. 1B. 2C. 3D. 3 210. 某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( ) A. 11142x+= B. 11111424x ⎛⎫++= ⎪⎝⎭ C. 1111142x ⎛⎫++= ⎪⎝⎭ D.11111442x ⎛⎫++= ⎪⎝⎭ 11. 如图,在菱形ABCD 中,60A ∠=︒,4AB =,动点M ,N 同时从A 点出发,点M 以每秒2个单位长度沿折线A B C --向终点C 运动;点N 以每秒1个单位长度沿线段AD 向终点D 运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x 秒,AMN 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A. B. C. D. 12. 如图,在正方形ABCD 中,点E 为边CD 的中点,连接AE ,过点B 作BF AE ⊥于点F ,连接BD 交AE 于点G ,FH 平分BFG ∠交BD 于点H .则下列结论中,正确的个数为( )①2AB BF AE =⋅;①:2:3BGF BAF S S =△△;①当AB a 时,22BD BD HD a -⋅=A. 0个B. 1个C. 2个D. 3个二、填空题.13. 因式分解:2x xy xz yz +--=_______.14.,则x 的取值范围是_______. 15. 在4张完全相同的卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是_________.16. 已知一元二次方程256x x x +=+的两根为1x 与2x ,则1211+x x 的值为_______. 17. 化简:2222142442x x x x x x x x x+--⎛⎫-÷= ⎪--+-⎝⎭_______. 18. 如图,O 的半径为2cm ,AB 为O 的弦,点C 为AB 上的一点,将AB 沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为_______.(结果保留π与根号)19. 如图,在平面直角坐标系中,ABC 与AB C ''△的相似比为12∶,点A 是位似中心,已知点(2,0)A ,点(,)C a b ,90C ∠=︒.则点C '的坐标为_______.(结果用含a ,b 的式子表示)20. 如图,ABC 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60︒得到CF .连接AF ,EF ,DF ,则CDF 周长的最小值是______.21. 在求123100++++的值时,发现:1100101+=,299101+=,从而得到123100++++=101505050⨯=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++=_______.(结果用含n 的代数式表示)22. 已知等腰ABC ,120A ∠=︒,2AB =.现将ABC 以点B 为旋转中心旋转45︒,得到A BC ''△,延长C A ''交直线BC 于点D .则A D '的长度为_______.三、解答题.23. 已知:点P 是O 外一点.(1)尺规作图:如图,过点P 作出O 的两条切线PE ,PF ,切点分别为点E ,点F .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,若点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒.求EDF ∠的度数. 24. 如图,直线MN 和EF 为河的两岸,且MN EF ∥,为了测量河两岸之间的距离,某同学在河岸FE 的B 点测得30CBE ∠=︒,从B 点沿河岸FE 的方向走40米到达D 点,测得45CDE ∠=︒.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D 点继续沿DE 的方向走12)米到达P 点.求tan CPE ∠的值.25. 某校组织师生参加夏令营活动,现准备租用A ,B 两型客车(每种型号的客车至少租用一辆).A 型车每辆租金500元,B 型车每辆租金600元.若5辆A 型和2辆B 型车坐满后共载客310人;3辆A 型和4辆B 型车坐满后共载客340人.(1)每辆A 型车,B 型车坐满后各载客多少人?(2)若该校计划租用A 型和B 型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A ,B 两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s (千米)与甲车行驶的时间t (小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t 为何值时两车相距25千米.26. 已知:四边形ABCD 为矩形,4AB =,3AD =,点F 是BC 延长线上的一个动点(点F 不与点C 重合).连接AF 交CD 于点G .(1)如图一,当点G 为CD 的中点时,求证:ADG FCG ≅△△.(2)如图二,过点C 作CE AF ⊥,垂足为E .连接BE ,设BF x =,CE y =.求y 关于x 的函数关系式. (3)如图三,在(2)的条件下,过点B 作BM BE ⊥,交FA 的延长线于点M .当1CF =时,求线段BM 的长.27. 如图,MN 为①O 的直径,且15MN =,MC 与ND 为圆内的一组平行弦,弦AB 交MC 于点H .点A 在MC 上,点B 在NC 上,90OND AHM ∠+∠=︒.(1)求证:MH CH AH BH ⋅=⋅.(2)求证:AC BC =.(3)在①O 中,沿弦ND 所在的直线作劣弧ND 的轴对称图形,使其交直径MN 于点G .若3sin 5CMN ∠=,求NG 的长.28. 如图,抛物线21y ax bx c =++的图象经过(6,0)A -,(2,0)B -,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E ,F ,B ,C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ⊥于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?2023年绥化市中考数学真题试卷答案一、单选题.1. C2. D3. B4. A5.D6. C7. D8. B9. C解:设()3,B m .①点B ,C 的横坐标都是3,2BC =,AC 平行于x 轴,点D 在AC 上,且其横坐标为1.①()()3,2,1,2C m D m ++.①32m m =+.解得1m =.①()3,1B .①313k =⨯=.故选C .10. B11. A解:如图所示,连接BD ,过点B 作BE AD ⊥于点E .当04t <<时,M 在AB 上.菱形ABCD 中,60A ∠=︒,4AB =.①AB AD =,则ABD △是等边三角形.①122AE ED AD ===,BE == ①2,AM x AN x ==. ①2AM AB AN AE==,又A A ∠=∠ ①AMN ABE ∽①90ANM AEB ∠=∠=︒①MN =.①212y x x = 当48t ≤<时,M 在BC 上.①1122y AN BE x =⨯=⨯=. 综上所述,04t <<时的函数图象是开口向上的抛物线的一部分,当48t ≤<时,函数图象是直线的一部分. 故选:A .12. D解:①四边形ABCD 是正方形.①90BAD ADE ∠=∠=︒,AB AD =①BF AE ⊥①90ABF BAF DAE ∠=︒-∠=∠①cos cos ABF EAD ∠=∠ 即BF AD AB AE=,又AB AD =. ①2AB BF AE =⋅,故①正确;设正方形的边长为a .①点E 为边CD 的中点.①2a DE =. ①1tan tans 2ABF EAD ∠=∠=. 在Rt ABE △中,AB a ==.①AF = 在Rt ADE △中,AE ==①2510EF AE AF a a a =-=-=. ①AB DE ∥①GAB GED ∽ ①2AG AB GE DE==①13GE AE ==①FG AE AF GE =--=--=①32AF FG == ①:2:3BGF BAF S S =△△,故①正确; ①AB a .①22222BD AB AD a =+=. 如图所示,过点H 分别作,BF AE 的垂线,垂足分别为,M N .又①BF AE ⊥.①四边形FMHN 是矩形.①FH 是BFG ∠的角平分线.①HM HN =.①四边形FMHN 是正方形.①FN HM HN ==①2,515BF AF a FG a === ①13MH FG BM BF == 设MH b =,则34BF BM FM BM MH b b b =+=+=+=在Rt BMH 中,BH .①BF =4b =解得:b =①102BH a a ==.①22222B a D BD HD a a =-⋅⨯=,故①正确. 故选:D .二、填空题.13. ()()x y x z +-14.5x ≥-且0x ≠ 15. 1216. 23-17. 12x -18. 22πcm 3⎛ ⎝ 解:如图所示,连接,OA OC ,设,AB CO 交于点D①将AB 沿弦AB 翻折,使点C 与圆心O 重合.①AC AO =,OC AB ⊥又OA OC =①OA OC AC ==.①AOC 是等边三角形.①60AOC ∠=︒,1OD CD ==.①AD =①阴影部分面积)226012π22πcm 36023AOC AOC S S =-=⨯-⨯=扇形故答案为:22πcm 3⎛- ⎝. 19. (62,2)a b --解:如图所示,过点,C C '分别作x 轴的垂线,CD C D ''垂足分别为,D D '.①ABC 与AB C ''△的相似比为12∶,点A 是位似中心,(2,0)A①2AD AD '=①(,)C a b .①2,AD a CD b =-=.①24,2A D a C D b '''=-=.①()224,0D a '-+①C '(62,2)a b --故答案为:(62,2)a b --.20. 3+解:①E 为高BD 上的动点. ①1302CBE ABC ∠=∠=︒ ①将CE 绕点C 顺时针旋转60︒得到CF .ABC 是边长为6的等边三角形.①,60,CE CF ECF BCA BC AC =∠=∠=︒=①CBE CAF ≌①30CAF CBE ∠=∠=︒.①F 点在射线AF 上运动.如图所示.作点C 关于AF 的对称点C ',连接DC ',设CC '交AF 于点O ,则=90AOC ∠︒ 在Rt AOC 中,30CAO ∠=︒,则132CO AC ==. 则当,,D F C '三点共线时,FC FD +取得最小值,即FC FD F C F D CD ''''+=+= ①6CC AC '==,ACO C CD '∠=∠,CO CD =①ACO C CD '≌①90C DC AOC '∠=∠=︒在C DC '中,C D '==①CDF 周长的最小值为3CD FC CD CD DC '++=+=+故答案为:3+21.22n n -解:依题意,()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-,.①123n a a a a ++++=()21432122n n n n n n +-==-=-. 故答案为:22n n -.22. 44+-解:如图所示,过点A 作AM BC ⊥于点M .①等腰ABC ,120BAC ∠=︒,2AB =.①30ABC ACB ∠=∠=︒.①112AM AB ==,BM CM ==①BC =如图所示,当ABC 以点B 为旋转中心逆时针旋转45︒,过点B 作BE A B '⊥交A D '于点E .①120BAC ∠=︒.①60DA B '∠=︒,30A EB '∠=︒.在Rt A BE '中,24A E A B ''==,BE ==①等腰ABC ,120BAC ∠=︒,2AB =.①30ABC ACB ∠=∠=︒.①ABC 以点B 为旋转中心逆时针旋转45︒.①45ABA '∠=︒.①180********DBE ∠=︒-︒-︒-︒=︒,1804530105A BD '∠=︒-︒-︒=︒在A BD '中,1801806010515D DA B A BD ∠=︒-∠-∠=︒-︒-︒=''︒.①D EBD ∠=∠. ①23EB ED ==.①423A D A E DE ''=+=+.如图所示,当ABC 以点B 为旋转中心顺时针旋转45︒,过点D 作DF BC '⊥交BC '于点F .在BFD △中,45BDF CBC ∠'=∠=︒.①DF BF =在Rt DC F '中,30C '∠=︒①'DF =①BC BF ==①3DF BF ==①26DC DF '==-①624A D C D A C ''''=-=-=-综上所述,A D '的长度为4-或4+故答案为:4-或4+三、解答题23. (1)见解析 (2)75EDF ∠=︒或105︒【小问1详解】解:如图所示.①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画弧,两弧交于点,M N 两点,作直线MN 交OP 于点A .①以点A 为圆心,OA 为半径画圆,与O 交于,E F 两点,作直线,PE PF . 则直线,PE PF 即为所求;【小问2详解】如图所示,点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒. ①,PE PF 是O 的切线.①90PEO PFO ∠=∠=︒.①360909030150EOF ∠=︒-︒-︒-︒=︒.当点D 在优弧EF 上时,1752EDF EOF ∠=∠=︒.当点D 在劣弧EF 上时,18075105EDF ∠=︒-︒=︒.①75EDF ∠=︒或105︒.24.(1)河两岸之间的距离是20米(2)5tan 2CPE ∠=【小问1详解】解:如图所示.过点C 作CM EF ⊥于点M ,设CM a =米.①30CBE ∠=︒①tan tan 303CM CBM PB ∠==︒=.①MB =.在Rt MCD △中,tan tan 451CM CDM MD∠==︒=. ①MD MC a ==①40BD MB MD a =-=-=解得:20a =答:河两岸之间的距离是20+米;【小问2详解】解:如图所示.依题意,4012)52PB BD DP =+=+=+①((20528MP MB PB =-=+=+在Rt CMP △中,5tan 2CM CPM MP ∠===. ①5tan 2CPE ∠=. 25. (1)每辆A 型车,B 型车坐满后各载客40人,55人(2)共有4种租车方案,租8辆A 型车,2辆B 型车最省钱(3)在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米 【小问1详解】解:设每辆A 型车,B 型车坐满后各载客x 人,y 人,由题意得 5231034340x y x y +=⎧⎨+=⎩ 解得4055x y =⎧⎨=⎩答:每辆A 型车,B 型车坐满后各载客40人,55人.【小问2详解】设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意得()()500600105500405510420m m m m ⎧+-≤⎪⎨+-≥⎪⎩ 解得:2583m ≤≤ m 取正整数.∴5m =,6,7,8∴共有4种租车方案设总租金为w 元,则500600(10)1006000w m m m =+-=-+1000-<w ∴随着m 的增大而减小∴8m =时,w 最小∴租8辆A 型车,2辆B 型车最省钱.【小问3详解】设s kt =甲,1s k t b =+乙.由题意可知,甲车的函数图象经过(4,300);乙车的函数图象经过(0.5,0),(3.5,300)两点. ①75s t =甲,10050s t =-乙25s s -=乙甲,即100507525t t --=解得3t =或3007525t -= 解得113t = 所以,在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米. 26. (1)见解析 (2)y =(或y = (3)3【小问1详解】证明:①四边形ABCD 为矩形.①AD BF ∥.①D DCF ∠=∠.①G 为CD 中点.①DG CG =,在ADG △和△FCG 中D GCF DG CGAGD FGC ∠=∠⎧⎪=⎨⎪∠=∠⎩①(ASA)ADG FCG △≌△;【小问2详解】①四边形ABCD 为矩形.①90ABC ∠=︒. ①CE AF ⊥.①90CEF ABC ∠=︒=∠. ①F F ∠=∠.①CEF ABF △∽△ ①CE CF AB AF=. ①4AB =,BF x =.①在Rt ABF 中,AF == ①CE y =. ①4y =①y =(或2(416x y x -=+); 【小问3详解】过点E 作EN BF ⊥于点N .①四边形ABCD 为矩形,且3AD =. ①3AD BC ==. ①4AB =,1CF =. ①AB BF =.①ABF △为等腰直角三角形. ①45CFE BAF ∠=∠=︒. ①CE AF ⊥.①CEF △为等腰直角三角形. ①45ECF ∠=︒ ①EN CF .①EN 平分CF . ①12CN NF NE ===. 在Rt BNE 中.①222BE BN EN =+.①BE == ①45ECF BAF ︒∠=∠=.①135BAM BCE ∠=∠=︒①BM BE ⊥.①90MBA ABE ∠+∠=︒.①90ABE EBC ∠+∠=︒.①MBA EBC ∠=∠.①BAM BCE △∽△. ①43BM BA BE BC ==.43=.①BM = 27. (1)见解析 (2)见解析(3)215【小问1详解】ABC ∠和AMC ∠是AC 所对的圆周角.∴ABC AMC .AHM CHB .①AMH CBH . ①AH MH CH BH=. ①MH CH AH BH ⋅=⋅.【小问2详解】连接OC ,交AB 于点F .MC 与ND 为一组平行弦,即:MC ND ∥.∴OND OMC .OM OC =.∴OMC OCM ∠=∠.90OND AHM ∠+∠=︒.∴90OCM AHM OCM CHB .∴90HFC ∠=︒.∴OC AB ⊥.∴OC 是AB 的垂直平分线.∴=AC BC .【小问3详解】连接DM ,DG ,过点D 作DE MN ⊥,垂足为E ,设点G 的对称点G ',连接G D ,G N '.DG DG '=,G ND GND .①'DM DG =.∴DG DM .∴DG DM =.∴DGM 是等腰三角形.DE MN ⊥.∴GE ME =.DN CM ∥.∴CMN DNM .MN 为直径.∴90MDN ∠=︒.∴90MDE EDN ∠+∠=︒.DE MN ⊥.∴90DEN ∠=︒.∴90DNM EDN . ∴3sin sin sin 5EDM DNM CMN . 在Rt MND △中,15MN =. ∴3sin 5MD DNM MN . ∴3155MD. ∴9MD =. 在Rt MED 中,3sin 5ME EDM MD . ∴395ME∴275ME. ∴2721215255NGMN MG MN ME ∴215NG 故答案为:215. 28. (1)211462y x x =++,36y x =+ (2)满足条件的E ,F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E -(3)当133m =时,12CD PD + 【小问1详解】解:把(6,0)A -,(2,0)B -,(0,6)C 代入21y ax bx c =++得36604206a b c a b c c -+=⎧⎪-+=⎨⎪=⎩解得1246a b c ⎧=⎪⎪=⎨⎪=⎪⎩①211462y x x =++ 把(2,0)B -代入6y kx =+得3k =①36y x =+【小问2详解】满足条件的E ,F 两点存在,1(8,2)E -,2(4,2)E -,3(4,4)E - 解:①当BC 为正方形的边长时,分别过B 点C 点作12E E BC ⊥,12F F BC ⊥,使12E B E B BC ==,12CF CF BC ==,连接11E F ,22E F .过点1E 作11E H x ⊥轴于1H .①1111,90BE CB BOC E H B E BC =∠=∠=︒=∠. 又111190BE H E BH CBO ∠=︒-∠=∠.①11(AAS)BE H CBO △≌△.①112E H BO ==,16H B OC ==①1(8,2)E -同理可得,2(4,2)E -①以BC 为正方形的对角线时,过BC 的中点G 作33E F BC ⊥,使33E F 与BC 互相平分且相等,则四边形33E BF C 为正方形.过点3E 作3E N y ⊥轴于点N ,过点B 作3BM E N ⊥于点M①3333,90CE BE CNE E MB =∠=∠=︒.又33390BE M CE N E CN ∠=︒-∠=∠①33(AAS)CE N E BM △≌△①3CN E M =,3BM E N =①BC =①3E G BG ==①3E B =在3Rt E NC △中,22233E C CN E N =+①222(6)CN CN =+-解得2CN =或4当4CN =时,3(2,2)E ,此时点E 在点F 右侧故舍去; 当2CN =时,3(4,4)E -.综上所述:1(8,2)E -,2(4,2)E -,3(4,4)E -【小问3详解】 ①211462y x x =++向右平移8个单位长度得到抛物线()()22184862y x x =-+-+ 当20y =,即()()21848602x x -+-+= 解得:122,6x x ==①(2,0)M ,(6,0)N①2y 过M ,N ,C 三点 ①221462y x x =-+ 在直线NC 下方的抛物线2y 上任取一点P ,作PH x ⊥轴交NC 于点H ,过点H 作HG y ⊥轴于点.G①(6,0)N ,(0,6)C①ON OC =①CON 是等腰直角三角形①45CHG ∠=︒,90GHP ∠=︒①45PHD ∠=︒又PD CN ⊥①HPD 是等腰直角三角形①2HD DP HP ==①点P 在抛物线2y 上,且横坐标为m①CG GH m ==①CH =①6CN y x =-+①(,6)H m m -+ ①2211646322HP m m m m m ⎛⎫=-+--+=-+ ⎪⎝⎭①22132242HD DP m m m m ⎛⎫==-+=-+ ⎪⎝⎭①211332222CD PD CH HD PD CH PD ⎛⎫+=++=+=+ ⎪ ⎪⎝⎭ 2138324m ⎫=--+⎪⎝⎭①当133m =时,12CD PD +的最大值为24.。
绥化中招数学试题及答案

绥化中招数学试题及答案一、选择题(本题共10小题,每小题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 如果一个角的度数是90°,那么这个角是:A. 锐角B. 直角C. 钝角D. 平角答案:B3. 一个数的平方根是它本身,这个数是:A. 1B. -1C. 0D. 4答案:C4. 若a > b > 0,则下列不等式中正确的是:A. a^2 > b^2B. a + b > 2√(ab)C. a/b > 1D. a/b < 1答案:B5. 一个圆的半径是5,那么这个圆的面积是:A. 25πB. 50πC. 75πD. 100π答案:B6. 一个等差数列的首项是3,公差是2,那么第5项是:A. 9B. 11C. 13D. 15答案:B7. 一个三角形的三边长分别是3, 4, 5,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 不能构成三角形答案:B8. 函数y = kx + b在x = 2时,y = 6,那么k + b的值是:A. 4B. 8C. 10D. 无法确定答案:A9. 若a, b, c是三角形的三边长,且满足a^2 + b^2 = c^2,那么这个三角形是:A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等边三角形答案:B10. 一个数的相反数是它本身,这个数是:A. 1B. -1C. 0D. 无法确定答案:C二、填空题(本题共5小题,每小题4分,共20分)11. 一个圆的直径是14,那么这个圆的周长是________。
答案:44π12. 若一个数的绝对值是5,那么这个数可以是________或________。
答案:5,-513. 一个数列的前3项是1, 1, 2,那么这个数列的第4项是________。
答案:314. 若一个三角形的内角和为180°,那么一个外角等于它相邻内角的________。
2023黑龙江省绥化市中考数学真题试卷和答案
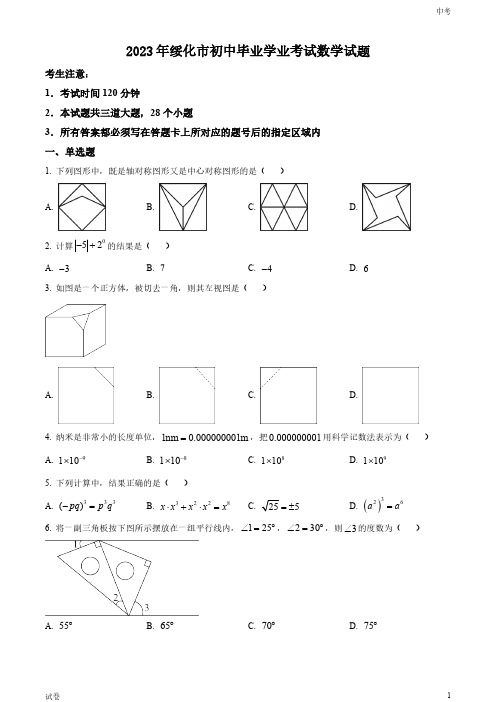
2023年绥化市初中毕业学业考试数学试题考生注意:1.考试时间120分钟2.本试题共三道大题,28个小题3.所有答案都必须写在答题卡上所对应的题号后的指定区域内一、单选题1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.2. 计算052-+的结果是( )A. 3- B. 7C. 4- D. 63. 如图是一个正方体,被切去一角,则其左视图是( )A. B. C. D.4. 纳米是非常小的长度单位,1nm 0.000000001m =,把0.000000001用科学记数法表示为( )A. 9110-⨯ B. 8110-⨯ C. 8110⨯ D. 9110⨯5. 下列计算中,结果正确的是( )A. 333()pq p q-= B. 3228x x x x x⋅+⋅= C.5=± D. ()326aa =6. 将一副三角板按下图所示摆放在一组平行线内,125∠=︒,230∠=︒,则3∠的度数为( )A. 55︒B. 65︒C. 70︒D. 75︒7. 下列命题中叙述正确的是( )A. 若方差22s s >乙甲,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上8. 绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是( )组别参赛者成绩A 7080x ≤<B 8090x ≤<C 90100x ≤<D 100110x ≤<E110120x ≤<A. 该组数据样本容量是50人B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D.110~120这组数据对应的扇形统计图的圆心角度数为51︒9. 在平面直角坐标系中,点A 在y 轴的正半轴上,AC 平行于x 轴,点B ,C 的横坐标都是3,2BC =,点D 在AC 上,且其横坐标为1,若反比例函数ky x=(0x >)的图像经过点B ,D ,则k 的值是( )的A. 1B. 2C. 3D.3210. 某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( )A.11142x+= B.11111424x ⎛⎫++= ⎪⎝⎭C.1111142x⎛⎫++= ⎪⎝⎭ D.11111442x⎛⎫++= ⎪⎝⎭11. 如图,在菱形ABCD 中,60A ∠=︒,4AB =,动点M ,N 同时从A 点出发,点M 以每秒2个单位长度沿折线A B C --向终点C 运动;点N 以每秒1个单位长度沿线段AD 向终点D 运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x 秒,AMN 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A. B. C. D.12. 如图,在正方形ABCD 中,点E 为边CD 的中点,连接AE ,过点B 作BF AE ⊥于点F ,连接BD 交AE 于点G ,FH 平分BFG ∠交BD 于点H .则下列结论中,正确的个数为( )①2AB BF AE =⋅;②:2:3BGF BAF S S =△△;③当AB a =时,22BD BD HD a -⋅=A. 0个B. 1个C. 2个D. 3个二、填空题13. 因式分解:2x xy xz yz +--=_______.14.x 的取值范围是_______.15. 在4张完全相同卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是_________.16. 已知一元二次方程256x x x +=+的两根为1x 与2x ,则1211+x x 的值为_______.17. 化简:2222142442x x x x x x x x x +--⎛⎫-÷=⎪--+-⎝⎭_______.18. 如图,O 的半径为2cm ,AB 为O 的弦,点C 为 AB 上的一点,将 AB 沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为_______.(结果保留π与根号)19. 如图,在平面直角坐标系中,ABC 与AB C ''△的相似比为12∶,点A 是位似中心,已知点(2,0)A ,点(,)C a b ,90C ∠=︒.则点C '的坐标为_______.(结果用含a ,b的式子表示)的20. 如图,ABC 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60︒得到CF .连接AF ,EF ,DF ,则CDF 周长的最小值是______.21. 在求123100++++ 的值时,发现:1100101+=,299101+= ,从而得到123100++++= 101505050⨯=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++= _______.(结果用含n 的代数式表示)22. 已知等腰ABC ,120A ∠=︒,2AB =.现将ABC 以点B 为旋转中心旋转45︒,得到A BC ''△,延长C A ''交直线BC 于点D .则A D '的长度为_______.三、解答题23. 已知:点P O 外一点.(1)尺规作图:如图,过点P 作出O 的两条切线PE ,PF ,切点分别为点E 、点F .(保留作图痕是迹,不要求写作法和证明)(2)在(1)的条件下,若点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒.求EDF ∠的度数.24. 如图,直线MN 和EF 为河的两岸,且MN EF ∥,为了测量河两岸之间的距离,某同学在河岸FE 的B 点测得30CBE ∠=︒,从B 点沿河岸FE 的方向走40米到达D 点,测得45CDE ∠=︒.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D 点继续沿DE 的方向走12)+米到达P 点.求tan CPE ∠的值.25. 某校组织师生参加夏令营活动,现准备租用A 、B 两型客车(每种型号的客车至少租用一辆).A 型车每辆租金500元,B 型车每辆租金600元.若5辆A 型和2辆B 型车坐满后共载客310人;3辆A 型和4辆B 型车坐满后共载客340人.(1)每辆A 型车、B 型车坐满后各载客多少人?(2)若该校计划租用A 型和B 型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A 、B 两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s (千米)与甲车行驶的时间t (小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t 为何值时两车相距25千米.26. 已知:四边形ABCD 为矩形,4AB =,3AD =,点F 是BC 延长线上的一个动点(点F 不与点C重合).连接AF 交CD 于点G .(1)如图一,当点G 为CD 的中点时,求证:ADG FCG ≅△△.(2)如图二,过点C 作CE AF ⊥,垂足为E .连接BE ,设BF x =,CE y =.求y 关于x 的函数关系式.(3)如图三,在(2)的条件下,过点B 作BM BE ⊥,交FA 的延长线于点M .当1CF =时,求线段BM 的长.27. 如图,MN 为⊙O 的直径,且15MN =,MC 与ND 为圆内的一组平行弦,弦AB 交MC 于点H .点A 在¼MC上,点B 在»NC 上,90OND AHM ∠+∠=︒.(1)求证:MH CH AH BH ⋅=⋅.(2)求证: AC BC=.(3)在⊙O 中,沿弦ND 所在的直线作劣弧 ND的轴对称图形,使其交直径MN 于点G .若3sin 5CMN ∠=,求NG 的长.28. 如图,抛物线21y ax bx c =++图象经过(6,0)A -,(2,0)B -,(0,6)C 三点,且一次函数6y kx =+的图象经过点B.的(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ⊥于点D .求m 为何值时,12CD PD+有最大值,最大值是多少?的2023年绥化市初中毕业学业考试数学试题考生注意:1.考试时间120分钟2.本试题共三道大题,28个小题3.所有答案都必须写在答题卡上所对应的题号后的指定区域内一、单选题1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.【答案】C 【解析】【分析】根据轴对称图形和中心对称图形的定义:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形;中心对称图形的定义:把一个图形绕着某一个点旋转180︒,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心,进行逐一判断即可.【详解】解:A 、是轴对称图形,不是中心对称图形,故A 选项不合题意;B 、是轴对称图形,不是中心对称图形,故B 选项不符合题意;C 、既是轴对称图形又是中心对称图形,故C 选项合题意;D 、不是轴对称图形,是中心对称图形,故D 选项不合题意.故选:C .【点睛】本题主要考查了轴对称图形和中心对称图形,解题的关键在于能够熟练掌握轴对称图形和中心对称图形的定义.2. 计算052-+的结果是( )A. 3- B. 7 C. 4- D. 6【答案】D 【解析】【分析】根据求一个数的绝对值,零指数幂进行计算即可求解.【详解】解:052-+516=+=,故选:D .【点睛】本题考查了求一个数的绝对值,零指数幂,熟练掌握求一个数的绝对值,零指数幂是解题的关键.3. 如图是一个正方体,被切去一角,则其左视图是( )A. B. C. D.【答案】B 【解析】【分析】根据左视图的意义判断即可.【详解】根据题意,该几何体的左视图为:,故选B .【点睛】本题考查了三视图的画法,熟练掌握三视图的空间意义是解题的关键.4. 纳米是非常小的长度单位,1nm 0.000000001m =,把0.000000001用科学记数法表示为( )A. 9110-⨯ B. 8110-⨯ C. 8110⨯ D. 9110⨯【答案】A 【解析】【分析】用科学记数法表示绝对值较小的数,一般形式为10n a -⨯,其中110a ≤<,n 为整数.【详解】解:90.000000001110-=⨯.故选:A .【点睛】此题主要考查了用科学记数法表示绝对值较小的数,一般形式为10n a -⨯,其中110a ≤<,n 为由原数左边起第一个不为零的数字前面的0的个数所决定,确定a 与n 的值是解题的关键.5. 下列计算中,结果正确的是( )A. 333()pq p q -= B. 3228x x x x x ⋅+⋅= C. 5=± D. ()326a a =【答案】D【解析】【分析】根据积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,进行计算即可求解.【详解】解:A. 333()pq p q =--,故该选项不正确,不符合题意;B. 43222x x x x x ⋅+⋅=,故该选项不正确,不符合题意;C. 5=,故该选项不正确,不符合题意;D. ()326a a =,故该选项正确,符合题意;故选:D .【点睛】本题考查了积的乘方与幂的乘方运算,同底数幂的乘法、合并同类项,算术平方根,熟练掌握以上运算法则是解题的关键.6. 将一副三角板按下图所示摆放在一组平行线内,125∠=︒,230∠=︒,则3∠的度数为( )A. 55︒B. 65︒C. 70︒D. 75︒【答案】C【解析】【分析】根据两直线平行内错角相等即可求解.【详解】解:依题意,190345∠+︒=∠+︒,∵125∠=︒,∴370∠=︒,故选:C .【点睛】本题考查了平行线的性质,熟练掌握两直线平行内错角相等是解题的关键.7. 下列命题中叙述正确的是( )A. 若方差22s s >乙甲,则甲组数据的波动较小B. 直线外一点到这条直线的垂线段,叫做点到直线的距离C. 三角形三条中线的交点叫做三角形的内心D. 角的内部到角的两边的距离相等的点在角的平分线上【答案】D【解析】【分析】根据方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,逐项分析判断即可求解.【详解】解:A. 若方差22s s >乙甲,则乙组数据的波动较小,故该选项不正确,不符合题意;B. 直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项不正确,不符合题意;C. 三角形三条中线的交点叫做三角形的重心,故该选项不正确,不符合题意;D. 角的内部到角的两边的距离相等的点在角的平分线上,故该选项正确,符合题意;故选:D .【点睛】本题考查了方差的意义,点到直线的距离,三角形的重心的定义,角平分线的性质,熟练掌握以上知识是解题的关键.8. 绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是( )组别参赛者成绩A7080x ≤<B8090x ≤<C90100x ≤<D100110x ≤<E 110120x ≤<A. 该组数据的样本容量是50人B. 该组数据的中位数落在90~100这一组C. 90~100这组数据的组中值是96D. 110~120这组数据对应的扇形统计图的圆心角度数为51︒【答案】B【解析】【分析】根据C 组的人数除以占比求得样本的容量,结合统计图求得8090x ≤<的人数为15,进而根据中位数的定义,即可判断B 选项,根据组中值为901002+=95,即可判断C 选项,根据110~120的占比乘以360︒,即可判断D 选项.【详解】解:A 、 该组数据的样本容量是1224%50÷=,故该选项不正确,不符合题意;B 、8090x ≤<的人数为:5041212715----=,41525+<,4151225++>,该组数据的中位数落在90~100这一组,故该选项正确,符合题意;C 、 90~100这组数据的组中值是95,故该选项不正确,不符合题意;D 、 110~120这组数据对应的扇形统计图的圆心角度数为736050.450⨯︒=︒,故该选项不正确,不符合题意;故选:B .【点睛】本题考查了样本的容量,条形统计图与扇形统计图信息关联,中位数的定义,求扇形统计图的圆心角的度数,求频数分布直方图组中值,从统计图表中获取信息是解题的关键.9. 在平面直角坐标系中,点A 在y 轴的正半轴上,AC 平行于x 轴,点B ,C 的横坐标都是3,2BC =,点D 在AC 上,且其横坐标为1,若反比例函数k y x=(0x >)的图像经过点B ,D ,则k 的值是( )A. 1B. 2C. 3D. 32【答案】C【解析】【分析】设()3,B m ,则()()3,2,1,2C m D m ++根据反比例函数的性质,列出等式计算即可.【详解】设()3,B m ,∵点B ,C 的横坐标都是3,2BC =,AC 平行于x 轴,点D 在AC 上,且其横坐标为1,∴()()3,2,1,2C m D m ++,∴32m m =+,解得1m =,∴()3,1B ,∴313k =⨯=,故选C .【点睛】本题考查了反比例函数解析式的确定,熟练掌握k的意义,反比例函数的性质是解题的关键.10. 某运输公司,运送一批货物,甲车每天运送货物总量的14.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物12天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x 天,由题意列方程,正确的是( )A. 11142x += B. 11111424x ⎛⎫++= ⎪⎝⎭C. 1111142x ⎛⎫++= ⎪⎝⎭ D.11111442x ⎛⎫++= ⎪⎝⎭【答案】B【解析】【分析】设乙车单独运送这批货物需x 天,由题意列出分式方程即可求解.【详解】解:设乙车单独运送这批货物需x 天,由题意列方程11111424x ⎛⎫++= ⎪⎝⎭,故选:B .【点睛】本题考查了列分式方程,根据题意找到等量关系列出方程是解题的关键.11. 如图,在菱形ABCD 中,60A ∠=︒,4AB =,动点M ,N 同时从A 点出发,点M 以每秒2个单位长度沿折线A B C --向终点C 运动;点N 以每秒1个单位长度沿线段AD 向终点D 运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x 秒,AMN 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A. B. C. D.【答案】A【解析】【分析】连接BD ,过点B 作BE AD ⊥于点E ,根据已知条件得出ABD △是等边三角形,进而证明AMN ABE ∽得出90ANM AEB ∠=∠=︒,当04t <<时,M 在AB 上,当48t ≤<时,M 在BC 上,根据三角形的面积公式得到函数关系式,【详解】解:如图所示,连接BD ,过点B 作BE AD ⊥于点E ,当04t <<时,M 在AB 上,菱形ABCD 中,60A ∠=︒,4AB =,∴AB AD =,则ABD △是等边三角形,∴122AE ED AD ===,BE ==∵2,AM x AN x ==,∴2AM AB AN AE==,又A A ∠=∠∴AMN ABE∽∴90ANM AEB ∠=∠=︒∴MN ==,∴212y x x =当48t ≤<时,M 在BC 上,∴1122y AN BE x =⨯=⨯=,综上所述,04t <<时的函数图象是开口向上的抛物线的一部分,当48t ≤<时,函数图象是直线的一部分,故选:A .【点睛】本题考查了动点问题的函数图象,二次函数图象的性质,一次函数图象的性质,菱形的性质,勾股定理,等边三角形的性质与判定,相似三角形的性质与判定,熟练掌握以上知识是解题的关键.12. 如图,在正方形ABCD 中,点E 为边CD 的中点,连接AE ,过点B 作BF AE ⊥于点F ,连接BD 交AE 于点G ,FH 平分BFG ∠交BD 于点H .则下列结论中,正确的个数为( )①2AB BF AE =⋅;②:2:3BGF BAF S S =△△;③当AB a =时,22BD BD HD a -⋅=A. 0个B. 1个C. 2个D. 3个【答案】D【解析】【分析】①根据题意可得90ABF BAF DAE ∠=︒-∠=∠,则cos cos ABF EAD ∠=∠,即BF AD AB AE=,又AB AD =,即可判断①;②设正方形的边长为a ,根据勾股定理求得AF ,证明GAB GED ∽,根据相似三角形的性质求得GE ,进而求得FG ,即可判断②;过点H 分别作,BF AE 的垂线,垂足分别为,M N ,根据②的结论求得BH ,勾股定理求得BD ,即可判断③.【详解】∵四边形ABCD 是正方形,∴90BAD ADE ∠=∠=︒,AB AD=∵BF AE⊥∴90ABF BAF DAE∠=︒-∠=∠∴cos cos ABF EAD∠=∠即BFADAB AE =,又AB AD =,∴2AB BF AE =⋅,故①正确;设正方形的边长为a ,∵点E 为边CD 的中点,∴2aDE =,∴1tan tans 2ABF EAD ∠=∠=,在Rt ABE △中,AB a ===,∴AF =在Rt ADE △中,AE ==∴EF AE AF =-==,∵AB DE∥∴GAB GED∽∴2AGABGE DE ==∴13GE AE ==∴FG AE AF GE =--=-=∴32AFFG ==∴:2:3BGF BAF S S =△△,故②正确;∵AB a =,∴22222BD AB AD a =+=,如图所示,过点H 分别作,BF AE 的垂线,垂足分别为,M N ,又∵BF AE ⊥,∴四边形FMHN 是矩形,∵FH 是BFG ∠的角平分线,∴HM HN =,∴四边形FMHN 是正方形,∴FN HM HN==∵2,BF AF FG ===∴13MH FG BM BF ==设MH b =,则34BF BM FM BM MH b b b=+=+=+=在Rt BMH中,BH ==,∵BF a =4b =解得:b =∴BH ==,∴2222B a D BD HD a a =-⋅=,故④正确.故选:D .【点睛】本题考查了解直角三角形,相似三角形的性质与判定,正方形的性质,熟练掌握相似三角形的性质与判定是解题的关键.二、填空题13. 因式分解:2x xy xz yz +--=_______.【答案】()()x y x z +-【解析】【分析】先分组,然后根据提公因式法,因式分解即可求解.【详解】解:2x xy xz yz +--=()()()()x x y z x y x y x z +-+=+-,故答案为:()()x y x z +-.【点睛】本题考查了因式分解,熟练掌握因式分解的方法是解题的关键.14. x 的取值范围是_______.【答案】5x ≥-且0x ≠##0x ≠且5x ≥-【解析】【分析】根据分母不为零,二次根式的被开方数是非负数,列出不等式计算即可.有意义,∴50x +≥且0x ≠,∴5x ≥-且0x ≠,故答案为:5x ≥-且0x ≠.【点睛】本题考查了分母不为零,二次根式的被开方数是非负数,熟练掌握二次根式和分式有意义的条件是解题的关键.15. 在4张完全相同的卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是_________.【答案】12##0.5【解析】【分析】根据题意列表法求概率即可求解.【详解】解:列表如下,1234111 1=1213142221=212=232142=333 1=32313=344441=42 2=43414=共有16种等可能结果,符合题意的有8种,∴第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是81162=,故答案为:12.【点睛】本题考查了列表法求概率,整除,熟练掌握列表法求概率是解题的关键.16. 已知一元二次方程256x x x +=+的两根为1x 与2x ,则1211+x x 的值为_______.【答案】23-【解析】【分析】根据一元二次方程根与系数的关系得出121246x x x x +==-,,将分式通分,代入即可求解.【详解】解:∵一元二次方程256x x x +=+,即2460x x --=,的两根为1x 与2x ,∴121246x x x x +==-,,∴1211+x x 12124263x x x x +===--,故答案为:23-.【点睛】本题考查了分式的化简求值,一元二次方程根与系数的关系,熟练掌握一元二次方程根与系数的关系是解题的关键.17. 化简:2222142442x x x x x x x x x +--⎛⎫-÷=⎪--+-⎝⎭_______.【答案】12x -##12x -+【解析】【分析】先根据分式的加减计算括号内的,同时将除法转化为乘法,再根据分式的性质化简即可求解.【详解】解:2222142442x x x x x x x x x+--⎛⎫-÷ ⎪--+-⎝⎭()()()()()2221242x x x x x x x x x +----=⨯--()()2222442x x x x xx x x ---+=⨯--12x =-;故答案为:12x -.【点睛】本题考查了分式的混合运算,熟练掌握分式的运算法则是解题的关键.18. 如图,O 的半径为2cm ,AB 为O 的弦,点C 为 AB 上的一点,将 AB 沿弦AB 翻折,使点C 与圆心O 重合,则阴影部分的面积为_______.(结果保留π与根号)【答案】22πcm3⎛- ⎝【解析】【分析】根据折叠的性质得出AOC 是等边三角形,则60AOC ∠=︒,1OD CD ==,根据阴影部分面积AOC AOC S S =- 扇形即可求解.【详解】解:如图所示,连接,OA OC ,设,AB CO 交于点D∵将 AB 沿弦AB 翻折,使点C 与圆心O 重合,∴AC AO =,OC AB⊥又OA OC=∴OA OC AC ==,∴AOC 是等边三角形,∴60AOC ∠=︒,1OD CD ==,∴AD ==,∴阴影部分面积)226012π22πcm 36023AOC AOC S S =-=⨯-⨯= 扇形故答案为:22πcm 3⎛- ⎝.19. 如图,在平面直角坐标系中,ABC 与AB C ''△的相似比为12∶,点A 是位似中心,已知点(2,0)A ,点(,)C a b ,90C ∠=︒.则点C '的坐标为_______.(结果用含a ,b 的式子表示)【答案】(62,2)a b --【解析】【分析】过点,C C '分别作x 轴的垂线,CD C D ''垂足分别为,D D ',根据题意得出2AD AD '=,则2,AD a CD b =-=,得出()224,0D a '-+,即可求解.【详解】解:如图所示,过点,C C '分别作x 轴的垂线,CD C D ''垂足分别为,D D ',∵ABC 与AB C ''△的相似比为12∶,点A 是位似中心,(2,0)A ∴2AD AD'=∵(,)C a b ,∴2,AD a CD b =-=,∴24,2A D a C D b '''=-=,∴()224,0D a '-+∴C '(62,2)a b --故答案为:(62,2)a b --.【点睛】本题考查了求位似图形的坐标,熟练掌握位似图形的性质是解题的关键.20. 如图,ABC 是边长为6的等边三角形,点E 为高BD 上的动点.连接CE ,将CE 绕点C 顺时针旋转60︒得到CF .连接AF ,EF ,DF ,则CDF 周长的最小值是______.【答案】3+3+【解析】【分析】根据题意,证明CBE CAF ≌,进而得出F 点在射线AF 上运动,作点C 关于AF 的对称点C ',连接DC ',设CC '交AF 于点O ,则=90AOC ∠︒,则当,,D F C '三点共线时,FC FD +取得最小值,即FC FD F C F D CD ''''+=+=,进而求得C D ',即可求解.【详解】解:∵E 为高BD 上的动点.∴1302CBE ABC ∠=∠=︒∵将CE 绕点C 顺时针旋转60︒得到CF .ABC 是边长为6的等边三角形,∴,60,CE CF ECF BCA BC AC=∠=∠=︒=∴CBE CAF≌∴30CAF CBE ∠=∠=︒,∴F 点在射线AF 上运动,如图所示,作点C 关于AF 的对称点C ',连接DC ',设CC '交AF 于点O ,则=90AOC ∠︒在Rt AOC 中,30CAO ∠=︒,则132CO AC ==,则当,,D F C '三点共线时,FC FD +取得最小值,即FC FD F C F D CD ''''+=+=∵6CC AC '==,ACO C CD '∠=∠,CO CD=∴ACO C CD' ≌∴90C DC AOC '∠=∠=︒在C DC ' 中,C D '===,∴CDF 周长的最小值为3CD FC CD CD DC '++=+=+故答案为:3+【点睛】本题考查了轴对称求线段和的最值问题,等边三角形的性质与判定,全等三角形的性质与判定,勾股定理,熟练掌握等边三角形的性质与判定以及轴对称的性质是解题的关键.21. 在求123100++++ 的值时,发现:1100101+=,299101+= ,从而得到123100++++= 101505050⨯=.按此方法可解决下面问题.图(1)有1个三角形,记作11a =;分别连接这个三角形三边中点得到图(2),有5个三角形,记作25a =;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作39a =;按此方法继续下去,则123n a a a a ++++= _______.(结果用含n 的代数式表示)【答案】22n n -##22n n -+【解析】【分析】根据题意得出()14143n a n n =+-=-,进而即可求解.【详解】解:依题意,()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-,,∴123n a a a a ++++= ()21432122n n n n n n +-==-=-,故答案为:22n n -.【点睛】本题考查了图形类规律,找到规律是解题的关键.22. 已知等腰ABC ,120A ∠=︒,2AB =.现将ABC 以点B 为旋转中心旋转45︒,得到A BC ''△,延长C A ''交直线BC 于点D .则A D '的长度为_______.【答案】44+-【解析】【分析】根据题意,先求得BC =,当ABC 以点B 为旋转中心逆时针旋转45︒,过点B 作BE A B '⊥交A D '于点E ,当ABC 以点B 为旋转中心顺时针旋转45︒,过点D 作DF BC '⊥交BC '于点F ,分别画出图形,根据勾股定理以及旋转的性质即可求解.【详解】解:如图所示,过点A 作AM BC ⊥于点M ,∵等腰ABC ,120BAC ∠=︒,2AB =.∴30ABC ACB ∠=∠=︒,∴112AM AB ==,BM CM ===∴BC =,如图所示,当ABC 以点B 为旋转中心逆时针旋转45︒,过点B 作BE A B '⊥交A D '于点E ,∵120BAC ∠=︒,∴60DA B '∠=︒,30A EB '∠=︒,在Rt A BE ' 中,24A E A B ''==,BE ==∵等腰ABC ,120BAC ∠=︒,2AB =.∴30ABC ACB ∠=∠=︒,∵ABC 以点B 为旋转中心逆时针旋转45︒,∴45ABA '∠=︒,∴180********DBE ∠=︒-︒-︒-︒=︒,1804530105A BD '∠=︒-︒-︒=︒在A BD ' 中,1801806010515D DA B A BD ∠=︒-∠-∠=︒-︒-︒=''︒,∴D EBD ∠=∠,∴EB ED ==∴4A D A E DE ''=+=+如图所示,当ABC 以点B 为旋转中心顺时针旋转45︒,过点D 作DF BC '⊥交BC '于点F ,在BFD △中,45BDF CBC ∠'=∠=︒,∴DF BF=在Rt DC F ' 中,30C '∠=︒∴'DF FC =∴BC BF =+=∴3DF BF ==∴26DC DF '==-∴624A D C D A C ''''=-=-=-,综上所述,A D '的长度为4-或4+,故答案为:4-或4+.【点睛】本题考查了旋转的性质,勾股定理,含30度角的直角三角形的性质,熟练掌握旋转的性质,分类讨论是解题的关键.三、解答题23. 已知:点P 是O 外一点.(1)尺规作图:如图,过点P 作出O 的两条切线PE ,PF ,切点分别为点E 、点F .(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,若点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒.求EDF ∠的度数.【答案】(1)见解析(2)75EDF ∠=︒或105︒【解析】【分析】(1)①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画圆,两圆交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O 交于,E F 两点,作直线,PE PF ,(2)根据切线的性质得出90PEO PFO ∠=∠=︒,根据四边形内角和得出150EOF ∠=︒,进而根据圆周角定理以及圆内接四边形对角互补即可求解.【小问1详解】解:如图所示,①连接PO ,分别以点,P O 为圆心,大于12PO 的长为半径画弧,两弧交于点,M N 两点,作直线MN 交OP 于点A ,②以点A 为圆心,OA 为半径画圆,与O 交于,E F 两点,作直线,PE PF ,则直线,PE PF 即为所求;【小问2详解】如图所示,点D 在O 上(点D 不与E ,F 两点重合),且30EPF ∠=︒,∵,PE PF 是O 的切线,∴90PEO PFO ∠=∠=︒,∴360909030150EOF ∠=︒-︒-︒-︒=︒,当点D 在优弧 E F 上时,1752EDF EOF ∠=∠=︒,当点D 在劣弧 E F 上时,18075105EDF ∠=︒-︒=︒,∴75EDF ∠=︒或105︒.【点睛】本题考查了切线的性质与判定,直径所对的圆周角是直角,圆内接四边形对角互补,圆周角定理,熟练掌握以上知识是解题的关键.24. 如图,直线MN 和EF 为河的两岸,且MN EF ∥,为了测量河两岸之间的距离,某同学在河岸FE 的B 点测得30CBE ∠=︒,从B 点沿河岸FE 的方向走40米到达D 点,测得45CDE ∠=︒.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D 点继续沿DE 的方向走12)+米到达P 点.求tan CPE ∠的值.【答案】(1)河两岸之间的距离是20米(2)5tan 2CPE ∠=【解析】【分析】(1)过点C 作CM EF ⊥于点M ,设CM a =米,在Rt MCB △中,MB =,在Rt MCD △中,MD MC a ==,根据40BD =,建立方程,解方程即可求解;(2)根据题意求得MP 的长,进而根据正切的定义,即可求解.【小问1详解】解:如图所示,过点C 作CM EF ⊥于点M ,设CM a =米,∵30CBE ∠=︒∴tan tan 30CMCBM PB ∠==︒=,∴MB =,在Rt MCD △中,tan tan 451CMCDM MD ∠==︒=,∴MD MC a==∴40BD MB MD a =-=-=解得:20a =+答:河两岸之间的距离是20米;【小问2详解】解:如图所示,依题意,4012)52PB BD DP =+=+=+,∴((20528MP MB PB =-=++=+在Rt CMP △中,5tan 2CM CPM MP ∠===,∴5tan 2CPE ∠=.【点睛】本题考查了解直角三角形的应用,熟练掌握三角函数关系是解题的关键.25. 某校组织师生参加夏令营活动,现准备租用A 、B 两型客车(每种型号的客车至少租用一辆).A 型车每辆租金500元,B 型车每辆租金600元.若5辆A 型和2辆B 型车坐满后共载客310人;3辆A 型和4辆B 型车坐满后共载客340人.(1)每辆A 型车、B 型车坐满后各载客多少人?(2)若该校计划租用A 型和B 型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A 、B 两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s (千米)与甲车行驶的时间t (小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t 为何值时两车相距25千米.【答案】(1)每辆A 型车、B 型车坐满后各载客40人、55人(2)共有4种租车方案,租8辆A 型车,2辆B 型车最省钱(3)在甲乙两车第一次相遇后,当3t =小时或113小时时,两车相距25千米【解析】【分析】(1)设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意列出二元一次方程组,解方程组即可求解;(2)设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意列出一元一次不等式组,解不等式组,求整数解即可得出m 的值,设总租金为w 元,根据一次函数的性质即可求解;(3)设s kt =甲,1s k t b =+乙,由题意可知,甲车的函数图像经过(4,300);乙车的函数图像经过(0.5,0),(3.5,300)两点.求出函数解析式,进而即可求解.【小问1详解】解:设每辆A 型车、B 型车坐满后各载客x 人、y 人,由题意得5231034340x y x y +=⎧⎨+=⎩解得4055x y =⎧⎨=⎩答:每辆A 型车、B 型车坐满后各载客40人、55人.【小问2详解】设租用A 型车m 辆,则租用B 型车(10)m -辆,由题意得()()500600105500405510420m m m m ⎧+-≤⎪⎨+-≥⎪⎩ 解得:2583m ≤≤ m 取正整数,∴5m =,6,7,8∴共有4种租车方案设总租金为w 元,则500600(10)1006000w m m m =+-=-+ 1000-<w ∴随着m 的增大而减小∴8m =时,w 最小∴租8辆A 型车,2辆B 型车最省钱.【小问3详解】。
2022年黑龙江省绥化市中考数学试题及答案解析

2022年黑龙江省绥化市中考数学试卷一、选择题(本大题共12小题,共36.0分)1.化简|−12|,下列结果中,正确的是( )A. 12B. −12C. 2D. −22.下列图形中,既是轴对称图形又是中心对称图形的是( )A. B. C. D.3.下列计算中,结果正确的是( )A. 2x2+x2=3x4B. (x2)3=x5C. √−233=−2 D. √4=±24.下列图形中,正方体展开图错误的是( )A.B.C.D.5.若式子√x+1+x−2在实数范围内有意义,则x的取值范围是( )A. x>−1B. x≥−1C. x≥−1且x≠0D. x≤−1且x≠06.下列命题中是假命题的是( )A. 三角形的中位线平行于三角形的第三边,并且等于第三边的一半B. 如果两个角互为邻补角,那么这两个角一定相等C. 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D. 直角三角形斜边上的中线等于斜边的一半7.如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA′,则点A′的坐标为( )A. (−5,2)B. (5,2)C. (2,−5)D. (5,−2)8.学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是( )A. 该组数据的中位数为98B. 该组数据的方差为0.7C. 该组数据的平均数为98D. 该组数据的众数为96和989.有一个容积为24m3的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径2倍的粗油管向油罐注油,直至注满,注满油的全过程共用30分钟.设细油管的注油速度为每分钟xm3,由题意列方程,正确的是( )A. 12x +124x=30 B. 15x+154x=24 C. 30x+302x=24 D. 12x+122x=3010.已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2−4ac与反比例函数y=4a+2b+cx在同一平面直角坐标系中的图象大致是( )A.B.C.D.11.小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为( )A. 2.7分钟B. 2.8分钟C. 3分钟D. 3.2分钟12.如图,在矩形ABCD中,P是边AD上的一个动点,连接BP,CP,过点B作射线,交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC= 5,AP=x,PM=y,其中2<x≤5.则下列结论中,正确的个数为( )(1)y与x的关系式为y=x−4x;(2)当AP=4时,△ABP∽△DPC;(3)当AP=4时,tan∠EBP=35.A. 0个B. 1个C. 2个D. 3个二、填空题(本大题共10小题,共30.0分)13.一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为14,则这个箱子中黄球的个数为______个.14.因式分解:(m+n)2−6(m+n)+9=______.15.不等式组{3x−6>0x>m的解集为x>2,则m的取值范围为______.16.已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为______.17.设x1与x2为一元二次方程12x2+3x+2=0的两根,则(x1−x2)2的值为______.18.定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α−β)=sinαcosβ−cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°)=√22×√32+√22×12=√6+√24,则sin15°的值为______.19.如图,正六边形ABCDEF和正五边形AHIJK内接于⊙O,且有公共顶点A,则∠BOH的度数为______度.20.某班为奖励在数学竞赛中成绩优异的同学,花费48元钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4元,乙种奖品每件3元.则有______种购买方案.21.如图,∠AOB=60°,点P1在射线OA上,且OP1=1,过点P1作P1K1⊥OA交射线OB于K1,在射线OA上截取P1P2,使P1P2=P1K1;过点P2作P2K2⊥OA交射线OB于K2,在射线OA上截取P2P3,使P2P3=P2K2…按照此规律,线段P2023K2023的长为______.22.在长为2,宽为x(1<x<2)的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x的值为______.三、解答题(本大题共6小题,共54.0分)23.已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.24.如图所示,为了测量百货大楼CD顶部广告牌ED的高度,在距离百货大楼30m的A处用仪器测得∠DAC=30°;向百货大楼的方向走10m,到达B处时,测得∠EBC=48°,仪器高度忽略不计,求广告牌ED的高度.(结果保留小数点后一位)(参考数据:√3≈1.732,sin48°≈0.743,cos48°≈0.669,tan48°≈1.111)) 25.在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,52两点,且与反比例函数y2=k2的图象在第一象限内交于P,K两点,连接OP,△OAPx的面积为5.4(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.26.我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.(1)如图一,在等腰△ABC中,AB=AC,BC边上有一点D,过点D作DE⊥AB于E,DF⊥AC于F,过点C作CG⊥AB于G.利用面积证明:DE+DF=CG.(2)如图二,将矩形ABCD沿着EF折叠,使点A与点C重合,点B落在B′处,点G为折痕EF上一点,过点G作GM⊥FC于M,GN⊥BC于N.若BC=8,BE=3,求GM+GN 的长.(3)如图三,在四边形ABCD中,E为线段BC上的一点,EA⊥AB,ED⊥CD,连接BD,且ABCD =AEDE,BC=√51,CD=3,BD=6,求ED+EA的长.27.如图所示,在⊙O的内接△AMN中,∠MAN=90°,AM=2AN,作AB⊥MN于点P,交⊙O于另一点B,C是AM⏜上的一个动点(不与A,M重合),射线MC交线段BA的延长线于点D,分别连接AC和BC,BC交MN于点E.(1)求证:△CMA∽△CBD.(2)若MN=10,MC⏜=NC⏜,求BC的长.(3)在点C运动过程中,当tan∠MDB=34时,求MENE的值.28.如图,抛物线y=ax2+bx+c交y轴于点A(0,−4),并经过点C(6,0),过点A作AB⊥y轴交抛物线于点B,抛物线的对称轴为直线x=2,D点的坐标为(4,0),连接AD,BC,BD.点E从A点出发,以每秒√2个单位长度的速度沿着射线AD运动,设点E的运动时间为m秒,过点E作EF⊥AB于F,以EF为对角线作正方形EGFH.(1)求抛物线的解析式;(2)当点G随着E点运动到达BC上时,求此时m的值和点G的坐标;(3)在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.答案解析1.【答案】A【解析】解:|−12|的绝对值是12,故选:A.利用绝对值的意义解答即可.本题主要考查了绝对值的意义,正确利用绝对值的意义是解题的关键.2.【答案】D【解析】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;B.是轴对称图形,不是中心对称图形,故本选项不符合题意;C.不是轴对称图形,是中心对称图形,故本选项不符合题意;D.既是轴对称图形,又是中心对称图形,故本选项符合题意.故选:D.根据中心对称图形与轴对称图形的概念进行判断即可.本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.3.【答案】C【解析】解:∵2x2+x2=3x2≠3x4,∴选项A不符合题意,∵(x2)3=x6≠x5,∴选项B不符合题意,∵√−233=−2,∴选项C符合题意,∵√4=2≠±2,∴选项D不符合题意,故选:C.利用合并同类项法则,幂的乘方的法则,立方根的意义,算术平方根的意义对每个选项进行分析,即可得出答案.本题考查了合并同类项,幂的乘方,立方根,算术平方根,掌握合并同类项法则,幂的乘方的法则,立方根的意义,算术平方根的意义是解决问题的关键.4.【答案】D【解析】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故D选项都不符合题意.故选:D.根据正方形的展开图得出结论即可.本题主要考查正方体展开图的知识,熟练掌握正方体的侧面展开图是解题的关键.5.【答案】C【解析】解:∵x+1≥0,x≠0,∴x≥−1且x≠0,故选:C.(a≠0)即可得出答案.根据二次根式的被开方数是非负数,a−p=1a p本题考查了二次根式有意义的条件,负整数指数幂,掌握二次根式的被开方数是非负数,a−p=1(a≠0)是解题的关键.a p6.【答案】B【解析】解:三角形的中位线平行于三角形的第三边,并且等于第三边的一半,故A是真命题,不符合题意;如果两个角互为邻补角,那么这两个角一定互补,故B是假命题,符合题意;从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,故C是真命题,不符合题意;直角三角形斜边上的中线等于斜边的一半,故D是真命题,不符合题意;故选:B.由三角形中位线定理,邻补角定义,切线长定理,直角三角形性质逐项判断即可.本题考查命题与定理,解题的关键是掌握教材上相关的概念和定理.7.【答案】A【解析】解:过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,如图,∵A点坐标为(2,5),∴OB−2,AB=5.由题意:∠AOA′=90°,OA=OA′.∴∠AOB+∠A′OC=90°.∵∠A′OC+∠A′=90°,∴∠A′=∠AOB.在△A′OC和△OAB中,{∠A′=∠AOB∠A′CO=∠OBA=90°OA′=AO,∴△A′OC≌△OAB(AAS).∴A′C=OB=2,OC=AB=5,∴A′(−5,2).故选:A.过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,利用旋转的性质和全等三角形的判定与性质解答即可.本题主要考查了图形的旋转与坐标的变化,点的坐标的特征,旋转的性质,全等三角形的判定与性质,利用点的坐标表示出相应线段的长度是解题的关键.8.【答案】D【解析】解:A、将这组数据从小到大排列为:96,96,97,98,98,中位数为97,故A选项不符合题意;C、平均数=96+96+97+98+985=97,故C选项不符合题意;B、方差=15×[(96−96)2×2+(97−96)2+(98−96)2×2]=1.8,故B选项不符合题意;D、该组数据的众数为96和98,故D选项符合题意;故选:D.根据中位数的定义判断A选项;根据算术平均数的计算方法判断C选项;根据方差的计算方法判断B选项;根据众数的定义判断D选项.本题考查了方差,算术平均数,中位数,众数,掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据是解题的关键.9.【答案】A【解析】解:24÷2=12(m3).设细油管的注油速度为每分钟xm3,则粗油管的注油速度为每分钟4xm3,依题意得:12x +124x=30.故选:A.设细油管的注油速度为每分钟xm3,则粗油管的注油速度为每分钟4xm3,利用注油所需时间=注油总量÷注油速度,即可得出关于x的分式方程,此题得解.本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.10.【答案】B【解析】解:∵二次函数y=ax2+bx+c的部分函数图象开口向上,∴a>0,∵二次函数y=ax2+bx+c的部分函数图象顶点在x轴下方,开口向上,∴二次函数y=ax2+bx+c的图象与x轴有两个交点,b2−4ac>0,∴一次函数y=ax+b2−4ac的图象经过第一,二,三象限,由二次函数y=ax2+bx+c的部分函数图象可知,点(2,4a+2b+c)在x轴上方,∴4a+2b+c>0,∴y=4a+2b+cx的图象经过第一,三象限,据此可知,符合题意的是B,故选:B.由二次函数y=ax2+bx+c的部分函数图象判断a,b2−4ac及4a+2b+c的符号,即可得到答案.本题考查一次函数,二次函数,反比例函数的图象,解题的关键是掌握三种图象的性质.11.【答案】C【解析】解:由图象可得,小明的速度为a12米/分钟,爸爸的速度为:a(12−4)÷2=a4(米/分钟),设小明出发m分钟两人第一次相遇,出发n分钟两人第二次相遇,a 12m=(m−4)⋅a4,a12n+a4[n−4−(12−4)÷2]=a,解得m=6,n=9,n−m=9−6=3,故选:C.根据题意和函数图象中的数据,可以先表示出两人的速度,然后即可计算出两人第一次和第二次相遇的时间,然后作差即可.本题考查一次函数的应用,解答本题的关键是明确题意,求出两人相遇的时间.12.【答案】C【解析】解:(1)过点P作PF⊥BC于点F,如图,∵四边形ABCD是矩形,PF⊥BC,∴四边形ABFP是矩形,∴PF=AB=2,BF=AP=x,∴AM=AP=PM=x−y.∵∠ABE=∠CBP,∠A=∠PFB=90°,∴△ABM∽△FBP,∴AMPF =ABBF,∴x−y2=2x.∴x2−xy=4.∴y=x−4x.∴(1)的结论正确;(2)当AP=4时,DP=AD−AP=5−4=1,∵ABAP =24=12,DBCD=12,∴ABAP =DPDC.∵∠A=∠D=90°,∴△ABP△DPC.∴(2)的结论正确;(3)由(2)知:当AP=4时,△ABP∽△DPC,∴∠ABP=∠DPC.∵∠BPA+∠ABP=90°,∴∠APB+∠DPC=90°.∴∠CPB=90°.∴∠BPE=90°.∴tan∠EBP=PEPB.由(1)知:PM=AP−4AP=3,BP=√AP2+AB2=2√5,CP=√CD2+DP2=√5.∵AD//BC,∴PMBC =PEEC.∴35=PE+√5,解得:PE=3√52,∴tan∠EBP=PEPB =3√522√5=34,∴(3)的结论错误,综上,正确的结论为:(1)(2),故选:C.利用矩形的性质,相似三角形的判定与性质,直角三角形的边角关系定理,勾股定理,平行线分线段成比例定理对每个选项的结论进行判断即可:(1)过点P作PF⊥BC于点F,利用矩形的判定与性质和相似三角形的判定与性质解答即可;(2)利用相似三角形的判定定理解答即可;(3)利用(1),(2)的结论利用勾股定理和平行线分线段成比例定理求得PB,PE,再利用直角三角形的边角关系定理即可求得结论.本题主要考查了矩形的性质,相似三角形的判定与性质,直角三角形的边角关系定理,勾股定理,平行线分线段成比例定理,灵活应用相似三角形的判定与性质是解题的关键.13.【答案】15【解析】解:设箱子中黄球的个数为x个,根据题意可得:5 5+x =14,解得:x=15,故答案为:15.直接利用概率公式得出红球个数小球总个数=14,进而得出答案.此题主要考查了概率公式,正确掌握概率求法是解题关键.14.【答案】(m+n−3)2【解析】解:原式=(m+n)2−2⋅(m+n)⋅3+32=(m+n−3)2.故答案为:(m+n−3)2.将m+n看作整体,利用完全平方公式即可得出答案.本题考查了因式分解−运用公式法,考查整体思想,掌握a2±2ab+b2=(a±b)2是解题的关键.15.【答案】m≤2【解析】解:由3x−6>0,得:x>2,∵不等式组的解集为x>2,∴m≤2,故答案为:m≤2.分别求出每一个不等式的解集,根据口诀:同大取大,结合不等式组的解集可得答案.本题考查了解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解题的关键.16.【答案】60πcm2【解析】解:圆锥的高为8cm,母线长为10cm,由勾股定理得,底面半径=6cm,侧面展开图的面积=πrl=π×6×10=60πcm2.故答案为:60πcm2.利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2.本题利用了勾股定理和圆锥的计算,圆锥的侧面积就是展开后扇形的面积,即S侧=πrl.17.【答案】20【解析】解:由题意可知:x1+x2=−6,x1x2=4,∴(x1−x2)2=(x1+x2)2−4x1x2=(−6)2−4×4=36−16=20,故答案为:20.根据根与系数的关系即可求出答案.本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系.18.【答案】√6−√24【解析】解:sin15°=sin(45°−30°)=sin45°cos30°−cos45°sin30°=√22×√32−√22×12=√64−√24=√6−√24.故答案为:√6−√24.把15°看成是45°与30°的差,再代入公式计算得结论.本题考查了解直角三角形,掌握特殊角的三角函数值是解决本题的关键.19.【答案】12【解析】解:如图,连接OA ,正六边形的中心角为∠AOB =360°÷6=60°,正五边形的中心角为∠AOH =360°÷5=72°,∴∠BOH =∠AOH −∠AOB =72°−60°=12°.故答案为:12.求出正六边形的中心角∠AOB 和正五边形的中心角∠AOH ,即可得出∠BOH 的度数. 本题主要考查正多边形与圆,会求正多边形的中心角是解题关键.20.【答案】3【解析】解:设购买x 件甲种奖品,y 件乙种奖品,依题意得:4x +3y =48,∴x =12−34y. 又∵x ,y 均为正整数,∴{x =9y =4或{x =6y =8或{x =9y =12, ∴共有3种购买方案.故答案为:3.设购买x 件甲种奖品,y 件乙种奖品,利用总价=单价×数量,即可得出关于x ,y 的二元一次方程,结合x ,y 均为正整数,即可得出共有3种购买方案.本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.21.【答案】√3(1+√3)2022【解析】解:由题意可得,P1K1=OP1⋅tan60°=1×√3=√3,P2K2=OP2⋅tan60°=(1+√3)×√3=√3(1+√3),P3K3=OP3⋅tan60°=(1+√3+√3+3)×√3=√3(1+√3)2,P4K4=OP4⋅tan60°=[(1+√3+√3+3)+√3(1+√3)2]×√3=√3(1+√3)3,…,P n K n=√3(1+√3)n−1,∴当n=2023时,P2023K2023=√3(1+√3)2022,故答案为:√3(1+√3)2022.根据题意和题目中的数据,可以写出前几项,然后即可得到P n K n的式子,从而可以写出线段P2023K2023的长.本题考查图象的变化类,解答本题的关键是发现P n K n的变化特点.22.【答案】1.2或者1.5【解析】解:第一次操作后的两边长分别是x和(2−x),第二次操作后的两边长分别是(2x−2)和(2−x).当2x−2>2−x时,有2x−2=2(2−x),解得x=1.5,当2x−2<2−x时,有2(2x−2)=2−x,解得x=1.2.故答案为:1.2或者1.5.本题中的x与(2−x)不知那个大,因此需要分类讨论,从而列方程求解.主要考查了含有字母的代数式的比较,关键是第二次操作后的边长,不知哪个是长,哪个是宽,所以分两种情况,不要丢掉任何一种.23.【答案】解:(1)如图,点O即为所求;(2)由题意,△ABC的面积=12×14×1.3=9.1(cm2).【解析】(1)作∠ABC,∠ACB的角平分线交于点O,点O即为所求;(2)△ABC的面积=12(a+b+c)⋅r计算即可.本题考查作图−复杂作图,三角形的内切圆与内心等知识,解题的关键掌握三角形的内心是角平分线的交点,属于中考常考题型.24.【答案】解:在Rt△ADC中,∠DAC=30°,AC=30米,∴CD=AC⋅tan30°=30×√33=10√3(米),∵AB=10米,∴BC=AC−AB=20(米),在Rt△BCE中,∠EBC=48°,∴EC=BC⋅tan48°≈20×1.111=22.22(米),∴DE=EC−DC=22.22−10√3≈4.9(米),∴广告牌ED的高度约为4.9米.【解析】在Rt△ADC中,利用锐角三角函数的定义求出CD的长,再利用已知求出BC的长,然后在在Rt△BCE中,利用锐角三角函数的定义求出EC的长,进行计算即可解答.本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.25.【答案】解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,52)两点,∴{5k1+b=0b=52,解得{k1=−12b=52.∴一次函数的解析式为:y1=−12x+52.∵△OAP的面积为54,∴12⋅OA⋅y P=54,∴y P=12,∵点P在一次函数图象上,∴令−12x+52=12.解得x=4,∴P(4,12).∵点P在反比例函数y2=k2x的图象上,∴k2=4×12=2.∴一次函数的解析式为:y1=−12x+52.反比例函数的解析式为:y2=2x.(2)令−12x+52=2x,解得x=1或x=4,∴K(1,2),由图象可知,当y2>y1时,x的取值范围为:0<x<1或x>4.(3)如图,作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,∵P(4,12).∴P′(4,−12).∴PP′=1,∴直线KP′的解析式为:y=−56x+176.令y=0,解得x=175.∴C(175,0).∴S△PKC=12⋅(x C−x K)⋅PP′=12×(175−1)×1=65.∴当PC+KC最小时,△PKC的面积为65.【解析】(1)根据待定系数法可求出直线AB的解析式,根据△OAP的面积可得出点P的坐标,代入反比例函数解析式可得出反比例函数的解析式;(2)联立一次函数和反比例函数的解析式,可得出点K的坐标,结合图象可直接得出x的取值范围;(3)作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,求出直线KP′的解析式,令y=0,可得出点C的坐标,再根据三角形的面积公式可得出结论.本题属于反比例函数与一次函数综合题,主要考查待定系数法求函数解析式,数形结合思想,轴对称最值问题,三角形的面积问题等知识,关键是求出一次函数和反比例函数的解析式.26.【答案】(1)证明:连接AD,∵S△ABC=S△ABD+S△ACD,∴12×AB×CG=12×AB×DE+12×AC×DF,∵AB=AC,∴DE+DF=CG;(2)解:∵将矩形ABCD沿着EF折叠,使点A与点C重合,∴∠AFE=∠EFC,AE=CE,∵AD//BC,∴∠AFE=∠CEF,∴∠CEF=∠CFE,∴CE=CF,∵BC=8,BE=3,∴CE=AE=5,在Rt△ABE中,由勾股定理得,AB=4,∴等腰△CEF中,CE边上的高为4,由(1)知,GM+GN=4;(3)解:延长BA、CD交于G,作BH⊥CD于H,∵ABCD =AEDE,∠BAE=∠EDC=90°,∴△BAE∽△CDE,∴∠ABE=∠C,∴BG=CG,∴ED+EA=BH,设DH=x,由勾股定理得,62−x2=(√51)2−(x+3)2,解得x=1,∴DH=1,∴BH=√BD2−DH2=√62−12=√35,∴ED+EA=√35.【解析】(1)连接AD,根据S△ABC=S△ABD+S△ACD,可得结论;(2)利用翻折的性质得,CE=CF,由勾股定理得,AB=4,则等腰△CEF中,CE边上的高为4,由(1)知,GM+GN=4;(3)延长BA、CD交于G,作BH⊥CD于H,利用△BAE∽△CDE,得∠ABE=∠C,则BG=CG,设DH=x,利用勾股定理列方程可得DH的长,从而得出BH,利用(1)中结论可得答案.本题是相似形综合题,主要考查了等腰三角形的判定与性质,翻折的性质,勾股定理,相似三角形的判定与性质,证明等腰三角形,利用(1)中结论是解决问题(2)、(3)的关键.27.【答案】(1)证明:连接BM ,如图:∵四边形ABMC 是⊙O 的内接四边形,∴∠DCA =∠ABM ,∵∠MAN =90°,∴MN 为⊙O 的直径,∵AB ⊥MN ,∴AM⏜=BM ⏜, ∴∠ABM =∠BAM ,∴∠DCA =∠BAM ,∵BM⏜=BM ⏜, ∴∠BAM =∠BCM ,∴∠DCA =∠BCM ,∴∠DCB =∠ACM ,∵AC⏜=AC ⏜, ∴∠DBC =∠AMC ,∴△CMA∽△CBD ;(2)解:连接OC ,如图:由AM=2MN,设AN=x,则AM=2x,∵MN为直径,∴∠NAM=90°,∴x2+(2x)2=102,解得x=2√5,∴AN=2√5,AM=4√5,∵AB⊥MN,∴2S△AMN=AN⋅AM=MN⋅AP,∴AP=BP=AN⋅AMMN =2√5×4√510=4,∴PM=√AM2−AP2=8,∵MC⏜=NC⏜,∴OC⊥MN,∵OC=OM,∴∠CMO=45°,∴△PDM是等腰直角三角形,CM=√2OM=5√2,∴PD=PM=8,∴BD=PD+BP=12,由(1)知△CMA∽△CBD,∴BCCM =BDAM,即5√2=4√5,∴BC=3√10;(3)解:连接CN交AM于K,连接KE,如图:∵MN 是⊙O 直径,∴∠MCN =90°=∠DPM ,∴∠CNM =90°−∠CMP =∠D ,∵tan∠MDB =34,∴tan∠CNM =34,∵AB ⊥MN ,∴AN⏜=BN ⏜, ∴∠KCE =∠KME ,∴C 、K 、E 、M 四点共圆,∵∠NCM =90°,∴∠KEM =90°=∠KEN ,而tan∠CNM =34,∴KE NE =34, 设KE =3m ,则NE =4m ,∵tan∠KME =KE EM =AN AM =12, ∴EM =6m ,∴ME NE =6m 4m =32. 【解析】(1)连接BM ,由四边形ABMC 是⊙O 的内接四边形,得∠DCA =∠ABM ,由∠MAN =90°,AB ⊥MN ,可得∠ABM =∠BAM ,即可得∠DCA =∠BCM ,从而∠DCB =∠ACM ,可证△CMA∽△CBD ;(2)连接OC ,由AM =2MN ,MN =10可得AN =2√5,AM =4√5,由面积法得AP =BP =AN⋅AM MN =2√5×4√510=4,即得PM =√AM 2−AP 2=8,根据MC⏜=NC ⏜,可得△PDM 是等腰直角三角形,CM =√2OM =5√2,即得PD =PM =8,BD =PD +BP =12,又△CMA∽△CBD ,可得BC =3√10;(3)连接CN 交AM 于K ,连接KE ,由tan∠MDB =34,可得tan∠CNM =34,根据AB ⊥MN ,得AN ⏜=BN ⏜,有∠KCE =∠KME ,即知C 、K 、E 、M 四点共圆,可得∠KEM =90°=∠KEN ,从而KE NE =34,设KE =3m ,则NE =4m ,而tan∠KME =KE EM =AN AM =12,得EM =6m ,故ME NE =6m 4m =32. 本题考查圆的综合应用,涉及相似三角形判定与性质,等腰直角三角形,锐角三角函数等知识,解题的关键是作辅助线,构造相似三角形.28.【答案】解:(1)∵抛物线的对称轴为直线x =2,D 点的坐标为(4,0),∴抛物线与x 轴的另一个交点为(−2,0),∴抛物线的解析式为:y =a(x +2)(x −6),将点A(0,−4)解析式可得,−12a =−4,∴a =13.∴抛物线的解析式为:y =13(x +2)(x −6)=13x 2−43x −4.(2)∵AB ⊥y 轴,A(0,−4),∴点B 的坐标为(4,−4).∵D(4,0),∴AB =BD =4,且∠ABD =90°,∴△ABD 是等腰直角三角形,∠BAD =45°.∵EF ⊥AB ,∴∠AFE =90°,∴△AEF 是等腰直角三角形.∵AE =2m ,∴AF =EF =√2m ,∴E(√2m,−4+√2m),F(√2m,−4).∵四边形EGFH 是正方形,∴△EHF 是等腰直角三角形,∴∠HEF =∠HFE =45°,∴FH是∠AFE的角平分线,点H是AE的中点.∴H(√22m,−4+√22m),G(3√22m,−4+√22m).∵B(4,−4),C(6,0),∴直线BC的解析式为:y=2x−12.当点G随着E点运动到达BC上时,有2×3√22m−12=−4+√22m.解得m=8√25.∴G(245,−125).(3)存在,理由如下:∵B(4,−4),C(6,0),G(3√22m,−4+√22m).∴BG2=(4−3√22m)2+(√22m)2,BC2=(4−6)2+(−4)2=20,CG2=(6−3√22m)2+(−4+√22m)2.若以B,G,C和平面内的另一点为顶点的四边形是矩形,则△BGC是直角三角形,∴分以下三种情况:①当点B为直角顶点时,BG2+BC2=CG2,∴(6−3√22m)2+(−4+√22m)2+20=(4−3√22m)2+(√22m)2,解得m=4√25,∴G(125,−165);②当点C为直角顶点时,BC2+CG2=BG2,∴20+(6−3√22m)2+(−4+√22m)2=(4−3√22m)2+(√22m)2,解得m=14√25,∴G(425,65 );③当点G为直角顶点时,BG2+CG2=BC2,∴(4−3√22m)2+(√22m)2+(6−3√22m)2+(−4+√22m)2=20,解得m=12√25或√2,∴G(3,−3)或(365,145);综上,存在以B,G,C和平面内的另一点为顶点的四边形是矩形,点G的坐标为(125,−165)或(425,65)或(3,−3)或(365,145).【解析】(1)根据抛物线的对称轴为直线x=2,可得出抛物线与x轴的另一个交点的坐标为(−2,0),列出交点式,再将点A(0,−4)可得出抛物线的解析式;(2)根据可得出△ABD是等腰直角三角形,再根据点E的运动和正方形的性质可得出点H,F,G的坐标,根据点B,C的坐标可得出直线BC的解析式,将点G代入直线BC的解析式即可;(3)若存在,则△BGC是直角三角形,则需要分类讨论,当点B为直角顶点,当点G为直角顶点,当点C为直角顶点,分别求解即可.本题属于二次函数综合题,主要考查待定系数法求函数解析式,正方形的性质与判定,矩形的性质与判定,等腰直角三角形的性质与判定,分类讨论等知识,解题关键是由点E的坐标得出点H,F,G的坐标.本题第(3)问当点B和点C为直角顶点时,也可通过一次函数和几何结合求解.。
2024绥化数学中考试题

2024绥化数学中考试题一、选择题(每题3分,共30分)1. 下列哪个数是正整数?A. -3B. 0C. 5C. 1.52. 如果\( a \)和\( b \)是两个连续的自然数,且\( a = 10 \),那么\( b \)的值是多少?A. 9B. 11C. 12D. 103. 一个直角三角形的两个直角边长分别是3和4,那么斜边的长度是多少?A. 5B. 7C. 8D. 94. 一个数的平方根是它自己,这个数可能是:A. 1B. 0C. -1D. 45. 下列哪个表达式的结果是一个负数?A. \( 2^3 \)B. \( -2^2 \)C. \( (-2)^3 \)D. \( (-2)^2 \)6. 如果一个圆的半径是5,那么它的面积是多少?A. 25B. 50C. 100D. 2007. 一个长方体的长、宽、高分别是2米、3米和4米,那么它的体积是多少?A. 24B. 36C. 48D. 608. 下列哪个选项是\( 2x + 3 = 11 \)的解?A. \( x = 4 \)B. \( x = 2 \)C. \( x = 5 \)D. \( x = 6 \)9. 一个数的绝对值是5,这个数可能是:A. 5B. -5C. 5或-5D. 都不是10. 下列哪个选项是方程\( 3x - 7 = 2x + 8 \)的解?A. \( x = -15 \)B. \( x = 1 \)C. \( x = 5 \)D. \( x = 15 \)二、填空题(每题2分,共20分)11. 如果一个数的立方是-27,那么这个数是______。
12. 一个数的相反数是-8,这个数是______。
13. 一个圆的直径是14厘米,那么它的周长是______厘米。
14. 如果\( a \)和\( b \)互为倒数,那么\( ab \)的值是______。
15. 一个等腰三角形的底边长为6厘米,如果它的周长是18厘米,那么它的腰长是______厘米。
黑龙江省绥化市2023年中考数学试卷((附参考答案))
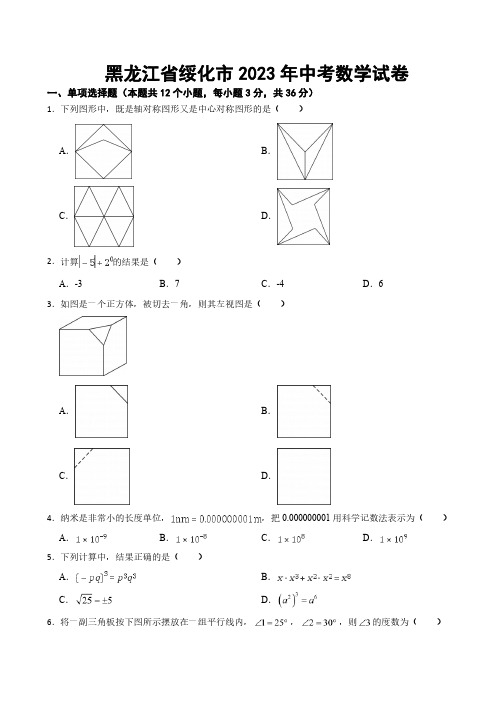
黑龙江省绥化市2023年中考数学试卷一、单项选择题(本题共12个小题,每小题3分,共36分)1.下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.2.计算的结果是()A.-3B.7C.-4D.63.如图是一个正方体,被切去一角,则其左视图是()A.B.C.D.4.纳米是非常小的长度单位,,把0.000000001用科学记数法表示为()A.B.C.D.5.下列计算中,结果正确的是()A.B.C.D.6.将一副三角板按下图所示摆放在一组平行线内,,,则的度数为()A.55°B.65°C.70°D.75°7.下列命题中叙述正确的是()A.若方差,则甲组数据的波动较小B.直线外一点到这条直线的垂线段,叫做点到直线的距离C.三角形三条中线的交点叫做三角形的内心D.角的内部到角的两边的距离相等的点在角的平分线上8.绥化市举办了2023年半程马拉松比赛,赛后随机抽取了部分参赛者的成绩(单位:分钟),并制作了如下的参赛者成绩组别表、扇形统计图和频数分布直方图.则下列说法正确的是()组别参赛者成绩ABCDEA.该组数据的样本容量是50人B.该组数据的中位数落在90~100这一组C.90~100这组数据的组中值是96D.110~120这组数据对应的扇形统计图的圆心角度数为51°9.在平面直角坐标系中,点A在y轴的正半轴上,平行于x轴,点B,C的横坐标都是3,,点D在上,且其横坐标为1,若反比例函数()的图象经过点B,D,则k的值是()A.1B.2C.3D.10.某运输公司,运送一批货物,甲车每天运送货物总量的.在甲车运送1天货物后,公司增派乙车运送货物,两车又共同运送货物天,运完全部货物.求乙车单独运送这批货物需多少天?设乙车单独运送这批货物需x天,由题意列方程,正确的是()A.B.C.D.11.如图,在菱形中,,,动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A-B-C向终点C运动;点N以每秒1个单位长度沿线段向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,的面积为y个平方单位,则下列正确表示y 与x函数关系的图象是()A.B.C.D.12.如图,在正方形中,点E为边的中点,连接,过点B作于点F,连接交于点G,平分交于点H.则下列结论中,正确的个数为()①②③当时,A.0个B.1个C.2个D.3个二、填空题(本题共10个小题,每小题3分,共30分)13.因式分解:.14.若式子有意义,则x的取值范围是.15.在4张完全相同的卡片上,分别标出1,2,3,4,从中随机抽取1张后,放回再混合在一起.再随机抽取一张,那么第二次抽取卡片上的数字能够整除第一次抽取卡片上的数字的概率是. 16.已知一元二次方程的两根为与,则的值为.17.化简:.18.如图,的半径为2,为的弦,点C为上的一点,将沿弦翻折,使点C与圆心O重合,则阴影部分的面积为.(结果保留π与根号)19.如图,在平面直角坐标系中,与的相似比为1∶2,点A是位似中心,已知点,点,.则点的坐标为.(结果用含a,b的式子表示)20.如图,是边长为6的等边三角形,点E为高上的动点.连接,将绕点C顺时针旋转60°得到.连接,,,则周长的最小值是.21.在求的值时,发现:,,从而得到.按此方法可解决下面问题.图(1)有1个三角形,记作;分别连接这个三角形三边中点得到图(2),有5个三角形,记作;再分别连接图(2)中间的小三角形三边中点得到图(3),有9个三角形,记作;按此方法继续下去,则.(结果用含n的代数式表示)22.已知等腰,,.现将以点B为旋转中心旋转45°,得到,延长交直线于点D.则的长度为.三、解答题(本题共6个小题,共54分)23.已知:点P是外一点.(1)尺规作图:如图,过点P作出的两条切线,,切点分别为点E、点F.(保留作图痕迹,不要求写作法和证明)(2)在(1)的条件下,若点D在上(点D不与E,F两点重合),且.求的度数.24.如图,直线和为河的两岸,且,为了测量河两岸之间的距离,某同学在河岸的B点测得,从B点沿河岸的方向走40米到达D点,测得.(1)求河两岸之间的距离是多少米?(结果保留根号)(2)若从D点继续沿的方向走米到达P点.求的值.25.某校组织师生参加夏令营活动,现准备租用A、B两型客车(每种型号的客车至少租用一辆).A型车每辆租金500元,B型车每辆租金600元.若5辆A型和2辆B型车坐满后共载客310人;3辆A型和4辆B型车坐满后共载客340人.(1)每辆A型车、B型车坐满后各载客多少人?(2)若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)在这次活动中,学校除租用A、B两型客车外,又派出甲、乙两辆器材运输车.已知从学校到夏令营目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地.下图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲乙两车第一次相遇后,t为何值时两车相距25千米.26.已知:四边形为矩形,,,点F是延长线上的一个动点(点F不与点C 重合).连接交于点G.(1)如图一,当点G为的中点时,求证:.(2)如图二,过点C作,垂足为E.连接,设,.求y关于x的函数关系式.(3)如图三,在(2)的条件下,过点B作,交的延长线于点M.当时,求线段的长.27.如图,为的直径,且,与为圆内的一组平行弦,弦交于点H.点A 在上,点B在上,.(1)求证:.(2)求证:.(3)在中,沿弦所在的直线作劣弧的轴对称图形,使其交直径于点G.若,求的长.28.如图,抛物线的图象经过,,三点,且一次函数的图象经过点B.(1)求抛物线和一次函数的解析式.(2)点E,F为平面内两点,若以E、F、B、C为顶点的四边形是正方形,且点E在点F的左侧.这样的E,F两点是否存在?如果存在,请直接写出所有满足条件的点E的坐标:如果不存在,请说明理由.(3)将抛物线的图象向右平移8个单位长度得到抛物线,此抛物线的图象与x轴交于M,N两点(M点在N点左侧).点P是抛物线上的一个动点且在直线下方.已知点P的横坐标为m.过点P作于点D.求m为何值时,有最大值,最大值是多少?答案1.【答案】C2.【答案】D3.【答案】B4.【答案】A5.【答案】D6.【答案】C7.【答案】D8.【答案】B9.【答案】C10.【答案】B11.【答案】A12.【答案】D13.【答案】14.【答案】且15.【答案】16.【答案】17.【答案】18.【答案】19.【答案】20.【答案】21.【答案】22.【答案】或23.【答案】(1)作法:如图所示①连接,分别以点P,O为圆心,大于长为半径画弧,两弧交于M,N两点作直线交于点A.②以点A为圆心,以为半径画弧(或画圆)与圆O交于E,F两点.作直线,、即为所求.(2)解:∵PE、PF分别为切线,∴∠PEO=∠PFO=90°,∴∠EOF=360°-∠PEO-∠PFO-∠EPF=150°,∴∠EDF=∠EOF=75°或∠EDF=180°-75°=105°.24.【答案】(1)解:过C作CH⊥EF于点H,∵tan∠CBH=,∴HB=CH.∵∠CDH=45°,∴CH=DH.∵BH-DH=BD=40,∴CH-CH=40,解得CH=+20,∴河两岸之间的距离是(+20)m.(2)解:∵HP=HD-PD=+20-(+12)=+8,∴tan∠CPE===.25.【答案】(1)设每辆A型车、B型车坐满后各载客x人、y人,由题意得解得答:每辆A型车、B型车坐满后各载客40人、55人.(2)设租用A型车m辆,则租用B型车辆,由题意得解得:∵m取正整数,∴,6,7,8∴共有4种租车方案设总租金为w元,则∵∴w随着m的增大而减小∴时,w最小∴租8辆A型车,2辆B型车最省钱.(3)设,.由题意可知,甲车经过;乙车经过,两点.∴,,即解得或解得所以,在甲乙两车第一次相遇后,当小时或小时,两车相距25千米. 26.【答案】(1)证明:∵四边形为矩形∴∴∵G为中点∴在和中∴(2)∵四边形为矩形∴∵∴∵∴∴∵,∴在中,∵∴∴(3)过点E作于点N∵四边形为矩形,且∴∵,∴∴为等腰直角三角形∴∵∴为等腰直角三角形∴∵∴平分∴在中,∵∴∵∴∵∴∵∴∴∴∴∴27.【答案】(1)证明:∵和是所对的圆周角∴∵∴∴∴(2)连接,交于点F∵与为一组平行弦(也可写成)∴∵∴∵∴∠∴∴∴(3)解:连接DM、DG,过D作DE⊥MN,垂足为E,设点G的对称点G′,连接G′D、G′N,∵DG=DG′,∠G′ND=∠GND,DG′=DM,弧DM=弧DG′,∴DG=DM,∴△DGM为等腰三角形.∵DE⊥MN,∴GE=ME.∵DN∥CM,∴∠CMN=∠DNM.∵MN为直径,∴∠MDN=90°,∴∠MDE+∠EDN=90°.∵DE⊥MN,∴∠DEN=90°,∴∠DNM+∠EDN=90°,∴sin∠EDM=sin∠DNM=sin∠CMN=.∵MN=15,∴sin∠DNM=,∴MD=9.∵sin∠EDM==,∴,∴ME=,∴NG=MN-MG=MN-2ME=.28.【答案】(1)解:把,,代入得解得∴把代入得∴(2)解:①当BC为正方形的边长时,分别过B、C作E1E2⊥BC,F1F2⊥BC,使E1B=E2B=BC,CF1=CF2=BC,连接E1F1、E2F2,过E1作E1H1⊥x轴于点H1,则△BE1H1≌△CBO(AAS),∴E1H1=OB=2,H1B=OC=6,∴E1(-8,2).同理可得E2(4,-2).②以BC为正方形的对角线时,过BC的重点G作E3F3⊥BC,使E3F3与BC互相平分且相等,则四边形E3BF3C为正方形,过E3作E3N⊥y轴于点N,过B作BM⊥E3N于点M,∴△CE3N≌△E3BM(AAS),∴CN=E3M,BM=E3N.∵BC=,∴E3G=BG=,∴E3B=.∵E3C2=CN2+E3N2,∴()2=CN2+(6-CN)2,解得CN=2或4.当CN=4时,E3(2,2),此时点E在点F右侧,舍去;当CN=2时,E3(-4,4),综上可得:E1(-8,2),E2(4,-2),E3(-4,4).(3)∵向右平移8个单位长度得到抛物线∴,∵过M,N,C三点∴在直线下方的抛物线上任取一点P,作轴交于点H,过点H作轴于点G.∵,∴∴是等腰直角三角形∵,∴又∴是等腰直角三角形∴∵点P在抛物线上,且横坐标为m∴∴∵∴∴∴∴∴当时,的最大值为.。
2022年黑龙江省绥化市中考数学试卷(解析版)

2022年黑龙江省绥化市中考数学试卷一、单项选择题(本题共12个小题,每小题3分,共36分)请在答题卡上用28铅笔将你的选项所对应的大写字母涂黑1.(3分)(2022•绥化)化简|﹣|,下列结果中,正确的是()A.B.﹣C.2D.﹣22.(3分)(2022•绥化)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.3.(3分)(2022•绥化)下列计算中,结果正确的是()A.2x2+x2=3x4B.(x2)3=x5C.=﹣2D.=±24.(3分)(2022•绥化)下列图形中,正方体展开图错误的是()A.B.C.D.5.(3分)(2022•绥化)若式子+x﹣2在实数范围内有意义,则x的取值范围是()A.x>﹣1B.x≥﹣1C.x≥﹣1且x≠0D.x≤﹣1且x≠0 6.(3分)(2022•绥化)下列命题中是假命题的是()A.三角形的中位线平行于三角形的第三边,并且等于第三边的一半B.如果两个角互为邻补角,那么这两个角一定相等C.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D.直角三角形斜边上的中线等于斜边的一半7.(3分)(2022•绥化)如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为()A.(﹣5,2)B.(5,2)C.(2,﹣5)D.(5,﹣2)8.(3分)(2022•绥化)学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是()A.该组数据的中位数为98B.该组数据的方差为0.7C.该组数据的平均数为98D.该组数据的众数为96和989.(3分)(2022•绥化)有一个容积为24m3的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径2倍的粗油管向油罐注油,直至注满,注满油的全过程共用30分钟.设细油管的注油速度为每分钟xm3,由题意列方程,正确的是()A.+=30B.+=24C.+=24D.+=3010.(3分)(2022•绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是()A.B.C.D.11.(3分)(2022•绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为()A.2.7分钟B.2.8分钟C.3分钟D.3.2分钟12.(3分)(2022•绥化)如图,在矩形ABCD中,P是边AD上的一个动点,连接BP,CP,过点B作射线,交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y,其中2<x≤5.则下列结论中,正确的个数为()(1)y与x的关系式为y=x﹣;(2)当AP=4时,△ABP∽△DPC;(3)当AP=4时,tan∠EBP=.A.0个B.1个C.2个D.3个二、填空题(本题共10个小题,每小题3分,共30分)请在答题卡上把你的答案写在相对应的题号后的指定区域内13.(3分)(2022•绥化)一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为,则这个箱子中黄球的个数为个.14.(3分)(2022•绥化)因式分解:(m+n)2﹣6(m+n)+9=.15.(3分)(2022•绥化)不等式组的解集为x>2,则m的取值范围为.16.(3分)(2022•绥化)已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为.17.(3分)(2022•绥化)设x1与x2为一元二次方程x2+3x+2=0的两根,则(x1﹣x2)2的值为.18.(3分)(2022•绥化)定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°)=×+×=,则sin15°的值为.19.(3分)(2022•绥化)如图,正六边形ABCDEF和正五边形AHIJK内接于⊙O,且有公共顶点A,则∠BOH的度数为度.20.(3分)(2022•绥化)某班为奖励在数学竞赛中成绩优异的同学,花费48元钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4元,乙种奖品每件3元.则有种购买方案.21.(3分)(2022•绥化)如图,∠AOB=60°,点P1在射线OA上,且OP1=1,过点P1作P1K1⊥OA交射线OB于K1,在射线OA上截取P1P2,使P1P2=P1K1;过点P2作P2K2⊥OA交射线OB于K2,在射线OA上截取P2P3,使P2P3=P2K2…按照此规律,线段P2023K2023的长为.22.(3分)(2022•绥化)在长为2,宽为x(1<x<2)的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x的值为.三、解答题(本题共6个小题,共54分)请在答题卡上把你的答案写在相对应的题号后的指定区域内23.(7分)(2022•绥化)已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.24.(8分)(2022•绥化)如图所示,为了测量百货大楼CD顶部广告牌ED的高度,在距离百货大楼30m的A处用仪器测得∠DAC=30°;向百货大楼的方向走10m,到达B处时,测得∠EBC=48°,仪器高度忽略不计,求广告牌ED的高度.(结果保留小数点后一位)(参考数据:≈1.732,sin48°≈0.743,cos48°≈0.669,tan48°≈1.111)25.(9分)(2022•绥化)在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数y2=的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.26.(9分)(2022•绥化)我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.(1)如图一,在等腰△ABC中,AB=AC,BC边上有一点D,过点D作DE⊥AB于E,DF⊥AC于F,过点C作CG⊥AB于G.利用面积证明:DE+DF=CG.(2)如图二,将矩形ABCD沿着EF折叠,使点A与点C重合,点B落在B'处,点G 为折痕EF上一点,过点G作GM⊥FC于M,GN⊥BC于N.若BC=8,BE=3,求GM+GN 的长.(3)如图三,在四边形ABCD中,E为线段BC上的一点,EA⊥AB,ED⊥CD,连接BD,且=,BC=,CD=3,BD=6,求ED+EA的长.27.(10分)(2022•绥化)如图所示,在⊙O的内接△AMN中,∠MAN=90°,AM=2AN,作AB⊥MN于点P,交⊙O于另一点B,C是上的一个动点(不与A,M重合),射线MC交线段BA的延长线于点D,分别连接AC和BC,BC交MN于点E.(1)求证:△CMA∽△CBD.(2)若MN=10,=,求BC的长.(3)在点C运动过程中,当tan∠MDB=时,求的值.28.(11分)(2022•绥化)如图,抛物线y=ax2+bx+c交y轴于点A(0,﹣4),并经过点C (6,0),过点A作AB⊥y轴交抛物线于点B,抛物线的对称轴为直线x=2,D点的坐标为(4,0),连接AD,BC,BD.点E从A点出发,以每秒个单位长度的速度沿着射线AD运动,设点E的运动时间为m秒,过点E作EF⊥AB于F,以EF为对角线作正方形EGFH.(1)求抛物线的解析式;(2)当点G随着E点运动到达BC上时,求此时m的值和点G的坐标;(3)在运动的过程中,是否存在以B,G,C和平面内的另一点为顶点的四边形是矩形,如果存在,直接写出点G的坐标,如果不存在,请说明理由.2022年黑龙江省绥化市中考数学试卷参考答案与试题解析一、单项选择题(本题共12个小题,每小题3分,共36分)请在答题卡上用28铅笔将你的选项所对应的大写字母涂黑1.(3分)(2022•绥化)化简|﹣|,下列结果中,正确的是()A.B.﹣C.2D.﹣2【分析】利用绝对值的意义解答即可.【解答】解:|﹣|的绝对值是,故选:A.【点评】本题主要考查了绝对值的意义,正确利用绝对值的意义是解题的关键.2.(3分)(2022•绥化)下列图形中,既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据中心对称图形与轴对称图形的概念进行判断即可.【解答】解:A.是轴对称图形,不是中心对称图形,故本选项不符合题意;B.是轴对称图形,不是中心对称图形,故本选项不符合题意;C.不是轴对称图形,是中心对称图形,故本选项不符合题意;D.既是轴对称图形,又是中心对称图形,故本选项符合题意.故选:D.【点评】本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后与自身重合.3.(3分)(2022•绥化)下列计算中,结果正确的是()A.2x2+x2=3x4B.(x2)3=x5C.=﹣2D.=±2【分析】利用合并同类项法则,幂的乘方的法则,立方根的意义,算术平方根的意义对每个选项进行分析,即可得出答案.【解答】解:∵2x2+x2=3x2≠3x4,∴选项A不符合题意,∵(x2)3=x6≠x5,∴选项B不符合题意,∵=﹣2,∴选项C符合题意,∵=2≠±2,∴选项D不符合题意,故选:C.【点评】本题考查了合并同类项,幂的乘方,立方根,算术平方根,掌握合并同类项法则,幂的乘方的法则,立方根的意义,算术平方根的意义是解决问题的关键.4.(3分)(2022•绥化)下列图形中,正方体展开图错误的是()A.B.C.D.【分析】根据正方形的展开图得出结论即可.【解答】解:由展开图的知识可知,四个小正方形绝对不可能展开成田字形,故D选项都不符合题意.故选:D.【点评】本题主要考查正方体展开图的知识,熟练掌握正方体的侧面展开图是解题的关键.5.(3分)(2022•绥化)若式子+x﹣2在实数范围内有意义,则x的取值范围是()A.x>﹣1B.x≥﹣1C.x≥﹣1且x≠0D.x≤﹣1且x≠0【分析】根据二次根式的被开方数是非负数,a﹣p=(a≠0)即可得出答案.【解答】解:∵x+1≥0,x≠0,∴x≥﹣1且x≠0,故选:C.【点评】本题考查了二次根式有意义的条件,负整数指数幂,掌握二次根式的被开方数是非负数,a﹣p=(a≠0)是解题的关键.6.(3分)(2022•绥化)下列命题中是假命题的是()A.三角形的中位线平行于三角形的第三边,并且等于第三边的一半B.如果两个角互为邻补角,那么这两个角一定相等C.从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角D.直角三角形斜边上的中线等于斜边的一半【分析】由三角形中位线定理,邻补角定义,切线长定理,直角三角形性质逐项判断即可.【解答】解:三角形的中位线平行于三角形的第三边,并且等于第三边的一半,故A是真命题,不符合题意;如果两个角互为邻补角,那么这两个角一定互补,故B是假命题,符合题意;从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角,故C是真命题,不符合题意;直角三角形斜边上的中线等于斜边的一半,故D是真命题,不符合题意;故选:B.【点评】本题考查命题与定理,解题的关键是掌握教材上相关的概念和定理.7.(3分)(2022•绥化)如图,线段OA在平面直角坐标系内,A点坐标为(2,5),线段OA绕原点O逆时针旋转90°,得到线段OA',则点A'的坐标为()A.(﹣5,2)B.(5,2)C.(2,﹣5)D.(5,﹣2)【分析】过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,利用旋转的性质和全等三角形的判定与性质解答即可.【解答】解:过点A作AB⊥x轴于点B,过点A′作A′C⊥x轴于点C,如图,∵A点坐标为(2,5),∴OB﹣2,AB=5.由题意:∠AOA′=90°,OA=OA′.∴∠AOB+∠A′OC=90°.∵∠A′OC+∠A′=90°,∴∠A′=∠AOB.在△A′OC和△OAB中,,∴△A′OC≌△OAB(AAS).∴A′C=OB=2,OC=AB=5,∴A′(﹣5,2).故选:A.【点评】本题主要考查了图形的旋转与坐标的变化,点的坐标的特征,旋转的性质,全等三角形的判定与性质,利用点的坐标表示出相应线段的长度是解题的关键.8.(3分)(2022•绥化)学校组织学生进行知识竞赛,5名参赛选手的得分分别为:96,97,98,96,98.下列说法中正确的是()A.该组数据的中位数为98B.该组数据的方差为0.7C.该组数据的平均数为98D.该组数据的众数为96和98【分析】根据中位数的定义判断A选项;根据算术平均数的计算方法判断C选项;根据方差的计算方法判断B选项;根据众数的定义判断D选项.【解答】解:A、将这组数据从小到大排列为:96,96,97,98,98,中位数为97,故A 选项不符合题意;C、平均数==97,故C选项不符合题意;B、方差=×[(96﹣96)2×2+(97﹣96)2+(98﹣96)2×2]=1.8,故B选项不符合题意;D、该组数据的众数为96和98,故D选项符合题意;故选:D.【点评】本题考查了方差,算术平均数,中位数,众数,掌握求一组数据的众数的方法:找出频数最多的那个数据,若几个数据频数都是最多且相同,此时众数就是这多个数据是解题的关键.9.(3分)(2022•绥化)有一个容积为24m3的圆柱形的空油罐,用一根细油管向油罐内注油,当注油量达到该油罐容积的一半时,改用一根口径为细油管口径2倍的粗油管向油罐注油,直至注满,注满油的全过程共用30分钟.设细油管的注油速度为每分钟xm3,由题意列方程,正确的是()A.+=30B.+=24C.+=24D.+=30【分析】设细油管的注油速度为每分钟xm3,则粗油管的注油速度为每分钟4xm3,利用注油所需时间=注油总量÷注油速度,即可得出关于x的分式方程,此题得解.【解答】解:24÷2=12(m3).设细油管的注油速度为每分钟xm3,则粗油管的注油速度为每分钟4xm3,依题意得:+=30.故选:A.【点评】本题考查了由实际问题抽象出分式方程,找准等量关系,正确列出分式方程是解题的关键.10.(3分)(2022•绥化)已知二次函数y=ax2+bx+c的部分函数图象如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=在同一平面直角坐标系中的图象大致是()A.B.C.D.【分析】由二次函数y=ax2+bx+c的部分函数图象判断a,b2﹣4ac及4a+2b+c的符号,即可得到答案.【解答】解:∵二次函数y=ax2+bx+c的部分函数图象开口向上,∴a>0,∵二次函数y=ax2+bx+c的部分函数图象顶点在x轴下方,开口向上,∴二次函数y=ax2+bx+c的图象与x轴有两个交点,b2﹣4ac>0,∴一次函数y=ax+b2﹣4ac的图象经过第一,二,三象限,由二次函数y=ax2+bx+c的部分函数图象可知,点(2,4a+2b+c)在x轴上方,∴4a+2b+c>0,∴y=的图象经过第一,三象限,据此可知,符合题意的是B,故选:B.【点评】本题考查一次函数,二次函数,反比例函数的图象,解题的关键是掌握三种图象的性质.11.(3分)(2022•绥化)小王同学从家出发,步行到离家a米的公园晨练,4分钟后爸爸也从家出发沿着同一路线骑自行车到公园晨练,爸爸到达公园后立即以原速折返回到家中,两人离家的距离y(单位:米)与出发时间x(单位:分钟)的函数关系如图所示,则两人先后两次相遇的时间间隔为()A.2.7分钟B.2.8分钟C.3分钟D.3.2分钟【分析】根据题意和函数图象中的数据,可以先表示出两人的速度,然后即可计算出两人第一次和第二次相遇的时间,然后作差即可.【解答】解:由图象可得,小明的速度为米/分钟,爸爸的速度为:=(米/分钟),设小明出发m分钟两人第一次相遇,出发n分钟两人第二次相遇,m=(m﹣4)•,n+[n﹣4﹣(12﹣4)÷2]=a,解得m=6,n=9,n﹣m=9﹣6=3,故选:C.【点评】本题考查一次函数的应用,解答本题的关键是明确题意,求出两人相遇的时间.12.(3分)(2022•绥化)如图,在矩形ABCD中,P是边AD上的一个动点,连接BP,CP,过点B作射线,交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y,其中2<x≤5.则下列结论中,正确的个数为()(1)y与x的关系式为y=x﹣;(2)当AP=4时,△ABP∽△DPC;(3)当AP=4时,tan∠EBP=.A.0个B.1个C.2个D.3个【分析】利用矩形的性质,相似三角形的判定与性质,直角三角形的边角关系定理,勾股定理,平行线分线段成比例定理对每个选项的结论进行判断即可:(1)过点P作PF ⊥BC于点F,利用矩形的判定与性质和相似三角形的判定与性质解答即可;(2)利用相似三角形的判定定理解答即可;(3)利用(1),(2)的结论利用勾股定理和平行线分线段成比例定理求得PB,PE,再利用直角三角形的边角关系定理即可求得结论.【解答】解:(1)过点P作PF⊥BC于点F,如图,∵四边形ABCD是矩形,PF⊥BC,∴四边形ABFP是矩形,∴PF=AB=2,BF=AP=x,∴AM=AP=PM=x﹣y.∵∠ABE=∠CBP,∠A=∠PFB=90°,∴△ABM∽△FBP,∴,∴.∴x2﹣xy=4.∴y=x﹣.∴(1)的结论正确;(2)当AP=4时,DP=AD﹣AP=5﹣4=1,∵,,∴.∵∠A=∠D=90°,∴△ABP△DPC.∴(2)的结论正确;(3)由(2)知:当AP=4时,△ABP∽△DPC,∴∠ABP=∠DPC.∵∠BP A+∠ABP=90°,∴∠APB+∠DPC=90°.∴∠CPB=90°.∴∠BPE=90°.∴tan∠EBP=.由(1)知:PM=AP﹣=3,BP==2,CP==.∵AD∥BC,∴.∴,解得:PE=,∴tan∠EBP===,∴(3)的结论错误,综上,正确的结论为:(1)(2),故选:C.【点评】本题主要考查了矩形的性质,相似三角形的判定与性质,直角三角形的边角关系定理,勾股定理,平行线分线段成比例定理,灵活应用相似三角形的判定与性质是解题的关键.二、填空题(本题共10个小题,每小题3分,共30分)请在答题卡上把你的答案写在相对应的题号后的指定区域内13.(3分)(2022•绥化)一个不透明的箱子中有5个红球和若干个黄球,除颜色外无其它差别.若任意摸出一个球,摸出红球的概率为,则这个箱子中黄球的个数为15个.【分析】直接利用概率公式得出=,进而得出答案.【解答】解:设箱子中黄球的个数为x个,根据题意可得:=,解得:x=15,故答案为:15.【点评】此题主要考查了概率公式,正确掌握概率求法是解题关键.14.(3分)(2022•绥化)因式分解:(m+n)2﹣6(m+n)+9=(m+n﹣3)2.【分析】将m+n看作整体,利用完全平方公式即可得出答案.【解答】解:原式=(m+n)2﹣2•(m+n)•3+32=(m+n﹣3)2.故答案为:(m+n﹣3)2.【点评】本题考查了因式分解﹣运用公式法,考查整体思想,掌握a2±2ab+b2=(a±b)2是解题的关键.15.(3分)(2022•绥化)不等式组的解集为x>2,则m的取值范围为m≤2.【分析】分别求出每一个不等式的解集,根据口诀:同大取大,结合不等式组的解集可得答案.【解答】解:由3x﹣6>0,得:x>2,∵不等式组的解集为x>2,∴m≤2,故答案为:m≤2.【点评】本题考查了解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解题的关键.16.(3分)(2022•绥化)已知圆锥的高为8cm,母线长为10cm,则其侧面展开图的面积为60πcm2.【分析】利用勾股定理易得圆锥的底面半径,那么圆锥的侧面积=底面周长×母线长÷2.【解答】解:圆锥的高为8cm,母线长为10cm,由勾股定理得,底面半径=6cm,侧面展开图的面积=πrl=π×6×10=60πcm2.故答案为:60πcm2.【点评】本题利用了勾股定理和圆锥的计算,圆锥的侧面积就是展开后扇形的面积,即S=πrl.侧17.(3分)(2022•绥化)设x1与x2为一元二次方程x2+3x+2=0的两根,则(x1﹣x2)2的值为20.【分析】根据根与系数的关系即可求出答案.【解答】解:由题意可知:x1+x2=﹣6,x1x2=4,∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(﹣6)2﹣4×4=36﹣16=20,故答案为:20.【点评】本题考查根与系数的关系,解题的关键是熟练运用根与系数的关系.18.(3分)(2022•绥化)定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ.例如:当α=45°,β=30°时,sin(45°+30°)=×+×=,则sin15°的值为.【分析】把15°看成是45°与30°的差,再代入公式计算得结论.【解答】解:sin15°=sin(45°﹣30°)=sin45°cos30°﹣cos45°sin30°=×﹣×=﹣=.故答案为:.【点评】本题考查了解直角三角形,掌握特殊角的三角函数值是解决本题的关键.19.(3分)(2022•绥化)如图,正六边形ABCDEF和正五边形AHIJK内接于⊙O,且有公共顶点A,则∠BOH的度数为12度.【分析】求出正六边形的中心角∠AOB和正五边形的中心角∠AOH,即可得出∠BOH的度数.【解答】解:如图,连接OA,正六边形的中心角为∠AOB=360°÷6=60°,正五边形的中心角为∠AOH=360°÷5=72°,∴∠BOH=∠AOH﹣∠AOB=72°﹣60°=12°.故答案为:12.【点评】本题主要考查正多边形与圆,会求正多边形的中心角是解题关键.20.(3分)(2022•绥化)某班为奖励在数学竞赛中成绩优异的同学,花费48元钱购买了甲、乙两种奖品,每种奖品至少购买1件,其中甲种奖品每件4元,乙种奖品每件3元.则有3种购买方案.【分析】设购买x件甲种奖品,y件乙种奖品,利用总价=单价×数量,即可得出关于x,y的二元一次方程,结合x,y均为正整数,即可得出共有3种购买方案.【解答】解:设购买x件甲种奖品,y件乙种奖品,依题意得:4x+3y=48,∴x=12﹣y.又∵x,y均为正整数,∴或或,∴共有3种购买方案.故答案为:3.【点评】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.21.(3分)(2022•绥化)如图,∠AOB=60°,点P1在射线OA上,且OP1=1,过点P1作P1K1⊥OA交射线OB于K1,在射线OA上截取P1P2,使P1P2=P1K1;过点P2作P2K2⊥OA交射线OB于K2,在射线OA上截取P2P3,使P2P3=P2K2…按照此规律,线段P2023K2023的长为(1+)2022.【分析】根据题意和题目中的数据,可以写出前几项,然后即可得到P n K n的式子,从而可以写出线段P2023K2023的长.【解答】解:由题意可得,P1K1=OP1•tan60°=1×=,P2K2=OP2•tan60°=(1+)×=(1+),P3K3=OP3•tan60°=(1+++3)×=(1+)2,P4K4=OP4•tan60°=[(1+++3)+(1+)2]×=(1+)3,…,P n K n=(1+)n﹣1,∴当n=2023时,P2023K2023=(1+)2022,故答案为:(1+)2022.【点评】本题考查图象的变化类,解答本题的关键是发现P n K n的变化特点.22.(3分)(2022•绥化)在长为2,宽为x(1<x<2)的矩形纸片上,从它的一侧,剪去一个以矩形纸片宽为边长的正方形(第一次操作);从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作);按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x的值为 1.2或者1.5.【分析】本题中的x与(2﹣x)不知那个大,因此需要分类讨论,从而列方程求解.【解答】解:第一次操作后的两边长分别是x和(2﹣x),第二次操作后的两边长分别是(2x﹣2)和(2﹣x).当2x﹣2>2﹣x时,有2x﹣2=2(2﹣x),解得x=1.5,当2x﹣2<2﹣x时,有2(2x﹣2)=2﹣x,解得x=1.2.故答案为:1.2或者1.5.【点评】主要考查了含有字母的代数式的比较,关键是第二次操作后的边长,不知哪个是长,哪个是宽,所以分两种情况,不要丢掉任何一种.三、解答题(本题共6个小题,共54分)请在答题卡上把你的答案写在相对应的题号后的指定区域内23.(7分)(2022•绥化)已知:△ABC.(1)尺规作图:用直尺和圆规作出△ABC内切圆的圆心O.(只保留作图痕迹,不写作法和证明)(2)如果△ABC的周长为14cm,内切圆的半径为1.3cm,求△ABC的面积.【分析】(1)作∠ABC,∠ACB的角平分线交于点O,点O即为所求;(2)△ABC的面积=(a+b+c)•r计算即可.【解答】解:(1)如图,点O即为所求;(2)由题意,△ABC的面积=×14×1.3=9.1(cm2).【点评】本题考查作图﹣复杂作图,三角形的内切圆与内心等知识,解题的关键掌握三角形的内心是角平分线的交点,属于中考常考题型.24.(8分)(2022•绥化)如图所示,为了测量百货大楼CD顶部广告牌ED的高度,在距离百货大楼30m的A处用仪器测得∠DAC=30°;向百货大楼的方向走10m,到达B处时,测得∠EBC=48°,仪器高度忽略不计,求广告牌ED的高度.(结果保留小数点后一位)(参考数据:≈1.732,sin48°≈0.743,cos48°≈0.669,tan48°≈1.111)【分析】在Rt△ADC中,利用锐角三角函数的定义求出CD的长,再利用已知求出BC 的长,然后在在Rt△BCE中,利用锐角三角函数的定义求出EC的长,进行计算即可解答.【解答】解:在Rt△ADC中,∠DAC=30°,AC=30米,∴CD=AC•tan30°=30×=10(米),∵AB=10米,∴BC=AC﹣AB=20(米),在Rt△BCE中,∠EBC=48°,∴EC=BC•tan48°≈20×1.111=22.22(米),∴DE=EC﹣DC=22.22﹣10≈4.9(米),∴广告牌ED的高度约为4.9米.【点评】本题考查了解直角三角形的应用,熟练掌握锐角三角函数的定义是解题的关键.25.(9分)(2022•绥化)在平面直角坐标系中,已知一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,且与反比例函数y2=的图象在第一象限内交于P,K两点,连接OP,△OAP的面积为.(1)求一次函数与反比例函数的解析式.(2)当y2>y1时,求x的取值范围.(3)若C为线段OA上的一个动点,当PC+KC最小时,求△PKC的面积.【分析】(1)根据待定系数法可求出直线AB的解析式,根据△OAP的面积可得出点P 的坐标,代入反比例函数解析式可得出反比例函数的解析式;(2)联立一次函数和反比例函数的解析式,可得出点K的坐标,结合图象可直接得出x 的取值范围;(3)作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,求出直线KP′的解析式,令y=0,可得出点C的坐标,再根据三角形的面积公式可得出结论.【解答】解:(1)∵一次函数y1=k1x+b与坐标轴分别交于A(5,0),B(0,)两点,∴,解得.∴一次函数的解析式为:y1=﹣x+.∵△OAP的面积为,∴•OA•y P=,∴y P=,∵点P在一次函数图象上,∴令﹣x+=.解得x=4,∴P(4,).∵点P在反比例函数y2=的图象上,∴k2=4×=2.∴一次函数的解析式为:y1=﹣x+.反比例函数的解析式为:y2=.(2)令﹣x+=,解得x=1或x=4,∴K(1,2),由图象可知,当y2>y1时,x的取值范围为:0<x<1或x>4.(3)如图,作点P关于x轴的对称点P′,连接KP′,线段KP′与x轴的交点即为点C,∵P(4,).∴P′(4,﹣).∴PP′=1,∴直线KP′的解析式为:y=﹣x+.令y=0,解得x=.∴C(,0).∴S△PKC=•(x C﹣x K)•PP′=×(﹣1)×1=.∴当PC+KC最小时,△PKC的面积为.【点评】本题属于反比例函数与一次函数综合题,主要考查待定系数法求函数解析式,数形结合思想,轴对称最值问题,三角形的面积问题等知识,关键是求出一次函数和反比例函数的解析式.26.(9分)(2022•绥化)我们可以通过面积运算的方法,得到等腰三角形底边上的任意一点到两腰的距离之和与一腰上的高之间的数量关系,并利用这个关系解决相关问题.(1)如图一,在等腰△ABC中,AB=AC,BC边上有一点D,过点D作DE⊥AB于E,DF⊥AC于F,过点C作CG⊥AB于G.利用面积证明:DE+DF=CG.(2)如图二,将矩形ABCD沿着EF折叠,使点A与点C重合,点B落在B'处,点G 为折痕EF上一点,过点G作GM⊥FC于M,GN⊥BC于N.若BC=8,BE=3,求GM+GN 的长.(3)如图三,在四边形ABCD中,E为线段BC上的一点,EA⊥AB,ED⊥CD,连接BD,且=,BC=,CD=3,BD=6,求ED+EA的长.【分析】(1)连接AD,根据S△ABC=S△ABD+S△ACD,可得结论;(2)利用翻折的性质得,CE=CF,由勾股定理得,AB=4,则等腰△CEF中,CE边上的高为4,由(1)知,GM+GN=4;(3)延长BA、CD交于G,作BH⊥CD于H,利用△BAE∽△CDE,得∠ABE=∠C,则BG=CG,设DH=x,利用勾股定理列方程可得DH的长,从而得出BH,利用(1)中结论可得答案.【解答】(1)证明:连接AD,∵S△ABC=S△ABD+S△ACD,∴=,∵AB=AC,∴DE+DF=CG;(2)解:∵将矩形ABCD沿着EF折叠,使点A与点C重合,∴∠AFE=∠EFC,AE=CE,∵AD∥BC,∴∠AFE=∠CEF,∴∠CEF=∠CFE,∴CE=CF,∵BC=8,BE=3,∴CE=AE=5,在Rt△ABE中,由勾股定理得,AB=4,∴等腰△CEF中,CE边上的高为4,由(1)知,GM+GN=4;(3)解:延长BA、CD交于G,作BH⊥CD于H,∵=,∠BAE=∠EDC=90°,∴△BAE∽△CDE,∴∠ABE=∠C,∴BG=CG,∴ED+EA=BH,设DH=x,由勾股定理得,62﹣x2=()2﹣(x+3)2,解得x=1,∴DH=1,∴BH==,∴ED+EA=.【点评】本题是相似形综合题,主要考查了等腰三角形的判定与性质,翻折的性质,勾股定理,相似三角形的判定与性质,证明等腰三角形,利用(1)中结论是解决问题(2)、(3)的关键.27.(10分)(2022•绥化)如图所示,在⊙O的内接△AMN中,∠MAN=90°,AM=2AN,作AB⊥MN于点P,交⊙O于另一点B,C是上的一个动点(不与A,M重合),射线MC交线段BA的延长线于点D,分别连接AC和BC,BC交MN于点E.(1)求证:△CMA∽△CBD.(2)若MN=10,=,求BC的长.(3)在点C运动过程中,当tan∠MDB=时,求的值.。
