物理化学经典例题
高中化学竞赛物理化学例题

例 题一. 选择题1. 一体系如图,隔板两边均充满空气(视为理想气体),只是两边压力不等,已知p 右<p 左,则将隔板抽去后应有: ( )(A) Q = 0 W = 0 ΔU = 0(B) Q = 0 W < 0 ΔU > 0(C) Q > 0 W < 0 ΔU > 0(D) ΔU = 0 , Q =W ≠ 02. 有一容器四壁导热,上部有一可移动的活塞,在该容器中同时放入锌块和盐酸,发生化学反应后活塞将上移一定距离,若以锌和盐酸为体系,Q -W =Δr U , 则: ( )(A) Q < 0 , W = 0 , Δr U < 0(B) Q = 0 , W > 0 , Δr U < 0(C) Q < 0 , W > 0 , Δr U = 0(D) Q < 0 , W > 0 , Δr U < 03. 恒容下,一定量的理想气体,当温度升高时内能将: ( )(A) 降低 (B) 增加(C) 不变 (D) 增加、减少不能确定4. 苯在一个刚性的绝热容器中燃烧,则: ( ) C 6H 6(l) + (15/2)O 2(g) 6CO 2+ 3H 2O(g)(A) ΔU = 0 , ΔH < 0 , Q = 0(B) ΔU = 0 , ΔH > 0 , W = 0(C) ΔU = 0 , ΔH = 0 , Q = 0(D) ΔU ≠0 , ΔH ≠0 , Q = 05. 当以5 mol H 2气与4 mol Cl 2气混合,最后生成2 mol HCl 气。
若以下式为基本单元,则反应进度ξ应是: ( ) H 2(g) + Cl 2(g)−−→2HCl(g)(A) 1 mol (B) 2 mol(C) 4 mol (D) 5 mol6. 若以B 代表化学反应中任一组分,0B n 和 n B 分别表示任一组分 B 在ξ= 0 及反应进度为ξ时的物质的量,则定义反应进度为: ( )(A) ξ= 0B n - n B (B) ξ= n B -0B n(C) ξ=(n B -0B n )/νB (D) ξ= (0B n -n B )/ νB7. 已知:Zn(s)+(1/2)O 2−−→ZnO Δc H m =351.5 kJ·mol -1Hg(l)+(1/2)O2−−→HgO Δc H m= 90.8 kJ·mol-1因此Zn+HgO−−→ZnO+Hg 的Δr H m是:( )(A) 442.2 kJ·mol-1(B)260.7 kJ·mol-1(C) -62.3 kJ·mol-1(D) -442.2 kJ·mol-18. 斜方硫的燃烧热等于( )(A)SO2(g)的生成热(B) SO3(g)的生成热(C) 单斜硫的燃烧热(D) 零9. 下述说法,何者正确? ( )(A) 水的生成热即是氧气的燃烧热(B) 水蒸气的生成热即是氧气的燃烧热(C) 水的生成热即是氢气的燃烧热(D) 水蒸气的生成热即是氢气的燃烧热10. 石墨的燃烧热( )(A) 等于CO生成热(B) 等于CO2生成热(C) 等于金刚石燃烧热(D) 等于零$:( )11. 298 K时,石墨的标准摩尔生成焓Δf Hm(A) 大于零(B) 小于零(C) 等于零(D) 不能确定12. 石墨(C)和金刚石(C)在25℃, 101 325 Pa下的标准燃烧焓分别为-393.4 kJ·mol-1和-395.3$(金刚石, 298 K)为:( ) kJ·mol-1,则金刚石的标准生成焓Δf Hm(A) -393.4 kJ·mol-1(B) -395.3 kJ·mol-1(C) -1.9 kJ·mol-1(D) 1.9 kJ·mol-113.在p ,273.15 K下水凝结为冰,判断体系的下列热力学量中何者一定为零?( )(A) ΔU (B) ΔH(C) ΔS(D) ΔG14.在绝热恒容的反应器中,H2和Cl2化合成HCl,此过程中下列各状态函数的变化值哪个为零?( )(A) Δr U m(B) Δr H m(C) Δr S m(D) Δr G m15.在标准压力下,90℃的液态水汽化为90℃的水蒸气,体系的熵变将:( )(A) ΔS体>0(B) ΔS体<0(C) ΔS体=0 (D) 难以确定16.水在100℃,p 下沸腾时,下列各量何者增加?( )(A) 熵(B) 汽化热(C) 吉布斯自由能(D) 蒸气压17.在N2和O2混合气体的绝热可逆压缩过程中,体系的热力学函数变化值在下列结论中正确的是: ( )(A) ΔU= 0 (B) ΔF = 0(C) ΔS = 0(D) ΔG = 018.将 1 mol 甲苯在101.325 kPa,110 ℃(正常沸点)下与110 ℃的热源接触,使它向真空容器中汽化,完全变成101.325 kPa 下的蒸气。
【精品】物理化学例子

热力学第一定律1、在绝热盛水容器中,浸入电阻丝,通电一段时间,通电后水及电阻丝的温度均略有升高,今以电阻丝为体系有:CA.W=0,Q<0,⊿U〈0B。
W〈0,Q〈0,⊿U>0C。
W〈(〉)0,Q〉0,⊿U>0D.W<0,Q=0,⊿U>02、下述说法中,哪一种正确?第一定律说明,封闭体系的D(A)吸热Q是状态函数(B)对外做功W是状态函数(C)Q+W是状态函数(D)热力学能U是状态函数3、下列叙述中,不具可逆过程特征的是(C)A。
过程的每一步都接近平衡态,故进行得无限缓慢B。
沿原途径反向进行时,每一小步系统与环境均能复原C。
过程的初态与终态必定相同D.过程中,若做功则做最大功,若耗功则耗最小功4、在293K时,1mol理气等温膨胀至体积增加一倍,则所做的最大功为(B)A。
733JB.1690JC—733JD.—1690JW=nRTln25、下列表示式中正确的是(A)A。
恒压过程ΔH=ΔU+pΔVB.恒压过程ΔH=0C.恒压过程ΔH=ΔU+VΔpD。
恒容过程ΔH=06、苯在一个刚性的绝热容器中燃烧,则:BC6H6(l)+(15/2)O2→(g)6CO2+3H2O (g)(A)ΔU=0,ΔH〈0,Q=0(B)ΔU=0,ΔH〉0,W=0(C)ΔU=0,ΔH=0,Q=0(D)ΔU≠0,ΔH≠0,Q=07、关于等压摩尔热容和等容摩尔热容,下面的说法中不正确的是(B)A.Cp,m与Cv,m不相等,因等压过程比等容过程系统多作体积功B。
Cp,m–Cv,m=R既适用于理想气体体系,也适用于实际气体体系C.Cv,m=3/2R适用于单原子理想气体混合D。
在可逆相变中Cp,m和Cv,m都为无限大8、对于理想气体,用等压热容Cp计算ΔH的适用范围为(C)A.只适用于无相变,无化学变化的等压变温过程B.只适用于无相变,无化学变化的等容变温过程C。
适用于无相变,无化学变化的任意过程D.以上答案均不正确9、0。
物理化学例题
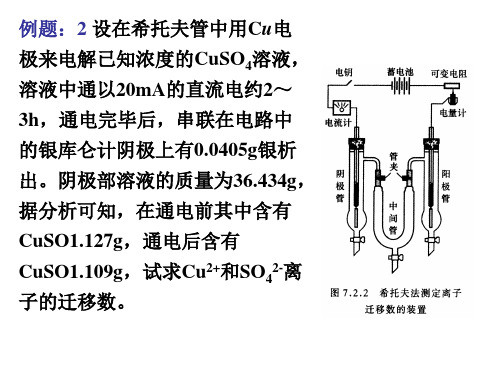
浓度的改变是由两种因素引起的, 解:阴极部Cu2+浓度的改变是由两种因素引起的, 阴极部 的迁入,( ,(2) 在阴极上发生还原反应, (1)Cu2+的迁入,( )Cu2+在阴极上发生还原反应, )
1 2+ 1 Cu (l ) + e Cu ( s ) → 2 2
阴极区,Cu2+的物质量变化前后之间的关系为: 的物质量变化前后之间的关系为: 阴极区
25℃时, ϕ (Q|H 2 Q) = 0.6995V − 0.05916V ipH ℃
通常将此电极与摩尔甘汞电极组成原电池: 通常将此电极与摩尔甘汞电极组成原电池: 醌氢醌饱和的溶液( 摩尔甘汞电极 || 醌氢醌饱和的溶液(pH<7.1)| Pt )
E = ϕ右 − ϕ左 = ( 0.6995 − 0.05916ipH − 0.2799 ) V
θ ∆ r Gm = −788.59kJ imol-1 ,则由定义可知: 则由定义可知:
θ θ θ ∆ r Gm = 2∆ f Gm {Au(s)} + 3∆ f Gm {H 2O(l)} θ θ − 3∆ f Gm {H 2 (g)} − ∆ f Gm {Au 2O2 (s)}
= −788.59kJimol-1
θ ∆ r Gm = − RTlnK θ , K θ = 2.98 × 10 −14
则
K = pO2 / p
θ
(
θ
)
3/ 2
,
pO2 = 9.612 × 10−8 kPa
−2 −4 −2
n迁移(+) 1.424 × 10 −4 = = 0.38 t+ = −4 n反应 3.754 × 10
t- = 1-t+ = 1-0.38 = 0.62 另一种解法是考虑SO 的浓度变化,先求t 另一种解法是考虑 42-的浓度变化,先求 - ,阴 极部SO42-的浓度变化仅仅是因 42-离子迁出造成 的浓度变化仅仅是因SO 极部 物质量的变化为: 的,故SO42-物质量的变化为: n电解后 = n电解前 − n迁移(-) 式中n表示 式中 表示
物理化学习题-含答案
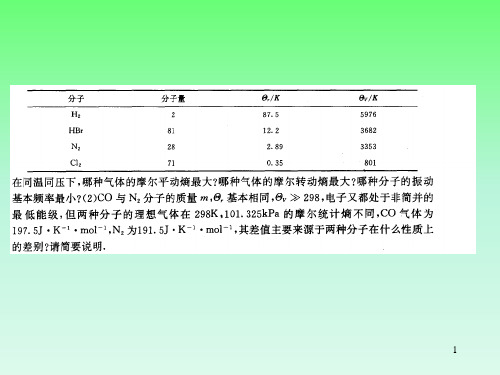
基态是单态。计算在298K、1atm下一氧化碳气体的 摩尔熵值。
7
解:由于CO气体为非定位体系,其熵公式为:
ln Q Q NkT S k ln N! T
N
ln Q Nk ln Q k ln N! NkT T
可将其看成是体系的平动熵、转动熵、振动熵及电子熵等之 和。可先分别求出各运动形式的熵、再求和而得体系的总熵 。上式的-k lnN! 项归入平动熵计算。
32
将题中给出的数据直接代入上式得:
Q转
2 8 1.1461045 1.381023 298 (3.1416 )
2 (6.62610
34 2
)
424
5
(3)如果将分子看成是谐振子,则有
Q振 1 1 e h kT 1 1 e h c kT
由题意知,
565cm1 565102 m1
~
1 代入上式得: Q振 6.6261034 565102 2.998108 1 exp[ ] 23 1.3810 298
1
1 e
2.73
1.07
6
计算题
2.已知一氧化碳分子的转动惯量是
I 1.451046 kg m2 ~ 1 基本振动波数 2170cm ,分子量为 28.0,其电子
2170cm1 217000 m1
ln Q h c e h c kT T kT2 1 e h c kT
12
将数据代入得
ln Q振 T
计算题
10.5 e10.5 0 10.5 298 (1 e )
S振 R ln Q振 RT T 8.314 ln 1 8.314 298 0 0
物理化学例题及习题

物理化学例题与习题解答习题1.1:5mol理气(300K,1013.25kPa)→5mol理气(300K,101.325kPa)求:体积功解:(1) 在101.325kPa的空气中膨胀了2dm3.W=-P外(V2-V1)=-101.325×2=-202.65J(2) 在恒外压101.325kPa下膨胀至终态.W=-P外(V2-V1)=-nRT(1-P2/P1)=-5×8.314×300(1-101.325/1013.25)=-11.224 kJ(3) 恒温可逆膨胀至终态。
W=nRTln(P2/P1)=5×8.314×300×ln101.325/1013.25 =-28.716 kJ习题1.2:2mol理气(373K,25dm3)→2mol理气(373K,100dm3)求:体积功解:(1) 向真空自由膨胀.W=-P外(V2-V1)=0(2) 在外压恒定为终态压强下膨胀至终态.W=-P外(V2-V1)=-nRT(1-P2/P1)=nRT(1-V2/V1)=2×8.314×373(1-100/25)=-4652 J(3) 恒温可逆膨胀至终态。
W=-nRTln(V2/V1)=2×8.314×373×ln100/25 =-8598 J=202.65 kPa;V1=10dm3,V2=20dm3;Q=1255J;求:△U习题1.3:恒外压压缩,P外(V2-V1)=-202.65×(20-10)=-2027 J解:W=-P外△U=Q+W=1255-2027=-772 J习题1.4:(1)可逆(2)恒外压100gH2(298K,101.325kPa)→100gH2(298K,506.625kPa)→100gH2(298K,101.325kPa) 求:体积功解:(1) 恒温可逆压缩n=100/2=50molW=nRTln(P2/P1)=50×8.314×298×ln506.625/101.325 =199.4 kJ(2)恒外压膨胀W=-P外(V2-V1)=-nRT(1-P2/P1)=-50×8.314×298(1-101.325/506.625)=-99.10 kJ习题1.5:(1)恒容(2)恒压1mol理气(10dm3,202.65kPa)→1mol理气(10dm3,2026.5kPa)→1mol理气(1dm3,2026.5kPa) 求:W Q △U △H解:因为P1V1=P3V3 , 所以T3=T1△U=△H=0W=-P2(V3-V2)=-2026.5(1-10)=18.2 kJQ=-18.2 kJ习题1.6:解:Q p=∫C pm dT=∫(26.78+0.04268T-146.4×10-7T2) dT=26.78(573-273)+0.04268/2(5732-2732)-146.4×10-7/3(5733-2733)=12.63 kJ△H= Q p=12.63 kJ△U=△H-nR△T=12.63-0.008314×(573-273)=10.14 kJW=Q+W=-2.49 kJ习题1.7:等温恒外压膨胀nmolN2(273K,2dm3,500kPa)→nmolN2(273K, 100kPa) 求:W、Q、△U、△H 解:△U=△H=0W=-P2(V2-V1) =-P1 V1 (1-P2/P1)=-500×2(1-100/500)=-800 JQ=800 J习题1.8:解:(1)恒容加热W=0Q v=△U= nC vm△T=1.5×8.314×(600-298)=3766 J△H= nC pm△T=2.5×8.314×(600-298)=6277 J(2)恒压加热Q p= △H=nC pm△T=2.5×8.314×(600-298)=6277 J△U= nC vm△T=1.5×8.314×(600-298)=3766 JW=△U-Q =-2511 J习题1.9:解:(1)恒温可逆膨胀△U=△H=0W=nRTln(P2/P1)=8.314×298×ln101.325/607.9 =-4439 JQ=4439 J(2)等温恒外压膨胀W=-P外(V2-V1)=-nRT(1-P2/P1)=-8.314×298(1-101.325/607.9)=-2065 JQ=2065 J习题13:苯在正常沸点353.4K下的蒸发焓为30.810 kJ/mol,求100g苯在正常沸点下等压蒸发的W Q △U △H。
物理化学教材例题解析供参考

物理化学教材例题解析供参考例1-1 设1mol 理想气体经下列三种途径,由298K 、500kPa 的始态变成298K 、100kPa 的终态。
试计算系统在这三个过程中所做的体积功。
(1)向真空膨胀;(2)在外压恒定为100kPa 时膨胀至终态;(3)先将外压恒定为300kPa ,膨胀至中间态,再由此中间态在外压恒定为100kPa 时膨胀至终态;试比较这三个过程的功,比较的结果说明了什么问题? 解(1)因,所以;(2)因,所以(3)系统分两步进行膨胀,第一步所做的功为 第二步所做的功为两步作功以上结果说明,始终态相同而途径不同时,系统对外所做的功不同;等温膨胀过程中,分步越多,系统反抗的外压越大,对环境所做的体积功越大。
0p =外0=W 2P P=外()2212211100kPa 111982J500kPa P nRT nRT W p V V p nRT nRT p p P ⎛⎫⎛⎫⎛⎫=--=--=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭外()11111111300kPa 11991J500kPa p nRT nRT W p V V p nRT nRT p p p ⎛⎫⎛⎫⎛⎫=--=--=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭外,外,外,中外,()222222100kPa 111652J 300kPa p nRT nRT W p V V p nRT nRT p p p ⎛⎫⎛⎫⎛⎫=--=--=--=--=- ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭外,中中中122643JW W W=+=-例1-2 在25℃、标准压力下,1molH 2与0.5molO 2生成1molH 2O (l),放热285.90kJ 。
设H2及O2在此条件下均为理想气体,求△U 。
若在此条件下将此反应改在原电池中进行,做电功为187.82kJ ,求Q 、W 、∆U 。
解(1)反应为:(恒温恒压)若忽略的体积,则,,所以(2)始、终态一致,则与(1)相同, 总功=电功+体积功,即此题为第一定律在化学反应中的应用.例1-3 水的蒸发热为40.593kJ·mol -1,1kg 水的体积为1.043dm 3,1kg 水蒸气的体积为1677dm 3。
物理化学习题集

第一章气体
1.内燃机排出的废气中含有一定量的NO + NO2。
将它们分离出来,得到30℃、169.21 kPa、100cm3的NO 和NO2混合气体0.219g。
若气体可视为理想气体,试求其中所含NO 的摩尔分数。
已知NO 和NO2的摩尔质量分别为30.01g·mol−1 和46.01g·mol−1。
2.25℃、101.325kPa 的干燥空气15.0dm3缓缓通过水并被水蒸气所饱和,已知空气带走的H2O (l) 的物质的量为0.01982mol。
试计算25℃时水的饱和蒸气压和通过水后湿空气的体积。
假设通入气体前后其总压保持不变。
3.300 K 时,把一定量的NO 气体引入1.055×10−3m3容器中,使其压力达到23.102 kPa。
然后将在容器内装有0.660 g Br2的小球打破。
当容器中NO、Br2与按2NO(g) + Br2 (g) = 2NOBr (g)反应生成的NOBr 达平衡后。
混合的三种气体总压力为25.737 kPa。
试求这三种气体在容器中的分压力各为多少?已知Br2的摩尔质量为159.81 g·mol−1。
4.在0℃、10132.5kPa 压力下氦的摩尔体积是0℃、101.325 kPa 压力下摩尔体积的0.011075。
物理化学题库及详解答案

物理化学题库及详解答案物理化学是一门结合物理学和化学的学科,它通过物理原理来解释化学现象,是化学领域中一个重要的分支。
以下是一些物理化学的题目以及相应的详解答案。
题目一:理想气体状态方程的应用题目内容:某理想气体在标准状态下的体积为22.4L,压力为1atm,求该气体在3atm压力下,体积变为多少?详解答案:根据理想气体状态方程 PV = nRT,其中P是压力,V是体积,n是摩尔数,R是理想气体常数,T是温度。
在标准状态下,P1 = 1atm,V1 = 22.4L,T1 = 273.15K。
假设气体摩尔数n和温度T不变,仅压力变化到P2 = 3atm。
将已知条件代入理想气体状态方程,得到:\[ P1V1 = nRT1 \]\[ P2V2 = nRT2 \]由于n和R是常数,且T1 = T2(温度不变),我们可以简化方程为:\[ \frac{P1}{P2} = \frac{V2}{V1} \]代入已知数值:\[ \frac{1}{3} = \frac{V2}{22.4} \]\[ V2 = \frac{1}{3} \times 22.4 = 7.46667L \]所以,在3atm的压力下,该气体的体积约为7.47L。
题目二:热力学第一定律的应用题目内容:1摩尔的单原子理想气体在等压过程中吸收了100J的热量,如果该过程的效率为40%,求该过程中气体对外做的功。
详解答案:热力学第一定律表明能量守恒,即ΔU = Q - W,其中ΔU是内能的变化,Q是吸收的热量,W是对外做的功。
对于单原子理想气体,内能仅与温度有关,且ΔU = nCvΔT,其中Cv 是摩尔定容热容,对于单原子理想气体,Cv = 3R/2(R是理想气体常数)。
由于效率η = W/Q,我们有:\[ W = ηQ \]\[ W = 0.4 \times 100J = 40J \]现在我们需要找到内能的变化。
由于过程是等压的,我们可以利用盖-吕萨克定律(Gay-Lussac's law)PV = nRT,由于n和R是常数,我们可以简化为PΔV = ΔT。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1. 下面有关统计热力学的描述,正确的是:( )A. 统计热力学研究的是大量分子的微观平衡体系B. 统计热力学研究的是大量分子的宏观平衡体系C. 统计热力学是热力学的理论基础D. 统计热力学和热力学是相互独立互不相关的两门学科B2.在研究N、V、U有确定值的粒子体系的统计分布时,令∑ni = N,∑niεi = U,这是因为所研究的体系是:( )A. 体系是封闭的,粒子是独立的 B 体系是孤立的,粒子是相依的C. 体系是孤立的,粒子是独立的D. 体系是封闭的,粒子是相依的C3.假定某种分子的许可能级是0、ε、2ε和3ε,简并度分别为1、1、2、3 四个这样的分子构成的定域体系,其总能量为3ε时,体系的微观状态数为:( ) A. 40 B. 24 C. 20 D. 28 A4. 使用麦克斯韦-波尔兹曼分布定律,要求粒子数N 很大,这是因为在推出该定律时:( ).!A、假定粒子是可别的 B. 应用了斯特林近似公式C.忽略了粒子之间的相互作用 D. 应用拉氏待定乘因子法A5.对于玻尔兹曼分布定律ni =(N/q)·gi·exp( -εi/kT)的说法:(1) n i是第i 能级上的粒子分布数; (2) 随着能级升高,εi 增大,ni 总是减少的; (3) 它只适用于可区分的独立粒子体系; (4) 它适用于任何的大量粒子体系其中正确的是:( ) A. (1)(3)B. (3)(4)C. (1)(2)D. (2)(4) C6.对于分布在某一能级εi上的粒子数ni,下列说法中正确是:( )A. n i与能级的简并度无关B.εi 值越小,ni 值就越大C. n i称为一种分布D.任何分布的ni 都可以用波尔兹曼分布公式求出B7. 15.在已知温度T时,某种粒子的能级εj = 2εi,简并度gi = 2gj,则εj 和εi 上分布的粒子数之比为:( )A. 0.5exp(εj/2kT)B. 2exp(- εj/2kT)C. ( -εj/kT)D. 2exp( 2εj/kT) C8. I2的振动特征温度Θv= 307K,相邻两振动能级上粒子数之n(v + 1)/n(v) = 1/2的温度是:( )A. 306 KB. 443 KC. 760 KD. 556 K B9.下面哪组热力学性质的配分函数表达式与体系中粒子的可别与否无关:( )《A. S、G、F、CvB. U、H、P、C vC. G、F、H、UD. S、U、H、G B10. 分子运动的振动特征温度Θv 是物质的重要性质之一,下列正确的说法是:( C )A.Θv 越高,表示温度越高B.Θv 越高,表示分子振动能越小C. Θv越高,表示分子处于激发态的百分数越小D. Θv越高,表示分子处于基态的百分数越小11.下列几种运动中哪些运动对热力学函数G与A贡献是不同的:( )A. 转动运动B. 电子运动C. 振动运动D. 平动运动D12.三维平动子的平动能为εt = 7h2 /(4mV2/3 ),能级的简并度为:( )A. 1B. 3C. 6D. 2 C的转动惯量J = ×10 -47 kg·m2 ,则O2 的转动特征温度是:( )A. 10 KB. 5 KC. KD. 8 K C;14. 对于单原子分子理想气体,当温度升高时,小于分子平均能量的能级上分布的粒子数:( )A. 不变B. 增多C. 减少D. 不能确定C15.在相同条件下,对于He 与Ne 单原子分子,近似认为它们的电子配分函数相同且等于1,则He 与Ne 单原子分子的摩尔熵是:( )A. Sm(He) > Sm (Ne)B. Sm (He) = Sm (Ne)C. Sm (He) < S m(Ne)D. 以上答案均不成立C二、判断题1.玻耳兹曼熵定理一般不适用于单个粒子。
(√)2.玻耳兹曼分布是最概然分布,但不是平衡分布。
(×)3.并不是所有配分函数都无量纲。
(×)4.在分子运动的各配分函数中平均配分函数与压力有关。
(√)-5.粒子的配分函数q 是粒子的简并度和玻耳兹曼因子的乘积取和。
(×)6.对热力学性质(U、V、N)确定的体系,体系中粒子在各能级上的分布数一定。
(×)7.理想气体的混合物属于独立粒子体系。
(√)8.量子统计认为全同粒子在不同的量子态中不可别。
(×)9.任何两个粒子数相同的独立粒子体系,不定因子a的值趋于一致。
(×)10.量热熵由量热实验结果据热力学公式算得。
(√)综合练习题一、选择题)1. 在统计热力学中,物系的分类常按其组成的粒子能否被辨别来进行,按此原则,下列说法正确的是:( )A. 晶体属离域物系而气体属定域物系B.气体和晶体皆属离域物系C.气体和晶体皆属定域物系D.气体属离域物系而晶体属定域物系D2. 某种分子的许多可能级是ε0、ε1、ε2,简并度为g0 = 1、g 1 = 2、g 2 = 1,5个可别粒子,按N0 = 2、N 1= 2、N2 = 1的分布方式分配在三个能级上,则该分布方式的样式为:A. 30B. 120C. 480D. 28 B3. 对热力学性质(U、V、N)确定的体系,下面描述中不对的是:( )A. 体系中各能级的能量和简并度一定B. 体系的微观状态数一定}C. 体系中粒子在各能级上的分布数一定D. 体系的吉布斯自由能一定C4.设一粒子体系由三个线性谐振子组成,体系的能量为(11/2)hν,三个谐振子分别在三个固定点a、b、c 上振动,体系总的微观状态数为:( )A. 12B. 15C. 9D. 6 B5. 式子∑Ni = N和∑Niεi = U的含义是:( )A. 表示在等概率假设条件下,密封的独立粒子平衡体系B. 表示在等概率假设条件下,密封的独立粒子非平衡体系C. 表示密闭的独立粒子平衡体系D. 表示密闭的非独立粒子平衡体系C6. 玻尔兹曼统计认为:( B )A. 玻尔兹曼分布不是最概然分布但却代表平衡分布B. 玻尔兹曼分布只是最概然分布但不代表平衡分布C. 玻尔兹曼分布不是最概然分布也不代表平衡分布D. 玻尔兹曼分布就是最概然分布也代表平衡分布【7. 如分子第一激发态的能量为400 kJ·mol-1,则体系中10%的分子被激发到第一激发态时,体系的温度(K)是:( )A. 2.1 × 104B. × 104C. × 103D. × 105 A8. I2 分子的振动能级间隔是×10-20 J,则在298 K时某一振动能级和其较低能级上分子数之比为:( )A. 1B. ×10-20C.D. 无法计算C9. 各种运动形式的配分函数中与压力有关的是:( )A. 电子配分函数B. 平动配分函数C. 转动配分函数D. 振动配分函数B10.下列哪个体系不具有玻尔兹曼-麦克斯韦统计特点:( B )A. 每一个可能的微观状态以相同的概率出现B. 各能级的各量子态上分配的粒子数,受保里不相容原理的限制/C. 体系由独立可别的粒子组成,U = ∑niεiD. 宏观状态参量N、U、V 为定值的封闭体系11. 下面对转动配分函数计算式的对称数σ差别理解不对的是:( B )A. 对配分函数的修正B. 对粒子等同性的修正C. 对量子态等同性的修正D. 对转动量子数的修正12. HI 的转动特征温度Θr= K,300 K 时HI 的摩尔转动熵为:( A )A. J·K-1·mol -1B. J·K-1 ·mol-1C. J·K-1·mol-1D. J·K-1 ·mol-113.对于单原子理想气体在室温下的物理过程,若要通过配分函数来求过程中热力学函数的变化:( )A. 必须知道qt、qR 、qv 、qn 各配分函数B.只须知道qt一个配分函数C. 必须知道qt、qn 配分函数D. 必须知道qt、q R、qv 配分函数B14. 巳知CO和N2分子的质量相同,转动特征温度基本相同,若电子处于非简并的基态,且振动对熵的贡献可忽略,那么:(D )>A. Sm(CO) < Sm (N 2)B. Sm (CO)与Sm (N2 ) 大小无法比较C. S m(CO) = Sm (N2 )D. S m(CO) > Sm (N 2)15. 玻耳兹曼熵定理一般不适用于:( )A. 独立子体系B.理想气体C. 量子气体D. 单个粒子D16. 非理想气体是:( )A.独立的等同粒子体系B. 相依的粒子体系C. 独立的可别粒子体系D. 定域的可别粒子体系B17. 下列各体系中属于独立粒子体系的是:( )A.绝对零度的晶体B.理想液体混合物C. 纯气体D. 理想气体的混合物D18.对于服从玻耳兹曼分布定律的体系,其分布规律为:( )(A) 能量最低的单个量子状态上的粒子数最多(B) 第一激发能级上的粒子数最多,(C) 视体系的具体条件而定(D) 以上三答案都不对A19. 近独立定域粒子体系和经典极限下的非定域粒子体系的( B )A. 最概然分布公式不同B. 最概然分布公式相同C. 某一能量分布类型的微观状态数相同D. 以粒子配分函数表示的热力学函数的统计表达示相同20. 在N 个NO 分子组成的晶体中,每个分子都有两种可能的排列方式,即NO 和ON,也可将晶体视为NO和ON的混合物,在0K 时该体系的熵值:( )A. S0 =0B. S0 =kln2C. S 0=Nkln2D. S0 =2klnN C21. 在平动、转动、振动运动对热力学函数的贡献中,下述关系式中错误的是:()A.Ar= Gr B.Uv= Hv C.CV,v=Cp,v D.Cp,t=CV, D22.分子的平动、转动和振动的能级间隔的大小顺序是:()A.振动能>转动能>平动能B.振动能>平动能>转动能C.平动能>振动能>转动能D.转动能>平动能>振动能A—23. 热力学函数与分子配分函数的关系式对于定域粒子体系和离域粒子体系都相同的是:( )A. G,F,SB. U,H,SC. U,H,CvD. H,G,Cv C24. 双原子分子的振动配分函数q ={1-exp(-h /kT)-1 是表示:( D )A. 振动处于基态B. 选取基态能量为零C. 振动处于基态且选基态能量为零D. 振动可以处于激发态,选取基态能量为零25. . 热力学函数与配分函数的关系式对于等同粒子体系和可别粒子体系都相同的是:( )A. U , F , SB. U , H, CvC. U , H, SD. H, F , Cv九、溶胶的聚沉和絮凝聚沉值:使溶胶发生明显聚沉所需电解质的最低浓度聚沉能力大小有以下规则:1.哈迪-舒尔兹(Hardy-Schulze)规则:*聚沉值与反离子价数成反比2. 感胶离子序:同价反离子,聚沉能力略有不同H+>Cs+ >Rb+ >NH4+ >K+ >Na+ >Li+ F->Cl->Br->NO3->I-3.同离子:当反离子相同时,同离子价数越高,聚沉能力越弱4.有机化合物离子有很强的吸附能力,因此有较强的聚沉能力。
