2004女子数学奥林匹克
国际奥林匹克数学竞赛

国际奥林匹克数学竞赛国际数学奥林匹克竞赛,英文名:International Mathematical Olympiad,简称:IMO。
“数学奥林匹克”的名称源自苏联,其将体育竞赛、科学的发源地——古希腊和数学竞赛相互关联。
在20世纪上半叶,不同国家相继组织了各级各类的数学竞赛,先在学校,继之在地区,后来在全国进行,逐步形成了金字塔式的竞赛系统。
从各国的竞赛进一步发展,自然为形成最高一层的国际奥林匹克竞赛创造了必要的条件。
1994年,美国奥数队首次创下了IMO历史上全队6人满分的出色成绩。
[6]2022年7月15日,2022年第63届IMO最终成绩公布,中国队6名选手全部获得满分,中国队以252分的成绩获得团队总分第一名。
1956年罗马尼亚数学家罗曼教授提出了倡议,并于1959年7月在罗马尼亚举行了第一次国际奥林匹克数学(International Mathematical Olympiad 简称IMO),当时只有保加利亚、捷克斯洛伐克、匈牙利、波兰、罗马尼亚和苏联参加。
以后每年举行(中间只在1980年断过一次),参加的国家和地区逐渐增多,参加这项赛事的代表队达80余支。
中国第一次参加国际数学奥林匹克是在1985年。
经过40多年的发展,国际数学奥林匹克的运转逐步制度化、规范化,有了一整套约定俗成的常规,并为历届东道主所遵循。
历届赛事编辑播报罗马尼亚的Brasov和布加勒斯特(1959),7个国家参赛罗马尼亚Sinaia(1960)匈牙利Veszprem(1961)捷克斯洛伐克Ceske Budejovice(1962)波兰的华沙和Wroclaw(1963)苏联莫斯科(1964)东德柏林(1965)保加利亚索菲亚(1966)南斯拉夫Cetinje(1967)苏联莫斯科(1968)罗马尼亚布加勒斯特(1969)匈牙利Keszthely(1970)捷克斯洛伐克Zilina(1971)波兰Torun(1972)苏联莫斯科(1973)德意志民主共和国的Erfurt和东柏林(1974)保加利亚的Burgas和索菲亚(1975)奥地利Linz(1976)南斯拉夫贝尔格勒(1977)罗马尼亚布加勒斯特(1978)英国伦敦(1979)美国华盛顿(1981)匈牙利布达佩斯(1982)法国巴黎(1983)捷克斯洛伐克布拉格(1984)芬兰Joutsa(1985)波兰华沙(1986)古巴哈瓦那(1987)澳洲坎培拉(1988)西德Brunswick(1989)中国北京市(1990),54个国家参赛瑞典Sigtuna(1991年7月12-23日),55个国家参赛俄罗斯莫斯科(1992年7月10-21日),56个国家参赛土耳其伊斯坦堡(1993年7月13-24日),73个国家参赛中国香港特别行政区(1994年7月8-20日),69个国家参赛加拿大多伦多(1995年7月13-25日),73个国家参赛印度孟买(1996年7月5-17日),75个国家参赛阿根廷马德普拉塔(1997年7月18-31日),82个国家参赛中国台湾省台北市(1998年7月10-21日),76个国家参赛罗马尼亚布加勒斯特(1999年7月10-22日),81个国家参赛大韩民国大田(2000年7月13-25日),82个国家参赛美国华盛顿(2001年7月1-14日),83个国家参赛英国格拉斯哥,84个国家参赛(2002年7月19-30日)日本东京(2003年7-19日),82个国家参赛希腊雅典(2004年6-18日),85个国家参赛墨西哥坎昆(2005年7月8-19日),98个国家参赛斯洛文尼亚卢布尔雅那(2006)越南(2007)西班牙(2008)德国不莱梅(2009)哈萨克斯坦首都阿斯塔纳(2010),95个国家的522名选手参赛荷兰阿姆斯特丹(2011)阿根廷马德普拉塔(2012)哥伦比亚圣玛塔(2013)南非开普敦(2014)泰国清迈(2015)中国香港(2016)巴西里约热内卢(2017)罗马尼亚克鲁日纳波卡(2018)英国巴斯(2019)挪威奥斯陆(2022)历届冠军编辑播报(1977-2019)[1]1977:美国1982:西德1983:西德1987:罗马尼亚1988:苏联1989:中国1990:中国1991:苏联1992:中国1993:中国1995:中国1996:罗马尼亚1997:中国1998:伊朗1999:中国/俄罗斯2000:中国2001:中国2002:中国2003:保加利亚2004:中国2005:中国2006:中国2007:俄罗斯2008:中国2009:中国2010:中国2011:中国2012:韩国2013:中国2014:中国2015:美国2016:美国2017:韩国2018:美国2019:中国[2]/美国2020:中国[3] 2022中国。
换元法在数学竞赛中的若干运用(李鑫)

换元法在数学竞赛中的若干运用摘要:在中学数学竞赛中,换元法作为一种重要的解题方法,有着能够将数学问题化繁为简,化难为易的作用。
本文论述换元法在中学数学竞赛中的若干种运用,主要从自身换元、局部换元、整体换元、常值换元、均值换元、参数换元、比值换元及其功能分类等八个方面来论述.关键词:换元法、数学竞赛Abstract前言从往年的竞赛试题看,初中竞赛和高中竞赛题需要用到换元法来求解的问题是相当多的。
在计算题、解高次方程、解无理方程、求函数解析式、不等式的证明、数列等题型中经常能过发挥重要的作用。
通过换元法可以达到化高次为低次,化分式为整式,化无理式为有理式,化超越式为代数式的转化。
这里我仅结合数学竞赛中常出现的一些题型来谈一谈它在数学竞赛中的一些运用.1.换元法的定义及其相关概念1.1换元法的定义所谓换元法(substitution method; substitution; changing yuan)是一种设辅助元素,把题中一个(些)字母的表达式用另外的一个字母(些)字母的表达式来代替,从而达到把要求解的问题简单化,建立已知和未知的联系的方法.在解决数学竞赛试题时,有时我们直接按原始的方法去解决问题会显得比较繁琐和困难,或者原问题所给已知条件不易得出最后结果,或者所给问题不好下手,那么这时如果我们能够引人新的“元”代替旧的“元”,使得建立在“新元”基础上的条件和问题得到了化繁为简、化难为易,容易得出最后的正确结果。
这就是换元法之所在.1.2换元法的基本思想化繁为简、化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式、化不熟悉为熟悉.1.3换元法的一般步骤①构造新元②解答③求出原解转化代价代换2.换元法的分类及典例分析2.1从结构上划分2.1.1自身换元法在数学竞赛中,我们经常会遇到一些很繁杂的计算题,如果按照原始的方法去计算,如果按照原始的方法去计算,将会使计算过程变的复杂难解,甚至不能得到最后的正确结果,这时我们常会用到“自身换元法”。
2004年首届中国东南地区数学奥林匹克竞赛考试试题

首届中国东南地区数学奥林匹克竞赛试题第一天(2004年7月10日 8:00 — 12:00 温州)一、设实数a 、b 、c 满足2223232a b c ++=,求证:39271a b c---++≥ 二、设D 是ABC ∆的边BC 上的一点,点P 在线段AD 上,过点D 作一直线分别与线段AB 、PB 交于点M 、E ,与线段AC 、PC 的延长线交于点F 、N 。
如果DE=DF , 求证:DM=DN三、(1)是否存在正整数的无穷数列{}n a ,使得对任意的正整数n 都有2122n n n a a a ++≥。
(2)是否存在正无理数的无穷数列{}n a ,使得对任意的正整数n 都有2122n n n a a a ++≥。
四、给定大于2004的正整数n ,将1、2、3、…、2n 分别填入n ×n 棋盘(由n 行n 列方格构成)的方格中,使每个方格恰有一个数。
如果一个方格中填的数大于它所在行至少2004个方格内所填的数,且大于它所在列至少2004个方格内所填的数,则称这个方格为“优格”。
求棋盘中“优格”个数的最大值。
第二天(2004年7月11日 8:00 — 12:00 温州)五、已知不等式63)cos()2sin 2364sin cos a a πθθθθ+-+-<++对于0,2πθ⎡⎤∈⎢⎥⎣⎦恒成立,求a 的取值范围。
六、设点D 为等腰ABC ∆的底边BC 上一点,F 为过A 、D 、C 三点的圆在ABC ∆内的弧上一点,过B 、D 、F 三点的圆与边AB 交于点E 。
求证:CD EF DF AE BD AF ⋅+⋅=⋅七、n 支球队要举行主客场双循环比赛(每两支球队比赛两场,各有一场主场比赛),每支球队在一周(从周日到周六的七天)内可以进行多场客场比赛。
但如果某周内该球队有主场比赛,在这一周内不能安排该球队的客场比赛。
如果4周内能够完成全部比赛,球n 的最大值。
注:A 、B 两队在A 方场地举行的比赛,称为A 的主场比赛,B 的客场比赛。
2004年度全国中学生数学奥林匹克竞赛全国决赛获奖名单
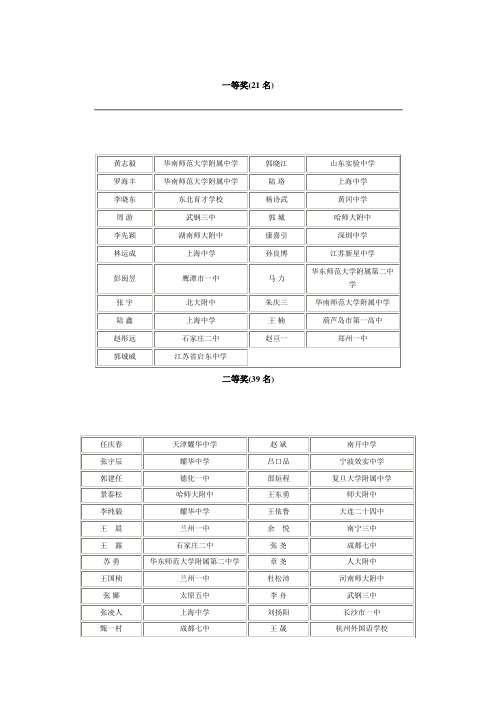
成都七中
苏勇
华东师范大学附属第二中学
章尧
人大附中
王国桢
兰州一中
杜松沛
河南师大附中
张娜
太原五中
李舟
武钢三中
张凌人
上海中学
刘扬阳
长沙市一中
甄一村
成都七中
王晟
杭州外国语学校
陈世腾
海南中学
赵琳博
北大附中
郑志诚
莆田一中
左力
陕西省西安中学
支持
镇海中学
胡 劲
华师一附中
祖鹏鹤
河南师大附中
李杨佳
长沙市一中
傅列
华东师大二附中
王枫
安师大附中
毛智超
西北工大附中
杨健慧
河师大附中
荣 膺
福州一中
曹楠
东北师大附中
万时凯
景德镇市一中
陈子娟
长沙市一中
魏崟泷
蚌埠二中
李思其
金陵中学
赵 沨
石家庄二中
林 嵩
深圳中学
张辉
利津一中
吴昊
北京二十二中
戴莽原
新疆实验中学
雷慧天
武钢三中
赵煦
北京二中
龙忠慧
湖南师大附中
周桐
山西大学附属中学
王一壘
绍兴一中
孙毅然
北京四中
陈宗文
上海中学
邢硕博
清华附中
茅越
江苏省启东中学
俞能昆
马鞍山二中
田 伟
石家庄二中
三等奖(31名)
杨磊
长沙市雅礼中学
藏经涛
哈师大附中
李邱华
江苏省启东中学
曹志敏
江苏省华罗庚中学
2004-2012历届女子数学奥林匹克试题PDF(无答案)

目录2002年女子数学奥林匹克 (1)2003年女子数学奥林匹克 (3)2004年女子数学奥林匹克 (5)2005年女子数学奥林匹克 (7)2006年女子数学奥林匹克 (9)2007年女子数学奥林匹克 (11)2008年女子数学奥林匹克 (13)2009年女子数学奥林匹克 (16)2010年女子数学奥林匹克 (19)2011年女子数学奥林匹克 (21)2012年女子数学奥林匹克 (24)2002年女子数学奥林匹克1.求出所有的正整数n,使得20n+2能整除2003n+2002.2.夏令营有3n(n是正整数)位女同学参加,每天都有3位女同学担任执勤工作.夏令营结束时,发现这3n位女同学中的任何两位,在同一天担任执勤工作恰好是一次.(1)问:当n=3时,是否存在满足题意的安排?证明你的结论;(2)求证:n是奇数.3.试求出所有的正整数k,使得对任意满足不等式k(aa+ab+ba)>5(a2+a2+b2)4.⊙O1和⊙O2相交于B、C两点,且BC是⊙O1的直径.过点C作⊙O1的切线,交⊙O2于另一点A,连结AB,交⊙O1于另一点E,连结CE并延长,交⊙O2于点F.设点H为线段AF内的任意一点,连结HE并延长,交⊙O1于点G,连结BG并延长,与AC的延长线交于点D.求证:AA AH=AA AC.5.设P1,P2,⋯,P n(n≥2)是1,2,⋯,n的任意一个排列.求证:1P1+P2+1P2+P3+⋯+1P n−2+P n−1+1P n−1+P n>n−1n+2.6.求所有的正整数对(x,y),满足x y=y x−y.7.锐角△ABC的三条高分别为AD、BE、CF.求证:△DEF的周长不超过△ABC周长的一半.8.设A1,A2,⋯,A8是平面上任意取定的8个点,对平面上任意取定的一条有向直线l,设A1,A2,⋯,A8在该直线上的摄影分别是P1,P2,⋯,P8.如果这8个射影两两不重合,以直线l的方向依次排列为P i1,P i2,⋯,P i8,这样,就得到了1,2,…,8的一个排列i1,i2,⋯,i8(在图1中,此排列为2,1,8,3,7,4,6,5).设这8个点对平面上所有有向直线作射影后,得到的不同排列的个数为N8=N(A1,A2,⋯88的最大值.图12003年女子数学奥林匹克1. 已知D 是△ABC 的边AB 上的任意一点,E 是边AC 上的任意一点,连结DE ,F 是线段DE 上的任意一点.设AC AA =x ,AA AA =y ,CH CA =z .证明: (1) S △ACH =(1−x )yzS △AAA ,S △AAH =x (1−y )(1−z )S △AAA ;(2) �S △ACH 3+�S △AAH 3≤�S △AAA 3.2. 某班有47个学生,所用教室有6排,每排有8个座位,用(i ,j )表示位于第i 排第j 列的座位.新学期准备调整座位,设某学生原来的座位为(i ,j ),如果调整后的座位为(m ,n ),则称该生作了移动[a ,a ]=[i −m ,j −n ],并称a +b 为该生的位置数.所有学生的位置数之和记为S .求S 的最大可能值与最小可能值之差.3. 如图1,ABCD 是圆内接四边形,AC 是圆的直径,BB ⊥AA ,AC 与BD 的交点为E ,F 在DA 的延长线上.连结BF ,G 在BA 的延长线上,使得BD ∥BB ,H 在GF 的延长线上,AC ⊥DB .证明:B 、E 、F 、H 四点共圆.图14.(1)证明:存在和为1的5个非负实数a、b、c、d、e,使得将它们任意放置在一个圆周上,总有两个相邻数的乘积不小于19;(2)证明:对于和为1的任意玩个非负实数a、b、c、d、e,总可以将它们适当放置在一个圆周上,且任意相邻两数的乘积均不大于19.5.数列{a n}定义如下:a1=2,a n+1=a n2−a n+1,n=1,2,⋯.证明:1−120032003<1a1+1a2+⋯+1a2003<1.6.给定正整数n(n≥2).求最大的实数λ,使得不等式a n2≥λ(a1+a2+⋯+a n−1)+2a n对任意满足a1<a2⋯<a n的正整数a1,a2,⋯,a n均成立.7.设△ABC的三边长分别为AB=b、BA=a、AA=a,a、b、c互不相等,AD、BE、CF分别为△ABC的三条内角平分线,且DE=DF.证明:(1)a b+c=b c+a+c a+b;(2)∠BAA>90°.8.对于任意正整数n,记n的所有正约数组成的集合为S n.证明:S n中至多有一半元素的个位数为3.2004年女子数学奥林匹克1.如果存在1,2,⋯,n的一个排列a1,a2,⋯,a n,使得k+a k(k=1,2,⋯,n)都是完全平方数,则称n为“好数”.问:在集合{11,13,15,17,19}中,哪些是“好数”,哪些不是“好数”?说明理由.(苏淳供题)2.设a、b、c为正实数.求a+3c a+2b+c+4b a+b+2c−8c a+b+3c的最小值.(李胜宏供题)3.已知钝角△ABC的外接圆半径为1.证明:存在一个斜边长为√2+1的等腰直角三角形覆盖△ABC.(冷岗松供题)4.一副三色纸牌,共有32张,其中红黄蓝每种颜色的牌各10张,编号分别是1,2,⋯,10;另有大小王牌各一张,编号均为0.从这副牌中任取若干张牌,然后按如下规则计算分值:每张编号为k的牌记为2k分.若它们的分值之和为2004,则称这些牌为一个“好牌组”.试求“好牌组”的个数.(陶平生供题)5.设u、v、w为正实数,满足条件u√vv+v√vu+v√uv≥1.试求u+v+v的最小值. (陈永高供题)6.给定锐角△ABC,点O为其外心,直线AO交边BC于点D.动点E、F分别位于边AB、AC上,使得A、E、D、F四点共圆.求证:线段EF在边BC上的投影的长度为定值.(熊斌供题)7.已知p、q为互质的正整数,n为非负整数.问:有多少个不同的整数可以表示为ii+jj的形式,其中i,j为非负整数,且i+j≤n.(李伟固供题)8.将一个3×3的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”.在一个10×11的棋盘上,最多可以放置多少个互不重叠的“十字形”(每个“十字形”恰好盖住棋盘上的5个小方格)?(冯祖明供题)2005年女子数学奥林匹克1.如图1,点P在△ABC的外接圆上,直线CP、AB相交于点E,直线BP、AC相交于点F,边AC的垂直平分线与边AB相交于点J,边AB的垂直平分线与边AC相交于点K.求证:AA2AH=AA⋅AA AA⋅AH.图1(叶中豪供题)2.求方程组�5�x+1x�=12�y+1y�=13(z+1z)xy+yz+zx=1,的所有实数解.(朱华伟供题)3.是否存在这样的凸多面体,它共有8个顶点、12条棱和6个面,并且其中有4个面,每两个面都有公共棱?(苏淳供题)4.求出所有的正实数a,使得存在正整数n及n个互不相交的无限整数集合A1,A2,⋯,A n满足A1∪A2∪⋯∪A n=Z,而且对于每个A i中的任意两数b>c,都有a−b≥a i.(袁汉辉供题)5.设正实数x、y满足x3+y3=x−y.求证:x2+4y2<1. (熊斌供题)6.设正整数n(n≥3).如果在平面上有n个格点P1,P2,⋯,P n满足:当�P i P j�为有理数时,存在P k,使得|P i P k|和�P j P k�均为无理数;当�P i P j�为无理数时,存在P k,使得|P i P k|和�P j P k�均为有理数,那么,称n是“好数”.(1)求最小的好数;(2)问:2005是否为好数(冯祖明供题)7.设m、n是整数,m>n≥2,S=�1,2,⋯,m�,T=�a1,a2,⋯,a n�是S的一个子集.已知T中的任两个数都不能同时整除S中的任何一个数.求证:1a1+1a2+⋯+1a n<m+n m. (张同君供题)8.给定实数a、b(a>a>0),将长为a、宽为b的矩形放入一个正方形内(包含边界).问正方形的边至少为多长?(陈永高供题)2006年女子数学奥林匹克1.设a>0,函数f:(0,+∞)→R满足f(a)=1.如果对任意正实数x、y,有f(x)f(y)+f�a x�f�a y�=2f(xy),求证:f(x)为常数.(朱华伟供题)2.设凸四边形ABCD的对角线交于点O.△OAD、△OBC的外接圆交于点O、M,直线OM分别交△OAB、△OCD的外接圆于点T、S.求证:M是线段TS的中点.(叶中豪供题)3.求证:对i=1,2,3,均有无穷多个正整数n,使得n,n+2,n+28中恰有i个可表示为三个正整数的立方和.(袁汉辉供题)4.8个人参加一次聚会.(1)如果其中任何5个人中都有3个人两两认识,求证:可以从中找出4个人两两认识;(2)试问:如果其中任何6个人中都有3个人两两认识,那么是否一定可以找出4个人两两认识?(苏淳供题)5.平面上整点集S=�(a,a)�1≤a,a≤5(a、a∈Z)�,T为平面上一整点集,对S中任一点P,总存在T中不同于P的一点Q,使得线段PQ上除点P、Q外无其它的整点.问T的元素个数最少为多少?(陈永高供题)6.设集合M={1,2,⋯,19},A={a1,a2,⋯,a k}⊆M.求最小的k,使得对任意的a∈M,存在a i、a j∈A,满足a=a i或a=a i±a j(a i、a j 可以相同).(李胜宏供题)7.设x i>0(i=1,2,⋯,n),k≥1.求证:∑11+x i n i=1⋅∑x i n i=1≤∑x i k+11+x i n i=1⋅∑1x i k n i=1. (陈伟固供题)8.设p为大于3的质数,求证:存在若干个整数a1,a2,⋯,a t满足条件−p2<a1<a2<⋯<a t<p2,使得乘积p−a1|a1|⋅p−a2|a2|⋅⋯⋅p−a t|a t|是3的某个正整数次幂.(纪春岗供题)2007年女子数学奥林匹克1.设m为正整数,如果存在某个正整数n,使得m可以表示为n和n的正约数个数(包括1和自身)的商,则称m是“好数”.求证:(1)1,2,⋯,17都是好数;(2)18不是好数.(李胜宏供题)2.设△ABC是锐角三角形,点D、E、F分别在边BC、CA、AB上,线段AD、BE、CF经过△ABC的外心O.已知以下六个比值AC CA、AA AA、AH HA、AH HA、AA AA、AC CA中至少有两个是整数.求证:△ABC是等腰三角形.(冯祖明供题)3.设整数n(n>3),非负实数a1,a2,⋯,a n满足a1+a2+⋯+a n=2.求a1a22+1+a2a32+1+⋯+a n a12+1的最小值.(朱华伟供题)4.平面内n(n≥3)个点组成集合S,P是此平面内m条直线组成的集合,满足S关于P中每一条直线对称.求证:m≤n,并问等号何时成立?(边红平供题)5.设D是△ABC内的一点,满足∠BAA=∠BAA=30°,∠BBA=60°,E是边BC的中点,F是边AC的三等分点,满足AF=2FC.求证:BD⊥DB.(叶中豪供题)6.已知a、a、b≥0,a+a+b=1.求证:�a+14(a−b)2+√a+√b≤√3(李伟固供题)7.给定绝对值都不大于10的整数a、b、c,三次多项式f(x)=x3+ ax2+ax+b满足条件�f(2+√3)�<0.0001.问:2+√3是否一定是这个多项式的根?(张景中供题)8.n个棋手参加象棋比赛,每两个棋手比赛一局.规定:胜者得1分,负者得0分,平局得0.5分.如果赛后发现任何m个棋手中都有一个棋手胜了其余m-1个棋手,也有一个棋手输给了其余m-1个棋手,就称此赛况具有性质P(m).对给定的m(m≥4),求n的最小值f(m),使得对具有性质P(m)的任何赛况,都有所有n名棋手的得分各不相同.(王建伟供题)2008年女子数学奥林匹克1.(1)问能否将集合�1,2,⋯,96�表示为它的32个三元子集的并集,且每个三元子集的元素之和都相等;(2)问能否将集合�1,2,⋯,99�表示为它的33个三元子集的并集,且每个三元子集的元素之和都相等.(刘诗雄供题)2.已知式系数多项式ϕ(x)=ax3+ax2+bx+d有三个正根,且ϕ(0)<0.求证:2a3+9a2d−7aab≤0. (朱华伟供题)3.求最小常数a(a>1),使得对正方形ABCD内部任一点P,都存在△P AB、△PBC、△PCD、△PDA中的某两个三角形,其面积之比属于区间�a−1,a�.(李伟固供题)4.在凸四边形ABCD的外部分别作正△ABQ、△BCR、△CDS、△DAP,记四边形ABCD的对角线的和为x,四边形PQRS的对角线中点连线的和为y.求y x的最大值.(熊斌供题)5.如图1,已知凸四边形ABCD满足AB=BC,AD=DA,E、F分别是线段AB、AD上一点,满足B、E、F、D四点共圆,作△DPE顺向相似于△ADC,作△BQF顺向相似于△ABC.求证:A、P、Q三点共线.图1 注:两个三角形顺向相似是指它们的对应顶点同按顺时针方向或同按逆时针方向排列.(叶中豪 供题)6. 设正数列x 1,x 2,⋯,x n ,⋯满足(8x 2−7x 1)x 17=8及x k+1x k−1−x k 2=x k−18−x k 8(x k x k−1)7(k ≥2).求正实数a ,使得当x 1>a 时,有单调性x 1>x 2>⋯>x n >⋯,当0<x 1<a 时,不具有单调性. (李胜宏 供题)7. 给定一个2008×2008的棋盘,棋盘上每个小方格的颜色均不相同.在棋盘的每一个小方格中填入C 、G 、M 、O 这4个字母中的一个,若棋盘中每一个2×2的小棋盘中都有C 、G 、M 、O 这4个字母,则称这个棋盘为“和谐棋盘”,问有多少种不同的和谐棋盘?(冯祖明 供题)8. 对于正整数n ,令f n =�2n √2008�+[2n √2009].求证:数列f 1,f 2,⋯中有无穷多个奇数和无穷多个偶数([x ]表示不超过实数x 的最大整数).(冯祖明 供题)B2009年女子数学奥林匹克1. 求证:方程aab =2009(a +a +b )只有有限组正整数解(a,b,c).(梁应德 供题)2. 如图1,在△ABC 中,∠BAA =90°,点E 在△ABC 的外接圆圆Γ的弧BC (不含点A )内,AE >EC .连结EC 并延长至点F ,使得∠DAA =∠AAB ,连结BF 交圆Γ于点D ,连结ED ,记△DEF 的外心为O .求证:A 、C 、O 三点共线.图1 (边红平 供题)3. 在平面直角坐标系中,设点集�P 1,P 2,⋯,P 4n+1�=�(x ,y )�x 、y 为整数,|x |≤n ,|y |≤n ,xy =0�,其中,n ∈N +.求(P 1P 2)2+(P 2P 3)2+⋯+(P 4n P 4n+1)2+(P 4n+1P 1)2的最小值.(王新茂 供题)4. 设平面上有n (n ≥4)个点V 1,V 2,⋯,V n ,任意三点不共线,某些点之间连有线段.把标号分别为1,2,⋯,n 的n 枚棋子放置在这n 个点处,每个点处恰有一枚棋子.现对这n 枚棋子进行如下操作:每B次选取若干枚棋子,将它们分别移动到与自己所在点有线段相连的另一个点处;操作后每点处仍恰有一枚棋子,并且没有两枚棋子在操作前后交换位置.若一种连线段的方式使得无论开始时如何放置这n 枚棋子,总能经过有限次操作后,使每个标号为k (k =1,2,⋯,n )的棋子在点V k 处,则称这种连线段的方式为“和谐的”.求在所有和谐的连线段的方式中,线段数目的最小值. (付云皓 供题)5. 设实数xyz 大于或等于1.求证:(x 2−2x +2)(y 2−2y +2)(z 2−2z +2)≤(xyz )2−2xyz +2 (熊 斌 供题)6. 如图2,圆Γ1、Γ2内切于点S ,圆Γ2的弦AB 与圆Γ1切于点C ,M 是弧AB (不含点S )的中点,过点M 作MN ⊥AB ,垂足为N .记圆Γ1的半径为r .求证:AA ⋅AB =2rMN .图2 (叶中豪 供题)7. 在一个10×10的方格表中有一个有4n 个1×1的小方格组成的图形,它既可被n 个“”型的图形覆盖,也可被n 个“”或“”型(可以旋转)的图形覆盖.求正整数n的最小值.(朱华伟供题)8.设a n=n√5−�n√5�.求数列a1,a2,⋯,a2009中的最大项和最小项,其中,[x]表示不超过实数x的最大整数.(王志雄供题)2010年女子数学奥林匹克1. 给定整数n (n ≥3),设A 1,A 2,⋯,A 2n 是集合�1,2,⋯,n�的两两不同的非空子集,记A 2n+1=A 1.求∑|A i ∩A i+1||A i |⋅|A i+1|2n i=1的最大值.(梁应德 供题)2. 如图1,在△ABC 中,AB =AA ,D 是边BC 的中点,E 是在△ABC 外一点,满足AD ⊥AB ,BD =BB .过线段BE 的中点M 作直线MB ⊥BD ,交△ABD 的外接圆的劣弧AD 于点F .求证:DB ⊥BB .图1 (郑焕 供题)3. 求证:对于每个正整数n ,都存在满足下面三个条件的质数p 和整数m :(1)i ≡5(mmd 6);(2)i ∤n ;(3)n ≡m 3(mmd i ).(付云皓 供题) 4. 设实数x 1,x 2,⋯,x n 满足∑x i 2=1(n ≥2)n i=1.求证:∑(1−k ∑ix i 2n i=1)2x k 2k n k=1≤(n−1n+1)2∑x k 2k n k=1,并确定等号成立的条件.(李胜宏供题)5.已知f(x)、g(x)都是定义在R上递增的一次函数,f(x)为整数当且仅当g(x)为整数.证明:对一切x∈R,f(x)−g(x)为整数.(刘诗雄供题)6.如图2,在锐角△ABC中,AB>AA,M为边BC的中点,∠BAA的外角平分线交直线BC于点P.点K、F在直线P A上,使得MB⊥BA,MM⊥PA.求证:BC2图2(边红平供题)7.给定正整数n(n≥3).对于1,2,⋯,n的任意一个排列P=(x1,x2,⋯,x n),若i<j<k,则称x j介于x i和x k之间(如在排列(1,3,2,4)中,3介于1和4之间,4不介于1和2之间).设集合S={P1,P2,⋯,P m}的每个元素P i(1≤i≤m)中都不介于另外两个数之间.求m的最大值.(冯祖鸣供题)8.试求满足下列条件的大于5的最小奇数a:存在正整数m1、n1、m2、n2,使得a=m12+n12,a2=m22+n22,且m1−n1=m2−n2.(朱华伟供题)2011年女子数学奥林匹克1.求出所有的正整数n,使得关于x,y的方程1x+1y=1n恰有2011组满足x≤y的正整数解(x,y) .(熊斌供题)2.如图1,在四边形ABCD的对角线AC与BD相交于点E,边AB、CD的中垂线相交于点F,点M、N分别为边AB、CD的中点,直线EF分别与边BC、AD相交于点P、Q,若MB⋅AB=NB⋅AB, BQ⋅BP=AQ⋅AP,求证:PQ垂直于BC.图1(郑焕供题)3.设正数a,a,b,d满足aabd=1,求证:1+1+1+1+9≥25(朱华伟供题)4.有n(n≥3)名乒乓球选手参加循环赛,每两名选手之间恰好比赛一次(比赛无平局).赛后发现,可以将这些选手排成一圈,使得对于任意三名选手A,B,C,若A,B在圈上相邻,则A,B中至少有一人战胜了C,求n的所有可能值.(付云皓供题)5.给定非负实数a,求最小实数f=f(a),使得对任意复数,Z1,Z2和实数x(0≤x≤1),若|Z1|≤a|Z1−Z2|,则|Z1−xZ2|≤f|Z1−Z2|.(李胜宏供题)6.是否存在正整数m,n,使得m20+11n是完全平方数?请予以证明.(袁汉辉供题)7.从左到右编号为B1,B2,⋯,B n的n个盒子共装有n个小球,每次可以选择一个盒子B k,进行如下操作:若k=1且B1中至少有1个小球,则可从B1中移1个小球至B2中;若k=n,且B n中至少有1个小球,则可从B n中移1个小球至B n-1中,若2≤k≤n-1且B k中至少有2个小球,则可从B k中分别移1个小球至B k-1和B k+1中,求证:无论初始时这些小球如何放置,总能经过有限次操作使得每个盒子中恰有1个小球.(王新茂供题)8. 如图2,已知⊙O 为△ABC 中BC 边上的旁切圆,点D 、E 分别在线段AB 、AC 上,使得BD ∥BA .⊙O 1为△ADE 的内切圆,O 1B 交DO 于点F ,O 1C 交EO 于点G .⊙O 切BC 于点M .⊙O 1切DE 于点N .求证:MN 平分线段FG .图2 (边红平 供题)A2012年女子数学奥林匹克1.设a1,a2,⋯,a n为非负实数,求证:11+a1+a1(1+a1)(1+a2)+⋯+ a1a2⋯a n−1(1+a1)(1+a2)⋯(1+a n)≤1.2.如图1所示,圆O1和O2外切于点T,点A、E在圆O1上,AB切圆O2于点B,ED切圆O2于点D,直线BD、AE交于点P.(1)求证:AB⋅DT=AT⋅DB;(2)求证:∠ATP+∠DTP=180°Array图13.求所有整数对(a,b),使得存在整数d>1,对任意的正整数n,都有d|a n+a n+1.4.在正十三边形的13个顶点上各摆放一枚黑子或者白子,一次操作是指将两枚棋子的位置交换.求证:无论开始时棋子是如何摆放的,总可以至多操作一次,使得各个棋子的颜色关于正十三边形的某一条对称轴是对称的.5.如图2所示,在△ABC中,I为内切圆圆心,D、E分别为AB、AC边上的切点,O为△BIC的外心,求证:∠OBB=∠ODA.图26. 某个国家有n (n ≥3)个城市,每两个城市间都有一条双向航线.这个国家有两个航空公司,每条航线由一家公司经营.一个女数学家从某个城市出发,经过至少两个其它城市,回到出发地.如果无论怎样选择出发城市和路径,都无法只乘坐一家公司的航班,求n 的最大值.7. 有一个无穷项的正整数数列a 1≤a 2≤a 3≤⋯.已知存在正整数k和r ,使得r a r =k +1,求证:存在正整数s ,使得s a s =k .8. 集合{0,1,2,⋯,2012}中有多少个元素k ,使得A 2012k 是2012的倍数.B。
数学奥林匹克问题

2
相交于点 Q ,割线 PEF 经过点 Q 交圆于 E 、 F. 证明 :
1
②
PE
+
1
PF
=
2
PQ
.
48
中 等 数 学
《中等数学》 2004 年总目次
数学活动课程讲座 ・ 初中・ 几何计数问题 ( 下) 存在性问题 好玩的平移 构造法在初中数学竞赛中的应用
a a + 8 bc
2
由于 EF ∥BC ,则 EB = FC. 从而 , ∠GAQ = ∠CA P , 即 A P 、 AQ 为 △ABC 的 ∠BAC 的外等角线 . 由三角形外等角线的性质定理得
AB B P・ BQ . 2 = CP・ CQ AC
2
①
又由三角形内角平分线性质定理得
AB BD = . AC CD
2 f ( f ( y ) ) = ( y - y + 1) f ( y ) .
④
f ( y) (y ≠ 在④ 中用 0) 代替 y ,并利用 ③ 得 y f f f ( y) y
=
y
f ( y) y
2
y
f ( y) +1 f y
f ( y) y
平 分
∠BA E , △L FM 、
3 2 ] f ( f ( y ) ) = ( f ( y2) ) - ( f ( y ) ) + f ( y )
由 ①、 ② 得
2 2
BD B P・ BQ , 2 = CP・ CQ CD
2
BD ・ CP・ CQ = CD ・ B P・ BQ , BD ( DP - CD) ( DQ - CD)
历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO

历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO(1985年,芬兰赫尔辛基)吴思皓(男)上海向明中学确规定铜牌上海交通大学王锋(男)北京大学(根据yongcheng先生提供的信息修订)目前作企业软件第27届IMO(1986年,波兰华沙)李平立(男)天津南开中学金牌北京大学方为民(男)河南实验中学金牌北京大学张浩(男)上海大同中学金牌复旦大学荆秦(女)陕西西安八十五中银牌北京大学,现在美国哈佛大学任教林强(男)湖北黄冈中学铜牌中国科技大学第28届IMO(1987年,古巴哈瓦那)刘雄(男)湖南湘阴中学金牌南开大学滕峻(女)北京大学附中金牌北京大学林强(男)湖北黄冈中学银牌中国科技大学潘于刚(男)上海向明中学银牌北京大学何建勋(男)广东华南师范大学附中铜牌中国科技大学高峡(男)北京大学附中铜牌北京大学,现在北大任教第29届IMO(1988年,澳大利亚堪培拉)团体总分第二陈晞(男)上海复旦大学附中金牌复旦大学,美国密苏里大学,美国哈佛大学,现在加拿大Alberta大学数学系任教授韦国恒(男)湖北武汉武钢三中银牌北京大学查宇涵(男)南京十中银牌北京大学,在中科院数学所任副研究员邹钢(男)江苏镇江中学银牌北京大学王健梅(女)天津南开中学银牌北京大学何宏宇(男)以满分成绩获第29届国际数学奥林匹金牌,1993年破格列入美国数学家协会会员,1994年获博士学位,现任亚特兰大乔治大学教授、博士生导师,从事现代数学研究前沿的《李群》《微分几何》等方向的研究,在《李群》的研究上已有重大突破。
第30届IMO(1989年,原德意志联邦共和国布伦瑞克)团体总分第一罗华章(男)重庆水川中学金牌北京大学俞扬(男)吉林东北师范大学附中金牌吉林大学霍晓明(男)江西景德镇景光中学金牌中国科技大学唐若曦(男)四川成都九中银牌中国科技大学颜华菲(女)北京中国人民大学附中银牌北京大学本科,1997年获美国麻省理工博士,现任Texax A&M Uneversity 数学系教授,美国数学会常务理事会成员,Mathematical Reviews评论员。
历届西部数学奥林匹克试题

目录2001年西部数学奥林匹克 (2)2002年西部数学奥林匹克 (4)2003年西部数学奥林匹克 (6)2004年西部数学奥林匹克 (7)2005年西部数学奥林匹克 (8)2006年西部数学奥林匹克 (10)2007年西部数学奥林匹克 (12)2008年西部数学奥林匹克 (14)2009年西部数学奥林匹克 (16)2010年西部数学奥林匹克 (18)2011年西部数学奥林匹克 (21)2012年西部数学奥林匹克 (23)2001年西部数学奥林匹克1.设数列{x n}满足x1=12,x n+1=x n+x n2n2.证明:x2001<1001.(李伟固供题)2.设ABCD是面积为2的长方形,P为边CD上的一点,Q为△P AB的内切圆与边AB的切点.乘积PP⋅PP的值随着长方形ABCD及点P 的变化而变化,当PP⋅PP取最小值时,(1)证明:PP≥2PB;(2)求PQ⋅PQ的值.(罗增儒供题)3.设n、m是具有不同奇偶性的正整数,且n>m.求所有的整数x,使得x2n−1x m−1是一个完全平方数.(潘曾彪供题)4.设x、y、z为正实数,且x+y+z≥xyz.求x2+y2+z2xyz的最小值.(冯志刚供题)5.求所有的实数x,使得[x3]=4x+3.这里[y]表示不超过实数y的最大整数.(杨文鹏供题)6.P为⊙O外一点,过P作⊙O的两条切线,切点分别为A、B.设Q为PO与AB的交点,过Q作⊙O的任意一条弦CD.证明:△PAB与△PCD有相同的内心. (刘康宁供题)7.求所有的实数x∈�0,π2�,使得(2−sss2x)sss�x+π4�=1,并证明你的结论.(李胜宏供题)8.我们称P1,P2,⋯,P n为集合A的一个n分划,如果(1)P1∪P2∪⋯∪P n=P;(2)P i∩P j≠Φ,1≤s<j≤s.求最小正整数m,使得对P={1,2,⋯,m}的任意一个14分划P1,P2,⋯,P14,一定存在某个集合P i(1≤s≤14),在P i中有两个元素a、b满足b<a≤43b. (冷岗松供题)2002年西部数学奥林匹克1.求所有的正整数n,使得s4−4s3+22s2−36s+18是一个完全平方数.2.设O为锐角△ABC的外心,P为△AOB内部一点,P在△ABC的三边BC、CA、AB上的射影分别为D、E、F.求证:以FE、FD为邻边的平行四边形位于△ABC内.3.考虑复平面上的正方形,它的4个顶点所对应的复数恰好是某个整系数一元四次方程x4+px3+qx2+rx+s=0的4个根.求这种正方形面积的最小值.4.设n为正整数,集合P1,P2,⋯,P n+1是集合{1,2,⋯,s}的n+1个非空子集.证明:存在{1,2,⋯,s+1}的两个不交的非空子集{s1,s2,⋯,s k}和{j1,j2,⋯,j m},使得P i1∪P i2∪⋯∪P i k=P j1∪P j2∪⋯∪P j m.5.在给定的梯形ABCD中,AD∥BC,E是边AB上的动点,O1、O2分别是△AED、△BEC的外心.求证:O1O2的长为一定值.6.设s(s≥2)是给定的正整数,求所有整数组(a1,a2,⋯,a n)满足条件:(1)a1+a2+⋯+a n≥s2;(2)a12+a22++a n2≤s3+1.7.设α、β为方程x2−x−1=0的两个根,令a n=αn−βnα−β,s=1,2,⋯.(1)证明:对任意正整数n,有a n+2=a n+1+a n;(2)求所有正整数a、b,a<b,满足对任意正整数n,有b整除a n−2sa n.8.设S=(a1,a2,⋯,a n)是一个由0,1组成的满足下述条件的最长的数列:数列S中任意两个连续5项不同,即对任意1≤s<j≤s−4,a i,a i+1,a i+2,a i+3,a i+4与a j,a j+1,a j+2,a j+3,a j+4不相同.证明:数列S 最前面的4项与最后面的4项相同.1. 将1,2,3,4,5,6,7,8分别放在正方体的八个顶点上,使得每一个面上的任意三个数之和均不小于10.求每一个面上四个数之和的最小值.2. 设2n 个实数a 1,a 2,⋯,a 2n 满足条件∑(a i+1−a i )2=12n−1i=1.求(a n+1+a n+2+⋯+a 2n )−(a 1+a 2+⋯+a n )的最大值.3. 设n 为给定的正整数.求最小的正整数u n ,满足:对每一个正整数d ,任意u n 个连续的正奇数中能被d 整除的数的个数不少于奇数1,3,5,⋯,2s −1中能被d 整除的数的个数.4. 证明:若凸四边形ABCD 内任意一点P 到边AB 、BC 、CD 、DA 的距离之和为定值,则ABCD 是平行四边形.5. 已知数列{a n }满足:a 0=0,a n+1=ka n +�(k 2−1)a n 2+1,s =0,1,2,⋯,其中k 为给定的正整数.证明:数列{a n }的每一项都是整数,且2k |a 2n ,s =0,1,2,⋯. 6. 凸四边形ABCD 有内切圆,该内切圆切边AB 、BC 、CD 、DA 的切点分别为A 1、B 1、C 1、D 1,连结A 1B 1、B 1C 1、C 1D 1、D 1A 1,点E 、F 、G 、H 分别为A 1B 1、B 1C 1、C 1D 1、D 1A 1的中点.证明:四边形EFGH 为矩形的充分必要条件是A 、B 、C 、D 四点共圆.7. 设非负实数x 1、x 2、x 3、x 4、x 5满足∑11+x i =15i=1.求证:∑x i4+x i 25i=1≤1. 8. 1650个学生排成22行、75列.已知其中任意两列处于同一行的两个人中,性别相同的学生都不超过11对.证明:男生的人数不超过928.1.求所有的整数n,使得s4+6s3+11s2+3s+31是完全平方数.2.四边形ABCD为一凸四边形,I1、I2分别为△ABC、△DBC的内心,过点I1、I2的直线分别交AB、DC于点E、F,分别延长AB、DC,它们相交于点P,且PE=PF.求证:A、B、C、D四点共圆.3.求所有的实数k,使得不等式a3+b3+c3+d3+1≥k(a+b+c+d)对任意a、b、c、d∈[−1,+∞)都成立.4.设s∈N+,用d(s)表示n的所有正约数的个数,ϕ(s)表示1,2,⋯,s 中与n互质的数的个数.求所有的非负整数c,使得存在正整数n,满足d(s)+ϕ(s)=s+c,且对这样的每一个c,求出所有满足上式的正整数n.5.设数列{a n}满足a1=a2=1,且a n+2=1a n+1+a n,s=1,2,⋯.求a2004.6.将m×s棋盘(由m行n列方格构成,m≥3,s≥3)的所有小方格都染上红蓝两色之一.如果2个相邻(有公共变)的小方格异色,则称这2个小方格为1个“标准对”.设期盼中“标准对”的个数为S.试问:S是奇数还是偶数有哪些方格的颜色确定?什么情况下S为奇数?什么情况下S为偶数?说明理由.7.已知锐角△ABC的三边长不全相等,周长为l,P是其内部一动点,点P在边BC、CA、AB上的射影分别为D、E、F.求证:2(PB+PD+ BB)=l的充分必要条件是:点P在△ABC的内心与外心的连线上.8.求证:对任意正实数a、b、c,都有1<a√a2+b2+b√b2+c2+c√c2+a2≤3√22.1. 已知α2005+β2005可表示成以α+β、αβ为变元的二元多项式.求这个多项式的系数之和.2. 如图1,过圆外一点P 作圆的两条切线P A 、PB ,A 、B 为切点,再过点P 作圆的一条割线分别与圆交于C 、D 两点,过切点B 作P A 的平行线分别交直线AC 、AD 于E 、F .求证:PB =PB .图13. 设S ={1,2,⋯,2005}.若S 中任意n 个两两互质的数组成的集合中都至少有一个质数,试求n 的最小值.4. 已知实数x 1,x 2,⋯,x n (s >2)满足|∑x i n i=1|>1,|x i |≤1(s =1,2,⋯,s ).求证:存在正整数k ,使得�∑x i k i=1−∑x i n i=k+1�≤1 5. 如图2,⊙O 1、⊙O 2交于A 、B 两点.过点O 1的直线DC 交⊙O 1于点D 且切⊙O 2于点C ,CA 且⊙O 1于点A ,⊙O 1的弦AE 与直线DC 垂直.过点A 作AF 垂直于DE ,F 为垂足.求证:BD 平分线段AF .图2P6.在等腰Rt△ABC中,BP=BP=1,P是△ABC边界上任意一点.求PP⋅PP⋅PB的最大值.7.设正实数a、b、c满足a+b+c=1.证明:10(a3+b3+c3)−9(a5+b5+c5)≥1.8.设n个新生汇总,任意3个人中有2个人互相认识,任意4个人中有2个人互不任何.试求n的最大值.2006年西部数学奥林匹克1. 设s (s ≥2)是给定的正整数,a 1,a 2,⋯,a n ∈(0,1).求∑�a i (1−a i+1)6n i=1的最大值,这里a n+1=a 1. 2. 求满足下述条件的最小正实数k :对任意不小于k 的4个互不相同的实数a 、b 、c 、d ,都存在a 、b 、c 、d 的一个排列p 、q 、r 、s ,使得方程(x 2+px +q )(x 2+rx +s )=0有4个互不相同的实数根. 3. 如图1,在△ABC 中,∠PPB =60°,过点P 作△PBC 的外接圆⊙O 的切线,与CA 的延长线交于点A .点D 、E 分别在线段PA 和⊙O 上,使得∠DPB =90°,PD =PE .连结BE 与PC 相交于点F .已知AF 、BP 、CD 三线共点.(1) 求证:BF 是∠PPB 的角平分线;(2) 求tas ∠PBP 的值.图14. 设正整数a 不是完全平方数.求证:对每一个正整数n ,S n =�√a�+�√a�2+⋯+�√a�n的值都是无理数.这里{x }=x −[x ],其中,[x ]表示不超过x 的最大整数.5. 设S =�s�s −1,s ,s +1都可以表示为两个正整数的平方和�.证明:若s ∈S ,则s 2∈S .C6. 如图2,AB 是⊙O 的直径,C 为AB 延长线上的一点,过点C 作⊙O 的割线,与⊙O 交于点D 、E ,OF 是△BOD 的外接圆⊙O 1的直径,连结CF 并延长交⊙O 1于点G .求证:O 、A 、E 、G 四点共圆.图27. 设k 是一个不小于3的正整数,θ是一个实数.证明:如果cms (k −1)θ和cms kθ都是有理数,那么,存在正整数s (s >k ),使得cms (s −1)θ和cms sθ都是有理数. 8. 给定正整数s (s ≥2),求|X |的最小值,使得对集合X 的任意n 个二元子集P 1,P 2,⋯,P n ,都存在集合X 的一个子集Y ,满足:(1)|Y |=s ;(2) 对s =1,2,⋯,s ,都有|Y ∩P i |≤1.这里,|P |表示有限集合A 的元素个数.A2007年西部数学奥林匹克1. 已知T ={1,2,⋯,8}.对于P ⊆T ,P ≠Φ,定义S (P )为A 中所有元素之和.问:T 有多少个非空子集A ,使得S (P )是3的倍数,但不是5的倍数?2. 如图1,⊙O 1、⊙O 2交于点C 、D ,过D 的一条直线分别与⊙O 1、⊙O 2交于点A 、B ,点P 在⊙O 1的AD 弧上,PD 与线段AC 的延长线交于点M ,点Q 在⊙O 2的BD 弧上,QD 与线段BC 的延长线交于点N ,O 是△ABC 的外心.求证:OD ⊥MN 的充要条件为P 、Q 、M 、N 四点共圆.图13. 设实数a 、b 、c 满足a +b +c =3.求证:15a −4a+11+15b −4b+11+15c −4c+11≤14. 4. 设O 是△ABC 内部一点.证明:存在正整数p 、q 、r ,使得|pOP +qOP +rOB |<12007.5. 是否存在三边长都为整数的三角形,满足以下条件:最短边长为2007,且最大的角等于最小角的两倍?O6.求所有的正整数n,使得存在非零整数x1,x2,⋯,x n,y,满足�x1+x2+⋯+x n=0,x12+x22+⋯+x n2=sy2.7.设P是锐角△ABC内一点,AP、BP、CP分别与边BC、CA、AB 交于点D、E、F,已知△DBB∼△PPB.求证:P是△ABC的重心. 8.将n枚白子与n枚黑子任意地放在一个圆周上.从某枚白子起,按顺时针方向依次将白子标以1,2,⋯,s.在从某枚黑子起,按逆时针方向依次将黑子标以1,2,⋯,s.证明:存在连续n枚棋子(不计黑白),它们的标号组成的集合为{1,2,⋯,s}.2008年西部数学奥林匹克1.实数数列{a n}满足a0≠0,1,a1=1−a0,a n+1=1−a n(1−a n)(s=1,2,⋯).证明:对任意的正整数n,都有a0a1⋯a n�1a0+1a1+⋯+1a n�=1.2.如图1,在△ABC中,AB=AC,其内切圆⊙I分别切边BC、CA、AB于点D、E、F,P为弧EF(不含点D的弧)上一点.设线段BP交⊙I于另一点Q,直线EP、EQ分别交BC于点M、N.证明:(1)P、F、B、M四点共圆;(2)EE EE=BB BB.图13.设整数m(m≥2),a1,a2,⋯,a m都是正整数.证明:存在无穷多个正整数n,使得数a1×1n+a2×2n+⋯+a m×m n都是合数.4.设整数m(m≥2),a为正实数,b为非零实数,数列{x n}定义如下:x1=b,x n+1=ax n m+b(s=1,2,⋯).证明:(1)当b<0且m为偶数时,数列{x n}有界的充要条件是ab m−1≥−2;(2)当b<0且m为奇数,或b>0时,数列{x n}有界的充要条件是ab m−1≤(m−1)m−1m m.5.在一直线上相邻的距离都等于1的四个点上各有一只青蛙,允许任意一只青蛙以其余三只青蛙中的某一只为中心跳到其对称点上.证明:无论跳动多少次后,四只青蛙所在的点中相邻两点之间的距离不能都等于2008.6.设x、y、z∈(0,1),满足�1−x yz+�1−y zx+�1−z xy=2.求xyz的最大值.7.设n为给定的正整数.求最大的正整数k,使得存在三个由非负整数组成的k元集P={x1,x2,⋯,x k},P={y1,y2,⋯,y k},B= {z1,z2,⋯,z k}满足对任意的j(1≤j≤k),都有x j+y j+z j=s.8.设P为正n边形P1P2⋯P n内的任意一点,直线P i P(s=1,2,⋯s)交正n边形P1P2⋯P n的边界于另一点P i.证明:∑PP i n i=1≥∑PP i n i=1.2009年西部数学奥林匹克1.设M是一个由实数集R去掉有限个元素后得到的集合.证明:对任意正整数n,都存在n次多项式f(x),使得f(x)的所有系数及n个实根都属于M.2.给定整数s≥3.求最小的正整数k,使得存在一个k元集合A和n 个两两不同的实数x1,x2,⋯,x n,满足x1+x2,x2+x3,⋯,x n−1+x n,x n+x1均属于A.3.设H为锐角△ABC的垂心,D为边BC的中点.过点H的直线分别交边AB、AC于点F、E,使得AE=AF,射线DH与△ABC的外接圆交于点P.求证:P、A、E、F四点共圆.4.求证:对任意给定的正整数k,总存在无穷多个正整数n,使得2n+3n−1,2n+3n−2,⋯,2n+3n−k均为合数.5.设数列{x n}满足x1∈{5,7}及当k≥1时,有x k+1∈{5x k,7x k}.试确定x2009的末两位数字的所有可能值.6.如图1,设D是锐角△ABC的边BC上一点,以线段BD为直径的圆分别交直线AB、AD于点X、P(异于点B、D),以线段CD为直径的元分别交直线AC、AD于点Y、Q(异于点C、D).过点A作直线PX、QY的垂线,垂足分别为M、N.求证△PMN∼△PPB的充分必要条件是直线AD过△ABC的外心.图17. 有s (s >12)个人参加某次数学邀请赛,试卷由十五道填空题组成,每答对一题得1分,不答或答错得0分.分析每一种可能的得分情况发现:只要其中任意12个人得分之和不少于36分,则这n 个人中至少有3个人答对了至少三道同样的题.求n 的最小可能值.8. 实数a 1,a 2,⋯,a n (s ≥3)满足a 1+a 2+⋯+a n =0,且2a k ≤a k−1+a k+1(k =2,3,⋯,s −1).求最小的λ(s ),使得对所有的k ∈{1,2,⋯s },都有|a k |≤λ(s )⋅max {|a 1|,|a n |}.B2010年西部数学奥林匹克1. 设m 、k 为给定的非负整数,p =22m +1为质数.求证: (1) 22m+1p k ≡1(mmd p k+1);(2) 满足同余方程2n ≡1(mmdp k+1) 的最小正整数n 为2m+1p k . (靳 平 供题)2. 如图1,已知AB 是⊙O 的直径,C 、D 是圆周上异于点A 、B 且在AB 同侧的两点,分别过点C 、D 作圆的切线,它们交于点E ,线段AD 与BC 的交点为F ,直线EF 与AB 交于点M .求证:E 、C 、M 、D 四点共圆.图1(刘诗雄 供题)3. 求所有的正整数n ,使得集合{1,2,⋯,s }有n 个两两不同的三元子集P 1,P 2,⋯,P n ,满足对任意的k (1≤s <j ≤s ),都有�P i ∩P j �≠1.(冯志刚 供题)4. 设非负实数a 1,a 2,⋯,a n 与b 1,b 2,⋯,b n 满足以下条件: (1) ∑a i +b i n i=1=1; (2) ∑s (a i −b i )n i=1=0; (3) ∑s 2(a i +b i )n i=1=10.求证:对任意的k(1≤k≤s),都有max{a k,b k}≤1010+k2. (李胜宏供题)5.设k为大于1的整数,数列{a n}定义如下:a0=0,a1=1,a n+1=ka n+a n−1(s=1,2,⋯).求所以满足如下条件的k:存在非负整数l、m(l≠m),及正整数p、q,使得a l+ka p=a m+ka q. (熊斌供题)6.如图2,在△ABC中,∠PBP=90°,以B为圆心、BC为半径作圆,点D在边AC上,直线DE切⊙B于点E,过点C垂直于AB的直线于直线BE交于点F,AF与DE交于点G,作AH∥BG于DE交于点H.求证GE=GH.图2(边红平供题)7.有s(s≥3)名选手参加乒乓球比赛,每两名选手之间恰比赛一场且没有平局.若选手A的手下败将不都是B的手下败将,则称A不亚于B.试求所有可能的n,使得存在一种比赛结果,其中每一名选手都不亚于其他任何一名选手.(李秋生供题)8.求所有的整数k,使得存在正整数a和b,满足b+1a+a+1b=k.(陈永高供题)2011年西部数学奥林匹克1. 已知0<x 、y <1.求xy (1−x−y )(x+y )(1−x )(1−y )的最大值.2. 设集合满足:M ⊆{1,2,⋯,2011}在M 的任意三个元素中都可以找到两个元素a 、b ,使得a |b 或b |a .求|M |的最大值(|M |表示集合M 的元素个数).3. 给定整数s ≥2.(1) 证明:可以将集合{1,2,⋯,s }的左右子集适当地排列为P 1,P 2,⋯,P 2n ,使得P i 与P i+1(s =1,2,,2n ,且P 2n +1=P 1)的元素个数恰相差1.(2) 对于满足(1)中条件的子集P 1,P 2,⋯,P 2n ,求∑(−1)i S (P i )2n i=1的所以可能值,其中,S (P i )=∑x x∈A i ,S (∅)=0. 4. 如图1,AB 、CD 是⊙O 中长度不相等的两条弦,AB 与CD 交于点E ,⊙I 内切⊙O 于点F ,且分别与弦AB 、CD 切于点G 、H .过点O 的直线l 分别于AB 、CD 交于点P 、Q ,使得EP =EQ ,直线EF 于直线l 交于点M .证明:过点M 且与AB 平行的直线是⊙O 的切线.图15. 是否存在奇数s (s ≥3)及n 个互不相同的质数p 1,p 2,⋯,p n ,使得p i +p i+1(s =1,2,⋯,s ,p n+1=p 1)都是完全平方数?请证明你的结论.6.设a、b、c>0.证明:(a−b)2(c+a)(c+b)+(b−c)2(a+b)(a+c)+(c−a)2(b+c)(b+a)≥(a−b)2a+b+c.7.在△ABC中,PP>PB内切圆⊙I与边BC、CA、AB分别切于点D、E、F,M是边BC的中点,PH⊥PB于点H,∠PPB的平分线AI分别与直线DE、DF交于点K、L.证明:M、L、H、K四点共圆. 8.求所有的整数对(a,b),使得对任意的正整数n都有s|(a n+b n+1).2012年西部数学奥林匹克1.求最小的正整数m,使得对任意大于3的质数p,都有:105|9p2−29p+m.2.证明:在正2s−1边形(s≥3)的顶点中,任意取出s个点,其中必有3个点,以它们为顶点的三角形为等腰三角形。
历届女子数学奥林匹克试题

目录2002年女子数学奥林匹克 (1)2003年女子数学奥林匹克 (3)2004年女子数学奥林匹克 (5)2005年女子数学奥林匹克 (7)2006年女子数学奥林匹克 (9)2007年女子数学奥林匹克 (11)2008年女子数学奥林匹克 (13)2009年女子数学奥林匹克 (16)2010年女子数学奥林匹克 (19)2011年女子数学奥林匹克 (21)2012年女子数学奥林匹克 (24)2002年女子数学奥林匹克1.求出所有的正整数n,使得20n+2能整除2003n+2002.2.夏令营有3n(n是正整数)位女同学参加,每天都有3位女同学担任执勤工作.夏令营结束时,发现这3n位女同学中的任何两位,在同一天担任执勤工作恰好是一次.(1)问:当n=3时,是否存在满足题意的安排?证明你的结论;(2)求证:n是奇数.3.试求出所有的正整数k,使得对任意满足不等式k(aa+ab+ba)>5(a2+a2+b2)4.⊙O1和⊙O2相交于B、C两点,且BC是⊙O1的直径.过点C作⊙O1的切线,交⊙O2于另一点A,连结AB,交⊙O1于另一点E,连结CE并延长,交⊙O2于点F.设点H为线段AF内的任意一点,连结HE并延长,交⊙O1于点G,连结BG并延长,与AC的延长线交于点D.求证:AA AH=AA AC.5.设P1,P2,⋯,P n(n≥2)是1,2,⋯,n的任意一个排列.求证:1P1+P2+1P2+P3+⋯+1P n−2+P n−1+1P n−1+P n>n−1n+2.6.求所有的正整数对(x,y),满足x y=y x−y.7.锐角△ABC的三条高分别为AD、BE、CF.求证:△DEF的周长不超过△ABC周长的一半.8.设A1,A2,⋯,A8是平面上任意取定的8个点,对平面上任意取定的一条有向直线l,设A1,A2,⋯,A8在该直线上的摄影分别是P1,P2,⋯,P8.如果这8个射影两两不重合,以直线l的方向依次排列为P i1,P i2,⋯,P i8,这样,就得到了1,2,…,8的一个排列i1,i2,⋯,i8(在图1中,此排列为2,1,8,3,7,4,6,5).设这8个点对平面上所有有向直线作射影后,得到的不同排列的个数为N8=N(A1,A2,⋯88的最大值.图12003年女子数学奥林匹克1. 已知D 是△ABC 的边AB 上的任意一点,E 是边AC 上的任意一点,连结DE ,F 是线段DE 上的任意一点.设AC AA =x ,AA AA =y ,CH CA =z .证明: (1) S △ACH =(1−x )yzS △AAA ,S △AAH =x (1−y )(1−z )S △AAA ;(2) �S △ACH 3+�S △AAH 3≤�S △AAA 3.2. 某班有47个学生,所用教室有6排,每排有8个座位,用(i ,j )表示位于第i 排第j 列的座位.新学期准备调整座位,设某学生原来的座位为(i ,j ),如果调整后的座位为(m ,n ),则称该生作了移动[a ,a ]=[i −m ,j −n ],并称a +b 为该生的位置数.所有学生的位置数之和记为S .求S 的最大可能值与最小可能值之差.3. 如图1,ABCD 是圆内接四边形,AC 是圆的直径,BB ⊥AA ,AC 与BD 的交点为E ,F 在DA 的延长线上.连结BF ,G 在BA 的延长线上,使得BD ∥BB ,H 在GF 的延长线上,AC ⊥DB .证明:B 、E 、F 、H 四点共圆.图14.(1)证明:存在和为1的5个非负实数a、b、c、d、e,使得将它们任意放置在一个圆周上,总有两个相邻数的乘积不小于19;(2)证明:对于和为1的任意玩个非负实数a、b、c、d、e,总可以将它们适当放置在一个圆周上,且任意相邻两数的乘积均不大于19.5.数列{a n}定义如下:a1=2,a n+1=a n2−a n+1,n=1,2,⋯.证明:1−120032003<1a1+1a2+⋯+1a2003<1.6.给定正整数n(n≥2).求最大的实数λ,使得不等式a n2≥λ(a1+a2+⋯+a n−1)+2a n对任意满足a1<a2⋯<a n的正整数a1,a2,⋯,a n均成立.7.设△ABC的三边长分别为AB=b、BA=a、AA=a,a、b、c互不相等,AD、BE、CF分别为△ABC的三条内角平分线,且DE=DF.证明:(1)a b+c=b c+a+c a+b;(2)∠BAA>90°.8.对于任意正整数n,记n的所有正约数组成的集合为S n.证明:S n中至多有一半元素的个位数为3.2004年女子数学奥林匹克1.如果存在1,2,⋯,n的一个排列a1,a2,⋯,a n,使得k+a k(k=1,2,⋯,n)都是完全平方数,则称n为“好数”.问:在集合{11,13,15,17,19}中,哪些是“好数”,哪些不是“好数”?说明理由.(苏淳供题)2.设a、b、c为正实数.求a+3c a+2b+c+4b a+b+2c−8c a+b+3c的最小值.(李胜宏供题)3.已知钝角△ABC的外接圆半径为1.证明:存在一个斜边长为√2+1的等腰直角三角形覆盖△ABC.(冷岗松供题)4.一副三色纸牌,共有32张,其中红黄蓝每种颜色的牌各10张,编号分别是1,2,⋯,10;另有大小王牌各一张,编号均为0.从这副牌中任取若干张牌,然后按如下规则计算分值:每张编号为k的牌记为2k分.若它们的分值之和为2004,则称这些牌为一个“好牌组”.试求“好牌组”的个数.(陶平生供题)5.设u、v、w为正实数,满足条件u√vv+v√vu+v√uv≥1.试求u+v+v的最小值. (陈永高供题)6.给定锐角△ABC,点O为其外心,直线AO交边BC于点D.动点E、F分别位于边AB、AC上,使得A、E、D、F四点共圆.求证:线段EF在边BC上的投影的长度为定值.(熊斌供题)7.已知p、q为互质的正整数,n为非负整数.问:有多少个不同的整数可以表示为ii+jj的形式,其中i,j为非负整数,且i+j≤n.(李伟固供题)8.将一个3×3的正方形的四个角上各去掉一个单位正方形所得到的图形称为“十字形”.在一个10×11的棋盘上,最多可以放置多少个互不重叠的“十字形”(每个“十字形”恰好盖住棋盘上的5个小方格)?(冯祖明供题)2005年女子数学奥林匹克1.如图1,点P在△ABC的外接圆上,直线CP、AB相交于点E,直线BP、AC相交于点F,边AC的垂直平分线与边AB相交于点J,边AB的垂直平分线与边AC相交于点K.求证:AA2AH=AA⋅AA AA⋅AH.图1(叶中豪供题)2.求方程组�5�x+1x�=12�y+1y�=13(z+1z)xy+yz+zx=1,的所有实数解.(朱华伟供题)3.是否存在这样的凸多面体,它共有8个顶点、12条棱和6个面,并且其中有4个面,每两个面都有公共棱?(苏淳供题)4.求出所有的正实数a,使得存在正整数n及n个互不相交的无限整数集合A1,A2,⋯,A n满足A1∪A2∪⋯∪A n=Z,而且对于每个A i中的任意两数b>c,都有a−b≥a i.(袁汉辉供题)5.设正实数x、y满足x3+y3=x−y.求证:x2+4y2<1. (熊斌供题)6.设正整数n(n≥3).如果在平面上有n个格点P1,P2,⋯,P n满足:当�P i P j�为有理数时,存在P k,使得|P i P k|和�P j P k�均为无理数;当�P i P j�为无理数时,存在P k,使得|P i P k|和�P j P k�均为有理数,那么,称n是“好数”.(1)求最小的好数;(2)问:2005是否为好数(冯祖明供题)7.设m、n是整数,m>n≥2,S=�1,2,⋯,m�,T=�a1,a2,⋯,a n�是S的一个子集.已知T中的任两个数都不能同时整除S中的任何一个数.求证:1a1+1a2+⋯+1a n<m+n m. (张同君供题)8.给定实数a、b(a>a>0),将长为a、宽为b的矩形放入一个正方形内(包含边界).问正方形的边至少为多长?(陈永高供题)2006年女子数学奥林匹克1.设a>0,函数f:(0,+∞)→R满足f(a)=1.如果对任意正实数x、y,有f(x)f(y)+f�a x�f�a y�=2f(xy),求证:f(x)为常数.(朱华伟供题)2.设凸四边形ABCD的对角线交于点O.△OAD、△OBC的外接圆交于点O、M,直线OM分别交△OAB、△OCD的外接圆于点T、S.求证:M是线段TS的中点.(叶中豪供题)3.求证:对i=1,2,3,均有无穷多个正整数n,使得n,n+2,n+28中恰有i个可表示为三个正整数的立方和.(袁汉辉供题)4.8个人参加一次聚会.(1)如果其中任何5个人中都有3个人两两认识,求证:可以从中找出4个人两两认识;(2)试问:如果其中任何6个人中都有3个人两两认识,那么是否一定可以找出4个人两两认识?(苏淳供题)5.平面上整点集S=�(a,a)�1≤a,a≤5(a、a∈Z)�,T为平面上一整点集,对S中任一点P,总存在T中不同于P的一点Q,使得线段PQ上除点P、Q外无其它的整点.问T的元素个数最少为多少?(陈永高供题)6.设集合M={1,2,⋯,19},A={a1,a2,⋯,a k}⊆M.求最小的k,使得对任意的a∈M,存在a i、a j∈A,满足a=a i或a=a i±a j(a i、a j 可以相同).(李胜宏供题)7.设x i>0(i=1,2,⋯,n),k≥1.求证:∑11+x i n i=1⋅∑x i n i=1≤∑x i k+11+x i n i=1⋅∑1x i k n i=1. (陈伟固供题)8.设p为大于3的质数,求证:存在若干个整数a1,a2,⋯,a t满足条件−p2<a1<a2<⋯<a t<p2,使得乘积p−a1|a1|⋅p−a2|a2|⋅⋯⋅p−a t|a t|是3的某个正整数次幂.(纪春岗供题)2007年女子数学奥林匹克1.设m为正整数,如果存在某个正整数n,使得m可以表示为n和n的正约数个数(包括1和自身)的商,则称m是“好数”.求证:(1)1,2,⋯,17都是好数;(2)18不是好数.(李胜宏供题)2.设△ABC是锐角三角形,点D、E、F分别在边BC、CA、AB上,线段AD、BE、CF经过△ABC的外心O.已知以下六个比值AC CA、AA AA、AH HA、AH HA、AA AA、AC CA中至少有两个是整数.求证:△ABC是等腰三角形.(冯祖明供题)3.设整数n(n>3),非负实数a1,a2,⋯,a n满足a1+a2+⋯+a n=2.求a1a22+1+a2a32+1+⋯+a n a12+1的最小值.(朱华伟供题)4.平面内n(n≥3)个点组成集合S,P是此平面内m条直线组成的集合,满足S关于P中每一条直线对称.求证:m≤n,并问等号何时成立?(边红平供题)5.设D是△ABC内的一点,满足∠BAA=∠BAA=30°,∠BBA=60°,E是边BC的中点,F是边AC的三等分点,满足AF=2FC.求证:BD⊥DB.(叶中豪供题)6.已知a、a、b≥0,a+a+b=1.求证:�a+14(a−b)2+√a+√b≤√3(李伟固供题)7.给定绝对值都不大于10的整数a、b、c,三次多项式f(x)=x3+ ax2+ax+b满足条件�f(2+√3)�<0.0001.问:2+√3是否一定是这个多项式的根?(张景中供题)8.n个棋手参加象棋比赛,每两个棋手比赛一局.规定:胜者得1分,负者得0分,平局得0.5分.如果赛后发现任何m个棋手中都有一个棋手胜了其余m-1个棋手,也有一个棋手输给了其余m-1个棋手,就称此赛况具有性质P(m).对给定的m(m≥4),求n的最小值f(m),使得对具有性质P(m)的任何赛况,都有所有n名棋手的得分各不相同.(王建伟供题)2008年女子数学奥林匹克1.(1)问能否将集合�1,2,⋯,96�表示为它的32个三元子集的并集,且每个三元子集的元素之和都相等;(2)问能否将集合�1,2,⋯,99�表示为它的33个三元子集的并集,且每个三元子集的元素之和都相等.(刘诗雄供题)2.已知式系数多项式ϕ(x)=ax3+ax2+bx+d有三个正根,且ϕ(0)<0.求证:2a3+9a2d−7aab≤0. (朱华伟供题)3.求最小常数a(a>1),使得对正方形ABCD内部任一点P,都存在△P AB、△PBC、△PCD、△PDA中的某两个三角形,其面积之比属于区间�a−1,a�.(李伟固供题)4.在凸四边形ABCD的外部分别作正△ABQ、△BCR、△CDS、△DAP,记四边形ABCD的对角线的和为x,四边形PQRS的对角线中点连线的和为y.求y x的最大值.(熊斌供题)5.如图1,已知凸四边形ABCD满足AB=BC,AD=DA,E、F分别是线段AB、AD上一点,满足B、E、F、D四点共圆,作△DPE顺向相似于△ADC,作△BQF顺向相似于△ABC.求证:A、P、Q三点共线.图1 注:两个三角形顺向相似是指它们的对应顶点同按顺时针方向或同按逆时针方向排列.(叶中豪 供题)6. 设正数列x 1,x 2,⋯,x n ,⋯满足(8x 2−7x 1)x 17=8及x k+1x k−1−x k 2=x k−18−x k 8(x k x k−1)7(k ≥2).求正实数a ,使得当x 1>a 时,有单调性x 1>x 2>⋯>x n >⋯,当0<x 1<a 时,不具有单调性. (李胜宏 供题)7. 给定一个2008×2008的棋盘,棋盘上每个小方格的颜色均不相同.在棋盘的每一个小方格中填入C 、G 、M 、O 这4个字母中的一个,若棋盘中每一个2×2的小棋盘中都有C 、G 、M 、O 这4个字母,则称这个棋盘为“和谐棋盘”,问有多少种不同的和谐棋盘?(冯祖明 供题)8. 对于正整数n ,令f n =�2n √2008�+[2n √2009].求证:数列f 1,f 2,⋯中有无穷多个奇数和无穷多个偶数([x ]表示不超过实数x 的最大整数).(冯祖明 供题)B2009年女子数学奥林匹克1. 求证:方程aab =2009(a +a +b )只有有限组正整数解(a,b,c).(梁应德 供题)2. 如图1,在△ABC 中,∠BAA =90°,点E 在△ABC 的外接圆圆Γ的弧BC (不含点A )内,AE >EC .连结EC 并延长至点F ,使得∠DAA =∠AAB ,连结BF 交圆Γ于点D ,连结ED ,记△DEF 的外心为O .求证:A 、C 、O 三点共线.图1 (边红平 供题)3. 在平面直角坐标系中,设点集�P 1,P 2,⋯,P 4n+1�=�(x ,y )�x 、y 为整数,|x |≤n ,|y |≤n ,xy =0�,其中,n ∈N +.求(P 1P 2)2+(P 2P 3)2+⋯+(P 4n P 4n+1)2+(P 4n+1P 1)2的最小值.(王新茂 供题)4. 设平面上有n (n ≥4)个点V 1,V 2,⋯,V n ,任意三点不共线,某些点之间连有线段.把标号分别为1,2,⋯,n 的n 枚棋子放置在这n 个点处,每个点处恰有一枚棋子.现对这n 枚棋子进行如下操作:每B次选取若干枚棋子,将它们分别移动到与自己所在点有线段相连的另一个点处;操作后每点处仍恰有一枚棋子,并且没有两枚棋子在操作前后交换位置.若一种连线段的方式使得无论开始时如何放置这n 枚棋子,总能经过有限次操作后,使每个标号为k (k =1,2,⋯,n )的棋子在点V k 处,则称这种连线段的方式为“和谐的”.求在所有和谐的连线段的方式中,线段数目的最小值. (付云皓 供题)5. 设实数xyz 大于或等于1.求证:(x 2−2x +2)(y 2−2y +2)(z 2−2z +2)≤(xyz )2−2xyz +2 (熊 斌 供题)6. 如图2,圆Γ1、Γ2内切于点S ,圆Γ2的弦AB 与圆Γ1切于点C ,M 是弧AB (不含点S )的中点,过点M 作MN ⊥AB ,垂足为N .记圆Γ1的半径为r .求证:AA ⋅AB =2rMN .图2 (叶中豪 供题)7. 在一个10×10的方格表中有一个有4n 个1×1的小方格组成的图形,它既可被n 个“”型的图形覆盖,也可被n 个“”或“”型(可以旋转)的图形覆盖.求正整数n的最小值.(朱华伟供题)8.设a n=n√5−�n√5�.求数列a1,a2,⋯,a2009中的最大项和最小项,其中,[x]表示不超过实数x的最大整数.(王志雄供题)2010年女子数学奥林匹克1. 给定整数n (n ≥3),设A 1,A 2,⋯,A 2n 是集合�1,2,⋯,n�的两两不同的非空子集,记A 2n+1=A 1.求∑|A i ∩A i+1||A i |⋅|A i+1|2n i=1的最大值.(梁应德 供题)2. 如图1,在△ABC 中,AB =AA ,D 是边BC 的中点,E 是在△ABC 外一点,满足AD ⊥AB ,BD =BB .过线段BE 的中点M 作直线MB ⊥BD ,交△ABD 的外接圆的劣弧AD 于点F .求证:DB ⊥BB .图1 (郑焕 供题)3. 求证:对于每个正整数n ,都存在满足下面三个条件的质数p 和整数m :(1)i ≡5(mmd 6);(2)i ∤n ;(3)n ≡m 3(mmd i ).(付云皓 供题) 4. 设实数x 1,x 2,⋯,x n 满足∑x i 2=1(n ≥2)n i=1.求证:∑(1−k ∑ix i 2n i=1)2x k 2k n k=1≤(n−1n+1)2∑x k 2k n k=1,并确定等号成立的条件.(李胜宏供题)5.已知f(x)、g(x)都是定义在R上递增的一次函数,f(x)为整数当且仅当g(x)为整数.证明:对一切x∈R,f(x)−g(x)为整数.(刘诗雄供题)6.如图2,在锐角△ABC中,AB>AA,M为边BC的中点,∠BAA的外角平分线交直线BC于点P.点K、F在直线P A上,使得MB⊥BA,MM⊥PA.求证:BC2图2(边红平供题)7.给定正整数n(n≥3).对于1,2,⋯,n的任意一个排列P=(x1,x2,⋯,x n),若i<j<k,则称x j介于x i和x k之间(如在排列(1,3,2,4)中,3介于1和4之间,4不介于1和2之间).设集合S={P1,P2,⋯,P m}的每个元素P i(1≤i≤m)中都不介于另外两个数之间.求m的最大值.(冯祖鸣供题)8.试求满足下列条件的大于5的最小奇数a:存在正整数m1、n1、m2、n2,使得a=m12+n12,a2=m22+n22,且m1−n1=m2−n2.(朱华伟供题)2011年女子数学奥林匹克1.求出所有的正整数n,使得关于x,y的方程1x+1y=1n恰有2011组满足x≤y的正整数解(x,y) .(熊斌供题)2.如图1,在四边形ABCD的对角线AC与BD相交于点E,边AB、CD的中垂线相交于点F,点M、N分别为边AB、CD的中点,直线EF分别与边BC、AD相交于点P、Q,若MB⋅AB=NB⋅AB, BQ⋅BP=AQ⋅AP,求证:PQ垂直于BC.图1(郑焕供题)3.设正数a,a,b,d满足aabd=1,求证:1+1+1+1+9≥25(朱华伟供题)4.有n(n≥3)名乒乓球选手参加循环赛,每两名选手之间恰好比赛一次(比赛无平局).赛后发现,可以将这些选手排成一圈,使得对于任意三名选手A,B,C,若A,B在圈上相邻,则A,B中至少有一人战胜了C,求n的所有可能值.(付云皓供题)5.给定非负实数a,求最小实数f=f(a),使得对任意复数,Z1,Z2和实数x(0≤x≤1),若|Z1|≤a|Z1−Z2|,则|Z1−xZ2|≤f|Z1−Z2|.(李胜宏供题)6.是否存在正整数m,n,使得m20+11n是完全平方数?请予以证明.(袁汉辉供题)7.从左到右编号为B1,B2,⋯,B n的n个盒子共装有n个小球,每次可以选择一个盒子B k,进行如下操作:若k=1且B1中至少有1个小球,则可从B1中移1个小球至B2中;若k=n,且B n中至少有1个小球,则可从B n中移1个小球至B n-1中,若2≤k≤n-1且B k中至少有2个小球,则可从B k中分别移1个小球至B k-1和B k+1中,求证:无论初始时这些小球如何放置,总能经过有限次操作使得每个盒子中恰有1个小球.(王新茂供题)8. 如图2,已知⊙O 为△ABC 中BC 边上的旁切圆,点D 、E 分别在线段AB 、AC 上,使得BD ∥BA .⊙O 1为△ADE 的内切圆,O 1B 交DO 于点F ,O 1C 交EO 于点G .⊙O 切BC 于点M .⊙O 1切DE 于点N .求证:MN 平分线段FG .图2 (边红平 供题)A2012年女子数学奥林匹克1.设a1,a2,⋯,a n为非负实数,求证:11+a1+a1(1+a1)(1+a2)+⋯+ a1a2⋯a n−1(1+a1)(1+a2)⋯(1+a n)≤1.2.如图1所示,圆O1和O2外切于点T,点A、E在圆O1上,AB切圆O2于点B,ED切圆O2于点D,直线BD、AE交于点P.(1)求证:AB⋅DT=AT⋅DB;(2)求证:∠ATP+∠DTP=180°Array图13.求所有整数对(a,b),使得存在整数d>1,对任意的正整数n,都有d|a n+a n+1.4.在正十三边形的13个顶点上各摆放一枚黑子或者白子,一次操作是指将两枚棋子的位置交换.求证:无论开始时棋子是如何摆放的,总可以至多操作一次,使得各个棋子的颜色关于正十三边形的某一条对称轴是对称的.5.如图2所示,在△ABC中,I为内切圆圆心,D、E分别为AB、AC边上的切点,O为△BIC的外心,求证:∠OBB=∠ODA.图26. 某个国家有n (n ≥3)个城市,每两个城市间都有一条双向航线.这个国家有两个航空公司,每条航线由一家公司经营.一个女数学家从某个城市出发,经过至少两个其它城市,回到出发地.如果无论怎样选择出发城市和路径,都无法只乘坐一家公司的航班,求n 的最大值.7. 有一个无穷项的正整数数列a 1≤a 2≤a 3≤⋯.已知存在正整数k和r ,使得r a r =k +1,求证:存在正整数s ,使得s a s =k .8. 集合{0,1,2,⋯,2012}中有多少个元素k ,使得A 2012k 是2012的倍数.B。
2002-2012女子数学奥林匹克CGMO

= R ( sin 2 C + sin 2 B) = 2 Rsin( B + C) cos( B - C) = 2 Rsin A·cos ( B - C) = acos( B - C) ≤a. 同理 , DE + EF ≤b , EF + DF ≤c.
将上述三式相加得
DE +
EF +
FD
≤1 2
(
a
矛盾. 故 c < a + b.
方法二 :构造函数
f ( x) = 5 x2 - 6 ( a + b) x + 5 a2 + 5 b2 - 6 ab.
则 f ( c) < 0.
因 f ( x) 在区间
3 5
(
a+
b)
,
+
∞
递增 ,且
f ( a + b) = 5 ( a + b) 2 - 6 ( a + b) ( a + b) + 5 a2 +
无正整数解. 所以 ,不存在满足题设要求的 n.
二 、(1) 当 n = 3 时 , 存在满足题意的安排. 具体
安排如下 (把 9 位女同学记为 1 ,2 , …,9) :
(1 ,2 ,3) , (1 ,4 ,5) , (1 ,6 ,7) , (1 ,8 ,9) , (2 ,4 ,6) ,
2004年全国小学数学奥林匹克竞赛成绩统计--
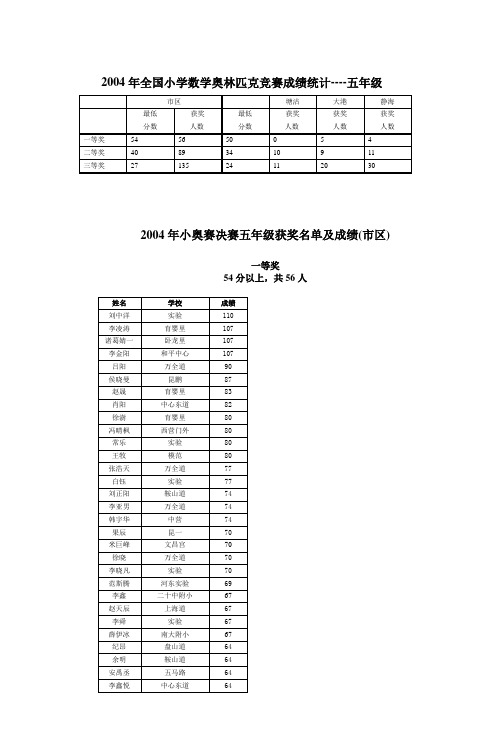
30
郑思远
红星
30
闫玮
红星
30
张绍琛
求真
30
张正
求真
30
郝苓淇
求真
30
夏岩
红桥实验
30
张月
佳园里
30
赵晓璐
咸阳北路
30
温馨
六一
30
陈睿
跃升里
30
田楚杰
鞍山道
30
芦钰
鞍山道
30
于梦薇
鞍山道
30
胡钧瀚
鞍山道
30
温元正
鞍山道
30
周明华
鞍山道
30
邢琨
昆鹏
30
孙宇
昆鹏
30
周翰驰
昆鹏
30
刘晓瑶
三水道
30
陈天用
大邱庄万全小学
30
郑秋臣
大邱庄津海小学
30
田洁
大邱庄津海小学
30
王竞颜
大邱庄尧舜实验
30
袁红超
陈官屯镇小集小学
25
张兴鹏
刘上道
25
孙中涵
实验小学
25
史凤强
蔡公庄惠丰小学
25
刘靓
静海镇孙家场
25
曲畅
大邱庄尧舜实验
25
高翠
团泊镇
24
曹月
静海镇三小
24
汤玉笑
静海镇四小
24
尚义嘉
大邱庄尧舜实验
24
五年级塘沽考点成绩汇总
团泊镇
34
三等奖
24分以上30人
张启文
沿庄镇
30
田祎伟
历届数学奥林匹克参赛名单

1985-2012年国际数学奥林匹克中国参赛人数按地区、学校统计国际数学奥林匹克(International Mathematical Olympiad,简称IMO)是世界上规模和影响最大的中学生数学学科竞赛活动。
由罗马尼亚罗曼(Roman)教授发起。
1959年7月在罗马尼亚古都布拉索举行第一届竞赛。
我国第一次派学生参加国际数学奥林匹克是1985年,当时仅派两名学生,并且成绩一般。
我国第一次正式派出6人代表队参加国际数学奥林匹克是1986年。
2012年第53届国际数学奥林匹克竞赛将于今年7月4日至16日在阿根廷马德普拉塔(Mar del Plata , Argentina)举行。
入选国家队的六名学生是:(按选拔成绩排名)陈景文(中国人民大学附属中学)、吴昊(辽宁师范大学附属中学)、左浩(华中师范大学第一附属中学)、佘毅阳(上海中学)、刘宇韬(上海中学)、王昊宇(武钢三中)---------------------------------------------------------历届IMO的主办国,总分冠军及参赛国(地区)数为:年份届次东道主总分冠军参赛国家(地区)数1959 1 罗马尼亚罗马尼亚71960 2 罗马尼亚前捷克斯洛伐克51961 3 匈牙利匈牙利 61962 4 前捷克斯洛伐克匈牙利71963 5 波兰前苏联81964 6 前苏联前苏联91965 7 前东德前苏联81966 8 保加利亚前苏联91967 9 前南斯拉夫前苏联131968 10 前苏联前东德121969 11 罗马尼亚匈牙利141970 12 匈牙利匈牙利141971 13 前捷克斯洛伐克匈牙利151972 14 波兰前苏联141973 15 前苏联前苏联161974 16 前东德前苏联181975 17 保加利亚匈牙利171976 18 澳大利亚前苏联191977 19 南斯拉夫美国211978 20 罗马尼亚罗马尼亚171979 21 美国前苏联231981 22 美国美国271982 23 匈牙利前西德301983 24 法国前西德321984 25 前捷克斯洛伐克前苏联341985 26 芬兰罗马尼亚421986 27 波兰美国、前苏联371987 28 古巴罗马尼亚421988 29 澳大利亚前苏联491989 30 前西德中国501990 31 中国中国541991 32 瑞典前苏联561992 33 俄罗斯中国621993 34 土耳其中国651994 35 中国香港美国691995 36 加拿大中国731996 37 印度罗马尼亚751997 38 阿根廷中国821998 39 中华台北伊朗841999 40 罗马尼亚中国、俄罗斯812000 41 韩国中国822001 42 美国中国832002 43 英国中国842003 44 日本保加利亚822004 45 希腊中国852005 46 墨西哥中国982006 47 斯洛文尼亚中国1042007 48 越南俄罗斯932008 49 西班牙中国1032009 50 德国中国1042010 51 哈萨克斯坦中国1052011 52 荷兰中国101------------------------------------------------------------------历届国际数学奥林匹克中国参赛学生分省市、分学校统计按学校排名(TOP16)1 武汉钢铁三中 152 湖南师大附中 113 华南师范大学附中 104 北大附中 94 人大附中 96 湖北黄冈中学 86 上海中学 88 上海华东师大二附中 5 8 东北育才学校 510 华中师大一附中 410 复旦大学附中 410 深圳中学 410 东北师范大学附中 4 14 上海向明中学 314 长沙市一中 314 哈尔滨师范大学附中 3 以下略。
2004年第3届中国女子数学奥林匹克(CGMO)真题及参考答案_wrapper

解:答案:15 个 首先证明最多可放 15 个“十字形”。用反证法,假设可放 16 个“十字形”。对每个“十 字形”,我们称其中心的方格为“心”(记为*)。将 10×11 的棋盘去掉周围一圈方格, 得到一个 8×9 的方格表,显然,每个“十字形”的“心”都只能出现在这个 8×9 的方 格表中。
E0M 0 F0 N 0
FN EM
. (2)
由(1),(2)得 E0 M 0 F0 N 0 E0 F0 M 0 N 0 (定值).
7
解:答案:如果记
A(
p,
q,
n)
(n 1)(n
第 3 届女子数学奥林匹克试题
第 3 届女子数学奥林匹克于 2004 年 8 月 11 日至 15 日在江西省南昌市举行,共有 45 个代表队的 179 名选手参加了此次竞赛,他们分别来自北京,上海等数十个城市以及美国, 俄罗斯,菲律宾,香港,澳门等国家和地区。竞赛共安排两天考试,每天四个小时,各考四 道题。通过竞赛,有 18 名选手获得金牌,39 名选手获得银牌,58 名选手获得铜牌。
k : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ak : 8 7 6 5 4 3 2 1 16 15 14 13 12 11 10 9 19 18 17
。
2 解:答案:最小值为 12 12 2
x a 2b c
令
y
a
b
2c
,则有
x
y
b,
现在,我们将 8×9 的方格表分为三个 8×3 的方格表,自左至右依次称它们为表(a), 表(b)和表(c)。由于 8×9 的方格表中共有 16 个“心”,所有必有一个 8×3 的方格 表中有 6 个“心” 如果在表(b)中有 6 个“心”,由于 8×3 的方格表中只有两种相互对称的放置 6 个“心” 的办法,故可不妨设 6 个“心”分布如下方左图:
2004年全国小学生奥林匹克竞赛预赛A试题讲解

第6页,共35页。
2004年全国小学生奥林匹克竞赛试题讲解 李彦波 主讲
第7页,共35页。
2004年全国小学生奥林匹克竞赛试题讲解
3、在下面的数之间适当填上+、-、×、÷运算符号 及括号,使算式的结果等于2004。
2222222222 2 2 2 2 - 2 2 2=2000 (2 2 2 2 - 2 2 2)+2+2=2004
李彦波 主讲
第14页,共35页。
⒍ 在12=1、22=4、32=9、42=16、…中,1、4、 9、16、…叫做“完全平方数”。从1到500这500 个整数中,去掉所有的“完全平方数”,剩下 的整数的和是 。
1+2+3+…+500=12750
有12注=1意、到222=242、=4382=4、9、23422==15629 找所到以规要律算+出连1续2+奇22数+32+…+222=? 52=25、62=36、72=49、82=64
第15页,共35页。
⒍ 在12=1、22=4、32=9、42=16、…中,1、4、 9、16、…叫做“完全平方数”。从1到500这500
个整数中,去掉所有的“完全平方数”,剩下的整
数的和是 。
1+2+3+…+500=12750
1+4+9+16+25+36+49+64+81+100
=385
121+144+169+196+225+256+289
第19页,共35页。
2004年全国小学生奥林匹克竞赛试题讲解
2004-2015东南数学奥林匹克试题及解答

参考答案
一 、由柯西不等式 ,有
( a + 2 b + 3 c) 2
≤(
2
1+
2
2+
2
3 )[(
1 a) 2 + (
2 b) 2 + (
3 c) 2 ] = 9 ,
则 a + 2 b + 3 c ≤3.
所以 ,3 - a + 9 - b + 27 - c ≥3 3 3 - ( a + 2 b + 3 c)
列的第 1 , 2 , …, i , n + i - 2 003 , n + i - 2 002 , …, n 行中有“ 3 ”. 当 i ≥2 004 时 , 第 i 列的第 i - 2 003 ,
i - 2 002 、…、i 行中有“ 3 ”. 所以 ,每行有 2 004 个方
格有“ 3 ”,每列也有 2 004 个方格有“ 3 ”. 所以 ,棋盘中“优格”个数的最大值是 n( n - 2 004) . 五 、设 sin θ+ cos θ= x. 则
格中填的数大于有“ 3 ”的方格中的任何一个数 , 所
以 ,棋盘 上 没 有“ 3 ”的 方 格 都 为“行 优 格”, 共 有
n ( n - 2 004) 个.
此时 ,每 行 有 2 004 个 方 格 有“ 3 ”, 每 列 也 有 2 004 个方格有“ 3 ”. 实际上 ,当 1 ≤i ≤2 003 时 ,第 i
①
因为 x ∈[1 , 2 ] ,所以 ,2 x - 3 < 0.
不等式 ①恒成立等价于
x+
2 x
-
a < 0 ( x ∈[1 ,
历年中国参加IMO选手(ZZ)

第26届IMO(1985年,芬兰赫尔辛基)吴思皓(男)上海向明中学确规定铜牌上海交通大学王锋(男)北京大学(根据yongcheng先生提供的信息修订)目前作企业软件第27届IMO(1986年,波兰华沙)李平立(男)天津南开中学金牌北京大学方为民(男)河南实验中学金牌北京大学张浩(男)上海大同中学金牌复旦大学荆秦(女)陕西西安八十五中银牌北京大学,现在美国哈佛大学任教林强(男)湖北黄冈中学铜牌中国科技大学第28届IMO(1987年,古巴哈瓦那)刘雄(男)湖南湘阴中学金牌南开大学滕峻(女)北京大学附中金牌北京大学林强(男)湖北黄冈中学银牌中国科技大学潘于刚(男)上海向明中学银牌北京大学何建勋(男)广东华南师范大学附中铜牌中国科技大学高峡(男)北京大学附中铜牌北京大学,现在北大任教第29届IMO(1988年,澳大利亚堪培拉)团体总分第二陈晞(男)上海复旦大学附中金牌复旦大学,美国密苏里大学,美国哈佛大学,现在加拿大Alberta大学数学系任教授韦国恒(男)湖北武汉武钢三中银牌北京大学查宇涵(男)南京十中银牌北京大学,在中科院数学所任副研究员邹钢(男)江苏镇江中学银牌北京大学王健梅(女)天津南开中学银牌北京大学彭建波(男)湖南师范大学附中金牌北京大学何宏宇(男)以满分成绩获第29届国际数学奥林匹金牌,1993年破格列入美国数学家协会会员,1994年获博士学位,现任亚特兰大乔治大学教授、博士生导师,从事现代数学研究前沿的《李群》《微分几何》等方向的研究,在《李群》的研究上已有重大突破。
第30届IMO(1989年,原德意志联邦共和国布伦瑞克)团体总分第一罗华章(男)重庆水川中学金牌北京大学俞扬(男)吉林东北师范大学附中金牌吉林大学霍晓明(男)江西景德镇景光中学金牌中国科技大学唐若曦(男)四川成都九中银牌中国科技大学颜华菲(女)北京中国人民大学附中银牌北京大学本科,1997年获美国麻省理工博士,现任Texax A&M Uneversity 数学系教授,美国数学会常务理事会成员,Mathematical Reviews评论员。
数学奥林匹克之路——我愿意做的事

2010年第11期49数学奥林匹克之路——我愿意做的事裘宗沪西部数学奥林匹克2000年初。
中国数学奥林匹克协作体刚成立不久,即已显现出强校恒强的趋势。
当时,国家教委制定了全国学科竞赛一等奖的获得者可以推荐保送上大学这一政策,这对东部地区的学校非常有利。
而西部地区的学校由于条件有限,在各大名牌学校的招生中也一直不太受重视。
因此,2001年在香港举行冬令营的时候,西部地区的各省市明显地表现出没有积极性。
其实,我早就意识到了数学奥林匹克活动在全国范围内的成绩强弱悬殊很大,也一直在想办法提高西部地区学校的积极性。
那时候,刚好中央强调要搞西部大开发,我就趁着这个良好的政治上的东风,提出来要举办一个西部地区的数学竞赛,目的是:一方面最大限度地调动西部地区各学校参与数学竞赛的积极性;另一方面希望能够给即将接替我们的年轻同志提供一个锻炼命题的机会。
事实上,西部竞赛确实是一个很好地锻炼新成员们命题、组织、协调等多种能力的良机。
当年,中国数学会普及工作委员会召开常委会会议的时候,我请吴建平同志向到会的同志们征求意见,结果大部分人对我的这个提议都不太理解,而不发表意见,甚至事后还有人说“老裘是疯了”。
我的一个朋友去问国务院西部办公室的意见,结果那里的工作人员非常热情,说只要是西部的活动就都支持。
这一鼓励无疑在众多非议和不理解的环境中e二十二)增强了我的信心。
我的朋友建议我说,西部竞赛要办就要办得有声势,建议在人民大会堂召开新闻发布会云云。
但我认为西部竞赛没有必要这么大张旗鼓地来搞,应该实事求是、踏踏实实地把每项工作做到位。
因此,2001年初,我特地去了一次香港,请梁哲云先生帮忙找一些财政支持。
梁先生找到了经营高级钟表的喜运佳公司总裁李福生先生,李先生本来就在内地有很多赞助的项目,听完我的介绍之后欣然同意赞助西部竞赛(赞助5万元港币)。
为了提高西部地区的学生参加数学竞赛的兴趣,我建议给每名参赛选手都颁发一个小型的电子产品,价值大概在400~500港元之间,李先生就用赞助的款项来采购这部分纪念品。
六年级成绩

黄居伟
西营门外
85
李玮
鞍山道
85
刘正阳
鞍山道
85
陈旭
昆鹏
85
韩宇华
中营
85
隋清宇
万全道
85
韩恺璠
实验
85
王睿
实验
85
张弋舟
南大附小
85
任炜烨
育婴里
80
刘璟彤
昆一
80
殷仲墨
邵公庄
80
宁一
鞍山道
80
王源
鞍山道
80
吕阳
万全道
80
李亚男
万全道
80
殷川
万全道
80
陈思文
天大附小
80
高悦
南开中心
80
陈乃馨
实验
55
赵凯强
上海道
55
张昭悦
上海道
55
刘天任
南大附小
55
三等奖
40分以上,共210人
王达
育婴里
50
张瑞桐
靶革当村
50
周瑞嘉
靶革当村
50
杨帅
靶革当村
50
刘俊
靶革当村
50
曹燕
春华
50
田彬
博安
50
高冉
铁一小
50
田霖
育婴里
50
袁野
友爱道
50
果辰
昆一
50
程超
中心东道
50
王鑫
盘山道
50
刘嘉轩
河东实验
50
凌翔
河东实验
40
吕鑫
求真
40
历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO

历年中国参加国际数学奥林匹克竞赛选手详细去向第26届IMO(1985年,芬兰赫尔辛基)吴思皓(男)上海向明中学确规定铜牌上海交通大学王锋(男)北京大学(根据yongcheng先生提供的信息修订)目前作企业软件第27届IMO(1986年,波兰华沙)李平立(男)天津南开中学金牌北京大学方为民(男)河南实验中学金牌北京大学张浩(男)上海大同中学金牌复旦大学荆秦(女)陕西西安八十五中银牌北京大学,现在美国哈佛大学任教林强(男)湖北黄冈中学铜牌中国科技大学第28届IMO(1987年,古巴哈瓦那)刘雄(男)湖南湘阴中学金牌南开大学滕峻(女)北京大学附中金牌北京大学林强(男)湖北黄冈中学银牌中国科技大学潘于刚(男)上海向明中学银牌北京大学何建勋(男)广东华南师范大学附中铜牌中国科技大学高峡(男)北京大学附中铜牌北京大学,现在北大任教第29届IMO(1988年,澳大利亚堪培拉)团体总分第二陈晞(男)上海复旦大学附中金牌复旦大学,美国密苏里大学,美国哈佛大学,现在加拿大Alberta大学数学系任教授韦国恒(男)湖北武汉武钢三中银牌北京大学查宇涵(男)南京十中银牌北京大学,在中科院数学所任副研究员邹钢(男)江苏镇江中学银牌北京大学王健梅(女)天津南开中学银牌北京大学何宏宇(男)以满分成绩获第29届国际数学奥林匹金牌,1993年破格列入美国数学家协会会员,1994年获博士学位,现任亚特兰大乔治大学教授、博士生导师,从事现代数学研究前沿的《李群》《微分几何》等方向的研究,在《李群》的研究上已有重大突破。
第30届IMO(1989年,原德意志联邦共和国布伦瑞克)团体总分第一罗华章(男)重庆水川中学金牌北京大学俞扬(男)吉林东北师范大学附中金牌吉林大学霍晓明(男)江西景德镇景光中学金牌中国科技大学唐若曦(男)四川成都九中银牌中国科技大学颜华菲(女)北京中国人民大学附中银牌北京大学本科,1997年获美国麻省理工博士,现任Texax A&M Uneversity 数学系教授,美国数学会常务理事会成员,Mathematical Reviews评论员。
2004年全国小学数学奥林匹克竞赛成绩统计---五年级

2004年全国小学数学奥林匹克竞赛成绩统计---五年级2004年全国小学数学奥林匹克竞赛成绩统计----五年级市区塘沽大港静海最低分数获奖人数最低分数获奖人数获奖人数获奖人数一等奖54 56 50 0 5 4二等奖40 89 34 10 9 11三等奖27 135 24 11 20 302004年小奥赛决赛五年级获奖名单及成绩(市区)一等奖54分以上,共56人姓名学校成绩刘中洋实验110李凌涛育婴里107诸葛婧一卧龙里107 李金阳和平中心107 吕阳万全道90侯晓曼昆鹏87赵晟育婴里83肖阳中心东道82徐澍育婴里80冯晴枫西营门外80 常乐实验80王牧模范80张浩天万全道77白钰实验77刘正阳鞍山道74李亚男万全道74韩宇华中营74果辰昆一70米巨峰文昌宫70徐晓万全道70李晓凡实验70范斯腾河东实验69 李鑫二十中附小67 赵天辰上海道67李舜实验67薛伊冰南大附小67 纪昂盘山道64余明鞍山道64安禹丞五马路64李鑫悦中心东道64 金晓求真64黄凯六纬路60程鹏昆一60孙思颖河东实验60李天玉河东实验60田文君鞍山道60于浩成中营60樊征征万全道60郑君倜万全道60赵旭万全道60吴楚申新华南路60李瑞琦万全道60李竞帅模范60王博文实验60宋博锴南大附小60翟宏堃洪湖里59缴万鑫河北实验57吕若辰实验57陈凯翔六一57王睿实验55王中冠桃花园54王雅娟鞍山道54吴双美和平中心54刘晓萌和平中心54郑轶河西中心54焦干轩南大附小54二等奖40分以上89人杨天予河北实验50徐越清源道50盛彧求真50刘畅求真50 李一丁新村小学50 陈圣六一50 杜裘伟长沙路50 王源鞍山道50 许诺鞍山道50 吕晟尧鞍山道50 徐文锐鞍山道50 王欣然万全道50 夏兴晖昆实50 王卓鞍山道50 郭奇岳阳道50 姜文睿华夏50 刘凯达实验50 贺坤南大附小50 黑喆六一49 杨梦育婴里47 王也五马路47 李珩中营47 张安琪岳阳道47 魏程鸣河西中心47 邸以文求真47 郭自轩靶革当村45 姜晨日求真45 刘晓伟六一45 梁宵练鞍山道45 苏孟鑫盘山道44 龙子昂六一44 王艺陶岳阳道44 齐天杰万全道44滕长久和平中心44隋清蕊四平东道44李想二师附小44孙宏六一44韩亚鑫新村小学43邵壮鞍山道43李鹏盘山道42俞宝智南大附小42孙元君育婴里40任梦育婴里40孟昭男靶革当村40朱双林铁一小40齐超铁一小40王洲河北实验40左罗钜缘诚40李炜恒中心东道40李宗鹏中心东道40迟昭河东实验40才胤松河东实验40赵磊福泉里40陈子昂正华40尹伟超南开小学40吕志超鞍山道40韩瑀昆鹏40任好昆鹏40吴浩宇昆鹏40陈博雅昆鹏40高嘉月三水道40 刘敬昊岳阳道40 牛津达万全道40 于超凡万全道40 于瑞琪天大附小40 李冠儒天大附小40 任成实验40凌菲彤北辰实验40 刘辰北辰实验40 郭嵩北辰实验40 姚远南开实验40 邢琮师大二附小40 刘兆丰实验40郭鸿宇闽侯路40 于博洋实验40李增辉闽侯路40 杨轶男实验40牟岸至师大附小40 朱慧鑫新华南路40 石盛楠育婴里40 陈筱河东务实40 郑慧求真40王权枫林路40樊峻石上海道40 李果南大附小40 李亦佳实验40张根实实验40尹嘉晟六一40祁皓男六一40三等奖27分以上,135人王一宁昆一39 刘畅闽侯路39 张伦榤模范39 季雨晨南大附小39 白昱铁一小37 张宇杰求真37 郎垚璞求真37 马鸿坤新村小学37 朱梦雅六一37 高胤中营37 刘晓源岳阳道37 国鑫万全道37 李明雪万全道37 白金晨和平中心37 刘培迪天大附小37 赵敏北辰实验37 黎宵宇闽侯路37 赵博远实验37 刘超逸二师附小35 仇戊强红桥小学35 杨宏生红桥小学35 戴瑞豪咸阳北路35 郝明茗中营35 郄意五马路35 韩笑逸阳35 张鸿宇铁一小34刘明远友爱道34李宸昆一34孙卓昆一34王奕均河东实验34陈理仁互助道34魏书圆河东实验34李思思红桥一号路34李洋万全道34门跃求真34张红太昆鹏34陈天一岳阳道34柴德天北辰实验34武泽台湾路34张晓涵风湖里34董禹鞍山道34杨正乐安里33张淼北仓小学33张麒益寿里30张洋益寿里30胡海涛育婴里30郭金诚育婴里30刘云鹏靶革当村30 刘震鹏铁一小30唐雯昆一30王慎语昆一30从双晨缘诚30杨学森缘诚30黎静北河东一中心30 盛煜辰河东一中心30 张航河东一中心30 何嘉宁中心东道30 刘思婷香山道30郑媛香山道30李静雅河东实验30 马良互助道30王晓明互助道30马志达互助道30王磊文昌宫30侯玥跃进里30马颖婕西站小学30 刘雨晴西站小学30 李漪涟正华30郑思远红星30闫玮红星30张绍琛求真30张正求真30郝苓淇求真30夏岩红桥实验30张月佳园里30赵晓璐咸阳北路30温馨六一30陈睿跃升里30田楚杰鞍山道30芦钰鞍山道30于梦薇鞍山道30胡钧瀚鞍山道30温元正鞍山道30周明华鞍山道30 邢琨昆鹏30 孙宇昆鹏30 周翰驰昆鹏30 刘晓瑶三水道30 陈天用昆明路30 姚政新华南路30 霍睿智六一30 杨艺万全道30 吕松臻六一30 兰嘉仪万全道30 王子彧和平中心30 姜文凯和平中心30 张津和平中心30 闫安和平中心30 刘梦妍和平中心30 于涛求真30 陈旭天大附小30 杜文雄实验30 王金城师大附小30 王梦雪北辰实验30 杨归一实验30 李晓常州道30 刘云恒昆鹏30 花城和平中心30 娄雅卉闽侯路30 张志千闽侯路30 黄逸凡台湾路30 马宏深上海道30孙靓实验30魏爱琳南大附小30汤骏杰南大附小30张鹏祥南大附小30张学伟南大附小30朱世博南大附小30张云龙昆实29袁翰求真29王峰求真29王浩宇模范29张宇二十中附小28王晖育婴里27王达昆一27薛媛河东实验27叶亦欣求真27刘浩天新村小学27黄家盛鞍山道27蔺吉军鞍山道27李思竹岳阳道27任轶岳阳道27赵瑞和平中心27马一翔逸阳27翟津铭实验272004年小学数学奥林匹克竞赛五年级大港区获奖名单及成绩一等奖(50以上,5人)姓名学校成绩王振宇大港一小70赵宸宇大港石化一小60许昕大港一小50赵玉瑾大港一小50缪则皓大港石化一小50二等奖34分以上9人陈婉莹大安47冯欣鑫大港一小47广浩宇第二小学44王宏达第二小学44王雪雯大港一小44梁元大港一小40于阔淼大港四小34蔺可大港三小34王一杰第二小学34三等奖24分以上20人张晓彤大港三小30袁文则大港三小30刘谨源第二小学30冯书桓第二小学30王晓瑜第二小学30张衷景大港一小30李雨翀大港一小30洪丹婷大港一小30魏书道大港一小30张丁允大港一小30张孟宇大港一小30孙璐大港一小30王逊大港石化一小30于玮嘉大港石化一小30于晗大港石化一小27王承啸大港实验25倪楚星大港实验25胡婷四公司一小24马宝良大港五小学24王斯羽大港一小242004年小奥赛静海获奖名单及成绩一等奖(50以上,4人)姓名学校成绩叶林大邱庄津海小学60李莹团泊镇54 李金桐实验小学50 李祖昌静海镇四小50二等奖34分以上11人刘媛陈官屯镇小集小学47王燃团泊镇47王超瀛海学校40贾晨实验小学40岳迪王口镇40刘广森子牙镇40王维璞大邱庄津海小学40 宋英林大邱庄津海小学40 郝艺岚实验小学35刘丽大邱庄津海小学35 刘如泽团泊镇34三等奖24分以上30人张启文沿庄镇30田祎伟六四六学校30张彤瀛海学校30张克璞瀛海学校30信浩然中旺镇30陈金铭中旺镇30丁鸿飞实验小学30刘云鹏实验小学30王睿实验小学30袁守山蔡公庄土河小学30 周德祥蔡公庄镇30刘洋王口镇30尚琪静海镇四小30陈绍军静海镇四小30李悦静海镇五小30张威大邱庄万全小学30郑秋臣大邱庄津海小学30田洁大邱庄津海小学30王竞颜大邱庄尧舜实验30袁红超陈官屯镇小集小学25张兴鹏刘上道25孙中涵实验小学25史凤强蔡公庄惠丰小学25刘靓静海镇孙家场25曲畅大邱庄尧舜实验25高翠团泊镇24曹月静海镇三小24汤玉笑静海镇四小24尚义嘉大邱庄尧舜实验24五年级塘沽考点成绩汇总二等奖(34分以上,10人)姓名学校成绩王晓晨实验44焦正辰浙江路小学44张博令上海道44李君妍实验40杨剑宇实验40刘昊宇浙江路小学40刘建宇浙江路小学40林汝慧上海道40张劭泰达一小40舒畅泰达一小40三等奖(24分以上,11人)周志浩实验30杜婕飞实验30吕淑琪实验30贺非实验30张乔浙江路小学30 蒋东吴上海道30 孙思齐二中心30 吕宏宁桂林路30 李响浙江路小学27 赵大地泰达一小27 王点泰达一小25。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6 . 给定锐角 △ABC ,点 O 为其外心 ,直线 AO 交
边 BC 于点 D . 动点 E 、 F 分别位于边 AB 、 AC 上 , 使 得 A、 E、 D、 F 四点共圆 . 求证 : 线段 EF 在边 BC 上 (熊 的投影的长度为定值 . 供题) 斌
7 . 已知 p 、 q 为互质的正整数 , n 为非负整数 .
= 45° , 作射线 OE , 使
( k + 1) ( k + 2) k ( k + 1) + 2 2
2 = ( k + 1) , k = 1 ,2 , …,1 002.
特别地 ,所求的 “好牌组” 的个数为
a2 004 = 1 003 = 1 006 009.
2
解法 2 :对于 n ∈ {1 ,2 , …,2 004} ,用 an 表示分值
1. 试求 u + v + w 的最小值 . uv≥ ( 陈永高 供题)
2. - 17 + 12 2 .
令 x = a + 2 b + c , y = a + b + 2c , z = a + b +
3 c ,则有 x - y = b - c , z - y = c . 由此可得
a + 3 c = 2 y - x , b = z + x - 2 y , c = z - y. a + 3c 4b 8c + a + 2b + c a + b + 2c a + b + 3c
2004 年第 6 期
b = (1 + 2) a , c = (4 + 3 2) a .
35
每张牌的分值都除以 2 , 就得到 “三王问题” 中的一 个分值之和为 k 的且允许包括有王牌的牌组 . 易见 , 这种对应是一一的 ,所以 ,这种牌组的个数为 uk .
(2) 若组内有王牌 , 则组内必有 2 张王牌 ( 大小
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
36
中 等 数 学
{ ip + ( n - i) q| i = n - p +1 , n - p + 2 , …, n} , n ≥p ; { ip + ( n - i) q| i = 0 ,1 , …, n} , n < p. 令 an = | A ( p , q , n) | ,有 =
的最小值 .
( 李胜宏 供题)
3 . 已知钝角 △ABC 的外接圆半径为 1. 证明 : 存
在一 个 斜 边 长 为 2 + 1 的 等 腰 直 角 三 角 形 覆 盖 ( 冷岗松 △ABC. 供题)
4 . 一副三色纸牌 , 共有 32 张 , 其中红黄蓝每种
(4) 17 是 “好 数” , 因 为 如 下 的 排 列 中 , k + ak ( k = 1 ,2 , …,17) 都是完全平方数 :
x + y + z = n.
(1 + 2 x + 3 x2 + …+ (2 k + 1) x2 k + … ) ,
故知 x 的系数为
2 a2 k = 1 + 3 + 5 + …+ ( 2 k + 1) = ( k + 1) , k = 1 ,2 , ….
2k
从而 ,所求的 “好牌组” 的个数为
a2 004 = 1 003 = 1 006 009.
4 5 6 7 8 9 10 11 12 13 5 4 3
ak : 8 2 13 12 11 10 9 1 7 6
(3) 15 是 “好 数” , 因 为 如 下 的 排 列 中 , k + ak ( k = 1 ,2 , …,15) 都是完全平方数 :
k : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ak : 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
亦即
a + b + 2 c = 2 ( a + 2 b + c) , a + b + 3 c = 2 ( a + 2 b + c) .
解此不定方程 ,得到
© 1994-2007 China Academic Journal Electronic Publishing House. All rights reserved.
2 2
现考虑原题中的 “两王问题” . 对于 n ∈{1 ,2 , …,2 004} ,用 an 表示分值之和为 n 的牌组的个数 . 当 n =2k ≤ 2 004 时 , 对于分值之和为 2 k 的任 一牌组 ,有 : (1) 若组内无王牌 ,则该牌组就是 “三王问题” 中 的一个分值之和为 2 k 的无王牌的牌组 . 如果将其中
un = C n + 2 =
2 2
2
+v
2
+w
2 1, uv ≥
≥u
vw + v
wu + w
( n + 1) ( n + 2) . 2
①
即 u v + vw + wu ≥ 1. 故 ( u + v + w) 2 = u2 + v2 + w2 + 2 uv + 2 vw + 2 wu
=
u +v
所以 ,所求的最小值为 - 17 + 12 2.
3 . 不妨设 ∠C > 90° ,于是 ,min{ ∠A , ∠B } < 45° .
不妨设 ∠A < 45° . 如图 1 , 以 AB 为 直径 , 在顶点 C 的同 侧 作 半 圆 ⊙O , 则 C 位于 半 圆 ⊙O 内 . 作 射线 AT 使 得 ∠BAT
an - a n - 1 = p, n+1, n ≥p ; n< p
综上所述 ,知 u + v + w 的最小值为 3.
6 . 如图 2 , 设 EF 在边 BC 上的投影为 E0 F0 ,过点 D 分别作
DM ⊥AB 于 M , DN ⊥ AC 于 N , 过点 M 、 N
注意到 a0 = 1 ,故对 n < p ,有
2
+
v +w
2
2
1
+
w + u
2
2
2
+ 2 uv + 2 vw + 2 wu
≥ 3 uv + 3 vw + 3 wu ≥ 3. 因此 , u + v + w ≥ 3. 另一方面 , u = v = w = 时 u + v + w = 3.
3 显然满足题中条件 ,此 3
易算出 ,对任何正实数 a , 只要 b = ( 1 + 2 ) a ,
c = (4 + 3 2 ) a ,就都有式 ① 中的等号成立 .
王牌都在组内) . 去掉王牌后 , 就化归为分值之和为
2 k - 2 的无王牌的牌组 . 从而 , 这种牌组的个数为
uk - 1 . 所以 , a2 k = uk + uk - 1 =
≥- 17 + 2 8 + 2
32 = - 17 + 12 2.
①
上式中的等号可以成立 . 事实上 ,由上述推导过程知 ,等号成立当且仅当 平均不等式中的等号成立 ,而这等价于
2
2 2 y =2x , y = 2x , 即 2 即 2 z y z =2y , z =2x , 4 =8 ,
个单位正方形所得到的图形称为 “十字形” . 在一个
5. 设 u 、 v、 w 为正实数 , 满足条件 u
v wu + w vw +
其中用到了轮换 (1 ,3 ,6 ,10 ,15) . (5) 19 是 “好 数” , 因 为 如 下 的 排 列 中 , k + ak
( k = 1 ,2 , …,19) 都是完全平方数 :
k : 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 ak : 8 7 6 5 4 3 2 1 16 15 14 13 12 11 10 9 19 18 17
0 2
1 2
3
1+ x
2 2
3
… 1 + x2
10
3
的展开式中 x 的系数 ( 约定| x | < 1) . 由于 f ( x) =
1 1+ x 1+ x 1+ x
3 1 2
1+ x
2 2
… 1 + x2
10
3
1 1 AB + 2 ・ AB 2 2
=
11 1 2 1- x (1 + x) (1 - x) 3
2
5.
3.
v+ w w+ u u+ v
由均值不等式和题中条件 ,知
u
由于任一非负整数的二进制表示方法惟一 , 所 以 ,一旦 x 、 y、 z 的值确定之后 , 红组 、 黄组 、 蓝组的 构成情况便惟一确定 . 而方程 x + y + z = n 的非负 整数解的组数等于 C n + 2 ,所以 ,
=
11 1 2 1- x (1 - x2 ) 1 - x) 2
