运输优化模型参考
运输线路优化---图上作业法

第2步 检查有无迂回现象。因为流向箭头都统一画 在线路右边,所以圈内圈外都画有一些流向。分别检 查每个小圈,如果内圈和外圈流向的总长度都不超过 全圈总长度的1/2,那么,全圈就没有迂回现象,这 个线路流向图就是最优的,对应的方案就是最优运输 方案。否则,转向第三步。
第3步 重新去段破圈,调整流向。在超过全圈总长 1/2的里(外)圈各段流向线上减去最小运量,然后在 相反方向的外(里)圈流向线上和原来没有流向线的 各段上,加上所减去的最小运量,这样可以得到一个 新的线路流向图,然后转到第二步检查有无迂回现象。 如此反复,直至得到最优线路流向图为止。
外圈流向总长=(25+18+23)km=66km
里圈流向总长=(23+36)km=59km
两者均没有超过全圈总的1/2,即85km,所以 调整后的新线路流向图所对应的方案为最优运 输方案。
之所以说调整后的新线路流向图所对应的方案为最优
运输方案,可以将它与初始运输方案进行对比:
按调整后的新方案组织运输,运力消耗为 (20×36+10×23+20×13+30×23+30×25+ 40×18+80×29+20×127)t·km
=8230t·km 按初始方案组织运输的运力消耗为 (20×45+10×23+50×25+80×29+20×127+20× 13+30×23+60×18)t·km =9270t·km
● 技能训练
任务实施 寻求最优运输方案
图3-2成圈的运输线路
做
图3-2是一个单位的运输 线路图。图中,①、 ③、 ⑥、 ⑧是产地, ②、 ④ 、 ⑤、⑦是销地。起运站 (目的地)之间线路旁括 号内标注的数字表示两点 之间的距离。如何找到最 优运输方案?
SCOR模型

SCOR模型供应链运作参考模型(Supply-Chain Operations Reference model,简称SCOR模型)目录[隐藏]• 1 什么是SCOR模型?• 2 SCOR的涵盖范围• 3 SCOR模型结构o 3.1 计划o 3.2 采购o 3.3 生产o 3.4 配送o 3.5 退货• 4 SCOR模型的三个层次o 4.1 第一层:绩效衡量指标o 4.2 第二层:配置层o 4.3 第三层:流程元素层• 5 SCOR的实施及收益• 6 SCOR的运用意义•7 SCOR模型用途[1]•8 SCOR模型案例分析o8.1 案例一:基于SCOR的汽车制造企业供应链运作模型的构建[2]o8.2 案例二:基于SCOR模型对绿色采购管理研究[3]o8.3 案例二:宝钢出厂物流的SCOR模型分析[4]•9 参考文献[编辑]什么是SCOR模型?SCOR (Supply-Chain Operations Reference-model) 是由国际供应链协会(Supply-Chain Council) 开发支持,适合于不同工业领域的供应链运作参考模型。
1996年春,两个位于美国波士顿的咨询公司——Pittiglio Rabin Todd & McGrath (PRTM) 和AMR Research (AMR) 为了帮助企业更好地实施有效的供应链,实现从基于职能管理到基于流程管理的转变,牵头成立了供应链协会(SCC) ,并于当年底发布了供应链运作参考模型(SCOR)。
SCOR是第一个标准的供应链流程参考模型,是供应链的诊断工具,它涵盖了所有行业。
SCOR使企业间能够准确地交流供应链问题,客观地评测其性能,确定性能改进的目标,并影响今后供应链管理软件的开发。
流程参考模型通常包括一整套流程定义、测量指标和比较基准,以帮助企业开发流程改进的策略。
SCOR不是第一个流程参考模型,但却是第一个标准的供应链参考模型。
第三方物流运输路径优化研究-以安吉汽车物流为例

第三方物流运输路径优化研究-以安吉汽车物流为例摘要第三方物流在汽车物流领域的迅猛发展,被誉为“未开发的经济领域”,是继原材料节约和劳动生产率提高后,公司的第三大盈利来源。
物流配送网络是一个由各个环节和运输路线组成的一个整体,其终极目标是满足终端客户,实现全供应链的价值。
物流配送网络的合理与否,将直接关系到整个物流体系的运行效率和成本,进而影响到企业的长期发展。
【关键词】第三方物流;优化方案;仓储作业1研究背景及意义当前经济发展迅速,商品流通的规模在逐渐扩大,在国内汽车行业的关税壁垒逐渐消除、汽车行业正在寻求新的途经来提高竞争力的大背景之下,现代物流作业规范、服务功能完善,具有便捷快速的优势,以及其一体化作业的流程使其可以较好地迎合时代的需要,作为第三利润源成为行业关注的热点,并迅速成长为我国国民经济中心的经济增长点,在经济全球化的大环境之中起着越来越重要的作用。
当下,在华投资的世界500强企业中有约90%的企业都选择了物流外包,足以说明第三方物流企业起到了极其重要的作用,随着经济发展的需要,汽车消费市场对整个汽车行业提出了新的要求,主要包括在不影响总体质量的前提之下,力求低价、更新周期缩短等,各生产厂商同样面临着降低成本、抢占行业地位的巨大压力,加之汽车制造厂也随着行业需求的提高而普遍开展订单式、JIT式等生产方式,这些都对汽车整车和零部件物流提出了更高的要求。
21世纪,作为新兴行业之一的现代物流业迅速发展,我国的物流业迅速崛起,并在此基础上形成了一种第三方物流企业。
与传统的物流公司相比,第三方物流具有更高的专业化、更低的综合成本和更高的配送效率,是当今世界物流业发展的必然趋势,也是社会化分工的必然趋势。
因此,从现代物流的视角,结合汽车产业的特性,对汽车的整车和零部件的运输进行研究,将会对汽车企业产生很大的影响。
物流运输管理优化通常源于物流配送系统,物流配送系统中又包含着方方面面,在以往的文献中不难发现对其中某个点的分析,比如信息平台、运输路径等,但是针对某一具休公司,对其进行一方面的优化却是少见,论文的研究摆脱了以往单方面研究的桎梏,进一步开拓了应用型的研究途径,从而为物流运输优化的理论学习做出贡献。
运输模型法的讲解

运输模型法的讲解
运输模型是一种数学模型,用于解决运输问题。
它的基本假设是,有若干个原产地和若干个目的地,原产地和目的地之间的运输需求和运输成本已知。
运输模型的目标是确定最佳的运输方案,即如何分配货物从原产地到目的地,以最小化总运输成本或最大化总运输利润。
运输模型的主要特点是基于线性规划方法进行求解,同时考虑了供需平衡和运输成本的影响。
在运输模型中,需要确定的主要变量有原产地到目的地的货物数量、货物的运输路径,以及每条运输路径上的运输成本。
同时,还需要满足原产地和目的地的供求平衡条件,即原产地的总供应量等于目的地的总需求量。
运输模型的求解过程通常包括如下步骤:
1. 建立数学模型:根据实际问题,确定运输路径、运输成本和供求平衡条件等参数,并将其用数学表达式表示为一个线性规划问题。
2. 求解线性规划问题:利用线性规划方法,求得最优解,即最小化总运输成本或最大化总运输利润。
3. 解释和应用结果:根据最优解,确定货物的最佳分配方案,并分析结果的可行性和经济效益。
运输模型通常有多种求解方法,包括西北角法、最小成本法、沃格尔法等。
这些方法都是通过不断迭代求解基本运输单元(通常是原产地和目的地),并更新运输路径和货物分配量来求解整个运输模型的最优解。
通过运输模型的求解,可以帮助企业和组织做出有效的运输决策,降低运输成本,提高货物的运输效率,优化供应链管理,并对相关的决策和政策制定提供支持和参考。
物流运输网络优化方案

物流运输网络优化方案第1章引言 (4)1.1 背景与意义 (4)1.2 目标与范围 (4)1.3 方法与步骤 (4)第2章物流运输网络现状分析 (4)2.1 我国物流运输网络发展概况 (4)2.2 现有物流运输网络存在的问题 (5)2.3 现状分析总结 (5)第3章物流运输网络优化理论 (6)3.1 物流运输网络优化概念 (6)3.2 物流运输网络优化方法 (6)3.2.1 网络设计方法 (6)3.2.2 网络改进方法 (6)3.2.3 网络优化算法 (6)3.3 物流运输网络优化模型 (6)3.3.1 线性规划模型 (6)3.3.2 整数规划模型 (6)3.3.3 非线性规划模型 (7)3.3.4 多目标优化模型 (7)3.3.5 随机规划模型 (7)第4章物流运输网络结构设计 (7)4.1 网络节点选址策略 (7)4.1.1 选址因素分析 (7)4.1.2 选址模型构建 (7)4.1.3 选址算法与求解 (7)4.2 网络线路规划方法 (7)4.2.1 线路规划目标 (7)4.2.2 线路规划模型 (8)4.2.3 线路规划算法 (8)4.3 物流运输网络结构优化 (8)4.3.1 结构优化目标 (8)4.3.2 结构优化方法 (8)4.3.3 结构优化策略 (8)第5章运输方式选择与优化 (8)5.1 常见运输方式分析 (8)5.1.1 公路运输 (8)5.1.2 铁路运输 (9)5.1.3 水路运输 (9)5.1.4 航空运输 (9)5.1.5 管道运输 (9)5.2 运输方式选择策略 (9)5.2.2 综合运输成本分析 (9)5.2.3 运输时效性要求 (9)5.2.4 运输距离与范围 (9)5.3 运输方式优化方法 (9)5.3.1 多式联运 (9)5.3.2 网络优化 (10)5.3.3 运输工具优化 (10)5.3.4 货物集散优化 (10)5.3.5 信息化管理 (10)第6章物流运输成本控制 (10)6.1 物流运输成本构成与影响因素 (10)6.1.1 运输成本 (10)6.1.2 仓储成本 (10)6.1.3 配送成本 (11)6.1.4 管理成本 (11)6.1.5 辅助成本 (11)6.2 成本控制策略 (11)6.2.1 运输成本控制策略 (11)6.2.2 仓储成本控制策略 (11)6.2.3 配送成本控制策略 (11)6.2.4 管理成本控制策略 (12)6.2.5 辅助成本控制策略 (12)6.3 成本优化方法 (12)6.3.1 运输成本优化方法 (12)6.3.2 仓储成本优化方法 (12)6.3.3 配送成本优化方法 (12)6.3.4 管理成本优化方法 (12)6.3.5 辅助成本优化方法 (12)第7章物流运输网络风险管理 (12)7.1 风险识别与评估 (12)7.1.1 自然灾害风险 (12)7.1.2 运输工具风险 (13)7.1.3 法律法规风险 (13)7.1.4 市场风险 (13)7.1.5 供应链风险 (13)7.2 风险防范与应对策略 (13)7.2.1 建立风险预警机制 (13)7.2.2 多元化运输渠道 (13)7.2.3 加强供应链协同 (13)7.2.4 优化运输路径 (13)7.2.5 增强法律法规意识 (13)7.3 风险管理优化 (13)7.3.1 建立健全风险管理组织 (14)7.3.3 加强风险培训与教育 (14)7.3.4 建立应急预案 (14)7.3.5 持续改进与优化 (14)第8章物流运输网络信息化建设 (14)8.1 信息化建设概述 (14)8.2 信息系统设计与实施 (14)8.2.1 设计原则 (14)8.2.2 设计内容 (14)8.2.3 实施步骤 (15)8.3 信息化管理与优化 (15)8.3.1 信息化管理 (15)8.3.2 优化措施 (15)第9章物流运输网络绩效评价 (15)9.1 绩效评价指标体系 (15)9.1.1 运输效率指标 (15)9.1.2 成本控制指标 (16)9.1.3 服务质量指标 (16)9.1.4 网络结构指标 (16)9.2 绩效评价方法 (16)9.2.1 指标权重设置 (16)9.2.2 数据处理与分析 (16)9.2.3 绩效评价模型 (16)9.3 绩效优化策略 (16)9.3.1 提高运输效率 (16)9.3.2 降低运输成本 (17)9.3.3 提升服务质量 (17)9.3.4 优化网络结构 (17)第10章物流运输网络优化方案实施与展望 (17)10.1 优化方案实施步骤与措施 (17)10.1.1 实施步骤 (17)10.1.2 实施措施 (17)10.2 优化方案预期效果分析 (18)10.2.1 成本降低 (18)10.2.2 效率提升 (18)10.2.3 服务质量改善 (18)10.3 未来发展趋势与展望 (18)10.3.1 智能化发展 (18)10.3.2 环保与绿色 (18)10.3.3 跨界融合 (18)10.3.4 国际化发展 (18)第1章引言1.1 背景与意义我国经济的快速发展和物流行业的不断壮大,物流运输网络作为物流体系的重要组成部分,其优化与调整已成为提高物流效率、降低物流成本的关键环节。
运输优化的方法-解释说明

运输优化的方法-概述说明以及解释1.引言1.1 概述概述运输是现代社会经济发展中不可或缺的环节之一,它涉及到各个行业和领域的物流运营和货物流转。
目前,随着市场竞争的加剧和全球化的发展,企业对运输效率和成本控制的需求也越来越高。
然而,传统的运输方法往往存在一些问题和挑战,例如路线规划不合理、运输量不均衡、成本过高等。
针对这些问题,运输优化成为了迫切需要解决的难题。
运输优化是通过科学的方法和技术手段,对现有的运输系统和运营流程进行分析和改进,以达到提高运输效率、降低运输成本、优化资源利用的目的。
它涉及到多个方面的因素,包括路线规划、货物配载、运输模式选择等。
本文将从传统运输方法的问题入手,探讨运输优化的重要性和基本原理。
同时,将介绍一些常用的运输优化方法,并通过案例分析来验证这些方法的有效性和可行性。
最后,对运输优化的未来发展进行展望,并对本文的结论进行总结。
通过本文的阐述,读者将能够深入理解运输优化的概念和意义,了解其基本原理和常用方法,并能够应用这些知识和技术来解决实际运输问题,提高运输效率和降低成本。
同时,本文也将启发读者对运输优化未来的发展趋势进行思考,以打造更加智能、高效的运输系统。
1.2 文章结构文章结构部分的内容可以包括以下信息:文章结构部分旨在介绍本篇长文的整体结构和组成部分,以帮助读者更好地理解文章的内容和逻辑。
本文主要分为四个部分:引言、正文、案例分析和结论。
引言部分(章节1)是文章的开头部分,它首先会给读者一个概述,简要介绍本文将要讨论的主题——运输优化的方法。
接着,引言部分会介绍文章的结构,并列出各个章节的主要内容。
最后,引言部分会提出文章的目的,即本文希望通过对运输优化的方法进行探讨,提供有关运输优化的实用方法和策略。
正文部分(章节2)是本文的核心部分,它详细介绍了传统运输方法、运输优化的重要性、运输优化的基本原理以及常用的运输优化方法等内容。
首先,正文部分会回顾传统运输方法,并分析其存在的问题和局限性。
数学建模:第五章 运筹与优化模型

1
例1、某工厂制造A.B两种产品,制造A每吨 需用煤9t,电力4kw,3个工作日;制造B每吨需 用煤5t,电力5kw,10个工作日。已知制造产品A 和B每吨分别获利7000元和12000元,现工厂只有 煤360t,电力200kw,工作日300个可以利用,问 A、B两种产品各应生产多少吨才能获利最大? 解:设 x1 x 2 ,(单位为吨)分别表示A、B产 品的计划生产数; f表示利润(单位千元) 则问题归结为如下线性规划问题:
a21 x1 a22 x2 a2 n xn (, )b2
am1 x1 am 2 x2 amn xn (, )bm
x1 , x2 ,, xn 0
7
例3:生产组织与计划问题 设有m种资源,第i(i=1,2…,m)种资源的现存量 为 bi ,现要生产n种产品,已知生产j(j=1,2…,n)种 产品时,每单位产品需要第i种资源量为 a ij ,而每 单位j种产品可得利润 c j ,问如何组织生产才能使 利润最大? 解:用 x j 表示生产第j(j=1,2,…,n)种产品 的计划数, 上述问题可归结为如下的数学问题:
z 14.3750
即 第1年项目A,D分别投资3.8268和6.1732(万元);
第2年项目A,C分别投资3.5436和3(万元);
第3年项目A,B分别投资0.4008和4(万元); 第4年项目A投资4.0752(万元); 第5年项目D投资0.4609(万元); 5年后总资金 14。375万元,即盈利43.75%.
x 模型建立 设该容器底边长和高分别为 x1米、 2米, 则问题的数学模型为
min f ( X ) 40 x1 x2 20 x1 (容器的费用)
2
x12 x 2 12, (容器体积) 2 s.t . 12 x1 x 2 2 x1 68, (容器重量) x 0, x 0. 2 1
冷链物流系统优化模型的建立与求解

冷链物流系统优化模型的建立与求解摘要:冷链物流是一种专门用于运输和储存温度敏感产品的物流模式。
为了提高冷链物流系统的效率和可靠性,需要建立优化模型来辅助决策,并通过合理的求解方法得到最佳解。
本文将介绍冷链物流系统优化模型的建立与求解方法。
一、引言冷链物流是农产品、药品、食品等温度敏感产品的运输过程中所采用的一种专门的物流模式。
它要求能够在整个运输链中保持特定的温度和湿度条件,以确保产品的品质和安全性。
为了提高冷链物流的效率和可靠性,需要建立优化模型来辅助决策。
二、冷链物流系统优化模型的建立1. 线性规划模型线性规划模型是一种常用的优化模型,适用于冷链物流系统中的一些简单问题。
该模型的目标是最小化或最大化一个线性函数,同时满足一组线性等式或不等式约束条件。
例如,可以利用线性规划模型来确定最佳的货物配送方案、最小化运输成本或最大化利润等。
2. 整数规划模型整数规划模型在线性规划模型的基础上增加了变量的整数限制,用于处理一些离散决策变量的问题。
在冷链物流系统中,比如需要确定最佳的仓库位置、最优的车辆调度方案等,这些问题往往涉及到离散的决策变量。
因此,整数规划模型可以更好地描述和求解这类问题。
3. 非线性规划模型非线性规划模型适用于冷链物流系统中一些存在非线性关系的问题。
例如,考虑到货物的温度和湿度对产品质量的影响,可以利用非线性规划模型来确定最佳的环境控制策略。
非线性规划模型可以更精确地描述和求解这类复杂的冷链物流问题。
三、冷链物流系统优化模型的求解方法1. 简单方法对于简单的冷链物流问题,可以使用一些经典的优化算法来求解,例如贪婪算法、动态规划算法等。
这些方法的优点是计算效率高,求解速度快,但只能得到局部最优解。
2. 近似算法近似算法是一类能够在合理时间内得到近似最优解的方法。
在冷链物流系统中,模拟退火算法、遗传算法、蚁群算法等都是常用的近似算法。
这些方法能够通过模拟自然界中的优化策略来求解复杂的冷链物流问题,具有较好的求解效果。
物资调运问题的优化模型

物资调运问题的优化模型肖凤莲 涂礼才 何三才摘 要:本题所说的是防洪抗涝物质调运问题。
在此问题中我们求各企业、物资仓库及国家级储备库之间物资的运费每一百件最少的路线,把附件2(生产企业,物资仓库及国家级储备库分布图)的分布图转化为数学直观简图(见模型求解中图1),所得图是连通图,设为()E V G ,=,各个边的权为相连两点每百件物资的运费。
我们利用“破圈法”和“最短路”求任意企业、物资仓库及国家级储备库两两之间及仓库与仓库之间的最优路线,显然我们建立的数学(简单图形)模型是可行的、合理的。
得出最优路线见表二、三、四、五。
我们根据实际情况,在保证国家级储备库的情况下,采用就近原则,在此基础上建立线性规划模型(如下):)))()(())()()(((min 1111111111∑∑∑∑∑∑∑∑∑∑=++==++==++=====⋅+⋅+⋅+⋅+⋅⨯=bi cb b k k i ki a i cb b k k i ikbi cb b k j i b i bj j i j i ji ai bj j i j i w zy xq w z w zy x p A F运用Lingo 软件对我们所建立线性规划问题进行计算。
再把天数为20带入上述线性规划,运用Lingo 运用软件进行计算,可以得到企业2—6—40—储备库1,其他中断路段对物资运输的路线无影响。
建立线性规划,运用Lingo 运用软件求解,其结果见问题4的求解。
此模型简单易懂,容易推广。
运用了LINGO 数学软件,提高了计算的速度。
解得的结果符合实际。
关键词:破圈法、最短路、线性规划模型、Lingo.一、问题的重述我国地域辽阔,气候多变,各种自然灾害频频发生,特别是每年在长江、淮河、嫩江等流域经常爆发不同程度的洪涝灾害,给国家和人民财产带来重大损失,防洪抗涝成为各级政府的一项重要工作。
某地区为做好今年的防洪抗涝工作,根据气象预报及历史经验,决定提前做好某种防洪抗涝物资的储备。
多车辆配送路线的优化---扫描法

表2-1 客户数据信息
客户 Di(吨) Xi Yi 1 1.9 20.0 4.80 2 2.8 18.8 5.17 3 4 5 2 6 3 18.6 5.88 7 2.25 19.5 5.98 8 2.5 9 1.8 10 2.15 19.5 4.55 11 1.6 18.7 4.55 12 2.6 19.5 5.19 13 1.5 20.3 5.20 3.15 2.4
各客户点的坐标位置, 并在每个客户编号旁边 的方框中标注出该客户
1.8 1.5 13
2.8 2 3 3.1 5
的货运量。 然后,以仓库为极坐标 原点,向右的水平线为
4
2.4 11 1.6
零角度线。
X
图 2-1
扫描法
Part2.3
Part 1 实例分析
【解析】
2.5 2.25 8 7 9 12 2.6 1 1.9 10 2.15 0
多车辆配送路线的优化
Part1.3
Part 1 如何求解多车辆配送路线的优化问题
原则
2、避免行车路线交叉
D (a)不交叉线路
D (b) 交叉线路
3.尽可能使用大载重量车辆,减少出车数量 4.取货/送货混合安排 5.从距仓库最远的站点开始设计线路
2.扫描法
扫描法
Part2.1
Part 1 何为扫描法
2.以零角度为极坐标轴,按顺时针或逆时针方向,依角度大
小开始扫描。 3.将扫描经过的客户点需求量进行累加,当客户需求总量达 到一辆车的载重量限制且不超过载重量极限时,就将这些客 户划分为一群,即由同一辆车完成送货服务。接着,按照同
样的方法对其余客户划分新的客户群,指派新的车辆。
4.重复步骤3,直到所有的客户都被划分到一个群中。 5.在每个群内部用TSP算法求出车辆行驶最短路径。
运输优化仿真方案

运输优化仿真方案
在运输优化方面,可以采用仿真来设计和评估不同方案的有效性和可行性。
以下是一个可能的仿真方案:
1. 数据收集:首先,收集相关的运输数据,如货物量、运输距离、运输时间、货车容量等。
这些数据可通过实地调研或历史数据分析获得。
2. 建模与参数设定:利用收集到的数据,建立运输优化的仿真模型。
根据实际情况,设定参数,如货车的最大载重量、最大行驶速度、装卸时间等。
确保模型的准确性和可靠性。
3. 场景设置:根据模型的需求,设置不同的运输场景,如货物量变动、运输路径调整等。
这些场景可以是已知的实际情况,也可以是理论上的假设场景,用于测试模型的鲁棒性。
4. 策略设计:根据运输目标,设计不同的优化策略,如最小化运输成本、最小化运输时间、最大化货车利用率等。
每个策略会有不同的约束条件,如货车的最大运行时间、每个地点的最大服务时间等。
5. 参数调优和模拟运行:通过对模型中的参数进行调优,优化策略的确定。
然后进行模拟运行,通过仿真模拟货车行驶路线、装卸货物等过程,评估每个策略的效果。
可以采用不同的评价指标,比较各策略的优劣。
6. 结果分析与优化:根据仿真结果的分析,评估所采用策略的
效果和运输的性能。
通过对仿真结果的优化分析,找出问题所在,并尝试提出改进方案,以进一步优化运输效率。
7. 结论与建议:根据仿真结果和优化分析,总结出具体的结论和建议,以供实际运输决策的参考。
以上是一个通用的运输优化仿真方案,具体实施过程中可以根据实际情况进行调整和补充。
【大学竞赛】数学建模 钢管订购和运输优化模型PPT

建模案例:钢管订购和运输优化模型
2000年“网易杯”全国大学生数学建模竞赛B
a
1
一.问题的提出
二.基本假设
1.沿铺设的主管道已有公路或者有施工公路. 2.1km 主管道钢管称为一单位钢管,在主管道上,每千
米卸1单位的钢管. 3.公路运输费用为1单位钢管每千米0.1万元
(不足整千米部分按整千米计算) 4.在计算总费用时,只考虑运输费用和购买钢管的费用, 而不考虑其他的费用(诸如中转费用)
5.假设钢管在铁路运输路程超过1000km,铁路每增加1 至100km,1单位钢管运输的运价增至5万元.
6.订购的钢管数量刚好等于需要铺设的钢管数量 7.销售价和运输价不受市场价格变化的影响
a
2
三. 符号说明
第 个钢厂, 第 个钢厂的最大产量,
输送天然气的主管道上的第 个点, 第 个钢厂 1 单位钢管的销售价格,
1)将图1转换为一系列以单位钢管的运输费用为权的赋权图.
所以可先求出钢厂 S i 到铁路与公路相交点 b j 的最短路径.如图3
a
4
1200
690
720
1100 202
20
1150
195
306
450 80
30 290
320 160
160
690
70
70
170 520
88
462
a
5
图-4
a
6
2)计算单位钢管从S 1 到 A j 的最少运输费用
x ij { 0 , [ 500 , s i ]}, i 1, 7
j1
7
x ij 1, j 1, 5171
i1
x ij { 0 ,1}, i 1, 7 , j 1, 5171
数学建模——码头货轮集装箱装卸的优化问题2

码头货轮集装箱装卸的优化问题摘要集装箱“货币化”已成为发展趋势,而港口发展渐渐滞后于集装箱的吞吐量,研究集装箱装卸的优化问题能有效扩大港口生产力,提高港口经济效益。
本文将建立集卡线路规划模型和岸桥、集卡与龙门吊协同优化模型,通过禁忌搜索算法进行求解,并通过青岛港的数据对模型进行实证分析。
对于提高装卸效率,降低装卸成本这一问题,我们将其分解为线路规划、协同优化和模型检验三个子问题进行分析。
针对问题一,我们建立了集卡线路规划模型。
通过对青岛港前湾港集装箱码头(QQCT)的航拍图和雷达图进行分析,画出了码头泊位到堆场的平面图,按照相应的比例尺,得到实际码头与堆场间的距离、各堆场间的相互距离。
通过集卡行驶的速度,计算得到集卡从码头到堆场的时间、集卡在各堆场之间行驶的相互时间和集卡从堆场返回码头的时间。
集卡在运输过程中,要尽量减少空集卡的行驶,即运送集装箱返回的途中携带需要装运到船上的集装箱。
利用第一阶段的禁忌搜索算法,当所需装卸集装箱位置确定后,最短的行驶路线也就计算出来。
针对问题二,我们建立了桥吊、集卡和龙门吊的协同优化模型。
问题一计算的集卡最佳线路分配结果,继续作为桥吊、集卡和龙门吊协同优化的条件。
第二阶段的禁忌搜素算法分析出最合适的桥吊、集卡与龙门吊的比例,桥吊在不等待集卡的情况下效率高。
通过协同优化,得到最高效率的设备分配比例。
针对问题三,我们汇总了附件中所有集装箱的装卸数据,对模型进行检验分析。
以青岛前湾港区为例,通过带入实际数据,得到如下比例关系,即桥吊:集卡:龙门吊为2:10:5。
2辆桥吊工作时配备10辆集卡,5辆轮式龙门吊;3辆桥吊工作时配备15辆集卡,7辆龙门吊;如此分配使相对成本与效率达到最大化。
本文的亮点在于:利用港口的雷达图和航拍图,绘制了港口的分布平面图,分析更贴近实际;以集卡线路规划为突破口,并以此为条件,建立了以集装箱类型为依据的集卡一站式服务(岸桥到堆场的线路标准化);对数据的分类处理,使计算简洁;协同了集卡、桥吊、龙门吊,采用两个阶段的禁忌搜索算法,将集装箱的装与卸混合在一起计算,比原来对集卡、桥吊,集卡、龙门吊等部分优化更加贴近实际,大大提升了港口的运行效率,并且降低的了成本。
线性规划模型在物流配送中的优化

线性规划模型在物流配送中的优化引言:将线性规划应用于物流配送中可以有效地解决运输成本、时间和资源利用效率等问题。
本文将探讨线性规划模型在物流配送中的应用,以及该方法所带来的优化效果。
一、线性规划模型的基本原理线性规划是一种优化方法,通过线性目标函数和一组线性约束条件来寻找最优解。
其基本原理是在约束条件的限制下,最大化或最小化目标函数的值,以实现优化目的。
在物流配送中,线性规划模型可以用来优化运输方案,以最大程度地减少成本、提高配送效率。
二、线性规划模型在物流配送中的应用1. 运输网络优化:线性规划模型可以用来确定最佳的运输路径和运输量分配,在保证满足需求和资源限制的条件下,最小化总运输成本。
通过考虑不同的供应地点、分销中心和客户需求等因素,可以建立适用于特定物流网络的线性规划模型,从而实现运输网络的优化。
2. 车辆路径规划:线性规划模型还可以用于车辆路径规划,以确定最短路径、最优路径或者满足特定条件的路径。
通过考虑不同的路径选择、配送点顺序等因素,可以建立适用于特定配送任务的线性规划模型,从而实现车辆路径规划的优化。
3. 货物装载优化:线性规划模型可以用来优化货物的装载,以最大程度地利用载重能力和空间,减少空运成本。
通过考虑不同的货物属性、运输工具的限制条件等因素,可以建立适用于特定货物装载任务的线性规划模型,从而实现货物装载的优化。
三、线性规划模型在物流配送中的优化效果1. 成本降低:通过应用线性规划模型,可以有效地降低物流配送过程中的运输成本。
该模型能够准确地计算不同运输方案的成本,并在满足需求的前提下,选择最经济的运输方案,从而降低了企业的运输成本。
2. 时间缩短:线性规划模型的应用可以有效地优化配送路径和运输量分配,从而减少配送过程中的距离和时间。
通过选择最优路径和合理的运输方案,可以缩短物流配送的时间,提高配送效率。
3. 资源利用效率提高:线性规划模型在物流配送中的应用可以更加充分地利用资源,如运输车辆、仓储设施等。
物流配送中的路径规划与调度优化模型

物流配送中的路径规划与调度优化模型第一章:引言物流配送作为现代供应链管理中的重要环节,对于提高运输效率、降低成本、提供优质服务具有重要意义。
在物流配送过程中,路径规划与调度优化模型的应用可以最大限度地提高配送效率和满足客户需求。
本文旨在探讨物流配送中的路径规划与调度优化模型,为相关研究和实践提供参考。
第二章:物流配送中的路径规划模型2.1 问题定义在物流配送中,路径规划的目标是确定合理的运输路径,使得货物可以以最短的时间和最低的成本到达目的地。
本节将详细介绍物流配送中的路径规划问题的定义。
2.2 路径规划算法路径规划算法是解决物流配送中路径选择问题的关键。
本节将介绍几种常用的路径规划算法,包括最短路径算法、遗传算法和模拟退火算法。
2.3 路径规划案例分析本节将通过一个实际的物流配送案例,使用路径规划算法进行路径优化,并对比不同算法的效果,验证模型的准确性和有效性。
第三章:物流配送中的调度优化模型3.1 问题定义在物流配送中,调度优化的目标是合理安排运输车辆的行驶路线和送货顺序,以最大程度地降低配送成本和提高配送效率。
本节将详细介绍物流配送中的调度优化问题的定义。
3.2 调度优化算法调度优化算法是解决物流配送中调度问题的重要方法。
本节将介绍几种常用的调度优化算法,包括遗传算法、禁忌搜索和粒子群算法。
3.3 调度优化案例分析本节将通过一个实际的物流配送案例,使用调度优化算法进行调度优化,并对比不同算法的效果,验证模型的准确性和有效性。
第四章:路径规划与调度优化模型综合应用4.1 综合模型构建路径规划与调度优化是物流配送中两个关键环节,综合应用能够更好地实现效率的提升。
本节将介绍路径规划与调度优化模型的综合应用构建过程。
4.2 综合应用案例分析本节将通过一个真实的物流配送案例,运用综合模型进行路径规划与调度优化,并对比不同方法的效果,验证模型的可行性和效果。
第五章:结论与展望5.1 结论总结本章对全文内容进行总结,归纳出物流配送中路径规划与调度优化模型的重要性和应用价值。
用lingo编程解决运输问题大全
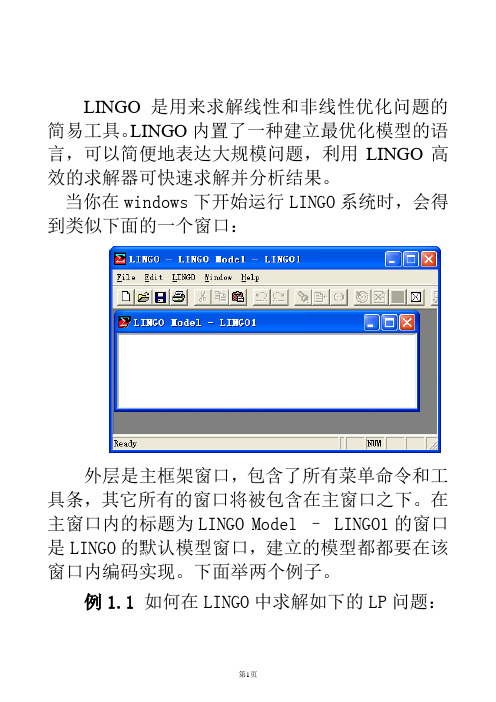
LINGO是用来求解线性和非线性优化问题的简易工具。
LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果。
当你在windows下开始运行LINGO系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1如何在LINGO中求解如下的LP问题:,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码:min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如下表。
销地产地B 1B 2B 3B 4B 5B 6B 7B 8产量A 1 6 2 6 7 4 2 5 9 60 A 2 4 9 5 3 8 5 8 2 55 A 3 5 2 1 9 7 4 3 3 51 A 4 7 6 7 3 9 2 7 1 43 A 5 2 3 9 5 7 2 6 5 41 A 6 5 5 2 2 8 1 4 3 52 销量3537223241324338使用LINGO软件,编制程序如下:model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity; vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I):volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J):volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38; cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
物流管理中的运输路径规划优化研究

物流管理中的运输路径规划优化研究一、引言在物流管理中,运输路径规划是一个重要的环节。
优化运输路径规划可以减少物流成本和时间,并提高运输效率。
本文从物流管理角度出发,深入研究运输路径规划优化问题。
二、运输路径规划的基本概念1.1 运输路径规划的定义运输路径规划是指在给定的运输网络中,找出一条或多条最优路径,以实现货物从出发地到目的地的快速、安全、低成本的运输。
1.2 运输路径规划的要素运输路径规划主要包括以下要素:运输网络、货物需求、运输距离和时间、运输成本。
三、运输路径规划优化方法2.1 经典算法经典算法是指一些经典的优化算法,如最短路径算法、遗传算法等。
这些算法通过数学模型,对运输路径进行优化,从而实现路径的最短和成本最低。
2.2 启发式算法启发式算法是指一类基于经验和直觉的优化算法,如蚁群算法、模拟退火算法等。
这些算法通过模拟物理过程或生物进化过程,寻找最优解或次优解。
2.3 智能算法智能算法是指一类仿生学和进化计算的算法,如人工神经网络、遗传算法等。
这些算法借鉴生物智能的特点,通过学习和优化来求解问题。
四、运输路径规划优化的实践案例3.1 货物配送中心的路径规划优化货物配送中心是一个典型的物流环节,对路径规划的优化有重要影响。
通过合理规划配送路径,可以减少配送时间和成本,提高配送效率。
3.2 运输大数据的应用随着物流信息化程度的提高,大量的运输数据可以被收集和分析。
通过对大数据的挖掘和分析,可以发现运输路径规划的优化空间,提高物流效益。
五、运输路径规划的挑战与未来趋势4.1 数据不完整和不准确在运输路径规划中,数据完整和准确性对结果至关重要。
然而,由于各种原因,数据可能存在缺失和错误,这给路径规划带来了挑战。
4.2 环境和时间的影响环境和时间因素对运输路径规划中的效果有重要影响。
如何在不同环境和时间条件下选择最优路径,是一个需要研究和解决的问题。
4.3 智能化和自动化技术随着智能化和自动化技术的发展,运输路径规划的优化趋势也向着智能化和自动化方向发展。
运筹学论文-产销不平衡运输

管理运筹学论文---产销不平衡运输摘要运输问题是运筹学中的一个重要问题,也是物流系统优化中常见的问题,同时也是一种特殊的线性规划问题。
怎么样尽可能的在产地与销地之间减少运输成本和降低运输费用是很多运输公司热切关注的话题。
本文涉及的是一个总产量大于总销量的产销不平衡运输问题,通过对产地与销售地车辆运输的建立模型,在运用表上作业迭代法(最小元素法)求解后,再根据模型用lingo软件编写程序进行求解。
然后对结果进行分析,以及运输问题的延伸。
最后证明用lingo 解决车辆运输的可行性。
关键字:运输问题,产销不平衡,表上作业法, lingo目录一、问题的提出与分析 (1)1.1问题提出 (1)1.2问题分析 (1)二、模型的建立与基本假设........................................................... . (1)2.1模型的建立 (1)2.2基本假设 (2)三、定义符号说明与表上作业法 (2)四、问题求解 (2)4.1、Lingo求解模型 (4)4.2、Lingo结果 (5)五、模型结果分析与改进 (10)参考文献 (11)一、问题的提出与分析1.1问题提出重庆有三家电子厂分别是新普,隆宇和恒华,生产的笔记本电脑将要运向北京,天津,广东,上海四个城市销售,其产量和销售量见下表:(单位:万台)表:1-1北京天津广东上海产量新普626730隆宇495325恒华881521销量15172212-问:哪种销售方案将会取得最少的运输费用,费用为多少?1.2问题分析图表数据显示产量总和为30+25+21=76万台,销量的总和为15+17+22+12=66万台,说明了此问题是一个总产量大于总销量的运输问题(76>66)。
该问题一方面要求满足北京,天津,广东,上海四个销售地的供货需求,而另一方面又要考虑新普,隆宇和恒华三个产地的运往销售地的运输费用,此外问题不但要求满足销售地分配要足,同时也要保证最大化的减少运输费用。
运筹优化常用模型、算法及案例实战PythonJava实现

作者对CPLEX和Gurobi这两款商业求解器的介绍也让我受益匪浅。通过了解 这两款工具的使用方法,我能够更好地将运筹优化算法应用到实际问题中。作者 还提供了Python和Java的API详解,让我能够更加方便地使用这些工具。这部分 内容不仅提高了我的编程能力,也增强了我对运筹优化算法的实际应用能力。
作者还详细介绍了两款常用的商业求解器——CPLEX和Gurobi的使用方法, 包括Python和Java的API详解,使得读者能够更好地理解和应用这些工具。
我被书中对运筹优化领域基本理论的介绍所吸引。作者通过清晰的语言和生 动的例子,让我对运筹优化有了更深入的理解。这部分内容不仅为后续的算法和 案例打下了坚实的基础,也使我对运筹优化在实际问题中的应用有了更清晰的认 识。
在算法部分,书中详细介绍了各种经典和现代的优化算法,如单纯形法、内 点法、遗传算法、模拟退火算法等。每种算法都给出了详细的步骤和 Python/Java代码实现,使读者能够亲自动手实践,加深对算法的理解和掌握。 例如,遗传算法是一种模拟生物进化过程的优化算法,通过选择、交叉和变异等 操作,逐步搜索到问题的最优解。
《运筹优化常用模型、算法及案例实战PythonJava实现》这本书是一本不可 多得的运筹优化学习指南。它不仅提供了丰富的理论知识和实用算法,还通过生 动的案例和实战演练,使读者能够真正掌握运筹优化的精髓和应用技巧。无论是 对于初学者还是有一定基础的读者来说,这本书都将是一本宝贵的参考资料和实 战宝典。
多种编程语言实现:本书提供了Python和Java两种编程语言的实现代码,适 应了不同读者的需求。Python语言简单易学,适合初学者快速上手;而Java语言 则更加成熟稳定,适合进行大型项目的开发。
案例实战丰富多样:本书选择的案例实战涵盖了多个领域,如物流管理、金 融投资、生产计划等,这些案例既具有代表性,又具有实际应用价值,能够帮助 读者更好地理解运筹优化的应用场景。
冷链物流配送的绿色车辆路径模型及其求解算法

内容摘要
物流配送车辆优化调度模型是在满足客户订单需求的前提下,合理调度车辆, 优化行驶路线,从而降低车辆空驶率、提高配送效率的一种方法。构建该模型需 要考虑订单量、客户分布、道路状况、车辆装载量等多种因素。
内容摘要
首先,我们需要收集和整理客户订单数据,明确每个客户的送货和需求量。 然后,根据实际情况设定车辆的装载量、速度、行驶限制等参数,以及路线的约 束条件,如不能绕行、必须经过某些节点等。接下来,利用数学建模的方法,我 们可以建立优化目标函数,如最小化总行驶距离、最小化总配送时间等。最后, 通过求解该优化目标函数,得到最佳的车辆调度方案。
一、绿色车辆路径模型
一、绿色车辆路径模型
在传统的车辆路径问题(VRP)中,主要考虑的是运输成本和时间约束,而很 少环境影响。为了解决这个问题,学者们提出了绿色车辆路径模型(Green Vehicle Routing Problem, GVRP)。GVRP在传统VRP的基础上,增加了对碳排 放、能源消耗等环境因素的考虑。
五、结论与展望
五、结论与展望
综上所述,冷链物流配送的绿色车辆路径模型及其求解算法是一种有效的解 决方案,可以帮助企业在保证产品质量的同时,降低能源消耗和环境污染。然而, 实际应用中仍存在许多挑战,如数据收集和处理、模型参数调整等。未来研究可 针对以下方向展开:
五、结论与展望
1、完善模型和算法:针对冷链物流配送的特性,进一步完善GVRP模型和求解 算法,提高求解效率和准确性。
五、结论与展望
2、考虑更多约束条件:在模型中考虑更多的实际约束条件,如车辆装载量、 行驶时间限制等,使模型更加贴近实际应用场景。
五、结论与展望
3、整合其他优化方法:将其他先进的优化方法,如强化学习、深度学习等, 与GVRP结合,形成更为强大的优化工具。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运输问题摘要本文根据运输公司提供的提货点到各个客户点的路程数据,利用线性规划的优化方法与动态优化模型——最短路径问题进行求解,得到相关问题的模型。
针对问题一 ,我们采用Dijkstra 算法,将问题转化为线性规划模型求解得出当运送员在给第二个客户卸货完成的时,若要他先给客户10送货,此时尽可能短的行使路线为:109832V V V V V →→→→,总行程85公里。
针对问题二,我们首先利用prim 算法求解得到一棵最小生成树:再采用Dijkstra 算法求得客户2返回提货点的最短线路为12V V →故可得到一条理想的回路是:121098436751V V V V V V V V V V V →→→→→→→→→→后来考虑到模型的推广性,将问题看作是哈密顿回路的问题,建立相应的线性规划模型求解,最终找到一条满足条件的较理想的的货车送货的行车路线:121098436751V V V V V V V V V V V →→→→→→→→→→。
针对问题三,我们首先直接利用问题二得一辆车的最优回路,以货车容量为限定条件,建立相应的规划模型并设计一个简单的寻路算法,最终可为公司确定合理的一号运输方案:两辆车全程总和为295公里(见正文);然后建立线性规划模型得出二号运输方案:两辆车全程总和为290公里(见正文);最后再进一步优化所建的线性规划模型,为运输公司针对问题四,我们首先用Dijkstra 算法确定提货点到每个客户点间的最短路线,然后结合一些限定条件建立一个目标模型,设计一个较好的解决方案进行求解可得到一种很理该方案得到运输总费用是645元。
关键字:Dijkstra 算法, prim 算法, 哈密顿回路问题重述某运输公司为10个客户配送货物,假定提货点就在客户1所在的位置,从第i个客户到第j个客户的路线距离(单位公里)用下面矩阵中的(,)i j(,1,,10)i j=L位置上的数表示(其中∞表示两个客户之间无直接的路线到达)。
1、运送员在给第二个客户卸货完成的时候,临时接到新的调度通知,让他先给客户10送货,已知送给客户10的货已在运送员的车上,请帮运送员设计一个到客户10的尽可能短的行使路线(假定上述矩阵中给出了所有可能的路线选择)。
2、现运输公司派了一辆大的货车为这10个客户配送货物,假定这辆货车一次能装满10个客户所需要的全部货物,请问货车从提货点出发给10个客户配送完货物后再回到提货点所行使的尽可能短的行使路线?对所设计的算法进行分析。
3、现因资源紧张,运输公司没有大货车可以使用,改用两辆小的货车配送货物。
每辆小货车的容量为50个单位,每个客户所需要的货物量分别为8,13,6,9,7,15,10,5,12,9个单位,请问两辆小货车应该分别给那几个客户配送货物以及行使怎样的路线使它们从提货点出发最后回到提货点所行使的距离之和尽可能短?对所设计的算法进行分析。
4、如果改用更小容量的车,每车容量为25个单位,但用车数量不限,每个客户所需要的货物量同第3问,并假设每出一辆车的出车费为100元,运货的价格为1元/公里(不考虑空车返回的费用),请问如何安排车辆才能使得运输公司运货的总费用最省?问题1【模型分析与假设】运送员在给第二个客户卸完货后,即从此处赶到第十个客户处,路程越短越好,是一个最短路径问题,为此我们采用Dijkstra算法,考虑到建模的方便我们将问题转化为线性规划模型进行求解。
下面是一些变量的假设与说明:X为0,1变量,其值为1代表行车路线经过第j个客户,为0则代表不经过。
1.ijC为题中给出的邻接矩阵对应位置的值。
2.ij3.为了表达的方便,将邻接矩阵的第一行与第二行互换,第一列与第二列互换。
(因为求的是客户2至客户10的最短线路,而非提货点至客户10)同时将矩阵中数据0或∞用一个足够大的数999代替。
(这是因为目标函数是求最小值)【模型建立与求解】建立问题的模型(1)是:将其转化为lingo代码(见附录[1])后,求解可得以下结果:Global optimal solution found at iteration: 19Objective value:Variable Value Reduced CostX( 1, 3)X( 3, 8)X( 8, 9)X( 9, 10)至此可以知道,运送员应该走的最好路线是:总行程为85公里。
【模型检验与评价】该模型是基于Dijkstra 算法的基础上转化为线性规划模型来求最短路径的模型,优点是实现较简单,也容易求解;但有个令人不是很满意的地方就是其模式固定,要求任两个客户点间最短距离时,需将其一客户的位置与提货点互换,另一个客户的位置则需与客户10的位置互换,将其看成原始的提货点到客户10最短距离的模型进行求解,这样较为烦琐,有待改进。
问题2【模型分析】很明显运输公司分别要对10个客户供货,必须访问每个客户,但问题要求我们建立相应模型寻找一条尽可能短的行车路线,首先不考虑送货员把10个客户所需的货送完货后不返回提货点的情2V (客户2)返回1V从上分析知送货员从提货点1出发,要走遍客户2,3,…,n 各至少一次,最后返提货点1。
为了更方便地建立起模型首先作以下假设与说明:1.ij X 为0,1整形变量,其值为1代表行车路线经过第j 个客户,为0则代表不经过。
2.ij C 为客户i 到j 的距离(题中给出的邻接矩阵的数据)。
3.为了数据的方便处理,先将邻接矩阵中的数据∞用一个足够大的数999代替。
4.访问客户i 后必须要有一个即将访问的确切客户;访问客户j 前必须要有一个刚刚访问过的确切客户。
故我们用以下条件来分别保证我们的假设。
到此我们得到了一个模型,它是一个指派问题的整数规划模型。
其目标是使式子:∑∑==*101101i j ij ij X C在约束条件下取得最小值。
5.哈密顿图优化问题[5],须添加一个额外变量()10,,3,2Λ=i u i,目的是为了更好的防止子巡回的产生,即须附加一个约束条件:到现在我就可以建立以下模型对问题求解了。
【模型建立与求解】可建立问题的模型(2)为:同样借助数学软件求解可得结果:从中可以找出一条较为理想的回路是:可见按此模型求解的结果与采用prim 算法求解的结果是一样的。
问题3【模型分析与猜想】用两辆容量为50单位的小货车运货,在每个客户所需固定货物量的情况下,要使得行程之和最短,我们假设每个客户的货物都由同一辆货车提供,这样只要找出两条尽可能短的回路,并保证每条线路客户总需求量在50个单位以内。
实际上这样的两条回路是存在的:由题二得到了一条哈密顿回路可根据货物需求量的大小将其分为前后两部分,并将之分别构成回路。
(注:由于提货点在客户1所在的位置,故不必考虑为客户1送货的情况。
)为了更好地建立模型,先作以下定义:『定义1:』 顺序集合⎭⎬⎫⎩⎨⎧→→→→→→→→→→=1221010998844336677551,,,,,,,,,V V V V V V V V V V V V V V V V V V V V N 代表由模型(2)求解得出的哈密顿回路的路径全集(集合中的元素是不可调换的,故称它为顺序集合);『定义2:』 函数()i N Get 为集合N 中第i 个元素终点所对应的下标。
(即若i=3,则,()73=N Get ) 『定义3:』 函数()i N U 为集合N 中第i 个元素终点所对客户的货物需求量(即若i=3则())(33N Get T N U =)其中(()10,,2,1,Λi T 为向量: ()9,12,5,10,15,7,9,6,13,8的第i 个分量的值)。
接下来我们设计一个简单的算法来寻找较好的路径:Step1:根据以下模型获得一个值k ;Step2:依k 的取值分两条路径:Step3:利用模型(1)分别求得()k N Get V 到1V 的最短路径:()1V V K N Get →→Λ 以及1V 到()1+K N Get V 的最短路径:()11+→→K N Get V V Λ依据模型很容易求得:k=5(因为根据模型(1)很容易可以确定4V 至1V 的最短路径是14V V →,1V 至8V 的最短路径是851V V V →→,但在代用模型(1)的时候须注意的是相应的客户位置的变换,可参照问题一的求解决方法。
)由此可得两车所行驶的距离之和(单位:公里):【结果优化】从以上得到的两条行车路线来看,两车得经过经过了客户5,根据算法二号车必客户5才能保证行程较短,而根据模型(1)易知路径71V V →优于751V V V →→,因此可优化一号车路线为:143671V V V V V V →→→→→,经检验优化后的两条行车路线上客户货物需求量总和分别是40与46均不超过货车的容量50,故认为此方案更优,这样我们可以给运输公司提供的一号很明显,以上猜想得到的模型来求解这一问题,存在着很大的缺陷,那就是没有更好说服力,不能让人感到很满意,不过这个结果也是很客观的,不会很差。
因此我们想通建立以下模型来弥补这一缺陷。
【模型建立与求解】若对以上猜得到的一种模型不够满意,我们同样可以建立相应的线性规划模型对以上的运输方案进一步优化,考虑到本问题与问题二有相似之处即要考虑回到提货点的情形,因此我们可以在模型(2)上进行改进, 在保证二号不超载(不超出容量)的前提下,先确定第一辆车的最优路径,首先对模型中将会用的变量作一些简单的定义或说明:1.j D 为每个客户的需货量,它是在向量()9,12,5,10,15,7,9,6,13,8的每j 个分量,据上分析知:5036101101≤*≤∑∑==j i j ij D X(不考虑客户1的需求量,因为它在提货点)。
2.由于这里是分两条路线分别给10个客户送货,就没有必要设计每条路线都能够访问每个客户点,但要保证送货员能回提货点,且均从提货点出发回到提货点,则送货员进入一个客户同时也必须出来。
故我们用以下条件来分别保证我们的假设:到此我们得到了一个模型,它是一个指派问题的整数规划模型。
其目标是使式子:∑∑==*101101i j ij ij X C在约束条件下取得最小值。
其余变量的假设与问题二的假设一致。
故可建立模型(3)如下:在5036≤≤jD 约束下,参加附录[3]的代码,在lingo 中求解可得以下结果:以上可视为确定首先确定的第一辆车的行车方案;则这两条路线所对的第二辆车最优路线的选择,(以长度为95公里的路线为例)只需将模型(3)中的条件:0101101∑∑===-j j ij ij X X 与∑∑==≥101101i j ij K X 改为条件()i j j Xij ≠==且10,6,4,3,21即要保证第二辆访问到所有第一辆车未访问过的客户,允许其访问第一辆车访问过的客户,故模型基本上不用改动。
