2016年全国大学生数学建模竞赛及全国第八届大学生数学竞赛
2016年全国大学生数学建模竞赛B题解题分析与总结

2016年全国大学生数学建模竞赛B题解题分析与总结2016年全国大学生数学建模竞赛B题解题分析与总结一、题目分析2016年全国大学生数学建模竞赛B题是一个与经济学、金融学相关的问题,要求参赛者通过对问题的深入分析和建模,以及对模型的求解和结果的解释,提出合理的结论。
二、问题描述本题的题目为《贷款利率调控模型》。
题目给出了一组数据,包括贷款利率、消费者价格指数、人均可支配收入、外汇储备等指标,要求参赛者针对这些指标进行分析,并建立合适的模型来解释这些指标之间的关系。
三、解题思路1. 数据分析:首先,我们需要对给定的数据进行分析。
通过绘制图表和计算一些统计量,我们可以对这些数据的变化和趋势进行初步了解。
2. 建立模型:在了解了数据的基本特征之后,我们需要以此为基础,建立起合适的数学模型。
这个模型应该能够描述贷款利率与消费者价格指数、人均可支配收入、外汇储备之间的关系,并能够进行预测。
3. 参数估计:建立好模型之后,我们需要对模型中的参数进行估计。
这需要依赖于数学推导和数据拟合的方法,通过最小二乘法等方法,确定模型的参数。
4. 模型求解:有了模型和参数之后,我们可以使用计算机软件进行模型的求解。
通过数值计算的方法,我们可以得到模型的解析解或数值解,并进行结果的分析和解释。
5. 结论与反思:最后,我们需要根据模型的结果,对问题进行结论和反思。
我们可以分析模型的合理性、可靠性,以及对解决实际问题的指导意义。
同时,我们也可以对模型的不足之处进行总结,并提出改进的建议。
四、模型建立与结果解释在解题的过程中,我们可以考虑建立如下的模型:贷款利率=消费者价格指数+人均可支配收入+外汇储备。
通过对这三个指标的分析,我们可以发现它们之间存在着一定的关系。
消费者价格指数和人均可支配收入可以反映经济的收入水平和购买力,而外汇储备可以反映国家的经济实力。
在建立了模型之后,我们可以对模型进行求解,并得到相应的结果。
根据模型的求解结果可以得出以下结论:贷款利率与消费者价格指数、人均可支配收入和外汇储备之间存在着一定的关系。
2016全国大学生数学建模竞赛获奖名单

2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。
2016 第八届全国大学生数学竞赛获奖名单

序号 姓名 性别 所在省份 专业(全称) 奖项
备注
1 侯思钦 男 陕西省
土木工程 一等奖 推荐参加全国总决赛
2
王娟
女
陕西省 水利水电工程(卓越)一等奖
3 王起亮 男
4
杨飞
男
非数学类 陕西省
陕西省
电子与信息工程 一等奖
自动化
一等奖
5 余聪聪 女 陕西省 光电信息科学与工程一等奖
98 肖瑞强 男
99
陈伟
男
100 殷乔刚 男
101 聂明秋 女
102 张蒙
女
103 邹以晴 女
104 刘琦
女
105 刘文涛 男
106 王宁
男
107 惠豪
男
108 陈源静 女
109 程丹妮 女
110 王兴旺 男 111 欧国平 男
112 姚旭豪 男
113 刘倩
女
114 马天梓 男
115 党佳琦 男
116 薛珂
6
刘帅
男 陕西省
自动化
一等奖
7 李燕鸿 女 陕西省 国际经济与贸易 一等奖
8 陈叶飞 男 陕西省
自动化
一等奖
9 余尚佳 男
10
刘乐
男
11 杨恺庆 女
12 丁有国 男
13 周兆吉 女
14
查浩
男
15 沈赛赛 男
16 卜宁
男
17 邓喜豪 男
18
徐昕
女
19 程书灿 男
20 杨涵
男
21 郭孟婷 女
22 汤碧瑶 女
陕西省 电气工程与智能控制三等奖 陕西省 给排水科学与工程 三等奖
2016全国大学生数学建模竞赛获奖名单
2016高教社杯全国大学生数学建模竞赛获奖名单(初稿)(异议期:2016年11月7日-2016年11月20日)
本科组高教社杯获得者:张滕翔、夏智康、郑安琪(东南大学)
专科组高教社杯获得者:吴伟龙、杨婷、段玲(湖南化工职业技术学院)
本科组MATLAB创新奖获得者:王毅然、纪昀红、张伟(中国人民大学)
专科组MATLAB创新奖获得者:刘苏生、祝王缘、王柏熙(海军蚌埠士官学校)
[注]以下每一获奖等级内,按赛区顺序排列(同一赛区内,按学校笔画顺序排列)。
本科组一等奖(共294名)
本科组二等奖(共1621名)
曹小
专科组一等奖(共60名)。
第八届全国大学生数学竞赛决赛(数学类3、4)参考答案一面

其中: x0 ∈ E , x2 ∈ E , · · · , xn ∈ E ; x1 ∈ / E, x3 ∈ / E, · · · , xn−1 ∈ / E. 构造如下: ∀n ⩾ 1, 先取 x0 = 0, x2 , x4 , · · · , xn−2 ∈ E, xn = 1
数学家
|χE (xi ) − χE (xi−1 )| → ∞, 即
因此, 当且仅当 a > 27 或 a < −37 时方程有虚根 ∫∫ ax dy dz + (x + a)2 dx dy √ (a > 0 为常数), 3. 计算曲面积分 I = x2 + y 2 + z 2 S √ 其中 S : z = − a2 − x2 − y 2 , 取上侧. I = π 答案:− a3 2 x2 + y 2 ⩽ a2 解: 令曲面 S1 : , 取下侧, 则 S1 ∩ S 为闭下半球的内侧. z = 0 令其内部区域为 Ω, 令 D 为 xOy 平面上的圆域 x2 + y 2 ⩽ a2 , 则利用高斯公式, 得 {∫ ∫ } ∫∫ [ ] 1 2 I= − axdy dz + (z + a) dxdy a S ∪S1 S1 [ ∫∫∫ ] ∫∫ 1 − (3a + 2z )dv + = a2 dxdy a Ω D [ ] ∫∫∫ 1 4 4 = −2πa − 2 z dv + πa a Ω ∫ ∫ a ∫ 0 2 2π = −πa3 − dθ rdr √ z dz a 0 0 − a2 −r 2 π = − a3 2
ˆ(x) ∈ S . 于是, 在 R 上有界, 从而 f ∫
A
数学家
−∞
ˆ(x)e2πixy dy 收敛, 而 f
2016年全国大学生数学建模竞赛题
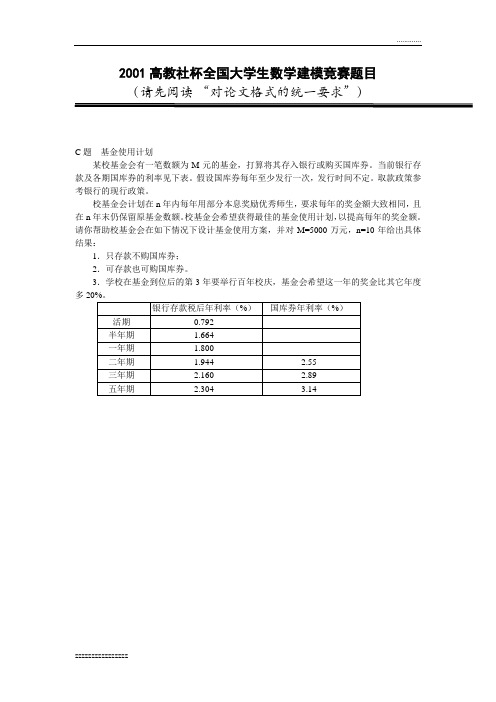
2001高教社杯全国大学生数学建模竞赛题目(请先阅读“对论文格式的统一要求”)C题基金使用计划某校基金会有一笔数额为M元的基金,打算将其存入银行或购买国库券。
当前银行存款及各期国库券的利率见下表。
假设国库券每年至少发行一次,发行时间不定。
取款政策参考银行的现行政策。
校基金会计划在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额。
校基金会希望获得最佳的基金使用计划,以提高每年的奖金额。
请你帮助校基金会在如下情况下设计基金使用方案,并对M=5000万元,n=10年给出具体结果:1.只存款不购国库券;2.可存款也可购国库券。
3.学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多摘要:运用基金M分成n份(M1,M2,…,Mn),M1存一年,M2存2年,…,Mn存n 年.这样,对前面的(n-1)年,第i年终时M1到期,将Mi及其利息均取出来作为当年的奖金发放;而第n年,则用除去M元所剩下的钱作为第n年的奖金发放的基本思想,解决了基金的最佳使用方案问题.关键词:超限归纳法;排除定理;仓恩定理1问题重述某校基金会有一笔数额为M元的基金,欲将其存入银行或购买国库券.当前银行存款及各期国库券的利率见表1.假设国库券每年至少发行一次,发行时间不定.取款政策参考银行的现行政策.表1 存款年利率表校基金会计在n年内每年用部分本息奖励优秀师生,要求每年的奖金额大致相同,且在n年末仍保留原基金数额.校基金会希望获得最佳的基金使用计划,以提高每年的奖金额.需帮助校基金会在如下情况下设计基金使用方案,并对M=5 000万元,n=10年给出具体结果:①只存款不购国库券;②可存款也可购国库券.③学校在基金到位后的第3年要举行百年校庆,基金会希望这一年的奖金比其它年度多20%.2模型的分析、假设与建立2.1模型假设①每年发放的奖金额相同;②取款按现行银行政策;③不考虑通货膨胀及国家政策对利息结算的影响;④基金在年初到位,学校当年奖金在下一年年初发放;⑤国库券若提前支取,则按满年限的同期银行利率结算,且需交纳一定数额的手续费;⑥到期国库券回收资金不能用于购买当年发行的国库券.2.2符号约定K——发放的奖金数;ri——存i年的年利率,(i=1/2,1,2,3,5);Mi——支付第i年奖金,第1年开始所存的数额(i=1,2,…,10);U——半年活期的年利率;2.3模型的建立和求解2.3.1情况一:只存款不购国库券(1)分析令:支付各年奖金和本金存款方案———Mij (i =1,…,10,i ;j 属于N ). 将各方案ij M 看成元素,构成集合A则ij M 属于A1,210;I =所以A 按I 取值分10行根据仓恩定理:分行集中,任何一单行有上界,则必包含一个极大元素。
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛(CUMCM)是面向全国各高校学生的大型数学建模类比赛。
在众多赛题中,B题以其复杂的实际问题背景和深入的应用数学知识引起了广泛关注。
本文旨在针对B题的解题过程进行详细分析,并做出相应的总结。
二、题目概述B题主要描述了一个实际生活中遇到的问题:基于网络平台的交通流量预测。
题目要求参赛者根据历史交通流量数据,分析交通流量的变化规律,并建立数学模型进行预测。
三、解题分析1. 数据收集与预处理首先,我们需要收集相关的历史交通流量数据。
这些数据可能包括时间、地点、交通流量等信息。
收集到的原始数据需要进行清洗和预处理,例如去除异常值、缺失值等,以获得更为准确的数据。
2. 建立数学模型根据数据的特点和问题需求,我们选择合适的数学模型进行建模。
考虑到交通流量与时间的关系较为密切,我们可以选择时间序列分析模型,如ARIMA模型等。
此外,考虑到不同地点之间的交通流量可能存在相互影响,我们还可以引入空间相关性分析,如空间自回归模型等。
3. 模型优化与验证建立数学模型后,我们需要对模型进行优化和验证。
这包括调整模型的参数、对模型进行诊断分析等。
我们可以通过对比模型的预测值与实际值,计算误差指标(如均方误差、平均绝对误差等)来评估模型的性能。
同时,我们还可以使用交叉验证等方法来验证模型的稳定性。
4. 模型应用与结果展示最后,我们将建立的数学模型应用于实际问题中,对未来的交通流量进行预测。
我们将预测结果以图表等形式进行展示,方便评委和观众理解。
同时,我们还可以对结果进行解释和讨论,说明模型的优点和局限性。
四、总结通过本文总结:经过详细的分析与探讨,针对2016年全国大学生数学建模竞赛B题,我们采取了有效的解决策略。
从数据收集与预处理到模型建立与优化,每一步都紧密联系实际,充分考虑了交通流量数据的特性和问题需求。
在建模过程中,我们选择了合适的时间序列分析模型和空间相关性分析模型,旨在捕捉交通流量的变化规律。
2016 第八届全国大学生数学竞赛获奖名单
自动化 一等奖 电气工程及其自 动化 二等奖 电气工程及其自 动化 二等奖 电气工程及其自 动化 二等奖 电气工程及其自 动化 二等奖 电气工程及其自 动化 二等奖 水利水电工程 二等奖
32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64
陕西省 电气工程及其自动化(电力) 三等奖 材料科学与工程 三等奖 车辆工程 电子信息工程 工程力学 工业工程 三等奖 三等奖 三等奖 三等奖 电子科学与技术 三等奖
陕西省 光信息科学与技术工程 三等奖 陕西省 机械设计制造及其自动化 三等奖
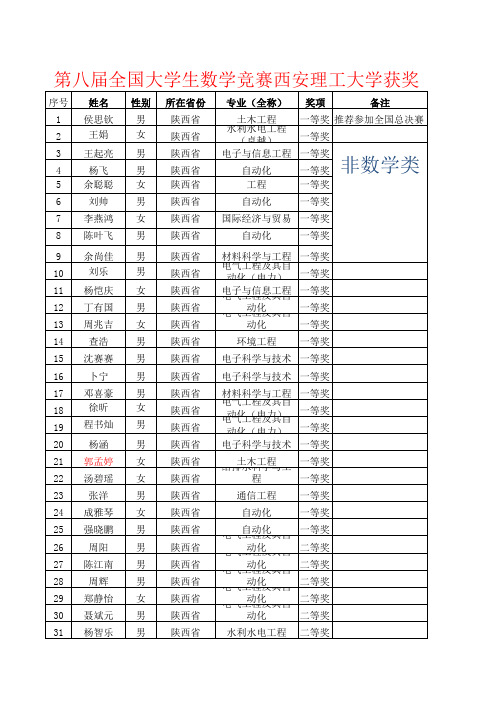
第八届全国大学生数学竞赛西安理工大学获奖
序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 姓名 侯思钦 王娟 王起亮 杨飞 余聪聪 刘帅 李燕鸿 陈叶飞 余尚佳 刘乐 杨恺庆 丁有国 周兆吉 查浩 沈赛赛 卜宁 邓喜豪 徐昕 程书灿 杨涵 郭孟婷 汤碧瑶 张洋 成雅琴 强晓鹏 周阳 陈江南 周辉 郑静怡 聂斌元 杨智乐 性别 男 女 男 男 女 男 女 男 男 男 女 男 女 男 男 男 男 女 男 男 女 女 男 女 男 男 男 男 女 男 男 所在省份 陕西省 陕西省 陕西省 陕西省 陕西省 陕西省 陕西省 专业(全称) 奖项 备注 土木工程 一等奖 推荐参加全国总决赛 陕西省 水利水电工程(卓越) 一等奖 电子与信息工程 一等奖 自动化 一等奖 光电信息科学与工程 一等奖 自动化 自动化 一等奖 一等奖 国际经济与贸易 一等奖
肖瑞强 陈伟 殷乔刚 聂明秋 张蒙 邹以晴 刘琦 刘文涛 王宁 惠豪 陈源静 程丹妮 王兴旺 欧国平 姚旭豪 刘倩 马天梓 党佳琦 薛珂Байду номын сангаас王帅洋 康洪玮 金梦辉 宋晨旭 王永超 宁静 张佳庆 贾蓉 许丁晖 王特
2016全国大学生数学建模A题
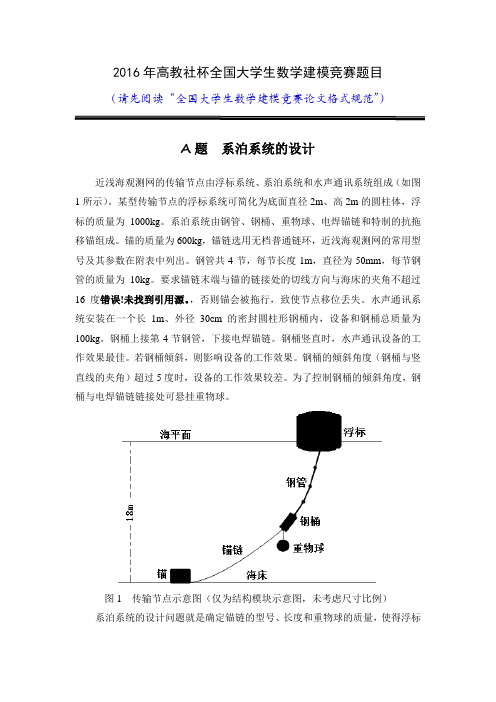
2016年高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度错误!未找到引用源。
,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外径30cm的密封圆柱形钢桶内,设备和钢桶总质量为100kg。
钢桶上接第4节钢管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
《2024年2016年全国大学生数学建模竞赛B题解题分析与总结》范文

《2016年全国大学生数学建模竞赛B题解题分析与总结》篇一一、引言2016年全国大学生数学建模竞赛(以下简称国赛)是中国大学最为盛大的数学建模比赛,汇集了来自全国各高校顶尖的数学建模团队。
在本次比赛中,B题题目独特且挑战性强,使得各队参赛选手展现出了超凡的建模和解决实际问题的能力。
本文旨在深入探讨该题的解题思路与总结,以便于为其他数学建模爱好者提供借鉴和参考。
二、B题概述题目B涉及到了金融领域的风险管理问题,主要考察了参赛选手在金融领域的数学建模和解决问题的能力。
具体来说,题目要求通过构建数学模型来分析不同类型股票之间的价格关系,以及在给定市场条件下如何确定风险阈值并有效地控制投资风险。
三、解题思路(一)明确问题在分析B题时,我们首先明确了题目的要求和目的,确定了对金融领域相关概念和理论的研究方向。
我们认识到这是一个典型的金融风险管理问题,需要运用数学建模的方法来分析股票价格之间的关系以及风险控制策略。
(二)数据收集与处理在收集了相关股票的历史数据后,我们进行了数据清洗和预处理工作,以确保数据的准确性和可靠性。
这包括剔除异常数据、填补缺失值、对数据进行归一化处理等。
(三)构建模型针对题目要求,我们选择了合适的方法和模型来分析股票价格之间的关系。
首先,我们使用相关性分析来探究不同股票之间的价格关系;其次,我们运用回归分析来建立股票价格与风险之间的数学模型;最后,我们利用蒙特卡洛模拟等方法来模拟市场环境并确定风险阈值。
(四)模型验证与优化在构建了数学模型后,我们通过实际数据对模型进行了验证和优化。
我们比较了模型的预测结果与实际市场数据,不断调整模型参数以优化模型的性能。
四、解题方法与技巧(一)熟悉金融领域相关知识在解决B题时,我们需要对金融领域的相关知识有充分的了解,包括股票价格的形成机制、风险控制策略等。
这有助于我们更好地理解题目要求并选择合适的建模方法。
(二)合理选择数学建模方法针对不同的金融问题,我们需要选择合适的数学建模方法。
2016年全国大学生数学建模竞赛B题解题分析与总结

2016年全国高校生数学建模竞赛B 题解题分析与总结专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,期望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请依据实际需要进行调整和使用,感谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、进修资料、教室资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想进修、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestyle materials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!2016年全国高校生数学建模竞赛B题解题分析与总结2016年全国高校生数学建模竞赛B题解题分析与总结引言:2016年全国高校生数学建模竞赛是我国高等教育中的一项重要赛事,也是高校生运用数学知识探究实际问题的一个重要平台。
2016年全国大学生数学建模竞赛河南赛区本科组获奖名单
马琼楠 张莉萌 秦一峰 时浩添 王利艳 贾雅萍 周兰兰 李亚爽 刘兴辰 王东旭 黄壮 姚百骏 程龙 雷达 韩静 李宏菊 宋国锋 张博冉 李征 刘文义 张亚 张泽旭 王烁 殷杰 高顾力 王鑫辉 王培鑫 刘海涛 沈旺 葛会新 要猛 邢云飞 梁理斌 张怀仁 高菡 吕彦昌 李政 王星贵 武飞飞 郑银龙 张芷丹 岳万昊 葛盛 董伍强 李雪 韩瑞 牛燕如
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92
河南师范大学 河南师范大学 河南师范大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南理工大学 河南科技学院 河南科技大学 河南科技大学 河南科技大学 河南科技大学 河南科技大学 河南工业大学 河南工业大学 河南工业大学 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南工程学院 河南大学 河南大学 河南大学 河南城建学院 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 河南财经政法大学 安阳学院 安阳师范学院 安阳师范学院 安阳师范学院
187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233
2016年全国大学生数学建模竞赛A题

2016年全国大学生数学建模竞赛A题2016年高教社杯全国大学生数学建模竞赛题目 ,请先阅读“全国大学生数学建模竞赛论文格式规范”,A题系泊系统的设计近浅海观测网的传输节点由浮标系统、系泊系统和水声通讯系统组成(如图1所示)。
某型传输节点的浮标系统可简化为底面直径2m、高2m的圆柱体,浮标的质量为1000kg。
系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成。
锚的质量为600kg,锚链选用无档普通链环,近浅海观测网的常用型号及其参数在附表中列出。
钢管共4节,每节长度1m,直径为50mm,每节钢管的质量为10kg。
要求锚链末端与锚的链接处的切线方向与海床的夹角不超过16度,否则锚会被拖行,致使节点移位丢失。
水声通讯系统安装在一个长1m、外00kg。
钢桶上接第4节钢径30cm的密封圆柱形钢桶内,设备和钢桶总质量为1 管,下接电焊锚链。
钢桶竖直时,水声通讯设备的工作效果最佳。
若钢桶倾斜,则影响设备的工作效果。
钢桶的倾斜角度(钢桶与竖直线的夹角)超过5度时,设备的工作效果较差。
为了控制钢桶的倾斜角度,钢桶与电焊锚链链接处可悬挂重物球。
图1 传输节点示意图(仅为结构模块示意图,未考虑尺寸比例)系泊系统的设计问题就是确定锚链的型号、长度和重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小。
问题1 某型传输节点选用II型电焊锚链22.05m,选用的重物球的质量为1200kg。
现将该型传输节点布放在水深18m、海床平坦、海水密度为1.025×103kg/m3的海域。
若海水静止,分别计算海面风速为12m/s和24m/s时钢桶和各节钢管的倾斜角度、锚链形状、浮标的吃水深度和游动区域。
问题2 在问题1的假设下,计算海面风速为36m/s时钢桶和各节钢管的倾斜角度、锚链形状和浮标的游动区域。
请调节重物球的质量,使得钢桶的倾斜角度不超过5度,锚链在锚点与海床的夹角不超过16度。
问题3 由于潮汐等因素的影响,布放海域的实测水深介于16m~20m之间。
2016年度学生学科竞赛获奖奖励名单
94
赛区二等奖
王威
100
95
赛区二等奖
张艳玲
100
96
赛区二等奖
刘秀伟
100
97
赛区二等奖
高航
100
98
赛区二等奖
姚鹏
100
99
赛区二等奖
魏成权
100
100
赛区二等奖
冯兴
100
101
赛区二等奖
张育坤
100
102
赛区二等奖
张守恒
100
103
赛区二等奖
邓昕岩
100
104
赛区二等奖
刘轩昂
100
105
70
赛区一等奖
郭斌
200
71
赛区一等奖
裴雪皓
200
72
赛区一等奖
王天阁
200
73
赛区一等奖
朱云龙
200
74
赛区一等奖
金嘉升
200
75
赛区一等奖
黄港港
200
76
赛区一等奖
周传波
200
77
赛区一等奖
石锋
200
78
赛区一等奖
焦侃
200
79
赛区一等奖
金雪萌
200
80
赛区一等奖
秦立峰
200
81
赛区一等奖
张雨晴
田新
100
250
省级二等奖
张娜术安琪张一晨
刘佳蒙辛星
100
251
省级三等奖
杨晨刘睿刘浪
屈椿柳润琪
50
252
2016年陕西省“福思特杯”大学生会计应用技能竞赛
2016年全国大学生数学建模竞赛获奖论文

小区开放对道路通行的影响评价模型摘要本文针对小区开放对道路的影响进行了研究,建立了层次分析模型、通行能力评价模型,使用了MATLAB、EXCEL等软件,得出小区开放在不同条件下会对道路交通产生不同的影响。
首先运用层次分析法,分析得出整体一般情况下小区开放有利于周边道路交通的结论。
之后构建了不同类型的小区,并分析得出小区开放的效果与小区结构及周边道路结构、车流量有关,因此小区开放不能盲目采取,要因地制宜。
最后根据分析结果,从交通通行的角度,向城市规划和交通管理部门提出了关于小区开放的合理化建议。
本文的突出特点是使用了层次分析法定量的比较了小区开放前后道路合理性,构建了对于研究该问题具有代表性的三种类型的小区,并建立了影响评估模型,客观的对不同小区结构及周边道路结构、车辆通行的影响进行评价。
针对问题一,首先查阅相关资料选取影响道路通行的指标,并对选取的指标进行筛选,然后运用各项指标进行层次分析,通过小区开放和小区封闭对道路交通和理性的判断来分析小区开放对道路通行的影响最后得出从整体看来,小区开放有利于道路通行。
针对问题二,通过查阅有关道路通行能力的相关资料建立了通行能力评价模型,首先根据模型求出道路基本通行能力的表达式,基本通行能力是理想状态下的通行能力,与实际情况分析对比存在差异。
因此基于差异,通过各实际因素对道路通行能力的影响进行修正,得到实际道路通行能力的数据。
最终计算出小区开放前后实际通行能力的相对系数。
针对问题三,构建了三种类型的小区,不同类型的小区具有不同的结构及不同的周边道路结构、车流量,应用问题二建立的模型分别对三种小区开放和封闭条件下周边道路的实际通行能力进行了计算,通过相对系数评价不同类型的小区开放对道路通行的影响,分析得出小区开放与地理位置、内部结构等因素有关,不能一概而论。
针对问题四,结合前述模型结果分析结果,从交通出行角度对城市规划部门和交通管理部门提出了合理化意见。
小区开放要合理的实施以体现小区开放的意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016年全国大学生数学建模竞赛及全国第八届大学生数学竞赛我校又创佳绩
2016年9月9日至9月12日,在教务处领导下,由基础科学学院组织的“全国大学生数学建模竞赛”圆满结束。
我校共选派了12个代表队,共计36名同学参加竞赛,参赛同学分别来自基础科学学院、轻工学院、计算机与信息工程学院、能源与建筑工程学院、会计学院、金融学院、财政学院和英才学院等。
经过竞赛组委会联评,我校获得省级一等奖4项,省级级二等奖与省级三等奖各2项,成功参赛奖4项。
2016年10月22日,在教务处领导下,我校选派了分别来自轻工学院、基础学院和计算机学院等11 个学院的74名同学参与全国第八届大学生数学竞赛。
经过竞赛组委会评审,我校所选派代表队共获得非数学专业组国家级奖项9项,省级奖项12项;数学专业组获国家级奖项及省级奖项各1项。
在此,让我们向以上获奖的同学及指导教师表示热烈的祝贺!获奖情况如下:
全国第八届大学生数学竞赛获奖情况(非数学专业组)
全国第八届大学生数学竞赛获奖情况(数学专业组)
教务处
基础科学学院
二〇一六年十二月六日。
